Submitted:
01 May 2024
Posted:
01 May 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
- ➢
- SDG 7: Affordable and Clean Energy: The focus on biomass gasification for hydrogen production contributes to the goal of ensuring access to affordable, reliable, sustainable, and modern energy sources. By exploring efficient and sustainable ways of producing hydrogen, we contribute to the transition towards clean energy systems.
- ➢
- SDG 9: Industry, Innovation, and Infrastructure: The utilization of computational and mathematical techniques, along with optimization strategies, demonstrates advancements in industry and innovation. These techniques can enhance the design and operation of biomass gasification processes, leading to more efficient and sustainable infrastructure for hydrogen production.
- ➢
- SDG 13: Climate Action: By reducing the dependence on fossil fuels and exploring alternative energy sources, such as biomass for hydrogen production, we contribute to mitigating climate change. Biomass gasification can significantly reduce greenhouse gas emissions and promote a low-carbon economy.
- ➢
- SDG 12: Responsible Consumption and Production: The research findings provide insights into optimizing biomass utilization, leading to more responsible and sustainable production practices. By maximizing the yield of hydrogen and utilizing co-generation approaches, we promote efficient resource utilization and minimize waste generation.
- ➢
- SDG 17:partnerships for the Goals: Collaboration between academia, industry, and policymakers is crucial for the successful implementation of sustainable energy solutions. The research findings can foster partnerships and knowledge-sharing among stakeholders, contributing to the achievement of the SDGs. Overall, the research findings discussed in this paper contribute to multiple SDGs, promoting sustainable energy, innovation, climate action, responsible production, and partnerships for sustainable development.
2. Methodology
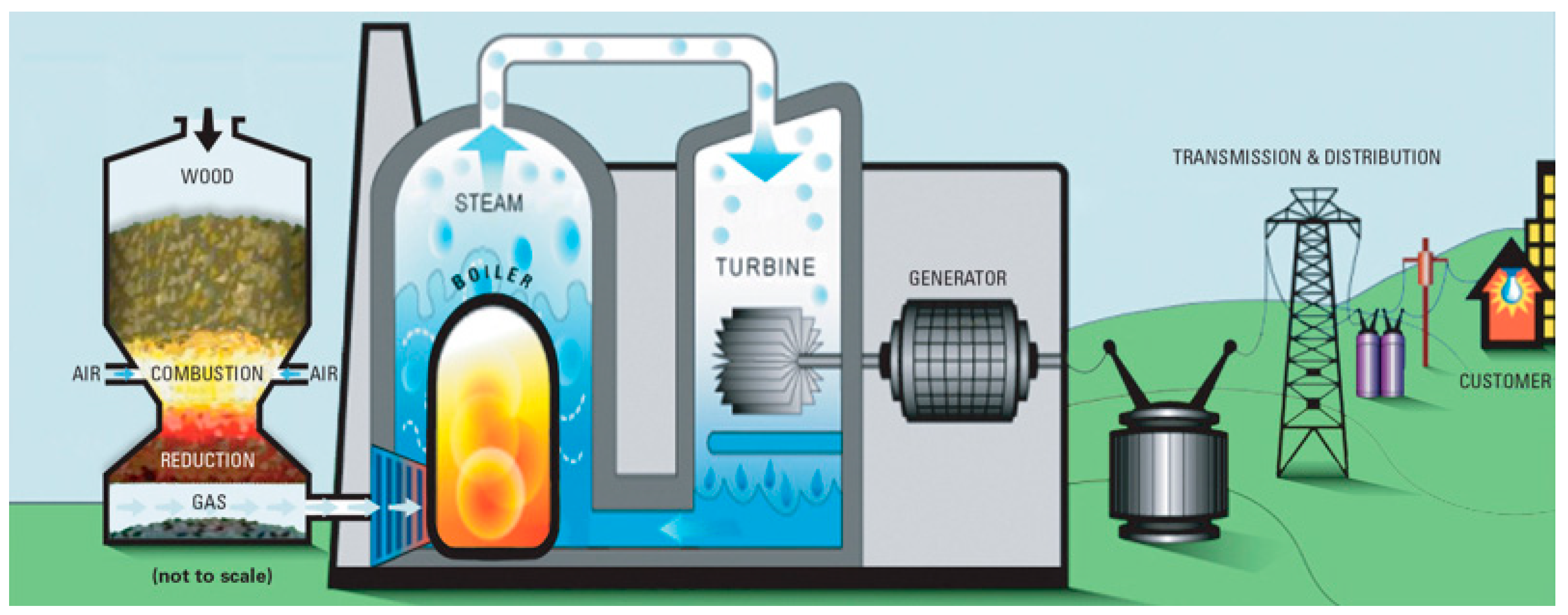
2.1. Biomass Conversion into Hydrogens
2.2. Gasification of Biomass into Hydrogen
2.3. Gasification Agents
- Air: Air is one of the most commonly used gasifying agents in gasification processes. It is readily available and cost-effective. However, the use of air as a gasifying agent can lead to the formation of nitrogen compounds in the syngas, reducing the overall heating value and increasing the volume of gas produced.
- Oxygen: Oxygen gasification, also known as oxygen-blown gasification, involves using pure oxygen or oxygen-enriched air as the gasifying agent. Oxygen gasification can result in higher syngas quality with a lower concentration of nitrogen compounds, leading to a higher calorific value of the produced gas. However, the use of oxygen can increase operational costs due to the need for oxygen separation processes.
- Steam: Steam gasification involves the injection of steam into the gasifier chamber to react with the solid feedstock. Steam acts as a gasifying agent by promoting the reaction of carbon with water vapor to produce hydrogen and carbon monoxide. Steam gasification can enhance the hydrogen content of the syngas, making it suitable for various applications, including hydrogen production.
- Carbon Dioxide (CO2): CO2 gasification, also known as dry reforming, involves reacting carbon-based feedstock with carbon dioxide to produce syngas. CO2 can act as a gasifying agent to promote the gasification reactions and increase the hydrogen content of the syngas. CO2 gasification is of particular interest for carbon capture and utilization applications, as it can contribute to reducing greenhouse gas emissions.
- Oxygen-steam: Oxygen-steam gasification combines the benefits of using oxygen and steam as gasifying agents. This approach can enhance the syngas quality by reducing nitrogen content and increasing hydrogen production. Oxygen-steam gasification is often employed in advanced gasification systems to optimize syngas composition and maximize energy efficiency. The selection of gasifying agents in gasification processes depends on factors such as feedstock characteristics, desired syngas composition, process efficiency, and economic considerations. By carefully choosing the appropriate gasifying agent and optimizing gasification conditions, researchers and engineers can tailor gasification processes to meet specific energy and environmental goals.
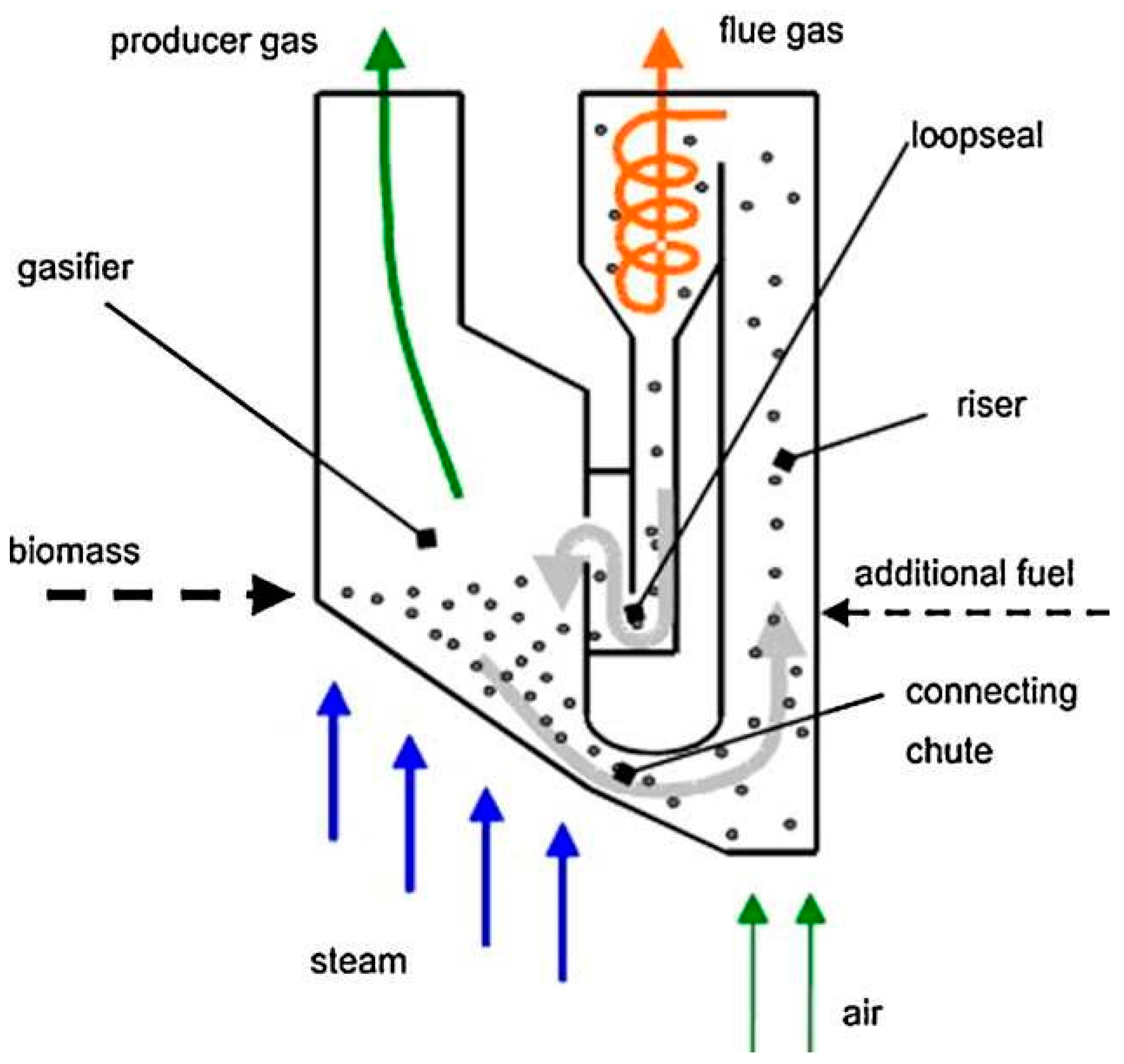
- Biomass is fed into the gasifier where it undergoes gasification to produce syngas.
- Steam and air are introduced into the gasifier to facilitate the gasification reactions.
- The produced gas flows out of the gasifier and is collected as product gas.
- Any remaining flue gas is directed out of the system.
- The gasification process takes place in a riser, providing a high-temperature environment for efficient conversion.
- Additional fuel may be added to supplement the energy input if needed.
- A loop seal and connecting chute help maintain the fluidized bed circulation within the reactor.

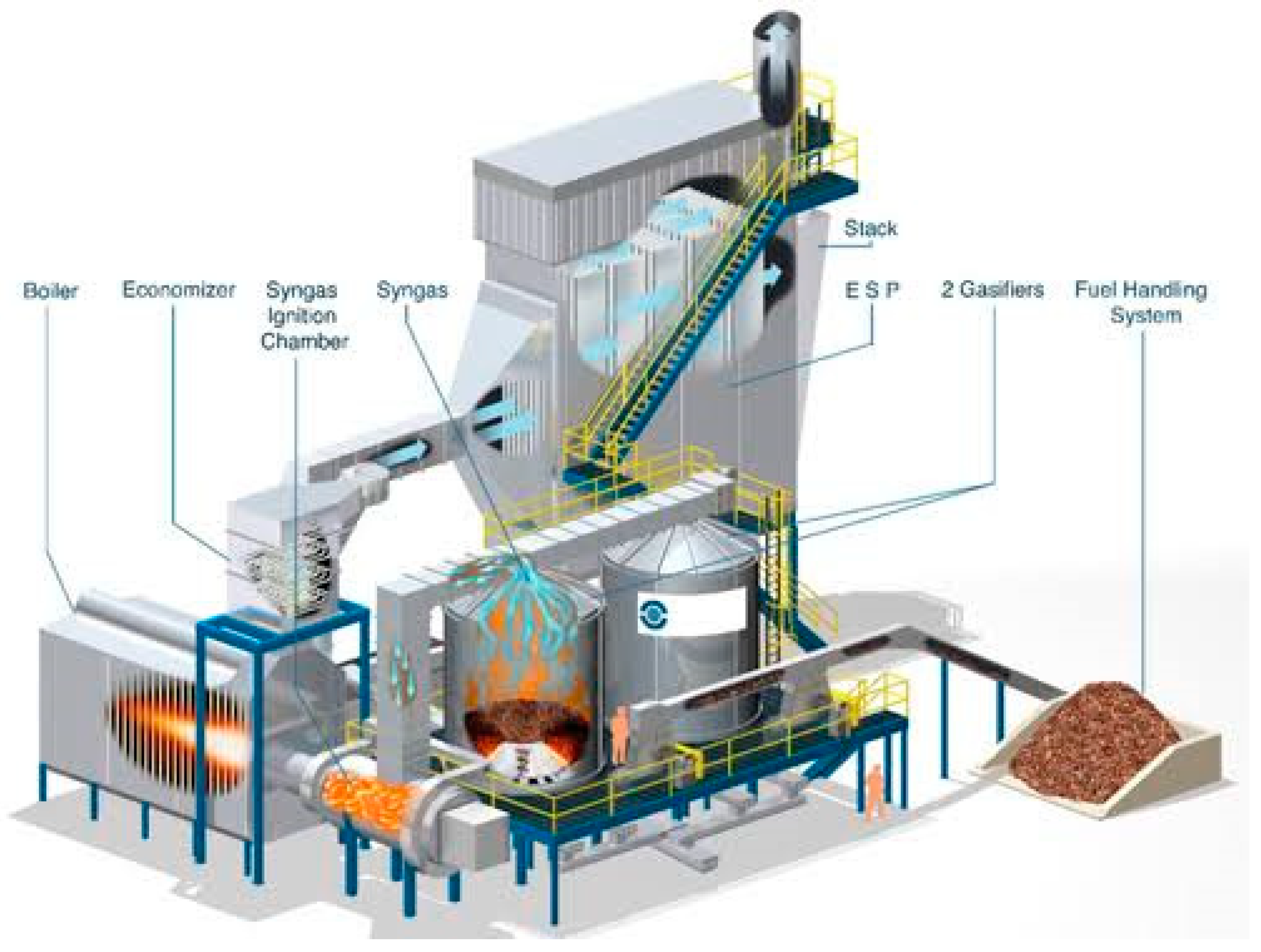
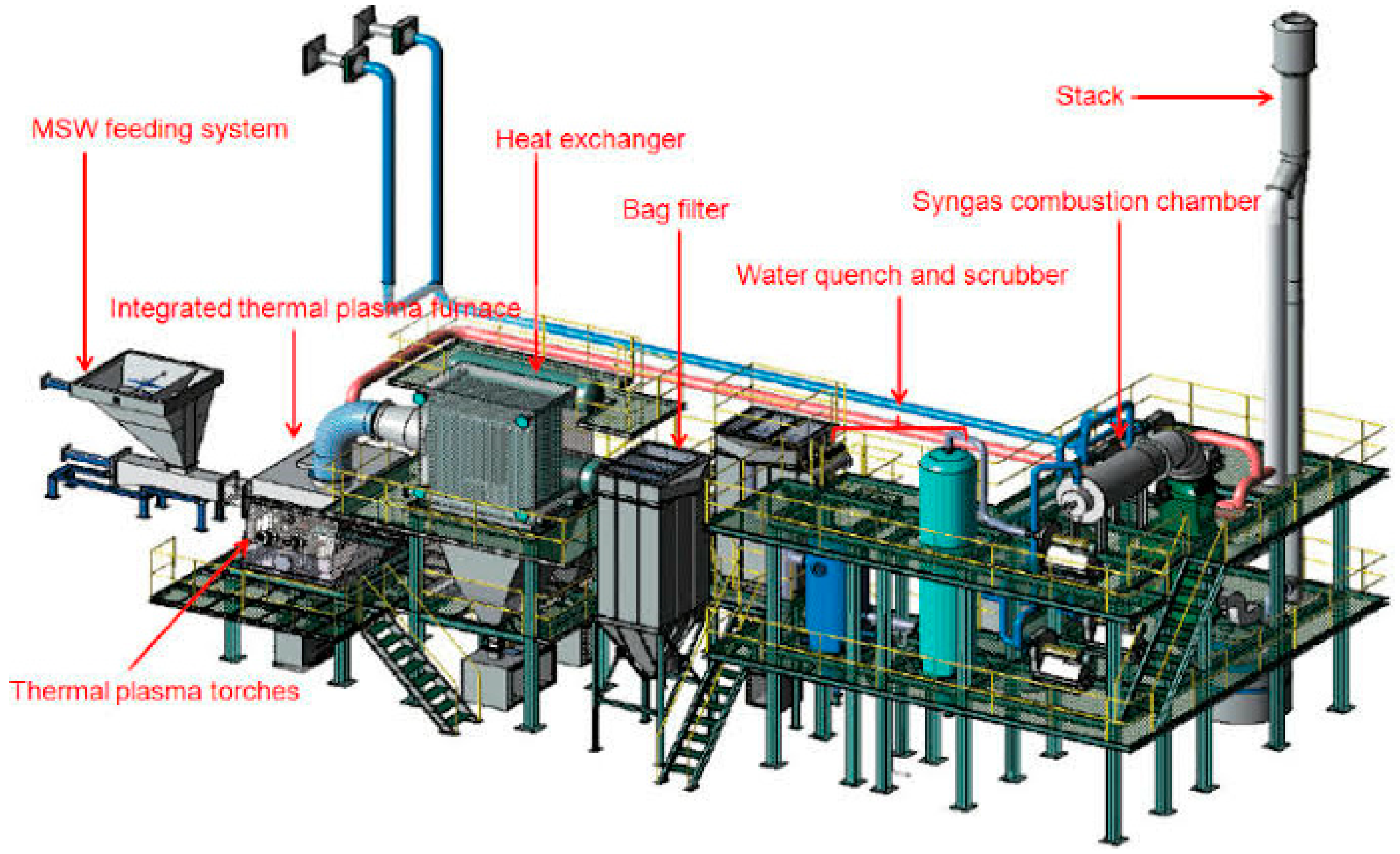
2.4. Type of Biomass Gasifiers
2.5. Numerical Model and Development
- ( C ) represents the concentration of a specific component in the gasifier reactor over time ( t ).
- ( F{i,in} ) and ( C{i,in} ) are the inlet flow rate and concentration of component ( i ) entering the reactor, respectively.
- ( F_{i,out} ) is the outlet flow rate of component ( i ) from the reactor.
- ( R_{bio} ) denotes the rate of biomass conversion reactions occurring within the reactor.
- ( E ) represents the energy content in the gasifier reactor over time ( t ).
- ( F{i,in} ) and ( H{i,in} ) are the inlet flow rate and enthalpy of component ( i ) entering the reactor, respectively.
- ( F{i,out} ) and ( H{i} ) are the outlet flow rate and enthalpy of component ( i ) leaving the reactor.
- ( Q{in} ) and ( Q{out} ) denote the energy input and output in the form of heat, respectively.
- ( \dot{W} ) represents the work done on or by the system.
- ( \dot{Q}_{bio} ) signifies the energy released or consumed due to biomass conversion reactions.
- ( C ) represents the concentration of a specific chemical species.
- ( t ) denotes time.
- ( u ) signifies the velocity field of the gas phase within the reactor.
- ( D ) is the diffusion coefficient of the species.
- ( R ) represents the net rate of generation or consumption of the species due to chemical reactions.
| 1. Mass Balance Equation |
| Describes the conservation of mass within the system, accounting for the inflow , outflow, and accumulation of mass. It is fundamental in understanding the distribution of species and reactants in biomass gasification processes. |
| 2. Energy Balance Equation |
| Governs the conservation of energy in the system, taking into account heat transfer , chemical reactions, and energy generation or consumption . This equation provides insights into the thermal behavior and energy requirements of the gasification process. |
| 3. Species Transport Equations |
| Models the transport of different species (e.g., gases, vapors, solids) within the reactor, considering diffusion, convection, and chemical reactions. These equations are essential for predicting the distribution and conversion of biomass components during gasification. |
| 4. Reaction Kinetics Equations |
| Describe the rates of chemical reactions taking place in the gasifier, including pyrolysis, combustion and gasification reactions. These equations elucidate the conversion of biomass into syngas and other byproducts, influencing overall process efficiency. |
| 5. Heat Transfer Equations |
| Govern the transfer of heat within the system, including conduction, convection, and radiation. These equations help in analyzing temperature profiles, thermal gradients, and heat distribution within the gasification reactor. |
| 6. Equilibrium Models |
| Utilize thermodynamic equilibrium assumptions to predict the composition of product gases at given operating conditions. These models simplify the complex gasification reactions by assuming equilibrium among species, providing valuable insights into gas composition and equilibrium constants. |
- Accumulation represents the rate of change of mass within the reactor over time.
- Inflow and Outflow denote the flow rates of biomass feedstock or gas species entering and leaving the reactor, respectively.
- Generation and Consumption refer to the rates at which products are generated or consumed due to chemical reactions within the reactor.
- ( E ) represents the total energy content within the reactor over time.
- ( F{i,in} ) and ( H{i,in} ) are the inlet flow rate and enthalpy of component ( i ) entering the reactor, respectively.
- ( F{i,out} ) and ( H{i} ) are the outlet flow rate and enthalpy of component ( i ) leaving the reactor.
- ( Q{in} ) and ( Q{out} ) denote the energy input and output in the form of heat, respectively.
- ( W_{shaft} ) represents the work done on or by the system.
- ( \dot{Q}_{bio} ) signifies the energy released or consumed due to biomass conversion reaction.
- ( C_i ) represents the concentration of species ( i ) at a given point in space and time.
- ( t ) denotes time.
- ( \rho ) is the density of the gas phase.
- ( u ) signifies the velocity field of the gas phase.
- ( \Gamma_i ) is the species diffusion coefficient.
- ( R_i ) represents the net rate of generation or consumption of species ( i ) due to chemical reactions.
- ( r ) is the reaction rate,
- ( k ) represents the rate constant,
- ( C ) denotes the concentration of reactants,
- ( n ) represents the reaction order.
2.6. Model and Kinetics
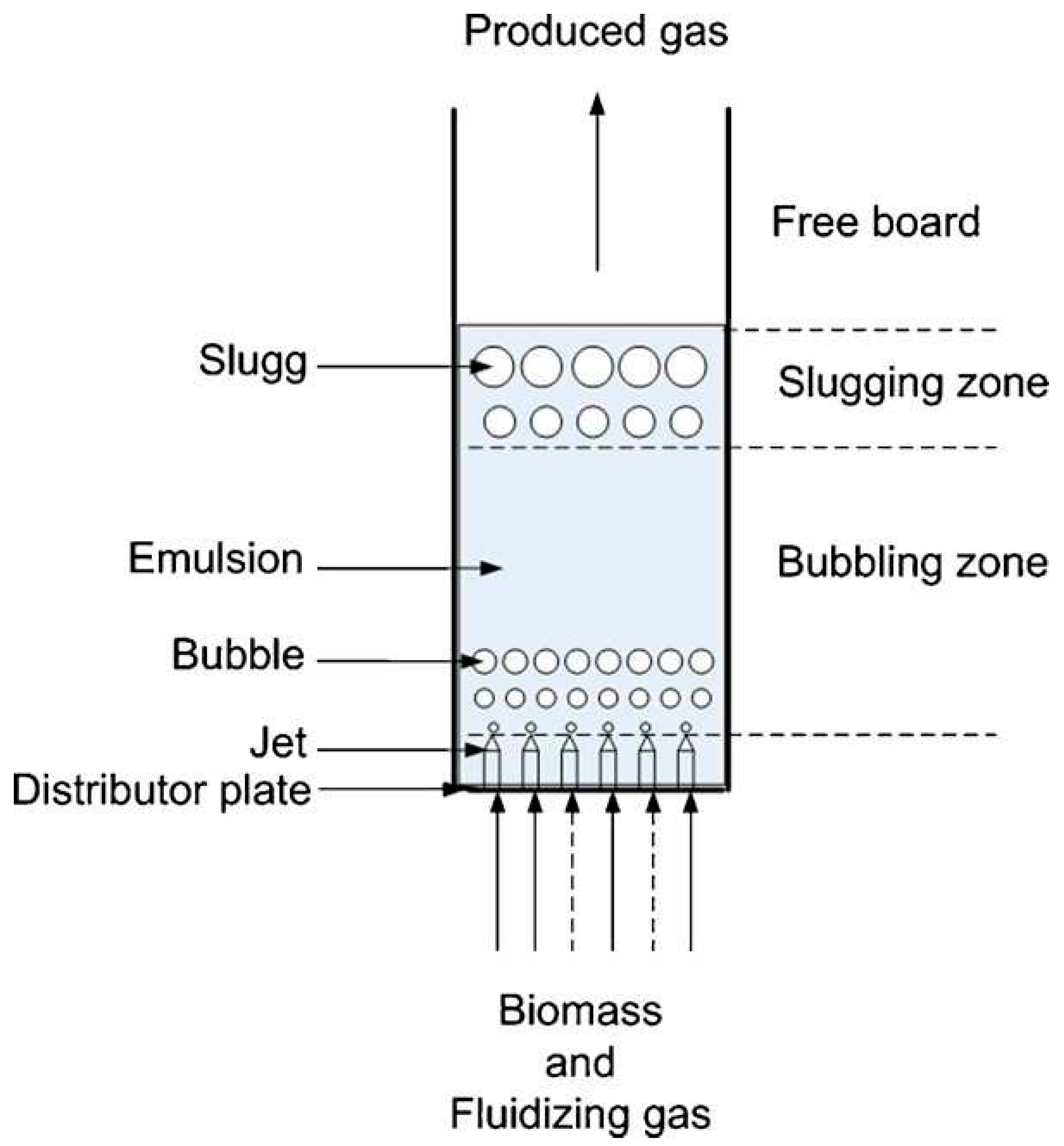
- Biomass and Fluidizing Gas Zone: This is where the raw biomass material is introduced along with the fluidizing gas, such as air or steam, which helps in fluidizing the bed of particles.
- Bubbling Zone: In this region, the fluidized bed exhibits bubbling behavior due to the gasification reactions and the circulation of gases and particles within the bed.
- Freeboard: The area above the fluidized bed where gasification reactions continue in the presence of oxygen, leading to the production of syngas.
- Slugging Zone: This zone may experience intermittent churning or slugging behavior, characterized by the movement of large clusters of particles and gases within the bed.
- Emulsion: Refers to the region where gas-solid mixing and reactions occur, facilitating the conversion of biomass into syngas.
- Distributor Plate: A component that helps in distributing the fluidizing gas evenly across the bed and maintaining the fluidized state.
- Jet: Represents the injection point for the fluidizing gas to enter the bed and maintain the desired fluidization characteristics.
- Slugs: Refers to the clusters or agglomerates of particles that move within the bed, impacting the gas-solid interactions and reaction kinetics.
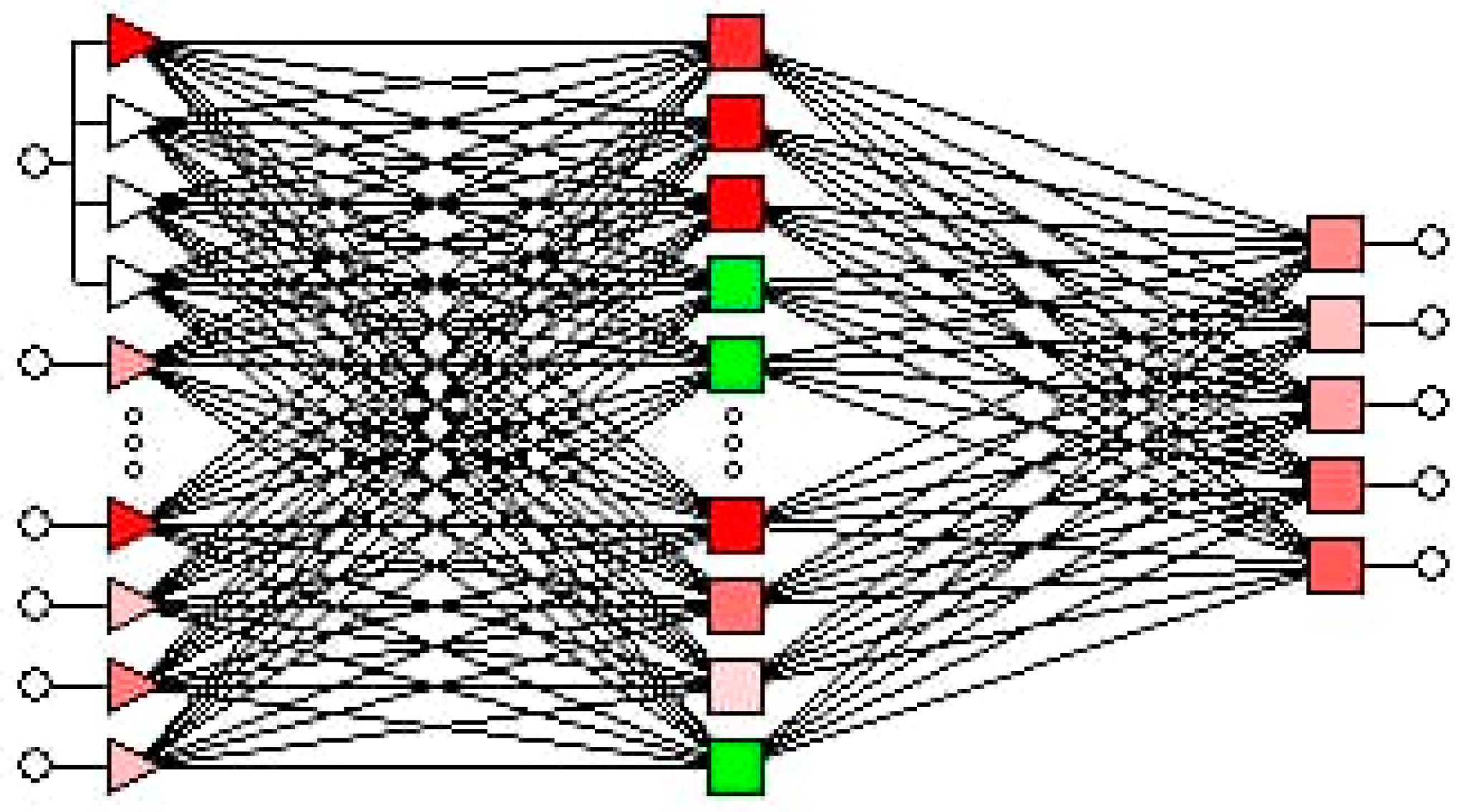
2.7. Artificial Neural Network Models
3. Results and Discussion
3.1. Model and Process Simulation
- ➢
- SuperPro Designer: SuperPro Designer is a comprehensive process simulation software that allows users to model and optimize a wide range of processes, including biomass conversion. It offers capabilities for designing process flowsheets, conducting mass and energy balances, and performing techno-economic analysis.
- ➢
- Pro/II: Pro/II is a powerful process simulation software widely used in the chemical and energy industries. It enables users to create detailed process models, simulate complex reactions, and analyze system performance. Pro/II can be applied to simulate biomass gasification processes and evaluate different operating scenarios.
- ➢
- ChemCad: ChemCad is another popular simulation software known for its chemical process modeling capabilities. It provides tools for simulating chemical reactions, heat and mass transfer, and equipment sizing. ChemCad can be utilized to model biomass gasification reactions and optimize process parameters.
- ➢
- MATLAB: MATLAB is a versatile programming environment that offers powerful numerical computation capabilities. It is often utilized for dynamic simulation of biomass gasification processes, where complex reaction kinetics, heat transfer, and mass transport phenomena need to be modeled and analyzed.
- ➢
- ANSYS Fluent and ANSYS CFX: ANSYS Fluent and ANSYS CFX are leading computational fluid dynamics (CFD) software packages used for simulating fluid flow, heat transfer, and chemical reactions. They are ideal for studying gas-solid interactions, combustion processes, and thermal behavior in biomass gasifiers.
- ➢
- CFD2000: CFD2000 is a specialized CFD software tailored for modeling combustion and gasification processes. It offers features for simulating fluidized bed reactors, particle dynamics, and chemical reactions, making it suitable for analyzing biomass gasification systems.
3.2. Analytical Fluid Dynamics Simulation Models
3.3. Heat Integration
3.4. Co-Generation Potential
4. Conclusion
4.1. Recommendation
Acknowledgments
References
- Börjesson, P., & Tjerneld, F. (2008). Life cycle assessment of biofuels in the European context (Vol. 42). Heidelberg: Springer Science & Business Media.
- Demirbas, A. (2004). Combustion characteristics of different biomass fuels. Progress in Energy and Combustion Science, 30(2), 219-230. [CrossRef]
- Hossain, M. A., & Davies, P. A. (2015). Biomass energy and the environmental impacts associated with its production and utilization. Environmental Sustainability, 3(1), 82-94.
- Knoef, H. A. M. (2005). Gasification: An alternative process for energy recovery and disposal of municipal solid wastes. Waste Management & Research, 23(4), 281-292.
- Mooney, C. A., Mansfield, S. D., & Beatson, R. P. (2002). Cellulose utilization for ethanol production: enzymatic hydrolysis of cellulosic biomass. Cellulose, 9(4), 445-450.
- Ometto, A. R., & König, A. (2017). Optimization of biomass gasification for power production: A combined numerical and experimental approach. Biomass and Bioenergy, 97, 153-165.
- Ptasinski, K. J., & Prins, M. J. (2011). Coverage of the biomass-to-power amendment by the Dutch renewable energy directive. Renewable Energy, 36(3), 1084-1086.
- Ramanan, R. N., Tan, K. T., Aroua, M. K., & Sulaiman, N. M. N. (2007). Utilization of oil palm as a source of renewable energy in Malaysia. Renewable and Sustainable Energy Reviews, 11(6), 1366-1377.
- Srinivas, T., & Reddy, B. V. (2012). Biomass gasification for decentralised power generation: The Indian perspective. Energy for Sustainable Development, 16(3), 237-244.
- Tabatabaei, M., & Kianmehr, M. H. (2015). A review on comprehensive thermo-economic analysis and optimization of biomass-based polygeneration systems. Renewable and Sustainable Energy Reviews, 52, 205-225.
- Tilman, D., Hill, J., & Lehman, C. (2006). Carbon-negative biofuels from low-input high-diversity grassland biomass. Science, 314(5805), 1598-1600. [CrossRef]
- Tiwari, P., Kumar, A., & Raheman, H. (2007). Biodiesel production from jatropha oil (Jatropha curcas) with high free fatty acids: an optimized process. Biomass and Bioenergy, 31(8), 569-575. [CrossRef]
- Uslu, A., & Faaij, A. (2010). Exploring the prospects for gasification-based energy systems in Turkey. Energy Policy, 38(11), 7151-7161.
- Van der Veen, S., & Junginger, M. (2011). Policy issues related to the development and diffusion of biofuels in the EU. Renewable and Sustainable Energy Reviews, 15(9), 4364-4384.
- Wang, H., Luo, Y., Fan, M., & Chen, L. (2007). Optimization of the biomass gasification process based on equilibrium calculations. Chemical Engineering Journal, 132(1-3), 119-124.
- Xue, J., Koo, Y., & Wu, C. (2012). Optimization of biofuels supply chain and land use under biomass price uncertainty. Biomass and Bioenergy, 46, 349-363.
- Yacob, S., Zhang, M., & Zhang, J. (2014). The prospects of biofuels in Malaysia. Bioresource Technology, 170, 495-503.
- Zainal, Z. A., Ali, R., Lean, C. H., & Seetharamu, K. N. (2001). Prediction of performance of a downdraft gasifier using equilibrium modeling for different biomass materials. Energy Conversion and Management, 42(12), 1499-1515. [CrossRef]
- Abada, E. H., & Avila, C. A. (2016). Techno-economic analysis of a biomass gasification-based power plant with polygeneration options. Energy Conversion and Management, 114, 23-38.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




