Unveiling the True Nature of Sliding Friction through Thermodynamic Principles

Preprint

Article

Unveiling the True Nature of Sliding Friction through Thermodynamic Principles

Altmetrics

Downloads

145

Views

101

Comments

Bohua Sun^*

This version is not peer-reviewed

Submitted:

30 May 2024

Posted:

31 May 2024

You are already at the latest version

Alerts

Abstract

Friction, one of the oldest technologies harnessed by humanity, has thus far eluded a theoretical model capable of predicting kinetic friction forces across a broad range of sliding velocities. This study employs the first principle of thermodynamics to delve into sliding friction. For the first time, a general expression for the friction force has been derived, revealing that the damping of sliding friction is inversely proportional to the relative sliding velocity between the two interfaces in motion, contrary to the assumption in traditional models that it is directly proportional to the relative velocity. To simplify the general result, the concept of a friction boundary layer is introduced. An approximate expression is found to reveal the mechanism for reducing friction, which involves increasing the sliding velocity while decreasing the vibration velocity of the object perpendicular to the sliding interface.

Keywords:

Subject: Physical Sciences - Thermodynamics

1. Introduction

Friction arises due to the relative movement between two objects; hence, frictional force is also considered a dissipative force existing at the interface of friction, converting mechanical kinetic energy into irreversible heat. Frictional fire-making is one of the oldest technology used by humankind [1,2,3,4,5,6], which signifies the active utilization of thermal energy by humans, aiding in the departure from the barbaric era of eating raw meat and drinking blood, and ushering in modern civilization. Friction plays a crucial role in our everyday lives, from walking to driving a car and from energy dissipation to triboelectric nanogenerators (TENG) [7,8].

The study of friction can be traced back to the Renaissance period, when figures such as Leonardo da Vinci, Amontons, and Coulomb proposed the famous laws of friction. The phenomenological Amontons-Coulomb friction law

F = μ_{k} N

states that kinetic friction force F is equal to a kinetic friction coefficient

μ_{k}

times the normal load N and is independent of contact area and relative sliding velocity. This description of frictional force is not derived from first principles, but rather an empirical summary of frictional phenomena [9,10,11,12].

As the accuracy of measuring instruments continues to improve, an increasing number of research results indicate that the three models of friction including the Amontons-Coulomb law, the classical Prandtl-Tomlinson (PT) [2,3] and Frenkel-Kontorova (FK) [4,5,6] models are not entirely accurate [9,10,11,12]. The Amontons’ law states that kinetic friction is independent of the sliding velocity while the Prandtl Tomlinson model suggests that damping is proportional to the relative sliding velocity between two contacting objects. To date, no theoretical model can predict the magnitude of frictional force, nor can it accurately predict the vibrations and noise induced by friction, making these aspects still unpredictable and elusive.

Recently, Huang et al. [12] discovered that the interfacial force is not a dissipative force. During the process of sliding friction, the interfacial interaction forces simply convert mechanical kinetic energy into the elastic potential energy of an elastic body, which is a process of conservation of mechanical energy. This potential energy continuously accumulates until it exceeds a specific threshold, at which point some of the accumulated potential energy is released in the form of phonons. The energy dissipation occurs throughout the entire elastic body, not just at the frictional interface. The energy dissipation of the entire elastic body can be described by an equivalent material damping. Therefore, the damping of sliding friction is directly proportional to the vibration velocity of the elastic body in sliding direction, rather than being proportional to the relative velocity of the two sliding interfaces, as assumed in traditional models such as the Prandtl-Tomlinson (PT). Based on this, Huang eta al. [12] has proposed the phonon friction model, which can predict the frictional forces measured by friction force microscopy, and this has been verified by molecular dynamics simulation models. The phonon friction model tries to explain long-standing puzzling tribological phenomena, such as the velocity weakening of frictional forces and the observed dependence of frictional forces on spring stiffness.

The work of Huang et al. [12] has subverted the traditional understanding that friction is a dissipative force at the interface, their phononic friction model deepens our understanding of the mechanism of frictional energy dissipation. However, the Amontons-Coulomb law has not been derived from their phononic friction model. The rational formulation of the Amontons-Coulomb law of friction is still an open problem.

In this Letter, we will take a different approach to considering the problem by treating two objects that are sliding past each other as elastic deformable bodies. The sliding interface is characterized by irregular roughness, and when the objects slide past each other, the irregularities of the rough surface undergo elastic deformation under pressure. The objects in motion obtain elastic potential energy, and then the issue of sliding friction is re-examined from the standpoint of energy conservation, in accordance with the first law of thermodynamics.

2. Thermodynamics of Friction Force

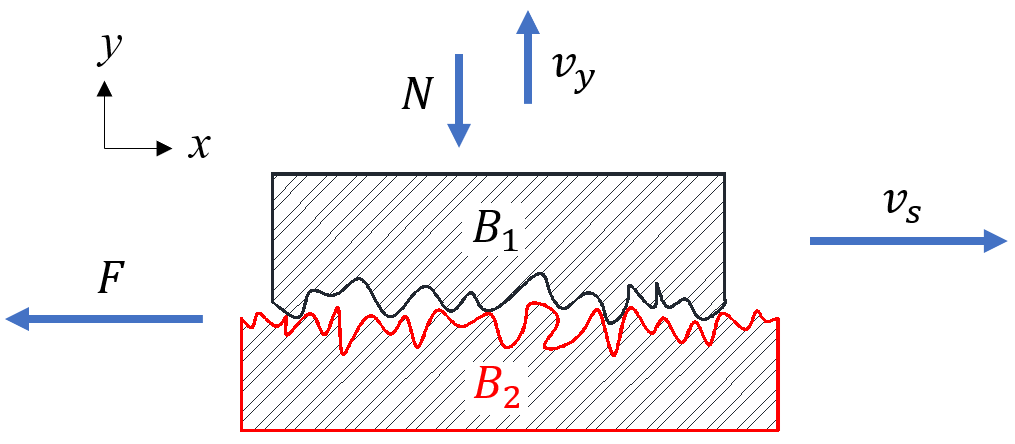
If we consider the two contact elastic objects

B_{1}

and

B_{2}

as a system

S = B_{1} + B_{2}

as shown in Figure 1, their relative sliding motion with the sliding velocity

v_{s}

causes the corrugated surface deformed under the pressure of the normal force N, the friction force F will resist the motion of the top object

B_{1}

if we assume the bottom object

B_{2}

is fixed. The problem becomes to find the kinetic friction force F under the pressure of N.

According to Huang et al. [12], the energy of sliding friction process is conservative. If the friction force does work

δ W

, and/or contact bodies absorb heat

δ Q

from its surroundings, then this corresponds to a net flow of energy

δ W - δ Q

across the boundary to the surroundings. In order to conserve the total energy E, there must be a counterbalancing change

δ E = δ Q - δ W

in the internal energy of the bodies. The first law provides a kind of strict energy accounting system in which the change in the energy account

δ E = {\int \int \int}_{V} \frac{1}{2} σ : ϵ d V

equals the difference between deposits

δ Q

and withdrawals

δ W

. Hence we have the 1st law of thermodynamics for the sliding friction as follows:

{\int \int \int}_{V_{1}} \frac{1}{2} σ : ϵ d V + {\int \int \int}_{V_{2}} \frac{1}{2} σ : ϵ d V = δ Q - F \cdot ℓ,

(1)

where

V_{1}

and

V_{2}

are the volume of the friction system

B_{1}

and

B_{2}

, respectively,

σ

is stress tensor,

ϵ

is strain tensor, ℓ is displacement vector of the friction motion.

By taking the time derivative of both sides of Equation (1) and considering that

\frac{d F}{d t} \cdot ℓ = 0

, we obtain

\frac{d F \cdot ℓ}{d t} = \frac{d F}{d t} \cdot ℓ + F \cdot \frac{d ℓ}{d t} = F \cdot \frac{d ℓ}{d t}

. This is because the derivative

\frac{d F}{d t}

is orthogonal to the displacement vector ℓ. Consequently, we have the rate form of the first law of thermodynamics.

{\int \int \int}_{V_{1}} σ : \dot{ϵ} d V + {\int \int \int}_{V_{2}} σ : \dot{ϵ} d V = δ \dot{Q} - F \cdot v_{s},

(2)

where

v_{s} = d l / d t

is sliding velocity.

Letting

θ

represent the angle between the force

F

and the velocity

v

, which are in opposite directions, we have

F \cdot v = - F v_{s} cos θ = - F v_{s}

since

θ = π

and

cos π = - 1

. Note that the Cauchy stress tensor

σ

governs the relation

σ : d \dot{ϵ} = σ : d

, where

d = \nabla v

denotes the deformation rate [13,14], where,

v

represents the velocity field of a deformable body, and ∇ is the gradient operator.

Hence Equation (2) becomes

{\int \int \int}_{V_{1}} σ : d d V + {\int \int \int}_{V_{2}} σ : d d V = δ \dot{Q} + F v_{s},

(3)

For kinetic sliding friction (

v_{s} \neq 0

), the kinetic friction force is given by

F = \frac{δ \dot{Q}}{v_{s}} + \frac{1}{v_{s}} ({\int \int \int}_{V_{1}} σ : d d V + {\int \int \int}_{V_{2}} σ : d d V),

(4)

which reveals that the friction force diminishes as the sliding velocity

v_{s}

increases, offering a plausible explanation for the observed phenomenon of friction weakening with increasing sliding velocity. This contradicts the assumption in conventional models that friction damping is directly proportional to the relative velocity between the sliding interfaces. Instead, it suggests an inverse relationship. Furthermore, Equation (4) suggests that the friction force is related to the rate of elastic energy, which is the capacity of an elastic body to mitigate vibration energy generated by sliding. This can be likened to a car traversing a bumpy road, where the shock absorbers provide damping. Equation (4) also implies that the rate of heat absorption,

δ \dot{Q}

, affects the friction force, with frictional heating potentially leading to a decrease in the friction force.

In the friction system depicted in Figure 1 as

B_{1} + B_{2}

, the friction force arises due to the interaction at the contact surface. Consequently, the deformation occurs exclusively within a minute boundary layer adjacent to the contact surface between

B_{1}

and

B_{2}

. The remainder of the system

B_{1} + B_{2}

maintains a strain-free state. This thin boundary layer can be identified as a friction boundary layer, and the associated simplification can be termed friction boundary layer modeling. Within this model, the elastic potential energy generated by the friction force is localized and confined to a thin layer encircling the contact surface.

3. Simplification

Building on this perspective and simplification, we can postulate that the rate of elastic energy density

(σ : d)

remains constant within the volume of the friction boundary layer, denoted as

V = l_{x} l_{y} l_{z}

, where

l_{x}, l_{y}, l_{z}

represent the dimensions of the friction boundary layer. Given that the stress tensor

σ

can be expressed as

σ = σ_{y y} e_{y} \otimes e_{y} = - \frac{N}{l_{x} l_{z}} e_{y} \otimes e_{y}

(with the convention that compression stresses are negative), and the deformation gradient d is defined as

d = d_{y y} e_{y} \otimes e_{y} = \frac{d v_{y}}{d y} e_{y} \otimes e_{y}

, where

l_{x} l_{z}

corresponds to the contact area. Consequently, we have

σ : d = σ_{y y} d_{y y}

. Consequently, if body

B_{1}

and body

B_{2}

has same materials, the friction force can be expressed as follows:

F = \frac{δ \dot{Q}}{v_{s}} - \frac{N}{v_{s}} l_{y} (\frac{d v_{y}}{d y}) |_{y = 0} .

(5)

Based on the concept of the friction boundary layer, we can assume the elastic body has bumping velocity

v_{{y |}_{y = 0}} = v_{y 0}

on the contact surface and decay to zero at

y = \infty

, namely

v_{y} = v_{y o} e^{- y / l_{y}}

, leads to the velocity gradient

\frac{d v_{y}}{d y} = - \frac{v_{y 0}}{l_{y}} e^{- y / l_{y}}

Substitute

\frac{d v_{y}}{d y} = - \frac{v_{y 0}}{l_{y}} e^{- y / l_{y}}

into Equation (5), we have the sliding fiction force as follows

F = \frac{δ \dot{Q}}{v_{s}} + \frac{v_{y o}}{v_{s}} N, v_{s} \neq 0 .

(6)

The fiction process can be consider as mass conservative or at constant volume, we have

δ \dot{Q} = C_{V} d \dot{T}

, where T is absolute temperature and

C_{V}

is the heat capacity at constant volume. Hence

\frac{δ \dot{Q}}{v_{s}} = C_{V} \frac{d \dot{T}}{v_{s}} = \frac{C_{V} d T / d t}{d l / d t} = C_{V} \frac{d T}{d ℓ}

, in which

\frac{d T}{d ℓ}

is the temperature gradient along the sliding direction ℓ, therefore the Equation (6) can further expressed as follows

F = C_{V} \frac{d T}{d ℓ} + \frac{v_{y o}}{v_{s}} N, v_{s} \neq 0,

(7)

in which the first term in the right hand represents frictional heating.

For sake of simplification, we can postulate that there is no friction heat generation (

δ \dot{Q} = 0

and or

\frac{d T}{d ℓ} = 0

), Equation (6) becomes

F = \frac{v_{y o}}{v_{s}} N, v_{s} \neq 0,

(8)

which can be easily understood from the power conservative point of view, that is the dissipation power equal to the potential power of the elastic body, namely

F v_{s} = N v_{{y |}_{y = 0}}

Equation (6) gives the kinetic friction coefficient as follows

μ_{k} = \frac{v_{y o}}{v_{s}} = \frac{bumping velocity}{sliding velocity},

(9)

which provides a clear picture for reducing friction that is to increase the sliding velocity while decreasing the vibration velocity of the object perpendicular to it.

It is noteworthy to point out that the kinetic friction coefficient

μ_{k}

typically depends on time and its value fluctuates in response to the velocity of surface roughness-induced vibrations.

4. Conclusions and Perspectives

The author is aware that this work represents the first theoretical framework for sliding friction within a physics context. By employing the thermodynamics of continuum media, this study offers a distinct physical understanding of sliding friction and reveals how to actively control friction. This approach represents a fundamental shift away from traditional models, which have been unable to reliably predict kinetic friction across a broad spectrum of sliding velocities.

Our findings reveal a surprising inverse relationship between the damping of sliding friction and the relative sliding velocity between the two interfaces. Contrary to the widely accepted belief that friction is directly proportional to the relative velocity, our theoretical model demonstrates that friction force is actually inversely proportional to the sliding velocity. This groundbreaking revelation has the potential to revolutionize our understanding of friction and could lead to the development of new technologies aimed at reducing friction and improving the efficiency of mechanical systems.

To clarify this overarching result and delve deeper into the underlying mechanisms, we introduce the concept of a friction boundary layer. Examining this layer allows us to derive an approximate expression that provides insight into methods for friction reduction. Notably, our analysis indicates that one effective strategy for reducing friction is to increase the sliding velocity while concurrently decreasing the vibration velocity of the object perpendicular to the sliding interface.

Conflicts of Interest

The authors declare that there are no competing financial interests.

References

D. Dowson, History of Tribology (Longman, New York, 1979). London, 1998). 63, 041506 (2001).
L. Prandtl, Ein Gedankenmodell Zur Kinetischen Theorie Der Festen Körper, J. Appl. Math. Mech. 8, 85 (1928).
G.A. Tomlinson, A molecular theory of friction, London, Edinburgh Philos. Mag. J. Sci. 7, 905 (1929).
T. Kontorova and J. Frenkel, On the theory of plastic deformation and twinning. II., Zh. Eksp. Teor. Fiz. 8, 1340 (1938).
M. Weiss and F.-J. Elmer, Dry friction in the Frenkel Kontorova-Tomlinson model: Static properties, Phys. Rev. B 53, 7539 (1996).
M. Weiss and F.-J. Elmer, Dry friction in the Frenkel Kontorova-Tomlinson model: Dynamical properties, Z. Phys. B Condens. Matter 104, 55 (1997).
Z.L. Wang, J. Song, Piezoelectric Nanogenerators Based on Zinc Oxide Nanowire Arrays, Science, 312 (2006), pp. 242-246.
Z.L. Wang, On the expanded Maxwell’s equations for moving charged media system - general theory, mathematical solutions and applications in TENG. Mater. Today 52, 348-363 (2021).
J. Krim, Friction at the atomic scale, Sci. Am. 275, No. 4, 74 (1996).
F. P. Bowden and D. Tabor, The Friction and Lubrication of Solids (Oxford University Press, Oxford, 2001).
M. Urbakh, J. Klafter, D. Gourdon, and J. Israelachvili, The nonlinear nature of friction, Nature (London) 430, 525 (2004).
S.Y. Huang, et al. Reexamination of damping in sliding friction, Phys.Rev.Lett. 132, 056203 (2024).
C. Truesdell and W. Noll, The Non-Linear Field Theories of Mechanics. Handbuch der Physik, Editor: S. Flügge, Vol. 3, Springer-Verlag Berlin,1969.
C. Truesdell and R. Toupin, Principles of Classical Mechanics and Field Theory. Handbuch der Physik, Editor: S. Flügge, Vol. 2, Springer-Verlag Berlin, 1960.

Figure 1. Schematic illustration of kinetic sliding friction. Friction force F is generated under pressure of the normal force N on the contact surface between body

B_{1}

and body

B_{2}

. Considering the two contact elastic objects

B_{1}

and

B_{2}

as a system

S = B_{1} + B_{2}

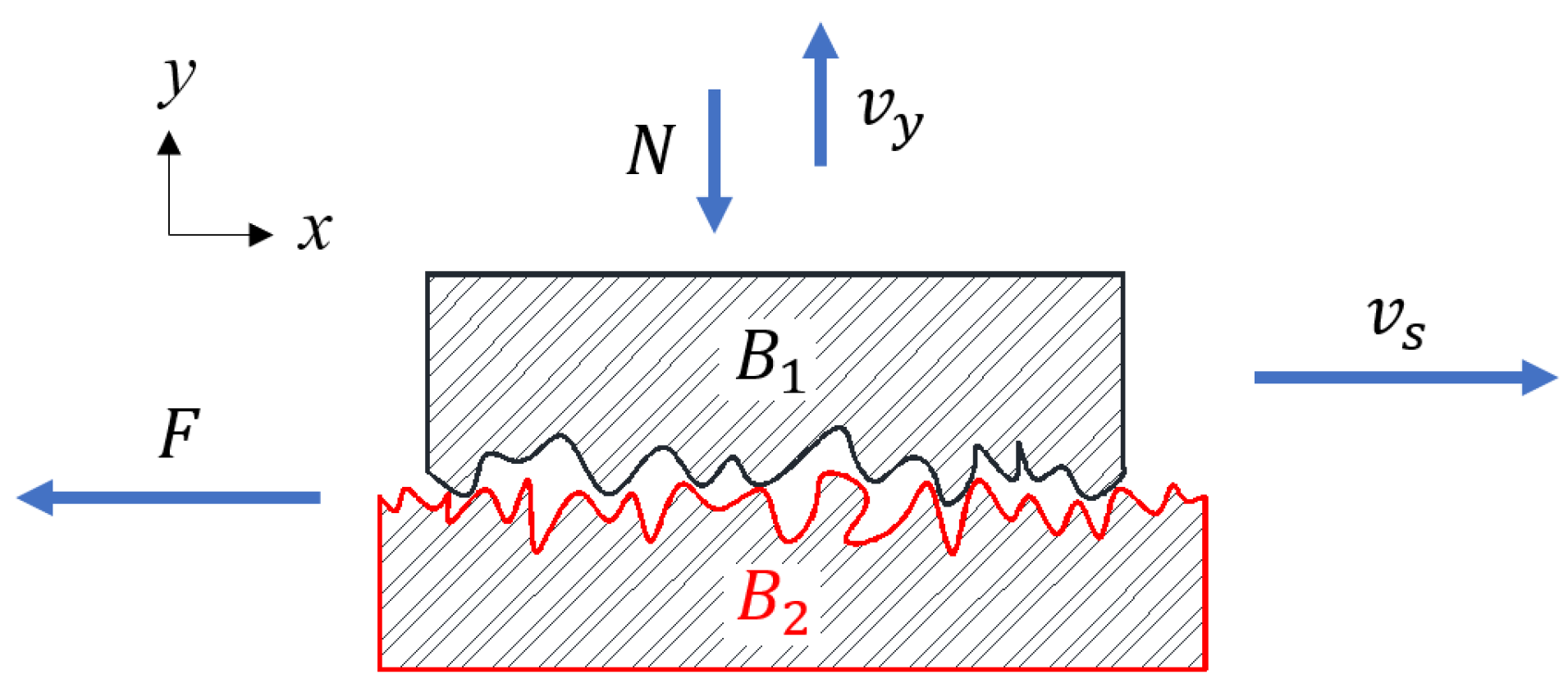
Figure 1. Schematic illustration of kinetic sliding friction. Friction force F is generated under pressure of the normal force N on the contact surface between body

B_{1}

and body

B_{2}

. Considering the two contact elastic objects

B_{1}

and

B_{2}

as a system

S = B_{1} + B_{2}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Unveiling the True Nature of Sliding Friction through Thermodynamic Principles

Abstract

1. Introduction

2. Thermodynamics of Friction Force

3. Simplification

4. Conclusions and Perspectives

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe