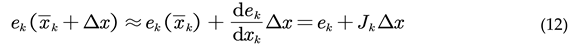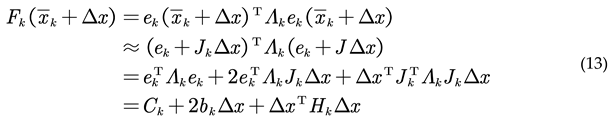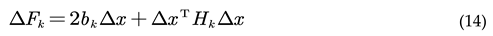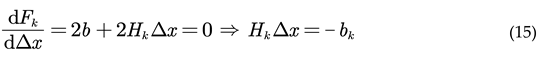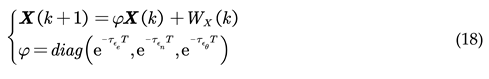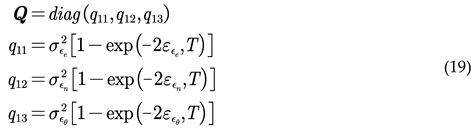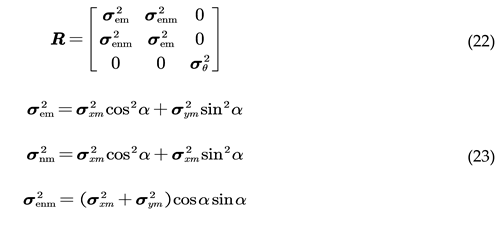1. Introduction
With the orderly opening of low-altitude airspace, the application of drones is becoming increasingly widespread in various fields, ranging from circuit inspection and logistics delivery to urban traffic management [
1]. The efficient use of drones has become a highlight of modern technological advancement. However, to ensure that drones can perform tasks safely and efficiently, precise positioning and navigation capabilities are essential. Currently, there are multiple positioning methods for drones, including the Global Positioning System (GPS), Inertial Navigation System (INS), Terrain-Aided Navigation (TAN), Doppler Velocity Log (DVL), odometer (OD), and Visual Navigation (VO) [
2]. Nevertheless, as application scenarios become more complex, the accuracy and robustness of the navigation system face severe challenges during high-speed maneuvers or prolonged flights.
Traditional drone positioning relies on a single sensor system, which may suffice in specific usage environments, but in complex environments, the interference from multipath effects, signal blockage, and environmental noise can lead to the accumulation of sensor noise and motion errors, impacting positioning accuracy. For instance, the Inertial Navigation System (INS) is a type of relative positioning technology that can only provide accurate solutions for a limited time, as errors in inertial sensors and integration drift can lead to solution divergence [
5]. Therefore, to enhance the positioning accuracy and system stability of drones, researchers have begun to explore multi-source and multimodal data fusion methods.
Data fusion technology [
7] involves the merging and processing of multiple complementary or similar information sources, where the merged information is more precise than any single source. The information fusion technique of combined navigation involves first converting the navigation data from various sensors to a unified coordinate system, then using appropriate mathematical estimation methods to fuse the data within this system, obtaining the system's optimal estimate [
8]. Thus, the data fusion process entails using mathematical optimal estimation algorithms to estimate the status of the navigation system. There are several categories of data fusion algorithms, among which analytical-based methods and learning-based methods are the most widely used. Analytical-based methods use analytical functions to simulate system states and external measurements, referred to as "estimation" in the literature [
10]. Many analytical-based methods are widely utilized, such as Kalman Filtering (KF) and Particle Filtering (PF), while several learning-based data fusion methods, such as Artificial Neural Networks (ANN), fuzzy logic, and Support Vector Machines (SVM), are also used because they can model systems without prior statistical information about the process and measurement noise. Since the introduction of the Kalman Filter (KF), it has been extensively used to address many challenging and complex information fusion problems [
9]. However, traditional Kalman Filtering can only be applied in linear systems. To apply federated Kalman Filtering in nonlinear systems, several improved KF methods have been proposed [
10]. Based on the changing Bayesian adaptive Kalman Filtering [
11], a method has been proposed to track the continuously varying noise variance in the Global Positioning System/Inertial Navigation System. Insufficient prior information can cause the filter to diverge [
13]. The Extended Kalman Filter (EKF) is a widely used method for integrating inertial/Global Positioning Systems. It linearizes nonlinear systems through a first-order Taylor expansion [
13]. For example, the fusion of visual sensors and IMU can be divided into loose and tight coupling [
6]. In loose coupling, the Extended Kalman Filter [
8] or the Unscented Kalman Filter (UKF) [
14] fuses the pose information obtained from the visual sensors and IMU as separate modules. The information fusion used in literature [
16] and [
17] is of loose coupling. Literature [
12] utilizes tight coupling, where the pose information obtained after processing the intermediate data from the visual and IMU sensors through filters has higher accuracy compared to loose coupling, but its robustness is poorer, and the failure of a sensor can paralyze the entire system. Additionally, for multi-sensor data fusion, the time synchronization of data directly affects the accuracy of the fusion. A method of sequential measurement updating has been proposed in the literature [
18], where the update timing nodes are the same as the IMU data measurement nodes. Other sensors act as auxiliary sensors to correct IMU data, and their update nodes must be on the IMU update nodes. Due to the different data acquisition frequencies of various sensors, it is necessary to synchronize the timing of various data at the fusion center, which can determine the best sequence for fusion [
19]. The pre-fusion processes add many complex processing and computational procedures to the multi-sensor data fusion process.
Digital Twin technology, as an innovative technology that has emerged in recent years, has demonstrated its significant application potential and value across multiple domains. For instance, in military operations, literature [
16] reflects on the construction of a digital twin battlefield, proposing a universal architecture for digital twin battlefields and providing feasible solutions for their construction. In drone-related fields, literature [
17] introduces an algorithm based on random finite sets, analyzing the system architecture and model, and demonstrating the application of digital twin robots in drone operations. Literature [
18] discusses and designs the digital twin framework for military large-scale drones using digital twin technology combined with cloud computing, analyzing its functions to some extent and providing solutions for constructing drone digital twin systems. In the area of drone positioning and navigation research, the introduction of digital twin technology offers new ideas and methods to address the challenges faced by traditional positioning systems. Digital twin technology creates a virtual drone model capable of real-time mapping and simulating the actual drone's state and behavior [
21]. This bridge between virtual and reality not only aids in predicting and analyzing drone performance but also provides more precise positioning and navigation support under complex environmental conditions.
However, although multi-source multimodal data fusion and digital twin technology theoretically hold significant potential, effectively integrating these technologies to achieve higher positioning accuracy and robustness remains a challenge in practical applications. Most existing studies focus on improving specific technologies or algorithms, lacking an in-depth exploration of how to effectively merge these different technologies to meet the positioning needs of drones in complex environments.
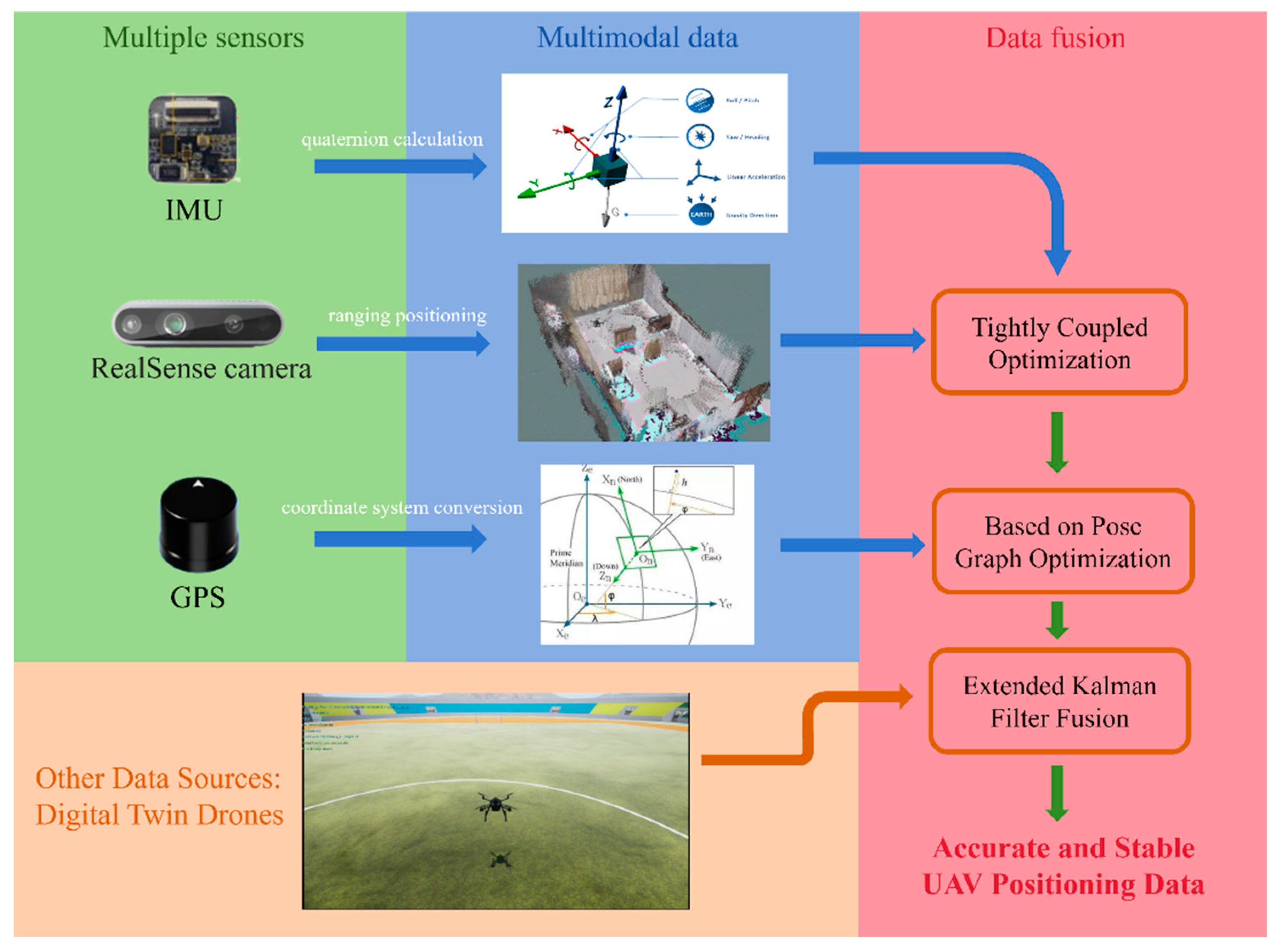
Therefore, this paper proposes a novel small drone positioning estimation method based on multi-source multimodal data fusion and digital twin technology. As shown in
Figure 1, this method first utilizes multiple sensors such as GPS, IMU, and visual sensors for multimodal data fusion, then employs the digital twin drone as a key data source, implementing data fusion between the real drone and its digital twin through the Extended Kalman Filter (EKF) algorithm. This fusion approach effectively eliminates the limitations of a single sensor and reduces the positioning deviations caused by sensor errors and external environmental changes. Moreover, the digital twin drone provides a simulation model that predicts the real drone under the same conditions, utilizing the predictive capabilities of the digital twin model to correct and optimize the sensor data of the real drone. Especially in cases where sensor data is unstable or severely interfered with, it provides a more accurate reference for real-time location information, allowing timely correction of positioning information when sensor data undergoes sudden changes, ensuring the stability and accuracy of the drone control system. This study not only offers new ideas and methods for precise positioning of small drones but also explores new possibilities for the practical application of digital twin technology in drone navigation and applications.
2. System and Model Construction
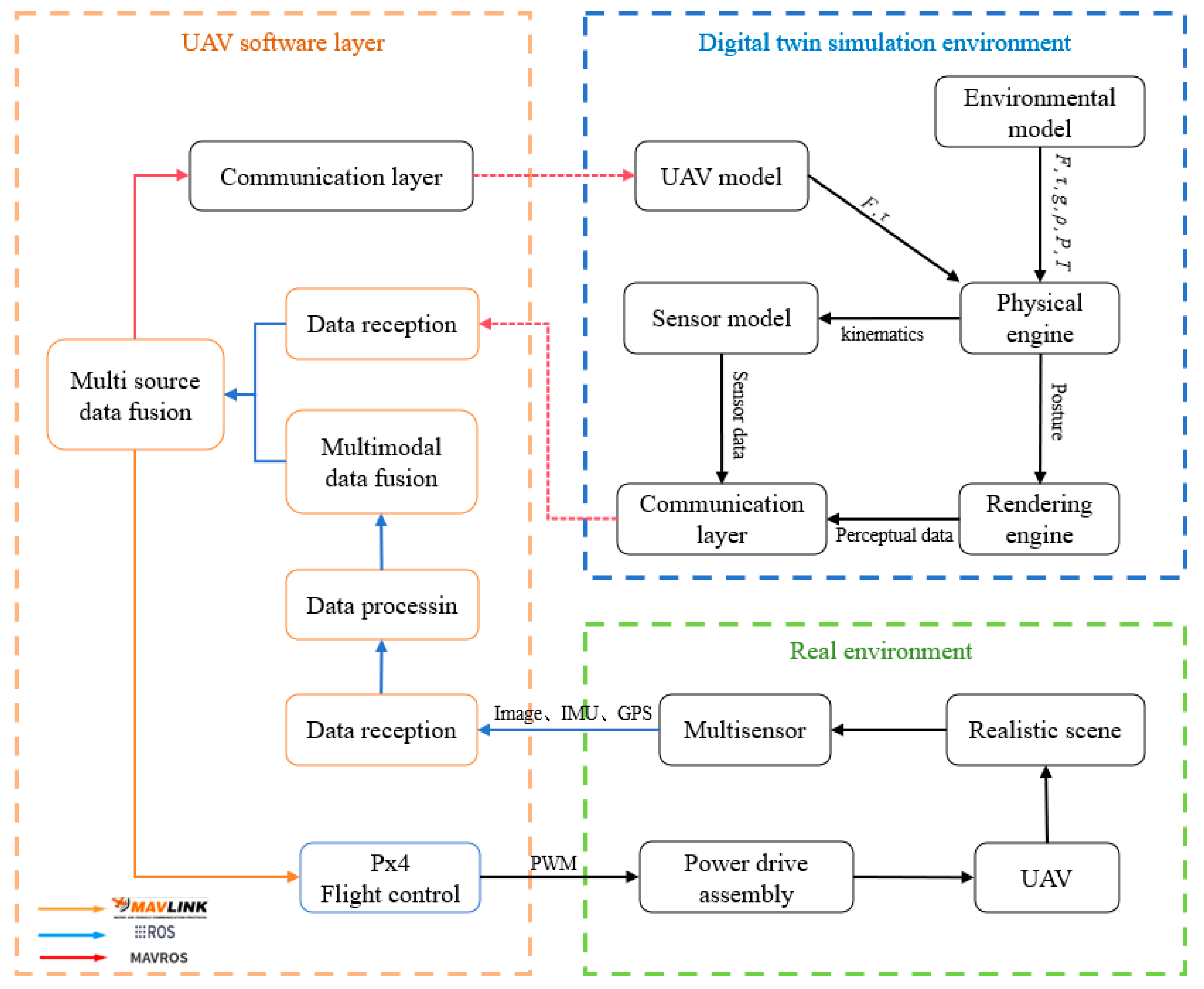
This paper establishes a data fusion system architecture based on digital twins for multi-source and multimodal data fusion methods, as illustrated in
Figure 2. This diagram depicts a multi-source and multimodal data fusion system primarily deployed in UAV software layers and digital twin simulations. During the digital twin simulation process, sensor models provide the UAV flight control with sensor information obtained from the simulation environment. The flight controller computes the current state estimates and outputs actuation signals to the UAV model, which calculates the required forces and torques and assigns motor voltages. Additionally, inputs such as drag, friction, gravity, and torque are used by the physical engine to compute the UAV's next motion state in the simulation environment, and the estimated data is relayed in real-time to the physical UAV. The UAV dynamics information, enriched with environmental model data like gravity, air density, atmospheric pressure, magnetic fields, and GPS coordinates, is then transmitted back to the sensor model, creating a feedback loop that captures sensor-acquired data. On the UAV's physical side, the system encompasses data collection, processing, and algorithmic fusion, utilizing raw data from IMUs and GPS, along with environmental information captured by depth cameras. It also receives real-time location estimates from the digital twin UAV, which are fed into the data fusion module. The data fusion and control execution section form the core of the system. Here, data from various sensors are integrated to enhance positioning accuracy and robustness. The fused information is used to generate precise flight control signals, which are subsequently transmitted back to the UAV flight control through the MavLink control protocol, achieving accurate flight control.
Through this architecture, the UAV can swiftly adapt to complex environments and effectively handle uncertainties, enhancing its operational stability and reliability in complex application scenarios. Additionally, the architecture supports modularity and distributed processing, offering flexibility and scalability for the further development of UAV technology.
To effectively simulate and predict the behavior and performance of physical unmanned aerial vehicles (UAVs) and achieve consistency between the digital twin UAV and the physical UAV, it is essential to construct a multidimensional and multiscale UAV model within the digital twin framework. This foundation supports the data interaction between the virtual and physical UAVs. The article will provide detailed explanations of the model parameters and model composition, and then construct a multidimensional and multiscale UAV model from three aspects: geometric, physical, and behavioral. This enables the digital twin UAV to simulate the physical properties, dynamic behaviors, and environmental interactions of the physical UAV in real time. Through such modeling, the digital twin acts as a critical tool in aligning the virtual operations with the real-world dynamics of UAVs, enhancing predictive maintenance and operational planning.
2.1. Geometric Model
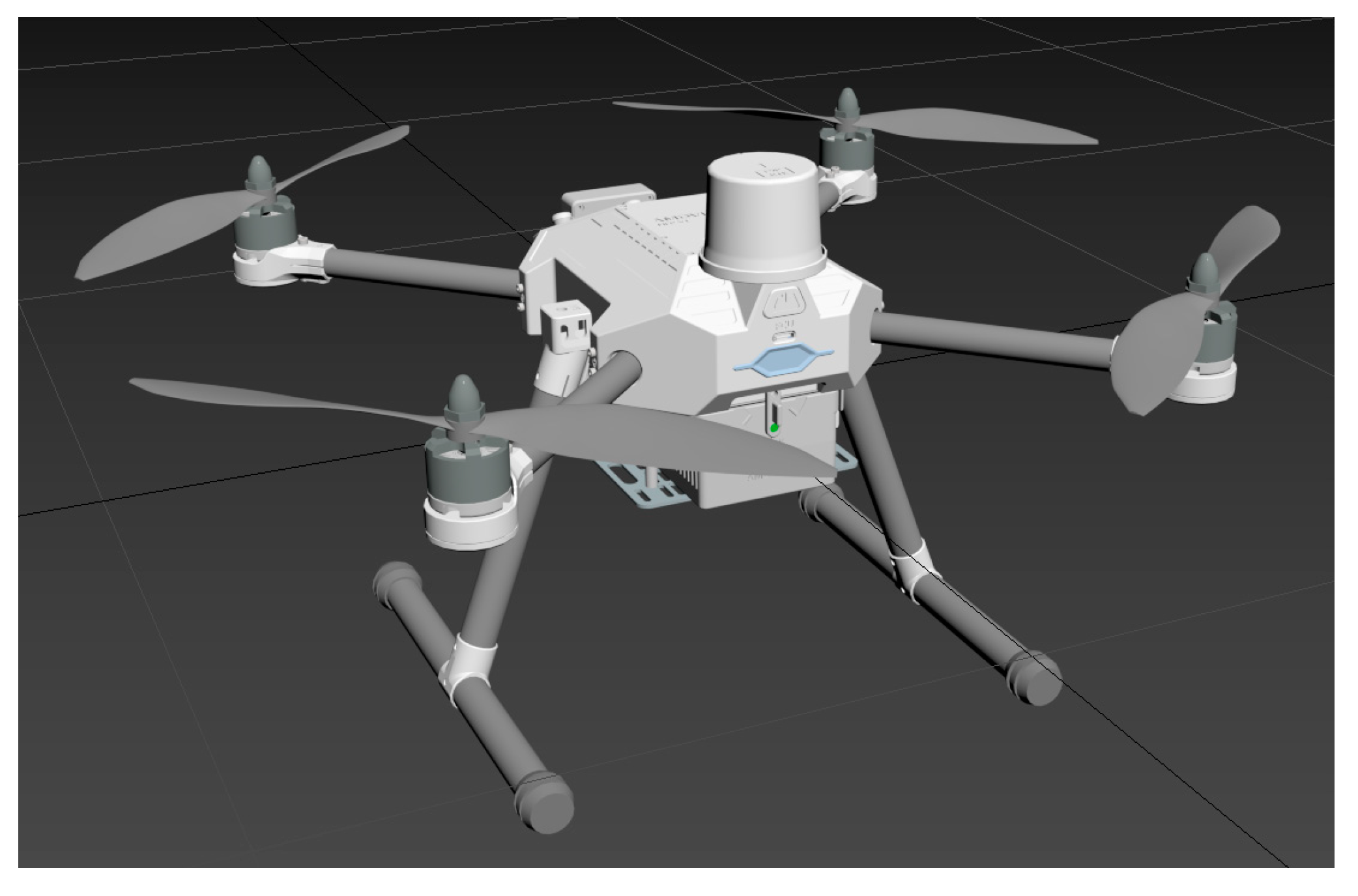
Incorporating the actual geometric dimensions and mass parameters of the unmanned aerial vehicle (UAV), a foundational model is developed using modeling software, based on the hardware architecture of the UAV as illustrated in
Figure 3. Particular emphasis is placed on the construction of critical components such as motors, propellers, flight controllers, and GPS modules, which are integral to the flight control stability of the UAV. Detailed attention is devoted to the assembly specifications of each UAV component, as demonstrated in
Figure 4, which depicts the UAV's external features, part dimensions, and material types, among other fundamental indicators. This process ensures a high-fidelity construction model of the physical UAV, enabling the digital twin system to accurately replicate the real UAV. This underpins subsequent digital twin UAV flight experiments by providing a fundamental model support, mitigating disparities between flight experimental results and actual conditions that may arise due to differences in geometric model parameters. Furthermore, it facilitates the development and testing of interfaces between the virtual and physical domains within digital twin technology.
2.2. Physical Model
The virtual drone entity model primarily consists of two parts: built-in sensors of the PX4 flight controller and physical connections. The built-in sensors mainly include a gyroscope, magnetometer, GPS, and barometer. The physical connection methods define the basic parameters for serial ports, local UDP, local TCP, remote TCP, QGC ground stations, and messaging protocols. The sensor module mainly contains devices such as gyroscopes, magnetometers, GPS, and barometers. The physical engine module mainly implements the dynamics modeling of quadrotor drones. A quadrotor drone with mass (m) is defined as a collection of four vertices , each vertex having a control input , where represents the position of the vertex relative to the centroid, and represents the corresponding control command. Finally, the control inputs (u_i) are mapped to the forces and torques at vertex equation. With the control input being a map to the angular velocity at each propeller located at the four vertices, and the local forces and torques at the four vertices are represented by equations (1) and (2):

Wherein,
and
represent the thrust coefficient and power coefficient calculated based on the physical characteristics of the propeller, respectively.
stands for air density,
is the propeller diameter, and
is the maximum angular velocity (rotations per minute). Based on the parameters of the physical drone and the experimental environment, this paper assumes the related parameters of the drone as shown in
Table 1.
2.3. Behavior Model
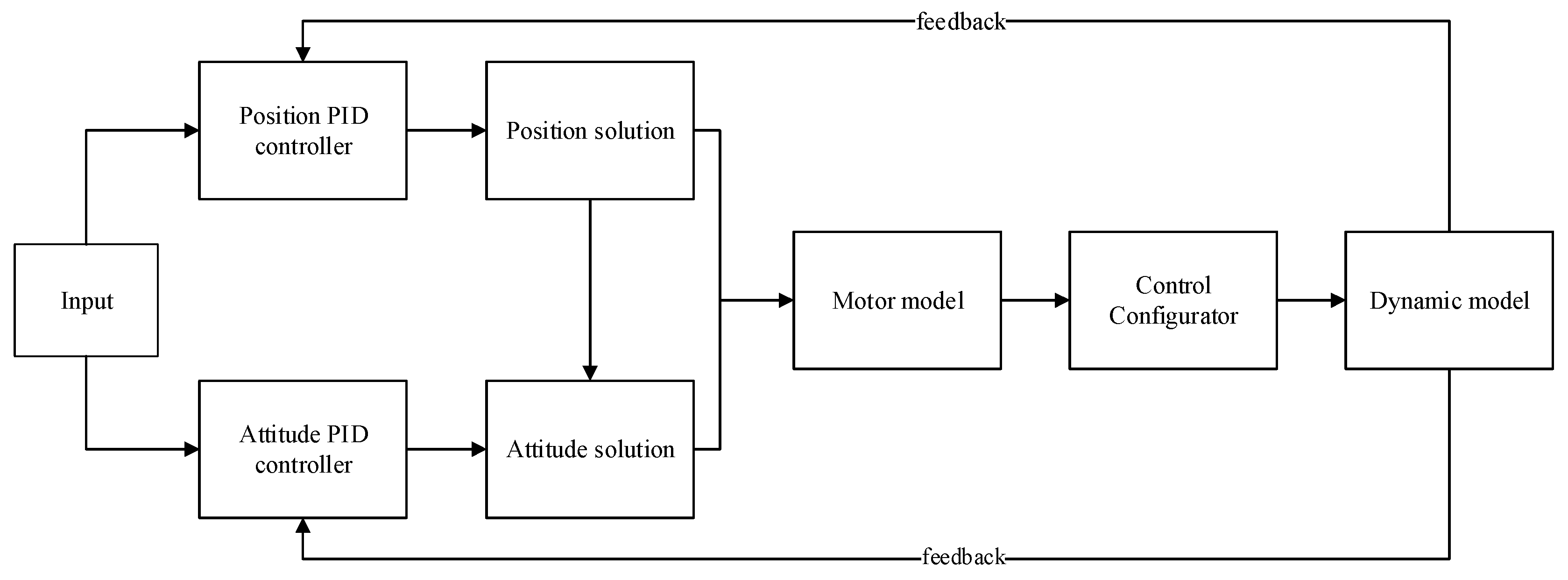
The behavioral model represents a precise control framework for UAV flight, and a PID (Proportional, Integral, Derivative) control loop is an effective method for regulating UAV flight. Building upon this, the paper proposes a design for a dual closed-loop cascaded PID control circuit, as shown in
Figure 5. In the diagram, the input signals, after filtration, are separately directed to the position PID controller and the attitude PID controller. The position PID controller takes the UAV's altitude value signal, which is linked to the UAV's NED (North East Down) coordinate system. The signal represents the difference between the set target altitude and the actual flight altitude, with the controller's output being the vertical acceleration. The attitude PID controller receives the UAV's horizontal displacement signals, which are related to its horizontal coordinates. Its values represent the discrepancies in the UAV's roll, pitch, and yaw angles from the set horizontal target values to their actual values, with the controller's output being the horizontal acceleration. Through position and attitude calculations, the system converts the input quantities allocated to each direction into PWM (Pulse Width Modulation) control signals, which are then sent to the motors. This process controls the motors, ensuring the precision of the UAV's flight control.
3. Multisource Multimodal Data Fusion
Navigating with only one type of sensor has its drawbacks. Due to the inherent differences among individual sensors, relying on a single sensor for navigation may lead to unsuitability for the environment, resulting in poor navigation accuracy. To address various complex environments, this paper adopts a navigation method using multiple sensors. The data collected by multiple sensors need to be fused, filtering out unnecessary data, extracting the required data, to achieve the best results.
3.1. Vision IMU Pose Fusion
Since pure visual positioning algorithms rely entirely on data obtained from cameras, they are susceptible to environmental lighting interference, resulting in low robustness. Cameras mounted on drones are prone to positioning failures during high-speed movements or rotational motions, making pure visual positioning highly dependent on environmental conditions and low in output frequency, which can lead to inaccurate pose estimation and cumulative errors. In contrast, IMUs (Inertial Measurement Units) offer good dynamic response performance and high pose update frequency but suffer from significant long-term cumulative errors, drift, and poor static characteristics. Therefore, to improve the accuracy and applicability range of pose estimation, this paper fuses the pose estimation results of visual odometry with those of the IMU, enhancing the robustness and real-time performance of drone pose estimation.
Visual-IMU fusion methods can be categorized into two types: loose coupling and tight coupling. The basic approach of loose coupling is to process the inertial measurement unit and visual sensors separately, which is relatively simple, requires less computation, and is highly scalable, but the accuracy of the fused pose estimation is relatively poor. The tight coupling approach combines image information with inertial navigation information and calculates the pose information through the fused data. This method is significantly more complex, requires more computation, but can effectively utilize information from each sensor, resulting in higher accuracy of the fused pose estimation. This paper adopts the tight coupling method to achieve the fusion of visual and inertial navigation information.
3.1.1. IMU Pre Integration
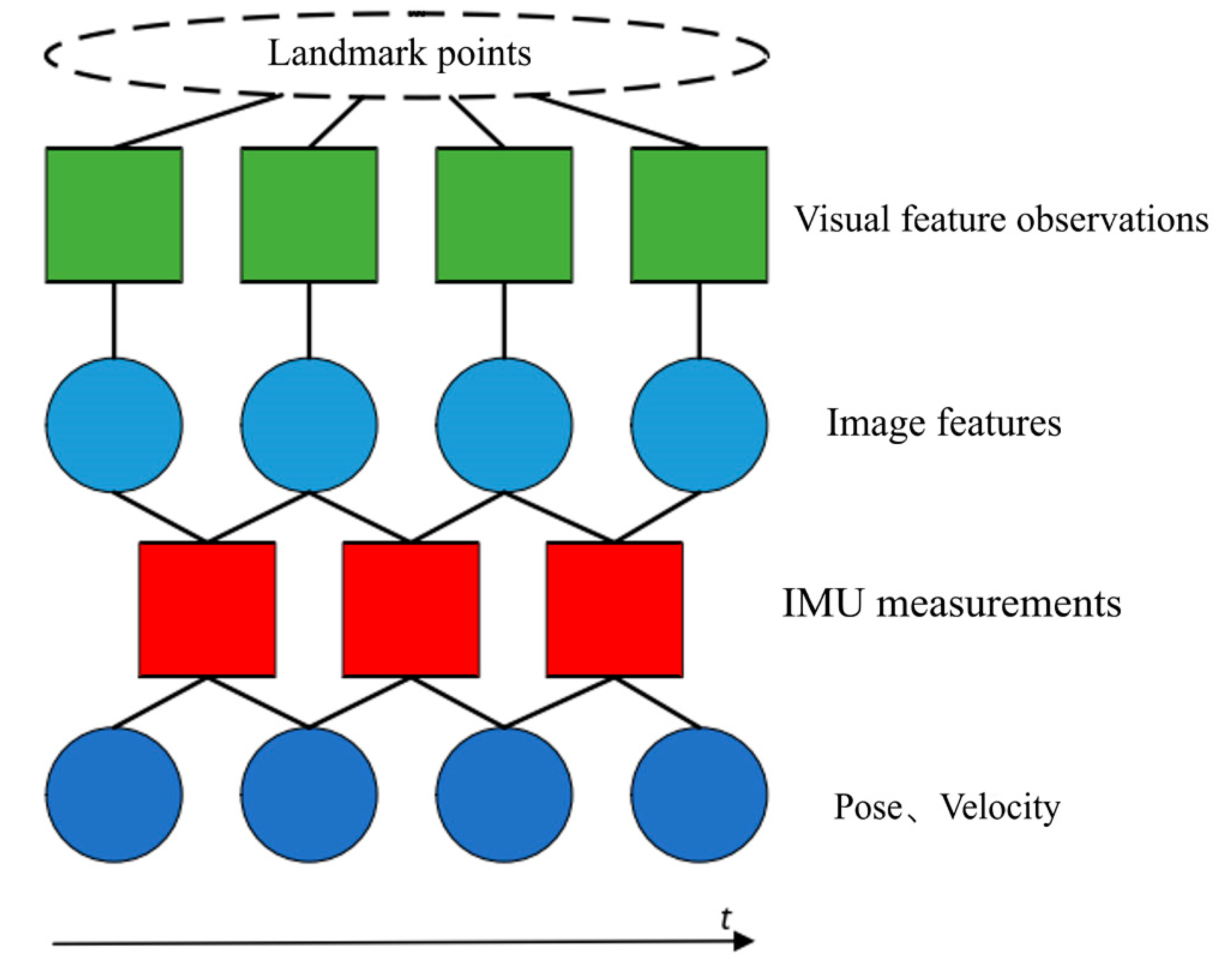
Given the disparity between the capture frequency of cameras and the signal frequency of IMUs, it is essential to consider time synchronization or measurement frequency before fusing IMU data with image information. The method of pre-integration is chosen to overcome the accumulation of errors in the world coordinate system, addressing the issue of the discrepancy in frequency between cameras and IMUs. The fundamental idea behind IMU pre-integration is to extract the invariant items during each optimization iteration beforehand, thereby reducing the workload of reintegration on each occasion. As depicted in
Figure 6, assume that we are in the global coordinate system of the camera, integrating each piece of IMU data from a previous keyframe (at time ( t_1 )) to a subsequent keyframe (at time ( t_2 )).
To optimize the poses and velocities at times (t_1) and (t_2), as well as the IMU bias (denoted as ba), where the IMU measurement is acceleration (ak), it can be deduced that:
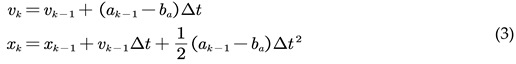
By integrating directly in the global coordinate system, it can be inferred:
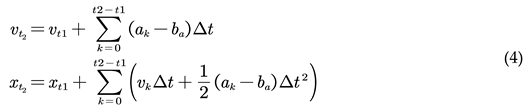
Since the drone operates in three-dimensional space, the velocity ( v ) is directional. Therefore, each time optimization occurs, updating the velocity (v_t1) in the global coordinate system requires recalculating the result within the summation sign.
The calculation is performed as a result of pre-integration. Then, the formula for calculating the position is modified to
Therefore, each time the velocity \(v_{t1}\) in the global coordinate system is updated, it is only necessary to substitute the results of pre-integration to obtain the new integration results.

This approach also reduces the necessity of recalculating when the original state information changes, significantly lowering computational complexity. By expanding according to formula (7) using the Euler integration method, the values of these three variables can ultimately be obtained. This completes the process of IMU value pre-integration. Subsequently, each optimization only requires multiplying the new velocity by time, thus greatly reducing the amount of computation required.
3.1.2. Tight Coupling Optimization Model of Vision Inertial Navigation
As illustrated in
Figure 7, visual feature measurements can be obtained through visual sensors. Subsequently, corresponding image feature information is derived using relevant algorithms. By integrating these with IMU measurements from the same time period, more accurate pose and velocity information can be acquired.
The specific steps for the visual-inertial fusion are as follows:
Based on the IMU motion model, integration can be performed on the IMU for the next image frame, obtaining a predicted value of the IMU increment;
The difference between the predicted pre-integration value of the IMU and the observed value obtained from the IMU measurement at the next image frame is calculated, yielding the residual of the inertial data;
The residual of the inertial data is introduced into the optimal cost function of visual SLAM, making the optimal cost function a sum of visual reprojection error and inertial data residual.
Equations (8) represent the motion equation and observation equation that describe the process of the body's motion. The motion state at time k+1, denoted as k+1, can be predicted based on the state at time k and the IMU measurements between time k and k+1. The observation equation is used to describe the process of the camera detecting visual features at time k+1.

The symbol Xk+1 = (Rk+1, pk+1, vk+1, bk+1g, bk+1a)T represents the system's state at time k+1, which encompasses the rotation information, velocity information, translation information, and the biases of the gyroscope and accelerometer from time k. The term uk+1 refers to the motion measurement provided by the IMU.
The kinematic process of a body is a cyclic iterative process. Based on the kinematic equations and inputs, it predicts the state at the next moment and uses the sensor's measurement equations to correct the state at the next moment. In the visual-inertial fusion algorithm, IMU data also act as an input, thereby allowing for more accurate predictions of the system's state using the kinematic equations. This process emphasizes the continuous integration of motion data and sensor measurements to refine the system's understanding of its state over time, leveraging both the predictive power of the motion model and the corrective insights from real-time sensor data.
3.2. GPS Fusion Based on Pose Graph Optimization
This section introduces a sensor fusion algorithm based on pose graph optimization, which is used to integrate GPS with the visual-inertial positioning algorithm introduced previously. It utilizes an optimization approach to complement the advantages of high local positioning accuracy and global positioning without cumulative errors.
After converting the absolute position data obtained from the GPS sensor into the coordinate system, the position under the East-North-Up (ENU) coordinate system, taking the position at the first moment as the origin, can be obtained to determine the drone's relative position. This is then aligned in time with the relative position data from the visual-inertial odometer obtained through the fusion of visual and IMU sensors, eliminating data with mismatched timestamps to ensure the correspondence of the data.
Figure 8.
Multi sensor data fusion time alignment.
Figure 8.
Multi sensor data fusion time alignment.
Since the relative poses from the visual-inertial odometer are quite accurate with minimal short-term drift, the covariance of the visual-inertial odometer is set to 0.1. The covariance of GPS is determined by the strength of the signal. In the fusion algorithm, the weights of the various sensors are dynamically allocated in real-time based on the covariance of GPS and the visual-inertial odometer to achieve better fusion effects.
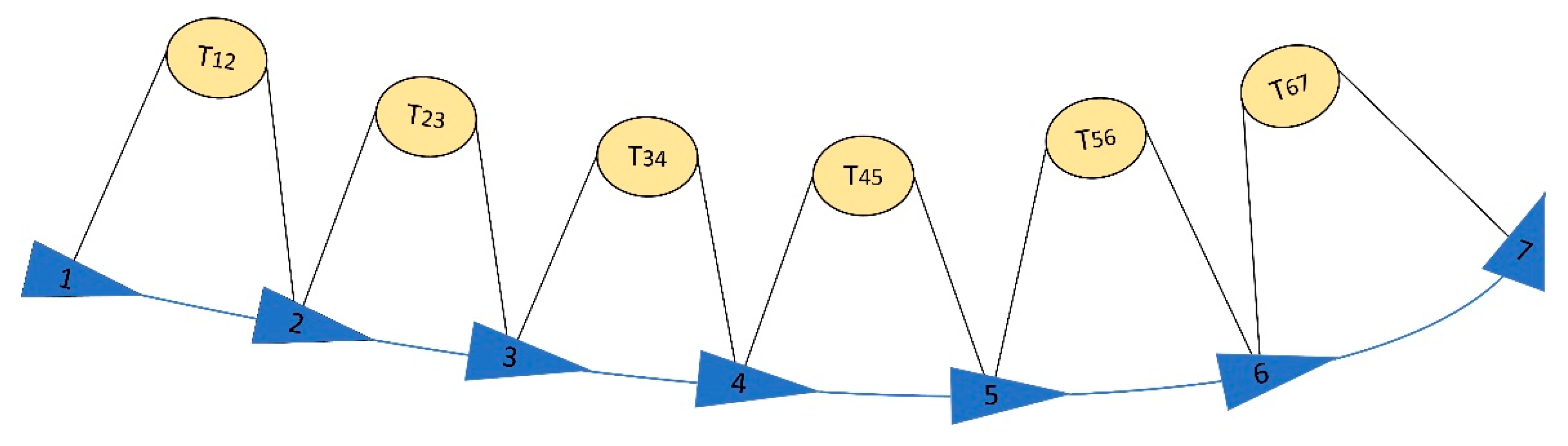
Pose graph optimization is a computational method used in SLAM to optimize the poses of robots. Compared to the commonly used Bundle Adjustment (BA) optimization in SLAM, pose graph optimization excludes the numerous three-dimensional space points considered in BA optimization, focusing only on the drone's position and attitude. This significantly reduces the scale of optimization and avoids unnecessary computational power consumption. Figure 10 illustrates the construction of the pose graph:
In
Figure 9, the triangles represent the drone's motion posture at each moment, referred to as nodes in the optimization process. The circles represent the change between two consecutive motion postures, known as relative measurements, and in the context of optimization problems, they are also called edges. In Bundle Adjustment (BA) optimization, the number of map points significantly exceeds the number of poses. If the system operates over a long duration, the number of nodes awaiting optimization increases, leading to slower solution speeds. To improve the solution speed, the concept of pose graph optimization emerged. The relative measurements between two motion states can be directly obtained through various sensors carried by the drone (inertial navigation, vision, GPS).
Assuming that the pose of the UAV at two times is Ti, Tj and the relative pose change of the UAV between these two times is ΔTji then there is the following formula:

Build an error term:

The objective function of pose graph optimization can be written as:
In the above equation,
λij
represents the information matrix, which is the inverse of the covariance,
indicating the weight of each error in the optimization function. If we set the
initial point of the optimization problem as
, and
consider an increment added on top of this initial point, then the estimated
value between state nodes becomes
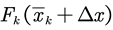
,
while the error value between nodes is
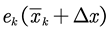
.
Subsequently, the overall error cost function is linearized for processing:
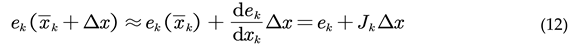
For the k-th edge, the optimization function is:
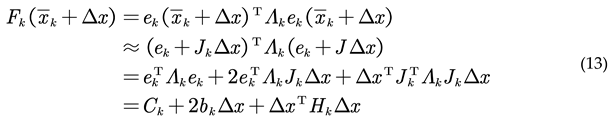
In the above formula, the constant term is sorted into Ck. in fact, the variation of the final optimization function is:
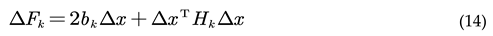
The core of solving the optimization problem is to find a state variable Δx to minimize the variation of the above formula, so the most direct way is to take the derivative of the above formula, and then make the derivative of Δx the smallest derivative in the definition domain, and then the optimal solution can be obtained:
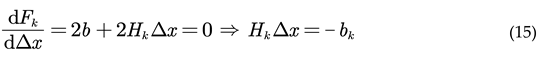
When Δx decreases to a certain extent, the iteration is stopped.
3.3. Digital Twin—Kalman Fusion Algorithm
In multi-sensor fusion positioning systems, although the addition of sensors can provide more sources of data, enhancing the system's perception of the external environment and positioning accuracy, it also introduces more complexity and uncertainty. From the perspectives of probability theory and systems engineering, as the number of sensors increases, the complexity of the system grows linearly or at an even higher rate, leading to a corresponding increase in the probability of failures. Each sensor could potentially become a point of failure, increasing the overall probability of system failure. Moreover, errors between different sensors may also accumulate or amplify each other, affecting the final data fusion quality and positioning accuracy. Therefore, this study introduces digital twin technology as an innovative strategy. By constructing a digital twin model of the real drone, it achieves real-time simulation of the real drone's flight status. This digital twin drone can not only predict and simulate the behavior and state of the real drone but also provide alternative positioning information in case the actual drone encounters sensor failures or data anomalies.
This paper will employ pose optimization techniques based on the Extended Kalman Filter (EKF) to improve the accuracy of the drone's motion posture. The core of pose optimization techniques based on the EKF lies in the fusion of different information sources. Applying the Kalman Filter to pose optimization involves using data generated by the digital twin model as estimated values, combined with real drone sensor data for posture prediction. Through the Extended Kalman Filter, the position information of the drone being measured in space is continuously corrected, and the filtered position information is fed back to the real drone, thereby enhancing the accuracy and robustness of the drone's motion posture and position information.
Take the attitude information of the UAV at the current time as:

The computational state update equation can be described as a first-order Markov process:

Where: θ′roll, θ′yaw, θ′pitch are the pose state of the target at the next moment respectively; τεe, τεn, τεθ are the reciprocal of the time constant of the noise process respectively; ωεe, ωεn, ωεθ are white noise with zero mean.
The discrete state equation of X from time k to time k+1 as:
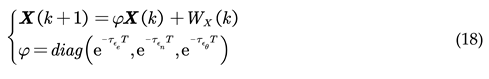
Where: T is the sampling period; WX(k) is white noise. Assuming that the state noise at each time is uncorrelated, the correlation state covariance matrix can be obtained as
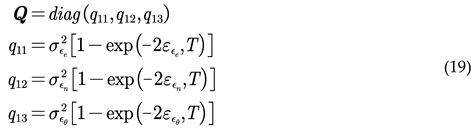
The position and attitude state of the previous state point Ω is the observation value

The discrete observation equation as

In the formula, H = diag(1,1,1); denotes the observation noise. The covariance matrix R of the observation noise is represented as
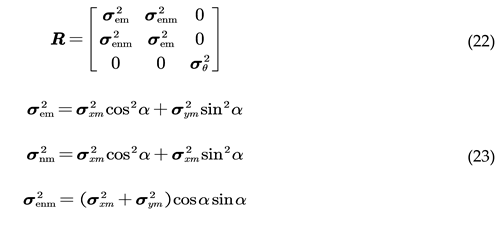
4. Experiments and Comparative Analysis
4.1. Introduction to Experimental Platform
For data collection and conducting real flight experiments, a quadcopter drone hardware platform was initially established, as illustrated in
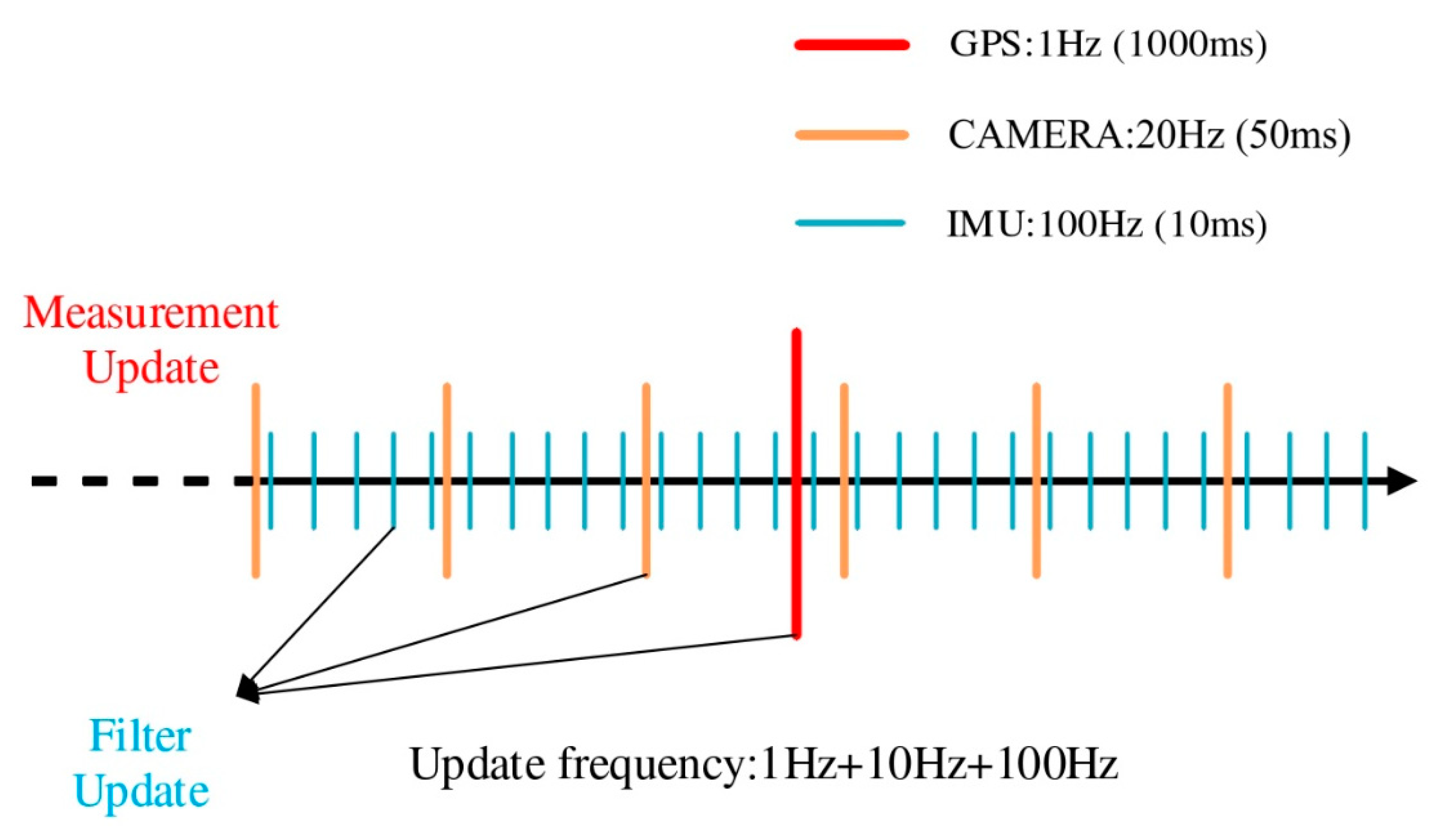
Figure 10. This platform was equipped with various sensors as previously described, including an Inertial Measurement Unit (IMU), GPS, and depth cameras. Simultaneously, the sensor models and measurement frequencies used in the digital twin simulation platform matched those of the actual sensors. The GPS provided coarse positioning information at a frequency of 1Hz, the IMU supplied high-speed dynamic attitude change data at 100Hz, and the visual sensors delivered visual-assisted positioning information at a rate of 20Hz.
Furthermore, to validate the effectiveness of the digital twin system, this study first established a virtual external testing environment as a primary prerequisite for digital twin testing. To conduct more accurate experiments with the drone digital twin system, the actual experiment environment the school playground was modeled in multiple dimensions. Three-dimensional scene real images and model diagrams are shown in
Figure 11:
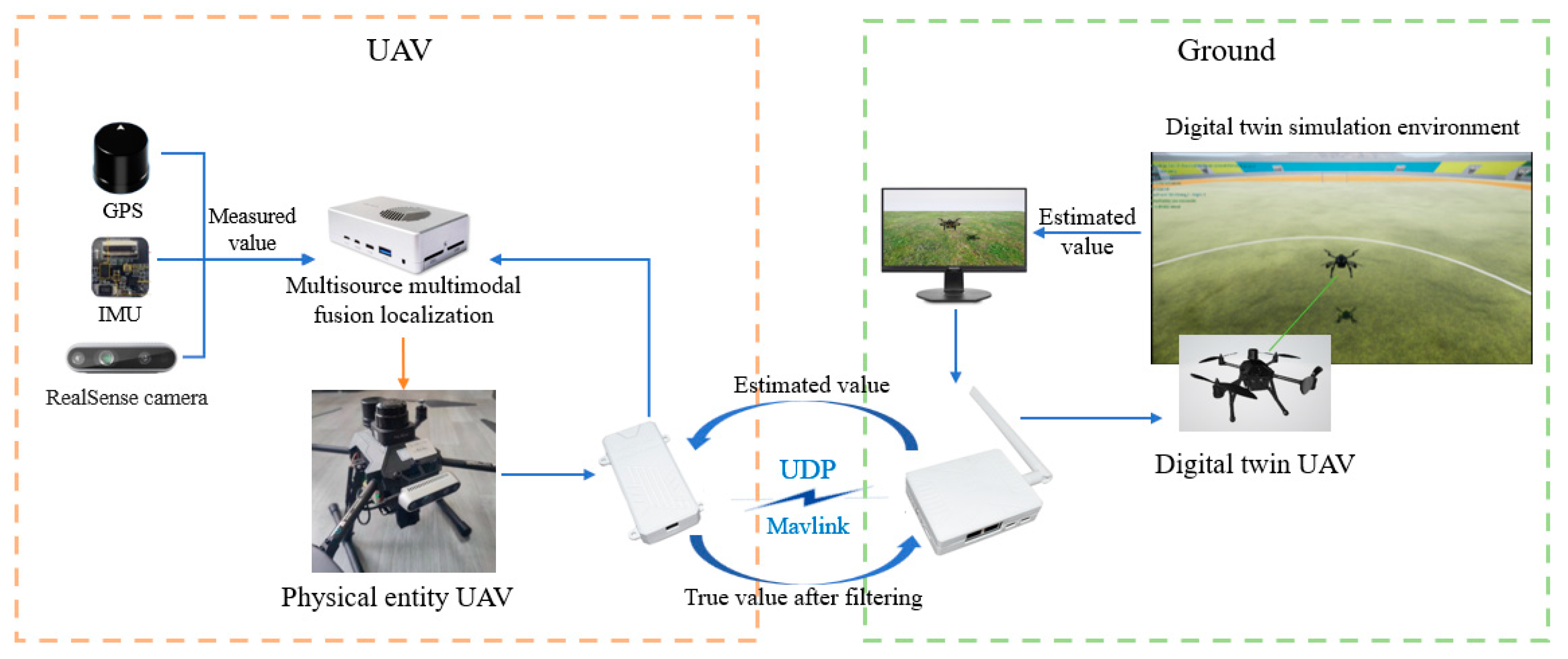
The experimental method employs a multi-source multimodal data fusion architecture based on digital twin technology, involving two main components: the physical drone and the digital twin platform, as illustrated in
Figure 12. On the physical drone end, various sensors such as GPS, IMU, and RealSense cameras collect pose data in real time. This data is transmitted to the drone's onboard computer for processing and multimodal fusion. The ground-based digital twin platform serves as the virtual part of the experiment, receiving the drone's location information in real time, using it as a reference value, and combining it with the digital twin model to calculate the drone's pose. The calculated pose information, in the form of estimated values, is transmitted back to the drone via data transmission modules using UDP network and MAVLink communication protocols. The drone's onboard computer receives these estimated values and further fuses them with the measurements obtained from its own multisensor fusion using the Extended Kalman Filter (EKF) algorithm to optimize the accuracy of pose estimation. The Extended Kalman Filter, through its iterative prediction and updating process, corrects the drone's real-time pose, thereby reducing estimation errors.
The entire experimental process forms a closed-loop system, where the real-time interaction between the physical drone and the digital twin platform ensures continuous synchronization and precise calibration of pose data. This method, by fusing physical multisensor data with virtual data from the digital twin platform, aims to enhance the accuracy of pose estimation and validate the effectiveness and reliability of multi-source multimodal data in practical applications.
4.2. Comparison of Integrated Navigation Experiments
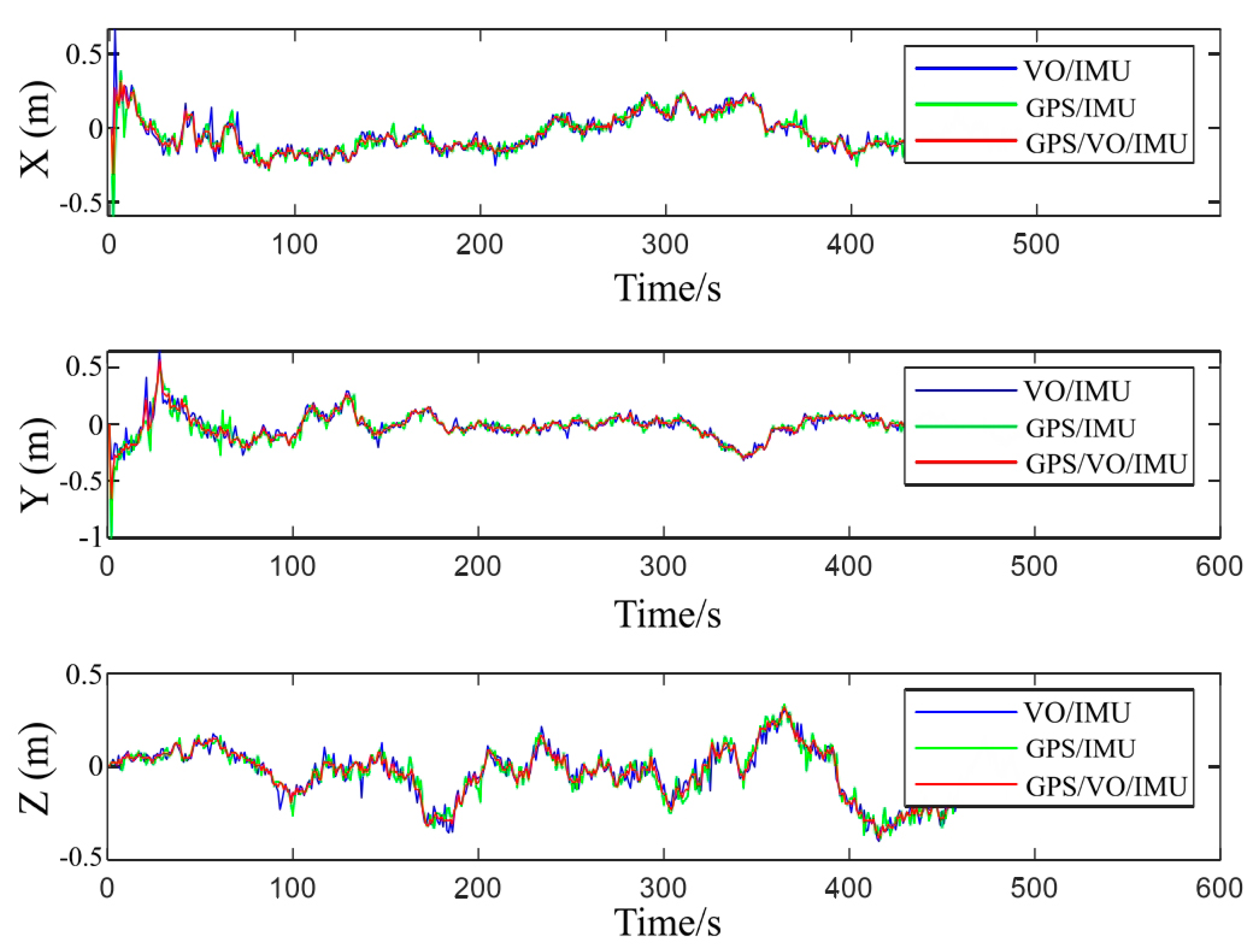
The digital twin environment for this experiment utilizes UE4 to simulate the real campus playground environment. While the real drone is conducting actual flight operations, the digital twin drone runs synchronously in the twin environment, collecting sensor data. The frequency of the sensors used in the digital twin simulation matches that of the real sensors: the inertial sensor sampling rate is 100Hz, the GPS sensor frequency is 1Hz, and the vision sensor frequency is 20Hz. This paper focuses on a comparative analysis of the integrated application of various combined navigation methods. It compares three different combination navigation strategies: Visual Odometry/Inertial Measurement Unit (VO/IMU), Global Positioning System/Inertial Measurement Unit (GPS/IMU), and Global Positioning System/Visual Odometry/Inertial Measurement Unit (GPS/VO/IMU). By analyzing their performance in positioning accuracy, theoretical foundations can be provided for the selection of UAV navigation systems.
The experimental results in
Figure 13 show that the GPS/VO/IMU combination navigation method exhibits smaller positioning errors and higher stability. This finding suggests that the fusion of GPS, VO, and IMU data in drone positioning can effectively suppress errors that may arise from individual systems, reduce positioning fluctuations caused by the performance variability of a single system, and significantly enhance overall navigation accuracy. Compared to using VO/IMU or GPS/IMU alone, the GPS/VO/IMU combination not only provides more accurate location information but also maintains stable system performance under complex environmental conditions.
These experimental results further confirm the importance of multimodal information fusion in improving the robustness of positioning systems. Especially when GPS signals are limited or the accuracy of the VO system is affected by indistinct environmental features, multisource information fusion ensures the continuity and accuracy of the system. Additionally, the GPS/VO/IMU combination navigation, by complementing the strengths and weaknesses of each system, not only enhances positioning accuracy but also improves the system's adaptability to dynamic changes and resistance to interference, providing strong support for the stable operation of drones in variable environments.
4.3. Analysis of Navigation Stability Experiment
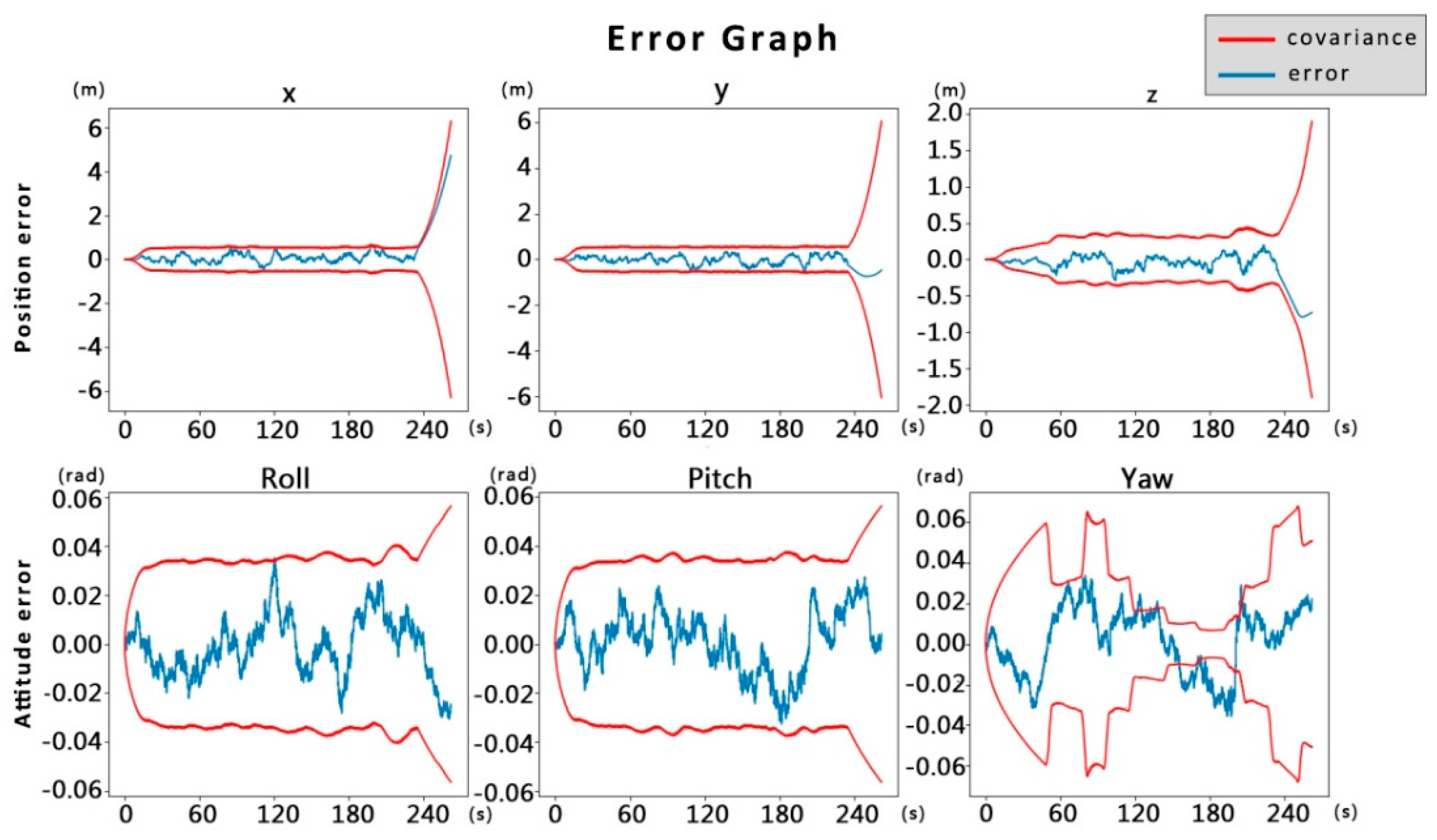
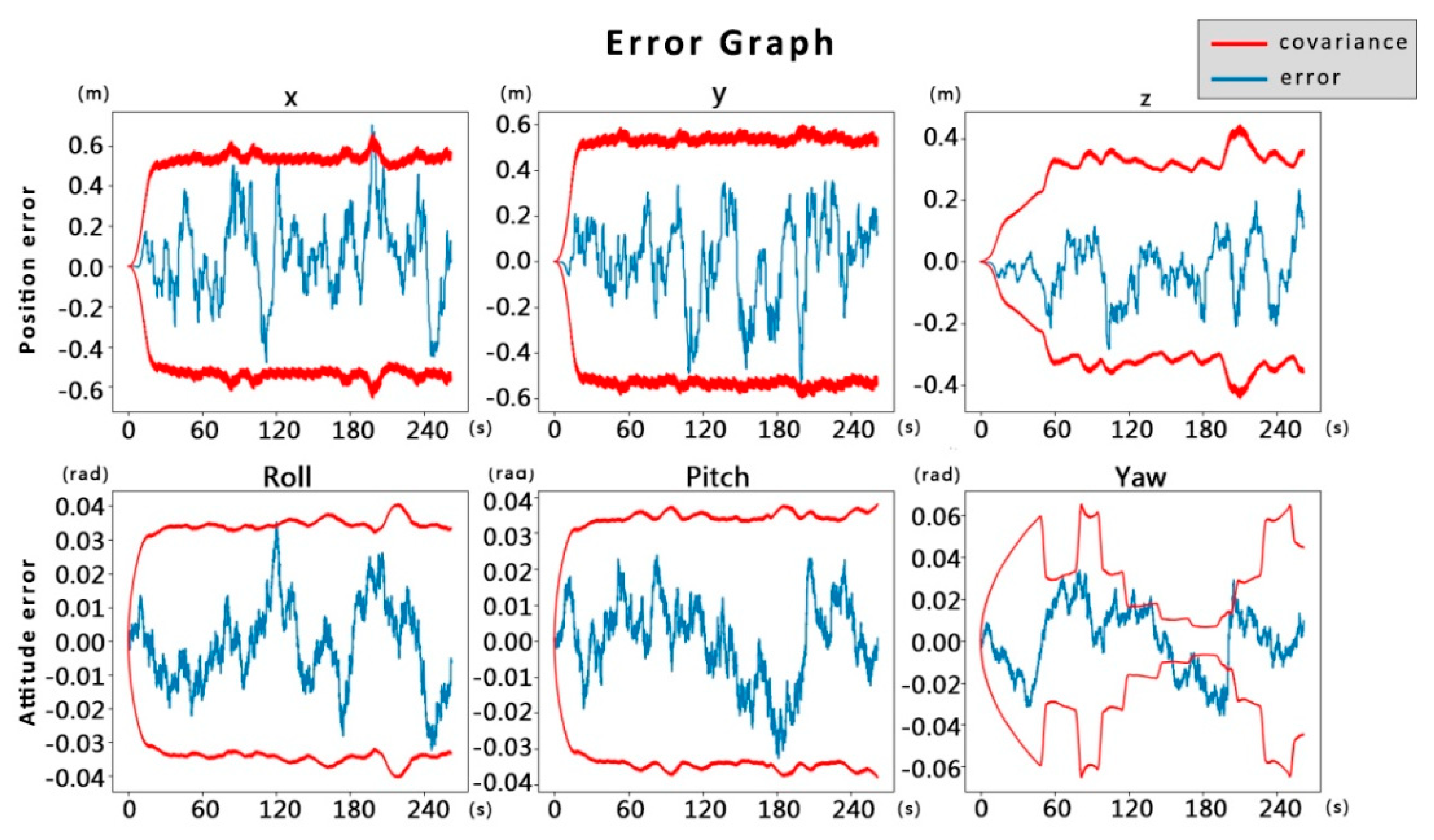
Figure 14 showcases the distribution of positional and attitudinal errors and covariance of the drone system before applying the data fusion technique proposed in this paper. From the figure, it can be observed that although the system can maintain errors within a relatively small range in the initial phase, indicating a certain degree of accuracy and stability in the short term, the errors in position and attitude exhibit a trend of gradual increase over time, manifesting as a systematic drift phenomenon. This drift leads to the divergence of covariance, reflecting an increase in the uncertainty of system state estimation. The performance degradation of the system indicates a lack of effective error correction mechanisms during long-term operation, ultimately leading to the inability of the drone's navigation system to maintain a normal working state, thereby validating the insufficiency of single sensor or unoptimized multisensor systems in maintaining long-term positioning stability.
In contrast,
Figure 15 shows the error distribution and covariance after implementing the data fusion method proposed in this study. Compared to
Figure 14, the covariance matrix maintained smaller fluctuations throughout the experiment period without significant divergence. This proves that the multimodal fusion positioning method proposed in this paper can effectively solve the problem of system state divergence caused by visual positioning errors, increasing the stability and robustness of state estimation, and improving accuracy based on actual operational results. This means that under diverse operational conditions and various disturbances that may be encountered, the drone's navigation system can still maintain high positioning accuracy, ensuring the reliability and safety of the drone's mission execution.
4.4. Experimental Analysis of Fault Tolerant Navigation
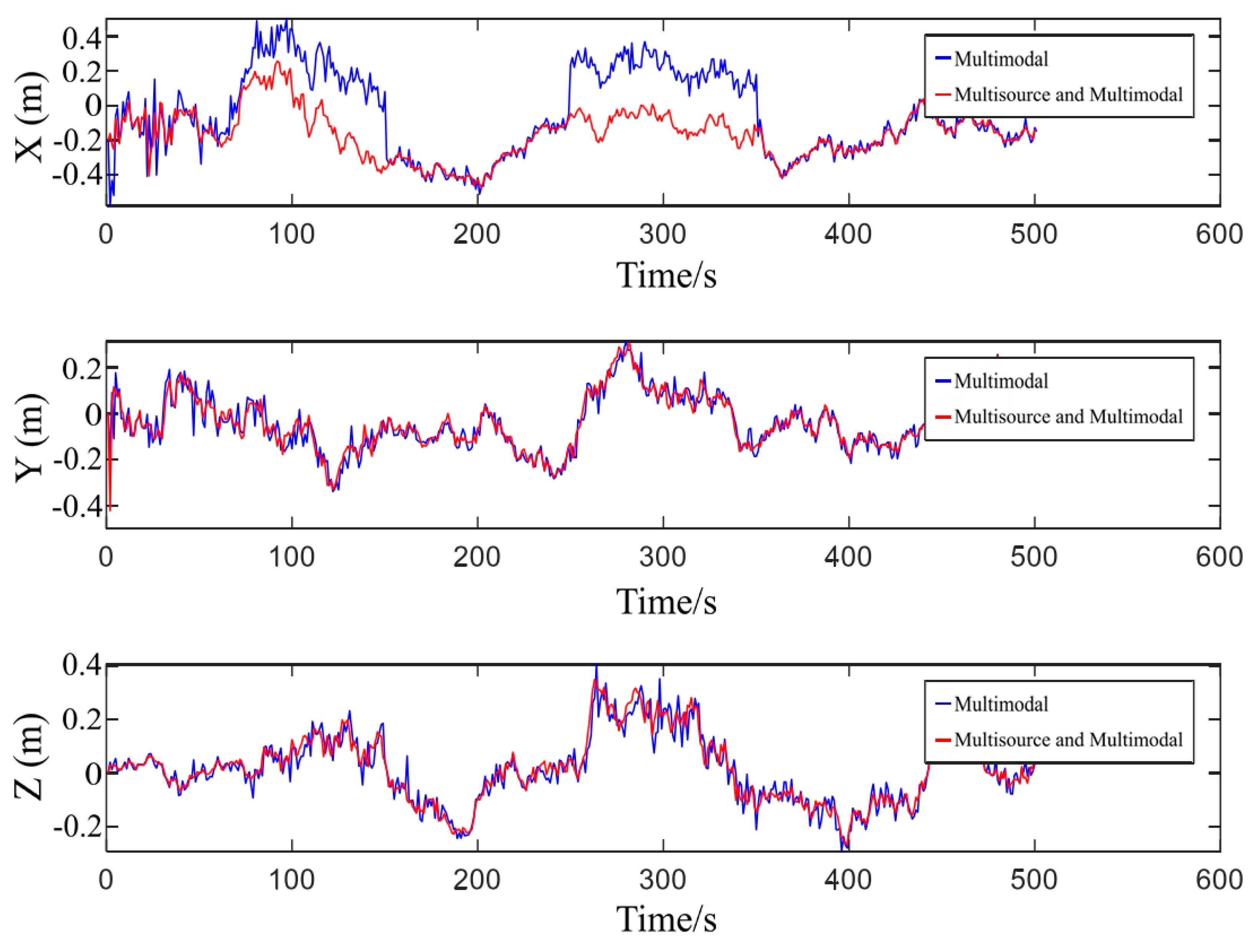
It is evident from
Figure 16 that a gradual fault was applied between 50s and 150s, while a sudden fault was applied between 250s and 350s. The component applied pertains to the drone's x-axis direction, with little difference observed in the y-axis and z-axis components. However, the occurrence of the fault and the distinction between the two can be clearly seen in the x-axis component.
In the absence of a digital twin drone data source and the utilization of a multisource multimodal navigation algorithm, the drone system experiences abrupt changes, especially in the x-axis direction, when subjected to the applied faults, leading to system instability. This instability manifests as rapid changes in position and attitude, thereby affecting the normal operation of the drone. However, the drone system, incorporating the multisource multimodal navigation algorithm, demonstrates significant stability. In the face of gradual faults, despite potential delays in detection that cause some variation in the response of the multisource multimodal navigation algorithm, the variation is minimal, and the system can quickly return to a stable state. In the case of sudden faults, the multisource multimodal navigation algorithm exhibits high robustness, with almost no impact, allowing for a smooth transition and ensuring the stability of the combined navigation system.
Specifically, the digital twin technology provides a robust reference for data fusion while simulating the real drone, by utilizing predictive data generated from the digital twin model and integrating it with real sensor data, the algorithm effectively combats instability caused by unexpected faults. In facing sensor errors or external disturbances, the system can adjust state estimates more stably. Moreover, this method also enhances positioning accuracy. As shown in
Figure 16, the fluctuation range of positional errors is relatively smaller and more concentrated, indicating the precision advantage of the fusion method.
5. Conclusions and Future Work
This paper first discusses the challenges of maintaining positioning accuracy and stability during continuous maneuvers of small drones in complex environments. To address this, it proposes a fusion positioning method that incorporates three different sensor technologies: GPS, inertial navigation, and visual navigation. After collecting relevant data from each sensor, a tightly coupled integration optimizes the fusion of visual and inertial data, which is then further integrated with GPS data based on pose graph optimization principles. Several experimental comparisons of navigation combinations and navigational stability analysis were carried out. The experiments prove that the combined navigation system utilizing GPS/VO/IMU enhances positional accuracy by leveraging the strengths and mitigating the weaknesses of each individual system. This combination not only provides more precise location information but also maintains a stable system performance in complex environmental conditions, resulting in a smoother UAV flight trajectory. However, as the number of sensors increases, the system's complexity grows linearly or even at a higher rate, which in turn increases the likelihood of system failures. Consequently, this research introduces a digital twin UAV data source. By using the data generated by the digital twin model as an estimation input, combined with real UAV sensor data via the Extended Kalman Filter (EKF) algorithm, the approach corrects for positional information deviations caused by sensor noise and environmental disturbances. The filtered positional information is then fed back into the control system of the real UAV to achieve real-time corrections of the UAV's movement attitude and positional information. The method has been empirically proven to significantly improve the UAV's positioning accuracy, exhibiting a high level of robustness and ensuring the stability of the combined navigation system and the reliability of the navigation data.
In summation, the data fusion technique propounded herein is validated both theoretically and experimentally for its efficacy in addressing UAV locational challenges within dynamically complex environments. The treatise delineates not only an efficacious strategy for amplifying locational precision and robustness in small UAVs but also carves new investigational trajectories for forthcoming UAV technological advancements. The induction of digital twin technology amplifies UAV locational system prowess and pioneers new possibilities for UAV application in labyrinthine settings, further spurring UAV technological innovation and evolution, and provisioning pivotal referential and investigational guidance for the conception and refinement of prospective UAV navigational frameworks.
Future inquiries shall pivot towards an enhanced exploration of fusion algorithm optimization tailored to accommodate more intricate environments and rigorous application demands, harnessing cutting-edge computational technologies such as edge computing or cloud computing to expedite data processing, diminishing system response latencies, and bolstering real-time application performance. An in-depth examination and refinement of the extant Kalman filter algorithms are envisaged to fortify their adaptability and precision in the management of data within high-dynamic and convoluted environmental contexts. Moreover, a deep-dive into the application of digital twin technology within UAV locational matrices, particularly within the realms of fault diagnostics and prognostic maintenance, is anticipated. The construction of digital twin models for UAVs will permit the real-time surveillance of UAV operational statuses, prognostication of potential malfunctions, and the pre-emptive enactment of preventative measures, thereby augmenting system stability and reliability.
Author Contributions
Conceptualization, S.Q. and Y.F.; methodology, J.C.; software, J.C.; validation, S.Q.; formal analysis, Y.Q.; investigation, Z.C.; resources, Y.F. and Z.C.; data curation, Y.Q. and X.M.; writing—original draft preparation, J.C.; writing—review and editing, S.Q.; visualization, X.M.; supervision, S.Q.; project administration, Y.F.; funding acquisition, Y.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the National Foreign Expert Program of the Ministry of Science and Technology (Grant No.G2023041037L), and the Shaanxi Natural Science Basic Research Project (Grant No.2024JC-YBMS-502).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest..
References
- Zhang Peng. Research and implementation of indoor autonomous navigation system for four-rotor UAV based on vision. University of Electronic Science and Technology of China, 2019.
- Tang Chunhua, Environmental Modeling and Exploration of small UAV based on RGB-D Data in Indoor Environment. Soochow University, 2020.
- Yan Gongmin, Weng Jun. Strapdown Inertial Navigation Algorithm and Integrated Navigation Principle. Xi 'an: Northwestern Polytechnical University Press, 2019; 127-128.
- Wang Tingting, Cai Zhihao, Wang Yingxun. Indoor vision/inertial navigation method for UAV. Journal of Beijing University of Aeronautics and Astronsutics 2018, 44, 176–186.
- Burri M, Oleynikova H, Achtelik M W, et al. Real-time visual-inertial mapping, re-localization and planning onboard MAVs in unknown environments. // 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, 2015: 1872-1878.
- Usenko V, Von Stumberg L, Pangercic A, et al. Real-time trajectory replanning for MAVs using uniform B-splines and a 3D circular buffer. //2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, Canada, 2017: 215-222.
- Alzugaray I, Teixeira L, Chli M. Short-term UAV path-planning with monocular-inertial SLAM in the loop. // 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 2017: 2739-2746.
- Bian Ruochen. Research on multi-source heterogeneous adaptive integrated navigation technology in complex environment. Shandong University,2020.
- Peng Jing. Research on UAV localization Technology based on Multi-perception information fusion. South China University of Technology,2020.
- Jin X B, Sun S, Wei H, et al. Advances in Multi-Sensor Information Fusion: Theory and Applications 2017. Sensors 2018, 18, 1162. [CrossRef]
- Pan Quan. Theory and Application of Multi-Source Information Fusion. Tsinghua University Press, 2013.
- Y. C. Paw, G. J. Balas. Development and application of an integrated framework for small UAVflight control development. Mechatronics 2011, 21, 789–802.
- Chen K, Zhang Z, Long J. Multisource Information Fusion: Key Issues,Research Progress and New Trends. Computer Science 2013, 40, 6–13.
- Wang R A, Chen Y B, Li Y C, et al. High-precision initialization and acceleration of particle filter convergence to improve the accuracy and stability of terrain aided navigation -ScienceDirect. ISA Transactions 2020, 110, 172–197. [CrossRef]
- Tang Luyang, Tang Xiaomei, Li Baiyu, et al. A review of fusion algorithms for multi-source fusion navigation systems. Global Positioning Systems 2018, 43, 39–44.
- Deng Ye, Feng Qilin, Zhao Jian. Discussion on digital twin battlefield construction. Protection Engineering 2020, 42, 58–64.
- WANG P, YANG M, ZHU J, et al. Digital Twin-Enabled Online Battlefield Learning with Random Finite Sets. computational intelligence and neuroscience 2021, 2021, 5582241–5582241. [CrossRef]
- Luo Hao, Zhang Jianfeng, Ning Yunhui, et al. Application requirements of digital twins in submarine combat system. Digital Ocean and Underwater Attack and Defense 2021, 4, 233–237.
- WANG Y-C, ZHANG N, LI H, et al. Research on Digital Twin Framework of Military Large-scale UAV Based on Cloud Computing. 2021. [CrossRef]
- YANG Y, MENG W, ZHU S. A Digital Twin Simulation Platform for Multi-rotor UAV. 2020.
- Wu Dongyang, Dou Jianping, Li Jun.Design of digital twin system for quad-rotor aircraft. Computer Engineering and Applications,: 1-11.
- Qiuying W, Xufei C, Yibing L, et al. Performance Enhancement of a USV INS/CNS/DVL Integration Navigation System Based on an Adaptive Information Sharing Factor Federated Filter. Sensors 2017, 17, 239. [CrossRef]
- W. Qiuying, G. W. Qiuying, G. Zheng, Z. Minghui, C. Xufei, W. Hui, J. Li, Research onpedestrian location based on dual MIMU/magnetometer/ultrasonic module, in:Position, Location and Navigation Symposium (PLANS), 2018 IEEE/ION, IEEE, 2018, pp. 565–570.
- J. Yan, G. J. Yan, G. He, A. Basiri, C. Hancock, Vision-aided indoor pedestrian dead reckoning, in: 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), IEEE, 2018, pp. 1–6.
- W. Xu, Y. Cai, D. He, J. Lin, F. Zhang, FAST-LIO2: Fast direct LiDAR-inertial odometry, IEEE Trans. Robot. 2022, 38, 2053–2073.
- Abdulrahman Soliman, Abdulla Al-Ali, Amr Mohamed, Hend Gedawy, Daniel Izham, Mohamad Bahri, Aiman Erbad, Mohsen Guizani, AI-based UAV navigation framework with digital twin technology for mobile target visitation, Engineering Applications of Artificial Intelligence 2023, 123, 106318. [CrossRef]
- L. Chen, X. Zhou, F. Chen, L.L. Yang, R. Chen, Carrier phase ranging for indoor positioning with 5G NR signals, IEEE Internet Things J. 2022, 9, 10908–10919. [CrossRef]
- Y. Zhuang, J. Yang, L. Qi, Y. Li, Y. Cao, N. El-Sheimy, A pervasive integration platform of low-cost MEMS sensors and wireless signals for indoor localization, IEEE Internet Things J. 2018, 5, 4616–4631. [CrossRef]
- Ben-Afia, L. Deambrogio, D. Salos, A.-C. Escher, C. Macabiau, L. Soulier, V. Gay-Bellile, Review and classification of vision-based localisation techniques in unknown environments, IET Radar Sonar Navig. 2014, 8, 1059–1072. [Google Scholar] [CrossRef]
- T. Hamel and C. Samson, ‘‘Position estimation from direction or range measurements,’’ Automatica 2017, 82, 137–144. [CrossRef]
- M. K. Al-Sharman, B. J. Emran, M. A. Jaradat, H. Najjaran,R. Al-Husari, and Y. Zweiri, ‘‘Precision landing using an adaptive fuzzy multi-sensor data fusion architecture,’’ Appl. Soft Comput. 2018, 69, 149–164. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

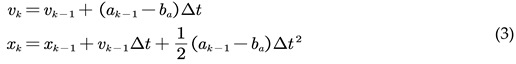
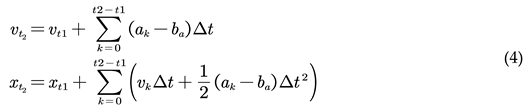
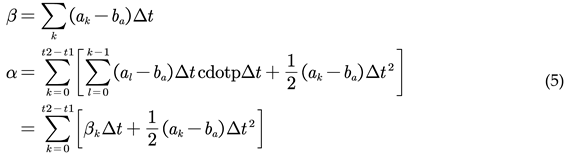
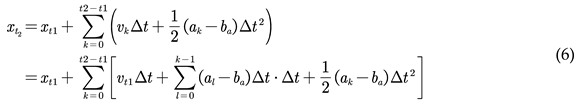




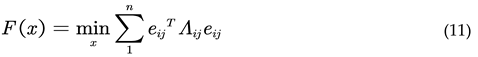
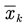 , and
consider an increment added on top of this initial point, then the estimated
value between state nodes becomes
, and
consider an increment added on top of this initial point, then the estimated
value between state nodes becomes 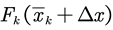 ,
while the error value between nodes is
,
while the error value between nodes is 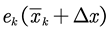 .
Subsequently, the overall error cost function is linearized for processing:
.
Subsequently, the overall error cost function is linearized for processing: