Preprint
Article
Quantifying Combat Effectiveness Through Frontline Variation: A Time-Series Analysis of the Russo-Ukrainian War
Altmetrics
Downloads
141
Views
34
Comments
0
Submitted:
01 May 2024
Posted:
02 May 2024
You are already at the latest version
Alerts
Abstract
Traditional methodologies for measuring combat effectiveness rely on various contribution factors, where the main challenge lies in the complexity and subjectivity of these factors. Using frontline variation to measure combat effectiveness circumvents the limitations of many previous methods regarding complexity and subjectivity. Employing this methodology, we have quantitatively measured the combat effectiveness of both parties in the Russo-Ukrainian War across various temporal scales. Utilizing the time series data derived from our measurements, we constructed Daily, Weekly, Monthly, and Annual Candlestick Charts to illustrate the variation trends in combat effectiveness between the two sides across different temporal scales. This comprehensive approach facilitated a nuanced and all-encompassing analysis of the conflict, capturing the intricate dynamics of individual military engagements and the broader strategic operations' context. This case underscores the distinctive utility of our method in quantifying combat effectiveness, offering detailed and strategically significant insights.
Keywords:
Subject: Social Sciences - Safety Research
Introduction
Combat effectiveness is not only the core of all military monographs; it is also crucial to establish whether theoretical military mathematical models and military simulation software can be applied to the real world. Lanchester (1916) became a pioneer in measuring combat effectiveness with his renowned Lanchester equations, which primarily assess the casualties of both sides based on the number of engaged combatants. The core limitation of Lanchester's equations lies in their reliance on explanatory variables to gauge combat effectiveness. In other words, within the framework of Lanchester's equations, the number of combatants is the independent variable, while combat effectiveness is the dependent variable.
However, the explanatory variables for combat effectiveness are multifarious and encompass numerous immeasurable, subjective factors. For instance, beyond the sheer count of combatants, explanatory variables for combat effectiveness also embrace, but are not limited to, the physical and mental prowess of troops, the prestige and tactical knowledge of military commanders, the quality of arsenal, and tactical adeptness in utilizing weaponry, logistics, intelligence, medical care, as well as terrain and weather conditions, and military budgets. Among these, elements such as morale and the quality of command and control are inherently subjective and defy easy quantification. Consequently, relying solely on the number of combatants fails to capture a comprehensive picture of combat effectiveness.
Lanchester's equations profoundly influenced subsequent researchers, especially prevalent from the 1960s to the 1990s. On the one hand, several variants of Lanchester's equations emerged, as seen in works by Dolanský (1964), Novikov (2013), and in the compilations by Przemieniecki (2000) and Tolk (2012), with the most notable among these being Helmbold (1997). Despite their advancements, these variants did not deviate from Lanchester's original approach of using the number of combatants as the explanatory variable for measuring combat effectiveness, merely incorporating more sophisticated mathematical treatments. On the other hand, researchers like Hayward (1968) attempted to add more explanatory variables beyond the number of participants, aiming to establish a mathematical model that included as many explanatory variables for combat effectiveness as possible. This approach was later adopted by Epstein (1985), Nevitt (1986), Krondak (2007), Kanatliev (2014), and Gordon (2014). However, these studies were unable to overcome two inherent flaws in the method of using explanatory variables for measurement mentioned earlier:
- The endless number of explanatory variables: Hayward admits, "Even the most thoroughgoing analysis will leave a rather large number of independent variables, the influence of which on combat effectiveness remains to be assessed" (Hayward, 1968, p.322).
- The inclusion of numerous subjective explanatory variables: As Nigel Perry notes, "the inability to measure parameters is a common shortcoming of all current combat models" (Perry, 2009, p.20).
Early-modern natural science encountered dilemmas similar to the conundrum of measuring combat effectiveness. For example, prior to the 17th century, there was no practical method for quantifying "force" either, as people then were also accustomed to using explanatory variables as the basis for measurement. However, the explanatory variables for "force" were endless. For instance, a physically strong person has more significant force, as does someone who has eaten well or is in an excited state of mind. There are numerous explanatory variables for "physical strength" alone, many of which involve subjective perceptions. Newton did not use these explanatory variables; instead, he approached the problem through outcome variables. The result of "force" is altering an object's state of motion. Objects are quantified by mass, and the state of motion is quantified by acceleration. Therefore, "m" (mass) and "a" (acceleration) as outcome variables successfully quantified "force." It was not merely a tiny improvement of previous measurement methods but a groundbreaking development that finally solved the problem. The "m×a" reflects the outcome variables of force, not the explanatory variables so that the equation can avoid the implications of complexity and sensory factors. In addition, it can be equivalent to the combined influence of all explanatory variables of force because regardless of its source, a force can be expressed as a change in acceleration (Hall, 1981, p.85). Dubarle defines this transformation as the new focus on the mathematization of effect rather than perceived causes (Dubarle 1988, p.300).
Through Table I, it is evident that since then, natural scientists have harnessed Newton's new pathway—measuring the second column using the third column in the table—to measure various physical quantities successfully. In contrast, the idea mentioned above of wanting to keep finding explanatory variables for combat effectiveness to measure combat effectiveness - the idea of using the first column in a table to measure combat effectiveness (the second column) - has tended to wane in recent years.
To address the deficiencies in military studies concerning the measurement of combat effectiveness, researchers in conflict studies have increasingly adopted the loss exchange ratio (LER) as a method for measuring combat effectiveness. The LER is the number of enemy casualties that can be inflicted for every loss on one's side. Pioneers in using this method include Desch (2002), Biddle and Long (2004), Biddle (2010), Beckley (2010), and Pilster and Bohmelt (2011), with its popularity growing in recent years. An example from recent literature is the study by Marius Mehrl (2022) on the Nepal civil war, which utilizes this approach:
To test hypothesis 2, I require a measure of the Maoists’ combat performance. For this, I use the loss exchange ratio (LER), which explicitly relates Maoist combat fatalities to battle deaths incurred by the security forces ... Crucially, the LER captures the notion of combat effectiveness as ‘destroying hostile forces while preserving one's own’ (Biddle and Long, 2004: 528) and is unaffected by the scale of fighting or the total number of fatalities, only by the relative fatality distribution over the belligerents.
Although the LER seems similar to Lanchester's equations in using numbers of soldiers as a basis for measurement—only substituting the number of combatants with the number of casualties—the two have a fundamental difference. The number of participants is the combat effectiveness's
- cause, or
- explanatory variable, or
- independent variable.
and the number of casualties is the combat effectiveness's
- effect, or
- outcome variable, or
- dependent variable.
Using outcome variables as a basis for measurement, it addresses the two major issues brought about by relying on explanatory variables: the endless number of explanatory variables and the inclusion of many immeasurable subjective explanatory variables. Measurement from the perspective of explanatory variables requires enumerating all variables, as overlooking any factor could fail to present a complete picture of combat effectiveness. However, this is not necessary from the perspective of outcome variables. Although a variable can have many outcome variables, only the most effective and objective result needs to be used to measure.
Measure temperature as an example. For temperature, solar radiation, geothermal energy, atmospheric conditions, human activity, and various natural or artificial chemical reactions are all
- causes, or
- explanatory variables, or
- independent variable.
It is like the relationship between the "number of combatants" and "combat effectiveness." To measure temperature using these explanatory variables, they must be integrated into a comprehensive mathematical model without omission. Missing any of these explanatory variables could lead to an incomplete temperature measurement. However, it is impossible to exhaustively account for these widely varying variables, especially considering the inherently unquantifiable subjectivity of human activity variables.Instead, for temperature, phase changes in water or alcohol, as well as different human perceptions of cold and heat, are all
- effects, or
- outcome variable, or
- dependent variable.
It is like the relationship between the "casualty numbers" and "combat effectiveness." There is no need to unify all these outcomes in one model; instead, selecting the most universal and objective among them—the phase transition of water—as the basis for measurement suffices. Indeed, this is the foundation upon which the Celsius and Fahrenheit temperature scales were established. As shown in Figure I.
So, the question arises: Is the loss exchange ratio (LER) the most suitable outcome variable for measuring combat effectiveness? We argue that it is not for two reasons. First, although the LER is one of the outcomes of combat, it is merely a result of killing within combat. The direct outcome of combat is "victory, defeat, or draw," with killing serving merely as one means to achieve victory in combat, thus making it a secondary outcome. Moreover, these two types of outcomes often do not align. Historically, there are countless examples where forces demonstrated valor, achieving disproportionate kill ratios yet ended in defeat, and instances where victories were clinched at the cost of significant sacrifices. Therefore, the LER is more suited to measure killing effectiveness, for which the direct outcome is the number of kills. Second, Obtaining accurate personnel casualty figures from battle reports remains a daunting challenge. These reports are often motivated to overstate enemy casualties while downplaying their own, to boost morale, undermine the enemy's confidence, and garner the trust of allies. Even the war loss data published long after the end of wars, while no longer motivated by the desire to hide one's casualties and exaggerate the enemy's, cannot be guaranteed for its truthfulness. It is because the officially released data often comes from frontline commanders' reports, and in these reports, reducing one's losses and exaggerating the enemy's casualties are advantageous for a commander's promotion.
Therefore, if a method could quantify the direct outcomes of combat—victory, defeat, or draw—in a way that does not rely on subjective data acquisition methods, then it would be more suitable for measuring combat effectiveness than the LER, which is the purpose of this paper.
Measuring Method
Frontline changes serve as a more suitable outcome variable for measuring combat effectiveness compared to casualty numbers, highlighting that the dynamics of the frontline encapsulate the ultimate results of war—victory, defeat, or stalemate. Clausewitz (1976, p. 90) articulates that the ultimate goal of war is to subjugate the adversary's territory under one's authority. So, the essence of warfare revolves around the contest for the "Sphere of Power Control," and the frontline fundamentally represents the spatial boundary of Power Control. The movement forward or backward of the frontline indicates victory or defeat and symbolizes the expansion or contraction of a political entity's Sphere of Power Control. This conceptualization aligns with traditional interpretations of military outcomes. When Party A's control effectively extends into Party B's domain, it denotes that Party A's frontline advances while Party B's recedes, manifesting what is commonly understood as victory for Party A and defeat for Party B. Conversely, when neither party can enforce their control within the opponent's territory, resulting in an unchanged frontline, this scenario is typically recognized as a draw.
On the other hand, the data acquisition for frontline changes possesses objectivity. In previous wars, the photographs taken by embedded journalists and the abundant relics left on-site make the changes in the frontline more public and verifiable compared to casualty numbers. More importantly, with the advent of modern satellite technology capable of capturing imagery of war zones from space and using short-wave infrared (SWIR) devices to monitor the operational positions of thermal weapons directly, the potential for falsification in frontline position data is significantly reduced. Modern satellite technology allows for collecting high-resolution imagery from space, providing unparalleled views of conflict zones. This capability ensures that the movements and changes in frontlines can be monitored accurately, offering real-time data critical for strategic decision-making. Furthermore, these satellites can bypass traditional limitations such as geographical barriers and access issues, providing a comprehensive battlefield overview. Short-wave infrared (SWIR) devices can detect heat signatures from various military weapons, including vehicles and weaponry, even under limited visibility conditions, such as smoke, fog, or darkness. Once both parties engage in combat using modern thermal weapons along the frontline, the engagement positions can be quickly and accurately captured by SWIR devices.
The next challenge is how to quantify the alterations in the front line. Previous researchers have typically used the distance or speed of their army's advancement within the enemy territory as a measure, such as those methods mentioned by Epstein (1985), Helmbold (1997), and Han (2016). However, this method of quantification is imperfect for at least two reasons:
Reason I. Due to the intricacy of military engagements, the trajectory of an army advancing within the enemy territory is complex and variable, as opposed to a constant forward movement. Let us assume we have two armies, A and B. Army A breaches the enemy's front, progressing slowly along the nearest transportation line until it captures the enemy's capital. On the other hand, after breaking through the enemy's front, Army B is pursued within the enemy territory, unable to establish a foothold, and therefore has to move at high speeds. Army A is more effective in altering the front line, yet its marching distance and speed are less than Army B.
Reason II. Even if we implement specific regulations regarding the distance and speed of the march, such as calculating only the march trajectory perpendicular to the front-line direction (or towards the enemy's capital or headquarters) and only accounting for its projection in the above direction for marches in other directions, many detours of Army B would offset each other, making the distance and speed of Army B's march slower than Army A's. However, even in this case, this quantitative method still has an imperfection: it fails to consider the multidimensional nature of the front line. To put it another way, profoundly penetrating enemy territory only changes one dimension of the front line - the vertical depth - while another crucial dimension of the front line is the width of the front. Let us consider two armies, C and D. Army C manages a breakthrough on a narrow front, a few hundred meters or kilometers wide, akin to a needle piercing into the enemy's front line. Conversely, Army D breaches the enemy's front line at the same advancing speed on a broad front stretching tens or even hundreds of kilometers, much like a wave crashing onto a shoreline at rise tide. The degree of change inflicted upon the enemy's front by Army C is much lower than that by Army D, although the distance and speed of both armies' marches are identical.
Indeed, a crude depiction of changes in the front line based on the distance or speed of the march has been employed in ancient Chinese military literature, such as Sun Tzu's Art of War, and Western classical military theory works like Clausewitz's On War. This method poses no problem in qualitative analyses that do not seek precision before introducing quantitative research into conflict studies. However, it is not suitable to use this approach for studying combat effectiveness measurement issues that require high precision.
Given that the issue with the quantification method in 'Reason II' resides in neglecting the multidimensional nature of the front-line changes, a slight adjustment incorporating consideration of the width of the front would be sufficient to quantify front-line changes accurately. The product of vertical depth and horizontal width is the area of the shape formed by the old and new fronts. This area essentially signifies the amount of change in the space covered by the powers of both parties (which can be referred to as the power space). This change is the result variable caused by combat effectiveness and can be used to measure combat effectiveness. The formula is as follows:
where CE is the combat effectiveness; ΔS represents changes in the frontline, which signifies the area of newly gained power space (if lost, it is represented as a negative value); t expresses the time required to alter frontline. Spatial changes are measured in square meters (sqm) and time in hours (h). Thus, the basic unit of measuring combat effectiveness is square meters/hour, expressed as sqm/h. In our analysis, we adhere to the International System of Units (SI) prefix symbols(M=106, k=103). Therefore, "1Msqm/h "means "1,000,000 square meters per hour", denoting one million square meters per hour.
Candlestick charts, widely recognized for their effectiveness in analyzing and predicting price movements in financial markets, have yet to be applied in conflict studies, primarily due to the challenges of obtaining time series data in conflict research. Our method, however, generates precisely this kind of data, enabling the innovative application of candlestick analytics to conflict analysis. We are equipped with a sophisticated analytical framework by applying candlestick chart analysis to the combat effectiveness data we have collected on the Russo-Ukrainian war. This framework enables us to conduct detailed analyses and make predictions regarding the progression of the Russo-Ukrainian war, achieving a level of analytical depth that is on par with those used in financial market research.
It is essential to clarify that our formulas quantify relative combat effectiveness; they assess the disparity in combat effectiveness between a political entity and its adversary. Thus, an outcome of 'CE = 0' does not signify that the combat effectiveness of both parties is nonexistent. Instead, it indicates that the gap in combat effectiveness is nonexistent, implying parity in combat effectiveness between the two sides. To ensure clarity and precision in our discussion, especially for those accustomed to considering combat effectiveness as an independent metric unrelated to the opponent, we will adopt the CERussia-Ukraine in all subsequent case studies. This specific designation delineates the differential in combat effectiveness between Russian and Ukrainian forces, succinctly expressed as CERussia-Ukraine = CERussia - CEUkraine. This terminological clarification eliminates potential ambiguity, facilitating a consistent and unambiguous comprehension across our analysis.
Daily Candlestick Chart Analysis of CERussia-Ukraine
A daily candlestick chart is a graphical graphical tool that meticulously captures the subtle dynamics of an asset; it delineates each day's price variations through a candlestick, marked by four essential points (two endpoints and two wicks), representing the opening, closing, highest, and lowest prices within that day. We have customized this technique in our study to shed light on the micro-trends of CERussia-Ukraine. Specifically, the apex or base of each candlestick indicates the CERussia-Ukraine at the start or conclusion of each day, echoing the financial notions of opening and closing prices. Our daily candlestick charts forgo the conventional upper and lower wicks because determining the highest and lowest points requires more granular data, a task complicated by the challenge of getting precise hourly territorial data. This omission of upper and lower wicks is specific to the daily candlestick charts. Because, with the daily CERussia-Ukraine data, our ensuing weekly, monthly, and yearly candlestick charts will incorporate the full array of wicks, thus providing a thorough depiction of temporal fluctuations.
The daily data for CERussia-Ukraine is derived from daily frontline change maps sourced from esteemed military analysis websites such as the Institute for the Study of War and Political Geography Now. These maps are meticulously compiled through a synergistic approach that combines traditional frontline reporting, high-resolution military satellite imagery, and the monitoring of fire points via shortwave infrared technology. Furthermore, military commentators like Poulet Volant and War Mapper, known for their diligent tracking of changes in Ukraine's territorial expanse and sharing their insights on Twitter, serve as invaluable corroborative sources for the accuracy of our data. The data collection timeline extends from the commencement of the conflict on February 24, 2022, to two years later on February 24, 2024, thus providing a comprehensive dataset of 730 time series samples.
Upon constructing the daily candlestick chart to analyze the two years of the Russo-Ukrainian War, we encountered a notable challenge: the overwhelming volume of candlesticks, when compressed together, became challenging to differentiate. To mitigate this issue, we focused exclusively on data from the first year of the war (February 24, 2022 - February 24, 2023) for our analysis. This period was chosen because the strength of daily candlestick charts lies in their ability to facilitate the identification and understanding of short-term, sudden strategic events. We will next analyze strategic events that had a profound impact in the short term, including "Russia's surprise attack strategy," "Russia's strategic withdrawal from Kyiv," "Ukraine's strategic counteroffensive in Kharkiv," and "Ukraine's strategic counteroffensive in the western Kherson," all of which occurred during this initial year of the war.
Figure II.
Daily Level CERussia-Ukraine Candlestick Chart (Feb 24, 2022 - Feb 24, 2023). Note: This chart was created using Python.
Figure II.
Daily Level CERussia-Ukraine Candlestick Chart (Feb 24, 2022 - Feb 24, 2023). Note: This chart was created using Python.
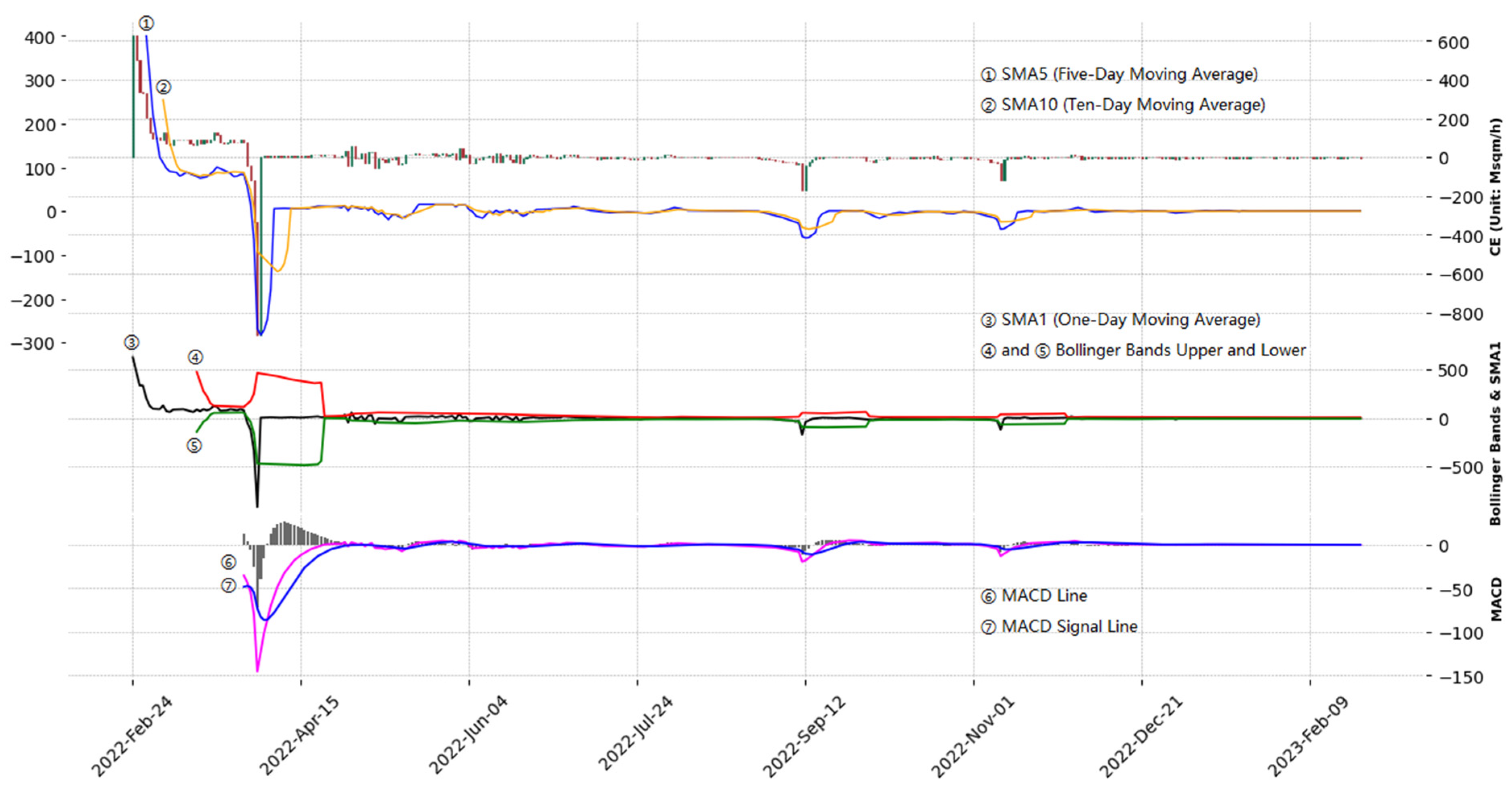
In the early stages of the war, Russia's sudden attack strategy and strategic withdrawal from Kyiv profoundly impacted the battlefield dynamics. This fact is vividly reflected in the candlestick charts. Russia's surprise attack strategy was to preemptively exert its offensive combat effectiveness before Ukraine's defensive combat effectiveness could be fully mobilized. This strategy was designed to amplify the disparity in combat effectiveness between Russia and Ukraine, enabling Russia to gain territory more quickly and extensively. The candlestick chart clearly shows that, at the beginning of the conflict, the CERussia-Ukraine displayed a significant upward candlestick, with a length nearing 400 Msqm/h. This unexpectedly rapid advancement of the front lines astonished global observers at that time. However, the swift mobilization by the Ukrainian government and its citizens and timely international support quickly made Russia's surprise attack strategy ineffective. This shift is clearly illustrated in the candlestick chart, where, following the initial large upward candlestick, a sequence of four declining candlesticks emerged, characterized by alternating 'small-big-small-big' patterns, forming a 'double evening star' formation. The evening star configuration is traditionally viewed as a solid bearish indicator, signaling the rapid depletion of upward momentum and establishing a downtrend—a notion further underscored by the emergence of a double evening star. Consequently, by early March, the CERussia-Ukraine had declined to approximately 150 Msqm/h, which means a more than 60% reduction in Russia's combat effectiveness advantage over Ukraine.
By mid-March, the CERussia-Ukraine experienced a modest increase. The critical question was whether this uptick represented a corrective rebound after a sharp decline or a downward trend reversal. This distinction was crucial at the time. The early victories of Russia in the conflict were not primarily due to the substantial investment of military resources but instead benefited significantly from its strategy of surprise attacks. Consequently, with the Ukrainian forces fully mobilized and international support stabilizing, Russia would only be able to cause a reversal of the downward trend in the CERussia-Ukraine by significantly escalating the conflict and deploying a greater quantity of combat effectiveness against Ukraine. Thus, accurately assessing this trend was vital to understanding Russia's intentions in the war. Upon examining the candlestick charts, it becomes apparent that the bullish candlestick that emerged in the third week of March was wholly and quickly overshadowed by an even larger bearish candlestick in the fourth week of March. Moreover, throughout March, the CERussia-Ukraine's five-day moving average repeatedly attempted to cross above the ten-day moving average to form a "golden cross" but consistently failed. The only successful crossover on March 20 was immediately followed by a downward cross, forming a "death cross." Furthermore, in early to mid-March, the daily moving average repeatedly attempted to break through the upper Bollinger Band without success; by late March, it had fallen below the lower Bollinger Band. Simultaneously, the MACD line crossed below the MACD signal line. These key indicators collectively suggested that Russia had no intention of escalating the conflict or increasing its military resource allocation to the Ukrainian battlefield. The rise in CERussia-Ukraine around mid-March was merely a technical rebound from the initial sharp decline at the beginning of the month, with a more significant downturn imminent.
When Russia announced troop withdrawal from Kyiv and Chernihiv on March 29, 2022, the combat effectiveness in these regions for Russia plummeted to zero, precipitating a rapid and significant decline in CERussia-Ukraine to negative values. This downturn in CERussia-Ukraine signaled the release of previously accumulated bearish factors. Despite Russia's failure to compensate for the ineffectiveness of its initial surprise attack strategy through a massive deployment of military resources, it adapted by concentrating its superior forces on a new strategy. Abandoning the aim to conquer the entirety of Ukraine, Russia focused its combat effectiveness on securing control over the eastern regions of Ukraine. CERussia-Ukraine, therefore, dispensed with the bearish factors and recovered and stabilized near the Fibonacci retracement support line (the 38.2% decline) in early April.
Following the mid-April redeployment of its combat effectiveness from Kyiv to the eastern regions of Ukraine, Russia's focused force concentration strategy led to a rapid escalation of CERussia in these regions, which means CERussia-Ukraine ascended in this area. To counter the continual rise of CERussia-Ukraine, which threatened territorial losses, Ukraine similarly redirected its combat effectiveness to Eastern Ukraine to bolster CEUkraine. This strategic adjustment initiated a period of intense confrontation between the main forces of both sides in this region, famously referred to by global media as the "Battle of Donbas." Owing to the simultaneous increase of CERussia and CEUkraine, the CERussia-Ukraine index remained unchanged. However, this equilibrium, marked by a high volume of engagements, was inherently unstable and poised for a directional shift in response to emerging influential factors. Just as a trading volume increase under a consolidation phase is unstable, the emergence of positive or negative factors can easily lead to a rise or fall in price.
Indeed, beginning in late August, a "descending triangle" pattern emerged on the chart, characterized by a gradual decline in the resistance line following a prolonged period of consolidation while the support line descended more markedly. This pattern suggested that it was becoming increasingly difficult for the Russian side (the bullish party) to maintain the stalemate, presaging a significant downturn in the CERussia-Ukraine. As anticipated, Ukrainian forces achieved a significant victory in Kharkiv in early September, nearly recapturing the entire region. This "descending triangle" emerged primarily due to newly mobilized troops being added to the Ukrainian. Although the international community has donated funds and supplies to Ukraine since March, replenishing qualified combat personnel, which Ukraine needed most, could not be as swiftly achieved as financial and material aid. From the outbreak of the war, Ukraine initiated a national mobilization. However, according to standard military experience, newly enlisted mobilized soldiers typically require approximately 4-5 months of training before genuinely contributing to combat effectiveness in live combat. Hence, until July, Ukraine had to rely on its existing combat effectiveness for resistance. Nevertheless, by August, with the supplementation of qualified mobilized soldiers to the Ukrainian military, especially those soldiers returning from NATO military training to join the combat, CEUkraine increased, signifying a decrease in CERussia-Ukraine. Besides the cause of the new add mobilized soldiers, the sharp decline in CERussia-Ukraine was also due to the Ukrainian military's implementation of a strategic deception tactic. By conducting feints in the southeastern regions of Ukraine, the Ukrainian command successfully misled the Russian command, causing the latter to misjudge the main direction of the Ukrainian counteroffensive towards the Zaporizhzhia area. As the Russian command redeployed troops from the northeastern regions to the south, the CERussia(Zaporizhzhia) increased. At the same time, the CERussia(Kharkiv) decreased, leading to a sharp decline in CERussia-Ukraine(Kharkiv) in early September.
A noteworthy shift occurred in mid-September. During this period, the ten-day moving average, which had previously diverged downward from the five-day moving average due to the Kharkiv offensive, saw a sudden ascent, nearly realigning with the five-day moving average. Concurrently, the one-day moving average, having breached the lower Bollinger Band in response to the Kharkiv offensive, swiftly ascended back to the median of the Bollinger Bands. The divergence from the signal line of the MACD, induced by the Kharkiv battle, was rapidly reconciled. Collectively, these pivotal technical indicators suggest that by mid-September, the battlefield dynamics had reverted to the equilibrium state observed before the Kharkiv offensive. In financial markets, such a scenario would be analogous to a potent force abruptly reverting security prices to their original positions. On the Russo-Ukrainian battlefield, an extrinsic formidable factor abruptly augmented CERussia, restoring equilibrium with CEUkraine. This factor is the Russia-Ukraine border. With the Ukrainian forces' significant success in the Kharkiv battle, the front lines in the northeast of Ukraine were restored to the pre-war borders. Given that Ukraine's strategy focused solely on regaining lost territory rather than offensive operations into Russian territory, coupled with Russia's repeated nuclear deterrence predicated on its homeland being attacked, these considerations prompted the Ukrainian military to cease further advancements into Russian territory using combat effectiveness voluntarily. This example illustrates the superiority of our method for measuring combat effectiveness. The concept of borders, as understood in international law, when considered alongside contemporary notions of territorial justice and the policy of first use of nuclear weapons, can impede combat effectiveness. Our measurement methodology adeptly captures this interference. In contrast, traditional approaches to measurement necessitate the acquisition of quantified impact coefficients regarding the influence of territorial justice perceptions and the policy of first use of nuclear weapons on the strategic decisions of the Ukrainian command—a notably impractical task.
Although disruptions due to factors along the Russia-Ukraine border prevented Ukraine from leveraging its combat effectiveness advantage in mid-September, this advantage did not vanish into thin air but merely needed to be redirected elsewhere. Over a month later, the Ukrainian command successfully transferred Ukraine's combat effectiveness advantage to the Kherson region. Technically, this shift manifested as the re-emergence of a "descending triangle" pattern in late October, closely mirroring the one observed in late August. Subsequently, in early November, an anticipated decline in the CERussia-Ukraine context unfolded, mirroring the downturn seen in early September. On the battlefield, this manifested as Russia losing control over the western Kherson region, including the regional capital, the city of Kherson.
It is worth noting that, consistent with the situation observed in mid-September, the technical pattern of a sudden increase in CERussia-Ukraine in mid-November due to a sudden drop in CEUkraine has reemerged. The previous was attributed to the Russia-Ukraine border, whereas the recent one was due to the Dnieper River. The precipitous decline in CERussia-Ukraine(west of the Dnieper River) made Ukraine's successful recapture of the western parts of Kherson, yet CERussia-Ukraine(east of the Dnieper River) failed to exhibit a synchronous uplift. This disparity can be attributed to the Dnieper River, Europe's fourth-largest river, whose expansive breadth significantly advantages the defending party by providing enhanced cover from the superior artillery strikes. Moreover, the threat posed by the potential deliberate breaching of the Nova Kakhovka Dam upstream adds a layer of complexity, impeding the offensive side's ability to deploy combat effectiveness across the river on a large scale. Traditional metrics fall short in quantifying the unique influences of the Dnieper River's hydrological environment and the anticipated dam breach upstream on combat effectiveness. Conversely, our measurement approach adeptly captures these. Furthermore, our analysis enables a comparative study of the impact magnitude captured at two different times. Comparing the rate at which the ten-day moving average reverts to the five-day moving average between mid-September and mid-November reveals that the latter rate is less than the former. It suggests that the weakening effect of the Dnieper River on Ukraine's combat effectiveness is less significant than that of the Russia-Ukraine border.
Despite the Dnipro River's role in hampering the full manifestation of Ukraine's combat effectiveness advantage, its effect, akin to the Russia-Ukraine border, merely constrains further advances along the front lines—limiting eastward progression due to the river and northeastward expansion due to the border. It does not obliterate Ukraine's advantage in combat effectiveness. Conventionally, it would be expected that a third significant victory akin to those in Kharkiv and Western Kherson would materialize shortly, with Ukraine reallocating its combat effectiveness advantage. Contrary to these expectations, the technical charts at the end of December failed to replicate the descending triangle pattern observed at the ends of August and October. Instead, Russia gained a slight upper hand during the battles in Bakhmut in late January and early February 2023. It indicates the emergence of a novel factor on the Russia-Ukraine battlefield capable of nullifying Ukraine's combat effectiveness advantage—namely, the participation of Russia's newly mobilized troops. Ukraine's substantial victory in Kharkiv in early September 2022 necessitated an increased allocation of military resources by Russia in Ukraine's theater. On September 21, Russia issued a partial mobilization order, its first since World War II, conscripting approximately 300,000 reservists. Like Ukrainian forces, these Russian mobilized troops required a 4-5 month training period to achieve combat effectiveness. By the end of January and the beginning of February 2023, the addition of Russia's newly mobilized troops increased CERussia, offsetting the rise in CEUkraine after the incorporation of Ukraine's recruits. Consequently, the sharp decline in the CERussia-Ukraine technical chart, previously observed on the Kharkiv and western Kherson battlefields, did not materialize for a third time.
Weekly Candlestick Chart Analysis of CERussia-Ukraine
A weekly candlestick chart is an essential tool in financial analysis, particularly adept at capturing trends at the sub-macro level of markets or specific sectors. Our approach to constructing the weekly candlestick chart uses data from daily candlestick charts to calculate the week's opening, closing, high, and low CEs. The weekly candlestick chart uncovers a distinct trend in CERussia-Ukraine: a complete classical five-wave decline pattern followed by a horizontal trend. The five-wave decline pattern, originating from the Elliott Wave Theory, which R.N. Elliott proposed in the 1930s, is a widely used technical analysis method in financial market analysis. This theory posits that market price trends undergo predictable, rhythmic reversals over specific periods. Our weekly candlestick charts specifically focus on the period from February 24, 2022, to February 24, 2023. This timeframe encapsulates the entire process of CERussia-Ukraine undergoing an entire five-wave decline pattern before leveling off into a horizontal trend.
Figure III.
Weekly Level CERussia-Ukraine Candlestick Chart (Feb 24, 2022 - Feb 24, 2023). Note: This chart was created using Python.
Figure III.
Weekly Level CERussia-Ukraine Candlestick Chart (Feb 24, 2022 - Feb 24, 2023). Note: This chart was created using Python.
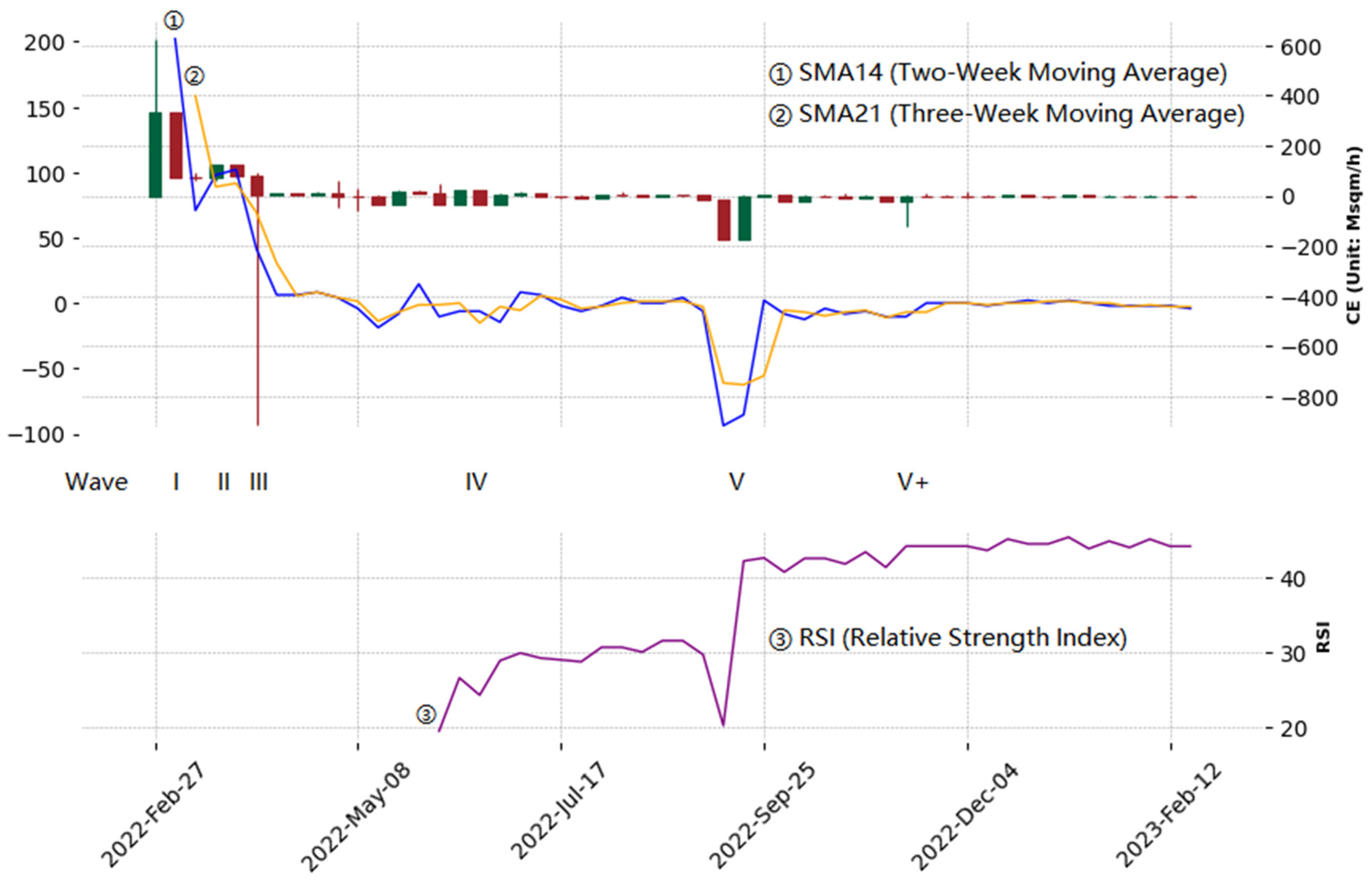
Based on the Elliott Wave Principle's five-wave decline pattern, the first wave signifies the establishment of a downward trend. In the context of the Russo-Ukrainian War, this wave is represented by the candlestick patterns observed in the first and second weeks, exhibiting distinct technical characteristics. The candlestick of the first week is a shooting star with a large upper shadow and no lower shadow, a professional term denoting a significant bearish reversal signal. This pattern strongly suggests an underlying bearish trend beneath a superficial rise, as the long upper shadow indicates a price spike while the close price suggests a fallback. In the context of the Russo-Ukrainian War, this foreshadows Russia's apparent victories (rapid frontline advances brought by surprise attack strategies) and the reversal of the underlying trend (rapid ineffectiveness of the surprise attack strategy due to Ukraine's swift mobilization and rapid international support). The second week's candlestick is a large "Black Marubozu" (or "Bearish Marubozu"), representing the main body of the first wave's decline. This formation's technical characteristic is the absence of upper and lower shadows, implying that from the beginning of the week (opening) to the end (closing), there was a continuous decline, reflecting that Russia's surprise attack strategy had utterly failed this week.
The second wave in the Five Wave Decline pattern represents a corrective and rebound phase against the first wave, characterized primarily by its peak being lower than the starting point of the first wave, indicating that the upward momentum is insufficient to alter the established downward trend. In the context of the Russo-Ukrainian War, this second wave commenced in the third week, marked by closing with a candlestick featuring a "short shadow gravestone doji," signaling the slow cessation of the downward trend. In the subsequent fourth and fifth weeks, closings featured two candlesticks of equal length, one bullish and one bearish, indicating that the fourth week was the main body of the second wave's rebound. Notably, the bullish candlestick of the fourth week fell significantly short of engulfing the bearish candlestick from the second week, illustrating the pronounced characteristic of a corrective rally in the second wave. From the perspective of other technical indicators, a brief crossover of the 2-week simple moving average (SMA14) above the 3-week simple moving average (SMA21) to form a "golden cross," which was quickly followed by a downturn to form a "death cross," further corroborates the temporary nature of this rise.
In the five-wave downward pattern context, the third wave is the most substantial and decisive decline, termed the "primary downtrend" or "primary bear market." By the end of March 2022, Russia's combat effectiveness, initially deployed at the onset of the war, has proved insufficient to execute its strategy to conquer all of Ukraine. Consequently, Russia was compelled to withdraw its forces from the Ukrainian western territories it had occupied. This retreat, symbolized in technical analysis by a hammer candlestick with a significantly long lower shadow, suggests that this maneuver was more likely a strategic adjustment than a total collapse; otherwise, the technical pattern would display a succession of Black Marubozu. The long hammer signifies that the buyers are attempting to exit the market by actively lowering the price. In early April, the frequency and intensity of the engagements between the two sides—akin to the volume indicator in stock market trading—dramatically decreased. It was because Russia focused on redeploying its troops to the eastern part of Ukraine while Ukraine was busy reclaiming the land vacated by Russian forces. These indicators suggest that this period resembled a trading halt in the stock market.
The fourth wave, akin to the second, serves as a corrective and rebound phase to the third wave, albeit with further diminished rebound momentum, manifested in a lower peak than the second wave. It aligns with the trajectory of the Russo-Ukrainian War. After a relative "pause" of approximately two weeks, Russia redeployed troops withdrawn from Kyiv to the eastern frontlines of Ukraine. From mid-April, this region became the epicenter of numerous intense battles, prominently dubbed the "Battle of Donbas" by global mainstream news media. The redeployment alleviated Russia's primary detrimental factor—dispersed forces—leading to an uptick in CERussia-Ukraine, culminating in the battle for Mariupol. However, chart analysis reveals that this peak did not surpass the second wave's high, indicating the temporary nature of the fourth wave's rebound. Further examination of technical indicators shows the two-week moving average crossing above the three-week moving average multiple times during this period, only to fall below it shortly after. It suggests that while Russia might have gained a marginal advantage, it could not return to its prior level of superiority, a hallmark characteristic of the fourth wave.
By July and August, there was a notable reduction in the battles' intensity (akin to trading volume) and the length of the CERussia-Ukraine candles (equivalent to price fluctuations), exemplifying a classic consolidation pattern in volume reduction. The emergence of this consolidation pattern signaled the conclusion of the fourth wave. At this juncture, it was time for the candlestick chart to select its future direction. Technically speaking, the proportion of bearish weekly candles in July and August increased by more than 55% compared to May and June (77.8% versus 50%). Furthermore, the RSI indicator consistently remained around 30 (the oversold territory) during July and August, indicating that the CERussia-Ukraine values had been overvalued. Ukraine had already secured the initiative to change the trend and was brewing a larger strategic counteroffensive plan. As previously mentioned, Ukraine's leverage to change the trend was the newly mobilized soldiers joining the fight in July and August, coupled with implementing deceptive tactics. Consequently, a new downtrend of CERussia-Ukraine began, manifesting as Ukraine's significant victory in the Kharkiv region in September 2022. This outcome astonished everyone at the time, yet it had been foreshadowed in the weekly candlestick charts of July and August.
Due to the Ukrainian forces not intending to cross the Russo-Ukrainian border to advance their front line further, the bearish factors of CERussia-Ukraine were not fully released. It is evidenced by the RSI on the weekly chart, which, despite a rapid ascent, only reached 40—a level still within the oversold territory—rather than the equilibrium point of 50, indicating that CERussia-Ukraine remained overvalued. Subsequently, Ukraine initiated a redeployment of its troops. Upon completion of the troop movements, the continuation of the downtrend established in early September was observed, with CERussia-Ukraine continuing the fifth wave decline until the recapture of western regions of Kherson in early November, including its capital, by Ukrainian forces forcibly halted the downtrend because of the Dnieper River. The RSI indicator's movement from 40 to 45, while still failing to reach 50, signifies that the advantage in combat effectiveness remained with the Ukrainian forces. However, after December, the fifth wave did not reappear for the third time. Russia initiated partial mobilization orders following the significant defeat in the Battle of Kharkiv in early September, which formed the new combat effectiveness in January- February 2023. This new positive factor offset the previous combat effectiveness advantage of Ukraine from July or August, which was reflected in the technical analysis by an equal number of bearish and bullish candlesticks during this period, with CERussia-Ukraine not breaking support levels as it had in previous battles in Kharkiv and Kherson, and the RSI rises approaching 50. These technical indicators suggest that the fifth wave has concluded.
On the battlefield around Bakhmut, while both sides engage in intense combat, the frontline experiences minimal shifts, with any territorial gains by one party swiftly counterbalanced by the other. This scenario of increased trading volume with price fluctuations within a very narrow range, essentially forming a nearly straight line, is known as "Price Squeeze." It signifies a rough equilibrium between buying and selling forces, with neither side being able to drive the market significantly toward a new direction. Additionally, the continuous maintenance of the RSI at 50 in the weekly candlestick chart and the daily moving average coinciding with both the upper and lower Bollinger Bands in earlier daily candlestick charts technically signifies this new trend. In the context of the Russo-Ukrainian War, this suggests that the combat effectiveness of the warring parties has reached a strategic point of dynamic equilibrium. In other words, CERussia≈CEUkraine implies CERussia-Ukraine≈0. It marks a distinct departure from the previous five-wave decline cycle, forming a more macroscopic cycle that is more aptly discussed in the context of monthly charts.
Monthly Candlestick Chart Analysis of CERussia-Ukraine
A monthly chart delineates the opening price of a month as the opening price on the first trading day and the closing price as that of the last trading day of the month, with the highest and lowest prices representing the peak and nadir of trading within the month, respectively. It is particularly adept at revealing macro trends by mitigating the noise of short-term fluctuations. Analyzing the monthly chart reveals that the macro trends in the CERussia-Ukraine over two years can be summarized as the sequential emergence of three fluctuation patterns: wide-range oscillation, box-range movement, and low volatility consolidation.
Figure IV.
Monthly Level CERussia-Ukraine Candlestick Chart (Feb 24, 2022 - Feb 24, 2024). Note: This chart was created using Python.
Figure IV.
Monthly Level CERussia-Ukraine Candlestick Chart (Feb 24, 2022 - Feb 24, 2024). Note: This chart was created using Python.
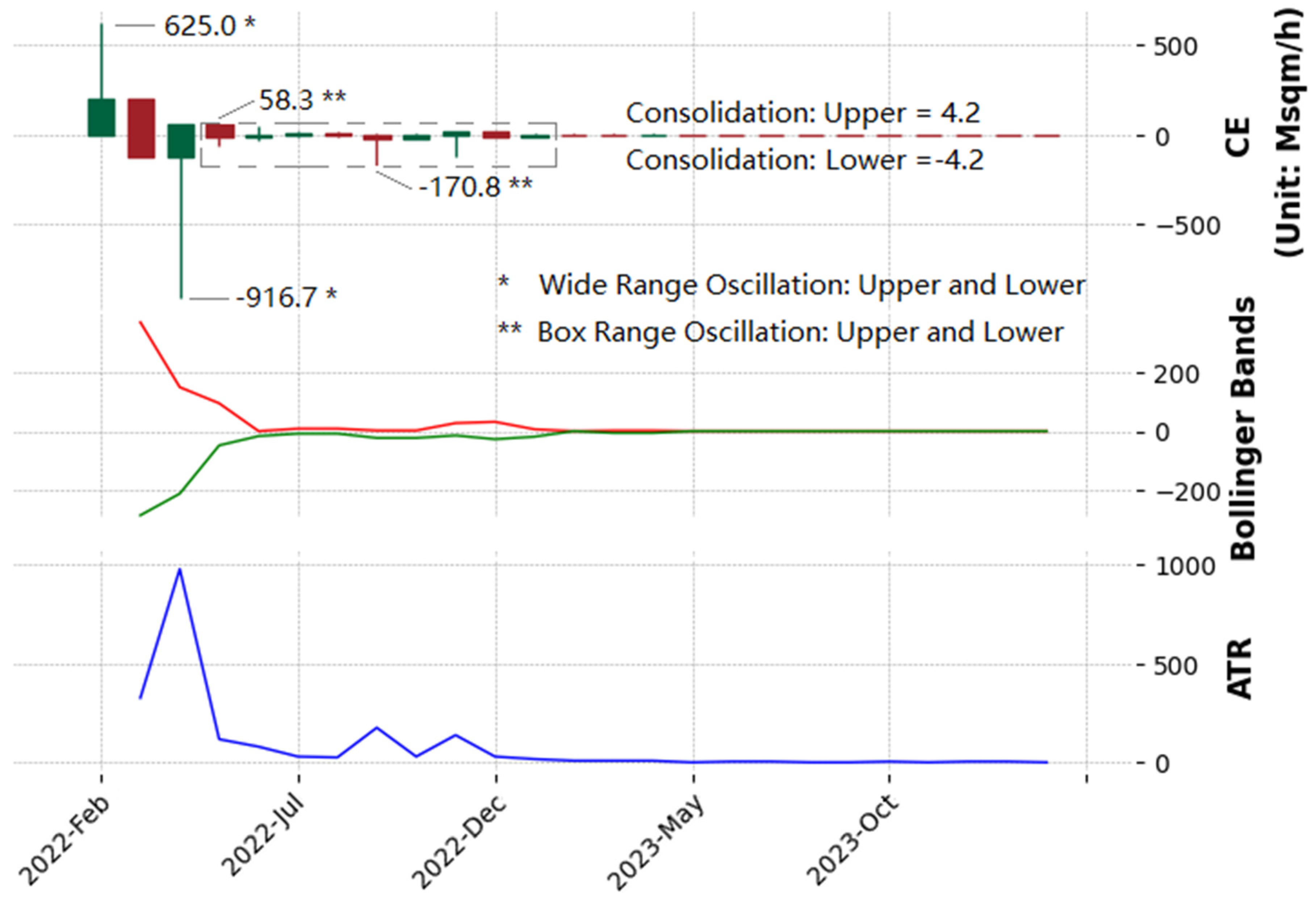
The phase of wide fluctuations is composed of candlestick charts from the initial three months, spanning from the outbreak of the war to Russia's withdrawal from Kyiv. This period is marked by significant CERussia-Ukraine swings, with a maximum volatility amplitude of 1500 Msqm/h. The opening, closing, highest, and lowest prices of the three candlestick charts have all varied significantly from each other, demonstrating the extreme volatility of CERussia-Ukraine. Additionally, the Bollinger Bands and ATR also show significant readings. The distance between the upper and lower Bollinger Bands can measure the degree of volatility. The chart shows that the upper band was above 200 and the lower band was below 200 in the previous three months, with a track difference exceeding 400. The ATR is a direct indicator of volatility, with higher values indicating greater volatility. The chart shows that the ATR for the past three months was consistently above 300, reaching as high as 1000 at its peak.
The box fluctuation phase consists of candlestick charts for months four to twelve, corresponding to the timeframe from the battle for Donbas to the defense of Bakhmut. Compared to the preceding three months, the maximum volatility amplitude of CERussia-Ukraine significantly decreased to around 220 Msqm/h during this phase. The differences between each candlestick's opening, closing, highest, and lowest prices have significantly narrowed, and most are confined within a range of ±60 Msqm/h. Correspondingly, during this stage, the upper Bollinger Band fell below 50, and the lower Bollinger Band rose above -50, which means the distance between the two bands was less than 100. The ATR also fell below 200 and even dropped to around 50 at one point.
The low volatility consolidation phase comprises 13-24 month candlestick charts, corresponding to the time range from the first to the second anniversary of the war's outbreak. The characteristic of this stage is the near disappearance of volatility phenomena in the CERussia-Ukraine index, with the maximum volatility amplitude not exceeding 10 Msqm/h. Additionally, the opening, closing, highest, and lowest prices of most candlesticks are at 0 Msqm/h, indicating that the battlefield situation has entered a stage of strategic stalemate. Correspondingly, during this phase, the upper and lower Bollinger Bands almost entirely overlap, meaning a difference of zero, and the ATR curve also almost entirely overlaps with the x-axis, which means a value of zero.
In summary, from a macro perspective, the overall strategic posture of the Russo-Ukrainian War over the past two years has been a process where CERussia-Ukraine has gradually stabilized through continuous probing and adjustment by both sides, eventually achieving strategic equilibrium. The fundamental reason behind this trend is that both warring parties possess factors that can neutralize each other's combat efficiency advantages. Specifically, Russia's war potential is significantly higher than Ukraine's, enabling it to realize combat effectiveness through continuous deployment of war resources. However, the Ukrainian forces' high morale and the international community's continuous support offset these advantages. These have fostered the development of a hyper-stable dual feedback loop on the battlefield of the Russo-Ukrainian War. This dual feedback loop can be macroscopically described as:
1. Russia makes strategic adjustments → 2. CERussia-Ukraine is higher than zero → 3. Russia advances the frontline → 4. The international community offers more assistance → 5. CERussia-Ukraine drops below zero → 6. Ukraine advances the frontline → 7. Russia is deploying more war resources, including increased personnel mobilization and military spending.→ 8. CERussia-Ukraine is higher than zero → and the cycle repeats and continues from stage 3.
To provide readers with a more intuitive understanding of this dual feedback loop, we have created Figure IV.
Figure V.
The Hyper-Stable Dual Feedback Loop in the Russo-Ukrainian War. Notes: 1. From left to right: schematic diagram and live diagram. 2.From top to bottom: changes in "War Resources", "Combat Effectiveness" and "Frontline" levels.
Figure V.
The Hyper-Stable Dual Feedback Loop in the Russo-Ukrainian War. Notes: 1. From left to right: schematic diagram and live diagram. 2.From top to bottom: changes in "War Resources", "Combat Effectiveness" and "Frontline" levels.
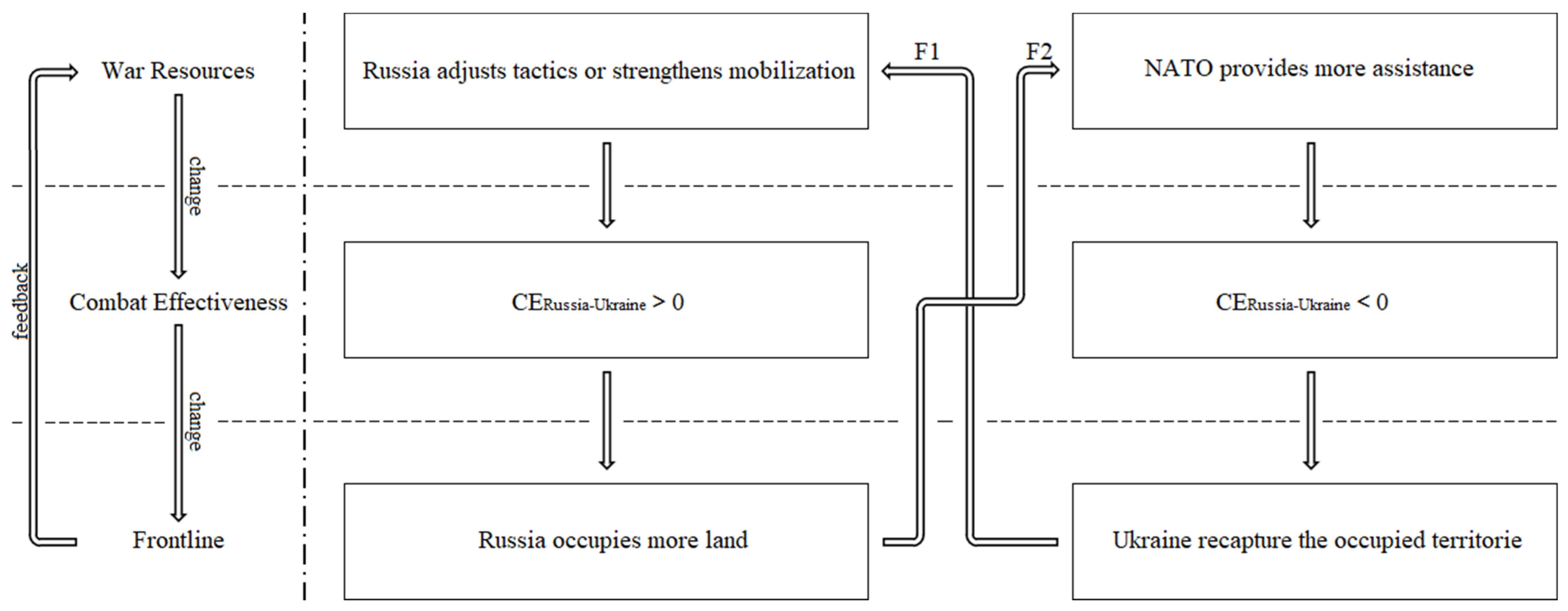
Table 1. in Figure V), which means that the losses Russia incurs from diplomatic isolation and economic sanctions outweigh the gains on the Ukrainian battlefield, leading Russia to withdraw troops in exchange for reacceptance by the international community. The potential outcomes of the Russo-Ukrainian War had been signed as early as April 2022. At the time, the retreat of Russian forces from Kyiv revealed evidence of atrocities against civilians in the capital's suburbs. This discovery led to a unanimous decision by the Senate to pass the Ukraine Democracy Defense Lend-Lease Act of 2022 on April 6, 2022. A strong will to fight and sufficient war resources are essential conditions for a protracted war. The Bucha incident profoundly and permanently ignited the Ukrainian nation's will to resist Russia, while the Lend-Lease Act provided Ukraine with a continuous supply of war resources. Therefore, the chain reaction initiated by Russia's withdrawal from Kyiv significantly enhanced Ukraine's will and capability to resist. Should Russia not withdraw from Ukraine proactively, the Russo-Ukrainian War could evolve into a protracted conflict disadvantageous to Russia, continuing until Russia withdraws due to the war costs exceeding the benefits.
The latter means the fracture of Feedback II (F2 in Figure V), which means Ukraine being defeated by Russia after losing international support, conceding the eastern regions of Ukraine. This possibility was initially far less likely than the former, as evidenced in the first year of the war: Russia's attempts to intimidate the international community with nuclear weapon threats aiming to disrupt Feedback II, but these threats have been ineffective. Conversely, the sentiment, "Your money is not charity; it is an investment in global security and democracy" (from Ukrainian President Zelensky's speech to the US Congress in December 2022), gained traction and resonated strongly with the international community. In his address in Warsaw on February 21, 2023, three days before the anniversary of the war's outbreak, President Biden declared unwaveringly and resolutely, asserting, "Our support for Ukraine will not waver, NATO will not be divided, and we will not tire." This speech minimized the risks of Feedback II fracturing. However, as the war entered a stalemate in its second year, Russia's short-term threats ceased to exist, and supporting Ukraine seemed to become an "economic burden" with diminishing returns, which suggested that the "Ukraine fatigue" – the notion that support for Ukraine from Western democracies might inevitably diminish over time, was gradually increasing. Nevertheless, the profound negative impact a Ukrainian defeat would have on global security rules makes it impossible for the international community to succumb to fatigue. On February 24, 2024, on the occasion of the second anniversary of the outbreak of the Russia-Ukraine war, the leaders of the Group of Seven (G7) emphasized in a statement from a video conference that they will continue to "unwaveringly support" Ukraine, reflecting the Transatlantic Alliance's elite vigilance and resistance to "Ukraine fatigue."
Annual Candlestick Chart Analysis of CERussia-Ukraine
Annual candlestick charts offer an ultra-macroscopic perspective, constructed by comparing daily combat effectiveness data, highlighting the opening, closing, highest, and lowest data each year. However, this methodology becomes limited in the context of the Russo-Ukrainian War, spanning only 2022, 2023, and 2024, resulting in just three candlesticks that provide limited analytical value. To enrich our analysis, we extend the timeframe to a decade, starting from 2014. The onset of Russian military operations in Crimea on February 20, 2014, marks the broader beginning of the Russo-Ukrainian War, as it laid the groundwork for all subsequent developments. Given the unavailability of precise daily combat effectiveness data for 2014 to 2021, our depiction relies on illustrating only the maximum and minimum values through the candlesticks' wicks, setting both opening and closing prices at zero.
Figure VI.
Annual Level CERussia-Ukraine Candlestick Chart (2014 - 2024). Note: This chart was created using Python.
Figure VI.
Annual Level CERussia-Ukraine Candlestick Chart (2014 - 2024). Note: This chart was created using Python.
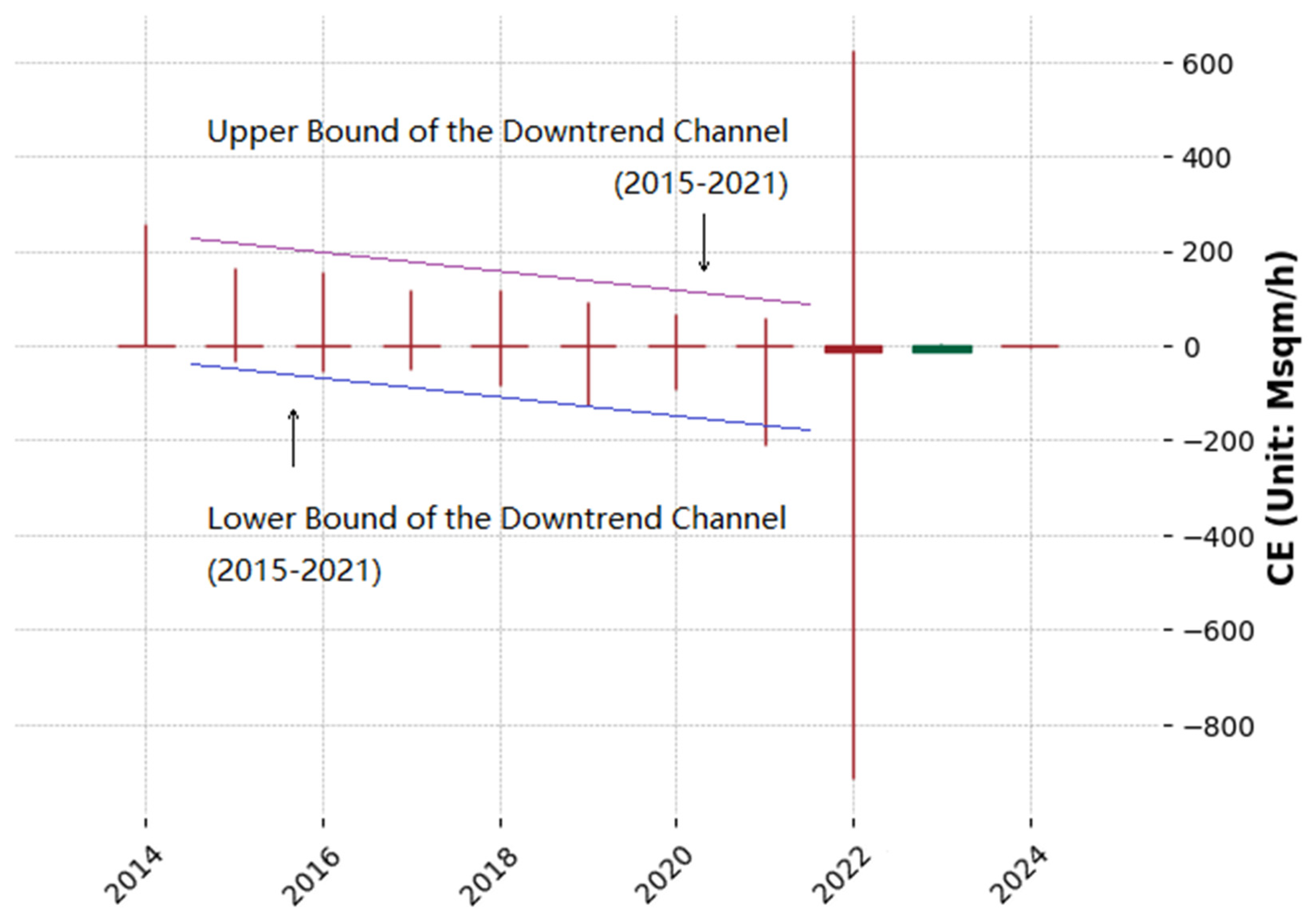
Based on the chart, excluding the years when Russian military forces were directly involved in combat, namely 2014 and 2022-2024, the remaining period from 2015 to 2021 formed a distinct downward channel in the candlestick chart. It is because the primary adversary of the Ukrainian government forces during this period was the Russian-backed separatists in Eastern Ukraine, against whom the combat effectiveness of Ukrainian government forces was higher than against Russian forces. The loss of Crimea catalyzed the bolstering of the spirit of national resistance and enhanced crisis awareness within Ukrainians, gradually improving the combat effectiveness of its forces year by year. Although the Russian-backed separatists received support from Russia, the gap in combat effectiveness between them and the Ukrainian government forces widened in the absence of direct Russian military involvement. Even when Russian military forces were directly engaged in combat in 2014 and 2022, the presence of long upper shadows in the candlestick charts was primarily facilitated by surprise. Moreover, not to mention, given the circumstances that precluded open intervention, Russia was relegated to offering only clandestine support. By 2019, the chart shows that the annual low for the CEseparatists-Ukrainian government forces had broken below the downward channel's lower boundary, indicating a potential for accelerated decline. Although the COVID-19 pandemic in 2020 caused a significant reduction in the number of engagements, preventing an accelerated decline, by 2021, as the impact of the pandemic gradually lessened, the conflict escalated anew. The downward trend of CEseparatists-Ukrainian government forces re-emerged with increased magnitude, with the annual low significantly breaking below the channel's lower boundary. In other words, by this time, if Russia did not intervene directly to support the separatists, they were on the brink of being decisively defeated.
Therefore, although Russia's sudden engagement in the conflict on February 24, 2022, took many by surprise, the candlestick charts and technical indicators had already concluded that unless Russia were willing to relinquish its aspirations for the eastern regions of Ukraine, it would inevitably intervene directly in the conflict. From both the perspectives of value conflicts and interest conflicts, the likelihood of Russia deploying troops was far greater than the possibility of willingly giving up the eastern regions of Ukraine. From the perspective of the conflict of values, the Russian Empire (1721-1917) was historically an expansionist state, similar to the Roman Empire (27 BC-AD 476), Arab (632-1258), Mongolian (1206-1635), and Ottoman Empires (1299-1922). After reaching its expansion peak, this type of empire is inevitably confronted with a solid centrifugal tendency until it disintegrates into numerous nation-states. Lenin and the October Revolution postponed the collapse of the Russian State, which seemed imminent at the beginning of the 20th century. The compromise from "self-determination and national alliance" delayed the inevitable until the end of the 20th century, ultimately completing the final piece of this long-term historical trend with the dissolution of the Soviet Union. However, the Russians' value system is unwilling to accept this historical trend. They still hold a nostalgic approach to the age of unity and nurture hopes to rebuild the empire of former days. For them, the eastern regions of Ukraine and the whole of Ukraine are considered natural parts of the empire. From the perspective of a conflict of interests, although Russia possesses a vast territory, the climate and soil in most regions are not conducive to agricultural production and industrial development. Ukraine boasts a solid industrial foundation and the Dnieper River Great Plains, which are suitable for agricultural production. The independence of the former Soviet republics led to eight of the top ten cities by population within the former Soviet Union falling outside Russia's control, with three of those in Ukraine. Occupying the eastern regions of Ukraine, or even the entire country, not only boosts economic progress but also provides strategic depth to buffer against NATO's military pressure.
It is evident that, when considered from both the perspectives of value conflicts and interest clashes, Russia is unlikely to relinquish its actual control over the eastern regions of Ukraine. The outbreak of war in early 2022 seemed almost inevitable. Russia's direct involvement and the consequent reverse chain reaction—significant international support for Ukraine—led to a comprehensive complication of the war's initial situation. Technically, this is represented by the 2022 annual candlestick chart exhibiting an exaggerated Long-Legged Doji, a pattern indicating an overall balance of power between buyers and sellers but marked by considerable uncertainty and volatility during the trading process. On the Russo-Ukrainian battlefield, this pattern implies that, despite significant uncertainty and volatility in the conflict's dynamics throughout 2022, subsequent probing and strategic adjustments have resulted in a de facto equilibrium in combat effectiveness between the two sides. This strategic balance trend dominated the Russo-Ukrainian battlefield's dynamics after that, technically reflected in the candlestick charts for 2023 and 2024, showing a Doji without legs. The emergence of a legless Doji following a Long-Legged Doji indicates that, after experiencing significant fluctuations, the battlefield forces have reached a dynamic equilibrium, mirroring the trend previously depicted by the monthly candlestick charts.
Conclusions
This paper introduces a concise, universally applicable, objective methodology for measuring combat effectiveness. The simplicity of this method is demonstrated by its requirement of only two parameters to measure the rate of frontline changes, which is the outcome of combat effectiveness. The universal applicability is evident across all wars, conflicts, power struggles, gang clashes in human history, and even territorial disputes in the animal kingdom, regardless of the era, region, or cultural background. They can all be measured for combat effectiveness by obtaining these two parameters. Its objectivity is reflected in the fact that these two parameters are objective physical data independent of human subjective emotions and value judgments.
Utilizing this methodology, we measured the daily combat effectiveness values of the Russo-Ukrainian War, creating a time series dataset. This dataset was then analyzed using candlestick charts across various time scales to discern trends. Moreover, the utility of time series data on combat effectiveness is not limited to visualization through candlestick charts; they also lend themselves to sophisticated statistical analyses such as Vector Autoregression (VAR) and Autoregressive Integrated Moving Average (ARIMA) models. Besides these modeling techniques exclusive to time series data, the combat effectiveness data obtained through our method can also be employed as explanatory or dependent variables in multivariate regression analyses, akin to panel data. It eliminates the need for reliance on loss exchange ratios as a substitute variable, which are more apt for measuring lethality or kill effectiveness rather than combat effectiveness.
References
- Beckley, Michael. 2010. “Economic Development and Military Effectiveness.” The Journal of Strategic Studies 33 (1): 43-79. [CrossRef]
- Biddle, Stephen, and Stephen Long. 2004. “Democracy and Military Effectiveness: A Deeper Look.” Journal of Conflict Resolution 48 (4): 525-46. [CrossRef]
- Biddle. 2010. “Military Power.” In Military Power. Princeton University Press.
- Clausewitz, C. von. 1976. On war. M. Howard & P. Paret, Eds.. Princeton University Press.
- Desch, Michael C. 2002. “Democracy and Victory: Why Regime Type Hardly Matters.” International Security 27 (2): 5-47.
- Dubarle, Dominique.1988. “Galileo's Methodology of Natural Science.”Galileo:Man of Science. Cranbury:The Scholar’s Bookshelf.
- Dupuy.1986.“Mythos or verity? The Quantified Judgment Model and German Combat Effectiveness.”Military Affairs: The Journal of Military History, including Theory and Technology, 204-210. [CrossRef]
- Epstein,Joshua.1985.The Calculus of Conventional War:Dynamic Analysis without Lanchester Theory.Washington DC:Brookings Institution Press.
- Fiedler,Fred.1955.“The influence of leader-keyman relations on combat crew effectiveness.” Journal of Abnormal Psychology,51(2),227-235. [CrossRef]
- Geoffrey, Barraclough.1989. The Times Atlas of World History. Times Βooks Limited.
- Glass,Albert.1949.“An attempt to predict probable combat effectiveness by brief psychiatric examination.”Am J Psychiatry,106(2), 81-90. [CrossRef]
- Hall,A.Rupert.1981.From Galileo to Newton.New York:Dover Publications, Inc.
- Han,Seung-Jo.2016.“Analysis of relative combat power with expert system.”Journal of Digital Convergence,14(6),143-150. [CrossRef]
- Hayward,Philip.1968. “The measurement of combat effectiveness”.Operations Research,16(2), 314-323. [CrossRef]
- Helmbold, Robert.1997. The Advantage Parameter:A Compilation of Phalanx Articles Dealing with the Motivation and Empirical Data.Army concepts analysis agency,Bethesda,MD.URL= <https://www.docin.com/p-1741779125.html>.
- Institute for the Study of War (ISW). (n.d.). Understanding War. URL= <https://www.understandingwar.org/>.
- Kanatliev,Rosen.2014.Improving Relative Combat Power Estimation:The Road to Victory.Army command and general staff college,Fort Leavenworth, KS.
- Krondak, W. J., Cunningham, R., Hunsaker, O., Derendinger, D., Cunningham, S., & Peck, M. (2007). Unit Combat Power (and Beyond). Presented at the 24th International Symposium on Military Operational Research (ISMOR), August 28-31, 2007.
- Lanchester,Frederick.1916.Aircraft in warfare:The dawn of the fourth arm.London:Constable Ltd.
- McKenna. A. Britannica Online, s.v. "combat-effectiveness", URL =<https://www.britannica.com/topic/combat-effectiveness>.
- Mehrl, M. 2022. Female combatants and rebel group behaviour: Evidence from Nepal. Conflict Management and Peace Science, 40(3). [CrossRef]
- Perry,Nigel.2009. Fractal Effects in Lanchester Models of Combat.Australian Joint Operations Division Defense Science and Technology Organization Report.URL = <https://www.onacademic.com/detail/journal_1000032543464210_151e.html>.
- Pilster, Ulrich, and Tobias Bohmelt. 2011. “Coup-Proofing and Military Effectiveness in Interstate Wars, 1967-99.” Conflict Management and Peace Science 28 (4): 331-50. [CrossRef]
- Political Geography Now (PolGeoNow). (n.d.). URL= <https://www.polgeonow.com/>.
- Poulet Volant. (n.d.). Twitter. URL= <https://twitter.com/Pouletvolant3>.
- Przemieniecki,Janusz Stanislaw.2000.Mathematical Methods in Defense Analyses.Reston:The American Institute of Aeronautics and Astronautics,Inc.
- Razma,Gintautas. 2019. ”A Modern Warfare Paradigm: Reconsideration of Combat Power Concept.” Journal of Security and Sustainability Issues,8(3),435-452. [CrossRef]
- Tolk,Andreas.2012. Engineering Principles of Combat Modeling and Distributed Simulation.Hoboken:John Wiley & Sons Inc.
- War Mapper. (n.d.). Twitter. URL= <https://twitter.com/war_mapper>.
Figure I.
Comparing Measurement Approaches: Causal Factors vs. Outcome Variables.
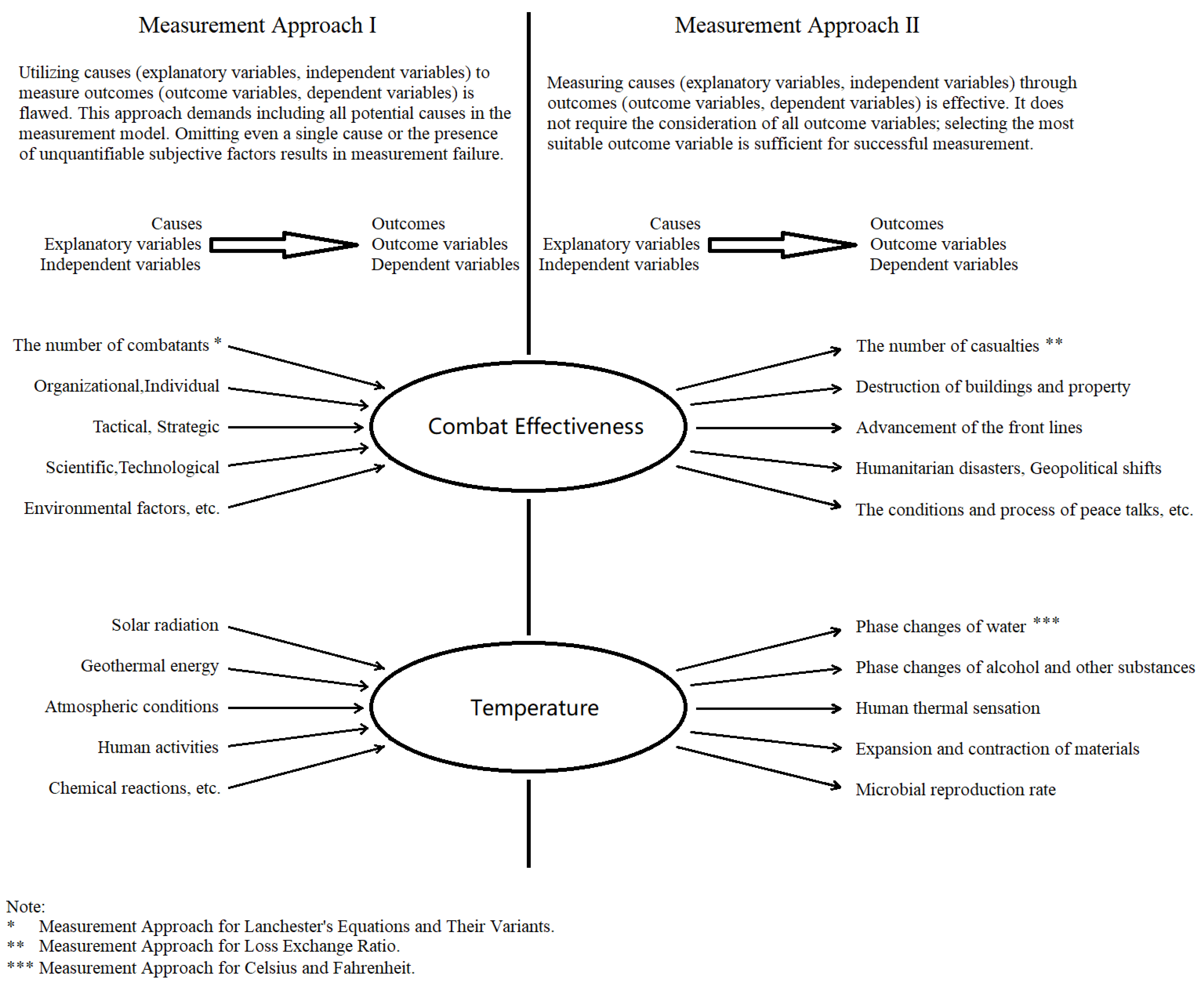
Table I.
Framework for Measuring Various Scientific Concepts through Explanatory and Outcome Variables.
Table I.
Framework for Measuring Various Scientific Concepts through Explanatory and Outcome Variables.
| Explanatory Variables | Measured Variable | Outcome Variables |
| Muscle development, high food intake, good mental state, etc. | Force | Change in the state of motion of an object (m) and acceleration (a) |
| Ambient heat, solar radiation, atmospheric pressure, etc. | Temperature | Phase change points of water |
| Greenhouse gas emissions, solar activity, Earth's albedo, etc. | Global Warming | Increase in global average temperature |
| Material type, ambient temperature, humidity, etc. | Resistance | Voltage (U) under a unit of current (I) |
| The material and purity of the radiation source, distance, and intervening objects, etc. | Radiation | Radiation energy absorbed per unit weight |
| Organizational,individual,tactical,strategic,scientific/technological,environmentalfactors, etc. | Combat Effectiveness | Combat outcomes (win, loss, draw) |
Note: Bolded Text indicates the measurement methods currently in use.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






