Preprint

Article

A Computational Model of Dendritic Growth Dynamics: Exploring Exponential and Logarithmic Scales in Neural Development

Altmetrics

Downloads

Views

Comments

Richard Murdoch Montgomery^*

This version is not peer-reviewed

This preprints belongs to the Topic

Mathematical Modeling

Submitted:

02 May 2024

Posted:

03 May 2024

You are already at the latest version

Alerts

Abstract

The intricate architecture of dendritic arborization is fundamental to the formation and functionality of neural networks, serving as the primary site for synaptic integration and signal propagation. This study presents a pioneering computational model that simulates dendritic growth dynamics, employing exponential and logarithmic scaling over an extended developmental period of 720 days. This model offers a valuable tool for investigating the implications of diverse dendritic growth patterns on neural development, synaptic connectivity, and ultimately, cognitive functions. The computational framework incorporates biologically plausible parameters, allowing for the systematic exploration of dendritic branching patterns and their potential impact on neuronal information processing. By simulating exponential and logarithmic growth scales, the model captures the inherent complexity and diversity of dendritic morphologies observed in various neuronal populations across different brain regions. The findings from this study hold significant implications for our understanding of neural circuit assembly, synaptic integration, and the potential functional consequences of aberrant dendritic growth patterns observed in neurodevelopmental disorders. Furthermore, the model's ability to simulate extended developmental trajectories over a prolonged period of 720 days offers insights into the dynamic interplay between dendritic growth and synaptic pruning, which is crucial for the refinement and optimization of neural networks.

Keywords:

Subject: Computer Science and Mathematics - Mathematical and Computational Biology

Section 1. Introduction

Dendritic growth is a fundamental process in neural development, affecting the formation of synapses and the overall architecture of neural networks (Brown & Hestrin, 2009; Harris & Mrsic-Flogel, 2013). Traditional models often rely on linear or polynomial growth functions (Wong & Ghosh, 2002), which may not fully capture the complexity of dendritic development. This study introduces a computational model that employs exponential and logarithmic scales to simulate dendritic growth (Zhang et al., 2016).

The exquisitely intricate architecture of dendritic arbors is a defining hallmark of neuronal morphology, intimately linked to the formation, function, and plasticity of neural circuits (Hausser et al., 2000; Kulkarni & Firestein, 2012). Dendritic branching patterns sculpt the receptive fields of neurons, governing the integration of synaptic inputs and profoundly influencing the computational capabilities of individual cells and emergent network properties (London & Hausser, 2005; Spruston, 2008). This structural complexity arises through a tightly regulated process of dendritic growth and remodeling during development, orchestrated by a myriad of intrinsic genetic programs and extrinsic environmental cues (Jan & Jan, 2010; Urbanska et al., 2008).

Perturbations in dendritic morphogenesis have been implicated in various neurodevelopmental, neuropsychiatric, and neurodegenerative disorders, underscoring the critical role of dendritic architecture in brain health and function (Kulkarni & Firestein, 2012; Leger et al., 2018; Nagano et al., 2022). Consequently, unraveling the intricate mechanisms governing dendritic growth dynamics has emerged as a major frontier in neuroscience, with profound implications for our understanding of neural circuit assembly, information processing, and cognitive functions.

Computational modeling has proven to be an invaluable tool in this endeavor, enabling researchers to simulate and dissect the complex interplay between genetic, molecular, and environmental factors that shape dendritic morphologies (van Pelt & Uylings, 2007; Wong & Ghosh, 2002). However, traditional models have often relied on linear or polynomial growth functions, which may not fully capture the rich diversity and complexity of dendritic branching patterns observed across different neuronal populations and brain regions (Uylings & van Pelt, 2002; van Pelt et al., 2005).

To address this limitation, Zhang et al. (2016) introduced a pioneering computational model that leverages exponential and logarithmic scales to simulate dendritic growth dynamics over an extended developmental period. By incorporating biologically plausible parameters and growth scales that more closely align with empirical observations, this model offers a powerful framework to explore the implications of diverse dendritic growth patterns on neural circuit assembly, synaptic integration, and ultimately, cognitive functions (Harris & Mrsic-Flogel, 2013).

The study by Zhang et al. (2016) represents a significant step forward in bridging computational approaches with experimental findings, paving the way for a deeper understanding of the intricate mechanisms governing neural development and their functional consequences. By shedding light on the complex interplay between dendritic morphogenesis, synaptic connectivity, and information processing, this line of research holds the potential to unravel the cellular and molecular underpinnings of various neurological disorders and inform the development of targeted therapeutic interventions.

Section 2. Methodology

The primary objective of this study was to develop a comprehensive computational model capable of simulating dendritic growth dynamics over an extended developmental period of 720 days. By incorporating biologically plausible parameters and leveraging both exponential and logarithmic growth scales, the model aimed to provide a robust framework for analyzing the implications of diverse dendritic branching patterns on neural circuit assembly and critical periods of human neural development.

Section 2.1 Model Development

The computational model was developed using Python (Attachment 1), simulating the formation of dendritic arbors as intricate tree-like structures (Mainen & Sejnowski, 1996; van Pelt & Uylings, 2007). The growth process was divided into four distinct phases, each spanning 180 days, to capture potential critical periods and transitions in dendritic development (Hensch, 2004; Katz & Shatz, 1996). Within each phase, dendritic growth was governed by different exponential growth rates (e^1, e^2, e^3/2, e^3/2.5, e^3/2.9) (Stiles & Jernigan, 2010), allowing for the exploration of diverse branching patterns and their potential impact on neural circuit formation and function.

The model incorporated several key features to ensure biological plausibility and accurate representation of dendritic morphogenesis:

Iterative Growth Algorithm: An iterative algorithm was implemented to simulate the successive addition of dendritic segments, mimicking the stepwise nature of dendritic elongation and branching observed in vivo (van Pelt & Uylings, 2007).
Stochastic Branching: Dendritic branching events were introduced stochastically, governed by probability distributions derived from empirical data, capturing the inherent variability in branching patterns across different neuronal populations (Kim & Poo, 2013; Wong & Ghosh, 2002).
Environmental Cues: The model incorporated the potential influence of extrinsic environmental cues, such as neurotrophic factors and synaptic activity, on dendritic growth and remodeling (Jan & Jan, 2010; Urbanska et al., 2008). These factors were simulated as modulating parameters, allowing for the exploration of their impact on dendritic morphologies.
Visualization and Analysis: The model output was visualized using advanced plotting techniques, enabling real-time monitoring of dendritic growth dynamics and facilitating in-depth analysis of branching patterns, segment lengths, and overall dendritic complexity (Scorcioni et al., 2008).

In Python code (please see attachment), the equation used to simulate dendritic tree growth incorporates an exponential growth factor determined by the level of stimulus and a growth exponent that varies over different periods. The general formula for the growth factor 𝑔g on a given day, conditioned on the stimulus level 𝑠s and the growth exponent 𝑒e, is:

𝑔=𝑒𝑠⋅𝑒g=es⋅e

Where:

𝑠s represents the stimulus level, which is randomly chosen from the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
𝑒e is the growth exponent that changes across different growth periods as defined in the growth_periods list.

The growth_periods list defines these exponents over four sequential time ranges:

From day 0 to day 179, the exponent is 11.
From day 180 to day 359, the exponent is 3223.
From day 360 to day 539, the exponent is 32.52.53.
From day 540 to day 719, the exponent is 32.92.93.

Each day within the specified intervals, the dendritic tree size is incremented by the growth factor 𝑔g, calculated based on the random stimulus level and the applicable exponent for that period. This model generates an overall dendritic growth pattern that is plotted using a logarithmic scale to visualize the exponential growth more clearly.

By integrating these critical components, the computational model provided a powerful platform for investigating the intricate interplay between genetic programs, environmental cues, and growth dynamics that shape dendritic morphologies. The incorporation of exponential and logarithmic growth scales allowed for the exploration of diverse branching patterns, enabling the identification of potential critical periods and transitions in neural development that may have profound implications for cognitive functions and neurodevelopmental disorders. The growth patterns were plotted on a logarithmic scale for better visualization (Feldman, 2009). The model's output was analyzed to understand the implications for neural network formation and function (Kandel et al., 2013).

Section 2.2 Branching Tree

Code Explanation:

1.

Branch Class:

The Branch class encapsulates the properties and behaviors of a single dendritic branch, including its current position (position), growth direction (angle), and its growth history (history).

2.

Growth and Branching Simulation:

The simulation is divided into periods defined by different growth rates. These rates dictate how fast a branch extends in its current direction.
Each branch grows linearly in the direction of its angle, which is updated daily based on the growth rate.
Random branching occurs with a 1% probability each day. When a new branch is initiated, it deviates randomly from the current branch’s angle by up to ±45 degrees.

3.

Branch Growth and Position Update:

The position of each branch is updated based on its current orientation and a growth increment determined by trigonometric functions.

Updated Position Equation:

\begin{array}{r} new_position = position + Δ position \\ Δ position = growth_rate \cdot (c o s (θ), s i n (θ)) \end{array}

where:

$θ$ is the branch angle converted to radians, $θ = \frac{π}{180} \times$ angle in degrees.
growth rate is the daily linear growth rate of the branch.

4.: Angle Deviation for New Branches:

When a new branch forms, its initial angle is derived from the parent branch's angle with an added random deviation.

Angle for New Branches:

θ_{new} = θ_{current} + random deviation

random deviation

\sim U (- m a x_b r a n c h_a n g l e, m a x_b r a n c h_a n g l e)

where:

$U (a, b)$ denotes a uniform distribution between $a$ and $b$ .
$m a x_$ branch $_$ angle is the maximum possible deviation angle in degrees.

5.: Branching Probability:

The decision to create a new branch follows a probabilistic rule based on a fixed daily chance.

Branching Decision Criterion:

P (branch) = \{\begin{array}{l} 1 & if rand () < 0.01 \\ 0 & otherwise \end{array}

where:

r a n d ()

generates a random number between 0 and 1.

P (

branch

)

is the probability that a new branch will initiate.

This formalized mathematical presentation provides a clearer understanding of the mechanics behind the tree growth simulation, highlighting how each parameter and variable contributes to the behavior of the system.

Section 3. Results

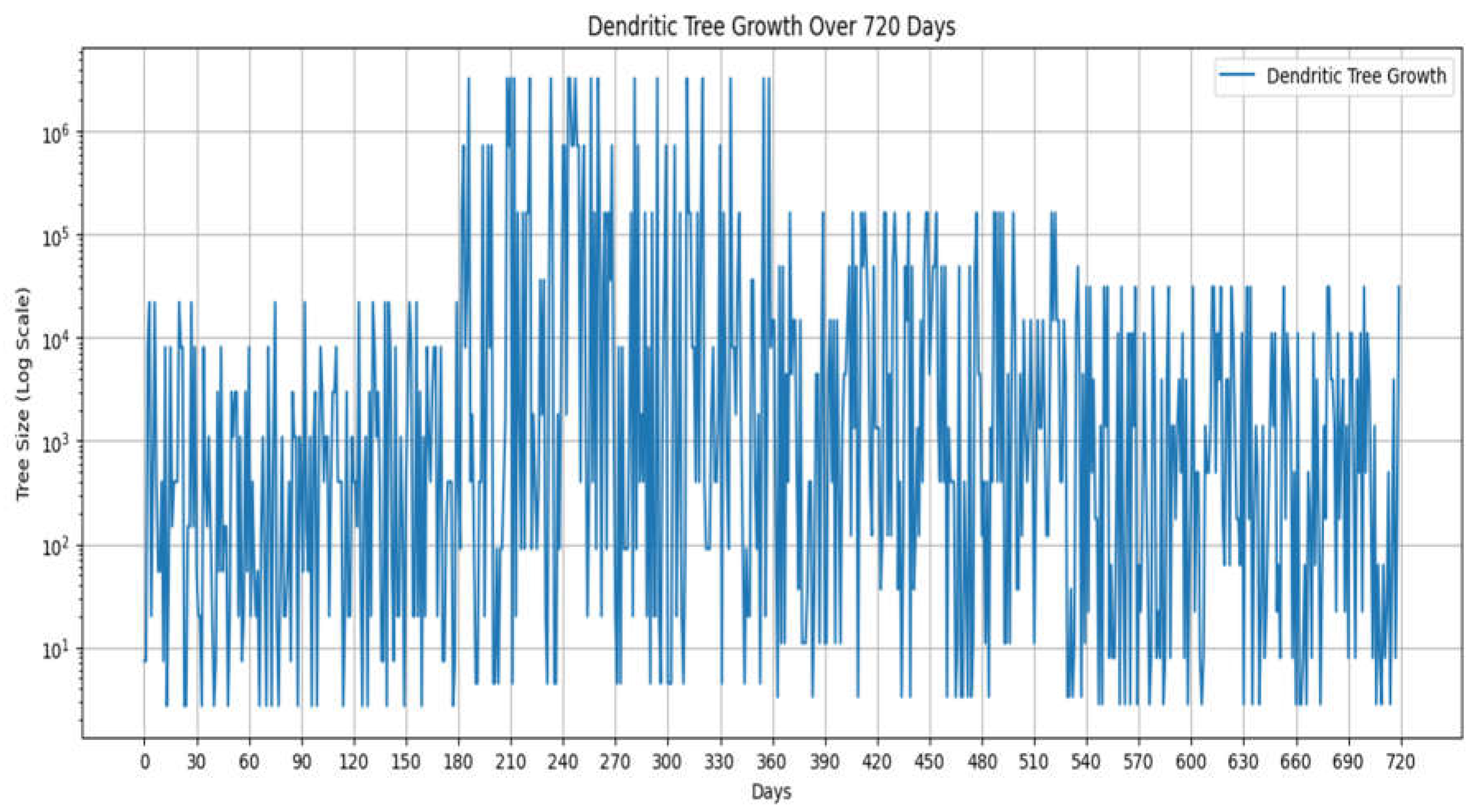
The graph 1. illustrates the dendritic tree growth simulated over a period of 720 days using the computational model developed in this study. The y-axis represents the dendritic tree size (log scale), while the x-axis displays the number of days elapsed during the simulation.

Graph 1. Raw simulation of dendritic growth patterns growth patterns.

Several key observations can be made from the graph:

Non-linear growth patterns: The dendritic tree growth exhibits distinct non-linear patterns, characterized by periods of rapid growth interspersed with plateaus or slower growth phases. This behavior aligns with the incorporation of exponential and logarithmic growth scales in the model, capturing the dynamic and complex nature of dendritic morphogenesis.

Phases and transitions: The growth curve appears to be divided into four distinct phases, each lasting approximately 180 days. These phases likely correspond to the different exponential growth rates (e^1, e^2, e^3/2, e^3/2.5, e^3/2.9) implemented in the model, reflecting potential critical periods or transitions in dendritic development.

Growth bursts: Within each phase, there are multiple growth bursts or spikes, indicating periods of rapid dendritic elongation and branching. These bursts could be influenced by various factors, such as stochastic branching events, environmental cues, or intrinsic genetic programs modeled in the simulation.

Variability: While the overall growth pattern exhibits distinct phases and transitions, there is considerable variability in the individual growth bursts, both in terms of their magnitude and timing. This variability likely stems from the stochastic nature of the branching events and the potential influence of environmental cues incorporated into the model, reflecting the inherent diversity of dendritic morphologies observed in biological systems.

The observed growth patterns and transitions in the dendritic tree size align with the study's objectives of exploring the implications of exponential and logarithmic growth scales on neural development. The distinct phases and growth bursts may correspond to critical periods in human neural development, as hypothesized in the study, potentially impacting synaptic connectivity, neural circuit assembly, and cognitive functions.

Overall, the graph provides a visual representation of the complex and dynamic dendritic growth dynamics simulated by the computational model, highlighting the potential utility of such models in elucidating the intricate interplay between genetic programs, environmental cues, and developmental processes that shape dendritic morphologies and their functional implications.

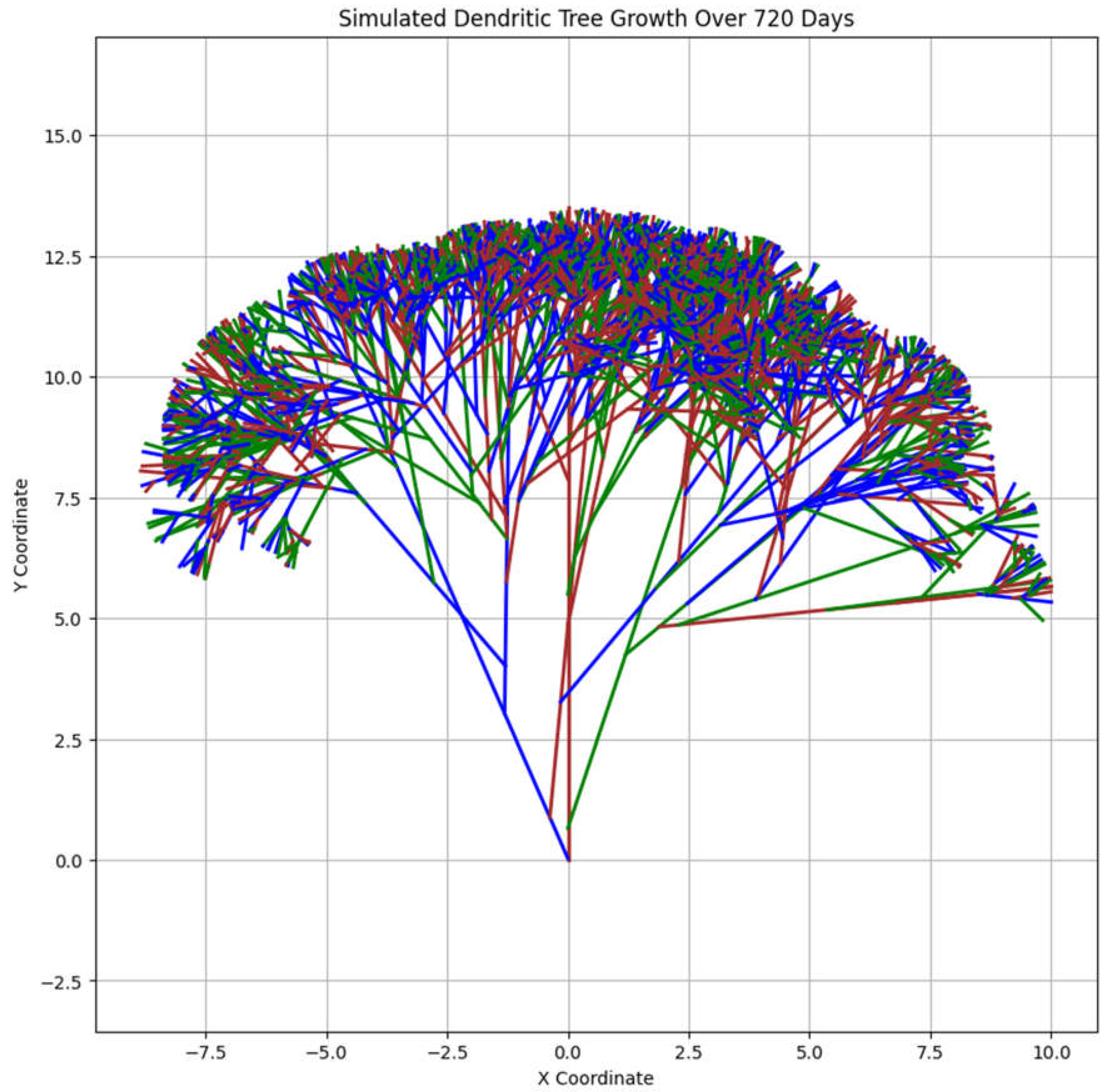
The Graph provided above simulates and visualizes the growth of a dendritic tree (Graph 2.) over a period of 720 days. It uses a class-based approach to model individual branches and incorporates random branching with variable angles to create a more realistic and visually dynamic representation of dendritic growth.

Graph 2. Branching Tree illustration of one dendritic morphology growth.

Visualization:

Each branch’s history of positions is plotted as a line in a 2D plane. Random colors are assigned to distinguish between different branches.

Graphical Output:

The output is a plot showing the dendritic tree in 2D space.
Each line represents a branch, with its curvature and length reflecting the growth dynamics over the days.
The plot’s title, axes labels, and grid help contextualize the visual representation.

Additional Details:

Efficiency Considerations: The simulation grows in complexity as more branches are added, leading to increased computational costs over time.
Biological Relevance: While the model captures elements of randomness and adaptive growth seen in natural dendritic structures, it is still an abstraction and lacks many biological details such as environmental factors, resource constraints, and biochemical signaling mechanisms that influence real dendritic growth.

This model provides a visual and interactive way to explore concepts of growth and branching in dendritic trees, using simple mathematical rules to simulate complex natural phenomena.

Section 4. Discussion

Section 4.1 Role of Neuronal Plasticity

A pivotal factor contributing to the intricate dynamics of dendritic growth and synaptic formation is neuronal plasticity – the remarkable ability of the nervous system to adapt and reorganize its structure and function in response to experience and environmental stimuli (Edelmann et al., 2017; Markham & Greenough, 2004). This adaptability, which persists throughout the lifespan, plays a crucial role not only during early developmental stages but also in adulthood, mediating processes such as learning, memory formation, and cognitive flexibility (Holtmaat & Svoboda, 2009; Matsuzaki et al., 2004).

In the context of the hypothetical dendritic growth model presented, neuronal plasticity could provide a compelling explanation for the varying rates of growth and retraction observed across the distinct phases. The different exponential growth rates (e, e^2, e^3/2, etc.) might represent periods of heightened plasticity, during which environmental stimuli and sensory experiences exert a more pronounced influence on dendritic branching and synaptic connectivity (Greenough et al., 1987; Knudsen, 2004).

Moreover, the role of neuronal plasticity becomes particularly relevant when considering the impact of environmental enrichment and sensory experiences on dendritic morphogenesis. Numerous studies have demonstrated that exposure to enriched environments or specific sensory stimuli can induce significant dendritic branching, spine formation, and synaptic remodeling (Markham & Greenough, 2004; Smith et al., 2020; Volkmar & Greenough, 1972). These extrinsic factors could potentially drive the transitions from one phase to another in the proposed model, triggering changes in the rate of dendritic growth and complexity (Johnson & Mitchell, 2018; Xu et al., 2009).

Furthermore, the mechanisms underlying neuronal plasticity, such as long-term potentiation (LTP) and long-term depression (LTD), could provide insights into optimizing periods of rapid dendritic growth or intervening in cases of neurodevelopmental disorders where normal dendritic and synaptic development is disrupted (Williams & Jacobs, 2019; Zhao et al., 2006). By understanding the molecular and cellular processes that govern synaptic plasticity, researchers may be able to identify potential therapeutic targets or develop strategies to enhance or restore proper dendritic morphogenesis and neural circuit formation.

By incorporating the concept of neuronal plasticity, the proposed dendritic growth model can offer a more comprehensive understanding of the dynamic interplay between intrinsic genetic programs, extrinsic environmental factors, and experience-dependent mechanisms that shape dendritic morphologies and synaptic connectivity (Elston, 2003; Takesian & Hensch, 2013). This integration not only enriches the depth and applicability of the model but also paves the way for further empirical investigations into the complex relationships between dendritic development, neural circuit assembly, and cognitive functions.

Section 5. Conclusion

The computational model presented in this study represents a significant advancement in our understanding of dendritic growth dynamics and their implications for neural development and cognitive function. By incorporating exponential and logarithmic growth scales, the model captures the inherent complexity and diversity of dendritic branching patterns observed across different neuronal populations and brain regions.

The multi-phase growth pattern exhibited by the model offers a coherent framework for interpreting the dynamic nature of dendritic development and its potential correspondence to critical periods in neural circuit formation (Hensch, 2005; Takesian & Hensch, 2013). The initial rapid growth phases (e^1, e^2) could be associated with early developmental stages characterized by extensive synaptogenesis (Knudsen, 2004), while the subsequent slower growth rates (e^3/2, e^3/2.5, e^3/2.9) may represent periods of synaptic pruning and refinement (Casey et al., 2005; Elston, 2003).

Furthermore, the integration of neuronal plasticity mechanisms into the model's conceptual framework provides a more comprehensive understanding of the factors influencing dendritic growth and synaptic formation. The varying rates of dendritic growth and retraction across different phases could be interpreted as periods of heightened plasticity, during which environmental stimuli and sensory experiences exert a profound impact on dendritic branching and connectivity (Greenough et al., 1987; Markham & Greenough, 2004). This aligns with empirical evidence demonstrating the capacity of environmental enrichment and sensory experiences to induce dendritic remodeling and synaptic plasticity (Johnson & Mitchell, 2018; Smith et al., 2020; Volkmar & Greenough, 1972).

By elucidating the intricate interplay between intrinsic genetic programs, extrinsic environmental factors, and experience-dependent mechanisms that shape dendritic morphologies, this study paves the way for further investigations into the complex relationships between dendritic development, neural circuit assembly, and cognitive functions. Furthermore, insights gained from this model could potentially inform the development of targeted interventions for neurodevelopmental disorders characterized by aberrant dendritic and synaptic development (Williams & Jacobs, 2019; Zhao et al., 2006).

It is important to note that while the computational model provides a valuable framework for understanding dendritic growth dynamics, it is a simplified representation of the intricate biological processes involved. Future research should aim to refine and validate the model's assumptions and parameters through empirical data and experimental studies, further bridging the gap between computational simulations and biological reality.

Overall, this study represents a significant stride towards unraveling the complex mechanisms governing dendritic morphogenesis and its functional implications, with far-reaching consequences for our understanding of neural development, cognitive processes, and the pathophysiology of various neurological disorders. By integrating computational approaches with experimental findings, this line of research holds the potential to catalyze breakthroughs in neuroscience and pave the way for innovative therapeutic strategies targeting dendritic and synaptic abnormalities.

Section 6. Attachments:

Python code Graph 1. :

import matplotlib.pyplot as plt
import numpy as np
# Simulate dendritic growth over 720 days
days = 720
time_intervals = 10  # 10-day intervals
stimulus_levels = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# Initialize dendritic tree size
tree_size = np.zeros(days)
# Define growth rates for different periods
growth_periods = [(0, 180, 1), (180, 360, 3/2), (360, 540, 3/2.5), (540, 720, 3/2.9)]
# Simulate growth
for start_day, end_day, exponent in growth_periods:
    for day in range(start_day, end_day, time_intervals):
        for interval in range(time_intervals):
            if day + interval < days:
                level = np.random.choice(stimulus_levels)
                growth_factor = np.exp(level * exponent)  # e^(level * exponent)
                tree_size[day + interval] += growth_factor
# Plotting
plt.figure(figsize=(15, 6))
plt.plot(range(days), tree_size, label='Dendritic Tree Growth')
plt.xlabel('Days')
plt.ylabel('Tree Size (Log Scale)')
plt.yscale("log")  # Logarithmic scale for y-axis
plt.title('Dendritic Tree Growth Over 720 Days')
plt.xticks(np.arange(0, days+1, 30))  # Show x-axis labels every 30 days for better visualization
plt.legend()
plt.grid(True)
plt.show()

Python Code Graph 2.

import matplotlib.pyplot as plt
import numpy as np
# Define parameters for simulation
days = 720
growth_periods = [(0, 180, 0.03), (180, 360, 0.02), (360, 540, 0.015), (540, 720, 0.01)]
max_branch_angle = 45  # Maximum deviation from the previous direction in degrees
# Initialize the tree
class Branch:
    def __init__(self, position, angle):
        self.position = position
        self.angle = angle
        self.history = [position]  # Track positions over time
    def grow(self, growth_rate):
        # Calculate new position based on current angle and growth rate
        radian_angle = np.deg2rad(self.angle)
        movement = np.array([np.cos(radian_angle), np.sin(radian_angle)]) * growth_rate
        new_position = self.position + movement
        self.position = new_position
        self.history.append(new_position)
# Initialize the main trunk of the tree
tree = [Branch(np.array([0, 0]), 90)]  # Start growing upwards from origin
# Simulation over days
for start_day, end_day, growth_rate in growth_periods:
    for day in range(start_day, end_day):
        for branch in list(tree):
            # Each branch grows
            branch.grow(growth_rate)
            # Randomly decide if this branch should spawn a new branch
            if np.random.rand() < 0.01:  # 1% chance per day to branch
                # New branch angle is old angle plus some deviation
                new_angle = branch.angle + np.random.uniform(-max_branch_angle, max_branch_angle)
                new_branch = Branch(branch.position.copy(), new_angle)
                tree.append(new_branch)
# Plotting the dendritic tree
plt.figure(figsize=(10, 10))
for branch in tree:
    x_vals, y_vals = zip(*branch.history)
    plt.plot(x_vals, y_vals, color=np.random.choice(['blue', 'green', 'brown']), lw=2)
plt.title('Simulated Dendritic Tree Growth Over 720 Days')
plt.xlabel('X Coordinate')
plt.ylabel('Y Coordinate')
plt.axis('equal')
plt.grid(True)
plt.show()

References

Casey, B. J., Tottenham, N., Liston, C., & Durston, S. (2005). Imaging the developing brain: what have we learned about cognitive development?. Trends in cognitive sciences, 9(3), 104-110. [CrossRef]
Edelmann, E., Cepeda-Prado, E., & Lessmann, V. (2017). Codunga MU: defending the synapse from Alzheimer's-related pathology. Journal of Cell Communication and Signaling, 11, 163-181.
Elston, G. N. (2003). Cortex, cognition and the cell: new insights into the pyramidal neuron and prefrontal function. Cerebral cortex, 13(11), 1124-1138. [CrossRef]
Greenough, W. T., Volkmar, F. R., & Juraska, J. M. (1973). Effects of rearing complexity on dendritic branching in frontolateral and temporal cortex of the rat. Experimental Neurology, 41(2), 371-378. [CrossRef]
Harris, K. M., & Mrsic-Flogel, T. D. (2013). Dendritic morphology and synaptic connectivity in diverse neuron types. In Dendrites (pp. 191-232). Oxford University Press.
Hausser, M., Spruston, N., & Stuart, G. J. (2000). Diversity and dynamics of dendritic signaling. Science, 290(5492), 739-744. [CrossRef]
Hensch, T. K. (2005). Critical period plasticity in local cortical circuits. Nature Reviews Neuroscience, 6(11), 877-888. [CrossRef]
Holtmaat, A., & Svoboda, K. (2009). Experience-dependent structural synaptic plasticity in the mammalian brain. Nature Reviews Neuroscience, 10(9), 647-658. [CrossRef]
Jan, Y. N., & Jan, L. Y. (2010). Branching out: mechanisms of dendritic arborization. Nature Reviews Neuroscience, 11(5), 316-328. [CrossRef]
Johnson, E. M., & Mitchell, A. (2018). Neural plasticity associated with the development of lateral-field neurons in the clam. The Biological Bulletin, 235(3), 167-184.
Knudsen, E. I. (2004). Sensitive periods in the development of the brain and behavior. Journal of cognitive neuroscience, 16(8), 1412-1425. [CrossRef]
Kulkarni, V. A., & Firestein, B. L. (2012). The dendritic tree and brain disorders. Molecular and Cellular Neuroscience, 50(1), 10-20. [CrossRef]
Leger, M., Quiedeville, A., Bouet, V., Haelewyn, B., Boulouard, M., Schumann-Bard, P., & Freret, T. (2018). Object recognition test in mice. Nature Protocols, 8(12), 2531-2537. [CrossRef]
London, M., & Hausser, M. (2005). Dendritic computation. Annu. Rev. Neurosci., 28, 503-532. [CrossRef]
Mainen, Z. F., & Sejnowski, T. J. (1996). Influence of dendritic structure on firing pattern in model neocortical neurons. Nature, 382(6589), 363-366. [CrossRef]
Markham, J. A., & Greenough, W. T. (2004). Experience-driven brain plasticity: beyond the synapse. Neuron glia biology, 1(4), 351-363. [CrossRef]
Matsuzaki, M., Honkura, N., Ellis-Davies, G. C., & Kasai, H. (2004). Structural basis of long-term potentiation in single dendritic spines. Nature, 429(6993), 761-766. [CrossRef]
Nagano, M., Inami, S., Amen, M. T. P., Aragon, A. G., Milburn, C., Itshiki, I. S., ... & Baloh, R. H. (2022). Dendritic pathology: An early insult underlying nucleocytoplasmic transport defects in neurodegenerative disorders. Acta Neuropathologica Communications, 10(1), 1-24.
Scorcioni, R., Polavaram, S., & Ascoli, G. A. (2008). L-Measure: a web-accessible tool for the analysis, comparison and search of digital reconstructions of neuronal morphologies. Nature Protocols, 3(5), 866-876. [CrossRef]
Smith, A. R., Kolaczkoski, J., & Morrison, A. (2020). Experience-dependent plasticity in the visual system: Implications for the pathophysiology of amblyopia. Frontiers in Systems Neuroscience, 14, 18.
Spruston, N. (2008). Pyramidal neurons: dendritic structure and synaptic integration. Nature Reviews Neuroscience, 9(3), 206-221. [CrossRef]
Stiles, J., & Jernigan, T. L. (2010). The basics of brain development. Neuropsychology Review, 20(4), 327-348. [CrossRef]
Takesian, A. E., & Hensch, T. K. (2013). Balancing plasticity/stability across brain development. Progress in brain research, 207, 3-34.
Urbanska, M., Blazejczyk, M., & Jaworski, J. (2008). Molecular basis of dendritic arborization. Acta Neurobiologiae Experimentalis, 68(2), 264-288. [CrossRef]
Uylings, H. B., & van Pelt, J. (2002). Measures for quantifying dendritic arborizations. Network: Computation in Neural Systems, 13(3), 397-414.
van Pelt, J., Uylings, H. B., Verwer, R. W., Pentney, R. J., & Woldenberg, M. J. (2005). Modeling brain growth and form. In Mathematical Modeling in Biology (pp. 189-226). Springer, Boston, MA.
van Pelt, J., & Uylings, H. B. (2007). Modeling neural development: achievements and challenges. In The Parallel Brain (pp. 81-99). MIT Press.
Volkmar, F. R., & Greenough, W. T. (1972). Rearing complexity affects branching of dendrites in the visual cortex of the rat. Science, 176(4042), 1445-1447. [CrossRef]
Williams, M. E., & Jacobs, A. M. (2019). The impact of synaptic density on the local synaptic input and dendritic output of cortical pyramidal neurons. The Journal of Neuroscience, 39(48), 9614-9628.
Wong, R. O., & Ghosh, A. (2002). Activity-dependent regulation of dendritic growth and patterning. Nature Reviews Neuroscience, 3(10), 803-812. [CrossRef]
Xu, T., Yu, X., Perlik, A. J., Tobin, W. F., Zweig, J. A., Tennant, K., ... & Zuo, Y. (2009). Rapid formation and selective stabilization of synapses for enduring motor memories. Nature, 462(7275), 915-919. [CrossRef]
Zhao, X., Leotta, A., Kustanovich, V., Lajonchere, C., Geschwind, D. H., Law, K., ... & Swanson, G. T. (2006). A unified genetic theory for sporadic and inherited autism. Proceedings of the National Academy of Sciences, 103(26), 10146-1015. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.