Solving Fuzzy Transportation Problem: Exploring a Novel Particle Swarm Optimization Approach

Preprint

Article

Solving Fuzzy Transportation Problem: Exploring a Novel Particle Swarm Optimization Approach

Altmetrics

Downloads

127

Views

Comments

Chrysanthi Aroniadi,

Grigorios N. Beligiannis^*

Chrysanthi Aroniadi,

Grigorios N. Beligiannis^*

This version is not peer-reviewed

Submitted:

02 May 2024

Posted:

03 May 2024

You are already at the latest version

Alerts

Abstract

The Fuzzy Transportation Problem (FTP) represents a significant extension of the Classical Transportation Problem (TP) by introducing uncertainly and imprecision into the parameters involved. Various algorithms have been proposed to solve the FTP, including fuzzy linear programming, metaheuristic algorithms and fuzzy mathematical programming techniques combined with Artificial Neural Networks. This paper presents the application of Trigonometric Acceleration Coefficients-PSO (TrigAc-PSO), a variation of the Classical Particle Swarm optimization algorithm, which is an innovative algorithm originally developed for solving the TP. TrigAC-PSO, has demonstrated remarkable success in optimizing various problem domains in crisp environments.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

In the realm of logistics and supply chain management, the Transportation Problem (TP) stands as a fundamental challenge, aiming to satisfy the distribution of goods from suppliers to consumers while minimizing overall transportation costs. Over the years, extensive research has been conducted to develop efficient algorithms and methods for solving various transportation problems with precise and deterministic values of supply and demand units such as transportation costs.

The NorthWest corner method (NWC) is one of the methods that discovers a basic feasible solution to various transportation problems [1]. The method is named after the fact that it stands from the northwest corner cell of the transportation table and proceeds in a systematic manner. Despite the fact that is an easy and applicable method, it does not always guarantee an optimal solution [1]. The Least Cost Method (LCM) is an alternative method, which focus on selecting the cell with the minimum cost during the allocation process [2]. Vogel’s Approximation Method (VAM) is known for yielding values relatively close to the optimum, often aligning precisely with it [3]. Although, VAM is more complex than the LCM, since it imposes penalties on cells characterized by high transportation costs, it tends to achieve more favorable initial solutions than LCM [3].

However, in real-world scenarios, it is difficult to predict supply and demand quantities “apriori” as they are inextricably linked by the season, by the trends, prevailing by consumers and the financial circumstances of each corporation. Equivalent situation unfolded with the prices of transportation which usually depends on factors such as fluctuating fuel prices, the weather, dynamic market conditions and varying transportation routes. To handle with these uncertainties, researchers have turned to fuzzy logic, a mathematical framework that allows for the representation of vagueness and ambiguity in decision-making processes. Going into further detail, fuzzy set theory provides a robust foundation for modeling and analyzing problems with imprecise information, emerged as a promising avenue to optimize transportation problems.

A Fuzzy Transportation Problem (FTP) is a variation of the traditional Transportation Problem in which the transportation cost, supply and demand are fuzzy quantities [4]. There are several researches relied on fuzzy environment, proving that fuzzy decision-making method is becoming paramount. The inspirers of the idea of decision-making in fuzzy environment were Bellman and Zadeh in 1970 [5]. Following their study, new findings emerged, with the most recent studies being noteworthy to be mentioned. Chanas et al., in 1996, introduced the concept of an optimal solution for the TP with fuzzy coefficients represented as fuzzy numbers and developed an algorithm to attain the optimal solution [6]. Ahmed, Khan and Uddin presented a new algorithm for finding an initial basic feasible solution of the TP when the transportation matrix contains both fuzzy and crisp numbers [7]. Another intriguing respective is offered by Chakraborty and Chakraborty in 2009 [8]. Their method was based on the minimization of transportation cost as well as time of transportation when the demand, supply and shipping cost per unit of the quantities are fuzzy [8]. Basirzadeh, two years later, introduced an approach for solving a wide range of transportation problems by transforming the fuzzy quantities into crisp values using their new method [9]. During the same year, Nagoor Gani et al. suggested their individual version for solving the fuzzy transportation problem utilizing the simplex algorithm [10]. Shanmugasundaram also worked on fuzzy exact algorithms. He successfully developed the fuzzy version of Vogel’s and MODI methods for obtaining the fuzzy initial basic solution and fuzzy optimal solution, respectively [11]. Balasubramanian and Subramanian formulated an alternative method for dealing with a special type of FTP, in which the cost depicted as triangular fuzzy number. In their research, they utilized ranking methods for numbers to evaluate the fuzzy objective values of the objective function and determine the optimal alternative [12]. Pandian and Natarajan introduced a novel algorithm known as the Fuzzy Zero Point method for finding a fuzzy optimal solution for FTP, where the transportation cost, supply and demand, are represented by trapezoidal fuzzy numbers [13]. Gani and Razak formulated a two-stage-cost-minimizing FTP, where supplies and demands are trapezoidal fuzzy numbers, while the costs remain crisp [14]. Malini and Kennedy introduced a method for solving FTP utilizing octagonal fuzzy numbers [15]. Ekanayake and Ekanayake, based their research, on the Yager’s robust ranking method [16]. They proposed an alternative algorithm for finding an initial basic solution to the fuzzy triangular and trapezoidal transportation problem [16].

In the literature, there are many other surveys consisted of problems which are solved by various methods via generalized trapezoidal fuzzy numbers. Specifically, generalized fuzzy numbers extend the concept of classical fuzzy numbers by introducing additional parameters to provide a more versatile representation of uncertainty. Kaur and Kuman, proposed a new approach for solving FTP using generalized fuzzy numbers, which had not been applied till that point [17]. Building upon the concept of Kaur and Kuman, Ali Ebrahimnejad, strived to diminish the computational complexity of the existing method. It was manifested that the technique applied in his study was simpler and computationally novel efficient than the proposed method by Kaur and Kuman [18]. Chen, contributed to the previously mentioned research, by proposing the concept of generalized fuzzy numbers when there are no prescribed limits on the membership function to the normal form [19].

FTP approximation is a crucial aspect in the realm of computational intelligence algorithms. Various optimization techniques including metaheuristic algorithms and mathematical programming approaches have been adapted or developed to handle with fuzzy transportation problems effectively. Lin solved the transportation problem with fuzzy coefficients using Genetic Algorithms (GA) [20]. Halder and Jana emphasized on 4-Dimensional multy-item TP through GA and Particle Swarm Optimization (PSO) [21]. New approaches in metaheuristics to solve the fixed TP in a fuzzy environment developed by Sadeghi-Moghaddamm et al. [22]. Gupta et al. design a hybrid GA-PSO algorithm to solve Traveling Salesman Problem (TSP) [23]. Last but not least, Singh and Singh, 2021, suggested an extension of PSO for solving FTP [24]. Their research, though, focused on solutions presented in a crisp form from fuzzy sets.

Motivated by the aforementioned applications of metaheuristic algorithms, this study focuses on the effective application of PSO to solve the FTP. Twenty eight distinct instances are tacked using ten well-established methods found in existing literature. The spotlight will be on the Trigonometric Acceleration Coefficients-PSO (TrigAC-PSO) algorithm, a variation of the classical PSO algorithm, introduced by Aroniadi and Beligiannis, in 2023 [25]. Extensive experimentation was carried out to assess the stability and the performance of the proposed algorithm in navigating transportation problems with fuzzy costs.

Furthermore, various particle configurations were examined to evaluate the TrigAC-PSO’s capacity to achieve optimal results, demonstrating its superior performance.

The contribution of the paper is as follows:

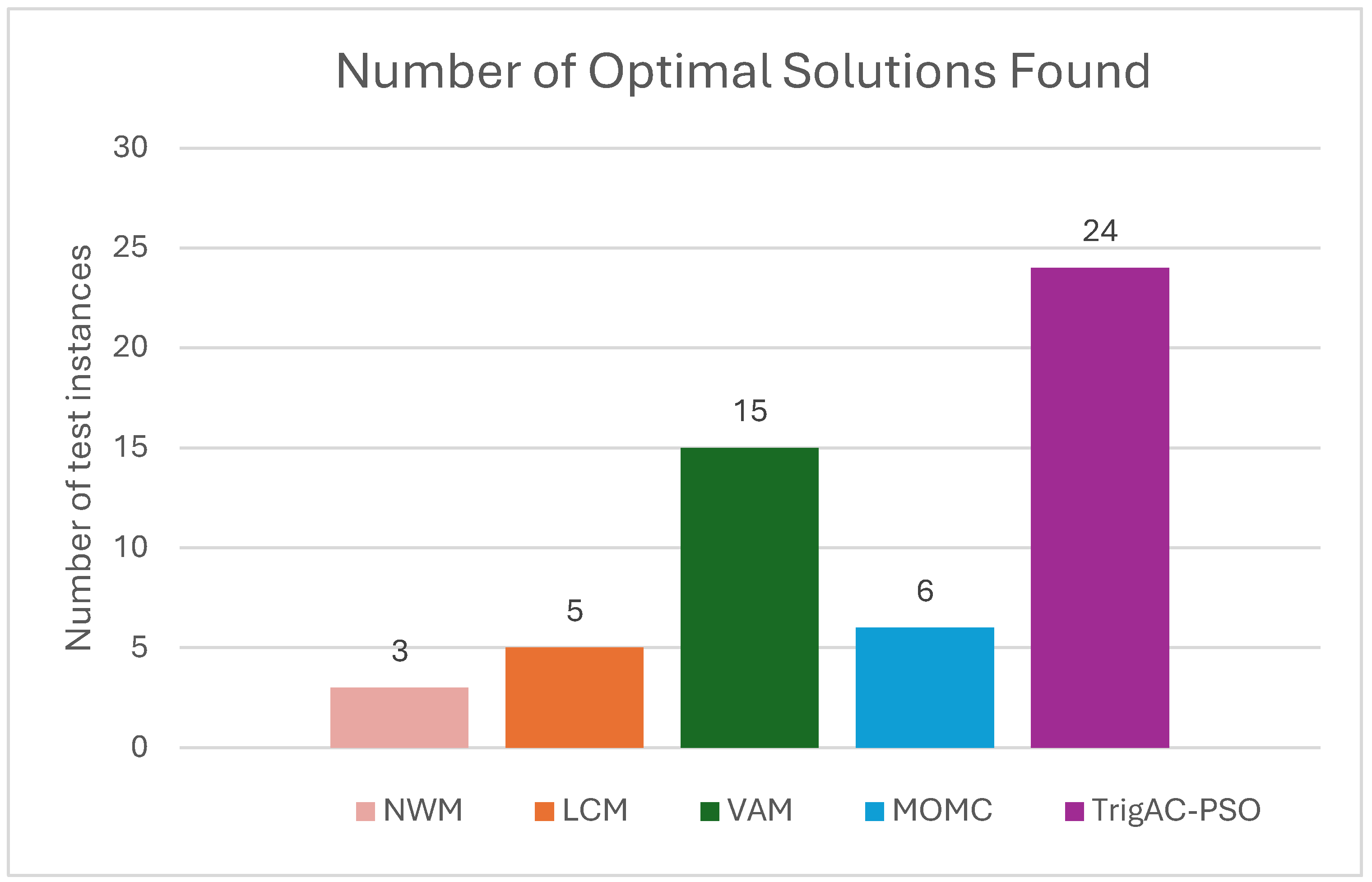
According to our knowledge, PSO has already been applied for solving the FTP. However, the conducted experiments lack depth in their data analysis, as they predominantly focus on individual problem instances rather than a diverse range of scenarios. Introducing a novel approach, the TrigAC-PSO is applied for the first time for solving the FTP, highlighting exceptional performance across a comprehensive set of instances.
Nevertheless, the selected problem instances encompass various types of fuzzy numbers such as triangular and trapezoidal fuzzy sets. Moreover, the fuzzy numbers extend beyond conventional representations, encompassing both classic fuzzy numbers and fuzzy generalized numbers, thereby adding depth and complexity to the study. It is the first time that fuzzy generalized numbers are applied to a particle swarm optimization variation.
The evaluation of results, from each method, is not based entirely on their attainment of the optimal solution. Instead, this study estimates the method’s performance according to the degree of membership in which their solutions approach optimality as determined by membership functions. Once more, the TrigAC-PSO method demonstrates remarkable completeness against other methods.

The remainder of the paper is organized as follows: Section 2 presents the mathematical formulation of TP. Definitions for fuzzy logic and fuzzy numbers are briefly described in Section 3. Section 4 presents the FTP. The PSO as well as TrigAC-PSO are represented in detail in section 5. An extensive and intriguing study case is conducted in section 6, solving the FTP by using the TrigAC-PSO algorithm. Subsequently, a comparative analysis is presented, comparing results obtained by the application of TrigAC-PSO against well-established methods documented in the respective literature. Lastly, conclusive remarks and future recommendations are presented in section 7.

2. Transportation Problem (TP)

The Transportation Problem (TP) is a classic optimization problem in the field of operation research and logistics. It deals with the optimal allocation of goods or resources from multiple suppliers to multiple consumers, in an effort to minimize the overall cost while satisfying supply and demand constraints. The TP is formulated as a liner programming problem.

Let’s denote the following:

$m = n u m b e r o f s u p p l i e r s$
$n = n u m b e r o f c o n s u m e r s$
$s_{i} = t h e c a p a c i t y o f s u p p l i e r i, i = 1,2, \dots m$
$d_{j} = t h e c a p a c i t y o f c o n s u m e r j, j = 1,2 \dots n$
$x_{i j} = n u m b e r o f u n i t s t o b e t r a n s p o r t e d f r o m s u p p l i e r i t o c o n s u m e r j$
$c_{i j} = c o s t o f t r a n s p o r t i n g$

The mathematical model of the TP can be formulated as follows

m i n Z = \sum_{i = 1}^{m} \sum_{j = 1}^{n} c_{i j} \cdot x_{i j}

(1)

\sum_{j = 1}^{m} x_{i j} \geq d_{j} f o r j = 1, 2, \dots, n

(2)

\sum_{j = 1}^{m} x_{i j} \leq s_{i} f o r i = 1, 2, \dots, m

(3)

x_{i j} \geq 0 f o r i = 1,2, \dots, m, j = 1,2, \dots, n

(4)

Equation (1) outlines the objective function that needs to be minimized. Equation (2) encompasses the supply constraints, ensuring that the available quantity at the source points is greater than or equal to the demanded quantity at the destination points. Similarly, equation (3) ensures that the sum of the quantities transferred from source

s_{i}

to destination

d_{j}

does not exceed the available quantity. Equation (4) introduces a necessary condition, specifying that the units

x_{i j}

must be positive integers. For the sake of simplicity, we assume a balanced condition model, where supplies and demands are equal in this paper.

As already mentioned, various algorithms and methods, such as the NorthWest Corner Method, the Least Cost Method and the Vogel’s Approximation Method have been developed for finding a basic feasible solution. In addition, extensions and variations of TP have emerged to enhance the model’s relevance across diverse scenarios.

3. Fuzzy Logic Definitions

In this section, fundamental definitions will be provided about fuzzy numbers, fuzzy sets and a variation of fuzzy numbers known as generalized fuzzy numbers. This variation will be explored in greater detail using specific examples in section 6.

3.1. Fuzzy Sets and Membership Functions

Definition 1. A fuzzy set

\tilde{A}

in the universe of discourse

X

could be defined as a set of ordered pairs.

\tilde{A} = \{(x, μ_{\tilde{A}} (x)) | x \in X\}

where

μ_{\tilde{A}} (x)

is called membership function of

\tilde{A}

. The membership function

μ_{\tilde{A}} (x)

defines all the information contained in a fuzzy set.

Definition 2. The fuzzy number

A

is an extension of a regular number in the sense that it does not refer to one single value but rather to a connected set of possible values, where each possible value has each own degree of membership between 0 and 1. The membership function

μ_{\tilde{A}} (x)

satisfies the following condition [5]:

i)

μ_{\tilde{A}} (x)

is piecewise continuous.

ii)

μ_{\tilde{A}} (x)

is convex fuzzy subset.

iii)

μ_{\tilde{A}} (x) : x \to [0,1],

where

$μ_{\tilde{A}} (x) = 1 i f x i s t o t a l l y i n A$ .
$μ_{\tilde{A}} (x) = 0 i f x i s n o t i n A$ .
$0 < μ_{\tilde{A}} (x) < 1 i f x i s p a r t l y i n A .$

Definition 3. A fuzzy number

\tilde{A} = (a, b, c)

, is said to be a triangular fuzzy number if its membership function is given by [5]

μ_{\tilde{A}} (x) = \{\begin{matrix} 0, i f x \leq a \\ \frac{x - a}{b - a}, i f a \leq x \leq b \\ \frac{c - x}{c - b}, i f b \leq x \leq c \\ 0, i f x \geq c \end{matrix}

Definition 4. A fuzzy number

\tilde{A} = (a, b, c, d

) is said to be a trapezoidal fuzzy number if its membership function is given by

μ_{\tilde{A}} (x) = \{\begin{matrix} \frac{x - a}{b - a}, a \leq x < b \\ 1, b \leq x \leq c \\ \frac{x - d}{c - d}, c < x \leq d \\ 0, o t h e r w i s e \end{matrix}

3.2. Generalized fuzzy numbers

In our comprehensive investigation of the TP involving a broad spectrum of fuzzy numbers, the exploration of generalized fuzzy numbers comprises an indispensable aspect of our research. Kaur and Kuman [17], had the idea of implying the generalized fuzzy numbers in the TP using exact algorithms. In our study, in some of the presented problems the transportation cost will be illustrated by generalized fuzzy numbers. Our basic aim is to assess their effectiveness following the implementation of TrigAC-PSO algorithm.

But how are generalized fuzzy numbers defined? Generalized fuzzy numbers extend the concept of classical fuzzy numbers by providing more specific details through additional parameters.

In [19], Chen represented a generalized trapezoidal fuzzy number

\tilde{A}

\tilde{A} = (a, b, c, d; w),

where

0 < w \leq 1

and

a, b, c, d

are real numbers.

According to Chen, the membership function of a fuzzy set

\tilde{A}

, has the following properties.

$μ_{\tilde{A}} : R \to [0, w]$ is continuous.
$μ_{\tilde{A}} (x) = 0$ for all $x \in (- \infty, a]u[d, \infty)$ .
$μ_{\tilde{A}} (x)$ is strictly increasing on $[a, b]$ and strictly decreasing on $[c, d] .$
$μ_{\tilde{A}} (x) = w,$ for all $x \in [b, c]$ where $0 < w \leq 1$ .

Definition 5. A fuzzy number

\tilde{A} = (a, b, c, d; w)

is said to be a generalized trapezoidal fuzzy number if its membership function is provided by

μ_{\tilde{A}} (x) = \{\begin{matrix} w \cdot \frac{x - a}{b - a}, a \leq x < b \\ w, b \leq x \leq c \\ w \cdot \frac{x - d}{c - d}, c < x \leq d \\ 0, o t h e r w i s e \end{matrix}

3.3. Arithmetic Operations

In this subsection, the method for defining the two basic mathematical operations, addition and multiplication, is provided. The following table (Table 1) defines these operations for triangular fuzzy numbers and trapezoidal fuzzy numbers, as well as generalized fuzzy numbers. The operator

\oplus

denotes addition in fuzzy sets, while the operator ⊗ denotes multiplication [17].

These arithmetic operations offer a systematic approach to combining and manipulating different types of fuzzy numbers, preserving their essential attributes of fuzziness and uncertainty that are fundamental to fuzzy logic. By performing addition and multiplication on fuzzy numbers, we generate new fuzzy numbers that encapsulate the collective or altered characteristics of the original fuzzy sets, as defined by their membership functions. This method empowers us to flexibly handle and analyze uncertain or imprecise data, enhancing our ability to model complex systems and make informed decisions across various domains. The numbers

{\tilde{A}}_{1}

and

{\tilde{A}}_{2}

are elements of the set of fuzzy numbers, while λ belongs to the set of real numbers.

4. Fuzzy Transportation Problem

The Fuzzy Transportation Problem (FTP) is an extension of the classical TP which introduces fuzzy sets and fuzzy numbers for representing transportation cost, supplies and demands [26]. Solving the FTP involves developing mathematical models and algorithms, which could affectively deal with the fuzzy nature of the input data.

In our study, we treat the supply and demand values as crisp numbers, whereas the transportation costs are represented as fuzzy sets. The solution of the objective function

\tilde{z}

is also depicted as a fuzzy number.

Let

{\tilde{c}}_{i j}

be the fuzzy cost of transporting one unit of product from warehouse

i

to consumer

j

Under changing circumstances, the mathematical model of the FTP could be structured is the following.

m i n \tilde{Z} = \sum_{i = 1}^{m} \sum_{j = 1}^{n} {\tilde{c}}_{i j} ⨂ x_{i j}

(5)

\sum_{j = 1}^{m} x_{i j} \geq d_{j} f o r j = 1, 2, \dots, n

(6)

\sum_{j = 1}^{n} x_{i j} \leq s_{i} f o r i = 1, 2, \dots, m

(7)

x_{i j} \geq 0 f o r i = 1, \dots, m, j = 1, \dots, n

(8)

5. Particle Swarm Optimization (PSO)

The Particle Swarm optimization (PSO) algorithm stands out as a contemporary and innovative heuristic approach, gaining widespread popularity over the years due to its straightforward implementation and ability to yield satisfactory solutions [27]. PSO algorithm is inspired from the collective behavior of animals, studying their interactions to function as a strong approach handling optimization challenge in various applications [28].

In the PSO framework, every potential solution is represented as a particle, and the complete set of particles constitutes the algorithm’s population, known as swarm. The optimization process heavily relies on collaboration and exchange of information, with the particles improving their effectiveness through active cooperation within the swarm. Sharing information within the swarm, particles are empowered to consistently enhance their performance, striving towards the optimal efficiency. In finer detail, each particle modifies its movement according to its own experience and its neighboring particle experience.

A particle is defined by three essential parameters:

Position, which indicates its location in the search space
Velocity, which dictates the direction and extent of particles movement
Its previous best position, which operates as a memory mechanism for the positions that the particle has already “visited”

Consequently, in n-dimensional search space, each particle of the swarm is represented by

x_{i j} = (x_{i 1,,} x_{i 2}, \dots, x_{i j})

and the equation of its position is as follows:

x_{i j} (t + 1) = x_{i j} (t) + v_{i j} (t + 1), i = 1, 2, n and j = 1,2, \dots n

(9)

where

$x_{i j} (t + 1)$ is its current position
$x_{i j} (t)$ is its previous position
$v_{i j} (t + 1)$ is the velocity in the current iteration $(t + 1)$

In sequence, the particle’s velocity is represented as

v_{i j}

and its expression is determined by the following equation:

v_{i j} (t + 1) = {w v}_{i j} (t) + c_{1} r_{1} ({p b e s t}_{i j} (t) - x_{i j} (t)) + c_{2} r_{2} ({g b e s t}_{i j} (t) - x_{i j} (t))

i = 1,2, \dots n and j = 1,2, \dots n

(10)

where $v_{i j} (t + 1)$ represents the velocity of the particle in the current iteration, while $v (t)$ is the velocity in the previous iteration.
$w$ denotes the inertia weight, balancing global and local exploitation by incorporating memory of the previous particles direction to prevent major changes in suggested directions.
$r_{1}$ and $r_{2}$ are variables, randomly generated from uniform distribution, in range $[0, 1] .$
${p b e s t}_{i j} (t)$ denotes the best position of the particle up to iteration $t$ , while ${g b e s t}_{i j} (t)$ is the finest position of the entire swarm up to the same iteration.
The term $c_{1} r_{1} ({p b e s t}_{i j} (t) - x_{i j} (t))$ is known as the cognitive component, acting as a form of memory storing the particle’s best previous positions. The cognitive component reflects the tendency of the particles to return to their best positions.
The term $c_{2} r_{2} ({g b e s t}_{i j} (t) - x_{i j} (t))$ is known as the social component. In this context, particles follow the guidance of the swarm’s best position, incorporating knowledge acquired from the swarm.
$c_{1}$ and $c_{2}$ are defined as acceleration coefficients, impacting the efficiency of the PSO method. More precisely, $c_{1}$ signifies the particle’s confidence in itself while $c_{2}$ expresses the particle’s confidence in the swarm.

The acceleration coefficients

c_{1}

and

c_{2}

, along with random variables

r_{1}

and

r_{2}

, significantly influence the evolution of the cognitive and social components, determining the velocity value, which is crucial for the search direction of the particles and the convergence of the algorithm. Furthermore, inertia weight plays a key role in the process of providing balance between exploration and exploitation. Periodically, several variations have been developed and introduced, successfully attaining a dynamic approach to the optimal solution by striking a balance between algorithm’s exploration and exploitation searches.

In our previous research [25], we introduced two new variations. They succeeded in finding the optimal solution under extensive experimental analysis and testing of different combinations of values for variables

c_{1}

c_{2}

and

w

5.1. Trigonometric Acceleration Coefficient – Particle Swarm Optimization (TrigAC-PSO)

Trigonometric Acceleration Coefficient – Particle Swarm Optimization (TrigAC-PSO), has been proved to be the variant yielding the most favorable outcomes in solving the Transportation Problem [25]. In fact, the TrigAC-PSO variation underwent testing across a set of 32 instances, and the outcomes were compared with widely recognized exact methods and some preceding variations of the PSO algorithm. In comparison to all other methods, the TrigAC-PSO variation achieved the best results [25].

In TrigAC-PSO, initially, each particle is guided by the collective knowledge and experience acquired by the swarm, were the value of

c_{2}

significantly exceeds the value of

c_{1}

. Subsequently, leveraging the learning mechanism, each particle formulates its unique strategy and accumulates individual experience, with the value of

c_{2}

decreasing while the value of

c_{1}

increases (refer to Equations 11 and 12). The adjustment of

c_{1}

and

c_{2}

continues until both parameters are equalized to 2 in the algorithm’s last generation.

The subsequent equations are employed to compute the cognitive and social acceleration parameters [25] :

c_{1} = \frac{c_{1 f}}{2} + \sin \frac{2 c_{1 i} \cdot t}{t_{m a x}} \cdot \frac{π}{2}

(11)

c_{2} = c_{2 i} + c o s \frac{c_{2 f} \cdot π \cdot t}{2 \cdot t_{m a x}} - \frac{1}{2}

(12)

In the initial iteration, the personal acceleration value $c_{1 i}$ , is set to 0.5, while the social acceleration value $c_{2 i}$ , is set to 3.5.
In the last iteration of the algorithm, both the personal $c_{1 f}$ and social $c_{2 f}$ acceleration values are adjusted to 2.
The inertia weight (w) is dynamic and depends on the current iteration $t$ and the maximum number of iterations $t_{m a x}$ and is defined by the following equation:

$w = \frac{t_{m a x} - t}{t_{m a x}}$

(13)

6. Case Studies and Experimental Results

In this section, the TrigAC-PSO algorithm will be utilized to solve the Fuzzy Transportation Problem. A total of twenty-eight numerical examples will be resolved with results derived from four other established methods. To ensure a thorough investigation, the numerical examples encompass both triangular and trapezoidal fuzzy numbers. Moreover, the inclusion of generalized fuzzy numbers in our domain adds a distinctive dimension, making the application of our variation particularly intriguing in this context.

Initially, the problems will be evaluated in comparison to methods whose reliability remains consistent over the years. In this context, the TrigAC-PSO algorithm will be assessed alongside the NorthWest Method, the Least Cost Method, the Vogel’s Approximation Method and the Maximum Supply with Minimum Cost Method (MOMC) which was introduced in 2015 by Giancarlo de Franca Aguiar et al. [29]. Their classification technique showed spectacular computation advantage characterized by higher processing speed and less use of memory. Both MOMC and the previously mentioned methods have been employed in attempting to solve the fuzzy transportation problem. This poses a challenge for us, as we strive to optimize the values of the given problems using the TrigAC-PSO.

At this stage, it would be beneficial to make a reference to the initialization process.

In the initial steps of Algorithm 1, two vectors, namely

S u p p l y

and

D e m a n d

, are created as input (line 1 and 2). Subsequently, variables

m

and

n

are calculated, representing the values of parameters

S u p p l y

and

D e m a n d

respectively. Then, a matrix is generated containing random Monte Carlo real numbers (line 7). Line 10 rounds the elements of the candidate solution matrix to the nearest integer, as the commodity quantities must be non-negative integers. The Subsequent lines of the algorithm commerce a process of realignment and redistribution of matrix

L

to align with the specified supply and demand amounts. In lines 11 and 12, the sum of all elements in each row of matrix L is stored in vector

S u m r o w

, and similarly, the sum of all elements in each column is stored in vector

S u m c o l

. Then, two new vectors,

s

and

d

, are created by subtracting

S u m r o w

from

S u p p l y

and

S u m c o l

from

D e m a n d

, respectively. Following this, for each cell in the final matrix, any discrepancies are identified and adjusted accordingly, ensuring that the excess amounts in vectors s and d are zeroed out.

Algorithm 1: Initialization algorithm

The output of Algorithm 1 is a matrix comprising the initial solution, known as Initial Basic Feasible Solution (IBFS). Subsequently, the PSO algorithm is employed to find the particle achieving the optimal position and its corresponding optimal transportation cost. The supply and demand values are crisp values, whereas transportation cost is depicted using fuzzy sets. However, the expanded positions of the particles, while adhering to demand and supply constraints, exhibited negative or fractional values. Such values are incompatible with the nature of the solution, which necessitates quantities represented solely by positive integers. Consequently, necessary adjustments were implemented to ensure the integrity of the particle’s positions. These sub-algorithms were presented in 2023 by Aroniadi and Beligiannis [25]. To derive the final solution, fuzzy operations outlined in Table 1, will be applied, culminating in the representation of the final iteration cost as a fuzzy number.

The entire algorithmic approach is implemented utilizing MATLAB R2021b. TrigAC-PSO, was tested on a set of different dimensional problems, both triangular and trapezoidal fuzzy sets as classical and generalized fuzzy numbers. Table 2, presents the 28 test instances that are examined in our research [16,18,26,30,31,32,33,34,35,36,37,38,39,40].

In Table 3 and Figure 1, provided bellow, the performance of both exact methods and Trig-PSO approach across 20 Monte Carlo runs is showcased. In every cell, the best value of each method is depicted using bold for the cases where the algorithms achieved the optimal solution. The last column provides the optimal solution for each numerical instance. The values highlighted in bold correspond to the optimal ones.

Figure 3. The number of equal solutions that every method achieved.

As illustrated, the NW method attains optimal solutions in 3 out of 28 test instances (10.71%). LCM achieved the optimal solution in 5 out of 28 instances (17.86%). VAM surpasses the previous methods, securing optimal solution in 15 out of 28 instances (53.57%). Despite being introduced later than the preceding methods, MOMC fell short of exceeding Vogel’s method, as it succeeded in identifying the optimal solution in 6 instances (21.43%). Notably, TrigAC-PSO method emerges as the most efficient, achieving optimal results in 24 out of 28 instances (81.71%).

The deviation measurement qualities the extent of variation between observed values and expected or target values. It provides a numerical representation of how much individual data values differ from the average or desired outcome and comprises a metric of each algorithm’s stability. Deviation is given by the following formula:

D e v = \frac{x_{i j} - o p t i m a l}{o p t i m a l}

(14)

where

x_{i j}

is the current solution.

Based on the data presented in Table 4, it is apparent that VAM, MOMC and TrigAC-PSO appear to be more efficient than the other methods. Therefore, the solutions achieved by NWC differ from the optimal solution by 27.3%, the results of LCM by 10.12% and MOMC by 7.5%. Vogel’s approximation method presented higher levels of efficiency since the average of the export solutions differ from the optimal solutions by 2.7%. TricAC-PSO method is now highlighted as the most efficient method, surpassing all other methods, with a percentage close to zero. This indicates its remarkable stability and accuracy in predicting the optimal value with near-perfect precision.

In Boolean (Classical) logic, transportation costs are represented as precise, fixed values. In fuzzy logic, transportation costs as supply and demand quantities are represented as approximate values, allowing for gradual transitions between costs and shipments.

The pivotal aspect of our study was the visual representation of the final solution using fuzzy numbers. In classical logic, a solution is deemed optimal only if its value aligns precisely with that of the optimal solution. However, the scientific quandary arises: How equitably is to discard other solutions even when their deviation from the optimal one is infinitesimal?

This quandary sparked our original concept: to represent the costs incurred by exact methods using fuzzy sets and to ascertain the degree of truth, inherent in each algorithm’s solution belonging to this set. Consequently, every solution is now endowed with its unique value, irrespective of its optimality status. The binary classification of classical logic, where 0 signifies non-optimality and 1 denotes optimality, is supplanted by a continuum with the interval

[0,1]

, wherein each number signifies the solution’s degree of belongingness to the fuzzy set. In this study, the Gaussian membership function will be employed to ascertain the truthfulness of each solution.

The Gaussian membership function, is defined by a bell-shaped curve characterized by its mean

(μ)

and standard deviation

(σ)

. The function assigns a degree of membership to each element in a fuzzy set, based on its proximity to the mean. Mathematically, the Gaussian membership function is given by the formula:

μ (x) = e^{\frac{- {(x - μ)}^{2}}{{2 σ}^{2}}}

(15)

where:

$x$ is the input value.
μ is the mean of the fuzzy numbers.
σ is the standard deviation of the fuzzy numbers.

The following table (Table 5) shows the degree of truth for each solution of the 28 problems.

We notice that among the methods that were unable to precisely identify the optimal solution, they achieved values that were remarkably close to the optimal cost. The degree of truth studies how closely the solution obtained by each method approaches our optimal solution offering a clearer perspective. When the degree of truth is 1, the The NWM solutions exhibited optimality with a degree of truth 0.6061 (equivalent to 60.61% optimality). In contrast, both LCM and MOMC attained optimality with a substantially higher degree, scoring 0.8261 (82.61% optimality) and 0.8546 (85.46% optimality) respectively, surpassing the NWM. While VAM succeeded in discovering the optimal solution in half of the instances, its remaining solutions were notably proximal, as VAM achieved the optimal with degree of truth as high as 0.9638 (96.38%). Yet again, TrigAC-PSO stands out significantly, having achieved the optimal solution in 24 out of 28 problems. However, in instances where TrigAC-PSO didn’t achieve the desired results, its attained solution diverged slightly from the optimal one, as indicated by the Gaussian membership function. TrigAC-PSO’s precision is evident, reaching the optimal solution with a remarkable truth score of 0.9991 (99.91% optimality).

The selection of these methods was deliberate, guided by two principal factors. Firstly, they were chosen because they have been established for years verified their reliability. Secondly, our intention was to demonstrate a compelling narrative: that despite their perceived obsolescence and occasional failure to attain optimality, these methods possess the potential for resurgence and redemption through the fuzzy sets, transcending the boundaries of classical logic to reclaim their erstwhile prominence.

Upon culmination of the exhaustive comparative analysis involving the aforementioned methods, it become apparent that TrigAC-PSO appeared as the best choice, distinguishing itself as the quintessential option. In a quest to examine further its rustiness and precision, TrigAC-PSO underwent additional tests against contemporaneous methods introduced concurrently. Firstly, the proposed algorithm is tested on twelve instances, from Table 2, against the algorithm introduced by Ekanayake and Ekanayake, in 2023 [16]. This algorithm was based on the Yager’s robust ranking method [17].

But how is a ranking function defined?

An efficient approach for comparing the fuzzy numbers is by the use of the racking function

R : F (R) \to R

where

F (R)

is a set of fuzzy numbers defined on a set of real numbers, which convents a fuzzy number into a crisp value, under specific circumstances [17].

The following table (Table 6) gives the formula of the ranking functions, which have been applied in this manuscript.

The subsequent table (Table 7), presents the outcomes of the solutions derived from both TrigAC-PSO and the research conducted by Ekanayake and Ekanayake [16].

Once more, TrigAC-PSO algorithm stands out by attaining the optimal solution with a membership degree of 1, demonstrating its superiority. Similarly, the method of Ekanayake and Ekanayake yield impressive outcomes, with an aggregated membership degree reaching 0.9995.

At this juncture, it is intriguing to delve into the realm of generalized fuzzy numbers, where the application of a metaheuristic approach to the FTP marks a pioneering endeavor. Five problems, from Table 2, will be subjected to comparison against TrigAC-PSO, shedding light at the algorithm’s adaptability and efficacy in undertaking challenges modelled by fuzzy generalized numbers [17,18,31,40].

The ensuing table (Table 8) illustrates the outcomes generated by four distinct methods applied to five of the aforementioned problem sets. These solutions are depicted as fuzzy numbers, subsequently subjected to defuzzification through the ranking function (Table 6). This process facilitates an in-depth analysis of the deviation from the optimal values, as shown in the Table 9, thus enhancing comprehension for the reader.

Upon reviewing the table above, the following conclusions can be drawn:

Ebrahimnejad, so as Thota and Raja’s approach exhibited zero deviation from the optimal solution, establishing it as the preferred method for solving the TP involving fuzzy generalized numbers.
TrigAC-PSO’s performance in this scenario was exceptional, yet again. This method reached almost the ultimate solution with a deviation rate of 1.71%.
Kaur and Kuman’s method demonstrated commendable efficiency with a deviation from the optimum standing at 2.89%
Conversely, the outcomes derived from Mathur’s method exhibited a substantial deviation from the optimal solution, amounting to 20.54%

Based on these assessments it is apparent that our method, TrigAC-PSO algorithm, ensures maximum accuracy, completeness and stability, adeptly handling both the classical TP and the more intricate FTP with remarkable proficiency.

Metaheuristic algorithms consistently emerge as optimal solutions for optimization problems with the PSO algorithm standing out as particularly advantageous. In our innovative variation, TrigAC-PSO, we have methodically designed the cognitive and social component to align with our philosophy, prioritizing the particle’s assimilation of swarm behavior and collective experience to follow its own decision-making process. Additionally, the inertia weight

w

, intricately intertwines with the number of iterations outlined in our algorithm. The remaining consideration is to assess whether the number of particles, comprising our swarm, influences the evolution and quality of our solutions. The solutions for 28 problems were figured using 20, 35 and 50 particles, generated by Algorithm 1. These solutions are summarized in the table below (Table 10). The highlighted indications show the cases where the method failed to identify the optimal solution but achieved a value very close to it.

A briefly examination reveals minimal deviation among solutions, often rendering them almost identical. However, a more thorough examination was deemed necessary. Each of the 28 problems was subjected to runs, with varying number of particles, conducting 20 tests for each instance.

Table 11, expands the accuracy rate of each algorithm for 20, 35 and 50 particles. The accuracy rate is commonly defined based on the relationship:

A c c u r a c y = \frac{T O R}{T R}

where

T O R

is the total number of runs where optimal solution was found and

T R

is generally the number of runs. In our scenario, the experiments will be carried out for 20 runs.

The data represented in table 11, indicates that the algorithm achieves an accuracy rate of 66.07% for 20 particles. For 35 particles, the algorithm’s accuracy rate improves to 74.03%. Furthermore, solutions obtained using 50 particles exhibit even higher accuracy, reaching 75.54%. This pattern indicates that, as the number of particles increases, there is enhanced interaction and information exchange within the swarm, resulting in higher solution accuracy rates. Figure 4, also reveals the high levels of accuracy.

In the following table (Table 12), the most important statistical measures for 20 independent runs are represented for 20, 35 and 50 particles, respectively.

The experimental findings highlight the remarkable stability of our proposed algorithm in solving the FTP. Across all scenarios, the mean values closely approximate the optimal solution, regardless of whether 20, 35, or 50 particles are utilized. This emphasizes not only the efficiency but also the robustness of the TrigAC-PSO method. Notably, the CV value, a crucial metric for measuring algorithm’s stability, remains consistently low. Specifically, for 20 particles, the mean CV is 1.82%, reducing to 1.53% for 35 particles, and further decreasing to 0.91% for 50 particles. This tendency suggests that increasing the number of particles improves algorithm’s stability. The consistently low CV values affirm the reliability of our algorithm, establishing it as a robust competitor among established methods.

7. Conclusions

In summary, the Transportation Problem stands as one of the pivotal challenges within the realm of operational research. While numerous methods have successfully solved it through advanced algorithms, the question remains: can these solutions be effectively implemented under non-ideal conditions in real-world scenarios? This question finds its answer in the realm of the Fuzzy Transportation Problem (FTP), where classical logic is supplanted by fuzzy logic.

In this publication, we solved the FTP using TrigAC-PSO algorithm, a variant of Particle Swarm Optimization (PSO), which effectively determined the classical Transportation Problem. Our method underwent rigorous testing across a spectrum of problem instances and was subsequently compared against well-established techniques documented in the respective literature. Our findings unequivocally demonstrate TrigAC-PSO’s superiority in terms of accuracy, negligible deviation from optimal solutions, and the quality of its solutions. Moreover, beyond traditional fuzzy numbers, TrigAC-PSO was tested under conditions where numbers were classical fuzzy and generalized fuzzy, respectively. In this context, TrigAC-PSO showed excellent performance. Based on comprehensive experimentation and meticulous research, it becomes noticeable that TrigAC-PSO emerges as the ideal option for resolving the complexities in the FTP.

As we look to the future, embracing and improving TrigAC-PSO presents hopeful opportunities for improving transportation logistics and management, thus enabling smoother and more productive operations in real-world scenarios, an aspect that presents a challenge for us to explore in our future research.

Author Contributions

Conceptualization, C.A. and G.N.B.; methodology, C.A. and G.N.B.; software, C.A.; validation, C.A. and G.N.B.; formal analysis, C.A. and G.N.B.; investigation, C.A. and G.N.B.; resources, C.A.; data curation, C.A.; writing—original draft preparation, C.A.; writing—review and editing, C.A. and G.N.B.; visualization, C.A.; supervision, G.N.B.; project administration, G.N.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data and the programming code used in this paper can be sent, upon request, to the interested reader. Please contact: gbeligia@upatras.gr.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Deshpande, V.A. An optimal method for obtaining initial basic feasible solution of the transportation problem. In Proceedings of the National Conference on Emerging Trends in Mechanical Engineering Patel College of Engineering & Technology (GCET), Vallabh Vidyanagar (ETME-2009), Vallabh Vidyanagar, India 2010, 20, 21.
Taha, H.A. Operations Research: An Introduction, 8th ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
Amaliah, B.; Fatichah, C.; Suryani, E. A new heuristic method of finding the initial basic feasible solution to solve the transportation problem. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 2298–2307. [Google Scholar] [CrossRef]
Basirzadeh, H. An approach for solving fuzzy transportation problem. Appl. Math. Sci. 2011, 5, 1549–1566. [Google Scholar]
Bellman, R.E.; Zadeh, L.A. Decision-making in fuzzy environment. Management Science 1970, 17, B141–B164. [Google Scholar] [CrossRef]
Chanas, S.; Kuchta, D. A concept of optimal solution of the transportation with Fuzzy cost coefficient. Fuzzy sets and systems 1996, 82, 299–305. [Google Scholar] [CrossRef]
Ahmed, N.; Khan, A.; Uddin, M. Solution of Mixed Type Transportation Problem: A Fuzzy Approach. 2015, 61, 19–31. [Google Scholar]
Chakraborty, A.; Chakraborty, M. Cost-time minimization in a transportation problem with fuzzy parameters: a case study. Journal of Transportation Systems Engineering and Information Technology 2010, 10, 53–63. [Google Scholar] [CrossRef]
Basirzadeh, H. An Approach for Solving Fuzzy Transportation Problem. Applied Mathematical Sciences 2011, 5, 1549–1566. [Google Scholar]
Gani, A.N. Simplex Type Algorithm for Solving Fuzzy Transportation Problem. Tamsui Oxford Journal of Information and Mathematical Sciences 2011, 27, 89–98. [Google Scholar]
Shanmugasundari, M.; Ganesan, K. A novel approach for the fuzzy optimal solution of fuzzy transportation problem. International Journal of Engineering Research and Applications 2013, 3, 1416–1421. [Google Scholar]
Balasubramanian, K.; Subramanian, S. Optimal Solution of Fuzzy Transportation Problems Using Ranking Function. International Journal of Mechanical and Production 2018, 8, 551–558. [Google Scholar] [CrossRef]
Pandian, P.; Natarajan, G. A new algorithm for finding a fuzzy optimal solution for fuzzy transportation problems. Applied Mathematical Sciences 2010, 4, 79–90. [Google Scholar]
Gani, A.; Razak, K.A. Two stage fuzzy transportation problem. Journal of Physical Sciences 2006, 10, 63–69. [Google Scholar]
Malini, S.; Kennedy, F. An approach for Solving Fuzzy Transportation Problem using Octagonal Fuzzy Numbers. 2013, 7, 2661–2673. [Google Scholar] [CrossRef]
Ekanayake, D.; Ekanayake, U. An Average Based Method for Finding the Basic Feasible Solution for the Fuzzy Transportation Problems. American Journal of Applied Scientific Research 2023, 9, 1–13. [Google Scholar]
Kaur, A.; Kumar, A. A new approach for solving fuzzy transportation problems using generalized trapezoidal fuzzy numbers. Applied Soft Computing 2012, 12, 1201–1213. [Google Scholar] [CrossRef]
Ebrahimnejad, A. A simplified new approach for solving fuzzy transportation problems with generalized trapezoidal fuzzy numbers. Applied Soft Computing 2014, 19, 171–176. [Google Scholar] [CrossRef]
Chen, S.H. Operations of fuzzy numbers with function principal. Tamkang Journal of Management Sciences 1985, 6, 13–25. [Google Scholar]
Lin, F.T. Solving the transportation problem with fuzzy coefficients using genetic algorithms. IEEE International Conference on fuzzy systems. 2009, 1468–1473. [Google Scholar]
Sharmistha, H.J.; Biswapati, J. Application of fuzzy programming techniques to solve solid transportation problem with additional constraints, Operations Research and Decisions, Wroclaw University of Science and Technology, Faculty of Management. 2020, 30, 67–84. [Google Scholar]
Sadeghi-Moghaddam, S.; Hajiaghaei-Keshteli, M.; Mahmoodjanloo, M. New approaches in metaheuristics to solve the fixed charge transportation problem in a fuzzy environment. Neural Comput & Applic 2019, 31 (Suppl 1), 477–497. [Google Scholar] [CrossRef]
Rajshri, G.; Onkar, C.; Dhawade, N. Optimizing Fuzzy Transportation Problem of Trapezoidal Numbers. 2017, 15–23. [Google Scholar]
Singh, G.; Singh, A. Extension of particle swarm optimization algorithm for solving transportation problem in fuzzy environment. Applied Soft Computing 2021, 110. [Google Scholar] [CrossRef]
Aroniadi, C.; Beligiannis, G.N. Applying Particle Swarm Optimization Variations to Solve the Transportation Problem Effectively. Algorithms 2023, 16, 372. [Google Scholar] [CrossRef]
Kumar, P.S. PSK Method for Solving Intuitionistic Fuzzy Solid Transportation Problems. International Journal of Fuzzy System Applications 2018, 7, 62–99. [Google Scholar] [CrossRef]
Rosendo, M.; Pozo, A. A hybrid particle swarm optimization algorithm for combinatorial optimization problems. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2017, 22, 387–408. [Google Scholar] [CrossRef]
29. Giancarlo de Franca Aguiar; Barbara de Cassia Xavier Cassins Aguiar, Volmir Eugenio Wilhelm. The MOMC method: a new methodology to find initial solution. Applied Mathematical Sciences 2015, 9, 901–914. [CrossRef]
Farikhin, M.S.; Bayu, S.; Bambang, I. Solving of Fuzzy Transportation Problem Using Fuzzy Analytical Hierarchy Process, Proceedings of the 2nd International Seminar on Science and Technology, Atlantis Press, (ISSTEC 2019), 10-15, 2352-5398. [CrossRef]
Mathur, N.; Srivastava, P. An Inventive Approach to Optimize Fuzzy Transportation Problem. International Journal of Mathematical, Engineering and Management Sciences 2020, 5, 985–994. [Google Scholar] [CrossRef]
Bisht, D.; Srivastava, P. One Point Conventional Model to Optimize Trapezoidal Fuzzy Transportation Problem. International Journal of Mathematical, Engineering and Management Sciences 2019, 4, 1251–1263. [Google Scholar] [CrossRef]
Muhammad, S.; Farikhin; Hariyanto; Soni; Surarso. Bayu Optimal solution of full fuzzy transportation problems using total integral ranking. Journal of Physics: Conference Series 2018, 983, 012075. [Google Scholar] [CrossRef]
Pandian, P.; Natarajan, G. ; An Appropriate Method for Real Life Fuzzy Transportation Problems. International Journal of Information Sciences and Application 2011, 3, 127–134. [Google Scholar]
Mathur, N.; Srivastava, P. K.; Paul, A. Trapezoidal fuzzy model to optimize transportation problem. International Journal of Modeling, Simulation, and Scientific Computing 2016, 07, 1650028. [Google Scholar] [CrossRef]
Singh, R.; Saxena, V. A new ranking based fuzzy approach for fuzzy transportation problem. Computer modelling and new technologies 2017, 21, 16–21. [Google Scholar]
Srinivasan, R.; Karthikeyan, N.; Renganathan, K.; Vijayan, D.V. Method for solving fully fuzzy transportation problem to transform the materials. Materials Today: Proceedings 2020. [Google Scholar] [CrossRef]
Hussain, R.; Jayaraman, P. Fuzzy Transportation Problem Using Improved Fuzzy Russells Method. International Journal of Mathematical Trends and Technology 2014, 5, 50–59. [Google Scholar] [CrossRef]
Kumar, P.S. A Simple Method for Solving Type-2 and Type-4 Fuzzy Transportation Problems. Int. J. Fuzzy Log. Intell. Syst. 2016, 16, 225–237. [Google Scholar] [CrossRef]
Thota, S.; Raja, P. New Method for Finding an Optimal Solution of Generalized Fuzzy Transportation Problems (June 15, 2020). Asian Journal of Mathematical Sciences 2020. Available at SSRN: https://ssrn.com/abstract=3813697. [Google Scholar]

Figure 1. Triangular Fuzzy number.

Figure 2. Trapezoidal Fuzzy number.

Figure 4. The accuracy of TrigAC-PSO for 20, 35 and 50 particles.

Table 1. Arithmetic Operations.

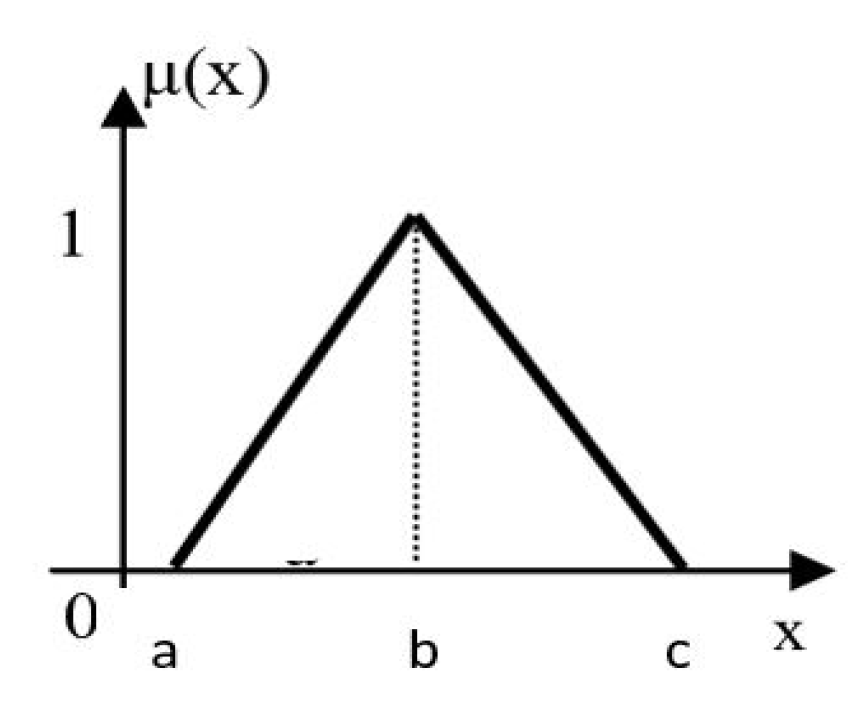
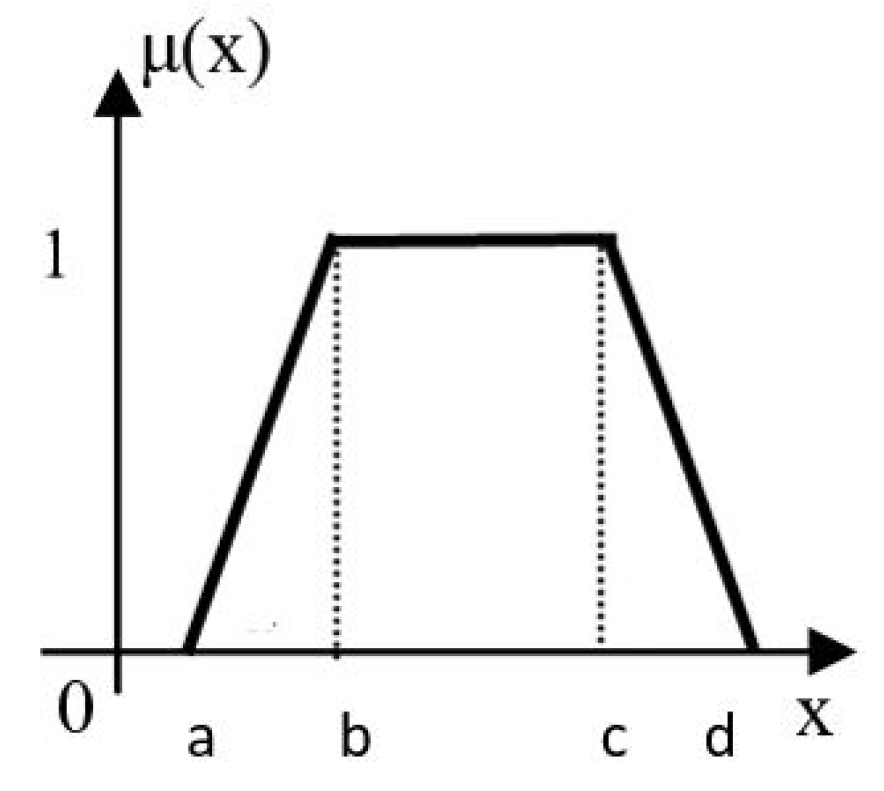
Triangular Fuzzy Numbers	Trapezoidal Fuzzy Numbers	Generalized Trapezoidal Fuzzy Numbers
$Let {\tilde{A}}_{1} = (a_{1}, b_{1}, c_{1})$ $and {\tilde{A}}_{2} = (a_{2}, b_{2}, c_{2})$ be two triangular fuzzy numbers then • ${\tilde{A}}_{1} \oplus {\tilde{A}}_{2} = (a_{1} + a_{2}, b_{1} + b_{2}, c_{1} + c_{2})$ • $λ \otimes {\tilde{A}}_{1} = ({λ a}_{1}, λ b_{1}, λ c_{1})$	$Let {\tilde{A}}_{1} = (a_{1}, b_{1}, c_{1}, d_{1})$ $and {\tilde{A}}_{2} = (a_{2}, b_{2}, c_{2}, d_{2})$ be two trapezoidal fuzzy numbers then • ${\tilde{A}}_{1} \oplus {\tilde{A}}_{2} = (a_{1} + a_{2,} b_{1} + b_{2}, c_{1} + c_{2}, d_{1} + d_{2})$ • $λ \otimes {\tilde{A}}_{1} = ({λ a}_{1}, λ b_{1}, λ c_{1}, {λ d}_{1})$	$Let {\tilde{A}}_{1} = (a_{1}, b_{1}, c_{1}, d_{1}; w_{1})$ $and {\tilde{A}}_{2} = (a_{2}, b_{2}, c_{2}, d_{2}; w_{2})$ be two generalized trapezoidal fuzzy numbers then • ${\tilde{A}}_{1} \oplus {\tilde{A}}_{2} = (a_{1} + a_{2}, b_{1} + b_{2}, c_{1} + c_{2}, d_{1} + d_{2}; m i n (w_{1}, w_{2}))$ • $λ \otimes {\tilde{A}}_{1} = ({λ a}_{1}, λ b_{1}, λ c_{1}, {λ d}_{1}; w_{1})$

Table 2. Details of the 28 test instances of the FTP.

No	From Journal	Name	Problem Size	Type	Optimal Solution
1	Ebrahimnejad (2014)	Pr. 01	3·3	Generalized Trapezoidal Fuzzy Number	64.35
2	Kumar and Subramanian (2018)	Pr. 02	4·4	Classic Triangular Fuzzy Number	853.35
3	Farikhin et al. (2020)	Pr. 03	3·4	Classic Triangular Fuzzy Number	817.17
4	Mathur and Srivastava (2020)	Pr. 04	3·4	Generalized Trapezoidal Fuzzy Number	196
5	Srivastava and Bisht (2018)	Pr. 05	3·3	Classic Triangular Fuzzy Number	166
6	Srivastava and Bisht (2018)	Pr. 06	3·4	Classic Triangular Fuzzy Number	101
7	Sam'an et al. (2018)	Pr. 07	3·3	Classic Trapezoidal Fuzzy Number	1770
8	Pandian and Natarajan (2011)	Pr. 08	3·4	Classic Trapezoidal Fuzzy Number	199
9	Mathur et al. (2016)	Pr. 09	3·3	Classic Trapezoidal Fuzzy Number	155.25
10	Singh and Saxena (2017)	Pr. 10	3·4	Classic Trapezoidal Fuzzy Number	126
11	Ekanayake and Ekanayake (2023)	Pr. 11	4·4	Classic Triangular Fuzzy Number	294
12	Ekanayake and Ekanayake (2023)	Pr. 12	3·4	Classic Triangular Fuzzy Number	65.8
13	Ekanayake and Ekanayake (2023)	Pr. 13	2·3	Classic Triangular Fuzzy Number	7735.5
14	Ekanayake and Ekanayake (2023)	Pr. 14	4·4	Classic Triangular Fuzzy Number	130.68
15	Srinivasan et al. (2020)	Pr. 15	6·6	Classic Triangular Fuzzy Number	2170
16	Ekanayake and Ekanayake (2023)	Pr. 16	3·3	Classic Trapezoidal Fuzzy Number	951.25
17	Ekanayake and Ekanayake (2023)	Pr. 17	4·3	Classic Trapezoidal Fuzzy Number	821.25
18	Ekanayake and Ekanayake (2023)	Pr. 18	3·4	Classic Triangular Fuzzy Number	149
19	Ekanayake and Ekanayake (2023)	Pr. 19	3·4	Classic Trapezoidal Fuzzy Number	67.25
20	Hussain and Jayaraman (2014)	Pr. 20	3·3	Classic Triangular Fuzzy Number	3640.56
21	Hussain and Jayaraman (2014)	Pr. 21	4·4	Classic Trapezoidal Fuzzy Number	3844
22	Ekanayake and Ekanayake (2023)	Pr. 22	3·3	Classic Triangular Fuzzy Number	295.9
23	Ekanayake and Ekanayake (2023)	Pr. 23	3·3	Classic Triangular Fuzzy Number	551.03
24	Ebrahimnejad (2014)	Pr. 24	4·6	Generalized Trapezoidal Fuzzy Number	4300.2
25	Kumar (2016)	Pr. 25	3·4	Classic Trapezoidal Fuzzy Number	68
26	Kumar(2016)	Pr. 26	3·4	Classic Trapezoidal Fuzzy Number	141
27	Thota and Raja (2020)	Pr. 27	3·3	Generalized Trapezoidal Fuzzy Number	91.45
28	Thota and Raja (2020)	Pr. 28	3·4	Generalized Trapezoidal Fuzzy Number	75.6

Table 3. The optimal solution of each method for the 28 test instances.

Pr	NWC	LCM	VAM	MOMC	TrigAC-PSO	Optimal
01	64.35	67.6	67.6	67.6	65.1	64.35
02	1046.67	870.05	853.35	855	853.35	853.35
03	861.53	894.66	817.17	1000.67	817.17	817.17
04	233	266.5	268	266.5	196	196
05	166	190	172	172	166	166
06	125	120.5	101	105	101	101
07	2025	1790	1770	1800	1770	1770
08	233	223	203	199	199	199
09	155.25	178.25	159.25	164.5	155.25	155.25
10	144.25	140	130	126	126	126
11	376	294	294	375	294	294
12	110.67	65.8	65.8	66	65.8	65.8
13	7736.67	7735.5	7735.5	7736.67	7735.5	7735.5
14	196	130.68	130.68	130.68	130.68	130.68
15	4285	2.455	2.310	2620	2261	2170
16	1035	971.25	951.25	951.25	951.25	951.25
17	967.5	887.5	821.25	826.25	821.25	821.25
18	176	152	149	150	149	149
19	93	67.25	67.25	77	67.25	67.25
20	5070.33	3740.58	3644.58	3944.34	3640.56	3640.56
21	4172	4172	4091	3932	3844	3844
22	486.67	339.92	295.9	340	295.9	295.9
23	592.67	557.71	557.71	581	551.03	551.03
24	6549.9	7567.8	4414.95	4452.9	4386.45	4300.2
25	93	73	70	68	68	68
26	169	148	141	141	141	141
27	108.8	97.5	97.45	97.5	91.45	91.45
28	134.175	95	75.6	95	82.5	75.6

Table 4. The deviation (dev) of the methods for the 28 test instances.

	NWM	LCM	VAM	MOMC	TrigAC-PSO
Pr.01	0	0.05050505	0.05050505	0.05050505	0.011655011
Pr.02	0.22654245	0.01956993	0	0.001933556	0
Pr.03	0.05428491	0.094827269	0	0.224555478	0
Pr.04	0.18877551	0.359693877	0.36734694	0.359693877	0
Pr.05	0	0.014457831	0.03614458	0.036144578	0
Pr.06	0.237623762	0.193069306	0	0.03960396	0
Pr.07	0.144067796	0.011299435	0	0.016949152	0
Pr.08	0.170854271	0.120603015	0.0201005	0	0
Pr.09	0	0.148148148	0.0257649	0.05958132	0
Pr.10	0.144841269	0.111111111	0.03174603	0	0
Pr.11	0.278911564	0	0	0.275510204	0
Pr.12	0.681914893	0	0	0.003039514	0
Pr.13	0.000151251	0	0	0.000151251	0
Pr.14	0.499846954	0	0	0	0
Pr.15	0.974654377	0.131336405	0.06060606	0.207373271	0.041935483
Pr.16	0.088042049	0.021019442	0	0	0
Pr.17	0.178082192	0.080669711	0	0.00608828	0
Pr.18	0.181208054	0.020134228	0	0.006711409	0
Pr.19	0.382899628	0	0	0.144981413	0
Pr.20	0.392733535	0.027523238	0.00110423	0.083443207	0
Pr.21	0.085327784	0.085327784	0.06425598	0.02289282	0
Pr.22	0.644711051	0.148766475	0	0.149036837	0
Pr.23	0.075567573	0.012122752	0.01212275	0.054389053	0
Pr.24	0.501813869	0.73852379	0.00533696	0.035509976	0.020057207
Pr.25	0.367647059	0.073529412	0.02941176	0	0
Pr.26	0.177304965	0.04964539	0	0	0
Pr.27	0.189721159	0.06615637	0.06560962	0.06615637	0
Pr.28	0.774801587	0.256613757	0	0.256613757	0.091269841
Average	0.27294034	0.101237633	0.02750198	0.075030869	0.005889912

Table 5. The Gaussian Membership Function for the 28 test instances.

No	NWM	LCM	VAM	MOMC	TrigAC-PSO
Pr. 01	1	0.9767	0.9767	0.9767	0.995
Pr. 02	0.7115	0.9985	1	0.9999	1
Pr. 03	0.6022	0.3488	1	0.0304	1
Pr. 04	0.7844	0.4699	0.4553	0.4699	1
Pr. 05	1	0.9137	0.9944	0.9944	1
Pr. 06	0.614	0.7183	1	0.9862	1
Pr. 07	0.7561	0.9983	1	0.9961	1
Pr. 08	0.8319	0.8319	0.9949	1	1
Pr. 09	1	0.9981	0.9697	0.9868	1
Pr. 10	0.7483	0.8445	0.9862	1	1
Pr. 11	0.6045	1	1	0.6139	1
Pr. 12	0	1	1	1	1
Pr. 13	0.998	1	1	0.998	1
Pr. 14	0.2271	1	1	1	1
Pr. 15	0	0.1311	0.6147	0.006	0.987
Pr. 16	0.9947	0.9951	1	1	1
Pr. 17	0.9974	0.9709	1	0.9995	1
Pr. 18	0.4868	0.9911	1	0.9999	1
Pr. 19	0.7559	1	1	0.9692	1
Pr. 20	0.4762	0.9924	0.9999	0.9665	1
Pr. 21	0.9999	0.9999	0.9999	0.9999	1
Pr. 22	0.9718	0.9921	1	0.992	1
Pr. 23	0.9093	0.9967	0.9967	0.9514	1
Pr. 24	0	0	0.9995	0.993	0.9999
Pr. 25	0.2235	0.9893	1	1	1
Pr. 26	0.259	0.975	1	1	1
Pr. 27	0.019	0.9998	0.9998	0.9997	1
Pr. 28	0	0	1	0	0.993
Average	0.606125	0.826146	0.963846	0.854621	0.999103571

Table 6. The formula of Ranking Functions.


Ranking function for two classical fuzzy numbers [7]	Ranking function for generalized trapezoidal fuzzy numbers [18]
• Let $\tilde{A} = (a, b, c)$ a triangular fuzzy number then, $R (\tilde{A}) = \frac{a + b + c}{3}$ • Let $A = (a, b, c, d)$ a trapezoidal fuzzy number then, $R (\tilde{A}) = \frac{a + b + c + d}{4}$	• Let ${\tilde{A}}_{1} = (a_{1}, b_{1}, c_{1}, d_{1}; w_{1})$ and ${\tilde{A}}_{2} = (a_{2}, b_{2}, c_{2}, d_{2}; w_{2})$ be two generalized trapezoidal fuzzy numbers and $w = \min (w_{1}, w_{2})$ . Then $R ({\tilde{A}}_{1}) = \frac{w \cdot (a_{1} + b_{1} + c_{1} + d_{1})}{4}$ and $R ({\tilde{A}}_{2}) = \frac{w \cdot (a_{2} + b_{2} + c_{2} + d_{2})}{4}$

Table 7. Comparison between Ekanayake and TrigAC-PSO method.

Pr.	Ekanayake Optimal Solution	TrigAC-PSO Optimal Solution	Ekanayake Membership Value	TrigAC-PSO Membership Value
Pr. 02	(400, 845, 1315)	(400, 845, 1315)	1	1
Pr. 11	(144, 285, 453)	(144, 285, 453)	1	1
Pr. 12	(20, 89, 89)	(20, 89, 89)	1	1
Pr. 13	(5960, 7620, 9630)	(5960, 7620, 9630)	1	1
Pr. 14	(64, 124, 206)	(64, 124, 206)	1	1
Pr. 16	(370, 735, 1145, 1595)	(370, 715, 1085, 1635)	0.9951	1
Pr. 17	(400, 640, 875, 1370)	(400, 640, 875, 1370)	1	1
Pr. 18	(105, 150, 195)	(104, 149, 194)	0.9999	1
Pr. 22	(148, 322, 418)	(148, 322, 418)	1	1
Pr. 23	(347, 566, 760)	(347, 554, 752)	0.995	1
Pr. 25	(12, 55, 88, 117)	(12, 55, 88, 117)	1	1
Pr. 26	(52, 106, 176, 230)	(52, 106, 176, 230)	1	1

Table 8. Comparison TrigAC-PSO among four established methods.

Pr.	Ebrahimnejad	Thota and Raja	Kaur and Kuman	Mathur et al.	TrigAC-PSO
Pr. 01	(117, 205, 352, 613; 0.2)	(117, 205, 35, 613; 0.2)	(147, 220, 382, 603; 0.2)	(197, 240, 382, 643; 0.2)	(147, 220, 382, 553; 0.2)
Pr. 04	(315, 810, 1220, 1575; 0.2)	(318, 813, 1220, 1582; 0.2)	(315, 810, 1220, 1575; 0.2)	(415, 970, 1460, 1865; 0.2)	(315, 810, 1220, 1575; 0.2)
Pr. 24	(5148, 6475, 7802, 9244; 0.6)	(5148, 6475, 7802, 9244; 0.6)	(5307, 6794, 7.872, 9460; 0.6)	(5307, 6794, 7.872, 9460; 0.6)	(3170.4, 4052.4, 4717.2, 5628; 0.6)
Pr. 27	(376, 436, 474, 543; 0.2)	(376, 436, 474, 543; 0.2)	(413, 459, 506, 572; 0.2)	(411, 455, 509, 563; 0.2)	(404, 460, 502, 559; 0.2)
Pr.28	(294, 348, 408, 462; 0.2)	(294, 348, 408, 462; 0.2)	(294, 348, 408, 462; 0.2)	(294, 348, 408, 462; 0.2)	(294, 348, 408, 462; 0.2)

Table 9. The deviation (dev) of the methods for 5 numerical examples.

Pr.	Thota and Raja	Kaur and Kuman	Mathur et al.	TrigAC-PSO
Pr.01	0	0.0505	0.136	0.0117
Pr.04	0.0028	0	0.2015	0
Pr.24	0	0.0278	0.0278	0.0213
Pr.27	0	0.0662	0.6617	0.0524
Pr.28	0	0	0	0
Average	0.00056	0.0289	0.2054	0.01708

Table 10. Solutions for 20, 35, 50 particles

Pr.	20 Particles	35 Particles	50 Particles	Optimal
01	65.1	65.1	65.1	64.35
02	853.35	853.35	853.35	853.35
03	817.17	817.17	817.17	817.17
04	200.5	196	196	196
05	166	166	166	166
06	101	101	101	101
07	1770	1770	1770	1770
08	199	199	199	199
09	155.25	155.25	155.25	155.25
10	126	126	126	126
11	294	294	294	294
12	65.8	65.8	65.8	65.8
13	7735.5	7735.5	7735.5	7735.5
14	130.68	130.68	130.68	130.68
15	2327	2330	2261	2170
16	951.25	951.25	951.25	951.25
17	821.25	821.25	821.25	821.25
18	149	149	149	149
19	67.25	67.25	67.25	67.25
20	3640.56	3640.56	3640.56	3640.56
21	3844	3844	3844	3844
22	295.9	295.9	295.9	295.9
23	551.03	551.03	551.03	551.03
24	4389.6	4386.45	4399.35	4392
25	68	68	68	68
26	141	141	141	141
27	96.25	96.25	96.25	96.25
28	82.5	82.5	82.5	75.6

Table 11. The accuracy of the 28 problems for 20, 35 and 50 particles.

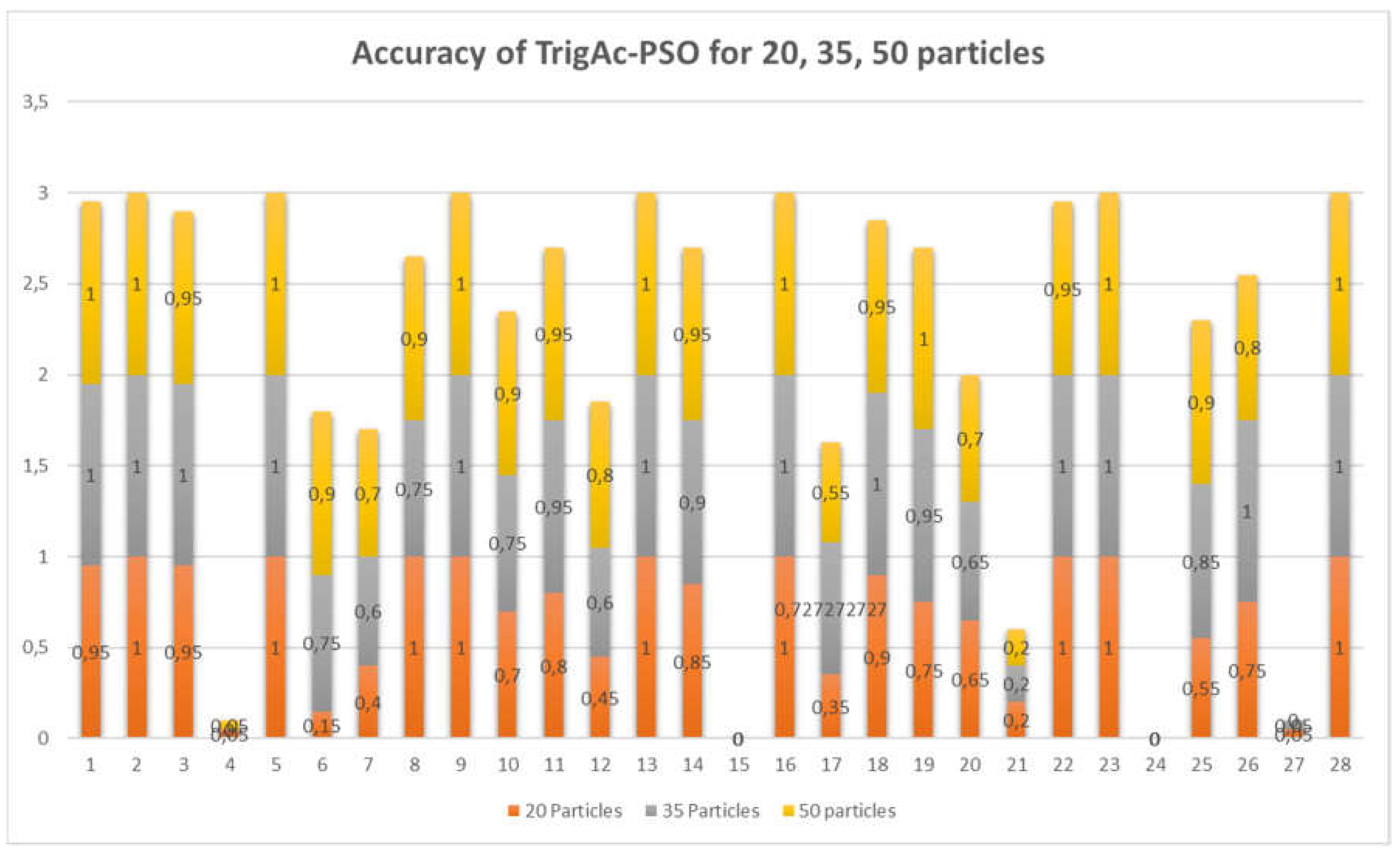
Pr.	20 Particles	35 Particles	50 particles
01	0.95	1	1
02	1	1	1
03	0.95	1	0.95
04	0.05	0	0.05
05	1	1	1
06	0.15	0.75	0.9
07	0.4	0.6	0.7
08	1	0.75	0.9
09	1	1	1
10	0.7	0.75	0.9
11	0.8	0.95	0.95
12	0.45	0.6	0.8
13	1	1	1
14	0.85	0.9	0.95
15	0	0	0
16	1	1	1
17	0.35	0.727273	0.55
18	0.9	1	0.95
19	0.75	0.95	1
20	0.65	0.65	0.7
21	0.2	0.2	0.2
22	1	1	0.95
23	1	1	1
24	0	0	0
25	0.55	0.85	0.9
26	0.75	1	0.8
27	0.05	0.05	0
28	1	1	1
Average	0.6607143	0.74026	0.755357

Table 12. Statistical measures for 20, 35 and 50 particles.

		20 particles	35 particles	50 particles
	Mean	65.225	65.1	65.1
	St.Dev	0.559016994	0	0
Pr.01	Min	65.1	65.1	65.1
	Max	67.6	65.1	65.1
	CV%	0.857059401	0	0
	Mean	853.35	853.35	853.35
	St.Dev	0	0	0
Pr.02	Min	853.35	853.35	853.35
	Max	853.35	853.35	853.35
	CV%	0	0	0
	Mean	817.659	817.17	817.49
	St.Dev	2.186874482	0	1.431083506
Pr.03	Min	817.17	817.17	817.17
	Max	826.95	817.17	823.57
	CV%	0.267455563	0	0.175058228
	Mean	204.285	203.225	200.765
	St.Dev	3.305700817	3.247002666	1.578898683
Pr.04	Min	200.5	196	196
	Max	210.2	210.1	203.4
	CV%	1.618180883	1.597737811	0.786441204
	Mean	166	166	166
	St.Dev	0	0	0
Pr.05	Min	166	166	166
	Max	166	166	166
	CV%	0	0	0
	Mean	102.575	101.45	101.2
	St.Dev	0.712205618	0.809483266	0.615587011
Pr.06	Min	101	101	101
	Max	103	103	103
	CV%	0.694326705	0.79791352	0.608287561
	Mean	1818.4125	1809.3875	1782.35
	St.Dev	76.91593476	69.08406754	26.25888321
Pr.07	Min	1770	1770	1770
	Max	2020	2020	1870
	CV%	4.229839751	3.818091345	1.473273106
	Mean	199	200.5	199.6
	St.Dev	0	2.66556995	1.846761034
Pr.08	Min	199	199	199
	Max	199	205	205
	CV%	0	1.329461322	0.925230979
	Mean	155.25	155.25	155.25
	St.Dev	0	0	0
Pr.09	Min	155.25	155.25	155.25
	Max	155.25	155.25	155.25
	CV%	0	0	0
	Mean	126.3	126.25	126.1
	St.Dev	0.470162346	0.444261658	0.307793506
Pr.10	Min	126	126	126
	Max	127	127	127
	CV%	0.37225839	0.351890422	0.24408684
	Mean	294.55	295.35	295.4
	St.Dev	1.234376041	6.037383539	6.260990337
Pr.11	Min	294	294	294
	Max	298	321	322
	CV%	0.419071818	2.044145434	2.119495713
	Mean	69.535	67.64	66.72
	St.Dev	6.309080757	2.312073574	1.887800168
Pr.12	Min	65.8	65.8	65.8
	Max	94.5	70.4	70.4
	CV%	9.073244779	3.418204574	2.829436702
	Mean	7735.5	7735.5	7735.5
	St.Dev	0	0	0
Pr.13	Min	7735.5	7735.5	7735.5
	Max	7735.5	7735.5	7735.5
	CV%	0	0	0
	Mean	132.418	132.3165	131.4825
	St.Dev	4.483441582	5.065924631	3.588889104
Pr.14	Min	130.68	130.68	130.68
	Max	147.39	148.71	146.73
	CV%	3.385824874	3.828641652	2.729556484
	Mean	2703.45	2738.7	2445.35
	St.Dev	251.6408207	400.1072356	138.7706457
Pr.15	Min	2327	2330	2261
	Max	3275	3585	2795
	CV%	9.308136665	14.60938532	5.674878675
	Mean	951.25	951.25	951.25
	St.Dev	0	0	0
Pr.16	Min	951.25	951.25	951.25
	Max	951.25	951.25	951.25
	CV%	0	0	0
	Mean	829.9	826.775	823.8125
	St.Dev	15.6005651	11.11983174	3.498002249
Pr.17	Min	821.25	821.25	821.25
	Max	878	868	834.75
	CV%	1.879812641	1.344964681	0.424611456
	Mean	149.45	149	149.15
	St.Dev	1.468081455	0	0.670820393
Pr.18	Min	149	149	149
	Max	155	149	152
	CV%	0.98232282	0	0.449762248
	Mean	68.1	67.4	67.25
	St.Dev	2.684507208	0.670820393	0
Pr.19	Min	67.25	67.25	67.25
	Max	79	70.25	67.25
	CV%	3.942007647	0.995282483	0
	Mean	3641.096	3641.297	3641.029
	St.Dev	0.801645676	1.265647743	0.786771551
Pr.20	Min	3640.56	3640.56	3640.56
	Max	3643.24	3644.58	3643.24
	CV%	0.022016604	0.034758157	0.021608494
	Mean	3896.4125	3896.4125	3896.4125
	St.Dev	53.85245896	53.85245896	53.85245896
Pr.21	Min	3844	3844	3844
	Max	4020	4020	4020
	CV%	1.382103639	1.382103639	1.382103639
	Mean	295.9	298.6665	295.9
	St.Dev	0	12.37216412	0
Pr.22	Min	295.9	295.9	295.9
	Max	295.9	351.23	295.9
	CV%	0	4.142467977	0
	Mean	551.03	551.03	551.03
	St.Dev	0	0	0
Pr.23	Min	551.03	551.03	551.03
	Max	551.03	551.03	551.03
	CV%	0	0	0
	Mean	4518.15	4465.515	4446.8775
	St.Dev	106.2485727	59.47704135	43.52466474
Pr.24	Min	4389.6	4386.45	4399.35
	Max	4857.3	4629	4580.55
	CV%	2.351594629	1.331918969	0.978769142
	Mean	70.4	68.15	68.2
	Var	4.159959514	0.366347549	0.695852374
Pr.25	Min	68	68	68
	Max	82	69	71
	CV%	5.909033401	0.537560599	1.020311399
	Mean	143.5	141	143.2
	St.Dev	4.442616583	0	4.583724066
Pr.26	Min	141	141	141
	Max	151	141	155
	CV%	3.095900058	0	3.200924627
	Mean	96.19	96.13	96.55
	St.Dev	1.198420012	1.343052297	0.53311399
Pr.27	Min	91.45	91.45	96.25
	Max	97.45	97.45	97.45
	CV%	1.245888359	1.397120875	0.552163635
	Mean	82.5	82.5	82.5
	St.Dev	0	0	0
Pr.28	Min	82.5	82.5	82.5
	Max	82.5	82.5	82.5
	CV%	0	0	0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Solving Fuzzy Transportation Problem: Exploring a Novel Particle Swarm Optimization Approach

Abstract

1. Introduction

2. Transportation Problem (TP)

3. Fuzzy Logic Definitions

3.1. Fuzzy Sets and Membership Functions

3.2. Generalized fuzzy numbers

3.3. Arithmetic Operations

4. Fuzzy Transportation Problem

5. Particle Swarm Optimization (PSO)

5.1. Trigonometric Acceleration Coefficient – Particle Swarm Optimization (TrigAC-PSO)

6. Case Studies and Experimental Results

7. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe