Submitted:
02 May 2024
Posted:
03 May 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction and Formalism
2. Results
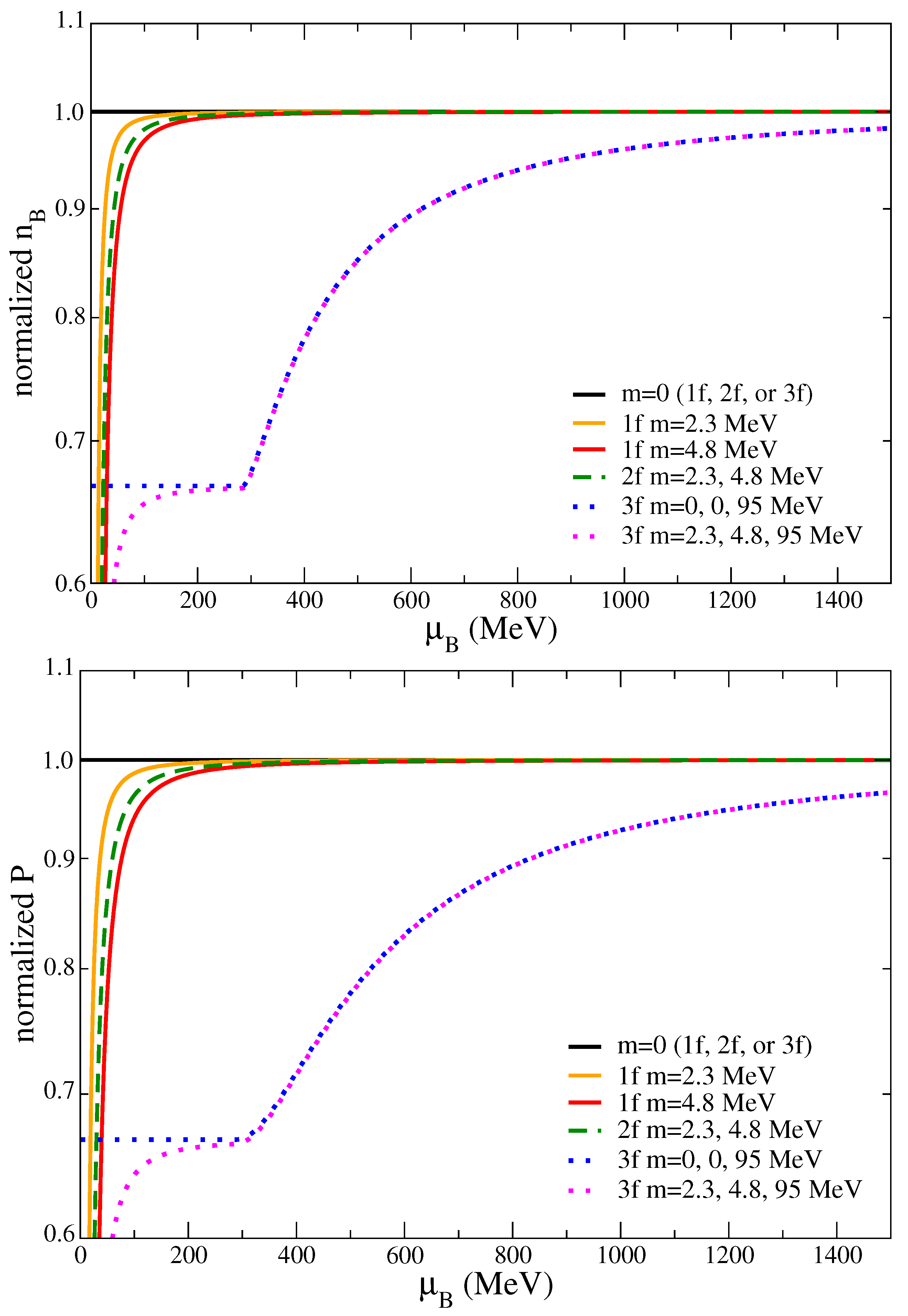
2.1. One Chemical Potential
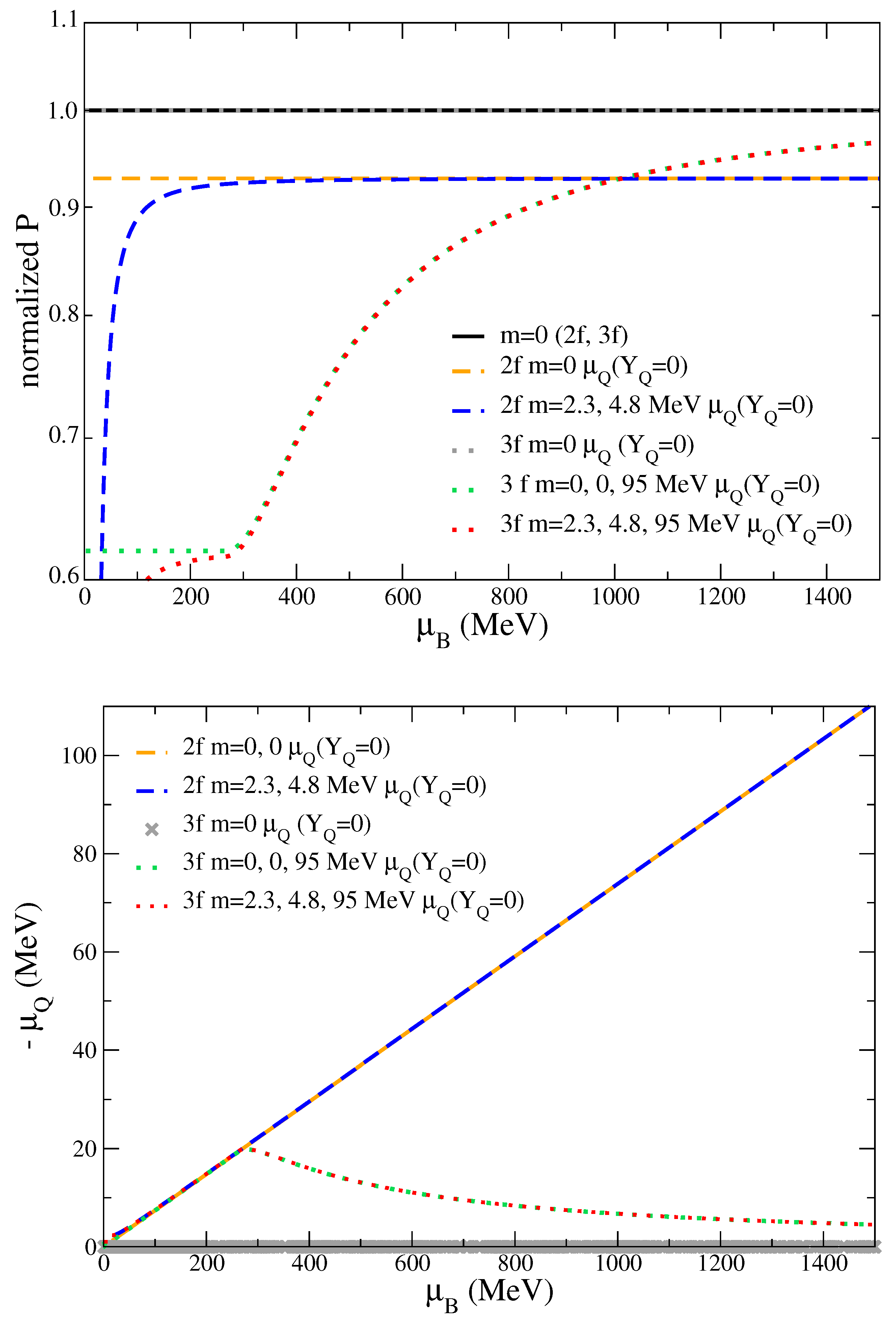
2.2. Two Chemical Potentials and
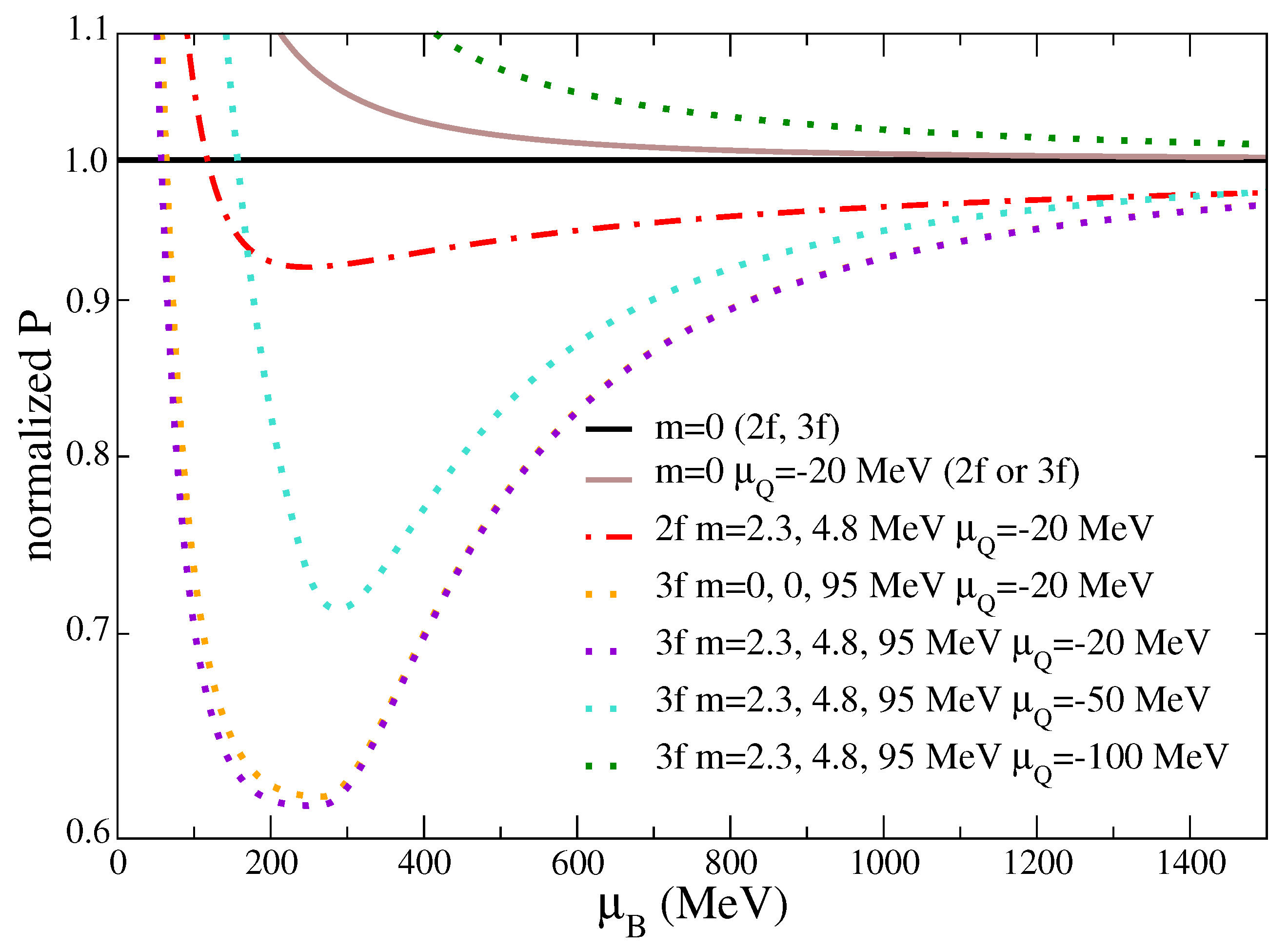
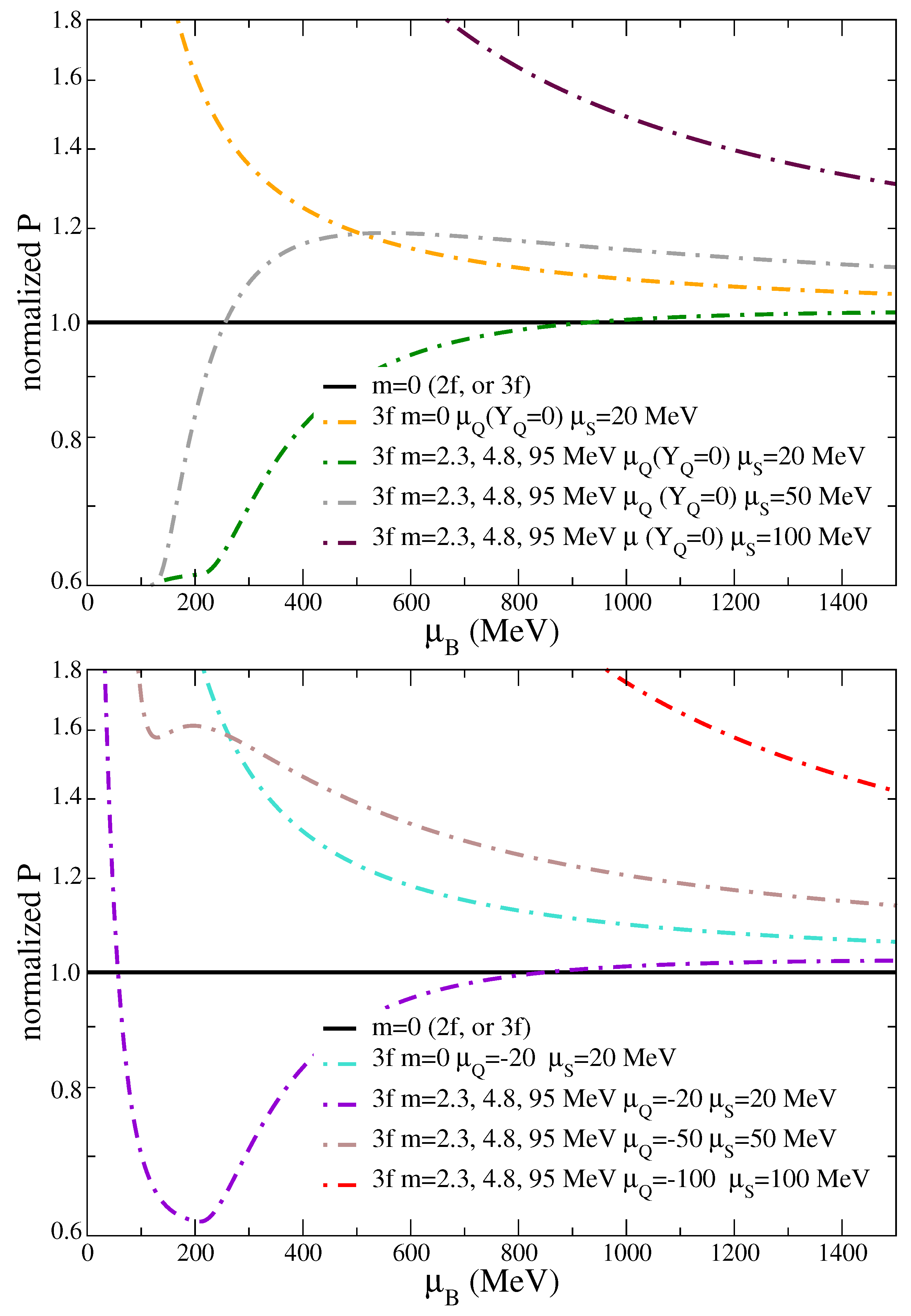
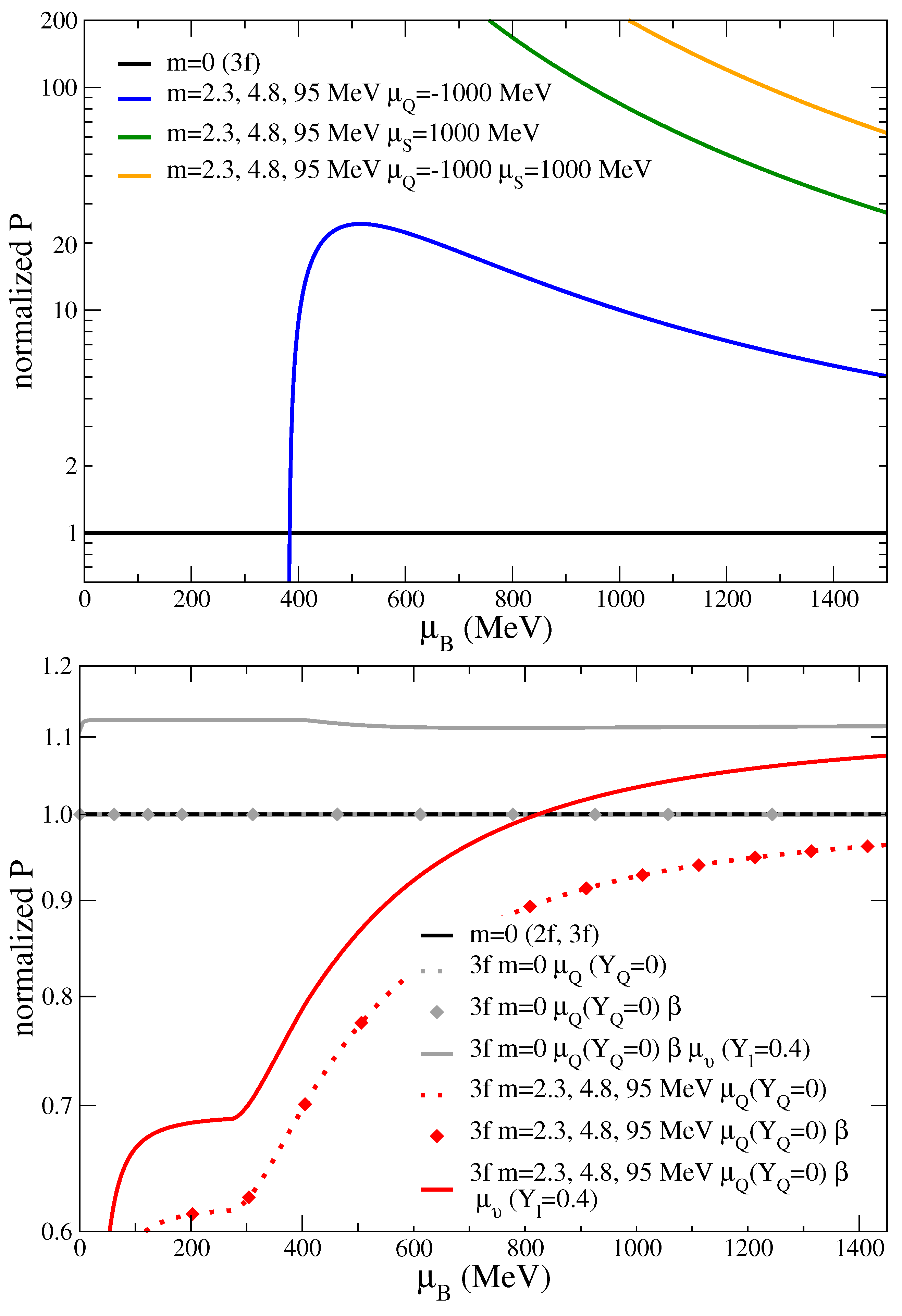
2.3. Three Chemical Potentials , , and or
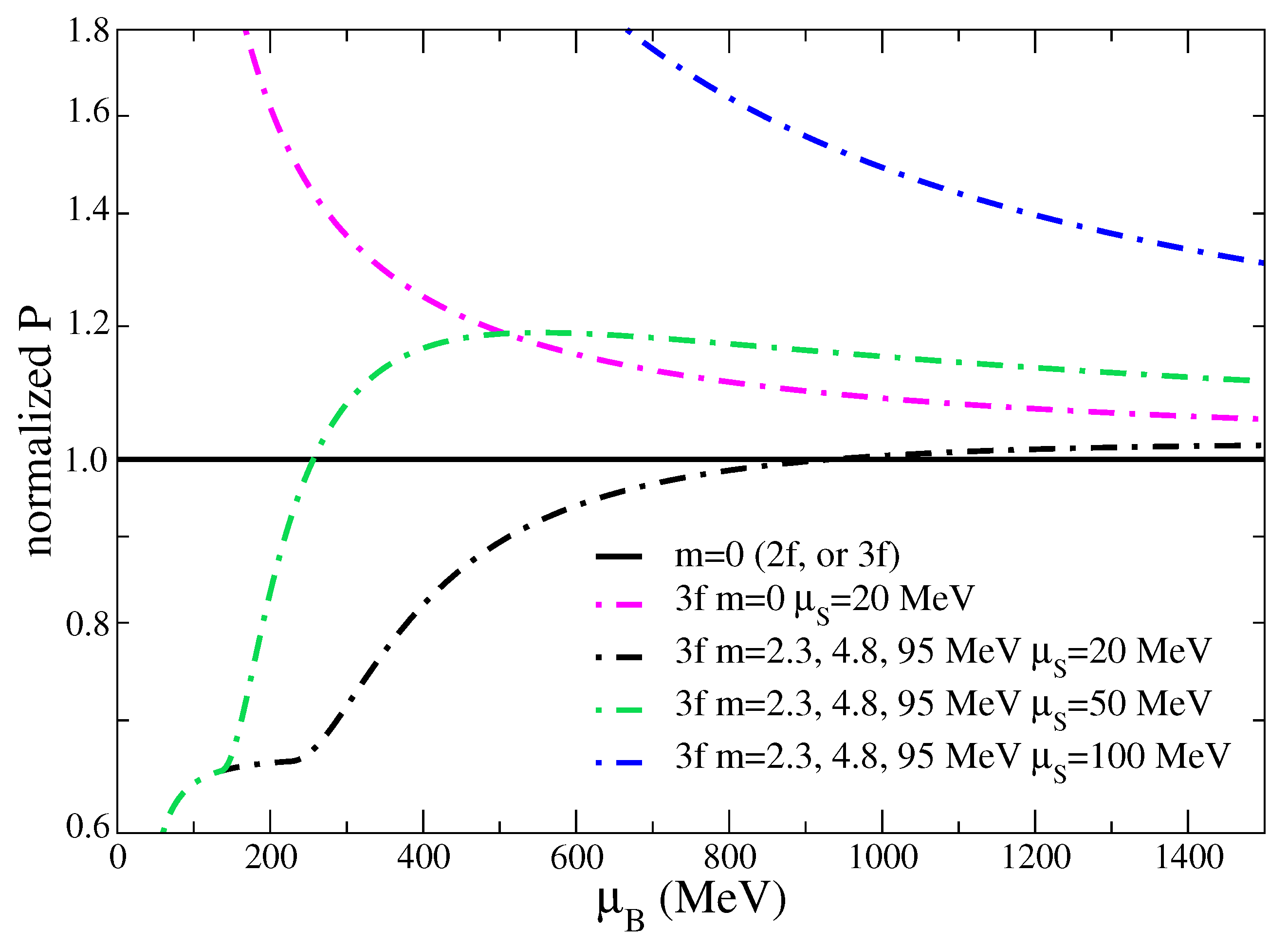
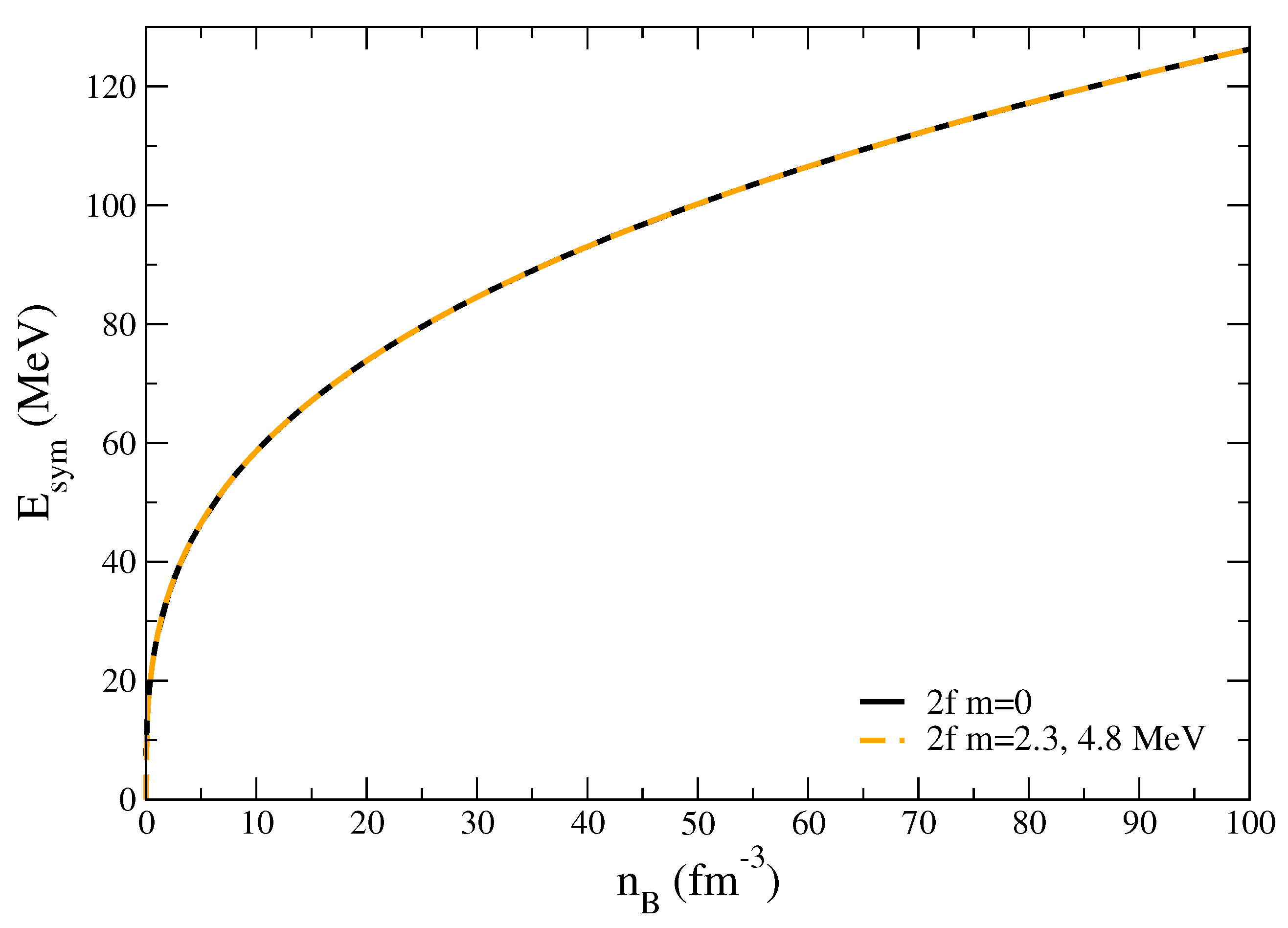
2.4. Symmetry Energy
3. Discussion and Conclusions
Acknowledgments
Abbreviations
Appendix A. General Expressions
Appendix B. Massless Quarks
- 2-flavor,
- 3-flavor, ,
- 2-flavor, fixed
- 2-flavor, from charge neutrality
- 3-flavor, fixed,
- 3-flavor, from charge neutrality,
- 3-flavor, zero net strangeness
- 3-flavor, fixed, fixed
- 3-flavor fixed
- 3-flavor, from charge neutrality, fixed
References
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Letessier, J.; Tounsi, A.; Heinz, U.W.; Sollfrank, J.; Rafelski, J. Strangeness conservation in hot nuclear fireballs. Phys. Rev. D 1995, 51, 3408–3435. [Google Scholar] [CrossRef]
- Chu, P.C.; Chen, L.W. Quark matter symmetry energy and quark stars. Astrophys. J. 2014, 780, 135. [Google Scholar] [CrossRef]
- Chen, L.W. Symmetry Energy in Nucleon and Quark Matter. Nucl. Phys. Rev. 2017, 34, 20–28. [Google Scholar] [CrossRef]
- Wu, X.; Ohnishi, A.; Shen, H. Effects of quark-matter symmetry energy on hadron-quark coexistence in neutron-star matter. Phys. Rev. C 2018, 98, 065801. [Google Scholar] [CrossRef]
- Thakur, S.; Dhiman, S.K. Temperature Effects in Quark Matter Symmetry Free Energy. DAE Symp. Nucl. Phys. 2017, 62, 696–697. [Google Scholar]
- Aryal, K.; Constantinou, C.; Farias, R.L.S.; Dexheimer, V. High-Energy Phase Diagrams with Charge and Isospin Axes under Heavy-Ion Collision and Stellar Conditions. Phys. Rev. D 2020, 102, 076016. [Google Scholar] [CrossRef]
- Yao, N.; Sorensen, A.; Dexheimer, V.; Noronha-Hostler, J. Structure in the speed of sound: From neutron stars to heavy-ion collisions. 2023; arXiv:nucl-th/2311.18819]. [Google Scholar]
- Burrows, A.; Lattimer, J.M. The birth of neutron stars. Astrophys. J. 1986, 307, 178–196. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Gorda, T.; Kurkela, A.; Paatelainen, R.; Säppi, S.; Vuorinen, A. Cold quark matter at N3LO: Soft contributions. Phys. Rev. D 2021, 104, 074015. [Google Scholar] [CrossRef]
- Gorda, T.; Kurkela, A.; Paatelainen, R.; Säppi, S.; Vuorinen, A. Soft Interactions in Cold Quark Matter. Phys. Rev. Lett. 2021, 127, 162003. [Google Scholar] [CrossRef] [PubMed]
- Kurkela, A.; Romatschke, P.; Vuorinen, A. Cold Quark Matter. Phys. Rev. D 2010, 81, 105021. [Google Scholar] [CrossRef]
- Graf, T.; Schaffner-Bielich, J.; Fraga, E.S. The impact of quark masses on pQCD thermodynamics. Eur. Phys. J. A 2016, 52, 208. [Google Scholar] [CrossRef]
- Gorda, T.; Säppi, S. Cool quark matter with perturbative quark masses. Phys. Rev. D 2022, 105, 114005. [Google Scholar] [CrossRef]
- Workman, R.L.; Others. Review of Particle Physics. PTEP 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Holdom, B.; Ren, J.; Zhang, C. Quark matter may not be strange. Phys. Rev. Lett. 2018, 120, 222001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




