Prerpints.org logo
Preprint
Article

Generation of Propagation-Dependent OAM Self-Torque with Chirped Spiral Gratings

Altmetrics

Downloads

82

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 May 2024

Posted:

06 May 2024

You are already at the latest version

Alerts
Abstract
The application of non-uniform spiral gratings to control structure, topological parameters and propagation of orbital angular momentum (OAM) beams was studied experimentally with coherent near-infrared light. Adapted digital spiral grating structures were programmed into the phase map of a high-resolution liquid-crystal-on-silicon spatial light modulator (LCoS-SLM). It is shown that characteristic spatio-spectral anomalies related to Gouy phase shift can be used as pointers to quantify rotational beam properties. Depending on sign and gradient of spatially variable periods of chirped spiral gratings (CSG), variations of rotation angle and angular velocity as a function of propagation distance were measured. Propagation-dependent self-torque is introduced in analogy to known local self-torque phenomena of OAM beams as obtained by the superposition of temporally chirped or phase modulated wavepackets.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

During the last few decades, the generation, detection and application of structured light [1,2] including orbital angular momentum (OAM) beams [3,4,5,6,7,8,9,10,11,12,13,14,15] were the subject of intensive research. In particular, wide spectral bandwidths and high intensities of ultrashort-pulsed lasers opened new prospects for optical communication, materials processing, nonlinear spectroscopy, metrology or particle manipulation. Characteristic anomalies in spectral and spatial domain in the vicinity of singularities, so-called “spectral eyes” [16,17,18,19,20,21], result from wavelength-dependent Gouy phase shift and spectral interference [22,23,24]. Related spectral re-distribution effects were previously detected by highly-resolved spectral mapping of femtosecond OAM laser pulses. The calculation of local (first order) and global (higher order) spectral statistical moments [25] was used to extract topological and rotational beam parameters. Moreover, the statistical formalism provides appropriate tools for advanced applications like, e.g., deep encryption, imaging, ranging, selective excitation, or optical processing. For the variable generation and manipulation of OAM beams by tunable phase and/or amplitude maps, the following approaches are of technical interest: (a) MEMS spiral phase plates (SPPs) [26], (b) digital mirror devices (DMD) [27], (c) liquid crystal spatial light modulators (SLMs) [28,29], and (d) cascaded [29] or combined [30,31] systems. Singularities in wave fields can be generated by phase dislocations in forked rectilinear or spiral grating structures [5,32,33,34,35]. Spiral phase gratings (SPGs) act as diffractive axicons with an axially extended focal zone and a helical wavefront [36,37,38]. SPG were developed for THz applications [39] and for the generation of acoustic vortices with electro-mechanical transducers [40,41,42,43,44,45,46,47,48].
For high-speed spatial phase modulation in optical range, DMDs are of interest because of one order of magnitude higher reported switching speed [49]. Phase stroke, linearity, fill factor and further parameters, however, are still not satisfying. A specific advantage of the liquid-crystal-on-silicon (LCoS)-SLM technique [50,51,52,53,54,55,56] consists in the large number of addressable small pixels with, at the same time, phase-shifting functionality at high dynamic range and calibrated phase. This combination is still not fully available with DMDs. Because of the high structural flexibility it is possible to write even complex reconfigurable diffractive optical elements (DOE) into advanced types of SLMs.
Recently we reported on first proof-of-principle experiments with high-resolution phase-only LCoS-SLMs as programmable non-uniform SPGs [57]. Here we present the results of continuing studies and a more detailed discussion. In particular, the concept of OAM self-torque is extended by a propagation-dependent acceleration or deceleration of angular rotation as an alternative approach.

2. Spiral Phase Gratings

The mechanism of axial beam shaping with spiral DOE is based on a radial-to-axial transformation. Radial variations of the grating period modulate the angular spectrum of interfering conical beams along the propagation path. If the rms radius of an illuminating Gaussian beam is held constant, the far-field divergence of OAM beams generated by grating dislocations scales linearly with the OAM [58]. The reflective operation of LCoS-SLM requires either to transform the shape of the programmed optical elements into its elliptical projection as a function of the angle of incidence, or to work at sufficiently small incident angles. In a slightly simplified picture, one can distinguish between selected cases of planar spiral gratings with respect to their silhouette (shape of edge):
A*) grating completely filling a circle
B*) grating completely filling an ellipse
C*) toroidal grating filling a single annulus (1 ring)
D*) grating filling center and annulus (center, 1 ring)
E*) multi-toroidal grating filling multiple annuli (N rings)
Furthermore, the uniformity and symmetry properties of spiral gratings can be described by the spatial distribution of the grating period p(r,θ) in polar representation with r and θ as the radial and azimuthal coordinates, respectively:
1*) constant grating period (uniform Archimedean grating)
2*) radially monotonically increasing spatial frequency (positive chirp)
3*) radially monotonically decreasing spatial frequency (negative chirp)
4*) grating period depending on θ (oscillating chirp)
Selected configurations with single spirals or composed uniaxial spirals of identical rotational orientation are, without claiming to be exhaustive, depicted in Figure 1. Recently, asymmetric elliptical gratings of type (C*,1*) were proposed for shaping toroidal vortex beams [59].
Previously it was demonstrated by experiments with stationary spiral axicons that the rotation of characteristic spectral features can be controlled via the grating period p(r) [23]. With SLMs, more free parameters and temporal modulation capability (within the limits of the cut-off frequency) become available. In particular, a continuous radial variation of p(r) as well as a discontinuous section-wise design can be used to obtain a propagation dependent rotation. The radial variation of the inverse period ν = p-1 is the signed spatial frequency chirp dν/dr.
Imaging properties, spectral response and diffraction efficiency of non-uniform binary gratings strongly depend on the individual phase structure of the grating, the angular spectrum of the illuminating beam, its frequency spectrum, polarization and coherence.
The m-th order convergence angle β of a reflective spiral axicon at small incident angles as a function of the wavelength λ and the period p(r) can approximately be described via the grating equation:
β ( r ) = sin − 1 ⁡ m · λ p ( r )
One should notice the convention that the angle β in eq. (1) is the half total convergence angle. For each β(r) one can define corresponding radially dependent “focal distances” f(r):
f ( r ) = r t a n sin − 1 ⁡ m · λ p r
A radially uniform Archimedean spiral grating axicon generates Bessel-like intensity profiles [33]. For non-uniform SPG, the propagation characteristics depend on the individual 2D phase envelope. In particular case (A*,3*), the outer parts of a continuous grating with smaller p diffract the light stronger than the parts closer to the center. This can lead to an overlap and interference of partial beams. Case 4*) is obtained by a grating transformation by linear stretching in one direction (mapping a circle to an ellipse) which is equivalent to illumination at oblique incidence [57]. In this case, p oscillates with increasing rotation angle ϕ and passes two maxima and two minima within every full rotational period of Δϕ = 2π. Therefore, one has to expect that the rotational parameters exhibit corresponding extrema at increasing propagation distance.

3. Propagation Dependent Self-Torque

In the spatial domain, the propagation-dependent Gouy rotation of “spectral eyes” of polychromatic OAM beams around singularities [22,23,24] can be described by a local angular gradient:
Ω ( z ) = ∂ φ ∂ z
where the rotational angle ϕ(𝑧) is the pointer position of a virtual connecting line between the centroids of two “spectral eyes” at a propagation distance z. This gradient results from the interference of all diffracted spectral contributions. In the temporal domain, one can formally define a corresponding angular velocity at a time t:
Ω t , z = ∂ φ ∂ t = c · Ω ( z )
(c = vacuum speed of light). For an ultrashort OAM pulse, eq. (4) describes the speed of angular rotation as a function of the pulse travel time. The temporal derivative of the angular velocity is a measure of rotational acceleration or deceleration and can be interpreted as a kind of “self-torque“[57]:
ξ t , z = ∂ Ω t , z ∂ t = ∂ 2 φ ∂ t 2 = c · ∂ Ω z ∂ t
Originally, the term “self-torque” was used for the temporal acceleration of an OAM at a fixed axial coordinate obtained by the superposition of frequency modulated wavepackets [60,61] or by interfering co-rotating wavepackets of different rotation speed [23]. The introduction of a propagation-dependent acceleration as described by eq. (5) enables to generalize the term “self-torque” covering both
(i) a local, interference-type, superposition-generated self-torque (SST)), and
(ii) a non-local, propagation-type self-torque (PST).
In special cases, these types can also appear simultaneously, e.g. by interference of overlapping contributions from SPG with positive chirp, as mentioned above.
SST is relevant for OAM-selective laser-matter interaction processes on ultrashort time scale and plays an important role, e.g., for high harmonics generation [60,61], the resonant excitation of quasi-particles by rotating ring-lattices [62], spin-to-orbit conversion, or optical spin-Hall effect in focused beams [63]. PST may also stimulate specific applications which require a sensibility against distances or pulse travel time.

4. Experimental Techniques

4.1. Experimental Setup

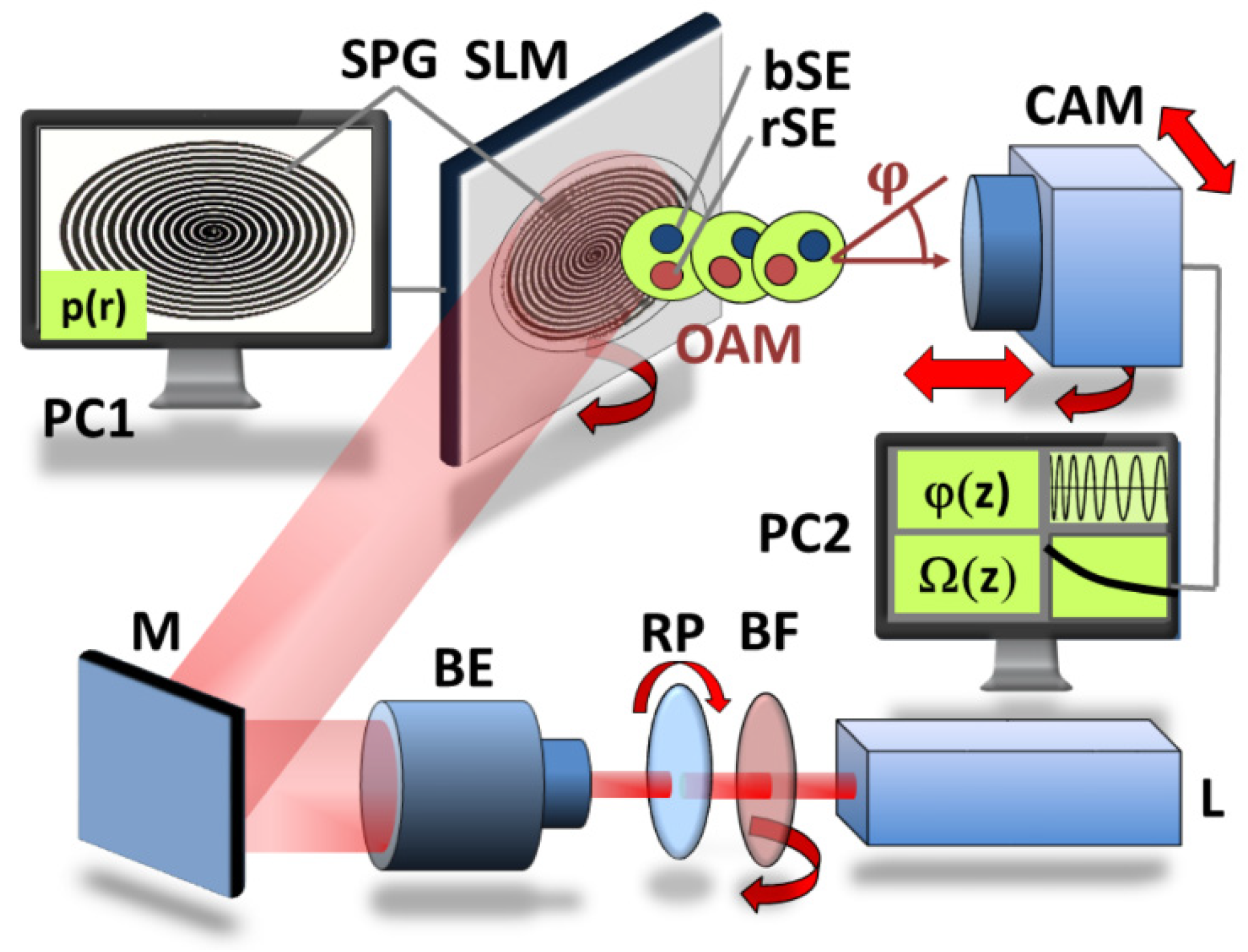
The experimental setup used for adaptive singular optics experiments is schematically drawn in Figure 2.
SPGs were programmed into the pixel matrix of a 10-megapixel (4K) phase-only reflective LCoS-SLM (GAEA, HOLOEYE Photonics, Berlin, Germany, pixel size 3.74 µm). Phase linearity was ensured by spectral calibration of grey scale values. Additionally, the contrast was optimized by adaptively varying the base level. The SLM was illuminated by a linearly polarized Ti:sapphire laser oscillator (center wavelength tunable between 780 and 810 nm) after 5x expanding the beam diameter to completely fill the active area of the microdisplay. A movable and rotatable near-infrared-enhanced, black-and-white CMOS camera (Thorlabs, Bergkirchen, Germany, DCC 324ONN, 1280 × 1024 pixels, pixel size 5.5 µm, 60 fps) served as a matrix detector. The spatial scale of the camera was adjusted and aberrations were evaluated by imaging the focal plane of a lithographically fabricated orthogonal microlens array (Heinrich Hertz Institute, Berlin) with 32 µm pitch as a reference. Saturation was avoided by attenuating the intensity with a rotatable polarizer. For programming SLM phase patterns and image analysis, two separate computers with related software packages were applied.
To characterize twist and self-torque phenomena of OAM beams, the spectral Gouy rotation [22,23,24] was exploited. The approach enables a direct visualization of spectrally resolved internal vortex structures instead of analyzing complex spiral interference patterns [64]. In contrast to time-consuming fiber-scanning techniques [25], single-shot detection of propagation-dependent azimuthal angles of spectral eyes with a matrix camera works much faster. From previous studies it was known that a channel bandwidth in few-nanometer range is sufficient to reliably separate spectral eyes [23]. Therefore, the spectral resolution of a tilted 10 nm metal interference bandpass filter for 794 nm (LC-HBP-794.9/1-25, Laser Components, Olching, Germany, total tilt range 20°) was used to identify the positions of spectral eyes and to adjust the transmission range.

4.2. Elliptical Continuously Chirped Gratings

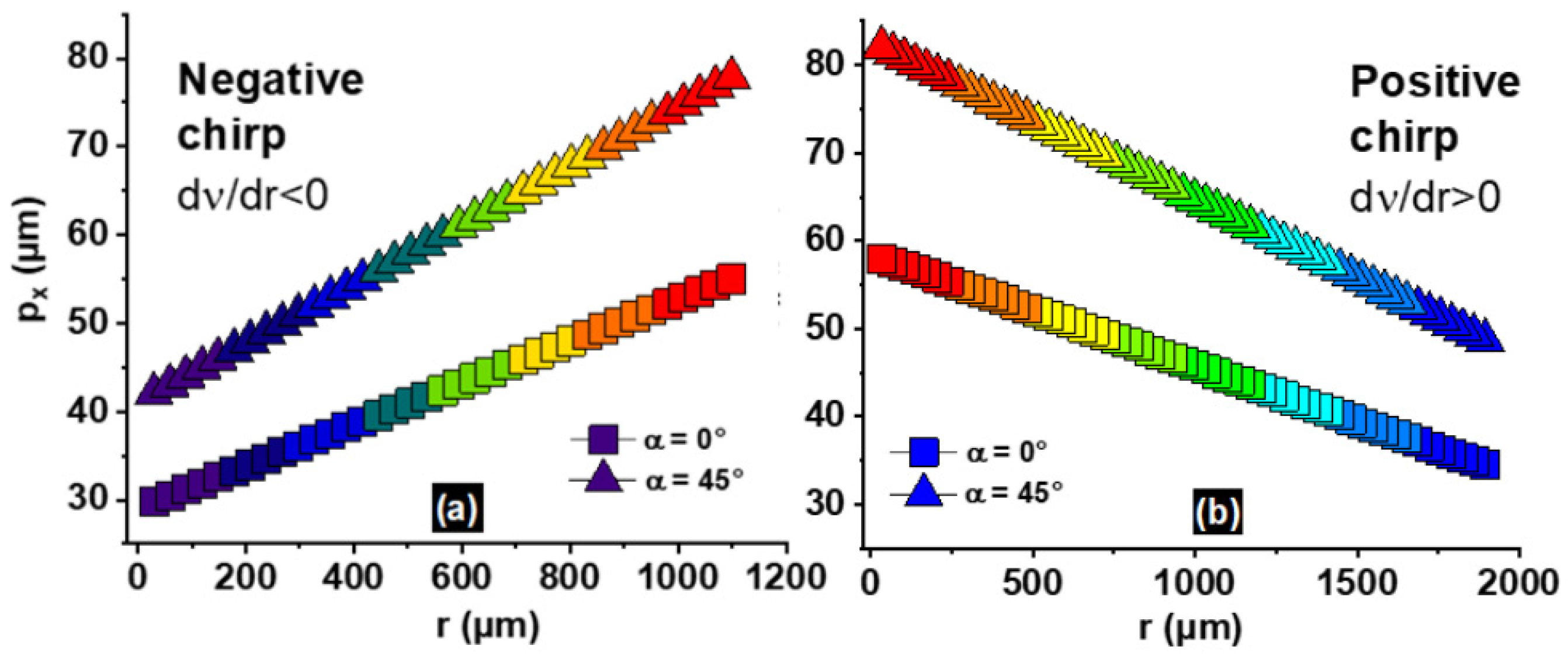
The radial change of the grating periods of spiral gratings with perfectly linear negative and positive spatial frequency chirp for realistic parameters is plotted in Figure 3a and Figure 3b, respectively.
To match non-zero tilt angles, the gratings have to be deformed to elliptical shape. The stretched periods expected for an incident angle of α = 45° can be compared to the case of normal incidence. The SPG with negative spatial frequency chirp was designed to be an Archimedean spiral with 37 windings and periods increasing from origin to the rim from 29 µm to 55 µm along the minor axis. The periods of the SPG with positive spatial frequency chirp along the minor axis were decrasing from 58 µm down to 34 µm along 55 windings. More details on the design strategy for linearly chirped SPGs can be found in the Appendix.
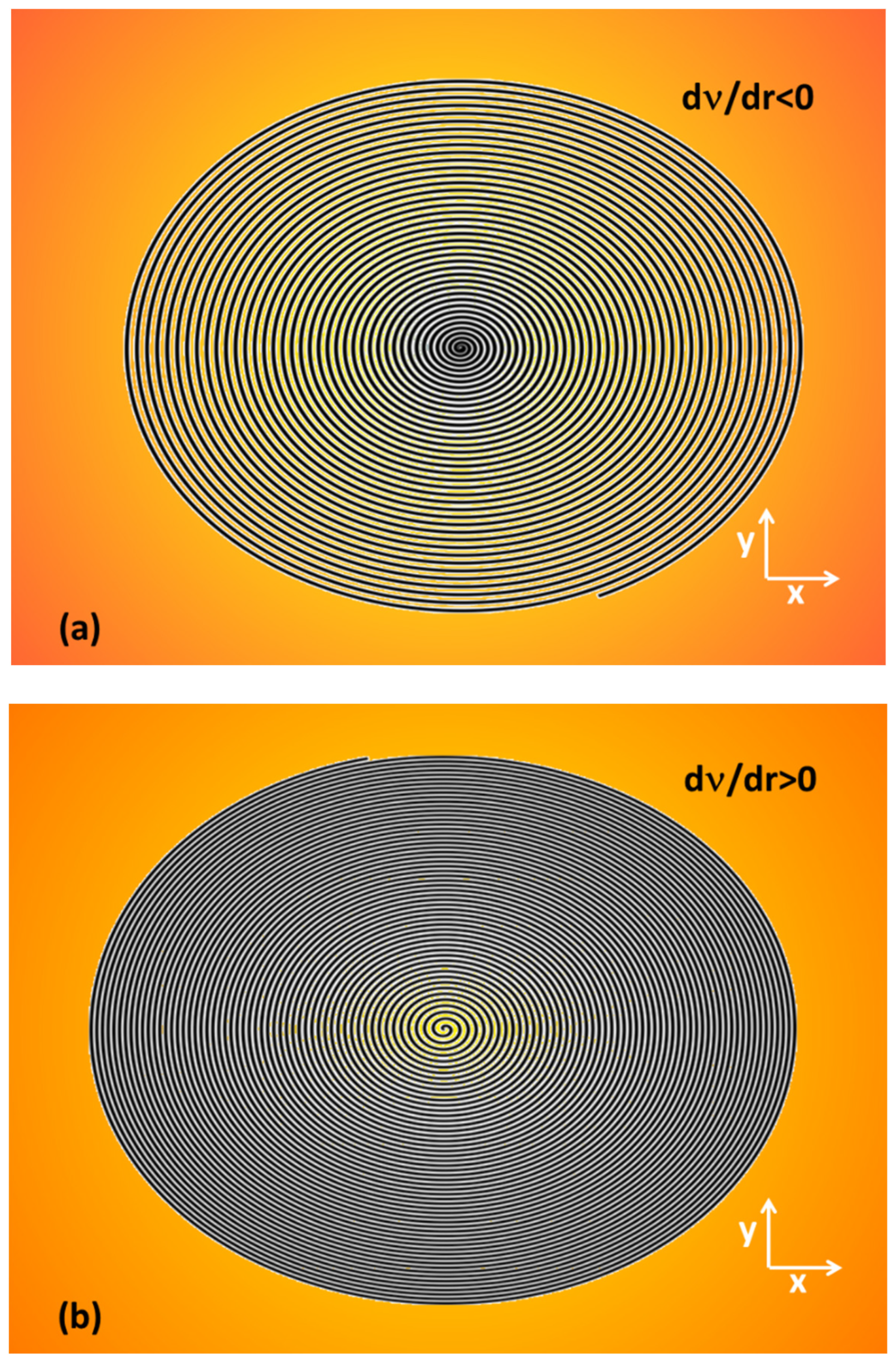
The spirals used in the experiments were generated with online available freeware (Inkscape 1.0x64). The resulting radial dependence of the grating periods deviated from perfect linear functions, in particular close to the center and the rim. The real radial chirp functions programmed into the SLM phase maps are plotted in Figure 4.
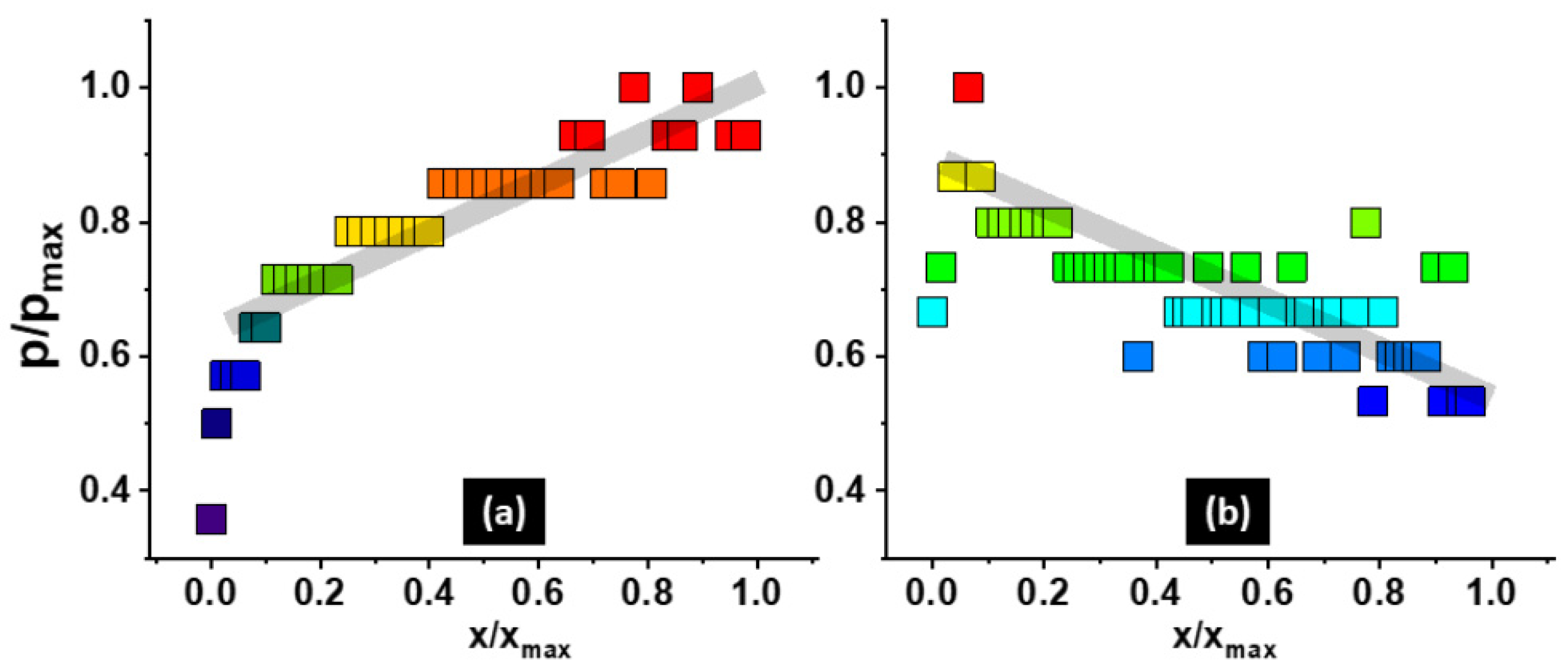
The real progression of periods (Figure 5) was determined by image processing software (ImageJ, Version 1.53k). The scattering of the data points along cuts is caused by the limited resolution of digital sampling at microscale.
Because of the pixel size of the SLM of 3.74 µm, the efficiency of the DOEs is limited by the Nyquist-Shannon sampling theorem. The design is less perfect at the highest spatial frequencies (grating periods < 30 µm) where the number of sampling points is < 5.
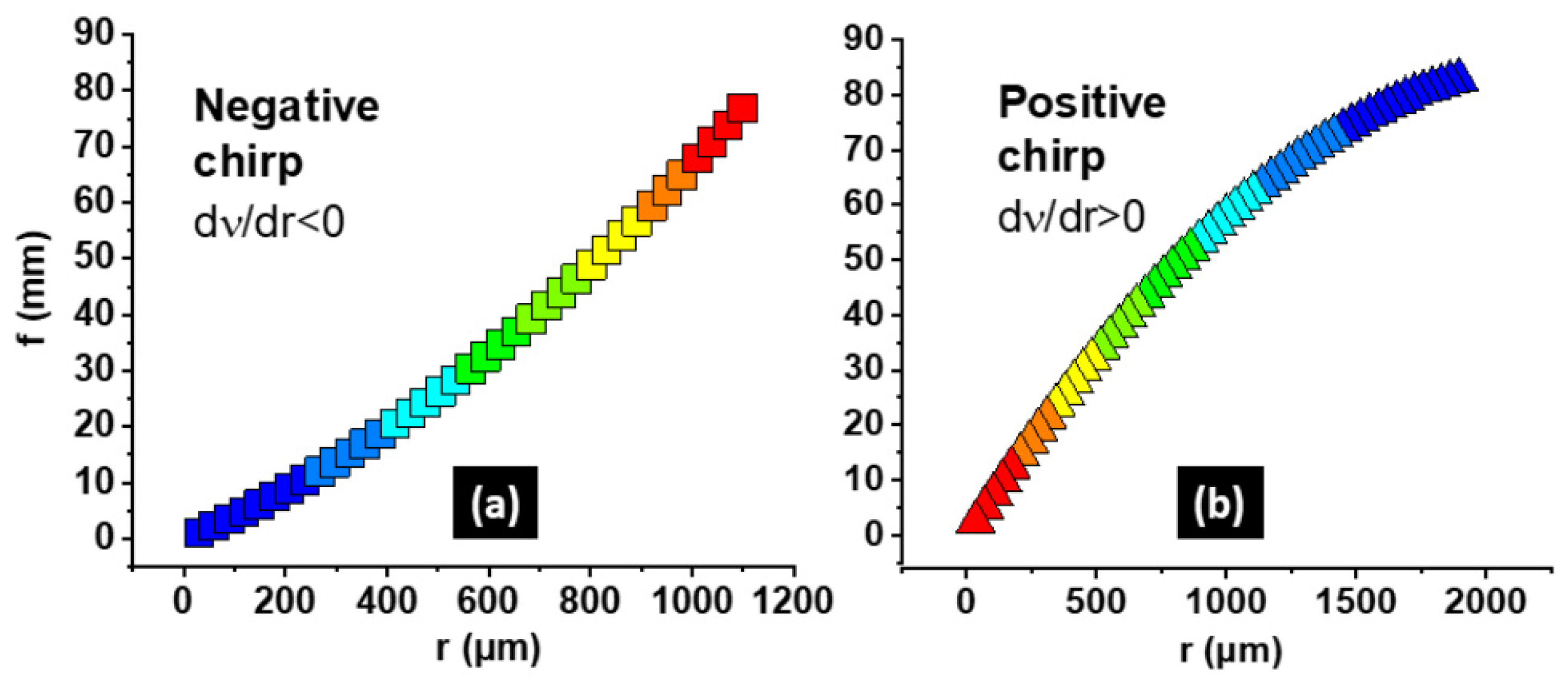
Figure 6 shows the “focal distances” in the m = 1st order as a function of SPG radii calculated by eq. (2) for perfect symmetric gratings with positive and negative chirp for a wavelength of 787 nm (spiral parameters see above). Despite of representing rough approximations, the graphs may give a qualitative indication of the expected axial beam shaping behavior.
One can recognize that the functions zF(r) are slightly nonlinear and, over the relevant spectral range of about 20 nm, nearly independent on the laser wavelengths (regarding the spectral bandwidth, see also paragraph 5.1).

4.3. Non-Uniform Toroidal Gratings

Alternative experiments were performed with SPGs consisting of an elliptical torus surrounding a central elliptical SPG. Figure 7 shows such a grating structure of type (D*,4*) (see Figure 1i). Both partial gratings are streched in one direction but, contrary to the SPGs in Figure 4a and Figure 4b, without spatial frequency chirp along radial cuts. The inner SPG, however, has a higher spatial frquency. The periods in the directions of minor and major axes are 17 µm and 45 µm for the inner elliptical SPG, for the surrounding torus 21 µm and 54 µm, respectively.
The partial gratings are not spatially chirped for each azimuthal angle but stretched in x-direction. The gap has a depth of about 0.56 times the torus width.

5.1. Spectral Filtering

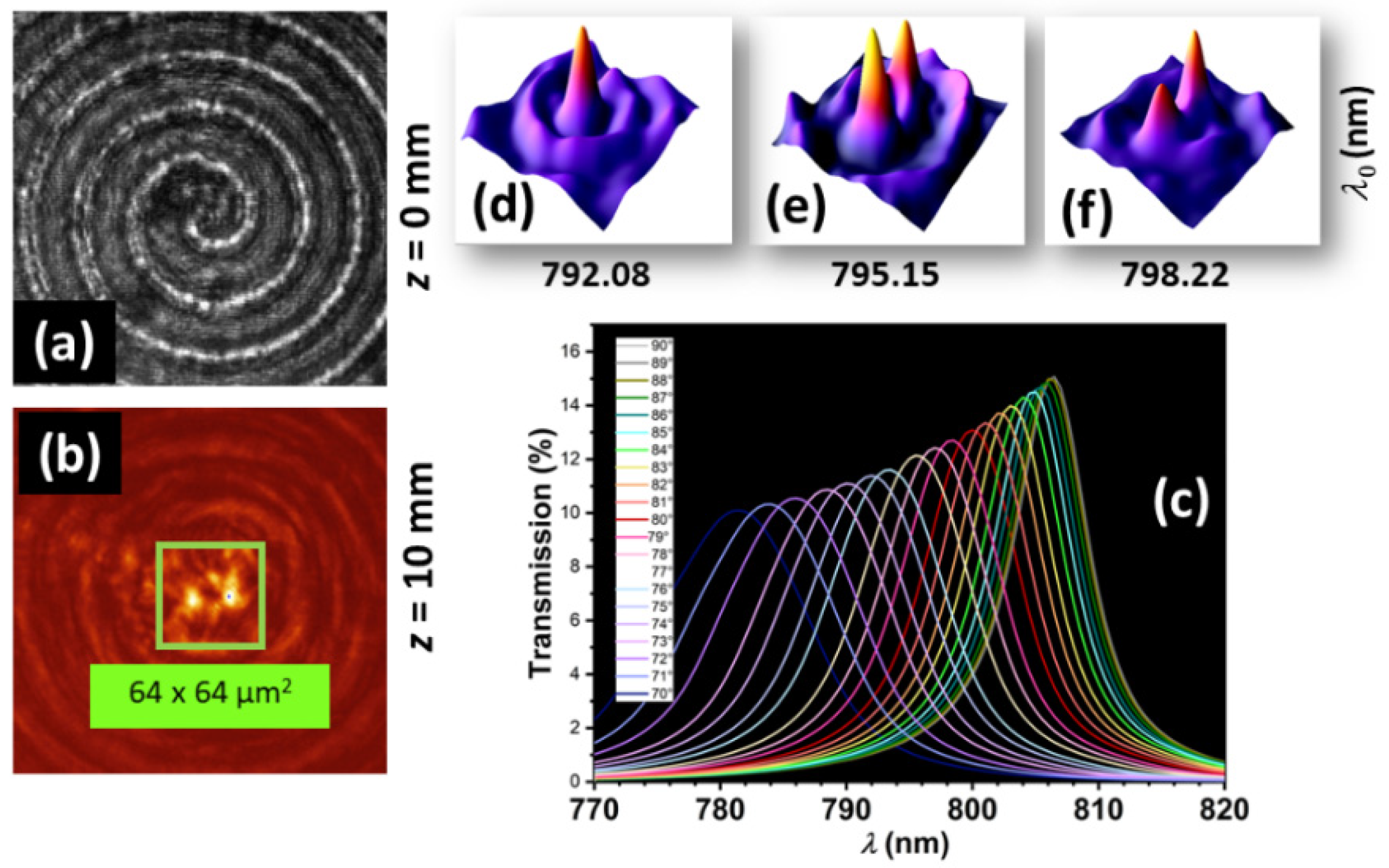
To select the characteristic “spectral eyes” as indicators for the spectral Gouy rotation, the spectral filter was adjusted to an appropriate tilt state at which the broadband background signal is attenuated whereas both the blue- and red-shifted parts around the singularity appear at comparable intensity. The selectivity was verified by alternatingly attenuating the different maxima by varying the tilt angle (Figure 8). Spectra were detected by a high-resolution spectrometer (HR 2000, Ocean Optics, Duiven, The Netherlands). This enabled to identify the spectral conditions for simultaneously detecting the blue- and red-shifted contributions at maximum intensity and contrast. An optimum wavelengths range was found between 784 nm and 787 nm at bandpass FWHM of about 7 nm.

5.2. Grating Aberrations at Oblique Incidence

The application of an SLM enables to adaptively correct for angular-dependent aberrations. From the literature it is known that spiral gratings at oblique incidence generate typical diamond-shaped light patterns [33]. In our investigations, we studied the response of this effect on the tilt angle at the relevant parameters. For an elliptically stretched SPG with a design angle of 45° it was found that the angular tolerance is critical. Even for an angular mismatch smaller than 2°, the rhomboidal distortion is clearly observed. The internal structure of the aberrated field looks complex and has some similarity to higher order laser modes. This effect and additionally the appearance of asymmetrically distributed higher grating diffraction orders are visible in Figure 9 for a misadjusted 45°-SPG illuminated at a central wavelength of about 790 nm.

5.3. Propagation Dependent Self-Torque

Propagation experiments with spectral selection were performed with the three types of non-uniform spiral gratings:
(1)
SPG-1 corresponding to Figure 4b (elliptical, negative chirp),
(2)
SPG-2 corresponding to Figure 4a (elliptical, positive chirp), and
(3)
SPG-3 corresponding to Figure 7 (elliptical and toroidal, different periods).
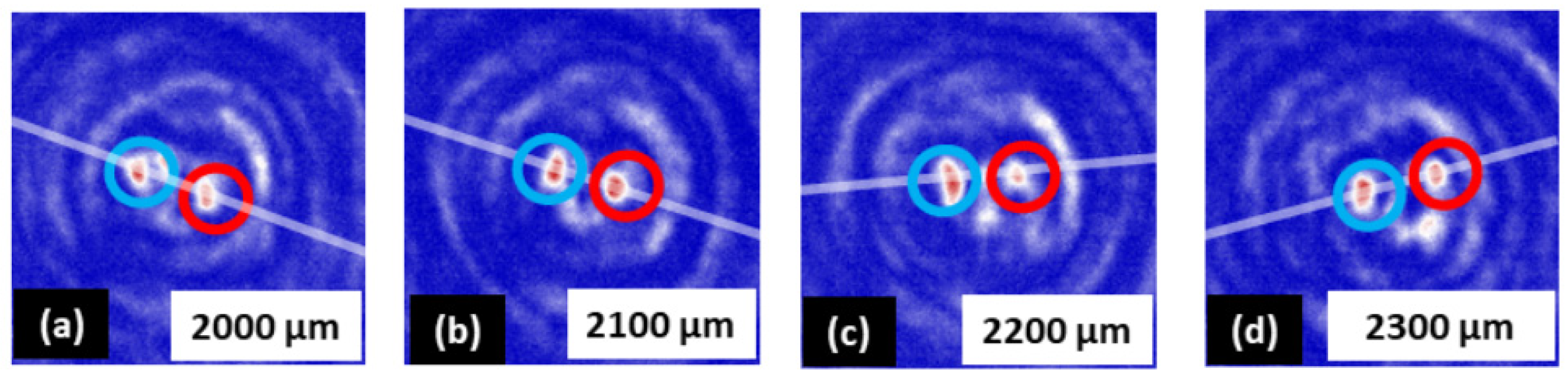
The spectral rotation was detected by measuring the rotation of the connecting lines between the “spectral eyes”. In accordance with the expected saw-tooth like axial oscillation of Gouy rotation caused by the accumulated phase anomaly [23,65], particular distance ranges with detectable rotation were identified. 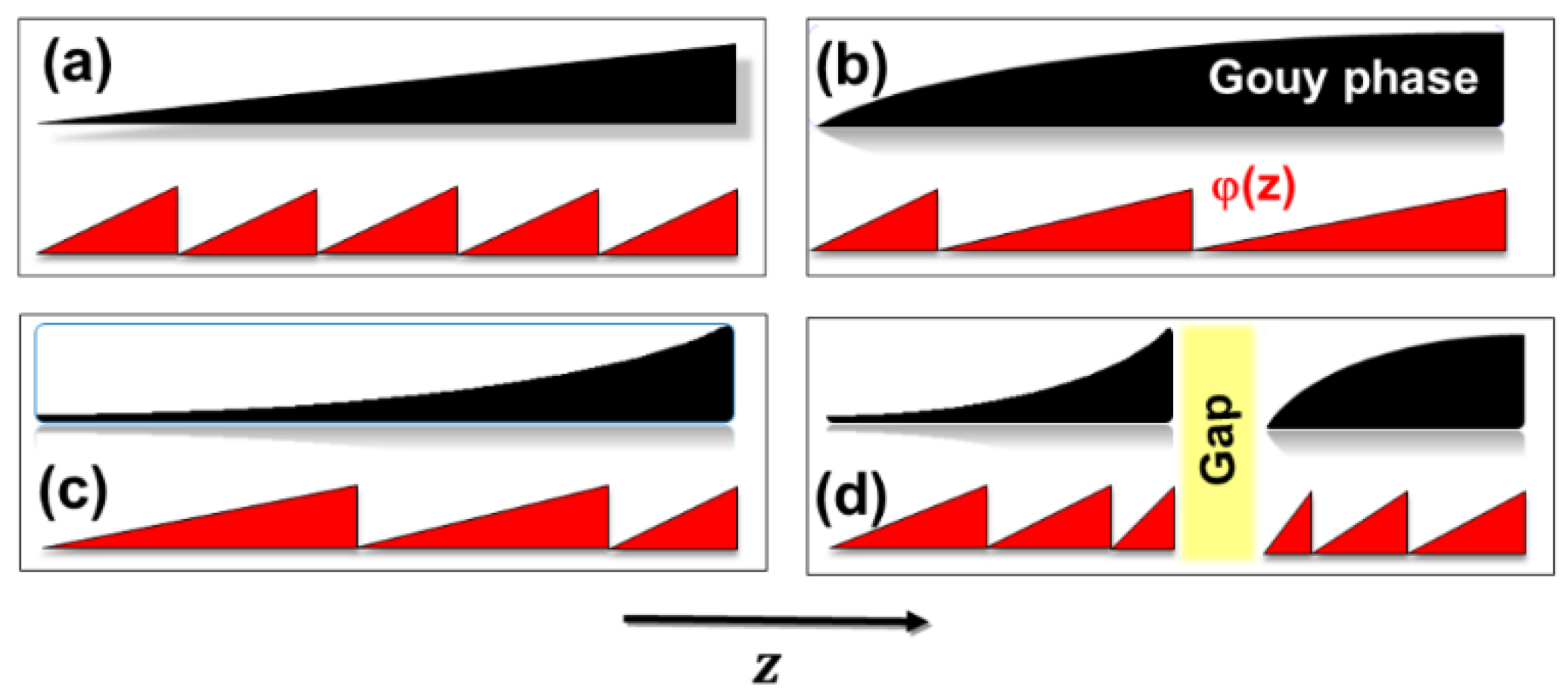Exemplary, a selected set of intensity maps for the elliptical SPG-1 with negative spatial frequency chirp is shown in Figure 10. The propagating intensity propagation was monitored for axial distances from z = 100 µm to z = 6000 µm. With increasing distance, however, the contrast went down so that meaningful measuring results were only obtained within the first part (few millimeters) of the interference zone. The detected pattern rotates counter-clockwise as expected from the programmed spiral orientation. In contrast to the case of radially constant grating periods, the changing focal distances of chirped spiral axicons generate accordion-like stretched angular compartments and thus correspondingly modified accumulated Gouy phase shifts. This phenomenon which is schematically depicted in Figure 11 also leads to an axial change of the ramps in the saw-tooth-like function ϕ(𝑧).
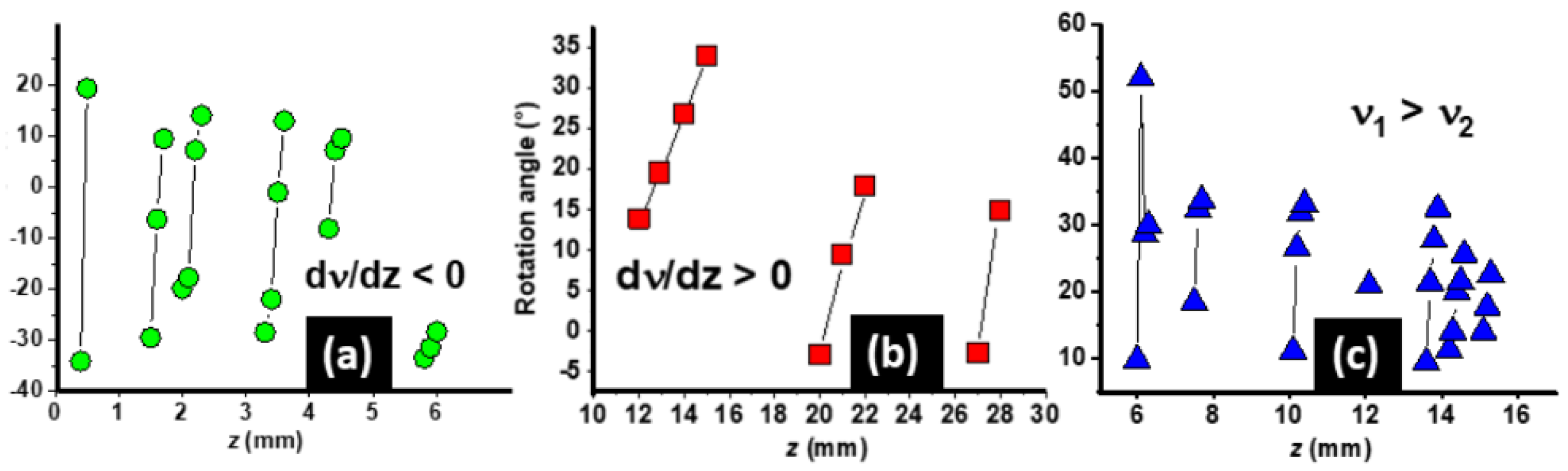
Figure 12a-c show the measured propagation-dependent rotational angles ϕ(z) for the three SPG-1, SPG-2 and SPG-3 (corresponding to the structures in Figure 4a, Figure 4b and Figure 7). The maximum measuring distances for the positively chirped SPG-2 and the composite SPG-3 were chosen to be 28 mm and 16.9 mm, repectively.
In all cases, a distinct rotational behavior was typically observed through discrete intervals in z-direction broken by zones of minimal rotation. The distortions result from the complex spatio-spectral interference caused by the detailed phase structure of the pixelated DOE (a particular factor for possible systematic distortions will briefly be discussed in paragraph 5.4).
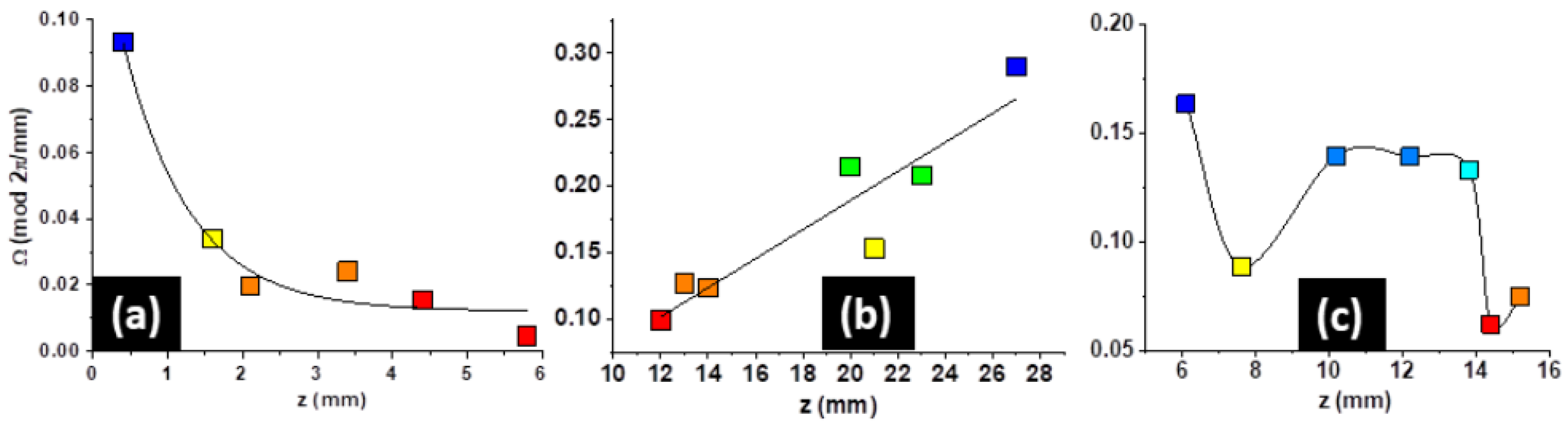
On the basis of the detected ramps of angular rotation, i.e. steep and nearly linearly increasing parts of ϕ(z), corresponding axial angular velocity gradients Ω(z) were calculated according to eq. (3). The resulting curves are plotted in Figure 13a-c.
The angular gradients confirm that the investigated types of non-uniform gratings enable to generate accelerating, decelerating and more complex spectral rotational behavior which can be interpreted as a specific, propagation-dependent kind of self-torque.

5.4. Influence of Grating Talbot Effect

The interaction of coherent light fields with periodical amplitude and/or phase objects like gratings leads to self-imaging effects [67]. Depending on the grating period p and the wavelength λ, the distances of planes with replicated periodicity (Talbot distances)
d T   ~   k · 2 p 2 λ   ( k = integer   number )
or fractal self-images can generate distortions in competition to the axially periodic Gouy phase effects. In our case, the grating periods have to be relatively large because of the sampling theorem. Because of the quadratic dependence on p, the resulting Talbot distances can be large enough to match the cycles of rotation. For example, the first Talbot planes for periods of 30 µm, 40 µm and 50 µm at a wavelength of 800 nm are expected to appear at distances of 2.25 mm, 4.0 mm and 6.25 mm, respectively.

6. Conclusions

In summary, it was demonstrated that the angular velocity of OAM beams can be controlled by programming digital non-uniform spiral gratings into the calibrated phase map of a reflective high-resolution LCoS-SLM. Propagation dependent rotation parameters were analyzed by detecting the spectral Gouy rotation, i.e. the twist of characteristic blue- and red-shifted areas around the singularity, on a matrix camera. A contrast optimization was obtained by an adaptive variation of the background gray level. The spectral signatures of the rotating spectral anomaly were clearly identified and separated by narrow band-pass filtering. The flexible generation of grating structures enables a radial variation of grating periods with positive or negative spatial frequency chirp, elliptical gratings and separated concentric rings of gratings. Resulting axial modulations of the angular velocity indicated accelerated and decelerated orbital angular momenta. The propagation dependent derivation of the speed of rotation is therefore interpreted as a specific type of self-torque in analogy to the local temporal self-torque which was previously reported in literature (see ref. [60,61]). This generalization enables to distinguish between local, nonlocal and mixed generation mechanisms of self-torque. Propagation-dependent self-torque could be of interest for specific applications like space-variant interaction scenarios for ultrafast space-time wavepackets, vortex metrology, or optical processing.
A more precise prediction of the axial light distribution requires to solve the complex diffraction problem, e.g. by starting from the Rayleigh-Fano equation for scattering from rough surfaces as it was shown for circular gratings. By Laplace and inverse Laplace transforms, the problem can be reduced to a tractable form [66]. An extended theoretical treatment including spatio-temporal propagation and dispersion effects, non-uniform phase envelope and specific aberrations, however, remains the subject of future studies.
Possible improvements with respect to the experimental methods could be obtained by replacing the combination of spectral filter and camera by a high-resolution hyperspectral camera. Moreover, the detailed study of the spatio-temporal dynamics of ultrashort-pulsed propagation-dependent self-torque phenomena, e.g. in nonlinear media, seems to be worthwhile.

Author Contributions

Conceptualization and methodology, R.G, M.L., M.B.; experiments R.G., M.J., M.L.; A.T.; data analysis, R.G., M.B.; writing—original draft preparation, R.G.; writing—review and editing, R.G., M.B.; visualization, R.G., M.L., M.J., M.B., A.T.; project ad-ministration and funding acquisition, R.G.; All authors have read and agreed to the pub-lished version of the manuscript. The authors declare that no support by AI was used.

Funding

This research was funded in parts by Deutsche Forschungsgemeinschaft (DFG), project MAXWELL III, grant number GR1782/16-2.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Measuring data can be provided by the authors.

Acknowledgments

Experimental resources including lab space and high-power laser systems were kindly provided by Prof. Elsaesser and Dr. Erik Nibbering (MBI). Prof. Jahns and his team (FernUniversity, Hagen) designed lithographic DOE structures which were used in preceding experiments with refractive-diffractive spiral axicon arrays. Advanced approaches were particularly inspired by this collaboration.

Conflicts of Interest

The authors declare no conflicts of interest. Funding agencies had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix: Design Parameters for Linearly Chirped SPG

The design of fully filled circular spiral gratings with radially linearly varying periods has to take into account the maximum radius rmax, the total number of windings N, the minimum period p0, and the linear increment Δp per winding:
r m a x = N · p 0 + ∆ p · ∑ j = 0 N − 1 j
The sum term provides
∑ j = 0 N − 1 j = N ( N − 1 ) 2
From eq. (7) and eq. (8) one obtains a maximum grating radius of
r m a x = N · p 0 + ∆ p · N 2 − N 2
For nonlinear types of spirals, the constant increment has to be replaced by a winding number dependent increment Δp(N), respectively

References

  1. Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M. V.; Dennis, M. R.; Andrews; D. L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light, J. Opt. 2017, 19, 133001. [CrossRef]
  2. Bliokh, K. Y.; Karimi, E.; Padgett, M. J., Alonso, M. A.; Dennis, M. R.; Dudley, A.; Forbes, A.; Zahedpour, S.; Hancock, S. W.; Milchberg, H. M.; et al. Roadmap on structured waves, J. Opt. 2023, 25, 103001. [CrossRef]
  3. Nye, J. F.; Berry, M. V. Dislocations in wave trains, Proc. R. Soc. Lond. 1974, 336, 165–190. [CrossRef]
  4. Coullet, P.; Gil, L.; Rocca, F. Optical vortices, Opt. Commun. 1989, 73, 403–408. [CrossRef]
  5. Soskin, M. S.; Vasnetsov, M. V. Singular optics, Progr. Opt. 2001, 42, 219–276. [CrossRef]
  6. Dennis, M. R.; O’Holleran, K.; Padgett, M. J. Singular optics: optical vortices and polarization singularities, Prog. Opt. 2009, 53, 293–363. [CrossRef]
  7. Yao, A.; Padgett, M. J. Orbital angular momentum: origins, behavior and applications, Adv. Opt. Photon. 2009, 3, 161–204 (2011). [CrossRef]
  8. Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation, Nanophoton. 2018, 7, 1533–1556. [CrossRef]
  9. Shen, Y.; Wang, Y.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities, Life Sci. & Appl. 2019, 8, 90. [CrossRef]
  10. Chen, R.; Zhou, H.; Moretti, M.; Wang, X.; Li, J. Orbital angular momentum waves: generation, detection and emerging applications, IEEE Communications Surveys & Tutorials 2020, 22, 840–868. https://ieeexplore.ieee.org/document/8894467.
  11. Zhang, K.; Wang, Y.; Yuan, Y.; Burokur, S. N. A review of orbital angular momentum vortex beams generation: from traditional methods to metasurfaces, Appl. Sci. 2020, 10, 1015. [CrossRef]
  12. Fatkhiev, D. M.; Butt, M. A.; Grakhova, E. P.; Kutluyarov, R. V.; Stepanov, I. V.; Kazanskiy, N. L.; Khonina, S. N.; Lyubopytov, V. S.; Sultanov, A.K. Recent advances in generation and detection of orbital angular momentum optical beams—a review, Sensors 2021, 21, 4988. [CrossRef]
  13. Bai, Y.; Lv, H.; Fu, X.; Yang, Y. Vortex beam: generation and detection of orbital angular momentum, Chin. Opt. Lett. 2022, 20, 012601. https://opg.optica.org/col/abstract.cfm?URI=col-20-1-012601.
  14. Zhu, L.; Wang, J. A review of multiple optical vortices generation: methods and application, Front. Optoelectron. 2019, 12, 52–68. [CrossRef]
  15. Forbes, A. Advances in orbital angular momentum lasers, IEEE J. Lightwave Technol. 2023, 41, 2079–2086. [CrossRef]
  16. Berry, M. V. Coloured phase singularities, New J. Phys. 2002, 4, 66.1–66.14. https://iopscience.iop.org/article/10.1088/1367-2630/4/1/366/pdf.
  17. Gbur, G.; Visser, T. D.; Wolf, E. Anomalous behavior of spectra near phase singularities of focus waves, Phys. Rev. Lett. 2002, 88, 013901. [CrossRef]
  18. Popescu, G.; Dogariu, A. Spectral anomalies at wave-front dislocations, Phys. Rev. Lett. 2002, 88, 183902. [CrossRef]
  19. Berry, M.V. Exploring the colours of dark light, New J. Phys. 2002, 4, 74.1–74.14. https://iopscience.iop.org/article/10.1088/1367-2630/4/1/374/pdf.
  20. Leach, J.; Padgett, M. J. Observation of chromatic effects near a white-light vortex, New J. Phys. 2003, 5, 154.1. https://iopscience.iop.org/article/10.1088/1367-2630/5/1/154/pdf.
  21. Zapata-Rodríguez, C. J. Analytical characterization of spectral anomalies in polychromatic aperture beams, Opt. Commun. 2006, 257, 9–15. Get rights and content. [CrossRef]
  22. Liebmann, M.; Treffer, A.; Bock, M.; Elsaesser, T.; Grunwald, R. Spectral anomalies and Gouy rotation around the singularity of ultrashort vortex pulses, Opt. Express 2017, 25, 26076–26088. [CrossRef]
  23. Liebmann, M.; Treffer, A.; Bock, M.; Wallrabe, U.; Grunwald, R. Ultrashort vortex pulses with controlled spectral Gouy rotation, Appl. Sci. 2020, 10, 4288. [CrossRef]
  24. Bock, M.; Liebmann, M.; Elsaesser T.; Grunwald, R. Gouy phase rotation in spectral maps of ultrashort vortex pulses, In Proc. Conference on Lasers and Electro-Optics/CLEO Europe-Conference on Lasers and Electro-Optics/Europe – European Quantum Electronics/EQEC, Munich, Germany, 25–29 June, 2017, EE-1.4. https://opg.optica.org/abstract.cfm?URI=EQEC-2017-EE_1_4.
  25. Liebmann, M.; Treffer, A.; Bock, M.; Seiler, T.; Jahns, J.; Elsaesser, T.; Grunwald, R. Spectral meta-moments reveal hidden signatures of vortex pulses, In Proc. XXI. Int. Conf. on Ultrafast Phenomena, Hamburg, Germany, 15–20 Jul. 2018, TUE.2B.6; online: EPJ Web of Conferences 2019, 205, 01005. [CrossRef]
  26. Bock, M.; Brunne, J.; Treffer, A.; König, S.; Wallrabe, U.; Grunwald, R. Sub-3-cycle vortex pulses of tunable topological charge, Opt. Lett. 2013, 38, 3642–3645. [CrossRef]
  27. Chen, Y.; Fang, Z.-X.; Ren, Y.-X.; Gong, L.; Lu, R.-D. Generation and characterization of a perfect vortex beam with a large topological charge through a digital micromirror device, Appl. Opt. 2015, 54, 8030–8035. [CrossRef]
  28. Guo, S. F.; Liu, K.; Sun, H. X.; Zhang, J. X.; Gao, J. R. Generation of high-order Laguerre-Guassian beams by liquid crystal spatial light modulators, J. Quantum Optics 2015, 21, 86–92. [CrossRef]
  29. Zhu, L.; Wang, J. Arbitrary manipulation of spatial amplitude and phase using phase-only spatial light modulators, Sci. Rep. 2014, 4:7441. [CrossRef]
  30. Grunwald, R.; Jurke, M.; Bock, M.; Liebmann, M.; Bruno, B. P.; Gowda, H.; Wallrabe, U. High-flexibility control of structured light with combined adaptive optical systems, Photonics 2022, 9, 42. [CrossRef]
  31. Grunwald, R.; Jurke, M.; Bock, M.; Liebmann, M.; Bruno, B. P.; Gowda, H.; Wallrabe, U. Structuring light by combining spatial modulation and fast angular shaping, Complex Light and Optical Forces XVII, Photonics West, 28 Jan. – 2 Feb. 2023 San Francisco, USA, In Proc. SPIE 2023, Vol. 12436, p. 1243606. [CrossRef]
  32. Brand, G. F. Phase singularities in beams, Am. J. Phys. 1999, 67, 55–60. [CrossRef]
  33. J. Dyson Circular and spiral diffraction gratings, Proc. Royal Soc. London, Ser. A, Math. And Phys. Sci. 1958, 248, 93–106. [CrossRef]
  34. Vasara, A.; Turunen, J.; Friberg, A. T. Realization of general nondiffracting beams with computer-generated holograms, J. Opt. Soc. Am. A. 1989, 6, 1748–1754. https://opg.optica.org/josaa/abstract.cfm?URI=josaa-6-11-1748.
  35. Abramochkin, E.; Volostnikov, V. Spiral-type beams, Opt. Commun. 1993, 102, 336–350. [CrossRef]
  36. Pereiro-García, J.; García-de-Blas, M.; Geday, M. A.; Quintana, X.; Caño-García, M. Flat variable liquid crystal diffractive spiral axicon enabling perfect vortex beams generation, Sci. Rep. 2023, 13:2385. [CrossRef]
  37. M. Musigmann, J. Jahns, M. Bock, and R. Grunwald, Refractive-diffractive dispersion compensation for optical vortex beams with ultrashort pulse durations, Appl. Opt. 2014, 53, 7304–7311. [CrossRef]
  38. Supp, S.; Jahns, J. Coaxial superposition of Bessel beams by discretized spiral axicons, J. Europ. Opt. Soc.–Rapid Pub. 2018, 14:18.
  39. Li, X.; Shen, Z.; Tan, Q.; Hu, W. High efficient metadevices for terahertz beam shaping, Front. Phys., 2021, 9, 1–7. https://www.frontiersin.org/articles/10.3389/fphy.2021.659747/full.
  40. Jiménez, N.; Picó, R.; Sánchez-Morcillo, V.; Romero-García, V.; García-Raffi, L. M.; Staliunas, K. Formation of high-order acoustic Bessel beams by spiral diffraction gratings, Phys. Rev. E 2016, 94, 053004. https://journals.aps.org/pre/abstract/10.1103/PhysRevE.94.053004.
  41. Wang, T.; Ke, M.; Li, W.; Yang, Q.; Qiu, C.; Liu, Z. Particle manipulation with acoustic vortex beam induced by a brass plate with spiral shape structure, Appl. Phys. Lett. 2016, 109, 123506. [CrossRef]
  42. Li, W.; Ke, M.; Peng, S.; Liu, F.; Qiu, C.; Liu, Z. Rotational manipulation by acoustic radiation torque of high-order vortex beams generated by an artificial structured plate, Appl. Phys. Lett. 2018, 113, 051902. [CrossRef]
  43. Zhou, H.; Li, J.; Guo, K.; Guo, Z. Generation of acoustic vortex beams with designed Fermat's spiral diffraction grating, J. Acoust. Soc. Am. 2019, 146, 4237–4243. [CrossRef]
  44. Jia, Y.; Sun, Z.; Li, J.; Zhao, L.; Liu, H.; Li, T.; Liu, S. MEMS Bessel beam acoustic transducer (MEMS-BBAT) with air-cavity lens based on spiral diffraction grating for particle trapping, IEEE Explore 2022, In Proc. IEEE Int. Ultrasonics Symp. (IUS), Venice, Italy, 10–13 Oct. 2022, https://ieeexplore.ieee.org/document/9958127.
  45. Li, J.; Sun, Z.; Jia, Y.; Li, T.; Lu, H.; Zhao, L.; Liu, H.; Liu, S. MEMS first-order Bessel beam acoustic transducer for particle trapping and controllable rotating, In Proc. IEEE MEMS Conf. 2023, Munich, Germany, 15-19 Jan. 2023, pp. 965–968. https://ieeexplore.ieee.org/document/10052542.
  46. Muelas-Hurando, R. D.; Ealo, J. L.; Volke-Sepúlveda, K. Electro-active diffraction gratings for the generation of acoustic vortex beams, IEEE Explore 2021, In Proc. IEEE Int. Ultrasonics Symp. (IUS), Xi'an, China, 11-16 September 2021, https://ieeexplore.ieee.org/document/9593669.
  47. Muelas-Hurtado, R. D.; Ealo, J. L.; Pazos-Ospina, J. F.; Volke-Sepúlveda, K. Generation of multiple vortex beam by means of active diffraction gratings, Appl. Phys. Lett. 2018, 112, 084101. [CrossRef]
  48. Muelas-Hurtado, R. D.; Ealo, J. L.; Pazos-Ospina, J. F.; Volke-Sepulveda, K. Acoustic analysis of a broadband spiral source for the simultaneous generation of multiple Bessel vortices in air, J. Acoust. Soc. Am. 2018, 144, 3252–3261. [CrossRef]
  49. Ketchum, R. S.; Blanche, P. A. Diffraction efficiency characteristics for MEMS-based phase-only spatial light modulator with nonlinear phase distribution, Photonics, 2021, 8, 62. [CrossRef]
  50. Serati, S. A.; Ewing, T. K.; Stockley, J. E. New developments in high-resolution liquid crystal spatial light modulators for wavefront control, Proc. SPIE 2002, 4825, 46–55. [CrossRef]
  51. Ohtake, Y.; Ando, T.; Fukuchi, N.; Matsumoto, N.; Ito, H.; Hara, T. Universal generation of higher-order multiringed Laguerre-Gaussian beams by using a spatial light modulator, Opt. Lett. 2007, 32, 1411–1413. [CrossRef]
  52. Matsumoto, N.; Ando, T.; Inoue, T.; Ohtake, Y.; Fukuchi, N.; Hara, T. Generation of high-quality higher-order Laguerre-Gaussian beams using liquid-crystal-on-silicon spatial light modulators, J. Opt. Soc. Am. A 2008. 25, 1642–1651. [CrossRef]
  53. Lazarev, G.; Hermerschmidt, A.; Krüger, S.; Osten, S. LCOS spatial light modulators: trends and applications; in: Osten, W.; Reingand, N. (Eds.) Optical Imaging and Metrology: Advanced Technologies, First Edition, Wiley-VCH 2012, Weinheim/Berlin, Germany, Part 1.2, 1–28. [CrossRef]
  54. Guo, S. F.; Liu, K.; Sun, H. X.; Zhang, J. X.; Gao, J. R. Generation of high-order Laguerre-Gaussian beams by liquid crystal spatial light modulators, J. Quant. Opt. 2015, 21, 86–92. [CrossRef]
  55. Gongjian, Z.; Man, Z.; Yang, Z. Wave front control with SLM and simulation of light wave diffraction, Opt. Express 2018, 26, 33543-33564. https://opg.optica.org/oe/fulltext.cfm?uri=oe-26-26-33543&id=402985.
  56. Gao, Y.; Chen, Z.; Ding; J.; Wang, H.-T. Single ultra-high-definition spatial light modulation enabling highly efficient generation of fully structured vector beams, Appl. Opt. 2019, 58, 6591–6596. https://opg.optica.org/ao/fulltext.cfm?uri=ao-58-24-6591&id=416758.
  57. Liebmann, M.; Treffer, A.; Bock, M.; Jurke, M.; Wallrabe, U.; Grunwald, R. Tailored spectral rotation of vortex pulses by non-uniform spiral phase gratings, In Proc. SPIE 2021, Vol. 11701, 117010V . [CrossRef]
  58. Padgett, M. J.; Miatto, F. M.; Lavery, M. P.; Zeilinger, A.; Boyd, R. W. Divergence of an orbital-angular-momentum-carrying beam upon propagation, New J. Phys. 2015, 17, 023011. https://iopscience.iop.org/article/10.1088/1367-2630/17/2/023011.
  59. Liu, W.; Cheng, J.; Wan, C. Generation of optical toroidal vortex with circular asymmetric gratings, arXiv preprint 2024, arXiv:2404.11921. [CrossRef]
  60. Dorney, K. M.; Rego, L; Brooks, N. J.; Nguyen, Q.; Liao, C.; Román, J. S.; Couch, D. E.; Liu, A.; Pisanty, E.; Lewenstein M.; et al. Attosecond extreme ultraviolet beams with time-varying orbital angular momentum: The Self-Torque of Light, In Conference on Lasers and Electro-Optics (CLEO), San José, USA, 5−10 May 2019, Optica Publishing Group, 2019, Tech. Digest, Postdeadline Session, JTh5C.10. [CrossRef]
  61. Rego, L.; Dorney, K. M.; Brooks, N. J.; Nguyen, Q.; Liao, C.-T.; Román, J. S.; Couch, D. E.; Liu, A.; Pisanty, E.; Lewenstein M.; et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum, Science 2019, 364, 1253 and eaaw9486. https://www.science.org/doi/10.1126/science.aaw9486.
  62. Yamane, K.; Sakamoto; M.; Murakami, N.; Morita, R.; Oka, K. Picosecond rotation of a ring-shaped optical lattice by using a chirped vortex-pulse pair, Optics Letters 2016, 41, 4597−4600. [CrossRef]
  63. Wu, Y.; Yu, P.; Liu, Y.; Wang, Z.; Li, Y.; Gong, L. Time-varying optical spin-orbit interactions in tight focusing of self-torqued beams, J. Lightwave Technol. 2023, 41, 2252−2258. [CrossRef]
  64. Grunwald, R.; Bock, M. Characterization of orbital angular momentum beams by polar mapping and Fourier Transform, Photonics 2024, 11, 296. [CrossRef]
  65. Kim, M.-S.; Scharf, T.; da Costa Assafrao, A.; Rockstuhl, C.; Pereira, S. F.; Urbach, H. P.; Herzig, H. P. Phase anomalies in Bessel-Gauss beams, Opt. Express 2012, 20, 28929−28940. [CrossRef]
  66. Elson, J. M. Mathematical analysis of gratings with circularly concentric grooves, J. Opt. Soc. Am. 1983, 73, 702–706. [CrossRef]
  67. Berry, M. V.; Klein, S. Integer, fractional and fractal Talbot effects, Journal of Modern Optics, 1996, 43, 2139–2164. [CrossRef]
Preprints 105515 g001
Figure 1. Selected types of uniform and non-uniform spiral gratings used in singular optics experiments in spectral domain (schematically); (a) case (A*,1*), (b) (A*,2*), (c) (B*,2*) and (B*,4*) with positive spatial chirp for each azimuthal angle, (d) (C*,1*), (e) (A*,3*) torus with negative spatial chirp, (f) (B*,3*), (g) (D*,1*), (h) (D*,3*), (i) (D*,4*). Patterns are transferred into calibrated SLM phase maps.
Figure 1. Selected types of uniform and non-uniform spiral gratings used in singular optics experiments in spectral domain (schematically); (a) case (A*,1*), (b) (A*,2*), (c) (B*,2*) and (B*,4*) with positive spatial chirp for each azimuthal angle, (d) (C*,1*), (e) (A*,3*) torus with negative spatial chirp, (f) (B*,3*), (g) (D*,1*), (h) (D*,3*), (i) (D*,4*). Patterns are transferred into calibrated SLM phase maps.
Preprints 105515 g001
Preprints 105515 g002
Figure 2. Experimental setup for the rotational control of OAM beams in spectral domain (schematically). (L = Laser, BF = rotatable narrow band-pass filter, RP = rotatable broadband polarizer, BE = beam expander, M = high-reflectance mirror, SLM = spatial light modulator, PC1 = computer for programming SLM, SPG = spiral phase grating, p(r) = radially dependent grating period, OAM = OAM beam, bSE and rSE = blue-shifted and red-shifted spectral eyes, CAM = movable camera, PC2 = computer for data processing,   φ (z) = local azimuthal rotation angle, Ω ( z ) = local angular velocity of spectral Gouy rotation).
Figure 2. Experimental setup for the rotational control of OAM beams in spectral domain (schematically). (L = Laser, BF = rotatable narrow band-pass filter, RP = rotatable broadband polarizer, BE = beam expander, M = high-reflectance mirror, SLM = spatial light modulator, PC1 = computer for programming SLM, SPG = spiral phase grating, p(r) = radially dependent grating period, OAM = OAM beam, bSE and rSE = blue-shifted and red-shifted spectral eyes, CAM = movable camera, PC2 = computer for data processing,   φ (z) = local azimuthal rotation angle, Ω ( z ) = local angular velocity of spectral Gouy rotation).
Preprints 105515 g002
Preprints 105515 g003
Figure 3. Theoretical perfectly linear curve progression of radially variable SPG periods with (a) negative (type B*,3*) and (b) positive spatial frequency chirp dν/dr (type B*,2*) (parameters for near-realistic conditions, number of spiral rotations: 37 µm and 55 µm, along minor axes: increasing periods between 29 µm and 55 µm, decreasing periods between 58 µm and 34 µm, respectively). Depending on incident angle α, the gratings are stretched in x-direction (perpendicular to the tilt-axis) by a factor cosα. Periods are compared for two tilt angles (α = 0°: circular SPG, α = 45°: elliptical SPG).
Figure 3. Theoretical perfectly linear curve progression of radially variable SPG periods with (a) negative (type B*,3*) and (b) positive spatial frequency chirp dν/dr (type B*,2*) (parameters for near-realistic conditions, number of spiral rotations: 37 µm and 55 µm, along minor axes: increasing periods between 29 µm and 55 µm, decreasing periods between 58 µm and 34 µm, respectively). Depending on incident angle α, the gratings are stretched in x-direction (perpendicular to the tilt-axis) by a factor cosα. Periods are compared for two tilt angles (α = 0°: circular SPG, α = 45°: elliptical SPG).
Preprints 105515 g003
Preprints 105515 g004
Figure 4. Programmed SPG periods as used in experiments for beam shaping with the SLM: (a) SPG-1 with negative spatial frequency chirp (type B*,3*), see Figure 1b, (b) SPG-2 with positive spatial frequency chirp number of spiral rotations, type (B*,2*), see Figure 1c, with (a) 37 periods, along minor axes increasing between 29 µm and 55 µm, (b) 55 periods, decreasing between 58 and 34 µm).
Figure 4. Programmed SPG periods as used in experiments for beam shaping with the SLM: (a) SPG-1 with negative spatial frequency chirp (type B*,3*), see Figure 1b, (b) SPG-2 with positive spatial frequency chirp number of spiral rotations, type (B*,2*), see Figure 1c, with (a) 37 periods, along minor axes increasing between 29 µm and 55 µm, (b) 55 periods, decreasing between 58 and 34 µm).
Preprints 105515 g004
Preprints 105515 g005
Figure 5. SPG periods as used in experiments determined by image analysis: (a) SPG with negative spatial frequency chirp (b) positive spatial frequency chirp number of spiral rotations: 37 and 55, along minor axes: increasing periods between 29 µm and 55 µm, decreasing periods between 58 and 34 µm, respectively).
Figure 5. SPG periods as used in experiments determined by image analysis: (a) SPG with negative spatial frequency chirp (b) positive spatial frequency chirp number of spiral rotations: 37 and 55, along minor axes: increasing periods between 29 µm and 55 µm, decreasing periods between 58 and 34 µm, respectively).
Preprints 105515 g005
Preprints 105515 g006
Figure 6. Radially dependent “focal distances” zF(r) (i.e. points of intersection of diffracted rays with the propagation axis) for perfect symmetric SPGs with negative and positive chirp for a wavelength of 787 nm (geometrical parameters see Figure 3a,b).
Figure 6. Radially dependent “focal distances” zF(r) (i.e. points of intersection of diffracted rays with the propagation axis) for perfect symmetric SPGs with negative and positive chirp for a wavelength of 787 nm (geometrical parameters see Figure 3a,b).
Preprints 105515 g006
Preprints 105515 g007
Figure 7. Composite grating of type (D*,4*) consisting of a central elliptical SPG centered in a surrounding toroidal SPG of different spatial frequency (periods in the directions of minor and major axes: 17µm and 45 µm for the inner SPG, 21 µm and 54 µm for the torus, respectively).
Figure 7. Composite grating of type (D*,4*) consisting of a central elliptical SPG centered in a surrounding toroidal SPG of different spatial frequency (periods in the directions of minor and major axes: 17µm and 45 µm for the inner SPG, 21 µm and 54 µm for the torus, respectively).
Preprints 105515 g007
Preprints 105515 g008
Figure 8. Selection of rotating spectral anomalies by an ultra-narrowband metal interference filter: (a) central region of an SPG (imaged plane at a distance z = 0 mm), (b) unfiltered intensity maxima, imaged plane at z = 18 mm (AOI: 115 x 115 µm2), (c) transmission of the filter as a function of tilt angle, (d)-(f) “spectral eyes” for three filter curves. Simultaneous detection of both the blue-shifted and red-shifted parts at highest contrast and maximum signal was found for wavelengths between 784 nm and 787 nm (indicated by a distinct double maximum in partial image i).
Figure 8. Selection of rotating spectral anomalies by an ultra-narrowband metal interference filter: (a) central region of an SPG (imaged plane at a distance z = 0 mm), (b) unfiltered intensity maxima, imaged plane at z = 18 mm (AOI: 115 x 115 µm2), (c) transmission of the filter as a function of tilt angle, (d)-(f) “spectral eyes” for three filter curves. Simultaneous detection of both the blue-shifted and red-shifted parts at highest contrast and maximum signal was found for wavelengths between 784 nm and 787 nm (indicated by a distinct double maximum in partial image i).
Preprints 105515 g008
Preprints 105515 g009
Figure 9. Aberrations for spiral gratings at oblique incidence with structural and angular mismatch: (a) diamond-shaped distortion and higher diffraction orders up to m = + 3 of a uniform, not adapted SPG at an incident angle of α = 45°, (b) distortion for a non-uniform SPG designed for α = 45° at an incident angle of α = 51°.
Figure 9. Aberrations for spiral gratings at oblique incidence with structural and angular mismatch: (a) diamond-shaped distortion and higher diffraction orders up to m = + 3 of a uniform, not adapted SPG at an incident angle of α = 45°, (b) distortion for a non-uniform SPG designed for α = 45° at an incident angle of α = 51°.
Preprints 105515 g009
Preprints 105515 g010
Figure 10. Angular rotation of “spectral eyes” generated with negatively chirped SPG-1 varying with increasing propagation distance for a selected sequence of intensity maps (AOI = 64 x 64 µm2, red and blue circles: red-and blue-shifted parts of the spectral anomaly, the line indicates the actual angle of rotation [57]).
Figure 10. Angular rotation of “spectral eyes” generated with negatively chirped SPG-1 varying with increasing propagation distance for a selected sequence of intensity maps (AOI = 64 x 64 µm2, red and blue circles: red-and blue-shifted parts of the spectral anomaly, the line indicates the actual angle of rotation [57]).
Preprints 105515 g010
Preprints 105515 g011
Figure 11. Accumulated Gouy phase shift (black) and Gouy rotation angle (red) (schematically) for SPGs with (a) constant period, (b) negatively chirped period, (c) positively chirped period, and (d) composite structure consisting of two zones with different constant periods separated by a spatial gap (yellow). A higher spatial frequency is assumed for the central part.
Figure 11. Accumulated Gouy phase shift (black) and Gouy rotation angle (red) (schematically) for SPGs with (a) constant period, (b) negatively chirped period, (c) positively chirped period, and (d) composite structure consisting of two zones with different constant periods separated by a spatial gap (yellow). A higher spatial frequency is assumed for the central part.
Preprints 105515 g011
Preprints 105515 g012
Figure 12. Experimentally determined propagation-dependent rotation angles ϕ(z): (a) SPG-1 (negative spatial frequency chirp, decreasing steepness (b) SPG-2 (positive spatial frequency chirp), increasing steepness, (c) SPG-3 (composite structure), complex dynamics. Characteristic ramps are caused by accumulated Gouy phase shift.
Figure 12. Experimentally determined propagation-dependent rotation angles ϕ(z): (a) SPG-1 (negative spatial frequency chirp, decreasing steepness (b) SPG-2 (positive spatial frequency chirp), increasing steepness, (c) SPG-3 (composite structure), complex dynamics. Characteristic ramps are caused by accumulated Gouy phase shift.
Preprints 105515 g012
Preprints 105515 g013
Figure 13. Angular gradients ϕ(z) calculated from angular rotation ramps in Figure 12a-c: a) SPG-1 (negative spatial frequency chirp, (b) SPG-2 (positive spatial frequency chirp), (c) SPG-3 (composite structure).
Figure 13. Angular gradients ϕ(z) calculated from angular rotation ramps in Figure 12a-c: a) SPG-1 (negative spatial frequency chirp, (b) SPG-2 (positive spatial frequency chirp), (c) SPG-3 (composite structure).
Preprints 105515 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated