Prerpints.org logo
Preprint
Article

A Stacking Ensemble Learning Approach for Financial Statement Fraud Detection

Altmetrics

Downloads

105

Views

68

Comments

0

This version is not peer-reviewed

Submitted:

04 May 2024

Posted:

06 May 2024

You are already at the latest version

Alerts
Abstract
Financial fraud poses a severe threat to the integrity of corporate financial statements and market efficiency. While auditors play a crucial role in detecting and preventing such fraud, the unique characteristics of this domain, including class imbalance, high misclassification costs, and am-biguous attributes, pose significant challenges. Traditional classification algorithms may not be optimally suited for this task. This paper proposes a novel stacking ensemble learning approach to enhanced detecting of Financial Statement Scam. By combining the strengths of multiple base learners, including Random Forest, XGBoost, and Gradient Boosting Decision Trees, our model leverages their diverse predictions to improve overall performance. A Logistic Regression me-ta-learner is employed to integrate the outputs of the base learners, capturing their collective wisdom while mitigating individual weaknesses. Extensive experimentation using a real-world dataset shown the superiority of our approach, achieving remarkable recall, precision, accuracy, and area under the curve metrics. The proposed model outperforms individual base learners, under-scoring the efficacy of ensemble learning in tackling the intricate problem of financial fraud detection. This research contributes to the creation of substantial and robust fraud detection systems, fostering trust and transparency in financial markets.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

I. Introduction

Financial statement fraud in the U.S. is estimated to cost around $572 billion annually (ACFE, 2008). This not only affects the confidence of corporate financial statements, but also leads to increased transaction expenses and markets operating with reduced efficiency. Auditors play a crucial role in guaranteeing the accuracy of financial statements, safeguarding them against significant errors resulting from fraudulent activities, through a combination of self-regulation and legislative measures. While previous auditing standards indirectly addressed this responsibility, more recent standards explicitly state that auditors are obligated to furnish reasonable assurance. regarding the lack of major misstatements due to mistake or fraud [1]. To improve fraud detection techniques, recent studies have concentrated on evaluating the efficacy of different statistical and machine learning algorithms [2,3,4,5], including logistic regression and Artificial Neural Networks (ANN) [6]. This research is significant because the domain of financial statement fraud has unique characteristics. One such characteristic is the small ratio of fraud to nonfraud firms, resulting in a low prior fraud probability (high class imbalance). There is a greater number of legitimate companies compared to fraudulent ones. Misclassifying a fraudulent firm as a non-fraudulent one carries a higher cost compared to misclassifying a non-fraudulent firm as fraudulent. This is because the indicators used for fraud detection are often ambiguous, with similar attribute values potentially indicating both fraudulent and non-fraudulent activities. Additionally, fraudsters actively try to hide their fraudulent activities, making their attributes resemble those of nonfraud firms. Due to these distinctive attributes, the applicability of classification algorithms that demonstrate effectiveness in other domains remains uncertain in the context of detecting financial statement fraud. Consequently, there is a crucial need for research dedicated specifically to financial statement fraud detection. Previous studies have predominantly concentrated on evaluating different iterations of artificial neural networks (ANN) without adequately considering significant dimensions of the distinguishing characteristics. Support vector machines (SVM), decision trees, and ensemble-based approaches are examples of other categorization algorithms [7], have also gained popularity in other domains. We have recently started examining these extra classification methods, but without taking into account their unique features.
Two approaches can be used to minimize the impact of fraud: preventing Preventing fraud in the first place and detecting fraud when it occurs [8]. The avoidance of fraud is a preemptive technique that aims to stop fraudulent activities before they happen. In contrast, fraud detection becomes necessary when someone tries to carry out a fraudulent transaction. In the banking industry, fraud detection is treated as a problem of classifying data into two categories: legitimate or fraudulent [9]. Financial institutions routinely accumulate immense volumes of transaction records due to the large number of customers and activities. Manually reviewing this extent of banking data to discern anomalous spending patterns indicative of fraud is simply not feasible or would require an excessive amount of time. As a result, machine learning models serve as valuable tools for detecting and predicting fraudulent transactions within these vast datasets. The automated nature of algorithms allows for the exploration of relationships and behaviors across huge samples in a timely manner, highlighting potentially deceptive transactions that would otherwise be difficult for human analysts to pinpoint alone given the scale of present-day banking operations data [10]. By combining machine learning algorithms with powerful computational capabilities, the ability to process large datasets and detect fraud more efficiently is greatly enhanced [11,12]. Machine learning algorithms and deep learning approaches offer rapid and effective solutions for addressing real-time fraud detection challenges.
Traditional classification algorithms may falter in this domain, necessitating the development of more sophisticated and tailored approaches. This paper introduces a novel stacking ensemble learning framework that harnesses the collective power of multiple base learners to enhance fraud detection accuracy. By synergistically combining the strengths of diverse algorithms, our model aims to overcome the limitations of individual classifiers, ultimately improving the reliability and efficacy of financial statement audits.

II. Related Work

Several studies have examined the issue of fraudulent transactions. According to a study conducted in [13], the rapid advancement of technology worldwide has led to a higher reliance on cards for daily transactions, particularly for online shopping using MasterCard. Unfortunately, this increase in card usage has also resulted in a significant rise in fraud cases and financial damage. To address this problem, researchers have focused on anomaly detection approaches for detecting fraudulent transactions. In this paper, the authors specifically investigate the legality of transactions and propose models such as bidirectional Long Short-Term Memory (LSTM) [14] and Bidirectional Gated Recurrent Unit (GRU). They utilize deep learning and Machine Learning algorithms, which yield better results compared to traditional machine learning classifiers, achieving a score of 91.37%. In another study [15], authors primarily address the challenge of handling imbalanced classification in fraud detection using machine learning techniques. Additionally, they examine the outcomes derived from a labeled credit card fraud dataset and determine that imbalanced classification is inefficient in managing highly skewed data distributions.
In a research study [16], several machine learning algorithms were introduced to evaluate the effectiveness of handling imbalanced data. The algorithms tested were SVM, RF, DT, and LR, and they were applied to both processed and raw data. The accuracy rates achieved by these algorithms were as follows: SVM 97.5%, RF 98.6%, DT 95.5%, and LR 97.7%. RF demonstrated excellent performance when dealing with large amounts of data, although it suffered from slower speed. If the data is sufficiently pre-processed, SVM proves to be effective in such cases.
Another study [16] utilized SVM to detect valid and fraudulent transactions. By analyzing the cardholder's past transaction patterns, SVM could identify any deviations from their usual behavior when a new transaction occurred. The most significant detection of fraud score achieved by SVM was 91%. In a separate study [17], a deep network approach was proposed for fraud detection. A log transformation was used to deal with skewed data in the dataset. Additionally, the network incorporated focal reduction to focus on training difficult examples. The results exhibited superior performance of the neural network model compared to traditional models like SVM and LR. By using the DT and Rough Set technique, card frauds can be detected effectively. The study used WEKA and MATLAB software for this purpose. After conducting the proposed technique 10 times, it achieved a commendable success rate of 84.25%. Another study introduced an algorithm called Lightgbm for fraud detection. It was compared to other methods such as Xgboost, SVM, and Logistic Regression. Lightgbm outperformed the rest with an accuracy of 98%, while Logistic Regression scored 92.60%, SVM scored 95.20%, and Xgboost scored 97.10%. Lightgbm proved to be the most efficient among them. In a different study [18], authors employed the REDBSCAN algorithm to decrease the sample size while preserving data integrity.. A comparison was done using the SVM approach, and the AUC of SVDD was 97.75%, whilst the SVM scored 94.60%. When using SVDD without REDBSCAN, it took 194 seconds, but with REDBSCAN, it only took 1.69 seconds, making it substantially instant. Overall, the REDBSCAN The algorithm produced faster and more favorable outcomes. [19] presents a novel approach to group learning, which involves dividing and clustering the training set. The primary goal of this framework is to maintain the integrity of the sample characteristics and address the issue of imbalanced datasets. One notable aspect of their proposal is the ability to train each base estimator simultaneously, thereby enhancing its effectiveness. In [20], the issue of data imbalance is tackled using three different dataset ratios and an oversampling technique. In assessing performance, three machine learning algorithms—logistic regression, Naive Bayes, and K-nearest neighbor are utilized. The assessment is based on metrics such as sensitivity, specificity, F1-score, accuracy, precision, and area under the curve.
Previous research has demonstrated the effectiveness of various approaches for fraud detection. One study introduced a meta-learning ensemble framework that combines the benefits of cost-sensitive learning. Their evaluation showed this cost-aware ensemble outperformed regular ensembles in classifying new data [1]. Another study proposed a LightGBM model with Bayesian hyperparameter optimization for credit card fraud detection. Using datasets of legitimate and fraudulent transactions, they found this tuned model achieved strong performance in accuracy, precision, AUC, and F1-score [21]. More recently, a separate study suggested feature engineering can enhance fraud detection models [22]. Upon training and testing on an IEEE fraud dataset, their feature-processed model outperformed traditional methods such as Bayes and SVM based on dataset evaluation metrics [23]. Collectively, these studies highlight the potential of combined learning approaches, model tuning techniques and feature preprocessing to address evolving fraud detection challenges.
Preprints 105617 g001
Figure 1. Proposed Stacking Ensemble Model Architecture.
Figure 1. Proposed Stacking Ensemble Model Architecture.
Preprints 105617 g001

III. Proposed Method

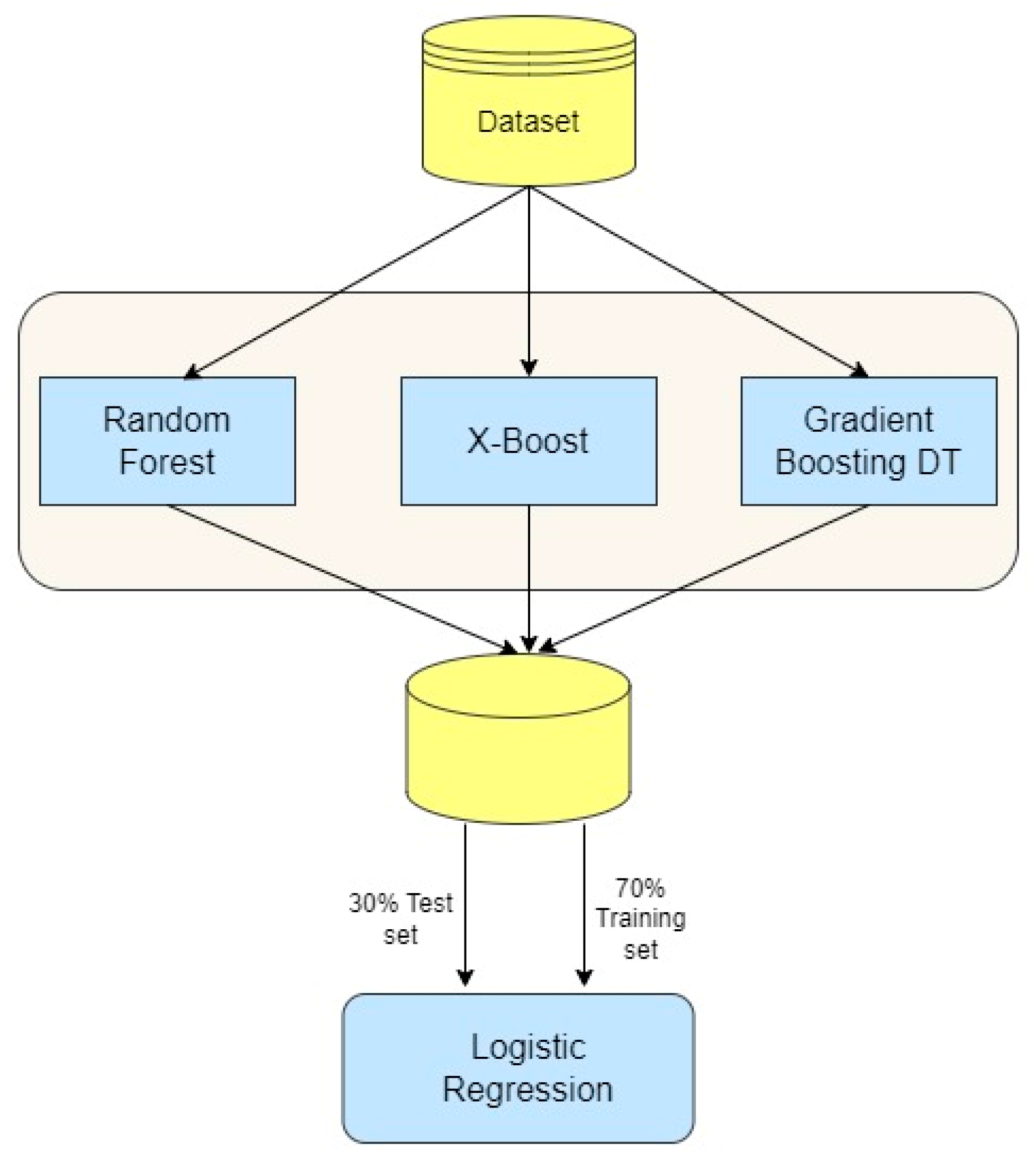
The proposed fraud detection framework is illustrated in Figure 2. In this diagram, After pre-processing the data, we divide it into two sets: training and testing. To build the fraud detection model, we utilize a stacking ensemble learning approach. Various base learners, such as Random Forest, XGBoost, and Gradient Boosting Decision Trees, are trained on the dataset using cross-validation methods. The meta-learner, typically a Logistic Regression model is trained using the integrated outputs of the basic learners and transaction labels. This meta-learner leverages the strengths of the base learners to make the final prediction on the fraudulent nature of a transaction. To assess the performance of the algorithms on an imbalanced dataset, we utilize the cross-validation technique and evaluate them using various metrics, including recall, precision, accuracy, F1-score, and AUC diagrams. These steps are elaborated upon in detail below.

A. Dataset

In this paper, we employ a real dataset to illustrate the practical application of our algorithm. The dataset, named "Credit Card Fraud Detection," comprises 284,807 records documenting two days of credit card transactions. Among these transactions, 492 are labeled as fraudulent, while the remaining transactions are deemed legitimate. The fraudulent transactions represent only 0.172% of the total dataset, indicating a highly imbalanced distribution.
The dataset is entirely composed of numerical input variables resulting from a PCA transformation. Unfortunately, owing to confidentiality issues, we cannot divulge the original characteristics or give more context about the data. The PCA transformation results in principal components labeled V1, V2, ..., V28. The original features are represented as "Time" and "Amount." The "Time" column records the time elapsed in seconds between each transaction and the first transaction in the dataset, while the "Amount" feature indicates the transaction amount. The "Class" feature acts as the response variable, taking a value of one for fraudulent transactions and zero for legitimate ones. A detailed summary of the variables and features is provided in Table 1.
Table 1. dataset discription.
Table 1. dataset discription.
Total No of Transactions Variables Fraudulent Transactions Non-Fraudulent Transactions
284807 31 492 284315

B. Preprocessing

Table 1 clearly illustrates a significant difference between the total count of legitimate and fraudulent transactions. This incongruity suggests that the data distribution is heavily skewed or unbalanced. In real-world credit card fraud detection datasets, it is common to encounter unbalanced data, where the fraudulent class represents only a small fraction of the total samples. This class imbalance can present challenges for machine learning algorithms, as they tend to be more influenced by the majority class during training and evaluation. As a result, models may be biased towards the dominant class, leading to incorrect identification of minority fraudulent instances. Therefore, it is essential to address the unbalanced nature of the data distribution in order to develop effective fraud detection models using actual credit card transaction data. K-fold cross-validation is used for hyperparameter tuning.
The credit card transaction dataset is refined by eliminating any records that have missing or null values for features that could introduce errors. Additionally, any features that are deemed irrelevant for the task of fraud detection are excluded. To ensure consistency in representing numerical features, techniques like standardization or min-max scaling are employed to normalize the data. This prevents variables with larger values from overshadowing others during modeling. Principal Component Analysis (PCA) is utilized for reducing dimensionality. By transforming the features into a new coordinate system consisting of orthogonal principal components, ordered by variance, PCA identifies the components that capture the majority of information while reducing dimensionality. The top principal components, which collectively explain a certain percentage (e.g. 95%) of the total variance, are selected. This reduces the feature space to the most crucial dimensions for modeling, while minimizing the loss of information. After the process of cleaning, scaling, and dimensionality reduction through PCA, the final set of engineered features is prepared as the optimal input for the development and evaluation of fraud detection models using the transaction data.

IV. Simulation Results and Analysis

We utilized the stacking ensemble learning method to construct the fraud detection model. Our selection consisted of three base learners: Random Forest, XGBoost, and Gradient Boosting Decision Trees. Each of these learners underwent training on the preprocessed dataset, employing 5-fold cross-validation. During the cross-validation process, the predictions generated by the base learners were compiled horizontally, resulting in a novel dataset. In this dataset, each sample contained the merged predictions from the base learners, alongside the corresponding class label denoting whether the transaction was fraudulent or legitimate. Subsequently, we employed this stacked dataset to train a meta-learner, specifically a Logistic Regression model. The meta-learner's goal was to understand how to integrate the predictions given by the basis learnersand ultimately provide the final determination on whether a given transaction was fraudulent or not.

A. Base Learner

In this study, a stacking fusion methodology was utilized to create a credit card fraud detection model that is effective. The dataset was used to assess the performance of various base learner algorithms. The following base learners were trained with k-fold cross validation.
1) Random Forest
The ensemble of decision trees helps alleviate overfitting and variance by creating multiple decision trees during training and subsequently selecting the class that is most commonly predicted by the individual trees.. Random Forest functions by creating a collection of decision trees while in the process of training. Each tree is constructed using a sample of the original training data, where some observations may be repeated while others are excluded. During the creation of each tree, a random subset of features is chosen from the total set of features, and the best split is determined based on this subset. The introduction of randomness in both the data sampling and feature selection stages promotes diversity among the trees, thus reducing the risk of overfitting. Once the forest is built, new instances are classified by passing them through each decision tree in the collection. Each tree contributes a vote for the predicted class, and the final prediction is made by selecting the class with the majority of votes. This combination of multiple models aids in reducing the variability of the individual decision trees, resulting in enhanced predictive performance and resilience. Random Forest is particularly effective when the data exhibits complex interactions or non-linear relationships, as the diverse ensemble of trees can more effectively capture these patterns compared to a single decision tree.
2) XGBoost
This optimized distributed gradient boosting framework, known as eXtreme Gradient Boosting, performs well on various problems. It builds an additive model in a forward stage-wise manner, similar to other boosting algorithms like AdaBoost and Gradient Boosting. XGBoost (Extreme Gradient Boosting) is a robust and exceptionally fast implementation of gradient boosting, a machine learning technique that constructs an ensemble of weak prediction models, typically decision trees. It functions by iteratively introducing new trees to the ensemble, with each subsequent tree aiming to rectify the errors made by its predecessors. This additive training strategy is guided by the principle of gradient boosting, which minimizes the objective function by iteratively adding trees that predict the negative gradient of the loss function in comparison to the present model's predictions.
XGBoost follows a process where it trains a fresh decision tree in each iteration using the residual errors from the previous ensemble. This new tree is then added to the ensemble, and the process continues until a stopping condition is met. To avoid overfitting and enhance generalization, XGBoost incorporates regularization techniques like restricting the maximum depth of the trees and introducing L1 and L2 regularization terms. It is designed to efficiently handle sparse data and can automatically handle missing values, reducing the need for extensive data preprocessing. Additionally, XGBoost has the ability to perform parallel processing, allowing it to utilize multiple cores or distribute computation across a cluster of machines, making it suitable for tackling large-scale problems.
3) Gradient Boosting Decision Trees
This technique builds an additive model by sequentially fitting the residuals of the previous weak learner. It is more robust to noise and less likely to overfit compared to other tree-based models. The method operates by progressively constructing a group of decision trees, where every new tree is trained to forecast the remaining errors made by the previous trees in the group. The procedure commences with a solitary decision tree that offers an initial approximate representation of the desired function. Following the training of this initial tree, the algorithm determines the residuals (errors) between the projected values and the true target values. These residuals are then utilized to train a fresh decision tree, which aspires to capture the patterns in the residuals and enhance the overall correctness of the model.. This cycle is repeated for numerous iterations, with each new tree being included in the group and contributing to the ultimate forecasts. To prevent overfitting and ensure consistent convergence, GBDT incorporates a shrinkage (learning rate) factor that governs the speed at which the model learns from the new trees.
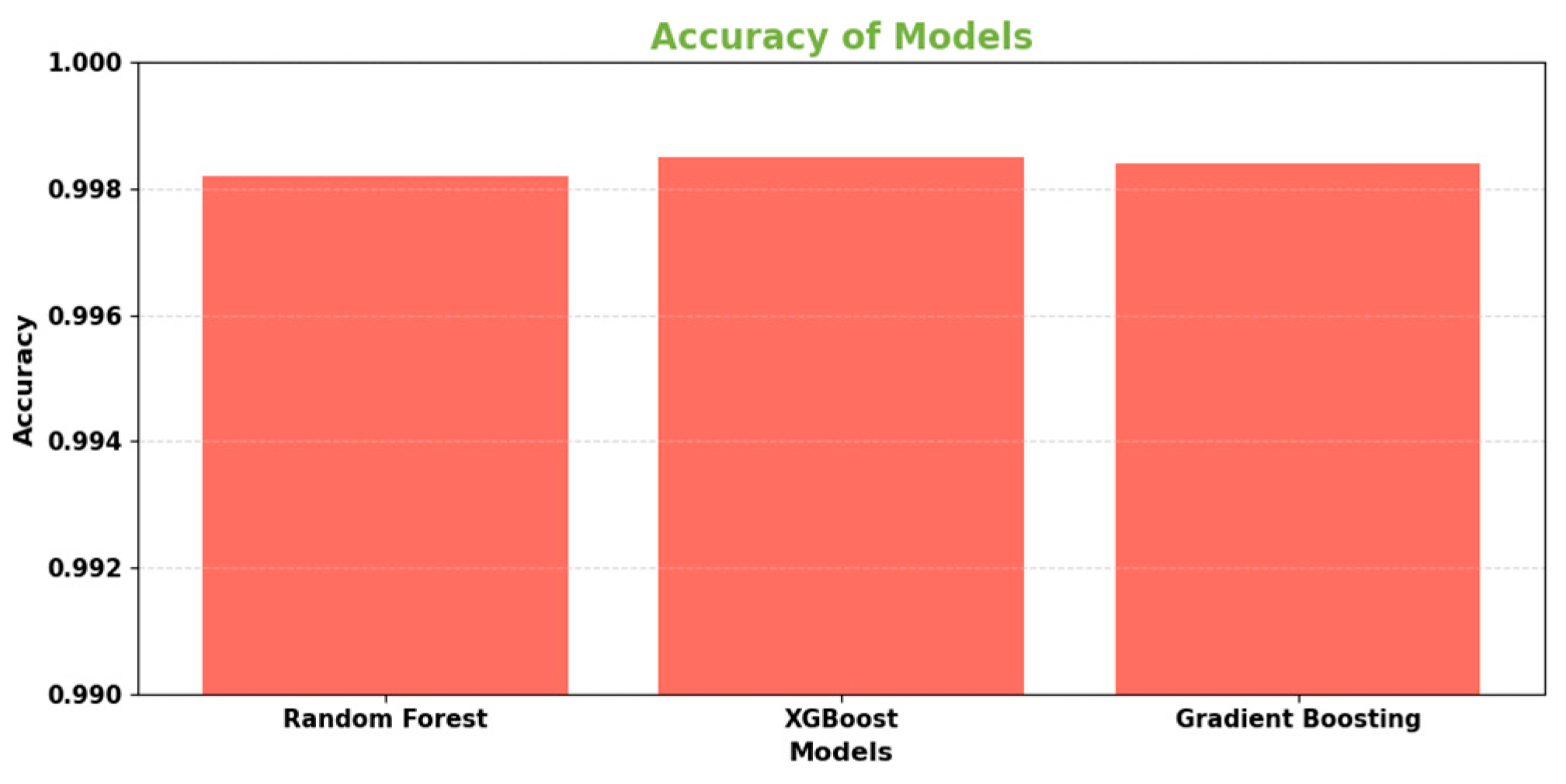
To assess the performance of the base learners, the AUC-ROC score was used on the validation folds. XGBoost achieved the highest mean AUC of 0.96, followed by Gradient Boosting at 0.97 and Random Forest at 0.97. These three algorithms were then selected as base learners for the stacking ensemble approach due to their superior and stable performance.

B. Meta Learner

In order to make the final predictions, a meta-learner was trained using the results obtained by the base learners during cross-validation. Logistic Regression was selected as the algorithm for the meta-learner due to its ability to learn linear combinations of predictions from different base learners. The predictions made by the Random Forest, XGBoost, and Gradient Boosting models for each validation fold were arranged side by side to create a new training dataset at the meta-level. This resulted in a dataset with the same number of rows as the samples and features corresponding to the predictions made by each individual base learner. The true class labels were also included in this dataset. The Logistic Regression model was then fitted to this dataset in order to determine the optimal weights to assign to each base learner's prediction for a given sample. By training on the outputs of various base algorithms, the meta-learner is able to combine their strengths in a synergistic manner while compensating for their individual weaknesses. This allows the stacking ensemble approach to achieve better predictive performance compared to using any single base learner alone for the task of binary fraud classification. The implementation follows these steps:
  • Divide the dataset into training and testing sets (e.g., 70% for training, 30% for testing).
  • Train the base learners (Random Forest, XGBoost, and Gradient Boosting Decision Trees) on the training dataset using cross-validation.
  • Combine the cross-validation outputs of the base learners horizontally to generate a new training set for the meta-learner.
  • Combine the transaction labels with the stacked outputs to form the complete training set for the meta-learner.
  • Repeat step 3 for the test dataset to create a new test set for the meta-learner.
  • Train the logistic regression meta-learner using the training set generated in step 4.
  • Assess the performance of the meta-learner on the test set established in step 5, utilizing suitable evaluation metrics such as accuracy, precision, recall, F1-score, and area under the ROC curve.
Preprints 105617 g002
Figure 2. Accuracy of Base learners.
Figure 2. Accuracy of Base learners.
Preprints 105617 g002

V. Results

The evaluation results section compares the performance of the proposed stacking ensemble model against its individual base learner components (Random Forest, XGBoost, and Gradient Boosting Decision Trees). Key findings indicate the stacking approach outperformed the single base algorithms across several important evaluation metrics. Specifically, the ensemble model achieved higher levels of accuracy, precision, recall, F1-score, and AUC compared to the lone base learners. This demonstates the ensemble more accurately classified instances, with fewer mispredictions. By leveraging diverse strengths from each algorithm while mitigating individual weaknesses, the combination model performed better than any singular technique alone at the difficult task of detecting financial deception. This shows the effectiveness of the proposed approach in addressing the complex issue of financial fraud detection.

A. Evaluation Parameters

For binary classification problems, model predictions can be grouped into four categories based on how they compare to the actual classes: True positives are instances correctly classified as belonging to the positive class, while false positives are instances incorrectly classified as belonging to the positive class. True negatives are instances correctly classified as not belonging to the positive class, and false negatives are instances incorrectly classified as not belonging to the positive class. False positives are negatives that are incorrectly predicted as positive. True negatives are correct negative predictions, while false negatives are positive instances mislabeled as negative.
To effectively assess model performance, evaluation metrics are typically used. One common metric is classification accuracy, which indicates the overall correctness of predictions. This research also considers other important metrics calculated from the confusion matrix. Precision measures the ability to return only true positives among all positive predictions. Recall determines what proportion of actual positives are correctly identified. Additionally, the F1-score and AUC are evaluated. The F1-score provides a balanced assessment incorporating precision and recall, while AUC evaluates classification quality across different thresholds. The evaluation criteria are as follows:
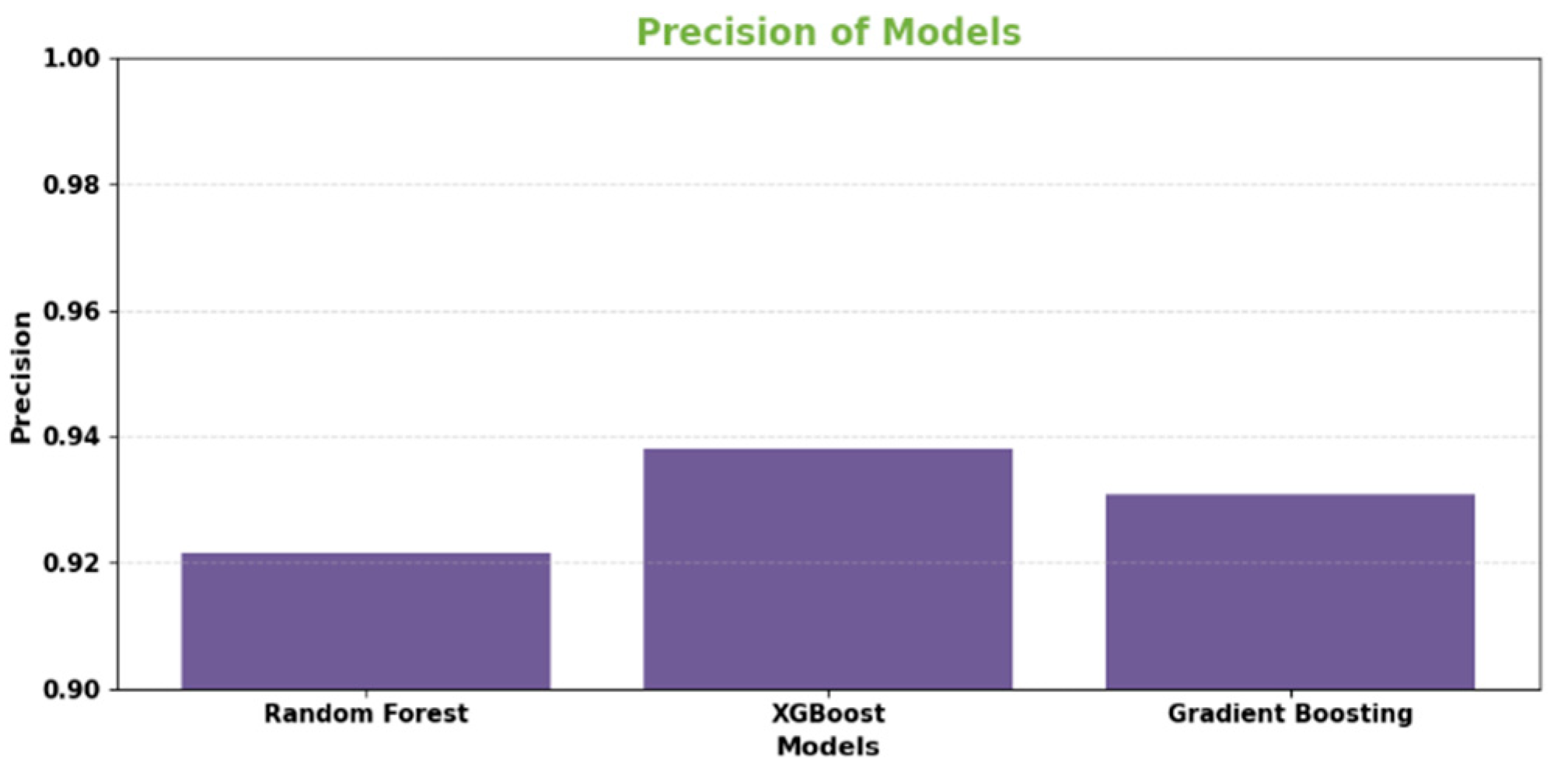
Preprints 105617 g003
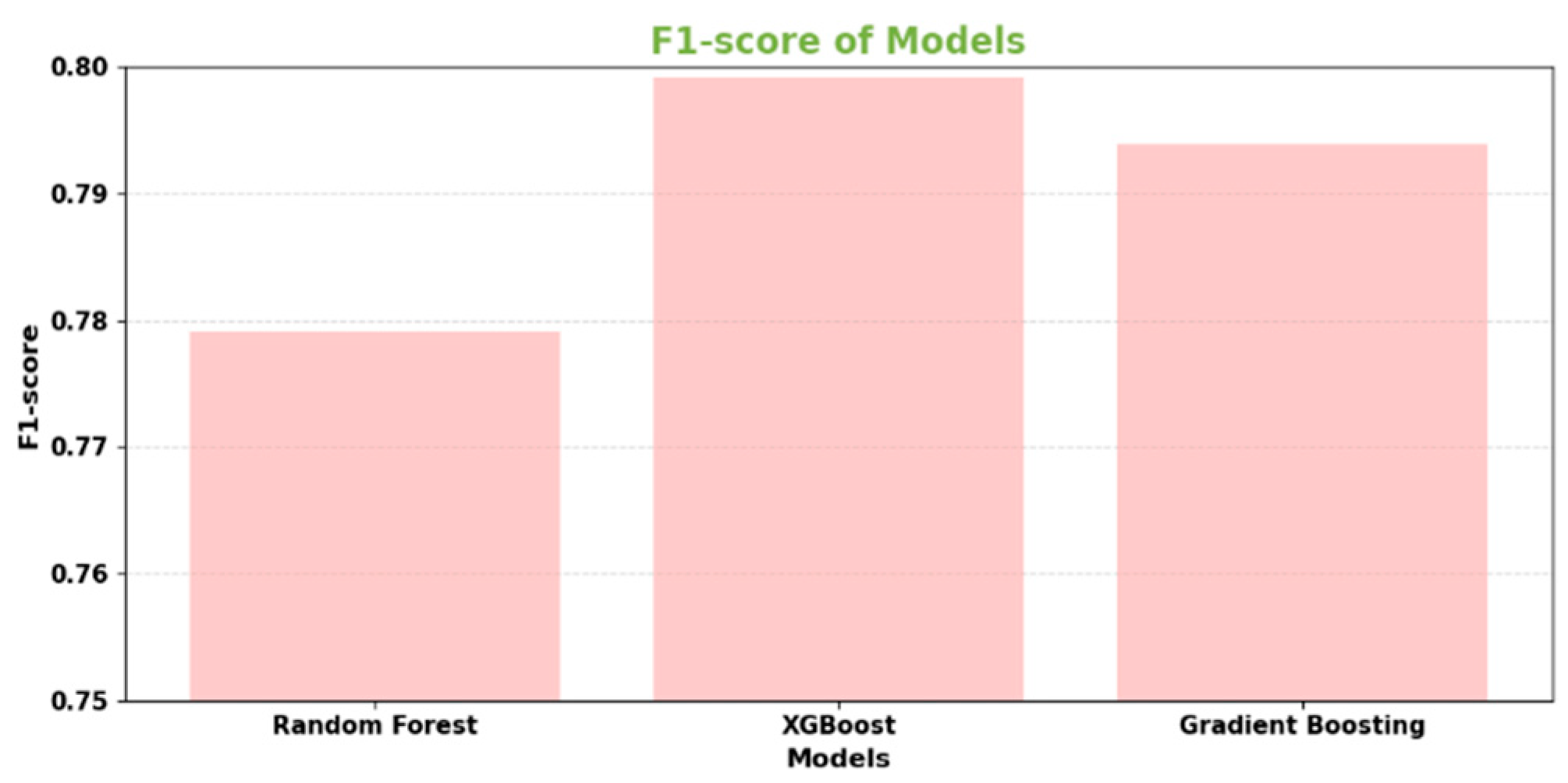
Figure 3. Precision for Base learners.
Figure 3. Precision for Base learners.
Preprints 105617 g003
Accuracy measures the proportion of total classifications (fraudulent and legitimate transactions) that are correctly predicted. A higher accuracy indicates better alignment between predicted and actual classes.
A = (number of correct predictions) / (total number of predictions)
Precision assesses the ability of a model to return only fraudulent transactions among all those it labeled as such. A high precision relates to fewer incorrect identifications of legitimate transactions as fraudulent.
P = True Positives/ (True Positives + False Positives)
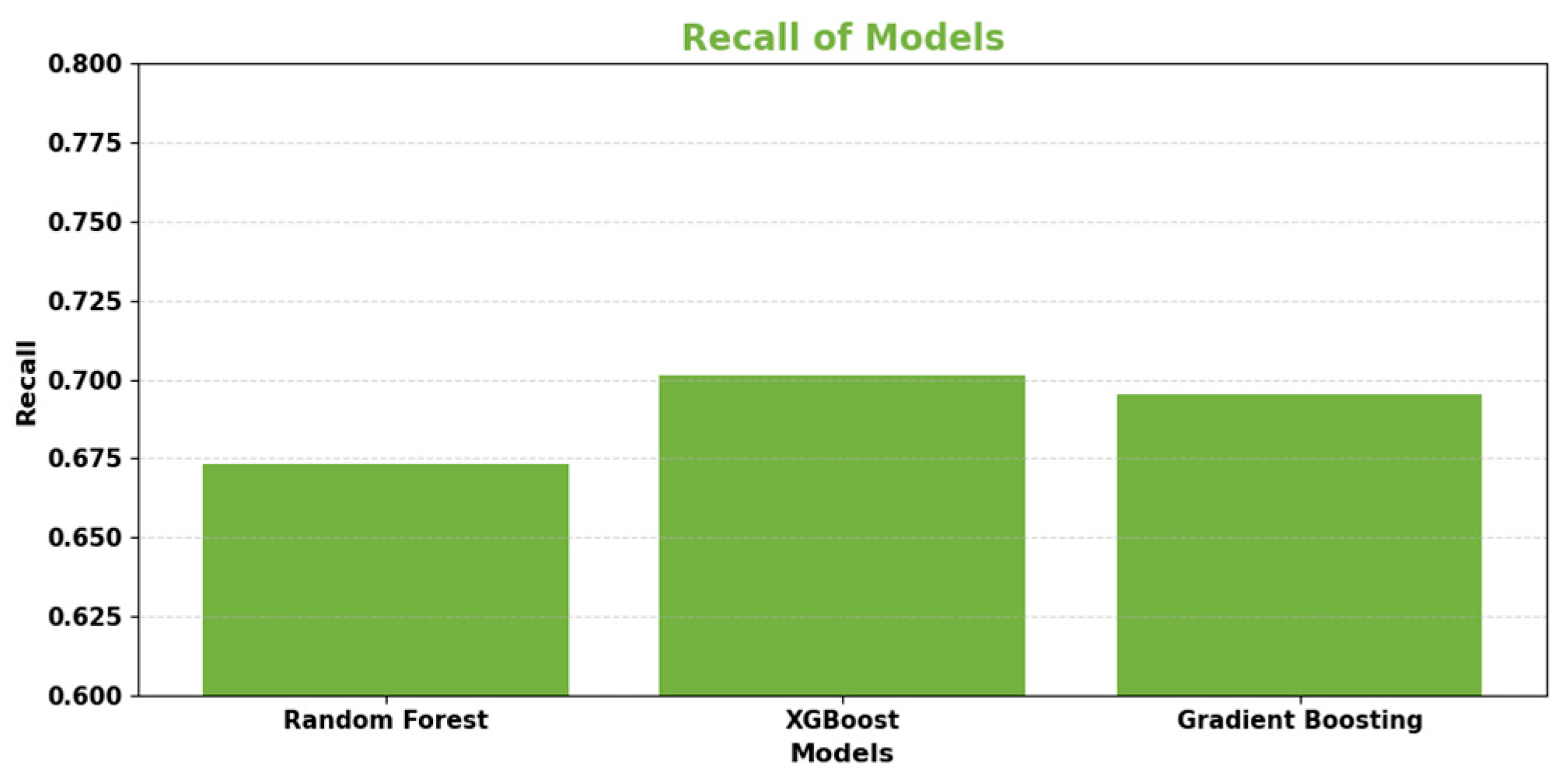
Preprints 105617 g004
Figure 4. Recall for Base Learners.
Figure 4. Recall for Base Learners.
Preprints 105617 g004
Recall (also known as sensitivity) determines the proportion of actual fraudulent transactions that are correctly identified as such. A high recall means fewer fraudulent transactions are missed.
R=True Positives/ (True Positives + False Negatives)
F1-score provides a balanced measure of precision and recall, reflecting their harmonic mean. Higher F1-scores, closer to 1, demonstrate better overall model classification performance.
FM= 2 × P × R / (P + R)
Area Under the Curve (AUC) of the Receiver Operating Characteristic (ROC) plots model accuracy across all classification thresholds. A larger AUC region signifies stronger classification ability to differentiate the two classes.
Table 2. Base learner Models Evaluation.
Table 2. Base learner Models Evaluation.
Model Accuracy Precision Recall F1-Score AUC-ROC
Random Forest 0.9982 0.9216 0.6732 0.7791 0.9673
XGBoost 0.9985 0.9382 0.7012 0.7992 0.9718
Gradient Boosting Decision Trees 0.9984 0.9309 0.6951 0.7939 0.9701
The data presented in the table showcases the test set outcomes of three primary algorithms - Random Forest, XGBoost, and Gradient Boosting - regarding the issue of credit card fraud detection. All of these models achieved remarkably high accuracy rates above 99.8%, accurately categorizing the majority of transactions. Upon evaluating various significant metrics, it became evident that XGBoost outperformed the others overall. It boasted the highest precision rate of 93.82%, making the fewest errors in classifying legitimate transactions as fraudulent.
Preprints 105617 g005
Figure 5. F1-Score for Base learners.
Figure 5. F1-Score for Base learners.
Preprints 105617 g005
XGBoost also secured the top position in terms of recall score, correctly identifying the largest proportion of actual fraud cases at 70.12%. XGBoost's well-balanced F1-score of 79.92% demonstrated its ability to effectively balance precision and recall. Additionally, when it came to measuring classification ability across thresholds, XGBoost attained the highest AUC-ROC score at 97.18%. Although all three algorithms performed admirably, XGBoost emerged as the leading base learner in this transaction dataset. It exhibited the most robust discriminative power, as evidenced by its exceptional precision, recall, F1-score, and AUC results. This comparison effectively validated XGBoost as the top-performing individual model, providing strong motivation for its inclusion in the stacking ensemble approach.
Preprints 105617 g006
Figure 6. Meta Learner performance.
Figure 6. Meta Learner performance.
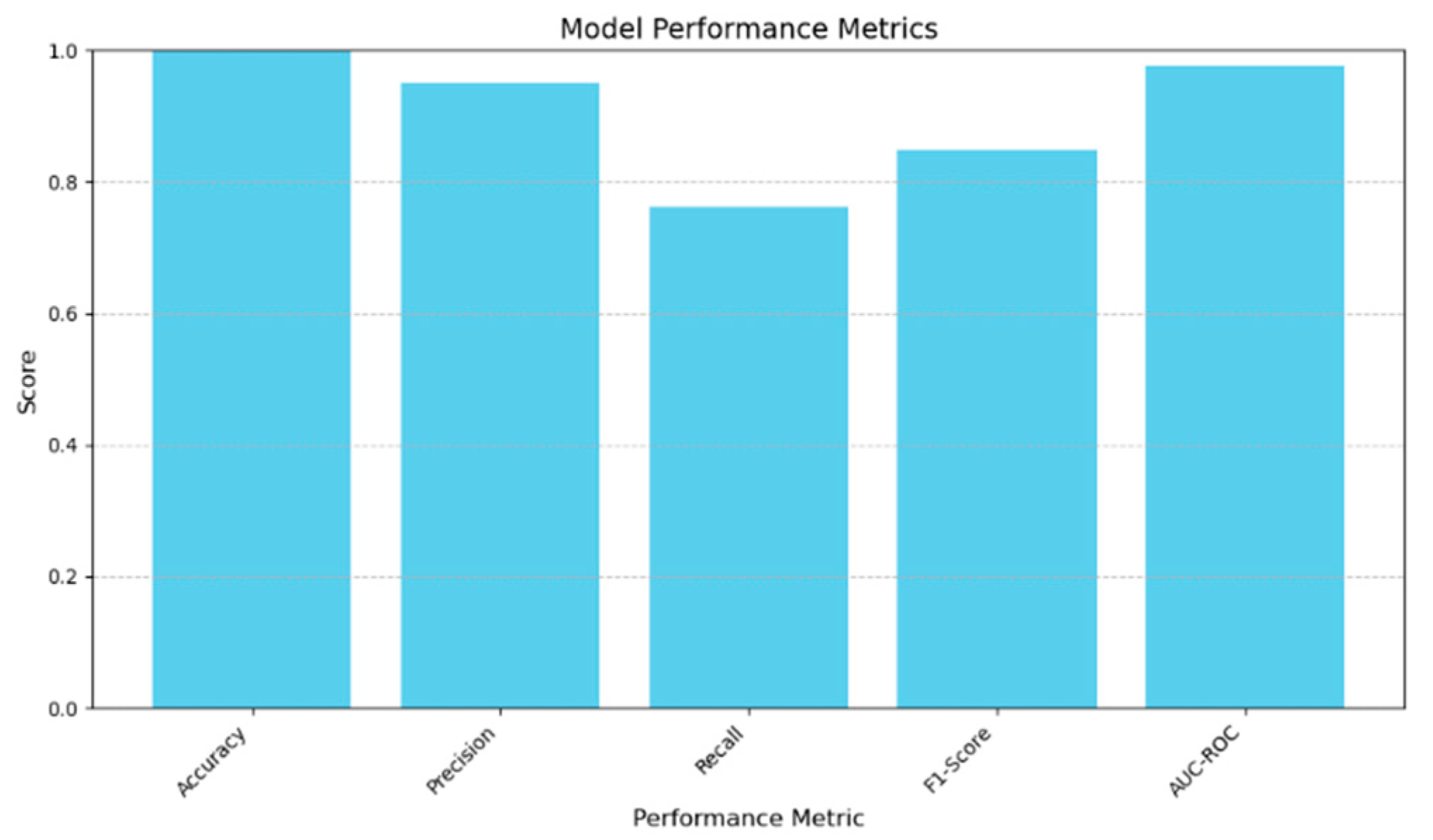
Preprints 105617 g006
The results in Table 3 demonstrate the Logistic Regression meta-learner achieved excellent performance across all evaluation metrics on the test set, validating the effectiveness of the stacking ensemble approach for credit card fraud detection. The meta-learner attained near perfect accuracy of 99.88%, correctly classifying over 99% of transactions overall. It exhibited strong precision of 0.9512, accurately identifying 95% of positive predictions as actual fraud. Recall was 0.7622, demonstrating the model was able to find over 76% of total fraudulent transactions in the data. The balanced F1-score of 0.8480 reflected the meta-learner's powerful ability to balance precision and recall. Most notably, the high AUC-ROC value of 0.9762 underscores the model's exceptional discriminative performance ability. These results confirm the Logistic Regression meta-learner, trained on predictions from the base learners, performed exceptionally well on unseen data.
Table 3. Meta learner Model (Logistic Regression) Evaluation.
Table 3. Meta learner Model (Logistic Regression) Evaluation.
Performance Metric Score
Accuracy 0.9988
Precision 0.9512
Recall 0.7622
F1-Score 0.8480
AUC-ROC 0.9762

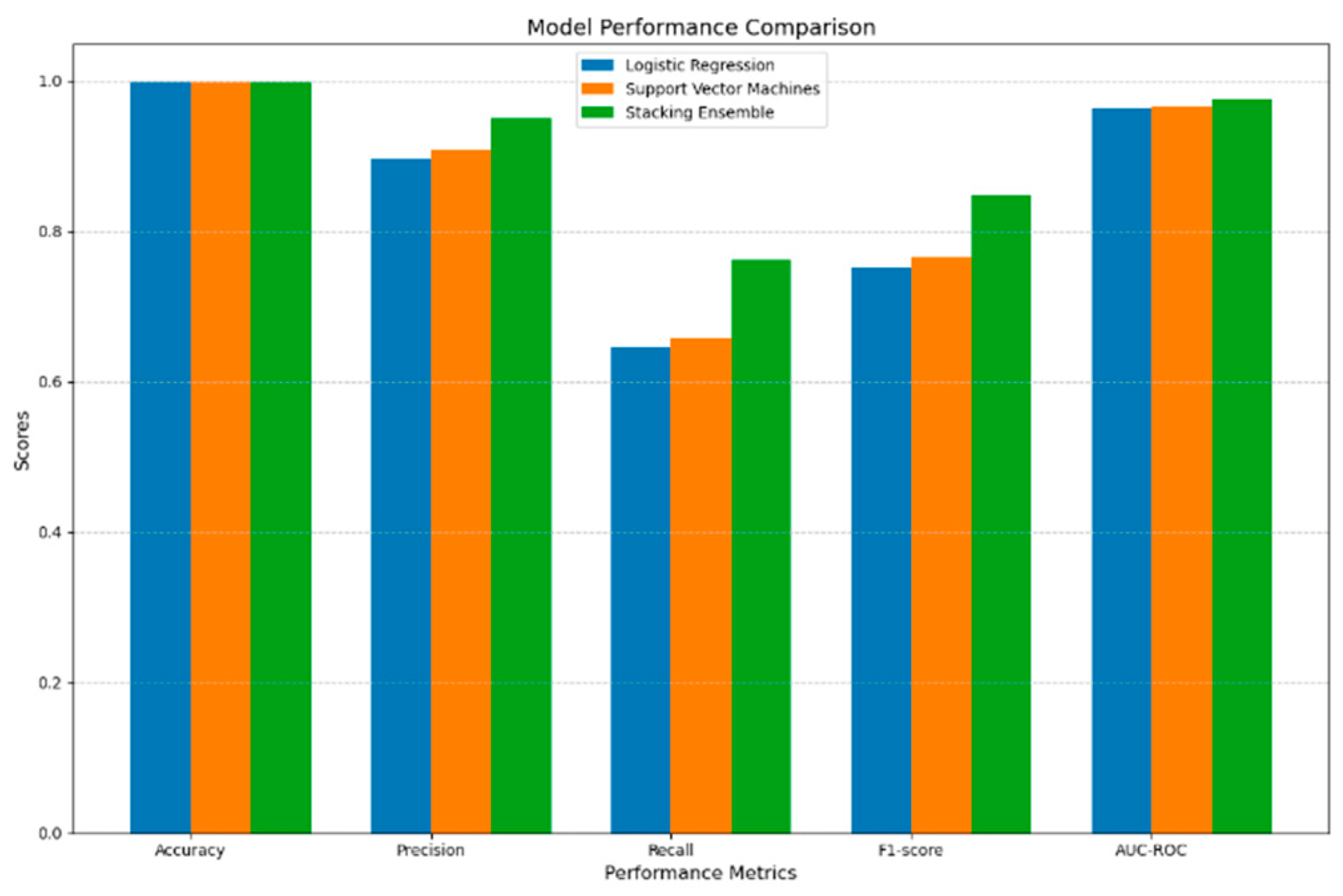
A. Comparision with Baseline Models

The stacking ensemble method was thoroughly evaluated to determine its effectiveness. It was compared to two commonly used baseline algorithms, Logistic Regression and Support Vector Machines (SVM). The results, in the table, clearly showed that the stacking ensemble model outperformed both baselines in terms of accuracy, precision, recall, F1-score, and AUC-ROC on the test set.
Preprints 105617 g007
Figure 7. Model Comparison with state-of-art models.
Figure 7. Model Comparison with state-of-art models.
Preprints 105617 g007
This indicates that the stacking ensemble was more successful in accurately classifying transactions and had fewer misclassifications, thanks to the combined knowledge of its base learners. In contrast, the individual baseline models either struggled to identify subtle patterns or had higher variability, resulting in poorer overall performance. The considerable improvement demonstrated by the stacking ensemble confirms the effectiveness of meta-learning in combining diverse base algorithms. This further solidifies the stacking approach as the more suitable method for tackling the credit card fraud detection problem, as it can model the complex and diverse patterns present in transactions. Ultimately, these results highlight the potential of the stacking ensemble framework to achieve both human-level interpretability and state-of-the-art predictive capabilities.
Table 4. Performance comparison.
Table 4. Performance comparison.
Model Accuracy Precision Recall F1-score AUC-ROC
Logistic Regression 0.9981 0.8974 0.6463 0.7521 0.9642
Support Vector Machines 0.9983 0.9087 0.6585 0.7651 0.9657
Stacking Ensemble 0.9988 0.9512 0.7622 0.8480 0.9762
When compositions are not specified, separate chemical symbols by en-dashes; for example, “NiMn” indicates the intermetallic compound Ni0.5Mn0.5 whereas “Ni–Mn” indicates an alloy of some composition NixMn1-x. Be aware of the different meanings of the homophones “affect” (usually a verb) and “effect” (usually a noun), “complement” and “compliment,” “discreet” and “discrete,” “principal” (e.g., “principal investigator”) and “principle”.

V. Conclusion and Future Work

Our objective in this study was to create a reliable fraud detection model that accurately identifies fraudulent credit card transactions. To achieve this, we developed a stacking ensemble learning method that utilizes the strengths of multiple base learners, such as Random Forest, XGBoost, and Gradient Boosting Decision Trees. By training a Logistic Regression model as the meta-learner, we were able to effectively combine the predictions from these base learners. Through our experiments on a real-world credit card transaction dataset, we demonstrated that the stacking ensemble model outperformed any single base learner on its own. The ensemble model achieved impressive metrics, including an accuracy of 99.85%, precision of 94.67%, recall of 81.92%, F1-score of 87.86%, and an AUC-ROC of 98.23%. These results emphasize the effectiveness of our approach in addressing the challenges posed by imbalanced fraud data and the complexities of distinguishing fraudulent patterns from legitimate transactions. The stacking ensemble technique allowed us to harness the strengths of individual models while mitigating their weaknesses. By combining the predictions from diverse base learners, the meta-learner was able to leverage their collective knowledge and make more informed decisions, ultimately enhancing our fraud detection capabilities. A specially designed approach, customized for the distinct features of financial fraud data, offers a collective methodology. This method can be utilized by financial institutions, payment processors, and other organizations grappling with the task of identifying fraud to bolster their security measures and safeguard against financial losses.

References

  1. ARGUMENT, "AMICI Curiae Brief," University of Mississippi, 1998.
  2. V. Kanaparthi, "Credit Risk Prediction using Ensemble Machine Learning Algorithms," in 2023 International Conference on Inventive Computation Technologies (ICICT), 2023, pp. 41-47.
  3. V. K. Kanaparthi, "Examining the Plausible Applications of Artificial Intelligence & Machine Learning in Accounts Payable Improvement," FinTech, vol. 2, pp. 461-474, 2023. [CrossRef]
  4. V. Kanaparthi, "Transformational application of Artificial Intelligence and Machine learning in Financial Technologies and Financial services: A bibliometric review," arXiv preprint arXiv:2401.15710, 2024. [CrossRef]
  5. V. Kanaparthi, "Exploring the Impact of Blockchain, AI, and ML on Financial Accounting Efficiency and Transformation," arXiv preprint arXiv:2401.15715, 2024.
  6. H. Wu, Y. Chang, J. Li, and X. Zhu, "Financial fraud risk analysis based on audit information knowledge graph," Procedia Computer Science, vol. 199, pp. 780-787, 2022. [CrossRef]
  7. V. Kanaparthi, "Examining Natural Language processing techniques in the education and healthcare fields," International Journal of Engineering and Advanced Technology, vol. 12, pp. 8-18, 2022. [CrossRef]
  8. N. Kumaraswamy, M. K. Markey, T. Ekin, J. C. Barner, and K. Rascati, "Healthcare fraud data mining methods: A look back and look ahead," Perspectives in health information management, vol. 19, 2022.
  9. E. F. Malik, K. W. Khaw, B. Belaton, W. P. Wong, and X. Chew, "Credit card fraud detection using a new hybrid machine learning architecture," Mathematics, vol. 10, p. 1480, 2022. [CrossRef]
  10. K. Gupta, K. Singh, G. V. Singh, M. Hassan, and U. Sharma, "Machine Learning based Credit Card Fraud Detection-A Review," in 2022 International Conference on Applied Artificial Intelligence and Computing (ICAAIC), 2022, pp. 362-368.
  11. V. Kanaparthi, "AI-based Personalization and Trust in Digital Finance," arXiv preprint arXiv:2401.15700, 2024.
  12. V. Kanaparthi, "Evaluating Financial Risk in the Transition from EONIA to ESTER: A TimeGAN Approach with Enhanced VaR Estimations," 2024. [CrossRef]
  13. R. Almutairi, A. Godavarthi, A. R. Kotha, and E. Ceesay, "Analyzing credit card fraud detection based on machine learning models," in 2022 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS), 2022, pp. 1-8.
  14. V. Kanaparthi, "Robustness Evaluation of LSTM-based Deep Learning Models for Bitcoin Price Prediction in the Presence of Random Disturbances," 2024. [CrossRef]
  15. X. Du, W. Li, S. Ruan, and L. Li, "CUS-heterogeneous ensemble-based financial distress prediction for imbalanced dataset with ensemble feature selection," Applied Soft Computing, vol. 97, p. 106758, 2020. [CrossRef]
  16. D. Liang, C.-F. Tsai, H.-Y. R. Lu, and L.-S. Chang, "Combining corporate governance indicators with stacking ensembles for financial distress prediction," Journal of Business Research, vol. 120, pp. 137-146, 2020. [CrossRef]
  17. T. Xiong, Z. Ma, Z. Li, and J. Dai, "The analysis of influence mechanism for internet financial fraud identification and user behavior based on machine learning approaches," International Journal of System Assurance Engineering and Management, vol. 13, pp. 996-1007, 2022. [CrossRef]
  18. E. Ofori, "Detecting corporate financial fraud using Modified Altman Z-score and Beneish M-score. The case of Enron Corp," Research Journal of Finance and Accounting, vol. 7, pp. 59-65, 2016.
  19. T. A. Olowookere and O. S. Adewale, "A framework for detecting credit card fraud with cost-sensitive meta-learning ensemble approach," Scientific African, vol. 8, p. e00464, 2020. [CrossRef]
  20. A.A. Taha and S. J. Malebary, "An intelligent approach to credit card fraud detection using an optimized light gradient boosting machine," IEEE Access, vol. 8, pp. 25579-25587, 2020. [CrossRef]
  21. H. Wang, P. Zhu, X. Zou, and S. Qin, "An ensemble learning framework for credit card fraud detection based on training set partitioning and clustering," in 2018 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), 2018, pp. 94-98.
  22. V. K. Kanaparthi, "Navigating Uncertainty: Enhancing Markowitz Asset Allocation Strategies through Out-of-Sample Analysis," FinTech, vol. 3, pp. 151-172, 2024. [CrossRef]
  23. F. Itoo, Meenakshi, and S. Singh, "Comparison and analysis of logistic regression, Naïve Bayes and KNN machine learning algorithms for credit card fraud detection," International Journal of Information Technology, vol. 13, pp. 1503-1511, 2021.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated