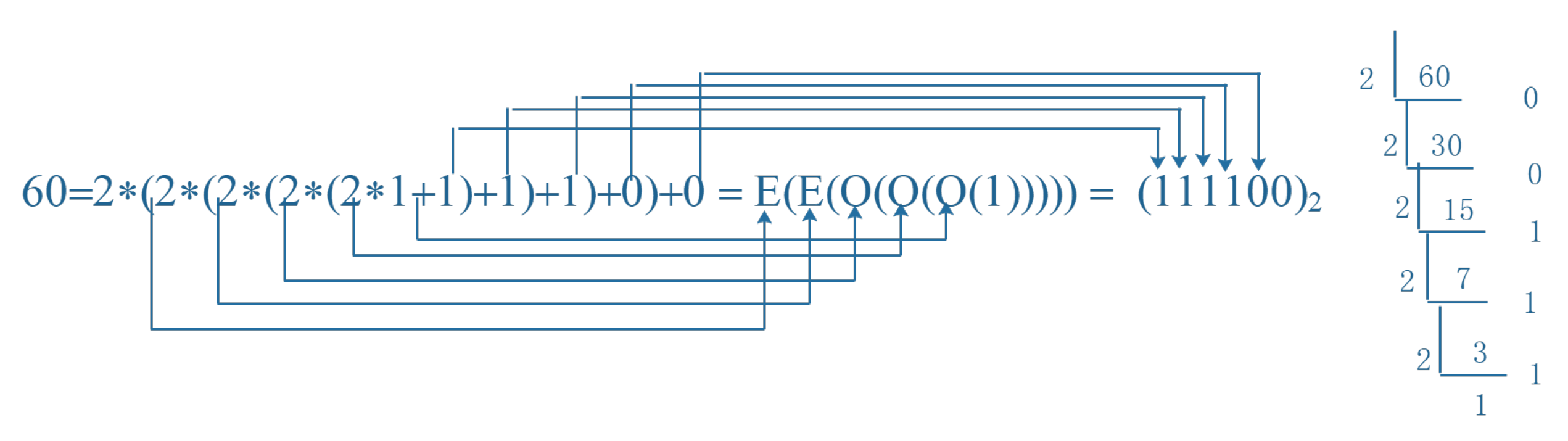Collatz Conjecture Is Analogous to an Inverse Function of Natural Number

Preprint

Article

Collatz Conjecture Is Analogous to an Inverse Function of Natural Number

Altmetrics

Downloads

144

Views

116

Comments

Jishe Feng^*

This version is not peer-reviewed

Submitted:

11 May 2024

Posted:

07 June 2024

You are already at the latest version

Alerts

Abstract

We introduce a full binary directed tree structure to represent the set of natural numbers, further categorizing them into three distinct subsets: pure odd numbers, pure even numbers, and mixed numbers. We adopt a binary string representation for natural numbers and elaborate on the composite methodology encompassing odd- and even-number functions. Our analysis focuses on examining the iteration sequence (or composition) of the Collatz function and its reduced variant, which serves as an analog to the inverse function, to scrutinize the validity of the Collatz conjecture. To substantiate this conjecture, we incorporate binary strings into an algebraic formula that captures the essence of the Collatz sequence. By this means, we transform discrete powers of 2 into continuous counterparts, ultimately culminating in the smallest natural number, 1. Consequently, the sequence generated through infinite iterations of the Collatz function emerges as an eventually periodic sequence, thereby validating an enduring 87-year-old conjecture.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

1. Introduction

In the study of number theory, odd and even numbers are a fundamental pair of ideas. Natural number sets can be parted to two different sets. There are many conjectures that attempt to generalize the fact of different kinds of natural numbers discovered in a restricted range to the entire infinite set of natural numbers. This article will proof the famous Collatz conjecture, which states that for each natural number n, if it is even, divided by 2, if it is odd, multiplied by 3, and added 1, and so on, the eventual value must be 1. It is also referred to as the

3 n + 1

conjecture and was put forth in 1937 by Lothar Collatz, also known as the

3 n + 1

problem. The mathematician Paul Erdos once said of this conjecture: "Mathematics may not be ready for such problems" [1,2].

For the Collatz conjecture, we can describe it as a function:

T (n) = \{\begin{matrix} 3 n + 1, & if n is odd number, \\ \frac{n}{2} & if n is even number . \end{matrix}

(1)

The following sequence is obtained via the composite function (iteration):

Λ = {n, T (n), T (T (n)), T (T (T (n))), \dots} = {n, T (n), T^{2} (n), T^{3} (n), \dots}

. Consequently, the Collatz conjecture can be stated as follows:

Collatz conjecture 1: For any natural number n, there is finite natural number m, the sequence

Λ

always leads to the integer 1, namely

T^{m} (n) = 1

The series

Λ

is an infinite sequence of ultimately period [3,4]. So we give another statement of the Collatz conjecture as the following.

Collatz conjecture 2: The series

Λ

is an infinite sequence of ultimately period, the preperiod

η (n)

varies with the initial value n, but the ultimately period is always

{1, 4, 2}

2. An Algebra and Graph Representation of Natural Numbers

2.1. The Composition of Odd-Number and Even-Number Functions

A natural number is considered even if it can be divided by 2; if not, it is considered odd. According to the Peano’s Axiom, the smallest natural number is 1. The set

N = {1, 2, 3, \dots}

of natural numbers can be divided into odd and even sets; in this paper, we will use the usual definition of natural numbers.

{natural number} = {odd number} ⋃ {even number}

In the set of natural numbers where 1 is the smallest odd number and 2 is the smallest even number, we can use the expression

n = 2 k - 1

to indicate that it is an odd, and the expression

n = 2 k

to indicate that it is an even, where k is any natural number.

We introduce two functions

O (x) = 2 x + 1

to express odd numbers greater than 1, and

E (x) = 2 x

to express even numbers, where x is any natural number in N.

We define a strictly increase monotonically piecewise function

f (n)

, from a natural number n it generates two cases: odd or even numbers:

f (n) = \{\begin{matrix} 2 n + 1 = O (n), & the value is odd number, \\ 2 n = E (n), & the value is even number . \end{matrix}

(2)

Definition 1 A natural number n is obtained by composition of the odd-number function

O (x) = 2 x + 1

and the even-number function

E (x) = 2 x

several times, namely

n = f (f (\dots f (1))) = f^{k} (1),

the function f is either odd-number function

O (x)

or even-number function

E (x)

For example,

f (1) = O (1) = 3, f (1) = E (1) = 2

7 = f^{2} (1) = 2 \cdot 3 + 1 = 2 \cdot (2 \cdot 1 + 1) + 1) = O (O (1))

189 = f^{7} (1) = 2 \cdot (2 \cdot (2 \cdot 4 + 1) = 2 \cdot (2 \cdot (2 \cdot (2 \cdot (2 \cdot (2 \cdot 1) + 1) + 1) + 1) + 1)) + 1 = E (O (O (O (O (E (O (1))))

Any natural integer n is the value of the finite times composite function of the odd-number and even-number functions beginning at 1. In particular, If

n = f (f (\dots f (1))) = f^{r} (1)

, then

f^{- r} (n) = 1

is the inverse function.

2.2. Use Binary String to Represent Natural Numbers

Using binary string to represent a natural number n, we can more clearly express the odd-number and even-number functions starting at 1 composite process of a natural number. The string indicates the order of composition of

O (x)

and

E (x)

; 0 implicates an even-number function, and 1 implicates an odd-number function.

A natural number’s binary string represents its odd-even composite function; from left to right, the

i (i > 0)

odd-number function

O (x)

is represented by the 1 in the

i (i > 0)

-bit, and the equivalent even-number function

E (x)

is represented by 0. For instance, the procedure of the composite function of 60 is displayed in Figure 1.

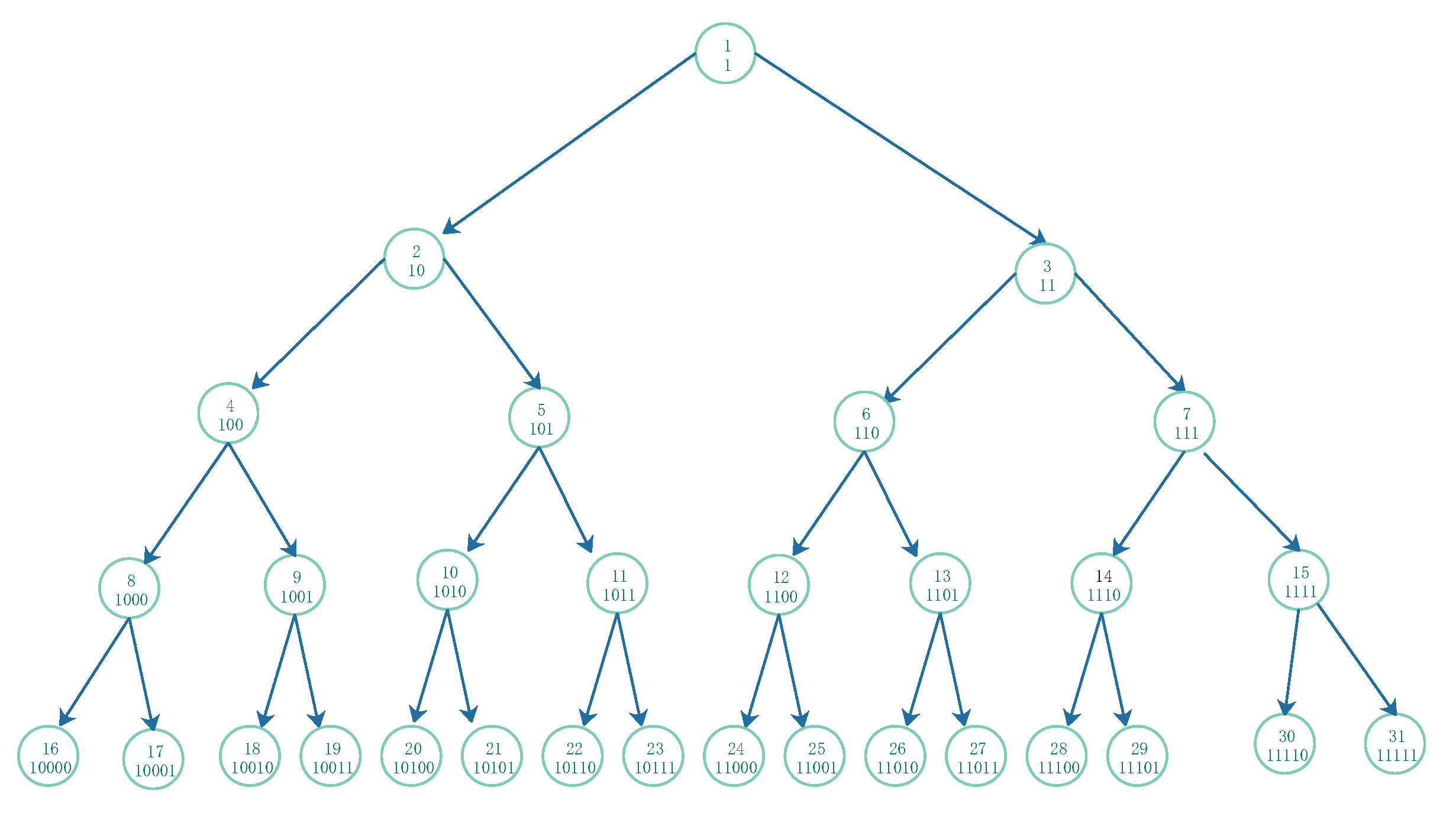
2.3. Use a Graph to Represent the Composite Procedure of the Natural Numbers

In order to give an intuitive impression, we provide a full binary directed tree to represent the natural number set, the root is the smallest number 1. For per vertex, its left-child is an even number which double itself, its binary string is appended by 0, right-child is an odd number which double itself and add 1, its binary string is appended by 1. For an natural number its binary string indicates the procedure of the composition of

O (x)

and

E (x)

from initial value 1 to the final accordingly binary string from the left to right. The full binary directed tree, as in Figure 2, is a very good representation of natural number N.

Proposition 1 A binary string’s length indicates its level in the full binary directed tree, and a binary string’s length minus one represents the number of times the odd- and even-number composite functions occur.

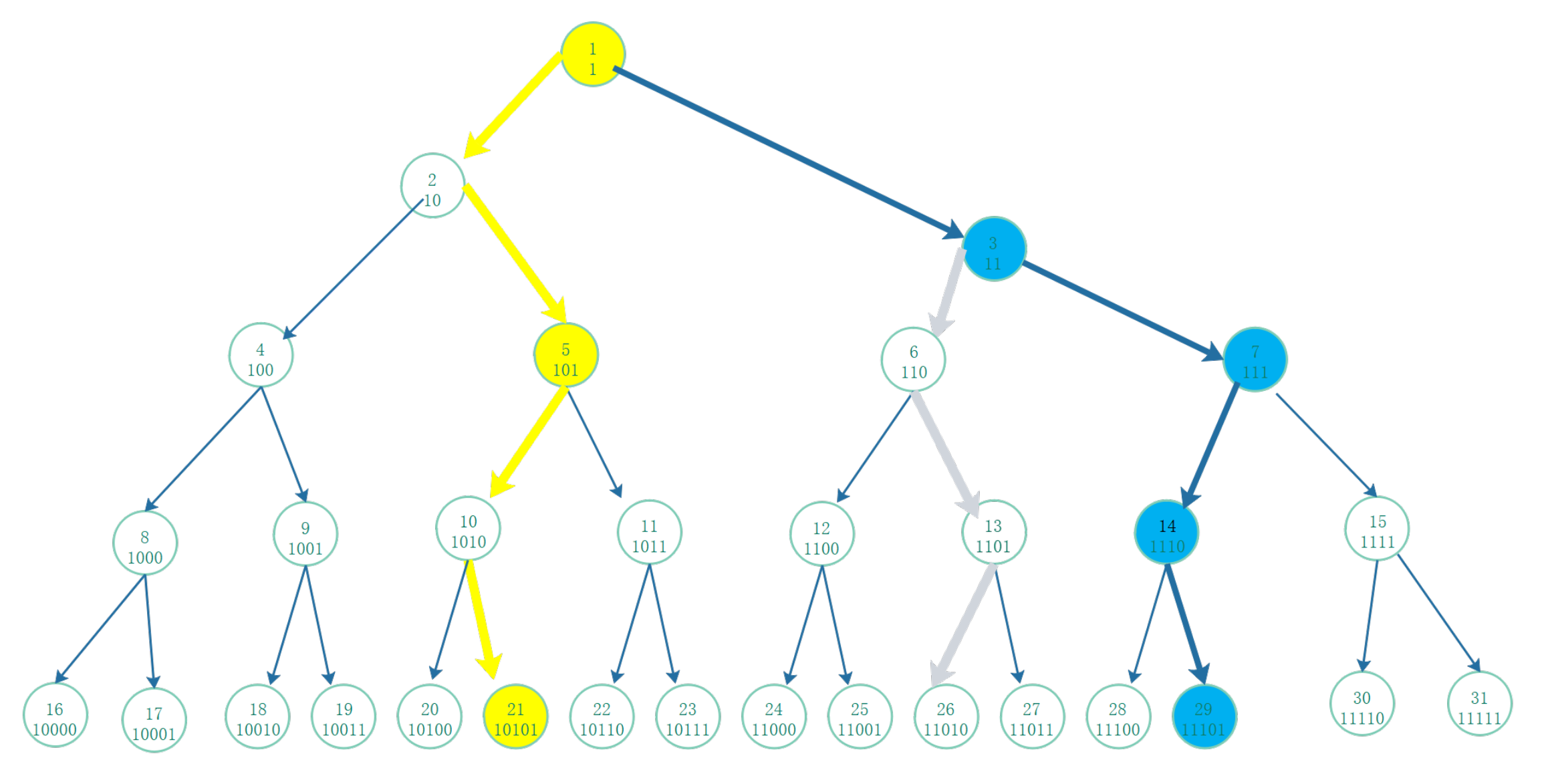
For given natural number n, its binary string from the second bit in left to right appending 0 or 1, indicates which comes from the root 1 of the full binary directed tree traversal according only one branch to itself. For instance, Figure 3 illustrates the procedures of composite odd-number and even-number of 21 and 29.

Given a natural number n, its binary string make of 0 or 1 from the second bit from left to right shows which originates from the root 1 of the full binary directed tree traversal, which only allows one branch to lead to itself. For example, the processes for the composite odd-number and even-number of 21 and 29 are shown in Figure 3.

2.4. Another Partition of the Natural Number Set

We give the definitions of three kinds of natural numbers:

Definition 2(i) A natural number,

O^{m} (1) = 2^{m} - 1 = 2^{m - 1} + 2^{m - 2} + \dots + 2 + 1 = {(11 \dots 1)}_{2}

, is obtained by applying the odd-number function

O (x)

m components. We call it as pure odd number. For instance, those are pure odd numbers:

3 = {(11)}_{2}, 7 = {(111)}_{2}, 15 = {(1111)}_{2}, 31 = {(11111)}_{2}, 63 = {(111111)}_{2}, \dots

. These are located in the full binary directed tree of Figure 2, which is the right leg of the isosceles triangle.

(ii) A natural number,

E^{m} (1) = 2^{m} = {(10 \dots 0)}_{2}

, is obtained by applying the even-number function

E (x)

m components. We call it as pure even number. For instance, those are pure even numbers:

2 = {(10)}_{2}

4 = {(100)}_{2}

8 = {(1000)}_{2}

16 = {(10000)}_{2}

32 = {(100000)}_{2}

64 = {(1000000)}_{2}

. Those are located in the left leg of the isosceles triangle, namely the full binary directed tree of the Figure 2.

(iii) The natural number obtained by the composition of odd function

O (x)

and even function

E (x)

, we call it mixed number. Such as,

18 = {(10010)}_{2}, 28 = {(11100)}_{2}, 67 = {(1000011)}_{2}, 309 = {(100110101)}_{2}

. Those are in the inside of the isosceles triangle, the full binary directed tree of the Figure 2.

In particular, the natural numbers obtained by the finite alternately composition of the odd function

O (x)

and the even function

E (x)

, namely,

{[E (O (1))]}^{m} = {(101 \dots 101)}_{2}

. Such as

5 = {(101)}_{2}, 21 = {(10101)}_{2}, 85 = {(1010101)}_{2}, 341 = {(101010101)}_{2}, 1365 = {(10101010101)}_{2}, 5461 = {(1010101010101)}_{2}, \dots .

We call hard numbers.

The traversal path in the full binary directed tree from the root to down along the arcs, for each natural integer n, is its binary string

1 \times \times

, where the left-child appended 0 for each vertex is an even number and the right-child appended 1 for each vertex is an odd number. For instance, in Fig. 3,

21 = {(10101)}_{2}

originates at the root 1 and proceeds down 2,5,10, ultimately reaching 21. To the vertexes,

1 \to 10 \to 101 \to 1010 \to 10101

, 0,1,0,1 are appended. In addition, for

29 = {(11101)}_{2}

, the appendix 1,1,0,1 is added to the vertexes,

1 \to 11 \to 111 \to 1110 \to 11101

, after it descends from the root 1 down 3,7,14, and ultimately reaches 29.

Property 2 The set of natural numbers can be partited into three different sets: {natural number}=

{pure even number}∪{pure odd number}∪{mixed number}, where {mixed number}={mixed even number}∪{mixed odd number}

Example 1 (1) 60, 97 are mixed numbers.

(2)

64, 1180591620717411303424

are pure even numbers.

(3)

63, 1180591620717411303423

are pure odd numbers.

When we convert those natural numbers from decimal to binary, the facts are obvious.

(1)

60 = {(111100)}_{2}

is a mixed-even number,

97 = {(1100001)}_{2}

is a mixed-odd number.

(2)

64 = 2^{6} = (1000000)

1180591620717411303424 = 2^{70} = (10000 \dots 0)

are pure even numbers:

63 = {(111111)}_{2}

1180591620717411303423 = 2^{70} - 1 = (11 \dots 1)

are pure odd numbers.

3. Two Functions Compare

In order to proof the Collatz conjecture 1 in Section 1, finding the beingness and finiteness of the number m in the expression

T^{m} (n) = 1

for a natural number n is the main challenge.

To visually represent the process of the composite functions of odd- and even-number functions, i.e.,

n = f^{k} (1)

, we propose a full binary directed tree. The following is the inverse functions

f^{- 1} (x)

f^{- 1} (n) = \{\begin{matrix} \frac{n - 1}{2}, & the value is odd number, \\ \frac{n}{2}, & the value is even number . \end{matrix}

(3)

The inverse function

f^{- 1} (x)

differs from the Collatz function

T (x)

, but so do the results of their own finite iterations. However, for infinite or a sufficiently large number of iterations, the iteration Collatz function’s value is the smallest number 1 to the cycle

{1, 4, 2}

If there is a formula

f^{k} (1) = n

for a given natural number n, we know that k is the length of the binary string of n minus 1. In decimal notation, we represent n, which obscures the composite process of odd- and even-number functions. When n is represented as a binary string, it can be used to understand how odd- and even-number functions work.

The iteration of the Collatz function is the key topic in discuss the proof procedure, we have the reduced Collatz function [2,5,6]

R T (x)

R T (n) = \{\begin{matrix} \frac{3 n + 1}{2^{m}}, & if n is odd number, \frac{3 n + 1}{2^{m}} is an odd number, \\ \frac{n}{2^{r}} & if n is even number, \frac{n}{2^{r}} is an odd number . \end{matrix}

(4)

There are many different points for piecewise functions when comparing the Collatz function

T (x)

with the function

f^{- 1} (x)

, the reduced Collatz function

R T (x)

, and the iteration function

f^{k} (x) = O (E (\dots (E (x)))

1) For any natural number x the function

f^{- 1} (x)

and

f^{- r} (x)

are strictly monotonically decreasing.

2) The function

T (x)

, which is strictly monotonically rising, is merely one case of the functions where x is purely even. The function

R T (x)

is wavy when x is a pure or mixed odd number. It is increasing at first, then goes through one or more decreasing processes, either as "increase – decrease – increase" or "increase – decrease ⋯ decrease – increase." For instance, the iterated sequence of Collatz functions is plotted in Figure 4 and Figure 5, where the beginning values are pure odd

255 = 2^{8} - 1 = {(11111111)}_{2}

and mixed odd number

97 = {(1100001)}_{2}

, respectively.

4. Proof the Collatz Conjecture

We have known that mathematics formula about geometric progression with initial term 1 and common ratio x, the sum of the first k terms is

x^{k} + x^{k - 1} + \dots + x + 1 = \frac{x^{k + 1} - 1}{x - 1}

(5)

when

x = 2

, there is a formula

2^{k} + 2^{k - 1} + \dots + 2 + 1 = 2^{k + 1} - 1

(6)

The substantive characteristics is that the powers of 2 must be continuous natural numbers, this is the key to our proof method to solve the Collatz conjecture.

Proof. (i) The conjecture states that if a given natural number

n = 2^{k}

is a pure even, then the smallest natural number 1 can be reached by simply repeating the k times Collatz function divided by 2.

(ii) When a natural number n is not pure even, that is, when it is either pure odd or mixed odd (a mixed even is eliminated since the end-substring 0 can become an odd number; hence, we do not include this case).

Given an odd number n, which can be expressed as follows in algebraic notation:

n = {(1 \times \dots \times 1)}_{2} = 2^{r} + 2^{m} + \dots + 1

, then

\begin{matrix} 3 n + 1 = 2 n + n + 1 \\ = 2^{r + 1} + 2^{m + 1} + \dots + 2 + 2^{r} + 2^{m} + \dots + 1 + 1 \\ = 2^{r + 1} + 2^{m + 1} + \dots + 2 + 2^{r} + 2^{m} + \dots + 2 \\ = 2^{r + 1} + 2^{r} + 2^{m + 1} + 2^{m} + \dots + \dots + 2^{h} \end{matrix}

If the length of the end-substring of n is 1, the length of end-substring of the binary string

3 x + 1

is either 1 or bigger than 1.

Two formulas,

2^{l} + 2^{l} = 2^{l + 1}

and above (6), can be used to modify the structure of the binary string n to the binary string

3 n + 1

. That is, there is an appended term

2^{r - h}

in two equivalent terms,

2^{r + 1 - h}

and

2^{m + 1 - h}

. When the zeros in the middle of a binary string are compared to a bubble, it means that these zeros are gradually being driven out of the rightmost end by

3 n + 1

. It is the same as progressively removing the bubbles hidden in the sponge using a means

3 n + 1

. Once 3n+1, 0 shifts one bit to the right, i.e., the length of the associated binary substring is reduced by one bit, when the length of the end-substring is greater than 1. The end-substring length of the binary string

3 x + 1

is either greater than or equal to 1 if the length of the end-substring of n is 1.

We shall then divide

3 n + 1

by the last term

2^{h}

\begin{matrix} \frac{3 n + 1}{2^{h}} = 2^{r + 1 - h} + 2^{r - h} + 2^{m + 1 - h} + 2^{m - h} + \dots + \dots + 2^{0} \end{matrix}

get another odd number, this is the value of reduced Collatz function (4). And so on, finitely steps after finally we get a pure even number

2^{t}

, this is the case in above (i), thus the Collatz conjecture hold on.

We illustrate the procedure by a mixed odd number

n = 67

and hard number set in the following,

\begin{matrix} 67 = {(1000011)}_{2} = 2^{6} + 2^{2} + 2^{0} \\ 3 \cdot 67 + 1 = 2 \cdot 67 + 67 + 1 = 2^{7} + 2^{2} + 2^{1} + 2^{6} + 2^{1} + 2^{0} + 2^{0} = 2^{7} + 2^{6} + 2^{3} + 2^{1} \\ 3 \cdot 101 + 1 = 2 \cdot 101 + 101 + 1 = 2^{7} + 2^{6} + 2^{3} + 2^{1} + 2^{6} + 2^{5} + 2^{2} + 2^{0} + 2^{0} = 2^{8} + 2^{5} + 2^{4} \\ 3 \cdot 19 + 1 = 2 \cdot 19 + 19 + 1 = 2^{5} + 2^{2} + 2^{1} + 2^{4} + 2^{1} + 2^{0} + 2^{0} = 2^{5} + 2^{4} + 2^{3} + 2^{1} \\ 3 \cdot 29 + 1 = 2 \cdot 29 + 29 + 1 = 2^{5} + 2^{4} + 2^{3} + 2^{1} + 2^{4} + 2^{3} + 2^{2} + 2^{0} = 2^{6} + 2^{4} + 2^{3} \\ 3 \cdot 11 + 1 = 2 \cdot 11 + 11 + 1 = 2^{4} + 2^{2} + 2^{1} + 2^{3} + 2^{1} + 2^{0} + 2^{0} = 2^{5} + 2^{1} \\ 3 \cdot 17 + 1 = 2 \cdot 17 + 17 + 1 = 2^{5} + 2^{1} + 2^{4} + 2^{0} + 2^{0} = 2^{5} + 2^{4} + 2^{2} \\ 3 \cdot 13 + 1 = 2 \cdot 13 + 13 + 1 = 2^{4} + 2^{3} + 2^{1} + 2^{3} + 2^{2} + 2^{0} + 2^{0} = 2^{5} + 2^{3} \\ 3 \cdot 5 + 1 = 2 \cdot 5 + 5 + 1 = 2^{3} + 2^{1} + 2^{2} + 2^{0} + 2^{0} = 2^{4} \\ 1 \end{matrix}

For a special class of mixed numbers, the hard number

\frac{4^{k} - 1}{3} = {(101 \dots 101)}_{2}

, then its Collatz sequent result is

\begin{matrix} a_{k} = \frac{4^{k} - 1}{3} = \frac{4^{k} - 1}{4 - 1} = 4^{k - 1} + 4^{k - 2} + \dots + 4 + 1 = {(101 \dots 101 \dots 101)}_{2}, \\ T (a_{k}) = 3 a_{k} + 1 = 4^{k} = 2^{2 k} = {(10 \dots 0)}_{2}, T^{2 k + 1} (a_{k}) = 1 . \end{matrix}

This means that the Collatz conjecture is valid for this case. Therefore we have proved the Collatz conjecture 1 at Section 1 of this paper. □

Proof.

For the smallest number

1 = 2^{0}

\begin{matrix} T (1) = 3 \times 1 + 1 = 2 \times 1 + 1 + 1 = 2^{1} + 2^{0} + 2^{0} = 2^{1} + 2^{1} = 2^{2} = 4, \\ T^{2} (1) = 2, \\ T^{3} (1) = 1, \end{matrix}

and so on, this is a cycle

{1, 4, 2}

, This is the Collatz conjecture 2 at Section 1 of this paper. □

5. Conclusions

From previous proof of the conjecture, it becomes a theorem.

Theorem 1 There exists a finite natural number m for every natural number n. The Collatz sequence always arrives at the integer 1, that is,

T^{m} (n) = 1

Theorem 2 For any positive integer n, the sequence of the iteration of the Collatz function is an ultimately periodic sequence, its preperiod

η (n)

is a related-to n, and the least period is

{1, 4, 2}

References

Lagarias, Jeffrey C. The Ultimate challenge: the 3x+1 problem; American Mathematical Society, Providence, RI, 2010. isbn=978-0-8218-4940-8.
Richard Kaufman. A reduced forward Collatz algorithm: How binary strings change their length under 3x+1. arXiv 2023, arXiv:2301.07466.
G. Ganesan. Linear recurrences over a finite field with exactly two periods. Advances In Applied Mathematics 2021. 102-108. [CrossRef]
D. Quijada. Periods of linearly recurring sequences. Bachelor thesis, Washingto and Lee University. 2015. isbn=978-0-8218-4940-8.
Bulent Sukusu Proof of the Collatz Conjecture. Theoret. Math. App. 2023, 13, 1-7. [CrossRef]
Jishe Feng. Proof the Collatz Conjecture by a new view of natural numbers, 2023. [CrossRef]
Eldar Sultanow, Christian Koch, Sean Cox, title=Collatz Sequencesinthe Light of Graph Theory. 2023. [CrossRef]

Figure 1. Natural number

60 = {(111100)}_{2}

is obtained starting 1 through the composition of five even-number and odd-number functions.

Figure 1. Natural number

60 = {(111100)}_{2}

is obtained starting 1 through the composition of five even-number and odd-number functions.

Figure 2. The representation of natural number set is a full binary directed tree.

Figure 3.

21 = {(10101)}_{2}

and

29 = {(11101)}_{2}

comes from the path from root 1 walk to 10101 and 11101 accordingly appending 1 or 0 to the vertexes in succession.

Figure 3.

21 = {(10101)}_{2}

and

29 = {(11101)}_{2}

comes from the path from root 1 walk to 10101 and 11101 accordingly appending 1 or 0 to the vertexes in succession.

Figure 4. Point plot of a sequence of 47 iterations of the Collatz function for pure odd 255.

Figure 5. Point plot of a sequence of 118 iterations of the Collatz function for mixed odd 97.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Collatz Conjecture Is Analogous to an Inverse Function of Natural Number

Abstract

1. Introduction

2. An Algebra and Graph Representation of Natural Numbers

2.1. The Composition of Odd-Number and Even-Number Functions

2.2. Use Binary String to Represent Natural Numbers

2.3. Use a Graph to Represent the Composite Procedure of the Natural Numbers

2.4. Another Partition of the Natural Number Set

3. Two Functions Compare

4. Proof the Collatz Conjecture

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe