Prerpints.org logo
Preprint
Article

Non-stationary Transformer Architecture: A Versatile Framework for Recommendation Systems

Altmetrics

Downloads

97

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 May 2024

Posted:

07 May 2024

You are already at the latest version

Alerts
Abstract
Recommendation systems are crucial in navigating the vast digital market. However, user data’s dynamic and non-stationary nature often hinders their efficacy. Traditional models struggle to adapt to the evolving preferences and behaviours inherent in user interaction data, posing a significant challenge for accurate prediction and personalisation. Addressing this, we propose a novel theoretical framework, the Non-stationary Transformer, designed to capture and leverage the temporal dynamics within data effectively. This approach enhances the traditional transformer architecture by introducing mechanisms accounting for non-stationary elements, offering a robust and adaptable solution for recommendation systems. Our experimental analysis, encompassing deep learning and reinforcement learning paradigms, demonstrates the framework’s superiority over benchmark models. The empirical results confirm the efficacy of our proposed framework, which not only provides significant performance enhancements, approximately 8% in Logloss reduction and up to 2% increase in F1 score but also underscores its potential applicability across accumulative reward scenarios. These findings advocate adopting Non-stationary Transformer models to tackle the complexities of today’s recommendation tasks.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In 2023, global e-commerce not only continued its robust growth, reaching a remarkable $6.3 trillion in sales, an increase of 10.4% from the previous year [1,2], but also witnessed the parallel rise of short video content, with the market for short video platforms anticipated to expand to USD 3.24 billion by 2030 [3]. In this rapidly evolving environment, effectively recommending relevant products and engaging video content to consumers has become vital. Consequently, the field of recommendation systems has witnessed accelerated development, with various platforms from online marketplaces to news aggregation sites and short video platforms deploying algorithms tailored to their unique requirements. These algorithms, often rooted in advanced methodologies such as deep learning-based models for predicting product click-through rates (CTR), such as Deep Factorisation Machines (DeepFM) [4], Wide & Deep [5], Deep Interest Evolution Network (DIEN) [6] and Behaviour Sequence Transformer (BST) [7] and reinforcement learning based models for sequential product recommendations, such as Exact-k [8] and traditional deep reinforcement learning algorithm: Double Deep Q-Network (DDQN) [9], Proximal Policy Optimisation (PPO) [10], Deep Deterministic Policy Gradient (DDPG) [11], aim to maximise overall utility.
The diversity in data dimensions across products, users, and interactions inherently introduces significant disparities within recommendation systems. Traditionally, these models, such as DIEN [6] and BST [7], standardise data into a normalised, quasi-normal distribution, which inadvertently ignores non-stationary data characteristics while enhancing computational efficiency. This loss of nuanced information can significantly diminish the effectiveness of recommendations, as models trained on stable datasets often perform well only within those controlled environments, which lack generalisation capability in real-time complicated recommendation systems. Therefore, finding a solution to the intricacies of non-stationary data is vital. Scholars across various fields have explored it, particularly in time-series modelling [12,13] and quantitative finance [14]. In these areas, the focus has often been on adapting models to handle the unpredictable nature of data over time, thereby enhancing predictive accuracy and robustness. In the specific context of recommendation systems, while there has been some focus on mitigating the effects of non-stationarity through techniques like data pruning [15,16], less attention has been given to restoring data to its original, untransformed state. This gap highlights an opportunity for innovation: developing methodologies that accommodate and capitalise on the inherent variability within data. By embracing non-stationarity, it may be possible to construct more adaptive, robust recommendation models that reflect the dynamic nature of user preferences and product features.
This paper addresses the challenge of preserving the intrinsic value provided by non-stationary data within recommendation systems. By introducing a novel mapping relationship within the Non-stationary Transformer architecture, we aim to enhance model robustness without sacrificing the utility of transformed data in different recommendation system tasks. In our experiments on the deep learning dataset TenRec [17] and the reinforcement learning dataset RL4RS [18], models incorporating our Non-stationary Transformer architecture consistently excelled in their respective tasks. Specifically, in the context of TenRec, we observed significant improvements in AUC and LogLoss metrics. Meanwhile, in RL-based tasks with the RL4RS dataset, the average cumulative rewards achieved by our models substantially surpassed those of the original reinforcement learning models. These results underscore the robust applicability and enhanced performance of our proposed framework across different domains of recommendation systems. The structure of this paper is organised into subsequent sections: Section 2 reviews related work on recommendation systems, spotlighting various methodologies currently employed to navigate the complexities of non-stationary data. Section 3, Methodology part, explains the construction of our model, detailing its integration within deep learning-based models and its application in reinforcement learning paradigms. Section 4 and Section 5 present an analytical discourse on our experimental findings, where through a series of diverse datasets, we validate our model’s efficacy in predicting click-through rates within deep learning contexts and its proficiency in forecasting cumulative rewards in reinforcement learning scenarios. We demonstrate our model’s superior performance on test datasets through comparative analysis, substantially enhancing its generalisation capabilities. Section 6 concludes our current discourse, reflecting on the work’s achievements while acknowledging its limitations and proposing directions for future research.

2. Related Work

We review the previous work related to recommendation systems from three perspectives. Initially, we discuss models based on deep learning, which have been widely adopted for their predictive accuracy and scalability. Following this, we explore reinforcement learning-based recommendation systems, highlighting how these models adapt and optimise user engagement over time. Finally, we discuss previous works on processing non-stationary data and introduce our Non-stationary Transformer architecture to address the challenges of non-stationary environments in recommendation systems.

2.1. Deep Learning-Based Recommendation System

The evolution of machine learning algorithms towards deep learning has significantly influenced the development of recommendation system models. Traditionally grounded in machine learning and statistical algorithms, such as Collaborative Filtering [19], Alternating Least Squares (ALS) [20], and Factorisation Machines (FM) [21], the field has witnessed the emergence of deep learning-based extensions that enhance these foundational models. The Factorisation-machine-supported Neural Network (FNN) [22] represents one of FM’s earliest deep learning expansions, laying the groundwork for subsequent innovations. For instance, the Wide & Deep model [5] merges the basic linear regression model with a Multi-Layer Perceptron (MLP) deep learning network, thereby harnessing memorisation and generalisation capabilities. Building on these advancements, Deep Factorisation Machines (DeepFM) [4] optimises the network structure further, integrating FM and deep neural networks to improve prediction accuracy. Attentional Factorisation Machines (AFM) [23] introduces an attention mechanism into the network, enabling the model to focus on relevant features dynamically. Additionally, Graph Factorisation Machines (GraphFM) [24,25] incorporates graph neural network modules, enhancing the model’s ability to leverage complex relational data. Parallel to these developments, deep learning-based sequence recommendation algorithms have also evolved, primarily leveraging Recurrent Neural Networks (RNNs). The Deep Interest Network (DIN) [26] enhances basic sequence models with an attention mechanism, focusing on capturing evolving user interests. This concept is further extended by the Deep Interest Evolution Network (DIEN) [6], which divides the model into layers for user behaviour sequences, interest extraction, and interest evolution, addressing the dynamic nature of user preferences. The introduction of the transformer model led to the development of the Behaviour Sequence Transformer (BST) [7], which employs the transformer encoder architecture to integrate user historical interaction data with user and item features. Furthermore, Bidirectional Encoder Representations from Transformer for Recommendation (BERT4Rec) [27] adapts the Bidirectional The Encoder Representations from Transformer (BERT) [28] model’s capabilities for recommendation systems showcase the adaptability of deep learning innovations in this domain. These models update their structure from RNN to transform to improve the robustness in prediction but lack details of recovering the data to their original status.

2.2. Reinforcement Learning-Based Recommendation System

In recommendation systems, reinforcement learning has been innovatively adapted from classical RL algorithms to address this field’s unique challenges and dynamics. These approaches leverage real-time user feedback and interactions to continually refine and optimise recommendation strategies, embodying a proactive approach to user engagement and satisfaction. This adaptation has led to the evolution of specialised models, branching from foundational RL algorithms like Deep Q-Network (DQN) [29], DDPG, and Soft Actor-Critic (SAC), each contributing distinct methodologies and applications within the recommendation ecosystem [30]. Adapting the DQN [31] framework has given rise to innovative models such as the Deep Recommender System (DEERS) [32], which models user interactions as a Markov Decision Process (MDP), dynamically adapting to positive and negative feedback to refine user experience. The deep reinforcement learning framework for news recommendation (DRN) [33], tailored for personalised online news recommendations, optimises future rewards by accounting for the fluctuating nature of news preferences and user engagement patterns. Integrating social network insights in the Social Attentive Deep Q-network (SADQN) [34] addresses data sparsity and cold start challenges, offering more precise recommendations by harnessing social influences and individual preferences. The deep reinforcement learning for online advertising impression in recommender systems (DEAR) [35] employs DQN to balance ad revenue generation with user experience in advertising, making strategic ad inclusion and placement decisions. Within the DDPG framework, models like DeepPage [36] utilise deep reinforcement learning to optimise digital page layouts, responding dynamically to user feedback to boost engagement on e-commerce platforms. The Knowledge-Guided Deep Reinforcement Learning (KGRL) [37] system combines RL with knowledge graphs, employing an actor-critic architecture to improve decision-making in interactive recommendation systems, surpassing traditional methods in performance. Supervised deep reinforcement learning recommendation framework (SRR) [38] addresses the challenge of prioritising top recommendations by blending supervised learning with RL, enhancing the efficacy of top-position recommendations without compromising long-term goals. The SAC [39] algorithm has inspired models such as Multi-Agent Soft Signal-Actor (MASSA) [40], which adopts a multi-agent cooperative RL approach for optimising module rankings in e-commerce settings without inter-module communication. Employing a signal network to generate coordination signals, this model fosters global policy exploration. Similarly, Multi-Agent Spatio-Temporal Reinforcement Learning (MASTER) [41] leverages a multi-agent spatio-temporal RL framework to recommend electric vehicle charging stations, considering long-term spatial and temporal dynamics and demonstrating enhanced performance in practical applications. The extension models from DQN, DDPG, and SAC are applied to different specific recommendation scenarios, focusing on adding more specific blocks to improve the prediction based on the stationary features.
In recommendation systems’ evolving domain, models based on deep learning and reinforcement learning typically process data into a standardised, stationary format, approximating a normal distribution to streamline model analysis. This standardisation, however, can inadvertently strip away unique data characteristics, potentially affecting analytical outcomes. Existing research has tried tailoring recommendation systems to adapt to the inherently non-stationary nature of user preferences and behaviours, introducing solutions to maintain system efficacy in such variability. Ye et al. introduce an adaptive case that employs a novel pruning algorithm for large-scale recommendation systems grappling with non-stationary data distributions, effectively balancing model adaptability and computational efficiency [15]. Huleihel et al. extend collaborative filtering techniques to accommodate the temporal variability in user preferences, enhancing recommendations’ relevance and personalisation [42]. Wu et al. propose a two-tiered hierarchical bandit algorithm to navigate the exploration-exploitation trade-off in environments characterised by non-stationarity and delayed feedback, facilitating more timely and contextually appropriate recommendations [43]. Chandak et al. address the challenge of delayed feedback in such settings with a stochastic, non-stationary bandit model that leverages intermediate observations to refine learning processes and decision-making [44]. Despite the notable advancements these studies contribute to the field, their application tends to be constrained by the specific contexts for which they were developed, limiting their generalisability. Our research aims to bridge this gap by reinstating the non-stationary attributes of data within a more universally applicable recommendation system framework. By integrating our model within both deep learning and reinforcement learning paradigms, we improved performance over traditional models that rely on stationary data processing. This enhancement not only underscores the robustness of our approach but also its versatility across a broad spectrum of complex data scenarios.

3. Methodology

In this section, we introduce the architecture of our Non-stationary Transformer [12,14], initially presenting its foundational structure. Following this, we combine it within deep learning and reinforcement learning-based recommendation systems, demonstrating the model’s versatility and wide applicability across various recommendation scenarios.

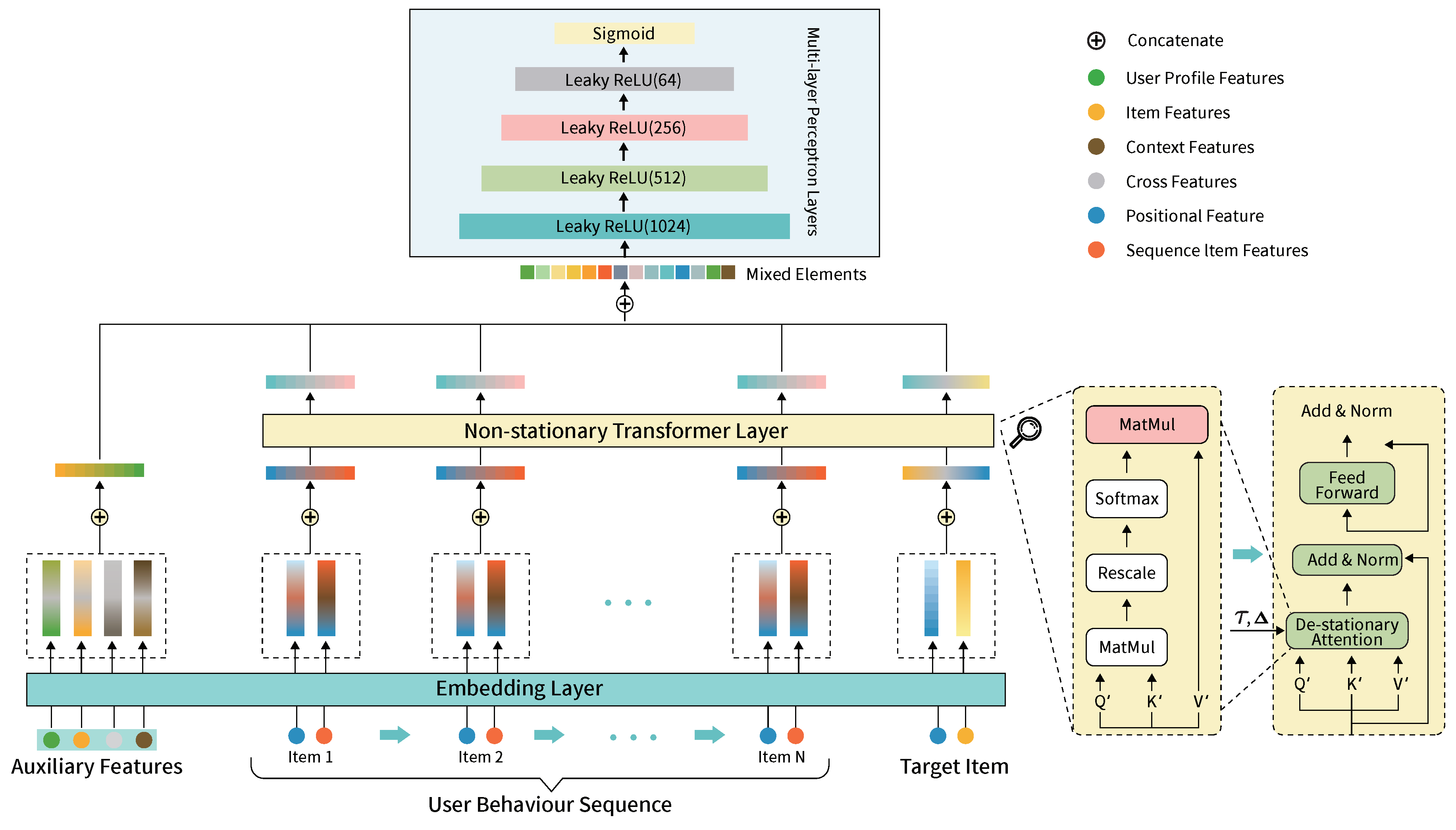
3.1. Non-stationary Transformer Structure

3.1.1. Projector Layer

The initiation point of our Non-stationary Transformer is the projector layer, essentially a framework designed to detect and adapt to the evolving patterns within sequential datasets. The adaptation process commences with:
X reduced = 1 T ∑ t = 1 T x t
where X reduced represents the dimensionally reduced data obtained through averaging over the temporal dimension T. Each x t corresponds to the data vector at time point t, capturing specific features. The index t runs from 1 to T, indicating the sequential nature of the averaged data points. Following this, the data is processed through a series of transformation layers, each comprising a dense neural network structure with Leaky ReLU activation, encapsulated as:
Y = Leaky ReLU ( W hidden · X reduced + b hidden )
where W hidden and b hidden denote the weights and biases of the hidden layers, respectively. Then the final output, incorporating the essence of the non-stationary features, is rendered through:
Z = tanh ( Y )
where tanh represents the hyperbolic tangent function, encapsulating the detected non-stationary aspects.

3.1.2. Transformer Encoder Layer

The transformer encoder layer is at the core of our structure, adding a self-attention mechanism specifically tailored for analysing complex sequential data. Integral to this encoder are the dynamic elements, namely scale_learner and shift_learner. These elements are crucial for adapting to changes in data over time, with the scale_learner adjusting the significance of different temporal features and the shift_learner accommodating shifts in the data’s patterns or distributions. Together, they ensure the model’s attention mechanism remains attuned to the evolving characteristics of the sequential data, as expressed by:
log τ = scale _ learner ( x raw , σ enc ) , Δ = shift _ learner ( x raw , μ enc )
where σ enc and μ enc denote the standard deviation and mean of the input sequences, respectively. The adapted attention mechanism in our dynamic structure is formulated to accommodate the intricacies of non-stationary data. Specifically, Q ′ , K ′ , and V ′ represent the stabilised versions of the queries, keys, and values obtained from the original dataset. The attention function is represented as:
Attn ( Q ′ , K ′ , V ′ , τ , Δ ) = Softmax τ ⊙ ( Q ′ K ′ ⊤ ) + Δ d k V ′
In Equation (5), the operation τ ⊙ ( Q ′ K ′ ⊤ ) effectively scales the dot product of the queries Q ′ and keys K ′ with the scaling factor τ , which is designed to adjust for time-varying aspects of the data. The term Δ introduces a shift to these scaled scores, further tailoring the attention scores to the non-stationary characteristics of the dataset. The normalisation factor d k , where d k denotes the dimensionality of the keys, ensures that the scaled dot products maintain a consistent variance, promoting stable gradients throughout the model. The softmax function is then applied to the resulting scores, converting them into a probability distribution. This step ensures that each value in the interval (0, 1) and the entire vector sums to 1. Finally, the attention scores are applied to the values V ′ through a weighted sum. This multiplication aggregates the information across all values, weighted by their relevance as determined by the attention scores, culminating in the output of the attention mechanism. This output serves as a contextually enriched representation that synthesises the most relative information from the input data, adjusted for both the temporal dynamics and the non-stationary features inherent in the dataset. A layer normalisation and dropout combination is applied to ensure stability and prevent model overfitting. We put the previous attention result in the dropout process and then use the layer normalisation in the process:
X final = LayerNorm X + Dropout Attn ( Q ′ , K ′ , V ′ , τ , Δ )
With its novel approach to handling non-stationary data through adaptive learning and dynamic adjustments, this architecture can be applied in designing transformers for complex and evolving datasets.

3.2. Fusion in the Deep Learning-based Recommendation System

We then integrate our Non-stationary Transformer architecture into the deep learning-based recommendation system framework, mainly focusing on refining the BST [7] algorithm. This integration involves replacing conventional transformer layers with our advanced Non-stationary Transformer modules to better capture temporal dynamics and distributional shifts in user behaviour sequences, see Figure 1.
Embedding Layer: The embedding layer initiates the adaptation process by transforming the multifaceted input data into compact, low-dimensional vector representations. The input data is categorised into three principal segments: (1) The core component comprises user behaviour sequence, encapsulating the dynamic interplay between users and items over time. (2) Auxiliary features encompass a broad spectrum of attributes, including user demographics, product specifications, and contextual information, enriching the model’s understanding beyond mere interaction patterns. (3) The target item features primarily focus on characteristics of new or prospective items that are subjects of prediction. Each of these segments undergoes a distinct embedding process, resulting in specialised embeddings that collectively form a comprehensive representation of the multifaceted input data within our model. This embedding strategy is crucial for capturing the nuanced relationships and attributes inherent in user behaviour sequences, auxiliary features, and target items. To preserve the sequential essence of user interactions, we employ positional features that assign temporal values based on the chronological distance between item interactions and the moment of recommendation.
Non-stationary Transformer Layer: We replace the BST algorithm’s standard transformer layers with our Non-stationary Transformer layers. This substitution improves the model’s ability to adapt to temporal variations and data distribution shifts, thereby enabling a deeper understanding of complex inter-item relationships and user interaction patterns within a dynamically changing context.
Multi-layer Perceptron Layers: The final part of our architecture is marked by a series of MLP layers coupled with a customised loss function designed for the binary classification task of predicting user clicks or the multi-classification task of predicting product scores. This final ensemble leverages the enriched feature set processed through the Non-stationary Transformer layers, facilitating precise and context-aware recommendations.
By adding the Non-stationary Transformer into the structure of the BST algorithm, our approach retains the original model’s capability to process user behaviour sequences. It significantly enhances the adaptability and predictive accuracy of user interaction. This novel integration represents a significant improvement in deep learning-based recommendation systems, promising superior performance in navigating the complexities of dynamic user behaviour patterns.

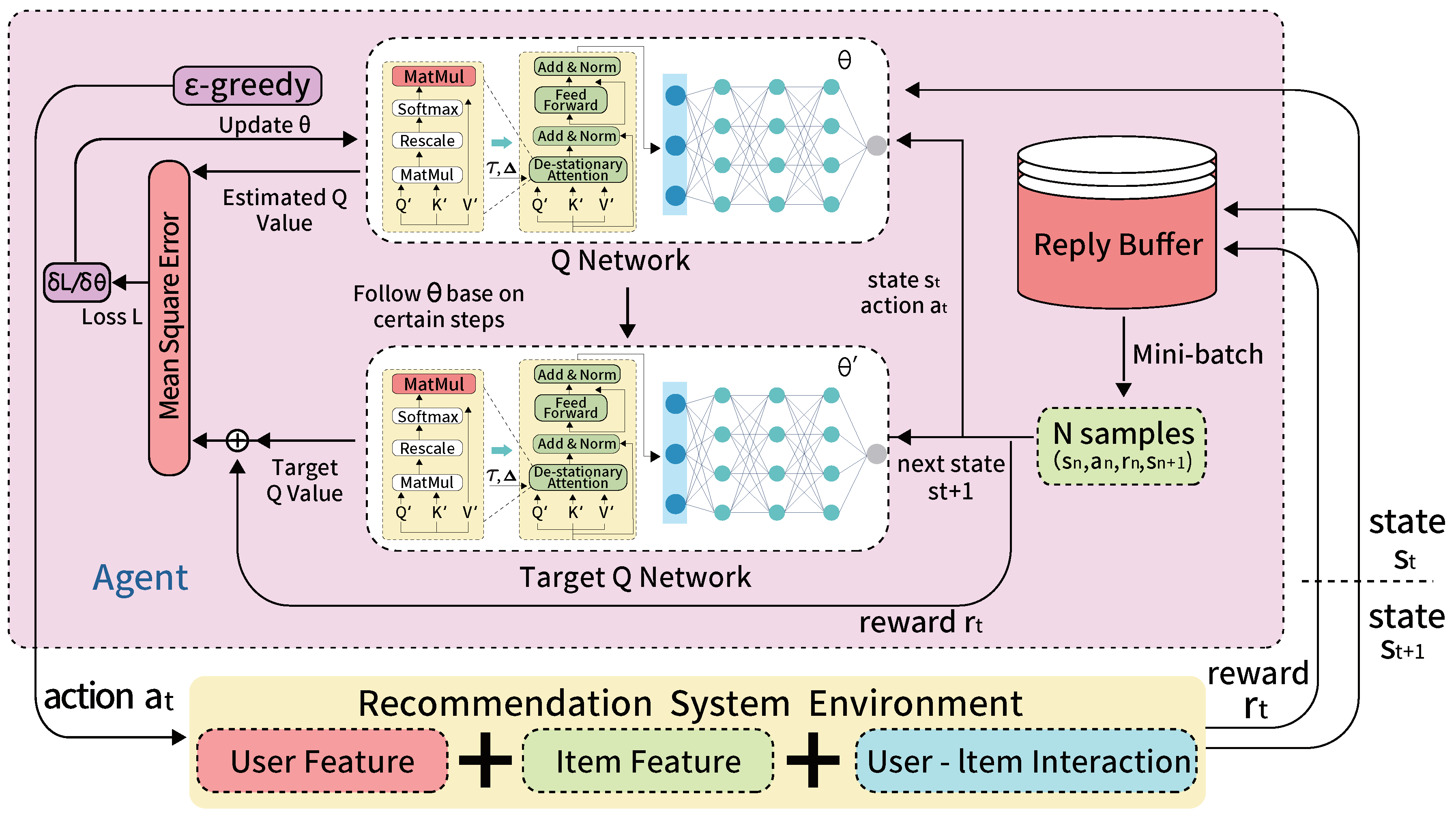
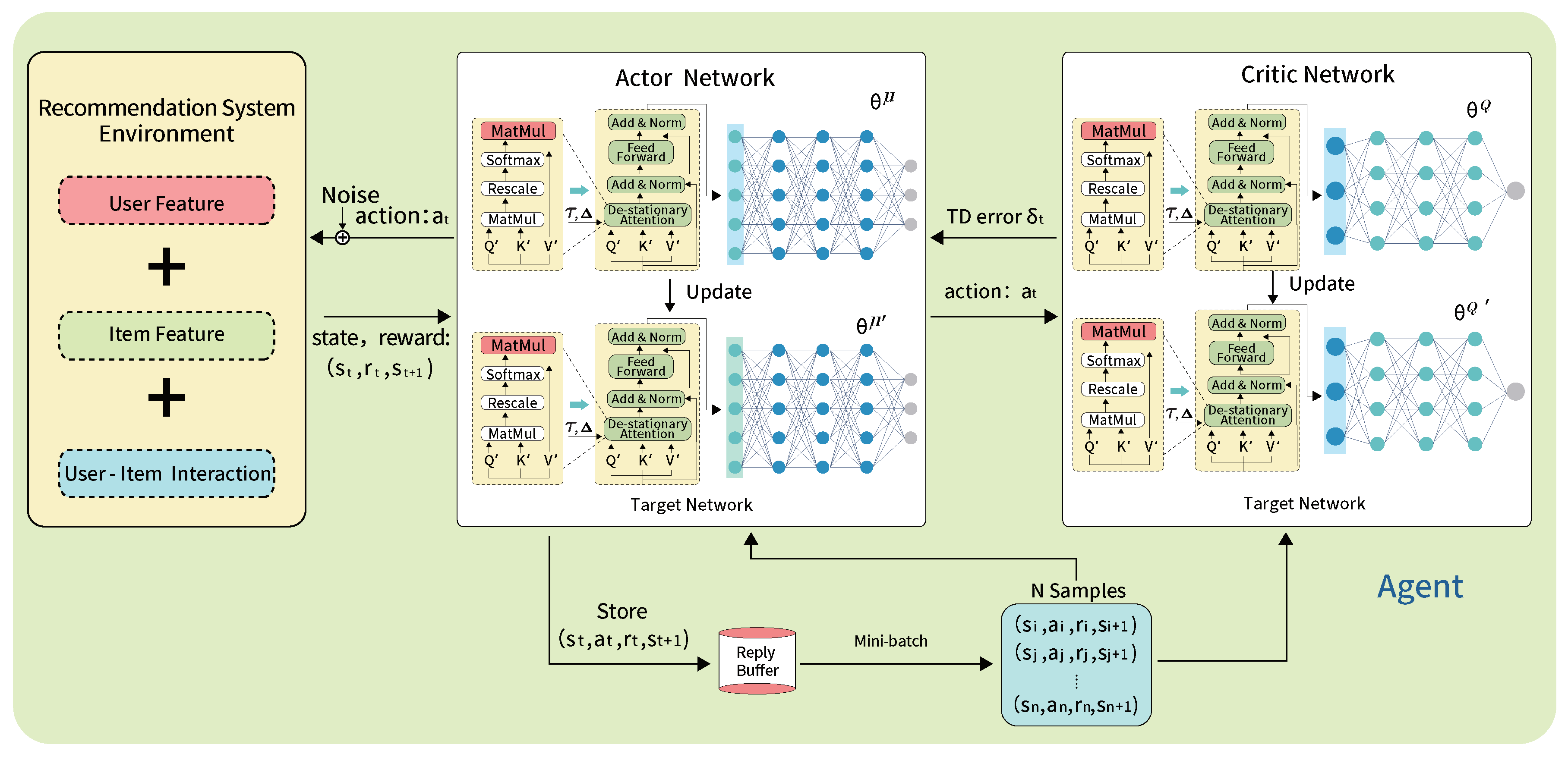
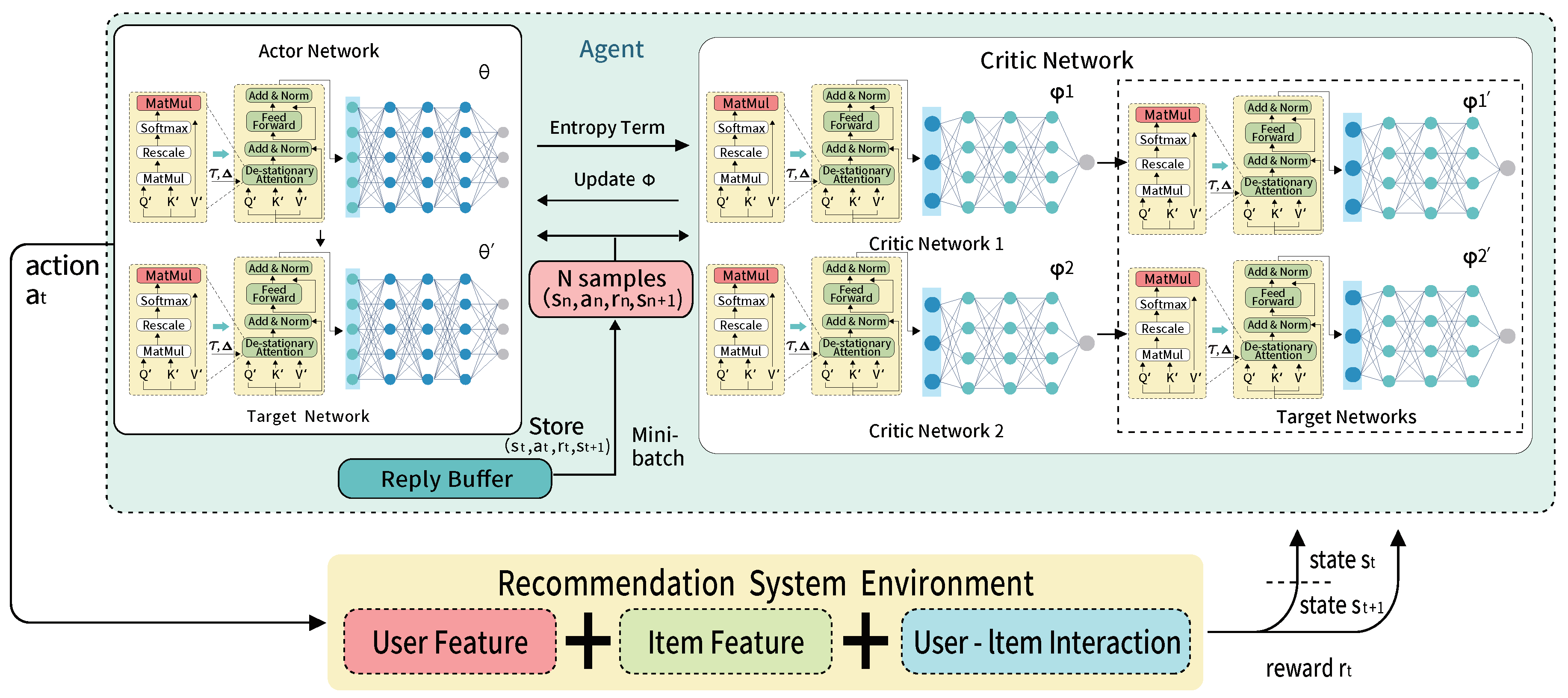
3.3. Fusion in the Reinforcement Learning-Based Recommendation System

We embedded our Non-stationary Transformer architecture into the core of reinforcement learning-based recommendation systems, specifically choosing the DDQN, DDPG, and SAC frameworks for integration. These frameworks are classic models within the field of reinforcement learning and represent different branches of the discipline, which showcases the versatility of our Non-stationary Transformer. By leveraging this architecture, we aim to enhance the models’ predictive capabilities and robustness, especially given their superior handling of non-stationary data characteristics. With their distinct mechanisms and strengths, the choice of DDQN, DDPG, and SAC provides a broad and comprehensive testing ground to demonstrate our approach’s enhanced adaptability and performance across various reinforcement learning scenarios.
Integration with DDQN: Integrating the Non-stationary Transformer within the DDQN framework substantially augments the model’s precision in value estimation and policy optimisation (Figure 2). DDQN [9], an extension of DQN [29], introduces a critical improvement by decoupling the selection and evaluation of the action in the Q-value update equation, thereby mitigating overestimation. The standard DQN update equation [45] is given by:
Q new ( s t , a t ) = Q ( s t , a t ) + α [ r t + 1 + γ max a Q ( s t + 1 , a ) − Q ( s t , a t ) ]
where s t and a t are the state and action at time t, r t + 1 is the reward received after taking action a t , α is the learning rate, and γ is the discount factor. In DDQN, this is modified to:
Q new ( s t , a t ) = Q ( s t , a t ) + α [ r t + 1 + γ Q target ( s t + 1 , arg max a Q ( s t + 1 , a ) ) − Q ( s t a t ) ]
where Q target represents the action-value function estimated by the target Q-network. In DDQN, we introduce a dual mechanism that significantly boosts the model’s ability to process and predict sequential datasets by embedding the Non-stationary Transformer into both the Q-network and the target Q-network. This is particularly relevant for recommendation systems where the goal is to sequentially recommend products on a page, with each recommendation considered an action. The DDQN, enhanced with our transformer, aims to maximise the overall layout’s utility, striving for the highest possible number of clicks or transactions through strategic product recommendations based on historical user-item interactions, product characteristics, and user profiles.
This enhanced approach allows the DDQN to more accurately anticipate the cumulative rewards associated with different action sequences, optimising the selection of items to present to the consumer at each step. The Non-stationary Transformer’s integration further empowers the DDQN to handle the temporal dynamics and non-stationary nature of recommendation system data, ensuring enhanced performance in environments characterised by rapidly evolving user preferences and interaction patterns.
Integration with DDPG: The augmentation of the DDPG [11] framework with the Non-stationary Transformer involves strategically embedding this architecture into the actor-network and the critic-network (Figure 3). This integration significantly enhances the model’s capacity to interpret and respond to recommendation system tasks’ complex, sequential nature.
In the Actor Network, the Non-stationary Transformer’s integration facilitates a more nuanced understanding of the current state, enabling the network to propose actions (e.g., product recommendations) that are not only optimal based on current knowledge but also adaptive to the evolving user preferences and behaviours. The transformer’s ability to process temporal sequences and adapt to data shifts allows the actor-network to make more informed decisions, especially in scenarios where user interactions with items change dynamically. Most importantly, it recovers the original non-stationary dataset distribution to reflect in the decision-making of the recommendation systems. For the Non-stationary Transformer integration within the DDPG framework, the actor-network update is defined by the following equation:
∇ θ μ J ≈ E ∇ a Q ( s , a | θ Q ) | s = s t , a = μ ( s t ) ∇ θ μ μ ( s | θ μ ) | s = s t
where ∇ θ μ J represents the gradient of the objective function J with respect to the actor parameters θ μ . This gradient is estimated as the expected value of the product of the gradient of the action-value function Q with respect to the action a, evaluated at the current state s t and the action proposed by the current policy μ ( s t ) and θ μ are the parameters of the Non-stationary Transformer integration DDPG’s actor-network. Equation (9) allows the actor-network to learn optimal policies over time by ascending the gradient of the performance criterion.
For the Critic Network, including the Non-stationary Transformer, empowers the network to more accurately estimate the future rewards associated with the actions proposed by the actor-network. This is particularly critical in recommendation systems, where the value of an action (e.g., the likelihood of a user clicking on a recommended item) can vary significantly over time. By capturing the temporal dynamics and distributional shifts in user-item interaction data, the critic-network can provide more reliable feedback to the actor-network, leading to continuous policy refinement. In the critic network of the Non-stationary Transformer-integrated DDPG model, the loss function L used for training is defined as follows:
L = E r + γ Q ( s ′ , μ ( s ′ | θ μ ′ ) | θ Q ′ ) − Q ( s , a | θ Q ) 2
where r is the reward received after executing action a in state s, and γ is the discount factor that weighs the importance of future rewards. The term Q ( s ′ , μ ( s ′ | θ μ ′ ) | θ Q ′ ) is the action-value predicted for the next state s ′ by the target policy μ and the target critic network, parameterised by θ μ ′ and θ Q ′ . Meanwhile, θ Q is the parameters of the critic-network.
Incorporating the Non-stationary Transformer into DDPG preserves DDPG’s advantages by offering smoother policy updates and reducing the variance in policy evaluation while significantly enhancing the model’s robustness and adaptability. By leveraging the transformer’s ability to process non-stationary data, our adapted DDPG framework exhibits superior performance in capturing the dynamic user-item interactions and evolving preferences, which are crucial for making precise and contextually relevant recommendations.
Integration with SAC: The SAC [39] algorithm, known for its stability and efficiency in continuous action spaces, employs an entropy-augmented reinforcement learning strategy that encourages exploration by maximising a trade-off between expected return and entropy. Integrating the Non-stationary Transformer into SAC involves embedding this advanced architecture into both actor-networks and critic-networks (Figure 4). It enhances their capability to process sequential decision-making tasks by capturing the complex dependencies in user-item interactions. The transformer’s ability to handle temporal dynamics and non-stationary data significantly improves the policy’s adaptability and the precision of action selection in dynamic recommendation environments. The core of enhanced SAC consists of two actor-networks π θ and π θ ′ , and four critic networks Q ϕ 1 , Q ϕ 1 ′ , Q ϕ 2 , and Q ϕ 2 ′ , where θ and ϕ denote the parameters of the actor and critic networks, respectively. Including the Non-stationary Transformer in the four critic networks enables a more nuanced valuation of the state-action pairs, considering the evolving nature of user preferences and item attributes. The objective function for the actor-network in enhanced SAC with Non-stationary Transformer is given by:
J π ( θ ) = E s t ∼ D , a t ∼ π θ min i = 1 , 2 Q ϕ i ( s t , a t ) − α log π θ ( a t | s t )
where D is the experience replay buffer, α is the temperature parameter that determines the importance of the entropy term, and s t and a t represent the state and action at time t, respectively. This comprehensive understanding of the data’s temporal and non-stationary aspects allows for a more accurate estimation of expected returns, facilitating more effective policy updates. The SAC equipped with the Non-stationary Transformer, sets a new benchmark for reinforcement learning-based recommendation systems, particularly in handling the complexities of sequential decision-making and adapting to the dynamic nature of recommendation tasks.
Through these strategic fusions, our Non-stationary Transformer improves the predictive accuracy of reinforcement learning models in recommendation systems. It enhances adaptability and robustness previously unattainable with conventional transformer architectures. This innovative approach promises to redefine the standards of reinforcement learning-based recommendation systems, accommodating the complex and dynamic nature of real-world user behaviour and preferences.

4. Experimental Analysis

4.1. Datasets

In our experimental analysis, we utilise two distinct datasets tailored to the specific needs of our study: Tenrec [17] for deep learning-based experiments and RL4RS [18] for reinforcement learning-based investigations.
Tenrec Dataset: Derived from Tencent’s renowned recommendation platforms, QQ BOW (QB) and QQ KAN (QK), the Tenrec dataset focuses on video recommendations, encapsulating a vast range of user interactions including clicks, likes, shares, and follows. The QK-video dataset alone boasts over 5 million users and 3.75 million items, resulting in a staggering 142 million clicks, alongside significant volumes of likes, shares, and follows. This extensive dataset, with its diverse feature set covering user demographics and item categories, is anonymised to ensure user privacy. Including both positive and negative feedback provides a holistic view of user preferences, which is pivotal for refining deep learning models within recommendation systems.
RL4RS Dataset: Originating from one of NetEase Games, the RL4RS dataset focuses on reinforcement learning applications in recommendation systems. Comprising two distinct subsets, RL4RS-Slate and RL4RS-SeqSlate, the dataset facilitates the exploration of single-page and sequential slate recommendations to maximise session rewards. The RL4RS-Slate dataset encompasses interactions from 149,414 users across 283 items, resulting in approximately 949 valid item slates per dataset variant, highlighting its complexity and potential for advancing reinforcement learning strategies in recommendation tasks. This comprehensive collection of interaction logs, user behaviours, and item features within the RL4RS dataset offers an unparalleled resource for investigating advanced recommendation strategies and sequential decision-making processes, further enriched by the detailed statistical insights provided.

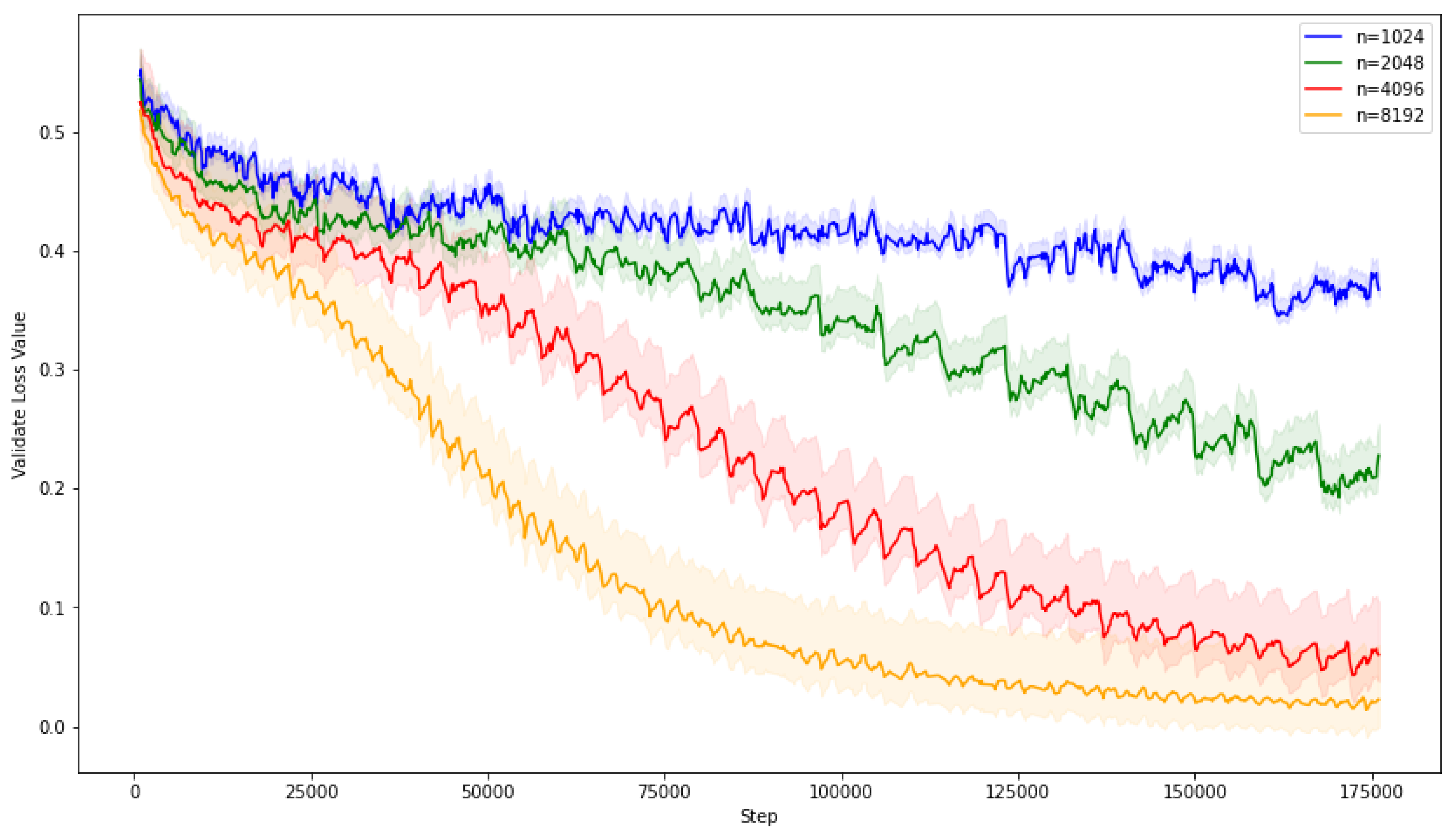
4.2. Deep Learning-Related Experiment

Using PyTorch as the computational framework, we used the Tenrec video dataset for the click-through rate prediction task, dividing it into three subsets: 70% for training, 15% for validation, and 15% for testing. Table 1 provides a summary of these splits. We trained two models on the training set: the baseline BST model and our enhanced version, which incorporated the Non-stationary Transformer. As depicted in Figure 5, the baseline BST model’s loss gradually converges to approximately 0.43, while the Non-stationary Transformer BST model demonstrates a more significant loss reduction, converging around 0.39. This notable difference indicates that our Non-stationary Transformer BST model achieves a lower train loss overall, suggesting an enhanced learning efficiency. Then, we plan to extend this comparative analysis to the test set to validate the models’ performance and ascertain whether the lower train loss translates to improved prediction accuracy on unseen data.
During the validation phase of our experiment, we conducted trials to determine the optimal batch size, considering the immense scale of the Tenrec video dataset, which contains over a hundred million records. Guided by Tenrec’s introduction, which suggests larger batch sizes for datasets of this magnitude, we experimented with batch sizes in powers of two: 1024, 2048, 4096, and 8192. Figure 6 indicates that larger batch sizes facilitated a more rapid decrease in loss. However, upon evaluating the largest batch size of 8192, we observed the loss diminishing to near zero, indicating a potential risk of severe overfitting. Consequently, based on these observations, we identified 4096 as the most suitable batch size for our experiments, balancing efficient learning with the need to avoid overfitting.
We utilise several performance metrics in the test, including Logloss, AUC and F1 score. We compare the models’ effectiveness with Tenrec data’s baseline models, such as Wide & Deep [5], DeepFM [4], Neural Factorisation Machines (NFM) [46], and Deep & Cross Network (DCN) [47], in which these baseline models are referenced in the original dataset. As Table 2 illustrates, our Non-stationary Transformer BST model not only aligns with but also significantly enhances the performance of the baseline BST model. It achieves an improvement in Logloss of 8.31%, an increase in AUC by 0.81%, and a rise in the F1 score of 2.79%. Moreover, compared with other benchmark models, our Non-stationary Transformer BST model demonstrated a clear advantage, yielding the lowest Logloss and the highest scores in both AUC and F1 metrics. Notably, it surpassed the Wide & Deep model by a substantial margin, with improvements of 14.89% in Logloss, 0.84% in AUC, and a significant 4.91% in the F1 score. Similar outperformance trends were observed against all metrics across the DeepFM, NFM and DCN models. These results underscore the exceptional ability of the Non-stationary Transformer BST model to effectively predict click-through rates, showcasing its strength in handling the complex and dynamic nature of the data inherent in recommendation systems. Integrating the Non-stationary Transformer within the BST framework enhanced its learning efficiency on the training data. It solidified its robustness and accuracy, making it a superior model for the CTR prediction task in practical applications.

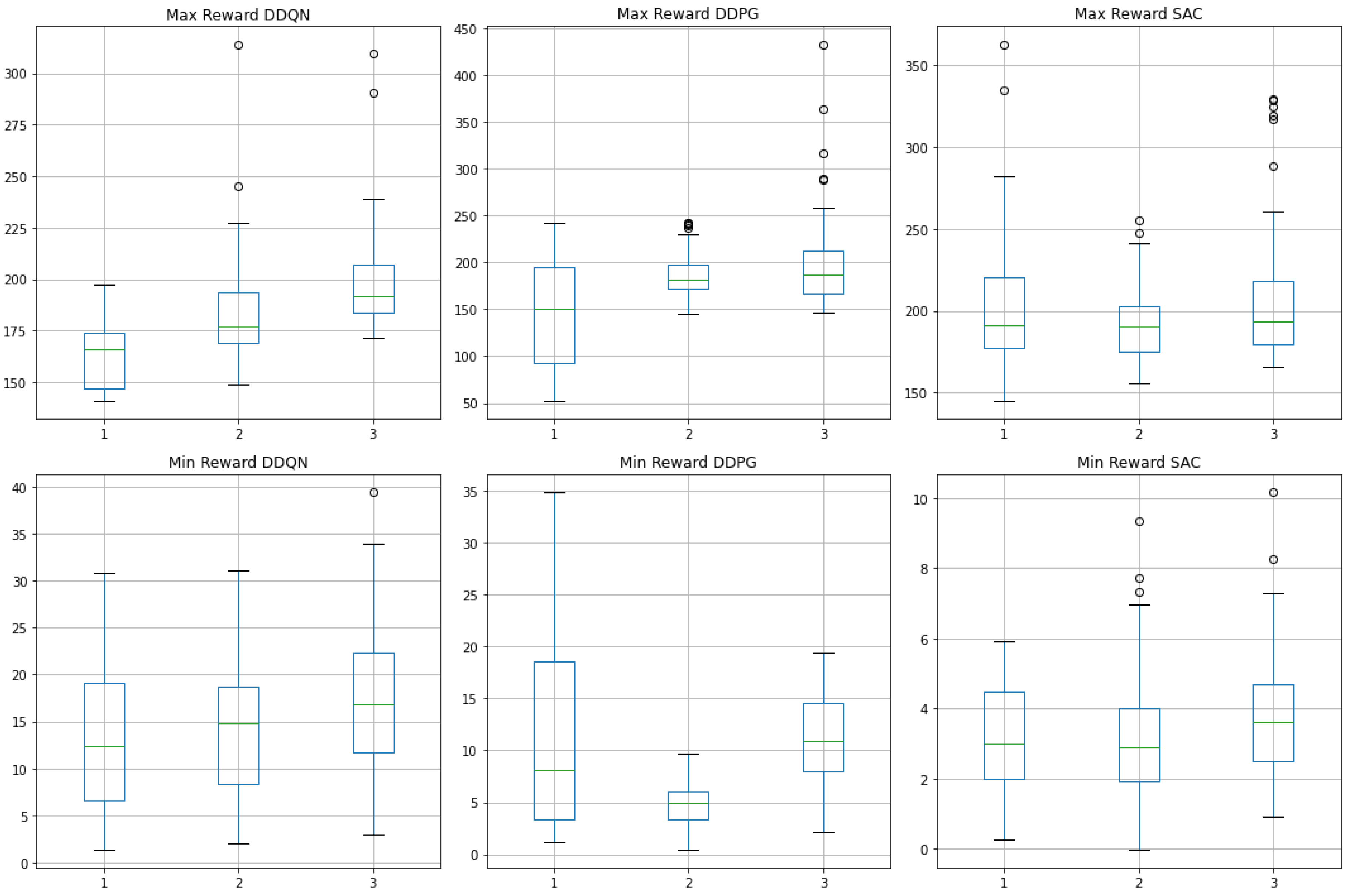
4.3. Reinforcement Learning-Related Experiment

For our reinforcement learning experiments, we employed the RL4RS-Slate dataset to train models across three distinct reinforcement learning frameworks: DDQN, DDPG, and SAC. These frameworks represent three classic types of models in the field of reinforcement learning. The experiments were conducted using the TensorFlow 1.15 environment. In each framework, we developed three models: one following the original framework architecture, the second integrating a transformer layer, and the third enhanced with a Non-stationary Transformer layer. To ensure comparability, we established a set of common hyperparameters for all models. The training configuration was as follows:
  • epochs: 10,000
  • maximum sequence length: 64
  • batch size: 64
  • action size: 284
  • number of classes: 2
  • number of dense features: 432
  • number of category features: 21
  • number of sequences: 2
  • embedding size: 128
  • hidden units: 128
For each model during the 10,000 epochs, we stored the optimal parameters. Then, post-training evaluations were conducted on the RL4RS-Slate dataset by recording the performance across 50 episodes for each model variant within the DDQN, DDPG, and SAC frameworks by randomly starting. We collected the maximum and minimum rewards for each episode and the average across the episodes. The results, depicted in Figure 7, exhibit the reward distribution for the original models, those with an added transformer layer, and those enhanced with the Non-stationary Transformer layer. The box plots in Figure 7 show that models incorporating the transformer layer (marked as “2” in each subplot) display a more concentrated range of rewards, suggesting that the transformer layer contributes to a more effective learning of the sequential patterns present in the dataset. However, this may come at the cost of losing some inherent data characteristics due to a stationary assumption. In contrast, the Non-stationary Transformer models demonstrate an extended range of maximum and minimum rewards, retaining the data’s non-stationary features and indicating their ability to maintain higher reward potential. An additional observation is that the maximum rewards achieved by DDPG and SAC models frequently surpass 200, a benchmark that only a minority of the DDQN episodes exceed. This outcome is attributed to the policy gradient nature of DDPG and SAC, which enables a more effective exploration of optimal strategies than DDQN. Moreover, SAC exhibits the smallest minimum rewards, often between 3 and 5, suggesting that incorporating entropy regularisation promotes exploration, occasionally leading to suboptimal strategies.
We further calculate the mean and standard deviation of average rewards across 50 episodes for each model variant. As detailed in Table 3, the Non-stationary Transformer models consistently outperformed the other two variants regarding average episodic rewards, irrespective of the underlying reinforcement learning framework employed. The models with the Non-stationary Transformer layer achieved the highest returns across all frameworks. Specifically, the Non-stationary Transformer DDQN model exhibited a remarkable average reward mean of 96.71 with a standard deviation of 7.72, while the corresponding figures for the original DDQN and Transformer DDQN were 61.93 with a standard deviation of 8.35, and 69.38 with a standard deviation of 6.84, respectively. This pattern of improved performance with the Non-stationary Transformer layer held for the DDPG and SAC models as well, with the Non-stationary Transformer DDPG model achieving an average reward mean of 115.08 and a standard deviation of 8.11, and the Non-stationary Transformer SAC model reaching 100.56 with a standard deviation of 8.71. The observed standard deviations indicate that the Non-stationary Transformer models achieve higher means and maintain performance stability close to the best-performing variants within each category. This robustness underscores the inherent strengths of the DDPG framework in maximising rewards within the reinforcement learning domain, potentially due to its policy gradient approach, which efficiently navigates the continuous action spaces typical of complex recommendation environments.

5. Discussion

Our comprehensive experimental analysis includes deep learning-related and reinforcement learning-based results in recommendation system algorithms.
Deep Learning-related Experiment: The deep learning experiments conducted using the Tenrec video dataset revealed the enhanced performance of the Non-stationary Transformer BST model over the baseline BST. Notably, the Non-stationary Transformer BST model achieved lower Logloss and higher AUC and F1 scores, indicating superior predictive accuracy and classification quality. This improvement suggests that accommodating the non-stationary aspects of user interaction data can significantly enhance the effectiveness of recommendation systems. Moreover, the observed benefits were consistent across various baseline models, emphasising the robustness and generalisability of our proposed approach.
Reinforcement Learning-related Experiment: In the reinforcement learning domain, the RL4RS-Slate dataset experiments demonstrated the effectiveness of incorporating Non-stationary Transformer layers into DDQN, DDPG, and SAC frameworks. The Non-stationary Transformer models consistently outperformed their standard and transformer-layer counterparts regarding average cumulative rewards. This outcome underlines the potential of Non-stationary Transformers in capturing the sequential decision-making nuances necessary for recommendation systems. The DDPG framework, in particular, showed the highest average reward means, suggesting that integrating Non-stationary Transformers is highly synergistic with policy gradient methods like DDPG.
These experiments collectively underscore the importance of considering temporal dynamics and non-stationarity in user data when designing algorithms for recommendation systems. The findings advocate for a paradigm shift toward models that process data effectively and adapt to its evolving nature. The superior performance of the Non-stationary Transformer enhanced models suggests that such architectures could be critical in the next generation of recommendation systems, which will require dealing with increasingly complex user behaviours and preferences. Firstly, this architecture enables the model to capture and leverage the intrinsic characteristics of the original data distribution more effectively. Secondly, data transformation through the Non-stationary Transformer introduces controlled noise to the training process. This inclusion of noise prevents premature convergence and enhances the generalisation ability of the models across diverse datasets. Future research could explore the scalability of Non-stationary Transformer models in even larger datasets and their adaptability across different domains. Additionally, investigating the interpretability of these models could yield further insights into the nature of the complex patterns they learn, potentially guiding the design of even more effective recommendation systems.

6. Conclusions

In this study, we provide a novel versatile framework that integrates the Non-stationary Transformer structure with both deep learning and reinforcement learning and presents an extensive examination of advanced model architectures for recommendation systems. The Non-stationary Transformer BST model demonstrated considerable superiority in deep learning experiments over the baseline BST and other benchmark models. Similarly, when applied to reinforcement learning across DDQN, DDPG, and SAC, the Non-stationary Transformer enhanced models consistently yielded higher rewards, indicating their robustness and efficiency in sequential decision-making tasks. The success of these models can largely be attributed to their ability to adapt to the non-stationary nature of user interaction data, capturing temporal dynamics that traditional models often overlook.
Despite these strengths, our study has certain limitations. The computational complexity of Non-stationary Transformer models is considerable, potentially complicating scalability in larger or distributed machine learning environments. Future work will explore integrating Non-stationary Transformer structures into a broader range of deep learning and reinforcement learning models and assess the feasibility of deploying these complex architectures in distributed systems for recommendation tasks.

Author Contributions

Y.L. contributed substantially to the conceptualisation, methodology, code development, validation, experiment analysis, and study investigation. He was also heavily involved in writing the original draft, its subsequent review and editing, and data visualisation. G.L., T.R.P., Y.Y., and K.L.M. were responsible for supervision and contributed to the review and editing of the writing. G.L., Y.Y., and K.L.M. also played a crucial role in acquiring funding for the project. All authors have read and agreed to the published version of the manuscript.

Funding

This work is partially supported by the XJTLU AI University Research Centre and Jiangsu Province Engineering Research Centre of Data Science and Cognitive Computation at XJTLU. Also, it is partially funded by the Suzhou Municipal Key Laboratory for Intelligent Virtual Engineering (SZS2022004) as well as funding: XJTLU-REF-21-01-002 and XJTLU Key Program Special Fund (KSF-A-17).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. E-commerce Sales by Country 2023. Available online: https://www.linkedin.com/pulse/ecommerce-sales-country-2023-julio-diaz-lg0be?trk=article-ssr-frontend-pulse_more-articles_related-content-card (accessed on 21 January 2024).
  2. Liu, Y.; Man, K.; Li, G.; Payne, T.R.; Yue, Y. Dynamic Pricing Strategies on the Internet. In Proceedings of the International Conference on Digital Contents: AICo (AI, IoT, and Contents) Technology, Dehradun, India, 2022; pp. 23–24. [Google Scholar]
  3. Global Short Video Platforms Market. Available online: https://www.grandviewresearch.com/press-release/global-short-video-platforms-market (accessed on 1 March 2023).
  4. Guo, H.; Tang, R.; Ye, Y.; Li, Z.; He, X. DeepFM: a factorization-machine based neural network for CTR prediction. In Proceedings of the 26th International Joint Conference on Artificial Intelligence; 2017; pp. 1725–1731. [Google Scholar]
  5. Cheng, H.-T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.; et al. Wide & deep learning for recommender systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems; 2016; pp. 7–10. [Google Scholar]
  6. Zhou, G.; Mou, N.; Fan, Y.; Pi, Q.; Bian, W.; Zhou, C.; Zhu, X.; Gai, K. Deep interest evolution network for click-through rate prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Volume 33, Number 01; 2019; pp. 5941–5948. [Google Scholar]
  7. Chen, Q.; Zhao, H.; Li, W.; Huang, P.; Ou, W. Behavior sequence transformer for e-commerce recommendation in Alibaba. In Proceedings of the 1st International Workshop on Deep Learning Practice for High-Dimensional Sparse Data; 2019; pp. 1–4. [Google Scholar]
  8. Gong, Y.; Zhu, Y.; Duan, L.; Liu, Q.; Guan, Z.; Sun, F.; Ou, W.; Zhu, K.Q. Exact-k recommendation via maximal clique optimization. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2019; pp. 617–626. [Google Scholar]
  9. Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Volume 30, Number 1; 2016. [Google Scholar]
  10. Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
  11. Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv, 2015; arXiv:1509.02971. [Google Scholar]
  12. Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationary transformers: Exploring the stationarity in time series forecasting. Advances in Neural Information Processing Systems 2022, 35, 9881–9893. [Google Scholar]
  13. Liu, Z.; Cheng, M.; Li, Z.; Huang, Z.; Liu, Q.; Xie, Y.; Chen, E. Adaptive normalization for non-stationary time series forecasting: A temporal slice perspective. Advances in Neural Information Processing Systems 2024, 36. [Google Scholar]
  14. Liu, Y.; Mikriukov, D.; Tjahyadi, O.C.; Li, G.; Payne, T.R.; Yue, Y.; Siddique, K.; Man, K.L. Revolutionising Financial Portfolio Management: The Non-Stationary Transformer’s Fusion of Macroeconomic Indicators and Sentiment Analysis in a Deep Reinforcement Learning Framework. Applied Sciences 2023, 14. [Google Scholar] [CrossRef]
  15. Ye, M.; Choudhary, D.; Yu, J.; Wen, E.; Chen, Z.; Yang, J.; Park, J.; Liu, Q.; Kejariwal, A. Adaptive dense-to-sparse paradigm for pruning online recommendation system with non-stationary data. arXiv, 2020; arXiv:2010.08655. [Google Scholar]
  16. Jagerman, R.; Markov, I.; de Rijke, M. When people change their mind: Off-policy evaluation in non-stationary recommendation environments. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining; 2019; pp. 447–455. [Google Scholar]
  17. Yuan, G.; Yuan, F.; Li, Y.; Kong, B.; Li, S.; Chen, L.; Yang, M.; Yu, C.; Hu, B.; Li, Z.; et al. Tenrec: A large-scale multipurpose benchmark dataset for recommender systems. Advances in Neural Information Processing Systems 2022, 35, 11480–11493. [Google Scholar]
  18. Wang, K.; Zou, Z.; Zhao, M.; Deng, Q.; Shang, Y.; Liang, Y.; Wu, R.; Shen, X.; Lyu, T.; Fan, C. RL4RS: A Real-World Dataset for Reinforcement Learning based Recommender System. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval; 2023; pp. 2935–2944. [Google Scholar]
  19. Koren, Y.; Rendle, S.; Bell, R. Advances in collaborative filtering. In Recommender Systems Handbook; Springer, 2021; pp. 91–142. [Google Scholar]
  20. Takács, G.; Tikk, D. Alternating least squares for personalized ranking. In Proceedings of the Sixth ACM Conference on Recommender Systems; 2012; pp. 83–90. [Google Scholar]
  21. Rendle, S. Factorization machines. In Proceedings of the 2010 IEEE International Conference on Data Mining; IEEE, 2010; pp. 995–1000. [Google Scholar]
  22. Zhang, W.; Du, T.; Wang, J. Deep Learning over Multi-field Categorical Data: –A Case Study on User Response Prediction. In Advances in Information Retrieval: 38th European Conference on IR Research, ECIR 2016, Padua, Italy, March 20–23, 2016. Proceedings 38; Springer, 20 March 2016; pp. 45–57. [Google Scholar]
  23. Xiao, J.; Ye, H.; He, X.; Zhang, H.; Wu, F.; Chua, T.-S. Attentional factorization machines: Learning the weight of feature interactions via attention networks. arXiv 2017, arXiv:1708.04617. [Google Scholar]
  24. Li, Z.; Wu, S.; Cui, Z.; Zhang, X. GraphFM: Graph factorization machines for feature interaction modeling. arXiv 2021, arXiv:2105.11866. [Google Scholar]
  25. Yang, F.; Yue, Y.; Li, G.; Payne, T.R.; Man, K.L. KEMIM: Knowledge-enhanced User Multi-interest Modeling for Recommender Systems. IEEE Access 2023. [Google Scholar] [CrossRef]
  26. Zhou, G.; Zhu, X.; Song, C.; Fan, Y.; Zhu, H.; Ma, X.; Yan, Y.; Jin, J.; Li, H.; Gai, K. Deep interest network for click-through rate prediction. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2018; pp. 1059–1068. [Google Scholar]
  27. Sun, F.; Liu, J.; Wu, J.; Pei, C.; Lin, X.; Ou, W.; Jiang, P. BERT4Rec: Sequential recommendation with bidirectional encoder representations from transformer. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management; 2019; pp. 1441–1450. [Google Scholar]
  28. Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
  29. Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
  30. Liu, Y.; Man, K.L.; Li, G.; Payne, T.R.; Yue, Y. Evaluating and Selecting Deep Reinforcement Learning Models for Optimal Dynamic Pricing: A Systematic Comparison of PPO, DDPG, and SAC. In Proceedings of the 2024 8th International Conference on Control Engineering and Artificial Intelligence; 2024; pp. 215–219. [Google Scholar]
  31. Liu, Y.; Man, K.L.; Li, G.; Payne, T.; Yue, Y. Enhancing sparse data performance in e-commerce dynamic pricing with reinforcement learning and pre-trained learning. In Proceedings of the 2023 International Conference on Platform Technology and Service (PlatCon); IEEE, 2023; pp. 39–42. [Google Scholar]
  32. Zhao, X.; Zhang, L.; Ding, Z.; Xia, L.; Tang, J.; Yin, D. Recommendations with negative feedback via pairwise deep reinforcement learning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2018; pp. 1040–1048. [Google Scholar]
  33. Zheng, G.; Zhang, F.; Zheng, Z.; Xiang, Y.; Yuan, N.J.; Xie, X.; Li, Z. DRN: A deep reinforcement learning framework for news recommendation. In Proceedings of the 2018 World Wide Web Conference; 2018; pp. 167–176. [Google Scholar]
  34. Lei, Y.; Wang, Z.; Li, W.; Pei, H.; Dai, Q. Social attentive deep Q-networks for recommender systems. IEEE Transactions on Knowledge and Data Engineering 2020, 34, 2443–2457. [Google Scholar] [CrossRef]
  35. Zhao, X.; Gu, C.; Zhang, H.; Yang, X.; Liu, X.; Tang, J.; Liu, H. Dear: Deep reinforcement learning for online advertising impression in recommender systems. In Proceedings of the AAAI Conference on Artificial Intelligence, Volume 35, Number 1; 2021; pp. 750–758. [Google Scholar]
  36. Zhao, X.; Xia, L.; Zhang, L.; Ding, Z.; Yin, D.; Tang, J. Deep reinforcement learning for page-wise recommendations. In Proceedings of the 12th ACM Conference on Recommender Systems; 2018; pp. 95–103. [Google Scholar]
  37. Chen, X.; Huang, C.; Yao, L.; Wang, X.; Zhang, W. Knowledge-guided deep reinforcement learning for interactive recommendation. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN); IEEE: pp. 1–8, 2020. [Google Scholar]
  38. Liu, F.; Tang, R.; Guo, H.; Li, X.; Ye, Y.; He, X. Top-aware reinforcement learning based recommendation. Neurocomputing 2020, 417, 255–269. [Google Scholar] [CrossRef]
  39. Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In International Conference on Machine Learning, 2018; PMLR: pp. 1861–1870.
  40. He, X.; An, B.; Li, Y.; Chen, H.; Wang, R.; Wang, X.; Yu, R.; Li, X.; Wang, Z. Learning to collaborate in multi-module recommendation via multi-agent reinforcement learning without communication. In Proceedings of the 14th ACM Conference on Recommender Systems; 2020; pp. 210–219. [Google Scholar]
  41. Zhang, W.; Liu, H.; Wang, F.; Xu, T.; Xin, H.; Dou, D.; Xiong, H. Intelligent electric vehicle charging recommendation based on multi-agent reinforcement learning. In Proceedings of the Web Conference 2021.
  42. Huleihel, W.; Pal, S.; Shayevitz, O. Learning user preferences in non-stationary environments. In Proceedings of the International Conference on Artificial Intelligence and Statistics; PMLR, 2021; pp. 1432–1440. [Google Scholar]
  43. Wu, Q.; Iyer, N.; Wang, H. Learning contextual bandits in a non-stationary environment. Proceedings of The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval; 2018; pp. 495–504. [Google Scholar]
  44. Chandak, Y.; Theocharous, G.; Shankar, S.; White, M.; Mahadevan, S.; Thomas, P. Optimizing for the future in non-stationary MDPs. In Proceedings of the International Conference on Machine Learning; PMLR, 2020; pp. 1414–1425. [Google Scholar]
  45. Watkins, C.J.C.H.; Dayan, P. Q-learning. Machine Learning 1992, 8, 279–292. [Google Scholar] [CrossRef]
  46. He, X.; Chua, T.-S. Neural factorization machines for sparse predictive analytics. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval; 2017; pp. 355–364. [Google Scholar]
  47. Wang, R.; Fu, B.; Fu, G.; Wang, M. Deep & Cross Network for Ad Click Predictions. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2017; pp. 1–7. [Google Scholar]
Preprints 105556 g001
Figure 1. Illustration of the Enhanced BST Model with Non-stationary Transformer Integration.
Figure 1. Illustration of the Enhanced BST Model with Non-stationary Transformer Integration.
Preprints 105556 g001
Preprints 105556 g002
Figure 2. Illustration of the Enhanced DDQN Model with Non-stationary Transformer Integration.
Figure 2. Illustration of the Enhanced DDQN Model with Non-stationary Transformer Integration.
Preprints 105556 g002
Preprints 105556 g003
Figure 3. Illustration of the Enhanced DDPG Model with Non-stationary Transformer Integration.
Figure 3. Illustration of the Enhanced DDPG Model with Non-stationary Transformer Integration.
Preprints 105556 g003
Preprints 105556 g004
Figure 4. Illustration of the Enhanced SAC Model with Non-stationary Transformer Integration.
Figure 4. Illustration of the Enhanced SAC Model with Non-stationary Transformer Integration.
Preprints 105556 g004
Preprints 105556 g005
Figure 5. Different Models Loss among Train Set.
Figure 5. Different Models Loss among Train Set.
Preprints 105556 g005
Preprints 105556 g006
Figure 6. Different Batch Sizes Loss among Validate Set.
Figure 6. Different Batch Sizes Loss among Validate Set.
Preprints 105556 g006
Preprints 105556 g007
Figure 7. Comparison of maximum and minimum rewards per episode across three reinforcement learning frameworks: DDQN, DDPG, and SAC. For each framework, we compare the original model (“1”), the model with an added transformer layer (“2”), and the model enhanced with the Non-stationary Transformer layer (“3”).
Figure 7. Comparison of maximum and minimum rewards per episode across three reinforcement learning frameworks: DDQN, DDPG, and SAC. For each framework, we compare the original model (“1”), the model with an added transformer layer (“2”), and the model enhanced with the Non-stationary Transformer layer (“3”).
Preprints 105556 g007
Table 1. Summary of the Tenrec Video Dataset Splits.
Table 1. Summary of the Tenrec Video Dataset Splits.
Set Records Users Items Video Categories User Features Seq Interactions
Train 84,239,614 998,993 2,027,521 3 3 10
Validate 18,051,346 985,099 1,104,613 3 3 10
Test 18,051,346 985,315 1,104,678 3 3 10
Table 2. Performance Comparison of Different Models.
Table 2. Performance Comparison of Different Models.
Model Logloss AUC F1 score
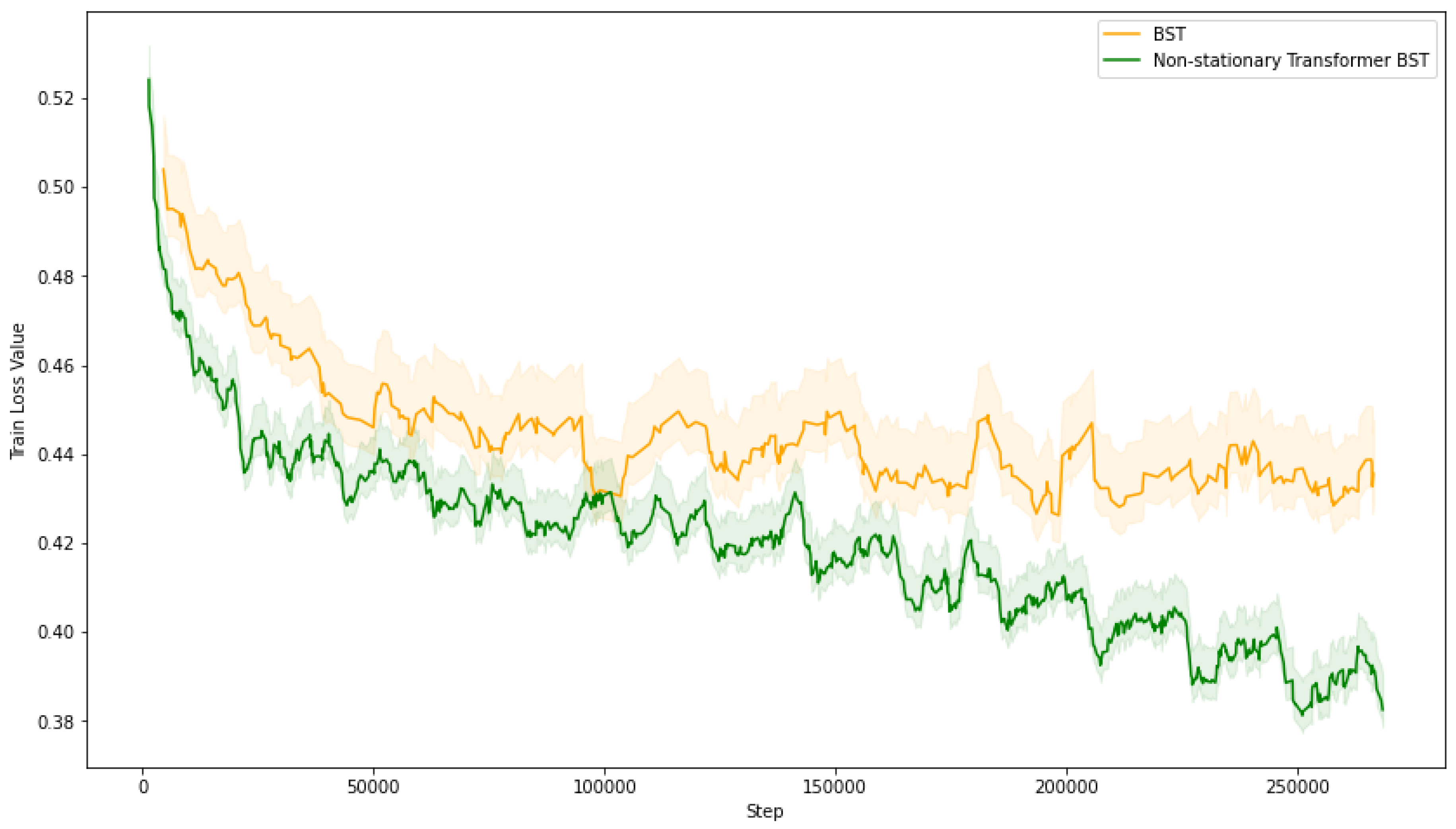
BST 0.4808 (+8.31%) 0.7921 (-0.81%) 0.7386 (-2.79%)
Non-stationary Transformer BST 0.4439 0.7986 0.7598
Wide & Deep 0.51 (+14.89%) 0.7919 (-0.84%) 0.7225 (-4.91%)
DeepFM 0.5083 (+14.51%) 0.793 (-0.70%) 0.7463 (-1.78%)
NFM 0.508 (+14.44%) 0.7957 (-0.36%) 0.7512 (-1.13%)
DCN 0.5092 (+14.71%) 0.7927 (-0.74%) 0.7261 (-4.44%)
Table 3. Summary of Episode Reward Mean and Standard Deviation for Various Algorithm Implementations.
Table 3. Summary of Episode Reward Mean and Standard Deviation for Various Algorithm Implementations.
Algorithm Episode Reward Mean Episode Reward Standard Deviation
Original DDQN 61.93 8.35
Transformer DDQN 69.38 6.84
Non-stationary Transformer DDQN 96.71 7.72
Original DDPG 107.33 9.94
Transformer DDPG 112.16 8.25
Non-stationary Transformer DDPG 115.08 8.11
Original SAC 68.85 9.21
Transformer SAC 84.07 8.63
Non-stationary Transformer SAC 100.56 8.71
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated