Prerpints.org logo
Preprint
Article

Shor-Term Forecasting of Photovoltaic Power Using MLPNN, CNN AND kNN

Altmetrics

Downloads

89

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 May 2024

Posted:

08 May 2024

You are already at the latest version

Alerts
Abstract
This work focuses on short-term forecasting of PV output power. The multilayer perception (MLP), convolutional neural networks (CNN), and k-nearest neighbour (kNN) neural networks have been used singly or in a hybrid (with other algorithms) to forecast solar PV power or global solar irradiance with good success. Their performances in forecasting PV power have been compared with other algorithms but not with themselves. The study aims to compare performance of a number of neural network algorithms in solar PV energy yield forecasting under different weather conditions. The performance of MLPNN, CNN and kNN are being compared using solar PV (hourly) energy yield data for Grahamstown, Eastern Cape, South Africa. The choice of location is part of the study parameters to provide insight into renewable energy power integration in specific areas in south Africa that may be prone to extreme weather conditions. The kNN algorithm was found to have RMSE value of 4.95% and MAE value of 2.74% at its worst performance, and RMSE value of 1.49% and MAE value of 0.85% at its best performance. It outperformed the others by a good margin and kNN could serve as a fast, easy, and accurate tool to forecast solar PV output power.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

The world’s energy suppliers are shifting towards using clean, renewable energy sources to reduce the pollution caused by fossil fuel energy sources. Photovoltaic and wind energy sources are the most favoured renewable energy sources because they have zero emissions, require minimal maintenance, and their initial installation cost is also coming down [1] recently. The output power of solar photovoltaic (PV) energy systems is highly dependent on constantly changing weather and environmental conditions like solar irradiance, wind speed, ambient temperature, module temperature, etc. There is need to forecast its output power to effectively plan and integrate the solar PV energy system into the main grid.
Many approaches and techniques have been used to predict solar PV output power. The physical models, the statistical models, and a hybrid (combination of physical statistical) models [2,3,4,5] are some of the major approaches which have been used to predict PV output power. The physical approach is designed using the global irradiance of the solar PV cells and a mathematical model describing the solar PV system [6]. The techniques produce high accuracy when the weather conditions are stable throughout the prediction period. The total sky imagers [7] and image technique [8] which analyses the solar surface irradiance of retrieved satellite images to make prediction are example of some implementations of the physical method. The statistical techniques are designed mostly for the principle of persistence. Using tested scientific processes, they predict the PV output power by establishing a relationship between the input variables (vectors) and the target output power. The weather parameters (solar irradiance, wind speed, ambient temperature, module temperature, rain, humidity etc.) which directly or indirectly affect the solar panels’ electricity generation constitute the input vectors, while the PV output power is the predicted output. Traditional statistical methods [9] use regression analyses to produce models that forecast the PV output power.
Artificial intelligence (AI) or machine learning (ML) is another way of applying this technique. A good example of the AI techniques which have been used to forecast PV output power is artificial neural networks (ANN) [10], long short-term memory (LSTM) [11,12], support vector machines (SVM) [9,10] etc. The multilayer perceptron (MLP) neural network [13], the convolutional neural network (CNN) [14,15], gated recurrent units (GRU) [16,17] and k-nearest neighbour (kNN) [17,18] are some instances of the ANN which have been successfully used to model and forecast solar PV output power. Ratshilengo et al. [19] compared the results of modelling the global solar irradiance with the generic algorithm (GA), recurrent neural network (RNN), and kNN techniques and showed that GA outperformed others in accuracy. Most of these researches focused on a single technique or forecasted solar irradiation (when they worked with more than one technique), but in this study, we will compare the results of modelling the actual solar PV output power using MLPNN, CNN and kNN algorithms and show that the kNN method had the best overall performance on our data. It is more important to model the output power instead of solar irradiance because the generated PV output power also captures the impact of the ambient and module temperatures, whose rise negatively affects the PV output power as well as the impart of other factors that affect solar irradiance. A comparative performance analysis has not been done on these modeling solar PV output power forecasting.
In Section 2 of this work, we present a brief review of PV power output forecasting, and in Section 3, we present a detailed review of the artificial neural network. Section 4 presents data description, variable selection, and evaluation metrics. Section 5 presents the results and discussion, while Section 6 considers the challenges of PV output power forecasting, while conclusions are drawn in Section 7.
Table 2. A summary literature review of PV power output forecasting showing references, forecast horizon, technique, and results.
Table 2. A summary literature review of PV power output forecasting showing references, forecast horizon, technique, and results.
Ref. Forecast horizon Target Forecast method Forecast error
[19] Short-term PV power LSTM RMSE=67.8 %, MAE=43.8%, NRMSE=0.19%
CNN RMSE=38.5%, MAE=4.0%, NRMSE=0.04%
CNN-LSTM RMSE=5.2%, MAE=2.9%, NRMSE=-0.03%
[19] Short-term Irradiance RNN RMSE=56.89%, MAE=20.18%, rRME=7.54%, rMAE-4.49%
KNN RMSE=57.48%, MAE=20.94%, rRME=7.58%, rMAE=4.58%
GA RMSE=35.50%, MAE=26.74%, rRME=5.95%, rMAE=5.17%
[23] Very-short-term PV power Persistence, MPL, CNN, LSTM RMSE=15.3%
[24] Short-term PV power Similarity algorithm, KNN, NARX, and smart persistence models RMSE=2.3%
[25] Short-term PV power Hybrid model of wavelet decomposition and ANN RMSE values between 7.193%−19.663%
[26] Short- and long-term PV power Prophet, LSTM, CNN,
C-LSTM		 MAE range 2.9 - 16730.3, RMSE range 5.2 - 21753.2 NRMSE range 0.0 - 30.59
[13] Short-term Irradiance MLPNN MAPE=6.15%
[27] Short-term Wind power K-means clustering method MAPE ≈ 11%

2. A Brief Overview of Solar PV Power Prediction in the Literature

Numerous studies have been published on forecasting PV output power. When solar panels receive irradiance, they convert the incident irradiance to electricity. Hence, solar irradiation strongly correlates with solar PV panels’ output power. Machine learning techniques like the ANN [20], support vector machines (SVMs) [21], kNN, etc., have been used to forecast solar irradiance. ML techniques are equipped with the ability to capture complex nonlinear mapping between input and output data. Efforts have been made to model solar PV output power with ANNs. Liu and Zhang [12] model the solar PV output power using kNN and analyse the performance of their model for cloudy, clear sky and overcast weather conditions. Ratshilengo et al. [19] compared the performance of generic algorithm (GA), recurrent neural networks (RNN) and kNN in modelling solar irradiance. They found GA outperformed the other two using their performance metrics. A combination of autoregressive and dynamic system approach for hour-ahead global solar irradiance forecasting was proposed by [22]. Table 1 summarises some previous study on solar PV output power prediction.
Some ways to forecast solar PV power are by modelling irradiance (indirectly modelling PV output power) or directly modelling the PV output power. A lot of research has been published in this regard.

2. Artificial Neural Network

ANN is one technique which has been used extensively to model and forecast solar PV output power with high accuracy [28,29]. This comes from its ability to capture the complex nonlinear relationship between the input features (weather and environmental data) and corresponding output power. ANN is a set of computational systems composed of many simple processing units inspired by the human nervous system. 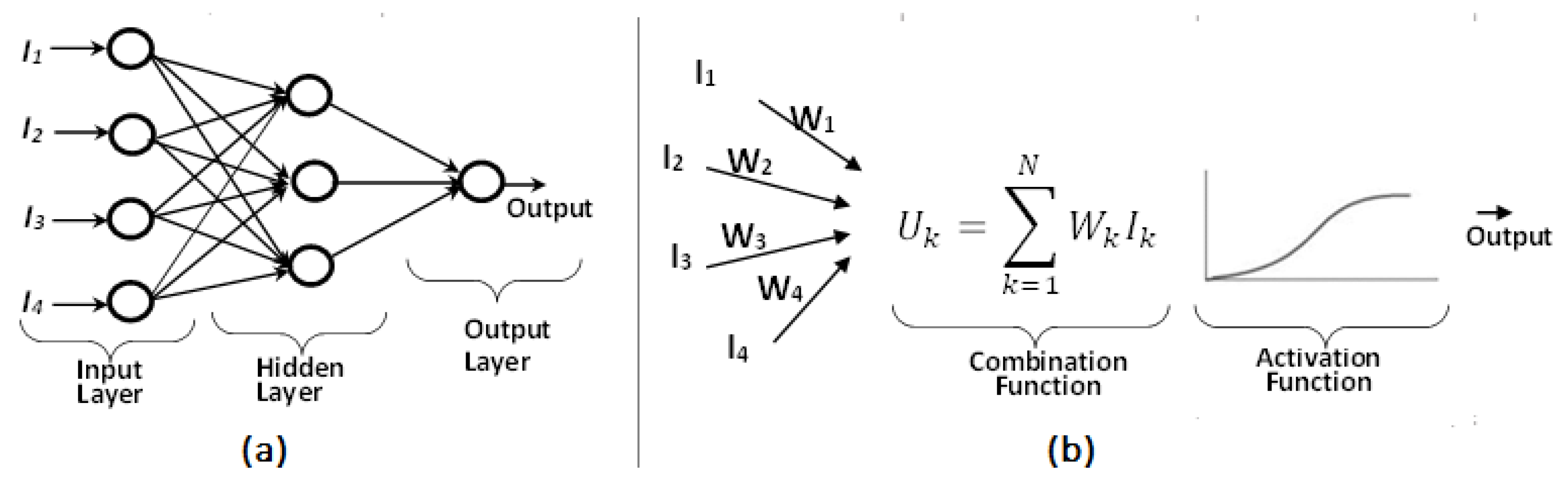Figure 1a shows a schematic representation of a basic ANN, with the input, hidden and output layers, connections, and neurons. Data of the (input) features are fed into the input layer. The hidden layer (which could be more than one) processes and analyses this input data. The output layer completes the process by finalising and providing the network output. The connections connect neurons in the adjacent layer together with the updated weights.
Figure 1b presents a pictural representation of basic ANN mathematics. It shows that the neuron of a basic ANN cell is made of two parts – the activation and combination functions. The network sums up all the input values using the activation function, making the activation function act like a squeezing transfer function on the input to produce the output results. Some commonly used activation functions are sigmoid, linear, hyperbolic tangent sigmoid, Gaussian radial basis, bipolar linear and unipolar step. The basic mathematical expression of an ANN is given as [30]:
U j = b + ∑ k = 1 N ( W k × I k ) ,
where Uj is the predicted network output, b is the bias weight, N is the number of inputs, Wk is the connection weight, and Ik is network input. There are many types of neurons and interconnections used in ANN. Some examples of this are feedforward and backpropagation NN. Feedforward NNs pass information/data in one forward direction only. The backpropagation NN allows the process to cycle through over again. it loops back, and information learnt in the previous iteration is used to update the hyperparameters (weights) during the next iteration to improve prediction. Deep learning is a type of ANN where its layers are arranged hierarchically to learn complex features from simple ones [14]. One weakness of the deep learning NN is that it takes a relatively long time to train the model.
There are two basic stages of the ANN – training and testing. The data for modelling PV output power is often split into training and test sets. Generally, 80% of the data is set aside for training, while 20% is reserved for testing. During the training stage, the neural network uses the training dataset to learn and find a mapping relationship between the input data by updating the synaptic weights. Prediction errors are calculated using the forecasted and measured values. The magnitude of the errors is used to update the weights and biases, and the process is repeated until the desired accuracy level is achieved. The testing dataset is used to test the final model produced in the training stage, and the ANN model’s performance is evaluated. A statistical approach that considers each experimental run as a test called the design of experiment approach, was described by [31] for use with ANNs.
Neural networks having a single hidden layer is usually enough to solve most data modelling problems but complex nonlinear mapping patterns between the input and output data may require the use of two or more hidden layers to obtain accurate results. Multilayer feedforward neural networks (MLFFNN) [32], adaptive neuro-fuzzy interface systems [33,34,35,36], multilayer perceptron neural networks (MLPNN) [13,37], convolutional neural networks (CNN) [14,37] are some examples of ANN with multiple layers. In this study, we will compare the results of modelling solar PV output power using ANN-MLPNN, CNN, gated recurrent units (GRU) and kNN models. Subsequent sections will present a brief overview of these techniques.

2.1.1. Multilayer Perceptron Neural Networks (MLPNN)

MLPNN is a special type of ANN that is organised in layers and can be used for classification and regression depending on the activation function used. A typical MLPNN has three layers like most ANN – the input, output and hidden layers. The hidden layer can have more than one hidden unit depending on the complexity of the problem at hand. Let I p be a p -th point in an N -dimensional input to MLPNN, the output be Y p , and the weight of on hidden layer be W h . To keep the discussion simple, take the case of a single-layer MLP. The output of the first hidden unit L 1 can be expressed as:
L 1 i = ∑ k = 1 N + 1 W h ( i , k ) I p ( k ) .
A linear activation function could be given as:
O p ( i ) = f ( L p i ) .
And the nonlinear activation function could be given as:
f ( L p i ) = 1 ( 1 + e − L p ( i ) ) .
MLPNN algorithm applies the weight of the previous iteration when calculating that of the next iteration. Let W 1 be the weight of the input to the hidden layer, and W 2 that of the hidden to the output layers. Then, the overall output Y p is given as [38]:
Y 1 i = ∑ k = 1 N + 1 W 1 ( i , k ) I p ( k ) + ∑ j = 1 N h W 2 ( i , j ) O p ( j ) .
Every layer of the MLP receives input from the previous layer and sends its output to the next layer, which receives it as input and so on. Hence, every layer has input, weight, bias, and output vectors. The input layer has an activation function but no thresholds. It connects and transfers data to successive layers. The hidden and the output layers have weights assigned to them together with their thresholds. At each layer, the input vectors are multiplied with the layers corresponding threshold and passed through the activations function, which could be linear or nonlinear [39]. Some of the advantages of MLPNN are that it requires no prior assumptions, no relative importance to be given to the input dataset and adjustment weights at the training stage [40,41].

2.1.2. Convolutional Neural Networks (CNNs)

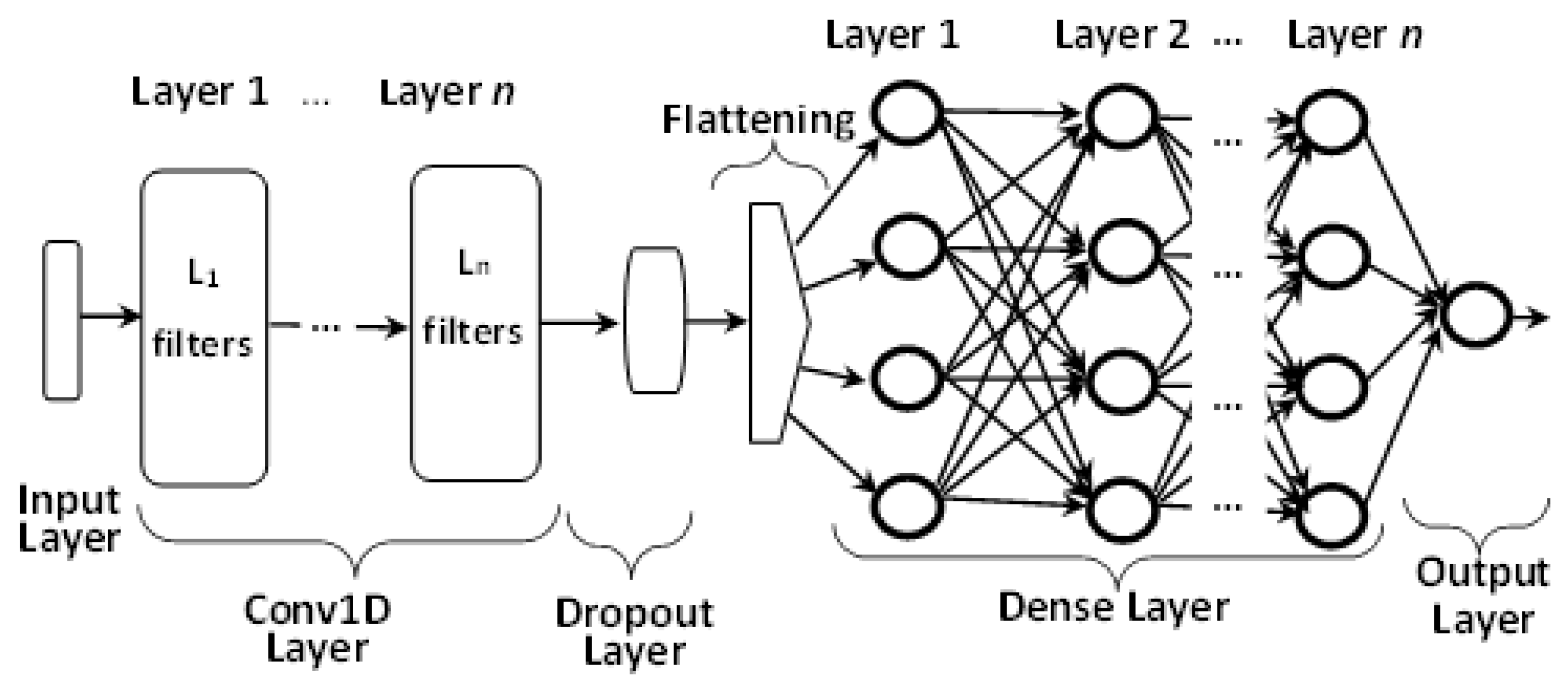
The CNNs are another commonly used deep learning feedforward NN used to model PV output power whose inputs are tensors. They have many hidden convolutional layers that can be combined with other types of layers, such as the pooling layer. CNN has been used effectively in image processing, signal process, audio classification and time series processing.
Figure 2 presents a schematic illustration of the CNN with a one-dimensional convolutional layer. It shows the input and a one-dimensional convolution layer, a dropout layer to prevent overfitting, a dense layer of fully connected neurons, a flattening layer, and the output layer.

2.1.3. k-Nearest Neighbour (kNN)

The kNN is a simple supervised ML algorithm that can be applied to solve regression and classification problems [42]. Supervised ML is a type of ML that require the use of labelled input and output data, while unsupervised ML is the process of analysing unlabeled data. The supervised ML model tries to learn the mapping relationship between the labelled input features and output data. The model is finetuned till the desired forecasting accuracy is achieved. The kNN algorithm, like most forecasting algorithms, works by using training data as the “basis” for predicting future values. In the algorithm, Neighbours are chosen from the basis and sorted depending on certain similarity criteria between the attributes of the training data and that of the testing data. The attributes are the training and testing data’s weather and PV output power data, while the target is the residual of the difference between them. The mean of the target values of the neighbours is used to forecast the PV power. The measure of similarity (e.g., the Manhattan distance) is given as [43]:
d j = ∑ k = 1 n W k x train , j , k − x test , k ) ,
where d j is the distance between the i -th training and test data, W k is the weight of the j -th attribute, and attribute values of the training and test are x train and x test , respectively. j and k are the indices of the training data and test attributes, respectively, while n is the number of attributes. The weights were calculated using the k-fold Cross Validation [44]. The k target values are used to forecasted residual F R as:
F R = ∑ k = 1 M v k D train , k ∑ k = 1 M v k ,
where D train is the training data-target value, k is the index of the neighbours’ chosen training data, and v k is the weight of the corresponding i -th target value. At the same time, M represents the total number of nearest neighbours. One advantage of the kNN is that it requires no training time. Another is that it is simple to apply, and new data samples can easily be added. The kNN also has a few disadvantages. These include that it is ineffective in handling very large data and it performs poorly with high dimension data. Another disadvantage is that it is sensitive to noisy data (having outliers and missing values).
The kNN algorithm works; thus, start by loading the dataset, then initialise K to the number of neighbours. For every record, calculate the distance between it and the current record, and add the distance and indices to an ascending ordered set of distances. Then, select the first K entries in the ordered list, retrieve the labels for the selected K entries, and return the average of the K labels in the case of regression (or return the mode of the K labels in the case of classification).

3. Data Description and Variable Selection

3.1. Data Description

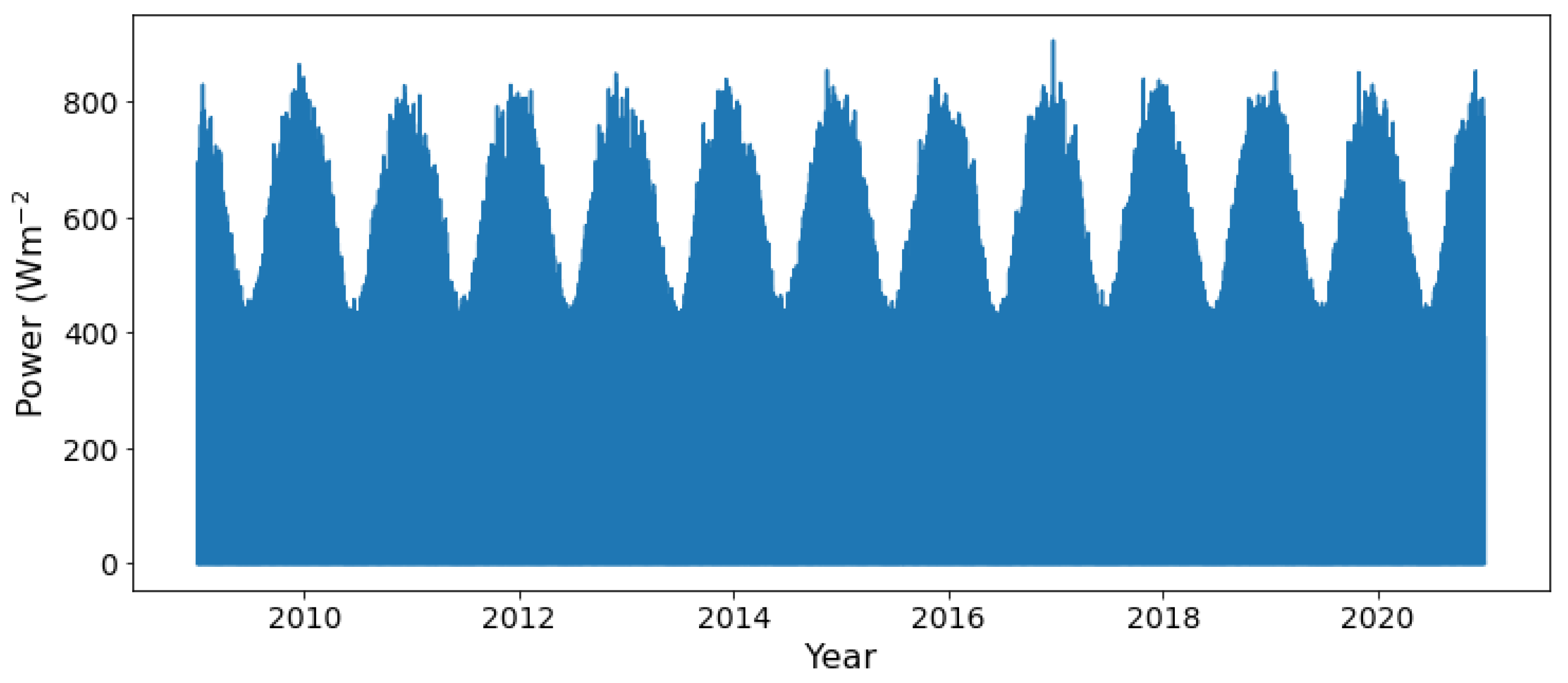
We have a time series hourly data having fields for PV output power, normal global irradiance, diffused irradiance, sun height, ambient temperature, reflected irradiance, wind speed, and 24-hour time cycle in Grahamstown, Eastern Cape, South Africa for the period from 2009 to 2020. Figure 3 presents the graph of the data – the PV output power.

3.2. Selecting Input Variables

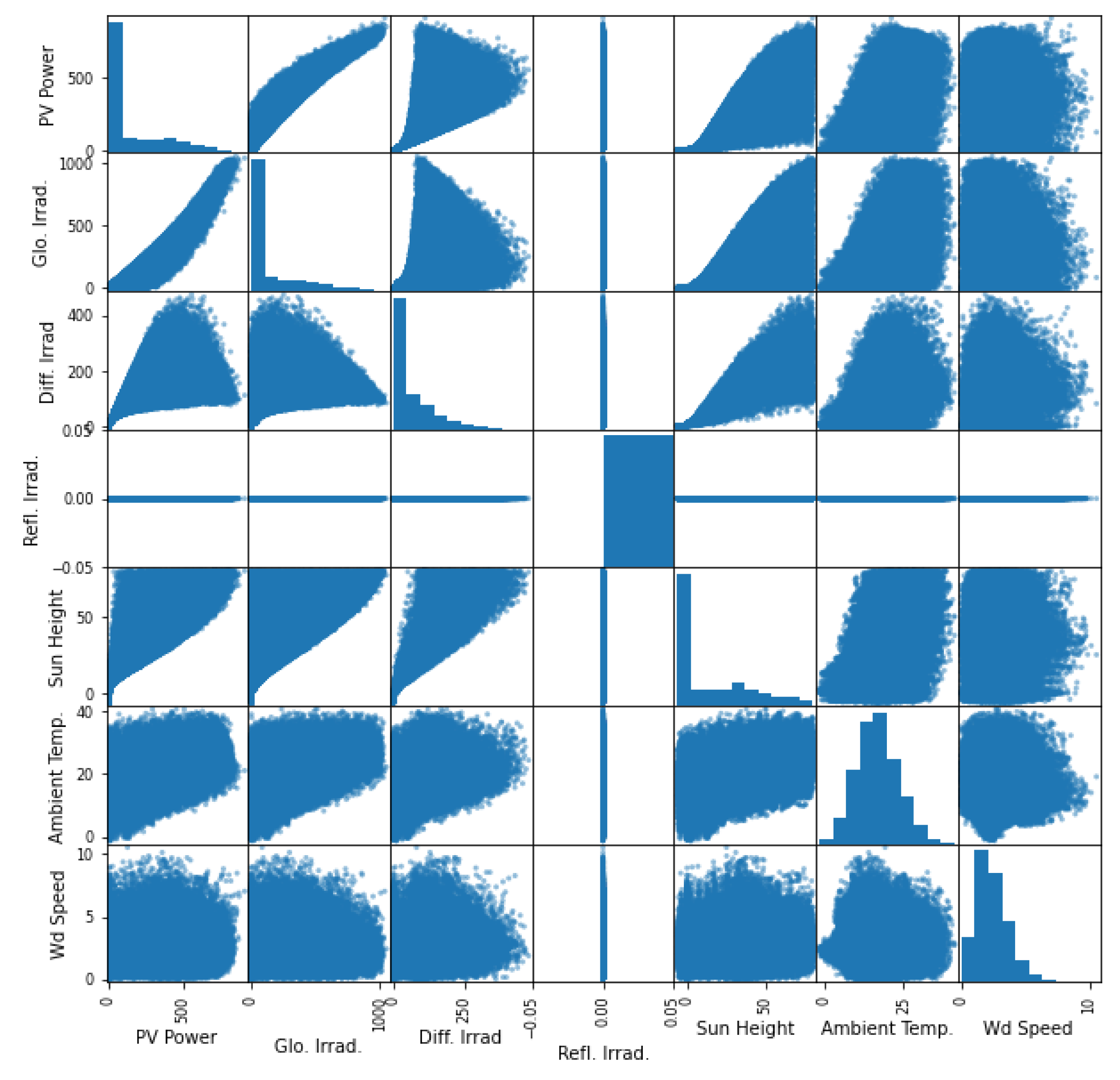
The more variables used as input, the better the performance of the algorithms but the higher the execution time and the higher the chances of overfitting. To select the variables that will serve as inputs to the algorithms, we consider the interaction between the variables and their correlation with the output power. Figure 4 presents scatterplots of all pairs of attributes. This figure can help one to see the relationship between the variables.
The diagonal plots display the Gaussian distribution of the values of each variable. As expected, there is a strong correlation between global (and the diffused) solar irradiance and PV power but no correlation between reflected irradiance and PV power. The fact will be demonstrated more quantitatively later using the Lasso regression analysis. One cannot precisely say for the other variables. We excluded the reflected solar irradiance from the list of input variables.

3.3. Prediction Intervals and Performance Evaluation

3.3.1. Prediction Intervals

The prediction interval (PI) helps energy providers and operators assess the uncertainty level in electrical energy they supply [45,46]. It is a great tool for measuring uncertainty in model predictions. We will subsequently take a brief look at prediction interval widths.
The prediction interval width ( PIW t ) is the estimated difference between the upper ( U t )and lower L t limits of the values given as:
PIW t = U t − L t           t = 1,2 , 3 , … . N .
The PI coverage probability (PICP) and PI normalised average width (PINAW) are used to assess the performance of the prediction intervals. The PICP is used to estimate the reliability of the PIs, while PINAW is used to assess the width of the PIs. These two are expressed mathematically as [47]:
P I C P = 1 N ∑ t = 1 N c t , c t = 1     i f       y t ∈ ( L t , U t ) 0             o t h e r w i s e ,
P I N A W = 1 N ∑ t = 1 N PIW t y max − y min ,
where y t is the data, y min and y max are the minimum and maximum values of PIW, respectively. The PIs are weighted against a predetermined confidence interval (CI) value. One has valid PIs values when the value of PICP is greater than or equal to that predefined CI value. The PI normarlised average deviation (PINAD) defines the degree of deviation from the actual value to the PIs and is expressed mathematically as [47]:
P I N A D = 1 N ( y max − y min ) ∑ t = 1 N c t , c t = L t − y t ,     i f       y t < L t 0       i f       L t ≤   y t ≤   U t y t − U t ,     i f       y t > U t .

3.3.2. Performance Matrices

A good number of performance measurement tools are available in the literature. Some are better fit for particular contexts and target objectives.
The mean absolute error (MAE) is the average of the absolute difference between the measured ( y t ) and predicted ( y ^ t ) data. For a total of N predictions, the MAE is given as:
M A E = 1 N ∑ t = 1 N | y t − y ^ t | ,
The relative MAE (rMAE) gives an MAE value is comparable to the measured values. The rMAE is given mathematically as:
r M A E = 1 N ∑ t = 1 N | y t − y ^ t | y t .
The root mean squared error (RMSE) is the average of the squared difference between the measured and predicted values. The average of the square of the prediction residual. It is always non-negative and is given as:
R M S E = 1 N ∑ t = 1 N ( y t − y ^ t ) 2 .
The relative RMSE (rRMSE) gives a percentage RMSE value. The rRMSE is given as:
r R M S E = 100 y ¯ 1 N ∑ t = 1 N ( y t − y ^ t ) 2 .
where y ¯ is the average of y t , t = 1,2 , 3 , … N . The smaller values for these error metrics, the more accurate the forecasted value.
The R2 score is another commonly used metric to measure the performance of a forecast. The R2 score can be expressed mathematically as:
R 2 = 1 ∑ t = 1 N ( y ^ t − y t ) 2 ∑ t = 1 N ( y ¯ t − y t ) 2 ,
The closer the value of R2 is close to 1, the more accurate the prediction is the true value.
It is common practice to normalise (or scale) data before passing through the training step, but we did not do this in our case because our data had a few missing records and outliers.

3.4. Selecting Input Variables

It is a common practice to use Lasso analysis to perform variable selection, which uses the l loss function penalty given as [4]:
β ^ Lasso λ = arg ⁡ m i n y → − Χ β ^ 2 2 + λ β ^ | | 1 .
In Table 2, we show the parametric coefficient of the Lasso regression analysis. All the variables except for the reflected irradiance are important forecasting variables.
Table 2. Parameter coefficient of Lasso regression.
Table 2. Parameter coefficient of Lasso regression.
Variables Coefficients
Global Normal irradiance 0.790206
Diffuse irradiance 0.902841
Reflected irradiance 0.000000
Sun Elevation -0.412872
Ambient Temperature -0.817793
Wind Speed 1.017501
24-hour time cycle 0.186437

4. Results

4.1. Prediction Results

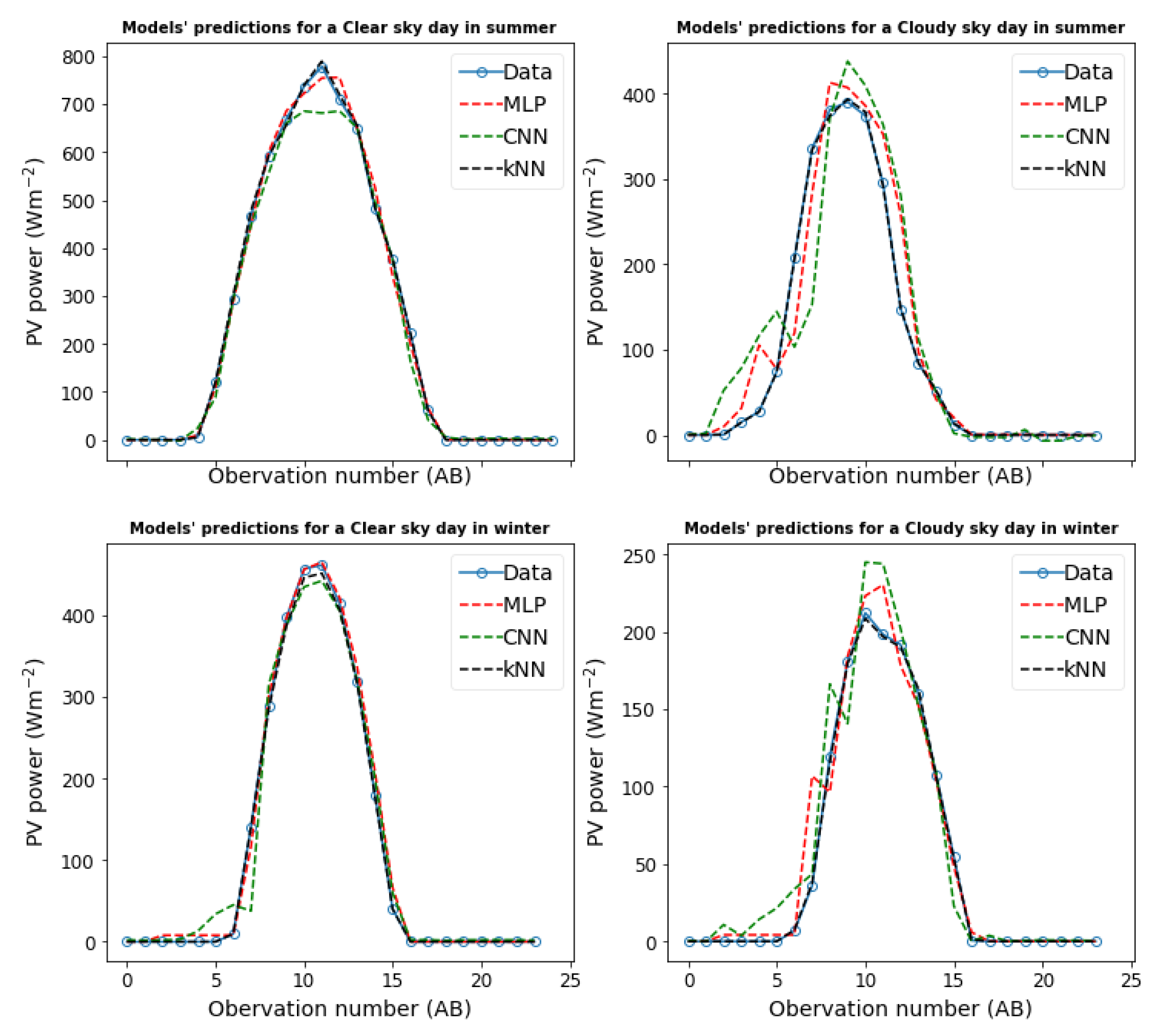
Figure 5 presents plots of the data and fits of the different models we used in this study for short-term forecasting (38 hours ahead) of the solar PV output power for two clear sky days and two cloudy days. The graph in blue is the measured data, while that in orange, green, red, and cyan are for MLPNN, CNN and kNN models’ forecast, respectively. We can see visually from these plots that the prediction produced by kNN best fits the data for these two conditions. MLPNN also produces a reasonably good fit on a clear sky day.
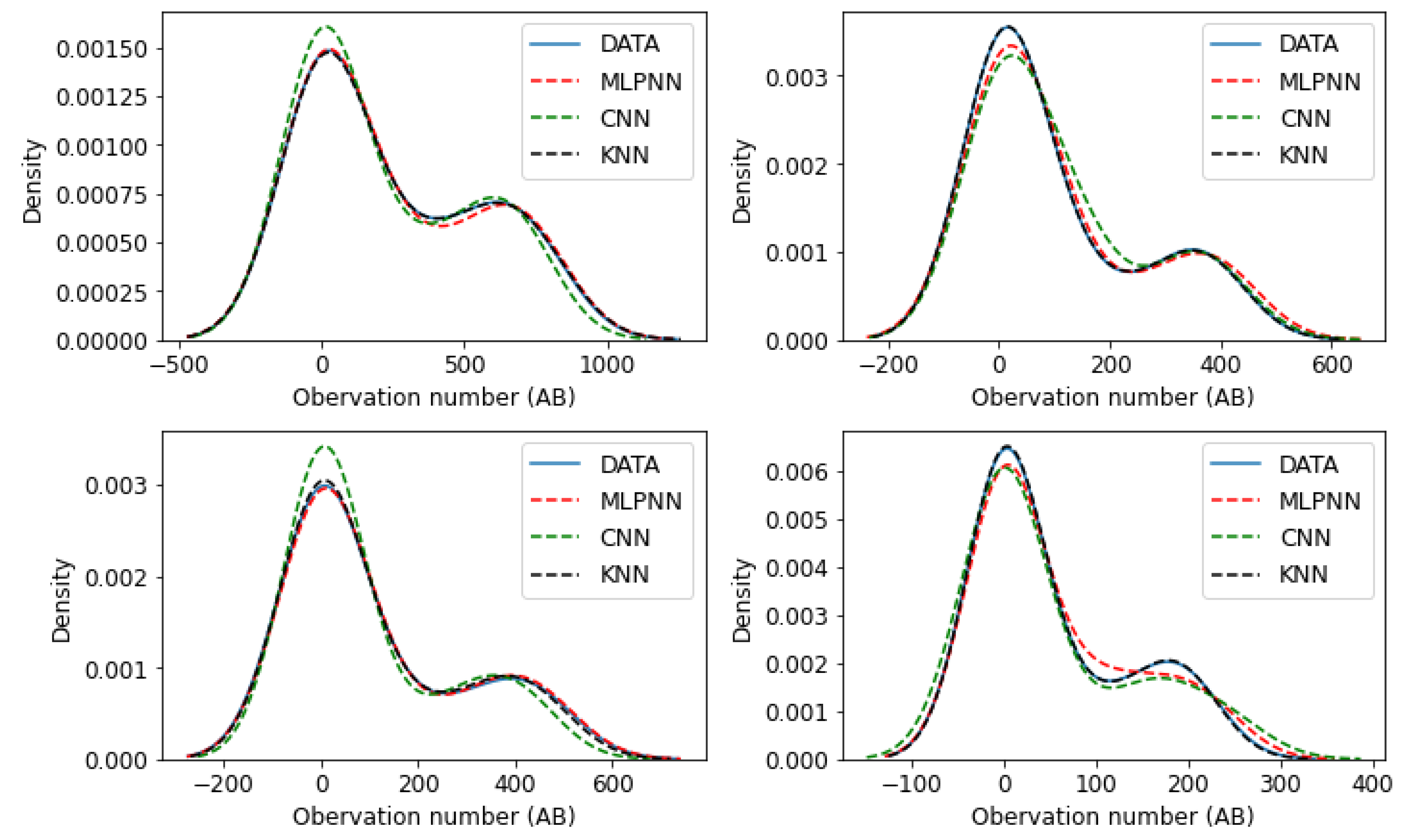
Figure 6 presents the measured solar PV output power together density plots and the different models’ predictions. The solid blue line graph is the measure data, while the dashed lines represent the models’ forecasts. From these graphs, it can be observed that kNN prediction best matches the data, followed closely by the MLPNN predictions. We will subsequently present a qualitative evaluation of these models’ performance.
Table 3. Evaluating models’ performances on summer (top panels) and winter (bottom panels) for clear and cloudy sky days (left and right columns respectively).
Table 3. Evaluating models’ performances on summer (top panels) and winter (bottom panels) for clear and cloudy sky days (left and right columns respectively).
Clear sky day in summer Cloudy sky day in summer
MLPNN CNN KNN MLPNN CNN KNN
RMSE 21.42 23.15 4.95 39.35 67.54 2.08
rRMSE 8.69 9.39 2.01 39.40 67.62 2.08
MAE 12.34 14.04 2.74 21.86 46.19 1.11
rMAE 0.49 0.56 0.11 0.91 1.92 0.05
R2 0.99 0.99 1.00 0.92 0.77 1.00
Clear sky day in winter Cloudy sky day in winter
MLPNN CNN KNN MLPNN CNN KNN
RMSE 10.96 25.69 4.11 17.22 20.09 1.49
rRMSE 9.71 22.77 3.64 32.59 38.04 2.82
MAE 6.47 14.09 2.00 8.18 12.88 0.85
rMAE 0.27 0.59 0.08 0.34 0.54 0.04
R2 1.00 0.98 1.00 0.95 0.93 1.00
Figure 6 presents the density plots of the measure solar PV output power together with the models’ predictions during the summer season (top row) on a clear sky day (in the left panel) and a cloudy day (in the right panel). The same is present for a winter clear sky day (left panel) and cloudy day (right panel) on the bottom row. The kNN model’s density graph produced the closest match to the measured data for all the four weather conditions under investigation.
In Table 3, we present the results of evaluating our models’ performance using MAE, rMAE, RMSE, rRMSE, and R2 metrics for the four weather conditions. The kNN has the overall best performance for these metrics, followed by the MLPNN, then CNN.

4.2. Prediction Accuracy Analysis

This section evaluates how the models’ predictions are centred using PIs and the forecast error distribution.

4.2.1. Prediction Interval Evaluation

In Table 4 we compare the performance confidence intervals of these modes’ predictions using PICP, PINAW and PINAD with a preset confidence level of 95%. Only the kNN model has a value of PICP greater than 95% on the clear sky days. The model with the lowest value for PINAD and the narrowest PINAW is the model that best fits the data [47]. kNN has the smallest PINAD and has the best overall performance with respect to these prediction interval matrices.
Table 4. Comparing the performance of the models using PICD, PINAW and PINAD on a confidence level set to 95% - on clear sky and cloudy days (top row left and right panels, respectively), while second row presents the same for a winter clear sky and cloudy days (bottom row left and right panels, respectively).
Table 4. Comparing the performance of the models using PICD, PINAW and PINAD on a confidence level set to 95% - on clear sky and cloudy days (top row left and right panels, respectively), while second row presents the same for a winter clear sky and cloudy days (bottom row left and right panels, respectively).
Clear sky day in summer Cloudy sky day in summer
MLPNN CNN KNN MLPNN CNN KNN
PICP 28.0 28.95 96 12.5 4.17 91.67
PINAW 0.631 0.622 0.637 0.561 0.633 0.511
PINAD 0.0520 0.0989 0.0002 0.4510 1.0619 0.0011
Clear sky day in winter Cloudy sky day in winter
MLPNN CNN KNN MLPNN CNN KNN
PICP 20.83 20.83 100.0 12.5 4.16 87.50
PINAW 0.507 0.455 0.481 0. 530 0.526 0.495
PINAD 0.0866 0. 2212 0.0000 0. 2769 0.5736 0.0016

4.2.2. Analysing Residuals

In Table 5, statistical analyses on the residuals of all the models’ predictions is presented for MLPNN, CNN, and kNN models (with a confidence level of 95%) on a summer clear sky day. The table shows that kNN has the smallest standard deviation among the three models under investigation, which implies that it produces the best fit for the data. MLPNN has the next best fit to the data. kNN and MLPNN have skewness close to zero meaning their errors have a normal distribution. All the models have a kurtosis value that is less than 3.
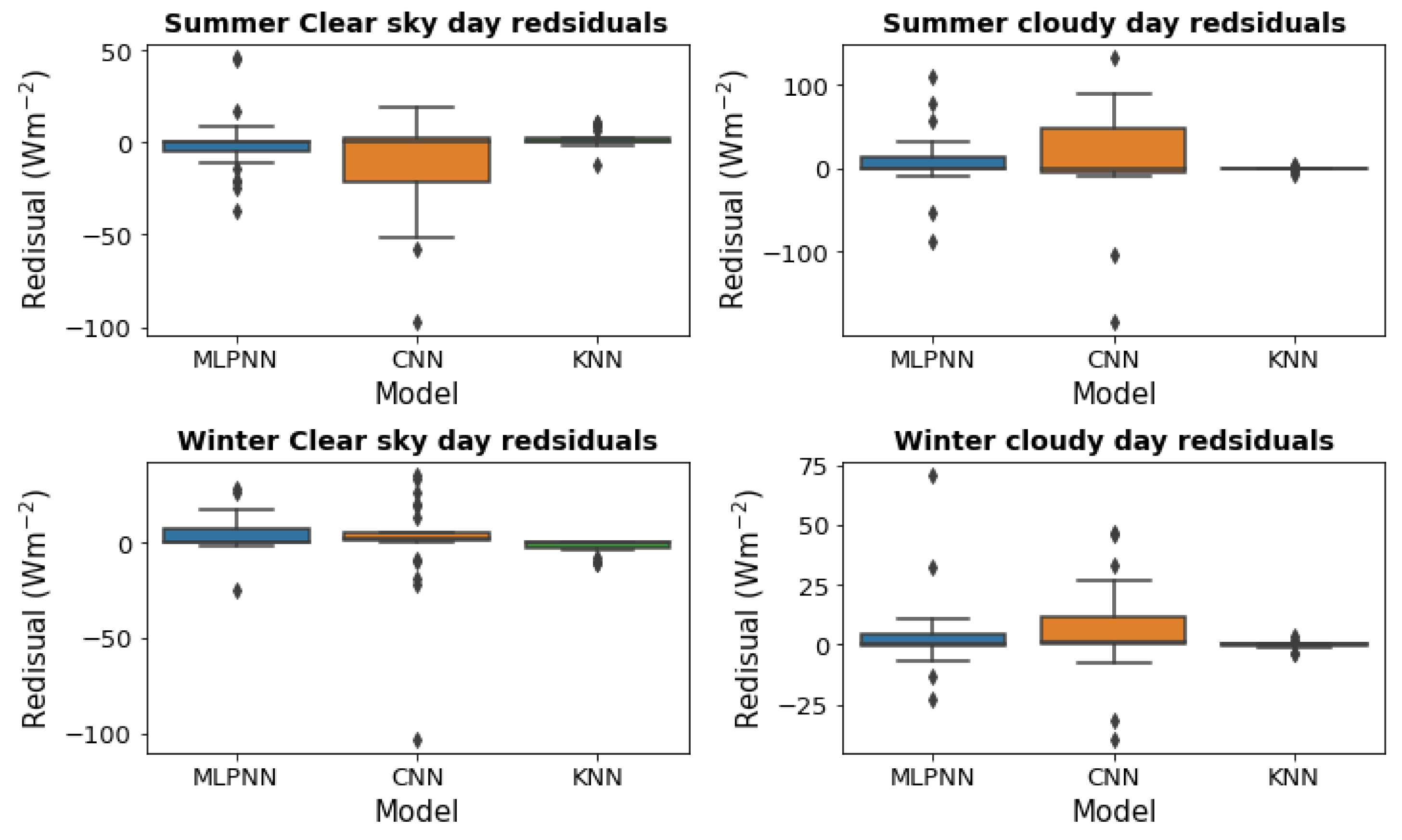
Figure 7 present the whisker and box plots of the residuals of the forecast made with the MLPNN, CNN and kNN models for clear sky and cloudy days during summer and winter seasons. The residual of the kNN model has the smallest tail compared to the others, followed by the forecast made with MLPNN although it made a worst prediction in the summer cloudy day under investigation. It also shows that the kNN model produced the best overall forecast.

4.2. Discussion of Results

This work has focused on modelling and forecasting solar PV output power (hourly) data for Grahamstown, Eastern Cape, South Africa. The data is from January 2009 to December 2020. Modelling this with MLPNN, CNN and kNN techniques, the kNN algorithm was found to produce the best model for this data based on RMSE, rRMSE, MAE, rMAE and R2 score metrics. The kNN is the best model for our data. Note that the data under investigation has very few spikes (or outliers) and missing records (and is not too noisy), so the kNN model perfectly predicted the data. Again, while MLPNN and CNN each takes several minutes to train their respective model, kNN has no training step. It goes straight into modelling the PV. So, when it comes to execution time, kNN still wins the contest.
We were inspired by the works of [4,20,48]. Mutavhatsindi et al. [48] analysed the performance of support vector regression, principal component regression, feedforward neural networks and LSTM network. Ratshilengo et al. [4] indeed compared the GA algorithm with the RNN and kNN algorithms models’ performance in forecasting global horizontal irradiance. They found the GA algorithm to have the best overall forecast performance. The kNN model applied in this study produced lower metric values for the kNN for RMSE, MAE, rRMSE and rMAE than those produced by [4].

5. Challenges of Photovoltaic Power Forecasting

Solar PV output power forecasting has a few challenges or limitations as with any other predictive analytics. One of the main limitations encountered is the accurate prediction of future weather condition when applying physical and indirect methods that require future weather parameters as input [49]. Another limitation is the issue of having a huge amount of data to be processed when applying statistical methods. Although a large amount of data allows this technique to make better prediction, processing the data consume a lot of machine resources which is also a weakness of this method. In addition, once large data is being processed, there is often a compromise on the output’s speed and accuracy, particularly for generation plants where real-time data output is required.
In most statistical and hybrid approaches, it is usually considered that a complex model will produce more accurate results. This is not always a guaranteed scenario, as a simpler technique may sometimes yield higher accuracy if the input parameters are properly filtered and preprocessed. This poses a challenge similar to the view expressed by the authors in [50] to selecting the right model and input parameters.
Furthermore, there is the challenge of cell/module degradation and site-specific losses, which negatively impact medium and long-term power forecasting estimates. Since forecasting models are based on input weather conditions, historical data or both, the forecasted data may deviate significantly when unexpected adverse weather conditions occur. The occurrence may accelerate the degradation of the installed solar cells/modules in a manner different from the predefined constant degradation factor that has been applied in the forecasting model. Thus, even when site-specific modelling has been done, there may be a need to constantly review the model’s input parameters over time based on the degradation of the solar PV modules.

6. Conclusions

This study has applied MLPNN, CNN and kNN methods to model solar PV output power for (solar PV installation in) Grahamstown, Eastern Cape, South Africa for a short-term forecast horizon. This study’s findings will be a useful tool for energy providers (both private and public) who want quick and easy but accurate forecast of their solar photovoltaic installation - to plan energy distribution and expansion of installations in a sustainable and environmentally friendly way.

Author Contributions

Conceptualization, K.J.I.; methodology, K.J.I.; formal analysis, K.J.I.; investigation, K.J.I.; writing—original draft preparation, K.J.I.; writing—review and editing, K.J.I. All authors have read and agreed to the published version of the manuscript.

Funding

Not applicable.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgements

We acknowledge the support of my spouse Chidinma, the University of Fort Hare and Rhodes University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Andrade, J.R.; Bessa, R.J. Improving Renewable Energy Forecasting With a Grid of Numerical Weather Predictions. IEEE Trans. Sustain. Energy 2017, 8, 1571–1580. [Google Scholar] [CrossRef]
  2. Sun, S.; Wang, S.; Zhang, G.; Zheng, J. A decomposition-clustering-ensemble learning approach for solar radiation forecasting. Sol. Energy 2018, 163, 189–199. [Google Scholar] [CrossRef]
  3. Yang, X.; Jiang, F.; Liu, H. Short-Term Solar Radiation Prediction based on SVM with Similar Data. 2nd IET Renewable Power Generation Conference (RPG 2013). LOCATION OF CONFERENCE, ChinaDATE OF CONFERENCE;
  4. Ratshilengo, M.; Sigauke, C.; Bere, A. Short-Term Solar Power Forecasting Using Genetic Algorithms: An Application Using South African Data. Appl. Sci. 2021, 11, 4214. [Google Scholar] [CrossRef]
  5. Iheanetu, K.J. Solar Photovoltaic Power Forecasting: A Review. Sustainability 2022, 14, 17005. [Google Scholar] [CrossRef]
  6. Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
  7. Zhang, J.; Florita, A.; Hodge, B.-M.; Lu, S.; Hamann, H.F.; Banunarayanan, V.; Brockway, A.M. A suite of metrics for assessing the performance of solar power forecasting. Sol. Energy 2015, 111, 157–175. [Google Scholar] [CrossRef]
  8. Blanc, P.; Remund, J.; Vallance, L. Short-term solar power forecasting based on satellite images. In Renewable Energy Forecasting; Woodhead Publishing: 2017; pp. 179–198.
  9. Wang, G.; Su, Y.; Shu, L. One-day-ahead daily power forecasting of photovoltaic systems based on partial functional linear regression models. Renew. Energy 2016, 96, 469–478. [Google Scholar] [CrossRef]
  10. C.F.M. Coimbra K., "Overview of solar-forecasting methods and a metric for accuracy evaluation," Boston: Academic Press, 2013, pp. 171–194.
  11. Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference, Systems, Man, and Cybernetics (SMC) 2016 - Conference Proceedings, Budapest, Hungary, 9 Octorber 2016. [Google Scholar] [CrossRef]
  12. Wang, H.; Yi, H.; Peng, J.; Wang, G.; Liu, Y.; Jiang, H.; Liu, W. Deterministic and probabilistic forecasting of photovoltaic power based on deep convolutional neural network. Energy Convers. Manag. 2017, 153, 409–422. [Google Scholar] [CrossRef]
  13. Lima, M.A.F.B.; Carvalho, P.C.M.; Braga, A.P.d.S.; Ramírez, L.M.F.; Leite, J.R. MLP Back Propagation Artificial Neural Network for Solar Resource Forecasting in Equatorial Areas. Renew. Energy Power Qual. J. 2018, 1, 175–180. [Google Scholar] [CrossRef]
  14. R.L.d.C. Costa, "Convolutional-LSTM networks and generalization in forecasting of household photovoltaic generation," Eng Appl Artif Intell, 2022, vol. 116, pp. 105458.
  15. Li, G.; Xie, S.; Wang, B.; Xin, J.; Li, Y.; Du, S. Photovoltaic Power Forecasting With a Hybrid Deep Learning Approach. IEEE Access 2020, 8, 175871–175880. [Google Scholar] [CrossRef]
  16. Wang, Y.; Liao, W.; Chang, Y. Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting. Energies 2018, 11, 2163. [Google Scholar] [CrossRef]
  17. Gao, B.; Huang, X.; Shi, J.; Tai, Y.; Xiao, R. Predicting day-ahead solar irradiance through gated recurrent unit using weather forecasting data. J. Renew. Sustain. Energy 2019, 11, 043705. [Google Scholar] [CrossRef]
  18. Tajmouati, S.; EL Wahbi, B.; Dakkon, M. Applying regression conformal prediction with nearest neighbors to time series data. Commun. Stat. - Simul. Comput. 2022; 1–11. [Google Scholar] [CrossRef]
  19. Ratshilengo, M.; Sigauke, C.; Bere, A. Short-Term Solar Power Forecasting Using Genetic Algorithms: An Application Using South African Data. Appl. Sci. 2021, 11, 4214. [Google Scholar] [CrossRef]
  20. M.A. Reyes-Belmonte, "Quo Vadis Solar Energy Research?" Applied Sciences, Mar 28, 2021, vol. 11, pp. 3015.
  21. Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Networks 2004, 17, 113–126. [Google Scholar] [CrossRef]
  22. Huang, J.; Korolkiewicz, M.; Agrawal, M.; Boland, J. Forecasting solar radiation on an hourly time scale using a Coupled AutoRegressive and Dynamical System (CARDS) model. Sol. Energy 2013, 87, 136–149. [Google Scholar] [CrossRef]
  23. El Hendouzi, A.; Bourouhou, A.; Ansari, O. The Importance of Distance between Photovoltaic Power Stations for Clear Accuracy of Short-Term Photovoltaic Power Forecasting. J. Electr. Comput. Eng. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
  24. Luo, X.; Zhang, D.; Zhu, X. Deep learning based forecasting of photovoltaic power generation by incorporating domain knowledge. Energy 2021, 225, 120240. [Google Scholar] [CrossRef]
  25. Zhu, H.; Li, X.; Sun, Q.; Nie, L.; Yao, J.; Zhao, G. A Power Prediction Method for Photovoltaic Power Plant Based on Wavelet Decomposition and Artificial Neural Networks. Energies 2016, 9, 11. [Google Scholar] [CrossRef]
  26. R.L.d.C. Costa, "Convolutional-LSTM networks and generalization in forecasting of household photovoltaic generation," Engineering Applications of Artificial Intelligence, Nov. 2022, vol. 116, pp. 105458.
  27. Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A Short-Term Wind Power Forecasting Approach With Adjustment of Numerical Weather Prediction Input by Data Mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291. [Google Scholar] [CrossRef]
  28. F. Aminzadeh and Paul De Groot, "Neural networks and other soft computing techniques with applications in the oil industry," Eage Publications, 2006.
  29. Hossain, S.; Ong, Z.C.; Ismail, Z.; Noroozi, S.; Khoo, S.Y. Artificial neural networks for vibration based inverse parametric identifications: A review. Appl. Soft Comput. 2017, 52, 203–219. [Google Scholar] [CrossRef]
  30. Zhang, Y.; Chen, G.; Malik, O.; Hope, G. An artificial neural network based adaptive power system stabilizer. IEEE Trans. Energy Convers. 1993, 8, 71–77. [Google Scholar] [CrossRef]
  31. Moreira, M.; Balestrassi, P.; Paiva, A.; Ribeiro, P.; Bonatto, B. Design of experiments using artificial neural network ensemble for photovoltaic generation forecasting. Renew. Sustain. Energy Rev. 2021, 135, 110450. [Google Scholar] [CrossRef]
  32. Malki, H.A.; Karayiannis, N.B.; Balasubramanian, M. Short-term electric power load forecasting using feedforward neural networks. Expert Syst. 2004, 21, 157–167. [Google Scholar] [CrossRef]
  33. Chen, S.-M.; Chang, Y.-C.; Chen, Z.-J.; Chen, C.-L. MULTIPLE FUZZY RULES INTERPOLATION WITH WEIGHTED ANTECEDENT VARIABLES IN SPARSE FUZZY RULE-BASED SYSTEMS. Int. J. Pattern Recognit. Artif. Intell. 2013, 27. [Google Scholar] [CrossRef]
  34. Yona, A.; Senjyu, T.; Funabashi, T.; Kim, C.-H. Determination Method of Insolation Prediction With Fuzzy and Applying Neural Network for Long-Term Ahead PV Power Output Correction. IEEE Trans. Sustain. Energy 2013, 4, 527–533. [Google Scholar] [CrossRef]
  35. Srisaeng, P.; Baxter, G.S.; Wild, G. An adaptive neuro-fuzzy inference system for forecasting Australia’s domestic low cost carrier passenger demand. Vilnius Gediminas Technical University 2015, 19, 150–163. [Google Scholar] [CrossRef]
  36. Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. An Efficient Fuzzy-Logic Based Variable-Step Incremental Conductance MPPT Method for Grid-Connected PV Systems. IEEE Access 2021, 9, 26420–26430. [Google Scholar] [CrossRef]
  37. Zhang, J.; Verschae, R.; Nobuhara, S.; Lalonde, J.-F. Deep photovoltaic nowcasting. Sol. Energy 2018, 176, 267–276. [Google Scholar] [CrossRef]
  38. Parvez, I.; Sarwat, A.; Debnath, A.; Olowu, T.; Dastgir, G.; Riggs, H. Multi-layer Perceptron based Photovoltaic Forecasting for Rooftop PV Applications in Smart Grid. in - 2020 SoutheastCon 2020, pp. 1–6.
  39. Hontoria, L.; Aguilera, J.; Zufiria, P. Generation of hourly irradiation synthetic series using the neural network multilayer perceptron. Sol. Energy 2002, 72, 441–446. [Google Scholar] [CrossRef]
  40. Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. CATENA 2017, 149, 52–63. [Google Scholar] [CrossRef]
  41. Parvez, I.; Sriyananda, M.G.S.; Güvenç, I.; Bennis, M.; Sarwat, A. CBRS Spectrum Sharing between LTE-U and WiFi: A Multiarmed Bandit Approach. Mob. Inf. Syst. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
  42. Horton, P. ; Y. Mukai and K. Nakai,.PROTEIN SUBCELLULAR LOCALIZATION PREDICTION:The Practical Bioinformatician, 2004.pp. 193, -05. 10.1142/9789812562340_0009.
  43. Liu, Z.; Zhang, Z. Solar forecasting by K-Nearest Neighbors method with weather classification and physical model. Sep 2016, pp. 1–6.
  44. Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1995, 97, 273–324. [Google Scholar] [CrossRef]
  45. C. Chatfield, "Calculating Interval Forecasts," Journal of Business & Economic Statistics, vol. 11, pp. 121–135, Apr 01.
  46. Gaba, A.; Tsetlin, I.; Winkler, R.L. Combining Interval Forecasts. Decis. Anal. 1993, 14, 1–20. [Google Scholar] [CrossRef]
  47. Sun, X.; Wang, Z.; Hu, J. Prediction Interval Construction for Byproduct Gas Flow Forecasting Using Optimized Twin Extreme Learning Machine. Math. Probl. Eng. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
  48. T. Mutavhatsindi; C. Sigauke and R. Mbuvha, Forecasting Hourly Global Horizontal Solar Irradiance in South Africa Using Machine Learning Models:IEEE Access, 2020. vol. 8, pp. 198872–198885, 10.1109/ACCESS.2020.3034690.stylefixSengupta, Manajit, Habte, Aron, Wilbert, Stefan, Gueymard, Christian,and Remund, Jan, "Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications: Third Edition," 2021.
  49. Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A Physical Hybrid Artificial Neural Network for Short Term Forecasting of PV Plant Power Output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef]
Preprints 105889 g001
Figure 1. (a) Schematic representation of a typical ANN - having the input, hidden and output layers. (b) A pictorial presentation of a mathematical model of an ANN cell [5].
Figure 1. (a) Schematic representation of a typical ANN - having the input, hidden and output layers. (b) A pictorial presentation of a mathematical model of an ANN cell [5].
Preprints 105889 g001
Preprints 105889 g002
Figure 2. Schematic representation of a convolutional network.
Figure 2. Schematic representation of a convolutional network.
Preprints 105889 g002
Preprints 105889 g003
Figure 3. Plot the PV output power from 2009 to 2020.
Figure 3. Plot the PV output power from 2009 to 2020.
Preprints 105889 g003
Preprints 105889 g004
Figure 4. Plots of the variables.
Figure 4. Plots of the variables.
Preprints 105889 g004
Preprints 105889 g005
Figure 5. Plots of the Sola PV output power (Data) superimposed with MLPNN, CNN, GRU and kNN models’ predictions (dash lines) on a summer clear sky day (top left panel) and cloudy day (top right panel). The same plots are show for a winter clear sky day (bottom left panel) and cloudy day (bottom right panel). The solid lines represent the measured data while dashed line the predictions.
Figure 5. Plots of the Sola PV output power (Data) superimposed with MLPNN, CNN, GRU and kNN models’ predictions (dash lines) on a summer clear sky day (top left panel) and cloudy day (top right panel). The same plots are show for a winter clear sky day (bottom left panel) and cloudy day (bottom right panel). The solid lines represent the measured data while dashed line the predictions.
Preprints 105889 g005
Preprints 105889 g006
Figure 6. Density plots of the measured data (data – solid line) together with the model’s forecast (dash lines). In the top row is the graph for the models’ predictions on a summer clear sky day (left panel) and cloudy day (right panel), while the bottom panel presents the same on a winter clear sky day (left panel) and cloudy day (right panel).
Figure 6. Density plots of the measured data (data – solid line) together with the model’s forecast (dash lines). In the top row is the graph for the models’ predictions on a summer clear sky day (left panel) and cloudy day (right panel), while the bottom panel presents the same on a winter clear sky day (left panel) and cloudy day (right panel).
Preprints 105889 g006
Preprints 105889 g007
Figure 7. Whisker and box plots of the residuals of the forecast made with MLPNN, CNN and kNN models on clear sky and cloudy days during the summer and winter seasons.
Figure 7. Whisker and box plots of the residuals of the forecast made with MLPNN, CNN and kNN models on clear sky and cloudy days during the summer and winter seasons.
Preprints 105889 g007
Table 5. Comparing residuals of the models’ prediction.
Table 5. Comparing residuals of the models’ prediction.
Median Min Max Mean Std. Dev. Skewness kurtosis
MLPNN 0.09 -57.31 67.73 -1.36 22.20 0.28 2.56
CNN 0.17 -77.58 30.96 -6.05 24.62 -1.31 1.68
kNN 0.00 -12.54 10.92 1.01 4.39 0.16 1.79
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated