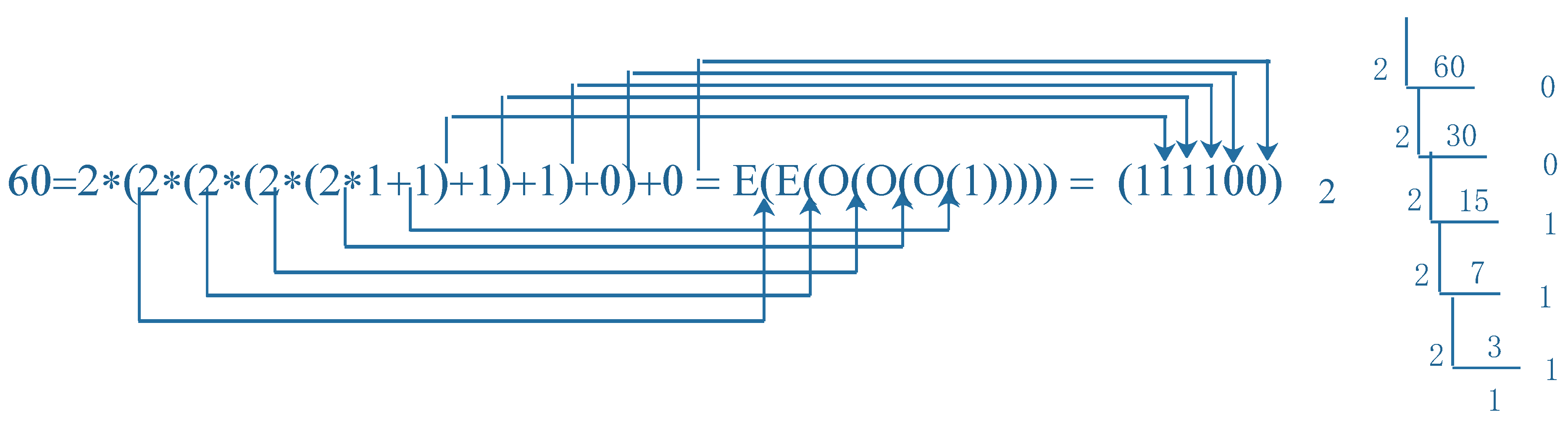Using Full Binary Directed Tree Proof the Collatz Conjecture

Preprint

Article

Using Full Binary Directed Tree Proof the Collatz Conjecture

Altmetrics

Downloads

105

Views

Comments

Jishe Feng^*

This version is not peer-reviewed

Submitted:

07 May 2024

Posted:

08 May 2024

You are already at the latest version

Alerts

Abstract

We use binary string to represent a natural number and show the composite procedure of odd-number and even-number functions, thus we propose full binary directed tree to represent the set of natural numbers and give another partition the natural number set to three sets: pure odd, pure even and mixed number. For the Collatz conjecture we make use of the parity of a natural number to analyse the sequence of iteration (or composite) of Collatz function and reduced Collatz function analog to the inverse function. We give tabular and binary strings to the algebra expression to state the sequence of Collatz, this is the key topic to proof the conjecture: the discrete powers of 2 can be changed to ultimately continuous powers of 2, finally get to pure even number and to the smallest number 1. The sequence created by the infinite iterations of the Collatz function becomes the ultimately periodic sequence if any natural number is the beginning value, proving the conjecture that has been held for 87 years.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

MSC: 03D20, 11B25, 11B83

In the study of number theory, odd and even numbers are a fundamental pair of ideas. Natural number set is parted into two different sets. Number theory frequently examines the connections between various numbers. There are many conjectures that attempt to generalize the facts of different kinds of natural numbers discovered in a restricted range to the entire infinite set of natural numbers. This article will examine the famous Collatz conjecture, which states that for each natural number n, if it is even, divide by 2, if it is odd, multiply by 3, add 1, and so on, the result must eventually reach 1. It is also referred to as the

3 n + 1

conjecture and was put forth in 1937 by Lothar Collatz, also known as the

3 n + 1

problem. The mathematician Paul Erdos once said of this conjecture: “Mathematics may not be ready for such problems”

^{[1, 2]}

The inconsistencies between the finite and the infinite, as well as the relation between various kinds, present difficulties in the study of number theory problems. We are talking about the connection between two different mathematical ideas: the iterated sequence is a ultimately periodic sequence whether the initial value is odd or even.

The finite and the infinite can be connected by the useful mathematical construct known as a function, and the value will also be finite and infinite. A special function that has particular significance in discrete mathematics is the piecewise function. Composite functions and piecewise functions combined is a highly clever mathematical trick. Particularly in number theory, which is the most fundamental idea and mathematical expression, the sequence of numbers is a close connection between functions and finite or infinite. Numerous conjectures are obtained through restricted iteration of an iterative algorithm, which is a widely used method in number theory, but people typically lack the tools to demonstrate the accuracy and reasoned nature of conjectures. A fresh technique or new knowledge is frequently used to support a hypothesis.

For the Collatz conjecture, we can describe it as a function:

T (n) = \{\begin{matrix} 3 n + 1, & if n is odd number, \\ \frac{n}{2} & if n is even number . \end{matrix}

(1)

The following sequence is obtained via the composite function (iteration):

A = {n, T (n), T (T (n)), T (T (T (n))), \dots} = {n, T (n), T^{2} (n), T^{3} (n), \dots}

. Consequently, the Collatz conjecture can be stated as follows:

Collatz conjecture 1: For any natural number n, there is finite natural number m, the sequence A always leads to the integer 1, namely

T^{m} (n) = 1

The series A is an infinite sequence of ultimately period

^{[9, 10]}

. So we give another statement of the Collatz conjecture as the following.

Collatz conjecture 2: The series A is an infinite sequence of ultimately period, the preperiod

η (n)

varies with the initial value n, but the ultimately period is always

{4, 2, 1}

The key problem is how find the beingness and finiteness of the natural number m. In order to solve the key problem, we propose full binary directed tree. Although there are binary tree and graphs in papers [5,13,14], comparing their binary tree and mine, there are many differences as the follows:

1) We use the full binary directed tree to represent the procedure of the composition of odd-number and even-number function from 1. Namely we visual represent the procedure of the function

n = f^{k} (1)

, k is the number of the level of the full binary directed tree, the function

f (n)

in (2.2).

2) By binary string of arbitrarily given natural, it is visual to the iteration procedure of the Collatz function, thats are the following two actions jump and trace accordingly two functions

3 n + 1

and

n / 2

1. An Algebra and Graph Representation of Natural Numbers

1.1. The Composition of Odd-Number and Even-Number Functions

If a natural number can be divided by 2, it is said to be an even number; otherwise, it is said to be odd number. The Peano’s Axiom states that 1 is the smallest natural number. The set of natural numbers

N = {1, 2, 3, \dots}

may be separated into odd and even sets, we will utilize the standard definition of natural numbers in this work.

{natural number} = {odd number} ⋃ {even number}

In the set of natural numbers where 1 is the smallest odd number and 2 is the smallest even number, we can use the expression

n = 2 k - 1

to indicate that it is an odd, and the expression

n = 2 k

to indicate that it is an even, where k is any natural number.

We introduce two functions

O (x) = 2 x + 1

to express odd numbers greater than 1, and

E (x) = 2 x

to express even numbers, where x is any natural number in N.

We define a strictly increase monotonically piecewise function

f (n)

, from a natural number n it generates two cases: odd or even numbers:

f (n) = \{\begin{matrix} 2 n + 1 = O (n), & the value is odd number, \\ 2 n = E (n), & the value is even number . \end{matrix}

(2)

Definition 1 A natural number n is obtained by composition of the odd-number function

O (x) = 2 x + 1

and the even-number function

E (x) = 2 x

several times, namely

\{\begin{matrix} n = f (f (\dots f (1))) = f^{k} (1), \end{matrix}

(3)

the function f is either odd-number function

O (x)

or even-number function

E (x)

For example,

f (1) = O (1) = 3, f (1) = E (1) = 2

7 = f^{2} (1) = 2 \cdot 3 + 1 = 2 \cdot (2 \cdot 1 + 1) + 1) = O (O (1)), 189 = f^{7} (1) = 2 \cdot (2 \cdot (2 \cdot 4 + 1) = 2 \cdot (2 \cdot (2 \cdot (2 \cdot (2 \cdot (2 \cdot 1) + 1) + 1) + 1) + 1)) + 1 = E (O (O (O (O (E (O (1))))

Any natural number n is the value of the finite times composite function of odd-number and even-number function. Namely if

n = f (f (\dots f (1))) = f^{r} (1)

, then the inverse function is

f^{- r} (n) = 1

1.2. Use Binary String to Represent Natural Numbers

An natural number is the value of composition of

O (x)

and

E (x)

, in order to more clearly express the odd-number and even-number functions composite process of a natural number, we use binary string to represent a natural number n, the string from right to left of 0 and 1 accordingly the procedure from top down to itself, it indicates the order of the composition of

O (x)

and

E (x)

, 0 implicate even-number function, and 1 implicate odd-number function.

The binary string of a natural number is a representation of its odd-even composite function, where the 1 in the

i (i > 0)

-bit from left to right is the

i (i > 0)

odd-number function

O (x)

, and 0 is the corresponding even-number function

E (x)

. For example, Figure 1 shows the decomposition of the composite function of 60.

The natural number n is then represented by the bring 0 and 1 string

a b c d e f

, we note in passing that the

f, e, d, c, b, a

are the remainders left after successive divisions of n by 2.

1.3. Use a Graph to Represent the Composite Procedure of the Natural Numbers

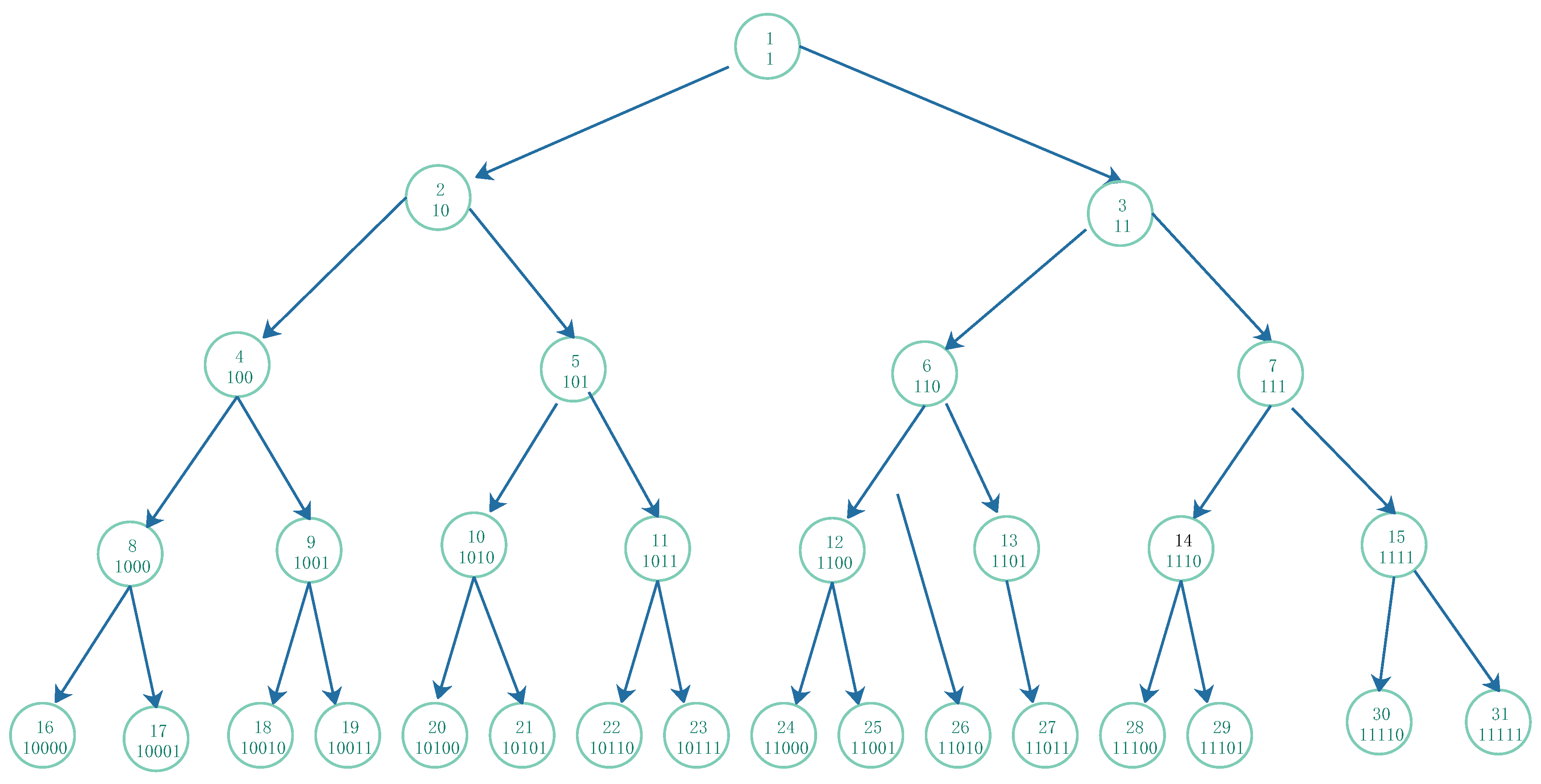
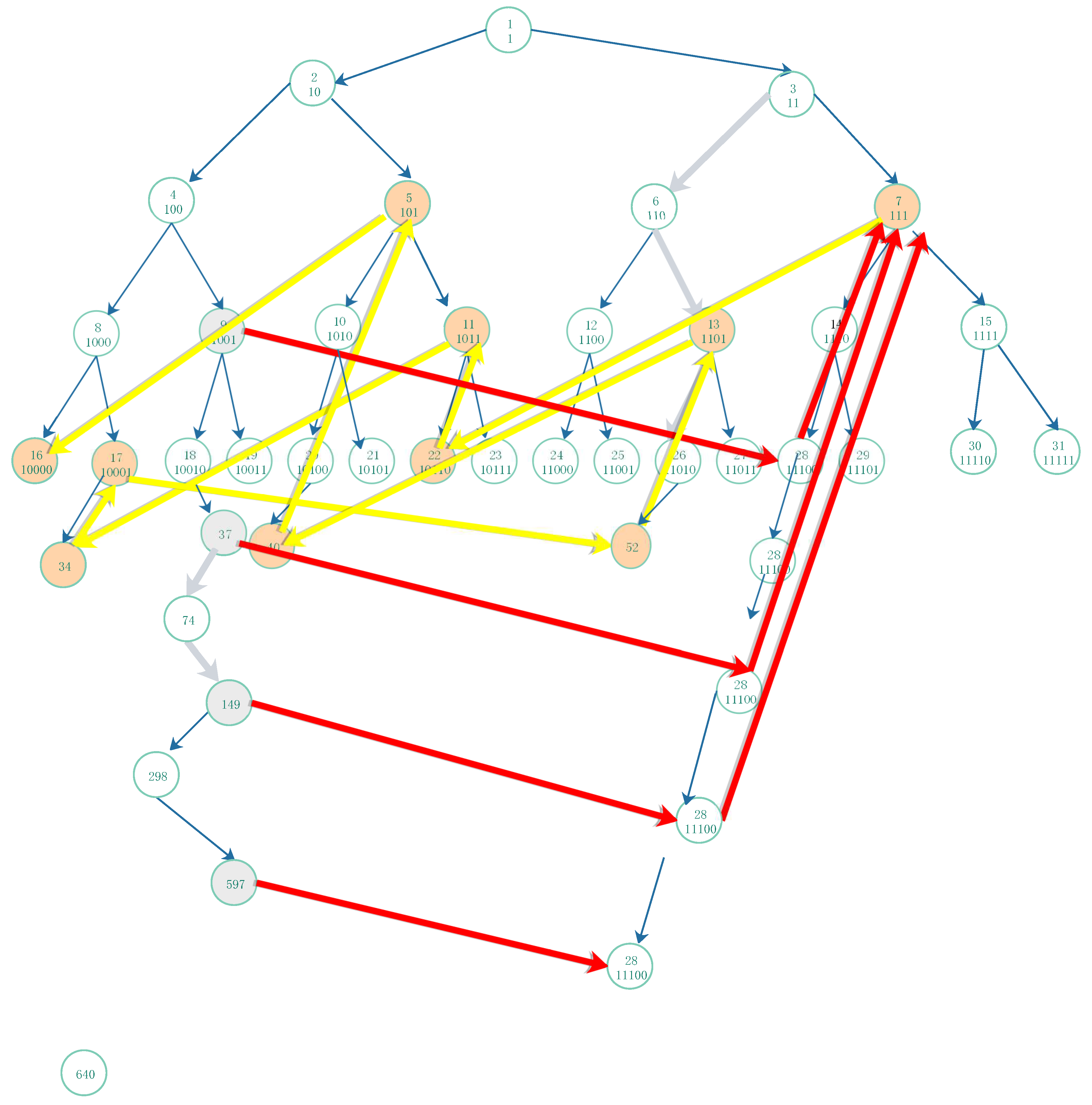
In order to give an intuitive impression, we provide a full binary directed tree to represent the natural number set, the root is the smallest number 1. For per vertex, its left-child is an even number which double itself, its binary string is appended by 0, right-child is an odd number which double itself and add 1, its binary string is appended by 1. For an natural number its binary string indicates the procedure of the composition of

O (x)

and

E (x)

from initial value 1 to the final accordingly binary string from the left to right. The full binary directed tree, as in Figure 2, is a very good representation of natural number N, it is infinitely isosceles triangle.

Proposition 1 The length of a binary string implies its level in the full binary directed tree, and the number of the times of composite of odd-number and even-number function is the length of a binary string minus 1.

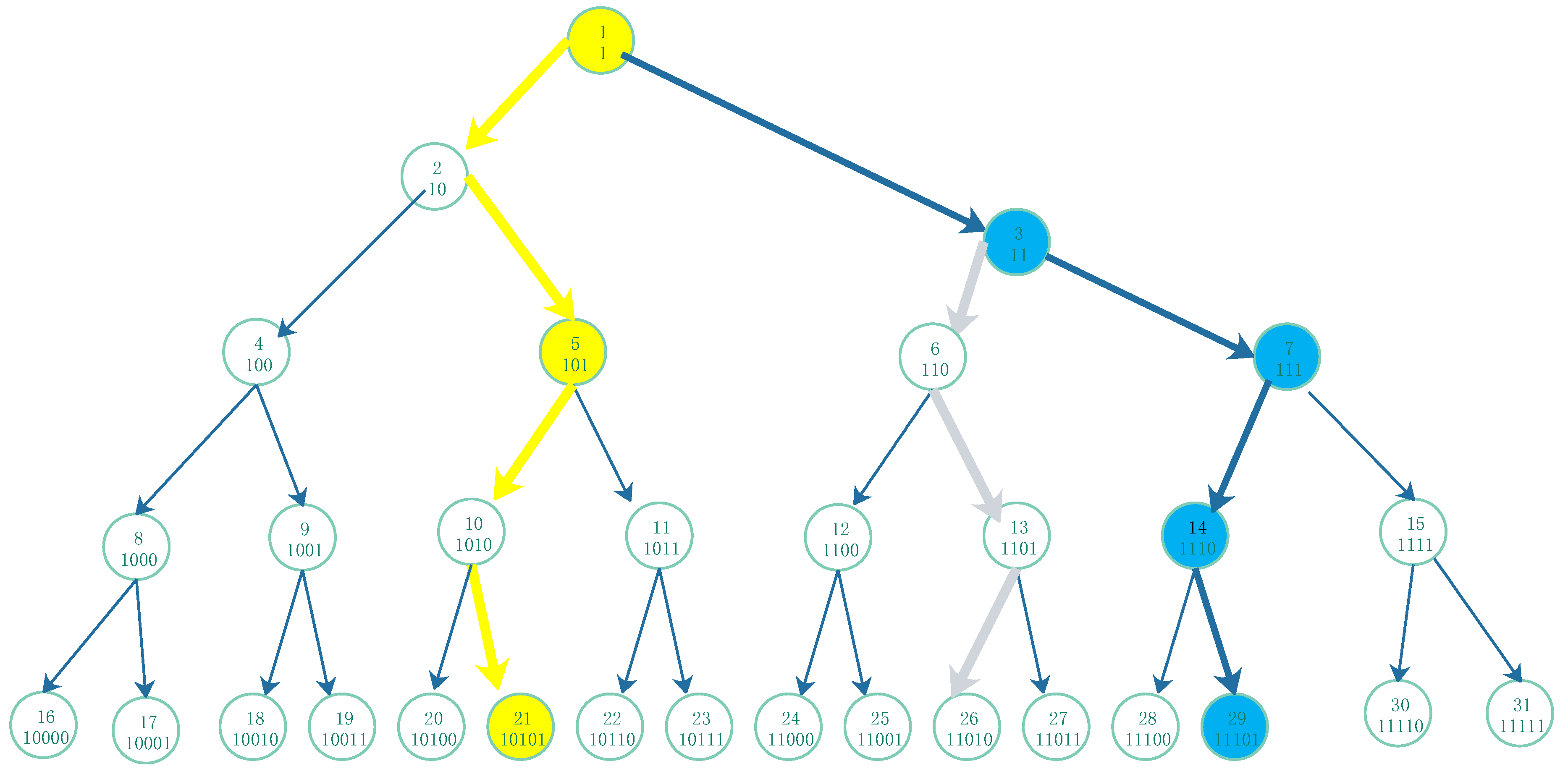
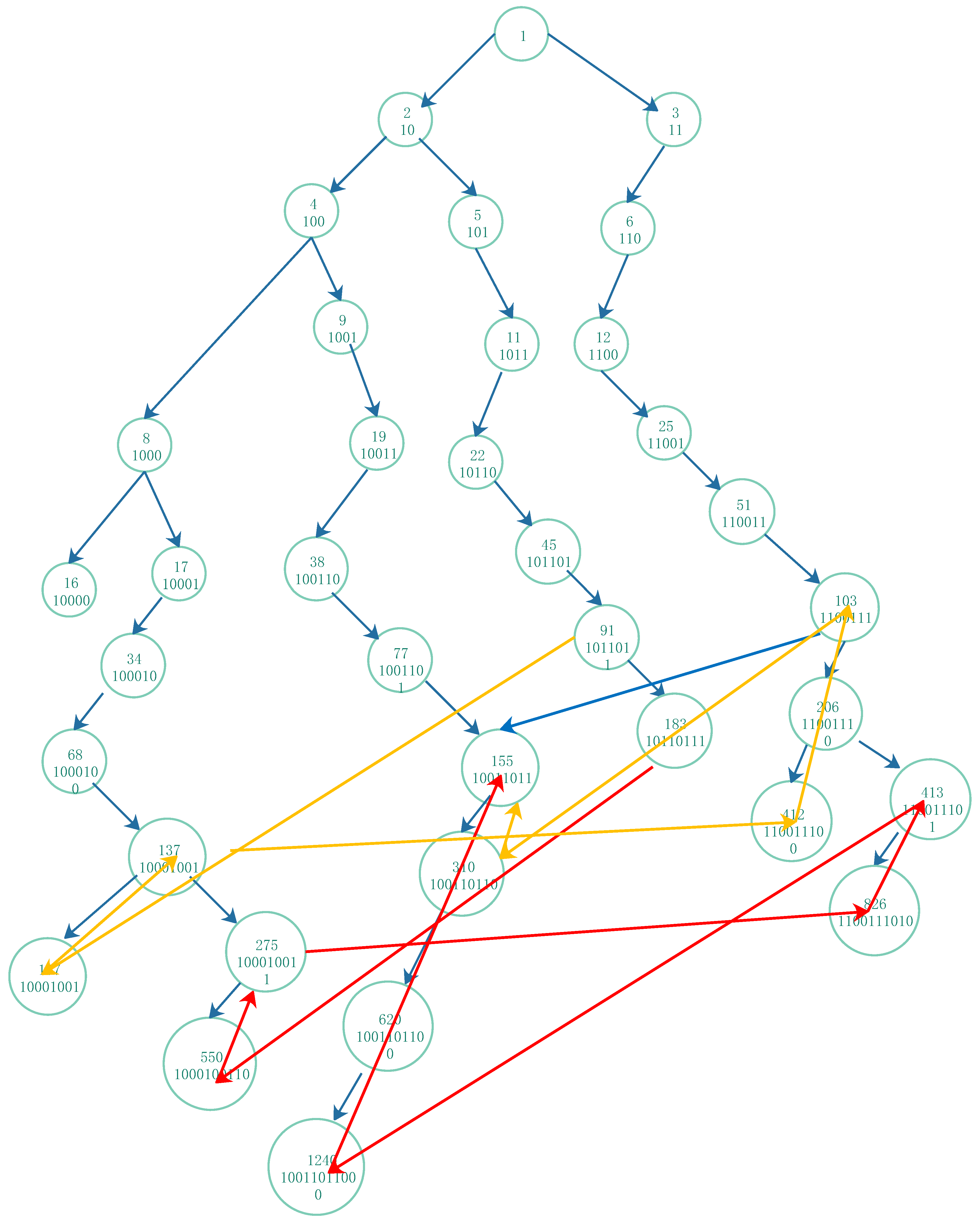
For given natural number n, its binary string from the second bit in left to right appending 0 or 1, indicates which comes from the root 1 of the full binary directed tree traversal according only one branch to itself. For instance, Figure 3 illustrates the procedures of composite odd-number and even-number of 21 and 29.

1.4. Another Partition of the Natural Number Set

We give the definitions of three kinds of natural numbers:

Definition 2(i) By applying the odd function

O (x)

m compositions, a natural number, namely

O^{m} (1) = 2^{m} - 1 = 2^{m - 1} + 2^{m - 2} + \dots + 2 + 1 = {(11 \dots 1)}_{2}

, is obtained. such as

3 = {(11)}_{2}, 7 = {(111)}_{2}, 15 = {(1111)}_{2}, 31 = {(11111)}_{2}, 63 = {(111111)}_{2}, \dots

, which we call it as pure odd number. Those are in the right leg of the isosceles triangle, namely the full binary directed tree of the Figure 2.

(ii) By applying the even function

E (x)

m compositions, a natural number, namely

E^{m} (1) = 2^{m} = {(10 \dots 0)}_{2}

, is obtained, such as,

2 = {(10)}_{2}, 4 = {(100)}_{2}, 8 = {(1000)}_{2}, 16 = {(10000)}_{2}, 32 = {(100000)}_{2}, 64 = {(1000000)}_{2}, \dots

, which we call it as pure even number.Those are in the left leg of the isosceles triangle, namely the full binary directed tree of the Figure 2.

(iii) The natural number obtained by the composition of odd function

O (x)

and even function

E (x)

, we call it mixed number. Such as,

18 = {(10010)}_{2}, 28 = {(11100)}_{2}, 67 = {(1000011)}_{2}, 309 = {(100110101)}_{2}

. Those are in the inside of the isosceles triangle, the complete directed binary tree of the Figure 2.

In particular, the natural numbers obtained by the finite alternately composition of the odd function

O (x)

and the even function

E (x)

, namely,

{[E (O (1))]}^{m} = {(101 \dots 101)}_{2}

. Such as

5 = {(101)}_{2}, 21 = {(10101)}_{2}, 85 = {(1010101)}_{2}, 341 = {(101010101)}_{2}, 1365 = {(10101010101)}_{2}, 5461 = {(1010101010101)}_{2}, \dots

, which we call hard numbers.

For a natural number n, if its binary string has

k + 1

bits, then the degree of composite function is k. The binary string of a pure odd number is made of all 1; and the binary string of a pure even number is all 0 besides 1 in left-most; the binary string of a mixed number is made of many 0 and 1.

Thus for any natural number n, its binary string

1 \times \times

is the traversal path in the full binary directed tree from the root to down along the arcs. For example in Fig 3, for

21 = {(10101)}_{2}

, it comes from the root 1 down 2,5,10, finally reach 21, it is appending 0,1,0,1 to the vertexes,

1 \to 10 \to 101 \to 1010 \to 10101

. And for

29 = {(11101)}_{2}

, it comes from the root 1 down 3,7,14, finally reach 29, it is appending 1,1,0,1 to the vertexes,

1 \to 11 \to 111 \to 1110 \to 11101

Property 2 The set of natural numbers can be divided into three different sets: {natural number}=

{pure even number}∪{pure odd number}∪{mixed number}, where {mixed number}={mixed even number}∪{mixed odd number}

Example 1 (1)60–97 are mixed numbers.

(2)64,1180591620717411303424 are pure even numbers.

(3)63,1180591620717411303423 are pure odd numbers.

When we convert those natural numbers from decimal to binary, the facts are obvious.

60 = {(111100)}_{2}

is a mixed-even number,

97 = {(1100001)}_{2}

is a mixed-odd number.

64 = 2^{6} = (1000000)

1180591620717411303424 = 2^{70} = (10000 \dots 0)

are pure even numbers:

63 = {(111111)}_{2}

1180591620717411303423 = 2^{70} - 1 = (11 \dots 1)

are pure odd numbers.

2. Study the Collatz Function

2.1. Using Tabular Form and Algebraic Expressions to Represent the Collatz Sequence

The reduced Collatz function [6] is an alternate form of the Collatz function that maps one odd number to the next odd number, so that only odd numbers are included in the Collatz sequence.

R T (n) = \{\begin{matrix} \frac{3 n + 1}{2^{m}}, & if n is odd number, \frac{3 n + 1}{2^{m}} is an odd number, \\ \frac{n}{2^{r}} & if n is even number, \frac{n}{2^{r}} is an odd number . \end{matrix}

(4)

where m and r are two natural number, and the result is an odd number. We use a table that has been modified from the tabular forms in [6], which is the process for iterating the Collatz function (1.1) on n. For instance, if

n = 117

, the tabular forms is as follows.

Line 0							117	$\frac{3^{5}}{2^{15}} \cdot 117$
Line 1	117→	352→	176→	88→	44→	22→	11	$\frac{3^{4}}{2^{15}}$
Line 2	11→	34→	17					$\frac{3^{3}}{2^{10}}$
Line 3	17→	52→	26→	13				$\frac{3^{2}}{2^{9}}$
Line 4	13→	40→	20→	10→	5			$\frac{3}{2^{7}}$
Line 5	5→	16→	8→	4→	2→	1		$\frac{1}{2^{4}}$
Line 6	1→	4→	2→	1

The tabular’s unique feature is that the first and last numbers in each row are all odd numbers. If x is the first odd number, then y in the same row can be represented by the formula

y = \frac{3 x}{2^{r}} + \frac{1}{2^{r}},

(5)

where r is the number of the arrows from the even number to last odd number in the same row. For instance, for the table on

n = 117

, there are the following,

Line 1	suppose $v = 117,$	there is the expression $\frac{3}{2^{5}} \cdot v + \frac{1}{2^{5}} = 11 = u,$
Line 2	suppose $u = 11,$	there is the expression $\frac{3}{2} \cdot u + \frac{1}{2} = 17 = z,$
Line 3	suppose $z = 17,$	there is the expression $\frac{3}{2^{2}} \cdot z + \frac{1}{2^{2}} = 13 = y,$
Line 4	suppose $y = 13,$	there is the expression $\frac{3}{2^{3}} \cdot y + \frac{1}{2^{3}} = 5 = x,$
Line 5	suppose $x = 5,$	there is the expression $\frac{3}{2^{4}} \cdot x + \frac{1}{2^{4}} = 1,$
Line 6	suppose $a = 1,$	there is the expression $\frac{3}{2^{2}} a + \frac{1}{2^{2}} = a = 1 .$

Substitute the expression in line 1 into the expression in line 2, we obtain

\frac{3}{2} \cdot (\frac{3}{2^{5}} \cdot v + \frac{1}{2^{5}}) + \frac{1}{2} = \frac{3^{2}}{2^{6}} \cdot v + \frac{3}{2^{6}} + \frac{1}{2} = z

We substitute this expression into the expression in line 3, get

\frac{3}{2^{2}} \cdot (\frac{3^{2}}{2^{6}} \cdot v + \frac{3}{2^{6}} + \frac{1}{2}) + \frac{1}{2^{2}} = \frac{3^{3}}{2^{8}} \cdot v + \frac{3^{2}}{2^{8}} + \frac{3}{2^{3}} + \frac{1}{2^{2}} = y

Using the same method, we get the following expressions,

\frac{3}{2^{3}} \cdot y + \frac{1}{2^{3}} = \frac{3}{2^{3}} \cdot (\frac{3^{3}}{2^{8}} \cdot v + \frac{3^{2}}{2^{8}} + \frac{3}{2^{3}} + \frac{1}{2^{2}}) + \frac{1}{2^{3}} = \frac{3^{4}}{2^{11}} \cdot v + \frac{3^{3}}{2^{11}} + \frac{3^{2}}{2^{6}} + \frac{3}{2^{5}} + \frac{1}{2^{3}} = x

\frac{3}{2^{4}} \cdot x + \frac{1}{2^{4}} = \frac{3^{5}}{2^{15}} \cdot v + \frac{3^{4}}{2^{15}} + \frac{3^{3}}{2^{10}} + \frac{3^{2}}{2^{9}} + \frac{3}{2^{7}} + \frac{1}{2^{4}} = 1

Thus, we have an algebraic expression

T^{20} (117) = \frac{3^{5}}{2^{15}} \cdot 117 + \frac{3^{4}}{2^{15}} + \frac{3^{3}}{2^{10}} + \frac{3^{2}}{2^{9}} + \frac{3}{2^{7}} + \frac{1}{2^{4}} = 1 .

(6)

In general, the algebraic expressions are obtained: Starting from the last row of the table and going up to the binary corresponding to the initial value n of the first row, the numerator is

3^{k}, k = 0, 1, 2, 3, \dots

, The denominator is

2^{r_{k}}

r_{0} = m_{0}, r_{k} = r_{k - 1} + m_{k}, k = 1, 2, 3, \dots

m_{k}

here for the before k lines at the end of the second column of binary string number 0. The details are expressed in the last column of the corresponding table.

The powers of 2 in the denominator are the sum of the numbers of arrows after the even numbers to the end of the row and the power of 2 in next row. We can see that in the last column of the table from the last row to the first row, the powers of 3 are 0,

1, 2, 3, \dots

in the numerator successively.

2.2. Discuss the Collatz Problem by Binary Strings

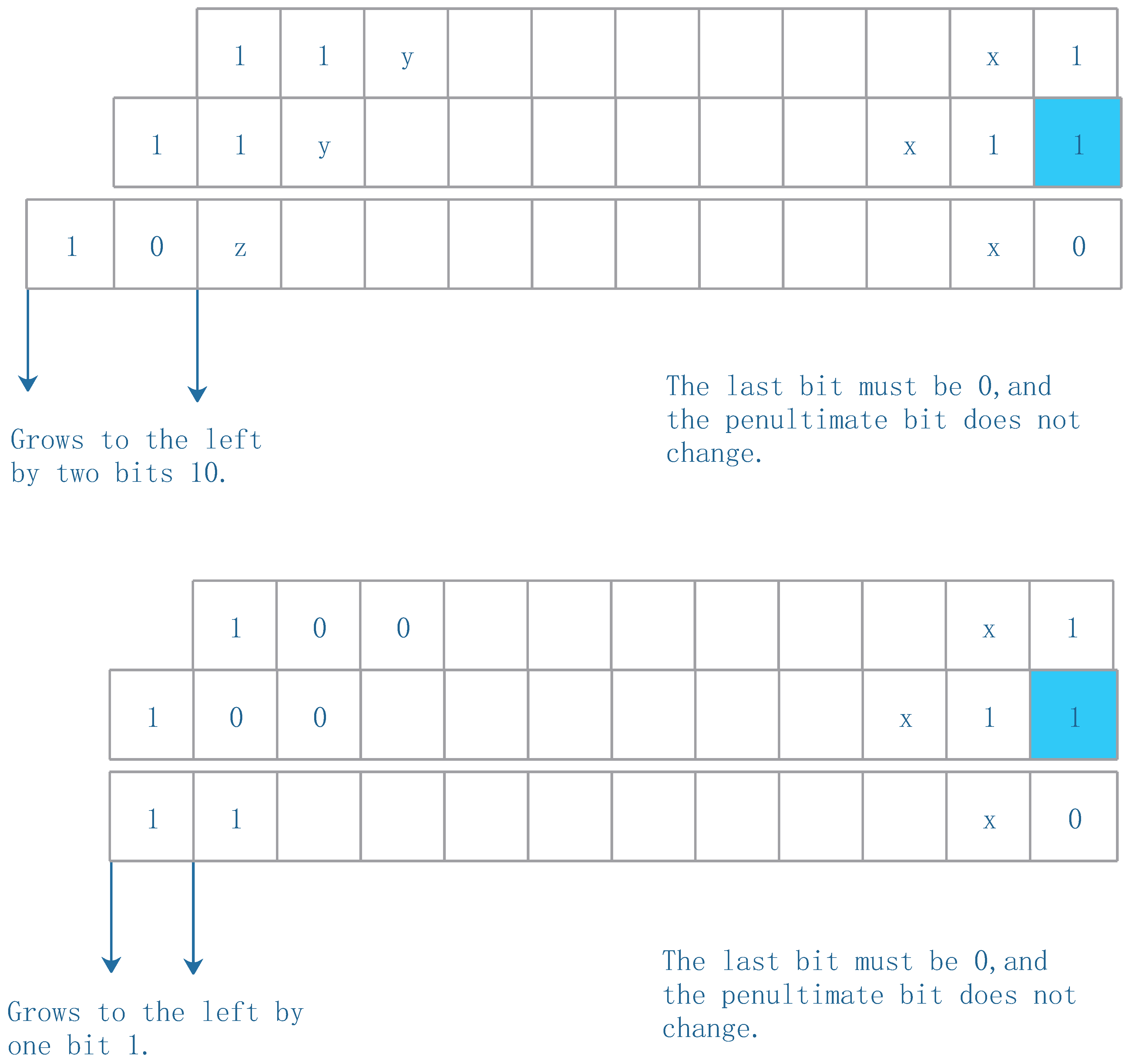
If the Collatz function (1.1) is expressed in binary form as

T (n) = \{\begin{matrix} {(11)}_{2} \cdot {(1 \times \dots \times 1)}_{2} + 1 = {(1 \times \times \times 10 \dots 0)}_{2}, & if n is odd number, \\ \frac{{(1 \times \dots \times 10)}_{2}}{{(10)}_{2}} = {(1 \times \dots \times 1)}_{2}, & if n is even number . \end{matrix}

(7)

The characteristics of the left side and right side and the penultimate of the binary string are illustrated by the Figure 4.

Then we use binary string to illustrate the reduced Collatz function (3.8) as the follows,

R T (n) = \{\begin{matrix} \frac{{(1 \times \times \times 10 \dots 0)}_{2}}{{(10 \dots 0)}_{2}} = {(1 \times \times \times 1)}_{2}, & if n is odd number, \frac{3 n + 1}{2^{m}} is an odd number, \\ \frac{{(1 \times \times \times 10 \dots 0)}_{2}}{{(10 \dots 0)}_{2}} = {(1 \times \times \times 1)}_{2} & if n is even number, \frac{n}{2^{r}} is an odd number . \end{matrix}

(8)

where × is 0 or 1.

In the Collatz squence, for the Collatz function

T (n)

, next

T^{2} (n)

, and next and next

T^{3} (n)

, so on, there have not unified formulas. If we use binary string to state the procedure

T^{k} (n)

, i.e.,

n \to R T (n)

, which is correspond to add 1 or 10 in the left side or delete all 0 in the right side. Thus we reduced the tabular form to the follows. For example, for

n = 67, 10027

one obtain the following tables.

1000011→	11001010→	1100101	$\frac{3^{8}}{2^{19}} \cdot 67$	$\frac{3^{7}}{2^{19}}$
1100101→	100110000→	10011		$\frac{3^{6}}{2^{18}}$
10011→	111010→	11101		$\frac{3^{5}}{2^{14}}$
11101→	1011000→	1011		$\frac{3^{4}}{2^{13}}$
1011→	100010→	10001		$\frac{3^{3}}{2^{10}}$
10001→	110100→	1101		$\frac{3^{2}}{2^{9}}$
1101→	101000→	101		$\frac{3}{2^{7}}$
101→	10000→	1		$\frac{1}{2^{4}}$
1

T^{27} (67) = T (8, 19, 67) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{13}} + \frac{3^{5}}{2^{14}} + \frac{3^{6}}{2^{18}} + \frac{3^{7}}{2^{19}} + \frac{3^{8}}{2^{19}} \cdot 67 = 1

		$\frac{3^{30}}{2^{61}} \cdot$ 10027
10027=(10011100101011) $_{2} \to$	(111010110000010) $_{2} \to$	(11101011000001) $_{2}$	$\frac{3^{29}}{2^{61}}$
15041=(11101011000001) $_{2} \to$	(1011000001000100) $_{2} \to$	(10110000010001) $_{2}$	$\frac{3^{28}}{2^{60}}$
11281=(10110000010001) $_{2} \to$	(1000010000110100) $_{2} \to$	(10000100001101) $_{2}$	$\frac{3^{27}}{2^{58}}$
8461=(10000100001101) $_{2} \to$	(110001100101000) $_{2} \to$	(110001100101) $_{2}$	$\frac{3^{26}}{2^{56}}$
3173=(110001100101) $_{2} \to$	(10010100110000) $_{2} \to$	(1001010011) $_{2}$	$\frac{3^{25}}{2^{53}}$
595=(1001010011) $_{2} \to$	(11011111010) $_{2} \to$	(1101111101) $_{2}$	$\frac{3^{24}}{2^{49}}$
893=(1101111101) $_{2} \to$	(101001111000) $_{2} \to$	(101001111) $_{2}$	$\frac{3^{23}}{2^{48}}$
335=(101001111) $_{2} \to$	(1111101110) $_{2} \to$	(111110111) $_{2}$	$\frac{3^{22}}{2^{45}}$
503=(111110111) $_{2} \to$	(10111100110) $_{2} \to$	(1011110011) $_{2}$	$\frac{3^{21}}{2^{44}}$
755=(1011110011) $_{2} \to$	(100011011010) $_{2} \to$	(10001101101) $_{2}$	$\frac{3^{20}}{2^{43}}$
1133=(10001101101) $_{2} \to$	(110101001000) $_{2} \to$	(110101001) $_{2}$	$\frac{3^{19}}{2^{42}}$
425=(110101001) $_{2} \to$	(10011111100) $_{2} \to$	(100111111) $_{2}$	$\frac{3^{18}}{2^{39}}$
319=(100111111) $_{2} \to$	(1110111110) $_{2} \to$	(111011111) $_{2}$	$\frac{3^{17}}{2^{37}}$
479=(111011111) $_{2} \to$	(10110011110) $_{2} \to$	(1011001111) $_{2}$	$\frac{3^{16}}{2^{36}}$
719=(1011001111) $_{2} \to$	(100001101110) $_{2} \to$	(10000110111) $_{2}$	$\frac{3^{15}}{2^{35}}$
1079=(10000110111) $_{2} \to$	(110010100110) $_{2} \to$	(11001010011) $_{2}$	$\frac{3^{14}}{2^{34}}$
1619=(11001010011) $_{2} \to$	(1001011111010) $_{2} \to$	(100101111101) $_{2}$	$\frac{3^{13}}{2^{33}}$
2429=(100101111101) $_{2} \to$	(1110001111000) $_{2} \to$	(1110001111) $_{2}$	$\frac{3^{12}}{2^{32}}$
911=(1110001111) $_{2} \to$	(101010101110) $_{2} \to$	(10101010111) $_{2}$	$\frac{3^{11}}{2^{29}}$
1367=(10101010111) $_{2} \to$	(1000000000110) $_{2} \to$	(100000000011) $_{2}$	$\frac{3^{10}}{2^{28}}$
2051=(100000000011) $_{2} \to$	(1100000001010) $_{2} \to$	(110000000101) $_{2}$	$\frac{3^{9}}{2^{27}}$
3077=(110000000101) $_{2} \to$	(10010000010000) $_{2} \to$	(1001000001) $_{2}$	$\frac{3^{8}}{2^{26}}$
577=(1001000001) $_{2} \to$	(11011000100) $_{2} \to$	(110110001) $_{2}$	$\frac{3^{7}}{2^{22}}$
433=(110110001) $_{2} \to$	(10100010100) $_{2} \to$	(101000101) $_{2}$	$\frac{3^{6}}{2^{20}}$
325=(101000101) $_{2} \to$	(1111010000) $_{2} \to$	(111101) $_{2}$	$\frac{3^{5}}{2^{18}}$
61=(111101) $_{2} \to$	(10111000) $_{2} \to$	(10111) $_{2}$	$\frac{3^{4}}{2^{14}}$
23=(10111) $_{2} \to$	(1000110) $_{2} \to$	(100011) $_{2}$	$\frac{3^{3}}{2^{11}}$
35=(100011) $_{2} \to$	(1101010) $_{2} \to$	(110101) $_{2}$	$\frac{3^{2}}{2^{10}}$
53=(110101) $_{2} \to$	(10100000) $_{2} \to$	(101) $_{2}$	$\frac{3}{2^{9}}$
5=(101) $_{2} \to$	(10000) $_{2} \to$	(1) $_{2}$	$\frac{1}{2^{4}}$

\begin{matrix} T^{91} (10027) & = & \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{14}} + \frac{3^{5}}{2^{18}} + \frac{3^{6}}{2^{20}} + \frac{3^{7}}{2^{22}} + \frac{3^{8}}{2^{26}} + \frac{3^{9}}{2^{27}} \\ + \frac{3^{10}}{2^{28}} + \frac{3^{11}}{2^{29}} + \frac{3^{12}}{2^{32}} + \frac{3^{13}}{2^{33}} + \frac{3^{14}}{2^{34}} + \frac{3^{15}}{2^{35}} + \frac{3^{16}}{2^{36}} + \frac{3^{17}}{2^{37}} + \frac{3^{18}}{2^{39}} \\ + \frac{3^{19}}{2^{42}} + \frac{3^{20}}{2^{43}} + \frac{3^{21}}{2^{44}} + \frac{3^{22}}{2^{45}} + \frac{3^{23}}{2^{48}} + \frac{3^{24}}{2^{49}} + \frac{3^{25}}{2^{53}} + \frac{3^{26}}{2^{56}} + \frac{3^{27}}{2^{58}} \\ + \frac{3^{28}}{2^{60}} + \frac{3^{29}}{2^{61}} + \frac{3^{30}}{2^{61}} \cdot 10027 \\ = & 1 \end{matrix}

\begin{matrix} T^{106} (31) & = & \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{14}} + \frac{3^{5}}{2^{18}} + \frac{3^{6}}{2^{20}} + \frac{3^{7}}{2^{22}} + \frac{3^{8}}{2^{26}} + \frac{3^{9}}{2^{27}} \\ + \frac{3^{10}}{2^{28}} + \frac{3^{11}}{2^{29}} + \frac{3^{12}}{2^{32}} + \frac{3^{13}}{2^{33}} + \frac{3^{14}}{2^{34}} + \frac{3^{15}}{2^{35}} + \frac{3^{16}}{2^{36}} + \frac{3^{17}}{2^{37}} + \frac{3^{18}}{2^{39}} \\ + \frac{3^{19}}{2^{40}} + \frac{3^{20}}{2^{42}} + \frac{3^{21}}{2^{43}} + \frac{3^{22}}{2^{44}} + \frac{3^{23}}{2^{47}} + \frac{3^{24}}{2^{49}} + \frac{3^{25}}{2^{50}} + \frac{3^{26}}{2^{51}} + \frac{3^{27}}{2^{52}} \\ + \frac{3^{28}}{2^{54}} + \frac{3^{29}}{2^{55}} + \frac{3^{30}}{2^{56}} + \frac{3^{31}}{2^{58}} + \frac{3^{32}}{2^{59}} + \frac{3^{33}}{2^{61}} + \frac{3^{34}}{2^{63}} + \frac{3^{35}}{2^{64}} + \frac{3^{36}}{2^{65}} \\ + \frac{3^{37}}{2^{66}} + \frac{3^{38}}{2^{67}} + \frac{3^{39}}{2^{67}} \cdot 31 \\ = & 1 \end{matrix}

\begin{matrix} T^{107} (63) & = & \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{14}} + \frac{3^{5}}{2^{18}} + \frac{3^{6}}{2^{20}} + \frac{3^{7}}{2^{22}} + \frac{3^{8}}{2^{26}} + \frac{3^{9}}{2^{27}} \\ + \frac{3^{10}}{2^{28}} + \frac{3^{11}}{2^{29}} + \frac{3^{12}}{2^{32}} + \frac{3^{13}}{2^{33}} + \frac{3^{14}}{2^{34}} + \frac{3^{15}}{2^{35}} + \frac{3^{16}}{2^{36}} + \frac{3^{17}}{2^{37}} + \frac{3^{18}}{2^{39}} \\ + \frac{3^{19}}{2^{40}} + \frac{3^{20}}{2^{42}} + \frac{3^{21}}{2^{43}} + \frac{3^{22}}{2^{44}} + \frac{3^{23}}{2^{47}} + \frac{3^{24}}{2^{49}} + \frac{3^{25}}{2^{50}} + \frac{3^{26}}{2^{51}} + \frac{3^{27}}{2^{52}} \\ + \frac{3^{28}}{2^{54}} + \frac{3^{29}}{2^{55}} + \frac{3^{30}}{2^{56}} + \frac{3^{31}}{2^{58}} + \frac{3^{32}}{2^{59}} + \frac{3^{33}}{2^{63}} + \frac{3^{34}}{2^{64}} + \frac{3^{35}}{2^{65}} + \frac{3^{36}}{2^{66}} \\ + \frac{3^{37}}{2^{67}} + \frac{3^{38}}{2^{68}} + \frac{3^{39}}{2^{68}} \cdot 63 \\ = & 1 \end{matrix}

\begin{matrix} T^{118} (97) & = & \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{14}} + \frac{3^{5}}{2^{18}} + \frac{3^{6}}{2^{20}} + \frac{3^{7}}{2^{22}} + \frac{3^{8}}{2^{26}} + \frac{3^{9}}{2^{27}} \\ + \frac{3^{10}}{2^{28}} + \frac{3^{11}}{2^{29}} + \frac{3^{12}}{2^{32}} + \frac{3^{13}}{2^{33}} + \frac{3^{14}}{2^{34}} + \frac{3^{15}}{2^{35}} + \frac{3^{16}}{2^{36}} + \frac{3^{17}}{2^{37}} + \frac{3^{18}}{2^{39}} \\ + \frac{3^{19}}{2^{40}} + \frac{3^{20}}{2^{42}} + \frac{3^{21}}{2^{43}} + \frac{3^{22}}{2^{44}} + \frac{3^{23}}{2^{47}} + \frac{3^{24}}{2^{49}} + \frac{3^{25}}{2^{50}} + \frac{3^{26}}{2^{51}} + \frac{3^{27}}{2^{52}} \\ + \frac{3^{28}}{2^{54}} + \frac{3^{29}}{2^{55}} + \frac{3^{30}}{2^{56}} + \frac{3^{31}}{2^{58}} + \frac{3^{32}}{2^{59}} + \frac{3^{33}}{2^{61}} + \frac{3^{34}}{2^{63}} + \frac{3^{35}}{2^{64}} + \frac{3^{36}}{2^{65}} \\ + \frac{3^{37}}{2^{66}} + \frac{3^{38}}{2^{69}} + \frac{3^{39}}{2^{70}} + \frac{3^{40}}{2^{71}} + \frac{3^{41}}{2^{73}} + \frac{3^{42}}{2^{75}} + \frac{3^{43}}{2^{75}} \cdot 97 \\ = & 1 \end{matrix}

We observe the procedure of composite reduced Collatz function (3,8), i.e., the Collatz sequences, that we pay close attention to the zeros in right side of binary strings of an even number and the end-substring between the first 0 encountered from right to left which is make of 1. There are many properties in the tabular expressions as the follows.

1. Column characteristic

1) In each row, the first column is always odd (empty when the initial value is even), i.e., the last bit of its binary string must be 1.

The second column must be even, its binary string must end with at least one 0, the number of subsequent even numbers must be as many as the number of zeros at the end of the second column’s binary string, and the number of zeros at the end of each even number to the right is one less than the previous one, until all zeros are deleted to become the last odd number in the row.

The last column must be odd, and the last bit of its binary string must be 1.

2) When there are only three numbers in a row, that is, only one even number, the last odd number must be greater than the first odd number (the first column); When there are more than three numbers in a row, that is, more than two even numbers, the last odd number must be smaller than the first odd number.

3) The preceding binary string is identical from the second column to the last column in one line, except for the all 0 at the end.

2. Row characteristic

From top to bottom, the binary string in the first column of two adjacent rows has the following two characteristics:

1) If the number of bits of 1 in the end-substring of the previous row is greater than 1, the number of bits of 1 in the end-substring of the next row is reduced by one, until it finally becomes only one; The corresponding number is greater than the number in the previous row;

2) If the end-substring of the binary string in a row contains only one bit of 1, then the end-substring of the binary string in the next row contains either one bit of 1 or many bits of 1, and the corresponding number is smaller than the number in the previous row;

3. Comprehensive characteristic

1) When the end-substring of the binary is 1, the corresponding digit of the decimal number can be any one of

1, 3, 5, 7, 9

. For instance,

161 = {(10100001)}_{2}

433 = {(110110001)}_{2}

325 = {(101000101)}_{2}

577 = {(1001000001)}_{2}

2429 = {(100101111101)}_{2}

2) The number ending in decimal is 9 and the corresponding binary number can end in any end-substrings of 1—for instance—

319 = {(100111111)}_{2}

479 = {(111011111)}_{2}

719 = {(1011001111)}_{2}

1079 = {(10000110111)}_{2}

1619 = {(11001010011)}_{2}

2429 = {(100101111101)}_{2}

3) When the last substring of binary is reduced by one bit from many, the corresponding decimal number’s unit’s digit are always reciprocated within the three groups of numbers:

{1, 7}

, or

{3, 5}

, and unit’s digit is always

{9}

2.3. Discuss the Collatz Sequences by Convert Function and Only Odd Numbers

Because the result of the reduced Collatz function (3.4) is only odd numbers, we talk three sets to divide the odd number set

O = {1, 3, 5, 7, 9, 11, 13, \dots}

. In [15,16] the odd number set can be divided into three sets

θ_{1}, θ_{3}, θ_{5}

θ_{1} = {6 i + 1 | i = 0, 1, 2, 3, \dots}

(9)

θ_{3} = {6 i + 3 = 3 (2 i + 1) | i = 0, 1, 2, 3, \dots}

(10)

θ_{5} = {6 i + 5 | i = 0, 1, 2, 3, \dots}

(11)

As [16] the authors call inverse Collatz function, if

a_{n} \equiv 1 (m o d 3)

, i.e.,

a_{n} \in θ_{1}

b_{m} = \frac{2^{2 m} \cdot a_{n} - 1}{3}, m = 0, 1, 2, 3, \dots

(12)

for each

a_{n}

we get infinite sequences of

B_{n}

sets as following:

1 \to B_{1} = {1, 5, 21, 85, 341, 1365, 5461, \dots}

7 \to B_{2} = {9, 37, 149, 597, 2389, 9557, 38229, \dots}

13 \to B_{3} = {17, 69, 277, 1109, 4437, 17749, 70997, \dots}

19 \to B_{4} = {25, 101, 405, 1621, 6485, 25941, 103765, \dots}

25 \to B_{5} = {33, 133, 533, 2133, 8533, 34133, 136533, \dots}

31 \to B_{6} = {41, 165, 661, 2645, 10581, 42325, 169301, \dots}

⋯

a_{n} \equiv 2 (m o d 3)

, i.e.,

a_{n} \in θ_{5}

c_{m} = \frac{2^{2 m - 1} \cdot a_{n} - 1}{3}, m = 0, 1, 2, 3, \dots

(13)

for each

a_{n}

we get infinite sequences of

C_{n}

sets as following:

5 \to C_{1} = {3, 13, 53, 213, 853, 3413, 13653, \dots}

11 \to C_{2} = {7, 29, 117, 469, 1877, 7509, 30037, \dots}

17 \to C_{3} = {11, 45, 181, 725, 2901, 11605, 46421, \dots}

23 \to C_{4} = {15, 61, 245, 981, 3925, 15701, 62805, \dots}

29 \to C_{5} = {15, 61, 245, 981, 3925, 15701, 62805, \dots}

35 \to C_{6} = {23, 93, 373, 1493, 5973, 23893, 95573, \dots}

⋯

B_{1}

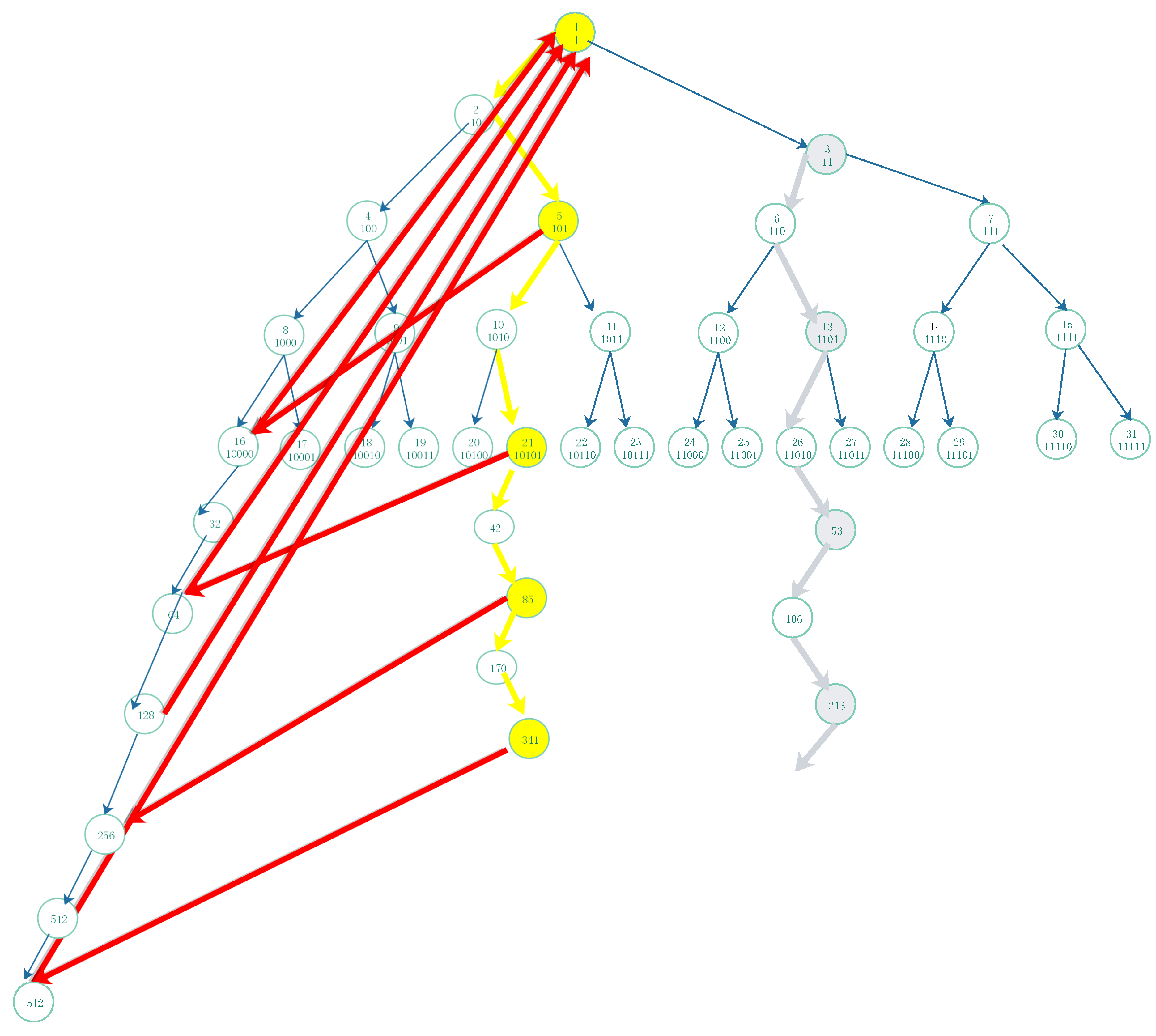
is the hard number set, they are in a zigzag branch which the start vertex is 1. The other set

B_{i}

C_{i}

are in the other zigzag branchs. For the per number in one set

B_{i}

C_{i}

the Collatz paths (corresponding Collatz sequence) from it to 1 are the same shape. It is shown in Figure 6.

For

a_{n} \equiv 0 (m o d 3)

, i.e.,

a_{n} \in θ_{3}

, we give a new formula

d_{m} = \frac{3 a_{n} + 1}{2^{r}}

(14)

which result is the odd set

{θ_{1}} ⋃ {θ_{5}}

. We observe (3.10) that

3 O = θ_{3}

3^{2} \cdot 1 + 1 = 10 = 2 \cdot 5, 1 \to 5

3^{2} \cdot 3 + 1 = 28 = 2^{2} \cdot 7, 3 \to 7

3^{2} \cdot 5 + 1 = 46 = 2^{2} \cdot 23, 5 \to 23

3^{2} \cdot 7 + 1 = 64 = 2^{6} \cdot 1, 7 \to 1

3^{2} \cdot 9 + 1 = 82 = 2 \cdot 41, 9 \to 41

3^{2} \cdot 11 + 1 = 100 = 2^{2} \cdot 25, 11 \to 25

3^{2} \cdot 13 + 1 = 118 = 2 \cdot 59, 13 \to 59

⋯

Thus we have two properties:

Proposition 3 The formulas (3.12) and (3.13) can map

θ_{1} ⋃ θ_{5}

to O.

Proposition 4 The formula (3.14) can map

θ_{3}

θ_{1} ⋃ θ_{5}

. Namely The formula

d_{m} = \frac{3^{2} a_{n} + 1}{2^{r}}

maps from O to

θ_{1} ⋃ θ_{5}

3. Discuss the Collatz Sequences by the Full Binary Directed Tree

In order to study the Collatz conjecture by the full binary directed tree, we call two cases

3 n + 1

and

\frac{n}{2}

as two actions jump and trace correspondingly in the full binary directed tree. An one jump is to walk down from a vertex to another vertex in another branch and another level of the tree. An one trace is to walk along the branch from current vertex back to its parent-vertex.

Proposition 5 A jump action is that from an odd vertex to an even vertex which is neither its child nor its descendant. A trace action is from even vertex back to its parent.

Proposition 6 For a given number n, applying the Collatz function (1.1) or the reduced Collatz function (3.4) or (3.8) gets the Collatz sequence has not common vertex until 1.

This means the path of the tree traversal by two actions jump and trace has not vertex of intersection until meets 1. Especially there is not the moment to jump to itself branch.

Proposition 7 In the sequence of the composites of Collatz function of natural number n, one jump action only down to next level or next adjacent level. There are not adjacent jump actions, namely two jump actions at least one trace action apart since

3 x + 1

is even number when x is odd.

Proposition 8 In the sequence of the composites of Collatz function of natural number n, one trace action only back to its parent. Two trace actions can adjacent, namely many trace actions can adjacent to find its ancestor. For instance, a pure even

64 = 2^{6}

, there are 6 trace actions adjacent to find its ancestor 1.

In the sequence of the composites of Collatz function of natural number n, we call the substring of a string encountered from right to left before the first 0 as end-substring.

Proposition 9 If the length of the end-substring of given odd number is one, the next odd must be smaller than itself. If the length of the end-substring of given odd number is bigger than one, the next odd must be bigger than itself.

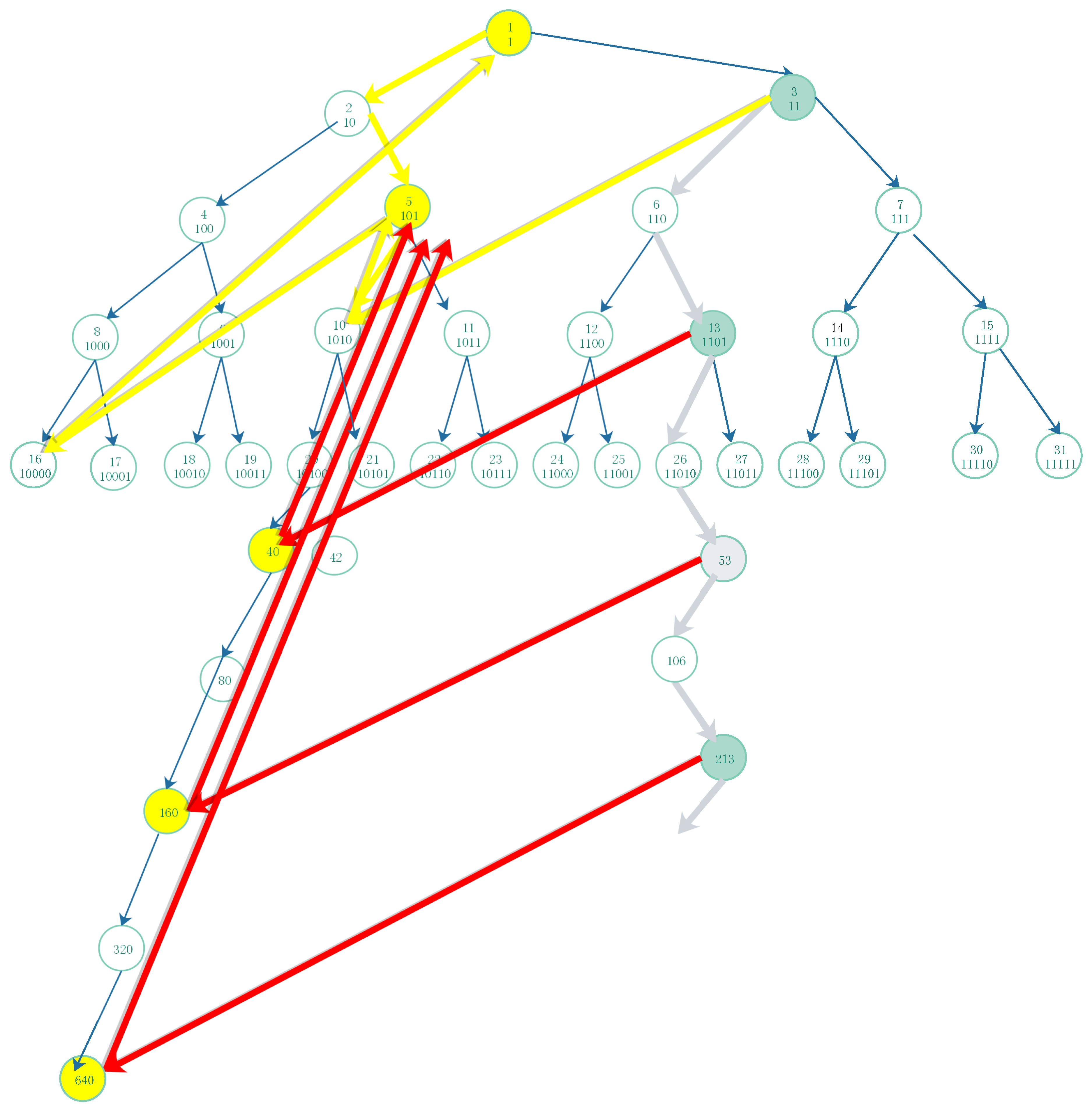
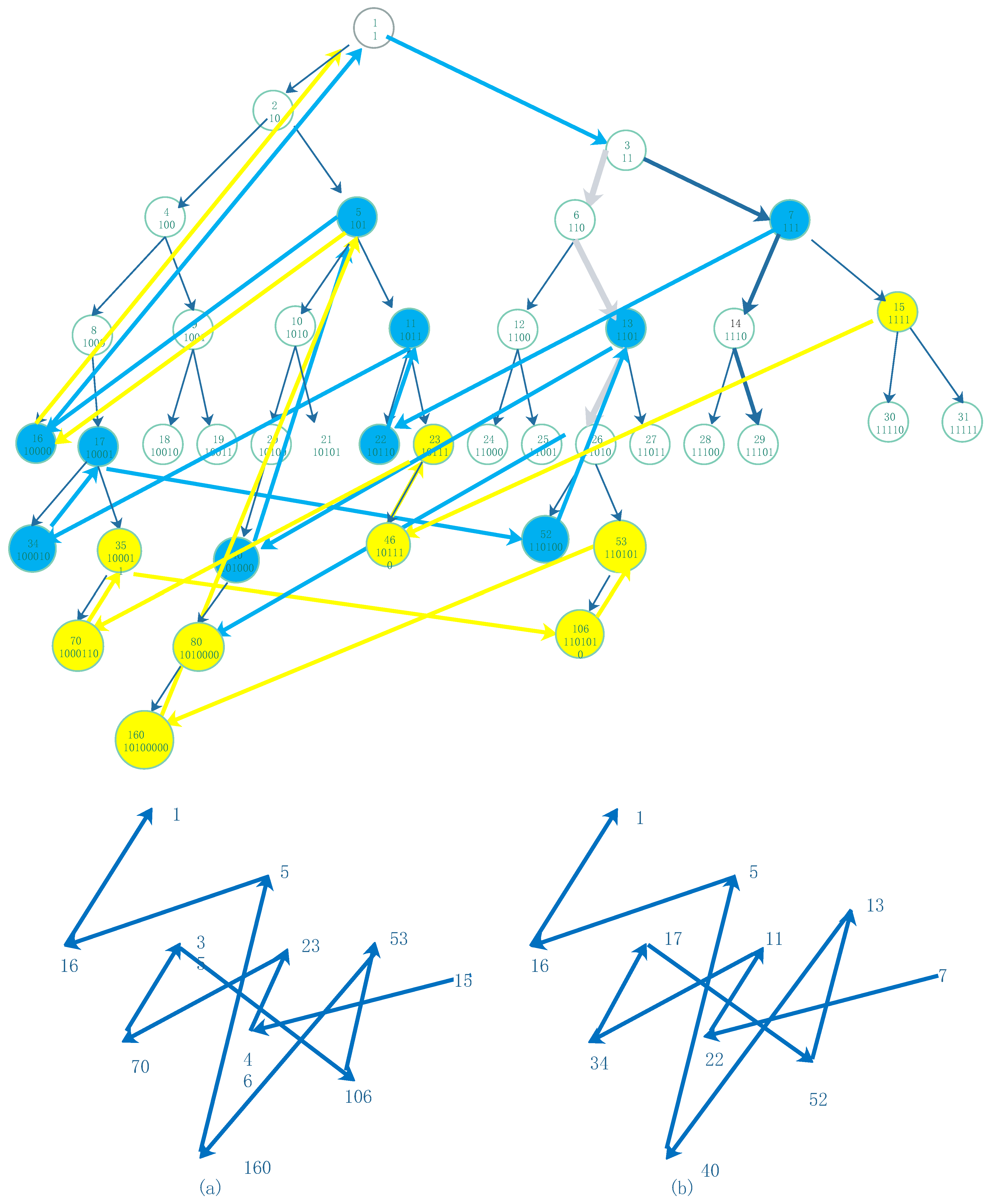
Proposition 10 As in [16], for adjacent pair pure numbers, in the full binary directed tree and the Collatz function (1.1) or reduced Collatz function (3.8). For a given odd number

r = 2 k - 1

, the pure odd

2^{r} - 1 = 2^{2 k - 1} - 1

, if there exists natural number m such that

T^{m} (2^{r} - 1) = T^{m} (2^{2 k - 1} - 1) = 1

, then for its right-child

2^{r + 1} - 1

have the relation

T^{m + 1} (2^{r + 1} - 1) = T^{m + 1} (2^{2 k} - 1) = 1

In the graph format, there is a similar invariants structures of two sequence of the (or reduced) Collatz function for a pure odd number with odd number lenght and its next pure number with even number length, as the Figure 6, Figure 7 and Figure 8.

4. Comparison of Two Piecewise Functions and the Proof of Collatz Conjecture

Comparing the Collatz function

T (x)

and the function

f^{- 1} (x)

, if their domain is defined as the set of natural numbers, we find that they have the following relation:

1) The function

f^{- 1} (x)

is strictly monotonically decreasing,

2) When x is purely even, the function

T (x)

is only one case of the functions, is strictly monotonically increasing;

3) When x is a pure or mixed odd number, the function

T (x)

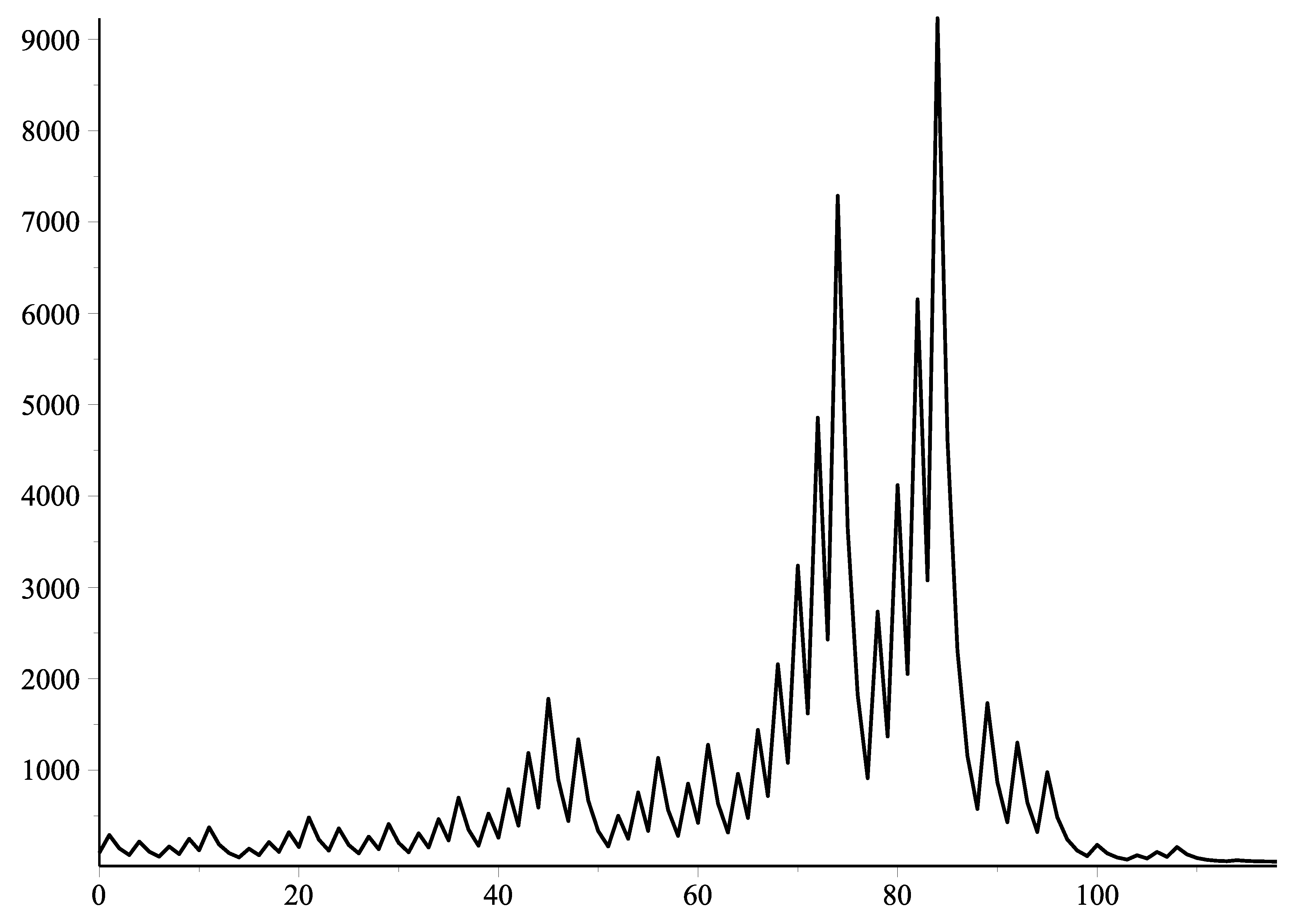
is wavy, which is increasing, followed by one or more decreasing processes, that is, “increase – decrease – increase”, or “increase – decrease ⋯ decrease – increase”. For example, Figure 3 and 4 are the plots of the iterated sequence of Collatz functions with initial values of pure odd

255 = 2^{8} - 1 = {(11111111)}_{2}

and mixed odd number

97 = {(1100001)}_{2}

, respectively.

Figure 10. Point plot of a sequence of 47 iterations of the Collatz function for pure odd 255.

Figure 11. Point plot of a sequence of 118 iterations of the Collatz function for mixed number 97.

Due to the fact that an odd number can be either pure or mixed, when x is odd, the Collatz function

3 x + 1

can be parted into two parts. i.e.,

3 x + 1 = 2 x + (x + 1)

(i) when x is a pure odd number, i.e.,

x = 2^{r} - 1

, The binary string

2 x = 2^{r + 1} - 2

is even, with just one 0 at the end, and the other part

x + 1 = 2^{r}

is pure even. As a result,

3 x + 1 = 2 x + (x + 1) = 2^{r + 1} + 2^{r} - 2

is a mixed even number with only one 0 in the last bit and

r - 1

bits 1 in the second-to-last substring, corresponding

\frac{3 x + 1}{2} = 2^{r} + 2^{r - 1} - 1 > x

, it means function T(x) is increase.

(ii) When x is a mixed odd number, it just has one 1 in the last binary substring, the value

\frac{3 x + 1}{2^{r}} < x, (r > 1)

is smaller odd than x, it means function T(x) is decrease. The last binary substring of number

\frac{3 x + 1}{2^{r}}, (r > 1)

has two kinds, which :

(a) There many 1 in the last binary substring. For example,

893 = {(1101111101)}_{2}

\frac{3 \times 893 + 1}{2^{3}} = 335 = {(101001111)}_{2} = 335

335 < 893

(b) Only 1 in the last binary substring. For example,

17 = {(10001)}_{2}

\frac{3 \times 17 + 1}{2^{2}} = {(1101)}_{2} = 13

13 < 17

When the end of the binary substring is 1, using × denotes either 1 or 0, we discuss the changes of the last substring three digits and four digits in the procedure of the Collatz function sequences:

\times 001 \to \times \times 100 \to \times \times 1

\times 101 \to \times 000 \to \times

\times 0101 \to \times \times 0000 \to \times \times

\times 1101 \to \times \times 1000 \to \times \times 1

3 x + 1

can adjust the structure of its binary substring, when the end of the binary substring is 1, the value of Collatz function

T (x) = \frac{3 x + 1}{2^{r}}, r > 1

decrease, thus the number of binary string digits decrease at least 2. This process continues several times, and eventually you can reach the minimum value of 1. The Collatz function shows that the Collatz conjecture holds.

We have known that mathematics formula

x^{k} + x^{k - 1} + \dots + x + 1 = \frac{x^{k + 1} - 1}{x - 1}

(15)

when

x = 2

, there is a formula

2^{k} + 2^{k - 1} + \dots + 2 + 1 = 2^{k + 1} - 1

(16)

The substantive characteristics is that the powers of 2 must be continuous natural numbers, this is the key to our proof method to solve the Collatz conjecture.

Proof. (i) If a given natural number

n = 2^{k}

is a pure even, it requires only an iteration of the k times Collatz function to reach the smallest natural number 1, that is the conjecture holds.

(ii) When a natural number n is not pure even, that is, when it is either pure odd or mixed odd (a mixed even is eliminated since the end-substring 0 can become an odd number; hence, we do not include this case).

Given an odd number n, which can be expressed as follows in algebraic notation:

n = {(1 \times \dots \times 1)}_{2} = 2^{r} + 2^{m} + \dots + 1

, then

\begin{matrix} 3 n + 1 = 2 n + n + 1 \\ = 2^{r + 1} + 2^{m + 1} + \dots + 2 + 2^{r} + 2^{m} + \dots + 1 + 1 \\ = 2^{r + 1} + 2^{m + 1} + \dots + 2 + 2^{r} + 2^{m} + \dots + 2 \\ = 2^{r + 1} + 2^{r} + 2^{m + 1} + 2^{m} + \dots + \dots + 2^{h} \end{matrix}

If the length of the end-substring of n is 1, the length of end-substring of the binary string

3 x + 1

is either 1 or bigger than 1.

Two formulas,

2^{l} + 2^{l} = 2^{l + 1}

and above (5.16), can be used to modify the structure of the binary string n to the binary string

3 n + 1

. That is, there is an appended term

2^{r - h}

in two equivalent terms,

2^{r + 1 - h}

and

2^{m + 1 - h}

. When the zeros in the middle of a binary string are compared to a bubble, it means that these zeros are gradually being driven out of the rightmost end by

3 n + 1

. It is the same as progressively removing the bubbles hidden in the sponge using a means

3 n + 1

. Once 3n+1, 0 shifts one bit to the right, i.e., the length of the associated binary substring is reduced by one bit, when the length of the end-substring is greater than 1. The end-substring length of the binary string

3 x + 1

is either greater than or equal to 1 if the length of the end-substring of n is 1.

We shall then divide

3 n + 1

by the last term

2^{h}

\begin{matrix} \frac{3 n + 1}{2^{h}} = 2^{r + 1 - h} + 2^{r - h} + 2^{m + 1 - h} + 2^{m - h} + \dots + \dots + 2^{0} \end{matrix}

get another odd number, this is the value of reduced Collatz function (4). And so on, finitely steps after finally we get a pure even number

2^{t}

, this is the case in above (i), thus the Collatz conjecture hold on.

We illustrate the procedure by a mixed odd number

n = 67

and hard number set in the following,

\begin{matrix} 67 = {(1000011)}_{2} = 2^{6} + 2^{2} + 2^{0} \\ 3 \cdot 67 + 1 = 2 \cdot 67 + 67 + 1 = 2^{7} + 2^{2} + 2^{1} + 2^{6} + 2^{1} + 2^{0} + 2^{0} = 2^{7} + 2^{6} + 2^{3} + 2^{1} \\ 3 \cdot 101 + 1 = 2 \cdot 101 + 101 + 1 = 2^{7} + 2^{6} + 2^{3} + 2^{1} + 2^{6} + 2^{5} + 2^{2} + 2^{0} + 2^{0} = 2^{8} + 2^{5} + 2^{4} \\ 3 \cdot 19 + 1 = 2 \cdot 19 + 19 + 1 = 2^{5} + 2^{2} + 2^{1} + 2^{4} + 2^{1} + 2^{0} + 2^{0} = 2^{5} + 2^{4} + 2^{3} + 2^{1} \\ 3 \cdot 29 + 1 = 2 \cdot 29 + 29 + 1 = 2^{5} + 2^{4} + 2^{3} + 2^{1} + 2^{4} + 2^{3} + 2^{2} + 2^{0} = 2^{6} + 2^{4} + 2^{3} \\ 3 \cdot 11 + 1 = 2 \cdot 11 + 11 + 1 = 2^{4} + 2^{2} + 2^{1} + 2^{3} + 2^{1} + 2^{0} + 2^{0} = 2^{5} + 2^{1} \\ 3 \cdot 17 + 1 = 2 \cdot 17 + 17 + 1 = 2^{5} + 2^{1} + 2^{4} + 2^{0} + 2^{0} = 2^{5} + 2^{4} + 2^{2} \\ 3 \cdot 13 + 1 = 2 \cdot 13 + 13 + 1 = 2^{4} + 2^{3} + 2^{1} + 2^{3} + 2^{2} + 2^{0} + 2^{0} = 2^{5} + 2^{3} \\ 3 \cdot 5 + 1 = 2 \cdot 5 + 5 + 1 = 2^{3} + 2^{1} + 2^{2} + 2^{0} + 2^{0} = 2^{4} \\ 1 \end{matrix}

For a special class of mixed numbers, the hard number

\frac{4^{k} - 1}{3} = {(101 \dots 101)}_{2}

, then its Collatz sequent result is

\begin{matrix} a_{k} = \frac{4^{k} - 1}{3} = \frac{4^{k} - 1}{4 - 1} = 4^{k - 1} + 4^{k - 2} + \dots + 4 + 1 = {(101 \dots 101 \dots 101)}_{2}, \\ T (a_{k}) = 3 a_{k} + 1 = 4^{k} = 2^{2 k} = {(10 \dots 0)}_{2}, T^{2 k + 1} (a_{k}) = 1 . \end{matrix}

This means that the Collatz conjecture is valid for this case. Therefore we have proved the Collatz conjecture 1 at section 1 of this paper. □

5. Conclusion

From previous proof of the conjecture, it becomes a theorem.

Theorem For any natural number n, if it is even, divide by 2, if it is odd, multiply by 3, add 1, and so on, the result must finally reach 1.

Theorem For any positive integer n, the sequence of the Collatz function is an ultimately periodic sequence, its preperiod

η (n)

is a related-to n positive, and the least period

{4, 2, 1}

ρ (n) = 3

References

Jeffrey, C. Lagarias. The 3x + 1 Problem and Its Generalizations. American Mathematical Monthly, Vol. 92, No. 1, 3–23(1985). [CrossRef]
Jeffrey, C. Lagarias. The 3x+1 Problem: An Overview. arXiv:2111.02635.
Li, T. , Yorke, J. A. Period three implies chaos. Am. Mat. Monthly, 82, 985–992 (1975). [CrossRef]
TERENCE TAO, Almost all orbits of the Collatz map attain almost bounded values. arxiv:1909.03562v5, 2022,1,15.
Alf Kimms. The structure of the 3x+1 problem, Electronic Journal of Graph Theory and Applications. 9(1)(2021)157–174.
Richard Kaufman. A reduced forward Collatz algorithm: How binary strings change their length under 3x+1. arXiv:2301.07466.
Patrick Chisan Hew. Collatz on the Dyadic rdtional in [0.5,1) with fractals: How bit strings change their length under 3x+1. Experimental Mathematics, 2021, 30(4): 481–488. [CrossRef]
G. Ganesan. Linear recurrences over a finite field with exactly two periods. Advances In Applied Mathematics 127(2021)102180. [CrossRef]
D. Quijada. Periods of linearly recurring sequences. Bachelor thesis, Washington and LeeUniversity, 2015.
Leonel Sternberg, Predictable trajectories of the reduced Collatz iteration and a possible pathway to the proof of the Collatz conjecture(Version 2), arXiv:2209.14230.
F. Jishe, Proof the Collatz Conjecture in Binary Strings. [CrossRef]
Eldar Sultanow, Christian Koch, Sean Cox, Collatz Sequences in the Light of Graph Theory. [CrossRef]
Bart Snapp, Matt Tracy, The Collatz Problem and Analogues. Journal of Integer Sequences, Vol. 11 (2008), Article 08.4.7.
Petro Kosobutskyy, Comment from article “Two different scenarios when the Collatz Conjecture fails”, Gen. lett. Math., 12(4) (2022),179-182.
Bulent Sukusu, Proof of the Collatz Conjecture, Theoret. Math. App., 13(3) (2023),1-17.
F. Jishe, Proof the Collatz Conjecture by a new view of natural numbers. [CrossRef]

Figure 1. Natural number 60 is obtained from 1 through the compositionof five even and odd functions its binary string is

{(111100)}_{2}

Figure 1. Natural number 60 is obtained from 1 through the compositionof five even and odd functions its binary string is

{(111100)}_{2}

Figure 2. The representation of natural number set is a infinite full binary directed tree.

Figure 3.

21 = {(10101)}_{2}

and

29 = {(11101)}_{2}

comes from the path from root 1 walk to 10101 and 11101 accordingly appending 1 or 0 to the vertexes in succession.

Figure 3.

21 = {(10101)}_{2}

and

29 = {(11101)}_{2}

comes from the path from root 1 walk to 10101 and 11101 accordingly appending 1 or 0 to the vertexes in succession.

Figure 4. Binary representation of the Collatz function, grows by appending 1 or 10 to the left side of the binary string delete at least one 0s in the right side of the binary string.

Figure 5. The zigzag branchs are the

B_{1}

set in full binary directed tree.

Figure 5. The zigzag branchs are the

B_{1}

set in full binary directed tree.

Figure 6. The zigzag branchs are the

C_{1}

set in full binary directed tree.

Figure 6. The zigzag branchs are the

C_{1}

set in full binary directed tree.

Figure 7. The same shapes paths for an odd-length pure odd and the next pure odd.

Figure 8. The representation of natural number set is a complete binary tree.

Figure 9. The representation of natural number set is a complete binary tree.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Using Full Binary Directed Tree Proof the Collatz Conjecture

Abstract

1. An Algebra and Graph Representation of Natural Numbers

1.1. The Composition of Odd-Number and Even-Number Functions

1.2. Use Binary String to Represent Natural Numbers

1.3. Use a Graph to Represent the Composite Procedure of the Natural Numbers

1.4. Another Partition of the Natural Number Set

2. Study the Collatz Function

2.1. Using Tabular Form and Algebraic Expressions to Represent the Collatz Sequence

2.2. Discuss the Collatz Problem by Binary Strings

2.3. Discuss the Collatz Sequences by Convert Function and Only Odd Numbers

3. Discuss the Collatz Sequences by the Full Binary Directed Tree

4. Comparison of Two Piecewise Functions and the Proof of Collatz Conjecture

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe