Submitted:
08 May 2024
Posted:
08 May 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
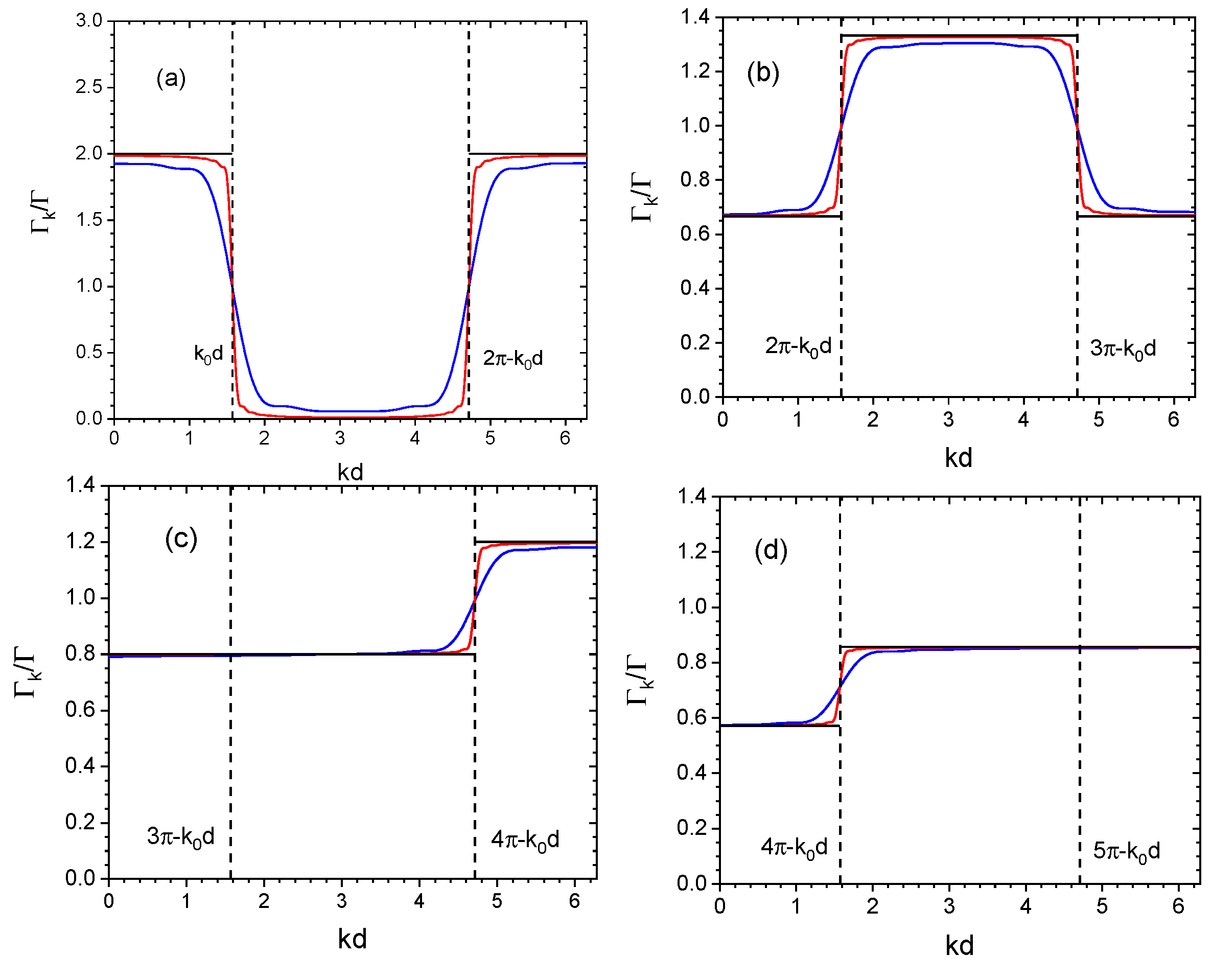
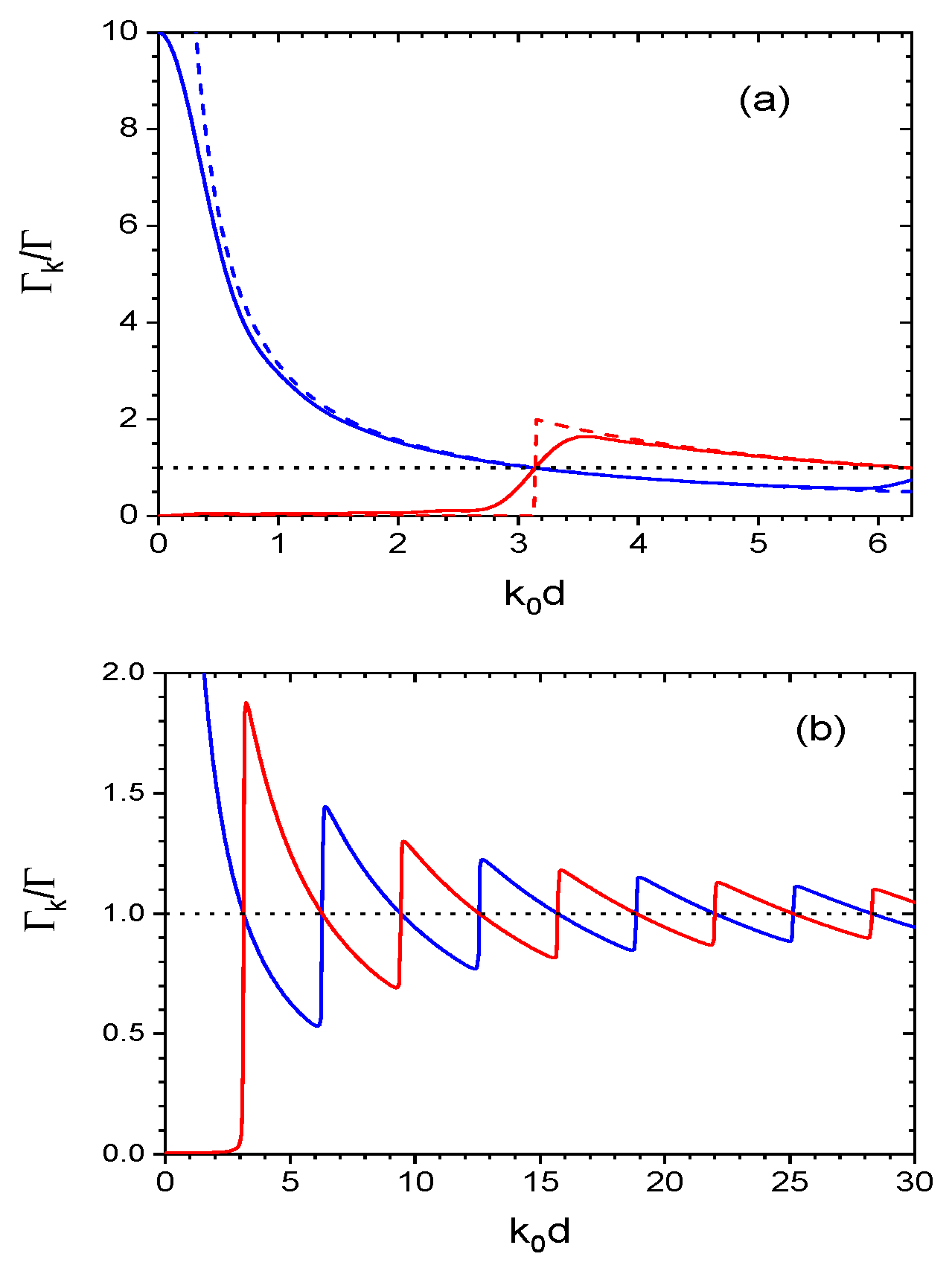
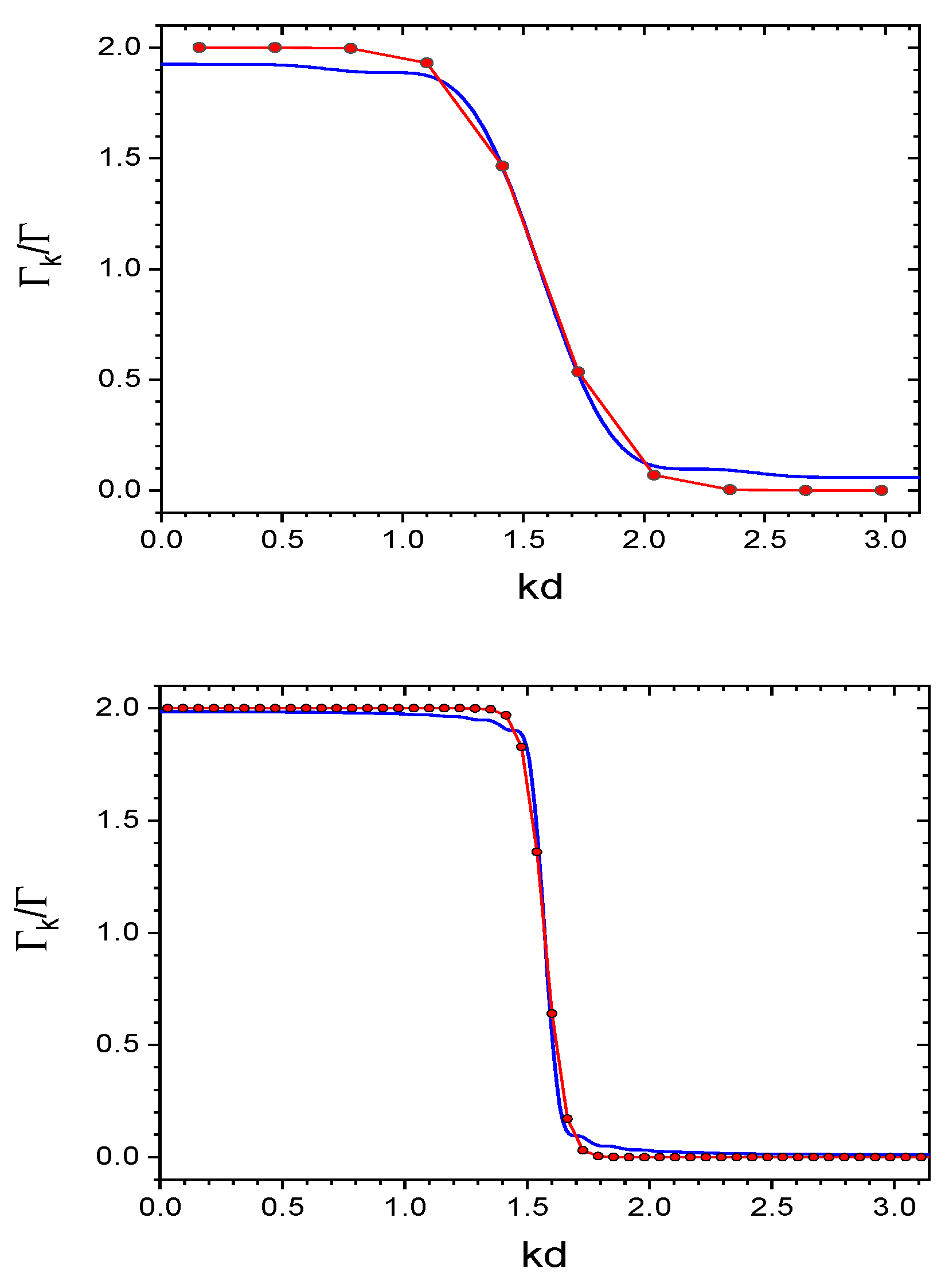
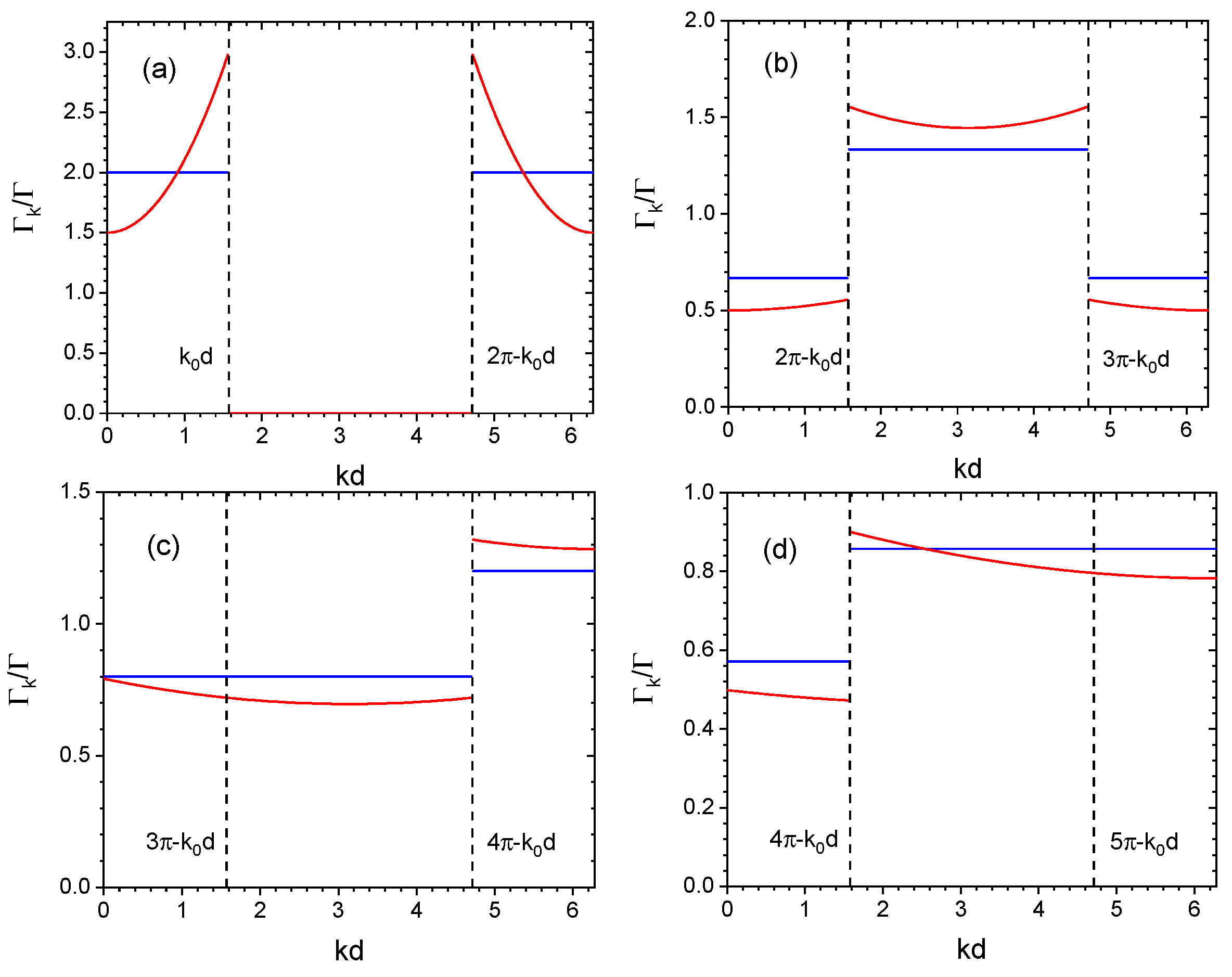
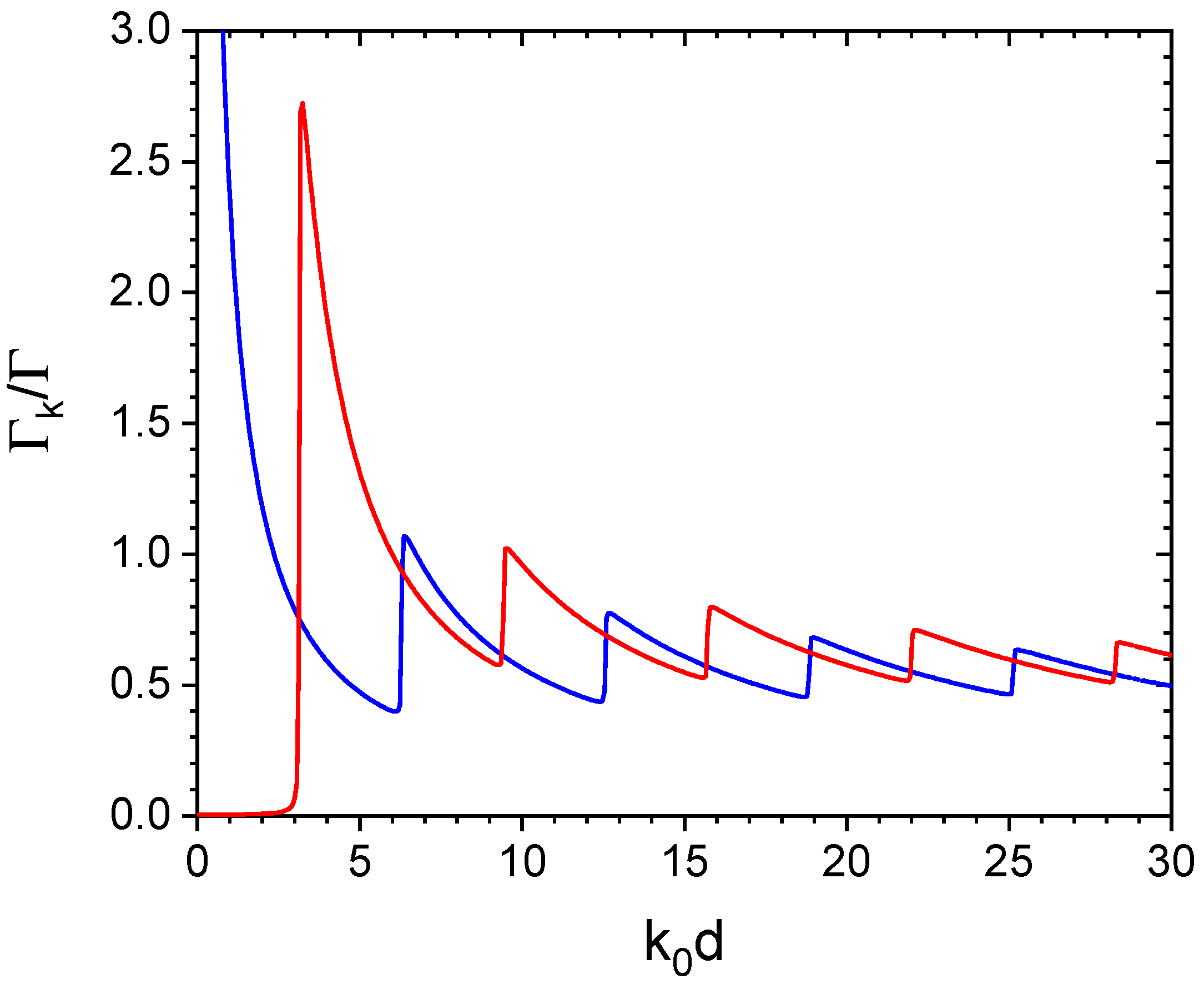
2. Scalar Model
3. Vectorial Model
4. Conclusions
Conflicts of Interest
References
- Dicke R., H. , Coherence in spontaneous radiation processes. Phys. Rev. 1954, 93, 99. [Google Scholar] [CrossRef]
- Lehmberg R., H. , Radiation from an N-Atom system, I. General formalism, Phys. Rev. A 1970, 2, 883. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An Essay on the Theory of Collective Spontaneous Emission. Phys. Rep. 1982, 93, 301. [Google Scholar] [CrossRef]
- Bonifacio, R.; Schwendimann, P.; Haake, F. Quantum Statistical Theory of Superradiance, I. Phys. Rev. A 1971, 4, 302. [Google Scholar] [CrossRef]
- Crubellier, A.; Liberman, S.; Pavolini, D.; Pillet, P. Superradiance and subradiance. I. Interatomic interference and symmetry properties in three-level systems. J. Phys. B: Atom. Mol. Phys. 1985, 18, 3811. [Google Scholar] [CrossRef]
- Bienaimé, T.; Piovella, N.; Kaiser, R. Controlled Dicke subradiance from a large cloud of two-level systems. Phys. Rev. Lett. 2012, 108, 123602. [Google Scholar] [CrossRef] [PubMed]
- Guerin, W.; Araùjo, M.O.; Kaiser, R. Subradiance in a Large Cloud of Cold Atoms. Phys. Rev. Lett. 2016, 116, 083601. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O. Single photon subradiance: quantum control of spontaneous emission and ultrafast readout. Phys. Rev. Lett. 2015, 115, 243602. [Google Scholar] [CrossRef]
- Jen, H.H.; Chang, M.S.; Chen, Y.C. Cooperative single-photon subradiant states Phys. Rev. A 2016, 94, 013803. [Google Scholar] [CrossRef]
- Facchinetti, G.; Jenkins, S.D.; Ruostekoski, J. Storing light with subradiant correlations in arrays of atoms. Phys.Rev. Lett. 2016, 117, 243601. [Google Scholar] [CrossRef]
- Asenjo-Garcia, A.; Moreno-Cardoner, M.; Albrecht A:; Kimble H. J.; Chang D. E. Exponential improvement in photon storage fidelities using subradiance and “selective radiance” in atomic arrays. Phys. Rev. X 2017, 7, 031024. [Google Scholar]
- Cech, M.; Lesanovsky, I.; Olmos, B. Dispersionless subradiant photon storage in one-dimensional emitter chains. Phys. Rev. A 2023, 108, L051702. [Google Scholar] [CrossRef]
- Needham, J.A.; Lesanovsky, I.; Olmos, B. Subradiance-protected excitation transport. New J. Phys. 2019, 21, 073061. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



