Study on Spatial Spillover Effect of Forest Carbon Sink Efficiency in China considering Multiple Output Benefits

Forests have multifunctional roles. They not only increase forest carbon sinks through afforestation and management, but also indirectly realize multiple benefits of "economy + ecology + society". Therefore, we construct a multiple output-benefit system of forest carbon sinks based on the development of forest carbon sinks in provinces of China. This system is also able to distinguish the importance of forest carbon sinks from other outputs. For the efficiency evaluation of multi-level output systems, this paper constructs a cross-evaluation model based on evidential reasoning method, the original efficiency information by conducting efficiency evaluation before information fusion. Further, the spillover effects and influencing factors of forest carbon sink efficiency are analyzed through a spatial regression model to explore the spatial characteristics of forest carbon sink efficiency in China. The results show that: (1) there is a large gap between the cross-efficiency levels of forest carbon sinks in various regions of China, with significant spatial correlation. For the perspective of direct output benefits, the cross-efficiency of the eastern region is higher, while the cross-efficiency of the northwestern region is lower; for the perspective of indirect output benefits, the cross-efficiency of the southeastern region is higher. (2) China's forest carbon sink has a significant positive spillover effect, and the indirect output cross-efficiency has a significant negative impact on the forest carbon sink in its own region. Further analyzing the impact of indirect output cross-efficiency, it is found that the cross-efficiency of the ecological dimension and the cross-efficiency of the social dimension have a significant negative impact on the forest carbon sink in its own region, and the economic dimension has a significant positive impact on the forest carbon sink in its own region. In conclusion, corresponding policy recommendations are proposed for the development of forest carbon sinks to promote the realization of the dual-carbon goal.

Keywords:

1. Introduction

Forests have systemic multifunctionality. Not only can they increase forest carbon sinks through afforestation and management, but they can also indirectly realize multiple benefits in terms of “economy + ecology + society”. Economically, the economic value can be realized through trading incremental carbon sinks. Ecologically, it can protect biodiversity and enhance the carrying capacity of the environment. In addition, socially, it can generate employment opportunities for forest farmers and promote the sustainable development of the local economy and society. Integrating directly produced forest carbon sinks with indirectly produced ecological, economic and social benefits is a crucial approach to assessing carbon sink benefits. For instance, in carbon trading, design documents of CCER forestry carbon sink projects not only require additional incremental forestry carbon sinks from anthropogenic operations but also require a comprehensive assessment of ecological, economic and social benefits during the development process of forestry carbon sink projects. Hua [1] explored the relationship between forestry carbon sink markets and economic performances in terms of institutional arrangements based on the characteristics of carbon sequestration project development. In the realm of green finance, the Intergovernmental Panel on Climate Change (IPCC) has recommended dynamic accounting of the multiple benefits of forest carbon sinks [2], and has also proposed quantifying the economic benefits of forestry carbon sequestration projects throughout the lifespan of investment project [3]. Therefore, improving the coordination level between economic, ecological and social systems can gradually enhance the carbon sequestration capacity of forests. Nevertheless, due to factors such as uneven economic development and disparities in natural resource endowments across China, the development degree of forest carbon sinks varies between regions, and there are significant differences in the coordination of different benefits. To achieve a regionally balanced development of forest carbon sinks, effective performance management systems have been implemented in various regions [4]. In terms of performance management, efficiency measures are designed to provide quantitative information on the performance of the evaluated object, enabling horizontal performance comparison as well as vertical performance monitoring. This provides a basis for formulating differentiated policies for the regional development of forest carbon sinks. Therefore, measuring forest carbon sink efficiency based on output orientation and studying the coupling and coordination degree and spatial distribution characteristics between economic, ecological, and social systems in forest carbon sink management based on efficiency results is a crucial scientific issue in forest carbon sink performance management.

From a systemic perspective, inputs and outputs, as interdependent and mutually constraining elements, jointly determine the level of performance of forest carbon sinks. Currently, there are two methods of performance measurement: one is to construct a comprehensive performance indicator by integrating information from the indicator system [5,6]; the other is to measure the efficiency of comparable units by utilizing data envelopment analysis (DEA) methods [7,8,9]. With the development of complex systems and diversification, many scholars combine these two methods to construct an efficiency measurement model with a multi-level indicator system, which can depict indicators from a multi-dimensional perspective, consider the input-output relationship, and form a more comprehensive efficiency measurement. However, for research on the input-output indicator systems of the forestry system, most scholars have only considered unilateral outputs [10]. Fewer scholars have selected output indicators from a comprehensive perspective, and these studies lack a distinction between direct and indirect outputs. Moreover, most of the traditional methods for measuring the efficiency of forestry systems are based on the self-assessment perspective, which leads to the decision-making unit (DMU) exaggerating its own efficiency [11,12]. Moreover, most efficiency evaluation studies of multilevel systems perform indicator fusion followed by efficiency evaluation, which can lead to partial loss of efficiency information of the original indicators [13].

This paper considers the direct benefits and multiple indirect benefits of forest carbon sinks, constructs a spatial model of a forest carbon sink cross-evaluation system based on Evidential Reasoning (ER), studies the spatial characteristics of multiple output benefits of China’s forest carbon sinks, and grasps the trend of forest carbon sinks based on the results of the study, so as to provide references for the relevant management decisions, ecological governance, and environmental management, and to promote the development of China’s green and low-carbon economy.

The marginal contributions of this study are: (1) the construction of a comprehensive indicator system of output benefits of forest carbon sinks by integrating the ecological, economic and social multiple output benefits of forest carbon sinks while distinguishing between the direct and indirect output benefits of forest carbon sinks. (2) for the multilevel output system, this paper proposes the evaluation idea of efficiency measurement before indicator fusion, which maximizes the retention of the original efficiency information. (3) the spatial distribution of the efficiency of forest carbon sinks and the spillover effect are studied, and the spatial distribution of the forest carbon sinks’ output systems are characterized from the social, economic and ecological perspectives under the perspective of efficiency.

2. Literature Review

DEA is a set of non-parametric efficiency evaluation methods, which can simultaneously consider multiple input and output indicators, without the need to specify a production function and directly assign weights to the indicators to measure efficiency. In recent years, scholars have used the CCR model [8], the BCC model [9], the SBM model [10,14,15,16], the DEA-Malmquist index model [10,12,17,18] and the inverse DEA model [19] to measure the efficiency of forest carbon sinks. In the existing literature, input indicators for measuring efficiency are mainly selected from the three factors of production: capital, land, and labour. Moreover, the selection of output indicators is more diversified. Some scholars take forest carbon sinks as the sole output indicator, while others consider only to the ecological benefits of forest carbon sinks or consider the comprehensive economic and ecological benefits of forest carbon sinks. They choose the total forestry output value and forest carbon sinks as the output indicators of forest carbon sinks. In addition to lacking a comprehensive perspective on the output benefits of forest carbon sinks, the forest carbon sink output indicator system constructed in the existing literature lacks a hierarchical structure. Constructing an evaluation indicator system with a hierarchical relationship would make the evaluation more comprehensive and reasonable.

Under the influence of the new socialist concept of ecological civilization, it is crucial to design a suitable indicator system for monitoring and evaluating forestry to promote its development. Selecting indicators from multiple dimensions to construct this indicator system will ensure a more comprehensive evaluation. In recent years, scholars’ research on the multidimensional evaluation indicator system of forestry has focused on high-quality development [20,21], sustainable development [22], and ecological security [23,24]. When it comes to multi-level indicator information processing, scholars first aggregate the indicators’ information to simplify it, and then evaluate efficiency subsequently. Combining the Analytic Hierarchy Process (AHP) with DEA [25] converts qualitative data into quantitative data, effectively measuring the effectiveness of decision-making units [26]. This approach also enables the determination of input and output indicators’ weights in DEA [27], and the estimation of missing data [28]. The integration of these two methods combines subjective judgments with objective choices, resulting in more accurate and rational results. Considering that data-driven-oriented information fusion methods are more objective, scholars combine ER with DEA to synthesize indicators using mathematical rationalization, which can reduce indicators while preserving as much original information as possible. Subsequently, DEA models were used to evaluate the efficiency of the fused indicators [5,6,13].

Since forest carbon sink is the process of absorbing and fixing carbon dioxide in the air, and the air has circulation, forest carbon sink has certain spatial correlation. Thus, exploring the development of forest carbon sink from the spatial perspective is an important research direction. Due to the differences in economic development and natural resource endowment, China’s forest carbon sinks have a large gap between regions, with incremental changes from the southern forest area to the southwest and northeast forest areas [29]. Among them, the southwest region has the highest carbon density, and its carbon stock and carbon stock density both increase faster than the northeast region [30]. As the development of forest carbon sinks between regions may be correlated, scholars have explored the spatial aggregation effect of forest carbon sinks using the Moran index [31], further, Xue et al. [32] and Fu et al. [33] analyzed the spatial spillover effect of forest carbon sinks from the national perspective, and Du et al. [34] further extended the scope of the study by discussing the cross-country spillover effect of forest carbon sinks from the global perspective. They all concluded that the development of forest carbon sinks is not always possible in isolation, and that the development of forest carbon sinks in each region may positively or negatively affect the development of forest carbon sinks in neighboring regions.

In summary, there are still the following shortcomings in current research on the development of forest carbon sinks: (1) most of the existing studies takes the forest carbon sinks as the only output indicator or some of the studies considers the output benefits of forest carbon sinks from multiple dimensions, but few of the studies characterizes them from the perspectives of direct and indirect benefits, which is not enough to meet the realistic needs of comprehensive evaluation of forestry carbon sinks’ output benefits and lacks a comprehensive consideration of the output benefits of forest carbon sinks in terms of ecological, economic and social aspects. (2) the efficiency measurement based on the indicator system of hierarchical structure consists of two processes: “efficiency evaluation” and “ indicators integration”. Most studies conduct “indicator fusion” before “efficiency evaluation”, which results in the loss of a part of the “efficiency information” from the original indicator data. (3) existing studies on spatial autocorrelation mainly focus on the uneven regional development of forest carbon sinks, while there is a lack of studies on spatial correlation studies based on the efficiency perspective.

3. Indicator System Construction and Data Sources

3.1. Construction of Input-Output Indicator System

According to the DEA method, it is necessary to select indicators from an input-output perspective. In terms of inputs, we select forestland area, forestry practitioners, and the completed amount of forestry investment as input indicators based on the three factors of production in economics - land, labour, and capital. During the process of forest management, in addition to the direct output benefits of forest carbon sinks, there are rich output benefits in ecological, economic and social aspects.

In the process of forest management, forest carbon sinks have rich output benefits in environmental, economic and social aspects in addition to direct output benefits. Considering the correlation between the developmental role of forest carbon sinks and output indicators, this paper categorizes the benefits into two types: direct output benefits and indirect output benefits. The forest carbon sink is the direct output benefit, while the indirect output benefit takes into account the ecological, economic and social benefits. The direct and indirect output benefits, as subsystems, respectively, together form a comprehensive output system for forest carbon sinks, where the indirect output system is constituted by multi-tiered indicators, as shown in Table 1.

From the perspective of ecological output benefits, the improvement of forest quality is firstly reflected in the increase in the quantity of forest resources. The improvement of forest quality is conducive to the formation of forest resources and can improve the ability of trees to resist pests and diseases [35]. Therefore, the area of forest conservation is chosen to represent the benefit of increasing forest resource quantity; the area of forest pest control is chosen to represent the benefit of pest control; and the area of afforestation is chosen to represent the benefit of increasing the forest area.

From the perspective of economic output benefits, forests can generate multiple types of economic income. For example, commercial forests in the forest can enter the market and generate economic value; the beautiful scenery and tranquil environment of the forest can attract travellers to visit, thus creating economic income [36]. Since the total forestry output value already includes the total value of final products and labour services produced by the forestry industry, for the convenience of categorization, we select the total output value of the primary industry, the total output value of the secondary industry and the total output value of the tertiary industry under the breakdown of the total forestry output value to represent the economic benefits.

From the perspective of social output benefits, forests have excellent carbon sequestration capacity, which can purify the air and create a more beautiful and livable living environment for human beings. The development of forests can drive the construction of local infrastructure and cultural services, as well as provide more employment opportunities and increase the wages of practitioners, enrich the spiritual and cultural life of human beings, and improve their material standard of living [37,38]. Therefore, the total number of forestry tourists is selected to represent the benefits of cultural service construction; the total amount of economic forest products is selected to represent the benefits of meeting people’s production and living needs; and the average annual salary of on-the-job employees in the forestry system is selected to represent the benefits in terms of employment and remuneration.

3.2. Spatial Regression Modelling Indicator System

Using spatial econometric models, forest carbon sinks were selected as the explanatory variables to explore the spatial spillover effects and influencing factors of forest carbon sink efficiency in China. Based on Table 1, forest carbon sink efficiency includes ecological output cross-efficiency, economic output cross-efficiency, social output cross-efficiency, and indirect output cross-efficiency, in which the indirect output efficiency is derived from the integration of social, ecological, and economic dimensions. As the growth of trees is closely related to environmental changes, plants absorb carbon dioxide through photosynthesis, which needs to be carried out under suitable water resources, temperature and light, thus annual precipitation, average annual temperature and annual sunshine hours were selected as control variables.

3.3. Sources of Data

In this paper, forestry data from 2009-2021 were used, and the data on forest carbon sinks were obtained from the China Forest Aboveground and Belowground Vegetation Carbon Stocks dataset of the National Tibetan Plateau Science Data Center., which was obtained by fusing high-resolution active microwave remote sensing, and long time-series passive microwave and optical remote sensing information by employing regression and machine learning algorithms [39]. The rest of the data were obtained from the China Forestry and Grassland Statistical Yearbook and the China Statistical Yearbook.

4. Spatial Modelling of Forest Carbon Sink Cross-Evaluation System Based on Evidence-Based Reasoning

In this section, 31 provinces in China are used as DMUs, and the cross-efficiency evaluation method is introduced to measure the cross-efficiency of forest carbon sinks under the multi-dimensional output indicator system, and then the ER model is used to synthesize the cross-efficiency of forest carbon sinks in each indirect output dimension and indirect output system to reduce the loss of efficiency information in the synthesis process. The spatial econometric model is then introduced to explore the spatial spillover effect and the influencing factors of China’s forest carbon sinks.

4.1. Measurement of Cross-Efficiency of Forest Carbon Sinks

In 1986, Sexton utilized optimal weights from the self-assessment perspective to develop a peer evaluation and referred to the method as the cross-efficiency evaluation method [7]. Currently, scholars have constructed multiple cross-evaluation strategy models based on decision-making needs and competition and cooperation relationships among peers [40,41,42]. Most traditional methods for measuring the efficiency of forestry systems are based on the self-assessment perspective, which exaggerates its efficiency. A two-by-two evaluation with a peer-to-peer perspective could make the results of the efficiency evaluation more applicable to the spatial analysis of forest carbon sinks between regions. We consider the competition and cooperation relationship between regions in the process of forest carbon sink development, and a neutral strategy was chosen for evaluation. Additionally, the efficiency is measured to maximize output benefits [40].

Taking 31 provinces in China as DMUs, each province has 3 forest carbon sink input indicators and 11 forest carbon sinks output indicators.

x_{i j} (i = 1, 2, 3; j = 1, 2, \dots, 31)

denotes the forest carbon sink input

i

of the province

j

\bar{Y_{j}} = {{y_{j}}^{D}, {y_{j}}^{E}, {y_{j}}^{F}, y_{j}^{S}}

denotes the outputs of the province

j

, where

{y_{j}}^{D}

denotes the forest carbon sink of the province

j

y_{j}^{E} = {{y_{i j}}^{E}} (i = 1, 2, 3)

denotes the forest carbon sinks output

i

under the ecological dimension of the province

j

y_{j}^{F} = {{y_{i j}}^{F}} (i = 1, 2, 3)

denotes the forest carbon sinks output

i

under the economic dimension of the

j

province and

y_{j}^{S} = {y_{i j}^{S}} (i = 1, 2, 3)

denotes the forest carbon sinks output

i

under the social dimension of the province

j

. For example, if we take the area of forest conservation as the only output, we can calculate the self-assessment efficiency of forest carbon sinks in the

k

(k = 1, \dots, n)

province using the following CCR model:

\begin{array}{l} M a x θ_{1, k k}^{E} = u_{1 k}^{E} y_{1 k}^{E} \\ s . t . \sum_{i = 1}^{3} v_{1, i k}^{E} x_{i j} - u_{1 k}^{E} y_{1 j}^{E} \geq 0, j = 1, 2, \dots, 31; \\ \sum_{i = 1}^{3} v_{1, i k}^{E} x_{i k} = 1; \\ v_{1, i k}^{E}, u_{1 k}^{E} \geq 0, i = 1, \dots, 3, r = 1, \dots, 3. \end{array}

(1)

where

θ_{1, k k}^{E}

denotes the self-assessment efficiency of forest carbon sinks in the province

k

based on the area of forest conservation as the only output, and the superscript

E

and subscript

1

together denote the

1 t h

output under the ecological dimension.

Using the optimal weights of the CCR model, a neutral strategy was established to calculate the cross-efficiency of each province based on the area of forest conservation as the only output:

\begin{array}{l} M i n & δ_{1}^{E} \\ s . t . & \sum_{i = 1}^{3} v_{1, i k}^{E} x_{i k} = 1, \\ u_{1 k}^{E} y_{1 k}^{E} = θ_{1, k k}^{E *}, \\ u_{1 k}^{E} y_{1 k}^{E} - \sum_{i = 1}^{3} v_{1, i k}^{E} x_{i j} \leq 0, j = 1, \dots, 31; j \neq k, \\ u_{1 k}^{E} y_{1 k}^{E} - δ_{1}^{E} \geq 0, \\ v_{1, i k}^{E} \geq 0, i = 1, \dots, 3, \\ δ_{1}^{E} \geq 0. \end{array}

(2)

Using cross-efficiency aggregation method based on interval conditional entropy proposed by Chen et al. [43], and using the forest conservation area as a single output as an example, the cross-efficiency of forest carbon sinks in the province

k

, the specific cross-efficiency assembly process is as follows:

The first step is to calculate the conditional entropy of each province. Let

θ_{1, k j}^{E}

denote the cross-efficiency of forest carbon sinks when

D M U_{k}

evaluating

D M U_{j}

, then the conditional entropy of

D M U_{k}

is calculated as follows：

H （ D |D M U_{k} ） = - \sum_{j = 1}^{n} P (θ_{1, k j}^{E}, θ_{1, j j}^{E}) \sum_{i = 1}^{n} P (θ_{1, k j}^{E}, θ_{1, i j}^{E}) \log_{2} P (θ_{1, k j}^{E}, θ_{1, i j}^{E})

(3)

where

\sum_{j = 1}^{n} P (θ_{1, k j}^{E}, θ_{1, j j}^{E})

denotes the uncertainty effect from

D M U_{j}

self-evaluation when

D M U_{k}

evaluates

D M U_{j}

P (θ_{1, k j}^{E}, θ_{1, i j}^{E}) = \frac{d (θ_{1, k j}^{E}, θ_{1, i j}^{E})}{d_{j}}

d_{j} =

\sum_{i = 1}^{n} d (θ_{1, k j}^{E}, θ_{1, i j}^{E})

and

d (θ_{1, k j}^{E}, θ_{1, i j}^{E}) = | θ_{1, k j}^{E} -

θ_{1, i j}^{E} |

P (θ_{1, k j}^{E}, θ_{1, i j}^{E}) \log_{2} P (θ_{1, k j}^{E}, θ_{1, i j}^{E})

denotes the uncertainty effect from

D M U_{k}

evaluating

D M U_{j}

when

D M U_{i}

evaluates

D M U_{j}

The second step is to calculate the aggregation weight of each province. The conditional entropy

H_{s} = {H (D | D M U_{1}), H (D | D M U_{2}), \dots, H (D | D M U_{n})}

of all provinces

U = {D M U_{1}, D M U_{2}, \dots, D M U_{n}}

is reordered in order from smallest to largest for the provinces to obtain an ordered set of conditional entropies

H_{s}^{*} = {H (D | D M U_{1}^{*}), H (D | D M U_{2}^{*}),

\dots, H (D | D M U_{n}^{*})}

, then the degree of fuzzy preference of

D M U_{i}

compared to

D M U_{j}

can be expressed as:

p_{i j}^{*} = \frac{1}{2} [1 + \frac{\sum_{t = 1}^{j} H (D | D M U_{t}^{*}) - \sum_{t = 1}^{i} H (D | D M U_{t}^{*})}{n - 1}]

(4)

The fuzzy preference matrix between provinces generated by Eq. (4) is clustered to obtain the clustering weights for each province:

ω_{i} = \frac{\sum_{j = 1}^{n} p_{j i}^{*} + \frac{n}{2} - 1}{n (n - 1)}, i = 1, 2, \dots, n .

(5)

The third step is to calculate the cross-efficiency of forest carbon sinks in each province.

E_{1, j}^{E} = \sum_{i = 1}^{n} ω_{i} θ_{1, i j}^{E}, j = 1, 2, \dots, n .

(6)

Then the final forest carbon sink cross-efficiency matrix for each province can be obtained:

E_{1, k j}^{E} = [\begin{matrix} E_{1, 11}^{E} & E_{1, 12}^{E} & \dots & E_{1, 1 n}^{E} \\ E_{1, 21}^{E} & E_{1, 22}^{E} & \dots & E_{1, 2 n}^{E} \\ ⋮ & ⋮ & ⋮ \\ E_{1, n 1}^{E} & E_{1, n 2}^{E} & \dots & E_{1, n n}^{E} \end{matrix}]

By analogy, it is possible to obtain a cross-efficiency matrix of forest carbon sinks for each of the remaining ten forest carbon sink tertiary output indicators as a single output, which is fused in the next section.

4.2. Information Fusion for Cross-Efficiency Based on ER

During the process of information fusion, indicators need to be weighted. The AHP relies on experts to assign weights based on their preferences, which can be influenced by the subjective factors of the experts themselves, thereby impacting the objectivity of the final weighting results. With a data-driven orientation, ER starts from the nature of the data source and extracts relevant evidence. Based on the set theory, the precise belief degree, belief degree and estimated belief degree of the evidence are described by introducing the concepts of belief function, likelihood of belief function, and class probability function. The set is then narrowed by synthesizing evidence using orthogonal summation methods. Therefore, in the multi-level indirect output benefit indicator system of forest carbon sinks, the cross-efficiency matrix under the three-level refinement is fused with information based on ER, and the cross-efficiency under the indirect output benefit of each province is measured. As shown in Table 1, the cross-efficiency of the ecological, economic as well as social dimensions is calculated first. The process of information fusion based on ER is specified below using the ecological dimension as an example:

Firstly, the cross-efficiency values were transformed into distributed confidence levels. The cross-efficiencies of the 31 provinces based on forest nursery area, forest pest control area, and afforestation area as single outputs were fused into efficiencies, where the range of values of

E_{1, j}^{E}

E_{2, j}^{E}

and

E_{3, j}^{E}

on the evaluation level

H_{d} (d = 1, 2, \dots, p)

[U_{d}, U_{d + 1})

, and the utility of the evaluation level

H_{d}

O_{d}

, and

β_{d, i, j}^{E} (j = 1, \dots, 31)

denotes the confidence of the cross-efficiencies of the province

j

based on the single output

i

on the evaluation level

H_{d}

β_{d, i, j}^{E} \geq 0

\sum_{d = 1}^{p} β_{d, i, j}^{E} \leq 1

. The distributed confidence of the province

j

on the distributed confidence level on the ecological dimension is denoted as [5,44,45]:

S (E_{i, k j}^{E}) = {(H_{d}, β_{d, i, k j}^{E}), d = 1, 2, \dots, p}

(7)

β_{d, i, k j}^{E} = \frac{U_{d + 1} - E_{i, k j}^{E}}{U_{d + 1} - U_{d}}, β_{d + 1, i, k j} = \frac{E_{i, k j}^{E} - U_{d}}{U_{d + 1} - U_{d}}

(8)

Secondly, a composite cross-efficiency matrix is generated.

m_{d, i, k j}^{E} = m_{i, k j}^{E} (H_{d}) = ω_{i}^{E} β_{d, i, j k}^{E}

(9)

m_{H, i, k j}^{E} = m_{i, k j}^{E} (H) = 1 - \sum_{d = 1}^{p} m_{d, i, k j}^{E} = 1 - ω_{i}^{E} \sum_{d = 1}^{p} β_{d, i, k j}^{E}

(10)

{\bar{m}}_{H, i, k j}^{E} = {\bar{m}}_{i, k j}^{E} (H) = 1 - ω_{i}^{E}

(11)

{\tilde{m}}_{H, i, k j}^{E} = {\tilde{m}}_{i, k j}^{E} (H) = ω_{i}^{E} (1 - \sum_{d = 1}^{p} β_{d, i, k j}^{E})

(12)

where

m_{d, i, j}^{E}

denotes the probability that the cross-efficiency

E_{i, j}^{E} (i = 1, 2, 3)

of the province

j

with a single output based on the output

i

of the ecological dimension is at evaluation level

H_{d}

{\bar{m}}_{H, i, j}^{E}

denotes the probability of uncertainty due to the indicator weight

ω_{i}^{E}

{\tilde{m}}_{H, i, j}^{E}

denotes the probability of uncertainty due to the structure of the output indicator based on the ecological dimension, and

m_{H, i, j}^{E}

denotes the probability of uncertainty of the total of the province

j

with a single output based on the output

i

of the ecological dimension.

The basic probability function of cross efficiency after fusion using the ER recursive algorithm is:

m_{d}^{E} = k^{E} [\prod_{i = 1}^{3} (m_{d, i, k j}^{E} + {\bar{m}}_{H, i, k j}^{E} + {\tilde{m}}_{H, i, k j}^{E}) - \prod_{i = 1}^{3} ({\bar{m}}_{H, i, k j}^{E} + {\tilde{m}}_{H, i, k j}^{E})]

(13)

{\tilde{m}}_{H}^{E} = k^{E} [\prod_{i = 1}^{3} ({\bar{m}}_{H, i, k j}^{E} + {\tilde{m}}_{H, i, k j}^{E}) - \prod_{i = 1}^{3} {\bar{m}}_{H, i, k j}^{E}]

(14)

{\bar{m}}_{H}^{E} = k [\prod_{r = 1}^{s} {\bar{m}}_{H, i, k j}^{E}]

(15)

k^{E} = {[\sum_{d = 1}^{p} \prod_{i = 1}^{3} (m_{d, i, k j}^{E} + {\bar{m}}_{H, i, k j}^{E} + {\tilde{m}}_{H, i, k j}^{E}) - (p - 1) \prod_{i = 1}^{3} ({\bar{m}}_{H, i, k j}^{E} + {\tilde{m}}_{H, i, k j}^{E})]}^{- 1}

(16)

where the confidence level of the cross-efficiency after synthesis can be expressed as:

β_{d, k j}^{E} = \frac{m_{d}^{E}}{1 - {\bar{m}}_{H}^{E}}, d = 1, 2, \dots, p

(17)

Then the cross-efficiency of the province after synthesis based on the ecological dimension is:

E_{k j}^{E} = O_{d} β_{d, k j}^{E}

(18)

4.3. Spatial Regression Model

Traditional regression models cannot examine the correlation between spatial units, thus, three commonly used spatial regression models are introduced in this paper [33]:

Spatial Lag Modelling (SLM):

y_{i t} = ρ \sum_{j = 1}^{n} w_{i j} y_{i t} + φ + x_{i t} β + μ_{i} + η_{i} + φ_{i t}

(19)

Spatial Error Modelling (SEM):

y_{i t} = φ + x_{i t} β + μ_{i} + η_{i} + φ_{i t}

(19)

φ_{i t} = λ \sum_{j = 1}^{n} w_{i j} φ_{i t} + ε_{i t}

(19)

Spatial Durbin Model (SDM):

y_{i t} = ρ \sum_{j = 1}^{n} w_{i j} y_{i t} + φ + x_{i t} β + \sum_{j = 1}^{n} w_{i j} x_{i j t} γ + μ_{i} + η_{i} + φ_{i t}

(19)

where

y_{i t}

w_{i j}

and

ρ

are the explanatory variables, spatial weight matrix and spatial autoregressive coefficients of province

i

in year

t

\sum_{j = 1}^{n} w_{i j} y_{i t}

represents the effect of the explanatory variables of neighbouring provinces on the local province,

x_{i j t}

is the explanatory variable,

β

is the vector of parameter estimates of the explanatory variables,

\sum_{j = 1}^{n} w_{i j} x_{i j t} γ

represents the effect of the explanatory variables of neighbouring provinces on the explanatory variables of the local province,

γ

is the matrix of spatial autocorrelation coefficients,

μ_{i}

η_{i}

and

φ_{i t}

are the spatial, temporal and error terms, respectively,

λ

is the spatial autocorrelation coefficient of the error term, and

ε_{i t}

is the independent and identically distributed error term that follows the distribution

(0, σ^{2})

In summary, the steps for constructing the spatial model for a forest carbon sink cross-evaluation system based on ER are as follows:

Step 1: Use the neutral cross-efficiency evaluation method to calculate the cross-efficiency of forest carbon sinks under the single output perspective. The self-assessment efficiency of forest carbon sinks of each province is obtained by using Eq. (1), and the cross-efficiency matrix of forest carbon sinks under the third-level single output indicator of each province is further calculated by Eqs. (2) and (6).

Step 2: Apply the cross-efficiency aggregation method based on conditional entropy to aggregate the above cross-efficiency matrix. Firstly, the distance between each element in the cross-efficiency matrix is calculated and the conditional entropy of each DMU is obtained by using formula (3). Then, the conditional entropy is converted into a fuzzy consistency preference matrix using Eq. (4), and then the aggregation weights of DMUs are calculated by Eq. (5). Finally, matrix aggregation is performed using Eq. (6).

Step 3: Use the ER method to fuse the cross-efficiency of forest carbon sinks under the third-level single output indicator into cross-efficiency under each indirect output dimension and indirect output system. The cross-efficiency values were converted into distributed confidence levels based on Eqs. (7) and (8), and the indicators were fused according to Eqs. (9)-(18) to obtain the cross-efficiency for the indirect output benefit system.

Step 4: Use spatial regression models to explore the spatial spillover effects and the influencing factors of forest carbon sinks. Firstly, the spatial autocorrelation of forest carbon sinks was investigated using the Moran index, and then the optimal spatial regression model (Eqs. (19)-(22)) was selected by using the cross-efficiency of indirect outputs as the core variable, and by using the Lagrange multiplier (LM) test, the likelihood ratio (LR) test, the Ward test and the Hausman test. The core variables were further expanded to cross-efficiency under ecological, economic and social output dimensions to explore the specific direction of indirect output cross-efficiency on forest carbon sinks.

In summary, the construction process of the spatial model of the forest carbon sink cross-evaluation system based on evidential reasoning is shown in Figure 1.

5. Results

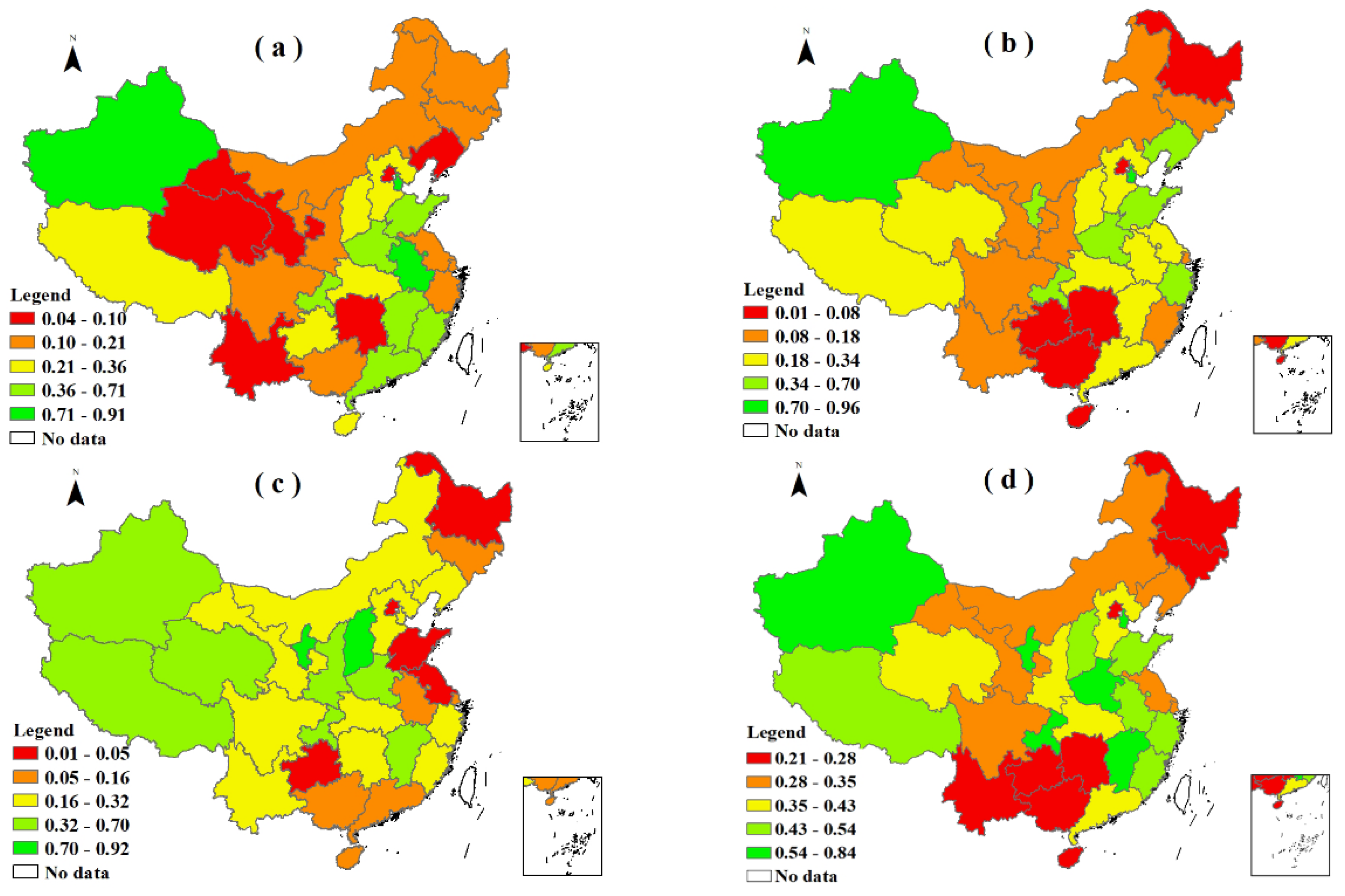
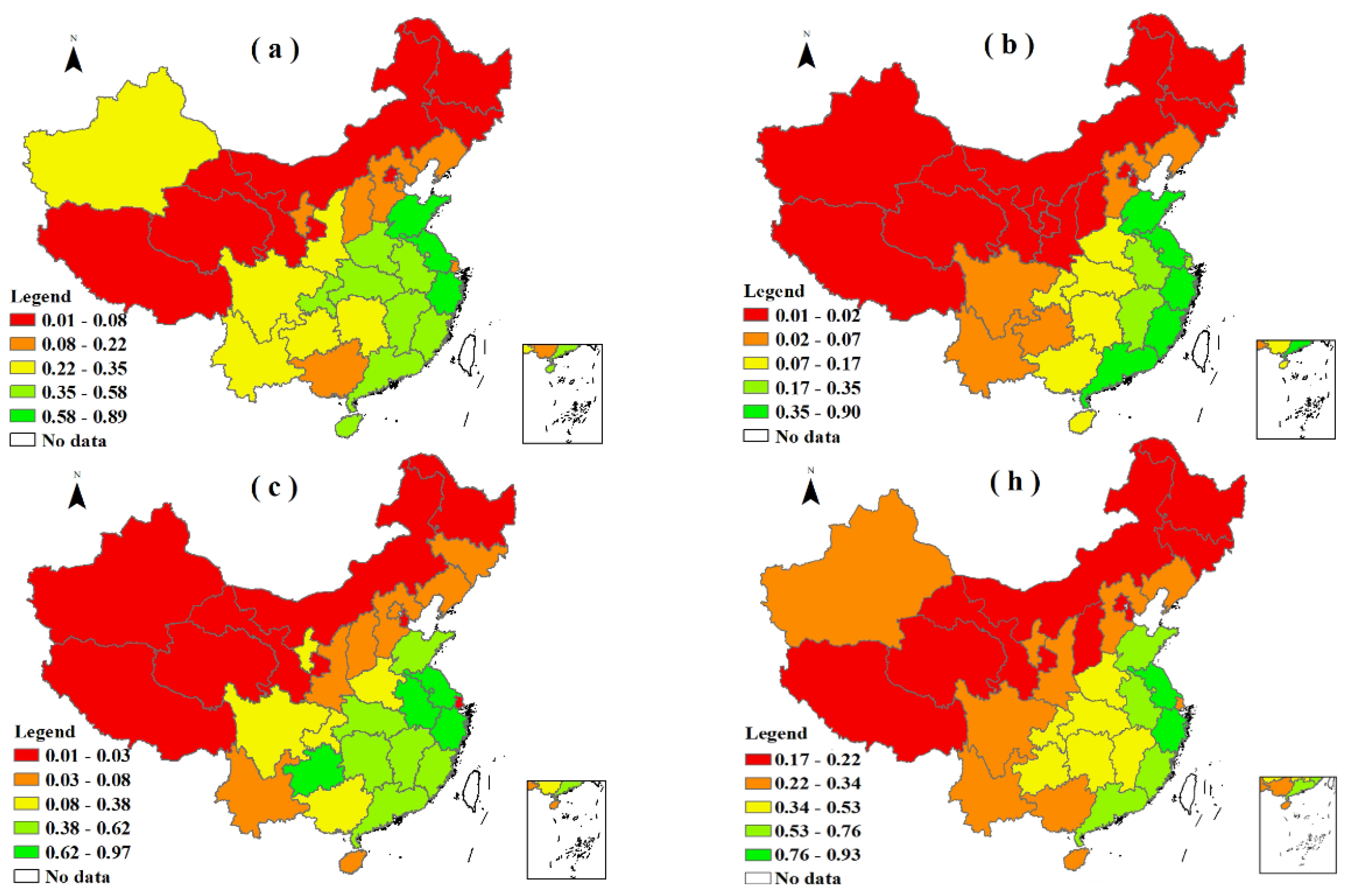
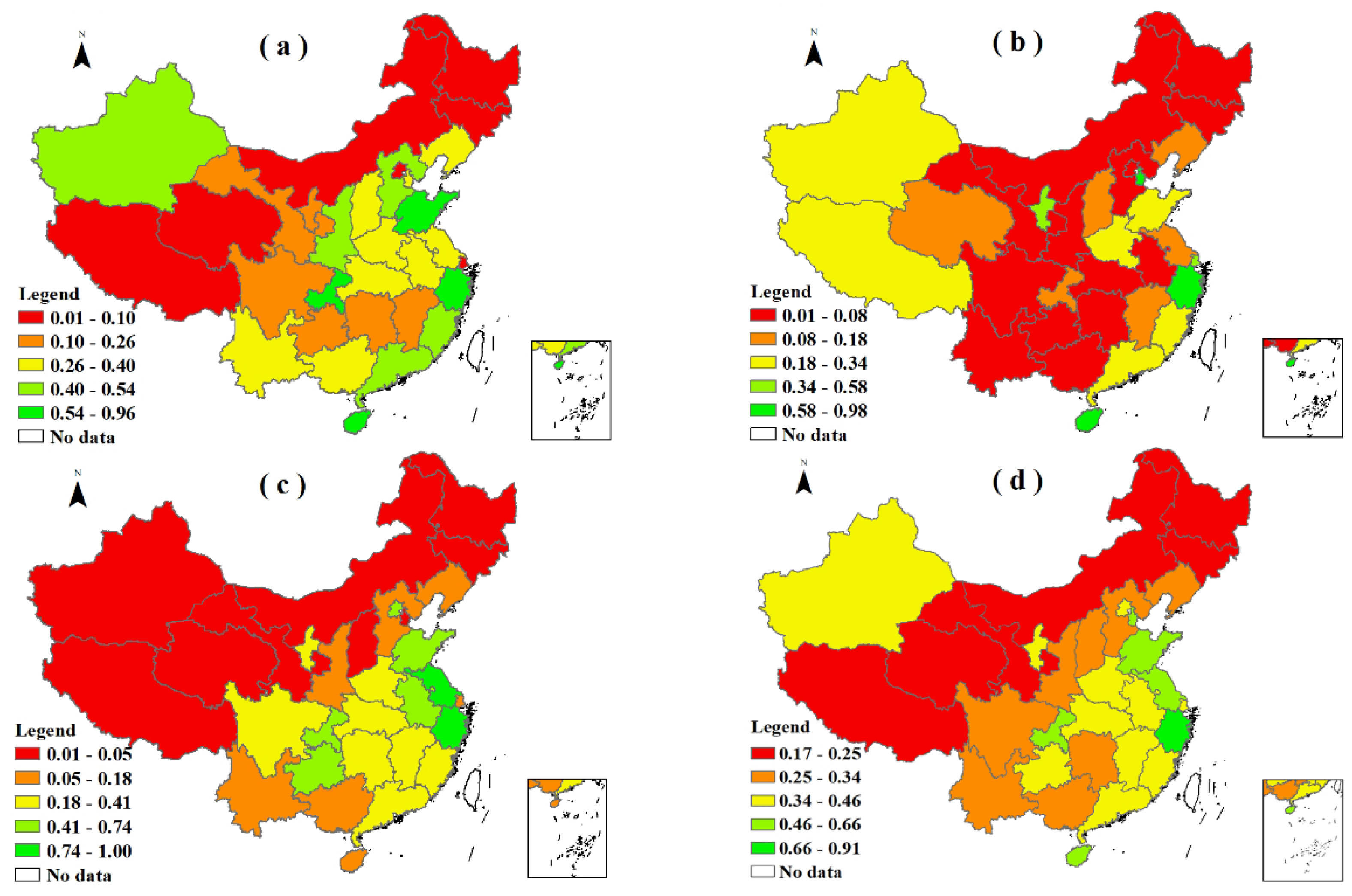
5.1. Results of Cross-Efficiency Evaluation of Forest Carbon Sinks

Based on the cross-efficiency calculation method outlined in Section 3.1 and the ER process discussed in Section 3.2, we have obtained the spatial distribution of the cross-efficiency levels for forest carbon sinks in each province. The specific results can be seen in Figures 2 through 6.

In terms of the cross-efficiency of the direct output dimension (i.e., forest carbon sink indicator), Yunnan and Heilongjiang have higher cross-efficiency, while Tianjin, Shandong, Qinghai and Ningxia have lower cross-efficiency. Heilongjiang is in the northeast forest area, which is the largest forest area in China, and Yunnan is located in the southwest forest area. Both provinces are rich in forest resources, which is conducive to the development of forest carbon sinks. While the terrain of Ningxia and Qinghai is too steep. The southern part of Ningxia is dominated by loess landforms eroded by flowing water, and the central and northern parts of Ningxia are dominated by arid stripping and wind erosion landforms; Qinghai belongs to the plateau region, with more than four-fifths of the area being a plateau, and the harsh environment makes it difficult to develop forest carbon sinks in Ningxia and Qinghai. Tianjin is in a plain and less forested area, with insufficient total forest resources and low forest quality, hindering the development of forest carbon sinks. Shandong, located in the North China Plain, is a major grain-producing province in China, with low forest cover, and the development of forest carbon sinks is subject to certain constraints.

Figure 3(a)-(c) show the spatial distribution of the cross-efficiency of forest carbon sinks in each province under the three levels of indicators belonging to the ecological dimension, respectively. The cross-efficiency of these three levels of indicators is fused by ER to obtain the cross-efficiency of forest carbon sinks in each province based on the ecological dimension, and its spatial distribution is shown in Figure 3(d). From the perspective of the overall ecological dimension, the cross-efficiency of all provinces is between 0.2 and 0.9, and the cross-efficiencies of Xinjiang and Tianjin are 0.840 and 0.776, respectively, which are far ahead of other provinces. Combined with Figure 3(a)-(c), Xinjiang and Tianjin are more efficient in forest conservation and forest pest control, which makes their overall ecological performance at an efficient level. Tianjin’s higher cross-efficiency is mainly because it puts in less investment in forestry and grassland fixed assets, forest area, and forestry employees, but the completed area of forest nourishment and forest pest control is at a medium level. The state has provided policy and financial support for the conservation management of forests in the mountainous areas of Xinjiang, which has promoted the conservation of forests in Xinjiang. However, due to the continuous growth of artificial afforestation areas in Xinjiang, the established artificial forests are mostly pure forests of single species and single structures, with simple insect community structures and a low number of natural enemies, such artificial forest ecosystems are very fragile, which leads to the occurrence and prevalence of forest pests and diseases, so Xinjiang attaches importance to the prevention and control of forest pests and diseases and has achieved remarkable results. Analyzed from the perspective of afforestation, Shanxi and Jiangxi have higher cross-efficiency. Relying on national and provincial forestry projects such as the “Three-North” project, the “Double” project, and the pilot demonstration project of land greening, Shanxi has formed a good situation of effective increase of newly afforested land and orderly afforestation of unforested land, further increasing the number of forested lands and increasing the number of forested lands. The good situation of the newly forested land has increased effectively and the unforested land has been forested in an orderly manner, which further improves the productivity of the forest land. Jiangxi in the grasp of mountain afforestation at the same time, vigorously implement afforestation greening “big four small” project, focusing on promoting the city, townships, rural areas, passages and industrial parks and other four aspects of the greening, promoting the effective growth of afforestation area in Jiangxi.

Figure 4(a)-(c) show the spatial distribution of forest carbon sink cross-efficiencies by province under the three levels of indicators belonging to the economic dimension, and the cross-efficiencies of these three levels of indicators are fused to obtain the cross-efficiencies of forest carbon sinks by province based on the economic dimension, and the spatial distribution is shown in Figure 4(d), which shows that the cross-efficiencies of Zhejiang and Jiangsu are the highest, While the cross-efficiencies of Tibet, Qinghai, and Inner Mongolia are the lowest. Combining the cross-efficiency of the total output value of the primary, secondary and tertiary forestry industries and the cross-efficiency of the fused economic dimensions, there are obvious spatial characteristics of the cross-efficiency, with the cross-efficiency of the southeastern region being significantly higher than that of the other regions, which indicates that the ER fusion of the indicators of the economic dimensions is more effective. This result is in line with the macro level of economic development, the provinces in the southeast coastal region are more prosperous, with higher economic levels and higher levels of forestry development, so the cross-efficiencies of forest carbon sinks in the economic dimension is higher; the western region is affected by the double effect of the poor economic conditions as well as ecological conditions, so the cross-efficiencies of forest carbon sinks in the economic dimension is low. Beijing and Shanghai, as the super first-tier cities in China, have strong economic strength, but their cross efficiency of forest carbon sinks under the economic dimension is not high, which is due to the low level of forestry construction in Beijing and Shanghai, which brings certain obstacles to the development of forest carbon sinks.

Figure 5(a)-(d) show the spatial distribution of the cross-efficiency of forest carbon sinks in each province under the three-level indicators of the social dimension, and the cross-efficiency of each province based on the social dimension is obtained by fusing the cross-efficiencies of the four three-level indicators into the ER, and the spatial distribution of the cross-efficiency of the social dimension is shown in Figure 5(e), which demonstrates that Zhejiang is much more efficient than other provinces in the social dimension. It indicates that compared with other provinces, Zhejiang’s forestry social development is better, which is more conducive to improving people’s satisfaction with forestry development; while Heilongjiang and Inner Mongolia have the lowest cross-efficiency, which has a lot of room for improvement. In terms of the number of forestry tourists, there are obvious regional differences in the cross-efficiency of forest carbon sinks, and the provinces with higher cross-efficiency are concentrated in the southeast region, where the climate is milder, the living environment is more comfortable, and the tourism industry is more developed, which leads to the development of the forestry tourism industry in a stronger way, whereas the western region lags behind in terms of forestry tourism due to its highland and basin topography, and its low forest coverage rate. In terms of the average annual wage of employees, Tianjin, Zhejiang and Hainan have higher cross-efficiency, while Guangxi has lower cross-efficiency. The low salary will make the employees less motivated, which is not conducive to the development of forest carbon sinks. In the total amount of economic forest products, Zhejiang and Shandong have higher cross-efficiency, while Jilin and Heilongjiang have lower cross-efficiency. Economic forest products mainly include fruits, dried fruits, forest beverages, forest seasonings, forest foods, woody medicinal herbs, etc., which play an important role in meeting people’s production and living needs.

Figure 6(a)-(c) show the spatial distribution of the cross-efficiency of forest carbon sinks in each province based on the ecological, economic and social dimensions, respectively, and the cross-efficiency of forest carbon sinks in these three dimensions is fused by ER to obtain the cross-efficiency of forest carbon sinks under the indirect output benefit system, and its spatial distribution is shown in Figure 6(d). The province with the largest forest carbon sink cross-efficiency under the indirect output benefit system is Zhejiang, and the next largest provinces are Shandong, Jiangsu, Chongqing, Anhui and Jiangxi. Guangdong’s cross-efficiency in both the economic and social dimensions is much larger than that of the other provinces, which makes its indirect output benefit system much more effective than that of the other provinces. Xinjiang has a larger cross-efficiency in the ecological dimension, but its smaller cross-efficiency in the economic and social dimensions prevents it from ultimately leading the way in cross-efficiency in the indirect output benefit system. In general, there is a significant spatial feature in the cross-efficiency of forest carbon sinks on the indirect output benefit system: the cross-efficiency in the eastern region is higher than that in other regions.

Figure 6. The spatial distribution of cross-efficiency of forest carbon sinks based on (a) ecological output benefits (b)economic output benefits (c) social output benefits (d) indirect output benefits.

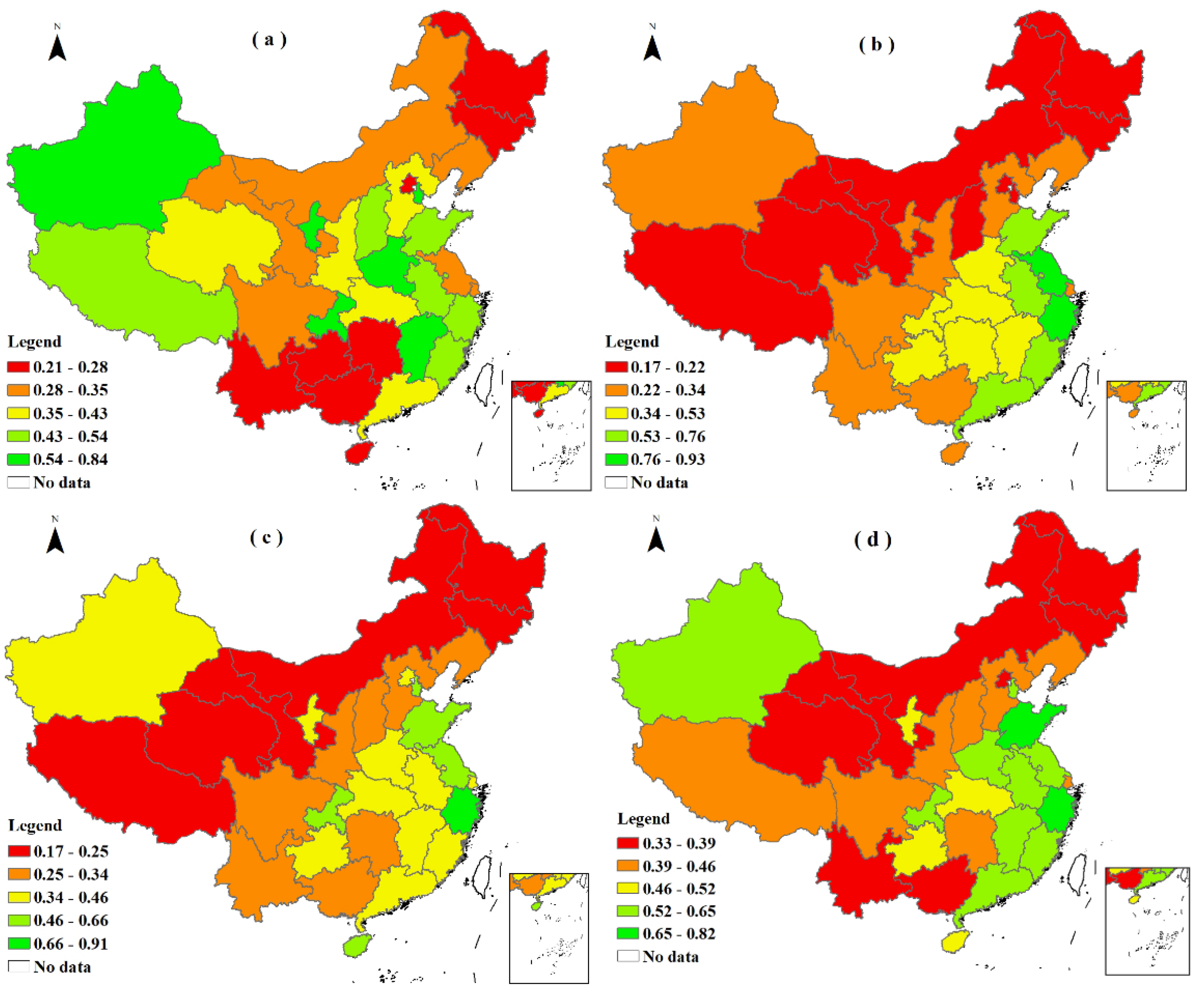
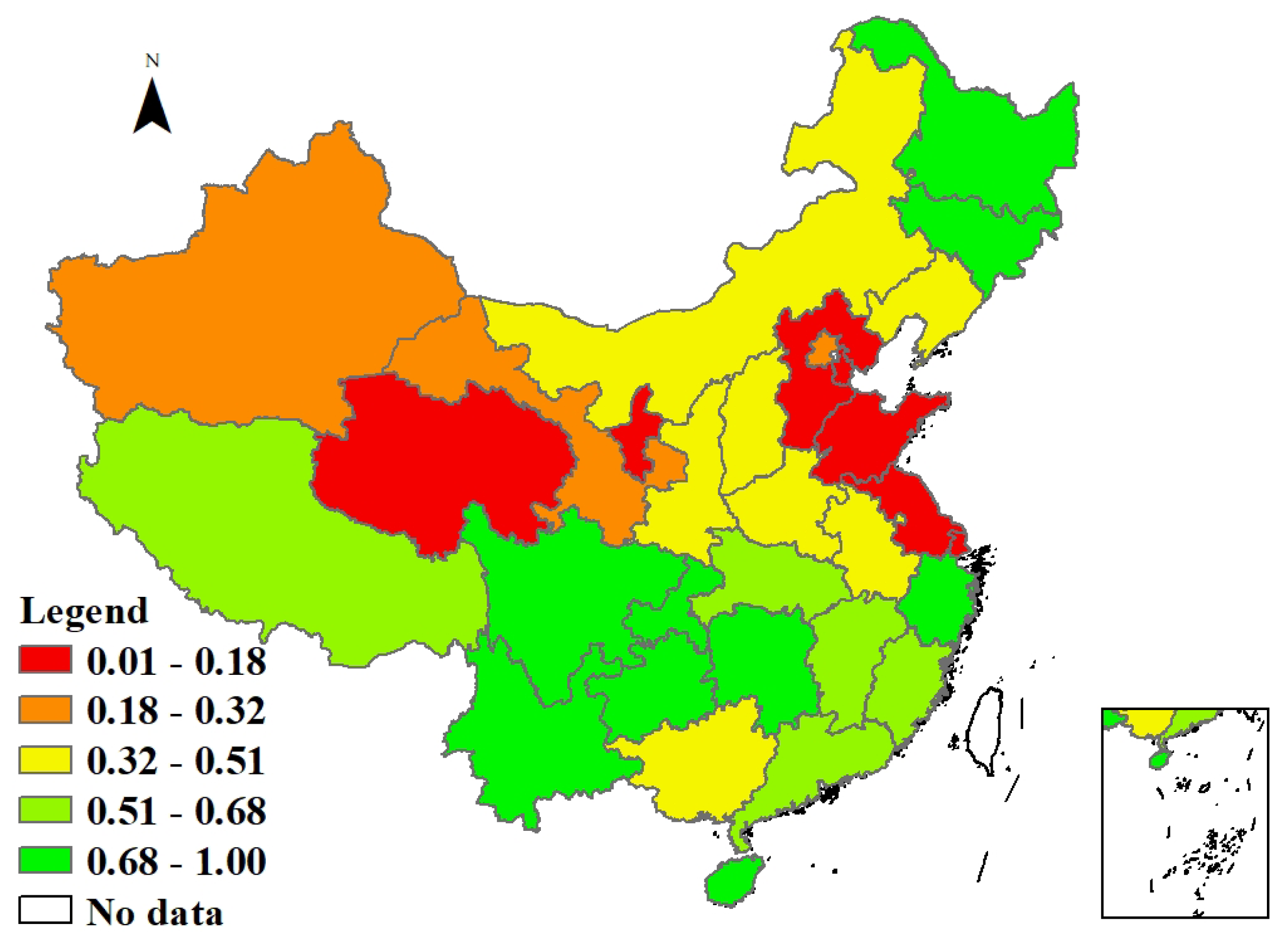
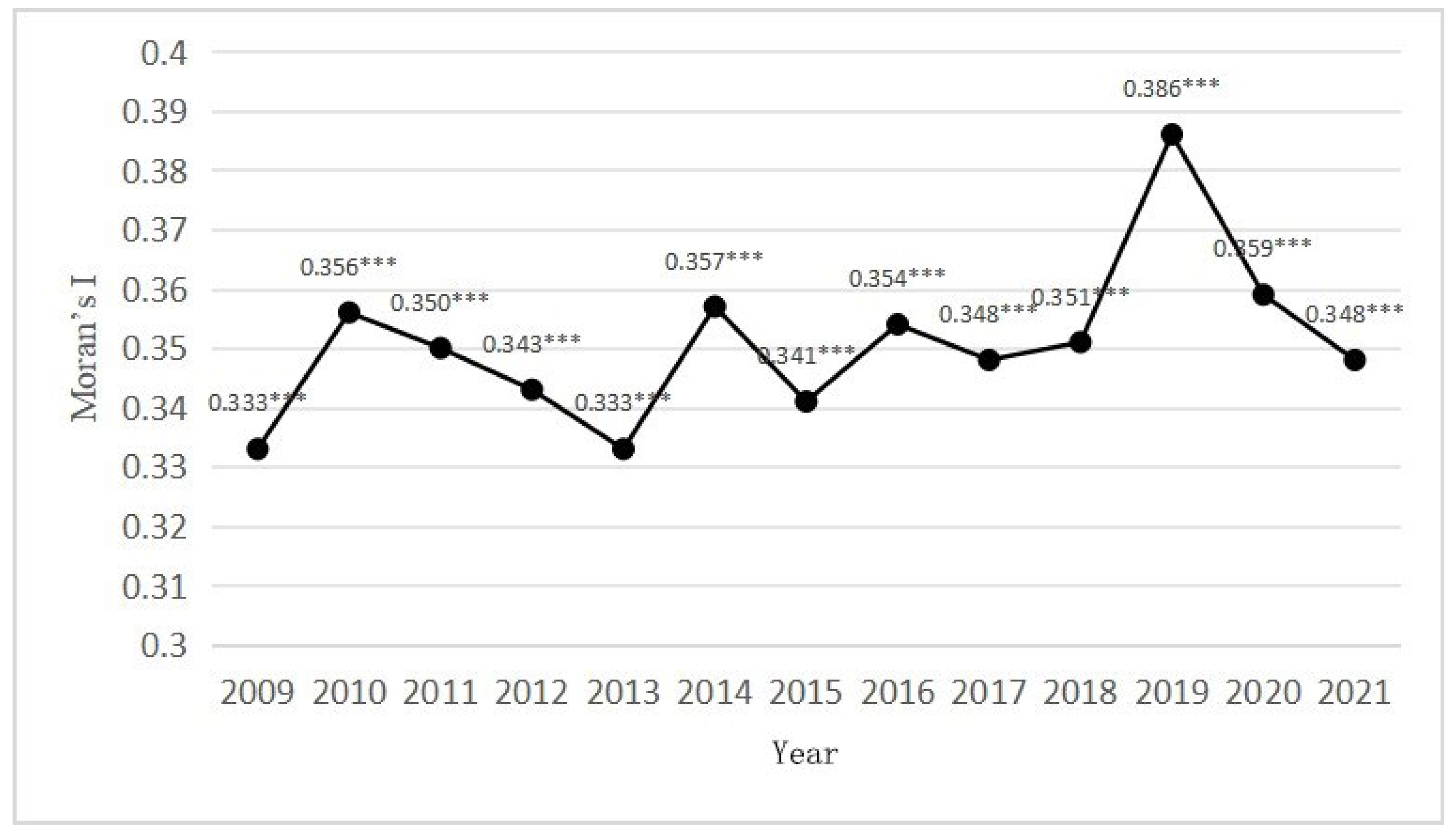
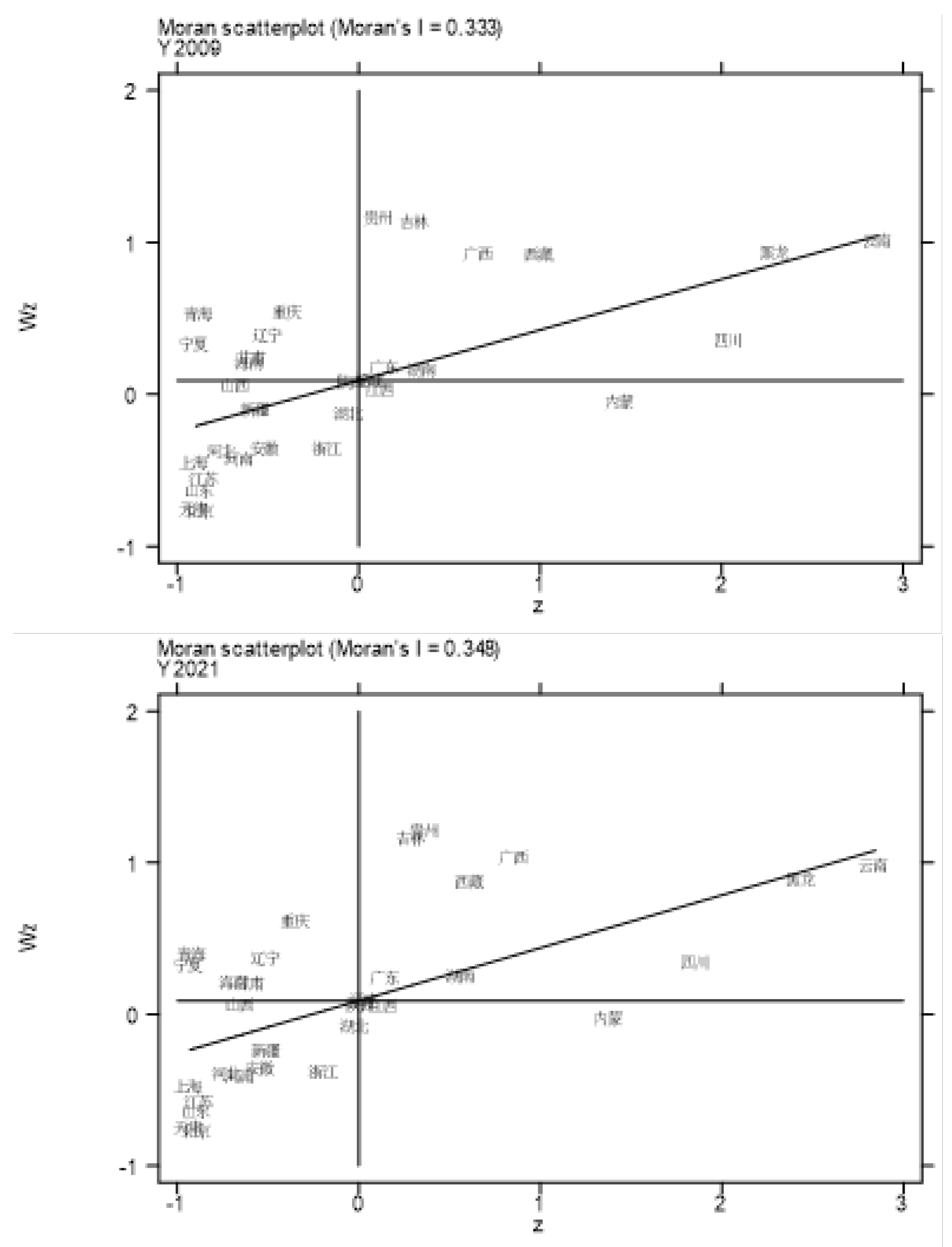
5.2. Spatial Regression Analysis of Forest Carbon Sinks in China

B In this paper, we use Stata18 to conduct Moran’s test on forest carbon sinks to examine whether there is spatial autocorrelation of forest carbon sinks in each province. The Moran’s I index and its significance level are shown in Figure 7, and it can be seen that Moran’s I indexes are all positive from 2009 to 2021, and all of them pass the 1% significance level test. It indicates that there is a significant positive spatial correlation of forest carbon sinks in China. Figure 8 shows the scatter plot of local Moran’s I index for forest carbon sinks in China in 2009 and 2021, in which most of the provinces are located in the first, second and third quadrants, and the provinces whose P-values passed the significance test in 2009 and 2021 are three, two high-high (Yunnan and Guizhou), and one low-low (Shandong), and most of the provinces show a trend of same high or same low forest carbon sinks.

According to the results of global and local spatial correlation, the spatial correlation of China’s forest carbon sinks in geospatial space is significant, and the spatial econometric model is used to analyze the spatial spillover effect of forest carbon sinks and the influencing factors. To determine the optimal spatial regression model, this paper carried out the Lagrange multiplier (LM) test, likelihood ratio (LR) test, Ward test and Hausman test, and the results are shown in Table 2. The p-values under the LM test and the Robust-LM test passed the significance test of 5% which indicates that there is a spatial error effect and spatial lag effect and rejects the use of mixed panel regression and the initial selection of the spatial Durbin model. Then the Hausman test to determine the use of fixed effects model or random effects model, In the test results, the p-value of Hausmann’s test is less than 0.05, which passes the 5% significance test, so the fixed-effects spatial Durbin model is finally chosen for the regression.

The results of regression analysis using the Spatial Durbin Model (SDM) in this paper are shown in Table 3. In the SDM model, the coefficient of the main parameter ρ is 0.385, which has an obvious positive effect and passes the significance test of 0.05, indicating that there is a spatial spillover effect between forest carbon sinks in various regions, and every 1% change in the level of forest carbon sinks in the neighbouring regions will promote forest carbon sinks in the local region to change by 0.385% in the same direction. The spatial effects of cross-efficiency of the indirect output system, annual precipitation, annual average temperature and annual sunshine hours are 2.071, -1.711, -3.814 and -4.075 respectively, indicating that the cross-efficiency of the indirect output system positively affects the forest carbon sinks in the neighbouring regions, while the annual precipitation, annual average temperature and annual sunshine hours negatively affect the forest carbon sinks in the neighbouring regions.

However, the regression coefficients of SDM are weak in reflecting the degree of influence of the explanatory variables on the explanatory variables and characteristics of spatial spillovers and need to be further measured in terms of the direct effect, indirect effect, and total effect, in which the direct effect reflects the influence of the independent variables in the region on the forest carbon sinks in the region, while the indirect effect indicates the indirect influence of the independent variables in the neighbouring regions on the forest carbon sinks in the local region, and the total effect is the sum of the direct and indirect effects, and the total utility is the sum of direct and indirect effects. The total utility is the sum of the direct effect and the indirect effect, and the measurement results are shown in Table 4.

From the impact coefficients of core variables on forest carbon sinks, the direct effect coefficients, indirect effect coefficients and total effect coefficients of the cross-efficiency of indirect output systems are -6.408, -0.948 and -7.356, respectively, which means that every 1% change in the cross-efficiency of indirect output systems will lead to a homogeneous change of forest carbon sinks in the local region by -7.356%, of which the part of the impact from the independent variables in the local region is -6.408% and -0.948% from the spillover effect of neighbouring regions, the direct and total effects passed the significance test, while the indirect effect did not pass the significance test. This result indicates that the indirect output system cross-efficiency will not hinder the development of forest carbon sinks in neighbouring regions although it will hurt forest carbon sinks in the local region.

From the coefficients of the control variables on forest carbon sinks, the direct effect coefficients, indirect effect coefficients and total effect coefficients of annual precipitation were 0.767, -2.175 and -1.408, respectively, and the direct and indirect effects passed the significance test, which indicated that annual precipitation would have a driving effect on forest carbon sinks in this region but would inhibit the growth of forest carbon sinks in the neighbouring regions. The direct effect coefficients, indirect effect coefficients and total effect coefficients of annual average temperature and annual sunshine hours are all significantly negative, with the direct effect coefficients, indirect effect coefficients and total effect coefficients of annual average temperature being -1.493, -6.628, and -8.121, and the direct effect coefficients, indirect effect coefficients and total effect coefficients of annual sunshine hours being -2.049, -7.494, and -9.543, indicating that these two factors have a negative effect on forest carbon sinks in the local region and the neighbouring regions. Hydrological function is a major function in forest ecosystems, and the circulation and distribution of water as a carrier in forest ecosystems integrates ecological functional processes such as energy flow and nutrient cycling. High temperatures and sunshine may accelerate the physiological activities of trees, thus causing an acceleration of transpiration, which results in water loss due to a poor supply of root uptake, disrupting the balance of tree metabolism and contributing to the wilting of plants; they may even cause forest fires, destroying forest resources, with destructive consequences for forests, and hindering the process of forest carbon sinks.

To further explore in depth the impact of the cross-cutting efficiency of indirect output systems on forest carbon sinks, due to the indirect output cross-efficiency is obtained from the cross-efficiency of the ecological dimension, economic dimension and social dimension through ER fusion, the core variables are replaced with the cross-efficiency of the ecological dimension, economic dimension and social dimension, and spatial regressions are re-conducted and the results obtained are as shown in Table 5 and Table 6.

In terms of the coefficient of influence of ecological dimension cross-efficiency on forest carbon sink, the direct effect coefficient, indirect effect coefficient and total effect coefficient are -2.161, 10.230 and 8.069 respectively, which means that every 1% change in ecological dimension cross-efficiency will lead to a change in the same direction of forest carbon sink in the local region by 8.069%, of which the part of the influence from the independent variable of the local region is -2.161% and the part of the influence from the spillover effect of neighbouring regions is 10.230% and the direct effect, indirect effect and total effect all pass the 1% significance test. The influence part of the spillover effect from neighbouring regions is 10.230% and the direct effect, indirect effect and total effect all passed the significance test of 1%. This result indicates that although the cross-efficiency of ecological dimensions will hurt the forest carbon sink in the local region, it has a driving effect on the improvement of the forest carbon sink in the neighbouring regions, which indicates that there is a mismatch between today’s ecological development mode and the forest carbon sink to a certain extent and that there may be a mismatch between the ecological resources that are not efficiently developed and utilized, and that do not adequately carry out the forest carbon sink, but instead inhibit the forest carbon sink Development.

In terms of the coefficient of influence of economic dimension cross-efficiency on forest carbon sinks, the direct effect coefficient, indirect effect coefficient and total effect coefficient are 1.620, -3.089 and -1.469, respectively, indicating that every 1% change in the cross-efficiency of the economic dimension will lead to a change in the same direction of forest carbon sinks in the local region by -1.469%, of which the part of the influence from the independent variable in the local region is 1.620% and the part of the influence from the spillover effect of neighbouring regions is 1.620%. spillover effects from the neighbouring regions are -3.089%. Among them, only the direct effect passed the 1% significance test, and neither the indirect effect nor the total effect passed the 10% significance test, i.e., the cross-efficiency of economic dimensions in the local region does not have a significant indirect effect on the forest carbon sinks in the neighbouring regions. Regions with high economic levels can invest more resources into the production of forest carbon sinks, thus positively affecting the change of forest carbon sinks. Further, economic growth promotes technological progress and optimises the production process of forest carbon sinks, which in turn promotes an increase in forest carbon sinks.

In terms of the coefficient of influence of social dimension cross-efficiency on forest carbon sinks, both the direct effect, indirect effect and total effect are all significantly negative, with the direct effect coefficient, indirect effect coefficient and total effect coefficient being -5.967, -9.180 and -15.147, respectively, which means that every 1% change in social dimension cross-efficiency will lead to a homogeneous change of forest carbon sinks in the local region by -15.147%. which the part of the effect from the independent variable of the local region is -5.967% and the part of the effect from the spillover effect of the neighbouring region is -9.180%. And the direct, indirect and total effects passed the 1% significance test. Excessive forestry tourism can lead to the destruction of the natural environment, on the one hand, the inappropriate behavior of tourists during tourism may lead to the destruction of natural resources, on the other hand, tourism developers may lead to the destruction of the forest land to develop the tourism project, resulting in an ecological imbalance, which will hurt the forest carbon sink.

6. Discussion

6.1. Theoretical Implication

With the deepening contradiction between economic growth and environmental concerns, coupled with the proposal of China’s “dual carbon” goal, the assessment of forest carbon sink development performance has gained paramount significance. The management of forests not only yields carbon sequestration benefits but also generates a spectrum of comprehensive advantages, including social, economic, and ecological benefits [38]. Therefore, this paper constructs a comprehensive multi-dimensional output indicator system, which contains the output benefits of forest carbon sinks in ecological, economic and social aspects, and can distinguish between direct and indirect output benefits. By constructing a spatial model of a forest carbon sink cross-evaluation system based on ER, this paper further investigates the spillover effects and the influencing factors of China’s forest carbon sinks under the perspective of cross-efficiency. The specific theoretical implications are as follows:

First, this paper constructs an input-output indicator system by considering the output benefits of forest carbon sinks in terms of ecology, economy and society, and at the same time considers the interactions between direct output benefits and indirect output benefits. Fewer studies in the existing literature construct a forest carbon sink indicator system through sub-dimensions from a comprehensive perspective, and the forest carbon sink indicator system constructed by Qiu et al. [30] only takes forest carbon sink as an output indicator, while the other indicators are used as environmental variables aimed at regulating the forest carbon sink. In the indicator system constructed by Huang et al. [13], the forest carbon sink indicator is categorised as an indicator under the ecological dimension. The indicator system constructed by the above study may not accurately reflect the full benefits brought by forest carbon sinks. Therefore, this paper constructs a more comprehensive and accurate forest carbon sink evaluation indicator system based on the full consideration of the comprehensive benefits of forest carbon sinks. In addition, a distinction is made between direct and indirect output benefits, emphasizing the importance of forest carbon sinks.

Second, this paper introduces neutral cross-evaluation and utilizes the cross- efficiency aggregation method based on conditional entropy to comprehensively consider the relationship between self-evaluation and peer evaluation of DMUs. Under the traditional self-evaluation perspective, DMUs may overestimate their own advantages when conducting self-evaluation, leading to exaggerated evaluation results [46]. Evaluating forest carbon sinks under this perspective may result in multiple areas being evaluated as effective, which is inconsistent with the reality and thus hinders decision-making [12,30]. In this paper, we measure the efficiency of forest carbon sinks based on the combined perspective of self-evaluation and peer evaluation, which solves the problem of exaggerated evaluation results.

Third, the efficiency measurement before indicator fusion in this paper can maximise the retention of the efficiency information of the indicators. The traditional method of measuring the efficiency of a multi-dimensional indicator system is generally to integrate the indicators first and then measure the efficiency [5,6,13], which will lose part of the indicator efficiency information and can only get the final efficiency results, which is not conducive to the development of specific decision-making programmed. In this paper, we first calculated the cross-efficiency of the three-level indicators, and based on this cross-efficiency, we used the ER method to integrate the indicators level by level. When evaluating the multiple output benefits of China’s forest carbon sinks based on this method, detailed decision-making analyses can be carried out based on the efficiency evaluation results of different dimensions.

Fourth, this paper analyses the spillover effects and influencing factors of China’s forest carbon sinks based on the cross-efficiency results. Although existing literature has paid attention to the spatial distribution characteristics of forest carbon sinks [29,30,47,48], there is a lack of spatial analyses of the development of forest carbon sinks under the perspective of efficiency evaluation. In this paper, the driving factors behind the development of forest carbon sinks in different regions are studied using the efficiency evaluation method, the development characteristics of forest carbon sinks in different types of regions are examined, and the results obtained can help to formulate further development plans for forest carbon sinks.

6.2. Policy Implications

Based on the conclusions drawn from the studies, the following recommendations can be considered when developing forest carbon sinks in China:

(1) Differentiated policies should be formulated about the performance level of forest carbon sinks.

Firstly, in regions with a low level of forest carbon sink performance, priority should be given to the development of forestry infrastructure, the implementation of afforestation activities, the improvement of forest cover and the enrichment of forest resources. At the same time, it focuses on improving the quality of forests, and in the process of cultivating forests, it pays attention to optimizing the structure of forest stands, selecting advantageous tree species for planting, improving the level of forest pest control, and strengthening the management of forests, to avoid the phenomenon of “focusing on afforestation but not on management, and focusing on planting but not on management and care”. Secondly, for regions with a high level of forest carbon sink performance, maintain the existing advantages of forest carbon sinks, explore the construction path of the carbon trading market, give full play to the economic value of forest carbon sinks, convert the advantages of forest carbon sinks into economic advantages, and then further improve the scientific and technological level of forest carbon sinks, to promote the more effective development of forest carbon sinks.

(2) Corresponding policy adjustments should be made for the results of the spatial spillover effect.

The social dimension of cross-efficiency on the total effect of forest carbon sinks is negative, indicating that to further improve the residents’ satisfaction with the development of forestry. Income is the material basis for improving the residents’ satisfaction, the government should actively formulate relevant policies to promote the simultaneous growth of the income of forestry employees, improve the mechanism of counterpart assistance, and give the family subsidies to forestry employees, to improve the work motivation of forestry employees. Vigorously promote forestry tourism, improve the infrastructure of forestry tourism, and promote the necessity of forest carbon sinks and the specific ways of energy saving and emission reduction to tourists during their visits, to increase people’s sense of identity. Ecological dimension cross efficiency on the region’s forest carbon sinks has a significant negative impact, indicating that today’s ecological environment development model to a certain extent and forest carbon sinks between the mismatch between the factors, failed well with the integration of forest carbon sinks development, the provinces should be tailored to the local conditions of forestry policy reform, combined with the province’s endowment of forest resources and topography and terrain of the forestry development of the spatial planning, the implementation of differentiated forestry policy, to promote the level of forest carbon sinks, the level of the forest carbon sinks. Each province should reform its forestry policy according to local conditions, consider its forest resource endowment and terrain, carry out spatial planning for forestry development, and implement differentiated forestry policies, to promote the enhancement of forest carbon sinks.

6.3. Shortcomings and Prospects

This paper evaluates the comprehensive benefits of forest carbon sinks in China and provides a spatial characterization based on the evaluation results. However, setting the weights of all indicators equal does not consider the different levels of importance of indicators in the evidential reasoning approach. The weighting information associated with the indicators could provide valuable insights into the development of decision-making scenarios for forest carbon sink development. In the future, a combination of subjective and objective methods could be used to assign weights, leading to a more nuanced understanding of how to maximize the overall benefits of forest carbon sinks, considering the spatial characteristics of the area.

7. Conclusion

Due to differences in economic development and natural resource endowments, there are significant imbalances in the regional development of forest carbon sinks in China. This paper proposes a spatial model to analyze the characteristics of China’s forest carbon sinks. Based on the cross-efficiency measurement of forest carbon sinks in each region of China from 2009 to 2021, this paper analyses the current situation and spatial characteristics of China’s forest carbon sinks. The results of the study show that:

(1) There is a large gap between the cross-efficiency levels of different regions in China, with significant spatial correlation. Based on the perspective of the direct output benefit, the cross-efficiency is higher in the eastern region and lower in the northwestern region; based on the perspective of the indirect output benefi, the cross-efficiency is higher in the southeastern region.

(2) The spatial regression model was used to explore the spatial spillover effects and influencing factors of forest carbon sinks in 31 provinces in China, and the results showed that China’s forest carbon sinks have a significant positive spillover effect, the cross-efficiency of indirect outputs, temperature and sunshine have a significant negative effect on forest carbon sinks in the local region, and the annual precipitation has a positive effect on forest carbon sinks in the local region; and the precipitation, temperature, and sunshine hurt the neighbouring regions. The effect of cross-efficiency of indirect outputs is further analyzed. Further analysis of the effects of indirect output cross-efficiency reveals that the ecological dimension cross-efficiency and social dimension cross-efficiency have a significant negative effect on forest carbon sinks in the local region, while the economic dimension has a significant positive effect on forest carbon sinks in the local region; the ecological dimension cross-efficiency has a positive effect on forest carbon sinks in neighbouring regions, while the social dimension hurts forest carbon sinks in neighbouring regions

Author Contributions

Conceptualization, Yan Huang and Siting Chen; Data curation, Siting Chen; Formal analysis, Siting Chen and Jiawei Wang; Funding acquisition, Yan Huang; Investigation, Jiawei Wang; Methodology, Yan Huang; Project administration, Yan Huang; Software, Siting Chen; Supervision, Yan Huang; Validation, Yan Huang; Visualization, Jinhuang Lin; Writing – original draft, Siting Chen; Writing – review & editing, Yan Huang. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by [the National Natural Science Foundation of China], grant number [72001042], [Fujian Agricultural and Forestry University Science and Technology Innovation Special Fund Project (Social Sciences)], grant number [CXZX2021029] and [Fujian Natural Science Foundation], grant number [FJ2022C045].

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Hua, Z.Q. Study on Shadow Price of Carbon Sinks under the Perspective of Compensation of Property Value of Forest Carbon Sinks--Taking Hunan Province as an Example. Seeker 2015, (02), 37–42. [Google Scholar]
Cai, B.F.; Zhu, S.L.; Yu, S.M.; Dong, H.M.; Zhang, C.Y.; Wang, C.K.; Zhu, J.H.; Gao, Q.X.; Fang, S.X.; Pan, X.B.; Zheng, X.H. The Interpretation of 2019 Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventory. Environmental Engineering 2019, 37, 1–11. [Google Scholar]
Roces-Díaz, J.V.; Vayreda, J.; Banqué-Casanovas, M.; Cusó, M.; Anton, M.; Bonet, J.A.; Brotons, L.; Cáceres, M.D.; Herrando, S.; Aragón4, J.M.D.; de-Miguel, S.; Martínez-Vilalta, J. Assessing the distribution of forest ecosystem services in a highly populated Mediterranean region. Ecological Indicators 2018, 93, 986–997. [Google Scholar] [CrossRef]
Xiong, S.W.; Yang, F.; Li, J.Y.; Xu, Z.N.; Ou, J.G. Temporal-spatial variation and regulatory mechanism of carbon budgets in territorial space through the lens of carbon balance: A case of the middle reaches of the Yangtze River urban agglomerations, China. Ecological Indicators 2023, 154, 110885. [Google Scholar] [CrossRef]
Ye, F.F.; Yang, L.H.; Wang, Y.M. An interval efficiency evaluation model for air pollution management based on indicators integration and different perspectives. Journal of Cleaner Production 2020, 245, 118945. [Google Scholar] [CrossRef]
Ye, F.F.; Yang, L.H.; Wang, Y.M. Estimation of Regional Environmental Pollution Intensity and Its Classified Management. Journal of Systems Science and Mathematical 2020, 40, 984–1003. [Google Scholar]
Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision-making units. European Journal of Operational Research 1978, 2, 429–444. [Google Scholar] [CrossRef]
Long, F.; Shen, Y.Q.; Wu, W.G.; Qi, H.B.; Zhu, Z.; Zhang, Z. Measurement and optimum design of carbon sequestration efficiency of regional forestland use process. Transactions of the Chinese Society of Agricultural Engineering 2013, 29, 251–261. [Google Scholar]
Wang, J.F.; Shi, K.H.; Hu, M.X. Measurement of Forest Carbon Sink Efficiency and Its Influencing Factors Empirical Evidence from China. Forests 2022, 13, 1909. [Google Scholar] [CrossRef]
Wei, J.M.; Shen, M.H. Analysis of the Efficiency of Forest Carbon Sinks and Its Influencing Factors—Evidence from China. Sustainability 2022, 14, 11155. [Google Scholar] [CrossRef]
Mlynarski, W.; Predki, A.; Kaliszewski, A. Efficiency and factors influencing it in forest districts in southern Poland: Application of Data Envelopment Analysis. Forest Policy and Economics 2021, 130. [Google Scholar] [CrossRef]
Yin, S.W.; Gong, Z.W.; Gu, L.; Deng, Y.J.; Niu, Y.J. Driving forces of the efficiency of forest carbon sequestration production: Spatial panel data from the national forest inventory in China. Journal of Cleaner Production 2022, 330, 129776. [Google Scholar] [CrossRef]
Huang, Y.; He, X.; He, S.Z.; Dai, Y.W. Efficiency evaluation of a forestry green economy under a multi-dimensional output benefit in China—Based on evidential reasoning and the cross efficiency model. sustainability 2022, 14, 13881. [Google Scholar] [CrossRef]
Qi, L.; Zhou, X.L. The Analysis of Forestry Investment Efficiency in China: Perspective of Climate Change. China Soft Science 2018, (06), 35–46. [Google Scholar]
Lin, B.Q.; Ge, J.M. Carbon sinks and output of China’s forestry sector: An ecological economic development perspective. Science of the total environment 2019, 655, 1169–1180. [Google Scholar] [CrossRef] [PubMed]
Lu, C.C.; Chiu, Y.H.; Lin, I.F.; Lin, T.Y. Dynamic total factors’ environmental efficiency in European Union countries. Environment, Development and Sustainability 2022. [Google Scholar] [CrossRef]
Xue, L.F.; Luo, X.F.; Wu, X.R. Carbon Sequestration Efficiency of Four Forest Regions in China: Measurement, Driving Factors and Convergence. Journal of Natural Resources 2016, 31, 1351–1363. [Google Scholar]
Shu, M.Y.; Wu, J.Z.; Li, C.Y.; Ding, S. Analysis of the Evolution of Forest Carbon Sinks Efficiency in Natural Forest Protection Project Regions. Issues of Forestry Economics 2022, 42, 490–497. [Google Scholar]
He, X.; Chen, L.Y.; Huang, Y. A Study of Forest Carbon Sink Increment from the Perspective of Efficiency Evaluation Based on an Inverse DEA Model. Forests 2022, 13, 1563. [Google Scholar] [CrossRef]
Chen, X.Y.; Guan, Z.J. Measurement of China’s Forestry High－quality Development Level and Analysis of Regional Differences. China Forestry Economics 2022, 172, 7–11. [Google Scholar]
Wen, S.S.; Guan, J.; Yang, Y. Construction of Evaluation Index System and Measurement of High-Quality Development of Forestry in China. Issues of Forestry Economics 2022, 42, 241–252. [Google Scholar]
Xu, M.; Chen, W.H.; Liu, J.C. Study on Evaluation Index System for Development of Green Economy in Forestry. Forestry Economics 2015, 37, 24–28. [Google Scholar]
Zhu, H.J.; Yao, S.B. Evaluation methodology for sustainable forestry development based on hybrid evaluation. Statistics & Decision 2015, 429, 64–67. [Google Scholar]
Sun, N.; Zhao, Z.; Wang, W.L. Study on the Evaluation of Forestry Sustainable Development in Weibei area of the Loess Plateau. Agricultural Research in the Arid Areas 2012, 30, 215–220. [Google Scholar]
Yang, T.; Kuo, C.W. A hierarchical AHP/DEA methodology for the facilities layout design problem. European Journal of Operational Research 2003, 147, 128–136. [Google Scholar] [CrossRef]
Lozano, S.; Villa, G. Multiobjective target setting in data envelopment analysis using AHP. Computers & Operations Research 2009, 36, 549–564. [Google Scholar]
Lin, M.I.; Lee, Y.D.; Ho, T.N. Applying integrated DEA/AHP to evaluate the economic performance of local governments in China. European Journal of Operational Research 2010, 209, 129–140. [Google Scholar] [CrossRef]
Saen, R.F.; Memariani, A.; Lotfi, F.H. Determining relative efficiency of slightly non-homogeneous decision-making units by data envelopment analysis: a case study in IROST. Applied Mathematics and Computation 2004, 165, 313–328. [Google Scholar] [CrossRef]
Xue, L.F.; Luo, X.F.; Li, R.R.; Yu, W.Z. Regional Differences and Dynamic Evolution of Forest Carbon Sink in China. Journal of China Agricultural University 2018, 23, 197–206. [Google Scholar]
Qiu, Z.X.; Feng, Z.K.; Song, Y.N.; Li, M.L.; Zhang, P.P. Carbon sequestration potential of forest vegetation in China from 2003 to 2050: Predicting forest vegetation growth based on climate and the environment. Journal of Cleaner Production 2020, 252, 119715. [Google Scholar] [CrossRef]
Liu, K.; Jiang, S.H.; Liu, W.Y. Estimation of Carbon Sequestration Value and Analysis of Space Effect of Forests in Guandong Province. Chinese Journal of Agricultural Resources and Regional Planning 2015, 36, 120–126. [Google Scholar]
Xue, L.F.; Luo, X.F.; Li, Z.L.; Wu, X.R. Spatial Spillover Effects and Influencing Factors of Forest Carbon Sink in China —Spatial Econometric Analysis Based on Forest Resources Inventory in 31 Provinces of the Mainland of China. Journal of Natural Resources 2017, 32, 1744–1754. [Google Scholar]
Fu, W.; Li, L.; Luo, M.C.; Chen, J.C.; Wang, F.L. Spatial spillover effects and influencing factors of forest carbon sink in China from a provincial perspective. Acta Ecologica Sinica 2023, 43, 4074–4085. [Google Scholar]
Du, Z.L.; Su, T.; Ge, J.M.; Wang, X. Towards the Carbon Neutrality: The Ｒole of Carbon Sink and Its Spatial Spillover Effects. Economic Research Journal 2021, 56, 187–202. [Google Scholar]
Liu, Y.; Yang, L.Y.; Zhang, J.; Zhang, J.Z.; Li, X.B.; Zhu, N.G.; Zhou, M.F. Evolution and assessment of forest carbon sink policy over the past 20 years. Acta Ecologica Sinica 2023, 43, 3430–3441. [Google Scholar]
Gu, J.L.; Lai, Y.M. Exploring and researching the mechanism of precision poverty alleviation by forest carbon sinks. China Soft Science 2022, (S1), 102–107. [Google Scholar]
Guan, B.; Shi, Z.; Ning, P.; Hou, M.M. The Enhancement Effect of Forest Carbon Sequestration on Yunnan Bridgehead Construction. Green Economy 2012, (07), 66–69. [Google Scholar]
Wu, G.Z.; Wang, H.P.; Zhou, N.D.; Li, Y.; Zeng, Q.B.; Yang, Y.M. Analysis of the Social Benefit of Forest Carbon Sequestration Industry Development in Hunan Province. Forestry Economics 2015, 37, 90–93. [Google Scholar]
Chen, Y.Z.; Feng, X.M.; Fu, B.J. Above- and belowground forest biomass carbon pool in China during 2002~2021. National Tibetan Plateau / Third Pole Environment Data Center 2023. [CrossRef]
Wang, Y.M.; Chin, K.S. A neutral DEA model for cross-efficiency evaluation and its extension. Expert Systems with Applications 2010, 37, 3666–3675. [Google Scholar] [CrossRef]
Doyle, J.; Green, R. Efficiency and Cross-efficiency in DEA: Derivations, Meanings and Uses. Journal of the Operational Research Society 1994, 45, 567–578. [Google Scholar] [CrossRef]
Wu, J.; Liang, L.; Yang, F.; Yan, H. Bargaining game model in the evaluation of decision-making units. Expert Systems with Applications 2009, 36, 4357–4362. [Google Scholar] [CrossRef]
Chen, S.T.; You, C.L.; Wu, N.; Huang, Y. Cross-efficiency Aggregation Based on Interval Conditional Entropy: An Application to Forest Carbon Sink Efficiency. Journal of Intelligent & Fuzzy Systems 2024, 46, 4397–4415. [Google Scholar]
Yang, J.B. Rule and utility-based evidential reasoning approach for multiattribute decision analysis under uncertainties. European Journal of Operational Research 2001, 131, 31–61. [Google Scholar] [CrossRef]
Wang, Y.M.; Yang, J.B.; Xu, D.L. Environmental impact assessment using the evidential reasoning approach. European Journal of Operational Research 2006, 174, 1885–1913. [Google Scholar] [CrossRef]
Sexton, T.R.; Silkman, R.H.; Hogan, A.J. Data Envelopment Analysis: Critique and Extensions. New Directions for Program Evaluation 1986, 32, 73–105. [Google Scholar] [CrossRef]
Ke, S.F.; Zhang, Z.; Wang, Y.M. China’s forest carbon sinks and mitigation potential from carbon sequestration trading perspective. Ecological Indicators 2023, 148, 110054. [Google Scholar] [CrossRef]
Lyu, X.; Li, X.B.; Wang, K.; Zhang, C.H.; Dang, D.L.; Dou, H.S.; Lou, A.R. Strengthening grassland carbon source and sink management to enhance its contribution to regional carbon neutrality. Ecological Indicators 2023, 152, 110341. [Google Scholar] [CrossRef]

Figure 1. Coupling model of forest carbon sinks cross-evaluation system based on ER.

Figure 2. Spatial distribution of cross-efficiency of forest carbon sinks based on forest carbon sinks.

Figure 3. Spatial distribution of cross-efficiency of forest carbon sinks based on (a) the area of forest conservation (b) forestry pest control area (c) afforestation area (d) ecological output benefits.

Figure 4. Spatial distribution of cross-efficiency of forest carbon sinks based on (a) the total output value of the primary industry (b) the total output value of the secondary industry (c) the total output value of the tertiary industry (d) economic output benefits.

Figure 5. Spatial distribution of cross-efficiency of forest carbon sinks based on (a) total forestry tourism (b) total economic forest products (c) wage of forest system employees (d) social output benefits.

Figure 7. Moran’s I index and its significance level.

Figure 8. Scatter plot of Moran’s I index for forest carbon sink localization in 2009, 2021.

Table 1. Comprehensive input-output indicator system of forest carbon sink.

Level 1	Level 2	Level 3
Inputs	Input (land)	Forest area
	Input (labor)	Forestry practitioners
	Input (capital)	Completion of investment in fixed assets in forestry
Direct output	Output (direct)	Forest carbon sinks
Indirect outputs	Output (ecological)	The area of forest conservation
		Forestry pest control area
		Afforestation area
	Output (economic)	The total output value of the primary industry
		The total output value of the secondary industry
		The total output value of the tertiary industry
	Output (social)	Total forestry tourism
		Total economic forest products
		Average annual wage of forest system employees on the job

Table 2. Non-spatial panel data estimation and LM test result.

inspect	statistic	p-value
LM test no spatial error	242.220***	0.000
Robust LM test no spatial error	41.020***	0.000
LM test no spatial lag	206.810***	0.000
Robust LM test no spatial lag	5.610**	0.018
LR lag	40.15***	0.000
LR Err	34.42***	0.000
Wald Lg	16.29***	0.003
Wald Err	18.37***	0.001
Hausman	72.92***	0.000

Table 3. Model regression result.

	OLS	SAR	SEM	SDM
X	-7.138***	-7.292***	-7.365***	-6.382***
X	(-8.54)	(-8.92)	(-9.04)	(-7.87)
lnD	1.062***	1.140***	1.157***	0.882***
lnD	(5.81)	(6.24)	(6.62)	(4.98)
lnE	-0.961***	-0.978***	-0.909***	-1.224***
lnE	(-2.94)	(-3.03)	(-2.89)	(-3.90)
lnF	-1.680***	-1.724***	-1.584***	-1.738***
lnF	(-4.8)	(-4.98)	(-4.74)	(-4.86)
W∙X				2.071
W∙X				(0.88)
W∙lnD				-1.711***
W∙lnD				(-3.13)
W∙lnE				-3.814***
W∙lnE				(-3.18)
W∙lnF				-4.075***
W∙lnF				(-3.01)
λ			0.330***
λ			(3.99)
ρ		0.208***		0.385***
ρ		(3.02)		(4.81)
sigma2_e		2.673***	2.605***	2.375***
sigma2_e		(14.16)	(14.06)	(14.01)
R^2	0.304	0.300	0.304	0.290

Note: *, **, *** are significant at 10%, 5% and 1% levels of significance, respectively, and the value in () is the Z-value.

Table 4. Decomposition of spatial effect.

	direct effect	indirect effect	total effect
X	-6.408***	-0.948	-7.356*
X	(-7.83)	(-0.26)	(-1.93)
lnD	0.767***	-2.175**	-1.408
lnD	(4.62)	(-2.47)	(-1.46)
lnE	-1.493***	-6.628***	-8.121***
lnE	(-4.19)	(-2.87)	(-3.21)
lnF	-2.049***	-7.494***	-9.543***
lnF	(-4.80)	(-3.23)	(-3.68)

Note: *, **, *** are significant at 10%, 5% and 1% levels of significance, respectively, and the value in () is the Z-value.

Table 5. Model regression result.

	OLS	SAR	SEM	SDM
A	-1.461**	-1.498***	-2.060***	-2.563***
A	(-2.51)	(-2.63)	(-3.46)	(-4.63)
B	1.365**	1.682**	1.641**	1.803***
B	(1.98)	(2.47)	(2.45)	(2.74)
C	-6.498***	-7.026***	-6.369***	-5.710***
C	(-7.34)	(-7.95)	(-7.40)	(-6.23)
lnD	0.751***	0.770***	-0.698***	0.568***
lnD	(3.62)	(3.73)	(3.53)	(2.85)
lnE	-0.618*	0.579*	-0.589*	-0.592*
lnE	(-1.92)	(-1.84)	(-1.94)	(-1.89)
lnF	-1.574***	-1.641***	1.543***	-1.617***
lnF	(-4.64)	(-4.94)	(-4.85)	(-4.73)
W∙A				8.127***
W∙A				-4.99
W∙B				-2.422
W∙B				(-0.97)
W∙C				-5.121*
W∙C				(-1.81)
W∙lnD				-0.114
W∙lnD				(-0.17)
W∙lnE				-0.687
W∙lnE				(-0.56)
W∙lnF				-2.172
W∙lnF				(-1.63)
λ			0.360***
λ			(4.28)
ρ		0.230***		0.313***
ρ		(3.44)		(3.7)
sigma2_e		2.440***	2.380***	2.124***
sigma2_e		(14.16)	(-4.85)	(14.07)
R^2	0.354	0.349	0.352	0.376

Note: *, **, *** are significant at 10%, 5% and 1% levels of significance, respectively, and the value in () is the Z-value.

Table 6. Decomposition of spatial effect.

	direct effect	indirect effect	total effect
A	-2.161***	10.230***	8.069***
A	(-4.13)	(4.22)	(3.36)
B	1.620***	-3.089	-1.469
B	(2.94)	(-0.97)	(-0.45)
C	-5.967***	-9.180***	-15.147***
C	(-6.48)	(-2.71)	(-3.92)
lnD	0.592***	0.130	0.722
lnD	(2.6)	(0.12)	(0.61)
lnE	-0.714*	-1.272	-1.986
lnE	(-1.87)	(-0.7)	(-0.98)
lnF	-1.767***	-3.683**	-5.450**
lnF	(-4.76)	(-1.72)	(-2.29)

Note: *, **, *** are significant at 10%, 5% and 1% levels of significance, respectively, and the value in () is the Z-value.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Study on Spatial Spillover Effect of Forest Carbon Sink Efficiency in China considering Multiple Output Benefits

Abstract

1. Introduction

2. Literature Review

3. Indicator System Construction and Data Sources

3.1. Construction of Input-Output Indicator System

3.2. Spatial Regression Modelling Indicator System

3.3. Sources of Data

4. Spatial Modelling of Forest Carbon Sink Cross-Evaluation System Based on Evidence-Based Reasoning

4.1. Measurement of Cross-Efficiency of Forest Carbon Sinks

4.2. Information Fusion for Cross-Efficiency Based on ER

4.3. Spatial Regression Model

5. Results

5.1. Results of Cross-Efficiency Evaluation of Forest Carbon Sinks

5.2. Spatial Regression Analysis of Forest Carbon Sinks in China

6. Discussion

6.1. Theoretical Implication

6.2. Policy Implications

6.3. Shortcomings and Prospects

7. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe