An Analytical Approach to Power Optimization of Concentrating Solar Power Plants with Thermal Storage

Preprint

Article

An Analytical Approach to Power Optimization of Concentrating Solar Power Plants with Thermal Storage

Altmetrics

Downloads

126

Views

Comments

A peer-reviewed article of this preprint also exists.

Andrii Cheilytko^*

,Spiros Orestis Alexopoulos,

Andriy Pozhuyev

,Oliver Kaufhold

Andrii Cheilytko^*

,Spiros Orestis Alexopoulos,

Andriy Pozhuyev

,Oliver Kaufhold

This version is not peer-reviewed

Submitted:

08 May 2024

Posted:

10 May 2024

You are already at the latest version

Alerts

Abstract

This paper deals with the problem of determining the optimal capacity of Concentrated Solar Power (CSP) plants, especially in the context of hybrid solar power plants. This work presents an innovative analytical approach to optimize the capacity of concentrated solar plants. The proposed method is based on the use of additional non-dimensional parameters, in particular the design factor and the solar multiple factor. The paper presents a mathematical optimization model that focuses on the capacity of concentrated solar power plants where thermal storage plays a key role in the energy source. The analytical approach provides a more complete understanding of the design process for hybrid power plants. In addition, the use of additional factors and the combination of the proposed method with existing numerical methods allows for a more refined optimization, which allows for a more accurate selection of the capacity for specific geographical conditions. Importantly, the proposed method significantly increases the speed of computation compared to traditional numerical methods. Finally, the authors present the results of the analysis of the proposed system of equations for calculating the levelized cost of electricity (LCOE) for hybrid solar power plants. The nonlinearity of the LCOE on the main calculation parameters is shown.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Current developments in the world once again demonstrate the need for reliable, readily available and predictable access to (electrical) energy. Solar energy can be a good source of long-term, reliable energy that is independent of specific market players. The fluctuating availability of the local energy supply via sunshine must be balanced in order to provide electrical energy according to the current demand from the grid. Concentrating Solar Power (CSP) provides relatively easy access to medium-term energy storage in the form of heat that can be converted to electricity on demand. There are line-focusing and point-focusing CSP systems.

Point source CSP plants concentrate sunlight from a large area via mirrors (heliostats) onto a small receiver aperture at the top of a tower, which can easily reach temperatures above 1000°C. Due to the potential to reach high temperatures, solar tower plants (STP) also offer good opportunities for chemical processing to produce substances that act as storage and/or fuel for other processes (ammonia, H2, etc.).

Line-focusing CSP plants use parabolic mirrors to concentrate sunlight onto receiver tubes through which a heat transfer fluid flow. Parabolic trough plants (PTP) typically operate in the 300-400°C temperature range.

In solar towers and parabolic troughs, the heat generated can be stored in molten salt storage tanks and converted into electricity by a power unit. The power unit consists of a heat engine using a thermodynamic cycle and a generator. The design of a CSP plant is mainly determined by the size of the solar field and receiver, the storage capacity, and the gross electrical rated output of the power unit.

The operating costs of generating electricity and meeting demand generally increase with the size of the components. At the same time, the capital cost per unit of electricity decreases. In addition, the estimation of these values is highly dependent on the daily and monthly variations of solar energy as well as the energy demand schedule. The balance between demand and generation is achieved by energy storage. Thus, the dependence of the cost of electricity on the capacity of the planned storage initially decreases with the increase of the storage capacity, and after reaching the optimum, it begins to decrease sharply. Therefore, finding the economically optimal design for a given site and demand profile becomes a non-trivial task that can be solved using optimization methods. In this article, a new analytical optimization approach is proposed to investigate the fraction of available solar energy that should be used by CSP at a given site, so that the rest can be covered by other systems (e.g. PV).

The object of the study is the projected concentrated solar power plant as a part of hybrid renewable power plants. The subject of the study is a functional dependence between the levelized cost of electricity and the fraction of the projected CSP power. The purpose of the article is to build a target function to determine the optimal integrated CSP capacity to obtain the minimum levelized cost of electricity.

2. Materials and Methods

The issue of power optimization in CSP plants is raised by different authors to determine the features of a hybrid CSP plant [1], to develop a strategy to mitigate the effects of high-power electricity shortages [2], to investigate the impact of weather forecast uncertainties [3] or to improve the efficiency of CSP cavity absorbers [4]. Optimization of the mirror field design is a trade-off between optical performance and cost. One of the most effective procedures for determining the characteristics of the mirror field is to determine the radial shift [5]. In this paper, it is proposed to consider the optimization of solar power plant capacity embedded in a hybrid system to determine the main parameters of influence on which to focus and to find new engineering solutions to improve CSP plants.

The main criteria for the implementation of solar power plants is the determination and comparison of the following values: levelized cost of electricity (LCOE), net present value of the project (NPV), benefit to cost ratio (BCR) and annual load satisfaction factor (ALSF) [6]. According to the authors, the most influential of the above criteria that affects the use of CSP and the construction of new plants is the price per kWh of electricity produced: the LCOE. At a given power consumption and the nature of the change in solar radiation during the year (given by the schedule of solar radiation per m² for the duration of the year), it is necessary to determine the characteristic parameters of the CSP (solar receiver, tower height, field size and layout, power block size, thermal energy storage (TES) size) considering the minimization of the price per kWh of electricity produced.

The available solar power of the solar power plant

N_{D N I}^{a v a i l}

and its geographically advantageous location are determined on the basis of GIS-assessment (geographical information system) using the average of the annual sums of direct normal irradiation (DNI) [7]. As a rule, this task is solved with the help of state-of-the-art tools to optimize LCOE of CSP plants like SAM (NREL) or Greenius from DLR [8,9].

SAM is a techno-economic computer model designed to facilitate decision making for people involved in the renewable energy industry [10]. For example, a model of SUPCON Delingha 50 MW MS ST plant was developed with SAM and a simulation took place in order to calculate the annual electrical output performance of the commercial power plant [11]. SAM is very useful tool making it possible for solar energy professionals to analyse photovoltaic systems and concentrating solar power parabolic trough systems in the same modelling platform using consistent financial assumptions.

Greenius is a simulation tool for the annual yield assessment of solar energy systems. It can be used to calculate the operation of a solar power plant depending on irradiance data in hourly or sub-hourly fidelity using a set of technical parameters to define the plant design as well as a predefined operation strategy. It is usually used to evaluate a typical operational year (TOY) of a solar power plant with operational results describing the plant state in every time step of a typical meteorological year (TMY). With the results of the TOY and additional economic parameters defining the costs and financing a detailed economic evaluation can be done, calculating the cash flow and key performance indicators like the levelized costs of electricity (LCOE) and the capacity factor (CF). The modeling in Greenius is based on energy flow between the components assuming a steady state behavior. Some transient effects in the scope of the time step size are accounted for using simplified equations. Such effects occur for components with large thermal inertia e.g. the heat up and cool down process of the solar field or the power block. To optimize a plant layout for a certain site, Greenius can be used to evaluate different plant designs via grid search with varying technical parameters and compare the results using the key performance indicators.

In contrast to the numerical solution, the authors propose here an analytical approach to optimization. The analytical approach is simple and fast to solve and allows minimizing the investment to obtain a profit close to the maximum. It also shows the capacity limit below which the construction of a CSP plant is not cost-effective. The analytical approach to the equation also allows the designer of a CSP plant to quickly perform a comprehensive analysis and find the conditions under which the LCOE at a given site will change its character. This, in turn, will allow to analyze how to change the conditions in order to change the optimum of the LCOE function. It is planned that the proposed analytical approach, in combination with existing LCOE calculation software, will allow a comprehensive analysis of the optimization of several variables in the design process of CSP plants.

The proposed analytical approach is centered around the incorporation of the design factor and the solar multiple factor into a mathematical optimization model. This model specifically targets the power capacity of concentrated solar power plants with thermal storage as the primary energy source.

Hybrid CSP systems that combine the best of CSP and PV renewable energy. By seamlessly integrating solar thermal and electrical conversion methods, these systems ensure a consistent and efficient power supply, harnessing the sun's energy from dawn to dusk. With the added benefit of energy storage integration, hybrid CSP systems promise uninterrupted power even during periods of low sunlight or high demand.

In optimization models, the input information is the load forecast data and the projected electricity demand. The amount of electricity to be generated is defined as:

E_{y e a r}^{n e e d} = E_{y e a r}^{C S P} + E_{y e a r}^{P V},

(1.1)

E_{y e a r}^{C S P} = \int_{0}^{τ} P d t = P_{C S P}^{m a x} {\cdot h}_{C S P}^{m a x}

(1.2)

where

τ

- the time period considered;

P_{C S P}^{m a x}

– Necessary electric power to fulfill the demand schedule from CSP;

h_{C S P}^{m a x}

- the number of hours of operation per year, according to which the amount of electricity produced will be equal to the yearly energy consumption.

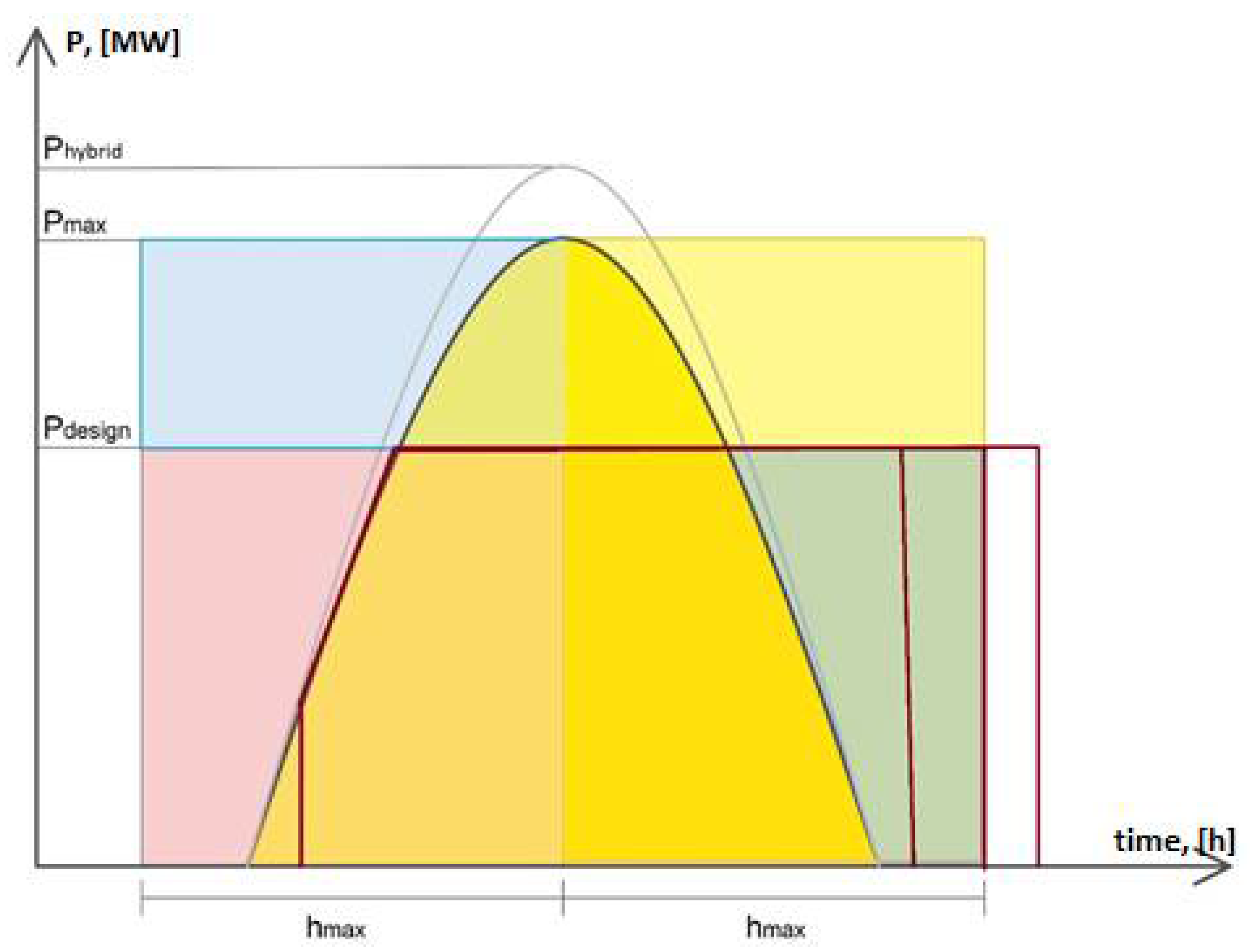
Figure 1 shows the main considerations regarding the dependence of the required CSP power demand on the CSP operating time. The area of the graph (dark yellow) corresponds to the CSP power demand. If we represent the selected area (the same amount of electricity generated) as a rectangle with a height of

P_{C S P}^{m a x}

, we obtain the imaginary number of hours h max that the CSP should operate to obtain

E_{y e a r}^{n e e d}

. If a CSP is designed with less than the required capacity for a given area

P_{C S P}^{d e s i g n}

, the lack of electricity can be compensated by energy storage and PV. Thus, the red line shows the theoretical operation of a CSP plant with a capacity of

P_{C S P}^{d e s i g n}

and possible three periods of plant shutdown (2, 4 and 6 hours of energy storage operation).

Therefore:

h_{C S P}^{m a x} = \frac{E_{y e a r}^{C S P}}{P_{C S P}^{m a x}}

(2)

Electricity generation per year:

E_{y e a r}^{d e s i g n} = P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x}

(3)

Electricity available generation per year is given through:

E_{y e a r}^{a v a i l a b l e} = P_{C S P}^{d e s i g n} \cdot h_{C S P}^{a v a i l a b l e}

(3)

where

h_{C S P}^{a v a l i b l e} -

the number of hours of rated operation per year depending on the available energy from the sun

After one receives:

E_{y e a r}^{a v a i l a b l e} = E_{y e a r}^{d e s i g n} \cdot \frac{h_{C S P}^{a v a i l a b l e}}{h_{C S P}^{m a x}}

(4)

h_{C S P}^{a v a l a b l e} = h_{C S P}^{m a x}

then

E_{y e a r}^{a v a i l a b l e} = E_{y e a r}^{d e s i g n}

The target function of the complex optimization of energy supply is the sum of the specific reduced costs of electricity, €/(MWh). For this approach, the concept of the levelized costs of electricity (LCOE) to define the economically viable specific costs of electricity production in €/MWh is used:

L C O E = \frac{\sum_{y = 0}^{Y} \frac{C_{y}}{{(1 + i)}^{y}}}{\sum_{y = 1}^{Y} \frac{E_{y}}{{(1 + i)}^{y}}}

(5)

where C_y – investment expenditures in period y;

E_y – produced energy in period y;

Y – total number of years considered for the operation of the plant;

i – considered discount rate.

Using the assumption of constant yearly operational costs defined as operational expenditures (OPEX) and the capital invested in the beginning defined as capital expenditures (CAPEX) as well as a constant yearly electricity production of E_year, the annuity factor to simplify the equation is introduced to:

L C O E = \frac{C R F \cdot C A P E X + O P E X}{E_{y e a r}}

(6)

The capital recovery factor

C R F = \frac{{(1 + i)}^{Y} \cdot i}{{(1 + i)}^{Y} - 1}

(7)

A weighted average cost of capital method [12] for the discount rate is used to depict the costs of equity

i_{e q u}

and debt

i_{d e b t}

less the income taxes:

W A C C = (1 - f_{d e b t}) \cdot i_{e q u} + f_{d e b t} \cdot (1 - r_{t a x, i n c}) \cdot i_{d e b t} .

(8)

To account for further tax costs the fixed charge rate FCR following [12] is introduced:

F C R = C R F \cdot \frac{1 - r_{t a x, i n c} \cdot P V_{d e p r}}{1 - r_{t a x, i n c}} .

(9)

The depreciable money benefits can be calculated depending on the present value of the depreciated cash flows assuming a linear depreciation schedule:

P V_{d e p r} = \sum_{y = 1}^{Y_{d e p r}} \frac{1}{Y_{d e p r} \cdot {(1 + W A C C)}^{y}}

(10)

To represent the optimal yearly electricity production in consideration of the production costs and the demand coverage ratio the LCOE is extended by further specific cost components in €/MWh representing the specific reduced cost due to the damage caused by the network failure flow

Z_{C S P}^{f a i l}

and costs due to penalties

Z_{C S P}^{p e n a l t i e s}

L C O E = \frac{F C R \cdot C A P E X + O P E X}{E_{y e a r}} + Z_{C S P}^{f a i l} + Z_{C S P}^{p e n a l t i e s} \to m i n

(11)

According to the life cycle assessment performed in the article [13] the operation phase decreases with increasing capital expenditures in CSP. So

O P E X = f (α_{C S P} {\cdot N}_{D N I}^{a v a i l})

. But there is still no specific model for building an optimization function for changing the cost of electricity from the power of the plant.

3. The Proposed Function of Optimization

3.1. The Mathematical Model

For CSP with thermal storage, it is necessary to design the solar field larger than the required thermal load for the power unit. Therefore, the solar multiple coefficient (SM) [14,15] is introduced as the ratio of the available thermal power from the solar field to the input thermal power of the power unit:

S M = \frac{{\dot{Q}}_{S F}^{m a x}}{{\dot{Q}}_{P B}^{d e s i g n}}

(12.1)

where

{\dot{Q}}_{S F}^{m a x}

– thermal power output of the solar field at reference DNI value;

{\dot{Q}}_{P B}^{d e s i g n}

– design nominal electric output power CSP according to its efficiency;

For averaged values:

S M = \frac{P_{C S P}^{m a x}}{P_{C S P}^{d e s i g n}} \frac{η_{C S P}^{d e s i g n}}{η_{C S P}^{m a x}}

(12.2)

where

η_{C S P}^{m a x}

and

η_{C S P}^{d e s i g n}

– the effectiveness CSP for

P_{C S P}^{m a x}

and

P_{C S P}^{d e s i g n}

η_{C S P}

– efficiency SCP, in this study is assumed to be linearly dependent on the receiver efficiency, then according to [16]

η_{C S P}

a \cdot l n (f_{j}) + b

here a,b- const a > 0, b < 1. Hence

η_{C S P}

does not depend on

α_{C S P}

The amount of electricity to be produced by the CSP plant is given by:

E_{y e a r}^{C S P} = E_{y e a r}^{d e s i g n} + E_{y e a r}^{T E S}

(13.1)

where

E_{y e a r}^{T E S}

– energy from thermal storage. So:

E_{y e a r}^{C S P} = P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x} + E_{y e a r}^{T E S}

(13.2)

To find the analytical optimization function, the concept of the design factor by analogy with a combined heat and power plant is introduced as in [17]. Here a coefficient equal to the ratio of the CSP capacity to the maximum required capacity of the power plant,

α_{C S P} \in [0, 1]

is defined as:

α_{C S P} = \frac{P_{C S P}^{m a x}}{P_{n e e d}^{m a x}}

(14)

where

P_{C S P}^{m a x}

– design nominal electric output power of the CSP according to its efficiency

P_{n e e d}^{m a x}

- maximum required electric output power of the hybrid plant from demand schedule

P_{n e e d}^{m a x} = I \frac{P_{C S P}^{m a x}}{α_{C S P}}

maximum required electric output power of the CSP plant from demand schedule (design power of the entire power plant), so

E_{y e a r}^{n e e d} = P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x} + E_{d a y}^{T E S} \cdot d a y + (1 - α_{C S P}) {\cdot P}_{n e e d}^{m a x} {\cdot h}_{C S P}^{m a x}

(15)

where

E_{d a y}^{T E S}

– energy from storage, MWh/day,

day – the number of days per year of CSP working time.

Storage capacity relative to the nominal thermal input power of the power block in h/day is calculated with:

C P_{T E S} = \frac{Q_{d a y}^{T E S}}{{\dot{Q}}_{P B}^{d e s i g n}} = \frac{Q_{d a y}^{T E S} \cdot η_{p o w}}{P_{C S P}^{d e s i g n}}

(16.1)

where

η_{p o w}

- efficiency of the power block;

Q_{d a y}^{T E S}

– thermal energy storage capacity in MWh/day,

Q_{d a y}^{T E S} = {E_{d a y}^{T E S} / η}_{T E S}

(16.2)

E_{y e a r}^{T E S} = E_{d a y}^{T E S} \cdot \frac{h_{C S P}^{m a x}}{24}

(16.3)

Therefore

E_{y e a r}^{n e e d} = P_{C S P}^{d e s i g n} \cdot h_{h y b r i d}^{m a x} + \frac{C P_{T E S}}{η_{p o w}} {\cdot P}_{C S P}^{d e s i g n} \cdot η_{T E S} \cdot \frac{h_{h y b r i d}^{m a x}}{24} + P_{C S P}^{m a x} \cdot \frac{1 - α_{C S P}}{α_{C S P}} {\cdot h}_{h y b r i d}^{m a x};

(17.1)

E_{y e a r}^{n e e d} = P_{C S P}^{d e s i g n} \cdot h_{h y b r i d}^{m a x} [1 + \frac{η_{T E S}}{η_{p o w}} \cdot C P_{T E S} \cdot \frac{1}{24} + S M \cdot \frac{η_{C S P}^{m a x}}{η_{C S P}^{d e s i g n}} \frac{(1 - α_{C S P})}{α_{C S P}}];

(17.2)

E_{y e a r}^{C S P + T E S} = P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x} [1 + \frac{η_{T E S}}{η_{p o w}} \cdot C P_{T E S} \cdot \frac{1}{24}];

(17.3)

h_{C S P}^{m a x} = \{\begin{matrix} h_{C S P}^{a v a i b l e}, if h_{C S P}^{m a x} > h_{C S P}^{a v a i b l e} \\ \frac{E_{y e a r}^{n e e d}}{P_{C S P}^{d e s i g n} [1 + \frac{η_{T E S}}{η_{p o w}} C P_{T E S} \cdot \frac{1}{24}]}, if h_{C S P}^{m a x} < h_{C S P}^{a v a a b l e} \end{matrix}

(17.2)

This equation shows the relationship between the necessary energy and the designed capacity of the CSP output unit through the parameters

C P_{T E S}, S M, α_{C S P}

and the efficiency of the plant. Assume, that depend of efficiency CSP on receiver efficiency is known. Then

P_{C S P}^{d e s i g n}

is dependent on three parameters

C P_{T E S}, S M a n d α_{C S P}

To reduce the number of input parameters, let's define the location where the CSP is designed. The electrical power of the CSP depends on the efficiency, the DNI value and the mirror area.

Area of solar field for range

P_{C S P}^{m a x}

A_{C S P}^{m a x} = S M {\cdot A}_{C S P}^{d e s i g n} = \frac{E_{y e a r}^{C S P}}{\int_{0}^{n} D N I^{n} d h \cdot η_{C S P}^{d e s i g n}}

(18)

where

d h -

hours of DNI data resolution.

Assuming a constant efficiency for the normalized available operating hours the following equation results:

h_{C S P}^{m a x} = \frac{\int_{0}^{n} D N I^{n} \cdot d h \cdot S M {\cdot A}_{C S P}^{d e s i g n}}{P_{C S P}^{m a x} {\cdot η}_{C S P}^{d e s i g n}}

(19)

where

A_{C S P}^{d e s i g n}

– area of the solar field for reach

P_{C S P}^{d e s i g n e}

To consider the minimum and maximum capacity of the power generation system during deviations from the selected average value

D N I^{n} = \{\begin{matrix} 0 f o r D N I^{n} \leq 10 % \cdot D N I^{d e s i g n} \\ D N I^{n} f o r {10 % \cdot D N I^{d e s i g n} \leq P}_{C S P}^{n} \leq 120 % \cdot D N I^{d e s i g n} \\ 120 % \cdot D N I^{d e s i g n} f o r D N I^{n} \geq 120 % \cdot D N I^{d e s i g n} \end{matrix}

(20)

Assuming that excess power is generated due to deviations between maximum power generation and design and is fed into the energy storage, the following equation results:

C P_{T E S} = \frac{(E_{y e a r}^{C S P} {- E}_{y e a r}^{d e s i g n}) \cdot η_{p o w}}{P_{C S P}^{d e s i g n} \cdot η_{T E S}} \frac{24}{h_{C S P}^{m a x}}

(21.1)

and use the equation 18:

C P_{T E S} = \frac{(S M {\cdot A}_{C S P}^{d e s i g n} \int_{0}^{n} D N I^{n} \cdot d h \cdot η_{C S P}^{d e s i g n} - P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x}) \cdot η_{p o w}}{P_{C S P}^{d e s i g n} \cdot η_{T E S}} \frac{24}{h_{C S P}^{m a x}}

(21.2)

Or suppose that the energy for the energy storage is extracted by increasing the area of the mirror field, then the following equation can be used:

C P_{T E S} = \frac{({P_{C S P}^{m a x} η_{C S P}^{d e s i g n} h}_{C S P}^{m a x} - P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x}) \cdot η_{p o w}}{P_{C S P}^{d e s i g n} \cdot η_{T E S}} \frac{24}{h_{C S P}^{m a x}}

(22.1)

C P_{T E S} = 24 \frac{(P_{C S P}^{m a x} η_{C S P}^{d e s i g n} - \frac{P_{C S P}^{m a x}}{S M} \frac{η_{C S P}^{d e s i g n}}{η_{C S P}^{m a x}}) η_{p o w}}{\frac{P_{C S P}^{m a x}}{S M} \frac{η_{C S P}^{d e s i g n}}{η_{C S P}^{m a x}} \cdot η_{T E S}}

(22.2)

C P_{T E S} = 24 \frac{(S M - 1) \cdot η_{p o w}}{η_{T E S}}

(22.3)

Given that the dependence

A_{C S P}^{d e s i g n}

is determined by the type and internal characteristics of the designed CSP, it is assumed that

{(\frac{A_{C S P}^{d e s i g n}}{P_{C S P}^{d e s i g n}})}_{r e f}

is known.

In reality, not all of the solar energy can be used because the storage has a maximum capacity and the components need to warm up and cool down. Depending on the storage size, the irradiance distribution, the sunshine hours and the solar multiplier, the real normalized operating hours can be defined as

h_{C S P}^{a v a i l a b l e} = h_{C S P}^{m a x} - f (f_{j}, h_{s d}, {D N I}^{r e f})

(24)

where

{D N I}^{r e f}

- reference DNI for the normalized value for operating hours;

h_{s d}

- sunshine duration, h/ year;

f_{j}

- relative load corresponding to the average arrival of solar radiation [18]

f_{j} = \frac{e x p (- β \cdot \frac{D_{j} - D_{m i n}}{D_{m a x} - D_{m i n}})}{\sum_{j = 1}^{J} e x p (- β \cdot \frac{D_{j} - D_{m i n}}{D_{m a x} - D_{m i n}})}

(25)

where

D_{m a x} a n d D_{m i n}

− denotes to the maximum and minimum distance among historical days to the current forecasting day, respectively.

β is a free parameter controlling the effective number of profiles which are averaged

Dj - is the distance between the current day and the historical day

The accuracy of load forecasting for CSP is directly affected by input uncertainties such as weather forecast. These are specified by black box models, or white box models, to provide a probabilistic load forecast [19]. Using Gaussian kernel density estimation, the procedure converts the point load forecast into a probabilistic load forecast based on historical data provided by the internal and external monitoring system.

3.2 The Function of Optimization

The target function is the following:

\begin{array}{l} L C O E = \frac{F C R \cdot C A P E X + O P E X}{P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x} [1 + \frac{η_{T E S}}{η_{p o w}} \cdot C P_{T E S} \cdot \frac{1}{24} + S M \cdot \frac{η_{C S P}^{m a x}}{η_{C S P}^{d e s i g n}} \cdot \frac{1 - α_{C S P}}{α_{C S P}}]} + Z_{C S P}^{f a i l} \\ + Z_{C S P}^{p e n a l t i e s} \to m i n \end{array}

(26)

where

Z_{C S P}^{f a i l}

- mathematical expectation of the specific impaired value due to losses caused by the flow of failures in the network;

Z_{C S P}^{p e n a l t i e s}

- the cost and the penalty function.

The CAPEX can be divided into overnight capital costs OCC and costs that for network connections

C_{t r a n s i t}

as well as costs for financing the construction

C_{f i n}

C A P E X = O C C + C_{t r a n s i t} + C_{f i n}

(27.1)

The EPC costs are divided into component costs, land costs including preparation and service costs and are extended by a contingencies factor

f_{c o n t}

. The OCC cost components all depend on the size of the plant and therefore on

α_{C S P}

. The scaling can be done using an exponential economy of scale relationship as described in [20].

O C C = {O C C}_{C S P} + {O C C}_{P V};

(27.2)

{O C C}_{C S P} = {(C}_{c o m p}^{m a x} \cdot {(α_{C S P})}^{s_{c o m p}} + C_{s e r v i c e}^{m a x} \cdot {(α_{C S P})}^{s_{s e r v i c e}} + C_{l a n d}^{m a x} \cdot α_{C S P}) \cdot f_{c o n t};

(27.3)

{O C C}_{P V} = {(C}_{c o m p}^{m a x} \cdot ({1 - α}_{C S P}) + C_{s e r v i c e}^{m a x} \cdot ({1 - α}_{C S P}) + C_{l a n d}^{m a x} \cdot (1 - α_{C S P})) \cdot f_{c o n t};

(27.4)

where C_comp – Capital investment for all components and equipment in €,

C_service – Capital investment for all engineering, procurement and construction services in €

C_{l a n d}

– Capital investment to purchase and prepare the land in €

f_cont – contingencies relative to the investment costs in %

s_comp – exponential scaling factor for component costs, s_comp in [0.7, 0.9] [20]

s_service – exponential scaling factor for service costs, s_service in [0.3, 0.5] [20]

C_{s e r v i c e}^{m a x} = C_{c o m p}^{m a x} \cdot f_{s e r v i c e}

(27.5)

where f_service – factor of service costs to component costs, usually around 5 % [20]

The transit costs are mainly associated with the construction of transit networks from the CSP to the distribution point:

C_{t r a n s i t} = К_{m a x}^{t r} \cdot n \cdot η_{t r} \cdot L_{в} + Z_{m i n}^{t r} \cdot E_{y e a r}^{n e e d}

(27.6)

where

К_{m a x}^{t r}

- capital investments in electricity transit networks, €/ m;

n - the number of parallel strands of wire 1 or 2;

η_{t r}

- network performance indicator;

L_{в}

- transit network length, m;

Z_{m i n}^{t r}

- minimum cost of the necessary equipment, €/MWh

The construction finance costs depend on the capital investment and therefore can be introduced relative to the OCC and transit costs. They include costs for up-front and commitment fees

r_{f e e s}

, for the interest during construction

i_{c o n s t r}

assumed to be accountable for half of the construction period

N_{c o n s t r}

and additional money loaned for reserve accounts

r_{r e s}

C_{f i n} = f_{d e b t} \cdot (O C C + C_{t r a n s i t}) \cdot (r_{f e e s} + i_{c o n s t r} \cdot \frac{N_{c o n s t r}}{2} + r_{r e s}) .

(27.6)

The annual operational expenditures OPEX are divided into fix and variable costs

C_{f i x}

and

C_{v a r}

, both in € and are introduced in [21].

O P E X = C_{f i x} + C_{v a r}

(28.1)

Fixed operating costs are the costs of land lease, insurance, personnel, operation and maintenance of components. They can be represented by a functional relationship to the electrical capacity of the plant

P_{C S P}^{d e s i g n}

C_{f i x} = c_{f i x} \cdot P_{C S P}^{d e s i g n}

(28.2)

where

c_{f i x}

– relative fixed OPEX costs per year in €/kW-yr.

Variable operational costs are costs in € depending on the yearly electricity produced, e.g. for auxiliary electric consumption or water use. This leads to

C_{v a r} = c_{v a r} \cdot E_{y e a r}

(28.3)

where

c_{v a r}

– relative variable OPEX costs per year in €/MWh-yr

The mathematical expectation of the specific reduced cost due to the damage caused by the network failure flow is given from the following equation

Z_{C S P}^{f a i l} = C_{S C P} n_{m i r r o r} \frac{1}{h_{C S P}^{m a x}} \times \{1 - \exp [- \frac{(ω_{m i r r o r} n_{m i r r o r}) \cdot h_{C S P}^{m a x}}{h_{y e a r}}]\} {+ C}_{P V} n_{P V} \frac{1}{h_{P V}^{m a x}} \times \{1 - \exp [- \frac{(ω_{P V} n_{P V}) \cdot h_{P V}^{m a x}}{h_{y e a r}}]\}

(29.1)

where

C_{C S P}, C_{P V}

- the cost of repairing a mirror unit or PV panel €/(pcs);

n_{m i r r o r}, n_{P V},

– number of mirrors or PV panels,

ω_{т}

- mirror failure rate, 1/(year);

A_{m i r r o r}

– the single mirror area.

\begin{array}{l} Z_{C S P}^{f a i l} = {S M \cdot C}_{т} \frac{A_{C S P}^{d e s i g n}}{A_{m i r r o r}} \frac{1}{h_{C S P}^{m a x}} \\ \times \{1 - \exp [- \frac{(ω_{m i r r o r} n_{m i r r o r}) \cdot h_{C S P}^{m a x}}{h_{y e a r}}]\} {+ C}_{P V} \frac{(1 - α_{C S P}) E_{y e a r}^{n e e d}}{P_{P V}^{p c s}} \frac{1}{h_{P V}^{m a x}} \\ \times \{1 - \exp [- \frac{(ω_{P V} n_{P V}) \cdot h_{P V}^{m a x}}{h_{y e a r}}]\} \end{array}

(29.2)

where

P_{P V}^{p c s}

- power of one panel, €/MWt

Using this equation, it should be noted, that

α_{C S P}

represents the ratio of the used plant size to the maximum plant size not only for the solar field but for all components and corresponding processes, influencing the costs as well as the yearly energy produced.

Function of costs and penalties is proposed and investigated by the authors in [22] for 50 MW CSP plant with molten-salt-based:

C_{C S P}^{p e n a l t i e s} = 7,69 € / M W h .

Given the theoretical support of the government for the introduction of a green tariff at which

Z_{C S P}^{p e n a l t i e s} < 0

C_{Z}

can be negative.

The target function has been

\begin{array}{l} L C O E = \frac{F C R \cdot C A P E X + O P E X}{E_{y e a r}} + {S M \cdot C}_{т} \frac{A_{C S P}^{d e s i g n}}{A_{m i r r o r}} \frac{1}{h_{C S P}^{m a x}} \\ \cdot \{1 - \exp [- \frac{(ω_{m i r r o r} n_{m i r r o r}) \cdot h_{C S P}^{m a x}}{h_{y e a r}}]\} {+ C}_{P V} \frac{(1 - α_{C S P}) E_{y e a r}^{n e e d}}{P_{P V}^{p c s}} \cdot \frac{1}{h_{P V}^{m a x}} \\ \cdot \{1 - \exp [- \frac{(ω_{P V} n_{P V}) \cdot h_{P V}^{m a x}}{h_{y e a r}}]\} \to m i n \end{array}

(30.1)

E_{y e a r}^{p r o d u c e} = P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x} [1 + \frac{η_{T E S}}{η_{p o w}} C P_{T E S} \cdot \frac{1}{24} + S M \frac{η_{C S P}^{m a x}}{η_{C S P}^{d e s i g n}} \frac{1 - α_{C S P}}{α_{C S P}}];

(30.2)

h_{C S P}^{m a x} = \{\begin{matrix} h_{C S P}^{a v i a b l e}, i f h_{C S P}^{m a x} > h_{C S P}^{a v i a b l e} \\ \frac{E_{y e a r}^{n e e d}}{P_{C S P}^{d e s i g n} [1 + \frac{η_{T E S}}{η_{p o w}} C P_{T E S} \cdot \frac{1}{24}]}, i f h_{C S P}^{m a x} < h_{C S P}^{a v i a b l e} \end{matrix};

(30.3)

\begin{array}{l} C P_{T E S} = \\ = \{\begin{matrix} \frac{(S M {\cdot A}_{C S P}^{d e s i g n} \int_{0}^{n} D N I^{n} d h \cdot η_{C S P}^{d e s i g n} - P_{C S P}^{d e s i g n} \cdot h_{C S P}^{m a x}) \cdot η_{p o w}}{P_{C S P}^{d e s i g n} \cdot η_{T E S}} \frac{24}{h_{C S P}^{m a x}} f o r S M = c o n s t \\ 24 \frac{(1 - \frac{1}{S M} \frac{1}{η_{C S P}^{m a x}}) η_{p o w}}{\frac{1}{S M} \frac{1}{η_{C S P}^{m a x}} \cdot η_{T E S}} f o r {\dot{Q}}_{P B}^{d e s i g n} = c o n s t \end{matrix} \end{array}

(30.4)

P_{C S P}^{m a x} {= α}_{C S P} P_{n e e d}^{m a x};

(30.5)

P_{C S P}^{d e s i g n} = \frac{P_{C S P}^{m a x}}{S M} \frac{η_{C S P}^{d e s i g n}}{η_{C S P}^{m a x}};

(30.6)

C A P E X = {O C C}_{C S P} + {O C C}_{P V} + C_{t r a n s i t} + C_{f i n};

(30.7)

{O C C}_{C S P} = {(C}_{c o m p}^{m a x} \cdot {(α_{C S P})}^{0.8} + C_{s e r v i c e}^{m a x} \cdot 0.05 \cdot {(α_{C S P})}^{0.4} + C_{l a n d}^{m a x} \cdot α_{C S P}) \cdot f_{c o n t};

(30.8)

{O C C}_{P V} = {(C}_{c o m p}^{m a x} \cdot {({1 - α}_{C S P})}^{0.8} + C_{s e r v i c e}^{m a x} \cdot 0.05 \cdot {({1 - α}_{C S P})}^{0.4} + C_{l a n d}^{m a x} \cdot (1 - α_{C S P})) \cdot f_{c o n t};

(30.9)

O P E X = C_{f i x} + c_{v a r_C S P} \cdot α_{C S P} \cdot E_{y e a r}^{n e e d} + c_{v a r_{P V}} \cdot ({1 - α}_{C S P}) \cdot E_{y e a r}^{n e e d} .

(30.10)

This function has three variables

S M, P_{C S P}^{d e s i g n}

and

α_{C S P}

4. Results and Discussions

The following results are calculated according to the proposed mathematical dependencies with different technical and economic indicators of the plant. A technical-economy analysis has been developed for 15-150 MW CSP which used the function of optimization in this research work. Storage capacity was been from zero to 10 hour.

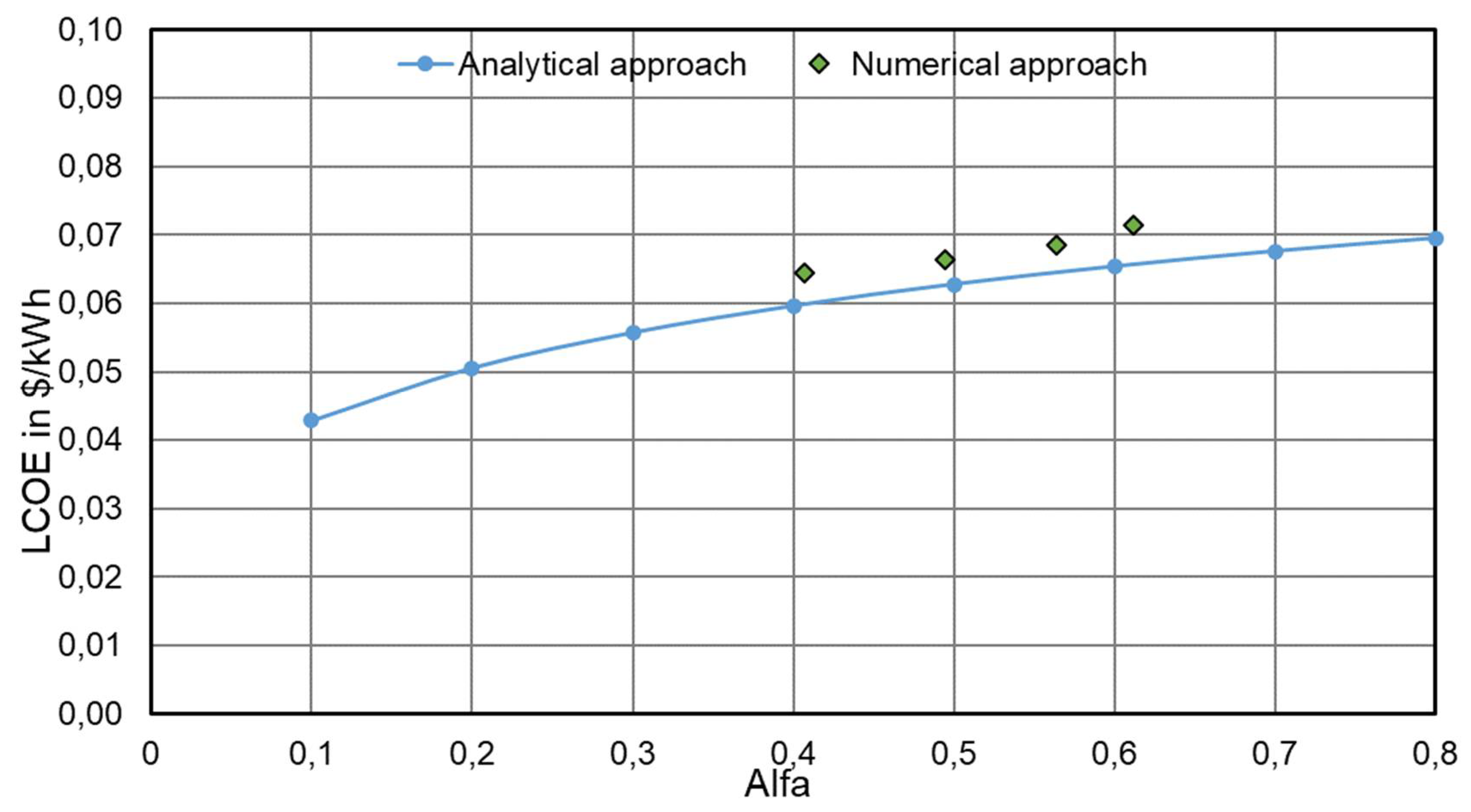
Type of CSP – solar tower. Solar multiple 1.5. Grid connection costs and costs of transit not included. Location – Almeria, Spain. Efficiency of CSP is a function of power capacity and the efficiency ratio of the TES is set at 0.9. Prices for equipment and service were chosen for 2022. Figure 2 shows the validation of the analytical model with the above parameters and the numerical model calculated by Greenius.

As can be seen from Figure 2, for the selected parameters, the data convergence is very high, which allows to recommend the selected analytical approach for building an optimization model of hybrid power plants.

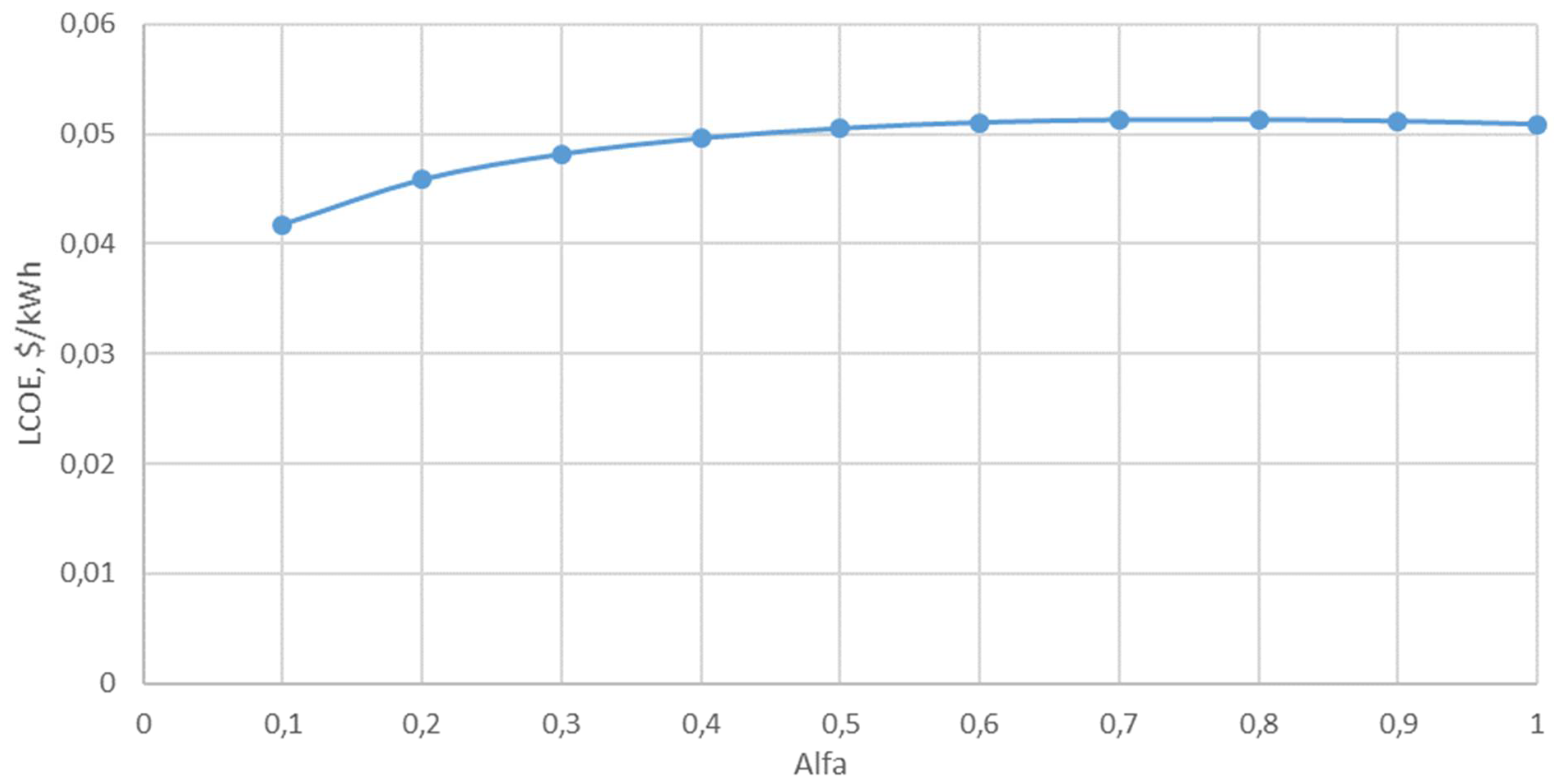
The same SPP parameters as before (without TES) and the same extremes of the function are obtained when the price of Battery Energy Storage Systems (BESS) for PV storage is added (Figure 3). From the analysis of Figure 2 and Figure 3, it can be seen that with the selected economic indicators, the optimization function has a minimum at the point

α_{C S P} = 0

. So, with lower PV prices, the higher the share of PV in the plant, the better. Therefore, the methods for finding the roots of the optimization function are not presented in this article. But this is true only for selected technical and economic indicators and may vary depending on the economic and political conditions of the area.

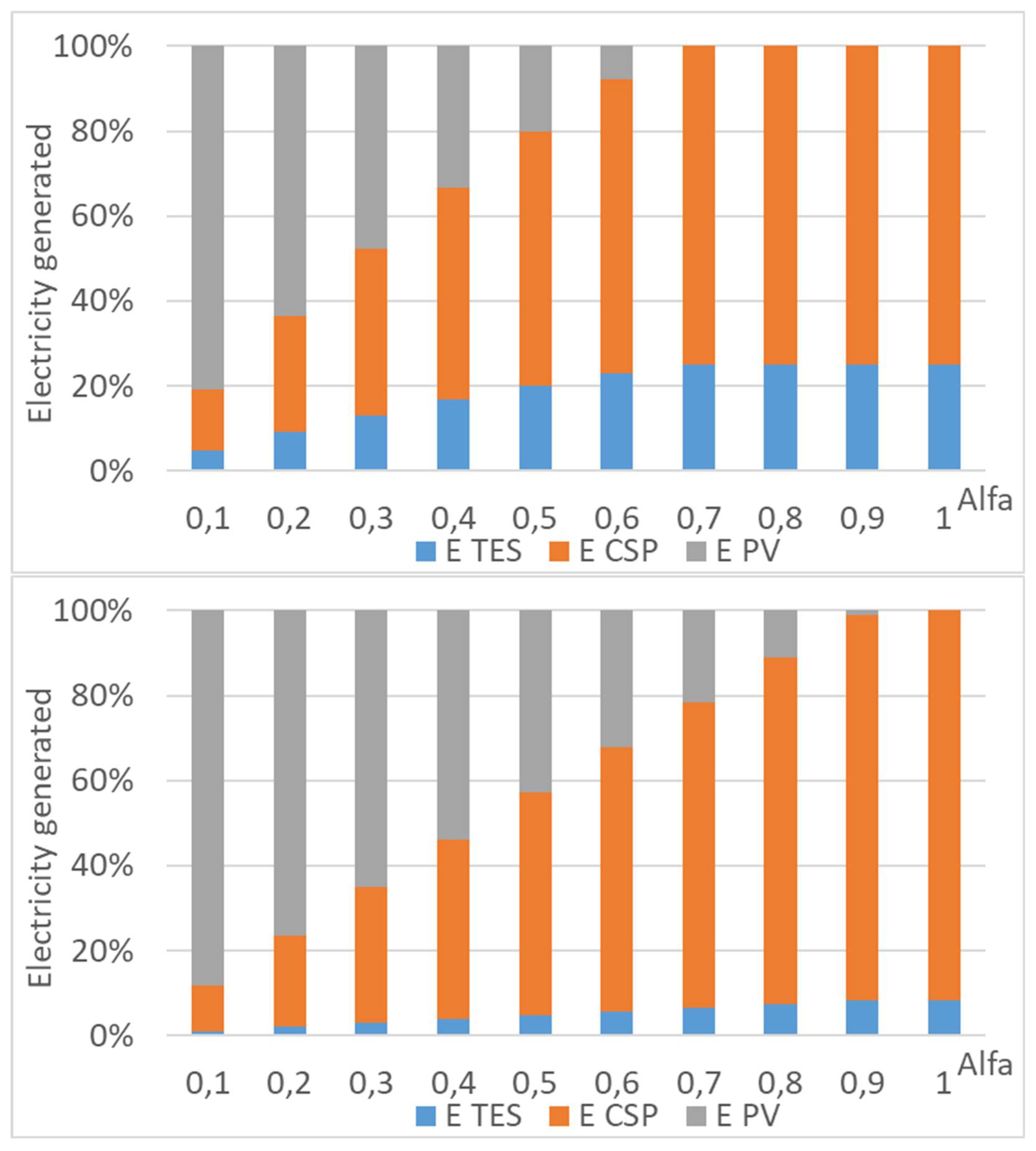
Figure 4 shows the percentage of electricity generated by different components of the hybrid power plant, calculated using the analytical model. In this case, it is assumed that all the excess energy from the SM goes to the energy storage, including additional energy loses. This figure shows that due to the TES thermal storage, the generation of electricity from the PV and CSP is not linear.

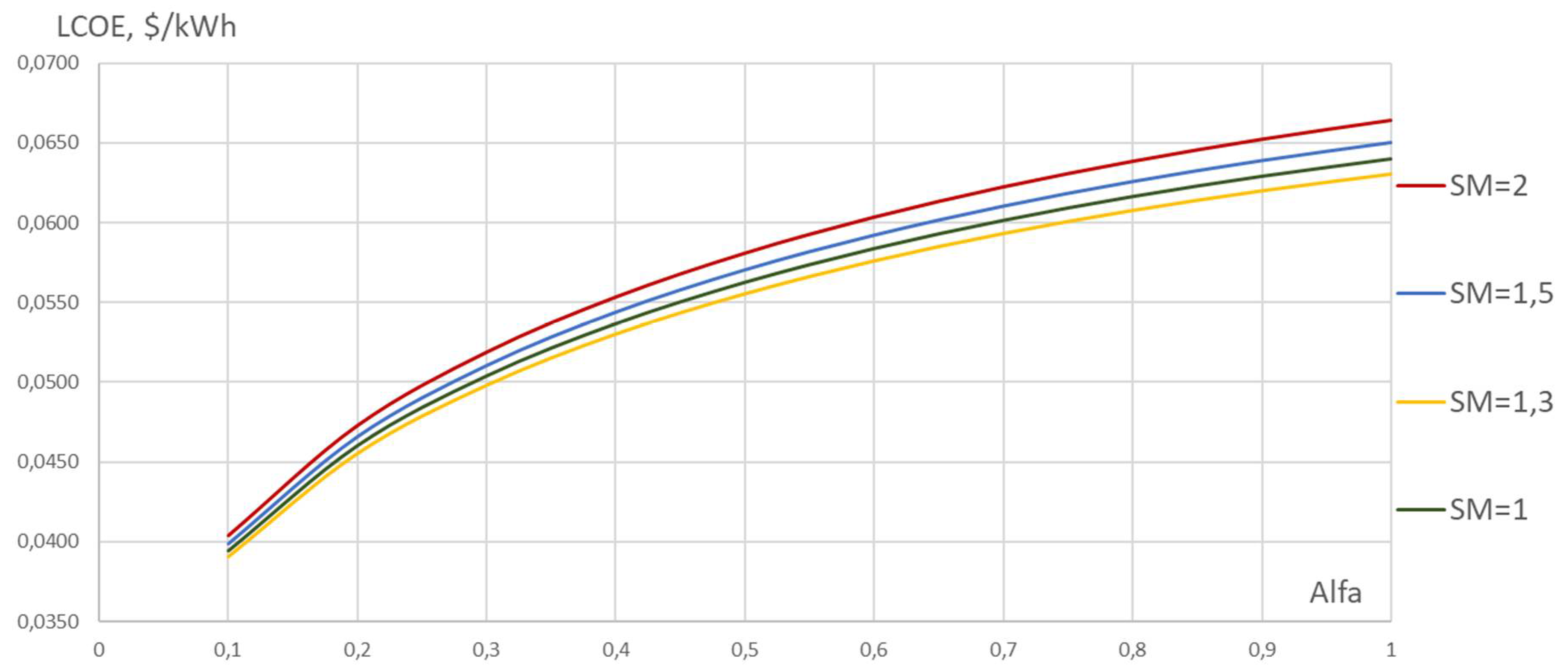
Since in the proposed analytical method the storage size function is set through the solar multiple factor, Figure 5 shows the change LCOE from design power capacity factor alfa. As the power of the concentrated station and the size of the mirror field increase, the size of the drive also increases, but the LCOE does not increase linearly. The non-linearity is caused by the difference in the cost of CP TES and the mirror field.

Despite the fact that the developed optimization model under current economic conditions has an optimum at

α_{C S P} \to 0

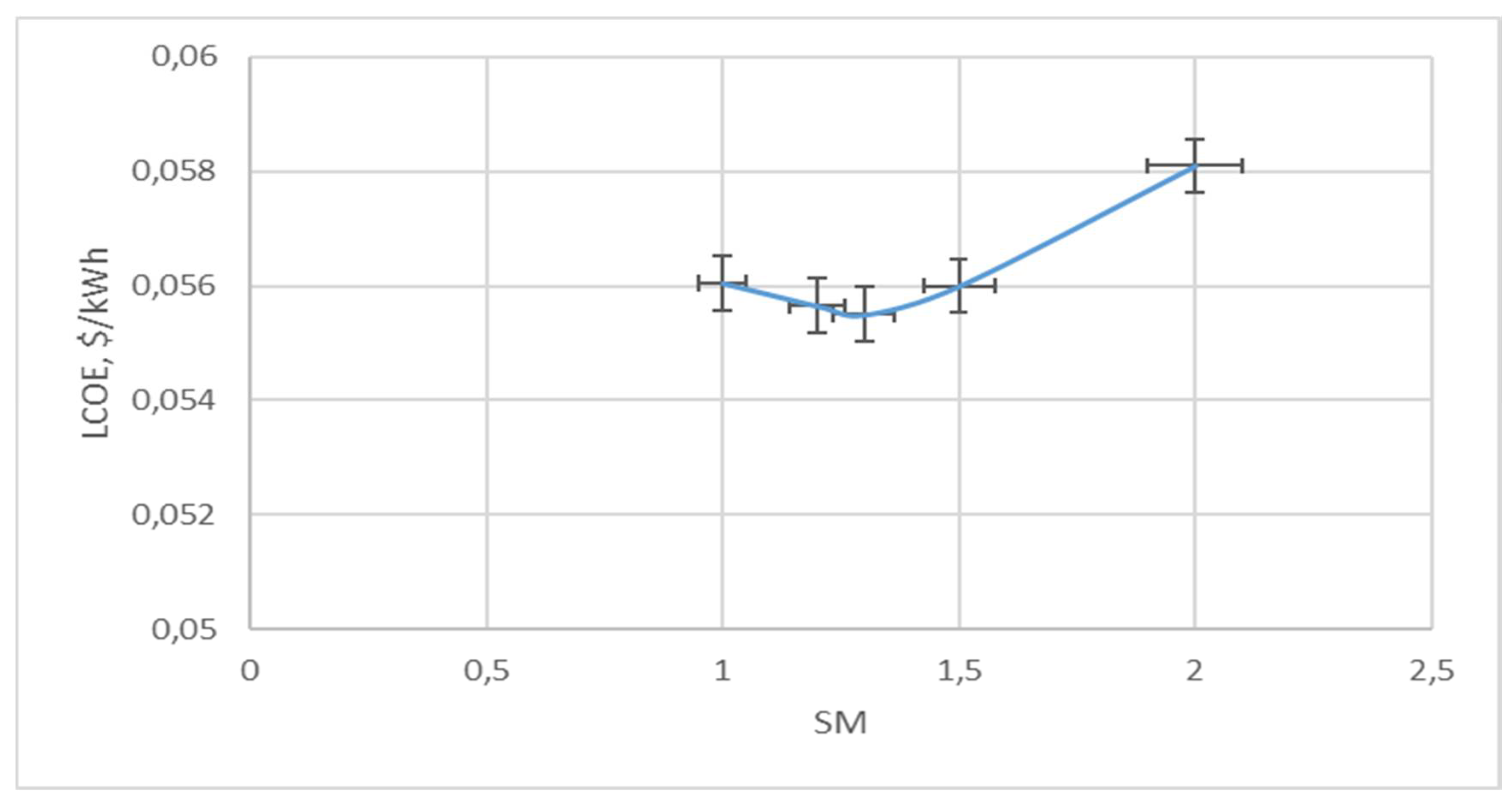
the very method of building this model allows to analyse various indicators of the designed hybrid power plant. Figure 6 also shows the existence of an SM optimum, which shows the importance of calculating the optimal capacity of a hybrid solar station for a specific geopolitical location in order to obtain the minimum LCOE.

5. Conclusions

This paper presents a novel analytical approach for optimizing the capacity of concentrated solar power plants in hybrid configurations. By incorporating the design factor and the solar multiple factor into a mathematical optimization model, the method provides a more detailed analysis of design possibilities while offering faster computational speeds. This advancement contributes to ongoing efforts to improve the efficiency and feasibility of concentrated solar power plants, particularly in hybrid systems.

The developed analytical approach to the performance optimization of CSP plants has shown that it is possible to use analytical functions to obtain the same results as those usually obtained by numerical methods.

The cost of electricity in a hybrid power plant has been analyzed. Hybrid power plants show a relative LCOE with increasing storage capacity, but the cost of the PV-BESS system increases significantly due to higher storage costs. The costs of heat production from CSP without storage and PV systems with an electric heater are comparable.

As the design factor increases, capital expenditures increase, but operating costs decrease. Further research in the field of analytical calculation of levelized costs of electricity for hybrid power plants is to calculate the threshold level of economic indicators for which the use of CSP will be economically more feasible and the function LCOE = f (α_CSP), α_CSP∈(0;1) will have an extreme.

The dependence LCOE = f (SM) is not linear and has a clear optimum (for the selected economic indicators at α_CSP = 1,3 in figure 5).

From the above, there are two different ways to determine the optimal storage capacity. The first way is to take the optimal SM value as a constant of the ratio of the mirror field area to the CSP capacity according to the CSP efficiency change graph, and direct the energy that is higher than this to the storage during peak hours. The second way is to take as constant the value of

{\dot{Q}}_{P B}^{d e s i g n}

the nominal electrical output power of CSP according to its efficiency and to increase the SM to obtain energy for the energy storage. According to the authors, the optimal start is to optimize these two functions using the regulator-simplex method.

Author Contributions

Cheilytko Andrii: Supervision; Methodology; Creation of models (the concept of design factor), Investigation, Writing, Original Draft; Spiros Alexopoulos: Writing – review &editing; Pozhuyev Andriy: Formal analysis, Validation; Oliver Kaufhold: Investigation (network failure flow).

Acknowledgments

Matthias Loevenich and Javier Iñigo-Labairu from DLR for their internal reviewers and comments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

De la Fuente, E. and M. Martin, Site specific process design for Hybrid CSP-Waste plants. Computers & Chemical Engineering, 2020. 135.
Wang, Q., et al., Mitigation Strategy for Duck Curve in High Photovoltaic Penetration Power System Using Concentrating Solar Power Station. Energies, 2019. 12(18). [CrossRef]
Ferretti, F., et al. Addressing Forecast Uncertainty Impact on CSP Annual Performance. in 22nd International Conference on Concentrating Solar Power and Chemical Energy Systems (SOLARPACES). 2016. Masdar Inst Sci & Technol, Abu Dhabi, U ARAB EMIRATES.
Moghimi, M.A., K.J. Craig, and J.P. Meyer, Optimization of a trapezoidal cavity absorber for the Linear Fresnel Reflector. Solar Energy, 2015. 119: p. 343-361. [CrossRef]
Rouibah, A., et al., Solar Tower Power Plants of Molten Salt External Receivers in Algeria: Analysis of Direct Normal Irradiation on Performance. Applied Sciences, 2018. 8(8): p. 1221. [CrossRef]
Shakeel, M.R. and E.M.A. Mokheimer, A techno-economic evaluation of utility scale solar power generation. Energy, 2022. 261. [CrossRef]
Djebbar, R., et al. Potential of concentrating solar power in Canada. in International Conference of the SolarPACES. 2013. Las Vegas, NE. [CrossRef]
Dersch, J., P. Schwarzbozl, and T. Richert, Annual Yield Analysis of Solar Tower Power Plants With GREENIUS. Journal of Solar Energy Engineering-Transactions of the Asme, 2011. 133(3). [CrossRef]
Inigo-Labairu, J., J. Dersch, and L. Schomaker, Integration of CSP and PV Power Plants: Investigations about Synergies by Close Coupling. Energies, 2022. 15(19). [CrossRef]
Blair, N., et al., System Advisor Model (SAM) General Description (Version 2017.9.5). . 2018: National Renewable Energy Laboratory.
Alexopoulos, S. and C. G., Modeling and Simulation of the 50 MW molten salt solar tower power plant in Delingha Real tower power plant simulation with SAM, in SolarPACES 2023. 2023.
Short, W., D. Packey, and T. Holt, A Manual for the Economic Evaluation of Energy Efficiency and Renewable Energy Technologies. 1995.
Gasa, G., et al., Life cycle assessment (LCA) of a concentrating solar power (CSP) plant in tower configuration with different storage capacity in molten salts. Journal of Energy Storage, 2022. 53: p. 105219. [CrossRef]
Coelho, B., et al., Optimization of an atmospheric air volumetric central receiver system: Impact of solar multiple, storage capacity and control strategy. Renewable Energy, 2014. 63: p. 392-401. [CrossRef]
Khosravi, A., et al., Design parameter modelling of solar power tower system using adaptive neuro-fuzzy inference system optimized with a combination of genetic algorithm and teaching learning-based optimization algorithm. Journal of Cleaner Production, 2020. 244: p. 118904. [CrossRef]
Rosenstiel, A., et al., Electrochemical Hydrogen Production Powered by PV/CSP Hybrid Power Plants: A Modelling Approach for Cost Optimal System Design. Energies, 2021. 14(12). [CrossRef]
Cheilytko, A., Vykorystannya vtorynnykh enerhoresursiv: navchalʹno–metodychnyy posibnyk dlya studentiv ZDIA napryamu 6.050601 “Teploenerhetyka” dennoyi i zaochnoyi formy navchannya. 2014: ZDIA, Ukraine.
Mohammadzadeh, N., et al., Model-predictive control for dispatch planning of concentrating solar power plants under real-time spot electricity prices. Solar Energy, 2022. 248: p. 230-250. [CrossRef]
Segarra, E.L., G.R. Ruiz, and C.F. Bandera, Probabilistic Load Forecasting Optimization for Building Energy Models via Day Characterization. Sensors, 2021. 21(9). [CrossRef]
Hirsch, T., et al., SolarPACES Guideline for Bankable STE Yield Assessment, T. Hirsch, Editor. 2017.
Ho, J., et al., Regional Energy Deployment System (ReEDS) Model Documentation. 2021.
Vasallo, M.J., et al., Economic MPC applied to generation scheduling in CSP plants. Ifac Papersonline, 2017. 50(1): p. 115-120. [CrossRef]

Figure 1. Schematic explanation of the calculation of

h_{C S P}^{m a x}

and the average annual energy produced by different types of hybrid power plant elements: yellow is a plan of electricity produced by CSP, pink is a projected CSP capacity, blue is an energy produced by thermal storage. The red line is the planned mode of operation.

Figure 1. Schematic explanation of the calculation of

h_{C S P}^{m a x}

Figure 2. Levelized Cost of Electricity as a Function of Capacity Factor for Hybrid Plant without BESS

Figure 3. Levelized Cost of Electricity as a Function of Design Factor with BESS for PV

Figure 4. Share of electricity generated. SM = 1.5 (up) and SM = 1.1 (down).

Figure 5. Dependence of levelized cost of electricity on design factor for different values of SM

Figure 6. Dependence of the levelized cost of electricity from the SM with alfa = 0.5

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Analytical Approach to Power Optimization of Concentrating Solar Power Plants with Thermal Storage

Abstract

1. Introduction

2. Materials and Methods

3. The Proposed Function of Optimization

3.1. The Mathematical Model

3.2 The Function of Optimization

4. Results and Discussions

5. Conclusions

Author Contributions

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe