Preprint

Article

Numerical Investigation of Heat Transfer Enhancement in Trapezoidal-Fin Heat Sinks

Altmetrics

Downloads

Views

Comments

Ya-Chu Chang^*

This version is not peer-reviewed

Submitted:

09 May 2024

Posted:

10 May 2024

You are already at the latest version

Alerts

Abstract

The objective of this work is to analyze the improvement of heat transfer in trapezoidal fin heat exchangers using numerical simulation. Heat exchangers are essential components frequently used in contemporary electronic gadgets to effectively disperse heat produced by high-power components. Nevertheless, as electronic devices continue to advance and become more powerful, the heat transfer capacity of heat exchangers is facing more requirements, therefore requiring enhanced heat dissipation efficiency. Afterwards, various fin angles were adjusted, and the heat transmission efficiency was compared. Modifying the angles can significantly improve the effi-ciency of convective heat dissipation. Moreover, it has been found that employing an optimized trapezoidal fin structure can further enhance the efficiency of heat transfer. The results indicate that trapezoidal fin heat exchangers provide superior heat dissipation efficiency compared to conventional heat exchangers. This is important for enhancing the thermal dissipation capabili-ties of electrical gadgets, hence guaranteeing steady functionality and extending their longevity. Subsequent study might explore supplementary methods to boost heat transmission in different heat exchanger configurations in order to meet the growing requirements for heat dissipation.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

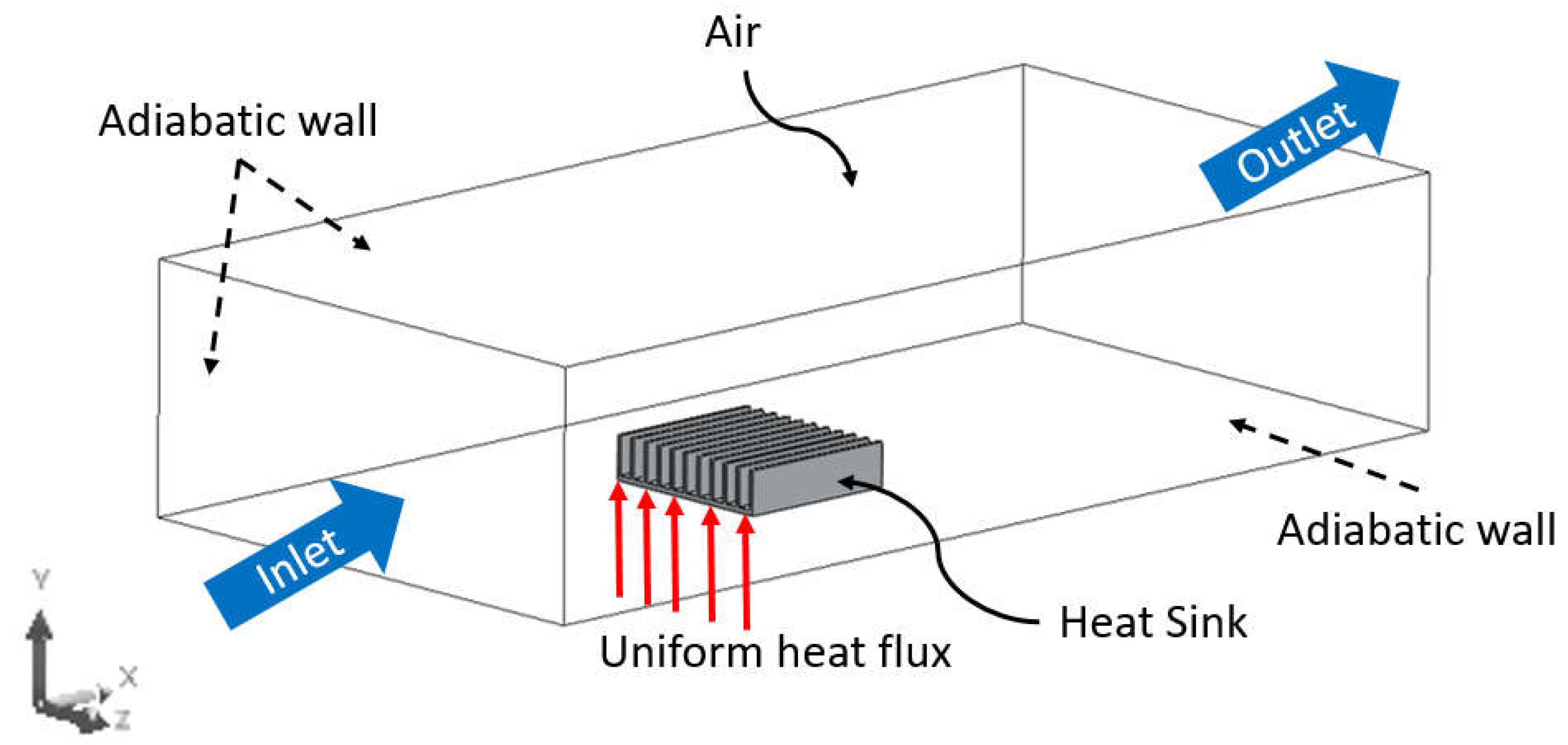
Effective thermal management is crucial for maintaining optimal operating temperatures and ensuring the dependability of microelectronics. To increase heat transfer from electronic components into the surrounding ambient environment, heat sinks are ubiquitously employed. Through an enlarged surface area, they permit conduction, while their form enhances convection by facilitating airflow across the surface. J.Y. Ho et al. [1] This model addresses the impact of airflow bypass and vortex effects, and its predictions exhibit outstanding consistency with experimental evidence. The findings of this work have great relevance for the design of electronic cooling, as they provide theoretical advice and prediction tools for adding aerodynamic wing-shaped fins to the cooling of integrated circuit boards. In summary, the article systematically investigates the heat transfer effects of fins with different profiles, explains the mechanisms by which aerodynamic wing-shaped fins enhance heat transfer, and establishes a corresponding predictive model, thus offering valuable resources for electronic cooling design. C-H Huang et al. [2] A unique construction consisting of a distorted array of sinusoidal fins is proposed in order to enhance heat dissipation. By maintaining the fin volume constant, the parameters of the deformed sinusoidal wave are modified to reduce the average temperature of the fin array baseplate. Comparative analysis demonstrates that the optimized de-formed sinusoidal wave fin array outperforms both straight fins and regular sinusoidal wave fins, resulting in a reduction of the baseplate average temperature by 8.78% and 1.35%, respectively. The optimization approach takes into consideration the impact of air-flow bypass and enhances heat transmission through increased surface area and vortex effects. Experimental validation shows the efficiency of the numerical optimization since the numerical findings fit well with the temperature distribution recorded during experimentation. Xiaoling Yu et al. [3] A unique composite heat sink has been produced by integrating cylin-drical fins into the flow channel, which is based on the flat plate heat sink. The numerical simulation data demonstrate that, when subjected to identical wind velocities, the thermal resistance of this composite radiator is lowered by 30% in contrast to the original flat radiator. The experimental measurements of the pressure drop in the composite radiator model coincide with the numerical simulation findings, therefore proving the efficacy of the numerical model. Under analogous input power levels, the composite radiator exhibits a cooling efficiency that is comparable to the optimized flat radiator. W. Yuan et al. [4] Research was undertaken on the thermal fluid properties of a flat-plate-cylindrical fin composite heat sink (PPFHS). The research studied how different elements, such as air speed, fin size, arrangement of fins, and proximity to the center of adjoining fins in the direction of flow, influenced PPFHS's efficiency. The numerical model's efficacy was proven, exhibiting a good correlation between the numerical computations and the empirical data. Findings demonstrate that the speed of the air and the diameter of the fins play a substantial role in performance, whereas the layout of the fins and their central distance exert a minor impact. S.E. Razavi et al. [5] Through numerical comparison, the characteristics of heat transfer and flow in a baffle-cylindrical fin heat sink were evaluated. Expanding on the basic structure of a cylindrical fin heat sink, a novel baffle-cylindrical fin heat sink (SPPFHS) was created, integrating a baffle located behind the cylindrical fins. Findings show that integrating a baffle, as opposed to a traditional cylindrical fin heat sink, can significantly lower both the pressure drop and the thermal resistance. By optimizing the movement around the cylindrical fins, the baffle decreases the reduction in pressure. Further, the larger surface area amplifies the effect of heat transport. Ambarish Maji et al. [6] The heat transfer characteristics of various shaped perforated fin configurations were quantitatively examined using 3D computational fluid dynamics (CFD) simulations, including fins with circular, diamond, and elliptical perforation holes. The impacts of parameters comprising hole number, shape, and size, as well as fin arrangement, on heat transfer performance and pressure drop were examined. The investigation found that within a certain range of hole number and size, the perforated fins demonstrated better heat transmission capacities compared to solid fins and that staggered fin arrangements beat in-line designs. YueRong Xu [7] A unique CPU cooler design featuring a U-shaped microchannel heat pipe array (U-MHPA) and rectangular fins was proposed. Its heat transfer and fluid flow resistance characteristics under varied air velocity and power input conditions were experimentally investigated using a wind tunnel system. The cooler structure might efficiently enhance heat dissipation. Experimental results indicated that under an ambient temperature of 20°C and a Reynolds number of about 1000, the cooler working temperature could be maintained at 75°C even when the power input reached 130 watts.Chirag R. Kharangate et al. [8] The development of a unique 3D heat exchanger, having both longitudinal and transverse interwoven flow channels, was recommended as a substitute for the standard straight aluminum fin heat exchangers in air-cooled condensers. Findings revealed that this 3D interwoven flow path heat exchanger beats the traditional straight alu-minum fin heat exchangers in terms of COP performance under different heat flux scenarios. Anil Kumar Rao [9] The author numerically examined the heat dissipation performance of fin plates with three different tilt degrees (1°, 2°, and 3°) against usually upright fin plates. It was determined that the fin plate slanted at 2° displayed the highest heat transfer performance, with a roughly 30% higher Nusselt number compared to the normally upright fin plate. The 2° inclined fin plate likewise demonstrated the lowest thermal resistance. Wadhah H. Aldoori [10] The influence of fin height on forced convection heat transfer in rectangular fin arrays was examined. The temperature difference between the fin array surface and the airflow was evaluated under varied fin height settings and various heat input power levels. Results showed that as the Reynolds number climbed, the overall heat transfer coefficient of the airflow increased. As heat input increases, the temperature difference increases under all Reynolds number circumstances. Fin height and position impact heat transfer performance and demand additional study. The heat transfer performance was best at a fin height of 0.67m. Abdüssamed Kabakus et al. [11] The cooling performance of electrospray cooling on smooth surface heat exchangers and finned heat exchangers was examined. The surface temperature, enhancement factor, and fin efficiency factor were studied between the smooth and finned heat exchangers. Although the two electrospray flow rates did not affect the spray modes, the 0.60 ml/min flow rate supplied more liquid to the heat exchanger surface, offering superior cooling enhancement 15–44% higher than 0.45 ml/min. Alhassan Salami Tijani et al. [12] The study focused on the thermal performance of through-hole pin fin heat sinks under forced convection circumstances. It compared the heat transfer performance of heat sinks with diverse geometrical structures, including solid pin fins, through-hole pin fins, solid flat plates, and through-hole flat plates. The results showed that the through-hole pin fin heat sink had the maximum heat transfer coefficient. Furthermore, the pressure drop in the through-hole pin fin heat sink was smaller than that in the solid pin fins, which can reduce the power required for fluid transmission and enhance the efficiency of heat dissipation. W-X Chu et al. [13] This study leverages deep reinforcement learning techniques to optimize and reduce the energy consumption of air-cooled server fans. We offer modified equations optimized to accurately estimate the thermal transfer and fluid dynamic behavior of plate-fin heat exchangers. The usefulness of these predictive models is emphasized by their precision, with the Nusselt number and pressure drop prediction errors maintained within a margin of 5% and 10%, respectively. Ammar A. Hussain et al. [14] The study investigated the cooling efficiency of flat-plate fin heat sinks under varied flow conditions. Through numerical simulations, the accuracy of the data for flat-plate fin heat sinks without rounded corners under impinging flow conditions was validated. The study then examined the baseplate temperature and thermal resistance of flat-plate fin heat sinks with and without rounded corners under impeding flow conditions. The results indicated that a parallel flow design with rounded corners, compared to the standard impinging flow design without rounded corners, greatly reduces the temperature and thermal resistance of the heat sink's baseplate, hence enhancing cooling efficiency. C-H Huang et al. [15] Numerical simulations and optimization methods were utilized to develop the ideal position, angle of attack, and perforation radius of vortex generators to decrease the average temperature of the heat sink's baseplate. The space between the vortex generator and the heat sink allows high-speed airflow to move along the edges of the heat sink, boosting cooling. The angle of attack determines the speed at which air enters the cooling channels, while perforations help minimize resistance. As the Reynolds number grows, the spacing between the vortex generator and the heat sink, the angle of attack, and the perforation radius must all be increased to ensure maximum cooling performance. Compared to a heat sink without vortex generators, the best-designed vortex generators can reduce the average temperature of the heat sink's baseplate by 11.2%. R. Bouchenafa et al. [16] A unique wave fin heat sink was designed and compared with a flat plate fin heat sink. The study evaluated the effects of the number of wave fins and wave amplitude on flow field distribution, pressure drop, and heat transfer coefficient. The results showed that, compared to flat plate fins, wave fins greatly enhance heat transfer performance but also increase the pressure drop. As the number of waves and amplitude rise, the heat transmission effect is further improved. A wave fin heat sink with a wavelength of 5 waves and an amplitude of 4mm displayed the lowest thermal resistance. Khurram Altaf et al. [17] This research studies the thermal transmission and fluid dynamics of heat sinks with different slot designs under conditions of forced convection. Employing a combination of numerical models and experimental approaches, we examined the efficacy of smooth heat sinks versus those with various slot layouts, characterized by changes in width, depth, and number. Findings reveal that the addition of slot patterns efficiently breaks the boundary layer flow on smooth heat sinks, thereby enhancing convective heat transfer. D-K Kim et al. [18] Experiments with varying flow rates and channel widths were conducted to measure the pressure drop and thermal resistance of flat plate fin and pin fin heat sinks. Based on the experimental data, a model to predict pressure drop and heat resistance was presented using the volume averaging method. This model was used to calculate the thermal resistance of improved flat plate fin and pin fin heat sinks under fixed pump power settings. Conversely, when the dimensionless pump power is high and the dimensionless length of the heat sink is small, the optimized flat plate fin heat sink exhibits lower thermal resistance. C-H Huang et al. [19] The goal is to design the op-timal pinhole width that minimizes the average temperature difference of the substrate and also minimizes the system pressure loss. Numerical simulation studies showed that the improved pinhole diameter arrays might reduce the average temperature of the substrate by 1.5–2.1%. The accuracy of the numerical findings was verified by experiments using an infrared thermometer, confirming the usefulness of the method in solving the optimal pinhole diameter design problem. Sakkarin Chingulpitak et al. [20] The study studied the impact of varied sizes and numbers of through-cut notches on the thermal resistance ratio of heat sinks. Experimental tests suggested that the heat sink displayed the lowest thermal resistance at a notch length of 1.5 mm. Numerical results further revealed that, for the same input power, the thermal resistance ratio was at its lowest when the notch length ranged between 1.5 and 2.0 mm. Additionally, increasing the number of through-cut notches was found to reduce the heat resistance ratio. Je-Doo Ryu et al. 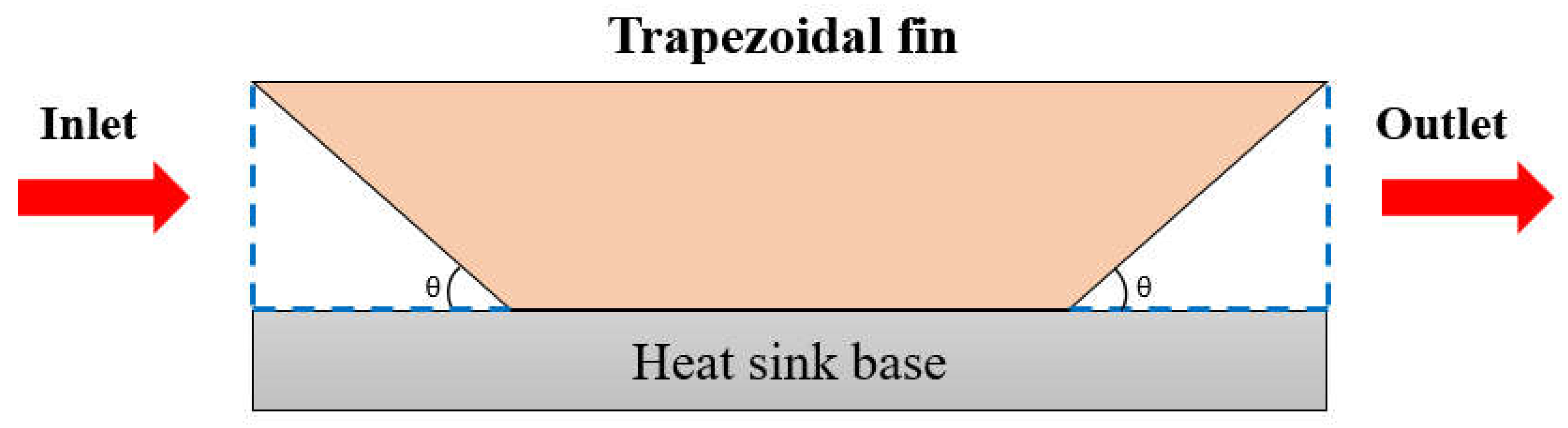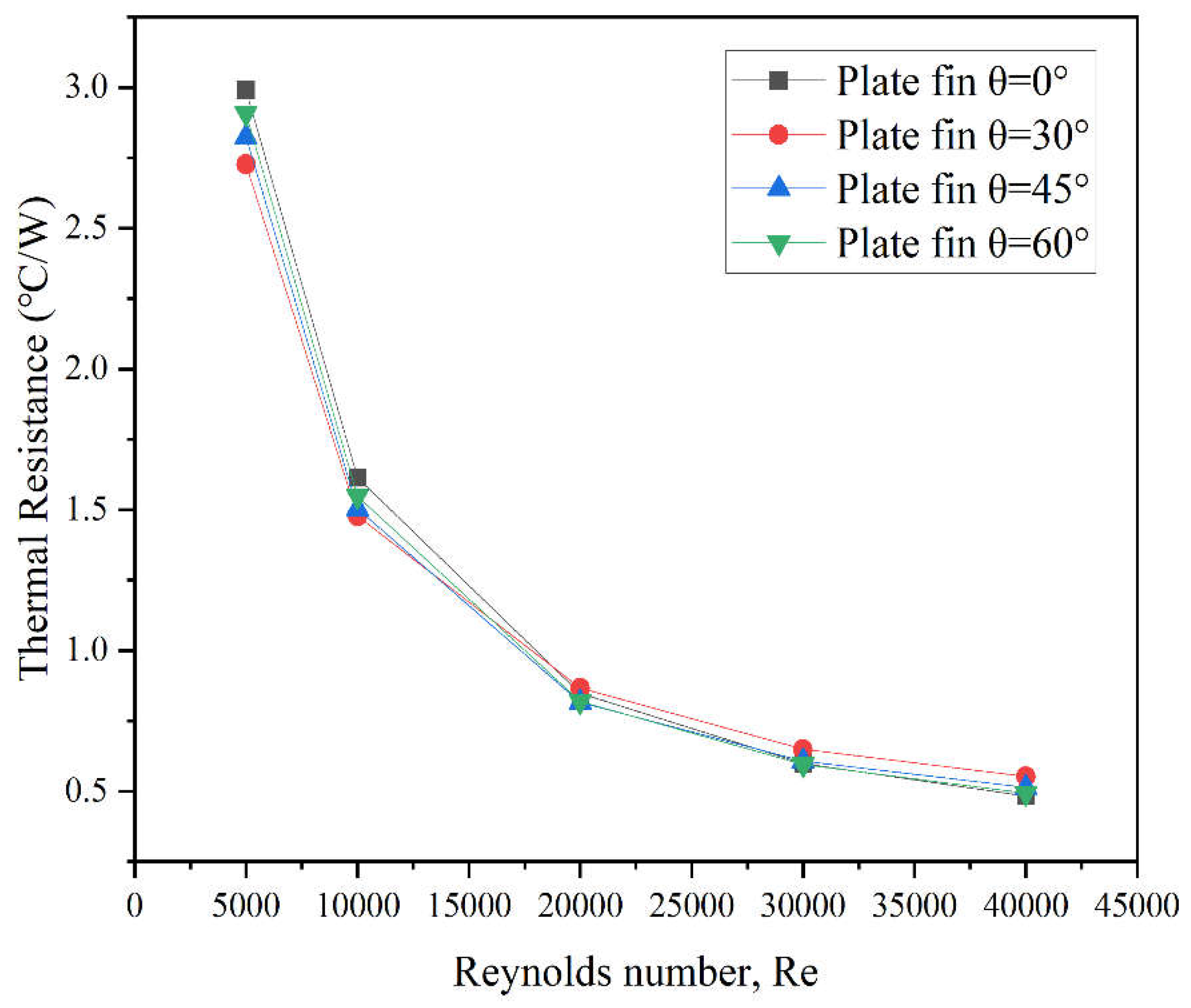[21]An investigation of jet flow fluid dynamics was conducted utilizing CFD numerical simulations and PIV experimental data. The numerical simulations were carried out using MIDAS NFX software, examining the velocity and pressure distributions under varied nozzle pressures. The PIV tests were conducted in a 22m x 3.5m x 3m water tank, utilizing a single-pulse laser and a high-speed camera to examine the jet flow field. The results suggest that while the velocity distribution patterns from both approaches showed comparable trends, there was a substantial variation in the maximum velocities. This shows that careful tuning of through-cut notch dimensions and numbers can greatly boost the thermal performance of heat sinks. The complete literature review demonstrates that various researchers have examined the thermal and dynamic features of plate-fin heat exchangers by applying approaches such as integrating plate and pin fins, introducing baffles, changing fin roughness, and implementing fin perforations. Contrasting these standard approaches, our numerical analysis presents an innovative design incorporating trapezoidal fins. This design intentionally employs angular modifications to increase cooling efficiency. When benchmarked against typical plate-fin heat exchangers, our trapezoidal fin design displays higher heat transfer efficacy, representing a significant improvement in heat exchanger technology.

2. Geometry and Mathematical Model

2.1. Problem Definition

Figure 1 and Figure 2 depict the geometry of the problem under study. Whereas the physical model in Figure 1 is a plate fin, the physical model in Figure 2 is a trapezoidal fin with changes via different angles. Table 1 shows the geometrical parameters.

2.2. Governing Equations

The fluid is assumed to be incompressible in this work, and the flow is turbulent, three-dimensional, and steady state. The effects of radiation, heat transport, and buoyancy are not taken into account. The following are the governing equations[22]:

2.2.1. Continuity Equation2.2.2. Momentum Equation2.2.3. Energy Equation

\frac{\partial ρ u_{i}}{\partial x_{i}} = 0

(1)

ρ u_{j} \frac{\partial ρ u_{i}}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} [(μ + μ_{t}) \frac{\partial u_{i}}{\partial x_{j}}] - \frac{\partial P}{\partial x_{i}} = 0

(2)

ρ u_{j} \frac{\partial T}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} [(\frac{μ}{\Pr} + \frac{μ_{t}}{\Pr_{t}}) \frac{\partial T}{\partial x_{j}}] = 0

(3)

2.3. Computational Domain and Boundary Conditions

Figure 3 displays the computational domain that corresponds to the study's boundary conditions. As depicted in Figure 3, while the expansion wall is insulated, the bottom of the heat sink maintains a constant heat flux (Q). Insulation has been put on the expansion wall. The fluid enters the channel with consistent velocity and temperature at the intake. The fluid can be safely assumed to be fully developed at the outlet, which means that the gradient of all variables is modest.

2.4. Characteristic Parameters

Estimate the ideal angle of the trapezoidal fins to produce the lowest average substrate temperature and pressure. The optimum angle of the fins. The following parameters need to be defined. The Nusselt number Nu, the convective heat transfer coefficient h, the pressure drop ΔP, as well as the Reynolds number Re_h and the channel hydraulic diameter Dh, are determined in the following equations [23]. The following equations are used:

N u = \frac{q D_{h}}{k_{a i r} ({\bar{T}}_{w} - \frac{T_{o u t} + T_{i n}}{2})}

(4)

h = \frac{N u k_{a i r}}{D_{h}}

(5)

Δ P = P_{i n} - P_{o u t}

(6)

{Re}_{h} = \frac{ρ {\bar{u}}_{0} D_{h}}{μ}

(7)

D_{h} = \frac{4 A}{P_{c}}

(8)

In the aforementioned equation,

{\bar{T}}_{w}

is the average bottom plate temperature, T_in and Tout represent the intake and outflow temperatures respectively, k_air is the thermal conductivity. k_air is the thermal conductivity of the air, D_h is the hydraulic diameter of the rectangular channel, ΔP is the pressure drop between the inlet pressure P_in and the outlet pressure P_out.

ΔP is the pressure drop between the inlet pressure P_in and the outlet pressure P_out;

{\bar{u}}_{0}

is the inlet velocity;

ρ

is the air density;

μ

is the air viscosity; A is the channel cross-section as the channel cross-sectional area; P_c is the channel perimeter.

2.5. Numerical Solution

The ANSYS FLUENT code was used to connect the energy and momentum equations. The SIMPLE methodology, or semi-implicit method, for the pressure dependent equations was used to solve the continuity equation. The solution of the energy equation is solved via second-order upwinding, and the resolution of the energy equation is regarded as having converged when the sum of the residuals is less than 10^-6. Solution of the continuity and momentum equations The solutions of the continuity and momentum equations are regarded as having converged when the sum of the residuals is less than 10^-4.

2.6. Grid Independent Test

The heat sink was divided into small, discrete components until grid independence was obtained. The numerical results for assessing the

{\bar{T}}_{w}

temperature with different grids are configured as given in Table 1. Four scenarios were investigated, i.e., plate-fin heat sink, Θ = 60°, Θ = 45°, and Θ = 30° trapezoidal fins. It is obvious from the tables that a considerable increase in the number of grid components does not lead to a major difference in the outcomes. According to Table 2, both plate-fin radiators and trapezoidal fin radiators with varying angles are grid-independent when the error value across iterations is less than 0.5%.

3. Results and Discussion

3.1. Nusselt Number

Figure 4 presents a graphical representation of the relationship between the Nusselt number and Reynolds number for both plate and trapezoidal fin heat exchangers. Across the range, there is a significant tendency toward increasing Nusselt numbers associated with rising Reynolds numbers. Upon studying the influence of changing fin angles, it becomes obvious that trapezoidal fins set at angles of Θ=60°, 45°, and 30° consistently outperform plate fins in terms of their Nusselt numbers. The convective heat transfer efficiency exhibited here is equivalent to that of standard plate-fin heat exchangers. Notably, when the fin angle widens, there is a marked escalation in convective heat transfer, peaking in the Θ=30° configuration. This enhancement in thermal transfer efficiency is related to the larger heat exchange surface area, reinforcing the premise that an increase in heat exchange surface directly adds to the augmentation of overall heat transfer capacity.

3.2. Thermal Resistance

The findings of thermal resistance versus Reynolds number are displayed in Figure 5, which clearly illustrates that thermal resistance is inversely related to the Reynolds number. It can also be shown that for the trapezoidal heat sink Θ = 30 ° in the Reynolds number 5000, the thermal resistance is the lowest; with the Reynolds number 40000, it is enough to slow down; on the contrary, the plate-fin heat sink is at the Reynolds number 40,000, the thermal resistance is the lowest. By adjusting the angle, the heat transmission to the air will rise, thereby raising the thermal resistance. By increasing, the amount of heat transported to the air increases; hence, the maximum temperature at the base of the radiator drops. The highest temperature at the base of the radiator lowers, resulting in a decrease in thermal resistance. This leads to a decrease in heat resistance. Radiator in the Reynolds numbers 5000 and 10000, the lowest thermal resistance is Θ = 30 ° in the sequence of Θ = 40 ° and Θ = 60 °, and the last is the plate-fin fin fins, and the Reynolds number reaches 20000 when Θ = 30 °. thermal resistance tends to flatten out from the Reynolds number of 20000 to start the turn of the tide, Θ = 40 °, Θ = 60 ° plate-fin fins, and the last Reynolds number of 40,000 when the plate-fin fins The thermal resistance is the lowest. The thermal resistance is decreased compared to other heat sinks. In addition, according to Eq. (7), when h increases, T will decrease, and subsequently, Tw will decrease, which will lead to the lowering of R_th.

4. Conclusions

The turbulent flow of air via a trapezoidal radiator has been examined statistically. Air flows through a trapezoidal radiator. The influence of angle on the hydrodynamic and thermal fields was researched and assessed. The finite volume formulation and SIMPLE method were utilized for solving the finite equations. The following conclusions can be drawn from the results:

(1): The use of trapezoidal heat sinks greatly improves heat transfer compared to plate heat sinks. Compared with plate heat sinks, trapezoidal heat sinks can greatly improve heat transfer efficiency.
(2): When Re = 5000, trapezoidal heat sink Θ = 30° can have the minimum thermal resistance; as the angle goes larger, Θ = 40° and Θ = 60° thermal resistance is less. When Re = 5000, the plate-fin heat sink has the smallest thermal resistance.

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflicts of interest.

References

Ho, J.; Wong, K.; Leong, K.; Wong, T. Convective heat transfer performance of airfoil heat sinks fabricated by selective laser melting. Int. J. Therm. Sci. 2017, 114, 213–228. [Google Scholar] [CrossRef]
Huang, C.-H.; Tung, P.-W. Numerical and experimental studies on an optimum Fin design problem to determine the deformed wavy-shaped heat sinks. Int. J. Therm. Sci. 2020, 151, 106282. [Google Scholar] [CrossRef]
Yu, X.; Feng, J.; Feng, Q.; Wang, Q. Development of a plate-pin fin heat sink and its performance comparisons with a plate fin heat sink. Appl. Therm. Eng. 2005, 25, 173–182. [Google Scholar] [CrossRef]
Yuan, W.; Zhao, J.; Tso, C.; Wu, T.; Liu, W.; Ming, T. Numerical simulation of the thermal hydraulic performance of a plate pin fin heat sink. Appl. Therm. Eng. 2012, 48, 81–88. [Google Scholar] [CrossRef]
Razavi, S.; Osanloo, B.; Sajedi, R. Application of splitter plate on the modification of hydro-thermal behavior of PPFHS. Appl. Therm. Eng. 2015, 80, 97–108. [Google Scholar] [CrossRef]
Maji, A.; Bhanja, D.; Patowari, P.K. Numerical investigation on heat transfer enhancement of heat sink using perforated pin fins with inline and staggered arrangement. Appl. Therm. Eng. 2017, 125, 596–616. [Google Scholar] [CrossRef]
Xu, Y.; Fan, H.; Shao, B. Experimental and numerical investigations on heat transfer and fluid flow characteristics of integrated U-shape micro heat pipe array with rectangular pin fins. Appl. Therm. Eng. 2020, 168, 114640. [Google Scholar] [CrossRef]
Kharangate, C.R.; Libeer, W.; Palko, J.; Lee, H.; Shi, J.; Asheghi, M.; Goodson, K.E. Investigation of 3D manifold architecture heat sinks in air-cooled condensers. Appl. Therm. Eng. 2020, 167. [Google Scholar] [CrossRef]
Rao, A.K.; Somkuwar, V. Investigation of taper sloped fin for heat transfer enhancement in plate fin heat sink. Mater. Today: Proc. 2021, 51, 422–429. [Google Scholar] [CrossRef]
Aldoori, W.H. The effect of fin height on forced convection heat transfer from rectangular fin array. Mater. Today: Proc. 2021, 80, 3181–3188. [Google Scholar] [CrossRef]
Kabakuş, A.; Yakut, K.; Özakın, A.N.; Yakut, R. Experimental determination of cooling performance on heat sinks with cone-jet electrospray mode. Eng. Sci. Technol. Int. J. 2020, 24, 665–670. [Google Scholar] [CrossRef]
Tijani, A.S.; Jaffri, N.B. Thermal analysis of eat sink under forced convection condition. Procedia Manufacturing 2018, 24, 290–298. [Google Scholar] [CrossRef]
Chu, W.-X.; Lien, Y.-H.; Huang, K.-R.; Wang, C.-C. Energy saving of fans in air-cooled server via deep reinforcement learning algorithm. Energy Rep. 2021, 7, 3437–3448. [Google Scholar] [CrossRef]
Hussaina, A.A.; Freegaha, B.; Khalafa, B.S.; Towsyfyan, H. Numerical investigation of heat transfer enhancement in plate-fin heat sinks: Effect of flow direction and fillet profile. Case Studies in Thermal Engineering 2019, 13, 1–14. [Google Scholar] [CrossRef]
Huang, C.-H.; Liu, L.-W. Optimal position and perforated radius of punched vortex generators for heat sink. Case Stud. Therm. Eng. 2022, 32, 101916. [Google Scholar] [CrossRef]
Bouchenafa, R.; Mohammed, H.A.; Saim, R. Numerical study of the thermal and hydraulic performances of heat sink made of wavy fins. Mech. Mech. Eng. 2019, 23, 150–161. [Google Scholar] [CrossRef]
Altaf, K.; Tariq, A.; Ahmad, S.W.; Hussain, G.; Ratlamwala, T.A.H.; Ali, H.M. Thermal and hydraulic analysis of slotted plate fins heat sinks using numerical and experimental techniques. Case Stud. Therm. Eng. 2022, 35. [Google Scholar] [CrossRef]
Kim, D.-K.; Kim, S.J.; Bae, J.-K. Comparison of thermal performances of plate-fin and pin-fin heat sinks subject to an impinging flow. Int. J. Heat Mass Transf. 2009, 52, 3510–3517. [Google Scholar] [CrossRef]
Huang, C.-H.; Liu, Y.-C.; Ay, H. The design of optimum perforation diameters for pin fin array for heat transfer enhancement. Int. J. Heat Mass Transf. 2015, 84, 752–765. [Google Scholar] [CrossRef]
Chingulpitak, S.; Chimres, N.; Nilpueng, K.; Wongwises, S. Experimental and numerical investigations of heat transfer and flow characteristics of cross-cut heat sinks. Int. J. Heat Mass Transf. 2016, 102, 142–153. [Google Scholar] [CrossRef]
Ryu, J.D.; Ha, K.N.; Lee, D.G.; Nam, K.S. Flow Analysis of Underwater Water Jet System Using Computational Fluid Dynamics and Particle Image Velocimetry. Proceedings of Engineering and Technology Innovation 2017, 6, 23–27. [Google Scholar]
Feng, Z.; Ivan, C. Numerical evaluation of flow and heat transfer in plate-pin fin heat sinks with various pin cross sections. Num. Heat Trans, Part A 2011, 60, 107–128. [Google Scholar]
Chin, S.-B.; Foo, J.-J.; Lai, Y.-L.; Yong, T.K.-K. Forced convective heat transfer enhancement with perforated pin fins. Heat Mass Transf. 2013, 49, 1447–1458. [Google Scholar] [CrossRef]

Figure 1. Schematic diagrams of heat sinks: Plate fin heat sink.

Figure 2. Schematic diagrams of heat sinks: Trapezoidal fin heat sink.

Figure 3. Computational domain and boundary conditions.

Figure 4. Nu as a function of Re for plate-fin and trapezoidal-fin heat sinks.

Figure 5. Thermal resistance of plate-fin and trapezoidal-fin heat sinks as a function of Re.

Table 1. Heat sinks dimensions.

Type	Area(mm²)	Photo
Plate fin	22710
Θ=60°	21021
Θ=45°	19513
Θ=30°	16966

Table 2. Grid independent test of flat plate heat sink.

Heat sink	Number of Elements	${\bar{T}}_{w}$ (°C)	Difference in temperature (%)
Plate fin	1164973	101.97	N/A
	1380587	101.60	0.36
	1581617	101.59	0.01
Θ=60°	1108711	95.27	N/A
	1323997	95.02	0.26
	2020562	95.03	0.01
Θ=45°	949468	97.23	N/A
	1227306	97.44	0.22
	1762147	97.45	0.01
Θ=30°	967400	99.91	N/A
	1063328	99.55	0.36
	1387000	99.56	0.01

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer