Model-Independent Odderon Results Based on New TOTEM Data on Elastic Pp Collisions at 8 TeV

1. Introduction

In 1973, Lukaszuk and Nicolescu [1] proposed that a noticeable crossing-odd contribution called Odderon may be present in the amplitude of elastic proton-proton ($pp$) and proton-antiproton ($p\overline{p}$) scattering at asymptotically high energies. In the field theory of strong interactions, quantum chromodynamics (QCD), Odderon exchange corresponds to the t-channel exchange of a color-neutral gluonic compound state consisting of odd number of gluons [2]. For more than 20 years since the theoretical prediction of the Odderon in the framework of QCD, and for more than 47 years since the Odderon concept has been introduced in Regge phenomenology, the odderon remained elusive until the time of 2019-2021, due to lack of a definitive and statistically significant experimental evidence of odderon exchange.

A direct way to probe odderon exchange in elastic scattering is by comparing the differential cross-section of particle-particle and particle-antiparticle scattering at the same and sufficiently high energy [3,4]. A search performed at the ISR energy of $\sqrt{s}=53$ GeV in 1985 [5] resulted in an indication of the Odderon at the 3.35 $\sigma$ significance level. That analysis, however, did not utilize all the available data in the overlapping acceptance of the $pp$ and $p\overline{p}$ measurements. Furthermore, at $\sqrt{s}=53$ GeV, Reggeon exchanges may play a significant role, rendering the Odderon search at the ISR energies rather inconclusive.

As far as we know, the first anonymously peer-reviewed publication of a statistically significant, at least 6.26 $\sigma$ signal of odderon exchange was published by the authors of the present manuscript, in the proceedings of the ISMD 2019 (Santa Fe, NM, USA), published in its final version in June 2020 [6]. This refereed conference contribution was backed up and detailed in our publication, published in its final form in February 2021, with the same statistical significance of at least 6.26 $\sigma$ signal for odderon exchange [7]. Our Hungarian-Swedish team introduced a new scaling function that turned out to be energy independent in the LHC energies of $\sqrt{s}=2.76-7.0$ TeV in elastic proton-proton ($pp$) collisions, based on a model-independent, direct data to data comparison [7].

These results as well as the model-independent investigation of the domain of validity of the $H(x,s|pp)$ scaling have been seconded by a theoretical paper of T. Csörgo, and I. Szanyi [8], increasing the statistical significance of the observation of odderon exchange to at least 7.08 $\sigma$. At the same time, this model-dependent investigation found that the domain of validity in s of the $H(x,s|pp)=H(x,s_0|pp)$ scaling (where $s_0$ stands for a fixed energy scale in the TeV region, e.g., $\sqrt{s_0}=7$ TeV) extends also to the top Tevatron energies of $\sqrt{s}=1.96$ TeV [8]. This theoretical work utilized a validated model, proposed in its first form by A. Bialas and A. Bzdak [9], however, the original model lacked a real part hence the possibility of odderon exchange. However, the so-called Real-extended Bialas-Bzdak (ReBB) model of Ref. [10] fixed these shortcomings and has been utilized in Ref. [8] to extrapolate not only the elastic proton–proton scattering data from the LHC energies of $\sqrt{s}=2.76$ and 7 TeV to the D0 energy of $\sqrt{s}=1.96$ TeV but also to extrapolate the elastic proton–antiproton scattering data from $\sqrt{s}=0.546$ and 1.96 TeV to the LHC energies of 2.76 TeV and 7 TeV. Evaluating the proton–proton data with a model increased the uncertainty and decreased the odderon signal from proton–proton scattering data alone, but this decrease was well over-compensated with the ability of the model to evaluate theoretically the proton–antiproton scattering at all the LHC energies. Overall, this procedure resulted in a model-dependent increase of the statistical significance from odderon exchange from 6.26 to 7.08 $\sigma$ [8] as published in final form in July 2021, but limited the comparison to the diffractive minimum and maximum region in the four-momentum transfer range, to the domain of verified validity of the ReBB model. More recently, these results were extended to the new TOTEM data on elastic $pp$ scattering at $\sqrt{s}=8$ TeV, published in March 2022 [11] in Ref. [8]. When TOTEM data on elastic $pp$ collisions at $\sqrt{s}=8$, 7, and 2.76 TeV are analyzed simultaneously with D0 data at $\sqrt{s}=$ 1.96 TeV in the framework of the ReBB model, a combined statistical significance greater than 32.4 $\sigma$ can be achieved, rendering the statistical significance of odderon observation, in any practical terms, to a certainty [8].

These studies utilized a series of important papers published by the TOTEM Collaboration investigating the properties of elastic $pp$ scattering in the LHC energy range between $\sqrt{s}=2.76$ and 13 TeV [12,13,14,15]. Most recently, the latest measurement performed by TOTEM at $\sqrt{s}=8$ TeV [11] extended the earlier analysis up to $\left|t\right|$-values of 1.9 GeV${ }^2$ [16]. An increase of the total cross section, ${\sigma }_{\mathrm{tot}}\left(s\right)$, associated with a decrease of the real-to-imaginary ratio, $\rho \left(s\right)$, with energy, first identified at $\sqrt{s}=13$ TeV [12,13] indicated a possible Odderon effect triggering an intense discussion in the literature (see e.g., Refs. [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]). The persistent diffractive minimum-maximum structure in the t-dependent profile of $d\sigma /dt$ in elastic $pp$ collisions observed by TOTEM at $\sqrt{s}$ = 2.76, 7, 8 and 13 TeV, and the lack of such structure in elastic $p\overline{p}$ collisions measured by D0 [35] at $\sqrt{s}=1.96$ TeV, indicate a qualitatively clear Odderon effect. The possibility of utilizing experimental data at the TeV energy scale for a search for a statistically significant odderon exchange has been proposed by Jenkovszky et al. in Refs. [4,19]. In 2020, the TOTEM collaboration made a qualitative conclusion about odderon exchange in Ref. [15] as follows: “Under the condition that the effects due to the energy difference between TOTEM and D0 can be neglected, the result provides evidence for a colourless 3-gluon bound state exchange in the t-channel of the $pp$ elastic scattering”. However, no statistical significance for this observation has been evaluated in Ref. [15].

More recently, in August 2021, a properly quantified statistical significance of the Odderon signal has been published by the TOTEM and D0 Collaborations [36] employing different methods and techniques, obtaining an at least 5.2 $\sigma$ combined statistical significance for an almost model independent observation of odderon exchange, a first statistically significant result obtained by two experimental collaborations. This result was based on the extrapolation of TOTEM experimental data of the differential cross-section of elastic $pp$ scattering from $\sqrt{s}=$ 13, 8, 7 and 2.76 TeV down to 1.96 TeV using an almost model independent technique and comparing the results with D0 data in a limited four-momentum transfer range, resulting in an at least 3.4 $\sigma$ signal for Odderon exchange. TOTEM also has measured the pair of the total cross-section and the real-to-imaginary ratio $({\sigma }_{tot},\rho )$ and compared it with a set of models without odderon exchange. When a partial combination of the TOTEM $({\sigma }_{tot},\rho )$ measurements is done at $\sqrt{s}=13$ TeV, the obtained partial significances range between 3.4 and 4.6 $\sigma$ for the considered models. The full combination of the signal of odderon exchange from TOTEM $({\sigma }_{tot},\rho )$ measurements at $\sqrt{s}=13$ TeV with the signal of the comparision of extrapolated TOTEM $pp$ data to $\sqrt{s}=1.96$ TeV with a subset of 8 out of 17 D0 datapoints [37] on elastic $p\overline{p}$ scattering leads to total significances ranging from 5.2 to 5.7 $\sigma$ for t-channel odderon exchange for each of the considered models [36].

The validity of this D0-TOTEM proof of Odderon exchange has been questioned in several published papers by now. Most importantly, the ATLAS collaboration [38] published a significantly different total cross-section hence a significantly different pair of $({\sigma }_{tot},\rho )$ at $\sqrt{s}=13$ TeV, questioning the significance of the signal of odderon exchange from these low $-t$ observations. Such a significant incompatibility between the ATLAS and TOTEM measurements of total cross-section and the ratio of real to imaginary part of the scattering amplitude, that is between the pairs of $({\sigma }_{tot},\rho )$ at $\sqrt{s}=13$ TeV as published by the ATLAS and by the TOTEM experiments has recently been confirmed by an independent analysis of Petrov and Tkachenko in Ref. [39]. Furthermore, Donnachie and Landshoff [40,41] stressed the point that phase of an elastic scattering amplitude is related to its energy variation, and as a consequence, they have questioned the validity of the D0-TOTEM signal of odderon exchange at $t=0$. Petrov and Tkachenko obtained results similar to that of Donnachie and Landshoff in Ref. [42], suggesting that the systematic error on the determination of the $\rho$ parameter at $\sqrt{s}=13$ TeV might have been slightly but significantly underestimated by TOTEM in Ref. [43]. Let us mention that Refs. [6,7] scale out the $t=0$ observables from their analysis of the $H(x,s|pp)$ scaling functions, while the low-t domain has been explicitely excluded from finding a statistically significant signal of odderon-exchange in Refs. [8,44]. Hence these odderon discovery papers are not affected by the above mentioned criticisms of the D0-TOTEM publication of a statistically significant, at least 5.2 $\sigma$ experimental observation of odderon exchange.

In addition to the criticism of the D0-TOTEM method of using $t=0$ data at $\sqrt{s}=13$ TeV for the observation of t-channel odderon exchange, Cui and collaborators [45] utilized a mathematical approach based on interpolation via continued fractions enhanced by statistical sampling and suggested that a model-independent extrapolation of TOTEM experimental data of the differential cross-section of elastic $pp$ scattering from $\sqrt{s}=$ 13, 8, 7 and 2.76 TeV down to 1.96 TeV and comparing the results with D0 data in a limited four-momentum transfer range, results in only an at least 2.2 $\sigma$ signal for Odderon exchange. This result alone decreases the significance of the D0-TOTEM combined result for odderon exchange from an at least 5.2 $\sigma$ to an at least 4.0 $\sigma$ signal for odderon exchange [45], suggesting that the D0-TOTEM method of proving the significance of odderon exchange is only on the level of an indication (defined as a significance between 3.0 $\sigma$ and 5.0 $\sigma$), but falls a little bit too short from being experimentally conclusive, definitive discovery as the corrected value falls short of the discovery threshold of 5 $\sigma$. Such an at least 2.2 $\sigma$ signal for Odderon exchange from extrapolating the TOTEM measured differential cross-sections of $\sqrt{s}=$ 8, 7 and 2.76 TeV down to 1.96 TeV confirms the model-dependent results of Refs. [8,44] as well.

A response to these published criticisms was given by the talk of K. Österberg, the physics coordinator of the TOTEM experiment at the ISMD 2023 conference in Gyöngyös, Hungary. We have good reasons to expect that a detailed D0-TOTEM response to the above criticisms will be submitted for a publication as soon as reasonably possible. Furthermore, we also second the suggestion of Petrov and Tkachenko in Ref. [39], calling for a joint ATLAS-TOTEM analysis to sort out the differences between their low-t measurements at $\sqrt{s}=13$ TeV, proposing also a comparison of ATLAS and TOTEM data at low $-t$ at $\sqrt{s}=7$ TeV [46,47,48] and the same comparison also at 8 TeV [49,50].

Let us note, that this ongoing debate in the literature focuses on questioning the validity of certain D0-TOTEM proofs of a statistically significant observation of odderon exchange, but this debate does not question the existence and statistical significance of Odderon exchange in all the four published papers on this topic at this energy scale. The statistically significant, well above the 5.0 $\sigma$ observations of a t-channel odderon exchange, as published in Refs. [6,7] as well as in Refs. [8,44], have not been affected by the above criticism and have not been challenged so far in other publications either, as far as we know. Furthermore, the statistical significance of Odderon exchange as determined from the ReBB model analysis has been increased by taking into account the new 8 TeV datapoints of the TOTEM experiment by I. Szanyi and T. Csörgő: In any practical terms, within the framework of the ReBB model, the signal for Odderon exchange in the limited $0.37\le -t\le 1.2$ GeV${ }^2$ and $1.96\le \sqrt{s}\le 8$ TeV kinematic region is so large that it amounts to not a probability, but a certainty [8].

In the present manuscript, we summarize our model-independent analysis of the statistical significance of the Odderon observation using the recently published [11] and extended [36] $\sqrt{s}=8$ TeV data set of the TOTEM Collaboration in elastic $pp$ collisions, together with earlier data from D0 [35] and TOTEM [14,15,51] Collaborations, extending our earlier scaling studies of the differential $pp$ scattering cross section at TeV energies up to 8 TeV.

Our approach is model independent in the sense that it does not rely on any fitting function or any theoretical input, it uses only linear and log-linear interpolation techniques between neighbouring datapoints, to allow for data to data comparison at the same values of the horizontal axes (using the scaling variable $x=-tB$). As we compare pairwise the $H(x,s|pp)$ scaling functions constructed at different energies based only upon the available data and look for statistically significant differences within any pair of TeV-scale $pp$ and $p\overline{p}$ data sets depending on the collision energy, we need to utilize rebinning that also includes model independent linear interpolation methods, as detailed in Ref. [7], where the basic concepts and methodology have been explained in detail.

Note that we have determined the domain of validity of the applicability of the $H(x,s|pp)$ scaling at $\sqrt{s}=1.96$ TeV so far model-dependently only, in Ref. [7], based on the ReBB model of Refs. [8,10,44]. The domain of validity of this $H\left(x\right|pp)$ scaling has been found to include $\sqrt{s}=1.96$, $2.76$, 7 and 8 TeV in a model-independent way as well, as presented at various conferences, e.g., [52], but these results go way beyond the scope of the present manuscript and will be detailed elsewhere.

2. $H\left(x\right)$ Scaling of 2.76, 7 and 8 TeV $pp$ Data of TOTEM

Our analysis is based on our recent discovery of a novel scaling law of elastic $pp$ scattering at TeV energies, referred to as $H\left(x\right)$ scaling, as described in ref [7]. The scaling function $H(x,s|pp)$ is defined for elastic proton-proton ($pp$) collisions as follows:

$$\begin{array}{ccc}\hfill H(x,s|pp)& =& \frac{1}{B{\sigma }_{\mathrm{el}}^{pp}}\frac{d{\sigma }^{pp}}{dt},\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill x& =& -tB,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill {\sigma }_{\mathrm{el}}^{pp}& =& {\int }_0^{\infty }d\left|t\right|\frac{d{\sigma }^{pp}}{dt},\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill B& =& \frac{d}{dt}ln\frac{d{\sigma }^{pp}}{dt}{|}_{t\to 0}\hfill \end{array}$$

(4)

A similar function $H(x,s|p\overline{p})$ can be introduced for elastic proton-antiproton ($p\overline{p})$ collisions. In Ref. [7] we have shown, that $H(x,s|pp)=H(x\left|pp\right)$ is independent of the energy in elastic $pp$ collisions, utilizing direct data to data comparison of elastic $pp$ data of the TOTEM Collaboration at $\sqrt{s}=2.76$ and 7 TeV, as described in Refs. [46,53,54]. In Ref. [7] we have also shown, in a model-dependent way, that this scaling extends down to $\sqrt{s}=1.96$ TeV, and we have also found that the scaling violations are significant already at $\sqrt{s}=13$ TeV. In the present study we investigate if the energy independence of this scaling is, within experimental errors, valid for the recently published TOTEM data at $\sqrt{s}=8$ TeV, or not, within the experimental errors as determined by the TOTEM collaboration in Ref. [11]. This question is particularly interesting as the elastic to total cross-section ratio increases with increasing energies, and at the LHC energies between 8 and 13 TeV it crosses significantly the important limit of $(1+{\rho }^2){\sigma }_{\mathrm{el}}/{\sigma }_{\mathrm{tot}}=1/4$, see Figure 4 of Ref. [55]. This ratio reaches such a critical value in the region of $\sqrt{s}=2.76$ – $7.0$ TeV and it clearly exceeds it at $\sqrt{s}=13.0$ TeV, where we find statistically significant violations of the $H(x,s|pp)=H(x,s_0|pp)$ scaling law. The search for the onset of the violation of $H(x,s|pp)=H(x,s_0|pp)=H(x,pp)$ scaling motivates our current investigation.

The $H\left(x\right|pp)$ scaling function was found to increase the statistical significance of the Odderon signal, based on a direct comparision of $H(x,s|pp)=H(x\left|pp\right)$ and $H(x,s|p\overline{p})$ at $\sqrt{s}=1.96$ TeV, due to at least two reasons. First of all, the overall normalization uncertainty, the largest source of the systematic error in differential cross-section measurements, cancels from $H(x,s|pp)$ (as well as from $H(x,s|p\overline{p})$ ) . Secondly, this $H\left(x\right|pp)$ scaling law reduces the collision energy related uncertainties in the data which consequently increases the precision of the extracted quantities. We may also mention that in the diffractive cone, expected to be valid at least up to $x=-Bt\ll 1$, the $H\left(x\right)$ scaling function is expected to start as $H\left(x\right)\approx exp(-x)$, with a well-defined normalization at the optical point:

$$H(x=0,s|pp)=H(x=0,s|p\overline{p})=1,$$

(5)

as follows from the definitions of this scaling function. This property of the scaling functions removes the uncertainty related to possible small differences between the optical points of the differential cross-sections in elastic $pp$ and $p\overline{p}$ collisions that may exist between $pp$ and $p\overline{p}$ elastic collisions even if they are measured at the same center of mass energies.

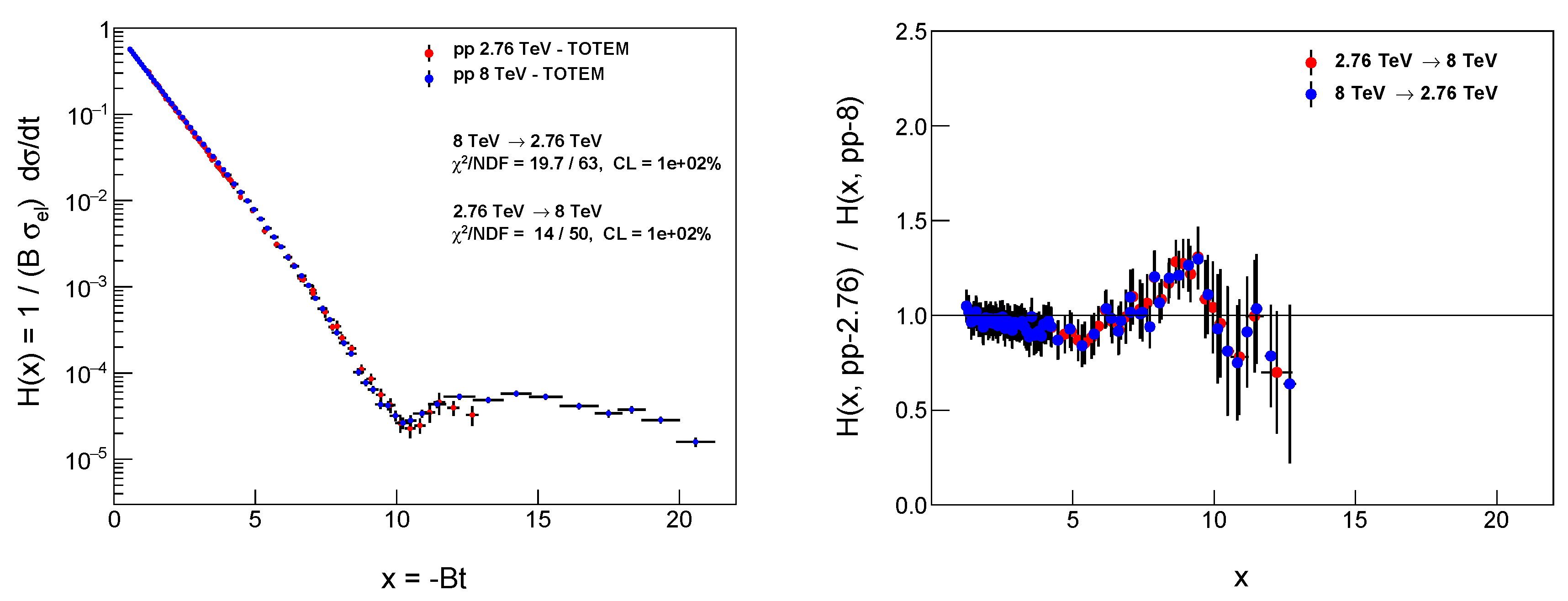
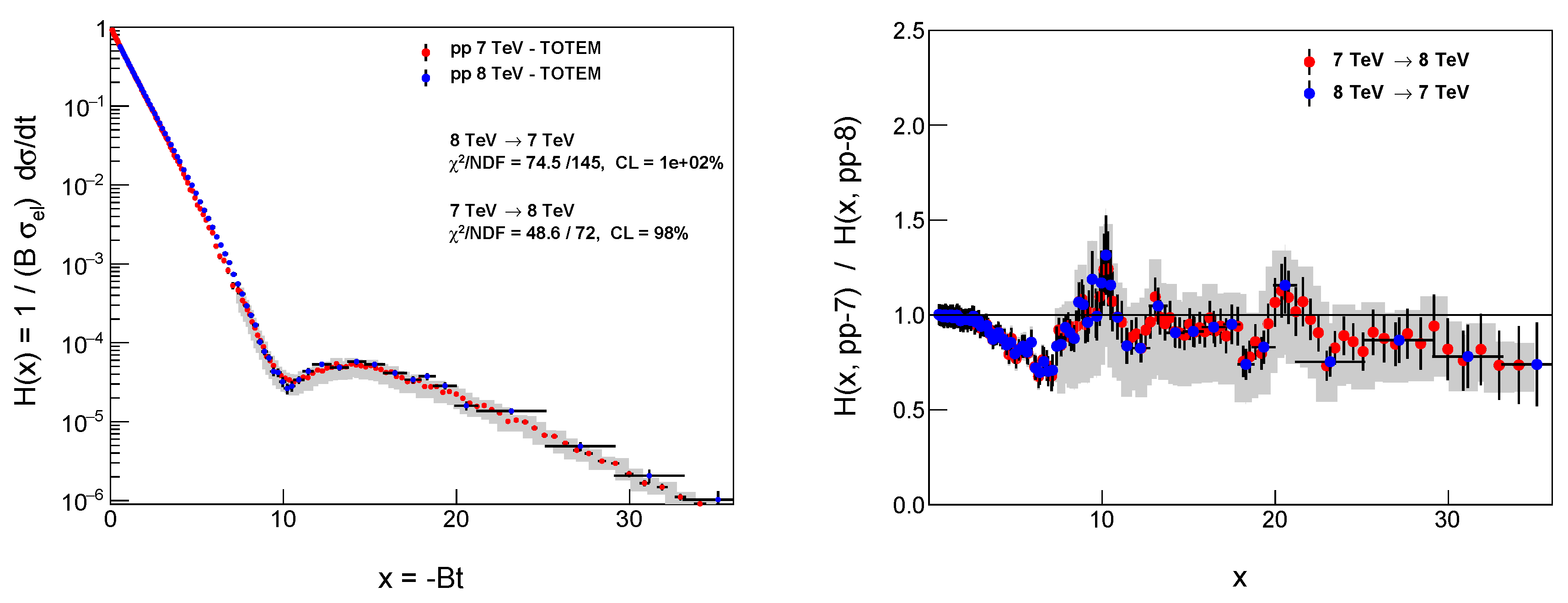
In the left panels of Figure 1 and Figure 2, we demonstrate the energy independence of the $H\left(x\right|pp)$-scaling within statistical errors, where the TOTEM datasets at $\sqrt{s}=2.76$ and 8 TeV as well as at $\sqrt{s}=7$ and 8 TeV are compared pairwise, respectively. The agreement between these datasets corresponds to a confidence level (CL) of at least 98% . Thus such a $H\left(x\right)$-scaling removes the trivial energy dependent terms, due to the known s-dependence of the elastic slope $B\left(s\right)$, the elastic and total cross-sections ${\sigma }_{\mathrm{el}}\left(s\right)$ and ${\sigma }_{\mathrm{tot}}\left(s\right)$, and the real-to-imaginary ratio $\rho \left(s\right)$ [55].

However, one should note that in a local low x (low $\left|t\right|$) interval one can see larger deviations than the reported data errors suggest: In case of the comparison of the $H(x,s|pp)$ scaling functions at $\sqrt{s}=7$ TeV and 8 TeV, we observe a partial disagreement beyond the published experimental errors in a small x range of about $\left|t\right|=[0.175-0.375]$ GeV${ }^2$, which points toward a possible adjustment problem of the two parts of the data sets measured with different optics (${\beta }^{*}=3.5$ m and ${\beta }^{*}=90$ m and published separately in Tables 5 and 4 of Ref. [46], respectively) and suggests the need of a further, more detailed investigation of the published systematic errors in the low $\left|t\right|=[0.175-0.375]$ GeV${ }^2$ range of the dataset measured by TOTEM at $\sqrt{s}=7$ TeV with the ${\beta }^{*}=90$ m LHC optics [46].

Difficulties of describing this part of the TOTEM data at $\sqrt{s}=7$ TeV have been reported in several earlier analyses, but these problems were typically attributed to the insufficiency of the applied analysis methods, for examples see Figs. 1 and 2 of Ref. [10] or Figure 2 of Ref. [4]. So, we suggest caution when using of the $\sqrt{s}=7$ TeV TOTEM data in the $\left|t\right|=[0.175-0.375]$ GeV${ }^2$ four-momentum transfer region.

Fortunately, this $-t$ range, when mapped to $x=-Bt$, overlaps only marginally with the D0 acceptance and data, at three points only, not impacting our conclusions about a model-independent observation of Odderon exchange Ref, [7] in a significant manner: the exclusion of these first three D0 data points at $\sqrt{s}=1.96$ TeV minimally modifies our earlier result of the Odderon significance given in Ref. [7]. We have repeated the analysis of Ref. [7] by leaving out the overlapping acceptance, by removing the first 3 D0 points, but in an otherwise unchanged manner as compared to Ref. [7], and we have found that the statistical significance of Odderon exchange decreased only slightly, from 6.26 to 6.10 $\sigma$, remaining safely well above the 5 $\sigma$ discovery threshold. This is due to the fact that most of the signal of odderon exchange arises from the kinematic range of the diffractive minimum and maximum. A more detailed investigation about this $-t$ range dependence of Odderon exchange has been presented by T. Csörgo in his invited talk at the XXXVth IWHEP conference [52].

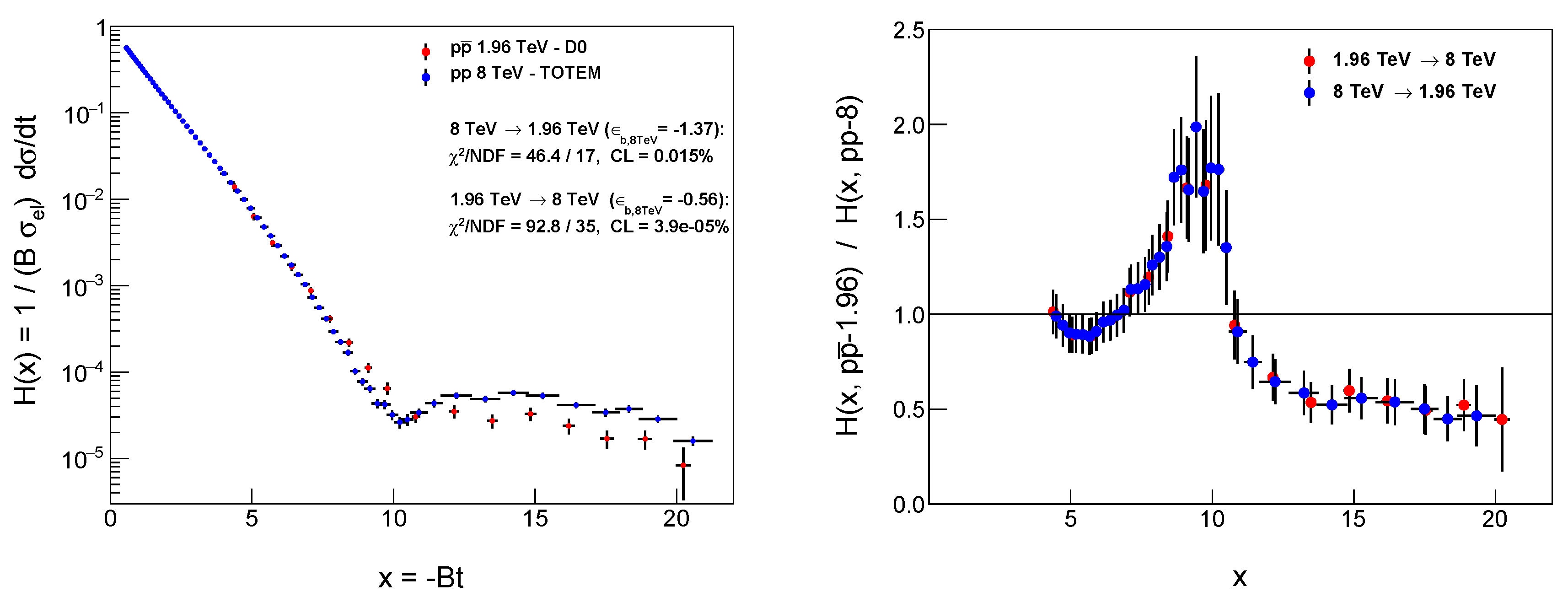
The $8\to 1.96$ TeV and $1.96\to 8$ TeV projections correspond to keeping the measured x values at $\sqrt{s}=$ 1.96 and 8 TeV, respectively, and determining by interpolation the $H(x,s)$ scaling functions at these x values, but at the other energy, $\sqrt{s}=$ 8 and 1.96 TeV, respectively. This procedure is described in full details in Ref. [7]. The left panel of Figure 3 compares the $H\left(x\right)$ scaling function of elastic $pp$ collisions at $\sqrt{s}=8$ TeV to that of $p\overline{p}$ collisions at $\sqrt{s}=1.96$ TeV. In this case, adopting the method of Ref. [56], the confidence level of the agreement of the $H\left(x\right)$ scaling functions is found to be lower then $0.015$%, with a minimum of ${\chi }^2/\mathrm{NDF}=46.4/17$. Hence, the difference between these scaling functions is statistically significant and represents our result for the Odderon observation from the comparison of the $\sqrt{s}=8$ TeV $pp$ and $\sqrt{s}=1.96$ TeV $p\overline{p}$ datasets to be an at least 3.79 $\sigma$ effect, in the $5\le x⪅20$ acceptance domain. This seems to be a conservative and robust result as we find that this value can only increase for variations both in the procedure itself and in the ${\chi }^2$ definition.

3. Quantification of Significance of Odderon-exchange

The quantification of the significance of Odderon is based on a method developed by the PHENIX collaboration in Ref. [56] using a specific ${\chi }^2$ definition that effectively diagonalizes the covariance matrix. In the case considered by the PHENIX Collaboration in Appendix A of Ref. [56], the experimental data are compared to a theoretical calculation. In our analysis, we adapt the PHENIX method [56] for a comparison of one set of data directly to another set of data, without using any theory or fitting functions. Following the PHENIX method, we classify the experimental errors of a given data set into three different types: (i) type A, point-to-point fluctuating (uncorrelated) systematic and statistical errors, (ii) type B errors that are point-to-point dependent, but 100% correlated systematic errors, and (iii) type C errors, that are point-to-point independent, but fully correlated systematic errors to evaluate the significance of correlated data [56], when the full covariance matrix is not publicly available. Since the t-dependent systematic errors in TOTEM measurements are almost 100 % correlated, we classified them as type B errors, while the t-independent overall normalization errors are type C errors, and the statistical errors are type A errors.

The covariance matrix has been published together with the differential cross-section of elastic scattering at $\sqrt{s}=13$ TeV by TOTEM [57] and on this dataset, we have checked with a Levy series expansion method [19], that a fit with the full covariance matrix and another fit with our adopted PHENIX method gave the same minimum, the same central values for the fit parameters and the same errors of these parameters, within one standard deviation. This suggests that indeed the two methods are equivalent in our case too, and we utilized and adapted the PHENIX method for the comparision of two datasets, where the covariance matrix of at least one of these datasets was not publicly available.

At $\sqrt{s}=2.76$ TeV, in Ref. [15], the TOTEM Collaboration published the $pp$ differential cross section data with separated type A and type B errors. The source of the TOTEM $pp$ differential cross section data, measured at $\sqrt{s}=7$ TeV, is Ref. [51]. In addition, the values of $\left|t\right|$ were determined together with their errors of type A and B as given in Table 5 of Ref. [46] and Table 3 of Ref. [58]. The t-independent, type C errors cancel from the $H\left(x\right)$ scaling functions, as they multiply both the numerator and the denominator of $H\left(x\right)$. The sources of the TOTEM $pp$ differential cross section data, measured at $\sqrt{s}=8$ TeV, are Refs. [11,16] with errors of type A and B. The second reference specifies data without horizontal errors, only the bin widths are given that significantly overestimate those errors. Therefore, we have performed calculations with more realistic but likely still well overestimated horizontal errors of half bin widths, as well, resulting in much higher significances. The D0 collaboration did not publish type B errors for its differential cross-section data at $\sqrt{s}=1.96$ TeV [35]. We have thus fixed the correlation coefficient of these D0 type B errors to zero. The input values of the nuclear slope parameters B and the elastic cross sections ${\sigma }_{\mathrm{el}}$ are summarized in Table 1, together with the appropriate references.

We define the significance of the agreement between the data set $D_1$ and the projection $D_{21}=D_2\to D_1$ of data set $D_2$ to $D_1$ in their overlapping acceptance, with the following ${\chi }^2$ definition [7]:

$$\begin{array}{ccc}\hfill {\chi }_{2\to 1}^2& =& \sum _{j=1}^{n_{21}}\frac{{(d_1^j+{ϵ}_{b,1}{e}_{B,1}^j-d_{21}^j-{ϵ}_{b,21}{e}_{B,21}^j)}^2}{{\left({\tilde{e}}_{A,1}^j\right)}^2+{\left({\tilde{e}}_{A,21}^j\right)}^2}+{ϵ}_{b,1}^2+{ϵ}_{b,21}^2,\hfill \\ \hfill {\tilde{e}}_{A,k}^j& =& e_{A,k}^j\frac{d_k^j+{ϵ}_{b,k}{e}_{B,k}^j}{d_k^j},\hfill \\ \hfill e_{M,k}^j& =& \sqrt{{\left({\sigma }_{M,k}^j\right)}^2+{\left(d_k^{\prime ,j}\right)}^2{\left({\delta }_{M,k}^{j}x\right)}^2},\hfill \end{array}$$

where $n_{21}$ is the number of data points $d_{21}^j$ in $D_{21}$ indexed by j, the same as in $D_1$ but remaining in the overlapping acceptance of $D_{1,2}$ sets, $e_{M,k}^j$, $k=1,21$, are the type $M=A,B$ errors found in terms of the type M vertical errors on data point j, ${\sigma }_{M,k}^j$, added in quadrature with the corresponding type M vertical errors that were evaluated from the corresponding errors on the horizontal axis x with the scaled variance method, $d_k^{\prime ,j}{\delta }_{M,k}^{j}x$, where $d_k^{\prime ,j}$ stands for the numerical derivative of the measured quantity in data set $D_k$ at the point j in the common acceptance and ${\delta }_{M,k}^{j}x$ is the j-dependent type M horizontal error. The overall correlation coefficients of the type B errors $e_{B,k}^j$ of $D_k$ data sets are denoted by ${ϵ}_{b,k}$. These coefficients are usually unknown, therefore we perform a scan of them to find the minimum of the ${\chi }^2$, whose corresponding values are indicated on the plots.

In the right panel of Figure 3 we present visible and statistically significant deviation from unity in the ratio of the scaling functions of $pp$ and $p\overline{p}$ elastic scattering. The ratio of the $H\left(x\right)$ scaling functions is shown for elastic $p\overline{p}$ collisions at $\sqrt{s}=1.96$ TeV over that of $pp$ collisions at $\sqrt{s}=8$ TeV. As a cross-check, we show the results of two different projection procedures: direct $1.96\to 8$ TeV and inverse $8\to 1.96$ TeV denoted by blue and red circle points, respectively. No significant variation with respect to the direction of projection has been found. In both ways, we observe an Odderon effect as a peak in the $5<x<10$ region, followed by a factor of two suppression or decrease from unity in a broad range of $10⪅x=-tB⪅20$. The statistical significance of the observed difference between the $pp$ and $p\overline{p}$ scaling functions has been found to be at least 3.79 $\sigma$, which corresponds to an indication but not alone a statistically significant proof of Odderon exchange from the comparison of these two datasets only. It is important to emphasize that this result is obtained by utilizing the scaling properties of $pp$ scattering without any reference to modelling and without removing (or adding to) any of the published D0 or TOTEM data points, that is all the available data (in particular all the 17 D0 points) were utilized in this analysis. This is in contrast to the D0-TOTEM publication on observation of Odderon exchange [61], where the analysis was limited to only 8 of all the 17 available D0 points [37].

4. Summary of Odderon-Exchange Significances

The significances of the model-independent Odderon-exchange observations in framework of the $H\left(x\right)$ scaling analysis are summarized in Table 2 based on the new results discussed in this paper and as well as on the ones in our previous paper, Ref. [7]. One can notice that no Odderon signal is observed when the $H(x,s_1|p\overline{p})$ scaling function calculated from the $\sqrt{s_1}=1.96$ TeV $p\overline{p}$ D0 data is compared to the $H(x,s_2|pp)$ scaling function calculated from the $\sqrt{s_2}=2.76$ TeV $pp$ TOTEM data. However, this small minimal significance value is due to the smaller acceptance domain in $-t$ of the 2.76 TeV data set which reflects the importance of having $pp$ data points possibly in the whole D0 acceptance. The $p\overline{p}$ 1.96 TeV vs. $pp$ 8 TeV $H\left(x\right)$ function comparison results in an Odderon signal that alone does not reach the 5 $\sigma$ discovery level significance limit. However, the comparison of the $H\left(x\right|s_1,p\overline{p})$ of 1.96 TeV and the $H\left(x\right|s_3,pp)$ data at $\sqrt{s_3}=7$ TeV $H\left(x\right)$ itself results in a statistically significant signal of Odderon exchange, that is well above the 5$\sigma$ discovery level significance limit [6,7,44].

What happens, if we combine significances obtained from various pairwise comparisons? The combined significances of Odderon exchange using the $H\left(x\right)$ scaling analysis are summarised in Table 3. For a combination of the significances two different methods are used: 1) summation of the individual ${\chi }^2$ and NDF values; 2) Stouffer’s method (used also by TOTEM in Ref. [36]). It is important to stress that, independently of the method used for a combination, the combined Odderon observation significance is well above the 5 $\sigma$ discovery level when all possible $pp$-$p\overline{p}$$H\left(x\right)$ scaling function comparisons are taken into account.

5. Conclusions

Using the ${\chi }^2$ method, the combined significance of Odderon exchange grows from 6.26 to 7.08 $\sigma$, as shown in Table 3, as obtained from TOTEM data on elastic $pp$ scattering at 7 and 8 TeV and all D0 data on elasttic $p\overline{p}$ scattering at 1.96 TeV. As also indicated in Table 3, Stouffer’s method for the combination of significances yields similar results, resulting in a 7.10 $\sigma$ combined statistical significance of odderon exchange using all the D0 elastic $p\overline{p}$ data at $\sqrt{s}=1.96$ TeV, Ref. [37] and all the TOTEM data at $\sqrt{s}=7$ and $\sqrt{s}=8$ TeV, Refs. [11,46]. Let us note, that the domain of validity of this $H(x,s|pp)$ scaling includes these three energies, but so far this property has been published only in a model-dependent way [8,44]. The domain of validity of this $H\left(x\right|pp)$ scaling has been found to include $\sqrt{s}=1.96$, $2.76$, 7 and 8 TeV in a model-independent way as well as presented at various conferences [52], but these results go well beyond the scope of the present manuscript and will be written up in full details in a separate publication.