Preprint
Article
Incremental Nonlinear Dynamics Inversion and Incremental Backstepping: Experimental Attitude Control of a Tail-sitter UAV
Altmetrics
Downloads
118
Views
48
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 May 2024
Posted:
09 May 2024
You are already at the latest version
Alerts
Abstract
Incremental control strategies provide undeniable advantages for controlling Uncrewed Aerial Vehicles (UAVs) due to their reduced model dependency and accurate tracking capacities. This is of particular relevance for hybrid UAVs, specially for tail-sitters, which perform complex manoeuvres when transitioning to and from aerodynamic flight. This paper summarizes the research undertaken in the application of the Incremental Nonlinear Dynamics Inversion (INDI) and Incremental Backstepping (IBKS) to a small tail-sitter UAV. After the application of these control strategies in a simulated scenario, the implementation in a Micro-Controller Unit was validated in a Hardware-in-the-Loop scenario. Following such validation, indoor experimental trials were undertaken in order to evaluate the capacity of these controllers to stabilize and control the real aircraft. The stabilization in the flight trials was successfully implemented and allow to conclude that both INDI and IBKS are control strategies suited to control a tail-sitter in vertical flight, providing accurate tracking capabilities under smooth actuation. Furthermore, it was found that the IBKS is significantly more computationally demanding than the INDI, although having a global proof of stability that is of interest in aircraft control.
Keywords:
Subject: Engineering - Control and Systems Engineering
1. Introduction
Hybrid Uncrewed Aerial Vehicles (UAVs) are a leading-edge research topic, aiming to combine the advantages of fixed-wing aircraft and multirotors - such as long endurance and high manoeuvrability - whilst avoiding their respective limitations [1]. These hybrid UAVs may be classified into multiple sub-categories, depending on the type and number of actuators, if these are fixed or rotatable, how the transition to and from aerodynamic flight is performed, among others [3,4]. In general, tail-sitters are the simplest hybrid aircraft in terms of actuation, owning their designation to the fact that they take off and land on their tails [2]. Tail-sitters may have several different configurations, but one of the most popular is the bi-rotor design[4], having two proprotors - which act simultaneously as propellers and rotors - and two elevons - which also have a double role of elevators and ailerons . They are suitable for high-endurance scenarios, as they can maintain control when gliding with minimal energy expenditure, thus allowing the coverage of large distances. Nevertheless, the transitions that this sort of UAVs are required to perform present are significantly complex, with the tail-sitter having to rely on the airspeed generated by its propellers to grant enough authority to the control surfaces to pitch the aircraft during these transition moments. As such, the automatic control of bi-rotor tail-sitters present remarkable and demanding challenges, as it requires that the aircraft should be stabilized not only in vertical or aerodynamic flight, but also during the transition maneuvers between these flight stages.
Linear control strategies are still common for both fixed-wing aircraft [5] and multi-rotors [6], much due to their simplicity of implementation and analytical proof of stability for the respective linearized models. In the case of aircraft that are capable of large altitudes or velocities, it is common to pair these linear controllers with a scheduling strategy, that changes the values of relevant parameters to account for these varying conditions [7]. Notwithstanding, this process is computationally demanding, and the assumptions and approximations that result from the linearization process may impact negatively the performance of the controller [2]. To counteract these aspects, nonlinear control strategies arise as strong alternatives, often including or cancelling the nonlinearities of the model of the system for the computation of the control action [4]. In aircraft control, the Nonlinear Dynamics Inversion (NDI) and the Backstepping (BKS) are undeniably two of the more acknowledged strategies [8], with examples of application in multi-rotors [9,10] fixed-wings [11,12] and, more recently, hybrid UAVs [13,14]. Consisting on an inversion of the model of the system to compute the stabilizing control action, the NDI strategy results in a straightforward yet effective control law, adequate for the stabilization of the attitude of aircraft. With a similar reasoning but having a stronger theoretical foundation, the Backstepping method is also common in UAV control, with the drawbacks of requiring for the model of a given system to be expressed in lower-triangular form whilst also having more intermediate computations when compared with NDI. Nevertheless, a successful application of BKS proves the global stability of the controlled system, which is a tempting aspect to consider when dealing with aircraft, due to the safety and security involved.
Although both NDI and BKS are suitable and common control strategies to stabilize the attitude of UAVs, these are still methods that rely greatly on the model of the system, which can be subject to significant uncertainty or may require expensive and demanding processes to be accurately identified [15]. Circumventing this limitation, incremental versions of these controllers - INDI and IBKS - have been gaining popularity as they require limited information of the model of the UAV to stabilize it, with a number of recent cases of applications in aircraft control [16,17,18,19,20]. The limited model dependency makes them ideal candidates for the challenges involved in controlling tail-sitters, due to the difficulty in modelling the complex aerodynamics during transitions and the propeller/control surface interaction.
Accounting for this introduction, this paper explores the application of the Incremental Nonlinear Dynamics Inversion and Incremental Backstepping in the vertical flight stabilization of the X-Vert VTOL [21], a small and lightweight radio-controlled tail-sitter. Building on previous research work [22], these two control strategies are developed in simulation and validated in a Hardware-in-the-Loop (HITL) setup. Following this validation, the INDI and IBKS controllers are implemented and evaluated in an experimental scenario, resorting to a Motion Capture System (MCS) to record the movement of the UAV during the flight trials.
2. Aircraft Model and Simulator
The simulator used in this work is based on a previous work [22], consisting of a simulated environment developed in MATLAB/Simulink 2023a. The aircraft model is largely based on the research work of [23], which modelled the X-Vert VTOL UAV as a rigid body under constant atmospheric properties, and complemented by the relevant sensor models [24]. The generic layout of the simulator is provided in Figure 1, which is briefly described afterwards.
2.1. UAV Nonlinear Model
The equations of motion (EOM) used in the aircraft model in [24,25] are
which encompass the expressions for the time derivatives of the linear and angular velocities relative to the ground, expressed in the body frame of the UAV, and , respectively, its position expressed in the North-East-Down frame, , and quaternion-expressed orientation in relation to this same frame, . The more-appropriate notation for would be as it represents a rotation from the body to the fixed frame, but the subscript is ommited not to overburden the notation. represents this same rotation, allowing to express the kinematics relationship between and , whilst is a skew-symmetric matrix for the rotational quaternion kinematics [24]. Lastly, the mass of the aircraft is denoted by , its inertia matrix by , and the resultant forces and moments by and , respectively, both expressed in the body frame.
The thirteen states in (1) - (4) are complemented by two others, , which represent the angular velocities of the right and left motors, forming the state vector used in the Simulink environment, . Likewise, the input vector is represented by , denoting the aileron and elevator deflections, and the rudder and thrust inputs. These can be gathered from the original left and right elevator deflections, and , and the left and right proprotor throttle signals, and , by the means of an appropriate transform [24].
Regarding and , these portray the influence of the aerodynamics, propulsion, ground-contact effects and gravity force in the aircraft model used in this work. In this model, the longitudinal aerodynamics were taken from [23], which is based on flat-plate theory [27,28] to derive the lift, drag and pitching moment curves for the X-Vert, and are complemented by the lateral aerodynamics and effects of aerodynamic derivatives described in [24]. For the purposes of this work, the assumption of the absence of wind is present, therefore resulting in a direct correspondence between ground and air velocities, and = [24,25]. The propulsion subsystem is also modelled in accordance to [23,26], with the difference that it included a Brushless Direct Current (BLDC) motor model, expressing the actuator dynamics between the throttle signals and the corresponding angular velocity of the motors . Finally, the ground-contact effects were modelled using a spring-damper analogy [23] accounting five contact points, and the gravity effects consist on a simple rotation of the inertial gravity vector into the body-frame, where represents the acceleration of gravity, taken as constant.
As this work focuses on the stabilization of a tail-sitter UAV in vertical flight, only the states of related with the attitude and vertical displacement are of relevance, forming the state vector subset:
It should be noted that the velocity is used to stabilize D as the aircraft is pitched up during vertical flight, with its x axis perpendicular to the ground plane. The vector in (5) represents the states that must be tracked for performing the vertical flight, arising in two instances, the first being the reference vector , and the second the corresponding measured or estimated states, , as shown in Figure 1.
2.2. Sensing and Estimation
In the previous research work [22], an accelerometer and gyroscope were combined in order to estimate the attitude using a quaternion-based complementary filter [29], providing the component of , and being obtained directly from the gyroscope. This method has a single design variable, , which determines the relative weight of the accelerometer in computation of the estimated quaternion, . Analogously, a sonar was paired with the accelerometer to estimate and D, but it was verified that the sonar would sometimes be partially blocked by the tail of the X-Vert when significant variations of attitude took place, resulting in the lack of reception of the required response signal. This caused the sensor to reach a timeout, assuming a much larger altitude, which caused unreliability of the altitude control action. Therefore, a barometer was considered for this iteration, and a simple atmosphere model was included in the simulator, illustrating the pressure P decrease with the altitude above sea-level, [24]:
where Pa and K represent the pressure and temperature at sea-level, K/m is the rate of temperature decrease in the lower atmosphere, and is an adimensional constant that summarizes the relevant air properties, available in [24]. Accounting for noise and bias present in its readings , the barometer model is given by
where is taken as a zero-mean Gaussian noise with variance , gathered from [24], and is assumed to be removed during the calibration process of the sensors, and therefore being zero for the simulation purposes. Together with the readings from the accelerometer and gyroscope, this results in the following output vector:
It should be noted that the components of are corrupted by noise in the simulation environment, attesting for the robustness of the control solutions to noise.
For the altitude estimation, the model in (6) can be simplified and inverted, and a low-pass filter (LPF) should be included to discard the effects of , resulting in the estimated Down position being
A second-order derivative filter [22] can be used to estimate , allowing to obtain this derivative from a noisy sensor, although introducing some delay, consequence of such filtering. In turn, is expressed in the body frame so that in can be used to provide a barometer-based estimation of the forward velocity , denoted by . Using both and as observations, a two-state Kalman filter [24] was designed in order to combine the information of the barometer and accelerometer in order to provide a more reliable estimation of and D. Therefore, the resulting tracking vector becomes
which includes all the the necessary variables - either estimated or measured - to track in order to perform vertical flight.
2.3. Affine form in hover conditions
Both the Nonlinear Dynamics Inversion and the Backstepping require for the equations of a given system to be expressed in affine form [30], which also holds true for its incremental variations, INDI and IBKS, explored in this work. For the attitude dynamics, the affine form of (2) becomes
where the subscript "" was used to denote dynamics, and represents the inputs for the attitude dynamics. For near hover conditions, the effects of the wing in can be neglected and can be taken as constant, as it is stated in [22]:
where , , , and respectively represent constants for the lift, drag, pitching moment, thrust and torque that result from a linearization at hover equilibrium conditions with a motor speed with throttle input , described in detail in the previous work [22]. Additionally, and represent the x and y coordinates of the aerodynamic centre of the right side of the wing in relation to the Centre of Gravity (COG) of the UAV, whilst is the analogous lateral position of the proprotor, and lastly is the Mean Aerodynamic Chord (MAC) of the tail-sitter.
In order to apply incremental control techniques, it is useful to express (11) in its incremental form under the assumptions that the input has a faster effect on the dynamics of this subsystem and a small sampling time is possible [31], resulting in
where k stands for the current time instant and the increment of the control input. Naturally, (14) requires that the acceleration of the previous time-step, , to be accessible, either via direct measurement or through a suitable estimation method.
For control purposes, the cross components of can be neglected, resulting in a simpler control effectiveness matrix, with the following numerical value for the X-Vert [22]:
Moving on to the attitude kinematics, (4) can also be expressed in affine form, this time considering as the input of this subsystem:
where the subscript "" symbolizes kinematics. Under this form, the vector takes only null values, and the respective varies with :
3. Incremental Control Methods for Attitude Stabilization
3.1. INDI Attitude Control
The increment of the INDI control law for the attitude dynamics can be directly deduced from the inversion of (14), taking as the desired dynamics of the system and as an Input Scaling Gain (ISG) [32]:
which must be added to the control input of the previous time-step, , to compute the final value. It should be noted that the subscript is omitted in (18) to not overburden the notation, as the INDI (and IBKS) is only applied to the attitude dynamics in this work. In (18), the desired dynamics are defined by
in which is the vectorial component of the error quaternion - defined by the quaternion product between the conjungate of the estimated quaternion, , and the respective reference quaternion to be tracked, - and and are diagonal gain matrices.
As stated before, the INDI control strategy assumes that is available. This vector can be estimated from at each time-step using the following second-order derivative filter [22,33]:
where the damping coefficient is constant, , making the cutoff frequency the only tunable parameter of (20).
It is also useful to include the possibility of a command filter, acting simultaneously as a saturation in ensuring that is bound to the limits of the actuators, and as a low-pass filter, with a time-constant [33], given by the expression
Therefore, for the INDI control strategy, , and assume the role of design variables that help shape the controller response, together with the two gain matrices, and .
3.2. IBKS Attitude Control
In this work, and similarly to the INDI strategy, the IBKS method is only applied to the attitude dynamics subsystem in (14), as it is the largest source of model uncertainties [34]. Therefore, the attitude kinematics is controlled using a standard Backstepping loop, which starts by defining the error variable of the kinematics subsystem [35], with its time-derivative being
where the additional subscript in is used to underline that this matrix is a function on the error quaternion , meaning that .
Proposing as the Candidate Lyapunov Function (CLF) for this subsystem, its time-derivative is given by
Defining as a stabilizing function to be tracked by , expressed by
it can be verified that becomes negative-definite for and a positive-definite matrix
thus resulting in asymptotic stability.
Defining now the second error variable as , its time-derivative is given by
where the incremental form of the attitude dynamics in (14) was already accounted for [34]. Incorporating the contribution of in , an augmented CLF can be formed such that , which has the following expression for its time-derivative
Accounting now for and , the final CLF can be rewritten so that it includes the expression for the stabilizing function in (24), becoming
which can be further simplified into
Similarly to , can be forced to be negative-definite by adequately designing [36], such as
where the subscript "" and a scaling gain were included, similarly to was done for the INDI controller.
It can be verified that substituting (30) into (29) yields , thus ensuring it always is negative-definite for positive-definite gain matrices and and , and grating asymptotic stability of the controlled system.
The last step required for the implementation of (30) is to determine the time-derivative of . For this research a decision was made to compute analytically, although assuming a time-scale separation between the dynamics and kinematics by considering to be constant at each time-step, resulting in
Similarly to the INDI controller, the incremental backstepping approach assumes that is available, and thus the second-order derivative filter in (20) was used for this purpose. The IBKS control strategy can also be paired with a command-filter, having an analogous set of design variables to INDI: , , , and .
4. Hardware-in-the-Loop Validation
In order to validate the INDI and IBKS control solutions for the tail-sitter UAV, these were first tested in the described Simulink environment, followed by the implementation on a Micro-Controller Unit (MCU) in order to perform Hardware-in-the-Loop (HITL) simulations. Some considerations about this implementation are now provided.
-
Altitude control:The incremental attitude control solutions were paired with the same altitude and vertical velocity controller, ensuring the same testing conditions. This control strategy starts by defining a desired forward force [23]where and are respectively the deviations of D and regarding their reference values, and , the adjustable gains for this controller. Knowing the desired forward force from (32), the propeller model can be inverted allowing for the computation of the angular velocities of the motors, which in then be used to determine the thrust input [22,23].
-
Setup description:As in the research work that preceded these developments [22], the setup used in HITL simulations consisted of a Arduino Nano 33 IOT [37] connected to a W5500 Ethernet module [38] via Serial Peripheral Interface (SPI) protocol. This enables sensor data from the simulated aircraft model in MATLAB to be sent to the MCU, together with the references , which proceeds to perform the necessary estimation steps and compute the control action . This is then sent back to MATLAB, effectively controlling the simulated UAV. The SPI connection allows for fast bi-directional data streaming via User Datagram Protocol (UDP) over Ethernet, enabling the HITL simulations to be run at seconds, which was also the sampling time used to run the Arduino board and to perform the discretization of the filters described in Section 2 and Section 3.
-
Numerical implementation:It was soon verified that the IBKS implementation was more computationally-demanding than the INDI one, mainly due to the multiple matrix over vector multiplications and matrix inversions present in (24), (30) and (31). Therefore, some care was taken to optimize the code in order to minimize these costly operations.The first step in such optimization process was to implement the different gain matrices - and in INDI, and and in IBKS - as simple multiplication of the different vector components by constants, taking advantage of these matrices being diagonal and avoiding unnecessary multiplications by zeros. For a generic 3-by-3 matrix with components , , in its diagonal and a vector , this results in . The same reasoning was applied when using , as its inverse is trivial when assumed as a diagonal matrix as illustrated in (13).The only exception to this procedure comes from matrix , which should not be simplified in order to accurately represent the attitude kinematics in (16). To avoid the computations required for its inversion at every instant, it was inverted symbolically resorting to MATLAB, and was implemented directly as a separate matrix, with the expressionwhich produced faster computations. Nevertheless, the matrix and vector multiplications that involved or were still complex, and thus a dedicated library - BasicLinearAlgebra [39] - was used to perform these computations.
4.1. Hardware-in-the-Loop Results
The hardware-in-the-loop simulations were run using the described setup, effectively allowing for the virtual UAV to be controlled by the Arduino board. The reference signals were the same as the ones in [22], starting by the take-off, followed by test rotations over the y, z and x axis of the UAV, and ending with the landing.
The estimation and altitude control tuning parameters were kept the same in the HITL simulations for both controllers, namely , and , and the filters described in Section 3 were discretized for s. Regarding the values for the parameters specific to each controller, these were:
- INDI: , , , ,
- IBKS: , , , , .
It should be noted that the HITL configuration introduces a noticeable delay when receiving the simulated sensor readings, which has a negative impact on the performance of incremental controllers mainly due to the estimation of , as the second-order derivative filter already introduces some delay. This was also the reason that motivated the absence of the command-filtering in the HITL simulations, evident by and , as it was noticed that that resulted in unwanted oscillations due to this delay. Therefore, the HITL simulations were faced as a merely qualitative validation step that preceded the experimental flight tests, and no particular effort was taken to tune the above parameters. Such validation was considered satisfactory, and the results are readily presented in Figure 2 and Figure 3, respectively for the INDI and for the IBKS controllers.
It can be verified that both incremental controllers track , with a certain degree of precision specifically for but with limited accuracy for and . Both control strategies present low actuator oscillation, even in the presence of significant noise in the sensors modelled in the simulator, demonstrating excellent robustness to it. Such conclusion had already been found in [22] for the INDI control strategy, but is now extended to the IBKS. Table 1 summarizes the results for the hardware-in-the-loop simulations, providing the Root Mean Square (RMS) values of the tracking errors and the actuator oscillation, both metrics having been previously described in detail in [22]. Inspecting this table, it can be stated that it effectively validates the implementations of these two incremental control strategies.
4.2. Analysis on Computational Resources
Despite the similarity in the results as illustrated by Table 1, the INDI and IBKS differ substantially in the complexity of the required computations to calculate the control increment . Assuming the estimation of and and the calculation of the error variables as common steps for both controllers, the INDI strategy can be implemented without any sort of matrix products, since , and are diagonal matrices. However, this is not the case for the IBKS, which requires several products of full 3-by-3 matrices, resulting in added computational effort. This was soon noticed in the HITL simulations, were it was found that the Arduino was struggling in performing the necessary computations for the IBKS controller under the specified sample time s. Although this is a clear evidence of a limitation of the chosen MCU, it was considered as an interesting aspect to analyse, as it explored a fundamental difference of two otherwise very similar control strategies. Figure 4 illustrates plots during HITL simulations, with the considered time-span being 5 seconds after take-off and 5 seconds before landing, to avoid any transient behaviour.
As can be seen, the Arduino board manages to perform the necessary computations for the INDI control law under the imposed sample time s, with just some occasional spikes. Contrasting with this, interval in the simulation using the IBKS kept oscillating between and seconds, evidencing that this is a more computationally demanding control law. These results are summarized by the mean value and standard deviation of for the INDI and IBKS controllers, shown in Table 2. Analysing this table, it can be concluded that the IBKS control law, although having the advantages of proof of its global stability, is clearly more demanding on computational resources, presenting a natural trade-off between these two aspects.
5. Experimental Validation
After the successful validation of the INDI and IBKS implementations in a HITL scenario, these controllers were tested to stabilize an experimental prototype, in indoor and controlled conditions.
5.1. Description of the Experimental Setup
5.1.1. Flight Controller
The flight controller (FC) used in this research work is an iteration of the one previously developed in [22], which was based on an Arduino Nano 33 IOT since it has both an onboard 6 Degree-of-Freedom (DOF) Inertial Measurement Unit (IMU), comprising an accelerometer and gyroscope, and Wi-Fi capabilities. However, as it was verified in this previous research, the Wi-Fi communications were demanding in terms of processing time, and thus radio communications were used instead. A low-cost and quite popular radio transceiver was used, the nRF24L01 by Nordic Semiconductor [40], together with the RF24 library [41] to enable its integration with the Nano 33 IOT. The second change made to the FC was the inclusion of a barometer for altitude estimation instead of a sonar, already mentioned in Section 2. The barometer chosen was the MS5611 [42], which was connected to the Arduino via Inter-Integrated Circuit (I2C) protocol as specified in the utilized library [43]. The final assembly of the flight controller used in the flight tests is shown in Figure 5.
The remaining electronic components were the same as the ones in [22], in particular the motors, the Electronic Speed Controllers (ESC), the Power Distribution Board (PDB) and the battery. It should however be noted that the PDB was included as part of the FC assembly, in order to save space in the fuselage of the X-Vert. Reflective markers were also distributed in the experimental prototype in order for a motion capture system (MCS) to be able to track its movement, as it will be described next. The experimental prototype is shown in Figure 6.
5.1.2. Ground Station
To accommodate the transition to radio communications, a suitable interface that allowed MATLAB to communicate with the FC had to be designed. A Raspberry Pi Pico [44] was chosen as the MCU of this ground station, mainly due to its dual-core 133 MHz processor, compatibility with the Arduino ecosystem [45], and two SPI ports. This allowed for the Pi Pico to be simultaneously paired with a W5500 Ethernet module and an antenna version of the nRF24L01 with independent SPI connections, and the final ground station assembly can be seen in Figure 7. It should be highlighted that the ground station was made to run at 100 Hz, so that it could perform the Ethernet/radio bridging without with losing data packets.
5.1.3. Ground Truth
The experimental trials were conducted in a indoor, net-protected area covered by a Qualisys MCS. Such system enabled the accurate and precise tracking of the movement and attitude of the X-Vert during the flight tests, providing the ground truth for evaluate of the performance of the controllers. Figure 8 shows an example of the tracking of the X-Vert by the MCS during the experimental flight trials.
5.2. Experimental Results
The flight trials were conducted using the experimental prototype shown in Figure 6, controlled by the Arduino board, which computed the estimated quaternion, altitude and the control action, and returned them to MATLAB via the previously-described ground station. The MCS was then used as a validation mechanism, allowing to track the attitude of the UAV with a separate and independent tool. A sample time of s was chosen in order to ensure that the MCU could perform the computations required by the IBKS controller in regular intervals, and the filters were re-designed accordingly. The parameters for the estimation methods and altitude controller were kept the same for both the INDI and IBKS,
ensuring that these would not influence the performance of the attitude controllers. On the other hand, the relevant controller-specific parameters have the following values:
- INDI: , , , , .
- IBKS: , , , , .
When it comes to the parameter tuning, it was soon verified that it was useful to specify a value for that would be satisfactory, and then choose in order to ensure a smooth, oscillation-free actuation. In turn, the gain matrices and ISG could be fine-tuned afterwards to achieve the desired control action. Nevertheless, the tuning of the IBKS demonstrated to be a challenge due to the influence of in the several steps of the implementation, whereas the and matrices for the INDI controller were easily fine-tuned separately.
Regarding the references to be tracked, the same decision taken in the previous research work [22] of exploring primarily the ability of tracking the longitudinal references in , due to its importance for future tail-sitter transition maneuvers and the relatively limited indoor area available for the flight tests. Nevertheless, a brief lateral non-zero reference for was introduced in the trials, to evaluate if the controllers could track it whilst already tracking . Accounting for this, the experimental results for the INDI controller are shown in Figure 9.
As can be seen from inspecting the aforementioned figure, the INDI controller tracks the reference with precision, whilst also responding to the request in . Some small overshoot moments are present, but these did not compromise the stabilization of the UAV during the flight trials. It should be noted that the discrepancy between the estimated and ground-truth values for and may be attributed to a subtle non-zero rotation before the take-off, which is only perceived by the MCS, as the Arduino assumes that both and are zero in the beginning of each trial. Regarding the actuation, it can be seen from the same figure that the INDI controller generates a fairly smooth control action, even in the presence of sensor noise, only having some small spikes in . Summarizing, it is possible to verify that the INDI controller manages to stabilize the aircraft in vertical flight and to track the provided references, whilst having a smooth actuation.
Moving on to the IBKS controller, the attitude tracking results for these flight tests are shown in Figure 10.
Inspecting Figure 10, it is clear that the IBKS controller demonstrates a much smoother tracking of and , but, when it comes to , its performance is less satisfactory, showing some significant overshoot, which highlights the aforementioned difficulty in tuning this controller. Regarding the actuation, the IBKS also allows for a smooth control action even in the presence of sensor noise, with minimal oscillation and without significant spikes. Therefore, it can be concluded that this controller was also able to stabilize the prototype in vertical flight and perform the desired maneuvers, demonstrating that it is fully capable of controlling a tail-sitter UAV, with robustness to sensor noise.
The experimental results for the attitude control are summarized in Table 3, where both the RMS of the quaternion tracking error and actuator oscillation are provided, similarly to what was done for the results for the HITL simulations. Inspecting this table, it can be seen that it agrees with the previous considerations, demonstrating that both controllers are capable of stabilizing the X-Vert and to track the provided references, evidenced by the relatively low values for . Furthermore, it can be concluded that both the INDI and IBKS control strategies allow for a smooth actuation due to the small values of , demonstrating excellent robustness to sensor noise.
The last aspect of the experimental flights to analyse is the altitude control which, altough not the focus of this research work, should also be the topic for some considerations. These results are shown in Figure 11, which comprises the altitude and throttle input plots for both the INDI and IBKS controllers.
As can be seen from the inspection of the aforementioned figure, none of the controllers tracks the reference altitude value with precision, and the experimental flight for the INDI controller has significant oscillation. Such oscillation may be attributed to the low-pass filtering used in obtaining the estimated altitude, but it was considered necessary in order to reduce the noise of the sensor measurements to acceptable values to be used in the altitude controller. The difficulty in tracking with more precision could be compensated with higher values for and , but it was found that it would cause additional oscillation, and therefore these results for altitude control were considered satisfactory as they enabled for successful take-off, altitude keeping, and landing. Furthermore, it allowed to verify with a smooth control action . Since it was verified that a sonar was not an ideal solution for altitude estimation by itself in the previous research work [22], it is now evident that the barometer should be paired with a similar distance measurement sensor in order to accurately track the altitude, specially in take-off and landing maneuvers. The application of incremental solutions to the altitude control should also be evaluated, as it is expected for them to be robust to the aforementioned sensor noise, whilst allowing for precise tracking.
6. Conclusions
The research involved in this work demonstrated that both the Incremental Nonlinear Dynamics Inversion and Incremental Backstepping are control strategies fully-capable of controlling a tail-sitter UAV in vertical flight. Once these controllers were implemented in simulation and validated with hardware-in-the-loop tools, the experimental flight trials took place, conducted in a indoor environment, performing simple maneuvers in vertical flight and demonstrating the tracking capabilities and excellent robustness to sensor noise.
Summarizing the comparison between these two control strategies, it can be stated that the INDI provides with a simple and straightforward control law, easy to implement and with low computational requirements, but it lacks a global asymptotic stability proof. The IBKS contrasts in these aspects, providing a global stability proof, but demanding several steps in obtaining the control law - all of which increase the computational demands of the MCU - and harder tuning of the controller parameters.
As future work, it is suggested to utilize a more capable MCU, preferably one capable of performing floating-point math for faster calculations, as opposed to the integer-based computations that the Arduino Nano 33 IOT employs. Furthermore, it is recommended to evaluate the application of both INDI and IBKS for aerodynamic flight, naturally also during transitions, so that their performance can be assessed for a full tail-sitter flight. This would demand for additional sensors to be included in an experimental prototype, and requires further investigation. Lastly, the altitude estimation and control should also be a topic of additional research, in order to ensure a robust and precise altitude tracking, whether it is by reintroducing a range sensor like a sonar, by applying incremental solutions for altitude control, or using both of these.
Author Contributions
Conceptualization, A.A., A.M. and J.R.A.; methodology, A.A., A.M. and J.R.A.; software, A.A. and J.R.A.; validation, A.M. and J.R.A.; formal analysis, A.A.; investigation, A.A.; resources, A.M.; data curation, A.A.; writing—original draft preparation, A.A.; writing—review and editing, A.M. and J.R.A.; visualization, A.A.; supervision, A.M. and J.R.A.; project administration, A.M.; funding acquisition, A.M.. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Funds by FCT – Fundação para a Ciência e Tecnologia, I.P. under project LAETA Base Funding (DOI: 10.54499/UIDB/50022/2020) and under project Eye in the Sky (DOI: 10.54499/PCIF/SSI/0103/2018).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Aerodynamic Center |
| AOA | Angle-of-attack |
| BKS | Backstepping |
| BLDC | Brushless Direct Current |
| CF | Complementary/Command Filter |
| CG | Center-of-Gravity |
| DOF | Degree-of-Freedom |
| ESC | Electronic Speed Controller |
| FC | Flight Controller |
| HITL | Hardware-In-The-Loop |
| I2C | Inter-Integrated Circuit |
| IMU | Inertial Measurement Unit |
| IBKS | Incremental Backstepping |
| INDI | Incremental Nonlinear Dynamics Inversion |
| ISG | Input Scaling Gain |
| LPF | Low-Pass Filter |
| LQR | Linear Quadratic Regulators |
| MAC | Mean Aerodynamic Chord |
| MCS | Motion Capture System |
| MCU | Micro-controller Unit |
| MDPI | Multidisciplinary Digital Publishing Institute |
| NDI | Nonlinear Dynamics Inversion |
| NED | North-East-Down |
| PCB | Prrinted Circuit Board |
| PID | Proportional Integral-Derivative |
| PWM | Pulse WidthModulation |
| QTM | Qualysis Track Manager |
| RMS | Root-Mean-Square |
| SD | Second-(order) Derivative |
| SPI | Serial Peripheral Interface |
| UAV | Uncrewed Aerial Vehicles |
| UDP | User Datagram Protocol |
| VTOL | Vertical Takeoff and Landing |
References
- Zhou, Y.; Zhao, H.; Liu, Y. An evaluative review of the VTOL technologies for unmanned and manned aerial vehicles. Computer Communications. 2020. [Google Scholar] [CrossRef]
- Saeed, A.S.; Younes, A.B.; Cai, C.; Cai, G. A survey of hybrid unmanned aerial vehicles. Prog. Aerosp. Sci. 2018, 98, 91–105. [Google Scholar] [CrossRef]
- Rakesh, D.; Kumar, N.A.; Sivaguru, M.; Keerthivaasan, K.V.R.; Janaki, B.R.; Raffik, R. Role of UAVs in innovating agriculture with future applications: A review. In Proceedings of the 2021 International Conference on Advancements in Electrical, Electronics, Communication, Computingand Automation (ICAECA), Coimbatore, India, 8–9 October 2021.
- Ducard, G.J.; Allenspach, M. Review of designs and flight control techniques of hybrid and convertible VTOL UAVs. Aerosp. Sci. Technol. 2021, 118, 107035. [Google Scholar] [CrossRef]
- Ziquan, Y. U.; Youmin, Z.; Bin, J. PID-type fault-tolerant prescribed performance control of fixed-wing UAV. Journal of Systems Engineering and Electronics. 2021. [Google Scholar] [CrossRef]
- Kazemi, M. H.; Tarighi, R. PID-based attitude control of quadrotor using robust pole assignment and LPV modeling. International Journal of Dynamics and Control. 2024. [Google Scholar] [CrossRef]
- Tunik, A. A.; Nadsadna, O. I. Robust digital gain-scheduling control of the UAV altitude. In 2017 IEEE 4th International Conference Actual Problems of Unmanned Aerial Vehicles Developments (APUAVD). 2017. [Google Scholar]
- Wang, J.; Holzapfel, F.; Peter, F. Comparison of nonlinear dynamic inversion and backstepping controls with application to a quadrotor. Proceedings of the EuroGNC, 1245-1263, 2013. [Google Scholar]
- Azinheira, J.R.; Moutinho, A. Hover Control of an UAV with Backstepping Design Including Input Saturations. IEEE Trans. Control. Syst. Technol. 2014, 16, 517–526. [Google Scholar] [CrossRef]
- Jang, K.; Bang, H.; Kim, Y. Mitigating Time-Delay in Nonlinear Dynamics Inversion for Multirotor Unmanned Aerial Vehicles. Journal of Guidance, Control, and Dynamics, 2024. [Google Scholar]
- Xin, H.; Chen, Q.; Xian, Y.; Wang, P.; Wang, Y.; Yao, X.; Hou, Z. Longitudinal Decoupling Control of Altitude and Velocity for a Fixed-Wing Aircraft. IEEE Transactions on Intelligent Vehicles 2024. [Google Scholar] [CrossRef]
- XKhanna, A.; Mukherjee, B. K. UAV Performing Level Turn Maneuver Under CG Offset: Backstepping Control Scheme. 10th IEEE Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), 2023. [Google Scholar]
- Lombaerts, T.; Kaneshige, J.; Schuet, S.; Hardy, G.; Aponso, B. L.; Shish, K. H. Nonlinear dynamic inversion based attitude control for a hovering quad tiltrotor eVTOL vehicle. AIAA Scitech 2019 forum 2019. [Google Scholar]
- Amiri, N.; Ramirez-Serrano, A.; Davies, R. J. Integral backstepping control of an unconventional dual-fan unmanned aerial vehicle. Journal of Intelligent & Robotic Systems, 2013. [Google Scholar]
- Cordeiro, R.A.; Azinheira, J.R.; Moutinho, A. Robustness of incremental backstepping flight controllers: The boeing 747 case study. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3492–3505. [Google Scholar] [CrossRef]
- Safwat, E.; Weiguo, Z.; Kassem, M.; Mohsen, A. Robust Nonlinear Flight Controller For Small Unmanned Aircraft Vehicle based on Incremental BackStepping AIAA Scitech 2020 Forum. 2020. [Google Scholar]
- Smeur, E.J.; Bronz, M.; de Croon, G.C. Incremental control and guidance of hybrid aircraft applied to a tailsitter unmanned air vehicle. J. Guid. Control. Dyn. 2020, 43, 274–287. [Google Scholar] [CrossRef]
- Wang, Y. C.; Chen, W. S.; Zhang, S. X.; Zhu, J. W.; Cao, L. J. Command-filtered incremental backstepping controller for small unmanned aerial vehicles. Journal of Guidance, Control, and Dynamics. 2018. [Google Scholar]
- Tal, E.; Karaman, S. Accurate tracking of aggressive quadrotor trajectories using incremental nonlinear dynamic inversion and differential flatness. IEEE Trans. Control. Syst. Technol. 2020, 29, 1203–1218. [Google Scholar] [CrossRef]
- Tal, E.A.; Karaman, S. Global trajectory-tracking control for a tailsitter flying wing in agile uncoordinated flight. In Proceedings of the AIAA Aviation 2021 Forum.
- E-Flite XVERT VTOL Webpage. Available online: https://www.horizonhobby.de/en_DE/product/x-vert-vtol-bnf-basic-504mm/EFL1850.html (accessed on 16 April 2024).
- Athayde, A.; Moutinho, A.; Azinheira, J.R. Experimental Nonlinear and Incremental Control Stabilization of a Tail-Sitter UAV with Hardware-in-the-Loop Validation. Robotics 2024, 13, 51. [Google Scholar] [CrossRef]
- Chiappinelli, R.; Nahon, M. Modeling and Control of a Tailsitter UAV. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice, 1st ed.; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Stevens, B.L.; Lewis, F.L. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Khan, W.; Nahon, M. Toward an accurate physics-based UAV thruster model. IEEE ASME Trans. Mechatron. 2013, 18, 1269–1279. [Google Scholar] [CrossRef]
- Khan, W.; Nahon, M. Real-time modeling of agile fixed-wing UAV aerodynamics. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015. [Google Scholar]
- Khan, W.; Nahon, M. Modeling dynamics of agile fixed-wing UAVs for real-time applications. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016. [Google Scholar]
- Madgwick, S.O.; Harrison, A.J.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011. [Google Scholar]
- Horn, J.F. Non-linear dynamic inversion control design for rotorcraft. Aerospace 2019, 6, 38. [Google Scholar] [CrossRef]
- Coelho, R. , Moutinho, A., ; Azinheira, J.R. Quadrotor Attitude Control using Incremental Nonlinear Dynamics Inversion. 2017. [Google Scholar]
- Azinheira, J.R.; Moutinho, A.; Carvalho, J.R. Lateral control of airship with uncertain dynamics using incremental nonlinear dynamics inversion. IFAC Pap. Online 2015, 48, 69–74. [Google Scholar] [CrossRef]
- Cordeiro, R.A.; Marton, A.S.; Azinheira, J.R.; Carvalho, J.R.; Moutinho, A. Increased robustness to delay in incremental controllers using input scaling gain. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1199–1210. [Google Scholar] [CrossRef]
- Acquatella, P.; van Kampen, E.; Chu, Q.P. Incremental backstepping for robust nonlinear flight control. In Proceedings of the EuroGNC 2013, Delft, The Netherlands, 10–12 April 2013. [Google Scholar]
- Oland, E.; Kristiansen, R. Quaternion-based backstepping control of a fixed-wing unmanned aerial vehicle. In IEEE Aerospace Conference, USA 2013.
- Van Ekeren, W.; Looye, G.; Kuchar, R.; Chu, Q.; Van Kampen, E. J. Design, implementation and flight-test of incremental backstepping flight control laws. AIAA Guidance, Navigation, and Control Conference, 2018, 2018.
- Arduino Nano 33 IOT Product Page. Available online: https://docs.arduino.cc/hardware/nano-33-iot/ (accessed on 16 April 2024).
- Wiznet W5500 Product Page. Available online: https://www.wiznet.io/product-item/w5500/ (accessed on 16 April 2024).
- Basic Linear Algebra Library Page, by Tom Stewart. Available online: https://github.com/tomstewart89/BasicLinearAlgebra (accessed on 16 April 2024).
- Nordic Semiconductor nRF24 Series Product Page. Available online: https://www.nordicsemi.com/Products/nRF24-series (accessed on 16 April 2024).
- NRF24L01 Library Page, by TMRh20. Available online: https://nrf24.github.io/RF24/ (accessed on 16 April 2024).
- MS5611 Barometer Product Page. Available online: https://www.okystar.com/product-item/gy-63-ms5611-atmospheric-pressure-sensor-module-height-sensor-module-iicspi-communication-oky3232/29/ (accessed on 16 April 2024).
- MS5611 Pressure and Temperature Sensor Library Page, by Rob Tillaart. Available online: https://www.arduino.cc/reference/en/libraries/ms5611/ (accessed on 16 April 2024).
- Raspberry Pi Pico Product Page. Available online: https://www.raspberrypi.com/documentation/ microcontrollers/raspberry-pi-pico.html (accessed on 16 April 2024).
- Raspberry Pi Pico Arduino Core Page, by Earle F. Philhower, III. Available online: https://arduino-pico.readthedocs.io/en/latest/ (accessed on 16 April 2024).
Figure 1.
Layout of the simulated environment [22].
Figure 1.
Layout of the simulated environment [22].
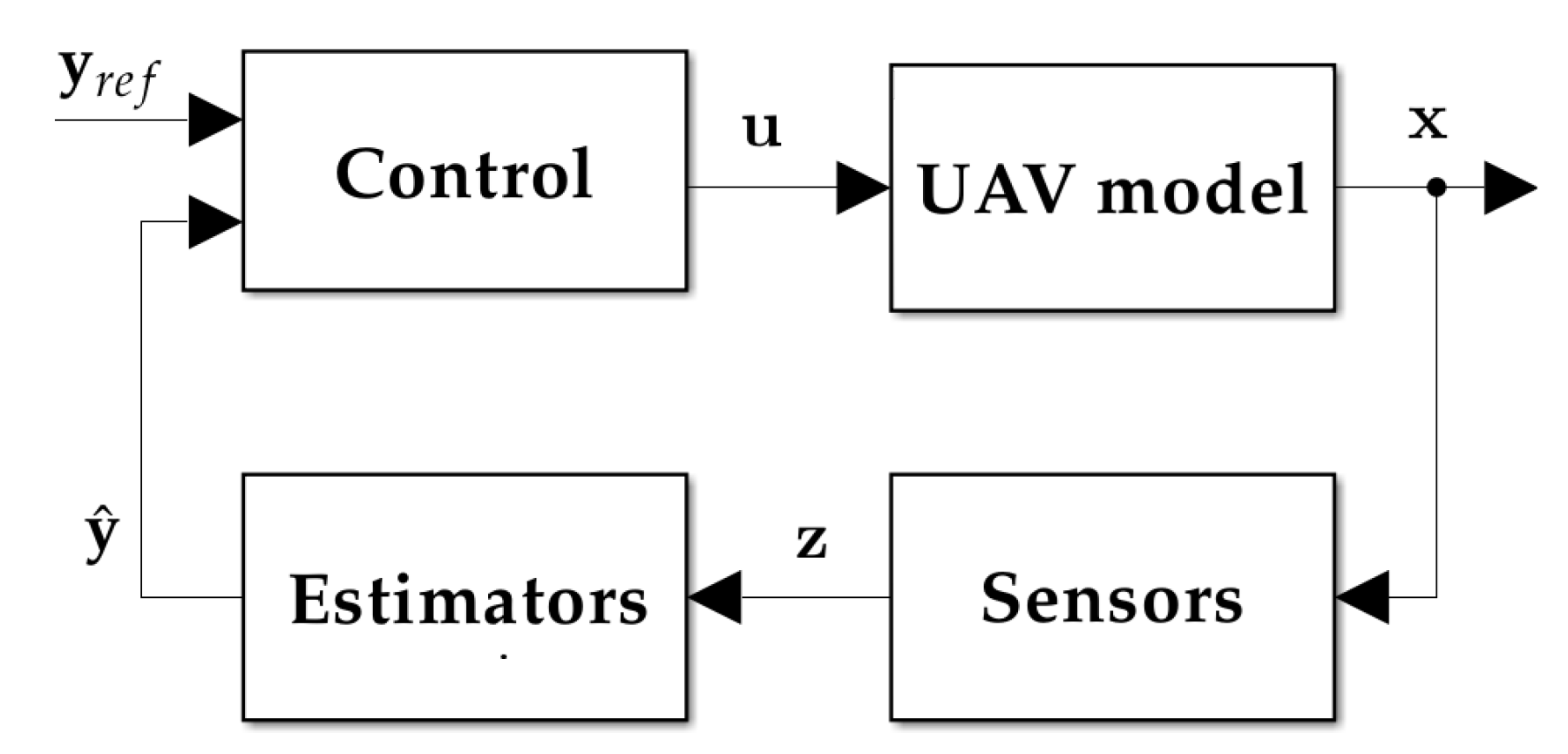
Figure 2.
Plots for the HITL simulations using the INDI controller.
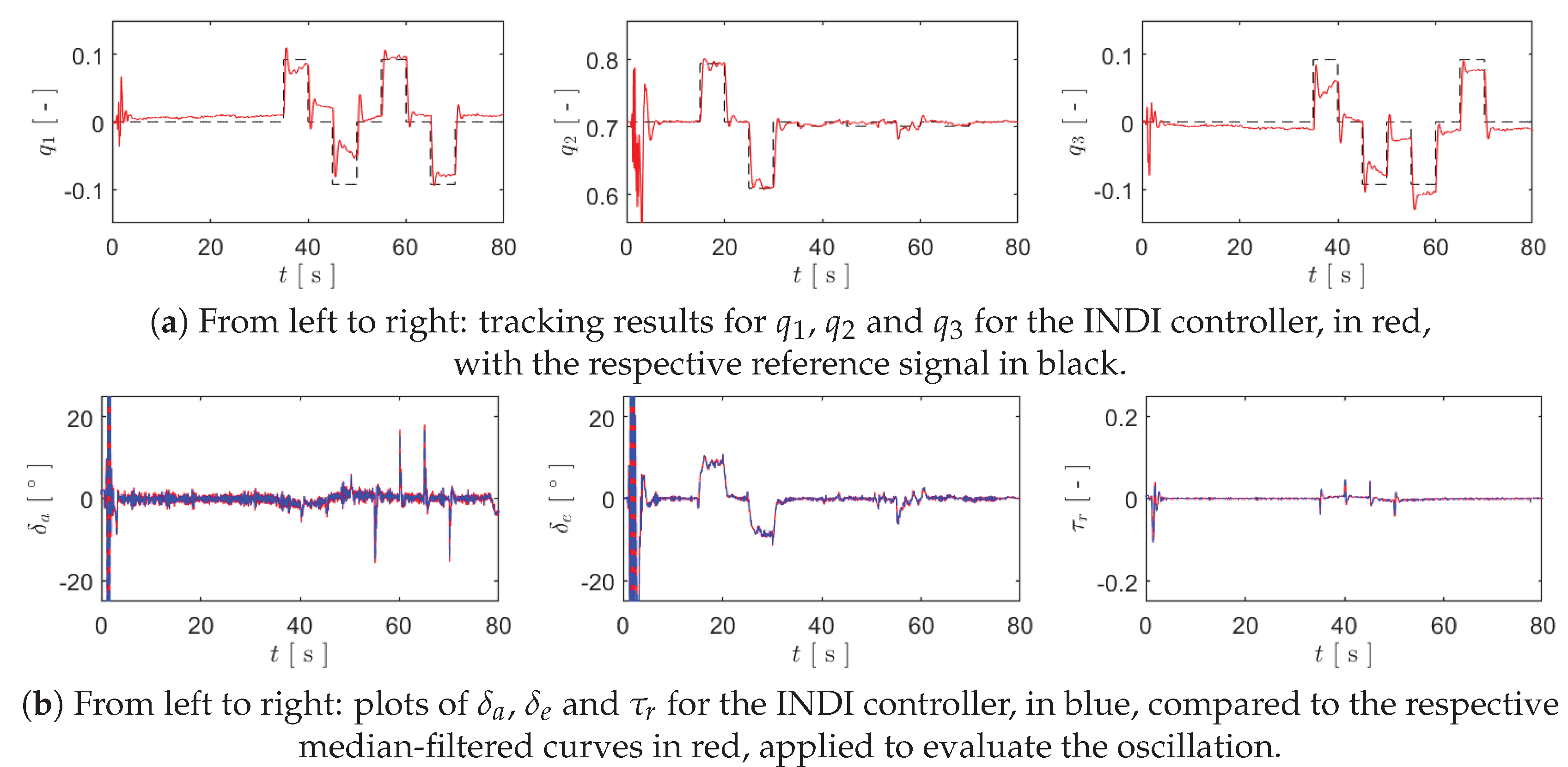
| (a) From left to right: tracking results for , and for the INDI controller, in red, |
| with the respective reference signal in black. |
| (b) From left to right: plots of , and for the INDI controller, in blue, compared to the respective |
| median-filtered curves in red, applied to evaluate the oscillation. |
Figure 3.
Plots for the HITL simulations using the IBKS controller.
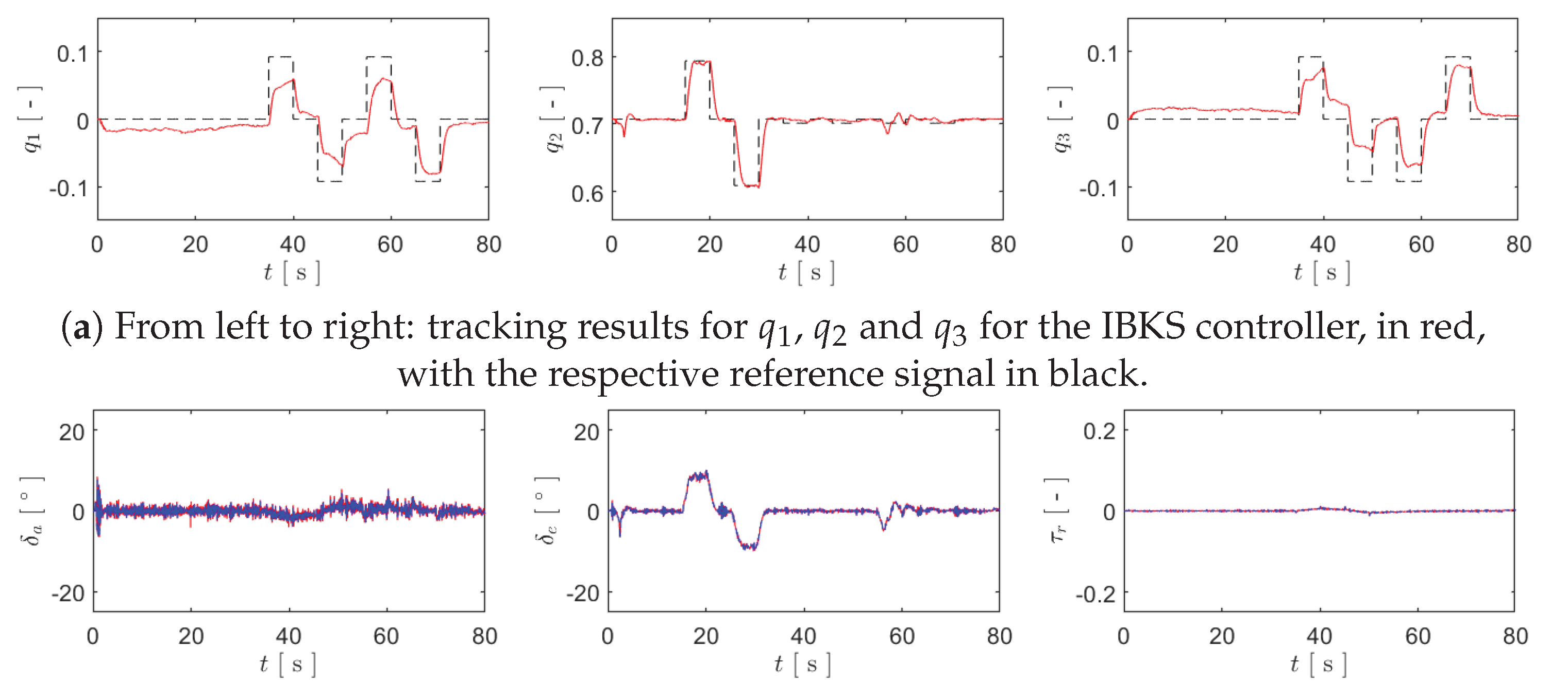
| (a) From left to right: tracking results for , and for the IBKS controller, in red, |
| with the respective reference signal in black. |
| (b) From left to right: plots of , and for the IBKS controller, in blue, compared to the respective |
| median-filtered curves in red, applied to evaluate the oscillation. |
Figure 4.
Plot of for the INDI hardware-in-the-loop simulation (left) and an analogous plot for the IBKS (right).
Figure 4.
Plot of for the INDI hardware-in-the-loop simulation (left) and an analogous plot for the IBKS (right).
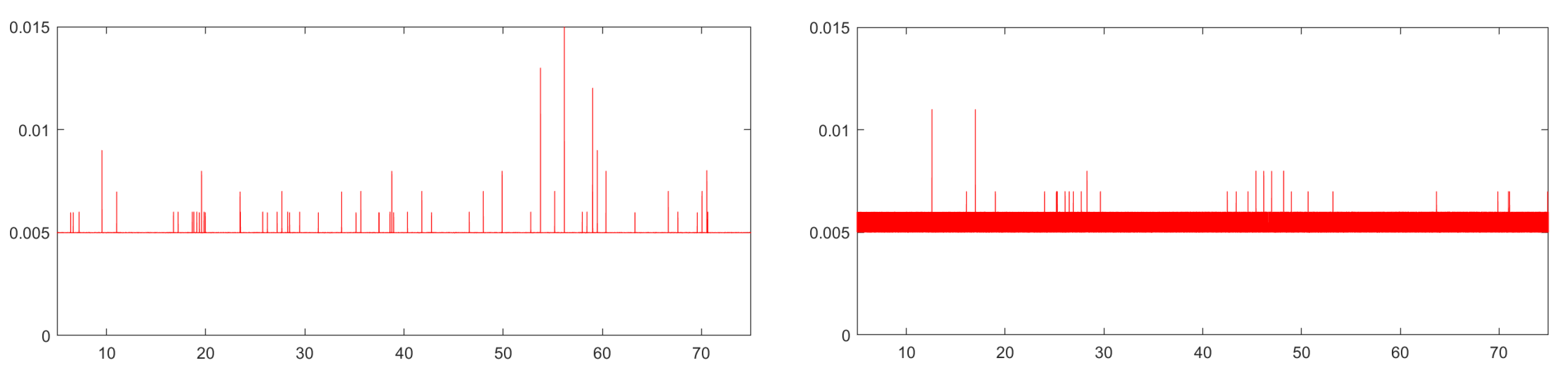
Figure 5.
Flight controller assembly used for the experimental trials.

Figure 6.
Experimental prototype based on the X-Vert VTOL.

Figure 7.
Disassembled ground station with the Raspberry Pi Pico and the W5500 Ethernet module (left) and the assembled version with the nRF24L01 (right).
Figure 7.
Disassembled ground station with the Raspberry Pi Pico and the W5500 Ethernet module (left) and the assembled version with the nRF24L01 (right).

Figure 8.
Reconstruction of the X-Vert using the MCS.
Figure 9.
Plots for the attitude control of the experimental flight test using the INDI controller.
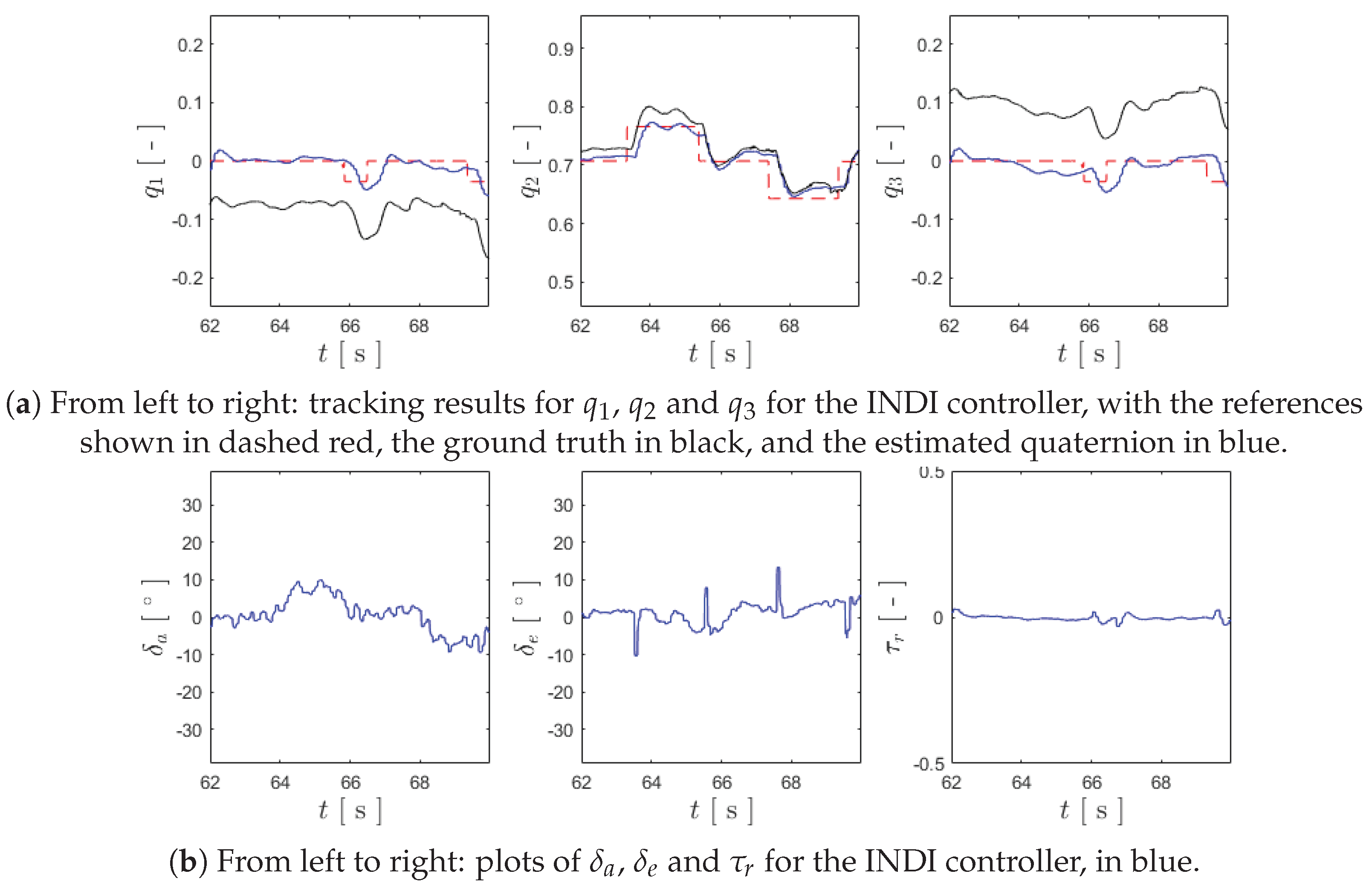
| (a) From left to right: tracking results for , and for the INDI controller, with the references |
| shown in dashed red, the ground truth in black, and the estimated quaternion in blue. |
| (b) From left to right: plots of , and for the INDI controller, in blue. |
Figure 10.
Plots for the attitude control of the experimental flight test using the IBKS controller.
Figure 10.
Plots for the attitude control of the experimental flight test using the IBKS controller.
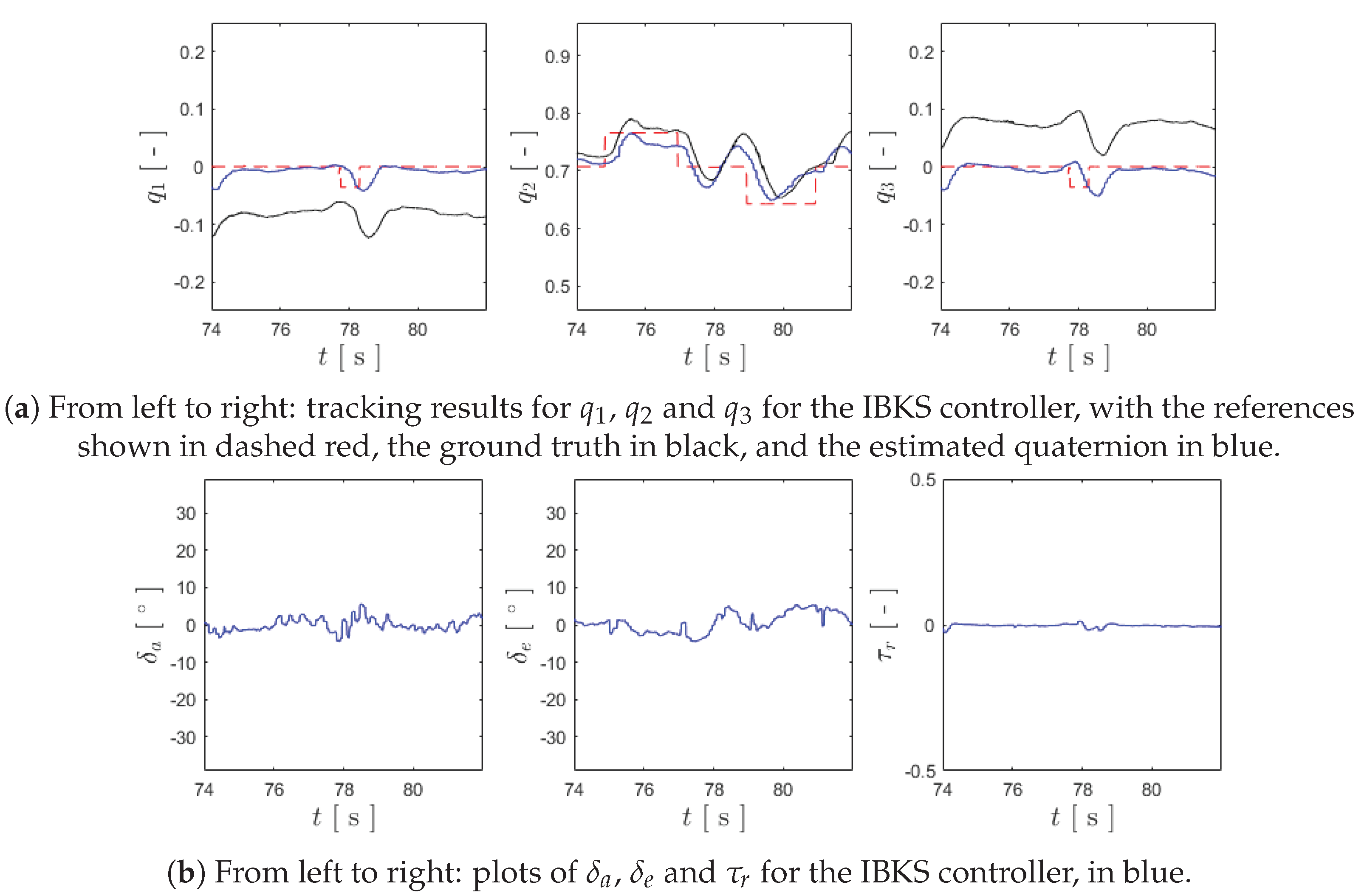
| (a) From left to right: tracking results for , and for the IBKS controller, with the references |
| shown in dashed red, the ground truth in black, and the estimated quaternion in blue. |
| (b) From left to right: plots of , and for the IBKS controller, in blue. |
Figure 11.
Plots for the experimental flight test using the IBKS controller.
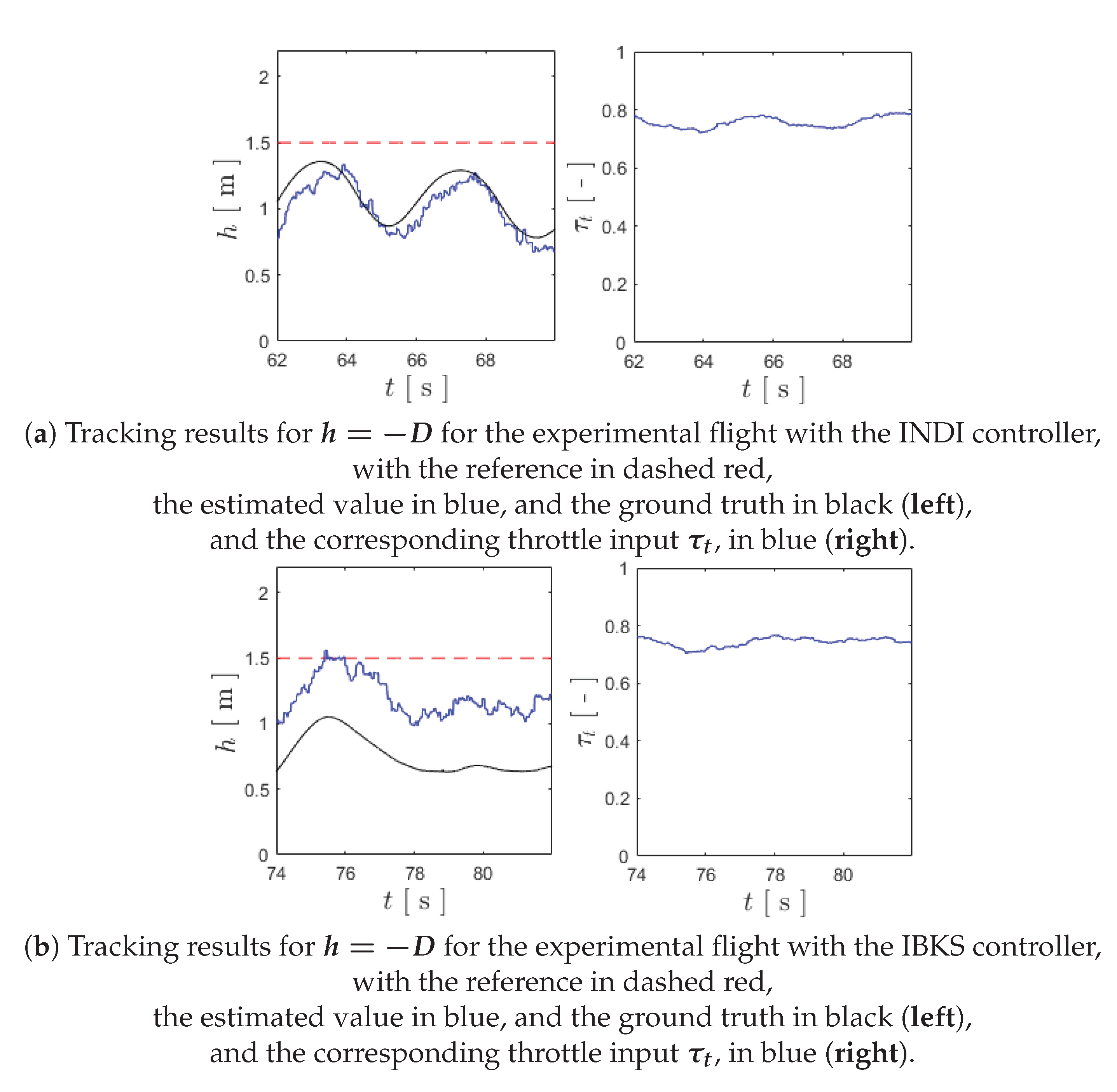
| (a) Tracking results for for the experimental flight with the INDI controller, |
| with the reference in dashed red, |
| the estimated value in blue, and the ground truth in black (left), |
| and the corresponding throttle input , in blue (right). |
| (b) Tracking results for for the experimental flight with the IBKS controller, |
| with the reference in dashed red, |
| the estimated value in blue, and the ground truth in black (left), |
| and the corresponding throttle input , in blue (right). |
Table 1.
Summary of the Hardware-in-the-loop results, expressed in the respective units.
| Cont. | ||||||||
|---|---|---|---|---|---|---|---|---|
| INDI | 0.0214 | 0.0125 | 0.0215 | 0.0185 | 0.0030 | 0.0009 | 0.0003 | 0.0014 |
| IBKS | 0.0299 | 0.0169 | 0.0289 | 0.0252 | 0.0033 | 0.0010 | 0.0003 | 0.0015 |
Table 2.
Summary of the Hardware-in-the-loop results.
| Cont. | [s] | [s] |
|---|---|---|
| INDI | 0.005008 | 0.000157 |
| IBKS | 0.005334 | 0.000483 |
Table 3.
Summary of the experimental results, expressed in the respective units.
| Cont. | ||||||||
|---|---|---|---|---|---|---|---|---|
| INDI | 0.0796 | 0.0283 | 0.1024 | 0.0701 | 0.0045 | 0.0081 | 0.0011 | 0.0046 |
| IBKS | 0.0822 | 0.0382 | 0.0769 | 0.0658 | 0.0042 | 0.0038 | 0.0007 | 0.0029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







