Modeling and Mitigating Gas Hazards during Potash Mine Closure

Preprint

Article

Modeling and Mitigating Gas Hazards during Potash Mine Closure

Altmetrics

Downloads

139

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 June 2024

Posted:

18 June 2024

You are already at the latest version

Alerts

Abstract

The planned closure of potash mines, achieved through the injection of highly mineralized brines into the worked-out area, is a complex and not fully studied process. A critical concern arises when brines obstruct the aerodynamic connections between the flooded mine's airspace and the atmosphere, potentially leading to the formation of closed cavities where explosive gases can accumulate. To address this hazard, it is imperative to develop systems capable of extracting the gas-air mixture from the unflooded domed portions of the worked-out area. This is the focus of this study, in which we analyze gas-dynamic processes within the potassium mine worked-out area during planned flooding. Two distinct scenarios are examined: the first involves controlled flooding with saturated brines, while the second contemplates flooding resulting from a hypothetical breakthrough of supra-salt strata, leading to the ingress of groundwater into the worked-out area. A novel mathematical model is introduced to predict the evolution of gas-air mixture parameters in the unflooded dome segment of the worked-out area. Utilizing this model, we assess the effectiveness of proposed measures designed to eliminate explosive gases from the worked-out area. Specifically, a pipeline system is proposed for the removal of gases, followed by their dilution below the maximum permissible concentrations in the effluent jet. The findings from this study contribute valuable insights into ensuring the safe and efficient closure of potash mines, shedding light on potential risks and effective mitigation strategies for gas-related hazards during planned flooding.

Keywords:

Subject: Engineering - Mining and Mineral Processing

Introduction

The closure of a potash mine represents the conclusive phase of its life cycle, which can occur either as a planned or emergency process. Planned mine closure is executed following the exhaustive extraction of balance reserves of minerals, the inability to recover off-balance reserves, or when the imminent threat of mine workings flooding exists, prevention of which is either technically unfeasible or economically impractical. During the planned closure of salt or potash mines, two methods are commonly employed: dry closure method and wet controlled closure method [1].

In the dry method, plugging the mine shafts is exclusively performed to thwart water inflows into the worked-out area of the mine. However, when faced with the risk of an emergency groundwater influx into a salt or potash mine, the wet controlled closure method is deemed more reliable to diminish the degree of pillar dissolution and the potential for failures [2]. The essence of this method involves pre-filling the worked-out area of the mine, followed by the introduction of saturated brine through specialized pipelines. The brine occupies the entire remaining volume of the mine voids without inducing complete pillar degradation. The higher density of the brine serves to impede the ingress of groundwater into the worked-out area.

Emergency closure of potash and salt mines arises from abrupt breakthroughs of fresh groundwater into mine workings through the water-protective layer [2]. The primary cause of such breakthroughs is the insufficient thickness of the water-protective layer considering the adopted mining parameters [3]. Uncontrolled flooding of a salt or potash mine typically results in the depletion of mineral reserves and various environmental issues [4,5,6].

Many researchers have analyzed real cases of flooding in potash mines, often involving emergency situations. For instance, Gendzwill and Martin [7] provided a practical example of emergency flooding in a potash mine near Saskatoon, Saskatchewan. The authors detailed various measures taken to slow down the flooding, such as grouting and the installation of bulkheads. Wittrup [8] conducted a hydrochemical analysis of groundwater involved in the flooding of Saskatchewan potash mines, categorizing three types of floodwaters based on the mine level.

Malovichko et al. [9] described a serious accident that occurred in the Berezniki-1 mine of the Verkhnekamskoye potassium-magnesium salt deposit (VPMSD). The waterproof stratum's integrity was compromised, leading to uncontrolled flooding. The authors employed a complex of geophysical methods to localize the inflow zone, estimate the expected sinkhole size, and monitor its development over time. Baryakh et al. [10] applied geomechanical methods to investigate ways to minimize the aftereffects of the large-scale accident connected with the flooding of Berezniki-1 potash mine. The authors constructed a synthesized geomechanical model of the flooded mine, illustrating mining conditions, salt rock dissolution processes, and the elastoplastic behavior of deformation and failure of the undermined rock mass over time. Kulikova and Ovchinnikova [11] mention a geochemical control method that allows one to determine the average concentrations of 40Ar isotope using laser spectroscopy. Argon isotopes can penetrate into the worked-out void atmosphere only if the integrity of the water-protective layer is damaged.

The most comprehensive overview of planned and emergency closures of potash mines is provided by Baryakh and Evseev [1]. The authors considered global experiences in mine commissioning, highlighting that most closures result from emergency breakthroughs of fresh water into the worked-out area. They analyzed the causes and consequences of accidents related to the entry of fresh water and brines into mine workings. Prugger and Prugger [6] described the history of water problems in the Saskatchewan potash industry. This study also summarizes the measures that are now commonly used to avoid these problems. The authors indicated the need to minimize the build-up of stress concentrations in the vicinity of mine rooms by adjusting room width, pillar size, extraction rate, mining sequence, the location of barrier pillars, and by utilizing stress-relief mining systems. Baryakh and Evseev [1] showed that an integral element of mine liquidation should be long-term comprehensive monitoring of the processes accompanying the flooding of mine workings. Zubov and Smychnik [12] proposed creation of backfill masses in worked-out areas to eliminate the possibility of dangerous water-conducting cracks between aquifers and productive formations.

Another important aspect related to the environmental impact of construction and closure of potash mines is given in review [13]. The authors concluded that the most effective measure to reduce the adverse environmental impact of potash mining at the VPMSD is hydraulic backfilling of worked-out area. This method protects underground mines from flooding, minimizes ground subsidence, and reduces the area of potash waste.

Some examples describing the impact of closed potash mines on the environment are also considered in [14,15]. Besnard and Pokryszka [14] noted that flammable and/or toxic gases or deoxygenated air can be transmitted to the surface through existing aerodynamic connections like abandoned shafts or galleries and fissures in rock mass. The authors provided an example of gas monitoring data on the surface near mine sites, where there is a risk of negative effects of gases released from a closed mine on humans. Vysotskaya and Piskun [15] considered the adverse impact of underground mining on the terrain and landscape of the Soligorsk mining district. The negative impact on the flora and fauna in the district consists of a complex effect from factors such as land acquisition for industrial sites, salt tailings piles, flooding, and waterlogging of lands due to subsidence of the earth's surface above the worked-out areas, salinization of territories adjacent to the enterprise by excess brines, and the impact of industrial dust and gas emissions.

Ponomarenko [16] considered the economic and social consequences of emergency flooding of potash mines using the example of the VPMSD. Katta et al. [17] investigated greenhouse gas mitigation pathways for the iron, gold, and potash mining sectors in Canada. Considering the potential to reduce greenhouse gas emissions for these subjects, the authors conducted cost-benefit analyses of implementable greenhouse gas reduction strategies.

A separate important area of research is the determination of the content of free and bound gases in salt rock masses. Zimmer et al. [18] studied the processes of fixation and migration of gases in evaporites of the Seam Hessen potash layer from the Werra-Fulda basin. Andreyko et al. [19] studied the gas content in the productive salt layers of the potash mines of the Starobinsk potassium-magnesium salt deposit. The authors analyzed the content of free and bound gas in various rocks, as well as the chemical composition of the free gas. Papulov et al.'s [20] study aimed to examine the relationship between the nature of the distribution of heavy hydrocarbon gases and geological disturbances and the subsequent prediction of the gas-dynamic situation during the development of potash reservoirs.

Baryakh et al. [21] studied factors that characterize the possibility of gas-dynamic roof fall in the stoping rooms. The authors established that natural gases in the working-out layers, host rocks, and non-working silvinite and carnallite layers located in between the layers, roof, and soil are distributed extremely unevenly. In practice, there are areas of potash layers that contain almost no gas, but there may also be local accumulations of free gases up to several thousand cubic meters in volume associated with areas of geological anomalies. The component content of gases from potash salt deposits is a complex mixture of combustible and inert gases, including nitrogen, methane, hydrogen, and methane-series hydrocarbons [14,22].

In general, the geographical distribution of the presented research is such that the main results were obtained by scientists from Canada, Russia and Belarus - countries where the largest modern deposits of potassium salts are being developed today. At the same time, contemporary literature extensively covers the emergency flooding of potash mines, yet there is a notable absence of studies on the planned and controlled flooding of these mines, particularly on the flooding of specific sections within potash mine fields.

This analytical gap becomes evident in the practical context of an operational mine within the VPMSD. This study delves into this gap, resulting in the development of design documentation for the controlled flooding of a potash mine field. The distinctive feature of the scenario under consideration is the existence of an unflooded section of the mine field, where regular mining operations continue.

The closed section of the mine is fortified with impermeable bulkheads, and saturated brine is introduced into the worked-out area through a dedicated pipeline. Ensuring gas safety during mining operations is crucial in this scenario. If aerodynamic connections between the mine upcast shaft and the flooded area are obstructed, gases released from the dissolved mass of salt rocks gradually accumulate. This process leads to the formation of closed cavities in the unflooded mined-out space (dome parts), where both brines and released gases persistently flow [11,22].

Without a mechanism to remove the gas-air mixture from these dome parts, the flow of brines continues until reaching an equilibrium state with the gas-air mixture. At this point, the pressure of the gas-air mixture equals the hydrostatic pressure of the rising brines. Under specific conditions, the total content of flammable gases, including methane and hydrogen, in these dome parts may exceed the maximum permissible limit (0.5% by volume).

Therefore, it is necessary to develop an effective system for diluting gas-air mixture in a flooded worked-out area. This measure is crucial to prevent the transition of the mixture into an explosive methane-air composition when enriched with flammable gases released during the dissolution of the adjacent salt rock mass. To address this need, we have developed and parameterized a mathematical model to elucidate the processes involved in filling the closed section of the mine with brine and the subsequent release of the gas-air mixture through a degassing pipeline. Subsequently, we explore two scenarios for the wet closure of the worked-out section of a potash mine: 1) controlled flooding with saturated brines and 2) emergency flooding due to a hypothetical breakthrough of the supra-salt strata and the ingress of groundwater into the worked-out area. In both scenarios, free and bound gases are released into the atmosphere of the closed section of the mine field, stemming from the partial dissolution of pillars and containing hydrogen and heavy hydrocarbon gases. These substances play a critical role in altering the lower concentration limit of the explosion of the methane-air mixture [20,22].

Methods

The object of study is the worked-out area in the southeastern section of the mine of the VPMSD. The mine field has total dimensions of 7700 m in the longitudinal direction and 7950 m in the latitudinal direction. The surface area of the mine field within the boundaries of the existing mining allotment is 66.15 km². Two industrial seams, AB and KrII, are being mined. The average depth of the AB seam in the mining area ranges from 250 m in the northwestern section of the mine field to 370 m in the southeastern section. Similarly, the depth of the KrII seam ranges from 260 m to 415 m.

Industrial seams are situated within the regional aquitard and are separated from the overlying aquifer and brine levels by a waterproof rock layer several tens of meters thick (waterproof layer), which naturally ensures their hydrogeological isolation.

Currently, the worked-out area in the southeastern section of the mine is conventionally divided into several mining panels, forming a complex interconnected network of mine airways (see Figure 1). Ventilation within the panels, as well as throughout the entire mine, follows a U-tube layout. Fresh air enters the mine through two shafts and is then divided into three streams along the northern, western and southern main directions. The air flow in the southern main direction, moving through the transport and conveyor airways, enters the panel airways in the southeastern section of the mine, providing ventilation to the working areas. Polluted air from the panel airways then enters the main return airways of the southern main direction and eventually reaches the upcast shaft. Air movement in the mine is ensured by the main fan, which is installed in a horizontal drift at the mouth of the upcast shaft.

The distance between the shaft inset and the panel airways in the southeastern section is considerable, approximately 2 km. The aerodynamic connection between the southeastern section and the rest of the mine is established through a limited number of airways, ranging from 2 to 5 at varying distances from the shaft inset. This aspect of the mine ventilation network presents the opportunity to close off the designated section of the mine by blocking the aerodynamic connections with solid, impenetrable bulkheads. This solution was outlined in the technical project for decommissioning mine airways at a hazardous production facility (considered mine section). According to the design, saturated brine is supplied to the closed section of the mine via a dedicated brine pipeline laid through the airway system and bulkheads.

To evacuate the gas-air mixture from the depleted space of the decommissioned section of the mine, a polyethylene pipeline is utilized. This pipeline facilitates the release of the gas-air mixture under pressure generated by the incoming brine, directing it into the existing main return airways, ventilated by the main fan. Subsequently, it travels through the upcast shaft to the surface. Figure 2 illustrates a schematic diagram of the connection between the closed section of the mine and the operational section. A dome-shaped area, partially filled with brine, represents the entire worked-out area of the southeastern section of the mine. Considering the topologically complex structure of this area, a more detailed spatial resolution seems unnecessary.

To estimate the duration of the process of removing the gas-air mixture from the worked-out area, as well as to calculate the change in the content of explosive gases in the outgoing stream, a new mathematical model of the degassing process was developed. The basis of this model is the degassing model proposed in [23]. However, we have supplemented it with an empirical time dependence of the volume of flammable gases released, taking into account the altitude of the incoming brine level. Previously, the rate of release of flammable gases was assumed to be constant. Now, the volume of release of flammable gases

V (h)

is determined based on actual geological data, considering both free and bound gases released during the dissolution of pillars located between absolute elevations of –180 m and –95 m (Figure 3). The perimeter part of the pillars was considered degassed by free gases to a depth of 0.5 m due to the development of technological fracturing [25,26].

To parameterize the model, the amount of free and bound gases contained in a unit volume of rocks under natural conditions was experimentally measured. According to experimental measurements [26], the amount of free and bound gases in the considered section of the mine field varies in the range from 0.64 m³/m³ to 0.06 m³/m³, with an average value of 0.25 m³/m³. The analysis was carried out in terms of equivalent methane, where the concentration is equal to the sum of the concentrations of methane and hydrogen in accordance with the regulatory rules adopted in Russia.

We describe the process of methane accumulation and removal in an isolated worked-out space using the following system of equations:

\frac{d V}{d t} = - q,

(1)

\frac{d M_{a}}{d t} = - \frac{M_{a}}{V} Q,

(2)

\frac{d M_{g}}{d t} = - \frac{M_{g}}{V} Q + γ (t) ρ_{g},

(3)

\frac{P V}{M_{a} + M_{g}} = \frac{P_{0} V_{0}}{M_{0}},

(4)

P - P_{0} = R Q_{i n}^{2},

(5)

Q_{o u t} = {\frac{P}{P_{0}} Q}_{i n}

(6)

with the initial conditions:

P (0) = P_{0} = 1

atm,

V (0) = V_{0} = 4.71 \cdot 10^{6}

m³,

M_{a} (0) = M_{0}

M_{g} (0) = 0

kg and

Q (0) = 0

m³/s. Here,

P

and

P_{0}

represent the current and initial (atmospheric) air pressures in the unflooded section of the worked-out space, respectively, Pa;

V

is the current volume of the unflooded section, m³;

M_{a}

and

M_{0}

are the current and initial masses of the air in the unflooded section, respectively, kg;

M_{g}

is the current mass of gas in the unflooded section, kg;

Q_{i n}

is the volumetric flow rate of the gas-air mixture entering the pipeline, m³/s;

Q_{o u t}

is the volumetric flow rate of the gas-air mixture leaving the pipeline in the main return airways, m³/s;

ρ_{g}

is the methane density, kg/m³;

γ (t)

is the intensity of flammable gas release in terms of equivalent methane, m³/s.

Equation (1) describes the decrease in the volume of the unflooded section resulting from the influx of brine. Equations (2) and (3) describe the reduction in the mass of air and gas, respectively, in the unflooded section of the worked-out space due to their removal through the pipeline. Equation (4) establishes a connection between the thermodynamic characteristics of the gas-air mixture using the ideal gas law and assumes that the compression process in the unflooded section is isothermal. This assumption is logical given that the processes considered in the problem progress relatively slowly (with characteristic times on the order of tens of days). Equation (5) describes the movement of the gas-air mixture through a pipeline with air resistance

R

under the influence of excess pressure of the gas-air mixture in the unflooded section. Equation (6) relates the volumetric flow rate of the gas-air mixture at the inlet and outlet of the pipeline, assuming the isothermal nature of the processes under consideration.

The air resistance of the pipeline was calculated using the following formula:

R = α \cdot \frac{Π \cdot L}{S^{3}},

(7)

where

α = 0.002

kg/m³ is the aerodynamic drag coefficient of the degassing pipeline, the value of which is calculated using the method described in [24];

L = 3900

m is the length of the degassing pipeline;

S

is the cross-sectional area of the degassing pipeline, m²;

Π

is the cross-section perimeter of the degassing pipeline, m.

In [23], it was demonstrated that the air resistance of the degassing pipeline and the 'back pressure' of the gas-air mixture in the closed section of the mine do not significantly affect the time it takes to fill the worked-out space with brine. Therefore, the current volume of the unfilled section is linearly dependent on time

t

V = V_{0} - q t .

(8)

The system of equations (2) – (8) with initial conditions can be reduced to a system of first-order nonlinear differential equations for the variables

M_{a}

M_{g}

\frac{d M_{a}}{d t} = - \frac{M_{a}}{V_{0} - q t} \sqrt{\frac{\frac{P_{0} (M_{a} + M_{g})}{ρ_{0} V} - P_{0}}{R}},

(9)

\frac{d M_{g}}{d t} = - \frac{M_{g}}{V_{0} - q t} \sqrt{\frac{\frac{P_{0} (M_{a} + M_{g})}{ρ_{0} V} - P_{0}}{R}} + γ (h (t)) ρ_{g}

(10)

with initial conditions

M_{a} (0) = M_{0}

M_{g} (0) = 0

kg. Here

ρ_{0} = M_{0} / V_{0} = 1.25

kg/m³ is the initial air density in the worked-out space.

Two different scenarios for flooding the closed section of the mine field were considered: scenario 1 involves controlled design flooding with brine supplied through a brine pipeline at a flow rate of

q = 300

m³/hour; scenario 2 entails a hypothetical breakthrough of fresh groundwater in the supra-salt strata with a flow rate of

q = 1700

m³/hour, corresponding to the predicted value obtained from the regional numerical geofiltration model of the supra-salt strata [27].

According to equation (8), the flooding time of the closed part of the mine under the planned scenario 1 is 654 days, while under scenario 2, it is 115 days. Additionally, considering equation (8) and the dependence of the volume of released flammable gases on the brine level height, as shown in Figure 3, the time dependencies of the intensity of the release of flammable gases, denoted as

γ (h (t))

, are plotted for both flooding scenarios in Figure 4. Thus, the intensity of gas release during flooding exhibits a strong nonlinear relationship, reaching a maximum of 0.0121 m³/s on day 276 for scenario 1 and 0.067 m³/s on day 50 for scenario 2.

The system (9) – (10) with initial conditions was numerically solved using the finite difference method in the computer algebra package Wolfram Mathematica. Based on the calculated values of

M_{a}

and

M_{g}

, the remaining characteristics of the degassing system were determined. To assess the effectiveness of the degassing system concerning the diameter and number of degassing pipelines, we further investigate the following three proposed options in this study:

One pipeline with a diameter of d = 0.153 m.
One pipeline with a diameter of d = 0.315 m.
Two pipelines with a diameter of d = 0.153 m.

Results and Discussion

The calculation results of the current values of the gas-air mixture flow rate emanating from the pipeline into the main return airways and the volume fraction of combustible gases in the process of flooding the closed section of the mine with brine according to scenario 1 are presented in Figure 5 and Figure 6, respectively. The flow rate of the gas-air mixture passing through the pipeline depends on the version of the degassing system. The greater the air resistance to the movement of the gas-air mixture the pipeline takes, the longer it takes for the mixture flow to reach a value close to the brine flow rate, denoted as

q

= 300 m³/hour = 0.083 m³/s, supplied to the closed section of the mine. The nonlinear behavior of the dependence in Figure 5 is associated with a similar nonlinear nature of the time dependence of the gas emission intensity (see Figure 4), while the peak values in Figure 5 correspond to the maximum gas emission intensity.

Figure 6 shows that the content of flammable gases in the gas-air mixture emanating from the pipeline gradually increases due to gas release from dissolved rocks, reaching a value of 24% by volume, which is almost five times higher than the lower explosive limit of methane. In this case, the time dynamics of the concentration of flammable gases practically do not depend on the version of the degassing system. At the same time, all three curves demonstrate a highly nonlinear increase in the average methane concentration in the unflooded section. This characteristic of the solution in our proposed model is logical, as there is a constant outflow of air through the degassing pipeline, while air replenishment does not occur in the unflooded section. Consequently, the methane concentration, determined by the ratio

c = \frac{\frac{M_{g}}{ρ_{g}}}{\frac{M_{g}}{ρ_{g}} + \frac{M_{a}}{ρ_{0}}}

increases nonlinearly with a decrease in the value of

M_{a}

The results of calculations of the pressure of the gas-air mixture in the unflooded section of the worked-out area, the flow rate of the gas-air mixture flow from the pipeline and the average volume fraction of combustible gases in the unflooded section according to scenario 2 are presented in Figure 7, Figure 8 and Figure 9 respectively.

The pressure of the gas-air mixture in the unflooded section of the worked-out area depends on the parameters of the degassing system. Figure 7 shows that over time, the pressure of the gas-air mixture increases significantly and, under certain parameters of the degassing system (such as a small number of pipelines and small diameter of pipelines), can lead to pressures of more than 2 atm. This is due to the insufficient rate of gas removal from the unflooded section. It also follows that when choosing the final layout of degassing pipelines, the material and thickness of the pipeline wall should be selected based on the maximum predicted pressures of the gas-air mixture in the unflooded section.

The flow rate of the gas-air mixture passing through the pipeline also depends significantly on the parameters of the degassing system (see Figure 8). The option with one degassing pipeline with a diameter of 0.315 m experiences the least air resistance, and within approximately 20 days after the start of closure, the gas-air mixture flow rate reaches a value close to the flow rate of brines, (

q

= 1700 m³/hour = 0.47 m³/s), supplied to the closed section of the mine. For the degassing system with two pipelines, each with a diameter of 0.153 m, the gas-air mixture flow rate grows more slowly. However, by the time the closed section of the mine is completely filled with brines, the maximum flow rate of the gas-air mixture reaches 0.65 m³/s. An even slower increase in the flow rate of the gas-air mixture is observed in the first days with a single pipeline of small diameter (0.153 m). However, an excess of gas-air mixture in the unflooded section of the worked-out space leads to the situation where, after 70 days, the consumption of the mixture begins to exceed the two previous options and grows rapidly until the end of flooding of the closed section. At the moment of complete flooding of the shaft section, the pipeline flow in this option is 1.1 m³/s.

The concentration of combustible gases in the gas-air flow originating from the pipeline, akin to scenario 1, steadily rises due to gas release from dissolved rocks. However, in the case of section closure under scenario 2, across different configurations of the degassing system, the peak concentrations of flammable gases range from 11.5 to 19% by volume, exceeding the lower explosion limit of methane by 2–4 times (Figure 9).

In both scenarios of section closure flooding, the concentration of gas in the outgoing stream will eventually surpass the lower explosive limit of methane, posing a hazard to mining operations. To reduce the gas concentration to a safe level, adequate fresh air must be supplied along the main return airways, where the gas-air mixture exits the degassing pipelines. The required amount of air can be calculated using the formula:

Q_{r e q} = \frac{C_{g}}{C_{t l v}} \cdot Q_{o u t}, m^{3} / s,

(11)

where

C_{g}

is the gas volume fraction, % vol;

C_{t l v}

is the gas concentration threshold limit value, which is 0.5 % vol. [17];

Q_{o u t}

is the gas-air mixture flow rate emanating through the pipeline from the worked-out space into the main return airways.

Figure 10 illustrates the results of calculating the required amount of fresh air to dilute combustible gases below the threshold limit value for both scenario 1 and scenario 2. In scenario 1, the required flow rate curve remains consistent regardless of the method of releasing the gas-air mixture and the layout of degassing pipelines outlined in the technical design for section closure. Therefore, Figure 10A depicts a single curve of the required flow rate versus time. However, in scenario 2, the intersection of the time dependence curves of the required amount of air in Figure 10B reflects different dynamics in the increase of the gas-air mixture flow rate at the pipeline outlet for various pipeline layout versions (refer to Figure 8 for details).

The calculations result for both scenarios of the mine section closure are summarized in the Table 1.

According to the obtained modeling results, in any scenario of flooding the decommissioned section of the mine, there is a possibility that a potentially explosive mixture of combustible gases will eventually escape from the worked-out area through the degassing pipeline and mix with fresh air flowing along the main return airways. Therefore, it is recommended to monitor the parameters of the gas-air mixture, such as flair velocity and concentration of combustible gases, both at the outlet of the degassing pipeline and in the main return airways, both before and after the uncontaminated air is mixed with the gas-air mixture.

Monitoring the parameters of the gas-air mixture can be achieved by employing an automated monitoring system. This system incorporates sensors for measuring air velocity and methane concentration. The collected data from these sensors is then transmitted to a control room computer located on the surface. If the system detects an exceeding of the maximum permissible concentration, an appropriate warning will be issued.

To prevent the accumulation of combustible gases in the existing mine airways, where their concentrations exceed the maximum permissible level, a separate measured should be implemented for the mine ventilation system. The return airways, into which the gas-air mixture will be released from the worked-out space of the flooded section, should receive a supply of fresh air with zero concentrations of combustible gases. Additionally, it is crucial to ensure that the gas-air mixture moving along the main return airways is effectively removed from the outgoing flow, eliminating the possibility of its recirculation and re-entry into the working areas of the mine.

Conclusion

The paper discusses two scenarios for the wet closure of the worked-out section of a potash mine. In the first scenario, the closed section is isolated with solid bulkheads, and a special pipeline is used to supply saturated brine to the worked-out space at an intensity of 300 m³/hour. The second flooding scenario involves a hypothetical breakthrough of the supra-salt strata, resulting in groundwater influx into the worked-out space at an intensity of 1700 m³/hour.

To remove the gas-air mixture from the worked-out space of the closed section, a degassing system is proposed, which consists of polyethylene pipelines. These pipelines allow the gas-air mixture to exit under the pressure created by the incoming brines and discharge it into the existing main return airways. These airways are ventilated by the main fan.

The paper presents a new mathematical model that describes the processes of filling the closed section of the mine with brine and the release of the gas-air mixture through the degassing pipeline. The simulation results reveal that in both scenarios, a potentially explosive mixture of combustible gases will eventually escape from the worked-out space through the degassing pipeline. Therefore, an additional calculation was performed to determine the required amount of fresh air to be supplied along the main return airways. This calculation ensures sufficient dilution of the gas-air mixture flow to maintain it below the threshold limit value.

Funding

The research was carried out with financial support from the Ministry of Education and Science of the Russian Federation (projects No. 122030100425-6 and No. 124020500030-7).

References

Baryah, A. A., & Evseev, A. V. (2019). Closure of potash and salt mines: Review and analysis of the problem. MIAB. Mining Inf. Anal. Bull, 9, 5-29. [CrossRef]
Laptev, B. V. (2011). Historiography of accidents during the development of salt deposits. Occupational Safety in Industry, (12), 41-46.
Laptev, B. V., & Kozachenko, M. G. (2004). On the problems of developing the Iletsk rock salt deposit. Occupational Safety in Industry, (6), 53-54.
Cocker, M. D., & Orris, G. J. (2012, April). World potash developments. In 48th Annual Forum on the Geology of Industrial Minerals Arizona Geological Survey. Scottsdale.
Whyatt, J., & Varley, F. (2008, July). Catastrophic failures of underground evaporite mines. In Proceedings of the 27th international conference on ground control in mining (Vol. 2008, p. 113). Morgantown, West Virginia: College of Engineering and Mineral Resources, West Virginia University.
Prugger, F. F., & Prugger, A. F. (1991). Water problems in Saskatchewan potash mining–what can be learned from them. CIM bulletin, 84(945), 58-66.
Gendzwill, D., & Martin, N. (1996). Flooding and loss of the Patience Lake potash mine. CIM bulletin, 89(1000), 62-73.
Wittrup, M. B. (1988). The origin of water leaks in Saskatchewan potash mines (Doctoral dissertation, University of Saskatchewan).
Malovichko, D. A., Dyagilev, R., Shulakov, D. Y., Butyrin, P., & Glebov, S. V. (2009). Seismic monitoring of large-scale karst processes in a potash mine. Controlling seismic hazard and sustainable development of deep mines, 2, 989-1002.
Baryakh, A. A., Devyatkov, S. Y., & Samodelkina, N. A. (2016). Theoretical explanation of conditions for sinkholes after emergency flooding of potash mines. Journal of Mining Science, 52, 36-45. [CrossRef]
Kulikova, A. A., & Ovchinnikova, T. I. (2021). On the issue of reducing geoecological risks at mining enterprises. MIAB. Mining Informational and Analytical Bulletin, (2-1), 251-262. [CrossRef]
Zubov, V. P., & Smychnik, A. D. (2015). The concept of reducing the risks of potash mines flooding caused by groundwater inrush into excavations. Journal of Mining Institute, 215, 29-37.
Ushakova, E., Perevoshchikova, A., Menshikova, E., Khayrulina, E., Perevoshchikov, R., & Belkin, P. (2023). Environmental Aspects of Potash Mining: A Case Study of the Verkhnekamskoe Potash Deposit. Mining, 3(2), 176-204. [CrossRef]
Besnard, K., & Pokryszka, Z. (2005, November). Gases emission monitoring in a post-mining context. In Symposium Post mining 2005 (p. NC).
Vysotskaya, N. A., & Piskun, E. V. (2020). The main factors of adverse environmental impact of potash production and methods of environmental protection. Mining Science and Technology (Russia), 4(3), 172-180. [CrossRef]
Ponomarenko, T. (2012). Ecological, economic and social consequences of emergencies on potash mines. Management Systems in Production Engineering, (2), 28.
Katta, A. K., Davis, M., & Kumar, A. (2020). Assessment of greenhouse gas mitigation options for the iron, gold, and potash mining sectors. Journal of Cleaner Production, 245, 118718. [CrossRef]
Zimmer, M., Strauch, B., Zirkler, A., Niedermann, S., & Vieth-Hillebrand, A. (2020). Origin and evolution of gas in salt beds of a potash mine. Advances in Geosciences, 54, 15-21. [CrossRef]
Andreyko, S. S., Ivanov, O. V., Nesterov, E. A., Golovatiy, I. I., & Beresnev, S. P. (2013). Research of salt rocks gas content of III potash layer in the Krasnoslobodsky mine field. Gorn. Zhurnal, 6, 69-73.
Papulov, A. S., Andreyko, S. S., & Ivanov, O. V. (2022, May). Influence of oil structures on the component composition of free gases of potash reservoirs at the BPPU-4 mine field of PJSC “Uralkali”. In IOP Conference Series: Earth and Environmental Science (Vol. 1021, No. 1, p. 012075). IOP Publishing. [CrossRef]
Baryakh, A. A., Andreiko, S. S., & Fedoseev, A. K. (2020). Gas-dynamic roof fall during the potash deposits development. Journal of Mining Institute, 246, 601-609. [CrossRef]
Zemskov, A. N., Kondrashev, P. I., & Travnikova, L. G. (2008). Natural gases of potash deposits and measures to combat them. Perm; 2008. 414 p.
Kolesov, E. V., Shalimov, A. V., & Semin, M. A. (2019). Development of the activities for explosive gases removal from the worked-out area in case of potash mine flooding. Occupational Safety in Industry, (12), 60-65. [CrossRef]
Mokhirev, N. N., & Radko, V. V. (2007). Engineering computation of mine ventilation. Construction. Reconstruction. Exploitation. Moscow, Nedra-Bisnestsentr, p. 324.
Andreyko, S. S., Ivanov, O. V., & Nekrasov, S. V. (2007). Formation of gas accumulations in the goaf of seam “B” during flooding of the BKPRU-1 mine. Gornoe echo, (3), 43-46.
Andreyko, S. S., & Ivanov, O. V. (2009). Assessment of the possibility of forming accumulations of free gases in the goaf of the carnallite seam "B" during flooding of the BKPRU-1 mine of OJSC "Uralkali". Gornaya mechanika, (3), 12-17.
Potapov, A. A. (2016). Regional groundwater flow numerical model southern Verkhnekamskoye deposit of potassium-magnesium salts. Vestnik of Saint-Petersburg University. Earth Sciences, (3), 4-23. [CrossRef]

Figure 1. Schematic diagram of the mine ventilation network.

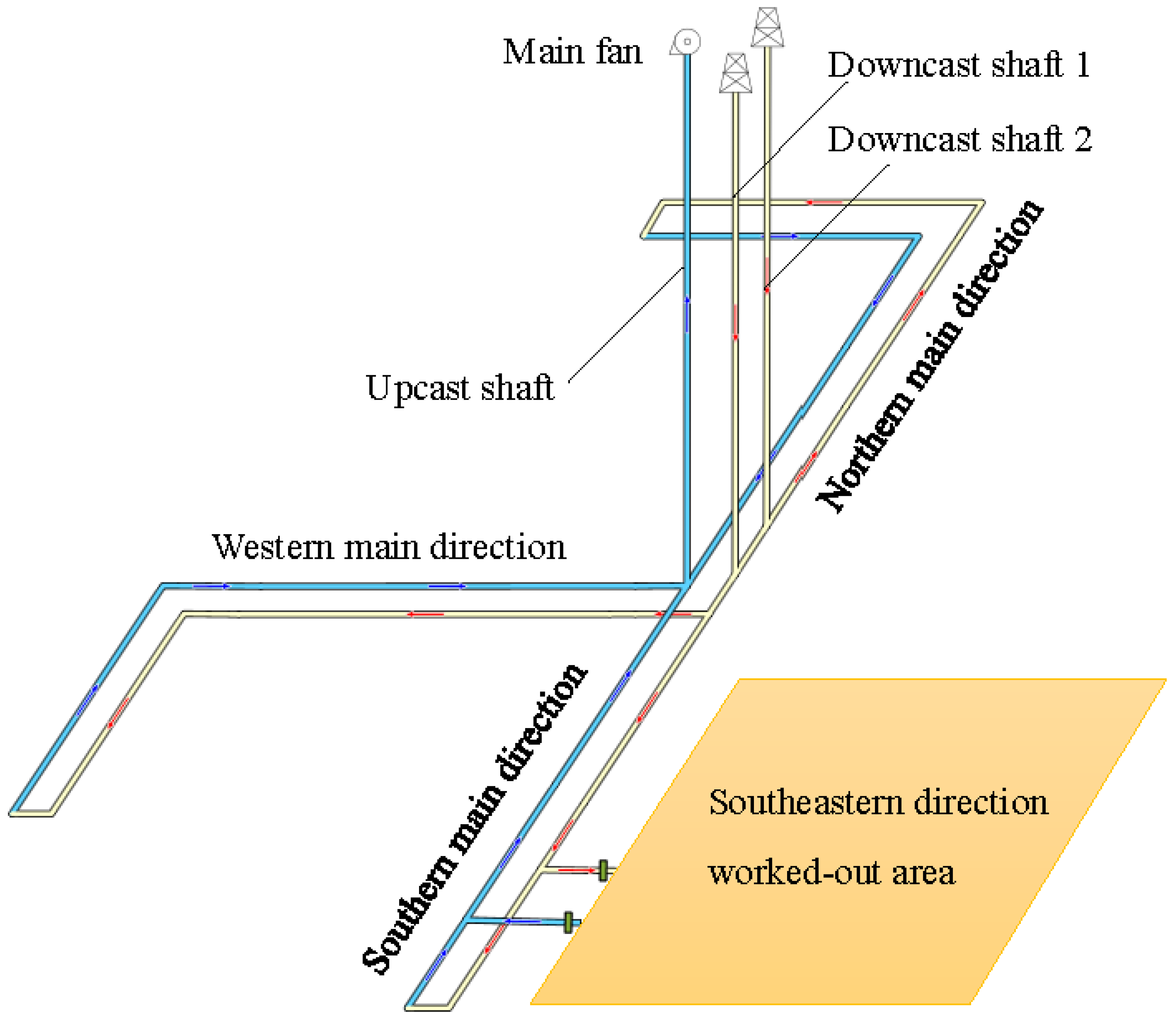
Figure 2. Schematic diagram of the closed section of the mine, brine and degassing pipelines.

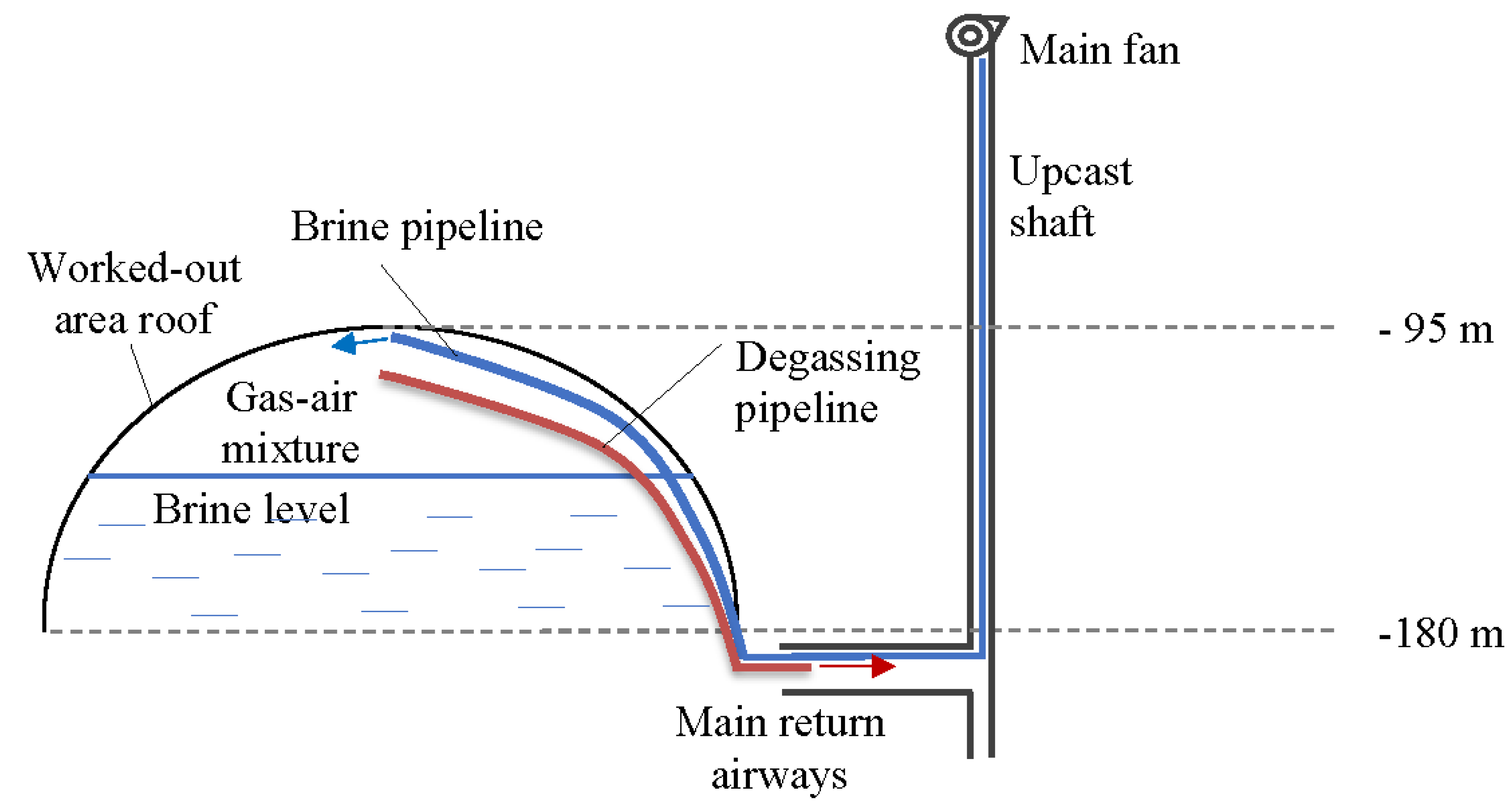
Figure 3. Dependence of the volume of flammable gases released during the dissolution of pillars on the brine level height.

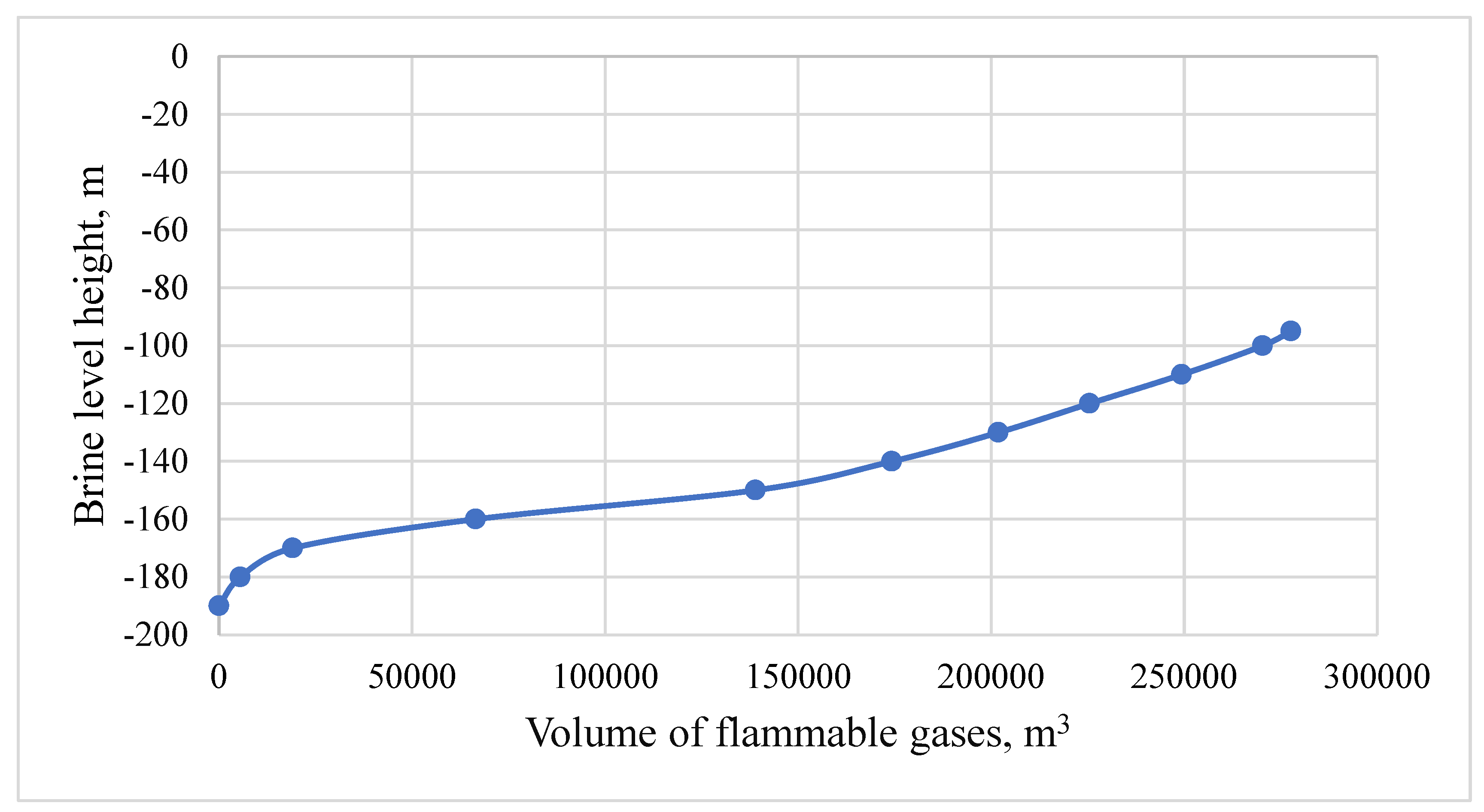
Figure 4. Time dependences of the intensity of flammable gas emissions in terms of conventional methane: A) for scenario 1; B) for scenario 2.

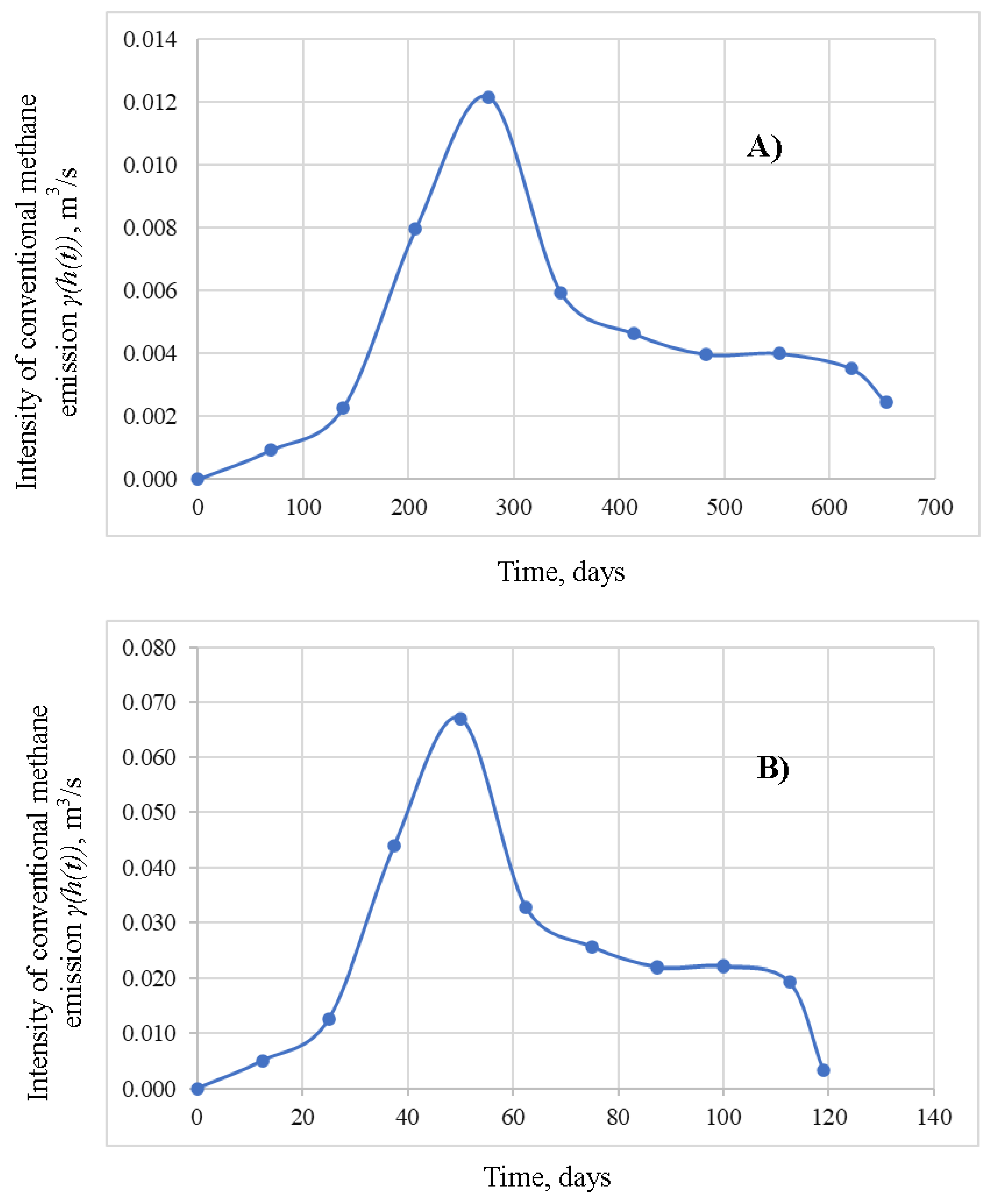
Figure 5. Time dependency of the gas-air mixture flow rate emanating from the pipeline.

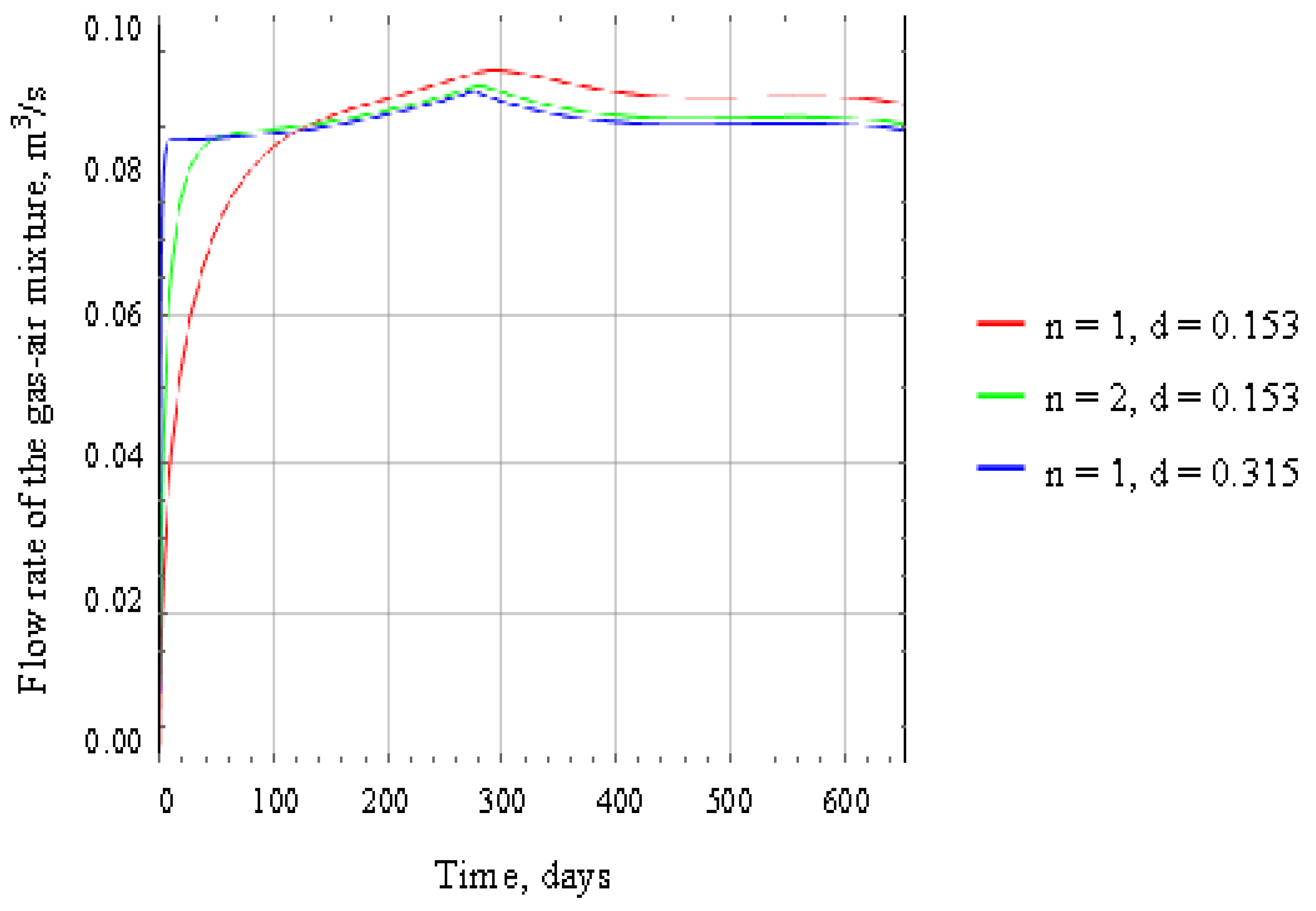
Figure 6. Time dependency of the gas concentration in the gas-air mixture emanating from the pipeline.

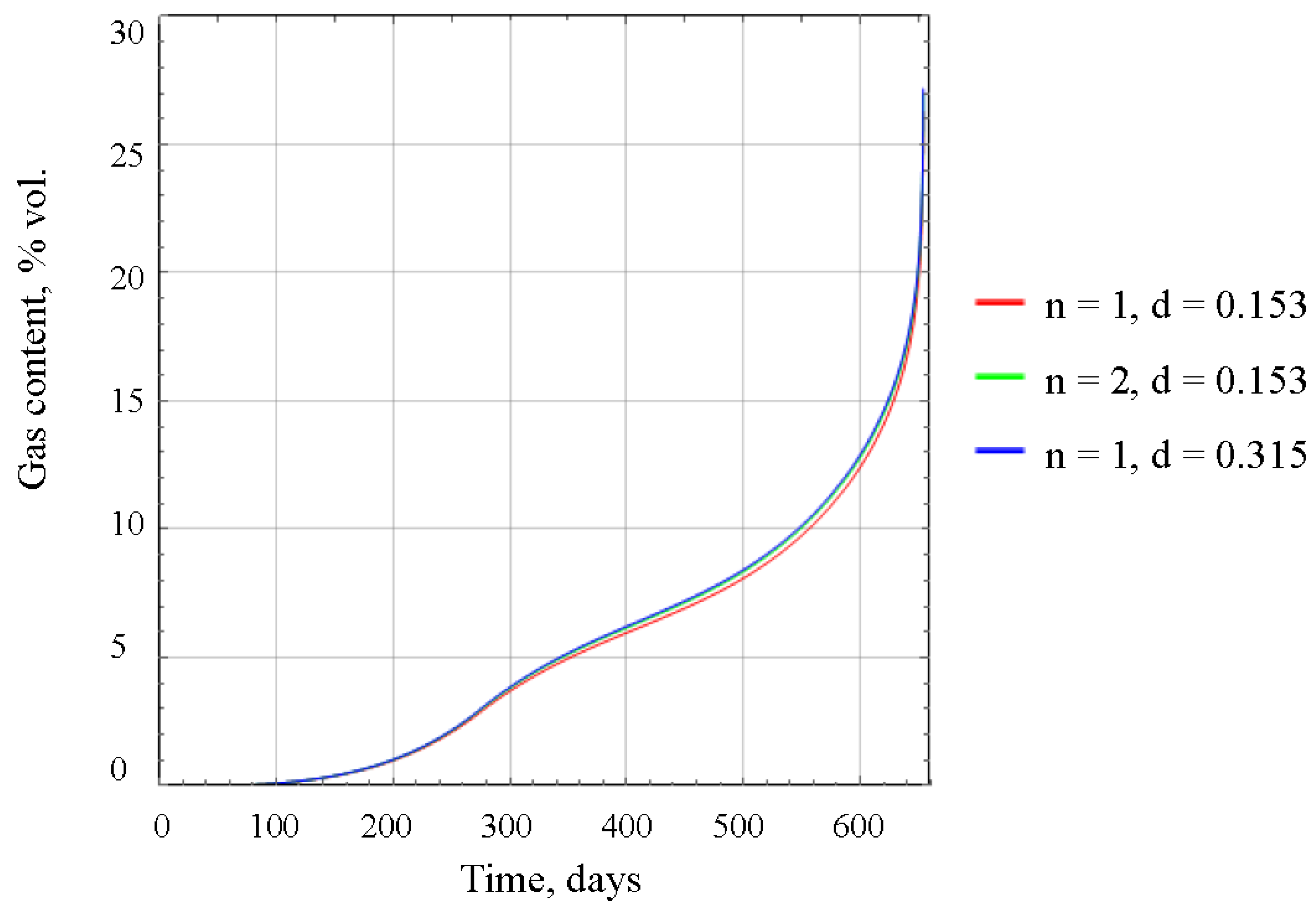
Figure 7. Time dependency of the gas-air mixture pressure in the unflooded section of worked-out area.

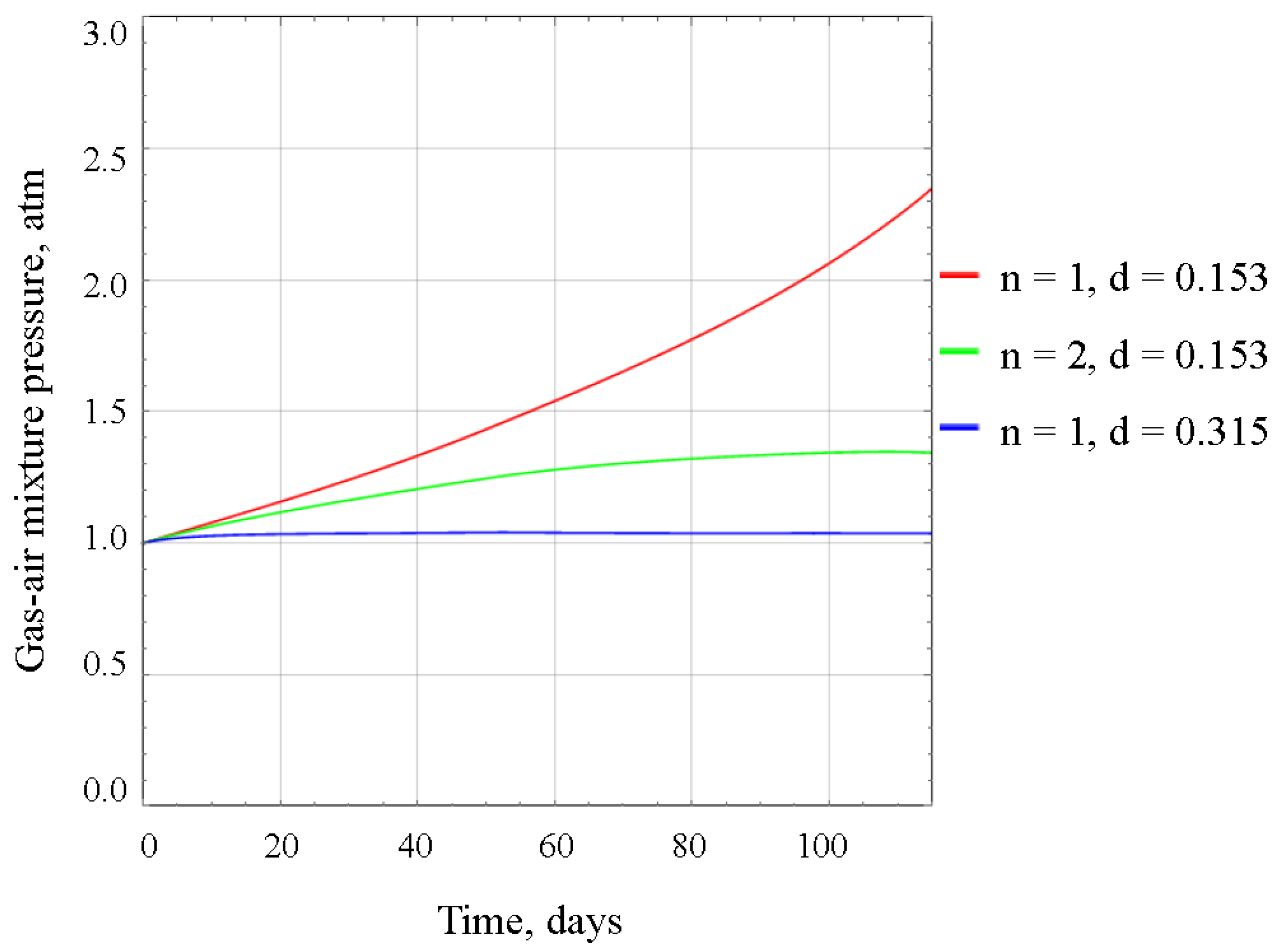
Figure 8. Time dependency of the gas-air flow rate emanating from the pipeline.

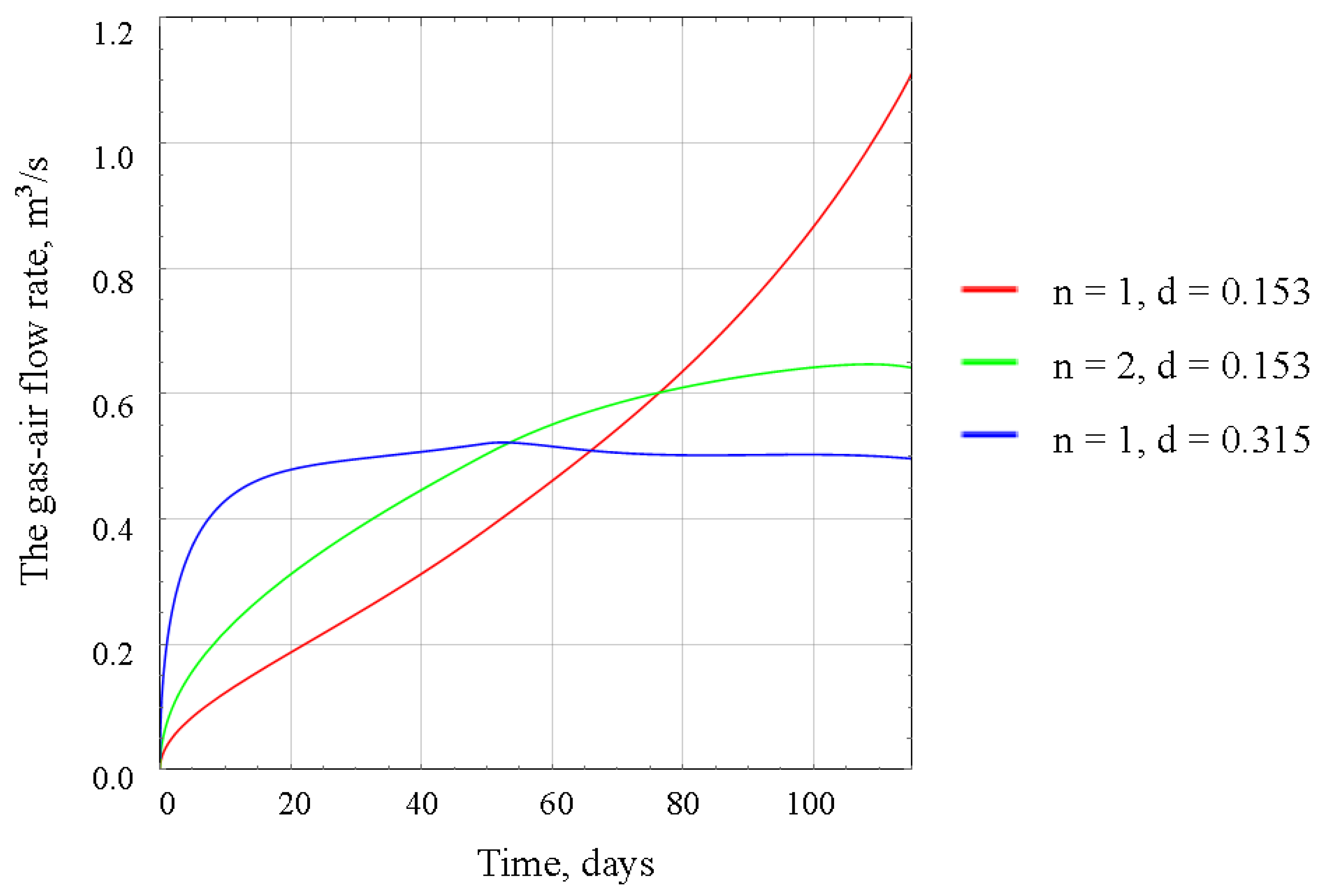
Figure 9. Time dependency of the gas concentration in the gas-air mixture emanating from the pipeline.

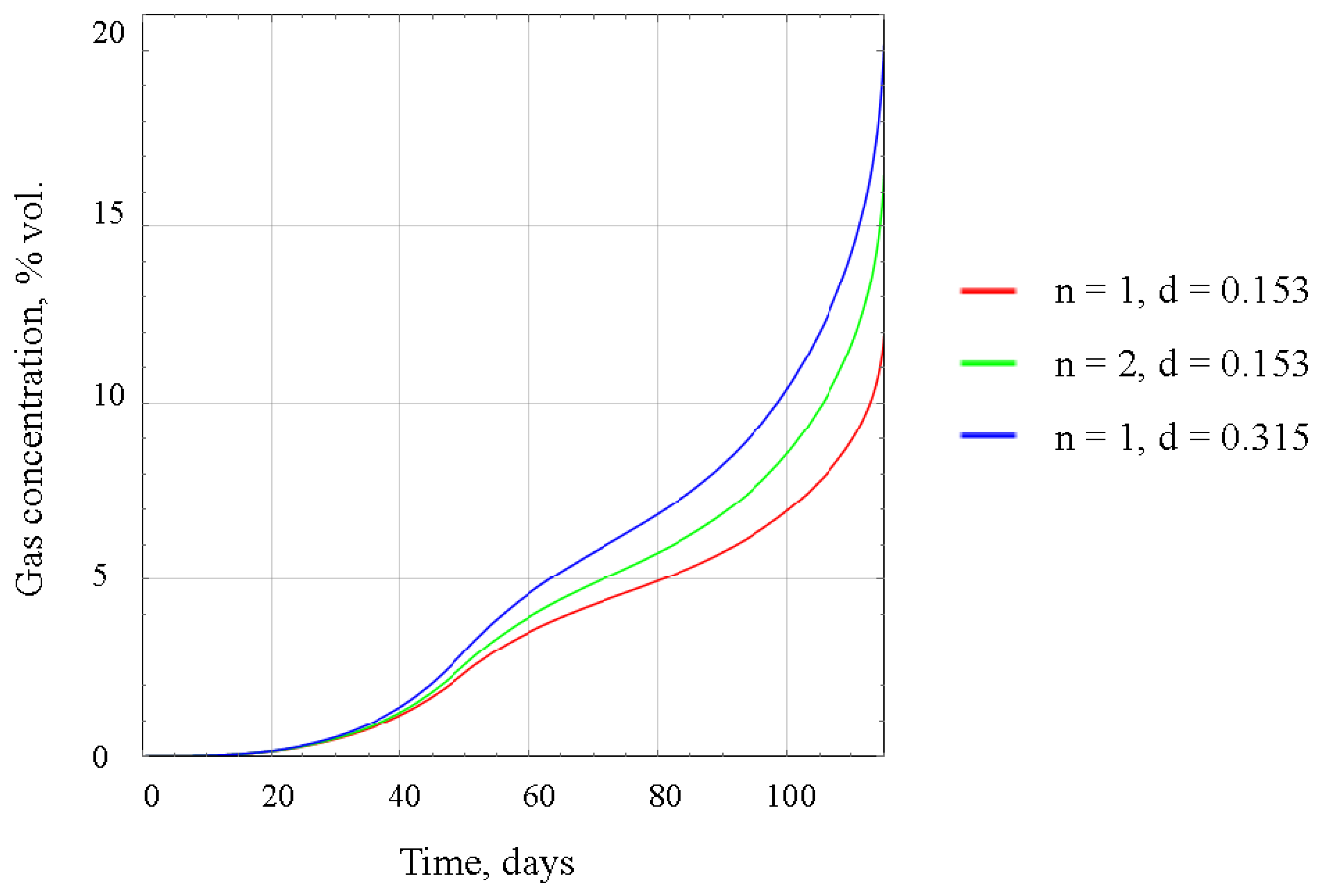
Figure 10. Required fresh air flow in ventilation working to dilute combustible gases to the threshold limit value: A) Scenario 1; B) Scenario 2.

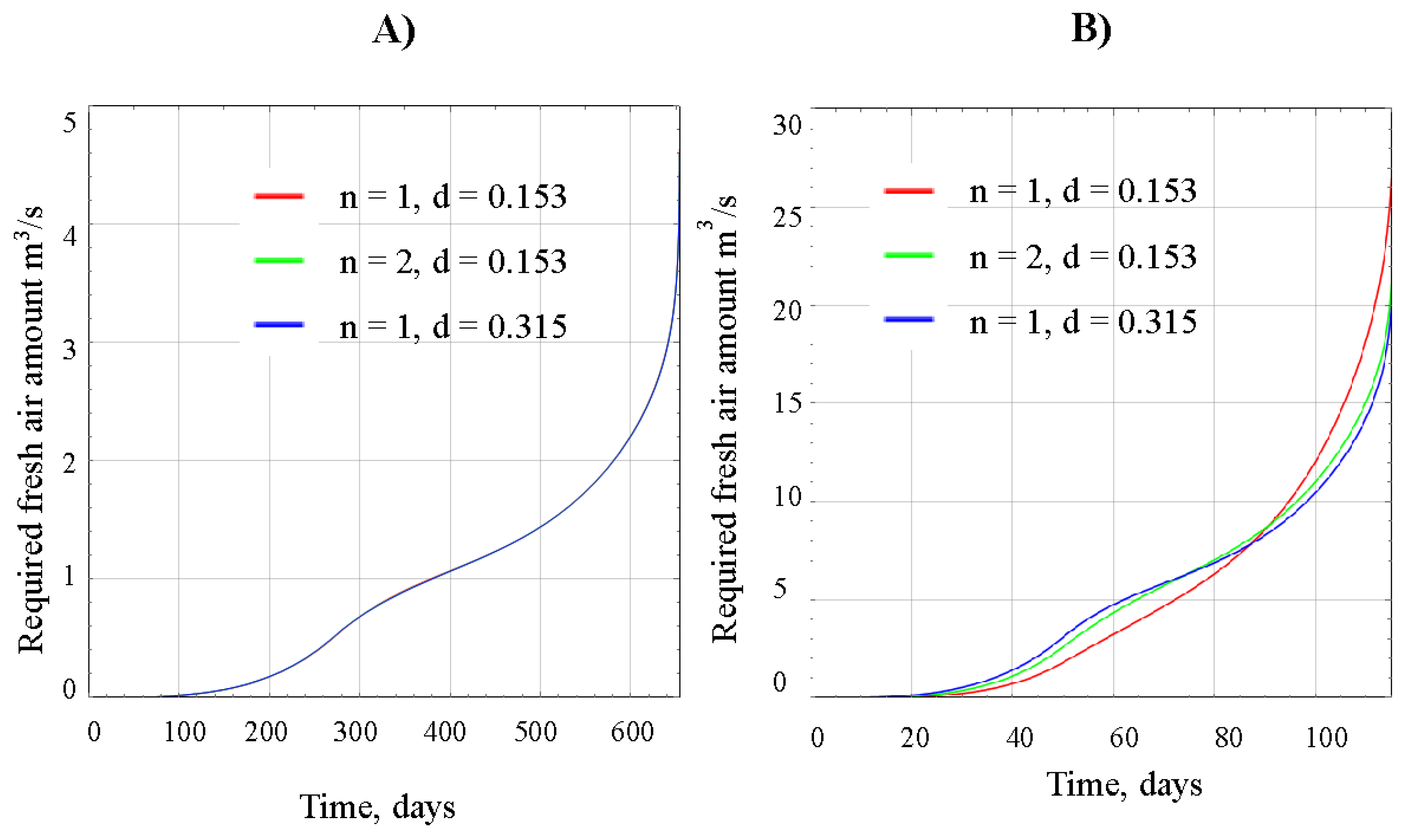
Table 1. Results of simulation of the closed section degassing.

Parameter	Scenario 1	Scenario 2
Worked-out area degassing time	654 days	115 days
Maximum gas concentration in worked-out area (in terms of equivalent methane)	26.3 –27.0 – 27.2 % vol.	11.9 – 16.4 – 20.1 % vol.
The maximum gas-air flow rate emanating from the pipeline	0.088 – 0.085 – 0.084 m³/s	1.1 – 0.6 – 0.5 m³/s
The required amount of fresh air in the main return airways to dilute combustible gases concentration below the threshold limit value	4.64 -4.62 – 4.61 m³/s	20.0 – 21.1 – 26.0 m³/s

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Modeling and Mitigating Gas Hazards during Potash Mine Closure

Abstract

Introduction

Methods

Results and Discussion

Conclusion

Funding

References

MDPI Initiatives

Important Links

Subscribe