Maximizing the Average Environmental Benefit of a Fleet of Drones under a Periodic Schedule of Tasks

Preprint

Article

Maximizing the Average Environmental Benefit of a Fleet of Drones under a Periodic Schedule of Tasks

Altmetrics

Downloads

Views

Comments

Supplementary Material

supplementary.pdf (1.51MB )

Eugene Levner^*,Vladimir Kats

This version is not peer-reviewed

This preprints belongs to the Topic

Innovation and Inventions in Aerospace and UAV Applications

Submitted:

09 May 2024

Posted:

10 May 2024

You are already at the latest version

Alerts

Abstract

Unmanned aerial vehicles (UAVs, drones) are not just a technological achievement based on modern ideas of artificial intelligence; they also provide a sustainable solution for green technologies in logistics, transport and material handling. In particular, using battery-powered UAVs to transport products can significantly decrease energy and fuel expenses, reduce environmental pollution, and improve the efficiency of clean technologies through improved energy-saving efficiency. We consider the problem of maximizing the average environmental benefit of a fleet of drones given a periodic schedule of tasks performed by the fleet of vehicles. To solve the problem efficiently, we formulate it as an optimization problem on an infinite periodic graph and reduce it to a special type of parametric assignment problem. We exactly solve the problem under consideration in O(n³) time, where n is the number of tasks performed by vehicles.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction

Transport by road and air is one of the largest contributors to the highest greenhouse gas emissions and fuel consumption in the logistics industry. In recent years, due to rising carbon dioxide emissions and fuel costs, the issue of sustainable daily scheduling of transport operations aimed at reducing environmental pollution, has attracted increasing interest and concern from large logistics companies. In such a situation, unmanned aerial vehicles (UAVs, drones) are not just a technological advancement based on modern ideas of artificial intelligence, but actually provide a sustainable solution to green technologies in logistics, transport and material handling In this light, the ability of UAVs to carry out sustainable autonomous deliveries efficiently and effectively has been researched and explored by large logistics companies (e.g., DHL Express, UPS), e-commerce retailers and companies (e.g., Walmart, Google) [1,2].

The environmental benefits of UAVs are universal and intertwined with economic and social benefits; their environmental friendliness has systematically improved in recent years as drone delivery technologies (e.g., batteries, autonomous navigation, obstacle avoidance and detection algorithms) have been greatly improved, and because drones are much smaller than trucks and airplanes, drones generally cost less and consume less energy and fuel per unit distance travelled. What’s more, most delivery drones consume electricity, which can be generated from clean energy sources such as solar or wind, so they emit fewer harmful emissions per unit of energy consumed compared to traditional trucks and airplanes, while also increasing the efficiency of clean technologies.

We observe that the environmental benefits of UAVs are mainly driven by the overall benefits and profits of modern digital and artificial intelligence-based technologies. They were comprehensively studied and classified by Dolgui and Ivanov [3,4]. Here, we select and highlight three main factors that directly lead to environmental benefits and economic profits:

Using battery-powered UAVs in the air instead of trucks on the road can significantly reduce energy and fuel expenses,
It reduces environmental pollution, carbon dioxide emissions and other negative impacts of transport processes on the environment,
It improves the efficiency of clean technologies by increasing energy saving efficiency.

A broader and more detailed categorization of the relevant environmental benefits of UAVs is beyond the scope of this article. The interested reader is referred to the available comprehensive surveys and studies in this area cited therein [1,2,5,6,7].

It is known that scheduling and routing of vehicles subject to external, in particular, environmental constraints, is a complex combinatorial problem, which, generally, is NP–hard, meaning it cannot be solved optimally for large instance sizes in reasonable (polynomial) computational time [8,9]. In this regard, a practical alternative would be either to obtain efficient exact algorithms for practically important special cases of the problem, or to develop fast and sufficiently effective approximation algorithms. Increased theoretical and practical interest in this problem and its applications has been noted, for example, in a number of excellent reviews [1,2,5,6,7]. In addition to the results presented in these surveys and the works cited therein, the main contribution of this work is as follows: we present and explore the problem of finding the optimal number of vehicles that maximizes the average UAV fleet profit per vehicle and thereby the fleet efficiency.

In what follows, we restrict our attention to the graph approach for maximizing the average fleet profit per vehicle and solve this optimization problem in strongly polynomial time, reducing it to a special type of parametric assignment problem.

For a detailed description of various problem formulations, models, and corresponding algorithms for the general drone fleet assignment problem, we refer the interested reader to the surveys [10,11,12,13,14,15], which provide excellent reviews of work in this area.

The rest of the article is organized as follows. In the next section we describe previous work. In Section 3 we describe the problem under study. In Section 4 we reformulate it as a graph-theoretic problem of maximizing the average total weight of a chain cover on an infinite graph; then we re-construct the infinite graph into an equivalent finite graph; as a result, the problem under consideration is reduced to the problem of covering the nodes of the last graph with a set of cycles that maximizes the average total weight. Section 5 reformulates the cycle-covering problem as a bi-matrix assignment problem and reduces the latter problem to a particular type of fractional assignment problem (FAP). Section 6 reduces FAP to a parametric assignment problem, and Section 7 solves it using Newton’s method. Section 8 improves the complexity of the latter algorithm. Section 9 concludes the paper.

2. Previous Work

Since we realize that the general problem under study is very complex (NP-hard in fact) and large in size, making it difficult to solve exactly, the challenge is to decompose it into smaller and simpler sub-problems that can be solved efficiently and thus provide the “building blocks” for solving the overall problem. We are interested in finding a special case that, on the one hand, makes the problem solvable, and, on the other hand, gives good upper/lower bounds on the objective functions of the general optimization problem.

The special case studied in this paper is an extension of the problem of minimizing the number of vehicles (airplanes, drones, robots, cars, etc.) needed to meet a fixed, periodically repeating schedule of tasks. This optimization problem has a long history in operations research. A non-periodic finite-horizon version of the problem, concerned with minimizing the number of tankers to meet a fixed schedule, was solved in 1954 by Dantzig and Fulkerson [16]. A few years later, Ford and Fulkerson [17] reduced that problem to finding a chain cover of minimum cardinality for finite partially ordered sets. Using an infinite periodic graph model and a chain covering, Karzanov and Livshits [18] elegantly reduced the periodic minimum-size vehicle problem to an assignment problem solvable in polynomial time. Kats [19] has modified and slightly simplified the Karzanov-Livshits algorithm. Orlin [20] proposed a chain covering algorithm for the periodic case where a finite number of tasks must be executed periodically over an infinite horizon and efficiently solved the problem as a finite network flow problem. Kats and Levner [21,22] proposed a periodic graph model that solved a similar scheduling problem with non-Euclidean distances. Orlin [23] has solved the more general problem of minimizing the average fleet cost per day of flying subject to a fixed number of aircraft; however, this optimization problem is different from the problem in this study, and besides this, it involves a solution technique induced from dynamic minimum-cost network flows which is substantially different from the technique presented here. Campbell and Hardin [24] considered the problem of minimizing the number of vehicles required to make periodic deliveries to a set of customers, under the assumption that each delivery requires the use of a vehicle for a full day; they thoroughly examined the problem structure, evaluated its complexity, and presented an algorithm that optimally solved the problem for some special cases. Extensive reviews of UAV fleet size optimization techniques and industrial applications are presented, for example, in [12,13,14,15].

In this paper, we present and explore a more general particular case of the vehicle scheduling problem, namely, our goal is to find the optimal number of vehicles that maximizes the average environmental fleet benefit per vehicle and thereby the UAV fleet environmental efficiency. Note that the optimal number of vehicles in the latter problem may be strictly greater than the minimum number of vehicles required to meet a given periodic schedule. We propose a new fast algorithm the logic and main stages of which are presented in Figure 1.

3. Description of the Problem

Let J₁, …, J_n be a set of n tasks (e.g., flights) that must be carried out periodically by a fleet of drones, and let p denote a given period length. Associated with task J_i are non-negative real numbers a_i and b_i such that a_i < p and b_i < p, where a_i and b_i are the start and finish time of task J_i in the time interval [0, p), respectively. If a_i < b_i, then the kth iteration (or instance) of task J_i is executed in the time interval [a_i + kp, b_i + kp). If a_i > b_i, then the kth iteration of task J_i is performed in the time interval [a_i + kp, b_i + (k + 1)p), for k = 0, 1, 2, … . Thus, the times a_i, b_i , i=1,…, n, define a predetermined periodic schedule for all tasks.

Any task can be done by any autonomous vehicle, and any vehicle can carry out any task. (We use this assumption to simplify the presentation of our algorithm; though, in fact, the proposed general graph approach can be extended to handle multiple aircraft types and solve efficiently other combinatorial problems). There is a known setup time r_ij between the sequential processing of instances of task J_i and task J_j by the same vehicle. The setup time r_ij is the required delay between the arrival of flight J_i and the departure of flight J_j, assuming the same aircraft is used for both flights. It is allowed that the arrival site s for flight J_i may differ from the departure site t for flight J_j; in this case, the setup time r_ij will include the deadhead time from s to t.

Unlike known models mentioned above, this study takes into account not only the size of the fleet, but simultaneously the environmental benefit (profit) accrued from using the UAV fleet, which depends on the fleet size and the assignment of tasks performed by the vehicles. Assume that profit e_ij is accrued from the use of an UAV when performing task J_j following task J_i; this quantity is known in advance, while the number of vehicles and the assignment of tasks to vehicles are the decision variables that need to be found.

Let K be the (unknown) number of vehicles required to meet periodic fixed schedule, and E be the total environmental profit obtained by all vehicles over period p. Then our problem to be solved is the following

Problem A.

Assign tasks to vehicles so as to maximize the ratio

E / K \frac{T o t a l e n v i r o n m e n t a l b e n e f i t a c c r u e d f r o m t h e u s e o f t h e U A V f l e e t o v e r p e r i o d p}{N u m b e r o f v e h i c l e s r e q u i r e d t o m e e t a f i x e d s c h e d u l e o f t a s k s},

that is, to maximize the average benefit obtained by the fleet of vehicles over the period, for a given task schedule, which is defined by the known times {a_i, b_i , i=1,…. n}.

Remark 1

In the above verbal formulation of Problem A, we do not reveal the explicit dependence of the total environmental benefit on the distribution of vehicles among tasks. This will be explained and formalized below in Problems D and FAP in the following sections.

Remark 2

The reader may notice that the problem under consideration in its current formulation resembles the well-known vehicle allocation problem. The latter problem in its various forms is known to be NP-hard (see, for example, [8,20,25,26]. However, in this paper we will prove that the problem under study can be solved in polynomial time; this is because this problem has a special structure that greatly reduces the problem complexity.

4. Reduction to Graph Problems

Consider an infinite weighted periodic graph G_∞ which is constructed as follows: G_∞= (N_∞, A_∞), where N_∞ is an infinite set of nodes and A_∞ is an infinite set of arcs. In this graph, node i_k ∈ N_∞ represents the kth iteration of task J_i. A directed arc (i_k, j_l)∈A_∞ leads from node i_k to node j_l iff the vehicle is able to carry out the lth iteration of task J_j after it has completed the kth iteration of task J_i. The weight of the arc (i_k, j_l) represents the profit e_ij collected by the vehicle from serving the task J_j following the task J_i. Let us formulate all profits e_ij in the form of the n×n matrix E = ║e_ij║.

Consider a periodic directed chain in the graph G_∞. Note that the period of such a chain can span several periods p defined in the previous section. The chain determines the schedule of an individual vehicle visiting a sequence of tasks, and the sum of its arc weights e_ij determines the profit earned by that vehicle during that period. The set of directed chains in G_∞ covering all nodes determines the total number of required vehicles, their schedule and the total environmental benefit obtained. Thus, the original allocation Problem A is reduced to the following graph-theoretic problem on the infinite graph G_∞:

Problem B

Find a periodic infinite chain cover of the graph G_∞ that maximizes the following average environmental benefit (profit) obtained by the UAV fleet:

E / K = \frac{T o t a l e n v i r o n m e n t a l p r o f i t o b t a i n e d b y t h e U A V f l e e t i n p e r i o d p}{N u m b e r o f v e h i c l e s r e q u i r e d} =

= \frac{S u m o f a r c w e i g h t s e_{i j} i n c h a i n c o v e r i n p e r i o d p}{N u m b e r o f d i r e c t e d c h a i n s c o v e r i n g n o d e s} .

The next step is to transform the infinite graph G_∞ into an equivalent finite graph. Due to the periodicity of the graph G_∞, we can roll up it into the so-called finite generating graph, G_gen = (N_gen, A_gen), defined as follows: node i∈N_gen represents all periodic implementations of task J_i; in other words, all nodes i_k ∈ N_∞, 0 ≤ k < ∞, of the infinite graph G_∞ are “packed” into one node i of the graph G_gen. Similarly, all arcs (i_k, j_l) ∈ A_∞ are “packed” into one arc (i, j)∈A_gen. Thus, every infinite, periodically repeated arc chain in the graph G_∞ can be transformed into a corresponding directed cycle in the graph G_gen. Knowing the generating graph G_gen, we can transform the problem B of covering the graph G_∞ with chains into the following problem C of covering the nodes of the graph G_gen with cycles. Let c denote a set of such cycles.

Problem C.

Find a covering of the nodes of the graph G_gen with a set of cycles c so as to maximize the ratio

E / K = \frac{\sum_{(i, j) c} e_{i j}}{N u m b e r o f r e q u i r e d v e h i c l e s}

Next, we associate two weights with each arc (i, j) ∈ A_gen. The first weight is the profit e_ij introduced above. The second weight, denoted k_ij, is needed to calculate the required number of vehicles. It is defined similarly to model in [20]; namely, k_ij is the number of periods p that must exist between an arbitrary departure iteration k(i) of a flight J_i and the departure iteration l(j) of the flight J_j that is closest to J_i in the graph G_∞, provided that the two flights are operated by the same aircraft; it is possible that j=i. Then

k_ij = l(j)– k(i).

(1)

For reader’s convenience, consider the definition of the weight k_ij in more detail. Let k(i ) be an arbitrary integer, and the symbol k(i) denotes that the flight J_i occurs during the k(i)-th period. Further, suppose that in the graph G_∞ there are arcs from the node representing the flight J_i to all other nodes representing iterations (repetitions) of the flight J_j; it is clear that then, in our notation, the numbers {k(j)} will denote the numbers showing in which periods those repetitions of J_j occur. Among these numbers k(j), choose the minimum one – this number is denoted as l(j). Then, as stated above, k_ij = l(j) - k(i). In other words, after completing the k(i)th iteration of task J_i, the vehicle does not have enough time to arrive and carry out the (l(j)–1)th iteration of task J_j but has time to successfully perform the l(j)th iteration of task J_j.

Remark 3.

Since the process under consideration is periodic, the found values k_ij are valid for all task iterations. As we will show shortly, the sum of k_ij over all cycles in any cycle-cover of the graph G_gen is equal to the number of vehicles required to meet a given schedule.

Remark 4.

Formally, the main property of the parameter l(j) can be presented as follows: Let d_i denote the duration of the flight J_i, that is,

d_i = b_i - a_i, if a_i < b_i and

d_i = b_i + p - a_i, if a_i > b_i.

Then the following inequalities hold:

a_j + (l(j) - 1)∙p < a_i + k(i)∙p + d_i + r_ij ≤ a_j + l(j)∙p.

Thus, we introduce the n×n matrix K = ║k_ij║ with the entries k_ij just described. If the arc (i, j) does not exist in the graph G_gen, then we set e_ij = 0 and k_ij = ∞. To obtain this matrix, we need O(n²) time.

Consider a small example to illustrate the above definition of k_ij in Eq.(1). Assume that we have three tasks J₁, J₂, J₃; p = 10, a(J₁) = a₁ = 5, b(J₁) = b₁ = 8; a(J₂) = a₂ = 9, b(J₂) = b₂= 2; a(J₃) = a₃ = 4, b(J₃) = b₃ = 9; r₁₂=2, r₁₃ =1, r₂₁=1, r₂₃=3. Let us consider, for example, the 12th iteration of these tasks, i.e. set k(1) =12, k(2) =12 and k(3) =12; then the task J₁ will be executed in the time interval [125, 128], the task J₂ - in the time interval [129, 132] and the tasks J₃ in the time interval [124, 129]. Therefore, the nearest iteration of task J₂ that can be performed by the same vehicle, which has performed the 12^th iteration of J₁, will be the 13^th iteration. Respectively, the nearest iteration of task J₃, that can be performed by the same vehicle following the 12^th iteration of J₁,will be also the13^th iteration. Hence, k₁₂ = k₁₃ =13 -12 =1. Similarly, we obtain that k₂₃ = 14-12 =2; k₂₁= 1.

At this point, let us recall a remarkable property of the weights k_ij in the periodic minimum-size vehicle problem, discovered by Karzanov and Livshits [18] in 1978 and independently by Orlin [20] in 1982, that establishes a direct connection between the minimum number of vehicles required and the minimum-weight cycle-cover of the graph G_gen, the arc weights of which are the weights k_ij defined by Eq. (1). Denote by c an arbitrary cycle cover of the generating graph G_gen, and S the set of all possible cycle covers of the graph G_gen.

The Karzanov-Livshits-Orlin Theorem.

A minimum-weight cycle-cover, having the total weight min_c_∈S ∑_(i,j)∈c k_ij, provides the minimum number of vehicles K_min required to perform a given task schedule: K_min =min_c_∈S ∑_(i,j)∈c k_ij.

For our further analysis, we need to extend the above claim to formulate it for the bi-matrix optimization problem C:

Proposition 1

Let c be an arbitrary cycle cover of the generating graph G_gen with two arc weights, e_ij and k_ij, where k_ij is the weight defined by Eq. (1). Then the total weight ∑_(i,j)∈c k_ij of the cycle-cover is equal to the number of vehicles K required to carry out all the tasks in the considered cycle-cover c in Problem C: K = ∑_(i,j)∈c k_ij.

Proof.

Let σ be a simple cycle entering the cycle cover c of the generating graph G_gen with two arc weights, and let s = ∑_(i,j)∈σ k_ij. Consider the periodic graph G_∞ that corresponds to the initial problem B, which has generated the generating graph G_gen. Recall, that each node i ∈ σ corresponds to an infinite number of nodes i_k in graph G_∞, 0 ≤ k < ∞. As proven in [20], a cycle σ can be unpacked into exactly s chains in the graph G_∞ such that no node in one chain is linked to a node in another chain. From the description of problem B and the definition of the cycle weight, it follows that each chain corresponds to one vehicle performing the tasks of the chain and then the value ∑_(i,j)∈σ k_ij is equal to the number of vehicles required to carry out all the tasks of the cycle σ. To complete the proof, it suffices to notice that the graph G_gen can be partitioned into a set c composed of a finite number of simple cycles and therefore the total number of chains ∑_(i,j)∈c k_ij corresponding to all simple cycles in partition c is equal to the number of vehicles required, which proves the claim.

From Proposition 1 it follows that Problem C reduces to the following Problem D.

Problem D.

Find a cycle-cover of the graph G_gen with a set of cycles c, so as to maximize the ratio E/K = ∑_(i,j)∈c e_{ij /}∑_(i,j)∈c k_ij.

The question remains: how to efficiently solve the resulting cycle-covering problem for the graph G_gen? We will answer this question in the following sections.

The illustrative example.

For reader’s convenience, consider a numerical example. It is adapted from the work of Orlin [20], who studied the problem of minimizing the number of aircraft to operate a fixed daily repeating set of flights; we generalize Orlin’s example for the problem of maximizing the average fleet profit.

Model of the Fixed Daily-Repeating Set of Drone Flights

Three daily flights are shown in Table 1.

It is also necessary to take into account the “deadhead” time, that is, the time that a given aircraft takes, after completing a flight, to reach the departure location of the next scheduled flight. The deadhead times are given in Table 2.

In the notation, introduced above, the input data from Table 1 and Table 2 are given in Table 3. Tasks J₁, J₂, and J₃ represent flights 1, 2 and 3, respectively.

We consider a daily-repeating schedule of flights, therefore, period length p is 24 hours.

Reduction to a Problem on a Periodic Graph

Let the profits be given by the following matrix E shown in Table 4.

Using the flight schedule given in Table 3, it is possible to plot the graph G_∞. A fragment of the graph G_∞ drawn for three consecutive periods, starting with period 1, is presented in Figure 2.

The nodes in Figure 2 depict the daily flights repeated for three periods; node i_k depicts flight i (i=1,2,3) during period k (k=1,2,3). Figure 2 shows only the arcs (i_k, j_l,) between the nearest iterations k and l of tasks J_i and J_j. Each arc (i_k, j_l) in G_∞ has the associated weight e(i_k, j_l), however, it is not shown in Figure 2 in order not to overload it. At this point, our initial fleet assignment problem is equivalent to finding the optimal number of infinite periodic disjoint paths covering all nodes and having maximum average profit per path per period.

Construction of the Generating Graph

According to the above description, the graph G_gen can be portrayed as follows (see Figure 3):

Each arc is double-weighted, and the weight of arc (i, j) has the form (e_ij, k_ij), where the number k_ij is determined by arc (i_k, j_l) in Figure 2, k_ij = l – k, (i, j = 1, 2, 3). Note that the generating network for the airplane scheduling example presented in [20] is different from the graph G_gen; namely, the arcs of the graph G_gen are double-weighted, whereas in the Orlin graph the weights on arcs (i, j) are specified by a single number.

Calculation of the Second Weight k_ij

According to the definition of the second weight k_ij and the data in Table 1, we see that flights 1 and 3 can be repeated every period (every day) by the same aircraft (the arc from node 1₁ to node 1₂ and the arc from node 3₁ to node 3₂ in Figure 2); therefore, k₁₁=k₃₃ =1. Flight 2 can be repeated by the same vehicle every two days; therefore, k₂₂ =2. Further, if an aircraft starts its flight no. 2 at 15:00 in the first period (node 2₁ in Figure 2), then it can start the nearest flight no. 3 only after 13+12 =25 hours, i.e. on the third day at 13:00 (node 3₃ in Figure 2); hence, k₂₃ = 3 – 1 = 2. Similarly, we compute all other values k_ij shown in Figure 3 and in Table 5.

The illustrative numerical example will be continued and completed in Section 7.

5. Reduction to the Fractional Assignment Problem

In this section, we reformulate Problem D as a fractional assignment problem. Recall that an assignment can be stated in the form of n×n matrix A whose entries, denoted a_ij, are 0 or 1, and a_ij =1 occurs in each row and each column of the matrix A exactly once.

Consider Problem D, defined in the previous section, and the corresponding cycle cover of the graph G_gen.

Proposition 2.

The set of all cycles in the cycle cover c= (C₁, C₂, …, C_q) of the graph G_gen, where q is the number of cycles in c, can be considered as an n×n assignment A in the matrix form defined as follows:

a_ij = 1 if and only if the arc (i,j) from G_gen belongs toc,and a_ij = 0, otherwise.

(2)

Indeed, from the definition of the cycle-cover it follows that the matrix A contains n rows and n columns, its elements are 1 or 0, and each a_ij =1 occurs exactly once for each row i and each column j (i, j =1,…, n), which proves the claim.

Given a profit matrix E, a weight matrixK and an arbitrary assignment matrix A, the profit and weight values corresponding to the assignment A are defined, respectively, as follows:

E(A) = ∑_(i,j)∈A e_ija_ij and K(A) = ∑_(i,j)∈A k_ija_ij.

In the above expression and wherever necessary, the notation (i,j)∈A denotes all pairs of indices i, j corresponding to entries a_ij = 1 of the assignment matrix A. For ease of notation, in the expressions E(A) and K(A) below we will omit the symbols a_ij. In what follows, in accordance with (2), instead of maximizing P = ∑_(i,j)∈c e_{ij /}∑_(i,j)∈c k_ij over all cycle covers of the graph G_gen (Problem D), we will focus on finding the optimal assignment that maximizes

P = E(A)/K(A) = ∑_(i,j)∈A e_ij/∑_(i,j)∈A k_ij.

Let us denote by C the set of all assignments A in the form of n×n matrices. Now Problem D in section 2 reduces to the following fractional assignment problem (FAP):

Problem FAP.

Given two n×n matrices E and K, find the optimal assignment A^*, common to the matrices E and K, that is, the one that maximizes the average fleet profit per vehicle P = E(A)/K(A):

P^* = E(A^*)/ K(A^*) = max_A_∈C E(A)/K(A) = max_A_∈C ∑_(i,j)_∈A e_ij /∑_(i,j)_∈A k_ij.

The following statement shows that the elements of matrix K in the considered problem are the small positive integers not exceeding 3; in fact, this is an important property that reduces the complexity of the problem by a factor of n.

Proposition 3

. If the arc (i, j) ∈ G_gen then, for any element k_ij of matrix K, it holds that k_ij ≤ 3.

Proof.

Сonsider the k(i)th iteration of task J_i that starts at time a_i + k(i)∙p, and let l(j) be the nearest iteration of task J_j that the vehicle can perform after the k(i)th iteration of task J_i. Consider two cases, a_i < b_i and a_i > b_i.

(i) a_i < b_i.

In this case, the k(i)th iteration of task J_i ends at time b_i + k(i)∙p. Then the nearest iteration of task J_j satisfies the following inequalities:

a_j + [l(j) – 1]∙p < b_i + k(i)∙p + r_ij ≤ a_j + l(j)∙p,

a_j + [l(j) - k(i) – 1]∙p < b_i + r_ij ≤ a_j + [l(j) - k(i)]∙p.

(ii) a_i > b_i.

In this case, the k(i)th iteration of task J_i ends at time b_i + [k(i) + 1]∙p. Then the nearest iteration of task J_j satisfies the following inequalities:

a_j + [l(j) – 1]∙p < b_i + [k(i) + 1]∙p + r_ij ≤ a_j + l(j)∙p,

a_j + [l(j) - k(i) – 1]∙p < b_i + p + r_ij ≤ a_j + [l(j) - k(i)]∙p.

From the definition of k_ij = l(j) - k(i) in Section 2, it immediately follows that each element k_ij is an integer satisfying the following relations:

a_j + (k_ij - 1)∙p < b_i + r_ij ≤ a_j + k_ij∙p, if a_i < b_i

and

a_j + (k_ij - 1)∙p < b_i + p + r_ij ≤ a_j + k_ij∙p, if a_i > b_i.

It means that, due to the given time constraints, the element k_ij is equal to the minimum number of periods p that the vehicle must skip before it can start task J_j after it have started task J_i. Since each task (flight) J_j is to be executed in every period p, the vehicle must skip k_ij instances of task J_j in the skipped periods.

It is natural to assume that all the setup times r_ij < p; then, from the definition of k_ij, we derive that the largest value of k_ij can appear only in the following inequalities

a_j + (k_ij - 1)∙p < b_i + p + r_ij ≤ a_j + k_ij∙p.

(3)

Suppose that b_i > a_j and p > r_ij > p – (b_i - a_j). Then, on the one hand, we have that

b_i + p + r_ij > b_i + p + p – (b_i - a_j) = a_j + 2p,

(4)

and, on the other hand, b_i < a_j + p; then we have that

b_i + p + r_ij ≤ (a_j + p) + p + p = a_j + 3p.

(5)

Comparing inequalities (3), (4) and (5), we find that in this case, k_ij = 3. Q.E.D.

6. Reduction to the Parametric Assignment Problem

In this section, we reduce the fractional assignment problem FAP with the objective function P defined above to a parametric assignment problem. Let us introduce a parameter λ, which for each assignment A from the set C of all assignments satisfies the following inequality:

∑_(i,j)∈A e_ij /∑_(i,j)∈A k_ij ≤ λ, for all A∈C.

(6)

Since the sum ∑_(i,j)_∈A k_ij is positive in any assignment A, inequalities (6) can be rewritten as follows:

∑_(i,j)∈A e_ij ≤ λ ∑_(i,j)∈A k_ij

0 ≤ λ ∑_(i,j)∈A k_ij - ∑_(i,j)∈A e_ij

and, finally,

0 ≤ ∑_(i,j)_∈A(λ k_ij - e_ij) for all A∈C

(7)

Thus, Problem FAP of finding the maximum average profit P^* presented in the previous section takes the following form:

To find the minimum λ that satisfies ( 6 ), or, equivalently, to find the minimum λ that satisfies ( 7).

Consider the matrix W(λ) = λ∙K - E with entries w_ij = (λ∙k_ij - e_ij), called arc costs, or simply costs. Consider some fixed value of λ. Let A^*(λ) denote the assignment with the minimum cost across all the assignments A∈C, defined as follows:

∑_{(i,j)∈ A*(λ)} (λ∙k_ij - e_ij) = min_A∈C ∑_(i,j)∈A (λ∙k_ij - e_ij),

(8)

and denote the latter function, called the minimum-cost function, by L(λ):

L(λ) = ∑ _{(i,j)∈ A*(λ)} (λ∙k_ij - e_ij).

(9)

Proposition 4 below states that the assignment problem of finding the maximum average fleet profit P^*, defined in Problem FAP, can be reduced to the following parametric minimum-cost assignment problem PAP:

Problem PAP

. Find the value of the parameter λ = λ^* for which the minimum-cost function L(λ) is equal to zero:

L(λ) = ∑ _(i,j)_{∈ A*}_(λ) (λ∙k_ij - e_ij) = 0,

(10)

and, further, together with the optimal value of the parameter λ^*, find the corresponding minimum-cost assignment A^*(λ^*) for the matrix W(λ^*); for the simplicity of notation we denote the latter assignment by Φ^*: Φ^* = A^*(λ^*).

Proposition 4

Let λ^* be the optimal solution to the problem PAP, and Φ^* = A^*(λ^*) be the corresponding minimum-cost assignment for the matrix W(λ^*). Then

λ^* = P^* = ∑_(i,j)∈A* e_ij/∑_{(i,j)∈ A*} k_ij = max_A∈C∑_(i,j)∈A e_ij/∑_(i,j)∈A k_ij,

and Φ^* = A^*,

that is, in meaningful terms, (i) the value of λ= λ^* defined by expression (10) is equal to the optimal profit value P^*, which we are looking for, and (ii) the assignment Φ^*, which is optimal for the problem PAP, coincides with the optimal assignment A^* for the maximum average fleet profit in the problem FAP.

Proof

From equation (10), we have:

L(λ^*) = ∑ _{(i,j)∈ A*(λ*)} (λ^*∙k_ij - e_ij) = 0.

(11)

In addition, from (8), we have:

∑_(i,j)_∈_A*_(λ*) (λ^*∙k_ij - e_ij) = min_A_∈_C∑_(i,j)_∈_A(λ^*∙k_ij - e_ij).

Then

∑_(i,j)_∈_A(λ^*∙k_ij - e_ij) ≥ 0 for all A∈C.

(12)

Thus, from (11), we obtain that

λ^* = ∑_(i,j)_∈ A*_(λ*) e_ij/∑_(i,j)_∈ A*_(λ*) k_ij,

and from (12), we have

λ^* ≥ ∑_(i,j)_∈_Ae_ij/∑_(i,j)_∈_Ak_ij for all A∈C,

that is, λ^* = P^* and Φ^*= A^*, which completes the proof.

The following claim is an extension of Proposition 4 that formulates a way of how we can optimally and efficiently solve the optimization problem PAP:

Corollary.

Let λ^* be the optimal parameter value, i.e., such that

L(λ^*) = ∑ _(i,j)_∈_A*_(λ) (λ∙k_ij - e_ij) = 0.

Then the parameter λ^* represents the maximum average profit per vehicle in the problem under study, and K(A^*) = ∑_(i,j)_∈A* k_ij is equal to the optimal number of required vehicles, where, A^* = A^*(λ^*).

In the following sections, we propose two strongly polynomial time algorithms for the parametric assignment problem under consideration, which in turn optimally solve the problem of maximizing the average profit of a fleet of identical vehicles.

7. A Newton-Type Algorithm for the Parametric Assignment Problem

Consider the cost value w(A, λ) = ∑_(i,j)_∈A(λ∙k_ij - e_ij) of an arbitrary assignment A, whose costs are the elements of the matrix W(λ). This value is a linear function w(A, λ) = (d_A λ – f_A) of the parameter λ, where d_A = ∑_(i,j)_∈A k_ij is the slope and f_A = ∑_(i,j)_∈A e_ij. In the UAV model considered, each k_ij ≤ 3, so d_A ≤ 3n. Let A be a collection of q cycles: A = (C₁, C₂, …, C_q). Consider an arbitrary cycle C ∈ (C₁, C₂, …, C_q). The sum of the elements k_ij over the cycle C is not less than one, ∑_(i,j)_∈C k_ij ≥ 1. Indeed, if C ={i₁, i₂ = j(i₁), i₃ = j(i₂), … , i_s = j(i_s-₁), i₁ = j(i_s)}, then after task J_i₁, the vehicle performs task J_i₂, and after task J_is, the vehicle again performs task J_i₁, but not at the same iteration as at the previous one. Two iterations of task J_i₁, carried out by the same vehicle, are separated by a time interval equal to ∑_(i,j)_∈C k_ij ≥ 1 periods. Therefore, 1 ≤ d_A ≤ 3n.

There is a set of linear functions corresponding to different assignments A of the matrix W(λ), each of which has the form:

∑_{(i,j)∈ A} (λ∙k_ij - e_ij), A ∈C.

According to (8) and (9), L(λ) is a lower bound for the costs of all assignments A∈C; it is an increasing concave piecewise linear function of the parameter λ with slope ∑_(i,j)_{∈ A*(λ)} k_ij. Since 1 ≤ ∑_(i,j)_{∈ A*(λ)} k_ij ≤ 3n, the number of pieces in L(λ) does not exceed 3n.

Let us select some arbitrary value λ = λ^′. Determine the corresponding minimum-cost assignment A′ = A^*(λ′) and the corresponding cost

L(λ^′) = ∑_{(i,j)∈ A′} (λ^′k_ij - e_ij).

(13)

Consider the function d_A′ λ – f_A′ = ∑_(i,j)_{∈ A′}(λ∙k_ij - e_ij). Let us select a starting value λ^′ such that it is so small that L(λ′) < 0, then λ′ < ∑_(i,j)_∈A′ e_ij/∑_(i,j)_{∈ A′} k_ij ≤ λ^*. The first inequality follows from (13); the second inequality follows from (12). Now we can set a new value of λ^′ that is equal to ∑_(i,j)_∈A′ e_ij/∑_(i,j)_∈A′ k_ij. Then determine the minimum-cost assignment for the updated λ = λ′. This procedure must be continued until the optimal solution λ^* of the problem PAP is found. The following algorithm A1 implements the described idea.

7.1. Algorithm A1

Initialization

Step 1. Solve the standard assignment problem for the known matrix K (using a standard assignment algorithm). Denote by I the obtained optimal (minimum-cost) assignment for this matrix.
Step 2. Calculate the average profit λ₀ received for the obtained assignment I:λ₀ = ∑ _(i,j)∈I e_ij/∑_(i,j)∈I k_ij.
(Note that at this stage λ₀ ≤ λ^*, where λ^* is the maximum average profit that we are looking for).
Step 3. Set i = 0.
Iterative procedure
Step 4. Find the minimum-cost assignment A^*(λ_i) for the matrix W(λ_i).
Step 5. Calculate the average profit λ_i+1 of the assignment A^*(λ_i):
λ_i+1 = ∑_{(i,j)∈A*(λi)} e_ij/∑ _{(i,j)∈ A*(λi)} k_ij.
Step 6. If λ_i+1 > λ_i then {set i = i + 1; go to Step 4},
else go to step 7.
Solution
Step 7. Set the maximum average profit per vehicle: P^* = λ^* = λ_i.
Set the optimal assignment Φ^* = A^*(λ_i)
Determine the optimal number of vehicles needed to meet the obtained schedule:
K = ∑_(i,j)∈Φ* k_ij.
End.

The proposed algorithm can be considered as a discrete version of Newton's optimization method adapted to solving equation (10).

7.2. Complexity of Algorithm A1

In Algorithm A1, in the iterative procedure (Steps 4-6 above) the slope of the minimum-cost function L(λ)in (9), ∑ _(i,j)_∈_A*(λi) k_ij, decreases, i.e.

∑ _{(i,j)∈ A*(λi)} k_ij > ∑ _{(i,j)∈ A*(λi+1)} k_ij.

Therefore, steps 4-6 return at most O(n) times. Each pass of the iterative procedure solves once the assignment problem. The complexity of solving the assignment problem is O(n³), which is repeated at most O(n) times. Thus, the overall complexity of algorithm A1 is O(n⁴).

The illustrative example (continued).

Reduction to the fractional FAP and parametric PAP problems.

Problem FAP. Given two n×n matrices E and K, defined at the previous step, find the optimal assignment A^*, common to the matrices E and K, that is, the one that maximizes the average fleet profit per vehicle P = E(A)/K(A):

P^* = E(A^*)/ K(A^*) = max_A_∈C E(A)/K(A) = max_A_∈C ∑_(i,j)_∈A e_ij /∑_(i,j)_∈A k_ij.

To solve this problem, we reduce it to the following parametric assignment problem:

Problem PAP. Find the value of the parameter λ = λ^* for which the minimum-cost function L(λ) is equal to zero: L(λ) = ∑ _(i,j)_{∈ A*}_(λ) (λ∙k_ij - e_ij) = 0, and find the corresponding minimum-cost assignment A^*(λ^*) for the matrix W(λ^*).

Solution of the parametric assignment problem by the Newton-type algorithm.

Let us solve the standard minimum-weight assignment problem with the matrix K. We can see that assignment I = {C₁ = [(1, 2), (2, 1)]; C₂ = (3, 3)} is optimal for this standard single-matrix problem, ∑_(i,j)_∈I k_ij = k_1,2 + k_2,1 + k_3,3 = 3. This is the minimum number of vehicles required to meet the given flight schedule.

Calculate the average profit received with the assignment I:

λ₀ = (900 + 600 + 300)/(1 + 1 + 1) = 600.

The value λ₀ can be taken as the lower bound of the desired maximum average profit P^*, 600 ≤ P^*.

Consider the matrix W(λ₀ =600) presented in Table 6:

The optimal assignment A^*(λ₀ =600) of the matrix W(λ₀ =600) is:

A^*(λ₀ =600) = {C = [(1, 2), (2, 3), (3, 1)]}.

The cost of the assignment A^*(λ₀ =600) at the point λ₀ =600 is negative, w(A^*, λ₀) = -300 + 0 + (-300) = - 600. Therefore, λ₀ =600 is not an optimal solution to the PAP problem considered. This means that the average profit λ₁ obtained with the assignment A^*(λ₀) is greater than λ₀: λ₁ = (900 + 1200 + 900)/(1 + 2 + 1) = 750

Now, in a similar way, consider the matrix W(λ₁ =750) presented in Table 7:

The optimal assignment A^*(λ₁ =750) of the matrix W(λ₁ =750) is the same as A^*(λ₀ =600). The cost of the assignment A^*(λ₁ =750) at the point λ₁ =750 is zero, w(A^*, λ₁) = -150 + 300 + (-150) = 0. Thus, λ^* = λ₁ = 750 is the optimal solution to our PAP problem, and according to , the maximum average profit per aircraft is P^*= λ^* = 750.

Solution of the original vehicle fleet optimization problem.

The optimal assignment A^*(λ₁ =750) consists of only one cycle C =[(1,2), (2,3), (3,1)]. It corresponds to the following optimal sequence of flights:

Flight 1 from Honolulu to Washington DC, then deadheading flight to New York, then
Flight 2 from New York to Tokyo, then deadheading flight to London, then
Flight 3 from London to Paris, then deadheading flight to Honolulu.

The considered circular route C takes four days, ∑_(i,j)_∈c k_ij = k_1,2 + k_2,3 + k_3,1 = 4. This schedule requires four aircraft, each repeating the same sequence of flights as the previous one, lagging behind it in time by a day. This is the optimal number of the aircraft in the considered example. Note that in this illustrative example, the optimal number of vehicles is four, and the minimum number of vehicles required to meet a given flight schedule is three; the optimal average fuel efficiency obtained in this example (i.e. for 4 vehicles) is 20 % better than the corresponding fuel efficiency for the minimum number of vehicles required: (750 - 600)/750 = 0.2.

Discussion. The Newton-type algorithm proposed in this section is relatively simple and easy to program. The question arises whether an algorithm of a similar or even better complexity can be obtained for the problem under study if one will exploit the existing polynomial algorithms for the general fractional assignment problem. Unfortunately, all polynomial algorithms for the general fractional assignment problem known to us (see, e.g., [26,27,28,29,30]) have the total running time similar or worse than O(n⁴), even in the case where the coefficients of the linear function in the denominator of the fractional objective are restricted to the values {0, 1}. However, unlike these studies, we found another way to speed up the solution time of the Newton type algorithm. In the next section, we present an improved algorithm that can solve the parametric assignment problem under study in O(n³) time, and, hence, can optimally solve the original max-benefit UAV fleet problem in O(n³) time.

8. A Faster Parametric Assignment Algorithm

8.1. Comparison of Two Parametric Assignment Problems

Reduction of the original aircraft profit maximization problem A to the special-type parametric assignment problem PAP formulated in Section 6 opens an opportunity to exploit another solution algorithm which is faster than the Newton-type algorithm proposed in the previous section. For this purpose, we adapt and use, after appropriate adaptation, a fast and elegant parametric assignment algorithm developed more than a decade ago by Elizabeth Gassner and Bettina Klinz [31].

Since the parametric assignment problem solved by Gassner and Klinz is somewhat different from our assignment problem PAP, we should make necessary changes to the Gassner-Klinz algorithm (GKA) to make the adapted version of GKA applicable to solve the PAP under consideration. We begin by comparing two related parametric assignment problems, focusing on their differences (see Table 8). Note that the significant difference between the two studies is that the present work is motivated and focused on the practical aircraft fleet assignment problem.

8.2. Brief Review of the Gassner-Klinz Algorithm and Its Adaptation

The GKA algorithm aims to solve the parametric assignment problem described in Table 8 for all possible values of parameter λ; its worst-case complexity is O(n³). that is, the same as that for the standard (non-parametric) linear assignment problem. In contrast to the Newton-type algorithm A1, the GKA does not solves each of O(n) assignment problems appearing in critical points, but, rather, solves an assignment problem only once and then transforms the obtained assignment into a new one with certain local operations so that that the minimum-cost assignments for all the values of λ are found in O(nm + n² log n) time, where m and n are the number of arcs and the number of nodes, respectively, in an underlying bipartite graph described below. We will follow the same idea of the GKA and adapt it, adding necessary changes, in order to take into account that the objective functions in the two problems are different (see Table 8).

Since the two optimization problems in Table 8 are very close, it suffices to replace c_λ(i, j) = (c_ij - λ∙b_ij) in the Gassner-Klinz problem by c′_λ(i, j) = (c′_ij - λ∙b′_ij) = (- e_ij - λ∙(-k_ij)) and then use the existing algorithm GKA. In this case the slope of the parametric objective function in the derived problem (which, obviously, in this case will be our PAP) will be positive and will decrease with the growth of parameter λ until L(λ) becomes zero, whereas the slope of the objective function in the original Gassner-Klinz problem is negative and its absolute value increases when the parameter increases to infinity (see Figure 4). Another observation is that in the original Gassner-Klinz problem b_ij ∈ {0, 1} whereas b′_ij are to be {0, -1, -2, -3}; however, this difference can be easily overcome and it does not influence the algorithm complexity. Finally, the starting point and the stopping rule are different in the GKA and in the modified algorithm. Indeed, when solving the PAP problem, one does not need to solve the assignment problems in all the critical points for all possible λ∈(-∞, +∞); rather, the modified algorithm starts with a known lower bound of the parameter and stop as soon as the cost L(λ) of a current assignment becomes zero.

Below, for the reader’s convenience, we review the proposed modification of the GKA and, in order to give a more complete picture, describe the steps of the adapted algorithm. For easier comparison, in this subsection we borrow graph-theoretic terminology from [31] to describe the modified algorithm.

Consider the parametric assignment problem as a minimum-cost matching problem in a bipartite graph G = (U, V, W), where the vertices U and V correspond, respectively, to the rows and columns of the matrix W(λ), |U|=|V| = n, |W| = m. Arc (i, j) ∈ W only if arc (i, j) exists in the graph G_gen. Arcs lead from set U to set V. The parametric cost of arcs (i, j) ∈ W is w(i, j) = (λ∙k_ij - e_ij), where i ∈ U and j ∈ V, i.e., the element of the matrix w_ij ∈ W(λ) is equal to the cost of the arc (i, j), w(i, j) = w_ij.

Let A^*(λ′) be a minimum-cost assignment in graph G for λ = λ′. Exactly as in [31], we associate with the graph G and assignment A = A^*(λ′) a residual graph N(A) = (U, V, W^*) constructed as follows: All the arcs (i, j) ∈ A, where i ∈ U and j ∈ V are replaced by backward arcs (j, i) of cost w(j, i) = - w(i, j) = (- λ∙k_ij + e_ij).

Note that it is at this point that we make changes needed to be taken because coefficients k_ij in our objective function have the opposite sign compared with the corresponding b_ij in the GKA.

The remaining arcs, called forward arcs, as well as their costs, remain the same as in the graph G. Graph N(A) has no cycles with a negative cost for λ = λ′. Let us increase parameter λ and let λ_c be the minimum value of λ such that in the residual graph N(A) there is a cycle C with zero cost, w(C, λ_c) = 0, and w(C, λ) < 0, when λ > λ_c. Value λ_c and cycle C are the critical point and critical cycle, respectively. The assignment A remains a minimum-cost assignment in the interval λ ∈ [λ′, λ_c]. Then, in the interval λ ∈ [λ_c, λ′_c], where λ′_c is a critical point next to the critical point λ_c, the minimum-cost assignment changes to A′ = (A\C′) ∪ (C′\A), where C′ is a subset of the arcs obtained from the C by replacing all the backward arcs with the corresponding forward arcs; the cost of A′ changes to w(A′, λ) = w(A, λ) + w(C, λ). It is worth to notice at this stage that the following essential property is valid: when the parameter λ increases, the objective function of our problem also increases while the objective function in the Gassner-Klinz problem decreases (see Figure 4). At point λ = λ_c the costs of assignments A and A′ are equal, w(A, λ_c) = w(A′, λ_c). By changing the cost and the direction of all the arcs in cycle C to opposite ones in the residual graph N(A), one obtains the residual graph N(A′).

The following question is crucial: how, starting with the minimum-weight assignment A for λ = λ′, one can determine the critical point λ_c. Recall that in the residual graph N(A), for λ = λ′ there are no cycles with a negative cost, and that, when the parameter λ increases, some cycle C with a zero cost appears only at the point λ = λ_c, w(C, λ_c) = 0. To determine this cycle, we follow the approach proposed in [31] and also use the parametric shortest path algorithm of Karp and Orlin [32] and its improved version in [33]. The steps of the modified GKA adapted for solving our PAP problem are the following:

Algorithm A2

Step 1. Initialization

1.1. Solve the initial standard assignment problem for the known matrix K. Denote by I the obtained optimal (minimum-cost) assignment.

1.2 Calculate the average profit λ₀ achieved with the obtained assignment I:

λ₀ = ∑ _(i,j)∈_I e_ij/∑_(i,j)∈_I k_ij.

//This step is different compared with the corresponding initialization step in the original GKA.

1.3. Find the minimum-cost assignment A = A^*(λ₀) in the graph G for λ = λ₀.

1.4. Construct the residual graph N(A).

Step 2. Finding the nearest critical point.

//In this step we take into account that in the objective function the term b′_ij = - k_ij is of opposite sign compared to the Gassner-Klinz assignment problem.

2.1. Apply the parametric shortest path algorithm to find the nearest critical point λ_c and the critical cycle C for which w(C, λ_c) = 0.

2.2. Calculate the cost of the assignment A at the point λ = λ_c:

w(A, λ_c) = λ_c ∑_(i,j)_∈_A k_ij - ∑_(i,j)_∈_A e_ij.

// When we increase the values of parameter λ from one critical point to the next one, we stop and go to Step 3.1 at the moment when we find (for the first time) a current assignment A such that w(A, λ_c) ≥ 0. According to Proposition 4 in Section 4, this assignment A maximizes the average fleet profit per vehicle.

2.3. If w(A, λ_c) ≥ 0, go to Step 3.

2.4. Create the new minimum-cost assignment A′ = (A\C′) ∪ (C′\A).

// C′ is a subset of arcs obtained from C by replacing all the backward arcs with the corresponding forward arcs.

2.5. Convert graph N(A) to graph N(A′); set N(A) := N(A′) and A := A′.

2.6. Return to Step 2.1.

Step 3.Solution of the vehicle scheduling problem

// This step is absent in the GKA because the max-benefit UAV fleet problem was not a subject studied by Gassner and Klinz.

//Let us denote by A* the optimal assignment, which maximizes the average fleet profit per vehicle; ∑_(i,j)∈_A* k_ij expresses the corresponding optimal number of the required vehicles.

3.1. Set the assignment that maximizes the average fleet profit per vehicle A^* := A.

Calculate the maximal average profit P^* = λ^* =∑_(i,j)_∈_A* e_ij/∑_(i,j)_∈_A* k_ij.

3.2. Calculate the optimal number of vehicles, which is ∑_(i,j)_∈_A* k_ij, to meet the given vehicle schedule.

End.

Evidently, the adapted version of GKA has the same complexity as the original GKA, and, hence, the original max-benefit UAV fleet problem is solved in O(n³) time.

9. Conclusion

In this article we consider the problem of scheduling/assigning periodically repeated flights performed by a fleet of UAVs/drones. We extend the known scheduling/assignment problem for minimizing the number of aircraft to a more general problem of maximizing the average drone fleet profit per vehicle.

The main contribution of the present study is two-fold. First, we formulate and optimally solve a new bi-matrix average fleet profit maximization model, using profit and capacity matrices, which is a special case of airline fleet assignment problems widely used in the airline industry. Secondly, the aircraft fleet profit optimization problem is reduced to a special type of the parametric assignment problem; moreover, we find a way to speed up the solution time of a Newton type algorithm and provide an improved algorithm that solves the initial aircraft assignment problem in question in O(n³) time. In addition to the above, the special case problem solved in this study clearly not only has its own merits, but can also serve as a “building block” for solving more complex problems. For example, it can be used to solve the mathematical programming-based model for periodic airline fleet assignment proposed in [34] using branch-and-bound strategies. Indeed, the maximum average profit decision represents a “warm start” and can also be used as a comprehensive upper bound on the maximum expected total fleet profit less penalties and costs of fleet use, which is the common objective function in [34].

A challenging open question for further research is to find other solvable cases of the general max–profit fleet assignment/scheduling problem. We believe that the proposed graph approach to problem analysis and algorithm design can be extended and applied to efficiently solve other combinatorial periodic assignment/scheduling problems, such as minimizing fuel consumption and CO2 emissions, planning recovery operations for unexpected disruptions, scheduling periodic and sporadic tasks in real time and others.

Author Contributions

Conceptualization, Vladimir Kats and Eugene Levner; Formal analysis, Vladimir Kats and Eugene Levner; Investigation, Vladimir Kats and Eugene Levner; Methodology, Vladimir Kats and Eugene Levner; Validation, Eugene Levner; Writing – original draft, Vladimir Kats and Eugene Levner; Writing – review & editing, Eugene Levner.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Engesser, V.; Rombaut, E.; Vanhaverbeke, L.; Lebeau, P. Autonomous delivery solutions for last-mile logistics operations: a literature review and research agenda. Sustainability 2023, 15, 2774. [Google Scholar] [CrossRef]
Rejeb, A.; Rejeb, K.; Simske, S.J.; Treiblmaier, H. Drones for supply chain management and logistics: a review and research agenda. International Journal of Logistics Research and Applications 2023, 26, 708–731. [Google Scholar] [CrossRef]
Dolgui, A.; Ivanov, D. Ripple effect and supply chain disruption management: New trends and research directions. International Journal of Production Research 2021, 59, 102–109. [Google Scholar] [CrossRef]
Dolgui, A.; Ivanov, D. 5G in digital supply chain and operations management: Fostering flexibility, end-to-end connectivity and real-time visibility through internet-of-everything. International Journal of Production Research 2021, 1–10. [Google Scholar] [CrossRef]
Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned aerial vehicles (UAVs): A survey on civil applications and key research challenges. IEEE Accesss 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; Müllerová, J. On the use of unmanned aerial systems for environmental monitoring. Remote sensing 2018, 10, 641. [Google Scholar] [CrossRef]
Maffezzoli, F.; Ardolino, M.; Bacchetti, A.; Perona, M.; Renga, F. Agriculture 4.0: A systematic literature review on the paradigm, technologies and benefits. Futures 2022, 142, 102998. [Google Scholar] [CrossRef]
Garey, M.; Graham, R.; Johnson, D. Some NP-complete geometric problems. Proceedings of the 8th Annual ACM Symposium on Theory of Computing 1976, 10–22. [Google Scholar]
Psaraftis, H.N.; Wen, M.; Kontovas, C.A. Dynamic vehicle routing problems: Three decades and counting. Networks 2016, 67, 3–31. [Google Scholar] [CrossRef]
Rave, A.; Fontaine, P.; Kuhn, H. Drone location and vehicle fleet planning with trucks and aerial drones. European Journal of Operational Research 2023, 308, 113–130. [Google Scholar] [CrossRef]
Zhang, K.; Lu, L.; Lei, C.; Zhu, H.; Ouyang, Y. Dynamic operations and pricing of electric unmanned aerial vehicle systems and power networks. Transportation Research Part C: Emerging Technologies 2018, 92, 472–485. [Google Scholar] [CrossRef]
Balac, M.; Vetrella, A.R.; Rothfeld, R.; Schmid, B. Demand estimation for aerial vehicles in urban settings. IEEE Intelligent Transportation Systems Magazine 2019, 11, 105–116. [Google Scholar] [CrossRef]
Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
Attenni, G.; Arrigoni, V.; Bartolini, N.; Maselli, G. Drone-Based Delivery Systems: A Survey on Route Planning. IEEE Access 2023, 11, 123476–123504. [Google Scholar] [CrossRef]
She, R.F. Design of freight logistics services in the era of autonomous transportation, 2023; (Doctoral dissertation, University of Illinois at Urbana-Champaign).
Dantzig, G.B.; Fulkerson, D.R. Minimizing the number of tankers to meet a fixed schedule. Naval Res. Logist. Quart. 1954, 1, 217–222. [Google Scholar] [CrossRef]
Ford, L.R.; Fulkerson, D.R. Flows in Networks. Princeton University Press, Princeton. 1962.
Karzanov, A.V.; Livshits, E.M. Minimal quantity of operators for serving a homogeneous linear technological process. Automation and Remote Control 1978, 39 Pt 2 Pt 2, 538–542. [Google Scholar]
Kats, V.B. An exact optimal cyclic scheduling algorithm for multi-operator service of a production line. Automation and Remote Control 1982, 43 Pt 2, 538–542. [Google Scholar]
Orlin, J.B. Minimizing the number of vehicles to meet a fixed periodic schedule. Operations Research 1982, 30, 760–776. [Google Scholar] [CrossRef]
Kats, V.; Levner, E. Minimizing the number of robots to meet a given cyclic schedule. Annals of Operations Research 1997, 69, 209–226. [Google Scholar] [CrossRef]
Kats, V.; Levner, E. Minimizing the number of vehicles in periodic scheduling: The non-Euclidean case. European Journal of Operational Research 1998, 107, 371–377. [Google Scholar] [CrossRef]
Orlin, J.B. Minimum convex cost dynamic network flows. Mathematics of Operations Research 1984, 9, 190–207. [Google Scholar] [CrossRef]
Campbell, A.M.; Hardin, J.R. Vehicle minimization for periodic deliveries. European Journal of Operational Research 2005, 165, 668–684. [Google Scholar] [CrossRef]
Kochenberger, G.A.; Glover, F.; Alidaee, B.; Rego, C. A unified modeling and solution framework for combinatorial optimization problems. OR Spectrum 2004, 26, 237–250. [Google Scholar] [CrossRef]
Kabadi, S.N.; Punnen, A.P. A strongly polynomial simplex method for the linear fractional assignment problem. Operations Research Letters 2008, 36, 402–407. [Google Scholar] [CrossRef]
Megiddo, N. Combinatorial optimization with rational objective functions. Mathematics of Operations Researh 1979, 4, 414–424. [Google Scholar] [CrossRef]
Gallo, G.; Grigoriadis, M.D.; Tarjan, R.E. A fast parametric maximum flow algorithm and applications. SIAM Journal on Computing 1989, 18, 30–55. [Google Scholar] [CrossRef]
Shigeno, M.; Saruwatari, Y.; Matsui, T. An algorithm for fractional assignment problems. Discrete Applied Mathematics 1995, 56, 333–343. [Google Scholar] [CrossRef]
Radzik, T. Newton's method for fractional combinatorial optimization. In Proceedings of the 33rd Annual Symposium on Foundations of Computer Science 1992, 659–669. [Google Scholar]
Gassner, E.; Klinz, B. A fast parametric assignment algorithm with applications in max-algebra. Networks: An International Journal 2010, 55, 61–77. [Google Scholar] [CrossRef]
Karp, R.M.; Orlin, J.B. Parametric shortest path algorithms with an application to cyclic staffing. Discrete Applied Mathematics 1981, 3, 37–45. [Google Scholar] [CrossRef]
Young, N.E.; Tarjan, R.E.; Orlin, J.B. Faster parametric shortest path and minimum balance algorithms. Networks 1991, 21, 205–221. [Google Scholar] [CrossRef]
Belanger, N.; Desaulniers, G.; Soumis, F.; Desrosiers, J. Periodic airline fleet assignment with time windows, spacing constraints, and time dependent revenues. European Journal of Operational Research 2006, 175, 1754–1766. [Google Scholar] [CrossRef]

Figure 1. Schematic diagram of the proposed fast algorithm.

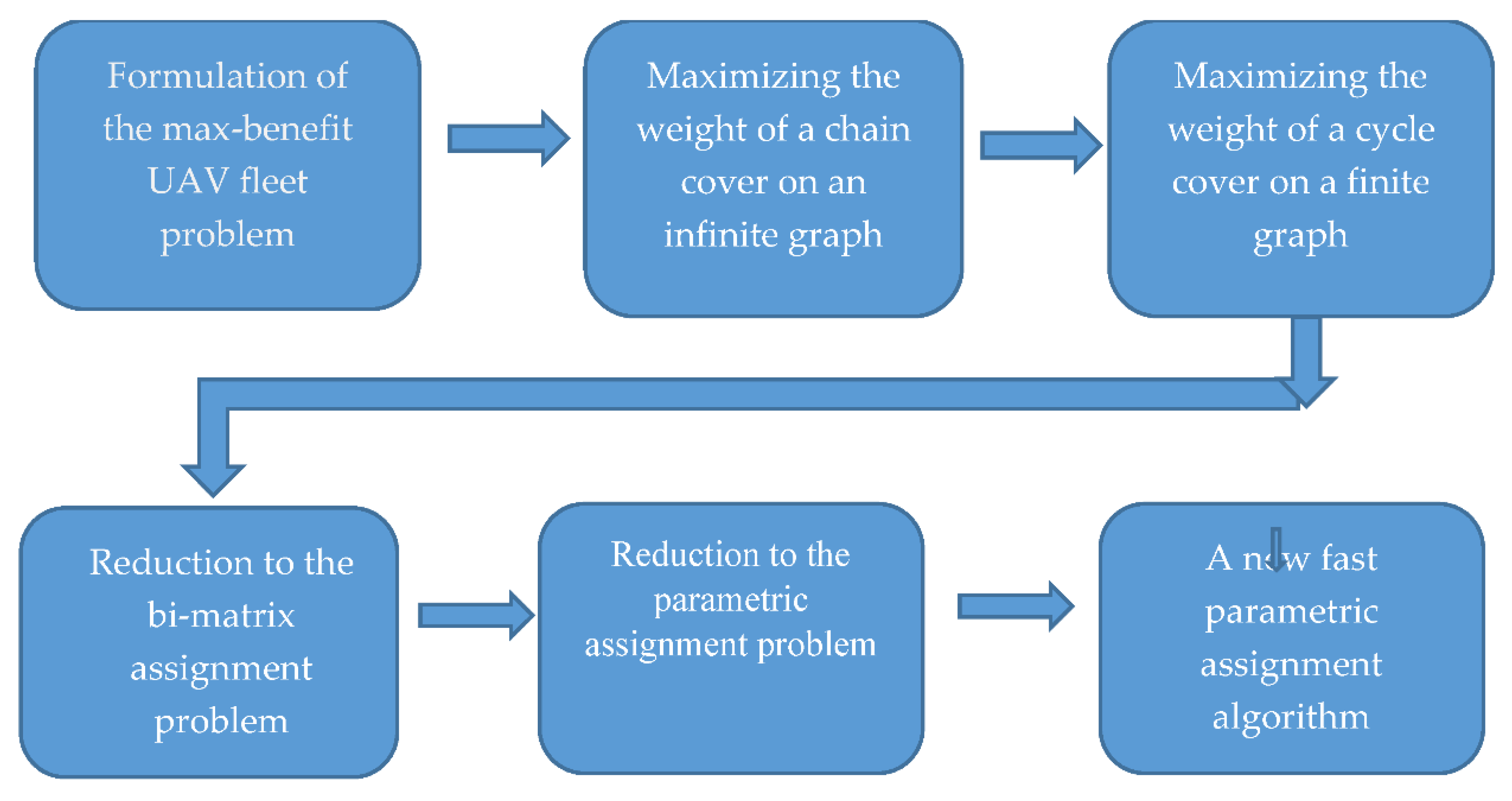
Figure 2. A 3-period fragment of the graph G_∞.

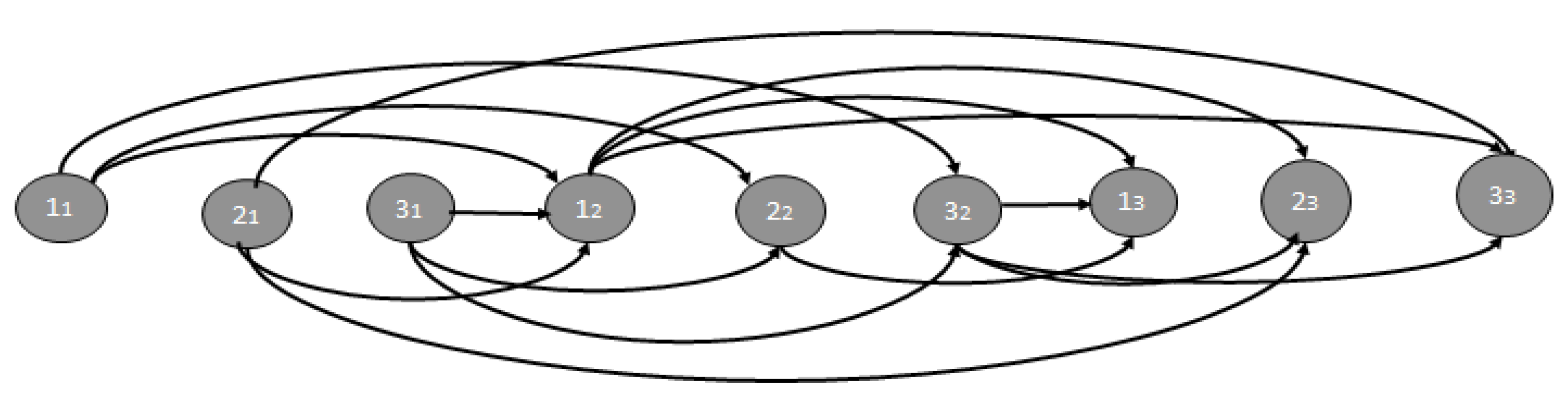
Figure 3. Generating graph G_gen.

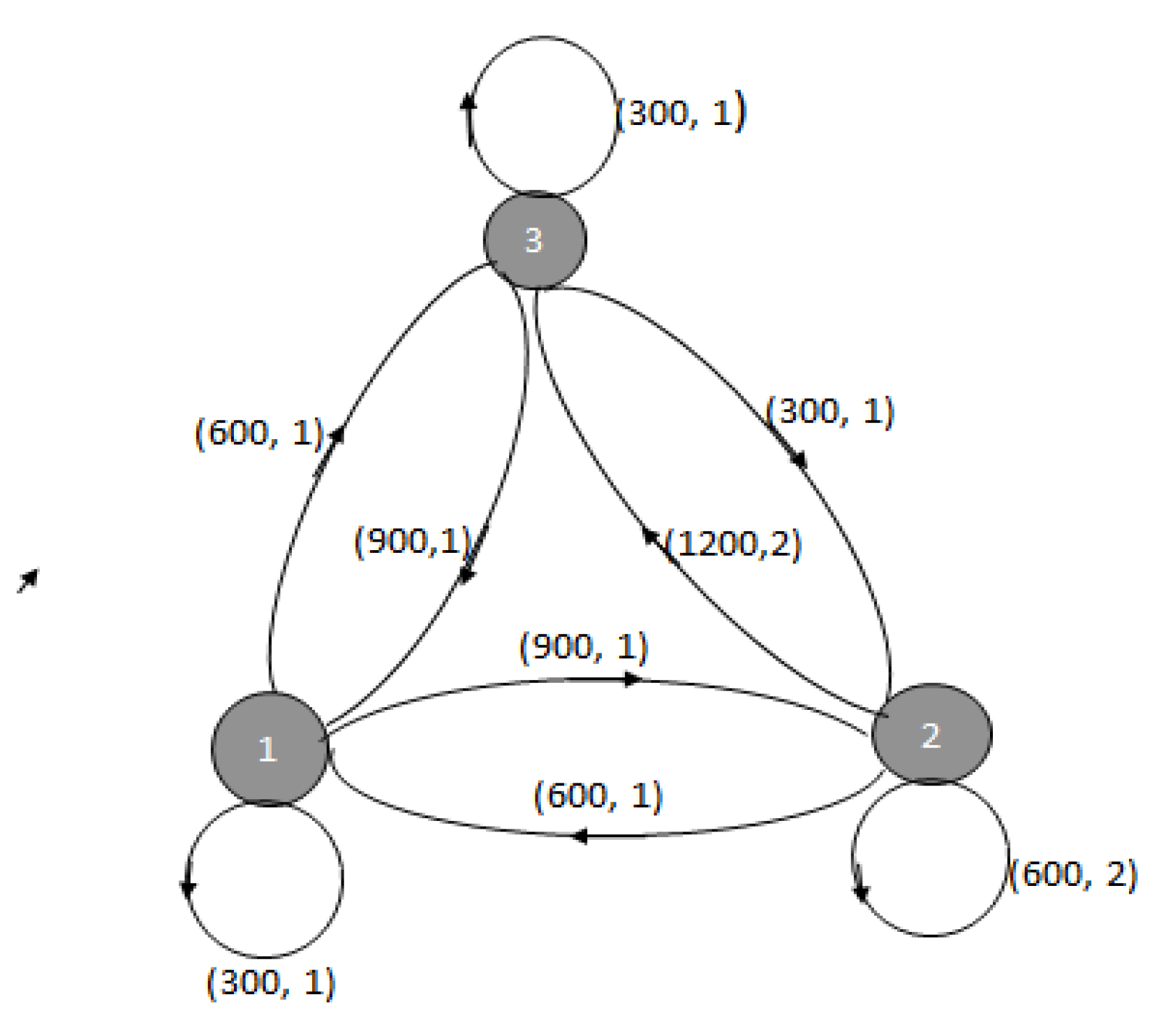
Figure 4. Graph of two objective functions, z(λ) of the Gassner-Klinz problem and L(λ) of the average fleet profit maximization problem.

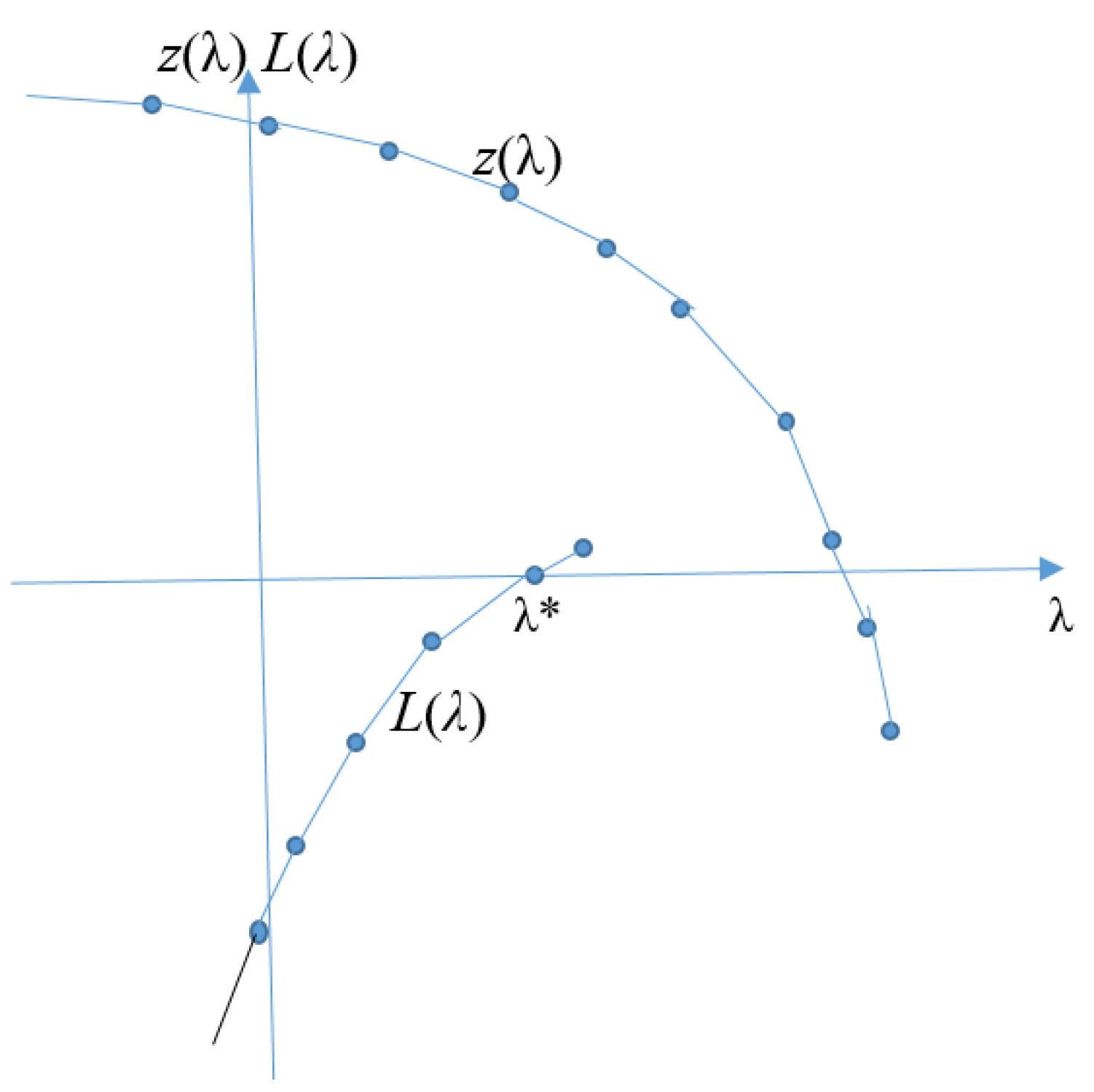
Table 1. Daily required flights.

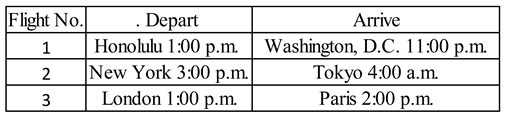Table 2. The deadhead flight times in hours.

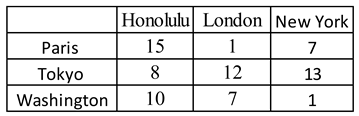Table 3. Input data.

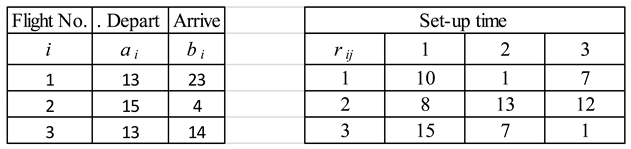Table 4. Matrix E.

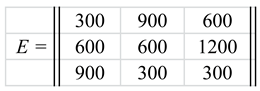Table 5. Matrix K.

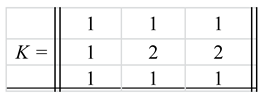Table 6. Matrix W(λ₀ =600).

Table 7. Matrix W(λ₁ =750).

Table 8. Comparison of two assignment problems.

	Gassner & Klinz [31]	Problem PAP in this paper
Problem formulation	Given a bipartite graph G and parametric arc costs c_λ(i, j) = (c_ij - λ∙b_ij), find the minimum of objective function z(λ) = {∑_(i,j)_∈A c_λ(i,j): A is an assignment in G}, for all λ∈R together with the corresponding optimal assignments	Given a matrix W with parametric entry costs w_λ(i, j) = (λ∙k_ij - e_ij) and the minimum cost function L(λ) defined as L(λ) = ∑ _(i,j)_∈A_(λ) (λ∙k_ij - e_ij), find a parameter value λ = λ^ for which the L(λ) = 0 and the corresponding optimal assignment A^(λ^) (see Figure 4)
Parametric arc costs	c_λ(i, j) = (c_ij - λ∙b_ij), where b_ij = 0, 1	w_λ(i, j) = (λ∙k_ij - e_ij), where k_ij = 0, 1, 2, 3
Decision to be found	To solve the problem for all λ in (-∞ +∞) and to find all the assignments	To find a single value λ^* and a single assignment, for which L(λ)=0
Practical application	To solve the problem of computing the characteristic max-polynomial of a matrix in the max-algebra.	To solve the problem of maximizing the average profit for a fleet of vehicles.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Maximizing the Average Environmental Benefit of a Fleet of Drones under a Periodic Schedule of Tasks

Abstract

1. Introduction

2. Previous Work

3. Description of the Problem

4. Reduction to Graph Problems

Model of the Fixed Daily-Repeating Set of Drone Flights

Reduction to a Problem on a Periodic Graph

Construction of the Generating Graph

Calculation of the Second Weight kij

5. Reduction to the Fractional Assignment Problem

6. Reduction to the Parametric Assignment Problem

7. A Newton-Type Algorithm for the Parametric Assignment Problem

7.1. Algorithm A1

7.2. Complexity of Algorithm A1

8. A Faster Parametric Assignment Algorithm

8.1. Comparison of Two Parametric Assignment Problems

8.2. Brief Review of the Gassner-Klinz Algorithm and Its Adaptation

9. Conclusion

Author Contributions

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

Calculation of the Second Weight k_ij