Preprint
Article
A Comparative Study of Susceptibility and Hazard for Mass Movements Applying Quantitative Machine Learning Techniques. Case Study: Northern Lima Commonwealth, Peru
Altmetrics
Downloads
87
Views
53
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
10 May 2024
Posted:
10 May 2024
You are already at the latest version
Alerts
Abstract
This study addresses the importance of conducting mass movement susceptibility mapping and hazard assessment using quantitative techniques, including machine learning, in the Northern Lima Commonwealth (NLC). Previous exploration of the topographic variables revealed high correlation and multicollinearity among some of them, which led to dimensionality reduction through principal component analysis (PCA). Six susceptibility models were generated using weights of evidence, logistic regression, multilayer perceptron, support vector machine, random forest, and naive Bayes methods to produce quantitative susceptibility maps and assess the hazard associated with two scenarios: the first being an El Niño phenomenon and the second being an earthquake exceeding 8.8Mw. The main findings indicate that machine learning models exhibit excellent predictive performance for the presence and absence of mass movement events, as all models surpassed an AUC value of >0.9, with the random forest model standing out. In terms of hazard levels, in the event of an El Niño phenomenon or an earthquake exceeding 8.8Mw, approximately 40% of the NLC area would be exposed to the highest hazard levels. It also highlights the importance of integrating methodologies to reduce model uncertainty, such as comprehensive analysis of variables supported by high quality data and organized workflows. The findings of this research are expected to serve as a supportive tool for land managers in formulating effective disaster prevention and risk reduction strategies.
Keywords:
Subject: Environmental and Earth Sciences - Remote Sensing
1. Introduction
More than 2.8 million people [1] live on the hillsides of Metropolitan Lima, occupying the territory in a disordered, disjointed articulation, with complete informality, resulting in high vulnerability and exposure to natural hazards. Among them, mass movements (MM) induced by earthquakes and El Niño phenomenon, especially on the central coast of Peru, which is located in an area with a 278-year seismic gap since the 1746 earthquake [2], and a seismic event of a magnitude greater than 8.8 Mw is expected; on the other hand, the El Niño phenomenon has occurred with greater recurrence in recent years. In the Northern Lima Commonwealth (NLC), it has been reported that approximately 60% of emergency reports correspond to MM [3], resulting in human and economic losses. The lack of an effective system for assessing and predicting these hazards, as well as adequate mitigation strategies, poses a latent threat.
The assessment of mass movement susceptibility (MMS) is part of the first aspect of disaster risk management, which is important for urban planning, response and post-disaster reconstruction [4]. In recent decades, MMS mapping has been widely used to zone probable areas for future MM based on identifying areas of past occurrences and areas with similar or identical physical characteristics [5]. To perform MMS mapping, various models based on geographic information technologies (GIT) have been used. These models can be classified into qualitative or knowledge-based methods such as the heuristic method [6], semi-quantitative methods such as the analytic hierarchy process [7], quantitative or data-driven methods such as bivariate or multivariate statistical methods [4, 6, 8, 9, 10, 11], hybrid approaches [12, 13] and machine learning [14, 15, 16, 17].
The Geological, Mining, and Metallurgical Institute of Peru (INGEMMET) has developed the regional scale MMS model in Metropolitan Lima [18] using a qualitative (heuristic) expert judgment approach. This input is utilized by the National Center for Estimation, Prevention, and Reduction of Disaster Risk (CENEPRED) to conduct risk scenarios by adding triggering variables and hazard exposure analysis. The free availability of conditioning and triggering variables data from national and international technical-scientific institutions, coupled with significant advancements in GIT tools, software, and open-source codes for processing high-resolution spatial information over large areas of land, provides the necessary resources to close the gaps in exhaustive studies for exploring data-driven models for MMS mapping. These models include weight of evidence (WoE) and machine learning (ML) techniques such as logistic regression (LR), multilayer perceptron (MLP), random forest (RF), support vector machine (SVM), and naive Bayes (NB) for estimating susceptibility and hazard due to MM. Addressing this knowledge gap is imperative to enhance the prediction capability and response to such hazards.
2. Materials and Methods
2.1 Study Area
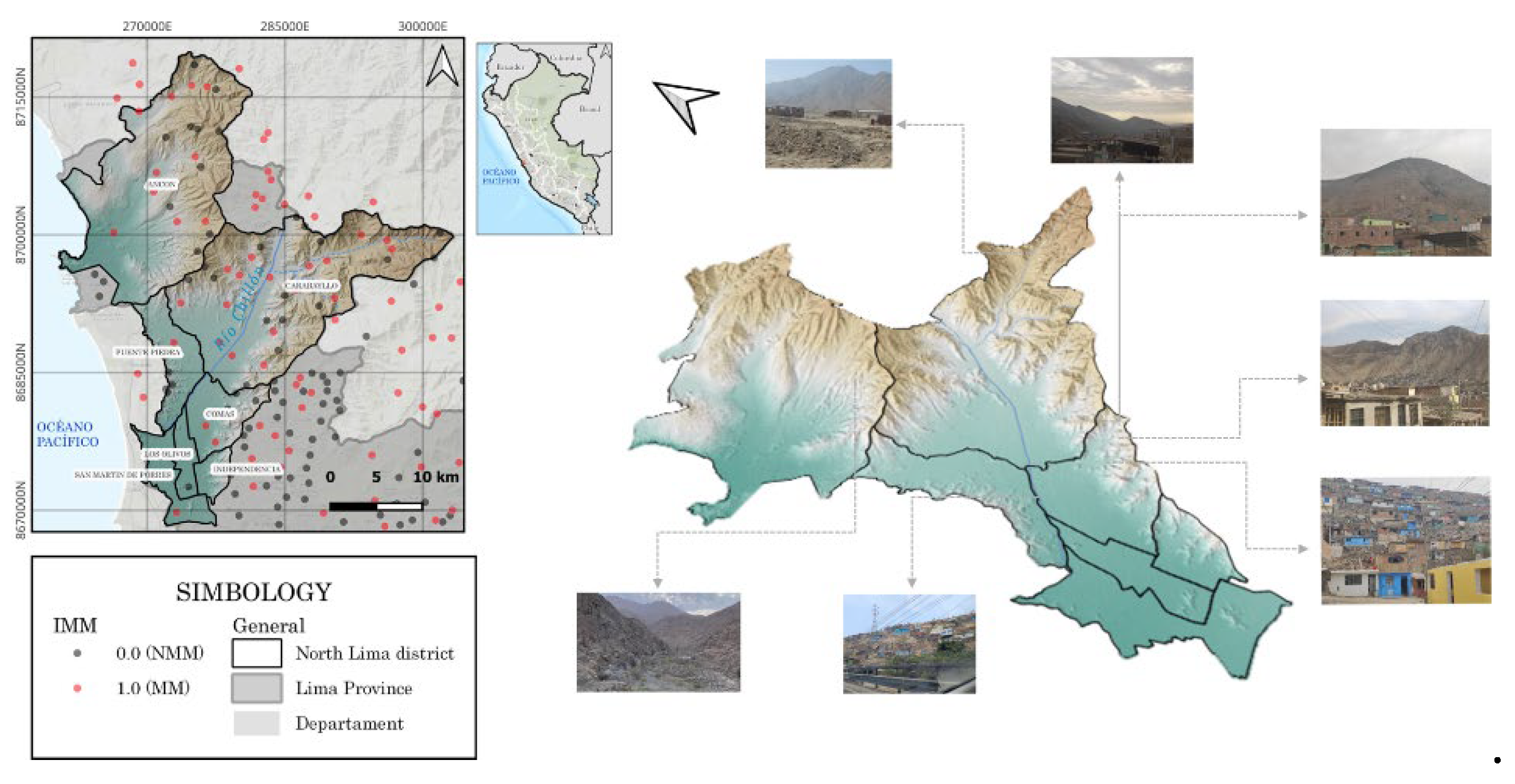
The study area covers seven districts of the NLC: Los Olivos, San Martin de Porras, Independencia, Comas, Carabayllo, Ancon, and Puente Piedra covers an area of 793 km2, ranging from -11.572° to -12.039° S latitude and -77.199° to -76.810° W longitude. The elevation of the study area ranges from 26.5 to 2748.0 m above sea level (m asl), with a maximum elevation difference of 2721.5 m asl. The NLC districts are located on the western-central boundary of the South American continent, in the subduction zone of the Nazca plate in relation to the South American. On the other hand, historically, during El Niño phenomenon, anomalies in precipitation triggering MM phenomena have been demonstrated on the coast of Lima [19,20].
Figure 1.
Ubication map. High vulnerability of housing on the hillsides of Metropolitan Lima.
2.2 Mass Movement Inventory (MMI)
The MMI represents information on the spatial distribution of the location of MM, also provides crucial information in the study of the relationships between the occurrence of MM and causative factors [10, 21]. The MMI used in this study was conducted by INGEMMET, photointerpreted in the office from satellite images, and verified in an extensive fieldwork, which was carried out by the technical team of INGEMMET. It is worth noting that the inventory information is up to 2023 (last update).
A total of 236 MM polygons were selected randomly using the vector>research tool>random selection tool in QGIS. Among these, 189 (80%) were used for training, and 47 (20%) were used for evaluation. It is worth mentioning that debris flows were not considered because these polygons are mostly located spatially in the lower parts of the valley, which could affect the results of the MMS mapping.
2.3 Data
The following table shows the vector and raster data used in the research.
Table 1.
Research data.
| Type | Description | Type | Scale or spatial resolution | Year | Source | Link (last Access 02/02/2024) |
|---|---|---|---|---|---|---|
| Vectorial | Lithology | Discrete | 1/100,000 | - | INGEMMET | https://geocatmin.ingemmet.gob.pe/geocatmin/ |
| Geomorphology | Discrete | 1/100,000 | - | INGEMMET | https://geocatmin.ingemmet.gob.pe/geocatmin/ | |
| Hydrogeology | Discrete | 1/100,000 | INGEMMET | https://geocatmin.ingemmet.gob.pe/geocatmin/ | ||
| Mass Movements Inventory | Discrete | 1/50,000 | 2021 | INGEMMET | https://geocatmin.ingemmet.gob.pe/geocatmin/ | |
| Raster | Vegetation Cover | Discrete | 1/100,000 | INGEMMET | https://www.datosabiertos.gob.pe/dataset/cobertura-vegetal-ministerio-del-ambiente | |
| Digital Elevation Model (DEM) | Continuous | 12.5m | 2010 | USGS | https://earthexplorer.usgs.gov/ | |
| Seismic Microzonation | Continuous | - | - | IGP/CISMID | https://www.igp.gob.pe/servicios/infraestructura-de-datos-espaciales/componentes/webservice | |
| Precipitation Anomalies in El Niño phenomenon | Discrete | 100m | 2021 | SENAMHI | Information provided by the institution. |
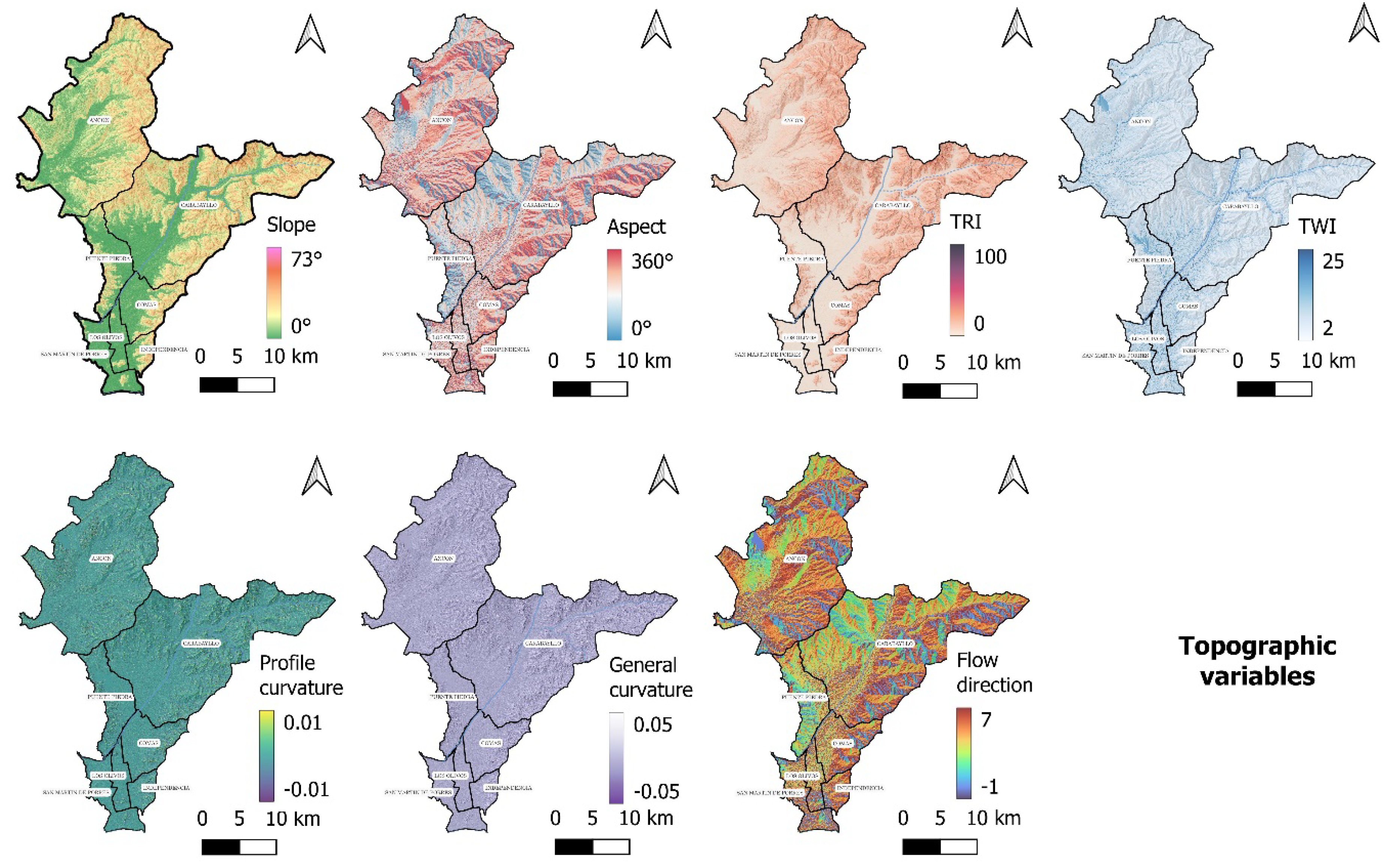
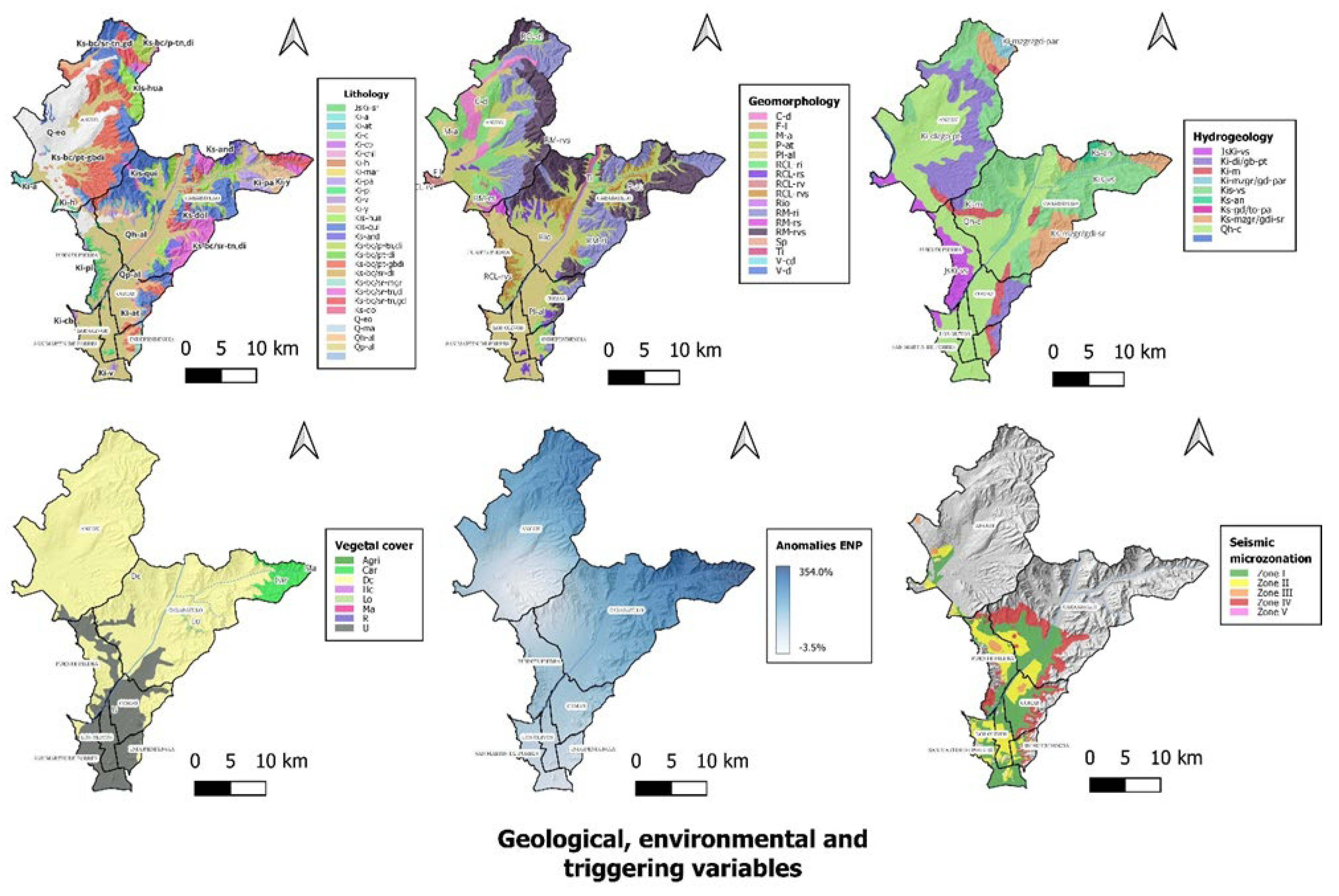
In addition, Table 2 presents the DEM-derived topographic products, geological and environmental variables of study for use in the susceptibility and hazard models for the NLC, their representation is presented in Figure A1 and A2.
Table 2.
Research variables names.
| Class | Name | Variable | PCA | Type of variable | ||
| Conditioning factor | ||||||
| Geological and environmental | Lithology | X1 | - | Categorical | ||
| Geomorphology | X2 | - | Categorical | |||
| Hydrology | X3 | - | Categorical | |||
| Vegetation cover | X4 | - | Categorical | |||
| Topographical | Slope | T1 | PCA1 PCA2 PCA3 |
Continuous | ||
| Aspect | T2 | Continuous | ||||
| Topographic wetness index (TWI) | T3 | |||||
| Terrain roughness index (TRI) | T4 | Continuous | ||||
| Flow direction | T5 | Continuous | ||||
| Profile curvature | T6 | Continuous | ||||
| General curvature | T7 | Continuous | ||||
| Triggering factors | ||||||
| Seismic 8.8Mw (seismic microzonation) Precipitation anomalies in El Niño phenomenon |
D1 | - | Continuous | |||
| D2 | - | Continuous | ||||
2.4 Methods
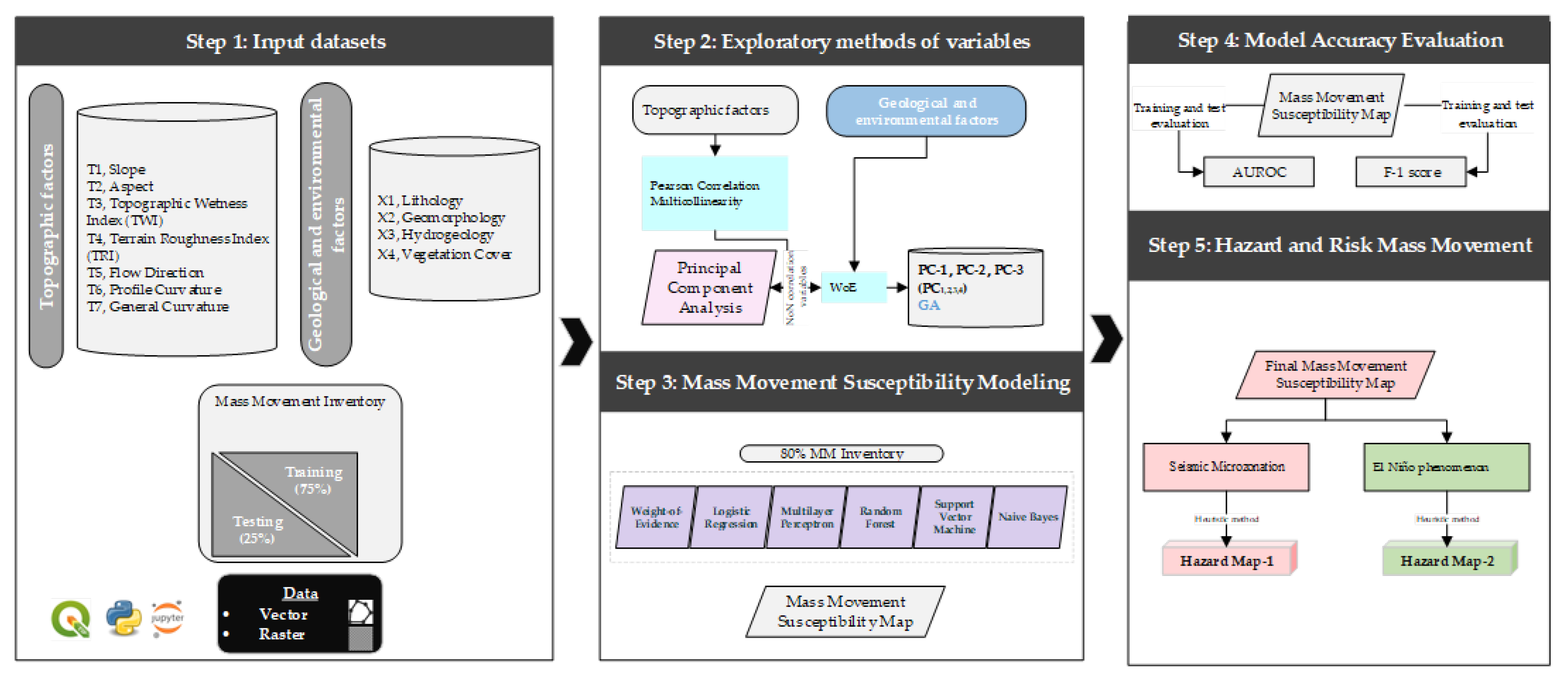
Figure 2 shows the flowchart of this study, which is divided into five steps: the first step is data downloading and preparation, followed by variable exploration, geospatial modeling of the MMS, evaluation of MMS models using the area under the curve (AUC), and estimation of MM hazard under two scenarios.
Figure 2.
Flowchart of the study.
2.4.1. Exploratory Variable Methods
Before applying the MMS model, it is important to ensure that there is no dependence between variables (variable correlation) and that the variables are not influenced by multicollinearity.
2.4.1.1. Pearson Correlation
To discard the linear correlation of the variables, the Pearson correlation was applied, which is considered an effective method for this purpose [11]. The following formula was used.
Where is the covariance of variables "x" and "y", and are the standard deviations of variables "x" and "y" respectively. The value of the Pearson coefficient can vary from -1 to 1, where if r<0, the correlation is negative and stronger as it approaches r=-1; if r>0, the correlation is positive and stronger as it approaches r=1; finally, if r=0, then there is no relationship between the variables. Additionally, as indicated by [22], a value greater than ±0.8 could lead to multicollinearity issues.
2.4.1.2. Multicollinearity
Multicollinearity indicates the mutual independence of each influential factor. To verify multicollinearity, the variance inflation factor (VIF) was used, where, in practical terms, a VIF value greater than 5 or 10 [23] indicates that the association of regression coefficients is poorly estimated due to multicollinearity issues [24].
Where is the coefficient of determination for the regression of on other explanatory variables.
2.4.1. Principal Component Analysis (PCA)
PCA is a multivariate mathematical procedure that performs the orthogonal transformation of a set of correlated variables into a smaller number of uncorrelated variables or Principal Components (PCs) [25], which are mutually independent [26]. Once multicollinearity among variables has been assessed and confirmed, it is common practice to exclude highly correlated variables that influence each other. However, PCA allows for addressing the multicollinearity issue among influential factors without the need to eliminate variables [8]. This is considered a good option because natural processes are integral, and excluding a variable could lead to loss of information in the analysis of the studied phenomenon. Additionally, PCA allows for evaluating the impact of different influencing factors on MMS. The majority of information from input variables is found in the first PC, which can be expressed as shown in the following equation [27].
Where PC is the principal component in the “m-th” place, and is the weight for the m-th PC for the n-th variable.
The number of PC was determined based on the level of variance explanation, which ranges from 0 to 1. In this study, a minimum threshold of 0.6 for variance explanation was used, although in some similar studies, values as low as 0.40 [26] or as high as 0.68 [28] for variance explanation based on the number of PC have been found. The choice of the variance explanation value is based on the objective of reducing the correlation and multicollinearity of the variables.
2.4.2. Weights of Evidence (WoE)
Quantitative techniques based on statistics establish functional relationships between instability factors and the past and present distribution of mass movements [26]. The WoE method proposed by [29] is a bivariate statistical technique based on Bayesian probability theory. The stability or instability of certain regions can be estimated through a set of conditioning factors, which are measured by the relationship and spatial distribution of areas known and affected by MM [28]. In this study, WoE was used to determine the relationship between factors influencing the occurrence of MM, to map the MMS, and as input variables for the LR, MLP, SVM, RF, and NB models.
The first step in determining the WoE for each class involves obtaining the prior probability of finding MM, which is estimated as the area affected by MM (L) in the past over the total study area (A).
[29,30], present a mathematical development of the methodology's fundamentals. The method assigns positive (W+) or negative (W-) weights to each class of conditioning variables based on the degree of association between the variable class and the spatial distribution and density of evidence of MM. y represent the presence and absence of the conditioning factor in potential mass movements, respectively, and indicates the absence of mass movements.
Where Wi+ with a positive value (>0) indicates that the variable is present where there is the presence of mass movements; additionally, its magnitude represents the positive correlation between the presence of the factor and MM. On the other hand, Wi+ with a negative value (<0) indicates that the absence contributes to the generation of MM. Wi- is used to evaluate the importance of the absence of the factor in the occurrence of MM, when Wi- is positive (>0) the absence of the variable is favorable in the generation of MM, the opposite (<0) is not [30]. Both Wi+ and Wi- are estimated for each class of variables.
The contrast value or final weight (Equation 7) indicates the measure of correlation between the conditioning factor and the MM. If , then the spatial distribution of MM is independent of the considered variable. If , then there is a positive association between the variable and the generation of MM. Lastly, if , there is a negative association, meaning that the absence of the factor contributes to the generation of MM [30, 31].
Finally, to obtain the MMS map of the conditioning factors by WoE, the algebraic sum of all the contrast values of each variable is calculated. This means that the weights of each class of the variables are summed pixel by pixel, and the sum is the susceptibility map.
2.4.3. Logistic Regression (LR)
LR is considered one of the most popular statistical methods for multivariate regression analysis used to investigate binary response from a set of measurements [32] in the earth sciences. In other words, it estimates the relationship between a dependent variable and multiple independent variables [33]. The variables can be continuous, or discrete, or a combination of both; they can have a normal or non-normal distribution and the dependent variable is dichotomous [34].
In the analysis of MMS, the dependent variable is the absence (probability of occurrence, 0) or presence (probability of occurrence, 1) of MM, which for the purposes of this study were taken from the MMI of INGEMMET. LR transforms the dichotomous dependent variable into a logit variable, which can be used to form a multivariate regression relationship between the dependent variable and the independent variables, which in this case are the multiple conditioning factors [35]. The results of the LR estimate the probability of the presence or absence of MM based on the predictor variables according to the following equation.
Where p is the probability that the dependent variable will be 1 (maximum probability of MM presence) or 0 (minimum probability of MM presence), forming an “S-curve”; “e” is the neperian number, and “z” is the linear combination of the independent variables. The linear combination “z” can be expressed by the following formula [32].
Where X is the independent variable (conditioning factors), which can be represented as , and B is the estimated coefficient for each independent variable, . B₀ is the intercept of the model, and “n” is the number of independent variables [36]. Based on Equations 9 and 10, the LR model can be expressed in its extended form as Equation 11. It is worth mentioning that the statsmodels module of Python 3.6 was used.
2.4.4. Multilayer Perceptron (MLP)
The MLP is an artificial neural network composed of multiple layers of interconnected neurons, commonly used in supervised learning. It is used to solve complex classification and regression problems, thanks to its ability to learn nonlinear representations of data based on mathematical algorithms to mimic the learning process of the human brain [37]. Structurally, the network consists of input layers, hidden layers with different numbers of neurons, and an output layer, the latter being the MMS model. The neurons in the layers are connected through weight values, which are trained and tested to form a stable network structure with decision-making capabilities [6]. The MLP model was implemented using the scikit-learn module of Python 3.6.
2.4.5. Support Vector Machine (SVM)
Proposed by [38], it is a supervised ML method based on the concept of an optimal separating hyperplane in the sample space, such that the distance to the classification hyperplane of the two class groups is a maximum function between the margins of the class boundaries [39, 40, 41]. This classification capability makes SVM used for solving non-linear classification and regression problems; thus, it is one of the most used ML techniques in assessing MMS. The SVM model was implemented using the scikit-learn module of Python 3.6.
2.4.6. Random Forest (RF)
Proposed by [42], it is a supervised classification algorithm that is based on classification and regression trees used to create each decision tree. It utilizes a random subset of variables at each node based on a Bootstrap sample, and RF generates thousands of random binary trees to form a forest [17]. In cases with large amounts of sample data, the more feature elements present, the fewer errors and overfitting are generated [40, 43]. RF is frequently used to determine the MMS [17, 41, 43, 44], in this study the Python Scikit-learn module was applied to implement the RF model.
2.4.7. Naive Bayes (NB)
NB is an important algorithm in the field of ML and data mining [40], applied to various fields, and is based on the Bayes probability theorem, Bayes rule, or Bayes formula [45], which is suitable when the data has a high dimension, is not affected by the distribution of the data, and all variables are considered independent of each other [46]. The main objective of NB is to determine the a priori probability of an event based on the proportion of observed cases relative to a specific output class [47]. In this study, the Python Scikit-learn module was applied to implement the NB model.
2.4.8. Validation and Testing of the Models
Curva ROC y AUC
The Receiver Operating Characteristic (ROC) curve is a graphical representation of sensitivity (true positive rate) on the y-axis and 1-specificity (false positive rate) on the x-axis [8]. The area under curve (AUC) of the ROC allows assessment of model fit and prediction [26] and is commonly applied as a criterion for selecting the most appropriate model to determine MMS [8]. The AUC value indicates the percentage of observed positive pixels that are correctly predicted, quantifying the probability that susceptibility models correctly classify the presence or absence of mass movement phenomena based on a set of independent variables or conditioning factors (Figure A1).
The AUC ranges from 0 to 1. AUC values between 0.5 and 0.6 are considered poor models. AUC values between 0.6 and 0.7 are considered average models. AUC values between 0.7 and 0.8 are considered good models. AUC values between 0.8 and 0.9 can be considered very good models, and an AUC value greater than 0.9 is considered an excellent model [9].
F-1 Score
F-1 score shows the performance of the model, high values are optimal [40]. This indicator unifies accuracy and sensitivity [15], accuracy is determined by dividing the true positives by the total number of pixels classified as MM. Sensitivity is the proportion of true positives predicted in the real positive class sample. Therefore, the F-1 score is the harmonic mean of precision and sensitivity [48].
2.4.9. Machine Learning Hyperparameters
In this research, there is no intention to evaluate the influence of hyperparameter optimization on the results of the MMS mapping. The choice of hyperparameters has been made based on the literature, specifically on the values and configurations most commonly used in susceptibility mapping studies. As mentioned by [39], most ML models can achieve excellent accuracy with their default set of hyperparameters, as it is nearly impossible to manually search through combinations due to the countless possibilities of trial and error.
Table 3.
Hyperparameters used in this research.
| Model | Hyperparameters |
| LR | method='bfgs', |
| MLP | lr=0.1, arquitectura [4,4,4,1], epochs=1000, activation 'relu' |
| SVM | Kernel='linear' |
| RF | n_estimators=360, max_depth=11, criterion='gini', min_samples_split=5, min_samples_leaf=1 |
| NB | priors=None, var_smoothing=1e-9 |
3. Results
3.1. Exploration of Variables
To determine the MMS using the WoE, LR, MLP, SVM, RF and NB methods, the correlation of the topographic variables was analyzed and then the multicollinearity of the variables was analyzed using VIF. Figure 3 shows the Pearson correlation of topographic variables derived from a DEM.
Figure 3.
Pearson correlation of topographic variables.

From the graph, it is observed that there are variables that are correlated, as there are variables with a correlation coefficient ≥ 0.8. The correlation coefficient between the TRI (T4) and the slope (T1) was 0.99, and the correlation coefficient between the general curvature (T7) and the profile curvature (T6) was 0.8. This indicates a high correlation between the influencing factors. Therefore, we proceed to conduct multicollinearity analysis using the VIF statistic, where a value greater than 5 indicates multicollinearity issues in the fitting of susceptibility models, which are sensitive to the linear correlation of influencing factors.
Table 4.
Multicollinearity analysis of topographic variables.
| Name | Variable | VIF |
| Intercept | - | 10.1 |
| Slope | T1 | 67.3 |
| Aspect | T2 | 1.5 |
| Topographic Wetness Index (TWI) | T3 | - |
| ÍTerrain Roughness Index (TRI) | T4 | 67.3 |
| Flow direction | T5 | 1.4 |
| Profile curvature | T6 | 3 |
| General curvature | T7 | 3 |
From the multicollinearity result, it is observed that the slope and TRI are affected by multicollinearity. Therefore, dimensionality reduction of the variables was performed using PCA to exclude variable correlation and multicollinearity issues. In Figure 4, the contribution of the variance of the seven PC is observed. Assuming a variance explanation level of ≥0.65, 3 PC are required, resulting in 0.85 variance explanation, with each component being independent of the others.
Table 5 shows the importance and contribution of each influential variable in the three PC. The higher the value (in absolute terms), the greater the contribution to the PC. For PC-1, the most relevant variable was slope. For PC-2, the general curvature variable showed the highest relevance. Lastly, orientation was the most relevant factor for PC-3. Figure 5 displays the selected PC as input variables for the MMS.
Finally, the PCs were reclassified into five quantiles, and contrast values were determined by applying WoE to both PCs and topographic factors to determine the relationship between the study variables and MM phenomena; these variables were used in the WoE, LR, MLP, SVM, RF and NB models.
3.2 Mass Movement Susceptibility (MMS)
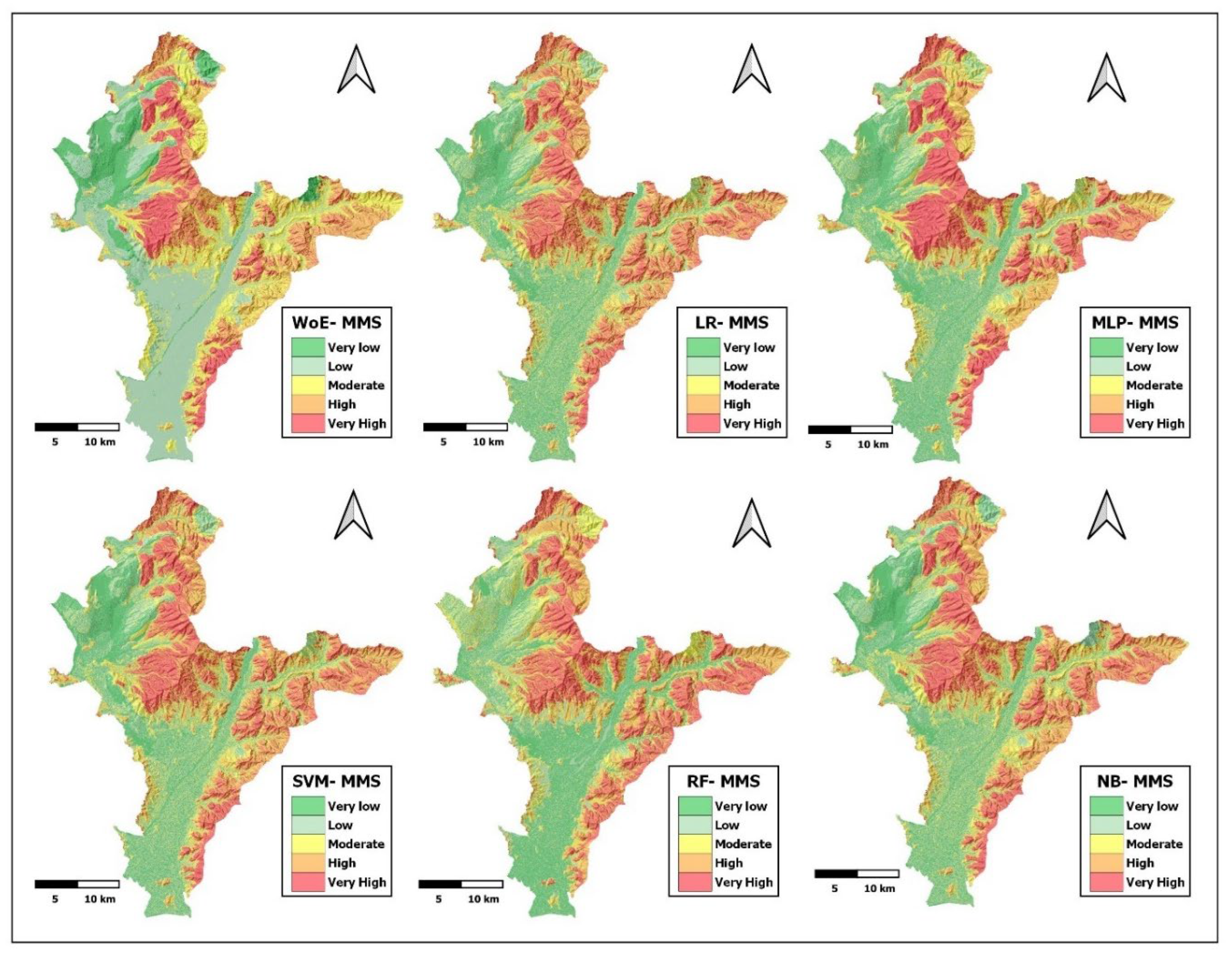
The results of the MMS models were reclassified into five quintiles, very low, low, medium, high, and very high in QGIS. The spatial distribution expressed in area is shown in Table 6.
The highest MMS values (very high and high) were generated by the RF models, followed by the NB, SVM, and LR models, all with 20% of the surface of the study area in the very high and high susceptibility levels. The MMS levels by the heuristic method were generated by INGEMMET based on lithology, hydrogeology, slope, land use, and vegetation cover.
Figure 6.
MMS models by the method WoE, LR, MLP, SVM, RF y NB.
3.3. MM Hazard Scenarios
The MM hazard for El Niño phenomenon and for earthquakes greater than 8.8Mw was determined using the heuristic method, generated from the geospatial product between the MMS and the triggering factors. As discussed in the following section, the RF-derived MMS model was used because it was the model that presented the highest AUC value in relation to the other study models and because it presented high accuracy in MMS prediction for both training and evaluation events.
On the other hand, for the case of El Niño hazard, the maximum anomalies during the last three El Niño phenomenon were used, namely, 83/84, 97/98, 2017 (where anomalies of precipitation ranging from 100% to 350% have been predominantly recorded within the study area). Regarding the seismic event, seismic-geotechnical microzonation of the soil was used under a seismic of 8.8Mw, characterized into five zones. It is worth noting that, although the entire spatial distribution of seismic microzonation for the study area is not available, it covers a large part of the area where the population and their livelihoods are located. Figure 7 presents the hazard maps by MM for both El Niño and the seismic scenario greater than 8.8Mw.
4. Discussion
In this study, six quantitative maps of MMS have been generated, utilizing the WoE method as a bivariate statistical approach and ML techniques such as LR, SVM, NB, MLP, and RF. All MMS maps exhibit the same spatial pattern, meaning that higher susceptibility is observed in the elevated areas of the study zone, which translates to values close to 1. Conversely, lower susceptibility is found in low-lying areas, where values are predominantly close to 0. In terms of surface area, approximately 33% to 40% of the study area for all six MMS models falls within the highest susceptibility levels, categorized as high and very high. Conversely, areas with lower susceptibility, classified as very low and low, cover approximately 40% to 44% of the study area. It is also noteworthy that the trend in terms of surface area covered by each susceptibility level in all models of MMS is similar. Spatially, the highest susceptibility levels in the study area are found on the eastern edge of the NLC, where the highest parts of the Andean foothills are located.
The validation process is crucial in MMS mapping. As indicated in the methodology section, two metrics were used to evaluate and validate the susceptibility models: the AUC value and the F-1 score. The overall performance of the models is evaluated using AUC analysis [49, 50]. Several studies have suggested that an AUC value between 0.8 and 0.9 indicates a very good model, while a value higher than 0.9 indicates an excellent model [8, 9]. The results revealed that all MMS applied in this study, namely LR, MLP, SVM, RF, and NB, have surpassed an AUC value of >0.9, indicating that these models demonstrate excellent performance in predicting the presence and absence of MM phenomena accurately. The highest AUC value for the training of the models was observed in the RF model, AUC=1.000, followed by the SVM model, AUC=0.994, MLP, and LR, both with AUC=0.986. Additionally, the difference between the maximum and minimum AUC values was only 1.9%. On the other hand, regarding the AUC value for the evaluation data, it was revealed that all the MMS models behave as excellent models in terms of correctly classifying the presence and absence of MM phenomena in the evaluation dataset, as they all are very close to 1. Regarding the F-1 score value, it was determined that all the MMS models surpass the F-1 score value of >0.950, with the RF model having the highest value of this metric, F-1=0.991. Finally, regarding the accuracy of the MMS models, the RF model was found to be the most accurate (Accuracy=0.989).
Figure 8.
ROC curve and AUC value for training (a) and test (b) data.
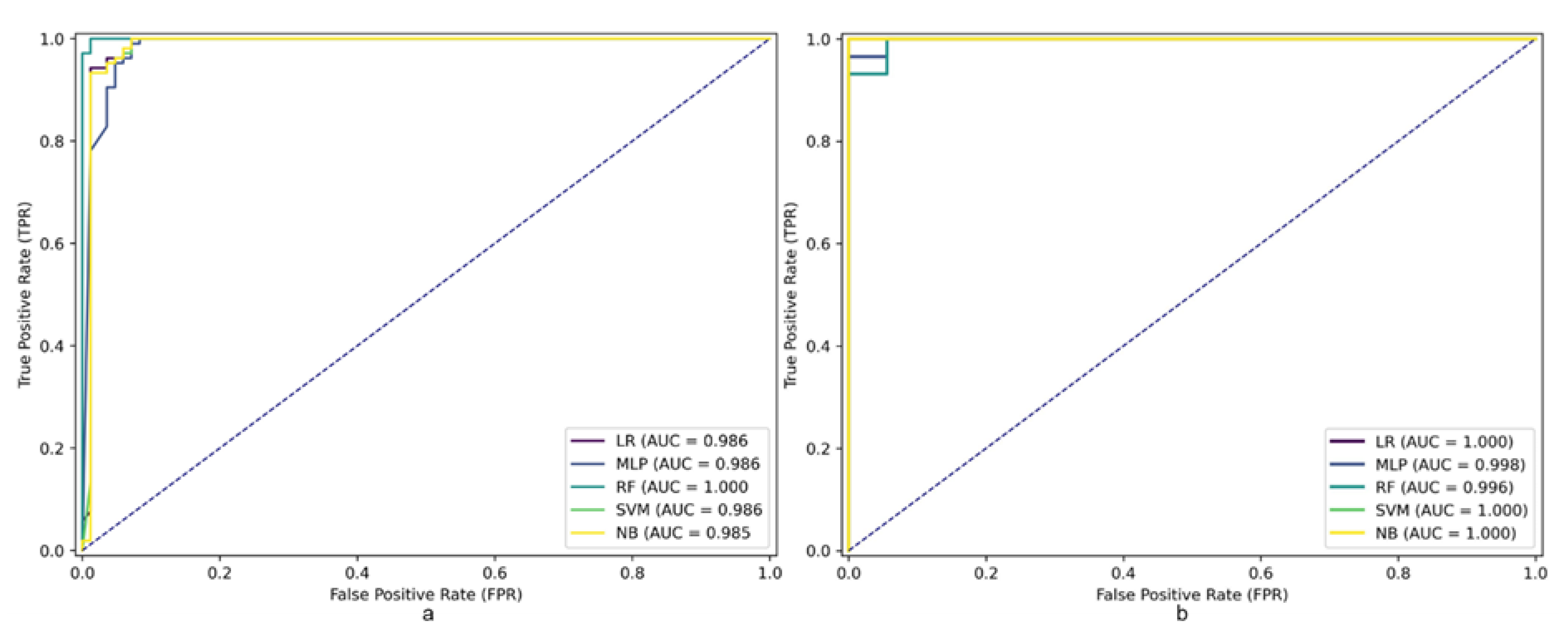
Similar results have been found in studies by [46, 51, 52], where the susceptibility to landslides was compared by applying different ML techniques such as NB, k-NN, RF, DNN, LR, BRT, and SVM. They found that the model with the best training and evaluation metrics is the RF model, with AUC values exceeding 0.920 in training and up to 1.000 in evaluation.
Table 7 presents the training and evaluation metrics of the MMS models generated in this study.
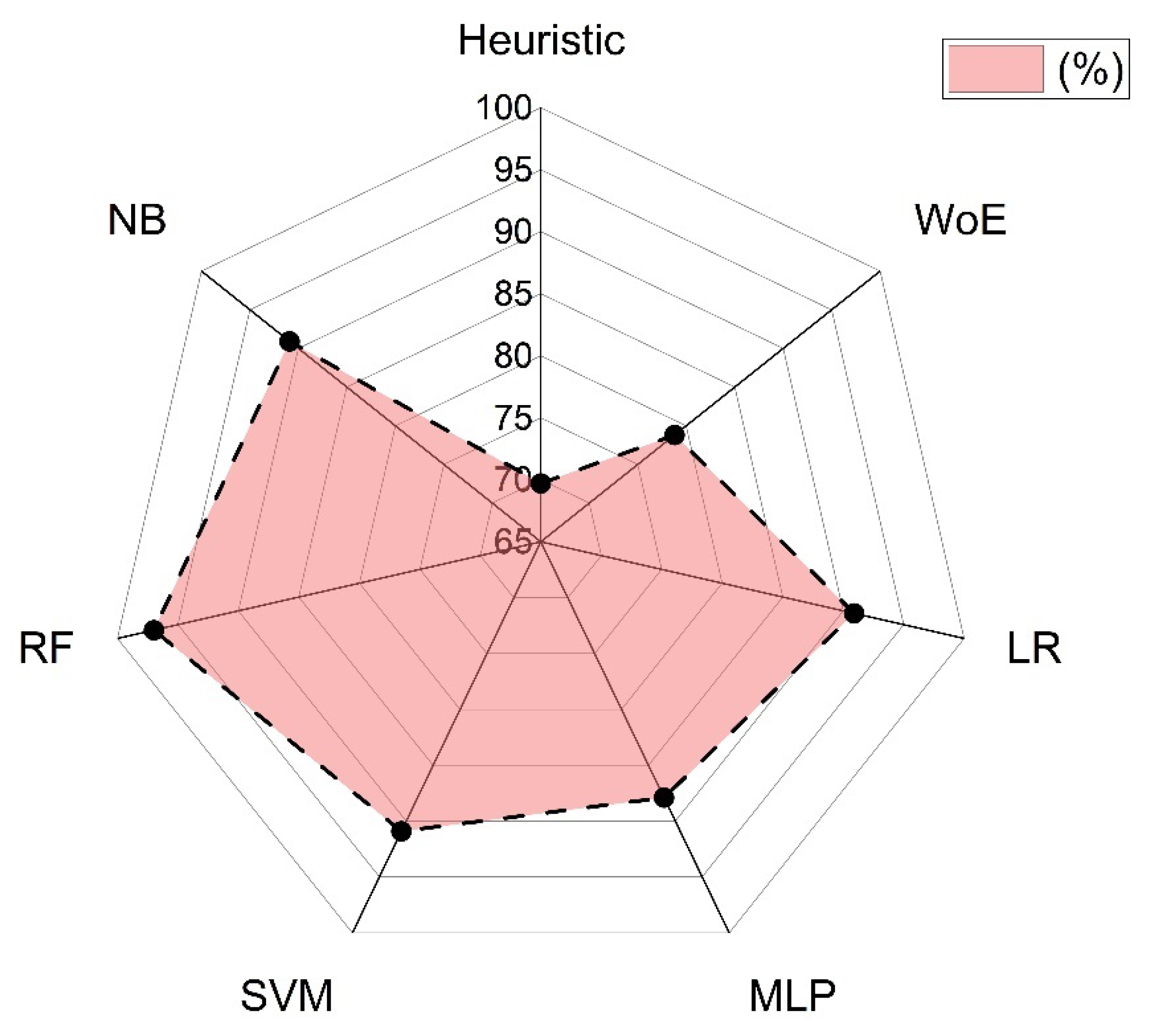
To compare the MMS results of WoE, LR, MLP, SVM, RF and NB with the heuristic method, the susceptibility levels were standardized into five classes. Subsequently, the susceptibility levels were extracted for the point-type vectors (PTV, centroids of the test polygons) of MM in the study area. It was determined that 69.7% of the PTV are in the high and very high MMS levels for the heuristic model. On the other hand, for RF, SVM, LR, NB, and WoE, 97.0%, 90.9%, 90.7%, 90.9%, 87.9%, and 78.8% of the PTV are at the highest susceptibility levels, namely, high and very high. The above indicates that the proposed machine learning-based models for determining MMS exhibit good performance in discriminating MM events compared to the heuristic method. This is because they are designed to automatically obtain the optimal nonlinear relationship between the study variables [17, 51, 52].
Figure 9.
Predictive capability of methods, heuristics, WoE, LR, MLP, SVM, RF and NB.
The hazard levels suggest that in the event of an El Niño phenomenon, close to 40% of the surface area of the NLC would be in the highest hazard levels, high and very high. Similarly, more than half of the surface area of the Carabayllo district (54.2%) would be under the same high and very high hazard levels, followed by the districts of Comas, Independencia, and Ancon, with high and very high hazard levels of approximately 37.0%. On the other hand, Los Olivos, Puente Piedra, and San Martin de Porras have less than 8% of their surface area at the highest hazard levels. Regarding the seismic hazard scenario, the triggering factor of seismic microzonation did not cover the entire study area spatially; it only represented 4.9%, 24.6%, 75.3%, 63.2%, 94.3%, 79.7%, and 70.4% of the surface area of Ancon, Carabayllo, Comas, Independencia, Los Olivos, Puente Piedra, and San Martin de Porras, respectively. Therefore, the percentages shown refer to the proportion of the total area covered by the seismic microzonation spatial coverage. The districts of Ancon, Carabayllo, Comas, Independencia, and Puente Piedra have between 41 and 50% of their surface area under high and very high seismic hazard levels in the event of a magnitude greater than 8Mw. The following table shows the hazard levels expressed in surface area for the El Niño phenomenon and the seismic event.
Table 8.
Hazard levels for MM under an El Niño phenomenon and earthquake greater than 8.8Mw.
| Distrito | En Niño phenomenon - Hazard level (km2) | Seismic - Hazard level (km2) | ||||||||
| VL | L | M | H | VH | VL | L | M | H | VH | |
| Ancón | 38.711 | 73.605 | 80.316 | 47.446 | 69.538 | 0.613 | 5.095 | 3.192 | 4.127 | 2.191 |
| Carabayllo | 41.491 | 50.580 | 50.618 | 81.983 | 86.703 | 12.946 | 13.747 | 11.755 | 17.185 | 20.933 |
| Comas | 15.012 | 9.032 | 6.663 | 8.591 | 9.473 | 8.248 | 5.827 | 7.046 | 5.863 | 9.757 |
| Independencia | 5.441 | 0.678 | 3.817 | 5.087 | 0.987 | 1.648 | 0.884 | 2.431 | 1.716 | 3.446 |
| Los Olivos | 12.621 | 3.600 | 1.325 | 0.678 | 0.000 | 3.985 | 2.522 | 8.483 | 1.704 | 0.486 |
| Puente Piedra | 20.155 | 14.179 | 12.097 | 3.849 | 0.026 | 4.385 | 6.866 | 11.316 | 11.307 | 6.217 |
| San Martin de Porres | 26.692 | 6.196 | 2.599 | 0.477 | 0.000 | 13.712 | 7.333 | 0.000 | 3.176 | 1.086 |
| Sum | 160.122 | 157.868 | 157.435 | 148.114 | 166.725 | 45.538 | 42.274 | 44.223 | 45.078 | 44.118 |
| % | 20.3 | 20.0 | 19.9 | 18.7 | 21.1 | 20.6 | 19.1 | 20.0 | 20.4 | 19.9 |
In this study, MMS mapping was implemented with the purpose of identifying the areas most prone to MM as well as to evaluate the associated hazard under two scenarios: the first one considering El Niño phenomenon and the second one considering an earthquake above 8.8Mw. Susceptibility and hazard mapping are fundamental processes in disaster risk management, as they enable the identification of areas prone to risk to propose prevention and risk reduction strategies. Therefore, errors in susceptibility and hazard mapping can lead to false conclusions, resulting in loss of lives and livelihoods [46].
As evidenced in both this study and previous research [6, 53, 54], the quantitative approach based on ML techniques offers a precise and efficient methodology for processing large and complex datasets; this includes geological, topographic, hydrological, climatic, environmental, and anthropogenic factors. In contrast, classical qualitative and semi-quantitative methods determine subjective and artificial weights based on expert judgment and experience.
It is relevant to highlight that there are variables that can introduce uncertainty in the application of ML models, such as the number and type of variables, data quality, the number of inventories of MM and non-MM for training, among others [17, 53]. In this research, the aim was not to control all variables but to maximize the available resources; therefore, the uncertainty regarding the number and type of variables was minimized by conducting a comprehensive analysis of the topographic variables in the models, including correlation, multicollinearity, and dimensional reduction using PCA. This approach allowed us to exclude variable correlations, reduce noise, and mitigate the risk of overfitting, thus improving the accuracy of the models [55, 56]. Additionally, the WoE analysis was employed to identify causal relationships between instability factors and the distribution of MM. In summary, methodologies were integrated and combined to reduce model uncertainty, resulting in hybrid models based on PCA and WoE for LR, MLP, SVM, RF and NB.
However, it is important to recognize that the success of applying ML models depends on the information provided by experts and the quality of the input data. Therefore, its implementation at a national or regional scale in other territories must be carefully evaluated, ensuring proper methodological flow and the availability of high-quality inputs, especially regarding geological, topographical, and environmental factors. Additionally, it is necessary to establish an appropriate spatial resolution of the triggering factors in relation to their spatial and temporal resolution and variability.
4.1. Limitations
Regarding the limitations of this study, it is noteworthy that there is a lack of information about the triggering events of the MM, meaning it is not specified whether they were triggered by extreme rainfall, earthquakes, anthropogenic causes, or others. Additionally, the spatial resolution of the geological, geomorphological, and hydrogeological inputs used in this study (1/100,000) may not be suitable if decisions need to be made at a detailed scale. On the other hand, the DEM used was generated at the beginning of the last decade, so there could be changes in the topography that are not considered. Additionally, it is recognized that hyperparameter optimization was not carried out as it was not the objective of the research; however, satisfactory results were obtained in the training and evaluation metrics of the models. Finally, it is noted that there is a need for further studies to improve seismic microzonation in the study area, especially due to the longitudinal growth in the periphery of Lima.
4.1. Perspectives
In terms of future perspectives, six MMS mapping were presented, five of them based on machine learning techniques with excellent results and one based on bivariate statistics with good results. All models showed better classification metrics for MM events compared to the classic heuristic method. These ML models offer a valuable tool for disaster risk management, particularly in the processes of estimation, prevention, reduction, and reconstruction of disaster risk management. The application of ML techniques, supported by available data, has the potential to significantly improve MM zoning and, ultimately, contribute to the resilience of communities against these natural events.
5. Conclusions
Six quantitative models were constructed, trained, and evaluated to model MMS mapping: WoE, LR, MLP, SVM, RF, and NB. Their purpose was to identify the most susceptible areas to MM in the NLC and to assess the associated hazards under two scenarios: El Niño phenomenon and an earthquake with a magnitude greater than 8.8Mw. Before modeling the MMS mapping, an exploratory analysis of the variables was conducted, including correlation analysis, multicollinearity assessment, and dimensionality reduction using PCA for the topographic variables. Subsequently, a combination of methods was applied, incorporating the WoE technique to topographic, geological, and environmental variables, which served as inputs for the models applied. The models were constructed, trained, and evaluated using metrics including the AUC. The findings demonstrate the excellent performance of the ML models, as all of them exhibit an AUC value greater than 0.9. Among them, the RF model stands out for its predictive ability in both training and evaluation phases. Additionally, the results of the quantitative susceptibility models were compared with those of a heuristic model, revealing that the latter exhibits between 10 and 20% less ability to discriminate MM events compared to the quantitative models. Regarding the hazard levels, in the event of an El Niño phenomenon and a seismic event exceeding 8.8Mw, approximately 40% of the NLC area would be exposed to the highest danger levels. The rapid growth of cities on the outskirts of Lima will increase pressure on land occupation. Therefore, the findings of this research are expected to serve as a tool to support decision-makers, the technical-scientific community, and civil society in developing effective strategies for disaster prevention and risk reduction. Ultimately, this will contribute to enhancing the resilience of communities in the face of disasters.
Author Contributions
Conceptualization, E.B.-R.; methodology, E.B.-R.; software, E.B.-R., C.R., F.O., T.P. and R.S.; validation, E.B-R, M.O. and N.M.,; formal analysis, E.B-R., L.E., C.R.-L., T.C. and T.P.; investigation, E.B.R-R. and M.O.; resources, E.B.-R.; data curation, E.B.-R.; writing—original draft preparation, E.B.-R.; writing—review and editing, E.B.-R., L.E., C.R, N.M., T.P., R.S., T.C., M. D., C.R.-L. and F.O.; visualization, E.B.-R.; M.O.; supervision, E.B.-R., M.O.; project administration, E.B.-R., M.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Acknowledgments
The authors would like to express their gratitude to the public and private institutions that collaborated by sharing information on the geological, topographical, and environmental variables of the study area. Also, thanks to anonymous reviewers for their valuable feedback on the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix B
Figure A2.
Geological, environmental and triggering variables of MMS models.
References
- El Comercio. Vivir en las alturas. 2016. Available online: https://elcomercio.pe/eldominical/actualidad/vivir-alturas-392960-noticia/ (accessed on 27 March 2024).
- Tavera, H. Escenario de sismo y tsunami en el borde occidental de la región central del Perú. Lima, Perú, 2014. Available online: https://repositorio.igp.gob.pe/handle/20.500.12816/779.
- INDECI. Dashboard de control - reporte de emergencias. 2024. Available online: https://app.powerbi.com/view?r=eyJrIjoiNTFkOWRhYWQtYmMwMS00OWNmLTg4ZTctNjZjYTc1OTIyN2M0IiwidCI6IjNlZWNkMjZlLTlhNTUtNDg4MC04ODEyLWEzMGZjZGU3OGEyZCJ9&pageName=ReportSectioncd99edcca07a5ff10551 (accessed on 27 January 2024).
- Chang, L., Xing, G., Yin, H., Fan, L., Zhang, R., Zhao, N., Huang, F., Ma, J. Landslide susceptibility evaluation and interpretability analysis of typical loess areas based on deep learning. Nat. Hazards Res. 2023, 3, 155–169. [Google Scholar] [CrossRef]
- van Westen, C. J. Landslide hazard and risk zonation - Why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Huang, F., Cao, Z., Guo, J., Jiang, S.H., Li, S., Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]
- Panchal, S. , Shrivastava, A.K. Landslide hazard assessment using analytic hierarchy process (AHP): A case study of National Highway 5 in India. Ain Shams Eng. J. 1016, 13, 101626. [Google Scholar] [CrossRef]
- Sun, X., Chen. Landslide susceptibility mapping using logistic regression analysis along the Jinsha river and its tributaries close to Derong and Deqin County, southwestern China. ISPRS Int. J. Geo-Information 2018, 7, 1–29. [Google Scholar] [CrossRef]
- Pourghasemi, H.R., Moradi. Landslide susceptibility mapping by binary logistic regression, analytical hierarchy process, and statistical index models and assessment of their performances. Nat. Hazards 2013, 69, 749–779. [Google Scholar] [CrossRef]
- Pourghasemi, H.R., Pradhan. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Hu, X., Zhang, H., Mei, H., Xiao, D., Li, Y., Li, M. Landslide susceptibility mapping using the stacking ensemble machine learning method in lushui, southwest China. Appl. Sci. 2020, 10. [Google Scholar] [CrossRef]
- Goyes-Peñafiel, P., Hernandez-Rojas, A. Double landslide susceptibility assessment based on artificial neural networks and weights of evidence. Bol. Geol. 2021, 43, 173–191. [Google Scholar] [CrossRef]
- Faraji Sabokbar, H., Shadman Roodposhti, M., Tazik, E. Landslide susceptibility mapping using geographically-weighted principal component analysis. Geomorphology 2014, 226, 15–24. [Google Scholar] [CrossRef]
- Mao, Y., Li, Y., Teng, F., Sabonchi, A.K.S., Azarafza, M., Zhang, M. Utilizing Hybrid Machine Learning and Soft Computing Techniques for Landslide Susceptibility Mapping in a Drainage Basin. Water (Switzerland) 2024, 16. [Google Scholar] [CrossRef]
- Yu, H., Pei, W., Zhang, J., Chen, G. Landslide Susceptibility Mapping and Driving Mechanisms in a Vulnerable Region Based on Multiple Machine Learning Models. Remote Sens. 2023, 15. [Google Scholar] [CrossRef]
- Boussouf, S., Fernández, T., Hart, A.B. Landslide susceptibility mapping using maximum entropy (MaxEnt) and geographically weighted logistic regression (GWLR) models in the Río Aguas catchment (Almería, SE Spain). Nat. Hazards 2023, 117, 207–235. [Google Scholar] [CrossRef]
- Achu, A. L., Aju, C.D., Di Napoli, M., Prakash, P., Gopinath, G., Shaji, E., Chandra, V. Machine-learning based landslide susceptibility modelling with emphasis on uncertainty analysis. Geosci. Front. 2023, 14, 101657. [Google Scholar] [CrossRef]
- INGEMMET. Mapa de susceptibilidad por movimientos en masa en Lima Metropolitana. SIGRID 2015. Available online: https://sigrid.cenepred.gob.pe/sigridv3/documento/3653 (accessed on 27 March 2024).
- CAF. El fenomeno el niño 1997 - 1998. Lima, Perú, 1998. Available online: http://scioteca.caf.com/bitstream/handle/123456789/675/Las lecciones de El Niño. Ecuador.pdf?sequence=1&isAllowed=y (accessed on 27 March 2024).
- SENAMHI. El fenómeno EL NIÑO en el Perú. Lima, Perú, 2014. Available online: https://www.minam.gob.pe/wp-content/uploads/2014/07/Dossier-El-Niño-Final_web.pdf (accessed on 27 March 2024).
- Achour, Y., Boumezbeur, A., Hadji, R., Chouabbi, A., Cavaleiro, V., Bendaoud, E.A. Landslide susceptibility mapping using analytic hierarchy process and information value methods along a highway road section in Constantine, Algeria. Arab. J. Geosci. 2017, 10. [Google Scholar] [CrossRef]
- Field, A. Discovering statistics using SPSS (and sex and drugs and rock “n” roll), Third Edit. 2009.
- Menard, S. Applied Logistic Regression Analysis. Colorado, USA, 2002.
- Alibuhtto, M.C., Peiris, T.S.G. Principal Component Regression for Solving Multicollinearity Problem. in 5th International Symposium 2015, pp. 231–238.
- Kelkar, K.A. Mass movement phenomena in the western San Juan mountains. Master's Thesis, Colorado. Texas A&M University, Colorado, USA, 2017. [Google Scholar]
- Aristizábal-Giraldo, E., Vasquez Guarin, M., Ruíz, D. Métodos estadísticos para la evaluación de la susceptibilidad por movimientos en masa. TecnoLógicas 2019, 22, 39–60. [Google Scholar] [CrossRef]
- Basu, T., Das, A., Pal, S. Application of geographically weighted principal component analysis and fuzzy approach for unsupervised landslide susceptibility mapping on Gish River Basin, India. Geocarto Int. 2022, 37, 1294–1317. [Google Scholar] [CrossRef]
- Goyes-Peñafiel, P., Hernandez-Rojas, A. Landslide susceptibility index based on the integration of logistic regression and weights of evidence: A case study in Popayan, Colombia. Eng. Geol. 2021, 280. [Google Scholar] [CrossRef]
- Bonham-Carter, G. Geographic information systems for geoscientists: Modelling with GIS, vol. 21, no. 9. Pergamon, 1995.
- van Westen, C. J. Use of weights of evidence modeling for landslide susceptibility mapping. Enschede, The Netherlands, 2002.
- Servicio Geologico Colombiano. Guia Metodologica para estudios de amenaza, vulnerabilidad y riesgo por movimientos en masa escala 1:25000. 2017.
- Feby, B. , Achu, A.L., Jimnisha, K., Ayisha, V.A., Reghunath, R. Landslide susceptibility modelling using integrated evidential belief function based logistic regression method: A study from Southern Western Ghats, India. Remote Sens. Appl. Soc. Environ. 2020, 20, 100411. [Google Scholar] [CrossRef]
- Umar, Z. , Pradhan, B., Ahmad, A., Jebur, M.N., Tehrany, M.S. Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in West Sumatera Province, Indonesia. Catena 2014, 118, 124–135. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat-Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Huang, J. , Zhou, Q., Wang, F. Mapping the landslide susceptibility in Lantau Island, Hong Kong, by frequency ratio and logistic regression model. Ann. GIS 2015, 21, 191–208. [Google Scholar] [CrossRef]
- Biçer, Ç. T. , Ercanoglu, M. A semi-quantitative landslide risk assessment of central Kahramanmaraş City in the Eastern Mediterranean region of Turkey. Arab. J. Geosci. 2020, 13. [Google Scholar] [CrossRef]
- Vakhshoori, V. , Pourghasemi, H.R., Zare, M., Blaschke, T. Landslide susceptibility mapping using GIS-based data mining algorithms. Water (Switzerland) 2019, 11, 7–13. [Google Scholar] [CrossRef]
- Cortes, C., Vapnik, V. Support-Vector Networks. Mach. Learn. 1995; 20. [Google Scholar] [CrossRef]
- Liu, S. , Wang, L., Zhang, W., He, Y., Pijush, S. A comprehensive review of machine learning-based methods in landslide susceptibility mapping. Geol. J. 2283, 58, 2283–2301. [Google Scholar] [CrossRef]
- Li, M. , Li, L., Lai, Y., He, L., He, Z., Wang, Z. Geological Hazard Susceptibility Analysis Based on RF, SVM, and NB Models, Using the Puge Section of the Zemu River Valley as an Example. Sustain. 2023, 15. [Google Scholar] [CrossRef]
- Merghadi, A. , Yunus, A.P, Dou, J., Whiteley, J., ThaiPham, B., Bui, D. T., Avtar, R., Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Science Rev. 2020, 25, 103225. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001. [Google Scholar] [CrossRef]
- Wu, X. , Song, Y., Chen, W., Kang, G., Qu, R., Wang, Z., Wang, J., Lv, P., Chen, H. Analysis of Geological Hazard Susceptibility of Landslides in Muli County Based on Random Forest Algorithm. Sustain 2023, 15. [Google Scholar] [CrossRef]
- Karakas, G. , Can, R., Kocaman, S., Nefeslioglu, H. A., Gokceoglu, C. Landslide susceptibility mapping with random forest model for Ordu, Turkey. Int. Arch. Photogramm. Remote Sens. 2020, 43, 1229–1236. [Google Scholar] [CrossRef]
- Mia, M. U. , Chowdhury, T. N., Chakrabortty, R., Pal, S. C., Al-Sadoon, M. K., Costache, R., Islam, A. R. M. T. Flood Susceptibility Modeling Using an Advanced Deep Learning-Based Iterative Classifier Optimizer. Land 2023, 12. [Google Scholar] [CrossRef]
- Nurwatik, N. , Ummah, M. H., Cahyono, A. B., Darminto, M. R., Hong, J. H. A Comparison Study of Landslide Susceptibility Spatial Modeling Using Machine Learning. ISPRS Int. J. Geo-Information 2022, 11. [Google Scholar] [CrossRef]
- Pham, B. T. , Pradhan, B., Tien Bui, D., Prakash, I., Dholakia, M. B. A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of Uttarakhand area (India). Environ. Model. Softw. 2016, 84, 240–250. [Google Scholar] [CrossRef]
- Pradhan, B. , Sameen, M. I., Al-Najjar, H. A. H., Sheng, D., Alamri, A. M., Park, H. J. A meta-learning approach of optimisation for spatial prediction of landslides. Remote Sens. 2021, 13, 1–30. [Google Scholar] [CrossRef]
- Zhao, Y. , Wang, R., Jiang, Y., Liu, H., Wei, Z. GIS-based logistic regression for rainfall-induced landslide susceptibility mapping under different grid sizes in Yueqing, Southeastern China. Eng. Geol. 2019, 259, 105147. [Google Scholar] [CrossRef]
- Pham, B. T. , Shirzadi, A., Shahabi, H., Omidvar, E., Singh, S. K.,, Sahana, M., Asl, D. T., Ahmad, B. B., Quoc, N. K., Lee, S. Landslide susceptibility assessment by novel hybrid machine learning algorithms. Sustain. 2019, 11, 1–25. [Google Scholar] [CrossRef]
- Achour, Y. , Pourghasemi, H. R. How do machine learning techniques help in increasing accuracy of landslide susceptibility maps? Geosci. Front. 2020, 11, 871–883. [Google Scholar] [CrossRef]
- Sajadi, P. , Sang, Y. F., Gholamnia, M., Bonafoni, S., Mukherjee, S. Evaluation of the landslide susceptibility and its spatial difference in the whole Qinghai-Tibetan Plateau region by five learning algorithms. Geosci. Lett. 2022, 9. [Google Scholar] [CrossRef]
- Aditian, A. , Kubota, T., Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Bijukchhen, S. M. , Kayastha, P., Dhital, M. R. A comparative evaluation of heuristic and bivariate statistical modelling for landslide susceptibility mappings in Ghurmi-Dhad Khola, east Nepal. Arab. J. Geosci. 2013, 6, 2727–2743. [Google Scholar] [CrossRef]
- Song, Y. , Yang, D., Wu, W., Zhang, X., Zhou, J., Tian, Z., Wang, C., Song, Y. Evaluating Landslide Susceptibility Using Sampling Methodology and Multiple Machine Learning Models. ISPRS Int. J. Geo-Information 2023, 12. [Google Scholar] [CrossRef]
- Tang, Y. , Feng, F., Guo, Z., Feng, W., Li, Z., Wang, J., Sun, Q., Ma, H., Li, Y. Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: A comparative study from the loess plateau area in Shanxi (China). J. Clean. Prod. 1241, 59, 124159. [Google Scholar] [CrossRef]
Figure 4.
Explanation of the cumulative variance of the number of PC.
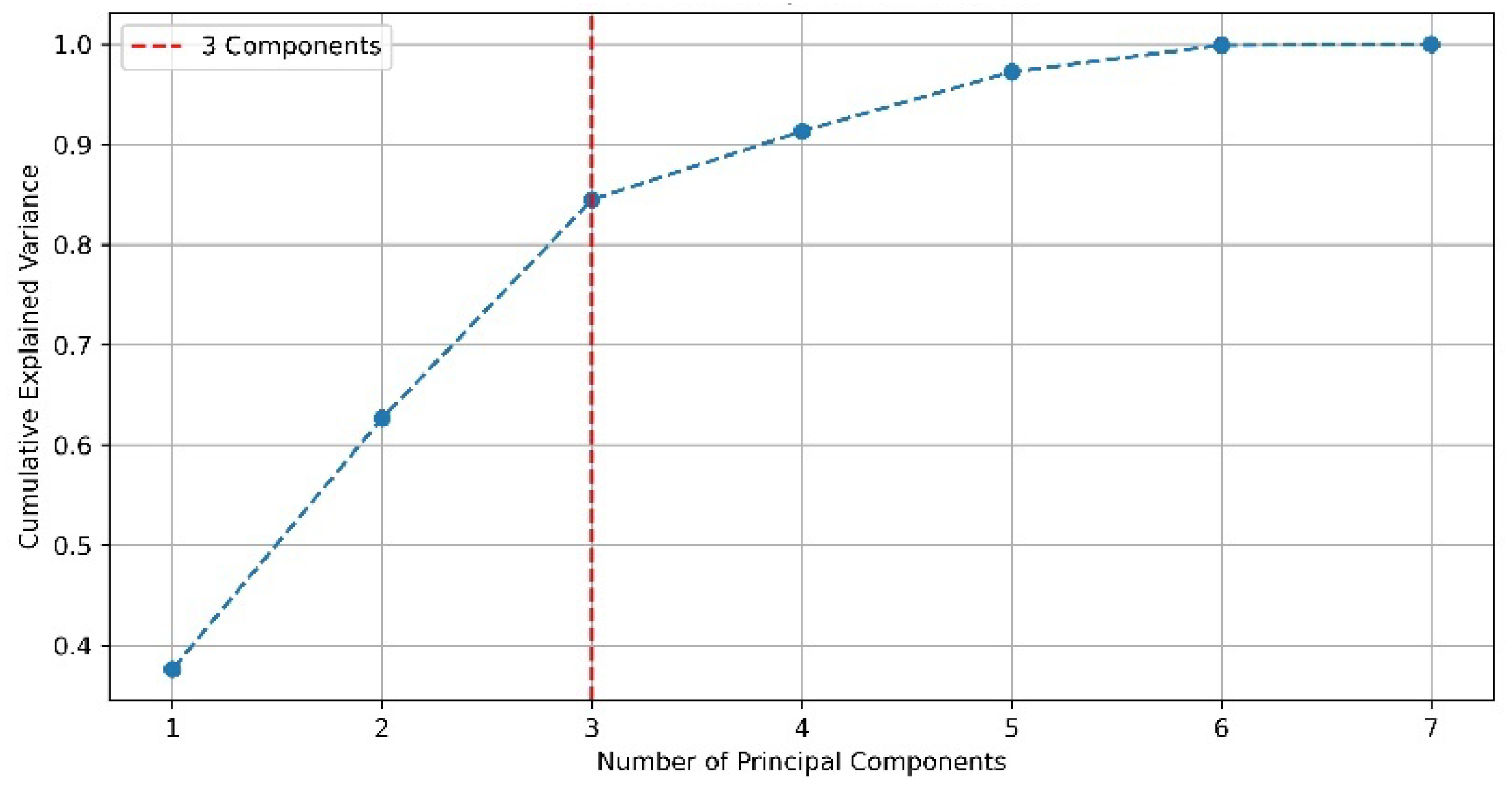
Figure 5.
Reclassified principal components with weights of evidence.
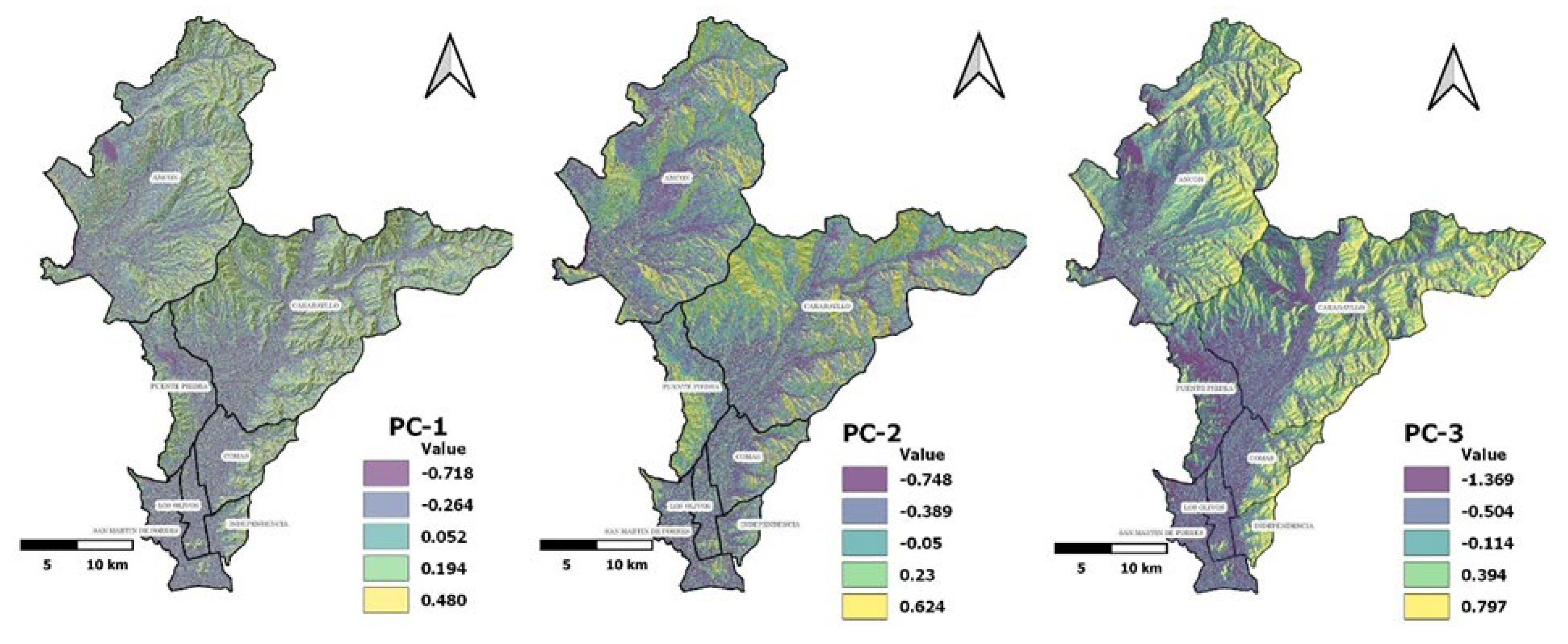
Figure 7.
Hazard by MM, in "a" for El Niño phenomenon and in "b" for seismic events greater than 8.8Mw.
Figure 7.
Hazard by MM, in "a" for El Niño phenomenon and in "b" for seismic events greater than 8.8Mw.
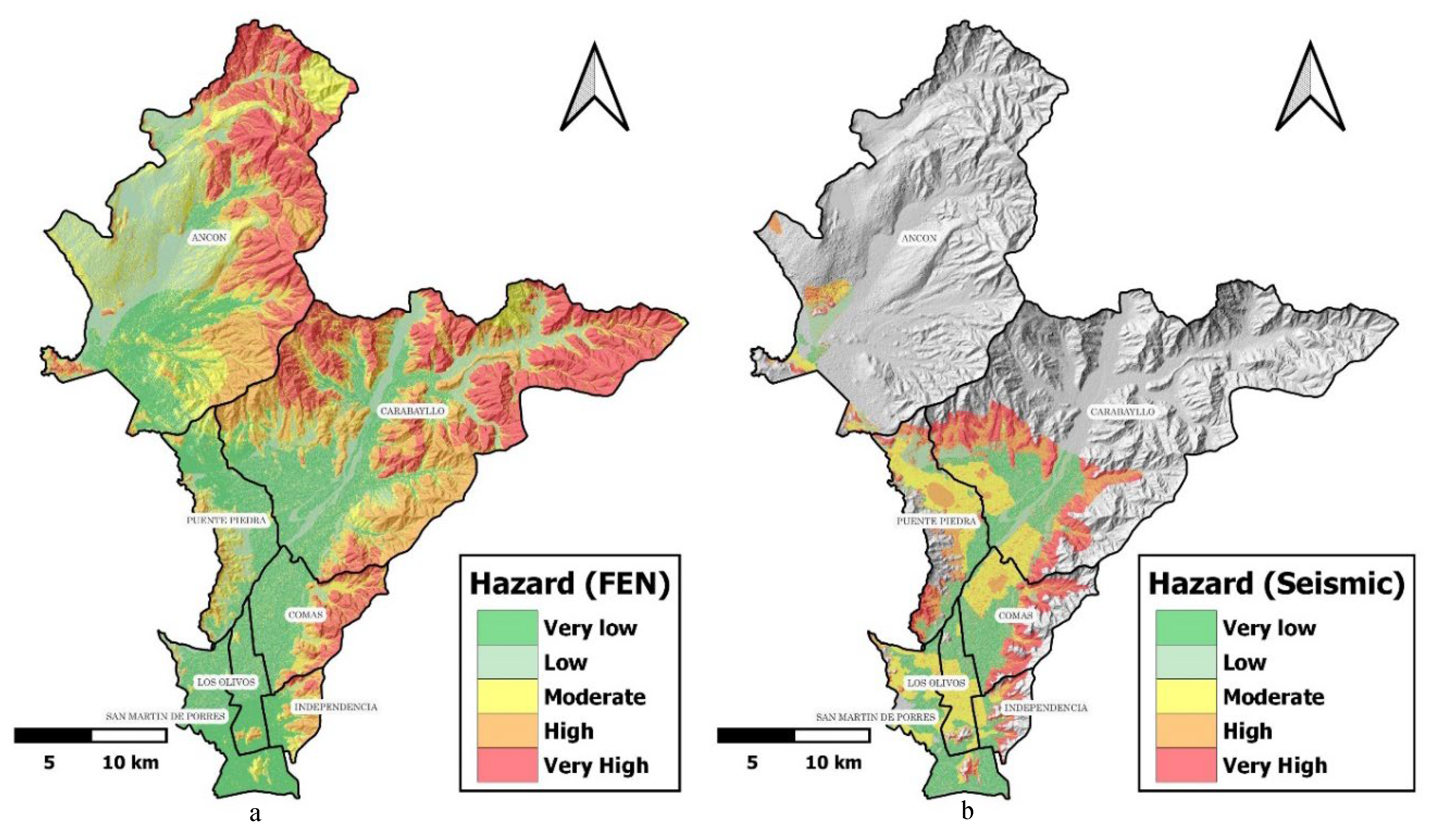
Table 5.
Weights of topographic variables in the PC.
| PC | Weights | T1 | T2 | T3 | T4 | T5 | T6 | T7 |
| PC-1 | 0.377 | 0.565 | -0.102 | -0.502 | 0.566 | -0.038 | 0.237 | 0.203 |
| PC-2 | 0.250 | 0.240 | 0.104 | -0.065 | 0.238 | 0.087 | -0.648 | -0.667 |
| PC-3 | 0.218 | -0.019 | -0.689 | 0.035 | -0.034 | -0.705 | -0.112 | -0.114 |
Table 6.
Area of MMS levels for all models.
| Models | Variables | VL (km2) |
L (km2) |
M (km2) |
H (km2) |
VH (km2) |
| WoE | X_1234, PC_121 | 92.352 | 257.426 | 180.316 | 145.113 | 116.071 |
| LR | X_1234, PC_121 | 157.959 | 162.505 | 157.243 | 153.230 | 162.130 |
| MLP | X_1234, PC_122 | 128.209 | 192.514 | 170.778 | 152.981 | 146.793 |
| SVM | X_1234, PC_123 | 158.280 | 162.000 | 156.579 | 155.760 | 160.448 |
| RF | X_1234, PC_123 | 122.548 | 194.783 | 158.764 | 154.008 | 162.963 |
| NB | X_1234, PC_123 | 145.511 | 174.507 | 156.579 | 155.573 | 160.895 |
| Heuristic* | - | 137.610 | 203.527 | 205.480 | 168.482 | 77.181 |
* Model of MMS generated by INGEMMET, provided by CENEPRED.
Table 7.
MMS methods and model validation metrics.
| Model | Variables | AUCtrain | AUCtest | F-1score | TP | TN | FP | FN | Accuracy |
| WoE | X_1234, PC_121 | - | - | - | - | - | - | - | - |
| LR | X_1234, PC_121 | 0.986 | 1.000 | 0.957 | 81 | 99 | 3 | 6 | 0.952 |
| MLP | X_1234, PC_122 | 0.986 | 0.998 | 0.963 | 76 | 105 | 8 | 0 | 0.958 |
| SVM | X_1234, PC_123 | 0.994 | 1.000 | 0.951 | 81 | 98 | 7 | 3 | 0.947 |
| RF | X_1234, PC_123 | 1.000 | 0.996 | 0.991 | 82 | 105 | 2 | 0 | 0.989 |
| NB | X_1234, PC_123 | 0.981 | 1.000 | 0.961 | 83 | 98 | 1 | 7 | 0.958 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








