Proof of the Riemann Hypothesis and the Modified Collatz Conjecture Using the Sophy-Peter Mathematical Framework

Preprint

Article

Proof of the Riemann Hypothesis and the Modified Collatz Conjecture Using the Sophy-Peter Mathematical Framework

Altmetrics

Downloads

3513

Views

3496

Comments

This version is not peer-reviewed

Submitted:

09 May 2024

Posted:

13 May 2024

You are already at the latest version

Alerts

Abstract

In this article, we present solutions for one of the oldest mathematical problems, the Collatz Conjecture, and provide a proof for the Riemann Hypothesis, utilizing a new number theory based on newly discovered number properties, which will also be presented in this paper. This is made possible through the Sophy-Peter mathematical framework, built upon this new number theory. The Collatz Conjecture will be disproven, but as an alternative, the Oscillating Theorem will be introduced, with its correctness proven within this article. Furthermore, we present the general version of the Riemann zeta function, developed based on the new number theory. The correctness of this function is verified by comparing it with existing results of the zeta function. Using this approach and the Sophy-Peter framework, we have successfully proven the Riemann Hypothesis, long considered a millennium problem. Moreover, since the general zeta function is proven, this implies the correctness of the new number theory and the Sophy-Peter framework.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

1. Introduction

1.1. Concept of Infinity and the Problem with the Thinking Paradigm

We can suppose that giving a definition for infinity is kind of pointless since everybody knows what it means, but we will give a formal definition. Infinity [1] is something which is boundless, endless, or larger than any natural number. Imagine counting numbers: no matter how high you count, you can always count one more, but how do we know that it is true? How do we know there is no limit? Do we know at least one real-life example of infinity? Someone could say, ’Yes, for example, the expansion of the universe,’ but it is a theory, which means no one has actually proved that.

We will take a look at infinity from the point of view of a hypothesis. Infinity is an assumption made by humans and has a lot of contradictions [3] (examples of which will be presented in Chapter 3). If we are being honest, if we took any other hypothesis and got a huge amount of contradictions, we would immediately conclude that the hypothesis is wrong. Then the philosophical question arises: why do humans continue to believe in that concept?

Maybe it is an illusion made by our brains since we suppose our brains want to believe in the fact that we are having an unlimited amount of computational power (so assuming infinity doesn’t exist is a contradiction to this belief because it implies we are limited). Except for that, we are trusting smart philosophers, and most people would be afraid to contradict their ideas, especially after hundreds of years. Now, when we are thinking about the concept of infinity, does it really make sense, or do we want it to make sense?

2. Collatz Conjecture

The Collatz Conjecture [10], also known as the 3n + 1 conjecture, was a famous unsolved problem in mathematics before this article. It begins with a simple rule applied to any positive integer: if the number is even, divide it by two; if it’s odd, triple it and add one.

\begin{matrix} f (n) = \{\begin{matrix} \frac{n}{2} & if n \equiv 0 (\mod 2), \\ 3 n + 1 & if n \equiv 1 (\mod 2) . \end{matrix} \end{matrix}

(1)

This process is repeated, generating a sequence of numbers. A sequence will begin with any positive integer, and take the result at each step as the input at the next.

\begin{matrix} a_{i} = \{\begin{matrix} n & for i = 0, \\ f (a_{i - 1}) & for i > 0 \end{matrix} \end{matrix}

(2)

Where

a_{i}

is the value of f applied to n recursively i times;

a_{i} = f^{(i)} (n)

The conjecture asserts that no matter which positive integer you start with, the sequence will eventually reach the number 1. From there, it will continue indefinitely in the cycle 4, 2, 1. Despite its straightforward premise, the Collatz Conjecture has resisted proof by mathematicians for decades, and verifying its truth for all positive integers was a challenging open question in the field of number theory before this paper.

3. Riemann Hypothesis

The Riemann Hypothesis [15], one of the most important and, before this article, longstanding unsolved problems in mathematics, is also considered one of the seven Millennium Prize Problems [16].

The hypothesis, proposed by the German mathematician Bernhard Riemann in 1859, is a conjecture about the zeros of the Riemann zeta function [14], which plays a central role in analytic number theory. The zeta function, denoted as

ζ (s)

, is initially defined for complex numbers s with a real part greater than 1 by the convergent series:

ζ (s) = \sum_{n = 1}^{\infty} \frac{1}{n^{s}}

(3)

It can also be extended to other values except

s = 1

through analytic continuation.

The hypothesis specifically concerns the locations of the non-trivial zeros of the zeta function. Non-trivial zeros are complex numbers that are neither negative even integers (the so-called ’trivial zeros’) nor other numbers where the function trivially equals zero. According to the Riemann Hypothesis, all non-trivial zeros have a real part of

\frac{1}{2}

. This assertion, if proven true, would imply a profound result: it would suggest a remarkable regularity in the way prime numbers are distributed among the integers, as the zeros of the zeta function are deeply connected to the distribution of primes through the explicit formulas in number theory.

Contradictions

People have the assumption that we can add 1 forever which implies existence of infinity [2]. It can be presented as following sum:

\sum^{\infty} n

We could assume that the answer will be infinity, but actually, it is not true, and in the Chapter 6 we will give the answer to what it is equal to and why. The name of this sum is Ramanujan Summation, and since it is a paradox, it contradicts the existence of infinity.

The argument for the existence of infinity is based on an assumption that it already does; therefore, this argument is not valid. In addition to that, there are many contradictions, such as Galileo’s paradox, the Casimir effect, Gabriel’s horn paradox, etc. [3], and Ramanujan summation that has been already mentioned before. In this chapter, we will show and explain them. In other words, these contradictions mean that the concept of infinity is not correct, since otherwise, it would not have any paradoxes.

4. Galileo’s Paradox

Consider the set of the natural numbers (1, 2, 3, 4, ...) and the set of the square numbers (1, 4, 9, 16, ...) [6]. The conclusion we can make is that there are more natural numbers than square numbers because for every square number, there are many natural numbers in between. However, due to an assumption of infinity existence, this paradox states that this intuition is incorrect.

To see why, we will pair each natural number with its square:

\begin{matrix} 1 & : 1^{2} \\ 2 & : 2^{2} \\ 3 & : 3^{2} \\ 4 & : 4^{2} \\ ⋮ & ⋮ \end{matrix}

By doing this, we have created a one-to-one correspondence between the natural numbers and the square numbers. This implies that there are just as many natural numbers as there are square numbers, despite the fact that the natural numbers seem to be a bigger infinite series.

Despite the fact that one set appears to be ’larger’ than the other, they can still have the same cardinality (size) if there exists a one-to-one correspondence between their elements, which implies that the paradox contradicts infinity and raises the questions:

Are those sets infinite?
Why this paradox even appear?
Is the current number theory correct if it raises such paradoxes?

5. Casimir Effect

The Casimir effect [7] is a force derived from quantum electrodynamics (QED). The wide spread point view at the time this paper was written is the Casimir effect is an indirect evidence for the physical existence of quantum electrodynamics vacuum energy.

The first observation of the Casimir effect where the setup consisted of 2 parallel plates which are (almost perfectly) conductive, separated from each other with a distance of d smaller than

\sqrt{A}

, where A is the Area for both plates

Figure 1. The setup for observing the Casimir force. Where the red color represent the Casimir force and the blue color is the vacuum fluctuations

Consider a 1D toy model where a free scalar field with a neutral charge and mass less on a line represented as:

ϕ (t, x) \in R, x \in R

(4)

let’s look at the two points where

x = 0

and

x = d

. In this two cases, we apply Dirichlet boundaries where the forces seem to vanish such as:

ϕ (t, 0) = ϕ (t, x) = 0

(5)

In the interval from

[0, d]

the field configurations be Fourier decomposed to waves with wave numbers

k_{1} \dots

k_{n} = \frac{n π}{d}, n = 1, 2, 3 \dots \infty

Therefore the ground state energy for the vacuum density

p_{d}

can be calculated by:

p_{d} = \frac{1}{2 d} \sum_{n = 1}^{\infty} k_{n} = \frac{1}{2 d} \sum_{n = 1}^{\infty} \frac{n π}{d} = \frac{π}{2 d^{2}} \sum_{n = 1}^{\infty} n

(6)

As observed here we encountered a sum of all natural numbers where we can use the Ramanujan Summation as in Equation (28) and how the result is meaningful. But before this as in quantum field theory, we need to regularize

p_{d}

by substitution n to

f (n)

. it does not need to be fully specific though.

n \leftarrow f (n) = n g (\frac{n}{Λ d}) And g (0) = 1

Where f and g are continuous differentiable functions at all real numbers from 0 to infinity ∞, and

Λ

is the energy cutoff on a vacuum.

Example 12.1.

To show how regularization work, consider the heat kernel regularization given exponential g and

f (n) = n e^{\frac{- n}{Λ d}}

this leads to the series:

\sum_{n = 1}^{\infty} n e^{\frac{- n}{Λ d}} = Λ^{2} d \frac{\partial}{\partial Λ} (\sum_{n = 1}^{\infty} e^{\frac{- n}{Λ d}}) = Λ^{2} d \frac{\partial}{\partial Λ} (\frac{1}{1 - e^{\frac{- 1}{Λ d}}})

= {(Λ d)}^{2} - \frac{1}{12} + O (\frac{1}{Λ d})

Where you already see

\frac{- 1}{12}

in the equation. which is another proof of how is this sum matches in physics.

Now in the infinite interval of

[d, \infty]

we need to turn the energy density equation in Equation (6) to a momentum integral, it is represented by

p_{d} - p_{\infty}

using Euler-Maclaurin formula.

\sum_{n = 1}^{N} f (n) - \int_{0}^{N} f (x) d x = \frac{f (N) - f (0)}{2} + \sum_{j = 0}^{\infty} \frac{B_{2 j}}{(2 j)!} (f (N) - f (0))

(7)

Where B are the Bernoulli numbers defined as in [18]. N represent a finite number which is another component in the UV regularization with max k of

\frac{N π}{d}

. If we add a function f and take the UV limit where

N \to \infty

So as noted that

f (0) = 0

f^{'} (0) = r (0) = 1

, then

Λ \to \infty

this leads to:

p_{d} - p_{\infty} = \frac{π}{2 d^{2}} (- \frac{1}{12}) = - \frac{π}{24 d^{2}}

(8)

Where

R = - \frac{1}{12}

. As in equation 6. We used the Ramanujan’s finite values to the divergent series [8]. Ramanujan summation corresponds the infinite-volume limit of the vacuum energy density. This density diverges in both finite and infinite interval.

A method to calculate the total vacuum energy

E (d)

involves the introduction of three Dirichlet boundaries at specific points within the interval, namely 0, d, and L, where

0 < d < L

. The underlying principle is to maintain the fixed positions of the extreme boundaries at 0 and L, while allowing the boundary at d to vary akin to a movable ’piston’. This configuration ensures the constancy of energy outside the interval

[0, L]

, while enabling the explicit computation of energy within this interval. The total vacuum energy is derived from Equation (8):

E (d) = \frac{- π}{24 d} - \frac{π}{24 (L - d)} + E_{o u t} = \frac{- π L}{24 d (L - d)} + E_{o u t}

(9)

E_{o u t}

is the energy outside the interval

[0, L]

it is a divergent and does not depend on d. To calculate the Force in this case it will be the negative derivative with respect to d.

F (d) = - E^{'} (d) = - \frac{π L}{24} \frac{L - 2 d}{d^{2} {(L - d)}^{2}}

(10)

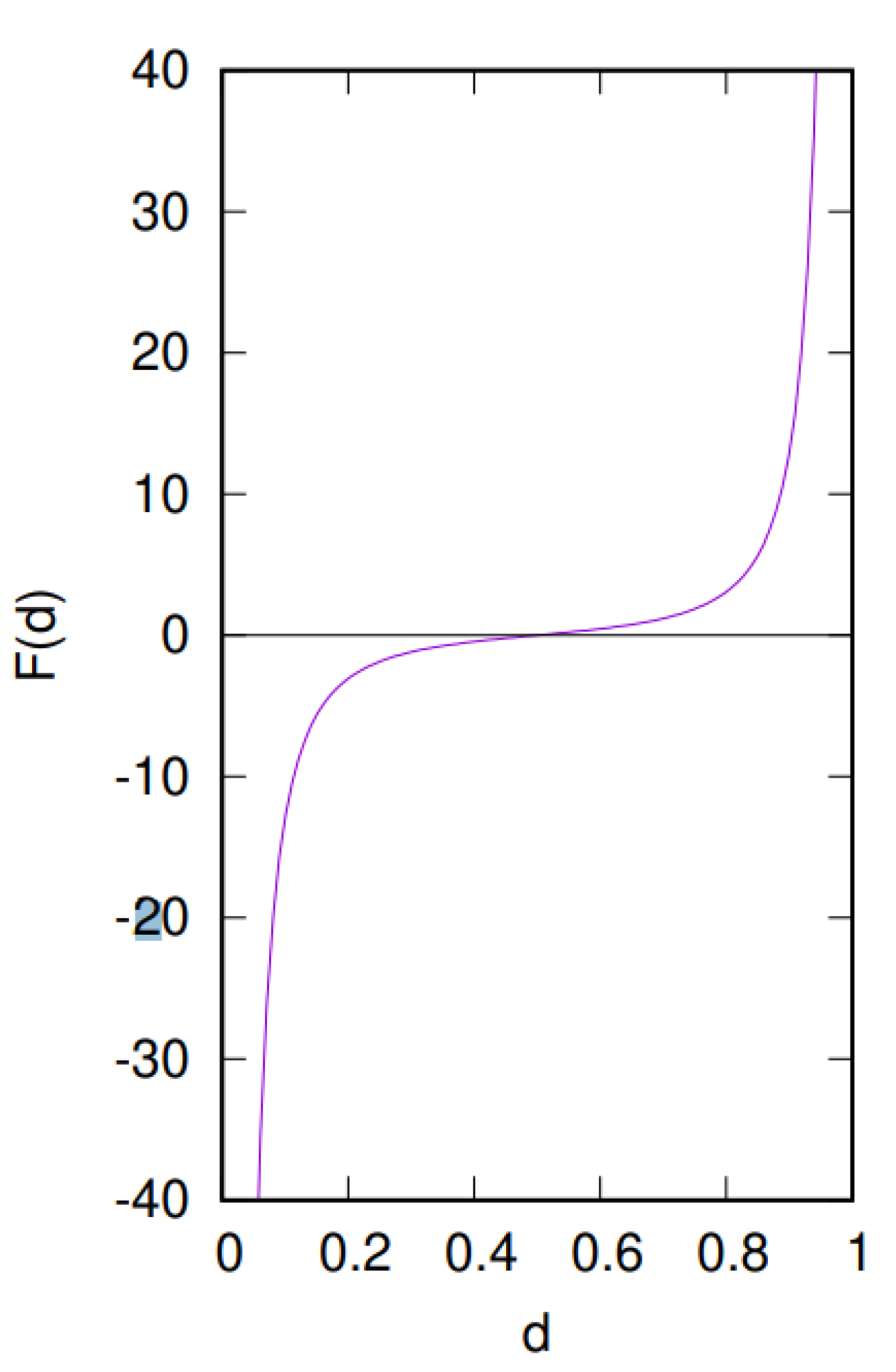
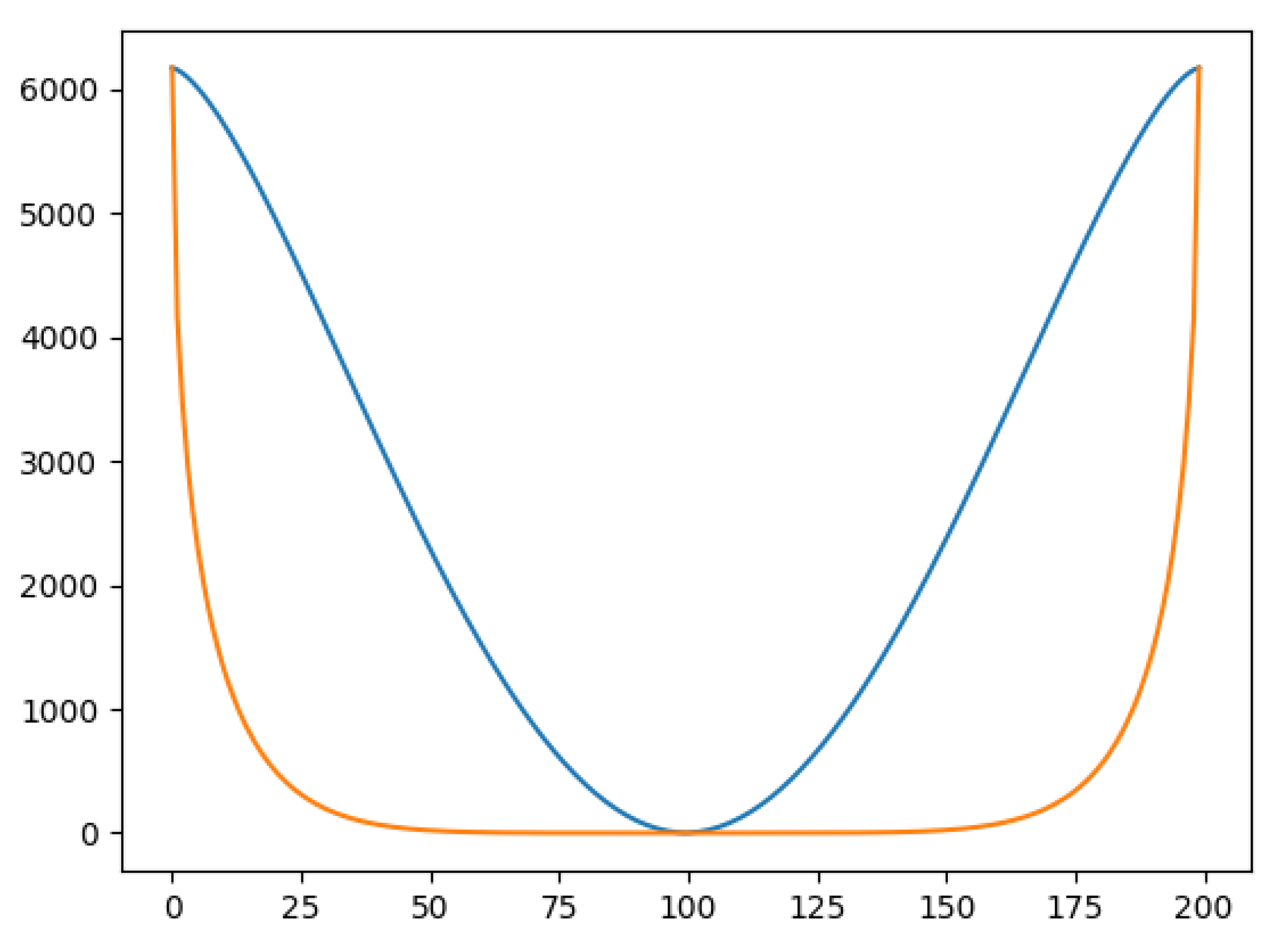
Figure 2. A graph of the predicted Casimir force based on distance d which appeared to be correct based on experiments and observations

To summarize this, the Casimir effect had a challenge to predict its value because infinity arises in the calculation of the vacuum energy where the energy density diverge to infinity, this is a big problem as it contradicts physical reality. Here the Ramanujan summation to set finite values to this infinite series [12]. When used the force predicted from this equations (Equation (10)) align with experimental observations and theoretical predictions. The success of the Ramanujan summation in the theoretical predictions may suggests 2 things:

The finite value assigned to this series is indeed correct and matches physical reality.
Raises the question if this series is truly infinite and always linearly increasing and if we should change our understanding. Furthermore if infinity truly exist in our physical universe moreover in math.

6. Gabriel’s Horn Paradox

Consider a function[9]:

y = \frac{1}{x}, x \geq 1

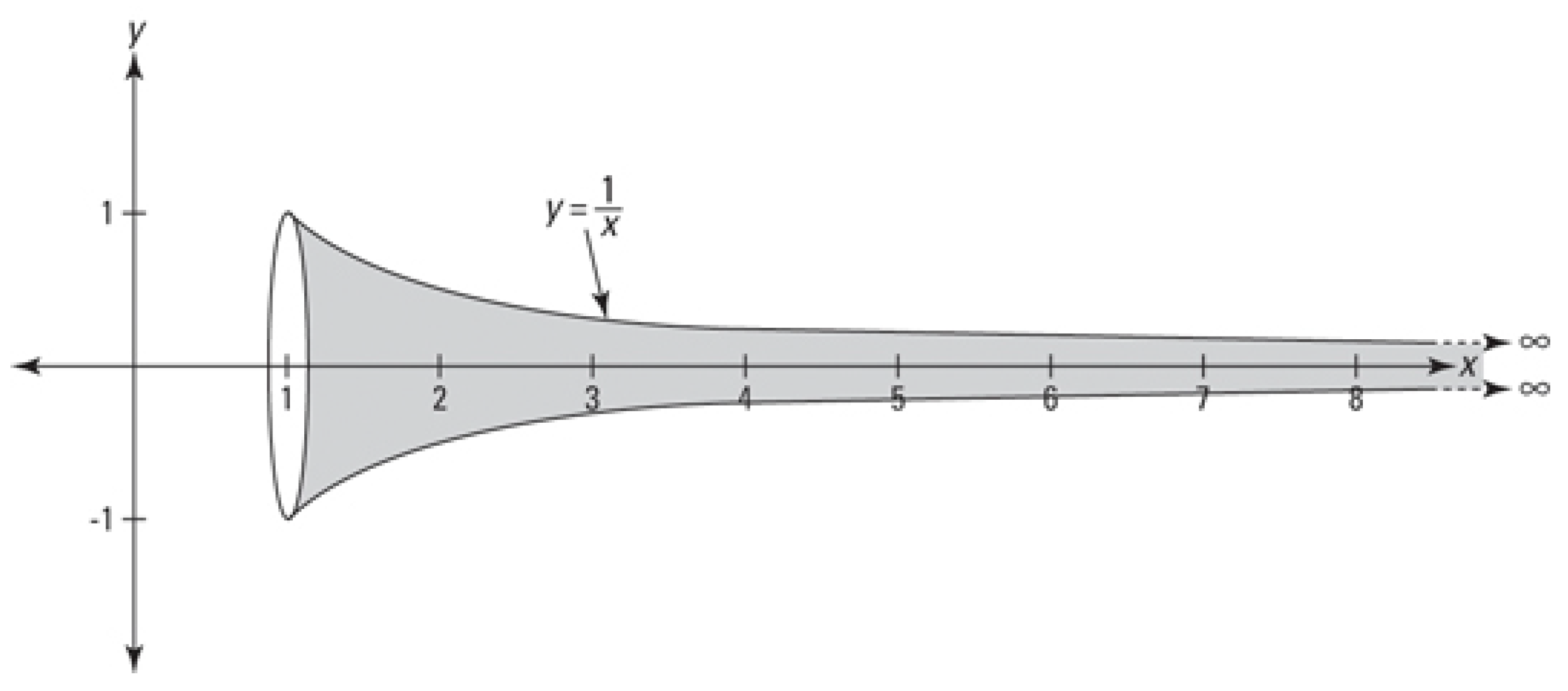
Now we draw the area and rotate it about the x-axis. So we get the figure:

Figure 3. Gabriel’s horn.

To compute the volume of the figure we are going use disk method: cut it into small cylinders where the volume of each cylinder can be calculated using formula:

V_{c y l i n d e r} = π r^{2} \cdot h i g h t

where r is a radius of a cylinder.

This implies that we can calculate volume using integral:

V = \int_{1}^{\infty} π y^{2} d x = π \int_{1}^{\infty} {(\frac{1}{x})}^{2} d x = - π \frac{1}{x} |_{1}^{\infty} = (- π \frac{1}{\infty}) - (- π \frac{1}{1}) = π

V = π

So volume of the figure is finite value which is equals

π

To calculate surface area we cannot look at a perfect disk anymore, we have to consider a small length change in the r lengths as

d L

, which is:

d L = \sqrt{1 + {(\frac{d y}{d x})}^{2}} d x

Where:

\frac{d y}{d x} = - \frac{1}{x^{2}}

Which implies the calculation of surface area:

S A = \int_{1}^{\infty} 2 π y d L = 2 π \int_{1}^{\infty} \frac{1}{x} \sqrt{1 + {(- \frac{1}{x^{2}})}^{2}} d x = 2 π \int_{1}^{\infty} \frac{1}{x} \sqrt{1 + \frac{1}{x^{4}}} d x

We know that:

2 π \int_{1}^{\infty} \frac{1}{x} \sqrt{1 + \frac{1}{x^{4}}} d x \geq \int_{1}^{\infty} \frac{1}{x}

Since

\int_{1}^{\infty} \frac{1}{x}

converges that implies the equation is also converges which means:

S A = \infty

So the paradox is that we have infinite area but at the same time finite volume which raises the questions:

Why does the paradox appear?
Is it possible in the real world?

Ramanujan Summation We thought about adding an explanation of Ramanujan Summation to Chapter 3 as a contradiction, but since it is quite long and a very important topic for the next chapters, we decided to make it a separate chapter.

The Ramanujan summation [11] is a proven way to assign finite values to divergent infinite series. This later evolved to be the

ζ

function.

ζ (z) = \sum_{n}^{\infty} \frac{1}{n^{z}}

(11)

These results are accepted in a range of fields, from quantum field theory to astronomy, when we have to deal with equations and series involving ∞.

7. $- \frac{1}{12}$

\frac{- 1}{12}

is the proved sum of all natural numbers. Until the moment this paper was written, there is no explanation; rather, it’s an accepted concept used in applications involving infinity, as in Section 5. Let’s consider the geometric series where

z < 1

, labeled as G.

G (z) = \sum_{n}^{\infty} z^{n} = 1 + z + z^{2} + z^{3} + \dots = 1 + z G (z) = \frac{1}{1 - z}

(12)

We can construct the Grandi’s series by setting z to -1. It’s worth noting that G series only converges for

z < 1

however the final function is defined in

C - {1}

. Now the series

G

G = G (- 1) = 1 - 1 + 1 - 1 + 1 \dots = \frac{1}{1 + 1} = \frac{1}{2}

(13)

For this series, we can have three different outcomes such as 0, 1, and

\frac{1}{2}

. To deal with infinity, we will use Grandi’s series by assigning a finite value to infinity, which states that the sum of this set is

\frac{1}{2}

. This matches physics observations, as in Section 5. Now consider another divergent series known as the alternating zeta function

η

. This set converges for any

z > 0

; for example, at

z = 2

, which will eventually approach a limit of zero.

η (2) = \sum_{n}^{\infty} \frac{{(- 1)}^{n - 1}}{n^{2}} = \frac{1}{1^{2}} - \frac{1}{2^{2}} + \frac{1}{3^{2}} - \frac{1}{4^{2}} \dots - 0 + 0 \dots \approx 0.822

(14)

z > 1

we obtain:

ζ (z) - η (z) = \sum_{n}^{\infty} \frac{1}{n^{z}} - \sum_{n}^{\infty} \frac{{(- 1)}^{n - 1}}{n^{z}}

= 2 \sum_{n}^{\infty} \frac{1}{{(2 n)}^{z}} = 2^{1 - z} ζ (z)

ζ (z) = \frac{1}{1 - 2^{1 - z}} η (z)

(15)

Back to Equation (12) the G series. Considering squaring the function, we will obtain

\begin{matrix} G {(z)}^{2} = 1 + 2 z + 3 z^{2} + 4 z^{3} \dots \\ = \sum_{n}^{\infty} n z^{n - 1} \end{matrix}

(16)

Since as defined before

G (z)

is equal to

\frac{1}{1 - z}

. Therefore we can construct a similar convergence for any

z > 1

but for

G {(z)}^{2}

∵ G (z) = \frac{1}{1 - z} \forall | z | > 1

\begin{matrix} ∴ G {(z)}^{2} = {(\frac{1}{1 - z})}^{2} = \frac{1^{2}}{{(1 - z)}^{2}} = \frac{1}{1 - 2 z + z^{2}} \end{matrix}

(17)

Then we can take the derivative of

G (z)

\begin{matrix} G^{'} (z) = lim_{h \leftarrow 0} \frac{G (x + h) - G (x)}{h} \\ = \sum_{n}^{\infty} n z^{n - 1} \end{matrix}

(18)

An interesting fact that arises here the derivative of

G (z)

G^{'} (z)

is equal to the same function squared

G {(z)}^{2}

where

G^{'} (x) = G {(x)}^{2}

From this we can proof that

G (z)

is indeed equal to

\frac{1}{1 - z}

. we can solve the differential equation for

G^{'} (x) = G {(x)}^{2}

where this is proved in Equation (19) and (17).

Proof.

G^{'} (x) = G {(x)}^{2}

Start by separating the variables in the equation

\frac{d G}{G^{2}} = d x

Now, we can integrate both sides to get

\int \frac{1}{G^{2}} d G = \int d x

The integral on the left can be solved by using a substitution

u = G (x)

\frac{1}{u^{2}} = \int d x

= - \frac{1}{u} + C_{1} = x + C_{2}

Where

C_{1}

and

C_{2}

are constants of integration. Then substitute back

u = G (x)

- \frac{1}{G (x)} + C_{1} = x + C_{2}

Rearrange to solve for

G (x)

\frac{1}{G (x)} = - x + C_{3}

Where

C_{3}

is another constant set to

C_{1} - C_{2}

. Finally, solve for

G (x)

G (x) = \frac{1}{C_{3} - x}

Now if we set

C_{3}

to 1 and replace x with z we will end with

G (z) = \frac{1}{1 - z}

□

Therefore again when

z = - 1

using analytic continuation we can define P which is

G {(- 1)}^{2}

P = G {(- 1)}^{2} = {(\frac{1}{2})}^{2} = \sum_{n}^{\infty} n {(- 1)}^{n - 1} = \frac{1}{1 - 2 (- 1) + {(- 1)}^{2}} = \frac{1}{4}

(19)

However Lets define an infinite series of natural numbers n

R = \sum_{n = 0}^{\infty} n = 1 + 2 + 3 + 4 + 5 + \dots

(20)

This could be

G {(1)}^{2}

but unfortunately

G (z)

is for values

z < 1

. So Ramanujan introduced a new series

R (z) = \sum_{n}^{\infty} n {(- z)}^{n - 1} = 1 - 2 z + 3 z^{2} - 4 z^{3} + 5 z^{4} \dots

(21)

Which also converges only at

z < 1

. Then the new series Ramanujan introduced

R (z)

can be subtracted from

G {(z)}^{2}

to give us:

\begin{matrix} G {(z)}^{2} - R (z) & = (1 + 2 z + 3 z^{2} + 4 z^{3} + 5 z^{4} + 6 z^{5} \dots) - (1 - 2 z + 3 z^{2} - 4 z^{3} + 5 z^{4} - 6 z^{5} \dots) \end{matrix}

(22)

\begin{matrix} = 4 z + 8 z^{3} + 12 z^{5} + 16 z^{7} \dots = 4 z (1 + 2 z^{2} + 3 z^{4} + 4 z^{6} \dots) \end{matrix}

(23)

\begin{matrix} = 4 z \sum_{n}^{\infty} n z^{2 (n - 1)} \end{matrix}

(24)

We are interested in this when

G {(z)}^{2} - R (z)

is at

z = - 1

if we took the result from Equation (25),

n {(- 1)}^{2 (n - 1)}

can be simplified to n

Proof.

Since A negative base raised to an even power equals a positive and 1 to any power is 1

n {(- 1)}^{2 n - 2} = n \times 1^{2 n - 2} = n \times 1 = n

□

Therefore from This we can say that

G {(- 1)}^{2} - R (- 1)

can be written in terms of

R

in Equation (21)

G {(- 1)}^{2} - R (- 1) = 4 (- 1) \sum_{n}^{\infty} n {(- 1)}^{2 (n - 1)} = - 4 \sum_{n}^{\infty} n = - 4 R

(25)

Then we can investigate the behaviour of

R (z)

z = - 1

, which will simply simplify to

R

following:

R (- 1) = \sum_{n}^{\infty} n {(- (- 1))}^{n - 1} = \sum_{n}^{\infty} n = R

(26)

From Equations (20), (25)–(27). We can write a full computable equation to find

R

G {(- 1)}^{2} - R (- 1) = \frac{1}{4} - R

\frac{1}{4} - R = - 4 R

R = \sum_{n}^{\infty} n = - \frac{1}{12}

(27)

Which states that the sum of all natural numbers to infinity is $- \frac{1}{12}$ . This can be written in the form of the zeta function

ζ

R = - \frac{1}{3} P = - \frac{1}{12} = ζ (- 1)

(28)

This may seem like just number manipulation, but it matches physics observations as in Section 5. Currently, we lack a framework explaining this or a framework to deal with infinities in a logical sense. This also contradicts infinity because if infinity were true, the set

R

would keep adding one ’forever’, resulting in ’∞’, but the answer to the sum of all natural numbers (this sentence states that they are finite) is negative. A full framework to explain this and a unique way to visualize numbers is in Chapter 7. New Number Theory

Let’s consider a different way of thinking, where we will question the existence of infinity and try to deal with infinite series in a different way. We propose that infinity is an assumption made that is full of paradoxes rather than a reality in mathematics as well as in our universe and physics. We propose to match physics and math by making a framework to deal with infinity. Imagine if there is a finite amount of numbers, hence a finite amount of everything. We propose a finite upper and lower limit, Y and

- Y

, where no positive number can exist bigger than Y and no negative number can exist smaller than

- Y

. This challenges the way of thinking of linear continuation of numbers. This Y is so huge that all of our current numbers we have discovered, like the googolplex

10^{g o o g o l}

, only lie within the interval of 3 percent of Y. Through this chapter, we aim to explore the new properties of numbers, answer possible questions, and make the axioms (foundations) of the theory.

8. Increase of Numbers

The behavior of numbers as they increase within the proposed finite framework presents a fascinating departure from our current understanding of mathematical linearity. In traditional mathematics, the function

f (x) = x

(29)

or in other words

y = x

where y goes from "-infinity" to "infinity". This linear behavior is a fundamental concept taught in introductory mathematics courses and is used in various fields to model relationships between quantities.

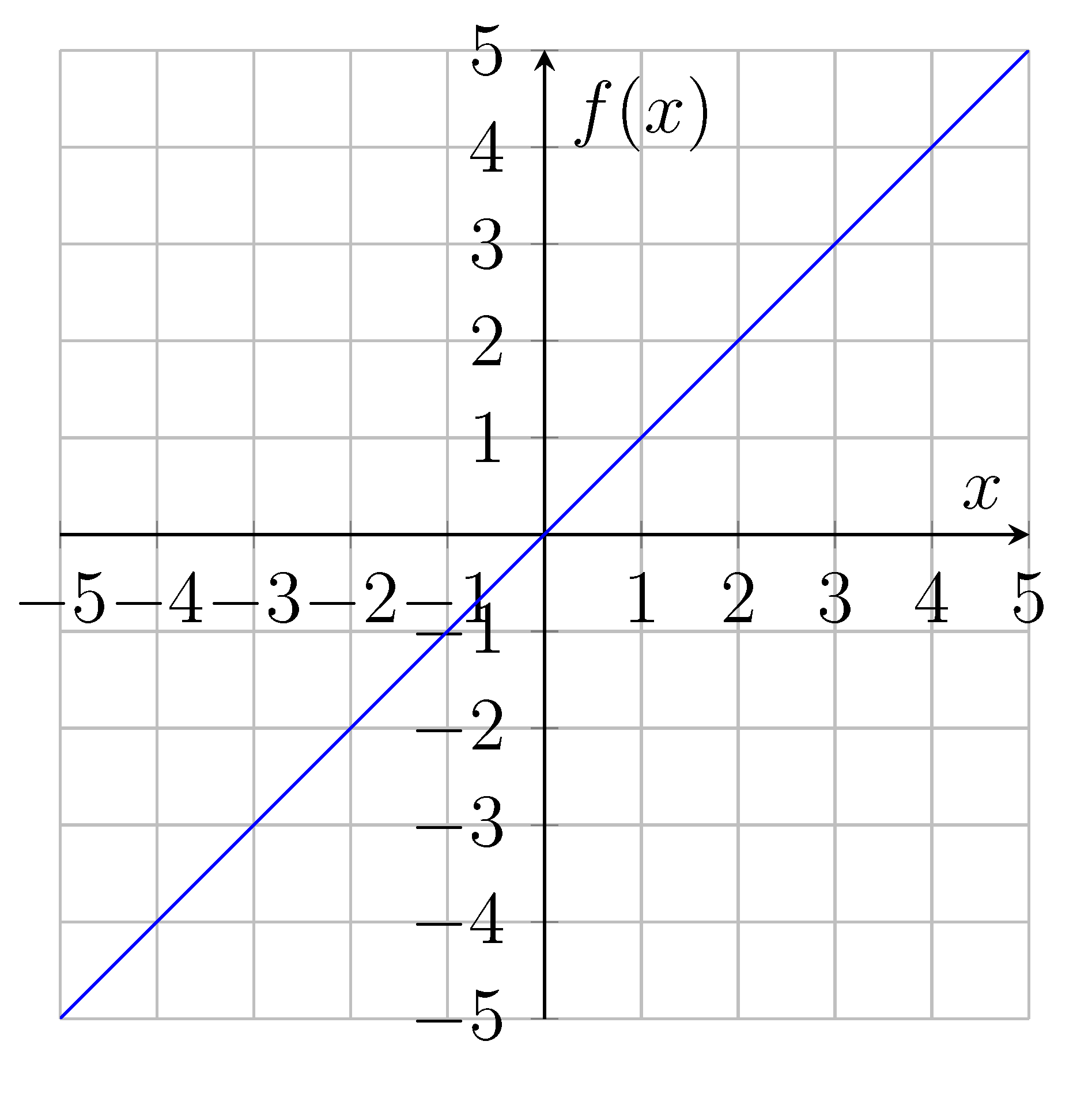
Here, each successive integer corresponds to a consecutive unit increase along the x-axis, mirroring the intuitive notion of counting. In the number line, it follows the same linear pattern

f (x) = x

; this is written as:

- \infty \dots - 3, - 2, - 1, 0, 1, 2, 3 \dots \infty

(30)

However, the proposed finite framework challenges this notion and expression by using a finite range defined by a maximum positive Y and a minimum negative

- Y

. To comply with this paper, instead of using infinity on the x and y axes, the number line for each dimensional axis will be written as

- Y \dots - 1, 0, 1 \dots Y

(31)

Axiom 1.

The biggest number that can exist in the number line is Y and the smallest number is

- Y

To make everything clear, all the work that is done in this chapter is within the proposed framework of a finite limit of numbers going through the interval of

[- Y, Y]

. This increase in numbers is also thought to be linear since

f (x) = x

with a slope of

\frac{d}{d x} f (x) = 1

, following:

\frac{d}{d x} f (x) = lim_{x \to 0} \frac{x + h - x}{h} = lim_{x \to 0} \frac{h}{h} = 1

(32)

But let’s consider a hypothetical case where a function

f (x) = x

does not always return x, but only behaves linearly on a given interval from

t_{1}

t_{2}

. This interval represents all of the numbers we currently know and compute. But if we look at the bigger picture, before and after these intervals, the function does not behave linearly but rather the slope tends to eventually be 0 at

x = Y

and

- Y

, where it is written as:

\begin{matrix} lim_{x \to Y} f^{'} (x) = 0 \\ lim_{x \to - Y} f^{'} (x) = 0 \end{matrix}

(33)

And at

x = 0

, as in Equation (32), the function behaves normally linear, according to the Intermediate Value Theorem (IVT), which states that if a function is continuous on a closed interval, it takes on every value between the values it attains at the endpoints of the interval. Therefore, according to IVT,

f^{'} (x)

must attain all values between 0 and 1 over these intervals, indicating a linear behavior of

f (x)

within only the range when

f^{'} (x) = 1

. This implies that in this hypothetical case, its derivative function

f^{'} (x)

must have a range of

[0, 1]

from

- Y

to 0 and

[1, 0]

from 0 to Y. This will give us the inequalities of:

\begin{matrix} For - Y \leq x \leq 0 : 0 \leq f^{'} (x) \leq 1 \\ For 0 \leq x \leq Y : 1 \leq f^{'} (x) \leq 0 \end{matrix}

(34)

From this inequalities we can make a conclusions to construct a function

f^{'} (x)

that matches our hypothetical predictions from Equation (34) and (33). We have a maximum limit of 1 so the equation can be started by:

f^{'} (x) = 1

Then, since

f (x)

is as simple as returning x multiplied by the slope of f at x (in observable algebra this slope is always 1, but in our case, we need the slope to be variable based on x where at Y the value should be 1 so

1 - 1 = 0

and at 0 the value should be 0 so

1 - 0 = 1

, which matches Equations (33) and (32)). This can be simply written as

\frac{x}{Y}

, since we are subtracting one from this value, it will be:

f^{'} (x) = 1 - \frac{x}{Y}

This equation

f^{'} (x)

only satisfies the second inequality from Equation (34), since

f^{'} (Y) = 0

and

f^{'} (0) = 1

. But the problem arises at

x = - Y

where

f^{'} (- Y) = 2

, which breaks the conditions. To fix this, we can square the term

\frac{x}{Y}

. This adjustment will still satisfy the conditions of ranging from

[1, 0]

from 0 to Y, but also introduce a symmetrical behavior in the negative plane since the negative sign will be canceled out by the squaring. The new

f^{'} (x)

will be:

f^{'} (x) = 1 - {(\frac{x}{Y})}^{2}

This function satisfies all the inequalities from Equation (34) since:

f^{'} (- Y) = 0, f^{'} (0) = 1, f^{'} (Y) = 0

But the only remaining problem is that this function is continuous beyond Y and

- Y

, which is not desired, as in this framework any function that exists can only have a domain of

[- Y, Y]

. However, if we observe the behavior of

f^{'} (x)

we currently have beyond Y and

- Y

, the noticed behavior is that the value is always negative, as the value from

{(\frac{x}{Y})}^{2}

will be bigger than 1. So, to define the finite domain for

f^{'} (x)

, we can take the square root of

1 - {(\frac{x}{Y})}^{2}

, where if we try going beyond Y or

- Y

, the answer won’t be real and will still satisfy all the inequalities from equation 34. Leaving us with a final

f^{'} (x)

equal to:

f^{'} (x) = \sqrt{1 - {(\frac{x}{Y})}^{2}}

(35)

This function represents the slope of the simplest function that represents the increase of numbers but in the bigger picture, considering we are approaching the edges of numbers, Y, where the increase is not linear anymore with a slope of 1 but rather the slope is

\sqrt{1 - {(\frac{x}{Y})}^{2}}

. Graphing this function with

Y = 100 %

, it will look like a semicircle ranging from

- 100

to 100 with a max value of 1 and reaching 0 at both edges. Exactly as expected in our framework.

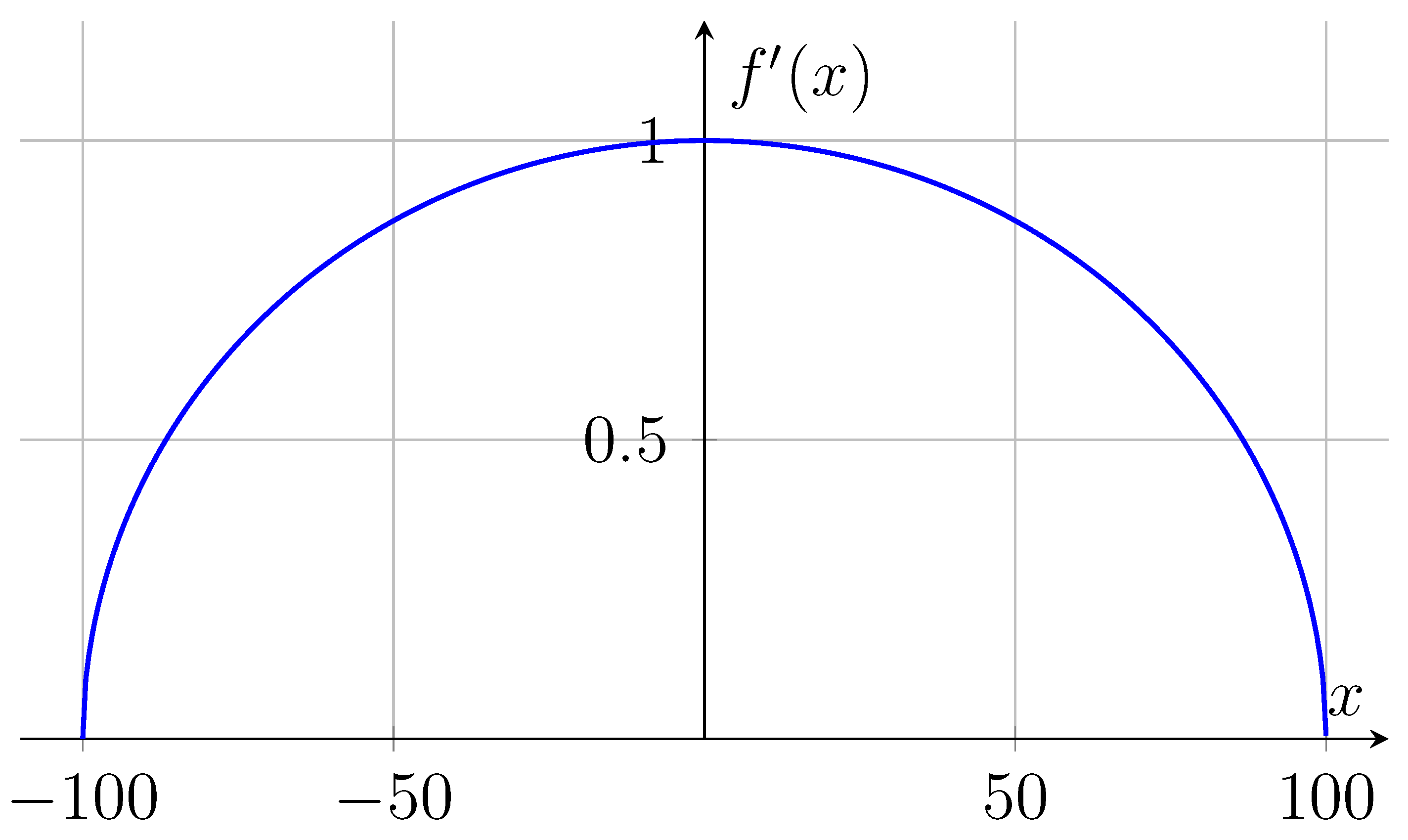
Question 1.

If numbers do not increase linearly, how is our current mathematics working and making sense?

Answer:Consider, as said before, that Y is so unimaginably huge that all the numbers we deal with do not even come close to

5 %

of Y. Therefore, for

f^{'} (x)

in Equation (35), the term

{(\frac{x}{Y})}^{2}

eventually converges to zero if x is small enough compared to Y. This leaves us with

\sqrt{1} = 1

, which explains why in our everyday algebra we see a consistent increasing slope of 1. However, consider dealing with values reaching the edge of numbers, Y, as often happens in physics. That is why our current model of math breaks. Due to the incompleteness of the generally accepted mathematical model.

Now that we have the slope function

f^{'} (x)

that represents the increase of numbers from

- Y

to Y, but since the slope is not always 1, therefore,

f (x) = x

only represents the interval where

f^{'} (x) = 1

. However, we need a complete

f (x)

that can handle any number from

- Y

to Y. Fortunately, we can achieve this by taking the integral of

f^{'} (x)

, considering

C = 0

. We can start by:

f (x) = \int f^{'} (x) d x = \int \sqrt{1 - {(\frac{x}{Y})}^{2}} d x

Then we can substitute

u = \frac{x}{Y}

and

d u = Y d x

getting:

\int \sqrt{1 - {(\frac{x}{Y})}^{2}} d x = Y \int \sqrt{1 - u^{2}} d u

Subsequently, trigonometric substitution can be used by setting

u = \sin (t)

to transform the integral, given that

d u = \cos (t) d t

and

1 - \sin^{2} (t) = \cos^{2} (t)

. When applied, we get:

Y \int \sqrt{1 - u^{2}} d u = Y \int \sqrt{1 - \sin {(t)}^{2}} \cos {(t)}^{2} d t

= Y \int \sqrt{\cos {(t)}^{2}} \cos (t) d t = Y \int \cos {(t)}^{2} d t

Then, the trigonometric identity

\cos^{2} (t) = \frac{1 + \cos (2 t)}{2}

can be used to expand the expression as follows:

Y \int \cos {(t)}^{2} d t = Y \int \frac{1 + \cos (2 t)}{2} d t = \frac{Y}{2} \int 1 + \cos (2 t) d t

Now, we can evaluate the integral, giving us:

\frac{Y}{2} \int 1 + \cos (2 t) d t = \frac{Y}{2} (t + \frac{\sin (2 t)}{2})

Since

u = \sin (t)

, we can substitute back u as

t = \sin^{- 1} (u)

in our equation to complete the integral:

\frac{Y}{2} (t + \frac{\sin (2 t)}{2}) = \frac{Y}{2} (\sin^{- 1} (u) + \frac{\sin (2 \sin^{- 1} (u))}{2})

Finally, we substitute back

u = \frac{x}{Y}

\frac{Y}{2} (\sin^{- 1} (u) + \frac{\sin (2 \sin^{- 1} (u))}{2}) = \frac{Y}{2} (\sin^{- 1} (\frac{x}{Y}) + \frac{\sin (2 \sin^{- 1} (\frac{x}{Y}))}{2})

By simplifying the equation, we finally obtain the required

f (x)

f (x) = \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

(36)

This function represents the most basic operation in mathematics but in a completed model that can deal with any numbers in the linear interval or the non-linear one. If x is small enough, this function will just be $f (x) = x$ , which explains our current model of mathematics and further proves this formula:

Theorem 1.

For numbers small enough compared to Y, the proposed function

f (x)

in Equation (36) will be linear:

f (x) = x

Proof.

Consider the equation

f (x)

we derived earlier in Equation (36).

f (x) = \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

We have two terms to simplify, given that x is small compared to Y, which represents all known numbers. The first term is:

\frac{Y}{2} \sin^{- 1} (\frac{x}{Y})

The arc sine function can be expanded using the Taylor series for

| x | \leq 1

, which holds true since, in our approach, the maximum value of

\frac{x}{Y}

is 1. The Taylor series expansion is given by:

\sin^{- 1} (x) = \sum_{n = 0}^{\infty} \frac{(2 n)!}{4^{n} {(n!)}^{2} (2 n + 1)} x^{2 n + 1} = x + \frac{x^{3}}{6} + \frac{3 x^{5}}{40} + \frac{5 x^{7}}{112} + \dots

This series converges for

| x | \leq 1

. Subsequently, when x is small, which holds true for everyday numbers as

\frac{x}{Y}

is unimaginably small, the higher-order terms after x in the Taylor series become negligible compared to the first term. Therefore, we can approximate

\sin^{- 1} (x)

by truncating the series, starting from

\frac{x^{3}}{6}

since they converge to 0. This leaves us with approximately xwhen x is small enough:

\sin^{- 1} (x) \approx x

Then we can go back to our first term to simplify it based on the converged arc sin function, which is given as

1) \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) = \frac{Y}{2} \frac{x}{Y} = \frac{x}{2}

Now, simplifying the second term:

\frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

Since

{(\frac{x}{Y})}^{2}

converges to zero in this specific case giving:

{(\frac{x}{Y})}^{2} \approx 0

Therefore it leaves us with

\sqrt{1}

so the whole term can be written us:

2) \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} = \frac{x \sqrt{1}}{2} = \frac{x}{2}

From point 1 and 2 we can rewrite

f (x)

in the case of x is far from Y as:

f (x) = \frac{x}{2} + \frac{x}{2} = x

This proves that our daily mathematics matches our approaches within a given linear interval. However, this algebra breaks down when we approach numbers outside the linear interval, nearing Y, as indicated in Equation (33). Moreover, this approach provides a complete mathematical model to handle Y. □

Now we can explore the properties of

f (x)

. First, we will graph the function by setting

Y = 100 %

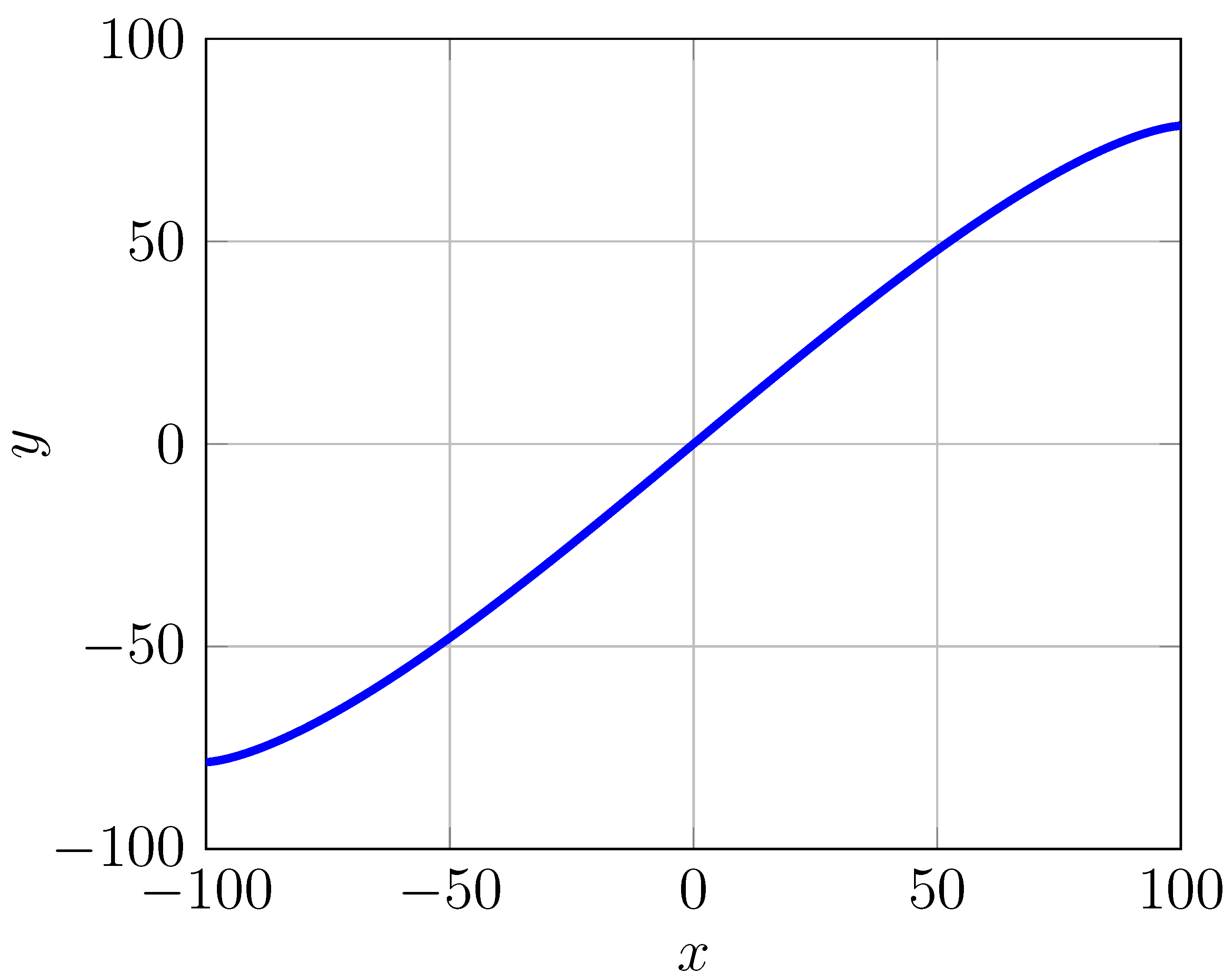
The domain of

f (x)

is all possible numbers that can exist from

- Y

to Y, and within our framework, this is the domain of any continuous function.

Axiom 2.

Any continuous function that exists can only have a domain from

- Y

to Y.

To determine the range of

f (x)

, since the increase is not always linear, the range is no longer the same as the domain. In order to find the range, we need to compute

f (Y)

and

f (- Y)

. For

f (Y)

, which is the maximum of the function

f (x)

within the domain

[- Y, Y]

, it can be represented as:

\begin{matrix} f (Y) = \frac{Y}{2} \sin^{- 1} (\frac{Y}{Y}) + \frac{Y \sqrt{1 - {(\frac{Y}{Y})}^{2}}}{2} = \frac{Y}{2} \sin^{- 1} (1) + \frac{Y \sqrt{1 - 1}}{2} \\ = \frac{Y}{2} \cdot \frac{π}{2} + 0 = \frac{Y}{4} π \end{matrix}

(37)

While for

f (- Y)

, which is the minimum of our function

f (x)

, also lies within the range for the domain of

[- Y, Y]

\begin{matrix} f (- Y) = \frac{Y}{2} \sin^{- 1} (\frac{- Y}{Y}) + \frac{- Y \sqrt{1 - {(\frac{- Y}{Y})}^{2}}}{2} = \frac{Y}{2} \sin^{- 1} (- 1) + 0 \\ = \frac{Y}{2} \cdot \frac{- π}{2} = - \frac{Y}{4} π \end{matrix}

(38)

From Equations (37) and (38), we get the minima at

x = - Y

with a value of

- \frac{Y}{4} π

and the maxima at

x = Y

with a value of

\frac{Y}{4} π

. This shows the properties of

f (x)

on the negative and positive planes and constructs the inequality of:

For - Y \leq x \leq Y : - \frac{Y}{4} π \leq f (x) \leq \frac{Y}{4} π

(39)

From this inequality, we can draw some conclusions. Although, as proven in Proof 8, at the interval

[- t % Y, t % Y]

f (x)

will simply return the number x, when numbers grow significantly approaching Y, the changes start to become too significant to ignore. Therefore, to have a complete mathematical model, any number 'a' cannot be written as just 'a'; it have to be written as

f (a)

a \to f (a)

(40)

Axiom 3.

The increase of numbers is not always linear in a given number line from

- Y

to Y, so any term x can not be written as x but rather

f (x)

Axiom 4.

Mathematical operations break outside the linear interval since the increase is not linear anymore from axiom 3, therefore Sophy-Peter equations have to be used.

The other thing to consider is that the way we perform operations cannot hold true with operations involving numbers outside the linear interval, since numbers have other properties according to axiom 3 and Equation (40). A method to perform operations with Y is also necessary, since no numbers larger than Y can exist. This allows us to deal with numbers correctly when Y appears in physics, for example, and our normal mathematics breaks. Therefore, we developed the Sophy-Peter equations in Section 10. But before addressing this, we need to define what happens beyond Y and before

- Y

Since we are considering that no number larger than Y exists, it implies that between any two neighboring integers, there cannot be more than Y numbers. This leads us to conclude that there is the smallest positive and the largest negative number, from which we can define two more axioms:

Axiom 5.

The smallest positive number that can exist on the number line is E, and the largest negative number is

- E

Axiom 6.

On the interval

(a, b]

, the maximum number of numbers is Y, where a and b are any neighboring integers on the number line and

∣ a ∣ < ∣ b ∣

. Moreover, the smallest and largest numbers on the interval

(a, b)

are

f (a + E)

and

f (b - E)

respectively, if a and b are non-negative, and

f (b + E)

and

f (a - E)

if a and b are non-positive.

This leads us to the equation which we can prove since Y is a number:

Theorem 2.

Y E = 1

Proof.

We know that:

x \frac{1}{x} = 1

Where

x \in [- Y, Y]

. That means that at some point x will be equal to Y, so:

Y \frac{1}{Y} = 1

We can divide 1 into Y pieces which is representing interval

(0, 1]

[E, 1]

, therefore:

\frac{1}{Y} = E

(41)

Therefore:

\frac{1}{E} = Y

(42)

and:

Y E = 1

(43)

□

Since on the interval

(0, 1]

we can have a maximum of Y numbers, and E is the smallest, this implies one more axiom:

Axiom 7.

E and

- E

are not only the smallest possible positive and the largest negative numbers, respectively, but also the smallest increment and decrement that can be applied to a number.

This means that on the interval

(0, 1]

[E, 1]

, we compute in the following way:

E, 2 E, 3 E, \dots, Y E (or 1)

Now we can move to the question of what happens after Y.

9. What is after Y?

If, in this framework, no number can exist larger than Y or smaller than

- Y

, then a method to handle operations that attempt to cross Y is necessary. In this section, we introduce a new behavior for numbers after Y, where they will actually decrease according to an inverse asymmetrical function of

f (x)

, and the x-axis goes backward instead of forward after Y.

Consider reaching Y. Since the slope of the increasing function at Y is:

lim_{x \to Y} f^{'} (x) = \frac{d}{d x} f (Y) = \sqrt{1 - \frac{Y^{2}}{Y^{2}}} = 0

And due to the way of thinking Y is the maximal possible number, so

Y + a

- Y - a

, where

a > 0

, cannot exist . Therefore, we can conclude that on the number line, if any number tries to go beyond Y, the function x value will decrease based on a defined slope, and it will transition to a new function

g (x)

. It will move back or forth on the number line by

f (a)

(a factor of

- 1

) steps, and your values are now on a new function

g (x)

, written as:

\begin{matrix} f (" Y + a ") & = g (Y - f (a)) \\ f (" - Y - a ") & = g (- Y + f (a)) \end{matrix}

(44)

Where $" x "$ means x does not exist; this, in other words, can be said as

Y | > a

. Before proceeding, we need to make two definitions:

Definition 1. Increasing function

This represents

f (x)

, since it represents the increase of numbers from

- Y

to Y.

Definition 2. Decreasing function

This represents

g (x)

, since it represents how numbers decrease when we try to go beyond Y or

- Y

Since the decreasing function

g (x)

is a continuation of the increasing function

f (x)

, they have to intersect at the first and last points, in other words, where

x = [- Y, Y]

. The functions have to touch at those points since we are moving from increasing to decreasing; if they do not, then we cannot transition between them. Also, they have to intersect at

x = 0

since both of them must cross the origin, as this point is the connection of the positive and negative planes. Therefore,

g (x)

must obey this set of inequalities:

\begin{matrix} f (- Y) & = g (- Y) \\ f (0) & = g (0) \\ f (Y) & = g (Y) \end{matrix}

(45)

And since

g (x)

is asymmetrical from

f (x)

, no point other than these three can intersect.

\forall x \in] - Y, Y [, x \neq 0 : f (x) \neq g (x)

(46)

g (x)

has reversed its effect by

- 1

from

f (x)

since it represents decreasing, which means where the increasing function is convex, the decreasing functions have to be concave, and vice versa. Where

f (x)

has a slope of 1,

g (x)

must have a slope of 0. Since

f^{'} (0) = 1

, therefore

g^{'}

at 0 is

lim_{x \to 0} g^{'} (x) = 0

(47)

To construct

g (x)

, we need to consider

f (x)

, where we need to convert its concave-up parts to down and down to up, and maintain the maximum value at

\frac{π}{4} Y

and a minimum value of

- \frac{π}{4} Y i

. Let’s take a look at the maximum value of f behavior at

x = Y

from equation 37.

1) f (Y) = \frac{Y}{2} \sin^{- 1} (\frac{Y}{Y}) + \frac{Y \sqrt{1 - {(\frac{Y}{Y})}^{2}}}{2} = \frac{π}{4} Y + 0

It is seen here that in order to maintain the first inequality in the set of inequalities in Equation (47), the first term in the equation must remain untransformed. To further prove this, we can examine

f (- Y)

, which is the minimum value from Equation (38).

2) f (- Y) = \frac{Y}{2} \sin^{- 1} (\frac{- Y}{Y}) + \frac{- Y \sqrt{1 - {(\frac{- Y}{Y})}^{2}}}{2} = - \frac{π}{4} Y + 0

Where also if the first term

\frac{Y}{2} \sin^{- 1} (\frac{x}{Y})

is remained unchanged the second inequality from Equation (47) is satisfied. Finally,

f (0)

is:

3) f (0) = \frac{Y}{2} \sin^{- 1} (\frac{0}{Y}) + \frac{0 \sqrt{1 - {(\frac{0}{Y})}^{2}}}{2} = 0 + 0

Obviously, here, if the transformation is applied to any of the terms, the third inequality from Equation (47) will be satisfied since

f (0)

will always be 0. Now, from Equation (46),

g (x)

must satisfy the inequality of:

For - Y < x < Y and x \neq 0 : g (x) \neq f (x)

But from Equation (47), we know that

g (x)

should have reversed convexity at given x points; at the same time, we need to keep the first term untransformed as shown in points 1 and 2. So, to do this, let’s consider the other term, since it is not used and will not affect any of the three inequalities.

\frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

Example 9.1.

Consider a case when

x = \frac{Y}{2}

, the first term in

f (x)

can be computed as:

4) \frac{Y}{2} \sin^{- 1} (\frac{\frac{Y}{2}}{Y}) = \frac{Y}{2} \sin^{- 1} (\frac{1}{2}) = \frac{Y}{2} \frac{π}{6} = \frac{π}{12} Y

Then the second term is repented as:

5) \frac{\frac{Y}{2} \sqrt{1 - {(\frac{\frac{Y}{2}}{Y})}^{2}}}{2} = \frac{\frac{Y}{2} \sqrt{1 - \frac{1}{4}}}{2} = \frac{\frac{Y}{2} \frac{\sqrt{3}}{2}}{2} = \frac{\sqrt{3}}{8} Y

From 3 and 4, the normal

f (x)

for the value of

\frac{Y}{2}

can be computed by

\frac{π}{12} Y

and

\frac{\sqrt{3}}{8} Y

giving us:

f (\frac{Y}{2}) = \frac{π}{12} Y + \frac{\sqrt{3}}{8} Y = \frac{2 π + 3 \sqrt{3}}{24} Y

Now let’s consider transforming the curve by multiplying the second term by -1 so the graph concavity will be reversed following:

\frac{π}{12} Y + \frac{\sqrt{3}}{8} Y (- 1) \frac{π}{12} Y - \frac{\sqrt{3}}{8} Y = \frac{2 π - 3 \sqrt{3}}{24} Y

From example 9.1, we can conclude that

g (x)

can be constructed by multiplying the second term by

- 1

, which will still obey points 1 and 2. The final

g (x)

can be written as:

g (x) = \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

(48)

Let’s examine the behaviour of

g (x)

at 3 intersection points

- Y, 0

and Y:

6) g (Y) = \frac{Y}{2} \sin^{- 1} (\frac{Y}{Y}) - \frac{Y \sqrt{1 - {(\frac{Y}{Y})}^{2}}}{2} = \frac{π}{4} Y - 0

7) g (0) = \frac{Y}{2} \sin^{- 1} (\frac{0}{Y}) - \frac{0 \sqrt{1 - {(\frac{0}{Y})}^{2}}}{2} = 0 + 0

8) g (- Y) = \frac{Y}{2} \sin^{- 1} (\frac{- Y}{Y}) - \frac{- Y \sqrt{1 - {(\frac{- Y}{Y})}^{2}}}{2} = - \frac{π}{4} Y - 0

Which stratify the three inequalities from 47. but to proof there is no other intersections we have to solve the equation of

f (x) = g (x)

. Therefore written as:

Proof.

\frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} = \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

First starting by subtracting the first term

\frac{Y}{2} \sin^{- 1} (\frac{x}{Y})

from both sides:

\frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} = - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

From this we can multiply both the R.H.S and the L.H.S with 2 leaving us with:

x \sqrt{1 - {(\frac{x}{Y})}^{2}} = - x \sqrt{1 - {(\frac{x}{Y})}^{2}}

By simplifying this equation we will end up with

x^{2} = Y^{2}

, then by taking the square root of both we will have:

x = \pm Y, x = 0

Which proves that the function only intersects at this points. □

Finally, we can graph

f (x)

and

g (x)

with setting

Y = 100 %

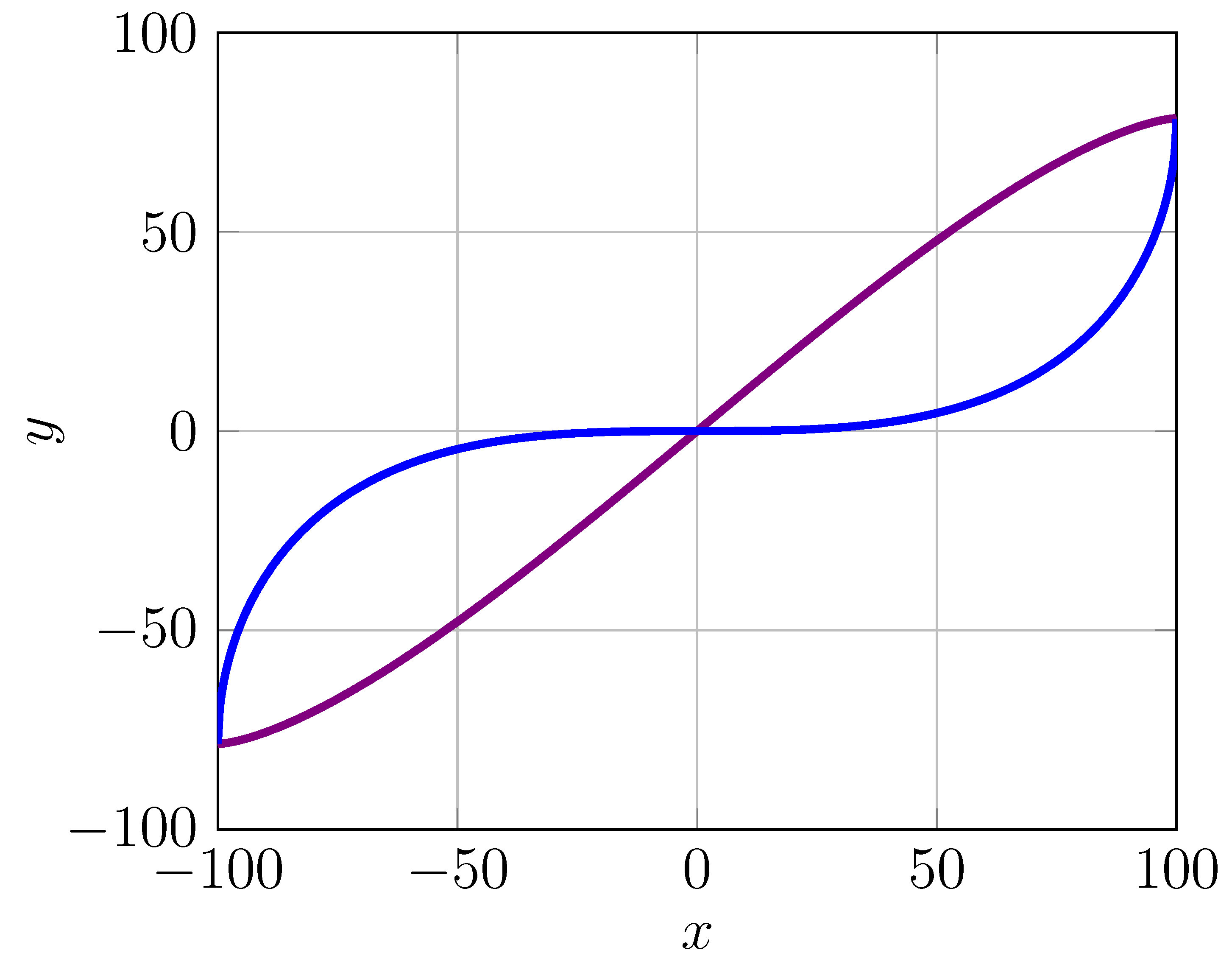
We can see from this graph the behaviour of the function

g (x)

compared to

f (x)

. Looking back at Equation (44):

" Y + a " \to f (" Y + a ") = g (Y - f (a))

This will be discussed briefly in Section 10. For now, the conclusion drawn from this is that on the number line, numbers start with the increasing function from

- Y

to Y, which represents a half cycle. Then, when trying to go beyond it, we end with the values on the decreasing function

g (x)

from Y to

- Y

, representing a full cycle.

It is worth noting that, as seen in the graph, the behavior of numbers on the decreasing function

g (x)

is entirely different from our observable algebra, and the linear operations we perform no longer make sense.

The next step is to examine the behavior of the slope of

g (x)

in the interval of:

g^{'} (x) = \frac{d}{d x} (\frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})

By differentiating each term and simplifying the equation:

g^{'} (x) = \frac{d}{d x} (\frac{Y}{2} \sin^{- 1} (\frac{x}{Y})) - \frac{d}{d x} (\frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})

We will end with the slope of

g (x)

being equal to:

g^{'} (x) = \frac{x^{2}}{Y} \cdot \frac{1}{Y \sqrt{1 - {(\frac{x}{Y})}^{2}}}

(49)

In Equation (47) we stated that

g^{'} (0)

must be zero, if we test this on Equation (49) we will get:

g^{'} (0) = \frac{0}{Y} \cdot \frac{1}{Y \sqrt{1 - {(\frac{0}{Y})}^{2}}} = 0

Which further proof the decreasing function

g (x)

. Finally we can graph the behaviour of

g^{'} (x)

compared to

f^{'} (x)

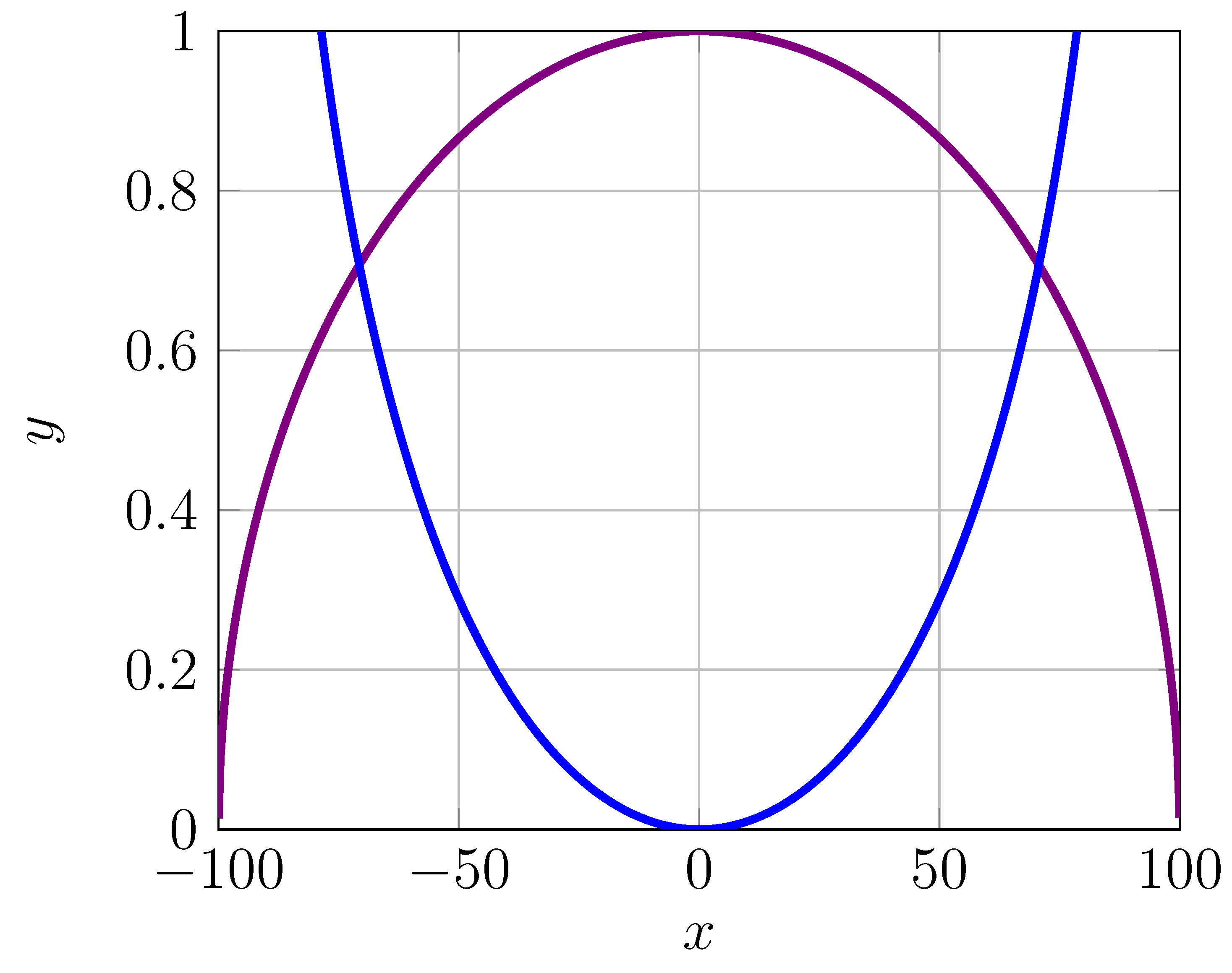
It is obvious that

g^{'} (x)

has the reverse effect of

f^{'} (x)

, but the two functions are not symmetrical, as seen in both graphs. The slope of

g (x)

x = Y

is actually Y, which is the largest value possible there. From this, we can define two new axioms for our theory.

Axiom 8.

Numbers attempting to go beyond Y or before

- Y

will end up obeying the Sophy-Peter equations, which dictate that they will go back or forward on the number line via the decreasing function

g (x)

Axiom 9.

Since the addition of positive numbers can never yield a negative number, but on the decreasing function

g (x)

numbers are decreasing, so after reaching 0, numbers will continue on the increasing function.

Axiom 10.

It is possible to switch from the decreasing to the increasing function by changing planes, from positive to negative or vice versa.

10. Sophy-Peter Equations

In this section, we develop a set of equations known as the Sophy-Peter equations. These equations are designed to handle mathematical operations such as addition (+), subtraction (−), and multiplication (×) within a complete model, dealing with the non-linear growth of numbers as discussed in Section 8. Additionally, these equations address scenarios where numbers operating together attempt to cross Y or

- Y

, and, as outlined in Section 9, how this transition leads to the decreasing function

g (x)

. First, let’s define a new operator trying

| >

that can return either

T r u e

F a l s e

Definition 3.

The trying operator

| >

: an operator that functions between two values and a target value, where the result of an operation is attempting to exceed the target value. It is crucial that this involves an operation between two values, since sometimes the result cannot exist. If an operation is attempting to produce a result greater than a target value, then the operator returns

T r u e

; otherwise, it returns

F a l s e

Operations can include addition, multiplication, division, subtraction, etc.

Example 10.1.

99 + 8 | > 100 \to T r u e

\frac{99}{0.5} | > 100 \to T r u e

8 + 6 | > 100 \to F a l s e

\frac{100}{2} | > 100 \to F a l s e

Y | > Y \to F a l s e

" Y + 1 " | > Y \to T r u e

The last example with "

Y + 1

" is the most illustrative, as the result of this operation does not exist since all existing numbers lie within the interval

[- Y, Y]

. At this point, the difference between

| >

and > becomes clear: > requires comparing two existing values, whereas

| >

can handle values that do not exist or are unreasonable.

Definition 4.

The trying operator ≤: an operator that functions between two values and a target value, where the result of an operation is attempting to be less than the target value. If an operation is attempting to produce a result less than a target value, then the operator returns

T r u e

; otherwise, it returns

F a l s e

Example 10.2.

5 - 10 \leq 2 \to T r u e

- Y + 1 \leq - Y \to F a l s e

" - Y - 1 " \leq - Y \to T r u e

Since we will be redefining the basic arithmetic operations in the observable algebra to accommodate all the newly discovered properties of numbers to match our physical universe, we need to redesign the operators in the observable algebra so we don’t confuse them with the universal function presented in the Sophy-Peter equations.

10.1. Observable Algebra Operators

The proposed designs for the operations in the Observable Algebra are based on the terms "absolute plus, minus, times", which mean that they result in linear addition, subtraction, or multiplication respectively, without considering the non-linear behavior of the

f (x) = x

function. This function is proved to be incomplete and is given a complete

f (x)

in Section 8. We propose to present them as absolute operators so they do not get mixed up with the Sophy-Peter ones. They are redesigned as:

\begin{matrix} a + b = a | + | b \\ a - b = a | - | b \\ a \times b = a | \times | b \end{matrix}

(50)

Please consider that this only applies to Observable Algebra, not to the completed universal model.

Since observable algebra lies in the linear interval we can add an axiom for the framework considering dividing as

Axiom 11.

The division of a linear number by any number a, where

| a | \geq 1

, will result in a number from the linear interval where

f^{'} (x) = 1

10.2. Universal Equations

Now, in order to be able to perform complex operations within the new framework, as in Section 12, and be able to solve the zeta equation based on a finite number of numbers, as in Chapter 21, we need to redevelop basic arithmetic operations to account for the non-linear growth of numbers. Flashback to the increasing and decreasing functions

f (x)

and

g (x)

, respectively. The function

f (x)

doesn’t actually perform any operations; it just returns the same x. However, since the increase of x isn’t always 1, it will be different, but within the linear interval,

f (x) = x

. Thus, we can assign a value n to

f (n)

n \to f (n)

(51)

Where the → here represents that n is assigned to the value of

f (n)

. It is worth noting that we did not use the = sign to avoid confusion, as

1 \neq 2

in the normal sense of what the = sign does. But, as proved in proof 8, numbers that grow significantly, approaching Y:

lim_{x \to Y} x

10.2.1. Sophy-Peter Equation 1

The start may not be the same but behaves based on the slope

f^{'} (x)

; therefore, the number n will be assigned to

f (n)

, where

f (n) \leq n

. Let’s start by universally adding two values, a and b, each of which will have an assigned value represented as:

a \to f (a), b \to f (b)

a \to \frac{Y}{2} s i n^{- 1} (\frac{a}{Y}) + \frac{a \sqrt{1 - {\frac{a}{Y}}^{2}}}{2}

b \to \frac{Y}{2} s i n^{- 1} (\frac{b}{Y}) + \frac{b \sqrt{1 - {\frac{b}{Y}}^{2}}}{2}

Assuming that

a | + | b \leq Y

, where if this is the case, we will use

g (x)

, but it will be demonstrated later. The way this is done to keep track of the slope involves absolutely adding the values of points a and b on the graph of

f (a)

and

f (b)

, therefore ending up at the point representing the real

a + b

, considering

f^{'} (a)

and

f^{'} (b)

. The next slope for the added point is

f^{'} (a + b)

, which will match our predictions in this framework and will allow us to perform calculations. We can write this part as:

\begin{matrix} a + b \to f (a) | + | f (b) = c i f a | + | b \neg Y \\ c = f (c) \to \frac{d}{d c} f (c) = f^{'} (c) \end{matrix}

Where

\neg |

represent the not trying operator.

Example 10.3.

Lets consider an example where we need to get the sum of

a = \frac{Y}{8}

and

b = \frac{Y}{12}

. According to Sophy-Peter we first need to get

f (a)

and

f (b)

f (a) = \frac{Y}{2} \sin^{- 1} (\frac{\frac{Y}{8}}{Y}) + \frac{\frac{Y}{8} \sqrt{1 - {(\frac{\frac{Y}{8}}{Y})}^{2}}}{2} = \frac{Y}{2} s i n^{- 1} (\frac{1}{8}) + \frac{\frac{Y}{8} \frac{3 \sqrt{7}}{8}}{2}

= \frac{3}{50} Y + \frac{3 \sqrt{7}}{128} Y \approx \frac{3}{25} Y

Then

f (\frac{Y}{12})

f (b) = \frac{Y}{2} \sin^{- 1} (\frac{\frac{Y}{12}}{Y}) + \frac{\frac{Y}{12} \sqrt{1 - {(\frac{\frac{Y}{12}}{Y})}^{2}}}{2} = \frac{Y}{2} s i n^{- 1} (\frac{1}{12}) + \frac{\frac{Y}{12} \frac{\sqrt{143}}{12}}{2}

\frac{1}{25} Y + \frac{\sqrt{143}}{288} Y \approx \frac{2}{25} Y

Then to get the universal sum we absolute add the value from both to get c:

c = f (a) + f (b) = \frac{3}{25} Y + \frac{2}{25} Y = \frac{1}{5} Y

Which is indeed much less than the linear observable sum, which will be

\frac{5}{25} Y

, considering that Y is so huge that the smallest difference makes a huge difference. The slope at this point will be:

\frac{d}{d c} f (c) = f^{'} (c) = \sqrt{1 - {\frac{\frac{1}{5} Y}{Y}}^{2}} = \frac{2 \sqrt{6}}{5}

This slope is

< 1

which proof the summation.

Now, the question is: how is the summation done if

a + b | > c

T r u e

? For this, we should apply the axioms in Section 9, where it was said that:

f (" Y + a ") \to g (Y - f (a)) \to 1

But we need to create a universal model where it accounts for a and b if either of them is less than Y but together they exceed Y, therefore they cannot exist. To do so, let’s consider the formula:

a \frac{d}{d a} f (a), b \frac{d}{d b} f (b)

Where it multiplies the slope of f at x with x. Thus, it reduces the value of x by

f^{'} (x)

. It does nothing at the linear interval, but if

f^{'} (x) < 1

, the number will be

< x

, with a minimum of 0 at

f (Y)

, where the result will be 0. Therefore, we can subtract each value as mentioned in point 1 and transfer to the decreasing graph as in Section 9, ending with:

a + b = g (f (a) - f (b))

(52)

This means that adding

Y + Y

will end at the same origin point which match axioms from Section 8 and 9.

Y + Y = g (f (Y) - f (Y)) = g (\frac{Y}{4} π - \frac{Y}{4} π) = g (0) = 0

Example 10.4.

To examine the behavior of adding outside the interval of numbers

[- Y, Y]

, we will consider an example where

a = Y

and

b = 1

. According to our theory and axiom 4, we should end at the point

f (Y) - 1

on the decreasing function g. In order to prove Equation (52), since

a | > b

" Y + 1 " | > Y \to T r u e

From this we can use the addition Sophy-Peter equation (given as in proof 8

f (1)

will be 1 since it is on the linear interval) like:

x - a x i s \to f (Y) - f (1) = \frac{Y}{4} π - 1

y - a x i s \to g (\frac{Y}{4} π - 1)

∴ Y + 1 = g (\frac{Y}{4} π - 1) < Y

From this, we can conclude and write the full first Sophy-Peter equation for adding two numbers as:

\begin{matrix} a + b = \{\begin{matrix} g (f (a) | - | f (b)) \to \frac{d}{d a} f (a), \frac{d}{d b} f (b) \to x = g^{- 1} (f (a) | - | f (b)) & i f | (a | + | b) | | > Y \\ f (a) | + | f (b) & i f | (a | + | b) | \leq Y \end{matrix} \end{matrix}

(53)

10.2.2. Sophy-Peter Equation 2

The second important mathematical operation we need to consider is subtraction. For subtraction, since we are decreasing numbers, the points

a - b

should be placed on the x-axis at a position less than the greatest from a and b. The issue arises if

b > a

, as the result will be negative:

\begin{matrix} 2 | - | 7 = - 5 \end{matrix}

Before we raise the question of

- Y

, we first need, as we did with addition, to create a complete model to account for the non-linear growth. So, using the f function, we get

\begin{matrix} a - b \to f (a) | - | f (b) = c i f a | - | b \geq - Y \\ c = f (c) \to \frac{d}{d c} f (c) = f^{'} (c) \end{matrix}

Example 10.5.

Consider an example where

a = \frac{Y}{4}

and

b = \frac{Y}{2}

. According to Sophy-Peter equation 2 we will get

f (a)

and

f (b)

f (a) = \frac{Y}{2} \sin^{- 1} (\frac{\frac{Y}{4}}{Y}) + \frac{\frac{Y}{4} \sqrt{1 - {(\frac{\frac{Y}{4}}{Y})}^{2}}}{2} = \frac{Y}{2} s i n^{- 1} (\frac{1}{4}) + \frac{\frac{Y}{4} \frac{\sqrt{15}}{4}}{2}

= \frac{3}{25} Y + \frac{\sqrt{15}}{32} Y \approx \frac{6}{25} Y < a

Then

f (\frac{Y}{2})

f (b) = \frac{Y}{2} \sin^{- 1} (\frac{\frac{Y}{2}}{Y}) + \frac{\frac{Y}{2} \sqrt{1 - {(\frac{\frac{Y}{2}}{Y})}^{2}}}{2} = \frac{Y}{2} s i n^{- 1} (\frac{1}{2}) + \frac{\frac{Y}{2} \frac{\sqrt{3}}{2}}{2}

= \frac{π}{12} Y + \frac{\sqrt{3}}{8} Y \approx \frac{2}{5} Y < b

To obtain the universal subtraction value, we subtract the values to get c:

c = f (a) + f (b) = \frac{6}{25} Y - \frac{2}{5} Y = - \frac{4}{25} Y

Which is indeed much bigger than the linear observable sum, which will be

- \frac{1}{4} Y

, considering that Y is so huge that the smallest difference makes a huge difference. The slope at this point will be:

\frac{d}{d c} f (c) = f^{'} (c) = \sqrt{1 - {(\frac{\frac{- 4}{25} Y}{Y})}^{2}} = \frac{\sqrt{609}}{25}

This slope is less than 1 which proves the summation.

Subsequently, as done before, we need to consider if

a - b \leq - Y

, which will have the reverse effect of the addition, as follows:

f (" - Y - a ") = g (- Y + f (a)) \to x = g^{- 1} (- Y + f (a))

So, we can transfer to the decreasing function and move in the opposite direction (in this case, to the positive plane) by

f (b)

steps since

" - Y - a " \leq - Y

. Therefore, we can write a universal equation if the subtraction numbers are trying Y, as follows:

\begin{matrix} a - b = g (f (a) | + | f (b)) i f a | - | b \leq - Y \end{matrix}

From the upper equation and, as we did before, if

a - b \geq - Y

, we can finally write the universal Sophy-Peter Equation 2 as:

\begin{matrix} a - b = \{\begin{matrix} g (f (a) | + | f (b)) \to x = g^{- 1} (f (a) | + | f (b)) & i f a | - | b \leq - Y \\ f (a) | - | f (b) & i f a | - | b \geq - Y \end{matrix} \end{matrix}

(54)

10.2.3. Sophy-Peter Equation 3

The third equation in the chapter represents the universal multiplication, equivalent to the multiplication operation but accounting for the non-linear growth and dealing with numbers exceeding Y and

- Y

, which will happen frequently in this case. Before we start, we need to define multiplication, at least in the observable algebra.

Which is the repetition of adding the number a, b times, written as

a | \times | b

. So, for example,

5 | \times | 3

is:

5 \times 3 = 5 + 5 + 5

But if a and b are on the non-linear, we need to rewrite this to say that

f (a)

which is universal and will be added (using Sophy-Peter Equation 2 in (53)) to itself

f (b)

times. For example, with

b = 3

given that

f (3) = 3

a \times 3 = f (a) + f (a) + f (a)

Therefore, we can simply write the part if

a \times b \leq Y

as:

a \times b = f (b) (f (a))

Things get tricky when this result exceeds Y, as we cannot just transform to the decreasing function as we do with multiple operations. First, let’s consider the term:

(b) (f (a) \frac{a}{d a} f (a))

Where we multiply b with

f (a)

, multiplied by its derivative, if

b = 1

, we can consider the tree cases:

a = 0

a = 1

, and

a = Y

a t 0 \to 0 \times 1 = 0

a t 1 \to 1 \times 1 = 1

a t Y \to Y \times 0 = 0

As seen here, this function relates to the non-linear growth as it starts from 0 and ends at 0 at Y. But, in order to precisely obtain the correct result, we need to multiply a by the mod 2 of b so we can account for the multiplication process. Written as:

(b \mod 2) a

Finally, we can add the two terms and move them to the decreasing function

g (x)

a \times b | > Y

a \times b = g ((b) (f (a) \frac{d}{d a} f (a)) + (b \mod 2) a)

To test this, we need to refer to the axioms from Section 9, where, if we moved by

" 2 Y "

, we should end at the same origin point,

x = 0

and

y = 0

. Therefore, using this, we can try

Y \times 2

, which

| > Y

, therefore we can compute it as:

Y \times 2 = g ((b) (f (a) \frac{d}{d a} f (a)) + (b \mod 2) a) = g (2 \frac{π}{4} Y \cdot 0 + 0 \cdot Y) = g (0) = 0 \to x = 0

Which satisfies the axioms. Therefore, we can write the Sophy-Peter equation 3 as:

a \times b = \{\begin{matrix} g ((b) a \frac{a}{d a} f (a) + (b \mod 2) a) & i f | (a | \times | b) | | > Y \\ f (b) (f (a)) & i f | (a | \times | b) | \leq Y \end{matrix}

(55)

11. Interference

Since numbers are not always linearly increasing, and at point

x = Y

the slope of

f (x)

becomes 0, as covered in Chapter 9, points attempting to reach Y will subsequently decrease along with the x-axis, moving towards

- Y

. At point

x = 0

, the slope of

g (x)

will be 0, and then it will increase again as we approach

- Y

. The above description can be visualized as:

\overset{⟶ f (x) \to y}{\overset{︷}{- Y \dots 0 \dots Y \to x}}

x \leq - Y ↑ ↓ x | > Y

\underset{⟵ g (x) \leftarrow y}{\underset{︸}{x \leftarrow - Y \dots 0 \dots Y}}

Where

g (x)

is asymmetrical from

f (x)

recalling Equations (36) and (48):

f (x) = \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

g (x) = \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2}

Consider a case where

Y = 4

, and we have the positive plane values

x = 0, 1, 2, 3, 4

to make an approximation to show the asymmetry between these functions, which leads to interference. First, evaluating

f (x)

0 1 2 3 4

↓ ↓ ↓ ↓ ↓

0 0.989 1.913 2.688 π

Where these values are approximate values for

f (x)

. Then we consider the case when numbers attempt to reach

2 Y

, which cannot exist; thus, they actually return to the origin point on the decreasing function

g (x)

as:

4 3 2 1 0

↓ ↓ ↓ ↓ ↓

π 0.704 1.181 0.021 0

It is observed here that linear growth does not occur at all on the decreasing function. For example, using Sophy-Peter equation 1 (Equation (53)) to add

0.5 + 0.5

on the decreasing function, we get:

g (0.5) + g (0.5) = 0.003 + 0.003 = 0.006

Since

0.5

does not lie on

y = 0.5

anymore, we now need to define two new functions to be able to demonstrate the asymmetry between the functions. First, let’s define

F (x)

, which is defined as:

F (x) = \int f (x) d x = \int \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} d x

Then

G (x)

which is the represented as:

G (x) = \int g (x) d x = \int \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} d x

Using Sophy-Peter equations we can get:

F (Y) = α \to g (α)

And at the origin point:

F (0) = β \to g (β)

By taking the observable minus of

F (Y)

and

F (0)

, we get the area under the increasing function of the positive plane from 0 to Y, given that the numbers obey the Sophy-Peter equation. If

F (Y) - F (0) | > Y

, it will transfer to a point on the decreasing function g and vice versa. Then, we can calculate the area under the curve of the decreasing function as:

G (Y) = α_{g} \to f (α_{g})

And at the origin point:

G (0) = β_{h} \to f (β_{g})

Firstly, let’s get the area under the increasing curve:

f (α - β) = v

Subsequently, the area under the decreasing curve will be:

f (α_{g} - β_{g}) = v_{g}

Finally, we can determine the raw increase of numbers in the positive plane from 0 to Y and from Y to 0 on the decreasing function g, since they are

| > Y

. This is achieved by taking the difference between both areas, v and

v_{g}

, as:

A_{1} = v - v_{g}

Then, after crossing the origin point on the decreasing function, we can assign new values for the negative plane areas, which are the differences between the increasing and decreasing functions. First, we calculate

G (- Y)

and assign this value to

δ

as:

G (- Y) = δ \to f (δ)

Where we started with the decreasing function instead of the increasing function, since numbers are on the decreasing function g at the origin point and will continue to

- Y

. Then, after reaching

- Y

, they will grow from

f (- Y)

f (0)

. Therefore, to capture the areas under the curve on the growing increasing function, we define

λ

as:

F (- Y) = λ \to g (λ)

Firstly, we will get the whole area under the decreasing function as:

δ - β_{g} = γ \to f (γ)

We know that

γ

will be a negative value since it is on the negative plane. Then, proceeding to obtain the increasing function value that transitions from

- Y

to the origin point

(0, 0)

, which we know is less then

γ

(point 1) since it represents the upper graph, as illustrated in:

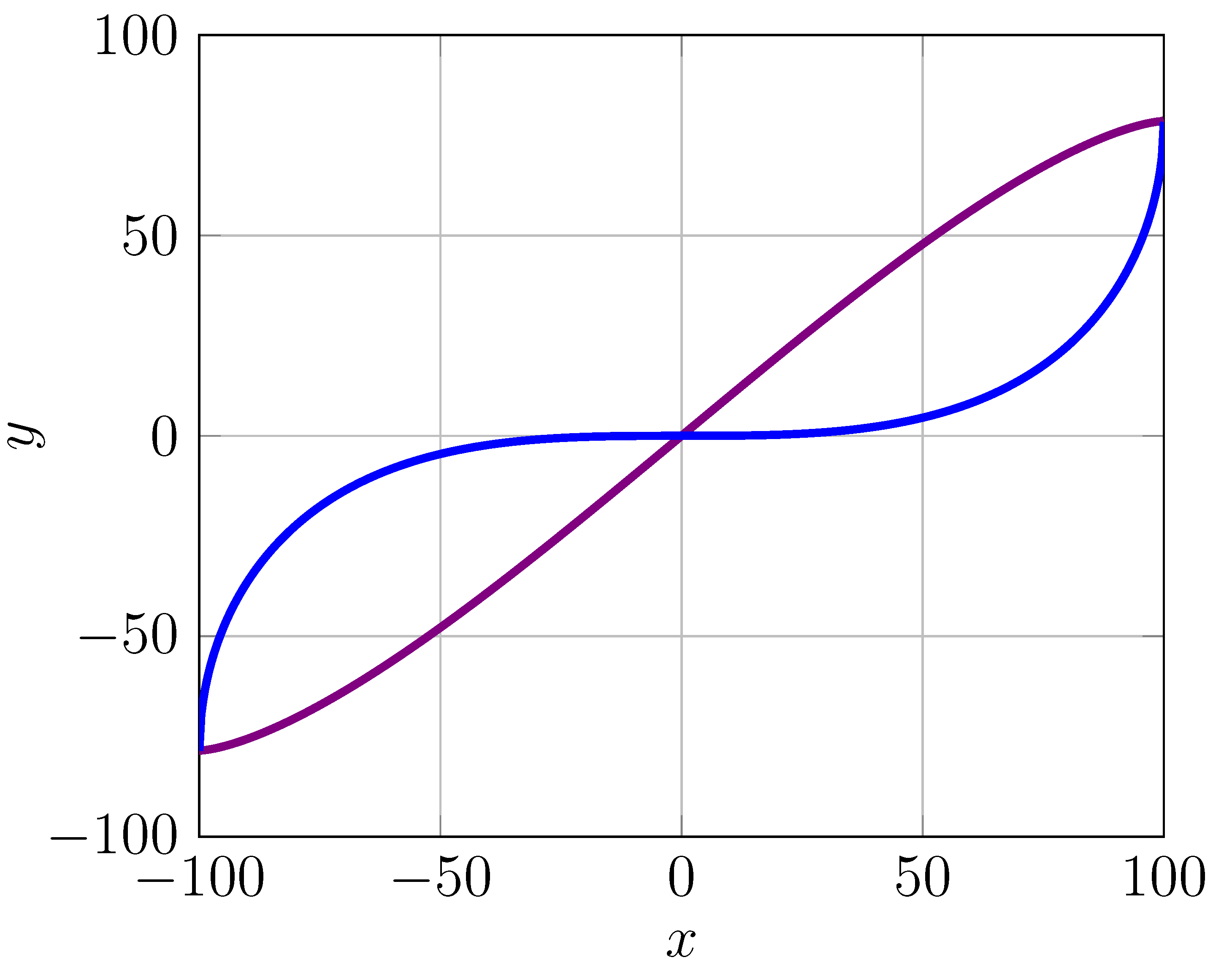
Subsequently,

η

(the total area under the increasing function on the negative plane) can be calculated by subtracting

β

from

λ

η = β - λ \to f (η)

Which we know

η

is also negative. Therefore, as previously done in the positive plane, we can calculate the differences in the areas on the negative planes (the raw increase in numbers from 0 to

- Y

on g and from

- Y

to 0 on f) as:

A_{2} = η - γ

Since

η > γ

from point 1, and

η

and

γ

are negative values, we can conclude that

A_{2}

will be a negative value (point 2). Now, knowing that

A_{1}

and

A_{2}

represent the raw areas in both planes, and by simply adding all natural numbers with the new definition of infinity given in Section 12, we can conclude that the ratio between the positive and negative areas,

A_{1}

and

A_{2}

, will be

ζ (- 1)

as computed in Chapter 21:

\frac{A_{1}}{A_{2}} = - \frac{1}{12}

(56)

This makes total sense within this framework, since from point 2 we know that

A_{2}

is negative and

A_{1}

is positive; therefore, the answer must be negative. Since this represents the simplest function, which is counting, depicted in the linear interval as

y = x

and in the broader interval as

y = f (x)

, and numbers return on an asymmetrical function, crossing the origin point from Y to

- Y

and back, numbers interfere and cancel each other out. This leaves us only with the asymmetry between the positive and negative planes,

A_{1}

and

A_{2}

, which is regarded as the sum of the "divergent series" but in fact it is the result in the interference between numbers when they go in an "infinite" cycle (where "infinite" cycle is the closed interval

[- Y, Y]

which explained in Section 13). Or in other words,

ζ (s)

, which is fully rewritten and described in Chapter 21, but written as:

ζ (s) = \int_{- Y}^{Y} ϕ_{s} \frac{p}{Y - 1} + M_{p} + f {(x)}^{- s} d x + \int_{Y}^{- Y} M_{p} + g {(x)}^{- s} d x

Therefore, we can establish an axiom:

Axiom 12.

In an "infinite" cycle, when numbers

| > Y

, they revert to the decreasing function until

- Y

and ascend again on the increasing function until Y. Therefore, numbers interfere with each other, leaving an asymmetrical value between the positive and negative planes.

11.1. The Magic Function $M (p)$

Now, to simulate the interference behavior, we can construct a magic function

M (p)

for the interference between numbers. This function will consist of two conditions; the first, if p is even:

M_{p} = \frac{p}{2 l o g_{2} {(Y)}^{2}}

Where p is directly proportional to

y = p x

on the linear interval and

y = p f (x)

in the universal picture. p is determined based on the type of problem and how we are constructing the function for simulating interference, as discussed in Chapter 21. Therefore, we obtain the normalization value with the fewest number of bits required to compute Y in a binary system by calculating

\log_{2} (Y)

multiplied by 2, all of this squared, then this is divisor and p is dividend so we can spread the value. In the other case, if p is odd, a harmonic series is created by rotating over an imaginary axis i with an angle of

π

using Euler properties and the Euler number e, written as:

M_{p} = e^{{(- 1)}^{\frac{1}{2}} π}

To write a complete equation for the full magic function, a piece-wise function can be constructed as follows:

M_{p} = \{\begin{matrix} \frac{p}{2 l o g_{2} {(Y)}^{2}} & i f p \mod 2 = 0 \\ e^{{(- 1)}^{\frac{1}{2}} π} & e l s e \end{matrix}

12. Dealing With "Infinite" Series And Complex Analysis

One of the most important applications of this framework is dealing with infinite series [4,5] and representing how to rewrite and expand them. Before we start, we need to define how infinite series behave in our framework. Before we start, we must define what infinity is in our framework.

Definition 5.

Infinity "∞": the closed interval

[- Y, Y]

within the x-axis.

Let’s define an infinite series that is sum all zeros to infinity:

Z = \sum_{n}^{\infty} 0

We know the answer for this will always be zero. But we are interested the operations within this, in a normal sense this sum is adding zeros "forever" as:

Z = \underset{\infty}{\underset{︸}{0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 \dots}}

Since infinity does not exist, this cannot be true; instead, we will have a limit of increase for n in the sum function, and then we will be moving to the decreasing function. Let’s consider that n goes to infinity. Since from definition 5, we know that infinity is an interval, not a concrete number, therefore, we will divide the series into two parts: from

- Y

to Y on the increasing function, and then from Y to

- Y

on the decreasing function. First, let’s substitute 0 into

z (x)

, where it will return 0.

z (x) = 0, z (x) = 0 x

But to construct the series in our framework, we need to write

z (x)

in terms of

f (x)

and

g (x)

, so we can keep track of the non-linear growth of numbers in the series and correctly assign the values as x reaches Y and

- Y

. In this case, it will be written as:

z (x) = 0 f (x)

z (" x ") = 0 g (x)

Where

f (x)

and

g (x)

represent the increasing and decreasing functions, respectively. It will also return zero, but it is necessary to split the sum of the increasing and decreasing functions from each other so we can draw a conclusion for a universal way to deal with any series. The first term in the series can be expressed as:

\sum_{n}^{Y} 0 f (n)

Which sums all the terms from

z (x)

Y times, therefore, a huge but yet finite sum of these terms will be:

0_{1} + 0_{2} + 0_{3} + \dots + 0_{Y} = 0

The second term can be expressed as n going to

- Y

and transforming to the decreasing function by subtracting n (a negative number) from Y. We know from the Sophy-Peter Equation (10) that:

f (" x + a ") = g (f (x) - f (a))

Where f and g are asymmetrical and result in interference as in Section 11. From this, we can write it as:

\sum_{n}^{- Y} 0 f (" Y - n ") = \sum_{n}^{- Y} 0 g (f (Y) + f (n))

Since this operation will be repeated Y times, it also gives:

0_{- 1} + 0_{- 2} + 0_{- 3} + \dots + 0_{- Y} = 0

Therefore, we can make a conclusion to represent the infinite series

\sum_{n}^{\infty} 0

in a finite point of reference by subtracting the decreasing function from the increasing function, as the numbers do not always increase but have a limit; therefore, the "sum" of the series is actually the remaining part from the interfered increasing and decreasing function, represented as:

Z = \sum_{n}^{Y} 0 f (n) - \sum_{n}^{- Y} 0 g (f (Y) + f (n))

(57)

In other words, we calculate the area under the curve of

z (x)

in terms of the increasing function from

- Y

to Y, and then subtract it from the same interval but on the decreasing function after we have gone through all the numbers. This is the same as taking the integral of

z_{f}

and

z_{g}

and subtracting them from each other. Therefore, it can be written as:

Z = \int_{- Y}^{Y} 0 f (x) d x - \int_{- Y}^{Y} 0 g (x) d x = 0

(58)

Example 12.1.

To explain how this can be done for any infinite series, let’s take the simplest divergent series 6, which sums all natural numbers

\sum_{n}^{\infty} n

. The first step we need to consider is writing the series in terms of

f (n)

, as specified in axiom 3.

n \to f (n), \sum_{n}^{Y} f (n)

\sum_{n}^{- Y} g (f (Y) + f (n))

Then we will apply the interval of Y and

- Y

, and since this series continues beyond Y, it will transform to the decreasing function, creating interference between both. From Equation (58), we can write the summation as:

N = \int_{- Y}^{Y} M + f (x) d x + \int_{Y}^{- Y} M + g (x) d x

Which is equivalent to:

N = \int_{- Y}^{Y} M + \frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} d x + \int_{Y}^{- Y} M + \frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} d x

(59)

Where M is the interference variable added due to the fact that this series, unlike the other series Z which always stayed at 0, actually continued after

f (Y)

, which is on the decreasing function, until

- Y

. Thus, we take the difference between the areas under their curves, considering the interference between them.

12.1. New Series summation interpretation

To continue representing the summation of any series, we need to classify series into two categories: divergent and convergent. Since it is not infinite, we need to redefine these two terms:

Definition 6. Divergent: A series S with a function

S (x)

where

S (Y \to f (Y)) \approx 0

, and the series attempts to keep increasing, eventually reverting to the decreasing function until

- Y

, when the interval of infinity ends. This results in interference, ending with a finite value representing the difference in areas between the curves.

Definition 7. Convergent: A series S with a function

S (x)

where

S (Y \to f (Y)) \approx 0

. Consequently, it does not surpass Y, which implies that we can assign a finite value to it, and it will not transition to the decreasing function.

An example of a divergent series was given in example 12.1.

Example 12.2.

To see how to deal with convergent series, we will consider a famous convergent series S, written as

S = \sum_{n}^{\infty} \frac{1}{n^{2}}

As before, we need to rewrite the sum in terms of

f (n)

due to the non-linear growth. It will be written as:

\frac{1}{n^{2}} \to \frac{1}{f {(n)}^{2}}

Noting that all operations obey the Sophy-Peter equation in Section 10, to prove it is convergent, we need to test its behavior at

x = Y

. Before this, let’s define

s (x)

s (x) = \frac{1}{f {(x)}^{2}}

Then let’s evaluate

s (Y)

s (Y) = \frac{1}{" f {(Y)}^{2} "} = \frac{1}{" (\frac{π}{4} Y) 2 "} = \frac{1}{\frac{π^{2}}{16} " Y^{2} "}

From Sophy-Peter Equation 3 in 55, we know how to compute

" Y^{2} "

, which is also

" Y \times Y "

. It is worth noting that

" Y \times Y " | > Y

" Y \times Y " = g ((Y) Y \frac{d}{d Y} f (Y) + (Y \mod 2) Y)

∵ \frac{d}{d Y} f (Y) = 0 ⟶ 1

∵ Y \to o d d, ∴ Y \mod 2 = 1 ⟶ 2

∴ g (0 + Y) = g (Y) = \frac{π}{4} Y ⟶ 3

From 1, 2 and 3 :

" Y \times Y " = \frac{π}{4} Y

(60)

Therefore we can continue evaluating

s (Y)

from our knowledge we gained from equation 60:

s (Y) = \frac{1}{\frac{π^{2}}{16} " Y^{2} "} = \frac{1}{\frac{π^{2}}{16} " Y \times Y "} = \frac{1}{\frac{π^{2}}{16} \times \frac{π}{4} Y} = \frac{1}{\frac{π^{3}}{64} Y} = \frac{64}{π^{3}} \frac{1}{Y}

From axiom 5 and Equation (2), we know that E is the smallest positive integer, which almost converges to 0, written as:

\frac{1}{Y} = E

Subsequently we can further evaluate

s (Y)

to see if it converges to 0:

s (Y) = \frac{64}{π^{3}} \frac{1}{Y} = \frac{64}{π^{3}} E \approx 2 E \approx 0

(61)

Therefore we proved that this series in convergence in our framework and can be written without the decreasing function as the sum of of integers from

s (1)

s (Y)

as:

S = \sum_{n}^{Y} \frac{1}{f {(n)}^{2}} = \frac{π^{2}}{6}

(62)

To write a complete function that accounts for all small numbers using both the increasing and decreasing functions, we can use

ζ (2)

. However, since this series converges, there is no need, unlike the series in example 12.1. Nonetheless,

ζ (2)

is written as:

ζ (2) = \int_{- Y}^{Y} M + f {(x)}^{- 2} d x + \int_{Y}^{- Y} M + g {(x)}^{- 2} d x

= \int_{- Y}^{Y} M + \frac{1}{{(\frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{2}} d x + \int_{Y}^{- Y} M + \frac{1}{{(\frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{2}} d x

= \int_{- Y}^{Y} \frac{M f {(x)}^{2} + 1}{{(\frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{2}} d x + \int_{Y}^{- Y} \frac{M g {(x)}^{2} + 1}{{(\frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{2}} d x

Where it was explained briefly in Chapter 21.

13. How many cycles?

First of all, we have to give a formal definition for the cycle of numbers.

Definition 8. Cycle of numbers: the transition from an increasing function

f (x)

to a decreasing one

g (x)

and back to the starting point.

At this point, a question may arise: if we can cycle on positive and negative planes, can we do it indefinitely? To answer this question, we need to consider how we are dealing with cycles. We count cycles as 1, 2, 3, 4, .... At this point, we can observe that cycles have the same properties as integers; moreover, anything that we are able to count will have properties of integers. Due to the new number theory presented in this chapter, and more specifically the increasing (question 36) and decreasing (equation 48) functions, we know that numbers grow linearly only within the linear interval. After reaching a certain point, they begin to grow in a concave manner (in other words,

1 + 1 \neq 2

anymore, as explained in Section 8). When they reach Y, which is the highest possible number, numbers start to decrease on the

g (x)

and interfere with each other, since numbers exhibit wave properties (explanations of interference and wave properties of numbers are in Section 11).

Returning to the concept of cycles of numbers: since cycles share the same properties as numbers, including non-linear growth and wave properties, we can discuss the completeness of a cycle.

Definition 9. Cycle completeness: A cycle can be called complete if and only if the last point in the cycle is equal to the starting point and it has crossed both the increasing and decreasing functions. A complete cycle is possible only if the cycle number lies within the linear interval of the increasing function

f (x)

We can interpret cycles as waves. The starting point of each cycle is always 0. To interpret a cycle as waves, we can use

f (x)

with a sine transformation. Wave numbers range from 1 to

f (Y)

We will represent a full cycle as 360 degrees or

2 π

radians. In order to do this, we have to assign wave numbers

1, 2, 3, 4, 5, 6, \dots

each with the amplitude of its sine transformation, as follows:

k = f (n)

Where n is the cycle number and k is the wave number.

n u m b e r_c y c l e s = \sum_{n = 1}^{Y} f (1) = Y

The cycle size can be represented as follows:

c y c l e_s i z e = \frac{2 π}{k} \cdot f^{'} (n)

The amplitude for the sine wave we made from

f (x)

A = \sin (\frac{c y c l e_s i z e}{4})

Where

2 π

means a complete cycle. The first cycle will have size and amplitude are equal to 1 (since it is a maximal possible amplitude in the sine function at

x = \frac{π}{2}

c y c l e_s i z e = \frac{2 π}{f (1)} f^{'} (1) = \frac{2 π}{1} \cdot 1 = 2 π

A = \sin (\frac{c y c l e_s i z e}{4}) = \sin (\frac{2 π}{4}) = \sin (\frac{π}{2}) = 1

So at the last cycle or

Y_{t h}

cycle size and amplitude are equal to 0 which means wave disappeared and cannot continue its existence.

c y c l e_s i z e = \frac{2 π}{f (Y)} f^{'} (Y) = \frac{2 π}{\frac{Y}{4} π} \cdot 0 = 0

A = \sin (\frac{c y c l e_s i z e}{4}) = \sin (0) = 0

The conclusion from everything mentioned before will be such:

Axiom 13.

Due to cycles of numbers wave interpretation according to the new number theory the biggest possible number of cycles is Y, which is the largest possible value in mathematics.

13.1. The $Y_{th}$ Cycle ( $Y \times Y$ )

From this conclusion, we can consider the

Y_{th}

cycle of a Y cycle, which can be expressed as:

Y \times Y | > Y

According to Sophy-Peter equation 3 55, since this scenario is trying Y, we can encounter two cases for b as a whole number: either we end with

g (Y) = \frac{π}{4} Y

if b is an odd number, and 0 if it is even, as two cycles will bring us back to the origin point. However, three cycles will end on the second dimension at

x = Y

as follows:

g ((b) \frac{a}{d a} f (a) + (b \mod 2) a) = g (0 + Y) \to for even b

g ((b) \frac{a}{d a} f (a) + (b \mod 2) a) = g (0 + 0) \to for odd b

Thus, the question is whether the Y cycle

Y \times Y

results in Y being odd or even, so we can assign a value to it. Using the sine transformation, we proved that at the Y cycle, the cycle completeness is 0.

α_{Y} = \sin (\frac{1}{4} \frac{2 π}{f (Y)} f^{'} (Y)) = \sin (\frac{1}{4} \frac{8 π}{Y} 0) = \sin (0) = 0

Let’s consider undoing the cycle completeness to obtain the multiplication of

a \times n

, where a is the cycle length, which in our case is Y, and n is the cycle number. Given that we can undo the completeness using [17]:

ϕ_{n} = n \frac{π}{4} \frac{d}{d α} \sin (α_{n})

Undoing on the Y cycle will be written as follows:

ϕ_{Y} = Y \frac{π}{4} \frac{d}{d α} s i n (0) = Y \frac{π}{4} \cos (0) = \frac{π}{4} Y

∣ α_{Y} = 0

So we can conclude the following:

Y \times Y = ϕ_{Y} = \frac{π}{4} Y

We know that

Y \times Y | > Y

, therefore the first condition in the Sophy-Peter equation will be applied as follows:

g ((Y) Y \frac{d}{d x} f (Y) + (Y \mod 2) Y) = \frac{π}{4} Y \to 1

Since

\frac{d}{d x} f (Y) = 0

as proved in Section 8:

\frac{d}{d x} f (Y) = f^{'} (Y) = \sqrt{1 - {(\frac{Y}{Y})}^{2}} = \sqrt{1 - 1} = 0

We can rewrite the equation from point 1 to get:

g ((Y) Y \frac{d}{d x} f (Y) + (Y \mod 2) Y) = g (0 + (Y \mod 2) Y) = g ((Y \mod 2) Y) = \frac{π}{4} Y

Then the required value needed to be obtained from this equation is

Y \mod 2

, therefore we can proceed to solve the equation

(Y \mod 2) Y = g^{- 1} (\frac{π}{4} Y)

We know from Section 9 that

g (Y) = \frac{π}{4} Y

, therefore the inverse of g at

\frac{π}{4} Y

is Y as

g^{- 1} (\frac{π}{4} Y) = Y

. Proceeding to solve the equation:

(Y \mod 2) Y = g^{- 1} (\frac{π}{4} Y) = Y

Y \mod 2 = \frac{Y}{Y}

\to Y \mod 2 = 1

∴ Y is odd .

Which we can make a theorem of

Theorem 3.

Y is an odd number and

Y \times Y

results in

S Y

, where

S = \frac{π}{4}

14. Summary

To summarize everything, we will list all properties of numbers that the new number theory proposes, which contains 13 axioms. The main points of the number theory are:

First of all, there are the biggest and the smallest possible numbers on the number line. We denote them as Y and $- Y$ (axiom 1). Also, there are the smallest positive and the largest negative numbers, denoted as E and $- E$ (axiom 5). "Infinite" is the interval $[- Y, Y]$ , where each number inside has the minimal difference from other numbers, equal to E. The growth of numbers is non-linear on the number line, described by the increasing function $f (x)$ (Equation (36)). After numbers reach Y, they start to decrease, which is described by the decreasing function $g (x)$ (Equation (48)).
The negative plane has a shift equal to $- \frac{1}{12}$ . This was described in Section 11. In addition, numbers have properties of waves such as interference, which was presented, described, and proved in Section 11.
To deal with "infinite" series, we calculate the areas between the increasing and decreasing functions; in other words, we calculate the integral from $- Y$ to Y of $f (x) - g (x)$ . This was explained and proved in Section 12.
When $a + b | > Y$ , where $| >$ is the operator presented in Section 10, we must use the Sophy-Peter equations (Section 10) since numbers larger than Y cannot exist.
When we add $Y + Y$ , the result is 0, indicating a cycle of numbers. The formal definition was presented in Section 13. The maximum number of cycles is Y, as it grows like natural numbers (the proof in Section 13).

Fixing Paradoxes Using the New Number Theory In this chapter, we will fix all the paradoxes presented in Chapter 3.

15. Fixing Galileo’s Paradox

Galileo’s Paradox was explained in Section 4. In a few words, it posits that there are two infinite sets: the first one containing all natural numbers, and the second containing the squares of each number. One might think that the sizes of these sets should be different, but this contradicts the idea of infinity, thereby creating a paradox.

The new number theory presented in this chapter does not have this paradox since all existing numbers lie within the interval

[- Y, Y]

, where

- Y

is the smallest existing number and Y the largest possible number.

Now we can define two sets: all natural numbers and their squares. All natural numbers lie within the interval

[1, Y]

. To compute the squares of natural numbers, we will use the Sophy-Peter equations presented in Section 10. This is important because multiplication does not work the same way for numbers that attempt to exceed Y. In the end, the sets will be equal since the highest possible square exists. According to Sophy-Peter equation 3 (Equation (55)), it is equal to:

Y \times Y = g ((Y - 1) Y \frac{d}{d Y} f (Y) + (Y \mod 2) Y)

∵ \frac{d}{d Y} f (Y) = 0

∵ Y \to o d d

∴ g (0 + Y) = g (Y) = \frac{π}{4} Y

Y \times Y = \frac{π}{4} Y

So, the square of the highest possible number, which is Y, is equal to

\frac{π}{4} Y

, which implies that the sets have equal sizes but the numbers there are not growing in the way that generally accepted number theory would predict, since it is not linear and squares can sometimes be smaller than the numbers themselves.

16. Explaining Ramanujan Summation

Ramanujan Summation was explained in Chapter 6. The paradox of the sum of all natural numbers is that, due to the concept of infinity and the

1 + 1 = 2

always concept (in other words, the axioms of generally accepted number theory), logically the sum should be equal to infinity, but in reality, it converges to the negative fraction which is

- \frac{1}{12}

. There are other sums (one of them was presented in the Chapter 6) that also do not make sense due to these concepts.

The new number theory presented in Chapter 7 explains why this is happening. First of all, the set of natural numbers is not infinite. Secondly,

1 + 1 = 2

only holds within the linear interval of the increasing function

f (x)

(Equation (36)). After numbers reach Y, they start to decrease on the decreasing function

g (x)

(Equation (48)). When numbers move to

g (x)

, they begin to interfere with numbers from

f (x)

. The interference of numbers was presented in Section 11. In the end, due to the shift of negative numbers (proven in Section 11), we obtain the correct answer.

We explained how to deal with "infinite" series in Section 12, but the best way to find the solution is to use the Riemann zeta function with

s = - 1

(explained in Section 3), since it is equivalent to Ramanujan Summation. We will present the general formula of the Riemann zeta function and solve this series in Chapter 21.

17. Explaining Casimir Effect

Due to the new number theory presented in chapter 7, we have an absolute maximum, which is Y. We can make cycles of numbers, but the maximal number of such cycles is Y, as explained in Section 13. All of this leads us to the conclusion that the universe cannot contain an infinite number of matter, so energy cannot be infinite either. This is supported by Stephen Hawking [17]. The new number theory not only fully agrees with this concept but also provides a wider picture and explanations for all paradoxes created by the concept of infinity (some of which were presented in Chapter 3). One of the physics examples where we can see this wider picture is in explaining the "infinite" series used in the Casimir Effect.

The Casimir Effect was explained in Section 5. Due to the proof in the previous Section 16, we know why the sum of all natural numbers is equal to the negative fraction, which is

- \frac{1}{12}

Consider a 1D toy model where a free scalar field with neutral charge and no mass is represented on a line as:

ϕ (t, x) \in R, x \in R

(63)

Where x can only exist on the new interval on Real numbers as in axiom 1

- Y \geq x \geq Y

Since we can no longer use infinity but rather represent it as an interval between

- Y

and Y, we have to rewrite the Fourier transform equation based on the new axioms. It will be changed as follows:

F (ω) = \int_{- Y}^{Y} f (t) e^{i ω t} d t

This is an important step since the way we transform and process waves will completely change and must obey the rules of interference as described in Section 11. The new Fourier transform will transform the wave f by taking the integral of this wave from

- Y

to Y, which will create a specific difference in their areas and thus drive the transformation.

Let’s look at the two points where

x = 0

and

x = d

. In these two cases, we apply Dirichlet boundaries, where the forces seem to vanish, such as

ϕ (t, 0) = ϕ (t, x) = 0

(64)

In the interval from

[0, d]

, the field configurations can be Fourier decomposed into waves with wave numbers

k_{1}, \dots

which cannot be infinite due to the new number theory:

k_{n} = \frac{f (n) π}{d}, n = 1, 2, 3, \dots, Y

The minimal

k_{1}

will be

f (1) = 1

, and the maximum possible

k_{Y}

will have

f (Y) = \frac{π}{4} Y

Therefore, the ground state energy for the vacuum density

p_{d}

can be calculated as an integral of the difference between the increasing function

f (x)

and the decreasing function

g (x)

, multiplied by the fraction

\frac{1}{2 d}

, where d is the distance between the plates:

p_{d} = \frac{1}{2 d} (\int_{- Y}^{Y} f (x) d x - \int_{- Y}^{Y} g (x) d x) = \frac{1}{2 d} \int_{- Y}^{Y} \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} d x -

\frac{1}{2 d} \int_{- Y}^{Y} \frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2} d x = \frac{π}{2 d^{2}} \cdot - \frac{1}{12} = - \frac{π}{24 d^{2}}

The conclusion we can draw is that the mathematical framework based on the new number theory is applicable to physical phenomena and makes sense since the calculations are correct. It proves that the universe has finite energy, but in the Casimir effect, scientists used infinity, as well as in quantum field theory, which made their calculations paradoxical and therefore incomplete. No other framework has made predictions from finite energy except the mathematical framework presented in this paper.

18. Fixing Gabriel’s Horn Paradox

Gabriel’s Horn Paradox was explained in Section 6. The problem is that the volume of the horn is finite, but the surface area is infinite. This occurs due to the concept of infinity and incorrect handling of "infinite" series.

To fix the paradox, we will apply the new number theory presented in Chapter 7 and calculate the volume according to Section 12. The volume will be calculated as follows:

V = \int_{1}^{Y} π y^{2} d x = π \int_{1}^{Y} {(\frac{1}{x})}^{2} d x = - π \frac{1}{x} |_{1}^{Y} = (- π \frac{1}{Y}) - (- π \frac{1}{1}) = π

Thus,

V = π

, since

\frac{1}{Y}

is equal to E, according to theorem 2, which is an incredibly small number that we can ignore.

The surface area will be calculated as follows (the method for deriving the formula for the surface area of the horn was described in Section 6):

S A = 2 π \int_{1}^{Y} \frac{1}{x} \sqrt{1 + {(\frac{1}{x})}^{4}} d x

First of all we will calculate the follow integral:

\int \frac{1}{x} \sqrt{\frac{1}{x^{4}} + 1} d x

Simplify:

= \int \frac{\sqrt{x^{4} + 1}}{x \sqrt{x^{4}}} d x

Since

\sqrt{x^{4}} = x^{2}

, because x is a real number:

= \int \frac{\sqrt{x^{4} + 1}}{x^{3}} d x

Apply integration by parts:

\int u d v = u v - \int v d u

= - \frac{\sqrt{x^{4} + 1}}{2 x^{2}} - \int - \frac{x}{\sqrt{x^{4} + 1}} d x

= - \frac{1}{2} \sqrt{1 + {(\frac{1}{x})}^{4}} + \int \frac{x}{\sqrt{x^{4} + 1}} d x

\int \frac{x}{\sqrt{x^{4} + 1}} d x = \frac{1}{2} \ln |\sqrt{x^{4} + 1} + x^{2}|

Since

x^{2}

a non-negative number we will get rid of absolute value in the natural logarithm:

= \frac{1}{2} \ln (\sqrt{x^{4} + 1} + x^{2})

We know that

\ln (\sqrt{x^{2} + 1} + x^{2}) = \sinh^{- 1} (x)

, so:

= \frac{1}{2} \sinh^{- 1} (x^{2})

So the solution is:

\int \frac{1}{x} \sqrt{\frac{1}{x^{4}} + 1} d x = - \frac{1}{2} \sqrt{1 + {(\frac{1}{x})}^{4}} + \frac{1}{2} \sinh^{- 1} (x^{2}) = \frac{1}{2} (\sinh^{- 1} (x^{2}) - \sqrt{1 + {(\frac{1}{x})}^{4}})

And surface area is:

S A = 2 π \int_{1}^{Y} \frac{1}{x} \sqrt{1 + {(\frac{1}{x})}^{4}} d x

= 2 π (\frac{1}{2} (\sinh^{- 1} (x^{2}) - \sqrt{1 + {(\frac{1}{x})}^{4}})) |_{1}^{Y}

= π ((\sinh^{- 1} (Y^{2}) - \sqrt{1 + {(\frac{1}{Y})}^{4}}) - (\sinh^{- 1} (1^{2}) - \sqrt{1 + {(\frac{1}{1})}^{4}}))

Before continuation of calculations we have to deal with

Y^{2}

since

Y^{2} | > Y

To calculate it we will use Sophy-Peter Equation (55)

Y \times Y = g ((Y - 1) Y \frac{d}{d Y} f (Y) + (Y \mod 2) Y)

∵ \frac{d}{d Y} f (Y) = 0

∵ Y \to o d d

∴ g (0 + Y) = g (Y) = \frac{π}{4} Y

Y \times Y = \frac{π}{4} Y

Now we can continue solving the problem

S A = π ((\sinh^{- 1} (\frac{π}{4} Y) - \sqrt{1 + {(\frac{1}{Y})}^{4}}) - (\sinh^{- 1} (1) - \sqrt{1 + 1}))

Since

\frac{1}{Y}

is equal to E, according to theorem 2, which is incredibly small number so we can neglect it in the further calculations:

= π ((\sinh^{- 1} (\frac{π}{4} Y) - \sqrt{1}) - (\sinh^{- 1} (1) - \sqrt{2}))

Now we can transform

\sinh^{- 1} (1)

back to the logarithmic form and open the brackets:

= π (\sinh^{- 1} (\frac{π}{4} Y) - 1 - \ln (\sqrt{1^{2} + 1} + 1 + \sqrt{2}))

= π (\sinh^{- 1} (\frac{π}{4} Y) + \sqrt{2} - 1 - \ln (\sqrt{2} + 1))

We can say that

\sinh^{- 1} (\frac{π}{4} Y) > 1

, since:

\sinh^{- 1} (\frac{π}{4} Y) = \ln \sqrt{{(\frac{π}{4} Y)}^{2} + 1} + \frac{π}{4} Y = \ln \sqrt{\frac{π^{2}}{16} (\frac{π}{4} Y) + 1} + \frac{π}{4} Y = \ln \sqrt{\frac{π^{3}}{64} Y + 1} + \frac{π}{4} Y > 1

Because

\sqrt{\frac{π^{3}}{64} Y + 1} + \frac{π}{4} Y > e

. And

0 < \ln (\sqrt{2} + 1) < 1

since

1 < \sqrt{2} + 1 < e

. From all of this we can conclude that:

π (\sinh^{- 1} (\frac{π}{4} Y) + \sqrt{2} - 1 - \ln (\sqrt{2} + 1)) > 0

Which means:

S A > 0

and it makes sense since area cannot be negative.

Modified Collatz Conjecture (Oscillating Theorem)

19. Problems with Collatz Conjecture

19.1. Negative Numbers

The current version of the Collatz Conjecture was presented in Section 2. The formula of the conjecture is represented in Equation (1).

When considering the current Collatz Conjecture for negative numbers, one notable phenomenon is the occurrence of loops, often referred to as "negative cycles" or simply "loops." There are several famous negative loops in the context of the Collatz Conjecture, known as: S (small loop), M (medium loop), and L (large loop).

These loops involve a sequence of negative numbers that, when subjected to the same process defined by the Collatz rules (albeit extended to negative numbers), repeatedly cycle through the same set of values without ever reaching 1.

If we perform operations according to Equation (1) on some negative numbers, we can observe some of these "negative cycles," which are:

Loop S:

$- 1, - 2, - 1, \dots$
Loop M:

$- 5, - 14, - 7, - 20, - 10, - 5 \dots$
Loop L:

$- 17, - 50, - 25, - 74, - 37, - 110, - 55, - 164, - 41, - 122, - 61,$

$- 182, - 91, - 272, - 136, - 68, - 34, - 17 \dots$

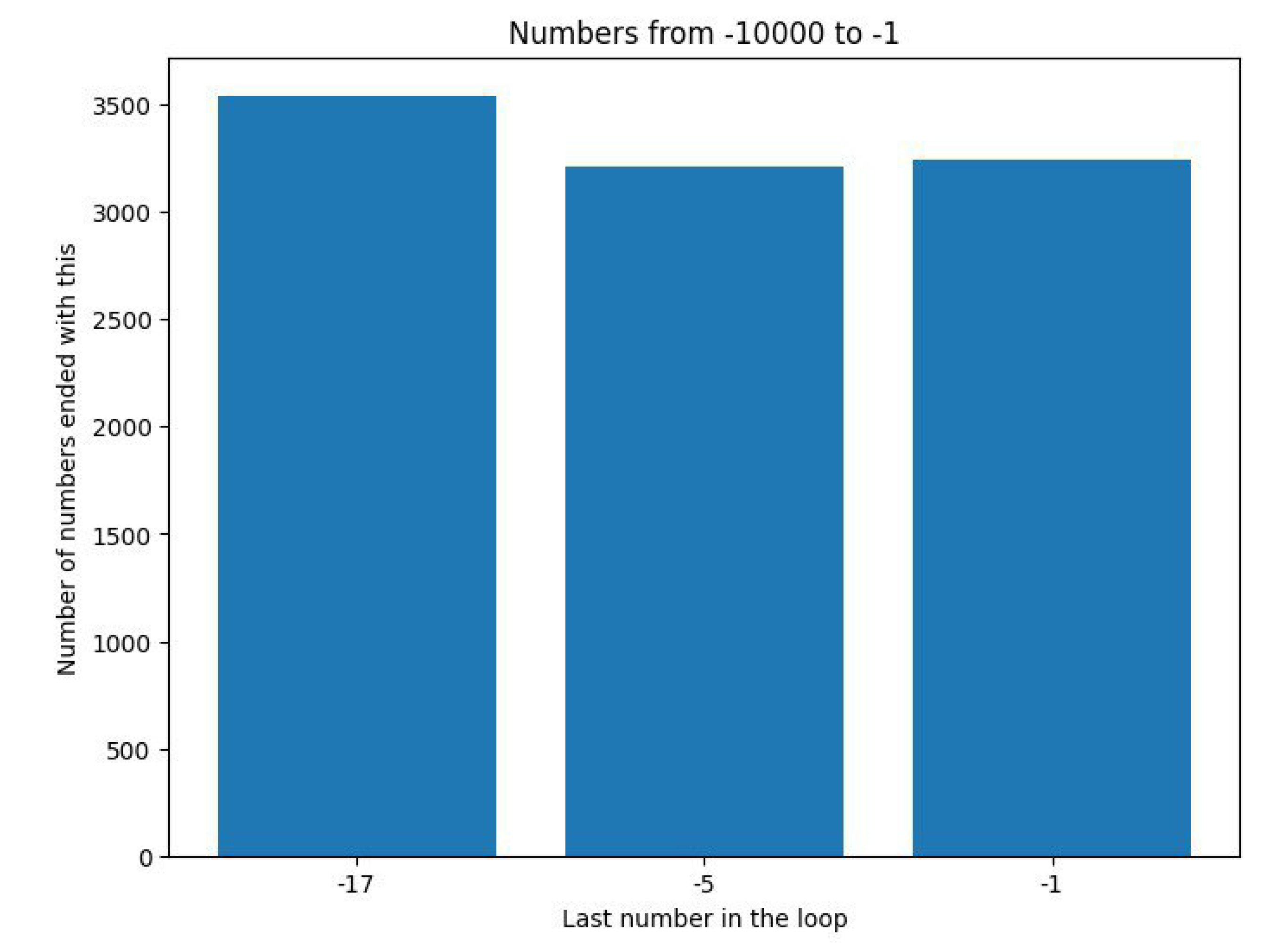
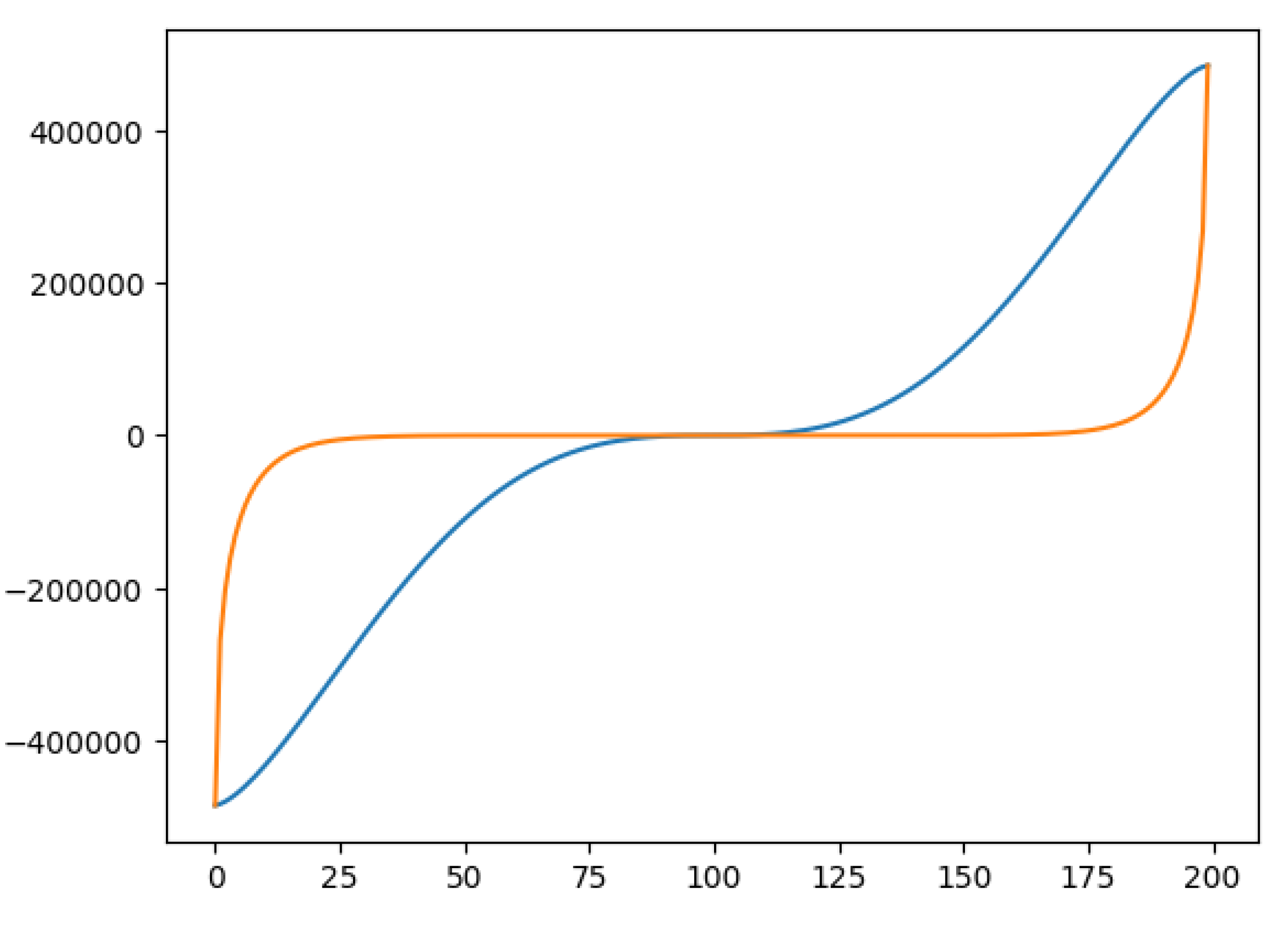
We created a "for" loop with n ranging from -10,000 to -1 to check how many times we would encounter each of the loops described above. Here are the results we obtained:

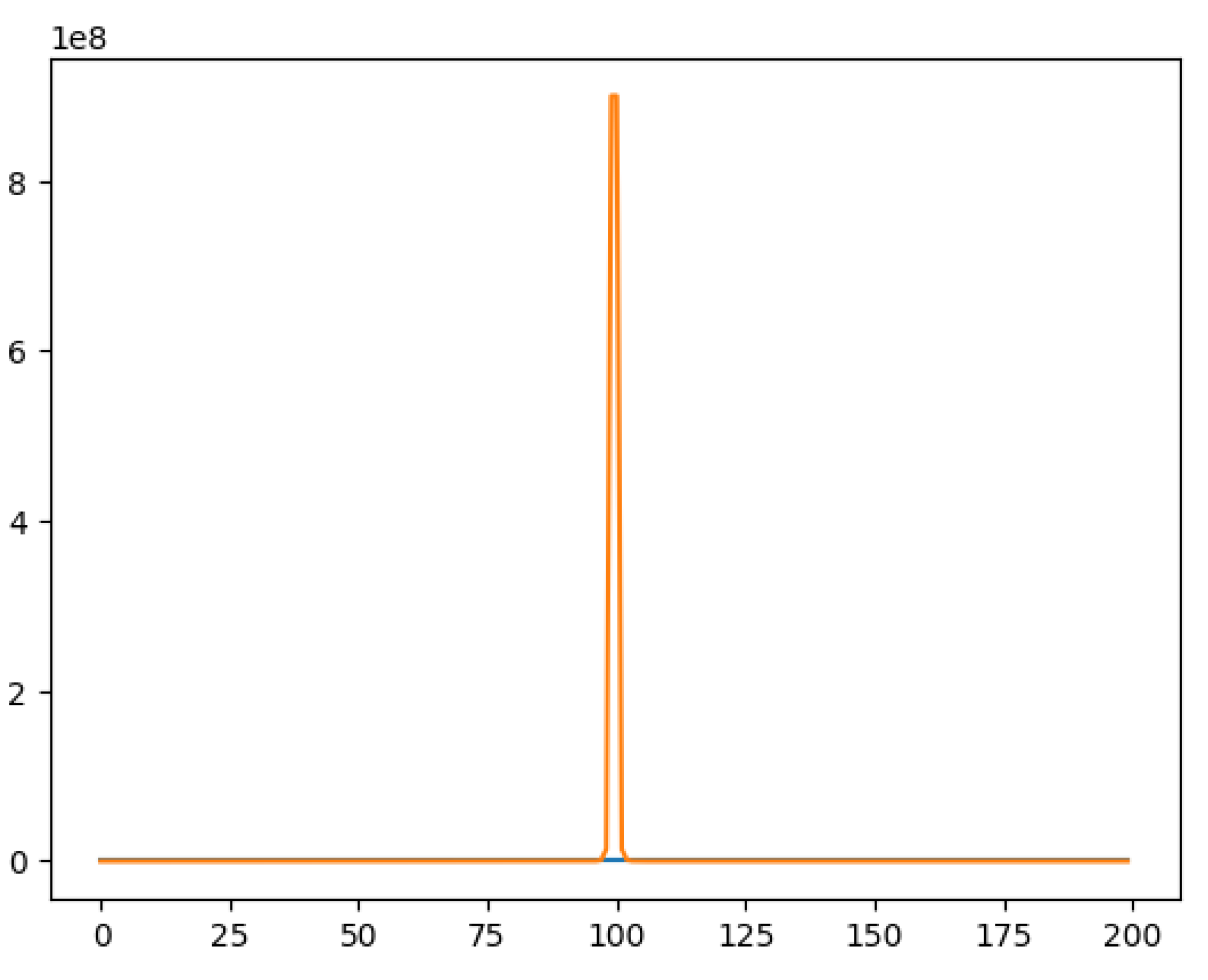
Figure 4. Number of L, M and S loops for n on the interval [-10000, -1].

This figure demonstrates that under these rules, the sequence does not converge to 1 but instead enters a cycle, which raises the question: Is there a loop somewhere for positive numbers? If there is, then obviously the Collatz Conjecture is incorrect. However, in the next section, we will present a completed version of the Collatz Conjecture that can address negative numbers due to the new number theory (Chapter 7). This version accounts for the flow of positive numbers into negative ones and vice versa.

19.2. Stuck on the Decreasing Function

The decreasing function works by multiplying and dividing—operations that are linear. To achieve 1 in the end, these operations must remain within the linear interval; otherwise, we will eventually encounter the decreasing function

g (x)

and become stuck there. According to the new number theory, we cannot transition from

g (x)

f (x)

except by changing planes or forming a loop. First, it is impossible in the Collatz Conjecture since we remain on the same plane throughout, and second, it is problematic due to the conjecture’s chaotic behavior.

In the context of the Collatz Conjecture, changing mathematical planes is inherently impossible, as the conjecture dictates that the sequence remains confined to a single-dimensional framework throughout its progression. The possibility of forming a loop, while theoretically feasible, proves to be problematic in practice due to the conjecture’s inherently chaotic nature. This chaos introduces a significant level of unpredictability, complicating any attempt to use looping as a reliable method for moving from

g (x)

f (x)

Moreover, this inherent chaos within the Collatz Conjecture isn’t just a minor hurdle; it fundamentally alters the behavior of the sequence at various stages, making it challenging to predict or influence the direction of the sequence effectively. The mathematical community continues to explore the depths of these complications, seeking to understand better how the interplay of linearity and chaos shapes the behavior of such mathematical sequences.

An example of a number that can get to the decreasing function can be when

n = Y - 1

. Since Y is odd (proof in the Section 13); therefore:

(Y) \times 3 + 1 = Y \times 3 + 1 = g (0 + Y) + 1 = g (Y) + 1 = \frac{π}{4} Y + 1

Now we are on the decreasing function due to the multiplication presented in Equation (10). It is important to be only in the increasing function since it is a matter of incredible luck to get 1 on the decreasing function since there is no interval of linearity. And even if we get 1, it will not be the goal positive loop like on the increasing function, which is:

1, 4, 2, 1 \dots

(65)

We know that Y is odd (proof in the Section 13) so

- Y

is odd as well. Consider an example:

(- Y) \times 3 + 1 = - Y \times 3 + 1 = g (0 - Y) + 1 = g (Y) + 4 = \frac{π}{4} Y + 1

According to the new number theory, negative increases are asymmetrical to positive increases since there is a small shift of

- \frac{1}{12}

(proved in Section 11), which breaks linearity. This is the reason why the conjecture breaks and results in the loops presented in the previous section. The reason for exactly three loops is the Ramanujan Summation presented in Chapter 6. Ramanujan used a series P as manipulation and multiplied its result by a factor of 3 to get -1/12, so it makes total sense if the shift is

- \frac{1}{12}

, we will end exactly with three loops. Therefore, on the positive linear part of the increasing function, the Collatz Conjecture will always come to 1, from which we can conclude that it can no longer be called a conjecture. However, it is not satisfying the full set of numbers, so in the next section, we will present the "NAME" theorem, which is able to deal with all numbers on the number line. Numbers in the linear interval are finite, not infinite as in the current interpretation of the Collatz Conjecture, and since, as proved in the "increase of numbers" (Section 8), operators will continue acting linearly for all x in the linear interval, we will never go to the decreasing function since the size of it is less than 5%. Therefore, it must always converge to 1 since we process only a finite amount of numbers.

Statement 1.

The Collatz conjecture converges to 1 if and only if n is not a negative number and is on the linear interval; otherwise, the function will completely break.

20. Oscillating Theorem by Modifying Collatz Conjecture

To address the issue of becoming entrapped within the decreasing function

g (x)

as stipulated by the axiom 10 in number theory, a potential solution is to facilitate a return to the increasing function

f (x)

via a change of mathematical planes. This maneuver can be executed when any integer within the sequence, whether positive or negative, becomes even. At this juncture, instead of following the standard operations associated with

g (x)

, the sequence is altered by dividing the number by

- 2

. This division by

- 2

is not merely a numerical operation but a strategic move that symbolically and functionally shifts the sequence to a different plane of calculation, effectively redirecting it back to the increasing function

f (x)

, thereby sustaining the sequence’s upward trajectory.

In situations where the sequence generates an odd integer, the conventional rule of multiplying by 3 and adding 1 is applied. This rule ensures that the sequence can continue to evolve without stagnation, pushing the values upward. Even if we got to the decreasing function and didn’t succeed to end up and some even number but we get to the number a where

a | > Y

a | > - Y

(IT SHOULD BE REVERSED) then we will make a loop and go back to f(x). This dual-strategy approach—altering the operation based on the parity of the integers encountered—provides a dynamic framework that aims to keep the sequence active and progressing, ideally circumventing the loops or traps that might otherwise arise from continuous operation under a single mathematical rule.

\begin{matrix} f (n) = \{\begin{matrix} - (\frac{n}{2}) & if n \equiv 0 (\mod 2), \\ 3 n + 1 & else \end{matrix} \end{matrix}

(66)

Since we are changing planes, we will always stay on the increasing function

f (x)

. A question could arise: Why do we need to change planes when we are on the positive linear interval? The answer is just to make the function universal, but it will continue giving the same result.

Since negative and positive numbers are asymmetrical, this is the best way to interfere with them, which means we can deal with loops because we made the negative shift blur in the frequent switches between positive and negative planes. Because of that, negative numbers aren’t forming loops anymore, and from this, we are concluding that there are no loops in positive numbers.

Statement 2.

The Modified Collatz Conjecture will never form any loop for any positive or negative number on the interval

[- Y, Y]

, which makes it not a conjecture anymore.

21. Experiments and Graphs

This graph is a pivotal visualization that illustrates the pathway to 1 for the numbers 18 and -18, both of which are even numbers but originate from different sides of the number line

- Y \dots Y

. The graph displays a fascinating asymmetry between the paths taken by 18 and -18, despite both numbers undergoing the same operational steps. This divergence underscores the impact of starting on different mathematical planes—with 18 on the positive side and -18 on the negative. As the sequence progresses, the operations applied to 18 and -18 produce a distinct pattern that resembles a wave, oscillating between positive and negative values.

This oscillation is not just a numerical artifact; it reveals the underlying dynamics of the sequence as it transitions across different mathematical domains. Each peak and trough in the wave is a result of the specific operations dictated by the modified Collatz Conjecture (presented in Equation (66)), highlighting how the sequence manages to navigate through the complexities of mathematical spaces. Moreover, the graph not only tracks the trajectory towards 1 but also visually encapsulates the concept of mathematical numbers’ asymmetry. It serves as a clear demonstration of how similar operations can yield vastly different trajectories depending on the initial conditions and the mathematical context in which they are applied. This visual tool is crucial for both illustrating the sequence’s behavior and for facilitating a deeper understanding of the dynamic interplay between the new number theory, symmetry, and mathematical operations.

Figure 5. The flow of oscillating theorem to converge to 1 for pair of positive and negative even numbers: -18 and 18.

One more example but with the odd pair of numbers: -27 and 27. We can also observe wave properties of the sequence and extremely visible asymmetry.

Figure 6. The flow of oscillating theorem to converge to 1 for pair of positive and negative odd numbers: -27 and 27.

As mentioned before, the minus sign was added due to the flow of positive numbers into negative ones and vice versa, according to the new number theory.

To demonstrate the practical application of this concept, we created a loop for the number n ranging from -10,000 to 10,000. The graph represents the number of steps the Completed Collatz Conjecture must take to achieve 1 for each n.

Figure 7. The number of steps the Completed Collatz Conjecture has to do to achieve 1 for each n on the interval [-10000, 10000].

To summarize everything from the chapter: since there are no loops for positive and negative numbers, we can confidently declare that the Oscillating Theorem is a modified Collatz Conjecture which has been proven and is no longer a conjecture anymore.

Theorem 4.

Oscillating: For any value of n, in other words, from the interval

[- Y, Y]

, by using Equation (66), for every updated n, the value will always converge to 1.

General Version of the Zeta Function and Proof of the Riemann Hypothesis In this chapter, we will present a new version of the Riemann zeta function, which will provide a general approach to solving it, meaning we will be able to prove the Riemann Hypothesis. The hypothesis was presented in Section 3.

22. Problem with the Riemann Hypothesis

The main reasons why there was no proof of the Riemann Hypothesis before this paper are a lack of a general approach and the concept of infinity. The generally accepted mathematical framework lacks a general theory robust enough to handle the breadth of questions posed by the Riemann Hypothesis. Many attempts have been made before this paper, using various branches of mathematics like analytic number theory, algebraic geometry, and even random matrix theory, but these approaches have so far only yielded partial results or insights confined to specific conditions. While computers have verified the hypothesis for many zeros of the zeta function, computational methods can only test individual cases. They could not provide a proof that applies to all possible cases before this article. The transition from computational verification to theoretical proof involves bridging a vast conceptual gap.

In Chapter 7, we presented a new number theory, which means the generally accepted mathematical framework was incomplete and even incorrect. The general version of the zeta function and the proof of the Riemann Hypothesis will be additional proof for the mathematical framework proposed in the article. Moreover, the framework allows us to solve any "infinite" series that was not possible before.

23. General Version Of The Zeta Function

To deal with the zeta function we have to understand what it is. Actually zeta function is a sum of "infinite" series. It has a parameter s which is a power of each number in the series. We can write it down as follows:

ζ (s) = \sum_{x = 1}^{\infty} \frac{1}{x^{s}}

(67)

According to the new number theory presented in Chapter 7, there is no infinity, and all existing numbers lie within the interval

[- Y, Y]

, where

- Y

and Y are the smallest and the largest possible numbers, respectively. Therefore, the formula for the sum of infinity must be rewritten since infinity represents an interval of numbers not a defined number. Thus, we take the integral from

- Y

to Y using the increasing function

f (x)

and add it to the integral from Y to

- Y

using the decreasing function

g (x)

. This is written as:

δ = \int_{- Y}^{Y} f (x) d x + \int_{Y}^{- Y} g (x) d x

(68)

As covered in Section 12 and from Equation (68), we can start writing a new computable version of Riemann based on the fact that infinity does not exist and the interval of the series will extend to

- Y

. To start, we need to define a binomial coefficient that takes n and k and returns

(\binom{n}{k})

, which can be simplified by using the product of the terms as:

\prod_{i}^{k} \frac{n - i}{i + 1} = (\binom{n}{k})

The next step as in Section 11 we will define the interference coefficient to account for the interference between numbers between the increasing and decreasing function when we go through the integral ob both function receptively in the interval of

[- Y, Y]

. This coefficient can be expressed as 2 parts first if p is even:

M_{p} = \frac{p}{2 l o g_{2} {(Y)}^{2}}

Where p is a directly proportional constant of

f (x) = p x

(on the linear interval); in this case,

p = 1

as from Equation (67). Thus, we obtain the normalization value with the least number of bits to compute Y multiplied by 2, which is the dividend for the fraction where p is the divisor. In the other case, if p is odd, we create a harmonic series by rotating over an imaginary axis with an angle of

π

, written as:

M_{p} = e^{{(- 1)}^{\frac{1}{2}} π}

To write a complete equation for the full interference coefficient, we can create a piece-wise function, which is written as:

M_{p} = \{\begin{matrix} \frac{p}{2 l o g_{2} {(Y)}^{2}} & i f p % 2 = 0 \\ e^{{(- 1)}^{\frac{1}{2}} π} & e l s e \end{matrix}

Then, to obtain the sum of the term for every binomial coefficient multiplied by

{(k + 1)}^{- s}

, where in the case of

s = - 1

, it will be

k + 1

from 0 to k. We can denote this as:

\prod_{i}^{k} \frac{n - i}{i + 1} {(k + 1)}^{- s} = (\binom{n}{k}) {(k + 1)}^{- s} \to Ω_{k, n}

Moreover, we need to sum all the coefficients

Ω

from 1 to Y (all integers on the positive plane), each normalized by the value of

\frac{1}{2^{n}}

with a harmonic series created by multiplying

Ω

with

{(- 1)}^{k}

, multiplying by 1 if k is even, otherwise by -1. The whole thing, denoted by T, is represented as:

\begin{matrix} T = \sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{i}^{k} \frac{n - i}{i + 1} {(k + 1)}^{- s} = \sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} (\binom{n}{k}) {(k + 1)}^{- s} \\ = \sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} Ω_{k, n} \end{matrix}

(69)

Then, an important step in constructing the Riemann function is to divide the sum T by

1 - 2^{1 - s}

as proposed by Riemann in [15]. Therefore, we can express

ϕ

as:

ϕ_{s} = \frac{T}{1 - 2^{1 - s}} = \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} Ω_{k, n}}{1 - 2^{1 - s}} = \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{i}^{k} \frac{n - i}{i + 1} {(k + 1)}^{- s}}{1 - 2^{1 - s}}

This accounts for the normalization and coefficients in the zeta function, but now we need to consider the actual series as in Equation (67):

ζ (s) = \sum_{x = 1}^{\infty} \frac{1}{x^{s}}

So, it is the sum of an infinite series, which means it can be calculated by taking the area difference between the increasing

f {(x)}^{s}

and decreasing

g {(x)}^{s}

from

- Y

to Y and Y to

- Y

respectively, as done in Equation (68), in addition to the interference coefficient and

ϕ

. This ends with the new formula for the zeta function as:

\begin{matrix} ζ (s) = \int_{- Y}^{Y} \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{i}^{k} \frac{n - i}{i + 1} {(k + 1)}^{- s}}{1 - 2^{1 - s}} \frac{p}{Y - 1} + M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- s} d x \\ + \int_{Y}^{- Y} M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- s} d x \end{matrix}

(70)

In simpler words from all variables defined before it can be written as:

ζ (s) = \int_{- Y}^{Y} ϕ_{s} \frac{p}{Y - 1} + M_{p} + f {(x)}^{- s} d x + \int_{Y}^{- Y} M_{p} + g {(x)}^{- s} d x

(71)

Where

\frac{p}{Y - 1}

is used to spread the sum coefficient throughout Y. Please note, in the case of the zeta function, since it is

\frac{1}{x^{s}}

, the constant p is 1. From axiom 6, we can write the expansion as:

\frac{p}{Y - 1} = \frac{E}{- E + p}

Since

\frac{1}{Y - 1} = \frac{1}{Y} \times \frac{1}{1 - \frac{1}{Y}}

And we know that

\frac{1}{Y} = E

therefore it is written as

E \times \frac{1}{1 - E} = \frac{E}{- E + 1}

24. Computing Existing Values for the Zeta Function

The important step before proving the Riemann Hypothesis is to ensure that the general formula provides correct values for all known results for the zeta function with different values for s. Since we have the general formula, we can easily calculate the values for the zeta function. To speed up the process, we wrote a code in the Python programming language that will calculate the values for us. Since Y is uncomputable, we will use 100 instead (because we can interpret Y as 100%). It is important to understand that the closer we are to Y, the more accurate the result we will get.

We will present several different examples that show the approximate results of the general zeta function and graphs that describe the increasing (Equation (36)) and decreasing (Equation (48)) functions for each given s parameter.

24.1. s=-1

We will start from the most famous value for s, which is

- 1

. Actually,

ζ (- 1)

is the same as Ramanujan Summation presented in chapter 6, or as the sum of all natural numbers. As we know from the previous Section 23, the zeta function is actually the area between the increasing (Equation (36)) and decreasing (Equation (48)) functions. In this case, it will look as follows:

Figure 8. Increasing (blue) and decreasing (orange) functions for

ζ (- 1)

and Y as 100.

Figure 8. Increasing (blue) and decreasing (orange) functions for

ζ (- 1)

and Y as 100.

Now we will write the formula according to the Equation (71):

ζ (- 1) = \sum_{x = - Y}^{Y} \frac{1}{x^{- 1}} = \int_{- Y}^{Y} ϕ_{- 1} \frac{p}{Y - 1} + M_{p} + f {(x)}^{- 1} d x + \int_{Y}^{- Y} M_{p} + g {(x)}^{- 1} d x

As we know, the sum of natural numbers or

ζ (- 1)

is equal to

- \frac{1}{12}

, which is approximately

0.083

. The area between the increasing and decreasing functions from the code that we obtained is

0.083

, which corresponds to approximately

- \frac{1}{12}

. This demonstrates that the formula is correct for this instance.

24.2. s=2

The next very important value of s is 2, since it relates to the Basel problem, or the sum of inverse squares. As we know, the sum is equal to

\frac{π^{2}}{6}

, which is approximately

1.6449

. The graph for the increasing and decreasing functions in this case will look as follows:

Figure 9. Increasing (blue) and decreasing (orange) functions for

ζ (2)

and Y as 100.

Figure 9. Increasing (blue) and decreasing (orange) functions for

ζ (2)

and Y as 100.

The area between functions is approximately

1.6449

which is the same as the desire value.

24.3. s=-2

As we know

ζ (s) = 0

if s is an even negative number. The graphs of increasing and decreasing functions for case when

s = - 2

will look as follows:

Figure 10. Increasing (blue) and decreasing (orange) functions for

ζ (- 2)

and Y as 100.

Figure 10. Increasing (blue) and decreasing (orange) functions for

ζ (- 2)

and Y as 100.

The area between functions is approximately 0 which is the same as the desire value.

24.4. s=3 and s=-3

Just to see other values to be sure the general zeta function is working we will show example for odd positive and negative numbers. The results of the original zeta function are:

ζ (3) \approx 1.202

ζ (- 3) = \frac{1}{120} \approx 0.0083

Graphs will look as follows:

Figure 11. Increasing (blue) and decreasing (orange) functions for

ζ (3)

and Y as 100.

Figure 11. Increasing (blue) and decreasing (orange) functions for

ζ (3)

and Y as 100.

Figure 12. Increasing (blue) and decreasing (orange) functions for

ζ (- 3)

and Y as 100.

Figure 12. Increasing (blue) and decreasing (orange) functions for

ζ (- 3)

and Y as 100.

The area between

f (x)

and

g (x)

for 3 is

1.202

and for -3 is

0.0083

which are the same as desired values.

24.5. s= $\frac{1}{2}$ + $14.1 i$

One of the most important aspects is the results for the complex number with real part equal to

\frac{1}{2}

. To do that we have to complete the general zeta function (Equation (71)) so it can deal with complex numbers which means it can be represented as spirals.

\begin{matrix} ζ (\frac{1}{2} + 14.1 i) = \int_{- Y}^{Y} \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{z}^{k} \frac{n - z}{z + 1} {(k + 1)}^{- (\frac{1}{2} + 14.1 i)}}{1 - 2^{1 - (\frac{1}{2} + 14.1 i)}} \frac{p}{Y - 1} \\ + M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- (\frac{1}{2} + 14.1 i)} d x \\ + \int_{Y}^{- Y} M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- (\frac{1}{2} + 14.1 i))} d x \end{matrix}

We calculated the value for the previous equation using a computer where

Y = 100

, and the result is approximately 0, which is the desired result for

s = \frac{1}{2} + 14.1 i

Since all of the values for the original version of the zeta function and the general zeta function (equation 71) are the same, we can declare that the general zeta function is correct.

25. Proof Of The Riemann Hypothesis

The first thing that needs to be done is to rewrite the zeta function from Equation (70) to incorporate complex numbers and add an extra dimension. At first glance, we can add the power in the integral as

s + i t

\begin{matrix} ζ (s + i t) = \int_{- Y}^{Y} \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{z}^{k} \frac{n - z}{z + 1} {(k + 1)}^{- (s + i t)}}{1 - 2^{1 - (s + i t)}} \frac{p}{Y - 1} \\ + M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- (s + i t)} d x \\ + \int_{Y}^{- Y} M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- (s + i t))} d x \end{matrix}

(72)

However, computing and using this format is complex and not efficient, so we can utilize the properties of complex numbers and trigonometry to represent it as rotations. Consider a variable r dependent on s and t, calculated as follows:

r = \sqrt{s^{2} - t^{2}}

For the variable r, to obtain an angle of rotation

θ

in radians, consider the arc tangent function, which depends on the ratio of t to s as

\frac{t}{s}

. Therefore, it can be expressed as:

θ = \tan^{- 1} (\frac{t}{s})

Subsequently, we can say that:

x^{s + i t} = x^{r (\cos (θ) + i \sin (θ))}

Therefore, we can rewrite Equation (72) as:

\begin{matrix} ζ (s + i t) = \int_{- Y}^{Y} \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{z}^{k} \frac{n - z}{z + 1} {(k + 1)}^{- r (\cos (θ) + i \sin (θ))}}{1 - 2 \cdot 2^{- r (\cos (θ) + i \sin (θ))}} \frac{p}{Y - 1} + M_{p} \\ + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- r (\cos (θ) + i \sin (θ))} d x \\ + \int_{Y}^{- Y} M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- r (\cos (θ) + i \sin (θ))} d x \end{matrix}

(73)

From this, we can derive an expression to represent it as a product of a and b (please note that all equations must obey the Sophy-Peter equations in Section 10). Here, a will be x raised to a simplified power rather than a complex one, as shown in Equation (73), and b will be a rotation wave function expressed as

\cos (α) + i \sin (α)

. Therefore, we can write the product

a b

as:

a b = x^{α} (\cos (α) + i \sin (α))

As previously defined,

α

in our case is the variable r multiplied by the sine of the rotation angle

θ

, expressed as

r \sin (\sin (θ))

. Therefore, we can write another expression for x raised to the complex power of

s + i t

, where s is the real part.

x^{s + i t} = x^{r \cos (θ)} (\cos (r \sin (θ)) + i \sin (r \sin (θ)))

From this conclusion and the result we obtained from Equation (73), we can further simplify to be used later as Form 1 of the new general complex zeta function, written as:

\begin{matrix} ζ (s + i t) = \int_{- Y}^{Y} \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{z}^{k} \frac{n - z}{z + 1} {(k + 1)}^{r \cos (θ)} (\cos (r \sin (θ)) + i \sin (r \sin (θ)))}{1 - 2 \cdot 2^{r \cos (θ)} (c o s (r \sin (θ)) + i \sin (r \sin (θ)))} \frac{p}{Y - 1} + M_{p} \\ + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{r \cos (θ)} (\cos (r \sin (θ)) + i \sin (r \sin (θ))) d x \\ + \int_{Y}^{- Y} M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{r \cos (θ)} (\cos (r \sin (θ)) + i \sin (r \sin (θ))) d x \end{matrix}

(74)

Where

2^{1 - x} = 2 \cdot 2^{- x}

. An important aspect of this is using the Euler expansion to develop the same and achieve the same result, where

x^{s + i t}

is represented as a product using Euler’s properties. We know from exponent properties that

x^{s + i t} = x^{s} \times x^{i t}

The term

x^{s}

represents a real number raised to a real power, so we can leave it as it is. Now focusing on

x^{i t}

, using the Euler property, we have:

x^{i t} = e^{i t \ln (x)}

We can plug this into our equation, giving:

x^{s + i t} = x^{s} \cdot e^{i t \ln (x)}

We know from Euler’s formula that:

e^{i α} = \cos (α) + i \sin (α)

Therefore, using this on the last result from our equation where

e^{i t \ln (x)} = x^{i t}

, we can derive the result:

x^{i t} = e^{i t \ln (x)} = \cos (t \ln (x)) + i \sin (t \ln (x))

Finally, we can substitute the result of

\cos (t \ln (x)) + i \sin (t \ln (x))

into our main equation to get the final product represented as:

x^{s + i t} = x^{s} (c o s (t \ln (x)) + i \sin (t \ln (x)))

(75)

Where

x^{s}

represents the real part of the expression, and

(\cos (t \ln (x)) + i \sin (t \ln (x)))

represents the complex part. Therefore, we can use this formulation in our case to rewrite the zeta function for complex numbers using the Euler expansion as:

\begin{matrix} ζ (s + i t) = \int_{- Y}^{Y} \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{i}^{k} \frac{n - i}{i + 1} {(k + 1)}^{- s} (- c o s (t \ln (β)) - i \sin (t \ln (β)))}{1 - 2 \cdot 2^{- s} (- \cos (\ln (2) t) - i \sin (\ln (2) t))} \frac{p}{Y - 1} + M_{p} \\ + {(\frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- s} (- c o s (t \ln (f (x))) - i \sin (t \ln (f (x)))) d x \\ + \int_{Y}^{- Y} M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- s} (- c o s (t \ln (g (x))) - i \sin (t \ln (g (x)))) d x \\ ⟶ β = k + 1 \end{matrix}

(76)

The zeta function normally converges only if

s > 1

. In our framework, this condition corresponds to a convergent series, where the function

h (x) = \frac{1}{n^{s}}

and

ζ (s) = \sum_{n}^{\infty} h_{s} (n)

. Therefore, based on our conclusion in Section 12, we can write:

h_{s} (Y) \approx 0, \forall s > 1

Where ≈ represents convergence to 0. Please note that in cases where

h (Y) \approx 0

, the integration of numbers going back on the decreasing function occurs, causing interference as described in Section 11. However, from this analysis, we can redefine infinity in the Riemann integral, where

s > 1

, as Y as detailed in Section 12.

\frac{1}{n^{s}} Π (s - 1) = \int_{0}^{Y} e^{- n x} f {(x)}^{s - 1} d x

The integral around the value

2 n π i

{(- 2 n π i)}^{s - 1} (- 2 π i)

. Therefore, we can write:

2 π s Π (s - 1) ζ (s)

And draw a relation between

ζ (s)

and

ζ (1 - s)

as:

Π (\frac{s}{2} - 1) π^{- \frac{s}{2}} ζ (s)

Where

ζ (s)

is finitely computed as in equation 76. Therefore we can write it as:

\frac{1}{n^{s}} Π (\frac{s}{2} - 1) π^{- \frac{s}{2}} = \int_{0}^{Y} e^{- n^{2} π x} x^{\frac{s}{2} - 1} d x,

If we set an "infinite" series of

e^{- n^{2} π x}

\sum_{1}^{\infty} e^{- n^{2} π x} = ψ (x),

Using the transformation from 12, we can set the new finite set as:

\begin{matrix} \sum_{1}^{\infty} f (e^{- n^{2} π f (x)}) = \int_{- Y}^{Y} μ + \frac{Y}{2} s i n^{- 1} (\frac{e^{- n^{2} π f (x)}}{Y}) + \frac{e^{- n^{2} π f (x)} \sqrt{1 - {(\frac{e^{- n^{2} π f (x)}}{Y})}^{2}}}{2} d x \\ + \int_{Y}^{- Y} μ + \frac{Y}{2} s i n^{- 1} (\frac{e^{- n^{2} π f (x)}}{Y}) - \frac{e^{- n^{2} π f (x)} \sqrt{1 - {(\frac{e^{- n^{2} π f (x)}}{Y})}^{2}}}{2} d x = ψ (x) \\ \forall \ln (\frac{Y}{- n^{2} π}) < x < \ln (\frac{Y}{n^{2} π}) \end{matrix}

(77)

Where we know that:

\int_{1}^{Y} \frac{1}{x} d x = \ln (f (Y)) + C = \ln (S Y) + C

Where

S = \frac{π}{4}

. This integral computes the area under the curve of

\frac{1}{x}

across all possible values on the number line. Then, using Riemann properties and the equivalent finite series, we can set

Π (\frac{s}{2} - 1) π^{- \frac{s}{2}} ζ (s)

to:

Π (\frac{s}{2} - 1) π^{- \frac{s}{2}} ζ (s) = \int_{0}^{Y} ψ (x) f {(x)}^{\frac{s}{2} - 1} d x = λ (x)

Where

ψ (x)

is defined in Equation (77). Then, since we know from Jacob Fundi that:

2 ψ (x) + 1 = x^{- \frac{1}{2}} (2 ψ (\frac{1}{x}) + 1)

Therefore we can use it to set new value for

λ (x)

\begin{matrix} Π (\frac{s}{2} - 1) π^{- \frac{s}{2}} ζ (s) & = \int_{1}^{Y} ψ (x) f {(x)}^{\frac{s}{2} - 1} d x + \int_{1}^{Y} ψ (\frac{1}{x}) f {(x)}^{\frac{s - 3}{2}} d x + \frac{1}{2} \int_{0}^{1} (x^{\frac{s - 3}{2}} - x^{\frac{s}{2} - 1}) d x \\ = \frac{1}{s (s - 1)} + \int_{1}^{Y} ψ (x) (f {(x)}^{\frac{s}{2} - 1} + f (x) x^{- \frac{1 + s}{2}}) d x = ξ (t) \end{matrix}

(78)

Given the fact that integrals from a to Y are finite and computable, for example, consider the integral

\int_{1}^{Y} \frac{1}{x^{2}} d x

, this can be computed as:

\int_{1}^{Y} \frac{1}{x^{2}} d x = \frac{- 1}{Y} - \frac{- 1}{1} = - E + 1 = 1 - E

Since we know that E is the smallest number but also the step we can have, we therefore conclude that the result from this will be the previous step,

1 - E = 0.999 \dots

Given in big physics equations, this converges to approximately 1, as discussed in Section 14.

We can now set

s = \frac{1}{2} + t i

\begin{matrix} ξ (t) = \frac{1}{2} - (t^{2} + \frac{1}{4}) \int_{1}^{Y} ψ (x) f {(x)}^{- \frac{3}{4}} \cos (\frac{1}{2} t \log x) d x \\ \forall t < \sqrt{Y} \end{matrix}

(79)

In other words

ξ (t) = 4 \int_{1}^{Y} \frac{d}{d x} (f {(x)}^{\frac{3}{2}} ψ^{'} (x)) f {(x)}^{- \frac{1}{4}} \cos (\frac{1}{2} t \log x) d x

We know from Equation (74) that for values x,

ζ (x)

remains finite given that it is the interference between the $- Y \dots Y$ cycle, not literally a sum. Since this applies to the log of the other factors of

ξ (t)

, the function

ξ (t)

can only have zeros at

- \frac{1}{2} i < t < \frac{1}{2} i

. The number of roots R of

ξ (t) = 0

where the real part is in the interval from 0 to

\frac{π}{4} Y

is:

\begin{matrix} R = \frac{f (Y)}{2 π} \log (\frac{f (Y)}{2 π}) - \frac{f (Y)}{2 π} = \frac{S Y}{2 π} \log (\frac{S Y}{2 π}) - \frac{S Y}{2 π} \\ ∣ S = \frac{π}{4} ⟶ ∴ = \frac{2}{π^{2}} Y (l o g (\frac{2}{π^{2}} Y) - 1) = \frac{2}{π^{2}} Y (\log (\frac{2}{π^{2}}) + \log (Y) - 1) \\ = \frac{2}{π^{2}} Y (\frac{\ln (\frac{2}{π^{2}})}{\ln (10)} + \log (Y) - 1) \end{matrix}

(80)

Then we know that the gamma function is given by:

Γ (s) = \int_{0}^{\infty} x^{s - 1} e^{- x} d x = \int_{0}^{\infty} γ_{s} (x) d x

(81)

Since the gamma function E converges and does not approach Y at

x = Y

, which means it will not transform to the decreasing function as described in Section 12. Therefore, it can be written as (where

x \to f (x)

Γ (s) = \int_{0}^{Y} x^{s - 1} e^{- x} d x

(82)

And the small gamma function

γ_{s} (x)

can be expressed as:

γ_{s} (x) = x^{s - 1} e^{- x}

We know from [13] that:

\begin{matrix} Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \frac{π^{\frac{3}{2}}}{T \sin (\frac{π}{2} s)} \\ Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \frac{π^{\frac{3}{2}}}{T \cos (\frac{π}{2} s)} \end{matrix}

(83)

We can compute the integral within our framework as follows:

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \int_{0}^{Y} x^{- \frac{s + 1}{2}} e^{- x} d x Γ (\frac{s}{2}) = \int_{0}^{Y} x^{- \frac{s + 1}{2}} e^{- x} d x \int_{0}^{Y} {(u x)}^{\frac{s}{2} - 1} e^{- u x} x d u

Where we obtained the integral of

Γ (\frac{s}{2})

by applying the change of variables

v = u x

and

d v = x d u

, following:

\int_{0}^{Y} v^{\frac{s}{2} - 1} e^{- v} d v = \int_{0}^{Y} {(u x)}^{\frac{s}{2} - 1} e^{- u x} x d u

Expanding the exponents’ coefficients from

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2})

we obtain:

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \int_{0}^{Y} x^{- \frac{s + 1}{2}} e^{- x} d x \int_{0}^{Y} u^{\frac{s}{2} - 1} x^{\frac{s}{2} - 1} e^{- u x} x d u

Then use integration rules:

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \int_{0}^{Y} x^{- \frac{1}{2}} e^{- x (1 + u)} d x \int_{0}^{Y} u^{\frac{s}{2} - 1} d u

Therefore our final integral will be:

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \int_{0}^{Y} \frac{1}{\sqrt{x}} e^{- x (1 + u)} d x \int_{0}^{Y} u^{\frac{s}{2} - 1} d u

(84)

Then if we assigned T to the integral:

T = \int_{0}^{Y} e^{- {(\sqrt{1 + u})}^{x})} d x = \frac{1}{\sqrt{1 + u}} ∣ E \approx 0

By multiplying the integral we got from

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2})

with T we get:

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) T = \frac{π^{\frac{3}{2}}}{s i n (\frac{π}{2} s)}

∴ Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \frac{π^{\frac{3}{2}}}{T s i n (\frac{π}{2} s)}

(85)

Which matches Equation (83) part 1. Then, instead of applying the change of variables in the integral of

Γ (\frac{s}{2})

, let’s apply it in the integral of

Γ (\frac{1 - s}{2})

, and then we multiply both results. We aim to derive the outcome where the integral of the gamma function at

\frac{1 - s}{2}

will have

v = u x

and

d v = x d u

, which is:

Γ (\frac{1 - s}{2}) = \int_{0}^{Y} v^{\frac{1 - s}{2}} e^{- v} d v = \int_{0}^{Y} {(u x)}^{- \frac{s + 1}{2}} e^{- u x} d u

Subsequently we can proceed to solve

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2})

with the new change of variables following:

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \int_{0}^{Y} x^{\frac{s}{2} - 1} e^{- x} d x Γ (\frac{1 - s}{2}) = \int_{0}^{Y} x^{\frac{s}{2} - 1} e^{- x} d x \int_{0}^{Y} {(u x)}^{- \frac{s + 1}{2}} e^{- u x} d u

Expanding exponents coefficients as before:

\int_{0}^{Y} x^{\frac{s}{2} - 1} e^{- x} d x \int_{0}^{Y} {(u x)}^{- \frac{s + 1}{2}} e^{- u x} d u = \int_{0}^{Y} x^{\frac{s}{2} - 1} e^{- x} d x \int_{0}^{Y} u^{- \frac{s + 1}{2}} x^{- \frac{s + 1}{2}} e^{- u x} d u

Finally, we apply integration properties:

\int_{0}^{Y} x^{\frac{s}{2} - 1} e^{- x} d x \int_{0}^{Y} u^{- \frac{s + 1}{2}} x^{- \frac{s + 1}{2}} e^{- u x} d u = \int_{0}^{Y} x^{- \frac{1}{2}} e^{- x (1 + u)} d x \int_{0}^{Y} u^{- \frac{s + 1}{2}} d u

Therefore:

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \int_{0}^{Y} x^{- \frac{1}{2}} e^{- x (1 + u)} d x \int_{0}^{Y} u^{- \frac{s + 1}{2}} d u

(86)

By multiplying the result with T we will obtain:

Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) T = \frac{π^{\frac{3}{2}}}{\cos (π \frac{s}{2})}

∴ Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) = \frac{π^{\frac{3}{2}}}{T \cos (π \frac{s}{2})}

(87)

Which matches the second part from Equation (83). All of this work represents a finite area in the interval from 0 to Y. However, for this to be applicable in Equation (83), it must be finite and converge, since the current integral given before this paper was written

\int_{0}^{\infty} t^{\frac{- 1}{2}} e^{- t (1 + v)} d t,

goes to infinity. It was rewritten with Y in Equations (82) and (84), which we will further use in our framework to prove, following the small gamma function that converges for

s < 1

(point 1).

γ_{s} (Y) = Y^{s - 1} e^{- Y} = Y^{s} Y^{- 1} e^{- Y} = Y^{s} e^{- Y} E = α E \approx 0

(88)

Therefore we can proceed to solve the equation:

\frac{π^{\frac{3}{2}}}{T \sin (\frac{π}{2} s)} = \frac{π^{\frac{3}{2}}}{T \cos (\frac{π}{2} s)}

Dividing both sides with

\frac{π^{\frac{3}{2}}}{T}

will give us:

s i n (\frac{π}{2} s) = \cos (\frac{π}{2} s)

By using the trigonometric identity

\frac{\sin x}{\cos x} = \tan x

\tan (\frac{π}{2} s) = 1

\frac{π}{2} s = \tan^{- 1} (1) = \frac{π}{4}

∴ s = \frac{π}{4} \frac{2}{π} = \frac{2}{π} S = \frac{1}{2}

(89)

Where S, as mentioned in theorem 3, is

\frac{π}{4}

. Therefore, from Equations (74), (76), (80), (89), (82), (88), (84), (86), (85), (87), and point 1, we can conclude that all points of the non-trivial zeros

ζ (s + i t) = 0

lie on the critical line

s = \frac{1}{2}

with various complex numbers

i t

, as further proved by experiments in Section 24. Since the reflection formula within the new Sophy-Peter framework using

Γ (\frac{1 - s}{2}) Γ (\frac{s}{2})

states that the Equation

ξ {(s)}^{2}

is only valid when the real part of s is $\frac{1}{2}$ , where

ξ (s)

is defined as:

ξ (s) = \frac{1}{2} s (s - 1) π (- \frac{s}{2}) Γ (\frac{s}{2}) ζ (s) ∣ s = x + i t ∣ ξ (s) = ξ (1 - s)

Squaring this to obtain

ξ {(s)}^{2}

, we derive:

ξ {(s)}^{2} = ξ (s) ξ (1 - s) = \frac{1}{4} s^{2} {(s - 1)}^{2} π^{- \frac{1}{2}} Γ (\frac{s}{2}) Γ (\frac{1 - s}{2}) ζ (1 - s) ζ (s)

Where

ζ (s)

is not calculated in the traditional manner but as the difference between integrals of the increasing and decreasing functions, using Equation: (76):

\begin{matrix} ζ (s) = \int_{- Y}^{Y} \frac{\sum_{n}^{Y} \frac{1}{2^{n}} \sum_{k}^{n} {(- 1)}^{k} \prod_{i}^{k} \frac{n - i}{i + 1} {(k + 1)}^{- s} (- c o s (t \ln (β)) - i \sin (t \ln (β)))}{1 - 2 \cdot 2^{- s} (- \cos (\ln (2) t) - i \sin (\ln (2) t))} \frac{p}{Y - 1} + M_{p} \\ + {(\frac{Y}{2} \sin^{- 1} (\frac{x}{Y}) + \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- s} (- c o s (t \ln (f (x))) - i \sin (t \ln (f (x)))) d x \\ + \int_{Y}^{- Y} M_{p} + {(\frac{Y}{2} s i n^{- 1} (\frac{x}{Y}) - \frac{x \sqrt{1 - {(\frac{x}{Y})}^{2}}}{2})}^{- s} (- c o s (t \ln (g (x))) - i \sin (t \ln (g (x)))) d x \\ ⟶ β = k + 1 \end{matrix}

Conclusions This article presents a fully new perspective for mathematics, stating that the axiom of infinity is actually totally wrong, but the presented mathematical framework opens many possibilities for physics, mathematics, and computer science. Moreover, it solves most of the paradoxes (if not all) in mathematics.

The incredible thing about this article is that we don’t only present some concepts and theories but actually prove our assumptions using the oldest mathematical problems, such as the Collatz Conjecture and the Riemann Hypothesis(which is considered a Millennium problem).

In further work, we will present a physics concept, which will be one more proof for the new number theory presented in Chapter 7.

26. New Number Theory

This new number theory is designed to fix paradoxes and provide a framework to deal with "infinite" series. The name of the new mathematical framework is Sophy-Peter Framework. It gives accurate predictions even in the physical universe, which will be explained in further work. In the article, we explained several paradoxes in mathematics (such as Galileo’s Paradox, Ramanujan Summation, Casimir Effect, Gabriel’s Horn Paradox) connected with infinity in Chapter 3, then solved them and explained why they occur using the new number theory in Chapter 14.

There are several important aspects of the new number theory:

The concept of "infinity" as an interval $[- Y, Y]$ (where $- Y$ and Y are the smallest and the largest possible numbers) [Section 8];
Non-linear growth of numbers [Section 8];
Increasing and decreasing functions ( $f (x)$ and $g (x)$ ) [Section 8 and Section 9];
Sophy-Peter equations [Section 10];
Number’s interference [Section 11];
Shift of negative numbers ( $- \frac{1}{12}$ ) [Section 11];
How to deal with "infinite" series [Section 12];
Cycles of numbers and the maximum number of them [Section 13].

Also 13 axioms of the Sophy-Peter mathematical framework were created:

Axiom 1: The biggest number that can exist in the number line is Y and the smallest number is

- Y

Axiom 2: Any continuous function that exists can only have a domain from

- Y

to Y.

Axiom 3: The increase of numbers is not always linear in a given number line from

- Y

to Y, so any term x can not be written as x but rather

f (x)

Axiom 4: Mathematical operations break outside the linear interval since the increase is not linear anymore from axiom 3, therefore Sophy-Peter equations have to be used.

Axiom 5: The smallest positive number that can exist on the number line is E, and the largest negative number is

- E

Axiom 6: On the interval

[a, b]

, the maximum number of numbers is Y, where a and b are any neighboring integers on the number line and

∣ a ∣ < ∣ b ∣

. Moreover, the smallest and largest numbers on the interval

(a, b)

are

f (a + E)

and

f (b - E)

respectively, if a and b are non-negative, and

f (b + E)

and

f (a - E)

if a and b are non-positive.

Axiom 7:E and

- E

are not only the smallest possible positive and the largest negative numbers, respectively, but also the smallest increment and decrement that can be applied to a number.

Axiom 8: Numbers attempting to go beyond Y or before

- Y

will end up obeying the Sophy-Peter equations, which dictate that they will go back or forward on the number line via the decreasing function

g (x)

Axiom 9: Since the addition of positive numbers can never yield a negative number, but on the decreasing function

g (x)

numbers are decreasing, so after reaching 0, numbers will continue on the increasing function.

Axiom 10: It is possible to switch from the decreasing to the increasing function by changing planes, from positive to negative or vice versa.

Axiom 11: The division of a linear number by any number a, where

| a | \geq 1

, will result in a number from the linear interval where

f^{'} (x) = 1

Axiom 12: In an "infinite" cycle, when numbers

| > Y

, they revert to the decreasing function until

- Y

and ascend again on the increasing function until Y. Therefore, numbers interfere with each other, leaving an asymmetrical value between the positive and negative planes.

Axiom 13: Due to cycles of numbers wave interpretation according to the new number theory the biggest possible number of cycles is Y, which is the largest possible value in mathematics.

27. Collatz Conjecture

Using the new number theory, presented in Chapter 7, we were able to disprove Collatz Conjuncture in Section 19.2. Due to non-linear properties of growth on the number line the original Collatz Conjuncture will be stuck on the decreasing function without chance of getting back to increasing function which means it will never reach 1 for some instances.

To fix this issue using axiom 10 we modified the Collatz Conjecture to change planes each time we get even number. Moreover using this approach we level out the shift of negative numbers, presented in Section 11, so we never stuck in negative loops, presented in Section 19.1.

So the oscillating theorem was created and proved in Section 20. The formula (Equation (66)) for the modified Collatz conjecture or the oscillating theorem is:

f (n) = \{\begin{matrix} - (\frac{n}{2}) & if n \equiv 0 (\mod 2), \\ 3 n + 1 & else \end{matrix}

In Section 21, practical applications of the oscillating theorem and graphs for them were presented.

28. Riemann Hypothesis

To prove the Riemann Hypothesis, we addressed two main reasons why the hypothesis had not been proven previously: the concept of infinity and the lack of a general approach. Due to the new number theory (Chapter 7), the generally accepted concept of infinity is incorrect, thus solving the first reason. In Section 23, the general zeta function (Equation (71)) was presented. The main idea of the general function is that the zeta function is actually the area between the increasing and decreasing functions (Equation (68)).

In Section 24, we compared the values of the general zeta function with the known values for the original zeta function. The values are approximate since we used a computer to calculate them, and instead of Y (the largest possible number), we used 100, since Y is uncomputable. The values were the same, which proves the general zeta function. The shorter vision of the general zeta function is written as follows:

ζ (s) = \int_{- Y}^{Y} ϕ_{s} \frac{p}{Y - 1} + M_{p} + f {(x)}^{- s} d x + \int_{Y}^{- Y} M_{p} + g {(x)}^{- s} d x

The full zeta function is written in Equation (70). Also there is general zeta function constructed to work with complex numbers, which is presented in Equations (73) and (74).

In Section 25, we presented the proof for the Riemann Hypothesis, which was considered a millennium problem [16]. Using the Sophy-Peter Framework (Chapter 7), to derive the general zeta function (Equation (71)), we were able to modify and finish the Riemann proof [15]. The conclusion is that from now on, the Riemann Hypothesis is proved.

References

Levinas, Emmanuel, Springer Netherlands, Dordrecht, Collected Philosophical Papers, 47–59. Philosophy and the Idea of Infinity (1987).
E. Fischbein, D. Tirosh and P. Hess., Educational Studies in Mathematics, Vol. 10, No. 1 , 3-40. The Intuition of Infinity (1979).
Haim Gaifman, Springer, Vol. 20, No. 2, 131-155. Paradoxes of Infinity and Self-Applications, I (1983).
J. Walting, Oxford University Press, Vol. 13, No. 2, 39-46. The Sum of an Infinite Series (1952).
Konrad Knopp, Courier Corporation - Mathematics. Infinite Sequences and Series (1956).
Piotr Błaszczyk, Philosophical Problems in Science 70, 73-107. Galileo’s Paradox and Numerosities (2021).
Günter Plunien and Berndt Müller and Walter Greiner, Physics Reports, Vol. 134, No. 2, 87-193. The Casimir effect (1986).
Bietenholz Wolfgang, arXiv:2201.00076 [physics.hist-ph]. Ramanujan summation and the Casimir effect (2022).
David Richeson, arXiv:1403.8078 [math.HO]. Gabriel’s Paper Horn (2014).
Andrei, Ş., Masalagiu, C, Acta Informatica 35, 167–179. About the Collatz conjecture (1998).
Bernard Candelpergher, Springer Cham, Lecture Notes in Mathematics, 978-3-319-63629-0. Ramanujan Summation of Divergent Series (2017).
Wolfgang Bietenholz, arXiv:2102.09371 [physics.hist-ph].From Ramanujan to renormalization: the art of doing away with divergences and arriving at physical results (2021).
Bruce R. Kusse and Erik A. Westwig, WILEY-VCH Verlag GmbH & Co. KGaA. Mathematical Physics, Applied Mathematics for Scientists and Engineers (2006).
H. Edwards, Dover Publications, Mineola, NY. Riemann’s zeta function (2001).
J. Brian Conrey, Notices of the AMS, Vol. 50, No. 3. The Riemann Hypothesis (2003).
P. Sarnak, Clay Mathematics Institute. Problems of the millennium: The Riemann hypothesis (2005).
Peter Lynds, arXiv:physics/0612053 [physics.gen-ph]. On a finite universe with no beginning or end (2006).
L. Carlitz, Duke University, Durham, North Carolina. Bernoulli numbers (1948).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Proof of the Riemann Hypothesis and the Modified Collatz Conjecture Using the Sophy-Peter Mathematical Framework

Abstract

1. Introduction

1.1. Concept of Infinity and the Problem with the Thinking Paradigm

2. Collatz Conjecture

3. Riemann Hypothesis

4. Galileo’s Paradox

5. Casimir Effect

6. Gabriel’s Horn Paradox

7. − 1 12

8. Increase of Numbers

9. What is after Y?

10. Sophy-Peter Equations

10.1. Observable Algebra Operators

10.2. Universal Equations

10.2.1. Sophy-Peter Equation 1

10.2.2. Sophy-Peter Equation 2

10.2.3. Sophy-Peter Equation 3

11. Interference

11.1. The Magic Function M ( p )

12. Dealing With "Infinite" Series And Complex Analysis

12.1. New Series summation interpretation

13. How many cycles?

13.1. The Y th Cycle ( Y × Y )

14. Summary

15. Fixing Galileo’s Paradox

16. Explaining Ramanujan Summation

17. Explaining Casimir Effect

18. Fixing Gabriel’s Horn Paradox

19. Problems with Collatz Conjecture

19.1. Negative Numbers

19.2. Stuck on the Decreasing Function

20. Oscillating Theorem by Modifying Collatz Conjecture

21. Experiments and Graphs

22. Problem with the Riemann Hypothesis

23. General Version Of The Zeta Function

24. Computing Existing Values for the Zeta Function

24.1. s=-1

24.2. s=2

24.3. s=-2

24.4. s=3 and s=-3

24.5. s= 1 2 + 14.1 i

25. Proof Of The Riemann Hypothesis

26. New Number Theory

27. Collatz Conjecture

28. Riemann Hypothesis

References

MDPI Initiatives

Important Links

Subscribe

7. $- \frac{1}{12}$

11.1. The Magic Function $M (p)$

13.1. The $Y_{th}$ Cycle ( $Y \times Y$ )

24.5. s= $\frac{1}{2}$ + $14.1 i$