Prerpints.org logo
Preprint
Article

Numerical Study of Concrete: A Mesoscopic Scale Simulation Methodology

Altmetrics

Downloads

67

Views

50

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 May 2024

Posted:

10 May 2024

You are already at the latest version

Alerts
Abstract
This study is dedicated to understanding and simulating the mechanical properties of concrete, with a specific focus on the mesoscopic scale. Investigating concrete at this level involves examining its composition as a heterogeneous amalgamation comprising mortar, aggregates, and the interfacial transition zone (ITZ). Such an approach provides a detailed examination of the material's behavior and attributes. Numerical models are utilized, leveraging the finite element method (FEM), to examine the behavior of concrete. The study employs MATLAB programming to develop three-dimensional models, subsequently subjected to FEM analysis. Various mesoscopic Representative Volume Elements (RVEs) are formulated, encompassing varied shapes and dimensions. The MATLAB framework generates input files for numerical FEM simulations, replicating compression strength tests. As complexity increases with the inclusion of the ITZ, prismatic RVEs are developed. The proposed mesoscopic model establishes a foundational framework for a numerical simulation methodology tailored to laboratory compression tests. It provides detailed insights into concrete behavior, elucidating deformation, and fracture mechanisms. Although not a complete substitute for experimental methods, these models offer a cost-effective and expeditious alternative, pinpointing vulnerable areas and exploring the implications of additional materials on concrete behavior. Experimental data and virtual tests pave the way for mitigating carbon footprint and improving concrete sustainability.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Concrete, widely employed in construction due to its cost-effectiveness, strength, and durability, has diverse applications in civil engineering. However, its highly heterogeneous microstructure complicates predictions solely based on experiments. Theoretical studies, employing micromechanics analysis, help deduce macroscopic constitutive behavior. Comprising different phases, concrete's behavior and properties exhibit variations across scales, ranging from the microscopic to the macroscopic scales [1,2].
At the microscopic level, concrete is a composition of cement particles and water, forming the intricate cement paste enveloping aggregates like sand and gravel. The microstructure of this paste is intricate, featuring porosities, micro-cracks, and other defects that can significantly influence its mechanical properties [3]. Zooming in to the mesoscopic level, concrete reveals itself as a material consisting of three crucial phases: the mortar, comprising cement, water, and fine aggregate; the interfacial transition zone (ITZ) found between the coarse aggregate and the mortar; and the coarse aggregates themselves [4,5]. Each of these phases contributes uniquely to the overall behavior of the material. At this level, parameters like shape, size, and distribution of coarse aggregates significantly impact concrete's mechanical behavior. This study aims to create random mesostructured models for concrete, considering aggregate particles' coordinates and sizes, then subjecting them to finite element method (FEM) analysis to understand their effects on macroscopic responses. At the macroscopic level, concrete is simplified as a single-phase material characterized primarily by its compressive strength, modulus of elasticity, and its flexural and tensile behavior. This macroscopic view is essential in the design process, where meticulous control and verification of these properties are imperative to ensure the safety and durability of constructed structures [6]. Engineers and architects rely on a thorough understanding of concrete's behavior at different scales to optimize its use in various applications, meeting the stringent demands of modern construction standards.
When examining concrete at the mesoscopic level, which deals with millimeter-scale dimensions, numerical models become valuable tools. These models enable a detailed analysis of how concrete behaves at the specimen level. The material's traits are intricately influenced by the properties of its key components: coarse aggregate, mortar, and the interface between them. Utilizing numerical models at this mesoscopic scale holds significant importance, offering insights into the mechanical aspects of concrete, such as its fracture toughness and ability to bear loads. This approach provides a nuanced understanding of concrete behavior, contributing to advancements in structural engineering and material science [7].
Several mesoscopic models have been developed, each examining material composition's influence on overall behavior [8,9,10]. Aggregate shapes, sizes, and distributions are essential factors affecting stress distribution and crack initiation. Various approaches, including truss models, lattice models, and finite element mesh simulations, have been employed to study concrete's microstructure. Notably, the choice of aggregate size distribution, often described by grading curves like the Fuller curve, plays a vital role in concrete mix design, affecting workability, mechanical strength, permeability, and durability of the material. In terms of simulating aggregate spatial distribution, different methods like take-and-place, divide-and-fill, stochastic-heuristic algorithms, and distinct element methods have been utilized. Meshing techniques, such as aligned and unaligned approaches, help discretize mesoscopic models for numerical analysis. The interfacial transition zone (ITZ) between aggregates and mortar is recognized as influential in microcrack initiation, prompting varied approaches in mesh generation considering ITZ domains [11].
The main novelties of the work have been in two aspects: concerning the algorithm used and regarding the numerical model. In the first case a Matlab code has been developed based on the take and place method, capable of designing Representative Volume Elements (RVE) in prismatic or cylindrical form, with filling characteristics as required in terms of aggregate percentage and size. Additionally, the Interfacial Transition Zone (ITZ) has been considered, and it is possible to account for the presence of pores, although this option has not been chosen in this instance. The geometric arrangement ensures that aggregates do not touch or overlap, thereby allowing the consideration of the specific properties of the ITZ. With respect to the numerical model, for mortar and ITZ, a nonlinear combined mathematical model of concrete based on the Drucker-Prager material model for compression stresses, and Willam and Warnke for tension stresses, is used to predict both material failure modes: cracking and crushing.
For the contact between coarse aggregates and ITZ, a pure penalty algorithm between deformable surfaces, with asymmetric behavior, is used.

2. Materials and Methods

The fact that concrete is brittle in tension but relatively strong in compression, that the strength of the mortar is higher than that of the concrete itself, and that this strength decreases as the size of the coarse aggregate increases, or that the permeability of high-density coarse aggregate concrete is higher than that of the cement paste, are questions about the behavior of concrete that are answered by the existence of the interfacial transition zone (ITZ) between the large aggregate particles and the hydrated cement paste [12]. Although it is composed of the same elements as the hydrated cement paste, the microstructure, and properties of the interfacial transition zone (ITZ) differ from the bulk hydrated cement paste. Therefore, it is treated as a separate phase in the microstructure of concrete.
Wittmann and his team [9] have delved into key aspects related to the Interfacial Transition Zone (ITZ) and the behavior of concrete at the mesoscopic level. They have crafted both 2D and 3D models, meticulously considering the interplay between mortar and aggregates, along with the geometric and mechanical characteristics inherent to each phase.
The mesoscopic model developed by Wittmann is based on the concept that concrete can be considered a composite material, formed by aggregates dispersed in a matrix of cement paste. In this model, concrete is divided into discrete elements called particles, representing the aggregates, and the cement paste. Each particle is individually modeled, considering its geometric and mechanical properties. For instance, aggregates can be represented as spherical or ellipsoidal particles with specific size and strength properties, while the cement paste can be modeled as a continuous matrix with elastic or viscoelastic properties. Wittmann's mesoscopic model allows for the simulation of the mechanical behavior of concrete by considering the interaction between particles [13,14]. External loads can be applied to study how forces are transmitted through the particles and the paste matrix. This allows the analysis of phenomena such as deformation, strength, fracture, and the long-term behavior of concrete. The model provides a more realistic representation of concrete behavior by considering the distribution and interaction of aggregates and allows the study of the influence of different parameters, such as the water-cement ratio, aggregate size, and material properties, on the mechanical properties of concrete. It is also useful for investigating the impact of defects and heterogeneities on material behavior. However, it is important to note that Wittmann's mesoscopic model is a simplification of reality and requires careful selection of parameters and properties for accurate results, and its application can require significant computational resources.
In this work, a detailed mesoscopic model has been devised to represent concrete, consisting of three distinct phases: mortar, coarse aggregate, and the transition zone (Figure 1).
To carry out a successful numerical approximation, experimental tests were conducted on cubic specimens measuring 50×50×50 mm made of concrete dosed with a water-to-cement ratio (w/c) of 0.5, and with CEM I 52.5 cement. All manufactured specimens incorporated the same number of coarse limestone aggregates corresponding to the particle size fractions 8/10 mm, 6/8 mm, and 4/6 mm to ensure, as much as possible, the best reproducibility among tests and the production of specimens very similar to those simulated numerically. Before the tests, the manufactured specimens were cured for 28 days in a humidity chamber with a relative humidity of 95% and at a temperature of 20°C.
The modeling was carried out in two stages: geometrical models are generated using our own Matlab code, and the numerical model is analyzed using FEM with the Ansys-Workbench program.

2.1. Stage 1: Geometrical Model Generation

To carry out the first stage of modeling, coarse aggregates have been spherical in shape, and three phases have been established: mortar, coarse aggregates, and the interfacial transition zone (ITZ). The effect of aggregate shape has been studied using spherical, ellipsoidal, and polyhedral shapes, while keeping the rest of the parameters fixed, and reaching the conclusion that the type of crack is independent of the shape of aggregates and voids. It was also concluded that the load capacity of concrete containing spherical and ellipsoidal aggregates is between 1% and 3% higher than that which includes polyhedral aggregates, perhaps since non-smooth aggregates have more mortar-aggregate interface elements and because the smooth edges of spherical and ellipsoidal aggregates have a more benign stress distribution that delays the fracture process and increases tensile strength [15].
In principle, the ITZ by subtracting the volume of two previously defined concentric spheres was generated: the inner sphere corresponds to the equivalent diameter of the coarse aggregate, and the outer sphere is designed with a diameter equal to that of the coarse aggregate plus twice the thickness of the ITZ. The shell, obtained by the difference between the larger and smaller spherical volumes, would precisely be this weaker zone (ITZ) of the concrete that is generated around the coarse aggregate particles. The programming in Matlab is carried out using the following input parameters:
  • The dimensions of the Representative Volume Element (RVE), which correspond to the dimensions of the specimens tested in the laboratory.
  • The diameters of the coarse aggregate particles, represented as spheres.
  • The mass percentage of each of the sizes of the coarse aggregate particles considered in relation to the total mass.
  • The coarse aggregate-cement ratio.
  • The volume fractions of cement, aggregates, and water.
  • The density of concrete.
The RVE generated in Matlab can be of different size and shape (cylinder, prism, cube). In the simulations carried out in this work, the coarse aggregate particles have diameters of 4, 6 and 8 mm, constituting 8%, 15% and 7% of the total mass, respectively [16]. These volumes have correspondence with those reflected in the Fuller parabola for the same particle sizes. The programming in Matlab has allowed to generate a random distribution of particles in the RVE so that they resemble that of the real concrete in a statistical sense. The position of each coarse aggregate particle within the (RVE) is done randomly, using the Take and Place method [9,17], arranging the spheres (particles), from the largest to the smallest, according to the mass percentages established in the initial data. The number of particles of each diameter i that is introduced in the RVE, is calculated by the expression:
n p i = V . p i v i 1 − c c 1 ρ c − r w c ρ w ,
where V is the volume in m3 of the RVE, p i is the mass fraction of the coarse aggregate of diameter, i with respect to the total mass, v i is the aggregate volume in m3, cc is the amount of cement per m3 of concrete, r w c is the water-cement ratio, ρ c is the density of cement (3150 kg/ m3), and ρ w is the density of water.
The amount obtained by the previous expression is rounded so that the number of particles is an integer. Next, a number of particles of each class is generated, higher than the one needed to introduce in the RVE, so that it meets the condition of the mass percentage previously indicated. Subsequently, the RVE is filled. A Cartesian coordinate system is used in the concrete sample, so that, when placing a coarse aggregate particle inside the considered concrete volume, its position is defined by the coordinates of its center. To be able to place a particle inside the RVE, two conditions must be met:
  • There must be no overlaps between two spheres, and they cannot be tangent to each other either.
  • All the particles (spheres) generated must have their entire volume inside the RVE.
A third condition establishes that each particle must be surrounded by a mortar layer with a minimum thickness. This implies that there must be a minimum distance between the boundary of a particle and the faces of the defined RVE, as well as a minimum space between two adjacent particles. This distance is defined by the following expression:
d r = 1 − α d c + d ,
where α is an influence parameter for each sphere, d c is the diameter of the sphere introduced, and d is the diameter of the next sphere that is intended to introduce.
The algorithm also introduces the parameter called particle radii Hsu’s whose value is 0.5. This value refers to the ability of the coarse aggregate to influence the properties and behavior of the concrete made with them. It depends on factors such as their size, shape, texture, and chemical composition. All particles for which d r < 0 are discarded.
The filling of the RVE begins with the particles of the largest diameter until the proportion of the agreed aggregate is obtained. Next, the particles of the successive diameters are placed in descending order of size.
As a test, the filling of many RVEs has been simulated. Different shape and sizes have been used, with different configurations of coarse aggregates, following the specifications established for the different volumetric fractions of each of the sizes of the coarse aggregate particles considered. Figure 2 illustrates three RVEs corresponding to a cube of 50 mm edge, a cylinder of 20 mm diameter and 40 mm height and a prism of 25 × 25 × 50 mm, which contain 345, 35 and 87 particles, respectively.
Once the specimen is filled with all the particles corresponding to the established different sizes, a file with the extensión .inp is generated in Matlab. This file contains the coordinates of the centers and the diameters of each of the coarse aggregate particles (spheres), as well as the dimensions of the Representative Volume Element (RVE). Subsequently, this file is transformed into another file with the extension .igs for export to Ansys. Ansys adapts the RVE generated by Matlab using the take and place method for subsequent application of the finite element method (Figure 3).

2.2. Stage 2: Numerical FEM Model

The second phase begins with importing the .igs file from the Ansys-Workbench FEM software. This file contains the geometry described in the first phase.
Once the file is imported, we proceed to generate the phase corresponding to the Interfacial Transition Zone (ITZ) using a Boolean operation. This operation allows us to differentiate the volumes of each pair of concentric spheres obtained in the previous phase. In this operation, we retain the sphere with the smaller diameter and assign it the properties of the aggregate material. The properties assigned to each of the considered phases were obtained experimentally.
Subsequently, we mesh the model. The meshing is done independently, using tetrahedral finite elements for the aggregates and hexahedral elements for the mortar and ITZ.
Considering the ITZ in the model introduces additional complexity due to coupling and assembly issues at the boundary separating the hexahedral elements used in the mortar phase and the ITZ. Initially, an ITZ thickness of 100 µm was established.
During the meshing process, the number of finite elements (FE) was limited to 1,5·106 to make the calculations feasible. To avoid exceeding these limits, a prismatic Representative Volume Element (RVE) was used, representing one-fourth of a cubic specimen with a 50 mm edge tested in the laboratory. Within this volume, the integrity of all included aggregates (spheres) is ensured (Figure 4).
The model has been modified by remeshing the coarse aggregates using tetrahedral finite elements and the rest of the Representative Volume Element (RVE) using hexahedral finite elements. The properties of the limestone aggregates used were assigned to the first group of elements. For the remaining elements in the model, the mortar properties were assigned, except for those in contact with the aggregates. Through programming in APDL, the properties of the Interfacial Transition Zone (ITZ) were assigned to these finite elements.

3. Finite Element Analysis

For finite element analysis, it is assumed that the material is linearly elastic, with its displacements u being infinitesimal and proportional to the applied force F . It is also assumed that the boundary conditions remain unchanged during the application of loads on the set of finite elements. With all of this, the equilibrium equations of the finite element obtained for static analysis are:
F = K · [ u ] ,
In practice, these assumptions allow us to state that the geometry of the finite elements remains unchanged during the loading process, hence first-order infinitesimal deformation approximations can be utilized. In real-world scenarios, it may be necessary to account for nonlinear deformations even when they are small and do not exceed the elastic limits of ordinary structural materials.
The Concrete Damage Plasticity (CDP) model used combines the theory of isotropic elastic damage with isotropic plasticity in tension and compression to simulate the inelastic behavior of concrete, as it is a quasi-brittle material. Additionally, this model is suitable for both mass and reinforced concrete and allows for static, cyclic, and dynamic loads. The CDP model considers two main fracture mechanisms: tensile cracking and compression crushing. The formulation of continuous damage in elasticity [18] can be expressed as:
σ = ( 1 − d ) D e : ( ε − ε i ) ,
where σ is the Cauchy stress tensor, d is the damage variable, D e is the undamaged elastic stiffness tensor, ε is the total strain tensor, and ε i is the inelastic strain tensor, which accounts for the irreversible nature of concrete cracking.
To evaluate the concrete structural behavior at mesoscale level we have used different finite elements as well as material and contact models.
With respect to the meshing, three different methods have been employed: a body-fitted Cartesian algorithm [19] is utilized for mortar and ITZ components, free meshing with specific sizing parameters is employed for coarse aggregate, and our own code with APDL programming is utilized for ITZ components. In detail, the above geometrical model has been meshed with linear FEM elements using a body-fitted Cartesian algorithm [19], with an element size ranging from 6·10-4 m for the coarse aggregate to 3·10-4 m for ITZ. The following element types have been used [20,21]:
  • The mortar and ITZ have been modeled using a solid type of tetrahedral finite element named SOLID65. This element is appropriate for simulating the nonlinear structural behavior of concrete. It has eight nodes with three degrees of freedom per node: translations in the X, Y, and Z directions.
  • The coarse aggregate is modeled by the SOLID185 element as a homogeneous structural solid defined by eight nodes with three degrees of freedom per node.
  • Contact between ITZ and coarse aggregate is modeled by the CONTA174 element. This element has eight nodes and three degrees of freedom per node. The contact element is used to simulate contact and sliding between both materials using a pure penalty algorithm between deformable surfaces.
On the other hand, drawing from other research works aimed to simulate the cracking and crushing of concrete [22,23,24,25,26,27,28], the following constitutive models have been employed by the authors:
  • For mortar and ITZ, a nonlinear combined mathematical model of concrete, incorporating the Drucker-Prager material model [29,30,31] for compression stresses and the Willam and Warnke model [32,33,34] for tension stresses, is utilized to predict both material failure modes: cracking and crushing.
The Drucker-Prager yield criterion, used to determine if a material has exceeded its
elastic limit, is:
F   ≡   α   I 1   +   J 2 − κ = 0 ,
where J 2 and I 1 are stress invariants:
I 1 = σ x + σ y + σ z ,
J 2 = 1 6 σ x − σ y 2 + σ y − σ z 2 + σ z − σ x 2 + τ x y 2 + τ z x 2 + τ y z 2
α is a parameter related to the internal friction angle φ:
α = 2 sin ⁡ φ 3 3 + sin ⁡ φ ,
and
κ = 6 c cos ⁡ φ 3 3 + sin ⁡ φ ,
where c is the cohesion angle, for which the following formula is proposed:
c = 0.231   l n E 0 d m a x 2 − 0.60
based on experience gained from finite element application to concrete.
The Drucker-Prager yield surface is a cone of revolution with its axis along the hydrostatic line ( σ x = σ y = σ z ) (Figure 5). Plastic deformations are given by:
d ε i j p = d λ ∂ F ∂ σ i j ,
where dλ is a scalar that provides the magnitude of plastic deformation. The vector of plastic deformations d ε → p is perpendicular to the yield surface. In this case, the volumetric plastic deformation is:
d ε v o l p = d ε x p + d ε y p + d ε z p = 3 α d λ ,
This model can be incorporated into the equations governing the behavior of mortar and ITZ as a yield condition in the nonlinear constitutive model [35].
The failure surface of Willam and Warnke reveals that the compressive strength of concrete subjected to multiaxial compressive stresses can be much greater than its uniaxial compressive strength. When considering σ x ≥ σ y ≥ σ z , the sign of σ z determines the mode of failure of concrete. For concrete to tend to fracture due to tension, σ z must be positive, and the crack will appear in the direction perpendicular to this principal stress. In cases where no stress is positive, crushing failure will occur. In Ansys, the failure criterion due to multiaxial stress state is:
F f c − S ≥ 0 ,
where F is a function of the principal stresses ( σ x , σ y , σ z ) , S is the failure surface, expressed as a function of the principal stresses, and f c is the uniaxial compressive strength, whenever the condition
σ h ≤ 3 f c ,
is met, where
σ h = σ x + σ y + σ z 3
since the remaining concrete strength parameters, Ansys takes them by default. For the complete definition of the material, in addition to the elastic modulus, Poisson's ratio, and the coefficients of transfer of shear stress for open and closed cracks must also be introduced.
With this model, if cracking occurs, Ansys nullifies the elastic modulus of the concrete element in the direction parallel to the principal tensile stress. Conversely, if crushing occurs, Ansys nullifies the elastic modulus of the concrete element in all directions, which is equivalent to removing the element from the model.
  • For coarse aggregate, a pure linear elastic model is employed due to its high strength. Besides, regarding the contact between coarse aggregates and ITZ, a pure penalty algorithm between deformable surfaces with asymmetric behaviour is used.
  • Furthermore, the relevant mortar material properties employed in the model include:
    Density of concrete, 2150 kg/ m3.
    Young’s modulus, 42000 MPa.
    Poisson’s ratio, 0.2.
    Nonlinear properties for the Drucker-Prager material model:
    Ultimate uniaxial crushing strength, 42 MPa.
    Angle of internal friction, 35°.
    Dilatancy angle, 35°.
  • The ITZ properties used in the model are:
    Young’s modulus, 25000 MPa.
    Ultimate uniaxial compressive strength, 37 MPa.
    Angle of internal friction, 35°.
    Dilatancy angle, 19°.
  • Additionally, the properties of the limestone aggregates employed in the model are:
    Young’s modulus, 65000 MPa.
    Poisson’s ratio, 0.18.
  • The following forces and boundary conditions to the FEM model are applied: a symmetry is applied to ZX and YZ faces, and an imposed displacement of -7·10-5 m applied to the XY face.
  • The numerical model, using a Newton-Raphson integration scheme with a force convergence parameter of a 2.5 with respect to the L2 Euclidean norm, with a minimum value of 0.01 N, is solved. The applied displacement, for each sub-step from the value of the previous load step ranging from 1% to a maximum value of 2%, is linearly interpolated.

4. Numerical and Experimental Results

Based on the above stages, four different numerical and experimental tests have been done. The main results are exposed in the following sections.

4.1. Experimental Results

In Figure 6, the setup for one of the experimental tests carried out can be observed. Two strain gauges attached to two opposite faces of the specimen, to determine the stress-strain curve of the material, are used.
In Figure 7, stress-strain curves of four experimental tests are shown. The first test shows an initial nearly linear phase that gradually curves as deformations increase. It achieves an ultimate tensile strength of 45,9 MPa with a strain close to 1,8 per thousand. In the second test, a slight deviation in the curve occurs when deformations exceed 8 per thousand due to a temporary malfunction in one of the strain gauges. Nonetheless, the test proceeds normally until failure, reaching deformation levels like the previous test and a tension slightly above (49,9 MPa). The third experimental test yields an ultimate tensile strength of 57,1 MPa at a strain close to 1.6 per thousand, with a less pronounced curvature compared to the previous tests. Finally, in the fourth test, a stress-strain curve characteristic of the material is observed, culminating in failure at a tension level akin to the first two tests (48,7 MPa) and a strain close to 1,7 per thousand.

4.2. Numerical FEM Results

The problem was solved in a workstation computer with a two Xeon 64-bit CPU E5630, 64 GB RAM memory, 6.0 TB hard disk and eight cores. The total elapsed average CPU time per nonlinear structural analysis was about 70,000 s and the total number of iterations to get convergence about 500. The Newton-Raphson method was used to solve the nonlinear mathematical model, both due to the constitutive model of the material and the contacts between the aggregates and the ITZ. The differences obtained between the values of "Force convergence" and "Force criterion" are very small, ranging from 1,4·10-7 to 31,7 N. Additionally, a smooth approximation of the iterations performed by the method until reaching the solution, indicating that the problem has been well-conditioned.
Figure 8 illustrates the curves derived from the four numerical simulations. Notably, all simulations exhibit an initial phase that is nearly linear, with almost the same slope in all of them. In simulations 1 and 4, the curve deviates at a stress level around 40 MPa, ac-companied by deformations of 1 per thousand. Conversely, simulations 2 and 3 depict cracking initiation at stress levels very close to 37,5 MPa, with deformations in both cases around 0,95 per thousand. Interestingly, the ultimate tensile strength in the first and fourth tests converges to similar failure values of 43 MPa, corresponding to strains of 1,2 per thousand and 1,3 per thousand, respectively. These discrepancies in ultimate tensile strength and strain among simulations are due to the different distributions of coarse aggregates in each of the geometric models employed to simulate the specimens, as generated using Matlab.
Cracking and crushing failures for different zones analyzed are shown in Figure 9 by means of elements in red color. Overall view, coarse aggregate, central section of the specimen and ITZ zone are showed in the same figure. It can be observed in the Figure 9 that failure occurs in the weakest part of the concrete, namely, in the ITZ (Interfacial Transition Zone).
In Figure 10, directional deformation along the z-axis from the fourth part of the prismatic specimen can be observed. Figure 11 depicts the total deformation experienced by the fourth part of a prismatic RVE.

4.3. Numerical and Experimental Comparison

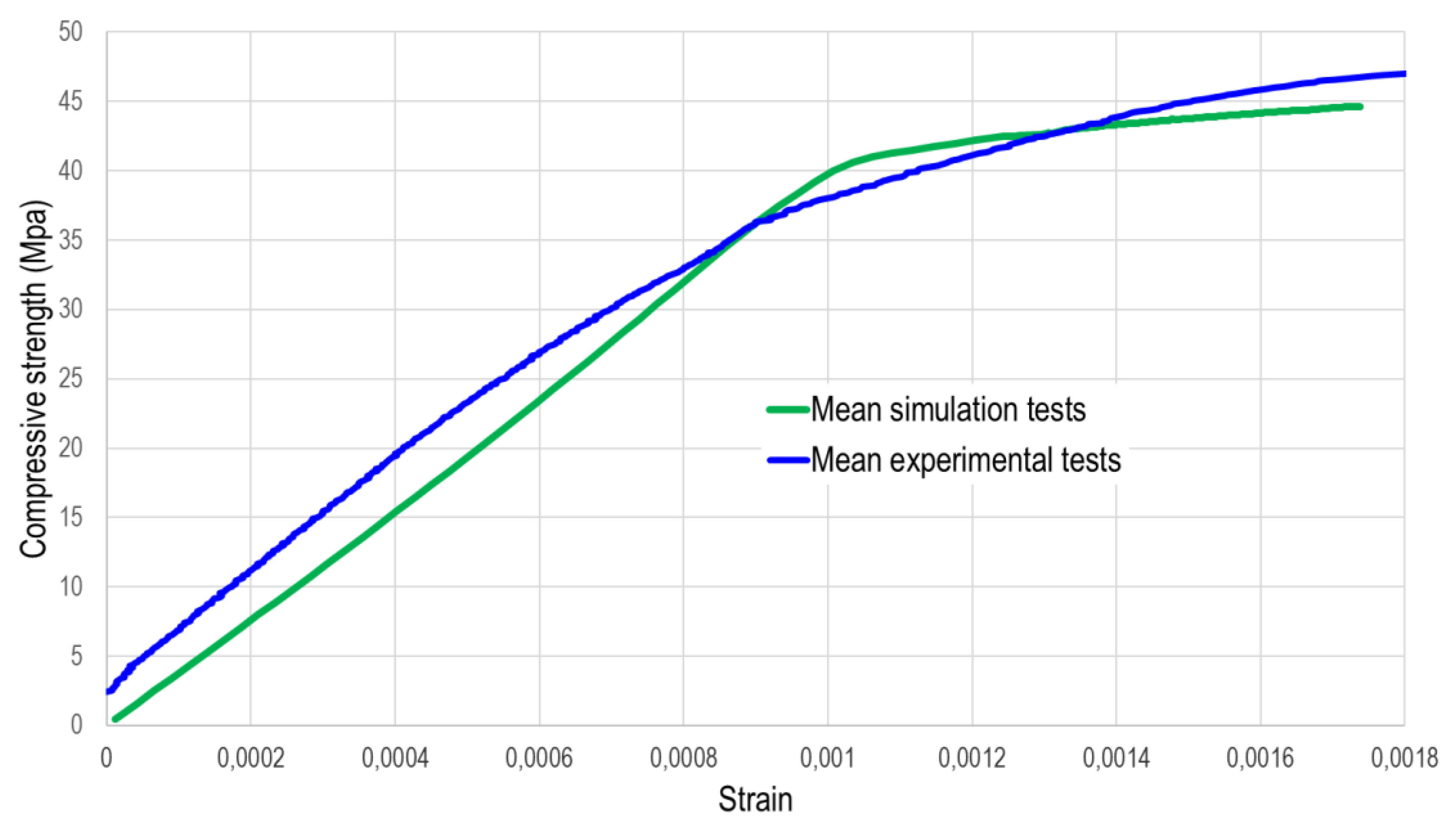
Figure 12 illustrates a strong agreement between the experimental findings and those derived from numerical simulation. In the latter case, the compressive strength measures 41,34 MPa with a strain of 1,04·10-3 m. Notably, the stress-strain curve from the laboratory tests aligns closely with this simulation data. Here is shown an advanced numerical model that provides reliable results based on four different FEM models, and which is intended to be used in the future to address more complex problems that require more effort, both experimental and computational.

5. Conclusions

The proposed model forms the groundwork for establishing a methodology aimed at the numerical simulation of compression tests, a commonplace in laboratory settings. Several key points arise in the discussion:
  • Detailed Insights into Mesoscopic Behavior: The model promises to deliver comprehensive insights into the mesoscopic-scale behavior of concrete. This detailed information is pivotal for unraveling deformation and fracture mechanisms, ultimately contributing to more informed and effective material design.
Cost-Effective and Rapid Evaluation: Mesoscopic numerical simulations present a cost-effective and time-efficient alternative for assessing concrete behavior. While they offer notable advantages, it is essential to acknowledge that they cannot entirely replace experimental methods. Both approaches complement each other, each with its unique strengths and limitations.
  • Identification of Failure-Prone Areas: Through these simulations, it becomes possible to identify areas within the material that are more susceptible to failure. This insight is invaluable for targeted improvements and reinforcement in structural design. The aim of this work is to compare numerical results with those obtained in the laboratory, hence we have not compared our numerical results with others obtained in a similar way, or with theoretical methods. In summary, the proposed mesoscopic model not only opens avenues for efficient simulation of compression tests but also holds the potential to deepen our understanding of concrete behavior, paving the way for advancements in material science and engineering.
  • The aim of the authors is to employ soon this methodology as a substitute for extensive experimental testing campaigns, which generate significant waste, by utilizing numerical simulations that yield comparable results.

Author Contributions

Conceptualization, Francisco Montero-Chacón, Juan José Del coz Díaz and Fernando López Gayarre.; methodology, Juan José del Coz-Diaz, Zulima Fernández Muñiz and Fernando López Gayarre; software, Zulima Fernández Muñiz, Juan José Del Coz Díaz, Mar Alonso Martínez.; validation, Fernando López Gayarre, Carlos López-Colina Pérez and Francisco Montero-Chacón.; formal analysis, Carlos López-Colina Pérez and Mar Alonso Martínez.; investigation, Zulima Fernández Muñiz Carlos López-Colina and Mar Alonso Martínez; writing—original draft preparation, Zulima Fernández Muñiz.; writing—review and editing, Zulima Fernández Muñiz, Juan José Del Coz Díaz and Fernando López Gayarre; supervision, Zulima Fernández Muñiz, Francisco Montero Chacón, Carlos López-Colina Pérez, Mar Alonso Martínez, Juan José Del Coz Díaz and Fernando López Gayarre. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Science and Innovation of the Government of Spain through the research projects grant numbers PID2021-122291OB-I00 and MCINN-22-TED2021-131976B-I00. Also, by the Foundation for Scientific and Technical Research of the Regional Government of Asturias through the research reference SV-PA-21-AYUD/2021/51328.

Acknowledgments

The authors also want to thank the support of the following in carrying out this study: Basf, Sika, the Ministry of Science and Innovation of the Government of Spain and the Foundation for Scientific and Technical Research of the Regional Government of Asturias. Furthermore, authors must acknowledge the academic use of the ANSYS-Workbench program.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bentz, A. Multiscale modelling of concrete: From nano to macro. Cement and Concrete Research 2008, 38 (2), 170-192.
  2. Meschke, G. Multiscale modelling of concrete structures. Journal of Structural Engineering 2011, 137 (12), 1469-1484.
  3. Cusatis, P.; Mola, F.; Berto, F. Multiscale modelling of concrete fracture: Bridging the gap between microscopic and macroscopic scales. Cement and Concrete Research 2011, 41 (11), 1109-1123.
  4. Krüger, M. Multiscale modelling of concrete: Bridging the gap between micro and macroscale. Journal of Engineering Mechanics, 2016, 142 (12), 04016077.
  5. Liu, Y., Ye, F., Cheng, X., Li, X., Li, C. A multiscale simulation approach for predicting the elastic modulus of concrete. Engineering Structures 2021, 242, 111952.
  6. Wang, X. Multiscale modelling of concrete: From microstructure to fracture mechanics. Engineering Fracture Mechanics 2018, 205, 295-313.
  7. Chateau, J.L.; La Borderie, R. A 3D mesoscopic model for concrete fracture analysis. Engineering Fracture Mechanics 2009, 76 (13), 1943-1962.
  8. Zhou, R.; Song, Z.; Lu, Y. 3D mesoscale finite element modelling of concrete, Computers and Structures 2017, 192, 96-113. [CrossRef]
  9. Wittmann, F.H.; Roelfstra, P.E.; Sadouki, H. Simulation and analysis of composite structures, Mater. Sci. Engng. 1984, 68 (2) 239-248.
  10. Bazant, Z.; Tabbara, M.; Kazemi, M.; Pijaudier-Cabot, G. Random Particle Model for Fracture of Aggregate or Fiber Composites, Journal of Engineering Mechanics 1990, 116:8 (1686). [CrossRef]
  11. Latifeh, S.E.H.; Khoei, A.R. An embedded cohesive crack model for modelling of fracture in concrete. Engineering Fracture Mechanics 2012, 85, 68-84.
  12. Mehta, P.; Monteiro, P. Concrete: Microstructure, Properties, and Materials 3rd Edition McGraw-Hill Professional, 2005. ISBN-13 978-0071462891.
  13. Wriggers, P.; Moftah, S.O. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elements in Analysis and Design 2006, 42, 623-636.
  14. Montero-Chacón, F., Marín-Montín, J., Medina, F. Mesomechanical characterization of porosity in cementitious composites by means of a voxel-based finite element model. Computational Materials Science, 2014, 90, 157-170.
  15. Xiaofeng, W., Mingzhong, Z, Andrey, P.J. Computational technology for analysis of 3D meso-structure effects on damage and failure of concrete. International Journal of Solids and Structures, 2016, 80, 310-333. [CrossRef]
  16. Cusatis, G., Bažant, Z. P., & Cedolin, L. (2003). Confinement-shear lattice model for concrete damage in tension and compression: I. Theory. Journal of engineering mechanics, 129(12), 1439-1448.
  17. Wang, Z.M.; Kwan, A.K.H.; Chan, H.C. Mesoscopic study of concrete I: generation of random aggregate structure and finite element mesh, Comput. Struct. 1999, 70 (5) 533–544.
  18. Marin Montin, J., Alcalde, M., Cifuentes, H., Montero-Chacón, F. Multiscale Analysis of the Influence of Steel Fiber Reinforcement on the Shear Strength of Post-Tensioned Dry Joints. Appl. Sci. 2020, 10, 5486. [CrossRef]
  19. Nadal, E.; Ródenas, J.J; Albelda, J.; Tur, M.; Tarancón, J.E.; Fuenmayor, F.J. Efficient Finite Element Methodology Based on Cartesian Grids: Application to Structural Shape Optimization, Abstract and Applied Analysis, vol. 2013, Article ID 953786, 19 pages. [CrossRef]
  20. Madenci, E.; Guven I. The finite element method and applications in engineering using ANSYS. New York: Springer; 2007.
  21. Moaveny, S. Finite element analysis: theory and applications with ANSYS. New York: Prentice Hall; 2007.
  22. Ranajay Bhowmick. Nonlinear Analysis of Tie Confined Columns. European Journal of Engineering Science and Technology, 2020 3(1), 130–138. [CrossRef]
  23. Gheitasi, A.; Harris, D.K.; Hansen, M. An experimental-computational correlated study for describing the failure characteristics of concrete across two scale levels: mixture and structural component. Experimental Mechanics, 2018 58, 11-32. [CrossRef]
  24. Zhou, F.; Wu, H. A novel three-dimensional modified Griffith failure criterion for concrete. Engineering Fracture Mechanics, 2023 284, 109287.
  25. Halahla, A. Study the behavior of reinforced concrete beam using finite element analysis. Proceedings of the 3rd World Congress on Civil, Structural, and Environmental Engineering (CSEE’18) Budapest, Hungary – April 8 - 10, 2018 Paper No. ICSENM 103. [CrossRef]
  26. Ulm, F. J.; Coussy, O.; Bažant, Z.P. The “Chunnel” fire. I: Chemoplastic softening in rapidly heated concrete. Journal of engineering mechanics, 1999, 125(3), 272-282.
  27. Wang, G.Y.; Wang, Z.P.; Yin, Y.; Wang, F.C. Bearing capacity of the corrosion reinforced concrete axial compression members. Advanced Materials Research, 2012, 430, 1830-1833.
  28. Turgay, T., Köksal, H.O.; Polat, Z.; Karakoç, C. Stress–strain model for concrete confined with CFRP jackets. Materials & Design, 2009, 30(8), 3243-3251.
  29. Bathe, K.J. Finite element procedures. Englewoods Cliffs (NJ): Prentice-Hall; 2007.
  30. Reddy, J.N. An introduction to non-linear finite element analysis. New York: Oxford University Press; 2004.
  31. Zienkiewicz, O.C., Taylor R.L. The finite element method for solid and structural mechanics. New York: Butterworth-Heinemann, 2005.
  32. Fuschi, P.; Dutko, M.; Peric, D.; Owen, D.R.J. On numerical integration of the five-parameter model for concrete. Comput & Structures 1994, 53(4), 825–38.
  33. Willam, K.J.; Warnke, E.D. Constitutive model for the triaxial behaviour of concrete. Proceedings of the international association for bridge and structural engineering, vol. 19. Bergamo (Italy): ISMES; 1975, 174–8.
  34. Del Coz Díaz, J.J., García Nieto, P.J., Álvarez Rabanal, F.P., Lozano Martínez-Luengas, A. Design and shape optimization of a new type of hollow concrete masonry block using the finite element method, Engineering Structures 2011, 33(1), 1-9.
  35. Doran, B., Köksal, H.O., Polat, Z., Karakoc, C. The use of Drucker-Prager criterion in the analysis of reinforced concrete members by finite elements, Teknik Dergi 1998, 9(2), 1617-1625.
Preprints 106119 g001
Figure 1. RVE. Mesoscopic model section detail.
Figure 1. RVE. Mesoscopic model section detail.
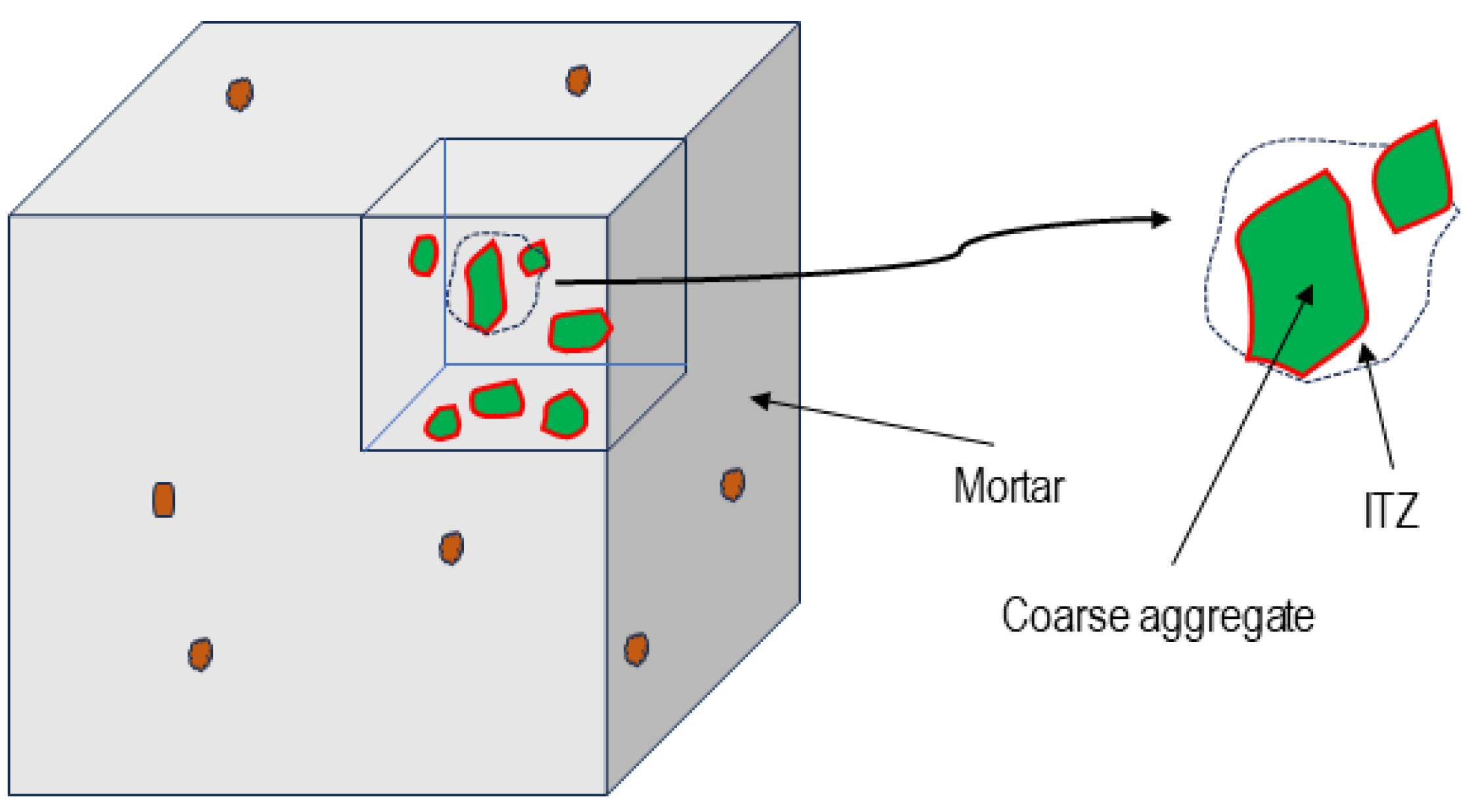
Preprints 106119 g001
Preprints 106119 g002
Figure 2. Different types of RVE used: (a) cubic, (b) cylindrical and (c) prismatic.
Figure 2. Different types of RVE used: (a) cubic, (b) cylindrical and (c) prismatic.
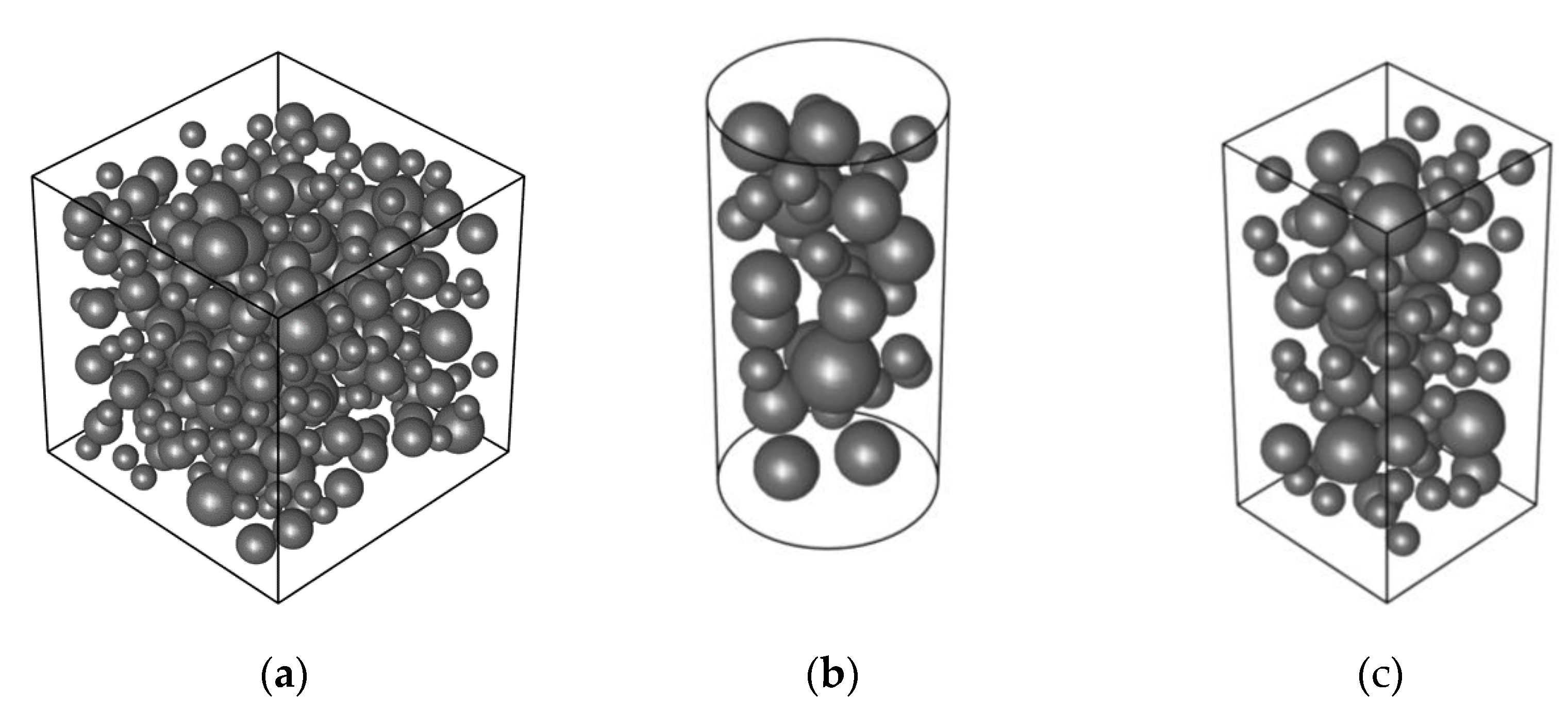
Preprints 106119 g002
Preprints 106119 g003
Figure 3. RVE generated by Matlab using the take and place method and adapted by Ansys.
Figure 3. RVE generated by Matlab using the take and place method and adapted by Ansys.
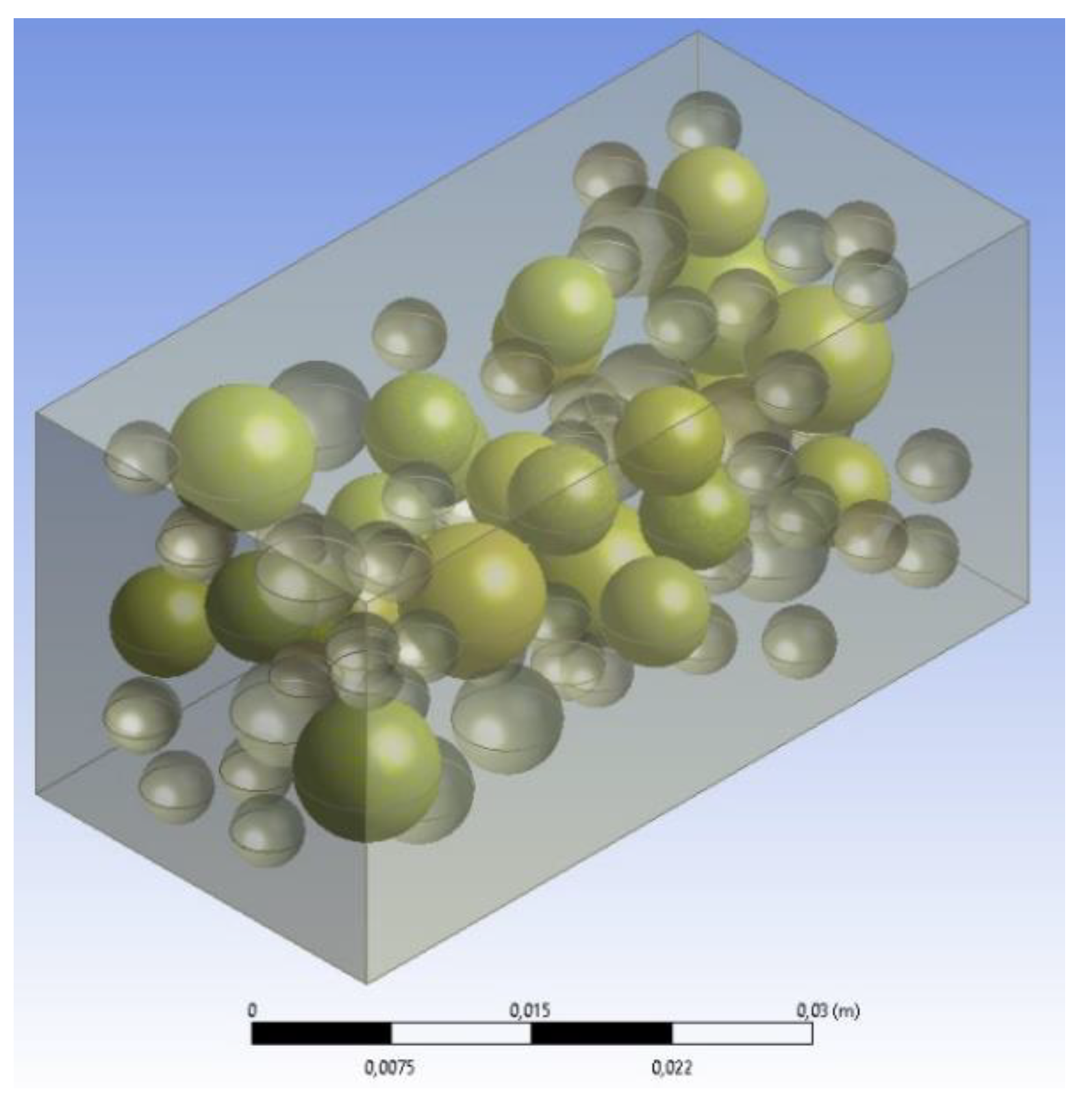
Preprints 106119 g003
Preprints 106119 g004
Figure 4. (a) Meshing of the considered Representative Volume Element (RVE). (b) Distribution and meshing of the aggregates in the specimen.
Figure 4. (a) Meshing of the considered Representative Volume Element (RVE). (b) Distribution and meshing of the aggregates in the specimen.
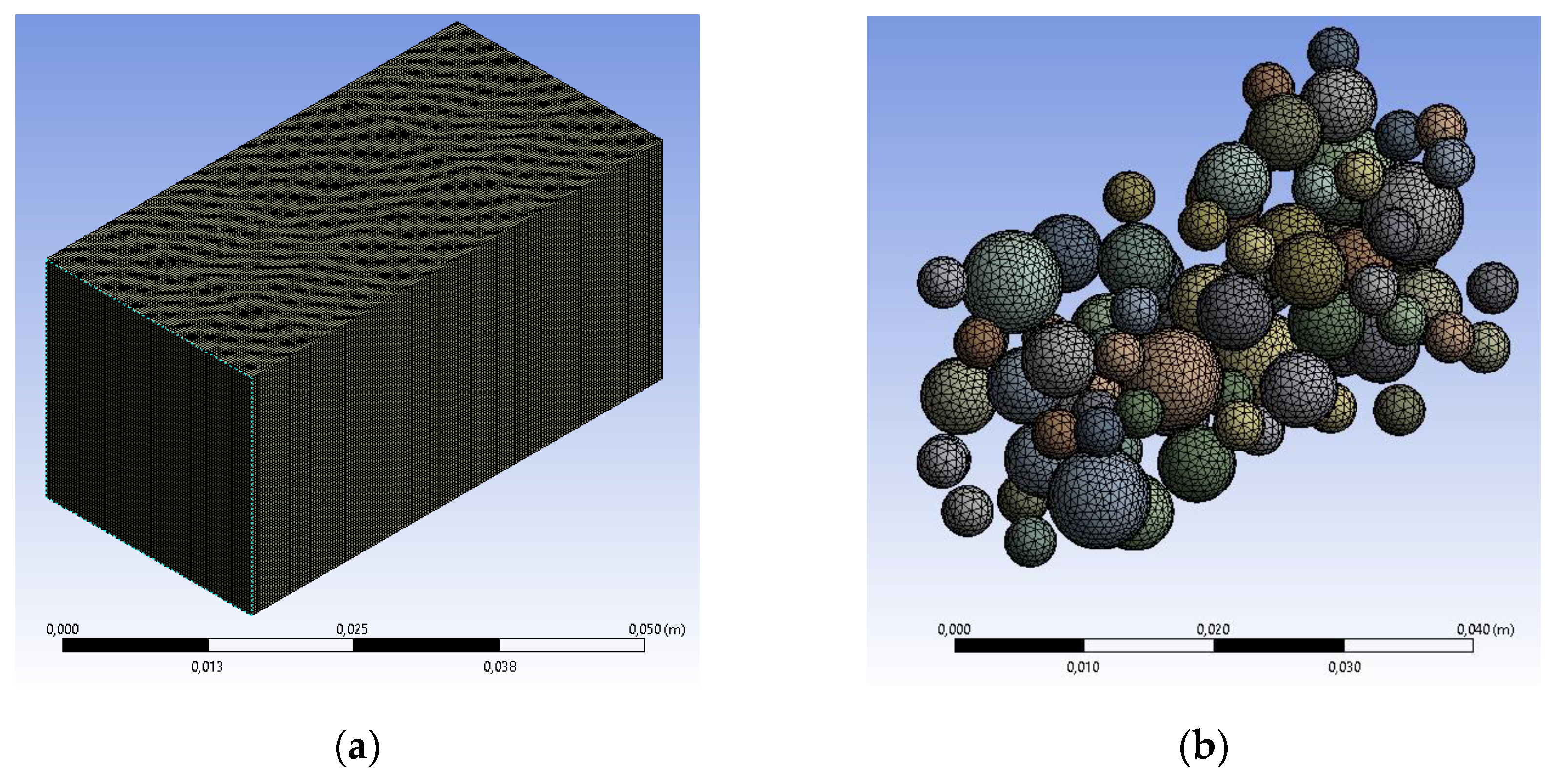
Preprints 106119 g004
Preprints 106119 g005
Figure 5. Drucker-Prager yield surface.
Figure 5. Drucker-Prager yield surface.
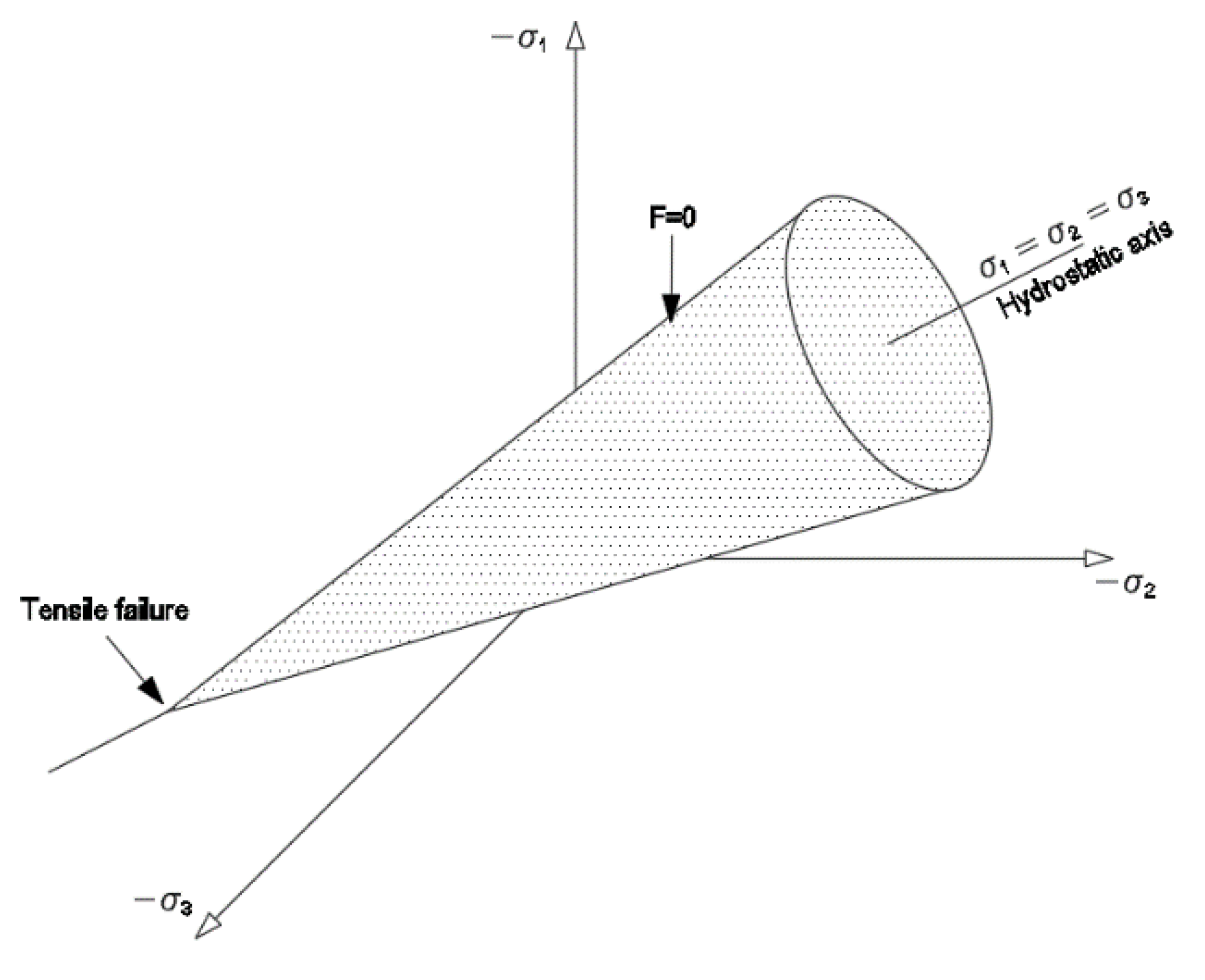
Preprints 106119 g005
Preprints 106119 g006
Figure 6. Experimental test using strain gauges.
Figure 6. Experimental test using strain gauges.
Preprints 106119 g006
Preprints 106119 g007aPreprints 106119 g007b
Figure 7. Stress-strain curves for the experimental tests.
Figure 7. Stress-strain curves for the experimental tests.
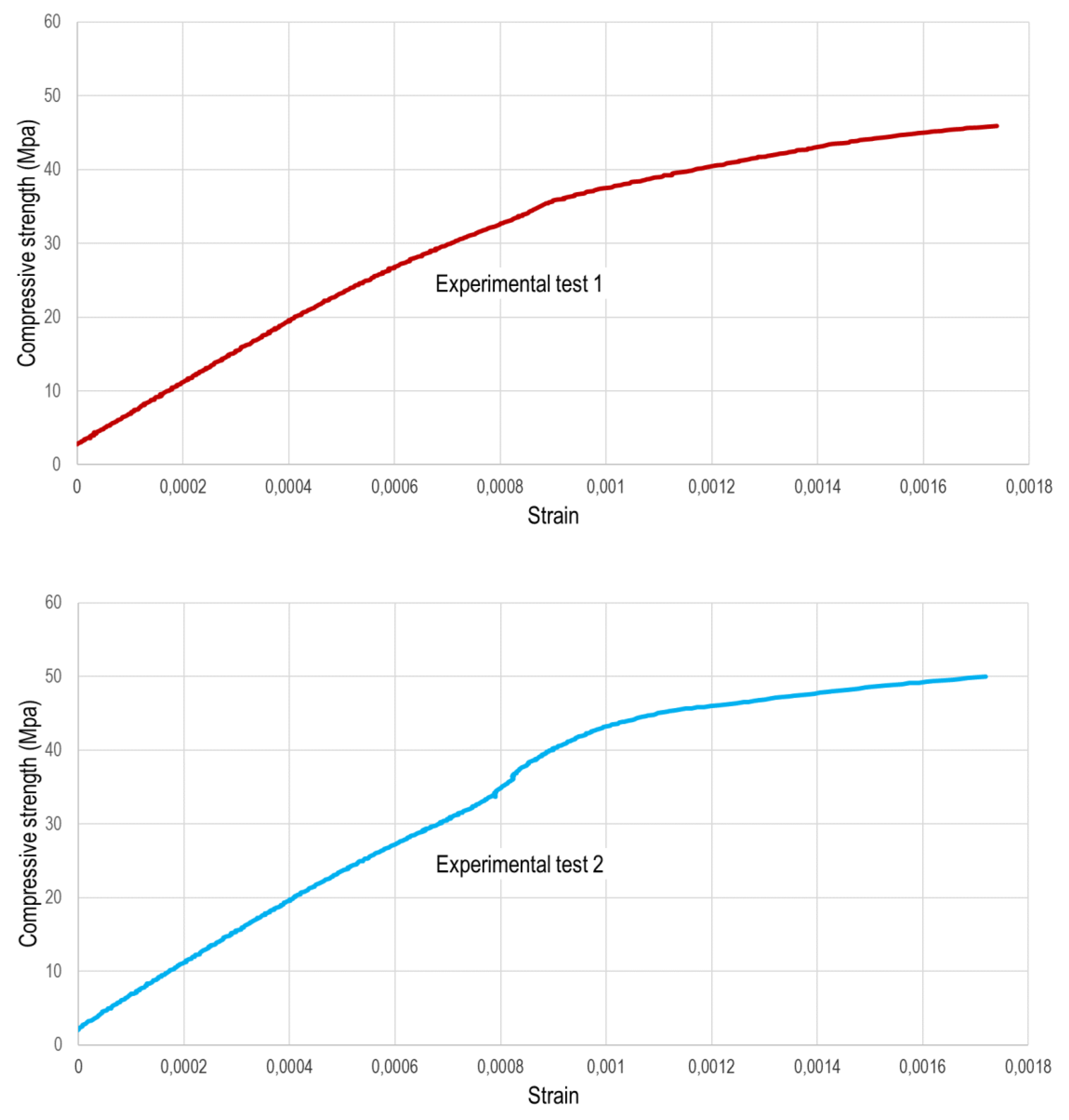
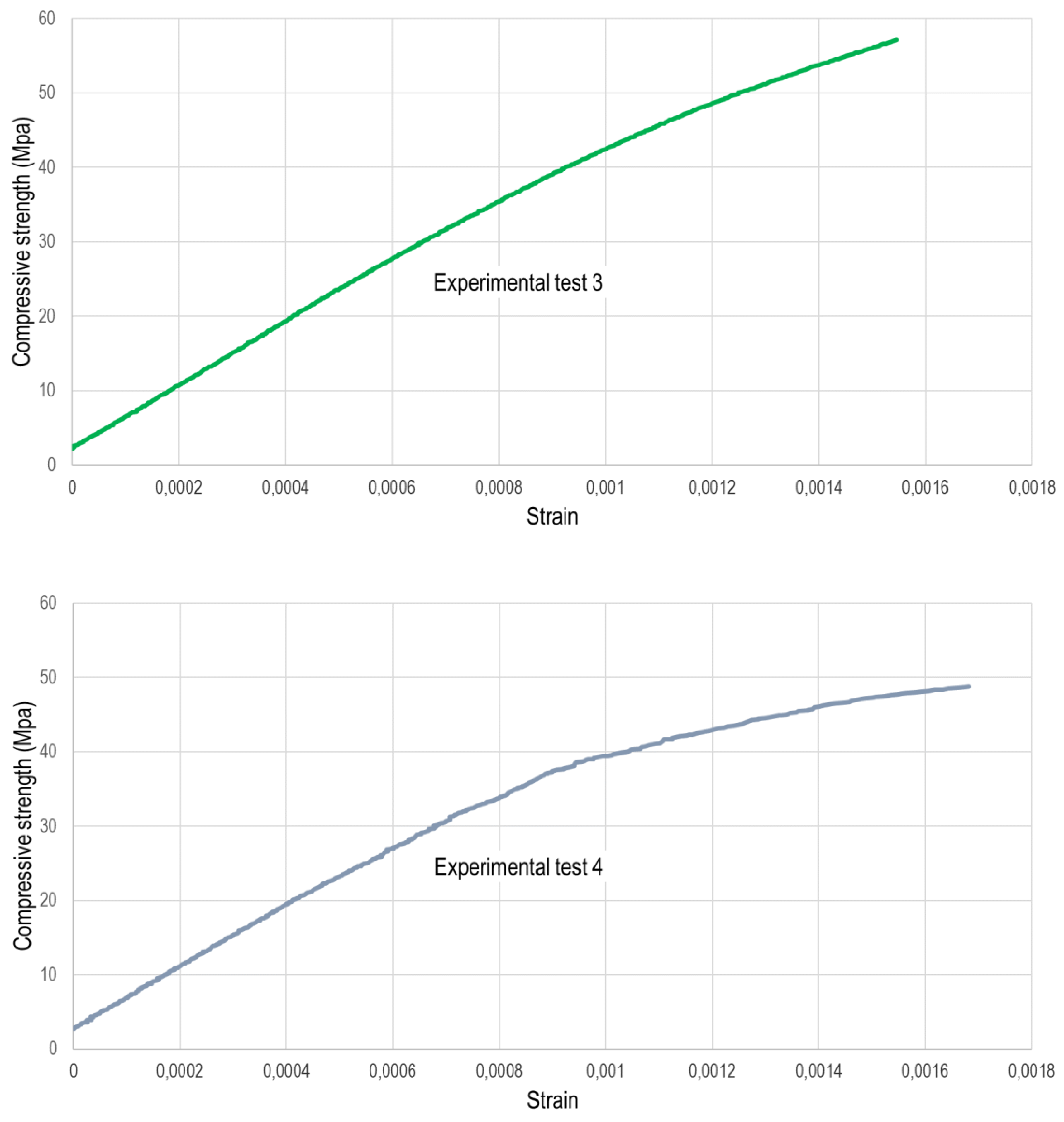
Preprints 106119 g007aPreprints 106119 g007b
Preprints 106119 g008aPreprints 106119 g008b
Figure 8. Stress-strain curves for the four numerical models.
Figure 8. Stress-strain curves for the four numerical models.
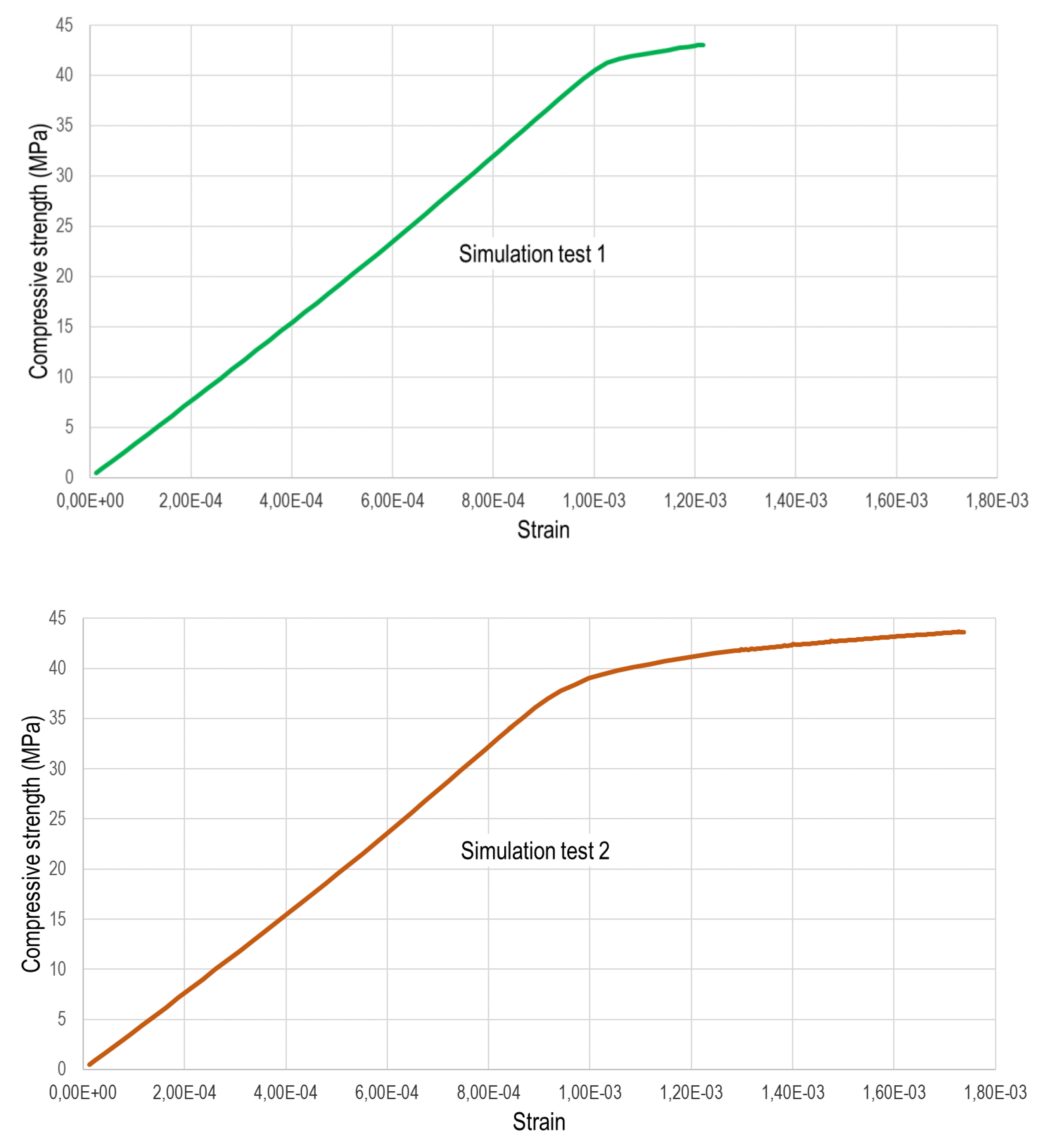
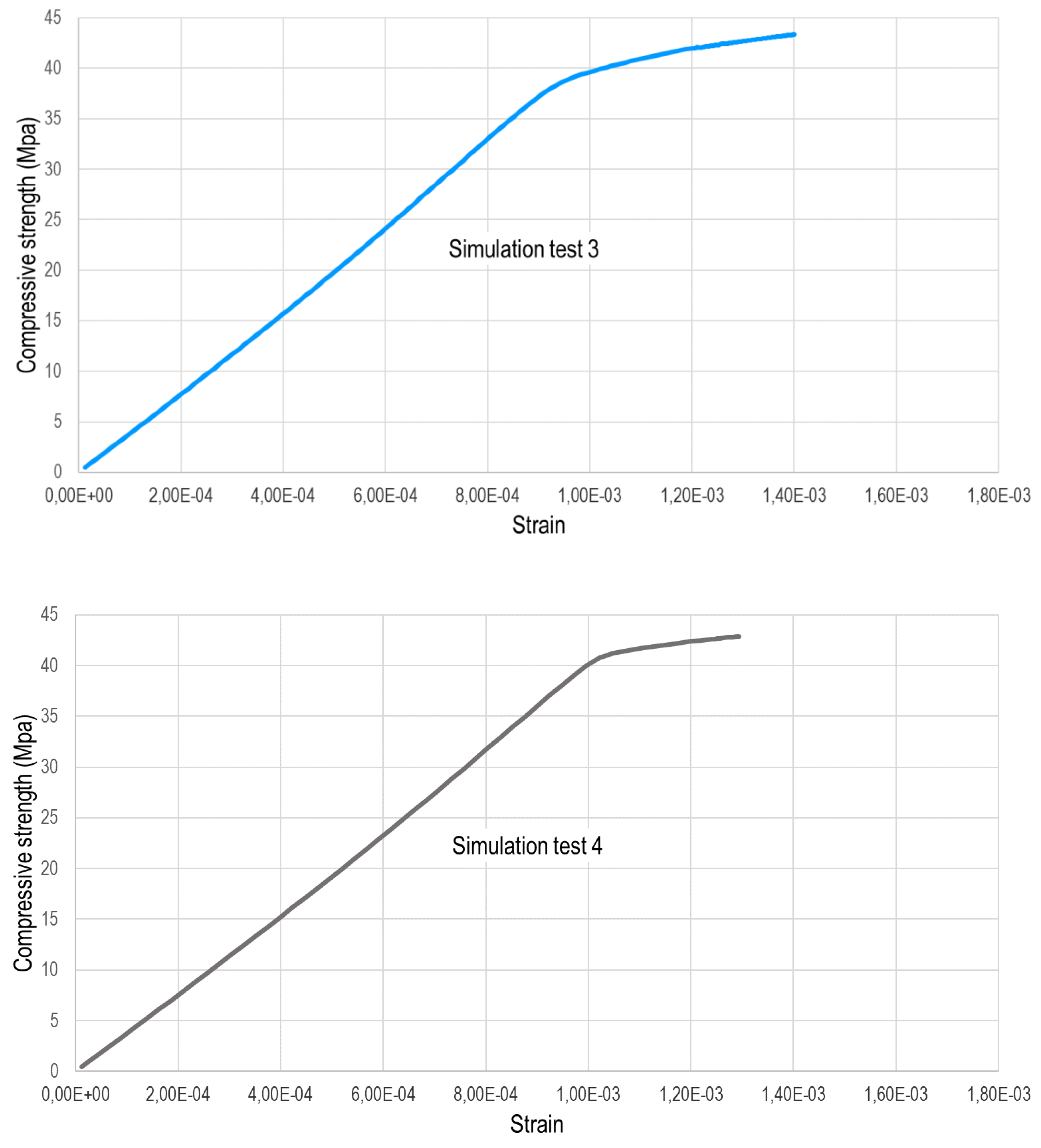
Preprints 106119 g008aPreprints 106119 g008b
Preprints 106119 g009aPreprints 106119 g009b
Figure 9. (a) Specimen. (b) Aggregates. (c) and (d) Cracking and crushing failures.
Figure 9. (a) Specimen. (b) Aggregates. (c) and (d) Cracking and crushing failures.
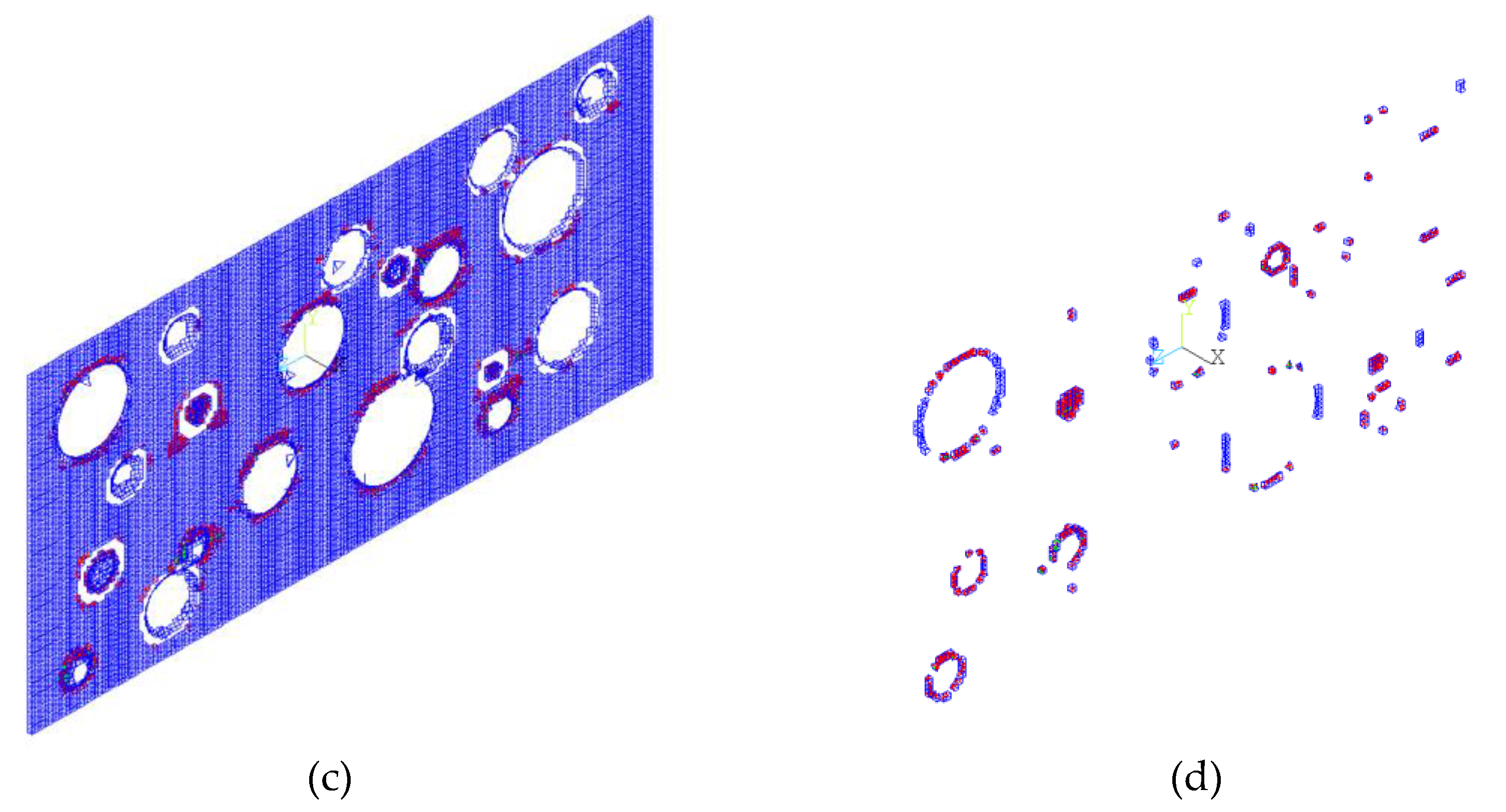
Preprints 106119 g009aPreprints 106119 g009b
Preprints 106119 g010
Figure 10. Directional deformation (along the longitudinal z axis) from the fourth part of the prismatic specimen.
Figure 10. Directional deformation (along the longitudinal z axis) from the fourth part of the prismatic specimen.
Preprints 106119 g010
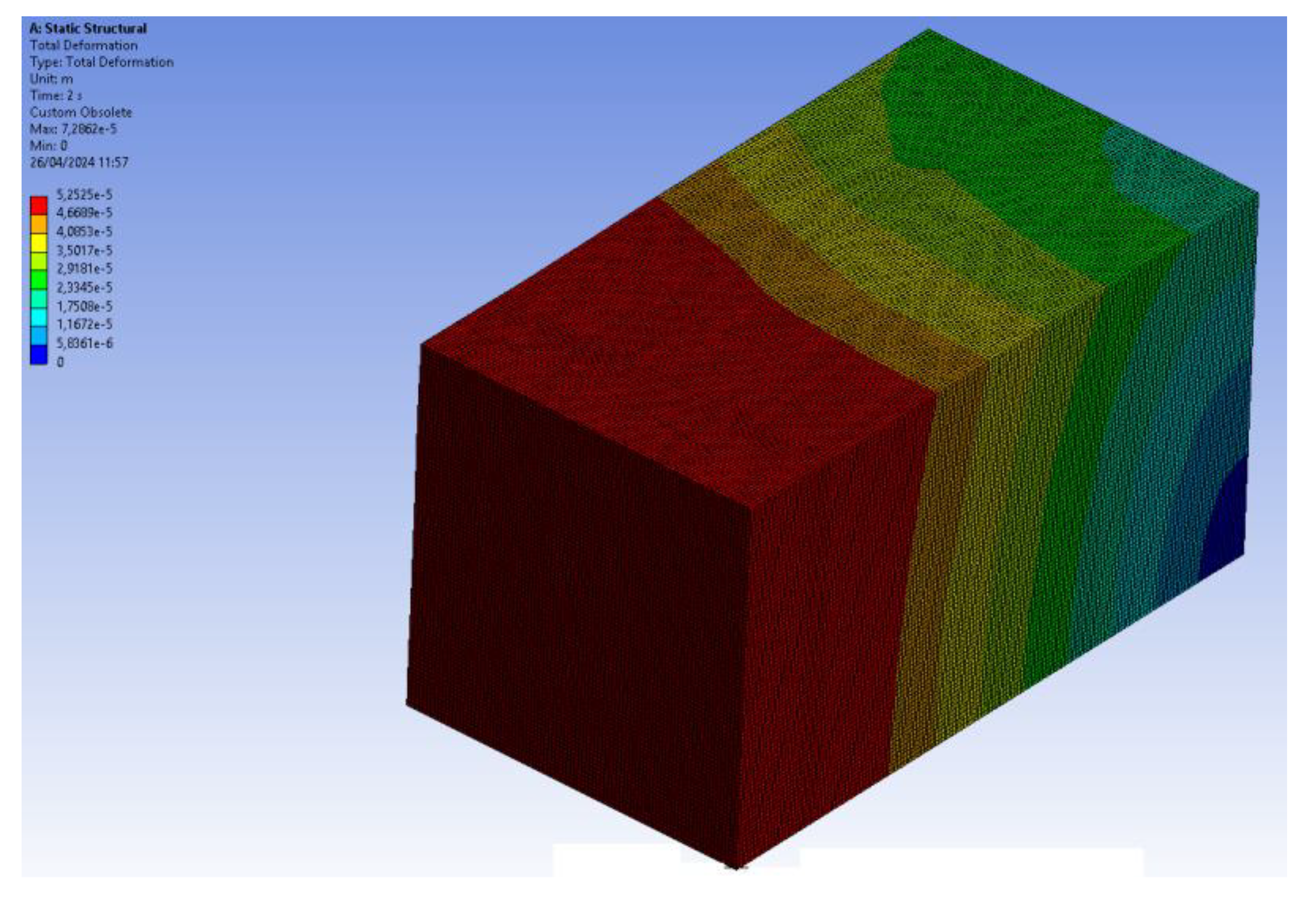
Preprints 106119 g011
Figure 11. Total deformation from the fourth part of the prismatic specimen.
Figure 11. Total deformation from the fourth part of the prismatic specimen.
Preprints 106119 g011
Preprints 106119 g012
Figure 12. Mean stress-strain curves to failure obtained in the laboratory and through numerical simulation.
Figure 12. Mean stress-strain curves to failure obtained in the laboratory and through numerical simulation.
Preprints 106119 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated