Preprint
Article
Rapid Modeling Method for Airborne FSS Radomes Based on Dynamic Customizable Primitives
Altmetrics
Downloads
74
Views
33
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
10 May 2024
Posted:
10 May 2024
You are already at the latest version
Alerts
Abstract
The digital model of airborne frequency selective surface radomes (AFSSRs) is the basis of design, simulation analysis, manufacturing, and other related research of AFSSRs. This paper proposes a rapid modeling method of AFSSRs based on dynamic customizable primitives. Firstly, a layered digital model construction scheme of AFSSR is presented based on the typical radome wall structure. Then, according to the characteristics of various surface configurations and complex wireframe information of AFSSRs, the dynamic primitives are raised to express the boundary and contour information of all kinds of radomes. Focusing on the undevelopable characteristics of the aero-dynamic shape surface of the AFSSR, the arrangement solution and mapping method for frequency selective elements on undevelopable surfaces are proposed. Furthermore, the imple-mentation logic of this method on the creation of each layer model and the assembly of the whole machine model is introduced. Finally, according to this method, a rapid modeling system (RMS) is established, and the modeling effect and efficiency of the RMS are demonstrated and compared, which verifies the feasibility and effectiveness of this method.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Modern war is essentially a battle for information control rights, electromagnetic (EM) control rights, and air control rights. Aviation weapons and equipment play a huge role in modern war and have become a crucial factor affecting the outcome of war. As the goggle of the airborne radar antenna, the airborne radome is a key structure to improve the aerodynamic shape of the airborne carrier and protect the radar antenna from working normally in extreme environments. It is widely used in typical airborne weapons platforms such as fourth-generation or fifth-generation fighters, unmanned aerial vehicles, and tactical missiles [1,2,3,4]. At the same time, to improve the penetration ability and survivability of our airborne weapon platforms and avoid the enemy's reconnaissance, detection, and interference, frequency selective surfaces (FSSs) technology is usually used to present the stealth performance of the airborne radome in a specific frequency band [5,6,7]. FSS refers to an aperture periodically arranged on the surface of a conductive metal or a metal patch arranged on the surface of a dielectric, which is essentially a spatial filter. Loading FSS onto the wall of the airborne radome will make the airborne radome have frequency selectivity, which can effectively improve the stealth ability of airborne weapon platforms [8,9,10,11].
Due to the important application value of airborne frequency selective surface radomes (AFSSRs) in the military field, the related technology of AFSSR has become a research hotspot at home and abroad. CHOI et al. [12] designed a low-observable composite sandwich structure radome composed of E-glass/epoxy or aramid/epoxy composite faces, polymethacrylimide foam core, and an FSS. The radome has good EM transmission characteristics in the X-band, and its mechanical properties are better than those of conventional composite radome. NARAYAN et al. [13] presented a Swastika-shaped novel metamaterial (MTM) element and designed an airborne hemispherical radome with an MTM-FSS structure based on this element. The radome has superior EM performance in the frequency range of 8.5-10.3 GHz, with high transmission efficiency (~ 0.30 dB insertion loss), and minimal boresight error (~ 4 mrad) in the entire beam steering range. LIU et al. [14] proposed an optimal design method for FSS radome. This method uses the pixel-overlap technique to improve the manufacturability of FSS layers and uses the binary particle swarm optimization algorithm to obtain the structural parameters of the FSS radome. A FSS radome is designed and simulated by using the optimized FSS element. When the incident angle reaches 50°, the trans-mission coefficient keeps above −2dB in the pass band and below −10dB in the stop band, indicating the method's feasibility. RAFIEIPOUR et al. [15] put forward a hybrid stacking sequence design of composites by using the complex proportional assessment method and considering the mechanical properties, EM performance, and moisture resistance of the experimental specimens. Combined with a genetic algorithm, an embedded FSS is designed. Compared with the traditional FSS performance, the design can not only achieve the maximum transmission at the resonance frequency but also enhance the transmission loss outside of the desired frequency band. However, the design and simulation of the FSS and the airborne radome loaded with the FSS under different conditions are generally based on the ideal plane model or flat plate sample, and the AFSSRs often have a specific aerodynamic shape (such as rotary type, duckbill type, prismatic shape, etc.) [16,17]. The EM performance of the airborne FSS radome designed based on the ideal conditions often fails to meet the initial design specifications in actual service.
WANG et al. [18] proposed a variable-thickness streamlined radome wall structure with graded dielectric multilayered walls for airborne applications. VINISHA et al. [19] designed a five-layer symmetrically cascaded radome wall structure with a dielectric constant gradually increasing from the outer layer to the inner layer. XU has done in-depth research on structural optimization, profile design, and EM performance of variable thickness radomes [20,21,22], and the EM performance and circular polarization application of inhomogeneous radomes [16,23,24]. DE LUCENA NÓBREGA et al. [25] designed a compact, dual-polarized FSS structure with a high-frequency compression coefficient (66.08%) and excellent angular stability by racializing the Sierpinski geometric structure. Inspired by fractal geometries, MURU-GASAMY et al. [26] presented a four-legged loaded loop element of third-order iteration and applied it to a 2.5-D FSS.YANG et al. [27] cascade the double-layer FSS and dielectric ceramic coating to form a radar absorber structure. One layer of FSS consists of square and circular metal period arrays that couple with each other, and another consists of period arrays with square patches. The structure has distinguished microwave-absorbing properties. At the structural level, AFSSRs are developing towards complex forms such as multilayer dielectric and metal stacking of the wall structure, variable thickness or inhomogeneous of the aerodynamic contour, fractal and mul-ti-dimensional FSS element, and cascade of multilayer FSS [28]. Nevertheless, the existing computer-aided design or engineering (CAD/CAE) model creation methods of FSS radomes (such as conventional manual modeling methods, HFSS-MATLAB combined modeling methods, etc.) and related EM simulation software (HFSS, CST, FEKO, etc.) are difficult to create models for diversified and complex structural design requirements.
The digital model of AFSSs is the research foundation of the development and design, simulation and analysis, manufacturing, testing and verification, maintenance and modification of AFSSs. Nonetheless, there is currently no systematic method or mature software available that can provide a solution for the digital modeling of AFSSRs, which limits the research of related technologies. Based on the research mentioned above challenges and technical obstacles in the digital modeling of AFSSRs, this paper proposes a rapid modeling method of AFSSRs based on dynamic customizable primitives, aiming to realize the customization, precision, automation, and rapid creation of the digital model of AFSSRs. This paper is structured as follows. Section 1 discusses the application background of AFSSRs and the shortcomings of existing research on the digital model of AFSSRs. Section 2 outlines the underlying support, logic implementation, and design goals of our proposed method, and presents its core idea. Section 3 introduces the modeling layered scheme of the solid-core and A-sandwich wall structure of AFSSRs. Then, according to the characteristics of various surface configurations and complex wireframe information of AFSSRs, the dynamic primitives are raised to express the boundary and contour information of all kinds of radomes. Focusing on the undevelopable characteristics of the aerodynamic shape surface of the AFSSR, the arrangement solution and mapping method for FSS elements on undevelopable surfaces are proposed. Finally, the implementation logic of this method on the creation of each layer model and the assembly of the whole machine model is introduced. Section 4 established a rapid modeling system (RMS) of AFSSRs based on this method. Meanwhile, The modeling effect and efficiency of the RMS are demonstrated and compared, which verifies the feasibility and effectiveness of this method. Lastly, conclusions are presented in Section 5.
2. Design Idea
The rapid modeling method of AFSSs based on dynamic customizable primitives utilizes the primitives' expression files (PEF) of the AFSSR's contour curves and the FSS element as the underlying support. The modeling functions of the dielectric layers and FSS layers, along with the assembly function of the whole machine model, serve as the logical implementation to achieve the application goal of creating a digital model of the AFSSR. The underlying support PEF adopts a file format that expresses the basic geometric elements and structural parameters of the contour curves and FSS element in the AFSSR's framework model. During the model creation process, model customization of the model is achieved by adjusting the PEF framework, while model precision is ensured through adjustments of the PEF's modeling parameters. The logical implementation is based on commercial CAD software application programming interfaces (APIs), incorporating rules for primitive expression, arrangement solution, and mapping method for FSS elements on undevelopable surfaces, manual modeling approaches, and manual modeling knowledge encapsulation into modeling functions of the dielectric layers and FSS layers, and assembly function of the whole machine model.
The design idea of this method is shown in Figure 1, which starts with the structural designers identifying the influencing factors for the EM design of the AFSSR. These factors include the EM indicators of antennas inside the radome and itself, environmental parameters during service, material parameters, processing indexes, strength requirements, and stiffness requirements [17,29,30]. Subsequently, based on these factors, the structural form and modeling parameters of the digital model for the AFSSR are determined, including the aerodynamic shape and dimension parameters of the AFSSR's body, the structure of the AFSSR's wall, the type and structural parameters of the FSS element, the periodic structure of the FSS, the number, and position of FSS loads. By analyzing the aerodynamic shape and integrating it with the dimensional parameters of the AFSSR's body, the PEF of the AFSSR's contour curves can be generated. Through analysis of the basic geometric elements of the FSS element and combining them with the structural parameters of the FSS element, the PEF of the FSS element can be created. Additionally, considering the structure of AFSSR's wall, and the number and position of FSS loads, a layered digital model construction scheme is established. According to the layered scheme of the AFSSR, the number of layers of the dielectric layers and the FSS layers in the digital model of the AFSSR and their interrelationships are determined. The dielectric layers or the FSS layers models are created by reading the corresponding PEF and calling the modeling functions of the dielectric layers or the FSS layers. Finally, by invoking the assembly function of the whole machine model and importing the sub-models of each layer for automated assembly, the integrated AFSSR model is generated, thereby achieving the customization, precision, automation, and rapidity creation of the digital model of the AFSSR.
3. Methodology
3.1. Modeling Layered Scheme
In the traditional radome structure design, the wall design of the solid-core structure is mainly used, such as the thin wall structure and the half-wave wall structure. The wall thickness of the thin wall structure is generally less than 1/10~1/20 of the wavelength, while the wall thickness of the half-wave wall structure is:
Where λ is the wavelength, ε is the relative permittivity of the dielectric material, and α is the incident angle [31].
To meet higher requirements for EM performance and mechanical prosperities, current AFSSRs often adopt a sandwich structure design for the radome wall, with common forms including A-sandwich, B-sandwich, and C-sandwich structures. Based on the typical wall structure forms of AFSSRs, and the number and position of FSS loads, a layered digital model construction scheme of AFSSRs is proposed. The layered scheme refers to the number of layers for the dielectric layers and the FSS layers in the digital model, as well as their interrelationships. For AFSSRs with solid-core wall structures, the FSS can be loaded on the inner side, outer side, or middle of the solid-core wall. Meanwhile, for AFSSRs with a sandwich wall structure, the FSS is typically placed at the skin-core junction or within the low-density layer [31,32]. Figure 2a illustrates the modeling layered scheme for the solid-core AFSSR wall structure, while Figure 2b demonstrates the modeling layered scheme for the A-sandwich AFSSR wall structure.
3.2. Expression Rules of Primitives
The wireframe model is a direct extension from the two-dimensional engineering drawings of geometric structures to three-dimensional space, composed of spatial points, lines, and curves, which represent the boundaries and contours of spatial geometric structures by transforming 2D plane lines and curves into 3D space lines and curves. In this paper, the basic geometric elements such as spatial points, lines, and curves are dynamically customized as primitives and combined with the modeling rules of commercial CAD software and the structure forms of AFSSRs. Considering the various surface configurations and complex wireframe information of AFSSRs' digital model, different geometric elements modeling semantics are raised to represent the boundaries and contours of AFSSRs, namely expression rules of primitives. The expression rules of different primitives are detailed below.
- Point primitivewhere ID represents the modeling identifier of the point primitive, X, Y, and Z are the x coordinate, y coordinate, and z coordinate of the point primitive modeling, respectively.
- Line primitivewhere ID represents the modeling identifier of the line primitive, , , and are the x-coordinate, y-coordinate, and z-coordinate of the starting point of the line primitive modeling, respectively, and , , and are the x-coordinate, y-coordinate, and z-coordinate of the ending point of the line primitive modeling, respectively.
- Circle primitivewhere ID represents the modeling identifier of the circle primitive, , , and are the x-coordinate, y-coordinate, and z-coordinate of the center of the circle primitive modeling, respectively, is the modeling radius of the circle primitive, denotes the starting point parameter of the circle primitive modeling, denotes the ending point parameter of the circle primitive modeling, and where and are within the range of [0, 1].
- Ellipse primitivewhere ID represents the modeling identifier of the ellipse primitive, , , and are the x-coordinate, y-coordinate, and z-coordinate of the center of the ellipse primitive modeling, respectively, , , and are the components of the major axis direction vector of the ellipse primitive along the x-axis, y-axis, and z-axis, respectively, is the modeling length of the major axis of the ellipse primitive, is the modeling length of the minor axis of the ellipse primitive, denotes the starting point parameter of the ellipse primitive modeling, denotes the ending point parameter of the ellipse primitive modeling, and where and are within the range of [0, 1].
- Spline primitiveWhere ID represents the modeling identifier of spline primitive, and is the set of point primitives that form spline primitive.
Before creating the digital model of AFSSRs, the boundary and contour information of the target AFSSR is extracted as a radome wireframe model, taking into consideration the structural form and modeling parameters of the designed AFSSR. The AFSSR's wireframe model is then meticulously dissected in three-dimensional space using basic geometric elements such as point elements, line elements, and curve elements, to derive the fundamental element composition of the wireframe model. Subsequently, the contour curves and FSS element of the radome are characterized as diverse primitive, resulting in their respective primitive expression. Equation 7 represents the general primitive expression of AFSSRs' contour curves, while equation 8 represents the broad primitive expression of FSS elements.
By combining the rules for point primitive, line primitive, and curve primitives described above, the primitive expressions of rotational airborne radomes' (RARs) generatrix, the shaping lines of duckbill-shaped airborne radomes (DSARs), the contour curves of airborne variable thickness radomes (AVTRs), and the FSS element of AFSSRs are presented. Figure 3 show the corresponding schematic diagrams, with primitive expressions provided in Equations (9) and (10), (12) and (13). By dynamically customizing the primitive of basic geometric elements, refining the expression rules of primitive, establishing standard primitive expressions for commonly used complex geometric shapes, creating PEFs for three-dimensional geometric structures, and adjusting the actual modeling parameters in PEFs, customization and precise modeling of complex spatial structures can be achieved.
3.3. Arrangement Solution for FSS Elements on Undevelopable Surfaces
Currently, the design and analysis of FSS on airborne radomes under different conditions are predominantly based on ideal plane models or ideal flat plate samples. In the ideal FSS model, the arrangement of FSS elements can be categorized into sparse and dense arrangements based on their density. Among these, sparse arrangements can further be classified into slanted grid arrangments and rectangular grid arrangements according to the angles between the connecting lines of each element center. FSS designed based on different densities and angles between element center connecting lines often exhibit varying transmission performances. However, in practical engineering applications, the aerodynamic shape of AFSSRs is undevelopable in most cases to satisfy the aerodynamic requirements of airborne weapon platforms. AFSSRs designed based on the arrangement of equivalent plane FSS elements may fail to meet the initial EM performance specifications in actual service environments. Therefore, to ensure the satisfactory EM performance of AFSSRs in practical service environments, the arrangement of FSS elements is necessary to be designed according to the aerodynamic shape of the radome. Hereafter, we will discuss the arrangement solutions of FSS elements for rotational radomes and non-rotational radomes, respectively.
3.3.1. Arrangement Solution of FSS Elements on Rotational Radomes
- Arrangement solution of FSS elements along the generatrix
In Figure 4a, Curve represents the generatrix of the rotational AFSSR generated by the conical evolution shape equation 14.
where is the diameter of the radome, and is the total length of the radome. Line is the rotational axis of the generatrix, and and are two points on . Two auxiliary points, and , can be determined based on and , where is the distance from the apexed FSS period to the top of the FSS layer, and is the distance from the terminal FSS period to the bottom of the FSS layer. The numerical values of and control the specific position of the apexed and terminal FSS period within the FSS layer of the radome. and are projected along the normal to onto to obtain points and . On undevelopable rotational surfaces such as the FSS of the rotational AFSSR, assuming a spacing between the centers of FSS elements along latitude circles and spacing of along generatrix, with a distance between and along , the theoretical number of FSS periods on the FSS can be determined as:
The is also the theoretical number of FSS elements along the generatrix. Let be an integer value denoted by , representing the actual number of FSS elements along . Taking as the reference point for arranging FSS elements along the generatrix, and as the parameter controlling the distance for the arrangement, the center points of each FSS element on can be sequentially determined as , where belonging to , and length is equal to , as illustrated in Figure 4a. Using as the central point allows for the mapping of FSS elements along the .
- 2.
- Arrangement solution of FSS elements along latitude circles
As shown in Figure 4a, center points of each FSS element on is projected along the normal direction of to obtain the center of the latitude circle of the FSS, with belonging to . The radius corresponding to any latitude circle is denoted as . By considering and , the theoretical number of FSS elements along can be determined as:
Let be an integer value denoted by , and considering as the actual number of FSS elements along , the actual distance between the centers of each FSS element along is calculated as:
The average distance error in the arrangement of FSS elements along , derived from the theoretical spacing along the latitude circle of FSS elements centers and the actual spacing , can be formulated as:
Taking the center of the FSS element on the generatrix of the airborne rotational FSS radome as an example, serves as the reference point for arranging FSS elements along latitude circle , with as the parameter controlling the distance for the arrangement, the center points of FSS elements along the of the FSS can be sequentially determined, as depicted in Figure 4b. As a consequence, this approach allows for the determination of center points for each FSS element on the rotational radome, enabling the arrangement of FSS elements on such undevelopable surfaces of the rotational AFSS- R. In the meantime, when customizing the modeling of the generatrix of rotational AFSS- Rs through the reading of the generatrix‘s PEF, control over the actual modeling parameters in the PEF, allows the circumference of each FSS period to precisely satisfy integer multiples of the theoretical spacing for centers of FSS elements along latitude circles, thereby distance error along latitude circles for each center of FSS elements are minimized.
3.3.2. Arrangement Solution of FSS Elements on Non-rotational Radomes
- Create a set of isoparametric curves
Figure 5b illustrates a schematic model of the metal FSS layer's substrate created from the PEF based on the shaping lines of the non-rotational AFSSR, where line represents the centerline of the radome, with lines and as well as curves and representing the shaping lines of the radome. and are symmetrical about the . By adjusting the shape of the shaping lines, the aerodynamic shape of the radome can be altered. On undevelopable non-rotational surfaces such as the FSS of non-rotational AFSSRs, isoparametric curves parallel to the and can be constructed on the surface of the radome as auxiliary lines for the arrangement of FSS elements. Isoparametric curves are a graphical representation of a dependent variable within a system where all parameters remain constant, and the curve varies only with the independent variable. In the digital modeling process of the non-rotational AFSSR, a set of isoparametric curves can be constructed by using the starting positions of FSS periods determined on or as the independent variable, with the starting positions of FSS periods and its tangential direction of the radome's outer surface in each frequency selection cycle as constant parameters.
Here taking as an example to determine the starting positions of FSS periods, further elaboration is as follows on the arrangement solution of FSS elements on non-rotational AFSSR. The plane in which Figure 5a is located is determined by and , where points and lie on , and length represents the total length of the radome. Two auxiliary points, and , can be determined based on and , where is the distance from the apexed FSS period to the top of the FSS layer, and is the distance from the terminal FSS period to the bottom of the FSS layer. The projection of and along the normal direction to onto the results in points and . On undevelopable non-rotational surfaces such as the FSS of the non-rotational AFSSR, assuming the spacing between the centers of FSS elements along isoparametric curves is and the spacing along shaping lines or is , and the spacing between and along is a distance , the theoretical number of FSS periods for the FSS can be obtained from and as follows:
Let be an integer value denoted by , with representing the actual number of FSS periods for the radome. Taking as the reference point for the starting position of FSS periods and as the parameter controlling the distance for each FSS period, the starting position point for each FSS period can be sequentially determined on , where belonging to , and length is equal to , as shown in Figure 5a. By considering as the independent variable for each isoparametric curve and the upper surface of the radome along with its tangential direction at as constant parameters, a set of isoparametric curves can be constructed on , as illustrated in Figure 5b.
- 2.
- Arrangement solution of FSS elements along isoparametric curves
Assuming the isoparametric curve determined by be denoted as , with the length of the being . The theoretical number of FSS elements along Ii can be obtained from and as follows:
Let be an integer value denoted by , representing the actual number of FSS elements along . The actual distance between the centers of each FSS element along the is calculated as:
The average distance error in the arrangement of FSS elements along isoparametric curve , based on the theoretical spacing and the actual spacing along the , can be formulated as:
Using the of each FSS period on the of the radome as the reference points for arranging FSS elements along the corresponding isoparametric curves Ii, with as the parameter controlling the distance for the arrangement, the center points of the FSS elements along the on the surface of the FSS layer can be sequentially determined, as shown in Figure 5b. As a result, this approach can determine the center points for FSS elements of each FSS period on the non-rotational radome, for the arrangement of FSS elements on such undevelopable surfaces of the non-rotational AFSSR. Moreover, when modeling the shaping lines of non-rotational AFSSRs based on PEF of the shaping lines, the curvature of the upper and lower surfaces can be controlled by the shaping line, ensuring that the lengths of each isoparametric curve are exactly integer multiples of theoretical spacing Dx for the center of FSS elements, thereby reducing the distance error of the center of each FSS elements along the corresponding iso-parameter curve.
3.4. Mapping Method of FSS Elements
Based on the above-mentioned arrangement solution of FSS elements on undevelopable surfaces, the center points of each FSS element on the metal substrate's surface of the FSS layer can be determined. The process of mapping planar elements into curved surface elements is described below, as shown in Figure 6. Firstly, a tangent plane is passed through the center point of any FSS element on the surface of the metal substrate of the FSS layer. Then, the planar model of the FSS element is carried out on the tangent plane. Finally, mapping the planar element onto the metal substrate of the FSS layer generates the FSS element on the undevelopable surface.
3.5. Implementation of sub-model and whole machine model
The logical implementation of this method is based on commercial CAD software's APIs, incorporating expression rules of primitives, arrangement solution and mapping method for FSS elements on undevelopable surfaces, manual modeling methods, and manual modeling knowledge encapsulation into modeling functions of the dielectric layers and FSS layers, and assembly function of the whole machine model. After determining the layered scheme for the digital model of AFSSRs, the modeling functions of the dielectric layers and the FSS layers are called separately to create models of dielectric layers and FSS layers. The assembly function of the whole machine model is then used to assemble each layer according to their inter-layer relationships, ultimately generating the whole machine model of the AFSSR. With this step, the digital modeling of the AFSSR is completed. Figure 7 and Figure 8 show the modeling algorithm flowchart for the submodels and the assembly algorithm flowchart for the whole machine model, respectively.
4. System Construction and Example Verification
4.1. Construction of Rapid Modeling System
Based on the rapid modeling solution for AFSSRs described above, this section utilizes CATIA software as the modeling tool and combines it with CATIA API, rules for primitive expression, arrangement solution, and mapping method for FSS elements on undevelopable surfaces, manual modeling methods, and manual modeling knowledge to establish a system for the rapid modeling of AFSSRs. As shown in Figure 9, the system's interactive interface includes an input area on the left for the structural form and modeling parameters of the target AFSSR and a modeling process display area for the modeling tool on the right. The rapid modeling of the target AFSSR using this system is divided into the following three phases:
- Modeling preparation phase.
Structural designers pre-determine the structural form and modeling parameters of the target AFSSR and construct PEFs of contour curves and FSS elements.
- 2.
- Human-computer interaction phase.
Structural designers open the system, select the desired structural form of the radome body, input modeling parameters, and import the PEFs built in the first phase in the interactive interface of the system. Then, they need to use the system to check whether the structural forms and modeling parameters meet the geometric conditions of the digital model of the target AFSSR. If satisfied, the modeling button is activated, leading to the third phase. If not satisfied, the structural form and modeling parameters of the target AFSSR need to be adjusted.
- 3.
- Modeling phase.
Clicking the modeling button activated in the second phase will call the modeling tool to automatically create the digital model of the target AFSSR in the modeling process display area.
4.2. Demonstration of Rapid Modeling Effect
Taking the modeling of a rotational AFSSR with an A-sandwich wall structure and dual-screen FSS as an example, the modeling effect of the system is demonstrated. The structural form and modeling parameters of the radome are exhibited in Table 1, and Figure 10a displays a schematic diagram of the FSS element of the radome. The content of the PEF for the FSS element is shown in Figure 10b.
Running the system on a computer configured with an Intel i5-13600KF processor and 32GB of memory, the data from Table 1 is input into the system's interactive interface, and the PEF is imported into the system. The exploded view of the digital model of the target AFSSR obtained is shown in Figure 11a. Figure 11b displays one of the dual-screen FSS models of the digital model, while Figure 11c illustrates the wall structural diagram of the target AFSSR. The total number of elements in the dual-screen FSS is 8589, and the modeling process took 14 minutes and 23 seconds.
4.3. Comparison of Rapid Modeling Efficiency
The efficiency of different modeling methods is compared by creating models with three different structural forms as follows, labeled as models A, B, and C. The structural forms and modeling parameters of models A, B, and C are shown in Table 1, Table 2 and Table 3 respectively, with schematic diagrams depicted in Figure 11, Figure 12 and Figure 13. Three models were created using manual modeling methods, HFSS-MATLAB combined modeling method, and the method described in this paper. The time consumed for each model creation is presented in Table 4. The research results indicate that, compared to conventional modeling methods, the method proposed in this study significantly reduces modeling time and enhances modeling efficiency.
Based on the research results of this section, it is evident that the rapid modeling method for AFFRs based on dynamic customizable primitives proposed in this paper not only achieves customization and precision of the radome model by defining expression rules of primitives, creating PEFs to represent contour curves and FSS element of target radome but also realizes the automation and rapidity of the radome modeling process by constructing modeling functions and setting up modeling systems.
5. Conclusions
This paper presents a rapid modeling method for AFFRs based on dynamic customizable primitives. This method relies on PEFs as underlying support to achieve customization and precision in the digital modeling of AFSSRs, and modeling functions for the dielectric layers, FSS layer, and whole machine, serve as the logical implementation to automate and rapid the modeling process. Subsequently, the construction of a rapid modeling system based on this method has demonstrated the following results through practical applications. Firstly, the representation of radome boundaries and contours is flexible and accurate through primitives. Secondly, the modeling process is autonomously completed by commercial CAD software. Lastly, compared to conventional modeling methods, a significant reduction in modeling time and enhanced efficiency is observed (with efficiency improvement ranging from approximately 20% to 99%, with efficiency increasing with the number of FSS elements). Future efforts will focus on refining types and representation rules of primitives, expanding the arrangement solution of FSS elements, optimizing modeling procedures and systems, and broadening the application of this method in the field of AFSSRs.
Author Contributions
Conceptualization, C.Q. and S.L.; methodology, C.Q.; software, C.Q.; validation, C.Q., X.L. and Z.Y.; formal analysis, Y.C.; investigation, S.S.; resources, L.S.; data curation, S.L.; writing—original draft preparation, C.Q.; writing—review and editing, C.Q.; visualization, C.Q.; supervision, W.Z.; project administration, S.L.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant U2241205.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The author would like to thank the editor-in-chief, associate editors and
reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, P.; Pedrycz, W.; Xu, W.; Song, L. Far-Field Pattern Tolerance Analysis of the Antenna-Radome System With the Material Thickness Error: An Interval Arithmetic Approach. IEEE Trans. Antennas Propag. 2017, 65, 1934–1946. [Google Scholar] [CrossRef]
- Wei, Z.; Zhou, C.; Zhang, F.; Zhou, C. Reliability Optimization of the Honeycomb Sandwich Structure Based on A Neural Network Surrogate Model. Materials 2023, 16, 7465. [Google Scholar] [CrossRef]
- Kishore Kumar Kandi, Nagaveni Thallapalli, and Surya Prakash Rao Chilakalapalli. "Development of Silicon Nitride-Based Ceramic Radomes — a Review." International Journal of Applied Ceramic Technology 12, no. 5 (2014): 909-20.
- Kenion, T.; Yang, N.; Xu, C. Dielectric and mechanical properties of hypersonic radome materials and metamaterial design: A review. J. Eur. Ceram. Soc. 2021, 42, 1–17. [Google Scholar] [CrossRef]
- Kim, P.C.; Gil Lee, D. Composite sandwich constructions for absorbing the electromagnetic waves. Compos. Struct. 2009, 87, 161–167. [Google Scholar] [CrossRef]
- Son, D.-S.; Hyun, J.-M.; Chaki, S.; Park, C.H.; Lee, J.-R. Evaluation of Mechanical/Electromagnetic Preformation of Single-Sided Active Frequency Selective Surface for Stealth Radomes. Int. J. Aeronaut. Space Sci. 2021, 22, 1235–1242. [Google Scholar] [CrossRef]
- Kim, P.C.; Lee, D.; Seo, I.S.; Kim, G.H. Low-observable radomes composed of composite sandwich constructions and frequency selective surfaces. Compos. Sci. Technol. 2008, 68, 2163–2170. [Google Scholar] [CrossRef]
- Wu, K.; Xu, W.; Li, P.; Zhou, J.; Li, W. Miniaturised element frequency selective surface design for high power microwave applications. IET Microwaves, Antennas Propag. 2023, 17, 846–856. [Google Scholar] [CrossRef]
- Ravi Panwar, Jung Ryul Lee "Progress in Frequency Selective Surface-Based Smart Electromagnetic Structures: A Critical Review." Aerospace Science and Technology 66 (2017): 216-34.
- Narayan, S.; Jha, R.M. Electromagnetic Techniques and Design Strategies for FSS Structure Applications [Antenna Applications Corner]. IEEE Antennas Propag. Mag. 2015, 57, 135–158. [Google Scholar] [CrossRef]
- Anwar, R.S.; Mao, L.; Ning, H. Frequency Selective Surfaces: A Review. Appl. Sci. 2018, 8, 1689. [Google Scholar] [CrossRef]
- Choi, I.; Lee, D.; Gil Lee, D. Hybrid composite low-observable radome composed of E-glass/aramid/epoxy composite sandwich construction and frequency selective surface. Compos. Struct. 2014, 117, 98–104. [Google Scholar] [CrossRef]
- Narayan, S.; Gulati, G.; Sangeetha, B.; Nair, R.U. Novel Metamaterial-Element-Based FSS for Airborne Radome Applications. IEEE Trans. Antennas Propag. 2018, 66, 4695–4707. [Google Scholar] [CrossRef]
- Liu, N.; Sheng, X.; Zhang, C.; Fan, J.; Guo, D. Design of FSS radome using binary particle swarm algorithm combined with pixel-overlap technique. J. Electromagn. Waves Appl. 2017, 31, 522–531. [Google Scholar] [CrossRef]
- Rafieipour, H.; Setoodeh, A.; Lau, A.K.-T. Mechanical and electromagnetic behavior of fabricated hybrid composite sandwich radome with a new optimized frequency-selective surface. Compos. Struct. 2021, 273, 114256. [Google Scholar] [CrossRef]
- Xu, W.; Duan, B.Y.; Li, P.; Qiu, Y. Study on the Electromagnetic Performance of Inhomogeneous Radomes for Airborne Applications—Part I: Characteristics of Phase Distortion and Boresight Error. IEEE Trans. Antennas Propag. 2017, 65, 3162–3174. [Google Scholar] [CrossRef]
- Raveendranath, U. Nair, and Rakesh M. Jha. "Electromagnetic Design and Performance Analysis of Airborne Radomes: Trends and Perspectives." IEEE Antennas and Propagation Magazine 56, no. 4 (2014): 276-98.
- Wang, Z.; Tang, L.; Zhou, L.; Jiang, Z.; Liu, Z.; Liu, Y. Methodology to Design Variable-Thickness Streamlined Radomes With Graded Dielectric Multilayered Wall. IEEE Trans. Antennas Propag. 2021, 69, 8015–8020. [Google Scholar] [CrossRef]
- Vinisha, C.; Yazeen, P.M.; Mahima, P.; Joy, V.; Nair, R. Multi-layered graded porous radome design for dual-band airborne radar applications. Electron. Lett. 2017, 53, 189–191. [Google Scholar] [CrossRef]
- Xu, W.; Duan, B.Y.; Li, P.; Hu, N.; Qiu, Y. Multiobjective Particle Swarm Optimization of Boresight Error and Transmission Loss for Airborne Radomes. IEEE Trans. Antennas Propag. 2014, 62, 5880–5885. [Google Scholar] [CrossRef]
- Xu, W.; Duan, B.Y.; Li, P.; Qiu, Y. A New Efficient Thickness Profile Design Method for Streamlined Airborne Radomes. IEEE Trans. Antennas Propag. 2017, 65, 6190–6195. [Google Scholar] [CrossRef]
- Xu, W.; Zong, Y.; Li, P.; Qiu, Y. Variable Thickness Airborne Radome Design Considering Thickness Profile Control and Additional Electromagnetic Performance. IEEE Trans. Antennas Propag. 2020, 69, 2443–2448. [Google Scholar] [CrossRef]
- Xu, W.; Duan, B.Y.; Li, P.; Qiu, Y. Study on the Electromagnetic Performance of Inhomogeneous Radomes for Airborne Applications—Part II: the Overall Comparison With Variable Thickness Radomes. IEEE Trans. Antennas Propag. 2017, 65, 3175–3183. [Google Scholar] [CrossRef]
- Xu, W.; Li, P.; Qiu, Y.; Wang, C.; Zhou, J. Electromagnetic Performance Analysis of Inhomogeneous Airborne Radomes for Circular Polarization Applications. IEEE Antennas Wirel. Propag. Lett. 2018, 18, 74–78. [Google Scholar] [CrossRef]
- Nóbrega, C.D.L.; Da Silva, M.R.; Silva, P.H.D.F.; D’assunção, A.G. A compact frequency selective surface with angular stability based on the Sierpinski fractal geometry. J. Electromagn. Waves Appl. 2013, 27, 2308–2316. [Google Scholar] [CrossRef]
- Lingeshwaran Murugasamy, and Ramprabhu Sivasamy. "A Novel Fractal Inspired Iterated Four-Legged Loaded Loop Elements Based 2.5-D Miniaturized Frequency Selective Surface." IEEE Transactions on Electromagnetic Compatibility 63, no. 6 (2021): 2164-67.
- Yang, Z.; Luo, F.; Zhou, W.; Jia, H.; Zhu, D. Design of a thin and broadband microwave absorber using double layer frequency selective surface. J. Alloy. Compd. 2017, 699, 534–539. [Google Scholar] [CrossRef]
- Solunke, Y.; Kothari, A. An ultra-thin, low-RCS, dual-bandpass novel fractal-FSS for planar/conformal C&X bands applications. AEU - Int. J. Electron. Commun. 2024, 175. [Google Scholar] [CrossRef]
- Li, P.; Xu, W.; Yang, D. An Inversion Design Method for the Radome Thickness Based on Interval Arithmetic. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 658–661. [Google Scholar] [CrossRef]
- Heydari, M.S.; Ghezavati, J.; Abbasgholipour, M.; Alasti, B.M. Various types of ceramics used in radome: A review. Sci. Iran. 2017, 24, 1136–1147. [Google Scholar] [CrossRef]
- Abanti Nag, R. Ramachandra Rao, and P. K. Panda. "High Temperature Ceramic Radomes (Htcr) – a Review." Ceramics International 47, no. 15 (2021): 20793-806.
- Zhou, L.; Wang, P.; Pei, Y.; Zeng, A.; Tang, L.; Liu, Z.; Liu, Y.; Jiang, Z.; Fang, D. Design and characterization for dual-band and multi-band A-sandwich composite radome walls. Compos. Sci. Technol. 2017, 149, 28–33. [Google Scholar] [CrossRef]
Figure 1.
The design idea of the rapid modeling method for AFSSRs based on dynamic customizable primitives.
Figure 1.
The design idea of the rapid modeling method for AFSSRs based on dynamic customizable primitives.
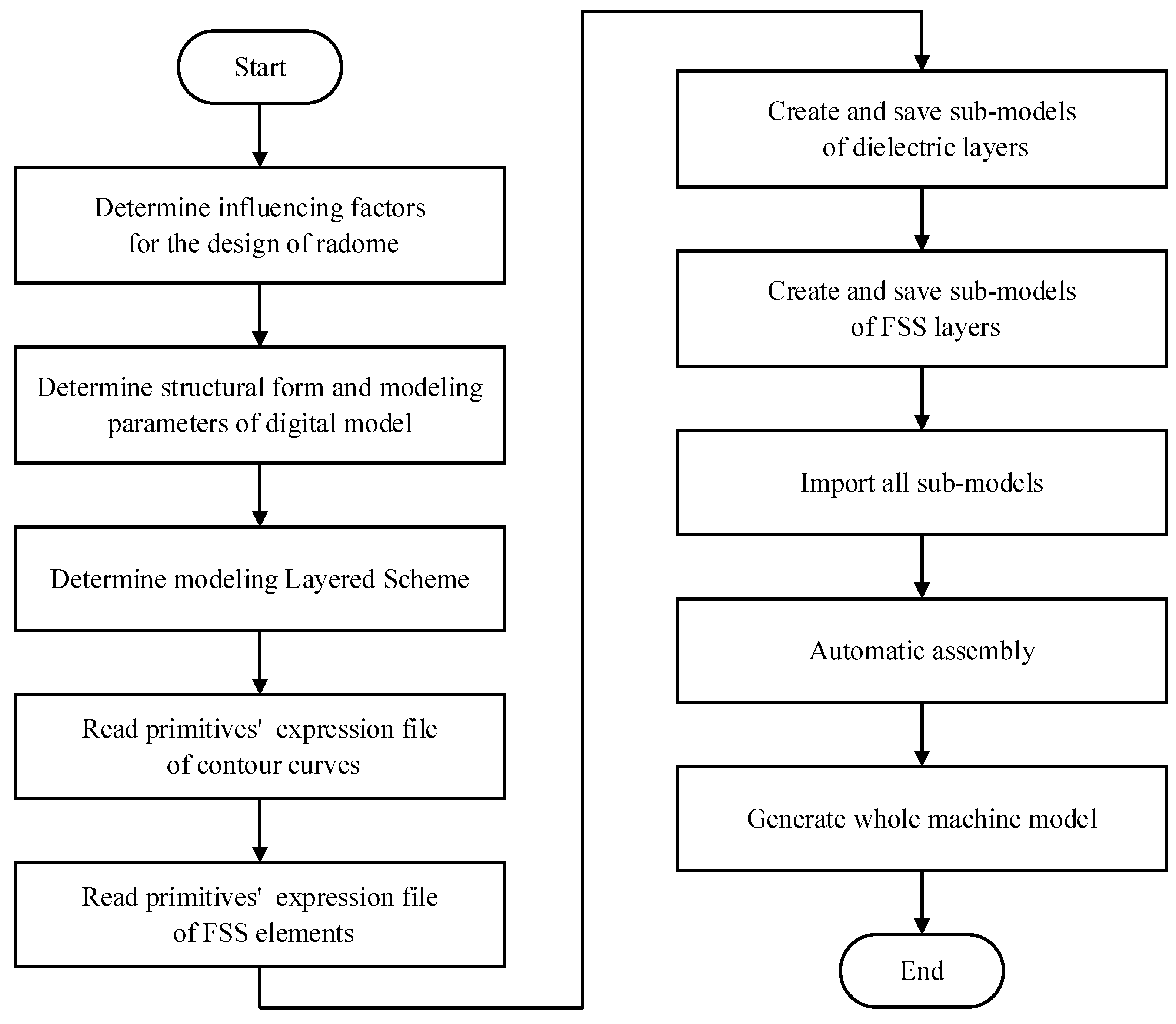
Figure 4.
Schematic diagrams of arrangement solution of FSS elements on Rotational Radomes. (a) Arrangement of FSS elements along the generatrix; (b) Arrangement of FSS elements along latitude circles.
Figure 4.
Schematic diagrams of arrangement solution of FSS elements on Rotational Radomes. (a) Arrangement of FSS elements along the generatrix; (b) Arrangement of FSS elements along latitude circles.
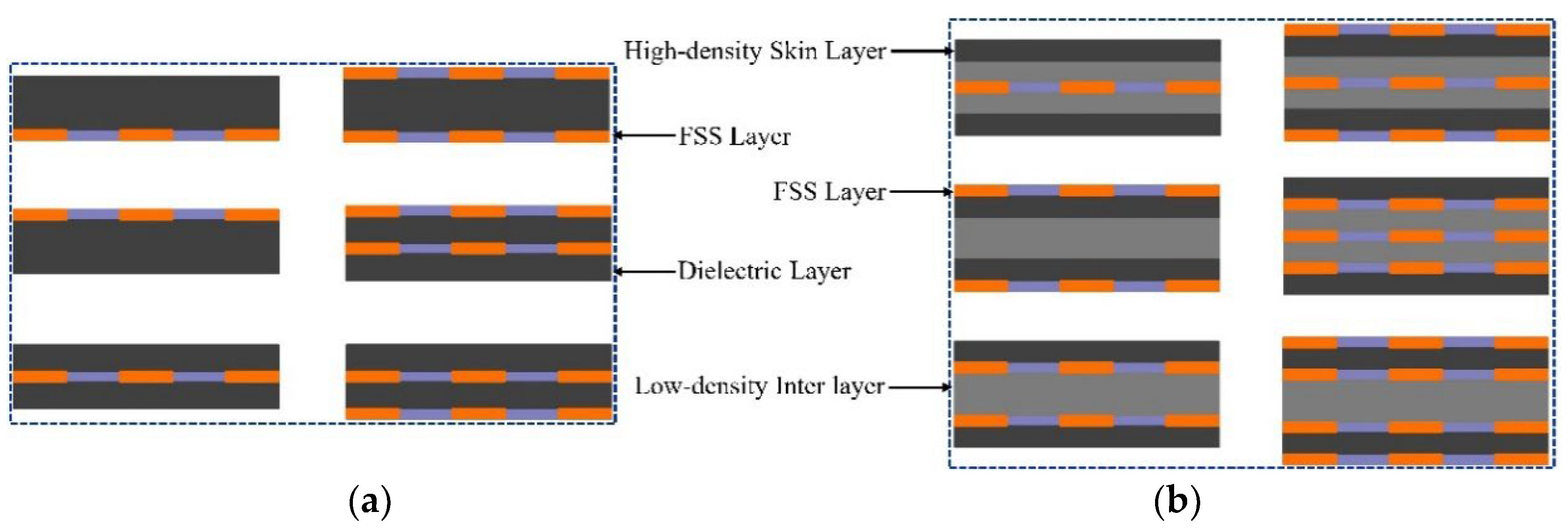
Figure 5.
Schematic diagrams of arrangement solution of FSS elements on non-rotational Radomes. (a) Schematic diagram of starting position points of isoparametric curves; (b) Arrangement of FSS elements along isoparametric curves.
Figure 5.
Schematic diagrams of arrangement solution of FSS elements on non-rotational Radomes. (a) Schematic diagram of starting position points of isoparametric curves; (b) Arrangement of FSS elements along isoparametric curves.
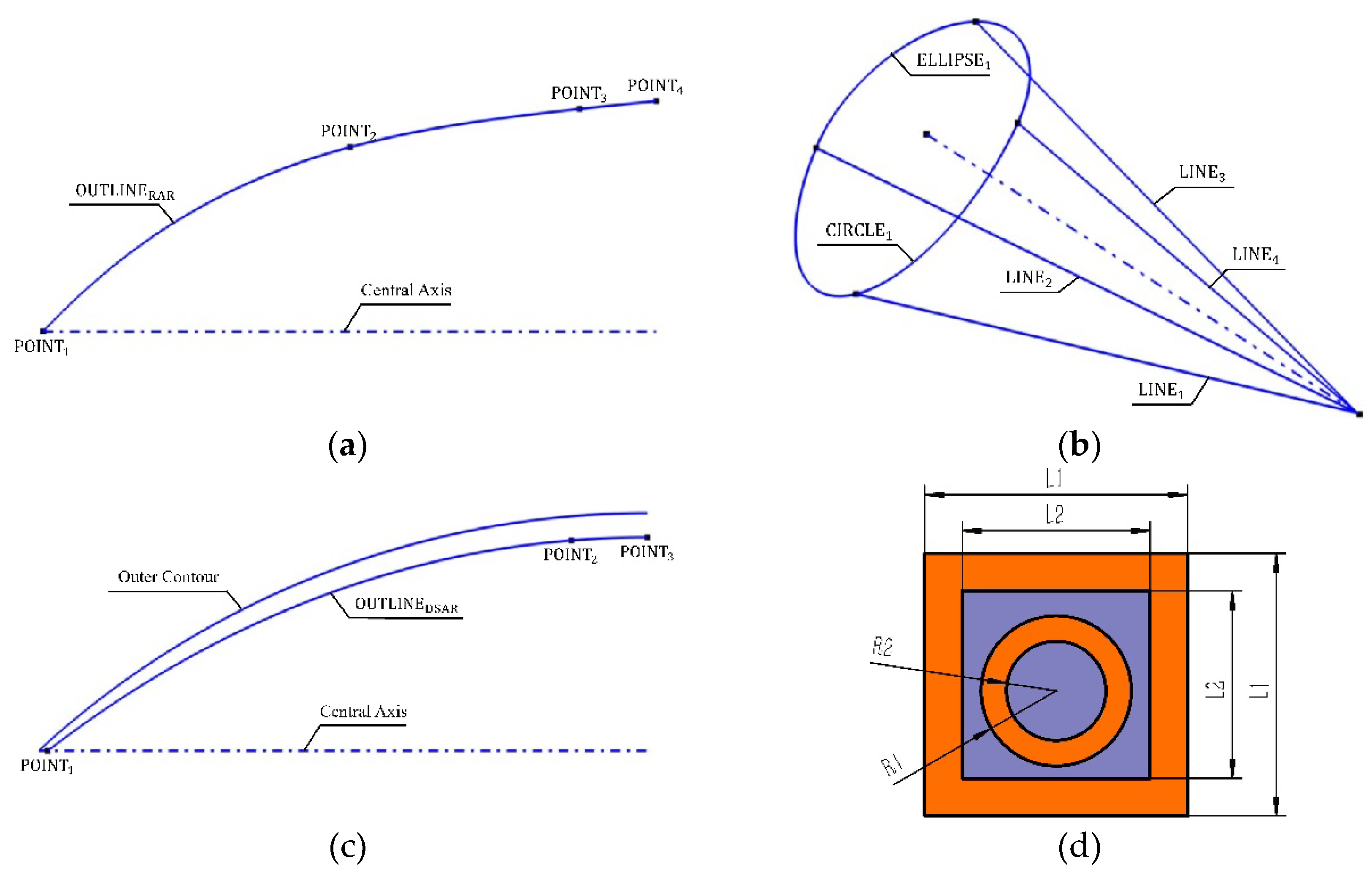
Figure 6.
Schematic diagram of mapping planar elements into curved surface elements.
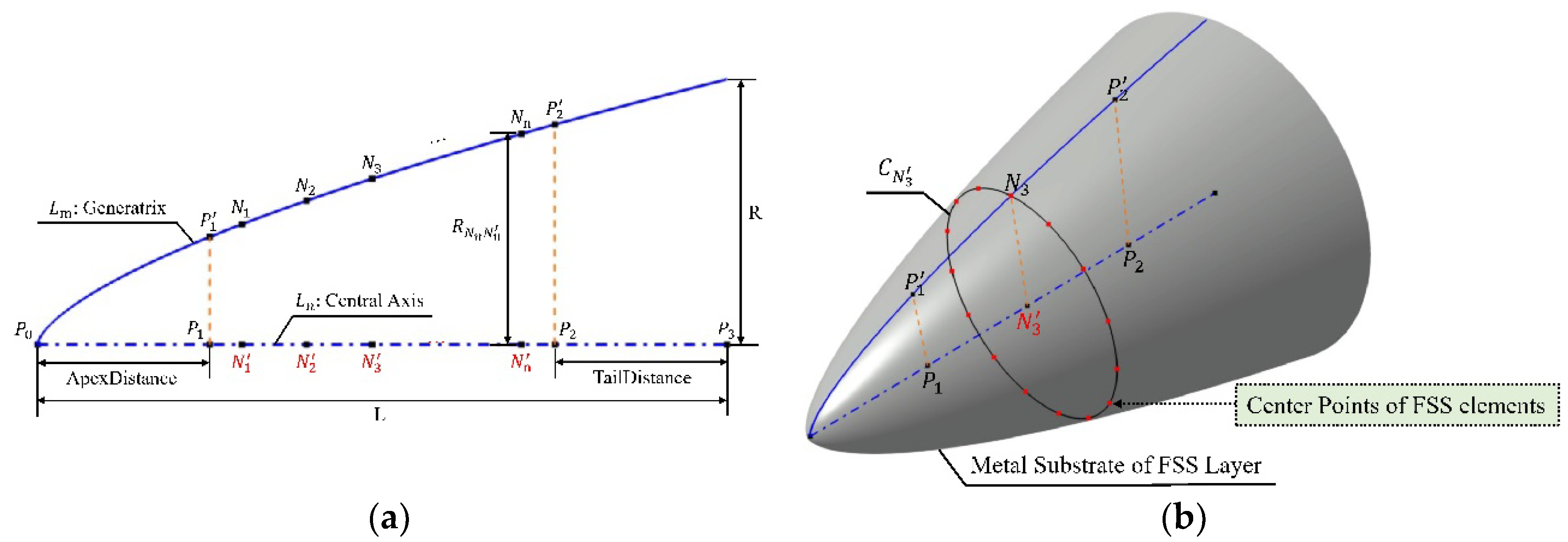
Figure 7.
Modeling algorithm flowchart for the sub-models.
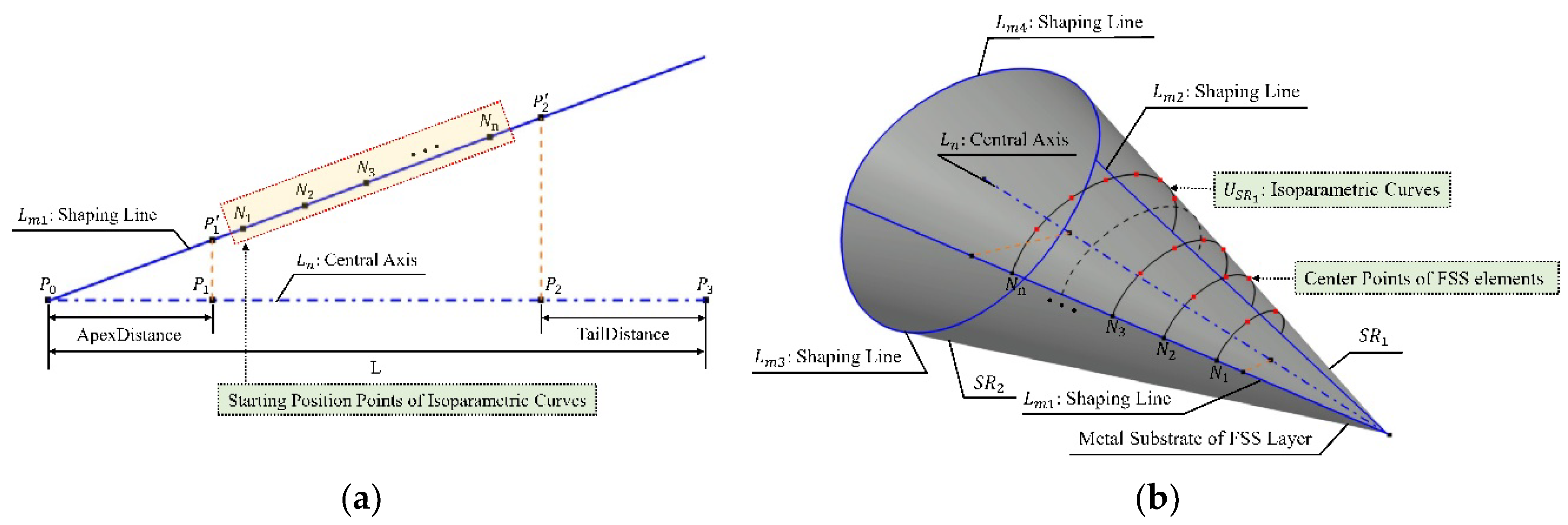
Figure 8.
Assembly algorithm flowchart for the whole machine model.
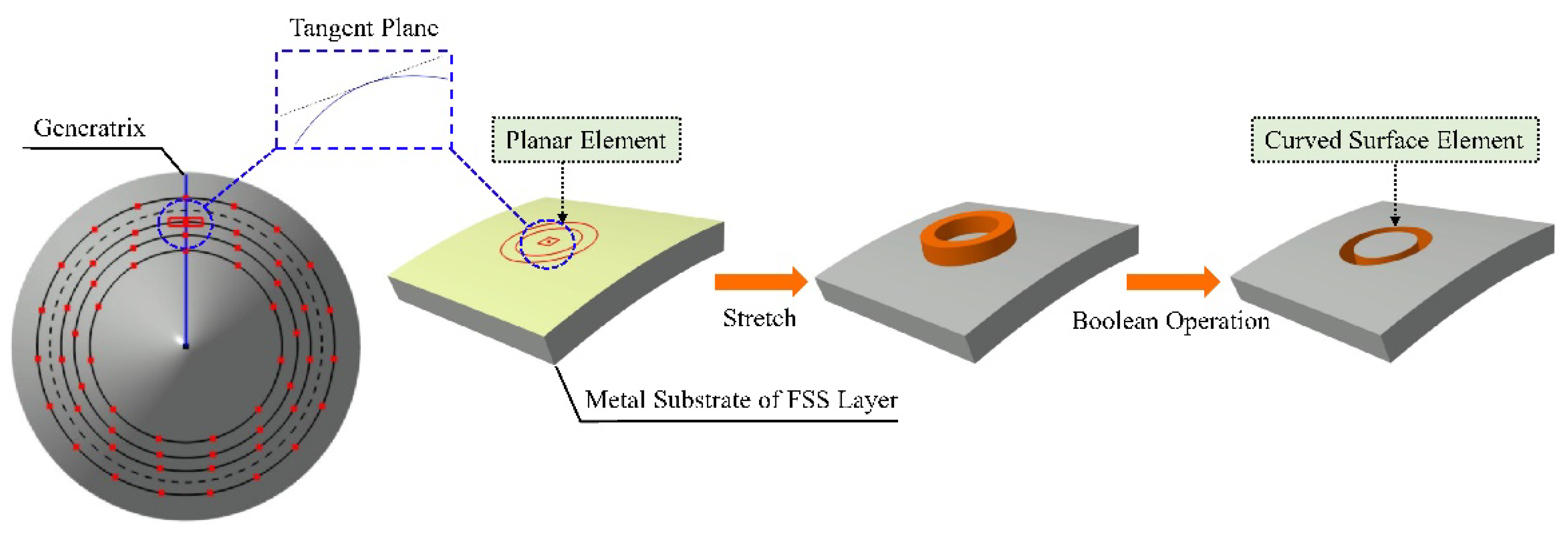
Figure 2.
Modeling layered scheme for typical radome wall structure (a) Modeling layered scheme for the solid-core AFSSR wall structure; (b) Modeling layered scheme for the A-sandwich AFSSR wall structure.
Figure 2.
Modeling layered scheme for typical radome wall structure (a) Modeling layered scheme for the solid-core AFSSR wall structure; (b) Modeling layered scheme for the A-sandwich AFSSR wall structure.
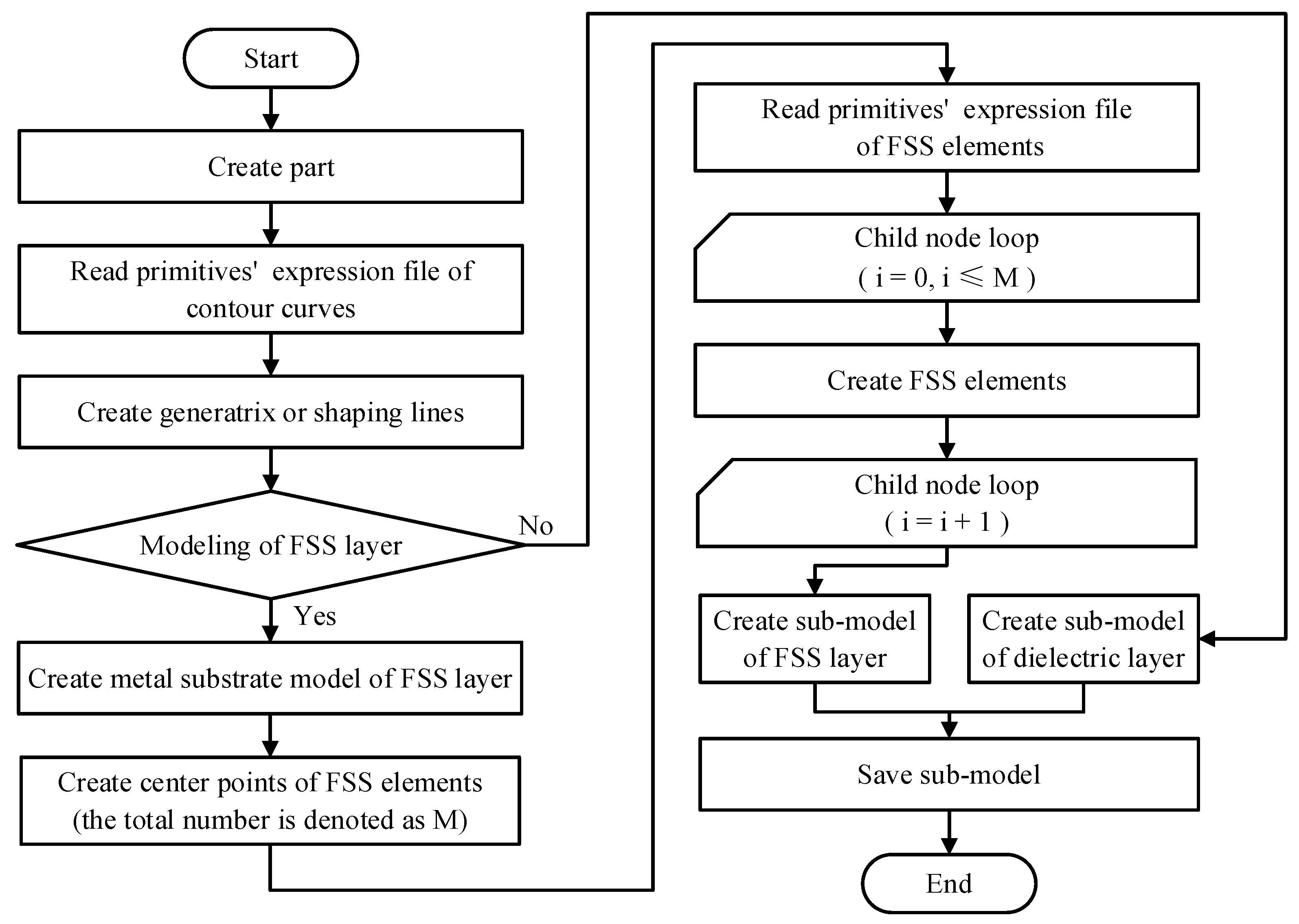
Figure 3.
Schematic diagrams of contour curves and FSS element for various radome. (a) Generatrix of rotational airborne radomes; (b) Shaping lines of duckbill-shaped airborne radomes; (c)Contour curves of airborne variable thickness radomes; (d) FSS element.
Figure 3.
Schematic diagrams of contour curves and FSS element for various radome. (a) Generatrix of rotational airborne radomes; (b) Shaping lines of duckbill-shaped airborne radomes; (c)Contour curves of airborne variable thickness radomes; (d) FSS element.
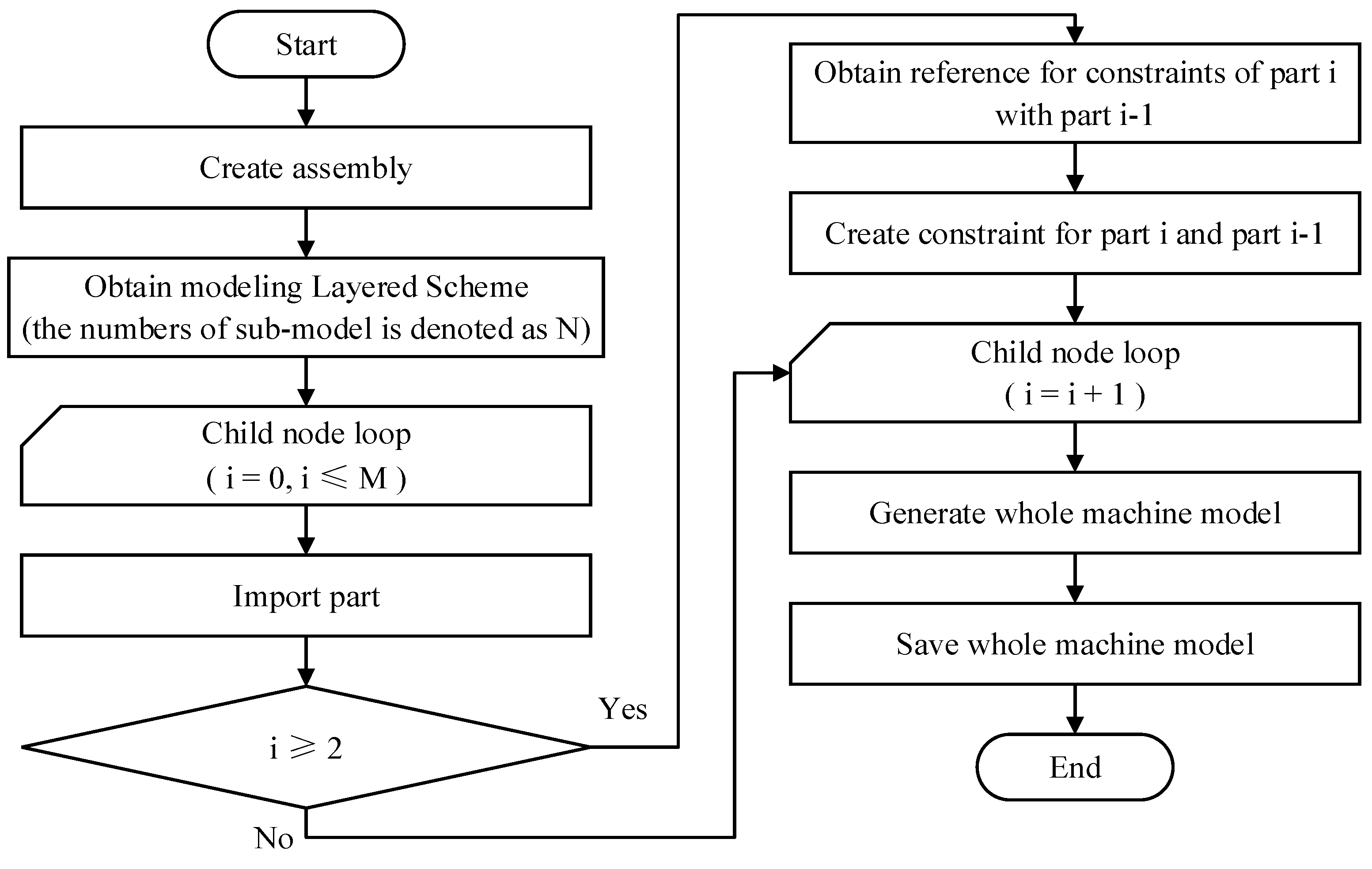
Figure 9.
Schematic diagram of the system's interactive interface.
Figure 10.
Schematic diagram of the FSS element and its PEF (a) FSS element; (b) Content of the PEF.
Figure 10.
Schematic diagram of the FSS element and its PEF (a) FSS element; (b) Content of the PEF.
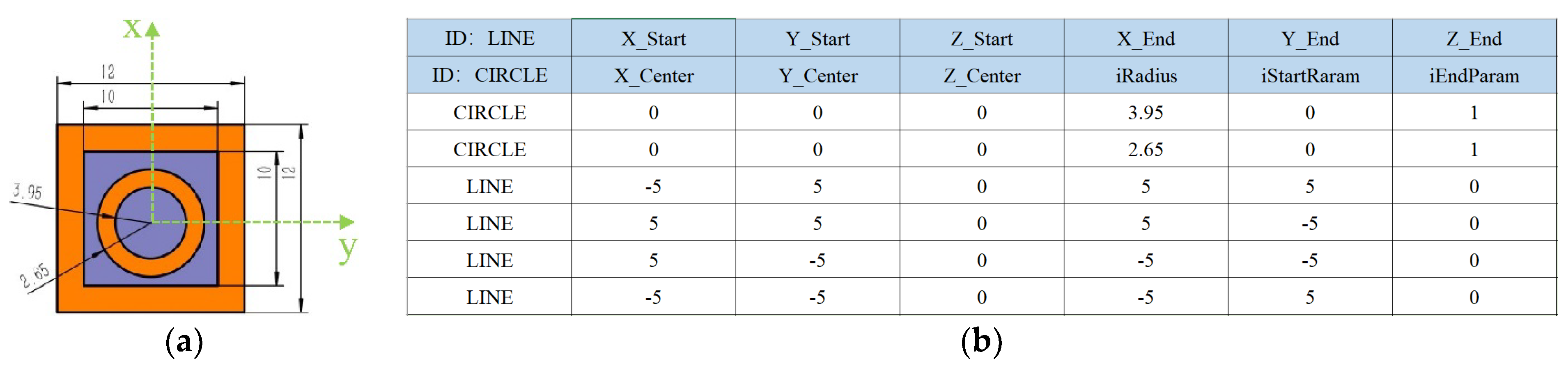
Figure 11.
Digital model of the rotational AFSSR with an A-sandwich wall structure and dual-screen FSS (a) Exploded view; (b) One of the dual-screen FSS models. (c) AFSSR wall structure.
Figure 11.
Digital model of the rotational AFSSR with an A-sandwich wall structure and dual-screen FSS (a) Exploded view; (b) One of the dual-screen FSS models. (c) AFSSR wall structure.
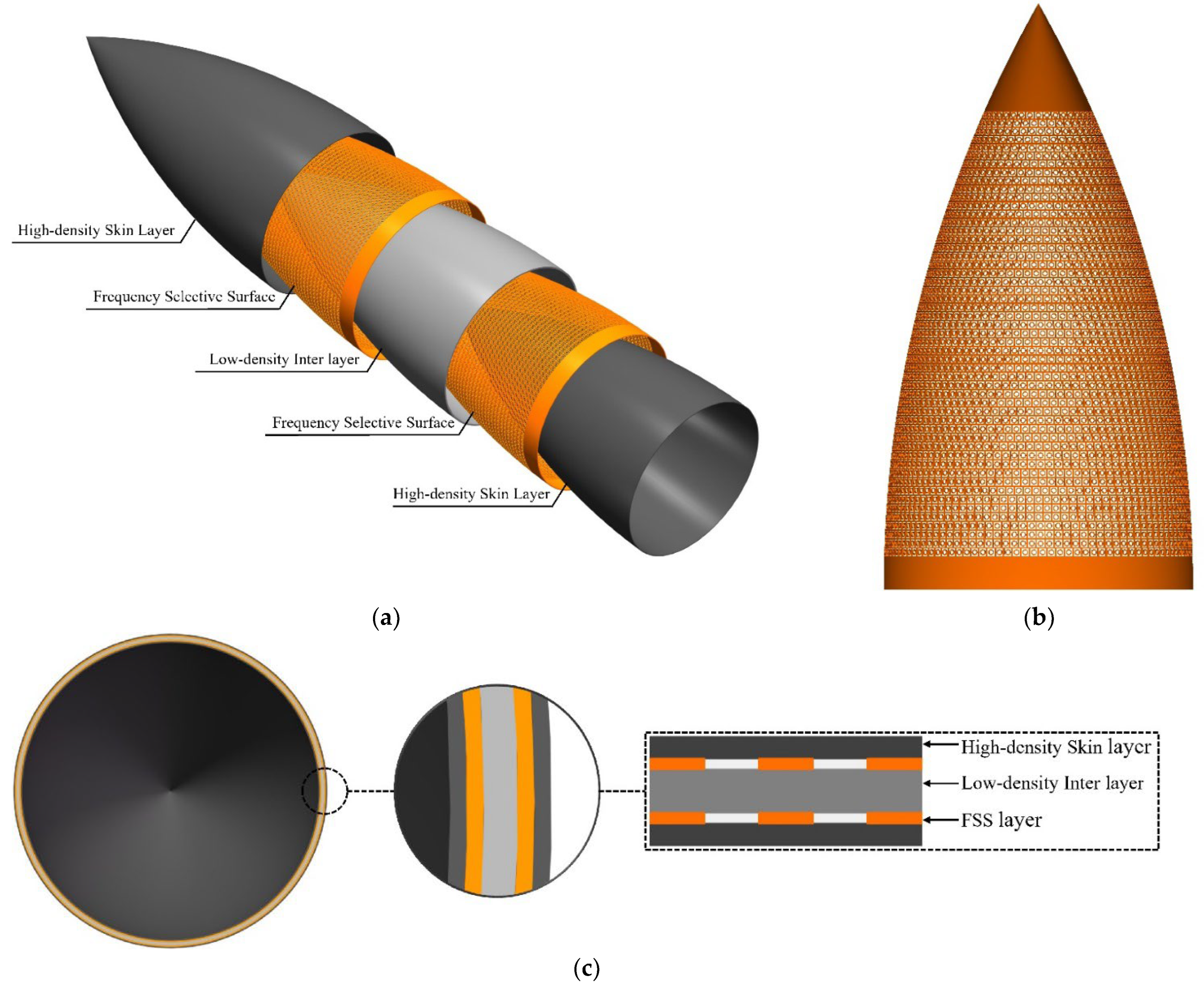
Figure 12.
Schematic diagram of the model B (a) Schematic diagram of the whole machine model; (b) Schematic of the interior of the radome.
Figure 12.
Schematic diagram of the model B (a) Schematic diagram of the whole machine model; (b) Schematic of the interior of the radome.
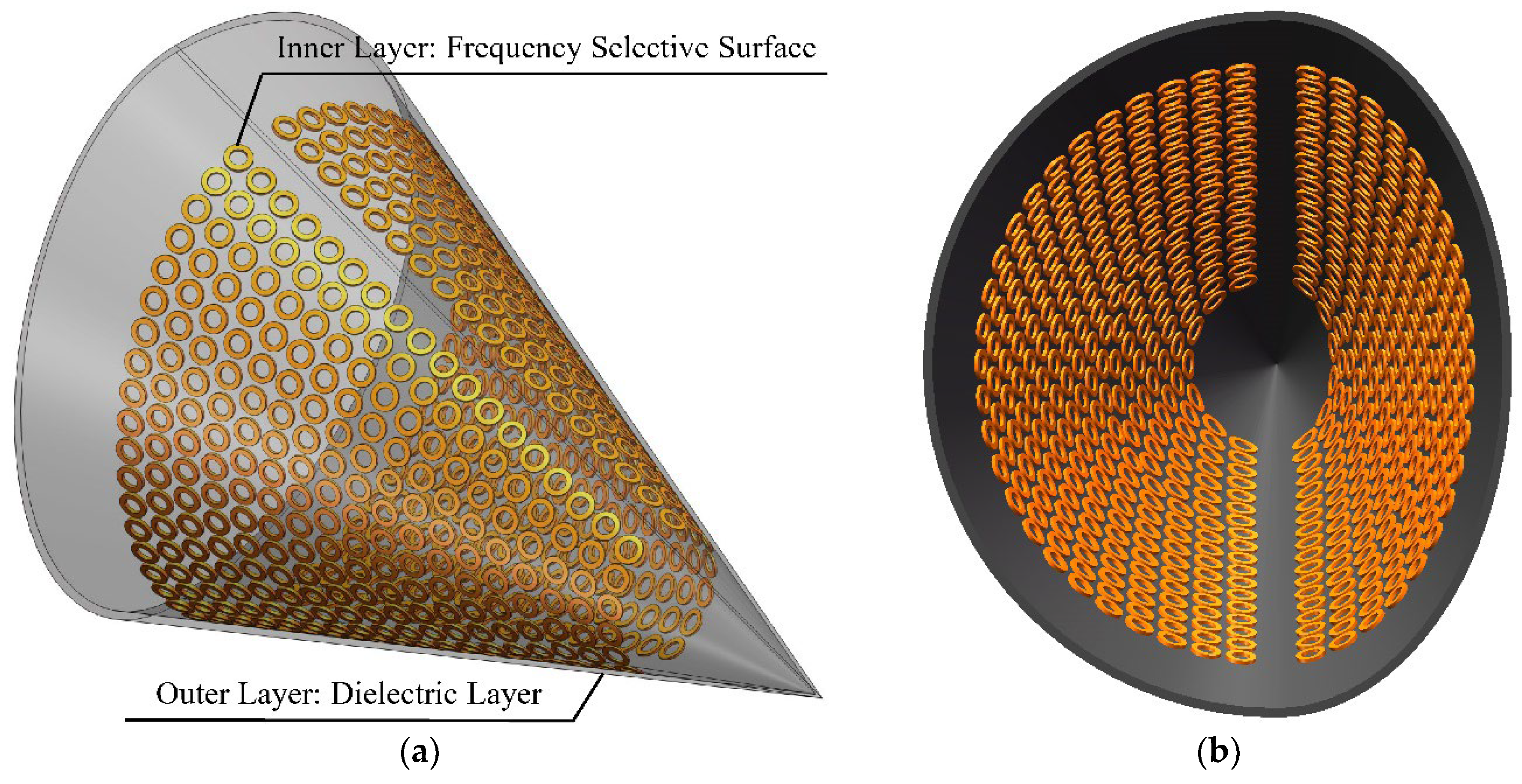
Figure 13.
Schematic diagram of the model C (a) Exploded view; (b) FSS layer.
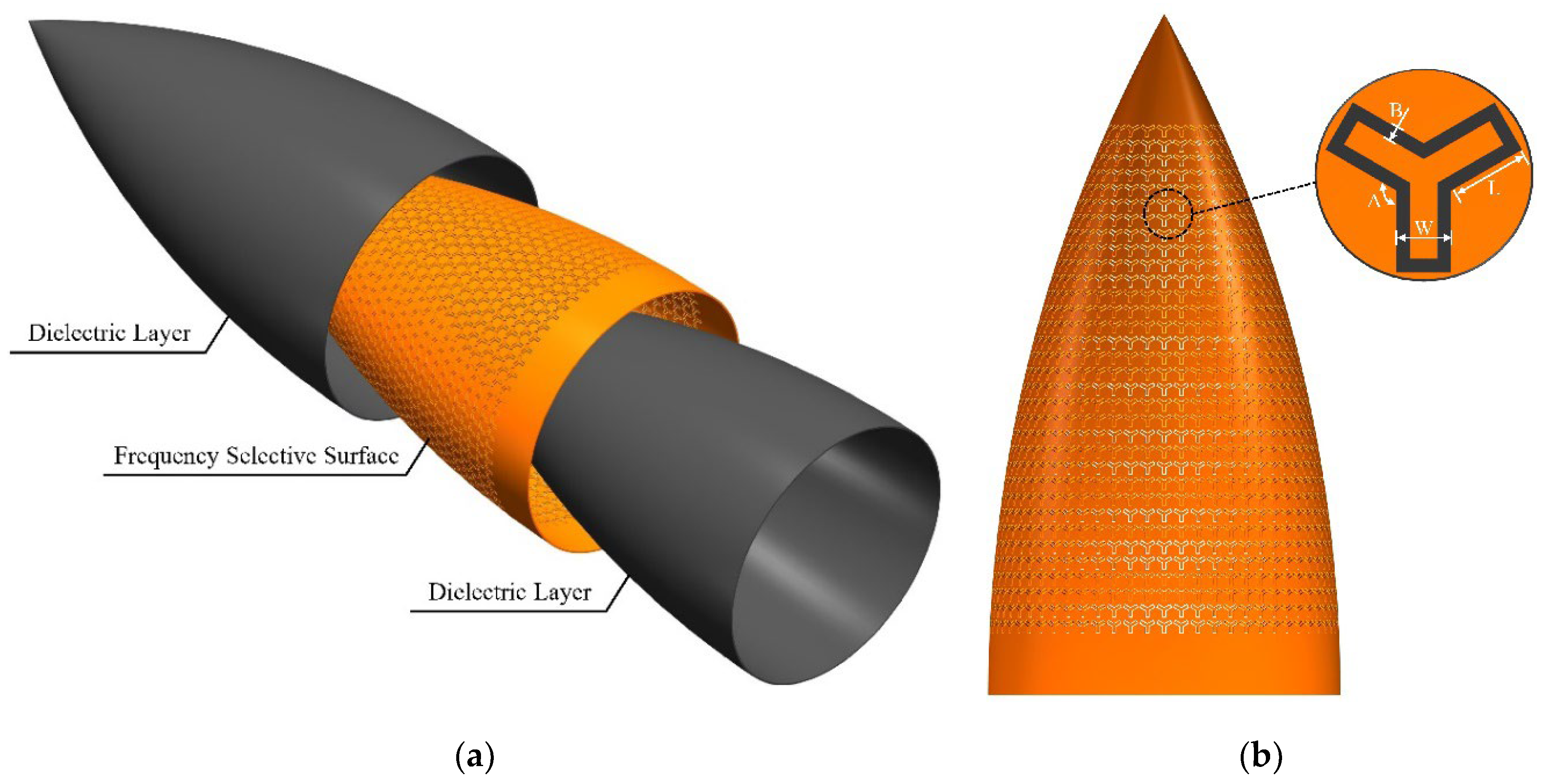
Table 1.
Modeling parameters of the rotational airborne frequency selective surface radome (AFSSR) with an A-sandwich wall structure and dual-screen frequency selective surface (FSS).
Table 1.
Modeling parameters of the rotational airborne frequency selective surface radome (AFSSR) with an A-sandwich wall structure and dual-screen frequency selective surface (FSS).
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| structural form | rotational | 150mm | |
| wall structure | A-sandwich | 50mm | |
| total length | 800mm | numbers of FSS layers | two-layer |
| total thickness | 12mm | position of FSS layers | skin-core junction |
| total caliber | 400mm | periodic structure of FSS | aperture |
| thickness of FSS layers | 2mm | 12mm | |
| thickness of skin layers | 2mm | 12mm | |
| thickness of inter layer | 4mm | numbers of FSS elements | 8589 |
Table 2.
Modeling parameters for Model B.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| structural form | non-rotational | 100mm | |
| wall structure | solid-core | 50mm | |
| total length | 400mm | periodic structure of FSS | patch |
| total thickness | 6mm | type of FSS elements | ring-shaped |
| total caliber | 250mm | size of FSS elements | R6.5mm*R4mm |
| thickness of FSS layers | 2mm | 15mm | |
| numbers of FSS layers | one-layer | 15mm | |
| position of FSS layers | middle | numbers of FSS elements | 530 |
Table 3.
Modeling parameters for Model C.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| structural form | rotational | 100mm | |
| wall structure | solid-core | 50mm | |
| total length | 600mm | periodic structure of FSS | aperture |
| total thickness | 6mm | type of FSS elements | Y-ring-shaped |
| total caliber | 300mm | size of FSS elements | L6mm*W4mm*B1mm*A60° |
| thickness of FSS layers | 2mm | 15mm | |
| numbers of FSS layers | one-layer | 14mm | |
| position of FSS layers | middle | numbers of FSS elements | 1582 |
Table 4.
Time required to build models A, B, and C by different methods.
| Manual Methods | HFSS-MATLAB刘Combined Method | Method Described刘in this Paper | |
|---|---|---|---|
| Model A | ≥300minutes | ≥180minutes | 15minutes≤ |
| Model B | ≥180 minutes | ≥10minutes | 8minutes≤ |
| Model C | ≥120minutes | ≥20minutes | 3minutes≤ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





