Preprint
Article
Integration of Laban Movement System’s Effort Theory in Biomechanical Analysis of Golf Swing: A Focus on the Initiation of the Downswing and Hip Turn Dynamics
Altmetrics
Downloads
108
Views
95
Comments
0
This version is not peer-reviewed
Submitted:
10 May 2024
Posted:
13 May 2024
You are already at the latest version
Alerts
Abstract
This study explores the application of the Laban/Bartenieff Movement System (® LBMS), particularly its Effort component, to analyze the biomechanical dynamics of the golf swing. Focusing on the initiation of the downswing, this paper investigates how the instantaneous screw axis (ISA) with rotational and linear motions contributes to subsequent movements, such as the hip turn. We propose that the physical forces generated by the golf club, characterized by mass moment inertia, extend beyond the body's boundaries, such as through the hand grip. A skilled golfer’s ability to 'allow' these forces to influence body dynamics without opposing them is analyzed through the lens of LBMS's Free Flow Effort, suggesting an indulgent and expansive use of movement energy.
Keywords:
Subject: Engineering - Bioengineering
1. Introduction
Golf is a sport that requires a complex interplay of physical, technical, and strategic skills. Among these, the biomechanical analysis of the golf swing stands out due to its critical role in performance enhancement and injury prevention. The golf swing is a dynamic movement that involves the entire body in a coordinated sequence, with the downswing phase being particularly crucial for the generation of speed and power. Traditionally, research in this area has focused on kinematic and kinetic aspects, such as body alignments, joint angles, and the forces exerted during the swing [1,2]. Researchers have reported on the kinematics and kinetics of the golf swing in terms of the relative contribution of each of the anatomical structures that are involved [3,4,5,6,7,8,9]. However, these mechanical descriptions often do not fully capture the qualitative aspects of movement fluidity and efficiency that distinguish skilled golfers.
Laban Movement Analysis offers a rich framework for the qualitative analysis of human movement. Developed by Rudolf Laban and colleagues, LMA describes body movements in terms of Body, Effort, Shape, and Space, collectively known as the Laban/Bartenieff Movement System (LBMS) [10]. Effort, or what Laban referred to as the dynamics of movement, involves understanding the dynamic intention and energy behind movements. The Effort category addresses the energetic expression of movement through four factors: Weight, Time, Space, and Flow, each with two polarities. For example, Flow can be either ‘Free’ or ‘Bound’, depicting how movement energy is either indulgently released or carefully controlled [11,12]. This effective aspect of movement analysis can provide novel insights into the qualitative aspects that make an efficient or powerful golf swing.
Despite the comprehensive nature of biomechanical models, there remains a research gap in how these models integrate qualitative movement descriptors that can differentiate between skill levels and identify movement efficiency. The application of LBMS, particularly its Effort component, offers a promising avenue to fill this gap. By analyzing golf swings through the lens of Effort qualities such as the Free or Bound nature of Flow, researchers can explore how these dynamics correlate with traditional biomechanical measurements, such as the instantaneous screw axis (ISA), which describes the rotation and translation of body segments [13]. One form of representing the club’s motion is the Instantaneous Screw Axes (ISA) [14,15].
Despite the potential applicability of LBMS in sports sciences, very few studies, if any, have utilized this rich analytical framework to understand and enhance the biomechanics of golf swings or other sports activities. This represents a significant research gap, as LBMS can provide novel insights into the qualitative aspects that make an efficient or powerful golf swing. Notably, the incorporation of LBMS into sports biomechanics remains largely unexplored, marking this study as a pioneering effort to integrate these qualitative descriptors with quantitative biomechanical models.
The current research aims to bridge this gap by applying LBMS’s Effort theory specifically to the biomechanical context of golf swings. By focusing on how the physical forces generated by the golf club (e.g., mass moment of inertia) are managed and utilized by the golfer, this study seeks to uncover the underlying dynamics that contribute to more efficient and powerful swings, particularly during the critical phase of the downswing [16]. This novel approach not only promises to enhance our understanding of the biomechanical aspects of golf swings but also opens the door for broader applications in sports science and rehabilitation.
2. Materials and Methods
2.1. Laban’s Effort Actions Theory to Refine and Communicate the Quality of Movement of the Golf Swing
Laban’s Eight Effort Actions, also known as Laban Effort Drives, are a key part of Rudolf Laban’s system for understanding and notating dance and movement, known as Laban Movement Analysis (LMA) [17,18]. These Effort Actions are used to describe the quality of movement and are organized according to Laban’s Effort-Shape theory, which considers both the inner intention and the outer shape of the movement. The eight Effort Actions are categorized into four pairs of opposite qualities, with each pair representing one of the factors of motion: Weight, Time, Space, and Flow (Figure 1). In refining the understanding of the golf swing, this study applies Rudolf Laban’s Eight Effort Actions, part of the Laban Movement Analysis (LMA), which characterizes movement through dynamic qualities. Each of these actions corresponds to a combination of Effort elements—Weight, Time, Space, and Flow—depicting how movement can be experienced and executed with varying intensities and intentions [19].
The golf swing, a sophisticated biomechanical action, encapsulates these Effort elements in its execution. The swing begins with a preparatory phase where the golfer aligns with the target, transitioning to the backswing, culminating in the powerful downswing. Each phase can be mapped to Laban’s Effort Actions, offering a qualitative lens through which to analyze and refine movement (Figure 2). The initial phase of the swing mirrors the ‘Float’ Effort Action—light, sustained, and indirect—where the golfer prepares, aligning body and mind with the intended direction and outcome. As the backswing progresses, the ‘Glide’ Effort Action—light, direct, and sustained—comes into play, signifying a smooth and controlled buildup of potential energy (Figure 3). As the golfer transitions into the downswing, the Effort Actions shift towards more dynamic qualities. The ‘Slash’ Effort Action—strong, indirect, and quick—aptly describes the initiation of the downswing. Here, the stored potential energy is released into kinetic energy, demonstrating the efficient and powerful execution of the swing. Throughout the swing, minimizing unnecessary muscular tension is vital. A ‘Free Flow’ Effort quality ensures that movements are executed with minimal restraint, allowing for better coordination and fluidity. This quality is particularly critical during the downswing, where excessive tension can lead to a disrupted kinetic chain and inefficient energy transfer.
Effort quality in the context of the swing also directly impacts efficiency and timing. For instance, a ‘Free Flow’ in the Effort Action ‘Press’—strong, direct, and sustained—can be seen in the even application of force through the impact with the ball, maximizing transfer of energy without unnecessary resistance. The implementation of LBMS in this context serves as an innovative method to convey the complex biomechanical and qualitative nuances of the golf swing. The inclusion of these Effort Actions within training regimens can enhance a golfer’s understanding of the physical and psychological elements at play, potentially leading to improved performance and a deeper appreciation for the subtleties of the sport.
As such, in this study, we seek to further explore these qualitative descriptors provided by Laban’s Effort Actions theory and apply them methodologically to analyze the intricate movements of the golf swing. Through this analysis, we aim to provide actionable insights that can be used to refine golf techniques and inform teaching and coaching practices.
2.2. Screw Representation of Line-Vector, Free-Vector, and the Spatial Inertia Tensor
This study employs screw theory [20] as a foundational mathematical framework to describe the spatial vector quantities relevant to the golf swing. Screw theory facilitates the representation of the six degrees of freedom of a rigid body (three translational and three rotational) in a unified manner. By defining the instantaneous screw axis (ISA) of the golf club, we capture both the rotational and translational dynamics essential for analyzing the complex movements in golf. We use Plücker coordinates [21] to represent these ISAs, allowing us to model the line of action and the moment around which the club rotates and translates during the swing. This approach provides a comprehensive understanding of the mechanical interactions between the golfer and the club, crucial for evaluating performance and technique.
The spatial Inertia tensor [22], a key concept from dynamics, is utilized to map the spatial acceleration space to the force space. Analogous to the error covariance tensor in estimation theory, this tensor encapsulates the inertia and mass properties of the golf club relative to the wrist joint, which is critical for understanding how golfers perceive and control the club during a swing. By decomposing the spatial inertia tensor into its geometric and constitutive components, we address complex eigenvalue problems that describe how different elements of the club’s inertia influence the swing dynamics. This decomposition allows us to explore the interaction between the golfer’s biomechanical inputs and the physical responses of the club.
In this section of our paper, therefore, we present a method of free-vector decomposition for the spatial rigid-body inertia tensor. The linear map from the spatial acceleration space to the spatial force space was defined as the spatial inertia tensor. This spatial inertia (of a rigid body) has been successfully represented by means of a set of principal screws of inertia [22]. Consider the situation in Figure 4: A club has a mass, m; its center of mass, CM, is given by the position vector, C; and the inertia tensor about its center of mass is J. The club is at rest, and experiences a force, f, acting along a line passing through the center of mass, and a couple, τC. The resulting acceleration is determined by an angular acceleration, α, along an axis passing through the center of mass (CM), the linear acceleration, aC, on CM.
The equation of motion is considered as a mapping from the twist-like screw acceleration to a wrench space [23].
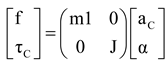 where
where 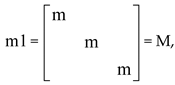 , and 1 is the 3×3 identity matrix.
, and 1 is the 3×3 identity matrix.
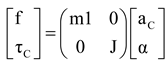
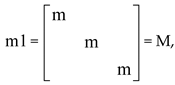 , and 1 is the 3×3 identity matrix.
, and 1 is the 3×3 identity matrix.Since all of the spatial quantities are referred to with respect to the center of mass, the linear and angular components of motion are decoupled – the linear acceleration being entirely due to the force, and the angular acceleration being a result of the couple. To transform Equation (1) into the origin of the joint axis (Figure 4), we obtain
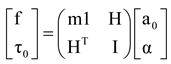 where
where 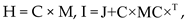 and C× is the anti-symmetric skew matrix corresponding to C.
and C× is the anti-symmetric skew matrix corresponding to C.
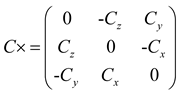
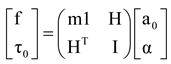
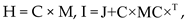 and C× is the anti-symmetric skew matrix corresponding to C.
and C× is the anti-symmetric skew matrix corresponding to C.
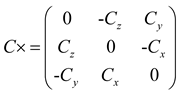
Due to its special 6×6 form, the spatial inertial tensor
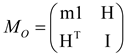 is expected to have special eigen structures.
is expected to have special eigen structures.
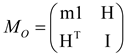
The spatial inertia tensor M0 represented at the origin is a symmetric, positive definite tensor and transforms to any point ‘A’ by the spatial Jacobian, Φ, according to
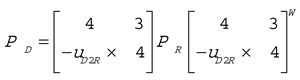 where
where 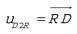 and
and 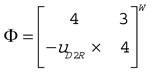 .
.

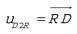 and
and 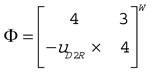 .
.The eigenvalue problem provides a unique decomposition of M0 as
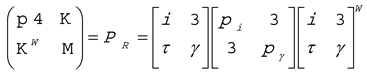 where mf and mγ are representing the eigen values of mass and mass moment of inertia, respectively (following the common notational tactics for the principal axes of inertia, we use
where mf and mγ are representing the eigen values of mass and mass moment of inertia, respectively (following the common notational tactics for the principal axes of inertia, we use 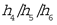 for mγ and, to the corresponding principal moment of inertia,
for mγ and, to the corresponding principal moment of inertia,  for γ).
for γ).
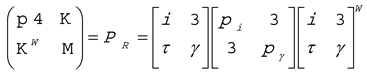
 for mγ and, to the corresponding principal moment of inertia,
for mγ and, to the corresponding principal moment of inertia,  for γ).
for γ).One might wonder whether the decomposition based on the solution for the free-vector eigenvalue problem would be different at another point A. We apply the transformation rule (Equation (5)) to the above decomposition (Equation (6)):
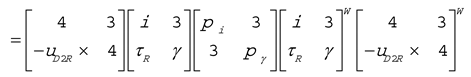
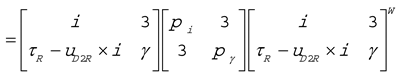
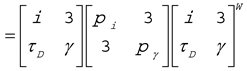 which shows that MA is decomposed by the same eigenscrews in the same manner, just represented at A. That is, no matter where the problem is posed, the same eigenscrews form the basis of the decomposition.
which shows that MA is decomposed by the same eigenscrews in the same manner, just represented at A. That is, no matter where the problem is posed, the same eigenscrews form the basis of the decomposition.
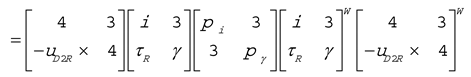
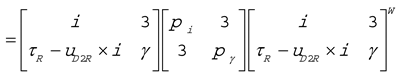
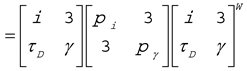
2.3. Instrumentation and Data Analysis
In this study, rather than collecting new empirical data, we utilized an existing dataset from previous research that detailed the golf swings of two female golfers with different skill levels [24] (Table 1). This dataset was chosen for its comprehensive capture of biomechanical movements using high-precision motion capture technology and ground reaction force measurements, making it highly suitable for our analysis.
The original data were collected using a sophisticated array of twelve high-speed Qualisys cameras, which accurately recorded the three-dimensional positions of reflective markers attached to the golfers and their clubs. This setup was designed according to the standards of the International Society for the Advancement of Kinanthropometry, ensuring that the biomechanical analysis adhered to high measurement accuracy and reliability (Figure 5). Ground reaction forces were measured using a Kistler force plate, providing essential data on the biomechanical forces exerted during the swings.
By reusing this existing dataset, we were able to directly apply our analytical models without the variability and resource constraints associated with new data collection. This approach also allowed us to focus on in-depth analysis using established data, ensuring that our study was both resource-efficient and grounded in reliable biomechanical metrics. The dataset included detailed annotations of each golfer’s movements and the corresponding biomechanical outputs, which facilitated a nuanced analysis of the swing mechanics.
Using the predefined anatomical coordinate system from the original study, which was based on key landmarks identified on the golfer and the club, we analyzed the motion data to extract the instantaneous screw axes (ISA) and their evolution during the downswing phase. This previously recorded data provided a robust basis for exploring how biomechanical properties such as the ISA correlate with golfer skill level and technique efficacy.
Reusing data from a well-designed previous study not only enhances the efficiency of the research process but also contributes to the sustainability of research practices by maximizing the utility of existing resources. This method ensures that the findings are built upon validated data, strengthening the reliability of the conclusions drawn from the analysis.
3. Results
3.1. A ‘Free’ Flow versus a ‘Bound’ Flow Based on Laban’s Effort Theory
Our analysis of the previously collected data revealed distinct differences in the golf swing mechanics between skilled and novice players, particularly in how they manage the physical forces during the downswing. Skilled golfers exhibited a profound synchronization between the instantaneous screw axis (ISA) and the dynamic forces exerted by the golf club’s inertia. This synchronization suggests a voluntary and strategic compliance with the natural forces, allowing these forces to guide the swing without opposition.
Figure 6 provides a dynamic visualization of the ISA paths during a novice golfer’s swing. The trajectories depicted by the solid lines and contrasted against the principal axes of inertia (dashed lines) illustrate a lack of alignment between perceived inertia and actual movement paths. This indicates a struggle with effective force management and synchronization, which is particularly evident from the disjointed ISA paths that exhibit abrupt changes in movement direction and speed. These perturbations suggest a resistance or a lack of coordination in allowing the inertia of the club to influence their body dynamics.
Conversely, Figure 7 illustrates the proficient golfer’s ability to synchronize her swing dynamics effectively. The alignment between the ISA (solid lines) and the e3 (dashed lines) demonstrates adept perception-action coupling, allowing her to voluntarily harness the club’s inertia to optimize swing mechanics and energy flow. This contrasted with the novice’s disjointed motion paths reveals significant insights into the qualitative differences in swing mechanics between different skill levels.
The movement patterns of skilled golfers demonstrated that their swings were not only synchronized in terms of timing but also optimized for energy utilization. The ISA paths in skilled golfers were smoother and showed a consistent alignment with the club’s inertia forces throughout the swing. This alignment allowed skilled players to maintain an efficient kinetic chain that enhanced both the power and fluidity of the swing, indicative of their ability to harness and modulate the club’s inertia effectively.
In contrast, novice golfers displayed multiple deviations from the ideal ISA path, with these deviations manifesting as abrupt changes in movement direction and speed. These perturbations indicate a resistance or a lack of coordination in allowing the inertia of the club to influence their body dynamics. The novice swings were characterized by a ‘Bound’ Flow, where the energy seemed restrained and movements were less fluid, likely resulting from a conscious or unconscious opposition to the inertia forces.
The spatiotemporal representation of the swings, especially the ISA paths, provided a vivid illustration of how the swing dynamics unfolded over time. For the skilled golfer, the ISA and the perceived inertia (e3 pathways) were closely aligned, suggesting a high degree of perceptual-motor integration. This integration enables proficient golfers to anticipate and adapt to the physical demands of the swing, allowing the natural progression of movement influenced by the club’s inertia. Conversely, the novice golfer’s e3 and ISA paths showed misalignment, indicating less effective perception-action coupling and a disjointed adaptation to the dynamic forces.
These results underscore the critical role of allowing physical forces to act naturally across the golfer’s biomechanical system, highlighting a fundamental difference in skill levels. The ability to voluntarily allow and adapt to these forces is a hallmark of proficiency in golf, reflecting a deeper kinesthetic awareness and a more refined control over the complex dynamics of the golf swing.
Figure 8 encapsulates the concept of gathering/scattering as a shaping movement in golf, akin to Dell’s description of accommodating the plastic character of objects and molding space like a sculptor with clay [18]. The sequence from phases 1 to 4 demonstrates the golf club’s dynamic downswing, where the club’s motion is adapted and refined in response to the forces and trajectory required for an effective strike. Each line traces the club’s path, illustrating the adaptation of form and the creative interaction with space, capturing the expressive and sculptural qualities inherent in skilled sports movements.
Sequential visualization of a golf club’s downswing, highlighting the dynamic envelope of club inertia. Phases 1 to 4 illustrate the progressive motion of the club head: starting from the initial downswing position (1), moving through the increasing acceleration (2, 3), and culminating in the final swing phase (4) where maximum velocity is achieved. The contour lines represent the club’s path, emphasizing how the inertia influences the trajectory and speed across the swing.
3.2. Motif Writing Using Laban Movement Analysis and Its Notation are Tied Closely to the Depiction of the Golf Swing
In this section, Laban Movement Analysis and its notation are tied closely to the depiction of the golf swing, emphasizing the continuous evolution of understanding human movement and its application to sports like golf. Laban Movement Analysis, inclusive of Labanotation, Motif Writing, Effort, and Space Harmony, constitutes an elaborate system for capturing the intricate and varied components of human movement. This comprehensive framework, originally developed by Rudolf Laban, was further enriched by Irmgard Bartenieff through her insightful contributions, particularly in the domain of Body Connectivity known as Bartenieff Fundamentals.
Labanotation, a component of this system, provides a sophisticated method for recording physical movements, as depicted in the figure which illustrates the nuanced choreography of a golf swing. It is through this notation that the qualitative aspects of the swing—its rhythm, fluidity, and dynamics—are meticulously transcribed, offering a visual lexicon of the movement.
The depicted Labanotation score is not merely a static representation but a dynamic blueprint that outlines the essential phases of a golf swing. It visually encodes the golfer’s posture, the sequential flow of the swing, the directionality of the club, and the shifting weight and balance of the golfer’s body through space and time.
By applying both the Labanotation and Bartenieff Fundamentals to the golf swing, the analysis becomes a living, evolving process. The systems work both separately and in unison, providing tools to capture and enhance the expressivity and functionality of the golfer’s movements. They enable a deeper investigation into how the golfer’s body engages with and navigates through the biomechanical demands of the swing, aiming for efficiency, power, and harmony. Thus, Figure 9 does not merely depict the mechanical sequence of the golf swing but embodies a deeper dialogue between the golfer and the swing—a synthesis of kinetic elegance and biomechanical precision, continually evolving as our understanding of movement deepens.
4. Discussion
The integration of Laban/Bartenieff Movement System’s Effort theory with biomechanical analysis reveals significant insights into the qualitative aspects of golf swings. This study’s findings underscore the nuanced way proficient golfers manage and interact with the physical forces during the swing. Unlike novice golfers who often resist or inefficiently channel these forces, proficient golfers demonstrate a voluntary and strategic allowance for the forces generated by the inertia of the golf club to act upon their bodies. This voluntary compliance facilitates a ‘Free’ Flow of movement, characterized by LBMS as indulgent and expansive, which correlates with more effective and fluid swing dynamics.
Our analysis indicated that proficient golfers’ ability to harness these forces without opposition is marked by their superior phase synchronization and reduced variability in their swings. This is particularly evident in the way these golfers manage the instantaneous screw axis (ISA) during the downswing, allowing the natural inertia and momentum of the club to guide their movements rather than forcing control. This approach not only enhances the smoothness and power of the swing but also contributes to a reduced risk of injury by aligning their movements more closely with the natural biomechanical pathways.
The insights gained from this study have profound implications for golf training and rehabilitation. Training programs that aim to develop a golfer’s ability to ‘allow’ rather than ‘control’ the forces during a swing could help in cultivating more proficient swings among novices and intermediates. Additionally, for rehabilitation, understanding the natural flow of forces and teaching injured golfers to harmonize with these forces could facilitate more effective recovery strategies, minimizing stress on the body while maximizing the efficiency of the swing.
These Effort Actions are not just theoretical; they are used in dance, theater, and other movement disciplines to refine and communicate the quality of movement. In fields like ergonomics and physical therapy, they can help in analyzing the efficiency of movement patterns and designing interventions for improvement. They can also be applied to animate characters in a more life-like and expressive manner in virtual environments, which is particularly relevant to our future work in VR and kinematics.
In our analysis, ‘Effort’ is considered the dynamic, qualitative aspect of the golf swing, encompassing the use of energy, the nuanced texturing of movement, emotional expression, and the internal attitude of the golfer. It is the ongoing interplay between the golfer (Weight), their movement (Flow), the surrounding environment (Space), and the temporal dynamics of the swing (Time) [19].
Unlike traditional biomechanical approaches that quantify movement in terms of angles, velocities, and accelerations, Effort in LBMS provides a qualitative perspective. It assesses how a golfer uses energy functionally and expressively throughout the swing. For instance, the functional Effort could be the golfer’s strength expressed in a weight shift that provides stability and power, lying beneath a lighter, more fluid upper body motion that guides the direction and shape of the swing.
Effort is analyzed through four motion factors: Flow, Weight, Time, and Space, with each factor ranging between two polarities that describe the quality of movement. For example, Flow may oscillate between free and bound, depicting the continuity or interruption of the golfer’s movement energy. A ‘Free’ Flow is continuous and unconstrained, reflecting a swing that is relaxed and adaptable. In contrast, a ‘Bound’ Flow is controlled and restrained, potentially signifying a swing that is more cautious or tense.
By examining the Effort elements of a golfer’s swing, we can better understand the subtle yet significant expressive nuances that contribute to performance. It allows us to identify the areas where a golfer’s movement may become inefficient or where energy is lost, offering a pathway to enhance the fluidity, power, and effectiveness of the swing.
Through this lens, we interpret the golf swing not just as a biomechanical event but as a rich, expressive action that is integral to the golfer’s interaction with the sport. It broadens our perspective beyond the physicality of the swing into the realms of personal expression and environmental interaction, thereby providing a holistic approach to analyzing and improving golf performance.
5. Conclusions
This research highlights the importance of integrating qualitative movement analysis with biomechanical metrics to achieve a deeper understanding of golf swing dynamics. By examining how proficient golfers voluntarily allow the inertia of the club to influence their movement, we uncover a critical aspect of sports performance that combines physical force management with psychological readiness to embrace these forces. Further investigations could extend these concepts to other sports and activities, broadening the impact of this approach across the fields of sports science and rehabilitation.
Author Contributions
Wangdo Kim: Conceptualized the study, led the original draft preparation, and performed the formal analysis. As the corresponding author, he oversaw the entire research project, ensuring all aspects of the manuscript preparation and submission were meticulously managed. Albert H. Vette: Contributed significantly to the writing, review, and editing of the manuscript. He was instrumental in acquiring funding for the project and provided substantial revisions to the scientific content, enhancing the depth and accuracy of the research. Wanda Ottes: Played a crucial role in providing resources and contributed to the writing, review, and editing of the manuscript. Her expertise in the Laban/Bartenieff Movement System was vital in interpreting the data and refining the methodology. Colleen Wahl: Contributed to the writing, review, and editing process, adding substantial intellectual content particularly in the application of movement analysis to the biomechanics of golf swings. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by PROCIENCIA under contract N° PE501080681-2022-PRO-CIENCIA Proyectos Especiales: Proyectos de Investigadores Visitantes.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors should like to acknowledge Miwon Kim, Sofia Camacho, and Professor Jorge Infante, for their help during data acquisition for this study. The first author should also like to thank Mr. Sangdo Kim for his stimulating discussions regarding the perfection of the golf swing.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Cochran, A.J. and J. Stobbs, The search for the perfect swing. (No Title), 1968.
- Neal, R.J. and B.D. Wilson, 3D kinematics and kinetics of the golf swing. Journal of Applied Biomechanics, 1985. 1(3): p. 221-232. [CrossRef]
- Horan, S.A., et al., Thorax and pelvis kinematics during the downswing of male and female skilled golfers. J Biomech, 2010. 43(8): p. 1456-62. [CrossRef]
- MacKenzie, S. and E. Sprigings, A three-dimensional forward dynamics model of the golf swing. Sports Engineering, 2009. 11(4): p. 165-175. [CrossRef]
- MacKenzie, S. and E. Sprigings, Understanding the mechanisms of shaft deflection in the golf swing. Sports Engineering, 2009. 12(2): p. 69-75. [CrossRef]
- Nesbit, S.M., A three dimensional kinematic and kinetic study of the golf swing. Journal of Sports Science and Medicine, 2005. 4: p. 499-519.
- Sprigings, E. and S.J. Mackenzie, Examining the delayed release in the golf swing using computer simulation. Sports Engineering, 2002. 5: p. 23-32. [CrossRef]
- Teu, K., et al., Using dual Euler angles for the analysis of arm movement during the badminton smash. Sports Engineering, 2005. 8(3): p. 171-178. [CrossRef]
- Teu, K.K., et al., The analysis of golf swing as a kinematic chain using dual Euler angle algorithm. Journal of Biomechanics, 2006. 39(7): p. 1227-1238. [CrossRef]
- Wahl, C., Laban/Bartenieff movement studies: Contemporary applications. 2019: Human Kinetics.
- Laban, R. and L. Ullmann, The mastery of movement. 1971.
- Bartenieff, I. and D. Lewis, Body movement: Coping with the environment. 2013: Routledge. [CrossRef]
- Fletcher, I.M. and M. Hartwell, Effect of an 8-week combined weights and plyometrics training program on golf drive performance. The Journal of Strength & Conditioning Research, 2004. 18(1): p. 59-62.
- Kiat Teu, K. and W. Kim, Estimation of the axis of a screw motion from noisy data—A new method based on Plücker lines. Journal of Biomechanics, 2006. 39(15): p. 2857-2862. [CrossRef]
- Kim, W. and S.S. Kohles, A reciprocal connection factor for assessing knee-joint function. Computer Methods in Biomechanics and Biomedical Engineering, 2011. [CrossRef]
- Sprigings, E.J. and S. Mackenzie, Examining the delayed release in the golf swing using computer simulation. Sports Engineering, 2002. 5(1): p. 23-32. [CrossRef]
- Berardi, G., Making connections: total body integration through Bartenieff fundamentals. Journal of Dance Medicine & Science, 2004. 8(3): p. 91-91. [CrossRef]
- Dell, C., A primer for movement description using effort-shape and supplementary concepts. (No Title), 1977.
- Konie, R. A brief overview of Laban Movement Analysis. in Movement That Has Meaning. http://movementhasmeaning. com/wp-content/uploads/2010/09/LMA-Workshop-Sheet. pdf. 2011.
- Ball, R.S., The Theory of Screws: A Geometrical Study of Kinematics, Equilibrium and Small Oscillations of a Rigid Body. The Transactions of the Royal Irish Academy, 1875. 25: p. 157-218.
- Hunt, K.H., Kinematic geometry of mechanism. 1990, Oxford: Clarendon Press.
- Ciblak, N., Analysis of Cartesian stiffness and compliance with applications. 1998, Georgia Institute of Technology, U.S.A.
- Featherstone, R., The Calculation of Robot Dynamics Using Articulated-Body Inertias. International Journal of Robotics Research, 1983. 2(1): p. 13-30. [CrossRef]
- Kim, W., et al., Haptic Perception-Action Coupling Manifold of Effective Golf Swing. International Journal of Golf Science, 2013. 2(1). [CrossRef]
Figure 1.
The accent sign, the / line, is the central notation graph; Effort is present when the accent sign is recorded. W = weight graph, with weight indications light and strong; F = flow graph, with flow indications free and bound; T = time graph, with time indications sustained and sudden; and S = space graph, with space indications flexible (indirect) and direct. The branches of the cross can be notated separately or together, each bearing the significance of a shade of the two factors: extension and control. The drawing of a combination of strokes and bars represents the Effort content of a movement and is called an Effort Graph.
Figure 1.
The accent sign, the / line, is the central notation graph; Effort is present when the accent sign is recorded. W = weight graph, with weight indications light and strong; F = flow graph, with flow indications free and bound; T = time graph, with time indications sustained and sudden; and S = space graph, with space indications flexible (indirect) and direct. The branches of the cross can be notated separately or together, each bearing the significance of a shade of the two factors: extension and control. The drawing of a combination of strokes and bars represents the Effort content of a movement and is called an Effort Graph.
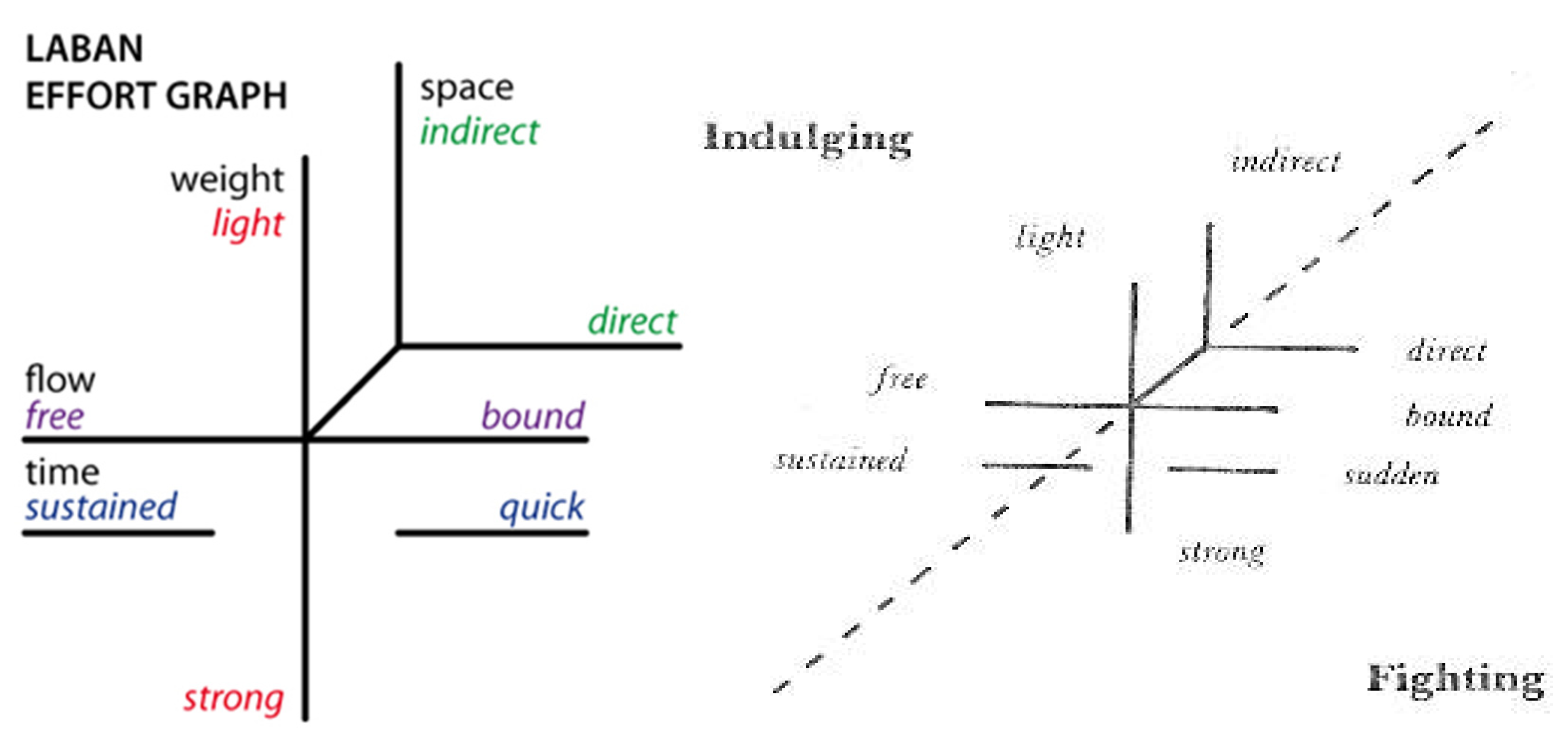
Figure 2.
This is the basic model Laban used to find his Effort Graph diagram with the three dimensions: (a) high/deep or the weight plane; (b) side-to-side or the space plane; (c) forward/backward or the time plane; (d) represents a two-dimensional projection of the Effort Cube, focusing on the movement within a single plane to simplify the analysis of dynamic qualities; (e) an X-marked schematic within the bounds of the Effort Cube, suggesting the intersection and interaction of Effort elements across different dimensions; (f) a clear view of the Effort Cube, emphasizing its structure and the confinement of movement dynamics within its boundaries; (g) displays a radial layout of various Effort elements and actions, illustrating the spectrum of possible movements and their classifications under Laban’s system; and (h) integrates the Effort Cube with a human figure, mapping the movement dynamics to the body, illustrating how different Effort actions can be expressed physically within the three-dimensional space of the cube.
Figure 2.
This is the basic model Laban used to find his Effort Graph diagram with the three dimensions: (a) high/deep or the weight plane; (b) side-to-side or the space plane; (c) forward/backward or the time plane; (d) represents a two-dimensional projection of the Effort Cube, focusing on the movement within a single plane to simplify the analysis of dynamic qualities; (e) an X-marked schematic within the bounds of the Effort Cube, suggesting the intersection and interaction of Effort elements across different dimensions; (f) a clear view of the Effort Cube, emphasizing its structure and the confinement of movement dynamics within its boundaries; (g) displays a radial layout of various Effort elements and actions, illustrating the spectrum of possible movements and their classifications under Laban’s system; and (h) integrates the Effort Cube with a human figure, mapping the movement dynamics to the body, illustrating how different Effort actions can be expressed physically within the three-dimensional space of the cube.
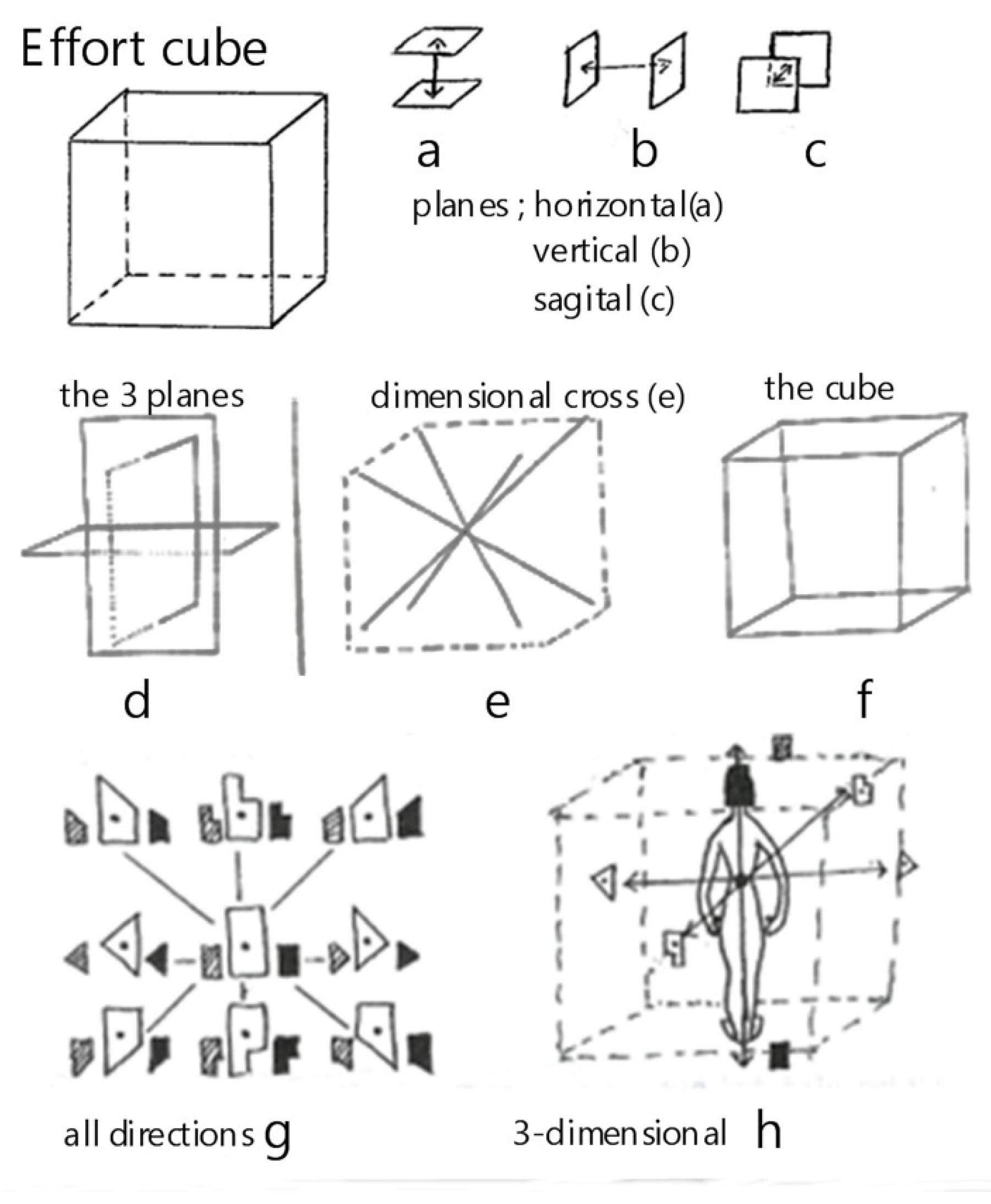
Figure 3.
As the golfer transitions into the downswing, the Effort Actions shift towards more dynamic qualities. The ‘Slash’ Effort Action—strong, indirect, and quick—aptly describes the initiation of the downswing.
Figure 3.
As the golfer transitions into the downswing, the Effort Actions shift towards more dynamic qualities. The ‘Slash’ Effort Action—strong, indirect, and quick—aptly describes the initiation of the downswing.
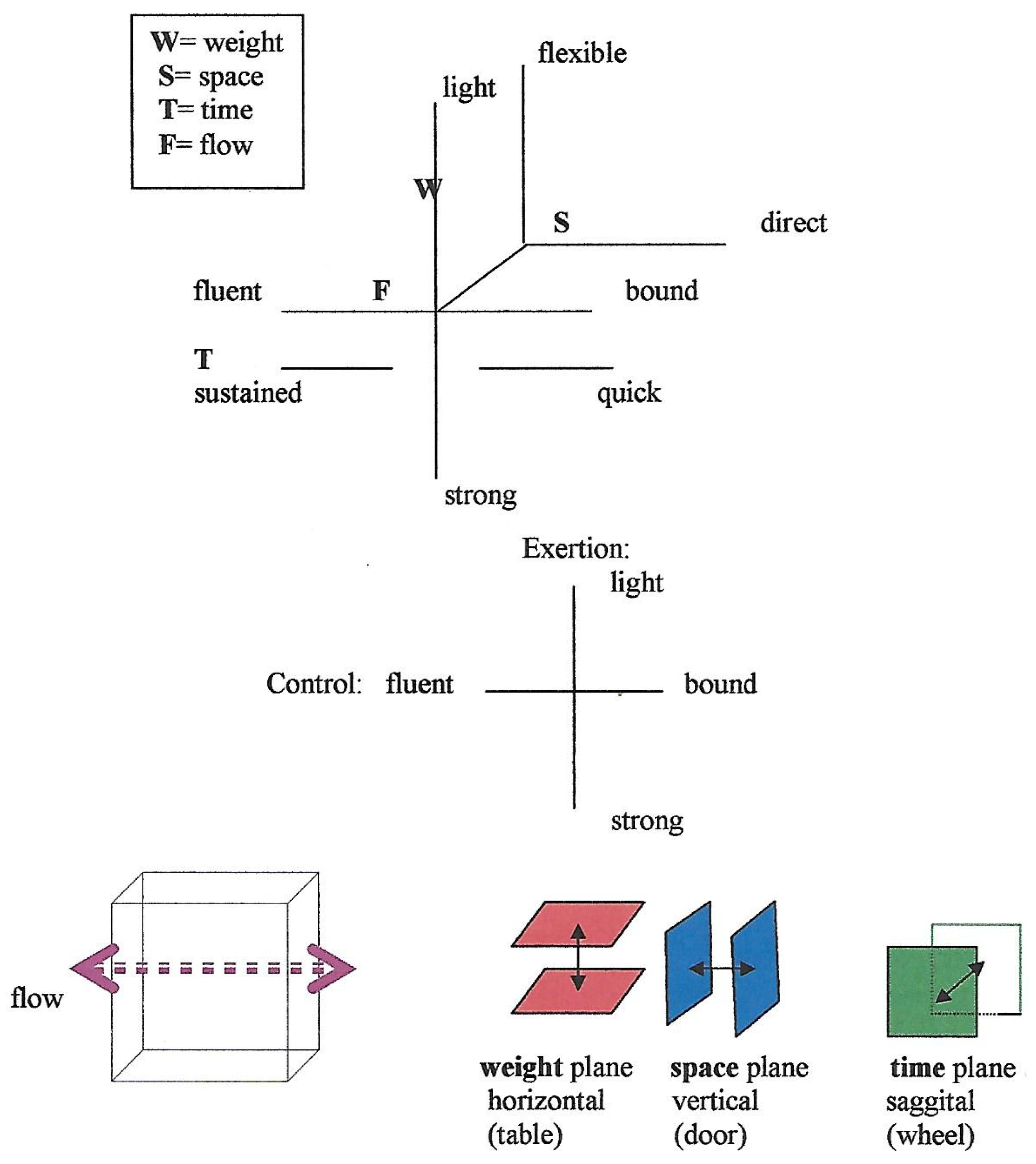
Figure 4.
This figure illustrates the grip reference frame attached at the center of the end of the club shaft. The spatial inertia tensor, computed with reference to the origin of the grip coordinate system, is depicted showing its principal axes and moments of inertia. This representation highlights how the inertia tensor transforms at any point along the wrist joint axis ‘A’, emphasizing the consistent eigenvalues irrespective of the positioning. The spatial arrangement allows us to explore how the inertia impacts the golfer’s control over the club during dynamic movements. The original values of quantities as well as the anatomical sketch that were originally published by [4] are used by permission of professor Sasho MacKenzie and are represented relative to the grip reference frame. (units in kg·cm2).
Figure 4.
This figure illustrates the grip reference frame attached at the center of the end of the club shaft. The spatial inertia tensor, computed with reference to the origin of the grip coordinate system, is depicted showing its principal axes and moments of inertia. This representation highlights how the inertia tensor transforms at any point along the wrist joint axis ‘A’, emphasizing the consistent eigenvalues irrespective of the positioning. The spatial arrangement allows us to explore how the inertia impacts the golfer’s control over the club during dynamic movements. The original values of quantities as well as the anatomical sketch that were originally published by [4] are used by permission of professor Sasho MacKenzie and are represented relative to the grip reference frame. (units in kg·cm2).
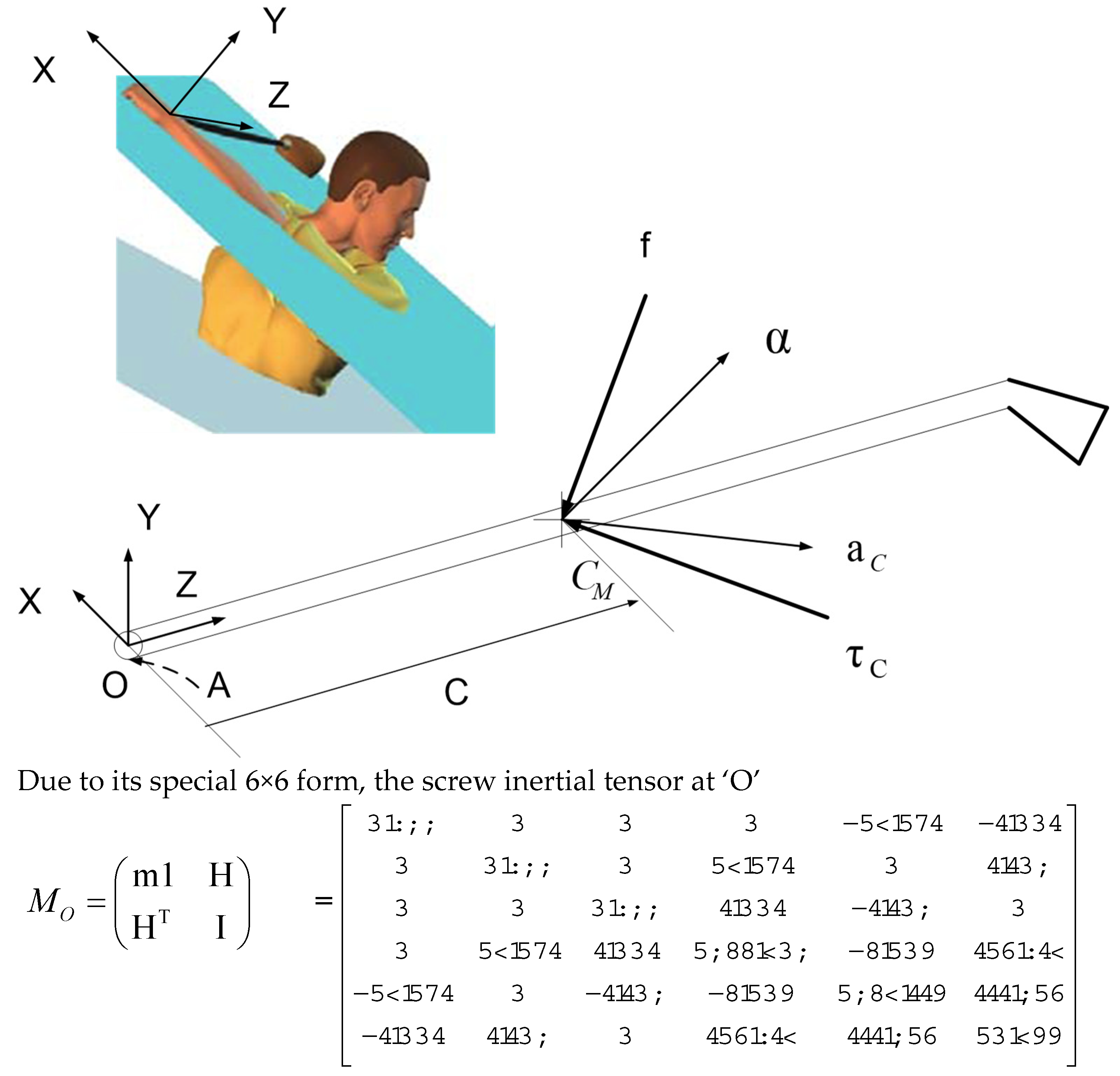
Figure 5.
Displayed here are the positions of reflective markers on a golfer at the moment the club addresses the ball. This setup was used to capture the biomechanical data originally recorded, detailing the anatomical landmarks critical for analyzing movement dynamics. The separate panel shows detailed placements on the hand, essential for understanding the grip dynamics and the resultant force transmission through the golfer’s body during the swing.
Figure 5.
Displayed here are the positions of reflective markers on a golfer at the moment the club addresses the ball. This setup was used to capture the biomechanical data originally recorded, detailing the anatomical landmarks critical for analyzing movement dynamics. The separate panel shows detailed placements on the hand, essential for understanding the grip dynamics and the resultant force transmission through the golfer’s body during the swing.
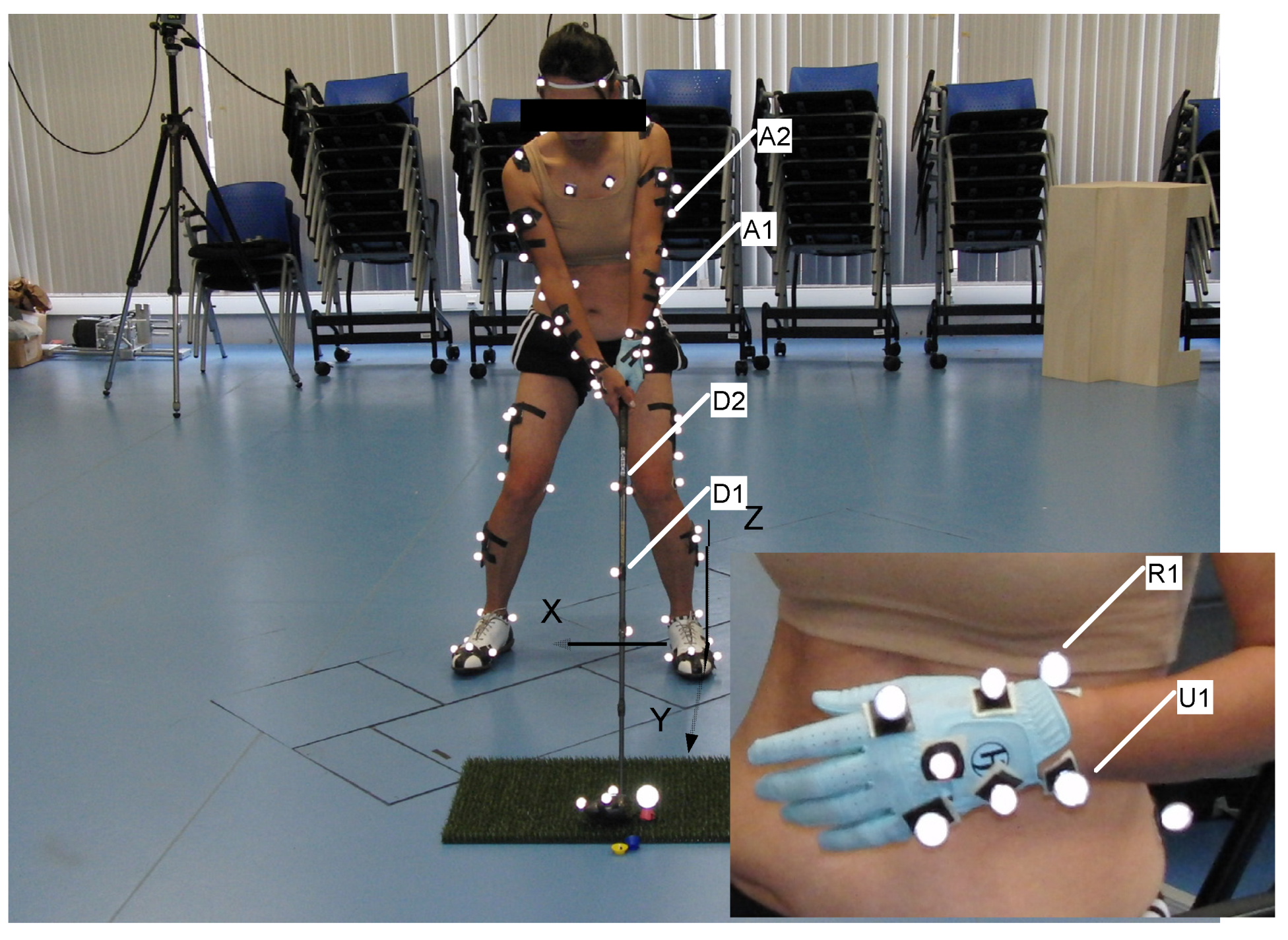
Figure 6.
This figure presents a three-dimensional spatiotemporal view of the ISA (solid lines) and the principal axes of inertia (e3 dashed lines) during a novice golfer’s swing. The paths projected onto the medial and superior sides illustrate the motion dynamics, showing the lack of alignment between perceived inertia and actual movement paths, indicative of the novice’s struggle with effective force management and synchronization. The arrow indicates where the subsequent axes have migrated at every 0.0333 second of time step (units in cm).
Figure 6.
This figure presents a three-dimensional spatiotemporal view of the ISA (solid lines) and the principal axes of inertia (e3 dashed lines) during a novice golfer’s swing. The paths projected onto the medial and superior sides illustrate the motion dynamics, showing the lack of alignment between perceived inertia and actual movement paths, indicative of the novice’s struggle with effective force management and synchronization. The arrow indicates where the subsequent axes have migrated at every 0.0333 second of time step (units in cm).
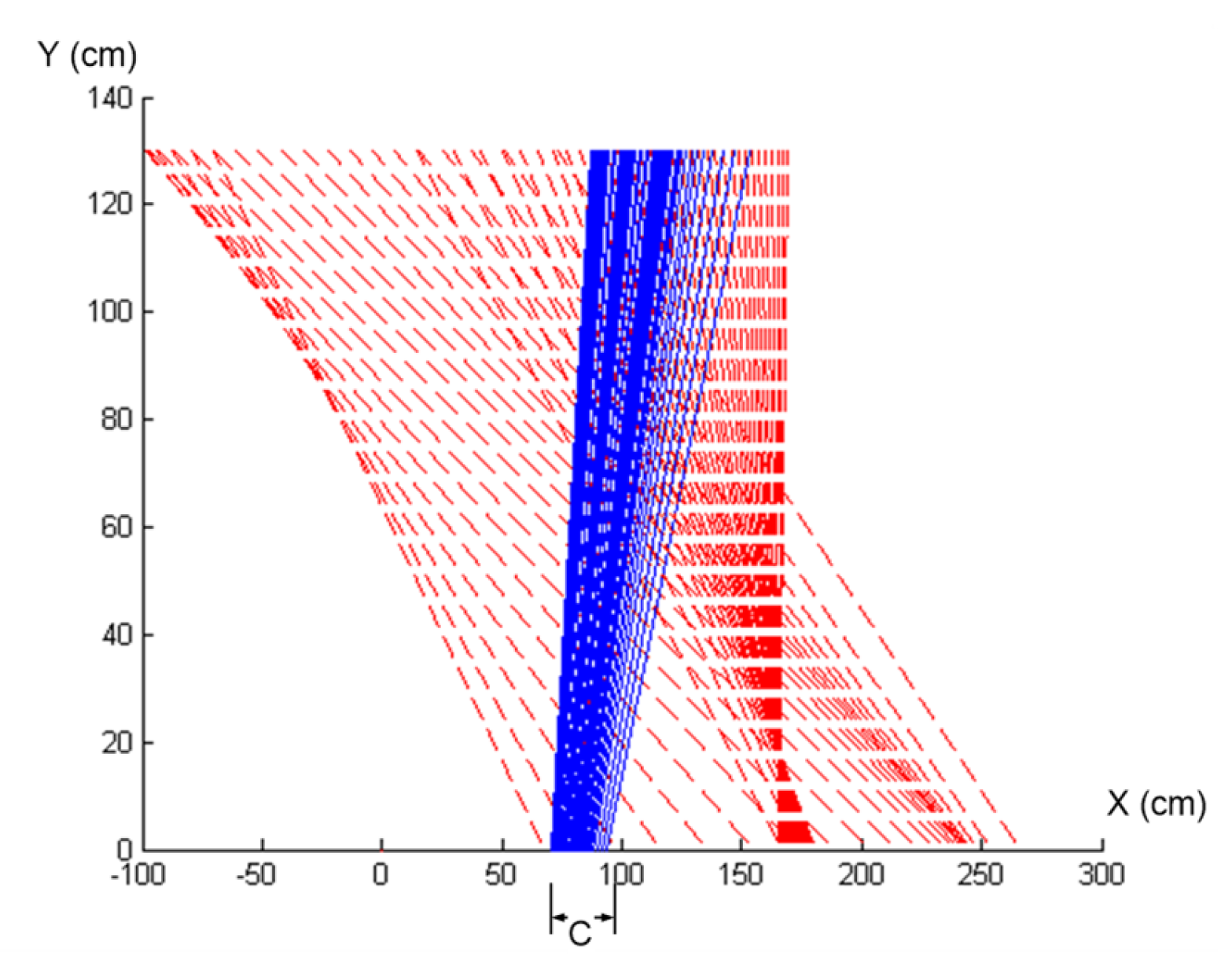
Figure 7.
Showcased here is the proficient golfer’s ability to synchronize her swing dynamics effectively, as evidenced by the alignment between the ISA (solid lines) and the e3 (dashed lines). This alignment demonstrates her adept perception-action coupling, allowing her to voluntarily harness the club’s inertia to optimize swing mechanics and energy flow, contrasted with the novice’s disjointed motion paths.
Figure 7.
Showcased here is the proficient golfer’s ability to synchronize her swing dynamics effectively, as evidenced by the alignment between the ISA (solid lines) and the e3 (dashed lines). This alignment demonstrates her adept perception-action coupling, allowing her to voluntarily harness the club’s inertia to optimize swing mechanics and energy flow, contrasted with the novice’s disjointed motion paths.
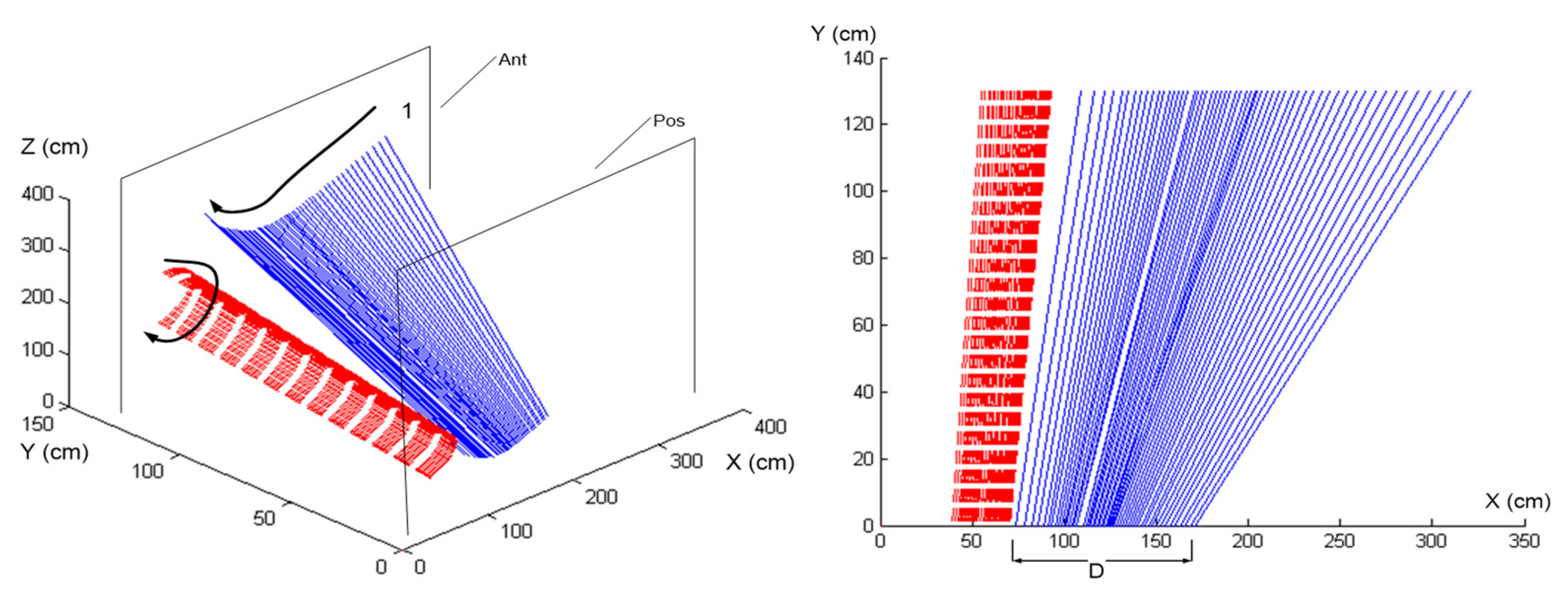
Figure 8.
This image embodies the application of Laban’s Body-Effort-Space-Shape framework, illustrating how the golfer’s body dynamically adapts to the contour of the club’s inertia envelope during the downswing. The red dashed contour marks the principal axis of inertia of the club, serving as a guide that the golfer’s movements mold around. This adaptive process, akin to a sculptor intuitively shaping clay, highlights the profound integration of body form with the evolving physical forces of the club, showcasing a sophisticated synchronization of movement and inertia for optimal swing efficiency.
Figure 8.
This image embodies the application of Laban’s Body-Effort-Space-Shape framework, illustrating how the golfer’s body dynamically adapts to the contour of the club’s inertia envelope during the downswing. The red dashed contour marks the principal axis of inertia of the club, serving as a guide that the golfer’s movements mold around. This adaptive process, akin to a sculptor intuitively shaping clay, highlights the profound integration of body form with the evolving physical forces of the club, showcasing a sophisticated synchronization of movement and inertia for optimal swing efficiency.
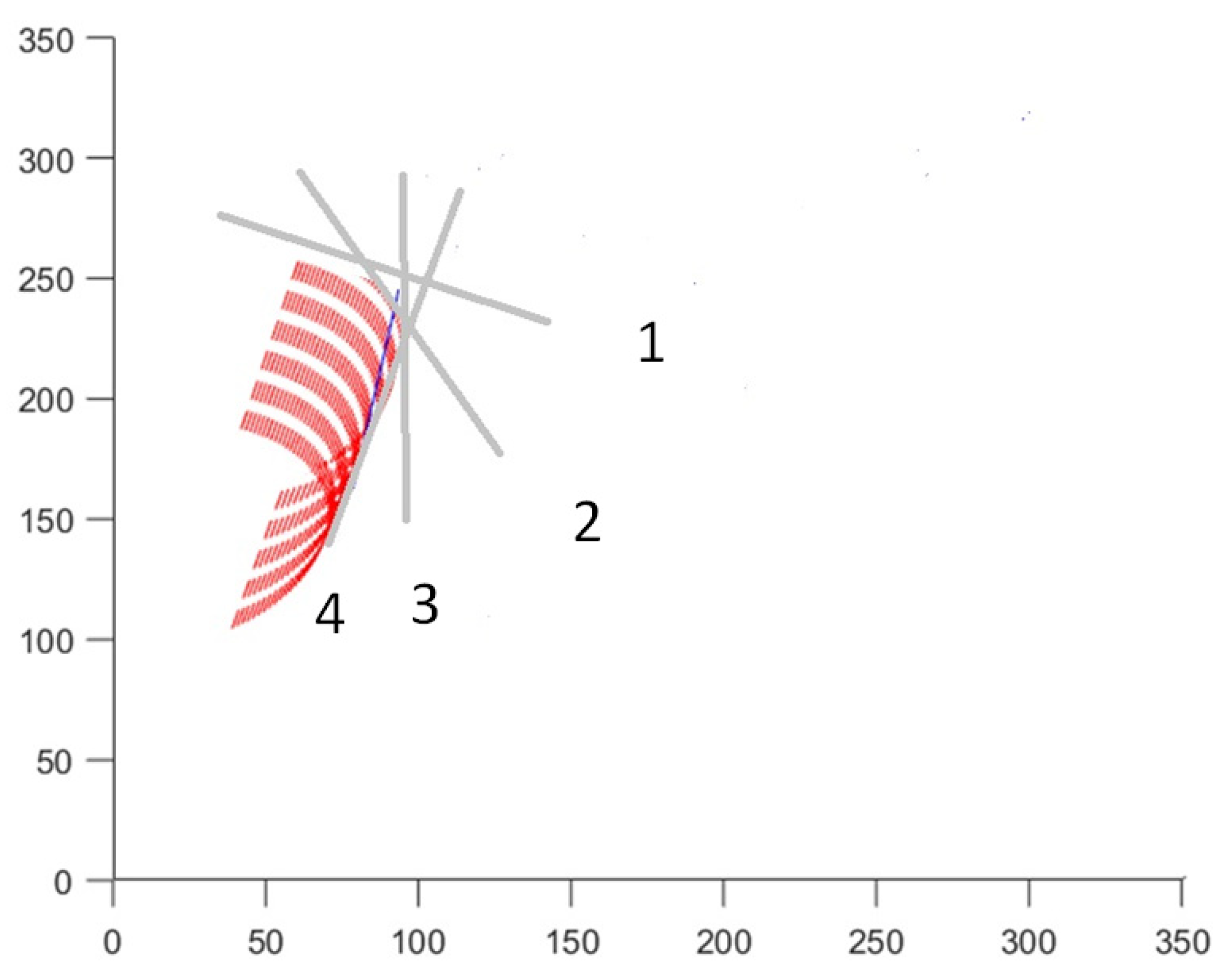
Figure 9.
The golf swing in Labanotation.
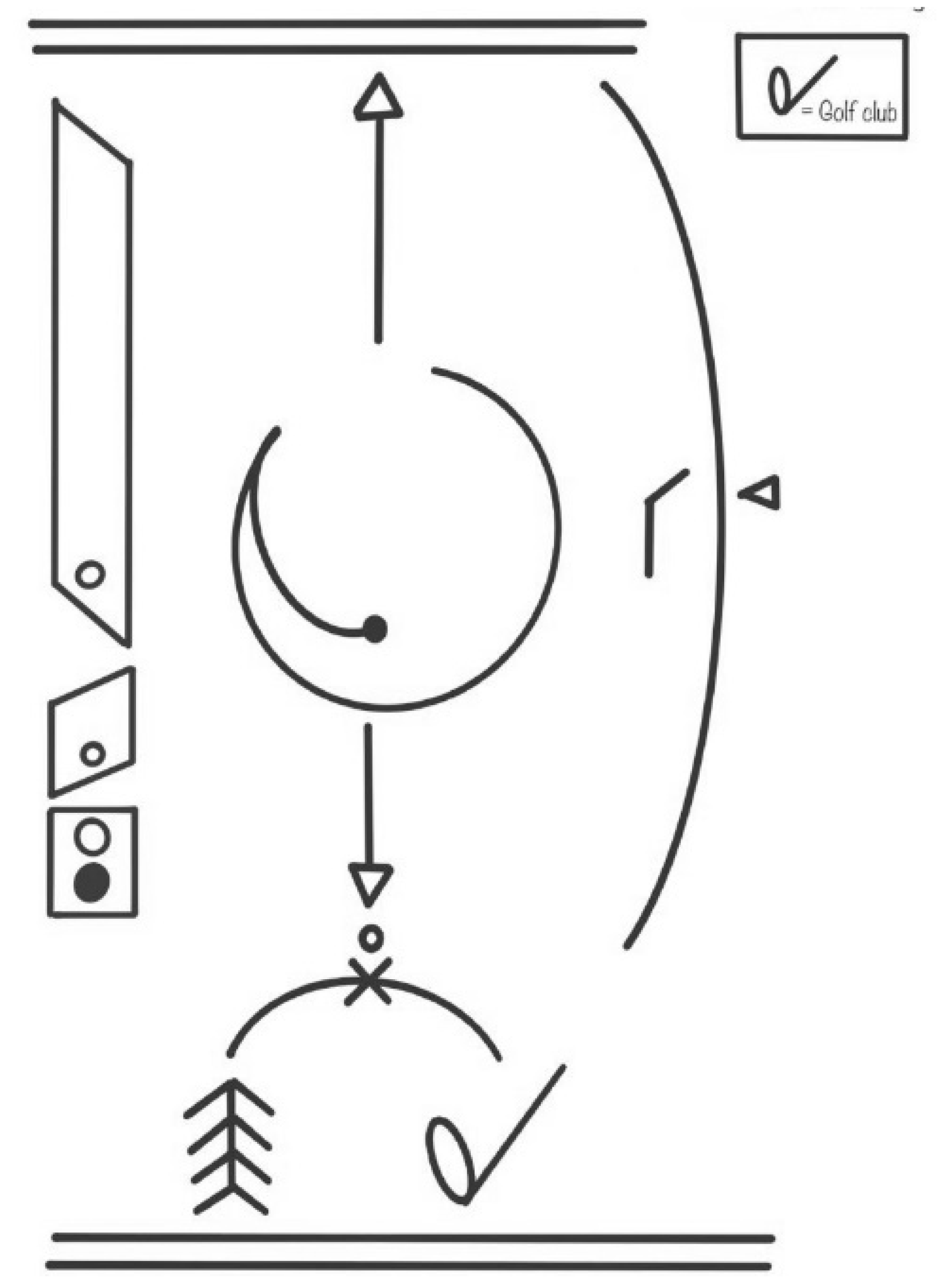
Table 1.
This table provides demographic and golfing background information for the two female golfers participated in the study. It includes age, height, mass, golfing handicap, experience, and annual rounds played, offering context for understanding the differences in their biomechanical data and performance outcomes.
Table 1.
This table provides demographic and golfing background information for the two female golfers participated in the study. It includes age, height, mass, golfing handicap, experience, and annual rounds played, offering context for understanding the differences in their biomechanical data and performance outcomes.
| Participant | Age | Height | Mass | Handicap | Experience | Rounds |
|---|---|---|---|---|---|---|
| (years) | (cm) | (kg) | (years) | (per year) | ||
| A | 17 | 167 | 54 | 32 | 1 | 10 |
| B | 51 | 165 | 55 | 8 | 15 | 110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







