Prerpints.org logo
Preprint
Article

Effects of Impurities and Deformations on Electronic Effective Mass in Quantum Revival Time within the Infinite Square Well

Altmetrics

Downloads

88

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 May 2024

Posted:

13 May 2024

You are already at the latest version

Alerts
Abstract
Quantum revival phenomena, wherein the wave function of a quantum system periodically returns to its initial state after evolving in time, are investigated in this study. Focusing on electrons confined within a quantum box with an impurity, both weak and strong coupling regimes are explored, revealing intricate relationships between impurity parameters and temporal dynamics. The investigation considers the influence of impurity position, impurity strength, and external factors such as aluminum concentration, temperature, and hydrostatic pressure on classical periods and revival times. Through analytical derivations and graphical analyses, the study elucidates the sensitivity of quantum revivals to these parameters, providing valuable insights into the fundamental aspects of quantum mechanics. While no specific physical applications are discussed, the findings offer implications for quantum heat engines and other quantum-based technologies, emphasizing the importance of understanding quantum revivals in confined quantum systems.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

Quantum revival refers to a phenomenon in which the wave function of a quantum system periodically returns to its initial state after evolving in time[1]. It arises in systems that are confined or periodic in nature, such as particles in a box or atoms in an optical lattice[2,3]. It is characterized by the recurrence of interference patterns in the probability density of finding the system in different states. Quantum revival is a fundamental aspect of quantum mechanics with applications in various fields, including quantum information processing[4,5] and condensed matter physics[6]. As is well known, it has counterparts in other branches of physics. One notable example is in the study of wave phenomena, where similar periodic behaviors can be observed. For instance, in classical wave physics, phenomena such as wave interference and diffraction can lead to periodic patterns in the intensity or amplitude of waves[7]. Additionally, in certain systems in classical mechanics, such as periodic mechanical oscillators or coupled pendulums, there can be periodic recurrences of specific states or motions due to the system’s inherent periodicity. While the underlying principles may differ between classical and quantum systems, the concept of periodic recurrence is a common thread across various branches of physics.
The time of quantum revival may be relevant not only for studies of electronic properties in quantum devices [8], but also for the study of quantum thermal machines [9]. The effects of topological defects on quantum revivals have been addressed in [10,11,12]. Recently, it was shown that the influence of spiral dislocation gives rise to a non-null revival time in the harmonic oscillator [13]. Additionally, the classical periods and revival times of electron currents in several bulk nanostructured semiconductor materials were computed in [14]. Quantum revivals within relativistic theory can be explored in [15], and further investigations concerning exact quantum revivals for the Dirac equation are detailed in [16].
Speaking of another topic of great current interest, in article [17], the authors investigated the impacts due to impurity in the quasi-static thermodynamics of thermal machines, with the quantum system of a particle in a box as the working substance. However, quantum thermodynamics aims to consider, in addition to thermal and quantum fluctuations, those due to processes with finite time. We shall not delve into these investigations at the moment, but rather focus on a fundamental aspect of quantum mechanics, which is quantum revival. Inspired by these works, in this contribution, we investigate the classical periods and revival times for the system mentioned at the beginning of this paragraph. Furthermore, we explore the impact of deformations on the electronic effective mass on these quantities, that is, we consider electrons in a G a A s / G a 1 − x A l x A s [18]. Effects of hydrostatic pressure, temperature, and aluminum concentration warrant attention due to pronounced modifications in physical quantities in electronic systems[19,20,21].
The paper is divided as follows: in Section II, we present the studied model and the eigenenergies for the electron in the impurity-doped box. In Section III, we present its effective mass as a function of temperature, hydrostatic pressure, and aluminum concentration. In Section IV, we calculate the revival times and perform graphical analyses to observe the effects of impurity position in the box and the effects of deformations in the effective mass on these times. Section V contains the conclusions of the work.

2. The model Hamiltonian and the eigenenergies

The Hamiltonian describing a particle of mass m confined within a 1-D infinite square well (ISW) of length L, featuring an impurity situated at position p L ( 0 ≤ p ≤ 1 ) inside the well, is expressed as follows:
H = H 0 + H ′ , where ,   H 0 = − ℏ 2 2 m ∇ 2 + V ( x ) , V ( x ) = 0 for 0 ≤ x ≤ L ∞ otherwise , and   H ′ = − λ δ ( x − p L ) .
Here, H 0 represents the Hamiltonian of the particle within the ISW, governed by the kinetic energy term and the potential energy function V ( x ) which is zero within the well and infinite elsewhere. The additional term H ′ introduces the effect of the impurity, modeled as a delta function potential with strength denoted by λ . The parameter p determines the precise location of the impurity within the well. A negative λ implies a repulsive impurity, behaving akin to a barrier, while a positive λ denotes an attractive impurity, creating a well-like potential. The schematic representation of the ISW potential featuring a repulsive impurity is depicted in Figure 1. Detailed solutions can be found in the article [17]. Here, we shall invoke the results of the eigenenergies in the cases of the perturbative solutions for the weak coupling regime and for the perturbative solution for the strong coupling regime.
The objective is to solve the time-independent Schrödinger equation H Ψ = E Ψ , where Ψ satisfies three boundary conditions:
lim x → p L − Ψ ( x ) = lim x → p L + Ψ ( x ) ,
lim x → p L + d Ψ ( x ) d x − lim x → p L − d Ψ ( x ) d x = − 2 m λ ℏ 2 Ψ ( p L ) ,
Ψ ( 0 ) = Ψ ( L ) = 0 .
For positive energies E = ℏ 2 k 2 2 m > 0 , the solution of the Schrödinger equation, satisfying the boundary conditions in Eqs. (2, ), is expressed as:
Ψ ( x ) = A sin ( k ( L − x ) ) sin ( k p L ) , for p L ≤ x ≤ L , A sin ( k x ) sin ( k L ( 1 − p ) ) , for 0 ≤ x < p L , 0 otherwise .
Here, A is the normalization constant for the wavefunction and k = 2 m E ℏ 2 .
By applying Eq. () and utilizing the wave function from Eq. (5), we obtain the dispersion relation as follows:
( k L ) f sin ( k L ) = 2 sin ( k p L ) sin ( k L ( 1 − p ) ) ,
where
f = ℏ 2 m λ L
is a dimensionless parameter representing the strength of the impurity. Thus, f < 0 ( f > 0 ) signifies a repulsive (attractive) δ potential.
We shall now direct our attention to two cases amenable to analytical solutions: the scenario of weak coupling regime and that of strong coupling regime. As indicated by reference [17], these arise for | f | ≥ 0.5 and | f | < < 1 , respectively.
We start by the perturbative eigenenergy correction for the weak-coupling regime up to the first order. It can be obtained through the application of Rayleigh-Schrödinger perturbation theory for time-independent systems. The initial energy correction at the first order is derived by treating H ′ as a perturbation within the framework of Eq. (1). Obtaining the eigenfunctions and eigenvalues of the infinite potential well without impurities is straightforward. These are given by:
Ψ n ( x ) = 2 L sin n π x L , E n = n 2 π 2 ℏ 2 2 m L 2 , n = 1 , 2 , 3 . . .
The first-order corrections to the energy eigenvalues caused by either attractive or repulsive δ function impurities can be readily computed[22]. These corrections yield:
E n , w ( 1 ) = ℏ 2 2 m L 2 n 2 π 2 − 4 sin n π p f .
The perturbative eigenenergy correction for the weak-coupling regime up to the second order can be obtained within a different approach. It is obtained from the expansion k = k 0 + λ k 1 + λ 2 k 2 + · · · . The details can be viewed in [17] and the eigenenergy up to the second order correction shall be given by
E n , w ( 2 ) = ℏ 2 2 m L 2 n 2 π 2 − 4 sin n π p f − 2 ℏ 2 sin n π p 4 1 + 2 n π 1 − 2 p cot n π p m L 2 n 2 π 2 f 2 .
In the context of strong coupling, a perturbative approach is employed to determine the energy eigenvalue by applying perturbation up to the first order in the strength parameter. Considering the case where f ≪ 0.1 , we expand k as k = k 0 + 1 λ k 1 + 1 λ 2 k 2 + ⋯ in the dispersion relation represented by Eq. 6. This expansion, as derived in [17], leads to the expression:
β sin ( β L ) = 2 m λ ℏ 2 sin ( β p L ) × sin ( β ( 1 − p ) L ) ,
where β = k 0 + 1 λ k 1 + 1 λ 2 k 2 + ⋯ . By calculating the power series expansion of sin and isolating terms with λ 1 on both sides, we arrive at:
sin ( k 0 p L ) sin ( k 0 ( 1 − p ) L ) = 0 .
This equation implies that either sin ( k 0 p L ) = 0 or sin ( k 0 ( 1 − p ) L ) = 0 . Then, two spectra for the energy were obtained, stemming from these two conditions(which we shall index by a and b). They are given by
E n , s t r ( a ) = ℏ 2 2 m L 2 n 2 π 2 p 2 + n f π p 3
and
E n , s t r ( b ) = ℏ 2 2 m L 2 n 2 π 2 ( 1 − p ) 2 + n f π ( 1 − p ) 3 .
In what follows, we shall consider the particle mass m given by the electronic effective mass denoted as m eff ( x , P , T ) , which depends on the aluminum concentration in the material, hydrostatic pressure, and temperature. Details regarding its dependence on these physical quantities for the material G a A s / G a 1 − x A l x A s shall be presented subsequently.

3. Effects of hydrostatic pressure, temperature and Al-concentration on the effective electron mass

The effective mass of an electron in a material is as real as its mass in in vacuum[23]. This way, we consider a case for electrons on a G a A s / G a 1 − x A l x A s . The effective mass of electrons in the conduction band, which is assumed to be dependent on x(aluminum concentration), P(hydrostatic pressure) and T(temperature), and can be expressed as [18]
m e f f x , P , T = m 0 1 + 28900 − 6290 x 3 2 E g Γ x , P , T + 1 E g Γ x , P , T + 314 − 66 x + ζ x − 1 ,
where m e = 9 , 11 × 10 − 31 K g is the electron mass at vacuum,
ζ x = − 3.950 + 0.488 x + 4.938 x 2 ,
and
E g Γ x , P , T = λ 1 + λ 2 x + λ 3 x 2 + a P − b T 2 T 0 + T ,
with λ 1 = 1519 m e V , λ 2 = 1360 m e V , λ 3 = 220 m e V , a = 107 m e V / G P a , b = 0.5405 m e V / K and T 0 = 204 K .
These deformations in the effective mass of the electron in this material shall be considered in the subsequent analyses. In the following, we shall denote m e f f ( x , P , T ) as m e f f for the purpose of simplifying notation.

4. Quantum Revivals

Quantum revivals manifest when the wave function regains its initial configuration, marking what is termed a "revival" moment. In quantum systems characterized by a single quantum number n, the energy eigenvalues can be expanded around the central value n 1 of this quantum parameter. This expansion yields the energy expressed as a Taylor series:
E n ≈ E n 1 + d E d n n = n 1 ( n − n 1 ) + 1 2 d 2 E d n 2 n = n 1 ( n − n 1 ) 2 + …
Consequently, distinct time scales emerge[1,24]: the classical period is determined by
t = 2 π ℏ d E d n n = n 1 .
while the revival time is defined as
τ = 4 π ℏ d 2 E d n 2 n = n 1 .
The energy levels (9) solely hinge on one quantum number.
From these definitions, and considering the energies described above(ene1,ene2,ene3,ene4), the classical periods and the revival times are obtained and described by:
t n , w ( 1 ) = 4 π m eff L 2 ℏ 2 n π 2 − 4 π p cos n π p f − 1 ,
t n , w ( 2 ) = 2 π 3 m eff L 2 n 3 f 2 A 1 + B 1 + C 1 − D 1 + E 1 ℏ ,
with A 1 ≡ 4 + π 4 − 8 p p − 1 / 2 π 2 , B 1 ≡ 2 8 p − 2 sin π p + π 2 p π cos π p , C 1 ≡ − 8 + 40 p p − 1 / 2 π 2 cos π p 2 , D 1 ≡ 16 sin π p p − 1 / 4 π cos π p 3 and E 1 ≡ 4 + π 4 − 8 p p − 1 / 2 π 2 ,
t n , s t r ( a ) = 4 π m eff L 2 ℏ 2 n π 2 p 2 + f π p 3 − 1 ,
t n , s t r ( b ) = 4 π m eff L 2 ℏ 2 n π 2 ( 1 − p ) 2 + f π ( 1 − p ) 3 − 1 ,
τ n , w ( 1 ) = 8 π m eff L 2 ℏ 2 π 2 + 4 π 2 p 2 sin n π p f − 1 ,
τ n , w ( 2 ) = 4 π 3 m eff L 2 n 4 f 2 A 2 + B 2 + C 2 − D 2 + E 2 + F 2 ℏ
whith
A 2 ≡ − 12 + π 4 f 2 n 4 + 24 p p − 1 / 3 n 2 π 2 ,
B 2 ≡ 2 π 4 sin n π p f n 4 p 2 ,
C 2 ≡ 80 sin n π p π n n 2 p 2 p − 1 / 2 π 2 − 3 / 5 p + 1 / 10 cos n π p ,
D 2 ≡ 24 − 120 p p − 1 / 3 n 2 π 2 cos n π p 2 ,
E 2 ≡ 128 sin n π p π n n 2 p 2 p − 1 / 2 π 2 − 3 / 8 p + 1 / 16 cos n π p 3 ,
F 2 ≡ − 12 + 96 p p − 1 / 3 n 2 π 2 cos n π p 4 ,
τ n , s t r ( a ) = 4 m eff L 2 p 2 π ℏ
and
τ n , s t r ( b ) = 4 m eff L 2 ( 1 − p ) 2 π ℏ .
In the case of weak coupling, the times depend both on this coupling and on the position of the impurity. This is not the case for strong coupling, which depends solely on the position of the impurity.
In the following analysis, we shall graphically examine these times with respect to classical periods and revival times for an electron in the box without the delta potential and with the effective mass of electrons in GaAs at x = T = P = 0 , given by m * = 0.067 × m e , where m e = 9.11 × 10 − 31 Kg is the electron mass in vacuum. They are given, respectively, by:
T 0 = 2 m * L 2 π ℏ n
and
τ 0 = 4 m * L 2 π ℏ .
The energy levels are inversely proportional to the effective mass of the electron in the box. Therefore, any increase in its value results in increased calculated times, as they become proportional to it. We analyze the classical periods and revival times versus the position of the impurity for the weak coupling regime in Figure 2. As the concentration of Al increases, the profile of the graphs does not change, but the times are increased. The same occurs for an increase in hydrostatic pressure (see Figure 3). The effects of temperature on the effective mass are the least pronounced, so we shall not plot them here. For f = ± 2 , the graphs show that the times behave non-monotonically as a function of the impurity’s position within the box and in the opposite way. For classical period and f = 2 , the lowest value of time occurs when the impurity is close to the infinite wall on the right, while the highest value is near p = 0.3 . For f = − 2 , this behavior inverts. As for the revival time, the highest value occurs when the impurity approaches the infinite wall on the left, while the lowest value is near p = 0.7 . The inversion in this behavior is also observed for f = − 2 . Notice that the classical periods calculated from the energy derived from second-order perturbation theory deviate, in 0.6 < p < 1 , towards slightly smaller values compared to the case for first-order perturbation. For the revival time, there is a peak time near p = 0.9 , but perhaps this region may not represent a physical value to be observed. Including more terms in the expansion could correct this situation, but we leave this open-ended.
Turning our attention to the strong coupling limit, for f ± 0.01 , the times behave monotonically, but in opposite ways for the two distinct energy spectra, which depend on the chosen condition (see Figure 4). Where one reaches the highest time, the other reaches the lowest value, and vice versa. The times are the same for p = 0.5 . One additional detail is that changes in f do not affect these times. In the case of revival time, it does not depend on this parameter, while for the classical period, it appears in a small term proportional to p 3 , which shall be irrelevant regardless of the value of f. Indeed, due to these details, both cases shall behave similarly, proportional to p 2 .
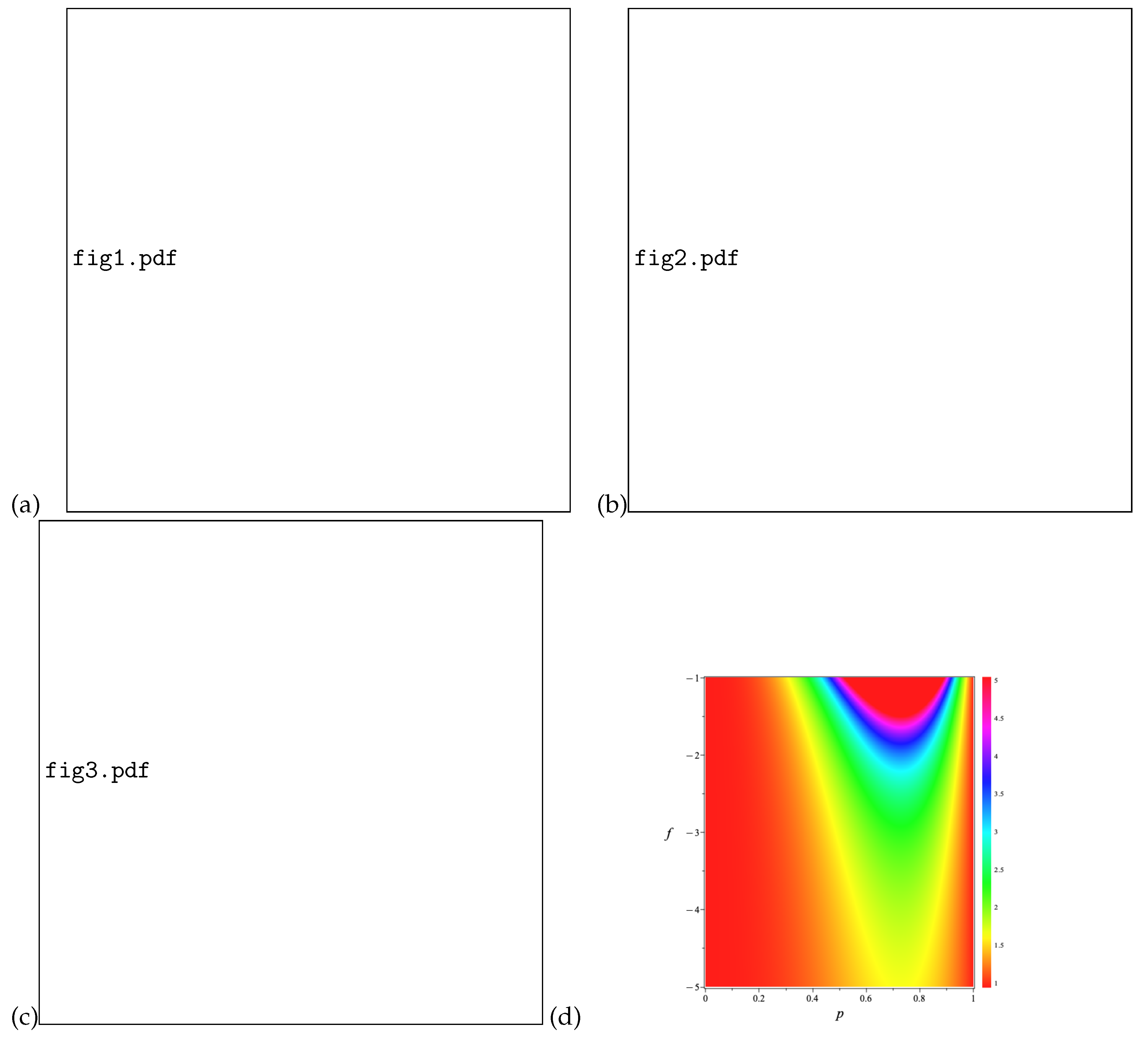
In Figure 5, we present a density plot of the calculated times for the first order energy correction in the weak regime coupling with impurity. We show only the case for electrons in GaAs because altering the aluminum concentration, temperature, and pressure results in an increase in effective mass, thereby increasing these times. For any other case, the profiles of these density plots remain the same. Firstly, we plotted the graphs for f > | 1 | because for f smaller than that up to | 0.5 | , the times have negative values and even divergences. Therefore, our study also suggests that the work [17] is better applied for values of this coupling constant f > | 1 | . As we can see, quantum revivals exhibit interesting behaviors for electrons in a quantum box, and the position of the impurity significantly affects them. The aluminum concentration in the sample causes these times to increase, as does the increase in hydrostatic pressure. We shall not make a physical application here, but this study should be important and particularly relevant for the case of quantum heat engines based on this physical system as a working substance.

5. Concluding Remarks

In conclusion, the investigation presented in this work delves into the realm of quantum revivals in systems featuring confined quantum particles, particularly electrons in a quantum box with an impurity. By exploring both weak and strong coupling regimes, the study unveils intricate relationships between impurity position, impurity strength, and the resulting classical periods and revival times. Notably, the effective mass of the electron, influenced by factors such as aluminum concentration, temperature, and hydrostatic pressure, plays a pivotal role in determining these temporal dynamics.
In the weak coupling regime, classical period and revival times exhibit nuanced behaviors as impurity position varies within the box. Additionally, changes in aluminum concentration and hydrostatic pressure lead to shifts in these times, underlining the sensitivity of quantum revivals to external conditions. Similarly, in the strong coupling limit, classical period and revival times display distinct trends depending on the chosen condition, emphasizing the complex interplay between impurity characteristics and temporal dynamics.
Moreover, the density plots provide insightful visualizations of these temporal phenomena, offering a comprehensive understanding of the intricate relationship between impurity parameters and quantum revival dynamics. Although no specific physical applications are discussed in this study, the findings hold potential implications for quantum heat engines and other quantum-based technologies, underscoring the relevance of understanding quantum revivals in confined quantum systems.
Overall, this investigation contributes valuable insights into the fundamental aspects of quantum mechanics, shedding light on the rich dynamics of quantum revivals and their dependence on impurity characteristics and external conditions.

Acknowledgments

This work was partially supported by the Brazilian agencies CNPq and FAPEMIG: C. Filgueiras and M. Rojas acknowledge FAPEMIG Grant No. APQ 02226/22. C. Filgueiras acknowledges CNPq Grant No. 310723/2021-3 and M. Rojas acknowledges CNPq Grant No 317324/2021-7.

References

  1. Robinett, R. Quantum wave packet revivals. Physics Reports 2004, 392, 1–119. [Google Scholar] [CrossRef]
  2. Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353–356. [Google Scholar] [CrossRef] [PubMed]
  3. Saif, F.; Fortunato. Quantum revivals in periodically driven systems close to nonlinear resonances. Phys. Rev. A 2001, 65, 013401. [Google Scholar] [CrossRef]
  4. Krizanac, M.; Altwein, D.; Vedmedenko, E.Y.; Wiesendanger, R. Quantum revivals and magnetization tunneling in effective spin systems. New Journal of Physics 2016, 18, 033029. [Google Scholar] [CrossRef]
  5. Kaur, T.; Kaur, M.; Arvind. ; Arora, B. Generating Sustained Coherence in a Quantum Memory for Retrieval at Times of Quantum Revival. Atoms 2022, 10. [Google Scholar] [CrossRef]
  6. Abanin, D.A.; Altman, E.; Bloch, I.; Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 2019, 91, 021001. [Google Scholar] [CrossRef]
  7. Dubois, M.; Lefebvre, G.; Sebbah, P. Quantum revival for elastic waves in thin plate. The European Physical Journal Special Topics 2017, 226, 1593–1601. [Google Scholar] [CrossRef]
  8. D’Errico, A.; Barboza, R.; Tudor, R.; Dauphin, A.; Massignan, P.; Marrucci, L.; Cardano, F. Bloch–Landau–Zener dynamics induced by a synthetic field in a photonic quantum walk. APL Photonics 2021, 6, 020802. [Google Scholar] [CrossRef]
  9. Hammam, K.; Hassouni, Y.; Fazio, R.; Manzano, G. Optimizing autonomous thermal machines powered by energetic coherence. New Journal of Physics 2021, 23, 043024. [Google Scholar] [CrossRef]
  10. Maia, A.; Bakke, K. Revival time and Aharonov–Bohm-type effect for a point charge in a uniform magnetic field under the spiral dislocation topology effects. Quantum Studies: Mathematics and Foundations 2022, 10. [Google Scholar] [CrossRef]
  11. Bakke, K. Topological effects of a disclination on quantum revivals. International Journal of Modern Physics A 2022, 37, 2250046. [Google Scholar] [CrossRef]
  12. Silva, W.; Bakke, K. On the effects of rotation and spiral dislocation topology on the persistent currents and quantum revivals in a cylindrical wire. The European Physical Journal Plus 2021, 136. [Google Scholar] [CrossRef]
  13. Maia, A.V.D.M.; Bakke, K. Topological Effects of a Spiral Dislocation on Quantum Revivals. Universe 2022, 8. [Google Scholar] [CrossRef]
  14. de los Santos, F.; Romera, E. Quantum recurrence times in nanostructures. Physics Letters A 2023, 483, 129062. [Google Scholar] [CrossRef]
  15. Strange, P. Relativistic Quantum Revivals. Phys. Rev. Lett. 2010, 104, 120403. [Google Scholar] [CrossRef] [PubMed]
  16. Chamizo, F.; Santillán, O.P. Exact quantum revivals for the Dirac equation. Phys. Rev. A 2024, 109, 022231. [Google Scholar] [CrossRef]
  17. Prakash, A.; Kumar, A.; Benjamin, C. Impurity reveals distinct operational phases in quantum thermodynamic cycles. Phys. Rev. E 2022, 106, 054112. [Google Scholar] [CrossRef] [PubMed]
  18. Reyes-Gómez, E.; Raigoza, N.; Oliveira, L.E. Effects of hydrostatic pressure and aluminum concentration on the conduction-electron g factor in GaAs-(Ga,Al)As quantum wells under in-plane magnetic fields. Phys. Rev. B 2008, 77, 115308. [Google Scholar] [CrossRef]
  19. Hernández, N.; López-Doria, R.; Fulla, M. Optical and electronic properties of a singly ionized double donor confined in coupled quantum dot-rings. Physica E: Low-dimensional Systems and Nanostructures 2023, 151, 115736. [Google Scholar] [CrossRef]
  20. Caicedo-Ortiz, H.; Castañeda Fernández, H.; Santiago-Cortés, E.; Mantilla-Sandoval, D. Energy Levels in a Single-Electron Quantum Dot with Hydrostatic Pressure. Acta Physica Polonica A 2018, 134, 570–573. [Google Scholar] [CrossRef]
  21. Xu, G.L.; Zhen, Z.; Shi, Y.S.; Guo, K.X.; Feddi, E.; Yuan, J.H.; Zhang, Z.H. Effects of hydrostatic pressure and temperature on the nonlinear optical properties of semiparabolic plus semi-inverse squared quantum wells*. Communications in Theoretical Physics 2021, 73, 085502. [Google Scholar] [CrossRef]
  22. Sakuray, J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press, 2017.
  23. Wang, Z.Y. Sagnac effect and EMF in heavy-electron materials: Revisitation of Coriolis force and Euler force. Results in Physics 2024, 56, 107117. [Google Scholar] [CrossRef]
  24. Bluhm, R.; Alan Kostelecký, V.; Tudose, B. Wave-packet revivals for quantum systems with nondegenerate energies. Physics Letters A 1996, 222, 220–226. [Google Scholar] [CrossRef]
Preprints 106230 g001
Figure 1. 1-D infinite square well with a Dirac delta barrier representing the potential induced by an impurity.
Figure 1. 1-D infinite square well with a Dirac delta barrier representing the potential induced by an impurity.
Preprints 106230 g001
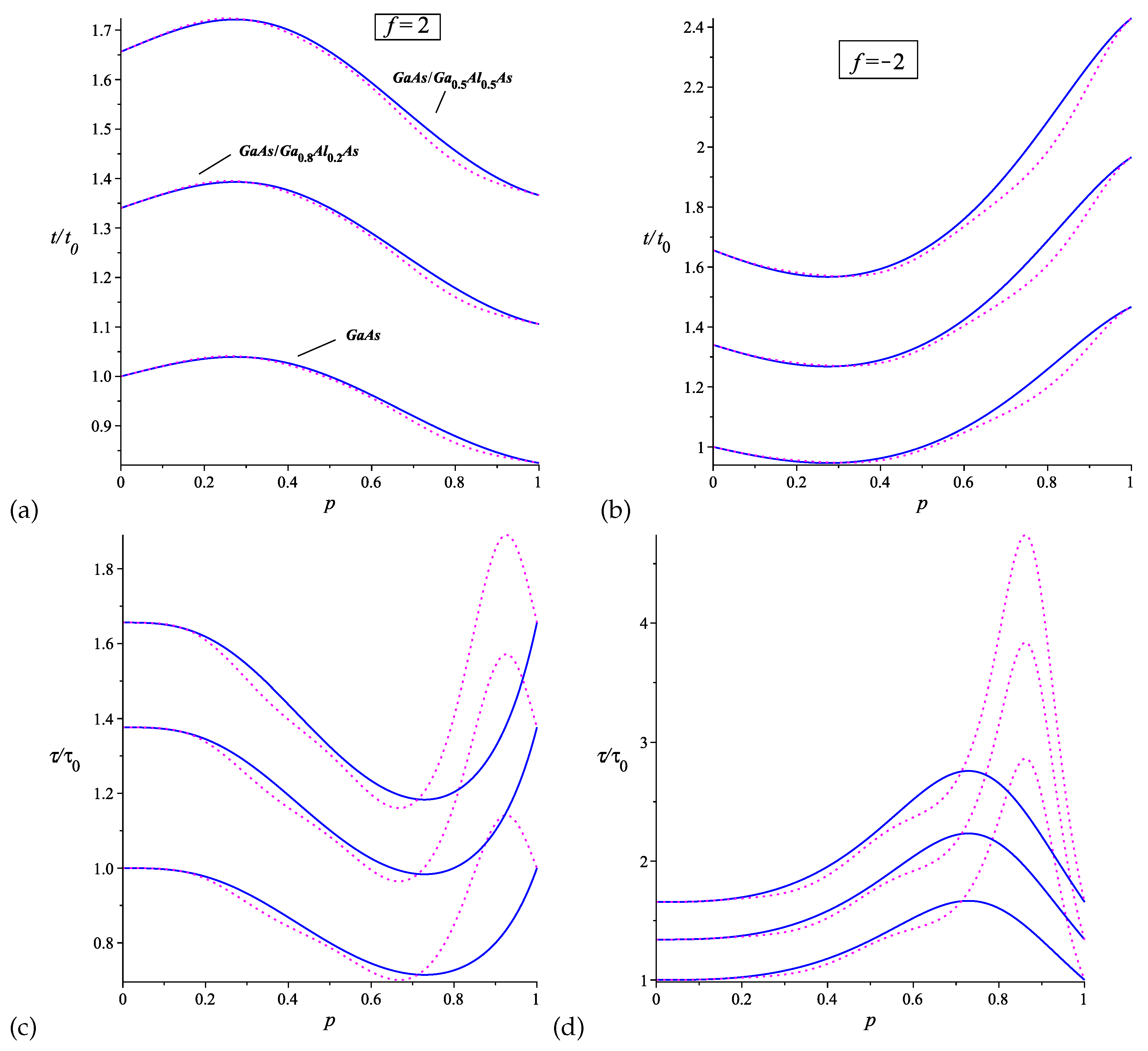
Preprints 106230 g002
Figure 2. The plots show the changes in classical period((a) and (b)) and revival times((c) and (d)) versus the impurity position in the box, for weak coupling with an impurity. As the concentration of A l increases, their profiles do not change, but the times shift to higher values. We considered T = 0.5 K , L = 25 n m and n = 1 .
Figure 2. The plots show the changes in classical period((a) and (b)) and revival times((c) and (d)) versus the impurity position in the box, for weak coupling with an impurity. As the concentration of A l increases, their profiles do not change, but the times shift to higher values. We considered T = 0.5 K , L = 25 n m and n = 1 .
Preprints 106230 g002
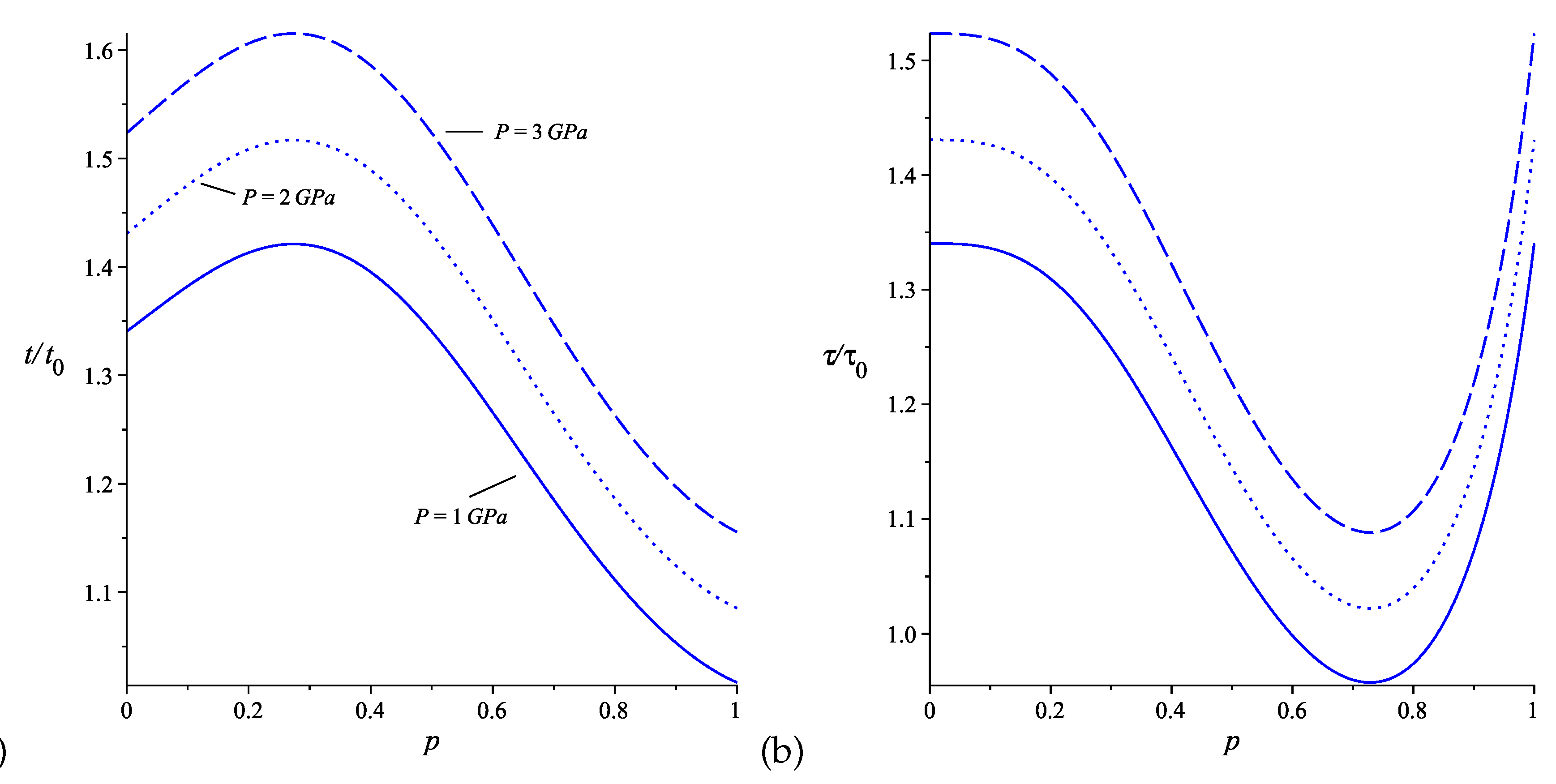
Preprints 106230 g003
Figure 3. The plots show the changes in classical period, (a), and revival times, (b), versus the impurity position in the box for different hydrostatic pressure, for weak coupling with an impurity. As it increases the times shift to higher values. We considered G a A s / G a 0.8 A l 0.2 A s , with f = 2 , T = 0.5 K , L = 25 n m and n = 1 .
Figure 3. The plots show the changes in classical period, (a), and revival times, (b), versus the impurity position in the box for different hydrostatic pressure, for weak coupling with an impurity. As it increases the times shift to higher values. We considered G a A s / G a 0.8 A l 0.2 A s , with f = 2 , T = 0.5 K , L = 25 n m and n = 1 .
Preprints 106230 g003
Preprints 106230 g004
Figure 4. The plots show the changes in classical period, (a), and revival times, (b), versus the impurity position in the box for the strong coupling with an impurity. As the concentration of A l increases, their profiles do not change, but the times shift to higher values. We considered f = 0.01 , T = 0.5 K , L = 25 n m and n = 1 . Solid lines are related to the eigenenergy 12 and doted lines to the eigenenergy 13.
Figure 4. The plots show the changes in classical period, (a), and revival times, (b), versus the impurity position in the box for the strong coupling with an impurity. As the concentration of A l increases, their profiles do not change, but the times shift to higher values. We considered f = 0.01 , T = 0.5 K , L = 25 n m and n = 1 . Solid lines are related to the eigenenergy 12 and doted lines to the eigenenergy 13.
Preprints 106230 g004
Preprints 106230 g005
Figure 5. The density plots of classical periods, (a) and (b), and revival times, (c) and (d), against the impurity position p and impurity strength f, in the weak coupling regime. We consider G a A s . Changing the effective mass of the electron shall keep their shapes consistent, but the color values shall increase.
Figure 5. The density plots of classical periods, (a) and (b), and revival times, (c) and (d), against the impurity position p and impurity strength f, in the weak coupling regime. We consider G a A s . Changing the effective mass of the electron shall keep their shapes consistent, but the color values shall increase.
Preprints 106230 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated