Prerpints.org logo
Preprint
Article

Benchmarking Time-Frequency Representations of PCG Signals for Classification Valvular Heart Diseases Using Deep Features and Machine Learning

Altmetrics

Downloads

122

Views

93

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 May 2024

Posted:

13 May 2024

You are already at the latest version

Alerts
Abstract
Heart sounds and murmurprovidecrucial diagnosis information for valvular heart diseases (VHD). Phonocardiogram (PCG) combined with modern digital processing techniques, provides a complementary tool for clinicians. This article proposes a benchmark different time-frequency representations, which are spectogram, mel-spectogram and cochleagram for obtaining images, in addition to the use of two interpolation techniques to improve the quality of the images, which are Bicubic and Lanczos. Deep features are extracted from a pre-trained model called VGG16 and for feature reduction the Boruta algorithm is applied. To evaluate the models and obtain more precise results, nested cross-validation is used. The best results achieved in this study were for coclegram with 99.2% accuracy and mel-spectogram representation with the bicubic interpolation technique which reached 99.4% accuracy, both having support vector machine (SVM) as classifier 10 algorithm. Overall, this study highlights the potential of time-frequency representations of PCG 11 signals combined with modern digital processing techniques and machine learning algorithms for 12 accurate diagnosis of VHD.
Keywords: 
Subject: Computer Science and Mathematics  -   Signal Processing

1. Introduction

Cardiovascular disorders (CVD) and valvular heart diseases (VHD) are the leading cause of mortality worldwide [1]. Recent studies have shown that AI capabilities have potential for health monitoring, automation of these tasks could free up clinicians for more complex work and improve access to health care [2]. Heart sound classification is an essential task for diagnosing and monitoring heart conditions.
VHD is a growing public health problem that should be addressed with appropriate resources to improve diagnosis and treatment [3]. Aortic stenosis (AS) is the most recurrent valvular disorder in developed countries (affecting 9 million people worldwide) [4], and its prevalence is increasing with the aging of the population and the increasing prevalence of atherosclerosis and it is characterized by a harsh, systolic ejection murmur that is best heard at the right upper sternal border[5]. Mitral regurgitation (MI) is one of the most common heart valve disorders worldwide, with an estimated prevalence of 1.7% [6] and it is characterized by a holosystolic murmur that is best heard at the apex and radiates to the axilla. Mitral stenosis (MS) is a common disease that causes a large number of diseases throughout the world. This disease is more recurrent in developing countries, but in developed countries it is becoming more common in atypical forms [7] and it is characterized by a low-pitched, diastolic rumble that is best heard at the apex with the patient in the left lateral decubitus position. Mitral valve prolapse (MVP) is a frequent condition that affects 2-3% of the general population and it is characterized by a mid-to-late systolic click followed by a late systolic murmur that is best heard at the apex and radiates to the axilla [3,8]. These common heart valve disorders with distinct characteristics and prevalences worldwide and each condition has a unique auscultation finding that helps in diagnosis.
Phonocardiography (PCG) is a diagnostic technique that analyzes heart sounds acquired at the chest wall to determine if the heart is functioning normally or if further diagnosis is required. Skilled cardiologists typically analyze these sounds, which result from muscle contractions and heart valve closure. However, this process can be affected by factors such as environmental noise, limitations in audible frequency range and the medical examiner’s expertise [9,10]. Given these problems, solutions have been developed over the last few years to help provide a better diagnosis, aided by technology for the analysis and classification. Based on previous work we can highlight 3 stages for the classification of PCG signals: pre-processing part, features extraction and classification. Cochleograms, spectrograms, mel-spectrograms, and scalograms are time-frequency multi-representations that provide a way to visualize the frequency content of PCG signals over time. A cochleogram is a time-frequency representation (TFR) that simulates the cochlea in the inner ear, which is responsible for frequency analysis in the auditory system [11,12]. A spectrogram is a time-frequency representation that uses a Fourier transform to convert a signal from the time domain to the frequency domain [13]. A mel-spectrogram is a TFR that uses a mel-scale filterbank to approximate the nonlinear human auditory system [14]. A scalogram is a TFR that uses a wavelet transform to provide a high resolution in both time and frequency [15]. These time-frequency representations allow a visualization of frequency content in PCG signals over time and their mathematical differences make a path to a benchmarking.
The use of bicubic and Lanczos interpolation methods for resizing the time-frequency representations is a significant contribution to this work [5,16]. These methods ensure the preservation of the original signal’s quality while providing uniform input dimensions for the classification models. By employing these high-quality resizing techniques, the performance and robustness of the classification models are enhanced, facilitating more accurate diagnosis and monitoring of valvular heart diseases.
The preprocessing, studies have been carried out for segmented signals as in [17] the segmentation is done synchronously and asynchronously with different sizes. Shannon energy envelope and zero crossing is a proposed algorithm for segmentation [18]. In this work we will not use signal segmentation since we may lose information from the signals.
The conventional methods of heart sound signal feature extraction like time domain as in [19] where the authors extract 12 features and to reduce them use feature reduction techniques, Matching Pursuit time-frequency decomposition using Gabor dictionaries [20]. Short-time Fourier transform (STFT) based spectrogram to represent patterns of the normal and abnormal PCG signals [21]. In [22] the authors use discrete wavelets transform (DWT) to extract features. Continue wavelet transforms based spectrogram (CWTS) [23], Hilbert-Huang transform (HHT) [24], Mel frequency cepstral coefficients (MFCC)[14,25]. Since manually the extraction of characteristics may not be as efficient, it is proposed use pretrained neural networks as Alexnet, VGG16, VGG19 to extract deep features [10,25].
In the last stage many types of machine learning for the classification of PCG signals to detect different types of CVD have been proposed. One dimension deep neural network (1-D DNN) with low parameters to detect abnormalities of Cardiovascular disease [26]. In [27] propose a combination of CNN and bi-directional long short-term memory (CNN-BiLSTM). In [28] they used five different types of Artificial neural network (ANN) named narrow, wide, tri-layered, bi-layered and medium. In [29] the residual neural network (Resnet) was used to avoid losing information from the previous layers.
In Table 1 shows the different techniques of feature extraction performance with the classifiers used by the authors where we can see the types of two-class and five-class classifications of PCG signals.
In this study, we present a benchmark of heart sound classification systems based on time-frequency multi-representations. The goal of this benchmark is to provide a comprehensive comparison of state-of-the-art heart sound classification systems and to identify the most effective TFR for detecting valvular heart diseases. The other contributions of this work are summarized in the following points:
  • Employ resizing techniques to TFRs to improve sorting performance.
  • Use of Boruta feature selector to narrow down the features to the most important ones.
  • Perform nested cross validation (nCV) approach that combines cross-validation with an additional model selection process.
  • Comparison of the classification performance of machine learning algorithms such as Decision Trees (DTs), K-Nearest Neighbors (KNN), Random Forest (RF) and Suport Vector Machine (SVM).
This paper is part of the research development in the area of biomedical engineering of the Universidad Nacional de San Agustin de Arequipa [30,31,32,33] for the Think Health project which seeks to improve medical assistance in the auscultation process.

2. Materials and Methods

2.1. Dataset

The heart sound database was acquired from an open source dataset made by Yanseen [22]. In Table 2 the database consists of a total of 1000 heart sound recordings (800 abnormal and 200 normal), gathered from various sources, sampled at a frequency of 8000Hz. There are 5 classes: aortic stenosis (AS), mitral regurgitation (MR), mitral stenosis (MS), mitral valve prolapse (MVP) and normal (N), each class having 200 recordings.

2.2. Proposed Methodology

This study proposes the use of various time-frequency representations (TFR) including spectrogram, mel-spectrogram and cochleogram to improve the accuracy of heart sound classification systems. The aim is to evaluate the performance of these different TFR methods in a comparative study with previous works.
To accomplish this, a dataset of heart sound recordings is collected and labeled for classification. The dataset consists of recordings from different patients, with various heart conditions, and collected from different sources. The heart sound signals are pre-processed to remove noise and artifacts. The output PCG filtered are then transformed into different time-frequency representations using the selected TFR methods.
In the next step, different classification algorithms are trained and tested using the dataset and the TFR methods. The algorithms include traditional machine learning methods, such as support vector machines (SVM) and random forests (RF), decision tree (DT) and K-nearest neighbor (KNN), as well as deep learning methods, such as convolutional neural networks (CNN). The performance of each algorithm is evaluated using standard evaluation metrics, such as accuracy, precision, MCC (Matthews Correlation Coefficient), recall, and F1-score.
Finally, a comparative analysis is performed to determine the effectiveness of each TFR method in improving the accuracy of heart sound classification. The analysis includes a comparison of the performance of the different algorithms using each TFR method. The results of the study can be used to guide the development of more accurate and efficient heart sound classification systems, with the potential to improve the diagnosis and treatment of heart disease.
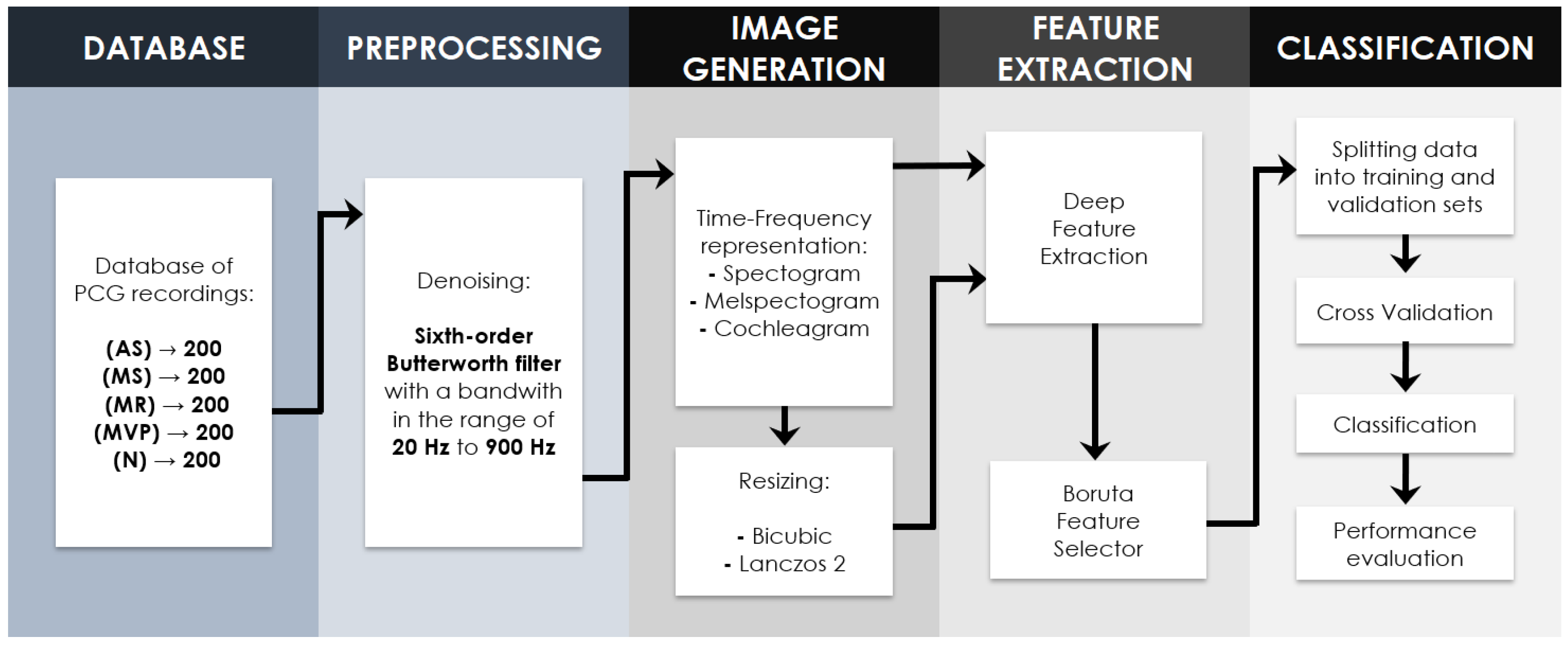
Preprints 106351 g001
Figure 1. Workflow chart of PCG classification based on Time-Frequency Representations.
Figure 1. Workflow chart of PCG classification based on Time-Frequency Representations.
Preprints 106351 g001

2.2.1. Signal Preprocessing

A Butterworth filter is an essential signal processing tool used for smoothing frequency responses and attenuating noise in various types of signals, including audio and biomedical data. In the case of processing PCG files, a 6th-order Butterworth filter with a passband of 20 Hz to 900 Hz can be highly effective in isolating heart sounds while minimizing external noise and artifacts as shown in Figure 2. This specific filter order and bandwidth selection is crucial for maintaining the integrity of the original signal while reducing unwanted frequency components, as higher-order Butterworth filters exhibit a steeper roll-off rate and a flatter response in the passband. For PCG signal processing, filtering out frequencies below 20 Hz helps to eliminate low-frequency noise, such as respiration and body movement artifacts, while attenuating frequencies above 900 Hz mitigates the impact of high-frequency noise like muscle contractions and electrical interference. [15] The application of a 6th-order Butterworth filter with a 20 Hz to 900 Hz passband is a well-established technique in the literature for extracting valuable diagnostic information from PCG signals, enabling healthcare professionals to analyze heart sounds and identify potential abnormalities more accurately.

2.3. Time-Frequency Representations

2.3.1. Spectrogram

The spectrogram serves as a valuable analytical tool for examining signals like the phonocardiogram, facilitating the visual depiction of energy distribution across various frequencies over time. Mathematically, the spectrogram is derived through [34] the Continuous Short-Time Fourier Transform (STFT), expressed as:
S ( f , t ) = ∫ − ∞ ∞ x ( τ ) w ( τ − t ) e − j 2 π f τ d τ
In this equation, S ( f , t ) denotes the spectrogram value at frequency f and time t. The function x ( τ ) represents the input signal, whereas w ( τ − t ) signifies an analysis window utilized to constrain the signal’s influence over a time interval centered around t. The component e − j 2 π f τ embodies a complex exponential function contingent upon frequency f and time τ .
The computation of the spectrogram involves the evaluation of this integral across diverse f and t values, furnishing an intricate portrayal of energy distribution within the time-frequency realm. This method is particularly advantageous for discerning temporal variations within the signal, a capability of paramount importance in the diagnosis of cardiac ailments such as valvular heart diseases.

2.3.2. Mel-Spectogram

The Mel spectrogram, akin to the conventional spectrogram, is a crucial tool in signal analysis, especially in domains like phonocardiography. It provides a detailed representation of signal energy distributed across frequencies over time, with a perceptually relevant frequency scale. Mathematically, the Mel spectrogram is computed by first transforming the signal into the Mel-frequency domain, followed by calculating the spectrogram using a Mel filterbank.
[35] The transformation into the Mel-frequency domain involves mapping the linear frequency scale (in Hertz) into the Mel scale, which is perceptually linear. This mapping is typically achieved using the formula:
M ( f ) = 2595 · ln ( 1 + f 700 )
Here, M ( f ) represents the Mel frequency corresponding to the linear frequency f.
After the signal is transformed into the Mel-frequency domain, the spectrogram is computed using a Mel filterbank. This involves applying a set of triangular filters, equally spaced in Mel-frequency, to the Mel-scaled signal. The energy within each filterbank is then calculated, resulting in the Mel spectrogram.
The Mel spectrogram provides a perceptually relevant representation of signal characteristics, making it particularly useful for tasks such as speech and audio processing. In the context of diagnosing conditions like valvular heart diseases, the Mel spectrogram can offer valuable insights into the temporal and spectral features of phonocardiographic signals, aiding in accurate diagnosis and analysis.

2.3.3. Cochleagram

The cochleagram is a specialized representation of auditory signals, particularly useful in analyzing phonocardiographic data. It mimics the processing that occurs in the human auditory system, providing a representation of signal energy that is sensitive to both frequency and time, akin to the functioning of the cochlea in the ear.
Mathematically, the cochleagram is computed by passing the signal through a bank of filters resembling the frequency response of the human cochlea. These filters are typically spaced on a logarithmic frequency scale to emulate the tonotopic organization of the cochlea. The signal’s energy within each filter is then computed, yielding a time-frequency representation akin to the human auditory system’s response to sound.
[36] The cochleagram computation involves several steps, beginning with the construction of the filterbank. Each filter’s response is designed to mimic the frequency selectivity of the corresponding region in the cochlea. The signal is then convolved with each filter in the bank, and the resulting energies are computed over time, yielding the cochleagram representation.
The cochleagram is mathematically expressed as:
C ( f , t ) = ∑ k = 1 N | x ( t ) * h k ( t ) | 2
Where C ( f , t ) denotes the cochleagram value at frequency f and time t, x ( t ) represents the input signal, and h k ( t ) represents the impulse response of the k-th cochlear filter in the bank. The sum is computed over all N filters in the cochlear filterbank.
The cochleagram offers a perceptually relevant representation of auditory signals, capturing both temporal and spectral features. In the context of diagnosing conditions like valvular heart diseases, the cochleagram can provide valuable insights into the acoustic characteristics of phonocardiographic signals, facilitating accurate diagnosis and analysis.

2.4. Resizing Image Techniques

The resize technique is an important component of audio signal processing, which allows us to adjust the size of the spectrogram, mel-spectrogram, and cochleagram representations. Two commonly used resize techniques are Lanczos and bicubic. The Lanczos resize technique provides a smoother resizing operation, which can help to preserve the quality of the original signal. The bicubic resize technique provides a sharper resizing operation, which can help to enhance the detail of the signal. In Figure 3 both resize techniques have been shown to improve the performance of various audio classification tasks, including speech recognition and music genre classification.

2.4.1. Bicubic

[37] Bicubic interpolation is a method commonly employed for resizing digital images, offering smoother transitions and reduced artifacts compared to linear interpolation techniques. It involves fitting a cubic polynomial to a 4x4 neighborhood of pixels surrounding each output pixel, allowing for more flexible and accurate estimation of pixel values.

2.4.2. Lanczos

[38] Lanczos interpolation, on the other hand, is a resampling technique that aims to maintain image fidelity while reducing aliasing artifacts. It utilizes a windowed sinc function to interpolate pixel values, providing high-quality results particularly suited for applications where preserving image details is crucial. The Lanczos kernel is defined as:
L ( x ) = sinc ( x ) · sinc x 4 , if | x | < 4 0 , otherwise
In this equation, sinc ( x ) = sin ( π x ) π x represents the sinc function, and x is the distance from the center of the kernel. Lanczos interpolation involves convolving the input image with this kernel, centered at the target pixel location, to compute the interpolated pixel value.

2.4.3. Deep Feature Extraction

There are many pre-trained models that were trained with one of the largest datasets of image recognition called ImageNet. In previous studies [15,29] they made use of different pre-trained models for deep feature extraction. In this study we take one of those models called VGG16 and change it from a classifier to a feature extractor for the different TFRs and their respective resize techniques.
In Figure 4 illustrates the modified structure of the VGG16, the images must have a size of 224x224, following the structure of the model we have thirteen convolutional layers, five max-pooling layers, after the last max-pooling layer we have a flatten layer to reduce the dimensions of the output and then we added two fully connected layers.The model operate with 134 million parameters At the output of the model we will have a vector of 4096 characteristics or deep features of each class of images that will serve as input for the classification algorithms.

2.4.4. Boruta Feature Selection Algorithm

As shown in previous studies [39] the selection of features increased the performance of the classification algorithms because some features may be redundant or unnecessary. In this work we use the boruta algorithm to do feature selection which works in conjunction with the random forest algorithm [40], for more information about the steps of the Boruta algorithm can be found in [41].

2.4.5. Nested Cross Validation

Nested cross-validation is a technique used to robustly and objectively evaluate and select models. In this approach, multiple cross validation iterations are performed: an external one to evaluate the performance of the model and an internal one to tune the model hyperparameters. Outer cross-validation is responsible for evaluating the performance of the final selected model, while inner cross validation is used to select the best hyperparameters of the model. This approach provides a more reliable assessment of model performance because it avoids overfitting of test data and ensures correct selection of hyperparameters [42].
In this case we use this type of cross-validation because we have a large number of characteristics for the analysis, therefore, given the number of classification algorithms, it was necessary to have the best parameters of each of them so that better results can be obtained. optimal Figure 5 explains how our nCV (Nested Cross Validation) works, composed of an inner loop and an outer loop. For the first case, a hyperparameter adjustment is made for each of the classifiers with already pre-established characteristics. This procedure is done as follows: 5-fold cross validation so that with the best characteristics of each classifier, we move to the outer loop where here each classification model is trained 10-fold cross validation, randomly distributing the testing and training data and then at the end being evaluated with the corresponding metrics such as Accuraccy, F1-Score, Precision, Recall and Matthews Correlation Coefficient (MCC).

2.4.6. Classifiers

Given that there is no absolute classification algorithm that will always perform best in any given situation, this paper uses several models of classification algorithms to evaluate the performance of each algorithm and get a general idea of which algorithm is better for each type of input. We propose the use of 4 classification algorithms which are: Decision trees (DTs) [43], K-nearest neighbor (KNN) [44], random forest (RF) [45] and support vector machines (SVM) [46].

2.4.7. Perfomance Evaluation Metrics

In assessing the outcomes of this study, we employed five distinct metrics for evaluation: Accuracy (Acc), Precision (Pre), Recall (Rec), F1-Score (F1), and Matthew correlation coefficient (MCC). These metrics provide various insights into the performance of each model and are calculated as follows:
A c c = T p + T n T p + T n + F p + F n
P r e = T p T p + F p
R e c = T p T p + F n
F 1 = 2 * P r e * R e c P r e + R e c
M C C = T p * T n − F p * F n ( T p + F p ) ( T p + F n ) ( T n + F p ) ( T n + F n )
True Positive (TP) signifies the count of correctly classified instances where diseased PCGs were correctly identified as diseased. False Positive (FP) represents instances where diseased PCGs were incorrectly classified as healthy. True Negative (TN) corresponds to instances where healthy PCGs were accurately classified as healthy. Finally, False Negative (FN) indicates instances where healthy PCGs were mistakenly classified as diseased.
In essence, TP and TN reflect correct classifications, while FP and FN indicate misclassifications. TP and TN capture instances where the classifier’s prediction aligns with the true status of the VHDs, whereas FP and FN illustrate cases where the classifier’s prediction deviates from the true status.

3. Results

The diagnosis of cardio-valvular diseases is a complex issue since the signals are not always obtained cleanly, which is why, as explained in Section 2.2.1, preprocessing is done for each type of signal that was used in this work. In the next stage, the TFRs were obtained from PCG signals of VHDs were given as input for the pre trained VGG16 model and given the large number of these obtained. In Table 3 shows the features confirmed, tentative and rejected for each type of TFR. The number of iterations performed for the selection was 10. The last part consisted of an nCV to obtain the best parameters of each classifier for each type of given input and obtain a correct classification. For this research, a machine with 16GB of RAM, Ryzen 5 3600 processor and an NVIDIA GeForce RTX 3060 video card was used. Obtaining characteristics as well as training each model were carried out in the Spyder 4.1.4 software with the libraries Tensorflow 2.12.0 and Tensorflow-GPU 2.10.0.
As previously indicated, this work seeks alternative ways of extracting features in order to improve the classification performance. Firstly, as we see in Table 4, different TFRs were used but without applying resize techniques, where initially a quantity of 4096 deep features was obtained. By then applying Boruta feature selection, confirmed deep features were obtained 1028 for Spectogram, 1007 for Mel Spectogram 1130 for and Cochleagram as shown in Table 3. The highest performance values were obtained using Cochleagram and SVM as classifier with the values of 99.2% precision, 99.2% recall, 99.19% F1 score, 99% Matthews correlation coefficient and 99.2% accuracy.
Another objective of this work was to apply resize techniques for the TFRs where in this case, as shown in Table 5, the bicubic resize technique was applied, which served as input for the VGG16 model, obtaining a row vector of 4096 deep features, then using Boruta in Table 3 the confirmed deep features were obtained 1031 for Spectogram, 936 for Mel Spectogram 1142 for Cochleagram. The highest performance values were obtained using Mel Spectogram and SVM as classifier with the values of 99.4% precision, 99.4% recall, 99.39% F1 score, 99.25% Matthews correlation coefficient and 99.4% accuracy.
And for the last part, each TFR obtained from the PCG signals, Lanczos resize technique was applied where a total of 4096 deep features were obtained and by applying Boruta feature selection in Table 3 the confirmed features were obtained 959 for Spectogram, 980 for Mel Spectogram 1124 for Cochleagram. The performance values shown in Table 6 were obtained using Mel Spectogram and SVM as classifier with the values of 99.2% precision, 99.2% recall, 99.19% F1 score, 99% Matthews correlation coefficient and 99.2% accuracy.
In our study, we observed that the cochleagram consistently outperformed other time-frequency representations in terms of accuracy, F1 score, recall, and precision. With a remarkable performance of 7 folds reaching 1.0 out of the other TFR and keep results in interpolation of itself, the cochleagram demonstrated its robustness and stability in diagnosing valvular heart diseases (VHD). Additionally, the mel-spectrogram representation, further highlighting the effectiveness of leveraging modern digital processing techniques. For spectograms in comparison to the others, are not stable and effective as the others two. These findings underscore the potential of time-frequency representations combined with advanced signal processing and machine learning algorithms for enhancing the accuracy of VHD diagnosis, as shown in Figure 6.
Our study’s findings demonstrate how well Support Vector Machine (SVM) classifiers perform when it comes to correctly identifying valvular heart disorders (VHD) from phonocardiogram (PCG) signals. SVM distinguished itself with an astounding accuracy rate of 98.76% among the classification algorithms examined, which included Decision Trees (DT), k-Nearest Neighbors (KNN), Random Forests (RF), and SVM. This remarkably high accuracy highlights SVM’s ability to distinguish between various heart sound patterns linked to VHD, making it a useful tool for clinical diagnosis.
The strong performance of Support Vector Machines (SVM) can be ascribed to its capacity to build ideal hyperplanes that optimize the margin of separation between distinct classes, hence permitting accurate PCG signal categorization. The input data is transformed into a higher-dimensional feature space by using a kernel function.
In this study, we evaluated the performance of Support Vector Machine (SVM) in Figure 7 classifiers using different time-frequency representations (TFRs) of phonocardiogram (PCG) signals. Specifically, we analyzed the effectiveness of three TFRs: spectrogram, mel-spectrogram, and cochleagram, each processed with two interpolation techniques—Bicubic and Lanczos. The results reveal compelling insights into the diagnostic accuracy of SVM classifiers across various TFRs and interpolation methods.
Starting with the spectrogram representation, SVM achieved an accuracy of 97.50%, with minor variations observed when applying Bicubic and Lanczos interpolation techniques. Despite slight fluctuations, SVM consistently demonstrated robust performance, highlighting its resilience in distinguishing between different heart sound classes.
Moving to the mel-spectrogram representation, SVM maintained a high accuracy of 99.00% across all interpolation methods. This indicates the effectiveness of mel-spectrogram features in capturing relevant information for VHD diagnosis, with SVM exhibiting exceptional discriminative capabilities.
In contrast, the cochleagram representation yielded even more impressive results, with SVM achieving an accuracy of 99.20%. Notably, this representation showcased superior performance compared to spectrogram and mel-spectrogram, emphasizing the importance of cochleagram features in accurately characterizing heart sound patterns associated with VHD.
Furthermore, when considering the interpolation techniques, both Bicubic and Lanczos methods resulted in comparable accuracies across all TFRs, underscoring their utility in enhancing image quality without compromising diagnostic performance.
Figure 8, shows confusion matrices for TFR using SVM classifier, due to last shown performance of SVM in classification.
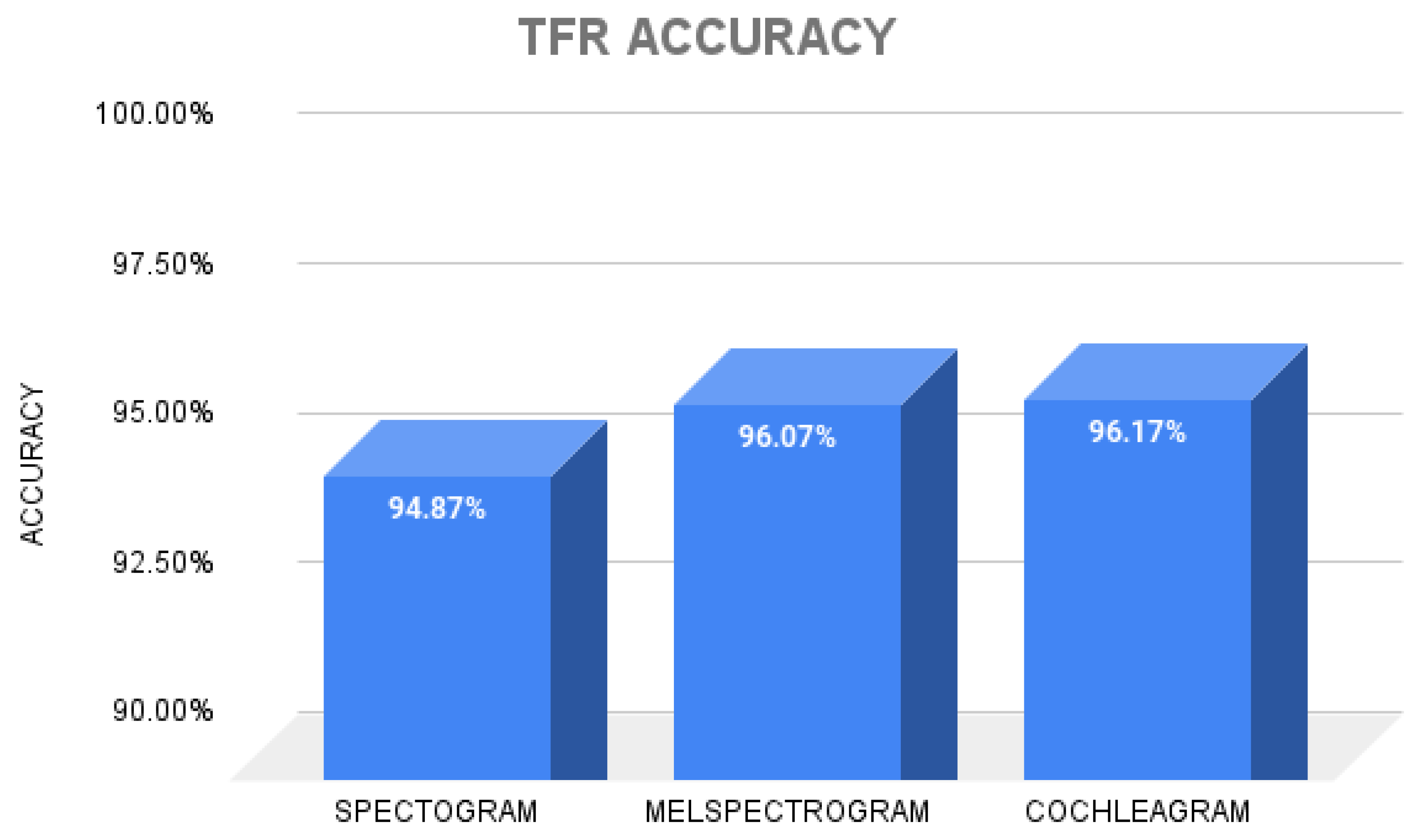
Our study delved into the efficacy of Time-Frequency Representations (TFRs) in accurately classifying valvular heart diseases (VHD) based on phonocardiogram (PCG) signals. Among the TFRs evaluated Spectrogram, Mel-Spectrogram, and Cochleagram emerged as the most promising, boasting an impressive accuracy rate of 96.07%. This notable accuracy underscores the effectiveness of Mel-Spectrogram in capturing and representing key features of PCG signals associated with different types of VHD.
The performance of Mel-Spectrogram can be attributed to its ability to provide a detailed and informative representation of PCG signals in both the time and frequency domains. By leveraging the Mel-scale to perceptually weight frequency bands, Mel-Spectrogram effectively highlights important spectral characteristics that are indicative of underlying heart abnormalities.
Furthermore, the high accuracy achieved by Cochelagram highlights its robustness and reliability in discriminating between different VHD classes, even in the presence of variations in signal quality or recording conditions. This robustness makes Cochleagram a valuable tool for automated VHD diagnosis, offering clinicians a dependable means of detecting and classifying heart abnormalities with high accuracy and confidence.
Overall, our findings underscore the potential of Cochleagram as a valuable tool for PCG-based VHD diagnosis. Its ability to consistently achieve high accuracy rates reaffirms its utility in clinical practice, providing clinicians with a reliable and efficient method for identifying and classifying VHD with precision and accuracy.
Preprints 106351 g009
Figure 9. Comparison of Time Frequency Representations accuracy considering previously shown classifiers.
Figure 9. Comparison of Time Frequency Representations accuracy considering previously shown classifiers.
Preprints 106351 g009
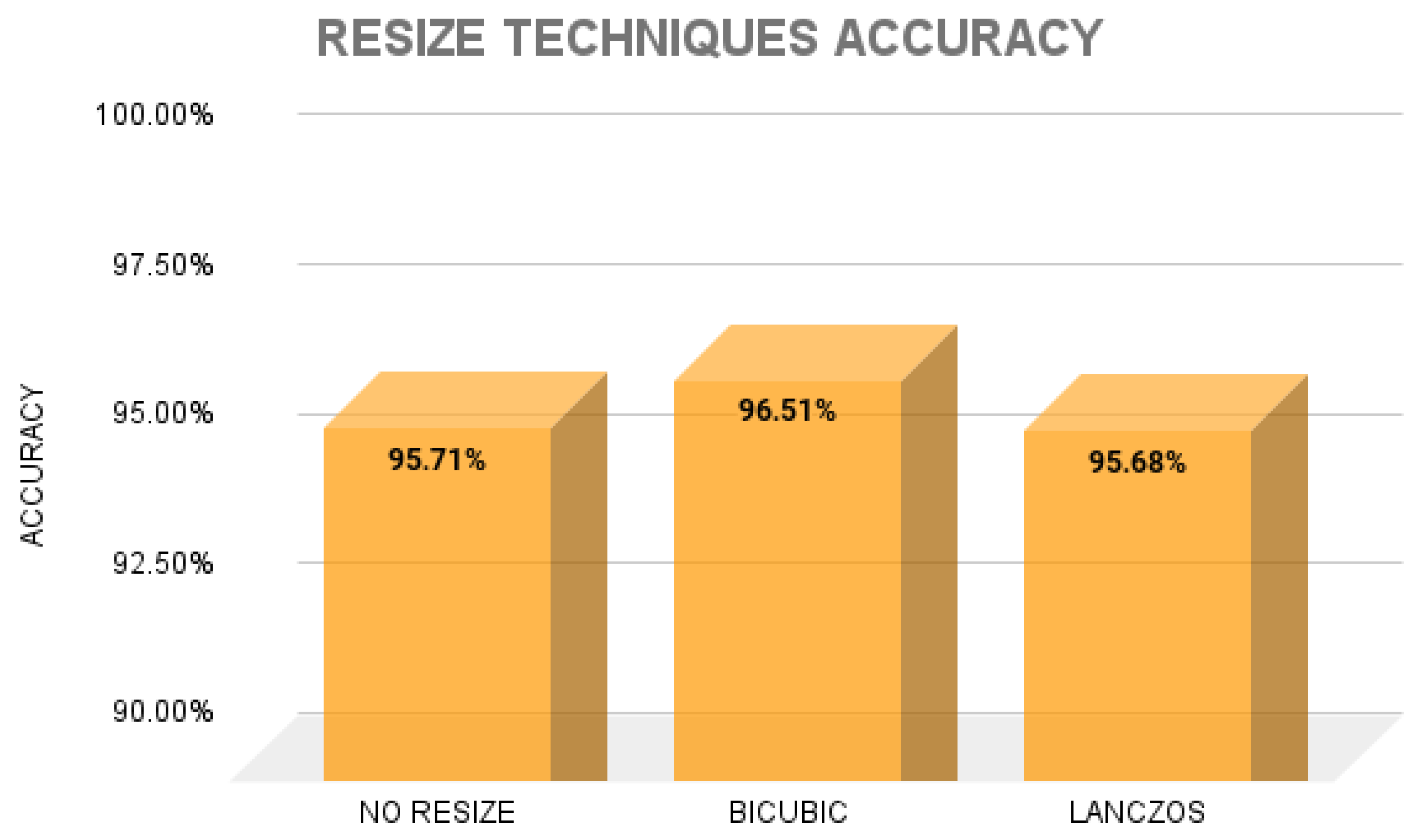
Our exploration into the effects of image resizing techniques on valvular heart disease (VHD) classification accuracy based on phonocardiogram (PCG) signals yielded noteworthy findings. Among the assessed techniques No Resize, Bicubic, and Lanczos Bicubic interpolation emerged as the standout performer, achieving an impressive accuracy rate of 96.51
The superior performance of Bicubic interpolation can be attributed to its capability to produce smooth and visually appealing resized images from the original PCG spectrograms. By employing sophisticated interpolation algorithms, Bicubic interpolation effectively preserves crucial features of the PCG signals while enhancing overall image quality.
Moreover, the high accuracy achieved with Bicubic interpolation underscores its effectiveness in enhancing the discriminative capability of PCG spectrograms for VHD classification. The refined image representations generated by Bicubic interpolation facilitate more precise feature extraction and classification, enabling accurate identification of various VHD classes.
These findings underscore the substantial impact of image resizing techniques on the accuracy of VHD classification from PCG signals. Bicubic interpolation, in particular, emerges as a valuable enhancement, providing clinicians with a reliable and efficient method of leveraging PCG spectrograms for accurate VHD diagnosis.
Preprints 106351 g010
Figure 10. Comparison of Resize Techniques accuracy considering previously shown TFRs.
Figure 10. Comparison of Resize Techniques accuracy considering previously shown TFRs.
Preprints 106351 g010

4. Discussion

The discussion of our findings unveils intriguing insights into the potential applications and implications of employing various time-frequency representations (TFRs) and image resizing techniques for valvular heart disease (VHD) classification based on phonocardiogram (PCG) signals. The meticulous evaluation of TFRs—specifically Spectrogram, Mel-Spectrogram, and Cochleagram—reveals nuanced differences in their effectiveness for capturing distinctive features indicative of different VHD classes. Notably, Mel-Spectrogram emerges as the most promising TFR, boasting a commendable accuracy rate of 96.07%. This underscores the importance of considering the spectral characteristics of PCG signals in VHD classification, with Mel-Spectrogram offering a rich representation conducive to accurate classification.
Furthermore, our investigation into the impact of image resizing techniques sheds light on the significance of preserving signal fidelity and enhancing image quality for improved classification outcomes. Among the evaluated techniques—No Resize, Bicubic, and Lanczos—Bicubic interpolation emerges as the optimal choice, achieving an impressive accuracy rate of 96.51%. This underscores the critical role of image preprocessing techniques in augmenting the discriminative power of PCG spectrograms, thereby facilitating more accurate VHD classification.
The observed superiority of Bicubic interpolation can be attributed to its ability to generate visually appealing resized images while preserving essential signal features, enabling more robust feature extraction and classification. This highlights the importance of leveraging advanced image processing techniques to enhance the diagnostic capabilities of PCG-based VHD classification systems.
Moreover, our study underscores the potential of machine learning algorithms, particularly Support Vector Machine (SVM), in effectively leveraging TFRs and resized images for accurate VHD classification. The consistently high accuracy rates achieved by SVM across different TFRs and resizing techniques underscore its robustness and suitability for VHD diagnosis.

5. Conclusions

The study conclusively underscores the remarkable superiority of the cochleagram over other time-frequency representations in detecting valvular heart diseases (VHD). Particularly, when coupled with the bicubic resizing technique, the cochleagram consistently outperformed its counterparts, yielding an impressive accuracy rate of 99.2%. This robust performance underscores its pivotal role as a frontline tool in analyzing phonocardiogram (PCG) signals for precise VHD diagnoses.
Furthermore, the synergistic integration of the cochleagram with machine learning algorithms, notably the Support Vector Machine (SVM), yielded outstanding results across all evaluated metrics. The synergy between the cochleagram and SVM exhibited exceptional diagnostic accuracy, surpassing 99% in several instances. Such findings highlight the efficacy of this integrated approach in delivering accurate and reliable diagnoses of VHD from PCG signals.
Moreover, the cochleagram’s consistency across various resizing techniques reinforces its prominence in PCG signals. While alternative time-frequency representations demonstrated commendable performance, the cochleagram maintained its superiority, underscoring its reliability and robustness in clinical applications. These findings collectively underscore the cochleagram’s role as a cornerstone tool in the accurate diagnosis and management of valvular heart diseases, offering promising prospects for enhancing clinical care and cardiovascular health.

Author Contributions

Conceptualization, Edwin M. Chambi and Jefry Cuela; methodology, Jefry Cuela; software, Edwin M. Chambi; validation, Edwin M.Chambi and Jefry Cuela; formal analysis Jorge Rendulich; investigation Edwin M. Chambi and Jefry Cuela; resources Edwin M. Chambi; writing—review and editing Edwin M. Chambi and Jefry Cuela; supervision, Erasmo Sulla and Milagros Zegarra; project administration, Jorge Rendulich and Erasmo Sulla; funding acquisition, Jorge Rendulich and Milagros Zegarra. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work is part of the research project "Development of a kit of Biomedical Instruments for a Basic Health Care Center and to assist in the study of chronic and congenital diseases" financed by the Universidad Nacional de San Agustin de Arequipa through contract number IBA- IB-44-2022-UNSA.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CVD Cardiovascular disorders
VHD Valvular heart diseases
PCG Phonocardiogram
AS Aortic stenosis
MI Mitral regurgitation
MS Mitral stenosis
MVP Mitral valve prolapse
MCC Matthews Correlation Coefficient

References

  1. Coffey, S.; Roberts-Thomson, R.; Brown, A.; Carapetis, J.; Chen, M.; Enriquez-Sarano, M.; Zühlke, L.; Prendergast, B.D. Global epidemiology of valvular heart disease. Nature Reviews Cardiology 2021, 18, 853–864. [Google Scholar] [CrossRef]
  2. Milne-Ives, M.; de Cock, C.; Lim, E.; Shehadeh, M.H.; de Pennington, N.; Mole, G.; Normando, E.; Meinert, E. The Effectiveness of Artificial Intelligence Conversational Agents in Health Care: Systematic Review. Journal of Medical Internet Research 2020, 22, e20346. [Google Scholar] [CrossRef] [PubMed]
  3. Domenech, B.; Pomar, J.L.; Prat-González, S.; Vidal, B.; López-Soto, A.; Castella, M.; Sitges, M. Valvular heart disease epidemics. The Journal of heart valve disease 2016, 25, 1–7. [Google Scholar] [PubMed]
  4. Aluru, J.S.; Barsouk, A.; Saginala, K.; Rawla, P.; Barsouk, A. Valvular Heart Disease Epidemiology. Medical Sciences 2022, 10. [Google Scholar] [CrossRef] [PubMed]
  5. Sharan, R.V.; Moir, T.J. Time-Frequency Image Resizing Using Interpolation for Acoustic Event Recognition with Convolutional Neural Networks. 2019 IEEE International Conference on Signals and Systems (ICSigSys), 2019, pp. 8–11.
  6. Zhou, J.; Lee, S.; Liu, Y.; Chan, J.S.K.; Li, G.; Wong, W.T.; Jeevaratnam, K.; Cheng, S.H.; Liu, T.; Tse, G.; Zhang, Q. Predicting Stroke and Mortality in Mitral Regurgitation: A Machine Learning Approach. Current Problems in Cardiology 2023, 48, 101464. [Google Scholar] [CrossRef] [PubMed]
  7. Shvartz, V.; Sokolskaya, M.; Petrosyan, A.; Ispiryan, A.; Donakanyan, S.; Bockeria, L.; Bockeria, O. Predictors of Mortality Following Aortic Valve Replacement in Aortic Stenosis Patients. Pathophysiology: The Official Journal of the International Society for Pathophysiology 2022, 29, 106–117. [Google Scholar] [CrossRef] [PubMed]
  8. Ghosh, S.K.; Ponnalagu, R.; Tripathy, R.; Acharya, U.R. Automated detection of heart valve diseases using chirplet transform and multiclass composite classifier with PCG signals. Computers in biology and medicine 2020, 118, 103632. [Google Scholar] [CrossRef] [PubMed]
  9. Maknickas, V.; Maknickas, A. Recognition of normal–abnormal phonocardiographic signals using deep convolutional neural networks and mel-frequency spectral coefficients. Physiological measurement 2017, 38, 1671. [Google Scholar] [CrossRef] [PubMed]
  10. Demir, F.; Şengür, A.; Bajaj, V.; Polat, K. Towards the classification of heart sounds based on convolutional deep neural network. Health information science and systems 2019, 7, 1–9. [Google Scholar] [CrossRef]
  11. Sharan, R.V.; Moir, T.J. Acoustic event recognition using cochleagram image and convolutional neural networks. Applied Acoustics 2019, 148, 62–66. [Google Scholar] [CrossRef]
  12. Das, S.; Pal, S.; Mitra, M. Deep learning approach of murmur detection using Cochleagram. Biomedical Signal Processing and Control 2022, 77, 103747. [Google Scholar] [CrossRef]
  13. Mutlu, A.Y. Detection of epileptic dysfunctions in EEG signals using Hilbert vibration decomposition. Biomedical Signal Processing and Control 2018, 40, 33–40. [Google Scholar] [CrossRef]
  14. Netto, A.N.; Abraham, L. Detection and Classification of Cardiovascular Disease from Phonocardiogram using Deep Learning Models. 2021 Second International Conference on Electronics and Sustainable Communication Systems (ICESC), 2021, pp. 1646–1651.
  15. Arslan, Ö. Automated detection of heart valve disorders with time-frequency and deep features on PCG signals. Biomedical Signal Processing and Control 2022, 78, 103929. [Google Scholar] [CrossRef]
  16. Moraes, T.; Amorim, P.; Da Silva, J.V.; Pedrini, H. Medical image interpolation based on 3D Lanczos filtering. Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization 2020, 8, 294–300. [Google Scholar]
  17. Hu, Q.; Hu, J.; Yu, X.; Liu, Y. Automatic heart sound classification using one dimension deep neural network. Security, Privacy, and Anonymity in Computation, Communication, and Storage: SpaCCS 2020 International Workshops, Nanjing, China, December 18-20, 2020, Proceedings 13. Springer, 2021, pp. 200–208.
  18. Varghees, V.N.; Ramachandran, K. A novel heart sound activity detection framework for automated heart sound analysis. Biomedical Signal Processing and Control 2014, 13, 174–188. [Google Scholar] [CrossRef]
  19. Nogueira, D.M.; Ferreira, C.A.; Gomes, E.F.; Jorge, A.M. Classifying heart sounds using images of motifs, MFCC and temporal features. Journal of medical systems 2019, 43, 168. [Google Scholar] [CrossRef] [PubMed]
  20. Ibarra-Hernández, R.F.; Bertin, N.; Alonso-Arévalo, M.A.; Guillén-Ramírez, H.A. A benchmark of heart sound classification systems based on sparse decompositions. 14th International Symposium on Medical Information Processing and Analysis. SPIE, 2018, Vol. 10975, pp. 26–38.
  21. Khan, K.N.; Khan, F.A.; Abid, A.; Olmez, T.; Dokur, Z.; Khandakar, A.; Chowdhury, M.E.; Khan, M.S. Deep learning based classification of unsegmented phonocardiogram spectrograms leveraging transfer learning. Physiological measurement 2021, 42, 095003. [Google Scholar] [CrossRef] [PubMed]
  22. Yaseen.; Son, G.Y.; Kwon, S. Classification of heart sound signal using multiple features. Applied Sciences 2018, 8, 2344. [CrossRef]
  23. Abbas, Q.; Hussain, A.; Baig, A.R. Automatic detection and classification of cardiovascular disorders using phonocardiogram and convolutional vision transformers. diagnostics 2022, 12, 3109. [Google Scholar] [CrossRef]
  24. Arslan, Ö.; Karhan, M. Effect of Hilbert-Huang transform on classification of PCG signals using machine learning. Journal of King Saud University-Computer and Information Sciences 2022, 34, 9915–9925. [Google Scholar] [CrossRef]
  25. Adiban, M.; BabaAli, B.; Shehnepoor, S. Statistical feature embedding for heart sound classification. Journal of Electrical Engineering 2019, 70, 259–272. [Google Scholar] [CrossRef]
  26. Baghel, N.; Dutta, M.K.; Burget, R. Automatic diagnosis of multiple cardiac diseases from PCG signals using convolutional neural network. Computer Methods and Programs in Biomedicine 2020, 197, 105750. [Google Scholar] [CrossRef]
  27. Alkhodari, M.; Fraiwan, L. Convolutional and recurrent neural networks for the detection of valvular heart diseases in phonocardiogram recordings. Computer Methods and Programs in Biomedicine 2021, 200, 105940. [Google Scholar] [CrossRef]
  28. Khan, M.U.; Samer, S.; Alshehri, M.D.; Baloch, N.K.; Khan, H.; Hussain, F.; Kim, S.W.; Zikria, Y.B. Artificial neural network-based cardiovascular disease prediction using spectral features. Computers and Electrical Engineering 2022, 101, 108094. [Google Scholar] [CrossRef]
  29. Jabari, M.; Rezaee, K.; Zakeri, M. Fusing handcrafted and deep features for multi-class cardiac diagnostic decision support model based on heart sound signals. Journal of Ambient Intelligence and Humanized Computing 2023, 14, 2873–2885. [Google Scholar] [CrossRef]
  30. Supo, E.; Galdos, J.; Rendulich, J.; Sulla, E. ; others. PRD as an indicator proposal in the evaluation of ECG signal acquisition prototypes in real patients. 2022 IEEE ANDESCON. IEEE, 2022, pp. 1–4.
  31. Sulla, T.R.; Talavera, S.J.; Supo, C.E.; Montoya, A.A. Non-invasive glucose monitor based on electric bioimpedance using AFE4300. 2019 IEEE XXVI International Conference on Electronics, Electrical Engineering and Computing (INTERCON). IEEE, 2019, pp. 1–3.
  32. Talavera, J.R.; Mendoza, E.A.S.; Dávila, N.M.; Supo, E. ; others. Implementation of a real-time 60 Hz interference cancellation algorithm for ECG signals based on ARM cortex M4 and ADS1298. 2017 IEEE XXIV International Conference on Electronics, Electrical Engineering and Computing (INTERCON). IEEE, 2017, pp. 1–4.
  33. Huisa, C.M.; Elvis Supo, C.; Edward Figueroa, T.; Rendulich, J.; Sulla-Espinoza, E. PCG Heart Sounds Quality Classification Using Neural Networks and SMOTE Tomek Links for the Think Health Project. Proceedings of Data Analytics and Management: ICDAM 2022; Springer; 2023; pp. 803–811. [Google Scholar]
  34. Ismail, S.; Ismail, B.; Siddiqi, I.; Akram, U. PCG classification through spectrogram using transfer learning. Biomedical Signal Processing and Control 2023, 79, 104075. [Google Scholar] [CrossRef]
  35. Leo, J.; Loong, C.; Subari, K.S.; Abdullah, N.M.K.; Ahmad, N.; Besar, R. Comparison of MFCC and Cepstral Coefficients as a Feature Set for PCG Biometric Systems. World Academy of Science, Engineering and Technology, International Journal of Medical, Health, Biomedical, Bioengineering and Pharmaceutical Engineering 2010, 4, 335–339. [Google Scholar]
  36. Das, S.; Pal, S.; Mitra, M. Deep learning approach of murmur detection using Cochleagram. Biomedical Signal Processing and Control 2022, 77, 103747. [Google Scholar] [CrossRef]
  37. Triwijoyo, B.; Adil, A. Analysis of Medical Image Resizing Using Bicubic Interpolation Algorithm. Jurnal Ilmu Komputer 2021, 14, 20–29. [Google Scholar] [CrossRef]
  38. Bentbib, A.; El Guide, M.; Jbilou, K.; Reichel, L. A global Lanczos method for image restoration. Journal of Computational and Applied Mathematics 2016, 300, 233–244. [Google Scholar] [CrossRef]
  39. Qiao, Q.; Yunusa-Kaltungo, A.; Edwards, R.E. Developing a machine learning based building energy consumption prediction approach using limited data: Boruta feature selection and empirical mode decomposition. Energy Reports 2023, 9, 3643–3660. [Google Scholar] [CrossRef]
  40. Kumar, S.S.; Shaikh, T. Empirical evaluation of the performance of feature selection approaches on random forest. 2017 international conference on computer and applications (ICCA). IEEE, 2017, pp. 227–231.
  41. Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. Journal of statistical software 2010, 36, 1–13. [Google Scholar] [CrossRef]
  42. Parvandeh, S.; Yeh, H.W.; Paulus, M.P.; McKinney, B.A. Consensus features nested cross-validation. Bioinformatics 2020, 36, 3093–3098. [Google Scholar] [CrossRef] [PubMed]
  43. Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE transactions on systems, man, and cybernetics 1991, 21, 660–674. [Google Scholar] [CrossRef]
  44. Sun, S.; Huang, R. An adaptive k-nearest neighbor algorithm. 2010 seventh international conference on fuzzy systems and knowledge discovery. IEEE, 2010, Vol. 1, pp. 91–94.
  45. Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
  46. Lau, K.; Wu, Q. Online training of support vector classifier. Pattern Recognition 2003, 36, 1913–1920. [Google Scholar] [CrossRef]
Preprints 106351 g002
Figure 2. PCG examplaries. (1) One PCG of AS; (b) one PCG of MS; (c) one PCG of MR; (d) one PCG of MVP; (e) one PCG of N.
Figure 2. PCG examplaries. (1) One PCG of AS; (b) one PCG of MS; (c) one PCG of MR; (d) one PCG of MVP; (e) one PCG of N.
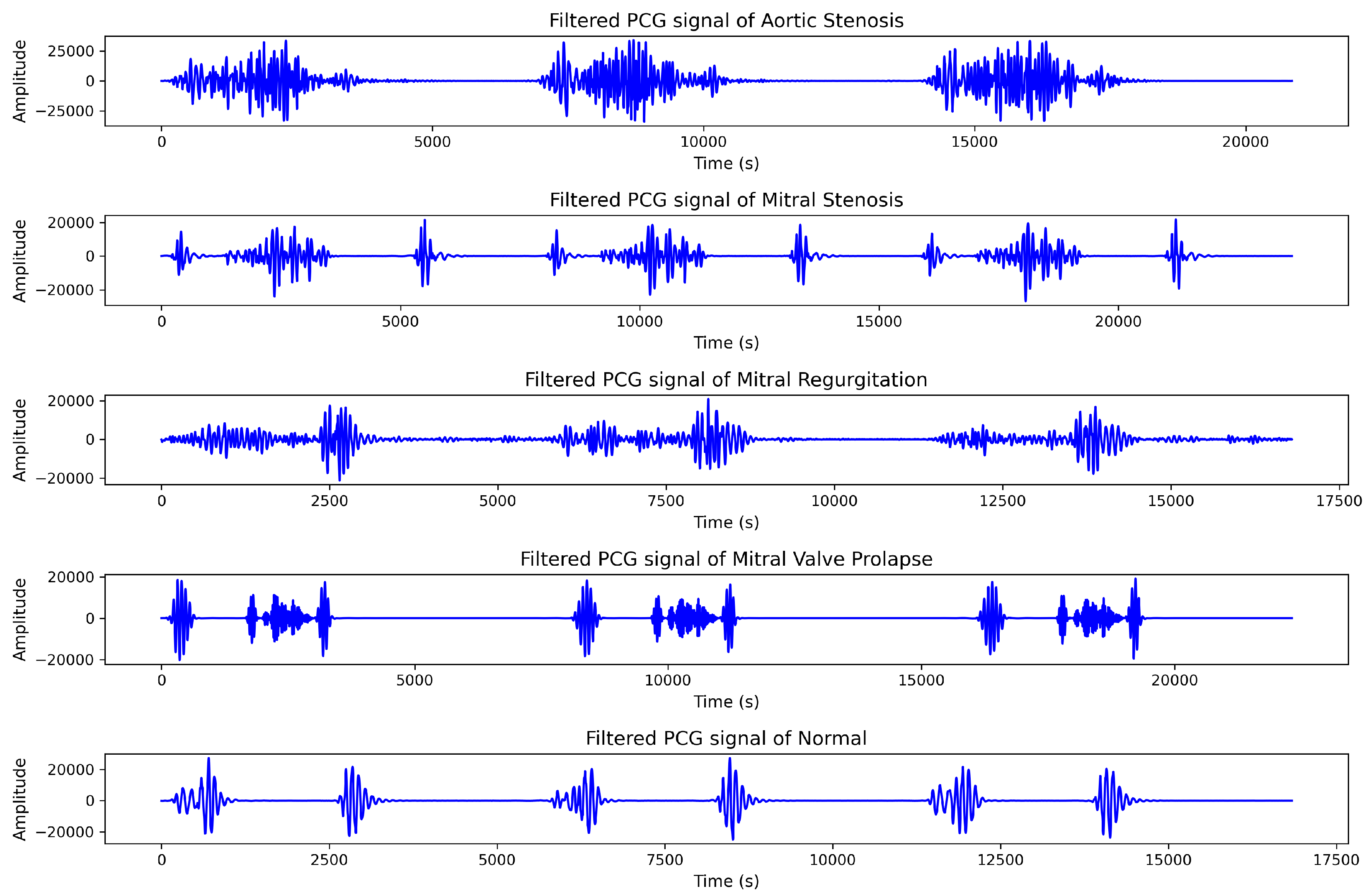
Preprints 106351 g002
Preprints 106351 g003
Figure 3. Time frequency representations. (1-5) Aortic Stenosis TFRs; (6-10) Mitral Stenosis TFRs; (11-15) Mitral Regurgitation TFRs; (16-20) Mitral Valve Prolapse TFRs; (20-25) Normal TFRs.
Figure 3. Time frequency representations. (1-5) Aortic Stenosis TFRs; (6-10) Mitral Stenosis TFRs; (11-15) Mitral Regurgitation TFRs; (16-20) Mitral Valve Prolapse TFRs; (20-25) Normal TFRs.
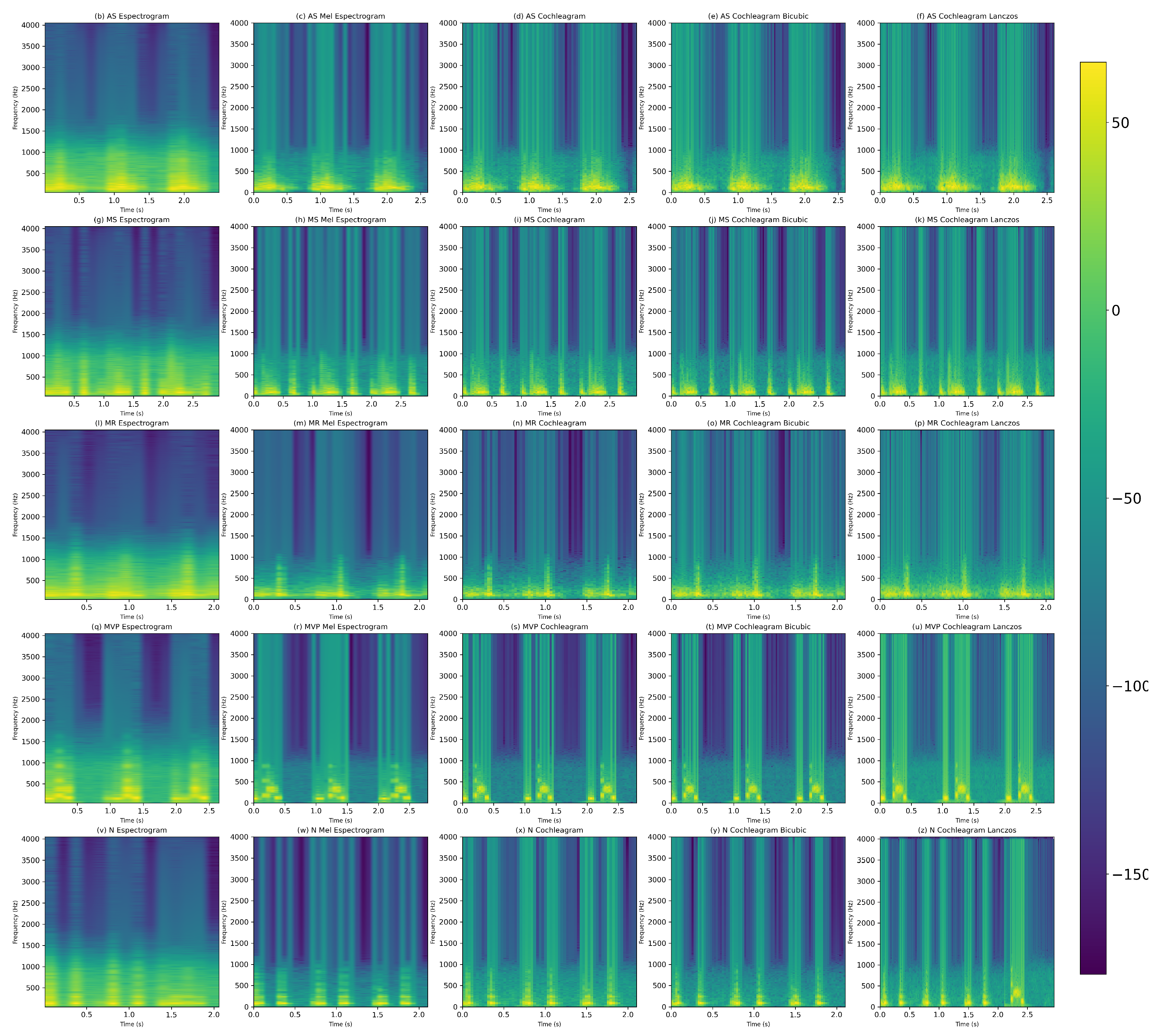
Preprints 106351 g003
Preprints 106351 g004
Figure 4. Model VGG16 modified estructure with all the parameters of the convolution layers frozen.
Figure 4. Model VGG16 modified estructure with all the parameters of the convolution layers frozen.
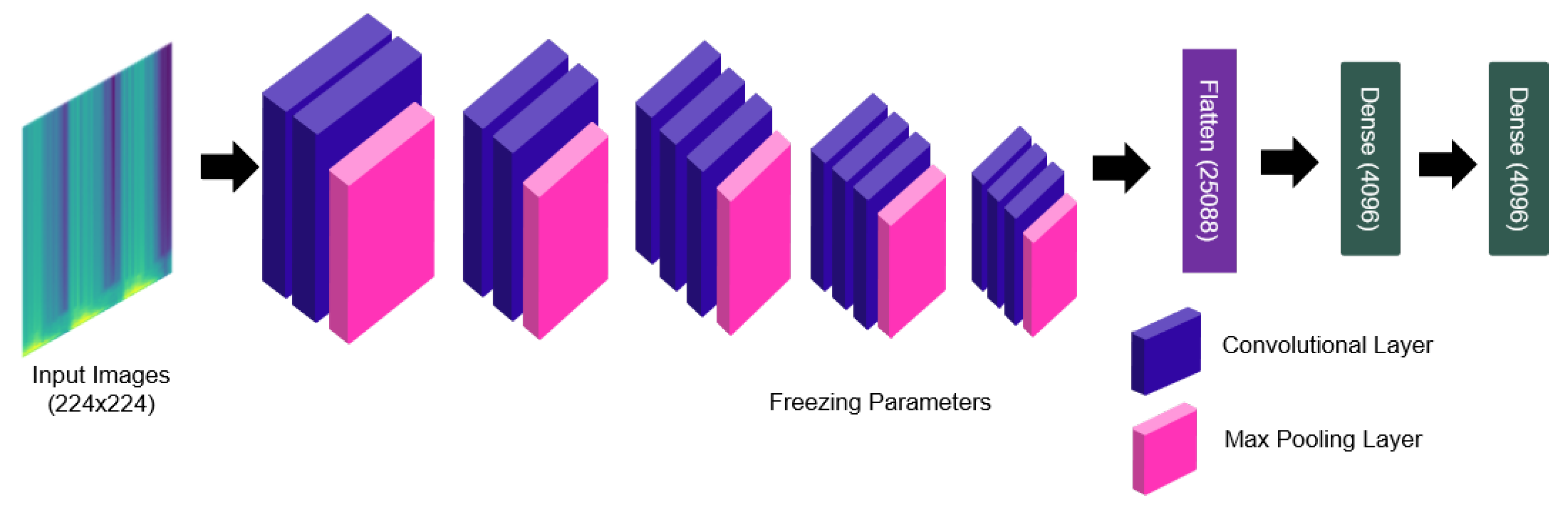
Preprints 106351 g004
Preprints 106351 g005
Figure 5. Operating diagram of nested cross validation for hyperparameter tuning and classification for each type of VHD
Figure 5. Operating diagram of nested cross validation for hyperparameter tuning and classification for each type of VHD
Preprints 106351 g005
Preprints 106351 g006
Figure 6. Parameters performance through folds.
Figure 6. Parameters performance through folds.
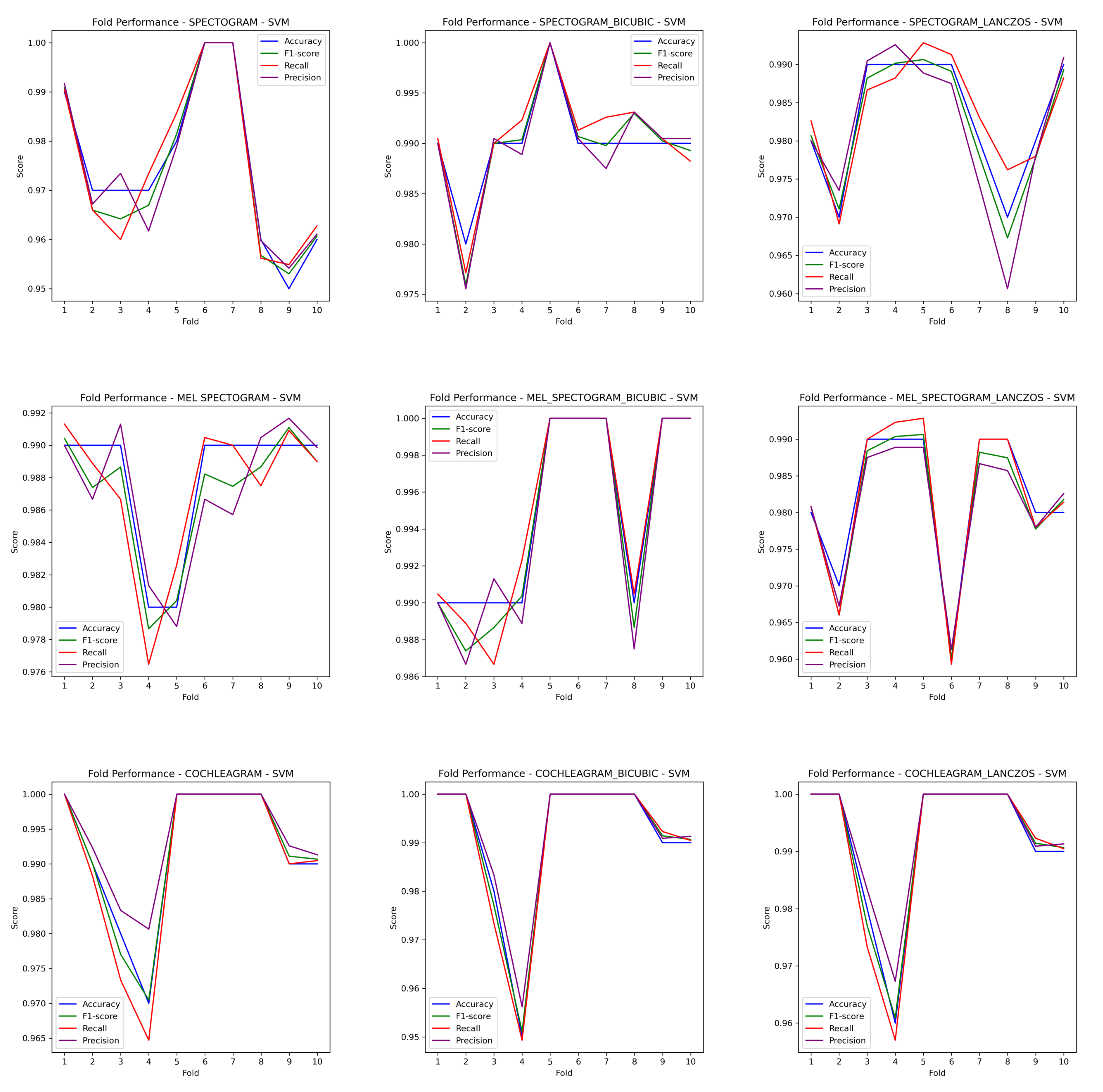
Preprints 106351 g006
Preprints 106351 g007
Figure 7. Comparison of Classifier Performance Using Different Time-Frequency Representations of Phonocardiogram Signals.
Figure 7. Comparison of Classifier Performance Using Different Time-Frequency Representations of Phonocardiogram Signals.
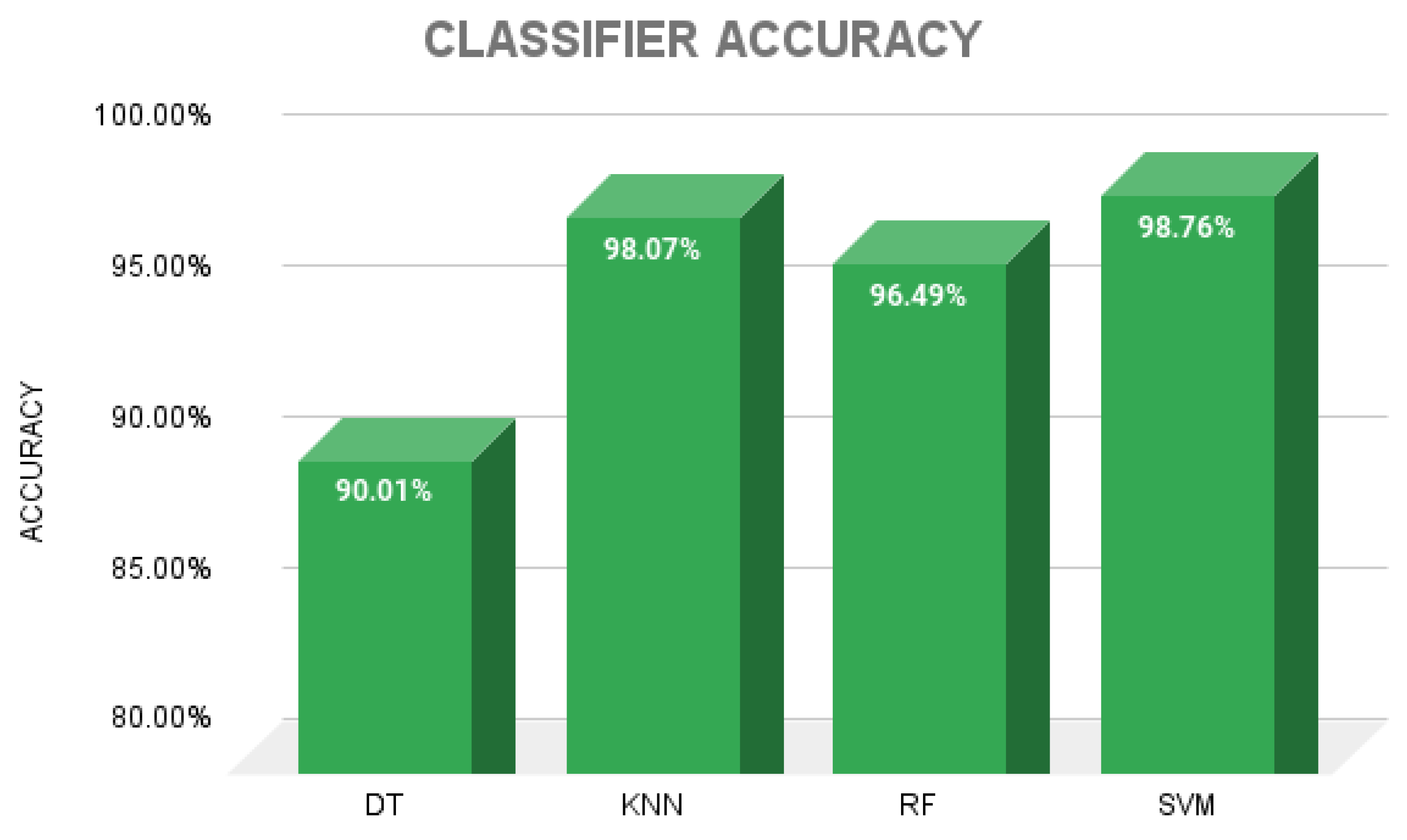
Preprints 106351 g007
Preprints 106351 g008
Figure 8. (a) Confusion Matrix for spectrogram using SVM classifier. (b) Confusion Matrix for spectrogram bicubic using SVM classifier. (c) Confusion Matrix for spectrogram lanczos using SVM classifier. (d) Confusion Matrix for mel-spectrogram using SVM classifier. (e) Confusion Matrix for mel-spectrogram bicubic using SVM classifier. (f) Confusion Matrix for mel-spectrogram lanczos using SVM classifier. (g) Confusion Matrix for cochleagram using SVM classifier. (h) Confusion Matrix for cochleagram bicubic using SVM classifier. (i) Confusion Matrix for cochleagram lanczos using SVM classifier.
Figure 8. (a) Confusion Matrix for spectrogram using SVM classifier. (b) Confusion Matrix for spectrogram bicubic using SVM classifier. (c) Confusion Matrix for spectrogram lanczos using SVM classifier. (d) Confusion Matrix for mel-spectrogram using SVM classifier. (e) Confusion Matrix for mel-spectrogram bicubic using SVM classifier. (f) Confusion Matrix for mel-spectrogram lanczos using SVM classifier. (g) Confusion Matrix for cochleagram using SVM classifier. (h) Confusion Matrix for cochleagram bicubic using SVM classifier. (i) Confusion Matrix for cochleagram lanczos using SVM classifier.
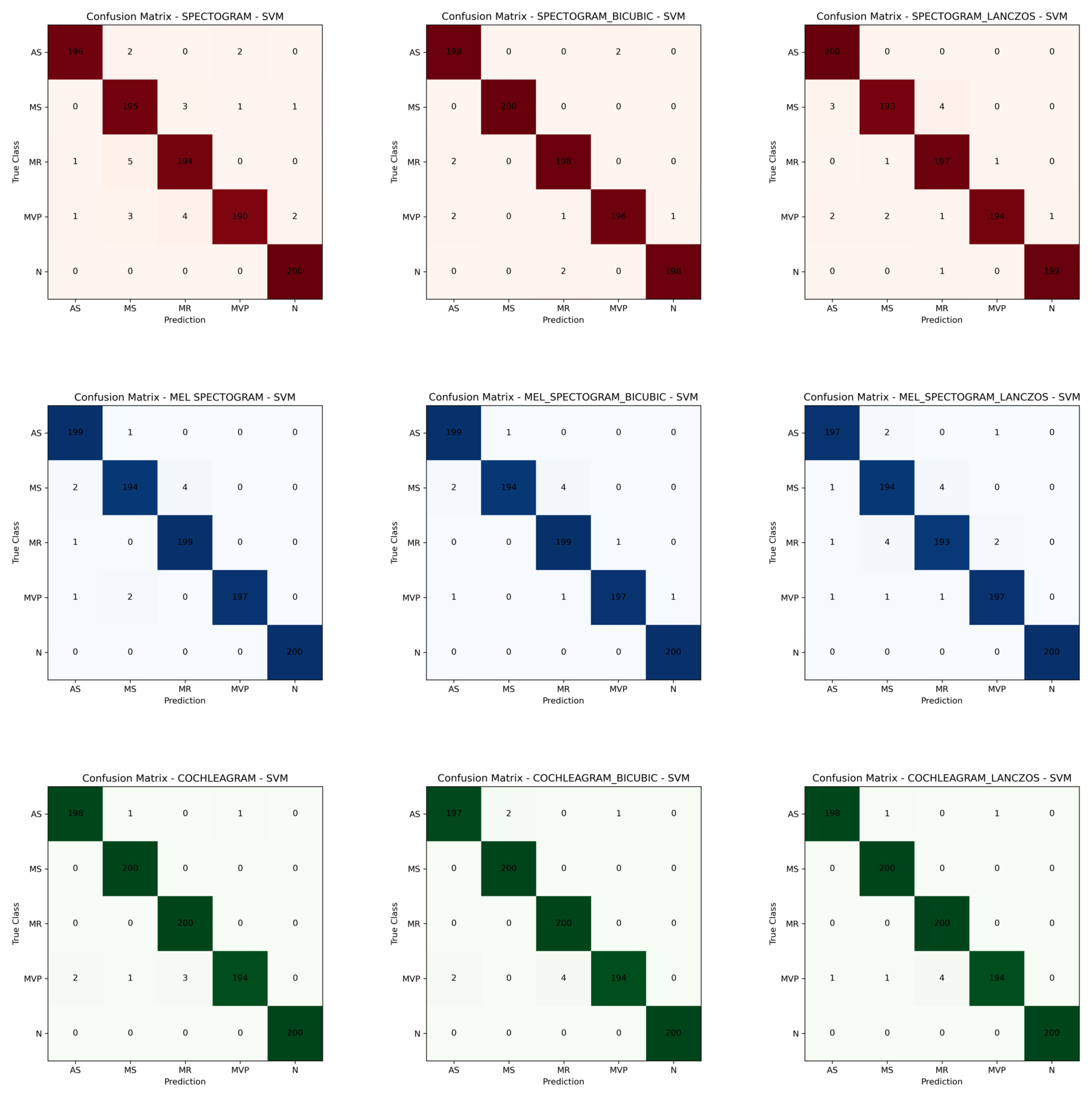
Preprints 106351 g008
Table 1. A Comparative performance of existing work for cardiac disease claassification.
Table 1. A Comparative performance of existing work for cardiac disease claassification.
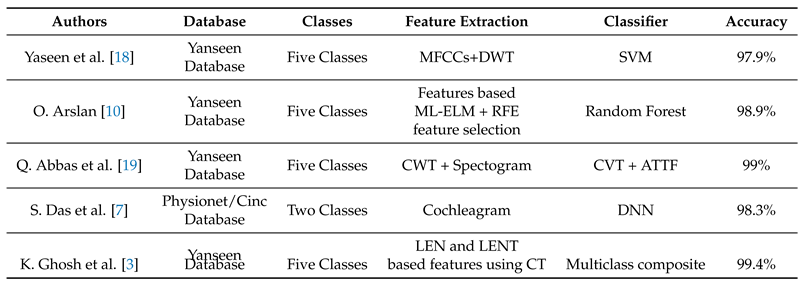
Preprints 106351 i001
Table 2. Table of heart disease sound files and sample sampling rate.
Table 2. Table of heart disease sound files and sample sampling rate.
Valve Heart Disease Files (wav.) amount Sample Frequency (Hz)
Aortic Stenosis (AS) 200 8000
Mitral Regurgitation (MR) 200 8000
Mitral Stenosis (MS) 200 8000
Mitral Valve Prolapse (MVP) 200 8000
Normal (N) 200 8000
Table 3. Boruta algorithm performance with 10 iterations.
Table 3. Boruta algorithm performance with 10 iterations.
TFRs Resize technique Confirmed Tentative Rejected
Spectogram - 1028 272 2796
Spectogram Bicubic 1031 154 2911
Spectogram Lanczos 959 198 2939
Mel-spectogram - 1007 394 2695
Mel-spectogram Bicubic 936 337 2823
Mel-spectogram Lanczos 980 300 2816
Cochleagram - 1130 400 2566
Cochleagram Bicubic 1142 398 2556
Cochleagram Lanczos 1124 410 2562
Table 4. Results for TFRs.
Table 4. Results for TFRs.
Methods/Algorithm Performances (%) for confirmed features
Pre Rec F1 MCC Acc
Spec/DT 86.36 86.30 86.31 82.88 86.20
Spec/KNN 96.71 96.70 96.70 95.87 96.70
Spec/RF 94.95 94.90 94.88 93.64 94.90
Spec/SVM 97.51 97.50 97.49 96.88 97.50
Mel/DT 91.50 91.50 91.47 89.39 91.50
Mel/KNN 97.95 97.90 97.89 97.39 97.90
Mel/RF 95.55 95.55 95.47 94.40 95.50
Mel/SVM 98.90 98.90 98.89 98.62 98.90
Coch/DT 91.04 91.00 91.01 88.75 91.00
Coch/KNN 98.61 98.60 98.59 98.25 98.60
Coch/RF 97.52 97.50 97.49 96.88 97.50
Coch/SVM 99.20 99.20 99.19 99.00 99.20
Table 5. Results for TFRs with Bicubic resize technique.
Table 5. Results for TFRs with Bicubic resize technique.
Methods/Algorithm Performances (%) for confirmed features
Pre Rec F1 MCC Acc
Spec+Bic/DT 91.59 91.60 91.59 89.50 91.60
Spec+Bic/KNN 98.90 98.90 98.89 98.62 98.90
Spec+Bic/RF 97.80 97.80 97.79 97.25 97.80
Spec+Bic/SVM 99.00 99.00 99.00 98.75 99.00
Mel+Bic/DT 93.83 93.70 93.72 92.14 93.70
Mel+Bic/KNN 99.30 99.30 99.29 99.12 99.30
Mel+Bic/RF 97.39 97.40 97.39 96.75 97.40
Mel+Bic/SVM 99.40 99.40 99.39 99.25 99.40
Coch+Bic/DT 91.81 91.80 91.80 89.75 91.80
Coch+Bic/KNN 98.51 98.50 98.49 98.13 98.50
Coch+Bic/RF 97.40 97.40 97.39 96.75 97.40
Coch+Bic/SVM 99.10 99.10 99.09 99.00 99.10
Table 6. Results for TFRs with Lanczos resize technique.
Table 6. Results for TFRs with Lanczos resize technique.
Methods/Algorithm Performances (%) for confirmed features
Pre Rec F1 MCC Acc
Spec+Lz/DT 85.55 85.60 85.56 82.00 85.60
Spec+Lz/KNN 96.80 96.80 96.79 96.00 96.80
Spec+Lz/RF 95.09 95.10 95.06 93.88 95.10
Spec+Lz/SVM 98.31 98.30 98.29 97.87 98.30
Mel+Lz/DT 88.98 88.91 88.9 86.13 88.90
Mel+Lz/KNN 97.40 97.40 97.41 96.75 97.40
Mel+Lz/RF 95.48 95.50 95.48 94.37 95.50
Mel+Lz/SVM 98.20 98.20 98.19 97.75 98.20
Coch+Lz/DT 90.77 90.60 90.64 88.27 90.60
Coch+Lz/KNN 98.52 98.50 98.49 98.13 98.50
Coch+Lz/RF 97.31 97.30 97.29 96.63 97.30
Coch+Lz/SVM 99.20 99.20 99.19 99.00 99.20
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated