Prerpints.org logo
Preprint
Article

IndustNerf: Accurate 3D Industrial Digital Twin based on Integrating Neural Radiance Fields using Unsupervised Learning

Altmetrics

Downloads

117

Views

48

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 May 2024

Posted:

13 May 2024

You are already at the latest version

Alerts
Abstract
Digital twin technology is revolutionizing traditional manufacturing paradigms. In modern manufacturing systems, digital twin technology is fraught with challenges due to the scarcity of labeled data. Specifically, existing supervised machine learning algorithms, with their reliance on voluminous training data, find their applicability constrained in real-world production settings. This paper introduces an unsupervised 3D reconstruction approach tailored for industrial applications, aimed at bridging the data void in creating digital twin models. Our proposed model, by ingesting high-resolution 2D images, autonomously reconstructs precise 3D digital twin models without the need for manual annotations or prior knowledge. Through comparisons with multiple baseline models, we demonstrate the superiority of our method in terms of accuracy, speed, and generalization capabilities. This research not only offers an efficient approach to industrial 3D reconstruction but also paves the way for the widespread adoption of digital twin technology in manufacturing.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Digital twins in the industrial realm serve as a vital bridge linking the physical and digital worlds within manufacturing systems. This innovative approach paves the way for real-time data exchange, monitoring, and advanced analytics, which are crucial for Industry 4.0 practices [1]. Among these, the three-dimensional (3D) digital twin models stand out for their significance in creating a holistic representation of products and processes.
These 3D models play an instrumental role in various industrial applications, especially in the areas of product design, simulation, testing, and production [2,3]. By providing a comprehensive digital representation of a physical asset, these models enable businesses to make better-informed decisions, reduce system downtime, and enhance product quality [4]. These models not only offer engineers and designers an intuitive tool that facilitates observing and refining designs in a virtual setting but also present the entire production team with a unified reference. Such references are invaluable in ensuring precision and consistency throughout the actual production process, leading to optimized workflows and improved product lifecycles [5,6].
Moreover, integrating digital twin models with other technologies like artificial intelligence and machine learning can further enhance predictive maintenance, resource optimization, and product customization [7,8]. In essence, 3D digital twin models herald immense opportunities for next-generation manufacturing systems, steering the industry towards a future characterized by smart, sustainable, and efficient practices [9,10].
However, the adoption of digital twin technology in current manufacturing systems encounters numerous challenges. One of the primary impediments stems from the conservative nature of manufacturing enterprises, which results in a scarcity of labeled data. This limitation hinders the application of state-of-the-art supervised machine learning algorithms known for their remarkable performance [11]. Additionally, the strong dependency of deep learning models on training data sets and their limited generalization pose significant problems. These models require the operational scenario to align closely with the data distribution from which they were trained [12]. In manufacturing systems, substantial data heterogeneity exists due to variations between different factories or even equipment, leading to exorbitant costs for data recollection. Such costs significantly obstruct the widespread adoption of deep learning models in real-world manufacturing applications [13].
Furthermore, with the advent of sophisticated technologies such as autonomous driving, robotics, and advanced automation systems in the manufacturing domain [14], there is an escalating demand for 3D digital twin models to achieve higher precision and real-time generation. Thus, there is an urgent need to develop models capable of automatic data labeling or those that can operate through unsupervised learning [15]. Enhancing the utility and generalization of models using unsupervised learning and improving their accuracy and computational speed remain focal points for both the academic and industrial communities.

2. Related Work

2.1. Digital Twins

Digital twins, at their core, represent a fusion of the physical and digital realms, enabling real-time data analysis and system monitoring. The term "digital twin" was initially introduced by Grieves, emphasizing its role as a virtual representation of a physical product or process, facilitating iterative development, testing, and optimization in a digital environment before real-world implementation [16].
In various industrial sectors, the adoption of digital twins has proved revolutionary. These virtual models have found extensive applications in sectors ranging from aerospace to manufacturing, assisting in tasks such as predictive maintenance, real-time monitoring, and fault detection. The integration of digital twins with IoT technologies has amplified operational efficiency, reducing system downtimes and refining product quality [3]. The real power of digital twins is realized when they are used to simulate real-world scenarios, thereby enabling preemptive problem identification and solution implementation.
Despite their immense potential, the deployment of digital twins in large-scale industrial systems is not without challenges. One major hurdle is the significant initial investment required in terms of infrastructure and expertise [5,17]. Furthermore, achieving synchronization between the physical and digital entities in real-time environments remains a technical challenge. Addressing data security concerns and ensuring seamless integration with existing systems are other challenges faced by industries. However, ongoing research and technological advancements promise solutions to these limitations, ensuring the wider adoption of digital twins in the future [18].

2.2. Unsupervised Learning

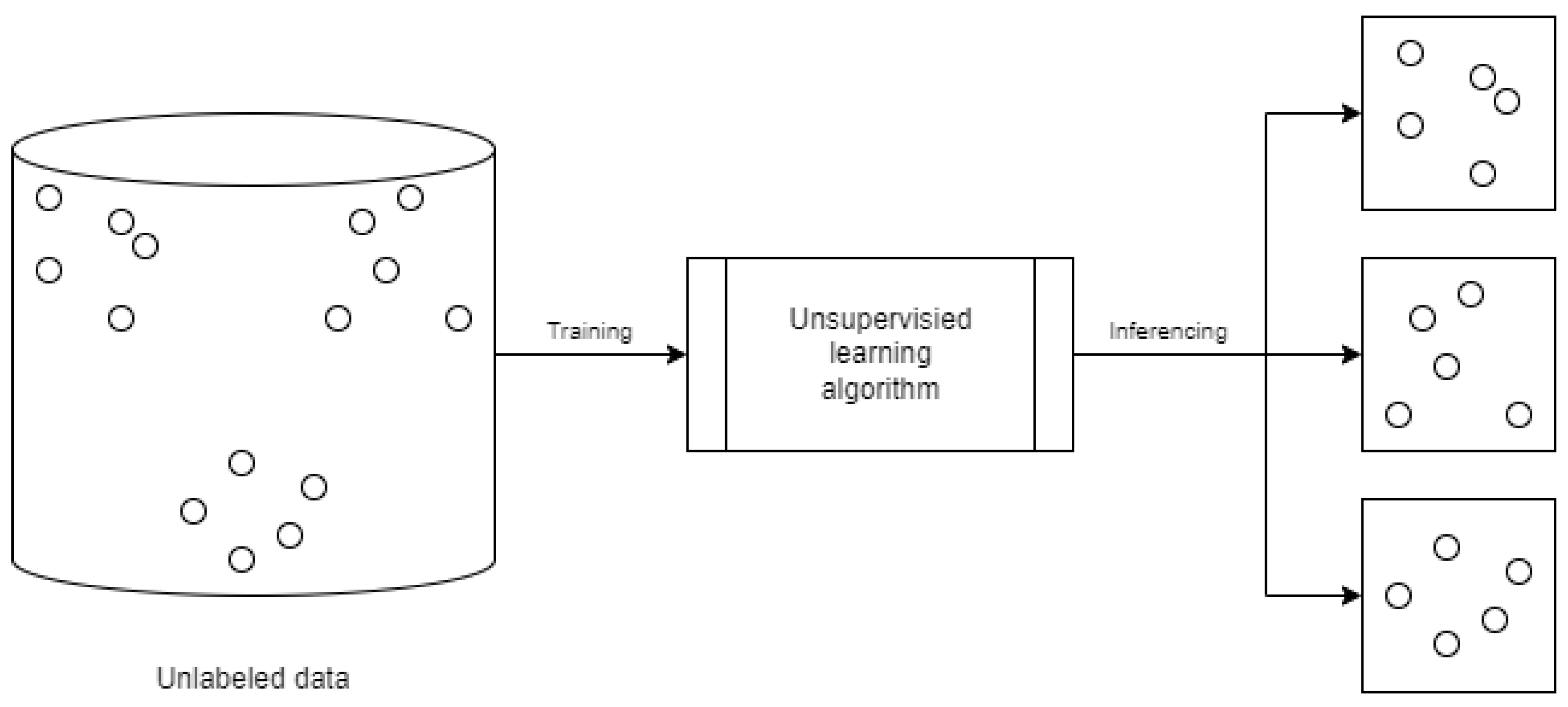
Unsupervised learning stands as one of the fundamental paradigms in machine learning, primarily focusing on deriving patterns and structures from data without labeled responses [19]. Contrasting with supervised learning, which relies on labeled datasets to make predictions or classifications, unsupervised learning delves into data’s intrinsic structures, offering the advantage of working with vast amounts of unlabelled data, making it particularly suitable for exploratory data analysis and feature discovery [20]. Figure 1 shows the process of unsupervised learning
Unsupervised learning has found myriad applications across industries, especially in scenarios with vast unlabelled datasets. In the manufacturing realm, it’s utilized for tasks like anomaly detection in machinery, where normal operations create a pattern and deviations from this pattern signal potential issues [21,22]. Additionally, it aids in segmenting market data for targeted product releases, allowing companies to better understand customer behaviors and preferences. Clustering methods, a subset of unsupervised learning, can be instrumental in grouping similar products or processes in manufacturing, optimizing resource allocation and production strategies [23].
While unsupervised learning presents novel opportunities, its deployment isn’t without challenges. A predominant concern is the interpretability of results, especially when complex algorithms like deep neural networks are employed [24]. The absence of labeled data can sometimes lead to spurious patterns or associations that may not have practical relevance. Ensuring data quality, handling high-dimensional data, and choosing the appropriate algorithm for specific tasks are further hurdles in the practical application of unsupervised learning. Researchers and practitioners are exploring ways to integrate domain knowledge to enhance the reliability and relevance of unsupervised models.
Recent advances in unsupervised learning have been driven by deep learning, with techniques like autoencoders and generative adversarial networks (GANs) leading the charge [25]. Variational autoencoders (VAEs) and transformers[26,27], especially in the context of natural language processing, have showcased the potential of unsupervised techniques in handling complex datasets and tasks. These state-of-the-art methods are continually being refined, promising even more potent applications in the future.

2.3. Neural Radiance Fields (NeRF)

Neural Radiance Fields, commonly referred to as NeRF, represent a novel approach in the realm of 3D reconstruction, employing deep neural networks to model volumetric scenes using sparse sets of 2D images [28]. This method capitalizes on the capability of neural networks to encode complex data relationships, thereby allowing for the generation of intricate 3D scenes. One of the main attractions of NeRF is its ability to produce high-fidelity and continuously viewable scenes without the necessity for mesh-based representations, setting it apart from conventional 3D modeling techniques.
NeRF has heralded significant advancements in the domain of 3D modeling and reconstruction [29]. By leveraging a scene’s sparse radiance samples and optimizing over-viewing angles and light directions, NeRF synthesizes novel views with impressive accuracy. Its applications span a diverse range, from virtual reality and augmented reality to film production and architectural visualization. Within an industrial context, NeRF can be especially advantageous for product modeling and prototyping, offering a more detailed and adjustable representation compared to traditional methods [30].
While NeRF presents remarkable capabilities, its implementation, particularly in large-scale industrial scenarios, presents challenges. The computational intensity of NeRF algorithms, given their reliance on deep neural networks, can lead to longer rendering times, which might be infeasible in real-time applications [31]. Additionally, the quality of the reconstruction can sometimes be contingent on the diversity and number of 2D input images. Researchers are actively exploring methods to enhance the efficiency of NeRF implementations and ensure consistent quality across diverse input conditions. Recent research has aimed at improving the computational efficiency of NeRF, leading to variants like FastNeRF and MicroNeRF that target real-time and embedded applications [32]. There’s also an ongoing exploration into combining NeRF with other 3D reconstruction techniques, aiming to harness the strengths of multiple methods. Given the rapid advancements in the field, NeRF and its derivatives are poised to redefine the landscape of 3D modeling and visualization in the forthcoming years.

3. Methodology

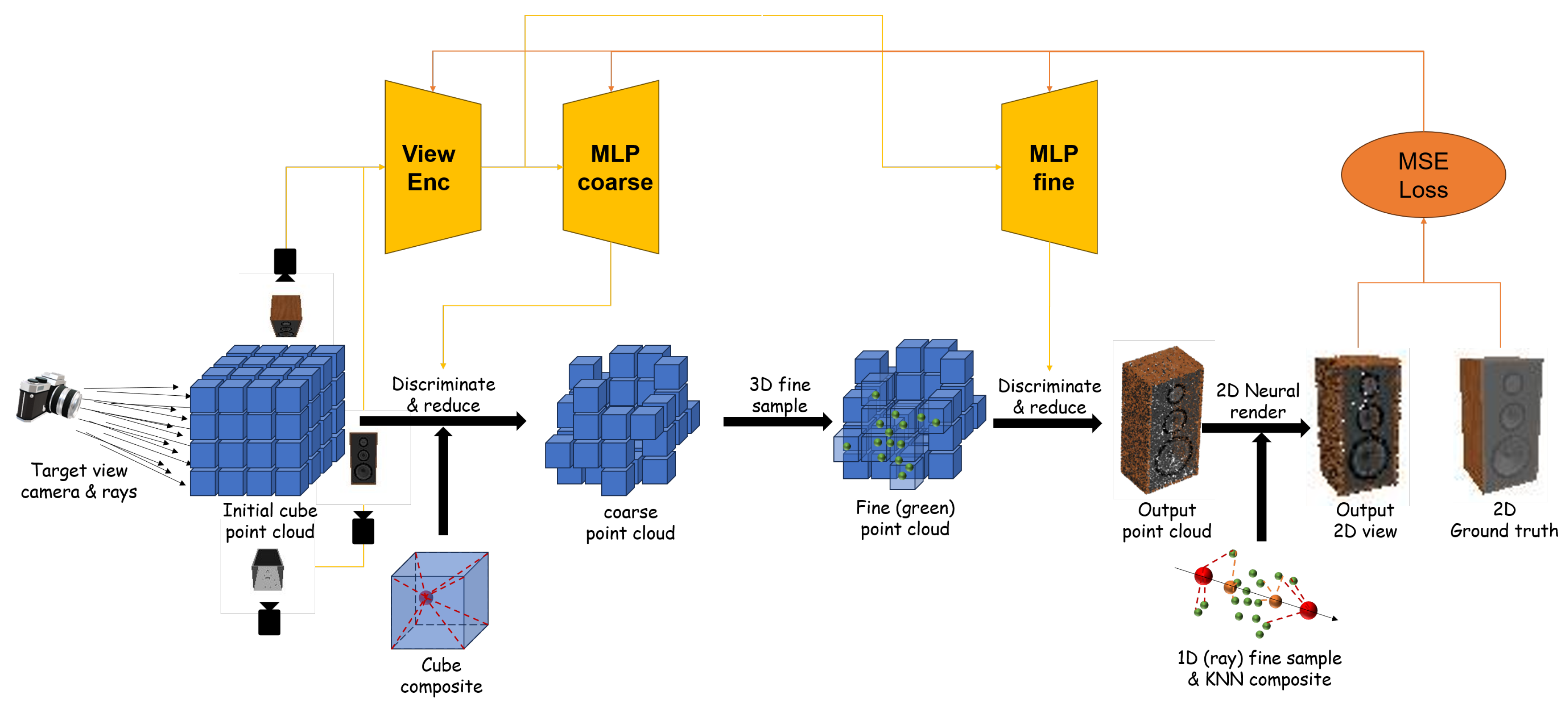
Preprints 106282 g002
Figure 2. The rendering pipeline of our model.
Figure 2. The rendering pipeline of our model.
Preprints 106282 g002

3.1. Initialization of Point Cloud and Color Discrimination Using NeRF

Given the input view-camera pose pairs ( I , P ) , and resolution hyperparameter r, an initial square point set X = S ( r ) of point count r 3 is generated, which facilitates axis-based indexing. Subsequently, based on the camera pose P, the initial point set X is transformed from the world coordinate system to the corresponding camera coordinate system of the view.
The points in the camera coordinate system undergo position encoding as per the formula referenced in [33] given by:
PosE ( p i ) = Concat ( p i x , p i y , p i z )
where:
p i x [ 2 j ] = sin ( α x i + β 6 j C )
and
p i x [ 2 j + 1 ] = cos ( α x i + β 6 j C )
Here, C represents the output dimension of position encoding, which is a multiple of 6, and j ∈ [ 0 , C 6 ] .
CNN features from the view are extracted into a feature map denoted as F = E ( I ) . Each point from the point set in the camera coordinate system is then projected onto this feature map, and the feature channels of the corresponding pixel, π ( F , P , X ) , serve as the view-associated feature of the point.
Finally, these image-associated features combined with position encoding features are input to the NeRF network, obtaining voxel density and color values:
( σ , rgb ) = N ( π ( F , P , X ) , PosE ( P ) )

3.2. 3D Coarse-to-Fine Sampling

The initial point set, once voxel densities are discerned, can be perceived as a 3D probability distribution, σ = P D F ( x , y , z ) . Inverse Transform Sampling (ITS) can be applied over this distribution. Given the ease of axis-based indexing of the initial point cloud, the distribution can be formulated as:
P D F ( x , y , z ) = σ i ∑ j σ j
where p i = ( x , y , z ) , and:
P D F ( x , y ) = ∑ z P D F ( x , y , z )
P D F ( x ) = ∑ y P D F ( x , y )
P D F ( y | x ) = P D F ( x , y ) P D F ( x )
P D F ( z | x , y ) = P D F ( x , y , z ) P D F ( x , y )
Using the ITS process, refined point cloud densities and colors are obtained.

3.3. 2D Neural Radiance Rendering

Points from subsections 3.1 and 3.2 with σ > 0 are termed cloud points. Using the target camera pose P; neural radiance points R = R ( P ) are sampled, and the cloud points are transformed into the target camera coordinate system. For each neural radiance point, the k-Nearest Neighbor algorithm captures a maximum of k points within its radius r. These points are then aggregated through inverse distance weighting to obtain the voxel density-color pairs. Using the neural rendering formula cited in [28], all neural points on the neural radiance line are aggregated to retrieve the target pixel color.

3.4. Point Cloud Confidence Based on Rerendering

For direct generation of a 3D point cloud instead of 2D images, the algorithm mentioned in 3.3 is typically not used. Our methodology facilitates the inclusion of multiple source views to generate a more precise point cloud, necessitating the introduction and aggregation of confidences.
By leveraging the principle of the algorithm from 3.3 for introducing and aggregating confidence across multiple views, our work possesses two unique characteristics:
  • The precision of the point cloud augments with an increase in the number of input views.
  • Different input views contribute varying confidences to the same point in the point cloud, and these contributions are interpretable.
This implies that our point cloud can achieve high precision given sufficient input and computational resources.
Given the exponential decrease of light intensity when a ray passes through a 3D object’s surface, this intensity is represented as:
T i = exp ( − ∑ j = 1 i − 1 σ j δ j )
should be lower for parts of the 3D point cloud reconstruction that are obscured from view and higher for visible portions.
The voxel confidence for the point cloud point at the neural radiance point T i is given by:
T i j = T i W i j max ( W i )
where W i j denotes the inverse distance weight.
By performing 2D neural radiance rendering on the point cloud using the camera poses from the source views, voxel confidences for these viewpoints are derived, alongside the neural rendered images from the source views. The color confidence is calculated as:
S i = max ( 1 − | | I i − O i | | L , 0 )
The aggregated point cloud confidence, combining voxel and color confidences, is given by:
t i j = S i T i W i j max ( W i )
In the case of multi-view aggregation, the confidence for each point is aggregated using the maximum value.

4. Experiment

4.1. Dataset Description

The primary dataset used in our experiments is a custom-assembled collection of industrial 3D models, which we shall refer to as the "Industrial 3D Twin Dataset". This dataset comprises approximately 100 distinct 3D models. Unlike conventional datasets available in the public domain, our collection has been meticulously curated and sourced through various online platforms. A significant preprocessing step involved in the preparation of this dataset was denoising, ensuring that our 3D models maintained a high level of fidelity and were devoid of any artifacts or anomalies often seen in publicly sourced data.
To facilitate the training process without the direct need for the 3D models, high-resolution images were captured from various angles of each 3D model. These images are of 512 × 512 resolution, serving as the primary input modality for our network, thereby simulating a real-world scenario where 3D models might not be readily available, but images can be easily sourced.

4.2. Experimental Environment and Model Implementation

All experiments were conducted on a workstation equipped with an NVIDIA RTX 3090 GPU. This high-performance GPU ensured swift training times and efficient resource utilization.
Our network architecture was designed and implemented using PyTorch. PyTorch was chosen because of its extensive library of pre-built modules and its capability to handle complex neural network designs. Subsequent sections will discuss a list of the hyperparameters and other pertinent training details.

4.3. Evaluation Metric: Earth Mover’s Distance (EMD)

The Earth Mover’s Distance (EMD), also known as the Wasserstein distance, is an effective measure for comparing two probability distributions. In our study, where we aim to evaluate the similarity between the reconstructed 3D point cloud and the ground truth, EMD provides a nuanced understanding of the differences in terms of geometry and density.
The primary reason behind selecting EMD as our evaluation metric is its ability to provide a more holistic view of the discrepancies between distributions, as opposed to simpler metrics that might only measure point-wise differences. EMD measures the minimum cost to transform one distribution into the other, which resonates well with the geometric nature of our task.
Mathematically, for two discrete distributions P and Q, the EMD is defined as:
E M D ( P , Q ) = ∑ i , j w i , j d ( p i , q j ) ∑ i , j w i , j
where w i , j represents the flow between points p i from P and q j from Q, and d ( p i , q j ) is the Euclidean distance between these points.

4.4. Baseline Models

4.5. Baseline Models

To ensure a comprehensive evaluation of our proposed methodology, we compare our results with three widely recognized supervised 3D reconstruction algorithms that serve as our baseline models:
  • 3D-R2N2: A deep residual network that uses convolutional layers to predict the 3D structure of an object from one or more 2D images. Developed by researchers at Stanford and Adobe, this model has become a benchmark in 3D reconstructions from 2D images.
  • AtlasNet: Proposed by Facebook AI, this model utilizes a collection of 2D patches, or atlases, to reconstruct the 3D geometry of objects. It leverages a PointNet encoder, demonstrating high proficiency in generating detailed 3D shapes.
  • Occupancy Networks: Occupancy Networks represent a novel approach to 3D
The rationale behind selecting these specific models as baselines is their prevalence in the domain of 3D reconstruction and their known efficacy in various scenarios. By juxtaposing our results with these established models, we aim to provide a clear benchmark for the capabilities of our proposed approach.

4.6. Experimental Results and Analysis

4.6.1. Model Performance Comparison

One of the primary metrics chosen for evaluating the performance of the proposed method against baseline models is the Earth Mover’s Distance (EMD). This section provides a comparative analysis based on the EMD metric for all the models.
The results, as presented in Table 1, indicate that the proposed model outperforms the baseline models in terms of the EMD score. Notably, the EMD score for the proposed model is lower than that of the 3D-R2N2, AtlasNet, and Occupancy Networks, suggesting a more accurate 3D reconstruction from the 2D images.
It is essential to understand that while the EMD score offers valuable insights into the performance of the models, the specific application context, and other qualitative factors also play a crucial role in determining the effectiveness of the 3D reconstruction.

4.6.2. Qualitative Analysis

Further to the quantitative results, visual inspections of the reconstructed 3D models also revealed the superiority of our proposed model. The baseline models, especially in the context of complex industrial objects, occasionally showed artifacts or lacked some minor details. In contrast, our proposed model maintained a consistent quality across diverse object categories. A part of the visual results of our method are presented in Figure 3. The loss scores of the visual results are shown in Table 2

4.6.3. Discussion

The proposed model’s improved performance can be attributed to its unique architecture and the robustness introduced by training on high-resolution industrial images. The model efficiently learns intricate details, enabling a more faithful reconstruction. However, it’s also important to consider computational efficiency and adaptability to real-world scenarios when deploying such models.

5. Conclusion

This study introduced a novel approach to 3D reconstruction using high-resolution industrial images. Through extensive experimentation, the proposed model demonstrated superior performance against notable baseline models like 3D-R2N2, AtlasNet, and Occupancy Networks, as measured by the Earth Mover’s Distance (EMD) metric. The results emphasize the potential of the proposed method in transforming 2D images into detailed 3D reconstructions, especially in the domain of complex industrial models.

5.1. Limitations and Future Work

While our model has shown promising results, it is essential to recognize its limitations:
  • Computational Efficiency: Although our model exhibits high accuracy, the computational demand, especially in terms of memory usage, might not be feasible for real-time applications or systems with limited resources.
  • Generalizability: The model was primarily trained and tested on industrial datasets. Its performance on diverse and more generic datasets remains to be explored.
  • Scalability: Handling larger or more intricate 3D models might require further optimizations, as the current architecture might not scale linearly with increasing complexity.
  • Noise Sensitivity: The model, though trained with denoised data, might be sensitive to noisy or imperfect input images. Robustness against such imperfections is crucial for real-world deployments.

5.2. Future Directions

Given the aforementioned limitations, future work can focus on:
  • Enhancing the computational efficiency, potentially through model pruning or adopting more lightweight architectures.
  • Broadening the dataset scope to ensure the model’s adaptability across various scenarios and objects.
  • Introducing noise augmentation during training to enhance robustness against imperfect input images.
  • Investigating multimodal input fusion techniques to leverage diverse data types for more detailed 3D reconstructions.
In conclusion, the journey of transforming 2D images into 3D models, especially in the industrial domain, is filled with challenges and opportunities. This study has paved one path, shedding light on potential methodologies and directions. As technology progresses, it is anticipated that 3D reconstruction will play an even more pivotal role in numerous applications, driving researchers and practitioners to innovate continuously. pt.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, Z.N. and L.Z.; methodology, Z.N.; software, J.X. and H.L.; validation, H.Z., J.X., and H.L.; formal analysis, H.Z.; investigation, H.Z.; resources, L.Z.; data curation, H.Z.; writing—original draft preparation, H.Z.; writing—review and editing, Z.N. and L.Z.; visualization, J.X.; supervision, Z.N.; project administration, L.Z.; funding acquisition, H.Z. and Z.N. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China under Grant No. 2020YFB1713200, and the National Natural Science Foundation of China under Grant number 72188101.

Data Availability Statement

We encourage all authors of articles published in MDPI journals to share their research data. In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study. Where no new data were created, or where data is unavailable due to privacy or ethical restrictions, a statement is still required. Suggested Data Availability Statements are available in the section “MDPI Research Data Policies” at https://www.mdpi.com/ethics.

Acknowledgments

In this section, you can acknowledge any support given that is not covered by the author’s contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors have no relevant financial or non-financial interests to disclose.

References

  1. Pang, T.Y.; Pelaez Restrepo, J.D.; Cheng, C.T.; Yasin, A.; Lim, H.; Miletic, M. Developing a digital twin and digital thread framework for an ‘Industry 4.0’Shipyard. Applied Sciences 2021, 11, 1097. [Google Scholar] [CrossRef]
  2. Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of digital twin about concepts, technologies, and industrial applications. Journal of Manufacturing Systems 2021, 58, 346–361. [Google Scholar] [CrossRef]
  3. Qi, Q.; Tao, F. Digital twin and big data towards smart manufacturing and industry 4.0: 360 degree comparison. Ieee Access 2018, 6, 3585–3593. [Google Scholar] [CrossRef]
  4. Lattanzi, L.; Raffaeli, R.; Peruzzini, M.; Pellicciari, M. Digital twin for smart manufacturing: A review of concepts towards a practical industrial implementation. International Journal of Computer Integrated Manufacturing 2021, 34, 567–597. [Google Scholar] [CrossRef]
  5. Haw, J.; Sing, S.L.; Liu, Z.H. Digital twins in design for additive manufacturing. Materials Today: Proceedings 2022, 70, 352–357. [Google Scholar] [CrossRef]
  6. Schleich, B.; Anwer, N.; Mathieu, L.; Wartzack, S. Shaping the digital twin for design and production engineering. CIRP annals 2017, 66, 141–144. [Google Scholar] [CrossRef]
  7. Feng, K.; Ji, J.; Zhang, Y.; Ni, Q.; Liu, Z.; Beer, M. Digital twin-driven intelligent assessment of gear surface degradation. Mechanical Systems and Signal Processing 2023, 186, 109896. [Google Scholar] [CrossRef]
  8. Zhang, R.; Zeng, Z.; Li, Y.; Liu, J.; Wang, Z. Research on Remaining Useful Life Prediction Method of Rolling Bearing Based on Digital Twin. Entropy 2022, 24. [Google Scholar] [CrossRef] [PubMed]
  9. Kenett, R.S.; Bortman, J. The digital twin in Industry 4.0: A wide-angle perspective. Quality and Reliability Engineering International 2022, 38, 1357–1366. [Google Scholar] [CrossRef]
  10. Yao, X.; Zhou, J.; Zhang, J.; Boër, C.R. From intelligent manufacturing to smart manufacturing for industry 4.0 driven by next generation artificial intelligence and further on. In Proceedings of the 2017 5th international conference on enterprise systems (ES). IEEE, 2017, pp. 311–318.
  11. Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Challenges and opportunities of deep learning models for machinery fault detection and diagnosis: A review. Ieee Access 2019, 7, 122644–122662. [Google Scholar] [CrossRef]
  12. Arjovsky, M.; Bottou, L.; Gulrajani, I.; Lopez-Paz, D. Invariant risk minimization. arXiv 2019, arXiv:1907.02893 2019. [Google Scholar]
  13. Zhao, J.; Papapetrou, P.; Asker, L.; Boström, H. Learning from heterogeneous temporal data in electronic health records. Journal of biomedical informatics 2017, 65, 105–119. [Google Scholar] [CrossRef] [PubMed]
  14. Leng, J.; Sha, W.; Lin, Z.; Jing, J.; Liu, Q.; Chen, X. Blockchained smart contract pyramid-driven multi-agent autonomous process control for resilient individualised manufacturing towards Industry 5.0. International Journal of Production Research 2023, 61, 4302–4321. [Google Scholar] [CrossRef]
  15. Bojanowski, P.; Joulin, A. Unsupervised learning by predicting noise. In Proceedings of the International Conference on Machine Learning. PMLR; 2017; pp. 517–526. [Google Scholar]
  16. Grieves, M. Intelligent digital twins and the development and management of complex systems. Digital Twin 2022, 2, 8. [Google Scholar] [CrossRef]
  17. Roy, R.B.; Mishra, D.; Pal, S.K.; Chakravarty, T.; Panda, S.; Chandra, M.G.; Pal, A.; Misra, P.; Chakravarty, D.; Misra, S. Digital twin: current scenario and a case study on a manufacturing process. The International Journal of Advanced Manufacturing Technology 2020, 107, 3691–3714. [Google Scholar] [CrossRef]
  18. Aheleroff, S.; Xu, X.; Zhong, R.Y.; Lu, Y. Digital twin as a service (DTaaS) in industry 4.0: An architecture reference model. Advanced Engineering Informatics 2021, 47, 101225. [Google Scholar] [CrossRef]
  19. Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
  20. Dike, H.U.; Zhou, Y.; Deveerasetty, K.K.; Wu, Q. Unsupervised learning based on artificial neural network: A review. In Proceedings of the 2018 IEEE International Conference on Cyborg and Bionic Systems (CBS). IEEE, 2018, pp. 322–327.
  21. Borghesi, A.; Bartolini, A.; Lombardi, M.; Milano, M.; Benini, L. Anomaly detection using autoencoders in high performance computing systems. In Proceedings of the Proceedings of the AAAI Conference on artificial intelligence, 2019, pp. 9428–9433.
  22. Meng, Q.; Wen, W.; Bai, Y.; Liu, Y. A Fault Detection Method for Electrohydraulic Switch Machine Based on Oil-Pressure-Signal-Sectionalized Feature Extraction. Entropy 2022, 24. [Google Scholar] [CrossRef] [PubMed]
  23. García-Escudero, L.A.; Gordaliza, A.; Matrán, C.; Mayo-Iscar, A. A review of robust clustering methods. Advances in Data Analysis and Classification 2010, 4, 89–109. [Google Scholar] [CrossRef]
  24. Chakraborty, S.; Tomsett, R.; Raghavendra, R.; Harborne, D.; Alzantot, M.; Cerutti, F.; Srivastava, M.; Preece, A.; Julier, S.; Rao, R.M.; et al. Interpretability of deep learning models: A survey of results. In Proceedings of the 2017 IEEE smartworld, ubiquitous intelligence & computing, advanced & trusted computed, scalable computing & communications, cloud & big data computing, Internet of people and smart city innovation (smartworld/SCALCOM/UIC/ATC/CBDcom/IOP/SCI). IEEE, 2017, pp. 1–6.
  25. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Advances in neural information processing systems 2014, 27. [Google Scholar]
  26. Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114 2013. [Google Scholar]
  27. Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, .; Polosukhin, I. Attention is all you need. Advances in neural information processing systems 2017, 30.
  28. Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. Nerf: Representing scenes as neural radiance fields for view synthesis. Communications of the ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
  29. Vinodkumar, P.K.; Karabulut, D.; Avots, E.; Ozcinar, C.; Anbarjafari, G. Deep Learning for 3D Reconstruction, Augmentation, and Registration: A Review Paper. Entropy 2024, 26. [Google Scholar] [CrossRef] [PubMed]
  30. Šlapak, E.; Pardo, E.; Dopiriak, M.; Maksymyuk, T.; Gazda, J. Neural radiance fields in the industrial and robotics domain: applications, research opportunities and use cases. arXiv 2023, arXiv:2308.07118 2023. [Google Scholar]
  31. Sengupta, S.; Gu, J.; Kim, K.; Liu, G.; Jacobs, D.W.; Kautz, J. Neural inverse rendering of an indoor scene from a single image. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019, pp. 8598–8607.
  32. Garbin, S.J.; Kowalski, M.; Johnson, M.; Shotton, J.; Valentin, J. Fastnerf: High-fidelity neural rendering at 200fps. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 14346–14355.
  33. Zhang, R.; Wang, L.; Wang, Y.; Gao, P.; Li, H.; Shi, J. Parameter is not all you need: Starting from non-parametric networks for 3d point cloud analysis. arXiv 2023, arXiv:2303.08134 2023. [Google Scholar]
Preprints 106282 g001
Figure 1. Unsupervised learning process.
Figure 1. Unsupervised learning process.
Preprints 106282 g001
Preprints 106282 g003
Figure 3. Experiment results.
Figure 3. Experiment results.
Preprints 106282 g003
Table 1. Comparison of EMD scores among various models. Lower EMD values indicate better performance.
Table 1. Comparison of EMD scores among various models. Lower EMD values indicate better performance.
Model EMD Score
Ours 0.0121665
3D-R2N2 0.0482132
AtlasNet 0.0759724
Occupancy Networks 0.0618715
Table 2. Comparison of EMD scores among various models. Lower EMD values indicate better performance.
Table 2. Comparison of EMD scores among various models. Lower EMD values indicate better performance.
Loss Score
Point Cloud (EMD) 0.0121665
RGB 2D (MSE) 0.0986291
Depth 2D (MSE) 0.0117503
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated