Submitted:
14 May 2024
Posted:
14 May 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Materials and Methods
3. Results
3.1. Nucleon Properties from Quantum Networks
3.1.1. Ground-State Quantum Vortex Neutron Model
3.1.2. Charge Arcs as Quantum Networks
3.1.3. Charge Arc Generation and Proton Charge-Exclusion Zone
3.1.4. Five Digit Precision
3.1.5. Nucleon Charge and Mass Coupling
3.2. Quarks and Neutron Decay
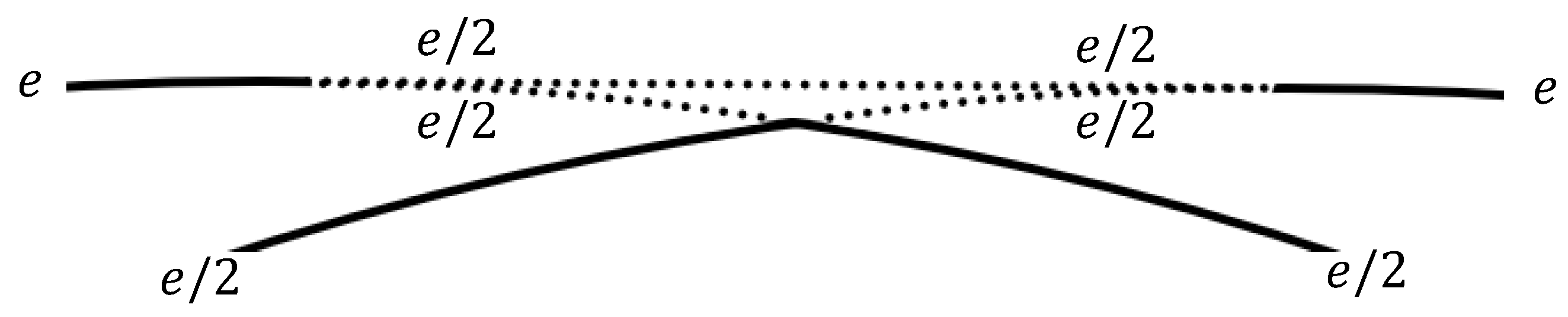
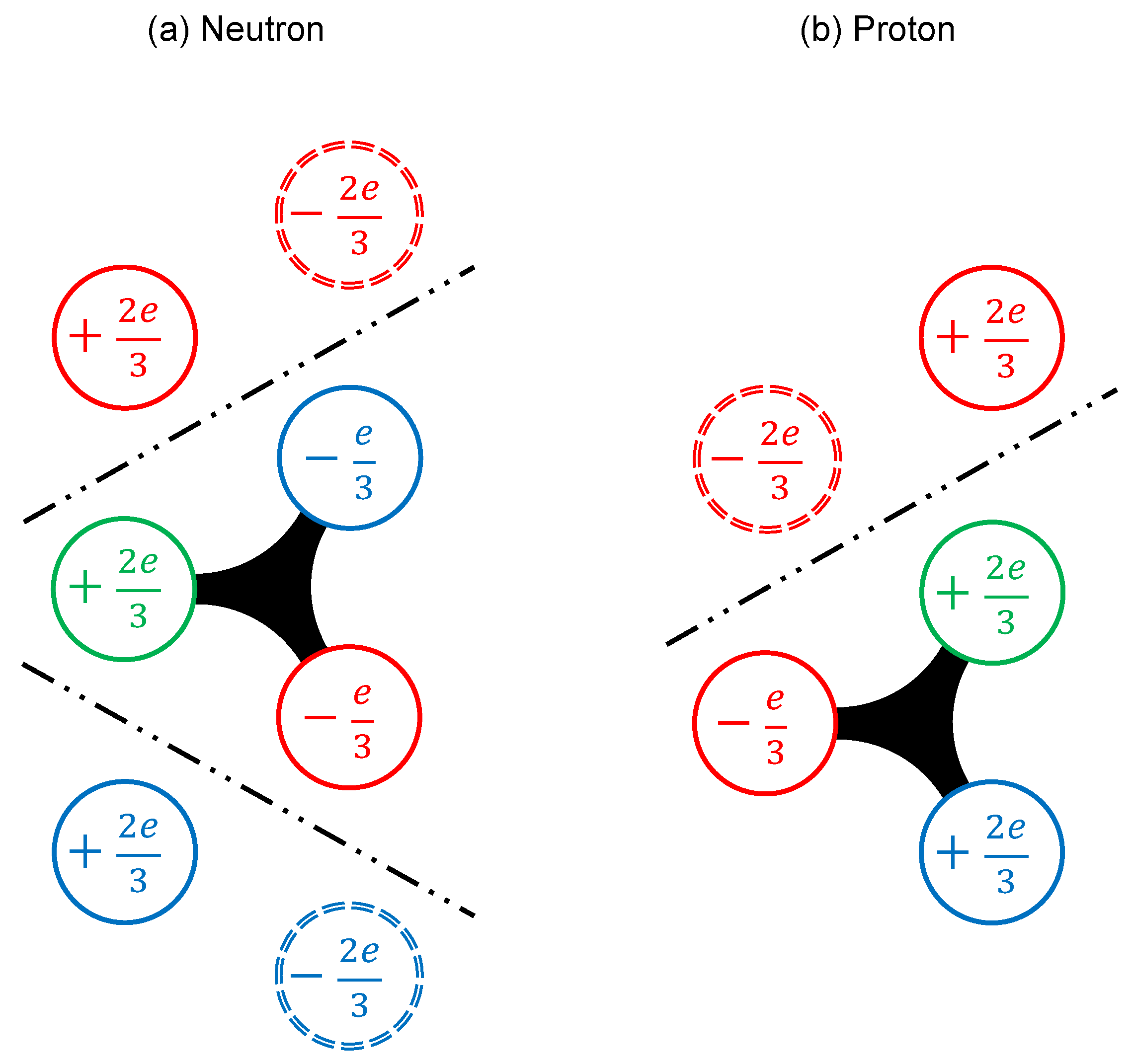
3.2.1. Quark Formation
3.2.2. Intrinsic Charm Quark Formation
3.2.3. Gluon Flux Tube Formation
3.2.4. Neutron Decay
- An outer charge arc decomposes into an intrinsic unbound quark pair. This quark pair either forms and emits a boson or annihilates with a quark pair that decomposes from an absorbed boson. This causes the decaying nucleon to initially lose mass equal to the sum of the bare masses of these intrinsic and d quarks. This results in an unstable structure that is less massive than, but of the same charge as, a proton;
- The inner charge arcs expand to become outer charge arcs and two new inner charge arcs form;
- Once this virtual optimal Möbius band structure has formed, the restabilizing nucleon is assumed to have the same angular charge distribution and equatorial speed as that of an unbound GSQV proton;
- Being less massive than a proton, this restabilizing nucleon will be larger than a proton. It will therefore have a lower charge density and larger magnetic moment compared to an unbound GSQV proton. Applying classical electromagnetism to this quantum system, the lower charge density is assumed to be associated with a lower tendency for outward expansion due to electrostatic forces. The larger magnetic moment is assumed to result in larger inward equatorial magnetic forces compared to an unbound GSQV proton [9];
- This larger inward equatorial compression, combined with reduced outward expansion, is assumed to cause the restabilizing nucleon to uniformly contract–and thereby increase its mass–to that of an unbound proton. An unbound GSQV proton is assumed to be a balanced system of internal quantum electromagnetic interactions [9].
3.2.5. W Boson Mass
3.3. Improved Unbound GSQV Proton Model
3.3.1. Theoretical Down Quark Mass
3.3.2. Perturbed Charge Distributions
3.3.3. Cosmic Origin of Quark Masses
3.3.4. Proton Magnetic Moment from a Charge Arc Geometry
3.3.5. Effective Proton Charge Radii
3.4. Precise Unbound GSQV Neutron Model
4. Discussion
- A consensus experimental estimate of proton rms charge radius that is statistically inconsistent with Equation (140);
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EFT | effective field theory |
| GDH | Gerasimov-Drell-Hearn |
| GSQV | ground state quantum vortex |
| QCD | quantum chromodynamics |
| QED | quantum electrodynamics |
| QFT | quantum field theory |
| QGP | quark-gluon plasma |
| ZIP | zitterbewegung inertial power |
Appendix A
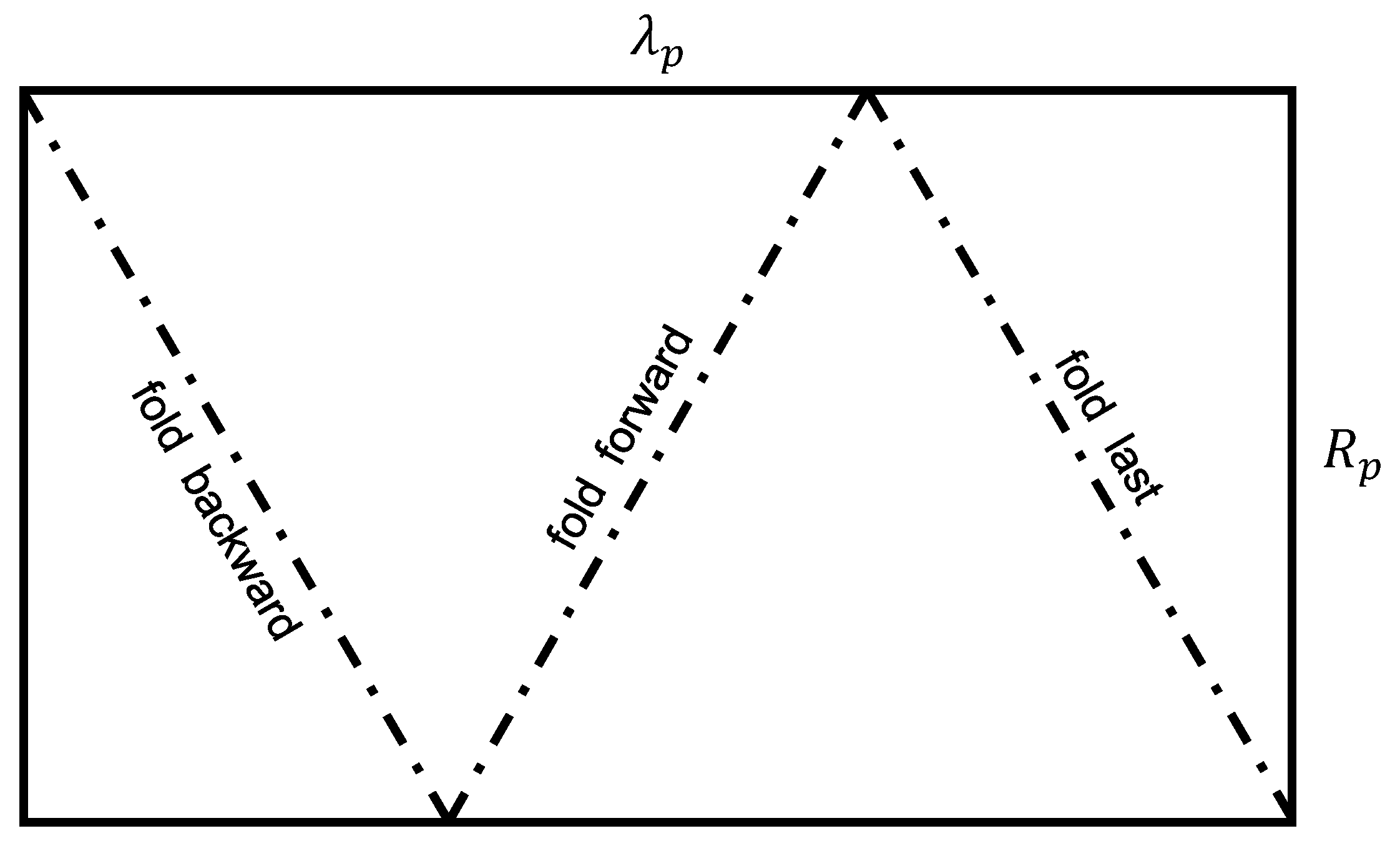
References
- NNPDF Collaboration. Evidence for intrinsic charm quarks in the proton. Nature 2022, 608, 483–491. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Lorcé, C. Nucleon relativistic polarization and magnetization distributions. Phys. Rev. D 2023, 107. [Google Scholar] [CrossRef]
- BABAR Collaboration. Study of e+e-→pp¯ via initial-state radiation at BABAR. Phys. Rev. D 2013, 87, 092005. [Google Scholar] [CrossRef]
- BESIII Collaboration. Oscillating features in the electromagnetic structure of the neutron. Nature Physics 2021, 17, 1200–1204. [Google Scholar] [CrossRef]
- Workman, R.L.; others. Review of Particle Physics. PTEP 2022, 2022. [Google Scholar]
- Peskin, M.; Schroeder, D. An Introduction to Quantum Field Theory; Westview Press, 1995.
- Oerter, R. The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics; Pi Press: New York, 2006. [Google Scholar]
- Sebens, C.T. The fundamentality of fields. Synthese 2022, 200. [Google Scholar] [CrossRef]
- Verrall, S.C.; Atkins, M.; Kaminsky, A.; others. Ground State Quantum Vortex Proton Model. Found. Phys. 2023, 53.
- Wunderlich, W. Über ein abwickelbares Möbiusband. Monatshefte für Mathematik 1962, 66, 276–289. [Google Scholar] [CrossRef]
- Halpern, B.; Weaver, C. Inverting a cylinder through isometric immersions and embeddings. Trans. Am. Math. Soc 1977, 230, 41–70. [Google Scholar] [CrossRef]
- Fuchs, D.; Tabachnikov, S. Mathematical Omnibus: Thirty Lectures on Classic Mathematics; Vol. 46, AMS, 2007.
- Schwartz, R.E. The Optimal Paper Moebius Band, 2023, [arXiv:math.MG/2308.12641].
- Amelino-Camelia, G.; Freidel, L.; Kowalski-Glikman, J.; Smolin, L. Amelino-Camelia, L. Freidel, J. Kowalski-Glikman, and L. Smolin. Principle of relative locality. Phys. Rev. D 2011, 84. [Google Scholar]
- Smolin, L. A Real Ensemble Interpretation of Quantum Mechanics. Found. Phys. 2012, 42, 1239–1261. [Google Scholar] [CrossRef]
- Cortês, M.; Smolin, L. Quantum energetic causal sets. Phys. Rev. D 2014, 90. [Google Scholar] [CrossRef]
- Cortês, M.; Smolin, L. The universe as a process of unique events. Phys. Rev. D 2014, 90. [Google Scholar] [CrossRef]
- Cortês, M.; Smolin, L. Spin foam models as energetic causal sets. Phys. Rev. D 2016, 93. [Google Scholar] [CrossRef]
- Smolin, L. Quantum Mechanics and the Principle of Maximal Variety. Found. Phys. 2016, 46, 736–758. [Google Scholar] [CrossRef]
- Smolin, L. The Dynamics of Difference. Found. Phys. 2018, 48, 121–134. [Google Scholar] [CrossRef]
- Smolin, L., Views, variety, and celestial spheres. In Time and Science - Volume 3: Physical Sciences And Cosmology; World Scientific, 2023; chapter 9, pp. 239–268.
- Greensite, J. An Introduction to the Confinement Problem; Springer: Germany, 2011. [Google Scholar]
- Achenbach, P.; Adhikari, D.; Afanasev, A.; others. The present and future of QCD. Nuclear Physics A 2024, 1047, 122874. [CrossRef]
- Beane, S.R.; Chang, E.; Cohen, S.; Detmold, W.; Lin, H.W.; Orginos, K.; Parreño, A.; Savage, M.J.; Tiburzi, B.C. Magnetic Moments of Light Nuclei from Lattice Quantum Chromodynamics. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef] [PubMed]
- Roberts, C.D.; Richards, D.G.; Horn, T.; Chang, L. Insights into the emergence of mass from studies of pion and kaon structure. Progress in Particle and Nuclear Physics 2021, 120. [Google Scholar] [CrossRef]
- Komarov, V.I. Structure of Nucleons and Their Interaction in the Concept of Nonperturbative QCD as a Pressing Issue of 21st-Century Physics. Phys. Part. Nuclei Lett. 2022, 19, 54–57. [Google Scholar] [CrossRef]
- Bernard, V.; Kaiser, N.; Meißner, U.-G. Bernard, N. Kaiser, and Ulf-G. Meißner. Chiral dynamics in nucleons and nuclei. Int. J. Mod. Phys. E 1995, 4, 193–344. [Google Scholar] [CrossRef]
- Zheng, X.; Deur, A.; Kang, H.; others. Measurement of the proton spin structure at long distances. Nat. Phys. 2021, 17, 736–741. [CrossRef]
- Sulkosky, V.; others. Measurement of the generalized spin polarizabilities of the neutron in the low-Q2 region. Nat. Phys. 2021, 17, 687–692. [Google Scholar] [CrossRef]
- Deur, A.; Chen, J.P.; Kuhn, S.E.; others. Experimental study of the behavior of the Bjorken sum at very low Q2. Physics Letters B 2022, 825. [Google Scholar] [CrossRef]
- Li, R.; others. Measured proton electromagnetic structure deviates from theoretical predictions. Nature 2022, 611. [Google Scholar] [CrossRef]
- Ruth, D.; Zielinski, R.; Gu, C.; others. Proton spin structure and generalized polarizabilities in the strong quantum chromodynamics regime. Nat. Phys. 2022, 18, 1441–1446. [Google Scholar] [CrossRef]
- Kegel, S.; others. Measurement of the α-Particle Monopole Transition Form Factor Challenges Theory: A Low-Energy Puzzle for Nuclear Forces? Phys. Rev. Lett. 2023, 130. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, S.; Cichy, K.; Constantinou, M.; Gao, X.; Metz, A.; Miller, J.; Mukherjee, S.; Petreczky, P.; Steffens, F.; Zhao, Y. Moments of proton GPDs from the OPE of nonlocal quark bilinears up to NNLO. Phys. Rev. D 2023, 108. [Google Scholar] [CrossRef]
- Tiesinga, E.; Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2018. Journal of Physical and Chemical Reference Data 2021, 50, 033105. [Google Scholar] [CrossRef] [PubMed]
- Tiesinga, E.; Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA recommended values of the fundamental physical constants: 2018. Rev. Mod. Phys. 2021, 93, 025010. [Google Scholar] [CrossRef]
- Hagen, W.F. Matter in the form of toroidal electromagnetic vortices. The Nature of Light: What are Photons? VI; Roychoudhuri, C.; Kracklauer, A.F.; Raedt, H.D., Eds. International Society for Optics and Photonics, SPIE, 2015, Vol. 9570.
- Niehaus, A. Trying an Alternative Ansatz to Quantum Physics. Found. Phys. 2022, 52. [Google Scholar] [CrossRef]
- Vassallo, G.; Kovacs, A. The Proton and Occam’s Razor. Journal of Physics Conference Series 2023, 2482, 1–24. [Google Scholar] [CrossRef]
- Brodsky, S.; Hoyer, P.; Peterson, C.; Sakai, N. The intrinsic charm of the proton. Physics Letters B 1980, 93, 451–455. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Peterson, C.; Sakai, N. Intrinsic heavy-quark states. Phys. Rev. D 1981, 23, 2745–2757. [Google Scholar] [CrossRef]
- The European Muon Collaboration. An experimental limit on the intrinsic charm component of the nucleon. Physics Letters B 1982, 110, 73–76. [Google Scholar] [CrossRef]
- NA 3 Collaboration. Experimental J/ψ hadronic production from 150 to 280 GeV/c. Z. Phys. C - Particles and Fields 1983, 20, 108–116. [Google Scholar] [CrossRef]
- R608 Collaboration. Production of Λc with large χF at the isr. Physics Letters B 1987, 199, 304–310. [Google Scholar] [CrossRef]
- Hobbs, T.J.; Londergan, J.T.; Melnitchouk, W. Phenomenology of nonperturbative charm in the nucleon. Phys. Rev. D 2014, 89, 074008. [Google Scholar] [CrossRef]
- Vogt, R.; Brodsky, S.; Hoyer, P. Systematics of J/ψ production in nuclear collisions. Nuclear Physics B 1991, 360, 67–96. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hoyer, P.; Mueller, A.; Tang, W.K. New QCD production mechanisms for hard processes at large x. Nuclear Physics B 1992, 369, 519–542. [Google Scholar] [CrossRef]
- LHCb Collaboration. Study of Z Bosons Produced in Association with Charm in the Forward Region. Phys. Rev. Lett. 2022, 128, 082001. [Google Scholar] [CrossRef]
- Vogt, R. Limits on intrinsic charm production from the SeaQuest experiment. Phys. Rev. C 2021, 103, 035204. [Google Scholar] [CrossRef]
- Vogt, R. Energy dependence of intrinsic charm production: Determining the best energy for observation. Phys. Rev. C 2022, 106, 025201. [Google Scholar] [CrossRef]
- Cai, T.; Moore, M.L.; Olivier, A.; others. Measurement of the axial vector form factor from antineutrino-proton scattering. Nature 2023, 614, 48–53. [Google Scholar] [CrossRef] [PubMed]
- Fulling, S.A. Nonuniqueness of Canonical Field Quantization in Riemannian Space-Time. Phys. Rev. D 1973, 7, 2850–2862. [Google Scholar] [CrossRef]
- Davies, P.C.W. Scalar production in Schwarzschild and Rindler metrics. J. Phys. A 1975, 8, 609–616. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870–892. [Google Scholar] [CrossRef]
- Dewitt, B.S. Quantum gravity: the new synthesis. General Relativity: An Einstein centenary survey; Hawking, S.W.; Israel, W., Eds., 1979, pp. 680–745.
- Takagi, S. Vacuum Noise and Stress Induced by Uniform Acceleration: Hawking-Unruh Effect in Rindler Manifold of Arbitrary Dimensions. Progress of Theoretical Physics Supplement 1986, 88, 1–142. [Google Scholar] [CrossRef]
- Unruh,W.G., Black holes, dumb holes, and entropy. In Physics meets Philosophy at the Planck Scale; Cambridge University Press, 2001; pp. 152–173.
- Matsas, G. The Fulling-Davies-Unruh Effect is Mandatory: The Proton’s Testimony. Int. J. Mod. Phys. D 2002, 11, 1573–1577. [Google Scholar] [CrossRef]
- Biermann, S.; Erne, S.; Gooding, C.; Louko, J.; Schmiedmayer, J.; Unruh, W.G.; Weinfurtner, S. Unruh and analogue Unruh temperatures for circular motion in 3 + 1 and 2 + 1 dimensions. Phys. Rev. D 2020, 102. [Google Scholar] [CrossRef]
- Lochan, K.; Ulbricht, H.; Vinante, A.; Goyal, S.K. Detecting Acceleration-Enhanced Vacuum Fluctuations with Atoms Inside a Cavity. Phys. Rev. Lett. 2020, 125. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, H. Entanglement harvesting for Unruh-DeWitt detectors in circular motion. Phys. Rev. D 2020, 102. [Google Scholar] [CrossRef]
- Lynch, M.H.; Cohen, E.; Hadad, Y.; Kaminer, I. Experimental observation of acceleration-induced thermality. Phys. Rev. D 2021, 104. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, J.; Yu, H. Entanglement dynamics for Unruh-DeWitt detectors interacting with massive scalar fields: the Unruh and anti-Unruh effects. J. High Energ. Phys. 2021. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, J.; Yu, H. Steady-state entanglement for rotating Unruh-DeWitt detectors. Phys. Rev. D 2022, 106. [Google Scholar] [CrossRef]
- Anastopoulos, C.; Savvidou, N. Coherences of accelerated detectors and the local character of the Unruh effect. J. Math. Phys. 2012, 53. [Google Scholar] [CrossRef]
- Ohanian, H.C.; Ruffini, R. Gravitation and Spacetime, third ed.; Cambridge University Press, 2013.
- Duran, B.; others. Determining the gluonic gravitational form factors of the proton. Nature 2023, 615. [Google Scholar] [CrossRef] [PubMed]
- Hansson, J. A simple explanation of the non-appearance of physical gluons and quarks. Can. J. Phys. 2002, 80, 1093–1097. [Google Scholar] [CrossRef]
- Coullet, P.; Gil, L.; Rocca, F. Optical vortices. Opt. Commun. 1989, 73, 403–408. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; others. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8. [Google Scholar] [CrossRef]
- Wan, C.; Cao, Q.; Chen, J.; others. Toroidal vortices of light. Nat. Photon. 2022, 16, 519–522. [Google Scholar] [CrossRef]
- Zdagkas, A.; McDonnell, C.; Deng, J.; others. Observation of toroidal pulses of light. Nat. Photon. 2022, 16, 523–528. [Google Scholar] [CrossRef]
- Breit, G. An Interpretation of Dirac’s Theory of the Electron. Proceedings of the National Academy of Sciences 1928, 14, 553–559. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, E. Über die kräftefreie Bewegung in der relativistischen Quantenmechanik. Sitzungsberichte der Preussischen Akademie der Wissenschaften. Physikali; , 1930; pp. 418–428.
- Schrödinger, E. Zur Quantendynamik des Elektrons. Sitzungsberichte der Preussischen Akademie der Wissenschaften. Physikali; , 1931; pp. 63–72.
- Barut, A.O.; Zanghi, N. Classical Model of the Dirac Electron. Phys. Rev. Lett. 1984, 52, 2009–2012. [Google Scholar] [CrossRef]
- Hestenes, D. The zitterbewegung interpretation of quantum mechanics. Found. Phys. 1990, 20, 1213–1232. [Google Scholar] [CrossRef]
- Greiner, W. Relativistic Quantum Mechanics, third ed.; Springer: Germany, 1995. [Google Scholar]
- Hestenes, D. Zitterbewegung in quantum mechanics. Found. Phys. 2010, 40, 1–54. [Google Scholar] [CrossRef]
- Niehaus, A. A Probabilistic Model of Spin and Spin Measurements. Found. Phys. 2016, 46, 3–13. [Google Scholar] [CrossRef]
- Kovács, A.; Vassallo, G.; Di Tommaso, A.O.; Celani, F.; Wang, D. Maxwell-Dirac Theory and Occam’s Razor: Unified Field, Elementary Particles, and Nuclear Interactions; 2019.
- Heisenberg, W. Über den Bau der Atomkerne. Zeitschrift für Physik 1932, 77, 1–11. [Google Scholar] [CrossRef]
- Wigner, E. On the Consequences of the Symmetry of the Nuclear Hamiltonian on the Spectroscopy of Nuclei. Phys. Rev. 1937, 51, 106–119. [Google Scholar] [CrossRef]
- Catillon, P.; Cue, N.; Gaillard, M.J.; others. A Search for the de Broglie Particle Internal Clock by Means of Electron Channeling. Found. Phys. 2008, 38, 659–664. [Google Scholar] [CrossRef]
- Wunderlich, C. Trapped ion set to quiver. Nature 2010, 463, 37–39. [Google Scholar] [CrossRef]
- Gerritsma, R.; others. Quantum simulation of the Dirac equation. Nature 2010, 463, 68–71. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, L.J.; others. Direct observation of zitterbewegung in a Bose-Einstein condensate. New J. Phys. 2013, 15. [Google Scholar] [CrossRef]
- Gaiotto, D.; Kapustin, A.; Seiberg, N.; others. Generalized global symmetries. J. High Energ. Phys. 2015, 172, 687–692. [Google Scholar] [CrossRef]
- Córdova, C.; Dumitrescu, T.T.; Intriligator, K.A. Exploring 2-group global symmetries. J. High Energ. Phys. 1–110. [CrossRef]
- Feynman, R.P. Space-Time Approach to Quantum Electrodynamics. Phys. Rev. 1949, 76, 769–789. [Google Scholar] [CrossRef]
- Feynman, R.P. Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction. Phys. Rev. 1950, 80, 440–457. [Google Scholar] [CrossRef]
- Feynman, R.P. QED: The Strange Theory of Light and Matter; Princeton University Press, 1985.
- van der Hulst, H.C. Radiogolven uit het wereldruim. Ned. T. Natuurk. 1945, 11. [Google Scholar]
- Shklovski, I.S. A monochromatic radio emission of the galaxy and the possibility of observing it. Astronomicheski Zhurnal SSSR 1948, 26. [Google Scholar]
- Ewen, H.I.; Purcell, E.M. Observation of a line in the galactic radio spectrum. Nature 1951, 168, 356. [Google Scholar] [CrossRef]
- Bloch, F.; Siegert, A. Magnetic Resonance for Nonrotating Fields. Phys. Rev. 1940, 57, 522–527. [Google Scholar] [CrossRef]
- Levitt, M.H. Spin Dynamics: Basics of Nuclear Magnetic Resonance; Wiley, 2001.
- Peleg, Y.; Pnini, R.; Zaarur, E.; Hecht, E. Schaum’s outline of theory and problems of quantum mechanics, second ed.; McGraw-Hill: New York, 2010. [Google Scholar]
- Guo, X.D.; Dong, L.; Yang, Y.G.; Shan, X.Y.; Zhan, J.M.; Lu, X.H. Detecting Larmor Precession of a Single Spin with a Spin-Polarized Tunneling Current. Chinese Physics Letters 2013, 30. [Google Scholar] [CrossRef]
- Gerasimov, S.B. A sum rule for magnetic moments and the damping of the nucleon magnetic moment in nuclei. Sov. J. Nucl. Phys. 1966, 2. [Google Scholar]
- Drell, S.D.; Hearn, A.C. Exact Sum Rule for Nucleon Magnetic Moments. Phys. Rev. Lett. 1966, 16, 908–911. [Google Scholar] [CrossRef]
- Drechsel, D.; Tiator, L. The Gerasimov-Drell-Hearn sum rule and the spin structure of the nucleon. Annual Review of Nuclear and Particle Science 2004, 54, 69–114. [Google Scholar] [CrossRef]
- Schumacher, M. Polarizability of the nucleon and Compton scattering. Progress in Particle and Nuclear Physics 2005, 55, 567–646. [Google Scholar] [CrossRef]
- Helbing, K. The Gerasimov-Drell-Hearn sum rule. Progress in Particle and Nuclear Physics 2006, 57, 405–469. [Google Scholar] [CrossRef]
- Adhikari, K.P.; others. Measurement of the Q2 Dependence of the Deuteron Spin Structure Function g1 and its Moments at Low Q2 with CLAS. Phys. Rev. Lett. 2018, 120. [Google Scholar] [CrossRef] [PubMed]
- Strakovsky, I.; Širca, S.; Briscoe, W.J.; Deur, A.; Schmidt, A.; Workman, R.L. Single-pion contribution to the Gerasimov-Drell-Hearn sum rule and related integrals. Phys. Rev. C 2022, 105. [Google Scholar] [CrossRef]
- Alvarez, L.W. Nuclear K Electron Capture. Phys. Rev. 1937, 52, 134–135. [Google Scholar] [CrossRef]
- Alvarez, L.W. Electron Capture and Internal Conversion in Gallium 67. Phys. Rev. 1938, 53, 606–606. [Google Scholar] [CrossRef]
- Alvarez, L.W. The Capture of Orbital Electrons by Nuclei. Phys. Rev. 1938, 54, 486–497. [Google Scholar] [CrossRef]
- Griffiths, D. Introduction to Elementary Particles; Wiley, 2008.
- Pourshahian, S. Mass Defect from Nuclear Physics to Mass Spectral Analysis. Journal of The American Society for Mass Spectrometry 2017, 28, 1836–1843. [Google Scholar] [CrossRef] [PubMed]
- Larmor, J. LXIII. On the theory of the magnetic influence on spectra; and on the radiation from moving ions. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1897, 44, 503–512. [Google Scholar] [CrossRef]
- Ren, H.; Weinberg, E.J. Radiation from a moving scalar source. Phys. Rev. D 1994, 49, 6526–6533. [Google Scholar] [CrossRef] [PubMed]
- Cozzella, G.; Fulling, S.A.; Landulfo, A.G.S.; Matsas, G.E.A. Uniformly accelerated classical sources as limits of Unruh-DeWitt detectors. Phys. Rev. D 2020, 102, 105016. [Google Scholar] [CrossRef]
- Portales-Oliva, F.; Landulfo, A.G.S. Classical and quantum reconciliation of electromagnetic radiation: Vector Unruh modes and zero-Rindler-energy photons. Phys. Rev. D 2022, 106, 065002. [Google Scholar] [CrossRef]
- Lynch, M.H.; Ievlev, E.; Good, M.R.R. Accelerated electron thermometer: observation of 1D Planck radiation. Progress of Theoretical and Experimental Physics 2023, 2024, 023D01. [Google Scholar] [CrossRef]
- Vacalis, G.; Higuchi, A.; Bingham, R.; Gregori, G. Classical Larmor formula through the Unruh effect for uniformly accelerated electrons. Phys. Rev. D 2024, 109, 024044. [Google Scholar] [CrossRef]
- Ievlev, E.; Good, M.R.R. Thermal Larmor Radiation. Progress of Theoretical and Experimental Physics 2024, 2024, 043A01. [Google Scholar] [CrossRef]
- Singh, T.P. Quantum gravity effects in the infrared: a theoretical derivation of the low-energy fine structure constant and mass ratios of elementary particles. Eur. Phys. J. Plus 2022, 137. [Google Scholar] [CrossRef]
- Diez, M.; Alkofer, R.; Kohlfürst, C. Identifying time scales in particle production from fields. Physics Letters B 2023, 844. [Google Scholar] [CrossRef]
- Sen, D. The Uncertainty Relations in Quantum Mechanics. Current Science 2014, 107, 203–218. [Google Scholar]
- McLerran, L.; Tribedy, P. Intrinsic fluctuations of the proton saturation momentum scale in high multiplicity p+p collisions. Nuclear Physics A 2016, 945, 216–225. [Google Scholar] [CrossRef]
- Pvoh, B.; Scholz, C.; Rith, K.; Zetsche, F. Particles and Nuclei; Springer, 2008.
- Leader, E.; Anselmino, M. A crisis in the parton model: Where, oh where is the proton’s spin? Z. Phys. C 1988, 41, 239–246. [Google Scholar] [CrossRef]
- European Muon Collaboration. A measurement of the spin asymmetry and determination of the structure function g1 in deep inelastic muon-proton scattering. Phys. Lett. B 1988, 206, 364–370. [Google Scholar] [CrossRef]
- Hansson, J. The "Proton Spin Crisis" — a Quantum Query. Prog. Phys. 2010, 3, 51–52. [Google Scholar]
- Heyde, K. Basic Ideas and Concepts in Nuclear Physics: An Introductory Approach, third ed.; Taylor & Francis, 2004.
- Conti, M.; Eriksson, L. Physics of pure and non-pure positron emitters for PET: a review and a discussion. EJNMMI Physics 2016, 3. [Google Scholar] [CrossRef] [PubMed]
- de Blas, J.; Ciuchini, M.; Franco, E.; Goncalves, A.; Mishima, S.; Pierini, M.; Reina, L.; Silvestrini, L. Global analysis of electroweak data in the Standard Model. Phys. Rev. D 2022, 106, 033003. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Measurement of the W-boson mass and width with the ATLAS detector using proton-proton collisions at TeV, 2024, [arXiv:hep-ex/2403.15085].
- Fazzini, T.; Fidecaro, G.; Merrison, A.W.; Paul, H.; Tollestrup, A.V. Electron Decay of the Pion. Phys. Rev. Lett. 1958, 1, 247–249. [Google Scholar] [CrossRef]
- Crawford, J.F.; Daum, M.; Frosch, R.; Jost, B.; Kettle, P.R.; Marshall, R.M.; Wright, B.K.; Ziock, K.O.H. Precision measurement of the pion mass difference mπ- − mπ0. Phys. Rev. D 1991, 43, 46–58. [Google Scholar] [CrossRef]
- Heald, M. Where is the “Wien peak”? Am. J. Phys. 2003, 71. [Google Scholar] [CrossRef]
- Fromerth, M.; Kuznetsova, I.; Labun, L.; Letessier, J.; Rafelski, J. From Quark-Gluon Universe to Neutrino Decoupling: 200 < T < 2 MeV. Acta Phys. Pol. B 2012, 43. [Google Scholar] [CrossRef]
- Schneider, G.; Mooser, A.; Bohman, M.; Schön, N.; Harrington, J.; Higuchi, T.; Nagahama, H.; Sellner, S.; Smorra, C.; Blaum, K.; Matsuda, Y.; Quint, W.; Walz, J.; Ulmer, S. Double-trap measurement of the proton magnetic moment at 0.3 parts per billion precision. Science 2017, 358, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Antognini, A.; others. Proton Structure from the Measurement of 2S − 2P Transition Frequencies of Muonic Hydrogen. Science 2013, 339, 417–420. [Google Scholar] [CrossRef] [PubMed]
- Greene, G.L.; Ramsey, N.F.; Mampe, W.; Pendlebury, J.M.; Smith, K.; Dress, W.B.; Miller, P.D.; Perrin, P. Measurement of the neutron magnetic moment. Phys. Rev. D 1979, 20, 2139–2153. [Google Scholar] [CrossRef]
- Sharda, A. Calculation and modeling of the neutron’s magnetic moment. Master’s thesis, University of Tennessee, 2021.
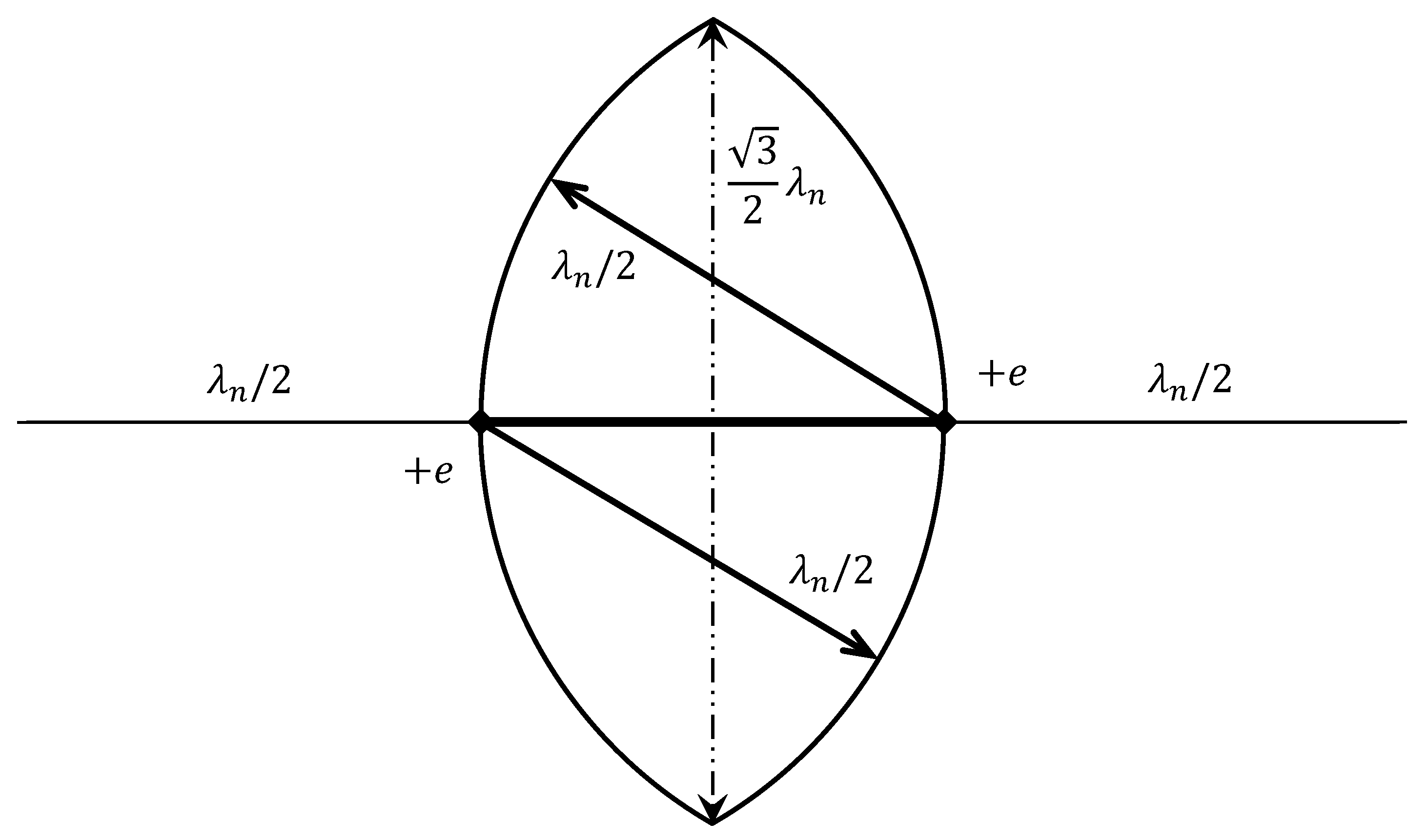
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




