Synthetic Ecosystems: From the Test Tube to the Biosphere

The study of ecosystems, both natural and artificial, has historically been mediated by population dynamics theories. In this framework, quantifying population numbers and related variables (associated with metabolism or biological-environmental interactions) plays a central role in measuring and predicting system-level properties. As we move towards advanced technological engineering of cells and organisms, the possibility of bioengineering ecosystems (from the gut microbiome to wildlands) opens several questions that will require quantitative models to find answers. Here, we present a comprehensive survey of quantitative modelling approaches for managing three kinds of synthetic ecosystems, sharing the presence of engineered strains. These include test tube examples of ecosystems hosting a relatively low number of interacting species, mesoscale closed ecosystems (or ecospheres), and macro-scale, engineered ecosystems. The potential outcomes of synthetic ecosystem designs and their limits will be relevant to different disciplines, including biomedical engineering, astrobiology, space exploration and fighting climate change impacts on endangered ecosystems. We propose a space of possible ecosystems that captures this broad range of scenarios and a tentative road map for open problems and further exploration.

Keywords:

Subject: Biology and Life Sciences - Ecology, Evolution, Behavior and Systematics

1. Introduction

Within ecology, particularly from the early works of Alfred Lotka [1,2], population dynamics has been its most relevant quantitative approximation [3]. Populations are naturally described in terms of abundance patterns in time and space, and common properties pervade their organization across scales [4]. Population dynamics provides a rationale for understanding how ecosystems work [5] and primarily illustrated by classic conservation biology [6], epidemic spreading [7] or invasion dynamics [8] where predicting the spread of a given population is a requirement for management decisions.

Not surprisingly, most textbooks in ecology start their approach to this broad field with simple models that describe the dynamics of a finite number of interacting species and their stability in terms of species abundances [9,10,11]. Along with them, it was soon realised that one way to approach ecological complexity could be to construct simpler instantiations of real, much more complex ecosystems, sometimes requiring little more than some initial diversity (Figure 1a). Those so-called microcosms [12] enclose small ecosystems held in containers that allow the study of small communities that can be systematically replicated. The experimental tractability of microcosms, together with recent advances in genetic engineering and (meta-)genomics techniques, made them an excellent asset to not only quantitatively testing theoretical predictions for community structure and dynamics [13,14,15,16], but also assessing how functional performance [17,18] depends on community composition—i.e. the taxonomic identity of community members [19]. On an intermediate scale, the same principles were extended into mesocosms [20, Figure 1b] and, at least in one case, to very large projects such as Biosphera 2 [21,22, Figure 1c].

Ecological communities are complex adaptive systems where different scales interact [23,24]. Because of their nonlinear nature, they display multiple alternative states, memory effects and breakpoints [5]. A large body of research has been developed around the population dynamics of microbial ecosystems, where the quest to a predictive understanding is a major issue [25]. These models have been traditionally instrumental in understanding natural communities, but their role has expanded into other kinds of ecosystems that, in one way or another, result from human interventions. This includes three types outlined in (Figure 1d-f), including (d) Ascension Island, which originated from an artificial combination of exotic species brought to the island [26], (e) marine ecosystems that develop on plastic debris [27] or (f) planetary colonization projects involving the building and maintenance of Life Support Systems (LSS, a class of closed ecosystems) [28].

With the rise of synthetic biology at the beginning of the 21st century, a whole new class of ecosystems became a reality: those designed from genetically modified organisms. Because of their designed nature, they can be used to interrogate the laws of ecological complexity. The importance of ecological thinking within synthetic biology is highlighted by the recurrent use of ecosystem-related concepts to understand the population-level behaviour of engineered communities [29,30]. This is particularly relevant when dealing with the stability and complexity of multicellular consortia, i.e., when different kinds of nonlinear interactions occur among engineered strains or between synthetic and natural cell populations. In Figure 1(g-h), we provide three examples of them, corresponding to competition between engineered yeast strains [31] (g) and cooperation between engineered E. coli strains [32] (h) during spatial population expansion on a Petri dish, and (i) engineered Cutibacterium acnes strains (in red) colonizing a hair foliculum [33]. In most of these systems, a full understanding of the (sometimes unexpected) spatiotemporal patterns is achieved using a suitable modelling approach.

There is a last scenario where synthetic ecosystems can play a crucial role: those associated with interventions, either within the domain of bioremediation [34,35,36] or as paths towards bioengineering the biosphere [37,38,39,40]. In both cases, a component of genetic design underlying a common goal is to restore or even modify extant ecosystems that have experienced—or can experience—degradation processes or collapse. In these cases, synthetic constructs are deployed in a habitat where a resident community is already present. Consequently, the final community will be "synthetic" if it incorporates the designed strains, which will coexist (perhaps indefinitely) within its host environment.

In this perspective, we aim to provide a comprehensive overview of various community types categorized as synthetic ecosystems using a population dynamics approach. These ecosystems involve the utilization of engineered strains to establish stable consortia. We situate them within the broader framework of artificial ecosystems to gain insight into their nature and potential applications within three spatial scales. Specifically, we examine three distinct classes of systems: (a) designed synthetic microbial communities, (b) closed ecosystems, and (c) terraformed ecosystems.

The first class encompasses a growing array of designed communities, primarily microbial, crafted through engineered gene networks. These cellular consortia allow us to interrogate the logic of ecological interactions and are the basis for synthetic ecosystem designs. The second class comprises mesoscale engineered closed habitats, i.e., modified to restrict effectively matter flows. Lastly, we explore the potential of large-scale synthetic ecosystems resulting from bioengineering efforts that extend the reach of bioremediation into the restoration of endangered or degraded ecosystems facing potential tipping points. In the three scenarios, systems biology approaches are required to guide our design efforts, and synthetic biology provides a robust path to designing predictable ecosystem architectures across scales.

2. Synthetic Microcosms

Microbial communities typically host many types of microorganisms that may engage in diverse interactions, from those providing cross-protection against toxins to competition for resources. These communities accumulate the vast majority of genetic diversity on Earth and perform pivotal ecological functions in the biosphere, such as nitrogen fixation and preventing soil erosion. Compared to communities of macro-organisms, these communities can host a large number of individuals in relatively small spaces—billions of bacterial cells can quickly grow in a single test tube—while presenting very rapid eco-evolutionary dynamics—bacterial generation times often span just a few dozen minutes. These features and recent developments in genetic engineering and sequencing techniques have made experimental microbial communities an ideal platform for quantitatively testing theoretical predictions and developing control over synthetic microcosms, i.e. the smallest synthetic ecosystems.

Understanding and controlling interactions between community members is crucial to managing the dynamics and functions of synthetic microcosms. Microbial interactions are typically categorized by their impact on the growth of the target species: negative, positive, or neutral. In turn, different classes of interaction pairs give rise to minimal interaction network motifs for (synthetic) microbial communities (see Figure 2). Below, we summarize the canonical examples of such motifs and their quantitative description regarding mathematical models. These minimal, synthetic interaction motifs are the basis for engineering more complex interaction networks in microbial communities.

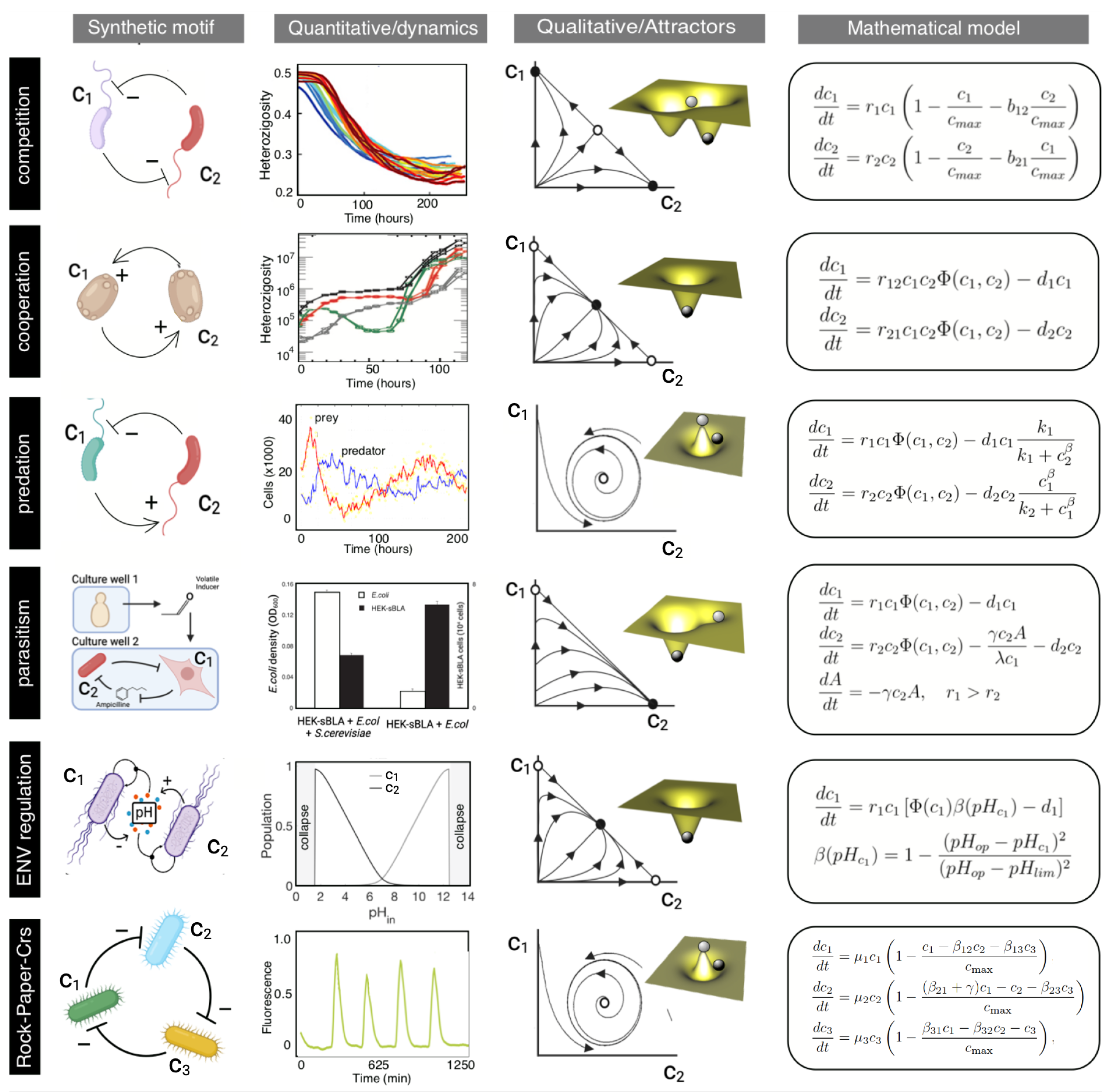
2.1. Competition

A classical model for competition between two populations is the competitive Lotka-Volterra (LV) model, which has played a central role in theoretical ecology since [41,42] and was tested in the lab [43] shortly after its introduction. In this model, two populations

c_{1}

and

c_{2}

compete for some common implicit resources as follows:

\begin{matrix} \frac{d c_{1}}{d t} & = μ_{1} c_{1} (1 - \frac{c_{1} + β_{12} c_{2}}{c_{\max}}), \\ \frac{d c_{2}}{d t} & = μ_{2} c_{2} (1 - \frac{c_{2} + β_{21} c_{1}}{c_{\max}}), \end{matrix}

(1)

where

μ_{i}

is the growth rate of population

c_{i}

, and

c_{\max}

is the carrying capacity of the system. The

β_{i j}

parameter is the inter-specific competition coefficient. It defines the intensity of competition between the two strains relative to the intra-specific competition coefficient (here normalized

β_{i i} = 1

). Setting all

β_{i j}

i \neq j

, to zero reduces the system to two independent logistic equations like equation (1).

The competitive LV model displays three qualitative outcomes: coexistence of the two species (only possible when intra-specific competition is stronger than inter-specific competition), competitive exclusion (one of the species always leads the other to extinction), and bistability (either species can exclude the other one depending on its initial relative abundance). In the case of exclusion (bistability), one (either) species is subject to an inter-specific competition stronger than the intra-specific one, eventually leading to diversity loss as one species reaches extinction.

In spatially extended systems, competitive exclusion could be avoided if competition occurs under local dispersal [44]. One way to visualize the effects of competitive dynamics using engineered strains (see Figure 1g) is to allow an initial inoculum of P. aeruginosa YFP- and CFP-labeled mutants [45]. Because they can interact only with nearest neighbours, a local amplification propagates outwards as the colony grows, indicating that each strain over-competes locally the other.

2.2. Cooperation

The presence of cooperative interactions appears to be a driving force behind evolutionary innovations and the preservation of biodiversity. A minimal cooperation scenario involves two strains displaying syntropic dependencies: one species requires the other for replication due to their shared need for a specific molecule produced by their partner species. This is also known as the hypercycle [46,47]. Synthetic, two-species mutualisms have been engineered in both eukaryotic [48] and prokaryotic [32,49,50] systems.

If we indicate by

c_{1}

and

c_{2}

cell population sizes, a pair of coupled equations allows us to model a two-population mutualism as follows:

\begin{matrix} \frac{d c_{1}}{d t} & = α_{12} c_{1} c_{2} (1 - \frac{c_{1} + c_{2}}{c_{\max}}) - δ_{1} c_{1} \\ \frac{d c_{2}}{d t} & = α_{21} c_{1} c_{2} (1 - \frac{c_{1} + c_{2}}{c_{\max}}) - δ_{2} c_{2} \end{matrix}

(2)

where

α_{i j}

is the replication rate of species

c_{j}

in the presence of the mutualistic partner

c_{j}

c_{\max}

is the carrying capacity of the system, and

δ_{i}

is the death rate of population

c_{i}

. As defined, we can see that no proliferation of any of the two partners will occur in the absence of the other due to the second-order kinetics that requires the product of the two concentrations.

2.3. Parasitism and Predator-Prey Interactions

Cooperators can out-compete other non-cooperative species [46,51], but they are vulnerable to disruption by a cheater (a parasite) [52]. In this scenario, models predicted that spatial structure can help cooperators to defeat parasites [53], and this was shown experimentally using E. coli engineered communities [32,50,54]. Cheaters can also have multiple effects (direct and indirect) on community dynamics. This is illustrated by an engineered multispecies community, where the presence of fungi leads to bacterial parasitism on mammalian cells Weber et al. [55].

Qualitatively, parasitic interactions display an identical interaction network motif – a positive interaction in one direction and a negative one in the other direction – to that of predator-prey interactions. Predator-prey systems can exhibit oscillatory behaviour regarding the temporal dynamics [42,56]. Its classical model is defined in terms of the interactions between prey (

c_{1}

) and predator (

c_{2}

) populations using two coupled differential equations, namely:

\frac{d c_{1}}{d t} = μ c_{1} - β c_{1} c_{2}

(3)

for the prey, which grows at a rate

μ

and is predated at a rate

β

, and

\frac{d c_{2}}{d t} = α c_{1} c_{2} - δ c_{2}

(4)

for the predator, which grows at a rate

α

and decays with a rate

δ

. In nature, microbial predators have evolved unique strategies to grow and acquire their resources from other living bacterial cells [57,58]. However, it is far from obvious how such an ecological motif can be implemented in a synthetic community.

The work by Balagaddé et al. [59] solved the problem by finding a way to reproduce the effective positive nonlinearities that appear in the previous model. The study involved the manipulation of two distinct strains of E. coli to establish a controlled predator-prey dynamic within a confined environment using quorum sensing (QS), which enables density-dependent induction of genes across populations [60].

In this case, prey cells consistently emit a QS compound. When this compound reaches high levels, predator cells generate an anti-toxin. Conversely, predator cells continually release a distinct QS compound, which (at higher concentration) stimulates prey cells to produce a toxin, causing DNA damage and eventual cell death. Additionally, predator cells continuously produce the same toxin, but in this case, they can counteract it by inducing the expression of the anti-toxin.

Given a population of prey cells

c_{1}

and a population of predator cells

c_{2}

, the cyclic orbits can be reproduced by the following system of differential equations (adapted from the original system in Balagaddé et al. [59] Supplementary Material):

\begin{matrix} \frac{d c_{1}}{d t} & = μ_{2} c_{1} (1 - \frac{c_{1} + c_{2}}{c_{\max}}) - δ_{1} c_{1} \frac{c_{2}^{β}}{K_{1}^{β} + c_{2}^{β}} \\ \frac{d c_{2}}{d t} & = μ_{2} c_{2} (1 - \frac{c_{1} + c_{2}}{c_{\max}}) - δ_{2} c_{2} \frac{K_{2}^{β}}{K_{2}^{β} + c_{1}^{β}} \end{matrix}

(5)

where

μ_{i}

is the effective growth rate of population

c_{i}

c_{\max}

is the carrying capacity,

δ_{i}

is the maximum death rate,

K_{i}

is the concentration of the complementary strain at which death rate is half the maximum value, and

β

is the Hill’s coefficient of the interaction coupling the strains.

In contrast to the system represented by original equations (3, 4), an increased concentration of prey provides cross-protection, reducing the effective death rate of predators. However, predators are toxic to the preys. This creates a cyclic succession of populations: prey growth triggers anti-toxin production in predators, allowing them to grow and replace the prey population by inducing toxin creation. As prey declines, predators start self-destructing as cross-protection diminishes, allowing prey to grow once again.

2.4. Environmental Self-Regulation

Ecological self-regulation is a fundamental concept in microbiology, encompassing the intricate mechanisms through which microbial communities maintain stability and balance within their ecosystems [61]. Microorganisms continuously interact with each other and their environment, dynamically adjusting their populations and behaviours to sustain ecological equilibrium. These interactions shape community structure, function, and resilience, ultimately influencing ecosystem dynamics [62,63].

One illustrative example of ecological self-regulation is the Daisyworld model [64], which serves as a simplified representation of a planetary ecosystem, where white and black daisies organisms regulate the planet’s temperature through their interactions with solar radiation.

Using synthetic biology, a possible implementation for a synthetic microbial Daisyworld was recently proposed by Maull et al. [65]. In this case, two cell populations growing in a chemostat, an acid-producer

c_{1}

and a base-producer

c_{2}

, can self-regulate the environment. This regulation stems from inherent feedback mechanisms: acidification favours the growth of base producers, while alkalinization provides an advantage to acid producers. The equations that are used to describe the cell dynamics are a coupled set of equations describing the growth of each cell type, similar to standard replicator equations from population genetics:

\begin{matrix} \frac{d c_{1}}{d t} & = μ_{1} c_{1} [β ({pH}_{1}) (1 - \frac{c_{1} + c_{2}}{c_{\max}}) - δ] \\ \frac{d c_{2}}{d t} & = μ_{2} c_{2} [β ({pH}_{2}) (1 - \frac{c_{1} + c_{2}}{c_{\max}}) - δ] \end{matrix}

(6)

where

μ_{i}

is the growth rate of population

c_{i}

c_{\max}

is the carrying capacity, and

δ

is the dilution rate. The function

β

describes the change in growth rate depending on the perceived pH,

β ({pH}_{i}) = 1 - \frac{{({pH}_{opt} - {pH}_{i})}^{2}}{{({pH}_{opt} \pm {pH}_{\lim})}^{2}} .

a symmetric, single-peaked function with its maximum located at the optimal growth pH, denoted as

{pH}_{opt}

, and positivity maintained across the interval

{pH}_{opt} \pm {pH}_{\lim}

. The perceived pH of each population deviates from the environmental pH, denoted

{pH}_{env}

due to the constant production of either an acid (a) or a base (b), slightly shifting the perception as follows:

\begin{matrix} {pH}_{1} & = {pH}_{env} - ω_{1} a, & {pH}_{2} & = {pH}_{env} + ω_{2} b, \end{matrix}

where

ω_{i}

is the sensitivity of the population

c_{i}

to the produced compound.

Despite given an external input of either acid or base,

{pH}_{in}

, the environmental pH is maintained close to the optimum by reorganizing the relative populations. The reorganization adjusts the production of acid and base, opposing the pH deviation due to the external perturbation.

2.5. Non-Transitive Interactions

Game theory has long been employed in theoretical biology to investigate critical evolutionary phenomena such as the development of cooperative behavior [66], strategies in conflicts and fights [67], interactions between hosts and parasites [68], and the evolution of biochemical pathways [69]. Some synthetic counterparts of these systems have been obtained using small toxins (bacteriocines) synthesized by certain bacteria, toxic to other bacteria, and often closely related. Their production confers a competitive advantage to the producer by hindering the growth or even killing others [70,71]. Toxin production typically entails some costs associated with synthesising toxin and the lysis protein necessary for its release from the cell. Moreover, the producing bacteria are exposed to their own toxin, requiring a heightened immunity response. These emergent dynamics resemble the one shown by the classic “Rock-Scissors-Paper” (RSP) game.

This game was designed using three engineered populations [72]: bacteriocin-producer cells (

c_{1}

), sensitive cells (

c_{2}

), and resistant cells (

c_{3}

). The game can be represented, following Neumann and Schuster [73] as:

\begin{matrix} \frac{d c_{1}}{d t} & = μ_{1} c_{1} (1 - \frac{c_{1} - β_{12} c_{2} - β_{13} c_{3}}{c_{\max}}), \\ \frac{d c_{2}}{d t} & = μ_{2} c_{2} (1 - \frac{(β_{21} + γ) c_{1} - c_{2} - β_{23} c_{3}}{c_{\max}}), \\ \frac{d c_{3}}{d t} & = μ_{3} c_{3} (1 - \frac{β_{31} c_{1} - β_{32} c_{2} - c_{3}}{c_{\max}}), \end{matrix}

(7)

where

μ_{i}

stands for the growth rate of population

c_{i}

c_{\max}

is the carrying capacity of the system and

β_{i j}

is the cross-competition coefficient between populations. The parameter

γ

represents the disadvantage of the sensitive population

c_{2}

when competing with the toxin-producer population

c_{1}

. RSP rules are obtained when

c_{2}

out-competes the slower growing population

c_{3}

c_{3}

out-competes the slowest growing population

c_{1}

, and

c_{1}

out-competes the fastest growing population

c_{2}

due to toxin production. This results in orbits converging to a limit cycle, characterized by a cyclical succession of dominant populations where

c_{1}

replaces

c_{2}

, then

c_{3}

replaces

c_{1}

, and

c_{2}

replaces

c_{3}

, thus starting the cycle anew.

These case studies capture the logic of ecological motifs, showing the potential for engineering them, but cannot capture the emergent patterns associated with whole communities. However, both in vitro and in silico paths can be followed to build and predict them [74,75]. In the next sections, we address the problem of how synthetic biology can help design living communities and the lessons provided by looking at these problems on a multiscale approach.

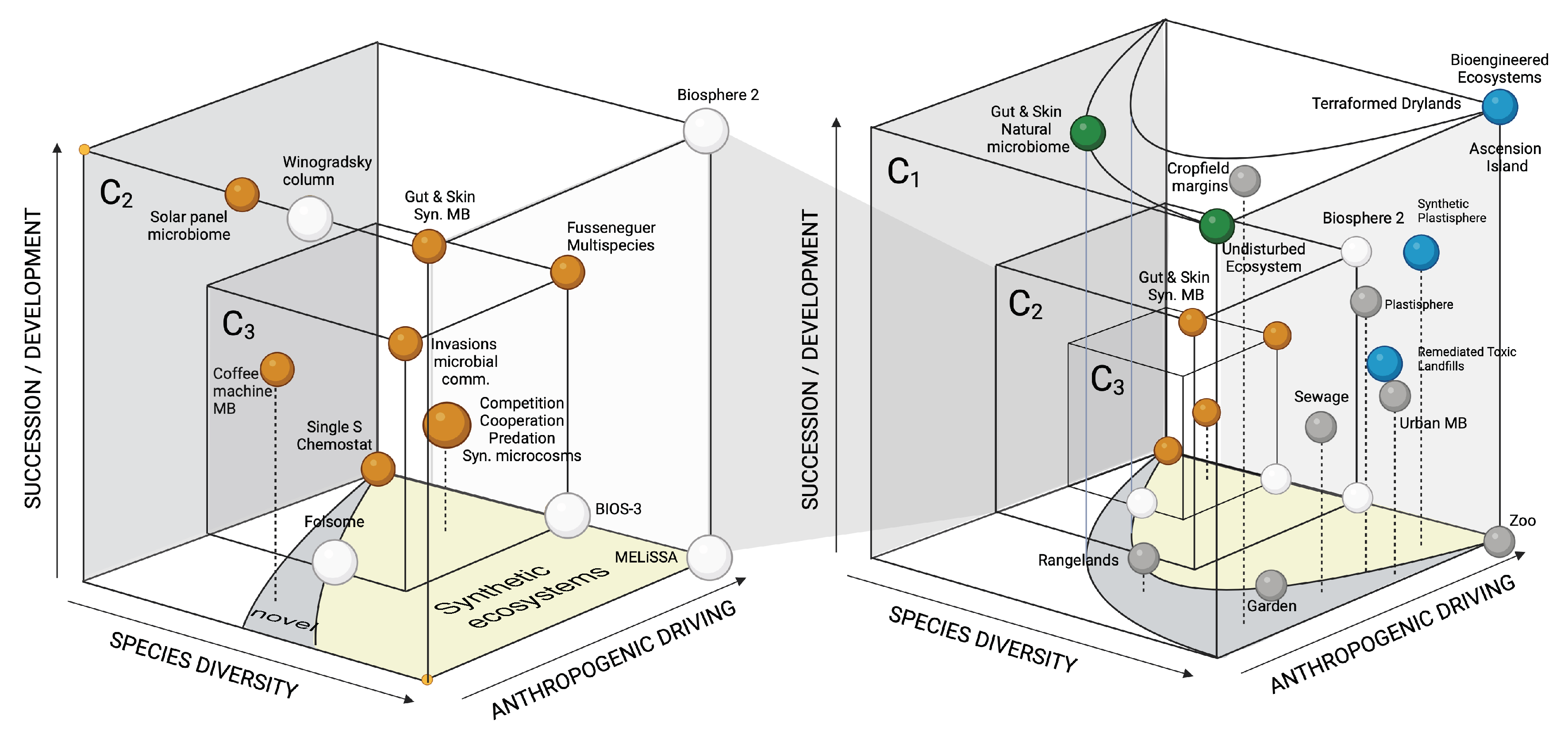
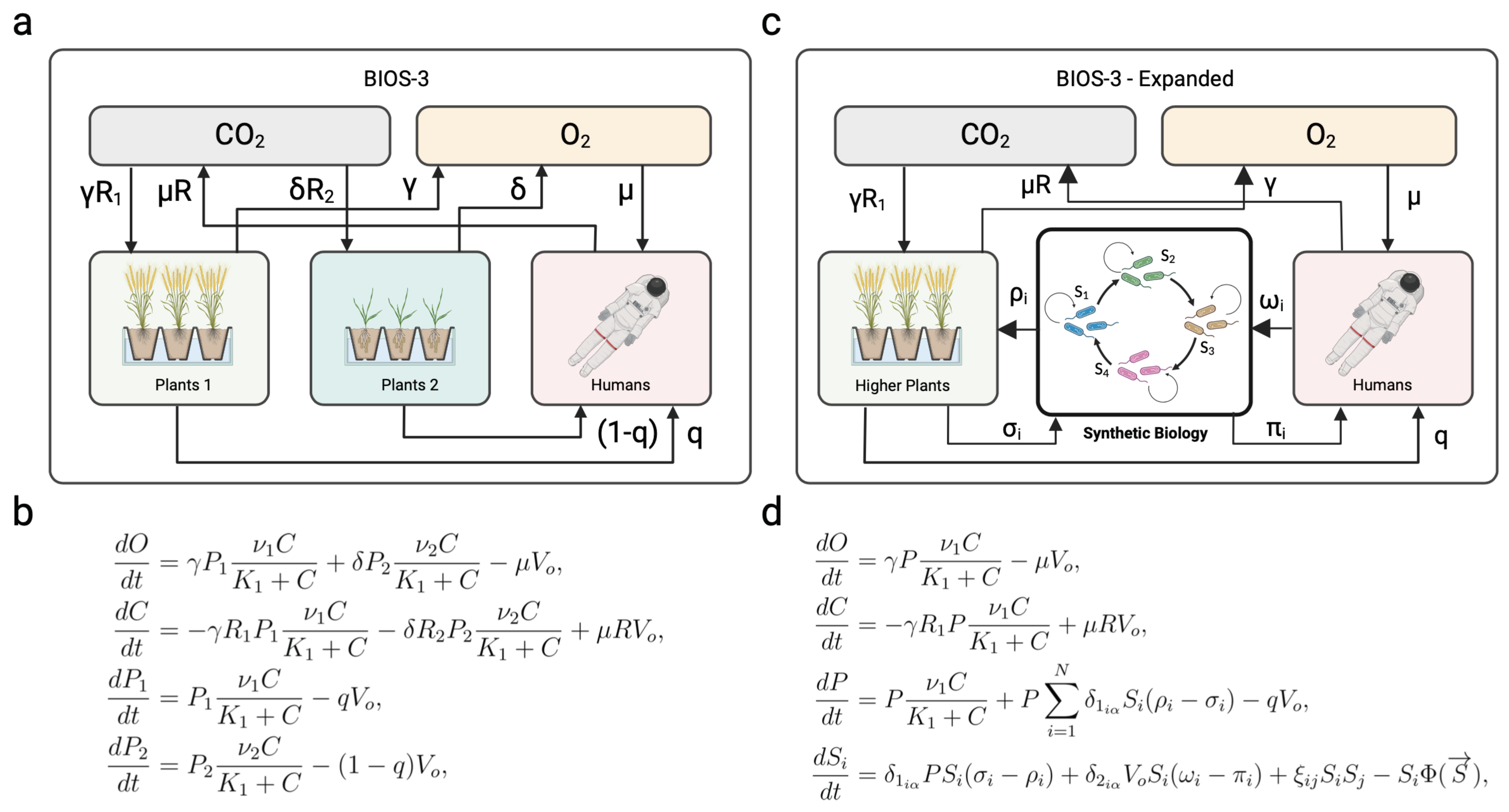
3. Closed Ecospheres and Space-Life Support Systems

The previous section illustrates the potential of synthetic biology and mathematical modelling to design building blocks of ecological interactions. In all those examples, the environment where the population dynamics occur is implicit: limiting resources are somehow available. However, once we move away from small-scale cell cultures and bioreactors, we must face new challenges associated with multispecies communities and their environmental constraints. In this section, we consider a mesoscale level that includes a range of well-defined case studies where we aim to build an artificial community within well-defined boundaries. These ecosystems share a common goal: building self-sustained so-called ecospheres that display stable metabolic cycles and rich community compositions in analogy with the biosphere.

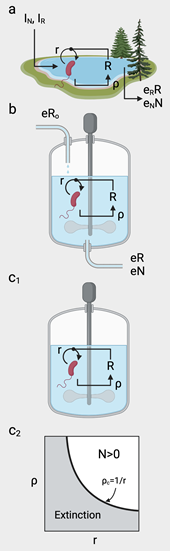
BOX 1. Critical thresholds for synthetic closed ecosystems
The simplest model approach to closed ecosystems includes a population of size N of a given species that exploits some limited (inorganic) resource R. In the open scenario (Figure a), the equations read:

\begin{matrix} \frac{d N}{d t} & = I_{N} - e_{N} N + r R N - N \\ \frac{d R}{d t} & = I_{R} - e_{R} R - R N + ρ N \end{matrix}

(8)

Where

I_{N}

and

I_{R}

stand for inputs of individuals and resources, respectively, they can leave the system (decay) at rates

e_{N}

and

e_{R}

. The recycling rate is defined by

ρ

. The pairwise terms with

R N

include the consumption of R and the resulting population growth. In a chemostat (Figure b) we would have

e_{N} = e_{R} = e

I_{N} = 0

and

I_{R} = e R_{0}

.
Mathematically, a closed ecosystem is a special case of the previous model, where the dilution rate is nonexistent (

e = 0

). Now (Figure c₁), the system only depends on the initial condition, the intrinsic growth dynamics of the species and the recycling rate of resource generation. Additionally, closure imposes a maximum carrying capacity, defined by logistic growth¹. The equations read:

\begin{matrix} \frac{d N}{d t} & = r R N (1 - N) - N \\ \frac{d R}{d t} & = - R N + ρ N \end{matrix}

(9)

What are the expected steady states for a closed system? The equilibrium (fixed) points are obtained from

d N / d t = d R / d t = 0

. The stability analysis of the system easily reveals two possible scenarios depending on the nature of the parameters. Establishment or extinction (Figure c₂). So we have

N^{*} = 1 - (1 / r ρ)

and the trivial point

N^{*} = 0

. A critical recycling rate

ρ_{c} = 1 / r

exists above which life can persist. As with other designed synthetic ecosystems, a closed system could be properly adjusted and maintained within the safe domain by adding a designed strain to the community.

These systems have been studied since the 1960s as part of the engineering efforts towards space exploration and the engineering of so-called Life Support Systems (LSS) [28], but also as a way to understand the requirements for a sustainable biosphere [21]. In many cases, the difficulties and failures associated with their design have provided important lessons on how to predict their dynamical evolution [76]. The potential for synthetic biology in harnessing these difficulties has shown that there is plenty of room for opportunities for addressing these problems while promoting novel microbial biotechnologies with broad implications [77,78]. Moreover, relevant lessons might be obtained by comparing these engineered ecosystems with microbial communities that have evolved within a host context [79].

Early studies on materially closed but energetically open ecospheres revealed that self-sustained, metabolically active communities (including prokaryotes, eukaryotes and metazoa) could persist over decades [80]. These closed ecosystems are, by definition, "synthetic": the requirement of a boundary that forbids matter flows violates the open, out-of-equilibrium nature of natural ecosystems. Not surprisingly, the closed character of one such ecology imposes severe limitations on the space of viable ecospheres, given the strong ties between microbial growth and resource recycling. Quantitative methods and mathematical models have been key to providing bounds to the potential feasibility conditions for closed ecosystems [81,82,83], but only a few -and yet illuminating- experimental studies have been performed so far [84,85,86]. One first estimation of the crucial conditions is sketched in Box 1 for a single species exploiting a single resource in a batch reactor. The general conclusion from this minimal model is that a critical boundary separates viable from non-viable life that balances microbial growth and recycling efficiency. Here comes one interesting and unexplored path to understanding and engineering closed ecospheres using synthetic biology: by assembling synthetic microbial communities [87,88,89], it would be possible to gain insight into the requirements for community-level complexity when matter flows are closed [78,90].

What can be learned from past and ongoing projects on LSS, and how can synthetic biology contribute to dealing with its limitations? The design of sustainable ecospheres for long-term space travel has been one of the main drivers for developing the science of closed ecosystems. It has inspired the emergence of a field, namely space synthetic biology [91]. The most iconic early research examples are BIOS-3 and Biosphere 2. BIOS-3 marked one of the pioneering endeavours towards achieving full atmosphere closure to sustain two to three humans by cultivating higher plants, thus fulfilling human metabolic requirements. This closed ecological system operated for five months under human supervision [92]. In contrast, Biosphere 2 encompassed an approximately 8000

m^{2}

sealed structure housing a scaled-down replica of various ecosystems, including rainforest, desert, steppe, ocean, field, and farm. Its ultimate goal was to establish a dynamic equilibrium capable of self-sustaining the enclosed environment and a team of eight scientists [12,93].

Any artificial closed environment, such as the ones outlined here, must have a set of reactions to perform cycles distributed among the species of the synthetic ecosystem interacting by metabolite exchange. These synthetic enclosed ecosystems must aim to zero matter loss, where all biochemical resources must be recyclable. In other words, the cycle of nutrients and matter must not be short-circuited by producing compounds that can not be biologically re-processed. Microbial biotechnologies and synthetic biology will be pivotal in filling the gaps in the reaction cycles and harnessing available volatiles and waste resources. Methanogenesis and electrolysis, nitrification and denitrification or stress responses are important space synthetic biology processes that can allow the production of propellant, food, biopolymers, and pharmaceutical products. At the same time, they can be used in the waste recycling processes and life-support environmental control. Thus increasing space exploration’s autonomy and long-term sustainability [77,78].

The pioneering design of BIOS-3 is very helpful in understanding the basic principles and how quantitative dynamical models can be formulated. In Figure 3a-b, we summarize the connection between biotic and abiotic components and a minimal model based on four key variables. Here, four variables capture the systems-level features, namely: (a) two key abiotic components (oxygen and carbon dioxide) and (b) two types of plants that regulate the “atmosphere” of the closed environment. Here, the human factor is encapsulated in the human metabolic rate

V_{o}

, excluding them from the mass conservation laws. Therefore, this model is completely closed regarding the atmosphere.

How could we modify the previously designed flows using synthetic biology? Again, quantitative population models can give us insight. The mathematical modeling of BIOS-3 (Figure 3b) reveals the presence of an equilibrium point, but also that this point is unstable under small disturbances [76]. This implies that some kind of external intervention to tune the parameters is a necessary requirement for system-level robustness. However, one interesting prediction from the synthetic environmental self-regulation (ENV regulation in Figure 2) might provide an alternative. The prediction [65] is that a diverse community (instead of simply two engineered strains) is much more likely to achieve environmental self-regulation. A full closure would be achievable with the addition of a rich synthetic community necessary to close the matter fluxes. Such a compartment (tagged as "synthetic biology" in Figure 3c) would allow the recycling of human and plant waste by a network of microorganisms that could be hybrid, i. e. including both natural or equipped with designed de novo capabilities. The reactions necessary for achieving complete closure, here considered sub-compartments, would be represented by formulating differential equations for N strains

S_{i}

, with

i = 1, . . . N

, where N denotes the total number of species involved in biochemical reactions. Remarkably, ongoing for over 30 years, there has been an endeavor to design and construct a hierarchically controlled ecological life support system facility, using microorganisms aimed at recovering resources from waste, known by the acronym MELiSSA [94,95,96]. Alternatively, The path towards LSS and ecospheres will require the formulation of ecological motifs that can cope with the potential outcomes of engineering designs, ensuring ecological resilience, long-term persistence and reliability. Network structures, like producer-consumer-reducer chains, could close a given system, where one species could reduce a given substrate to feed the next [97]. One key approximation would be the exploitation of mutualistic cycles, so called hypercycles [98,99]; where all species involved in the ecosystem are entangled in a closed catalytic architecture, ensuring this way their persistence, see Figure 3d. As discussed in [99] within the context of synthetic biology, the mutual dependencies between the members of the hypercycle (indicated by the terms

ξ_{i j} S_{i} S_{j}

in Figure 3d) guarantee the presence of all the components. By distributing over different strains a given number of functionalities, their persistence would guarantee their functional contribution to the system’s performance. Such a synthetic multispecies community could be engineered using the appropriate syntrophic interactions [100].

Finally, we could wonder which are the candidates for such engineered communities? Particularly outstanding ones are cyanobacteria. Along with microalgae, they have been proposed as key components for photobioreactors [101]. Desert cyanobacteria, particularly those adapted to extreme environments have been shown to be highly resistant to the harsh conditions of space and Martian simulated conditions [102,103]. Enhancement of these strains would be obtained using synthetic biology and not only allow for oxygen production but also to obtain energy, food, fuel and a variety of materials [104]. Their relevance will be highlighted when discussing synthetic ecosystems on the largest scales, as discussed in the next section.

4. Synthetic Biospheres

Our previous examples reveal the potential for interrogating the nature of ecological interactions by implementing micro- and mesoscale synthetic systems and their associated mathematical descriptions. They can also provide valuable insights into our understanding of planetary boundaries and novel ways of thinking about the future of our biosphere. The environmental regulation motif (Figure 2) offers a unique opportunity for small-scale experimental testing of questions regarding Earth systems science. In particular, it would help understand the interplay between microbial community responses to externally changing environments and how feedback loops can generate homeostasis.

In the previous section, we have also touched on this problem as we considered the limitations imposed by how a sustainable closed ecosystem would allow for persistent communities. In both cases, systems and synthetic biology approaches shed light on potential conditions for ecological persistence. Here, mathematical models are helpful to define the causal connections between different variables and to predict the likelihood of success for a given engineered design. The feasibility domains obtained from these models also provide a no less critical feature: their boundaries define the conditions for tipping points. Can this conceptual framework address the ongoing biodiversity and climate crisis?

The existence of tipping points in natural ecosystems was early raised within the ecological literature [105,106] and has become a significant research area in the last decades [107,108]. Due to diverse effects of Anthropogenic origin (global warming, contamination, habitat loss and intensive agriculture), many extant ecosystems face the possibility of rapid degradation as key environmental parameters cross critical thresholds [109,110]. Far from happening in the distant future, these events will likely become a reality over the next decades [111]. Along with much-needed policies regarding conservation, sustainable growth and the transition towards green energy sources, it has also been proposed that synthetic biology could play a relevant role [36,37,38,112] as an alternative to geoengineering scenarios. Because these bioengineering strategies require the inoculation of engineered microorganisms in extant habitats, this terraformation approach is an intervention scenario that could give rise to new communities. This path towards the use of synthetic biology to modify ecosystems has been gaining momentum, and microbial biotechnology is now a largely unexplored but very promising alternative that has been proposed within the context of bioremediation [39], coral reef restoration [113], dryland preservation [114,115], carbon sequestration [116,117] or biodiversity conservation [37,118]

One particular case study involves arid and semiarid ecosystems. These so-called Drylands cover around

45 %

of emerged lands and host more than one-third of the human population, and they are expanding while being threatened by global warming [119,120,121]. A very important contribution to dryland stability and resilience is the soil microbiome [122,123,124]. In this context, some particular species, such as cyanobacteria, are known to play a key role and have been used in restoration efforts where their inoculation can enhance carbon sequestration [125,126,127,128]. Not surprisingly, the potential for synthetic biology as an enhancer of this process has also been suggested [114].

Along with field studies (sometimes hand in hand), mathematical models have successfully addressed the problem of the origin of alternative states and catastrophic shifts [129,130]. One example is the so-called green-desert transition, where aridity values larger than

a = 0.8

trigger a shift from a vegetated state to a desert-like state. Recent studies on global drylands have shown that several regime shifts seem to be involved in the response of drylands to aridity levels [120]. We can illustrate this phenomenon using a toy model that captures some key components responsible for these shifts, where the population cover of a given area is indicated as x and modelled as a nonlinear equation:

\frac{d x}{d t} = r x^{2} (1 - \frac{x}{K}) - α x

(10)

K is the carrying capacity, while r and

α

are plants’ growth and death rates, respectively. Notice a quadratic term in the growth function characteristic of systems that exhibit facilitation: plants enhance the growth of other plants [131] usually mediated by soils. Because of this nonlinear term, the response of this system to external stress, quantified by

α

, is abrupt1. Specifically, if

α < α_{c} = r / 4

, a stable vegetation cover will be observed but will vanish for

α > α_{c}

. It can be shown that the system shifts from a state

x = K / 2

(thus displaying a half-covered area) to the desert (

x^{*} = 0

) state.

Dedicated quantitative and theoretical efforts have revealed that collapse is a likely future scenario for facilitation-driven communities, such as drylands [129]. Can such undesirable shifts be avoided or at least prevented? Are there potential ways of reducing the impact of aridification or even halting these systems in a safe state, avoiding catastrophic transitions? Is there room for synthetic biology as a way to stop ecosystem shifts? The answer to these questions requires considering the problem of multiple ecological scales [39].

In this terraformation scheme, synthetic strains allow us to bypass an obvious limitation of most geoengineering designs: the "machines" do not need to be built since each engineered cell can replicate itself. This advantage from biology makes it possible to spread on a given scale [37]. This, of course, raises several issues regarding safety [35,132,133]: can these interventions have “unintended consequences”? Interestingly, the answer to this question must be found in the collective behaviour of ecological networks. Under this view [65,134] engineering is designed to enhance biodiversity, and biodiversity defines the conditions for containment.

This engineering departs from the standard, top-down picture aimed at predictable control over the system properties. Instead, the terraformation scheme is an emergent engineering approach that follows two essential design principles. First, a resident community member is chosen as the candidate species to be modified [38]. The best choice here would be some species of cyanobacteria, which have a well-known impact in dryland ecosystems [128]. More importantly, they are ecosystem engineers: they have a specially disproportionate impact on the flows of matter and energy of the dryland soils. The term is especially relevant within ecology [135,136] and provides a helpful guide to identifying keystone species to define restoration strategies [137]. In other words, we define a terraformation strategy grounded in engineering ecosystem engineers.

The reason for choosing a microbial species from the resident community is that, as a member of a coevolved ecological network, we expect this species to display some stability [134]. Once the candidate has been isolated and modified, it is returned to the original community equipped with a given, designed functionality while preserving the wild-type interactions with other species.

The second part of this approach is based on a systems-level property strongly tied to ecosystem health: biodiversity [138], which plays a leading role (along with soil organic carbon) in preserving drylands [139,140]. While most studies within synthetic biology have addressed the problem of containment by actively pursuing gene-level control of growth [141,142], here we suggest that biodiversity, as well known from invasion ecology studies [143,144], will act as a firewall.

BOX 2. Emergent bioengineering: systems biology of ecosystem terraformation

What can be expected if we inoculate a given synthetic strain in a community? Mathematical models help predict the outcome of this intervention and the role played by biodiversity. One general scenario involves a set of species , namely

N_{i}

where

i = 1, 2, . . . n

, and a set of resources

{R_{k}}

, where

k = 1, 2, . . . m

. The growth rates for each resource and species are represented by

ρ \in (0, 1)

and

η \in (0, 1)

, respectively [138]. One is a strain (

N_{s y n}

) engineered from a resident species, thus sharing all the ecological interactions with the wild type. This synthetic strain can reduce the loss of a given, shared resource. The equations read:

\frac{d N_{i}}{d t} = η_{i} N_{i} (\sum_{k = 1}^{m} ξ_{i k} R_{k}) - σ_{i} N_{i}

(11)

for the species populations, whereas the resources will change in the following:

\frac{d R_{k}}{d t} = ρ_{k} - (\sum_{i = 1}^{n} ξ_{k i} N_{i}) R_{k} - \frac{β_{k} R_{k}}{1 + δ_{k α} (\frac{N_{s y n}}{λ})}

(12)

Whereas most of the previous set of equations corresponds to the standard resource-consumer models, the last term in (13) introduces the effect of the synthetic strain (

N_{s y n}

). As we can see, it has an inhibitory effect on the loss of the

α

-th resource (here

δ_{k α} = 1

k = α

and zero otherwise) whereas, in the absence of the synthetic strain (i. e. if

N_{s y n} = 0

R_{k}

decays at a rate

β_{k}

. By modelling these populations, it has been shown that, under the proposed engineering scheme, biodiversity acts as a firewall for expanding the synthetic strain, which performs its function and improves the community without species loss. Because of this shared resource’s effective decay, there is an emergent community-level readjustment: we do not intend to predict (as in a top-down scenario) how different species will behave. Instead, the fact that biodiversity enhances ecosystem functionality as an indicator of health makes it the target of the intervention.

Figure 4. Synthetic ecosystems for dryland restoration and conservation. A visual summary of the three levels of analysis. Here, we include, from bottom to top, (1) competitive synthetic pair in liquid media, theoretically described by standard ode models. This level is the most basic implementation in the test tube (2) micro/mesocosms implementation of cooperation among synthetically engineered microorganisms and the soil crust, where cooperative interactions in the mathematical model are now extended to include the feedback with environmental forcing. Finally, the biosphere and (3) large-scale systems can be approached using formal models involving a network-level description. As we move from one level to another, new, emergent properties must be considered. Feedback across scales may indeed exist, however, each level possesses its own dynamics significant enough to elucidate its basic functioning independently, without necessarily considering the others. Therefore, bidirectionally, for example, such as from the mesocosm to the biosphere and vice versa, illustrate the feasibility of employing various mathematical approximations to address broader or community-specific inquiries at each level.

Figure 5. Synthetic ecosystems in context. Using three axes, namely: (a) the degree of community development to achieve their stationary state, (b) species (strain) diversity, and (c) the amount of human intervention required to build the ecosystem. Each sphere represents a given system, and the three scales (not represented in proportion) considered in this paper appear as three nested cubes (

C_{1} \subset C_{2} \subset C_{3}

). Each case study is located relative to others (it is not a metric space). Systems close to the cube’s floor are designed, constructed, or require an initial condition that allows them to achieve their organization. Novel and synthetic domains are indicated by the grey and yellow areas, respectively. Anthropogenic actions create conditions for the emergence of so-called novel ecosystems[145]. Beyond, synthetic ecosystems span out of design effort. In (a), we have the test-tube scale designs that involve standard motifs, small-scale microbiomes living in man-made artefacts (coffee machines or solar panels) and mesocosm experiments that involve synthetic biology and life support systems. These two scales are shown within the larger cube

C_{1}

in (b) that contains undisturbed and designed (terraformed) ecosystems as two corners on the right upper part. Grey spheres stand for human-driven ecosystems that are highly controlled (bottom floor) to the urban microbiome. Blue marbles indicate potential scenarios of ecosystem intervention.

C_{1} \subset C_{2} \subset C_{3}

C_{1}

What kind of extra functionality can be used? An example of drylands would be a genetic construct that helps fight aridity by reducing water losses. Once again, cyanobacteria are known to secrete extracellular polysaccharides that contribute to soil health in different ways, from the increase in organic carbon to the improvement of soil stability and water retention [146,147,148]. Water losses could be reduced by engineering a strain to produce a more efficient extracellular molecule, and the possibility of an undesirable ecosystem shift could be prevented (Box 2). As shown in [138], the population-level impact on the rest of the community is typically negligible. All species remain basically in the same state, with very rare extinctions and, in some cases, showing augmentation. This is the first evidence that the risks associated with engineering in the wild employing synthetic biology might have been overestimated. As the population model suggests, the potential unintended consequences might be negligible under our emergent engineering approach. Here, experiments in micro- and mesocosms under controlled conditions will be required to test the validity of the model approximations and its predictions. In this context, the lessons provided by small- and medium-scale engineered communities (the two lower layers in Figure 4) and those from the fields of invasion ecology can inform us about the feasibility of these interventions.

5. Discussion

Understanding natural ecosystems, repairing dysbiotic microbiomes, planning for future space missions, and even engineering our biosphere are examples of the wide range of problems where synthetic biology can play a role within ecosystems across scales. This paper synthesises ideas and case studies concerned with ecological communities that are fully designed using genetic engineering or built as hybrid assemblies. This includes fully engineered microcosms, augmented ecospheres or terraformed ecosystems. A common thread in our analysis involves using mathematical models that help us understand the implications of nonlinear interactions and predict potential outcomes. This systems biology view connects with the traditional quantitative study of ecological assemblies through population dynamics.

Although each scale is valuable (and, to a point, self-contained) in itself, they are by no means disconnected. Fundamental dynamical and structural properties of simple ecological motifs are crucial to predicting the expected outcomes of some types of interactions within more complex communities. Simple regulatory feedbacks provide evidence for potential designs of microbial assemblies that could offer enhanced resilience to closed or semi-closed ecospheres. The lessons learned from studying these hybrid mesocosms could be instrumental in future scenarios of ecological engineering based on our terraformation scheme. This rich range of designs and scales is summarized in Figure 5 using the concept of a morphospace [149,150,151]. In a nutshell, we define a three-dimensional space where the axes involve (1) the degree of human intervention (from no intervention to complete engineering), (2) the richness of species or strains, and (3) the role of development in generating the outcome.

Within this space, each case study is represented by a sphere and their location is defined relative to others (and thus, there is no metric). We use two highlighted areas indicating synthetic ecosystems and the so-called novel ecosystems. The latter is associated with losing valuable, historical habitats. These include communities that result from non-historical networks of species arising from human-disturbed habitats, environmental change or species invasions [145,152,153]. Figure 5a shows the microscale systems and the mesoscale ecosphere cubes (

C_{3}

and

C_{2}

). In contrast, Figure 5b shows their location within the broader context, including complex ecosystems (

C_{1}

). As we have seen in the previous sections, the relevance of synthetic biology percolates across scales.

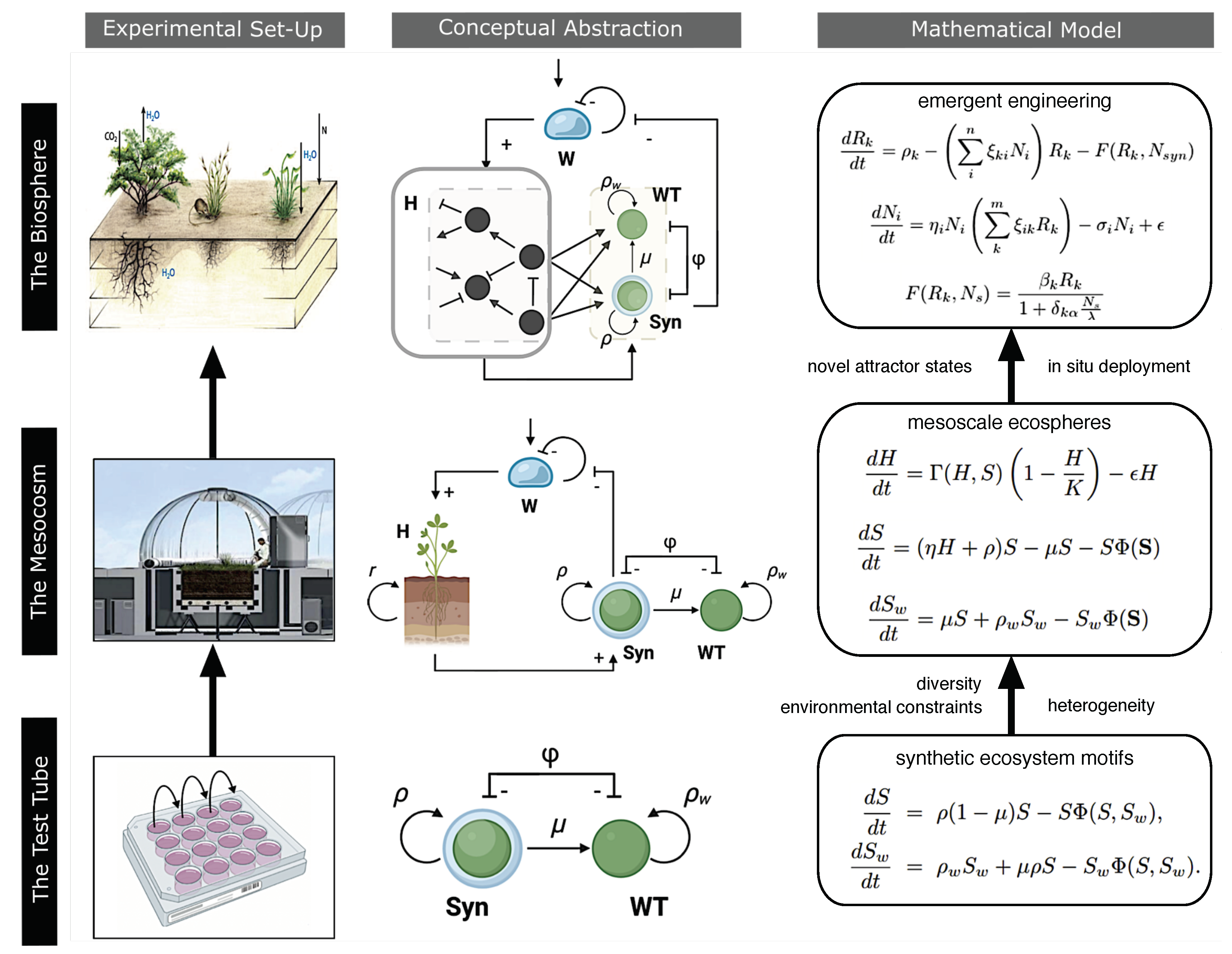
The study and modelling of synthetic ecosystems can be extended into multiple directions, each addressing relevant questions. Here, we provide a list of potential paths for exploration:

Although the microbial consortia described above follow the logic of ecological interactions in nature, this constraint does not necessarily limit the potential design principles, particularly when engineering computations with living cells [154]. In particular, it has been shown that complex functionalities can be built on engineered consortia that do not follow either biological or standard engineering designs [155]. What are the corresponding motifs and the alternative designs for ecological engineering?
Who needs to be targeted when modifying ecospheres or whole communities in the wild? If we keep the single-species scenario described above, ecosystem engineers are a clear choice. However, considering single-species changes is one particular scenario within engineering complex communities, which can be obtained using either synthetic biology [87,156] or directed evolution [157]. Importantly, despite the success of microbiome transplants (which would be the non-engineered counterpart of our proposal) little is known in terms of theoretical models about how these transplants actually work. Developing synthetic models to address this problem would benefit both biomedical research and new ecosystem bioengineering strategies.
Detailed quantitative models of ecological communities require estimates about the sign and weight of species-species interactions. This is a challenging problem that has received much attention and mathematical models involving several (n) species can be easily defined using generalised Lotka-Volterra equations, namely:

$\frac{d c_{i}}{d t} = μ_{i} c_{i} (1 + \frac{1}{c_{\max}} \sum_{k = 1}^{N} β_{i k} c_{k}) .$

(13)

[158,159] This is the standard model used in most quantitative analyses of microbiome dynamics, particularly the gut microbiome [160,161,162,163,164]. The challenge here is to deal with appropriate estimates of the matrix $B = (β_{i j})$ that captures the strength of competitive interactions [165]. Of particular importance if to determine the resilience of these communities and their responses to engineering them. Recent work on community transitions [166] provides a useful estimate of these properties (based on an entropy measure) that could be used as a quantitative approach to determine the likelihood of microbiome shifts.
Engineering efforts affecting extant communities, such as drylands, present an important challenge in terms of the strategies to be followed given the interactions between scales. The microbiome affects soil carbon content, which influences plant cover and the quality of the plant community influences back soil properties. On the other hand, we are considering changes that can percolate across whole landscapes, which can display several sources of heterogeneity. The simple scheme summarized in table 2 might require an extended approach that considers all these sources of variability. In this context, future efforts might benefit from machine learning techniques that can provide a system-level integration of data-driven information about responses across scales. Future models of terraformation should address this multiscale picture.
In our previous examples, we assumed that synthetic biology has microbial candidates as potential chassis for engineered designs, and the population dynamics occur at the bacterial-resource scale. Viruses, on the other hand, and despite their tiny contribution to biomass, are acknowledged as crucial players in the dynamics of microbiomes, and they are largely understudied [167]. The impact of viruses and their potential role as vectors for ecosystem engineering should be explored using mathematical models that introduce the virome in an explicit manner [168].
Under an evolutionary perspective, the nature of innovations (or major evolutionary transitions, see [169]) is one particularly relevant one. These transitions include for example the origins of the first cells and early forms of multicellularity. It has been proposed that an approach to these questions can be grounded in considering "Synthetic transitions" [170] where potential paths to innovation could be recreated using synthetic biology, artificial life or evolutionary robotics. Along with the standard list of MET, it has been suggested that synthetic ecosystems can shed light into a variety of open problems regarding the evolution of complexity beyond the species level [171]. Here too, ongoing efforts to build and augment in vitro synthetic interaction networks [172,173,174], along with new population dynamics models could help define scenarios of ecosystem transitions and the role played by contingency versus robust network properties on the tempo and mode of microbiome evolution.

The ecological perspective within many domains of the life sciences, from cancer to biomedicine makes the study of synthetic ecosystems an extremely useful bridge between models and reality. Following the tradition of building microcosms as partial, and yet representative in vitro approximations of natural communities, synthetic biology stands as a unique framework to bring together experimental studies and mathematical models. Moreover, they will help bring together different scales and conceptual frameworks, connecting domains as diverse as invasion ecology and metabolomics. We believe that the lessons to be learned from biomedical studies on the gut microbiome will inform the application of synthetic biology to restoration and conservation efforts, while the system perspective associated to the latter might strongly benefit our understanding of organismal-level ecology. In all these scenarios, theoretical models are likely to play a pivotal role in achieving unifying principles.

Acknowledgements

The authors want to thank Fernando Maestre, Víctor de Lorenzo, James Sharpe and the members of the Complex Systems Lab for useful discussions and support and Charlie Hutchison and Salaria Kea for inspiration. This work was supported by the Planetary Biology EMBL program (RS, NC), the PR01018-EC-H2020-FET-Open MADONNA project and funded by the Ajuntament de Barcelona and “la Caixa” Foundation (RS, VM). A PID2019-111680GB-I00 grant from the Spanish government (RS, NC), an AGAUR 2021 SGR 00751 grant (RS), AGAUR FI-SDUR 2020 grant (VM) and a PRE2020-091968 grant from the Spanish government (JPM). D.R.A acknowledges support from the program ANR-22-CPJ2-0064-01 by the French “Agence Nationale de la Recherche”. R.S. thanks the Santa Fe Institute, where much of this work was done.

References

Lotka, A.J. Elements of mathematical biology; Dover Publications: Mineola, NY, 1956. [Google Scholar]
Bacaër, N. Histoires de mathématiques et de populations; Cassini, 2008. [Google Scholar]
Vandermeer, J.H.; Goldberg, D.E. Population Ecology, 2 ed.; Princeton University Press: Princeton, NJ, 2013. [Google Scholar]
Weitz, J.S. Quantitative Biosciences: Dynamics Across Cells, Organisms, and Populations; Princeton University Press, 2024. [Google Scholar]
Sole, R.V.; Bascompte, J. Self-organization in complex ecosystems.; Monographs in Population Biology, Princeton University Press: Princeton, NJ, 2006. [Google Scholar]
Botsford, L.W.; Wilson White, J.; Hastings, A. Population dynamics for conservation; Oxford University Press: London, England, 2019. [Google Scholar]
Anderson, R.M.; May, R.M. Infectious diseases of humans; Oxford science publications, Oxford University Press: London, England, 1991. [Google Scholar]
Lockwood, J.L.; Hoopes, M.F.; Marchetti, M.P. Invasion Ecology, 2 ed.; Wiley-Blackwell: Chichester, England, 2013. [Google Scholar]
Odum, E.P.; Barrett, G.W.; others. Fundamentals of ecology, Vol. 3, Saunders Philadelphia, 1971.
Pimm, S.L. The balance of nature?: ecological issues in the conservation of species and communities; University of Chicago Press, 1991. [Google Scholar]
May, R.M. Stability and complexity in model ecosystems; Princeton Landmarks in Biology, Princeton University Press: Princeton, NJ, 2001. [Google Scholar]
Beyers, R.J.; Odum, H.T. Ecological Microcosms, 1993 ed.; Springer Advanced Texts in Life Sciences, Springer: New York, NY, 1993. [Google Scholar]
De Roy, K.; Marzorati, M.; Van den Abbeele, P.; Van de Wiele, T.; Boon, N. Synthetic microbial ecosystems: an exciting tool to understand and apply microbial communities. Environmental microbiology 2014, 16, 1472–1481. [Google Scholar] [CrossRef]
Friedman, J.; Gore, J. Ecological systems biology: The dynamics of interacting populations. Current Opinion in Systems Biology 2017, 1, 114–121. [Google Scholar] [CrossRef]
Goldford, J.E.; Lu, N.; Bajić, D.; Estrela, S.; Tikhonov, M.; Sanchez-Gorostiaga, A.; Segrè, D.; Mehta, P.; Sanchez, A. Emergent simplicity in microbial community assembly. Science 2018, 361, 469–474. [Google Scholar] [CrossRef] [PubMed]
Hu, J.; Amor, D.R.; Barbier, M.; Bunin, G.; Gore, J. Emergent phases of ecological diversity and dynamics mapped in microcosms. Science 2022, 378, 85–89. [Google Scholar] [CrossRef] [PubMed]
Skwara, A.; Gowda, K.; Yousef, M.; Diaz-Colunga, J.; Raman, A.S.; Sanchez, A.; Tikhonov, M.; Kuehn, S. Statistically learning the functional landscape of microbial communities. Nature Ecology & Evolution 2023, 7, 1823–1833. [Google Scholar]
Arya, S.; George, A.B.; O’Dwyer, J.P. Sparsity of higher-order landscape interactions enables learning and prediction for microbiomes. Proceedings of the National Academy of Sciences 2023, 120, e2307313120. [Google Scholar] [CrossRef] [PubMed]
Shoemaker, W.R.; Grilli, J. Investigating macroecological patterns in coarse-grained microbial communities using the stochastic logistic model of growth. bioRxiv 2023, 2023–03. [Google Scholar]
Odum, E.P. The Mesocosm. BioScience 1984, 34, 558–562. [Google Scholar] [CrossRef]
Nelson, M.; Burgess, T.L.; Alling, A.; Alvarez-Romo, N.; Dempster, W.F.; Walford, R.L.; Allen, J.P. Using a closed ecological system to study Earth’s biosphere: Initial results from Biosphere 2. Bioscience 1993, 43, 225–236. [Google Scholar] [CrossRef]
Cohen, J.E.; Tilman, D. Biosphere 2 and Biodiversity–The Lessons So Far. Science 1996, 274, 1150–1151. [Google Scholar] [CrossRef]
Levin, S.A. Ecosystems and the Biosphere as Complex Adaptive Systems. Ecosystems 1998, 1, 431–436. [Google Scholar] [CrossRef]
Levin, S.A. Multiple Scales and the Maintenance of Biodiversity. Ecosystems 2000, 3, 498–506. [Google Scholar] [CrossRef]
Widder, S.; Allen, R.J.; Pfeiffer, T.; Curtis, T.P.; Wiuf, C.; Sloan, W.T.; Cordero, O.X.; Brown, S.P.; Momeni, B.; Shou, W.; others. Challenges in microbial ecology: building predictive understanding of community function and dynamics. The ISME journal 2016, 10, 2557–2568. [Google Scholar] [CrossRef]
Wilkinson, D.M. The parable of Green Mountain: Ascension Island, ecosystem construction and ecological fitting, 2004.
Amaral-Zettler, L.A.; Zettler, E.R.; Mincer, T.J. Ecology of the plastisphere. Nature Reviews Microbiology 2020, 18, 139–151. [Google Scholar] [CrossRef]
Schwartzkopf, S.H. Design of a controlled ecological life support system. Bioscience 1992, 42, 526–535. [Google Scholar] [CrossRef]
Escalante, A.E.; Rebolleda-Gómez, M.; Benítez, M.; Travisano, M. Ecological perspectives on synthetic biology: insights from microbial population biology. Frontiers in microbiology 2015, 6, 126260. [Google Scholar] [CrossRef]
Zomorrodi, A.R.; Segrè, D. Synthetic ecology of microbes: mathematical models and applications. Journal of molecular biology 2016, 428, 837–861. [Google Scholar] [CrossRef]
Müller, M.; Neugeboren, B.; Nelson, D.; Murray, A. Genetic drift opposes mutualism during spatial population expansion. Proc Natl Acad Sci 2014, 111, 1037–42. [Google Scholar] [CrossRef]
Amor, D.R.; Montañez, R.; Duran-Nebreda, S.; Solé, R. Spatial dynamics of synthetic microbial mutualists and their parasites. PLOS Computational Biology 2017, 13, e1005689. [Google Scholar] [CrossRef]
Knödlseder, N.; Fábrega, M.J.; Santos-Moreno, J.; Manils, J.; Toloza, L.; Marín Vilar, M.; Fernández, C.; Broadbent, K.; Maruotti, J.; Lemenager, H.; others. Delivery of a sebum modulator by an engineered skin microbe in mice. Nature Biotechnology 2024, 1–6. [Google Scholar] [CrossRef]
de Lorenzo, V. Systems biology approaches to bioremediation. Current opinion in biotechnology 2008, 19, 579–589. [Google Scholar] [CrossRef] [PubMed]
Schmidt, M.; de Lorenzo, V. Synthetic constructs in/for the environment: managing the interplay between natural and engineered biology. FEBS letters 2012, 586, 2199–2206. [Google Scholar] [CrossRef] [PubMed]
de Lorenzo, V. Environmental Galenics: large-scale fortification of extant microbiomes with engineered bioremediation agents. Philosophical Transactions of the Royal Society B 2022, 377, 20210395. [Google Scholar] [CrossRef] [PubMed]
Solé, R. Bioengineering the biosphere? Ecological Complexity 2015, 22, 40–49. [Google Scholar] [CrossRef]
Solé, R.V.; Montañez, R.; Duran-Nebreda, S. Synthetic circuit designs for earth terraformation. Biology Direct 2015, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
de Lorenzo, V.; Marliere, P.; Sole, R. Bioremediation at a global scale: from the test tube to planet Earth. Microbial biotechnology 2016, 9, 618–625. [Google Scholar] [CrossRef] [PubMed]
Conde-Pueyo, N.; Vidiella, B.; Sardanyés, J.; Berdugo, M.; Maestre, F.T.; De Lorenzo, V.; Solé, R. Synthetic biology for terraformation lessons from mars, earth, and the microbiome. life 2020, 10, 14. [Google Scholar] [CrossRef] [PubMed]
Lotka, A.J. The growth of mixed populations: two species competing for a common food supply. Journal of the Washington Academy of Sciences 1932, 22, 461–469. [Google Scholar]
Volterra, V. Fluctuations in the Abundance of a Species considered Mathematically. Nature 1926, 118, 558–560. [Google Scholar] [CrossRef]
Gause, G.F. Experimental Studies on the Struggle for Existence: I. Mixed Population of Two Species of Yeast. The Journal of Experimental Biology 1932, 9, 389–402. [Google Scholar] [CrossRef]
Solé, R.V.; Bascompte, J.; Valls, J. Stability and complexity of spatially extended two-species competition. Journal of theoretical Biology 1992, 159, 469–480. [Google Scholar] [CrossRef]
Mitri, S.; Clarke, E.; Foster, K.R. Resource limitation drives spatial organization in microbial groups. The ISME journal 2016, 10, 1471–1482. [Google Scholar] [CrossRef] [PubMed]
Eigen, M.; Schuster, P. The Hypercycle; Springer: Berlin, Germany, 1979. [Google Scholar]
Sardanyés, J.; Solé, R.V. Bifurcations and phase transitions in spatially extended two-member hypercycles. Journal of Theoretical Biology 2006, 243, 468–482. [Google Scholar] [CrossRef] [PubMed]
Shou, W.; Ram, S.; Vilar, J.M. Synthetic cooperation in engineered yeast populations. Proceedings of the National Academy of Sciences 2007, 104, 1877–1882. [Google Scholar] [CrossRef] [PubMed]
Hosoda, K.; Suzuki, S.; Yamauchi, Y.; Shiroguchi, Y.; Kashiwagi, A.; Ono, N.; Mori, K.; Yomo, T. Cooperative Adaptation to Establishment of a Synthetic Bacterial Mutualism. PLoS ONE 2011, 6, e17105. [Google Scholar] [CrossRef] [PubMed]
Momeni, B.; Waite, A.J.; Shou, W. Spatial self-organization favors heterotypic cooperation over cheating. Elife 2013, 2, e00960. [Google Scholar] [CrossRef] [PubMed]
Szathmáry, E. The origin of replicators and reproducers. Philosophical Transactions of the Royal Society B: Biological Sciences 2006, 361, 1761–1776. [Google Scholar] [CrossRef] [PubMed]
Smith, J.M. Hypercycles and the origin of life. Nature 1979, 280, 541–541. [Google Scholar] [CrossRef]
Boerlijst, M.C.; Hogeweg, P. Spiral wave structure in pre-biotic evolution: hypercycles stable against parasites. Physica D: Nonlinear Phenomena 1991, 48, 17–28. [Google Scholar] [CrossRef]
Pande, S.; Kaftan, F.; Lang, S.; Svatoš, A.; Germerodt, S.; Kost, C. Privatization of cooperative benefits stabilizes mutualistic cross-feeding interactions in spatially structured environments. The ISME Journal 2016, 10, 1413–1423. [Google Scholar] [CrossRef]
Weber, W.; Daoud-El Baba, M.; Fussenegger, M. Synthetic ecosystems based on airborne inter- and intrakingdom communication. Proceedings of the National Academy of Sciences 2007, 104, 10435–10440. [Google Scholar] [CrossRef] [PubMed]
Lotka, A.J. Contribution to the Theory of Periodic Reactions. The Journal of Physical Chemistry 1910, 14, 271–274. [Google Scholar] [CrossRef]
Martin, M.O. Predatory prokaryotes: an emerging research opportunity. Journal of Molecular Microbiology and Biotechnology 2002, 4, 467–478. [Google Scholar] [PubMed]
Pérez, J.; Moraleda-Muñoz, A.; Marcos-Torres, F.J.; Muõz Dorado, J. Bacterial predation: 75 years and counting! Environmental Microbiology 2016, 18, 766–779. [Google Scholar] [CrossRef] [PubMed]
Balagaddé, F.K.; Song, H.; Ozaki, J.; Collins, C.H.; Barnet, M.; Arnold, F.H.; Quake, S.R.; You, L. A synthetic Escherichia coli predator-prey ecosystem. Molecular Systems Biology 2008, 4. [Google Scholar] [CrossRef] [PubMed]
Whiteley, M.; Diggle, S.P.; Greenberg, E.P. Progress in and promise of bacterial quorum sensing research. Nature 2017, 551, 313–320. [Google Scholar] [CrossRef] [PubMed]
Barabás, G.; Michalska-Smith, M.J.; Allesina, S. Self-regulation and the stability of large ecological networks. Nature Ecology & Evolution 2017, 1, 1870–1875. [Google Scholar] [CrossRef] [PubMed]
Konopka, A.; Lindemann, S.; Fredrickson, J. Dynamics in microbial communities: unraveling mechanisms to identify principles. The ISME Journal 2014, 9, 1488–1495. [Google Scholar] [CrossRef] [PubMed]
Ranheim Sveen, T.; Hannula, S.; Bahram, M. Microbial regulation of feedbacks to ecosystem change. Trends in Microbiology 2024, 32, 68–78. [Google Scholar] [CrossRef] [PubMed]
Watson, A.J.; Lovelock, J.E. Biological homeostasis of the global environment: the parable of Daisyworld. Tellus B: Chemical and Physical Meteorology 1983, 35, 284. [Google Scholar] [CrossRef]
Maull, V.; Pla Mauri, J.; Conde Pueyo, N.; Solé, R. A synthetic microbial Daisyworld: planetary regulation in the test tube. Journal of The Royal Society Interface 2024, 21. [Google Scholar] [CrossRef] [PubMed]
Axelrod, R.; Hamilton, W.D. The Evolution of Cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
Smith, J.M.; Price, G.R. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
Frank, S.A. Models of Parasite Virulence. The Quarterly Review of Biology 1996, 71, 37–78. [Google Scholar] [CrossRef] [PubMed]
Pfeiffer, T.; Schuster, S. Game-theoretical approaches to studying the evolution of biochemical systems. Trends in Biochemical Sciences 2005, 30, 20–25. [Google Scholar] [CrossRef] [PubMed]
Riley, M.A.; Wertz, J.E. Bacteriocins: Evolution, Ecology, and Application. Annual Review of Microbiology 2002, 56, 117–137. [Google Scholar] [CrossRef]
Granato, E.T.; Meiller-Legrand, T.A.; Foster, K.R. The Evolution and Ecology of Bacterial Warfare. Current Biology 2019, 29, R521–R537. [Google Scholar] [CrossRef] [PubMed]
Kerr, B.; Riley, M.A.; Feldman, M.W.; Bohannan, B.J.M. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature 2002, 418, 171–174. [Google Scholar] [CrossRef] [PubMed]
Neumann, G.; Schuster, S. Continuous model for the rock-scissors-paper game between bacteriocin producing bacteria. Journal of Mathematical Biology 2007, 54, 815–846. [Google Scholar] [CrossRef]
van den Berg, N.I.; Machado, D.; Santos, S.; Rocha, I.; Chacón, J.; Harcombe, W.; Mitri, S.; Patil, K.R. Ecological modelling approaches for predicting emergent properties in microbial communities. Nature Ecology & Evolution 2022, 6, 855–865. [Google Scholar] [CrossRef]
Shetty, S.A.; Smidt, H.; de Vos, W.M. Reconstructing functional networks in the human intestinal tract using synthetic microbiomes. Current Opinion in Biotechnology 2019, 58, 146–154. [Google Scholar] [CrossRef]
Bartsev, S.; Okhonin, V. Potentialities of theoretical and experimental prediction of life support systems reliability. Advances in Space Research 1999, 24, 407–412. [Google Scholar] [CrossRef] [PubMed]
Menezes, A.A.; Cumbers, J.; Hogan, J.A.; Arkin, A.P. Towards synthetic biological approaches to resource utilization on space missions. Journal of the Royal Society interface 2015, 12, 20140715. [Google Scholar] [CrossRef] [PubMed]
Santomartino, R.; Averesch, N.J.; Bhuiyan, M.; Cockell, C.S.; Colangelo, J.; Gumulya, Y.; Lehner, B.; Lopez-Ayala, I.; McMahon, S.; Mohanty, A.; others. Toward sustainable space exploration: a roadmap for harnessing the power of microorganisms. Nature communications 2023, 14, 1391. [Google Scholar] [CrossRef]
Foster, K.R.; Schluter, J.; Coyte, K.Z.; Rakoff-Nahoum, S. The evolution of the host microbiome as an ecosystem on a leash. Nature 2017, 548, 43–51. [Google Scholar] [CrossRef] [PubMed]
Folsome, C.E.; Hanson, J.A. The emergence of materially-closed-system ecology. Ecosystem Theory and Application, 1986; 269–299. [Google Scholar]
Ulanowicz, R.E. Identifying the structure of cycling in ecosystems. Mathematical Biosciences 1983, 65, 219–237. [Google Scholar] [CrossRef]
Loreau, M. Material cycling and the stability of ecosystems. The American Naturalist 1994, 143, 508–513. [Google Scholar] [CrossRef]
Rillig, M.C.; Antonovics, J. Microbial biospherics: The experimental study of ecosystem function and evolution. Proceedings of the National Academy of Sciences 2019, 116, 11093–11098. [Google Scholar] [CrossRef] [PubMed]
Shoemaker, W.R.; Jones, S.E.; Muscarella, M.E.; Behringer, M.G.; Lehmkuhl, B.K.; Lennon, J.T. Microbial population dynamics and evolutionary outcomes under extreme energy limitation. Proceedings of the National Academy of Sciences 2021, 118, e2101691118. [Google Scholar] [CrossRef]
de Jesús Astacio, L.M.; Prabhakara, K.H.; Li, Z.; Mickalide, H.; Kuehn, S. Closed microbial communities self-organize to persistently cycle carbon. Proceedings of the National Academy of Sciences 2021, 118, e2013564118. [Google Scholar] [CrossRef]
Goyal, A.; Flamholz, A.I.; Petroff, A.P.; Murugan, A. Closed ecosystems extract energy through self-organized nutrient cycles. Proceedings of the National Academy of Sciences 2023, 120, e2309387120. [Google Scholar] [CrossRef] [PubMed]
McCarty, N.S.; Ledesma-Amaro, R. Synthetic biology tools to engineer microbial communities for biotechnology. Trends in biotechnology 2019, 37, 181–197. [Google Scholar] [CrossRef] [PubMed]
Sanchez, A.; Bajic, D.; Diaz-Colunga, J.; Skwara, A.; Vila, J.C.; Kuehn, S. The community-function landscape of microbial consortia. Cell Systems 2022, 14, 122–134. [Google Scholar] [CrossRef] [PubMed]
Diaz-Colunga, J.; Catalan, P.; San Roman, M.; Arrabal, A.; Sanchez, A. Full factorial construction of synthetic microbial communities. bioRxiv 2024, 2024–05. [Google Scholar]
Ben Said, S.; Or, D. Synthetic microbial ecology: engineering habitats for modular consortia. Frontiers in microbiology 2017, 8, 252185. [Google Scholar] [CrossRef] [PubMed]
Menezes, A.A.; Montague, M.G.; Cumbers, J.; Hogan, J.A.; Arkin, A.P. Grand challenges in space synthetic biology. Journal of The Royal Society Interface 2015, 12, 20150803. [Google Scholar] [CrossRef] [PubMed]
Gitelson, I.; Terskov, I.; Kovrov, B.; Lisovskii, G.; Okladnikov, Y.N.; Sid’Ko, F.Y.; Trubachev, I.; Shilenko, M.; Alekseev, S.; Pan’kova, I.; others. Long-term experiments on man’s stay in biological life-support system. Advances in Space Research 1989, 9, 65–71. [Google Scholar] [CrossRef] [PubMed]
Gitelson, J.I.; Lisovsky, G.M.; MacElroy, R.D. Man-Made Closed Ecological Systems; Earth space institute book series; CRC Press: London, England, 2002. [Google Scholar]
Fulget, N.; Poughon, L.; Richalet, J.; Lasseur, C. MELISSA: global control strategy of the artificial ecosystem by using first principles models of the compartments. Advances in Space Research 1999, 24, 397–405. [Google Scholar] [CrossRef] [PubMed]
Lasseur, C.; Brunet, J.; De Weever, H.; Dixon, M.; Dussap, G.; Godia, F.; Leys, N.; Mergeay, M.; Van Der Straeten, D. MELiSSA: the European project of closed life support system. Gravitational and Space Research 2010, 23. [Google Scholar]
Ciurans, C.; Bazmohammadi, N.; Poughon, L.; Vasquez, J.C.; Dussap, C.G.; Gòdia, F.; Guerrero, J.M. Hierarchically controlled ecological life support systems. Computers & Chemical Engineering 2022, 157, 107625. [Google Scholar]
Bartsev, S. Stoichiometric constraints and complete closure of long-term life support systems. Advances in Space Research 2004, 34, 1509–1516. [Google Scholar] [CrossRef]
Eigen, M.; Schuster, P. The hypercycle: a principle of natural self-organization, Springer Science & Business Media, 2012.
Conde-Pueyo, N.; Vidiella, B.; Sardanyés, J.; Berdugo, M.; Maestre, F.T.; De Lorenzo, V.; Solé, R. Synthetic biology for terraformation lessons from mars, earth, and the microbiome. life 2020, 10, 14. [Google Scholar] [CrossRef]
Mee, M.T.; Collins, J.J.; Church, G.M.; Wang, H.H. Syntrophic exchange in synthetic microbial communities. Proceedings of the National Academy of Sciences 2014, 111, E2149–E2156. [Google Scholar] [CrossRef] [PubMed]
Mapstone, L.J.; Leite, M.N.; Purton, S.; Crawford, I.A.; Dartnell, L. Cyanobacteria and microalgae in supporting human habitation on Mars. Biotechnology Advances 2022, 59, 107946. [Google Scholar] [CrossRef] [PubMed]
Billi, D.; Baqué, M.; Smith, H.; McKay, C.; others. Cyanobacteria from extreme deserts to space. Advances in Microbiology 2013, 3, 80–86. [Google Scholar] [CrossRef]
Billi, D. Desert cyanobacteria under space and planetary simulations: a tool for searching for life beyond Earth and supporting human space exploration. International Journal of Astrobiology 2019, 18, 483–489. [Google Scholar] [CrossRef]
Verseux, C.; Baqué, M.; Lehto, K.; de Vera, J.P.P.; Rothschild, L.J.; Billi, D. Sustainable life support on Mars–the potential roles of cyanobacteria. International Journal of Astrobiology 2016, 15, 65–92. [Google Scholar] [CrossRef]
Holling, C.S. Resilience and stability of ecological systems. Annual review of ecology and systematics 1973, 4, 1–23. [Google Scholar] [CrossRef]
May, R.M. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 1977, 269, 471–477. [Google Scholar] [CrossRef]
Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef]
Scheffer, M. Critical transitions in nature and society; Vol. 16, Princeton University Press, 2020.
Rockström, J.; Steffen, W.; Noone, K.; Persson, Å.; Chapin III, F.S.; Lambin, E.; Lenton, T.M.; Scheffer, M.; Folke, C.; Schellnhuber, H.J.; others. Planetary boundaries: exploring the safe operating space for humanity. Ecology and society 2009, 14. [Google Scholar] [CrossRef]
Turner, M.G.; Calder, W.J.; Cumming, G.S.; Hughes, T.P.; Jentsch, A.; LaDeau, S.L.; Lenton, T.M.; Shuman, B.N.; Turetsky, M.R.; Ratajczak, Z.; others. Climate change, ecosystems and abrupt change: science priorities. Philosophical Transactions of the Royal Society B 2020, 375, 20190105. [Google Scholar] [CrossRef] [PubMed]
Solé, R.; Levin, S. Ecological complexity and the biosphere: the next 30 years, 2022.
Jansson, J.K.; McClure, R.; Egbert, R.G. Soil microbiome engineering for sustainability in a changing environment. Nature Biotechnology 2023, 41, 1716–1728. [Google Scholar] [CrossRef] [PubMed]
Cavicchioli, R.; Ripple, W.J.; Timmis, K.N.; Azam, F.; Bakken, L.R.; Baylis, M.; Behrenfeld, M.J.; Boetius, A.; Boyd, P.W.; Classen, A.T.; others. Scientists’ warning to humanity: microorganisms and climate change. Nature Reviews Microbiology 2019, 17, 569–586. [Google Scholar] [CrossRef] [PubMed]
Maestre, F.T.; Sole, R.; Singh, B.K. Microbial biotechnology as a tool to restore degraded drylands. Microbial biotechnology 2017, 10, 1250–1253. [Google Scholar] [CrossRef] [PubMed]
Vidiella, B.; Sardanyés, J.; Solé, R.V. Synthetic soil crusts against green-desert transitions: a spatial model. Royal Society open science 2020, 7, 200161. [Google Scholar] [CrossRef] [PubMed]
DeLisi, C. The role of synthetic biology in climate change mitigation. Biology Direct 2019, 14, 1–5. [Google Scholar]
Goodchild-Michelman, I.M.; Church, G.M.; Schubert, M.G.; Tang, T.C. Light and carbon: Synthetic biology toward new cyanobacteria-based living biomaterials. Materials Today Bio 2023, 19, 100583. [Google Scholar] [CrossRef] [PubMed]
Piaggio, A.J.; Segelbacher, G.; Seddon, P.J.; Alphey, L.; Bennett, E.L.; Carlson, R.H.; Friedman, R.M.; Kanavy, D.; Phelan, R.; Redford, K.H.; others. Is it time for synthetic biodiversity conservation? Trends in ecology & evolution 2017, 32, 97–107. [Google Scholar]
Maestre, F.T.; Eldridge, D.J.; Soliveres, S.; Kéfi, S.; Delgado-Baquerizo, M.; Bowker, M.A.; García-Palacios, P.; Gaitán, J.; Gallardo, A.; Lázaro, R.; others. Structure and functioning of dryland ecosystems in a changing world. Annual review of ecology, evolution, and systematics 2016, 47, 215–237. [Google Scholar] [CrossRef]
Berdugo, M.; Delgado-Baquerizo, M.; Soliveres, S.; Hernández-Clemente, R.; Zhao, Y.; Gaitán, J.J.; Gross, N.; Saiz, H.; Maire, V.; Lehmann, A.; others. Global ecosystem thresholds driven by aridity. Science 2020, 367, 787–790. [Google Scholar] [CrossRef]
Berdugo, M.; Vidiella, B.; Solé, R.V.; Maestre, F.T. Ecological mechanisms underlying aridity thresholds in global drylands. Functional Ecology 2022, 36, 4–23. [Google Scholar] [CrossRef]
Pointing, S.B.; Belnap, J. Microbial colonization and controls in dryland systems. Nature Reviews Microbiology 2012, 10, 551–562. [Google Scholar] [CrossRef] [PubMed]
Maestre, F.T.; Delgado-Baquerizo, M.; Jeffries, T.C.; Eldridge, D.J.; Ochoa, V.; Gozalo, B.; Quero, J.L.; García-Gómez, M.; Gallardo, A.; Ulrich, W.; others. Increasing aridity reduces soil microbial diversity and abundance in global drylands. Proceedings of the National Academy of Sciences 2015, 112, 15684–15689. [Google Scholar] [CrossRef] [PubMed]
Coleine, C.; Delgado-Baquerizo, M.; DiRuggiero, J.; Guirado, E.; Harfouche, A.L.; Perez-Fernandez, C.; Singh, B.K.; Selbmann, L.; Egidi, E. Dryland microbiomes reveal community adaptations to desertification and climate change. The ISME Journal 2024, 18, wrae056. [Google Scholar] [CrossRef] [PubMed]
Maestre, F.T.; Martín, N.; Díez, B.; Lopez-Poma, R.; Santos, F.; Luque, I.; Cortina, J. Watering, fertilization, and slurry inoculation promote recovery of biological crust function in degraded soils. Microbial Ecology 2006, 52, 365–377. [Google Scholar] [CrossRef] [PubMed]
Muñoz-Rojas, M.; Román, J.; Roncero-Ramos, B.; Erickson, T.; Merritt, D.; Aguila-Carricondo, P.; Cantón, Y. Cyanobacteria inoculation enhances carbon sequestration in soil substrates used in dryland restoration. Science of the Total Environment 2018, 636, 1149–1154. [Google Scholar] [CrossRef] [PubMed]
Rossi, F.; Li, H.; Liu, Y.; De Philippis, R. Cyanobacterial inoculation (cyanobacterisation): Perspectives for the development of a standardized multifunctional technology for soil fertilization and desertification reversal. Earth-Science Reviews 2017, 171, 28–43. [Google Scholar] [CrossRef]
Chamizo, S.; Mugnai, G.; Rossi, F.; Certini, G.; De Philippis, R. Cyanobacteria inoculation improves soil stability and fertility on different textured soils: gaining insights for applicability in soil restoration. Frontiers in Environmental Science 2018, 6, 49. [Google Scholar] [CrossRef]
Kéfi, S.; Rietkerk, M.; van Baalen, M.; Loreau, M. Local facilitation, bistability and transitions in arid ecosystems. Theoretical population biology 2007, 71, 367–379. [Google Scholar] [CrossRef]
Borgogno, F.; D’Odorico, P.; Laio, F.; Ridolfi, L. Mathematical models of vegetation pattern formation in ecohydrology. Reviews of geophysics 2009, 47. [Google Scholar] [CrossRef]
Brooker, R.W.; Maestre, F.T.; Callaway, R.M.; Lortie, C.L.; Cavieres, L.A.; Kunstler, G.; Liancourt, P.; Tielbörger, K.; Travis, J.M.; Anthelme, F.; others. Facilitation in plant communities: the past, the present, and the future. Journal of ecology 2008, 18–34. [Google Scholar]
Wright, O.; Stan, G.B.; Ellis, T. Building-in biosafety for synthetic biology. Microbiology 2013, 159, 1221–1235. [Google Scholar] [CrossRef] [PubMed]
Lensch, A.; Lindfors, H.A.; Duwenig, E.; Fleischmann, T.; Hjort, C.; Kärenlampi, S.O.; McMurtry, L.; Melton, E.D.; Andersen, M.R.; Skinner, R.; others. Safety aspects of microorganisms deliberately released into the environment. EFB Bioeconomy Journal 2023, 100061. [Google Scholar]
Maull, V.; Solé, R. Network-level containment of single-species bioengineering. Philosophical Transactions of the Royal Society B 2022, 377, 20210396. [Google Scholar] [CrossRef] [PubMed]
Samson, F.B.; Knopf, F.L.; Jones, C.G.; Lawton, J.H.; Shachak, M. Organisms as ecosystem engineers. Ecosystem management: selected readings, 1996; 130–147. [Google Scholar]
Jones, C.G.; Lawton, J.H.; Shachak, M. Positive and negative effects of organisms as physical ecosystem engineers. Ecology 1997, 78, 1946–1957. [Google Scholar] [CrossRef]
Byers, J.E.; Cuddington, K.; Jones, C.G.; Talley, T.S.; Hastings, A.; Lambrinos, J.G.; Crooks, J.A.; Wilson, W.G. Using ecosystem engineers to restore ecological systems. Trends in ecology & evolution 2006, 21, 493–500. [Google Scholar]
Maull, V.; Solé, R. Biodiversity as a Firewall to Engineered Microbiomes for Restoration and Conservation. Royal Society open science 2024. ?, ?. [Google Scholar]
Delgado-Baquerizo, M.; Maestre, F.T.; Reich, P.B.; Jeffries, T.C.; Gaitan, J.J.; Encinar, D.; Berdugo, M.; Campbell, C.D.; Singh, B.K. Microbial diversity drives multifunctionality in terrestrial ecosystems. Nature communications 2016, 7, 10541. [Google Scholar] [CrossRef]
Delgado-Baquerizo, M.; Eldridge, D.J.; Ochoa, V.; Gozalo, B.; Singh, B.K.; Maestre, F.T. Soil microbial communities drive the resistance of ecosystem multifunctionality to global change in drylands across the globe. Ecology letters 2017, 20, 1295–1305. [Google Scholar] [CrossRef]
Stirling, F.; Bitzan, L.; O’Keefe, S.; Redfield, E.; Oliver, J.W.; Way, J.; Silver, P.A. Rational design of evolutionarily stable microbial kill switches. Molecular cell 2017, 68, 686–697. [Google Scholar] [CrossRef]
Rottinghaus, A.G.; Ferreiro, A.; Fishbein, S.R.; Dantas, G.; Moon, T.S. Genetically stable CRISPR-based kill switches for engineered microbes. Nature communications 2022, 13, 672. [Google Scholar] [CrossRef]
Case, T.J. Invasion resistance arises in strongly interacting species-rich model competition communities. Proceedings of the National Academy of Sciences 1990, 87, 9610–9614. [Google Scholar] [CrossRef]
van Elsas, J.D.; Chiurazzi, M.; Mallon, C.A.; Elhottovā, D.; Krištůfek, V.; Salles, J.F.a. Microbial diversity determines the invasion of soil by a bacterial pathogen. Proceedings of the National Academy of Sciences 2012, 109, 1159–1164. [Google Scholar] [CrossRef] [PubMed]
Hobbs, R.J.; Higgs, E.; Harris, J.A. Novel ecosystems: implications for conservation and restoration. Trends in Ecology & Evolution 2009, 24, 599–605. [Google Scholar] [CrossRef] [PubMed]
Tamaru, Y.; Takani, Y.; Yoshida, T.; Sakamoto, T. Crucial role of extracellular polysaccharides in desiccation and freezing tolerance in the terrestrial cyanobacterium Nostoc commune. Applied and environmental microbiology 2005, 71, 7327–7333. [Google Scholar] [CrossRef] [PubMed]
Mager, D. Extracellular polysaccharides from cyanobacterial soil crusts and their role in dryland surface processes. PhD thesis, University Manchester Metropolitan, 2008.
Adessi, A.; de Carvalho, R.C.; De Philippis, R.; Branquinho, C.; da Silva, J.M. Microbial extracellular polymeric substances improve water retention in dryland biological soil crusts. Soil Biology and Biochemistry 2018, 116, 67–69. [Google Scholar] [CrossRef]
Ollé-Vila, A.; Duran-Nebreda, S.; Conde-Pueyo, N.; Montañez, R.; Solé, R. A morphospace for synthetic organs and organoids: the possible and the actual. Integrative Biology 2016, 8, 485–503. [Google Scholar] [CrossRef]
Avena-Koenigsberger, A.; Goñi, J.; Solé, R.; Sporns, O. Network morphospace. Journal of the Royal Society Interface 2015, 12, 20140881. [Google Scholar] [CrossRef] [PubMed]
Solé, R.; Ollé-Vila, A.; Vidiella, B.; Duran-Nebreda, S.; Conde-Pueyo, N. The road to synthetic multicellularity. Current Opinion in Systems Biology 2018, 7, 60–67. [Google Scholar] [CrossRef]
Hobbs, R.J.; Higgs, E.S.; Hall, C. Novel Ecosystems: Intervening in the New Ecological World Order; Wiley-Blackwell: Hoboken, NJ, 2013. [Google Scholar]
Morse, N.B.; Pellissier, P.A.; Cianciola, E.N.; Brereton, R.L.; Sullivan, M.M.; Shonka, N.K.; Wheeler, T.B.; McDowell, W.H. Novel ecosystems in the Anthropocene: a revision of the novel ecosystem concept for pragmatic applications. Ecology and Society 2014, 19. [Google Scholar] [CrossRef]
Goñi-Moreno, Á. Biocomputation: Moving Beyond Turing with Living Cellular Computers. Communications of the ACM 2024. [Google Scholar] [CrossRef]
Solé, R.V.; Macia, J. Expanding the landscape of biological computation with synthetic multicellular consortia. Natural Computing 2013, 12, 485–497. [Google Scholar] [CrossRef]
Johns, N.I.; Blazejewski, T.; Gomes, A.L.; Wang, H.H. Principles for designing synthetic microbial communities. Current Opinion in Microbiology 2016, 31, 146–153. [Google Scholar] [CrossRef] [PubMed]
Chang, C.Y.; Vila, J.C.; Bender, M.; Li, R.; Mankowski, M.C.; Bassette, M.; Borden, J.; Golfier, S.; Sanchez, P.G.L.; Waymack, R.; others. Engineering complex communities by directed evolution. Nature ecology & evolution 2021, 5, 1011–1023. [Google Scholar]
Saavedra, S.; Rohr, R.P.; Bascompte, J.; Godoy, O.; Kraft, N.J.; Levine, J.M. A structural approach for understanding multispecies coexistence. Ecological Monographs 2017, 87, 470–486. [Google Scholar] [CrossRef]
Saavedra, S.; Medeiros, L.P.; AlAdwani, M. Structural forecasting of species persistence under changing environments. Ecology Letters 2020, 23, 1511–1521. [Google Scholar] [CrossRef] [PubMed]
Marino, S.; Baxter, N.T.; Huffnagle, G.B.; Petrosino, J.F.; Schloss, P.D. Mathematical modeling of primary succession of murine intestinal microbiota. Proceedings of the National Academy of Sciences 2013, 111, 439–444. [Google Scholar] [CrossRef] [PubMed]
Stein, R.R.; Bucci, V.; Toussaint, N.C.; Buffie, C.G.; Rätsch, G.; Pamer, E.G.; Sander, C.; Xavier, J.a.B. Ecological Modeling from Time-Series Inference: Insight into Dynamics and Stability of Intestinal Microbiota. PLoS Computational Biology 2013, 9, e1003388. [Google Scholar] [CrossRef] [PubMed]
Buffie, C.G.; Bucci, V.; Stein, R.R.; McKenney, P.T.; Ling, L.; Gobourne, A.; No, D.; Liu, H.; Kinnebrew, M.; Viale, A.; Littmann, E.; van den Brink, M.R.M.; Jenq, R.R.; Taur, Y.; Sander, C.; Cross, J.R.; Toussaint, N.C.; Xavier, J.B.; Pamer, E.G. Precision microbiome reconstitution restores bile acid mediated resistance to Clostridium difficile. Nature 2014, 517, 205–208. [Google Scholar] [CrossRef] [PubMed]
Coyte, K.Z.; Schluter, J.; Foster, K.R. The ecology of the microbiome: Networks, competition, and stability. Science 2015, 350, 663–666. [Google Scholar] [CrossRef] [PubMed]
Joseph, T.A.; Shenhav, L.; Xavier, J.B.; Halperin, E.; Pe’er, I. Compositional Lotka-Volterra describes microbial dynamics in the simplex. PLOS Computational Biology 2020, 16, e1007917. [Google Scholar] [CrossRef]
Remien, C.H.; Eckwright, M.J.; Ridenhour, B.J. Structural identifiability of the generalized Lotka-Volterra model for microbiome studies. Royal Society Open Science 2021, 8, 201378. [Google Scholar] [CrossRef]
Long, C.; Deng, J.; Nguyen, J.; Liu, Y.Y.; Alm, E.J.; Solé, R.; Saavedra, S. Structured community transitions explain the switching capacity of microbial systems. Proceedings of the National Academy of Sciences 2024, 121, e2312521121. [Google Scholar] [CrossRef] [PubMed]
Jansson, J.K. Soil viruses: Understudied agents of soil ecology. Environmental Microbiology 2023, 25, 143. [Google Scholar] [CrossRef] [PubMed]
Weitz, J.S. Quantitative viral ecology: dynamics of viruses and their microbial hosts; Princeton University Press, 2016. [Google Scholar]
Smith, J.M.; Szathmary, E. The major transitions in evolution; OUP Oxford, 1997. [Google Scholar]
Solé, R. The major synthetic evolutionary transitions, 2016.
Sole, R. Synthetic transitions: towards a new synthesis. Philosophical Transactions of the Royal Society B: Biological Sciences 2016, 371, 20150438. [Google Scholar] [CrossRef] [PubMed]
Venturelli, O.S.; Carr, A.V.; Fisher, G.; Hsu, R.H.; Lau, R.; Bowen, B.P.; Hromada, S.; Northen, T.; Arkin, A.P. Deciphering microbial interactions in synthetic human gut microbiome communities. Molecular systems biology 2018, 14, e8157. [Google Scholar] [CrossRef] [PubMed]
Weiss, A.S.; Burrichter, A.G.; Durai Raj, A.C.; von Strempel, A.; Meng, C.; Kleigrewe, K.; Münch, P.C.; Rössler, L.; Huber, C.; Eisenreich, W.; others. In vitro interaction network of a synthetic gut bacterial community. The ISME journal 2022, 16, 1095–1109. [Google Scholar] [CrossRef]
Cheng, A.G.; Ho, P.Y.; Aranda-Díaz, A.; Jain, S.; Feiqiao, B.Y.; Meng, X.; Wang, M.; Iakiviak, M.; Nagashima, K.; Zhao, A.; others. Design, construction, and in vivo augmentation of a complex gut microbiome. Cell 2022, 185, 3617–3636. [Google Scholar] [CrossRef]

A closed microbial system confined in a container would easily impose a carrying capacity due to space constraints, i.e. proximity-dependent inhibition. Conversely, an unbounded scenario would present a much more restrictive solution, being

1 = r ρ

the only condition for long-term

N^{*} > 0

This is a simple mathematical model of the Allee effect, where a population will thrive, provided that minimal population size is achieved. This is obtained here by first finding the fixed points of the dynamics, i.e., the

x^{*}

, such that

d x / d t = 0

. In this case, one solution is the extinction (desert) state

x^{*} = 0

, whereas two extra states

x_{\pm}

are found by solving the quadratic equation

x^{2} - K x + α K / r = 0

. The solutions of this equation exist only if

1 - 4 α / r \geq 0

, which gives the critical condition.

Figure 1. Microcosms, novel and synthetic ecosystems. Simplified communities have been studied within the context of (a) micro- and (b) mesocosm experiments, while a large-scale scenario is provided by biosphere 2 (c), where different habitats and their associated ecosystems have been recreated. On the other hand, new kinds of human-related ecosystems have also been obtained from the assembly of many exotic species, as is the case of Ascension Island (d), or have emerged within an Anthropogenic waste, such as plastic (e), providing a new habitat to a whole class of marine assembly (the so-called Plastisphere). Future developments within space missions and planetary colonisation (f) present extra challenges associated with the constraints imposed by closed environments. Synthetic biology offers a whole range of ways to both interrogate natural ecosystems, as it occurs with competition (g) and cooperation (h) in the Petri dish, but also as ways to modify extant communities, such as (i) the skin microbiome.

Figure 2. Minimal synthetic ecological networks. Here, we display six types of distinct SE and their characterization using quantitative analyses, qualitative stability properties and candidate mathematical models. In each case, the nature of the species-species interactions is indicated. At the same time, quantification of their underlying behaviour is illustrated by both time series (for the three first examples) and statistical, stationary measures for the last two. Beyond the specific quantitative results, each motif displays some class of generic behaviour that can be described in terms of attractor states. Here we display, on a

(c_{1}, c_{2})

space, the trajectories exhibited by the system, which connect stable (filled circles) and unstable (open circles) states. In some systems, alternative states are accessible from different initial conditions, in others there is a single, global attractor states and in some systems the dynamics approaches a periodic orbit. These attractors are often represented as marbles on a landscape with two axes associated with the two populations. Here, stable and unstable states (darker and lighter spheres, respectively) correspond to the bottom of valleys (the basins of attraction) and peaks. Simple mathematical models (right column) provide a mechanistic explanation of how nonlinear interactions generate different kinds of attractor states. In most cases, these models are based on systems of coupled nonlinear differential equations.

(c_{1}, c_{2})

Figure 3. Systems and synthetic biology for Life Support Systems. In (a), the BIOS-3 design of a closed ecosphere is represented here as a graph (including the closed cycling of

O_{2}

and

{CO}_{2}

, along with higher plants and humans). This coarse-graining allows defining a set of equations (b) that describe the system [76]. Here

O = [O_{2}]

C = [C O_{2}]

and

P_{k}

indicate plant abundance;

V_{o}

is the rate of human metabolism;

ν_{1 | 2}

stands for plant maximum growth rate;

γ

and

δ

rate of plant growth;

μ

is rate of human metabolism related to oxygen consumption;

R_{1 | 2}

is the assimilation quotients for plants; R stands for human respiratory quotient and q the fraction of human metabolism supported by plants. Synthetic biology could enhance and stabilize this design, achieving a fully closed system and recycling plant and human waste as food and fertilizer are produced (c). Here, an extra compartment is added. The tag "Synthetic Biology" stands for the necessary closure of metabolic pathways, here to be conducted in bioreactor tanks. The corresponding mathematical model (d) is obtained from (b) by adding

S_{i}

, where

i = 1, . . . N

, where N is the number of species performing biochemical reactions. Here we could propose a closed catalytic architecture, i.e. hypercycle dynamics governing

S_{i}

. Here

δ_{1_{i α}}

and

δ_{2_{i α}}

stand for Dirac’s delta function to tag who is producing or recycling from or to plant and human compartment, respectively; i. e.

δ_{i α} = 1

when

i = α

and zero otherwise. The catalytically-assisted replication species j provides to i is denoted by

ξ_{i j}

. Recycling and production rates are

ω_{i}

σ_{i}

and

π_{i}

ρ_{i}

, respectively. The last term,

Φ (\vec{S})

, is the dilution outflow that keeps the population constant by competition between species.

Figure 3. Systems and synthetic biology for Life Support Systems. In (a), the BIOS-3 design of a closed ecosphere is represented here as a graph (including the closed cycling of

O_{2}

and

{CO}_{2}

, along with higher plants and humans). This coarse-graining allows defining a set of equations (b) that describe the system [76]. Here

O = [O_{2}]

C = [C O_{2}]

and

P_{k}

indicate plant abundance;

V_{o}

is the rate of human metabolism;

ν_{1 | 2}

stands for plant maximum growth rate;

γ

and

δ

rate of plant growth;

μ

is rate of human metabolism related to oxygen consumption;

R_{1 | 2}

S_{i}

, where

i = 1, . . . N

, where N is the number of species performing biochemical reactions. Here we could propose a closed catalytic architecture, i.e. hypercycle dynamics governing

S_{i}

. Here

δ_{1_{i α}}

and

δ_{2_{i α}}

stand for Dirac’s delta function to tag who is producing or recycling from or to plant and human compartment, respectively; i. e.

δ_{i α} = 1

when

i = α

and zero otherwise. The catalytically-assisted replication species j provides to i is denoted by

ξ_{i j}

. Recycling and production rates are

ω_{i}

σ_{i}

and

π_{i}

ρ_{i}

, respectively. The last term,

Φ (\vec{S})

, is the dilution outflow that keeps the population constant by competition between species.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Synthetic Ecosystems: From the Test Tube to the Biosphere

Abstract

1. Introduction

2. Synthetic Microcosms

2.1. Competition

2.2. Cooperation

2.3. Parasitism and Predator-Prey Interactions

2.4. Environmental Self-Regulation

2.5. Non-Transitive Interactions

3. Closed Ecospheres and Space-Life Support Systems

4. Synthetic Biospheres

5. Discussion

Acknowledgements

References

MDPI Initiatives

Important Links

Subscribe