Prerpints.org logo
Preprint
Article

Reducing Model Complexity in Neural Networks by Using Pyramid Training Approaches

Altmetrics

Downloads

92

Views

100

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 May 2024

Posted:

14 May 2024

You are already at the latest version

Alerts
Abstract
Throughout the evolution of machine learning, the size of models has steadily increased as researchers strive for higher accuracy by adding more layers. This escalation in model complexity necessitates enhanced hardware capabilities. Today, state-of-the-art machine learning models have become so large that effectively training them requires substantial hardware resources, which may be readily available to large companies but not to students or independent researchers. To make the research on machine learning models more accessible, this study introduces a size reduction technique that leverages stages in Pyramid Training and Similarity Comparison. Our results demonstrate that pyramid training can reduce model complexity while maintaining accuracy of conventional full-sized models, offering a scalable and resource-efficient solution for researchers and practitioners in hardware-constrained environments.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

In the rapidly evolving field of machine learning, Convolutional Neural Networks (CNNs) are extensively used for visual information processing, playing pivotal roles in areas such as image classification [1,2], object detection [3,4], facial recognition [5], medical imaging [6,7], and autonomous driving [8]. As these tasks grow in complexity, so too do the models designed to tackle them, often resulting in increased model size and computational demands. Consequently, state-of-the-art models require significant hardware resources, which can be prohibitively expensive for individual researchers or small organizations.
Addressing the challenge of CNN model size optimization has spurred a variety of strategies. Techniques such as quantization [9], pruning [10], knowledge distillation [11], weight sharing [12], factorization [13], low-rank approximation [14] and dynamic network surgery [15] have been developed to manage model complexity by reducing size either before or after training. However, these methods often require trade-offs between model performance and efficiency.
This study introduces a novel "pyramid training" methodology, an innovative approach designed to dynamically adjust and optimize CNNs during the training process itself. Pyramid training involves building smaller networks incrementally—starting with a simple model (A) and progressively integrating it with other networks (B, C, etc.) to form larger, more complex structures. This method not only conserves resources but also adapts to increasing accuracy demands without the exponential growth in computational load typically associated with larger models.
A distinctive feature of our methodology is the implementation of a feature size reduction strategy during network combination. By employing a similarity comparison between features using a cosine similarity matrix, our approach identifies and merges similar feature maps. This process not only helps in condensing the network’s complexity efficiently but also ensures that essential information is preserved, optimizing both the model size and its computational efficiency.
The contributions of this study are summarized as follows:
  • Introduction of the pyramid training paradigm for efficient optimization of CNNs.
  • Detailed methodology for iterative network construction and integration to progressively achieve desired accuracy.
  • Implementation of a feature size reduction strategy using a similarity matrix and averaging technique to enhance the network’s architectural efficiency.

2. Related Work

Quantization has garnered significant attention in machine learning due to its potential to reduce model size without substantially compromising accuracy, a crucial factor in on-device applications where balance between accuracy and latency is vital [9,16]. It is also effective in large-scale multimedia retrieval, managing high-dimensional data efficiently [17]. Pruning techniques enhance neural network efficiency by removing redundant model components, thereby reducing computational overhead without affecting accuracy. Innovative approaches, such as the formulation by Molchanov et al., have made significant contributions to efficient inference [18,19]. Further, studies by Frankle et al. emphasize its utility in removing unnecessary network structures post-training, improving performance [20].
Knowledge Distillation involves training a smaller, more efficient "student" model to emulate a larger "teacher" model, thereby accelerating and compressing machine learning models without losing predictive power, proving especially useful in domains like computer vision and natural language processing [11,21].Weight Sharing reduces the number of parameters in a neural network, enhancing generalization and reducing overfitting. It has shown particular promise in Neural Architecture Search (NAS), where careful management of weight sharing can significantly impact model performance [12,22].
Low-Rank Approximation techniques streamline the training of deep neural networks by leveraging the inherent structures within the data. Hsieh et al.’s method of low-rank matrix factorization exemplifies how these techniques facilitate efficient training processes by focusing on the most expressive features of the data [14]. Additionally, the adaptive quantization method introduced by Nakata integrates low-rank approximations to reduce computational burdens, which is crucial in resource-constrained settings [9].
Dynamic Network Surgery (DNS), an advanced form of model optimization, combines network pruning and growth strategies to dynamically adjust network architecture during training. This method, pioneered by Liu et al., allows for adaptive model refinement, enhancing performance while maintaining or even reducing computational requirements [15]. It has been effectively applied in medical image segmentation, demonstrating its versatility across different domains [6].

3. Methodology

In this section, the information about proposed and complementary techniques will be given in great detail.

3.1. Pyramid Training

Pyramid training in this study refers to a novel approach that diverges from traditional multiresolution pyramids, commonly used in object detection and other tasks requiring scale variance [25,26]. Our methodology involves iteratively training and combining smaller, less computationally intensive networks to progressively build up a model capable of achieving the accuracy of much larger networks. By initially training a small network (A) and systematically integrating it with additional networks (B, C, etc.), we construct a larger and more capable model without the substantial resource requirements typically associated with large-scale neural networks. This hierarchical approach not only optimizes computational resources but also allows for fine-tuning of individual network segments before they are integrated, enhancing overall model performance and efficiency.

3.2. Similarity Comparison

During the convolutional layers of a CNN, feature maps are generated that encapsulate the essential characteristics of the input data. These maps often exhibit redundancy, especially in deeper layers of the network, which can be computationally wasteful and detract from model efficiency. To address this, we employ a similarity comparison strategy using cosine similarity metrics to identify and consolidate redundant features [12].
Cosine similarity measures the cosine of the angle between two vectors (feature maps in this context), providing a value between -1 and 1 that indicates how similar the feature maps are in terms of their information content. The formula is given by:
cos ine similarity ( A , B ) = A · B ∥ A ∥ · ∥ B ∥
Here, A · B denotes the dot product of vectors A and B, and ∥ A ∥ and ∥ B ∥ represent their respective magnitudes. This measure allows us to quantify the degree of similarity between pairs of feature maps. Feature maps that exhibit a high degree of similarity (cosine similarity close to 1) are considered redundant. These are then combined using averaging techniques, reducing the overall number of feature maps and, consequently, the model’s complexity and computational load.
To illustrate this concept, an example feature map representation from the MNIST dataset is shown in Figure 1. This visualization demonstrates how similar feature maps, which emerge naturally during the training of convolutional layers, can be identified and merged. By highlighting these redundancies through the feature maps of the well-known digit images, we underline the potential for significant reductions in network complexity through our similarity comparison technique.
Let’s assume we have a set of 16 features, represented as vectors F 1 , F 2 , … , F 16 . To evaluate the similarity between these feature vectors, we calculate the cosine similarity for each pair, which measures the cosine of the angle between two vectors in a multi-dimensional space. The cosine similarity is particularly useful as it normalizes the feature scale, focusing solely on the information content.
Preprints 106434 i001
As an alternative to cosine similarity, Euclidean distance can also be used to measure the similarity between features. Euclidean distance calculates the straight-line distance between two points in a multidimensional space, making it a geometric measure of similarity. It is defined by the following equation:
Euclidean Distance ( A , B ) = ∑ i = 1 n ( A i − B i ) 2
Here, A and B represent the feature vectors, n is the number of dimensions, and A i and B i are the i t h components of vectors A and B respectively. Unlike cosine similarity, which normalizes the vectors and focuses solely on their orientation, Euclidean distance takes into account both the magnitude and direction of the vectors. This characteristic means that Euclidean distance is sensitive to the scale of the vector components, which can be both an advantage and a limitation depending on the application.
While Euclidean distance provides a direct measure of the physical ’distance’ between feature vectors, it may not be as effective in high-dimensional spaces where different features may vary widely in scale or where the direction of the vectors is more informative than their magnitude. In contrast, cosine similarity, by normalizing vector magnitude, offers resilience to variations in scale and is often preferred in applications such as text analytics and other forms of semantic similarity where the direction of the feature vector (i.e., the angle between vectors) is more critical than their length.
Therefore, the choice between Euclidean distance and cosine similarity should be guided by the specific characteristics of the dataset and the requirements of the application. Euclidean distance may be more suitable for datasets with uniform feature scales and where the magnitude of the data points carries significant meaning. On the other hand, cosine similarity might be the better option when dealing with features of varying magnitudes or when the orientation of the data points is of greater importance than their absolute values.

3.3. Size Reduction

Feature size reduction, also known as feature selection or dimensionality reduction, plays a vital role in machine learning by enhancing model efficiency and generalization capabilities. A primary advantage of this technique is its ability to mitigate the curse of dimensionality. High-dimensional feature spaces often lead to increased computational complexity and a higher risk of overfitting.
In our approach, a similarity matrix facilitates the identification of redundant features, guiding the selection of feature pairs that exceed a predefined similarity threshold. These pairs are deemed combinable. The merging of similar features is accomplished by replacing the original features with their mean or another suitable aggregation method, effectively reducing the number of features iteratively until no additional pairs meet the threshold. This results in a dataset with a minimized set of features, maintaining essential information while eliminating redundancies.
To manage the dimensionality reduction dynamically, we introduce a ’reduction scale’ parameter. This parameter adjusts according to the evolving feature set; starting low when feature numbers are small and incrementing as the feature count increases. This adaptive mechanism allows the reduction process to become more aggressive as the complexity of the dataset grows, thereby ensuring efficient handling of varying feature spaces and achieving more optimized reductions as necessary.
The mean method is commonly used in this reduction process:
μ = 1 n ∑ i = 1 n F i
where n is the number of similar features to be combined, and F i represents the i t h feature. While this method is straightforward and maintains the central tendencies of the features, it may not account for variations in feature importance and is susceptible to outliers. An alternative is the weighted mean method, which provides a more nuanced combination:
μ = ∑ i = 1 n w i · F i ∑ i = 1 n w i
where w i represents the weight assigned to the ith feature, allowing for differential importance among features. This method enhances adaptability and allows for customization according to the specific characteristics of the dataset.
Both methods serve to consolidate multiple features into a single, composite feature. The choice between these methods should be dictated by the dataset’s characteristics and the specific goals of the analysis. A systematic approach involving experimentation and validation is essential to determine the most effective method for a given scenario.
Let’s assume we have features of shape ( B , N , H , W ) where B represents the batch size, N represents the feature size, H represents the height and W represents the width. The the general formulation of feature size reduction for both mean and weighted mean methods can be seen below.
Mean Reduction ( X ) i , j = 1 N ∑ f = 1 N X i , j , f
Weighted Mean Reduction ( X , W ) i , j = ∑ f = 1 N W f · X i , j , f ∑ f = 1 N W f
Here, W represents the weight vector for each feature, and the equation calculates the weighted mean reduction at each spatial location (i,j) considering the importance assigned by the weights. In both equations, X i , j , f denotes the feature map value at position (i,j) for the f-th feature, and n is the total number of features in the tensor. The weighted mean reduction incorporates the weights W f associated with each feature for a more nuanced reduction process.

3.4. Quantization

Quantization in machine learning is a critical technique employed to reduce model sizes, thereby enhancing memory efficiency and accelerating inference times. This process involves approximating numerical values with fewer bits, which decreases the precision of parameters but significantly boosts computational efficiency.

3.4.1. Fixed-Point Quantization

Fixed-point quantization simplifies the representation of weights by using a fixed number of bits for both integer and fractional parts. This method is characterized by the use of a scaling factor 2 k where k indicates the number of fractional bits. Weights are then quantized by rounding them to the nearest fixed-point value based on this scaling factor. The mathematical formulation is as follows:
Q ( x ) = Round ( x × 2 k ) × 2 − k
Fixed-point quantization is particularly beneficial for hardware implementations that support fixed-point arithmetic, leading to more efficient computations than floating-point operations.

3.4.2. Integer Quantization

Integer quantization further simplifies the model by quantizing weights to integer values, which can be extremely beneficial for reducing memory footprint. This method converts weights by rounding them to the nearest integer, thus simplifying computations and storage requirements:
Q ( x ) = Round ( x )
This technique is often used in scenarios where extreme memory constraints exist, such as in embedded systems or mobile devices where storage and processing power are limited.

3.4.3. Vector Quantization

Vector quantization groups weights into vectors and quantizes each vector to a centroid that represents the group. This method reduces the number of unique weight values by assigning multiple weights to a single centroid, thus compacting the model’s memory usage. The quantization process is defined by:
Q ( x i ) = argmin j | x i − c j |
Vector quantization is especially useful in neural networks where redundancy across weights can be leveraged to minimize the overall model size without substantial loss in accuracy. It is suitable for applications requiring models with a small footprint but where some loss of precision is acceptable.

3.5. Experimental Fields

In this section, we explore the application of feature size reduction across different machine learning fields, each presenting unique challenges and opportunities for efficiency improvements. We delve into classification, semantic segmentation, and object detection to evaluate the impact of our proposed methodologies.

3.5.1. Classification

Classification is a foundational task in machine learning, pivotal for decision-making processes in intelligent systems. It involves training models to accurately assign predefined labels to input data instances. We apply feature size reduction to a convolutional neural network (CNN) specifically designed for this purpose, which includes layers for hierarchical feature extraction, spatial down-sampling, and high-level abstraction. Our primary objective is to evaluate the influence of feature size reduction on model performance and efficiency, as illustrated in Figure 2, which depicts the integration of pyramid training and feature size reduction within the network.

3.5.2. Semantic Segmentation

Semantic segmentation involves detailed pixel-wise classification, crucial for tasks such as medical image analysis. We employ the U-Net architecture [28], known for its efficacy in detailed segmentation tasks, to implement feature size reduction. The U-shaped architecture of U-Net, which includes skip connections that help preserve spatial hierarchies, poses unique challenges when integrating feature size reduction. These complexities necessitate adaptations in our pyramid training approach to ensure that crucial spatial information is not lost during feature reduction. The tailored approach and its architectural nuances are detailed in Figure 3.

3.5.3. Object Detection

Object detection requires identifying and localizing objects within images, a task we approach by adapting the Faster R-CNN framework [29]. This model uses a two-stage process involving region proposal networks (RPNs) and deep CNNs for refining and classifying proposals. We modify the Faster R-CNN’s backbone to incorporate feature size reduction within its convolutional layers, carefully balancing the trade-offs between detection accuracy and computational demands. The modifications aim to maintain detection performance while enhancing processing speed and reducing memory usage, as detailed in Figure 4.

3.6. Individual Blocks

In the pyramid training framework, the term ’Block’ refers to the smallest trainable and combinable unit within the network. These blocks are fundamental components that serve as the building blocks of our modular network architecture. Blocks in pyramid training offer a modular and iterative approach to constructing neural networks. Each block can be independently trained and optimized before being combined with others to form a more complex and capable network structure. This modular nature not only facilitates fine-tuning at a granular level but also simplifies the management of computational resources. While the typical strategy involves training individual blocks separately and then assembling them, an alternative approach is to combine blocks first and then train the resultant larger structure. This method allows for the joint optimization of interactions between blocks, potentially leading to better integrated system performance. However, each approach has its trade-offs, with the separate training method providing more control over individual block optimization and the combined training method potentially achieving better overall system integration. Using a block-based design addresses several challenges in scaling neural networks. It allows for incremental improvements and updates without the need to retrain the entire network, which can be resource-intensive. Additionally, it provides a systematic way to expand network capacity and complexity by adding new blocks, thereby enabling the construction of a pyramid-like architecture that can achieve comparable accuracy with potentially lower computational overhead. Detailed specifications of two sample blocks used in our experiments are provided in Table 1 and Table 2. For a comprehensive understanding of how these blocks are integrated into the general pyramid training architecture, refer to Section 3.7.

3.7. Method Description

In the pyramid training framework, we begin by training two foundational blocks, Block 1 and Block 2, which are designed to capture and process diverse features from the input data. The training starts with Block 1, which focuses on extracting primary features and patterns essential for the initial stages of learning. After training Block 1, we discard its fully connected (FC) layers to prevent any loss of spatial information when integrating with Block 2. This step is crucial as it allows for the preservation of spatial relationships that are vital for the network’s performance. The convolutional layers of Block 1, which contain hierarchically processed features, are then seamlessly integrated with Block 2. To address potential dimensional mismatches—such as the one observed between the output of Conv2 in Block 1 (32 feature maps) and the input requirements of Conv3 in Block 2 (16 feature maps)—we employ a feature size reduction strategy. This involves constructing a similarity matrix to identify highly correlated feature maps from Conv2. By applying a mean reduction method to the most similar feature maps, we effectively reduce the feature map count, ensuring compatibility and enhancing the network’s capacity to handle complex patterns. The combined architecture, now consisting of Block 1 and Block 2, undergoes further training to refine and enhance the feature representations. This iterative process of training and combining blocks continues until the network achieves the desired level of accuracy. Each cycle of this process not only enriches the network’s feature understanding but also optimizes its overall performance. The entire pyramid training process is visually depicted in Figure 2, which illustrates the structured progression of combining and refining blocks. Through this methodical approach, the pyramid training model leverages both hierarchical learning and feature size reduction to construct a robust and efficient network. This process not only enhances the network’s adaptability to new and complex data sets but also optimizes computational resources, making it an effective solution for scaling deep learning architectures.

4. Experiments

This section elucidates the outcomes of the experiments conducted to validate our proposed methods. It details the datasets used, the tasks performed, and the setup for the experiments.

4.1. Dataset and Task

The experiments span three principal areas: classification, segmentation, and object detection.
  • Classification: We utilized the CIFAR-10 dataset [27], a benchmark for image classification tasks, to evaluate the effectiveness of our pyramid training and feature reduction techniques.
  • Segmentation: For segmentation tasks, the KITTI dataset [32], which is broadly employed for object detection, tracking, and segmentation, was used.
  • Object Detection: The Penn-Fudan Database for Pedestrian Detection [33] was chosen for object detection experiments. This dataset, comprising diverse urban scenes, focuses on pedestrian detection, offering a challenging testbed for our methodologies.

4.2. Experimental Setup

Experiments were executed on two platforms:
1.
A local GPU setup powered by an RTX-3060 with 6GB of memory.
2.
A cloud-based Google Colab session configured to utilize the T4 GPU runtime.
The following metrics were tracked across all experiments to assess performance:
  • Test set accuracy for classification tasks.
  • Training loss and validation loss for segmentation tasks.
  • Various loss metrics (Loss Box Reg, Loss Classifier, Loss RPN Box Reg, Total Loss) for object detection tasks.
  • Training time and model size, measured in megabytes (MB) or gigabytes (GB).

4.3. Experimental Configurations

Different network configurations were tested to examine the impact of feature size reduction and quantization:
  • BaseNetwork: This configuration serves as a control, comprising Block 1 and Block 2 combined without any feature size reduction steps.
  • ReducedNetwork: Incorporates a feature size reduction step between Conv2 and Conv3 layers. This network undergoes iterative pyramid training, progressively refining the model and reducing its complexity by minimizing redundant feature representations.
  • Quantization: Both BaseNetwork and ReducedNetwork are subjected to quantization to compress model size and enhance computational efficiency.
  • Reduced+Quantization: This setup investigates the synergistic effect of combining feature size reduction with quantization, focusing on the rate of model size reduction and operational efficiency.
  • U-Net: Employed for semantic segmentation, this network’s architecture is designed to efficiently segment images by progressively reducing and then expanding the resolution of intermediary representations.
  • U-Net-Reduced:A simplified variant of U-Net, where feature size reduction techniques are applied to decrease the complexity and computational demands of the network while aiming to maintain effective segmentation performance.
  • Faster R-CNN: Utilizes a two-stage approach for object detection, combining region proposal networks with a CNN classifier. The backbones used in these experiments include CustomBackbone and VGG16, adapted for this framework.
  • Faster-RCNN-Reduced: A reduced-complexity version of Faster R-CNN, where feature size reduction techniques are implemented within the convolutional layers of the backbone to explore potential benefits in scenarios with limited computational resources.
These configurations are designed to systematically evaluate the effectiveness of our methods across different network architectures and tasks. The results of these experiments, detailed in the subsequent sections, validate the advantages of our approach in terms of efficiency and performance.

4.4. Results

The outcomes of our experiments are comprehensively documented in Table 4, Table 5 and Table 6, which summarize the performance across various configurations and tasks.
For the classification task, the ReducedNetwork, which integrates feature size reduction and pyramid training, demonstrates a balance between reducing the model size and slightly decreasing test set accuracy relative to the BaseNetwork. This configuration underscores the network’s enhanced adaptability and efficiency, enabling it to capture detailed patterns effectively. Applying quantization to both networks further minimizes the model sizes, with the Reduced + Quantization setup achieving the most substantial size reduction—a sixfold decrease. However, this compactness results in a minor reduction in test set accuracy, showcasing the trade-offs involved in aggressive model compression techniques. These results validate the effectiveness of our methods and their potential synergy with other size reduction strategies.
In the segmentation experiments, the performance metrics for U-Net and U-Net-Reduced are detailed in Table 5. U-Net-Reduced, with feature size reduction applied, shows a lower training loss of 0.6522 compared to U-Net’s 1.004 but incurs a slightly higher validation loss of 0.8945. Although the training time increases for the reduced model, the model size is significantly decreased to 7 MB, compared to 31 MB for the standard U-Net. These findings illustrate the inherent trade-offs between model complexity, efficiency, and size, particularly relevant in segmentation tasks where maintaining high accuracy is critical.
The object detection task results are summarized in Table 6. For the CustomBackbone model, while the Reduced variant exhibits a modest increase in individual loss components, leading to a total loss of 1.223 compared to 1.14 for the non-reduced model, it shows improved resource efficiency with shorter training times and reduced memory requirements. Similarly, the VGG16-Reduced model, although experiencing a slight increase in total loss to 0.4377 from 0.216, demonstrates significant gains in resource efficiency.
The resource utilization metrics indicate that CustomBackbone-Reduced requires less memory (10.31 GB vs. 15.84 GB) and longer training times (823 seconds vs. 460 seconds) compared to its non-reduced counterpart. The VGG16-Reduced also shows a reduction in memory usage (9.96 GB vs. 16.04 GB) and an increase in training time (1100 seconds vs. 653 seconds). These results offer critical insights into the performance and efficiency trade-offs associated with implementing feature size reduction in complex object detection frameworks.

5. Conclusion

Our exploration of the pyramid training schema, along with the strategic computation of feature size reduction using similarity comparison, has yielded valuable insights into enhancing neural network architectures for classification tasks. The iterative pyramid training process, combined with feature size reduction, has proven to be an effective strategy in refining the model’s adaptability and computational efficiency. The ReducedNetwork, which integrates these methodologies, demonstrated a commendable reduction in model size while maintaining comparable test set accuracy to the BaseNetwork.
The application of quantization, a model compression technique, to both BaseNetwork and ReducedNetwork, further underscored the versatility of our approach. The combination with quantization in the Reduced+Quantization configuration achieved the smallest model size with a sixfold reduction rate. Although this considerable reduction in size introduced a marginal decrease in test set accuracy, it illustrates the potential for substantial model optimization.
The incorporation of similarity comparison techniques in feature size reduction provides several advantages:
  • Efficiency: It significantly reduces redundancy and enhances computational efficiency, crucial for environments with limited computational resources.
  • Information Preservation: This method ensures that essential features are retained, which is vital for maintaining the effectiveness of the model.
  • Scalability: Similarity comparison is flexible and can be applied across different network layers and architectures, making it widely applicable.
  • Energy Conservation: Particularly beneficial for mobile and embedded systems, reducing computational demands helps in conserving energy.
For segmentation tasks, U-Net and its reduced variant, U-Net-Reduced, were evaluated. The U-Net-Reduced demonstrated improved efficiency with a significantly lower model size of 7 MB compared to the original U-Net’s 31 MB, showcasing the effectiveness of feature dimensionality reduction. However, this reduction in size was accompanied by a slight increase in validation loss, highlighting the typical trade-offs between model complexity and performance.
In object detection tasks, CustomBackbone and VGG16, along with their reduced versions, exhibited notable reductions in model size and memory allocation, demonstrating their potential for resource-efficient deployment. The reduced variants showed increased losses, which underscores the delicate balance required when scaling down model complexity to fit resource constraints.
Ultimately, the trade-offs between model size reduction and potential increases in loss scores are critical considerations for deploying complex networks in resource-constrained environments. The experimental results, especially with the reduced variants of U-Net and CustomBackbone, demonstrate that feature dimensionality reduction techniques can significantly decrease model size, enabling the operation of sophisticated networks in settings with limited memory and computational resources. This trade-off suggests that sacrificing marginal accuracy for resource efficiency could be a viable strategy, particularly when the computational demands of larger models are prohibitive in real-world applications.
Through this study, the effectiveness of similarity comparison in feature size reduction has been highlighted as not only enhancing efficiency but also ensuring the practical deployment of advanced neural architectures in various computational environments. Looking ahead, refining feature size reduction algorithms to enhance efficiency without sacrificing accuracy could yield more robust models. Additionally, future efforts could also focus on optimizing the training process to reduce the considerable increase in training times associated with our method.

Author Contributions

Conceptualization, Methogology, Writing Paper., S.G.K.; Formal analysis, supervision, B.S.; Providing research ideas, supervision, F.N.; review, supervision, A.O.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, A. Rabinovich, "Going Deeper with Convolutions," in 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015. [CrossRef]
  2. S. Sladojević, M. Arsenović, A. Anderla, D. Ćulibrk, D. Stefanović, "Deep Neural Networks Based Recognition of Plant Diseases by Leaf Image Classification," Computational Intelligence and Neuroscience, vol. 2016, pp. 1–11, 2016. [CrossRef]
  3. J. Redmon, S. Divvala, R. Girshick, A. Farhadi, "You Only Look Once: Unified, Real-Time Object Detection," in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016. [CrossRef]
  4. Z. Zhao, P. Zheng, S. Xu, X. Wu, "Object Detection with Deep Learning: A Review," IEEE Transactions on Neural Networks and Learning Systems, vol. 30, no. 11, pp. 3212–3232, 2019. [CrossRef]
  5. A. Khan, A. Sohail, U. Zahoora, A. Qureshi, "A Survey of the Recent Architectures of Deep Convolutional Neural Networks," Artificial Intelligence Review, vol. 53, no. 8, pp. 5455–5516, 2020. [CrossRef]
  6. P. Malhotra, S. Gupta, D. Koundal, A. Zaguia, W. Enbeyle, "Deep Neural Networks for Medical Image Segmentation," Journal of Healthcare Engineering, vol. 2022, pp. 1–15, 2022. [CrossRef]
  7. S. Singh, L. Wang, S. Gupta, H. Goli, P. Padmanabhan, B. Gulyás, "3D Deep Learning on Medical Images: A Review," Sensors, vol. 20, no. 18, p. 5097, 2020. [CrossRef]
  8. M. Junaid, Z. Szalay, Á. Török, "Evaluation of Non-Classical Decision-Making Methods in Self-Driving Cars: Pedestrian Detection Testing on a Cluster of Images with Different Luminance Conditions," Energies, vol. 14, no. 21, p. 7172, 2021. [CrossRef]
  9. K. Nakata, D. Miyashita, J. Deguchi, R. Fujimoto, "Adaptive Quantization Method for CNN with Computational-Complexity-Aware Regularization," in 2021 IEEE International Symposium on Circuits and Systems (ISCAS), 2021. [CrossRef]
  10. Y. Cai, W. Hua, H. Chen, G. Suh, C. Sa, Z. Zhang, "Structured Pruning Is All You Need for Pruning CNNs at Initialization," 2022. Available: https://arxiv.org/abs/2203.02549.
  11. G. Hinton, O. Vinyals, J. Dean, "Distilling the Knowledge in a Neural Network," arXiv preprint arXiv:1503.02531, 2015.
  12. Y. LeCun, L. Bottou, Y. Bengio, P. Haffner, "Gradient-Based Learning Applied to Document Recognition," Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998. [CrossRef]
  13. A. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang, T. Weyand, M. Adam, "MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications," 2017. Available: https://arxiv.org/abs/1704.04861.
  14. C.-J. Hsieh, M. A. Sustik, I. S. Dhillon, P. Ravikumar, "Low-Rank Matrix Factorization for Deep Neural Network Training with High-Dimensional Output Targets," arXiv preprint arXiv:1611.05725, 2017.
  15. Z. Liu, M. Sun, T. Zhou, G. Huang, T. Darrell, "Dynamic Network Surgery for Efficient DNNs," arXiv preprint arXiv:2003.02389, 2019.
  16. B. Jacob, S. Kligys, B. Chen, M. Zhu, M. Tang, A. Howard, H. Adam, D. Kalenichenko, "Quantization and training of neural networks for efficient integer-arithmetic-only inference," in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018. [CrossRef]
  17. J. Chen, W. K. Cheung, "Similarity preserving deep asymmetric quantization for image retrieval," in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, no. 01, pp. 8183-8190, 2019. [CrossRef]
  18. P. Molchanov, S. Tyree, T. Karras, T. Aila, J. Kautz, "Pruning convolutional neural networks for resource efficient inference," 2016. Available: https://arxiv.org/abs/1611.06440.
  19. H. Li, A. Kadav, I. Durdanovic, H. Samet, H. P. Graf, "Pruning filters for efficient convnets," 2016. Available: https://arxiv.org/abs/1608.08710.
  20. J. Frankle, G. K. Dziugaite, D. M. Roy, M. Carbin, "Stabilizing the lottery ticket hypothesis," 2019. Available: https://arxiv.org/abs/1903.01611.
  21. J. Gou, B. Yu, S. J. Maybank, D. Tao, "Knowledge distillation: a survey," International Journal of Computer Vision, vol. 129, no. 6, pp. 1789-1819, 2021. [CrossRef]
  22. Y. Zhang, Z. Lin, J. Jiang, Q. Zhang, Y. Wang, H. Xue, C. Zhang, Y. Yang, "Deeper insights into weight sharing in neural architecture search," 2020. Available: https://arxiv.org/abs/2001.01431.
  23. Y. Koren, R. M. Bell, C. Volinsky, "Matrix factorization techniques for recommender systems," Computer, vol. 42, no. 8, pp. 30-37, 2009. [CrossRef]
  24. . [CrossRef]
  25. J. Gibson, H. Oh, "Mutual information loss in pyramidal image processing," Information, vol. 11, no. 6, p. 322, 2020. [CrossRef]
  26. J. Mao, M. Niu, H. Bai, X. Liang, H. Xu, C. Xu, "Pyramid R-CNN: Towards Better Performance and Adaptability for 3D Object Detection," 2021. Available: https://arxiv.org/abs/2109.02499.
  27. A. Krizhevsky, V. Nair, G. Hinton, "CIFAR-10 (Canadian Institute for Advanced Research)," 2009. Available: https://www.cs.toronto.edu/~kriz/cifar.html.
  28. O. Ronneberger, P. Fischer, T. Brox, "U-Net: Convolutional Networks for Biomedical Image Segmentation," in Medical Image Computing and Computer-Assisted Intervention (MICCAI), 2015.
  29. S. Ren, K. He, R. Girshick, J. Sun, "Faster R-CNN: Towards real-time object detection with region proposal networks," in Advances in Neural Information Processing Systems (NeurIPS), 2015.
  30. K. He, X. Zhang, S. Ren, J. Sun, "Deep Residual Learning for Image Recognition," in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 770–778.
  31. K. Simonyan, A. Zisserman, "Very Deep Convolutional Networks for Large-Scale Image Recognition," arXiv preprint arXiv:1409.1556, 2014.
  32. A. Geiger, P. Lenz, R. Urtasun, "The KITTI Vision Benchmark Suite," in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2012.
  33. L. Wang, J. Shi, G. Song, I.-F. Shen, "Object detection combining recognition and segmentation," in Proceedings of the 8th Asian Conference on Computer Vision - Volume Part I, Springer-Verlag, 2007, pp. 189–199. [CrossRef]
Preprints 106434 g001
Figure 1. Visual representation of feature maps extracted from a convolutional layer of a neural network trained on MNIST dataset [12]. These maps highlight the potential for similarity-based feature reduction, as several maps exhibit similar activation patterns.
Figure 1. Visual representation of feature maps extracted from a convolutional layer of a neural network trained on MNIST dataset [12]. These maps highlight the potential for similarity-based feature reduction, as several maps exhibit similar activation patterns.
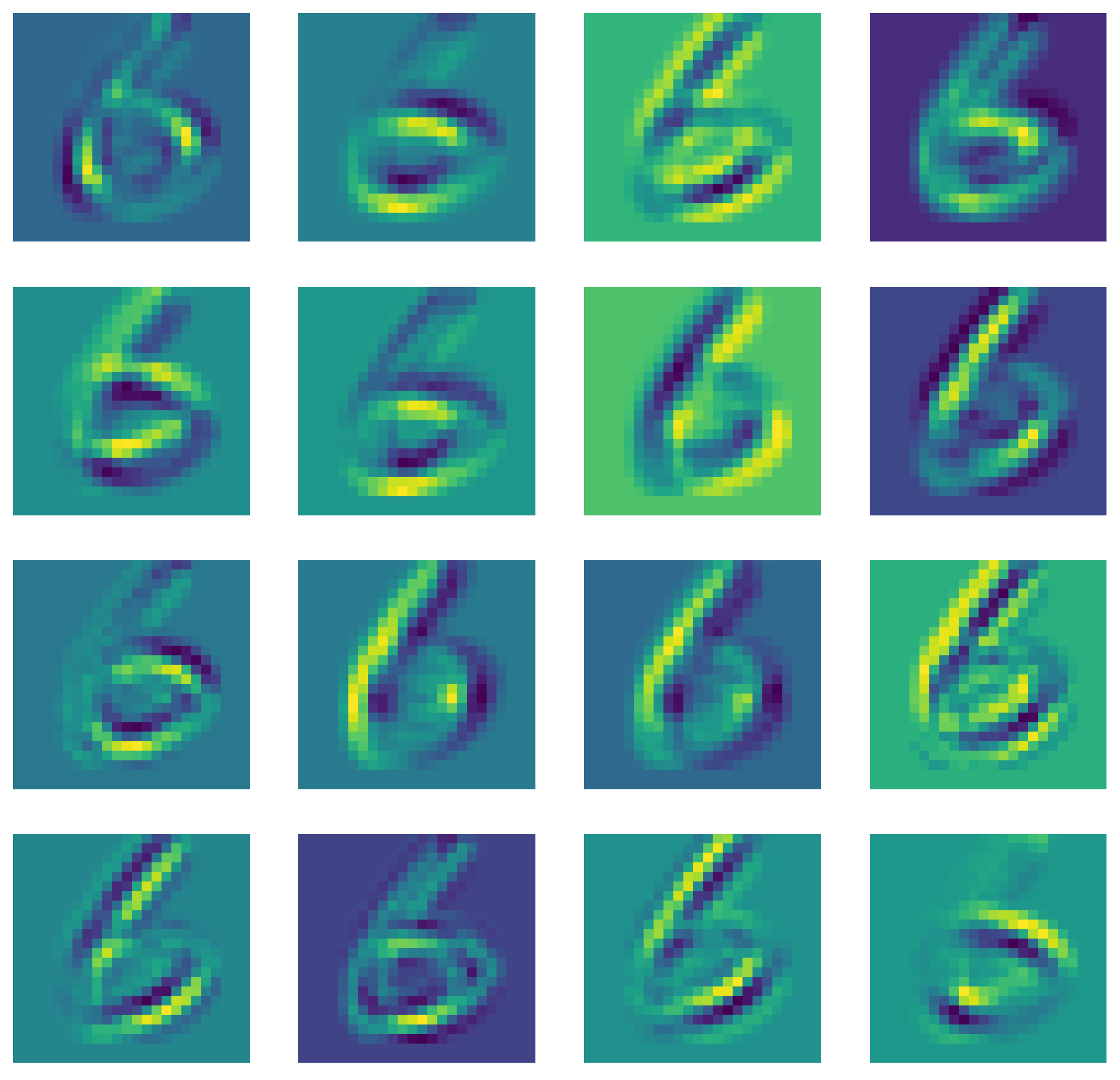
Preprints 106434 g001
Preprints 106434 g002
Figure 2. The general architecture of Pyramid training used in Classification Task.
Figure 2. The general architecture of Pyramid training used in Classification Task.
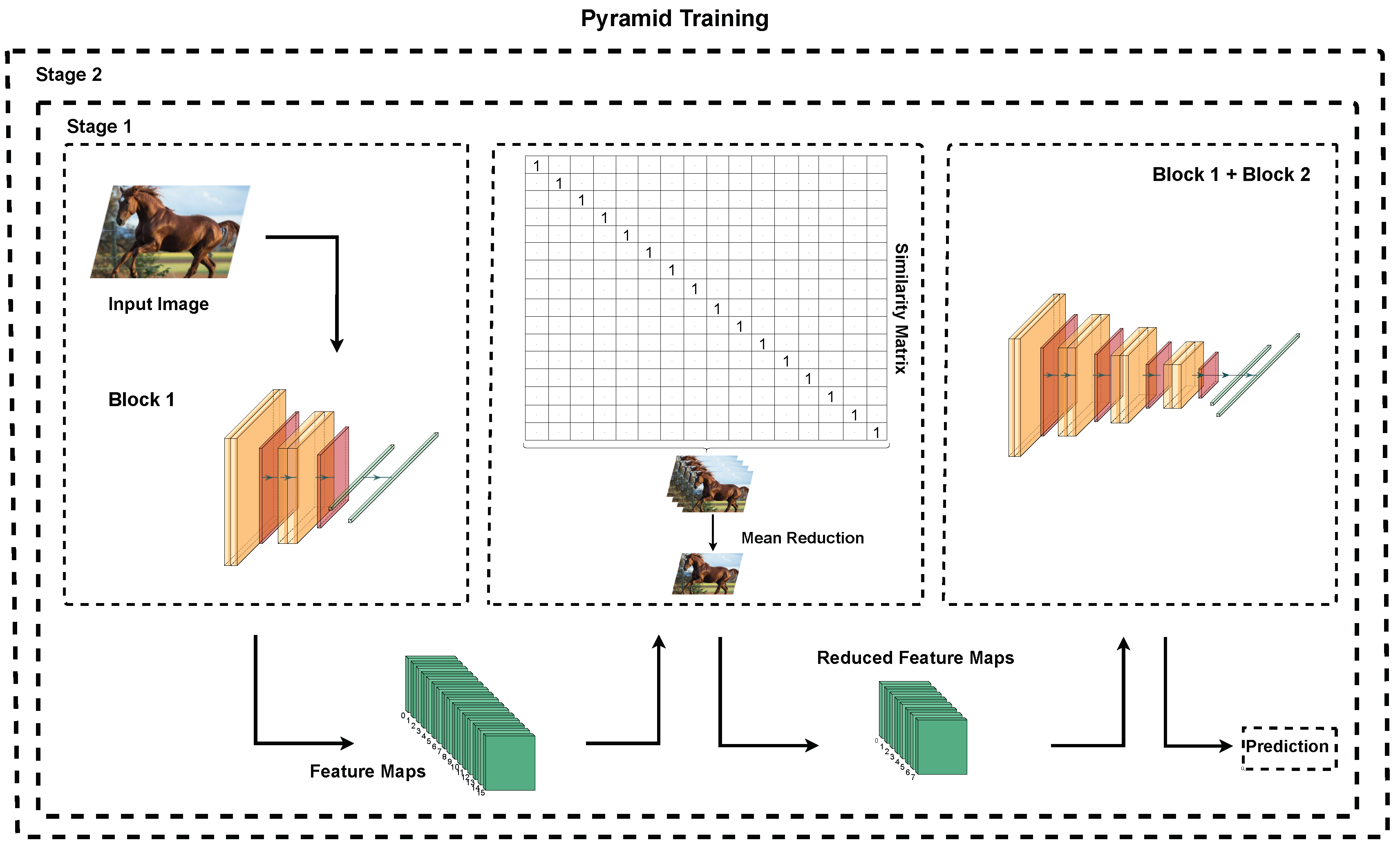
Preprints 106434 g002
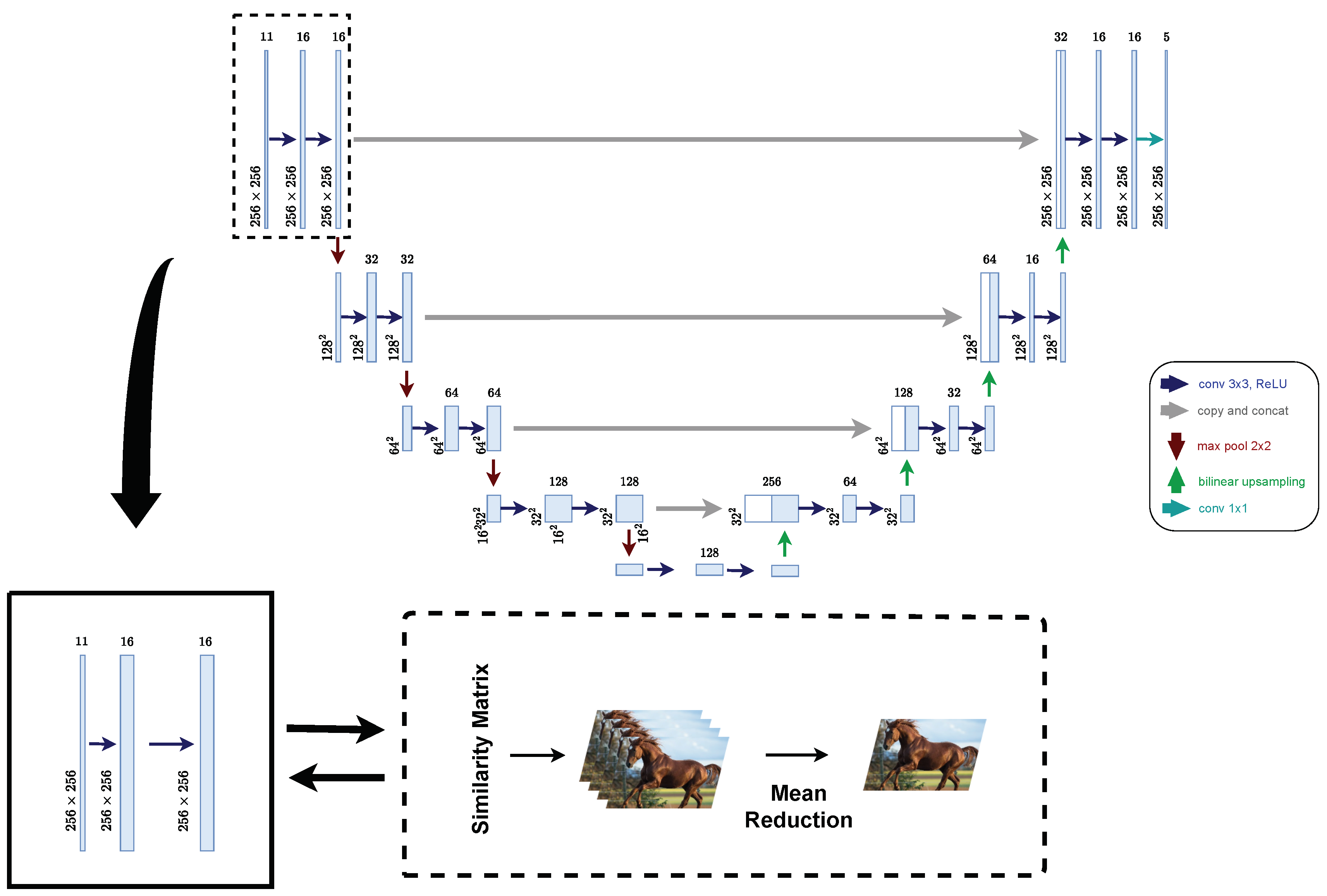
Preprints 106434 g003
Figure 3. The application of feature dimensionality reduction to U-Net Architecture.
Figure 3. The application of feature dimensionality reduction to U-Net Architecture.
Preprints 106434 g003
Preprints 106434 g004
Figure 4. The application of feature dimensionality reduction to Fast R-CNN Architecture.
Figure 4. The application of feature dimensionality reduction to Fast R-CNN Architecture.
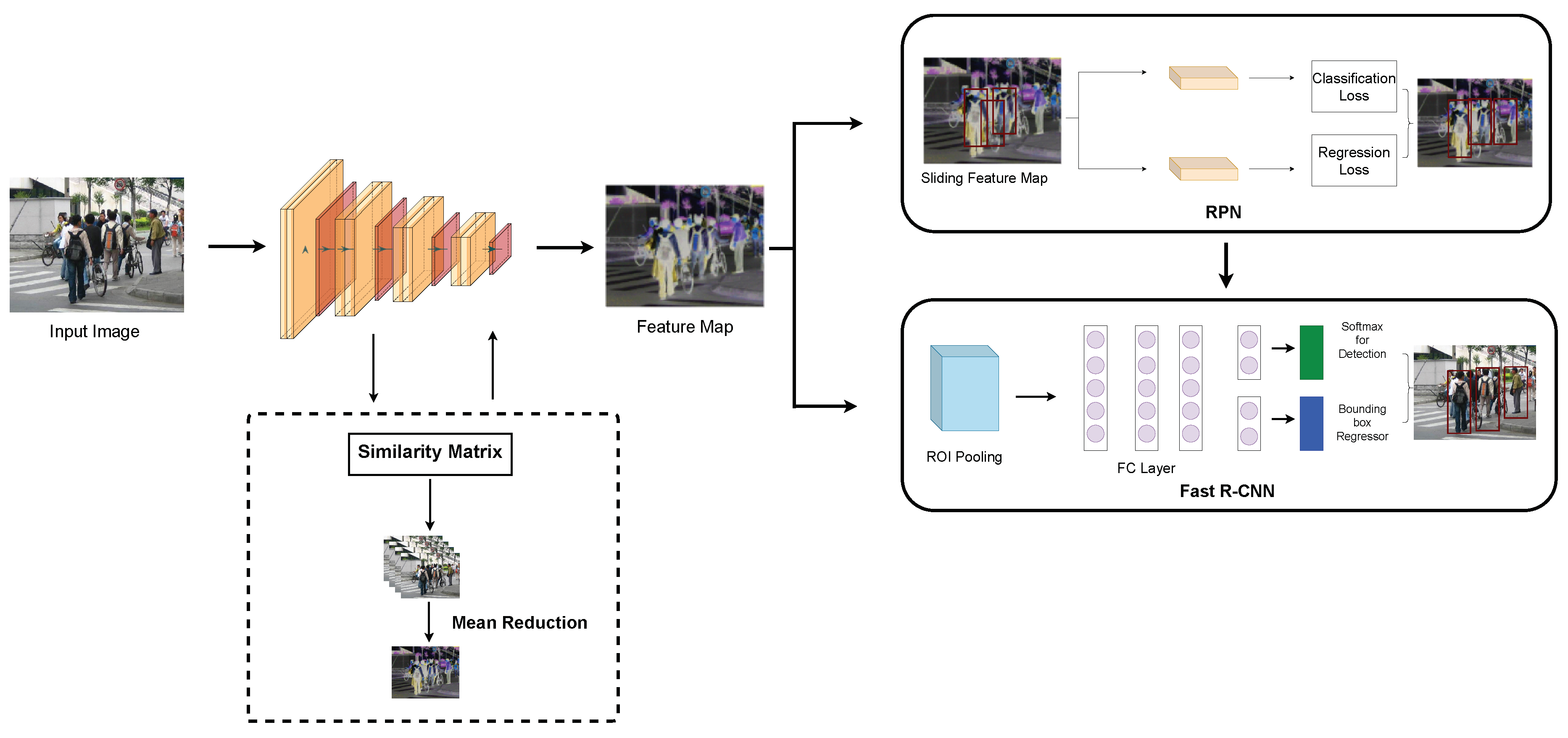
Preprints 106434 g004
Table 1. Block 1 Model Details.
Table 1. Block 1 Model Details.
Layer Type Input Channels Output Channels Kernel Size Stride Padding
Conv1 Conv2d 3 16 3x3 1 1
Pool1 MaxPool2d - - 2x2 2 0
Conv2 Conv2d 16 32 3x3 1 1
Pool2 MaxPool2d - - 2x2 2 0
FC1 Linear - 128 - - -
FC2 Linear - 10 - - -
Table 2. Block 2 Model Details.
Table 2. Block 2 Model Details.
Layer Type Input Channels Output Channels Kernel Size Stride Padding
Conv3 Conv2d 16 32 3x3 1 1
Pool1 MaxPool2d - - 2x2 2 0
Conv4 Conv2d 32 128 3x3 1 1
Pool2 MaxPool2d - - 2x2 2 0
FC3 Linear - 128 - - -
FC4 Linear - 10 - - -
Table 3. Block 1 Combined with Block2 Model Details.
Table 3. Block 1 Combined with Block2 Model Details.
Layer Type Input Channels Output Channels Kernel Size Stride Padding
Conv1 Conv2d 3 16 3x3 1 1
Pool1 MaxPool2d - - 2x2 2 0
Conv2 Conv2d 16 32 3x3 1 1
Pool2 MaxPool2d - - 2x2 2 0
Conv3 Conv2d 16 32 3x3 1 1
Pool1 MaxPool2d - - 2x2 2 0
Conv4 Conv2d 32 128 3x3 1 1
Pool2 MaxPool2d - - 2x2 2 0
FC3 Linear - 128 - - -
FC4 Linear - 10 - - -
Table 4. Experimental Results on Classification Task.
Table 4. Experimental Results on Classification Task.
Network Training Time (s) Test Set Accuracy (%) Size (MB)
BaseNetwork 366.51 77.31 0.65
ReducedNetwork 613.78 74.77 0.17
Quantization+BaseNetwork 343.25 76.51 0.32
Reduced+Quantization 601.47 73.53 0.10
Table 5. Experimental Results for Segmentation Task.
Table 5. Experimental Results for Segmentation Task.
Networks Train Loss Validation Loss Training Time (s) Size (MB)
U-Net 1.004 0.8484 1683 31 MB
U-Net-Reduced 0.6522 0.8945 2562 7 MB
Table 6. Experimental Results for Object Detection Task.
Table 6. Experimental Results for Object Detection Task.
Networks Loss Box Reg Loss Classifier Loss RPN Box Reg Loss Training Time (s) Memory Allocation (GB)
CustomBackbone a 0.3894 0.4018 0.3894 1.14 460 15.841
CustomBackbone-Reduced 0.4402 0.4343 0.4402 1.223 823 10.312
VGG16 b 0.1043 0.0701 0.1043 0.216 653 16.04
VGG16-Reduced 0.1894 0.1394 0.1894 0.4377 1100 9.96
a Custom CNN model; b VGG model.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated