Prerpints.org logo
Preprint
Article

3D – 2D Crossover and Phase Shift of Beats of Quantum Oscillations of Interlayer Magnetoresistance in Quasi-2D Metals

Altmetrics

Downloads

88

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 May 2024

Posted:

14 May 2024

You are already at the latest version

Alerts
Abstract
Magnetic quantum oscillations (MQO) are traditionally applied to investigate the electronic structure of metals. In layered quasi-two-dimensional (Q2D) materials the MQO have several qualitative features giving additional useful information, provided their theoretical description is developed. Within the framework of the Kubo formula and the self-consistent Born approximation, we reconsider the phase of beats in the amplitude of Shubnikov oscillations of interlayer conductivity in Q2D metals. We show that the phase shift of beats of the Shubnikov (conductivity) oscillations relative to the de Haas - van Alphen (magnetization) oscillations is larger than expected previously and, under certain conditions, can reach the value of π/2, as observed experimentally. We explain the phase inversion of MQO during the 3D - 2D crossover and predict the decrease of relative MQO amplitude of interlayer magnetoresistance in a strong magnetic field, larger than the beat frequency.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Layered quasi-two-dimensional (Q2D) metals (see Figure 1 for illustration) represent a wide class of materials, intermediate between the various two-dimensional (2D) electron systems and usual three-dimensional (3D) compounds. The Q2D materials attract enormous research interest due to the variety of new electronic phenomena and diverse potential applications. They include high-temperature superconductors, organic metals, van der Waals crystals, artificial heterostructures, etc. An experimental study of their electronic structure, in addition to ab initio calculations, is crucial for the understanding and utilizing their properties. Although the angle-resolved photoemission spectroscopy (ARPES) provides visual data on electronic bands and Fermi surface (FS), more traditional tools, such as magnetic quantum oscillations (MQO) [1], usually have higher accuracy and availability.
The MQO originate from the Landau-level (LL) quantization of electron spectrum in a magnetic field B and appear in all thermodynamic and transport quantities as their periodic dependence on 1 / B . The standard MQO theory, based on the Lifshitz-Kosevich (LK) formula [1], is often applied even in Q2D metals and gives the FS extremal cross-section areas S i = 2 π e ℏ F i / c from the fundamental MQO frequencies F i . Such data, collected at various directions of the magnetic field B , helped to determine the FS of most known metals. Less accurate, the LK theory also describes the damping of MQO amplitude by temperature and disorder as a function of magnetic field strength B, which allows the estimate of electron effective mass and mean free time for each band [1].
The strong anisotropy of layered Q2D metals introduces special features to MQO. The Q2D electron dispersion, obtained in the tight-binding approximation for the interlayer z direction, is given by
ϵ 3 D ( k ) = ϵ ‖ k ‖ − 2 t z cos ( k z d ) ,
where ϵ ‖ k ‖ is the intralayer electron dispersion, t z is the interlayer transfer integral of electrons, and d is the lattice constant along the z-axis. Often in Q2D metals the Fermi energy μ ≫ t z , and the FS is a warped cylinder with two close cross-section areas corresponding to the ”neck” and ”belly” of the FS (see Figure 1b). According to the LK theory, at B | | z the MQO have two close fundamental frequencies F 1 = F − Δ F / 2 and F 2 = F + Δ F / 2 . As the MQO amplitudes with these two frequencies are also close, the resulting MQO at frequency F have amplitude modulations with frequency Δ F , called beats. The beat frequency Δ F is proportional to the interlayer transfer integral: Δ F / F ≈ 4 t z / μ . It non-monotonously depends on the direction of magnetic field, which follows the angular magnetoresistance oscillations (AMRO) [2,3,4,5] and the can be used to determine the in-plane Fermi momentum [4,5] and even high harmonics of FS warping [6,7].
Even when the MQO are weak, the interlayer electron transport in Q2D metals exhibits several unique properties, such as the aforementioned AMRO [2,3,4,5] and longitudinal interlayer magnetoresistance [8,9,10]. There are even more new features of MQO in Q2D metals which are not described within the standard L-K theory. The interplay between the angular and quantum magnetoresistance oscillations is nontrivial [11,12] and leads to the angular modulations of MQO amplitude [12]. The so-called difference or slow oscillations (SO) of magnetoresistance [13,14,15,16] at frequency 2 Δ F appear and survive at much higher temperature than the usual MQO. The SO help to determine the type of disorder and give other useful information, such as the interlayer transfer integral. Another feature beyond the L-K theory is the phase shift of beats between the MQO of thermodynamic and transport quantities [14,17]. This phase shift increases with magnetic field strength B, as observed in various Q2D metals [17,18,19] and substantiated theoretically [14,17]. The experimentally observed phase shift of beats Δ ϕ e x p , usually, considerably exceeds the theoretical prediction Δ ϕ t h e o r (e.g., see Figure 3 of Ref. [14] or Figure 6 of Ref. [18]). In the present paper we explain this inconsistency and develop a more accurate theory of this effect.
The beatings of MQO amplitude due to the interlayer electron hopping were observed in many other layered materials [4,5,20,21,22,23,24]. Note that the phase shift of beats is observed not only between the SdH and dHvA effect, but also between the oscillations of other quantities, e.g., the interlayer magnetoresistance and thermopower [21], or magnetoresistance and specific heat [25]. The MQO of magnetization and of interlayer conductivity were also measured simultaneously in the Dirac semimetals BaGa2 [26]. There are many other combined SdH and dHvA measurements in layered metals where the MQO beats are observed [27,28,29,30]. Similar beating effects may also appear in artificial heterostructures and multilayer topological insulators [31,32], as well as in layered Weyl semimetals [25].
Another interesting feature of the 3D - 2D crossover, driven by the parameter λ = 4 Δ F / B z , is the phase inversion of MOQ of conductivity as compared to those of the electronic density of states (DoS) at the Fermi level and, hence, of all thermodynamic quantities. At low magnetic field the MQO of conductivity and of DoS have opposite phases, because the former is proportional to the electron mean free time which is inversely proportional to the DoS [33,34], according to the golden Fermi rule or the Born approximation. However, in a high magnetic field B z ≫ Δ F in Q2D metals, when the Landau levels (LLs) become separated and the DoS between the LLs is zero, the MQO phase of conductivity and DoS coincide. The latter follows both from the direct observations [9,35,36] and calculations [8,9,10,16,37], being supported by the simple qualitative argument that if the DoS at the Fermi level is zero the conductivity must also be zero at low temperature. However, in spite of a general understanding, the quantitative description of this phase inversion is absent. Below we show how this phase inversion during the 3D - 2D crossover is described by analytical formulas. The understanding of this MQO phase inversion is helpful for experimental studies of the Berry phase using MQO measurements [38,39,40,41].

2. Available Experimental Observations and their Description

The MQO have been extensively investigated in various Q2D metals, including the cuprate [42,43,44,45] and iron-based [46,47] high-Tc superconductors, organic metals [4,5], van-der-Walls layered crystals, artificial heterostructures, and many other materials. The two most common MQO experiments are the measurements of magnetization and conductivity oscillations, i.e., the de Haas - van Alphen (dHvA) and the Shubnikov - de Haas (SdH) effect. However, the observation of the phase shift between their beats is less common because it requires the measurements of both these effects on the same sample.
In Ref. [18] the Fermi surface of a layered organic metal (BEDT-TTF)4[Ni(dto)2] was studied by measuring the quantum oscillations of both magnetization and interlayer conductivity. The authors have shown that the standard Lifshitz-Kosevich theory (LK) [1] well describes the results on magnetization oscillations. The detected positions of the beat nodes of the de Haas - van Alphen oscillation amplitude are well fitted by the formula
B n o d e = 4 4 n − 1 Δ F , n = 1 , 2 , 3 …
where Δ F is the beat frequency giving the FS warping. However the observed position of the beat nodes of the Shubnikov oscillation amplitude in Ref. [18] are strongly shifted and well fitted by another formula
B n o d e = 4 4 n + 1 Δ F , n = 0 , 1 , 2 …
A similar difference in the positions of beat nodes of de Haas van Alphen oscillations and Shubnikov oscillations was also observed in κ − ( BEDT − TTF ) 2 Cu [ N ( CN ) 2 ] Br [19]. The LK theory does not explain this clearly observed phase shift of beat nodes about π / 2 between the oscillations of magnetization and interlayer conductivity.
The 3D → 2D crossover in MQO behavior happens [9] when B ∼ Δ F , i.e., when the LL separation ℏ ω c becomes comparable to the interlayer bandwidth 4 t z , where ω c = e B / ( m * c ) is the cyclotron frequency, e – the elementary charge, c – the speed of light, m * – the effective electron mass, ℏ – the Planck constant. The phase shift between the MQO beats of dHvA and SdH effects is considerable when ℏ ω c ≳ 4 t z , i.e., during this 3D → 2D crossover.
The expressions for interlayer conductivity derived [13,17] in the tau approximation strongly underestimate the observed phase shift ϕ b between the beats of magnetization and interlayer conductivity, giving
ϕ b = arctan [ ℏ ω c / ( 2 π t z ) ] ,
This formula always predicts ϕ b < π / 2 , which does not explain the experimental data from [18]. Note that the phase shift of beats observed in Ref. [17] is also ∼ 2.4 times larger than the prediction of this formula. Indeed, substituting the known parameters in the quasi-two-dimensional organic metal β -(BEDT-TTF)2IBr2, namely, the cyclotron mass m * = 4.2 m e , as obtained from the temperature dependence of MQO amplitude, and the interlayer bandwidth 4 t z = 1.15 meV, as extracted from the ratio between the beating and fundamental MQO frequencies, to Equation (4) one obtains the 2.4 times smaller slope of the linear dependence of tan ϕ b on B z than the experimental data in Figure 4 of Ref. [17].
The calculations of interlayer conductivity using the Kubo formula predict a larger phase shift of beats, given by [14]
tan ϕ b = ℏ ω c 2 π t z 1 + 2 π 2 k B T D ℏ ω c = ℏ ω c 2 π t z 1 + π ω c τ ≡ ℏ ω c 2 π t z 1 + γ 0 ,
where T D ≡ ℏ / ( 2 π k B τ ) is the so-called Dingle temperature, τ is the electron mean free time, and γ 0 = π / ( ω c τ ) is the dimensionless parameter. These quantities enter the Dingle factor R D 0 = exp ( − γ 0 ) = exp [ − 2 π 2 k B T D / ( ℏ ω c ) ] , describing the damping of MQO by crystal disorder (see Equations (6)-(8) below). However, even this enhanced phase shift of beats, given by Equation (5), is still insufficient to describe quantitatively the effect observed in Refs. [17,18].
Note that the electron mean free time τ measured from the MQO is, usually, shorter than the transport mean free time τ t r and than the mean-free time τ * arising from short-range disorder only and measured from the damping of slow magnetoresistance oscillations [13]. This difference, τ < τ * ≈ τ t r , appears because the MQO are damped not only by short-range disorder but also by long-range sample inhomogeneities which smear the Fermi energy similar to the temperature effect [9,13,14,15,16]. The opposite case when the transport mean free time τ t r < τ ≲ τ * is also possible in heterogeneous conductors, where there are rare but strong inhomogeneities as, e.g., domain walls or linear crystal defects. Then inside each domain of the size larger than the Larmor radius the material is a clean metal with a large τ ∼ τ * , but the electronic transport across the sample is difficult because of its heterogeneity, which corresponds to a short τ t r . As follows from the calculations in Refs. [14,16], it is τ * rather than τ enters the Equation (5).

3. Materials and Methods

The materials to which our study is applicable are the strongly anisotropic layered quasi-2D metals, where the interlayer transfer integral t z is of the same order of magnitude as the LL separation ℏ ω c . For the comparison of our formulas with experiment we take the data from Refs. [17,18] obtained on the organic metals (BEDT-TTF)4[Ni(dto)2] and β -(BEDT-TTF)2IBr2.
Below we take the magnetic field B perpendicular to conducting layers, so that B = B z . We will use the expressions for the MQO of magnetization and interlayer conductivity from Refs. [14,16,48,49] obtained in the self-consistent Born approximation. In the leading order of the expansion in powers of the Dingle factor R D 0 at temperature T, the oscillating parts of the magnetization is equal to (see Equation (33) of Ref. [48] or Equation (6) of Ref. [49])
M ˜ ≈ e μ 2 π 2 ℏ c d R D 0 R T J 0 ( λ ) sin α ¯ + λ α ¯ J 1 ( λ ) cos α ¯ ,
and of interlayer conductivity is (see Equation (18) of Ref. [14] or Equation (64) of Ref. [16])
σ z z Q O ≈ 2 σ ¯ z z ( 0 ) cos α ¯ R D 0 R T R z σ , R z σ = J 0 λ − 2 λ 1 + γ 0 J 1 λ ,
where R D 0 = exp ( − γ 0 ) is the Dingle factor, γ 0 ≡ 2 π Γ 0 / ( ℏ ω c ) = π / ( ω c τ ) , λ = 4 Δ F / B z = 4 π t z / ( ℏ ω c ) , α ¯ = 2 π μ / ( ℏ ω c ) , J 0 , J 1 – the Bessel functions of zero and first order, σ ¯ z z ( 0 ) – the interlayer conductivity without magnetic field, R T = 2 π 2 k B T / ( ℏ ω c ) / sinh ( 2 π 2 k B T / ( ℏ ω c ) ) is the temperature damping factor of MQO.
At strong Q2D anisotropy, when 2 t z / μ = λ / α ¯ ≪ 1 and the beats of MQO are the most pronounced, the last term in the square brackets of Equation (6) can be omitted, and the oscillating part of magnetization simplifies to
M ˜ ≈ e μ 2 π 2 ℏ c d sin α ¯ R D 0 R T R M , R M = J 0 ( λ ) .
The MQO correspond to the rapidly oscillating factors sin α ¯ or cos α ¯ in Equations (6)-(8), while the factors R M and R z σ describe the beats of MQO amplitudes and are the subject of our study.

4. Analysis and Results

Let us first consider the limit of λ ≫ 1 , corresponding to a rather large electron interlayer transfer integral 4 π t z ≫ ℏ ω c or weak magnetic field. Then one can use the large-argument asymptotic expansions of the Bessel functions in Equations (7) and (8). As a result, the beating factors of the MQO amplitudes in Equations (7) and (8) simplify to
R M = 2 π cos λ − π 4 λ ,
R z σ = 2 π cos λ − π 4 λ + ( 16 γ 0 + 15 ) cos λ + π 4 4 2 π λ 3 / 2 .
At λ ≫ 2 ( γ 0 + 1 ) the second term in Equation () is negligibly small, and we get the same beating factors of the MQO of magnetization and interlayer conductivity,
R z σ ≈ 2 π cos λ − π 4 λ = R M .
Hence, in this limit the phase shift of beats is absent, ϕ b ≈ 0 .
In the opposite limit of strong MQO damping by disorder, γ 0 ≫ λ / 2 , the first term in Equation () can be omitted, and one obtains
R z σ ≈ 2 3 / 2 γ 0 cos λ + π 4 π λ 3 / 2 .
Comparing Equations (9) and (12) we see that at γ 0 ≫ λ / 2 the MQO beats of interlayer conductivity are shifted from those of magnetization by the phase ϕ b = π / 2 . As follows from Equation (9), the beat nodes of magnetization oscillations M ˜ in Equation (8) are located at λ ≈ − π / 4 + π n , and from Equation (12) it follows that the beat nodes of the interlayer conductivity oscillations σ z z Q O given by Equation (7) are shifted by π / 2 and located at λ ≈ π / 4 + π n , where n ≥ 1 is an integer number. These λ give the same position of the beat nodes as the expressions (2) and (3) for n ≥ 1 and Δ F = λ | B z | / π , corresponding to the fit of experimental data in Ref. [18]. Hence, Equations (9) and (12) describe well the experimental observations in Ref. [18]. However, Equation (12) assumes γ 0 ≫ λ / 2 , while γ 0 ∼ λ in the experiment in Ref. [18]. The Dingle temperature extracted from the experimental data in Ref. [18] is T D ≈ 0.5 K. The beat frequency in the organic metal (BEDT-TTF)4[Ni(dto)2] studied in Ref. [18] is Δ F ≈ 4.5 T, which corresponds to the interlayer transfer integral t z = 0.06 meV ≈ 0.7 K. Hence, the ratio γ 0 / λ = 2 π 2 T D / ( 4 π t z ) = π T D / ( 2 t z ) ≈ 1.12 in Ref. [18]. Hence, to improve the quantitative description of the observed phase shift of MQO beats we need to consider the case λ ∼ γ 0 ∼ 1 more accurately.
Preprints 106469 g002
Figure 2. The beating factors R z σ ≡ J 0 λ − 1 + γ 0 ( λ ) J 1 λ / λ and R M ≡ J 0 ( λ ) , describing the MQO amplitudes of interlayer conductivity σ z z Q O and magnetization M ˜ (brown solid curve), as a function of the inverse magnetic field 1 / | B z | . Here Δ F = 4 t z B z / ( ℏ ω c ) is the beat frequency, and the ratios γ 0 / λ = 0.1 , 1.12 , 2 , 3 correspond to the blue thick long-dashed, red short-dashed, green long-dashed and black dotted curves for R z σ .
Figure 2. The beating factors R z σ ≡ J 0 λ − 1 + γ 0 ( λ ) J 1 λ / λ and R M ≡ J 0 ( λ ) , describing the MQO amplitudes of interlayer conductivity σ z z Q O and magnetization M ˜ (brown solid curve), as a function of the inverse magnetic field 1 / | B z | . Here Δ F = 4 t z B z / ( ℏ ω c ) is the beat frequency, and the ratios γ 0 / λ = 0.1 , 1.12 , 2 , 3 correspond to the blue thick long-dashed, red short-dashed, green long-dashed and black dotted curves for R z σ .
Preprints 106469 g002
The phase shift ϕ b of MQO beats becomes even stronger than that given by Equations (9) and (12) if one applies Equations (7) and (8) without the asymptotic expansions of the Bessel functions at large argument, i.e., without the assumption λ ≫ 1 , which is more relevant to the experiment in Ref. [18]. In Figure 2, using Equations (7) and (8) at γ 0 ( λ ) = { 0.1 , 1.12 , 2 , 3 } λ , we plot the beating factors R M and R z σ , describing the MQO amplitudes of magnetization and conductivity without the Dingle and temperature damping factors. The theoretical curves in Figure 2 correspond to four values γ 0 / λ = { 0.1 , 1.12 , 2 , 3 } to describe the experimental data from Refs. [17] and [18] where γ 0 / λ ≈ 0.1 and γ 0 / λ ≈ 1.12 correspondingly. In Figure 2 we take a special scale of the abscissa axis so that the zeros of both curves, called the beat nodes, fall into integer values. From Figure 2 we see that the beat nodes for interlayer conductivity oscillations σ z z Q O are shifted relative to the magnetization M ˜ beat nodes by a quarter of the period λ ≈ π Δ F / | B z | .1 The beat nodes of magnetization oscillations M ˜ given by Equation (8) in Figure 2 are located at 4 λ / π ≈ { 3 , 7 , 11 , 15 } . This coincides with the prediction of simplified limiting-case formula (9) and agrees perfectly with the experimental data from Ref. [18], fitted by Equation (2). At γ 0 ( λ ) = 0.1 λ , the positions of beat nodes of the amplitude of conductivity oscillations are close to the position of the beat nodes of the amplitude of magnetization oscillations. The beat nodes of interlayer conductivity oscillations σ z z Q O given by Equation (7) and plotted in Figure 2 at γ 0 ( λ ) = { 1.12 , 2 , 3 } λ are located at 4 λ / π ≈ { 0 , 5 , 9 , 13 } . For n ≥ 1 they coincide with Equation (3), which fits the experimental data from Ref. [18].
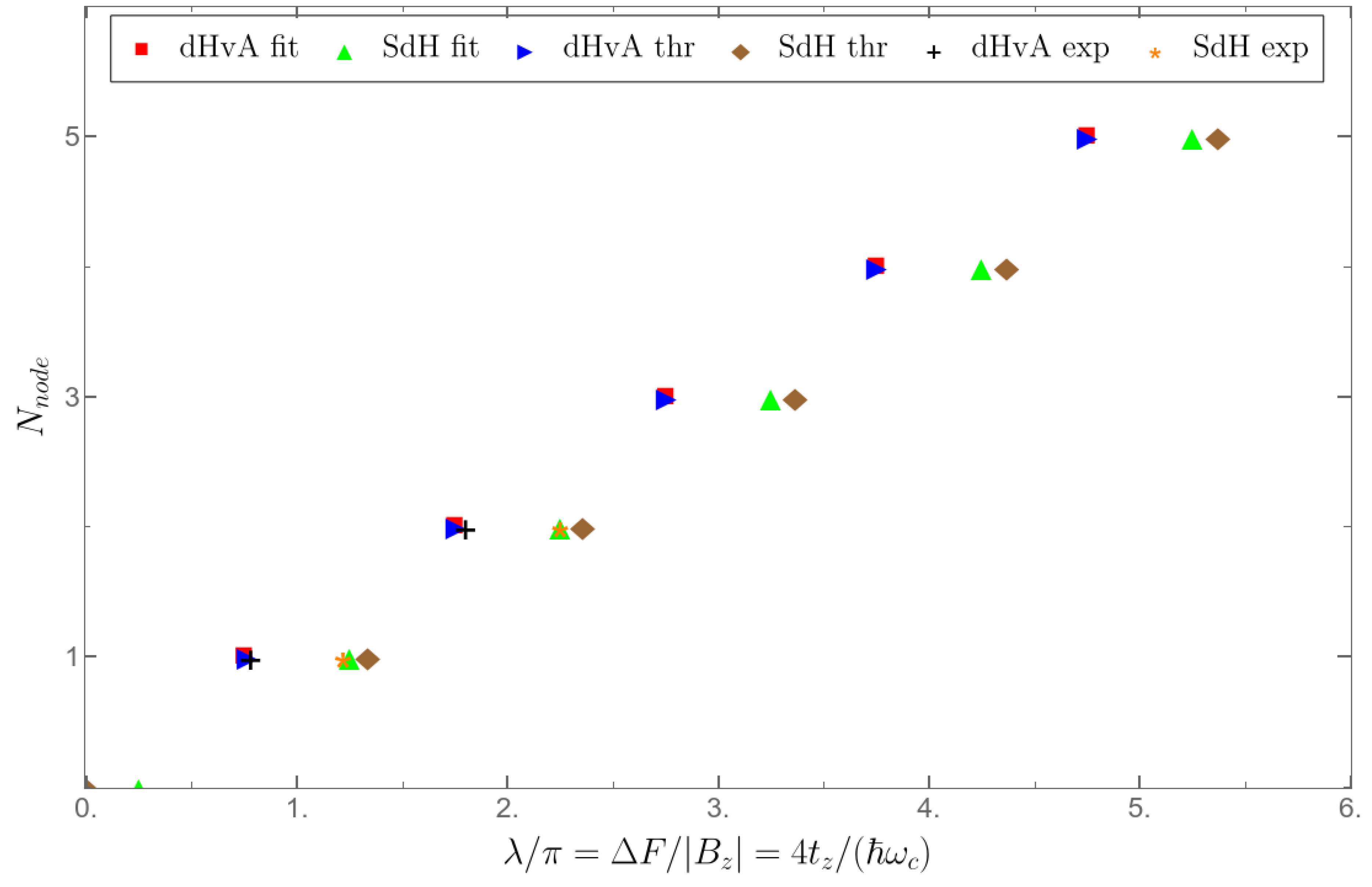
Equations (7) and (8) also perfectly agree with the experimental data from Ref. [17]. In Figure 3 we plot the measured positions of magnetization and conductivity beat nodes from the experiments in Refs. [17,18] together with the theoretical predictions from formulas (7) and (8). The measured positions of the beat nodes in Ref. [18] at n ≥ 1 are very well described by Equations (2) and (3) and, therefore, denoted by ”dHvA fit” and ”SdH fit” in Figure 3. The points ”dHvA exp” and ”SdH exp” in Figure 3 are taken from the experimental data in Figure 2 or 3 of [17]. The prediction of Equations (7) and (8) are denoted by ”SdH thr” and ”dHvA thr” in Figure 3. From Figure 3 we see a perfect agreement between the above theory and the experimental data from Refs. [17,18] for the beat-node positions with number n ≥ 1 . These beat-node positions for the MQO of magnetization and interlayer conductivity are fitted well by two straight lines parallel to each other. Hence, we conclude that Equations (8) and (7) describe very well the beating nodes with n ≥ 1 .
Preprints 106469 g003
Figure 3. The dependence of the beat-node number N n o d e of the MQO of σ z z Q O and M ˜ on the inverse magnetic field 1 / | B z | at γ 0 = 1.12 λ . Points <<dHvA fit>> and <<SdH fit>> refer to the fit expressions (2) and (3) from Ref. [18]. Points <<dHvA exp>> and <<SdH exp>> refer to the experimental data from Figure 2 and 3 of Ref. [17]. Points <<dHvA thr>> are found from the zeros of expression (9), while points <<SdH thr>> are found numerically from the solution of equation R z σ = J 0 λ − 1 + γ 0 ( λ ) J 1 λ / λ = 0 .
Figure 3. The dependence of the beat-node number N n o d e of the MQO of σ z z Q O and M ˜ on the inverse magnetic field 1 / | B z | at γ 0 = 1.12 λ . Points <<dHvA fit>> and <<SdH fit>> refer to the fit expressions (2) and (3) from Ref. [18]. Points <<dHvA exp>> and <<SdH exp>> refer to the experimental data from Figure 2 and 3 of Ref. [17]. Points <<dHvA thr>> are found from the zeros of expression (9), while points <<SdH thr>> are found numerically from the solution of equation R z σ = J 0 λ − 1 + γ 0 ( λ ) J 1 λ / λ = 0 .
Preprints 106469 g003
The position λ = 0 of the zeroth beating node given by Equation (7) holds at any ratio γ 0 / λ , as illustrated in Figure 2 and can be shown analytically. Indeed, in a very high magnetic field λ → 0 , the ratio γ 0 / λ = ℏ / ( 4 τ t z ) → c o n s t , and the beating nodes are given by the equation
R z σ = J 0 λ − 2 λ 1 + γ 0 J 1 λ ≈ − γ 0 λ λ + γ 0 − 1 8 λ 2 = 0 .
λ = 0 is the root of this equation at any ratio γ 0 / λ . The second root λ = 8 γ 0 / γ 0 − 1 of Equation (13) is physically irrelevant as it gives a too large value
λ = 1 + 1 + 32 γ 0 2 / λ 2 2 γ 0 / λ > 2 2
much beyond the limit λ ≪ 1 where the expansion (13) holds.
The position of the very first beat node at n = 0 differs in Equations (3) and (7). According to Equation (3), the beating node N n o d e = 0 of σ z z Q O oscillations should be at 4 λ / π = 1 , which does not coincide with the position B = ∞ or λ = 0 of the zeroth beating node given by Equation (7) and shown in Figure 2. As we just have shown, the origin of this difference is not a ”wrong” choice of the parameter γ 0 / λ , entering Equation (7).
In fact, the position λ = π / 4 of the zeroth beating node n = 0 , predicted by the ”fit” Equation (3), has not been observed experimentally. The beat frequency in the organic metal (BEDT-TTF)4[Ni(dto)2] studied in Ref. [18] is Δ F ≈ 4.5 T. According to Equation (3) the zeroth beating node is at B = 4 Δ F ≈ 18 T. In Ref. [18] the experimental data on the SdH oscillations in (BEDT-TTF)4[Ni(dto)2] are shown up to B = 6 T only in Figure 6 of Ref. [18], while the data up to B = 28 T are given only for dHvA oscillations in Figure 3 of Ref. [18]. In Figure 6.1 of Ref. [50] the SdH data up to B = 28 T are shown for the same organic metal (BEDT-TTF)4[Ni(dto)2], and no beating nodes are observed in the magnetic-field interval 4 < B < 28 T. A similar difference in the beat-node positions of de Haas - van Alphen and Shubnikov oscillations in κ − ( BEDT − TTF ) 2 Cu [ N ( CN ) 2 ] Br [19] was also detected by the non-observation of the SdH beat node in the magnetic-field interval 16 < B < 28 T. Hence, Equation (7) describes very well the available experimental data on the MQO beats of interlayer conductivity.
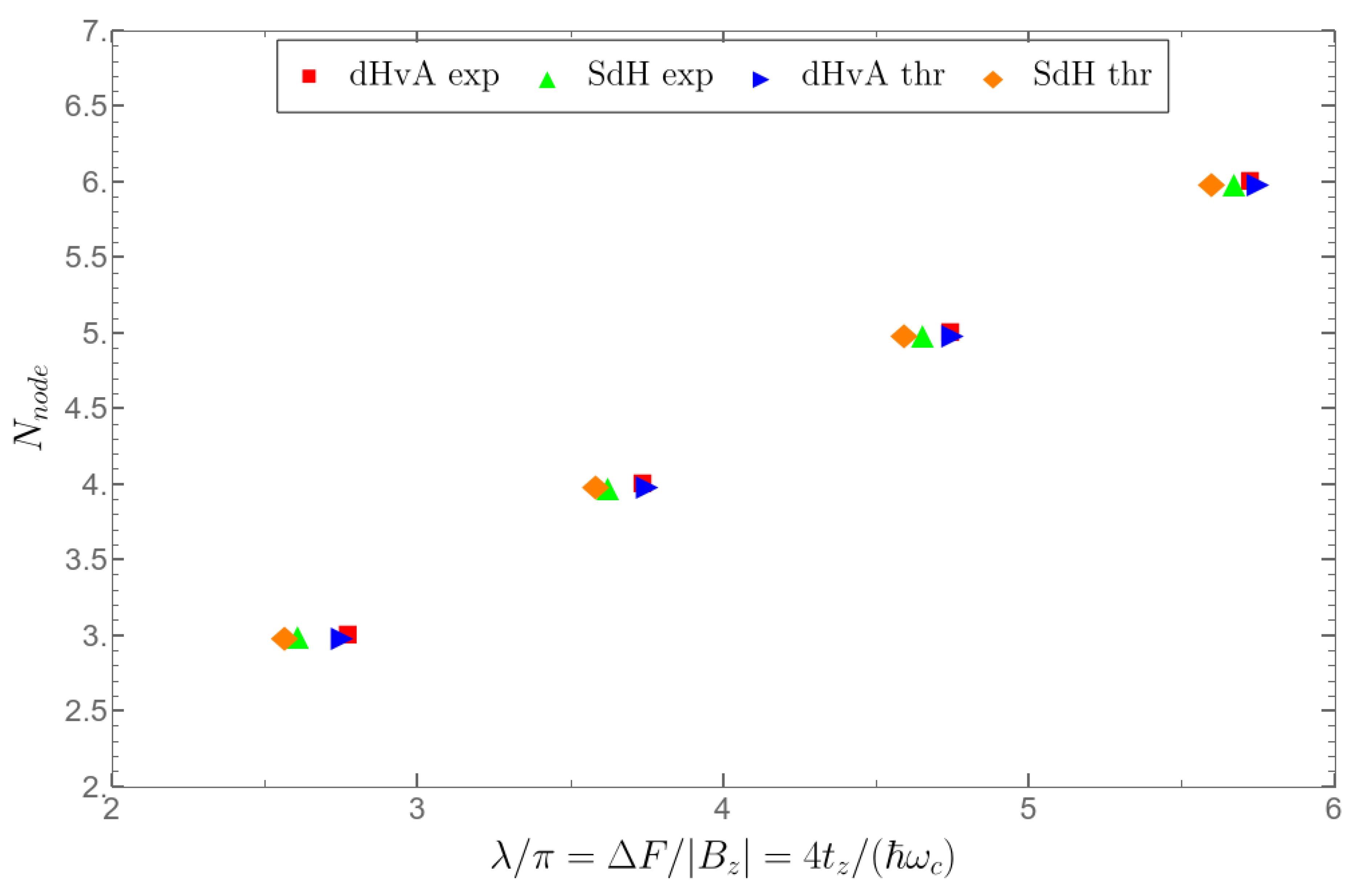
In Ref. [17] the Dingle temperature extracted from the experimental data is T D = 0.8 K, but the Dingle temperature from the scattering by short-range disorder is T D * = 0.15 K (see Figure 4 of Ref. [13]). The beat frequency Δ F ≈ 40.9 T in the organic metal β -(BEDT-TTF)2IBr2 studied in Ref. [17] is much larger than in (BEDT-TTF)4[Ni(dto)2] studied in Ref. [18]. It corresponds to the interlayer transfer integral t z = 1.15 meV ≈ 13.3 K and γ 0 / λ ≈ 0.1 . For γ 0 ≪ λ / 2 3 / 2 the expression for R z σ λ in Equation () is approximately equal to that in Equation (11). Since formulas (9) and (11) are similar, this means that the beat nodes for magnetization M ˜ and conductivity oscillations σ z z Q O in this limit are close to each other. In Figure 4 we show that the beat nodes found at γ 0 = 0.1 λ fit well with the experimental data on the position of beat nodes from Figure 3 of Ref. [17]. The higher is the number N n o d e of the MQO beat nodes of magnetization and interlayer conductivity, the shorter is the distance between them along the abscissa axis in the units of Δ F / | B z | .
Preprints 106469 g004
Figure 4. The dependence of the number N n o d e of the beat node of magnetic quantum oscillations of σ z z Q O and M ˜ on the inverse magnetic field 1 / | B z | at γ 0 ( λ ) = 0.1 λ . The points <<dHvA exp>> and <<SdH exp>> refer to the experimental points taken from the Figure 3 of [17]. The points <<dHvA thr>> are found from the zeros of expression (9), while the points <<SdH thr>> are found numerically from the solution of equation R z σ = J 0 λ − 1 + γ 0 ( λ ) J 1 λ / λ = 0 . Here Δ F = 4 t z B z / ( ℏ ω c ) .
Figure 4. The dependence of the number N n o d e of the beat node of magnetic quantum oscillations of σ z z Q O and M ˜ on the inverse magnetic field 1 / | B z | at γ 0 ( λ ) = 0.1 λ . The points <<dHvA exp>> and <<SdH exp>> refer to the experimental points taken from the Figure 3 of [17]. The points <<dHvA thr>> are found from the zeros of expression (9), while the points <<SdH thr>> are found numerically from the solution of equation R z σ = J 0 λ − 1 + γ 0 ( λ ) J 1 λ / λ = 0 . Here Δ F = 4 t z B z / ( ℏ ω c ) .
Preprints 106469 g004

5. Discussion

The above analytical formulas describe the interlayer conductivity σ z z . They can also be applied to describe the first MQO harmonic of interlayer magnetoresistance ρ z z = 1 / σ z z , if the MQO are not very strong so that the non-linear effects in MQO amplitude are not important [51]. If only the first MQO harmonic is kept and the higher-order terms in the MQO amplitude are negligible, one can safely apply the relation ρ z z = σ z z − 1 to describe the interlayer magnetoresistance [51]. However, for strong MQO their averaging over temperature and long-range disorder differs [9,51] for ρ z z and σ z z .
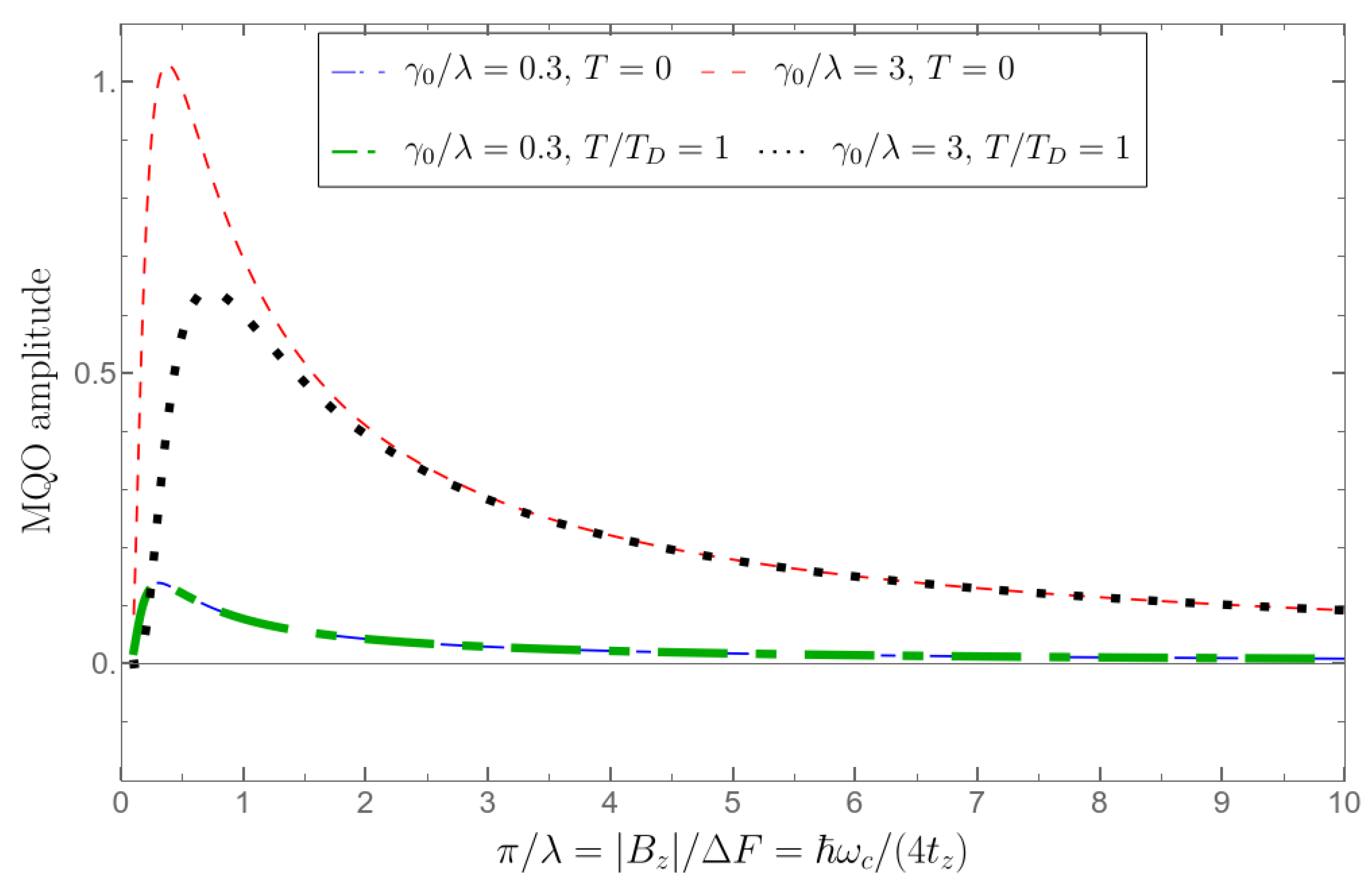
Above we have shown that the developed theory and Equation (7) describe very well the available experimental data on the MQO beats of interlayer conductivity σ z z . They also predict some new interesting and observable features. In particular, Equation (7) predicts a strong decrease of the MQO beating factor R z σ of interlayer conductivity with the increase of magnetic field, corresponding to λ → 0 . This decrease of R z σ is partially compensated by the Dingle factor R D 0 and by the temperature damping factor R T . However, the product R D 0 R T R z σ , describing the MQO amplitude of interlayer conductivity, may still be non-monotonic in high field, in contrast to the amplitude of magnetization MQO described by Equation (8), which always monotonically increases in a very high field at ℏ ω c ≫ t z . This nonmonotonic magnetic-field dependence of the MQO amplitude of interlayer conductivity in a high field is rather robust to the variation of material parameters, e.g, to variations of the ratio γ 0 / λ = π k B T D / ( 2 t z ) = ℏ / ( 4 t z τ ) . In Figure 5 we show this non-monotonic dependence of the R z z MQO amplitude ( − 1 ) R D 0 R T R z σ on π / λ = | B z | / Δ F for two different ratios γ 0 / λ and temperatures T. At the small ratio γ 0 / λ < 0.1 the increase of temperature up to the Dingle temperature T D has almost no effect on the graph. The predicted decrease of MQO amplitude of the interlayer conductivity in a high field is somewhat counterintuitive, being opposite to what is observed in magnetization, but it can be easily tested experimentally in various Q2D layered compounds, such as organic metals, van der Waals crystals, artificial heterostructures, etc. We suppose that the proposed decrease of MQO amplitude in a high field was actually observed in many experiments but mistaken for the non-existing beat node at a high magnetic field beyond the available range. For example, as we mentioned in the previous section, in Refs. [18,19,50] the beating node n = 0 of the SdH effect was not observed but assumed from some decrease of MQO amplitude in a very high field. This decrease may be considered as the experimental indication of the predicted high-field non-monotonic behavior of the MQO amplitude of interlayer conductivity, but further experimental studies of this interesting effect are required to compare with our theoretical predictions and to determine the range of parameters where it is observed.
Another amazing prediction of our theoretical analysis is that all the curves in Figure 2, describing the MQO amplitudes, periodically cross at the same points. It can also be checked experimentally. However, this experimental test is less obvious and convenient than the above prediction of the monotonic magnetic-field dependence of R z z MQO amplitude, because the corresponding experimental data for M ( B z ) and R ( B z ) magnetic oscillations must be properly normalized for this comparison.
Now we consider the MQO phase of interlayer conductivity. For the Q2D electron spectrum (1) in a magnetic field one can easily calculate [48,49] the one-particle DoS ρ . If we neglect higher harmonics, the DoS oscillations are given by [48,49]
ρ ˜ ≈ ρ 0 2 R D R ρ cos α ¯ , R ρ = − J 0 ( λ ) ,
where ρ 0 = m * / ( 2 π ℏ 2 d ) is its nonoscillating part per one spin component. The phase of DoS oscillations is strictly tied to that of magnetization given by Equation (8), because the beating factors R M = − R ρ . In a weak magnetic field, when λ ≫ 1 corresponding to the 3D limit, the second term in the beating factor R z σ of interlayer conductivity given by Equation 7 is much smaller than its first term. Then we have R z σ ≈ R M = J 0 ( λ ) = − R z ρ , and the MQO phases of the interlayer conductivity σ z z and of the DoS ρ are strictly opposite, as predicted by the 3D theory of SdH effect [33,34]. In the opposite case λ < π , corresponding to the 3D →2D crossover or nearly 2D limit, the SdH beating factor R z σ < 0 is negative, as follows from Equation 7 and illustrated in Figure 5. Since R ρ = − R M < 0 is also negative at λ < 1 , at the 3D →2D crossover B ≳ Δ F or in the almost 2D limit B ≫ Δ F the quantum oscillations of the electronic DoS and of the interlayer conductivity have the same phase. We see that our theory describes the phase inversion of the SdH oscillations during the 3D →2D crossover.
The above analysis is generic to layered Q2D metals and can be applied to a very large class of layered compounds, which are actively studied by MQO till nowadays [24,26,27,28,29,52,53,54,55].

6. Conclusions

Above we developed the quantitative theoretical description of the beating phase of magnetic quantum oscillations of interlayer magnetoresistance and magnetization in quasi-2D metals, which are traditionally used to extract useful information about the electronic properties. This theory agrees very well with the available experimental data and explains the long-standing puzzle of the observed too large phase shift of beats between the MQO of thermodynamic and transport electronic properties. In addition, our theory also makes several new predictions which can be tested experimentally. The most unexpected prediction is the non-monotonic field dependence of the MQO amplitude of interlayer magnetoresistance in a high magnetic field B z ∼ Δ F , where Δ F is the beat frequency. Naively one may expect a monotonic growth of MQO amplitude of interlayer conductivity in a strong magnetic field | B z | > Δ F , similar to magnetization, but we predict its decrease at | B z | > Δ F in the regime of 3D → 2D crossover, as illustrated in Figure 5. Our analytical formulas also explain and describe the phase inversion of the SdH oscillations during the 3D →2D crossover.

Author Contributions

Conceptualization, P.D.G.; methodology, P.D.G. and T.I.M.; validation, I.V., V.D.K. and T.I.M.; formal analysis, T.I.M.; investigation, P.D.G. and T.I.M.; writing—original draft preparation, T.I.M.; writing—review and editing, P.D.G.; supervision, P.D.G.; funding acquisition, I.Y.P. and P.D.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation grant #22-42-09018. V.D.K. acknowledges the Foundation for the Advancement of Theoretical Physics and Mathematics ”Basis” for grant # 22-1-1-24-1 and NUST "MISIS" grant No. K2-2022-025.

Data Availability Statement

Dataset available on request from the authors.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
MQO Magnetic quantum oscillations
Q2D Quasi-two-dimensional
FS Fermi surface
LK Lifshitz-Kosevich
dHvA de Haas - van Alphen
SdH Shubnikov - de Haas

References

  1. Shoenberg, D. Magnetic Oscillations in Metals; Cambridge University Press: Cambridge, England, UK, 1984. [Google Scholar] [CrossRef]
  2. Yagi, R.; Iye, Y.; Osada, T.; Kagoshima, S. Semiclassical Interpretation of the Angular-Dependent Oscillatory Magnetoresistance in Quasi-Two-Dimensional Systems. J. Phys. Soc. Jpn. 1990, 59, 3069–3072. [Google Scholar] [CrossRef]
  3. Moses, P.; McKenzie, R.H. Comparison of coherent and weakly incoherent transport models for the interlayer magnetoresistance of layered Fermi liquids. Phys. Rev. B 1999, 60, 7998–8011. [Google Scholar] [CrossRef]
  4. Kartsovnik, M.V. High Magnetic Fields: A Tool for Studying Electronic Properties of Layered Organic Metals. Chem. Rev. 2004, 104, 5737–5782. [Google Scholar] [CrossRef] [PubMed]
  5. Wosnitza, J. Fermi Surfaces of Low-Dimensional Organic Metals and Superconductors; Springer Berlin: Berlin, 2013. [Google Scholar]
  6. Bergemann, C.; Julian, S.R.; Mackenzie, A.P.; NishiZaki, S.; Maeno, Y. Detailed Topography of the Fermi Surface of Sr2RuO4. Phys. Rev. Lett. 2000, 84, 2662–2665. [Google Scholar] [CrossRef] [PubMed]
  7. Grigoriev, P.D. Angular dependence of the Fermi surface cross-section area and magnetoresistance in quasi-two-dimensional metals. Phys. Rev. B 2010, 81, 205122. [Google Scholar] [CrossRef]
  8. Grigoriev, P.D. Weakly incoherent regime of interlayer conductivity in a magnetic field. Phys. Rev. B 2011, 83, 245129. [Google Scholar] [CrossRef]
  9. Grigoriev, P.D.; Kartsovnik, M.V.; Biberacher, W. Magnetic-field-induced dimensional crossover in the organic metal α-(BEDT-TTF)2KHg(SCN)4. Phys. Rev. B 2012, 86, 165125. [Google Scholar] [CrossRef]
  10. Grigoriev, P.D. Longitudinal interlayer magnetoresistance in strongly anisotropic quasi-two-dimensional metals. Phys. Rev. B 2013, 88, 054415. [Google Scholar] [CrossRef]
  11. Grigoriev, P.D.; Mogilyuk, T.I. Angular dependence of magnetoresistance in strongly anisotropic quasi-two-dimensional metals: Influence of Landau-level shape. Phys. Rev. B 2014, 90, 115138. [Google Scholar] [CrossRef]
  12. Grigoriev, P.D.; Mogilyuk, T.I. False spin zeros in the angular dependence of magnetic quantum oscillations in quasi-two-dimensional metals. Phys. Rev. B 2017, 95, 195130. [Google Scholar] [CrossRef]
  13. Kartsovnik, M.V.; Grigoriev, P.D.; Biberacher, W.; Kushch, N.D.; Wyder, P. Slow Oscillations of Magnetoresistance in Quasi-Two-Dimensional Metals. Phys. Rev. Lett. 2002, 89, 126802. [Google Scholar] [CrossRef] [PubMed]
  14. Grigoriev, P.D. Theory of the Shubnikov–de Haas effect in quasi-two-dimensional metals. Phys. Rev. B 2003, 67, 144401. [Google Scholar] [CrossRef]
  15. Grigoriev, P.D.; Ziman, T. Magnetic oscillations measure interlayer coupling in cuprate superconductors. Phys. Rev. B 2017, 96, 165110. [Google Scholar] [CrossRef]
  16. Mogilyuk, T.I.; Grigoriev, P.D. Magnetic oscillations of in-plane conductivity in quasi-two-dimensional metals. Phys. Rev. B 2018, 98, 045118. [Google Scholar] [CrossRef]
  17. Grigoriev, P.D.; Kartsovnik, M.V.; Biberacher, W.; Kushch, N.D.; Wyder, P. Anomalous beating phase of the oscillating interlayer magnetoresistance in layered metals. Phys. Rev. B 2002, 65, 060403. [Google Scholar] [CrossRef]
  18. Schiller, M.; Schmidt, W.; Balthes, E.; Schweitzer, D.; Koo, H.J.; Whangbo, M.H.; Heinen, I.; Klausa, T.; Kircher, P.; Strunz, W. Investigations of the Fermi surface of a new organic metal: (BEDT-TTF)4[ Ni(dto)2]. Europhys. Lett. 2000, 51, 82. [Google Scholar] [CrossRef]
  19. Weiss, H.; Kartsovnik, M.V.; Biberacher, W.; Balthes, E.; Jansen, A.G.M.; Kushch, N.D. Angle-dependent magnetoquantum oscillations in κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 1999, 60, R16259–R16262. [Google Scholar] [CrossRef]
  20. Kang, W.; Jo, Y.; Noh, D.Y.; Son, K.I.; Chung, O.H. Appearance of Beating in the Shubnikov–de Haas Oscillations of the Organic Conductor κ-(BEDT-TTF)2Cu(NCS)2 under Pressure. Journal of the Physical Society of Japan 2010, 79, 044716. [Google Scholar] [CrossRef]
  21. Krstovska, D. Quantum Oscillations of the Interlayer Magnetothermopower in a Q2D Organic Conductor. Journal of the Physical Society of Japan 2011, 80, 044701. [Google Scholar] [CrossRef]
  22. Audouard, A.; Fortin, J.Y.; Vignolles, D.; Lyubovskii, R.B.; Drigo, L.; Shilov, G.V.; Duc, F.; Zhilyaeva, E.I.; Lyubovskaya, R.N.; Canadell, E. Non-Lifshitz–Kosevich field- and temperature-dependent amplitude of quantum oscillations in the quasi-two dimensional metal θ-(ET)4ZnBr4(C6H4Cl2). Journal of Physics: Condensed Matter 2015, 27, 315601. [Google Scholar] [CrossRef]
  23. Arnold, F.; Naumann, M.; Rosner, H.; Kikugawa, N.; Graf, D.; Balicas, L.; Terashima, T.; Uji, S.; Takatsu, H.; Khim, S.; Mackenzie, A.P.; Hassinger, E. Fermi surface of PtCoO2 from quantum oscillations and electronic structure calculations. Phys. Rev. B 2020, 101, 195101. [Google Scholar] [CrossRef]
  24. Oberbauer, S.; Erkenov, S.; Biberacher, W.; Kushch, N.D.; Gross, R.; Kartsovnik, M.V. Coherent heavy charge carriers in an organic conductor near the bandwidth-controlled Mott transition. Phys. Rev. B 2023, 107, 075139. [Google Scholar] [CrossRef]
  25. Wang, J.F.; Dong, Q.X.; Huang, Y.F.; Wang, Z.S.; Guo, Z.P.; Wang, Z.J.; Ren, Z.A.; Li, G.; Sun, P.J.; Dai, X.; Chen, G.F. Quantum oscillations in the magnetic Weyl semimetal NdAlSi arising from strong Weyl fermion–4f electron exchange interaction. Phys. Rev. B 2023, 108, 024423. [Google Scholar] [CrossRef]
  26. Xu, S.; Bao, C.; Guo, P.J.; Wang, Y.Y.; Yu, Q.H.; Sun, L.L.; Su, Y.; Liu, K.; Lu, Z.Y.; Zhou, S.; Xia, T.L. Interlayer quantum transport in Dirac semimetal BaGa2. Nature Communications 2020, 11, 2370. [Google Scholar] [CrossRef] [PubMed]
  27. Hornung, J.; Mishra, S.; Stirnat, J.; Raba, M.; Schwarze, B.V.; Klotz, J.; Aoki, D.; Wosnitza, J.; Helm, T.; Sheikin, I. Anomalous quantum oscillations of CeCoIn5 in high magnetic fields. Phys. Rev. B 2021, 104, 235155. [Google Scholar] [CrossRef]
  28. Zeng, X.Y.; Dai, Z.Y.; Xu, S.; Zhao, N.N.; Wang, H.; Wang, X.Y.; Lin, J.F.; Gong, J.; Ma, X.P.; Han, K.; Wang, Y.T.; Cheng, P.; Liu, K.; Xia, T.L. Quantum oscillations and weak anisotropic resistivity in the chiral fermion semimetal PdGa. Phys. Rev. B 2022, 106, 205120. [Google Scholar] [CrossRef]
  29. Luo, X.; Ma, X.; Zhang, J.; Xing, Y.; Shen, A.; Ye, H.; Shen, S.; Peng, J.; Cao, S.; Dong, S.; Li, L. Investigation of de Haas–van Alphen and Shubnikov–de Haas quantum oscillations in PrTe3. Phys. Rev. B 2024, 109, 035121. [Google Scholar] [CrossRef]
  30. Daschner, M.; Grosche, F.M.; Liu, C.; Gudac, B.; Novak, M.; Kokanović, I. Probing the Fermi surface with Quantum Oscillation Measurements in the Dirac semimetal TaNiTe5, 2024, [arXiv:cond-mat.mes-hall/2403.12921].
  31. Leeb, V.; Polyudov, K.; Mashhadi, S.; Biswas, S.; Valentí, R.; Burghard, M.; Knolle, J. Anomalous Quantum Oscillations in a Heterostructure of Graphene on a Proximate Quantum Spin Liquid. Phys. Rev. Lett. 2021, 126, 097201. [Google Scholar] [CrossRef]
  32. Alisultanov, Z.Z.; Abdullaev, G.O.; Grigoriev, P.D.; Demirov, N.A. Quantum Oscillations of Interlayer Conductivity in a Multilayer Topological Insulator. Journal of Experimental and Theoretical Physics 2023, 136, 353–367. [Google Scholar] [CrossRef]
  33. Abrikosov, A.A. Fundamentals of the theory of metals; North-Holland Sole distributors for the USA and Canada, Elsevier Science Pub. Co: Amsterdam New York New York, NY, USA, 1988. [Google Scholar]
  34. Ziman, J.M. Principles of the theory of solids; Cambridge University Press: Cambridge England, 1972. [Google Scholar]
  35. Wosnitza, J.; Wanka, S.; Hagel, J.; Löhneysen, H.v.; Qualls, J.S.; Brooks, J.S.; Balthes, E.; Schlueter, J.A.; Geiser, U.; Mohtasham, J.; Winter, R.W.; Gard, G.L. Field-Induced Metal-Insulator Transition in a Two-Dimensional Organic Superconductor. Phys. Rev. Lett. 2001, 86, 508–511. [Google Scholar] [CrossRef]
  36. Laramee, B.; Ghimire, R.; Graf, D.; Martin, L.; Blundell, T.J.; Agosta, C.C. Superconductivity and Fermi Surface Studies of β"-(BEDT-TTF)2[(H2O)(NH4)2Cr(C2O4)3]·18-Crown-6. Magnetochemistry 2023, 9. [Google Scholar] [CrossRef]
  37. Champel, T.; Mineev, V.P. Magnetic quantum oscillations of the longitudinal conductivity σzz in quasi-two-dimensional metals. Phys. Rev. B 2002, 66, 195111. [Google Scholar] [CrossRef]
  38. Datta, B.; Adak, P.C.; Shi, L.k.; Watanabe, K.; Taniguchi, T.; Song, J.C.W.; Deshmukh, M.M. Nontrivial quantum oscillation geometric phase shift in a trivial band. Sci. Adv. 2019, 5. [Google Scholar] [CrossRef] [PubMed]
  39. Xu, X.; Kang, Z.; Chang, T.R.; Lin, H.; Bian, G.; Yuan, Z.; Qu, Z.; Zhang, J.; Jia, S. Quantum oscillations in the noncentrosymmetric superconductor and topological nodal-line semimetal PbTaSe2. Phys. Rev. B 2019, 99, 104516. [Google Scholar] [CrossRef]
  40. Zhao, W.; Wang, X. Berry phase in quantum oscillations of topological materials. Advances in Physics: X 2022. [CrossRef]
  41. Nie, Y.; Tu, W.; Yang, Y.; Chen, Z.; Wang, Y.; Pan, S.; Mei, M.; Zhu, X.; Lu, W.; Ning, W.; Tian, M. Quantum oscillations and nontrivial topological properties of layered metal SrAg4Sb2. Appl. Phys. Lett. 2023, 123. [Google Scholar] [CrossRef]
  42. Sebastian, S.E.; Harrison, N.; Lonzarich, G.G. Towards resolution of the Fermi surface in underdoped high-Tc superconductors. Reports on Progress in Physics 2012, 75, 102501. [Google Scholar] [CrossRef] [PubMed]
  43. Vignolle, B.; Vignolles, D.; Julien, M.H.; Proust, C. From quantum oscillations to charge order in high-Tc copper oxides in high magnetic fields. Comptes Rendus Physique 2013, 14, 39–52. [Google Scholar] [CrossRef]
  44. Helm, T.; Kartsovnik, M.V.; Bartkowiak, M.; Bittner, N.; Lambacher, M.; Erb, A.; Wosnitza, J.; Gross, R. Evolution of the Fermi Surface of the Electron-Doped High-Temperature Superconductor Nd2-xCexCuO4 Revealed by Shubnikov–de Haas Oscillations. Phys. Rev. Lett. 2009, 103, 157002. [Google Scholar] [CrossRef]
  45. Breznay, N.P.; Hayes, I.M.; Nair, N.L.; Helm, T.; Analytis, J.G.; McDonald, R.D.; Zhu, Z.; Krockenberger, Y.; Irie, H.; Yamamoto, H.; Modic, K.A.; Frano, A.; Shafer, P.; Arenholz, E. Interplay of structure and charge order revealed by quantum oscillations in thin films of Pr2CuO4±δ. Phys. Rev. B 2019, 100, 235111. [Google Scholar] [CrossRef]
  46. Carrington, A. Quantum oscillation studies of the Fermi surface of iron-pnictide superconductors. Reports on Progress in Physics 2011, 74, 124507. [Google Scholar] [CrossRef]
  47. Coldea, A.I.; Braithwaite, D.; Carrington, A. Iron-based superconductors in high magnetic fields. Comptes Rendus Physique 2013, 14, 94–105. [Google Scholar] [CrossRef]
  48. Champel, T.; Mineev, V.P. de Haas–van Alphen effect in two- and quasi-two-dimensional metals and superconductors. Philos. Mag. B 2001, 81, 55–74. [Google Scholar] [CrossRef]
  49. Grigoriev, P.D. The influence of the chemical potential oscillations on the de Haas-van Alphen effect in quasi-two-dimensional compounds. J. Exp. Theor. Phys. 2001, 92, 1090–1094. [Google Scholar] [CrossRef]
  50. Balthes, E. Electron correlations in the 2D multilayer organic metal k-(BEDT-TTF)2I3 in magnetic fields. Habilitation, University of Stuttgart, Germany, 2004. [CrossRef]
  51. Grigoriev, P.D.; Mogilyuk, T.I. Magnetic quantum oscillations of in-plane Hall conductivity and magnetoresistance tensor in quasi-two-dimensional metals, 2023. [CrossRef]
  52. Krstovska, D.; Choi, E.S.; Steven, E. Giant Angular Nernst Effect in the Organic Metal α-(BEDT-TTF)2KHg(SC N)4. Magnetochemistry 2023, 9. [Google Scholar] [CrossRef]
  53. Rehfuss, Z.; Broyles, C.; Graf, D.; Li, Y.; Tan, H.; Zhao, Z.; Liu, J.; Zhang, Y.; Dong, X.; Yang, H.; Gao, H.; Yan, B.; Ran, S. Quantum oscillations in kagome metals CsTi3Bi5 and RbTi3Bi5. Phys. Rev. Mater. 2024, 8, 024003. [Google Scholar] [CrossRef]
  54. Sakai, H.; Nakagawa, K.; Tsuruda, K.; Shiogai, J.; Akiba, K.; Tokunaga, M.; Kimura, S.; Awaji, S.; Tsukazaki, A.; Murakawa, H.; Hanasaki, N. Variation of Landau level splitting in the Fermi level controlled Dirac metals (Eu,Gd)MnBi2. Phys. Rev. B 2023, 108, 115142. [Google Scholar] [CrossRef]
  55. Zhang, W.; Wang, L.; Tsang, C.W.; Liu, X.; Xie, J.; Yu, W.C.; Lai, K.T.; Goh, S.K. Emergence of large quantum oscillation frequencies in thin flakes of the kagome superconductor CsV3Sb5. Phys. Rev. B 2022, 106, 195103. [Google Scholar] [CrossRef]
1
In [16] we used different definition of Δ F ≈ 2 t z B z / ( ℏ ω c ) = λ B z / π .
Preprints 106469 g001
Figure 1. Schematic representation of a layered Q2D metal (a) and its Fermi surface (b).
Figure 1. Schematic representation of a layered Q2D metal (a) and its Fermi surface (b).
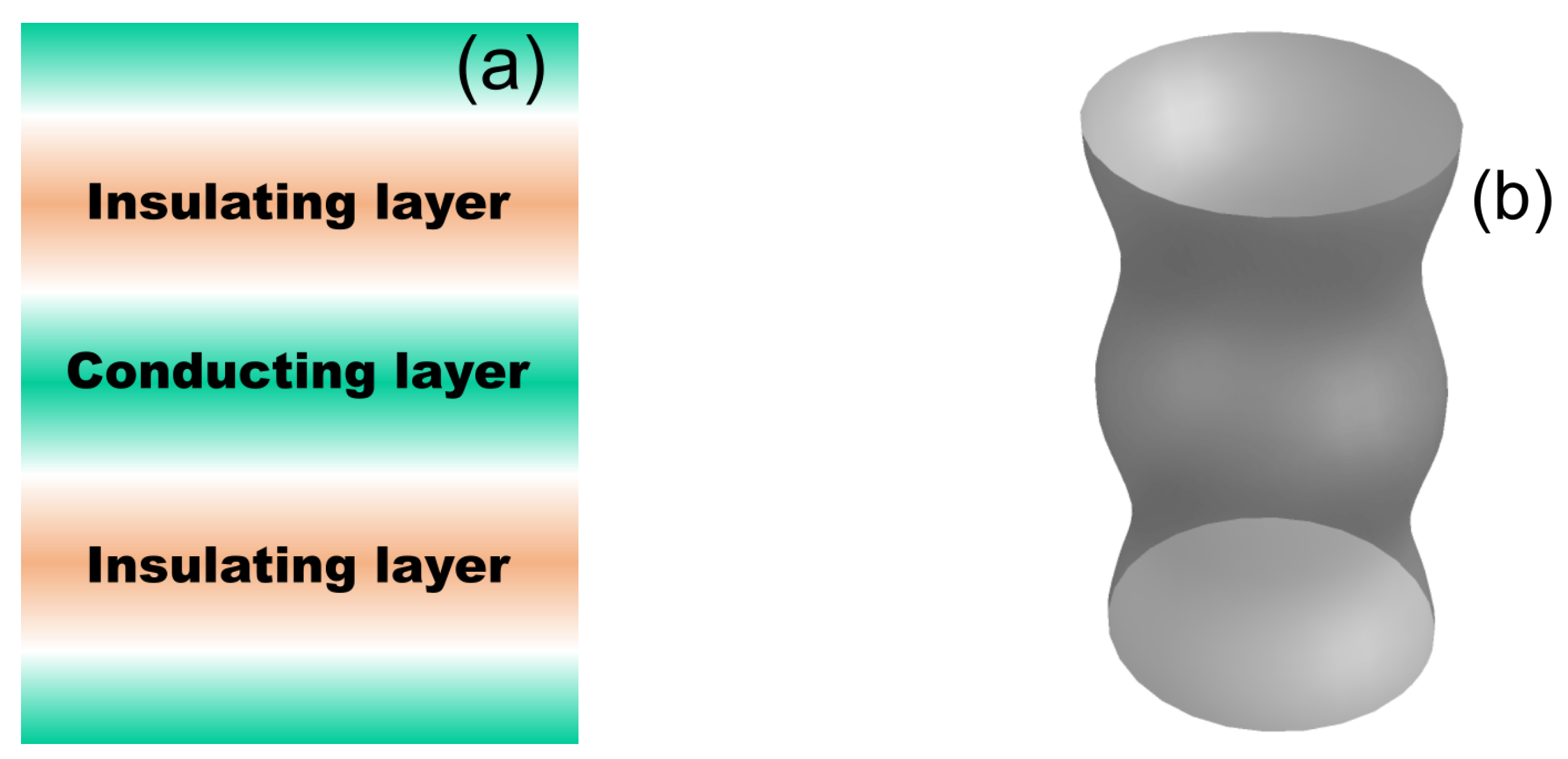
Preprints 106469 g001
Preprints 106469 g005
Figure 5. Dependence of the value ( − 1 ) R D 0 R T R z σ on the magnetic field for γ 0 = { 0.3 , 3 } λ for temperature T = { 0 , 1 } T D , where Dingle temperature is equal to T D ≡ ℏ / ( 2 π k B τ ) .
Figure 5. Dependence of the value ( − 1 ) R D 0 R T R z σ on the magnetic field for γ 0 = { 0.3 , 3 } λ for temperature T = { 0 , 1 } T D , where Dingle temperature is equal to T D ≡ ℏ / ( 2 π k B τ ) .
Preprints 106469 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated