Prerpints.org logo
Preprint
Article

Novel Spectrometer Designs for Laser Driven Ion Acceleration

Altmetrics

Downloads

170

Views

121

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 May 2024

Posted:

14 May 2024

You are already at the latest version

Alerts
Abstract
We propose novel spectrometer designs that aim to enhance the measured spectral range 1 of ions on a finite-sized detector. In contrast to the traditional devices that use uniform magnetic 2 field, in which the deflection of particles increases inversely proportional to their momentum, in a 3 gradient magnetic field, the deflection of particles will be decreased due to the reduction of the 4 magnetic field along their propagation. Low energy ions are particularly impacted, as they are 5 deflected less and are more likely to reach the detector compared to being driven out of it while 6 using a uniform magnetic field. By the means of a gradient magnetic field, the nonlinear dispersion 7 of ions in a homogeneous magnetic field can approach a nearly linear dispersion. Nonetheless, 8 the dispersion of low energy ions in a homogeneous magnetic field remains unnecessarily high. 9 In this article, we explore linear, quadratic, and higher-order field profiles in comparison to the 10 homogeneous field case. We discuss the employed methodology and present simulation results of 11 the spectrometer with an extended ion spectral range, focusing on the minimum detectable energy 12 (energy dynamic range) and energy resolution
Keywords: 
Subject: Physical Sciences  -   Other

1. Introduction

The development of ultrahigh-power laser systems [1,2] in the last two decades has led to enormous scientific achievements in the field of laser-plasma based research. Nowadays, laser intensities even above 10 22 W · c m − 2 [3] have become available for experiments opening new perspectives for science and applications [4,5].
It becomes essential to develop advanced diagnostics that allow detailed measurements of plasma properties in this new interaction regime. It requires scaling up the range of available parameters in ion spectrometers, detectors and calibrations in order to be ready to measure effects that are not even thought of today.
This paper is focused on spectrometric methods of particles diagnostics that allow extending the measured spectral range of accelerated ions phenomena. The analyses of multi-species ion emission with the spectrometer is well described in the literature [6]. Several modifications have been made in the spectrometer design that allowed temporally [7] and spatially resolved [8] detection of accelerated ion spectral distributions, the simultaneous measurement of ion and electron spectra along the same observation direction [9], precise measurements of the proton/ion trajectories [10] for proton deflectometery [11] and tomography applications [12]. Another important modification in the Thomson spectrometer allowed simultaneous measurements of the charged particles and X-rays emitted from the target [13]. The trapezoidal-shaped electric field plates have been used to circumvent the spectral clipping at the low energy end of the ion spectra [14,15]. All these changes [16,17,18,19,20,21] immensely support an extensive and thorough research of relevant laser-plasma processes.
The spectrometer becomes uniquely valuable if high sensitive, active detector is used, such as micro-channel-plate (MCP) detector [22] coupled to a phosphor screen and a CCD camera [23]. It allows particularly online recording the particle spectrum on a single laser shot basis and at repetition rate of more than 10 Hz [24,25]. Nevertheless, due to the finite size of the detector, the measured spectral range of ions and species resolution will be restricted. Thus, in order to have a decent energy resolution at high particle energies (nowadays, laser generated proton energies are more than 100 MeV [26,27]) the dispersion must be increased, which will reduce the spectral range covered by the detector.
In this article, we provide guidelines for new ion spectrometer designs, that uses a linear gradient magnetic field. This makes possible to decrease the dispersion of ions at low energies, bring them back to the detector, while the dispersion at high energies will be almost as high as can be achieved with a dipole magnet.
The paper is structured as follows: Section 2 provides a description of the conceptual design of the new spectrometer. Following that, Section 3 presents the implemented model system along with its initial assumptions. In Section 4, we delve into the investigation of spectrometer parameter tuning for two distinct proton energy range scenarios: (1) the low energy range, ranging between a few keV up to 100 MeV, and (2) the high energy range that goes from a few tens of MeV up to hundreds of MeV. In conclusion, we thoroughly discuss and summarize the advantages and limitations of our theoretical approach, while also analyzing the potential replacement of a dipole with various non-homogeneous magnetic profiles.

2. Conceptual Approach

In the ion spectrometer, the particles are deflected in the homogeneous parallel magnetic (B) and electric (E) fields [28]. The particle position on the trace depends on its energy, as higher the particle energy as less it is deflected from the so-called zero point, where undeflected plasma emission (mainly x-ray) hits the detector.
The spectra of ions with the same charge-to-mass ratio (Z/m) will trace a parabola and particles with different (Z/m) will follow different parabolic traces. In the approximation of small deflections and not relativistic particles[17], the electric and magnetic deflections are:
x = Z e E L e l 2 E i D E
y = Z e B L m a g n 2 m 0 E i D B
In the case of non-relativistic speeds, the expression for kinetic energy is given by E i = ( γ − 1 ) m 0 c 2 , where γ represents the Lorentz factor. The variables m 0 and c correspond to the rest mass and the speed of light, respectively. We have D E = L d e t + L e l / 2 , which denotes the distance between the detector plane and the midpoint of the electric field, Additionally, D B = L d e t + L e l + L d i s + L m a g n / 2 stands for the distance between the center of the magnetic field and the detector. L d e t represents the distance between the electric field and the detector, while L e l is the length of the electric field. In this case, L m a g n corresponds to the length of the magnetic field, and L d i s is the distance between the electric field and the magnetic field (see Figure 1).
The deflection of particles from "zero point" is not linearly increasing y ∼ 1 / ( E i ) (see Equation (2)), as the particle’s energy is decreasing. This limits the measurable spectral range of ions due to the limited size of the detector [15,17].
Our conceptual approach aims at reducing the dispersion of “low energy” ions, which is often excessively high. To achieve this, we suggest employing a magnetic field gradient instead of an homogeneous magnetic field. In comparison to the homogeneous magnetic field, where particle deflection increases inversely with momentum, a gradient magnetic field results in the reduction of particle deflection due to decreasing magnetic field strength along their path. This impact on low energy ions, as they experience less deflection and are more likely to reach the detector rather than being pushed out when a uniform magnetic field is used. As a result, the use of a gradient magnetic field enables the achievement of an almost linear dispersion behaviour.

3. Model System

The magnetic field of an in-homogeneous magnet can be expanded as a function of its multi-pole components [29,30,31] :
B x ( 0 , y ) = B 0 ρ ∑ n = 0 ∞ K n ( s ) y n ( n )
The magnetic rigidity of a particle with momentum p 0 and charge e is given by the equation B 0 ρ = p 0 / e , where ρ represents the gyroradius of the particle in the presence of the magnetic field. The term K n ( s ) is defined as:
K n ( s ) = 1 B ρ 1 n ! ∂ n B y ∂ y n
For pure multi-pole fields, the expression of the magnetic field is given by:
B x ( 0 , y ) = 1 n ! ∂ n B y ∂ y n y n
The term ∂ n B y / ∂ y n is referred as the field gradient. In the case of a dipole n=0, we have the magnetic field B 0 on the central y-axis, while n=1 represents the linear field gradient achieved in a single segment of the magnetic quadrupole configuration. Throughout the rest of the article, we denote G = ∂ n B y / n ! ∂ y n .
The particles are injected along the z-axis into the magnetic element, perpendicular to (xy) plane, at the point y= r 0 where the field is the highest. We ignore the width of the particle beam and assume that the magnetic field lines are perpendicular to the trajectory of the particle. These particles disperse perpendicular to the y-axis, where B x = 0 (refer to Figure 1). It is assumed that a parallel proton beam is formed by the entrance pinhole of the spectrometer neglecting its divergence. This is justified by the fact that ions are usually detected within the nsr solid angle [17,23]. Additionally, the charge density is considered to be low, so that the interactions between the charged particles and therefore the beam space charge effects can be safely ignored.
The force acting on a charged particle is given by the Lorentz force:
F = d p → d t = q ( E → + v → × B → ) ,
where E is the electric field, B is the magnetic field.
The particle traces from the source to the detector screen are obtained by integrating the equation of motion numerically by a second-order Runge-Kutta (RK) method [32].
The particle deflection in the magnetic field can be obtained by solving Hill’s equations, taking into account relativistic effects and ignoring the space-charge effects. The electric and magnetic fields are assumed to have linear components (up to quadrupole field) while preserving the particle impulse. These calculations can be done analytically [29,33] :
x " + K x ( s ) x = 0 y " + K y ( s ) y = 0
where x ′ ′ = d 2 x / d s 2 and y ′ ′ = d 2 y / d s 2 respectively, due to the change of variable d / d t = v 0 d / d s .
Using the transfer matrix methodology, the transport matrices are defined as follows [29,33]:
u ( s ) u ( s ′ ) =
c o s ( κ . L m a g n ) 1 κ s i n ( κ . L m a g n ) − κ s i n ( κ . L m a g n ) c o s ( κ . L m a g n ) . 1 D B 0 1 . y 0 p 0
where u(s) stands for the particle position, u(s’) for the particle momentum, y 0 is the injection point into the quadrupole field (see Figure 1), L m a g n is the magnet length, κ = G · Z e / p 0 with p 0 relativistic impulse of the particles and γ is the Lorentz factor.
The analytical expression of the electric field is taken from [15], whereas, the magnetic deflection on the detector plane for our quadrupolar spectrometer is given by:
x = Z e γ γ 2 − 1 E 0 L e l m 0 c 2 ( L d e t + L e l / 2 ) , y = [ c o s ( κ L m a g n ) − D B . κ . s i n ( κ . L m a g n ) ] · y 0
From the magnetic field equation one can see clearly that changing D B results in a linear re-scaling of the y-component, while the factor κ L m a g n tailor the non-linear contribution of the magnetic particle deflection. Therefore, the longer the dispersive field (or G ) the larger the non-linear dispersion.

4. Particle dispersion in a radially inhomogeneous magnetic field

The proposed ion spectrometer is illustrated in Figure 1. The performance of the spectrometer with magnetic gradient fields is investigated for the proton beams with 100 MeV [26,27] and 700 MeV cutoff energies [34]. The proton spectra obtained in the detector plane for homogeneous and the quadrupolar magnetic fields are compared.

4.1. Optimized Design for Proton Spectrum with 100 MeV Cut-Off Energy

It is considered as input a point source proton beam in the energy range from 0.5 MeV to 100 MeV [26,27].
The main spectrometer parameters are summarized in Table 1. The pinhole size was chosen as typical, about 100 μ m (see e.g., [23]). The detector size (in our case an MCP) is typically about 8 cm [22] and the ”zero point” is set about 5 mm from the edge of the detector in order to do not loose the signal.
The particles enter the magnetic field at a distance r 0 from the bottom edge of the magnet, where magnetic field is the highest B 0 = 0.9 T.
The retrieved value of G resembles the typical gradient values employed for the design of laser-driven proton beamlines [35,36]. The distance to the detector plane L d e t is tuned in order to obtain the magnetic deflection for 100 MeV protons at 1 cm on the detector. This would reasonably avoid the overlapping of the spectral trace with a “zero point”. This requirement is applied to all the cases [37].
Figure 2A illustrates the particle deflection in the detector plane for both the homogeneous (red) and linear-gradient (blue) cases. The detector screen is indicated by the horizontal black line. The double arrows point to the protons with the same energies.
The spectrometer with the dipole will be detecting protons in the energies range from 2-100 MeV, compared with the linear-gradient design case, which can record the whole proton spectrum from 0.5 MeV and even lower.
We evaluate the normalized resolution of the spectrometers in both cases and they are shown in Figure 2B.
The uncertainties of the ion position on a detector limit the energy resolution of a conventional Thomson Parabola (TP). Since the projection of the ion pinhole on the detector screen has a given size δ R p , the energy resolution is a function of the displacement of the particles from the zero point.
This distance from the neutral point is calculated as R= x 2 ( E ) + y 2 ( E ) , at z = z 0 (our propagation axis). The energy uncertainty is thus given by:
R e s = δ E r e s E = d E δ R δ R p E ,
where δ Rp depends on the pinhole size [18,23,38].
The overall energy resolution for the total analyzed energy range, i.e., from a few keV up to 100 MeV, slightly decreases, as expected in the case of the linear gradient. We highlight in the inset of Figure 2B the energy resolution in the range between 0.5 up to 6 MeV, which corresponds to the same energy shown by the arrows.
The difference is of the order of 0.4 % for the low energy region of interest, whereas has a value of 0.2% for the high energy.
Hence, the results of Figure 2 show that, using a linear gradient (quadrupole) field enlarges the detectable dynamic energy range at a reasonable cost in term of energy resolution.

4.2. Optimized Design for Proton Spectrum with 700 MeV Cut-Off Energy

For these set of simulations, it is considered as input a proton beam with 700 MeV cutoff energy. The 1 cm deflection point is found for a magnetic field strength of B 0 = 1.9 T at a distance L d e t = 11 cm. Please note that a dipole magnet of 1.9 T is extremely bulky.
In the linear gradient case, the field gradient is G ≃ 100 T/m and the beam is injected in the magnetic field at r 0 =1.9 cm. All design parameters are summarized in Table 2.
In Figure 3A, the particle dispersion is shown for a dipolar field of 1.9 T (dashed black lines), for quadrupolar field (black line) and for a reference dipole field of 0.9 T (red lines).
The dipole case of B 0 = 0.9 T has been added, tuning, accordingly the L d e t , that is increased up to 16.5 cm, in order to take 5 MeV protons to the detector screen. The color bar on the right-hand side represents the correspondent energy range (from a few keV up to a maximum of 700 MeV[34]). The double arrows in Figure 3 are connecting points of equal proton energy shown for 10, 20, 30, 40, 60, 80 MeV. Furthermore, the normalized energy resolutions have been calculated using the Equation (10).
As it can be seen in Figure 3B the energy resolution changes between a minimum of 0.2% up to maximum 0.8%, comparing the quadrupolar gradient and the dipole cases. In this case, there is a significant increase of the energy dynamic range of the detected protons of almost 10 MeV, substituting the dipolar field B 0 = 1.9 T with a quadrupolar field.
In Figure 3A it can be observed that in the case of the reference dipole with B 0 =0.9 T, not only an increase in distance from the detector is needed, but also the measurable proton energy range goes from 5 MeV (our lower limit) up to 250 MeV, while in the case of the quadrupolar field we can extend it up to 700 MeV and keep the total spectrometer size more compact.
For completeness, we have also studied the same three cases described before, fixing the proton energy cut-off at 700 MeV on the detector (indicated in red in Figure 4A).
As it has been already done in refs [16,19], it is possible to tune the drift between the electric field to the detector L d e t with the aim of modifying the detectable energy spectra. The value of L d e t =30 cm in order to achieve the 1 cm magnetic deflection for 700 MeV protons (line 3 in Figure 4A). In Figure 4A, it can be observed a larger energy dynamic range in the linear gradient design case compared to dipole ones. The energy resolutions are very close to each other and the difference between the three cases goes up to maximum 0.5%, as shown in Figure 4B.
In summary, we have shown that dispersion of the high energetic particles is not changed by the use of the quadrupolar fields, whereas it affects the most the low energetic particles. The overall proton energy dynamic range can be enlarged by replacing the constant dipolar field with linear gradient design cases, preserving accuracy.

5. High Order Magnetic Field Profiles

We further study the effects of the replacement of a homogeneous magnetic field with different magnetic field profiles, such as decapolar and octupolar profiles.
A set of simulations have been implemented in order to investigate the minimum achievable detectable proton energy with these modifications. A point source of protons that goes from a few keV up to 100 MeV has been used as input. The quadrupolar parameters are the same reported in SubSection 4.1. The results are shown in Figure 5A.
For consistency, the same distance between the spectrometer and the detector L d e t = 5 cm and the same distance between the electric and magnetic field L d i s = 1 cm have been used for all the cases.
The cut-off minimal proton energy as a function of the gradient power, i.e., n= 0,1,3,5,7 is reported in Figure 5 (B) to investigate the change of the lowest detectable energy. The values n are odd integer number of the magnetic field profiles used in Equation (5). The magnetic field profiles were chosen to reach a maximum magnetic field of B = 0.9 T at the injection point. This corresponds to a quadrupolar G q ≃ 45 T / m , an octupolar G o c t = 8.5 · 10 4 T / m 3 , a decapolar G d e c =1.7· 10 8 T / m 5 and multipolar G m u l t = 3.6 · 10 11 T / m 7 of order 7.
We are aware that these values are very demanding, but they align with our initial assumptions. In this way, the highest detectable energy is preserved for all magnetic field profiles, whereas the lowest detectable energy changes as a function of the field gradient power.
Please note that when a charged particle passes through a magnetic field profile with an odd power index n, particles are deflected back when crossing the zero point. In principle, the traces of the back deflected particle could be used for determining its energy (see Figure 5A). These particles are excluded to determine the lowest detectable energy and avoid potential crossing of different ion species on the detector screen. This is, in practice, easily achievable by blocking particles crossing the central axis.
In the case of the spectrometer composed by a dipole, the energy spectral information achievable and observable on the detector screen, goes from 1.891 MeV (∼ 2 MeV) up to 100 MeV, while for the magnetic field profiles, the achievable spectral information increases from 1.891- 100 MeV to 0.392-100 MeV (case n=1), 0.15 - 100 MeV (case n=3), 0.008-100 MeV (case n= 5) and 0.0061-100 MeV (case n= 7).
The results of Figure 5B show that the replacement of a constant magnetic field with the considered magnetic field profiles increases the achievable energy dynamic range, without introducing significant losses at high energy. The reduction of the magnetic field of the dipole is obviously possible, but it is unavoidable to lose in high energy particle dispersion. As expected, there is a proportionality between the increase in the order of the elements and the respective increase in minimum detectable energy information.
However, after the third order (decapole) there is not a significant improvement in terms of capture of the low energy particles compared to the previous orders, as can be seen in Figure 5B.

6. Discussions and Conclusions

In this paper, we presented the theoretical study of novel types of spectrometers with the aim of investigating the enhancement of detectable energy dynamic range, compared to existing ones.
We have implemented different sets of simulations, studying the replacement of different gradient field profiles instead of a constant dipole field in a TP design, for two proton energy range scenarios. Our results offer valuable insights into the benefits and constraints of the proposed designs.
In Section 4.1, we have shown that a higher energy spectral range can be achieved, without significant losses in terms of energy resolution. This “new” detectable low proton energy range is particularly relevant for applications, such as the ones in cultural heritage [39,40], laser driven proton boron fusion [41,42] and towards the perspective of low divergent MeV-class proton beam with micrometer source size driven by a few-cycle laser pulse [38]. The minimum detectable proton energy value, for the TP geometry that we are proposing, becomes 0.38 MeV.
For proton energy range that goes from a few keV up to hundreds of MeV, such as the ones obtained with conventional accelerators [29,34], we show in Section 4.2 that we can obtain considerable improvements in terms of detectable proton energy dynamic range.
It is evident that this enhancement is easily scalable, tweaking the quadrupolar field parameters. We also investigate the possibility to use more sophisticated magnetic devices, with strong gradients. However, after the third-order magnetic field profile that corresponds to a decapole element, there is no significant improvement.
In conclusion, the quadrupolar magnetic field profile is the most reliable, suitable and feasible (easy to manufacture and assemble [43]) case, among the analyzed ones. In laser driven proton acceleration, the use of quadrupole (e.g., doublet and/or triplet) is not new because they have been implemented, as reported in refs [35,44], downstream laser-plasma interaction point for manipulating and adapting laser proton sources for applications.
The versatility and the tunability of the linear gradient field profile, close to the quadrupole, in our spectrometer designs, compared to the existing combinations, e.g., the tuning of the length of the drift between spectrometer and detector in combination with a TP [16,20], allows to enlarge the detectable energy range, without significant looses in energy resolution and gaining compactness of the total spectrometer structure. All the modifications that can be applied to a TP spectrometer design are not mutually exclusive, i.e., the length of the drift between spectrometer and detector and the tuning of both electric and magnetic sections can be implemented at the same time, as reported in [17].
In summary, we can conclude that, according to the constraints of the different experimental setups and the needed detectable proton energy of interest, the proposed spectrometer designs can represent alternative and versatile proton diagnostic devices for both laser applications and other radiation sources.

Author Contributions

Conceptualization, K.N and S.T-A.; methodology, K.N,M.M. and A.M.; software, K.A and A.M.; validation, all authors; investigation, all authors; data curation K.N and A.M.;writing—original draft preparation, A.M.; writing—review and editing, all authors; supervision, K.N,M.M,S.T-A; All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

ELI-ALPS is supported by the European Union and co-financed by the European Regional Development Fund (GINOP-2.3.6-15-2015-00001). This work is supported by the IMPULSE project which receives funding from the European Union Framework Programme for Research and Innovation Horizon 2020 under grant agreement No 871161.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mourou, G.A.; Barry, C.P.; Perry, M.D. Ultrahigh-intensity lasers: Physics of the extreme on a tabletop. Physics today 1998, 51, 22–28. [Google Scholar] [CrossRef]
  2. Albert, F.; Couprie, M.; Debus, A.; Downer, M.C.; Faure, J.; Flacco, A.; Gizzi, L.A.; Grismayer, T.; Huebl, A.; Joshi, C.; others. 2020 roadmap on plasma accelerators. New Journal of Physics 2021, 23, 031101. [Google Scholar] [CrossRef]
  3. Yoon, J.W.; Jeon, C.; Shin, J.; Lee, S.K.; Lee, H.W.; Choi, I.W.; Kim, H.T.; Sung, J.H.; Nam, C.H. Achieving the laser intensity of 5.5× 10 22 W/cm 2 with a wavefront-corrected multi-PW laser. Optics express 2019, 27, 20412–20420. [Google Scholar] [CrossRef] [PubMed]
  4. Daido, H.; Nishiuchi, M.; Pirozhkov, A.S. Review of laser-driven ion sources and their applications. Reports on progress in physics 2012, 75, 056401. [Google Scholar] [CrossRef] [PubMed]
  5. Macchi, A. A review of laser-plasma ion acceleration. arXiv 2017, arXiv:1712.06443 2017. [Google Scholar]
  6. Bolton, P.; Borghesi, M.; Brenner, C.; Carroll, D.; De Martinis, C.; Fiorini, F.; Flacco, A.; Floquet, V.; Fuchs, J.; Gallegos, P.; Giove, D.; Green, J.; Green, S.; Jones, B.; Kirby, D.; McKenna, P.; Neely, D.; Nuesslin, F.; Prasad, R.; Reinhardt, S.; Roth, M.; Schramm, U.; Scott, G.; Ter-Avetisyan, S.; Tolley, M.; Turchetti, G.; Wilkens, J. Instrumentation for diagnostics and control of laser-accelerated proton (ion) beams. Physica Medica 2014, 30, 255–270. [Google Scholar] [CrossRef]
  7. Ter-Avetisyan, S.; Schnürer, M.; Nickles, P.V. Time resolved corpuscular diagnostics of plasmas produced with high-intensity femtosecond laser pulses. Journal of Physics D: Applied Physics 2005, 38, 863. [Google Scholar] [CrossRef]
  8. Schreiber, J.; Ter-Avetisyan, S.; Risse, E.; Kalachnikov, M.; Nickles, P.; Sandner, W.; Schramm, U.; Habs, D.; Witte, J.; Schnürer, M. Pointing of laser-accelerated proton beams. Physics of plasmas 2006, 13, 033111. [Google Scholar] [CrossRef]
  9. Ter-Avetisyan, S.; Schnürer, M.; Busch, S.; Risse, E.; Nickles, P.; Sandner, W. Spectral dips in ion emission emerging from ultrashort laser-driven plasmas. Physical review letters 2004, 93, 155006. [Google Scholar] [CrossRef]
  10. Ter-Avetisyan, S.; Schnürer, M.; Nickles, P.; Sokollik, T.; Risse, E.; Kalashnikov, M.; Sandner, W.; Priebe, G. The Thomson deflectometer: A novel use of the Thomson spectrometer as a transient field and plasma diagnostic. Review of Scientific Instruments 2008, 79, 033303. [Google Scholar] [CrossRef]
  11. Sokollik, T.; Schnürer, M.; Ter-Avetisyan, S.; Nickles, P.; Risse, E.; Kalashnikov, M.; Sandner, W.; Priebe, G.; Amin, M.; Toncian, T.; others. Transient electric fields in laser plasmas observed by proton streak deflectometry. Applied Physics Letters 2008, 92, 091503. [Google Scholar] [CrossRef]
  12. Ter-Avetisyan, S.; Schnürer, M.; Nickles, P.; Sandner, W.; Nakamura, T.; Mima, K. Correlation of spectral, spatial, and angular characteristics of an ultrashort laser driven proton source. Physics of Plasmas 2009, 16, 043108. [Google Scholar] [CrossRef]
  13. Ter-Avetisyan, S.; Ramakrishna, B.; Doria, D.; Sarri, G.; Zepf, M.; Borghesi, M.; Ehrentraut, L.; Stiel, H.; Steinke, S.; Priebe, G.; others. Complementary ion and extreme ultra-violet spectrometer for laser-plasma diagnosis. Review of Scientific Instruments 2009, 80, 103302. [Google Scholar] [CrossRef] [PubMed]
  14. Gwynne, D.; Kar, S.; Doria, D.; Ahmed, H.; Cerchez, M.; Fernandez, J.; Gray, R.; Green, J.; Hanton, F.; MacLellan, D.; others. Modified Thomson spectrometer design for high energy, multi-species ion sources. Review of Scientific Instruments 2014, 85, 033304. [Google Scholar] [CrossRef] [PubMed]
  15. Alejo, A.; Kar, S.; Tebartz, A.; Ahmed, H.; Astbury, S.; Carroll, D.; Ding, J.; Doria, D.; Higginson, A.; McKenna, P.; others. High resolution Thomson Parabola Spectrometer for full spectral capture of multi-species ion beams. Review of Scientific Instruments 2016, 87, 083304. [Google Scholar] [CrossRef] [PubMed]
  16. Torrisi, L.; Costa, G. Compact Thomson parabola spectrometer for fast diagnostics of different intensity laser-generated plasmas. Physical Review Accelerators and Beams 2019, 22, 042902. [Google Scholar] [CrossRef]
  17. Alejo, A.; Gwynne, D.; Doria, D.; Ahmed, H.; Carroll, D.; Clarke, R.; Neely, D.; Scott, G.; Borghesi, M.; Kar, S. Recent developments in the Thomson Parabola Spectrometer diagnostic for laser-driven multi-species ion sources. Journal of Instrumentation 2016, 11, C10005. [Google Scholar] [CrossRef]
  18. Jung, D.; Hörlein, R.; Kiefer, D.; Letzring, S.; Gautier, D.; Schramm, U.; Hübsch, C.; Öhm, R.; Albright, B.; Fernandez, J.; others. Development of a high resolution and high dispersion Thomson parabola. Review of Scientific Instruments 2011, 82, 013306. [Google Scholar] [CrossRef]
  19. Teng, J.; He, S.; Deng, Z.; Zhang, B.; Hong, W.; Zhang, Z.; Zhu, B.; Gu, Y. A compact high resolution Thomson parabola spectrometer based on Halbach dipole magnets. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2019, 935, 30–34. [Google Scholar] [CrossRef]
  20. Kojima, S.; Inoue, S.; Dinh, T.H.; Hasegawa, N.; Mori, M.; Sakaki, H.; Yamamoto, Y.; Sasaki, T.; Shiokawa, K.; Kondo, K.; others. Compact Thomson parabola spectrometer with variability of energy range and measurability of angular distribution for low-energy laser-driven accelerated ions. Review of Scientific Instruments 2020, 91, 053305. [Google Scholar] [CrossRef]
  21. Salgado-López, C.; Apiñaniz, J.I.; Henares, J.L.; Pérez-Hernández, J.A.; de Luis, D.; Volpe, L.; Gatti, G. Angular-Resolved Thomson Parabola Spectrometer for Laser-Driven Ion Accelerators. Sensors 2022, 22, 3239. [Google Scholar] [CrossRef]
  22. Microchanel plates-photonics website. url:https://www.photonis.com/products/microchannel-plates.
  23. Jeong, T.W.; Singh, P.; Scullion, C.; Ahmed, H.; Kakolee, K.; Hadjisolomou, P.; Alejo, A.; Kar, S.; Borghesi, M.; Ter-Avetisyan, S. Experimental evaluation of the response of micro-channel plate detector to ions with 10s of MeV energies. Review of Scientific Instruments 2016, 87, 083301. [Google Scholar] [CrossRef] [PubMed]
  24. Morrison, J.T.; Feister, S.; Frische, K.D.; Austin, D.R.; Ngirmang, G.K.; Murphy, N.R.; Orban, C.; Chowdhury, E.A.; Roquemore, W. MeV proton acceleration at kHz repetition rate from ultra-intense laser liquid interaction. New Journal of Physics 2018, 20, 022001. [Google Scholar] [CrossRef]
  25. Xu, N.; Streeter, M.; Ettlinger, O.; Ahmed, H.; Astbury, S.; Borghesi, M.; Bourgeois, N.; Curry, C.; Dann, S.; Dover, N.; others. Versatile tape-drive target for high-repetition-rate laser-driven proton acceleration. High Power Laser Science and Engineering 2023, 11, e23. [Google Scholar] [CrossRef]
  26. G&#xF6, *!!! REPLACE !!!*; thel, I.; Assenbaum, S.; Bernert, C.; Brack, F.E.; Cowan, T.; Dover, N.; Gaus, L.; Kluge, T.; Kraft, S.; Kroll, F.; others. Laser-driven high-energy proton beams from cascaded acceleration regimes. https://www.researchsquare.com/article/rs-2841731/v1 2023. [Google Scholar] [CrossRef]
  27. Higginson, A.; Gray, R.; King, M.; Dance, R.; Williamson, S.; Butler, N.; Wilson, R.; Capdessus, R.; Armstrong, C.; Green, J.; others. Near-100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme. Nature communications 2018, 9, 724. [Google Scholar] [CrossRef] [PubMed]
  28. Thomson, J.J. XXVI. Rays of positive electricity. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1911, 21, 225–249. [Google Scholar] [CrossRef]
  29. Reiser, M.; O’Shea, P. <italic>Theory and design of charged particle beams</italic>; Vol. 312, Wiley Online Library, 1994.
  30. Jackson, J.D. Classical electrodynamics, 1999.
  31. Fano, U.; Racah, G. Irreducible tensorial sets. Irreducible tensorial sets 1959. [Google Scholar] [CrossRef]
  32. Butcher, J.C. <italic>The numerical analysis of ordinary differential equations: Runge-Kutta and general linear methods</italic>; Wiley-Interscience, 1987.
  33. Wiedemann, H.; others. <italic>Particle accelerator physics</italic>; Vol. 314, Springer Berlin, 2007.
  34. Evans, L.; Bryant, P. LHC machine. Journal of instrumentation 2008, 3, S08001. [Google Scholar] [CrossRef]
  35. Morabito, A.; Scisciò, M.; Veltri, S.; Migliorati, M.; Antici, P. Design and optimization of a laser-PIXE beamline for material science applications. Laser and Particle Beams 2019, 37, 354–363. [Google Scholar] [CrossRef]
  36. Ter-Avetisyan, S.; Schnürer, M.; Polster, R.; Nickles, P.; Sandner, W. First demonstration of collimation and monochromatisation of a laser accelerated proton burst. Laser and Particle Beams 2008, 26, 637–642. [Google Scholar] [CrossRef]
  37. Morabito, A. Transport and manipulation of laser driven proton beams for diagnostics and applications. PhD thesis, Universita’ la Sapienza di Roma, 2021. https://iris.uniroma1.it/handle/11573/1695964.
  38. Singh, P.K.; Varmazyar, P.; Nagy, B.; Son, J.G.; Ter-Avetisyan, S.; Osvay, K. Low divergent MeV-class proton beam with micrometer source size driven by a few-cycle laser pulse. Scientific Reports 2022, 12, 1–2. [Google Scholar]
  39. Barberio, M.; Veltri, S.; Scisciò, M.; Antici, P. Laser-Accelerated Proton Beams as Diagnostics for Cultural Heritage. Scientific Reports 2017, 7, 40415. [Google Scholar] [CrossRef] [PubMed]
  40. Mirani, F.; Maffini, A.; Casamichiela, F.; Pazzaglia, A.; Formenti, A.; Dellasega, D.; Russo, V.; Vavassori, D.; Bortot, D.; Huault, M.; others. Integrated quantitative PIXE analysis and EDX spectroscopy using a laser-driven particle source. Science Advances 2020, 7, eabc8660. [Google Scholar] [CrossRef] [PubMed]
  41. Margarone, D.; Bonvalet, J.; Giuffrida, L.; Morace, A.; Kantarelou, V.; Tosca, M.; Raffestin, D.; Nicolai, P.; Picciotto, A.; Abe, Y.; others. In-target proton–boron nuclear fusion using a PW-class laser. Applied sciences 2022, 12, 1444. [Google Scholar] [CrossRef]
  42. Giuffrida, L.; Belloni, F.; Margarone, D.; Petringa, G.; Milluzzo, G.; Scuderi, V.; Velyhan, A.; Rosinski, M.; Picciotto, A.; Kucharik, M.; others. High-current stream of energetic α particles from laser-driven proton-boron fusion. Physical Review E 2020, 101, 013204. [Google Scholar] [CrossRef] [PubMed]
  43. Eichner, T.; Grüner, F.; Becker, S.; Fuchs, M.; Habs, D.; Weingartner, R.; Schramm, U.; Backe, H.; Kunz, P.; Lauth, W. Miniature magnetic devices for laser-based, table-top free-electron lasers. Physical Review Special Topics - Accelerators and Beams 2007, 10, 082401. [Google Scholar] [CrossRef]
  44. Milluzzo, G.; Petringa, G.; Catalano, R.; Cirrone, G. Handling and dosimetry of laser-driven ion beams for applications. The European Physical Journal Plus 2021, 136, 1170. [Google Scholar] [CrossRef]
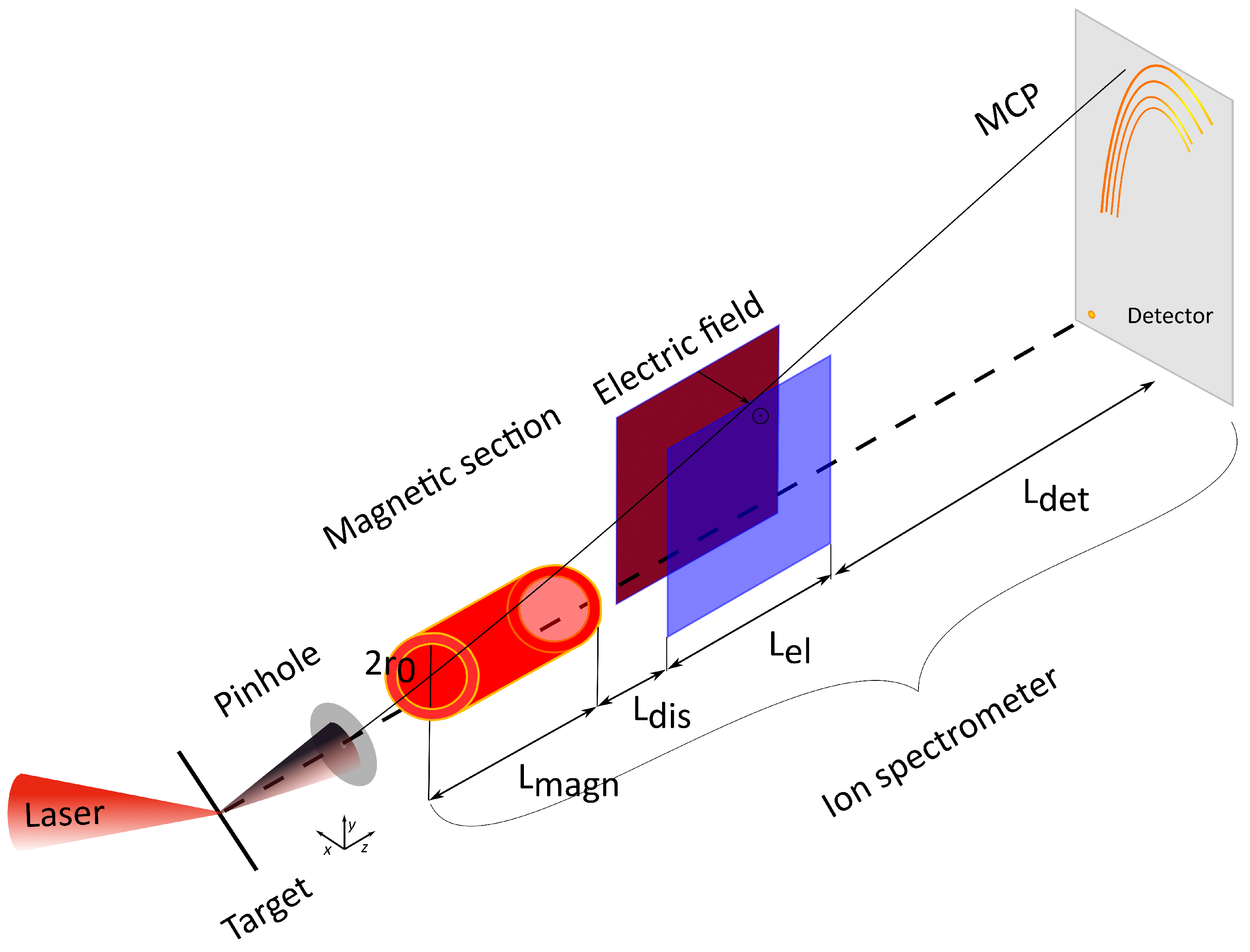
Preprints 106478 g001
Figure 1. Scheme of the spectrometer, that is composed of a pinhole, a magnetic section, that is depicted as a cylinder with length L m a g n and bore radius r 0 , separated by a distance L d i s from the electric field with length L e l . The distance between the exit of the electric field and the ion detector (MCP) is labeled L d e t .
Figure 1. Scheme of the spectrometer, that is composed of a pinhole, a magnetic section, that is depicted as a cylinder with length L m a g n and bore radius r 0 , separated by a distance L d i s from the electric field with length L e l . The distance between the exit of the electric field and the ion detector (MCP) is labeled L d e t .
Preprints 106478 g001
Preprints 106478 g002
Figure 2. Figure (A) The comparison of particle deflection in dipole and linear-gradient (quadrupole) magnetic fields with the parameters given in Table 1. The color bar on the right-hand side indicates the initial proton energy range. Figure (B) Energy resolution calculated according to eq. 10 for homogeneous and linear gradient cases. The inset shows a zoom onto the lowest energetic particles.
Figure 2. Figure (A) The comparison of particle deflection in dipole and linear-gradient (quadrupole) magnetic fields with the parameters given in Table 1. The color bar on the right-hand side indicates the initial proton energy range. Figure (B) Energy resolution calculated according to eq. 10 for homogeneous and linear gradient cases. The inset shows a zoom onto the lowest energetic particles.
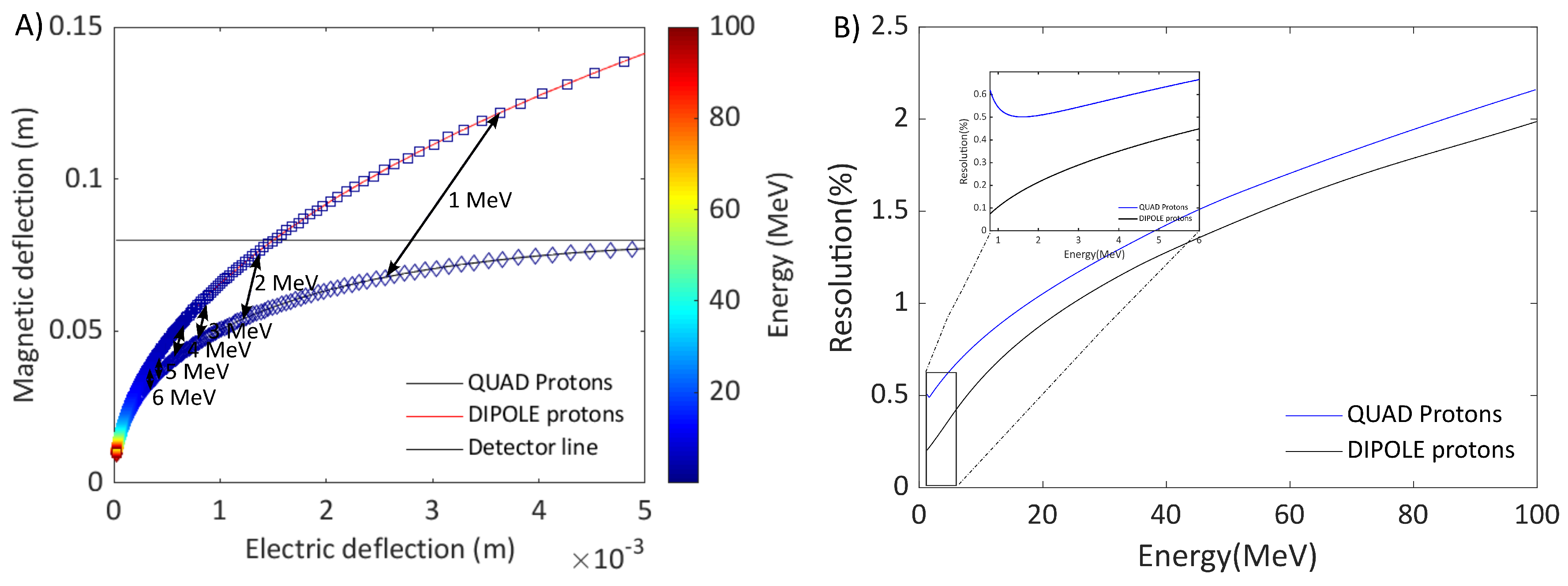
Preprints 106478 g002
Preprints 106478 g003
Figure 3. (A) The comparison of particles deflection in a dipole (line 1) and quadrupolar (line 2) magnetic fields with the parameters given in Table 2 and a dipole (line 3) field with B 0 = 0.9 T, L m a g n = 10 cm, L d e t = 16.5 cm. On the x axis it is shown the electric deflection in m, whereas on the y axis it is shown the magnetic deflection, also in m. (B) The comparison between the energy resolutions (y axis) versus proton energy range (x axis in MeV) for both the cases of the dipoles and the case of the quadrupolar field.
Figure 3. (A) The comparison of particles deflection in a dipole (line 1) and quadrupolar (line 2) magnetic fields with the parameters given in Table 2 and a dipole (line 3) field with B 0 = 0.9 T, L m a g n = 10 cm, L d e t = 16.5 cm. On the x axis it is shown the electric deflection in m, whereas on the y axis it is shown the magnetic deflection, also in m. (B) The comparison between the energy resolutions (y axis) versus proton energy range (x axis in MeV) for both the cases of the dipoles and the case of the quadrupolar field.
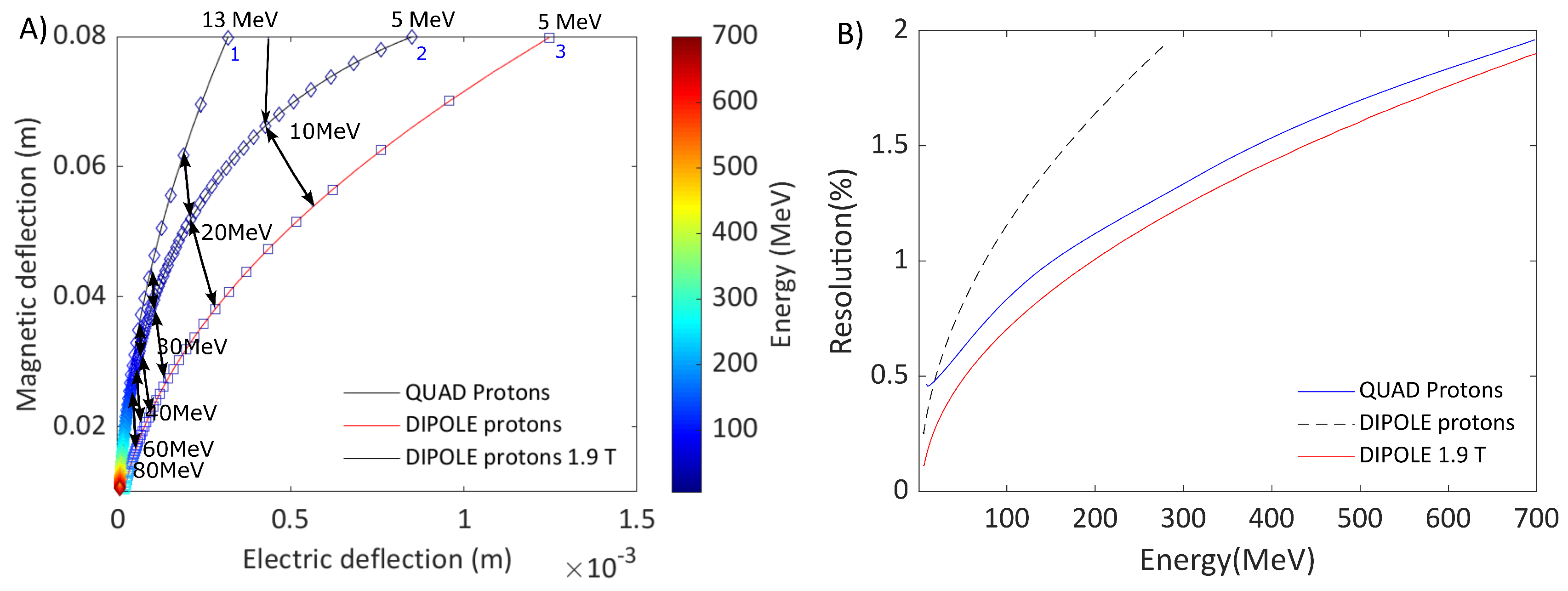
Preprints 106478 g003
Preprints 106478 g004
Figure 4. (A) The comparison of particles deflection in a dipole (line 1) and quadrupolar magnetic fields (line 2) with the parameters given in Table 2 and the dipole (line 3) field with B 0 = 0.9 T, L m a g n = 10 cm, L d e t = 30 cm. On the x axis we plot the electric deflection in m, while on the y axis we plot the magnetic deflection, that is also in m. (B) Comparison between the energy resolutions (y axis) versus proton energy range(x axis) expressed in in MeV, for both the cases of the dipoles and the case of the magnetic field profile of the quadrupole.
Figure 4. (A) The comparison of particles deflection in a dipole (line 1) and quadrupolar magnetic fields (line 2) with the parameters given in Table 2 and the dipole (line 3) field with B 0 = 0.9 T, L m a g n = 10 cm, L d e t = 30 cm. On the x axis we plot the electric deflection in m, while on the y axis we plot the magnetic deflection, that is also in m. (B) Comparison between the energy resolutions (y axis) versus proton energy range(x axis) expressed in in MeV, for both the cases of the dipoles and the case of the magnetic field profile of the quadrupole.
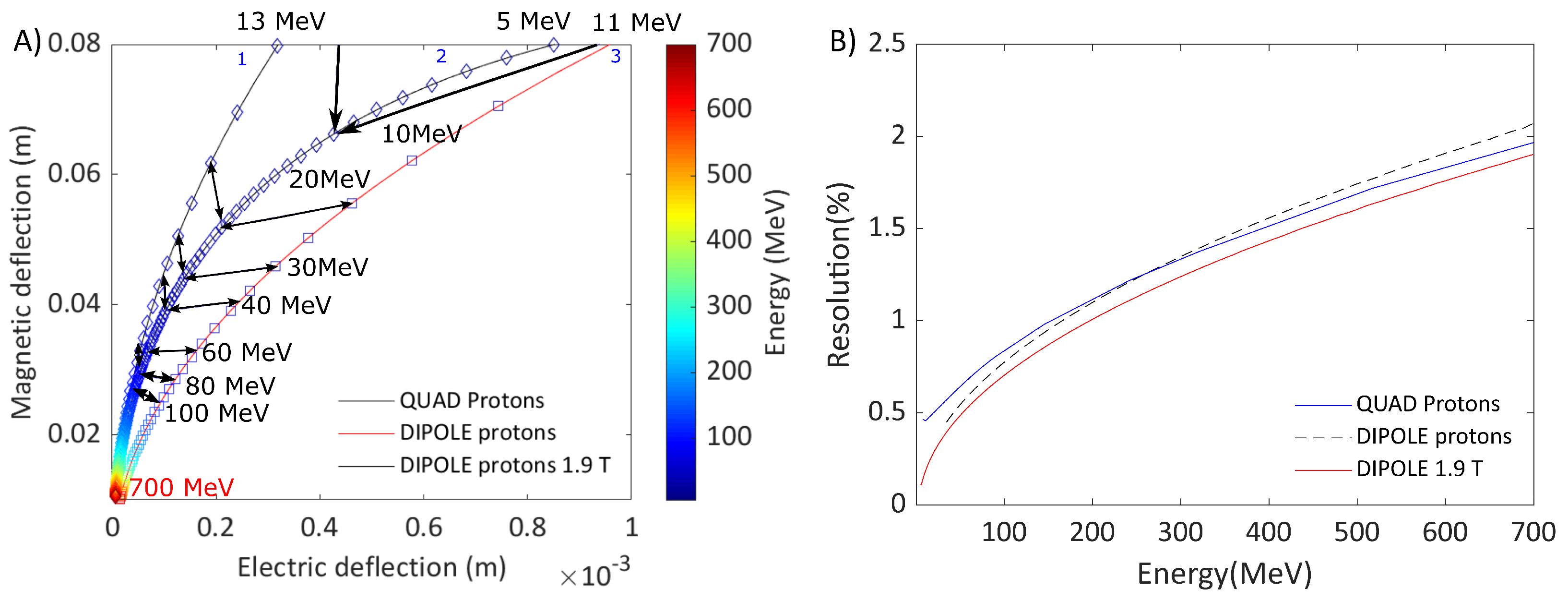
Preprints 106478 g004
Preprints 106478 g005
Figure 5. (A) The overlap of the different magnetic profiles compared to the case of the dipole is shown. The continuous black line represents the detector line. The dashed black line represents the magnetic deflection of the reference case of the dipole, while the blue, red, green and magenta lines represent the cases of the not linear magnetic profiles. Both the x axis and the y axis are in a logarithmic scale. On the x axis the proton energy range is in MeV, while on the y axis, the magnetic deflection is in m units. (B) The scaling law is shown. We illustrate the different orders (n) of the magnetic profiles vs the minimum detectable energy in MeV.
Figure 5. (A) The overlap of the different magnetic profiles compared to the case of the dipole is shown. The continuous black line represents the detector line. The dashed black line represents the magnetic deflection of the reference case of the dipole, while the blue, red, green and magenta lines represent the cases of the not linear magnetic profiles. Both the x axis and the y axis are in a logarithmic scale. On the x axis the proton energy range is in MeV, while on the y axis, the magnetic deflection is in m units. (B) The scaling law is shown. We illustrate the different orders (n) of the magnetic profiles vs the minimum detectable energy in MeV.
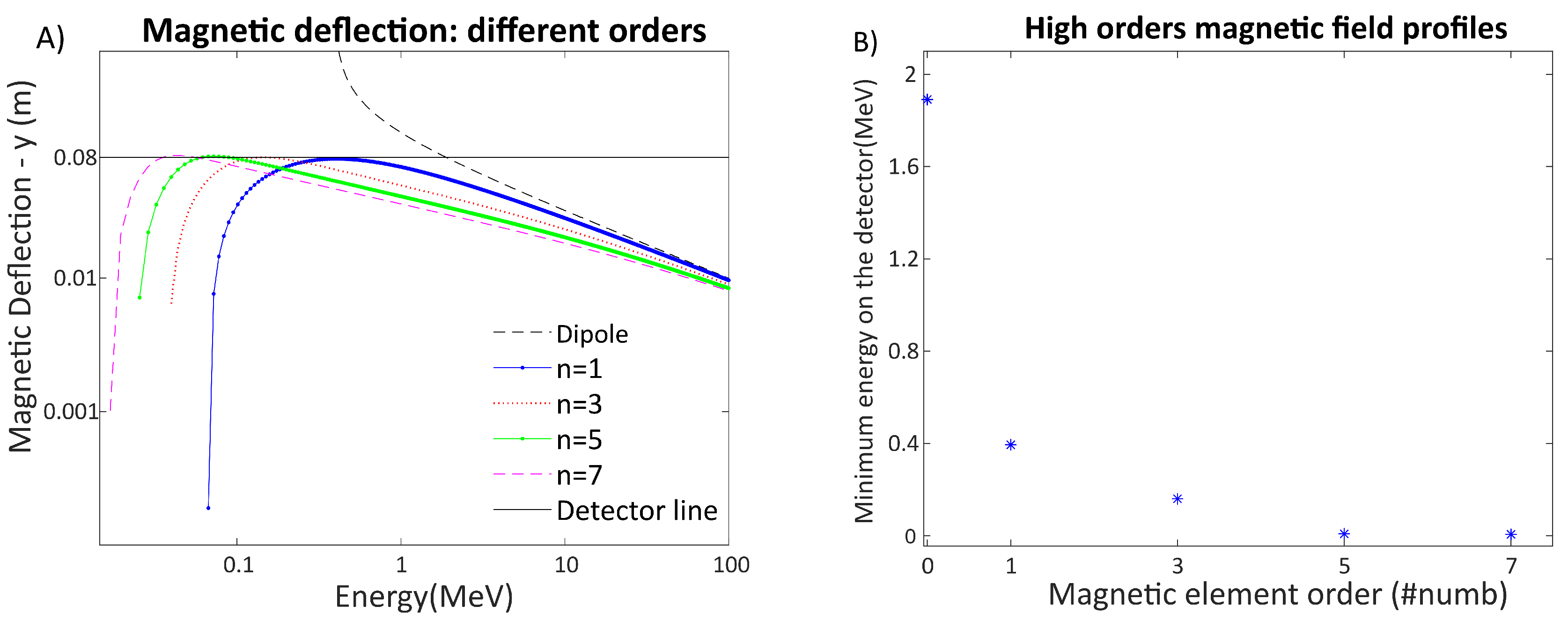
Preprints 106478 g005
Table 1. Optimized design parameters for low energy protons.
Table 1. Optimized design parameters for low energy protons.
Element B 0 / G L m a g n E L e l L d e t
Dipole 0.9 T 10 c m 12 k V / c m 5 c m 5 c m
Quadrupole 45 T / m at r 0 =2.2 c m 10 c m 12 k V / c m 5 c m 5 c m
Table 2. Optimized design parameters for high energy protons
Table 2. Optimized design parameters for high energy protons
Element B 0 / G L m a g n E L e l L d e t
Dipole 1.9 T 10 c m 12 k V / c m 5 c m 11 c m
Quadrupole 100 T/m at r 0 =1.9 cm 10 c m 12 k V / c m 5 c m 11 c m
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated