Prerpints.org logo
Preprint
Article

Seismic Nowcasting: A Holistic Artificial Neural Network Predictive Model

Altmetrics

Downloads

161

Views

576

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 August 2024

Posted:

16 August 2024

You are already at the latest version

Alerts
Abstract
A contemporary technique for calculating seismic risk is earthquake nowcasting (EN), which analyzes the progression of the earthquake (EQ) cycle in fault systems. 'Natural time' is a novel idea of time that serves as the foundation for EN assessment. The earthquake potential score (EPS), which has been discovered to have useful uses regionally and worldwide, is a unique tool EN uses to predict seismic risk. For the estimation of the EPS for the occurrences with the highest magnitude among these applications, we have since 2021 concentrated on Greece territory, applying sophisticated Artificial Intelligence (AI) algorithms, both wise (semi)supervised and unsupervised models, along with a customized dynamic sliding window technique that performs as a stochastic filter able to fine-tune the geo seismic occurrences. Long short-term memory (LSTM) neural networks, random forests, and clustering (geospatial) models are three machine learning techniques that are particularly good at finding patterns in vast databases and may be used to enhance earthquake prediction performance. In this study, we attempt to forecast whether practical Machine-learning and AI/Game-theoretic-based approaches can help predict big earthquakes and the normal future seismic cycle for 6-12 months. Specifically, we focus on answering two questions for a given region: (1) Is there a chance that a significant earthquake—say, one with a magnitude of M ≥ 6.0 will happen in the upcoming year? (2) What is the largest earthquake magnitude predicted in the upcoming year, and with which exact geographic coordinates (GCS)? Our results are quite promising and project a high precision accuracy score (≥ 98%) for seismic nowcasting in terms of four predictive parameters: the approximate (a) latitude, (b) longitude, (c) focal depth, and (d) magnitude of the phenomena.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

One of the worst natural disasters on the planet, earthquakes frequently result in significant loss for the human race. As a result, it is imperative to foresee when and where they will occur, albeit doing so is difficult because of their inherent randomness [1].
The frequently used earthquake prediction methods nowadays can be categorized into four groups, according to [2]. The first two strategies, namely 1) mathematical tools like FDL [3] and 2) precursor-based techniques that retrieve geographic features like seismic anomalies [4], cloud images [5], and animal behavior [6], were well-liked when there was a dearth of earthquake data. Then, as more and more earthquakes produced larger datasets, machine learning techniques entered the picture. Maria Moustra et al. [7] used an artificial neural network, one of them, to predict an earthquake in 2011. The model’s accuracy was just about 70%, which was not very good then. It was determined from the research that fewer attributes in the dataset, as well as the class imbalance, led to unsatisfying results.
Finally, deep learning techniques have recently been used to forecast earthquakes. A deep neural network (DNN) model that assessed earthquake magnitudes due to occur within the next seven days using a newly introduced parameter Fault Density (based on the concept of spatial effect) was tested by Mohsen Yousefzadeh et al. [8]. DNN performed better than other machine learning models, with a test accuracy of about 79% on magnitudes greater than 8. To detect the epicenters of earthquakes that occurred in the past two months, Luana Ruiz et al. [9] developed a network called the Graph Convolutional Recurrent Neural Network (GCRNN) by combining the properties of convolutional neural networks (CNN) and recurrent neural networks. GCRNN used convolutional filters to maintain the independence of the trained parameter count from the input time sequences. For both the 30-second and 60-second waves, GCRNN achieved an accuracy of about 33% with fewer characteristics being taken into account. In addition, Q. Wang et al. [2] used a long short-term memory (LSTM) variation of the recurrent neural network to learn the temporal-spatial dependencies of seismic signals and, consequently, forecast earthquakes. Even though they only used seismic data from the previous year as input, the accuracy was about 75%. A CNN-LSTM hybrid network was also suggested by Parisa Kavianpour et al. [10] to learn the spatial-temporal dependencies of earthquake signals. They used the total number of earthquakes that occurred in a single month between 1966 and 2021 as their input to evaluate the model’s effectiveness in nine regions of the Chinese mainland. They also included other earthquake-related factors, such as latitude and longitude. They compared the results of several models, including MLP and SVM, and found that CNN-LSTM scored the highest. In [11], the Author(s) focuses on predicting an earthquake in the next 30 seconds. Even though a long-term prediction’s outcome is likely erroneous (not accurate to a single day), 30 seconds allows individuals enough time to react and prevent an unthinkable tragedy. They, finally, deploy different time series models (vanilla RNN, LSTM, and Bi-LSTM) compared with one another in the same study question.
More recent research studies outline alternative neural network technologies. In recent years, neural networks, including LSTM and convolution neural networks, have been widely used in the research of time series and magnitude prediction [7,12]. As mentioned earlier, using LSTM networks to record spatiotemporal correlations among earthquakes in various places, the authors of [3] developed a novel method for earthquake prediction. Their simulation findings show that their strategy performs better than conventional methods. It has been demonstrated that earthquake prediction accuracy can be increased using seismicity indicators as inputs in machine learning classifiers [13]. Results from using this methodology in four Chilean cities show that reliable forecasts may be made by thoroughly examining how specific parameters should be configured. [14] describes a proposed methodology trained and tested for the Hindu Kush, Chile, and Southern California regions. It is based on the computation of seismic indicators and GP-AdaBoost classification. Compared to earlier studies, the derived prediction results for these regions show improvement. [15] explores how artificial neural networks (ANNs) can be used to predict earthquakes. The results from applying ANNs to Chile and the Iberian peninsula are presented, and the findings are compared with those of other well-known classifiers. Adding a new set of inputs improved all classifiers, but according to the conclusion, the ANN produced the best results of any classifier.
Seven different datasets from three areas have been subjected to a methodology for identifying earthquake precursors using clustering, grouping, building a precursor tree, pattern extraction, and pattern selection [16]. Results compare favorably to the previous edition regarding all measured quality metrics. The authors propose that this method could be improved and used to predict earthquakes in other places with various geophysical characteristics.
The authors of [17] employ machine learning techniques to identify signals in a correlation time series that predict future significant earthquakes. Decision thresholds, receiver operating characteristic (ROC) techniques, and Shannon information entropy are used to assess overall quality. They anticipate that the deep learning methodology would be more all-encompassing than earlier techniques and won’t require guesswork upfront about whether patterns are significant. Finally, their findings in [18] demonstrate that the LSTM technique only provides a rough estimate of earthquake magnitude, whereas the random forest method performs best in categorizing major earthquake occurrences. The Author(s) conclude that information from small earthquakes can be used to predict larger earthquakes in the future. Machine learning offers a potential way to enhance earthquake prediction.

1.1. Research Contribution

To technically elaborate and materialize this claim, a study was conducted by utilizing (four) seismic features ((°N), (°E), (km), (Mag.)) based on seismic catalogs from the National Observatory of Athens (NOA), Greece containing the full list (i.e., small and large magnitude occurrences) of past earthquake events and for a specific year frame. This input was granted to construct a solicit time-scaled "sliding-window" (SW) mathematical technique that, if co-deployed with advanced Machine-learning and Game-theoretic algorithms, would significantly impact increasing the future precision accuracy of the earthquake predictability. Additionally, the capability of having architectured a synthesized seismic predictability framework that is capable of endorsing Machine Learning (both (semi)supervised and unsupervised), Game-theory solving models (i.e., OpenAI Gym, which is a toolkit for developing and comparing reinforcement learning (RL) algorithms), as well as the adaptation of the SW model in seismic short and long term casting was explored. The research investigation emphasized two crucial questions:
  • Will there be a strong event (M ≥ 6.0, 7.0, or 8.0) forecasted in the next year among the specific studied geographical region?
  • Can we obtain the scientific ability to predict the nearly exact 4-tuple ((°N), (°E), (km), (Mag.)) output of such future major event, as well as the (implicit) almost exact time frame of its occurrence?

2. Proof of Methods

Greece is a natural seismology laboratory because it has the highest seismicity in Europe and statistically produces an earthquake of at least M6.0 almost every year [19]–21]. The short repeat time in the area also makes it possible to study changes in regional seismicity rates over "earthquake cycles." Here, we provide the outcomes of the novel earthquake nowcasting approach (EN) developed by Rundle, Turcotte, and colleagues [22]. With this approach, we counted the number of tiny EQs since the most recent major EQ to determine the region’s current hazard level. The term "natural time," which was coined by Varotsos et al. [23,24,25,2627], refers to event counting as a unit of "time" as opposed to clock time. According to Rundle et al. [22], applying natural time to EQ seismicity offers the following two benefits: In addition, when computing nowcasts, the concept of natural time—counts of small EQs—is used as a measure of the accumulation of stress and strain between large EQs in a defined geographic area. First, it is not necessary to declutter the aftershocks because natural time is uniformly valid when aftershocks dominate, when background seismicity dominates, and when both contribute.
In other words, the use of natural time is the foundation of nowcast. As previously mentioned, there are two benefits to using natural time: first, there is no need to separate the aftershocks from the background seismicity; second, only the natural interevent count statistics are used, as opposed to the seismicity rate, which also takes into account conventional (clock) time. Instead of focusing on recurrent events on particular faults, the nowcasting method defines an "EQ cycle" as the recurring large EQs in a vast seismically active region composed of numerous active faults. Following Pasari [28] (see also Pasari et al. [29]), we may say that although the concept of "EQ cycle" has been used in numerous earlier seismological investigations [30],31]32], the idea of "natural time" is unique in its properties.
The estimation of seismic risk in large cities around the world [33], the study of induced seismicity [34], the study of temporal clustering of global EQs [35], the clarification of the role of small EQ bursts in the dynamics associated with large EQs [36], the understanding of the complex dynamics of EQ faults [37], the identification of the current state of the "EQ cycle" [38,39,40], the nowcasting of avalanches [41]. The Olami-Fe Here, using the earthquake potential, we examined the greatest events in Greece between January 1 and February 6, 2023, with MW(USGS) 6 (see Figure 1 and Table 1), utilizing the earthquake potential score (EPS) (see below).
Natural time analysis (NTA), which was discussed in [27] and more recently in [42], in general, displays the dynamical evolution of a complex system and pinpoints when it hits a critical stage. As a result, NTA can play a significant role in foreseeing approaching catastrophic occurrences, such as the emergence of massive EQs. In this regard, it was used in situations of EQ in Greece [23,25,26,43,44,45,46,47,48,49], the USA [50,51], Mexico [70,71], the Eastern Mediterranean [55,56], and globally [57,58,59]. We observe that NTA permits the insertion of an entropy, S, which is a dynamic entropy [24] that demonstrates positivity, concavity, and experimental stability for Lesche [64,65]. Recently, the research of EQs in Japan [67,68,69,70] and Mexico [71,72] has used complexity metrics [66] based on natural temporal entropy and S itself, with encouraging results [73]. In particular, two quantities—which are discussed below—have lately been stated in the Preface of [43] and have emerged through natural time analysis to be crucial in determining whether and when the critical moment (mainshock, the new phase) is approaching.
First, let’s talk about seismicity’s order parameter κ 1 . Its value ( = 0.070 ) indicates when the system reaches the critical stage, and its variations’ minimum indicates when the Seismic Electric Signals (SES) [74,75,76,77,78,79] activities start [80]. The SES amplitude is crucial because it allows for estimating the impending mainshock’s magnitude. The epicentral area is determined using the station’s SES selectivity map, which records the pertinent SES (using this methodology, a successful prediction for a M W = 6.4 E Q that occurred on June 8, 2008, in the Andravida area of Greece was made [44,46,81]).
Second, the entropy change, Δ S , under time reversal: its value, when minimized a few months in advance, denotes the beginning of precursory phenomena; as for its fluctuations (when the minimum of Δ S appears), they show a clear increase, denoting the time when the E Q preparation begins, as explained by the physical model that served as the basis for the SES research [79].
The M W = 9.0 Tohoku E Q on March 11, 2011, which was the largest event ever recorded in Japan, and the M W = 8.2 Chiapas E Q on September 7, 2017, which was the largest EQ in Mexico in more than a century, were used to study precursory phenomena before the two subsequent major EQs.

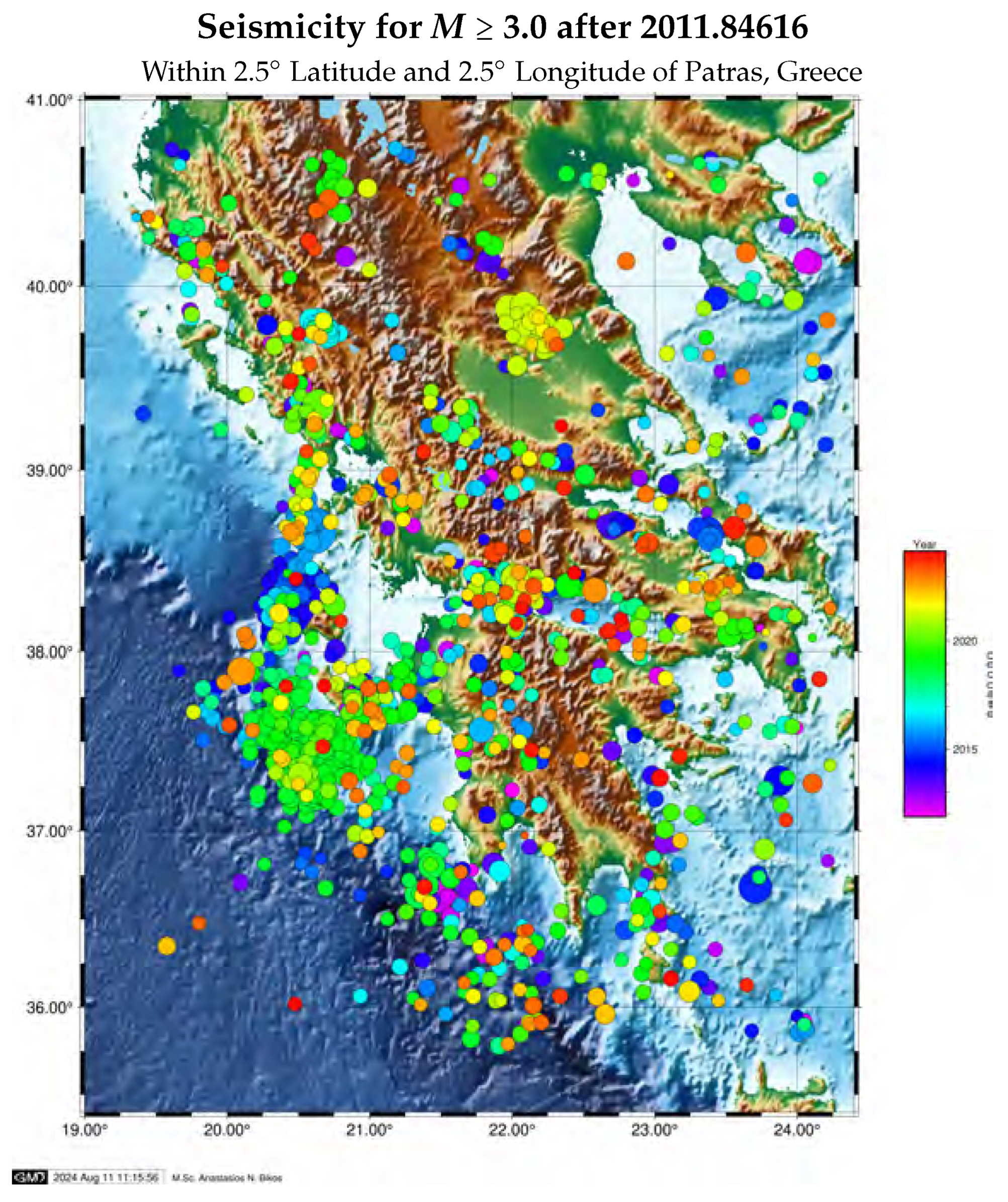
3. Datasets and Feature Engineering

The seismic input catalog used in this research study was provided by the Greece National Observatory of Athens (NOA), (https://www.gein.noa.gr/services/cat.html, last accessed on 1 January 2024) and includes earthquake events with a magnitude greater than 2.0 in the Greek geographic region from 1950 to 2024. Using feature engineering, several statistical principles were used to create the seismic activity parameters for a specific experimentation trial set; rather than using the original seismic catalog, these parameters obtained from it were utilized as the input features for earthquake prediction.
Numerous seismic properties obtained from earthquake catalogs have been shown in previous studies to be useful in earthquake prediction. The number and maximum/mean magnitude of previous earthquakes, seismic energy release, magnitude deficit, seismic rate fluctuations, and the amount of time since the last significant earthquake are some of these characteristics. Other elements include an ’a’ and a ’b’ value in the Gutenberg-Richter (GR) law. Typical related research work seismic features also include the probability of an earthquake occurring, the divergence from the Gutenberg-Richter rule, and the standard deviation of the estimated b value. The equation of the GR property, which describes the fractal and/or power law magnitude distribution of earthquakes in the defined region and in the defined time interval, is given by the following formula: l o g 10 N = α − b M , is a very nice illustration scenario where we applied, as part of the scope of our ANN framework, a quite accurate Machine-learning logistic regression library to predict the next mathematical future value (of the GR rule), with strict preconditional property of holding at least 3 decimal digits of numerical accuracy in the fractional part of the predicted value.

4. Methodologies

This section begins with an introduction to ad-hoc deep-learning neural networks that we customized and leveraged inside our Artificial Neural Network framework architecture and a discussion of their suitability for earthquake prediction. Next, a detailed explanation of the metrics used to assess the networks’ performances will be provided.

4.1. Deep Learning Approach

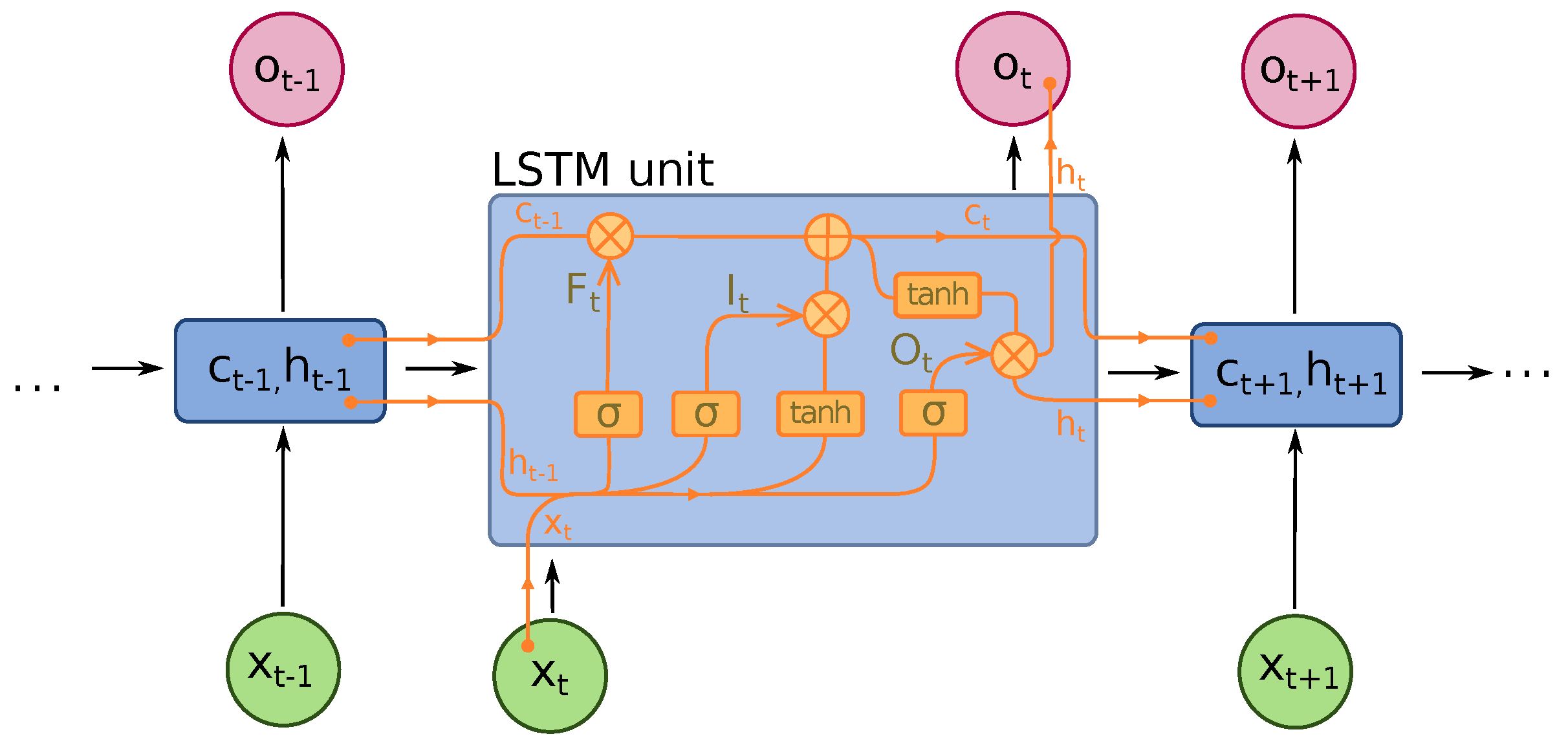
4.1.1. Recurrent Neural Networks: an elemental LSTM artificial neural network

One of the two major categories of artificial neural networks, recurrent neural networks (RNNs), are distinguished by the direction of information flow between their layers. It is a bi-directional artificial deep-learning neural network, which allows the output from some nodes to influence consecutive input to the same nodes instead of a uni-directional feedforward neural network. They are useful for tasks like our RNG approximation because they can handle arbitrary input sequences using internal state (memory). We mainly focus on the LSTM (Long short-term memory) version of such RNNs.
A deep learning system that overcomes the vanishing gradient problem is called long short-term memory (LSTM). Recurrent gates called "forget gates" are typically added to LSTM. Backpropagated mistakes are not allowed to explode or vanish, thanks to LSTM. Errors can instead travel backward through an infinite number of virtual layers that are spread out in space. Therefore, LSTM can be trained to perform tasks that call for memories of past events that occurred hundreds or millions of discrete time steps ago. LSTM-like topologies that are tailored to a certain problem can evolve. Long time intervals between important events do not affect the performance of LSTM, and it can handle signals that combine low- and high-frequency components. To discover an RNN weight matrix capable of maximizing the likelihood of the label sequences in an application, many employ fragmented stacks of LSTM RNNs and train them using Connectionist Temporal Classification (CTC).
We illustrate the exact LSTM cell network diagram we exploit in our ANN framework in Figure 2.
The analytical forms of the equations for the forward pass of an LSTM cell while attaching a forget gate are:
f t = σ g ( W f x t + U f h t − 1 + b f ) i t = σ g ( W i x t + U i h t − 1 + b i ) o t = σ g ( W o x t + U o h t − 1 + b o ) c ˜ t = σ c ( W c x t + U c h t − 1 + b c ) c t = f t ⊙ c t − 1 + i t ⊙ c ˜ t h t = o t ⊙ σ h ( c t )
where the preliminary values are c 0 = 0 and h 0 = 0 and the operator ⊙ assumes the Hadamard product (element-wise product). The subscript t indexes the (next) time step.
Variables
  • x t ∈ R d : input vector to the LSTM unit
  • f t ∈ ( 0 , 1 ) h : forget gate’s activation vector
  • i t ∈ ( 0 , 1 ) h : input/update gate’s activation vector
  • o t ∈ ( 0 , 1 ) h : output gate’s activation vector
  • h t ∈ ( − 1 , 1 ) h : hidden state vector also known as output vector of the LSTM unit
  • c ˜ t ∈ ( − 1 , 1 ) h : cell input activation vector
  • c t ∈ R h : cell state vector
  • W ∈ R h × d , U ∈ R h × h and b ∈ R h : weight matrices and bias vector parameters which need to be learned during the training period where the superscripts d and h refer to the number of input features as well as the number of hidden units, correspondingly.
Intrinsic activation functions
  • σ g : sigmoid function.
  • σ c : hyperbolic tangent function.
  • σ h : hyperbolic tangent function, or σ h ( x ) = x .

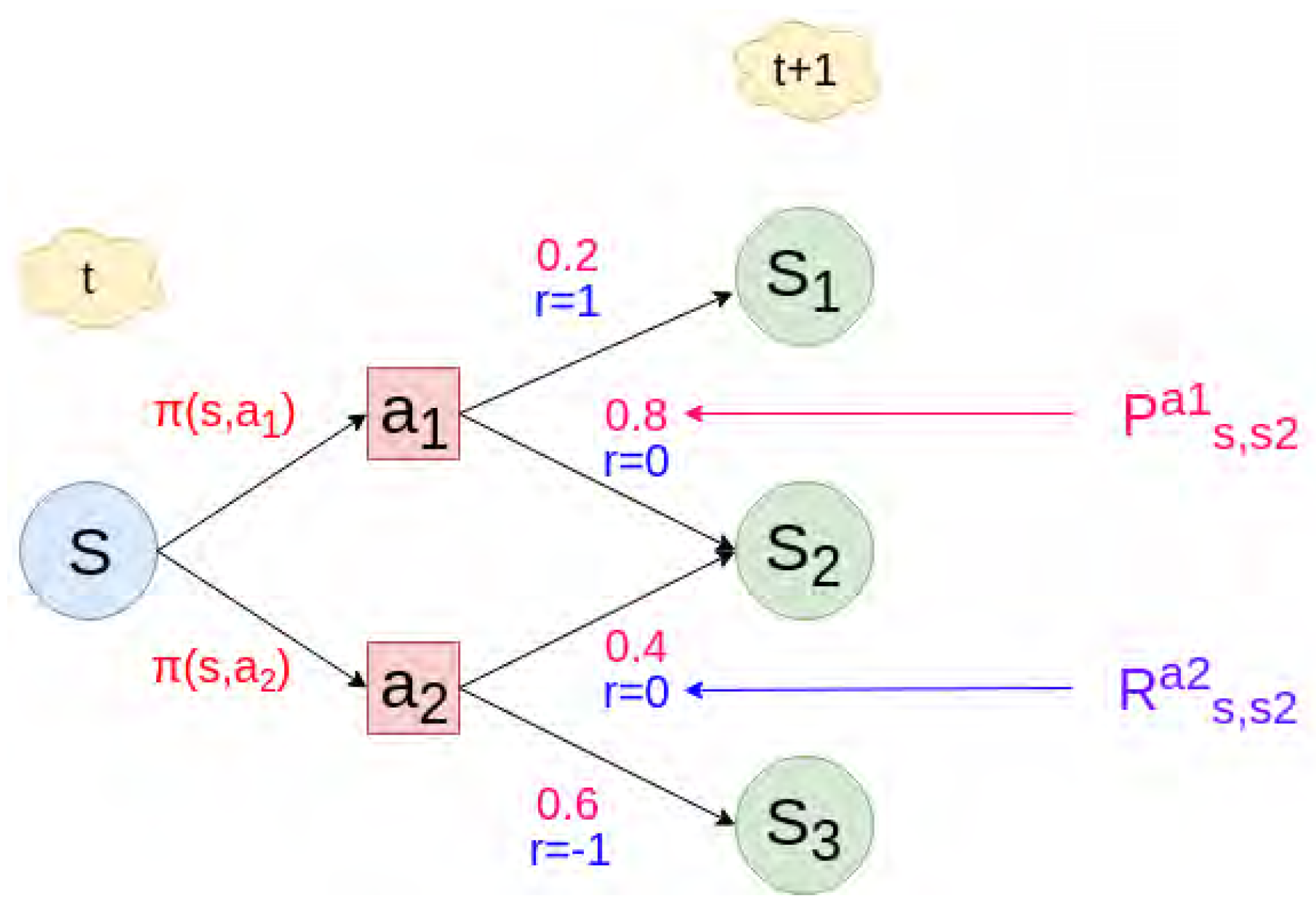
4.1.2. (Customized) Reinforcement Learning Rule

Our seismic predictive analytics framework incorporates artificial neural networks, as shown above, that can work with rewards and penalties after each decision process, thus achieving better and faster equilibrium. Our entirely ad hoc and game-theoretic-based reinforcement learning rule uses Q-learning mathematics. Modern Reinforcement Learning, a Machine Learning (ML) paradigm, is called Q-learning (Q==Quality). Most recently, an AI robot was taught to play a game using reinforcement learning (Google DeepMind, Atari, etc.).
Markov chains are mathematical models for predicting state transitions using probabilistic rules (e.g., 70% chance of coming to state A, initially commencing from the state E). A Markov Decision Process (MDP) is a leverage extension of the Markov chain for modeling complex environments, allowing choices at each state and aggregating rewards for actions taken. This is the primary reason we refer to such instances as a stochastic, non-deterministic environment (randomized), e.g., for the same action performed in the same state, we may obtain various results (understand and do not comprehend (notifications)).
In our deployed reinforcement learning, that can be considered the manner we model a game or antagonistic environment, and our primary goal will be to maximize the reward we receive from that environment (Game-Theory). Our ultimate goal is to maximize the total reward as highly as possible. However, trying to define the reward this way leads to two major issues:
  • This sum can potentially diverge (go to infinity), which does not make sense since we want to converge it into maximization.
  • We are considering as much for future rewards as we do for (inter)immediate rewards values.
One way to correct these problems is to use a dropping factor for future rewards. A policy is a utility function that informs what action to take while in a certain specialized state. This function is usually depicted as π ( s , a ) and holds the probability of acting a in such state s. We want to retrieve the policy that maximizes the whole reward function. Moreover, as a probability distribution, the sum over all the possible actions must strictly be equal to 1.
∑ α π ( s , α ) = 1
Two well-defined “value functions” do exist. The state value function, on the one hand, and the action value function, on the other. These functions are a good manner to estimate the “value,” or how good some state is, or how good some action is, adjacently. The following equation describes the former: V π ( s ) = E [ R t | s t = s ] , and the value of each state is the expected total reward we can receive from that exact state. It relies on the policy, which tells how to make decisions. The latter is shown with the following equation: Q π ( s , α ) = E [ R t | s t = s , α t = α ] , and the value of an action considered in some state is the expected total reward we can receive, starting from that state and making that action. It also relies on the exact policy.
Now, we can depict the mathematical standards for our whole ANN environment. Observing the following diagram (see Figure 3) during the calculation can help us understand the (custom) reward-penalty process. This form of the Q-value is very abstract. It tackles stochastic environments, but we could translate it into a deterministic version. We finish in the same next state whenever we act and get the same reward. In that manner, we are not required to utilize a weighted sum with probabilities, and the equation finally becomes:
Q ( s , α ) = r + γ max α ′ Q ( s ′ , α ′ )

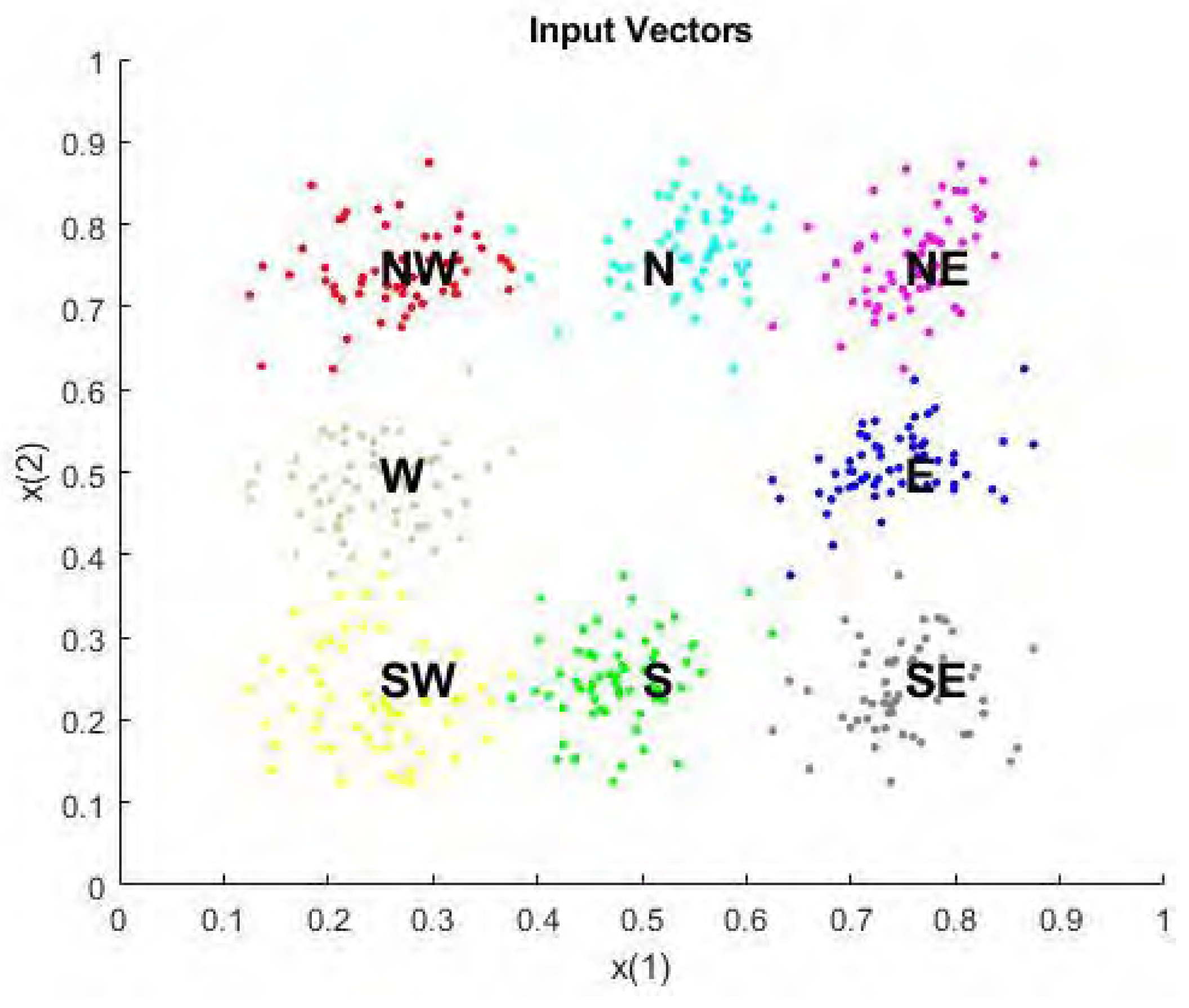
4.1.3. Competitive Learning

In this study’s scope, we underlined that competitive learning neural networks proved extremely accurate as clustering algorithmic candidates for earthquake prediction. Artificial neural networks use competitive learning and unsupervised learning in which nodes fight to respond to a portion of the input data. Competitive learning, a variation of Hebbian learning, functions by making every node in the network more specialized. It works effectively for locating clusters in data. Models and methods such as vector quantization and self-organizing (Kohonen maps) are founded on competitive learning.
Neural networks with a hidden "competitive layer" layer are typically used to implement competitive learning. Every competitive neuron is described by a vector of weights w i = ( w i 1 , ⋯ , w i d ) T , i = 1 , ∏ , M and calculates the similarity measure between the input data x n = ( x n 1 , ⋯ , x n d ) T ∈ R d and the weight vector w i .
The competitive neurons "compete" with one another for each input vector, trying to determine the most comparable to that specific input vector. Neuron m, the winner, sets its output o m = 1 and all the other competitive neurons set their output o i = 0 , i = 1 , ∏ , M , i ≠ m .
Typically, the inverse of the Euclidean distance is used to calculate similarity: | | x − w i | | between the input vector x n and the weight vector w i .
So the question arises: how can an ad-hoc deep learning technique, based on competitive learning, be developed for identifying geo-location regions with seismic events? Neurons in a competitive layer learn to represent different regions of the input space where input vectors occur. P is a set of randomly generated but clustered test data points. Here, the data points are plotted. A competitive network will be used to classify these points into natural classes. The following strategy will be to map our 2D input plane (6x10 matrix) to the output plane, which will be an 8-bit Boolean vector, with one TRUE-bit enabled each time. All rest bits will be FALSE, which corresponds to a new random direction (dis)placement (N, W, S, E, NW, NE, SW, SE) of the seismic event (re)occurrence upon the physical terrain. The neural network enabled to do so will be a competitive learning net with clustering; the network will be provided with re-enforcement learning capability from the co-output of the evaluation function f(•), that will reward or penalize the initial decisions of the random_configuration.
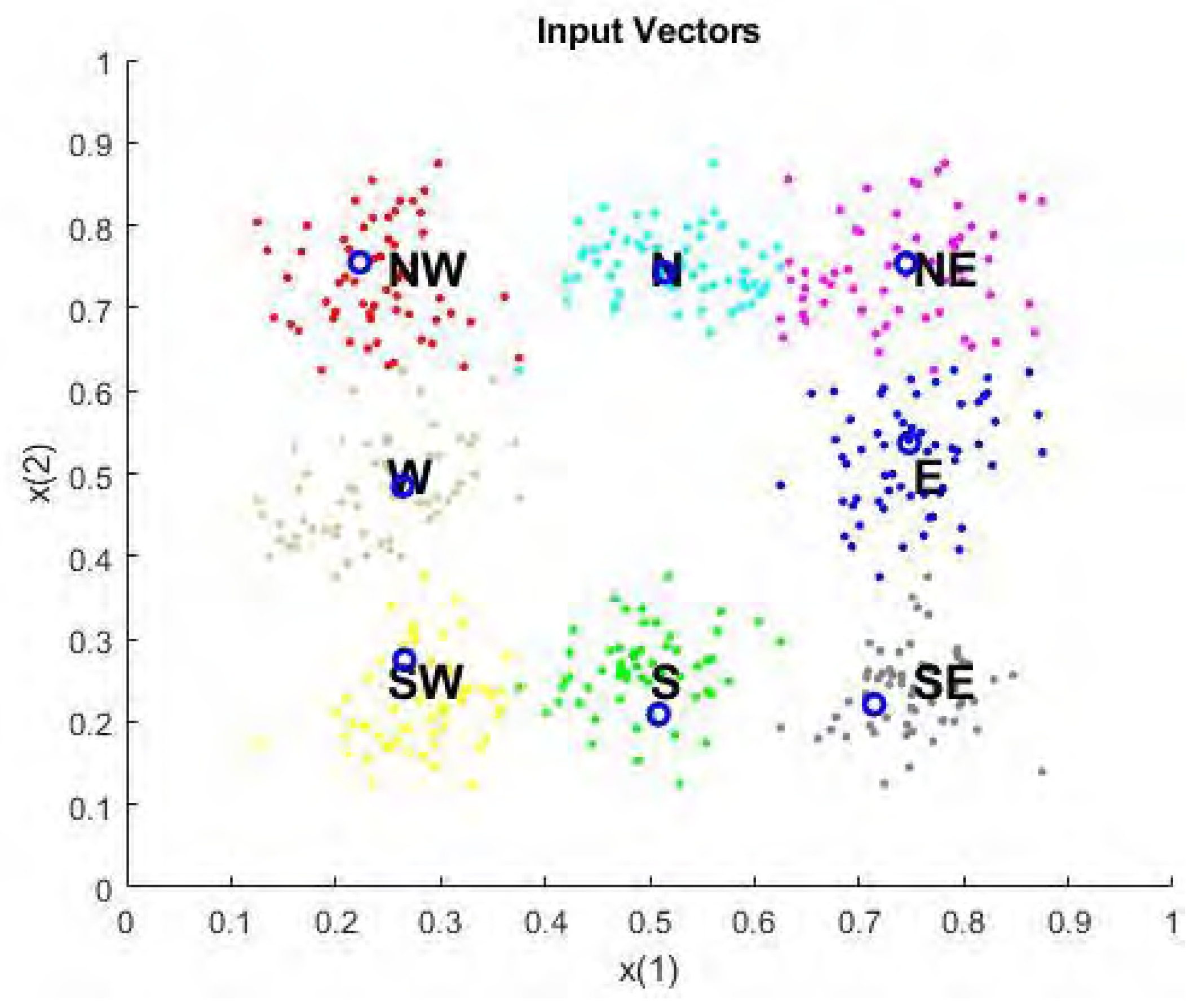
  • First, we simulate (create) the eight horizon directions with a (custom) Matlab code (see Figure 4).
  • Next, we set the number of epochs to train before stopping and training this competitive layer(which may take several seconds). We plot the updated layer weights on the same graph (Figure 5).
  • Finally, let us predict a new prediction instance: i.e., by creating a prediction input that is North-directed (e.g., with value ranges spaced around XY coordinates of the ‘N’ direction), the network will correctly classify the input to the fifth cluster, which is North, most of the times.
    o u t = [ 0 0 0 0 1 0 0 0 ]

4.2. Game-theoretic Learning Approach

That way, we conclude with the Bellman equation in the Q-Learning context. It outputs that the total value of an action a in some state s is the intermediate reward for taking that action, to which we sum the maximum expected reward we can receive in the next state. We define a custom equilibrium-based game in our ANN framework. The purpose of the game, the primary utility function in our Q-Learning model, is to use the reward as efficiently as possible to understand the appropriate action to perform. After each stage, the agent or player receives a 0 - No guess submitted (only after reset), 1 - Guess is lower than the target, 2 - The guess equals the target, or 3 - The guess is greater than the target. The value(s) ( ( m i n ( a c t i o n , s e l f . n u m b e r ) + s e l f . b o u n d s ) / ( m a x ( a c t i o n , s e l f . n u m b e r ) + s e l f . b o u n d s ) ) * * 2 are the predicted rewards. This is the squared proportion of how the agent estimated toward the objective. In an ideal world, a player can predict the ’taste’ of a higher reward and increase the pace at which his predictions in that direction until the prize is reached; the reward reaches its maximum equilibrium. If an agent can learn the reward dynamics, it is possible to attain the maximum reward in two steps (one to detect the direction of the goal and the second to jump directly to the target based on the reward).

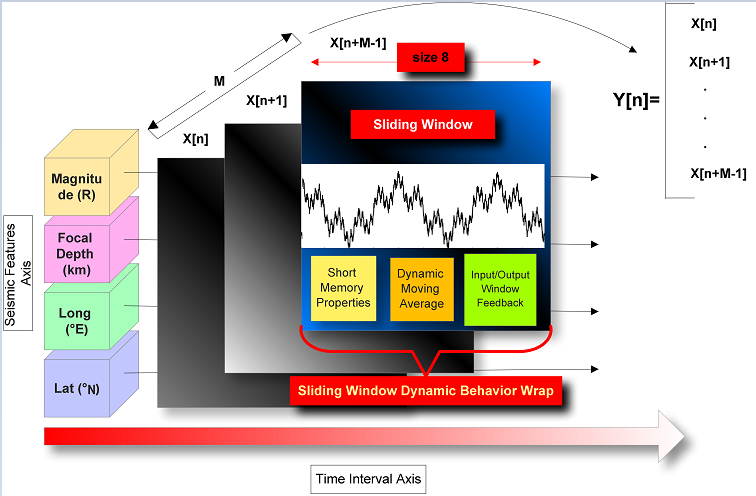
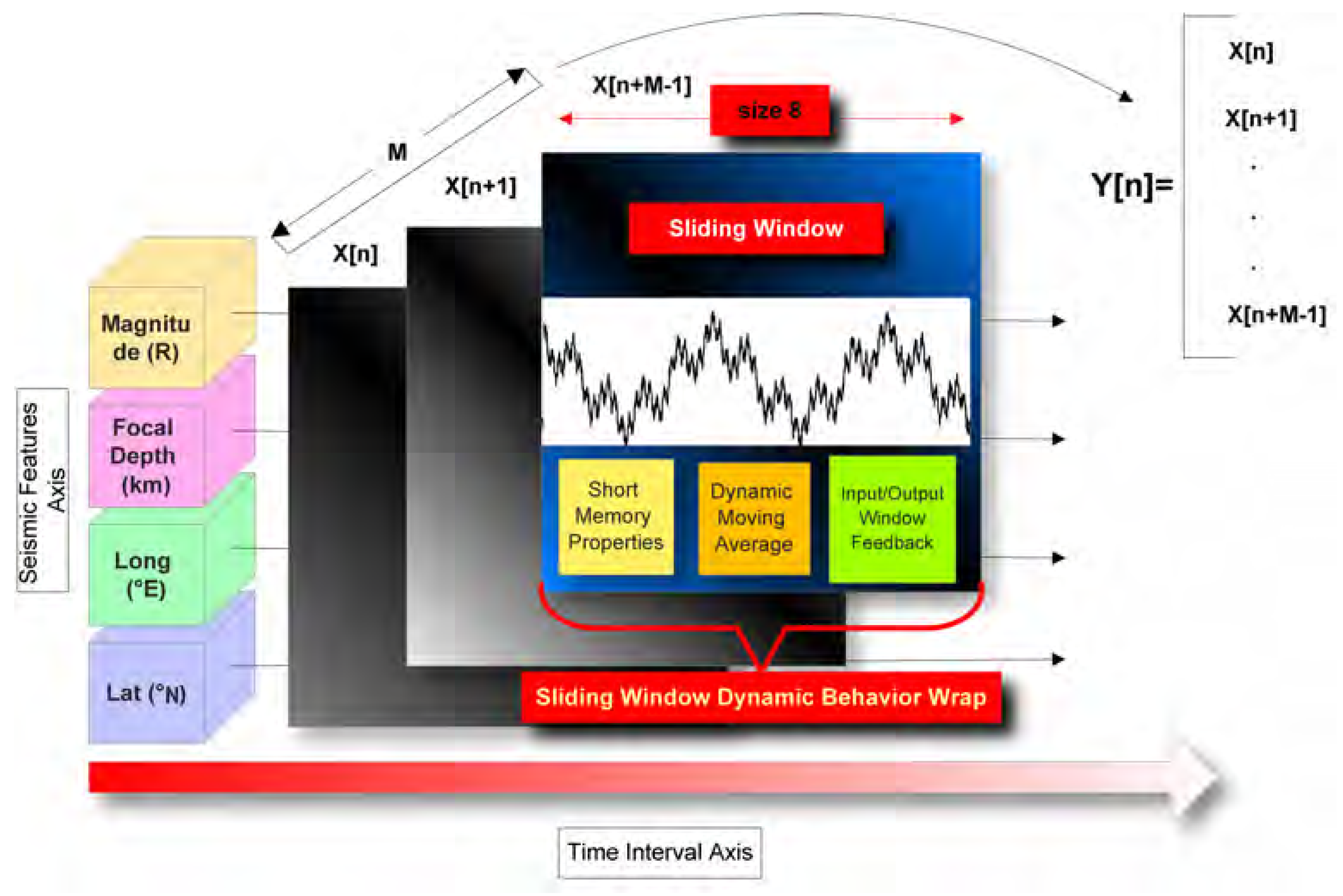
4.3. Sliding-Window Learning Approach

Our ad-hoc Sliding Window method is similar to the moving average computation procedure. A moving or rolling average is an estimate used in statistical analysis to evaluate data points by analyzing a sequence of averages, or means, of flexible subsets of the entire data set. Additional dynamic aspects of our method include left/right feedback (at the window’s inputs/outputs), memory properties, and sliding average properties. As seen in Figure 6, the "moving" window inputs the resource monitoring metrics and fully feeds back all of its complex outcomes in recursive cycles. It slides stochastically across the time axis (with an empirical static size of 8 value). Interestingly, the window travels sequentially (with a step size of 1) despite having an 8-size amidst the earlier axes. Such behavior of our SW can be seen as an example of a low-pass filter used in signal processing, and it can readily resemble a form of dynamic convolution.
Prior research on convolutional sliding windows exists, but almost none has been applied to geophysics. In [85] the Author(s) are performing deep acceleration of Gaussian Filter using short sliding window length, by deploying Discrete Cosine Transform (DCT-1). In this paper, a fast constant-time Gaussian filter (O ( 1 ) GF) with a low window length is shown. The constant-time (O ( 1 ) in this filter indicates that the computational complexity per pixel is independent of the filter window length. The concept of O ( 1 ) GF based on Discrete Cosine Transform (DCT) forms the basis of the Author(s) method’s extensive design. This framework uses a sliding transform to convolve each cosine term in O ( 1 ) per pixel, so it approximates a Gaussian kernel by a linear sum of cosine terms. If the window length is brief, DCT-1 comprises readily computed cosine values, namely 0 , ± 1 2 , and ± 1 . Other DCT kinds do not satisfy this behavior. Because of this, the Author(s) have developed a method that uses DCT-1 to accelerate the sliding transform while concentrating on short windows. Thus, an example proof-of-concept sliding transform of the DCT-3 method, with versatile use-case input features (either pixels or geological-oriented features), is given as:
x ^ t − 1 ( k ) + x ^ t + 1 ( k ) = 2 C 1 ( k ) x ^ t ( k ) + C N − 1 ( k ) X t , N

5. Evaluation Results

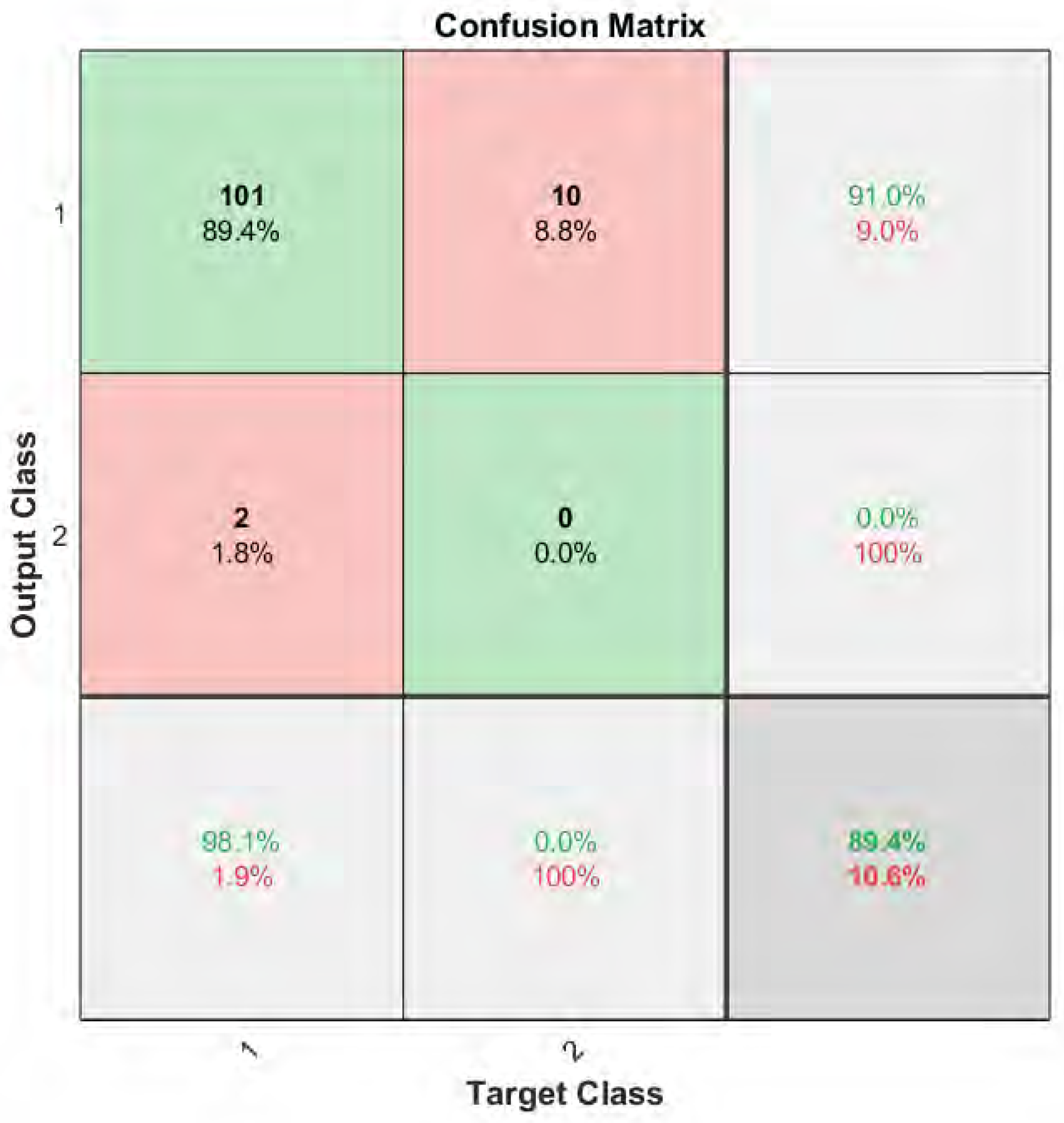
5.1. Performance Evaluation Metrics

The networks we established above have only two possible outcomes: 0 indicates that an earthquake is not predicted to occur, and 1 indicates that an earthquake is expected to occur. We generally select the confusion matrix as one of the assessment criteria for such binary classifiers [81]. Each matrix element’s actual meaning in the earthquake prediction task is listed.
  • True Positives (TP): The quantity of times the model accurately forecasts the occurrence of an earthquake within the following experimental time frame.
  • True Negatives (TN): The quantity of times the model accurately forecasts that there won’t be an earthquake during the following experimental time frame.
  • False Positives (FP): The frequency with which the model incorrectly forecasts the occurrence of an earthquake within the following experimental time frame.
  • False Negatives (FN): The quantity of times the model incorrectly forecasts that there won’t be an earthquake during the following experimental time frame.
Since an earthquake would result in enormous loss if it is not foreseen to occur, we contend that FN presents the most serious issues. In the interim, we will also keep the readers updated regarding FP. If the earthquake is anticipated but does not happen, it may cause societal problems during the evacuation drill. Thus, in our scenario, among the important evaluation metrics produced from the confusion matrix, the true positive rate linked to FN (TPR, also known as sensitivity or recall) and positive predictive value connected to FP (PPV, also known as precision) are chosen. They have the following definitions.
Precision = T P T P + F P
Recall = T P T P + F N
According to how the formulas are interpreted, precision is the proportion of actual earthquakes to anticipated ones. The term recall refers to the proportion of projected earthquakes to actual earthquakes. Every time there is an FN, the recall rate decreases. Similarly, each time an FP occurs, the accuracy rate suffers. Recall and precision are therefore anticipated to be as high as possible to minimize the penalty resulting from FN and FP. Another statistic, the f1-score, is used to counterbalance recall and precision’s effects on the evaluation. It is described as the precision and recall’s harmonic mean:
F1 score = 2 T P 2 T P + F P + F N
Lastly, presuming that the dataset is reasonably balanced, test accuracy is included in the metrics to illustrate the model’s overall performance on unseen data clearly. It can be expressed as the proportion of accurate forecasts using the test data.
Accuracy = T P + T N T P + T N + F P + F N
Illustratively enough, we can tabulate the above Machine-learning model evaluation metrics in the following table:
Table 1. Confusion matrix of the binary classification problem.
Table 1. Confusion matrix of the binary classification problem.
Predicted Seismic Condition Is Positive Predicted Seismic Condition Is Negative
Actual seismic condition is positive True Positive (TP) False Negative (FN)
Actual seismic condition is negative False Positive (FP) True Negative (TN)
Lastly, we are particularly interested in the RMSE metric. Mean square error (MSE), mean absolute error (MAE), and root mean square error (RMSE) are computed to assess the model’s prediction accuracy for magnitude prediction. The prediction error is represented by MSE, the degree of variation between the expected and true values is reflected by RMSE, and the average absolute error (AUE) between the predicted and observed values is represented by MAE. The following formula is used to determine the RMSE index:
RMSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2
where n is the number of predicted values, y i is the true value, and y ^ i is the predicted value.

5.2. Forecast Results

Inside the full scope of our artificial neural network framework’s predictive dynamics potential capabilities, we performed a prior (before the real seismic occurrence did take place) and a posterior (afterward) on several occasions. We mainly focused on Greece’s geospatial territory and specific geodynamic areas with extensive seismic faults that can produce mega-earthquakes, like in 2021.

5.2.1. Predicting the next-day GR-law value

In the first experimental dataset, we aimed to forecast the next decimal value (with extremely low fractional relative tolerance - to avoid loss of prediction accuracy) by using customized XGBoost (eXtreme Gradient Boosting) libraries along with solving a Game equilibrium to achieve maximum numerical efficiency for the next 24-hours GR-rule mathematical value. Unlike gradient boosting, which operates as gradient descent in function space, XGBoost operates as Newton-Raphson; the connection to the Newton-Raphson method is made using a second-order Taylor approximation in the loss function. We efficiently deployed an ad-hoc algorithm for generic unregularized XGBoost that acted as a (hyper)logistic regressor, or extrapolator. We targeted the geographical area of South Greece, specifically nearby Arkalochori, Crete (island), where on the 27th of September 2021, at 09:17 a.m.. local time, a major seismic event took place of the estimated magnitude of M W = 6.0 . Figure 7 depicts the major event, and it shows the progression of the time series of all the earthquake phenomena from 27/9 until 07/10/2021, as NOA, Greece, provided the data.
When inputting the exact numerical data (interpolated and normalized) from the National Observatory of Athens (NOA) b-value(s) database catalogue(s) into our custom library, we managed to extract the result of the next GR-law value for the 2021 . 764 timestep, as shown and compared to Table 2. It is worth noticing that the calculated RMSE value we received for the prediction data was 0.077438 .

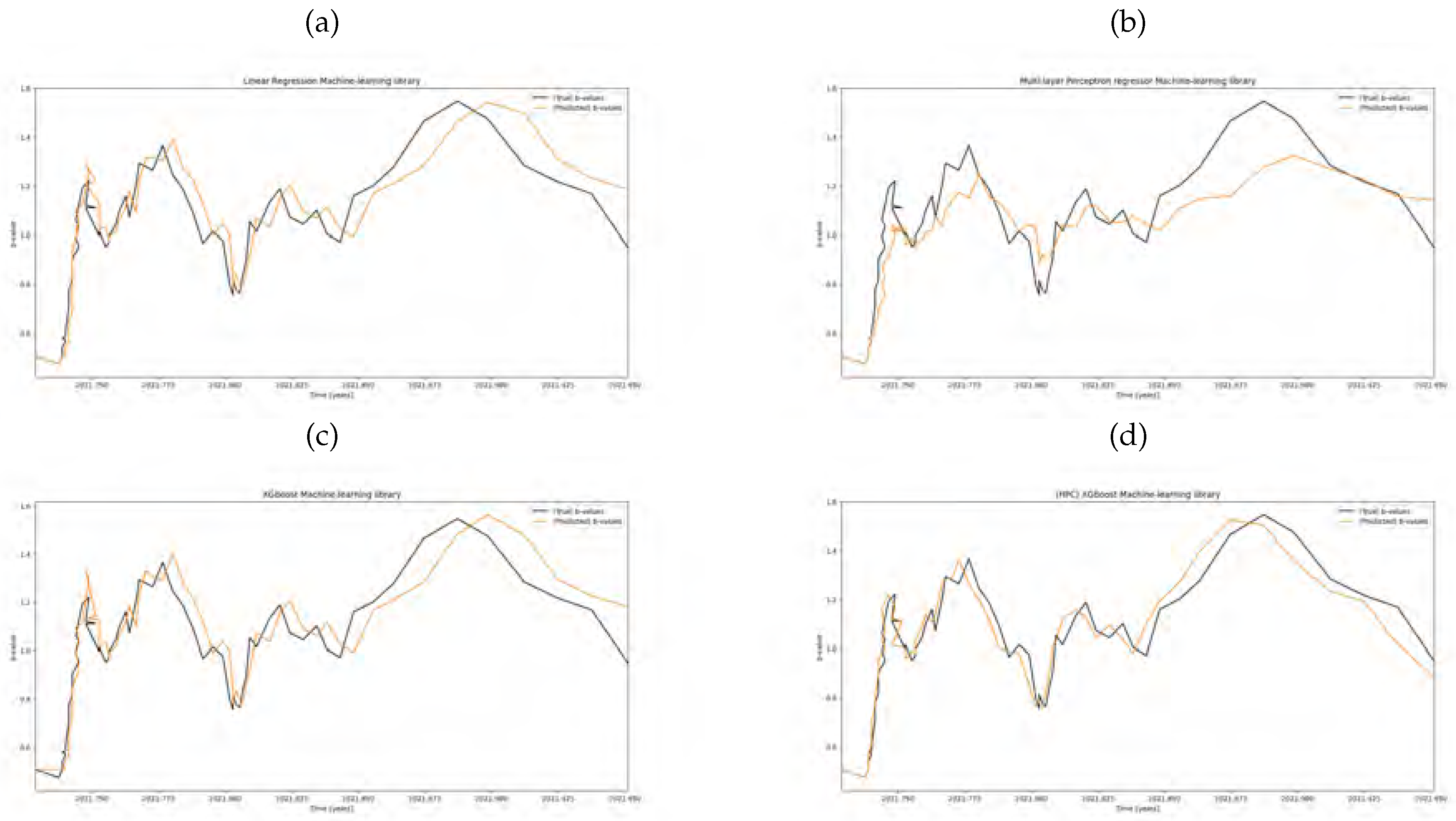
5.2.2. Predicting future GR-law values

This experimental section emphasized the gravity of the future predictability of the progressive b-value(s). As already mentioned in earlier sections, Earthquake Nowcasting (EN) evaluation is based on a new concept of time, termed ’natural time.’ Since counts of tiny events reflect a physical or natural time scale that characterizes the system’s behavior, event count models are also known as natural time models in physics. The basic premise is that enormous earthquakes (EQs) will eventually occur to compensate for a lack of EQs in a local region enclosed inside a broader seismically active zone. The theory states that over long periods and across wide spatial domains, the statistics of smaller regions will be equal to those of the larger region. Hence, small events can serve as a form of "clock" to indicate the "natural time" that separates the big events [83]. This has been particularly the observed case for the Arkalochori, Crete, Greece (2021) seismic case study, as per the regions’ b-values. Thus, it remains crucial for seismologists to be able to forecast the future "trend" of the GR-law estimates both before and after major EQ events.
In this context, we applied four Machine-learning methodologies to project such potency from our ANN framework. The primary ML library (a) had been a standard linear regression model with weak exogeneity. This means that inputted values, instead of being viewed as random variables, the predictor variables x might be treated as fixed values. This implies that the predictor variables, for instance, are thought to be error-free or free of measurement errors. The second (b) ML library model was a Multi-layer Perceptron Regressor with 2 thousand hidden layer-sized nodes and a 3-dimensional hidden layer network. The MLP regressor is trained iteratively because the parameters are updated at each time step by computing the partial derivatives of the loss function concerning the model parameters. The loss function may also include a regularization term that reduces the model’s parameters to avoid overfitting. Dense and sparse numpy arrays of floating point values are the data types this implementation uses. The (c) ML model deployed had been a conventional XGBoost library, whereas in (d), we decided to invoke a High-Performance Computing (HPC), or the most efficient deep learning network of separate XGBoost libraries both wise optimized in terms of precision, recall, and accuracy.
Our overall (future) fitting accuracy depends mainly on the efficacy of (extreme) gradient tree boosting [84]. It is not possible to optimize the tree ensemble model in the regularized learning objective of the conventional tree boosting in Euclidean space using conventional optimization techniques since it has functions as parameters. Rather, the model undergoes additive training. Formally, we will need to add feet to minimize the following objective: let y ^ i ( t ) be the forecast of the i-th occurrence at the t-th iteration.
L ( t ) = ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t )
This indicates that, by the regularized learning objective of the conventional tree boosting, we add the foot greedily if it most improves our model. The objective can be easily optimized in the generic setting using second-order approximation. The previous equation can be applied as a grading function to assess a tree structure q’s quality. This score is produced for a wider variety of objective functions than the impurity score used to evaluate decision trees. Generally speaking, it is impossible to list all potential tree structures q. Instead, a greedy algorithm is employed, which begins with a single leaf and iteratively builds branches to the tree. We observe the four ML models in Table 2. From all the benchmarks above, (d) HPC-XGBoost has the highest accuracy because it works like a segmented network of connected optimized (c) individual XGB libraries. On the contrary, the least accurate ML methodology belongs to the MLP regressor (b), probably due to minor overfitting issues.
Table 2. Machine-learning (ML) prediction methods of the progressive b-value(s) for Arkalochori, Crete, Greece (year 2021) - (a) LinearRegression, (b) MLP Regressor, (c) XGBoost, and (d) (HPC) XGBoost.
Table 2. Machine-learning (ML) prediction methods of the progressive b-value(s) for Arkalochori, Crete, Greece (year 2021) - (a) LinearRegression, (b) MLP Regressor, (c) XGBoost, and (d) (HPC) XGBoost.
Preprints 115154 i001

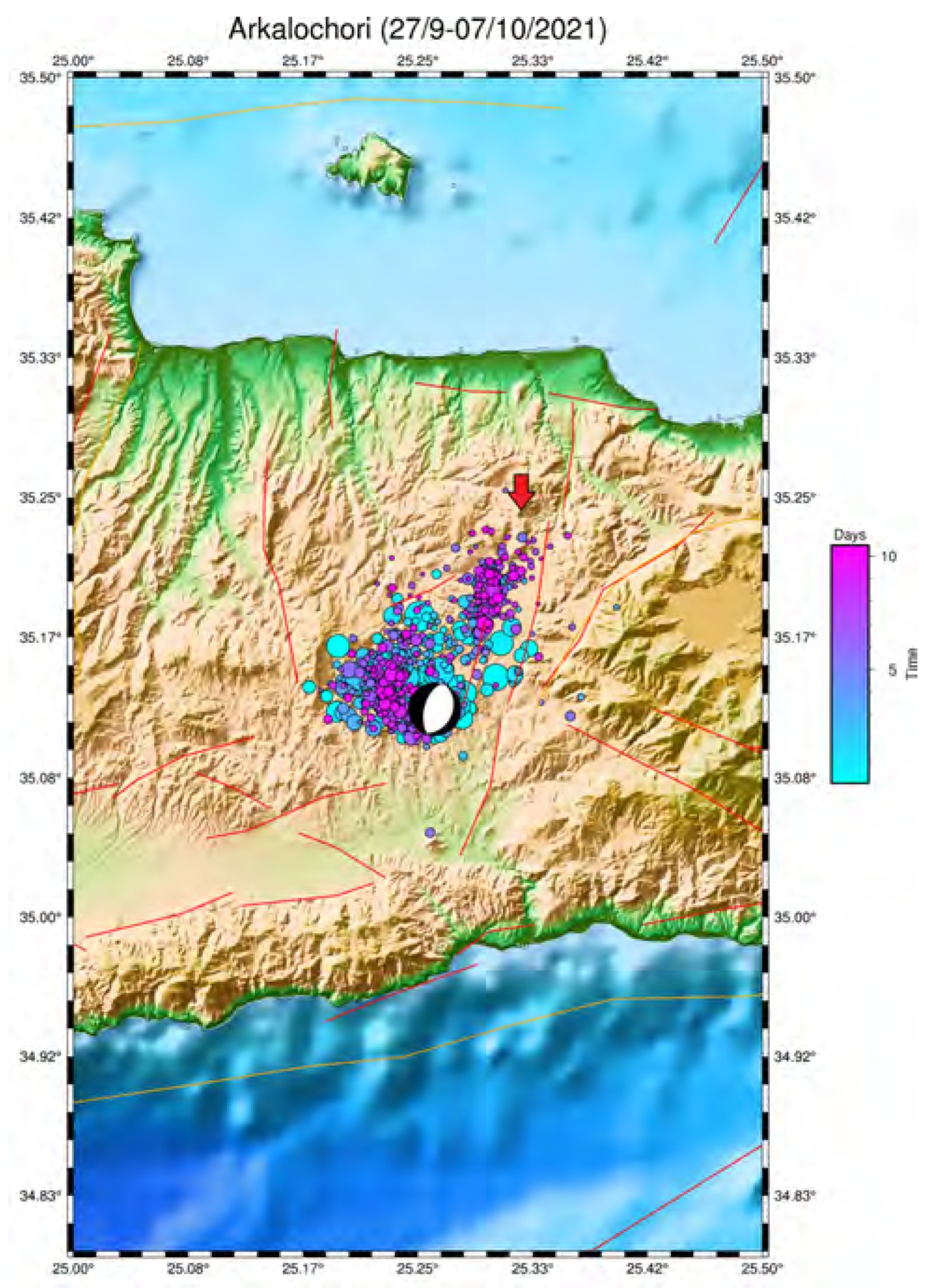
5.2.3. Next-Day Seismic Prediction for Arkalochori, Crete, Greece

In the second experimental trial set, we applied the competitive learning features of our nowcasting seismic architecture embedded with the LSTM potentials and the sliding window technique we described before. Again, we selected the same geographical area of Greece (Arkalochori, Crete) during a calmer earthquake activity period (arbitrary selection). We aimed to predict the 4-tuple feature set ((a) latitude, (b) longitude, (c) focal depth, and (d) magnitude) of the next 24 hours potential seismic activities. Figure 8 projects the forecasted and the real events that took place regarding the seismic centroids. The level of earthquake nowcasting accuracy, in this scenario, seems compelling.
However, even after the main EQ event time slot, we followed the exact Natural Time methodology concept, as per [83], to project the predictability of our software framework for aftershocks. There were two technical reasons for this approach. First, the seismicity’s order parameter, k_1: its minimum, indicates when the Seismic Electric Signals (SES) activities begin, and its value (=0.070) indicates when the system reaches the critical stage. There is an aftershock k_1 interval period, which we approximated in this trial hereby. The second is the entropy change, or Δ S , under time reversal: its value, when minimized a few months ahead of time, indicates the beginning of precursory phenomena; its fluctuations, when the Δ S minimum appears, show a clear increase, indicating the beginning of the EQ preparation, as explained by the physical model that served as the inspiration for the SES research.
These two quantities were intrinsically utilized to study precursory, particularly the metacursory phenomena following the major EQs in Arkalochori (year 2021). One of the main withholding concepts of our ANN framework is the "topological" and "chronological" locality of reference, as derived from the previous meta-information parameters of the natural time technique (k_1, and Δ S ). Specifically, despite the high, but not maximum-arising entropy levels of the NT-EQ prediction, the stochasticity of the phenomena leaves us the opportunity to predict, via the holistic artificial neural network strategy, location/time occurrences that happened recently with the ML possibility to occur again in the nowcasted future (Geo/Time-locality of reference property).

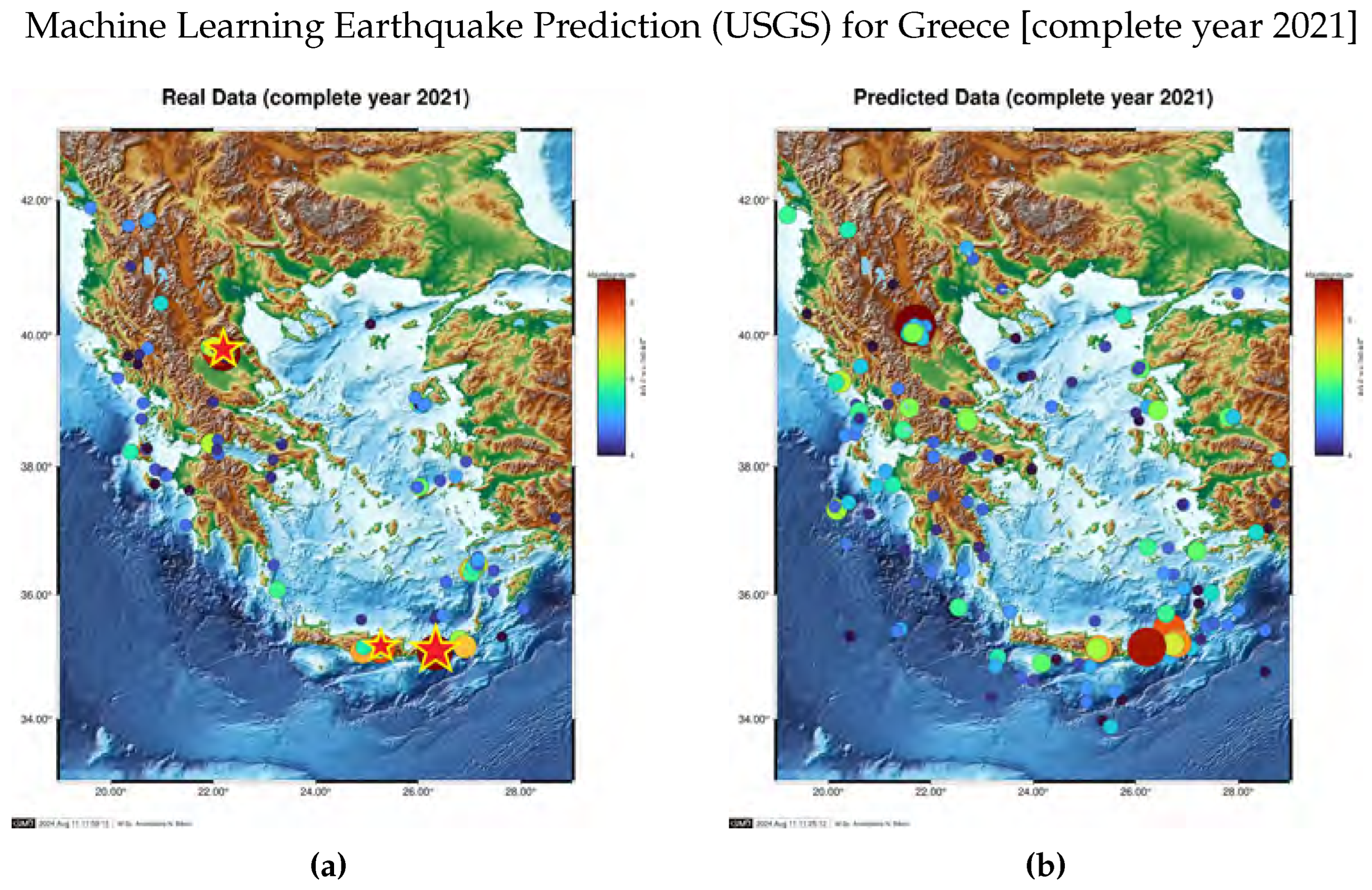
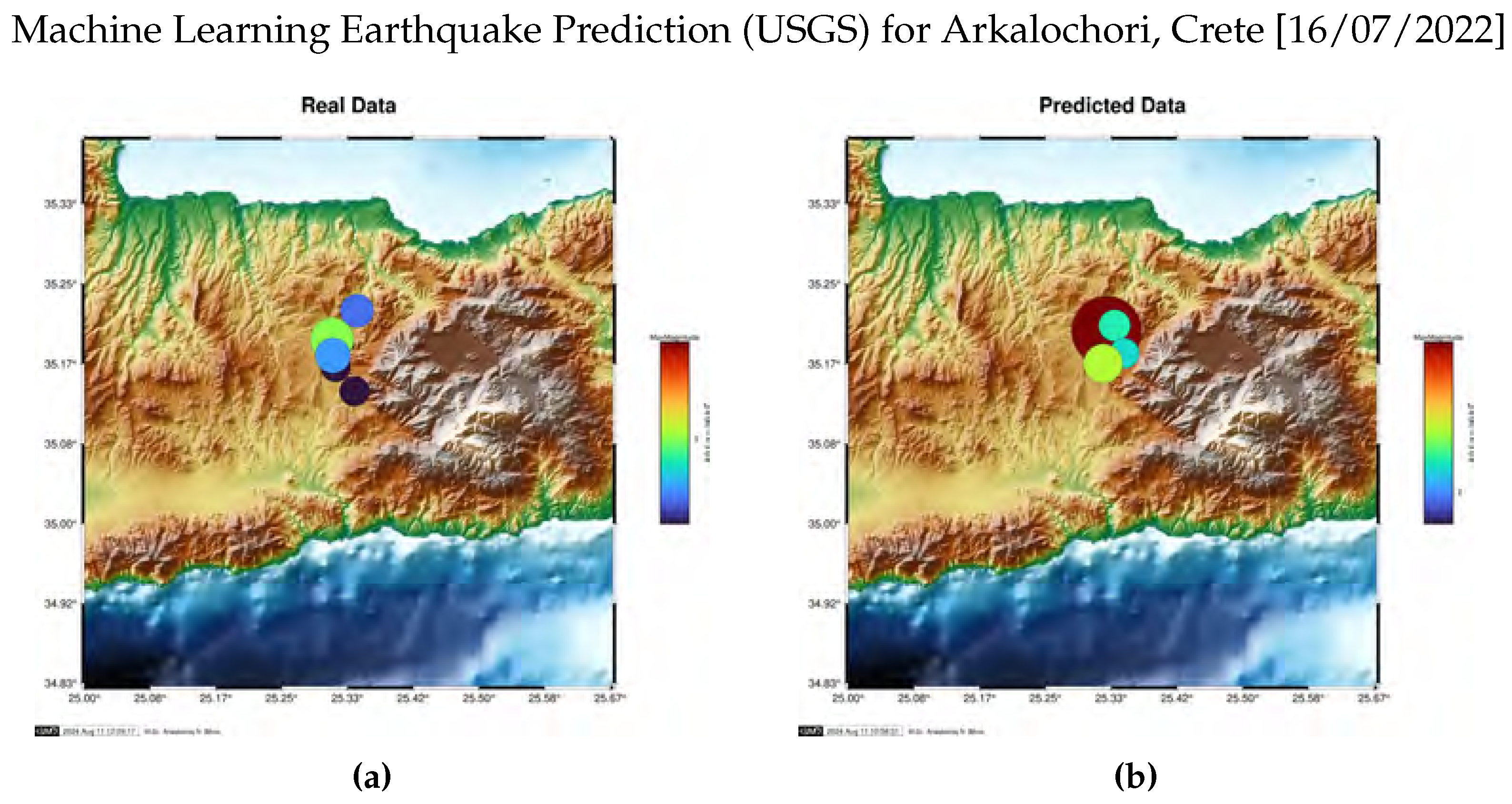
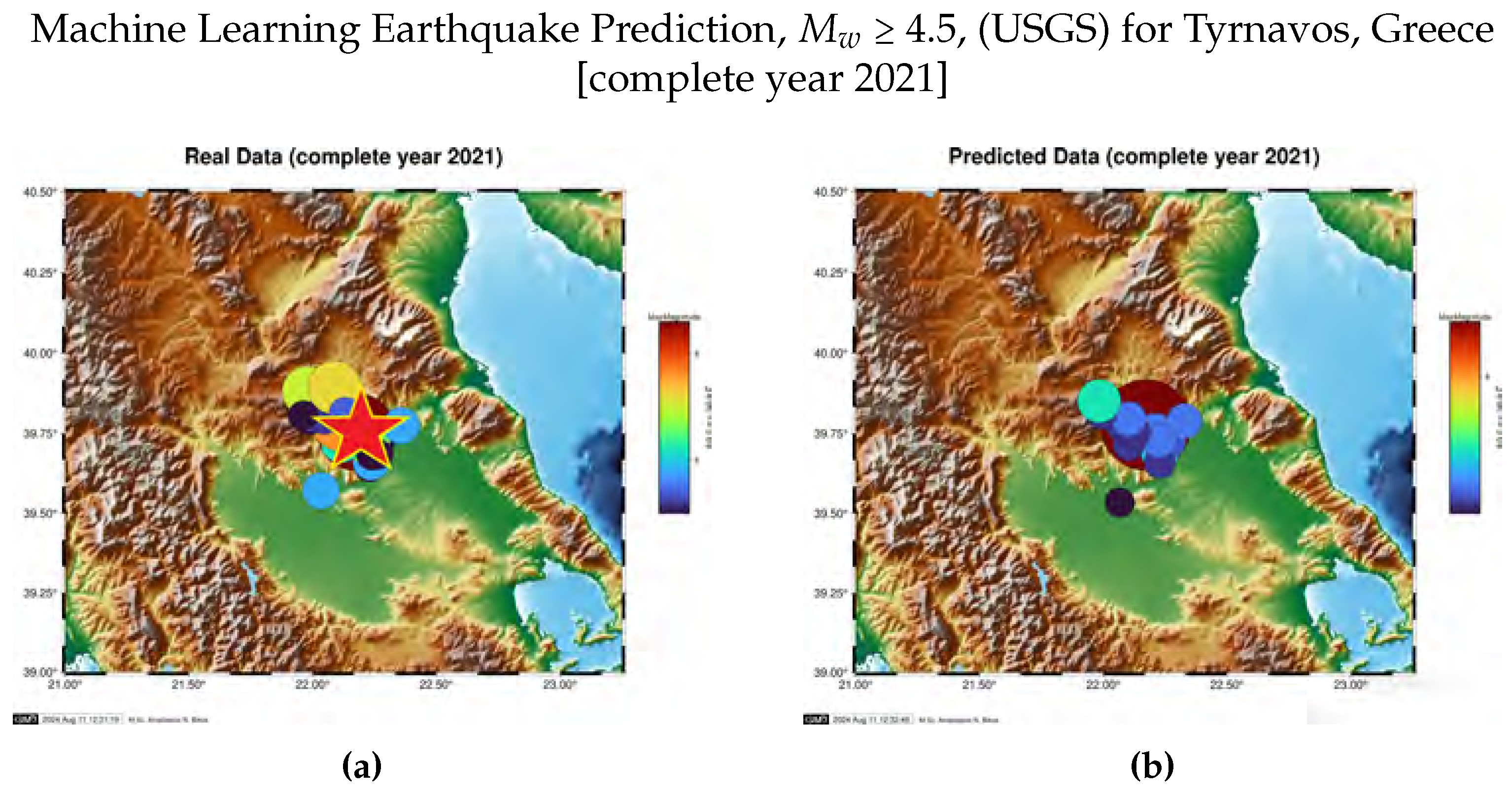
5.2.4. Long-Term Seismic Prediction

(1) Theva, Voitiea, Central Greece
Perhaps the most paramount and citizen life-critical applicability scenario of a highly accurate seismic forecasting mechanism is to be capable of making agile seismic predictions for major events on any geographical territory as early as possible before the phenomena take place. On 28/12/2022 at 12:24:21 local Greece time, a moderate earthquake shock occurred near Theva, in Voitiea district, Greece, measured at M W = 4.9 , afterward by the NOA instruments. Even from the date back to the 24th of October 2022, our Artificial Neural Network framework successfully predicted the exact 4-tuple seismic feature set with extreme accuracy, as shown below, both graphically and numerically.
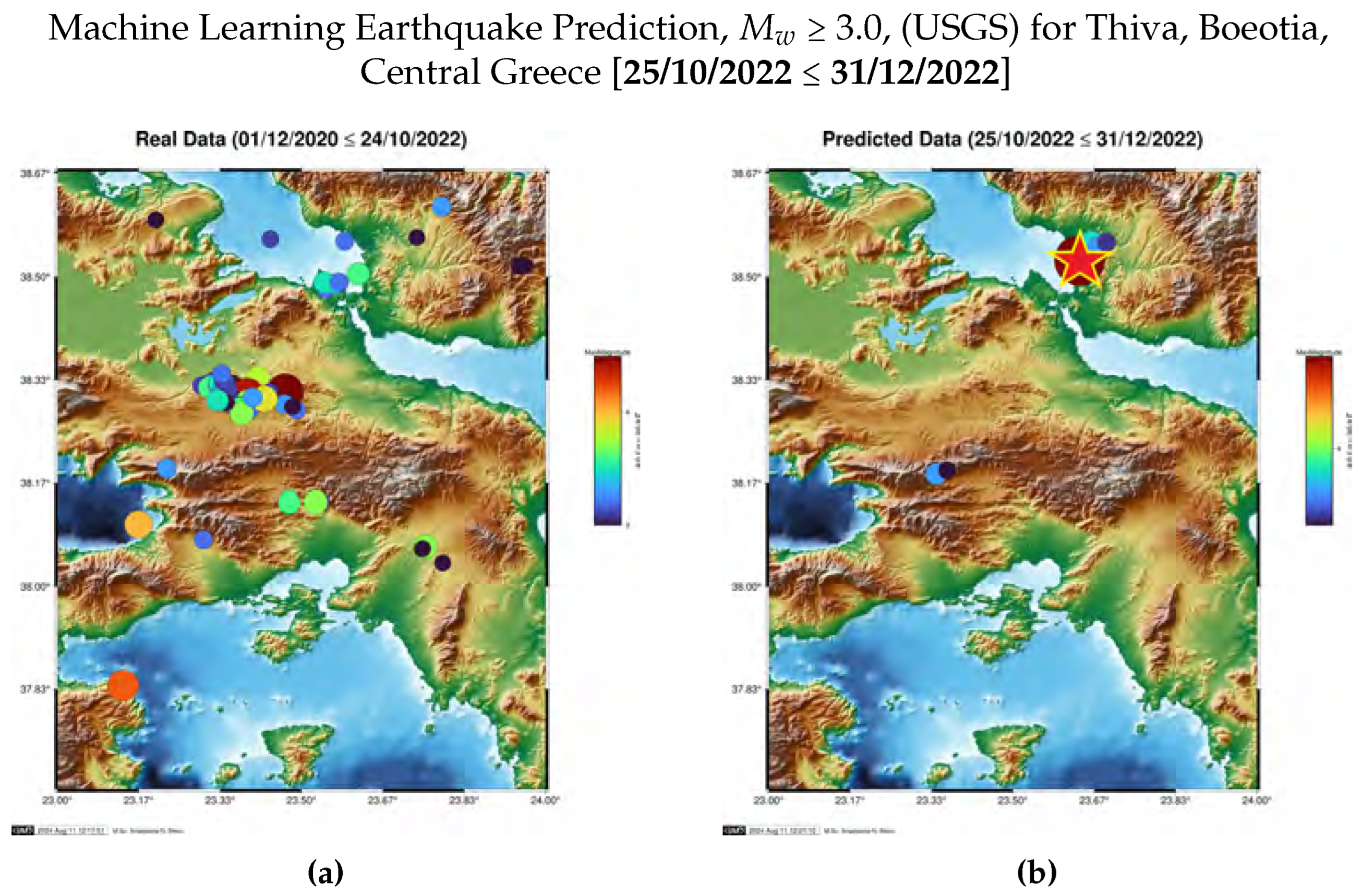
Preprints 115154 g009
Figure 9. Real (a) & Forecasted (b) major shock (★) [28/12/2022 12:24:21 (GMT)], Theva, Voitiea, Greece.
Figure 9. Real (a) & Forecasted (b) major shock (★) [28/12/2022 12:24:21 (GMT)], Theva, Voitiea, Greece.
Preprints 115154 g009
Table 3. Numerical comparison matrix of the seismic forecasting accuracy of the (★) [28/12/2022 12:24:21 (GMT)] event, Theva, Voitiea, Greece.
Table 3. Numerical comparison matrix of the seismic forecasting accuracy of the (★) [28/12/2022 12:24:21 (GMT)] event, Theva, Voitiea, Greece.
Lat (°N) Long (°E) Focal Depth (km) Magnitude (R)
Predicted data* 38.5267 23.6367 8.0 5.1
Real data 38.5652 23.6906 13.0 4.9
* Date of exact Machine-learning seismic prediction: 24/10/2022
(2) Sitia, Crete, South Greece
The seismic year 2021 in Greece was particularly active, with three main EQs occurring in different (sub)regions with different geophysical traits and seismic fault indications. The M w = 6.4 in Sitia Crete EQ on 12 October 2021 was one of those. In this particular use case, we "backtested" our ANN software with historical datasets 15 years before this exact EQ occurred in the same nearby geographical region as input datasets. We project and analyze the competitive learning (+sliding window/NTA) deep-learning results in Figure 10. Again, the numerical accuracy of the magnitude scale, time prediction interval, and especially the longitude/latitude precision seems quite emphatic.
Natural time analysis (NTA), examined in earlier sections, is useful for determining whether a complex system has reached a critical stage and for revealing the system’s dynamical evolution. Because of this, NTA can be extremely helpful in anticipating future catastrophic catastrophes, such as the advent of huge EQs. In this research effort, we demonstrate that if NTA analysis is co-deployed with advanced Machine-learning and Game-theoretic mathematical techniques, it can project real practicality not only to nowcasting but also forecasting efforts for the applied predictive seismology.
(3) Tyrnavos, North Greece
Our next studied seismic use case, one of the major EQ events that shocked Central Greece in 2021, was in Tyrnavos. The main event occurred with M W = 6.3 in Tyrnavos on 3 March 2021. Again, we performed a backtest validation analysis of our predictive software and depicted the real and predicted comparison results in Figure 11. Same as before, the overall 4-tuple ((a) latitude, (b) longitude, (c) focal depth, and (d) magnitude) numerical accuracy, or match, between what "would" happen and what "really" happened is quite interesting. Besides the forecasting accuracy of the main shock, the predictability capabilities of the aftershocks that took place from our ANN software architecture are also worth noticing.
Here, we furthermore utilized (as proof of comparison) the most recent version of the Megacities Earthquake Nowcasting software [86] (see also [39,83]). Based on the NTA equations in the Introduction section and the assumption that M s = M c in each catalog case, we calculated the EPS using the empirical CDF computed in the large region. We also considered the epicenter of each of the strong EQs in 2021 as the center of the circular zone. To estimate the EPS for EQs of magnitude more than or equal to M λ = 6.5, Rundle et al. [39,83] estimated R 0 = 400 km and D 0 = 200 km around the Greek capital, Athens, taking into account their Figure 1.
(4) Comprehensive Forecast Analysis for whole Greece territory - year 2021
In this Section, we holistically deployed and mapped our seismic nowcasting software to foresee if we could "pick" the 3 major EQs events that shocked Greece in the quite active year of 2021 ((1) (EQ Name) Tyrnavos (EQ Date) 3 March 2021 (Lat) 39.8 (Long) 22.2 ( M w ) 6.3 (EPS) 98.5, (2) (EQ Name)Arkalohorion Crete(EQ Date) 27 September 2021 (Lat) 35.2 (Long) 25.3 ( M w ) 6.0 (EPS) 62.0, and (3) (EQ Name)Sitia Crete(EQ Date) 12 October 2021 (Lat) 35.2 (Long) 26.2 ( M w ) 6.4 (EPS) 34.3). Our competitive learning neural networks made it feasible to forecast both EQ occurrences for the same year (2021) time-frame. Alongside, more moderate to minor magnitude scaled events were predicted across the Greek territory, with some non-avoidable FP/FN instances appearing alike in the same right-most sub-plot figure. What we can conclude from this trial case is that both atomically (as shown in the case studies before) as well as comprehensively, the ANN (NTA-based) predictive software can spot-trace moderate ( M w ≥ 4.0) and mega-earthquake events with considerable (4-tuple) accuracy.
Preprints 115154 g012
Figure 12. Real (a) & Predicted (b) major and minor-shock event(s), Greece (2021).
Figure 12. Real (a) & Predicted (b) major and minor-shock event(s), Greece (2021).
Preprints 115154 g012

5.2.5. Error Validation Analysis

Based on what we discussed and assumed in Section 5.1, we depict in Figure 13 the 2-dimensional confusion matrix of our holistic framework for clustering in seismic nowcasting. Hereby, we attach the True Positive(s) and other accuracy estimation metrics. We can safely claim that our Machine-learning methodology (co-deployed with the sliding-window technique) can reach even a (beyond) 6-month long-term earthquake forecasting accuracy of at least 90%. By continuing to work and improving our models and their hyperparameters, we are optimistic we can obtain even higher precision-recall accuracy.

6. Discussion and Future Work

The scientific luxury of obtaining a network of seismographic instruments and next-generation Internet-of-Things microseismic sensors that can aggregate in real time a massive amount of earthquake data from beneath the earth’s surface would be an add-on for any research attempts like the one above that aims to leverage state-of-the-art Artificial Intelligence (AI) to predict shock events in the short and long term. At first glance, we can increase the number of layers in each network to enable each network to learn more consecutive properties from the data. Then, improving the hyperparameters is another choice.
As Future Work for our research project, we will deploy explicit next-generation (hybrid) Transformer networks, focusing on exploiting eXplainable AI (XAI) techniques and building Large Language Models (LLMs). The latter are known to possess extreme potency in language detection and language generation. The research field of predicting earthquakes via generative AI (GPT-4) would be quite interesting to construct and experiment on.
Ultimately, the investigation showed that earthquake prediction remains a difficult issue. Various deep learning techniques can be applied separately or in combination to determine the best approach for these time series forecasting problems.

7. Conclusions

In this work, we investigated the feasibility of applying various fully ad-hoc machine learning techniques and an LSTM/Competitive learning deep neural network to forecast the maximum magnitudes and frequency of earthquakes in the Greek area. As input features, we computed and retrieved seismicity metrics associated with earthquake occurrence from the catalog. The outcomes demonstrated that the research potential has been quite promising at categorizing significant earthquakes.
The results provide evidence in favor of the theory that small earthquakes can provide useful information for forecasting larger earthquakes in the future and present a viable method for doing so. Furthermore, the results offer valuable insights into which physical interpretation-consistent elements are critical for earthquake prediction.
While this study has plenty of space for improvement and scientific speculations, it offers a possible route for raising earthquake prediction accuracy in the future.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ANN Artificial Neural Network
LSTM Long Short-Term Memory
SW Sliding Window
XGBoost eXtreme Gradient Boosting
EQ EarthQuake

References

  1. T. Bhandarkar et al. "Earthquake trend prediction using long short-term memory RNN". In: International Journal of Electrical and Computer Engineering 9.2 (2019), p. 1304, 2019.
  2. Q. Wang et al. "Earthquake prediction based on spatio-temporal data mining: an LSTM network approach". In: IEEE Transactions on Emerging Topics in Computing, 2017.
  3. A.Boucouvalas, M.Gkasios, N.Tselikas, and G.Drakatos. "Modified fibonacci-dual-lucas method for earthquake prediction". In Third International Conference on Remote Sensing and Geoinformation of the Environment, pages 95351A-95351A. International Society for Optics and Photonics, 2015.
  4. Chouliaras, G. "Seismicity anomalies prior to 8 June 2008 earthquake in Western Greece". Nat. Hazards Earth Syst. Sci., 9 (2): 327-335, 2009. [CrossRef]
  5. J. Fan, Z. Chen, L. Yan, J. Gong, and D. Wang. "Research on earthquake prediction from infrared cloud images". In Ninth International Symposium on Multispectral Image Processing and Pattern Recognition (MIPPR2015), pages 98150E-98150E. International Society for Optics and Photonics, 2015.
  6. M. Hayakawa, H. Yamauchi, N. Ohtani, M. Ohta, S. Tosa, T. Asano, A. Schekotov, J. Izutsu, S. M. Potirakis, and K. Eftaxias. "On the precursory abnormal animal behavior and electromagnetic effects for the kobe earthquake (m 6) on april 12, 2013". Open Journal of Earthquake Research, 5(03):165, 2016.
  7. M. Moustra, M. Avraamides, and C. Christodoulou. "Artificial neural networks for earthquake prediction using time series magnitude data or seismic electric signals". Expert systems with applications, 38(12):15032-15039, 2011.
  8. Mohsen Yousefzadeh, Seyyed Ahmad Hosseini, Mahdi Farnaghi. "Spatiotemporally explicit earthquake prediction using deep neural network". Soil Dynamics and Earthquake Engineering, Volume 144, 2021. [CrossRef]
  9. Luana Ruiz, Fernando Gama and Alejandro Ribeiro. "Gated Graph Convolutional Recurrent Neural Networks". arXiv:1903.01888, 2019.
  10. Parisa Kavianpour, Mohammadreza Kavianpour, Ehsan Jahani, Amin Ramezani. "A CNN-BiLSTM Model with Attention Mechanism for Earthquake Prediction". arXiv:2112.13444, 2021.
  11. Du, Xiangyu (2022). Short-term Earthquake Prediction via Recurrent Neural Network Models: Comparison among vanilla RNN, LSTM and Bi-LSTM.
  12. Panakkat, A.; Adeli, H. Neural network models for earthquake magnitude prediction using multiple seismicity indicators. Int. J. Neural Syst. 2007, 17, 13–33. [Google Scholar] [CrossRef] [PubMed]
  13. Asencio-Cortes, G.; Martinez-Alvarez, F.; Morales-Esteban, A.; Reyes, J. A sensitivity study of seismicity indicators in supervised learning to improve earthquake prediction. Knowl.-Based Syst. 2016, 101, 15–30. [Google Scholar] [CrossRef]
  14. Asim, K.M.; Idris, A.; Iqbal, T.; Martinez-Alvarez, F. Seismic indicators based earthquake predictor system using Genetic Programming and AdaBoost classification. Soil Dyn. Earthq. Eng. 2018, 111, 1–7. [Google Scholar] [CrossRef]
  15. Martinez-Alvarez, F.; Reyes, J.; Morales-Esteban, A.; Rubio-Escudero, C. Determining the best set of seismicity indicators to predict earthquakes. Two case studies: Chile and the Iberian Peninsula. Knowl.-Based Syst. 2013, 50, 198–210. [Google Scholar] [CrossRef]
  16. Florido, E.; Asencio Cortes, G.; Aznarte, J.L.; Rubio-Escudero, C.; Martinez-Alvarez, F. A novel tree-based algorithm to discover seismic patterns in earthquake catalogs. Comput. Geosci. 2018, 115, 96–104. [Google Scholar] [CrossRef]
  17. Rundle, J.B.; Donnellan, A.; Fox, G.; Crutchfield, J.P. Nowcasting Earthquakes by Visualizing the Earthquake Cycle with Machine Learning: A Comparison of Two Methods. Surv. Geophys. 2022, 43, 483–501. [Google Scholar] [CrossRef]
  18. Wang, X., Zhong, Z., Yao, Y., Li, Z., Zhou, S., Jiang, C., & Jia, K. (2023). Small Earthquakes Can Help Predict Large Earthquakes: A Machine Learning Perspective. Applied Sciences, 13(11), 6424.
  19. Chouliaras, G. Investigating the earthquake catalog of the National Observatory of Athens. Nat. Hazards Earth Syst. Sci. 2009, 9, 905–912. [Google Scholar] [CrossRef]
  20. Mignan, A.; Chouliaras, G. Fifty Years of Seismic Network Performance in Greece (1964–2013): Spatiotemporal Evolution of the Completeness Magnitude. Seismol. Res. Lett. 2014, 85, 657–667. [Google Scholar] [CrossRef]
  21. National Observatory of Athens, Institute of Geodynamics. Recent Earthquakes. Available online: http://www.gein.noa.gr/en/seismicity/recent-earthquakes (accessed on 6 February 2023).
  22. Rundle, J.B.; Turcotte, D.L.; Donnellan, A.; Grant Ludwig, L.; Luginbuhl, M.; Gong, G. Nowcasting earthquakes. Earth Space Sci. 2016, 3, 480–486. [Google Scholar] [CrossRef]
  23. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Spatio-Temporal complexity aspects on the interrelation between Seismic Electric Signals and Seismicity. Pract. Athens Acad. 2001, 76, 294–321. Available online: http://physlab.phys.uoa.gr/org/pdf/p3.pdf (accessed on 6 February 2023).
  24. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Long-range correlations in the electric signals that precede rupture. Phys. Rev. E 2002, 66, 011902. [Google Scholar] [CrossRef]
  25. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Seismic Electric Signals and Seismicity: On a tentative interrelation between their spectral content. Acta Geophys. Pol. 2002, 50, 337–354. Available online: http://physlab.phys.uoa.gr/org/pdf/d35.pdf (accessed on 6 February 2023).
  26. Varotsos, P.A.; Sarlis, N.V.; Tanaka, H.K.; Skordas, E.S. Similarity of fluctuations in correlated systems: The case of seismicity. Phys. Rev. E 2005, 72, 041103. [Google Scholar] [CrossRef]
  27. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time. Precursory Seismic Electric Signals, Earthquakes and Other Complex Time-Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
  28. Pasari, S. Nowcasting Earthquakes in the Bay of Bengal Region. Pure Appl. Geophys. 2019, 176, 1417–1432. [Google Scholar] [CrossRef]
  29. Pasari, S.; Verma, H.; Sharma, Y.; Choudhary, N. Spatial distribution of seismic cycle progression in northeast India and Bangladesh regions inferred from natural time analysis. Acta Geophys. 2023, 71, 89–100. [Google Scholar] [CrossRef]
  30. Utsu, T. Estimation of parameters for recurrence models of earthquakes. Bull. Earthq. Res. Inst. Univ. Tokyo 1984, 59, 53–66. Available online: http://basin.earth.ncu.edu.tw/download/courses/seminar_MSc/2009/02252_Estimation%20of%20parameters%20for%20recurrence%20models%20of%20earthquakes.pdf (accessed on 6 February 2023).
  31. Pasari, S.; Dikshit, O. Distribution of Earthquake Interevent Times in Northeast India and Adjoining Regions. Pure Appl. Geophys. 2015, 172, 2533–2544. [Google Scholar] [CrossRef]
  32. Pasari, S.; Dikshit, O. Earthquake interevent time distribution in Kachchh, Northwestern India. Earth Planets Space 2015, 67, 129. [Google Scholar] [CrossRef]
  33. Rundle, J.B.; Luginbuhl, M.; Giguere, A.; Turcotte, D.L. Natural Time, Nowcasting and the Physics of Earthquakes: Estimation of Seismic Risk to Global Megacities. Pure Appl. Geophys. 2018, 175, 647–660. [Google Scholar] [CrossRef]
  34. Luginbuhl, M.; Rundle, J.B.; Hawkins, A.; Turcotte, D.L. Nowcasting Earthquakes: A Comparison of Induced Earthquakes in Oklahoma and at the Geysers, California. Pure Appl. Geophys. 2018, 175, 49–65. [Google Scholar] [CrossRef]
  35. Luginbuhl, M.; Rundle, J.B.; Turcotte, D.L. Natural Time and Nowcasting Earthquakes: Are Large Global Earthquakes Temporally Clustered? Pure Appl. Geophys. 2018, 175, 661–670. [Google Scholar] [CrossRef]
  36. Rundle, J.B.; Donnellan, A. Nowcasting Earthquakes in Southern California With Machine Learning: Bursts, Swarms, and Aftershocks May Be Related to Levels of Regional Tectonic Stress. Earth Space Sci. 2020, 7, e2020EA001097. [Google Scholar] [CrossRef]
  37. Rundle, J.; Stein, S.; Donnellan, A.; Turcotte, D.L.; Klein, W.; Saylor, C. The Complex Dynamics of Earthquake Fault Systems: New Approaches to Forecasting and Nowcasting of Earthquakes. Rep. Prog. Phys. 2021, 84, 076801. [Google Scholar] [CrossRef]
  38. Rundle, J.B.; Donnellan, A.; Fox, G.; Crutchfield, J.P. Nowcasting Earthquakes by Visualizing the Earthquake Cycle with Machine Learning: A Comparison of Two Methods. Surv. Geophys. 2022, 43, 483–501. [Google Scholar] [CrossRef]
  39. Rundle, J.B.; Donnellan, A.; Fox, G.; Crutchfield, J.P.; Granat, R. Nowcasting Earthquakes: Imaging the Earthquake Cycle in California with Machine Learning. Earth Space Sci. 2021, 8, e2021EA001757. [Google Scholar] [CrossRef]
  40. Rundle, J.; Donnellan, A.; Fox, G.; Ludwig, L.; Crutchfield, J. Does the Catalog of California Earthquakes, with Aftershocks Included, Contain Information about Future Large Earthquakes? Earth Space Sci. 2023, 10, e2022EA002521. [Google Scholar] [CrossRef]
  41. Perez-Oregon, J.; Angulo-Brown, F.; Sarlis, N.V. Nowcasting Avalanches as Earthquakes and the Predictability of Strong Avalanches in the Olami-Feder-Christensen Model. Entropy 2020, 22, 1228. [Google Scholar] [CrossRef] [PubMed]
  42. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time, Part II. Advances in Disaster Prediction Using Complex Systems; Springer: Berlin/Heidelberg, Germany, 2023; in press; ISBN 978-3-031-26005-6. [Google Scholar]
  43. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Fluctuations, under time reversal, of the natural time and the entropy distinguish similar looking electric signals of different dynamics. J. Appl. Phys. 2008, 103, 014906. [Google Scholar] [CrossRef]
  44. Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S.; Varotsos, P.A. Investigation of seismicity after the initiation of a Seismic Electric Signal activity until the main shock. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2008, 84, 331–343. [Google Scholar] [CrossRef]
  45. Uyeda, S.; Kamogawa, M. The Prediction of Two Large Earthquakes in Greece. Eos Trans. AGU 2008, 89, 363. [Google Scholar] [CrossRef]
  46. Uyeda, S.; Kamogawa, M. Comment on ‘The Prediction of Two Large Earthquakes in Greece’. Eos Trans. AGU 2010, 91, 163. [Google Scholar] [CrossRef]
  47. Uyeda, S.; Kamogawa, M.; Tanaka, H. Analysis of electrical activity and seismicity in the natural time domain for the volcanic seismic swarm activity in 2000 in the Izu Island region, Japan. J. Geophys. Res. 2009, 114, B02310. [Google Scholar] [CrossRef]
  48. Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Nagao, T.; Kamogawa, M.; Tanaka, H.; Uyeda, S. Minimum of the order parameter fluctuations of seismicity before major earthquakes in Japan. Proc. Natl. Acad. Sci. USA 2013, 110, 13734–13738. [Google Scholar] [CrossRef] [PubMed]
  49. Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Nagao, T.; Kamogawa, M.; Uyeda, S. Spatiotemporal variations of seismicity before major earthquakes in the Japanese area and their relation with the epicentral locations. Proc. Natl. Acad. Sci. USA 2015, 112, 986–989. [Google Scholar] [CrossRef]
  50. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Uyeda, S.; Kamogawa, M. Natural time analysis of critical phenomena: The case of Seismicity. Europhys. Lett. 2010, 92, 29002. [Google Scholar] [CrossRef]
  51. Skordas, E.S.; Christopoulos, S.R.G.; Sarlis, N.V. Detrended fluctuation analysis of seismicity and order parameter fluctuations before the M7.1 Ridgecrest earthquake. Nat. Hazards 2020, 100, 697–711. [Google Scholar] [CrossRef]
  52. Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Ramírez-Rojas, A.; Flores-Márquez, E.L. Natural time analysis: On the deadly Mexico M8.2 earthquake on 7 September 2017. Physica A 2018, 506, 625–634. [Google Scholar] [CrossRef]
  53. Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Ramírez-Rojas, A.; Flores-Márquez, E.L. Identifying the Occurrence Time of the Deadly Mexico M8.2 Earthquake on 7 September 2017. Entropy 2019, 21, 301. [Google Scholar] [CrossRef] [PubMed]
  54. Perez-Oregon, J.; Varotsos, P.K.; Skordas, E.S.; Sarlis, N.V. Estimating the Epicenter of a Future Strong Earthquake in Southern California, Mexico, and Central America by Means of Natural Time Analysis and Earthquake Nowcasting. Entropy 2021, 23, 1658. [Google Scholar] [CrossRef]
  55. Mintzelas, A.; Sarlis, N. Minima of the fluctuations of the order parameter of seismicity and earthquake networks based on similar activity patterns. Phys. A 2019, 527, 121293. [Google Scholar] [CrossRef]
  56. Varotsos, P.K.; Perez-Oregon, J.; Skordas, E.S.; Sarlis, N.V. Estimating the epicenter of an impending strong earthquake by combining the seismicity order parameter variability analysis with earthquake networks and nowcasting: Application in Eastern Mediterranean. Appl. Sci. 2021, 11, 10093. [Google Scholar] [CrossRef]
  57. Sarlis, N.V.; Christopoulos, S.R.G.; Skordas, E.S. Minima of the fluctuations of the order parameter of global seismicity. Chaos 2015, 25, 063110. [Google Scholar] [CrossRef] [PubMed]
  58. Sarlis, N.V.; Skordas, E.S.; Mintzelas, A.; Papadopoulou, K.A. Micro-scale, mid-scale, and macro-scale in global seismicity identified by empirical mode decomposition and their multifractal characteristics. Sci. Rep. 2018, 8, 9206. [Google Scholar] [CrossRef]
  59. Christopoulos, S.R.G.; Varotsos, P.K.; Perez-Oregon, J.; Papadopoulou, K.A.; Skordas, E.S.; Sarlis, N.V. Natural Time Analysis of Global Seismicity. Appl. Sci. 2022, 12, 7496. [Google Scholar] [CrossRef]
  60. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Attempt to distinguish electric signals of a dichotomous nature. Phys. Rev. E 2003, 68, 031106. [Google Scholar] [CrossRef]
  61. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Entropy in Natural Time Domain. Phys. Rev. E 2004, 70, 011106. [Google Scholar] [CrossRef] [PubMed]
  62. Varotsos, P.A.; Sarlis, N.V.; Tanaka, H.K.; Skordas, E.S. Some properties of the entropy in the natural time. Phys. Rev. E 2005, 71, 032102. [Google Scholar] [CrossRef]
  63. Lesche, B. Instabilities of Renyi entropies. J. Stat. Phys. 1982, 27, 419. [Google Scholar] [CrossRef]
  64. Lesche, B. Renyi entropies and observables. Phys. Rev. E 2004, 70, 017102. [Google Scholar] [CrossRef]
  65. Sarlis, N.V. Entropy in Natural Time and the Associated Complexity Measures. Entropy 2017, 19, 177. [Google Scholar] [CrossRef]
  66. Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. A remarkable change of the entropy of seismicity in natural time under time reversal before the super-giant M9 Tohoku earthquake on 11 March 2011. EPL (Europhys. Lett.) 2018, 124, 29001. [Google Scholar] [CrossRef]
  67. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Tsallis Entropy Index q and the Complexity Measure of Seismicity in Natural Time under Time Reversal before the M9 Tohoku Earthquake in 2011. Entropy 2018, 20, 757. [Google Scholar] [CrossRef] [PubMed]
  68. Skordas, E.S.; Sarlis, N.V.; Varotsos, P.A. Identifying the occurrence time of an impending major earthquake by means of the fluctuations of the entropy change under time reversal. EPL (Europhys. Lett.) 2019, 128, 49001. [Google Scholar] [CrossRef]
  69. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Self-organized criticality and earthquake predictability: A long-standing question in the light of natural time analysis. EPL (Europhys. Lett.) 2020, 132, 29001. [Google Scholar] [CrossRef]
  70. Ramírez-Rojas, A.; Flores-Márquez, E.L.; Sarlis, N.V.; Varotsos, P.A. The Complexity Measures Associated with the Fluctuations of the Entropy in Natural Time before the Deadly Mexico M8.2 Earthquake on 7 September 2017. Entropy 2018, 20, 477. [Google Scholar] [CrossRef]
  71. Flores-Márquez, E.L.; Ramírez-Rojas, A.; Perez-Oregon, J.; Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Natural Time Analysis of Seismicity within the Mexican Flat Slab before the M7.1 Earthquake on 19 September 2017. Entropy 2020, 22, 730. [Google Scholar] [CrossRef]
  72. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Order Parameter and Entropy of Seismicity in Natural Time before Major Earthquakes: Recent Results. Geosciences 2022, 12, 225. [Google Scholar] [CrossRef]
  73. Varotsos, P.; Alexopoulos, K. Physical Properties of the variations of the electric field of the Earth preceding earthquakes, I. Tectonophysics 1984, 110, 73–98. [Google Scholar] [CrossRef]
  74. Varotsos, P.; Alexopoulos, K.; Nomicos, K.; Lazaridou, M. Earthquake prediction and electric signals. Nature 1986, 322, 120. [Google Scholar] [CrossRef]
  75. Varotsos, P.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals. Tectonophysics 1991, 188, 321–347. [Google Scholar] [CrossRef]
  76. Varotsos, P.; Alexopoulos, K.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals, II. Tectonophysics 1993, 224, 1–37. [Google Scholar] [CrossRef]
  77. Varotsos, P. The Physics of Seismic Electric Signals; TERRAPUB: Tokyo, Japan, 2005; p. 338. [Google Scholar]
  78. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Phenomena preceding major earthquakes interconnected through a physical model. Ann. Geophys. 2019, 37, 315–324. [Google Scholar] [CrossRef]
  79. Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Seismic Electric Signals: An additional fact showing their physical interconnection with seismicity. Tectonophysics 2013, 589, 116–125. [Google Scholar] [CrossRef]
  80. Chouliaras, G. Seismicity anomalies prior to 8 June 2008, MW = 6.4 earthquake inWestern Greece. Nat. Hazards Earth Syst. Sci. 2009, 9, 327–335. [Google Scholar] [CrossRef]
  81. Shaikh, S.A.. "Measures Derived from a 2 x 2 Table for an Accuracy of a Diagnostic Test". Journal of biometrics biostatistics, 2, pp. 1-4, 2011.
  82. Kim, J., & Yang, I. (2019). Hamilton-Jacobi-Bellman Equations for Q-Learning in Continuous Time. ArXiv, abs/1912.10697.
  83. Chouliaras, G.; Skordas, E.S.; Sarlis, N.V. Earthquake Nowcasting: Retrospective Testing in Greece. Entropy 2023, 25, 379. [Google Scholar] [CrossRef]
  84. Chen, T., & Guestrin, C. (2016). XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.
  85. Yano, T., Sugimoto, K., Kuroki, Y., & Kamata, S. (2018). Acceleration of Gaussian Filter with Short Window Length Using DCT-1. 2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), 129-132.
  86. Rundle, J. Megacities Earthquake Nowcasting V4.0. Zenodo 2023.
Preprints 115154 g001
Figure 1. Map with the seismic events of “higher” EQs scale within a specific Greece megacity. Large EQ comes from “smaller” events within the circular radius region.
Figure 1. Map with the seismic events of “higher” EQs scale within a specific Greece megacity. Large EQ comes from “smaller” events within the circular radius region.
Preprints 115154 g001
Preprints 115154 g002
Figure 2. The Long Short-Term Memory (LSTM) cell
Figure 2. The Long Short-Term Memory (LSTM) cell
Preprints 115154 g002
Preprints 115154 g003
Figure 3. Bellman Equation for Q-Learning diagram example [82]
Figure 3. Bellman Equation for Q-Learning diagram example [82]
Preprints 115154 g003
Preprints 115154 g004
Figure 4. As clearly shown, we have eight clusters. The effort will be to map (train) each (6x10) matrix instance from the nn (e.g., nn=10000) Monte-Carlo instances into one only cluster. If re-enforcement learning is consistent, together with the DNN parameters, etc., 98% of the prediction time, the evaluation function should output a positive evaluation metric, for that prediction input.
Figure 4. As clearly shown, we have eight clusters. The effort will be to map (train) each (6x10) matrix instance from the nn (e.g., nn=10000) Monte-Carlo instances into one only cluster. If re-enforcement learning is consistent, together with the DNN parameters, etc., 98% of the prediction time, the evaluation function should output a positive evaluation metric, for that prediction input.
Preprints 115154 g004
Preprints 115154 g005
Figure 5. As depicted from the image, classification has been successful. And the network has correctly classified the centroids of each cluster. The process demonstrates the competitive learning capabilities to cluster-classify the input.
Figure 5. As depicted from the image, classification has been successful. And the network has correctly classified the centroids of each cluster. The process demonstrates the competitive learning capabilities to cluster-classify the input.
Preprints 115154 g005
Preprints 115154 g006
Figure 6. The sliding-window concept.
Figure 6. The sliding-window concept.
Preprints 115154 g006
Preprints 115154 g007
Figure 7. Major earthquake event (★) (R6.0) & aftershocks for Arkalochori, Crete, Greece (2021).
Figure 7. Major earthquake event (★) (R6.0) & aftershocks for Arkalochori, Crete, Greece (2021).
Preprints 115154 g007
Preprints 115154 g008
Figure 8. Real (a) and Nowcasted (b) seismic events for Arkalochori, Crete, Greece.
Figure 8. Real (a) and Nowcasted (b) seismic events for Arkalochori, Crete, Greece.
Preprints 115154 g008
Preprints 115154 g010
Figure 10. Real (a) & Predicted (b) major shock (★) (R6.4), Sitia, Crete, Greece (2021)
Figure 10. Real (a) & Predicted (b) major shock (★) (R6.4), Sitia, Crete, Greece (2021)
Preprints 115154 g010
Preprints 115154 g011
Figure 11. Real (a) & Predicted (b) major shock (★) (R6.3), Tyrnavos, Greece (2021).
Figure 11. Real (a) & Predicted (b) major shock (★) (R6.3), Tyrnavos, Greece (2021).
Preprints 115154 g011
Preprints 115154 g013
Figure 13. Confusion error matrix of our framework.
Figure 13. Confusion error matrix of our framework.
Preprints 115154 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated