Preprint
Article
Quasi-Analytical Solution of Kepler’s Equation as an Explicit Function of Time
Altmetrics
Downloads
96
Views
61
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
15 May 2024
Posted:
15 May 2024
You are already at the latest version
Alerts
Abstract
Although the empirical Kepler’s laws can be proven by applying Newton’s laws to the dynamics of two particles attracted due to the gravitational interaction, there is no explicit formula for the motion as a function of time. In this paper, a quasi-analytical solution for this problem is proposed. It approximates the real behavior of celestial bodies with an acceptable degree of accuracy. All calculations involved require a low computational cost. This problem is closely related to Kepler’s equation, since, the solution for the equations of motion as a function of time gives us the solution to Kepler’s equation as well. The results are presented for each planet of the solar system (including Pluto), and the solution is compared against the real orbits.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
Kepler’s laws provide an empirical mathematical model to describe the dynamics of the motion of the planets around the Sun (later proven by Newton’s analytical results [1,2]. Therefore, they are of fundamental importance in astrophysics, celestial mechanics, and earth science [3]. In this way and under the Copernican hypothesis, where the Earth rotates on itself and around the Sun, phenomena such as the apparent motion of the stars and the flattening of the Earth, among others, could be explained. Nevertheless, Kepler’s fundamental problem is the motion of a planet over time as it traverses through its orbit. As we shall see, it is the so-called Kepler’s equation (KE) that provides the explicit time dependence of the fundamental quantities of the problem. Since this equation was first established by Kepler in 1609, until the present day, several solutions of different types have been proposed [2,4,5,6]. Due to its inherent nature, it has not yet been possible to obtain an exact explicit solution, and a large number of calculations must be made to improve the approximate solutions. It is hardly possible to refer here to all the relevant works. Some of the procedures give satisfactory approximations, but they are very complex and often require many terms in order to obtain a solution with a given degree of accuracy and may involve high computational cost [3,7]. These solutions normally consist of calculating infinite series, or high-order iterative approaches [3,7,8,9,10,12,14] and by integral solutions [13]. Recently, some methods which use artificial intelligence were proposed [11].
In this work, we present a quasi-analytical solution that gives the explicit equations of motion as a function of time. This solution is quasi-analytical because even though it gives explicit formulas, it depends on six numerical coefficients, which in turn depend on the eccentricity. As mentioned above, this result provides an explicit solution to KE.
1.1. The Orbit Equation
The classical problem begins then, with the description of the motion of the planets according to the following equations [15]:
where
has been used. Here, are the coordinates of the planet in the polar coordinate system, with the origin at the Sun, t is the time, is the eccentricity, and , , and l are the focal parameter, the reduced mass, and the angular momentum, respectively [2]. The angle is called the true anomaly, defined as at the pericenter [14].
The inverse of the solution of Eq. (1), is closely related to KE:
where E is the eccentric anomaly and M is the mean anomaly, expressed as:
T being the orbital period. As was pointed out before, usually, E needs to be estimated by series expansions [16] or iterative methods [6]. Thus, the accuracy of the position and/or velocity of the celestial object moving in the Keplerian orbit, which may be obtained from the solution of KE, depends on the approximation method used. Figure 1 illustrates the variables involved in the problem.
Equations (1) and (3) are both transcendental. The solution of Eq. (1) gives the solution of the Eq. (3), and vice-versa, which has led to a vast literature concerning alternative approaches [3]. A detailed description of the different works presented in the literature on this problem can be found in [3,14].
The remainder of this paper is structured as follows. In Section 2 we present in detail, step by step, the quasi-analytical solution of Eq. (1). In Section 3 the results are presented and compared with the real orbit of each planet of the solar system. In Section 4 we present the solution to KE based on the solution of Eq. (1). Finally, in Section 5 we give a brief discussion and conclusions about the results obtained in this work.
2. Methodology
In the present section, the quasi-analytical method is established for solving Eq. (1). For clarity, we divide the method into sections that we will call steps. All calculations and graphics were performed with MATLAB 2020b. Now we briefly describe each step.
Step 0. In this step we integrate Eq. (1) and introduce a normalized time which maps the real time t from the interval to the interval , which leads us to Eq. (7) for .
Step 1. In this step we separate into two parts, and . Based on the observation that resembles the behavior of (especially for small values of ), and, taking into account its analytical form, we find the inverse of , as our zeroth approximation for .
Step 2. Assuming the exact solution has the form of Eq. (14), we introduce the true argument of the arctangent function, , which gives the exact solution. Then, we introduce the function (Eq. (17)) as the quotient of the true argument and the argument of the zeroth approximation, . Finally, we define the first approximation by adjusting the argument of the arctangent function which appears in the zeroth approximation . The main idea is to make a series of adjustments in such a way that the quotient mentioned above approaches 1 as closely as possible.
Step 3. Following the logic of Step 2, we introduce the function (Eq. (22)) and the argument (Eq. (25)) in order to obtain the second approximation (Eq. (26)). First, we propose two kinds of approximations for : linear and harmonic. This gives the approximations and (Eqs. (27) and (28)), respectively. This approximations give the corresponding precision of 3,400 km and 470 km, respectively, for the position of the Earth. This formulas are completely analytical, and may be used in some applications which do not require high precision.
Next, we proceed to improve the function as an analytical expression (Eq. (29)), involving an arctangent function, with an argument which, in turn, is an expression that depends on six numerical coefficients (Eq. (30)). In order to calculate these coefficients, we propose two methods, namely, Method A and Method B.
Method A consists in calculating the coefficients for fixed values of the eccentricity, while Method B allows us to express these coefficients as an analytic function with other numeric coefficients calculated for ranges of the eccentricity.
2.1. Step 0
This solution is valid on the interval . In order to make the solution valid on the interval , we need to apply the following correction:
In order to avoid complications related with the periodicity of the functions of involved, and the monotony of time, in what follows, we focus our work only on the half-period of the orbit, namely, . The second half of the orbit may be obtained from the first part using the symmetry of the orbit.
We now propose the following change of variable:
So, Eq. (5), in terms of and has the form:
Let us seek for the solution to Eq. (7) in the form on the interval , and, as deduced from Eq. (7), in .
Note the relationship between and the mean anomaly M:
2.2. Step 1
Figure 2 shows the behavior of , and with as parameter.
As we can see, Figure 2 shows how is similar to , therefore, as our zeroth approximation , we will solve the following equation:
To solve the Eq. (12) we apply the tangent function to both parts. Solving for , we obtain:
2.3. Step 2
We introduce the functions and as follows:
so that:
Now, we introduce another function , defined on the open interval :
Appendix B proves the following limits (the former is used immediately to introduce the function , and the latter is used in step 3):
and
We define the approximation one, as follows:
Figure 4 shows plots of and with as parameter.
2.4. Step 3
We introduce a new function, , defined on the open interval :
Figure 5 shows the plot of with as parameter.
We introduce the function as follows:
The definition of as the product of and leads us to an apparent logical paradox, since, as it follows from Eq. (22), . The solution to this paradox is the fact that is an unknown function, which we are trying to approximate with the best precision possible. The existence of such a function is obvious, for it can be theoretically constructed point-wise. However, in this work we are looking for a quasi-analytic expression for , since the exact analytic expression for it, in principle, may not even exist.
Now, we define the approximation two, as follows:
It should be noted that the approximation (Eq. (21)) can be considered as the approximation with . For small values of , such as Earth’s () has a small range (for the Earth, it will be of [0.9997, 1]) so that the approximation already gives us an acceptable result for certain applications. Thus, for the Earth, the maximum error of is of rad, which, translated to the error in the position, taking into account the average distance from the Earth to the Sun as km, is equivalent to 27,000 km, which is a little more than two diameters of the Earth. Now, approximating in a linear form, and, as a cosine with period and amplitude adjusted to the range [, 1] the following corresponding approximations are obtained:
The approximation gives a maximum error of rad, which translates to 3400 km in the position (slightly more than half the Earth’s radius), and the approximation gives a maximum error of rad, which corresponds to approximately 470 km in the position.
In Figure 5, we notice that the shape of the curves resembles an arctangent function, with a mapping of the argument from (, ∞) to (,0), with the range mapping from (, ) to (), and with the behavior of the argument being asymmetric and nonlinear. By the aforementioned, we search for the approximation of the function in the following form:
where:
with y () being functions of .
In order to evaluate the coefficients and (the six numerical coefficients mentioned in the introduction), two methods were developed, Method A and Method B. In Method A, the coefficients are calculated for each value of , while in Method B, they are expressed as analytic functions which, in turn, depend on other numeric coefficients, that are calculated for ranges of . As will be seen further, Method A is more accurate, but less general, while Method B is slightly less accurate (especially after a certain value of ), but more general and easier to use in applications.
2.4.1. Method A
The coefficients and were calculated numerically for each eccentricity value, corresponding to every planet of the solar system, by means of RMSE (Root Mean Square Error) minimization, using MATLAB 2020b.
Figure 6 shows the behavior of and in the range of ∈ (0, 0.5) (this range was selected because some absolute values of and grow drastically after , which does not allow us to appreciate the behavior before ).
Table 1 shows the values of and , as well as the error of for the Earth and Pluto, in radians, where ME is the Maximum absolute Error, MAE is the Mean Absolute Error and RMSE is the Root Mean Square Error.
Since Table 1 serves just for illustrative purposes, the values of and were rounded to three decimal places. A detailed table including more accurate values for all planets will be shown in the section of Results. For now let us mention that the absolute maximum error in the position of the Earth is 915 meters and approximately 39,000 kilometers (close to the value of the circumference of the Earth, or 16 Pluto diameters) for the position of Pluto (the average distance of Pluto to the Sun is approximately 5.9 billion kilometers).
2.4.2. Method B
Analyzing Figure 6, it can be seen that the shapes of the curves have a behavior of a cubic polynomial, so we search for the coefficients and in the following form:
where repeated indices imply summation.
We introduce the approximation with the same form of given by Eqs. (26), (29), (30), where now Eq. (31) is used to approximate the and in Eq. (30).
The attempt to calculate the coefficients and in the complete range of ∈ (0,1) was not successful. Thus, it was decided to divide the range into five intervals, ∈ (0,0.1], ∈ (0.1,0.25], ∈ (0.25,0.5], ∈ (0.5,0.7] and ∈ (0.7,1). In the next section, we will present the values of and by ranges, and compare the precision of the approximation , which uses values of calculated using Method A, with that of .
3. Results
We now compare the results of our quasi-analytical solution with the real orbits of the planets of the solar system. First, we resume the results obtained above in the following equations. By the change of variable:
the equations of motion in the polar coordinate system with the origin at the Sun, and in the interval of time ∈, ∈ are the following:
where is given by the following expression:
being and functions of . In what follows we present the two methods developed for the calculation of the coefficients and .
3.1. Method A
As mentioned above, in this method, the values of and were calculated for each eccentricity by means of RMSE minimization in MATLAB 2020b. Table 2 shows the values of and , ME, MAE, and RMSE errors in , in radians, being the average distance of the planet to the Sun in kilometers and is the maximum error of the position in kilometers with respect to the real orbit.
The results of Table 2 show that for small values of , the accuracy is high. However, for values of the error increases significantly.
3.2. Method B
As was pointed out before, in this method we calculate the coefficients of a third-degree polynomial (Eq. (31)) by minimizing the RMSE, for the ranges of . So, in this case, it is not necessary to calculate the and for each value of the eccentricity. Table 3 shows the values of the coefficients and for the different ranges of . Obviously, using this method results in errors greater than those of Method A.
Figure 7 shows the comparison of the errors between methods A and B. As can be seen, the error in Method B is slightly higher (especially for ME) up to values of . For values of the errors of Method B increase significantly with respect to those of Method A.
3.3. Equations of Motion for the Planets
Finally, let us express the equations of motion of both position and velocity in the Cartesian coordinate system, with the origin at the Sun.
The equations for the velocity are:
where:
and
The function defined in the interval ∈ is given by Eq. (35) and its derivative is the following:
Figure 8 shows the comparison plot between the real orbit, calculated numerically using Eq. (7), and the orbit obtained by numerical integration of Eq. (37) (where Method A was used). Additionally, the velocity vectors are shown at an arbitrary scale at some points of the trajectory.
As can be seen in Figure 8, the integrated orbit closely resembles the behavior of the real orbit. This shows that our Method A is sufficiently accurate even for eccentricities of the order up to .
4. Solution to Kepler’s Equation
As can be seen from Figure 1b, it is trivial to obtain the following expression, which gives the formula for E (the eccentric anomaly), appearing in Eq. (3) as a function of the polar coordinates with the center in the focus F. In what follows, we set the major semi-axis equal to one ():
where (Figure 1b). As is well known from the theory of conic sections, , since we set . Thus, Eq. (42) acquires the following form:
Due to the normalization , the expression for is as follows:
Now, in order to obtain the final explicit expression for the solution of KE, , we need to express and as functions of M (the mean anomaly given by Eq. (4)). So far, and r are functions of (where is given by Eq. (6)). Thus, by expressing as a function of M, and r automatically become functions of M. The expression for is the following:
In order to obtain as a function of M, we use Kepler’s third law to express a as follows:
5. Remarks and Conclusions
In this work, we obtained a quasi-analytical solution for the motion of the celestial bodies as an explicit function of time in four steps. We called this solution quasi-analytical, due to dependency on some numerical coefficients, which, in turn, themselves depend on the eccentricity. We proposed two methods for evaluating these coefficients, Method A and Method B. The former gives a higher degree of accuracy, but involves calculations for each value of the eccentricity, while the ladder is less accurate (especially for values of ), but more practical, since it works for ranges of the eccentricity. All of our calculations involve low computational cost, and provide a high degree of accuracy for the motion of celestial bodies. Using our results, we obtained an explicit solution to KE without the need of calculating infinite series, or using numeric iterative methods.
Author Contributions
The first two A.N. Beloiarov and V.A. Beloiarov developed the theory and worked on the redaction together with the authors, R.C. Cruz-Gómez and C.O. Monzón. J.L. Romero collaborated in the theoretical revision of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Integration of Eq. (1)
To solve the integral, we propose the Weierstrass change of variable:
From Eq. (1.1) it follows that:
Substituting Eq. (1.2) into Eq. (1), and with a little algebra, we obtain the following:
which will be left undefined for now, and will eventually be evaluated in the original variables. Here and . To facilitate the integration, the integrand is simplified using partial fractions, leaving the integral as follows:
Doing a bit of algebra, and making the trigonometric substitution
where . Finally, Eq. (1.4) reads:
The latter integral is trivial, and the former is solved using the identity , such that is left as:
Returning to the variable u, recalling that and doing some algebra, Eq. (1.6) reads:
Finally, recalling Eq. (1.1), expressing a and b in terms of , doing algebra, and evaluating the limits of integration, we arrive at our final result:
which is in agreement with Eq. (5).
Appendix B. Proofs of limits Eq. (18) and Eq. (19)
We begin by solving for from Eq. (14):
Next, in Eq. (15), we substitute by the expression Eq. (7):
We introduce the variable as follows:
For the sake of ease, we will evaluate the limit instead of .
In order to prove limit Eq. (18), we will use the Taylor expansion about zero of the following functions:
Using Eq. (2.4), we obtain:
which is equivalent to:
which agrees with Eq. (18).
In order to demonstrate Eq. (19), we use the following trigonometric identity:
Using Eq. (2.4) and Eq. (2.6), we have:
which is equivalent to:
which agrees with Eq. (19).
References
- K. Krisciunas, Demonstrating the elliptical orbit of Mars using naked eye data, Am. J. Phys. (2019). [CrossRef]
- H. Goldstein, Classical Mechanics, 2nd ed. Addison-Wesley, Reading. (2020).
- W. Baisheng, Y. Zhou, C. Lim and H. Zhong, A new solution approach via analytical approximation of the elliptic kepler equation, Acta Astronautica (2023). [CrossRef]
- P. Colwell, Solving Kepler’s Equation over Three Centuries, Willman-Bell, Inc., Richmond (1993).
- L. D. Landau and E. M. Lifshitz, Mechanics, 3rd ed. Elsevier Butterworth-Heinemann, Burlington (1976).
- A. W. Odell and R. H. Gooding, Procedures for solving Kepler’s equation, Cel. Mech. (1986).
- O. González-Gaxiola and S. Hernández-Linares, An Efficient Iterative Method for Solving the Elliptical Kepler’s Equation, Int. J. Appl. Comput. Math (2021). [CrossRef]
- G. G. Elenin and T. G. Elenina, Parametrization of the Solution of the Kepler Problem and New Adaptive Numerical Methods Based on This Parametrization, Diff Equat (2018). [CrossRef]
- F. L. Markley, Kepler Equation solver, Celestial Mech Dyn Astr (1995). [CrossRef]
- A. Simha, An algebra and trigonometry-based proof of Kepler’s first law, Am. J. Phys. (2021). [CrossRef]
- M. Zheng, J. Luo and Z. Dang, Machine learning-based solution of Kepler’s equation, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series (2022). [CrossRef]
- R. W. Easton, R. L. Anderson and M. W. Lo, Conic transfer arcs for Kepler’s problem, Am. J. Phys. (2022). [CrossRef]
- M. Calvo, A. Elipe and L. Rández, On the integral solution of elliptic Kepler?s equation, Celest. Mech. Dyn. Astron. (2023). [CrossRef]
- F. Orlando, C. Farina de Souza, C. Zarro and P. Terra, Kepler’s equation and some of its pearls, Am. J. of Phys. (2018). [CrossRef]
- J. B. Marion, Kepler’s equation and some of its pearls, Academic Press Inc. 1st Edition (1965).
- S. A. Mikkola, A cubic approximation for Kepler’s equation, Cel. Mech. (2018). [CrossRef]
Figure 1.
Illustration of the relative position of the Sun and planet (a) and Kepler’s equation (b).
Figure 1.
Illustration of the relative position of the Sun and planet (a) and Kepler’s equation (b).
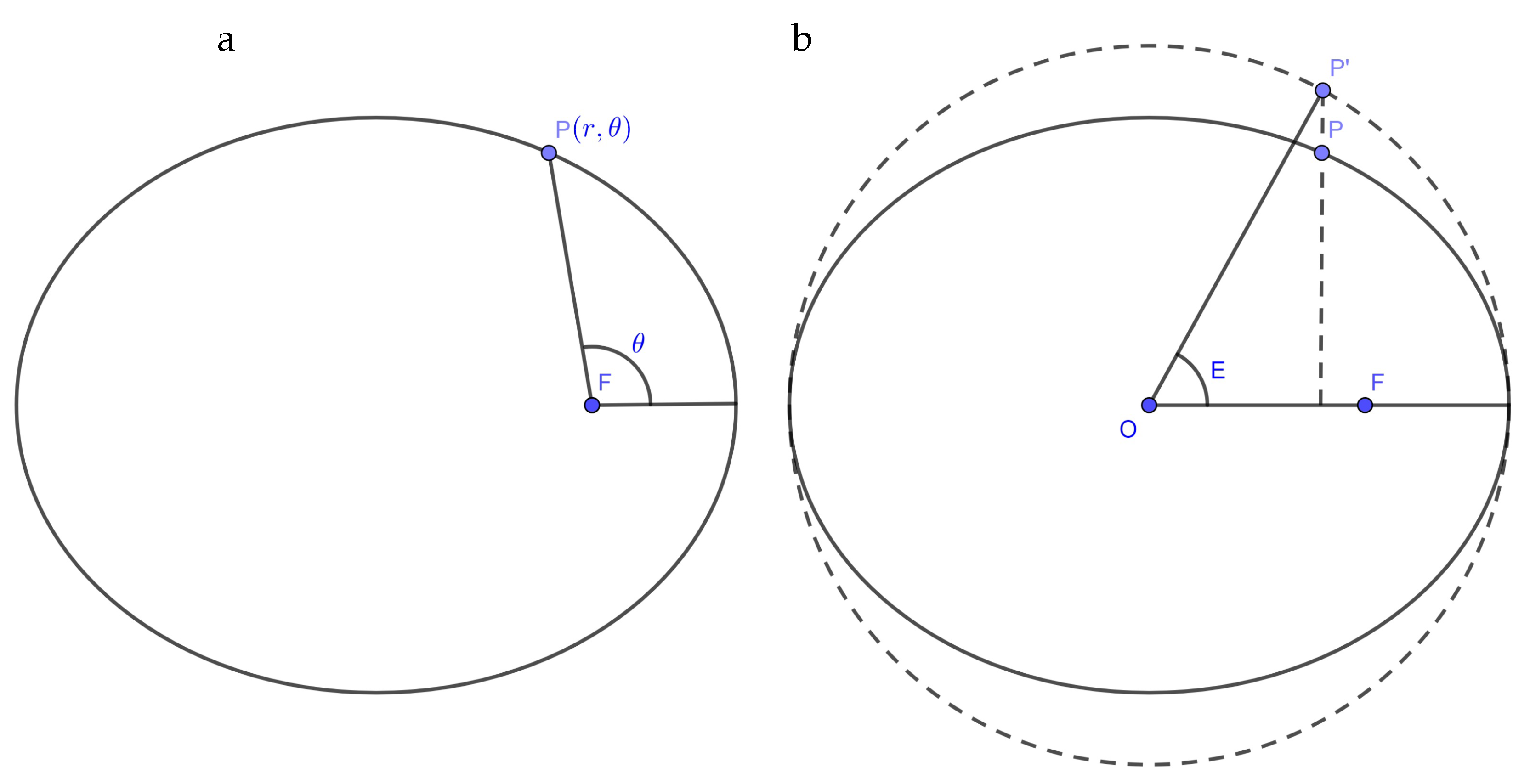
Figure 2.
Plots of , and with = 0.1 (left) and = 0.5 (right).
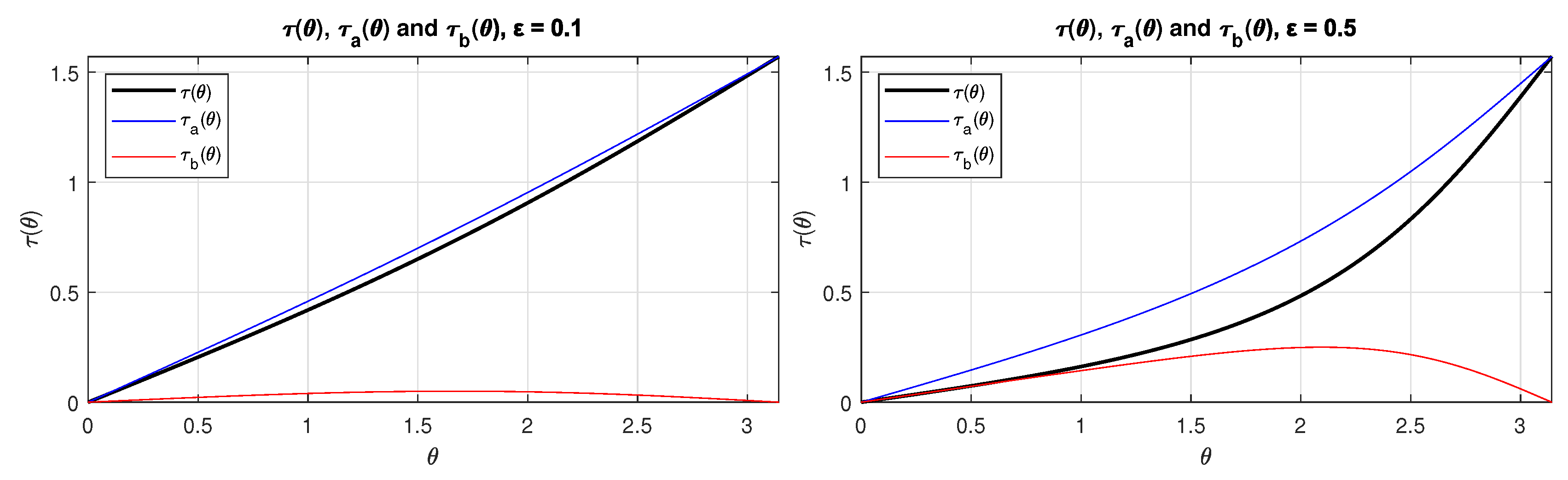
Figure 3.
Plots of and with = 0.1 (left) y = 0.5 (right).
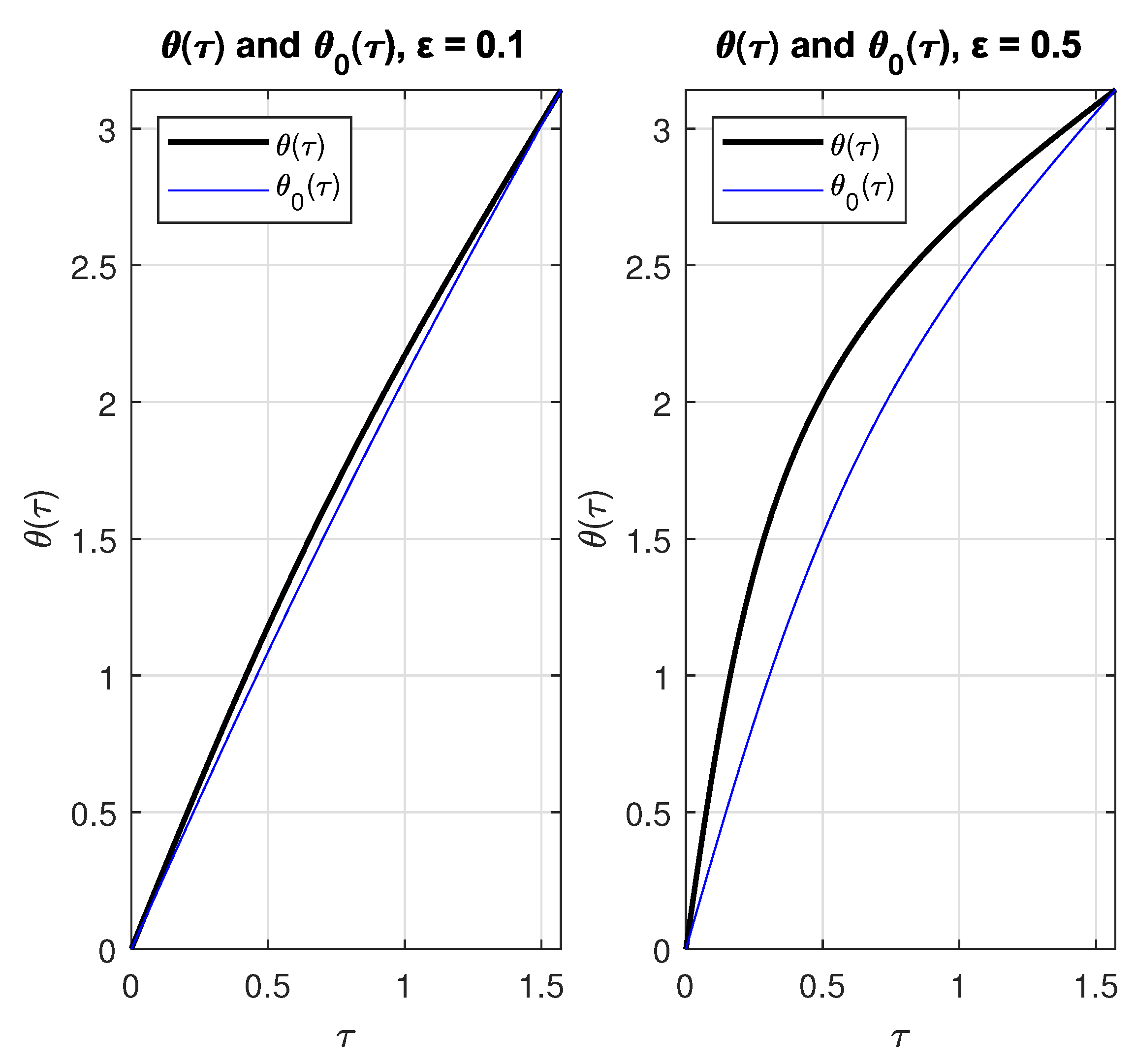
Figure 4.
Plots of and with = 0.1 (left) and = 0.5 (right).
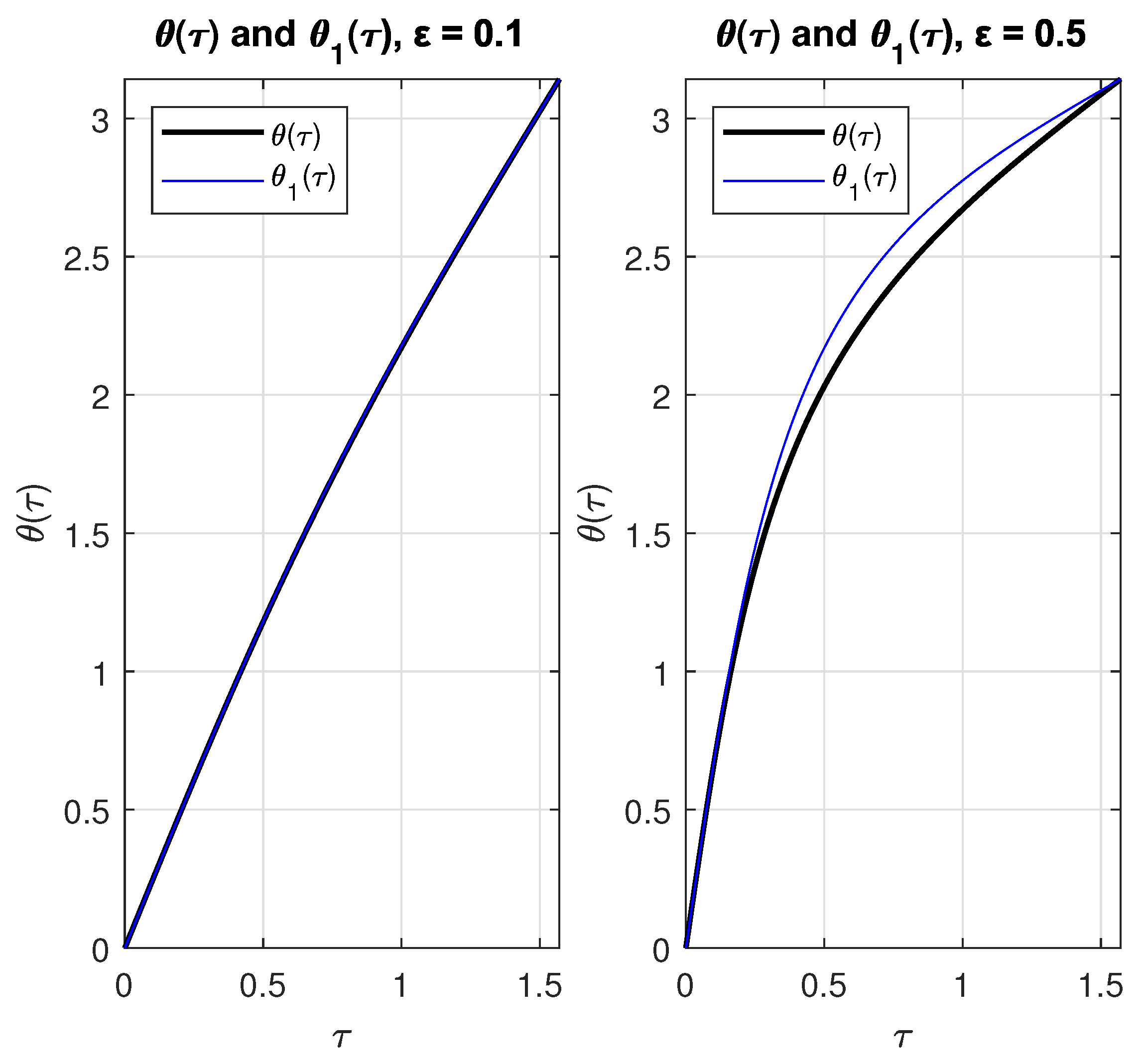
Figure 5.
Plot of with as parameter.
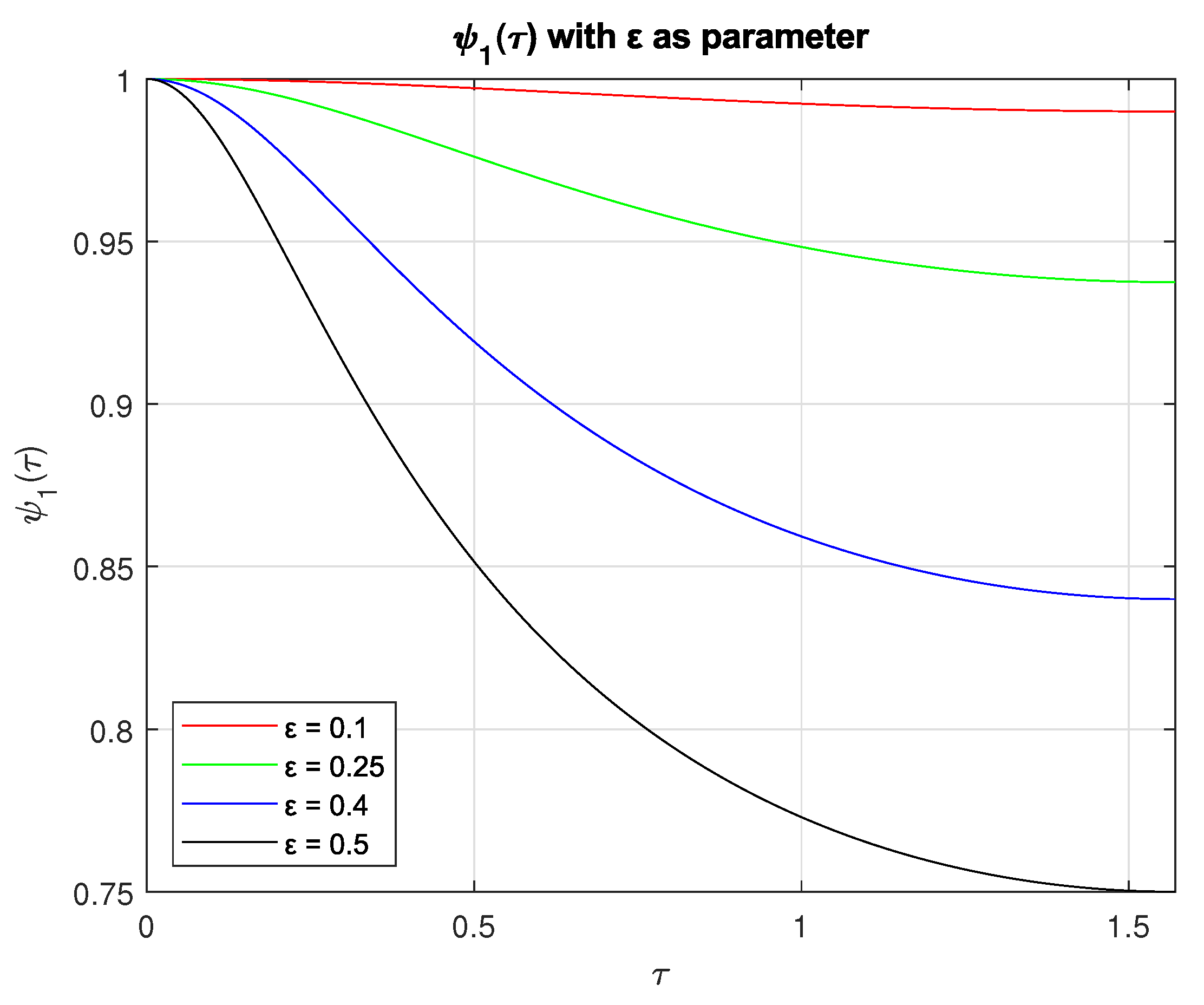
Figure 6.
Plots of (left) and (right).
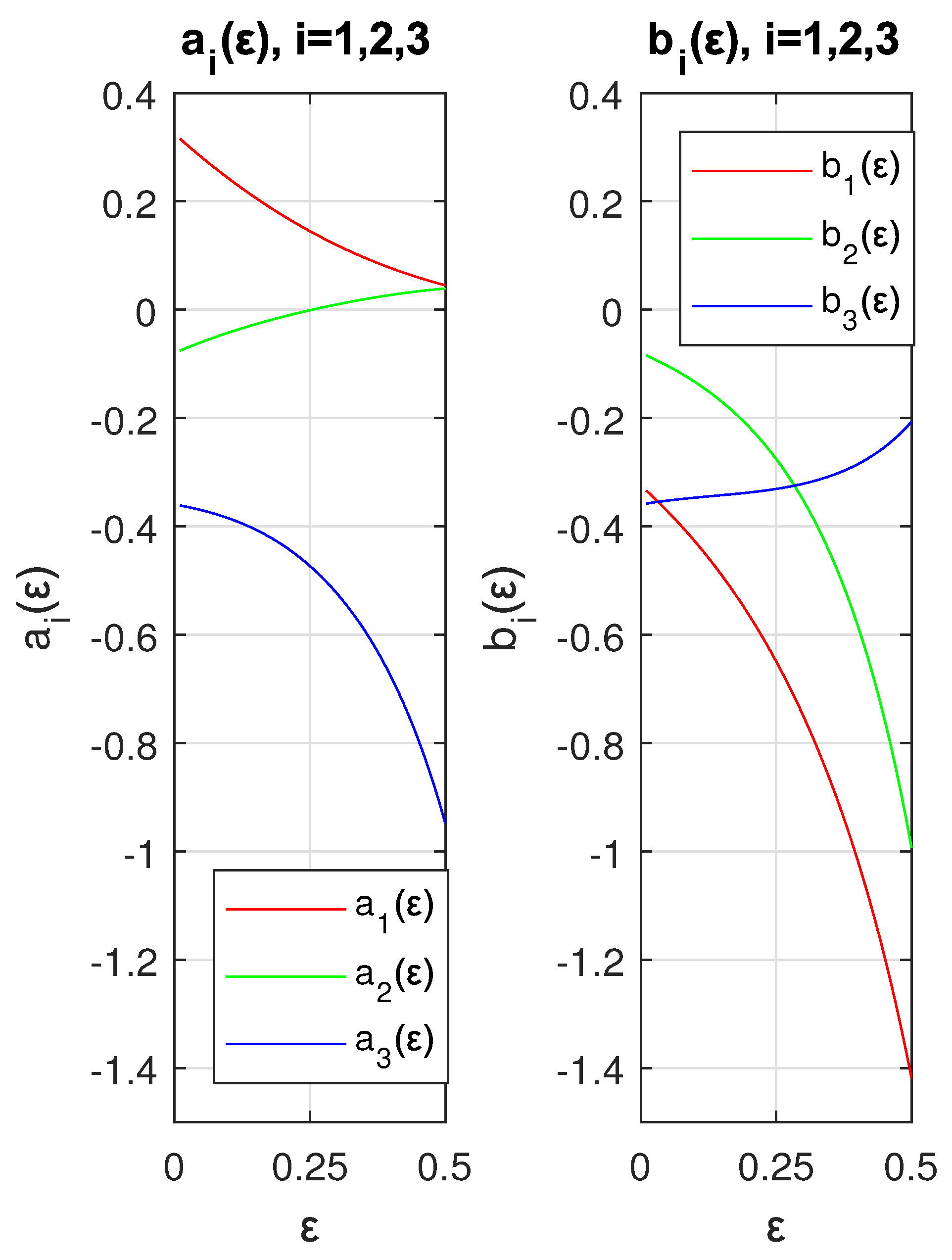
Figure 7.
Logarithmic plots of the error in as a function of for both methods.
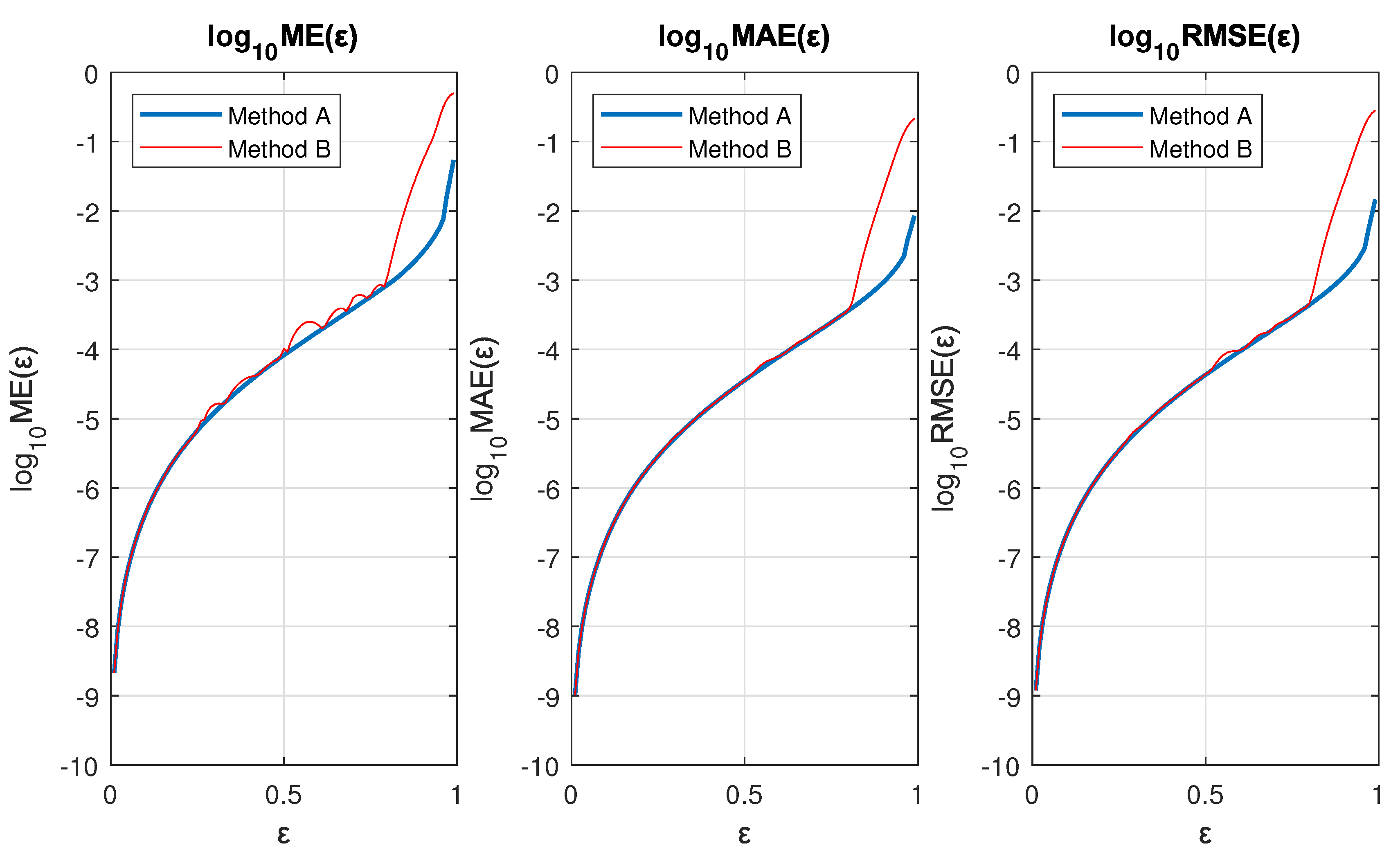
Figure 8.
Plot of the orbits, real and integrated, with and .
Table 1.
Values of and and error in for the Earth and Pluto.
| Planet | ME | MAE | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Earth | 0.0167 | 0.310 | -0.073 | -0.363 | -0.340 | -0.087 | -0.357 | |||
| Pluto | 0.2488 | 0.146 | -0.001 | -0.472 | -0.647 | -0.274 | -0.331 |
Table 2.
Values of and , errors in and absolute position.
| Mercury | Venus | Earth | Mars | Jupiter | Saturn | Uranus | Neptune | Pluto | |
|---|---|---|---|---|---|---|---|---|---|
| 0.2056 | 0.0067 | 0.0167 | 0.0935 | 0.0489 | 0.0565 | 0.0457 | 0.0113 | 0.2488 | |
| 0.17053517 | 0.31862395 | 0.30977503 | 0.24694331 | 0.28234256 | 0.27609996 | 0.28499728 | 0.31453377 | 0.14561949 | |
| -0.01166110 | -0.07705003 | -0.0728542 | -0.04432541 | -0.06014655 | -0.05731287 | -0.06135776 | -0.07510434 | -0.0012376 | |
| -0.43861374 | -0.36086494 | -0.36274460 | -0.38289299 | -0.36985666 | -0.37179675 | -0.36907139 | -0.36171170 | -0.47217706 | |
| -0.57282655 | -0.33074668 | -0.34005421 | -0.42023391 | -0.37170483 | -0.37957121 | -0.36843946 | -0.33499871 | -0.64694223 | |
| -0.22240872 | -0.08288098 | -0.08742593 | -0.12920751 | -0.10334339 | -0.10741403 | -0.10166725 | -0.08494978 | -0.27396065 | |
| -0.33681377 | -0.35855961 | -0.35697508 | -0.34764211 | -0.35253989 | -0.35161930 | -0.35294044 | -0.35781706 | -0.33108759 | |
| ME | |||||||||
| MAE | |||||||||
| RMSE | |||||||||
| 208 | 0.11 | 0.92 | 80 | 52 | 131 | 163 | 12 | 39,000 |
Table 3.
Values of and calculated in ranges of .
| Range of | (0,0.1] | (0.1,0.25] | (0.25,0.5] | (0.5,0.7] | (0.7,1.0) |
|---|---|---|---|---|---|
| 0.32464090 | 0.32455984 | 0.32493519 | 0.33117795 | 0.34799892 | |
| -0.90342437 | -0.90136299 | -0.90443788 | -0.94434644 | -1.02378174 | |
| 0.79798292 | 0.77956682 | 0.78688870 | 0.87179816 | 0.99672027 | |
| -0.24897861 | -0.19074605 | -0.19470806 | -0.25486105 | -0.32027157 | |
| -0.07992819 | -0.07920359 | -0.07197522 | -0.06646582 | -0.11098658 | |
| 0.43404410 | 0.41648507 | 0.33665965 | 0.29615322 | 0.50088661 | |
| -0.64017363 | -0.49188569 | -0.19208276 | -0.09396227 | -0.40748236 | |
| 0.75341116 | 0.31132787 | -0.07256170 | -0.15093252 | 0.00894242 | |
| -0.35968044 | -0.35742442 | -0.15675162 | 6.29837377 | 154.50791377 | |
| -0.17220655 | -0.22278632 | -2.20357719 | -41.92862343 | -715.24316797 | |
| -0.64666864 | -0.26055305 | 6.28024901 | 87.40520959 | 1105.82612363 | |
| -1.78408496 | -2.80408480 | -10.06884121 | -65.08749455 | -577.96129585 | |
| -0.32463507 | -0.32142203 | -0.09294215 | 6.21933680 | 138.39317241 | |
| -0.90434048 | -0.97722350 | -3.24616805 | -42.18802414 | -643.15766068 | |
| -1.11071449 | -0.54525397 | 7.00356134 | 86.74796714 | 996.53861794 | |
| -1.63153199 | -3.15712303 | -11.61829996 | -65.86504267 | -524.44755555 | |
| -0.07992299 | -0.07527391 | 0.29080466 | 11.97863173 | 287.23614950 | |
| -0.43571269 | -0.54094614 | -4.16198706 | -76.07319110 | -1326.12648115 | |
| -0.78063318 | 0.03353877 | 12.02291626 | 158.84151291 | 2048.91985911 | |
| -2.10660888 | -4.29567159 | -17.65734989 | -117.20310761 | -1068.68369232 | |
| -0.35968350 | -0.36025835 | -0.44346730 | -3.54853992 | -81.17535211 | |
| 0.17171182 | 0.18402819 | 0.99888552 | 20.06864682 | 372.42195877 | |
| -0.59524043 | -0.68312683 | -3.34688052 | -42.20159066 | -574.67488149 | |
| 1.45594036 | 1.66666199 | 4.58818969 | 30.87266047 | 298.77577747 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






