Preprint

Article

Principles of Reasoning Dynamics

Altmetrics

Downloads

136

Views

Comments

Yingrui Yang^*

This version is not peer-reviewed

This preprints belongs to the Topic

Social Sciences and Intelligence Management

Submitted:

15 May 2024

Posted:

15 May 2024

Read the latest preprint version here

Alerts

Abstract

This paper proposes a new dynamic analysis of reasoning. It makes the following contributions. First, the current states of the psychology of reasoning are critically reviewed from theoretical and empirical perspectives. The long-standing controversies between logicians and psychologists are clarified by introducing the gauge theoretic structure. The debates between the mental logic theory and the mental models theory are carefully reviewed by identifying the problem types used in the empirical studies. Certain mental fluctuations are found and a quantum theoretic solution is examined. Second, it solves the measurement problem within the Hamiltonian framework. The modeling structure underlying reasoning dynamics is the electrodynamics. They are both the single-charge dynamic systems sharing the U(1) symmetry. The mental logic theory and the mental models theory are now characterized as wavefunctions in a unified account of the dynamic analysis with the yes/no measurements. The stochastic sampling method is introduced to solve the measurement problem, which has a wide range of applications in social sciences. Third, a novel metatheoretic framework of reasoning dynamics within Lagrangian framework is proposed. It solves the “Man vs. Men” problem via gauge theoretic modeling, by making the distinction between the global level and the local level. At each level, the gauge transformations are applied to achieve the global symmetry and the local gauge symmetry. It explains the meanings of the gauge principle and the Nether theorem. Fourth, the special theory of relativity is applied to address the “Man vs. Men” problem. It explains how to draw the global language cone and the individualized local language cones. Finally, it points out that borrowing modeling methods from physics has a long tradition in psychology. The present work utilizes the conceptual and modeling methods found in modern theoretical physics.

Keywords:

Subject: Social Sciences - Cognitive Science

1. Introduction

Reasoning is one of the core capacities of human cognition. In this domain, there are longstanding controversies between logicians and psychologists, and there are hard debates between their different psychological approaches. There also exist empirical mysteries in reasoning research, which need to be explained. These issues demand careful reviews. This paper proposes a new theoretical framework by introducing both the dynamic analysis of reasoning and the gauge theoretical approach via formation of the gauge structure. It establishes the concepts of global symmetry and local symmetry. At the global level, it characterizes the gauge potential and strength of the general reasoner. At the local level, it characterizes the individual differences and the connections of reasoners.

Here, the dynamic analysis is the sourced reasoning dynamics, of which the source is the logic charge. The moving logic charge produces the logical current, which is accompanied by a cognitive field. During the reasoning process, hesitation is a significant mental phenomenon. Such mental activities are not directly observable, but they may be characterized by the wavefunctions. In this case, the wavefunction is single-valued. However, for the evaluation tasks used in reasoning experiments, the participants need to answer “Yes or else No” for a given putative conclusion, indicating that it is actually a two-valued measurement. This is the reasoning version of the so-called measurement paradox.

This dynamic analysis mainly studies two quantities which are modeled as the Hamiltonian and/or the Lagrangian. In any reasoning problem, the reasoner must possess a certain internal text comprehension capacity to read through the problem and understand the contents. In other words, a certain amount of mental energy must be expended by the reasoner to process a problem. This mental energy is represented by potential energy, denoted by

V

. Accordingly, for a given wavefunction, the potential energy is denoted by

V_{ψ}

. Chomsky made the distinction between ‘competence’ and ‘performance.’ The reasoning competence includes the knowledge of logic, the skills of applying inference schemas, and the ability to construct mental models. These competences are modeled as potentials. The reasoning performance involves actually activating certain inference schemas or constructing mental models when working on reasoning tasks. These performances cost mental kinetic energy, denoted by

E_{ψ}

In the dynamic analysis, the Hamiltonian, written

H = E + V

and the Lagrangian, written

L = E - V

must each hold invariant in form for a dynamic system. The two forms are logically equivalent, but have different applications. For the Hamiltonian, the initial state is given but the final state is open. So, the evolution of the wavefunction follows the Schrödinger equation. For the Lagrangian, both the initial state and the final state are given, and the perturbation theory applies. The present paper aims to solve the measurement problem in reasoning within the Hamiltonian framework, and to solve the “Man vs. Men” puzzle within the Lagrangian framework.

The topics and contents of the present paper can be read in three parts as follows:

Part I. Revisits the current reasoning research. Section 2 reviews the theoretical issues, including the debates between the mental logic theory and the mental models theory. Section 3 reviews the associated empirical issues and looks further into the varying problem types used by different approaches within their reasoning experiments. It also highlights a mystery phenomenon, called the cognitive traffic effect. Section 4 explains the difference between the inward observation of psychology and the outward observation of physics. It points out that both traditional psychophysics and Newtonian physics are by a low degree of disturbance in observations, while both higher cognition and quantum physics are characterized by a high degree of disturbance in observations. These differences generate the orthogonal law and the diagonal rule.

Part II deals with Hamiltonian modeling and the measurement paradox of reasoning. Section 5 explains concepts such as the logic charge, cognitive field, hesitation, wavefunction of reasoning, and the Yes/No measurement. It also addresses the issue of the measurement problem. Section 6 introduces a new stochastic sampling method, which solves the measurement problem.

Part III deals with Lagrangian modeling and the role language plays in reasoning. Section 7 first explains the gauge transformation of the first kind, which establishes the global symmetry of the reasoner. Then it explains the gauge transformation of the second kind, which establishes the local symmetry of reasoners. It shows that reasoning dynamics satisfies the mathematical U(1) symmetry. Section 8 explains the role that language plays in reasoning from relativistic perspectives. It first shows that language functions like light in reasoning. It then characterizes the language cone for the reasoner at the global level, and the individualized proper language cone at the local level. It also introduces three particle-alike concepts from quantum field theoretic perspectives. The notion of syntactic reasoning field is defined as the Synon; the notion of semantic reasoning field is defined as the Semon; the notion of the reason language field is defined as the Langon. Then, it studies the interaction of the three fields. Finally, Section 9 provides some general discussion and further research topics.

2. Theoretical Controversies and the Gauge Structure

2.1. Reasoning is One of the Core Capacities of Human Cognition

It places a critical role in text comprehension, knowledge acquisition, and decision making. The study of reasoning is related to logic and psychology. Logicians regard logic as the structure of thought. Logic is largely related to languages, including natural language, mathematical language, and even the language of thought [1]. Note that there are many logic systems, which were all created by logicians. In other words, logic is a manmade result. Psychology of reasoning is interested in mental representations, mental processes, and reasoners’ reasoning performances. Nevertheless, not only are there certain controversies between logicians and psychologists, but there are also long-standing debates within the community of psychologists. The reasoning dynamics is a new approach aimed at providing a unified framework for the above, which accounts for logic, psychology of reasoning, and beyond. Dynamic analyses are sourced analyses. The source of reasoning dynamics is the “logic charge,” which is analogous to the electric charge in physics.

2.2. Historical Controversies and Debates

Logic studies the definition of reasoning, while psychology of reason studies how people themselves reason. There is a longstanding debate between logicians and psychologists. Psychologists found that human reasoning significantly violates standard logic [2,3,4,5]. Thus, they often claim that the study of reasoning does not need logic. This is actually an illusion. By and large, we can hardly study human reasoning without logic. Below are four reasons that support this statement. First, there are many cognitive channels in human thinking. Reasoning is one of the modes of human cognition. Logic is responsible for identifying which mode is a reasoning task. Theoretically, why do we call some experiments the reasoning experiments, but not decision-making experiments? This is due to the fact that certain logical structures are embodied in experimental items and in order to achieve the correct answer to this question, the reasoner needs to make inferences logically.

Second, the experiment designs require logic from empirical research perspectives. For instance, in mental logic research [6], in order to predict the degree of problem difficulty, schema weights must be generated. The method to obtain such schema weights is to ask subjects to report their perceived relative difficulty ratings immediately upon solving each reasoning problem. This introspective data can then be used to produce schema weights by applying a statistical method known as linear regression. This type of experimental design requires that the set of testing items covers the whole distribution of relative difficulty. Otherwise, it is difficult to judge whether the testing items are skewed to the easy problems, or else skewed to the hard problems. Thus, the whole range of inference structures must be designed systematically, and all possibilities exhausted. More systematically designed testing items result in higher quality experiments. One may imagine that this can hardly be done without logic.

Third, and even more sensitively, standardized educational testing, such as the SAT and the GRE need logic. The SAT and the GRE are high profile selection tests. Hence, the degree of pre-evaluated item difficulty is important to the organization of a particular set of testing items. This is a sensitive issue to maintain the fairness of a standard test. In particular, the testing items in the section of logical inference have different logical structures. Thus, before we apply psychological theories of human reasoning, we need to first disclose the logical structure of each item [7,8,9].

Fourth, there are two major competing approaches in psychology of reasoning, namely, the mental logic theory and the mental models theory. Mental logic theory claims that people reason by applying inference schemas, akin to formal rules of logic [9]. Hence, the mental logic theory can be treated as a syntactic approach from a logic perspective. Mental models theory claims that people reason by constructing mental models, based on reasoners’ understanding of the meanings of given premises [10]. Hence, the mental models theory can be treated as a semantic approach from a logic perspective. How individuals reason is a subject of major controversy between the two competing approaches [11,12].

Fifth, psychological theories of reasoning are compatible with logic. Logicians used to regard logic as the science of validity in a certain sense. In fact, both the mental logic theory and the mental models theory are partially compatible with logic. For example, consider two inference forms. One is Modus Ponens (MP): from premises

p \to q a n d p,

we can infer

q

。The other is Modus Tollens MT): from premises

p \to q a n d \neg q,

we can infer

\neg p

. Both MP and MT are valid inferences. The empirical evidence shows that people rarely make an error in doing MP [13], but often commit rather high error rates in doing MT [14]. Hence, the mental logic theory selects MP as an inference schema, but not MT. The MP is also referred to as the cognitive meaning of “if-then” [15]. If a reasoner makes an error in doing MP, it is likely that such a reasoner does not know what if-then means. We can see from here that the mental logic theory is a psychological partial selection of logic from the syntactic perspective.

Mental models theory is a principled theory [16], and has its own symbolic representations of mental models. For instance, it holds the principle of truth, meaning that given very limited working memory, reasoners tend to only cope with what is true but not with what is false. In particular, let us consider the truth semantics of propositional logic. In the truth table, each binary operator has four possibilities. For instance, the conjunction

(p \land q)

has only one true possibility, that is when both disjuncts are true. Thus, it has one mental model, written

(p, q)

. While for the conditional statement,

p \to q,

there is only one possibility which makes it false. This occurs when its antecedent

p

is true but the consequence

q

is false. By the principle of truth, this false possibility is not construed in mental models. For the true possibility when both

p a n d q

are true, we have an explicit model

(p, q)

. For the other two true possibilities where the antecedent

p

is false and still by the principle of truth, the reasoner would find discomfort in reasoning from a false antecedent. Thus, the reasoner only makes an implicit mental footnote, denoted by

(\dots)

. Unless it is absolutely necessary this implicit model would be ignored. In this case, we can see that the conjunction and the conditional would share one explicit mental model

(p, q)

. Hence, the reasoner would often understand the meaning of the conditional as the same as the conjunction. Thus, the mental models theory predicts a wide range of illusory inferences. From the above analyses, we see how the mental models theory is compatible with logic. In this sense, the mental models theory is a psychological partial selection of logic from the semantic perspective.

In addition, note that ideally any standard logic system needs to satisfy certain metaproperties such as consistency and completeness. Consistency requires that all the proofs are valid argument forms, and completeness requires that all the valid argument forms are provable. This is the bridge between the formal syntax and the formal semantics. Now, because the mental logic theory and the mental models theory are psychological partial selections of logic, the bridge connecting the syntactic side and the semantic side is broken. An interesting topic is how to rebuild this bridge from psychological perspectives [17].

2.3. Gauge Structure

The contents described above are concerned with the multi-factors in reasoning. Moreover, we did not even mention the various pragmatic approaches to reasoning. This situation is not satisfactory. Here we introduce a mathematical structure which provides a unified model of the multi-reasoning components. This structure is called the gauge structure, borrowed from the gauge field theory [18].

Gauge structure is a two-by-two structure. It first makes a clear distinction between the global level and the local level. In our context, the global level has nothing to do with the individual differences, while the local level must take individual differences into account. At each level, it makes a distinction between the potential and the field strength. We now introduce the reasoning components into this gauge structure.

At the global level, the global potential is composed of logicians and psychologists of reasoning. Call all them the logician and the psychologist. The global field strength are logic systems (such as propositional logic and quantified predicate logic) made up by the logician, or psychological theories of reasoning (such as the mental logic theory and the mental models theory) made up by the psychologist. Obviously, here neither the global potential nor the global field strength is concerned with individual differences. In other words, they place all of the individuals in the symmetric position. This is referred to as global symmetry. Note that for empirical sciences, all the theories may only be hypothetical and may only need to be supported by empirical evidence, that which involves empirical research.

At the local level, it must take individual difference into account. It is well-known that Chomsky makes the distinction between the competence and the performance. Here the individual reasoning capacities or logical skills serve as the local potential, and the individual performances serve as the local field strength. Due to these individual differences, to achieve the local symmetry the so-called gauge transformation is required. This will be introduced in Section 7, where we will see that the gauge theory is the language of conducting dynamic analyses. We then can have:

Principle 2.1 (gauge structure) The factors in the domain of reasoning can be fitted into the gauge structure.

The relation between the global symmetry and the local symmetry is governed by the gauge principle, which states that if the global symmetry is broken, then the local symmetry cannot be achieved. For example, consider the standardized educational testing. If any amount information regarding the testing items was leaked to someone before the test, it would break the global symmetry among the test takers. Then, as a result, the testing scores would no longer reflect correct information on the distribution of individual differences.

3. An Empirical Puzzle and the Quantum Theoretic Solution

3.1. An Empirical Puzzle

Both the mental logic theory and the mental models theory are supported by significant empirical evidence. Nevertheless, careful review find that two different types of reasoning problems were used in the mental logic experiment and in the mental models experiment. Below is an example of a Type 1 problem used in the mental logic research [6].

Type 1 problem:

All the beads are wooden or metal

The wooden beads are red

The metal beads are green

The square beads are not red

Are the square beads green?

Note that this problem type contains only straight statements. The mental logic theory predicts that reasoners can solve the Type 1 problem by applying inference schemas almost errorlessly, effortlessly, and universally (across different languages). The experimental results show that the accuracy is higher than 90%. Below is a Type 2 problem used in mental models research [19,20].

Type 2 problem:

Only one of the following statements is true:

Some of the plastic beads are not red, or	(Premise 1)
None of the plastic beads are red	(Premise 2)

Is it possible that none of the red beads are plastic?

By the principle of truth, the mental models theory predicts that this is an illusory problem with a low accuracy rate. The experimental results show that the accuracy rate is below 30%, which significantly supports the predictions of the mental models theory. Note that the Type 2 problem has a more complex surface structure. It has a heading statement which involves the truth values of the premises. Thus, the correct strategy to solve a Type 2 problem must consider two possible cases: when the first premise is true and the second premise is false, and vice versa. Moreover, its putative conclusion is a modal statement. From the above empirical results, one can see that the issue of how people reason remains.

3.2. Failed Mental Metalogic and the Quantum Lightening

Mental metalogic [17] attempts to reestablish the bridge between the mental logic theory and the mental models theory from the metalogical perspective. The theoretical idea is as follows. Assume A is a psychological theory of reasoning, and

A^{*}

is a problem type used in the empirical research under theory A. Assume B is another psychological theory of reasoning, and

B^{*}

is another problem type used in the empirical research under theory B. If the integration of

A^{*}

and

B^{*}

can produce a new problem type

C^{*}

and

C^{*}

is testable as an ordinary verbal task from the experimental perspective, then we say that the problem types

A^{*}

and

B^{*}

are empirically consistent. Meanwhile, if theories A and B can be integrated into a new theory C, which can predict the results of testing

C^{*}

, then we say that C is complete for

C^{*}

. Let A be the mental logic theory and B be the mental models theory. Accordingly, C denotes Problem Type 1 and

C^{*}

denotes Problem Type 2. We can construct the compound Problem Type 3 by simply combining Problem Type 1 and Problem Type 2. An example is given below.

Problem Type 3:

The premises given below are either all true or all false:

All the beads are wooden or metal;

The wooden beads are red;

The metal beads are green;

The square beads are not red.

Q1: Is it possible that the square beads are green?

Q2: Is it necessary that the square beads are green?

To solve this problem correctly, the reasoner needs to consider two possible cases: All the premises are either true or else all the premises are false. Subjects are supposed to solve this problem by applying inference schemas or by constructing mental models at different steps. This problem has two versions. One is the possibility version (See Q1) and the other is the necessity version. The possibility version is predicted as a control problem with high accuracy, while the necessity problem is predicted as an illusory problem with low accuracy. However, the experimental results show that the accuracy is roughly 60% [17]. A largescale cross-language experiment in Chinese also confirmed this result [21]. This result cannot be explained by the mental metalogic theory, by the mental logic theory, nor by the mental models theory. It is an empirical puzzle in psychology of reasoning.

One post hoc explanation pertaining to the above puzzle is that it is caused by mental traffic. When two cognitive channels (e.g., the mental logic channel and the mental models channel) are attempting to merge by various reasons (including psychologists themselves), some mental fluctuations occur. At this point, the reasoner has to spend extra energy to manage the cognitive traffic light. Eventually a formula was found to calculate the results:

\frac{1}{2} (90 %) + \frac{1}{2} (30 %) = 60 %

. This formula is called the No. 1 formula in the quantum mechanics by Feynman [22]. This observation shines a ray of quantum theoretic insight. People might wonder how this could happen and if this is a coincident? The explanations are given in the next section, where we discuss scientific observations. The rest of the paper will build upon the gauge theoretic framework of reasoning. This approach was not only motivated by theoretical interests, but mostly by the empirical push. We have:

Principle 3.1 (quantum calculation). Reasoning processes involve mental fluctuations, of which the results can be calculated by quantum theoretic formulations.

Note that Problem Type 3 is just a simple compound integration of the Type 1 structure and the Type 2 structure. Reasoning problems can be rather complex. Below is a logical reasoning problem selected from the GRE.

The Lobster Problem (LP)

Lobsters usually develop one smaller cutter claw and one large crusher claw. To show that exercise determines which claw becomes the crusher, researchers placed young lobsters in tanks and repeatedly promoted them to grab a probe with the same randomly selected claw. For most of the lobsters the grabbing claw became the crusher. However, in a second similar experiment, when lobsters were promoted to use both claws equally for grabbing, most matured with two cutter claws, even though each claw was exercised as much as the grabbing claws had been in the first experiment.

Which of the following is best supported by the information above?

(A) Young lobsters usually exercise one claw more than the other.

(B) Most lobsters raised in captivity will not develop a crusher claw.

(D) Cutter claws are more effective for grabbing than the crusher claws.

(E) Young lobsters that do not exercise either claw will nevertheless usually develop one crusher and one cutter claw.

The correct answer is A. In a large-scale experiment by using the think-aloud method [23], more than 800 think-aloud protocols were coded and analyzed. The analyses disclosed a number of multi-strategies on the way people are solving GRE reasoning items [8]. It also shows that researchers apply different methods to model complex reasoning problems [7,9].

3.4. A Set of New Questions

Now we want to ask a different set of questions:

Question 1. What force drives the reasoner to go through a challenging logical inference problem?

Question 2. In the domain of reasoning, can we provide a unified account of the rational reasoner and reasoners with the bounded rationality? This is called the “Man vs. Men” problem.

Question 3. Assume that the mental processes of human reasoning are not directly observable, but can be measured by Yes/No questions. Can we formulate a unified mathematical model in this situation? This is called the measurement problem.

Question 4. What role does language play in reasoning? Can we construct a unified model to capture the interactions of language, inference schemas, and mental models? This is called the two-leg structure game.

Question 5. The standardized educational test is a selection test and the individual differences in logical reasoning are significant. How do we connect one individual score to another, and how should we model it mathematically? etc.

These questions are fundamental. We can borrow some modeling methods from modern theoretical physics, and more specifically from the mathematical gauge field theory which calls for a new framework of dynamic analysis for reasoning. Parts II and III are devoted to answering these questions.

4. Why Do We Need a Quantum Model?

4.1. The Directness of Observations

We must understand why and how the fields of psychology and physics can share the same mathematical model. Both psychology and physics are the empirical sciences per se. Yet, both mind and matter have been and continue to be studied scientifically. While cognitive psychology is a much younger field than physics and its partner, mathematics, it is well known that traditional psychophysics was heavily influenced by classical Newtonian mechanics and its conceptual framework. On the other hand, it must be conceded that higher-order cognitive research (such as the study of reasoning, decision making and behavioral game theory) has been lagging behind lower-order cognitive research, such as the study of perception, sensation, and action. Simply put, the reason for this lag is that when it comes to higher-order cognition, classical mechanics is the wrong branch of physics to leverage. This paper presents an alternative approach, which goes beyond classical mechanics and delves into quantum realm. What is the theoretical foundation for our new line of modeling?

Though a great part of the human mind is not directly observable, psychologists have not stopped trying to observe the seemingly unreachable portions of the mental world. Researchers want to scientifically investigate and rigorously model how the mind works (including, but not limited to, mental equipment, mental representations, and mental processes). Yet we must be wary of the fact that most theories relating to the mind are hypothetical and need to be empirically justified; the hypotheses in these theories can only be represented in a statistical language. Therefore, by its very nature, cognitive psychology is an empirical science. A well-trained professional in this domain would never say, “I have proven something.” Proofs are notions used in analytical methods, which are at the heart of mathematics and logic. A well-trained professional is suitably circumspect and would therefore say that the empirical evidence “tends to confirm” the predictions made by the model, and thus, the theory is rendered more plausible.

Under these constraints, an important question arises: as cognitive psychologists, what method do we have at our disposal that allows us to study the mental world as rigorously as physicists modeling the physical world? In other words, what can psychological modeling share with theoretical physics? One thing that it can share can be described in terms of observation. Here, we propose a useful distinction as our first working conceptualization without further argument for it. The scientific observations can be classified in the following two ways: we have outward observations of the physical world, and we have inward observations of the mental world. Accordingly, we assume this as our first working hypothesis:

Principle 4.1 (observational directions): Scientific observations are directional. The inward observation of the mental world and the outward observation of the physical world are in opposite observational directions.

Scientific observations are performed through carefully designed experiments. This is the second thing that cognitive psychology shares with physics. Similar to experimental designs in physics (and to other natural sciences), good experimental designs in psychology require various kinds of experimental controls including testing materials, procedures, and participants. Critics sometimes blame psychologists for putting too many experimental controls in their experiments. This sort of attitude constitutes unfair treatment of the empirical research of the mind. Indeed, physicists would acknowledge that in their experiments, the experimental controls are very important. So, it seems unfair to question these controls, when they are in fact positive reinforcements used in psychological experimentation. A good experimental design in psychology of reasoning aims to use well-worded testing items with clear inference structures, as stimuli to be entangled with the targeted cognitive capacity. We assume that when the target capacity is accelerated, the original mental (phenomenological) world collapses.

Another fact, which we assume as a presupposition, is that there is always certain friction against the body with respect to mental processes. We cannot stop people from getting tired when exerting sustained cognitive effort for the simple fact that the human species has limited mental energy for effective thinking. This is why experimental sessions usually last no more than a single hour.

4.2. Types of Experimentations

Given the limitations of experimental methodologies, both in the research of psychology and physics, there are generally certain degrees of disturbance in observation. Often, in books written to introduce nonclassical physics, such as quantum theory or theories of relativity to nonexperts, some cartoons or personified examples are given in order to illustrate how the mind perceive physical phenomenon beyond everyday intuition (e.g., Hawking, 1996, 2001). For example, when a father goes out to do yard work, his two boys are peacefully watching TV; when he returns to the house, the boys are still watching TV peacefully. In between these observations however, the boys have a fight while he works in the yard. This phenomenon can be seen as a type of quantum fluctuation (Greene, 1999). Similarly, different kinds of quantum fluctuations occur when inward observations are performed. For example, when it takes longer than a minute for a participant to complete an experimental trial, say solving an SAT item, there is generally a five-second mental daydreaming break or bout of confusion to disturb observation when the latency data is being collected. In certain types of experiments, this disturbance is small and can be ignored; in others however, it matters greatly. Taking this into account and following the insight of Dirac (1930/1958), we have:

Principle 4.2 (disturbance): The higher the degree of disturbance in the experiment, the smaller the world can be observed.

What kind of experiment has a low degree of disturbance, and what kind of experiment has a high degree of disturbance? The principle of disturbance actually provides a way of distinguishing two very general types of experiments. One can be characterized as the smooth type of experiment with a low degree of disturbance; the other can be characterized as the Yes/No type of experiment (von Neumann, 1955; Penrose, 2004), with a high degree of disturbance. The principle of disturbance allows us to draw the chart below.

Here, we provide an intuitive way to understand the levels of scientific observation. As an example, imagine a picture of an iceberg. This image allows us to distinguish three levels of research. The first level takes place on top of the iceberg and enables the researcher to make a map of the parts floating above the water line. This can be compared with behavioral research in psychology as well as in economics. For the second level, assume that a boat equipped with advanced measurement technologies is near the iceberg. Imagine that this technology allows for the possibility of simulations, aimed at approximating the properties of the iceberg beneath the water, to take place. This can be compared with cognitive computational modeling research in cognitive science. Both the first and the second levels of observation have a relatively low degree of disturbance and are accordingly treated as “smooth” experiments. For the third level, suppose that the boat is within a certain distance from the iceberg and that it only allows us to see the top of the frozen mass. This third level of observation carries a high degree of disturbance and shall be treated as the Yes/No type of experiment. It is this type of experimentation that this paper focuses on. Why is the third level of research as important as the first two levels?

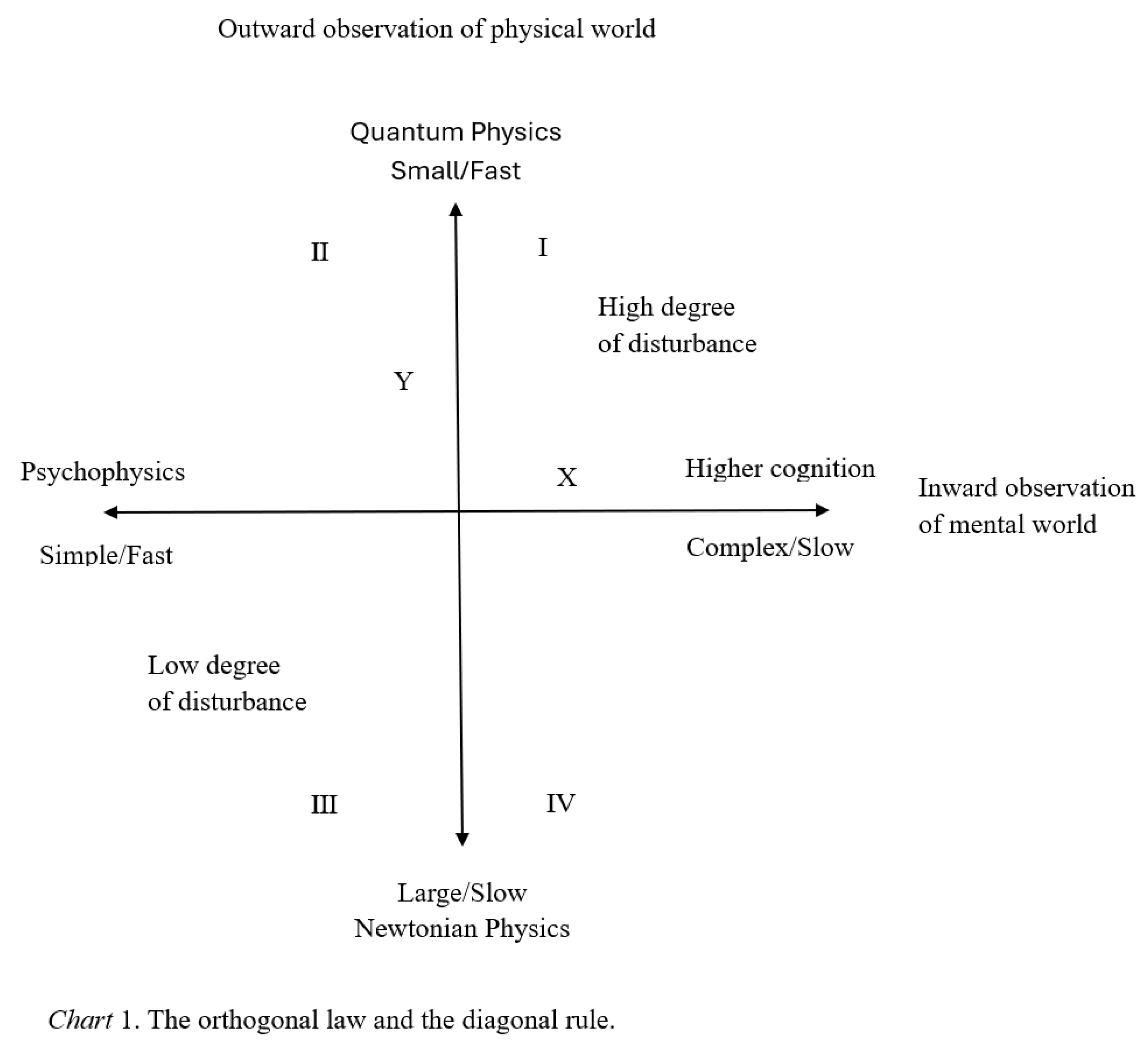
4.3. The Orthogonal Law and the Diagonal Rule

The distinction between the smooth experiments and the Yes/No experiments should be general enough to cross observations of the physical world and observations of the mental world. Given this distinction, we are now ready to address some key ideas.

Principle 4.3 (orthogonal): Experiments in the study of higher-order cognition and experiments in the study of quantum physics are within the spectrum of the same type of Yes/No measurement, and share a great deal of the same kind of mathematical analyses.

The orthogonal principle only spells out half of what can be called the diagonal rule. To spell it out fully, let us start by zooming in on Chart 1. In doing so, we obtain the four cases below.

Case 1. Consider the classic Newtonian mechanics that use outward observation of the physical world. Here, the target moves slow and has a larger size; the degree of disturbance in the experiment is low, and it can be described by a smooth curve. It is about the macro-world for observation via Principle 4.2.

Case 2. Consider the traditional psychophysics that uses inward observation of the mental world. It mostly studies sub-domains of lower cognition, such as vision, audition, sensation, perception, human-computer interaction, etc. The experiments mostly use computerized simulation and priming tasks, in which each single trial is simple and in while milliseconds matter. Thus, the degree of disturbance in these experiments is relatively low. Accordingly, in an hour-long experimental session, a large number of trials can be tested. Given the high density of trials, the distribution of raw data can be approximated as a smooth learning curve, and characterized as a differentiable function.

Thus, from the experimental perspective, the above tradition of psychophysics is about the observational macro-world, and it shares a great deal of mathematical elements with classical Newtonian mechanics. Here, the term lower cognition has a new meaning: viz., some cognitive tasks having a lower degree of disturbance when observed. This paper is not about the orthogonal Case 1 and Case 2; rather, this paper is about the following orthogonal pair of cases found below:

Case 3. Consider quantum mechanics, which uses the outward observation of the physical world. It is well known that target physical particles, which are accelerating, are very small in size and move fast. By Dirac (1930/2004), the degree of disturbance in quantum experimentations is high; thus, such experimentation is about the microworld by Principle 4.2.

Case 4. Consider the new reasoning dynamics, which this paper is devoted to. Reasoning dynamics applies inward observations to the mental world. It investigates a particular higher-order cognitive task; i.e., reasoning. Below are several characteristics of the inward observation on reasoning.

First, the experimental items used in these domains are designed with formal structures, reflecting the normative theories, which are more complex than the priming trials used in lower-order cognition experiments. Second, the predictions are made based on the corresponding psychological models, which are compatible with normative theories. Third, the experimental items are verbal tasks, given in natural language(s). Fourth, it is to be measured in seconds or minutes (contrary to the case of priming tasks, where milliseconds matter). And finally, the number of trials (experimental items) is relatively small in an hour-long session—much shorter than that of lower-order cognitive experiments. These characteristics allow various kinds of thinking fluctuations during the information-processing period. In this sense, the experiment is with a high degree of disturbance; thus, by Principle 4.2, the corresponding observational world is micro, meaning the degree of what is observable is low. (As a general, extreme case, one can imagine the logical reasoning items found in standardized tests, such as the GRE or SAT, as implications.)

Because the mental representations and mental processes in higher-order cognitive tasks are not directly observable, the tests of this kind are typical Yes/No experiments. In most reasoning experiments, the so-called evaluation tasks are performed. Given a set of premises, the participant is asked to mark “Yes” or else “No” for a putative conclusion provided. In addition, in the experiments of decision making and behavioral game theory, the preference order is a binary relation. In preferring A to B, it means that one is marking A yes and B no. Even multiple-choice problems can be considered Yes/No type problems.

Given the initial descriptions of the Cases 3 and 4, we should get some basic insights into the reason why new mental dynamics can share the Yes/No type of experimentation with quantum mechanics. Consequently, as we later demonstrate, the field of mental dynamics shares a great deal of its formal and mathematical tools with that of quantum mechanics.

In a more abstract sense, the orthogonal law reflects a symmetric relation between inward and outward observations of the characteristics of observational targets across physical and mental worlds, as can be seen from the Table 4.1 below.

The phenomenon represented in the table above deserves some more general observations. To summarize the contents in the table above, we can generate a very useful rule, called the Diagonal Rule in modeling.

Principle 4.4 (the diagonal rule). 1. Reasoning and quantum physics both feature high disturbance in their observations such that they share the same type of mathematical modeling methods. 2. Traditional psychophysics and classical Newtonian physics both have low disturbance in their observations such that they share a different type of mathematical modeling methods.

It is helpful to understand the relationship between physics and cognitive science to better grasp the diagonal rule. As we mentioned earlier, both physics and cognitive science/psychology are empirical sciences. They both study observables as well as non-observables; the border between observables and non-observables seems to continuously change as experimental technologies advance. T. D. Lee once gave some great insights, “Indeed, all symmetries are based on assuming that it is impossible to observe certain basic quantities, which we shall call ‘non-observables and non-observables imply symmetry” [39].

Part II. The Hamiltonian and the measurement problem

5. The Wavefunction and the Measurement Problem

5.1. Reasoning Dynamics: The U-Procedure

If we think carefully, we would find that the human mind can navigate all kinds of reasoning processes from solving simple problems to rather complex ones. Is there any force that leads us to do so? The discussions in the following sections involve a great deal of theoretical physics and mathematics. The formal descriptions of these contents would go beyond the scope and the size of this paper. We try to keep the theoretical points informal and brief.

5.2. Logic Charge and Cognitive Field

Dynamic analysis is the sourced analysis. This source is called charge. For example, the electric charge in the electrodynamics. For building up the reasoning dynamic framework, we first assume the following as our working hypothesis.

Postulate 5.1 (logic charge). People reason because they are charged, called this charge the logic charge, denoted by

e

The logic charge can be the syntactic (e.g., the mental logic channel), denoted by

e^{-}

. The logic charge can also be semantic (e.g., the mental models channel), denoted by

e^{+}

. We assume that

e^{-}

and

e^{+}

share the equal mass in the sense that they have the same representational demand (as explained earlier about schema weights).

Definition 5.1 (syntactic charge).

e^{-}

= [Intention to apply inference schemas, problem],

Definition 5.2 (semantic charge).

e^{+}

= [Intention to construct mental models, problem],

Logic charge is a two-components unit, which contains a reasoning problem and the intention to solve it either syntactically by applying inference schemas, or semantically by constructing mental models. The moving logic charge creates logic current, which may be strong or weak. Logic current produces the cognitive field simultaneously. The cognitive field can be characterized by the magnetic field in the electromagnetic theory [24]. The reasoner’s cognitive efforts include reading through the contents in order to understand the premises and the conclusion, thinking about which schemas to activate, how to construct mental models, and other pragmatic matters. For the evaluation task, the reasoner needs to mark the putative conclusion. This decision is polarized by the cognitive field, which is analogical to magnetic field in physics. The cognitive field is a closure around the logic current. Thus, we have the following

Postulate 5.2 (The logical-cognitive potential). Together, the intention carried by the logic charge and the cognitive capacity form the logic-cognitive potential, which is characterized by a vector, called the vector potential [30]. The field strength is the gradient field of the logic potential and the curl of the cognitive potential, such as the degree of mental energy spent by a moving logic charge and the strength of cognitive efforts. Obviously, this postulate is comparable to the electromagnetic potential originally proposed by Maxwell [25].

5.3. Hesitation, Spin, and Dynamic Phase

Reasoning is directional. To solve a reasoning problem correctly, the reasoner needs to solve the problem logically, which is the right direction to proceed. Particularly for deductive reasoning, the reasoner needs to infer a conclusion from a set of premises step by step; each step must be an application of some inference schema or the construction of some mental models. In theory, at each deductive step, the reasoner may have two basic directions to go: completing the step correctly or incorrectly. However, in practice, the reasoner may hesitate between two basic directions. Hence, as in quantum superposition, all other directions are possible from the hesitation state and the linear combination rules. Consider a high-profile test, to reason incorrectly could be costly; naturally, the hesitation is a significant phenomenon in human reasoning. In fact, as we have all experienced, most of the mental energy involved in reasoning in spent in the hesitation state. In general, the more complex and demanding a reasoning task is, the more hesitations that occurs. Thus, we have

Postulate 5.3 (spin). We assume as our working hypothesis that the reasoner has an internal space, in which the hesitation is an intrinsic property characterized by the notion of spin. Each hesitating direction is characterized by a vector, which is a complex number. We also assume all the vectors are bounded within the unit-circle; Hence, the complex numbers have the exponential form,

e^{i θ}

of which the phase

θ

is called the dynamic phase.

Definition 5.3 (the state Born probability). Let

z

be the complex number representing a state of the wavefunction. The Born probability of this state is the squared modulus of

z

, write

{|z|}^{2}

Obviously, during the reasoning processes, mental activities such as activating inference schemas, constructing mental models, perceiving relative difficulties by self-reporting introspective data, hesitating among different directions, etc. are not directly observable. These are called the non-observables. Thus, reasoning states are characterized by the wavefunction. Each state is represented by a complex number, which involves a real component and an imaginative component. The imaginative “i” has two meanings: the observer I and the information may be obtained. Whether or not the information reflects reality is a philosophical issue. In any case, in the quantum theory that the states of the wavefunction are characterized by, complex numbers are not optional, but required. Thus, the dynamic phase is a crucial concept in quantum theoretic modeling.

5.4. The U-Procedure and the R-Procedure

From reasoning experimentation, we may obtain two kinds of raw data. The first kind is objective data, i.e., the accuracy or error rate. However, objective data does not tell us how the reasoner solved the problem. In the mental logic research, in order to make theoretical predictions about problem difficulty, it is necessary to generate schema weights. For doing so, the participants are asked to rate the perceived relative difficulty right after solving each problem. This is the data of the second kind, i.e., the self-reporting introspective data [6]. Moreover, the subjective data and objective data control each other. The perceived difficulty rating makes sense only when the accuracy is high. Otherwise, if a participant solves a problem wrongly, but rate it as a relatively easy problem, it would make little sense. Also, in the mental models research about illusory inferences, the participants are asked to report the degree of confidence [19]. This is introspective data, too. If a participant solves a problem incorrectly but with a low degree of confidence, it should be counted as a mistake, but not an illusion. The illusory inference means that the reasoner solves a problem incorrectly, but with a high degree of confidence. In this paper, the reasoning dynamics are characterized by the so-called wavefunction in quantum theory [26]. The wavefunction consists of two procedures, namely, the U-procedure (U standing for unitary), and the R-procedure (R standing for reduction) [27], which will be explained shortly. Subjective data belongs to the U-procedure while objective data belongs to the R-procedure. Reasoning is a special kind of mental activity. When the reasoner works toward the conclusion, the processes are not directly observable, called the non-observables. When the reasoner makes a conclusion, it becomes observable.

Reasoning is special due to the fact that it has a normative theory, namely, the logic. From the problem types discussed above, we can observe that they all have the right answers. The “right” answers are right because they are logical. That is the reason why, for a reasoning experimental task, subjects are asked to mark a putative conclusion as yes or else no. In other words, based on logic, reasoning has two eigenstates, being right or being wrong. Accordingly, it has only two eigenvalues, i.e., yes or else no. While during the reasoning processes before making the final judgement, the reasoning states are superpositions of yes or no. This is the quantum nature of reasoning dynamics. During such a reasoning process, the reasoner experiences all kinds of hesitations, hesitating back and forth in different frequencies and strengths, which constitute all kind of superposition states. Not hard to imagine that hesitations cost not only cognitive efforts, but also mental energy.

5.5. Mental Energy

By the intuitionistic logic [28], each symbol needs to be constructed. For example, a propositional variable p is an atomic sentence in the propositional logic, and p demands a construction. Accordingly,

\neg p

demands two constructions, one for p and another for

\neg p

. Thus, we have:

Postulate 5.4 (the mental energy quantization). We assume as our working hypothesis that in the reasoning process, mental energy is quantized and denoted by h.

We assume that the mental logic processes and the mental models processes share equal mental energy in the sense that they have the same representational demand. Some evidence for this assumption is based on the observations explained in Table 5.1 below. Table 5.1 lists 10 inference schemas. For each schema, the first line is the mental logic representation of the schema and the second line is the mental model representation of the schema. The schema weight is generated from the mental logic research. It shows that the number of symbols divided by 10 is exactly the schema weights.

From the above, one can observe that the schema weights can be reduced to three levels: 0.5, 1.0, and 1.5. It suggests that the 10-parameter model may be reduced to a 3-parameter model. The statistical analyses show that the 3-parameter model has the same predictive power as the 10-parameter model. It hints that the mental energy in reasoning can be quantized into three levels, or in other words, it can be characterized by three and only three equivalent curves.

5.6. The Yes/No Type Measurement

The Yes/No type measurement was originally proposed by von Neuman [26] and outlined in detail by Penrose [27]. R-procedure stands for the reduction procedure in quantum mechanics. Psychology of reasoning is naturally an empirical science, which must be based on observations. Psychological theories may propose various hypothetical accounts to human reasoning, but mental processes are not directly observable. This is due to various kinds of experimental limitations; in physics this is called the disturbance in our observation. Paul Dirac [29] says that the higher the degree of the disturbance in our observation, the smaller the world we can observe. In this sense, the observation of how people reason is a special kind of micro-observation. For example, the mental traffic mentioned earlier is usually not directly observable, but we still want to measure it. This is what reduction means. In other words, the world of cognitive fluctuations is a microworld. Quantum physicist John Wheeler once said, quantum experiments are playing the 20-questions game with nature. Here we need to play the 20-questions game with the reasoner’s mind. In reasoning experiments, the evaluation task is most often used. The participants are asked to mark Yes or else No for the given putative conclusions. What we can observe directly is whether the reasoners get it right or else wrong. This is a special kind of the Yes/ No type measurement.

The Yes/No (Y/N) type measurement can be characterized by the projector E, which projects an answer to yes or else no. The function of E-projector can be first characterized by the Dirac

δ

-function below.

δ (x) = \{\begin{matrix} \infty, x = x_{0} \\ 0, x \neq x_{0} \end{matrix}

(1)

\int_{- \infty}^{\infty} δ (x) d x = M

(2)

In measurement theory,

δ (x)

in (2) is called a testing function, and

x_{0}

in (1) is called the supporting point of

δ (x)

[30]. We can immediately recognize that

x_{0}

can stand for the right answer in a reasoning task. Interestingly, the formula (2) makes such a commitment that no matter the reasoner’s answer is right or wrong, as long as the reasoner marked yes or no, the reasoner made his/her effort. In other words, the reasoning process exists. Now we look at an important property of the

δ

-function.

Let

ψ (x)

be an any given one-dimensional wavefunction. Assume (

x_{0} + ε

) is a R-interval. Then we have

\int_{x_{0}}^{x_{0} + ε} ψ (ξ) δ (x_{0} + ε) d x = ψ (x_{0})

(3)

This is called the selectiveness property of the Dirac

δ

-function. In the gauge field theory, the integral is the potential, the integrand is the field strength. Formula (3) shows that the reasoner has a potential to get the right answer. This also shows the existentiality of reasoning.

6. The R-Procedure and a Solution of the Measurement Problem

6.1. The Measurement Problem

The R-procedure is about the measurement, which concerns with observations. In order to understand R-procedure, we need a deeper understanding of wavefunction. The quantum theoretic experiments can be characterized in terms of Dirac bra-ket formalism [29]. Let

ψ

be a wavefunction. A state of

ψ

is denoted by

| ψ⟩

, which represents a vector in Hilbert space. This can be seen as a syntactic representation. The semantic meaning of a state is called the amplitude, which is characterized by the squared modulus of a complex number

z

, write

{|z|}^{2}

, which is also called the Born probability (density). As Dirac regards, the probability is the squared possibility. The wavefunction is single-valued and linear. The states of a wavefunction satisfy superposition operation.

The quantum theoretic experimentation can be characterized by the Dirac bra-ket formalism as follows:

⟨φ| A_{i}| ψ⟩

, where

ψ

is a sample state,

φ

is a reasoning experiment, and

A_{i}

is a set of reasoning tasks used in the experiment

φ

. When

A_{i}

are used to keep stimulate reasoners one by one, the reasoners are required to provide answers one after one. Thus,

ψ

becomes a function of

φ

, write

ψ (φ)

, which supposes to be a wavefunction. As Feynman characterized,

| ψ⟩

is the initial state while

⟨φ |

serves as the final state of the experiment [22]. However, as explained earlier, for the evaluation task used in reasoning experiments, such a wavefunction has two eigen values, yes or else no. In other words, it is two-valued, which is inconsistent with the single-value requirement. This is the long-standing measurement problem (or paradox, by Penrose) in quantum theory [26].

6.2. Stochastic Sampling

To solve the measurement problem of reasoning experiments, we propose a new approach called stochastic sampling [31], which is introduced in the following step by step.

Let H be the population of all potential reasoners. Let us consider an any given wavefunction

φ

(x), where x ranges over all of the potential reasoners. We assume that

φ

(x) is one-dimensional without loss of generality for multi-dimensions. Thus, the corresponding Hilbert space we are currently discussing is one-dimensional, denoted by H. Hence, we may treat all the vectors in H as space points also without loss of generality. Now, it introduces an observation operator Q, which is defined below.

Definition 6.1. (the observation operator). For any given a,

a \in H

Q a = a

. We call that

a

is the observational conjugate of

a

. Accordingly, we define

H^{*} = {x

x

ranges over all possible observational

a

. Call

H^{*}

the observational dual space of

H

The necessity of the distinction between the space points and the observational points is analytical to the distinction between the intuitive natural numbers and the set-theoretic enumerers in Gödel’s work [6].

Consider the power set of

H

w r i t e P (H)

. Now, we start to select the elements from

P (H)

. Notice that this selection process is countable, but the cardinal number of

P (H)

is an uncountable infinity. We may reasonably assume this selection process is stochastic.

Definition 6.2. (the internal variable of a sample). We introduce a new variable

x^{j}

x^{j} \in P (H)

. Of course, we also have

x^{j} \subset H

, so we can introduce another variable

x_{i}^{j}

, where the superscript j indicates the j^th element stochastically selected from

P (H)

, the subscript i indicates that x ranges over only those space points within

x^{j}

. It is easy to see that

x_{i}^{j}

connects

H

and

P (H)

. Accordingly, we have

Definition 6.3. (sampling operator). We introduce a new operator

\hat{Q}

, called the sample generator.

F o r a n y g i v e n x_{i}^{j}, \hat{Q} (x_{i}^{j}) = A_{i}^{j}

，

{w h e r e A}_{i}^{j} {\in P (H}^{*})

. Call

A_{i}^{j}

the testing adjoint of

x_{i}^{j}

Definition 6.4 (the stochastic sampling). 1. For any given

{f i n i t e x}_{i}^{j},

once a

x_{i}^{j}

is stochastically selected, its adjoint

A_{i}^{j}

becomes a testing sample. 2. For any

x_{i}^{j}

, if it has not been selected, then its adjoint

A_{i}^{j}

is not a testable sample yet.

Note, this definition is comparable to the expressibility in Gödel’s work [6]. (Hint, the notion of expressibility is necessary to bridge the relations in Piano arithmetic and functions in the first order theory.) While here the definition of stochastic sampling process is necessary to bridge any

{x_{i}^{j} a n d A}_{i}^{j}

from sampling perspectives.

Definition 6.5 (the R-procedure). Let

ψ

stand for an any given sample

A_{i}^{j}

φ

denote a Yes/No type experiment, and q be a Yes/No type stimuli that

φ

can use to test

ψ

. By Dirac bra-ket formalism, we can write this structure as

⟨ ψ ⟩

. When

φ

gives the stimulus q to

ψ

, each operational conjugate

a_{i}^{j}

ψ

returns a Yes/No type response. Thus,

ψ

is a function of

φ, w r i t e ψ (φ)

. This is called the R-procedure of the wavefunction. Note, this idea is from Feynman, who calls

⟨ φ |

the final state and

| ψ ⟩

the initial state of a quantum theoretic experiment.

Definition 6.6 (the sample space). The sample space for the Yes/No type measurement is two-valued, i.e.,

S = [Y e s, N o] .

This means the E-projector has two and only two eigenstates, of which the eigenvalues are Yes and No.

Definition 6.7 (the sample phase). Consider projector E, for each proper sample of Yes/No type measurement,

{E (a}_{i}^{j}) c o n d u c t s a y e s r e s p o n s e o r e l s e a n o r e s p o n s e . T h u s, {E (A}_{i}^{j})

produces a pair of the yes-number c and the no-number d, which in turn produces a sample phase

θ^{j}

with respect to the exponential form of

(c + i d)

. All the possible sample phases form an

U (1)

group, write it G. From Definitions 1 to 4, it is easy to see that G is originally generated from the wavefunction

ψ (x)

, so we write G as

G_{ψ (R)}

Because

G_{ψ} o b v i o u s l y s a t i s f i e s U (1)

symmetry, the stochastic sampling here satisfies the required conservativeness. It is worth mentioning that, in addition to the well-documented dynamic phase and Berry phase in the literature of dynamic analysis, the sample phase introduced here is the third kind of phase. This is one significant character of the R-procedure. For the U-procedure, we have the dynamic phase potential group, write it as

G_{ψ (U)}

Definition 6.8 (Linearization). The linearization operator L is defined by

L (c, d) = (c + i d

Definition 6.9 (the sample Born probability). For any given testing sample

A^{j}

, which produces a yes-number

c

and a no-number

d

. The sample Born probability is defined by

{P (A}^{j}) = | {(c + i d) |}^{2} .

(4)

Born probability is a kind of explanation, which serves as a semantics for the evolution of wavefunction. As Penrose points out [1], the U-procedure and R-procedure must share the same semantics, i.e., the squared magnitude of two eigenvalues.

Theorem 1. (Born rule) The Born probability defined by Definition 9 obeys Born rule.

Proof. Let

A_{i}^{j} = \hat{Q} (x_{i}^{j})

be a testing sample.

E {(A}_{i}^{j}) h a s t w o

eigenstates, Yes or else No. Assume the eigenvalue for Yes is c and the eigenvalue for No is d. Then, by Definition 8, we have

L (c, d) = (c + i d

). Hence, by Definition 9, we have

p (c + i d) = {| ⟨ (c + i d) | A^{j} ⟩ |}^{2} .

(5)

This shows that Definition 6.8 is conformal with respect to the Born rule.

Part III. The Lagrangian and the “Man vs. Men” problem

7. Gauge Symmetries and Gauge Transformations

7.1. The Gauge Invariance

The Lagrangian modeling studies the minimum action, which is defined with respect to the integral of the Lagrangian density function. In order to make this definition hold, the form of the Lagrangian density function has to be conformal. Thus, this section focuses on the so-called gauge transformation and gauge symmetry. Recall that in Section 2.3, we introduced the gauge structure, which is a two-by-two structure. First, it makes clear distinction of the global level and the local level. Second, at each level, it makes clear distinction of the gauge potential and the gauge strength. Note that from the gauge potential to calculate the gauge strength, some differential operations must be applied. The easiest way to explain the gauge potential and gauge strength is through the indefinite integration

\int f (x) d x + C .

In this formula, the whole integration is the gauge potential, the gauge integrand

f (x)

is the gauge field strength. The any given constant

C

is called the gauge freedom. The gauge freedom may be a value function in market dynamics, a pragmatic function in reasoning dynamics, etc. The gauge freedom can be vanished when the appropriate differential operation applied.

From the modeling perspectives, the gauge theory has significant descriptive power. In the gauge theoretic modeling, it makes a clear distinction of the global level and the local level. At the global level, we consider the general reasoner without taking the individual deferences into account. Thus, the dynamic phase of the wavefunction can be an any given constant, write

θ = C

. At the local level, we are talking reasoners and it must take individual differences into account. Hence, the dynamic phase becomes a function, write

θ (x),

where

x

ranges over all the potential individual reasoners. Note that when we talk about individual reasoners, it is not counting them as persons, but the reasoning potentials, including their knowledge bases, trainings, skills, intentions, etc. Holistically, in mathematical terms, it is about the reasoning capacity neighborhood of each individual reasoner. This neighborhood of x is denoted as

∆ x

. Thus, we have

Postulate 7.1 (differentiability). The wavefunction of reasoning is continuous and differentiable. Accordingly, the phase function

θ (x)

is also differentiable.

Recall that in Section 5.1, we claim that the notion of reasoning intention and cognitive effort always go together, and they interact with each other to behave as one force: the logic-cognitive force. The gauge potential,

A_{μ} = (φ, A)

, serves as the field for logic-cognition interaction to occur.

The strength field tensor

F_{μ ν}

is constructed with the complete anti-symmetric structure in order to make the form of Lagrangian density invariant (under Lorentz transformation); we have

L = - \frac{1}{4} F_{μ ν} F^{μ ν},

T r (F_{μ ν} F^{μ ν}) = - \frac{1}{2} i (E^{2} - B^{2}) ψ .

Here,

L

must be a scalar. Indeed, Lagrangian density is what we shall call the margin density in reasoning. Notice that the structure in

F_{μ ν}

involves applying the differential operators to the logic and cognitive potentials respectively, as well as their interactions. So, in the gauge field theory, a state is generally represented by

(\emptyset, \partial_{μ})

. To keep the form

F_{μ ν}

invariant, it requires the gauge symmetries at both the global level and at the local level. In order to satisfy this requirement, we need to introduce the gauge transformations.

7.2. The Global Gauge Symmetry

Postulate 7.2 (the rational reasoner). We assume as our working hypothesis that there exists the fully rational man, called the rational reasoner, who holds the global symmetry in reasoning.

At the global level, the gauge potential of the rational reasoner is the collective abstraction of logicians, psychologists of reasoning, or the ETS (The Center for Standard Educational Testing, Princeton), etc. while the gauge field strength consists of particular logic systems, psychological theories of reasoning, and testing items of logical inferences, prospectively. Obviously, the notion of the rational reason is independent of individual differences among real reasoners. In other words, all the particular reasoners are symmetric to the rational reasoner.

Mathematically, all the discussions so far can be seen as only referring to the internal space of the rational reasoner. Thus, when it moves from one state of the rational reasoner’s potential to another state, we need to make the potential transformation, write

ψ \to ψ' = e^{i θ} ψ

Consider that the dynamic phase is an any given constant,

θ = C

, so

e^{i θ}

is also a constant. Then, in order to keep the forms of Lagrangian density function invariant, we can expect:

\partial_{μ} ψ^{'} = \partial_{μ} (e^{i θ} ψ) = e^{i θ} \partial_{μ} ψ

Note that

e^{i θ}

is kept at the left side of

ψ

as well as

\partial_{μ} ψ

; this is what makes the gauge transformation conformal. This is called the gauge transformation of the first kind, which implies the global gauge symmetry.

The gauge transformation of the first kind seems very simple, but the global symmetry is crucial. Before a GRE test is given, the testing items have to be kept untouchable to each and every test taker. If the item information was leaked, it would break the global symmetry. If the experimental items were leaked, the results would become invalid. Likewise, a logic system must be constructed independent of any individual reasoner. In general, the non-observables or untouchables imply the global symmetry.

7.3. The Local Gauge Symmetry

At the local level, for all kinds of bounded rationality, the individual differences of reasoners are sensitive. We have

Postulate 7.3 (the bounded rational reasoners). We assume as our working hypothesis that there are individual differences of real reasoners. Each reasoner has different gauge potentials and gauge strength in reasoning.

Each particular reasoner has different reasoning potential, including reasoning skills, language capacities, preparations for taking a reasoning test, etc. Accordingly, each individual reasoner may perform differently in taking a reasoning task. For example, the GRE is a high-profile selection test. Of which, the logic inference items are used to disclose the individual differences. These differences become more significant and sensitive. Thus, at the local level, we must pay attention to individual differences.

Recall the notion of the wavefunction

ψ (x),

where x ranges over all the possible reasoners. Accordingly, when we consider the individual differences of the reasoners’ potential, the

θ

is no longer a constant but becomes a phase function

θ (x)

. Consequently, when the potential transforms from one state to another state

ψ (x) \to e^{i θ (x)} ψ (x)

, we have the strength transformation

\partial_{μ} (e^{i θ (x)} ψ (x)) = (e^{i θ (x)} i \partial_{μ} θ (x)) ψ (x) + e^{i θ (x)} \partial_{μ} ψ (x) .

On the right side of the equation, the first term is not what we would expect there, so it makes the transformation no longer conformal. In other words, the standard derivative does not work at the local level. To solve this problem, we need to introduce the new mathematical tools [18], namely, the covariate derivative

D_{μ}

and the gauge field

A_{μ}

, which are defined as below, respectively,

D_{μ} = \partial_{μ} + 𝑖 𝑔 A_{μ}

A_{μ}^{'} = A_{μ} - \frac{1}{g} \partial_{μ} 𝜃 .

Then, we can see below that the gauge transformation at the local level becomes conformal

ψ \to ψ^{'} = e^{i θ} ψ,

{D_{μ} e^{i θ} ψ \to e}^{i θ} D_{μ} ψ

This is called the gauge transformation of the second kind. For those readers who are not familiar with the gauge field theoretic modeling, the derivations below would be helpful. Note that for convenience, the individual variable x is omitted from both 𝜓 and

θ

D_{μ} e^{i θ} 𝜓 = (\partial_{μ} + 𝑖 𝑔 A_{μ}^{'}) e^{i θ} 𝜓 = \partial_{μ} (e^{i θ} 𝜓) + i g {(A}_{μ} - \frac{1}{g} \partial_{μ} θ) e^{i θ} 𝜓 = \partial_{μ} (e^{i θ} 𝜓) + 𝑖 𝑔 A_{μ} e^{i θ} 𝜓 - 𝑖 𝑔 \frac{1}{g} (\partial_{μ} 𝜃) e^{i θ} 𝜓 = (\partial_{μ} e^{i θ}) 𝜓 + e^{i θ} \partial_{μ} 𝜓 + 𝑖 𝑔 A_{μ} e^{i θ} 𝜓 - i (\partial_{μ} θ) e^{i θ} 𝜓 = 𝑖 e^{i θ} (\partial_{μ} 𝜃) 𝜓 + e^{i θ} (\partial_{μ} + 𝑖 𝑔 A_{μ}) 𝜓 - 𝑖 (\partial_{μ} 𝜃) e^{i θ} 𝜓 = e^{i θ} (\partial_{μ} + 𝑖 𝑔 A_{μ}) 𝜓 = e^{i θ} D_{μ} 𝜓

The above derivation is given step by step (which is usually not fully spelled out in textbooks but is by all means a key effort to make for interested social scientists.)

7.4. The “Man vs. Men” Problem

The above discussions can be captured by a general issue in social sciences, which is named the “Man vs. Men” problem. Here, the Man can stand for the rational reasoner, the logician, the psychologist, or a theory at the global level, while the Men may stand for individual reasoners with bounded rationality at the local level. Understandably, the gauge theoretic modeling provides a unified account the Man and the Men.

In Section 2.1, we mentioned the gauge principle, which states that we can’t established the local symmetry without the global symmetry. Here is the original version of the gauge principle: If the gauge transformation of the first kind does not hold, then the gauge transformation of the second kind could not be held. The gauge principle is rooted in an even deeper idea, which is named the Nöether theorem in mathematical physics.

Briefly, the Nöether theorem says that the non-observable implies symmetry, and symmetry implies conservation. In our context, it tells us that the rational reasoner is untouchable for the ordinary reasoners. Such an untouchability makes all the ordinary reasoners symmetric. In turn, such a symmetry keeps the reasoning dynamic system conservative. More intuitively, consider the reasoning section in the GRE. The information of testing items has to be kept untouchable before the test is given. This makes all the test takers in a symmetric position. In turn, such a symmetry protects the credibility and sustainability of the GRE.

Finally, the reasoning dynamics we have constructed is a single-charge dynamic system. It only admits one charge which is the logic charge. Thus, as we explained earlier, it satisfies the mathematical

U (1)

symmetry group. Such a symmetry solves the “Man vs. Men” problem in the domain of reasoning.

8. The Language Cones and the Relativistic Phase Function

8.1. The Language as an Invariant

In most situations, reasoning is a verbal task. As mentioned earlier, the mental logic theory claims that people can automatically activate inference schemas during the text comprehension. The mental models theory posits that people reason by constructing mental models, based on their understanding of the meaning of the premises. Either way, both theories claim that human reasoning is language oriented. Thus, the language, natural or symbolic, mental or verbal, plays the fundamental role in reasoning. This idea is comparable to the light-alike property in special theory of relativity. We propose

Postulate 7 (the invariant). We assume as our working hypothesis that the language, natural or symbolic, mental or verbal, is invariant with highest speed in reasoning, denoted by

c

Here we construct a model of reasoning from the special relativistic perspectives. This is necessary but we will try to make it intuitive and to keep it brief. The mathematics of special relativity is the so-called four-dimensional Minkowski spacetime.

8.2. Interval and the Global Cone

Now we characterize the Minkowski spacetime in terms of reasoning. Each point stands for a permissible reasoner. The neighborhood of a point is called a reasoning event. The main structure is called the interval, which is defined as follows,

(∆ {s)}^{2} = c^{2} {(∆ t)}^{2} - {(∆ x)}^{2} - {(∆ y)}^{2} - {(∆ z)}^{2}

with gauge,

g_{μ ν} = (+, -, -, -)

. The interval format is invariant. In special relativity, on the right side of this equation, the first term can be seen as the energy term. The next three terms are space position terms. The reasoning can be characterized suitably in terms of an interval. We discussed about the mental energy in reasoning in Section 4, and discussed about the relative difficulty of a reasoning take in Section 3. Now let

(∆ {s)}^{2}

stand for reasoning,

c^{2} {(∆ t)}^{2}

stand for the mental energy, and

{(∆ x)}^{2} - {(∆ y)}^{2} - {(∆ z)}^{2}

stand for the relative difficulty of a reasoning task, we may propose

Postulate 8.1 (reasoning). Reasoning can be characterized as the mental energy of the reasoner minus the relative difficulty of a reasoning task. In other words, reasoning is a two-component structure, one is the reasoner, the other is a reasoning task.

We assume as our hypothesis that language travels with the highest but limited speed. Also, the timeframe allowed to solve a reasoning task may be longer or shorter, while the relative difficulty can be greater or smaller. Thus, the performance of reasoning can have three possible cases:

(∆ {s)}^{2} = 0, (∆ {s)}^{2} > 0, a n d (∆ {s)}^{2} < 0 .

This situation can be characterized by a figure, called the light cone. In our context, it should be treated as the global language cone, which is given below.

Figure 1. Shows three possible cases. Case 1, the event is within the cone,

(∆ {s)}^{2} > 0

, called the time-like event. It means that the reasoner has more than enough language energy to solve a reasoning problem with certain degree of the relative difficulty. Case 2, the event is on the surface of the cone,

(∆ {s)}^{2} = 0

, called the null event. It means that the reasoner has just enough (no more, no less) language energy to solve a reasoning problem with certain degree of the relative difficulty. Case 3, the event is within the cone,

(∆ {s)}^{2} < 0

, called the space-like event. It means that the reasoner does not have enough language energy to solve a reasoning problem with certain degree of the relative difficulty. Note that in the global language cone, the cone phase is an any given constant;

i . e ., θ = C .

It is not concerned with individual differences.

Figure 1. Shows three possible cases. Case 1, the event is within the cone,

(∆ {s)}^{2} > 0

(∆ {s)}^{2} = 0

(∆ {s)}^{2} < 0

i . e ., θ = C .

It is not concerned with individual differences.

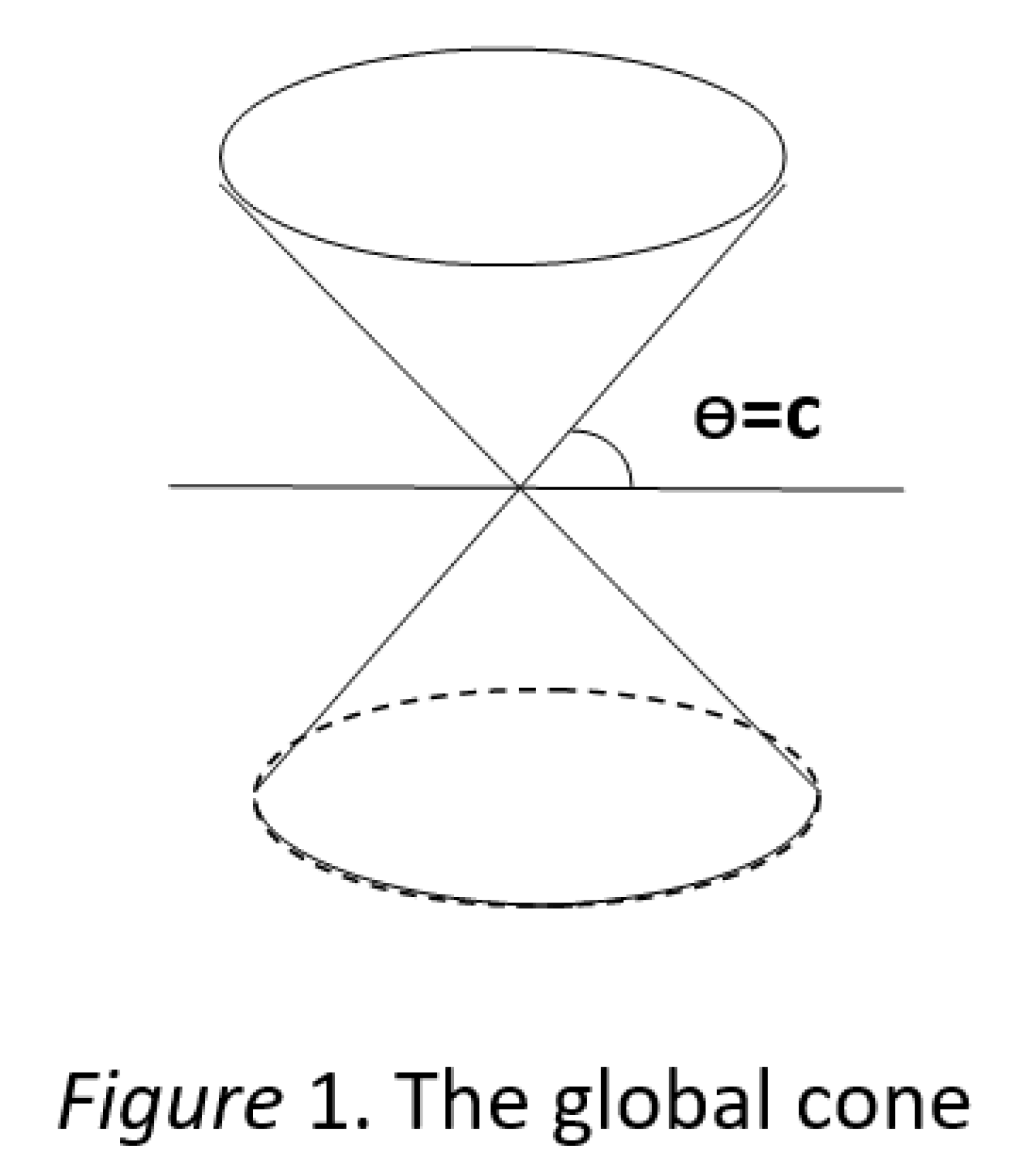
8.3. The Proper Language Cones and the Individual Differences

Language skills play a sensitive role in reasoning. At the local level, there is a lot of the language related individual differences in human reasoning. The reasoner may have different degree of language influence; e.g., the native English speakers have certain advantages over most non-native English speakers in solving logical inference items of GRE or SAT. The reasoners may have different logic skills in solving reasoning problems in a reasoning experiment as well as in everyday life. In many cases, reasoning is sensitive to the timeframe allowed. This is significant to the in-class exams or to any standard educational tests. For a given reasoning problem with certain degree of relative difficulty, such as the lobster problem given in Section 3, the stronger the language capacity a reasoner has, the faster this reasoner is able to solve the problem. In other words, the faster a reasoner can solve a reasoning problem, the shorter the time needed. This time is called the proper time, denoted by

τ

, which is also called the clock time. Different from the absolute time t shared by everyone, the proper time is individualized, so it shall be denoted by

τ_{i}

when necessary. The proper time is defined by

- d τ^{2} = d s^{2}

; thus, the proper time is inverse proportional to the speed of solving a problem. Using proper time, we can define the notion of momentum, also called the four-velocity vector denoted by u as follows

u = \frac{{(∆ S)}^{2}}{τ_{i}} = {[c}^{2} (∆ t)^{2}] / τ_{i} - ({∆ x)}^{2} / τ_{i} - ({∆ y)}^{2} / τ_{i} - ({∆ z)}^{2} / τ_{i}

This idea, borrowed from the special relativity theory, enables us to draw the proper language cones with different shapes for different reasoners, showing below,

In Figure 2a, the individual reasoner has stronger language skills, the shape of the language cone becomes flatter and wider, so it is with a smaller phase

θ_{1}

. The wider

d_{1}

indicates that for a given time frame, this reasoner has a greater chance to solve the problem correctly. In Figure 2b, the individual reasoner has weaker language skills, the shape of the language cone becomes thinner and longer, so it is with a greater phase

θ_{2}

. The narrow

d_{2}

indicates that for the same time frame, this reasoner has a lesser chance to solve the problem correctly. Note, here the key point is that we have generated a relativistic phase function,

θ (x)

, where the variable x ranges over all the possible individual reasoners.

8.4. Wittgenstein and the Language Game

Wittgenstein characterizes the communication as playing the language game. He also realizes that the language game is based on some psychological game. What psychological game do people play for reasoning? In psychology of deductive reasoning, we may image that the game is similar to “The Servant of Two Masters,” by Carlo Goldoni.

The natural language has its syntax (grammar) and semantics. The formal language of a logic system has its formal syntax and formal semantics. In psychology of reasoning, as we mentioned in Section 2, the mental logic theory claims that people reason by applying inference schemas akin to inference rules. This can be classified as a syntactic approach. Call it the Master Synon, denoted by

e^{-}

. The mental models theory claims that people reason by constructing mental models based on the understanding of the meaning of premises. This can be classified as a semantic approach. Called it the Master Semon, denoted by

e^{+}

. Here the language naturally plays the role of the servant, called the Servant Langon, denoted by

λ . T h e i n t e r a c t i o n s o f

three starts can be shown in Figures 3a,b below.

Table 32. In quantum theory, the spin is an intrinsic property of particles. The syntax and the semantics form the two-leg structure of language. Imagine that when the reasoning process is running, one leg is forward and the other is backward, and they reciprocate. Briefly, on one hand, this means that each leg, either Master Synon or Master Semon spins one second (

s p i n \frac{1}{2})

. On the other hand, no matter which leg is moving forward, the language is always moving forward. It means that the Servant Langon spins one (spin 1).

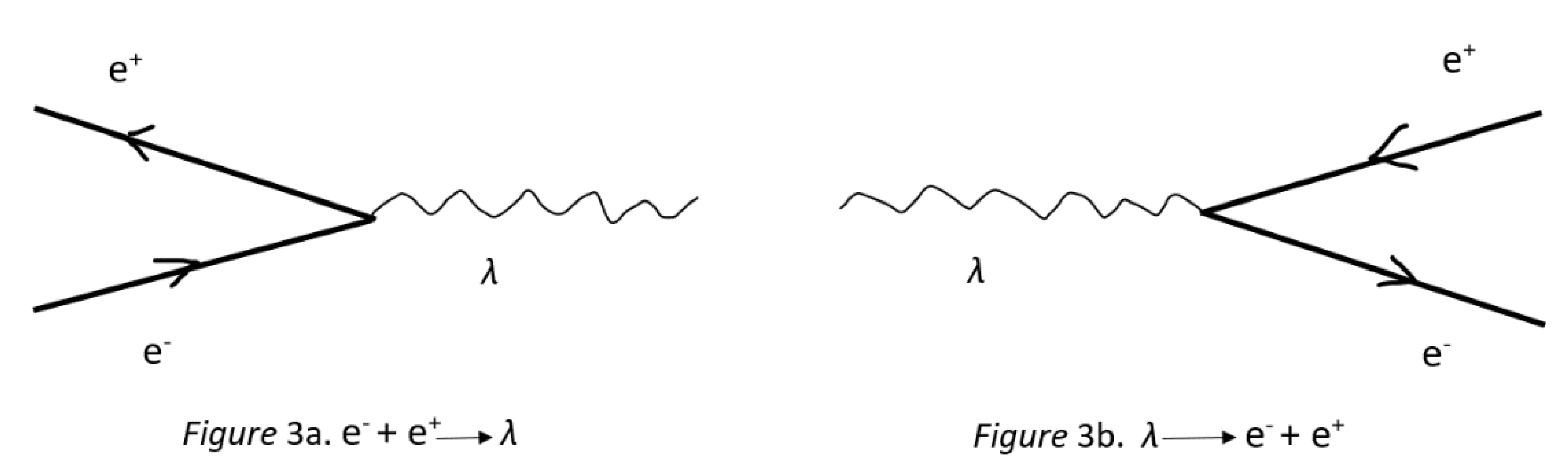
9. General discussion

9.1. An Outline of the Contributions

We made the following contributions in the work presented in this paper. First, the current states of the psychology of reasoning are critically reviewed from theoretical as well as empirical perspectives. The long-standing controversies between logicians and psychologists are clarified by introducing the gauge theoretic structure. The debates between the mental logic theory and the mental models theory are carefully reviewed by identifying the problem types used in the empirical studies. Certain mental fluctuations are found and a quantum theoretic solution is examined.

Second, we proposed a novel framework of the reasoning dynamics. It solved the measurement problem within the Hamiltonian framework. The modeling structure underlying reasoning dynamics is the electrodynamics. They are both single-charge dynamic systems sharing the U(1) symmetry. The mental logic and the mental models theory are hypothetical theories, which are now characterized as wavefunctions in a unified account of the dynamic analysis with Yes/No measurements. We solved the measurement problem of higher cognition research with Yes/No measurements. The stochastic sampling method is introduced, which will have a wide range of applications in social sciences.

Third, we proposed a novel metatheoretic framework of reasoning dynamics within Lagrangian framework. It solved the “Man vs. Men” problem by gauge theoretic modeling, which makes the distinction of the global level and the local level. At each level, the gauge transformations are applied to achieve the global symmetry and the local gauge symmetry. It explains the meanings of the gauge principle and the N

ö

ether theorem. Here, the key concepts are the covariate derivative and the gauge field.

Fourth, the special theory of relativity is applied to address the “Man vs. Men” problem. This is necessary because the quantum field theory applied in this paper is an integration of the quantum mechanics and special relativity. It explains how to draw the global language cone and the individualized local language cones. Here, the key concept is the relativistic phase function.

Finally, it is worth to point out that borrowing modeling methods from physics has a long tradition in psychology. The classical psychophysics borrowed a great deal from the Newtonian physics. Theses Newtonian methods have certain advantages for perception research but disadvantages to higher cognition research. The modern physics including the quantum physics and the theories of relativity has developed more than a century. However, psychology has rarely utilized these new developments in modern theoretical physics. Note that the reasoning dynamics proposed in this paper shares the structure of the quantum electrodynamics. At this point, it is a breakthrough. Let us make it clear that borrowing conceptual and modeling tools from theoretical physics is strengthening psychological research, but no intention to make it as physics. This idea is from the Bourbaki structuralism. An excellent earlier example is the Piaggi approach to study cognitive structures.

9.2. The Directions for Future Work

The approach of dynamic analysis developed in this paper has future work directions. These directions are briefly described below.

1. Human reasoning is heterogeneous [33]. This paper is mostly focused on deductive reasoning. There are a number of other reasoning domains, such as induction, abduction, causal reasoning, reasoning with pragmatic perspectives, deontic reasoning, etc. The framework of reasoning dynamics can be well extended to these reasoning domains.

2. The higher cognition research has three major domains, namely, reasoning, decision making, and game theoretic interactions. Each subdomain has its normative theory, namely, logic, standard decision theory, and game theory. Thus, the three subdomains share certain characteristics in observations. First, the corresponding mental processes are not directly observable. Second, the observations are mostly Yes/No measurements. Third, using verbal tasks, we studied decision with underlying reasoning processes and game theoretic interactions with underlying reasoning processes [34]. In the domain of decision, there are controversies between the standard decision theory [35] and psychology of decision making [36]. In the domain of game theoretic interactions, there are controversies between the standard game theory [37] and the behavioral game theory [38]. Thus, these domains all need to deal with the measurement problem, as well as the “Man vs. Men” problem. Thus, applying the dynamic analysis described above to these domains remains an interesting challenge.

3. We solved the measurement problem within the Hamiltonian picture, and we also solved the “Man vs. Men” puzzle within the Lagrangian picture. We know that both the Hamiltonian and the Lagrangian are based on the generalized coordinates with independent variables, which are friendly to apply in social sciences. Their shared mathematical foundation is the Grassmann algebra. Introducing these topics would go beyond the scope of the present paper. Nevertheless, why the measurement problem and the “Man vs. Men” problem are always tied with each other is a topic concerning deeper issues which deserves more careful thinking.

References

J. Forder (1975), The language of thought. Harvard University Press.
M. D.S. Braine (1978). On the relation between the natural logic of reasoning and standard logic. Psychological Review, 85: 1-21. [CrossRef]
L. J. Rips (1983). Cognitive processes in propositional reasoning. Psychological Review, 90(1), 38. [CrossRef]
P.N. Johnson-Laird (1983). Mental Models. Cambridge University Press.
Holyoak, K.J. and Glass, A. (1975). The role of contradictions and counter examples in the rejection of false sentences. Journal of Verbal Learning and Verbal Behavior. 14, 215-239. [CrossRef]
Y. Yang, M. D. S. Braine, and D. O’Brien (1998). Some empirical justifications of a mental predicate logic. Chapter 12, in M.D.S. Braine and D.P. (Eds.), Mental Logic. Mahwah, NJ: Lawrence Erlbaum Associates.
Yang, Y., Bringsjord, S., and Bello, P. (2006). Mental possible world mechanism: A new method for analyzing logical reasoning problems on the GRE. Journal of Experimental and Theoretical Artificial Intelligence. Vol. 18 No. 2 157-168.
Van der Henst, J-B, Yang, Y. and Johnson-Laird, P.N. (2002). Strategies in sentential reasoning. Cognitive Science, 26, 425-468. [CrossRef]
Yang, Y. and Johnson-Laird, P.N. (2001). Mental models and logical reasoning problems in the GRE. Journal of Experimental Psychology: Applied. 7 (4), 308-316.
M.D.S. Braine and D.P. (Eds., 1998), Mental Logic. Mahwah, NJ: Lawrence Erlbaum Associates.
P. N. Johnson-Laird and R. M. J. Byrne (1991), Deduction. Mahwah, NJ: Lawrence Erlbaum Associates.
O'Brien, D.P., Braine, M.D.S., & Yang, Y. (1994). Propositional reasoning by mental models? Simple to refute in principle and in practice. Psychological Review, 101,711-724.
P.N. Johnson-Laird, Ruth M. J. Byrne, and Walter Schaeken (1994). Why models rather than rules give a better account of propositional reasoning: A reply to Bonatti and to O’Brien, Braine, and Yang. Psychological Review 101 (4), 734-739.
Braine, M.D.S., O'Brien, D.P., Noveck, I.A., Samuels, M.C, Lea, R., & Yang, Y. (1995). Predicting intermediate and multiple conclusions in propositional logic inference problems: Further evidence for a mental logic. Journal of Experimental Psychology: General, 124, 263-292.
Ray. S. S. Jackendoff (1990). Semantic structure. MIT Press, Cambridge, Mass.
Philip Johnson-Laird (2006/2008). How we reason. Oxford University Press Inc. New York.
Yang, Y. and Bringsjord, S. (2003). Some initial empirical justifications for mental metalogic: The case of reasoning with quantifiers and predicates. In R. Alterman & D. Kirsh (Eds.): The Proceedings of the Twenty-fifth Annual Conference of the Cognitive Science Society, 1275-1280. Mahwah, NJ: Lawrence Erlbaum Associates.
David Bailin and Alexander Love (1986/2019). Introduction to gauge field theory. CRC Press.
Yang, Y. and Johnson-Laird (2000). Illusions in quantified reasoning: How to make impossible seem possible, and vice versa. Memory & Cognition. 28 (3), 452-465.
Yang, Y. and Johnson-Laird, P.N. (2000). How to eliminate illusions in quantified reasoning. Memory & Cognition, 28 (6), 1050-1059. [CrossRef]
Yang, Y., Zhao, Y., Zeng, J., Guo J., Ju, S. and Bringsjord, S. (2005). Some empirical justifications for the universalness of the mental logic/model paradigm. In B. Bara, L. Barsalou, & M. Bucciarelli (Eds.), Proceedings of the Twenty-Seventh Annual Conference of the Cognitive Science Society, 2399-2404. Mahwah, NJ: Lawrence Erlbaum Associates.
R. Feynman, R. B. Leighton, and M. Sands (1971). The Feynman lectures on physics, Vol. 3. Addison Wesley.
Allen Newell and Herbert Simon (1972). Human Problem solving. Echo Point Books & Media, LLC.
R. Feynman (1971). Quantum electrodynamics. Basic Books.
C. N. Yang (2014). The conceptual origins of Maxwell’s equations and gauge theory. Physics Today, November, 2014. [CrossRef]
von Neuman (1955/1983), The Foundations of Quantum Mechanics. Princeton University Press, Princeton, New Jersey.
R. Penrose (2004), The Road to Reality: A Complete Guide to the Laws of Universe. Random House Inc., New York.
Bell, John and Machover, Moshe (1977). A Course in Mathematical Logic. North Holland Publisher.
P. A. M. Dirac (1930/1958), Principles of Quantum Mechanics. Oxford University Press, Pearson Education Inc. New York.
D. H. Griffel (1981/2002), Applied Functional Analysis. Dover Publications, Inc. Mineola, New York.
Y. Yang (2024). The revised Schrödinger equation as a solution of measurement paradox: A unified model of the U-procedure and R-procedure. Under review, Annals of Mathematics, Princeton.
Feynman, R. (1985/2006). QED, the strange theory of light and matter. Princeton University Press. Princeton, New Jersey. [CrossRef]
Bringsjord S. and Yang, Y. (2006). Human reasoning is heterogeneous – as Jon Barwise informed us. Journal of Experimental and Theoretical Artificial Intelligence. Vol. 18, No. 2, 117-119.
Yang, Y. (2006). Toward a mental decision logic of the small-grand problem: Its decision structure and.
arithmetization. In R. Sun and N. Miyake (Eds.), Proceedings of the Twenty-Eighth Annual Conference of the Cognitive Science Society, Mahwah, NJ: Lawrence Erlbaum Associates.
Savage, Leonard (1954/1972). The foundations of statistics. Dover Publications.
Kahneman, Daniel (2011). Thinking, fast and slow. Farrar, Straus and Giroux. New York, New York.
Osborne, Martin and Rubinstein, Ariel (1994). A course in game theory. MIT Press.
Camerer, Colin (1999). Behavioral game theory. Princeton University Press. Princeton, New Jersey.
Lee, T. D. (1988). Symmetries, asymmetries, and the world of particles. The University of Washington Press, Seattle.

Table 4. 1.

		Experimental Characteristics
	Disturbance	Low Macro-world	High Micro-world
Observation
Outward		Slow / Large	Fast / Small
Inward		Fast / Simple	Slow / Complex

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Principles of Reasoning Dynamics

Abstract

1. Introduction

2. Theoretical Controversies and the Gauge Structure

2.1. Reasoning is One of the Core Capacities of Human Cognition

2.2. Historical Controversies and Debates

2.3. Gauge Structure

3. An Empirical Puzzle and the Quantum Theoretic Solution

3.1. An Empirical Puzzle

3.2. Failed Mental Metalogic and the Quantum Lightening

3.4. A Set of New Questions

4. Why Do We Need a Quantum Model?

4.1. The Directness of Observations

4.2. Types of Experimentations

4.3. The Orthogonal Law and the Diagonal Rule

5. The Wavefunction and the Measurement Problem

5.1. Reasoning Dynamics: The U-Procedure

5.2. Logic Charge and Cognitive Field

5.3. Hesitation, Spin, and Dynamic Phase

5.4. The U-Procedure and the R-Procedure

5.5. Mental Energy

5.6. The Yes/No Type Measurement

6. The R-Procedure and a Solution of the Measurement Problem

6.1. The Measurement Problem

6.2. Stochastic Sampling

7. Gauge Symmetries and Gauge Transformations

7.1. The Gauge Invariance

7.2. The Global Gauge Symmetry

7.3. The Local Gauge Symmetry

7.4. The “Man vs. Men” Problem

8. The Language Cones and the Relativistic Phase Function

8.1. The Language as an Invariant

8.2. Interval and the Global Cone

8.3. The Proper Language Cones and the Individual Differences

8.4. Wittgenstein and the Language Game

9. General discussion

9.1. An Outline of the Contributions

9.2. The Directions for Future Work

References

MDPI Initiatives

Important Links

Subscribe