Prerpints.org logo
Preprint
Article

An Efficient Shunt Modulated AC Green plug - Switched Filter Compensation Scheme for Nonlinear Loads

Altmetrics

Downloads

75

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (1.01MB )

Submitted:

15 May 2024

Posted:

15 May 2024

You are already at the latest version

Alerts
Abstract
Nonlinear loads, a crucial component of power systems grids, pose a challenge due to harmonics injection. Our research tackles this issue with a novel approach - a modified green plug / switched filter compensation scheme using fuzzy logic controllers. This innovative scheme, presented in the paper, utilizes dual action pulse width modulation to ensure switching functions from harmonic reduction and capacitive compensation for inrush nonlinear type AC loads.  The scheme's multi-loop regulations and online switching effectively handle dynamic type slow acting inrush, motorized and other rectifier type-nonlinear loads, enhancing power factor, power quality at source and load buses, and reducing total harmonic distortion at key source and sensitive nonlinear load buses. A simulation model in the MATLAB/SIMULINK software environment demonstrates the efficiency of the proposed FACTS technique. The results show that voltage, current, active power, reactive power, power factor regulation, and effective energy utilization are achievable with the designed FACTS-MFCC-SFC. The switched modulated AC green plug filter significantly improves power quality and enhances power factor in the case of inrush and nonlinear loads.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Over the past two decades, power quality issues have become increasingly prevalent in electrical power transmission and distribution systems. Numerous devices connected to microgrids, and modern distribution systems contribute to power quality issues, including harmonics distortions in the grids. Key sources of harmonics in modern distribution systems include motor drives, electric vehicle chargers, Compact Fluorescent Lamps (CFLs), LEDs, and inverters utilized as interfaces for storage systems and Distributed Generation (DG) units [1]. Flexible Alternating Current Transmission Systems (FACTS) devices offer a viable solution to improve power quality by addressing various issues such as long and short duration voltage variations, voltage imbalance, waveform distortion, voltage fluctuation, and power frequency variations, primarily caused by loads connected to electric supply systems [2,3]. Power outages, generator malfunctions, frequency control challenges, and unplanned prolonged blackouts are among the commonly encountered issues. Modern automation and industries rely on sensors, microprocessors, relays, and other sophisticated electrical equipment. While these devices enable complex operations, they are highly sensitive to power quality. As a result, utilities, customers, and load device suppliers all face financial implications [3].
The advantageous point of the proposed scheme is its performance by adding the fuzzy logic control typ-2 scheme that reduces harmonics and improves power factor as well as reduces transient over voltage conditions with FACTS-MFCC-SFC [4,5].
Various capacitor banks, including fixed, switched, and modulated types, have been widely deployed in modern electrical systems to mitigate feeder active and reactive power losses and enhance the system response to events like faults, load switching, and short circuits [6]. Fixed power filters, known for their cost-effectiveness and simple structure, are commonly used in industrial networks to enhance power quality [7]. However, these fixed-parameter power filters and capacitor banks may have limited effectiveness for dynamic loads and can potentially lead to resonance issues in certain scenarios [8,9].
The paper introduces an innovative AC switched filter compensation method employing dual-action pulse width modulation. This approach facilitates the switching functionality for both harmonics reduction and capacitive compensation, particularly suitable for addressing inrush-type nonlinear AC loads. The novel multi-loop regulations and online switching mechanisms are designed to effectively mitigate the effects of dynamic and reduce the acting of inrush current [10]. This compensation strategy aims to improve power factor and power quality at source and load buses and reduce total harmonic distortion at critical source and sensitive nonlinear load buses.
Moreover, paper delves into Type-2 fuzzy logic, an advancement from Type-1 fuzzy logic, which addresses uncertainties in defining membership functions by introducing an uncertainty zone between upper and lower membership functions. This enables each data point to possess two degrees of membership when mapped using interval Type-2 fuzzy sets, managed by governing rules. However, direct defuzzification becomes impractical due to added encoded data, necessitating reduction techniques to simplify algorithm complexity [11]. We utilize the defuzzification process from Type-1 Fuzzy Logic to generate crisp values, employing triangle membership functions in our study. Shifting to dynamic controllers, we explore their enhanced functionality with additional loops operating in an error-sequential manner. Our research also investigates an innovative tri-loop regulation setup at the common source bus, strategically addressing changes in voltage and current. Leveraging a modulated filter capacitive compensator and a fast PWM-modulated switching system, we effectively reduce voltage transients and minimize inrush current ripple, addressing various scenarios arising from load-switching and short-term faults [12]. The fuzzy logic controller is flexible as it can deal with hidden nonlinearities in the loads and other inrush transient load behaviors. The flexibility is busted by fast response and tolerance to hidden nonlinear load dynamics [13].
The present paper proposes a novel low-cost FACTS-MFCC-SFC device that will improve the system performance. The proposed device is validated in a MATLAB-Simulink -2023b software environment using Type-2 FLC controller for voltage stabilization and power delivery to the load. This FACTS-MFCC-SFC device uses switches for implementing dynamic error-driven control strategies, thereby achieving improved response. The study also compares operation for both with and without the MFCC-FACTS device, tests for harmonic reduction, power quality and improvements in power factor correction.

2. Literature Review

Chao, Wujie, et al. delved into the limitations of passive filters in LCC-HVDC projects, particularly regarding harmonic filtering and system impedance dependence. Conversely, they introduced Hybrid Active Power Filters (HAPF) as a versatile solution offering high controllability and effective compensation for various harmonics, flicker suppression, and reactive power compensation. Unlike passive filters, HAPF's characteristics remain stable regardless of system impedance, mitigating resonance risks. The adaptive function enables automatic harmonics tracking and compensation, as evidenced by its successful application in the Fujian Guangdong DC interconnection project, indicating its suitability for high-voltage environments and future DC projects [14]. In a different vein, Wang, Lianjie, et al. presented a TPMP Si & SiC hybrid inverter coupled with a specialized compensating current modulation strategy. This approach effectively addressed large low-frequency harmonic currents, showcasing high efficiency and comparable performance to all SiC-MOSFET inverters. The proposed hybrid inverter offered cost savings and compact filter volumes, validated by simulation results [15].
Furthermore, Catata, Elmer O. Hancco, et al. explored the presence of stroke components in the electrical grid and proposed in-line adaptive filters for DC-link voltage control loops. These filters aimed to mitigate stroke frequency components from Synchronous Reluctance Generators (SRG), reducing distortion in grid current waveforms. Experimental results demonstrated the effectiveness of these adaptive filters in adapting to SRG stroke frequencies and minimizing distortion, particularly when integrated with voltage compensators [16]. Similarly, Singh, Vikram, et al. addressed harmonic currents generated by nonlinear loads and evaluated the performance of a Shunt Active Power Filter (SAPF) in power distribution systems using MATLAB/Simulink. They implemented SAPF with a combination of hysteresis current control (HCC) and Pulse Width Modulation (PWM) Generator, effectively maintaining total harmonic distortion (THD) of supply currents below specified limits [17].
Moreover, Lima, Vitor Leobet, and Tiago Jackson May Dezuo proposed an adaptation to existing switching rule design methods to address time-varying nonlinearities in Shunt Active Power Filters (APF). This modification aimed to improve harmonics compensation and power factor correction when dealing with nonlinear loads, outlining future research directions for extending the approach to three-phase systems and minimizing sensor information requirements [18]. Additionally, Lin, Hongyi, et al. tackled limitations in traditional high-power Active Power Filters (APF) using IGBT by proposing a novel approach employing Proportional-Integral (PI) and repetitive control with shorter sampling times. Simulation results demonstrated improved harmonic compensation with higher switching frequencies, ensuring accurate compensation even for high-order harmonics and dynamic load changes [19].
Furthermore, Daftary, Dhrumil, and M. T. Shah focused on modeling and simulating Hybrid Active Power Filters (HAPF) to reduce the kVA rating of Shunt Active Power Filters (SAPF), leading to improved power quality and reduced VA rating. Their findings suggested the potential of hybrid power filters to enhance power quality in grid systems [20]. Lastly, Nolasco, Diego HS, et al. introduced an automatic power quality diagnosis method based on the online estimation of voltage and current total harmonic distortions indices. This method utilized a fuzzy system to assess the impact of harmonic distortions on power quality, providing linguistic and quantitative diagnoses without requiring external expertise [21].

3. System Description

The Single-line diagram of AC system sample study of three-phase AC system supplying loads is shown in Figure 1. Figure 2 shows the FACTS-MFCC-SFC Scheme of the AC Three-phase system grid network. It represents Simulink MATLAB software of the novel dynamic error-driven tri-loop FLC applied to lower switching transients, current inrush excursions, as well as in the low voltage utilization system for effective power/energy utilization and power quality improvement for the type of load depicted in [22,23].
The Single-line diagram sample study of a three-phase AC system consists of the comprises a synchronous generator (driven by Source) that delivers the power to a local hybrid load (Linear, DC ARC, and Induction Motor Load) and is connected to an infinite bus through a 10km transmission line. The main components of the AC system are:
  • Three-phase AC Grid Source.
  • Novel Modulated Filter-Capacitor compensator MFCC-SFC Filter scheme.
  • Novel dynamic error-driven tri-loop Type-2 FLC.
  • Three different Electrical Hybrid Nonlinear Loads.
  • Transformers for voltage change from 138 kv to 25kv and then 25kv to 4.16 kv.
The best way to ensure high efficiency is to minimize the active power loss during the power transmission process. Active power loss reduction strategies with power factor regulation efforts can lead to a more efficient power transmission system [24,25]. At the same time, regulating the power factor (PF) is crucial during power transmission, as the PF contributes substantially to transmission efficiency (T.E) [26,27]. Minimizing losses and maintaining reliability play a crucial role in providing end-consumers a stable and cost-effective electricity supply while also contributing to sustainable energy practices [28].
Transmission efficiency is the power obtained at the receiving end of a transmission line, which is generally less than the sending end power due to active power losses in the line resistance. The ratio of the receiving end power to the sending end power of a transmission line is known as the transmission efficiency of the line, as shown in Equation 1.
% T .   E . , η T = Receiving end power Sending end power × 100
= V R I R cos ⁡ ф R V S I S cos ⁡ ф S × 100
Where: V R ,   I R are the receiving end voltage and current.
cos ф R is the receiving end power factor (Lagging).
V S , I S are the sending end voltage and current.
cos ф S is the sending end power factor.

4. FACTS-MFCC-SFC Scheme

The proposed Low-Cost FACTS-MFCC-SFC dynamic voltage stabilization device is a member of the switched capacitor compensator and modulated switching/modulated power filter family [29]. Using a double-switched shunt capacitor bank and two shunt-linked fixed capacitors for the proposed FACTS-MFCC-SFC minimizes the overall harmonics distortion and improves power quality and power factor. Moreover, the system's ground is linked to a tuned arm filter to improve the overall performance. FACTS-MFCC-SFC has two modes of operation: a capacitive compensation mode and a tuned arm filter mode that utilizes the controlled IGPT switches S1 and S2 as shown in Figure 2.
The MFCC filter acts as a modulated admittance and point of connection, usually near nonlinear loads. The duty cycle ratio is adjusted online using the multi regulation total error to ensure dynamic matching to fast and slow-acting nonlinear variations. The dual function of the tuned arm filter is complemented by the adjusted capacitive compensation level for nonlinear reactive loads, motorized inrush loads, and cyclical loads.

5. Type-2 Fuzzy Logic Controller

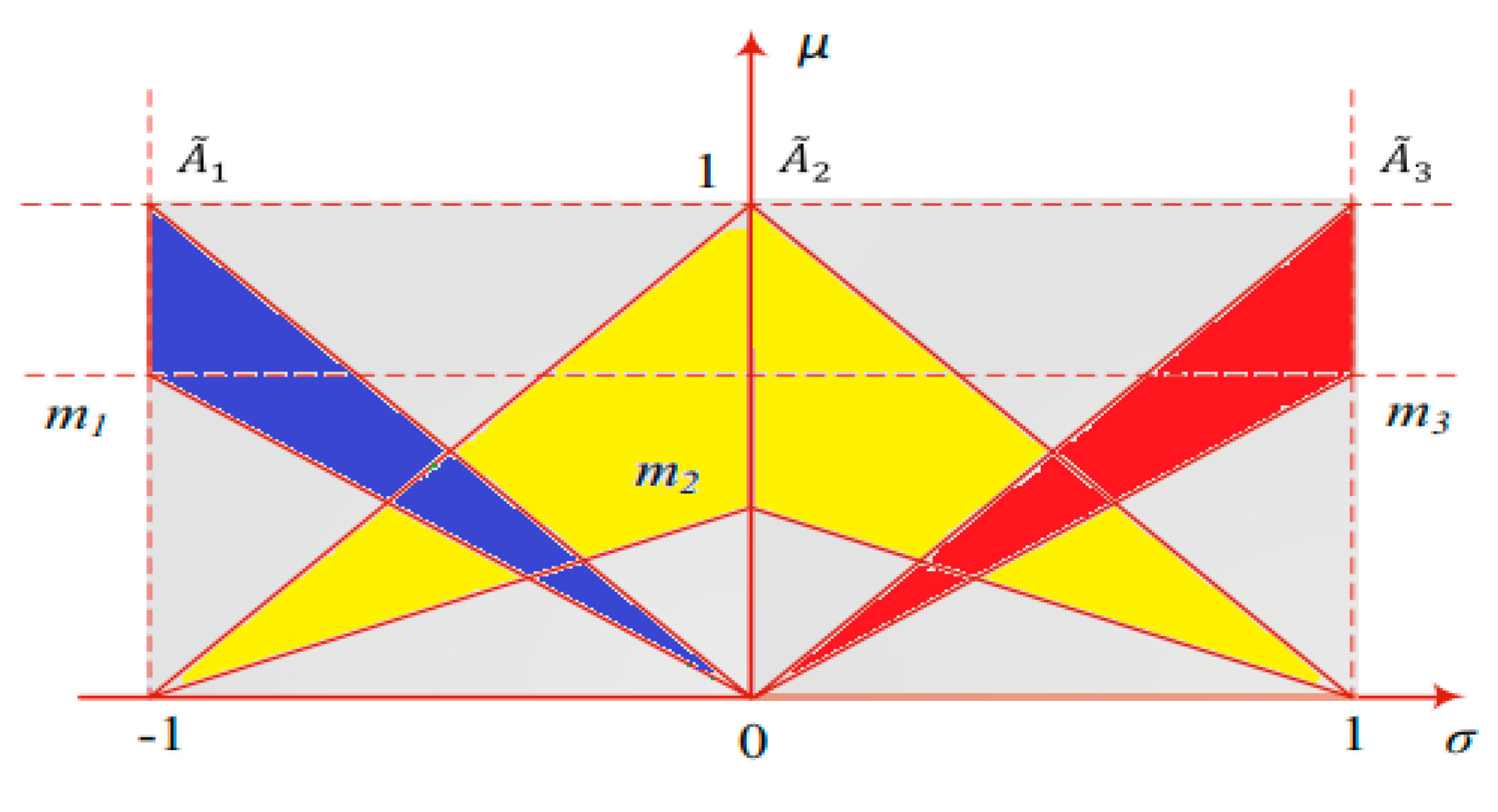
The fuzzy logic controller is flexible as it can deal with hidden nonlinearities in the loads and other inrush transient load behaviors. The flexibility is busted by fast response and tolerance to hidden nonlinear load dynamics [13]. The purpose of type-2 fuzzy logic, which is an expanded form of type-1 fuzzy logic, is to capture the ambiguities involved in defining type-1 fuzzy membership functions. To perform this task, a footprint of uncertainty is introduced in the type-1 Fuzzy sets. Between the upper and lower fuzzy membership functions lies this ambiguous imprint. Consequently, when mapping real-world data using interval type-2 fuzzy sets, any such data will now have two degrees of membership [30]. The fuzzification procedure is now completed. The fuzzified lower and upper membership levels function according to rules, and each rule is assessed sequentially. Since there is an additional encoded data, defuzzification is not possible to be accomplished directly. As a result, a particular kind of reduction technique is presented to lessen the algorithm's complexity. There are many other kinds of reduction algorithms, and the Karnik-Mendel technique is the most used one. Nevertheless, due to the complexity of this procedure, some computationally less expensive techniques have also been proposed. The same defuzzification process used for type-1 Fuzzy Logic is used to generate crisp value following this kind of reduction. In our study, we have represented upper and lower fuzzy sets using triangle membership functions as shown in Figure 5 and Figure 6 [31,32].
The main loops are used to keep the monitor out for any errors in the voltage or current of the bus. The controller's time delay and scaling parameters are chosen using offline guided trial and error.
It is possible to mitigate any inrush, dynamic, sudden excursion changes that may appear in the bus voltage and current using the innovative tri-loop regulation set-up at the common source bus. In the meantime, loop decoupling in a dominant voltage stabilization loop is guaranteed by loop-weighing factors. This methodology guarantees a prompt reaction and a minimal quantity of errors in general. [33]. Using a modulated filter capacitive compensator, this method takes advantage of optimal switching based on system requirements. Furthermore, a fast PWM-modulated switching system consisting of a dynamic multi-regulation time-descaled error-driven controller is used for the green plug filter [34]. This design provides lower damped voltage transients, reduced inrush current ripple content, and dynamic interface bus voltage regulation by alternating between static capacitive compensation and the tuned arm filter. These situations can result from load-switching, fluctuations in the wind pattern, self-excited capacitor banks within the system, and/or short-term in the SC and OC faults.
Dynamic controllers with extra loops activated in an error-sequential method. The dynamic quad-loop controller is made up of two main loops and two sub-loops, as shown in Figure 3. The inputs and/or outputs of the interval type-2 FLC are represented by interval type-2 fuzzy sets [35,36]. Real-time robot FLC design is made possible using interval type-2 FLC, which simplifies calculation compared to general type-2 FLC, which is computationally demanding [37,38]. The structure of an interval type-2 FLC and the Fuzzifier, Inference Engine, Rule Base, Type-Reducer and a De-Fuzzifier are shown in Figure 4.
Preprints 106553 g003
Figure 3. Dynamic Tri-Loop Tri-regulation Controller for the AC SFC Filter Compensator.
Figure 3. Dynamic Tri-Loop Tri-regulation Controller for the AC SFC Filter Compensator.
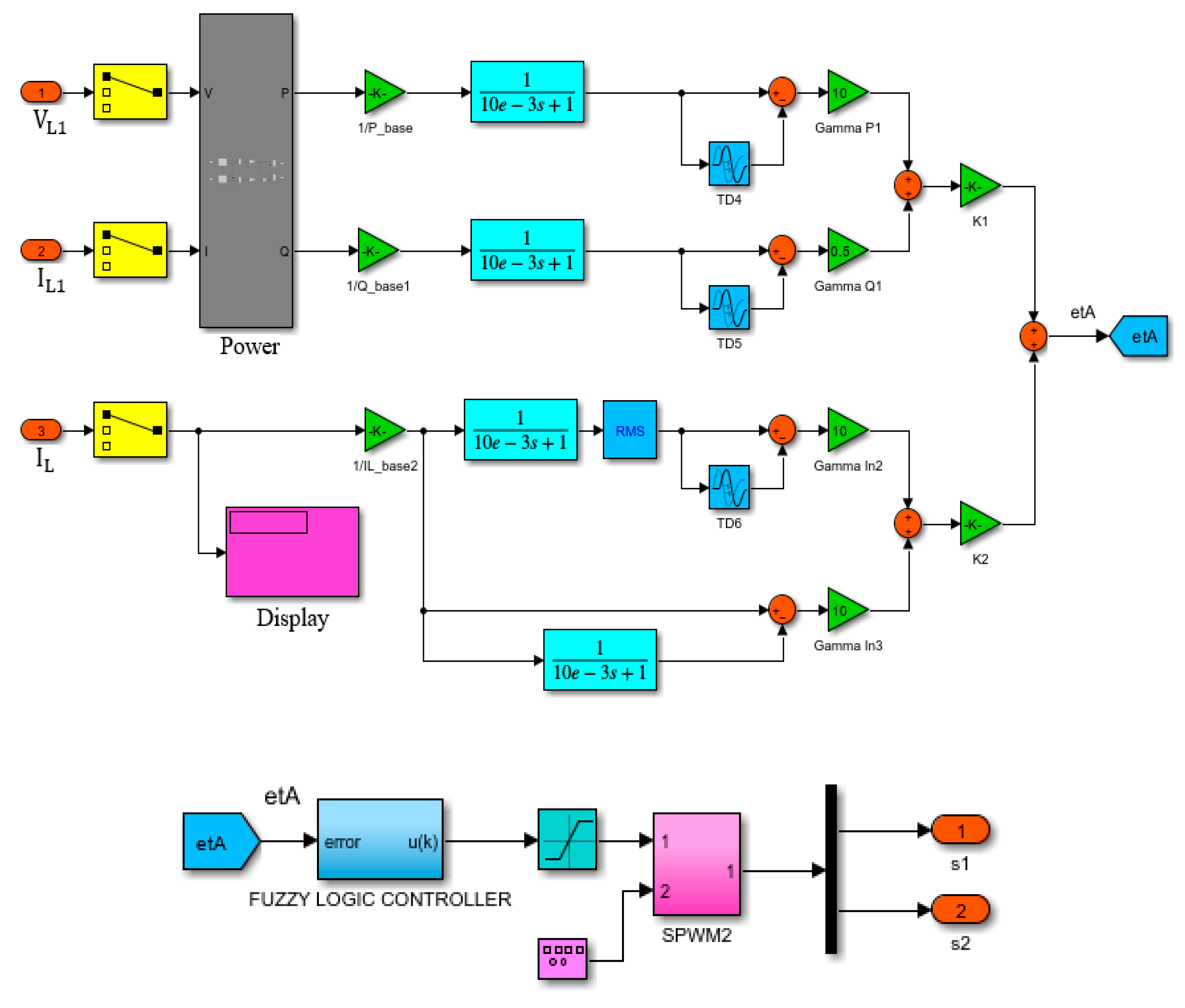
Preprints 106553 g003
Preprints 106553 g004
Figure 4. Structure Flow of Interval Type-2 Fuzzy system.
Figure 4. Structure Flow of Interval Type-2 Fuzzy system.
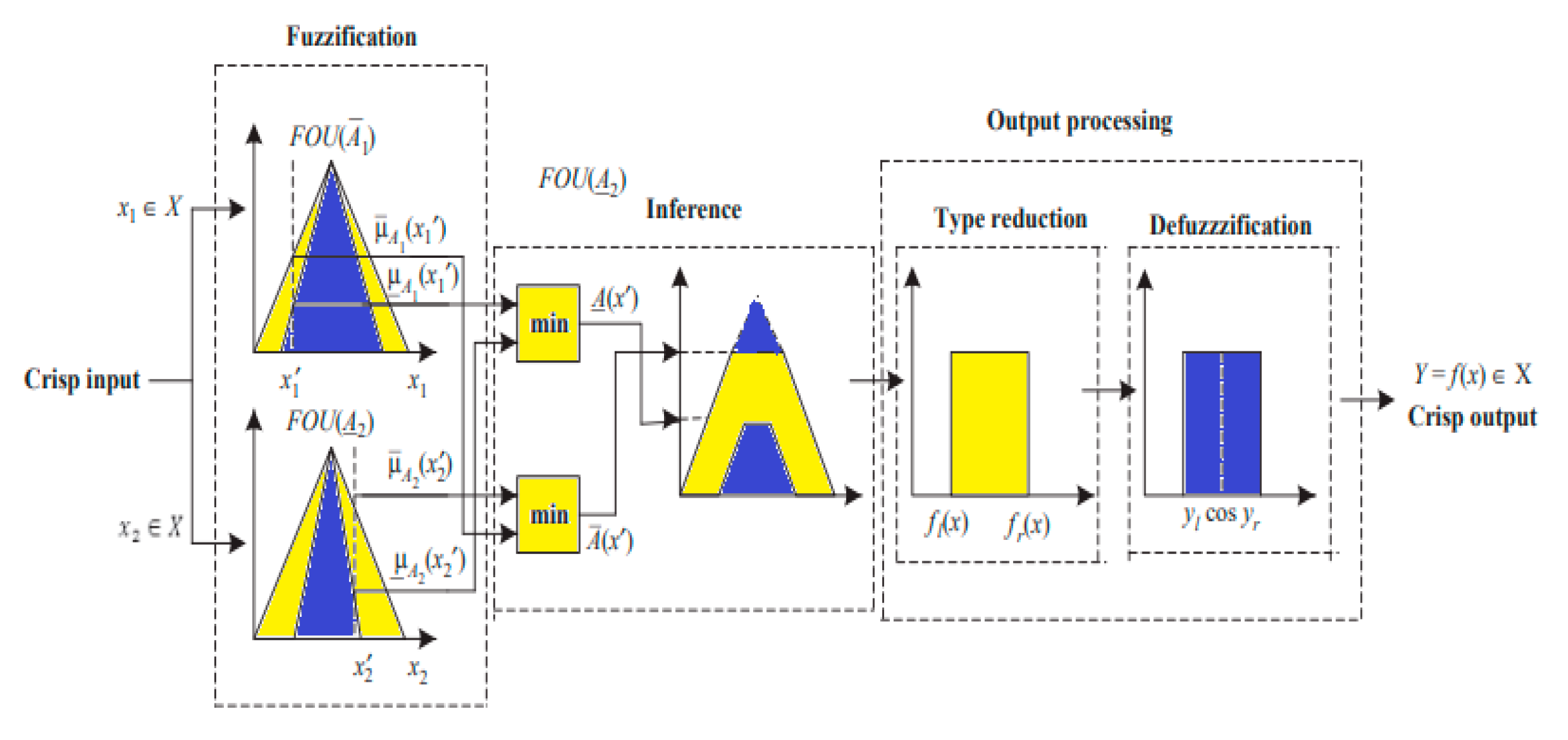
Preprints 106553 g004
Preprints 106553 g005
Figure 5. An Interval Gaussian type-2 fuzzy set.
Figure 5. An Interval Gaussian type-2 fuzzy set.
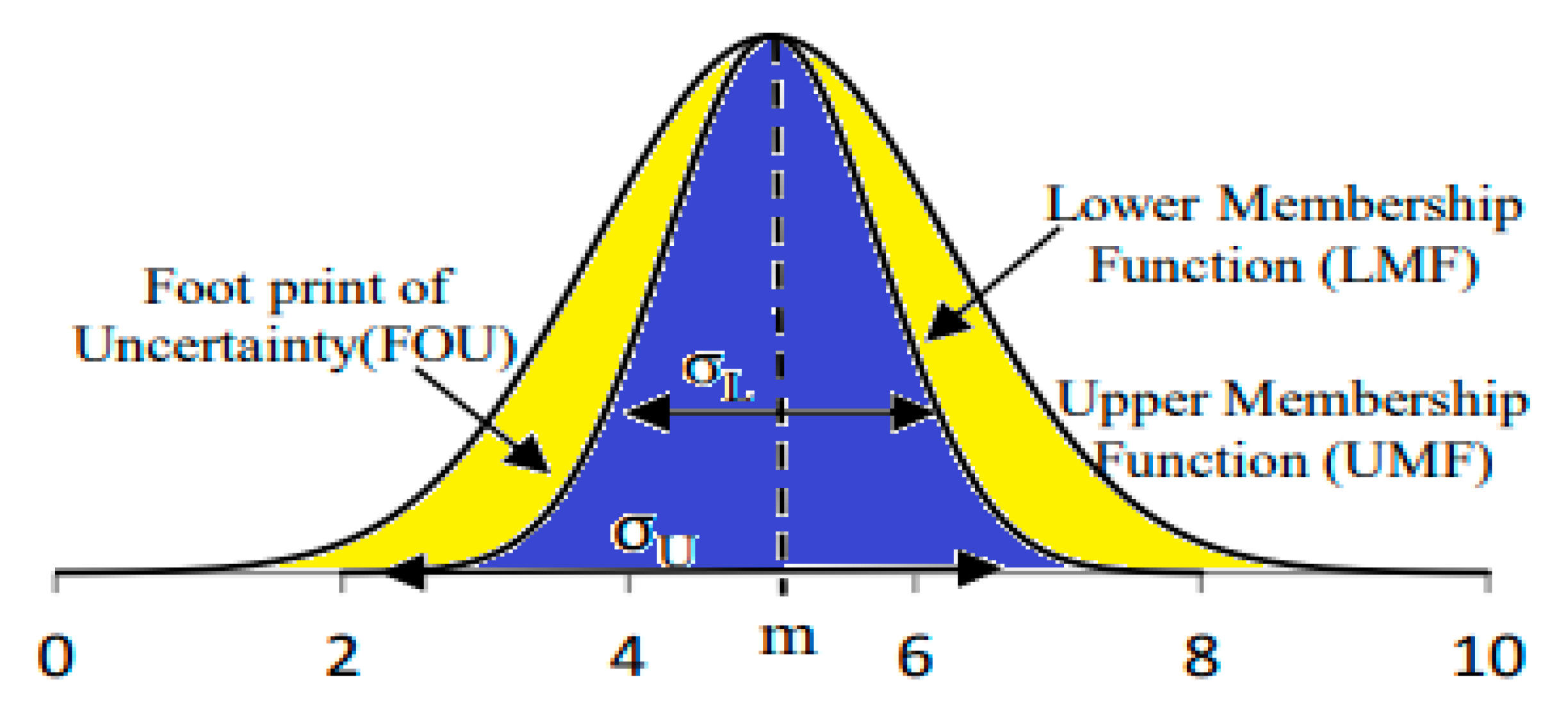
Preprints 106553 g005
Preprints 106553 g006
Figure 6. Triangular IT2-FSs.
Figure 6. Triangular IT2-FSs.
Preprints 106553 g006
The input type-2 fuzzy sets are created by fuzzifying the crisp inputs from the input sensors. Since singleton fuzzification is easy to apply and works well with embedded processors and real-time applications, it is typically employed in interval type-2 FLC applications [39]. The inference engine and the rule base are then triggered by the input type-2 fuzzy sets to generate output type-2 fuzzy sets as shown in Figure 5 [40].
The Rule structure of each S1-IT2-FLC is as follows as shown in Figure 6:
R i : IF σ is   A ~ i THEN φ is B i , i = 1,2 , 3
μ ¯ A ~ i Described in terms of an upper membership function.
μ _ A ~ i Described in terms of the lower membership function.
σ It is the standard deviation.
B i It is crisp consequents 1,2,3.
The equations describing the type-2 fuzzy logic are described as:
φ = m 1 = m 3 = 1 − α m 2 = α
Where:
m 1 , m 2   a n d   m 3 represent the height of the lower membership function.
Eq (4) describes the Fuzzy rule base.
φ = φ ᶥ + φ r 2
Equation (5) describes the type of reduction mechanism of type-2 Fuzzy controller.
Where:
φ ᶥ and φ r are the end points of the type of reduced set which are described as follows:
φ l = ∑ i = 1 L μ ¯ A ~ i σ B i + ∑ i = L + 1 N μ _ A ~ i σ B i ∑ i = 1 L μ ¯ A ~ i σ + ∑ i = L + 1 N μ _ A ~ i σ φ r = ∑ i = 1 R μ _ A ~ i σ B i   + ∑ i = R + 1 N μ ¯ A ~ i σ B i ∑ i = 1 R μ _ A ~ i σ + ∑ i = R + 1 N μ ¯ A ~ i σ
Where:
L & r are switching points.
Equation (6) describes the type of reduction mechanism of type-2 Fuzzy controller as shown in Figure 6 and Figure 7.

6. Simulation Results and Discussion

Figure 8 shows the sample research AC System along with certain supplementary, FACTS-MFCC. It is connected to the infinite bus - 138KV, Substation bus through the 10 km feeder and consists of a local hybrid load, which includes linear, nonlinear, and induction motor type loads. Appendices A and B show the unified AC system, FACTS-MFCC, and the dynamic control parameters, respectively.
  • 6.1. V, I, P, Q and PF at Source bus with Short Circuit Operation
    Preprints 106553 g009aPreprints 106553 g009b
    Figure 9. V, I, P, Q and PF at Source bus with Short Circuit, duration in (100ms to 200ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform at Source bus.
    Figure 9. V, I, P, Q and PF at Source bus with Short Circuit, duration in (100ms to 200ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform at Source bus.
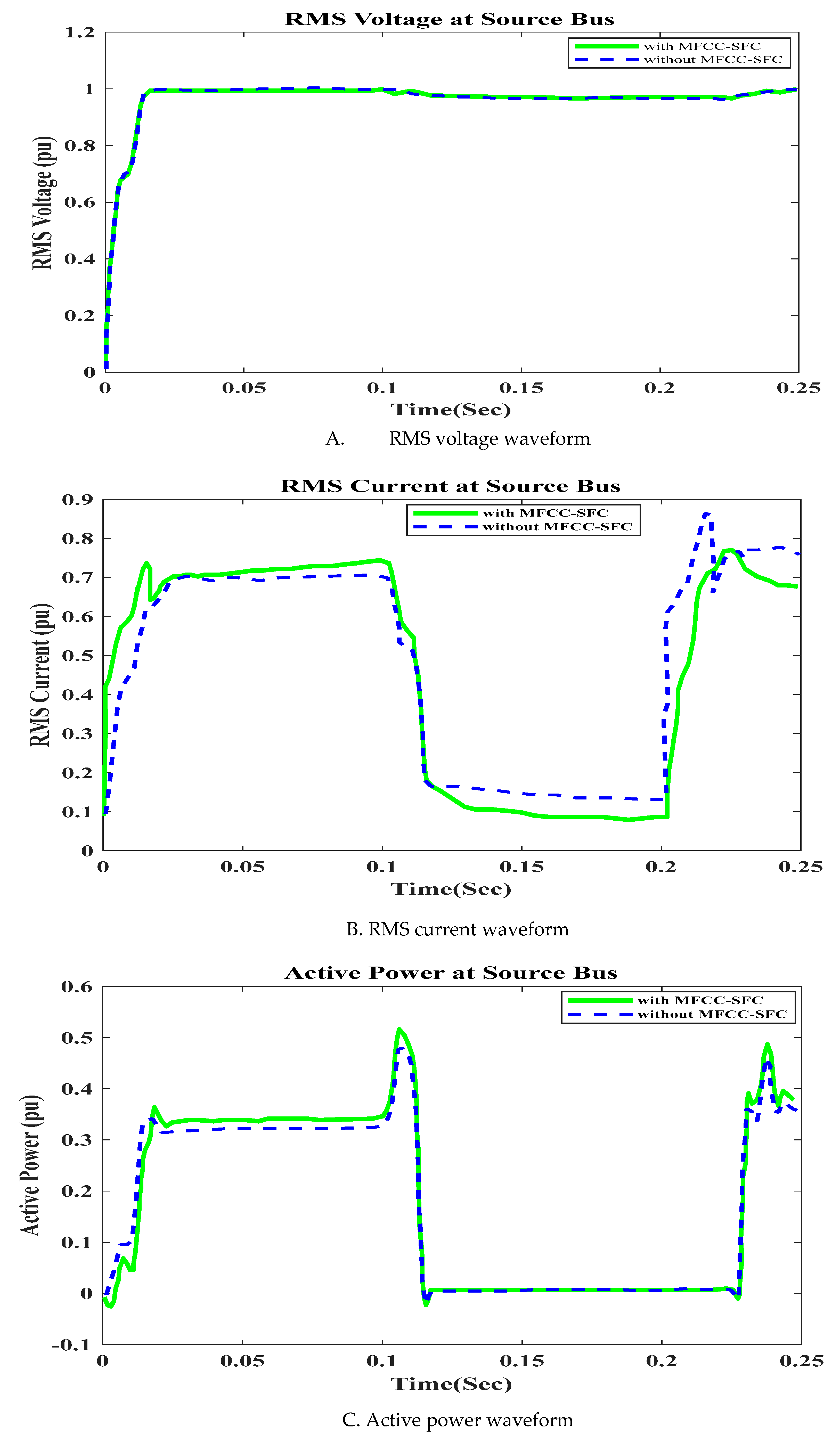
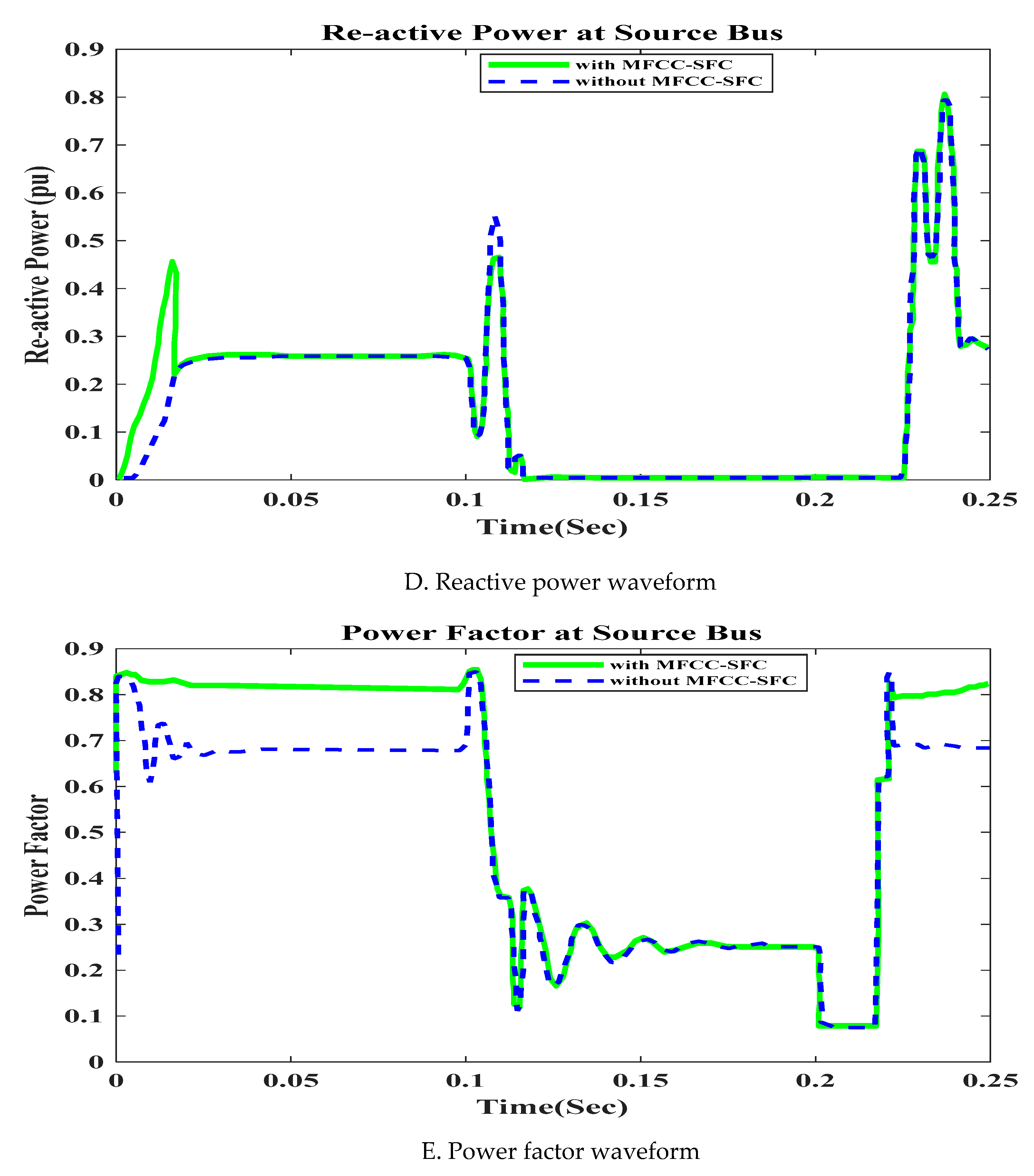
    Preprints 106553 g009aPreprints 106553 g009b
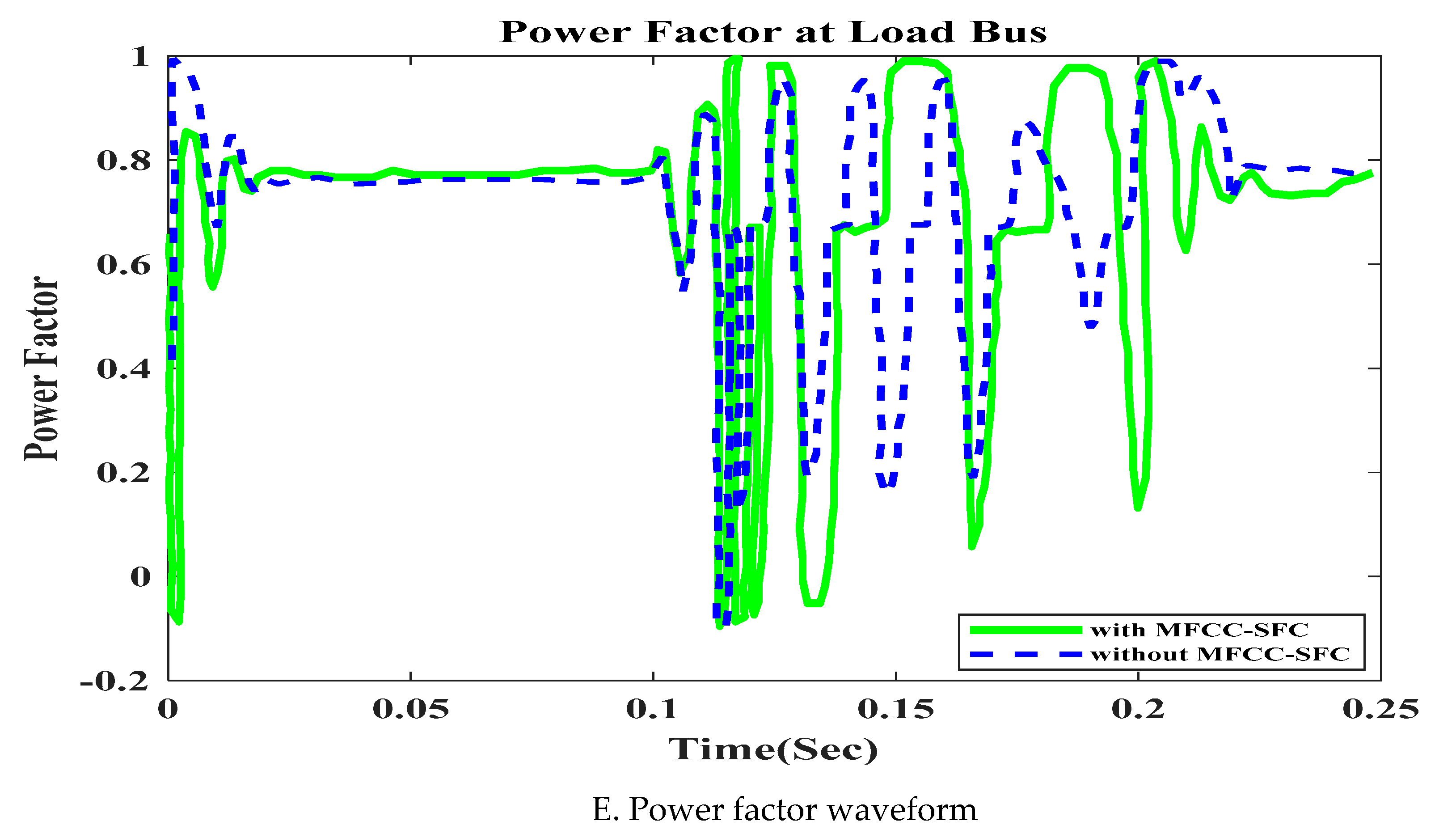
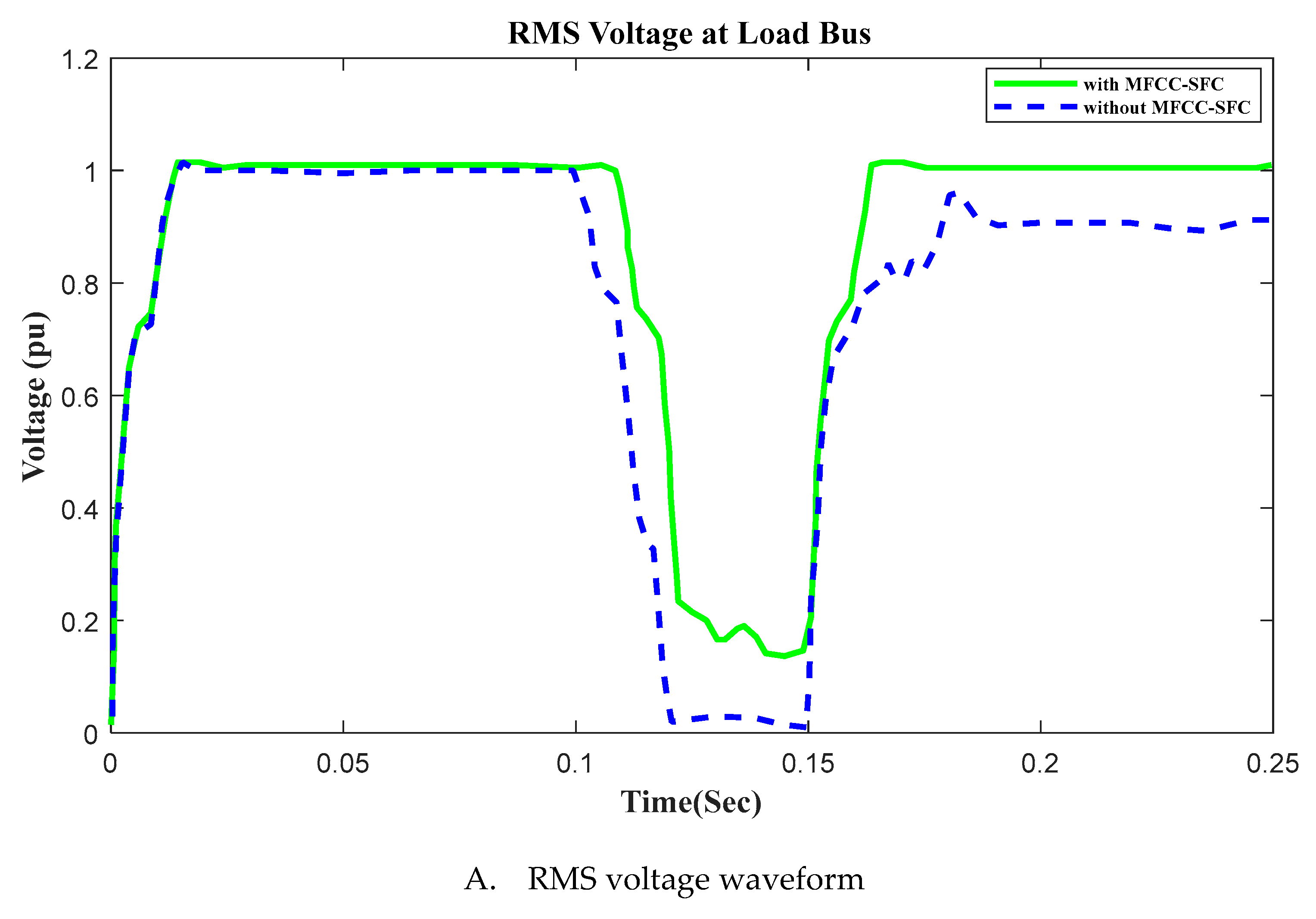
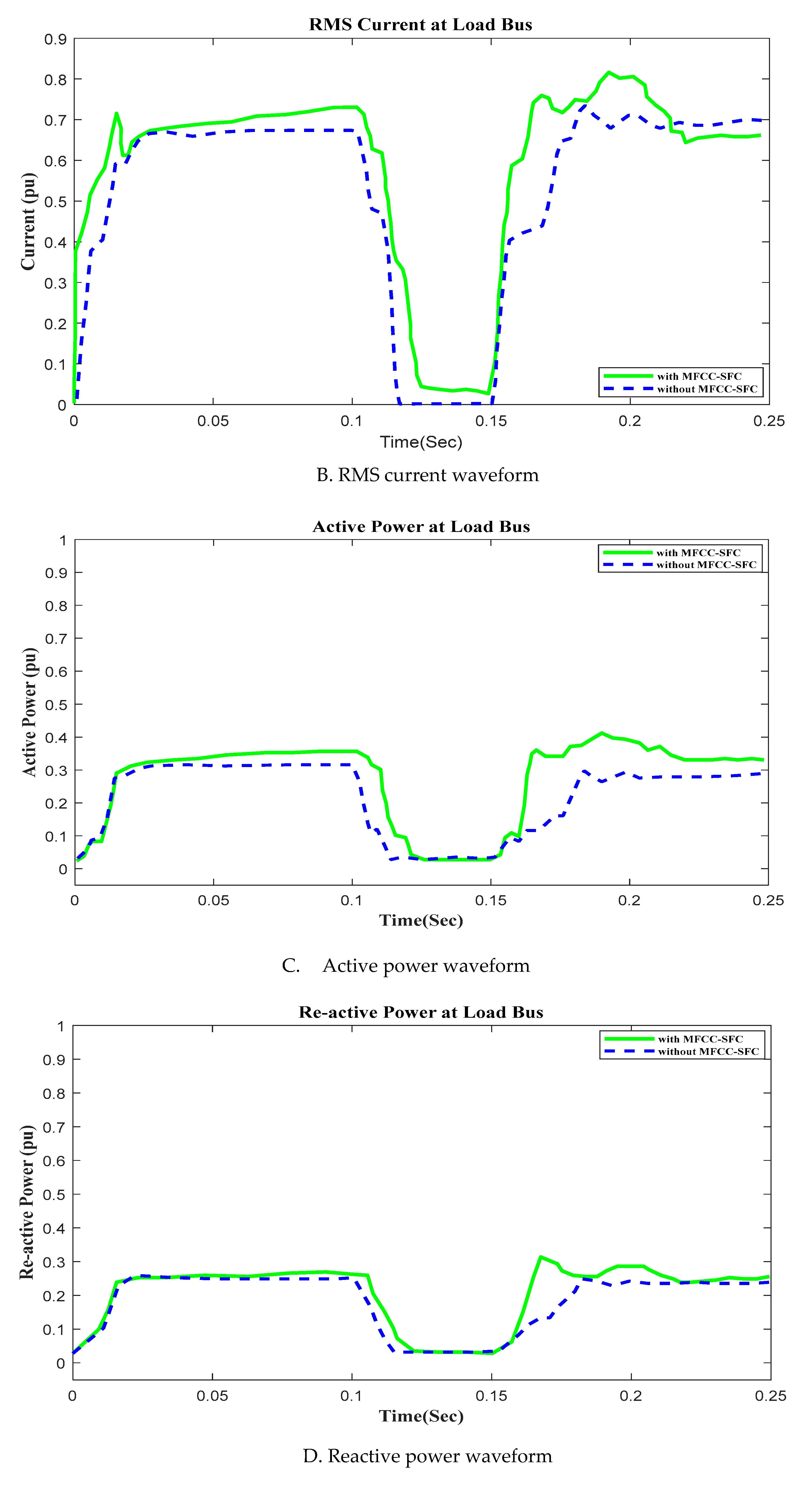
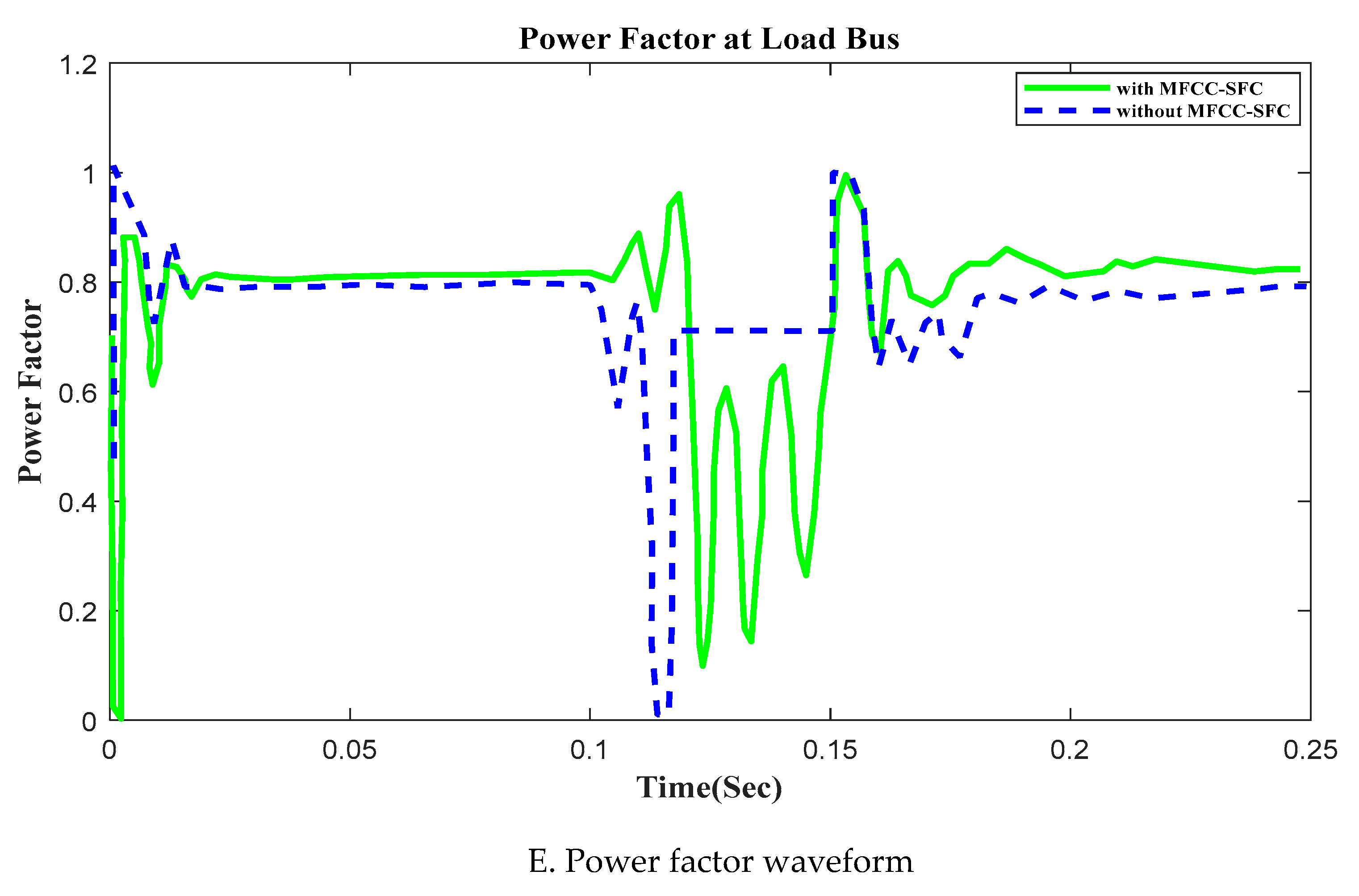
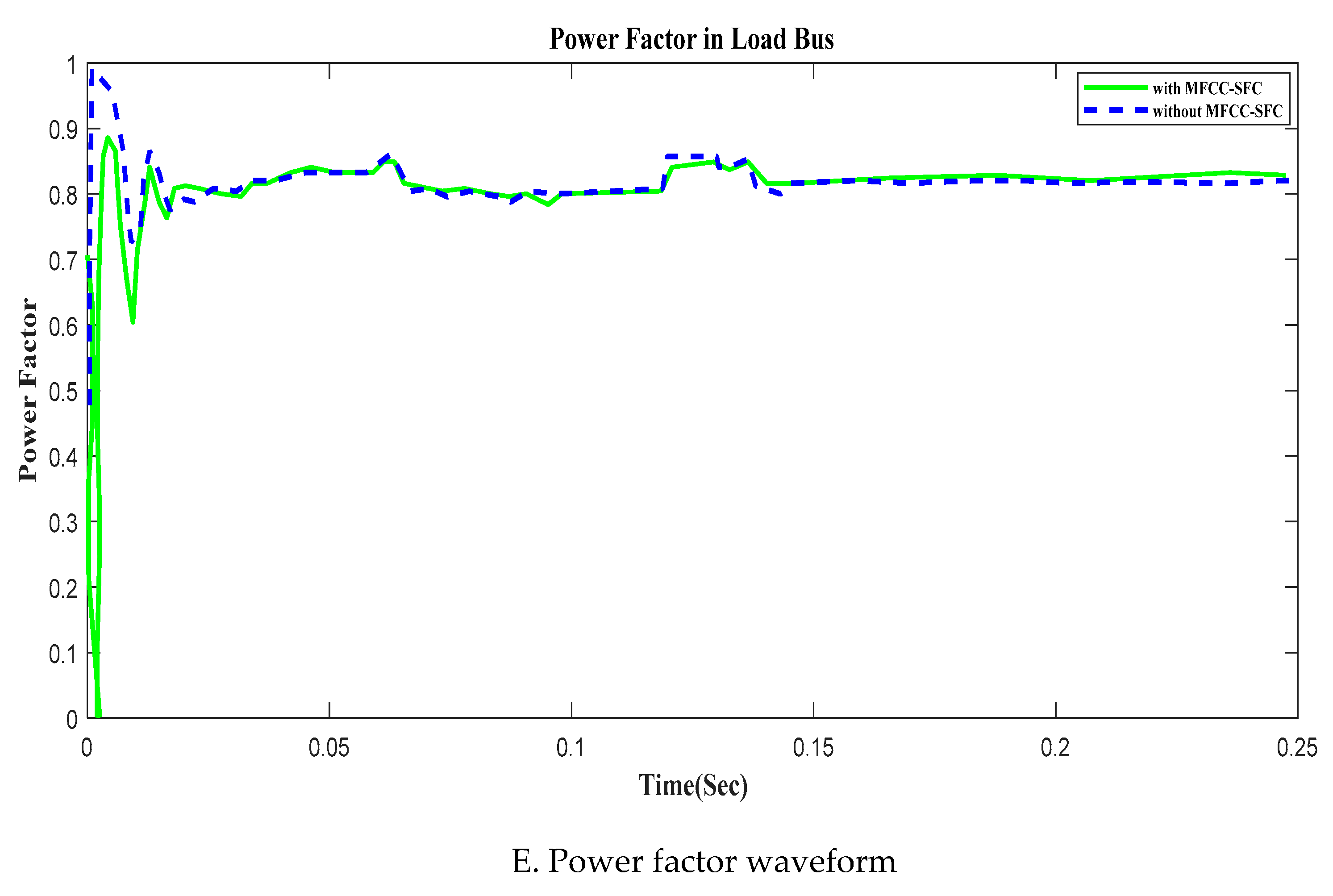
  • 6.2. V, I, P, Q and PF at Load bus with Short Circuit Operation
    Preprints 106553 g010aPreprints 106553 g010bPreprints 106553 g010c
    Figure 10. V, I, P, Q and PF at Load bus with Short Circuit, duration in (100ms to 200ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform at Load bus.
    Figure 10. V, I, P, Q and PF at Load bus with Short Circuit, duration in (100ms to 200ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform at Load bus.
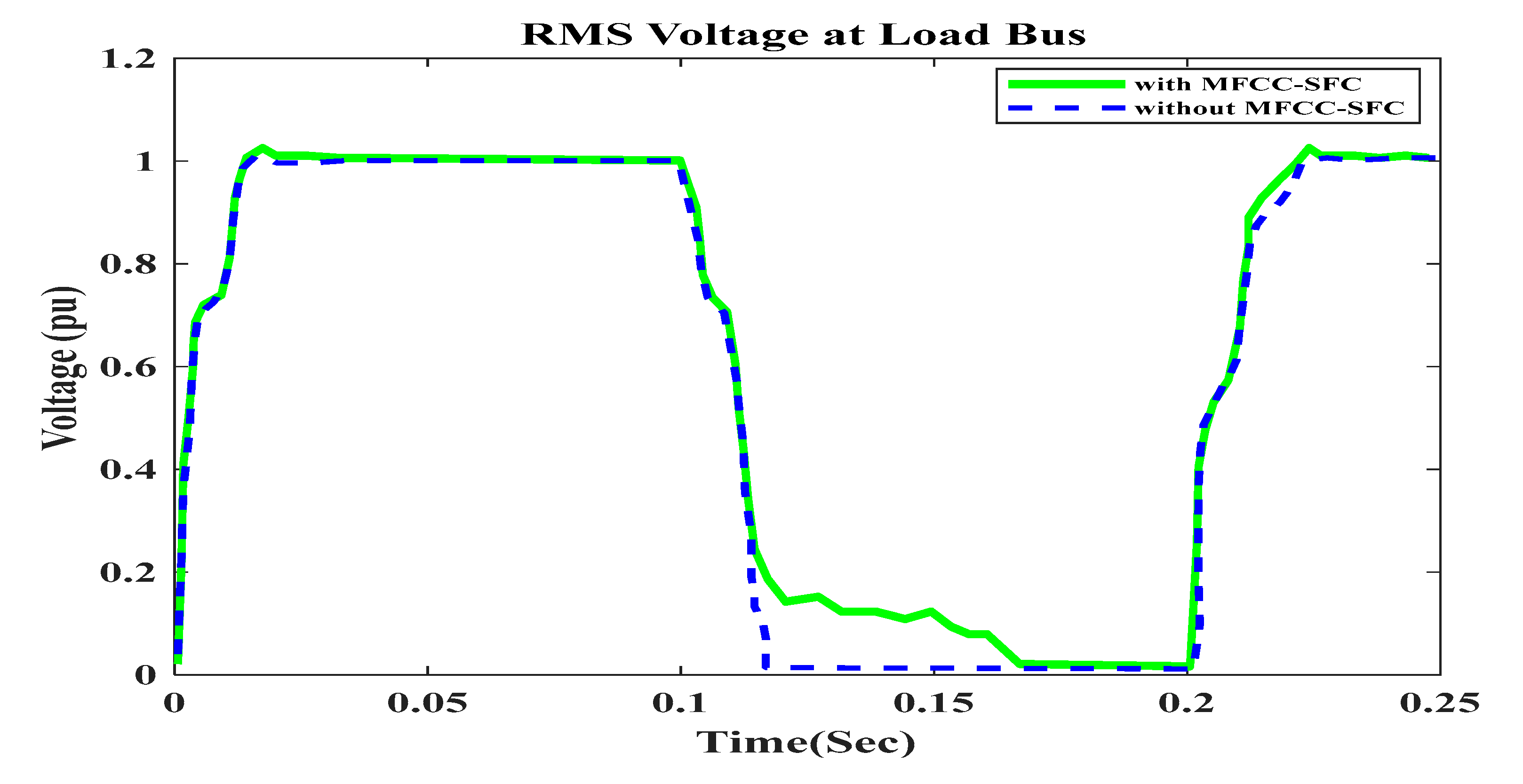
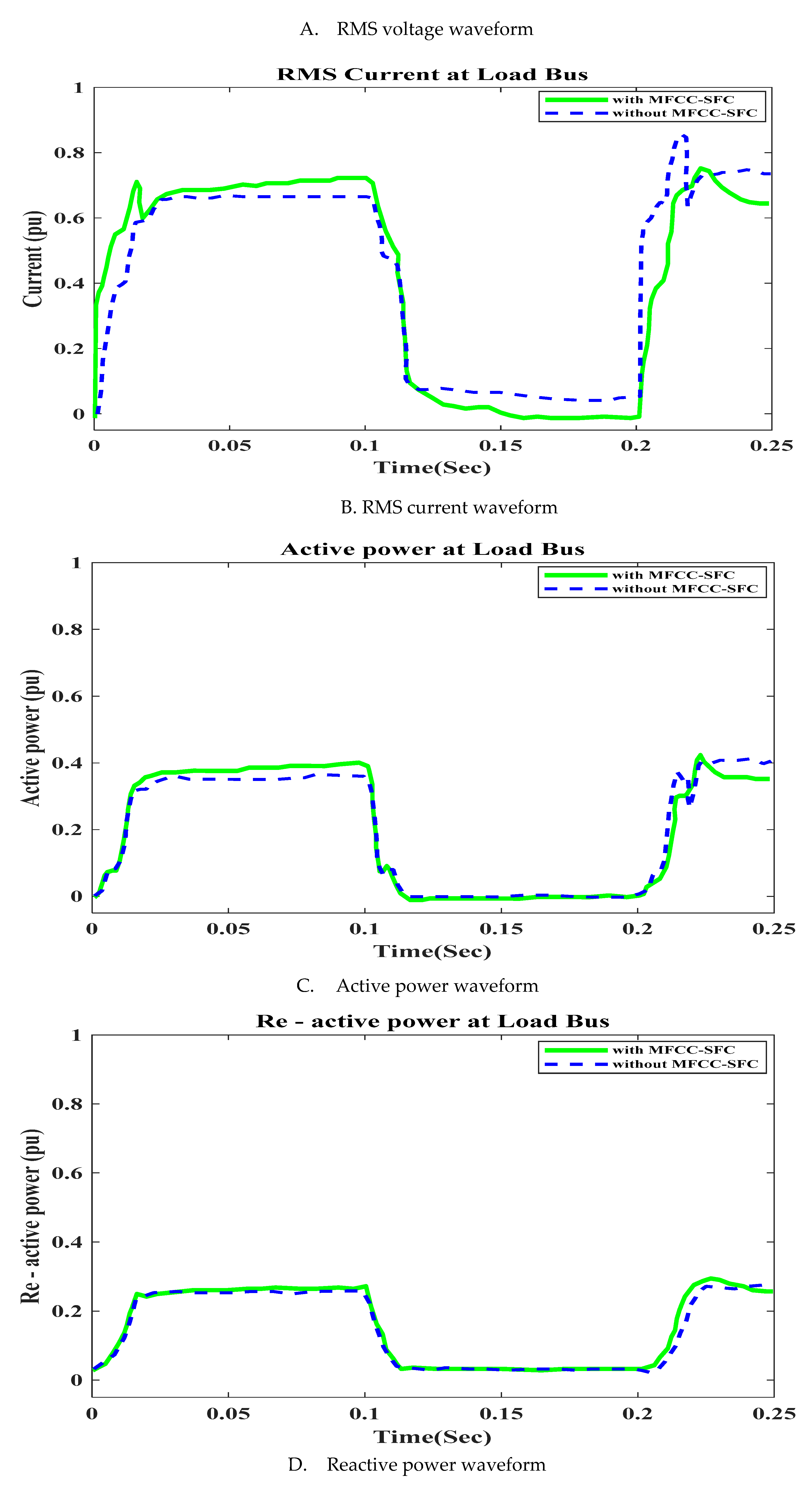
    Preprints 106553 g010aPreprints 106553 g010bPreprints 106553 g010c

7. Application Short Circuit Condition

To demonstrate that the low-cost FACTS-MFCC Scheme dynamic stabilization and efficient energy utilization work as intended, the proposed control schemes for stabilizing the host smart grid under short circuit (SC), open circuit (OC), and other conditions are tested. All digital simulations used the MATLAB/SIMULINK-2023b Software Environment, which introduced a 3-phase short circuit to the load bus of the AC grid at time of 100ms and cleared after 200ms. Figure 9 and Figure 10 demonstrate the outcomes of the simulations under the short circuit situation. Furthermore, the FACTS-MFCC-SFC scheme has improved its efficiency in lowering inrush currents during short and open circuit failures, which helps enhancing power factor and stabilizing bus voltages in the case study.
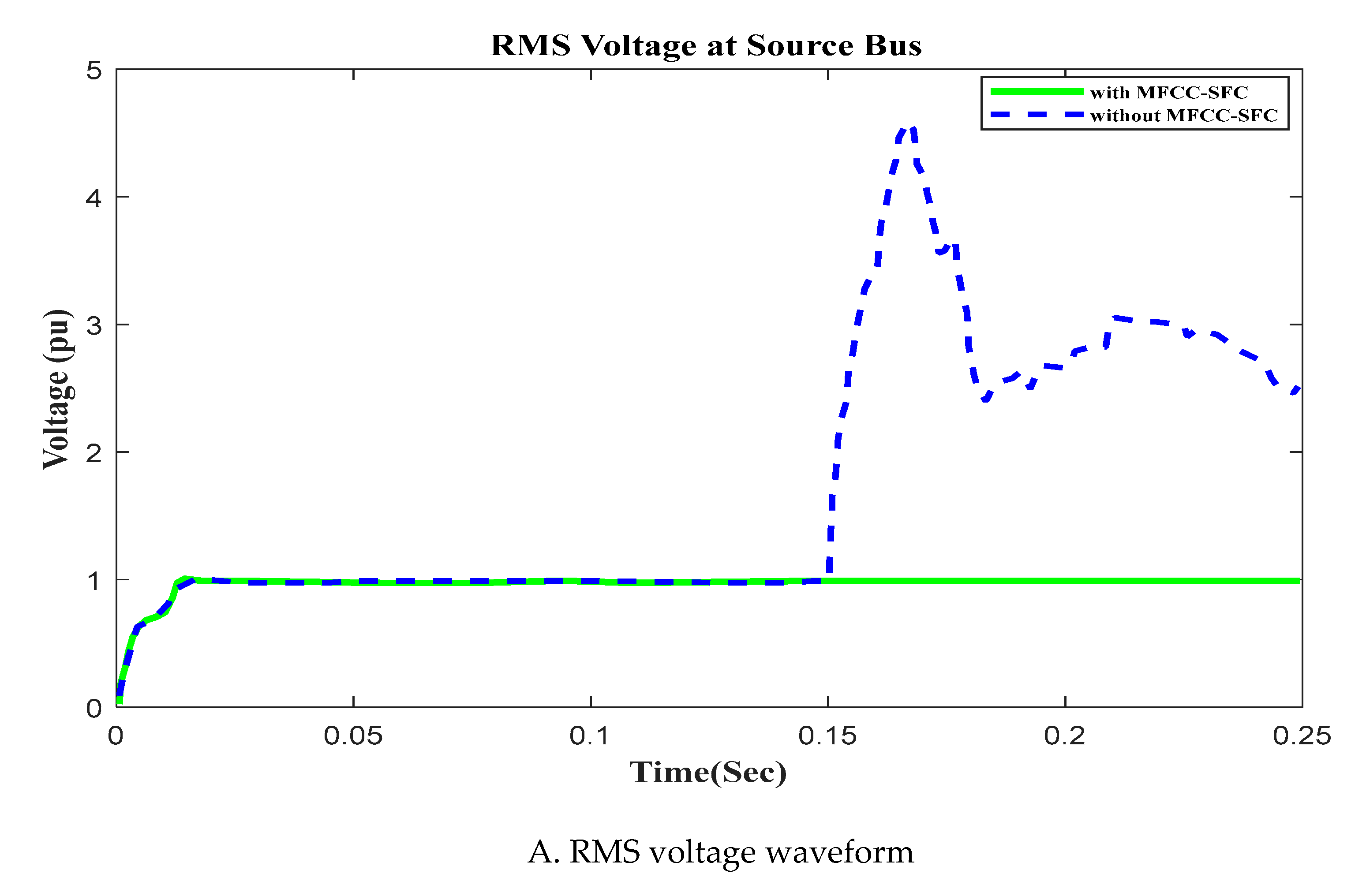
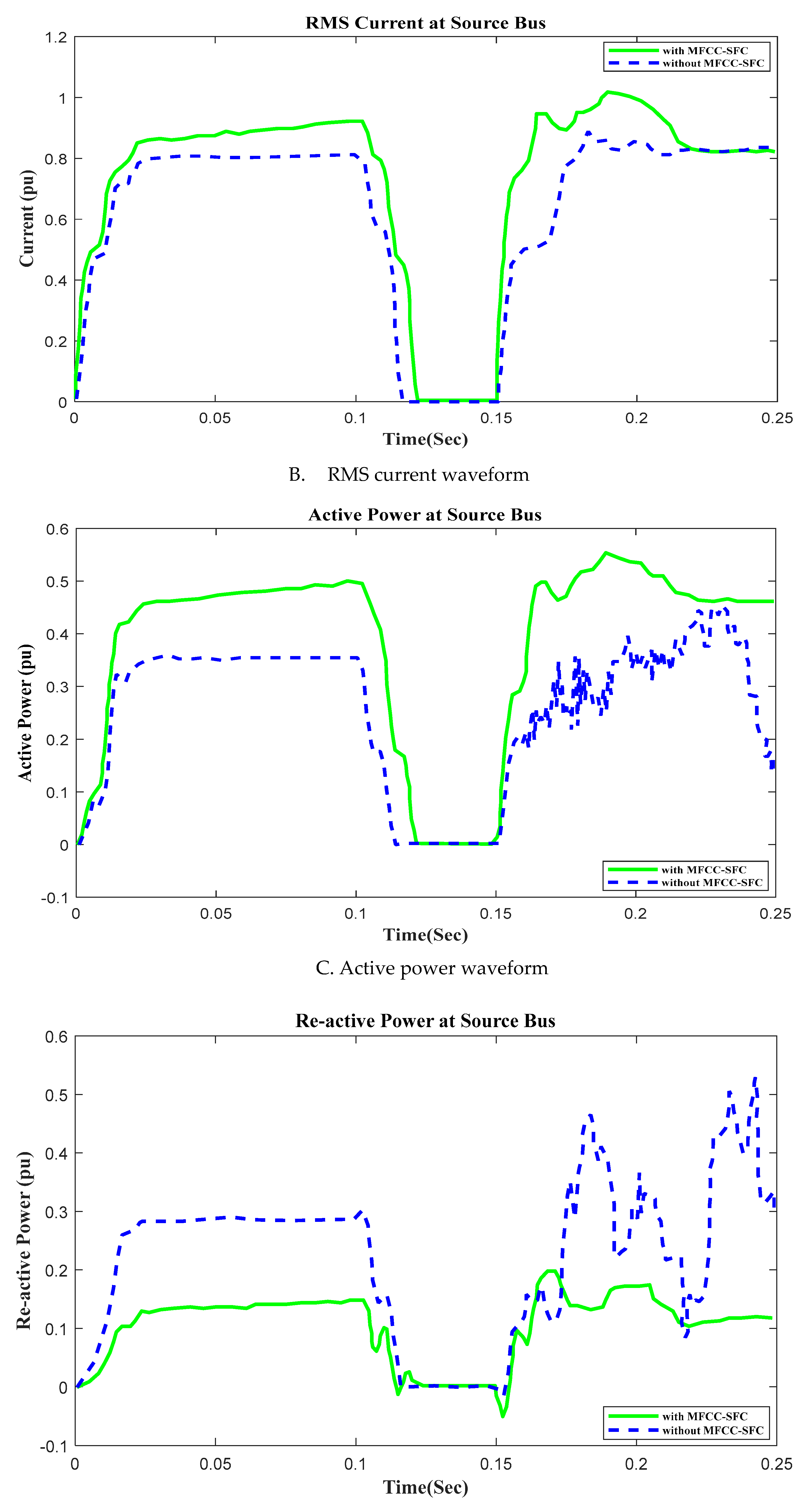
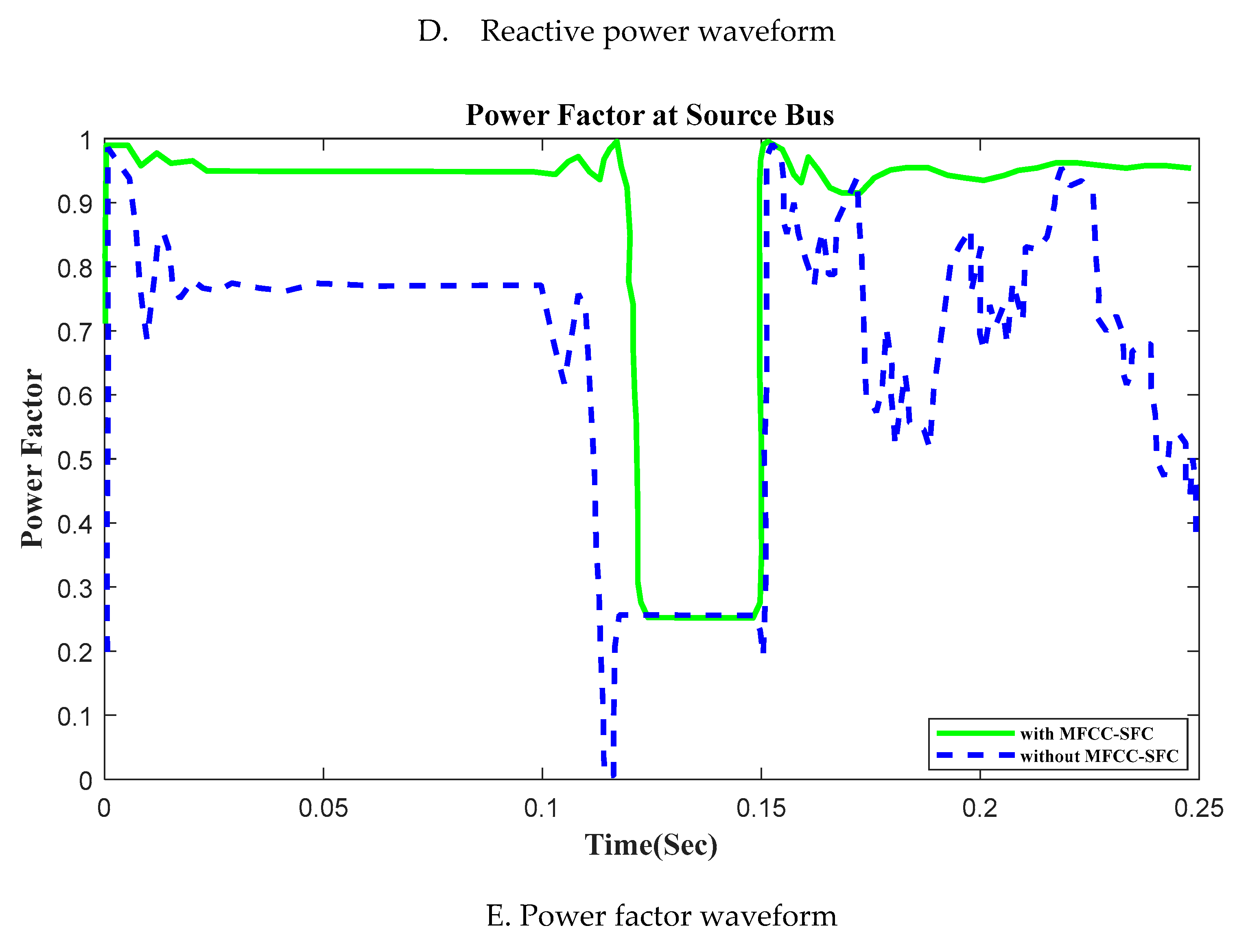
  • 6.4. V, I, P, Q and PF at Source bus with Open Circuit Operation
    Preprints 106553 g011aPreprints 106553 g011bPreprints 106553 g011c
    Figure 11. V, I, P, Q and PF at Source bus with Open Circuit, duration in (100ms to 150ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform at Source bus.
    Figure 11. V, I, P, Q and PF at Source bus with Open Circuit, duration in (100ms to 150ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform at Source bus.
    Preprints 106553 g011aPreprints 106553 g011bPreprints 106553 g011c
  • 6.5. V, I, P, Q and PF under at Load bus with Open Circuit Operation
    Preprints 106553 g012aPreprints 106553 g012bPreprints 106553 g012c
    Figure 12. V, I, P, Q and PF at Load bus with Open Circuit, duration in (100ms to 150ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform at Load bus.
    Figure 12. V, I, P, Q and PF at Load bus with Open Circuit, duration in (100ms to 150ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform at Load bus.
    Preprints 106553 g012aPreprints 106553 g012bPreprints 106553 g012c

8. Application Open Circuit Condition

In this section of the work, an open circuit occurs close to the load, and the altering of a critical parameter is demonstrated. All digital simulations used the MATLAB/SIMULINK-2023b Software Environment, which introduced a 3-phase open circuit to both buses (Source and Load) of the AC grid at time 100ms and cleared after 150ms. Figure 11 and Figure 12 demonstrate the outcomes of the simulations under the open circuit situation. Furthermore, as can be seen, both buses (Source and Load) now have better dynamic response and power quality. Additionally, there aren't many fluctuations in the power factor in open circuit faults with FACTS-MFCC-SFC in essential buses, particularly the Source bus.
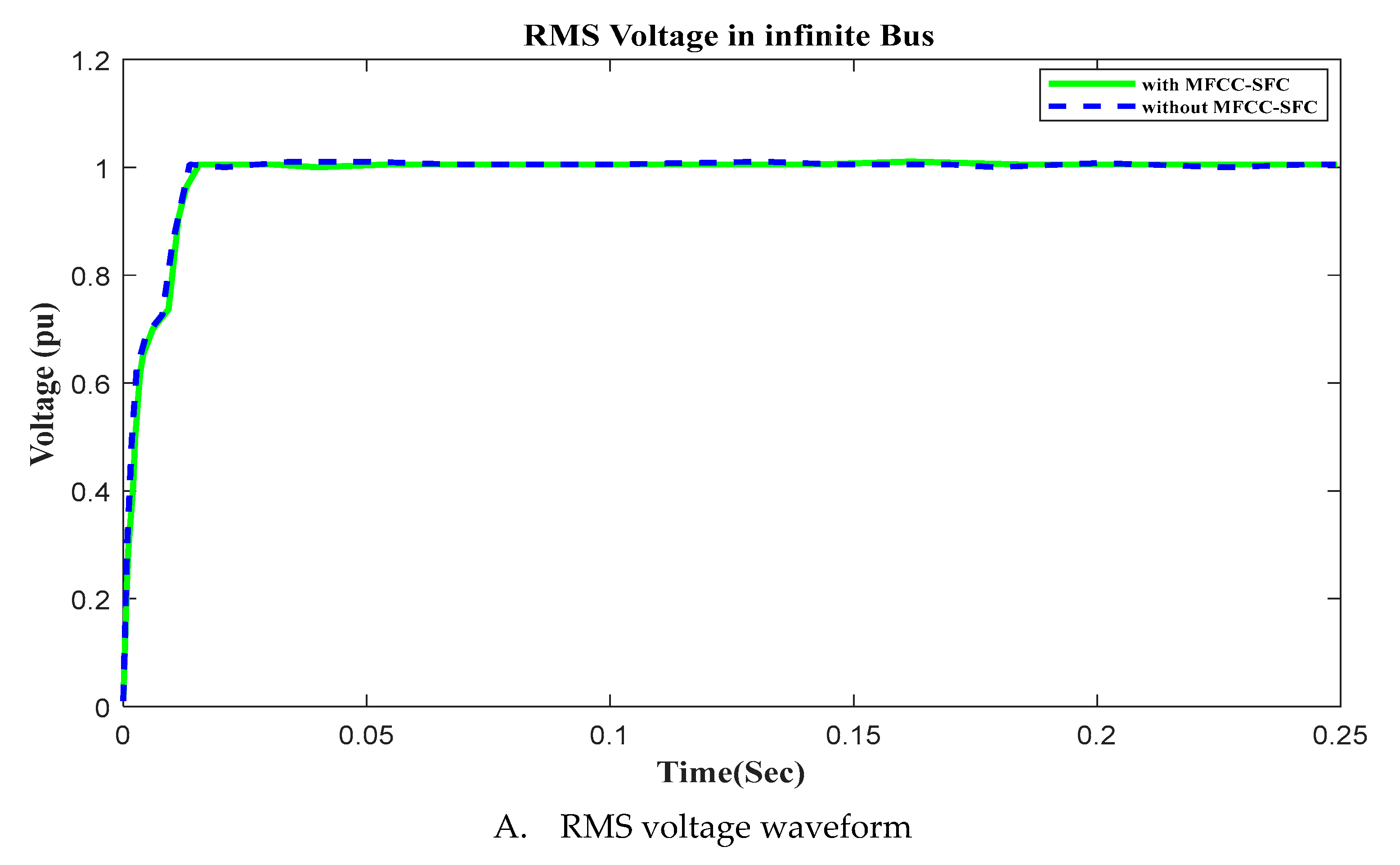
  • 6.7. V, I, P, Q, and PF in infinite bus
    Preprints 106553 g013aPreprints 106553 g013bPreprints 106553 g013c
    Figure 13. V, I, P, Q and PF at infinite bus with Open Circuit, duration in (100ms to 150ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform in infinite bus.
    Figure 13. V, I, P, Q and PF at infinite bus with Open Circuit, duration in (100ms to 150ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform and E. Power factor waveform in infinite bus.
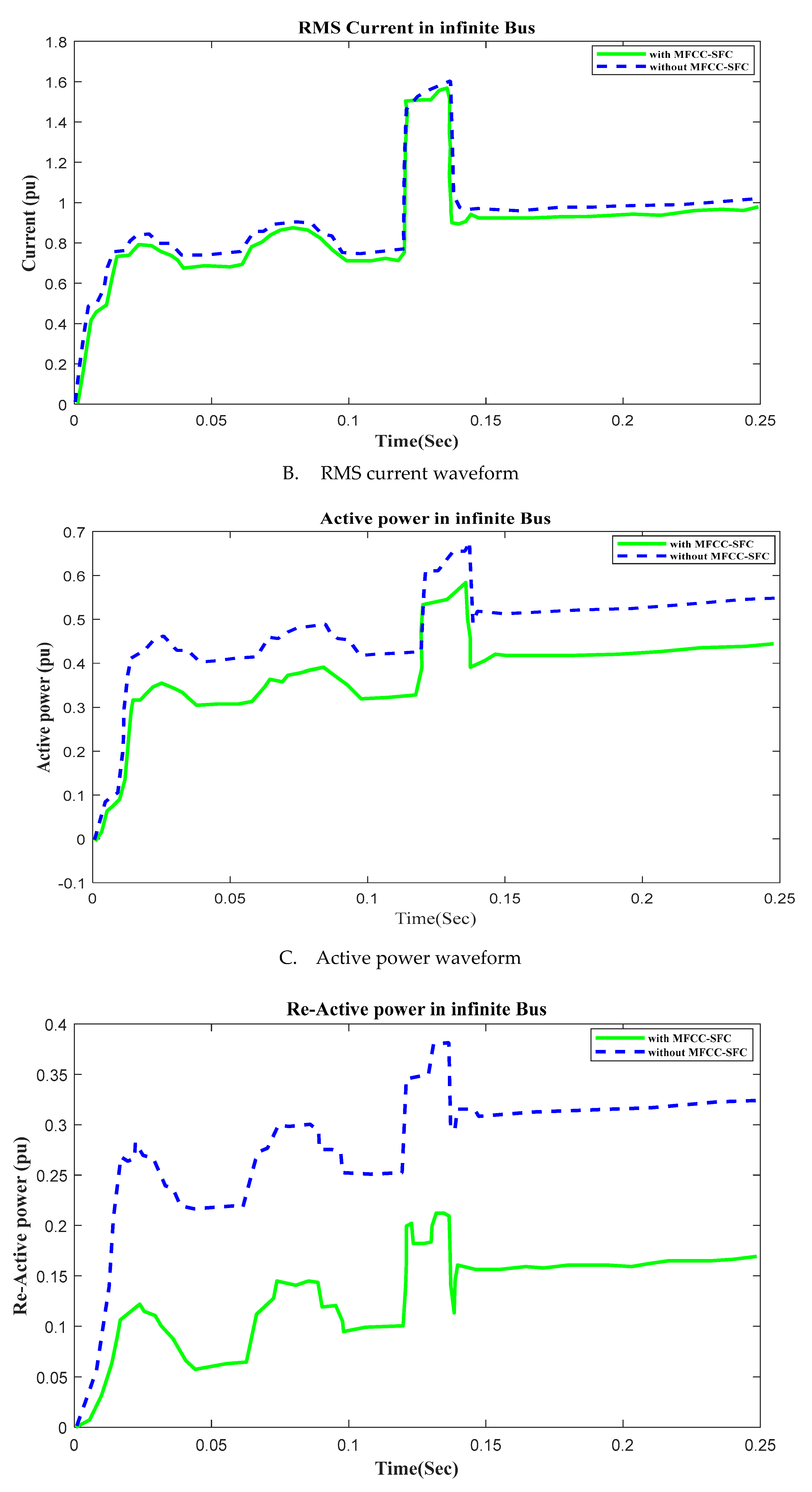
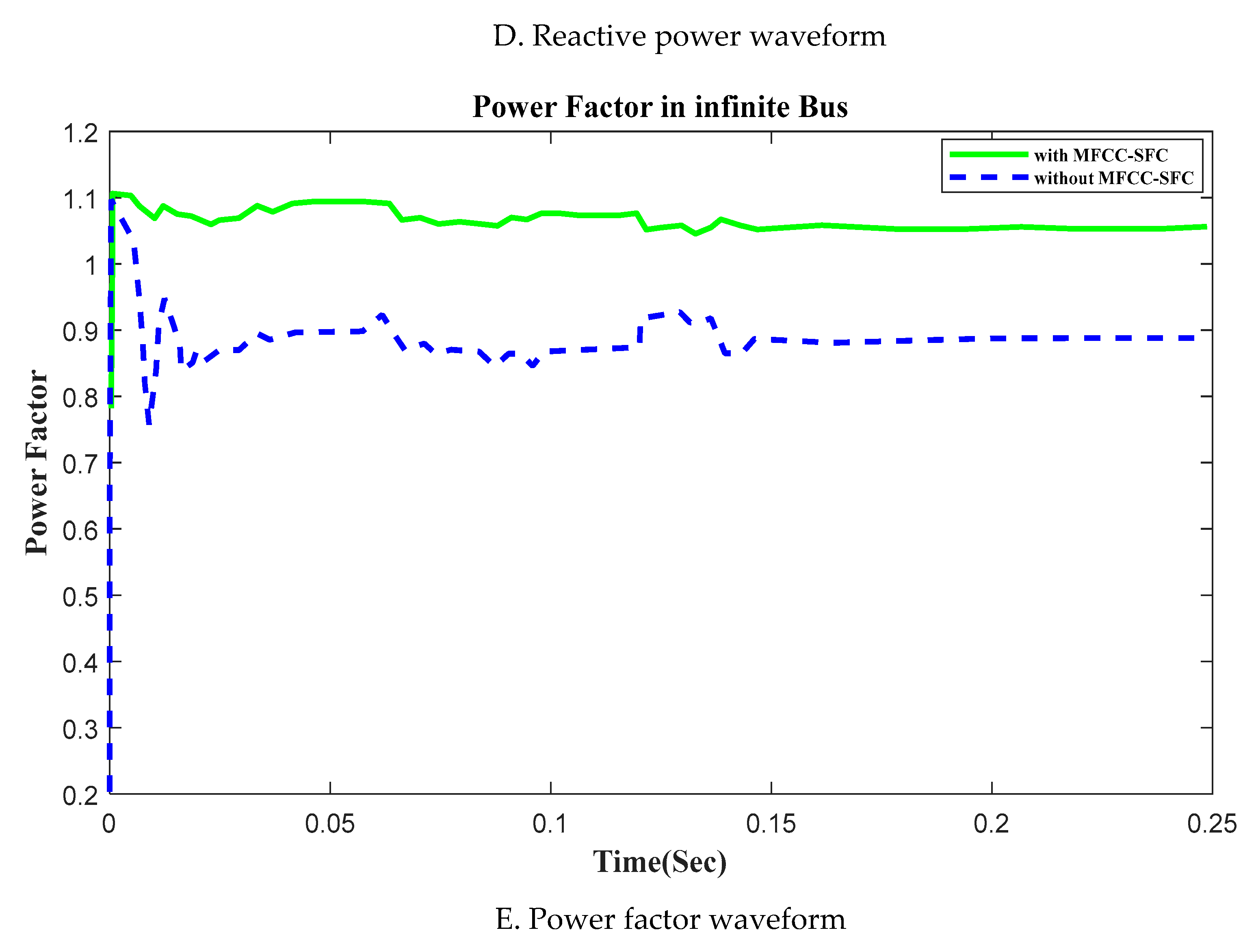
    Preprints 106553 g013aPreprints 106553 g013bPreprints 106553 g013c
  • 6.6. V, I, P, Q and PF in Load bus
    Preprints 106553 g014aPreprints 106553 g014bPreprints 106553 g014c
    Figure 14. V, I, P, Q, and PF at Load bus with Open Circuit, duration in (100ms to 150ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform, and E. Power factor waveform in Load bus.
    Figure 14. V, I, P, Q, and PF at Load bus with Open Circuit, duration in (100ms to 150ms). A. RMS voltage waveform, B. RMS current waveform, C. Active power waveform, D. Reactive power waveform, and E. Power factor waveform in Load bus.
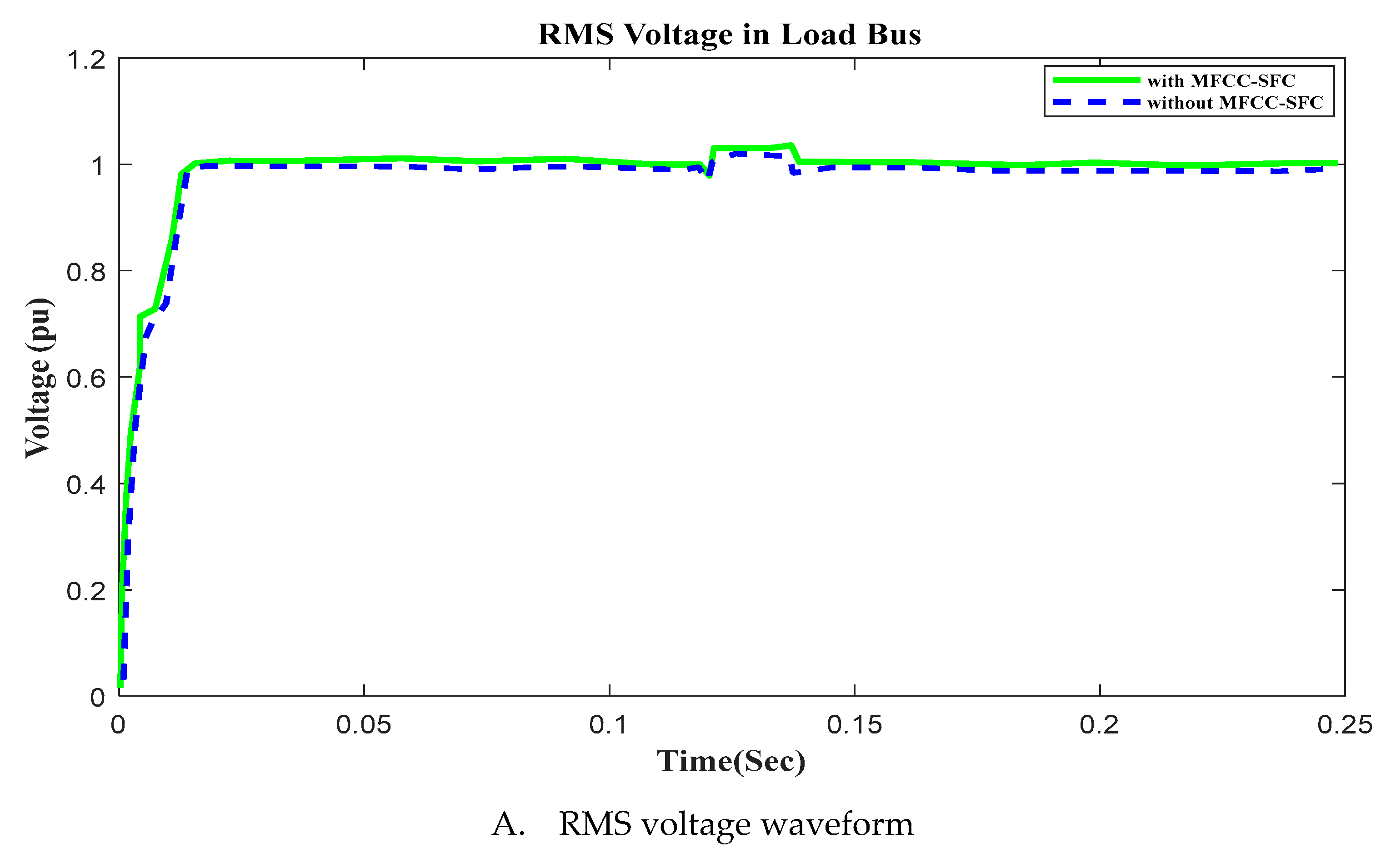
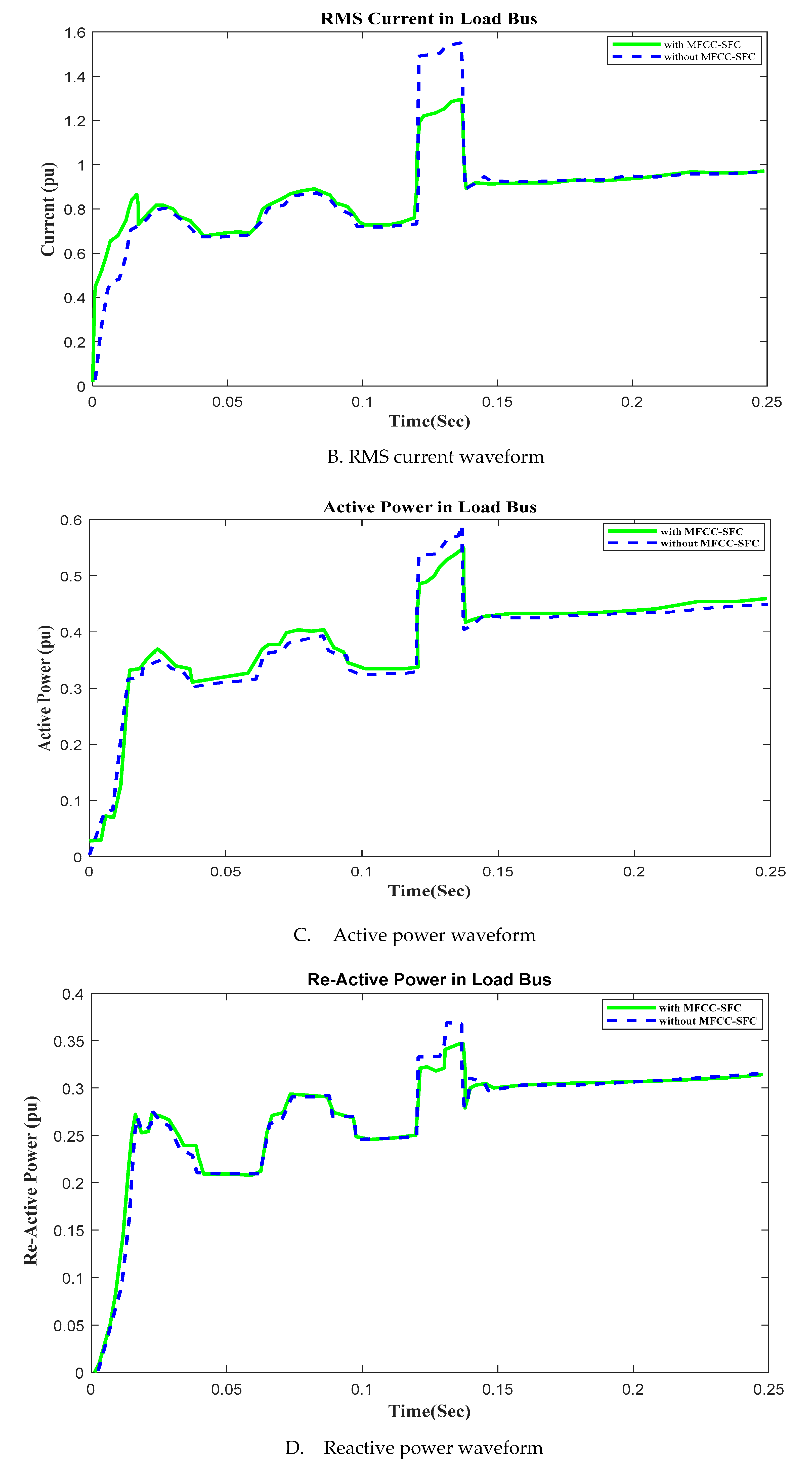
    Preprints 106553 g014aPreprints 106553 g014bPreprints 106553 g014c

9. Open and Close Circuits

We used the breakers on/off as seen on Simulink model and the position of the Breaker in series to close to ground at open circuit and parallel at short circuit and the operation for both open circuit and short circuit were done at AC source and load bus for a duration of short circuit 100ms to 200ms and open circuit duration of 100ms to 150ms as shown in Table 1 and Table 2. Figure 9 shows the V, I, P, Q and PF at Source side with Short Circuit Operation and Figure 10 shows the V, I, P, Q and PF at load side with Short Circuit Operation at 100ms to 200ms. Figure 11 shows the V, I, P, Q and PF at Source side with open Circuit Operation and Figure 12 shows the V, I, P, Q and PF at load side with open Circuit Operation at 100ms to 150ms.

10. Hybrid Load Variations

The grid is subjected to the following situations in order to study how the AC grid reacts to load excursions both with and without the FACTS-MFCC. The results for both current and voltage values are shown in Figure 13 and Figure 14. Linear pressure is disconnected at 117 ms and then reconnected at 134 ms. Nonlinear demand is disconnected at 100 ms and then reconnected at 45 ms. Motor load torque drops at 170 ms by 50% and continues for a duration of 45 ms. Motor load torque rises by 50% at 250 ms seconds for a duration of 45 ms.

11. Power Systems Harmonics Analysis

One useful metric for estimating the harmonics in voltage or current waveforms is the total harmonic distortion or THD. The harmonics effect of the voltage and current load bus are discussed in this section. The voltage and current THD of the load bus without FACTS-MFCC-SFC as a function of time are seen in , respectively. The rate of THD has increased for constant series compensation, as shown in Figure 15 and Figure 17 because the nonlinear loads are used on power systems; however, THD of the line current terminal voltage in the load bus is improved, as shown in Figure 16 and Figure 18, by employing the FACTS-MFCC-SFC [41,42].

12. Discussions of Digital Simulation Results

There are many reasons to propose a new equipment device and the use of the low-cost structure of the dual Mode modulated filter is necessitated by the need to dual tuned arm filter plus capacitive compensation for dynamic inrush nonlinear loads. The function of the modulated pulse width duty cycle switching scheme is to dynamically cater the nonlinear loads and inrush current variations and reactive compensation tasks to stabilize the AC voltages at key load buses with FACTS-MFCC-SFC as shown in Table 1 and Table 2.

13. Conclusion and Extended Work

The paper validated the concept of AC plug switched filter modulated action using pulse width modulation based on multi-loop self-adjusted modified weighted PID structure controller and FLC. The modulated filter AC green plug ensures enhanced efficient operation, power quality, reduced harmonics, and improved power factor operation at nonlinear type motorized inrush and rectifier nonlinear loads. For strong interfacing to the smart AC grid, the same filter structure MFCC-SFC device with different control techniques is currently being extended for hybrid renewable wind and micro-hydro green energy systems and applications such as using virtual inertia static synchronous machines and Energy Storage System (ESS) DC- AC utility grid systems. The digital simulation results validate the quick flexibility and efficiency of the proposed FACTS-MFCC-SFC scheme in improving voltage regulation, reducing inrush current conditions, and altering power factor. The AC green plug filter is validated as an effective voltage stabilization and power factor improvement tool in case of slow dynamic nonlinear and inrush type loads. The PWM switching-modulation index is dynamically modified to modulate the tuned arm filter apparent admittance and capacitive VAR - compensation level using the multi-loop multi regulation fuzzy logic fast dynamic controller. The fuzzy logic fast dynamic multi loop multi regulator controller was validated as an effective tool in voltage stabilization, power factor improvement and power quality enhancements.

Appendix A

Parameters Value
AC Utility Grid Parameters
Nominal Voltage 138 KV (L-L), 100 MW
Ratio X/R 10
Base Power Vs Bus 100 MVA
Base Power VL Bus 200 MVA
Frequency 1.750 KHz
FACTS-MFCC Parameters
CF 275µF
RD, RF, LF 1Ω, 0.15Ω, 3mH
Width Modulation Proportional Integral Derivative (WMPID) Controller Parameters
Ke, Kp, Ki, Ki, γ e , γ R 0.7, 5, 1.5, 0.5, 0.5, 0.1
Transmission Line
Feeder 25 kv(L-L),10 km
R/km, L/km 0.4Ω, 0.45Ω

Appendix B

Parameters Value
Transformer Parameters
Power Transformer 1 138 KV to 25kv, 5 MW
Power Transformer 2 25 KV to 4.16kv, 5 MW
Hybrid AC Load Parameters
Induction Motor 2.5 MVA, 4 poles
Rs=0.02765pu, Ls=0.0498 pu
Rr=0.01807pu, Lr=0.0497 pu
Lm=1.354 pu
Linear Load P=2500 KW, Q= 2 MVAr
Nonlinear Load P=1250 KW, Q= 2 MVAr

References

  1. Kazemi-Robati, E.; Hafezi, H.; Sepasian, M.S.; Silva, B. Probabilistic planning of virtually-hybrid harmonic filters inmodern distribution systems. in 2023 International Conference on Smart Energy Systems and Technologies (SEST), 2023.
  2. Aly, H.H.H. A proposed intelligent short-term load forecasting hybrid models of ANN, WNN and KF based on clustering techniques for smart grid. Electr. Power Syst. Res. 2020, 182, 106191. [Google Scholar] [CrossRef]
  3. Das Biswas, S.; Chowdhury, S.; Nandi, C.; Das, B. Power quality improvement with hybrid shunt active power filter. In Proceedings of the 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 17–20 December 2023. [Google Scholar]
  4. Elbakush, E.; Sharaf, A.M.; Altas, I.H. A novel Green Plug Filter Compensation scheme for electric vehicle DC drive. In Proceedings of the 2011 International Symposium on Innovations in Intelligent Systems and Applications, Istanbul, Turkey, 15–18 June 2011; pp. 599–605. [Google Scholar]
  5. Sharaf, A.M.; Khaki, B. A novel FACTS hybrid modulated filter/capacitor compensator. In Proceedings of the 2012 International Conference on Smart Grid (SGE), Oshawa, ON, Canada, 27–29 August 2012; pp. 1–6. [Google Scholar]
  6. Golla, M.; Thangavel, S.; Simon, S.P.; Padhy, N.P.; Pannala, S. An improved hybrid control strategy for UAPF- based microgrid system for active power line conditioner with power flow control. in 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE).
  7. R. S. Yallamilli and M. K. Mishra, "Instantaneous symmetrical component theory based parallel grid side converter control strategy for microgrid power management. IEEE Trans. Sustain. Energy 2019, 10, 682–692. [Google Scholar] [CrossRef]
  8. Naqvi, S.B.Q.; Singh, B. A PV-battery system resilient to weak grid conditions with regulated power injection and grid supportive features. IEEE Trans. Sustain. Energy 2022, 13, 1408–1419. [Google Scholar] [CrossRef]
  9. Şahin, Mustafa Ergin, and Adel Mahmoud Sharaf. "A Robust Decoupled Microgrid Charging Scheme Using a DC Green Plug-Switched Filter Compensator." In Fast Charging and Resilient Transportation Infrastructures in Smart Cities, pp. 89–116. Cham: Springer International Publishing, 2022.
  10. Ayman, F.; Sharaf, A. A novel filter compensation scheme for hybrid (photovoltaic–fuel cell)-dc utilization systems. Int. J. Adv. Renew. Energy Res. 2012, 1, 283–291. [Google Scholar]
  11. Sharaf, Adel M., and Mohamed A. El-Sayed. "A novel hybrid Photovoltaic/Wave energy utilization system for island electricity." In 2009 16th IEEE International Conference on Electronics, Circuits and Systems-(ICECS 2009), pp. 571–574. IEEE, 2009. [CrossRef]
  12. Mohammed, A. Performance enhancement of stand-alone photovoltaic systems with household loads. In 2019 2nd International Conference on Computer Applications & Information Security (ICCAIS), pp. 1–6. IEEE, 2019.
  13. Fry, Sophia, Mahir Irtiza, Alexa Hoffman, and Yousef Sardahi. "Fuzzy Logic Control for Flexible Joint Manipulator: An Experimental Implementation.". International Journal of Mechanical and Mechatronics Engineering 2024, 18, 16–20.
  14. Chao, Wujie; et al. "Research on Hybrid Active Power Filter and Its Control and Protection System for LCC-HVDC." 2023 IEEE 11th Joint International Information Technology and Artificial Intelligence Conference (ITAIC). Vol. 11. IEEE, 2023. [CrossRef]
  15. Wang, Lianjie; et al. "A Three-Phase-Module-Parallel Si & SiC Hybrid Inverter with Smaller Filter Size and Low Cost." 2022 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific). IEEE, 2022. [CrossRef]
  16. Catata, Elmer O. Hancco; et al. "In-Loop Adaptive Filters to Improve the Power Quality of Switched Reluctance Generator in WECS.". IEEE Access 2021, 10, 2941–2951. [CrossRef]
  17. Singh, Vikram; et al. "Performance Evaluation of A Shunt Active Power Filter For Current Harmonic Elimination." 2021 IEEE Region 10 Symposium (TENSYMP). IEEE, 2021. [CrossRef]
  18. Lima, Vitor Leobet, and Tiago Jackson May Dezuo. "Robust Switching Rule Design for Single-Phase Shunt Active Power Filter." 2021 Brazilian Power Electronics Conference (COBEP). IEEE, 2021. [CrossRef]
  19. Lin, Hongyi; et al. "Shunt active power filter using SiC-MOSFET with high accuracy compensation." 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia). IEEE, 2020. [CrossRef]
  20. Daftary, Dhrumil, and M. T. Shah. "Design and analysis of hybrid active power filter for current harmonics mitigation." 2019 IEEE 16th India Council International Conference (INDICON). IEEE, 2019. [CrossRef]
  21. Nolasco, Diego HS; et al. "Application of Fuzzy Systems in Power Quality: Diagnosis of Total Harmonic Distortions." 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE). IEEE, 2018.
  22. Mohammad Nurul Absar, Md Fokhrul Islam, Ashik Ahmed “Power quality improvement of a proposed grid-connected hybrid system by load flow analysis using static VAR compensator. Heliyon journal, 2023. [CrossRef]
  23. Solanki, A.Y.; Vyas, S.R. A review on power quality enhancement using custom power devices. Int. Res. J. Eng. Technol. 2021, 8, 287–290. [Google Scholar]
  24. A.M. Bloul; A.M. Sharaf; H.M. Mosbah; M.E. El-Hawary, “A robust fuzzy logic controller for a green plug-switched filter for nonlinear loads’’ IEEE International Canadian Conference on Electrical and Computer Engineering (CCECE), 2015. [CrossRef]
  25. Sharaf, A.M.; Huang, H.; Chang, L. Power quality and nonlinear load voltage stabilization using error driven switched passive power filter. IEEE Proc. on International Symposium on Industrial Electronics 1995, 616–621. [Google Scholar] [CrossRef]
  26. Sharaf, A.M.; Gandoman, F.H. A Flexible Facts Based Scheme for Smart Grid-PV-Battery Storage Systems. Int. J. Distrib. Energy Resour. 2014, 10, 261–271. [Google Scholar]
  27. Desale, P.A.; Dhawale, V.J.; Bandgar, R.M. Brief review paper on the custom power devices for power quality improvement. International Journal of Electronic and Electrical Engineering 2014, 7, 723–733. [Google Scholar]
  28. Nejabatkhah, F.; Li, Y.; Tian, H. Power quality control of smart hybrid AC/DC Microgrids: An Overview”, IEEE conference. Translations and content mining, 2169-3536, 2019. [CrossRef]
  29. Bloul, A.M.; Sharaf, A.M.; Aly, H.H.; Gu, J. An Energy Efficient Green Plug Filter Compensation Scheme for Hybrid Nonlinear Loads. International Journal of Engineering Innovation & Research IJEIR 2023, 12, 69–88. [Google Scholar]
  30. Amal Dendouga, Abdelhakim Dendouga, Najib Essounbouli, “Performance Enhancement of Wind Turbine Systems using Type-2 Fuzzy Logic Control: Comparative study’’ 19th International Multi-Conference on Systems, Signals & Devices (SSD'22), 2022. [CrossRef]
  31. Al-Bashayreh, Q.; Kiftaro, A.; Alsheikh, M.; Jaradat, M.A. An Intelligent Controller for an Assisted Electric Wheelchair based on Interval Type-2 Fuzzy Logic. IEEE Advances in Science and Engineering Technology International Conferences (ASET) 2023. [Google Scholar]
  32. Jianan Zhang, Lei Zhang, Fengchun Sun and Zhenpo Wang, An Overview on Thermal Safety Issues of Lithium-ion Batteries for Electric Vehicle Application. IEEE Special Section on Battery Energy Storage and Management Systems 2018. [CrossRef]
  33. Dong, H.; Xi, J. Model Predictive Longitudinal Motion Control for the Unmanned Ground Vehicle with a Trajectory Tracking Model. IEEE Trans. Veh. Technol. 2022, 71. [Google Scholar] [CrossRef]
  34. Seema Agrawal, Deepika Sharma, Vijay Kumar Gupta and R. K. Somani, “Performance Evaluation of 3-Phase 4-Wire SAPF based on Synchronizing EPLL with Fuzzy Logic Controller’’ 2nd IEEE International conference on power Electronics, Intelligent Control and Energy systems, ICPEICES.2018. [CrossRef]
  35. Ahmed, F. Zobaa, Shady H. E. Abdel Aleem (ed.), Power quality in future electrical power systems, Energy Engineering, IET Digital Library, 2017, pp. 200-230.
  36. Hagras, H. A Hierarchical type-2 Fuzzy Logic Control Architecture for Autonomous Mobile Robots. IEEE Transactions on Fuzzy Systems 2004, 12, 524–539. [Google Scholar] [CrossRef]
  37. Mahdi M EI-Arini, MT Youssef, Hamed H Hendawy “Voltage sag analysis and its reduction to improve power system performance" IEEE Eleventh International Middle East Power Systems Conference, (2006).
  38. Mendel, J.; Hagras, H.; Tan, W.-W.; Melek, W.W.; Ying, H. Introduction to Type-2 Fuzzy Logic Control: Theory and Applications, John Wiley & Sons, Inc., Hoboken, New Jersey (2014).
  39. Mendel, J.; John, R. Type-2 Fuzzy Sets Made Simple. IEEE Transactions on Fuzzy Systems 2002, 10, 117–127. [Google Scholar] [CrossRef]
  40. Mukhtar Fatihu Hamza, Hwa Jen YAP and Imtiaz Choudhury. Advances on the Use of Meta-Heuristic Algorithms to Optimize Type-2 Fuzzy Logic Systems for Prediction, Classification, Clustering and Pattern Recognition. Journal of Computational and Theoretical Nanoscience 2016, 13, 96–109. [CrossRef]
  41. Mukhtar Fatihu Hamza, Hwa Jen YAP and Imtiaz Choudhury. Advances on the Use of Meta-Heuristic Algorithms to Optimize Type-2 Fuzzy Logic Systems for Prediction, Classification, Clustering and Pattern Recognition. Journal of Computational and Theoretical Nanoscience 2016, 13, 96–109. [CrossRef]
  42. Bloul, A.; Sharaf, A.; El-Hawary, M. An energy saving green plug device for nonlinear loads. IOP Conf. Ser. Earth Environ. Sci. 2018, 127, 012016. [Google Scholar] [CrossRef]
Preprints 106553 g001
Figure 1. AC Grid Study system with hybrid loads and Interface hybrid FACTS-Switched Filter.
Figure 1. AC Grid Study system with hybrid loads and Interface hybrid FACTS-Switched Filter.
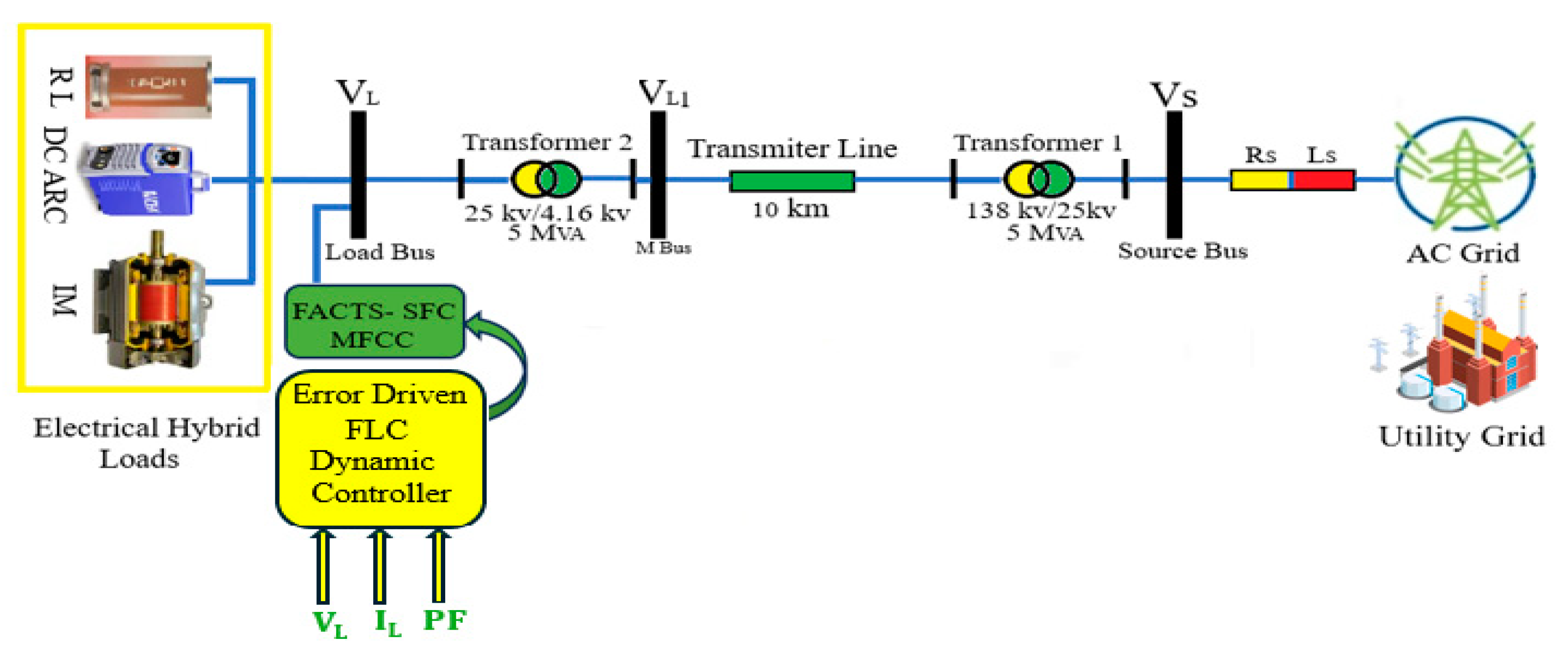
Preprints 106553 g001
Preprints 106553 g002
Figure 2. The MFCC-SFC device.
Figure 2. The MFCC-SFC device.
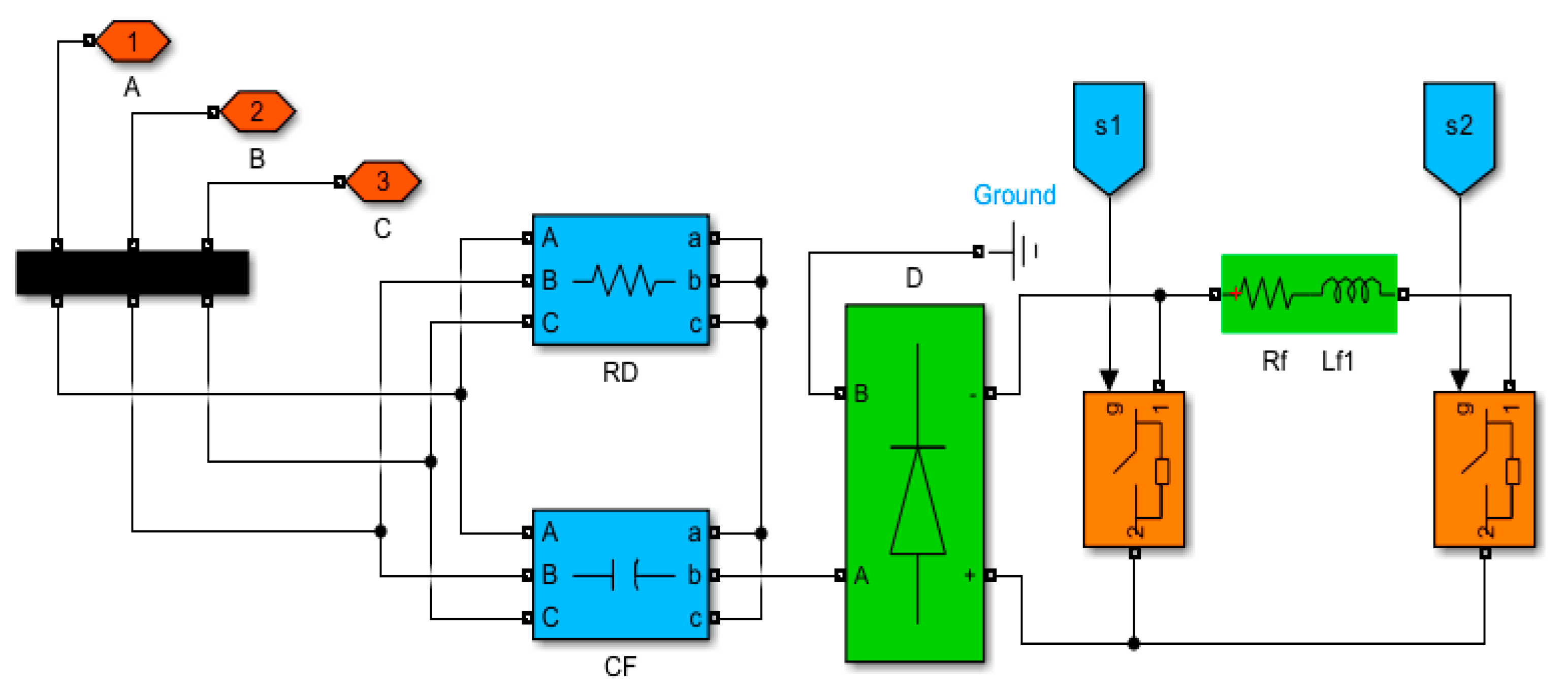
Preprints 106553 g002
Preprints 106553 g007
Figure 7. Type-2 Fuzzy Information Processing.
Figure 7. Type-2 Fuzzy Information Processing.
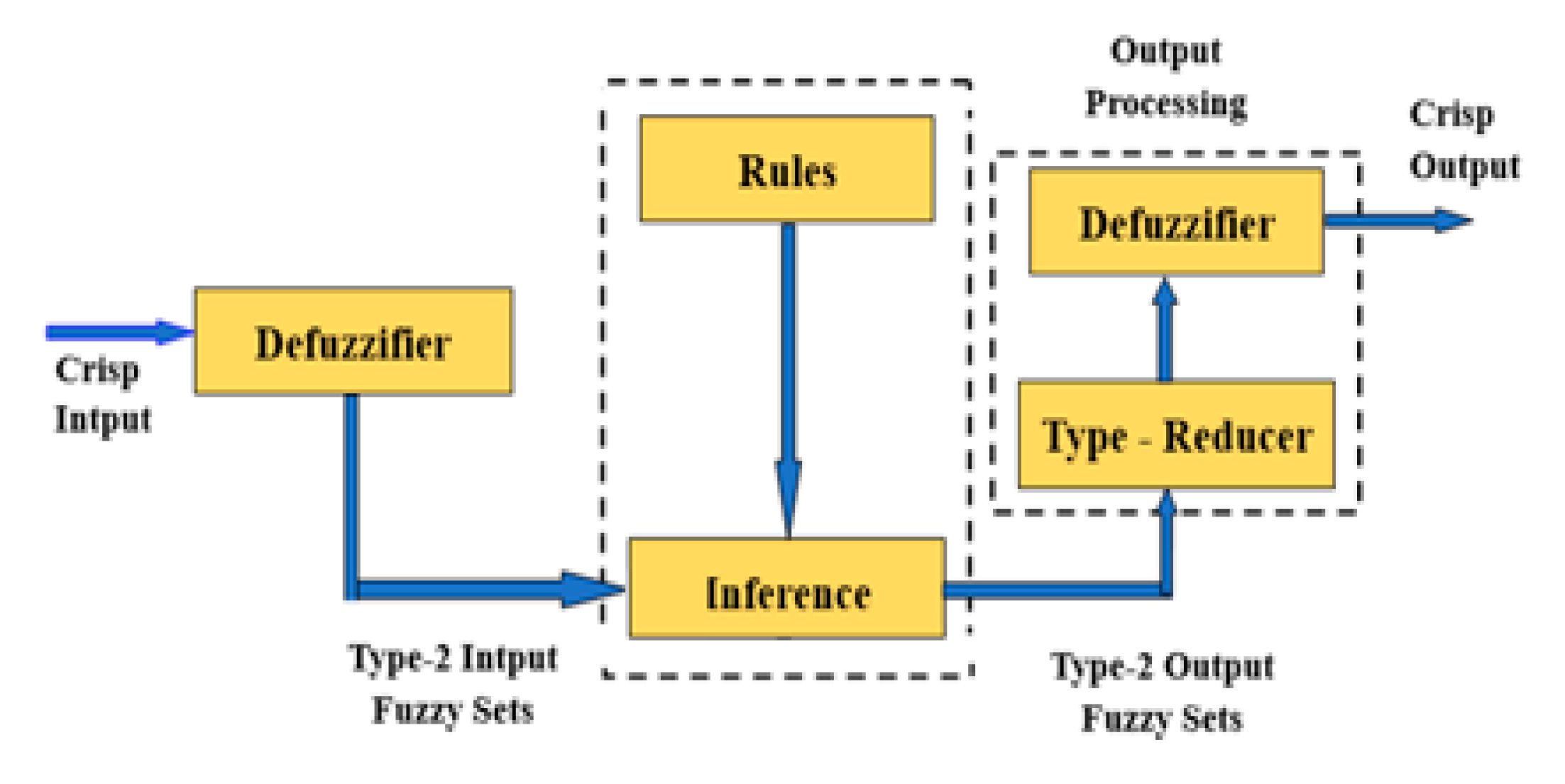
Preprints 106553 g007
Preprints 106553 g008
Figure 8. Radial AC Study system with FACTS -MFCC at Load Bus.
Figure 8. Radial AC Study system with FACTS -MFCC at Load Bus.
Preprints 106553 g008
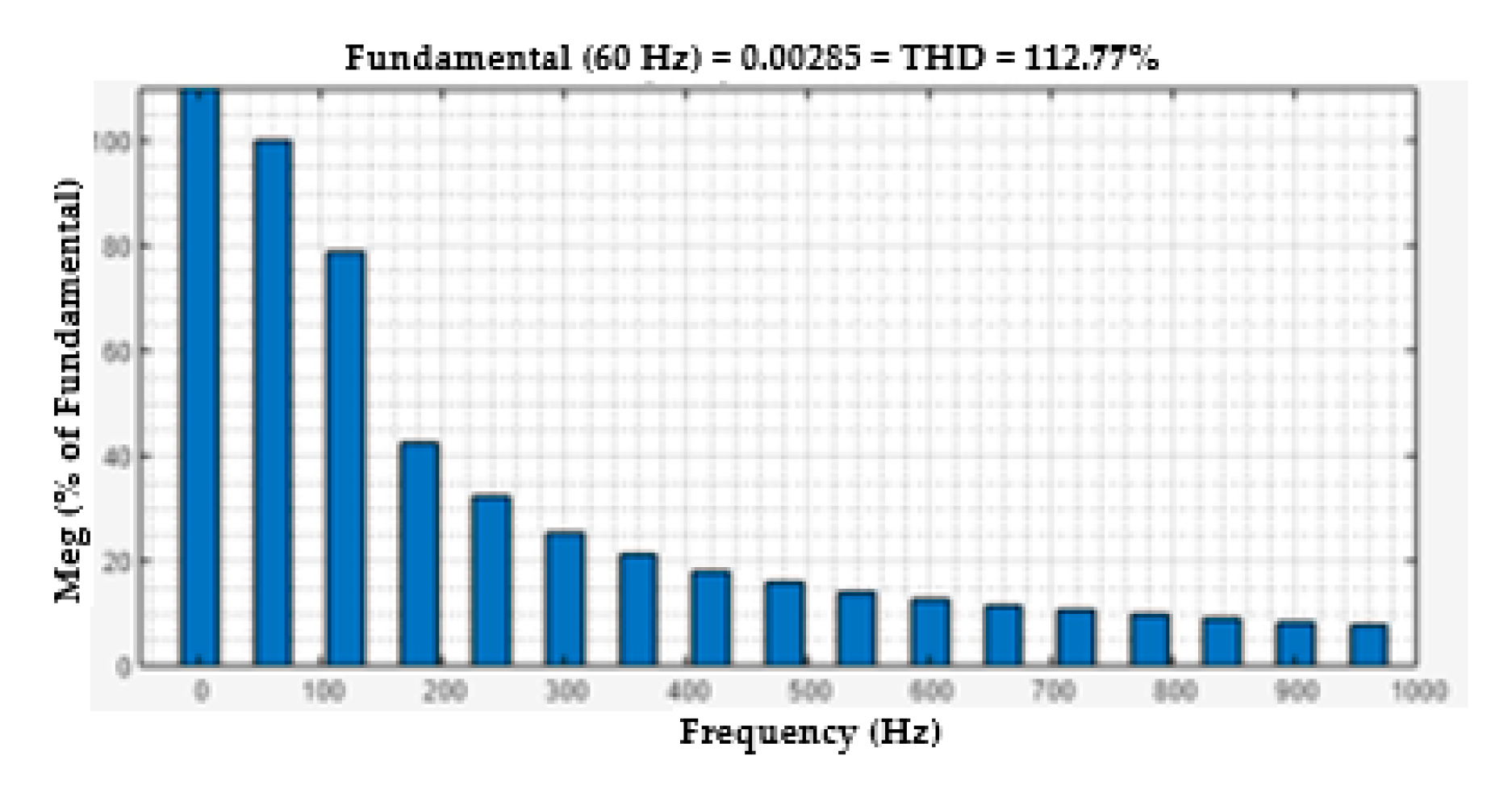
Preprints 106553 g015
Figure 15. FFT analysis of voltage at load Bus without FACTS-MFCC for load-changing operation.
Figure 15. FFT analysis of voltage at load Bus without FACTS-MFCC for load-changing operation.
Preprints 106553 g015
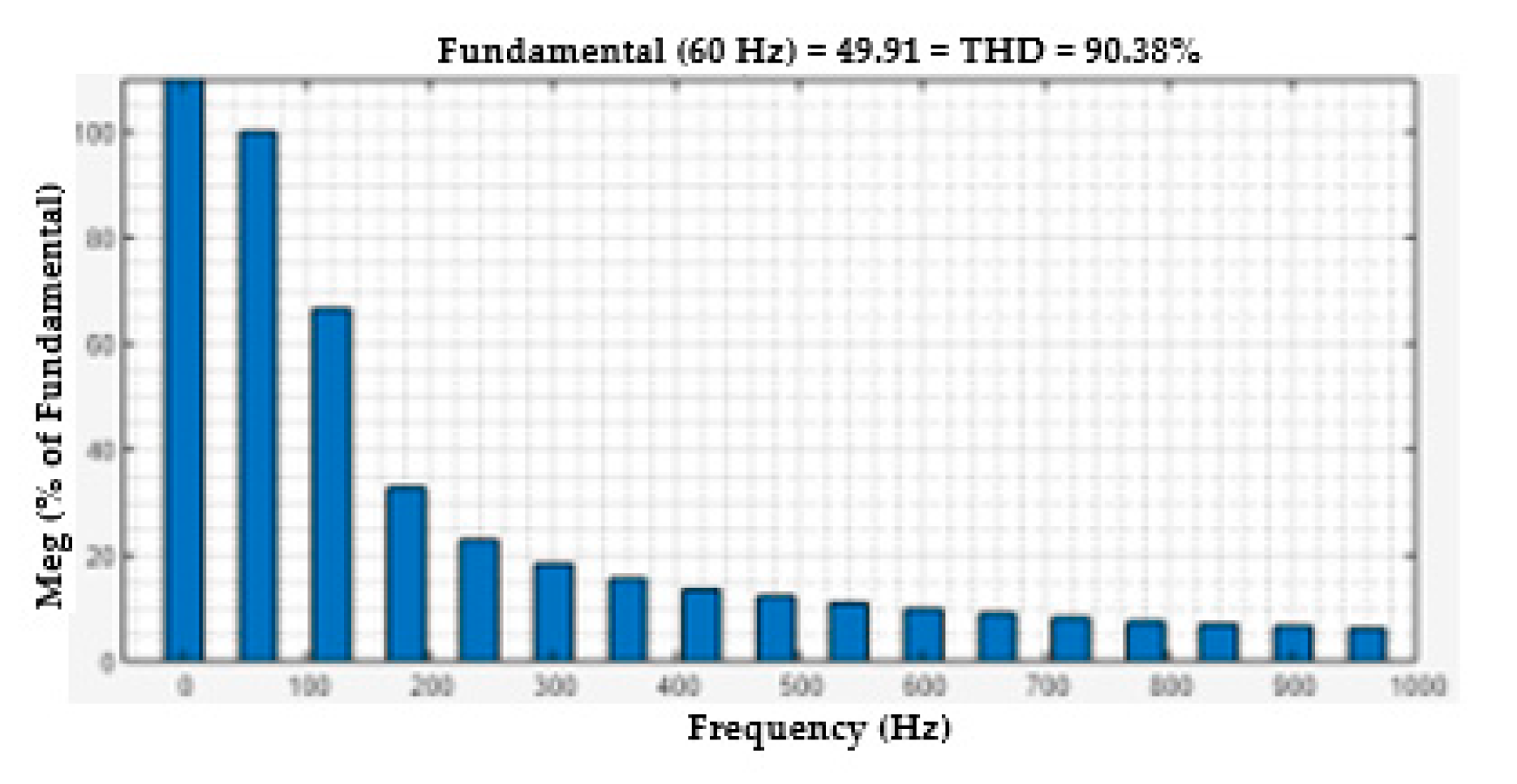
Preprints 106553 g016
Figure 16. FFT analysis of voltage at load Bus with FACTS-MFCC for load-changing operation.
Figure 16. FFT analysis of voltage at load Bus with FACTS-MFCC for load-changing operation.
Preprints 106553 g016
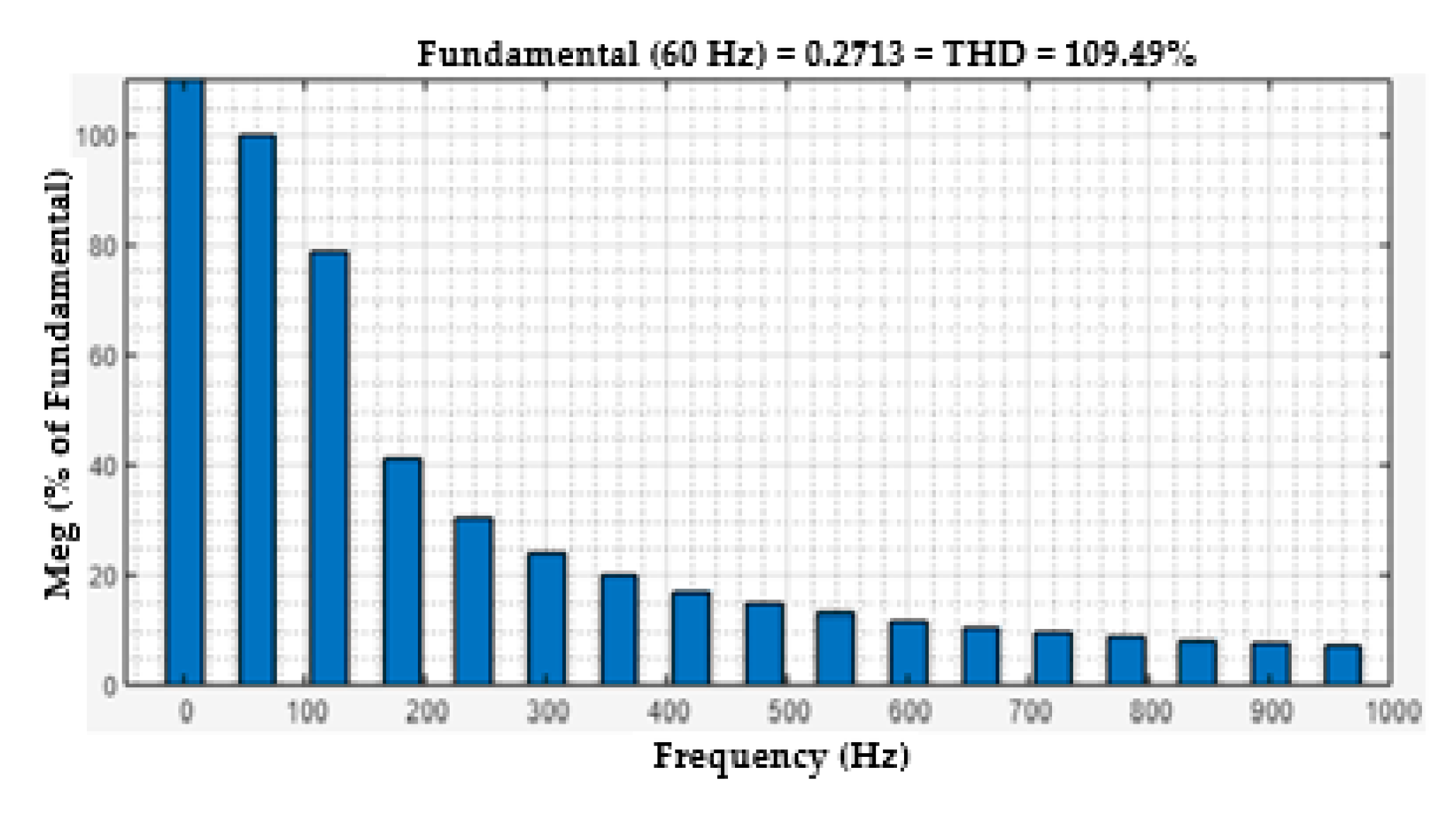
Preprints 106553 g017
Figure 17. FFT analysis of Current at load Bus without FACTS-MFCC for load-changing operation.
Figure 17. FFT analysis of Current at load Bus without FACTS-MFCC for load-changing operation.
Preprints 106553 g017
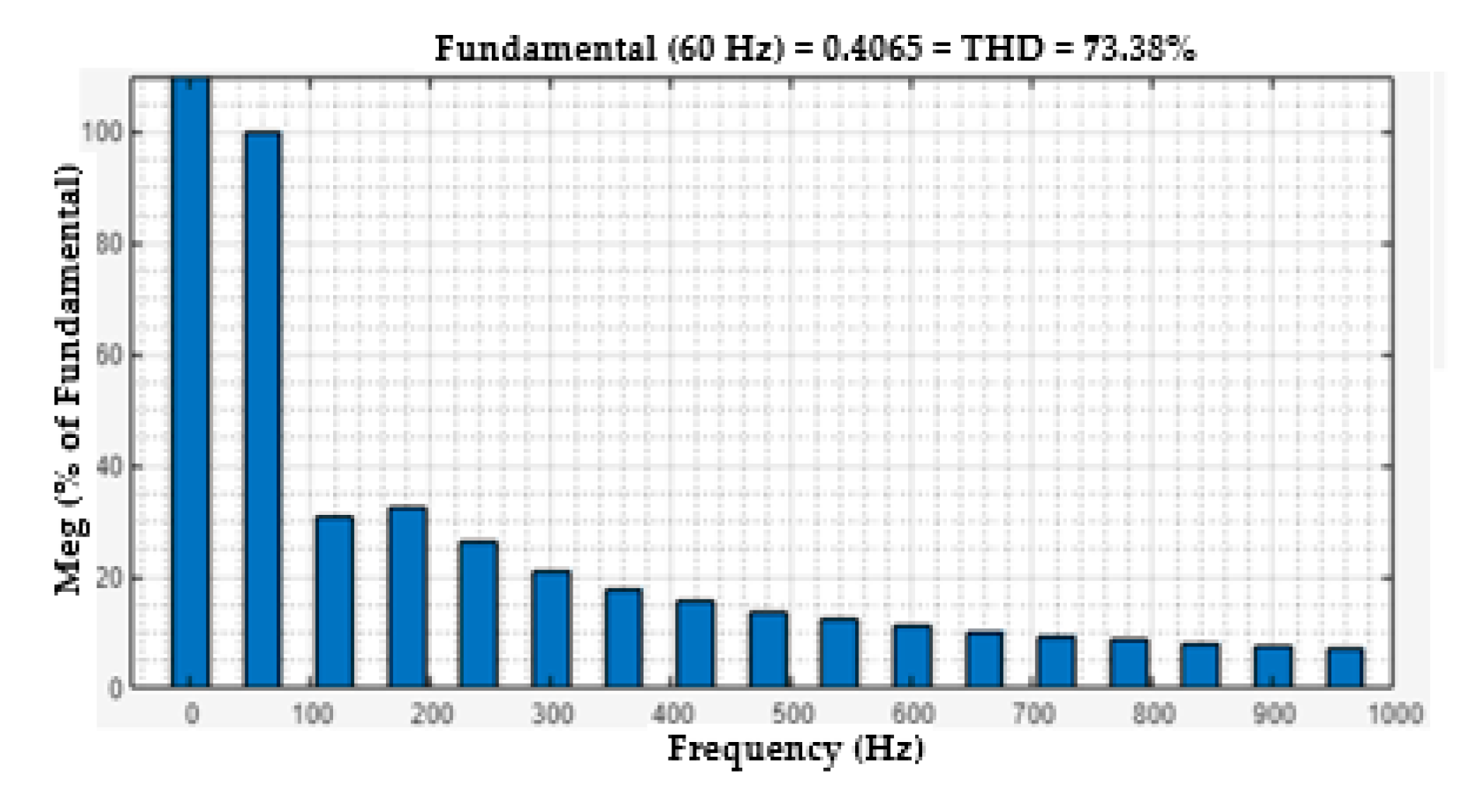
Preprints 106553 g018
Figure 18. FFT analysis of Current at load Bus with FACTS-MFCC for load-changing operation.
Figure 18. FFT analysis of Current at load Bus with FACTS-MFCC for load-changing operation.
Preprints 106553 g018
Table 1. Voltage, Current, Active power and Power Factor Values at Source and Load Buses without and with MFCC device Under SC.
Table 1. Voltage, Current, Active power and Power Factor Values at Source and Load Buses without and with MFCC device Under SC.
Buses Source bus, Vs (pu) Load bus, VL (pu)
V I P PF V I P PF
Without MFCC 1.0 0.7 0.46 0.68 1.0 0.65 0.35 0.75
With MFCC 1.01 0.75 0.52 0.8.2 1.05 0.7 0.4 0.79
Improvement 0.01 0.05 0.06 0.14 0.05 0.05 0.05 0.04
% Improvement 1% 5% 6% 14% 5% 5% 5% 4%
Table 2. Voltage, Current, Active power and Power Factor Values at Source and Load Buses without and with MFCC device Under OC.
Table 2. Voltage, Current, Active power and Power Factor Values at Source and Load Buses without and with MFCC device Under OC.
Buses Source bus, Vs (pu) Load bus, VL (pu)
V I P PF V I P PF
Without MFCC 1.0 0.8 0.35 0.78 0.8 0.68 0.3 0.8
With MFCC 1.01 0.9 0.5 0.98 1.0 0.75 0.4 0.98
Improvement 0.01 0.1 0.15 0.2 0.2 0.05 0.1 0.18
% Improvement 1% 10% 15% 20% 20% 7% 10% 18%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated