Prerpints.org logo
Preprint
Article

SU(2)-Symmetric Exactly Solvable Models of Two Interacting Qubits

Altmetrics

Downloads

108

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 May 2024

Posted:

15 May 2024

You are already at the latest version

Alerts
Abstract
A two-qubit Hamiltonian model exhibiting an SU(2) symmetry is considered. The related dynamical problem results to be then exactly solvable both in the time-independent and in the time-dependent case. Basing on the formal, general form of the related time evolution operator, the time-dependence of the level of entanglement of some initial conditions is studied within both the Rabi and the Landau-Majorana-Stückelber-Zener scenarios.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. Introduction

It is well known how the two-level approximation (namely, when the dynamics of a quantum system can be restricted to only two of its states) is ubiquitous and finds a plethora of applications in physics [1,2,3] and chemistry [4,5,6]. For example, it has been recently shown how the two-level formalism turns out to be suitable to adequately describe the dynamics of charge transfer [7,8] and of molecules in optical cavities [3]. Moreover, in the last decades the two-level quantum dynamical problem has become fundamental in quantum technologies, such as quantum computing [9,10,11], quantum sensing [12,13], quantum information processing [14,15], and quantum metrology [16,17].
Besides appropriately implementing qubits, in quantum computing it deserves to initialize and measure them precisely. As this aspect is concerned, the quantum control becomes critical. Quantum control Hamiltonians are conceived to be time-dependent Hamiltonians characterized by an external driving used to govern the qubit dynamics. Consequently, the identification of single-qubit exactly solvable scenarios, that is, of time-dependent Hamiltonians whose time evolution operator can be analytically derived, has become crucial. Indeed, several mathematical approaches and methods has been developed in order to individuate exactly solvable two-level dynamical problems [18,19,20,21,22,23,24,25], since solving the Schrödinger equation with a time-dependent Hamiltonian is not an easy task, in general. Among different exactly solvable scenarios, the most famous are undoubtedly the Rabi [26] and the Landau-Majorana-Stückelberg-Zener (LMSZ) [27,28,29,30] ones for their wide ranges of applications in physics. The interest of such a kind of research is shown also by its across-the-board validity. For example, the analytical solutions for a single two-level system have proved to be useful also in more complex systems not composed by spin variables [31], as well as, analogous approaches have been used for obtaining exact solutions for non-Hermitian two-level dynamical problems [32].
In some many-qubit scenarios, however, the coupling between different effective two-level systems (TLSs) cannot be neglected [33,34]. In other contexts, instead, such as in quantum computation, it is fundamental to tune the interaction between the TLSs in order to perform quantum logic gates aimed at generating entangled states of the system [35,36,37]. Entanglement is indeed a resource for quantum computation [38]. Therefore, great attention has been payed to the simplest many-qubit physical system which is of course the two-qubit scenario: two TLSs interacting either directly (exchange, Heisenberg, and Dzialoshinskii-Moriya interactions) or indirectly (photon-mediated interaction). This fact is confirmed, for example, by the huge amount of works focused on performing quantum gates and logic operational protocols on two-qubit systems implemented through different platforms [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57].
Of course, in order to fully control the dynamics of two interacting qubits, the development of strategies for solving the dynamical problem related to two-qubit time-dependent Hamiltonians are crucial as well. In Ref. [58], for example, the original two-qubit dynamical problem is decomposed into two independent single-qubit (sub)problems related to two dynamically invariant subspaces stemming from the existence of a specific symmetry of the Hamiltonian (and then of a constant of motion). In this way, on the basis of the knowledge of exact solutions for the single-qubit scenario, exact solutions for the two-qubit problem have been derived. The integrability of the two-qubit Hamiltonian model has been then exploited to bring to light physical effects in both the closed [59,60,61] and the open [62] case.
In this work, instead, our scope is to individuate a, generally time-dependent, two-qubit Hamiltonian model which presents no integrals of motion, and whose related time evolution operator can be still formally written and, for specific cases, analytically derived. To this end, we have relied on the Group Theory, focusing, in particular, on the SU(2) group. The possibility of exactly solving the dynamical problem has been exploited to investigate the exact time dependence of the concurrence (which measures the level of entanglement between the two qubits) in three different cases: the time-independent, the Rabi, and the LMSZ scenarios. It is shown how controlled generation of entanglement is possible both periodically and asymptotically in adiabatic and non-adiabatic regimes.
The work is organized as follows. In Section 2, after recalling some basics aspects of the SU(2)-symmetry group, the new two-qubit Hamiltonian model is derived. In Section 3 three possible solutions of the dynamical problem are discussed, and the related time behaviour of the two-qubit concurrence is investigated in Section 4. Finally, conclusive remarks are given in Section 5.

2. The Model

2.1. SU(2) Symmetry

The SU(2)-symmetric group is a compact group whose lowest-dimensional matrix representation consists in the set of all two-dimensional unitary matrices of the form
U 2 = a b − b * a * ,
with a and b two complex parameters satisfying | a | 2 + | b | 2 = 1 . The generators of this 2 × 2 representation of the SU(2) group are the well known Pauli matrices: σ x , σ y , and σ z . The most general generator, combination of the three Pauli matrices, can be then written as
H 2 = ω x σ x + ω y σ y + Ω σ z = Ω ω ω * − Ω ,
with ω ≡ ω x − i ω y , and the matrix is represented in the basis of σ z . It is worth underlining that H 2 are the generators of U 2 in the sense that U 2 are the solutions of the equation i U ˙ = H U , which is nothing but the Schrödinger ( ℏ = 1 ) equation for a physical system described by the Hamiltonian H. This holds when the the Hamiltonian is both time-dependent and time-independent (the time plays the role of the group parameter). In the time-independent case, the expressions of a and b can be easily derived by diagonalizing the Hamiltonian. In case of time-dependence of H, instead, the solution of the system for a and b, stemming form the Schrödinger equation, could be a not easy task. However, several examples of exactly solvable dynamical problems related to time-dependent Hamiltonians exist [18,19,20,21,22,23,24,25,26,27,30,58].
Matrix representations of the same SU(2) group in higher dimensions are also possible. The three-dimensional representation, for example, consists in all 3 × 3 unitary matrices whose generators are linear combinations of the three spin-1 Pauli matrices. The peculiarity at the basis of all representations is that they are always characterized by two independent parameters. It means that we can formally write the entries of the higher-dimensional unitary matrices of SU(2) as specific combinations of the two parameters a and b. The three-dimensional matrices, e.g., can be cast as
U 3 = a 2 2 a b b 2 − 2 a b * a a * − b b * 2 a * b b * 2 − 2 a * b * a * 2 .
As physical problems are concerned, this aspect is extremely relevant from a dynamical point of view, since it implies that high-dimensional SU(2)-symmetric dynamical problems can be solved by solving the related analogous 2 × 2 SU(2) dynamical problem.
In this work the 4 × 4 representation of the SU(2) group is considered. The 4 × 4 unitary matrices constituting the set read
U 4 = a 3 3 a 2 b 3 a b 2 b 3 − 3 a 2 b * a ( | a | 2 − 2 | b | 2 ) b ( 2 | a | 2 − | b | 2 ) 3 a * b 2 3 a b * 2 − b * ( 2 | a | 2 − | b | 2 ) a * ( | a | 2 − 2 | b | 2 ) 3 a * 2 b − b * 3 3 a * b * 2 − 3 a * 2 b * a * 3 .
The related generators are the spin-3/2 operators and the most general linear combination, in the basis of S z , results to be
H 4 = 3 Ω / 2 3 ω / 2 0 0 3 ω * / 2 Ω / 2 ω 0 0 ω * − Ω / 2 3 ω / 2 0 0 3 ω * / 2 − 3 Ω / 2 .
Also in this case, of course, the matrix U 4 is the formal solution of the equation i U ˙ 4 = H 4 U 4 . Of course, depending on the forms of Ω and ω (in general time-dependent), we obtain different expressions of a and b, solutions of the two independent equations stemming from the Schrödinger equation.

2.2. SU(2) Two-Qubit Model

We can interpret H 4 , that is the 4 × 4 matrix representation of the generic generator of the SU(2) group, in terms of two spin-qubits. In other words, we can interpret the Hamiltonian H 4 as written in the composite basis of the two qubits { | + + 〉 , | + − 〉 , | − + 〉 , | − − 〉 } , with σ z | ± 〉 = ± | ± 〉 . It is possible to verify that the resulting two-qubit model read
H 4 = Ω σ 1 z + Ω 2 σ 2 z + 3 2 ω x σ 2 x − ω y σ 2 y + ω x 2 σ 1 x σ 2 x + σ 1 y σ 2 y + ω y 2 σ 1 x σ 2 y − σ 1 y σ 2 x .
It describes two qubits interacting through an Heisenberg term depending on ω x and a Dzialoshinsky-Moriya (DM) term [63,64] characterized by a the DM vector d = ( 0 , 0 , 2 ω y ) (since the DM interaction is commonly written as d · S 1 × S 2 [65], with S j = ℏ / 2 { σ j x , σ j y , σ j z } , j = 1 , 2 ). The first qubit is subjected to a magnetic field along the z direction, namely ( 0 , 0 , 2 Ω ) , while the second one is subjected to a different magnetic field with nonvanishing components on the three directions, precisely ( 3 ω x , 3 ω y , Ω ) . We see that, in order to obtain the SU(2) form, specific relations between the parameters of the two-qubit Hamiltonian exist. In particular, it is interesting to note the link between the strength of the magnetic field on the x − y plane (on the second spin) and the interaction parameters, as well as the z-magnetic field on the first spin which doubles the one on the second spin. We stress that the magnetic fields written before, compared to the terms in the Hamiltonian, lack of a factor 1 / 2 since the Hamiltonian terms describe the coupling between the magnetic field and the spin magnetic moment which, for a spin-1/2, is characterized by a pre-factor 1 / 2 ( ℏ = 1 ) in front of the Pauli matrices, namely s = σ ^ / 2 .
As discussed above, the dynamical problem related to such a two-qubit model can be solved by finding the solutions of a and b which can be derived by solving the analogous two-dimensional dynamical problem. In the following three dynamical scenarios are considered.

3. Dynamical Scenarios

3.1. Time-Independent Case

First, consider the case where the three Hamiltonian parameters are time-independent, namely Ω = Ω 0 , ω = ω 0 e i ϕ 0 [where ω 0 = ω x 2 + ω y 2 , and ϕ 0 = − arctan ( ω y / ω x ) ]. In this case we can speak of eigenenergies of the system and they read
E 1 = − 3 2 k , E 2 = − 1 2 k , E 3 = 1 2 k , E 4 = 3 2 k , k ≡ Ω 0 2 + ω 0 2 .
The expression of a and b can be analytically derived and it is possible to verify that they results to be
a ( t ) = cos ( k t ) − i Ω 0 k sin ( k t ) , b ( t ) = − i ω 0 k sin ( k t ) .
We see that the parameter ϕ 0 does not play any role in the dynamics since it does not appear in the above expressions of a and b. This fact is physically reasonable since we can unitarily transform the Hamiltonian by performing a rotation in the x-y plane in order to obtain ϕ 0 ′ = 0 , that is, ω x ′ = ω 0 and ω y ′ = 0 .

3.2. Rabi Scenario

The Rabi scenario is characterized by a precessing magnetic field with a constant component along the z axis and a rotating field on the x-y plane, that is
Ω ( t ) = Ω 0 , ω x ( t ) = ω 0 cos ( ν 0 t ) , ω y ( t ) = ω 0 sin ( ν 0 t ) ,
where ν 0 is the precession frequency of the field. In this case a and b obtain the following expressions [26]
a ( t ) = cos ( ν R t ) − i Δ ν R sin ( ν R t ) e − i ν 0 t , b ( t ) = − i ω 0 ν R sin ( ν R t ) e − i ν 0 t ,
with Δ = Ω 0 − ν 0 being the detuning and ν R = Δ 2 + ω 0 2 the Rabi frequency. Δ = 0 corresponds to the well known resonance condition for which the Rabi oscillations of the populations in a two-level system are characterized by the maximum amplitude [26]. It is important to underline that the realization of a Rabi scenario for the two-qubit model under scrutiny could be challenging from an experimental point of view since the transverse magnetic field on the second spin and the coupling between the two qubits must be varied accordingly in order to maintain the SU(2) symmetry of the Hamiltonian. However, through trapped ion and superconducting circuit technologies both parameters can be appropriately managed [66].

3.3. Landau-Majorana-Stückelberg-Zener Scenario

The LMSZ scenario [27,30] is characterized by a constant transverse field, i.e. ω ( t ) = ω 0 , and a longitudinal ramp, that is a linearly varying magnetic field along the z direction, namely Ω ( t ) = α t (with α > 0 being the slope of the ramp), from negative to positive infinite values [ t ∈ ( − ∞ , + ∞ ) ]. To consider negative values of time is a mathematical trick to formally describe the experimental procedure consisting in the inversion of the magnetic field. Precisely, the passage from negative to positive values means that the magnetic field is initially set along a specific direction and its modulus is linearly decreased in time until it vanishes. At this point the modulus starts to be linearly increased in the opposite versus of the same direction. The instant when the field vanishes is then the inversion point.
The related dynamical problem cannot be solved in general, but only for specific initial states [27,30]. Moreover, it is not physically meaningful both from a theoretical and experimental point of view since an infinite field implies infinite energies as well as an infinite process. However, the dynamical problem related to a ‘finite’ LMSZ scenario, that is a ramp starting and ending at finite instants, i.e. t ∈ ] − t 0 , + t 0 [ , can be generally solved as well [67]. The expressions of a and b, although complicated, can be analytically derived and read [67]
a = Γ f ( 1 − i β ) 2 π × [ D i β ( 2 e − i π / 4 τ ) D − 1 + i β ( 2 e i 3 π / 4 τ i ) + D i β ( 2 e i 3 π / 4 τ ) D − 1 + i β ( 2 e − i π / 4 τ i ) ] , b = Γ f ( 1 − i β ) 2 π β e i π / 4 × [ − D i β ( 2 e − i π / 4 τ ) D − 1 + i β ( 2 e i 3 π / 4 τ i ) + D i β ( 2 e i 3 π / 4 τ ) D − 1 + i β ( 2 e − i π / 4 τ i ) ] ,
where β = ω 0 2 / α , Γ f is the gamma function, D ν ( z ) are the parabolic cylinder functions [68] and τ ≡ α t is a time dimensionless parameter (we stress that since ℏ = 1 then [ α ] = s − 2 ); τ i identifies the initial time instant. It is interesting to stress that in this case one can consider also non-symmetric time windows, that is τ i ≠ − τ f ; it is particularly relevant the case in which τ i = 0 [67] which can generate entangled states of two-qubit [59] and two-qutrit [69] systems through an adiabatic change of the field ( α ≪ 1 ).

4. Concurrence Dynamics

The level of entanglement of a two-qubit system can be quantified through the concurrence [70], which, in case of a generic normalized pure state | ψ 〉 = c + + | + + 〉 + c + − | + − 〉 + c − + | − + 〉 + c − − | − − 〉 , acquires the following analytical form
C = 2 | c + + c − − − c + − c − + | .
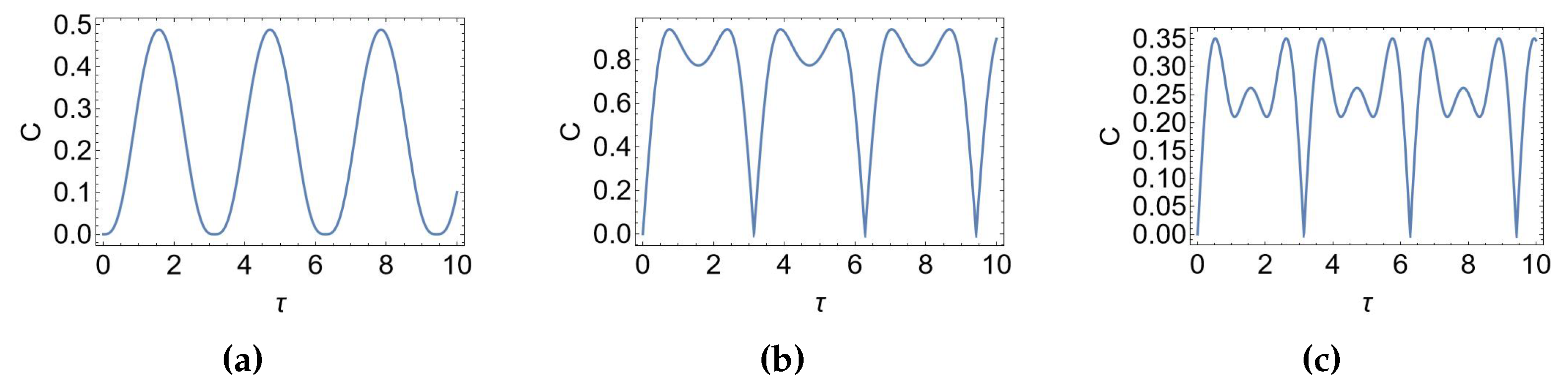
In Figure 1 (Figure 2) the Concurrence is calculated for different initial conditions, namely when the two-qubit system is initialized in the state | − − 〉 , | + − 〉 , and ( | + + 〉 + | + − 〉 ) / 2 (in the subplots ( a ) , ( b ) , and ( c ) , respectively) for the time-independent (Rabi) scenario. We see that the behaviour of the concurrence is qualitatively similar in the two cases. This is due to the fact that the expressions of a and b for the Rabi scenario closely resemble the ones related to the time-independent case. This circumstance stems from the fact that the Rabi Hamiltonian can be unitarily transformed to a time-independent one by changing the reference frame from the laboratory one to the frame rotating with the precessing magnetic field. The time behaviours of the concurrence practically consists in periodic oscillations. It can be noted that the subplots ( a ) of Figure 1 and Figure 2 are identical since in that case, that is for the initial condition | − − 〉 , the concurrence results to be C = 4 | ( a * ) 3 | | b 3 | . In this instance the factor e − i ν 0 t , appearing in the expressions of a and b for the Rabi scenario, does not play any role, contrarily to what occurs in the other cases (subplots ( b ) and ( c ) in the two figures) which present slight differences.
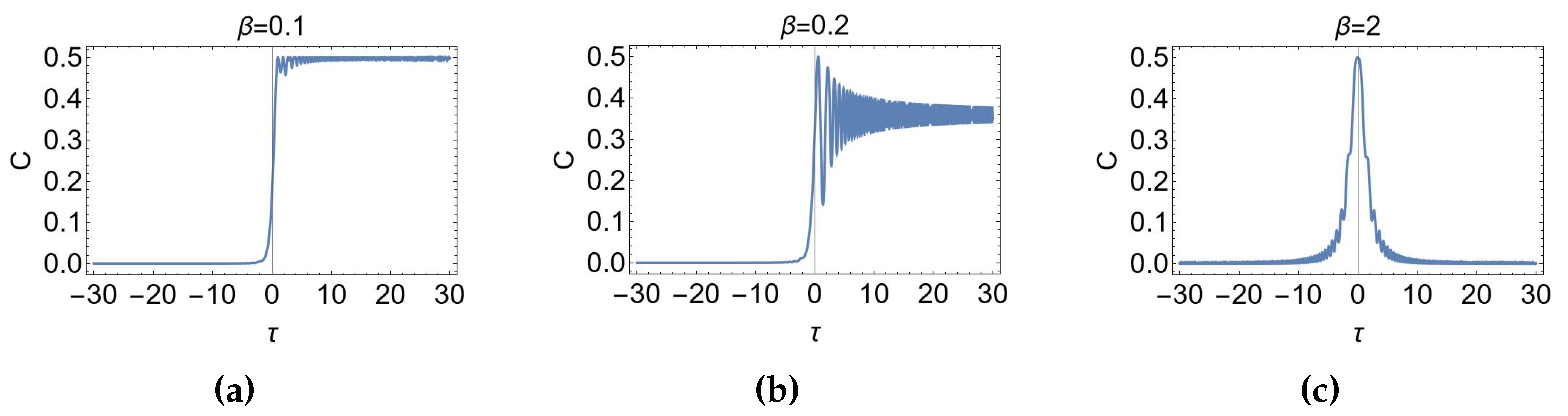
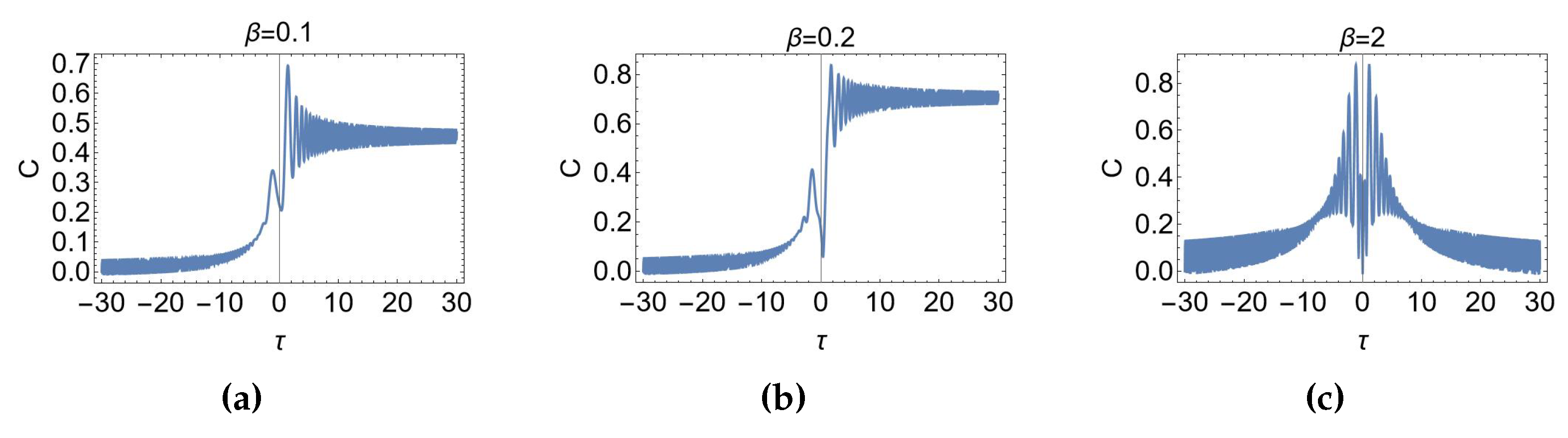
In Figure 3, Figure 4, Figure 5, the time behaviour of the concurrence in the LMSZ scenario is plotted for the three initial conditions | ψ 1 ( t i ) 〉 = | − − 〉 , | ψ 2 ( t i ) 〉 = | + − 〉 , and | ψ 3 ( t i ) 〉 = ( | + + 〉 + | + − 〉 ) / 2 , respectively. The value of β = ω 0 2 / α determines the level of adiabaticity of the dynamics. In particular, for β < 1 ( β > 1 ) the system is driven by a non-adiabatic (adiabatic) process.
The differences between the cases related to β = 0.1 and β = 0.2 in the three figures are only quantitative. The system starts indeed from a vanishing concurrence (since the considered initial conditions are separable) and then, after the inversion of the field, an amount of entanglement is generated between the two qubits.
A qualitatively different behaviour is instead obtained for the plots with β = 2 . In this case, for the three initial conditions, the maximum level of entanglement is generated at or near the central point (the inversion point of the field). At large times the concurrence tends to zero again, meaning that the system comes back to a separable state. This can be seen by explicitly writing the evolved states at time t, obtaining
| ψ 1 ( t − t i ) 〉 = U 4 ( t − t i ) | ψ 1 ( t i ) 〉 = b 3 | + + 〉 + 3 a * b 2 | + − 〉 + 3 ( a * ) 2 b | − + 〉 + ( a * ) 3 | − − 〉 , | ψ 2 ( t − t i ) 〉 = U 4 ( t − t i ) | ψ 2 ( t i ) 〉 = 3 a 2 b | + + 〉 + a ( | a | 2 − 2 | b | 2 ) | + − 〉 − b * ( 2 | a | 2 − | b | 2 ) | − + 〉 + 3 a * ( b * ) 2 | − − 〉 , | ψ 3 ( t − t i ) 〉 = U 4 ( t − t i ) | ψ 3 ( t i ) 〉 = 1 2 ( a 3 + 3 a 2 b ) | + + 〉 + [ a ( | a | 2 − 2 | b | 2 ) − 3 a 2 b * ] | + − 〉 − [ 3 a ( b * ) 2 − b * ( 2 | a | 2 − | b | 2 ) ] | − + 〉 + ( 3 a * ( b * ) 2 − ( b * ) 3 ) | − − 〉 ,
and by taking into account that for adiabatic dynamics ( β > 1 ) a ( t ≫ t ) → 0 and b ( t ≫ t ) → 1 . In this limit it is possible to see that | ψ 1 ( t ≫ 1 ) 〉 , | ψ 2 ( t ≫ 1 ) 〉 , and | ψ 3 ( t ≫ 1 ) 〉 obtain a separable form, namely
| ψ 1 ( t ≫ 1 ) 〉 = | + + 〉 , | ψ 2 ( t ≫ 1 ) 〉 = | − + 〉 | ψ 3 ( t ≫ 1 ) 〉 = | − + 〉 + | − − 〉 2 ,
justifying the vanishing concurrence at large times. We note that, such a kind of dynamics practically consists in the fully state-inversion, that is in flipping the spin-states. Contrarily, for non-adiabatic dynamics ( β < 1 ) the state at large times is not separable presenting a non-vanishing level of entanglement.
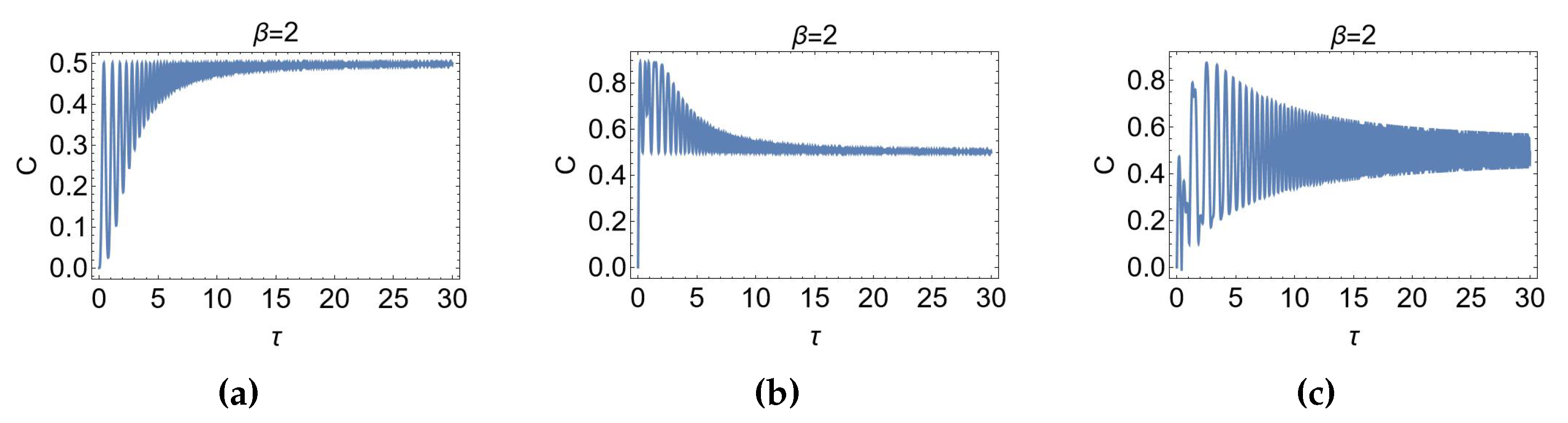
However, it is interesting to show that it is possible to generate entanglement also through adiabatic dynamics. In this case it is sufficient to modify the procedure of application of the magnetic field; namely, it deserves only to modify the time window, leaving unchanged the linear time-dependence of the ramp. Indeed, for a half-ramp, that is, a magnetic field initially vanishing and then linearly increased, the production of of entanglement can be appreciated in Figure 6. We see that in the three cases the concurrence, starting from a vanishing value, asymptotically tends to a (almost) constant value, namely 0.5 . In the transient, for the cases in subplots Figure 6(b) and Figure 6(c), high level of entanglement, corresponding C ≈ 0.9 , are reached by the two-qubit system during the adiabatic dynamics.
Finally, it is important to stress that the fast oscillations clearly visible in all of the plots related to the LMSZ scenario are not due to approximations adopted to obtain the plots. Rather, they are related to the fast oscillating cylinder functions appearing in the analytical solutions of the LMSZ model, given in Eqs. (11).

5. Conclusions

In this work a model of two interacting qubits has been presented and studied. The model has been derived by initially considering the finite four-dimensional representation of the general generator of the SU(2) group. Such a 4 × 4 matrix can be written in an operatorial form through spin-3/2 Pauli operators. In this case one simply obtains a model of a single spin-3/2 (a four-level system) subjected to a magnetic field with, in general, non-vanishing components on the three independent directions.
The same 4 × 4 matrix, however, can be read also in terms of the Pauli matrices of two spin-1/2 (TLSs or qubits). By performing such a ‘translation’ in the new language of the two TLSs, we have obtained a model of two qubits interacting through both an exchange and a Dzialonshinskii-Moriya interaction terms. The two qubits are also subjected to different local magnetic fields. Precisely, the first qubit is subjected only to a longitudinal (z) magnetic field, while the second spin is subjected to both a longitudinal and a transverse (on the x-y plane) magnetic field. Of course, in order to respect the SU(2)-symmetry form of the generator, specific relations between the different Hamiltonian parameters exist. Namely, the longitudinal magnetic field on the first qubit doubles the one on the second qubit, and the coupling strength of the interaction parameters are closely related to the magnitude of the transverse magnetic field on the second qubit.
The importance of an SU(2)-symmetric model relies on the fact that we know the general structure of the operator U generated by the generator H (the Hamiltonian) through U = e − i H t ( ℏ = 1 ); in physical terms, U is then the time evolution operator. The general structure of the operator U, which is dependent only on two generally complex parameters (which can be found by solving the related Schrödinger equation), is valid when the Hamiltonian parameters are both time-dependent and not. While the time-independent case is of course easily solvable, the time-dependent one depends on the specific time-dependence of the field and, in general, to find exact solutions is not an easy task. However, thanks to the SU(2) symmetry, we can obtain exact solutions for our two-qubit problem from the known solutions of the single-qubit dynamical problem. This circumstance considerably simplifies our task since several exactly solvable single-qubit scenarios (for which analytical solutions of the Schrödinger equation can be found) exist in literature [18,19,20,21,22,23,24,25,26,27,28,29,30,58]. It means that for all of these scenarios we can derive the exact dynamics of the two qubits. From a physical point of view, such a circumstance implies that, for such scenarios, we can have a full control of the evolution of the two-qubit system. Moreover, we could analogously take advantage from specific applications developed for single two-level systems [71,72,73,74,75,76] and applying them in two-qubit scenarios.
Besides the time-independent case, we have considered the most famous exactly solvable time-dependent scenarios: the Rabi and the LMSZ ones. The exact expressions of the two parameters defining the time evolution operator have allowed us to derive the analytical form of the evolved states of some initial (separable) conditions taken into account. We have analysed, in particular, the time evolution of the concurrence, being a measure of the entanglement established between the two qubits. High level of entanglement can be generated through such a kind of interaction model and the considered scenarios. Further, we have highlighted how it is possible, in the case of the LMSZ scenario, to generate high values of concurrence in a different way depending on the level of adiabaticity of the procedure (that is, depending on the slope of the magnetic field).
Finally, it is worth pointing out that the relevance of the present work relies also on the fact that it opens the possibility to analogously investigate: 1) other possible exactly solvable scenarios for the same model; 2) other finite representations of the SU(2)-symmetry group which can be interpreted in terms of more complex systems of interacting qubits [77,78] and/or qudits (N-level systems) [69,79,80]. For example, the 6 × 6 representation matrix can be written in terms of a qubit coupled to a qutrit (three-level system), as well as the eight-dimensional matrix can be expressed in terms of three interacting qubit operators.

Acknowledgments

RG warmly thanks Antonino Messina for fruitful discussions. RG acknowledges financial support by the PNRR MUR project PE0000023-NQSTI.

References

  1. Dell’Anno, F.; De Siena, S.; Illuminati, F. Multiphoton quantum optics and quantum state engineering. Physics Reports 2006, 428, 53–168. [Google Scholar] [CrossRef]
  2. Shevchenko, S.; Ashhab, S.; Nori, F. Landau–Zener–Stückelberg interferometry. Physics Reports 2010, 492, 1–30. [Google Scholar] [CrossRef]
  3. Ivakhnenko, O.V.; Shevchenko, S.N.; Nori, F. Nonadiabatic Landau–Zener–Stückelberg–Majorana transitions, dynamics, and interference. Physics Reports 2023, 995, 1–89. [Google Scholar] [CrossRef]
  4. Newton, M.D. Quantum chemical probes of electron-transfer kinetics: the nature of donor-acceptor interactions. Chemical Reviews 1991, 91, 767–792. [Google Scholar] [CrossRef]
  5. Gupta, S.; Yang, J.H.; Yakobson, B.I. Two-level quantum systems in two-dimensional materials for single photon emission. Nano letters 2018, 19, 408–414. [Google Scholar] [CrossRef] [PubMed]
  6. Wang, D.; Kelkar, H.; Martin-Cano, D.; Rattenbacher, D.; Shkarin, A.; Utikal, T.; Götzinger, S.; Sandoghdar, V. Turning a molecule into a coherent two-level quantum system. Nature Physics 2019, 15, 483–489. [Google Scholar] [CrossRef]
  7. Migliore, A. Nonorthogonality problem and effective electronic coupling calculation: Application to charge transfer in π-stacks relevant to biochemistry and molecular electronics. Journal of Chemical Theory and Computation 2011, 7, 1712–1725. [Google Scholar] [CrossRef]
  8. Migliore, A.; Messina, A. Controlling the charge-transfer dynamics of two-level systems around avoided crossings. The Journal of Chemical Physics 2024, 160. [Google Scholar] [CrossRef]
  9. McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S.C.; Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 2020, 92, 015003. [Google Scholar] [CrossRef]
  10. Koch, C.P.; Boscain, U.; Calarco, T.; Dirr, G.; Filipp, S.; Glaser, S.J.; Kosloff, R.; Montangero, S.; Schulte-Herbrüggen, T.; Sugny, D.; others. Quantum optimal control in quantum technologies. Strategic report on current status, visions and goals for research in Europe. EPJ Quantum Technology 2022, 9, 19. [Google Scholar] [CrossRef]
  11. Chiavazzo, S.; Sørensen, A.S.; Kyriienko, O.; Dellantonio, L. Quantum manipulation of a two-level mechanical system. Quantum 2023, 7, 943. [Google Scholar] [CrossRef]
  12. Chu, Y.; Liu, Y.; Liu, H.; Cai, J. Quantum Sensing with a Single-Qubit Pseudo-Hermitian System. Phys. Rev. Lett. 2020, 124, 020501. [Google Scholar] [CrossRef] [PubMed]
  13. Hönigl-Decrinis, T.; Shaikhaidarov, R.; de Graaf, S.; Antonov, V.; Astafiev, O. Two-Level System as a Quantum Sensor for Absolute Calibration of Power. Phys. Rev. Appl. 2020, 13, 024066. [Google Scholar] [CrossRef]
  14. Jafarizadeh, M.; Naghdi, F.; Bazrafkan, M. Time optimal control of two-level quantum systems. Physics Letters A 2020, 384, 126743. [Google Scholar] [CrossRef]
  15. Feng, T.; Xu, Q.; Zhou, L.; Luo, M.; Zhang, W.; Zhou, X. Quantum information transfer between a two-level and a four-level quantum systems. Photon. Res. 2022, 10, 2854–2865. [Google Scholar] [CrossRef]
  16. Yang, Y.; Liu, X.; Wang, J.; Jing, J. Quantum metrology of phase for accelerated two-level atom coupled with electromagnetic field with and without boundary. Quantum Information Processing 2018, 17, 1–15. [Google Scholar] [CrossRef]
  17. Pezzè, L.; Smerzi, A.; Oberthaler, M.K.; Schmied, R.; Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 2018, 90, 035005. [Google Scholar] [CrossRef]
  18. Bagrov, V.G.; Gitman, D.M.; Baldiotti, M.C.; Levin, A. Annalen der Physik 2005, 14, 764–789.
  19. Kuna, M.; Naudts, J. Reports on Mathematical Physics 2010, 65, 77–108.
  20. Barnes, E.; Sarma, S.D. Physical review letters 2012, 109, 060401.
  21. Messina, A.; Nakazato, H. Journal of Physics A: Mathematical and Theoretical 2014, 47, 445302.
  22. Markovich, L.; Grimaudo, R.; Messina, A.; Nakazato, H. An example of interplay between Physics and Mathematics: Exact resolution of a new class of Riccati Equations. Ann. Phys. (NY) 2017, 385, 522–531. [Google Scholar] [CrossRef]
  23. Liang, H. Generating arbitrary analytically solvable two-level systems. Journal of Physics A: Mathematical and Theoretical 2023. [Google Scholar]
  24. Castaños, L. Simple, analytic solutions of the semiclassical Rabi model. Optics Communications 2019, 430, 176–188. [Google Scholar] [CrossRef]
  25. Castaños, L. A simple, analytic solution of the semiclassical Rabi model in the red-detuned regime. Physics Letters A 2019, 383, 1997–2003. [Google Scholar] [CrossRef]
  26. Rabi, I.I. Space Quantization in a Gyrating Magnetic Field. Phys. Rev. 1937, 51, 652–654. [Google Scholar] [CrossRef]
  27. Landau, L.D. A theory of energy transfer II. Phys. Z. Sowjetunion 1932, 2, 19. [Google Scholar]
  28. Majorana, E. Atomi orientati in campo magnetico variabile. Il Nuovo Cimento (1924-1942) 1932, 9, 43–50. [Google Scholar] [CrossRef]
  29. Stückelberg, E.C.G. Atomi orientati in campo magnetico variabile. Helv. Phys. Acta 1932, 5. [Google Scholar]
  30. Zener, C. Non-adiabatic crossing of energy levels. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 1932, 137, 696–702. [Google Scholar]
  31. Grimaudo, R.; Man’ko, V.I.; Man’ko, M.A.; Messina, A. Dynamics of a harmonic oscillator coupled with a Glauber amplifier. Phys. Scr. 2019, 95, 024004. [Google Scholar] [CrossRef]
  32. Grimaudo, R.; de Castro, A.S.M.; Nakazato, H.; Messina, A. Analytically solvable 2×2PT-symmetry dynamics from su(1,1)-symmetry problems. Phys. Rev. A 2019, 99, 052103. [Google Scholar] [CrossRef]
  33. Calvo, R.; Abud, J.E.; Sartoris, R.P.; Santana, R.C. Collapse of the EPR fine structure of a one-dimensional array of weakly interacting binuclear units: A dimensional quantum phase transition. Phys. Rev. B 2011, 84, 104433. [Google Scholar] [CrossRef]
  34. Napolitano, L.M.B.; Nascimento, O.R.; Cabaleiro, S.; Castro, J.; Calvo, R. Isotropic and anisotropic spin-spin interactions and a quantum phase transition in a dinuclear Cu(II) compound. Phys. Rev. B 2008, 77, 214423. [Google Scholar] [CrossRef]
  35. Kang, Y.H.; Chen, Y.H.; Wu, Q.C.; Huang, B.H.; Song, J.; Xia, Y. Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics. Scientific reports 2016, 6, 36737. [Google Scholar] [CrossRef]
  36. Lu, M.; Xia, Y.; Song, J.; An, N.B. Generation of N-atom W-class states in spatially separated cavities. J. Opt. Soc. Am. B 2013, 30, 2142–2147. [Google Scholar] [CrossRef]
  37. Li, J.; Paraoanu, G.S. Generation and propagation of entanglement in driven coupled-qubit systems. New Journal of Physics 2009, 11, 113020. [Google Scholar] [CrossRef]
  38. Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
  39. Morzhin, O.V.; Pechen, A.N. Optimal state manipulation for a two-qubit system driven by coherent and incoherent controls. Quantum Information Processing 2023, 22, 241. [Google Scholar] [CrossRef]
  40. Ding, L.; Hays, M.; Sung, Y.; Kannan, B.; An, J.; Di Paolo, A.; Karamlou, A.H.; Hazard, T.M.; Azar, K.; Kim, D.K.; others. High-fidelity, frequency-flexible two-qubit fluxonium gates with a transmon coupler. Physical Review X 2023, 13, 031035. [Google Scholar] [CrossRef]
  41. Schäfter, D.; Wischnat, J.; Tesi, L.; De Sousa, J.A.; Little, E.; McGuire, J.; Mas-Torrent, M.; Rovira, C.; Veciana, J.; Tuna, F.; others. Molecular one-and two-qubit systems with very long coherence times. Advanced Materials 2023, 35, 2302114. [Google Scholar] [CrossRef] [PubMed]
  42. Mills, A.R.; Guinn, C.R.; Gullans, M.J.; Sigillito, A.J.; Feldman, M.M.; Nielsen, E.; Petta, J.R. Two-qubit silicon quantum processor with operation fidelity exceeding 99%. Science Advances 2022, 8, eabn5130. [Google Scholar] [CrossRef] [PubMed]
  43. Petit, L.; Russ, M.; Eenink, G.H.; Lawrie, W.I.; Clarke, J.S.; Vandersypen, L.M.; Veldhorst, M. Design and integration of single-qubit rotations and two-qubit gates in silicon above one kelvin. Communications Materials 2022, 3, 82. [Google Scholar] [CrossRef]
  44. Noiri, A.; Takeda, K.; Nakajima, T.; Kobayashi, T.; Sammak, A.; Scappucci, G.; Tarucha, S. A shuttling-based two-qubit logic gate for linking distant silicon quantum processors. nature communications 2022, 13, 5740. [Google Scholar] [CrossRef]
  45. Moskalenko, I.N.; Simakov, I.A.; Abramov, N.N.; Grigorev, A.A.; Moskalev, D.O.; Pishchimova, A.A.; Smirnov, N.S.; Zikiy, E.V.; Rodionov, I.A.; Besedin, I.S. High fidelity two-qubit gates on fluxoniums using a tunable coupler. npj Quantum Information 2022, 8, 130. [Google Scholar] [CrossRef]
  46. Bresque, L.; Camati, P.A.; Rogers, S.; Murch, K.; Jordan, A.N.; Auffèves, A. Two-qubit engine fueled by entanglement and local measurements. Physical Review Letters 2021, 126, 120605. [Google Scholar] [CrossRef] [PubMed]
  47. Cai, T.Q.; Han, X.Y.; Wu, Y.K.; Ma, Y.L.; Wang, J.H.; Wang, Z.L.; Zhang, H.Y.; Wang, H.Y.; Song, Y.P.; Duan, L.M. Impact of spectators on a two-qubit gate in a tunable coupling superconducting circuit. Physical review letters 2021, 127, 060505. [Google Scholar] [CrossRef] [PubMed]
  48. Blümel, R.; Grzesiak, N.; Nguyen, N.H.; Green, A.M.; Li, M.; Maksymov, A.; Linke, N.M.; Nam, Y. Efficient stabilized two-qubit gates on a trapped-ion quantum computer. Physical Review Letters 2021, 126, 220503. [Google Scholar] [CrossRef] [PubMed]
  49. Gu, X.; Fernández-Pendás, J.; Vikstål, P.; Abad, T.; Warren, C.; Bengtsson, A.; Tancredi, G.; Shumeiko, V.; Bylander, J.; Johansson, G.; others. Fast multiqubit gates through simultaneous two-qubit gates. PRX Quantum 2021, 2, 040348. [Google Scholar] [CrossRef]
  50. Foxen, B.; Neill, C.; Dunsworth, A.; Roushan, P.; Chiaro, B.; Megrant, A.; Kelly, J.; Chen, Z.; Satzinger, K.; Barends, R.; others. Demonstrating a continuous set of two-qubit gates for near-term quantum algorithms. Physical Review Letters 2020, 125, 120504. [Google Scholar] [CrossRef]
  51. Xu, Y.; Chu, J.; Yuan, J.; Qiu, J.; Zhou, Y.; Zhang, L.; Tan, X.; Yu, Y.; Liu, S.; Li, J.; others. High-fidelity, high-scalability two-qubit gate scheme for superconducting qubits. Physical review letters 2020, 125, 240503. [Google Scholar] [CrossRef] [PubMed]
  52. von Lüpke, U.; Beaudoin, F.; Norris, L.M.; Sung, Y.; Winik, R.; Qiu, J.Y.; Kjaergaard, M.; Kim, D.; Yoder, J.; Gustavsson, S.; others. Two-qubit spectroscopy of spatiotemporally correlated quantum noise in superconducting qubits. PRX Quantum 2020, 1, 010305. [Google Scholar] [CrossRef]
  53. Hendrickx, N.; Franke, D.; Sammak, A.; Scappucci, G.; Veldhorst, M. Fast two-qubit logic with holes in germanium. Nature 2020, 577, 487–491. [Google Scholar] [CrossRef] [PubMed]
  54. Wie, C.R. Two-qubit bloch sphere. Physics 2020, 2, 383–396. [Google Scholar] [CrossRef]
  55. Watson, T.; Philips, S.; Kawakami, E.; Ward, D.; Scarlino, P.; Veldhorst, M.; Savage, D.; Lagally, M.; Friesen, M.; Coppersmith, S.; others. A programmable two-qubit quantum processor in silicon. nature 2018, 555, 633–637. [Google Scholar] [CrossRef]
  56. Veldhorst, M.; Yang, C.; Hwang, J.; Huang, W.; Dehollain, J.; Muhonen, J.; Simmons, S.; Laucht, A.; Hudson, F.; Itoh, K.M.; others. A two-qubit logic gate in silicon. Nature 2015, 526, 410–414. [Google Scholar] [CrossRef] [PubMed]
  57. DiCarlo, L.; Chow, J.M.; Gambetta, J.M.; Bishop, L.S.; Johnson, B.R.; Schuster, D.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.; others. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 2009, 460, 240–244. [Google Scholar] [CrossRef]
  58. Grimaudo, R.; Messina, A.; Nakazato, H. Exactly solvable time-dependent models of two interacting two-level systems. Phys. Rev. A 2016, 94, 022108. [Google Scholar] [CrossRef]
  59. Grimaudo, R.; Vitanov, N.V.; Messina, A. Coupling-assisted Landau-Majorana-Stückelberg-Zener transition in a system of two interacting spin qubits. Phys. Rev. B 2019, 99, 174416. [Google Scholar] [CrossRef]
  60. Ghiu, I.; Grimaudo, R.; Mihaescu, T.; Isar, A.; Messina, A. Quantum Correlation Dynamics in Controlled Two-Coupled-Qubit Systems. Entropy 2020, 22. [Google Scholar] [CrossRef]
  61. Grimaudo, R.; Isar, A.; Mihaescu, T.; Ghiu, I.; Messina, A. Dynamics of quantum discord of two coupled spin-1/2’s subjected to time-dependent magnetic fields. Results Phys. 2019, 13, 102147. [Google Scholar] [CrossRef]
  62. Grimaudo, R.; de Castro, A.S.M.a.; Messina, A.; Solano, E.; Valenti, D. Quantum Phase Transitions for an Integrable Quantum Rabi-like Model with Two Interacting Qubits. Phys. Rev. Lett. 2023, 130, 043602. [Google Scholar] [CrossRef]
  63. Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. Journal of Physics and Chemistry of Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
  64. Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
  65. Weil, J.A.; Bolton, J.R. Electron paramagnetic resonance: elementary theory and practical applications; John Wiley & Sons, 2007.
  66. Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting qubits. Applied physics reviews 2019, 6. [Google Scholar] [CrossRef]
  67. Vitanov, N.V.; Garraway, B.M. Landau-Zener model: Effects of finite coupling duration. Phys. Rev. A 1996, 53, 4288–4304. [Google Scholar] [CrossRef] [PubMed]
  68. Abramowitz, M.; Stegun, I.A. Handbook of mathematical functions with formulas, graphs, and mathematical tables; Vol. 55, US Government printing office, 1968.
  69. Grimaudo, R.; Vitanov, N.V.; Messina, A. Landau-Majorana-Stückelberg-Zener dynamics driven by coupling for two interacting qutrit systems. Phys. Rev. B 2019, 99, 214406. [Google Scholar] [CrossRef]
  70. Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Physical Review Letters 1998, 80, 2245. [Google Scholar] [CrossRef]
  71. Cafaro, C.; Alsing, P.M. Continuous-time quantum search and time-dependent two-level quantum systems. International Journal of Quantum Information 2019, 17, 1950025. [Google Scholar] [CrossRef]
  72. Cafaro, C.; Gassner, S.; Alsing, P.M. Information Geometric Perspective on Off-Resonance Effects in Driven Two-Level Quantum Systems. Quantum Reports 2020, 2, 166–188. [Google Scholar] [CrossRef]
  73. Cafaro, C.; Alsing, P.M. Information geometry aspects of minimum entropy production paths from quantum mechanical evolutions. Phys. Rev. E 2020, 101, 022110. [Google Scholar] [CrossRef]
  74. Gassner, S.; Cafaro, C.; Ali, S.A.; Alsing, P.M. Information geometric aspects of probability paths with minimum entropy production for quantum state evolution. International Journal of Geometric Methods in Modern Physics 2021, 18, 2150127. [Google Scholar] [CrossRef]
  75. Casado-Pascual, J.; Lamata, L.; Reynoso, A.A. Spin dynamics under the influence of elliptically rotating fields: Extracting the field topology from time-averaged quantities. Phys. Rev. E 2021, 103, 052139. [Google Scholar] [CrossRef] [PubMed]
  76. Cafaro, C.; Ray, S.; Alsing, P.M. Complexity and efficiency of minimum entropy production probability paths from quantum dynamical evolutions. Phys. Rev. E 2022, 105, 034143. [Google Scholar] [CrossRef]
  77. Grimaudo, R.; Lamata, L.; Solano, E.; Messina, A. Cooling of many-body systems via selective interactions. Phys. Rev. A 2018, 98, 042330. [Google Scholar] [CrossRef]
  78. Grimaudo, R.; Magalhães de Castro, A.S.; Messina, A.; Valenti, D. Spin-Chain-Star Systems: Entangling Multiple Chains of Spin Qubits. Fortschritte der Physik 2022, 70, 2200042. [Google Scholar] [CrossRef]
  79. Grimaudo, R.; Messina, A.; Ivanov, P.A.; Vitanov, N.V. Spin-1/2 sub-dynamics nested in the quantum dynamics of two coupled qutrits. J. Phys. A Math. Theor. 2017, 50, 175301. [Google Scholar] [CrossRef]
  80. Grimaudo, R.; Belousov, Y.; Nakazato, H.; Messina, A. Time evolution of a pair of distinguishable interacting spins subjected to controllable and noisy magnetic fields. Ann. Phys. 2018, 392, 242–259. [Google Scholar] [CrossRef]
Preprints 106575 g001
Figure 1. Time-dependence of the concurrence for the initial condition: a) | − − 〉 , b) | + − 〉 , and c) ( | + + 〉 + | + − 〉 ) / 2 , in the time-independent case when Ω 0 = 2 ω 0 as a function of the dimensionless time τ = k t .
Figure 1. Time-dependence of the concurrence for the initial condition: a) | − − 〉 , b) | + − 〉 , and c) ( | + + 〉 + | + − 〉 ) / 2 , in the time-independent case when Ω 0 = 2 ω 0 as a function of the dimensionless time τ = k t .
Preprints 106575 g001
Preprints 106575 g002
Figure 2. Time-dependence of the concurrence for the initial condition: a) | − − 〉 , b) | + − 〉 , and c) ( | + + 〉 + | + − 〉 ) / 2 , in the Rabi scenario when Ω 0 / 2 = 2 ν 0 = ω 0 as a function of the dimensionless time τ = ν R t .
Figure 2. Time-dependence of the concurrence for the initial condition: a) | − − 〉 , b) | + − 〉 , and c) ( | + + 〉 + | + − 〉 ) / 2 , in the Rabi scenario when Ω 0 / 2 = 2 ν 0 = ω 0 as a function of the dimensionless time τ = ν R t .
Preprints 106575 g002
Preprints 106575 g003
Figure 3. Time-dependence of the concurrence in the LMSZ scenario, as a function of the dimensionless time τ = α t , for the initial condition | − − 〉 , when: a) β = 0.1 , b) β = 0.2 , c) β = 2 .
Figure 3. Time-dependence of the concurrence in the LMSZ scenario, as a function of the dimensionless time τ = α t , for the initial condition | − − 〉 , when: a) β = 0.1 , b) β = 0.2 , c) β = 2 .
Preprints 106575 g003
Preprints 106575 g004
Figure 4. Time-dependence of the concurrence in the LMSZ scenario, as a function of the dimensionless time τ = α t , for the initial condition | + − 〉 , when: a) β = 0.1 , b) β = 0.2 ,c) β = 2 .
Figure 4. Time-dependence of the concurrence in the LMSZ scenario, as a function of the dimensionless time τ = α t , for the initial condition | + − 〉 , when: a) β = 0.1 , b) β = 0.2 ,c) β = 2 .
Preprints 106575 g004
Preprints 106575 g005
Figure 5. Time-dependence of the concurrence in the LMSZ scenario, as a function of the dimensionless time τ = α t , for the initial condition ( | + + 〉 + | + − 〉 ) / 2 , when: a) β = 0.1 , b) β = 0.2 , c) β = 2 .
Figure 5. Time-dependence of the concurrence in the LMSZ scenario, as a function of the dimensionless time τ = α t , for the initial condition ( | + + 〉 + | + − 〉 ) / 2 , when: a) β = 0.1 , b) β = 0.2 , c) β = 2 .
Preprints 106575 g005
Preprints 106575 g006
Figure 6. Time-dependence of the concurrence in the LMSZ scenario, as a function of the dimensionless time τ = α t , for the initial condition: a) | − − 〉 , b) | + − 〉 , and c) ( | + + 〉 + | + − 〉 ) / 2 , and for adiabatic procedures, namely β = 2 .
Figure 6. Time-dependence of the concurrence in the LMSZ scenario, as a function of the dimensionless time τ = α t , for the initial condition: a) | − − 〉 , b) | + − 〉 , and c) ( | + + 〉 + | + − 〉 ) / 2 , and for adiabatic procedures, namely β = 2 .
Preprints 106575 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated