Energy, Exergetic and Thermoeconomic Analyses of Hydrogen-Fueled 1-kW Proton Exchange Membrane Fuel Cell

Exergy analysis evaluates the efficiency of system components by quantifying the rate of entropy generation. In general, the exergy destruction rate or irreversibility rate was directly obtained through the exergy-balance equation. However, this method cannot determine the origin of the component's entropy generation rate, which is a very important factor in system design and improvement. In this study, a thorough energy, exergy thermoeconomic analysis of a proton exchange membrane fuel cell (PEMFC) was performed, providing the heat transfer rate, entropy generation rate and cost loss rate of each component. The irreversibility rate of each component is obtained by the Gouy-Stodolar theorem. Detailed and extensive exergy and thermoeconomic analyses of PEMFC system have determined that water cooling units experience the greatest heat transfer among the components in the studied PEMFC system, resulting in the greatest irreversibility and thus the greatest monetary flow loss.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Proton exchange membrane fuel cells (PEMFCs) are suitable for small scale distributed power generation because of their high electrical efficiency at low operating temperatures and zero emission of air pollutants [1]. In addition, the PEMFC-cooling, heating and power (CHP) system [2,3], which has a fast response to load changes, was confirmed to be the most effective system for residential use through dynamics analysis [4]. For more effective residential applications, a combined cooling, heating and power (CCHP) system that integrates absorption cooling systems and the low and high temperature PEMFC system have been proposed [5]. For instance, a CCHP system integrated with a high-temperature PEMFC was proposed for data center applications with a constant cooling demand [6]. A demonstration of a residential CHP system based on PEMFC was performed by Gigliucci et al. [1], and the seasonal optimal operation of a 1kW PEMFC-based cogeneration system in an apartment complex was also calculated [7]. As surveyed above, applicability of various types of PEMFC to our daily lives is increasing, and accordingly, efficiency analysis of PEMFC components is required.

Exergy analysis predicts the thermodynamic performance of an energy system and the efficiency of system components by accurately quantifying the entropy generation of components [8]. Therefore, it is essential to utilize exergy analysis for thermal systems to improve the efficiency of components or to identify the origins of inefficiencies in components. Recently, exergy analysis has been applied in the diagnosis of defective components in power plants [9,10,11], PEMFC systems [12], and air conditioning systems [13,14]. In previous exergy analyses [10,15], the amount of exergy destruction of a component was simply calculated by subtracting the product (output) exergy from the fuel (input) exergy. However, heat transfer interactions are found to play an important role in increasing the irreversibility of malfunction cases in PEMFC systems [12]. Meanwhile, the difference between entropy inflow and outflow plays an important role in increasing the irreversibility of the devices in power plants where heat transfer from components to the environment is negligible [16].

In this study, the heat transfer rate and entropy generation of a component were evaluated from the first and second law of thermodynamics, respectively. The entropy generation rate, which can calculate the irreversibility rate by the Gouy-Stodolar theorem [17], can be obtained from the entropy flow into and out of the component and the heat transfer between the component and the surroundings. Additionally, a detailed exergetic and thermoeconomic analysis of the PEMFC system can identify the components that lose the most money flow due to irreversibility rates, and these findings can suggest modifications to the system.

2. Energy and Exergy Analysis of Thermal Systems

2.1. Energy Conservation

The first law of thermodynamics for any thermal component at the steady flow condition may be written as

{\dot{Q}}_{c v} + \sum_{i n} {\dot{H}}_{i} = \sum_{o u t} {\dot{H}}_{i} + {\dot{W}}_{c v}

(1)

where

{\dot{Q}}_{c v}

in the first term in Eq. (1) denotes the heat transfer interaction between a component and the environment,

{\dot{H}}_{i} = \dot{m} h_{i}

is the enthalpy flow rate of i species at the inlet or outlet, and

{\dot{W}}_{c v}

is the work flow rate in the component. The amount of heat transfer,

{\dot{Q}}_{c v}

which is not usually measured, can be obtained from Eq. (1) using known values of the enthalpy flow rates at the inlet and outlet and the work-flow rate

2.2. Exergy-Balance Equation and the Second Law of Thermodynamics

A general exergy-balance equation that can be applied to any component of thermal systems was formulated by Oh et al. [18]. With the inclusion of the exergy losses due to the heat transfer through the non-adiabatic components, the general exergy-balance equation may be written as Eq. (2) by separating the material stream into thermal and exergy streams [16]:

{\dot{E}}_{x}^{C H E} + (\sum_{i n l e t} {\dot{E}}_{x, i}^{T} - \sum_{o u t l e t} {\dot{E}}_{x, i}^{T}) + (\sum_{i n l e t} {\dot{E}}_{x, i}^{P} - \sum_{o u t l e t} {\dot{E}}_{x, i}^{P}) + T_{o} (\sum_{i n l e t} {\dot{S}}_{i} - \sum_{o u t l e t} {\dot{S}}_{i} + {\dot{Q}}_{c v} / T_{o}) = {\dot{E}}_{x}^{W}

(2)

where

{\dot{E}}_{x, i} (= \dot{m} e_{x, i})

, and

{\dot{S}}_{i} (= {\dot{m}}_{i} s_{i})

denote the exergy or entropy flow rates of i species, respectively, and T_o is ambient temperature. The superscripts CHE, T, P, and W represent chemical, thermal, and mechanical exergy, and work, respectively. The terms of

{\dot{E}}_{x}^{C H E}

and

{\dot{E}}_{x}^{W}

denote the exergy flow rate of the fuel and work-flow rate, respectively. The fourth term is the negative value of the rate of work loss or irreversibility due to entropy generation. The exergy-balance equation given in Eq. (2) can also be obtained by directly combining the first and second laws of thermodynamics (See Appendix A).

The entropy generation rate that appeared in the exergy-balance equation, was obtained using the second law of thermodynamics under steady-state flow conditions:

{\dot{S}}_{g e n} = \sum_{o u t l e t} {\dot{S}}_{i} - \sum_{i n l e t} {\dot{S}}_{i} - {\dot{Q}}_{c v} / T_{o}

(3)

The irreversibility rate

\dot{I}

can be obtained from the Gouy-Stodolar theorem [16]. That is:

\dot{I} = T_{o} {\dot{S}}_{g e n} = T_{o} (\sum_{o u t} {\dot{S}}_{i} - \sum_{i n} {\dot{S}}_{i}) - {\dot{Q}}_{c v}

(4)

This equation states that the exergy destruction rate is directly related to the rate of entropy flow into and out of the component (entropy flow part) and the rate of heat transfer from the component to the environment (heat transfer part).

If we do not separate the exergy flow into thermal and mechanical parts, the exergy-balance equation shown in Eq. (2) is simplified to

{\dot{E}}_{x}^{C H E} + (\sum_{i n l e t} {\dot{E}}_{x, i} - \sum_{o u t l e t} {\dot{E}}_{x, i}) + T_{o} (\sum_{i n l e t} {\dot{S}}_{i} - \sum_{o u t l e t} {\dot{S}}_{i} + {\dot{Q}}_{c v} / T_{o}) = {\dot{E}}_{x}^{W}

(5)

The exergy appeared in Eqs. (2) and (5) can be defined as

{\dot{E}}_{x} = \dot{m} e_{x} = \dot{m} [(h - T_{o} s) - (h_{o} - T_{o} s_{o})]

(6)

where the subscript “o” denotes reference values, usually taken as ambient temperature (T_o) and pressure (P_o).

By substituting the exergy definition into the exergy-balance equation given in Eq. (5), one can fine that the exergy-balance equation becomes the first law of thermodynamics. This outcome is rational because the exergy-balance equation can be obtained directly from the first and second laws of thermodynamics (See Appendix A).

The exergy-balance equation given in Eq. (5) can be rewritten as

{\dot{E}}_{x}^{C H E} + \sum_{i n l e t} {\dot{E}}_{x, i} = \sum_{o u t l e t} {\dot{E}}_{x, i} + {\dot{E}}_{x}^{W} + {\dot{E}}_{x}^{D}

(7)

Therefore, the irreversibility rate,

\dot{I}

or exergy destruction rate,

{\dot{E}}_{x}^{D}

can be determined by Eq. (7) without information on the heat transfer of the components. In the previous exergy studies by numerous researchers, the irreversibility rate was obtained through the above exergy-balance equation. The left side of Eq. (7) represents “fuel” or input exergy, and the right side represents “product’ or output exergy.

The exergy stream defined in Eq. (6) is calculated by following Eq. (8) including enthalpy (h) and entropy (s) per unit mass.

{\dot{E}}_{x} = \dot{m} e_{x} = \dot{m} {[h (T, P) - h_{o} (T_{o}, P_{o})] - T_{o} [s (T, P) - s_{o} (T_{o}, P_{o})]}

(8)

where T is temperature, and P is pressure. The exergy stream per unit mass (ex) can be further recognized as the combination of its thermal and mechanical components, which are described as superscripts, T and P, respectively, as follows [19]:

e_{x} = e_{x}^{T} + e_{x}^{P}

(9)

and

e_{x}^{T} = [h (T, P) - h (T_{o}, P)] - T_{o} [s (T, P) - s (T_{o}, P)]

(10)

e_{x}^{P} = [h (T_{o}, P) - h_{o} (T_{o}, P_{o})] - T_{o} [s (T_{o}, P) - s_{o} (T_{o}, P_{o})]

(11)

The energy conservation equation and exergy-balance equation for each component of the hydrogen-fueled 1kW PEMFC system can be obtained by applying Eqs. (1) and (2), respectively.

2.3. Exergy Cost-Balance Equation

In the modified production structure analysis (MOPSA) method [16], a cost-balance equation corresponding to the exergy-balance equation can be obtained by assigning a unit cost to each exergy flow. For example, the unit cost of C_o is assigned to the chemical exergy flow. The resulting exergy cost-balance equation corresponding to the exergy-balance equation is given by Eq. (2):

{\dot{E}}_{x}^{C H E} C_{o} + (\sum_{i n l e t} {\dot{E}}_{x, i}^{T} - \sum_{o u t l e t} {\dot{E}}_{x, i}^{T}) C_{T} + (\sum_{i n l e t} {\dot{E}}_{x, i}^{P} - \sum_{o u t l e t} {\dot{E}}_{x, i}^{P}) C_{P} + T_{o} (\sum_{i n l e t} {\dot{S}}_{i} - \sum_{o u t l e t} {\dot{S}}_{i} + {\dot{Q}}_{c v} / T_{o}) C_{S} + \dot{Z} = {\dot{E}}_{x}^{W} C_{W}

(12)

where C_T, C_P are the unit cost of thermal and mechanical exergies, respectively, C_S is the unit cost of lost work and C_W is the unit cost of work or electricity. When Eq. (12) is applied to a component of a thermal system to obtain the exergy cost-balance for that device, a new unit cost is assigned to the main product of that component and is displayed in Gothic letters. In Eq. (12),

{\dot{Z}}_{i}

is the flow of capital cost per unit time including the initial purchase cost and operating cost of the i-th compopnent, and can be obtained by the following equation [20]

{\dot{Z}}_{i} = ϕ_{i} \cdot {\dot{C}}_{i} / δ_{i}

(13)

In Eq. (13),

ϕ_{i}

and

δ_{i}

are the maintenance factor and the annual operating hours, respectively. On the other hand,

{\dot{C}}_{i}

is the initial purchase cost of the equipment converted into an annual equivalent cost and is given as follows.

{\dot{C}}_{i} = [C_{i} - S V \cdot P W F (i, n)] \cdot C R F (i, n)

(14)

In Eq. (14), C_i is the initial purchase cost of the equipment, SV is the depreciation cost after n years of life of the equipment, and PWF and CRF are the present worth factor and capital recovery factor, respectively. Maintenance costs are taken into account with a coefficient,

ϕ_{i}

=1.06 for each component assuming an expected life of 10 years. The annual interest rate is assumed to be 5% in this study.

3. Hydrogen-Fueled 1-kW PEMFC System

A schematic of the hydrogen-fueled 1-kW PEMFC system considered is shown in Figure 1. The main system consists of 9 components: an air blower (1), a humidifier (2), an anode (3), a cathode (4), a heat exchanger (HTX) for the fuel cell stack (FCS) (5), an FCS (6), a HTX for deionized (DI) water (7), an DI water tank (8), and a pump (9). To cool the DI water heated in the FCS, a cooling device consisting of HTX for coolant (10), a coolant tank (11), and a pump (12) is used. FCS is an artificial device that generates power and heat through an electrochemical reaction of hydrogen.

3.1. Energy Conservation and Exergy-Balance and Exergy Cost-Balance Equations for PEMFC System

The following energy conservation and exergy-balance equations can be obtained by applying the first law of thermodynamics shown in Eq. (1) and the general exergy-balance equation given in Eq. (2) to each component in the hydrogen fueled PEMFC system. The exergy cost-balance equation can be obtained by applying Eq. (12) to each component. In describing both exergy and cost-balances, the first digit in the subscript indicates a specific fluid stream 1 for air, 2 for hydrogen, and 5 for water. The second and third digits denote a digital number that represents the inlet or outlet of points in the components. The number in the bracket indicates each component of PEMFC system. In the exergy cost-balance equation, the number in the unit cost subscript indicates the component number. For each component of the PEMFC, the first law of thermodynamics and the exergy-balance and exergy cost-balance equations are:

1.Air blower

{\dot{H}}_{101} + {\dot{Q}}_{[1]} = {\dot{H}}_{102} + {\dot{W}}_{[1]} (= {\dot{E}}_{x, [1]}^{W})

(15-1)

\begin{array}{l} ({\dot{E}}_{x, 101}^{T} - {\dot{E}}_{x, 102}^{T}) + ({\dot{E}}_{x, 101}^{P} - {\dot{E}}_{x, 102}^{P}) + ({\dot{E}}_{x, 101}^{C} - {\dot{E}}_{x, 102}^{C}) \\ + [T_{o} ({\dot{S}}_{101} - {\dot{S}}_{102}) + {\dot{Q}}_{[1]}] = {\dot{E}}_{x, [1]}^{W} \end{array}

(15-2)

\begin{array}{l} ({\dot{E}}_{x, 101}^{T} - {\dot{E}}_{x, 102}^{T}) C_{T} + ({\dot{E}}_{x, 101}^{P} - {\dot{E}}_{x, 102}^{P}) C_{1 P} + ({\dot{E}}_{x, 101}^{C} - {\dot{E}}_{x, 102}^{C}) C_{C} \\ + [T_{o} ({\dot{S}}_{101} - {\dot{S}}_{102}) + {\dot{Q}}_{[1]}] C_{S} + {\dot{Z}}_{[1]} = {\dot{E}}_{x, [1]}^{W} C_{W} \end{array}

(15-3)

2.Humidifier

{\dot{H}}_{102} + {\dot{H}}_{104} + {\dot{Q}}_{[2]} = {\dot{H}}_{103} + {\dot{H}}_{105}

(16-1)

\begin{array}{l} [({\dot{E}}_{x, 102}^{T} - {\dot{E}}_{x, 103}^{T}) + ({\dot{E}}_{x, 104}^{T} - {\dot{E}}_{x, 105}^{T})] + [({\dot{E}}_{x, 102}^{P} - {\dot{E}}_{x, 103}^{P}) + ({\dot{E}}_{x, 104}^{P} - {\dot{E}}_{x, 105}^{P})] \\ + [({\dot{E}}_{x, 102}^{C} - {\dot{E}}_{x, 103}^{C}) + ({\dot{E}}_{x, 104}^{C} - {\dot{E}}_{x, 105}^{C})] + [T_{o} ({\dot{S}}_{102} - {\dot{S}}_{103} + {\dot{S}}_{104} - {\dot{S}}_{105}) + {\dot{Q}}_{[2]}] = 0 \end{array}

(16-2)

\begin{array}{l} [({\dot{E}}_{x, 102}^{T} - {\dot{E}}_{x, 103}^{T}) + ({\dot{E}}_{x, 104}^{T} - {\dot{E}}_{x, 105}^{T})] C_{2 T} + [({\dot{E}}_{x, 102}^{P} - {\dot{E}}_{x, 103}^{P}) + ({\dot{E}}_{x, 104}^{P} - {\dot{E}}_{x, 105}^{P})] C_{P} \\ + [({\dot{E}}_{x, 102}^{C} - {\dot{E}}_{x, 103}^{C}) + ({\dot{E}}_{x, 104}^{C} - {\dot{E}}_{x, 105}^{C})] C_{C} + [T_{o} ({\dot{S}}_{102} - {\dot{S}}_{103} + {\dot{S}}_{104} - {\dot{S}}_{105}) + {\dot{Q}}_{[2]}] C_{S} \\ + {\dot{Z}}_{[2]} = 0 \end{array}

(16-3)

3.Anode

{\dot{H}}_{206} + {\dot{Q}}_{[3]} = {\dot{H}}_{207}

(17-1)

({\dot{E}}_{x, 206}^{T} - {\dot{E}}_{x, 207}^{T}) + ({\dot{E}}_{x, 206}^{P} - {\dot{E}}_{x, 207}^{P}) + [T_{o} ({\dot{S}}_{206} - {\dot{S}}_{207}) + {\dot{Q}}_{[3]}] = 0

(17-2)

({\dot{E}}_{x, 206}^{T} - {\dot{E}}_{x, 207}^{T}) C_{3 T} + ({\dot{E}}_{x, 206}^{P} - {\dot{E}}_{x, 207}^{P}) C_{P} + [T_{o} ({\dot{S}}_{206} - {\dot{S}}_{207}) + {\dot{Q}}_{[3]}] C_{S} + {\dot{Z}}_{[3]} = 0

(17-3)

4.Cathode

{\dot{H}}_{103} + {\dot{Q}}_{[4]} = {\dot{H}}_{104}

(18-1)

({\dot{E}}_{x, 103}^{T} - {\dot{E}}_{x, 104}^{T}) + ({\dot{E}}_{x, 103}^{P} - {\dot{E}}_{x, 104}^{P}) + ({\dot{E}}_{x, 103}^{C} - {\dot{E}}_{x, 104}^{C}) + [T_{o} ({\dot{S}}_{103} - {\dot{S}}_{104}) + {\dot{Q}}_{[4]}] = 0

(18-2)

\begin{array}{l} ({\dot{E}}_{x, 103}^{T} - {\dot{E}}_{x, 104}^{T}) C_{T} + ({\dot{E}}_{x, 103}^{P} - {\dot{E}}_{x, 104}^{P}) C_{P} + ({\dot{E}}_{x, 103}^{C} - {\dot{E}}_{x, 104}^{C}) C_{4 C} \\ + [T_{o} ({\dot{S}}_{103} - {\dot{S}}_{104}) + {\dot{Q}}_{[4]}] C_{S} + {\dot{Z}}_{[4]} = 0 \end{array}

(18-3)

5. HTX in FCS

{\dot{H}}_{509} + {\dot{Q}}_{[5]} = {\dot{H}}_{510}

(19-1)

({\dot{E}}_{x, 509}^{T} - {\dot{E}}_{x, 510}^{T}) + ({\dot{E}}_{x, 509}^{P} - {\dot{E}}_{x, 510}^{P}) + [T_{o} ({\dot{S}}_{509} - {\dot{S}}_{510}) + {\dot{Q}}_{[5]}] = 0

(19-2)

({\dot{E}}_{x, 509}^{T} - {\dot{E}}_{x, 510}^{T}) C_{5 T} + ({\dot{E}}_{x, 509}^{P} - {\dot{E}}_{x, 510}^{P}) C_{D P} + [T_{o} ({\dot{S}}_{509} - {\dot{S}}_{510}) + {\dot{Q}}_{[5]}] C_{S} + {\dot{Z}}_{[5]} = 0

(19-3)

6. FCS

P_{t h e r m} = {\dot{E}}_{x}^{C H E} (= {\dot{E}}_{x, i n}^{C H E} - {\dot{E}}_{x, o u t}^{C H E}) - {\dot{E}}_{x, [6]}^{W}

(20-1)

{\dot{E}}_{x, [6]}^{D} = η P_{t h e r m}

(20-2)

{\dot{E}}_{x}^{C H E} C_{o} + (P_{t h e m} - {\dot{E}}_{x}^{D}) C_{T} + {\dot{E}}_{x}^{D} C_{S} + {\dot{Z}}_{[6]} = {\dot{E}}_{x, [6]}^{W} C_{6 W}

(20-3)

7. HTX for DI

{\dot{H}}_{510} + {\dot{H}}_{513} + {\dot{Q}}_{[7]} = {\dot{H}}_{511} + {\dot{H}}_{514}

(21-1)

\begin{array}{l} ({\dot{E}}_{x, 510}^{T} - {\dot{E}}_{x, 511}^{T}) + ({\dot{E}}_{x, 513}^{T} - {\dot{E}}_{x, 514}^{T}) + ({\dot{E}}_{x, 510}^{P} - {\dot{E}}_{x, 511}^{P}) + ({\dot{E}}_{x, 513}^{P} - {\dot{E}}_{x, 514}^{P}) + \\ [T_{o} ({\dot{S}}_{510} - {\dot{S}}_{511} + {\dot{S}}_{513} - {\dot{S}}_{514}) + {\dot{Q}}_{[7]}] = 0 \end{array}

(21-2)

\begin{array}{l} [({\dot{E}}_{x, 510}^{T} - {\dot{E}}_{x, 511}^{T}) + ({\dot{E}}_{x, 513}^{T} - {\dot{E}}_{x, 514}^{T})] C_{7 T} + [({\dot{E}}_{x, 510}^{P} - {\dot{E}}_{x, 511}^{P}) + ({\dot{E}}_{x, 513}^{P} - {\dot{E}}_{x, 514}^{P})] C_{P} + \\ [T_{o} ({\dot{S}}_{510} - {\dot{S}}_{511} + {\dot{S}}_{513} - {\dot{S}}_{514}) + {\dot{Q}}_{[7]}] C_{S} + {\dot{Z}}_{[7]} = 0 \end{array}

(21-3)

8. DI water tank

{\dot{H}}_{511} + {\dot{Q}}_{[8]} = {\dot{H}}_{508}

(22-1)

({\dot{E}}_{x, 511}^{T} - {\dot{E}}_{x, 508}^{T}) + ({\dot{E}}_{x, 511}^{P} - {\dot{E}}_{x, 508}^{P}) + [T_{o} ({\dot{S}}_{511} - {\dot{S}}_{508}) + {\dot{Q}}_{[8]}] = 0

(22-2)

({\dot{E}}_{x, 511}^{T} - {\dot{E}}_{x, 508}^{T}) C_{8 T} + ({\dot{E}}_{x, 511}^{P} - {\dot{E}}_{x, 508}^{P}) C_{P} + [T_{o} ({\dot{S}}_{511} - {\dot{S}}_{508}) + {\dot{Q}}_{[8]}] C_{S} + {\dot{Z}}_{[8]} = 0

(22-3)

9. Pump 1

{\dot{H}}_{508} + {\dot{Q}}_{[10]} = {\dot{H}}_{509} + {\dot{W}}_{[9]} (= {\dot{E}}_{x, [9]}^{W})

(23-1)

({\dot{E}}_{x, 508}^{T} - {\dot{E}}_{x, 509}^{T}) + ({\dot{E}}_{x, 508}^{P} - {\dot{E}}_{x, 509}^{P}) + [T_{o} ({\dot{S}}_{508} - {\dot{S}}_{509}) + {\dot{Q}}_{[9]}] = {\dot{E}}_{x, [9]}^{W}

(23-2)

({\dot{E}}_{x, 508}^{T} - {\dot{E}}_{x, 509}^{T}) C_{T} + ({\dot{E}}_{x, 508}^{P} - {\dot{E}}_{x, 509}^{P}) C_{9 P} + [T_{o} ({\dot{S}}_{508} - {\dot{S}}_{509}) + {\dot{Q}}_{[9]}] C_{S} + {\dot{Z}}_{[9]} = {\dot{E}}_{x, [9]}^{W} C_{W}

(23-3)

10. HTX for coolant

{\dot{H}}_{515} + {\dot{Q}}_{[10]} = {\dot{H}}_{516} + {\dot{W}}_{x, [10]}

(24-1)

({\dot{E}}_{x, 515}^{T} - {\dot{E}}_{x, 516}^{T}) + ({\dot{E}}_{x, 515}^{P} - {\dot{E}}_{x, 516}^{P}) + [T_{o} ({\dot{S}}_{515} - {\dot{S}}_{516}) + {\dot{Q}}_{[10]}] = {\dot{W}}_{x, [10]}

(24-2)

({\dot{E}}_{x, 510}^{T} - {\dot{E}}_{x, 507}^{T}) C_{10 T} + ({\dot{E}}_{x, 510}^{P} - {\dot{E}}_{x, 507}^{P}) C_{P} + [T_{o} ({\dot{S}}_{510} - {\dot{S}}_{507}) + {\dot{Q}}_{[10]}] C_{S} + {\dot{Z}}_{[10]} = 0

(24-3)

11. Coolant water tank

{\dot{H}}_{518} + {\dot{Q}}_{[11]} = {\dot{H}}_{512}

(25-1)

({\dot{E}}_{x, 518}^{T} - {\dot{E}}_{x, 512}^{T}) + ({\dot{E}}_{x, 518}^{P} - {\dot{E}}_{x, 512}^{P}) + [T_{o} ({\dot{S}}_{518} - {\dot{S}}_{512}) + {\dot{Q}}_{[11]}] = 0

(25-2)

({\dot{E}}_{x, 518}^{T} - {\dot{E}}_{x, 512}^{T}) C_{11 T} + ({\dot{E}}_{x, 518}^{P} - {\dot{E}}_{x, 512}^{P}) C_{P} + [T_{o} ({\dot{S}}_{518} - {\dot{S}}_{512}) + {\dot{Q}}_{[11]}] C_{S} + {\dot{Z}}_{[11]} = 0

(25-3)

12. Pump 2

{\dot{H}}_{512} + {\dot{Q}}_{[12]} = {\dot{H}}_{513} + {\dot{W}}_{[12]} (= {\dot{E}}_{x, [12]}^{W})

(26-1)

({\dot{E}}_{x, 512}^{T} - {\dot{E}}_{x, 513}^{T}) + ({\dot{E}}_{x, 512}^{P} - {\dot{E}}_{x, 513}^{P}) + [T_{o} ({\dot{S}}_{512} - {\dot{S}}_{513}) + {\dot{Q}}_{[12]}] = {\dot{E}}_{x, [12]}^{W}

(26-2)

({\dot{E}}_{x, 512}^{T} - {\dot{E}}_{x, 513}^{T}) C_{T} + ({\dot{E}}_{x, 512}^{P} - {\dot{E}}_{x, 513}^{P}) C_{12 P} + [T_{o} ({\dot{S}}_{512} - {\dot{S}}_{513}) + {\dot{Q}}_{[12]}] C_{S} + {\dot{Z}}_{[12]} = {\dot{E}}_{x, [12]}^{W} C_{W}

(26-3)

As explained in the previous section, the heat transfer rate obtained from the first law of thermodynamics can be used to obtain the irreversibility rate from the exergy-balance equation. The chemical exergy of various gases [4,21] was only considered for the FCS. The hydrogen flow at the anode is considered a mass flow.

Twelve exergy cost-balance equations are obtained from 12 components, but there are 17 unknown unit costs in those equations. The unknown unit costs of C_1P, C_2T, C_3T, C_4C, C_5T, C_6W, C_7T, C_8T, C_9P, C_10T, C_11T, C_12P, C_T, C_P, C_C, C_W and C_S in those equations. T_o solve for these 17 unknown unit costs, we need the following auxiliary cost-balance equations for the junctions of various exergies:

Thermal exergy junction:

\begin{array}{l} [\begin{array}{l} ({\dot{E}}_{x, 102}^{T} - {\dot{E}}_{x, 103}^{T}) + ({\dot{E}}_{x, 104}^{T} - {\dot{E}}_{x, 105}^{T}) + ({\dot{E}}_{x, 206}^{T} - {\dot{E}}_{x, 207}^{T}) + ({\dot{E}}_{x, 509}^{T} - {\dot{E}}_{x, 510}^{T}) + \\ ({\dot{E}}_{x, 510}^{T} - {\dot{E}}_{x, 511}^{T} + {\dot{E}}_{x, 513}^{T} - {\dot{E}}_{x, 514}^{T}) + ({\dot{E}}_{x, 511}^{T} - {\dot{E}}_{x, 508}^{T}) + ({\dot{E}}_{x, 510}^{T} - {\dot{E}}_{x, 507}^{T}) + ({\dot{E}}_{x, 518}^{T} - {\dot{E}}_{x, 512}^{T}) \end{array}] C_{T} \\ = [({\dot{E}}_{x, 102}^{T} - {\dot{E}}_{x, 103}^{T}) + ({\dot{E}}_{x, 104}^{T} - {\dot{E}}_{x, 105}^{T})] C_{2 T} + ({\dot{E}}_{x, 206}^{T} - {\dot{E}}_{x, 207}^{T}) C_{3 T} + ({\dot{E}}_{x, 509}^{T} - {\dot{E}}_{x, 510}^{T}) C_{5 T} + \\ ({\dot{E}}_{x, 510}^{T} - {\dot{E}}_{x, 511}^{T} + {\dot{E}}_{x, 513}^{T} - {\dot{E}}_{x, 514}^{T}) C_{7 T} + ({\dot{E}}_{x, 511}^{T} - {\dot{E}}_{x, 508}^{T}) C_{8 T} + ({\dot{E}}_{x, 510}^{T} - {\dot{E}}_{x, 507}^{T}) C_{10 T} + \\ ({\dot{E}}_{x, 518}^{T} - {\dot{E}}_{x, 512}^{T}) C_{11 T} \end{array}

(27)

Mechanical exergy junction:

\begin{array}{l} [({\dot{E}}_{x, 101}^{P} - {\dot{E}}_{x, 102}^{P}) + ({\dot{E}}_{x, 508}^{P} - {\dot{E}}_{x, 509}^{P}) + ({\dot{E}}_{x, 512}^{P} - {\dot{E}}_{x, 513}^{P})] C_{P} = ({\dot{E}}_{x, 101}^{P} - {\dot{E}}_{x, 102}^{P}) C_{1 P} + \\ ({\dot{E}}_{x, 508}^{P} - {\dot{E}}_{x, 509}^{P}) C_{9 P} + ({\dot{E}}_{x, 512}^{P} - {\dot{E}}_{x, 513}^{P}) C_{12 P} \end{array}

(28)

Chemical exergy junction:

({\dot{E}}_{x, 103}^{C} - {\dot{E}}_{x, 104}^{C}) C_{C} = ({\dot{E}}_{x, 103}^{C} - {\dot{E}}_{x, 104}^{C}) C_{4 C}

(29)

Work exergy junction:

{\dot{E}}_{x, [6]}^{W} C_{W} = {\dot{E}}_{x, [6]}^{W} C_{7 W}

(30)

Boundary:

\begin{array}{l} - [({\dot{E}}_{x, 101}^{T} - {\dot{E}}_{x, 105}^{T}) + ({\dot{E}}_{x, 206}^{T} - {\dot{E}}_{x, 207}^{T})] C_{T} - [({\dot{E}}_{x, 101}^{P} - {\dot{E}}_{x, 105}^{P}) + ({\dot{E}}_{x, 206}^{P} - {\dot{E}}_{x, 207}^{P})] C_{P} - ({\dot{E}}_{x, 101}^{C} - {\dot{E}}_{x, 105}^{C}) C_{C} \\ - T_{o} ({\dot{S}}_{101} - {\dot{S}}_{105} + {\dot{S}}_{206} - {\dot{S}}_{207}) C_{S} = 0 \end{array}

(31)

3.2. Energy Conservation and Exergy-Balance of FCS

Special attention was paid on obtaining the energy conservation equation and exergy-balance equations of FCS. The sum of the thermal exergy and the lost work in the exergy balance equation for FCS is expressed as the chemical exergy (P_therm) which is not converted to electric power. Since the chemical exergy of the fuel depends on the amount of condensation of the water product, the mole fraction of water in the water vapor produced during the electrochemical reaction of FCS must be determined. By introducing the mole fraction (y) of liquid water in the total water vapor produced in FCS, the chemical exergy pf the fuel entering FCS can be presented by Eq. (32) [12].

\begin{array}{l} e_{x}^{C H E} = (1 - y) L H V + y H H V \\ = L H V + y h_{f g} \end{array}

(32)

where h_fg is the latent heat of H₂O at given temperature. Since the consumed chemical exergy in FCS is presented by the difference between input and output chemical exergy, the energy conservation equation of FCS can be written as:

P_{t h e r m} = {\dot{E}}_{x}^{C H E} (= {\dot{n}}_{H_{2}} \cdot e_{x}^{C H E}) - {\dot{E}}_{x, [7]}^{W}

(33)

The terms in the left-hand side (P_therm) represents the chemical energy which is not converted to electric power in the FCS. The mole flow rate of the fuel consumed in the FCS, or mole flow rate of hydrogen at the membrane level [22], can be obtained by the following equation.

{\dot{n}}_{H_{2}} = I \cdot N_{c e l l} / (2 F)

(34)

where I is current and N_cell is the number of cells in the stack. The Faraday constant in Eq. (34) is 26801.48 A∙h/kmol.

The value of P_therm was substituted by following equation in the exergy-balance equation.

P_{t h e r m} = {\dot{E}}_{x, [7]}^{D} + {\dot{E}}_{x}^{T}

(35)

The exergy destruction rate in the FCS should be determined.

3.3. Exergy Cost-Balance Equation for Overall System

The overall exergy cost-balance equation of the system can be obtained by summing all the exergy cost-balance equations of the components and the cost-balance equations for the various exergy junctions and boundary, which is presented by summation of all the cost-balance equations of equations (15-3) to (26-3) and equations (27) to (31). The exergy cost-balance equation for the overall system is:

{\dot{E}}_{x}^{C H E} C_{o} + [\sum_{i} {\dot{Q}}_{[i]}] C_{S} + \sum_{i} {\dot{Z}}_{i} = \sum_{i} {\dot{E}}_{x, i}^{W} C_{W}

(36)

The second term on the left-hand side is the lost cost flow due to the heat transfer of all components of the PEMFC system. However, the contribution of this term is negligible comparing to other terms, such that Eq. (36) can be simplified as:

{\dot{E}}_{x}^{C H E} C_{o} + \sum_{i} {\dot{Z}}_{i} = \sum_{i} {\dot{E}}_{x, i}^{W} C_{W}

(37)

In the case of a thermal energy system that produces one product, such as electricity, it is known that the unit cost of the product can be obtained using Eq. (37) [16]. However, a detailed thermo-economic analysis is needed to evaluate the costing process of the system and loss of monetary flow in a particular process or device. The unit cost of a product estimated by some type of thermoeconomic method must equal to the unit cost calculated using Eq. (37).

4. Calculation Results and Discussion

The energy, exergy, and thermoeconomic analyses were conducted based on the experimental data obtained from a hydrogen-fueled 1-kW PEMFC system operated at Korea Institute of Energy Research, Korea [12]. The PEMFC system consists of 24 cells in the stack with effective cell area of 220 cm2, producing 820 W of electricity under 100 % current load. The measured thermodynamic properties, such as molar flow rate, temperature, and pressure, as well as the calculated thermal and mechanical exergy flow rates and entropic flow rates at the various inlets and outlets of the components are presented in Table 1 for the case of operation at 100% current load. A dataset for the mole flow rate, temperature and pressure was obtained by averaging 300 data measured over 5 min at 1-s intervals.

Table 2 lists the energy conservation for each component of the PEMFC system operating at full load conditions using the data shown in Table 1. Components of FCS are not listed in this table because they have no material flow. The second and third columns show the enthalpy flows into and out of each component, respectively. The fourth and fifth columns show work-flow rate and thermal interaction of the components with their environment. The null values of the sum of the incoming and outgoing enthalpy flow, heat and work-flow rates indicate that energy conservation is maintained in each component. The plus sign in the heat transfer rate indicates the heat flow from the component to the environment or another component, thus increasing the entropy production of the component. This is not the traditional symbolic convention for heat transfer that can be obtained from the first law of thermodynamics given in Eq. (1). The sixth column shows the irreversibility rate for each component calculated from the difference between the outgoing and incoming entropy flows. The seventh column represents the total irreversibility of the component, which is the sum of the irreversibility originating from the heat transfer and the irreversibility due to the entropy flow. The largest irreversibility occurs in the HTX for coolant (10), which is approximately 310.6 kJ/h as results of heat transfer interaction between the component and the environment.

The net flow rates of exergies crossing the boundary of each component in the PEMFC system at a 100% current load are listed in Table 3. Positive exergy indicates the exergy flow rate of 'product' (the right-hand side of Eq. 7), while negative values indicate the exergy flow rate of 'resources' or 'fuel' (the left-hand side of Eq. 7). Irreversibility acts as a “product” in the exergy balance equation, as can be clearly seen in Eq. (7). The irreversibility rates of each component, shown in sixth column, were obtained from the exergy-balance equation given of Eq. (7). The irreversibility rate of each component can be obtained from Eq. (7) without any information about the heat transfer rate. The irreversibility value matched well with those of calculated by the Gouy-Stodolar theorem presented in Table 2. One exception is the cathode component, where the molar flow at the inlet is different from the molar flow at the outlet. The negative irreversibility rates of the cathode, and HTX in FCS indicate that heat flows into the components resulting in the decrease of the rate of entropy generation. As clearly seen in Table 2 and 3, the highest irreversibility (310.6 kJ/h) occurs in the HTX for coolant (10) due to heat transfer to the environment. The sum of the exergy flow rates of products and resources is zero for each component, indicating that perfect exergy balance has been met.

Table 4 shows the unit cost for the primary product in each component as shown in in the exergy cost-balance equations. The unit cost of exergy was obtained by solving the 17 cost-balance equations simultaneously for the components and junctions. A hydrogen unit cost of $25/GJ ($3.0/kg H₂) was used in this calculation. The input molar flow rate of hydrogen was taken as the consumed hydrogen in FCS (0.00196 kmol/h) rather than the molar flow rate of hydrogen coming in at 206 state point (0.00275 kmol/h). The mole fraction of water condensate at the GDL layer was taken to be 0.35, which is a typical value for normal operation of the PEMFC system [12]. The electrical unit cost of C_6W ($270.3/GJ) was obtained by adjusting the irreversibility value of the FCS to match the system production cost obtained by Eq. (37). The unit cost of entropy destruction (CS) is -$4483.0/GJ.

In Table 5, the initial investment costs for all components are also listed in the seventh column of the table. The total investment cost for the PEMFC system is approximately $23,800. The sixth column of this table lists the investment cost flow rate for each component, which can be calculated by Eq. (13). The cost flow rate for each component required to solve the cost balance equation acts as an input cost (negative sign) as shown in the table.

The cost flow rate for each exergy of each component at 100% current load is given in Table 5. For example, the second row in Table 5 numerically expresses the following exergy cost-balance equation for the air blower. That is:

\begin{array}{l} {\dot{E}}_{x, [1]}^{W} C_{W} + ({\dot{E}}_{x, 102}^{T} - {\dot{E}}_{x, 101}^{T}) C_{T} + ({\dot{E}}_{x, 102}^{P} - {\dot{E}}_{x, 101}^{P}) C_{1 P} + ({\dot{E}}_{x, 102}^{C} - {\dot{E}}_{x, 101}^{C}) C_{C} \\ + [T_{o} ({\dot{S}}_{102} - {\dot{S}}_{101}) - {\dot{Q}}_{[1]}] C_{S} - {\dot{Z}}_{[1]} = 0 \end{array}

(15-3’)

The cost flow rate can be calculated using the exergy flow rates shown in Table 3 and the unit costs of the primary product listed in Table 4. The same sign convention for the cost flow rates related to the products and resources was used as the case of exergy balances shown in Table 2. The monetary cost flow rate and the lost cost flow rate due to the entropy production rate in a component, which are negative value, are consumed cost, while the cost flow rate for the electricity produced in FCS, which is positive value, is a production cost. The fact that the sum of the cost flow rates of each component becomes zero shows that all the cost-balances for the components are satisfied.

As can be seen in Table 5, the cost flow rate to net electricity production rate is about 0.78 $/h, and the net electricity production rate is about 2883.19 kJ/h as shown in Table 3. The estimated electricity unit cost from these results is approximately $270.53/GJ. As shown in Table 5, the total lost cost flow rate whose amount is approximately 0.455 $/h. This total lost cost flow rate is about 58% of the total cost flow rate of initial investment of 0.778 $/h. In particular, capital losses incurred by HTX for coolant (10) amount to $1.392/h, indicating that this equipment requires modification of component. Heat transfer from the HTX to the environment by forced convection of air must be recovered by water flow to improve the performance of the PEMFC system.

5. Conclusions

Energy, exergy and thermoeconomic analyses were conducted for a 1-kW hydrogen fueled proton exchange membrane fuel system. A detailed energy, exergy and thermoeconomic analysis of the PEMFC system shows that HTX for coolant has the greatest irreversibility and highest cost loss of all components. The irreversibility rate of the component was obtained using the Gouy-Stodola theorem, which states that the irreversibility rate depends on the difference in entropy flow rates entering and leaving the component and the heat transfer rate to the environment. Typically, the irreversibility rate of system components is obtained directly from the exergy balance equations without thermal interaction information. However, this method cannot determine the origin of entropy generation, which is a very important factor in system design and improvement. With help of the Gouy-Stodola theorem, the irreversibility occurred in the HTX for coolant is due to the forced convection of air. The heat transfer to the environment must be recovered to increase the efficiency of the PEMFC system. In residential applications of PEMFC systems [1,6], the heat gained in cooling the stack is recovered by the water stream.

Acknowledgments

This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE), (20213030030190, Development of Smart DPO (Design, Production, Operation) Open Platform for Fuel Cell System).

Appendix

Consider a thermal system (or a component) which is in thermal contact with ambient temperature T_o and another heat reservoir of temperature T_L. Assuming that the system has heat source, the first law of thermodynamics is written as

\frac{d E_{c v}}{d t} = {\dot{Q}}_{s o u r c e} + {\dot{Q}}_{o} + {\dot{Q}}_{L} + \sum_{i n} {\dot{m}}_{i} h_{i} - \sum_{o u t} {\dot{m}}_{i} h_{i} - {\dot{W}}_{c v}

(A-1)

where

{\dot{Q}}_{o}

and

{\dot{Q}}_{L}

are the heat transfer interactions with the environment and thermal reservoir at temperatures of T_o and T_L, respectively. In Eq. (A-1),

{\dot{W}}_{c v}

is the work flow rate,

h_{i}

is the enthalpy per mass and

{\dot{m}}_{i}

is the mass flow rate.

The second law of thermodynamics for the system is given by

\frac{d S_{c v}}{d t} = \sum_{i n} {\dot{m}}_{i} s_{i} - \sum_{o u t} {\dot{m}}_{i} s_{i} + \frac{{\dot{Q}}_{o}}{T_{o}} + \frac{{\dot{Q}}_{L}}{T_{L}} + {\dot{S}}_{g e n}

(A-2)

where S_i is the entropy per mass and

{\dot{S}}_{g e n}

is the entropy generation rate.

We can obtain the heat transfer interaction with environment,

{\dot{Q}}_{o}

from the second law of thermodynamics [18]. In such case, Eq. (A-2) can be written by

{\dot{Q}}_{o} = T_{o} (\sum_{o u t} {\dot{m}}_{i} s_{i} - \sum_{i n} {\dot{m}}_{i} s_{i}) + T_{o} \frac{d S_{c v}}{d t} - \frac{T_{o}}{T_{L}} {\dot{Q}}_{L} - T_{o} {\dot{S}}_{g e n}

(A-3)

Substituting

{\dot{Q}}_{o}

to Eq. (A-1), we obtain the following combined form of the first and second laws of thermodynamics.

{\dot{Q}}_{s o u r c e} + T_{o} (\sum_{o u t} {\dot{m}}_{i} s_{i} - \sum_{i n} {\dot{m}}_{i} s_{i}) + (\sum_{i n} {\dot{m}}_{i} h_{i} - \sum_{o u t} {\dot{m}}_{i} h_{i}) + {\dot{Q}}_{L} (1 - \frac{T_{o}}{T_{L}}) + \frac{d}{d t} ({\dot{E}}_{c v} - T_{o} {\dot{S}}_{c v}) - T_{o} {\dot{S}}_{g e n} = {\dot{W}}_{c v}

(A-4)

Equation (A-4) can be rearranged using the definition of exergy given in Eq. (6). That is

{\dot{Q}}_{s o u r c e} + (\sum_{i n} {\dot{m}}_{i} e_{x, i} - \sum_{o u t} {\dot{m}}_{i} e_{x, i}) + {\dot{Q}}_{L} (1 - \frac{T_{o}}{T_{L}}) + \frac{d}{d t} ({\dot{E}}_{c v} - T_{o} {\dot{S}}_{c v}) - T_{o} {\dot{S}}_{g e n} = {\dot{W}}_{c v}

(A-5)

The second law of thermodynamics provides the following lost work rate or irreversibility rate.

- T_{o} {\dot{S}}_{g e n} = - \dot{I} = T_{o} (\sum_{i n} {\dot{m}}_{i} s_{i} - \sum_{o u t} {\dot{m}}_{i} s_{i} + \frac{{\dot{Q}}_{o}}{T_{o}} + \frac{{\dot{Q}}_{L}}{T_{L}}) + T_{o} \frac{d S_{c v}}{d t}

(A-6)

Assuming that the flow is steady-state and the component is only in thermal contact with the ambient, Eq. (A-6) is the same as Eq. (4). It should be noted that the third term,

- {\dot{Q}}_{L} \cdot T_{o} / T_{L}

in Eq. (A-5) appears only when the component is in thermal contact with the thermal reservoir of temperature T_L.

References

Gigliucci G, Petruzzi L, Cerelli E, Garzisi A, La Mendola A, Demonstration of a residential CHP system based on PEM fuel cells, J Power Sources 2004; 131: 62-68. [CrossRef]
Chen JC, Chen XH, Chen LW, Guo JC. An available method exploiting the waste heat in a proton exchange membrane fuel cell system. Int J Hydrogen Energy 2011; 36: 6099-104.
Hwang JJ, Zou ML, Chang WR, Su A, Weng FB, Wu W. Implementation of a heat recovery unit in a proton exchange membrane fuel cell system. Int J Hydrogen Energy 2010; 35: 8644-53.
Barelli L, Bidini G, Gallorini F, Ottaviano, An exergetic-exergetic analysis of a residential CHP system based on PEM fuel cell. Appl Energy 2011; 88: 4334-4342.
Chen X, Gong G, Wan Z, Luo L, Wan J. Performance analysis of 5 kW PEMFC based residential micro-CCHP with absorption chiller. Int J Hydrogen Energy 2015; 40: 10647-57.
Seo, S.-H., Oh, S.-D., Kwak, H., Thermodynamic, exergetic and thermoeconomic analyses of double-effect LiBr-water absorption refrigeration systems with a 5 kW high temperature PEMFC as heat source for data center applicaions. Energies 2022; 15:3101.
Oh SD, Kim KY, Oh SB, Kwak H, Optimal operation of a 1-kW PEMFC-based CHP system for residential applications, Appl. Energy, 95, 93-101, 2012.
Ebadi MJ, Gorji-Bandpy M, Exergetic analysis of gas turbine plants. Int J Exergy 2005; 2 : 31-39.
Valero A, Lerch F, Serra L, Royo J. Structural theory and thermoeconomic diagnosis Part II: Application to an actual power plant. Energy Conversion and Management, 2002;43:1519-1535.
Wang L, Fu P, Wang N, Morosuk T, Yang Y, Tsatsaronis G. Malfunction diagnosis of thermal power plants based on advanced exergy analysis: The case with multiple malfunctions occurring simultaneously, Energy Conver and Manage 2017; 144: 1453-1467.
Oh HS, Lee Y, Kwak H. Diagnosis of combined cycle power plant based on thermoeconomic analysis: A computer simulation study. Entropy, 2017; 19: 643.
Seo S.H., Oh S.-D., Oh H, Kim M, Lee WY, Kwak, H. Thermal management for a hydrogen-fueled 1-kW PEMFC based on thermoeconomic analysis. Int J Hydrogen Energy 2019; 44: 24934-24946.
Piacentino A, Talamo M, Critical analysis of conventional thermoeconomicapproaches to the diagnosis of multiple faults in air conditioning units: Capabilities, drawbacks and improvement directions. A case studu for an air-cooled system with 120 kW capacity. Int. J. Refrigeration 2013; 36: 24-44.
Yoo, Y., Oh, H.-S., Uysal, C., Kwak, H., Thermoeconomic diagnosis of an air-cooled air conditioning systems. Int. J. Exergy 2018, 26 393-417.
Morosuk, T.; Tsatsaronis,G. A new approach to the exergy analysis of absorption refrigeration machines. Energy 2008, 33, 890-907.
Kwak H, Kim DJ, Jeon JS. Exergetic and thermoeconomic analyses of power plant, Energy 2003; 28: 343-360.
Bejan A. Advanced Engineering Thermodynamics, John Wiley and Sons, 1997.
Oh S, Pang H, Kim S, Kwak H. Exergy analysis for a gas turbine cogeneration system, J Eng Gas Turbine and Power. 1996; 118: 782–791.
Kotas J. The Exergy Method of Thermal Plant Analysis, Krieger; 1995.
Moran, J. Availability Analysis: A Guide to Efficient Energy Use, Prentice Hall, Inc., Englewood Cliffs, 1982.
Ye L, Du Q, Yin Y. Exergy analysis of high-temperture proton exchange membrane fuel cell systems. Int J Green Energy 2015; 12: 917-929.
Müller EA, Stefanopoulou AG, Analysis, modeling, and validation for the thermal dynamics of a polymer electrolyte membrane fuel cell, Proceedings of Fuel Cell 2008, Third International Conference on Fuel Cell Science, Engineering and Technology, FUELCELL2005-74050, 2005.

Figure 1. Schematic of hydrogen-fueled 1-kW PEMFC system.

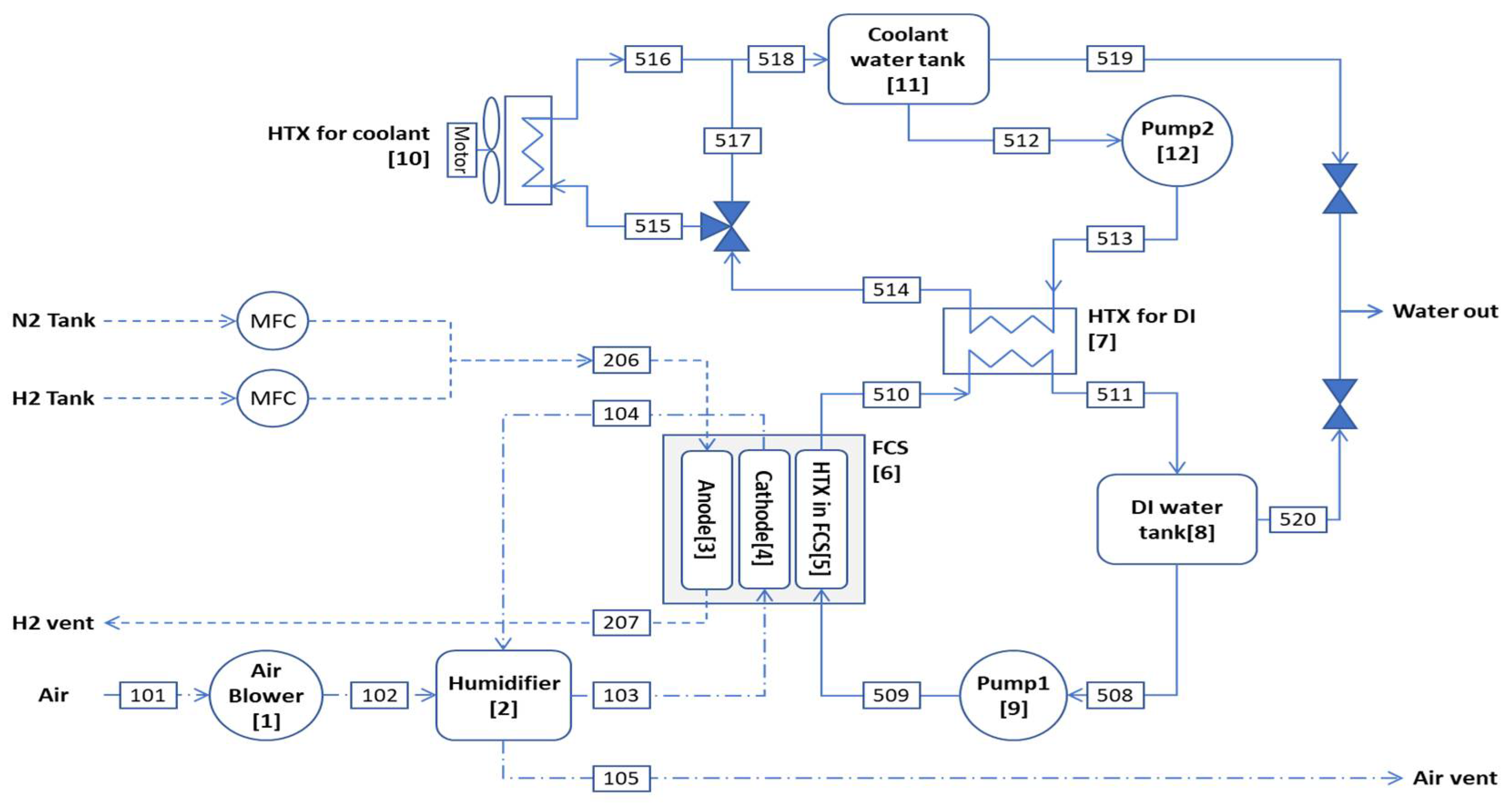
Table 1. Measured property values, and calculated enthalpy, entropy and exergy flow rates at various state points in the hydrogen-fueled 1-kW PEMFC under 100% current load.

States	$\dot{n}$ (kmol/h)	$P$ (kPa)	$T$ (K)	$\dot{H}$ (kJ/h)	$\dot{S}$ (kJ/h/K)	${\dot{E}}_{x}$ (kJ/h)
101	0.0846	100.90	299.40	3.0821	0.471	-1.186
102	0.0846	113.36	305.99	19.340	0.443	23.461
103	0.0846	105.40	322.14	59.280	0.621	10.214
104	0.0748	102.28	332.99	76.067	0.540	35.345
105	0.0748	102.42	312.52	31.335	0.407	30.376
206	0.0275	103.98	299.97	1.443	0.005	0.0
207	0.0079	102.05	326.10	6.368	0.020	0.002
508	4.8295	99.80	325.69	19136.736	64.053	435.754
509	4.8295	143.63	325.59	19103.614	63.940	436.496
510	4.8295	122.48	333.13	21846.193	72.273	694.585
511	4.8295	110.48	326.14	19301.256	64.555	450.631
512	2.2926	102.35	303.10	5185.052	17.998	7.057
513	2.2926	114.85	303.03	5173.442	17.958	7.378
514	2.2926	105.72	331.47	10082.861	33.445	299.545
515	2.2926	103.72	331.47	10082.791	33.445	299.463
516	2.2926	101.75	303.05	5176.401	17.970	6.891
518	2.2926	100.75	302.05	5003.788	17.400	4.340

Table 2. Energy conservation for each component in the PEMFC system.

	Enthalpy flow in	Enthalpy flow out	Work- flow	Heat flow	$T_{o} ({\dot{S}}_{o u t} - {\dot{S}}_{i n})$	Irreversibility rate
Air blower	-3.082	19.340	-16.258	0.0	-8.389	-8.389
Anode	-1.443	6.368	0.0	-4.925	4.648	-0.277
Cathode	-59.280	76.067	0.0	-16.787	-24.097	- 40.884
Humidifier	-95.408	90.615	0.0	4.793	13.484	18.277
HTX for FCS	-19103.614	21486.193		-2742.579	2484.490	-258.089
HTXDI	-27019.635	29384.117	0.0	-2364.482	2316.269	-48.213
DIWT	-19301.256	19136.736		164.521	-149.644	14.877
Pump 1	-19136.736	19103.614	-5.503	38.625	-33.864	4.762
HTXWC	-10082.791	5176.401	-18.000	4924.390	-4613.819	310.572
Hot WT	-5003.788	5185.052	0.0	-181.264	178.548	-2.716
Pump 2	-5185.052	5173.442	-0.645	12.255	-11.931	0.324

* Unit is kJ/h. The Entropy generation rate was calculated using the second law of thermodynamics, and irreversibility rate was calculated using the Gouy-Stodolar theorem.

Table 3. Exergy-balance for each component in hydrogen-fueled 1-kW PEMFC at 100% current load. Irreversibility rate was calculated using the exergy-balance equation given in Eq. (7).

Component	Net exergy flow rates (kJ/h)				Irreversibility
	${\dot{E}}_{(k)}^{W}$	${\dot{E}}_{x}^{C H E}$	${\dot{E}}_{x}^{T}$	${\dot{E}}_{x}^{P}$	rate (kJ/h),
Air blower	-16.258	0.0	0.244	24.403	-8.389
Anode	0.0	0.0	1.622	-1.620	-0.002
Cathode	0.0	0.0	31.651	-6.521	-25.131
Humidifier	0.0	0.0	-1.381	-16.834	18.215
HTX in FCS	0.0	0.0	259.935	-1.845	-258.090
FCS	2923.596	-5666.175	(2642.475)	0.0	100.104
HTX DI			49.638	-1.425	-48.213
DIWT	0.0	0.0	-13.945	-0.932	14.877
Pump 1	-5.503	0.0	-3.083	3.824	4.762
HTXWC	-18.0	0.0	-292.490	-0.082	310.572
Hot WT			2.650	0.066	-2.716
Pump 2	-0.645		-0.196	0.518	0.324
Total	2883.19	-5666.175	(2677.12)	-0.448	106.313

Table 4. Unit cost of various exergies in the cost-balance equations for the PEMFC system. (Unit is USD/MJ)

C_1P	C_2T	C_3T	C_4C		C_5T	C_6W	C_7T
-0.8955	-230.52	102.99	-86238.0		-4.173	0.2703	-3.9587
C_8T	C_9P	C_10T	C_11T	C_12P		C_T	C_P
5.80	94.494	-4.790	2.065		52.719	114.76	12.759
C_C	C_W	C_S
-86238.0	0.2703	-4.483

Table 5. Exergy cost-balance for each component in hydrogen-fueled 1-kW PEMFC at 100% current load. Unit is USD/h.

Component	Electricity cost flow	Thermal exergy cost flow	Mechanical exergy cost flow	Lost cost flow	Invest cost flow	Investment (USD)
Air blower	-0.004	0.028	-0.022	0.038	-0.039	1431.5
Anode		0.167	-0.021		-0.146	5332.4
Cathode	-3.515*	3.632	-0.083	0.113	-0.146	5332.4
Humidifier		0.318	-0.215	-0.082	-0.022	800.0
HTX in FCS		-1.085	-0.024	1.157	-0.049	1775.3
FCS	0.790			-0.449	-0.342	7856.6
HTX DI		-0.197	-0.018	0.216	-0.001	52.2
DIWT		0.081	-0.012	-0.067	-0.002	84.2
Pump 1	-0.001	-0.354	0.361	-0.001	-0.005	168.4
HTXWC	-0.005	1.401	-0.001	-1.392	-0.003	111.1
Pump 2		-0.022	0.027	-0.0	-0.005	168.4
Hot WT		0.005	0.001	0.012	-0.018	673.7
Total	-2.735(0.78+)	3.974	-0.007	-0.455	-0.778	23786.2

*Chemical exergy, + Net electrical exergy

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Energy, Exergetic and Thermoeconomic Analyses of Hydrogen-Fueled 1-kW Proton Exchange Membrane Fuel Cell

Abstract

1. Introduction

2. Energy and Exergy Analysis of Thermal Systems

2.1. Energy Conservation

2.2. Exergy-Balance Equation and the Second Law of Thermodynamics

2.3. Exergy Cost-Balance Equation

3. Hydrogen-Fueled 1-kW PEMFC System

3.1. Energy Conservation and Exergy-Balance and Exergy Cost-Balance Equations for PEMFC System

3.2. Energy Conservation and Exergy-Balance of FCS

3.3. Exergy Cost-Balance Equation for Overall System

4. Calculation Results and Discussion

5. Conclusions

Acknowledgments

Appendix

References

MDPI Initiatives

Important Links

Subscribe