Deterministic Quantum Mechanics – Part II – The Linearized Temporal-Azimuthal Wave Solution

Preprint

Article

Deterministic Quantum Mechanics – Part II – The Linearized Temporal-Azimuthal Wave Solution

Altmetrics

Downloads

100

Views

Comments

Peter Vadasz^*

This version is not peer-reviewed

Submitted:

15 May 2024

Posted:

16 May 2024

You are already at the latest version

Alerts

Abstract

This is the second paper in a series introducing a deterministic quantum mechanics theory that is shown to be consistent with the current mainstream statistical quantum theory as well as with classical physics. The first paper in this series demonstrated how causality, physical reality, and determinism are restored and concerns that were raised by results from the current mainstream statistical quantum theory were explained in simple form. The meaning of particle-wave duality and complementarity, the possibility of a particle, like the electron, to cross through the nucleus as it does when the angular momentum of the electron is zero, the possibility of a point-size particle to have an “intrinsic spin”, the possibility of “quantum jumps” as the electron transitions instantaneously from one stable orbital to another and does that at irregular time intervals, the natural collapse of the wave function as part of the solution, as well as consistency with the phenomenon of entanglement were some of the results that emerged from the proposed deterministic quantum mechanics theory. While the first paper presented overwhelming evidence of the latter, the present paper is the first to produce actual solutions that are consistent with current mainstream quantum theory as well as with classical physics. Analytical solutions are presented via a linear stability method. The Bohr-Schrödinger energy levels leading to the experimentally confirmed spectral lines, as well as the fine structure constant emerge directly from the solution of the equations governing the proposed deterministic quantum mechanics. Recommended follow-up solutions as well as generalizations are being presented at the end of the paper.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

This paper is the second in a series of papers introducing a deterministic quantum mechanics theory that is shown to be consistent with the current mainstream probabilistic quantum theory as well as classical physics. The first paper in this series [1] introduced the conceptual framework and presented overwhelming evidence to support the proposed theory. The proposed deterministic quantum mechanics uses only one postulate, i.e. that the electron and most likely other subatomic particles are in reality compressible fluids. In the first instance the proposed theory focuses on the electron in the hydrogen atom. As such, the governing equations are the inviscid Navier-Stokes equations (Euler equations) for compressible fluids (Landau and Lifshitz [2] and the Maxwell equations (Griffiths [3], Jackson [4]) for electro-magnetism. Generalizations are straightforward and will be presented at the end of the present paper. Since the electron-fluid mass density and electric charge density can vary in space and time one can introduce a definition of the center of mass. By introducing the definition of the center of mass of the electron-fluid it becomes possible to regard the motion of the center of mass as the motion of the quantum “particle”, while the electron-fluid itself represents the detailed wave motion. The link and equivalence between the definition of the center of mass of the electron-fluid based on the proposed deterministic quantum theory, and the expectation of finding the electron in a specific location as applicable in the statistical interpretation of the current mainstream quantum mechanics (Born [5]) was demonstrated in [1]. In addition, it was shown that the center of mass (electron-particle) of the electron-fluid can pass through the nucleus as Eiseberg and Resnick [6] indicated, while the electron-fluid material remains outside the nucleus at all times, a fact that is consistent with zero angular momentum. For the same reason the electron-fluid can have a “spin” in addition to orbital motion, a consequence of magnetic effects, and this spin can be associated then with the center of mass, i.e. with the electron-particle. Also, in [1] it was shown that the inviscid Navier-Stokes (Euler) equations are equivalent to the Schrödinger equation [7–11]. A slightly modified version of the Schrödinger equation that resulted by including the pressure term from the inviscid Navier-Stokes equations (Euler equations) via an additional potential to the Schrödinger equation converts the latter into a nonlinear form. Consequently, this causes the natural collapse of the wave function because a superposition of the individual eigenstates is not anymore possible as a general solution due to the nonlinearity. “Quantum jumps” postulated by Bohr [12–16] indicating that the electron radiates as it moves from one stable orbit to another stable orbit but can never pass through the space between these orbits during these “jumps” were shown to be plausible solutions of the governing equations representing shock waves, as typically occurs in compressible fluid dynamics. Like in compressible flow it was shown in [1] that an electron-fluid Mach number is a dimensionless group controlling the occurrence of the shock wave. The specific fact that the electron does pass through the space in between the orbitals when such shock waves occur was supported by the recent experimental evidence provided by Minev et al. [17], which reveals the latter by “catching and reversing a quantum jump mid-flight”. The fact that such jumps occur at irregular time intervals (Baggot [18]) was explained in terms of the possibility of having chaotic solutions, which are typical too in fluid dynamics. Electro-magnetic induction as well as electrostatic pressure distribution were shown to be the reason that a free electron cannot spread indefinitely but rather expected to produce an expansion-compression oscillatory motion or a stationary solution instead. The reason for the instantaneous “communication” between two entangled electrons (or photons) was established as the fact that the measurement of the spin (polarization in the case of photons) consists of measuring locally a global property. The spin being such a global property was demonstrated in [1].

The governing equations for the dynamics of the electron-fluid in the hydrogen atom that were introduced in [1] can be solved numerically in three dimensions. There is available commercial software for 3D computational fluid dynamics that might need some adaptation to the specific application considered here. However, prior to undertaking numerical experiments it is always advisable to perform analytical work that provides insight into the expected type and form of solutions. The applied methodology follows the proven sequence that is applied successfully for the solution of nonlinear natural convection problems such as Malkus and Veronis [19], Segel [20], Newell and Whitehead [21], Daniels [22], Vadasz [23]. This sequence consists of performing a linear stability analysis of a basic stationary solution that produces eigenvalues and eigenfunctions essential for the next step. It also produces stability conditions for the basic stationary solution. The linear stability solution does not produce the values of the amplitudes of the solutions, and not the final quantitative values of the frequency of oscillations, when oscillations are anticipated solutions. The next step is undertaking a weak nonlinear analysis based on the results of the linear stability solutions. The weak nonlinear analysis is an asymptotic method using asymptotic expansions to produce solutions for the amplitudes and frequencies (or frequency corrections) related to the linear stability solutions. A third step can be a further development of a spectral system of equations to represent more accurately the dynamics of the problem as well as extend the validity domain of the solutions beyond the asymptotic limit of the weak nonlinear method. This third step requires information that is obtained from the weak nonlinear solutions. This specific methodology is to be applied in the present paper consisting of the first step, i.e. obtaining the linear stability solutions as well as the stability conditions. The information obtained will be used in follow-up papers for the next two steps as indicated above. The focus in the present paper is in demonstrating possible solutions that extend beyond just stationary states and possibly represent even transitions between orbitals when excited. The Bohr-Schrödinger energy levels leading to the experimentally confirmed spectral lines, as well as the fine structure constant emerge directly from the solution of the equations subject to one assumption. The anticipation is that eventually as the complete solution is obtained, the Plank constant [24]

h = 6.62607 \cdot 10^{- 34} [J \cdot s]

will emerge naturally from this solution, and consequently Bohr radius [12, 13,14,15,16], and energy levels will emerge too without any assumptions. Note that the latter emerge from the solution to the Schrödinger equation only because Plank constant appears explicitly in the equation. The governing equations to be used in this and follow-up papers do not include explicitly or implicitly the Plank constant or Bohr radius as they are expected eventually as part of the solution.

The multiplicity of symbols imposes severe restrictions on the available choices. Therefore, for clarity, subscripts are being used to distinguish among different variables. For example while

E_{e}

is the electric field due to the electron-fluid and

E_{p}

is the electric field due to the proton, the symbol

E

refers to total energy, and

E_{n}

to the energy in the

n^{t h}

orbital. Also for volume the use of a tilde above the symbol

\tilde{V}

distinguishes it from the symbol representing the potential energy

V

. Asterisks as subscripts are being introduced to represent initially dimensionless variables but they are being dropped eventually for clarity of the presentation when all derivations are being performed using dimensionless variables and equations. At some following stages when dimensional variables are being reintroduced a tilde above the symbol will reflect that it is dimensional.

2. Governing Equations and the Basic Equilibrium Stationary Solution

2.1. Electron-Fluid (Subatomic-Fluid) Governing Equations

The proposed deterministic quantum mechanics uses only one postulate, i.e. that the electron and most likely other subatomic particles are in reality compressible fluids. They posses mass density

ρ (x, t) [kg / m^{3}]

, and if they are charged particles like the electron they posses electric charge density too

ρ_{e} (x, t) [C / m^{3}]

, both allowed to vary in space as well as in time. As the mass density is space dependent it becomes appealing to define the center of mass

x_{c m}

in the same form as applied to rigid bodies

x_{c m} = \frac{\int_{{\tilde{V}}_{o}} ρ (x, t) x d \tilde{V}}{\int_{{\tilde{V}}_{o}} ρ (x, t) d \tilde{V}}

(1)

where the electron-mass contained in the volume

{\tilde{V}}_{o}

is the denominator in equation (1) and it is therefore constant. For one electron system this is

m_{e} = \int_{{\tilde{V}}_{o}} ρ (x, t) d \tilde{V} = const .

(2)

where

m_{e} = 9.11 \cdot 10^{- 31} [kg]

is the mass of the electron. The center of mass of the electron-fluid (1) is defined as the electron-particle.

The equations will be presented for application to the one-electron one-proton hydrogen atom. The generalization for multi-electrons multi-protons atoms as well as to molecules is straightforward and will be presented at the end.

The equations governing the flow and electro-magnetic effects due to the motion of the electron-fluid are the inviscid Navier-Stokes (Euler) equations (Landau and Lifshitz [2]) from fluid dynamics and Maxwell equations (Griffiths [3], Jackson [4]) from electro-magnetism. The inviscid Navier-Stokes (Euler) equations represent conservation of mass and linear momentum per unit volume of fluid. It is assumed that there are no shear stresses present, the latter causing dissipation effects and we lack evidence of such effects being present at the subatomic level at the leading order. Also the electron-fluid occupies the empty space and therefore using Maxwell equations for empty space is appropriate. The electric current density (charge flux)

J_{e}

[A / m^{2}]

in Maxwell equations is identical to the charge density multiplied by the electron-fluid velocity, i.e.

J_{e} = ρ_{e} v

, where

v (x, t) [m / s]

is the electron-fluid velocity. Consequently, we have the following governing equations of mass and charge continuity, linear momentum, Coulomb law in field form, Ampere law, Faraday law of induction, and Gauss law for the magnetic field.

\frac{\partial ρ}{\partial t} + \nabla \cdot (ρ v) = 0 (a); \frac{\partial ρ_{e}}{\partial t} + \nabla \cdot (ρ_{e} v) = 0 (b)

(3)

ρ [\frac{\partial v}{\partial t} + (v \cdot \nabla) v] = - \nabla P + ρ_{e} E_{e} + ρ_{e} E_{p} + ρ_{e} (v \times B)

where

E_{e} (x, t)

[N / C]

is the dependent variable representing the intrinsic electrostatic field due to forces that differential electron-fluid elements impress on each other,

E_{p}

[N / C]

is the electrostatic field impressed on an electron-fluid position by the nucleus’s proton,

B (x, t)

[T]

is the dependent variable representing the magnetic flux density, and

P (x, t)

[Pa]

is the pressure resulting from the normal components in the stress tensor. The combination of the terms

ρ_{e} E_{e} + ρ_{e} E_{p} + ρ_{e} (v \times B)

represents the Lorenz force per unit volume.

\nabla \cdot E_{e} = \frac{1}{ε_{o}} ρ_{e} (a) \nabla \cdot E_{p} = \frac{1}{ε_{o}} ρ_{p} (b)

(5)

where

ε_{o} = 8.854 \cdot 10^{- 12} [F / m]

is the permittivity of vacuum, and where the proton electric charge density is

ρ_{p} = \{\begin{array}{l} \begin{array}{l} \frac{3 q_{p}}{4 π r_{N}^{3}} = \frac{3 |e|}{4 π r_{N}^{3}} f o r r \leq r_{N} \end{array} \\ 0 f o r r > r_{N} \end{array}

(6)

and where

q_{p} = |e| = 1.6022 \cdot 10^{- 19} [C]

is the electric charge of the proton (assumed in the first instance to be homogeneously distributed within the nucleus), and

r_{N} = 8.783 \cdot 10^{- 16} [m]

is the radius of the nucleus. Solving the proton electric field equation for

E_{p}

in spherical coordinates, i.e.

(1 / r^{2}) [d (r^{2} E_{r}) / d r] = ρ_{p} / ε_{o}

gets the familiar form of Coulomb law

E_{p} = [|e| / (4 π ε_{o} r^{2})] {\hat{e}}_{r}

where

e = - 1.6022 \cdot 10^{- 19} [C]

is the electron charge.

(7)

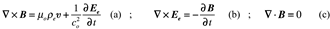where the term

\partial E_{p} / \partial t

in (7a) was removed because it vanishes identically when using the solution for

E_{p} (r)

and the term including

E_{p} (r)

in (7b) was removed because

\nabla \times E_{p} (r) = 0

identically when using the solution for

E_{p} (r)

. Not all the equations need to be solved, as it is simple to show that satisfying equations (5a) and (7a) leads to identical satisfaction of equation (3b) as they are equivalent.

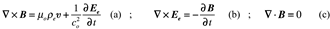
Also the following additional assumption is being made

β_{e} = \frac{ρ}{|ρ_{e}|} = \frac{m_{e}}{|e|} = 5.685 \cdot 10^{- 12} [k g / C]

(8)

Equation (8) implies that the ratio between the mass density and electric charge density is constant and equals to the ratio between the electron mass and the electron charge. The justification for this assumption lies in the fact that it is difficult to imagine the electric charge moving independently of the mass sustaining it. One cannot have an electric charge in the electromagnetic sense without a mass carrying it. If a different relationship exists, then equation (8) will represent a first order Taylor expansion of such a relationship. A relaxation of this assumption might be needed in due course. An additional approximation is needed to reflect the constitutive relationship between the mass density and pressure in a compressible barotropic fluid (i.e. mass density depends on pressure only). For macro-level fluids such relationships have been established experimentally. For the electron-fluid this relationship is unknown and therefore a linear approximation is adopted in the form

ρ = ρ_{o} [1 + β_{p} (P - P_{o})]

, where

P_{o}

and

ρ_{o}

are reference values of pressure and

β_{P} = (\partial ρ / \partial P) / ρ_{o} =

1 / ρ_{o} v_{o}^{2}

= const .

[{Pa}^{- 1}]

is the compression coefficient which is constant, and

v_{o} = \sqrt{\partial P / \partial ρ} [m / s]

is the constant “speed of propagation of the electron-fluid wave” in analogy to compressible fluids, assuming isentropic wave propagation as customary in compressible fluid dynamics. The inverse relationship needed for substitution into the momentum equation (4) is obtained in the form

P = P_{o} + \frac{1}{ρ_{o} β_{P}} (ρ - ρ_{o}) = P_{o} + v_{o}^{2} (ρ - ρ_{o})

(9)

Taking the gradient of equation (9) and substituting it into the momentum equation (4) produces the following equation

ρ [\frac{\partial v}{\partial t} + (v \cdot \nabla) v] = - v_{o}^{2} \nabla ρ + ρ_{e} E_{e} + ρ_{e} E_{p} + ρ_{e} (v \times B)

(10)

Substituting equation (8) into equation (10) leads to

- β_{e} ρ_{e} [\frac{\partial v}{\partial t} + (v \cdot \nabla) v] = β_{e} v_{o}^{2} \nabla ρ_{e} + ρ_{e} E_{e} + ρ_{e} E_{p} + ρ_{e} (v \times B)

(11)

where

v_{o}^{2} = 1 / ρ_{o} β_{P}

. By neglecting the magnetic field, the latter being a second order effect leading to the “fine structure” [18,25] the electron-fluid equations (7a) and (11) become

ε_{o} \frac{\partial E_{e}}{\partial t} + ρ_{e} v = 0

(12)

- β_{e} ρ_{e} [\frac{\partial v}{\partial t} + (v \cdot \nabla) v] = β_{e} v_{o}^{2} \nabla ρ_{e} + ρ_{e} E_{e} + ρ_{e} E_{p}

(13)

with the solution for

E_{p} = E_{p r} {\hat{e}}_{r}

as presented in the text preceding equation (7).

2.2. Basic equilibrium stationary solution

A spherical coordinate system is being considered for the electron-fluid hydrogen atom as presented in Figure 1, where

φ \in [0, 2 π]

is the azimuthal angle, and

θ \in [0, π]

is the polar angle. Assuming the existence of an electro-static equilibrium such that the mass and charge densities

ρ

and

ρ_{e}

vary in the radial direction only, i.e. the mass and charge densities distribution in the angular directions

φ

and

θ

is homogeneous, and consequently

v = 0, E_{e φ} = E_{e θ} = 0,

\partial (\cdot) / \partial θ = \partial (\cdot) / \partial φ = 0

and

E_{e} = E_{e r} (r) {\hat{e}}_{r}

ρ \equiv ρ (r)

ρ_{e} \equiv ρ_{e} (r)

when substituted into (12) yields

\partial E_{e} / \partial t = 0

, and when substituted into (13) and (5a) leads to

β_{e} v_{o}^{2} \frac{d ρ_{e}}{d r} + ρ_{e} E_{e r} + ρ_{e} E_{p r} = 0

(14)

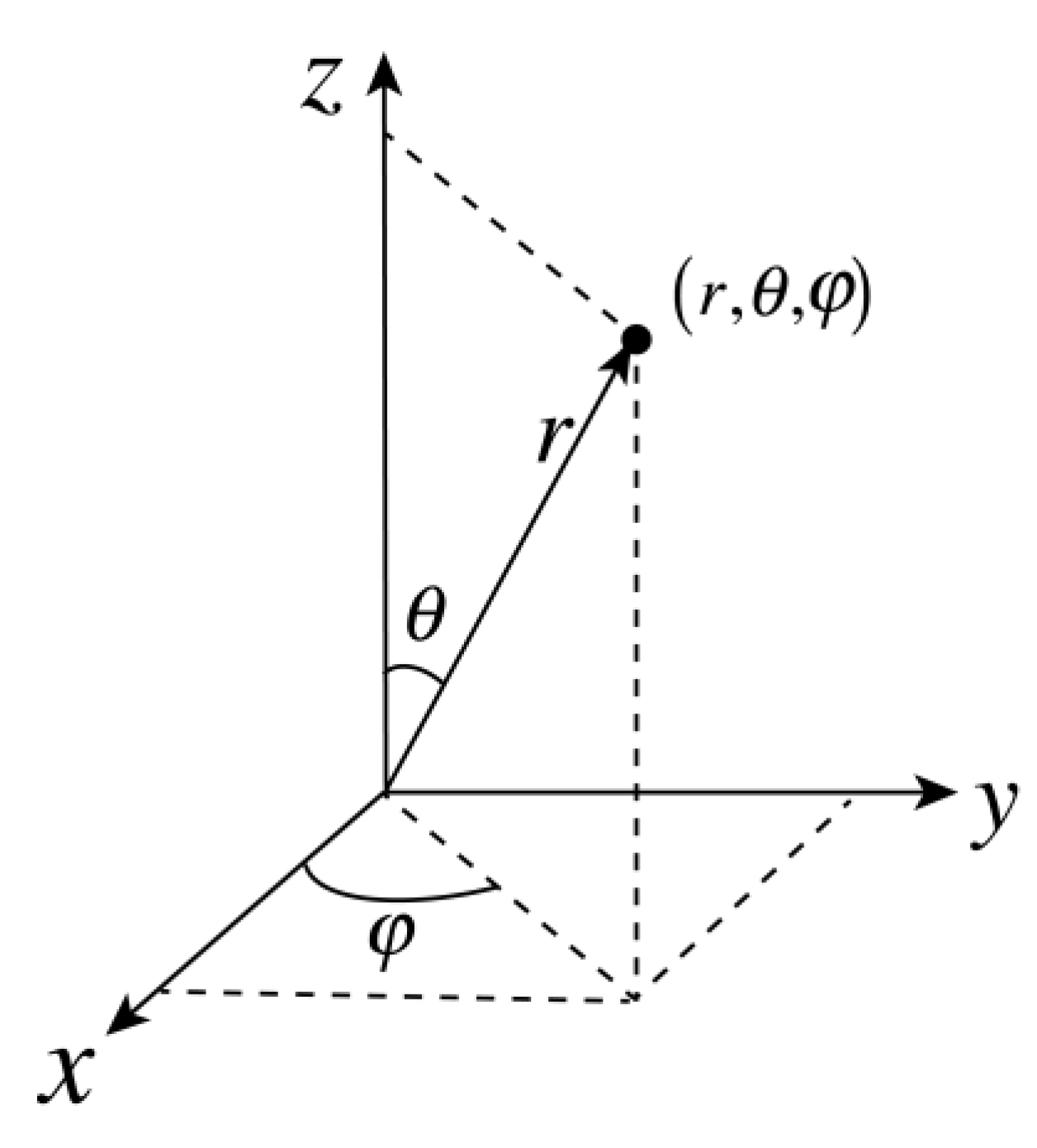
Figure 1. The spherical system of coordinates.

\frac{1}{r^{2}} \frac{d (r^{2} E_{e r})}{d r} = \frac{1}{ε_{o}} ρ_{e}

(15)

Substituting (15) into (14) leads to

β_{e} v_{o}^{2} \frac{d}{d r} [\frac{1}{r^{2}} \frac{d (r^{2} E_{e r})}{d r}] + (E_{e r} + E_{p r}) \frac{1}{r^{2}} \frac{d (r^{2} E_{e r})}{d r} = 0

(16)

and substituting the solution for

E_{p} (r)

into (16) gives

β_{e} v_{o}^{2} \frac{d}{d r} [\frac{1}{r^{2}} \frac{d (r^{2} E_{e r})}{d r}] + (E_{e r} + \frac{|e|}{4 π ε_{o}} \frac{1}{r^{2}}) \frac{1}{r^{2}} \frac{d (r^{2} E_{e r})}{d r} = 0

(17)

The solutions for

ρ_{e} (r)

and

E_{e r} (r)

have to comply with the following boundary and integral conditions

r \to \infty : ρ_{e} = 0; E_{e r} = 0

(18)

\int_{{\tilde{V}}_{o}} ρ_{e} d \tilde{V} = 4 π \int_{r_{N}}^{\infty} ρ_{e} (r) r^{2} d r = e

(19)

\int_{r_{N}}^{\infty} ρ_{e} (r) r^{2} d r = \frac{e}{4 π}

(20)

Using the following notations in equation (17)

b_{1} = β_{e} v_{o}^{2}; b_{2} = \frac{|e|}{4 π ε_{o}}; ξ = r^{2} E_{e r}

(21)

produces the equation

b_{1} \frac{d}{d r} [\frac{1}{r^{2}} \frac{d ξ}{d r}] + (ξ + b_{2}) \frac{1}{r^{4}} \frac{d ξ}{d r} = 0

(22)

An equivalent form of equation (22) can be obtained by expanding the first term and multiplying the whole equation by

r^{4} / b_{1}

leading to

r^{2} \frac{d^{2} ξ}{d r^{2}} + (\frac{ξ + b_{2}}{b_{1}} - 2 r) \frac{d ξ}{d r} = 0

(23)

Equation (23) is a nonlinear ordinary differential equation and might possibly have multiple solutions. One such solution is obtained by observation that the coefficient of the term

d ξ / d r

can be zero, i.e.

(ξ + b_{2}) / b_{1} - 2 r = 0

leading to the solution

ξ = 2 b_{1} r - b_{2}

(24)

This can be a solution to equation (23) only if the remaining term is also zero and the boundary and integral conditions (18) and (20) are also satisfied, i.e.

r^{2} \frac{d^{2} ξ}{d r^{2}} = 0

(25)

The solution

ξ = C_{1} r + C_{2}

to equation (25) can be identical to solution (24) if the integration constants are

C_{1} = 2 b_{1} = 2 β_{e} v_{o}^{2}

and

C_{2} = - b_{2} = - |e| / 4 π ε_{o}

, therefore the solution (24) is a solution to equation (22). Reverting back to

E_{e r}

by using (21) into (24) yields

E_{e r} = \frac{2 β_{e} v_{o}^{2}}{r} - \frac{|e|}{4 π ε_{o} r^{2}}

(26)

and this solution for

E_{e r}

satisfies the boundary condition (18) for

E_{e r} = 0

r \to \infty

. Substituting (26) into (14) leads to

\frac{d ρ_{e}}{d r} + \frac{2}{r} ρ_{e} = 0

(27)

Integrating (27) produces the solution

ρ_{e} = \frac{C_{3}}{r^{2}}

(28)

The anticipation is that the integration constant

C_{3}

can be evaluated from the integral condition (20). Introducing (28) into the integral condition (20) leads to

C_{3} \int_{r_{N}}^{\infty} d r = \frac{e}{4 π}

(29)

However, it is obvious that this integral diverges. The conclusion is that there must exist a finite external radius so that the electron-fluid is confined within it. By introducing this finite radius as

r_{\infty}

the integral condition (29) converts to

C_{3} \int_{r_{N}}^{r_{\infty}} d r = \frac{e}{4 π}

(30)

and the integration constant is then evaluated to be

C_{3} = e / 4 π (r_{\infty} - r_{N})

generating the solution for

ρ_{e}

in the form

ρ_{e} = \frac{e}{4 π (r_{\infty} - r_{N}) r^{2}}

(31)

By using the relationship (8) between

ρ_{e}

and

ρ

one obtains the solution for the mass density at the basic equilibrium as

ρ = \frac{m_{e}}{4 π (r_{\infty} - r_{N}) r^{2}}

(32)

Equations (26), (31) and (32) could have been the equilibrium solution, however, substituting (26) into (15) produces a positive value for the electron charge density and certainly not consistent with the negative solution (31). This result would be the first manifestation of how the equations have the ability to produce results consistent with annihilation and creation of particles, e.g. annihilation of the electron and creation of a positron under certain conditions. However, since for now the aim is at investigating the usual behavior of the electron in the hydrogen atom such an equilibrium as obtained should be avoided. Consequently, the electric field due to the electron charge at leading order (i.e. at static equilibrium) is to be excluded, producing

E_{e} = 0

at equilibrium. Such a choice is consistent with a weak compressibility assumption, i.e. the mass density

ρ

is assumed constant everywhere except in the momentum equation (10). The charge density at equilibrium will be established from the balance to the proton electric field only. Substituting

E_{e r} = 0

in equation (14) and solving the differential equation subject to

E_{p} = E_{p r} {\hat{e}}_{r} = [|e| / (4 π ε_{o} r^{2})] {\hat{e}}_{r}

produces the equilibrium solution

ρ_{e} = \frac{e}{4 π I_{e q}} e^{r_{o} / r}

(33)

where

(34)

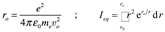
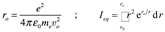
The necessity of keeping a finite radius

r_{\infty}

confining the electric charge remained, as the integral in (34) diverges when

r_{\infty} \to \infty

. From (33) the mass density is evaluated by using (8) leading to

ρ = \frac{m_{e}}{4 π I_{e q}} e^{r_{o} / r}

(35)

Equations (33), and (35) represent the basic equilibrium solutions for the electron-fluid in the hydrogen atom. The basic equilibrium solution for the electron-fluid mass density has the same shape as the solution for the ground state obtained from the Schrödinger equation, i.e.

ψ_{100} ψ_{100}^{*}

although not identical. The next step is to evaluate the stability of these basic equilibrium solutions by invoking a linear stability analysis. The objective of this analysis is mainly to derive the azimuthal solution and test the consistency with the projected framework presented in [1].

2.3. Dimensionless Governing Equations

As the following derivations and solutions are being undertaken in a dimensionless form it is sensible to render the basic equilibrium solutions into dimensionless form at this point. While originally the only known length scale was the nucleus radius, the basic equilibrium solution and the integral condition imposed the existence of an external radius

r_{\infty}

and consequently it will be used as a characteristic length scale

r_{c} = r_{\infty}

. Introducing the additional characteristic values or scales

ρ_{o} = ρ_{c} = m_{e} / r_{\infty}^{3}

ρ_{e c} = |e| / r_{\infty}^{3}

for mass density scale and electric charge density scale, respectively,

Δ P_{c} = ρ_{o} v_{o}^{2} = m_{e} v_{o}^{2} / r_{\infty}^{3}

for pressure scale,

t_{c} = {(m_{e} r_{\infty}^{3} ε_{o} / e^{2})}^{1 / 2}

for time scale,

v_{c} = {(e^{2} / m_{e} ε_{o} r_{\infty})}^{1 / 2}

for velocity scale,

E_{c} = |e| / ε_{o} r_{\infty}^{2}

for electric field scale,

B_{c} = {μ_{o} e^{2} / (m_{e} ε_{o} r_{\infty}^{5})}^{1 / 2}

for the magnetic flux density scale, and

(e^{2} / ε_{o} r_{\infty})

for energy scale. An asterisk

{(\cdot)}_{*}

as a subscript will be used initially to represent dimensionless quantities and variables. Therefore,

r_{*} = r / r_{\infty}

ρ_{*} = ρ r_{\infty}^{3} / m_{e}

ρ_{e *} = ρ_{e} r_{\infty}^{3} / |e|

P_{*} = r_{\infty}^{3} P / m_{e} v_{o}^{2}

t_{*} = t e / {(m_{e} r_{\infty}^{3} ε_{o})}^{1 / 2}

v_{*} = v {(m_{e} ε_{o} r_{\infty})}^{1 / 2} / e

E_{e *} = E_{e} ε_{o} r_{\infty}^{2} / |e|

E_{p *} = E_{p} ε_{o} r_{\infty}^{2} / |e|

, and

B_{*} = B {(m_{e} ε_{o} r_{\infty}^{5})}^{1 / 2} / μ_{o} e^{2}

are the dimensionless variables. Consequently, the integral conditions (2) and (19) can be presented in the following dimensionless form

\int_{{\tilde{V}}_{o *}} ρ_{*} (x_{*}, t_{*}) d {\tilde{V}}_{*} = 1 (a); \int_{{\tilde{V}}_{o *}} ρ_{e *} (x_{*}, t_{*}) d {\tilde{V}}_{*} = - 1 (b)

(36)

For the basic equilibrium solution these conditions convert into

\int_{r_{N *}}^{1} ρ_{*} r_{*}^{2} d r_{*} = \frac{1}{4 π} (a); \int_{r_{N *}}^{1} ρ_{e *} r_{*}^{2} d r_{*} = - \frac{1}{4 π} (b)

(37)

The dimensionless form of the basic equilibrium solutions (33), and (35) is (

E_{e r *} = 0

)

ρ_{e *} = - \frac{1}{4 π I_{e q *}} e^{r_{o *} / r_{*}} (a); ρ_{*} = \frac{1}{4 π I_{e q *}} e^{r_{o *} / r_{*}} (b)

(38)

where

I_{e q *} = \int_{r_{N *}}^{1} r_{*}^{2} e^{r_{o *} / r *} d r_{*}; r_{o *} = \frac{M a^{2}}{4 π}

(39)

and the electron-fluid Mach number emerged and is defined by

M a^{2} = \frac{v_{c}^{2}}{v_{o}^{2}} = \frac{e^{2}}{m_{e} ε_{o} r_{\infty} v_{o}^{2}}

(40)

and

r_{N *} = r_{N} / r_{\infty}

is the dimensionless nucleus radius.

The relevant governing equations (5a), the solution for

E_{p} (r)

in the text prior to equation (7), as well as equations (7a,b), (11), and (8) expressed in a dimensionless form are

\nabla_{*} \cdot E_{e *} = ρ_{e *} (a); E_{p *} = \frac{1}{4 π} \frac{1}{r_{*}^{2}} {\hat{e}}_{r} (b)

(41)

\frac{\partial E_{e *}}{\partial t_{*}} + ρ_{e *} v_{*} = \nabla \times B_{*} (a); \nabla_{*} \times E_{e *} = - \frac{1}{M_{e}^{2}} \frac{\partial B_{*}}{\partial t_{*}} (b)

(42)

ρ_{e *} \frac{\partial v_{*}}{\partial t_{*}} + ρ_{e *} (v_{*} \cdot \nabla_{*}) v_{*} = - \frac{1}{M a^{2}} \nabla_{*} ρ_{e *} - ρ_{e *} E_{e *} - ρ_{e *} E_{p *} - \frac{1}{M_{e}^{2}} ρ_{e *} (v_{*} \times B_{*})

(43)

ρ_{*} = - ρ_{e *}

(44)

where the magnetic number

M_{e}

emerged as an additional dimensionless parameter in the form

M_{e}^{2} = \frac{m_{e} r_{\infty}}{μ_{o} e^{2}}

(45)

Neglecting magnetic terms that are second order effects leading to the fine structure yields

\frac{\partial E_{e *}}{\partial t_{*}} + ρ_{e *} v_{*} = 0 (a); \nabla_{*} \times E_{e *} = 0 (b)

(46)

ρ_{e *} \frac{\partial v_{*}}{\partial t_{*}} + ρ_{e *} (v_{*} \cdot \nabla_{*}) v_{*} = - \frac{1}{M a^{2}} \nabla_{*} ρ_{e *} - ρ_{e *} E_{e *} - ρ_{e *} E_{p *}

(47)

3. Linear Stability Equations

As from now on the derivations and solutions are presented in dimensionless form by using equations (36)-(38) and (46)-(47) the asterisk is being dropped understanding that all variables are now dimensionless. When reverting in some specific circumstances to dimensional variables an identification of the dimensional variables will be then specified.

Taking the time derivative of equation (47) and using equation (41b) leads to

ρ_{e} \frac{\partial^{2} v}{\partial t^{2}} + \frac{\partial v}{\partial t} \frac{\partial ρ_{e}}{\partial t} + \frac{\partial (ρ_{e} v \cdot \nabla) v}{\partial t} = - [\frac{1}{M a^{2}} \nabla + E_{e} + E_{p}] \frac{\partial ρ_{e}}{\partial t} - ρ_{e} \frac{\partial E_{e}}{\partial t}

(48)

At this stage the linear stability analysis is being pursued by assuming a two-dimensional solution in the

r

and

φ

directions, evaluating the equations as an “average” over the

θ

direction allocated at

θ = π / 2

. In two-dimensional spherical coordinates

E_{e} = E_{e r} {\hat{e}}_{r} + E_{e φ} {\hat{e}}_{φ}

v = v_{r} {\hat{e}}_{r} + v_{φ} {\hat{e}}_{φ}

, and the position vector is

x = r {\hat{e}}_{r}

, where

{\hat{e}}_{r}

and

{\hat{e}}_{φ}

are unit vectors in the radial

r

, and azimuthal

φ

directions, respectively. Introducing perturbations around the basic static equilibrium (38) in the form

E_{e r} = E_{e r}^{(1)} (r, φ, t) (a) .; E_{e φ} = E_{e φ}^{(1)} (r, φ, t) (b)

(49)

ρ_{e} = ρ_{e}^{(o)} (r) + ρ_{e}^{(1)} (r, φ, t) (a); ρ = ρ^{(o)} (r) + ρ^{(1)} (r, φ, t) (b)

(50)

v_{r} = v_{r}^{(1)} (r, φ, t) (a); v_{φ} = v_{φ}^{(1)} (r, φ, t) (b)

(51)

where

ρ_{e}^{(o)} (r)

, and

ρ^{(o)} (r)

are the basic static equilibrium solutions (38a), and (38b) respectively, and

E_{e r}^{(1)} (r, φ, t)

ρ_{e}^{(1)} (r, φ, t)

ρ^{(1)} (r, φ, t)

E_{e φ}^{(1)} (r, φ, t)

v_{r}^{(1)} (r, φ, t)

, and

v_{φ}^{(1)} (r, φ, t)

are the small perturbations around the basic equilibrium solutions, leads to the linear stability equations. Note that superscripts in parenthesis, e.g.

{(\cdot)}^{(1)}

, represent asymptotic orders and not powers, the latter appearing without the parenthesis. Substituting (49)-(51) into equation (41a), (46a), and (48), using the basic equilibrium solutions (38a,b), and neglecting terms that are products of perturbations that are of second order and therefore negligible at the linear stability order, leads to the following linearized equations

\nabla \cdot E_{e}^{(1)} = ρ_{e}^{(1)}

(52)

\frac{\partial E_{e}^{(1)}}{\partial t} + ρ_{e}^{(o)} v^{(1)} = 0

(53)

ρ_{e}^{(o)} \frac{\partial^{2} v^{(1)}}{\partial t^{2}} = - [\frac{1}{M a^{2}} \nabla + E_{p}] \frac{\partial ρ_{e}^{(1)}}{\partial t} - ρ_{e}^{(o)} \frac{\partial E_{e}^{(1)}}{\partial t}

(54)

Substituting (52) into (54) yields

ρ_{e}^{(o)} \frac{\partial^{2} v^{(1)}}{\partial t^{2}} = - [\frac{1}{M a^{2}} \nabla + E_{p}] \nabla \cdot (\frac{\partial E_{e}^{(1)}}{\partial t}) - ρ_{e}^{(o)} \frac{\partial E_{e}^{(1)}}{\partial t}

(55)

and substituting (53) into (55) leads to a linear equation for the velocity perturbation in the form

ρ_{e}^{(o)} \frac{\partial^{2} v^{(1)}}{\partial t^{2}} = [\frac{1}{M a^{2}} \nabla + E_{p}] \nabla \cdot (ρ_{e}^{(o)} v^{(1)}) + {(ρ_{e}^{(o)})}^{2} v^{(1)}

(56)

where the basic equilibrium solution

ρ_{e}^{(o)} (r)

appears as coefficients. Dividing (56) by

ρ_{e}^{(o)}

leads to the final form of the linear stability equations to be solved, presented explicitly in scalar component form

\frac{\partial^{2} v_{r}^{(1)}}{\partial t^{2}} = [\frac{1}{M a^{2} ρ_{e}^{(o)}} \frac{\partial}{\partial r} + \frac{1}{4 π r^{2}}] [\frac{1}{r^{2}} \frac{\partial (r^{2} ρ_{e}^{(o)} v_{r}^{(1)})}{\partial r} + \frac{1}{r} \frac{\partial (ρ_{e}^{(o)} v_{φ}^{(1)})}{\partial φ}] + ρ_{e}^{(o)} v_{r}^{(1)}

(57)

\frac{\partial^{2} v_{φ}^{(1)}}{\partial t^{2}} = \frac{1}{M a^{2} ρ_{e}^{(o)} r} \frac{\partial}{\partial φ} [\frac{1}{r^{2}} \frac{\partial (r^{2} ρ_{e}^{(o)} v_{r}^{(1)})}{\partial r} + \frac{1}{r} \frac{\partial (ρ_{e}^{(o)} v_{φ}^{(1)})}{\partial φ}] + ρ_{e}^{(o)} v_{φ}^{(1)}

(58)

4. Linear Stability Method of Solution

4.1. Separation of Variables

In solving equations (57) and (58) the method of separation of variables is employed in the form

v_{r}^{(1)} = T (t) Y_{r} (φ) R_{r} (r)

(59)

v_{φ}^{(1)} = T (t) Y_{φ} (φ) R_{φ} (r)

(60)

Substituting (59) and (60) into (57) and (58) and dividing (57) by

T Y_{r} R_{r}

and (58) by

T Y_{φ} R_{φ}

produces the following equations separated between the time dependent variables and the space dependent variables

\frac{\ddot{T}}{T} = \frac{1}{ρ_{e}^{(o)} R_{r}} [\frac{1}{M a^{2}} \frac{d}{d r} + \frac{1}{4 π r^{2}}] [\frac{1}{r^{2}} \frac{d (r^{2} ρ_{e}^{(o)} R_{r})}{d r}] + \frac{1}{M a^{2} ρ_{e}^{(o)} R_{r}} \frac{d}{d r} (\frac{ρ_{e}^{(o)} R_{φ}}{r}) + \frac{R_{φ}}{4 π r^{3} R_{r} Y_{r}} \frac{d Y_{φ}}{d φ} + ρ_{e}^{(o)}

(61)

\frac{\ddot{T}}{T} = \frac{1}{M a^{2} r^{3} ρ_{e}^{(o)} R_{φ}} \frac{d (r^{2} ρ_{e}^{(o)} R_{r})}{d r} \frac{1}{Y_{φ}} \frac{d Y_{r}}{d φ} + \frac{1}{M a^{2} r^{2} Y_{φ}} \frac{d^{2} Y_{φ}}{d φ^{2}} + ρ_{e}^{(o)}

(62)

where the Newtonian notation for time derivatives was used, i.e.

\ddot{T} = d^{2} T / d t^{2}

4.2. The Solution in Time

The left-hand-side of equations (61) and (62) are functions of time only, while the right-hand-side are functions of the space variables

r

and

φ

only. Consequently, each side has to be equal to a separation constant

χ

. From the left-hand-side of both equations one obtains the equation for the variations in time in the form

\frac{d^{2} T}{d t^{2}} - χ T = 0

(63)

where the separation constant can be real or complex. The solution to equation (63) produces two eigenvalues

\pm \sqrt{χ}

4.2.1. $χ$ is real

χ

is real there are two possibilities, namely

χ < 0

and

χ > 0

with the special case of

χ = 0

separating between the two.

The case of $χ < 0$ produces imaginary eigenvalues $\pm i \sqrt{|χ|}$ leading to the oscillatory solution

$T = a_{1} e^{i \sqrt{|χ|} t} + a_{2} e^{- i \sqrt{|χ|} t}$

(64)

and the basic equilibrium solution represented by equations (38a) and (38b) is neutrally stable. This neutrally stable equilibrium will have oscillatory perturbations in time that do not decay, nor amplify.
The case of $χ > 0$ produces real eigenvalues $\pm \sqrt{χ}$ leading to the solution

$T = a_{1} e^{\sqrt{χ} t} + a_{2} e^{- \sqrt{χ} t}$

(65)

The $+ \sqrt{χ} t$ term causes the exponential term to diverge, and consequently the basic equilibrium solution is unstable.

Therefore the stability condition for this case is $χ < 0$ for real values of $χ$ .

4.2.2. $χ$ is complex

When

χ

is complex it can be represented in the form

χ = χ_{r} + i χ_{i}

(66)

where

χ_{r}

and

χ_{i}

are real. Then

\sqrt{χ} = σ_{r} + i σ_{i}

(67)

where

σ_{r}

and

σ_{i}

are real. This yields the solution

T = e^{σ_{r} t} (a_{1} e^{i σ_{i} t} + a_{2} e^{- i σ_{i} t})

(68)

There are two regions to consider, i.e.

χ_{r} > 0

and

χ_{r} < 0

separated by the special case of

χ_{r} = 0

The case of $χ_{r} > 0$ produces

$σ_{r} = \pm \frac{χ_{r}^{1 / 2}}{\sqrt{2}} {[1 + \sqrt{1 + \frac{χ_{i}^{2}}{χ_{r}^{2}}}]}^{1 / 2} \forall χ_{r} > 0$

(69)

$σ_{i} = \pm \frac{χ_{i}}{\sqrt{2} χ_{r}^{1 / 2} {[1 + \sqrt{1 + \frac{χ_{i}^{2}}{χ_{r}^{2}}}]}^{1 / 2}} \forall χ_{r} > 0$

(70)

From (69) it is evident that the positive root causes the solution (68) to grow indefinitely leading the basic solution to be unstable with a basic frequency given by (70).

The case of $χ_{r} < 0$ produces

$σ_{r} = \mp \frac{{|χ_{r}|}^{1 / 2}}{\sqrt{2}} {[\sqrt{1 + \frac{χ_{i}^{2}}{χ_{r}^{2}}} - 1]}^{1 / 2} \forall χ_{r} < 0$

(71)

$σ_{i} = \mp \frac{χ_{i}}{\sqrt{2} {|χ_{r}|}^{1 / 2} {[\sqrt{1 + \frac{χ_{i}^{2}}{χ_{r}^{2}}} - 1]}^{1 / 2}} \forall χ_{r} < 0$

(72)

From (71) it is evident that the positive root causes the solution (68) to grow indefinitely leading the basic solution to be unstable with a basic frequency given by (72).

The separation special case of $χ_{r} = 0$ produces

$σ_{r} = σ_{i} = \pm \frac{1}{\sqrt{2}} χ_{i}^{1 / 2} \forall χ_{i} \geq 0$

(73)

Even at marginal stability, when

χ_{r} = 0

, perturbations still grow as one of the roots

σ_{r} = + χ_{i}^{1 / 2} / \sqrt{2}

is positive as long as

χ_{i} > 0

. Only when

χ_{i} = 0

both

σ_{r} = σ_{i} = 0

creating neutral stability.

Since the case when

χ

is complex causes the basic equilibrium solution to be unstable with perturbations growing with a frequency proportional to

χ_{i}

and neutral stability is established only if

χ_{i} = 0

it is sufficient to focus on the case when

χ

is real because the basic frequency for complex

χ

vanishes at neutral stability and the actual frequency is to be obtained from the solution to the weak nonlinear solution. While the same conclusion can be drawn for the case when

χ

is real the latter includes a neutrally stable solution for

χ < 0

that is important to explore even before pursuing a weak nonlinear solution.

At this point it becomes appealing to comment that when solving the Schrödinger equation the time solution imposes a frequency

\sqrt{|χ|} = ν = E_{n} / ℏ

, where

ℏ = h / 2 π

is the reduced Plank constant and

E_{n}

represents the separation constant eigenvalues that correspond to the energy levels. In our case imposing such a condition is avoided in an attempt to eventually cause the Plank constant to emerge naturally from the complete solution.

4.3. The Solution in Space

For the solution in space one considers the right-hand side of equations (61) and (62) to be equal to the same separation constant

χ

, leading to

M a^{2} χ = \frac{1}{ρ_{e}^{(o)} R_{r}} [\frac{d}{d r} + \frac{M a^{2}}{4 π r^{2}}] [\frac{1}{r^{2}} \frac{d (r^{2} ρ_{e}^{(o)} R_{r})}{d r}] + \frac{1}{ρ_{e}^{(o)} R_{r}} \frac{d}{d r} (\frac{ρ_{e}^{(o)} R_{φ}}{r}) + \frac{M a^{2} R_{φ}}{4 π r^{3} R_{r} Y_{r}} \frac{d Y_{φ}}{d φ} + M a^{2} ρ_{e}^{(o)}

(74)

M a^{2} χ = \frac{1}{r^{3} ρ_{e}^{(o)} R_{φ}} \frac{d (r^{2} ρ_{e}^{(o)} R_{r})}{d r} \frac{1}{Y_{φ}} \frac{d Y_{r}}{d φ} + \frac{1}{r^{2} Y_{φ}} \frac{d^{2} Y_{φ}}{d φ^{2}} + M a^{2} ρ_{e}^{(o)}

(75)

4.3.1. The Azimuthal Solution

From equation (75) in order to separate the functions of

r

from the functions of

φ

one needs to require that

(d^{2} Y_{φ} / d φ^{2}) / Y_{φ} = - κ_{φ}^{2} = constant

, producing the following ordinary differential equation

\frac{d^{2} Y_{φ}}{d φ^{2}} + κ_{φ}^{2} Y_{φ} = 0

(76)

that generates the eigenvalues

\pm i κ_{φ}

and the solution for

Y_{φ}

Y_{φ} = B e^{i κ_{φ} φ} + B^{*} e^{- i κ_{φ} φ}

(77)

where

B^{*}

is the complex conjugate of

B

that is required by the fact that the velocity and consequently

Y_{φ}

have to be real functions. Therefore, the solution (77) can be expressed in terms of trigonometric functions in the form

Y_{φ} = b_{1} \sin (κ_{φ} φ) + b_{2} \cos (κ_{φ} φ)

(78)

The boundary conditions for the azimuthal solution are just continuity and smoothness for all values of

φ

. This implies that

Y_{φ}

and its derivative

d Y_{φ} / d φ

φ = 0

are identical to their values at

φ = 2 π

, i.e.

{(Y_{φ})}_{φ = 0} = {(Y_{φ})}_{φ = 2 π} and {(\frac{d Y_{φ}}{d φ})}_{φ = 0} = {(\frac{d Y_{φ}}{d φ})}_{φ = 2 π}

(79)

Applying the boundary conditions (79) to the solution (78) produces an equation for the eigenvalues of

κ_{φ}

in the form

\cos (2 π κ_{φ}) = 1

(80)

leading to the following eigenvalues

κ_{φ} = m \forall m = 0, \pm 1, \pm 2, \pm 3, ...

(81)

The eigenvalues (81) are identical to the ones obtained from the solution to the Schrödinger equation (Griffiths [25]). The specific eigenvalue of

m = 0

produces a constant solution for

Y_{φ}

, a result that would have been obtained from (76) directly if

κ_{φ} = 0

and applying the continuity boundary conditions (79). This constant solution for

Y_{φ}

is consistent with an orbital motion that does not depend on

φ

and its details will be presented in a following section. Substituting (81) into (78) yields

Y_{ϕ} = b_{1} \sin (m φ) + b_{2} \cos (m φ)

(82)

If we can set the origin of

φ

in such a way that

Y_{φ} = 0

when

φ = 0

then the solution (79) can be presented in the simpler form

Y_{φ} = b_{1} \sin (m φ) \forall m = \pm 1, \pm 2, \pm 3, ...

(83)

which applies to

m \neq 0

. For

m = 0

the solution is

Y_{φ} = b_{2} {[\cos (m φ)]}_{m = 0} = b_{2} \forall m = 0

(84)

4.3.2. The Radial Equation

Returning now to equation (75) one needs to impose also that

(d Y_{r} / d φ) / Y_{φ} = κ_{r φ} = constant

, leading to

d Y_{r} / d φ = κ_{r φ} b_{1} \sin (m φ)

and establishing the solution for

Y_{r} (φ)

in the form

Y_{r} = - (κ_{r φ} / m) b_{1} \cos (m φ)

(85)

Substituting (83) and (85) into equation (75) allows expressing

R_{ϕ}

in terms of the remaining terms that are functions of

r

only

R_{φ} = f_{φ 1} \frac{d (r^{2} ρ_{e}^{(o)} R_{r})}{d r}

(86)

where

f_{φ 1} = \frac{κ_{r φ}}{r ρ_{e}^{(o)} [m^{2} + M a^{2} r^{2} (χ - ρ_{e}^{(o)})]}

(87)

Also by using (83) and (85) one can find the term

(d Y_{φ} / d φ) / Y_{r} = - m^{2} / κ_{r φ}

. Substituting (83), (85), and (86) into (74) produces an equation for

R_{r}

(1 + r f_{φ 1} ρ_{e}^{(o)}) \frac{d^{2} η}{d r^{2}} + [r f_{φ 2} - \frac{2}{r} + \frac{M a^{2}}{4 π r} (\frac{1}{r} + κ_{φ r} f_{φ 1} ρ_{e}^{(o)})] \frac{d η}{d r} + M a^{2} (ρ_{e}^{(o)} - χ) η = 0

(88)

where

η = r^{2} ρ_{e}^{(o)} R_{r}

(89)

and

f_{φ 2} = - \frac{κ_{r φ} [2 m^{2} + M a^{2} r^{2} (4 (χ - ρ_{e}^{(o)}) - r \frac{d ρ_{e}^{(o)}}{d r})]}{r^{3} {[m^{2} + M a^{2} r^{2} (χ - ρ_{e}^{(o)})]}^{2}}

(90)

The radial solution to equation (88) is the objective of a separate discussion. The focus of the linear stability in this paper is in deriving the time and azimuthal eigenfunctions and demonstrating their combined result.

5. Combined Solution in Space and Time

5.1. The Electron-Fluid Standing Waves

Meanwhile it is appealing to investigate the combination of the azimuthal solution with the time solution for any radial solutions

R_{r} (r)

and

R_{φ} (r)

. Considering the solution in time that is consistent with a neutrally stable basic equilibrium, i.e.

χ < 0

and using the notation

ω = \sqrt{|χ|}

one obtains from substituting (64) and (82) into (59) and (60) for

m \neq 0

v_{r}^{(1)} = R_{r} (r) \{A_{1} [\sin (ω t - m φ) + \sin (ω t + m φ)] + A_{2} [\cos (ω t - m φ) - \cos (ω t + m φ)]\}

(91)

v_{φ}^{(1)} = R_{φ} (r) \{B_{1} [\cos (ω t - m φ) - \cos (ω t + m φ)] + B_{2} [\sin (ω t - m φ) - \sin (ω t + m φ)]\}

(92)

The solutions (91) and (92) represent standing waves just as the solution to the Schrödinger equation yields standing waves. The latter result is applicable for

m \neq 0

. For

m = 0

the solutions are

v_{r}^{(1)} = 0; v_{φ}^{(1)} = R_{φ} (r) [A_{1} \sin (ω t) + A_{2} \cos (ω t)] \forall m = 0

(93)

Substituting solutions (91) and (92) as well as (38a) into (53) and integrating the result leads to the solution for

E_{e r}^{(1)}

and

E_{e φ}^{(1)}

in the form

E_{e r}^{(1)} = \frac{m ρ_{e}^{(o)} R_{r} (r)}{κ_{φ r} ω r^{2}} \{A_{2} [\sin (ω t - m φ) - \sin (ω t + m φ)] - A_{1} [\cos (ω t - m φ) + \cos (ω t + m φ)]\}

(94)

E_{e φ}^{(1)} = \frac{ρ_{e}^{(o)} R_{φ} (r)}{ω r^{2}} \{B_{2} [\sin (ω t - m φ) - \sin (ω t + m φ)] - B_{1} [\cos (ω t - m φ) + \cos (ω t + m φ)]\}

(95)

Substituting (94) and (95) into (52) produces the solution for

ρ_{e}^{(1)}

in the form

ρ_{e}^{(1)} = - F_{1} (r) [\sin (ω t - m φ) - \sin (ω t + m φ)] - F_{2} (r) [\cos (ω t - m φ) + \cos (ω t + m φ)]

(96)

and then by using (38) and (50b)

ρ = ρ^{(o)} (r) + ρ^{(1)} (t, r, φ) = \frac{1}{4 π I_{e q}} e^{r_{o} / r} + ρ^{(1)} (t, r, φ)

(97)

where

ρ^{(1)} = F_{1} (r) [\sin (ω t - m φ) - \sin (ω t + m φ)] + F_{2} (r) [\cos (ω t - m φ) + \cos (ω t + m φ)]

(98)

and

F_{1} (r)

F_{2} (r)

are

F_{1} (r) = [\frac{A_{2}}{κ_{φ r} r^{2}} \frac{d (r^{2} ρ_{e}^{(o)} R_{r} (r))}{d r} - \frac{B_{1} ρ_{e}^{(o)} R_{φ} (r)}{r}]

(99)

F_{2} (r) = - [\frac{A_{1}}{κ_{φ r} r^{2}} \frac{d (r^{2} ρ_{e}^{(o)} R_{r})}{d r} + \frac{B_{2} ρ_{e}^{(o)} R_{φ} (r)}{r}]

(100)

The solutions (91), (92), (93), (94), (95), (96) and (97) provide the evidence of the “wave” part from the “wave-particle” duality. The next section will focus on identifying the “particle” motion. The solution (97) for the mass density is presented graphically in Figure 3 as density plots at a constant value of

r

. From the figure one can observe two branches of the electron-fluid density each compressing and expanding periodically in the azimuthal

φ

direction. More discussion on this figure will follow in section 5.3.

5.2. The Electron-Fluid Linear and Angular Momentum, and Kinetic Energy

The local linear momentum of the electron-fluid, i.e. the linear momentum per unit volume is defined by

p_{f} = ρ^{(o)} v^{(1)} = p_{r} {\hat{e}}_{r} + p_{φ} {\hat{e}}_{φ}; where p_{r} = ρ^{(o)} v_{r}^{(1)}; p_{φ} = ρ^{(o)} v_{φ}^{(1)}

(101)

The total linear momentum

p

is then the integral of the local linear momentum over the whole volume occupied by the electron-fluid

p = \int_{{\tilde{V}}_{o}} ρ^{(o)} v^{(1)} d \tilde{V} = \int_{{\tilde{V}}_{o}} ρ^{(o)} v_{r}^{(1)} d \tilde{V} {\hat{e}}_{r} + \int_{{\tilde{V}}_{o}} ρ^{(o)} v_{φ}^{(1)} d \tilde{V} {\hat{e}}_{φ}

(102)

where

d \tilde{V} = r^{2} \sin θ d r d θ d φ

The local angular momentum of the electron-fluid, i.e. the angular momentum per unit volume is defined by

L_{f} = x \times ρ v = (r {\hat{e}}_{r}) \times ρ v^{(1)} = r v_{φ}^{(1)} [ρ^{(o)} (r) + ρ^{(1)} (t, r, φ)] {\hat{e}}_{θ} = ρ^{(o)} v_{φ}^{(1)} r {\hat{e}}_{θ}

(103)

The last term in (95), i.e.

r v_{φ}^{(1)} ρ^{(1)}

is of second order of magnitude and is therefore discarded at the linear stability level.

The total angular momentum

L

is then the integral of the local angular momentum over the whole volume occupied by the electron-fluid, which for the two-dimensional system considered is given by

L = 2 \int_{0}^{2 π} d φ \int_{r_{N}}^{1} r^{2} L_{f} (t, r, φ) d r = 2 \int_{0}^{2 π} d φ \int_{r_{N}}^{1} ρ^{(o)} v_{φ}^{(1)} r^{3} d r {\hat{e}}_{θ}

(104)

By substituting the solution for

ρ^{(o)} = (1 / 4 π I_{e q}) e^{r_{o} / r}

from equation (38b) and

v_{φ}^{(1)}

from equation (92) into (104) leads to (applicable for

m \neq 0

)

L = \frac{1}{4 π I_{e q}} \int_{0}^{2 π} f_{φ} (φ) d φ \int_{r_{N}}^{1} e^{r_{o} / r} R_{φ} (r) r^{3} d r {\hat{e}}_{θ} \forall m \neq 0

(105)

where

f_{φ} (φ) = B_{1} [\sin (ω t - m φ) + \sin (ω t + m φ)] + B_{3} [\cos (ω t - m φ) - \cos (ω t + m φ)]

(106)

The integral in

φ

vanishes as

\int_{0}^{2 π} \cos (ω t \pm m φ) d φ = \int_{0}^{2 π} \sin (ω t \pm m φ) d φ = 0

, except when

m = 0

in which case

v_{φ}^{(1)} = R_{φ} (r) [A_{1} \sin (ω t) + A_{2} \cos (ω t)]

from (93) leading to

L = \frac{I_{L o}}{I_{e q}} [A_{1} \sin (ω t) + A_{2} \cos (ω t)] {\hat{e}}_{θ} \forall m = 0

(107)

where

I_{L o} = \int_{r_{N}}^{1} e^{r_{o} / r} R_{φ} (r) r^{3} d r

(108)

However, even in this case of

m = 0

an average over the period of oscillation

2 π / ω

still produces a vanishing total angular momentum. Then consequently the total angular momentum for

m \neq 0

is zero as is the total angular momentum averaged over a period of oscillations for

m = 0

, i.e.

L = 0

(109)

We will see that the total kinetic energy is in all these cases non-zero, and the meaning of this result will be presented and discussed in connection with the motion of the electron-particle, i.e. the center of mass of the electron-fluid.

The local kinetic energy

K_{f}

of the electron-fluid, i.e. the kinetic energy per unit volume is defined by

K_{f} = \frac{1}{2} ρ^{(o)} v^{(1)} \cdot v^{(1)} = \frac{1}{2} ρ^{(o)} [{(v_{r}^{(1)})}^{2} + {(v_{φ}^{(1)})}^{2}]

(110)

For

m = 0

the total kinetic energy becomes

K_{f} = \frac{1}{2} ρ^{(o)} {(v_{φ}^{(1)})}^{2} = \frac{e^{r_{o} / r} R_{φ}^{2} (r)}{8 π I_{e q}} [A_{1}^{2} \sin^{2} (ω t) + A_{2}^{2} \cos^{2} (ω t) + A_{1} A_{2} \sin (2 ω t)] \forall m = 0

(111)

and for

m \neq 0

the local kinetic energy is

\begin{array}{l} K_{f} = \frac{1}{2} ρ^{(o)} {(v_{φ}^{(1)})}^{2} = \frac{e^{r_{o} / r} \sin^{2} (ω t)}{8 π I_{e q}} \{(a_{1}^{2} R_{r}^{2} + a_{3}^{2} R_{φ}^{2}) \cos^{2} (m φ) + \\ (a_{2}^{2} R_{r}^{2} + a_{4}^{2} R_{φ}^{2}) \sin^{2} (m φ) + (a_{1} a_{2} R_{r}^{2} + a_{3} a_{4} R_{φ}^{2}) \sin (2 m φ) \end{array} \forall m \neq 0

(112)

The total kinetic energy

K

is then the integral of the local kinetic energy over the whole volume occupied by the electron-fluid, which for the two-dimensional system considered is given by

K = 2 \int_{0}^{2 π} d φ \int_{r_{N}}^{1} r^{2} K_{f} d r = \int_{0}^{2 π} d φ \int_{r_{N}}^{1} ρ^{(o)} v^{(1)} \cdot v^{(1)} r^{2} d r {\hat{e}}_{θ} \forall m \neq 0

(113)

For

m = 0

the total kinetic energy becomes

K = \frac{I_{K o}}{2 I_{e q}} [A_{1}^{2} \sin^{2} (ω t) + A_{2}^{2} \cos^{2} (ω t) + A_{1} A_{2} \sin (2 ω t)] \forall m = 0

(114)

where

I_{K o} = \int_{r_{N}}^{1} e^{r_{o} / r} R_{φ}^{2} (r) r^{2} d r

(115)

and the average of the total kinetic energy over a period of oscillation

2 π / ω

K_{a v} = \frac{I_{K o} π}{2 I_{e q} ω} (A_{1}^{2} + A_{2}^{2}) \neq 0 \forall m = 0

(116)

For

m \neq 0

the total kinetic energy becomes

K = \frac{I_{K}}{4 I_{e q}} \sin^{2} (ω t) \neq 0 \forall m \neq 0

(117)

where

I_{K} = \int_{r_{N}}^{1} [A_{1}^{2} R_{r}^{2} (r) + A_{2}^{2} R_{φ}^{2} (r)] e^{r_{o} / r} r^{2} d r

(118)

An average of the total kinetic energy over a period of oscillation

2 π / ω

K_{a v} = \frac{I_{K} π}{4 I_{e q} ω} \neq 0 \forall m \neq 0

(119)

All values of the total kinetic energy for the values of

m = 0, m = \pm 1, \pm 2, \pm 3, ...

ended up non-zero, while their angular momenta are all zero. The explanation of how this can occur is presented in the next section dealing with the motion of the electron-particle, i.e. the motion of the center of mass of the electron-fluid.

5.3. The Electron-Particle Motion as the Electron-Fluid Center of Mass

The center of mass of the electron-fluid is regarded as the electron-particle and is defined in the form (1) that is presented in spherical coordinates as follows

x_{c m} = r_{c m} {\hat{e}}_{r} = \frac{\int_{0}^{π} d θ \sin θ \int_{0}^{2 π} d φ \int_{r_{N}}^{1} d r r^{3} ρ (t, r, φ)}{\int_{0}^{π} d θ \sin θ \int_{0}^{2 π} d φ \int_{r_{N}}^{1} d r r^{2} ρ (t, r, φ)} {\hat{e}}_{r}

(120)

The denominator represents the mass of the electron, which has a dimensionless value of 1, consequently (120) becomes

x_{c m} = r_{c m} {\hat{e}}_{r} = \int_{0}^{π} d θ \sin θ \int_{0}^{2 π} d φ \int_{r_{N}}^{1} d r r^{3} ρ (t, r, φ) {\hat{e}}_{r}

(121)

and for the two-dimensional problem considered it is presented in the form

x_{c m} = r_{c m} {\hat{e}}_{r} = 2 \int_{0}^{2 π} d φ \int_{r_{N}}^{1} d r r^{3} ρ (t, r, φ) {\hat{e}}_{r}

(122)

By substituting the solution for

ρ^{(o)} = (1 / 4 π I_{e q}) e^{r_{o} / r}

from equation (38b) and substituting (97) into (122) yields

x_{c m} = r_{c m} {\hat{e}}_{r} = [I_{e q o} + 2 \int_{0}^{2 π} d ϕ \int_{r_{N}}^{1} r^{3} ρ^{(1)} (t, r, ϕ) d r] {\hat{e}}_{r}

(123)

where

I_{e q o} = I_{o} / I_{e q}

For

m = 0

the value of

ρ^{(1)} = 0

and therefore the center of mass is

x_{c m} = r_{c m} {\hat{e}}_{r} = I_{e q o} {\hat{e}}_{r}

(124)

For other values of

m

one can use equation (97) into (123) to evaluate the center of mass, i.e.

x_{c m} = [I_{e q o} + \frac{2 m \cos (ω t)}{ω} \{\int_{0}^{2 π} [\sin (m φ)] d φ \int_{r_{N}}^{1} F_{1} (r) r^{3} d r - \int_{0}^{2 π} [\cos (m φ)] d φ \int_{r_{N}}^{1} F_{2} (r) r^{3} d r\}] {\hat{e}}_{r}

(125)

The integrals in

φ

from (125) vanish resulting in the radial location of the center of mass identical to equation (124).

However, in order to establish the motion of the center of mass, if any, one needs to convert the location of the center of mass to Cartesian coordinates before evaluating the integrations, as follows

d r = d r {\hat{e}}_{r} = d r [\cos φ {\hat{e}}_{x} + \sin φ {\hat{e}}_{y}]

(126)

where

{\hat{e}}_{x}

{\hat{e}}_{y}

are unit vectors in the x and y directions, respectively, and

x_{c m} = x_{c m} {\hat{e}}_{x} + y_{c m} {\hat{e}}_{y}

. Then equation (123) becomes

x_{c m} = [\frac{1}{2 π I_{e q}} \int_{0}^{2 π} [\cos φ {\hat{e}}_{x} + \sin φ {\hat{e}}_{y}] d φ \int_{r_{N}}^{1} e^{r_{o} / r} r^{3} d r + 2 \int_{0}^{2 π} [\cos φ {\hat{e}}_{x} + \sin φ {\hat{e}}_{y}] d φ \int_{r_{N}}^{1} r^{3} ρ^{(1)} (t, r, φ) d r]

(127)

Since for

m = 0

the value of

ρ^{(1)} = 0

, the location of the center of mass in Cartesian coordinates is at the center of the nucleus, i.e.

x_{c m} = 0 {\hat{e}}_{x} + 0 {\hat{e}}_{y} = 0

However, for

m = \pm 1, \pm 2, \pm 3, ...

the location of the center of mass in Cartesian coordinates is evaluated from (127) to become

\begin{array}{l} x_{c m} = r_{c m} {\hat{e}}_{r} = \frac{2 m}{ω} \cos (ω t) \int_{0}^{2 π} \{I_{c m 1} [\cos (φ) {\hat{e}}_{x} + \sin (φ) {\hat{e}}_{y}] \sin (m φ) - \\ I_{c m 2} [\cos (φ) {\hat{e}}_{x} + \sin (φ) {\hat{e}}_{y}] \cos (m φ)\} d φ \forall m \neq 0 \end{array}

(128)

leading after integration to

x_{c m} = x_{c m} {\hat{e}}_{x} = \frac{2 π}{ω} [I_{c m 1} {\hat{e}}_{x} \pm I_{c m 2} {\hat{e}}_{y}] \cos (ω t) \forall m = \pm 1

(129)

and

x_{c m} = x_{c m} {\hat{e}}_{x} = 0 {\hat{e}}_{x} + 0 {\hat{e}}_{y} \forall m = \pm 2, \pm 3, ...

(130)

where

I_{c m 1} = \int_{r_{N}}^{1} F_{1} (r) r^{3} d r; I_{c m 2} = \int_{r_{N}}^{1} F_{2} (r) r^{3} d r

(131)

and

F_{1} (r), F_{2} (r)

are defined by equations (99) and (100). Equation (129) describes the motion of the electron particle in the horizontal direction from one side to the other of the circle of radius

I_{F} π

for

I_{F} = 2 \sqrt{I_{c m 1}^{2} + I_{c m 2}^{2}} / ω

, showing that the electron-particle while oscillating crosses the nucleus with the electron-fluid itself being at all times outside the nucleus, as Eiseberg and Resnick [6] described. This horizontal motion is described in Figure 2 as well as in Figure 3, where the electron-particle motion overlaps the electron-fluid motion presented as a density plot of the mass density solution on an annulus in the

φ

direction. The density plot of the electron-fluid motion was accomplished by using Mathematica^™ (Wolfram [29]). From Figure 3 it can be observed that the electron-fluid performs an “embracing” motion as its differential elements repel each other in the

φ

direction. At the same time the electron-particle (center of mass) follows a horizontal motion from one side of the annulus to the other and back (from

φ = 0

φ = π

and back horizontally). The third and seventh of the annuli in Figure 3 show the electron-particle located at the center of the nucleus, while the electron-fluid is outside the nucleus at all times. The radial mass density variations are omitted here for clarity purposes. For

m = \pm 2, \pm 3, ...

the center of mass in Cartesian coordinates is obtained from performing the integrations in (128). The latter causes the integral to vanish and as a consequence the Cartesian coordinates location of the center of mass is

x_{c m} = 0 {\hat{e}}_{x} + 0 {\hat{e}}_{y} = 0

Figure 2. The electron-particle motion (center of mass).

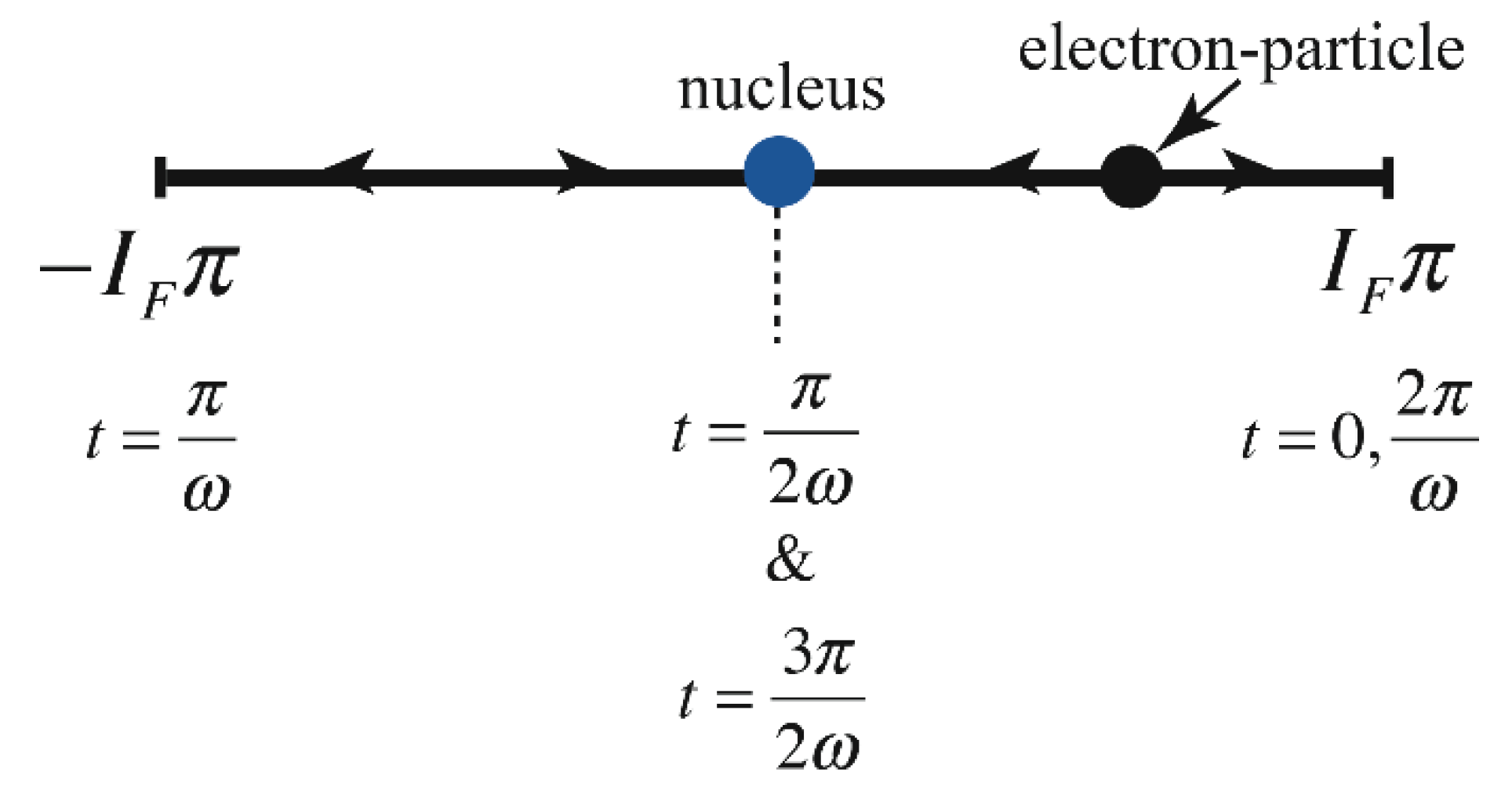
Figure 3. The electron-particle motion (center of mass) overlapping the electron-fluid motion presented as a density plot on an annulus in the

φ

direction.

Figure 3. The electron-particle motion (center of mass) overlapping the electron-fluid motion presented as a density plot on an annulus in the

φ

direction.

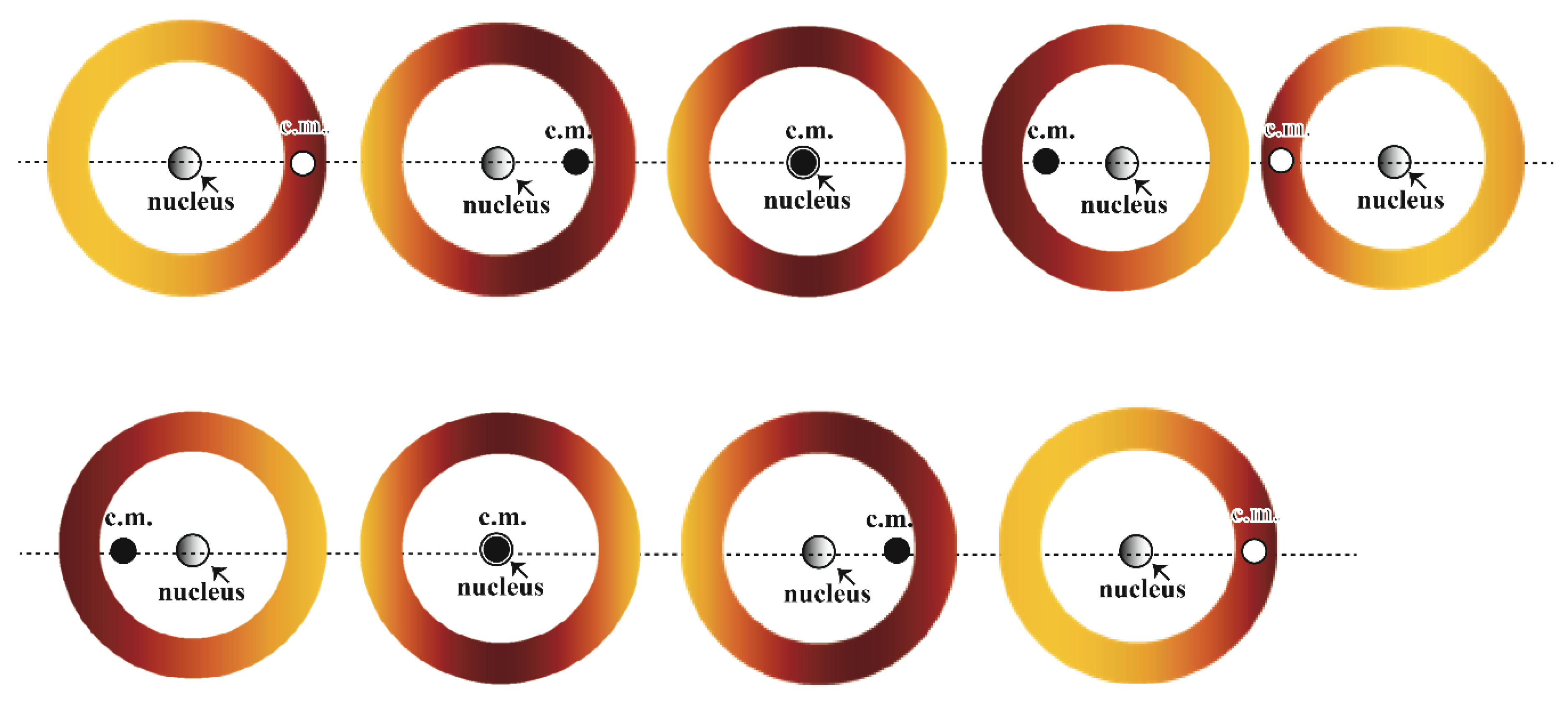
The results show that in the cases of

m = 0

and

m = \pm 2, \pm 3, ...

the electron-particle is stationary and located at the center of the nucleus, a result that was seen as “objectionable” by Einstein while criticizing Bohm’s position regarding “de Broglie-Bohm pilot wave theory” (Bohm [26], Myrvold [27], Einstein [28]). The classical visualization presented in this paper demonstrates how the “static” electron-particle is perfectly consistent with the orbital motion of the electron-fluid, making the results “unobjectionable”.

5.4. Consistency of the Results with the Solution to the Schrödinger Equation, the Binding Energy Levels, and the Fine Structure Constant

It is difficult to compare the results obtained so far with the solution to the Schrödinger equation because of three reasons. First, the results presented in this paper are for a two-dimensional model. Second, the amplitudes of the solutions obtained in this paper from the linear stability analysis are undefined yet. They will be defined once the next step of the finite amplitude weak nonlinear analysis is undertaken. Third, the Schrödinger equation was shown in [1] to be identical to the inviscid Navier-Stokes (Euler) equations in the limit of large values of the electron-fluid Mach number

M a > > 1

. In the present paper the electron-fluid Mach numbers are of unit order of magnitude and therefore not complying with the latter condition. Nevertheless, there are already quite a few similarities that are worth identifying.

In order to do so one needs to convert back some of the results to dimensional form. The following notation is then used to provide a distinction between the dimensionless variables and the dimensional ones. The dimensional variables will be identified by a tilde

{(\cdot)}_{}^{~}

over the symbol. For example,

r_{c m}

is the dimensionless center of mass, while

{\tilde{r}}_{c m}

is the dimensional counterpart. The result for the radial location of the center of mass of the electron fluid for all values of

m

was equation (124), i.e.

r_{c m} = I_{e q o}

. The dimensional counterpart is

{\tilde{r}}_{c m} = I_{e q o} {\tilde{r}}_{\infty}

(132)

If the radial location of the center of mass obtained from the present model corresponds to the orbital location obtained from the Schrödinger equation (i.e. the highest expectation value) then

{\tilde{r}}_{c m} = {\tilde{r}}_{o, n} = \frac{4 π ε_{o} ℏ^{2}}{m_{e} e^{2}} n^{2} = {\tilde{r}}_{B} n^{2}

(133)

where

n = 1, 2, 3, ...

is the principal quantum number, and

{\tilde{r}}_{B}

is Bohr radius. Combining (132) with (133) defines

{\tilde{r}}_{\infty}

{\tilde{r}}_{\infty} = \frac{{\tilde{r}}_{B}}{I_{e q}} n^{2} for n = 1, 2, 3, ...

(134)

Evaluating now the binding energy of the electron-fluid by adding the potential energy

\tilde{U}

due to the proton Coulomb potential to the total kinetic energy

\tilde{K}

evaluated in the previous section, i.e. converted back into a dimensional form, produces

\tilde{U} = - \frac{e^{2}}{4 π ε_{o} {\tilde{r}}_{c m}} (a); \tilde{K} = \frac{b_{K} π}{2 ω I_{e q}} \frac{e^{2}}{ε_{o} {\tilde{r}}_{\infty}} (b)

(135)

b_{K} = I_{K o} (A_{1}^{2} + A_{2}^{2}) \forall m = 0; I_{K o} = \int_{r_{N}}^{1} r^{2} e^{r_{o} / r} R_{φ}^{2} (r) d r

(136)

(137)

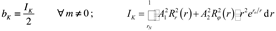
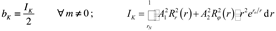
The binding energy is then expressed in the form which upon substitution of (134) and (135) and

{\tilde{r}}_{B} = 4 π ε_{o} ℏ^{2} / m_{e} e^{2}

from (133) becomes

{\tilde{E}}_{n} = \tilde{U} + \tilde{K} = [\frac{4 π^{2} b_{K}}{ω I_{e q}} - \frac{2}{I_{e q o}}] {(\frac{e^{2}}{4 π ε_{o}})}^{2} \frac{m_{e}}{2 ℏ^{2}} \frac{1}{n^{2}}

(138)

Therefore, if the amplitudes of the solution from the forthcoming weak nonlinear analysis were such that

b_{K} = ω I_{e q} (2 I_{e q} - I_{o}) / 4 π^{2} I_{o}

, then the binding energy of the hydrogen atom obtained from the current model is identical to the ones obtained from the Schrödinger equation as well as to the ones obtained from the Bohr model of the atom that were confirmed experimentally, i.e. equation (138) becomes

{\tilde{E}}_{n} = - {(\frac{e^{2}}{4 π ε_{o}})}^{2} \frac{m_{e}}{2 ℏ^{2}} \frac{1}{n^{2}} for n = 1, 2, 3, ...

(139)

Substituting the value of

{\tilde{r}}_{\infty}

from (134) and using

{\tilde{r}}_{B} = 4 π ε_{o} ℏ^{2} / m_{e} e^{2}

from (133) into the emerged magnetic number

M_{e}

in equation (45) reveals the fine structure constant,

α = 7.2976 \times 10^{- 3} \sim 1 / 137

, the latter being related to the reciprocal of

M_{e}

in the form

M_{e} = \frac{n}{\sqrt{2 π I_{e q}}} (\frac{4 π ε_{o} ℏ c}{e^{2}}) = \frac{n}{\sqrt{2 π I_{e q}} α} \forall n = 1, 2, 3, ...

(140)

Therefore, these derivations show that the fine structure constant emerged naturally as a dimensionless parameter in the momentum and the Faraday law equations. This occurred only by assuming that the center of mass of the electron-fluid is identical to the orbital radius obtained from the solution to the Schrödinger equation and from Bohr’s model of the atom.

6. Generalizations and Follow-Up Solutions

The model presented in this paper applies to the hydrogen atom, i.e. one-electron and one-proton system. This can be easily extended to multi-electron and multi-proton systems. The neutrons have no impact on the model as long as gravitational effects are neglected.

To include effects of multi-electrons one needs only to adjust the integral conditions related to the total electron-mass and total electron-charge in the system, i.e. equations (2) and (19)

N_{e} m_{e} = \int_{{\tilde{V}}_{o}} ρ (x, t) d \tilde{V} = const .

(141)

N_{e} e = \int_{{\tilde{V}}_{o}} ρ_{e} (x, t) d \tilde{V} = const .

(142)

where

N_{e}

is the number of electrons.

To include effects of multi-protons in the nucleus one needs to evaluate the electric field due to the protons by accounting for the latter, i.e. the amended equation becomes

E_{p} = \frac{N_{p} |e|}{4 π ε_{o}} \frac{1}{r^{2}} {\hat{e}}_{r}

(143)

where

N_{p}

is the number of protons in the nucleus.

The model can also be extended to consider multiple atoms as molecules by geometrically locating one or more atoms in the vicinity of each other and transform the coordinates in such a way that the different effects included in the present model are reflected in the coordinates transformed system adequately.

Further work on the three-dimensional version of the model presented in this paper, the inclusion of the magnetic effects, as well as the follow-up weak nonlinear analysis is anticipated to provide the amplitudes of the solutions that the linear stability analysis cannot do. In addition, the results for the frequency of oscillations are anticipated from such an analysis. The weak nonlinear analysis is an asymptotic method that introduces expansion of all dependent variables in terms of a small parameter

ε (M a^{2}, M_{e}^{2})

. At order

ε

it is anticipated to obtain the linear set of equations solved at the linear stability level with the value of

χ = 0

, i.e. on the neutral stability curve. The

O (ε^{2})

equations will then produce a non-homogeneous version of linear equations sharing the same homogeneous operator as the

O (ε)

solution leading to additional particular solutions due to the non-homogeneous forcing. The final step occurs at order

ε^{3}

where a solvability condition in the form of a nonlinear ordinary differential equation emerges. This equation is anticipated to be of the form of a nonlinear oscillator that will provide the frequency of the oscillations in addition to the amplitudes of the

O (ε)

solutions. Another possible extension of the present work beyond the weak nonlinear analysis is deriving a spectral system associated with the fundamental modes of the solution and their evolution in time. These solutions while removing the weak compressibility assumption form also part of the follow-up investigation.

A separate research effort is to be dedicated to the solution of the current problem as well as a free electron while including magnetic effects that were neglected in the current model. The latter is expected to reveal the electron-spin as well as the spread-less solutions of the free electron-fluid, that were described in [1] based on the properties of the governing equations.

Solutions to the complete system of governing equations that include excitation via external forcing are then anticipated to demonstrate the “quantum jump” from one orbital to another via a shock-wave as it is common in compressible fluid dynamics. Eventually, numerical solutions are anticipated to reveal the complete details.

7. Conclusions

The solution presented in this paper revealed results that seem “objectionable” [27,28] and even “absurd” [30] when obtained via the statistical main-stream quantum theory or via the “de Broglie-Bohm” pilot wave theory, such as the electron crossing via the nucleus or a static electron, respectively. Simple explanations of such solutions were presented in the present paper, which show how these solutions are perfectly consistent with classical mechanics as well as common sense. The linear stability solutions presented in the present paper showed how one can observe the motion of the electron-fluid and then convert it into the motion of the electron-particle (i.e. the corresponding center of mass), i.e. from local variables to global properties. The solutions that were obtained are in large part consistent with the solutions obtained from the Schrödinger equation. In particular, the energy levels obtained were shown to be identical to the ones obtained from the solution to the Schrödinger equation by assuming a certain value for the amplitude, the latter being anticipated from the solution to the weak nonlinear formulation. The fine structure constant emerged naturally from the equations subject to the only assumption that the position of the center of mass of the electron-fluid as derived from the present model is identical to the Bohr- Schrödinger orbital radius.

Acknowledgments

The author wishes to thank the National Science Foundation for supporting this research under grant no. CBET-1804251.

References

Vadasz, P. , “Deterministic Quantum Mechanics – Part I – Conceptual Framework”, submitted for publication (linked to this submission).
Landau, L.D. , Lifshitz, E.M., “Fluid Mechanics”, translated from Russian by Skyes, J.B., and Reid, W.H., Pergamon Press, Oxford, New York, Toronto, Sydney, Paris, Frankfurt, 1978.
Griffiths, D. J. , “Introduction to Electrodynamics”, Third Edition, Prentice Hall, Inc., Upper Saddle River NJ, 1999.
Jackson, J.D. , “Classical Electrodynamics”, Third Edition, John Wiley & Sons, Inc., 1999.
Born, M. Quantenmachanik der Stoßvorgänge, Zeitschrift für Physik. 1926; 38, 803–827. [Google Scholar]
Eisberg, R. Resnick, R., “Quantum physics of atoms, molecules, solids, nuclei, and particles”, 2nd edition, John Willey & Sons Inc., New York, Chichester, Brisbane, Toronto, Singapore, 1985, p. 254.
Schrödinger, E. , “Quantisierung als Eigenwertproblem”, Annalen der Physik, 1926, 384, 361–376. (Part I).
Schrödinger, E. , “Quantisierung als Eigenwertproblem”, Annalen der Physik, 1926, 384, 489–527, (Part II).
Schrödinger, E. , “Quantisierung als Eigenwertproblem”, Annalen der Physik, 1926, 385, 437–490, (Part III).
Schrödinger, E. , “Quantisierung als Eigenwertproblem”, Annalen der Physik, 1926, 386, 109–139. (Part IV).
Schrödinger, E. , “21 Collected Papers on Wave Mechanics”, New York: Chelsea Publishing Company, 1982.
Bohr, N. On the constitution of atoms and molecules, Part I, Philosophical Magazine. 1913; 26, 1–24. [Google Scholar]
Bohr, N. On the constitution of atoms and molecules, Part II Systems containing a single nucleus. Philosophical Magazine. 1913; 26, 476–502. [Google Scholar]
Bohr, N. On the constitution of atoms and molecules, Part III Systems containing several nuclei. Philosophical Magazine. 1913; 26, 857–875. [Google Scholar]
Bohr, N. The spectra of helium and hydrogen. Nature. 1914; 92, 231–232. [Google Scholar]
Bohr, N. , “Atomic structure”, Nature 1921, 106, 104–107.
Minev, Z.K. , Mundhada, S. O., Shankar, S., Reinhold, P., Gutiérrez-Jáuregui, R., Schoelkopf, R.J., Mirrahimi, M., Carmichael, H.J., and Devoret, M.H., “To catch and reverse a quantum jump mid-flight”, Nature, 2019, 570, 200–204. [Google Scholar]
Baggot, J. , “The meaning of quantum theory”, Oxford University Press Inc., New York, 1992 (reprinted 2004).
Malkus, W.V.R. and Veronis, G. , “Finite amplitude cellular convection”, Journal of Fluid Mechanics 1958, 4, 225–260. [Google Scholar] [CrossRef]
Segel, L.A. , “Distant side-walls cause slow amplitude modulation of cellular convection”, Journal of Fluid Mechanics 1969, 38, 203–224. 38.
Newell, A.C. and Whitehead, J. A., “Finite bandwith, finite amplitude convection”, Journal of Fluid Mechanics, 1969, 38, 279–303. [Google Scholar]
Daniels, P.G. “Roll pattern evolution in finite amplitude Rayleigh-Benard convection in a two-dimensional fluid layer bounded by distant sidewalls”, Journal of Fluid Mechanics, 1984, 143, 125–152. 143.
Vadasz, P. , “Centrifugal buoyancy in a rotating fluid layer next and distant from the rotation axis”, Physics of Fluids 2021, 33, 034123. 33.
Planck, M. , “Ueber das Gesetz der Energieverteilung in Normalspectrum” (translation: On the law of distribution of energy in the normal spectrum), Annalen der Physik, 1901, 4, 553–563. 4.
Griffiths, D.J. , “Introduction to Quantum Mechanics”, Second Edition, Pearson Education Inc., Upper Saddle River, NJ, 2005, p. 145-146.
Bohm, D. , “A suggested interpretation of quantum theory in terms of ‘hidden variables’ I”, Physical Review, 1952, 85, 166–179. 85.
Mirvold, W.C. “On some early objections to Bohm’s theory”, International Studies in the Philosophy of Science, 2003, 17.
Einstein, A. , “Elemantäre Überlegungen zur Interpretation der Grundlagen der Quanten-Mechanik”, in Scientific Papers to Max Born (New York, Hafner), pp. 33–40, 1953.
Wolfram, S. , Mathematica: A System for Doing Mathematics by Computer, 2nd edn, Wolfram Research Inc., Addison-Wesley, Redwood City, California, 1991.
Bohm, D. , “Quantum Theory”, Prentice Hall Inc., 1951, (David Bohm 1979, Dover publication 1989, p.44.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Deterministic Quantum Mechanics – Part II – The Linearized Temporal-Azimuthal Wave Solution

Abstract

1. Introduction

2. Governing Equations and the Basic Equilibrium Stationary Solution

2.1. Electron-Fluid (Subatomic-Fluid) Governing Equations

2.2. Basic equilibrium stationary solution

2.3. Dimensionless Governing Equations

3. Linear Stability Equations

4. Linear Stability Method of Solution

4.1. Separation of Variables

4.2. The Solution in Time

4.2.1. χ is real

4.2.2. χ is complex

4.3. The Solution in Space

4.3.1. The Azimuthal Solution

4.3.2. The Radial Equation

5. Combined Solution in Space and Time

5.1. The Electron-Fluid Standing Waves

5.2. The Electron-Fluid Linear and Angular Momentum, and Kinetic Energy

5.3. The Electron-Particle Motion as the Electron-Fluid Center of Mass

5.4. Consistency of the Results with the Solution to the Schrödinger Equation, the Binding Energy Levels, and the Fine Structure Constant

6. Generalizations and Follow-Up Solutions

7. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe

4.2.1. $χ$ is real

4.2.2. $χ$ is complex