Prerpints.org logo
Preprint
Article

Influence of Local Thermodynamic Non-Equilibrium to Photothermally Induced Acoustic Response of Complex Systems

Altmetrics

Downloads

106

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 May 2024

Posted:

16 May 2024

You are already at the latest version

Alerts
Abstract
In this paper, the time-resolved model of photoacoustic signal for samples with a complex inner structure is derived including local non-equilibrium of structural elements with multiple degrees of freedom, i.e. structural entropy of the system. The local non-equilibrium is taken into account through the fractional operator. By analyzing the model for two types of time-dependent excitation, a very short pulse and a very long pulse, it is shown that the rates of non-equilibrium relaxations in complex samples can be measured by applying the derived model and time-domain measurements. Limitations of the model and further directions of its development are discussed.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Photoacoustic (PA) and other photothermal (PT) techniques are non-destructive experimental methods based on recording of detectable phenomena produced by optically induced heat transfer across the illuminated sample [1,2,3,4,5,6,7,8]. These techniques have been developed for the last half century and are increasingly being applied in measuring the thermal properties of various samples [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26].
In PA measurement, the pressure fluctuations in gaseous surrounding of the optically heated sample are recorded [1,2,3,28]. They are proportional to surface temperature variations of optically excited sample [1,26,27,28,29,30,31]. To relate these fluctuations with sample properties it is necessary to develop the theoretical description of heat transfer across the illuminated sample and to calculate surface temperature variations based on this description.
Classical heat conduction theory [32] was established more than 150 years ago and is still found in textbooks and most engineering and scientific literature related to the problem of heat transport because it is consistent with the basic laws of thermodynamics. However, classical thermodynamics contains some assumptions that limit its domain of validity [33,34]. One of these assumptions is the local equilibrium assumption for non-equilibrium situations such as heat transport. Namely, classical thermodynamics considers that all sub-systems of a thermodynamic system are in local equilibrium while the system is not in equilibrium [33]. This assumption is valuable only if all subsystems relax with rates much larger than the rate of system enthalpy changes [35,36]. Otherwise, the influence of local relaxations must be taken into account [35,36,37,38,39,40].
The rates of subsystem relaxations in crystal solids are large [41]. Therefore, one doesn’t expect their influence on heat transfer in the usual measurement ranges of standard experiments based on heat transfer such as photoacoustic and other PT techniques. The theoretical estimations of the relaxation rates in complex systems are much less reliable due to large structural entropy of these systems however it is expected to be much slower than in crystals [35,41,42]. Besides, many calorimetric experiments show that the heat transport within complex systems such as glasses, liquid crystals, polymers, biopolymers, biological tissues, etc. deviates from the corresponding standard Fourier’s theory of heat conduction [37,38,42,43,44,45,46,47,48,49] indicating a possible influence of non-equilibrium relaxations in the usual measurement range of PT techniques.
In this paper, we derive the generalized model of photothermally induced acoustic signal including local relaxation in the sample with the complex inner structure. Our objective is to investigate do PA measurements could be employed in the estimation of non-equilibrium relaxation rates of complex systems.
The structure of the paper is as follows. After this introductory chapter, in Chapter 2 we briefly presented the fractional theory of heat conduction, which includes kinetic relaxations due to local non-equilibrium. We showed that kinetic relaxations can be connected with a microscopic approach based on fractional statistical physics and the kinetic memory of substantial media. Using the proposed fractional theory, in Chapter 3, a model of the spectral function of the PA signal was derived by applying the Laplace transform. After that, by applying the inverse Laplace transform to the spectral function of the PA signal for a thin sample, a model of the time-dependent PA signal generated by optical pulse excitation was derived. In Chapter 4, the time-dependent PA signal was analyzed for samples with a complex internal structure of different thicknesses. It has been shown that kinetic relaxations affect the slope and magnitude of the time-resolved PA signal indicating that this measurement technique can be employed in observation of local non-equilibrium in complex systems.

2. Theory of Heat Conduction Including the Non-Equilibrium Relaxation

The classical theory of heat conduction is based on the law of conservation of energy (First Law of Thermodynamics Eq.1) and Fourier’s constitutive relation Eq.2, which satisfies the Second Law of Thermodynamics [32,50]:
ρ C p ∂ T ( x , t ) ∂ t + d i v q → ( x , t ) = 0
q → ( x , t ) = − k ∂ T ( x , t ) ∂ x
The first term of Eq.1 denotes the rate of internal energy ∂ e ( x , t ) / ∂ t [39] while the second term, the divergence of the heat flux caused by the appearance of a temperature gradient inside the sample Eq.2, refers to the dissipation of energy inside the sample and is related to the increase in entropy of the system during process of energy exchange between system and its environment [51]. Heat capacity of a system Cp tell us how much heat per unit volume the system will absorb from its surrounding if we change its temperature by a small amount. Symbols T ( x , t ) and ρ signify system temperature and mass density, respectively.
Substituting Eq.2 into Eq.1 gives the classic heat conduction equation [32]:
∂ 2 T ( x , t ) ∂ x 2 − 1 D ∂ T ( x , t ) ∂ t = 0
where D denotes thermal diffusivity of the system and it is defined as ratio of thermal conductivity k and heat capacity C p , D = k / C p .
Eq.3 has been used for more than a century to describe heat transport processes in the condensed phase and to explain and process dynamic calorimetric experiments [32]. However, numerous dynamic calorimetric experiments performed in the last fifty years on systems with a complex internal structure, such as polymers, glasses, liquid crystals, biological tissues, etc., cannot be explained by the application of classical theory [42,43,44,45,46,47,48,49]. A number of such experiments are explained by the introduction of complex thermal capacitance [35,37,38,39,40,43,48,49], indicating that in the First Law of Thermodynamics given by Eq.1 there is an approximation that limits the domain of applicability of the classical theory [37,38,39,40].
From a thermodynamic point of view, the First Law of Thermodynamics given in the form of Eq.1 assumes that the exchange of energy between a system and its environment is a reversible process when the dissipation due to the appearance of a temperature gradient is neglected (e.g., in the case of small-sized samples) [51]. This further means that in this case the increase in entropy due to the thermodynamic process of energy exchange is ignored [35], that is, this law assumes the local equilibrium of all subsystems even though the whole system is not in thermodynamic equilibrium with the environment [33]. This approximation can be removed by introducing one more state variable (in addition to pressure and temperature), which is called affinity [35,52,53].
Generally, at constant temperature and pressure, affinity can be regarded as the advancement of internal parameter (internal degree of freedom) of the system [35] or as thermodynamic potential for the system undergoing a physic-chemical transformation i.e., as generalized driving force, which vanishes when the system is at equilibrium. Prigogine, De Groot and Mazur [52,53] defined an internal space of configuration of the system, where each degree of freedom is represented by a continuing variable representing a coordinate of the internal space. By analogy with heat diffusion in classical theory where heat is lost along the spatial direction defined by hot and cold points, in this representation, heat is lost by diffusion along the coordinate defined by the degree of freedom inside the internal space of configuration which participates to the entropy productions [35,42]. It could be related with kinetic memory of the system [41] which comes to expression when the time scale of observing the process (of experiment) is approximately equal to or less than the relaxation time of kinetic relaxations [33,35,37]. The rates of subsystem relaxations in crystal solids are large [41]. Therefore, one doesn’t expect their influence on heat transfer in the usual measurement ranges of standard experiments based on heat transfer such as photoacoustic and other photothermal techniques. The theoretical estimations of the relaxation rates in complex systems are much less reliable due to large structural entropy of these systems however it is expected to be much slower than in crystals [42,54] and it could be expected that there is influence of these relaxations to AC calorimetry.
When the complex system in which there are internal degree of freedom absorbs energy from (or releases to) environment it is in non-equilibrium state but if this state is close to equilibrium, the internal energy can be described through convolution integral as it is done in linear response theory [37,38,39,40]:
e ( x , t ) − e 0 = ρ C p [ Φ ( 0 ) T ( x , t ) + ∫ 0 t d Φ ( t , ) d t , T ( x , t − t , ) d t , ]
where C p is the equilibrium heat capacity and Φ ( t ) is memory kernel that describes relaxations of internal degrees of freedom (subsystems) that must satisfies relations Φ ( t = 0 ) = 1   Φ ( t → ∞ ) = 0 [39].
In essence, the above integral relation introduces a phase lag between change of internal energy and change of temperature [41] caused by local non-equilibrium of internal degree of freedom i.e., by kinetic of subsystems and their relaxations in equilibrium state, e ( x , t + τ ) ∼ T ( x , t ) .
The assumption about exponentially fading memory kernel leads to generalized theory of heat conduction with complex heat capacity that is widely used in analysis of calorimetric measurement of complex system [37,38,39,40,41].
However, microscopis approach of heat conduction suggests power law fading memory to explanation anomalous diffusive effects that leads to the following fractional relation between temperature rate and internal energy rate [55,56,57,58,59,60]:
∂ e ( x , t ) ∂ t = ρ C p γ ∂ υ T ( x , t ) ∂ t υ
where the Riemann–Liouville definition of fractional derivative is used [61]:
∂ υ f ( x , t ) ∂ t υ ≜ { 1 Γ ( 1 − υ ) ∂ ∂ t ∫ 0 t f ( x , t , ) ( t − t , ) υ d t , 0 < υ < 1 1 Γ ( − υ ) ∂ ∂ t ∫ 0 t f ( x , t , ) ( t − t , ) υ + 1 d t , υ < 0  
and Γ ( υ ) is Gamma function. With C p υ is denoted fractional heat capacity C p υ = ρ C p τ υ − 1 and τ is kinetic relaxation time.
A fractional order differential calculus is a generalization of the integer order integral and derivative to real or even complex order [62,63]. This idea first emerged at the end of the seventeenth century and has been developed in the area of mathematics throughout the eighteenth and nineteenth centuries. More recently, by the end of the twentieth century, it turned out that some physical phenomena can be modeled more accurately when fractional calculus is used [62,63,64,65,66,67,68,69,70,71,72,73,74]. A good review of various applications of fractional calculus in physics can be found in [62].
By substituting Eq.5 into Eq.1 and by substituting Eq.2 into Eq.1, a generalized description of heat conduction through complex systems is obtained, which includes local non-equilibrium through the fractional exponent υ and fractional heat capacity C p υ :
C p υ ∂ υ ϑ ( x , t ) ∂ t υ − k ∂ 2 ϑ ( x , t ) ∂ x 2 = 0
while the constitutive relation that satisfies the Second Law of Thermodynamics remains the same Eq.2.
In the Eq.7, ϑ ( x , t ) = T ( x , t ) − T 0 is the temperature variation of the system with respect to the temperature at which the sample was in thermodynamic equilibrium with the environment, and T 0 signifies temperature of ambient.
It is important to note that the same generalized equation of heat conduction Eq.7, was derived from the point of view of statistical physics by using various approaches [55,56,75].

3. Model of PA Signal Including Local Thermal Non-Equilibrium in the Sample

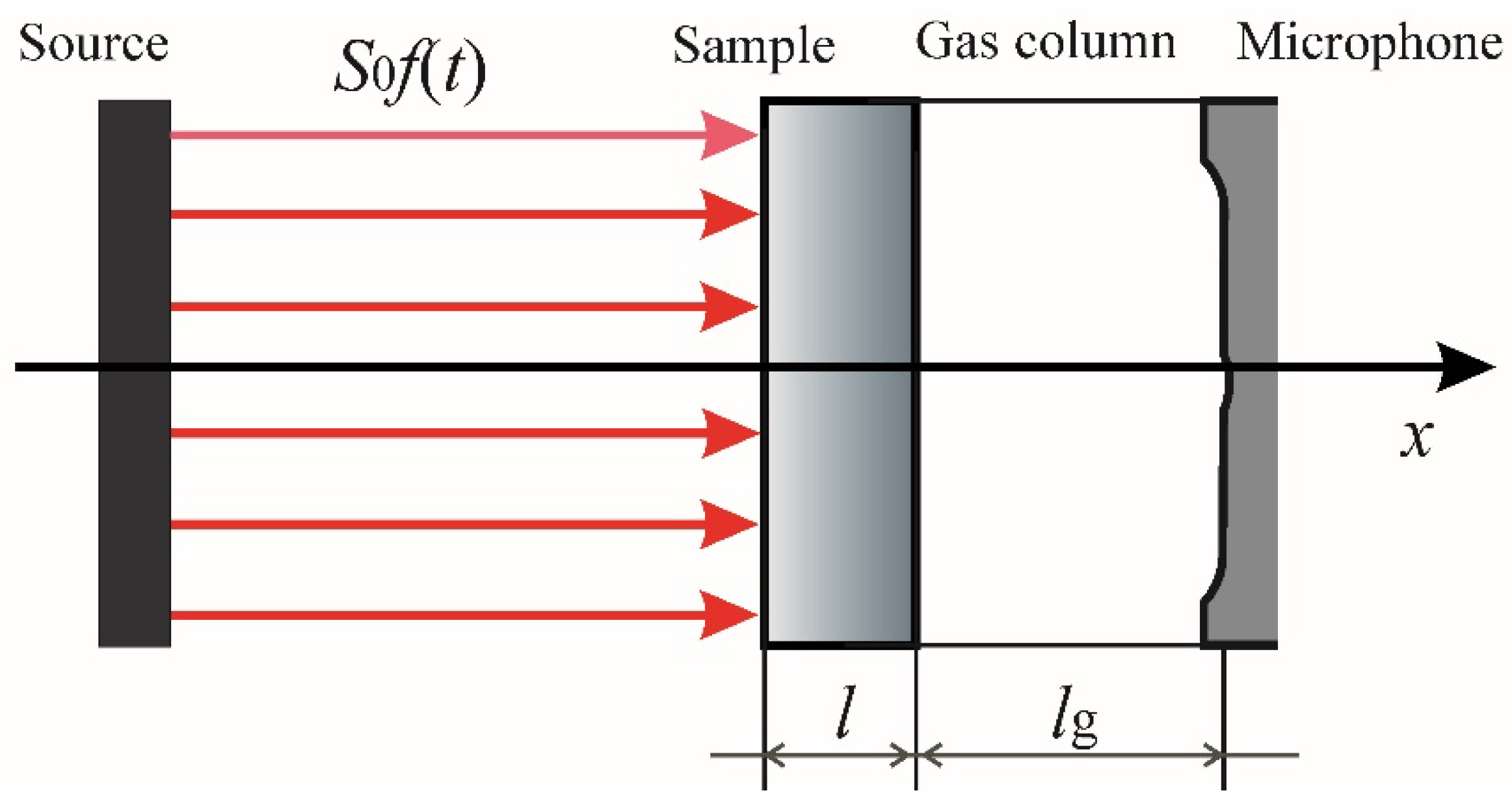
We observe an optically opaque sample that is illuminated homogeneously over the entire surface Figure 1.
The sample is surrounded by air, and air conducts heat much more poorly than the sample [42,76]. We consider that the time dependence of the optical excitation can be described by δ -function for very short optical pulse:
f ( t ) = δ ( t ) = { 1 t = 0 0 t ≠ 0
and by Heaviside function for very long optical pulse:
f ( t ) = h ( t ) = { 1 t ≥ 0 0 t < 0
Therefore, for t < 0 , the system was in thermodynamic equilibrium with the environment at ambient temperature T 0 . When the sample is illuminated, the part of the excitation EM energy is absorbed and part of the absorbed energy is converted into heat on the surface of the sample (due to the fact that the sample is optically opaque). In other words, the excitation optical beam leads to the formation of an excitation heat flux on the illuminated surface of the sample, which follows the dynamics of the optical excitation due to very fast (infinitely fast) de-excitation-relaxation processes [76,77].
Inside the sample, a perturbation of the thermodynamic state occurs and heat flow and heat flux appear, which tend to bring the system into a new thermodynamic equilibrium with the environment [5]. Based on the theoretical model presented in the previous section, the propagation of optically generated heat through the sample can be described by the following system of partial differential equations:
S ( x , t ) = ( 1 − R ) η I 0 δ ( x ) f ( t ) = S 0 δ ( x ) f ( t )
Symbol δ ( x ) in Eq.9 signifies unity δ function:
δ ( x ) = { 1 x = 0 0 x ≠ 0
Inside the sample, a perturbation of the thermodynamic state occurs and heat flow and heat flux appear, which tend to bring the system into a new thermodynamic equilibrium with the environment [5]. Based on the theoretical model presented in the previous section, the propagation of optically generated heat through the sample can be described by the following system of partial differential equations:
∂ 2 ϑ ( x , t ) ∂ x 2 − 1 D υ ∂ υ ϑ ( x , t ) ∂ t υ = 0
q ( x , t ) = − k ∂ ϑ ( x , t ) ∂ x
where D υ = k / C p υ is fractional heat diffusivity.
We suppose zero initial conditions and inhomogeneous boundary conditions:
j ( x = 0 , t ) = S 0 f ( t )
j ( x = l , t ) = 0
The heat transfer is described in the 1d spatial dimension due to the fact that the heat source appears as a surface source in a homogeneously illuminated sample [42,76].
Based on Eqs.11-14, it can be seen that the entire problem is described by fractional linear integro-differential equations. Such equations, as well as integer linear integro-differential equations, can be solved using the Laplace transform [61,68,69,70,71,72,73,74,78].
By applying the Laplace transform to Eqs.11-14 [61,74], the above system of equations is reduced to a system of linear differential equations with complex coefficients
d 2 ϑ ¯ ( x ) d x 2 − σ ¯ 2 ϑ ¯ ( x ) = 0
q ¯ ( x ) = − 1 σ ¯ Z ¯ d ϑ ¯ ( x ) d x
with complex boundary conditions:
q ¯ ( x = 0 ) = S 0 F ( s )
q ¯ ( x = l ) = 0
where F ( s ) is Laplace transform of time-dependent function that describes evolution of optical excitation Eqs.8a-8b.
Parameters σ ¯ (complex coefficient of heat transfer) and Z ¯ (complex thermal impedance) are defined as:
σ ¯ = s υ D υ
Z ¯ = D υ k 1 s υ
By solving the above system of equations Eqs.15-16, with the boundary conditions Eqs.17-18, the spectral function of the profile of temperature variations in the sample is obtained, as well as surface temperature variations on the non-illuminated surface of the sample (sample/air boundaries):
ϑ ¯ ( x ) = S 0 Z ¯ c h ( σ ¯ ( l − x ) ) s h ( σ ¯ l ) F ( s )
ϑ ¯ ( l ) = S 0 Z ¯ 1 s h ( σ ¯ l ) F ( s )
If the local non-equilibrium is not taken into account and heat transfer is described by Eqs.1-3, the classical model of the spectral function of the PA signal is obtained, where only the thermal impedances and the complex propagation coefficient differ than parameters given by Eqs.19-20. In the classic model, these complex parameters are defined by the following expressions [26,42]:
σ ¯ c l a s s = s D
Z ¯ c l a s s = D k 1 s
Based on RG theory [1], and papers [8,27], pressure fluctuations in the gaseous environment of an optically heated sample, if the length of the gas column is much larger than the thermal diffusion length in the gas, depend on temperature variations at the sample/air:
p ¯ = p 0 T 0 D g l g 1 s ϑ ¯ ( l )
In Eq.25 the following symbols are introduced: p 0 and T 0 are normal pressure and temperature of ambient, D g is thermal diffusivity in air, and l g is air column length in PA cell Figure 1.
Substituting Eq.22 into Eq.25, the spectral function of pressure fluctuations in the gaseous environment of the sample is obtained:
p ¯ = S 0 p 0 T 0 D g l g 1 s Z ¯ 1 s h ( σ ¯ l ) F ( s )
The model given by Eq.26 can be obtained from Generalized Cattaneo Fractional Model GCEIII for thermal piston component of PA signal presented in paper [79] if inertial relaxations are neglected and if one find limit for optically opaque sample.
Taking into account that the microphone, which records pressure fluctuations, behaves as a differentiator of these fluctuations [32,80], the spectral function of the recorded PA signal is described by the expression:
S ¯ ( s ) = A S 0 p 0 T 0 D g l g s s Z ¯ 1 s h ( σ ¯ l ) F ( s )
where A signifies the gain of electrical signal recorded by microphone.
To calculate time dependent PA signal for thin samples we used the development function s h ( σ ¯ l ) / σ ¯ l in Taylor order [81]:
s h ( y ) y = 1 + y 2 3 ! + y 4 5 ! + ....
By substituting Eqs.28,19, and 20 in Eq.27, an approximate spectral function of the PA signal is obtained, which includes the local non-equilibrium in complex systems:
S ¯ ( s ) = K a a 1 s υ − 0.5 1 s υ + a F ( s )
where:
K = A S 0 p 0 T 0 D g k l g
a = 6 D υ l 2
In order to compare our model with the classical model, we first calculated the spectral function of the PA signal based on the classical theory of heat conduction. Substituting Eqs.28, 23 and 24 in Eq.27 gives:
S ¯ c l a s s ( s ) = K a 1 a 1 1 s 1 s + a 1 F ( s )
where:
K 1 = K = A S 0 p 0 T 0 D g k l g
a 1 = a = 6 D l 2
In further analysis, time-domain PA signals normalized to the gain constant, K will be considered:
S ¯ n ( s ) = a a s υ − 0.5 1 s υ + a F ( s )
S ¯ n c l a s s ( s ) = a a s 1 s + a F ( s )
Considering that Laplace transforms of optical pulse given by Eq.8a is F ( s ) = 1 [82] we obtain spectral functions of PA signals for very short optical pulse predicted by fractional and classical theory:
S ¯ n ( s ) = a a s υ − 0.5 1 s υ + a
S ¯ n c l a s s ( s ) = a a s 1 s + a
Similarly, for very long optical pulse described by Eq.8b we have F ( s ) = 1 / s [82], and consequently, spectral functions of PA signals become (from Eqs.35-36)):
S ¯ n ( s ) = a a s υ + 0.5 1 s υ + a
S ¯ n c l a s s ( s ) = a a s s 1 s + a
Normalized PA signals in the time domain were obtained by finding the inverse Laplace transform of Eqs.37-40.
As it can be seen from Eqs.38, and 40, the spectral functions predicted by the classical model are described by the product of fractional operator and rational function 1 / ( s + a ) which inverse Laplace transforms are known (given in Table 1) [82].
As it is known, product in s-space is convolution in time. Inverse Laplace transform of spectral function given by Eq.38 is obtained by solution of convolution integral:
S n c l a s s ( t ) = a a ∫ 0 t 1 π τ e − a ( t − τ ) d τ = a a e − t 2 ∫ 0 t e ( a τ ) 2 d τ
Using the results of the paper [83], the above solution can be represented via the two-parameter Mittag-Leffler function [84,85,86]:
S n c l a s s ( t ) = a a t υ − 0.5 E υ , υ + 0.5 ( − a t υ )
where Mittage Leffler function is defined by [62,83,85]:
E α , β γ ( z ) = ∑ k = 1 ∞ ( γ ) k Γ ( α k + β ) z k k !
with Pochhammer symbol defined by:
( γ ) k = γ ( γ + 1 ) ( γ + 2 ) ... ( γ + k − 1 )
The inverse Laplace transform of the function given by Eq.40, (PA signal for long optical puls) is found by solving the following convolution integral:
S n c l a s s ( t ) = a a ∫ 0 t h ( t − τ ) τ υ − 0.5 E υ , υ + 0.5 ( − a τ υ ) d τ
Using the properties of the Mittage-Leffer function [62,83,84,85], the solution of the above integral is again a two-parameter Mittage-Leffler function:
S n c l a s s ( t ) = a a t υ + 0.5 E υ , υ + 1.5 ( − a t υ )
The spectral functions of the PA signal for the fractional model are given by Eqs.37 and 39, for very short optical pulse and for long optical pulse, respectively. As can be seen from these expressions, both functions are given as a product of functions described by irrational operators. To find their inverse Laplace transform, the general solution [86] given in Table 2 was used.
The spectral functions of the PA signal for the fractional model are given by Eqs.37 and 39, for very short optical pulse and for long optical pulse, respectively. As can be seen from these expressions, both functions are given as a product of functions described by irrational operators. To find their inverse Laplace transform, the general solution [86] given in Table 2 was used
By using Eq.37 and Table 2, the time-domain PA signal for very short optical pulse is given by:
S n ( t ) = a a t 2 υ − 1.5 E υ , 2 υ − 0.5 ( − a t υ )
In a similar way, the time domain PA signal generated by long optical pulse which spectral function is given by Eq.39 is obtained:
S n ( t ) = a a t 2 υ − 0.5 E υ , 2 υ + 0.5 ( − a t υ )

4. Discussion

By comparing the expressions describing the PA signal predicted by the fractional model Eqs.47-48 with the expressions describing the PA signal predicted by the classical model Eqs.42 and 46, for both types of optical impulse excitation, it is shown that the fractional models reduce to the classical for υ = 1 [80].
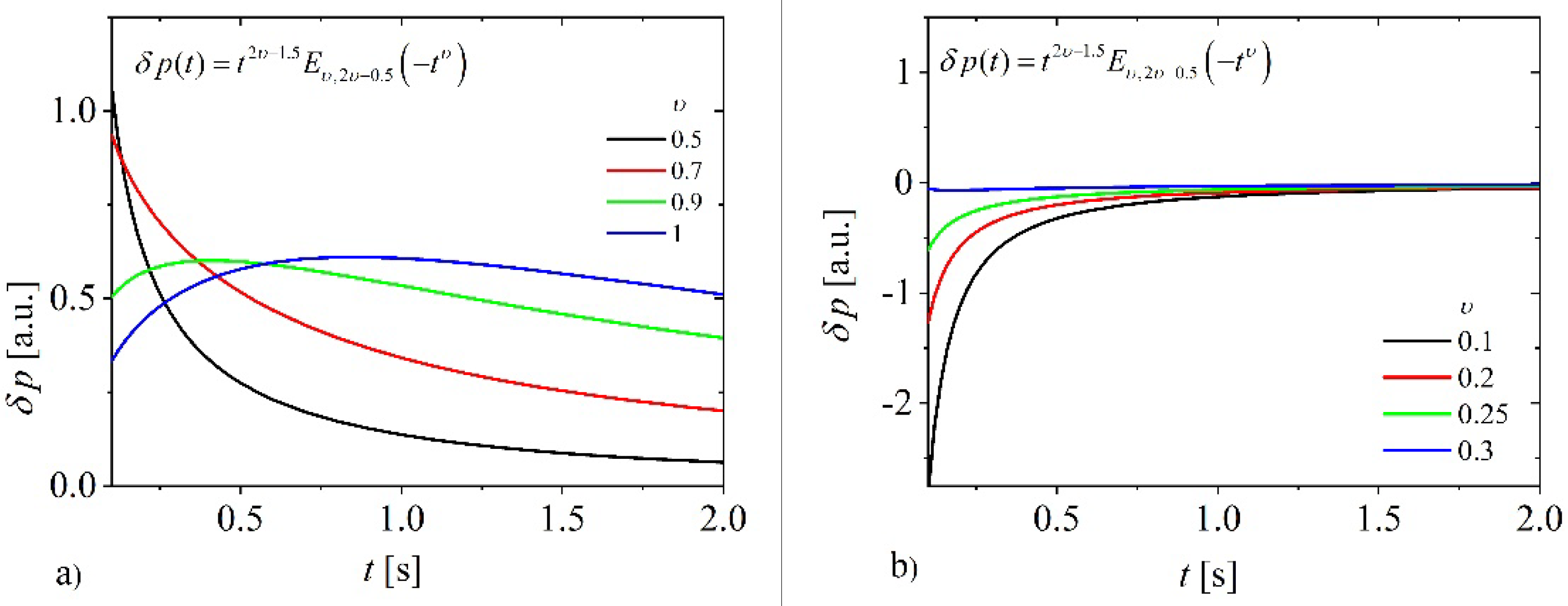
In order to examine the influence of the local non-equilibrium represented by the fractional exponent υ on the time-domain PA signal generated by a very short optical excitation, we illustrated the PA signals described by Eq.47 in Figure 2 for a = 1 and several values of the fractional exponent υ from the range (0,1).
b) υ < 0.3 .
It can be seen from Figure 2a that for t < 0.5 s and 0.3 < υ < 0.8 the fractional model predicts a completely different behavior of the PA signal (steep decline) than the classic diffusion model (
,blue line in Figure 2), while in long time domain both models, fractional for υ > 0.3 and classical predict decreasing signal. This result can be explained by the fact that Eq.5 with the Riemann-Liouville definition of the fractional derivative Eq.6, is not equivalent to the integral representation of the First Law of Thermodynamics Eq.4 for any initial conditions as discussed in [87]. Riemann-Liouville fractional derivatives are non-local operators that are non-invariant under time reversal and can be recognized as infinitesimal generators of a coarse grained microscopic time evolution in long-time limits [87,88,89]. This means that the derived model can be applied to the consideration of PA signals in the long time domain if υ > 0.3 . In this domain, the fractional model predicts smaller signal values and their rapid decline towards a steady value. The classical model predicts a decreasing function proportional to 1 / t , while fractional models predict a decreasing function proportional to 1 / t 1.5 − υ in long time domain. Physically, it means the following: if the fractional exponent υ decreases, the kinetic relaxations become slower leading to an increase in the diffusion length of heat and more rapid convergence to steady state after very short pulse excitation.
For υ < 0.3 , the derived model predicts completely non-physical behavior of PA signal (see Figure 2b). It seems that system can be optically cooled generating sub-pressure in air environment if there are structural elements that slowly relax. However, we think that the flow of heat in a medium in which there are very slow relaxations, i.e., large degrees of freedom of the structural elements, cannot be well physically described either short time domain or long time domain without taking into account non-zero initial conditions (see consideration of Fourier’s and Maxwell’s materials [39,40]). From point of view of material physics, it means that for υ < 0.3 there is phase transition of solids in some more fluid phase indicating different description of heat transfer. It means that domain of validity of derived model is limited to systems with fractional exponents υ > 0.3 .
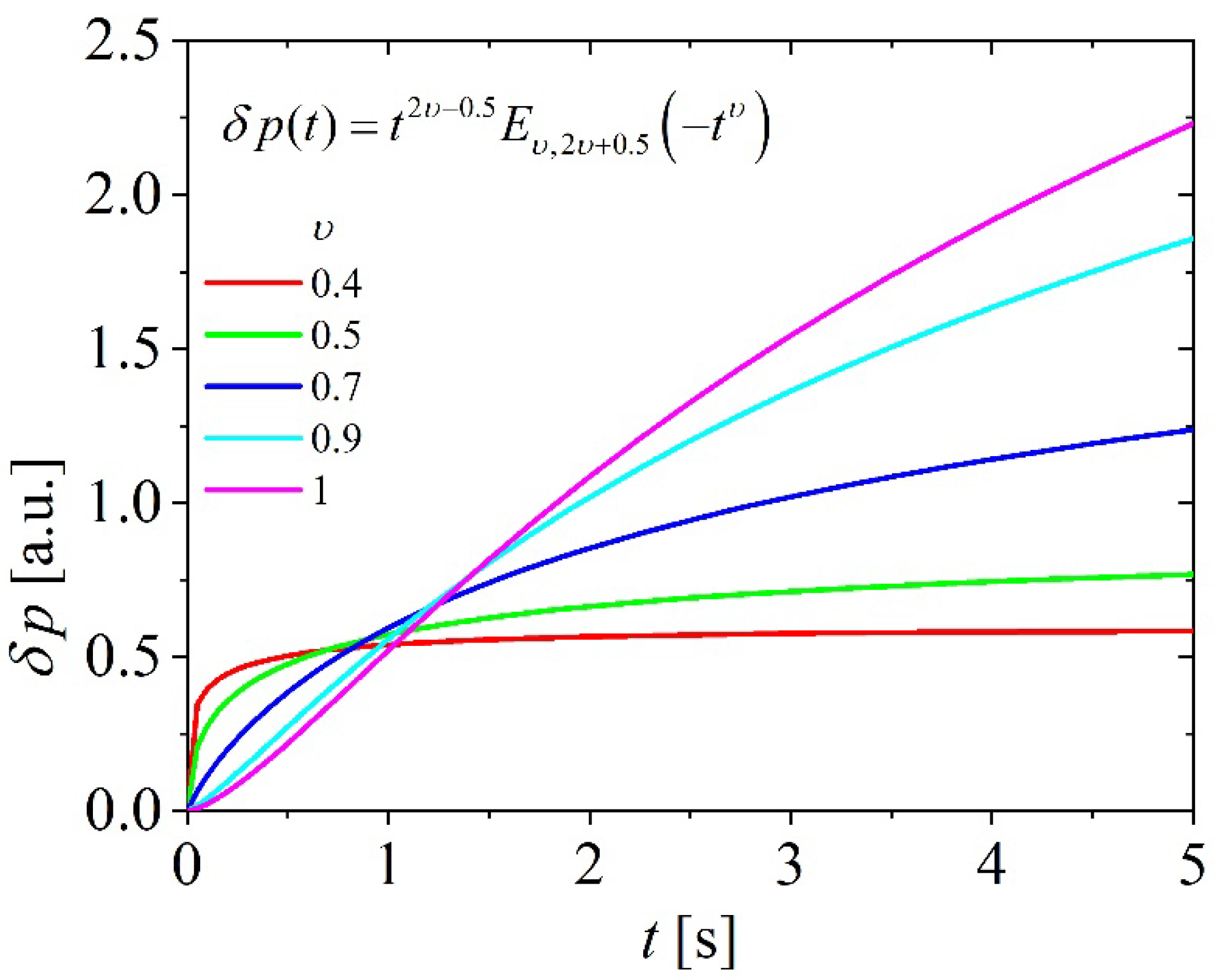
From Figure 3, it can be seen that the PA signal excited by a very long optical pulse in the long time domain grows more slowly than predicted by the classical model ( υ = 1 ). As υ decreases, the time constant of the PA signal increases. The smaller the fractional exponent υ the kinetic relaxation the slower, as discussed below Figure 2, and this has the effect of increasing the heat diffusion length as well as increasing the thermal impedance. As with very long excitation, low harmonics are dominant in the long time domain. The influence of thermal impedance on these harmonics is strong causing the smaller slope of the PA signal and its higher time constant.
and several values of the fractional exponent υ from the range ( 0 , 1 ) .
It is important to note that fractional as well as the classical model predict PA signal divergence in the long time domain Figure 3. We think that the cause of this behavior is related to the limitations of the thermal piston model [1,8,30]. Namely, this model, as discussed in [27,80], presupposes that the diffusion length of heat in the gas is much smaller than the dimensions of the cells. This assumption is completely justified for harmonics whose frequency is higher than 100 Hz [1], but for lower harmonics of very long pulse excitation, whose influence becomes expressed in the long-time domain, this assumption is not justified, and for a complete analysis of the PA signal, it is necessary to use a generalized model of transformation of variations temperature at the sample/gas boundary in pressure fluctuations in a PA cell of finite length [80].
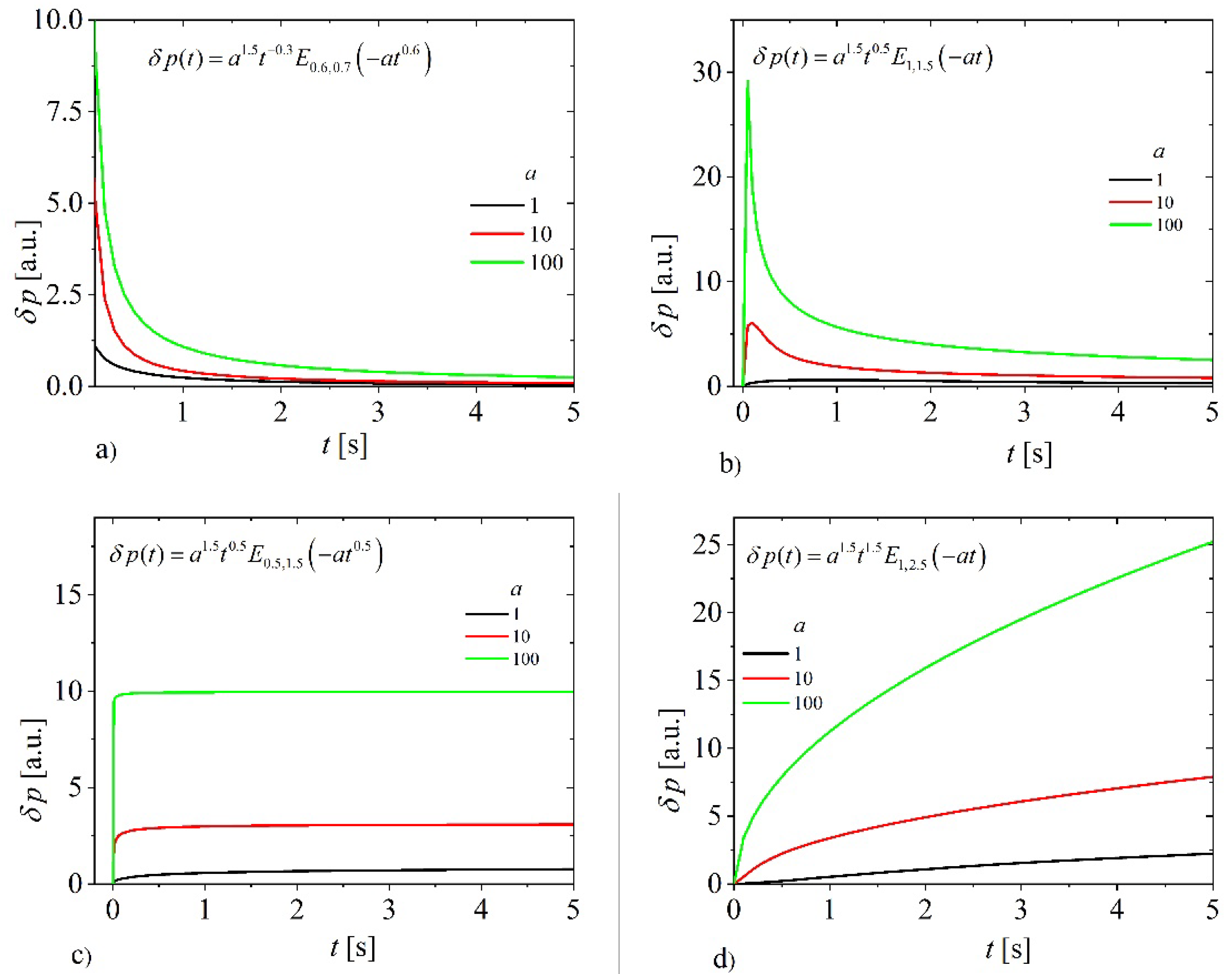
The influence of sample thickness on PA signals excited by very short optical pulse and very long optical pulse are illustrated in Figure 4.
, short pulse excitation; b) υ = 1 , short pulse excitation, c) υ = 0.5 , long pulse excitation; d) υ = 1 , long pulse excitation.
As it could be seen from Figure 4a,b, for a very short excitation pulse, decreasing the thickness of the sample affects the shift of the boundary between the short time and long time domains to the right opposite to the effect of decreasing the fractional exponent Figure 2. However, for long excitation pulse, the reduction of the sample thickness affects the shift of the boundary between the short time and long time domains towards a shorter time interval compared to the initial moment Figure 4c, independently on magnitude of fractional coefficient Figure 4d. The similar effect can be observed in Figure 3 if the fractional exponent decreases.
For both type of excitation, the sample the thinner (higher parameter a) the PA signal the higher in each moment. Besides, the signal pattern is similar for each thickness and follows the excitation shape.

5. Conclusion

In the paper, a generalized theoretical description of optically excited surface temperature variations in samples with a complex internal structure is performed, taking into account the local non-equilibrium of subsystems with large kinetic degrees of freedom, which are expected to exist in such complex samples. In that case, the local non-equilibrium is taken into account through the fractional exponent and fractional thermal diffusivity.
It is shown that the obtained theoretical description can coincide with the one obtained in the framework of statistical physics, which is based on the consideration of anomalous diffusion effects, i.e., the deviation of the mean sqare displacement of heat carriers from the linear law. Using a generalized description of heat conduction, a fractional model of the spectral function of surface temperature variations and pressure fluctuations in the gaseous environment of the optically excited sample was derived. Derived expressions are validated by comparison with classical model and previous fractional models for harmonical excitation.
Based on the fractional model of the spectral function of pressure fluctuations, a time-domain PA signal was derived for very short and very long pulse excitation. Comparing with the classical model, it was shown that the derived model reduces to the classical one when the fractional exponent is equal to unity.
Analysis of the PA signal for very short optical excitation showed that the domain of validity of derived fractional model is limited to υ > 0.3 and long-time domain. For such excitations, fractional models predict a smaller time constant of the signal than the classic one due to the influence of local non-equilibrium on the increase of the thermal diffusion length of the sample with a complex internal structure.
The analysis of the PA signal for very long optical excitation pointed out the shortcomings of the classic heat piston model, which is widely used in frequency photoacoustics. For pulsed excitations, low harmonics of time-dependent temperature variations at the sample/air interface, whose diffusion length is greater than the cell dimensions, must be taken into account. However, in the long-time limit, it can be clearly observed that the local non-equilibrium affects the higher time constant of the PA signal, which is related to the subdiffusion nature of heat propagation through the sample with a complex internal structure.
The sample thickness influences to magnitude of PA signal. The sample the thinner the signal the larger.
Our results show that time-domain photoacoustic could be applied to the estimation of the rate of non-equilibrium relaxations in complex systems but it request further development of the model of PA signal in time domain as well as fractional model of heat conduction.

Author Contributions

Conceptualization, S.G.; methodology, S.G.; software, A.DJ.; validation, S.G, A. DJ., B.K. K.DJ. and D.C.; formal analysis, S.G, A. DJ., B.K. K.DJ. and D.C.; investigation, S.G, A. DJ., B.K. K.DJ. and D.C.; resources, S.G, A. DJ., B.K. K.DJ. and D.C.; data curation, D.C; writing—original draft preparation, S.G; writing—review and editing, S.G, K.DJ. and D.C.; visualization, A.DJ., K.DJ.; supervision, S.G., K.DJ.; project administration, D.C; funding acquisition, D.C All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The authors are grateful to the Ministry of Science, Technological Development and Innovations of the Republic of Serbia (Contract No. 451-03-47/2024-01/200017) for the financial support.

Conflicts of Interest

The authors declare no conflicts of interest

References

  1. Rosencwaig, A.; Gersho, A. Theory of the photoacoustic effect with solids. J. Appl. Phys. 1976, 47(1), 64-69. [CrossRef]
  2. Tam, A.C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 1986, 58(2), 381-431. [CrossRef]
  3. Park H.K.; Grigoropoulos C.P.; Tam A.C. Optical measurements of thermal diffusivity of a material. Int. J. Thermophys. 1995, 16(4), 973-995. [CrossRef]
  4. Vargas, H.; Miranda, L.C.M. Photoacoustic and related photothermal techniques. Phys. Rep. 1988, 161(2), 43-101. [CrossRef]
  5. Bialkowski, S. Photothermal Spectroscopy Methods for Chemical Analysis, John Wiley, New York, 1996. ISBN: 978-1-119-27907-5.
  6. Sarode, A.P.; Mahajan, O.H. Theoretical Aspects of Photoacoustic Effect with Solids: A Review. IJSART 2018, 4(2), 1237-1242. [CrossRef]
  7. Isaiev, M.; Mussabek, G.; Lishchuk, P.; Dubyk, K.; Zhylkybayeva, N.; Yar-Mukhamedova G.; Lacroix, D.; Lysenko, V. Application of the Photoacoustic Approach in the Characterization of Nanostructured Materials. Nanomaterials 2022, 12(4), 708. [CrossRef]
  8. Mandelis A.; Royce B.S.H. Time-domain photoacoustic spectroscopy of solids. J. Appl. Phys. 1979, 50(6), 4330-4338. [CrossRef]
  9. Mandelis, A.; Hess, P. Semiconductors and Electronic Materials. SPIE Opt.Eng.Press: Belingham, Washington, 2000. ISBN0819435066.
  10. Markushev, D.D.; Rabasović, M.D.; Todorović, D.M.; Galović, S.; Bialkowski, S.E. Photoacoustic signal and noise analysis for Si thin plate: Signal correction in frequency domain. Rev. Sci. Instrum. 2015, 86(3), 035110. [CrossRef]
  11. Astrath, N.G.C.; Astrath, F.B.G.; Shen, J.; Lei, C.; Zhou, J.; Sheng L.Z., Navessin, T.; Baesso, M.L.; Bento, A.C. An open-photoacoustic-cell method for thermal characterization of a two-layer system. J. Appl. Phys. 2010, 107(4), 043514. [CrossRef]
  12. Olenka, L.; Nogueiran, E.S.; Medina, A.N.; Baesso, M.L.; Bento, A.C.; Muniz, E.C.; Rubira, A.F. Photoacoustic study of PET films and fibers dyed in supercritical CO2 reactor. Rev. Sci. Instrum. 2003, 74(1), 328-330. [CrossRef]
  13. Pichardo-Molina J.L.; Gutiérrez-Juárez G.; Huerta-Franco R.; Vargas-Luna M.; Cholico, P.; Alvarado-Gil, J.J. Open Photoacoustic Cell Technique as a Tool for Thermal and Thermo-Mechanical Characterization of Teeth and Their Restorative Materials. Int. J. Thermophys. 2005, 26(1), 243-253. [CrossRef]
  14. Djordjević, К.Lj.; Galović, S.P.; Ćojbašić, Ž.M.; Markushev, D.D.; Markushev, D.K.; Aleksić, S.M.; Pantić, D.S. Electronic characterization of plasma-thick n-type silicon using neural networks and photoacoustic response. Opt. Quantum Electron. 2022, 54(8), 485. [CrossRef]
  15. Djordjević, К.L.; Galović, S.P.; Popović, M.N.; Nešić, M.V.; Stanimirović, I.P.; Stanimirović, Z.I.; Markushev, D.D. Use neural network in photoacoustic measurement of thermoelastic properties of aluminum foil. Measurement 2022, 199, 111537. [CrossRef]
  16. Lishchuk, P.; Isaiev, M.; Osminkina, L.; Burbelo, R.; Nychyporuk, T.; Timoshenko, V. Photoacoustic characterization of nanowire arrays formed by metal-assisted chemical etching of crystalline silicon substrates with different doping level. Physica E Low Dimens. Syst. Nanostruct. 2019, 107, 131-136. [CrossRef]
  17. Lishchuk, P.; Andrusenko, D.; Isaiev, M.; Lysenko, V.; Burbelo, R. Investigation of Thermal Transport Properties of Porous Silicon by Photoacoustic Technique. Int. J. Thermophys. 2015, 36(9), 2428-2433. [CrossRef]
  18. Dubyk, K.; Nychyporuk, T.; Lysenko, V.; Termentzidis, K.; Castanet, G.; Lemoine, F.; Lacroix, D.; Isaiev, M. Thermal properties study of silicon nanostructures by photoacoustic techniques. J. Appl. Phys. 2020, 127(22), 225101. https://hal.science/hal-03418227v2.
  19. Dubyk, K.; Borisova, T.; Paliienko, K.; Krisanova, N.; Isaiev, M.; Alekseev, S.; Skryshevsky, V.; Lysenko, V.; Geloen, A. Bio-distribution of Carbon Nanoparticles Studied by Photoacoustic Measurements. Nanoscale Res. Lett. 2022, 17(1), 127. [CrossRef]
  20. Wang, X.; Pang, Y.; Ku, G.; Xie, X.; Stoica, G.; Wang, L.V. Noninvasive laser-induced photoacoustic tomography for structural and functional in vivo imaging of the brain. Nat. Biotechnol. 2003, 21(7), 803-806. [CrossRef]
  21. Li, C.; Wang, L.V. Photoacoustic tomography and sensing in biomedicine. Phys. Med. Biol. 2009, 54(19), 59-97. [CrossRef]
  22. Somer, A.; Camilotti, F.; Costa, G.F.; Bonardi, C.; Novatski, A.; Andrade, A.V.C.; Kozlowski, V.A.; Cruz, G.K. The thermoelastic bending and thermal diffusion processes influence on photoacoustic signal generation using open photoacoustic cell technique. J. Appl. Phys. 2013, 114(6), 063503. [CrossRef]
  23. Somer, A.; Galovic, S.; Lenzi, E.K.; Novatski, A.; Djordjevic, K. Temperature profile and thermal piston component of photoacoustic response calculated by the fractional dual-phase-lag heat conduction theory, Int. J. Heat Mass Transf. 2023, 203, 123801. [CrossRef]
  24. Somer, A.; Popovic, M.N.; Da Cruz G.K.; Novatski, A.; Lenzi, E.K.; Galovic, S.P. Anomalous thermal diffusion in two-layer system: The temperature profile and photoacoustic signal for rear light incidence. Int. J. Therm. Sci. 2022, 179, 107661. [CrossRef]
  25. Pichardo-Molina, J.L.; Alvarado-Gil, J.J. Heat diffusion and thermolastic vibration influence on the signal of an open photoacoustic cell for two layer systems. J. Appl. Phys. 2004, 95(11), 6450-6456. [CrossRef]
  26. Šoškić, Z.; Ćirić-Kostić, S.; Galović, S. An extension to the methodology for characterization of thermal properties of thin solid samples by photoacoustic techniques. Int. J. Therm. Sci. 2016, 109, 217-230. [CrossRef]
  27. Bein, B.; Pelzl, J. Theory of signal generation in a photoacoustic cell. J. Phys. Colloq. 1983, 44, 6-27. https://hal.science/jpa-00223163.
  28. Galović, S.; Kostoski, D. Photothermal wave propagation in media with thermal memory, J. Appl. Phys. 2003, 93(5), 3063-3070. [CrossRef]
  29. Hu, H.; Wang, X.; Xu, X. Generalized theory of the photoacoustic effect in a multilayer material. J. Appl. Phys. 1999, 86(7), 3953-3958. [CrossRef]
  30. Domanowska, A.; Bukowski, R.J. Theoretical Analysis of Pulsed Photoacoustic Effect in Solids. Int. J. Thermophys. 2009, 30(5), 1536-1556. [CrossRef]
  31. Bonno, B.; Zeninari, V.; Joly, L.; Parvitte, B. Study of a Thermophysical System with Two Time Constants Using an Open Photoacoustic Cell. Int. J. Thermophys. 2011, 32(3), 630-640. [CrossRef]
  32. Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids. Oxford University Press: Oxford, UK, 1959. ISBN 0 19 8533 68 3.
  33. Sobolev, S.L. Local non-equilibrium transport models. Physics-Uspekhi 1997, 167(10), 1095-1106. [CrossRef]
  34. Sobolev, S.L.; Dai, W. Heat Transport on Ultrashort Time and Space Scales in Nanosized Systems: Diffusive or Wave-like? Materials 2022, 15(12), 4287. [CrossRef]
  35. Garden, J.L. Macroscopic non-equilibrium thermodynamics in dynamic calorimetry. Thermochim. Acta 2007, 452(2), 85–105. [CrossRef]
  36. Garden, J.L., Richard, J., Saruyama, Y. Entropy production in TMDSC J. Therm. Anal. Calorim 2008, 94(2), 585-590. https://hal.science/hal-00311748.
  37. Birge, N.O. Specific-heat spectroscopy of glycerol and propylene glycol near the glass transition. Phys. Rev. B 1986, 34(3), 1631–1642. [CrossRef]
  38. Birge, N.O.; Nagel, S.R. Specific-heat spectroscopy of the glass transition. Phys. Rev. Lett.1985, 54,2674–2677. [CrossRef]
  39. Novikov, A.; Kolpashikov, V.L.; Shnipp, A.I. Reophysics and Thermophysics of Nonequliubrium Systems (Minsk, Russia, 1991), 58.
  40. Novikov, I.A. Harmonic thermal waves in materials with thermal memory. J. Appl. Phys. 1997, 81(3), 1067–1072. [CrossRef]
  41. Tzou, D.Y. Macro-to-Microscale Heat Transfer: The Lagging Behavior. Washington DC, USA, Taylor and Francis; 1996, 323-332. https://lib.ugent.be/catalog/rug01:001873084.
  42. Djordjevic, K.Lj., Milicevic, D., Galovic, S.P., Suljovrujic, E., Jacimovski, S.K., Furundzic, D., Popovic, M. Photothermal Response of Polymeric Materials Including Complex Heat Capacity, Int. J. Thermophys., 43(5) (2022) 68. [CrossRef]
  43. Wunderlih, B. Thermal Analysis of Polymeric Materials. Springer: Berlin, Heidelberg, New York, 2005.
  44. Roetzel, W., Putra, N., Das S.K. Experiment and analysis for non-Fourier conduction in materials with non-homogeneous inner structure. Int. J. Therm. Sci 2003, 42(6), 541-552. [CrossRef]
  45. Dixon, P.K. Specific-heat spectroscopy and dielectric susceptibility measurements of salol at the glass transition. Phys. Rev. B 1990, 42(13), 8179-8186. [CrossRef]
  46. Scherrenberg, R., Mathot, V., Steeman, P. The Applicability of TMDSC to Polymeric Systems General theoretical description based on the full heat capacity formulation J. Therm. Anal. Calorim 1998, 54(2), 477-499.
  47. Saiter, A., Couderc, H., Grenet, J. Characterisation of structural relaxation phenomena in polymeric materials from thermal analysis investigations. J. Therm. Anal. Calorim 2007,88(2),483-488. [CrossRef]
  48. Saruyama, Y. AC calorimetry at the first order phase transition point. J. Therm. Anal. 1992,38(8),1827-1833. [CrossRef]
  49. Liu, K.C., Wang, Y., Chen, Y. Investigation of the bioheat transfer with dual phase lag effect. Int. J. Therm. Sci. 2012,58,29-35. [CrossRef]
  50. Jou, D., Casas-Vazquez, J., Lebon, G. Extended irreversible thermodynamics. Rep. Prog. Phys. 1988, 51, 1105-1179. [CrossRef]
  51. Davies, R.O. The Macroscopic Theory of Irreversibility. Rep. Prog. Phys. 1956, 19(1), 326-367.
  52. De Groot, S.R., Mazur, P. Non-Equilibrium Thermodynamics. North-Holland publishing company: Amsterdam, Holland,1962. ISBN0486153509.
  53. Prigogine I. Introduction to thermodynamics of irreversible processes. John Wiley and Sons: New York, USA, 1968. ISBN0470699280.
  54. Mitra, K., Kumar, S., Vedavarez, A., Moallemi, M.K. Experimental Evidence of Hyperbolic Heat Conduction in Processed Meat. J. Heat Transfer, 1995,117(3), 568-573 . [CrossRef]
  55. Metzler, R., Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339(1),1-77. [CrossRef]
  56. Korabel, N., Klages, R., Chechkin, A.V., Sokolov, I.M., Gonchar, V.Yu. Fractal properties of anomalous diffusion in intermittent maps, Phys. Rev. E, 2007, 75, 036213. [CrossRef]
  57. Bouchaud, J.-P., Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications, Phys. Rep. 1990, 195(4-5), 127-293. [CrossRef]
  58. Liang, Y., Wang, W., Metzler, R. Anomalous diffusion, non-Gaussianity, and nonergodicity for subordinated fractional Brownian motion with a drift, arXiv:2302.04872v1 [cond-mat.stat-mech] 9 Feb 2023.
  59. Metzler, R.; Rajyaguru, A.; Berkowitz, B. Modelling anomalous diffusion in semi-infinite disordered systems and porous media, New J. Phys. 2022, 24, 123004. [CrossRef]
  60. Sposini, V.; Krapf, D.; Marinari, E.; Sunyer, R.; Ritort, F.; Taheri, F.; Selhuber-Unkel, C.; Benelli, R.; Weiss, M.; Metzler, R.; Oshanin, G. Towards a robust criterion of anomalous diffusion. Commun. Phys. 2022, 5(1), 305. ). [CrossRef]
  61. Comptey, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A: Math. Gen. 1997, 30, 7277–7289. [CrossRef]
  62. Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications, Springer-Verlag Berlin Heidelberg 2014. ISBN 978-3-662-43930-2 (eBook). [CrossRef]
  63. Kiryakova, V.S. Generalized Fractional Calculus and Applications. Longman Scientific and Technical: Harlow, UK, 1994.
  64. Podlubny, I. Fractional differential equations. Academic Press: San Diego, USA, 1999.
  65. Fernández, A.D.; Charchar, P.; Cherstvy, A.G.; Metzler R.; Finnis, M.W. The diffusion of doxorubicin drug molecules in silica nanoslits is non-Gaussian, intermittent and anticorrelated, Phys.Chem.Chem.Phys.,2020, 22, 27955.
  66. Tateishi, A.A.; Lenzi, E.K.; Da Silva, L.R.; Ribeiro, H.V.; Picoli, S.; Mendes, R.S. Different diffusive regimes, generalized Langevin and diffusion equations. Phys. Rev. E 2012, 85(1), 011147. [CrossRef]
  67. Dzielinski, A.; Sierociuk, D.; Sarwas, G. Some applications of fractional order calculus. Bull. Polish Acad. Sci. Tech. Sci. 2010, 58, 583–592. [CrossRef]
  68. Lenzi, E.K.; Somer, A.; Zola, R.S.; Da Silva, R.S.; Lenzi, M.K.A. Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids 2003, 8, 34. [CrossRef]
  69. Caputo, M.; Fabrizio, M. Admissible frequency domain response functions of dielectrics. Math. Method Appl. Sci. 2014, 38, 930–936. [CrossRef]
  70. Saxena, R.K.; Saxena, R.; Kalla, S.L. Solution of space time fractional schroedinger equation occurring in quantum mechanics, Fract. Calc. Appl. 2010, 13, 190–201. http://hdl.handle.net/10525/1648.
  71. Del Castillo Negrete, D.; Carreras, B.A.; Lynch, V.E. Fractional diffusion in plasma turbulence. Phys. Plasmas 2004, 11, 3854–3864. [CrossRef]
  72. Magin, R.L. Fractional Calculus in Bioengineering. Begell House Publishers: New York, USA, 2006.
  73. Caputo, M. Diffusion of fluids in porous media with memory. Geothermics 1999, 28, 113–130. [CrossRef]
  74. Čukić, M.; Galovic, S. Mathematical modeling of anomalous diffusive behavior in transdermal drug-delivery including time-delayed flux concept. Chaos, Solitons & Fractals 2023, 172, 113584. [CrossRef]
  75. Bouchaud, J.-P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. 1990, 195(4-5), 127–293. [CrossRef]
  76. Galović, S.; Šoškić, Z.; Popović, M.; Čevizović, D.; Stojanović, Z. Theory of photoacoustic effect in media with thermal memory. J. Appl. Phys. 2014, 116, 024901. [CrossRef]
  77. Sablikov, V.A., Sandomirskii, V.B. The Photoacoustic effect in semiconductors. Phys. Stat. Solidi (a), 1983, 120(2); 471-480. [CrossRef]
  78. Polyanin, A.D., Sorokin, V.G., Zhurov, A.I. Delay ordinary and partial differential equation, CRC Press, Boca Raton, 2024. [CrossRef]
  79. Somer, A., Novatski, A., Lenzi, E.K. Theoretical predictions for photoacoustic signal: Fractionary thermal diffusion with modulated light absorption source, Eur. Phys. J. Plus, 134(12), 593, (2019). [CrossRef]
  80. Galovic, S.P.; Djordjevic, K.L.; Nesic, M.V.; Popovic, M.N.; Markushev, D.D.; Markushev, D.K.; Todorovic, D.M. Time-domain minimum-volume cell photoacoustic of thin semiconductor layer. I. Theory. J. Appl. Phys. 2023, 133. [CrossRef]
  81. Galovic, S.; Soskic, Z.; Popovic, M. Analysis of photothermal response of thin solid films by analogy with passive linear electric networks. Therm. Sci. 2009, 13(4), 129-142.
  82. Roberts, G. E.; Kaufman, H. Table of Laplace Transform, W. B. Saunders Company, Philadelphia and London, 1966.
  83. Saenko, V.V. Integral Representation of the Mittag-Leffler Function, Russian Mathematics, 2022, 66(4), 43–58. [CrossRef]
  84. Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler Functions and Their Applications. J. Appl. Math. 2011, 1–51. [CrossRef]
  85. Baumann, G. Sinc Based Inverse Laplace Transforms, Mittag-Leffler Functions and Their Approximation for Fractional Calculus. Fractal Fract. 2021, 5, 43. [CrossRef]
  86. Chen, Y.Q.; Petras, I.; Vinagre, B.M. A list of Laplace and inverse Laplace transforms related to fractional order calculus. [online] http://www.steveselectronics. com/petras/foc laplace.pdf, 2007.
  87. Hilfer, R. Fractional Diffusion Based on Riemann-Liouville Fractional Derivatives. J. Phys. Chem. B. 2000, 104(16), 3914–3917. [CrossRef]
  88. Abdon, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus, 2018, 133(4), 166. [CrossRef]
  89. Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of the fractional time-derivative operators in anomalous diffusion. Front. Phys. 2017, 5, 1-5. [CrossRef]
Preprints 106594 g001
Figure 1. Geometry of the problem.
Figure 1. Geometry of the problem.
Preprints 106594 g001
Preprints 106594 g002
Figure 2. Photoacoustic signal induced by very short optical pulse Eq.47, for a) υ > 0.3
Figure 2. Photoacoustic signal induced by very short optical pulse Eq.47, for a) υ > 0.3
Preprints 106594 g002
Preprints 106594 g003
Figure 3. The PA signals excited by very long optical pulse described by Eq.48 for a = 1
Figure 3. The PA signals excited by very long optical pulse described by Eq.48 for a = 1
Preprints 106594 g003
Preprints 106594 g004
Figure 4. The dependence of photoacoustic signal on sample thickness a) υ = 0.6
Figure 4. The dependence of photoacoustic signal on sample thickness a) υ = 0.6
Preprints 106594 g004
Table 1. Table of inverse Laplace transform of some fractional-ordered and rational functions.
Table 1. Table of inverse Laplace transform of some fractional-ordered and rational functions.
Laplace transform G(s) Inverse Laplace transform L-1 [G(s)]
1 s 1 π t
1 s s 2 t π
1 s + a e − a t
Table 2. Inverse Laplace transform of some irrational-order functions [86].
Table 2. Inverse Laplace transform of some irrational-order functions [86].
Laplace transform F(s) Inverse Laplace transform L-1 [F(s)]
s α γ − β ( s α + a ) γ t β − 1 E α , β γ ( − a t α )
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated