Prerpints.org logo
Preprint
Article

Port Accessibility Depends on Cascading Interactions between Fleets, Policies, Infrastructure, and Hydrodynamics

Altmetrics

Downloads

85

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 May 2024

Posted:

16 May 2024

You are already at the latest version

Alerts
Abstract
Reducing waiting times is crucial for ports to be efficient and competitive. Important causes of waiting times are cascading interactions between realistic hydrodynamics, accessibility policies, vessel-priority rules, and detailed berth availability. The main challenges are determining the cause of waiting and finding rational solutions to reduce waiting time. In this study, we focus on the role of the design depth of a channel on the waiting times. We quantify the performance of channel depth for a representative fleet rather than the common approach of a single normative design vessel. It relies on a mesoscale agent-based discrete-event model that can take processed Automatic Identification System and hydrodynamic data as its main input. The presented method’s validity is assessed by hindcasting one year of observed anchorage area laytimes for a liquid bulk terminal in the Port of Rotterdam. The hindcast demonstrates that the method predicts the causes of 73.4% of the non-excessive laytimes of vessels, thereby correctly modelling 60.7% of the vessels-of-call. Following a recent deepening of the access channel, cascading waiting times due to tidal restrictions were found to be limited. Nonetheless, the importance of our approach is demonstrated by testing alternative maintained bed level designs, revealing the method’s potential to support rational decision-making in coastal zones.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Access channels and waterways form the gateway to seaports and simultaneously an important element of coasts and estuaries [1]. An ‘accessible’ port assures the safe and efficient transit of the calling (sea-going) vessels through the channel. Downtime of the access channel can cause significant waiting times for vessels, which decreases the port’s efficiency. Tide-related accessibility restrictions are a common cause of downtime, especially for the largest vessels, and therefore considered important for port authorities from a nautical-logistical perspective. A port can moreover be congested, meaning that the capacity of its infrastructure is overloaded. Port congestion and downtime are interconnected, which can lead to cascading effects that increase waiting times and thereby further decrease the port’s efficiency [2].
So far such cascading effects have rarely been considered in port design, as common guidelines typically focus on (the largest) design vessels only [3]. The most common approach to quantify port accessibility is the method described in the Harbour Approach Channels Design Guideline [4]. It quantifies accessibility as the percentage of accessible tides for the deepest-draughted vessel(s) in the calling fleet (see also [5,6]). Although realistic hydrodynamics and detailed accessibility policies form the basis of this method, it ignores nautical traffic and, consequently, waiting times due to congestion and cascading effects.
Beyond the approach suggested by PIANC [4], various simulation approaches are available that do resolve waiting times, at varying scales, ranging from micro- to macroscopic approaches [7]. Most models in the literature are microscopic, meaning they resolve detailed manoeuvres including vessel-vessel and vessel-infrastructure interactions. They tend to focus on waiting times caused by single components of the port network/infrastructure. Examples include heuristic algorithms that minimize congestion-related waiting times at various types of terminals (i.e., [8,9,10]), and on the waterway (i.e., [11,12]). Furthermore, analytical agent-based models are available that describe vessel motions and behaviour in waterways (i.e., [13,14,15,16,17]), and discrete-event models that focus on land-based terminal operations (i.e., [18,19,20,21,22]).
Although successful in estimating the delays of individual vessels at specific components of the port, microscopic models are typically unable to cover the entire port network or the full extent of the traffic, due to computational constraints. Furthermore, they rarely include (realistic) hydrodynamics, detailed accessibility policies, specific berth layouts, and berth allocation policies.
In contrast to the amount of microscopic models, only a few macroscopic shipping models are discussed in the literature. These models focus on traffic flows rather than the behaviour of individual vessels. Koldborg Jensen et al. [23] used a mathematical model to calculate the efficiency of a waterway, while Tasseda and Shoji [24] developed a framework to unravel the vessel traffic streams in Tokyo Bay. Queuing theory is another type of macroscopic model [25,26].
Macroscopic models, while good at scale, lack resolution to resolve the detailed causes of waiting times. Typically they also don’t include realistic hydrodynamics, detailed accessibility policies, and berth availability information.
Mesoscopic models aim for a compromise where the behaviour of large numbers of individual agents can be simulated but their behaviour is aggregated to the level of objectively distinguishable events (e.g., mooring, (un)loading, unmooring, anchoring). This allows for a realistic representation of important port processes at scale while keeping computation times at acceptable levels. One of the first mesoscopic simulation models for port operations was developed by Hansen [27] and later expanded by Park and Noh [28]. These models focused mainly on land-based terminal operations, typically ignoring hydrodynamic aspects like currents and tides. Similar models were presented by Kondratowicz [29], Hassan [30], Demirci [31], Howard et al. [32], Arango et al. [33], Ugurlu and Yükseky [34].
Mesoscopic simulation models with a more prominent focus on nautical traffic, schematize the wet infrastructure as a network of nodes and edges, over which vessels sail and interact. An early model by Clark et al. [35] studied the Suez Canal, excluding port operations. Some later case-specific nautical traffic models that did include port operations did not include tidal restrictions, such as the work presented by Van de Ruit et al. [36] who studied the Maasvlakte of the Port of Rotterdam (PoR), and Yeo et al. [37] who studied the North Harbor of the Port of Busan. Furthermore, the models of Fransen et al. [38] and Nikghadam [39] focused on waiting times related to the availability of tugs and pilots in the PoR, but these approaches did not include downtime related to hydrodynamic restrictions.
More complete nautical traffic models with a clear focus on congestion and downtime were designed by Groenveld [40], whose HarbourSim model did consider the interactions between calling vessels and the port’s infrastructure in detail, including terminals and (tidal) downtime. This model was applied to the Rio de la Plata in the work by Frima [41]. Moser et al. [42] created the similar HarborSym. Other comparable models were presented by Macquart [43], Rayo [44], Piccoli [45]. Tang et al. [46] developed a similar approach, albeit with a different process interaction-based approach. Furthermore, some case-specific nautical traffic models were constructed by Thiers and Janssens [47] for the Scheldt Estuary, by Almaz and Altiok [48] for the Delaware River, and by Scott et al. [49] for the Port of Geraldton. Last, various in-house discrete-event models are known to exist in practice, such as DPCM® [50] and SiFlow21 [51], that claim to include detailed port congestion and tidal downtime, but no detailed information on these models is available in the open literature.
The use of Automatic Identification System (AIS) data to assess waiting times in port and waterway systems is a relatively new trend. Franzkeit et al. [52] and Ma et al. [53] focused on vessel waiting times in anchorage areas, Martinicic et al. [54] analysed arrival and turnaround times of vessels in the Port of Piraeus, Jafari Kang et al. [55] studied congestion in the Port of Houston, and Steenari et al. [56] investigated the performance of berths in the Port of Brest. A standalone AIS data analysis, however, is typically insufficient to unravel the detailed causes of vessel waiting times. This is due to the complex dependencies that exist between vessels and port infrastructure that cannot be deduced in full from AIS data alone without additional data and/or simulations [57].
Although most of the above-mentioned mesoscale nautical traffic models are, in principle, able to resolve the cascading effects due to congestion and (tidal) downtime, none of the openly available models simultaneously accounts for (1) realistic hydrodynamics, (2) detailed accessibility policies, (3) realistic vessel properties, (4) cascading effects of vessel-priority rules, (5) detailed waterway and berth layouts and (6) concrete berth allocation policies. Also, none of the pre-mentioned studies provides a detailed decomposition of the causes for waiting times, let alone validates the predicted waiting times against actually observed vessel data. This paper adresses this gap by presenting a method that relies on a combination of data analysis and mesoscopic modelling.
We analyse one year of AIS data for a liquid bulk terminal in the 3rd Petroleumhaven (3rd PET) in the PoR. Based on these observations we quantify vessel arrivals, laytimes in the anchorage and at the terminals, and vessel departures. Furthermore, we determine sailing speeds, turning times, and the effect of tidal restrictions. We subsequently adapt and use the open-source mesoscopic nautical traffic model OpenTNSim [58,59] to reproduce the observed vessels’ behaviour through a hindcast study. The simulation allows us to analyse the effect of detailed hydrodynamics, Under Keel Clearance (UKC) regulations, reported vessel draughts, vessel-priority rules, waterway and berth layouts, and berth allocation policies. We compare the predicted laytimes in the anchorage area with those observed in the AIS data, and unravel which causes contributed to these laytimes, accounting for tidal restrictions, congestion of port infrastructure, and priority in berth allocation. The approach improves our understanding of port performance, which in turn enhances our capability to suggest improvements to port operations and infrastructure (component) design.
Section 2 describes the materials and methods used to set up and validate the nautical traffic model. Section 3 compares the model results to the AIS data and demonstrates the model’s potential through a brief study of alternative Maintained Bed Level (MBL) designs for the 3rd PET’s entrance channel. Section 4 and Section 5 provide a discussion and our conclusions respectively.

2. Materials and Methods

To decompose the waiting times for the liquid bulk terminal in the 3rd PET harbour in the PoR we apply a mesoscale simulation model to hindcast a period for which observed AIS data is available. The following information is required for the model set-up:
  • a geospatial graph of the port network, including:
    -
    schematizations of relevant port infrastructure,
    -
    governing UKC policies,
    -
    priority rules and berth allocation policies; and
  • the calling vessels in the form of agents, including:
    -
    dimensions (i.e., length, beam, and draught), and
    -
    followed trajectories to derive:
    *
    origin-destination information,
    *
    speeds, and
    *
    laytimes in various port areas; and
  • realistic hydrodynamics over the port network, including:
    -
    tidal elevations as a function of time and space, and
    -
    current velocities at critical locations.
The required information can be derived from available geospatial data, AIS data, and hydrodynamic data (see Figure 1).
SubSection 2.1 describes the case study. Section 2.2 describes the data sources. Section 2.3 describes processing steps applied to the AIS data (Figure 1-I). Section 2.4 describes the additional steps that are needed for simulation and validation (II). Section 2.5 describes the nautical traffic model that was applied (III).

2.1. Case Study: 3rd Petroleum Harbour

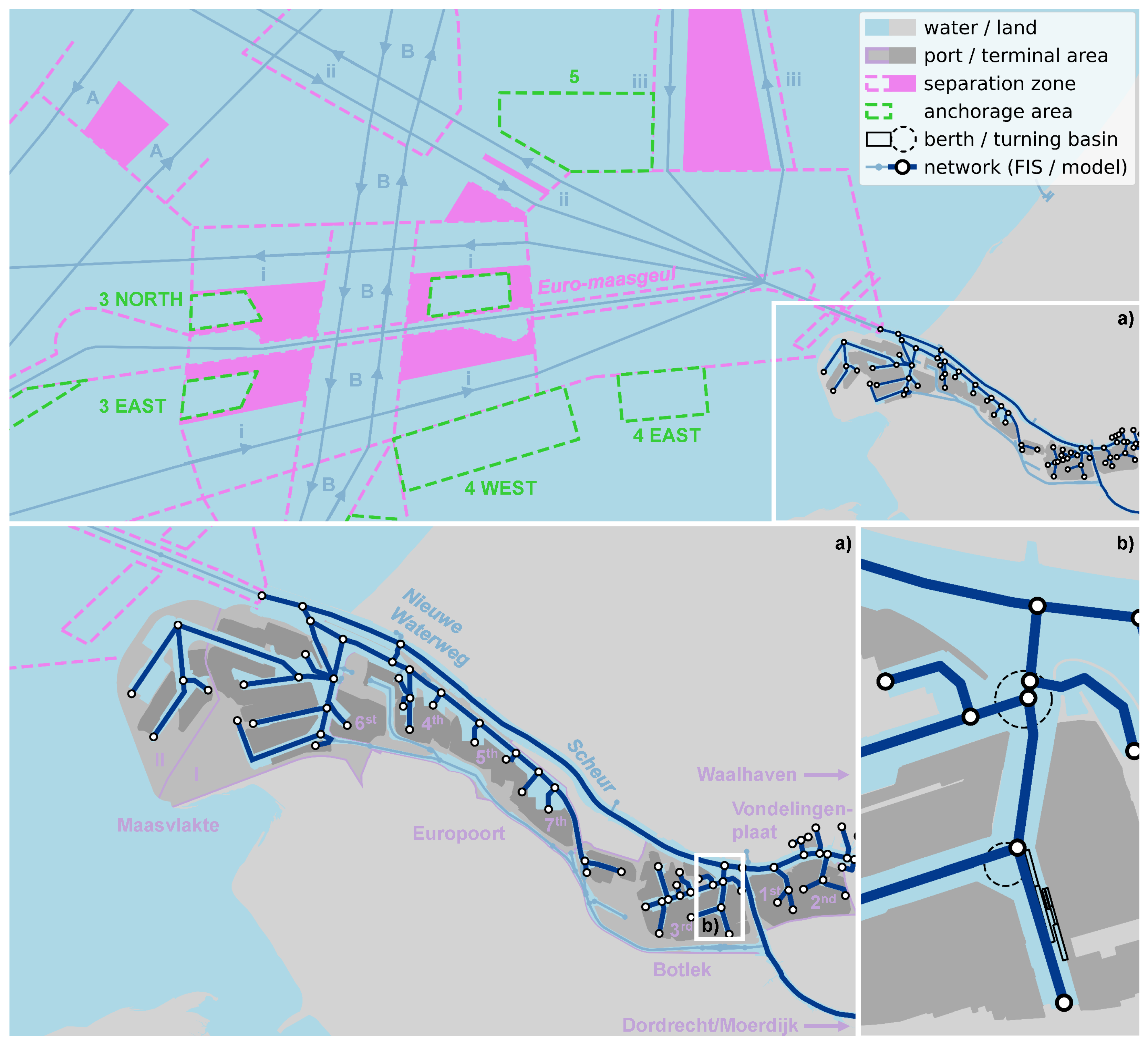
The PoR is the largest seaport in Europe and serves as a transfer location of various types of cargo (mainly containers and liquid bulk) to other modalities bound for other destinations in Northern and Central Europe. An overview of the nautical infrastructure of the PoR is given in Figure 2. Sea-going vessels arrive at the port’s Traffic Separation System (TSS) through which they sail to the port entrance, possibly visiting one of the anchorage areas. There are three routes to the port entrance. There is a west-east corridor (i), a north-south corridor (ii), and a north-west-north-east corridor (iii). The southern (northern) and western (eastern) lanes are dedicated to inbound (outbound) traffic, while the deepest-draughted vessels make use of the central access channel, called the Euro-Maasgeul, and its dedicated anchorage areas. There are two deep-sea routes (A and B) that cross the TSS from north(-east) to south(-west).
The 3rd PET is an important transfer hub within the petrochemical cluster of the PoR. Constructed in the 1960s as part of the Botlek expansion, the basin is located along the main waterway, the Nieuwe Waterweg and Scheur (hereafter jointly called Nieuwe Waterweg), 21.5 km inland. Various terminals are located in the basin, facilitating both sea-going and inland vessels. The Botlek Harbour is an important hub as it defines the MBL of the NWW. In 2018, the NWW, and Botlek Harbour have been deepened from 14.5 m to 16.2 m to facilitate partially loaded New Panamax and Suezmax-type vessels up to a draught of 15.0 m. This research focuses on one of the liquid bulk terminals in the 3rd PET that operates these vessels. It has various dedicated jetties and quays for deep-sea vessels, coasters, and barges, with varying MBL and lengths.
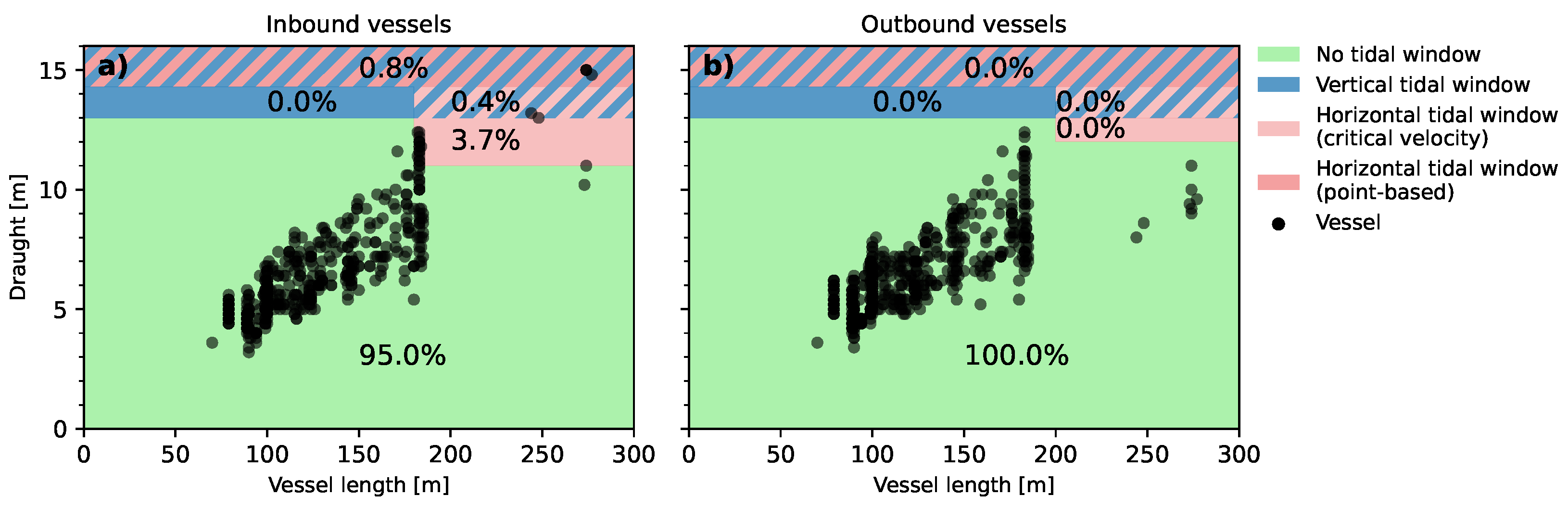
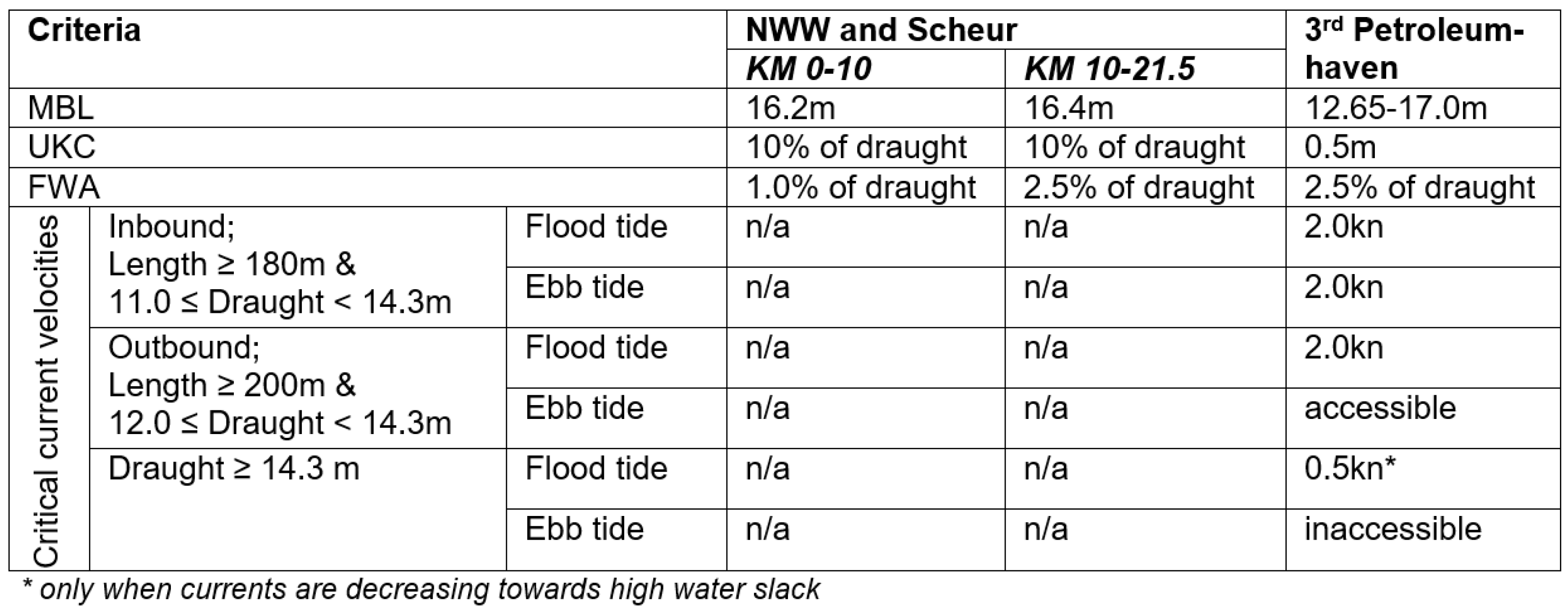
To enter the 3rd PET, vessels are prone to a tidal restriction policy, which is summarized in Table 1. During navigation over the NWW, a vessel is obliged to have an UKC of 10% of its draught, increased with a Fresh Water Allowance (FWA) of 1.0% of the draught up to halfway the waterway and 2.5% of the draught in the remaining part of the channel. 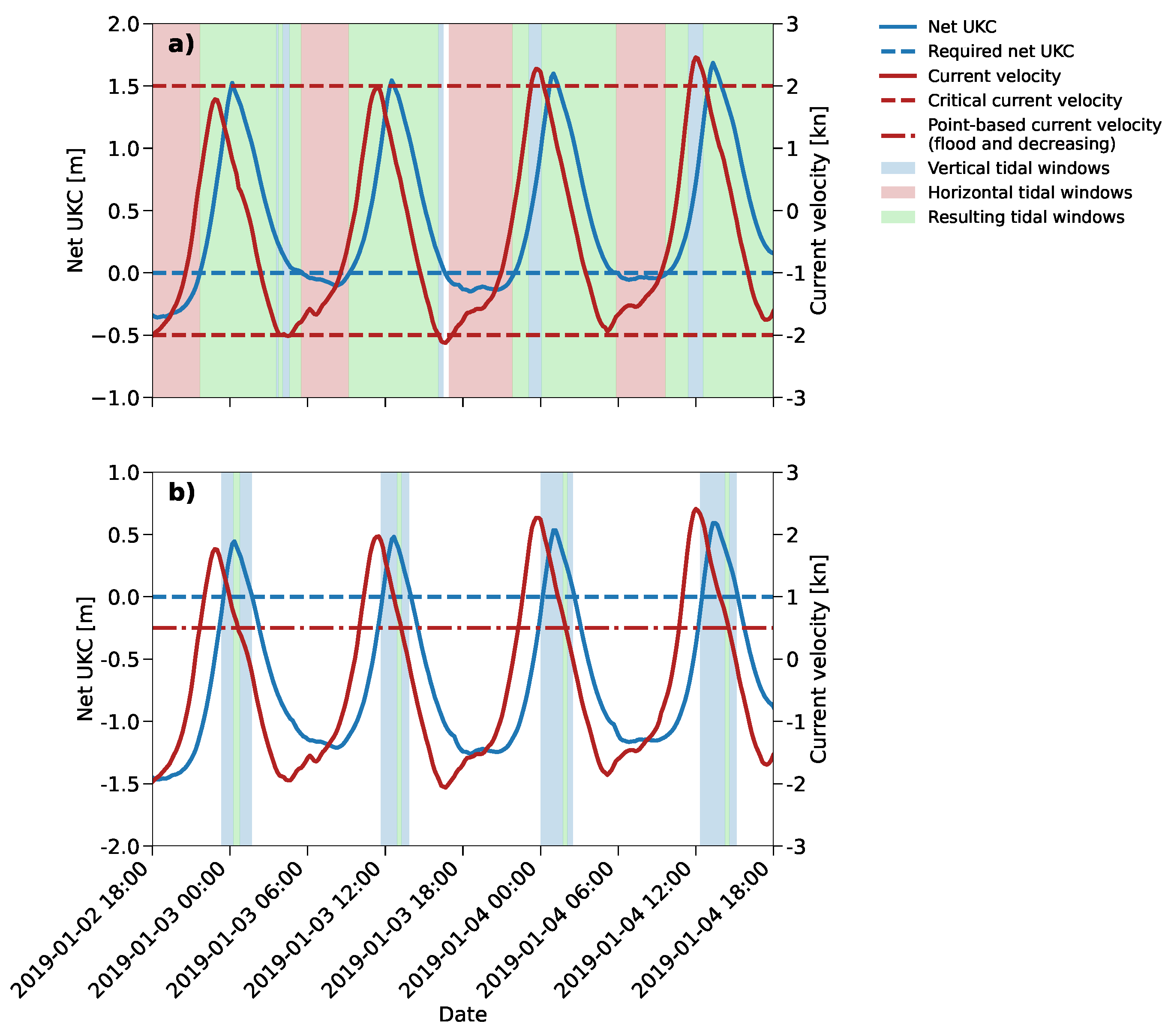The maintained bed level of the NWW is optimized for the deepest-drafted vessels [60], and varies from 16.2 m MBL in the first half to 16.4 m in the second half of the channel. Given this information, vessels with a draught of 13.0 m or more are prone to a vertical tidal window. Additionally, some vessels are prone to a horizontal tidal window when entering the 3rd PET. Vessels with a length equal to and greater than 180 m and a draught ranging from equal to and greater than 11.0 m (inbound) or 12.0 m (outbound) up to 14.3 m are in principle only allowed to enter or leave when the tidal currents are less than or equal to 2.0 kn. Outbound vessels, however, are exempt from this condition during ebb tide, which is fully accessible. In contrast, vessels with a draught equal to and greater than 14.3 m are only allowed to enter or leave during flood tide when the currents are 0.5 kn and decreasing (ebb tide inaccessible).

2.2. Data Sources

2.2.1. Geospatial Data

Geospatial data is a collective term for all data with a specified geometry. For the approach discussed here, we are interested in a schematic representation of the port’s wet infrastructure.
On the one hand, this relates to the network of waterways that is schematized in the nautical traffic model as a graph, typically consisting of connected lines (edges) and points (nodes). Various geospatial processing tools, such as Shapely, are available in Python to derive such networks from shapes that mark the fairways and water bodies. Moreover, spatial-temporal processing tools, such as the Python-based MovingPandas, are able to derive networks by aggregating observed tracks in the AIS data (see Section 2.2.2). In many cases, more formal versions of such nautical traffic graphs exist. For the Netherlands, for instance, Rijkswaterstaat provides the latest information on the state of its waterways via the Fairway Information System (FIS) (vaarweginformatie.nl). This network is used in the case study of the 3rd PET (see Figure 2).
On the other hand, this relates to information on important port infrastructure, such as anchorage areas, fairways, turning basins, and berths. Generally, it is sufficient to specify such infrastructure in the form of shapes that specify their position and outline. In some cases further metadata is needed, e.g. the capacity of an anchorage area or berth, the applicable UKC policy for a fairway section. Port authorities may also have accurate geospatial datasets including metadata that can be used. In this research the geometric extents of the 3rd PET, the PoR and the areas of the TSS (see Figure 2) were obtained from OpenStreetMap using the open data mining tool Overpass turbo. A polygon containing a specific area between the breakwaters, used in the AIS analysis in Section 2.3.1, was created using GoogleEarth. Specific geospatial data with metadata on MBL and FWA was obtained via PoR, through its Port Map application.

2.2.2. AIS Data

The AIS is an automatic vessel tracking system that is primarily used to guarantee safety in waters with heavy traffic. It consists of time series of various types of messages that contain either static vessel properties (e.g. the vessel’s unique Maritime Mobile Service Identity (MMSI) number, the vessel type, the vessel’s dimensions) or dynamic vessel properties (e.g. location, Speed Over Ground (SOG), Course Over Ground (COG)). The dynamic data is transmitted with a higher frequency than the static data; every 2–10 seconds a message is transmitted for a sailing vessel, increasing to 180 seconds for an idle vessel. By combining the static and dynamic components, the transit information of each individual vessel can be gathered, stored, and researched. Raw AIS data is available in National Marine Electronics Association (NMEA) encoding. The open-source Python package PyAIS can be used to decode this raw data and convert it into readily usable dataframes (i.e. Pandas, MovingPandas). Ready-to-use, pre-decoded, and cleaned AIS data products may in some cases be available from organisations like the coast guard or the local water authority. For this study, decoded, anonymized AIS data for the entire area of the PoR, including the TSS, for the entire year of 2019 was provided by Rijkswaterstaat. The anonymization algorithm ensured that the vessels maintained a unique vessel ID. The data processing that was applied to this AIS data is discussed in Section 2.3.

2.2.3. Hydrodynamic Data

Hydrodynamic data is required for the calculation of the vertical (water levels) and horizontal tidal windows (current velocities), where and if applicable. The data can furthermore be used to determine the vessels’ sailing speed over water. A useful data source should specify this hydrodynamic data as a function of time in at least two strategic locations. Data from measurement stations could be interpolated to relevant locations, e.g. to key nodes of the nautical traffic network. More measurement stations increase the accuracy. Another option, that is applied in this research, is the use of a well-calibrated and validated hydrodynamic model. The PoR makes current hydro-meteo data available via its Weather, Tides and Water Depths platform. An important tool in this platform is the Operationeel Stromingsmodel Rotterdam (OSR) that calculates water levels and currents, while constantly being re-calibrated with the most recent measurement data. This numerical model calculates the present hydrodynamic situation and makes a 24-hour prediction on a daily basis. Furthermore, hindcast simulations can be made with the model, which was done for this study. Hydrodynamic data on relevant locations was acquired by adding monitoring points to the model’s computational grid. The model output was made available in NetCDF-files for further processing.

2.3. Data Processing (I)

The decoded AIS data contains information on all types of vessels, including barges, and tugs and pilot boats which constitute the majority of the data received. For our study, we are primarily interested in the behaviour of sea-going cargo vessels. To arrive at the desired level of detail the AIS data had to be filtered and trajectorised, and outliers had to be removed. For this sequence of algorithms, we followed the basic principle of performing the most computationally demanding algorithms on as little data as possible. The processing was performed using the multi-core Planetary Computer of Microsoft.

2.3.1. Filtering of the AIS Data

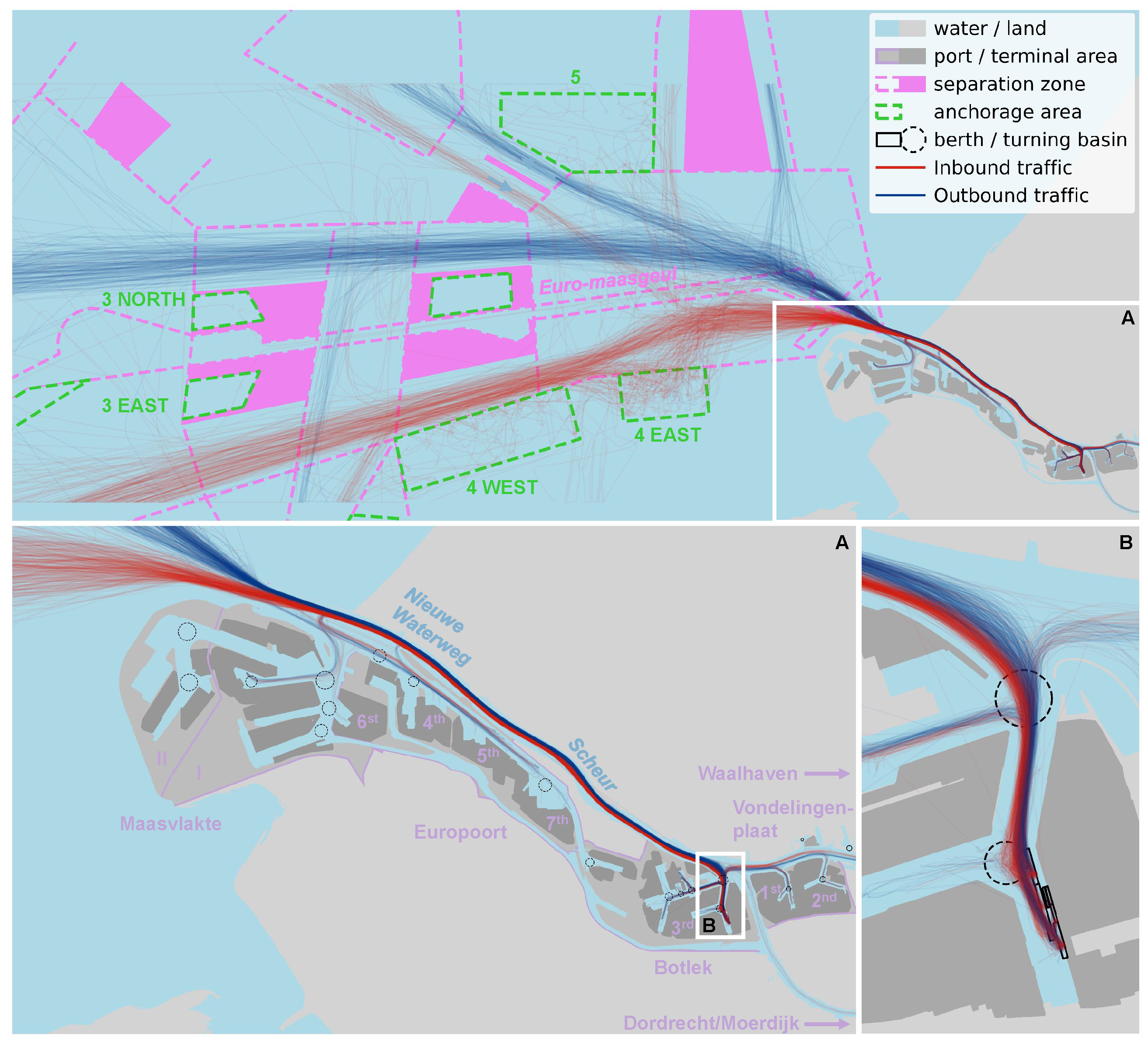
Figure 1a shows some first filtering steps that were applied to arrive at the AIS data of interest. By filtering on vessel type, we reduced the overall dataset to cargo vessels and tankers. Next, we used a polygon encompassing the access channel between the breakwaters through which inland barges will not sail. This allowed us to further trim down the dataset to only the sea-going cargo vessels that call at the port. A combined polygon encompassing the berths of the specific liquid bulk terminal in the 3rd PET was used to select only those sea-going vessels that called at the liquid bulk terminal at least once during the entire year of 2019.

2.3.2. Trajectorization into Voyages and Trips

Next, Figure 1b shows the subsequent steps that were taken to process the AIS data. First we ‘trajectorized’ the now filtered AIS data based on a unique static vessel property (i.c., vessel name). For each vessel, this resulted in a tabulated chronological overview of all time-position combinations in the 2019 AIS data. For each time-position combination, instantaneous vessel properties like speed, heading, and acceleration were added to the table for later use.
Since the total trajectory of one vessel for a given year generally consists of several voyages (or port calls) that in turn can consist of multiple trips (origin-destination combinations), the next processing step is to split the vessel trajectories into ‘voyages’ and ‘trips’.
A ‘voyage’ (or port call) is defined as a vessel’s in- and outbound time-of-stay within the port infrastructure, including the TSS. To distinguish between voyages we made use of a time gap without any messages in a vessel’s trajectory data. The open-source Python package MovingPandas provides the so-called ObservationalGapSplitter method for this purpose. We used a gap of 6 hours to distinguish between voyages in a vessel’s trajectory data. Each individual voyage was assigned a unique ID for purposes of later analysis.
A ‘trip’ is defined as a subset of a vessel’s trajectory (or voyage) data that can be demarcated by a clear origin and destination. The start and stop of each voyage are taken as origin and destination, respectively. To distinguish between trips within each voyage we made use of the time that a vessel stays at a fixed location. The StopSplitter method of MovingPandas can be used for this purpose. It creates splits based on the condition that a vessel stays within a certain radius for a minimum duration. Based on trial-and-error we used a diameter of 25 meters and a minimum duration of 30 minutes to identify intermediate stops in each voyage. Each individual trip was assigned a unique ID for purposes of later analysis.
As the StopSplitter operation proved to be time-consuming, we separated the trajectory data of each vessel into sub-sets of roughly equal size. This allowed for parallel processing, which greatly reduced the processing time. One artifact of this approach, however, was that artificial splits were created at the boundaries between the sub-sets. To resolve this, a merge step was required to rejoin sub-trips that belonged together. Another artifact was that the StopSplitter method deletes the trajectory data that falls within its search radius. As a consequence, the start and end points of subsequent trips would no longer match. In some cases, this caused significant shifts in a vessel’s position from the end of one trip to the start of the next, which in turn caused problems in the subsequent analysis. To resolve this issue the deleted data was retrieved and restored.
To focus on the in- and outbound traffic of the 3rd PET, we used the combined polygon of the 3rd PET berths to reject all trips that did not stop or start in this area. The remaining trips were sorted based on their start time, classified as in- or outbound depending on their start- and endpoint, and combined into round trips. If the inbound trip had one of the anchorage areas as its origin, the preceding trip that had this anchorage as its destination was added to the round trip. This resulted in 255 individual ships that undertook a total of 481 unique voyages, consisting of one or two inbound trips to the 3rd PET (depending on whether the vessel laid in one of the anchorage areas) and a single outbound trip from this terminal. Vessel properties such as length, beam, and draught, as derived from the AIS data, were added to each trip dataset. The difference in draught between the in- and outbound trips was added as the (un)loading quantity to each voyage.

2.3.3. AIS Data Outlier Removal

Unfortunately, AIS data is known to contain errors. Some of the AIS fields rely on manual input, so human error is to be expected here. But other fields rely on sensors, such as the vessel’s location as a function of time, as well as its SOG, COG, and derived speeds and accelerations. The last data processing step is to remove errors in this latter kind. Since this is a very time-consuming row-by-row operation this step was performed at the very end on the minimum subset of relevant voyages and trips. The following four conditions for sailing vessels, proposed by Abreu et al. [61], were used to classify whether a data point was considered anomalous: stop, drift, acceleration, and turning. Based on trial and error the condition for sailing vessels was set to a speed of 2 kn minimum. Suspected outliers were removed accordingly.

2.4. Simulation and Validation Preparation (II)

The processed data from the previous subsection (I) can now be used to generate inputs for the nautical traffic simulation and validation.

2.4.1. Origins, Destinations and Other Trip Data

The ‘real world’ coordinates of origins and destinations can be extracted straightforwardly from the voyage and trip datasets. Next to origins and destinations, each simulation needs at least the following information for each calling vessel: arrival time, sailing speeds along the route, projected turning time in the turning basins, designated berth(s), and the (un)loading time at the berth(s). Also, the vessel’s actual laytime at the anchorage area must be recorded to validate the simulation results.
The designated berths of call are determined using the stoppage data between the in- and outbound ‘trips’. An algorithm counts the number of AIS points that fall inside the different berths and selects the berth with the most hits as the vessel’s most likely berth of call. The unloading times at these berths are estimated from the stoppage intervals between the in- and outbound trips. The time for (de)berthing is assumed to be included in these intervals.
Turning times are estimated with an algorithm that determines the time of stay in the turning basins that the sailing vessel passes during its voyage. The algorithm selects the turning time with the maximum time of stay, as the vessel only needs to turn once during its voyage. This may be during its inbound or outbound trip.
The laytimes in the anchorage areas are determined similarly to the unloading times at the berth, though with the start time of the second part of an inbound trip and the end time of the first inbound trip, starting and ending in the anchorage area respectively. If the vessel did not visit an anchorage area, the laytime is set to zero.

2.4.2. Mapping Locations to the Graph

The nautical traffic model requires the origin and destination nodes for each trip, rather than the ‘real world’ coordinates, to enable routing on the network graph.
To map the trajectories of the AIS trips onto the routing graph we used an algorithm that finds the nearest directional edge in the graph for each coordinate of the trajectory. Since this is a time-consuming operation for large amounts of data and complex, extensive networks, the algorithm was initially only applied to special way-points. These way points were derived based on a running criterion on cumulative distance (1000 m) and cumulative course difference (30 degrees). Based on the identified nearest directional edges of two consecutive way-points, a significantly smaller sub-graph could be defined, which was used for the search of the nearest directional edge for the coordinates between those way-points.
The origin and destination nodes of the trips were determined through a similar nearest-node algorithm. Accordingly, the timestamp of the AIS message closest to the origin node of the first trip was set as the arrival time at the port of the vessel. As vessels may originate from, or are bound for, another location within the port, the origin and destination of a voyage are not necessarily at the TSS. Since we decided to omit the modelling of traffic in the TSS (see Section 2.5.1), for those vessels that did arrive from, or depart to, this area we decided to set the origin (including the arrival time) or destination to the node at the port entrance between the breakwaters. The observed arrival times of the vessels at this newly defined port entrance are of vessels that were cleared by the vessel traffic service to enter the port, as vessels originating from the TSS will wait in an offshore anchorage area for a tidal window and berth availability. Hence, to be able to quantify and resolve the waiting times in the anchorage areas, the arrival times had to be corrected (brought forward) for the time that the vessel waited in the anchorage area. Thus, if a waiting time is required for a vessel it will be ordered to wait at the port entrance in the nautical traffic model.
Now that the actual routes of the vessels are mapped onto the graph, we can identify speed distributions for each individual directional edge that was covered by the vessels of call. For the simulations in this study, we assumed, that vessels maintain their average speed over the edges. However, since the routes on the graph and AIS trips do not map exactly in space, the actual average speed of the vessel differs from the average vessel speed over the edge. For this study we concluded that the vessel’s average speed over the edge would be the most accurate, meaning that the edge length and arrival time at and departure time from the edge are used to determine the average network speeds. This information was added to the graph so that it would be available for the vessels during the simulation. The vessel speed over the network is important in the calculation of the tidal windows. The slower the vessel sails, the smaller these windows will be.

2.4.3. Adding Tidal Information to the Graph

Next to speeds, the simulations also require hydrodynamic data to be available on the network’s nodes to enable the determination of tidal windows. Table 1 shows that different tidal restrictions apply for flood and ebb tidal periods. Determining the start and end times of these flood and ebb periods in astronomic tidal hydrodynamic data requires a tidal analysis. We performed a Fourier analysis on the water levels and current velocities, and a (preceding) Principal Component Analysis (PCA) on the current velocity magnitudes and directions. The tidal component analysis is performed using the Hatyan package. The tidal periods were derived based on the intersection points of the abscissa (current velocity magnitude = 0 kn), i.e. the slack tides.

2.5. Nautical Traffic Model (III)

For our nautical traffic simulations we used the open source Python package OpenTNSim, which is an agent-based discrete-event simulation package that is based on SimPy. OpenTNSim provides a library of standardised ‘mixin’ classes that can be combined to create agents or infrastructure components with user-specified properties and behaviour.
Adding the ‘Identifiable’ mixin to an agent, for example, allows the user to give that agent a name and/or a Universal Unique Identifier (UUID). Adding the ‘Movable’ mixin gives that agent the ability to move at a predefined speed. The ‘Routeable’ mixin, which implies ‘Movable’, allows an agent to move over a graph following a specified route with an origin, intermediate waypoints, and a destination. The ‘VesselProperties’ mixin allows the user to specify agent properties, such as length (L), beam (B), draught (T), payload, etc. The ‘Log’ mixin ensures that key information is logged for later inspection.
The same mixins can be used to define infrastructure components in the transport network. Components like anchorage areas, turning circles, berths, jetties, quays, etc. can be named by adding the ‘Identifiable’ mixin. The user can furthermore specify how many vessels can make use of that object at the same time by adding the ‘HasResource’ mixin. If the maximum number has been achieved, i.e. a jetty can handle one vessel at a time and is already occupied, then the next vessel that wants to call on that jetty has to wait until it is available. Waiting is typically done in one of the ports anchorage areas.
Specifically for this study, we developed various new mixins. Most noteworthy are the VesselTrafficService-mixin and a PortInfrastructure-mixin. When these mixins are added to an object, it allows to request information from a port authority, i.e., regarding the availability of a berth, and the availability of a tidal window. The mixins communicate berth availability in advance, meaning that a vessel can already enter the port to sail to their berth of call when a vessel that is occupying this berth is scheduled to leave before the arrival of the next vessel.
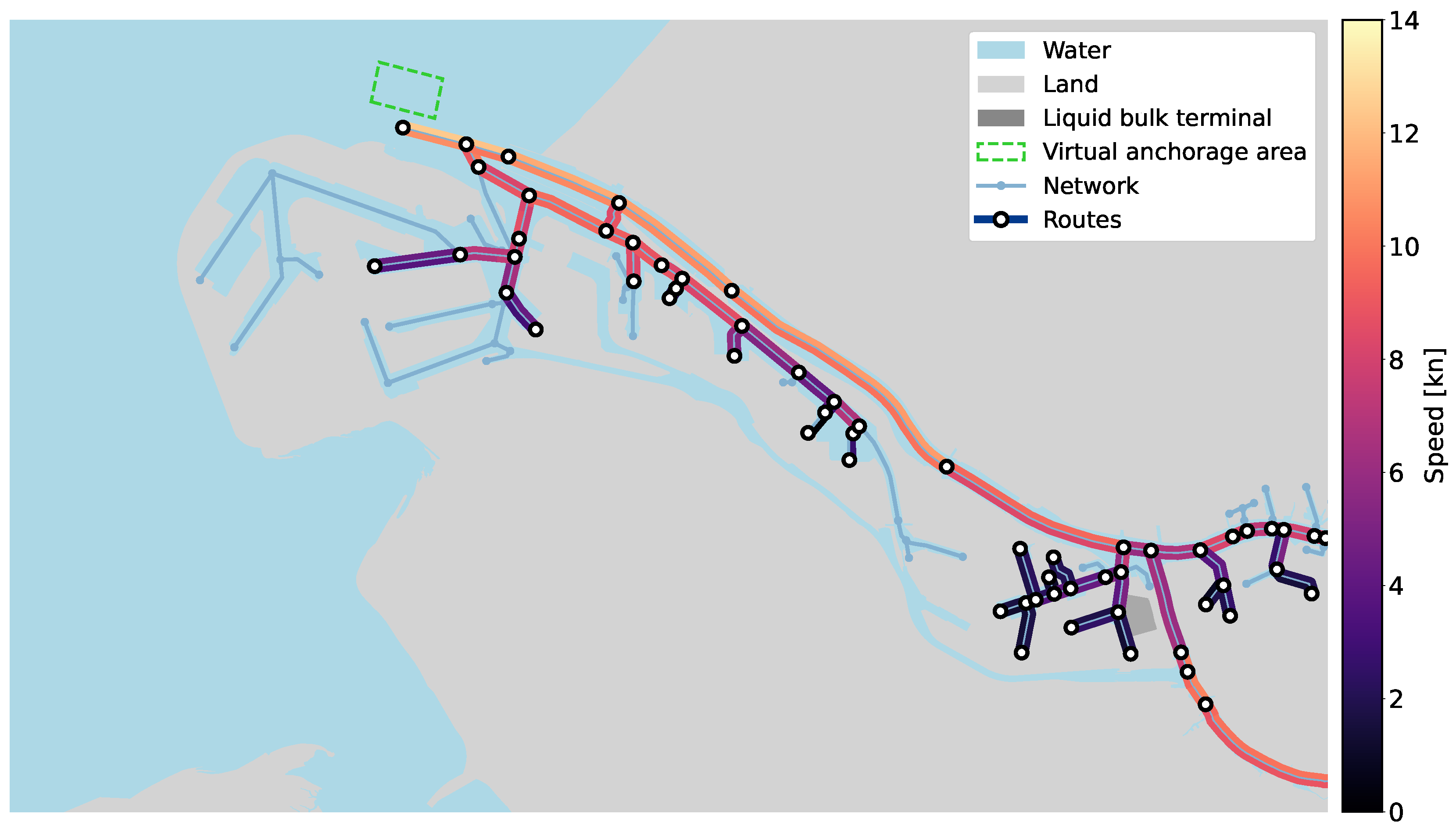
The minimum required input for a simulation consists of the port infrastructure network and the generated vessels with their routing information and realistic properties. To achieve this paper’s aim we added the following specifics to the network: the detailed accessibility policies that apply at the different edges (i.e., tidal restrictions, vessel-priority rules), the average vessel speeds per edge, and the hydrodynamic data at key nodes to determine when vertical and horizontal tidal windows are available. The details of the nautical traffic simulation are discussed according to Figure 3.

2.5.1. Port Infrastructure Network

The waterway network in Figure 3 was extracted from Rijkswaterstaat’s FIS that includes the PoR area (see also Figure 2). For simplicity, the TSS was not included. The complex vessel behaviour in the TSS is challenging to mimic and does not affect the waiting times of the vessels that sail to the 3rd PET. Since the TSS contains (the routes to) the anchorage areas, we placed a virtual anchorage at the port entrance to serve as the vessel waiting area. Vessels originating or departing to the TSS were modelled to be bound from/to the port entrance between the breakwaters. The arrival times of the vessels were corrected accordingly (see Section 2.4.2).
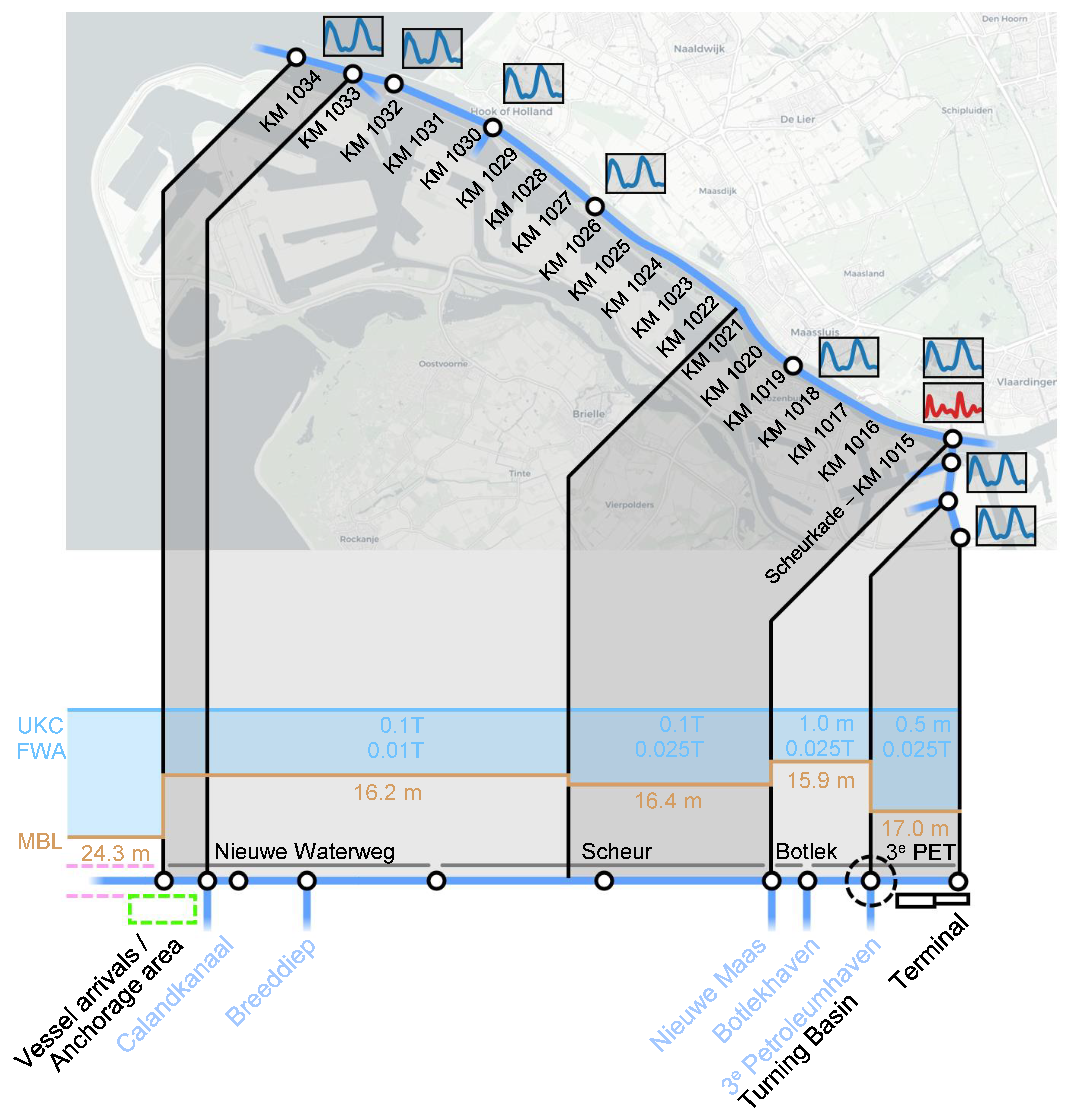
The port infrastructure that was added to this network consists of the port entrance on the most seaward node with the virtual anchorage area, the waterways towards the Botlek area schematised as nodes and edges, the dedicated turning basin for the 3rd PET (for vessels up to a length of 290 m) on the penultimate node, and the liquid bulk terminal in the 3rd PET on the last edge with its various berths for sea-going vessels. The turning time does not contribute significantly to the total turnaround time, however, vessels waiting for other vessels to turn or to pass the turning basin before they can turn can slightly contribute to the waiting times of the vessels.
Key properties of these objects were specified using the OpenTNSim mixin classes. Anchorages, waterways and turning basins were modelled using the ‘HasResource’ mixin. The virtual anchorage area is assumed to have an infinite capacity to prevent vessels from entering the anchorage area and leaving the port without being processed. The waterway edges were also assumed to have an infinite capacity, and they were modelled as bi-directional edges to account for two-way traffic. It was assumed that a safe distance is maintained by the vessels so that encountering does not lead to a reduction in speed. Overtaking by the sea-going vessels is assumed not to occur, as these vessels are sailing over the network with similar speeds. The turning basin can handle one vessel at a time, and the manoeuvre of the vessels is modelled to occur during the inbound trip. Outbound vessels can still occupy the turning basin, as they have to pass through it when leaving the port. The berths of the liquid bulk terminal are modelled using the FilterStore class from SimPy [3]. This concept works as a store of products (berths) with each their own properties, such as a name, a MBL, and a maximum ship length that they can operate. The liquid bulk terminal has a few quays that do not have a unit capacity, like jetties, but that have a finite length. These quays, however, contain a limited number of fixed pumping facilities and are therefore modelled similarly to jetties. For simplicity, we assume empty berths at the start of the simulation.
Water level data was added to relevant nodes, and the governing MBL and the UKC policies were added to the edges (see Figure 3). Current velocity data was included at the critical point along the route where the vessels turn (KM 1015 at the Scheurkade). The water level and current information are used to calculate the tidal windows according to the governing rules that are summarized in Table 1.

2.5.2. Generated Vessels

For our model implementation, vessels have to be generated with the following required information:
  • length and draught per trip in the voyage,
  • origin, intermediate waypoints and destination nodes that constitute the route of the voyage and trips over the network,
  • arrival time at the vessel’s origin node,
  • designated berth(s) of call,
  • turning time in the turning basin,
  • the (un)loading time(s) at the designated berth(s), and
  • the change in draught at the berths.
Since we perform a hindcast study, we replicate the observed traffic using the processed AIS data (see in Section 2.4). Each vessel travels past the nodes that are specified in its route. Between these specified nodes the route is determined with Dijkstra’s shortest path algorithm if needed. The route leads to the designated berth. In reality, berths can be assigned freely based on their properties and restrictions that prevent small vessels from berthing at the deep-sea berths (e.g. a minimum vessel length or draught requirement), which also could have been included in the model.

2.5.3. Modelling Strategy

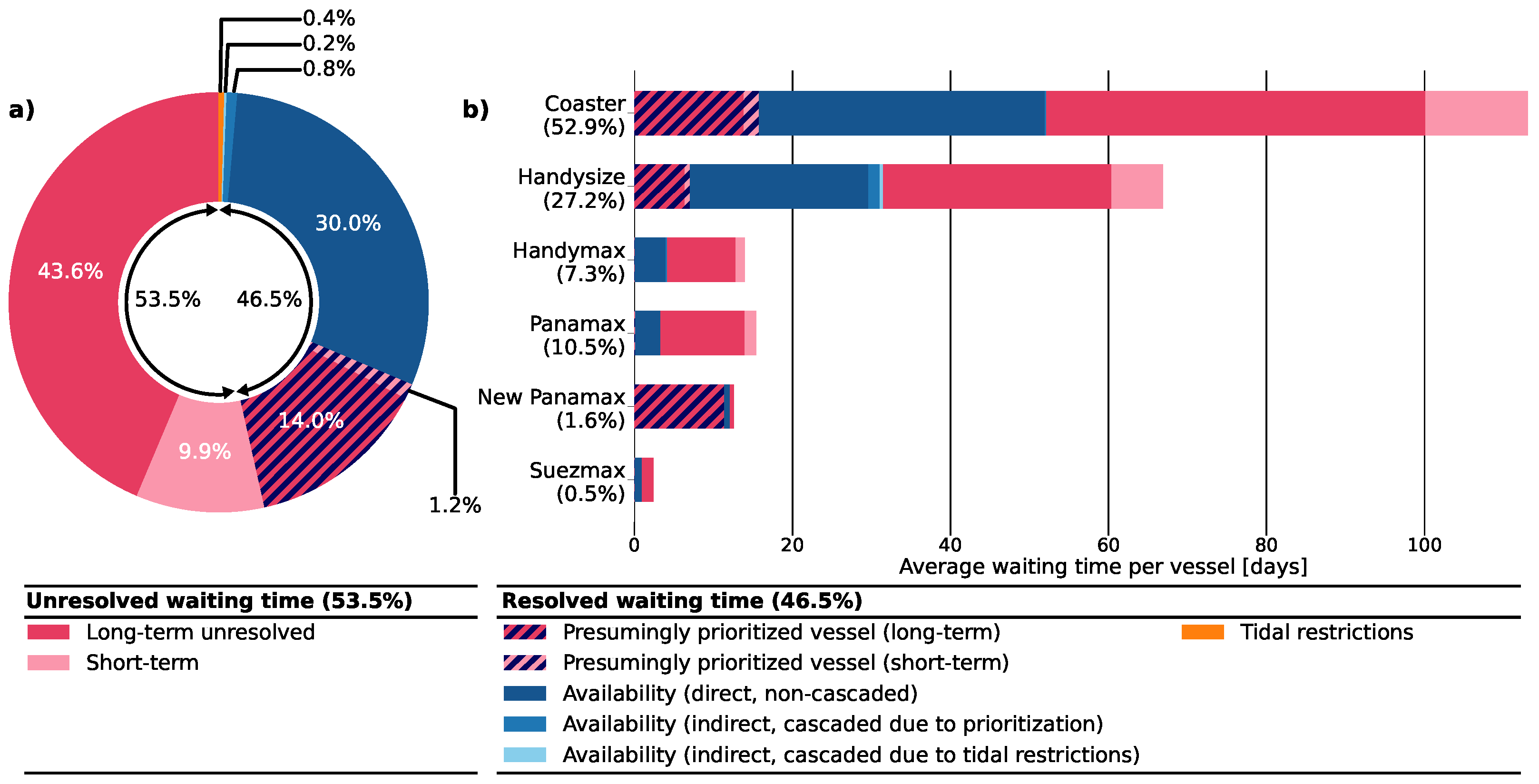
After the port infrastructure network and the generated vessels have been specified, SimPy works out how these vessels, together, move through the network. The simulation resolves where and when which vessel needs to wait and for how long. Waiting times in the anchorage area will occur if a vessel has to wait on either a tidal window or unavailable (congested) port infrastructure, either directly or indirectly through cascading effects. Priority rules to be included in the berth planning strategy to minimize the demurrage costs of vessels were omitted in this research but can be included in the model. Instead, the sporadically observed behaviour of newly calling vessels jumping ahead in the queue, over already waiting vessels, was mimicked by giving additional waiting times to these latter vessels. This waiting time equalled the difference between the arrival time between the two vessels and was presumed to be due to the priority rules. To quantify the individual contributions of the tidal restriction, berth unavailability and priority rules to the waiting times of vessels, as well as the cascading effects of these causes, the simulation was also run without tidal windows and prioritization. Besides the reference situation, the model is applied to test alternative MBL designs for the NWW.

3. Results

We first describe behaviour that can be observed in the AIS data. Next, we describe the results from the hindcast made with the nautical traffic model.

3.1. AIS Data

The processed AIS data is visualized in Figure 4. A total of 481 voyages were identified, made by 255 different vessels. 52.8% of these voyages were operated by vessels that can be classified as coasters, while 23.1% were of the Handysize class, 9.1% of the Handymax class, and 12.5% were vessels of the Panamax class. Only 2.3% of the voyages were made with New Panamax-class vessels and a single Suezmax-class vessel called at the terminal. From this dataset, we could also derive origin-destination patterns and length-draught distributions. For example, 80.7% of the inbound trips used the NWW, of which 5.2% is tide-bound (83.3% of the total tide-bound vessels). Figure 5 shows histograms and distributions for a number of key aspects of the observed traffic: laytime at the offshore anchorage areas, sailing times for inbound and outbound vessels over the NWW, turning times for inbound and outbound vessels, and laytime at the terminal. Figure 6 shows the distribution of speed information over the network.

3.1.1. Laytime at the Anchorage

The laytime of vessels at the anchorage area will be used to validate the model. 39.7% of the voyages included laytime in the anchorage area. 89.5% of these voyages originated from offshore. Based on expert judgment, it is expected that voyages originating from other areas in the Port of Rotterdam claim internal anchorage areas or, less likely, wait at their terminal, and only visit an offshore anchorage area if the internal anchorage areas or terminal are not available or waiting in internal anchorage areas is impossible. Furthermore, 59.7% of the voyages with laytime in an anchorage used the closest anchorage to the port along their route, 4 EAST. 88.4% of these voyages arrived from the southwest. 13.1% of the voyages with waiting time used anchorage 5, of which all vessels from offshore arrived from the northwest. Out of the deepest-draughted vessels (14.8 m ≤ draught ≤ 15.0 m) the four New Panamax-class vessels were obliged to navigate the Euro-Maasgeul. Two of these vessels had a laytime in the dedicated anchorage areas of 3 North and 3 South.
From the probability density function (pdf) in Figure 5a, we observe that 56.5% of the voyage that had laytime in the anchorage area did not wait for more than a day. Voyages with larger vessels tend to wait shorter, as only 29.2% exceed a laytime of a day. The longest observed laytime was found for a New Panamax class vessel that waited over 13 days. The second longest was found for a Coaster that waited almost 5 days. Such long laytimes of over 2 days occurred frequently for voyages with smaller vessels (16.2%).

3.1.2. Sailing Time

The sailing time over the NWW, presented in Figure 5b, is important to estimate the delay in arrival time at the terminal and to determine the tidal windows in the model. We observe that the speeds contain significant spreading with transit times ranging from 50 to 120 minutes. We observe that inbound vessels, on average, sail with lower speeds than outbound vessels; the modal traveling times are in the order of 75 and 65 minutes, respectively. This bias may be because most trips occurred during ebb tide, as well as that outbound vessels on average had less draught; larger vessels were observed to sail with lower speeds than smaller vessels with modal differences of around 10 minutes. However, a clear correlation between the tide and the sailing speed was not found. Observed variation is expected to be due to captain behaviour, ambient traffic, the strength of (tidal) currents and winds, etc.
The above-mentioned behaviour can also be observed in the average in- and outbound speeds over the network as visualised in Figure 6. Over the NWW and the Scheur the average vessel speed is nearly constant: 9.9 knots for inbound vessels and 11.1 knots for outbound vessels. Towards the Botlek and the New Meuse, the average speeds drop due to decelerating (from 8.3 to 5.9 kn, on average) and accelerating vessels (from 7.4 to 9.5 kn, on average) that are sailing in and out of the Botlekhaven, respectively. The contrary holds for the entrance of the Port of Rotterdam, in which outbound vessels seem to accelerate further to 12.5 kn. Inside the harbour basins the average speeds are low, below 5.0 kn (in the 3rd PET), as expected, and decreasing further towards the ends of the harbour basins as a consequence of the vessel manoeuvres.

3.1.3. Turning Time

Figure 5c shows the turning times of the vessels of call, i.e., when a vessel is occupying the entrance to the terminal and inhibits other traffic from entering/leaving the 3rd PET. They range from a minute up to tens of minutes with a maximum of 43 minutes (not shown in the figure). However, from the pdf, we can observe that 91.1% of the voyages have a turning time of less than 10 minutes. The turning times of vessels larger than coasters follow a positively skewed distribution with a modal duration of around 6 minutes. Most vessels (84.2% of the total) turn during their inbound trip, which is according to common practice, as this was previously mandatory based on safety regulations. There is no significant increase in the modal turning time with vessel size, although the longest turning times are observed for larger vessels. Most probably, the outliers are caused by severe winds. Since coasters are more manoeuvrable, most of these vessels are believed not to turn at the turning basin, but rather manoeuvre at the berth, thereby passing the turning basin without actually turning. They affect the overall distribution severely.

3.1.4. Laytime at the Terminal

The observed time at the berth of the vessels is presented in Figure 5d. Note that during this time, the vessel occupies the berth during which other vessels cannot make use of this berth. The pdf follows a positively skewed distribution with a lot of spreading ranging from a few hours to several days. The modal laytime of all vessels of call is slightly longer than a full day. For smaller vessels, especially coasters, the distribution shifts more to shorter laytimes of around half a day, while for the largest vessels (Panamax class and larger) the distribution shifts to longer times with a mode of around one-and-a-half day. Understandably, these differences are caused by varying transshipment volumes of liquid bulk between the vessel and the terminal that increase with vessel size. The standard deviation, however, is large compared to the average laytime for all types of vessels. Based on expert judgment, this is presumably caused by varying onboard pumping capacities and the number of storage compartments that need to be (un)loaded.

3.1.5. Tidal Restrictions

Figure 7 shows the draught and length combinations of the incoming and outgoing vessels of call at the liquid bulk terminal. Only 8.5% of the inbound trips were prone to tidal windows during the voyage, while none of the outbound voyages were affected by a tidal window. During 7.7% of these trips, vessels had long-lasting horizontal tidal windows, based on a critical velocity. Only for 5.4% of these vessels (with a draught greater than and equal to 13.0 m), the tidal windows started to be shortened further by the vertical tidal constraint. For these vessels, the accessibility was, however, fully determined by the criterion of the critical tidal velocity. The resulting tidal windows, combining the vertical and horizontal tidal windows, are visualized in Figure 8a for a vessel with 14.2 m of draught. For vessels with such (deeper) draughts, the horizontal tidal windows are severely (more) shortened by the vertical tidal constraint. This combination still resulted in adequately long tidal windows. For 9.8% of the inbound trips that are restricted by the tide, vessels are prone to a narrow tidal window, consisting of a strict, governing point-based horizontal tidal window within a tight vertical tidal window (see Figure 8b). Only during 0.6% of the voyages, vessels were observed to have the maximum design draught of 15.0 m, which had to fully exploit the MBL design of the NWW, Scheur, and the Botlek, including the 3rd PET. Based on the observation that the most deep-draughted vessels left the terminal with less draught, we can consider the terminal to be an import terminal. This claim is, moreover, further signified by the fact that most incoming coasters (up to a draught of 8.6 m and a length of 120 m) arrive with less draught compared to their departure.

3.2. Nautical Traffic Model

3.2.1. Estimation of the Total Waiting Time

To align the nautical traffic model with the AIS data analysis, we simulated the 481 voyages of 255 vessels in the nautical traffic model and observed that 46.5% of the total laytimes in the anchorage areas could be resolved (see Figure 9a); 53.5% of the observed laytimes, consisting of the pink slices in this figure (43.6%+9.9%), were unresolved. For 60.7% of voyages, the laytimes at the anchorage area were modelled in exact accordance with the observations (less than 10 minutes of difference). Additionally, the model correctly estimated any form of waiting time for 18.7% of other voyages with observed laytime in the anchorage area, however, with some discrepancy. Hence, for the remaining 20.6% of voyages, the model could not resolve any of the observed laytime in the anchorage area.
For 99.0% of voyages that were modelled correctly, the vessels did not have any observed laytime in the anchorage area, which was, hence, confirmed by the model. The nautical traffic model furthermore predicted only once an exceedance of the observed laytime (no laytime was observed) by 6 minutes and 40 seconds due to waiting time for a tidal window. The remaining 1.0% of the correctly modelled voyages were made by New Panamax-class vessels that did have observed waiting time in the anchorage area.

3.2.2. Underlying Causes for the Waiting Time

From Figure 9 we observe that congestion due to berth unavailability (30.0%) contributes most to the resolved laytimes and is partly caused by prioritization (14.0% + 1.2% + 0.8% cascading). Tidal restrictions (0.4% + 0.2% cascading) are of secondary importance for the laytimes. This is according to the expectations, as the NWW are designed for vessels with draughts up to 15.0 m, which led to only 4.9% of the vessels of the inbound trips being prone to tidal restrictions. Partly as a consequence, cascading effects contributed to 1.0% of the resolved laytimes in the anchorage area. The unavailability of the turning time did not result in additional waiting times, but this waiting time may be hidden in additional laytime of vessels at the terminal.
The model implied that 18.7% of the voyages were subject to waiting time due to terminal congestion. Most of these voyages were executed by coasters (53.3%) and Handysize-class vessels (33.3%), while the rest of the waiting time due to berth unavailability was found for voyages made by Handymax-class vessels (4.4%), Panamax-class vessels (6.7%), New Panamax-class vessels (1.1%), and Suezmax-class vessels (1.1%). This distribution is slightly shifted to the smaller vessels, compared to fleet composition (see Section 3.1). The main cause of this congestion was found to be the irregular arrival time of vessels, rather than the excessive laytimes at the terminal for some vessels, as we observed in the AIS data. These extreme laytimes of more than 2 days that caused other vessels to wait at the anchorage area only contributed to 6.2% of the total waiting time due to terminal congestion. Although the underlying causes for the excessive laytimes at the terminal are not known, the majority is expected to occur during no active call for the specific berth at which the vessel is laying (idle). Unwanted excessive laytimes may have been caused by breakdowns of terminal equipment or vessel, or spills. However, these do not occur frequently.
During 36.7% of the voyages with waiting time due to berth congestion, the vessel presumably gave priority to other vessels; during 8.5% of the total trips, a vessel moved ahead at the expense of another vessel. It is, however, debatable whether prioritization is the main reason for this waiting time. This was confirmed by experts in the field, as the vessels are in principle scheduled according to First Come First Serve (FCFS). First, only half of the time ‘priority’ was given to a larger vessel. Second, long additional waiting times of on average more than 17 hours were found for which prioritizing may not pay off. Third, a considerable amount of waiting time due to prioritization was found for a New Panamax-class vessel, which waited over 11 days in the anchorage area. It was estimated that in only 1.0% of the voyages, prioritization could potentially have been a motive to wait in the anchorage area, explaining only 1.2% of the total observed laytime in the anchorage, rather than the full 15.2%. In this case, cascading effects due to prioritization would not occur. We assume that none of the vessels gave priority in reality, and consider the resolved waiting time due to prioritization as unresolved waiting time. An additional run without prioritization shows that the resolved laytime of vessels in the anchorage areas drops to 37.3%.
Only 1.2% of the total voyages were predicted by the model to have a waiting time due to the tidal restrictions, leading to very little waiting time in the anchorage area. The horizontal tidal restrictions were found to be governing; 50.0% of the vessels that had to wait for these restrictions were limited by a critical tidal current velocity, while the other 50.0% vessels experienced waiting time due to the strict point-based tidal window, with a maximum of 9 hours and 41 minutes. Since this contributed to 9.7% of the total turnaround time of this specific vessel, tidal accessibility remains important at vessel level. Since two of the four vessels, which were prone to a strict tidal window of only 20 minutes per tide, did not have to wait more than an hour, we expect that most of the waiting time in the anchorage area due to tidal windows is prevented due to careful prior planning in which vessels adjust their sailing speed at sea to arrive at the port during a tidal window.
Cascading effects were mainly triggered by vessels that presumably let other vessels go ahead (prioritization). Also, the waiting times due to tidal restrictions caused additional waiting times for non-tide-bound vessels.

3.2.3. Discrepancies with the Observed Waiting Time

Accounting for only congestion (30.0%) and tidal windows (0.4% + 0.2% cascaded), 69.6% of the total observed laytimes in the anchorage area could not be resolved by the model. The observed discrepancies can be subdivided into long-term (43.6% + 14.0%) and short-term (9.9% + 1.2%) unresolved waiting times, and loading and unloading vessels (see Figure 10). These categories are discussed below based on feedback from experts of the PoR.
In Figure 10, we see that most unresolved waiting time is for loading vessels (76.8%) of which 56.5% is long-term with an average waiting time of around 16 hours. 94.9% of the long-term waiting vessels are coasters (53.8%), Handysize class (33.3%), and Handymax class (7.7%) vessels (see Figure 10b). We observe a wide distribution of waiting times up to long waiting times for vessels that are to be loaded. These long, excessive laytimes are expected to be mainly caused by (a combination of) contractual obligations, and availability of the cargo/facilities at the terminal. For vessels that are hired by a party to load new cargo, sailing to the port as early as possible may be part of contractual obligations. These vessels arrive at the port and wait for the actual order to be fulfilled. Furthermore, since the terminal is processing the liquid bulk products, it may occasionally occur that the cargo is not yet ready to be shipped. Moreover, cargo may be lacking as the terminal is awaiting an import transshipment of another vessel. Since we could deduce that the liquid bulk terminal is an import terminal, mainly smaller vessels are expected to be subject to these forms of waiting time. The shorter-term unresolved laytimes for loading vessels, which contribute to 43.5% of the total (see Figure 10), can also be explained by the above-mentioned processes. This form of waiting time is also dominated by the smaller vessel classes (96.7%). Like the long-term unresolved waiting time, this is because bigger class vessels constitute only 3.3% of the loading vessels. Relatively, these latter vessels contribute most to the long-term unresolved waiting time, while the short-term contribution is more or less equal to vessels of smaller vessel classes.
On the other hand, we observe in Figure 10 that only 23.2% of the unresolved laytime is found for unloading vessels, of which 41.2% was found to be long-term. 38.2% of this long-term unresolved laytime belongs to the Panamax class (28.6%), New Panamax class (4.8%), and Suezmax class (4.8%) vessels. These long-term unresolved laytimes may be related to price speculations and negotiations. Especially the larger, loaded (to be unloaded) liquid bulk carriers may want to anchor for an additional time as the market price for the transshipped cargo may rise. Next to these speculations, negotiations about the final price may not have been terminated before the arrival of the vessel. An example may be the Suezmax class vessel, which waited for an extra day and a half. In addition to the readiness of the cargo, the larger vessels may be prone to the unavailability of facilities at the terminal, such as the storage tanks. The long wait of 11 days for the New Panamax-class vessel may have been related to the above reasons (see Figure 9). Smaller vessel classes, contributing to 61.8% of the long-term unresolved waiting time, are also prone to these waiting times. However, most unresolved waiting times for the unloading vessels of smaller classes are generally short-term and are more pronounced than the long-term waiting times. For the larger vessel classes, the unresolved waiting times are more or less equally divided between short- and long-term.
The (long-term) discrepancies can also be composed of a combination of frequent short-term disruptions. First, based on interviews with captains of tanker vessels, performed by Römers [62], delays due to poor communication and coordination with the shore may cause small waiting times for vessels in the anchorage. For example, updates on berth availability are rarely provided to these waiting vessels. This causes additional waiting times that are not resolved with the model, as the communication in this model is assumed to be optimal. 40% of vessels that would be loading at the terminal, had a short-term unresolved waiting time of less than 4 hours, while having resolved waiting time due to berth congestion (see Figure 10a).
Second, congestion due to the limited availability of tugs and pilots occurs frequently in the PoR. This waiting time will typically not last longer than 2 hours and waiting for towage is reported to be the most frequent cause for waiting time [39]. During busy periods and extremely windy conditions, the increased demand for tugs and pilots may even cause waiting times of 3 to 4 hours. It is questionable whether this effect is major for this particular terminal, as most vessels with unresolved laytimes do not require tug assistance (classes smaller than Handymax class). Waiting for pilotage, however, could contribute to the waiting times of the other types of vessels; in total 10 Panamax-class vessels have short-term unresolved waiting times (see Figure 10). Another potential reason for the short-term discrepancy in waiting times is due to congestion of the waterway.
Third, vessels could have potentially waited during the downtime of the port due to other consequences than tidal restrictions, such as fog, wind, or storms. The importance of this downtime is debatable as its occurrence is infrequent. Other downtimes may theoretically be caused by daylight and working hours of the terminal, but this is not influential for this terminal; departures and arrivals occur almost uniformly over the full period of the day. Less frequent reasons for the long-term discrepancies may be the unavailability of berths due to barges, special operations, and calamities. It is, however, believed that sea-going vessels do have priority over barges. Special operations such as lightening operations of large vessels that are otherwise not able to enter the port directly due to draught restrictions, are not applicable for the PoR. Calamities of vessels that are broken down, and required reparations could have potentially caused additional waiting times, but this is very unlikely.

3.2.4. Testing Alternative Maintained Bed Level Designs

We saw that terminal congestion explains most of the waiting time of the fleet, while tidal windows are less important for the fleet. This is in accordance with the port policy that states that 99.0% of the tides should be accessible for any inbound vessel with a draught of 15.0 m. Our model found that the current MBL design of the channel is slightly underdimensioned with a tidal accessibility of 98.4%.
Applying the validated model to the previous MBL design of the NWW (14.5 m instead of 16.2 m), we found that the four deepest-draughted vessels of 14.8 and 15.0 m of draught could not enter the 3rd PET. Furthermore, assuming that the tidal restrictions will now apply to vessels with a draught of 9.3 m (11.0 m minus 1.7 m), more inbound trips (9.0% instead of 4.6%) will be prone to these rules. The total waiting time due to tidal restrictions, however, decreases from about 21.5 hours to about 19.5 hours. This is because most vessels fall in the lenient window-based current velocity regime. The percentage of vessels prone to the strict point-based current velocity tidal window decreased from 8.3% to 4.2% (with port accessibility for design vessels with draughts of 13.5 m of about 99%).
In case the exclusion of the four deepest-draughted vessels may be unacceptable, a more moderate reduction of 0.5 m in MBL of the Nieuwe Waterweg and Scheur could be undertaken. The model found that this will result in a degree of accessibility of 59.1% for the design vessel, leading to an increase of the total modelled waiting times of 33.6%. This increase consists of 73.4% of waiting time due to cascading effects of the tidal window; the rest (26.6%) is waiting time directly caused by the tidal restrictions. On the contrary, based on Figure 7, we see that more considerable gains in the reduction of the MBL can be obtained by redirecting the deepest-draughted New Panamax and Suezmax class vessels to other deep-sea terminals (i.e. Maasvlakte). The model found that by diverting the 9 deepest-drafted vessels, the desired service level could be achieved with MBLs that are 3.0 m higher than the current MBLs. More vessels will then be prone to a tidal window, but the increase in the total waiting time will only be 2.7%, while dredging costs are likely substantially lower.

4. Discussion

4.1. Further Challenges to Overcome the Approach’s Limitations

Although the results on the quantification of the waiting times are promising, we still found significant discrepancies between the modelled and observed laytimes of vessels in the anchorage area. The method has several limitations that may have to be addressed in future studies.
First, the model presented here relies on an extensive set of geospatial, hydrodynamic, and AIS data. In other case studies, these datasets may be unavailable. The availability of hydrodynamic data, for instance, depends on measurement campaigns and/or numerical models, which may be lacking and are costly to set up. Moreover, AIS data may be protected or absent (i.e., for new ports or future scenarios). While the availability of these datasets is expected to improve the results significantly, the simulation model can be also used with synthetic data.
Second, although the processing and analysis of AIS data successfully resulted in the required information, the dependency of the model on AIS is not fully reliable and could have potentially led to errors in the set-up and validation of the hindcast simulation with the nautical traffic model. AIS data is known to contain errors in the manual, static (i.e., draught) and dynamic (i.e. Global Positioning System (GPS), SOG) information, which was also observed in this research. As severe Global Positioning System (GPS) errors caused idle vessels to drift in space, our method could occasionally not distinguish idle from sailing vessels. These errors have potentially resulted in erroneous laytimes of vessels at the wrong infrastructure. Contributing to this problem was the fact that AIS data was sometimes lacking around the berth areas, seemingly caused by the operators of the vessel that forgot to switch on the AIS. We limited these errors by removing outliers based on the SOG, but this parameter was found to include inadequacies as well. The outlier removal process could therefore not be fully relied upon, and some errors remained to be present. A more extensive analysis may be required for further studies.
Third, various port processes have been neglected in this model that may explain part of the discrepancies and/or may be required in different case studies but were deemed out of scope in this research. Most prominently, the land-based terminal operations were disregarded. These are thought to have a significant effect on the waiting times of vessels, as, based on expert judgement, cargo is occasionally not ready to be (un)loaded. For example, preceding vessels that provide the cargo have not called at the terminal yet, or substances have not been processed by the terminal and cannot be discharged yet. This may lead to long-term, cascading waiting times in the order of several hours to days. Omitted processes that could have resulted in resolving more short-term waiting times are waterway congestion due to ambient traffic, congestion due to limited tug and pilot availability, and downtime due to other external environmental conditions. These processes may interact with each other, as more adverse weather conditions (i.e., strong winds from particular directions) may lead to a higher demand for tugs and pilots, which can exceed their capacity during peak traffic flows. Other neglected processes that affect the speed of vessels, and could have led to delays in the order of several minutes, are vessel encounters and overtaking, vessel properties (i.e., draught), and meteo-hydrological conditions (i.e., currents and winds). Modelling the correct speed for tide-bound vessels is important to calculate the tidal windows. In this study, due to the short distances and few tide-bound vessels, this would not have led to different results. However, we believe that the above-mentioned processes can in fact be included in the discrete-event simulation environment of the model, should a specific case demand this.
Last, the mapping of the AIS tracks onto the network has led to errors in vessel speed. Vessels did not necessarily follow the simplified network. This has contributed to errors in the delays in the order of several minutes. Future research may need to overcome this simplification for cases where small deviations like this are considered problematic.
Still, it is important to note that the majority of the waiting times discussed in this study are not caused by the physical limitations of the port and waterway infrastructure.

4.2. Significance of the Method for New Applications

Although many improvements to the model are possible, we want to stress that our data-driven modelling approach already gives very promising results. By including realistic hydrodynamics, detailed accessibility policies and berth availability information, the model was able to rapidly quantify and resolve the fleet’s laytime in the anchorage area due to the cascading delays of terminal congestion and tidal restrictions. Furthermore, we were able to create a relation between the degree of accessibility of ports, which for the 3rd PET was in accordance with De Jong [60], and the waiting time of vessels. Therefore, our approach is able to test alternative MBL designs based on the impact of the fleet’s waiting time, rather than on the accessibility percentage of a single design vessel. This is a significant advantage over design-vessel approaches. In particular, the quantification of the cascading effects proved to be highly important for this. Although these effects have a limited effect on the fleet’s waiting time in the current situation, we observed that they become increasingly important when the MBL become shallower and more vessels are affected by the tidal restrictions.
We would also like to mention that the open-source environment of the nautical traffic model enables an excellent opportunity to include further improvements to the model, in joint development with other researchers and stakeholders. We expect that the model is capable of incorporating omitted port processes and infrastructure (i.e., container and dry bulk terminals) with minor additions and alterations. Besides, the model is not limited to the hindcast study that was presented in this paper. We foresee that the model can be implemented in worldwide port and waterway systems for various other purposes. The model could namely be used as an operational tool for real-time modelling or nowcasting to, for example, optimize short-term planning of operations. Moreover, the model can be applied as a forecasting tool on tactical (medium-term) and strategical (long-term) levels, namely to test alternative traffic regulations, accessibility policies, vessel-priority rules, waterway and berth layouts, and the effect of changing fleets of call on the port. Probabilistic and machine-learning tools on AIS data may be required to assist in these model applications. Most distinctively, the model is also suitable for integral design in areas with multiple stakeholders, as it is coupled with a hydrodynamic model. This is particularly useful when modelling alternative port infrastructure designs and port expansions, which may alter the hydrodynamics (i.e. channel deepening, and construction of new harbour basins). Such interventions may lead to enhanced salt intrusion and additional sedimentation, which are important for the functioning of ports and the local society.

5. Conclusions

The work in this paper was triggered by the observation that port accessibility designs are typically based on design vessels while neglecting or simplifying important, cascading waiting times for a representative fleet of vessels due to congestion and port downtime. Such strategies may lead to sub-optimal port and waterway designs.
To investigate this, a method was envisioned that simultaneously accounts for (1) realistic hydrodynamics, (2) detailed accessibility policies, (3) realistic vessel properties, (4) cascading effects of vessel-priority rules, (5) detailed waterway and berth layout, and (6) concrete berth allocation policies. It was postulated that such a method does not as yet exist. Therefore, we developed a discrete-event model that simulates nautical traffic by including these aspects of tidal downtime and infrastructure congestion. The model requires a geospatial graph of the port network, resources that schematise the port infrastructure (i.e., terminals, anchorage areas, and turning basins), agents with properties that represent the vessels of call (i.e., arrival times, draughts, laytimes at the terminal and turning basins), and tidal and traffic restrictions, including vessel speeds and realistic hydrodynamics over the graph. We applied the simulation model to a real-world case study of a liquid bulk terminal in the 3rd PET of the PoR. To derive the required information for this model, we jointly analysed geospatial data, AIS data, and hydrodynamic data from a numerical model. The approach was designed to result in a detailed decomposition of the causes of the fleet’s waiting time, which were validated against the observations in AIS data.
Using the mentioned data sources, we could successfully deploy the nautical traffic model, leading to a reproduction of 73.4% of the non-excessive laytimes, modelling 60.7% of the vessels-of-call in accordance with the observations. 98.0% of the observed waiting time was resolved by the model as terminal congestion while waiting time due to tidal restrictions was limited to only 2.0% of the observed waiting time. This finding met our expectations, as the channel’s MBL is designed for the deepest draughted design vessel that comprises 0.6% of the fleet. Consequently, only 5.0% of the fleet was prone to tidal restrictions, with 1.2% of the fleet having consequential waiting times. The resolved waiting time that was allegedly caused by vessel priority rules was excluded, as experts confirmed that such rules are not in place. Therefore, the cascading effects of tidal restrictions and vessel priority rules were limited for this specific case study. However, by running various alternative MBL designs, these cascading effects became important, highlighting the added value of the modelling approach of a fleet over a design vessel approach.
Still, a discrepancy of 69.2% between the modelled and observed laytimes was found. Most of this waiting time is expected not to be related to the wet infrastructure, but due to (cascading) congestion in cargo flows and other economic considerations. For further studies, improvements to the model may therefore be required. The open-source, and modular structure of the nautical traffic model is highly suitable for this. Despite these potential improvements, the model’s current performance is satisfactory. We have high confidence that our modelling approach will eventually enable us to analyse the inefficiency of the total port system while uncovering the specific, underlying contribution of each specific component. In this way, we can make rational improvements to the port’s wet infrastructure.

Author Contributions

Conceptualization, F.P.B., S.W., F.B., A.K, S.W. and M.K; methodology, F.P.B.; software, F.P.B., S.W., F.B., M.K.; validation, F.P.B.; formal analysis, F.P.B.; investigation, F.P.B.; resources, F.P.B. and S.W.; data curation, F.B.; writing—original draft preparation, F.P.B.; writing—review and editing, S.W., F.B., A.K, S.W. and M.K; visualization, F.P.B.; supervision, M.K.; project administration, M.K.; funding acquisition, M.K.

Funding

The work for this publication is part of SALTISolutions, which is a Perspective Programme (partly) funded by the Dutch Research Council (NWO). More specifically the work presented here is part of P18-32 Project 7 “Design and operation of nature-based SALTISolutions”

Data Availability Statement

The original data presented in the study are reproducible using the presented simulation model in OpenTNSim at [https://github.com/TUDelft-CITG/OpenTNSim/tree/SALTISolutions]. Restrictions apply to the availability of the raw data. Data were obtained from Rijkswaterstaat and the Port of Rotterdam

Acknowledgments

We would like to express our gratitude to the Port of Rotterdam which provided part of the geospatial data and, in particular, Lamber Hulsen, who provided the hydrodynamic data. Furthermore, we would like to thank Rijkswaterstaat for providing the AIS data and the FIS graph.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
3rd PET 3rd Petroleumhaven
AIS Automatic Identification System
GPS Global Positioning System
FIS Fairway Information System
FWA Fresh Water Allowance
pdf Probability Density Function
MBL Maintained Bed Level
NWW New Waterway
PoR Port of Rotterdam
SOG Speed Over Ground
TSS Traffic Separation Scheme
UKC Under Keel Clearance

References

  1. Siemes, R.; Duong, T.M.; Willemsen, P.; Borjse, B.; Hulsche, S. Morphological Response of a Highly Engineered Estuary to Altering Channel Depth and Restoring Wetlands. Journal of Marine Science and Engineering 2023. [Google Scholar] [CrossRef]
  2. Van Koningsveld, M.; Verheij, H.; Taneja, P.; De Vriend, H. Ports and Waterways: navigating the changing world; TU Delft Open, 2023.
  3. Bakker, F.P.; Van Koningsveld, M. Optimizing bed levels in ports based on port accessibility. Proceedings of the International Conference on Coastal Engineering (ICCE) in Sydney, Australia, 2023, Vol. 37, p. 11. [CrossRef]
  4. PIANC. Harbour Approach Channels - Design Guidelines. Technical report, Permanent International Commission for Navigation Congresses (PIANC), Brussels, Belgium, 2014.
  5. Bos, M.; Koop, O.; Bolt, E. Safety Level of a Probabilistic Admittance Policy. Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering OMAE, Rotterdam, The Netherlands, June 19-24 2011, pp. pp. 263–271. [CrossRef]
  6. Vantorre, M.; Candries, M.; Verwilligen, J. Optimization of Tidal Windows for Deep-Drafted Vessels by Means of ProToel. International Workshop on Next Generation Nautical Traffic Models;, 2013.
  7. Masalaci, B.; Zorba, Y. An application of agent-based traffic flow model for maritime management evaluation. International Journal of Maritime Engineering 2023, 165. [Google Scholar] [CrossRef]
  8. De Alvarenga Rosa, R.; Ribeiro, G.M.; Mauri, G.R.; Fracaroli, W. Planning the berth allocation problem in developing countries with multiple cargos and cargo priority by a mathematical model and a clustering search metaheuristic. International Journal of Logistics Systems and Management 2017, 28, 397–418. [Google Scholar] [CrossRef]
  9. Venturini, G.; Iris, Ç.; Kontovas, C.A.; Larsen, A. The multi-port berth allocation problem with speed optimization and emission considerations. Transportation Research Part D: Transport and Environment 2017, 54, 142–159. [Google Scholar] [CrossRef]
  10. Kramer, A.; Lalla-Ruiz, E.; Iori, M.; Voß, S. Novel formulations and modeling enhancements for the dynamic berth allocation problem. European Journal of Operational Research 2019, 278, 170–185. [Google Scholar] [CrossRef]
  11. Jia, S.; Li, C.L.; Xu, Z. Managing navigation channel traffic and anchorage area utilization of a container port. Transportation Science. [CrossRef]
  12. Zhang, B.; Zheng, Z.; Wang, D. A model and algorithm for vessel scheduling through a two-way tidal channel. Maritime Policy and Management 2020, 47, 188–202. [Google Scholar] [CrossRef]
  13. Xiao, F.; Ligteringen, H.; Van Gulijk, C.; Ale, B. Nautical traffic simulation with multi-agent system. Proceedings of the 16th International IEEE Annual Conference on Intelligent Transportation Systems. ITSC 2013.; IEEE: The Hague, 2013; pp. 1245–1252.
  14. Bellsolà Olba, X.; Daamen, W.; Vellinga, T.; Hoogendoorn, S.P. Estimating Port Network Traffic Capacity. Scientific Journals of the Maritime University of Szczecin 2015, 42, 45–53. [Google Scholar] [CrossRef]
  15. Shu, Y.; Daamen, W.; Ligteringen, H.; Hoogendoorn, S. Operational model for vessel traffic using optimal control and calibration. Scientific Journals of the Maritime University of Szczecin 2015, 42, 70–77. [Google Scholar]
  16. Xin, X.; Liu, K.; Yang, X.; Yuan, Z.; Zhang, J. A simulation model for ship navigation in the “ Xiazhimen ” waterway based on statistical analysis of AIS data. Ocean Engineering 2019, 180, 279–289. [Google Scholar] [CrossRef]
  17. Durlik, I.; Gucma, L.; Miller, T. applied sciences Statistical Model of Ship Delays on the Fairway in Terms of Restrictions Resulting from the Port Regulations : Case Study of Swinoujscie-Szczecin Fairway. Applied Sciences 2023, 13. [Google Scholar] [CrossRef]
  18. Cartenì, A.; Luca, S.D. Tactical and strategic planning for a container terminal: Modelling issues within a discrete event simulation approach. Simulation Modelling Practice and Theory 2012, 21, 123–145. [Google Scholar] [CrossRef]
  19. Iannone, R.; Miranda, S.; Prisco, L.; Riemma, S.; Sarno, D. Proposal for a flexible discrete event simulation model for assessing the daily operation decisions in a Ro-Ro terminal. Simulation Modelling Practice and Theory 2016, 61, 28–46. [Google Scholar] [CrossRef]
  20. Wahed, M.A.; Faghri, A.; Li, M. An innovative simulation model for the operations of a multipurpose seaport: A case study from Port of Wilmington, USA. International Journal of Simulation and Process Modelling 2017, 12, 151–164. [Google Scholar] [CrossRef]
  21. Leal, L.R. Stochastic Simulation of an Oil Terminal To Reduce the Turnaround Time of Tankers Through Pipeline Operability. Proceedings of the Brazilian Symposium on Operations Research, 2018.
  22. Neagoe, M.; Hvolby, H.H.; Taskhiri, M.S.; Turner, P. Using discrete-event simulation to compare congestion management initiatives at a port terminal. Simulation Modelling Practice and Theory 2021, 112, 102362. [Google Scholar] [CrossRef]
  23. Koldborg Jensen, T.; Gamborg Hansen, M.; Lehn-Schiøler, T.; Melchild, K.; Mølsted Rasmussen, F.; Ennemark, F. Free flow-efficiency of a one-way traffic lane between two pylons. The Journal of Navigation 2013, 66, 941–951. [Google Scholar] [CrossRef]
  24. Tasseda, E.H.; Shoji, R. Statistical Modeling Framework of Vessel Traffic Streams in Tokyo Bay. Transactions of Navigation 2018, 3, 31–42. [Google Scholar]
  25. Dragovic, B.; Zrnic, N.; Twrdy, E. Ship Traffic Modeling and Performance Evaluation in Container Port. Analele Universităţii “Eftimie Murgu” reşiţa 2012, XVII, 127–138.
  26. Navarro, M.; Bano, R.; Cheng, M.; Torres, M.; Y.B., K.; Gutierrez, T. Queuing Theory Application using Model Simulation : Solution to address Manila Port congestion. Proceedings of the Asia Pacific Industrial Engineering & Management Systems Conference, 2015, pp. 1109–1114.
  27. Hansen, J.B. Optimizing Ports through Computer Simulation Sensitivity Analysis of Pertinent Parameters. Operational Research Quarterly (1970-1977) 1972, 23, 519–530. [Google Scholar] [CrossRef]
  28. Park, C.S.; Noh, Y.D. An interactive port capacity expansion simulation model. Engineering Costs and Production Economics 1987, 11, 109–124. [Google Scholar] [CrossRef]
  29. Kondratowicz, L.J. Methodological solutions for increased efficiency of modelling and simulation of seaports and inland freight terminals. Maritime Policy and Management 1992, 19, 157–164. [Google Scholar] [CrossRef]
  30. Hassan, S.A. Port activity simulation : An overview. ACM SIGSIM Simulation Digest 1993, December, 17–36. [Google Scholar] [CrossRef]
  31. Demirci, E. Simulation Modelling and Analysis of a Port Investment. Simulation 2003, 79, 94–105. [Google Scholar] [CrossRef]
  32. Howard, D.L.; Bragen, M.J.; Burke, J.F.; Love, R.J. PORTSIM5: Modelling from a Seaport Level. Mathematical and Computer Modelling 2004, 39, 715–731. [Google Scholar] [CrossRef]
  33. Arango, C.; Cortés, P.; Muñuzuri, J.; Onieva, L. Berth allocation planning in Seville inland port by simulation and optimisation. Advanced Engineering Informatics 2011, 25, 452–461. [Google Scholar] [CrossRef]
  34. Ugurlu, Ö.; Yükseky, E. Simulation Model on Determining of Port Capacity and Queue Size : A Case Study for BOTAS Ceyhan Marine Terminal. the International Journal on Marine Navigation and Sefety of Sea Transportation 2014, 8, 143–150. [Google Scholar] [CrossRef]
  35. Clark, T.; Kabil, M.; Moussa Mostafa, M. An analysis and simulation of an experimental suez canal traffic control system. Proceedings of the 1983 Winter Simulation Conference, 1983, pp. 311–318.
  36. Van de Ruit, G.; Van Schuylenburg, M.; Ottjes, J. Simulation of shipping traffic flow in the Maasvlakte port area. Proceedings of the European SImulation Multiconference (ESM);, 1995.
  37. Yeo, G.T.; Roe, M.; Soak, S.M. Evaluation of the Marine Traffic Congestion of North Harbor in Busan Port. Journal of Waterway, Port, Coastal, and Ocean Engineering 2007, 133, 87–93. [Google Scholar] [CrossRef]
  38. Fransen, R.; Tilanus, P.; de Jong, J.; Davydenko, I. Swarmport agent-based simulation model description and documentation. Technical report, TNO, 2021.
  39. Nikghadam, S. Cooperation between Vessel Service Providers for Port Call Performance Improvement. PhD thesis, Delft University of Technology, 2023. [CrossRef]
  40. Groenveld, R. HARBORSIM: a generally applicable harbour simulation model. Technical report, Delft University of Technology, Department of Civil Engineering, Hydraulig Engineering Group, 1983.
  41. Frima, G. Capacity study for the Rio de la Plata waterway, Argentina. Master’s thesis, Delft University of Technology, 2004.
  42. Moser, D.; Hofseth, K.; Heisey, S.; Males, R.; Rogers, C. HARBORSYM: a data-driven Monte Carlo simulation model of vessel movement in harbors. Technical report, Institude for Water Resources U.S. Army Corps of Engineers Alexandria, Virginia, Alexandria, Virginia, 2004.
  43. Macquart, A. Simulation model to assess the effective capacity of the wet infrastructure of a port. Master’s thesis, Delft University of Technology, 2007.
  44. Rayo, S. Development of a simulation model for the assessment of approach channels - The Tasman Seaport case. Master thesis, Delft University of Technology, 2013.
  45. Piccoli, C. Assessment of Port Marine Operations Performance by Means of Simulation. Case study: The Port of Jebel Dhanna/Ruwais–UAE. Master’s thesis, Delft University of Technology, 2014.
  46. Tang, G.; Wang, W.; Song, X.; Guo, Z.; Yu, X.; Qiao, F. Effect of entrance channel dimensions on berth occupancy of container terminals. Ocean Engineering 2016, 117, 174–187. [Google Scholar] [CrossRef]
  47. Thiers, G.; Janssens, G. A Port Simulation Model as a Permanent Decision Instrument. Simulation 1998, 71, 117–125. [Google Scholar] [CrossRef]
  48. Almaz, O.A.; Altiok, T. Simulation modeling of the vessel traffic in Delaware River: Impact of deepening on port performance. Simulation Modelling Practice and Theory 2012, 22, 146–165. [Google Scholar] [CrossRef]
  49. Scott, D.; Taylor, D.; El-solh, S.; Elliott, T. Port Simulation Modelling and Economic Assessment. Journal of Marine Science and Engineering 2016, 4, 1–16. [Google Scholar] [CrossRef]
  50. Curtis, B. An Integrated Approach to Port Planning, Operations & Risk Management through Technology. PIANC-World Congress Panama City, Panama, 2018.
  51. Ayuso, C.; Redondo, R.; Atienza, R.; Ramón, J. Paper CA1201 - SIFLOW21. Simulación predictiva de capacidad basado en análisis de datos AIS. XII Congreso Argentino de Ingeniería Portuaria;, 2022.
  52. Franzkeit, J.; Pache, H.; Jahn, C. Investigation of Vessel Waiting Times. Dynamics in Logistics, Proceedings of the 7th International Conference LDIC 2020, Bremen, Germany, 2020, pp. 70–78. [CrossRef]
  53. Ma, J.; Zhou, Y.; Zhu, Z. Identification and analysis of ship waiting behavior outside the port based on AIS data. Nature, Scientific Reports 2023, 13, 1–12. [Google Scholar] [CrossRef]
  54. Martinicic, T.; Stepec, D.; Costa, J.P.; Cagran, K.; Chaldeakis, A. Vessel and Port Efficiency Metrics through Validated AIS data. Global Oceans;, 2020. [CrossRef]
  55. Jafari Kang, M.; Zohoori, S.; Hamidi, M.; Wu, X. Study of narrow waterways congestion based on automatic identification system (AIS) data: A case study of Houston Ship Channel. Journal of Ocean Engineering and Science 2022, 7, 578–595. [Google Scholar] [CrossRef]
  56. Steenari, J.; Lwakatare, L.; Nurminen, J.; Tolonen, J.; Manderbacka, T. Mining port operation information from AIS Data. Proceedings of the Hamburg International Conference of Logistics (HICL), 2022, Vol. 33, pp. 657–678. [CrossRef]
  57. Van der Werff, S.; Baart, F.; Van Koningsveld, M. Vessel Behaviour under Varying Environmental Conditions in Coastal Areas. Proceedings to the 35th PIANC World Congress, Cape Town, 2024.
  58. Van Koningsveld, M.; Den Uijl, J. OpenTNSim v0.0.1, 2019. [CrossRef]
  59. Baart, F.; Jiang, M.; Bakker, F.P.; Frijlink, T.; Van Koningsveld, M. OpenTNSim v1.2.0, 2022. Zenodo. [CrossRef]
  60. De Jong, S. Assessing Maintained Bed Levels in ports. Master’s thesis, Delft University of Technology, Delft, The Netherlands, 2020.
  61. Abreu, F.H.; Soares, A.; Paulovich, F.V.; Matwin, S. A trajectory scoring tool for local anomaly detection in maritime traffic using visual analytics. ISPRS International Journal of Geo-Information 2021, 10. [Google Scholar] [CrossRef]
  62. Römers, I.E.M. Port Call Optimization in three oil shipping markets. Master’s thesis, Erasmus University Rotterdam, Rotterdam, The Netherlands, 2013.
Preprints 106439 g001
Figure 1. Information flows for the set-up and validation of the nautical traffic model, consisting of data processing (I), simulation and validation preparation (II), and nautical traffic modelling (III).
Figure 1. Information flows for the set-up and validation of the nautical traffic model, consisting of data processing (I), simulation and validation preparation (II), and nautical traffic modelling (III).
Preprints 106439 g001
Preprints 106439 g002
Figure 2. Nautical infrastructure of the PoR (a), including its TSS, and the 3rd Petroleumhaven (b). The TSS consists of three routes to the port (i, ii, and iii); two deep-sea routes are crossing the system (A and B).
Figure 2. Nautical infrastructure of the PoR (a), including its TSS, and the 3rd Petroleumhaven (b). The TSS consists of three routes to the port (i, ii, and iii); two deep-sea routes are crossing the system (A and B).
Preprints 106439 g002
Preprints 106439 g003
Figure 3. Overview of the nautical traffic model based on an extraction of the graph following the route to the 3rd PET. The MBL, UKC, and FWA policies are added, which may be constant or dependent on the draught (T) of the vessel. The water levels (blue time series) and current velocities (red time series) are added to the nodes of the network.
Figure 3. Overview of the nautical traffic model based on an extraction of the graph following the route to the 3rd PET. The MBL, UKC, and FWA policies are added, which may be constant or dependent on the draught (T) of the vessel. The water levels (blue time series) and current velocities (red time series) are added to the nodes of the network.
Preprints 106439 g003
Preprints 106439 g004
Figure 4. Overview of the processed AIS data: inbound and outbound vessels are show that are navigating the TSS. Two close-ups are added of the trips’ track through the NWW (A) and the 3rd PET (B).
Figure 4. Overview of the processed AIS data: inbound and outbound vessels are show that are navigating the TSS. Two close-ups are added of the trips’ track through the NWW (A) and the 3rd PET (B).
Preprints 106439 g004
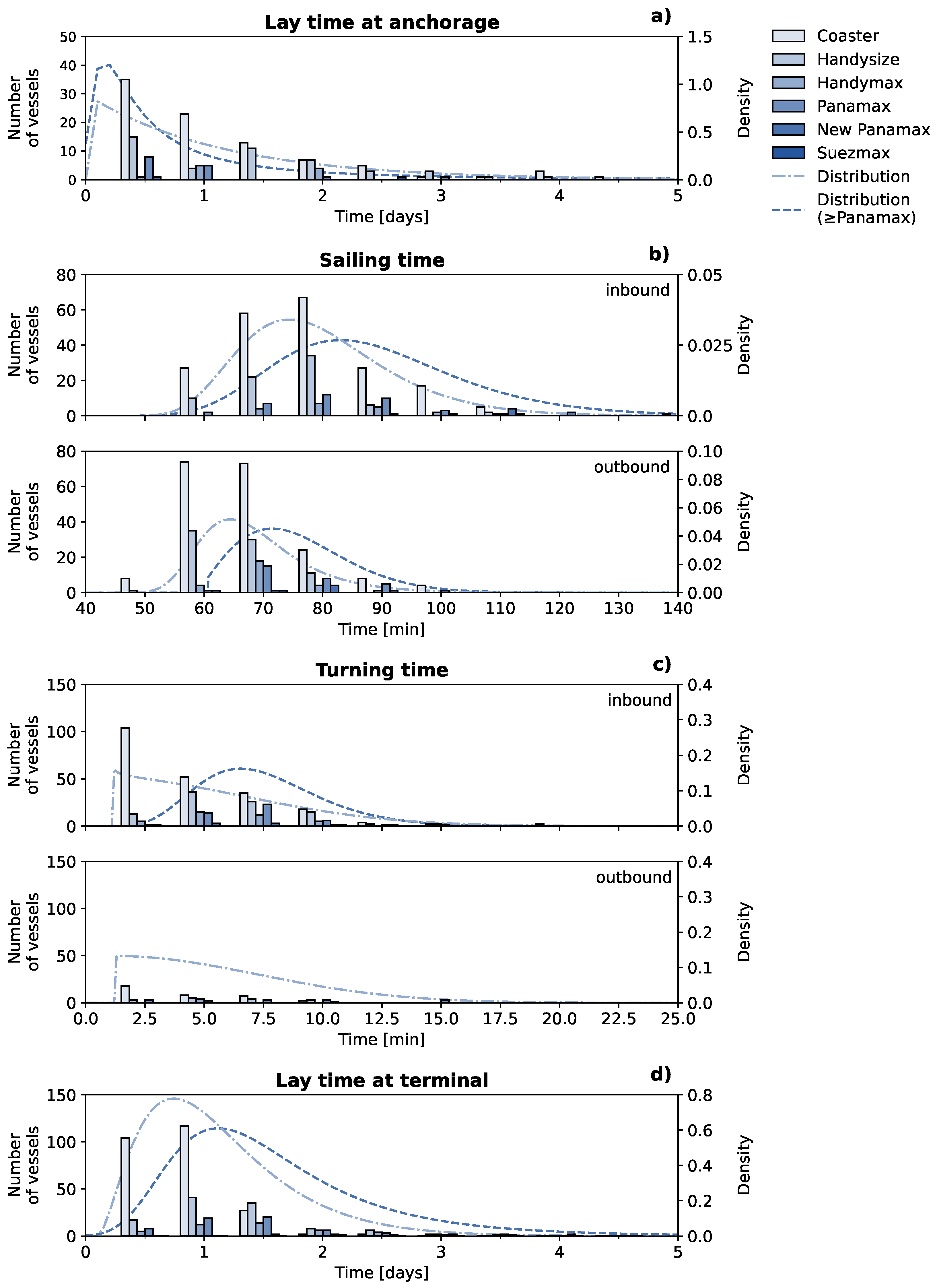
Preprints 106439 g005
Figure 5. Histograms and distributions of the calibration data derived from the processed AIS data: laytime at the offshore anchorage areas (a), sailing time for inbound and outbound vessels over the NWW and Scheur (b), turning time for inbound and outbound vessels (c), and the laytime at the terminal (d).
Figure 5. Histograms and distributions of the calibration data derived from the processed AIS data: laytime at the offshore anchorage areas (a), sailing time for inbound and outbound vessels over the NWW and Scheur (b), turning time for inbound and outbound vessels (c), and the laytime at the terminal (d).
Preprints 106439 g005
Preprints 106439 g006
Figure 6. Speed distributions over network derived from mapped AIS data.
Figure 6. Speed distributions over network derived from mapped AIS data.
Preprints 106439 g006
Preprints 106439 g007
Figure 7. Tidal restrictions of the incoming (a) and outgoing (b) vessels, based on the vessel’s length and draught, according to Table 1.
Figure 7. Tidal restrictions of the incoming (a) and outgoing (b) vessels, based on the vessel’s length and draught, according to Table 1.
Preprints 106439 g007
Preprints 106439 g008
Figure 8. Examples of a tidal window calculation: vertical tidal windows, governed by the net UKC (left axis; a positive value means excess water depth), with a horizontal tidal window based on a critical (panel a, current velocity should be smaller and equal to 2 kn) and a point-based (panel b, the current velocity should be 0.5 kn with a positive and negative spreading of both 30% based on practice) current velocity (right axis).
Figure 8. Examples of a tidal window calculation: vertical tidal windows, governed by the net UKC (left axis; a positive value means excess water depth), with a horizontal tidal window based on a critical (panel a, current velocity should be smaller and equal to 2 kn) and a point-based (panel b, the current velocity should be 0.5 kn with a positive and negative spreading of both 30% based on practice) current velocity (right axis).
Preprints 106439 g008
Preprints 106439 g009
Figure 9. The causes of the laytimes of the vessels of call in the anchorage area for the base case and for the scenario without inclusion of prioritization.
Figure 9. The causes of the laytimes of the vessels of call in the anchorage area for the base case and for the scenario without inclusion of prioritization.
Preprints 106439 g009
Preprints 106439 g010
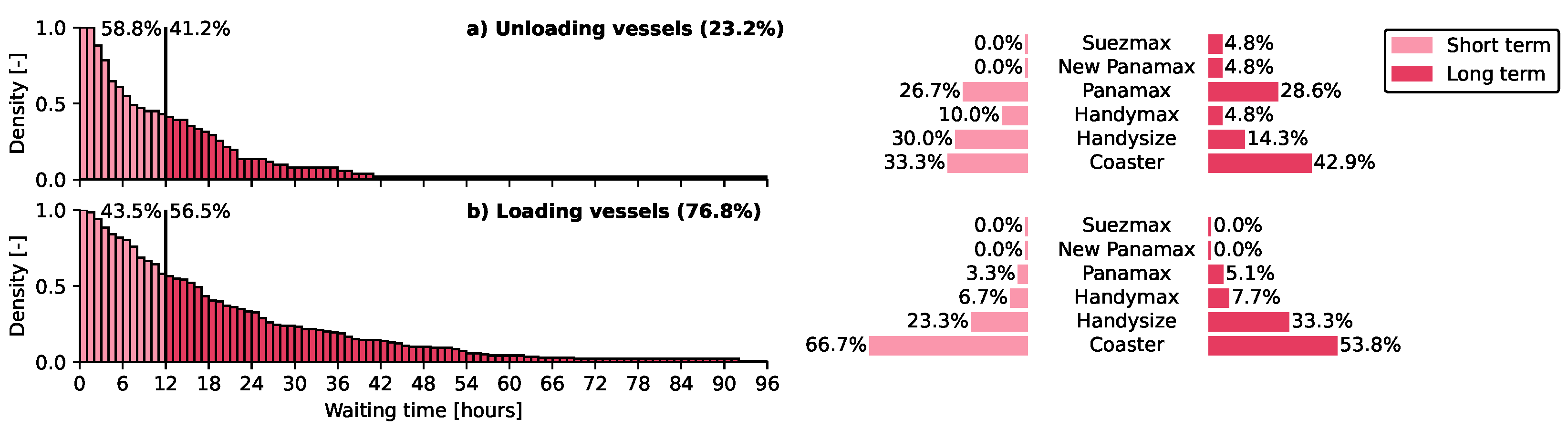
Figure 10. Inverse cumulative distributions of the discrepancies of unloading (a) and loading (b) vessels, including the number of vessels that had unresolved waiting times
Figure 10. Inverse cumulative distributions of the discrepancies of unloading (a) and loading (b) vessels, including the number of vessels that had unresolved waiting times
Preprints 106439 g010
Table 1. Entrance policy for tide-bound vessels to the 3rd Petroleumhaven.
Table 1. Entrance policy for tide-bound vessels to the 3rd Petroleumhaven.
Preprints 106439 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated