Prerpints.org logo
Preprint
Article

A Dual Hilbert-Space Formalism for Consciousness; Memory Experiments

Altmetrics

Downloads

107

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 May 2024

Posted:

17 May 2024

You are already at the latest version

Alerts
Abstract
Inspired by works of W. H. Zurek and others, a mathematical, physical theory, entirely within a quantum mechanical formalism, is proposed for cognitive processes in terms of an abstract Hilbert-space for the conscious state that is an exact replica of the Hilbert-space for the neuronic physical state. Thus, any actual state of consciousness arises by its formal alignment (identification) with some-one in the set of the neuronic states, with the latter undergoing perpetual changes in the wake of life-long experiences. It is posited that these changes become expressed by an increase in the number of ordered, coherent neuronic states at the expense of the pre-ordinal random neuronic states. Changes, transitions between states are induced by a Gorini-Kossakowski-Sudarshan-Lindblad formalism, which is also instrumental in the effect of the conscious state on bodily actions. The paradigmatic findings of R.N. Shepard (1958 - 2011) and of S. Sternberg (1966 - 2016) for long- and short-term recalls are interpreted within the model.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. Introduction

[Defn.: Briefly, Hilbert space in quantum mechanics (q. m.) is the space of all possible states of a given system.]
Consciousness was defined in NEB (1980), quoting John Locke, as "the perception of what passes in one’s mind", and similarly as "the intuitive perception of experience and the flow of inner time" by Atkinson ( 2011), or in a more nuanced form as "sentience, awareness, subjectivity, qualia, the ability to experience or to feel, wakefulness, having a sense of self-hood, and the executive control system of the mind" (Farthing 1992). Regarding consciousness in animals other than humans, the jury is still out, notwithstanding a weighty declaration that the neural conditions in animals are also favorable for it (Low 2012).
Historically, Tononi and Edelman (1998) with their concept of a re-entrant functioning of the mind (reminiscent of "mean field" theories of phase transitions in physics), may be regarded as the prime movers of a scientific, mathematical study of consciousness, an approach that has further been continued more recently by e.g., Lamme (2006). With a growth of research activities in the field, both experimental and theoretical, more kinds of different theories of consciousness have come to be recognized: e.g., nominally three in one version (Link 2022) and over twenty in another survey (Seth and Bayne 2022). The theorizing concern with consciousness spans several disciplines: philosophy, psychology, neurology, biology, chemistry, information sciences and, more recently, physics. Distinct approaches include higher order theories (HOT), by which consciousness emerges as the result of some higher order mental activity (Rosenthal 2005). Then, one has global workspace theories (Baars 1988, Dehaene and Nacache 2001),which associate with the conscious state the propensity to give it an outward expression, e.g., by talking, deliberate acting, etc. Additionally, other views relate consciousness to a unique combination of electro- and chemical- processes, these taking place exclusively in the brain (Levine 1983, Block 2009). A more exhaustive account of the further, numerous theoretical approaches to interpret mental activities erstwhile in terms of the neural framework is beyond the scope of this paper and so is the assignment of the different types of mental events to their location in the brain or the specification of any brain component [e.g., synapses, microtubules (Hameroff and Penrose 2014)] primarily involved in cognition.
Attributions of quantum aspects to mental activities, as in the present study, are not new and are on the increase as of late, but it is here that a formal and inclusive formalism is offered anew. In the past, looking backwards over several decades, one might recall a proposed interaction in reverse between cognition and q.m. due to E. P. Wigner, who sought the solution for the infinite regress problem of quantum mechanical observation in the mind of the observer (Wigner 1961). An association of intelligent decisions with quantum mechanics was proposed early by Asano et al (2011), continued by Khrennikov (2019) and Khrennikov and Asano (2020). Previous work on quantum mechanical aspects of cognitive processes was categorized by Hu and Wu (2010). Notably, a formal identification between quantum mechanics and psychology was made by Khrennikov (2019), where, in Equation (20), the wave-mechanical function Ψ made his appearance for the mental state. Quantum entanglement in bipartite systems and violations of Bell-inequalities were pinpointed in psychological events by Aerts and collaborators (2019). Noting some phenomenological aspects of decision making in human affairs both by human individuals and collectives, the authors of a series of papers, in e.g., Pothos and Busemeyer (2013), Busemeyer and Bruza (2012), Wang et al (2013) showed that these obeyed quantum mechanical rules of probabilities, rather than classical, Boolean or Bayesian ones. Specifically, this conclusion was reached on the basis of empirical evidences relating to non-commutativity (i.e. temporal order effects) in decision making, complementarity (interference between different decision path-ways, such as in binocular rivalry), super-positions (of alternative choices) and the bistable perception of ambiguous events, all of which feature in processes of choice and decision. Other instances mentioned were the so-called conjunctions fallacy, for whose resolution the authors in Pothos and Busemeyer (2013) resort to an expression in terms of a quantum state function. The "Linda paradox" of Kahanman and Tversky (1983), illustrating a falsely conceived dichotomy between her being a feminist and a bank-teller, is further quoted there as pertaining to the quantum domain. A related outcome of the identification with quantum mechanics is the derivation of a generalized Jarzynski equality and a generalized Crooks’ theorem for decision-making (Braun-Moya, Krüger and Braun 2018), in which the energy is replaced by the "utility function".
All these motivate the present authors to propose a formulation of mental activities in a fully quantum setting, touching also, but not solving (or intending to solve), the mind-body problem. What follows, then, is a quantum mechanical description of cognitive processes, with prospects of future extensions and empirical predictions, not as yet provided.

2. Formalism

We formalize these findings, by postulating three disjoint Hilbert spaces, together with their representatives (state functions) at any instant of time (t), consisting of a) the physical state of the neurons [ ϕ f ( n , t ) ] , b) the actual mental state involved in any cognitive process [ ψ p ( m , t ) ] , c) the physical state of the rest of the bodily organs, excluding the neurons [ χ k ( b , t ) ] . for N n e u neuronic degrees of freedom (DOF). Thus the state-function is written in a basis of a product:
Ψ f , p , k ( n , m , b , t ) = ϕ f ( n , t ) ψ p ( m , t ) χ k ( b , t ) ≡ Ψ i
with the vectorial sub-indexes f , p , k mapped onto the single vectorial index i and omission of time, for brevity.
There being a multitude of neurons and of bodily organs, each with its own multitude of DOF, the functions in a) and c) are representations of long product functions (assuming at this stage independence between the DOF), with the possibility of entangled super-positions of product functions taking, as bases, the following form:
ϕ f ( n , t ) = ϕ ^ f 1 ( q 1 ) ϕ ^ f 2 ( q 2 ) . . . ϕ ^ f N n e u ( q N n e u )
for N n e u neural DOF (the q’s). Analogous products form the bases for the function χ in c), involving the bodily organs numbering, say, N o r g and it will turn out after our introduction of the "alignment" later in this section that for the mental state functions represented in b) the bases are in correspondence with (in fact, duals of) those in the equation 2 above.
The employment of a quantum mechanical formalism for the first and third factors in the above need hardly to be commented on, insomuch as they relate to physical objects (essentially, molecules although of an immensely large number and of a complicated kind.) The following quote by the noted cognitive psychologist, R.N. Shepard is in order: "Human beings and all other animals are themselves physical systems and, as such, operate in compliance with physical laws" (Shepard 2004). A more explicit quote stressing the physics background of neural activities is due to Zurek (2014):
"... the higher mental processes all correspond to well-defined but, at present, poorly understood information processing functions that are carried out by physical systems, our brains. Described in this manner, awareness becomes susceptible to physical analysis. In particular, the process of decoherence is bound to affect the states of the brain: Relevant observables of individual neurons, including chemical concentrations and electrical potentials, are macroscopic. They obey classical, dissipative equations of motion. Thus any quantum superposition of the states of neurons will be destroyed far too quickly for us to become conscious of quantum goings-on: Decoherence applies to our own "state of mind"."
This is followed there by an evolutionary hypothesis :
"One might still ask why the preferred basis of neurons becomes correlated with the classical observables in the familiar universe. The selection of available interaction Hamiltonians is limited and must constrain the choices of the detectable observables. There is, however, another process that must have played a decisive role: Our senses did not evolve for the purpose of verifying quantum mechanics. Rather, they developed through a process in which survival of the fittest played a central role. And when nothing can be gained from prediction, there is no evolutionary reason for perception. Moreover, only classical states are robust in spite of decoherence and therefore have predictable consequences. Hence one might argue that we had to evolve to perceive classical reality."
[Though, not everyone shares this view. Thus T. Nagel (202) writes:"The existence of consciousness seems to imply that the physical description of the universe, in spite of its richness and explanatory power, is only part of the truth, and that the natural order is far less austere than it would be if physics and chemistry accounted for everything. If we take this problem seriously, and follow out its implications, it threatens to unravel the entire naturalistic world picture".]
What needs to be stated clearly is that the first factor-function ϕ , representing the neuronic state is the potential and actual repository of all human experiences. The Hilbert space for this factor is of course of a prodigiously large dimensionality: thus, by supposing just two possible states for every neuron (e.g., off and on), the Hilbert space of the first factor is 2 to-the-power of the number of neurons in the brain (estimated at 86 billion for humans). Furthermore, it seems possible to posit as a guiding idea, that a "virgin", un-experienced brain is composed of collective neuronic states in which diverse neurons are connected by the connecticomal architecture in the brain, possibly in an entangled form, but in essentially random, disorganized arrangements, i.e. with no regular correlations between individual neuron states in anyone collective state. An experience or external stimulus causes a collective state to become organized, regular, orderly in a way that resembles a paramagnetic-to-ferromagnetic phase-transition. Further experiences do the same for additional collective states, so that there is a one-to-one correspondence between the experiences and the number of orderly collective states, all this happening without regard to the energy of the states or to the prevailing temperature.
This model of cooperative transition is supported by researchers of an extensive observation on 40 retinal ganglion cells of salamander (Schneidmanet al 2006), (further confirmed for monkey eyes (Shlens et al 2014)), who found that a model of weakly correlated neuronic units is equivalent to the Ising model with pairwise coupling in Statistical Physics. Their conclusion is reached after noting that the observed frequency of collective spiking is many order of magnitudes larger than that arising from a model of independent neurons. Clearly, such coordinated spiking is a hallmark of a coherent collective neuronic state. Subsequent work in Tkacik et al (2014) on up to 200 retinal cells reinforced the model and led to the authors’ writing: "It is widely agreed that ....percepts, thoughts, and actions require the coordinated activity of many neurons in a network, not the independent activity of many individual neurons".
The quoted dictum of R.N. Shepard (2004) holds equally well for the third factor-function χ , that represents the bodily state after the mental process, such as uttering a sound (in speaking), moving a finger or taking a step. Admittedly these activities are more parsimoniously described classically, e.g., by Mechanics of muscular action, nevertheless, for consistency we choose to stay within a quantum formalism to formulate also bodily activities. In this formalism, the dynamics is represented as transitions between quantum states, of which later. Alternatively, a mental process may be followed not by a bodily change, but by a subsequent mental activity (like thinking, contemplating) or an altered feeling (e.g. being afraid or elated); in this case third factor stays constant and it is the middle state-factor that undergoes change(s). We now turn to this item, which, in its form, is essentially the newcomer in the theory (although the several cited works in the "Introduction" have paved the way to its inclusion into a fully quantum formulation.)
The middle factor-function ψ is a vector in the Hilbert-space of all mental states. In the theory this space is posited to be in a one-to-one correspondence with the actual, momentarily prevailing neuronic Hilbert space (and therefore possesses the same dimensionality as that). At any moment the mental state occupied (meaning, sensed by the person) is one that is the reflection of one, single neuronic state. If this neuronic state is the creation of a past experience, etc., that is to say ordered, the mental state will qualify as a conscious state; if however the mental state is aligned with a random, un-organized neuronic state, then the possessor of this mental state will be lacking consciousness at that moment.
Putting in numbers, if one associates the conscious states with thoughts in the mind, one may find an estimate for the the maximal number of conscious states achievable in a human lifetime, as 10 8 - 10 9 , based on 10k-100k thoughts per day. Now, this number is infinitesimally small compared to the astronomically large number of neuronic state. In an alternative estimation, if one may associate the collective coherent states with the meta-stable correlated states, the number of the former grows exponentially with the number of neurons N n e u , roughly as 0.1 x 10 0.03 N n e u , which again is much smaller than the number of neuronic states [This is based on Figure 10 in Tkacik et al(2014)]. How is it, then, that human beings are thoughtful most of the day? The answer seems to lie in the evolutionary hypothesis of Zurek (2014) quoted above.
The postulated neuron-consciousness correspondence has its analogue in the mapping, erstwhile put forward by John Maynard-Smith, between genotypes (the stored biological information) and phenotypes (functional or observed properties), allowing in that case for a redundancy (many-to-one correspondence) quantified in Greenbury et al (2016) and recently discussed critically in Sappington and Mohanty (2023). Our model of a single-mode alignment is a null hypothesis, which may be modified without essentially altering the main concept.
The above process of alignment between the state of consciousness and a neuronic state, or their duality, that is central to the theory, is just one of the transitions taking place and will be treated in the next section under "Dynamics of Cognition". Alignment between states in different Hilbert spaces is not without parallel, in as much as it forms the critical step in von Neumann’s quantum measurement theory, through the process of aligning the states of the microscopic observable with the states of the pointer (E.g., equation (2.5) in Leggett 1980). As is well known (e.g., Moreira-Almeida et al 2018), there are two main approaches to the mind-body problem: Pysicalism, according to which mind is a material or physical process, a product of the functioning of the brain. In contrast, dualism claims that mind is something other than, and could exist apart from, the brain. The here proposed alignment mechanism bridges between the two approaches.

3. Dynamics of Cognition

Life means changes (activity) (Marx 1867). Irreversible changes in physical systems are currently described by the Gorini-Kossakowski-Sudarshan-Lindblad (GKSL) formalism , which is an extension of the time-dependent Schrödinger equation for the density matrix of systems in interaction with their surrounding, such that the densities are non-negative and their trace sums to unity at all times (Gorini et al 1976, Lindblad 1976). The density matrix arises as the components of the density operator:
ρ ≡ | Ψ > < Ψ |
being a function of time.
The range and conditions of validity of the GKSL-equation have been the subject of numerous investigations, in which the equation is derived for a microscopic system coupled to a macroscopic environment. In most of the treatments this coupling is postulated as weak, in the sense of its lying below the energy spread of the system’s Hamiltonian. In the derivation of the GKSL-equation in Pearle (2012), this requirement is not noted. But in Kosloff (2013) the weak system-bath coupling limit is explicitly postulated, additionally to a thermalization time that is slower than the inverse energy spread in the system. In this limit, the system-environment interaction energy may be neglected. The uniqueness of the Lindblad formalism was studied in Barra and Liedo (2018). In an extensive review by Rivas and Huelga (2018), one finds a sally in their section 7.3 to the strong coupling, non-Markovian regime with a generator of the Lindbladian form that preserves positivity.
We recall Lindblad’s equation for the time varying density of states operator ρ as being of the following form:
∂ ρ ∂ t = − i ℏ [ H , ρ ] + ∑ n γ n ( L n ρ L n † − 1 2 ( L n † L n ρ + ρ L n † L n ) )
in which the gamma’s are cofactors and L n are the Lindblad operators for a set of n’s. We now postulate having a single summand in the second term, conventionally named "Dissipator" D ( ρ ) , and rewrite this in the bra-ket form as:
D ( ρ ) ≡ Ω L ∑ i , j P j P i [ | Ψ i > < Ψ j | ρ | Ψ j > < Ψ i | − 1 2 ( | Ψ j > < Ψ i | Ψ i > < Ψ j | ρ + ρ | Ψ j > < Ψ i | Ψ i > < Ψ j | ) ]
with the P i in the cofactors to be specified presently. The circular frequency Ω ( ≡ 2 π f , with f the frequency) characteristic of the system is inserted, so as to make L , the strength of the system-environment coupling, dimensionless.
The "first application" of the GKSL formalism in cognitive psychology was made in Asano et al. (2012) for decision problems of the type of the prisoner’s dilemma. In the present work we formalize the time history of a general mental process by the same method. The task is to describe the following chain of processes: I) perception, II) bringing the mental state to a conscious awareness of a perception, III) activating some bodily process consequent upon the awareness. Alternative to this flow of events is that of contemplation or deliberation, in which case III is absent and II is followed by another conscious mental state, say II’. Recall, or pure retrieval to memory is effected by the interaction of I with II, again leading to a new conscious state, i.e. replacing II by II’. In an instinctive action, essentially equivalent to Kahanman’s "fast thinking" (Kahanman 2013), a change in III (→ III’) proceeds with the omission of II. Actually, the perception process in I is preceded by III, e.g. by the seeing, or hearing, or sensing by any other means, some happening in the external world. The two modes of mental processes, extensively treated in Sloman (1996) and Evans (2003) will be treated below in Section 4.
By a simple device on the Dissipator as given in Eq. 5, one can guide the course of transitions of a quantum system, when connected to a macroscopic apparatus, from an arbitrary initial quantum state (pure or mixed) to any arbitrary final state (also pure or mixed). This involves putting P i = 0 for all states that are absent in the final state and letting P i = 1 for the state to which Ψ i converges at long times.(In numerical work, vanishing values for P i yield infinities eventually cancelling out, so one must put infinitesimally small values for the nominally vanishing parameters.) A formal theory for quantum transitions induced by Lindblad operators (as above in equation 5) has been proposed in Englman and Yahalom (2023). There the P i ’s take the values of the Born probabilities, and their origin was attributed to a non-Markovian process in the coupling between the measured system and the measuring apparatus. The interplay between these two was previously posited for quantum transitions (again) by Zurek (1991):
"The preferred basis of the detector — or, for that matter, of any open quantum system — is selected by the dynamics. Not all aspects of this process are completely clear (added italics), but the detector-environment interaction Hamiltonian certainly plays a decisive role. In particular, when the interaction with the environment dominates, the reduced density matrix ends up being diagonal in the eigenspace of an observable A [on the pointer (added by us for clarity)] that commutes with the interaction Hamiltonian, [ A , H i n t ] = 0 . This commutation relation has a simple physical interpretation: It guarantees that the pointer observable A will be a constant of motion of the interaction Hamiltonian. Thus when a system is in the eigenstate of A, interaction with the environment will leave it unperturbed." We now specify the procedure for each of the above mental processes:
(I)
Perception, change in the neuronic state: neuronic state index in Eq 1 changing from f to f ′ , with other indices invariant.
(II)
Consciousness, recognition of neuronic change: p (aligned to f) → p ′ (aligned to f ′ ).
(III)
Bodily activity: k → k ′ ⟶ k " . . . . .
(IV)
Instinctive action: Process I → process I I I without intervention of process I I .
(V)
Other unconscious activity, including dreaming and one satisfying a Turing test: Process I → process I I I without intervention of process I I .

4. An Illustration

We assume that the density of states ρ for the neuronic states Ψ i in equation (1) may be written at some initial time t = − ∞ in a diagonal representation (and, similarly, for the analogous functions of the consciousness). To mimic the effect of an experience starting at t = 0 on ρ , we suppose that one of the factors, say the first, in Ψ i represents a partially disordered neuronic state, with the rest of the factors spanning any arbitrary number of ordered states, bearing the imprint of previous sense impressions. Suppose now, further, that the new experience changes this first factor into an ordered neuronic state. If the two, initial and final, neuronic states are labelled respectively ρ i n and ρ f i n , this simply means that the occupation numbers (probabilities) 1 and 0 for ρ i n and for ρ f i n are interchanged due to the new experience. In the present theory this transition is driven by a Lindblad operator.
In Figure 1 we illustrate the working of the Lindblad operator for a toy-example involving only a paltry of five neuronic states (instead of the myriad in a realistic situation). The occupation probabilities of the neuronic states are shown by a green curve line for the initially excited state, being replaced upon some experience by the ultimately occupied component ρ f i n , whose probabilities are drawn in red. This process is then followed, after a delay of about one-tenth of a second, by the acquisition of an awareness (consciousness) of the new neuronic state, with the respective occupation probabilities drawn horizontal initial and full final blue lines, for before and after the acquisition of awareness. The cognitive delay 0.1 s is in line with the empirical observations, "the Libet delay" in Libet et al. (1983). As an outcome, the actual state of consciousness is aligned with the actual neuronic state (i.e., identical in their respective Hilbert-spaces).

5. The Coupling

At the backbone of the theory lies the role of the Lindbladian term, which primes each of the stages I-IV, bringing about the transitions. The source of this term as arising from an interaction between the neuronic framework and the surrounding is not identified at this stage, but seems to reside in the unity of the neuronic system with its broad surrounding. Such unity has been called into play for the interpretation of the quantum mechanical measurement process already by N. Bohr (1958): "The answer that we get is built up from the combined interaction of [the observer’s] state and the object of interrogation". and more recently in several works: Thus one may find from John Bell that "The answer that we get is built up from the combined interaction of [the observer’s] state and the object of interrogation". (Bell (1990); from Asher Peres "A measurement both creates and records a property of the system" (Peres 1998), and further by Anthony Leggett: "...under these conditions the macroscopic apparatus, and more generally any part of the macro-world which has suffered changes in the course of the measurement process, does not end up in a state with definite macroscopic properties at all,... This change in the course of a measurement affects also the environment outside the observed system" Leggett (1980). Lately, Zurek coined the term "Einselection" for the environment-assisted alignment of the state of the measuring apparatus with the property of the system to be investigated. His approach is expressed by the following excerpts quoted from his recent review in Zurek (2022):
"... Information transfer — nature of the coupling to the measuring device — determines [the] preferred set...These states are (ein)selected by the dynamics of the process of information acquisition...Pointer states — terminal states for quantum jumps — are determined by the dynamics of information transfer. They define the outcomes independently of the instantaneous reduced density matrix of the system and of its initial state. Fixed outcomes define events, and call for the derivation of probabilities."

6. Observational Impacts

6.1. Memory Recall Experiments

There are a number of experimentally observed effects in psychological behavior possessing quantitative description that a theory of consciousness is called upon to explain. We list these now, noting that they are many decades old and that, yet, they are subject to dispute.
First is Shepard’s "Generalized Universal Law" for the relationship of the distance between a pair of items and the probability that the pair will be perceived as similar (Shepard 1958, Shepard 1987, Shepard 2001 Shepard 2004). Specifically, this probability is empirically found to be a negative exponential function of the distance between the pair of items, with the distance (e.g., the variation of plume color in a bird) in general defined in a psychological space. (Shepard 1987, Shepard 2011). An extension of the law was more recently proposed, so as to hold also for multiple subsequent stimuli with arbitrary representational structure. (Tenenbaum and Griffiths 2001). A further generalization in terms of an algorithmic information distance is due to to Chater and Vitányi (2003).
Another remarkable development, also due to Shepard and summarized in Shepard (2004), is that the time required to determine that two things are identical, in spite of their apparent difference, linearly increases with their transformational separation ("distance") in the space of possible positions. On the other hand, the time required to determine that two things are different, despite their apparent similarity, decreases non-linearly, upward concavely as function of their separation in the space of possible objects. As the guiding principle for clustering together in human perception of widely different stimuli (sources of experience), Shepard (2001) proposed that, "[these] generally form a connected local region in the space of possible objects, despite appreciable differences among individual objects of that kind in size, shape, position, motion, or color". We shall reformulate this broad "juxtaposition" idea of Shepard, originally pertaining to some undefined space (his "appropriate representational space") to apply to the Hilbert spaces that constitute the basic elements of the present theory. Passing from a continuous representation of different stimuli (as in rotationally different stimuli) to those that differ in a discontinuous, discrete way, Shepard notes that one would still obtain an exponential type of fall-off of generalization with distance, where distance is now defined in terms of the sum of the weights of the features that differ between the two objects or, if the features are all equal in weight, simply in terms of the number of differing features.
Noting the above two apparently discordant assertions by Shepard, [that the reaction time (RT) for affirmative response increases linearly with distance, whereas on the contrary, the discriminatory RT falls off according to a decreasing, concave-upward function of distance between stimuli in representational space], we shall now demonstrate how in the present formulation of transitions the two findings may be reconciled.
As a preliminary, one bears in mind that quantitatively the RT differs by a so-called "response time" from (is less than) the actual experimental delay time (the time that has elapsed between the presentation of the task to the subject and the instant of the subject giving his decision). Then, for the explanation of affirmative responses, we simply utilize a protocol due to Sternberg (Sternberg 1966), of which more later, which predicates that for a decision involving several items, the system declares its decision after scanning all items, and not at any interim stage, thereby resulting in a RT that is proportional to the number of items. If we now conjecture that the distance in Shepard’s experiments is represented by the number of states in the Hilbert spaces, the proportionality of RT to the distance follows for affirmative decisions.
When an affirmative answer is not forthcoming, as when the subject discriminates between the presented and the task items, the decision time is composed of two times; the first, during which the subject scans all the relevant items, as in the case of an affirmative decision, but now reaching a negative result followed by a further search. Such a search had been investigated some long time ago, e.g. for discriminating sounds as functions of both frequencies and intensities. It was found, e.g., by Chocholle (1940), that the discrimination time decreases as some inverse power of the sound intensity, with the exponent varying between − 0.50 and − 0.25 (with a dependence on the sound frequencies). Other experiments (both pre-dating and post-dating Chocholle’s), including also those with light, gave similar results. A detailed theoretical study (Luce and Green 1972) interpreted the stage of decision making by the neural system as one at which the incoming pulse-signals in the brain reach some saturation. A stochastically varying mode was analyzed which then in some limiting approximation led to the result for the mean reaction time
R T = 2 a r r i v a l t i m e o f t h e s i g n a l s S o u n d i n t e n s i t y
The intuitive meaning of the result, derived by the authors of (Luce and Green 1972) is that when the intensity is large, proportionately less time is needed to saturate the system with information. The inverse power relation in the above expression is to be noted, agreeing with the empirical findings.
In a further series of studies of the latency time of short term memory, pioneered by S. Sternberg (1966), subjects were first given a set of terms or symbols and then tested by a further term or symbol, and asked whether or not this was one of the test terms? Remarkably, their mean reaction time (RT) increased linearly with the length of the sequence. The linearity and slope of the reaction time was hypothesized by the author as implying the existence of an internal serial-comparison process with an average rate of 25-30 symbols per second. Similar rates were found for positive and negative answers by the subjects, which finding led the author to his theory that in short-term memory experiments the subject scans all preliminarily presented items, before making a response. Subsequently, some discrepancies from linearity were noted, e.g., when the experiments were repeated with differing ordering of the test terms, as in Derosa and Morin (1970), with Sternberg (2016) replying with a vigorous defence of his position.

7. Theoretical

7.1. Short-Term Recall Experiments

Saul Sternberg’s serial exhaustive scanning paradigm, proposed for the explanation of short -term memory experiments reconciling positive and negative responses, implies an information transfer between that part of the collectives of neuronal states which was created by the pre-presented items and the consciousness state in the brain that elicits the response. Formally, in the dual Hilbert space model, this may be represented in the most transparent way in terms of a coupling between the neural and consciousness spaces through interaction terms in the Hamiltonian, written in a second quantization description, in the form, n i n j † c i c j † for which the letters and their daggered version in n , n † , c , c † represent respectively destruction and creation operators in the neuronic and consciousness Hilbert spaces. In physical terms, the information transfer is effected by some further entities, whose nature is not known as of now, these being the cognitive counter-parts of mRNA featuring in the the central dogma of biology for the formation of peptides from DNA. In this the translational elongation is achieved through the scanning of the full length of mRNA by the ribosome, this being done at a rate of abot 1.5 codon per second (Heinrich and Rapoport 1980). It stands to reason that through some entities Nature employs the same stratagem for the analogous scanning in the brain for the information transfer, this being done at a rate of items per second higher by a factor of about 20. (The factor is likely due to the correspondingly higher complexity along a linear dimension in the brain, in comparison to other bodily organs).

7.2. Long-Term Memory Results

By the time that the recall experimentation takes place at some instant after the short-term memory times (this being of the order of 10 ms), as in the Shepard type of investigations of identification or discrimination between tests and probe items, the neuronic wave functions have changed their character, due to the decohering interaction with the environment, from the coherent entangled form of the foregoing section, to mixed quantum states. These are now subject to a diffusive process, whose time dependent occupation probability was given in Eq. [13] of Shepard (1987) as function of the distance D i k = | x i − x k | between test and probe items and of time t by the Gaussian
P r i k ( t ) = 2 π V t e − ( x i − x k ) 2 2 V t
in which V is a diffusion constant. A convolution integration is then shown by Shepard (1987) to lead to a negative exponential dependence of the time integrated probability for the affirmative identification between the test and probe items as function of their distance. This establishes the theoretical basis of Shepard’s "Universal Law of Generalization".
The foregoing Gaussian (modified, as described below) is now proposed as the criterion for the time (RT)-distance relation found in identification-discrimination experiments (resulting in a positive-negative response respectively), distance being a measure of dissimilarity between sample and probe. For a qualitative understanding one notes that in a diffusion process along an infinite line (and similarly for higher dimensions) starting at the origin, the occupation probability at some distance away at first increases, as the diffuser makes its way randomly away from the origin to this point, but then decreases as the diffuser proceeds to farther away. It is now postulated that as the growing occupation probability exceeds a certain significantly large critical value (to be denoted p 0 , meaning that P r → p 0 + 0 ) a recognition is attained and likewise when it later again decreases to beyond a critical small value p 1 (which is different from the former critical value) of the occupation probability, P r → p 1 − 0 a discrimination (negative response) has come into force. In the dual Hilbert space model of this article, the diffusive motion takes place among the locations of the states in the neural function space, with the consciousness’ Hilbert space "contacted", aligned whenever the critical occupation values are in place. To account for the empirical finding that the reaction time (RT) for affirmative response increases linearly with distance, whereas on the contrary, the discriminatory RT falls off according to a decreasing, concave-upward function of distance between stimuli in representational space, we hypothesize a time dependent diffusion parameter V ( t ) in Shepard’s Gaussian probability function, replacing his constant V. This assumed variable diffusion parameter is such that the width of the Gaussian, instead of steadily increasing as in standard diffusion theories, first increases and then drops off. The physical meaning of this is that the basic diffusion step is not constant, but rather diminishes as the scanning proceeds. Variable diffusion steps of a different kind are known as Levy-walks.
Examples of the postulated widths are depicted in Figure 2. Algebraically they take the form:
R o o t − m e a n − s q u a r e − w i d t h = 2 t t 0 2 t 2 + t 0 2
Affirmative answers for identifying probes slightly dissimilar from samples take place when the diffusional probability reaches a critical value p 0 . The two curves in Figure 3, with the choices p 0 = 0.5 in blue and p 0 = 1 in red show reaction times (RT) in ms, as function of distance. A linear relation is shown with broken lines, recalling Shepard’s paradigmatic findings, that the reaction time (RT) for affirmative response increases linearly with distance.
At a contrary extreme of large dissimilarities the RT for discrimination takes large values. These are shown in Figure 4, again with two choices of the p 1 criterion, p 1 = 0.5 , and 0.1 meaning that when the diffusive occupation probability decreases down to this value, the subject concludes that there is no similarity. Due to the time dependent width, this discriminatory RT falls off according to a decreasing, concave-upward function of distance between stimuli and probe in representational space, as found empirically by Shepard (1987). Qualitatively, the curves are robust in both parameters, p 1 and the t 0 .

8. Conclusion

Mental states are postulated to be represented by quantum states, thereby constituting a Hilbert space of their own, distinct from the physical Hilbert-space of the neural network, but being a mirror image (dual) of the latter. Thus, any actual mental state is at any time in correspondence with (aligned to) a neural state, this being a particular vector in the neural Hilbert space. The neural space is under perennial development under external experiences, such that out of the multitude of initially disordered neuronic set of states ordered, coherent neuronic sets are formed, one at a time, for each external stimulus. Then the states of mental awareness (consciousness) are associated with alignment to the ordered neuronic quantum states. Changes in both the neuronic and mental states are effected by a Gorini-Kossakowski-Sudarshan-Lindblad formalism, originally formulated to describe changes (dissipations) of quantum systems induced by a macroscopic environment. Several components in the postulated theory (as e.g., the quantum formulation of mental states, the transition to ordered neuronic sets) are based on experimental evidence, as documented by the publications (and quotes) cited in this article, but their sawing together as attempted here to represent generic mental processes as fully quantum-like is novel, and requires factual confirmation.
Two kinds of memory experiments, for short and long term memory re-calls, had led S. Sternberg and R. N. Shepard, respectively, to semi-quantitative descriptions regarding cognitive processes in the brain. These are interpreted within the dual Hilbert space model of this paper, coupled with a proposal of a copying process analogous to the DNA-to-peptide translation in biology and, further, through a diffusive process with time variant decrease of the diffusion parameter. The latter leads to an experimentally verifiable prediction of a time-asymptotic narrowing of the probability-distribution of recalls.

Conflicts of Interest

The authors have no competing interest.

References

  1. Aerts,D., Aerts Argu’elles,J., Beltran, L., Geriente1, S., Sassoli de Bianchi1, M., Sozzo, S. and Veloz, T. (2019) Quantum entanglement in physical and cognitive systems: A conceptual analysis and a general representation. European Phys. J. Plus 134, Article 493, pp.1-20.
  2. Asano, M. , Ohaya, M.,Tanaka, Y., Basieva, I. and Khrennikov, A. (2011) Quantum-like model of brain’s functioning: Decision making from decoherence. J. Theoretical Biol. 281 pp.56-64.
  3. Asano, M. , Ohya, M., Tanaka, Y. and I. Basieva,I.(2012) On application of Gorini-Kossakowski-Sudarshan-Lindblad equation in Cognitive Psychology. Open Systems & Information Dynamics 18(1)pp. 55-69.
  4. Atkinson, S., ed. (2011) The Philosophy Book (DK Publisher Dorling Kindersley, London) p. 227.
  5. Baars, B.J. (1988) A Cognitive Theory of Consciousness. (Cambridge University Press, Cambridge, U.K.
  6. Barra, F. and Liedo, C. (2018) The smallest absorption refrigerator: The thermodynamics of a system with quantum local detailed balance. European Journal of Physics Special Topics 231-246.
  7. Bell, J. (1990) Against measurements. Physics World, 3 pp.33-41.
  8. Block, N. (2009) Comparing the major theories of consciousness, in M. Cazzaniga, ed. The Cognitive Neuroscience (MIT press, Cambridge MA) pp.111-122.
  9. Bohr, N. (1958) Atomic Physics and Human Knowledge. (Wiley, New York).
  10. Bruckmaier, G., Krauss, S., Binder, K., Hilbert, S. & Brunner, M. (2021)Tversky and Kahneman’s cognitive illusions: Who can solve them, and why? Front. Psychol., Article 584689, pp.1-23;
  11. Busemeyer, J.R. and Bruza, P.D. (2012) Quantum Models of Cognition and Decision. (Cambridge University Press, Cambridge UK).
  12. Chater, N. and Vitányi, P. M. B. (2003) The generalized universal law of generalization. Journal of Mathematical Psychology 47 (3) pp.346–369. [CrossRef]
  13. Chocholle, R. (1940) Variations ds temps de réactions audits en fonction de l’intensit’e a diverse frequences. L’Année Psychologique 41 pp.65-124.
  14. Dehaene, S. and Nacache, L. (2001) Towards a cognitive science of consciousness: basic evidence and a workspace framework. Cognition 79 pp.1-37.
  15. Englman, R. and Yahalom, A. (2023) A Lindbladian-induced alignment in Quantum measurements. Foundations of Physics, 53 pp.9-31.
  16. Evans, J.St.B.T. (2003) In two minds: Dual process accounts of reasoning. Trends in Cognitive Sciences, 7 pp.454-459.
  17. Farthing, G. (1992) The Psychology of Consciousness. (Prentice Hall, New York), ISBN 978-0-13-728668-3.
  18. Gorini, V. , Kossakowski, K. and Sudarshan,E.C. G. (1976) Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 17pp.821-5.
  19. Grau-Moya, J. , Krüger, M. and Braun, D.A. (2018) Non-equilibrium relations for bounded rational decision-making in changing environments. Entropy, 20 pp.1-14.
  20. Greenbury, S. F. , Schaper, S., Ahnert, S. E. and Loui, A.A. (2016) Correlations greatly increase mutational robustness and can both reduce and enhance evolvability. PLOS Computational Biology 12 e1004773.
  21. Hameroff, S. and Penrose, R. (2014) Consciousness in the universe: A review of the ‘Orch OR’ theory. Physics of the Life Reviews 11 (1) pp. 39-78.
  22. Heinrich, R. and Rapaport, T.A. (1980) Mathematical modelling of translation of mRNA in Eucaryotes; Steady states, time-dependent processes. J. Theor. Biol. 86 pp.279-313.
  23. Hu, H. and Wu, M. (2010) Landscape and Future Direction of Theoretical & Experimental Quantum Brain/Mind/Consciousness Research. Journal of Consciousness Exploration and Research 1 (8) pp.888-897.
  24. Kahneman, D. (2013)Thinking, Fast and Slow.(Columbia, Farrar, Straus and Giroux, Columbia USA).
  25. Khrennikov, A. and Asano, M. (2020) A Quantum-like model of Information processing in the brain. Applied Sciences - Basel 10(2) pp.707-17, doi.org/10.3390/app10020707.
  26. Khrennikov, A. (2019) Classical and quantum mechanics on information spaces with applications to cognitive, psychological, social and anomalous phenomena. Foundations of Physics, 29 pp. 1065-98.
  27. Kosloff, R. (2013) Quantum Thermodynamics: A dynamical viewpoint. Entropy 15 (12) pp. 2100-18; ArXiv:1305.2268.
  28. Lamme, V.A. (2006) Towards a true neuronic stance on consciousness. Trends Cogn. Sci. 10 pp.494–501.
  29. Leggett, A.J. (1980) Macroscopic quantum systems and the quantum theory of measurement. Suppl. Progress Theor. Phys. 69, 80-96.
  30. Levine, L. (1981) Materialism and Qualia: The explanatory gap. Pacific Philosophical Quarterly, LXIV (4) pp. 354-361.
  31. Libet, B., Gleason,C.A., Wright, E.W. and Pearl, D.K., 1983 Time of conscious intention to act in relation to onset of cerebral activity (Readiness-Potential) - The unconscious initiation of a freely voluntary act. Brain 106 (3) pp.623-642. [CrossRef]
  32. Lindblad, G. (1976) On the generators of quantum dynamical semigroups. Commun. Math. Phys., 48 pp. 112-30.
  33. Link, M. (2022) Everything and more: the prospects of whole brain simulation, J. Philosophy 1908 pp. 444-459.
  34. Low, P. (2012) The Cambridge Declaration on Consciousness, Ed. J. Panksepp et al.
  35. Luce, R. D. and Green, D. M. (1972) A neural timing theory for response times and the psychophysics of intensity. Psychological Review 79 pp. 14-57.
  36. Marx, K. (1867) "...the life processes of definitive individuals, as they are in reality,... acting and materially producing." Das Kapital : Kritik der politischen Oekonomie. Hamburg : Verlag von Otto Meissner, ETH-Bibliothek Zürich, Rar 6494, doi.org/10.3931/e-rara-25622.
  37. Moreira-Almeida, A, de F. Araujo, S. and Cloninger C.R. (2018) The presentation of the mind-brain problem in leading psychiatry journals. Braz. J. Psychiatry, 43(3) pp.35-42.
  38. NEB (1980) New Encyclopaedia Britannica. 3 p.251.
  39. Pearle, P. , (2012)Simple derivation of the Lindblad equation. European Journal of Physics, 33(4), 805-22.
  40. Peres, A. (1988) Quantum Theory: Concepts and Methods. (Kluwer Academic, Norwell MA).
  41. Pothos, E.M. and Busemeyer,J.R. (2013) Can quantum probability provide a new direction for cognitive modeling? Behav. Brain. Sci. 36 pp. 255-274.
  42. Rivas, A. and Huelga, S. F. (2012) Open quantum systems. An introduction, ArXiv:104.5242v2 9Feb2012 pp. 1-100.
  43. Nagel, T. (2012) Mind and Cosmos: Why the Materialist Neo-Darwinian Conception of Nature Is Almost Certainly False.(Oxford University, Oxford,2012) p.35.
  44. NEB (1980) New Encyclopaedia Britannica, 3 p.251.
  45. Pearle, P. , (2012) Simple derivation of the Lindblad equation. European Journal of Physics, 33(4), 805-22.
  46. Peres, A. (1988) Quantum Theory: Concepts and Methods. (Kluwer Academic, Norwell MA).
  47. Pothos, E.M. and Busemeyer, J.R. (2013) Can quantum probability provide a new direction for cognitive modeling? Behav. Brain. Sci. 36 pp. 255-274.
  48. Rivas, A. and Huelga, S. F. (2012) Open quantum systems. An introduction. ArXiv:104.5242v2 9Feb2012 pp. 1-100.
  49. Rosenthal, D. (2005) Consciousness and Mind. (Oxford University Press, N.Y.
  50. Sappington, A. and Mohanty, V. (2023) Probabilistic genotype-phenotype maps reveal mutational robustness of RNA folding, spin glasses, and quantum circuits. ArXiv:2301.01847 (05 Jan 2023).
  51. Schneidman, E. , Bery II, M.J., Segev, R. and Bialek, W. (2006) Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440 pp. 2007-201.
  52. Seth, A.K. and Bayne, T. (2012) Theories of consciousness. Nature Rev. Neuroscience 23 pp. 439-455.
  53. Shepard, R. N. (1958) Stimulus and response generalization: Deduction of the generalization gradient from a trace model. Psychological Review, 56 (4) pp. 242–256. [CrossRef]
  54. Shepard, R.N.(1987) Towards a universal law of generalization for psychological science. Science 237 pp. 1317-1323.
  55. Shepard, R.N. (2001) On the possibility of universal mental laws: A reply to my critics. Behavioral and Brain Sciences. 24 pp. 712-748. [CrossRef]
  56. Shepard, R.N. (2004) How a cognitive psychologist came to seek universal laws.Psychonomic Bulletin Review. 11 (1) pp. [CrossRef]
  57. Shepard, R.N. (2011) Perceptual-cognitives universals as reflections of the world. Behavorial and Brain Sciences 24 pp. 581-601.
  58. Sloman, S.A. (1996) The empirical case for two systems of reasoning. Psychological Bulletin pp. 119 3-22.
  59. Sternberg, S. (1966) High-Speed scanning in human memory. Science 153 pp.652-654.
  60. Sternberg, S. (1969). Memory-scanning: Mental processes revealed by reaction-time experiments. American Scientist, 57, 421–457.
  61. Sternberg, S. (1975) Memory scanning: new findings and current controversies. Quart. J. Exp.Psychol. 27 pp.1-32. [CrossRef]
  62. Sternberg, S. (2011) Modular processes in mind and brain.Cognitive Neuropsychology 28 pp. 156-208, PMID 22185235.
  63. Sternberg, S. (2016) In defence of high-speed memory scanning. Quarterly Journal of Experimental Psychology 69(10) pp. 2020-2075.
  64. Tenenbaum, J.B. and Griffiths, T.L. (2001) Generalization, similarity, and Bayesian inference. Behavioral and Brain Sciences 24 pp. 629-40.
  65. Tkačik, G. , Marre, O., Amodei, D., Schneidman, E., Bialek, W. and. Berry II, M.J. (2014) Searching for collective behavior in a large network of sensory neurons. PLoS Comput Biol. Jan. 2014. [Google Scholar]
  66. Tononi, G. and Edelman, G.M. (1998) Consciousness and complexity. Science 282 (5395) pp. 1846-51 , doi: 10.1126/science.282.5395.1846. [CrossRef]
  67. Tversky A. and Kahneman, D. (1983) Extensional versus intuitive reasoning: the conjunction fallacy in probability judgment. Psychol. Rev. 90 pp.293–315. [CrossRef]
  68. Wang, D. et al. (2013) The potential of using quantum theory to build models of cognition. Topics Cogn. Sci. 5 pp.672-688.
  69. Wigner, E.P. (1961) Remarks on the mind-body question, in A Scientist speculates, An anthology on partly baked ideas. (Heinemann, London).
  70. Zurek, W.H. (1991) Decoherence and the transition from quantum to classical. Physics Today, October 1991, pp.36-44.
  71. Zurek, W. (2014) Quantum Darwinism, classical reality, and the randomness of quantum jumps. Physics Today, October 2014, 67 pp.44-50.
  72. Zurek, W. H. (2022) Quantum theory of the classical: Einselection, Quantum Darwinism and Extantons. Entropy 24 (11) pp. 1529-1618, doi.org/10.390/e24111520.
Preprints 106715 g001
Figure 1. Mental state probabilities: The initially (at negative times) excited neuronic state (shown for positive times in green) with low information content is replaced upon a new experience (taking place at t = 0 ) by a neuronic state of higher information content whose occupation probability is drawn with a red line. Subsequently, after about 0.1 s , the awareness of the new experience develops (as shown with the blue curve) in exchange from the unaware state (whose occupation probability is drawn with a horizontal blue line). The continuous transitions are brought about with Lindblad operators coupling five states.
Figure 1. Mental state probabilities: The initially (at negative times) excited neuronic state (shown for positive times in green) with low information content is replaced upon a new experience (taking place at t = 0 ) by a neuronic state of higher information content whose occupation probability is drawn with a red line. Subsequently, after about 0.1 s , the awareness of the new experience develops (as shown with the blue curve) in exchange from the unaware state (whose occupation probability is drawn with a horizontal blue line). The continuous transitions are brought about with Lindblad operators coupling five states.
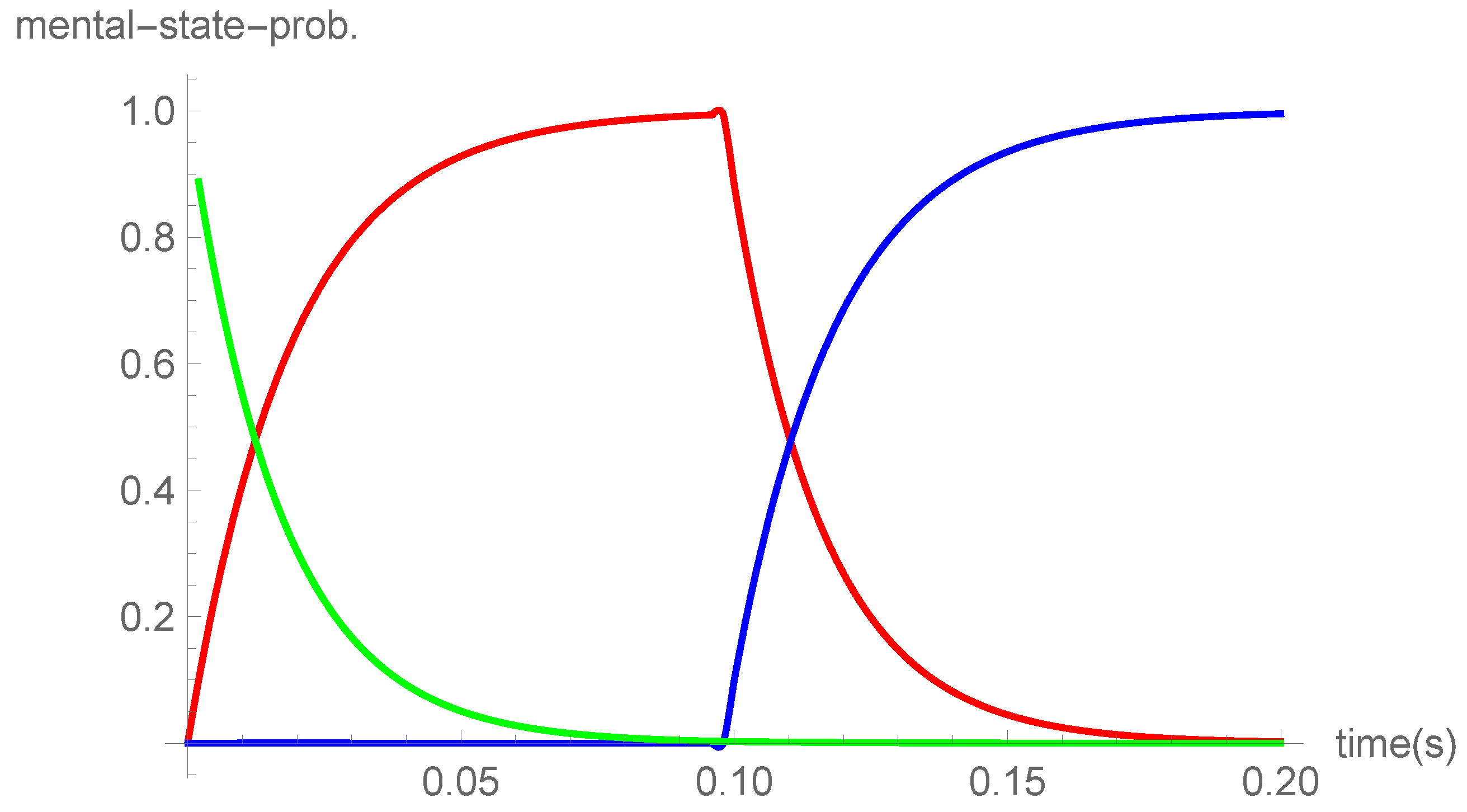
Preprints 106715 g001
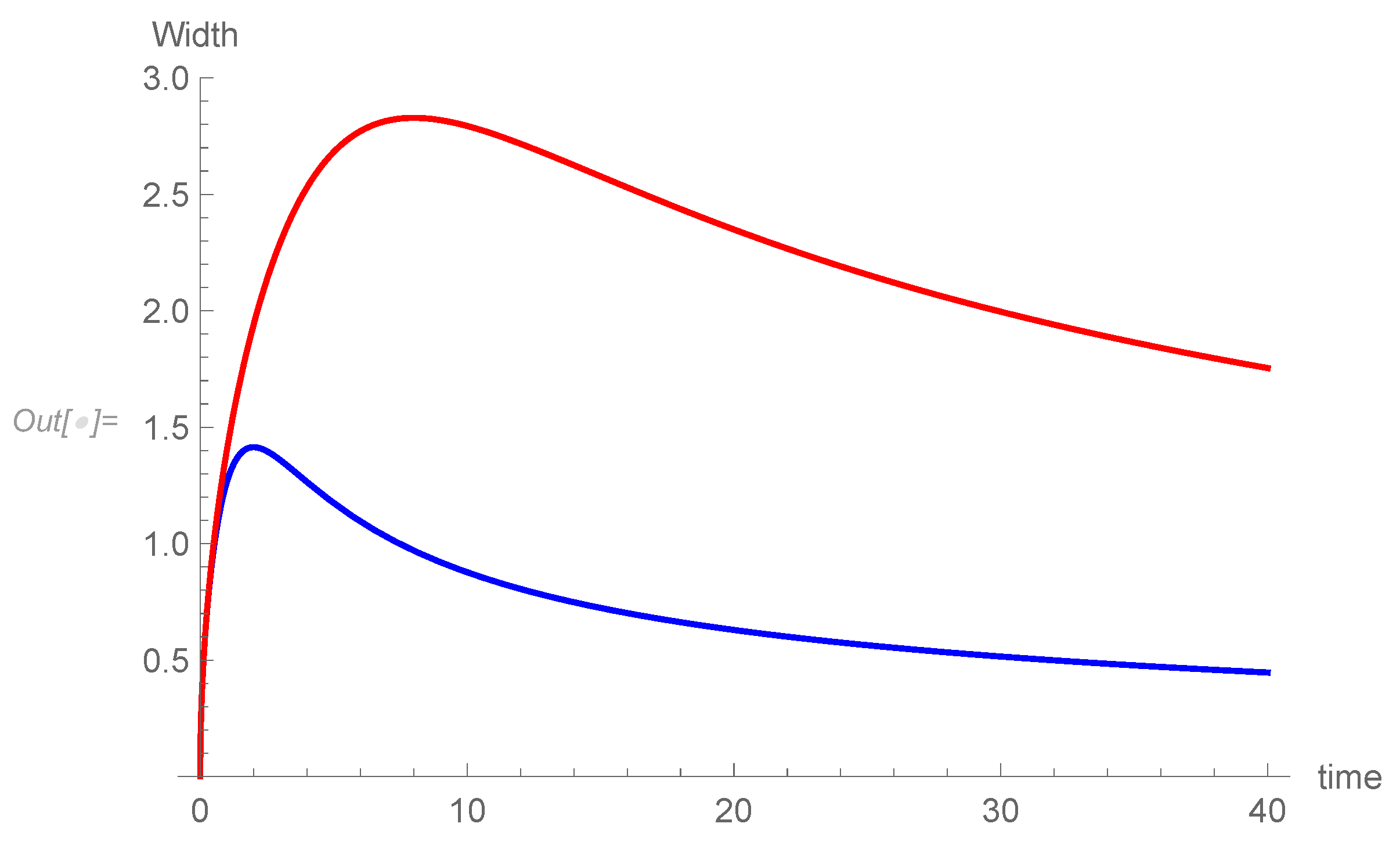
Preprints 106715 g002
Figure 2. Postulated root - mean -square - width in diffusion as function of time in ms. Parameters in Eq. 8 are as follows. Blue: t 0 = . 05 ; Red : t 0 = . 1 .
Figure 2. Postulated root - mean -square - width in diffusion as function of time in ms. Parameters in Eq. 8 are as follows. Blue: t 0 = . 05 ; Red : t 0 = . 1 .
Preprints 106715 g002
Preprints 106715 g003
Figure 3. Early reaction times in units of milliseconds for confirmation. Blue: p 0 ( c r i t i c a l p r o b a b i l i t y d e n s i t y ) = 0.5 , t 0 = 2 ; Red : p 0 = . 1 , t 0 = 8 . A linear relation is shown with broken lines for comparison.
Figure 3. Early reaction times in units of milliseconds for confirmation. Blue: p 0 ( c r i t i c a l p r o b a b i l i t y d e n s i t y ) = 0.5 , t 0 = 2 ; Red : p 0 = . 1 , t 0 = 8 . A linear relation is shown with broken lines for comparison.
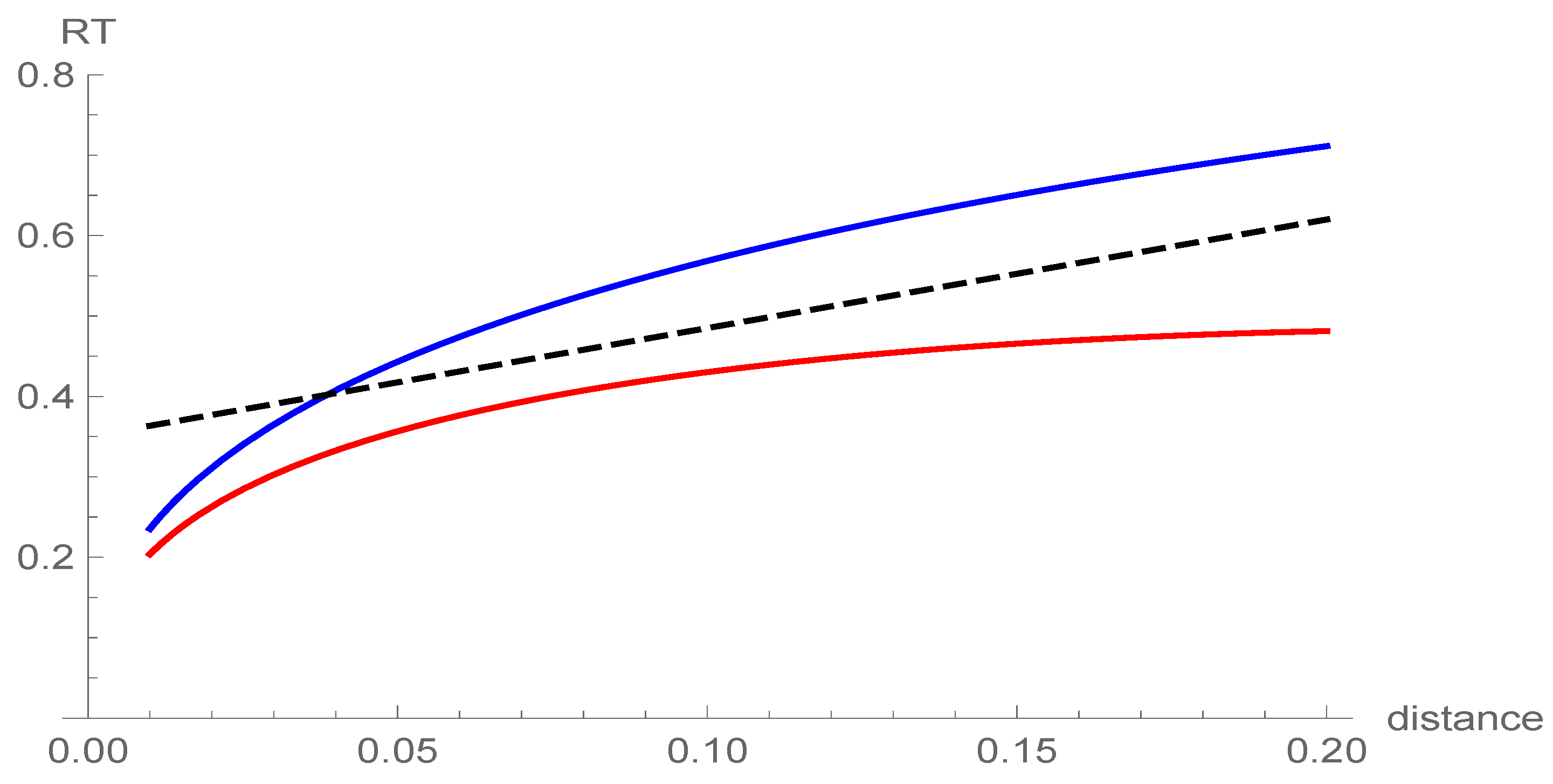
Preprints 106715 g003
Preprints 106715 g004
Figure 4. Reaction times for discrimination. Parameters in equation Figure 2: p 1 ( c r i t i c a l p r o b a b i l i t y d e n s i t y ) = 0.05 , t 0 = 2 blue; p 1 = 0.1 , t 0 = 8 (red). An inverse power of time curve is shown by broken lines for comparison.
Figure 4. Reaction times for discrimination. Parameters in equation Figure 2: p 1 ( c r i t i c a l p r o b a b i l i t y d e n s i t y ) = 0.05 , t 0 = 2 blue; p 1 = 0.1 , t 0 = 8 (red). An inverse power of time curve is shown by broken lines for comparison.
Preprints 106715 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated