Prerpints.org logo
Preprint
Article

Dynamic Slicing and Reconstruction Algorithm for Precise Canopy Volume Estimation in 3D Citrus Tree Point Clouds

Altmetrics

Downloads

132

Views

48

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 May 2024

Posted:

17 May 2024

You are already at the latest version

Alerts
Abstract
Crop phenotyping data collection is the basis for precision agriculture and smart decisionmaking applications. In this study, a dynamic slicing and reconstruction canopy volume (DR) algorithm is proposed to accurately estimate citrus canopy volume. The algorithm dynamically slices nearby slices based on their proportional area change and density difference, subsequently conducting AS reconstruction and volume calculation for each slice using an iterative mean point spacing as the α-value. Compared with six point cloud-based reconstruction algorithms, the DR approach achieved the best results in removing perforations and lacunae (0.84) and exhibited volumetric consistency (1.53) that closely aligned with the growth pattern of citrus trees. The DR algorithm effectively addresses the challenges of adapting the thickness and number of canopy point cloud slices to the shape and size of the canopy in the ASBS and CHBS algorithms, as well as overcoming inaccuracies and incompleteness in reconstructed canopy models caused by limitations in capturing detailed features using the PCH algorithm. It offers improved adaptive ability, finer volume computations, better noise reduction, and anomaly removal. In conclusion, we recommend selecting appropriate operating environments for each algorithm based on their principles, geometric properties, volumetric values, running time, and linear relationships with one another to guide orchard mechanization and intelligent operation.
Keywords: 
Subject: Computer Science and Mathematics  -   Data Structures, Algorithms and Complexity

1. Introduction

Citrus cultivation plays a pivotal role in the rural revitalization strategy of southern China, with China leading globally in terms of both total output and planting area. However, there are persistent challenges, such as inadequate intelligence and mechanization levels, as well as incomplete information construction[1]. The collection of crop phenotyping data serves as the fundamental basis for intelligent decision-making applications in agriculture. The canopy of a fruit tree constitutes the primary section responsible for light absorption during respiration and photosynthesis. It encompasses the majority of branches, leaves, and fruits that provide the essential nutrients and energy required for growth. The fruit tree canopy plays a crucial role in the growth and productivity of trees, making it an essential indicator for monitoring tree biomass, estimating growth, predicting yield, estimating water consumption, monitoring health status, and tracking long-term productivity [2,3,4,5,6]. Moreover, this approach enables the quantification of pruning effects and the evaluation of tree characteristics. This approach enables the quantification of pruning effects and the evaluation of tree characteristics. Recognizing citrus canopy features is vital in citrus tree production, breeding, and management. It is inextricably associated with orchard precision management projects such as irrigation and fertilization practices, moisture detection techniques, fruit crop breeding, and yield assessment methods[7]. At the same time, accurate canopy volume measurements can serve as a foundation for determining crop pesticide doses and making decisions[8,9], as well as technical assistance for pruning robots[10], assisting managers in making sound agricultural production decisions[11,12,13]. As a result, the rapid and accurate estimation of canopy features plays a crucial role in monitoring fruit tree growth dynamics and enhancing orchard management optimization[14].
Citrus trees are evergreen perennials, and their canopy characteristics are essential for understanding how they grow. These features can make it easier to analyze how they relate to yield, physiological markers, and growth circumstances[15]. Currently, the most common methods for measuring canopy volume are manual measurement and noncontact automatic measurement. Manual measurements often entail measuring the height and width of fruit trees with equipment such as tape and height rulers. The crown is then approximated to a corresponding geometric model based on its shape and structure, and its volume is calculated using the geometric model’s volume formula. Miranda-Fuentes et al.[16] estimated canopy volume for olive trees by assuming an ellipsoidal shape. Zheng et al.[17] Computed crown volume for Hamlin sweet orange trees assuming an uneven columnar shape. Scapin et al.[18] determined crown volume by measuring the contour shape of citrus trees along their rows and combining that information with crown height data. Lee et al.[19] introduced a novel approach for accurately measuring the geometric features of tree crowns by slicing the crown horizontally at a 20 cm spacing, measuring the circumference of the slices with a PVC pipe around the tree, and multiplying the area of the sliced circle by the height to determine the slice’s volume. Li et al.[20] the formula for calculating the volume of slices in this method was changed to a formula for calculating the volume of circular platforms and then used to calculate the volume of citrus trees, which was more accurate than the previous method of comparing the entire fruit tree to a single geometric model and more responsive to the volume of the actual fruit tree. Although manual measurements are simple and convenient, they are prone to errors due to subjective factors, and there is also a significant difference between the model used and the canopy’s true form; moreover, no model can completely and accurately simulate the canopy’s true form.
Researchers have tried and developed a variety of noncontact automatic measurement methods to meet the requirements of efficient and accurate measurements. Dong et al.[21] employed a camera-carrying drone to capture photos, reconstruct a single fruit tree and extract its area and diameter. Jurado et al.[22] employed a camera to capture numerous overlapping photos to estimate plant height and volume. Cameras for 3D reconstruction have the benefit of being low-cost and rich in texture. Cameras, on the other hand, have the disadvantage of being readily limited by light and climatic conditions, requiring a high level of equipment and technology, complex data processing, and the necessity for vast amounts of data capture. Dong et al.[23] collected canopy volume, trunk diameter, tree height, and fruit number in an orchard by putting an RGB-D depth camera on a pole to gather data from a horizontal or top-down view, and then 3D reconstructed an apple tree using photos on both sides. Subsequently, they utilized these data to reconstruct a three-dimensional model of an apple tree by employing images taken from multiple angles. Yin et al.[24] employed depth cameras to generate a three-dimensional reconstruction of a cherry tree and perform volume calculations. Although depth cameras are more precise and accurate in 3D reconstruction and are more sensitive to changes in light than are standard cameras, they nevertheless have drawbacks, including low-quality depth images and a small measuring range. A system built using wireless networks and ultrasonic sensors was created by Yu et al.[25] to achieve three-dimensional reconstruction and volume extraction from fruit tree canopy. H Maghsoudi et al.[26] Ultrasonic sensors at various heights were placed on a sprayer to detect canopy information in real time, and then a multilayer perceptual neural network technique was used to calculate canopy volume. Measuring data using ultrasonic measurement technology has the advantages of being noncontact, highly efficient, and highly accurate; however, in practice, measurement results are easily influenced by environmental noise and temperature changes, and the detection range is limited, necessitating the use of multiple devices and complex technology. Zhang et al.[27] used tilt photography to create a linear relationship between the crop volume model and manually determined biomass. Zhu et al.[28] used tilt photography to determine the canopy structural parameters of maize. Tilt photography has the advantages of wide range and quick speed, but its measurement accuracy is greatly influenced by lighting conditions, background interference, camera distortion, and other variables. Because of the complicated canopy structure of fruit trees, tilt photography cannot reconstruct the bottom of the canopy and is easily influenced by environmental changes during acquisition.
LiDAR (Light Detection and Ranging) can be employed with effective information management to characterize tree canopy and generate canopy point clouds at various viewing angles and spatial resolutions [29]. This method has the advantages of high accuracy, long-distance measurement, high density, lack of light, and fast data acquisition and is widely used in agriculture. Liu et al.[30] employed a handheld laser scanner to achieve 3D canopy reconstruction and volume extraction of pomelo trees. Wang et al.[31] developed a dynamic grid division of fruit tree canopy volume LiDAR online detection method for determining the canopy contour and volume of peach groves. Pagliai et al.[32] created a terrestrial LiDAR-based canopy volume assessment algorithm that uses a tractor in conjunction with terrestrial LiDAR and GNSS technology to achieve exact vineyard spraying, which has the advantages of being faster and requiring fewer postprocessing computations. Yu et al.[33] utilized a handheld mobile laser scanner, scanned and reconstructed 367 blueberry plants, and collected height, breadth, and volume data for each. The usefulness of these data was then assessed statistically by examining the extracted canopy size and shape characteristics to identify the best shrub structure for mechanical harvesting.
The following algorithms are commonly used by researchers for point cloud-based canopy reconstruction. Lee et al.[19] employed a convex hull approach to determine the volume of Hamlin sweet orange trees, resulting in more valuable information for predicting tree growth and productivity. Xu et al.[34] employed a convex hull slicing approach to determine the predicted volume and surface area of the canopy, lowering the computational error of complicated canopy structures. Colaço et al.[35] used the alpha-shape algorithm and the convex hull algorithm to reconstruct the surface of citrus trees and compared it to artificial measurements based on cylinders or cubes. The experiment revealed that the use of the alpha-shape algorithm may better describe the distributions of the canopy and provide a more realistic representation of the canopy. Mahmud et al.[36] employed the alpha-shape algorithm to estimate the volume of a fruit tree, with the canopy volume calculated by this algorithm showing a significant correlation with the physically counted foliage. Chakraborty et al.[37] employed a handheld 3D LiDAR scanning device to determine the volume of a grapevine canopy, and they found that the voxel-based algorithm more accurately accounts for changes in canopy structure than does the convex hull algorithm. Fernández-Sarría et al.[38] used seven methods reconstruct the canopy of Platanus hispanica trees. They assessed the leftover biomass produced by pruning faster by analyzing the volume and runtime of multiple techniques, which will aid future management. Wang Jia et al.[39] the tree crown was split into many uneven platforms, and the crown volume was obtained, but viewing the crosssection of each point cloud slice as circular or elliptical resulted in a large deviation in the calculation results. Yang et al.[34] improved this platform method to determine the volume of the platform by calculating the area of the convex packet of each crown point cloud slice, and high-precision and fast reconfiguration of the canopy structure was achieved. Yan et al.[40] developed an adaptive sliced convex hull approach, achieving street tree reconstruction and volumetric computation. Liu et al.[30] proposed a slice-based alpha shape algorithm for canopy reconstruction and volume calculation of pomelo trees.
Most agricultural researchers still use manual measurements of the volume of citrus, the world’s number one fruit crop, which not only is time-consuming and laborious but also has a large deviation from the true volume, which is not conducive to further analysis by researchers. We summarize six typical point cloud reconstruction algorithms(PRAs) for reconstructing a citrus circle with 160 orange trees and propose a set of preprocessing procedures for 3D reconstruction of a large-scale citrus orchard using a hand-held laser scanner. These algorithms include Convex Hull (CH), Alpha-Shape (AS), Platform Convex Hull (PCH), Voxel-based (VB), Convex Hull by Slices (CHBS), with Alpha-Shape by Slices (ASBS). We then synthesize the principles, geometric properties, volume values, runtime, and linear relationships between each algorithm to analyze the reconstruction effectiveness and problems. The efficacy and issues of each algorithm’s outputs are evaluated. The findings demonstrate that even with the best performance of these six algorithms(the ASBS algorithm) is used to reconstruct an orange tree, the thickness and number of canopy point cloud slices are not always able to match the size and shape of the canopy itself. Accordingly, we developed a dynamic slicing and reconstruction canopy volume algorithm (DR), which, compared to existing algorithms, dynamically slices nearby slices based on their proportional area change and density difference, better capturing and reflecting the actual growth characteristics of the tree canopy. Finally, we integrate the benefits of each algorithm to identify acceptable operating fields for them, providing an effective reference for the intelligent mechanization of orchards in the future. Section 2 describes the preprocessing process of segmenting a single fruit tree, as well as the principle method and implementation process of each algorithm; Section 3 describes the experimental process and results with a detailed analysis; Section 4 discusses the influence of the number of slices on the reconstruction effect, followed by the application scenarios of each algorithm; and Section 5 concludes this paper’s work and contributions.

2. Materials and Methods

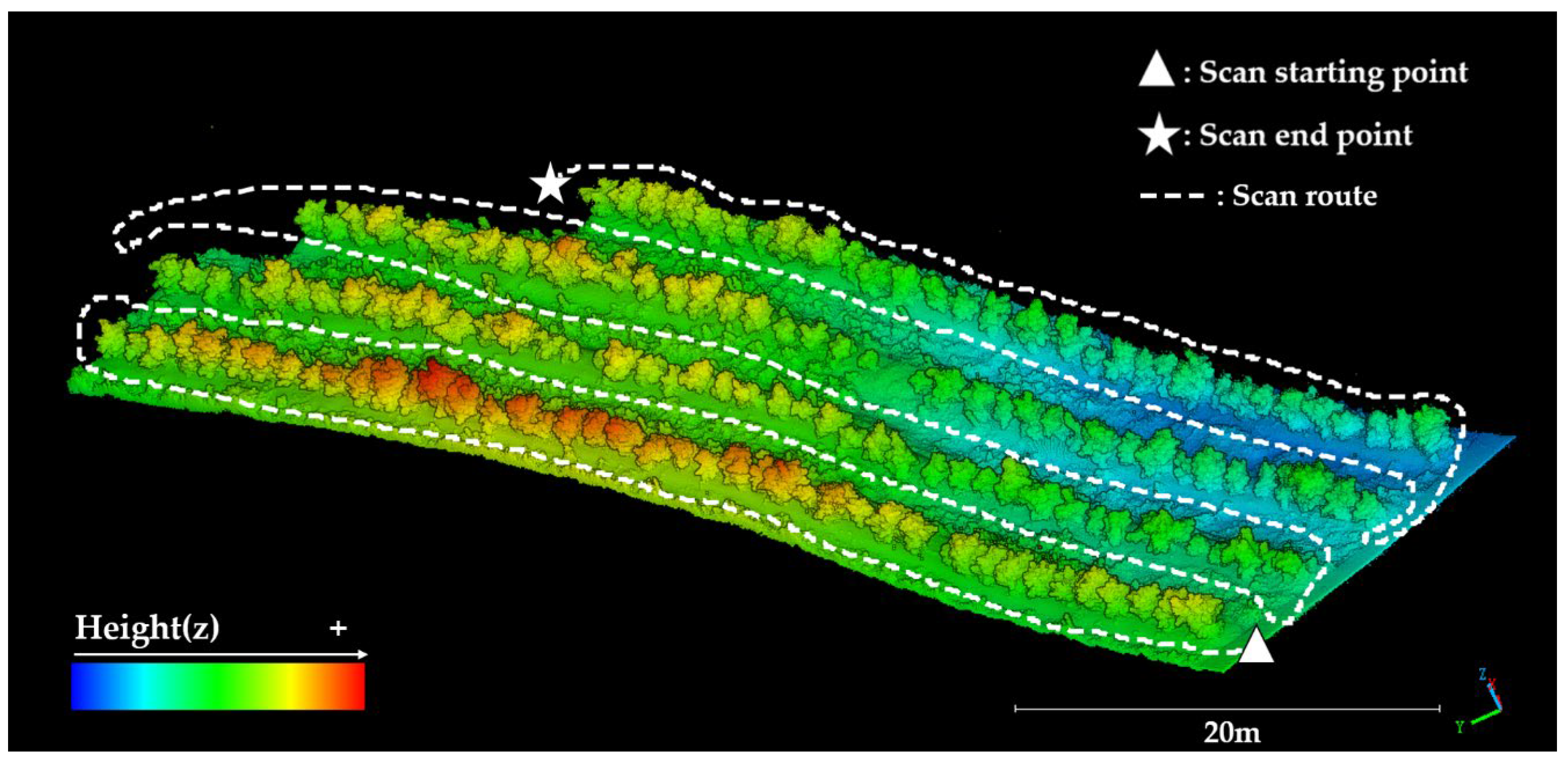
2.1. Test Area

The experimental citrus variety used was late-maturing blood orange No. 8, a trifoliate orange rootstock with a tree age of 3 years. Blood orange no. 8 is a bud mutation discovered in the descendants of Italian Tarocco blood oranges and is a late-maturing type among blood oranges[41]. Its main cultivation areas are in Sichuan Province and Chongqing Municipality, China. The trees are vigorous, with tree forms including round-headed, main stem shapes, and open-hearted. The experimental orchard has a spacing between rows of 5.5 m, a tree standing of approximately 2.5 m, and a plant distance of 2 m. The base adopts the method of high ridges with deep furrows for soil bundling, with the height of the ridges ranging from 0.3-0.6 m. The blood orange tree has a natural round head structure, which is more compact and full, with a slightly open posture, and the middle-length branches easily droop. The crown is more rounded, the branches are evenly distributed, and the bottom of the crown is densely foliated; however, there are also many holes and gaps. The experiment was conducted in December 2023 in Jingba village, Jielong town, Fushun County. The local area (29°12.78’ N, 105°5.97’ E) features an average altitude of 310 m above sea level, a mean yearly precipitation of 1081.69 mm, and a typical yearly temperature of 19.82°C. It is located in the southwest Sichuan Basin and has a shallow hill landscape, a subtropical humid monsoon climate, abundant rainfall, abundant light, a lengthy frost-free period and four distinct seasons. 4 rows totaling 160 blood orange trees were selected as the subjects of this experiment. Figure 1 shows the experimental site.

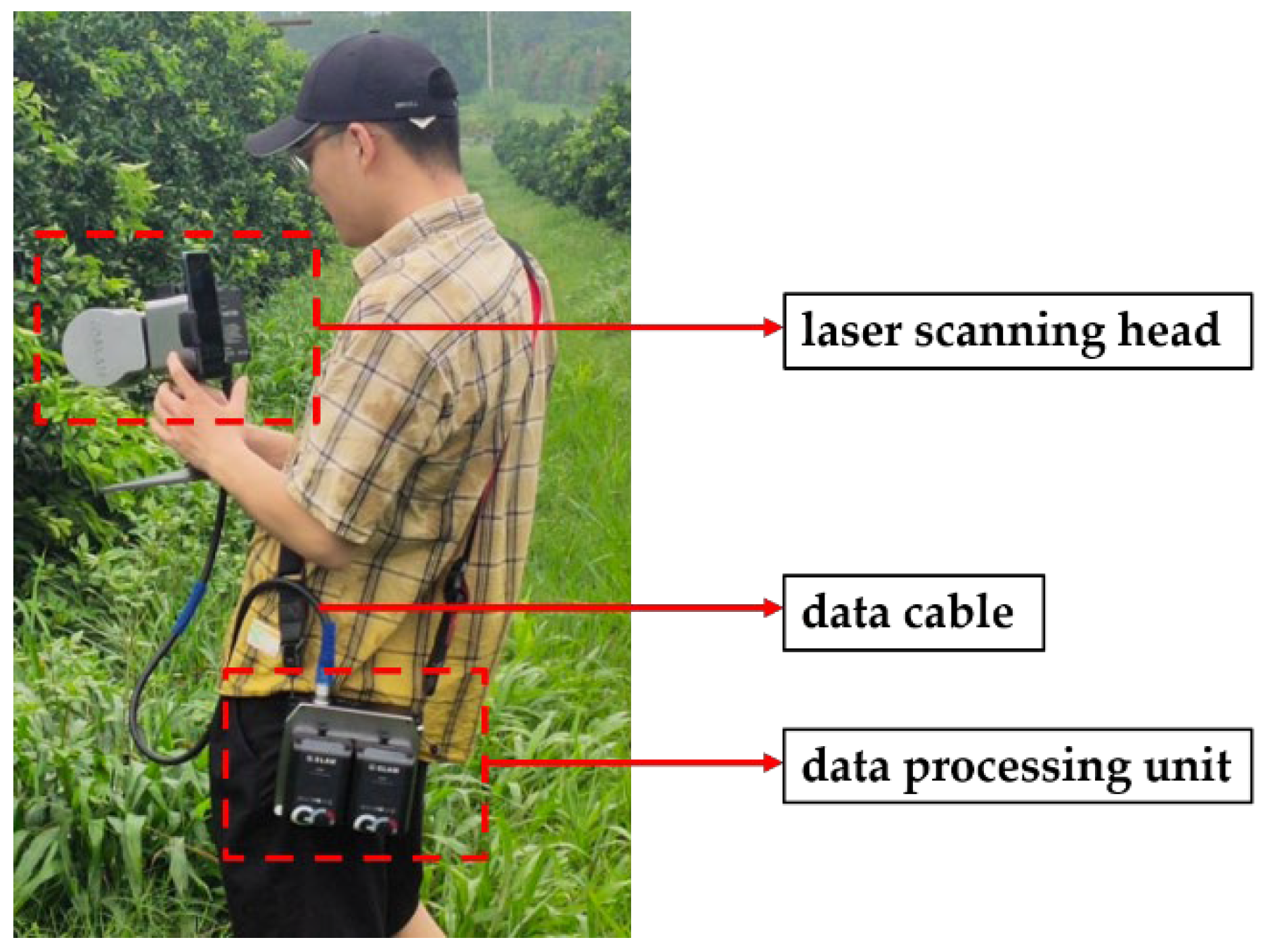
2.2. Acquisition Device and Acquisition Method

The handheld 3D LIDAR scanning device (GoSLAM RS100) consists of a laser scanning head and a data processing unit (Figure 2). The laser scanning head is made up of a laser emitter, receiver, and scanning mirror that allows quick scanning of the target surface. The data processing unit consists of an inertial measurement unit (IMU) for measuring device acceleration and angular velocity and a microcomputer for data processing, map generation, localization, and navigation activities. This device scans a distance of 120 m, a scanning rate of 650,000 points/second, a point accuracy of 1 cm, 32 lines of laser lines, a scanning range of 360° × 285°, and two lithium batteries, allowing the LIDAR system to work continuously for 4 hours.
The experimenter used a handheld LiDAR scanning device to collect scanning data in a closed loop around the experimental site line by line, and the roadmap of the collection is shown in Figure 3. The laser scanner scans the experimental area along with the nearby environment during operation. The figure was taken after the experimental test area was delineated using the point cloud cropping and slicing function in the GoSLAM Studio point cloud processing software.

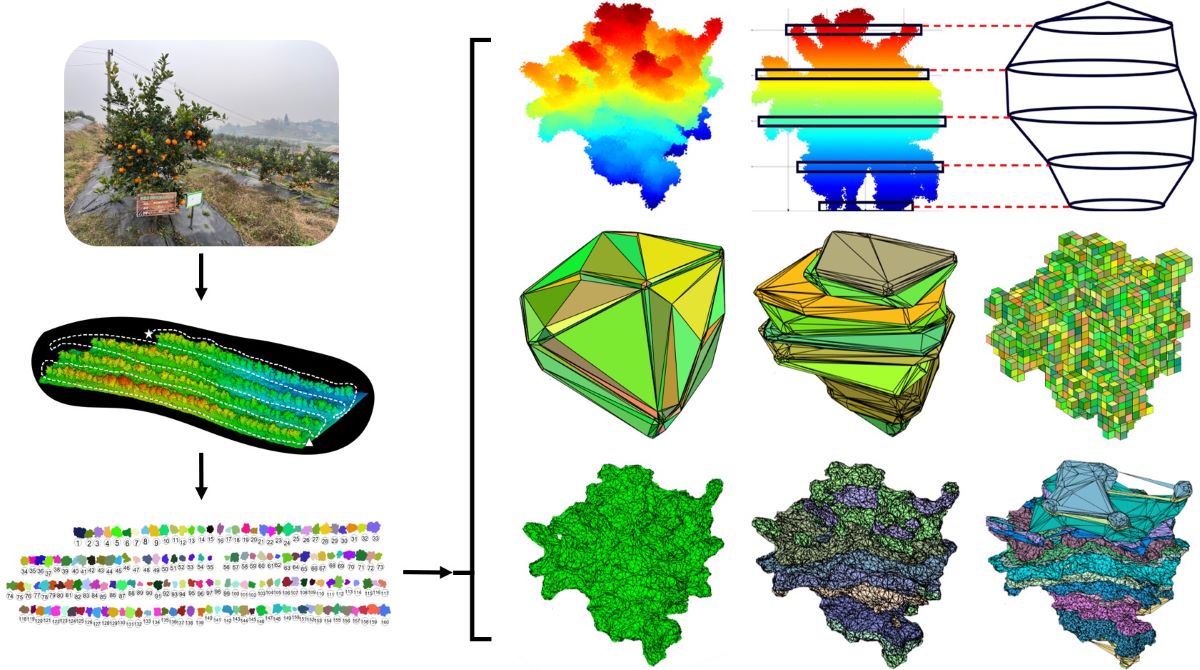
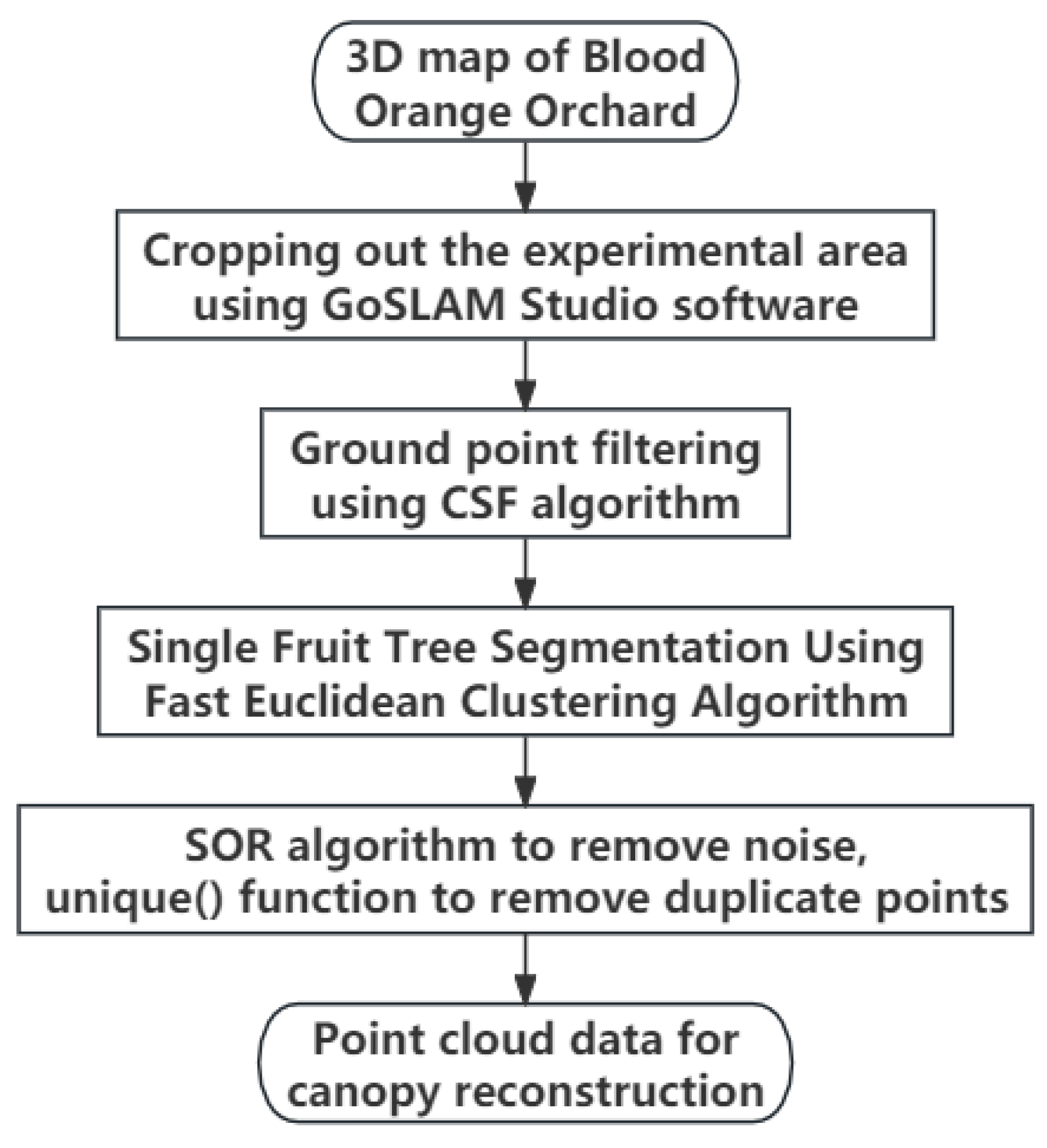
2.3. Preprocessing for Canopy Reconstruction

The canopy reconstruction preprocessing flow can be found in Figure 4. Initially, a 3D model of a blood orange orchard was created utilizing a LiDAR scanner. The experimental area was then cropped using GoSLAM Studio software. The CSF algorithm was employed to filter ground points, followed by the application of the fast Euclidean clustering algorithm for segmenting individual fruit trees. Finally, the SOR algorithm was utilized to eliminate noisy points, and the unique() function was used to remove repetitive points.

2.3.1. Ground Filtering

To facilitate the subsequent extraction of fruit tree information, it is necessary to select a suitable algorithm to filter the ground points in the test area. Common algorithms include least squares plane fitting (LSPF)[42], random sample consensus (RANSAC)[43], and the cloth simulation framework (CSF)[44]. The LSPF fits the ground plane model by minimizing the distance between the point and the plane. RANSAC is primarily used to fit the model and remove outliers, and it is commonly used to recognize simple geometric objects (such as planes and straight lines). Since the test area is a blood orange orchard with high ridges and deep furrows, the LSPF algorithm assumes that the ground is planar and cannot accurately identify ground points for orchard ground with irregular ground surfaces or large elevation variations. The RANSAC algorithm is also unable to accurately fit a complex ground model, is sensitive to noise and occlusions, and has high computational complexity and difficulty in parameter selection. The CSF algorithm can fully consider the local and global characteristics of point cloud data to better cope with complex orchard terrain. Through regional growth and point cloud segmentation technology, ground points can be accurately identified, a reliable ground model can be extracted, and a reliable database can be constructed. This paper thus employs the CSF algorithm.
The lidR package in RStudio includes the CSF function, which contains four parameters. sloop_smooth determines whether the point cloud is smoothed to decrease the impact of noise. The class_threshold function is used to modify the accuracy and stability of ground extraction by adjusting the threshold for dividing ground and nonground points. The cloth_resolution parameter is used to control the grid resolution of ground point cloud data to balance processing efficiency and ground extraction accuracy. The time_step parameter is used to control the rate at which the amount of ground points increases. This study employed four feature values: TRUE, 0.4, 1, and 1. Figure 5 shows the filtered results. Although certain dispersed weeds and ground points remain unfiltered, they have no effect on subsequent single-tree segmentation.

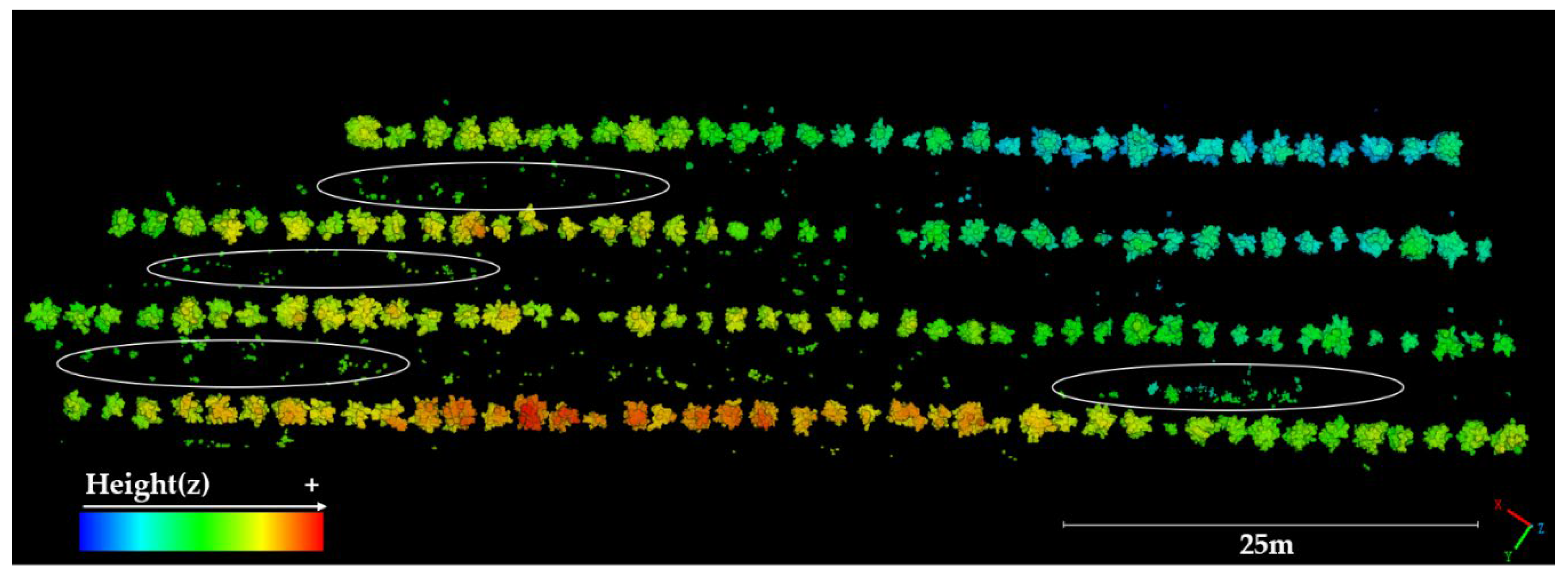
2.3.2. Single-Fruit Tree Splitting

After finishing the ground filtering, the point cloud should be segmented by clustering using appropriate clustering algorithms in conjunction with the crop growth characteristics and the size of the test area to get each fruit tree’s point cloud data. Among the frequently employed clustering algorithms are the region expanding algorithm[45], Kmean clustering[46], DBSCAN clustering[47] and Euclidean clustering[48] algorithms. The point cloud is split up by the region expanding algorithm into different regions based on the similarity between neighboring points to form point clusters with continuity. The Kmean clustering algorithm separates the point cloud data into a set of groups, with the centroid of each representing a grouping result. The DBSCAN clustering algorithm identifies and segments clusters based on the density of points. The Euclidean algorithm for clustering classifies point cloud data into discrete clusters based on their physical closeness, allowing for the identification and separation of unique objects or features within the dataset. Considering that there are 160 fruit trees in the test area, the point cloud file has close to 30 million points, the file size is 1 GB, the computational complexity of the area growth algorithm is high, the Kmean clustering requires a certain number of groups, and it requires numerous testing for fruit trees of various forms and densities and is highly reactive to noise. The DBSCAN algorithm is more sensitive to parameter selection, and the processing of large files is too time-consuming. Therefore, they are not suitable for processing large files of blood orange orchard point clouds. Liu et al.[30] have chosen to use Euclidean clustering for single tree segmentation of pomelo orchards containing 36 fruit trees and achieved good segmentation results, which shows that compared with traditional Euclidean clustering algorithms, Euclidean clustering algorithms are more suitable for citrus orchards. Yu et al.[49] proposed fast Euclidean clustering algorithms to optimize the data structure and algorithmic flow of the Euclidean clustering algorithm. clustering data structure and algorithmic process, avoids constantly traversing each point, and has higher efficiency and speed when dealing with large-scale point cloud data; therefore, this experiment adopts the fast Euclidean clustering algorithm for single tree segmentation.
The fast_euclidean_cluster() function is implemented in the open3d library in the Python environment, and the function contains four parameters. The tolerance parameter specifies the search range of the closest search. The parameter max_n represents the maximum number of points for a nearby search. The choice of this value affects the speed and accuracy of the clustering. The min_cluster_size parameter determines the smallest amount of points required for a group of points. The parameter max_cluster_size determines the largest amount of points required for a group of points. Based on the real planting tree spacing, plant distance, and the number of points between the smallest and largest fruit trees within each row of the blood orange orchard, this paper sets the values of the four parameters to 0.08, 800, 18,000, and 600,000, respectively. Figure 6 shows the clustering results after the algorithm has been run; each different color represents a fruit tree segmented out, and from the results, the fast Euclidean clustering method also removes those scattered weeds and ground point clouds from the point cloud.

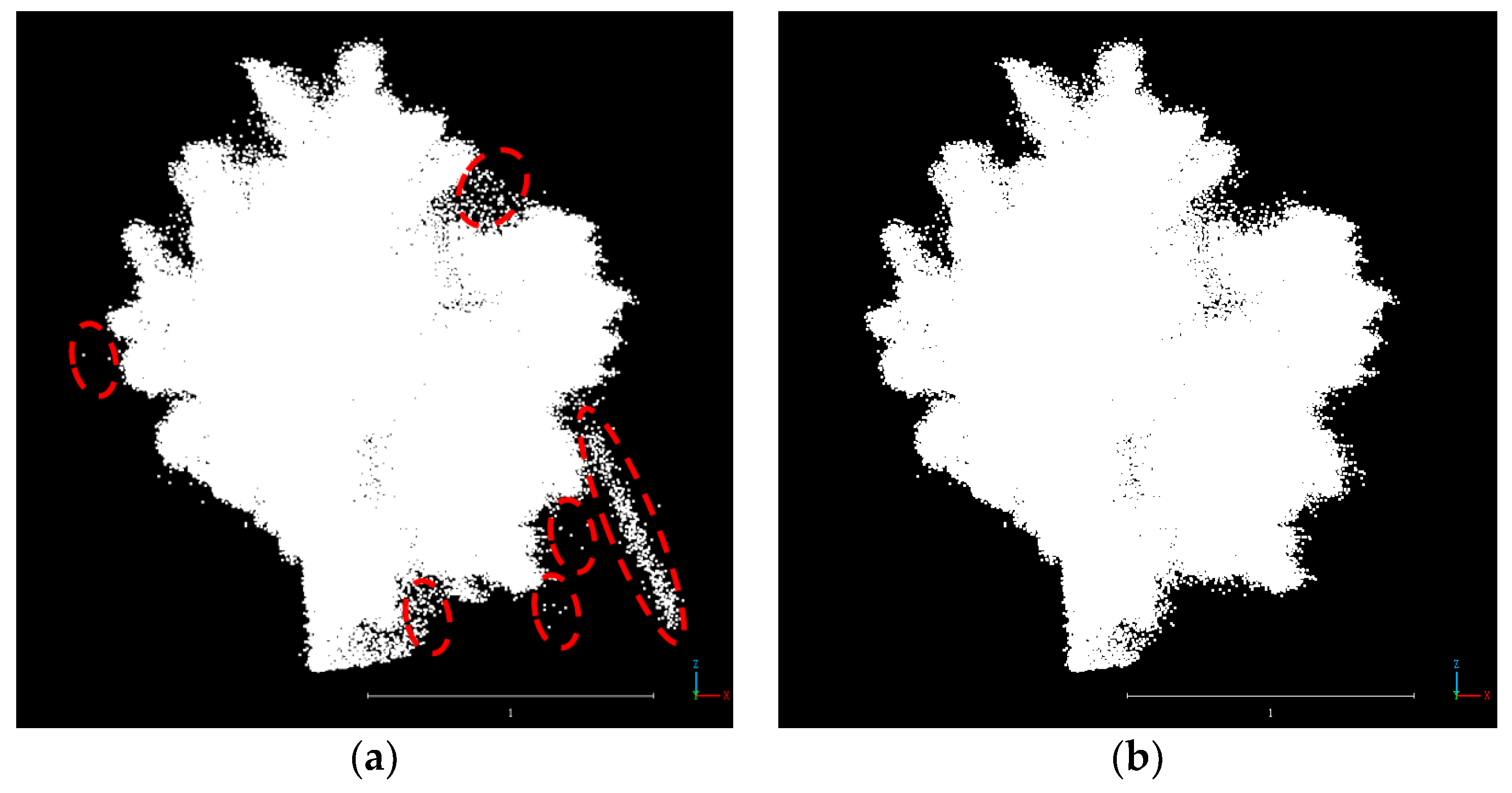
2.3.3. Point Cloud Denoising and Deduplication

Laser scanning typically produces point cloud datasets of nonuniform density, and errors in measurements and environmental disturbances can also lead to the appearance of sparse outliers. Statistical Outlier Removal (SOR) algorithm[50] is used to remove obvious outliers, which indicates that a point cloud is considered invalid if it is less than a certain density. The SOR algorithm requires that the parameters k and n be set. The number of neighborhood points taken into account when determining the mean distance for each point is indicated by the expression “k number of nearest neighbors.” The notation “n multiple of standard deviation” means that the algorithm, after determining the average distance between every single point, examines the distribution of distances for each point from a point cloud. If a point’s distance exceeds the mean plus n multiplied by the norm deviation, that is thought to be an anomaly. In this study, it is experimentally found that when k=600 and n=3, not only are the noise points around the citrus tree point cloud effectively removed but also the original structure of the citrus tree point cloud is completely preserved. Figure 7 compares the data before and after denoising.
Due to the movement of the scanner or the intricate structure inside the tree canopy, when scanning citrus trees with a laser scanner, the scanning region overlaps. This means that points at the same position are scanned more than once, resulting in duplicate points. Repetitive points can generate data bloat and impact the accuracy and efficiency of the reconstruction algorithm throughout further processing and analysis, particularly during AS reconstruction. Repetitive points make the algorithm process more data and cause the reconstruction results to have undesired concavities, convexities, or discontinuities. Point cloud duplicate points were removed using the unique (pointCloud, ‘rows’) function in MATLAB, which takes every single point from the point cloud as a row afterwards to locate the unique point within it. Duplicate points were removed for 160 test trees, with an average of 52 duplicate points removed per tree and an average time of 0.19 s per tree.

2.4. Calculating the Canopy Height and Width of Fruit Trees

Assessing the physical properties of fruit trees (e.g., tree height, crown spread, and canopy volume) is essential in agricultural studies and is increasingly a significant subject in precision agriculture[29]. Horticulturists can use accurate morphological estimates to evaluate the impact of these characteristics on crop output, wellness, and growth. Growers, such as experimenting with various root stocks, determine which rootstock produces the most per unit volume in a given geographic region. They also utilize parameters such as the height of trees and crown spread when predicting fruit yield. This approach of assessment requires significant human effort and frequently lacks precision[23]. These geometric features for phenotyping are now available for extraction via LiDAR scanning. To assess the accuracy of the current scanner acquisition data, we manually measured the plant height and east‒west and north‒south crown widths of 160 blood orange fruit trees using a tape measure. For the LiDAR-scanned and preprocessed point clouds of individual fruit trees, we used CloudCompare software to calculate the minimum AABB box. The box’s x and y lengths indicate the fruit tree’s two canopy widths (W), and the z length indicates the fruit tree’s height (H).
The H was determined uniformly with the following formula(1):
H = Z max − Z min
where Z max and Z min represent the highest and lowest points of the Z elevation.
The W was calculated uniformly using the following formula (2):
W = W H + W V 2
where W H represents the horizontal width and W V represents the vertical width.
A comparative analysis of the canopy height (Table 1) and width (Table 2) measured by the two methods revealed that the errors between the manual measurement method and the LiDAR scanning data were very small (RE of 0.039 for H and 0.081 for W), and the minimum RE values for H and W even reached 0.005 and 0.003, respectively. Therefore the data processed using LiDAR scanning more accurately represent the real fruit tree morphology, which provides an accurate basis for later canopy volume calculations.

2.5. Canopy Reconstruction and Volume Calculations

The fruit canopies of the trees were reconstructed using the MM and 7 types of PRAs to compute canopy volume. These PRA algorithms were run using MATLAB R2023a.

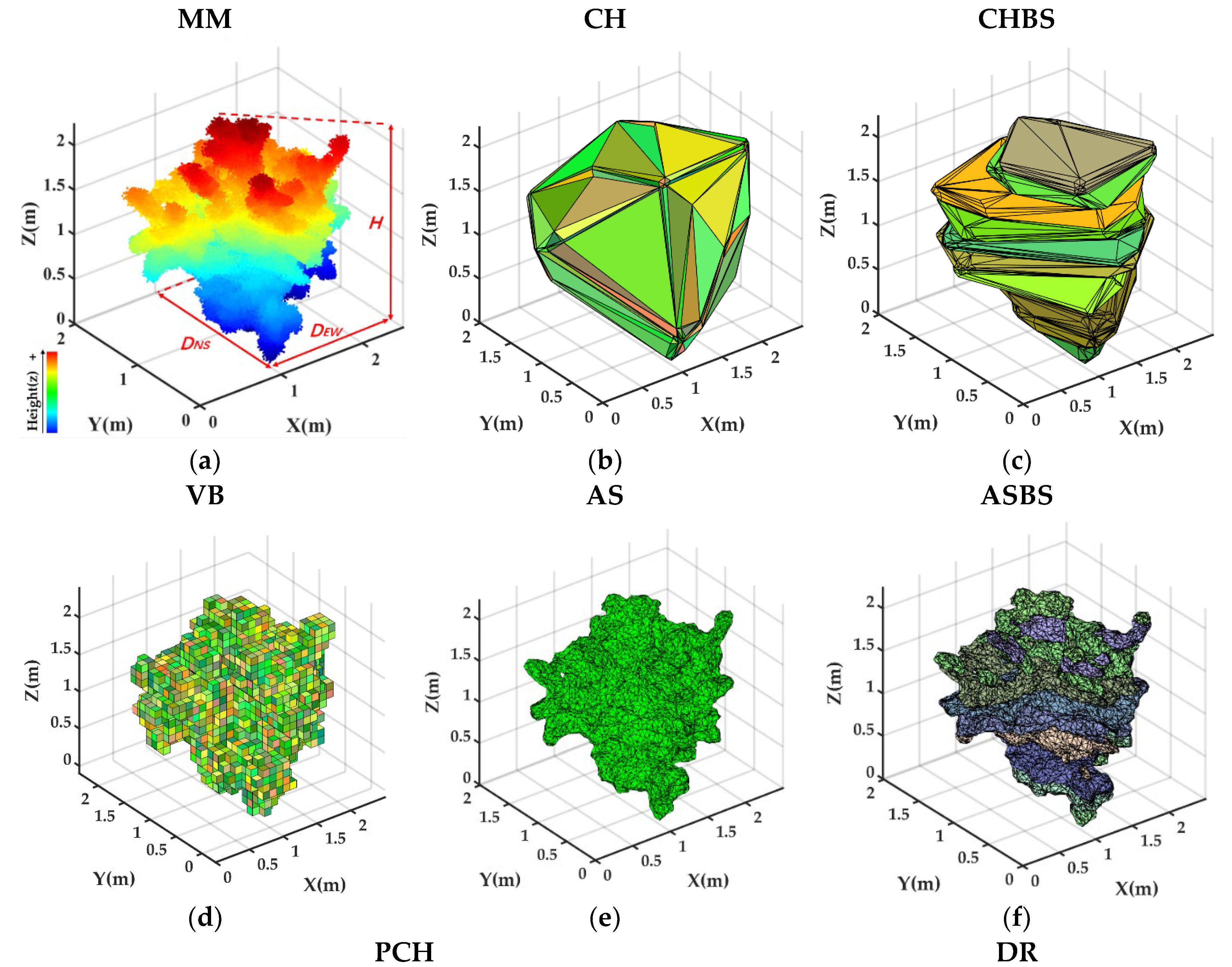
2.5.1. MM Approach

Ellipsoidal models are frequently utilized by researchers as geometric models for typical citrus canopy trees[51]; hence, in this study, the ellipsoidal formulation was employed as the MM approach to determine the canopy volume of blood orange trees. The volume was computed with the following equation(3):
V = π ⋅ W 2 ⋅ H 6
where W is crown width and H is the plant height, both of which were measured by the CloudCompare software above.
Figure 8a shows a picture with manual method.

2.5.2. CH Approach

In computer graphics, a convex packet is the smallest convex set containing a finite set P of points in an arbitrary dimensional space. It consists of convex hull vertices and behaves like a convex solid in a three-dimensional environment. In this study, the QuickHull method was used to determine the volume of a convex hull on the surface of a citrus tree. Figure 8b depicts the canopy reconstruction effect diagram using a CH algorithm.

2.5.3. CHBS Approach

The CHBS approach works by taking a specific amount N of equally spaced slices of the point cloud in the z-direction after running the CH algorithm on each segmented point cloud slice to determine the slice volume. Finally, the total volume within the canopy is computed by adding the volumes of the individual slices. Various numbers of slices had varying effects on the experimental results, and Yan initially selected a 15 cm spacing in his slice investigation since estimating the volume using the CH or AS algorithms required at least three points per slice[40]. In this study, the mean value of H was 1.835 m (Table 1); hence, the value of N was set at 10. Figure 8c depicts the canopy reconstruction effect diagram using the CHBS algorithm.

2.5.4. VB Approach

The VB approach works on the premise of segmenting the tree crown in the tree height direction in k steps of equal distance. The points in each segment of the canopy are projected onto a plane perpendicular to the tree height direction, and then the plane is divided into image elements of size k*k. Determined by the number of dots projected into every graphic element, the validity of the image element is judged, and the number of valid image elements is counted T. Finally, the volume of the canopy can be expressed as the sum of the T k*k*k voxel elements. Lecigne[52] proposed that when k equals one-tenth of the width of the canopy, the calculations are stable. In this investigation, the mean value of W was 1.619 m (Table 2); hence, the value of k was set to 0.1 m. Figure 8d depicts the canopy reconstruction effect diagram using the VB algorithm.

2.5.5. PCH Approach

The PCH algorithm views the entire canopy of a fruit tree from bottom to top as a geometry composed of many platforms and a cone[53]. First, the canopy’s point cloud data are sliced based on elevation. Subsequently, every slice is created into a convex packet of planar point sets using the Graham convex packet algorithm. The area of the convex packet (S) is then determined using Green’s formula; thus, the volume of each platform is obtained. Finally, the canopy’s total volume is calculated by combining the platform and cone volumes. In this investigation, we fixed the segmented platform thickness (h) to 0.2 m and the thickness of the slice to 0.04 m. Figure 8g depicts the canopy reconstruction effect diagram using a PCH algorithm. The calculation methods are shown in formulas (4) and (5).
S = 1 2 ∑ k = 1 m x k y k + 1 − x k + 1 y k
where m is the number of endpoints and （ x k y k + 1 ） and （ x k + 1 y k ） are the plane coordinates of the kth and k + 1th endpoints, respectively.
V = 1 3 ∑ i = 1 n − 1 S i + S i + 1 + S i S i + 1 h i + 1 3 S n h n + 1
In the formula, S i S i + 1 signifies the area of the i, i+1th layer of point cloud slices, n signifies the number of slices, h i defines the spacing between neighboring slices, h n + 1 denotes the cone’s height, and V denotes the canopy volume.

2.5.6. AS Approach

The AS approach is a classic method for edge extraction. The core idea is to rotate a sphere with radius α inside the specified point set S. When α is sufficiently large, the ball will only roll tangent to the point set’s boundary rather than into its interior. At this moment, the points the ball has rolled through come together to create the point set S’s boundary (convex hull). Every point could be a border point if α is small enough.
The parameter α influences the fineness of the surface reconstruction results. After reconstructing the experimental fruit trees, it was discovered (Figure 9) that when α = 0.05, the reconstruction effect contains more details and characteristics, making the overall 3D model more realistic and fine. When α = 0.25, there are several flaws, such as insufficient details, particularly for small-scale structures, which can be disregarded, resulting in information loss. When α = 0.5, there is excessive smoothing, which causes blurring of the surface’s concave and convex parts as well as the loss of precise branching characteristics. When α = 0.75, an oversimplification develops, resulting in a significant loss of surface details and a structure that is not realistic or exact enough. This research suggested that varying α has a significant impact on the spatial form, compactness, and branching properties of the fruit tree canopy model. Therefore, a value of 0.05 was used in this study (Figure 8e).

2.5.7. ASBS Approach

The ASBS algorithm works on an identical basis to the CHBS method. The AS algorithm uses α = 0.05 for each segmented point cloud slice, which is the only variation. The value of N was set at 10, as is the case with the CHBS algorithm; the ASBS method results are given in Figure 8f.

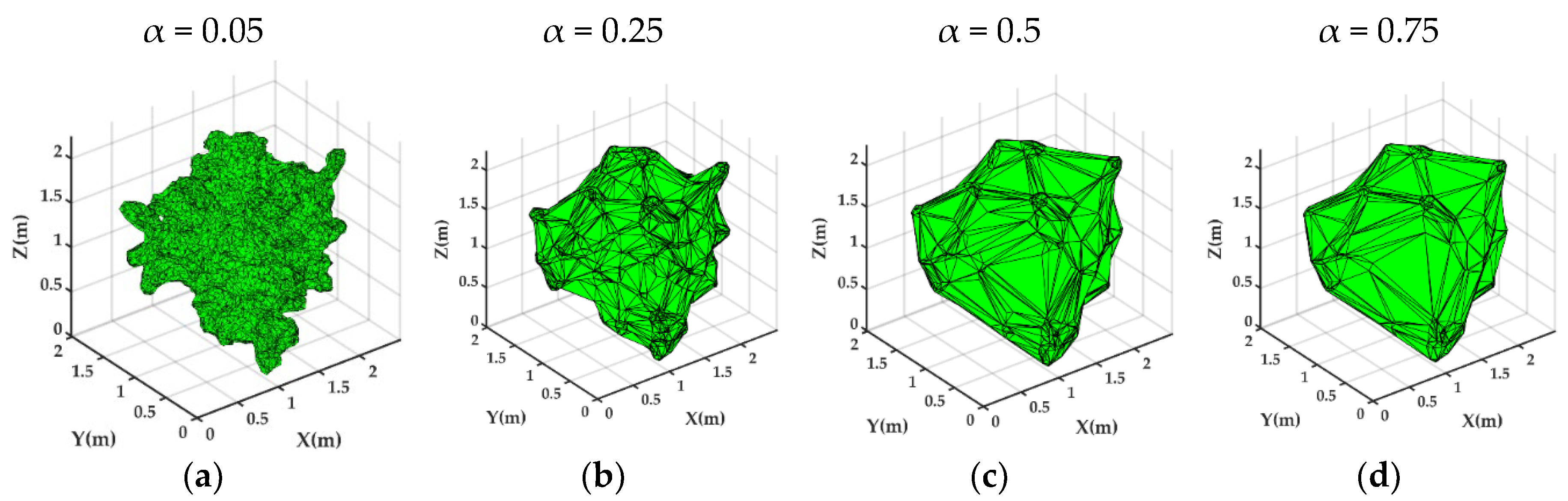
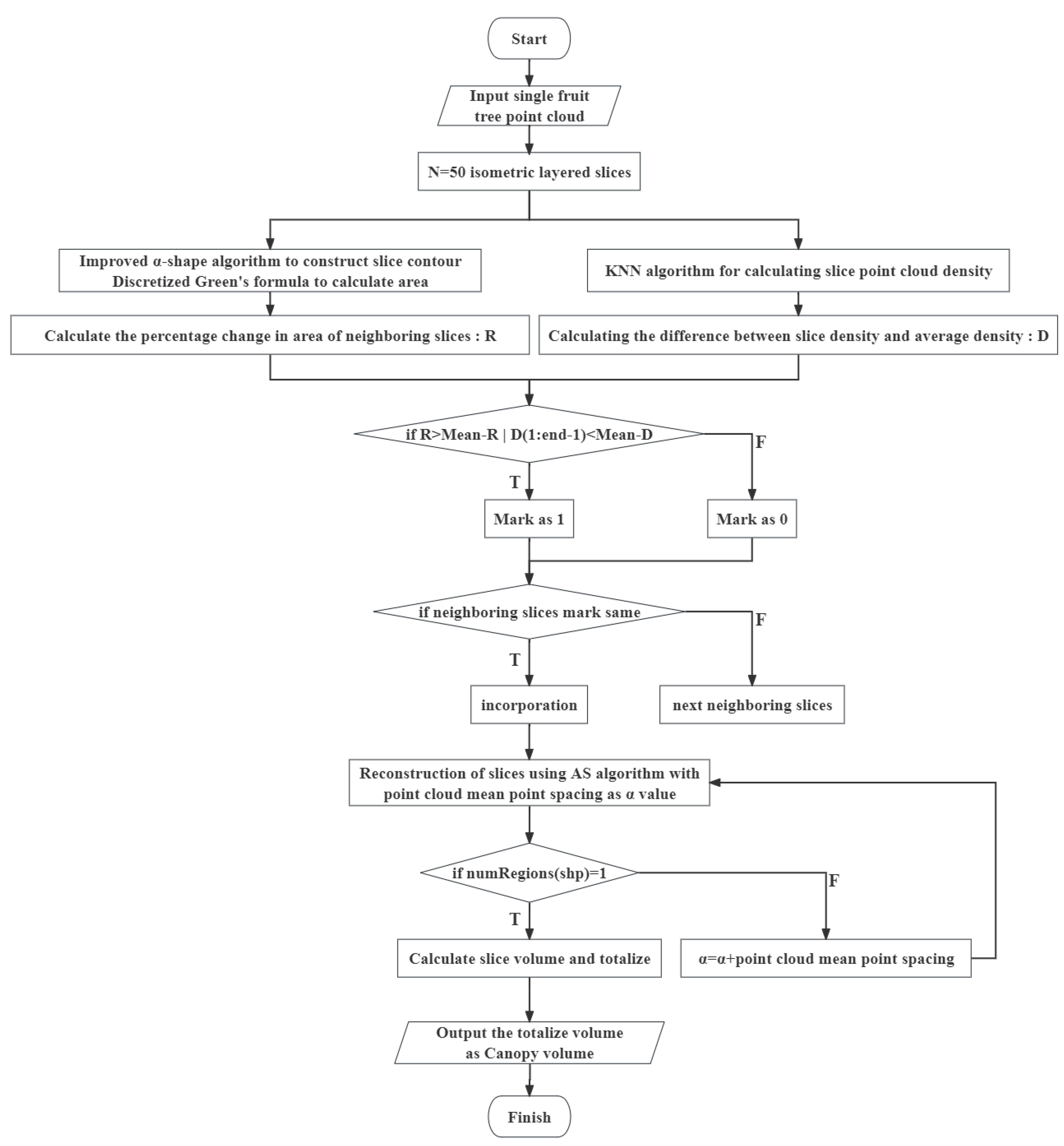
2.5.8. DR Approach

Although ASBS performs well in determining canopy volume, due to the varied shapes and sizes of each citrus tree’s canopy, slicing the canopy vertically with a consistent thickness has the following disadvantages: it is unable to adapt to the irregular shapes of the canopy, especially at the edges or the top of the canopy, which can lead to over- or underslicing; slicing the center of the canopy generates too many data points; it does not accurately reflect the complex structures and cavities inside the canopy; and it may ignore some details and properties of the canopy, including branching and density of the foliage; thus, it can comparatively overestimate the volume. Furthermore, it has been established[54] that in the canopy slicing zone, the relatively moderate change in the area of nearby canopy point cloud slices does not necessitate a separate layer. As a result, the slicing method must be adjusted so that it can be used on citrus trees of various shapes and sizes, as well as to compute canopy volume more correctly.
The experimental fruit trees range in height from 0.83 m to 2.616 m, and the number of slices per tree is variable, typically between 10 and 30 after adaptive slicing, whereas citrus trees are dense and morphologically complex, with varying densities of branching structure and distribution. When the fixed value of α=0.05 is still applied, the problem of volume underestimation occurs due to the smooth surface transition in some locations and the lack of detail in the reconstruction results or the loss of information due to excessive denoising. Using the point cloud’s average point spacing as α better reflects the distribution and adapts to point cloud files with different densities, preserving the characteristics of the original point cloud files and reconstructing a volume that is more adaptable, accurate, and reliable.
Cheng et al.[53] developed the triangular mesh growth algorithm and proposed a dynamic threshold improvement α-shape algorithm considering the boundary point cloud density. This algorithm was used with the platform algorithm to compute the volume of the tree, and while it can produce a relatively accurate canopy slice contour, its simple geometric shape reconstruction by using the platform algorithm means that it is unable to capture the features of complex shapes or scenes with many details, which results in inaccurate reconstruction results and a certain amount of holes and gaps. In this paper, based on the above features and obstacles, we propose a dynamic slicing and reconstruction algorithm for tree canopy volume (DR). The algorithm flowchart is illustrated in Figure 10. The algorithm’s particular phases are listed below:
1) The canopy point cloud was split into 50 equally spaced slices.
2) According to the literature[55], when using the α-shape algorithm to construct a contour, a threshold is present α b ; with α ≥ α b , the boundary shape formed can include all points from the point set P. The enhanced α-shape approach proposed in the literature[53] iteratively searches for the threshold value αb of each point cloud slice and obtains the area of the slice’s outside geometries under this threshold using the following iterative formula(6):
α i + 1 = α i + Δ α   ( i = 1 , 2 , ⋯ , n )
where Δ α denotes the increment size of each iteration and i denotes the iteration count. In this study, the initial α is set to 0.05, and i is set to 0.1.
3) Calculate the percentage change in area, R, for each neighboring slice with the following formula:
R i = A i A i + 1 − 1
where A i A i + 1 indicates the area ratio of adjacent slices.
4) Calculate the overall density of each slice using the KNN algorithm:
  localDensity i = k m e a n ( p d i s t 2 ( Data i , Data idx i [ 2 : end ] ) )   density i = m e a n ( localDensity )
k is the number of nearest neighbors; here, 10 is used. Data i is the data point of the ith slice. idxi is the index of the nearest neighbor of the ith slice. p d i s t 2 ( Data i , Data idx i [ 2 : end ] ) denotes the distance from the ith slice to its k closest neighbors (excluding itself).
The difference between the slice density and the average density is then calculated:
D i = | d e n s i t y i − m e a n ( d e n s i t y ) |
5) If the percentage change in the area of two neighboring slices R is greater than the average neighboring slice’s percentage of area Mean-R or if the difference between the density of two neighboring slices and the average density D is less than the overall average difference Mean-D, the slice is labeled 1; otherwise, it is labeled 0.
6) If the markers of two neighboring slices are the same, then these two slices are merged; otherwise, the next slice is traversed until all slices are traversed.
7) The slices are reconstructed by employing the AS algorithm, using the mean point interval distance of the point cloud in the current slice as the α value. The α value is updated until a complete region is generated, and then the volume of that reconstructed region is calculated. The mean point interval distance is as follows: first, the kd-tree structure was utilized to swiftly determine the nearest neighbor of each point in the current slice of the point cloud, and the total distances among each spot were calculated. The average distance was determined by multiplying the total distance by the total number of points in the point cloud.
8) The total canopy volume was calculated by summing the volumes of all slices.
Figure 8h depicts the performance visualization for crown reconstruction using a DR algorithm, and its performance will be reviewed in Section 3.3.3.

3. Experiment and Results

3.1. Canopy Reconstruction

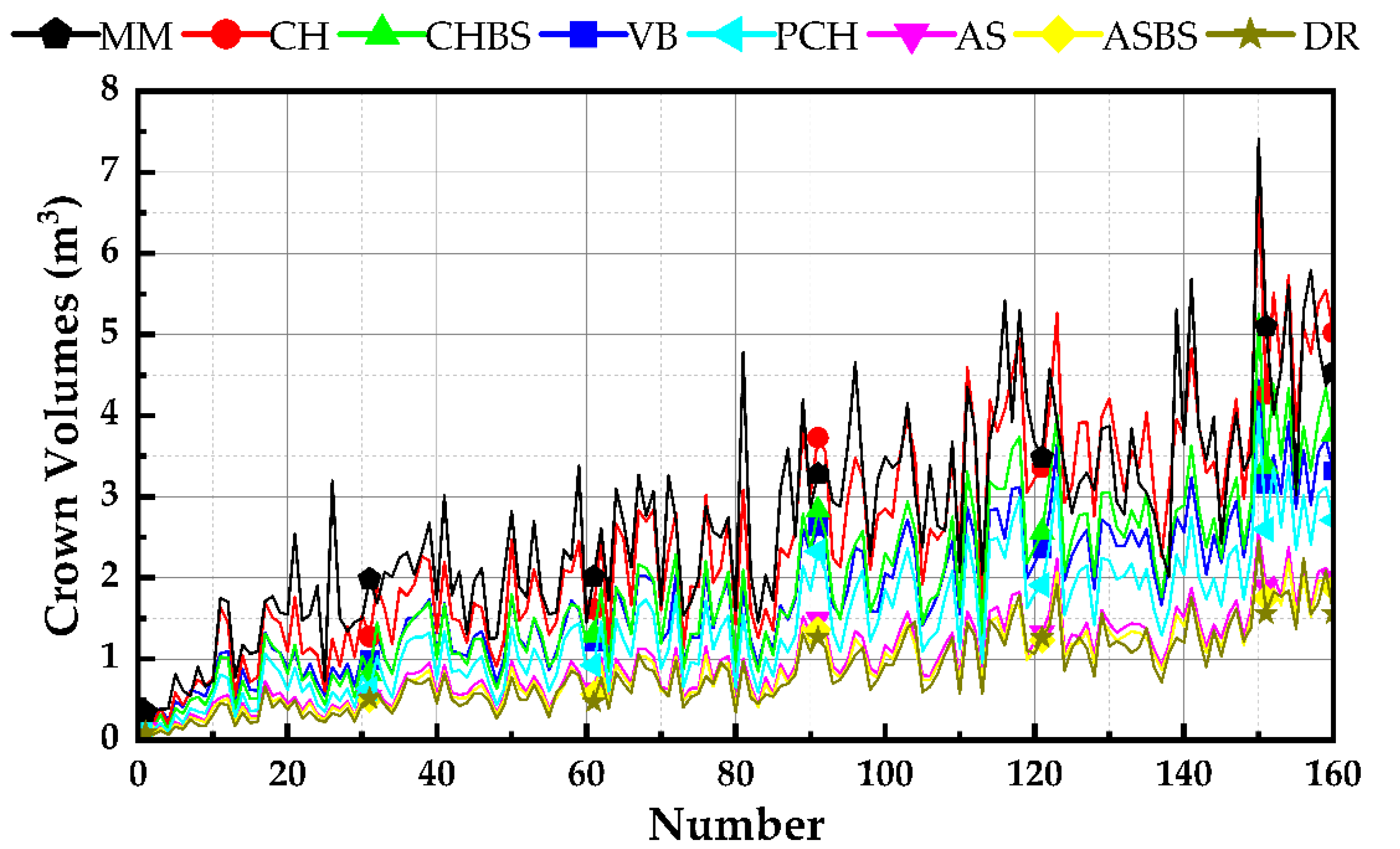
3.1.1. Comparative Analysis of Volumetric Values Using Various Approaches

Figure 11 shows that the relationships between the volumes measured by the six algorithms and the MM method are VMM>VCH>VCHBS>VVB>VPCH>VAS>VASBS. Of these, the MM method’s calculation of crown volume was greater than that of all PRAs calculations ( V ¯ MM=2.72m3). This is because the MM method considers the crown to be an oval, whereas the morphology of blood orange fruit trees is frequently complex and irregular. This simplified model accounts for both the external space between the ellipsoid model and the crown’s holes and crevices. Consequently, the volume values calculated using the MM method are significantly greater than the canopy’s actual volume. Because the CH algorithm treats the fruit tree as a convex polyhedron and accounts for the holes, cracks, and depressions inside the canopy, as well as produces convex packets larger than the canopy contour, it yields the largest calculation result of all PRAs ( V ¯ CH=2.51m3). The result still overestimates the canopy volume ( V ¯ CHBS=1.87m3) even after the CHBS algorithm partially closes the gaps and holes introduced by the CH algorithm. This is because CHBS also has the problem of the nature of the CH algorithm. Although the VB algorithm considers the cubes on the surface of the canopy, because it is difficult to choose the right size of cubes for each fruit tree with a different canopy width and because the cubes’ shape and layout cannot be sufficiently adapted to the canopy morphology, its final volume ( V ¯ VB=1.76m3) is larger than the results of the subsequent algorithms. The PCH algorithm can determine three-dimensional canopy information by fully utilizing external geometric features. It is a simple, fast, and effective method for measuring the volume of a canopy. However, this approach simplifies the canopy morphology to a certain degree and ignores the details of the internal holes, which leads to an increase in the error of volume estimation ( V ¯ PCH=1.42m3). The AS algorithm can accurately extract the boundaries of the canopy point cloud with a reasonable setting of α. The ASBS can eliminate perforations and lacunae in trees with some degree of success, so the AS algorithm calculates a smaller volume ( V ¯ AS=0.97 m3), and the ASBS algorithm calculates the smallest volume ( V ¯ ASBS=0.90 m3).

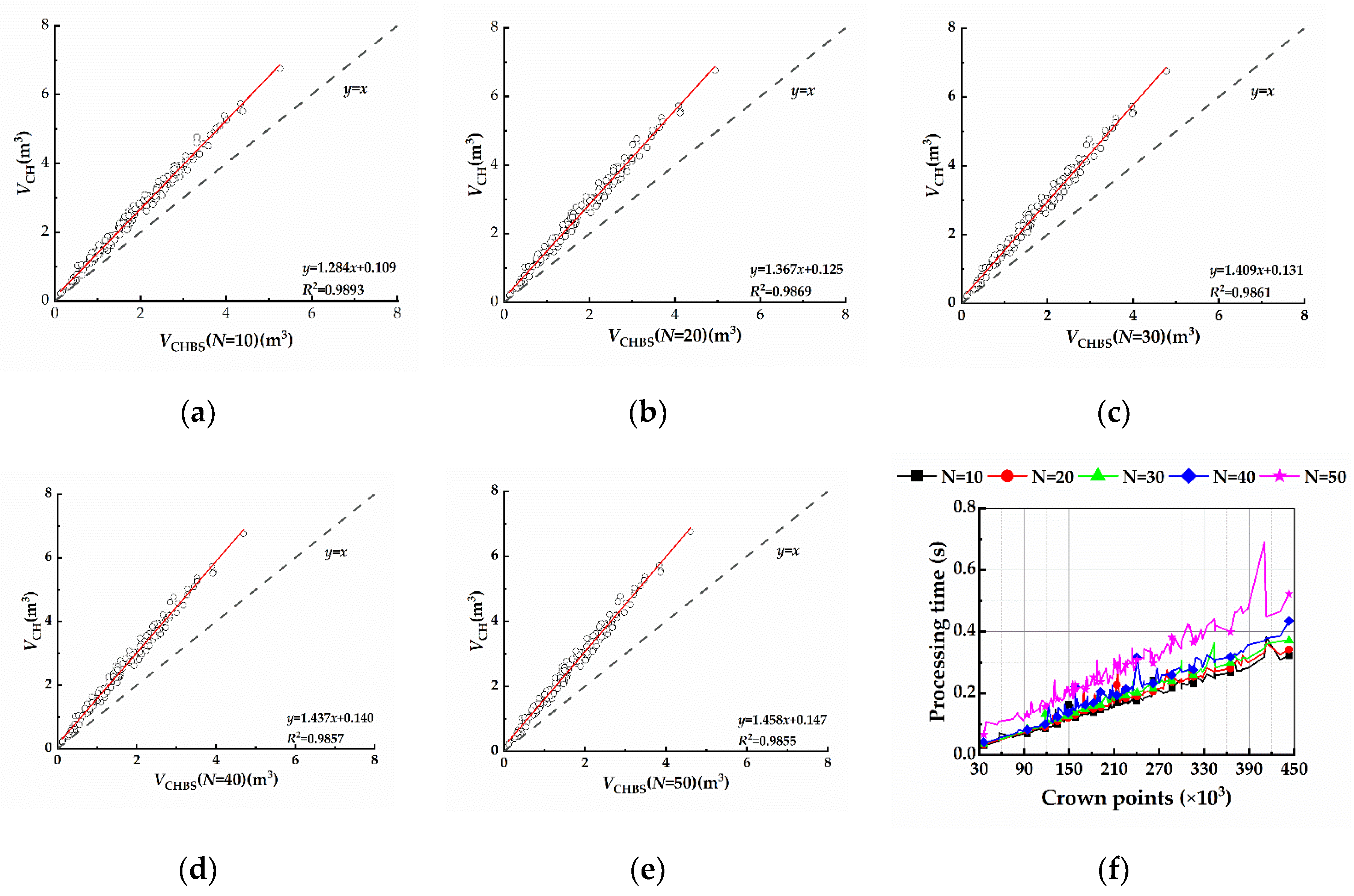
3.1.2. Comparative Analysis of R2 and Regression Coefficients for Various Approaches

The volume fits calculated by the eight methods are shown in Table 3 to investigate the associations between the different methods, with the R2 values of MM and PRAs being relatively low, ranging from 0.802 to 0.854, and the R2 values of the seven types of PRAs ranging from 0.962 to 0.999. The R2 and regression equation for various approaches in Table 3 agree with the quantitative connections in Figure 11.
A boost in the variation in regression coefficients between the VMM and the volume measurements of the other methods implies a boost in the variation in the VMM and the volume measured by the other methods. The VMM ‘s linear fit R2 to other methods’ volume measurements decreases as the volume discrepancy increases. This is because the ellipsoid model takes into account both the perforations and lacunae inside the trees as well as the exterior space between the canopy and the oval model, resulting in a significant overestimation of canopy volume. The CH algorithm removed some of the outside area surrounding the canopy and the ellipsoid model, the CHBS algorithm removed some of the holes and gaps, and the subsequent algorithms all progressively removed more holes and gaps to some degree to optimize the details of extracting the canopy boundaries. The changes in the regression coefficients and R2 that were previously discussed are thus the result of the continuous growth in the disparity between the measured MM and PRAs.
The lower R2 of the CH algorithm compared to that of the other algorithms suggests that its predictive power is relatively weak, and the larger intercepts of the regression equations of the CH and CHBS algorithms compared to the smaller intercepts of the other algorithms imply that the CH and CHBS algorithms overestimate the volume of the tree crowns more than do the other algorithms. The VB algorithm is a voxel-based algorithm that does not compute a cube’s volume when there is no point cloud present, which is why VCHBS is larger than VVB. The PCH algorithm fits the data well, with moderate slopes and minor intercepts in the fitted equations and a significant correlation with the AS method, indicating that its estimated volumes are relatively accurate. The CH and AS algorithms have substantial differences in terms of reconstruction effectiveness and accuracy. The CH algorithm simplifies the canopy shape and ignores internal details and holes. The AS algorithm, on the other hand, can generate canopy shapes with varying degrees of fineness based on the parameter α. This algorithm is more sensitive to external details and can accurately reconstruct the canopy shape. The intercepts of the AS and ASBS algorithms with the other algorithms are small (between 0.013-0.91), and only with the VB algorithm are the intercepts the largest (0.161 and 0.183), which suggests that the VB algorithm does not represent the genuine fruit tree structures with the details of the contours very well using small cubes and overestimates the volume of the canopy. The R2 values for the AS and ASBS are 0.999, and both the intercepts and the slopes are very small, indicating that they are strongly correlated; since the ASBS has the smallest volume, its slope (1.068-2.690) is greater than that of all the other algorithms.

3.1.3. Comparative Analysis of DR Algorithms

Figure 1b shows that the natural round-headed type of citrus tree will have branches that naturally droop when fruiting, with fruit moving toward the bottom and central sections of the canopy, with the lower part usually having more fruit and branches and leaves concentrated in the elevated and central sections of the tree. Because the experimental fruit tree is a blood orange fruit tree that was grafted and planted in 2021 and is still in the process of cultivating the second layer of the tree, the majority of the top is covered with new, unfruitful branches, and it is quite sparse. The DR algorithm dynamically merges slices by taking into account the ratio of area change and density difference of neighboring slices: the change in the area of slices tends to reflect the actual shape and growth characteristics of the canopy; if the ratio of area change of a slice is larger than the average area change ratio, it means that the canopy in that part is growing more vigorously; these areas may be new-growing branches or foliage or rapidly growing fruits; if a slice’s density difference is less than the average density difference, this suggests that the health of that portion of the canopy is more stable and that the growth is more balanced.
Following the analysis of the agronomic traits, the side-by-side reconstruction view of the DR algorithm (Figure 12) shows that the dynamic slices more thoroughly consider the area and density characteristics of the slices, making it easier to identify the areas of dense foliage and branches, areas of concentrated fruit, and areas of sparse density in the roots and tops of trees. The best α values for these regions are automatically determined by the constant iteration of point spacing α values: for the branch- and fruit-rich regions, a smaller α value is used to refine the reconstruction (0.0244-0.0775), which better captures the detailed contour and structure of the branches, leaves, and fruits, making the model more structurally realistic; for the root and top slices of the tree, which are sparsely populated with branches and fruits, a slightly larger α value is used for a looser reconstruction (0.1161-0.3306), which is able to capture the overall shape and structure, resulting in a smoother and more stable overall contour of the canopy;
Because the true volume of the canopy is not available, we used the ASBS algorithm, which performs better than the other six algorithms; the PCH algorithm, which is widely applicable; and the CHBS algorithm, which also uses a slicing method, for comparison with our proposed algorithm. We used the four methods to compute the average number of slices per tree ( n ¯ ) , the average value of α per slice   ( α ¯ ), the average value of volume consistency ( V C ¯ ), and the average value of volume per slice ( v ¯ ) for the 160 blood orange fruit trees. The volume consistency of a tree is obtained by multiplying the standard deviation of the slice volume by the mean value of the slice volume as follows:
  volumeConsistency = 1 n ∑ m = 1 n V m − V ave 2 V ave
where n represents the number of slices, V m denotes the current slice volume, and V ave denotes the average slice volume.
As shown in Table 4, both CHBS and ASBS used a fixed number of slices (10) in each tree and reconstructed each slice in the same way, resulting in extremely consistent volume consistency (0.556 and 0.665). However, the growth pattern of citrus trees is inherently inhomogeneous, and the density and volume of each part (for example, the root, middle, and top of the canopy) vary greatly, which CHBS and ASBS did not account for in the stratification, resulting in reconstructed models that are too consistent and stable to accurately represent citrus tree growth. Because the PCH divides the circular platform at a height of 0.4 m, it dynamically stratifies the citrus trees to some extent. Specifically, it divides each tree’s top into a conical shape and platform slicing of the remaining area according to the height of the canopy. As a result, its volume consistency is closer to the citrus distribution pattern (0.710) than that of ASBS and CHBS, but because it still relies on a basic geometric model to calculate volume, the volume that is obtained will be on the large side and will not be able to adequately remove the holes and gaps. DR dynamically stratified each fruit tree and used different a-values for different parts of the tree. According to the results (1.532), DR better represented the growth characteristics and morphological features of various parts of the citrus tree (e.g., canopy densities, branch/fruit distributions), as well as more continuous and smoother reconstruction results and alpha shapes that better matched the original data to obtain a more accurate canopy volume.
According to the density and shape of the point cloud files, DR dynamically modifies the thickness of the slices and the α-value to more closely resemble the real canopy situation when processing the point cloud data, effectively eliminating holes and gaps. As shown in Figure 11, the volumetric values measured by the DR on the 160 experimental trees tended to be stable, and the volumetric mean value was lower than that of all six algorithms (VDR=0.84). Table 3 shows that DR has more significant slopes and intercepts in the regression equations with other algorithms (the intercepts are more significant than the effects of PCH, AS, and ASBS examined in the previous section). Additionally, the previous analysis revealed that the R2 value of the fit with MM is lower for algorithms that are more accurate because ellipsoidal models differ significantly from the actual volume of the crown, which ignores the fact that every tree is distinct, with varying fruit distributions, branch and leaf densities, and gaps and holes between canopies (which the CH algorithm does as well). The R2 for DR and the other algorithms is approximately 0.96, indicating that the volume derived by the algorithm is stable and that the goodness of fit is satisfactory. The R2 is lower than that of the ASBS and other algorithms because DR begins with the canopy’s internal structure, using the correlation between density and area to dynamically slice the slices and iteratively searching for the optimal a-value for reconstruction based on the distribution of branches, leaves, and fruits in each slice. Conventional algorithms all utilize a simple uniformized slicing and reconstruction approach rather than dynamically correcting changes from the underlying structure of the canopy, as does DR; hence, R2 is greater among numerous other algorithms, while DR is lower. This information is crucial for analyzing citrus tree growth patterns and forecasting fruit supply in the future.

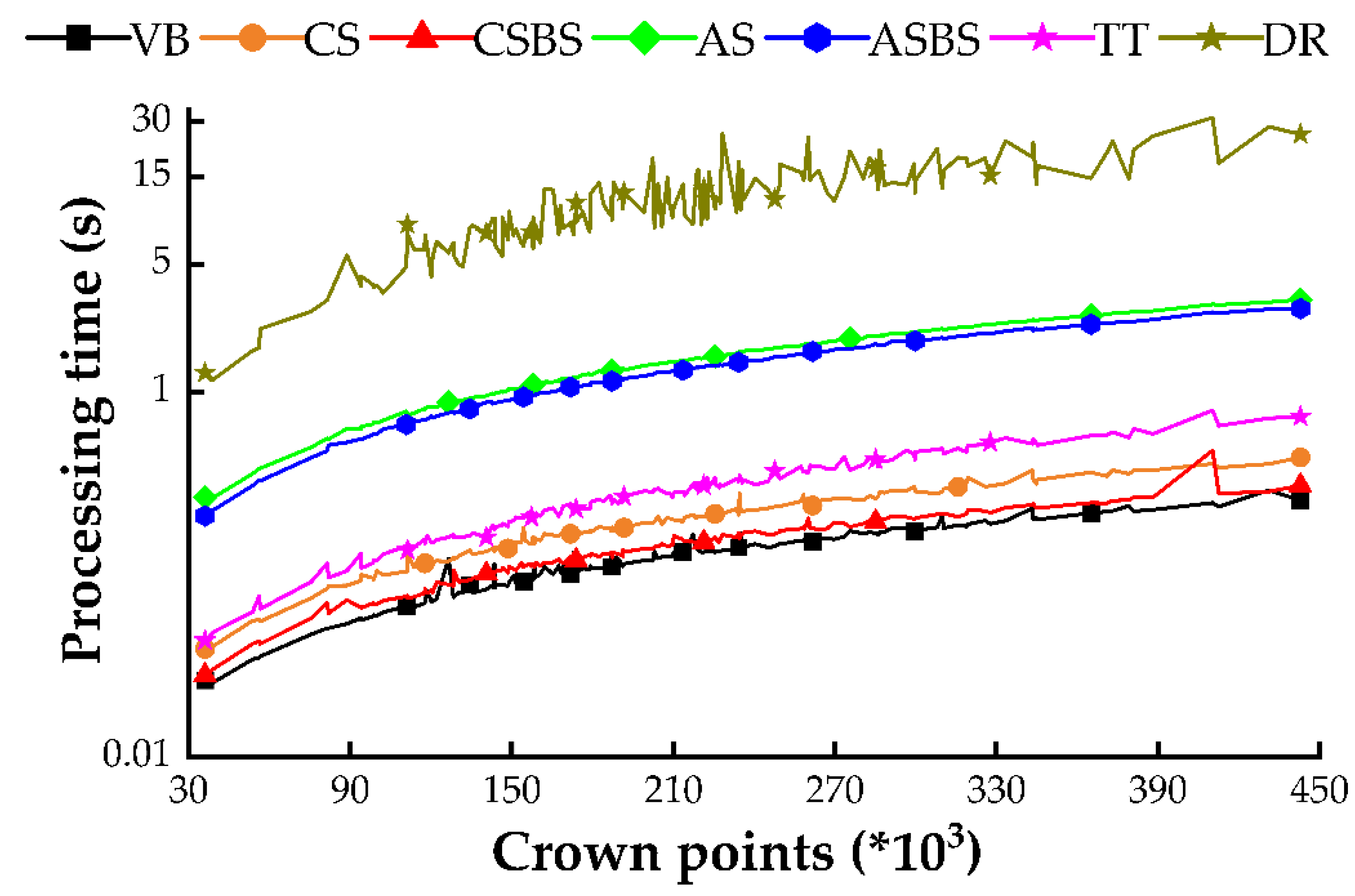
3.1.4. Comparative Analysis of Algorithm Runtimes for Various Approaches

MATLAB R2023a software was used for running seven PRA programs on a Dell computer (processor Intel Core i9-12900 @2.40 GHz, Samsung DDR5 4800 MHz 16 GB × 2 RAM, 512 GB SSD). All other background processes were closed during the program execution. The running times of several algorithms are displayed in Figure 10.
Figure 13 illustrates the link between the running times of the seven volume-finding algorithms as follows: TVB<TCHBS<TCH<TPCH<TASBS<TAS<TDR. VB employs a simple data structure (3D labeled array) and a straightforward traversal technique with low processing complexity. In the loop, only one traversal of the point cloud files is performed, and each point is assigned to the appropriate rectangle. Due to its simplicity, this procedure takes the most quickly to complete ( T ¯ VB=0.126). Although CHBS requires an additional slicing phase, the small amount of data in each slice results in a very fast computation of the CH. Sliced data can often make greater use of the computer’s memory architecture, such as caches, perhaps leading to faster computations. Because the sliced dataset is smaller, it fits more easily into the cache and allows for faster data reading and manipulation during processing ( T ¯ CHBS=0.145). In comparison, applying the CH method ( T ¯ CH=0.2) directly to the complete point cloud data will have a higher computational complexity because it needs to process a larger quantity of data; hence, the CH takes slightly longer than the CHBS. Similarly, the ASBS algorithm ( T ¯ ASBS=1.294) outperforms the AS algorithm ( T ¯ AS=1.457) according to the same principle. Slicing also streamlines the calculation process and minimizes the overall computational effort when considering hardware environments such as processor multicore architecture and memory access efficiency. Because the DR algorithm executes many lookup and iteration operations, it is the longest running algorithm among the PRAs ( T ¯ DR=11.429).

4. Discussion

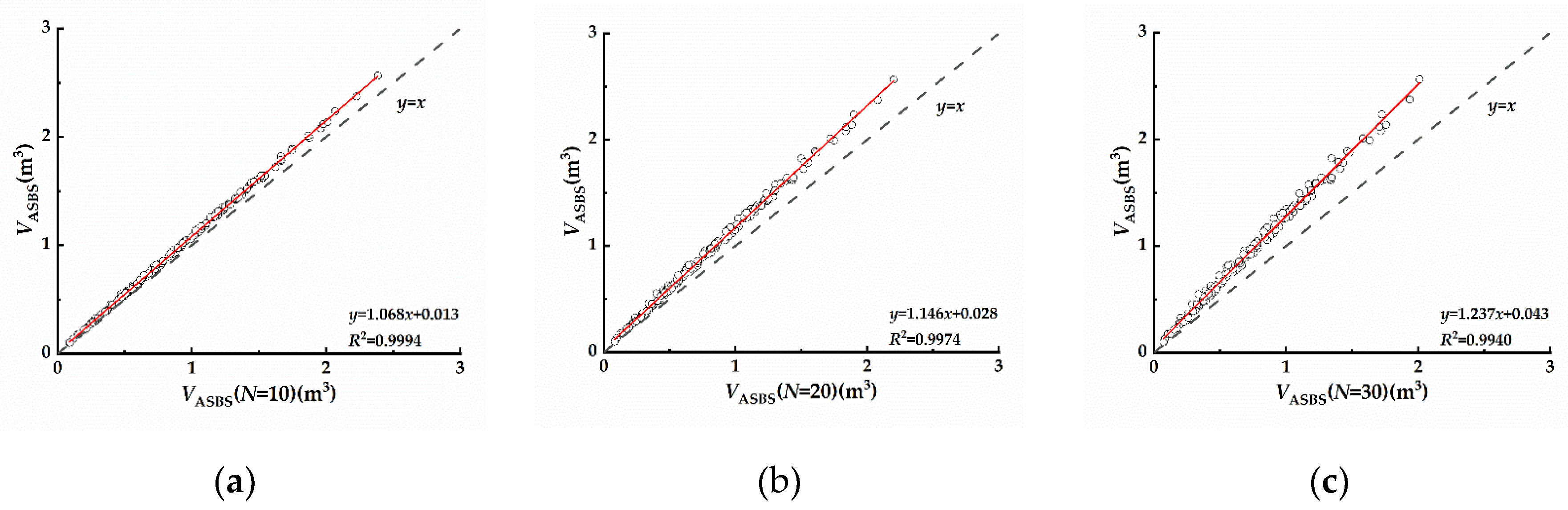
4.1. Discussion of the Number of Slices

Based on earlier investigations[30,40] on the number of slices, five distinct numbers of slices (N = 10, 20, 30, 40, and 50) were selected for the discussion of how the number of slices affects the outcomes of ASBS and CHBS reconstructions in terms of both volume and runtime.

4.1.1. CHBS

Figure 14 demonstrates how the amount of slices affects the reconstructed volume in the CHBS. The percentages of perforations and lacunae eliminated by the original CH algorithm were 26.4%, 31.3%, 33.7%, 35.3%, and 36.5%, respectively, when varying numbers of slices were used (N = 10, 20, 30, 40, 50). As the number of slices increased, the regression coefficients (slope and intercept) between CHBS and CH slowly increased, and the weak change in R2 suggested that increasing the number of slices from the interval of 20-50 did not significantly improve CH.
Figure 14f shows that when the number of processed point clouds increases, the CHBS algorithm running time increases progressively. The runtime climbs by 0.02 seconds for every 10 extra slices in terms of the number of slices and by 0.07 seconds when the number of slices climbs from 40 to 50. According to this linear relationship, the computational cost of the algorithm increases with the number of slices, and this increase becomes more noticeable as the number of slices increases.

4.1.2. ASBS

Figure 15 depicts the effect of the amount of slices on the reconstructed volume in the ASBS. The percentages of perforations and lacunae eliminated by the original AS algorithm were 8.0%, 16.1%, 23.7%, 30.7%, and 36.9%, respectively, when varying numbers of slices were used (N = 10, 20, 30, 40, 50). The trends and reasons for the regression coefficients and R2 values of VAS and VASBS were identical in terms of VCH and VCHBS, but the regression coefficients of ASBS versus AS increased more with the number of slices, and the R2 values decreased faster, indicating that the AS algorithm was more successful at eliminating perforations and lacunae than the CH algorithm.
With regard to execution time, T ¯ ASBS takes 2 seconds more than the T ¯ CHBS algorithm in processing the same amount of points. When the amount of points computed increases, the running time shows a stable linear increase, indicating that the execution time of the ASBS approach remains constant across a range of point cloud file sizes. Interestingly, as the number of slices increases, the running time of the ASBS algorithm decreases, and this decrease becomes increasingly obvious as the number of points increases (Figure 15f). We predict that this is associated with the peculiarities of citrus tree point cloud data as well as the working concept of AS. Citrus tree point cloud data have a high density and volume, and increasing the number of slices reduces the size of individual slices, reducing the processing time per slice. Furthermore, because citrus tree point cloud data contain some overlap and continuity, increasing the number of slices reduces the degree of overlap between slices and unnecessary calculations, resulting in increased efficiency. AS typically reconstructs surfaces by identifying local geometric structures in the point cloud data and then utilizes the geometric structures to generate smooth surface representations. Increasing the number of slices will provide more local geometric information, which will help to reconstruct the surface more accurately, thus reducing the time for subsequent processing. This is also related to the possible optimization of the hardware environment and MATLAB version, as mentioned before.

4.2. Discussion on the Application Scenarios for Each Algorithm

When selecting relevant algorithms, different application scenarios and needs must be considered to provide valuable data support and decision-making references for connected businesses. We discuss this phenomenon after a thorough analysis of the reconstruction effect, algorithm principle, volume, and running time.
The MM volume is significantly greater than the real volume of the tree canopy; this approach is laborious and complicated, and it is weaker than a point cloud-based approach. CHBS reduces some of the flaws and gaps of the CH method, making it less significant than overestimation, and it also keeps the fruit tree shape contour while improving the runtime, with an average runtime that is only 0.02 slower than that of the VB approach. In the case of real-time obstacle avoidance in agricultural robots, which requires quick and precise volume and contour information from the tree canopy, CHBS combines fast slice-volume computation with an accurate convex bagging technique, making it an excellent candidate. The VB can determine the volume of tree crowns rapidly and precisely, making it useful for measuring leaf area and analyzing plant health. It also has uses in urban greening planning and forest resource management. The PCH algorithm has a strong mathematical foundation and reliability, is resistant to data noise and interference, and the computational process is relatively simple, resulting in high computational efficiency and certain advantages in large-scale data processing and real-time monitoring. It can be used to examine the development and canopy structure of forest vegetation, as well as to offer data for forest preservation and resource utilization. ASBS is an optimization of the AS algorithm that produces more accurate results than previous algorithms and is appropriate for large-scale spray volume estimation. DR can better describe the canopy shape and density distribution, and it can also be used to assess crop growth status and the exact volume of the plant canopy, allowing agricultural producers to adjust management measures such as irrigation and fertilization in real time to increase crop yield and quality.

5. Conclusions

This study presents a DR algorithm for citrus tree canopy reconstruction and volume estimation, which was analyzed along with six mainstream algorithms. The specific research is summarized below:
(1)
A collection of processing procedures is offered for three-dimensional reconstruction designed to use handheld laser scanners on large-scale citrus farms. Detailed procedures and parameters for the reconstruction of pretreatment are provided, especially for high ridges and deep furrows for soil bundling in southern hilly areas. The accuracy of the handheld laser scanner precision was demonstrated by measuring the parameters of 160 blood orange trees. It was also shown that the MM method is time-consuming and subject to subjective influences, that the volume obtained by ellipsoidal modeling is grossly biased, and that PRAs proved to be a fast and reliable method of canopy measurement.
(2)
Six popular canopy reconstruction algorithms were evaluated and tested on orange trees, and their reconstruction effects were examined. The merits and disadvantages of each algorithm are examined by combining the principle, geometric qualities, volume value, runtime, and linear relationship between each algorithm, and appropriate operating environments are proposed for each algorithm. For example, CHBS, which has a shorter runtime, is excellent for obstacle avoidance for agricultural robots that require fast real-time sensing. VB can be used to measure leaf area and estimate plant health, PCH can be used to assess forest vegetation growth and canopy structure, and ASBS can be used for large-scale, accurate spraying volume estimation.
(3)
Only when N=10 did shifting did the amount of slices significantly affect the volumetric values calculated by the CH algorithm, and the running time was reduced compared to that of CH, but as the number of slices increased, this effect became weaker and the running time increased; therefore, the CHBS algorithm with N=10 is recommended for citrus tree reconstruction. The AS algorithm had a considerable effect on the volumetric values after increasing the number of slices, and this effect became more steady and significant as the number of slices increased. Furthermore, adding slices to the AS algorithm enhanced the operational efficiency, indicating that slicing-based optimization of the AS algorithm is useful for citrus tree reconstruction.
(4)
A dynamic slicing and reconstruction algorithm is developed to determine the volume of the citrus canopy; this algorithm integrates the percentage change in the area of the citrus tree point cloud with the density difference, better captures and reflects the actual shape and growth characteristics of the canopy, and adopts the iterative point cloud average point spacing in the reconstruction to find the appropriate α-value for each slice, which can reconstruct the parts of the citrus tree more accurately to obtain a more realistic three-dimensional model.

Author Contributions

Conceptualization, W.J. and Y.Z.; Data curation, W.J., Z.H. and H.W.; Formal analysis, W.J., H.W. and Z.B.; Funding acquisition, Y.Z.; Investigation, W.J., B.T. and Q.Y.; Methodology, W.J., B.T. and Y.Z.; Project administration, W.J. and Y.Z.; Resources, W.J. and Q.Y.; Software, W.J., B.T. and Z.H.; Supervision, Y.Z.; Validation, W.J. and Z.B.; Visualization, W.J.; Writing – original draft, W.J. and Y.Z.; Writing – review & editing, W.J. and Y.Z.. All authors have read and agreed to the published version of the manuscript.

Funding

The National Natural Science Foundation of China (31972991), the earmarked fund for the China Agriculture Research System (CARS-26), the Key Research and Development Project of Southwest University Pilot Plan (SWU-XDZD22004), and the Technology Innovation and Application Development Project in Chongqing (CSTB2023TIAD-LUX0001 )

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Wang, T.; Li, J.; He, L.; Deng, L.; Yongqiang, Z.; Yi, S.; Xie, R.; Lyu, Q. Citrus canopy volume estimation using UAV oblique photography. International Journal of Precision Agricultural Aviation 2021, 1, 22–28. [Google Scholar] [CrossRef]
  2. Pommerening, A.; Sánchez Meador, A.J. Tamm review: Tree interactions between myth and reality. Forest Ecology and Management 2018, 424, 164–176. [Google Scholar] [CrossRef]
  3. Li, F.; Cohen, S.; Naor, A.; Shaozong, K.; Erez, A. Studies of canopy structure and water use of apple trees on three rootstocks. Agricultural Water Management 2002, 55, 1–14. [Google Scholar] [CrossRef]
  4. Pereira, A.R.; Green, S.; Villa Nova, N.A. Penman–Monteith reference evapotranspiration adapted to estimate irrigated tree transpiration. Agricultural Water Management 2006, 83, 153–161. [Google Scholar] [CrossRef]
  5. Villalobos, F.J.; Testi, L.; Hidalgo, J.; Pastor, M.; Orgaz, F. Modelling potential growth and yield of olive (Olea europaea L.) canopies. European Journal of Agronomy 2006, 24, 296–303. [Google Scholar] [CrossRef]
  6. Zaman, Q.; Schumann, A.; Hostler, H. Estimation of citrus fruit yield using ultrasonically-sensed tree size. Applied Engineering in Agriculture 2006, 22. [Google Scholar] [CrossRef]
  7. Primo-Capella, A.; Molina-Nadal, M.D.; Catalá-Senent, L.; de Miguel-Moreno, A.; Forner-Giner, M.Á.; Martínez-Cuenca, M.-R. Response to Deficit Irrigation of ‘Orogrande’ Mandarin Grafted onto Different Citrus Rootstocks in Spain. Horticulturae 2024, 10, 37. [Google Scholar] [CrossRef]
  8. Guo, S.; Chen, C.; Du, G.; Yu, F.; Yao, W.; Yubin, L. Evaluating the use of unmanned aerial vehicles for spray applications in mountain Nanguo pear orchards. Pest Management Science 2024. [Google Scholar] [CrossRef] [PubMed]
  9. Abbas, I.; Liu, J.; Faheem, M.; Noor, R.S.; Shaikh, S.A.; Solangi, K.A.; Raza, S.M. Different sensor based intelligent spraying systems in Agriculture. Sensors and Actuators A: Physical 2020, 316, 112265. [Google Scholar] [CrossRef]
  10. Kolmanič, S.; Strnad, D.; Kohek, Š.; Benes, B.; Hirst, P.; Žalik, B. An algorithm for automatic dormant tree pruning. Applied Soft Computing 2021, 99, 106931. [Google Scholar] [CrossRef]
  11. Ye, X.-J.; Sakai, K.; Asada, S.I.; Sasao, A. Inter-Relationships Between Canopy Features and Fruit Yield in Citrus as Detected by Airborne Multispectral Imagery. Transactions of the ASABE (American Society of Agricultural and Biological Engineers) 2008, 51, 739–751. [Google Scholar] [CrossRef]
  12. Marín-Buzón, C.; Pérez-Romero, A.; Tucci-Álvarez, F.; Manzano-Agugliaro, F. Assessing the Orange Tree Crown Volumes Using Google Maps as a Low-Cost Photogrammetric Alternative. Agronomy 2020, 10, 893. [Google Scholar] [CrossRef]
  13. Krajewski, A.; Schumann, A.; Ebert, T.; Oswalt, C.; Ferrarezi, R.; Waldo, L. Management of Citrus Tree Canopies for Fresh-Fruit Production. EDIS 2021, 2021. [Google Scholar] [CrossRef]
  14. Mu, Y.; Fujii, Y.; Takata, D.; Zheng, B.; Noshita, K.; Honda, K.; Ninomiya, S.; Guo, W. Characterization of peach tree crown by using high-resolution images from an unmanned aerial vehicle. Horticulture research 2018, 5. [Google Scholar] [CrossRef] [PubMed]
  15. De-Yu, H.; Xue-Feng, L.; Shao-Lan, H.; Rang-Jin, X.; Chun, Q.; Qiang, L.; Shi-Lai, Y.; Yong-Qiang, Z.; Lie, D. Effect of plant canopy transformation on chlorophyll fluorescence characteristics and fruit yield and quality in closed citrus orchard. Scientia Agricultura Sinica 2017, 50, 1734–1746. [Google Scholar]
  16. Miranda-Fuentes, A.; Llorens, J.; Gamarra-Diezma, J.L.; Gil-Ribes, J.A.; Gil, E. Towards an optimized method of olive tree crown volume measurement. Sensors 2015, 15, 3671–3687. [Google Scholar] [CrossRef] [PubMed]
  17. Zheng, Y.; Deng, L.; He, S.; Zhou, Z.; Yi, S.; Mao, S.; Zhao, X. Effects of seven rootstocks on tree growth, yield and fruit quality of’Hamlin’sweet orange in south China. Acta Horticulturae Sinica 2010, 37, 532–538. [Google Scholar]
  18. Scapin, M.d.S.; Behlau, F.; Scandelai, L.H.M.; Fernandes, R.S.; Silva Junior, G.J.; Ramos, H.H. Tree-row-volume-based sprays of copper bactericide for control of citrus canker. Crop Protection 2015, 77, 119–126. [Google Scholar] [CrossRef]
  19. Lee, K.; Ehsani, R. A laser scanner based measurement system for quantification of citrus tree geometric characteristics. Applied Engineering in Agriculture 2009, 25, 777–788. [Google Scholar] [CrossRef]
  20. Li, P.; Zhang, M.; Wang, T.; Zheng, Y.; Yi, S.; Lü, Q. Real-time estimation of citrus canopy volume based on laser scanner and irregular triangular prism module method. Scientia Agricultura Sinica 2019, 52, 4493–4504. [Google Scholar]
  21. Dong, X.; Zhang, Z.; Yu, R.; Tian, Q.; Zhu, X. Extraction of information about individual trees from high-spatial-resolution UAV-acquired images of an orchard. Remote Sensing 2020, 12, 133. [Google Scholar] [CrossRef]
  22. Jurado, J.M.; Ortega, L.; Cubillas, J.J.; Feito, F. Multispectral mapping on 3D models and multi-temporal monitoring for individual characterization of olive trees. Remote Sensing 2020, 12, 1106. [Google Scholar] [CrossRef]
  23. Dong, W.; Roy, P.; Isler, V. Semantic mapping for orchard environments by merging two-sides reconstructions of tree rows. Journal of Field Robotics 2020, 37, 97–121. [Google Scholar] [CrossRef]
  24. Yin, Y.; Liu, G.; Li, S.; Zheng, Z.; Si, Y.; Wang, Y. A Method for Predicting Canopy Light Distribution in Cherry Trees Based on Fused Point Cloud Data. Remote Sensing 2023, 15, 2516. [Google Scholar] [CrossRef]
  25. Yu, L.; Hong, T.; Zhao, Z.; Huang, J.; Zhang, L. 3D-reconstruction and volume measurement of fruit tree canopy based on ultrasonic sensors. transactions of the chinese society of agricultural engineering 2010, 26, 204–208. [Google Scholar]
  26. Maghsoudi, H.; Minaei, S.; Ghobadian, B.; Masoudi, H. Ultrasonic sensing of pistachio canopy for low-volume precision spraying. Computers and Electronics in Agriculture 2015, 112, 149–160. [Google Scholar] [CrossRef]
  27. Zhang, J.; Xie, T.-J.; Wei, X.-N.; Wang, Z.-K.; Liu, C.-T.; Zhou, G.-S.; Wang, B. Estimation of feed rapeseed biomass based on multi-angle oblique imaging technique of unmanned aerial vehicle. 2021.
  28. Zhu, B.; Li, M.; Liu, F.; Jia, A.; Mao, X.; Guo, Y. Modeling of canopy structure of field-grown maize based on UAV images. Trans. Chin. Soc. Agric. Mach 2021, 52, 170–177. [Google Scholar]
  29. Rosell, J.; Sanz, R. A review of methods and applications of the geometric characterization of tree crops in agricultural activities. Computers and electronics in agriculture 2012, 81, 124–141. [Google Scholar] [CrossRef]
  30. Liu, X.; Wang, Y.; Kang, F.; Yue, Y.; Zheng, Y. Canopy parameter estimation of citrus grandis var. Longanyou based on Lidar 3d point clouds. Remote Sensing 2021, 13, 1859. [Google Scholar] [CrossRef]
  31. Wang, M.; Dou, H.; Sun, H.; Zhai, C.; Zhang, Y.; Yuan, F. Calculation method of canopy dynamic meshing division volumes for precision pesticide application in orchards based on lidar. Agronomy 2023, 13, 1077. [Google Scholar] [CrossRef]
  32. Pagliai, A.; Sarri, D.; Lisci, R.; Lombardo, S.; Vieri, M.; Perna, C.; Cencini, G.; De Pascale, V.; Ferraz, G.A.E. Development of an algorithm for assessing canopy volumes with terrestrial LiDAR to implement precision spraying in vineyards. 2022.
  33. Jiang, Y.; Li, C.; Takeda, F.; Kramer, E.A.; Ashrafi, H.; Hunter, J. 3D point cloud data to quantitatively characterize size and shape of shrub crops. Horticulture research 2019, 6. [Google Scholar] [CrossRef]
  34. Xu, W.-H.; Feng, Z.-K.; Su, Z.-F.; Xu, H.; Jiao, Y.-Q.; Deng, O. An automatic extraction algorithm for individual tree crown projection area and volume based on 3D point cloud data. Spectroscopy and Spectral Analysis 2014, 34, 465–471. [Google Scholar] [PubMed]
  35. Colaço, A.F.; Trevisan, R.G.; Molin, J.P.; Rosell-Polo, J.R.; Escolà, A. Orange tree canopy volume estimation by manual and LiDAR-based methods. Advances in Animal Biosciences 2017, 8, 477–480. [Google Scholar] [CrossRef]
  36. Sultan Mahmud, M.; Zahid, A.; He, L.; Choi, D.; Krawczyk, G.; Zhu, H.; Heinemann, P. Development of a LiDAR-guided section-based tree canopy density measurement system for precision spray applications. Computers and Electronics in Agriculture 2021, 182, 106053. [Google Scholar] [CrossRef]
  37. Chakraborty, M.; Khot, L.R.; Sankaran, S.; Jacoby, P.W. Evaluation of mobile 3D light detection and ranging based canopy mapping system for tree fruit crops. Computers and Electronics in Agriculture 2019, 158, 284–293. [Google Scholar] [CrossRef]
  38. Fernández-Sarría, A.; Martínez, L.; Velázquez-Martí, B.; Sajdak, M.; Estornell, J.; Recio, J. Different methodologies for calculating crown volumes of Platanus hispanica trees using terrestrial laser scanner and a comparison with classical dendrometric measurements. Computers and electronics in agriculture 2013, 90, 176–185. [Google Scholar] [CrossRef]
  39. Wang Jia, W.J.; Yang HuiQiao, Y.H.; Feng ZhongKe, F.Z. Tridimensional green biomass measurement for trees using 3-D laser scanning. 2013.
  40. Yan, Z.; Liu, R.; Cheng, L.; Zhou, X.; Ruan, X.; Xiao, Y. A Concave Hull Methodology for Calculating the Crown Volume of Individual Trees Based on Vehicle-Borne LiDAR Data. Remote Sensing 2019, 11, 623. [Google Scholar] [CrossRef]
  41. Quan, C.; Songlin, X.; Mei, Y.; Jinhui, H. Effect of Different Pruning on Growth and Fruit Bearing of ‘Blood Orange No.8’. Molecular Plant Breeding 2023, 1-15.
  42. ZENG, Q.; MAO, J.; LI, X.; LIU, X. Planar-fitting filtering algorithm for LIDAR points cloud. Geomatics and Information Science of Wuhan University 2008, 33, 25–28. [Google Scholar]
  43. Fischler, M.A.; Bolles, R.C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
  44. Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sensing 2016, 8, 501. [Google Scholar] [CrossRef]
  45. Hojjatoleslami, S.; Kittler, J. Region growing: a new approach. IEEE Transactions on Image processing 1998, 7, 1079–1084. [Google Scholar] [CrossRef] [PubMed]
  46. Hu, C.; Pan, Z.; Zhong, T. Leaf and wood separation of poplar seedlings combining locally convex connected patches and K-means++ clustering from terrestrial laser scanning data. Journal of Applied Remote Sensing 2020, 14, 018502–018502. [Google Scholar] [CrossRef]
  47. Ferrara, R.; Virdis, S.G.; Ventura, A.; Ghisu, T.; Duce, P.; Pellizzaro, G. An automated approach for wood-leaf separation from terrestrial LIDAR point clouds using the density based clustering algorithm DBSCAN. Agricultural and forest meteorology 2018, 262, 434–444. [Google Scholar] [CrossRef]
  48. Gamal, A.; Wibisono, A.; Wicaksono, S.B.; Abyan, M.A.; Hamid, N.; Wisesa, H.A.; Jatmiko, W.; Ardhianto, R. Automatic LIDAR building segmentation based on DGCNN and euclidean clustering. Journal of Big Data 2020, 7, 1–18. [Google Scholar] [CrossRef]
  49. Cao, Y.; Wang, Y.; Xue, Y.; Zhang, H.; Lao, Y. FEC: Fast Euclidean Clustering for Point Cloud Segmentation. Drones 2022, 6, 325. [Google Scholar] [CrossRef]
  50. Rusu, R.B.; Marton, Z.C.; Blodow, N.; Dolha, M.; Beetz, M. Towards 3D Point cloud based object maps for household environments. Robotics and Autonomous Systems 2008, 56, 927–941. [Google Scholar] [CrossRef]
  51. Schinor, E.H.; Cristofani-Yaly, M.; Bastianel, M.; Machado, M.A. Sunki mandarin vs Poncirus trifoliata hybrids as rootstocks for Pera sweet orange. Journal of Agricultural Science 2013, 5, 190. [Google Scholar] [CrossRef]
  52. Lecigne, B.; Delagrange, S.; Messier, C. Exploring trees in three dimensions: VoxR, a novel voxel-based R package dedicated to analysing the complex arrangement of tree crowns. Annals of Botany 2017, 121, 589–601. [Google Scholar] [CrossRef] [PubMed]
  53. Cheng, G.; Wang, J.; Yang, J.; Zhao, Z.; Wang, L. Calculation Method of 3D Point Cloud Canopy Volume Based on Improved α-shape Algorithm. Trans. Chin. Soc. Agric. Mach 2021, 52, 175–183. [Google Scholar]
  54. ZHOUHeng-ke; LIHai-wang; ZHAOXing; GUOCai-ling; LIBai-lin. A Tree Crown Volume Calculation Method Based on Adaptive Slice of Point Cloud. Journal of Northwest Forestry University 2023, 38, 189-195+202.
  55. Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Transactions on Information Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
Preprints 106744 g001
Figure 1. Photographs of the experimental area: (a) Satellite image of a blood orange orchard; (b) ground-level image of a blood orange orchard.
Figure 1. Photographs of the experimental area: (a) Satellite image of a blood orange orchard; (b) ground-level image of a blood orange orchard.
Preprints 106744 g001
Preprints 106744 g002
Figure 2. Constituent part of the handheld 3D LIDAR scanning system (GoSLAM RS100).
Figure 2. Constituent part of the handheld 3D LIDAR scanning system (GoSLAM RS100).
Preprints 106744 g002
Preprints 106744 g003
Figure 3. 3D LiDAR map of the blood orange orchard. The gradient color by z value indicates altitude; the white dashed line represents the path traveled by the LiDAR scanning equipment during the scan, and the triangle and star markers indicate the starting and ending points of the scan paths, respectively.
Figure 3. 3D LiDAR map of the blood orange orchard. The gradient color by z value indicates altitude; the white dashed line represents the path traveled by the LiDAR scanning equipment during the scan, and the triangle and star markers indicate the starting and ending points of the scan paths, respectively.
Preprints 106744 g003
Preprints 106744 g004
Figure 4. Preprocessing for canopy reconstruction flowchart. Note: CSF, cloth simulation framework algorithm; SOR, Statistical Outlier Removal algorithm.
Figure 4. Preprocessing for canopy reconstruction flowchart. Note: CSF, cloth simulation framework algorithm; SOR, Statistical Outlier Removal algorithm.
Preprints 106744 g004
Preprints 106744 g005
Figure 5. The experimental area after completing CSF ground filtering, with some weeds and ground points still present (indicated by white circles).
Figure 5. The experimental area after completing CSF ground filtering, with some weeds and ground points still present (indicated by white circles).
Preprints 106744 g005
Preprints 106744 g006
Figure 6. Clustering results for the blood orange orchard 3D map. Each different color represents a split fruit tree, manually numbered on the original image, indicating trees from 1-160.
Figure 6. Clustering results for the blood orange orchard 3D map. Each different color represents a split fruit tree, manually numbered on the original image, indicating trees from 1-160.
Preprints 106744 g006
Preprints 106744 g007
Figure 7. Comparison of the data before and after denoising: (a) The data before denoising. The red dashed circle shows a few obvious noise points (including the stick used to support the branch); (b) The state after denoising.
Figure 7. Comparison of the data before and after denoising: (a) The data before denoising. The red dashed circle shows a few obvious noise points (including the stick used to support the branch); (b) The state after denoising.
Preprints 106744 g007
Preprints 106744 g008aPreprints 106744 g008b
Figure 8. Canopy reconstruction effect diagram with (a) manual method (MM); (b) convex hull (CH); (c) convex hull by slices (CHBS); (d) voxel-based (VB); (e) alpha-shape (AS) (f) alpha-shape by slices (ASBS); (g) platform convex hull (PCH); (h) dynamic slicing and reconstruction (DR) algorithms. Note: x, y, and z denote the horizontal width, vertical width, and height, respectively.
Figure 8. Canopy reconstruction effect diagram with (a) manual method (MM); (b) convex hull (CH); (c) convex hull by slices (CHBS); (d) voxel-based (VB); (e) alpha-shape (AS) (f) alpha-shape by slices (ASBS); (g) platform convex hull (PCH); (h) dynamic slicing and reconstruction (DR) algorithms. Note: x, y, and z denote the horizontal width, vertical width, and height, respectively.
Preprints 106744 g008aPreprints 106744 g008b
Preprints 106744 g009
Figure 9. Effect of the AS algorithm reconstruction for varying α values.
Figure 9. Effect of the AS algorithm reconstruction for varying α values.
Preprints 106744 g009
Preprints 106744 g010
Figure 10. Flowchart of the DR algorithm.
Figure 10. Flowchart of the DR algorithm.
Preprints 106744 g010
Preprints 106744 g011
Figure 11. Comparative plot of volumetric values of 160 blood orange trees measured by the MM method and 7 PRAs.
Figure 11. Comparative plot of volumetric values of 160 blood orange trees measured by the MM method and 7 PRAs.
Preprints 106744 g011
Preprints 106744 g012
Figure 12. Lateral angle of the reconstruction using the DR algorithm. Note: α, the α-value used for AS reconstruction from the slice; Sum(V) signifies the total volume from the canopy; V, sliced point cloud volume.
Figure 12. Lateral angle of the reconstruction using the DR algorithm. Note: α, the α-value used for AS reconstruction from the slice; Sum(V) signifies the total volume from the canopy; V, sliced point cloud volume.
Preprints 106744 g012
Preprints 106744 g013
Figure 13. Comparison plot of run times for 7 PRAs measuring 160 blood orange trees.
Figure 13. Comparison plot of run times for 7 PRAs measuring 160 blood orange trees.
Preprints 106744 g013
Preprints 106744 g014
Figure 14. Impact of the amount of slices (N) on the reconstruction volume in the CHBS approach. (a) N is set to 10; (b) 20; (c) 30; (d) 40; (e) 50; (f) Impact of various numbers of slices on the running time of the CHBS approach.
Figure 14. Impact of the amount of slices (N) on the reconstruction volume in the CHBS approach. (a) N is set to 10; (b) 20; (c) 30; (d) 40; (e) 50; (f) Impact of various numbers of slices on the running time of the CHBS approach.
Preprints 106744 g014
Preprints 106744 g015aPreprints 106744 g015b
Figure 15. Impact of the amount of slices (N) on the reconstruction volume in the ASBS approach. (a) N is set to 10; (b) 20; (c) 30; (d) 40; (e) 50; (f) Impact of various numbers of slices on the running time of the ASBS approach.
Figure 15. Impact of the amount of slices (N) on the reconstruction volume in the ASBS approach. (a) N is set to 10; (b) 20; (c) 30; (d) 40; (e) 50; (f) Impact of various numbers of slices on the running time of the ASBS approach.
Preprints 106744 g015aPreprints 106744 g015b
Table 1. Comparison of height values measured by manual and CC methods.
Table 1. Comparison of height values measured by manual and CC methods.
H(m) Manual CC Absolute Error Relative Error
Mean 1.835 1.814 0.072 0.039
Var. 0.118 0.130 0.004 0.001
Max 2.590 2.616 0.397 0.178
Min 0.880 0.83 0.001 0.0005
Table 2. Comparison of the measured width between the manual and CC methods.
Table 2. Comparison of the measured width between the manual and CC methods.
W(m) Manual CC Absolute Error Relative Error
Mean 1.619 1.719 0.131 0.081
Var. 0.087 0.114 0.011 0.004
Max 2.400 2.460 0.513 0.343
Min 0.730 0.793 0.0005 0.0003
Table 3. R2 and regression equation for various approaches.
Table 3. R2 and regression equation for various approaches.
Eq./R2 VMM VCH VCHBS VVB VPCH VAS VASBS VDR
VMM y=0.884x+0.495 y=1.124x+0.615 y=1.345x+0.341 y=1.460x+0.642 y=2.199x+0.575 y=2.353x+0.600 y=2.346x+0.750
VCH 0.854 y=1.284x+0.109 y=1.536x-0.201 y=1.664x+0.145 y=2.516x+0.061 y=2.690x+0.091 y=2.678x+0.265
VCHBS 0.827 0.989 y=1.195x-0.242 y=1.297x+0.025 y=1.963x-0.042 y=2.097x-0.017 y=2.088x+0.118
VVB 0.819 0.979 0.989 y=1.078x+0.233 y=1.646x+0.161 y=1.759x+0.183 y=1.743x+0.304
VPCH 0.820 0.977 0.995 0.989 y=1.509x-0.048 y=1.611x-0.027 y=1.602x+0.077
VAS 0.802 0.962 0.978 0.994 0.982 y=1.068x+0.013 y=1.053x+0.090
VASBS 0.805 0.964 0.977 0.994 0.980 0.999 y=0.985x+0.072
VDR 0.794 0.948 0.962 0.968 0.962 0.965 0.964 DR
Table 4. Comparative analysis of DR with CHBS, PCH, and ASBS.
Table 4. Comparative analysis of DR with CHBS, PCH, and ASBS.
Algorithm n ¯ α ¯ v ¯ V C ¯ V ¯
CHBS 10 No 0.187 0.556 1.872
PCH 5 No 0.254 0.709 1.339
ASBS 10 0.05 0.09 0.664 0.901
DR 13.806 0.085 0.065 1.532 0.84
Note: the average number of slices per tree, n ¯ ; the average value of α per slice, , α ¯ ; the average value of volume consistency, V C ¯ ; and the average value of volume per slice, v ¯ .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated