Prerpints.org logo
Preprint
Article

An Uncertainty Relation for Retarded Gravity

Altmetrics

Downloads

68

Views

38

Comments

0

This version is not peer-reviewed

Submitted:

16 May 2024

Posted:

17 May 2024

You are already at the latest version

Alerts
Abstract
In recent years retarded gravity has explained many of the mysteries surrounding the "missing mass" related to galactic rotation curves, the Tully-Fisher relations, and gravitational lensing phenomena. Indeed a recent paper analyzing 143 galaxies, has demonstrated that retarded gravity will suffice to explain the galaxies rotation curves without the need to postulate dark matter for multiple types of galaxies. Moreover, it also demystified the "missing mass" related to galactic clusters and elliptic galaxies in which excess matter wad derived through the virial theorem. Here we give a mathematical criterion which specifies the cases for which retardation is important for gravity (and when it is not). The criterion takes the form of an "uncertainty" relation.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

From a practical standpoint, general relativity (GR) has been validated by numerous observations spanning various fields. However, its current status presents challenges. While supported by substantial observational evidence, GR faces significant hurdles. Its verifications in cosmology and astrophysics are under scrutiny, primarily because it relies on unproven concepts like dark matter and energy to explain phenomena on a large scale, such as galaxies and the universe. Often, these unconfirmed elements are employed while simultaneously overlooking a crucial aspect of GR: retardation, which contradicts Newtonian principles of action at a distance. This discrepancy may be connected to the problems we have understanding of gravitational interactions on cosmic scales.
The mystery surrounding dark matter has long been a topic of discussion within the astronomical community, dating back to the 1930s, and possibly even earlier in the 1920s when it was referred to as the "question of missing mass." Over time, this enigma has only grown more prominent, particularly as the need for dark matter (and the tendency to overlook retardation) has increased on larger scales under examination. Despite extensive and costly efforts, including a forty-year search conducted underground and using accelerators, dark matter’s existence remains unproven. Recent years have only added to the challenge, as the Large Hadron Collider’s failure to detect any super-symmetric particles—a favored form of dark matter among astro-particle physicists—poses further complications. These particles are not only crucial for understanding dark matter but also play a pivotal role in string theory, which is anticipated to provide insights into the quantization of gravity.
As far back as 1933, Zwicky observed anomalies in the velocities of galaxies inside the Coma Cluster that exceeded predictions based on Newtonian theory. He calculated [1,2] that the required amount of matter to explain these velocities could be about 400 times greater than that of visible matter, although later adjustments mitigated this discrepancy to some extent. Had Zwicky utilized the concept of retarded gravity in his calculations, this issue might have been resolved without significant complication [3]. In 1959, Volders [4] noted similar discrepancies on a smaller scale within the outer parts of the nearby spiral galaxy M33, where velocities did not follow the expected 1 r pattern. This observation was corroborated in subsequent years by Rubin and Ford [5,6], who demonstrated that velocities at the outer rim of many spiral galaxies either plateaued or continued to increase, each at a different velocity. Previous studies have indicated that such velocity patterns can be directly inferred from general relativity (GR) if retardation effects are considered [7,8,9,10,11,12,13,14]. The mechanism underlying retardation is intricately linked to the dynamics of the matter density within galaxies, specifically to the second derivative of density. Changes in density may result from various factors, including gas depletion in surrounding intergalactic gas [12] or dynamic processes such as star formation and supernova explosions [10,11]. These processes can be characterized by three different typical length scales: the density gradient length, velocity field gradient length, and dynamical length scale. The importance of retardation is determined by the shortest among these length scales [15].
The famous Tully-Fisher relation [16], which links the baryonic mass of a galaxy to the fourth power of its rotational velocity at the outer rim, can also be derived from the principles of retarded gravity [17]. It was shown that the effects of retarded gravity extend beyond just slowly moving particles and also apply to photons. While there may be some differences in the mathematical analysis for each case, it is ultimately concluded that the observed "dark mass" inferred from galactic rotation curves must be identical in both the lensing and rotation curves scenarios [15,18].
While the prevailing notion of dark matter remains prominent, the current circumstances warrant consideration of the case that this prevailing paradigm may need to be reevaluated. Several challenges cast doubt on this common idea:
Firstly, in order to align with observed phenomena and structure formation simulations, a set of properties has been assigned to dark matter (DM) [2]. However, despite being over 50 years since its inception, dark matter has yet to be directly observed, nor have any known particles been identified that match its purported properties.
Secondly, simulations involving dark matter often encounter what is known as the core-cusp problem. The Navarro-Frenk-White (NFW) [19] profile, derived from Cold Dark Matter (CDM) simulations and commonly used to fit rotation curves, is a prime example. However, this profile faces challenges, particularly when applied to Low Surface Brightness galaxies (LSBs). Derivations made using the NFW profile regarding rotational velocities frequently diverge from actual observations, leading to discrepancies. Specifically, while the NFW profile anticipates a "cuspy" internal region for a dark halo (where density changes rapidly), observations tend to favor a "core-like" behavior (where density remains approximately constant). Efforts to address this issue have often relied on specific and somewhat contrived adjustments, raising doubts about whether these solutions were devised primarily to maintain the current paradigm.
Thirdly, Sancisi’s Law [20] presents a significant and broadly applicable observation. It suggests that changes in the luminosity profile of a galaxy correspond to changes in its rotation curve, and vice versa. This phenomenon applies to various types of dark halos. However, from a dark matter perspective, this relationship is unexpected: the dark halo is typically assumed to be much more massive than the baryonic matter. Consequently, fluctuations in the distribution of baryonic matter should not significantly affect the velocity distribution, contrary to what is observed. This discrepancy is particularly pronounced in LSBs, where the dark halo is believed to dominate at every radius, yet the velocity distribution exhibits fluctuations corresponding to each "baryonic bump." This suggests that, somehow, the overall velocity distribution is influenced by small fluctuations in baryonic matter.
Hence, the current retarded gravity proposition offers a unique perspective. Unlike alternative theories that propose modifications to general relativity, such as Milgrom’s Modified Newtonian Dynamics (MOND) [21], Mannheim’s Conformal Gravity [22,23], or Moffat’s Modified Gravity (MOG) [24], our approach does not seek to alter the fundamental framework of general relativity. Instead, we adhere strictly to the principle of Occam’s razor, as advocated by both Newton and Einstein. Our objective is to replace the need for dark matter with phenomena inherent within standard General Relativity itself (retardation). It’s worth noting that recent research has shed light on the relationship between retardation and MOND [25], demonstrating how criteria for low acceleration MOND can be deduced from retardation theory, and how the MOND interpolation function can approximate retarded gravity effectively.
It’s essential to highlight that significant retardation effects are not contingent upon high velocities of matter within galaxies, although higher velocities may enhance these effects. In reality, the majority of galactic constituents, such as stars and gas, move relatively slowly compared to the speed of light. This is indicated by the ratio of the velocity v to the speed of light in vacuum c, denoted as v c , which is much smaller than 1. For instance, typical velocities within galaxies are around 100 km/s, resulting in a ratio of 0.001 or smaller. This will be discussed in more details in the sections that follow.
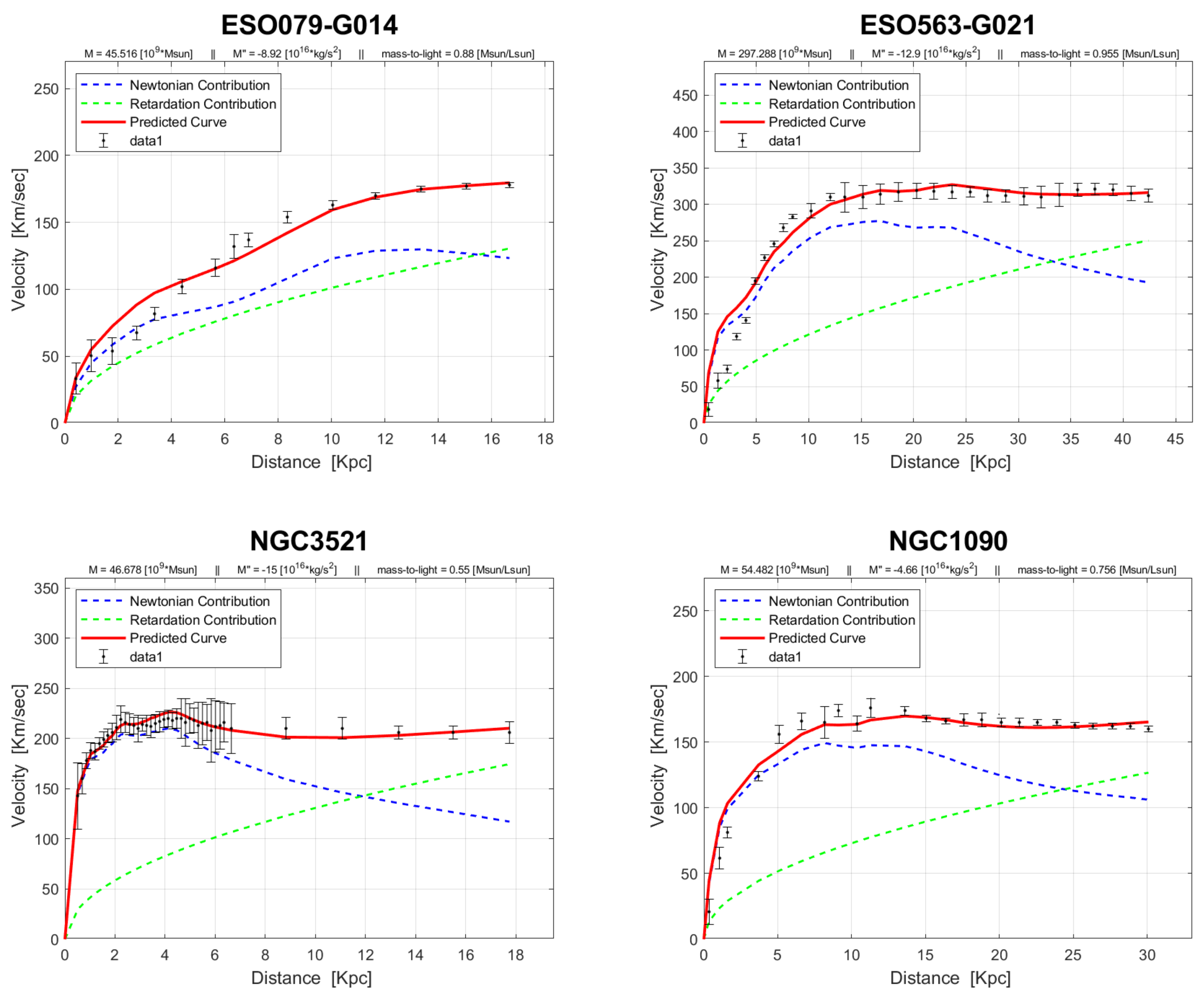
In contrast to the solar system, where retardation effects are considered negligible [26,27], observations of galaxies’ velocity curves suggest that these effects become significant beyond a certain distance [10,11,12]. Recent research [28] has expanded the empirical basis for the theory of retarded gravity. Building upon previous studies that analyzed eleven galaxies [11], the latest research extends its scope to a larger sample of 143 galaxies sourced from the SPARC Galaxy collection. These galaxies vary in type, size, and luminosity. The analysis indicates that in most cases, an excellent fit to the observed data is achieved without the need to postulate dark matter or modify general relativity (see Figure 1 for some examples).
As we shall show below this is not an accident but is rather dictated by general relativity.

2. A Discrete Model

Retarded gravity emerges from the weak field approximation of general relativity [12]. In this framework, the metric perturbation h 00 can be expressed in terms of a retarded potential ϕ as follows [12,15]:
ϕ = − G ∫ ρ ( x → ′ , t − R c ) R d 3 x ′ , ϕ ≡ c 2 2 h 00 , h 00 = 2 c 2 ϕ
where G represents the gravitational constant, x → denotes the location where the potential is calculated, x → ′ signifies the whereabout of the mass element producing the potential, R → ≡ x → − x → ′ , R ≡ | R → | , and ρ represents the mass distribution. The characteristic duration R c for galaxies might span a few tens of thousands of years, but small relative to the timescale over which galactic density significantly changes. Therefore, we can express the density using a Taylor series expansion:
ρ ( x → ′ , t − R c ) = ∑ n = 0 ∞ 1 n ! ρ ( n ) ( x → ′ , t ) ( − R c ) n , ρ ( n ) ≡ ∂ n ρ ∂ t n .
By substituting rhotay into Equation photonequastartpoint and retaining the first three terms, we can derive:
ϕ = − G ∫ ρ ( x → ′ , t ) R d 3 x ′ + G c ∫ ρ ( 1 ) ( x → ′ , t ) d 3 x ′ − G 2 c 2 ∫ R ρ ( 2 ) ( x → ′ , t ) d 3 x ′
The initial term in the series is referred to as the Newtonian potential:
ϕ N = − G ∫ ρ ( x → ′ , t ) R d 3 x ′
The second term doesn’t influence the force acting on subluminal particles since its gradient is zero. As for the third term, it serves as a lower-order ammendment to the Newtonian potential.
ϕ r = − G 2 c 2 ∫ R ρ ( 2 ) ( x → ′ , t ) d 3 x ′
The geodesic equation governing the motion of a "slow" test particle in the given space-time metric can be evaluated by utilizing the force per unit mass [12]:
a → ≡ d v → d t = − ∇ → ϕ .
The total acceleration is thus:
a → = a → N + a → r a → N ≡ − ∇ → ϕ N = − G ∫ ρ ( x → ′ , t ) R 2 R ^ d 3 x ′ , R ^ ≡ R → R , a → r ≡ − ∇ → ϕ r = − G 2 c 2 ∫ ρ ( 2 ) ( x → ′ , t ) R ^ d 3 x ′
Now, let’s examine a point particle with a mass m j positioned at r → j ( t ) . The particle will possess a mass density given by:
ρ j = m j δ ( 3 ) ( x → ′ − r → j ( t ) )
Here, δ ( 3 ) represents a three-dimensional Dirac delta distribution. This particle induces a Newtonian potential given by:
ϕ N j = − G m j R j ( t ) , R → j ( t ) = x → − r → j ( t ) , R j ( t ) = | R → j ( t ) |
and a retardation potential in the following form:
ϕ r j = − G m j 2 c 2 ∂ 2 ∂ t 2 R j ( t ) = G m j 2 c 2 R ^ j · a → j − v → j 2 − ( v → j · R ^ j ) 2 R j ( t ) , R ^ j ≡ R → j R j , v → j ≡ d r → j d t , a → j ≡ d v → j d t .
A test particle at the vicinity of particle j will be accelerated as follows:
a → T j = a → N j + a → r j a → N j = − ∇ → ϕ N j = − G m j R j 2 R ^ j , a → r j = − ∇ → ϕ r = G m j 2 R j 2 c 2 R j a → ⊥ j + R ^ j v → ⊥ j 2 − 2 ( v → j · R ^ j ) v → ⊥ j a → ⊥ j ≡ a → j − ( a → j · R ^ j ) R ^ j , v → ⊥ j ≡ v → j − ( v → j · R ^ j ) R ^ j .
in which the reader should not confuse the acceleration of the point particle j denoted a → j and the acceleration caused by particle on a test particle located at point x → denoted a → T j .

3. The Uncertainty Relation of Retarded Gravity

First we notice that:
a N j = | a → N j | = G m j R j 2 ⇒ a → r j = a N j R j a → ⊥ j + R ^ j v → ⊥ j 2 − 2 ( v → j · R ^ j ) v → ⊥ j 2 c 2
For non relativistic matter:
β ≡ v c ≪ 1 ,
hence we may write approximately:
a → r j ≃ a N j R j a → ⊥ j 2 c 2 , a → T j = a → N j + a → r j ≃ a N j − R ^ j + R j a → ⊥ j 2 c 2 .
Thus in order for retarded gravity to have a significant effect R j a → ⊥ j 2 c 2 must be of the order of unity ( | R ^ j | = 1 ) or larger, this leads to the retarded gravity "uncertainty" type relation:
R j a ⊥ j 2 c 2 > 1 ⇒ R j a ⊥ j > 2 c 2 ⇒ a ⊥ j > a c = 2 c 2 R j .
Consider a point mass located on a circle which serves as border of the M33 galaxy, then we may ask what will be the amount of acceleration suffered by the point mass that will cause a retardation effect on a test particle located across the diameter of the galaxy (which is the furthest point on the imaginary circle from the point mass). Now the radius of the galaxy M33 is R s ≃ 30 , 000 light years = 2.8 10 20 meters. Hence we will need an acceleration of about:
a c = 2 c 2 R j = 2 c 2 2 R s = c 2 R s ≃ 0.00032 m / s 2
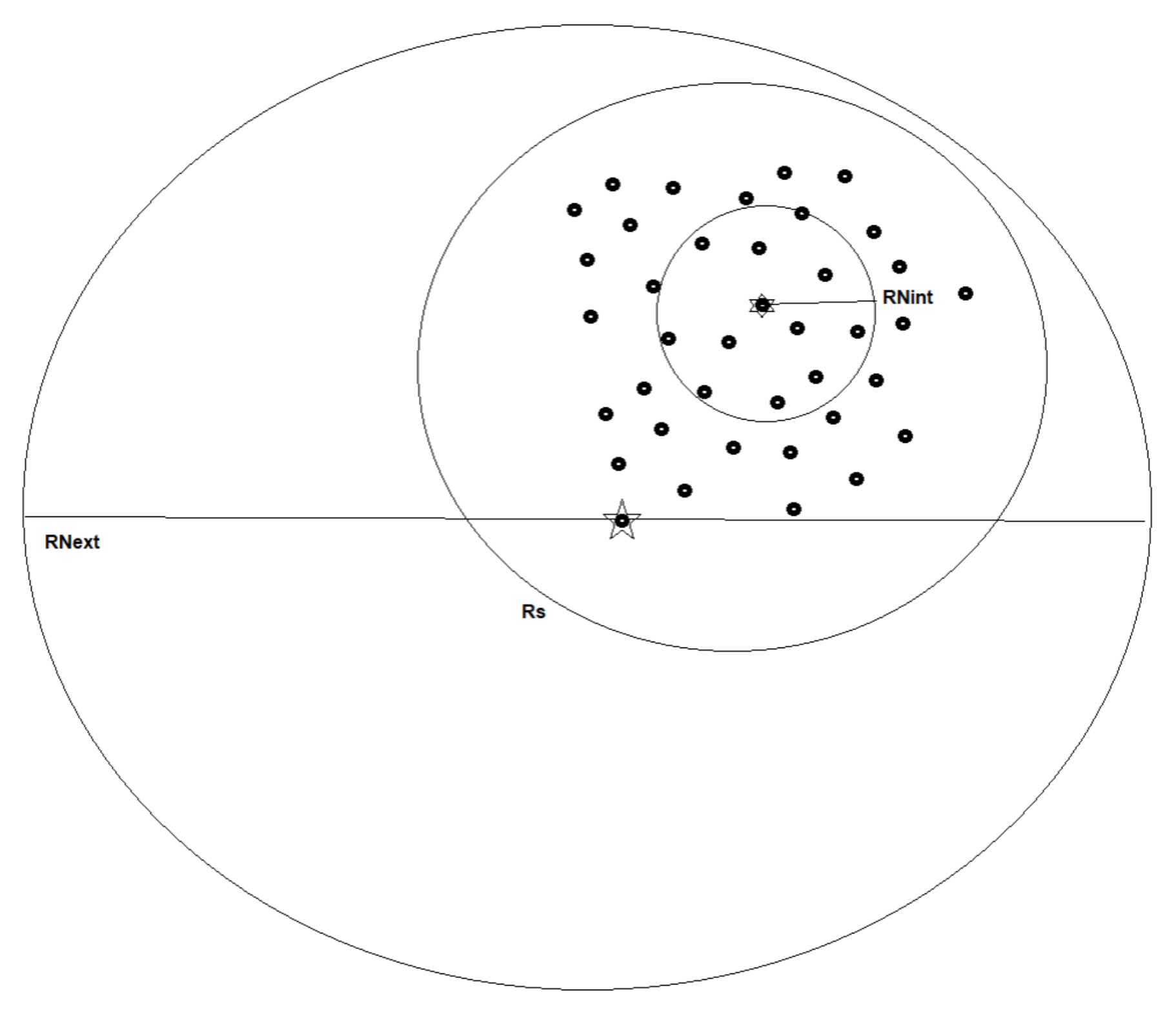
to observe the effect of retarded gravity. This does not seem to be such a huge acceleration and many point masses (atoms, molecules etc.) in the galaxy may have accelerations that need to be considered in the total galactic balance of gravitational forces. From this point of view we may partition the galactic point masses in to two classes: Newtonian gravity particles and retarded (+Newtonian) gravity particles the difference depends on how big is the Newtonian radius (which depends on the particle’s acceleration):
R j a ⊥ j 2 c 2 < 1 R j < R N j ≡ 2 c 2 a ⊥ j .
This reality is depicted in Figure 2. Of course each test particle in not affected by just one massive particle but by all N p massive particles this leads to the equation:
a → T = ∑ j = 1 N p a → T j = ∑ j = 1 N p a → N j + a → r j = ∑ j = 1 N p a → N j + ∑ j = 1 N p a → r j ≃ ∑ j = 1 N p a → N j + ∑ j = 1 , j ∈ RG N p a N j R j a → ⊥ j 2 c 2
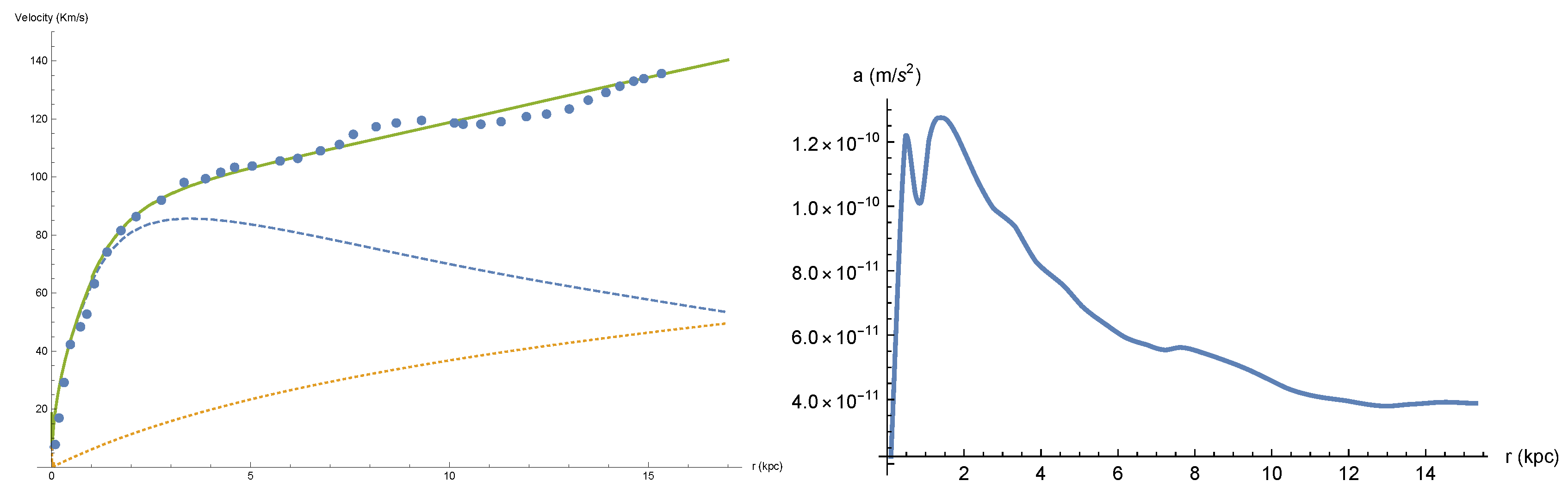
in which RG means particles that have a retarded influence in point x → , that is particles in which point x → is outside their Newtonian radius. We point out that the stellar component of disk galaxies is not responsible for the retardation effects. To see this look at the velocity & acceleration curves of the M33 galaxy depicted in Figure 3:
Assuming stars (and gas) moving in circles we obtain accelerations which do not exceed 1.4 10 − 10 m/s2 yielding a Newtonian Radius not smaller R N ≃ 4 10 7 kpc, hence the effects of those stars and rotating gas is completely Newtonian within the galaxy. Thus to obtain retardation corrections one must look at other processes taking place in galaxy like stellar winds, supernovae explosions [11] and the depletion of gas in the intergalactic medium [12] leading to the deceleration of the rate of mass accretion by the galaxy and to an attractive gravitational retardation effect.

4. Evidence for the Gas Depletion Model

A recent paper [30] (see also [31,32,33]) highlights that recent measurements of gas speed in the outer regions of galaxies at high redshifts indicate a prevalence of steeply declining rotation curves, contrasting with the nearly universal flat rotation curves observed in nearby galaxies. This aligns with the proposition put forth by [12], suggesting that gas depletion plays a role in generating significant M ¨ and implies that older galaxies should not exhibit significantly smaller M ¨ , resulting in steep rather than flat rotation curves. Furthermore, the paper suggests that once a smooth stellar disk forms within the baryonic matter, resembling properties of high-redshift galaxies, the computed rotation curves consistently remain relatively flat at large radii in the gas disk. Strikingly, only simulations devoid of a dark matter halo successfully replicate observed rotation curves. This finding supports our theory, which dismisses the presence of dark matter. Moreover, the paper implies that the flat rotation curves observed in low-redshift galaxies may either result from dark matter falling into the galactic potential well or necessitate an alternative explanation apart from dark matter. Indeed, an alternative explanation, considering retardation, is plausible.

References

  1. Zwicky, F. On a New Cluster of Nebulae in Pisces. Proc. Natl. Acad. Sci. USA 1937, 23, 251–256. [Google Scholar]
  2. de Swart, J.G.; Bertone, G.; van Dongen, J. How dark matter came to matter. Nature Astronomy 2017, 1, 0059. [Google Scholar]
  3. Yahalom, A. The Virial Theorem for Retarded Gravity. International Journal of Modern Physics D 2023, 32, 2342013. [Google Scholar] [CrossRef]
  4. L.M.J.S. Volders, "Neutral Hydrogen in M33 and M101," Bull. astr. Inst. Netherl., vol. 14, 323, 1959. V.C. Rubin, W.K. Ford Jr., N. Thonnard, and M.S. Roberts, "Motion of the Galaxy and the Local Group Determined from the Velocity Anisotropy of Distant Sc I Galaxies. I. The Data and II. The Analysis for the Motion," Astrophys. J., vol. 81, 687 and 719, 1976.
  5. Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379–487. [Google Scholar] [CrossRef]
  6. Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Rotational Properties of 21 Sc Galaxies with a Large Range of Luminosities and Radii from NGC 4605 (R=4kpc) to UGC 2885 (R=122kpc). Astrophysical Journal 1980, 238, 471–487. [Google Scholar] [CrossRef]
  7. Yahalom, A. The effect of Retardation on Galactic Rotation Curves. J. Phys. Conf. Ser. 2019, 1239, 012006. [Google Scholar] [CrossRef]
  8. Yahalom, A. Retardation Effects in Electromagnetism and Gravitation. In Proceedings of the Material Technologies and Modeling the Tenth International Conference, Ariel University, Ariel, Israel, 20–24 August 2018. [Google Scholar]
  9. Yahalom, A. Dark Matter: Reality or a Relativistic Illusion? In Proceedings of Eighteenth Israeli-Russian Bi-National Workshop 2019, Ein Bokek, Israel, 17–22 February 2019.
  10. Wagman, M. Retardation Theory in Galaxies. Ph.D. Thesis, Senate of Ariel University, Samria, Israel, 23 September 2019. [Google Scholar]
  11. Michal Wagman, Lawrence P. Horwitz, and Asher Yahalom "Applying Retardation Theory to Galaxies" 2023 J. Phys.: Conf. Ser. 2482 012005. Proceedings of the 13th Biennial Conference on Classical and Quantum Relativistic Dynamics of Particles and Fields (IARD 2022), 05/06/2022 - 09/06/2022 Prague, Czechia. [CrossRef]
  12. Asher Yahalom "Lorentz Symmetry Group, Retardation, Intergalactic Mass Depletion and Mechanisms Leading to Galactic Rotation Curves" Symmetry 2020, 12(10), 1693. [CrossRef]
  13. Yahalom, A. Effects of Higher Order Retarded Gravity. Universe 2021, 7, 207. [Google Scholar] [CrossRef]
  14. Yahalom, A. The Cosmological Decrease of Galactic Density and the Induced Retarded Gravity Effect on Rotation Curves" Proceedings of IARD 2020. J. Phys. Conf. Ser. 1956, 012002. [Google Scholar] [CrossRef]
  15. Yahalom, A. Lensing Effects in Retarded Gravity. Symmetry 2021, 13, 1062. [Google Scholar] [CrossRef]
  16. Tully, R.B.; Fisher, J.R. A New Method of Determining Distances to Galaxies. Astronomy and Astrophysics 1977, 54, 661–673. [Google Scholar]
  17. A. Yahalom "Tully - Fisher Relations and Retardation Theory for Galaxies" International Journal of Modern Physics D, (2021), Volume No. 30, Issue No. 14, Article No. 2142008 (8 pages). ©World Scientific Publishing Company.
  18. A. Yahalom "Lensing Effects in Galactic Retarded Gravity: Why "Dark Matter" is the Same for Both Gravitational Lensing and Rotation Curves" IJMPD Vol. 31, No. 14, 2242018 (10 pages), received 23 May 2022, Accepted 31 August 2022, published online 30 September 2022.
  19. Navarro, Julio F.; Frenk, Carlos S.; White, Simon D. M. The Structure of Cold Dark Matter Halos. The Astrophysical Journal. 1996, 462, 563-575. arXiv:astro-ph/9508025. [CrossRef]
  20. Renzo Sancisi "The visible matter - dark matter coupling" proceedings of IAU Symposium 220, "Dark Matter in Galaxies", eds. S. Ryder, D.J. Pisano, M. Walker and K. Freeman, Publ. Astron. Soc. Pac. [CrossRef]
  21. Milgrom, M. 1983, The Astrophysical Journal, 270, 371.
  22. Mannheim, P.D. 1993, The Astrophysical Journal, 419, 150.
  23. Mannheim, P.D. Local and global gravity. Foundations of Physics 1996, 26, 1683–1709. [Google Scholar]
  24. Moffat, J.W. Scalar-Tensor-Vector Gravity Theory. Journal of Cosmology and Astroparticle Physics 2006, 2006, 4. [Google Scholar] [CrossRef]
  25. Yahalom, A. MOND & Retarded Gravity. Bulgarian Journal of Physics 2024, 51, 5–20. [Google Scholar] [CrossRef]
  26. A. Yahalom "The weak field approximation of general relativity, retardation, and the problem of precession of the perihelion for mercury" Proceedings of the International Conference: COSMOLOGY ON SMALL SCALES 2022 Dark Energy and the Local Hubble Expansion Problem, Prague, 21-24 September 2022. Edited by Michal Krizek and Yuri V. Dumin, Institute of Mathematics, Czech Academy of Sciences.
  27. Yahalom, A. The Weak Field Approximation of General Relativity and the Problem of Precession of the Perihelion for Mercury. Symmetry 2023, 15, 39. [Google Scholar] [CrossRef]
  28. Glass, Yuval, Tomer Zimmerman, and Asher Yahalom. 2024. "Retarded Gravity in Disk Galaxies" Symmetry 16, no. 4: 387. [CrossRef]
  29. Corbelli, E. Dark matter and visible baryons in M33. MNRAS 2003, 342, 199–207. [Google Scholar] [CrossRef]
  30. Nelson, A.H.; Williams, P.R. Recent Observations of the Rotation of Distant Galaxies and the Implication for Dark Matter. arXiv 2023, arXiv:2401.13783. [Google Scholar]
  31. Genzel, R. , et al. 2017, Nature, 543, 397.
  32. Lang, P. , 2017, ApJ, 840, 92.
  33. Lang, P. , 2018, KMOS@5 Workshop, ESO Garching. [CrossRef]
Preprints 106683 g001
Figure 1. Some rotation curves of ’Sbc’ type galaxies.
Figure 1. Some rotation curves of ’Sbc’ type galaxies.
Preprints 106683 g001
Preprints 106683 g002
Figure 2. Point particles in the galaxy and their Newtonian spheres of influence. For some point particles R N i n t is within the galaxy of Radius R s hence retarded gravity due to those particles does effect the galaxy dynamics, while for other particles R N e x t contains the entire galaxy hence those particle cause only gravitational Newtonian effects.
Figure 2. Point particles in the galaxy and their Newtonian spheres of influence. For some point particles R N i n t is within the galaxy of Radius R s hence retarded gravity due to those particles does effect the galaxy dynamics, while for other particles R N e x t contains the entire galaxy hence those particle cause only gravitational Newtonian effects.
Preprints 106683 g002
Preprints 106683 g003
Figure 3. Rotation & Acceleration curves for M33 [29]. In the left hand side we have the complete rotation curve, depicted by the solid line, represents the combined effect of two contributions: the dotted line represents the contribution from retardation, while the dashed line represents the contribution from Newtonian gravity [12]. In the right hand side the acceleration assuming that the stars and gas move in circles around the galactic center and thus have an acceleration of v 2 r , were r denotes the distance from the galactic center.
Figure 3. Rotation & Acceleration curves for M33 [29]. In the left hand side we have the complete rotation curve, depicted by the solid line, represents the combined effect of two contributions: the dotted line represents the contribution from retardation, while the dashed line represents the contribution from Newtonian gravity [12]. In the right hand side the acceleration assuming that the stars and gas move in circles around the galactic center and thus have an acceleration of v 2 r , were r denotes the distance from the galactic center.
Preprints 106683 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated