Prerpints.org logo
Preprint
Article

Investigation of Variability of Flaw Strength Distributions on a Brittle SiC Ceramic

Altmetrics

Downloads

74

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 May 2024

Posted:

17 May 2024

You are already at the latest version

Alerts
Abstract
The present paper investigates flaw strength distributions established using various flexural tests on batches of SiC bar test specimens: 4-point bending as well as 3-point bending with different span lengths. Flaw strength is given by the elemental stress operating on the critical flaw at fracture of a test specimen. Fracture inducing flaws and their locations are identified by fractography. A single population of pores was found to dominate fracture. The construction of diagrams of p-quantile vs elemental strengths was aimed at assessing the Gaussian nature of flaw strengths. Then, empirical cumulative distributions of strengths were constructed using the normal distribution function. Weibull cumulative probability distributions were derived from the mean and the standard deviation using the first moment equation. Agreement was obtained between both Weibull and normal flaw strengths distributions. The cumulative distributions for the different bending tests were predicted satisfactorily from the flaw strength density function using the elemental strength model. Flaw strength distributions that include potential weaker flaws encountered in larger test pieces are extrapolated using the p-quantile diagrams. Implications are discussed about the pertinence of an intrinsically representative flaw strength distribution, about failure predictions, about size effects, and about the significance of flaw spatial distributions.
Keywords: 
Subject: Chemistry and Materials Science  -   Ceramics and Composites

1. Introduction

Microstructural flaws that act as stress concentrators cause the fracture of many brittle materials including ceramics. The flaws generated during manufacturing of ceramic and glass pieces are generally distributed randomly, and they may exhibit wide variability in severity, as a result of variability in shape, nature and size. As a consequence, stress-induced fracture is a stochastic event, and fracture stress is a variate. The strength of brittle ceramics is commonly characterized by statistical distribution functions, which allows the interpretation of strength variability and the prediction of component reliabilty.
Statistical variability of ceramic strength is commonly characterized by the Weibull distribution function, which is based on a power law. Then, statistical-probabilistic approaches can be used to the fracture stress of specimens or components containing flaws. For this purpose, they should enable the use of laboratory data to infer the probability of fracture of a component under more complicated stress states encountered in service (nonuniform polyaxial stress states, transient stress states). Which requires considerable extrapolation to larger sizes as well as to more complex stress states than those encountered with specimens usually tested under uniaxial stresses. Therefore appropriate distribution functions and statistical-probabilistic approaches are required to describe specimen size effects on strength.
According to Weibull, « the only merit of the distribution function he proposed, is to be found in the fact that it is the simplest mathematical expression of the appropriate form, which satisfies the necessary general conditions. » [1] However, authors raised questions about the validity of the Weibull distribution for ceramic strengths, owing to variation of estimated statistical parameters, and bias introduced by the method of estimation of Weibull parameters [2,3,4,5,6,7,8,9,10]. They have compared various distribution functions, and no consensus emerged on the proper form. Thus, for instance, an outcome of the detailed statistical analysis of the flexural strength data [11] using various probability models including Weibull, normal, log-normal, gamma and generalized exponential distributions, was that the gamma or log-normal distribution function, in contrast to Weibull distribution, may describe more appropriately, in certain cases, the experimentally measured strength data. The normal distribution was assumed by a few researchers on bulk ceramics and ceramic fibers [11,12,13,14,15,16]. However, it was also reported that the fitted Weibull and normal distributions of flexural strengths behave quite similarly [11,12]. The similarity of normal and Weibull distributions has also been established on fiber tows made of very large numbers (up to more than 1000) of filaments [15,16].
It is difficult to decide whether the strength data follow a Weibull distribution or not when small sample sizes and a single batch of specimens of the same dimensions are considered. The validity of a distribution function implies that the statistical parameters are constant whatever the specimen size and the stress-state. In the case of small diameter ceramic fibers tested under tensile load, the estimated Weibull parameters pertinent to flaw strengths display variation depending on various factors, including the methods of analysis of experimental strength data [15,16,17], the sample size and also the selection of test specimens (sampling) from a tow [15,16]. Sampling dictates the populations of critical flaws present in the tows. As reported in [18], authors did not agree on the most appropriate method of accurate determination of Weibull distribution function for brittle matrials.
In a recent paper on ceramic fibers [16], it was shown that the linearity of the p-quantile vs. flaw strength relation indicates that critical flaw strength in a fiber tow is a Gaussian variable. This approach was applied to various fiber types, including SiC, carbon, glass, basalt and alumina fibers [16], to construct empirical flaw strength distributions. It was shown to avoid some of the above sources of bias for the estimation of Weibull statistical parameters [16]. This approach was applied to a monolithic ceramic in the present paper.
There are two main types of probabilistic-statistical approaches to predict the fracture stress of specimens or components containing flaws [2]:
-
The phenomenological and macroscopic approaches which consider specimen strengths, like the Weibull model ;
-
The approaches that consider the flaws as physical entities [2,19,20,21,22,23,24,25]. They are more fundamental. They are based on the flaw strength density function. The severity of a flaw is measured either using flaw strength or flaw size. The flaw strength is defined as the critical value of the local stress operating on a volume element containing a single flaw (also referred to as elemental stress) that causes extension of the flaw. Failure probability of a test piece is derived from the flaw strength density function using the following equation [21,22,23,24,25].
P = 1 − e x p ⁡ − ∫ d V ∫ 0 S g S d S
where g(S) is the flaw strength density function, S is the elemental strength and V is the stressed volume.
A power law equation is generally selected for g(S) because it can be integrated easily for the calculation of probability using equation (1). Determination of the parameters of the power law requires the experimental distribution of flaw strengths. However, unlike fibers, the determination of this empirical distribution of flaw strengths is not straightforward for bulk ceramics since tensile tests are percluded due to practical difficulties. Bending tests are commonly used on ceramics. Therefore, most analyses and predictions of strength distributions are based on specimen strength data (macroscopic approach), neglecting the sources of fracture (the microstructural flaws). The approach proposed in the present paper, is different in essence since the strength of the fracture inducing flaws was considered. The location of critical flaws was identified and flaw strength was derived from measured data.
The present paper investigates flaw strength distributions in a bulk SiC ceramic, with the intent to propose an approach based on p-quantile diagrams to anticipate specimen size effects on the flaw strength density function with a view to predict specimen strength using the elemental strength model under various stress-states and volumes. The Weibull distributions of flaw and flexural strengths were considered for comparison purposes.

2. Materials and Methods

Flaw strengths were determined using flexural tests on SiC bending bars and fractography. The construction of p-quantile diagrams allowed the normal distribution to be assessed, which permitted the construction of unbiased cumulative distribution functions (CDF) and probability density functions (PDF). The Weibull distribution function was then compared to the reference normal distribution. A power law for g(S) was derived from 4-point bending tests. Flexural strength distributions at different 3-pt bending conditions were then predicted using equation (1) and Weibull equation. Then, broader flaw strength distributions that incorporate potential weaker flaws that were not not present nor activated due to their location with respect to stress gradient in bending bars, were constructed using the p-quantile diagrams,

2.1. Generation of Flaw Strength Data

Fracture tests were performed in three and four point bending on sintered silicon carbide bars at a constant displacement rate of 1mm/mn. A servohydraulic Instron machine was used. Long and short span lengths were selected for the 3-point bending tests in order to vary the stressed volume. The long spans induce a predominantly uni-axial stress state, whereas appreciable shear stresses may exist in the section of the short span specimens.
The bar specimens were machined out of plates having dimensions of 40x40x10 mm3. The 3 batches of 70 bar test specimens comprised specimens from the different plates. After machining, all the specimens were bevelled and polished on the opposite faces using diamond disks. The specimen dimensions are given in Table 1.
The stresses at fracture origins (flaw strengths) were derived from the maximum stress:
-   3 - point   bending :​     σ z = σ m a x ( l − z l ) ( x d )
Where σ  denotes the stress parallel to longitudinal axis Oz at flaw location, σmax is the maximum stress in the outer surface σ m a x = 3 F l 4 b d 2 ; x is the distance from the neutral plane, 2d is the specimen thickness, z is the distance from the loading plane, 2l is the span length.
-   4 - point   bending :​     σ z = σ m a x ( x d )
Where σ  denotes the stress at flaw location parallel to longitudinal axis Oz, between the loading pins, σmax is the maximum stress in the outer surface between the loading pins σ m a x = 3 F l 2 4 b d 2 , l2 = l-l1, x is the distance from the neutral plane, 2d is the specimen thickness.
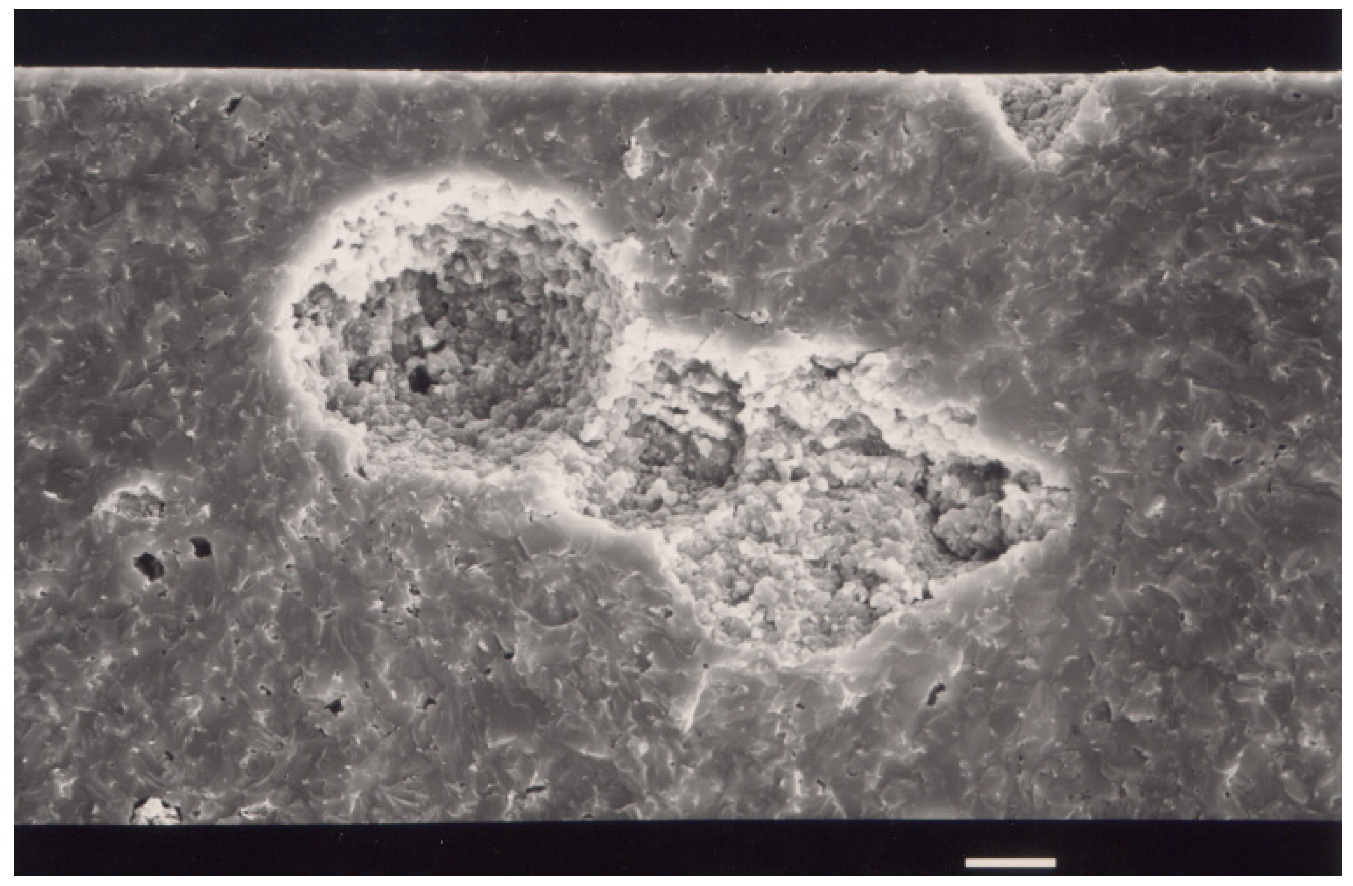
Fracture mirrors showed the locations of fracture inducing flaws. The plane of fracture origin was always perpendicular to the σz direction. Processing flaws consisting of pores dominated fracture (> 91%). The strengths of the other flaw types were distributed evenly. Therefore these data were kept. Figure 1 shows an example of pore fracture origin identified in the fracture surface of a 3-pt bending specimen. Fractographic analysis showed that fracture occurred always in the central loaded region of specimens, perpendicular to the direction of longitudinal tensile stress σz. For the 4-point bending specimens it occurred in the part of specimens located between the loading pins and close to the outer surface. Therefore, for the 4-point bending tests, the flaw strengths coincided with flexural strengths.
Preprints 106700 g001
Figure 1. Pores in the fracture surface of a silicon carbide specimen. The scale bar indicates 10 micrometers.
Figure 1. Pores in the fracture surface of a silicon carbide specimen. The scale bar indicates 10 micrometers.
Preprints 106700 g001

2.2. Analysis of Flaw Strength Data

2.2.1. p-Quantile Diagrams and Normal Distribution [16].

The approach based on p-quantile diagram was proposed in a previous paper to demonstrate that filament flaw strength is a Gaussian variable [16]. It is a graphical method for comparing a Gaussian distribution to a set of data. When X is a Gaussian variable, with μ = mean and s = standard deviation, and N is a variable of the standard normal distribution, it comes:
P X < x = P X − μ s < x − μ s = P N < z = Φ ( z )
Where P (.) is probability, z = x − μ s (5), Φ  is the cumulative standard normal distribution of variable z.
Thus, when linearity of relation z(x) (equation (5)) is observed for a set of xi data, one may assume that the xi data are occurrences of the same Gaussian variable. Then, the plot of p-quantile zp vs. σp indicates whether the strength is a Gaussian variable.
z p = Φ − 1 p = σ p − μ s
where p=i/(n+1). zp can be extracted easily from Φ using a computer or tables available in text books.

2.2.2. Analysis Using the Normal Distribution.

The reference CDFs were calculated using the cumulative normal distribution function (equation (7)) for the values of mean μ and standard deviation s of the sets of experimental strength data:
P n σ = 1 s 2 π ∫ 0 σ e x p ⁡ ( − ( t − μ ) 2 2 s 2 ) d t
The normal CDF are referred to as reference distributions because they provide unbiased graphical representation of the empirical distribution, unlike Weibull plot.

2.2.3. Analysis Using the Elemental Strength Model.

The equation of elemental strength model relates probability to flaw strength density by equation (1). This equation was used to calculate probabilities under the various bending conditions. As detailed in [2], after introduction of power-law expression of g(S), equation (1) becomes:
P = 1 − e x p ⁡ [ − 1 V 0 ∫ d V ( σ 1 S 0 ) λ I ( λ , σ 2 σ 1 , σ 3 σ 1 ) ]
where σ1, σ2, σ3 are the principal stresses, λ and S0 are statistical parameters. I( .) is a function of local and principal stresses. In the present bending tests, σ1=σz, σ2= σ3=0 ; I λ , σ 2 σ 1 , σ 3 σ 1 = I λ , 0,0   [2].
After introduction of S as a function of  max (equations (2) and (3)) into equation (1), it comes after integration:
P = 1 − e x p ⁡ ( − V E ( λ ) I ( λ ,   0,0 ) σ S 0 λ )
VE(λ) results from integration of equations (2) or (3). For the 3-point bending specimens:
V E ( λ ) = V 2 ( λ + 1 ) 2
For the 4-point bending specimens:
V E (​ λ ) = V (​ λ + 2 ) 2 (​ λ + 1 ) 2
VE(λ) is the statistically equivalent volume subject to S = σz operating uniformly.

2.2.4. Analysis Using the Weibull Model

Weibull distributions of strength data were calculated using the statistical parameters derived from the experimental strength data. The Weibull distributions functions were compared to the reference normal distribution functions for assessment purpose.
The general equations of probability density function and cumulative distribution Weibull function are respectively:
f σ = m σ z σ σ z m − 1 e x p − σ σ s m
P σ = 1 − e x p − σ σ s m
Where m is the Weibull parameter, σ is the strength and σs is the characteristic strength.
For the analysis of the influence of dimensions on strengths, the following equation of Weibull distribution was used for flexural tensile stress-state:
P = 1 − e x p − ∫ 1 V 0 ( σ σ 0 ) m d V
Introducing the expressions (2) or (3) of the stress-state and integrating over the stressed volume it comes:
P = 1 − e x p − V E ( m ) V 0 ( σ m a x σ 0 ) m
where σR = σmax is the flexural strength of specimens, σ  is the scale factor, VE(m) is the above statistically equivalent volume for m and σmax = σz operating uniformly, V0 is a reference volume.
The parameters of the Weibull cumulative distribution functions (CDF) were estimated using the Maximum Likelihood Estimation Method and the Moment Method [18,26,27].
(a) Maximum Likelihood Estimation (MLE)
The parameter estimates obtained using the maximum likelihood technique are unique (for a two-parameter Weibull distribution), and they are claimed to statistically approach the true values of the population more efficiently than other parameter estimation techniques as the size of the sample increases. They are derived from equations (16) and (17):
∑ j = 1 n ( σ R j ) m L n σ R j ∑ j = 1 n ( σ R j ) m − 1 n ∑ j = 1 n L n σ R j − 1 m = 0
σ s = 1 n ∑ j = 1 n ( σ R j ) m 1 m
where σ R j is the jth strength in the set of data
(b) Method of moments (MM)
This method has the advantage of involving closed-form equation that can be handled for analysis purposes. The statistical parameters are related to the mean and variance expressions derived from the first moment of the Weibull distribution. The following expressions are used for estimating the Weibull parameters:
C V = s μ = Γ 1 + 2 m Γ 2 1 + 1 m − 1
σ s = μ Γ ( 1 + 1 m )
where CV is the coefficient of variation, Γ(.) is the Gamma function.

3. Results

3.1. The p-Quantile Diagrams

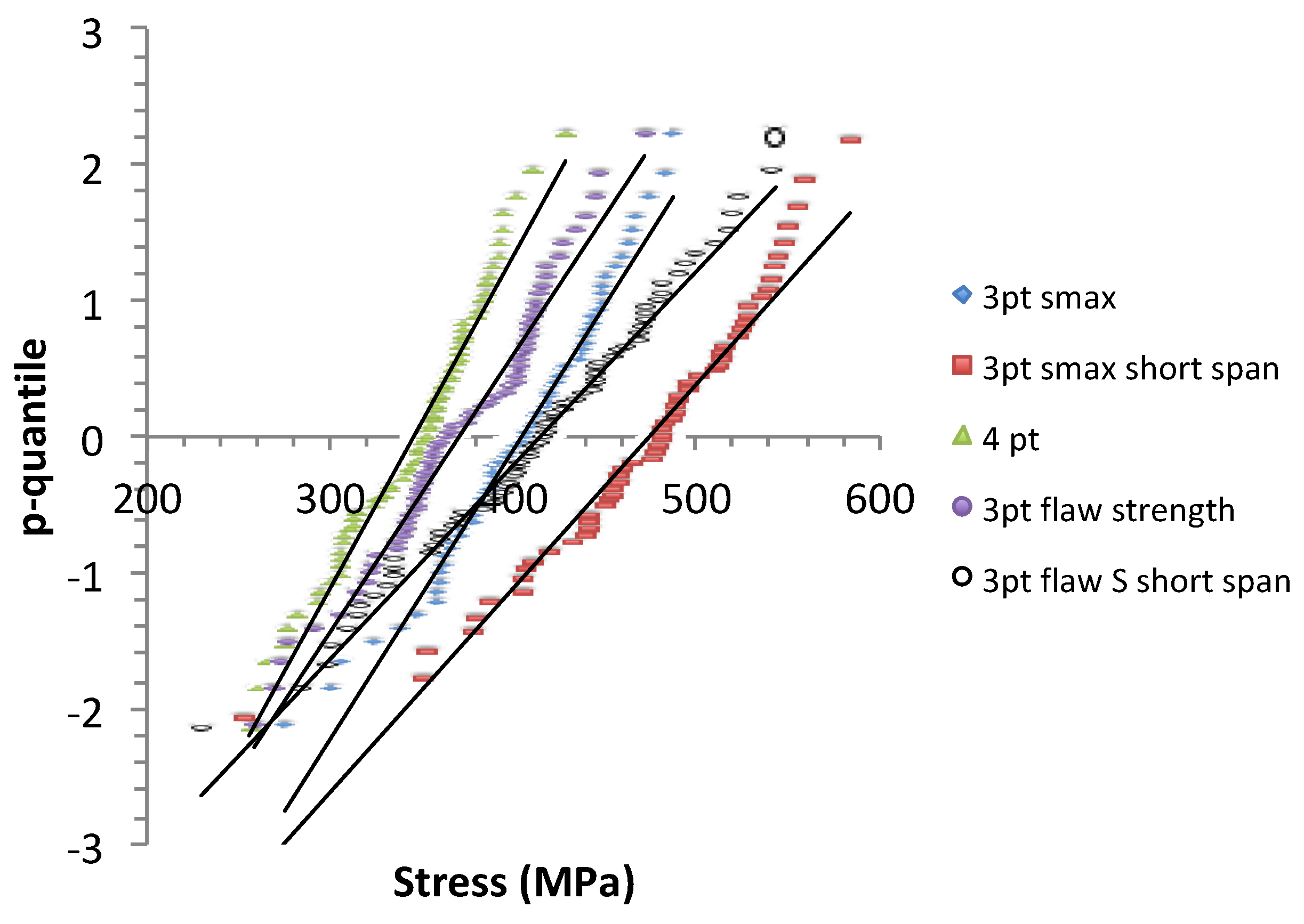
The p-quantile vs. strength diagrams display linearity (Figure 1) with a high value of correlation coefficient (Table 2). This indicates that the flexural stengths and the flaw strengths follow normal distribution.
The p-quantile vs flaw strength diagrams were distinct and depend on the bending mode. It can be noted that the difference between the distributions was larger for the flexural strengths than for the flaw strengths. The increase of the slope of the p-quantile diagrams (=1/s) with increasing VE indicates that more weak flaws were present in the 4 –pt bending specimens (larger equivalent volume VE), whereas stronger flaws were present in the short span 3-pt bending specimens (smaller VE). The long span specimens are an intermediate case. The values of VE are given in Table 3. When the effective volume increased the high extreme values of flaw strengths decreased, whereas the low extreme values were quite similar (Table 4). The p-quantile diagrams of flaw strengths intersect at the same minimum strength (of about 250 MPa). Thus, the Figure 1 reflects shrinkage of flaw strength distribution. This indicates that weaker critical flaws did not appear when the effective volume was increased. This may be related to the stress gradient, so that bigger flaws would not be activated by a sufficiently large stress owing to their location. This may also indicate that the spatial distribution of flaws was not reproducible or uniform.
The Weibull parameters were determined using both MM and MLE approaches except for the elemental strength model. Table 3 shows that both methods give very close parameter estimates. The statistical parameters of the elemental strength models were determined by fitting equation (9) to the reference normal distribution of 4-pt bending strength data. The statistical parameters are given in Table 3. There is a discrepancy between the estimated statistical parameters of Weibull distribution of flexural strengths and flaw strengths. This was logically expected since there is no unique relation between flaw location and flexural strengh. The statistical parameters show dependence on loading mode and equivalent volume VE. With increasing VE, mean strengths μ  standard deviation s and characteristic strength σ  decrease, whereas the scale factor and the Weibull modulus of flaw strength distribution increase.
Preprints 106700 g020
Figure 1. p-quantile diagrams obtained for the sets of flaw strength data obtained on the bending tests. The solid lines indicate the regression lines.
Figure 1. p-quantile diagrams obtained for the sets of flaw strength data obtained on the bending tests. The solid lines indicate the regression lines.
Preprints 106700 g020

3.2. Distributions of Flaw Strengths

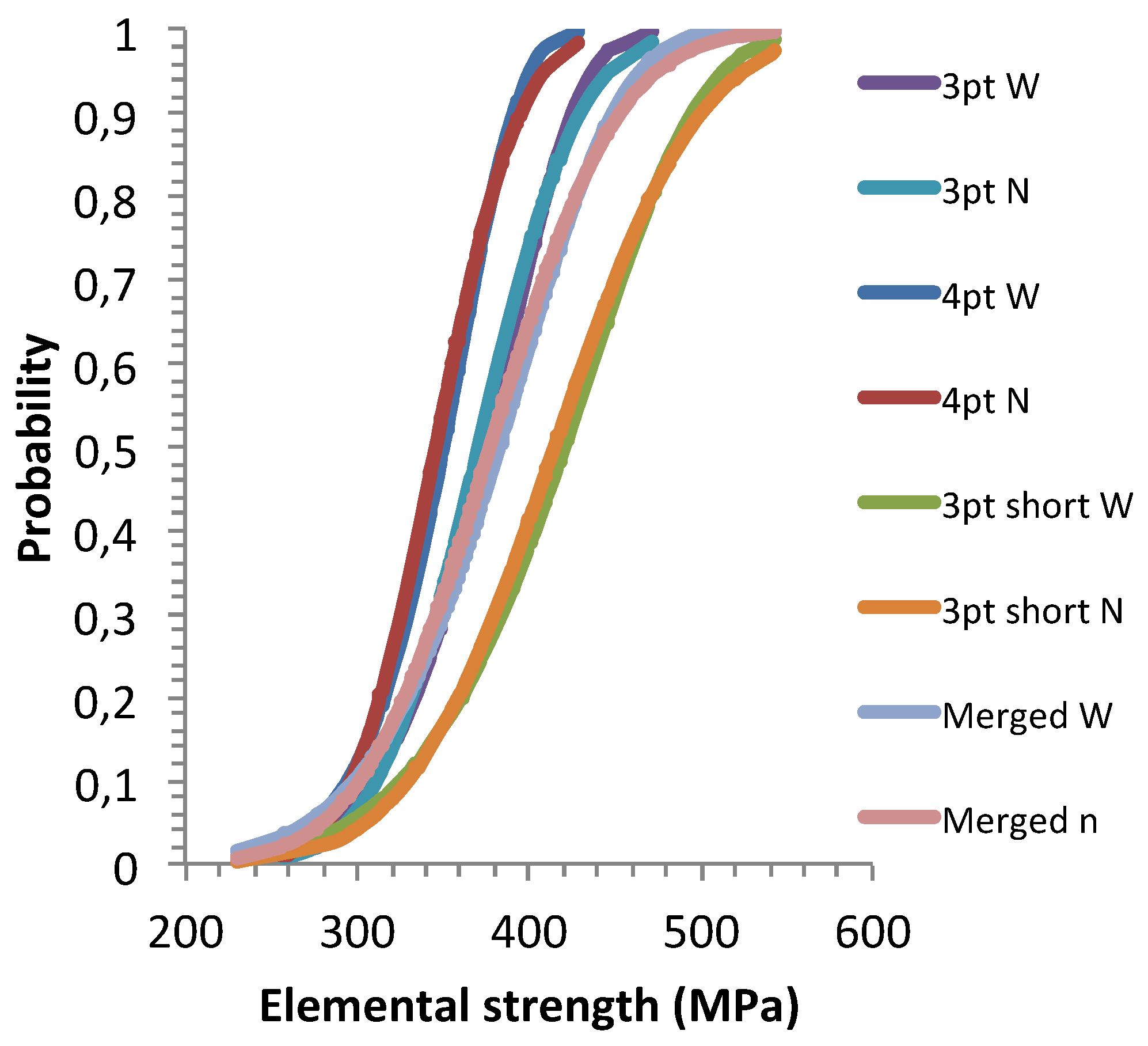
Normal flaw strength CDF were calculated using equation (7), and the Weibull CDF were calculated using equation (13) for the parameters given in Table 3. Figure 2 shows excellent agreement of Weibull distributions with the normal reference ones. The values of correlation coefficients given in Table 2, highlight a good agreement, which indicates that the distributions of flaw strengths can be described by Weibull functions.
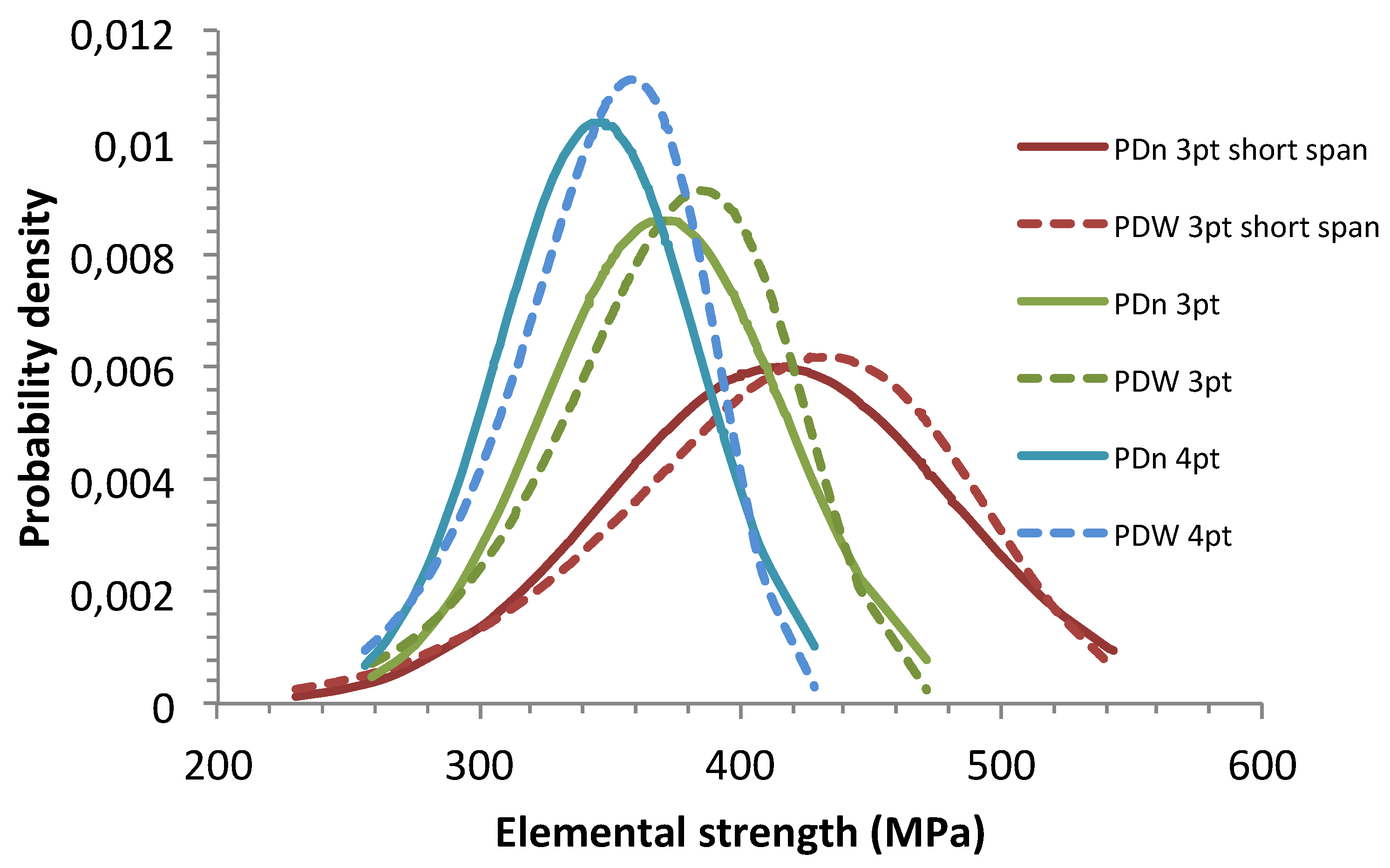
Discrepancy between Gauss and Weibull probability density functions (PDF) can be noted on Figure 3. These curves amplify subtle differences between the normal and Weibull cumulative distributions that did not appear distinctly on Figure 2. This result moderates the above conclusion on correlation between normal and Weibull functions for the flaw strengths. Therefore, it can be considered that the Weibull distribution may be regarded only as an acceptable approximation of a flaw strength distribution.
The PDFs show the same trends as above on the dependence of flaw strengths on the loading mode and the effective volume size. The peak probability density increased with the effective volume size, whereas the flaw strength interval decreased towards the same low strength extreme (Table 1). Like the p-quantile diagrams, this trend describes shrinkage of the flaw strength interval.

3.3. Predictions of CDFs

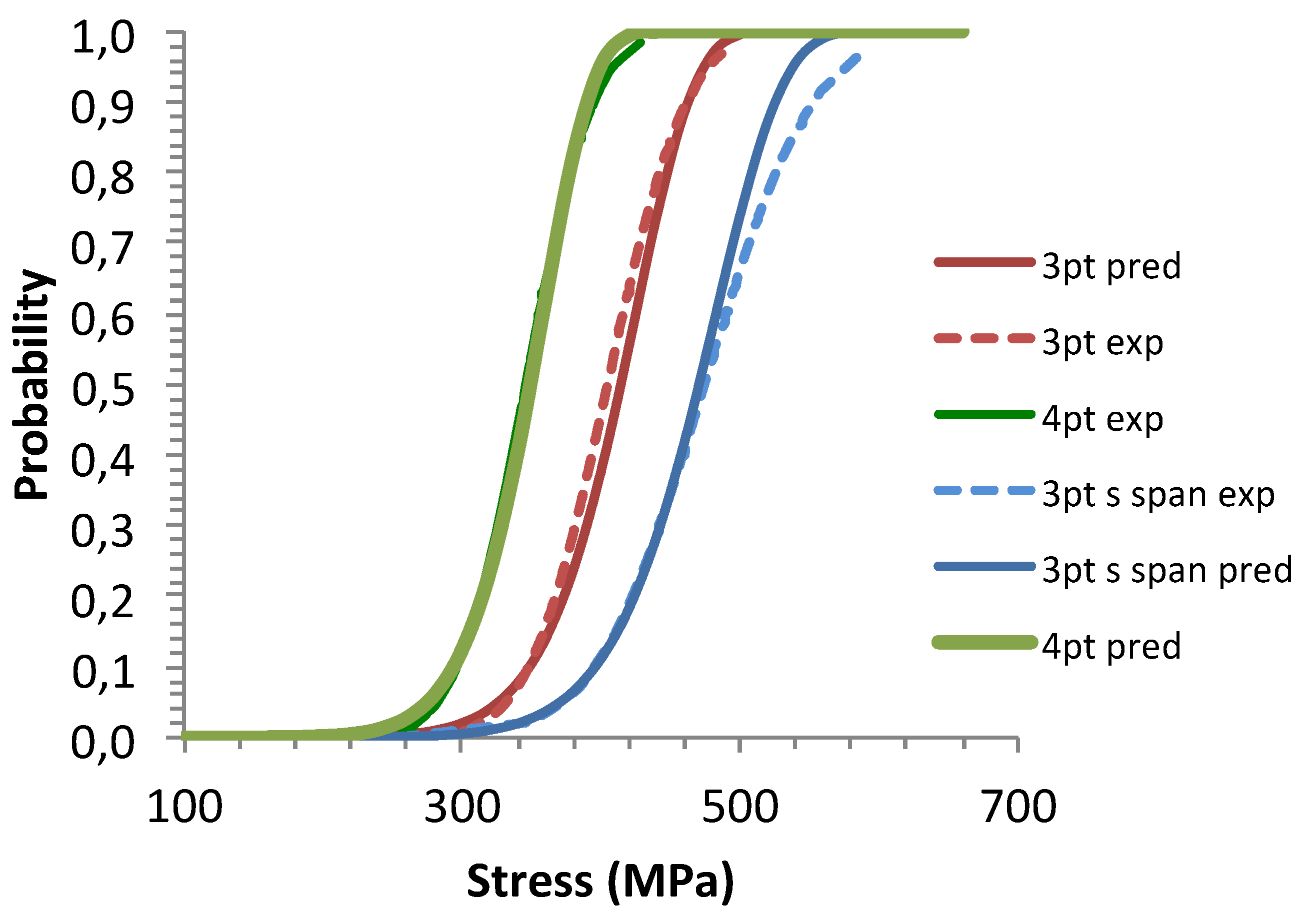
Failure probabilities were calculated using equations (9) and (15) and the statistical parameters derived from the 4pt-bending tests given in Table 3. The predicted CDFs were compared with the reference distributions of flexural (Figure 4 and Figure 5) and of flaw strengths (Figure 6). The 4-pt bending CDF was well fitted by the elemental strength model for the parameters λ and S0 given in Table 3 and for I(λ, 0, 0) = 0.25 [2] (Figure 4). The 3-pt bending CDFs were satisfactorily predicted by the elemental strength model for these latter values of λ, S0 and I(λ, 0,0) (Figure 4). 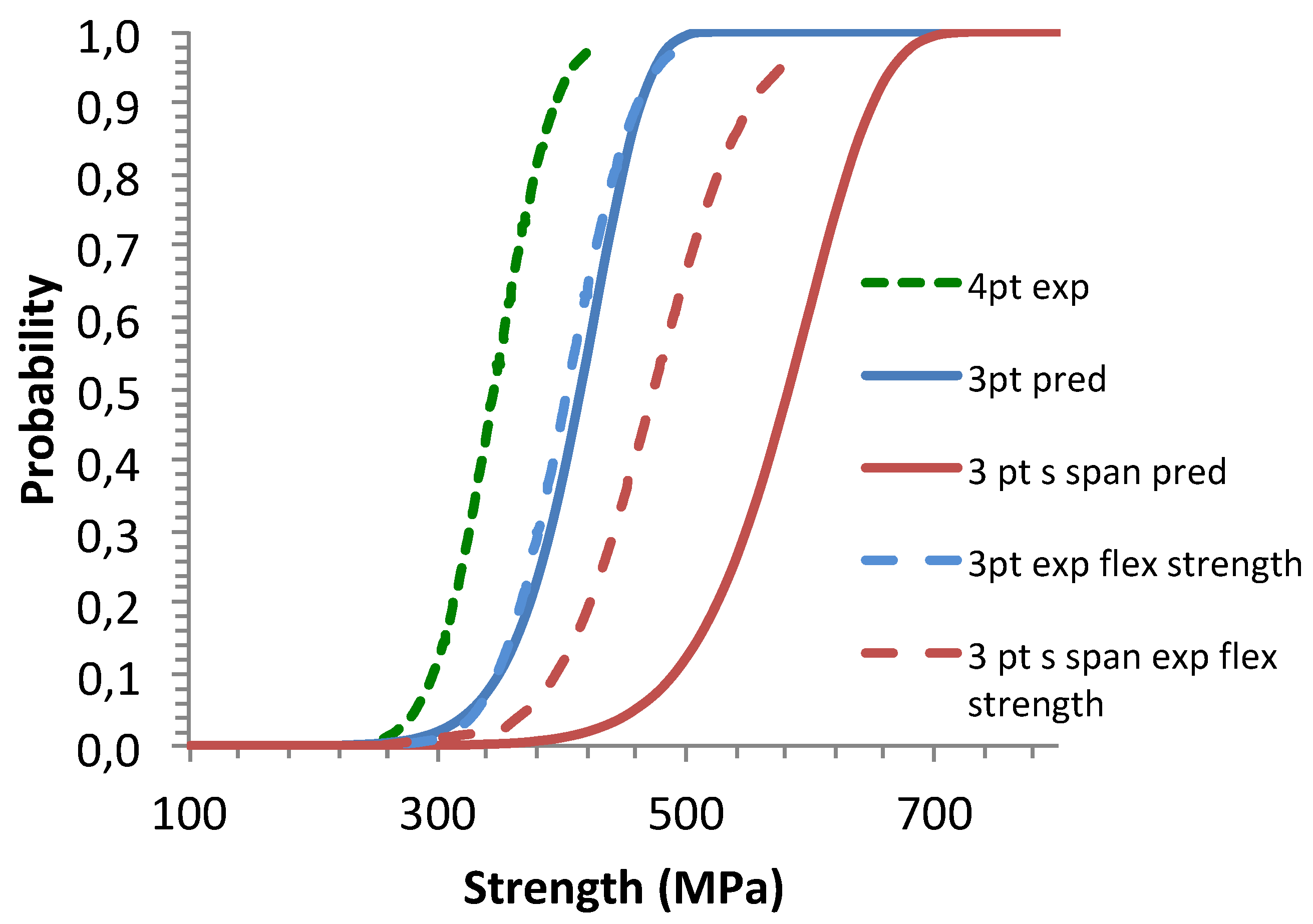Figure 5 shows satisfactory Weibull predictions of CDF for the 3-point bending strengths (long span) from the 4-pt bending parameters. 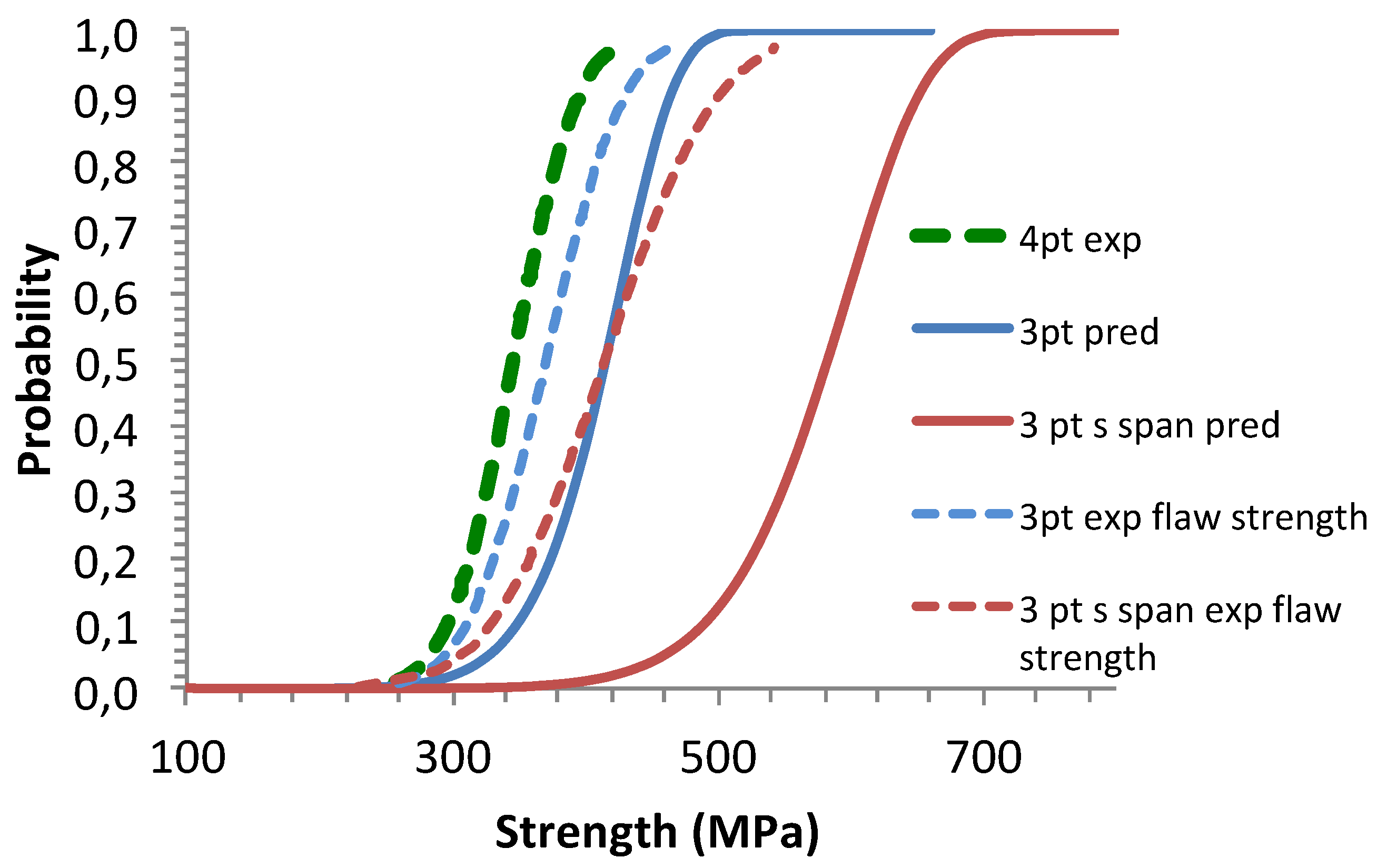By contrast, the Weibull model underestimated failure probabilities for the short span flexural strengths (Figure 5) and did not describe properly the evolution of flaw strengths when the effective volume decreased (Figure 6).

4. Discussion : Implications

4.1. Merged Flaw Strength Distribution

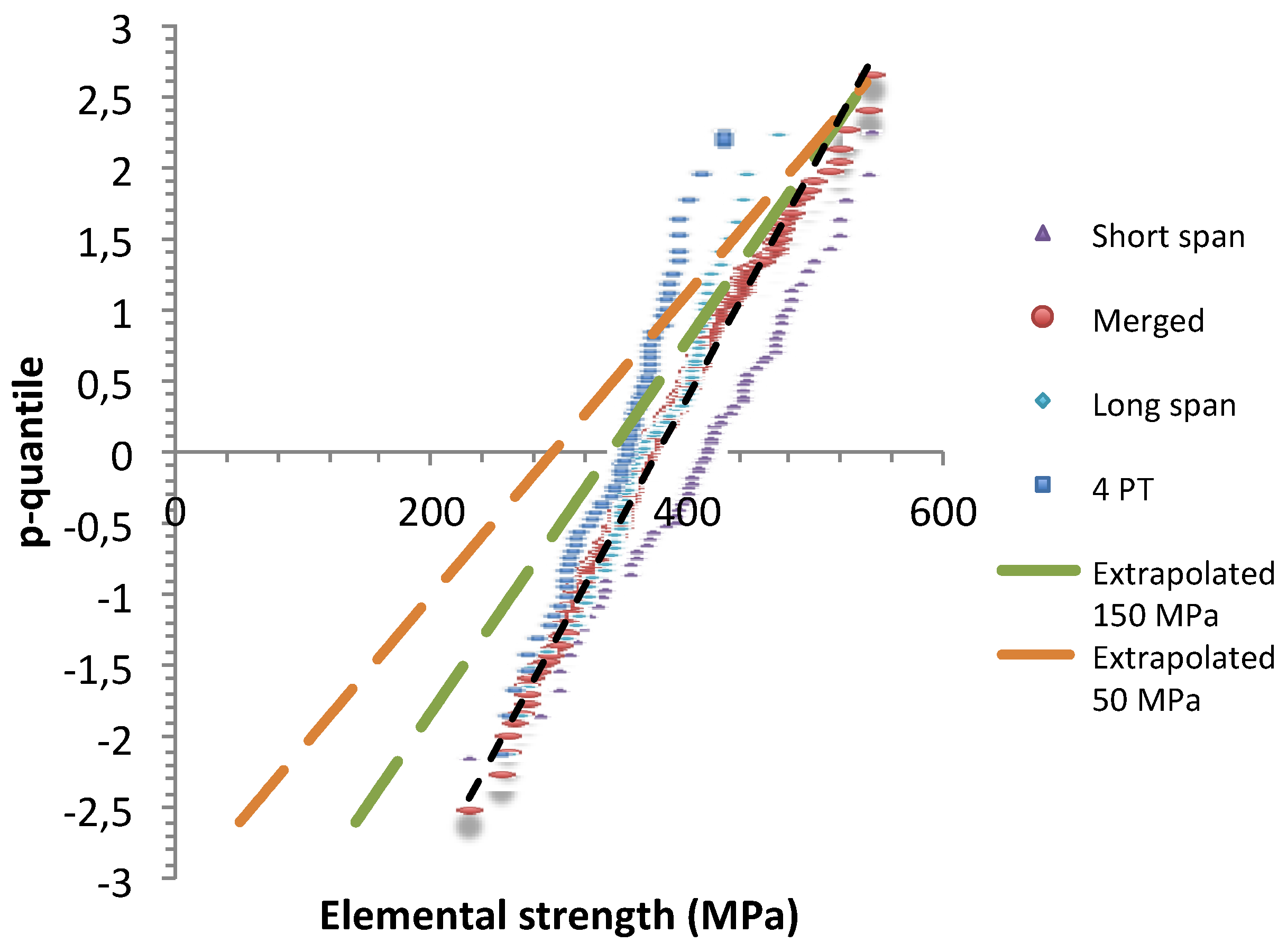
The elemental strengths are independent of volume size, being strengths of flaws. Therefore, the three flaw strength data sets were merged. The outcome gives a linear p-quantile diagram (Figure 7) with a high correlation coefficient (Table 2). The result indicates that the merged diagram follows also a single normal distribution function and thus that all the flaws belong to the same family (Figure 7). This allows us to infer that the populations of flaw strengths in test specimens are subsets of a wider set of data. The merged population may characterize the whole population for the batches of test specimens of the present paper, as suggested by the same value for the lowest flaw strengths. However, it may not include more severe flaws that were not activated owing to the stress state that activates unequally the flaws.
The statistical parameters are given in Table 3. They are close to the parameters of the flaw strength distribution derived from the short span 3-point bending tests.

4.2. Extrapolated Flaw Strength Distribution

The comparison of flaw strengths on PDF, or p-quantile diagrams indicates that the underlying flaw populations displayed variation. Thus, they cannot be regarded as representative of the material type. On the basis of the above results, it seems logical to think that the flaw strength distributions obtained on various batches of specimens belong to a unique distribution characteristic of the whole flaw population existing in the material at larger volume size. The existence of a material characteristic flaw strength distribution was evidenced on fiber tows in [28]. Thus, it was shown that there exists a critical tow size above which the flaw strength distribution is invariant. Therefore, an attempt was made to construct a flaw strength distribution that would be representative of the SiC ceramic of the present paper. This population would be obtained on a larger volume such that the underlying flaw population includes flaws weaker than those characterized on the bending specimens and present in the original plates. The extrapolation to distributions including weaker flaws was carried out using the p-quantile diagrams.
A linear p-quantile diagram is symmetrical to the mean strength per construction since zpmax and zpmin are symmetrical to zp=0. These remarkable features enable to construct extrapolated p-quantile diagrams with broader flaw strength distributions.
zpmax and zpmin depend on the number of data through equations :
z p m a x = Φ − 1 n n + 1
z p m i n = Φ − 1 1 n + 1
The slope of the p-quantile diagram is :
z p m a x − z p m i n S m a x − S m i n = 1 s
Predictions of p-quantile diagrams and CDF for a specified value of Smin were carried out as follows. The value of n is selected first. Then zpmax and zpmin are calculated using equations (20) and (21). Then, the values of Smin and Smax allow the definition of the p-quantile straight line. The value of μ corresponds to zp = 0 and the standard deviation is derived from the slope (= 1/s) (equation (22)). From μ and s one can derive the Weibull parameters m and Ss (equations (18) and (19)).
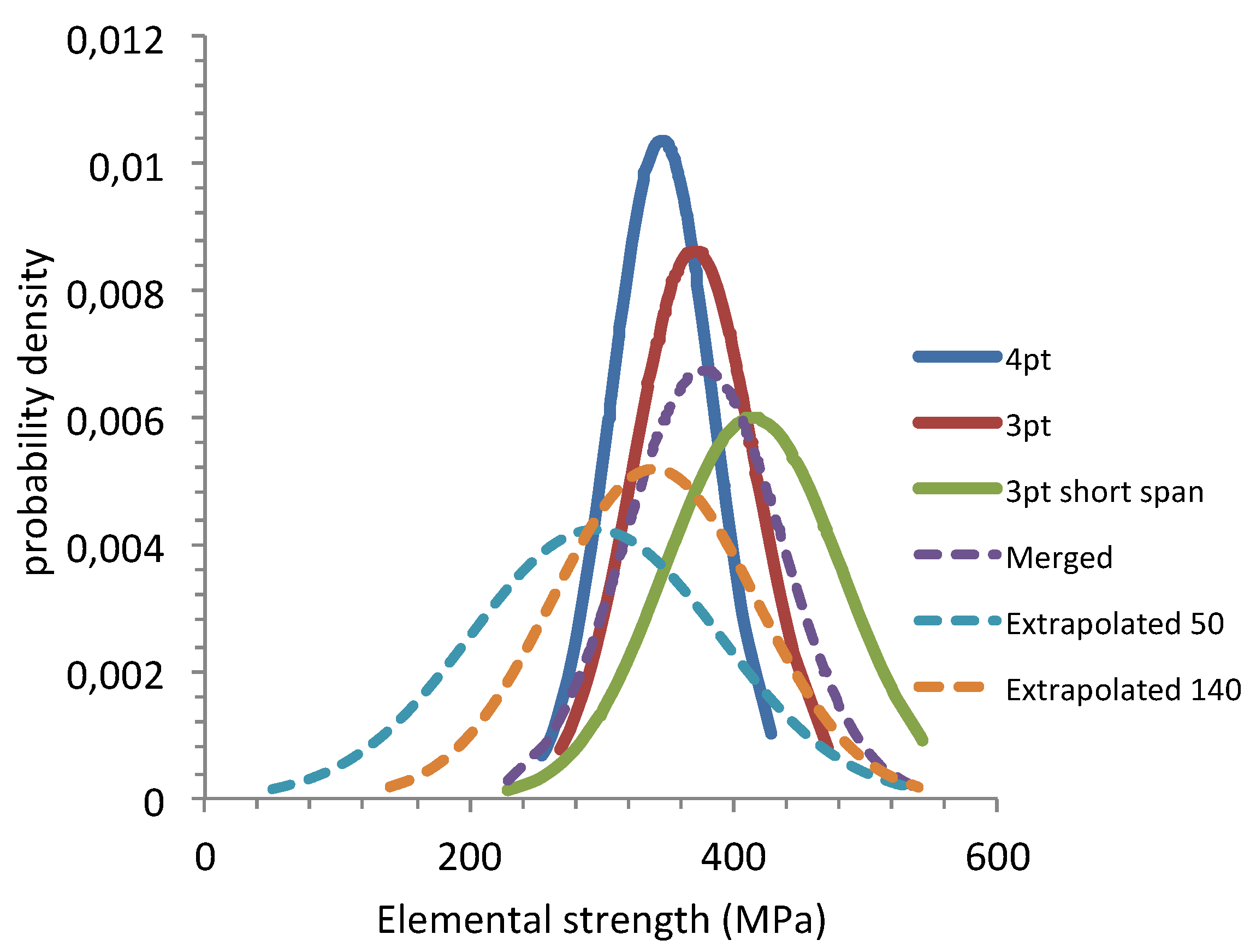
Figure 7 shows the extrapoled p-quantile diagrams for zpmax =-zpmin =2.6, n=210, Smin=50 and 140 MPa, Smax=540 MPa. Figure 8 and Figure 9 show the corresponding normal CDFs and the PDFs. These CDFs give the probability of existence of a flaw strength in a piece of material containing flaws having strengths larger than 50 or 140 MPa. Smin = 140 MPa, is the strength of a 1mm flaw, and Smin = 50 MPa, is the strength of a 8 mm flaw, when KIC= 5 MPa√m. 8 mm is quite large with respect to the thickness of the initial plates. However, it may be considered as a conservative limit. The value of low strength extreme can be refined using non destructive testing methods to detect and eliminate those specimens with flaws larger than a given value. Smax was taken as the high strength extreme of the merged distribution.
Such representative function would be useful for comparison purposes of materials. It also allows anticipation of appropriate flaw strength distribution for the prediction of strength at large volumes. If the critical volume size existed above which the piece contains the whole population of flaws, there would not be size effect above the critical volume size. Below the critical volume size, representative distribution of flaw strengths depends on the reproducibility of the flaw strength distribution.

4.3. Influence of n and Size

The p-quantile diagrams depend on the following parameters: the boundaries of the zp interval determined by n the number of strength data and the boundaries of the elemental strength interval. These values define the p-quantile diagram, the normal statistical parameters s and μ, and the Weibull parameters.
In an uniform tensile stress state, the increase of volume size may be regarded as equivalent to an increase of the number of flaw strength data n. In the presence of a stress gradient, this trend may be affected, as weak flaws may not be activated due to their location with respect to stress magnitude, whereas stronger flaws may be activated instead. A larger number of bending specimens is thus required to increase the chance that a broader spectrum of flaws is activated.

4.3.1. Influence of n on p-Quantile Maximum Values

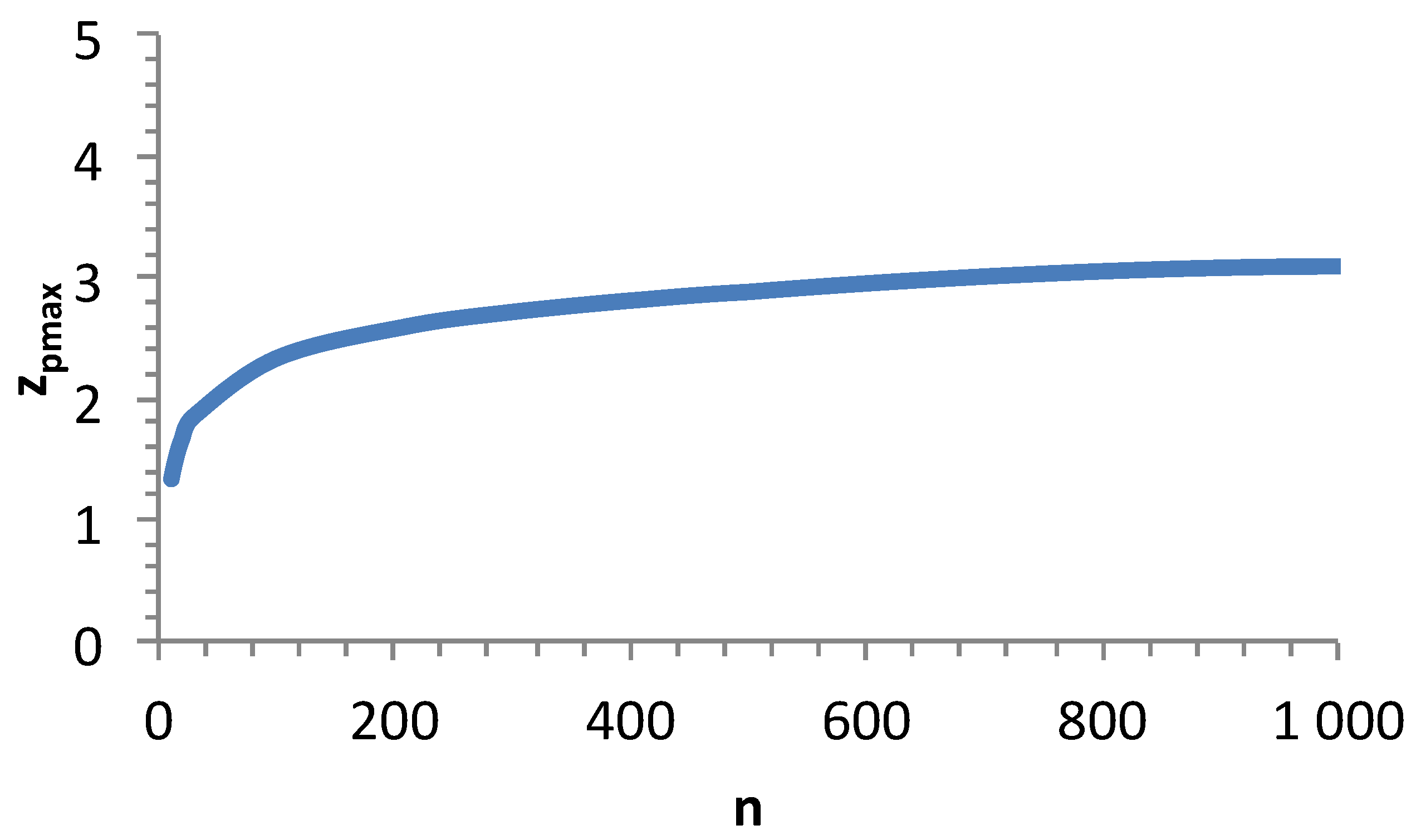
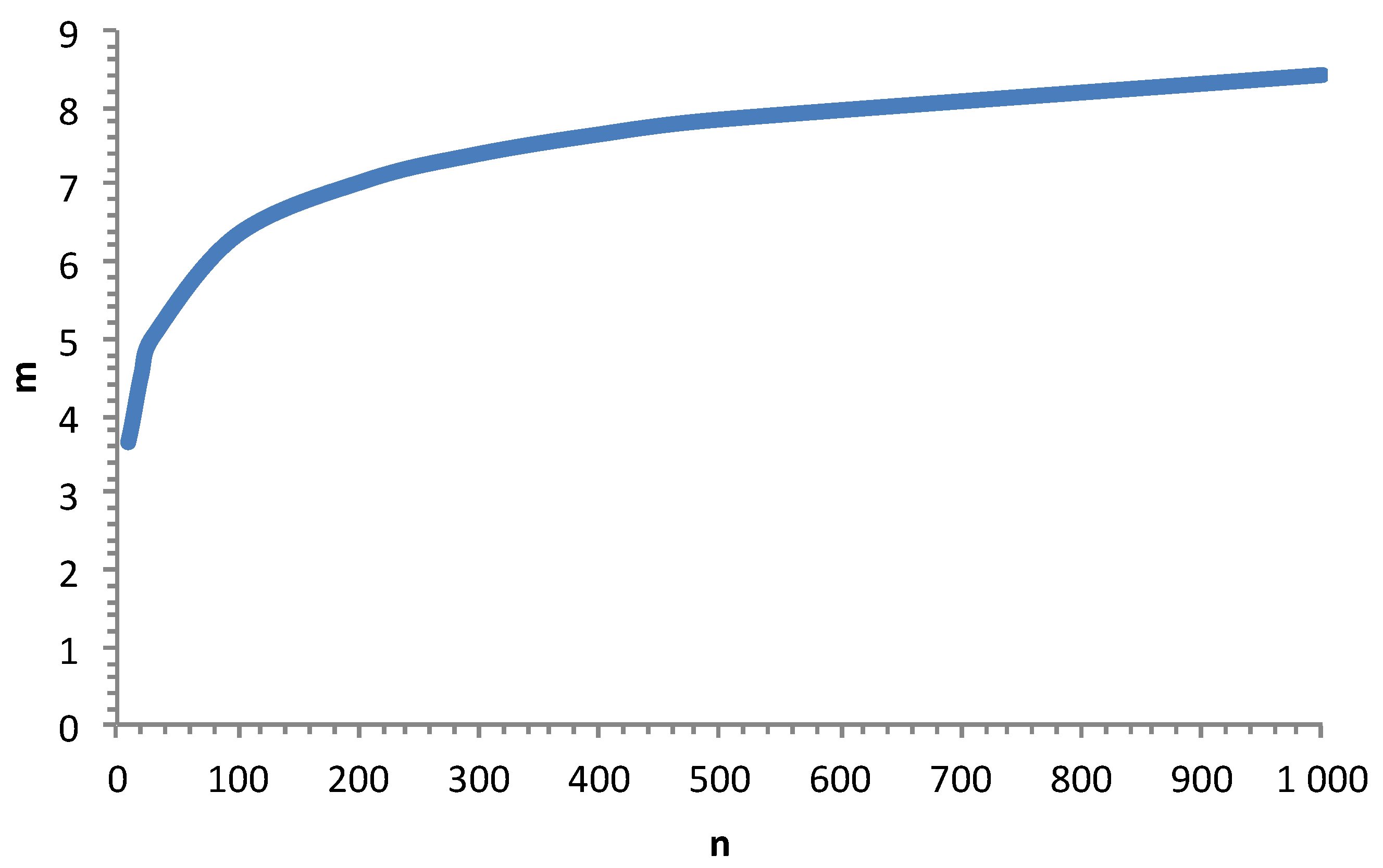
The influence of n on zpmax =-zpmin was calculated using equation (20). Figure 10 indicates that zpmax increases slowly with n, for n> 200. But, there is no limit.

4.3.2. Influence of n and Volume on Statistical Parameters

From the equation (26) of the slope of the p-quantile diagram it comes for standard deviation:
s = S m a x − μ z p m a x = S m a x − μ Φ − 1 n n + 1
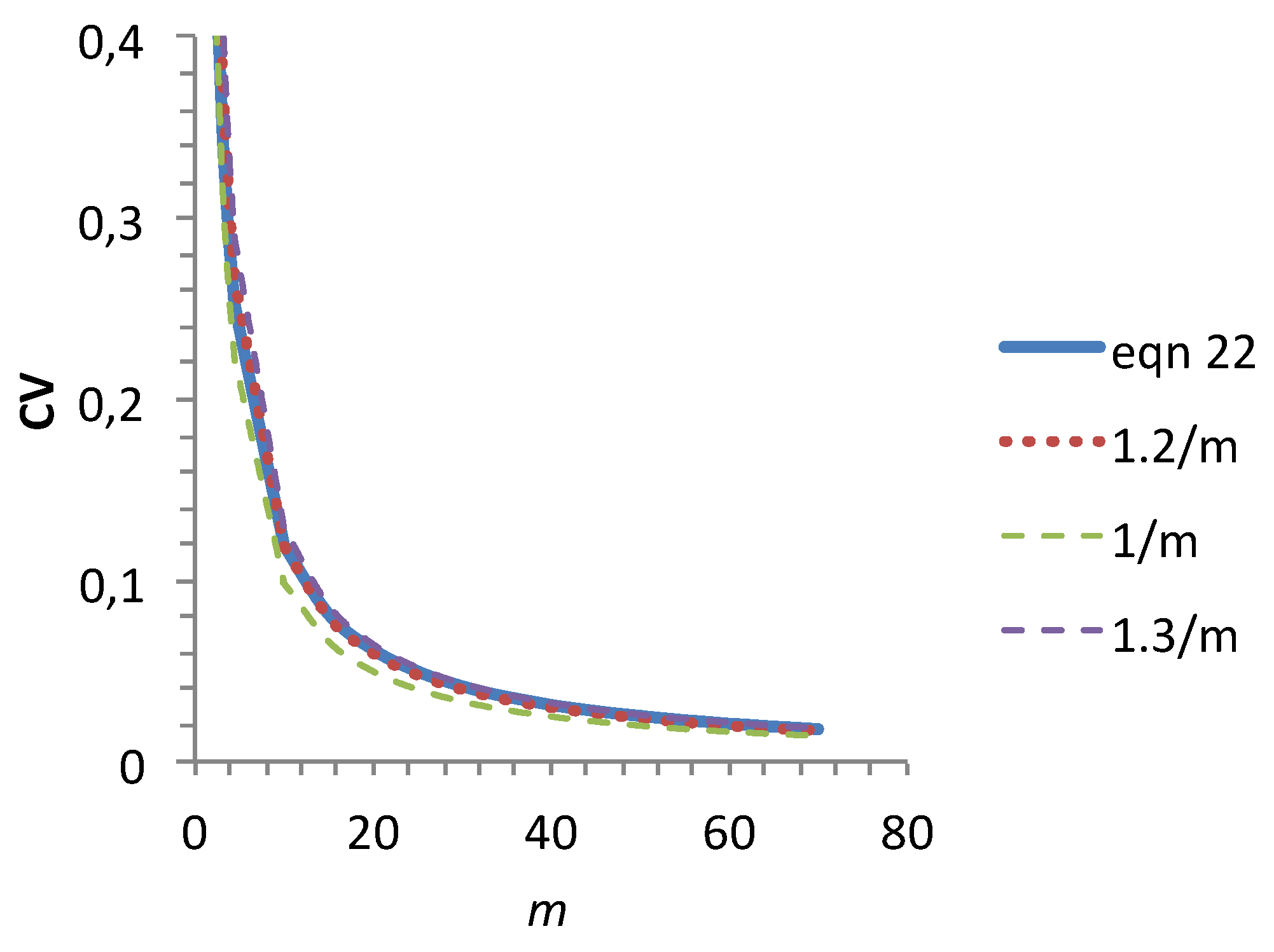
Figure 11 shows that equation (24) is a good approximation of coefficient of variation (CV= μ/s ; equation (18)) for the range of m values observed on ceramics. It is not significantly affected by variation of constant around 1.2.
C V = 1.2 m
Trends in statistical parameters variation with the value of n or of volume size were determined using equations (23) and (24). Main results are reported in Table 5.
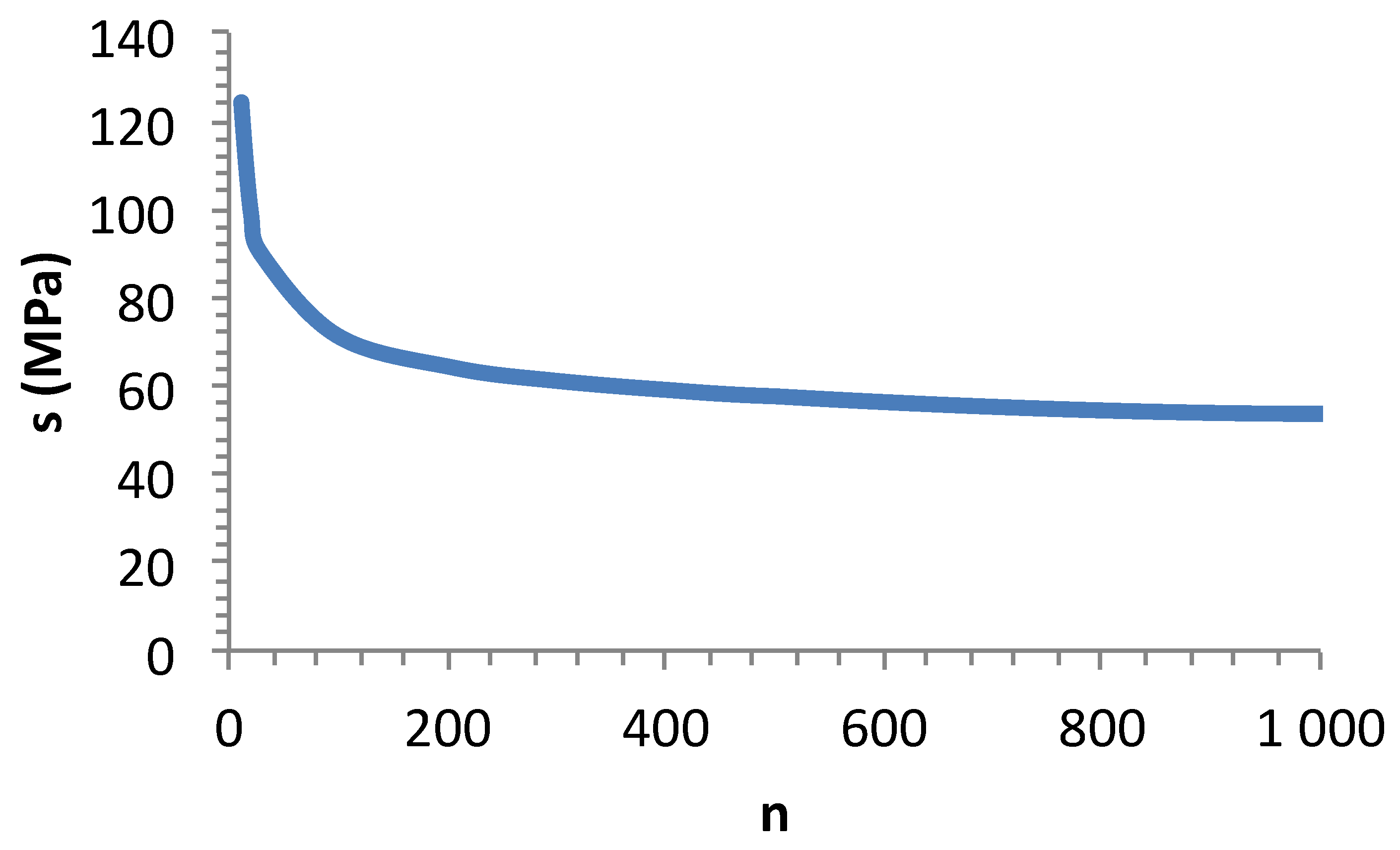
When the flaw strength interval and μ are constant, s is a decreasing function of increasing n (Figure 12). As a consequence, the Weibull modulus increases with n as shown by Figure 13. It appears that there is no maximum value for m. Thus, it may be difficult to identify an appropriate estimate of m. For the purpose of comparison of different distributions, it is thus necessary to consider batches of identical numbers of specimens.
When the flaw strength interval is constant and shifted towards lower values, μ decreases and s is a decreasing function as the slope increases with n. The trend in Weibull modulus variation is undeterminate on the basis of equation (24) (Table 5). m may increase, decrease or remain constant. It remains constant only if μ and s remain proportional. If n is constant, the slope and s are constant so that m decreases according to equation (24). This latter case was not reported in Table 5.
When the flaw strength interval is changed and shifted to lower values, μ decreases and s may increase or decrease with increasing n. m decreases with s increase. Then, its variation is indeterminate when s decreases (Table 5). As before, it remains constant only if μ and s remain proportional.
Both latter cases can be encountered at constant or increasing volume. Thus it appears that m does not take unique value. It depends on the variability of the underlying flaw strength population in the test specimens from batch to batch, characterized by the variation in standard deviation (Table 5). m constant requires that μ and s are proportional according to equations (18) and (24). It can be anticipated that this requirement implies a reproducible spatial distribution of the flaws.
These results are consistent with many papers that reported a big variation of m estimates from various laboratories testing different batches of specimens. Obviously, this is an issue for the prediction of the volume dependence of strengh. For this reason, the determination of a characteristic flaw strength distribution as proposed in this paper, is an interesting alternative that provides the probability of presence of flaws in the material and not only in small specimens. It can be used for comparison purposes of materials or components when those components with flaws larger than a given value have been eliminated. Furthermore failure predictions on the components can be performed with the appropriate parameters instead of the parameters estimated on small specimens that may display significant variability.

4.4. Validity of the Uniaxial Analysis for Short Span

In a previous paper [29] it was shown that the shear components can be reasonably neglected when d/l=0.4. At short span local perturbations can arise in the vicinity of supports and loading point. It was found that the equation of the elementary beam theory provides a satisfactory value of strength [24]. The possible effect of loading points is not detrimental since it concerns local compressive stresses. Fractography of the broken specimens clearly showed that failure occurred from the tensile part of specimens. Furthermore the plane of fracture origin was always perpendicular to the longitudinal stress. This suggests that the elemental strength was parallel to the longitudinal stress. This supports the validity of the uniaxial elemental strength model for the short span specimens of this paper.

5. Conclusion

The p-quantile diagrams showed that the flaw strength data followed normal distributions in different non uniform stress states, as well as when they were merged into a single set. The flexural strengths also shown normal distribution.
The strength data also followed Weibull distribution functions. Maximum Likelihood and Moment Method gave very close estimates of Weibull distribution parameters.
The fit of Weibull distributions to normal distributions was acceptable.
The elemental strength model permitted satisfactory predictions of flexural strength distributions from the flaw strength distribution of the 4-point bending specimens. .
Weibull predictions from 4-pt bending strength distributions overestimated the 3-pt bending flaw strength distributions and the short span flexural strength distributions.
The strength distribution may characterize only the batch of test specimens used for the determination of strength data. The distribution of critical flaw strengths, may vary from batch to batch. The population of critical flaws is characterized by the size given by the number of flaw strength data (n), the weakness given by the strength interval (Smin, Smax), and the mean strength (μ), the dispersion given by the standard deviation (s), the reproducibility given by CV. The Weibull modulus variability results from the variation of these parameters. It remains constant when n or V increase only if μ and s remain proportional (constant CV).
The extrapolation of experimental p-quantile diagrams by including weaker flaw strengths is an alternative approach to size effects based on the probability of existence of critical flaw strengths. It allows also anticipating flaw strength distributions in larger specimens for failure predictions using the elemental strength model.
The critical specimen size for which the flaw strength population is representative of the total critical flaw population inherent to the material type can be approached using p-quantile diagrams and a technique of detetection of the most deleterious flaws.

References

  1. Weibull, W. A statistical distribution function of wide applicability. J Appl Mech 1951, 18, 293–297. [Google Scholar] [CrossRef]
  2. Lamon, J. Fracture and Damage of Brittle Materials and Composites Statistical-Probabilistic Approaches, ISTE Press – Elsevier, U. K, 2017, ISBN 9781785481215.
  3. Gong, J. A new probability index for estimating Weibull modulus for ceramics with least square method. J Mater Sci Lett 2000, 19, 827–29. [Google Scholar] [CrossRef]
  4. Barnett, V. Probability plotting methods and order statistics. J R Statist Soc 1975, C24, 95–108. [Google Scholar] [CrossRef]
  5. Watson, A.S.; Smith, R.L. An examination of statistical theories for fibrous materials in the light of experimental data. J. Mater. Sci. 1985, 20, 3260–3270. [Google Scholar] [CrossRef]
  6. Paramonov, Y; Andersons J. A family of weakest link models for fiber strength distribution. Composites Part A 2007, 38, 1227–1233. [CrossRef]
  7. Phani, K.K. A new modified Weibull distribution function for the evaluation of the strength of silicon carbide and alumina fibres. J. Mater. Sci. 1988, 23, 2424–2428. [Google Scholar] [CrossRef]
  8. Amaniampong, G.; Burgoyne, C. J. Statistical variability in the strength and failure strain of aramid and polyester yarns. J. Mater. Sci. 1994, 29, 5141–5152. [Google Scholar] [CrossRef]
  9. Bergman, B. On the estimation of the Weibull modulus. J. Mater Sci. Let. 1984, 3, 689–692. [Google Scholar] [CrossRef]
  10. Sullivan, J.D.; Lauzon, P.H. Experimental probability estimators for Weibull plots, J. Mat. Sci. Letters 1986, 5, 1245–1247. [Google Scholar] [CrossRef]
  11. Basu, B.; Tiwari, D.; Kundu, D.; Prasad, R. Is Weibull Distribution the Most Appropriate Statistical Strength Distribution for Brittle Materials? Ceramics International 2009, 35, 237-246. doi.org/10.1016/j.ceramint.2007.10.003. [CrossRef]
  12. Lu, C.; Danzer, R.; Fischer, F. D. Fracture statistics of brittle materials: Weibull or normal distribution. Physical Review E 2002, 65, 06702. [Google Scholar] [CrossRef]
  13. Peirce, F. T. Tensile Tests for Cotton Yarns- The Weakest Link. J. Textile Inst., Trans. 1926, 17, 355–368. [Google Scholar]
  14. Epstein, B. Application of the theory of extreme values in fracture problems. J Am Statist Assoc 1948, 43, 403–412. [Google Scholar] [CrossRef]
  15. R’Mili, M.; Godin, N. ; Lamon.J. Flaw strength distributions and statistical parameters for ceramic fibres: The Normal distribution. Phys. Rev. E, 2012; 85, 1106–1112. [Google Scholar]
  16. Lamon, J.; R’Mili, M. Investigation of flaw strength distributions from tensile force-strain curves of fiber tows. Compos. Part A 2021, 145, 106262. [Google Scholar] [CrossRef]
  17. Lissart, N.; Lamon, J. Statistical analysis of failure of SiC fibers in the presence of bimodal flaw populations. J. Mater. Sci. 1997, 32, 6107–6117. [Google Scholar] [CrossRef]
  18. Chi-Cong Vu; Hong-Hai Tran. Performance analysis of methods to estimate Weibull parameters for the compressive strength of concrete. Case Studies in Construction Materials 2023, 19. [CrossRef]
  19. Freudenthal A. Chapter 6 in Fracture; Liebowitz, H. Academic Press, New York, 1968, Volume II.
  20. Gumbel, E. Statistics of Extremes, Columbia University Press, New York, 1968.
  21. Jayatilaka, A. De S.; Trustrum, K. Statistical approach to brittle fracture. J. Mat. Sc. 1977, 10, 1426–1430.
  22. Argon, A.S.; McClintock, F.A. Mechanical Behavior of Materials. Addison-Wesley, Reading, MA, USA, 1966.
  23. Batdorf, S.B.; Crose, J.G. A statistical theory for the fracture of brittle structures subjected to nonuniform polyaxial stresses. J. Applied Mech. Transactions of the ASME 1974, 459–464. [Google Scholar] [CrossRef]
  24. Lamon, J. Ceramics reliability : statistical analysis of multiaxial failure using the Weibull approach and the Multiaxial Elemental Strengh model. Journal of the American Ceramic Society 1990, 73, 2204–2212. [Google Scholar] [CrossRef]
  25. Lamon, J.; Evans, A.G. The statistical analysis of bending strengths for brittle solids: a multiaxial fracture problem. J. Am. Ceram. Soc. 1983, 66, 177–182. [Google Scholar] [CrossRef]
  26. Paritosh Bhattacharya; Rakhi Bhattacharjee. A study on Weibull distribution for estimating the parameters. Journal of Applied Quantitative Methods 2010, 5, 234–241.
  27. Bin Deng, B.; Wang, X.; Jiang, D. ; Gong, J. Description of the statistical variations of the measured strength for brittle ceramics: A comparison between two-parameter Weibull distribution and normal distribution, Processing and Application of Ceramics 2020, 14, 293-302. [CrossRef]
  28. Lamon, J.; R’Mili, M. Investigation of Specimen Size Effects on P-Quantile Diagrams and Normal Distributions of Critical Flaw Strengths in Fiber Tows. J. Compos. Sci. 2022, 6, 171. [Google Scholar] [CrossRef]
  29. Lamon, J. Statistical analysis of fracture of Silicon Nitride using the short span bending technique. International Journal of Turbo and Jet Engines 1988, 5, 13–22. [Google Scholar] [CrossRef]
Preprints 106700 g002
Figure 2. Comparison of Weibull (referred to as W) and normal (referred to as N) cumulative distribution functions for the elemental strengths.
Figure 2. Comparison of Weibull (referred to as W) and normal (referred to as N) cumulative distribution functions for the elemental strengths.
Preprints 106700 g002
Preprints 106700 g003
Figure 3. Comparison of Weibull (PDW) and Gauss (PDn) probability density functions.
Figure 3. Comparison of Weibull (PDW) and Gauss (PDn) probability density functions.
Preprints 106700 g003
Preprints 106700 g004
Figure 4. Size effects: Predictions of flexural strengths by the multiaxial elemental strength model equation for the flaw strength parameters derived from 4 –pt bending tests. Comparison with the experimental flexural strength distributions.
Figure 4. Size effects: Predictions of flexural strengths by the multiaxial elemental strength model equation for the flaw strength parameters derived from 4 –pt bending tests. Comparison with the experimental flexural strength distributions.
Preprints 106700 g004
Preprints 106700 g005
Figure 5. Size effects: Predictions of flexural strengths by the Weibull model equation for the statistical parameters derived from the 4 –pt bending tests. Comparison with the experimental flexural strength distributions.
Figure 5. Size effects: Predictions of flexural strengths by the Weibull model equation for the statistical parameters derived from the 4 –pt bending tests. Comparison with the experimental flexural strength distributions.
Preprints 106700 g005
Preprints 106700 g006
Figure 6. Size effects: predictions of flaw strengths by the Weibull model for the flaw strength parameters derived from 4 –pt bending tests. Comparison with the experimental flaw strength distributions.
Figure 6. Size effects: predictions of flaw strengths by the Weibull model for the flaw strength parameters derived from 4 –pt bending tests. Comparison with the experimental flaw strength distributions.
Preprints 106700 g006
Preprints 106700 g007
Figure 7. Merged and extrapolated p-quantile – flaw strength diagrams. Comparison with those obtained from the 3-point and 4-point bending tests.
Figure 7. Merged and extrapolated p-quantile – flaw strength diagrams. Comparison with those obtained from the 3-point and 4-point bending tests.
Preprints 106700 g007
Preprints 106700 g008
Figure 8. Normal CDFs derived from the merged and extrapolated p-quantile – flaw strength diagrams.
Figure 8. Normal CDFs derived from the merged and extrapolated p-quantile – flaw strength diagrams.
Preprints 106700 g008
Preprints 106700 g009
Figure 9. Gaussian PDFs derived from the merged and extrapolated p-quantile – flaw strength diagrams.
Figure 9. Gaussian PDFs derived from the merged and extrapolated p-quantile – flaw strength diagrams.
Preprints 106700 g009
Preprints 106700 g010
Figure 10. Influence of the number of flaw strength data n on the extreme values zpmax (=-zpmin).
Figure 10. Influence of the number of flaw strength data n on the extreme values zpmax (=-zpmin).
Preprints 106700 g010
Preprints 106700 g011
Figure 11. Variation of coefficient of variation (equation (18)) with m. Comparison with functions 1/m, 1.2/m and 1.3/m.
Figure 11. Variation of coefficient of variation (equation (18)) with m. Comparison with functions 1/m, 1.2/m and 1.3/m.
Preprints 106700 g011
Preprints 106700 g012
Figure 12. Influence on n on standard deviation when the flaw strength interval and μ are constant.
Figure 12. Influence on n on standard deviation when the flaw strength interval and μ are constant.
Preprints 106700 g012
Preprints 106700 g013
Figure 13. Influence of n on m when the strength interval and the mean strength are kept constant.
Figure 13. Influence of n on m when the strength interval and the mean strength are kept constant.
Preprints 106700 g013
Table 1. Test specimen dimensions.
Table 1. Test specimen dimensions.
Length (mm) Thickness 2d (mm) Width b (mm) upper span 2l1 (mm) lower span 2l (mm)
3 pt long span 45 4 4 0 40
3 pt short span 20 4 4 0 10
4 pt 45 4 4 20 40
Table 2. Coefficients of correlation of p-quantile vs strengths, normal vs. Weibull cumulative (Pn or PW respectively) or probability distributions (PDn or PDW respectively).
Table 2. Coefficients of correlation of p-quantile vs strengths, normal vs. Weibull cumulative (Pn or PW respectively) or probability distributions (PDn or PDW respectively).
p-quantile vs strength Pn vs PW PDW vs PDn
4pt 0.985 0.99 0.93
3pt flex strength 0.988 0.997
3pt flex strength
short span		 0.97 0.997
3pt flaw strength 0.988 0.997 0.90
3pt flaw strength short span 0.99 0.998 0.95
Merged flaw strength 0.995 0.998
Table 3. Statistical parameters of the normal and Weibull distributions of flexural and flaw strengths. Also given are the statistical parameters of the elemental strength model for the 4pt flaw strengths. Also given are the statistically equivalent stressed volumes VE. Except for the elemental strength model, the parameters of the strength distributions were determined using both MM and MLE methods.
Table 3. Statistical parameters of the normal and Weibull distributions of flexural and flaw strengths. Also given are the statistical parameters of the elemental strength model for the 4pt flaw strengths. Also given are the statistically equivalent stressed volumes VE. Except for the elemental strength model, the parameters of the strength distributions were determined using both MM and MLE methods.
μ 
     		 s
(MPa)		 m Weibull λ σs (1)
(MPa)
Weibull		 scale factor
(MPa) Weibull		 S0
(MPa)
elemental model		 VE (10-9 m3)
4pt flaw strength 345.67 38.46 10.9
(MM)
10.8
(MLE)		 10.9 362.06
(MM)
362.44
(MLE)		 64.9 57 7.29
3pt flexural strength 404.67 44.26 11.1
(MM)
10.97
(MLE)		 423.73
(MM)
424,20
(MLE)		 66.03 1.09
3pt flexural strength
short span		 474.27 61.26 9.3
(MM)
9.9
(MLE)
 499.23
(MM)
499.0
(MLE)		 48.42 0.38
3pt flaw strength 370.3 46.2 9.63
(MM)
9.35
(MLE)		 389.82
(MM)
390.1
(MLE)		 46.99 1.42
3pt flaw strength
short span		 414.8 66.55 7.36
(MM)
7.29
(MLE)		 442.22
(MM)
442.2
(MLE)		 24.54 0.57
Merged flaw strength 377.15 59.12 7.56
(MM)
6.64
(MLE)		 401.65
(MM)
402.93
(MLE)		 33
extrapolated
flaw strength		 340 76.92 5.08 369.97
extrapolated
flaw strength		 295.28 94.34 3.5 328,09
(1) V0 = 1 m3.
Table 4. Values of parameters that define the p-quantile vs. strength diagrams.
Table 4. Values of parameters that define the p-quantile vs. strength diagrams.
Smin (MPa) Smax (MPa) zp n
4pt flaw strength 256 429 +/- 2.2 69
3pt flexural strength +/- 2.2 68
3pt flexural strength
short span		 +/-2.13 70
3pt flaw strength 259 472 +/2.18 68
3pt flaw strength
short span		 230 544 +/- 2.2 70
Merged flaw strength 230 544 +/- 2.59 207
extrapolated flaw strength 140 544 +/- 2.6 210
extrapolated flaw strength 50 544 +/- 2.6 210
Table 5. Main trends in the influence of n and V changes on Weibull modulus.
Table 5. Main trends in the influence of n and V changes on Weibull modulus.
n, V Smin Smax mean μ slope 1/s s          m
n↗    V=cst constant constant constant ↗ ↘ ↗
n↗  V=cst constant ↗ ↗ ↗ ↘ ↗
n=cst V↗ constant ↘ ↘ ↗ ↘ indeterminate
V↗  n↘ constant ↘ ↘ ↘ ↗           ↘
V↗ ↘ ↘ ↘ ↗ ↘ indeterminate
V↗ ↘ ↘ ↘ ↘ ↗        ↘
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated