A New Alternating Suboptimal Dynamic Programming Algorithm with Applications for Feature Selection

Preprint

Article

A New Alternating Suboptimal Dynamic Programming Algorithm with Applications for Feature Selection

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 May 2024

Posted:

20 May 2024

You are already at the latest version

Alerts

Abstract

Feature selection is predominantly used in machine learning tasks, such as classification and regression. It selects a subset of features (relevant attributes of data points) from a larger set that contributes as optimally as possible to the informativeness of the model. There are exponentially many subsets of a given set, and thus, the exhaustive search is only practical for problems with at most a few dozen features. In the past, there have been attempts to reduce the search space using dynamic programming. However, models that consider similarity in pairs of features besides the quality of individual features do not provide the required optimal substructure. As a result, algorithms, which we will call suboptimal dynamic programming algorithms, find a solution that may deviate significantly from the optimal one. In this paper, we propose a dynamic programming algorithm with an iterative upgrade where the order of feature processing is inverted in each iteration. Such an alternating approach allows for improving the optimization function by using the score from the previous iteration to estimate the contribution of unprocessed features. The iterative process is proven to converge and terminate when the solution does not change in three successive iterations or when the number of iterations reaches the threshold. Results in more than 90 % of tests align with those of the exhaustive search, being competitive and often superior to the reference greedy approach. The validation was done by comparing the scores of output feature subsets and examining the accuracy of different classifiers learned on these features. In the context of feature selection, the proposed algorithm can be characterized as a filter method. However, we expect that the idea of alternating suboptimal optimization will soon be generalized to tasks beyond feature selection.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Nowadays, in the Internet of Things era, social media platforms, Earth observation, crowdsourcing, medical imaging equipment, various biomedical signals measurement devices, wearable sensors, digital twins, etc., we are flooded with vast amounts of data. Those measurable characteristics used as attributes or input variables to describe an object of interest are called features, while individual data points (objects of interest) represent feature vectors. Each feature thus corresponds to a dimension in the vector. Vast amounts of data allow the creation of a large repertoire of features, but usually, not all are relevant for further processing objects of interest. They often slow it down, direct it towards a wrong solution, or even make it infeasible. In order to address these challenges, feature selection approaches were introduced that select a subset of the most informative features while discarding irrelevant or redundant ones [1]. Feature selection plays a vital role in model construction in statistical analysis, dimensionality reduction, signal processing, pattern recognition, data visualization, and, particularly, in various machine learning tasks, such as classification, regression, and clustering. It is aimed to improve the model’s performance, including its accuracy, generalisability, and interpretability, and reduce overfitting and computational cost [2].

Feature selection methods can be grouped into three categories [1]. Filter methods evaluate candidate subsets with independent criteria that exploit essential characteristics of the training data. They are fast, but the solution may deviate significantly from the optimal one. A wrapper approach uses a learning algorithm for subset evaluation, such as a classifier or regressor. Its performance is usually better but also much slower than the filter approach. Embedded methods interact with a learning algorithm but at a lower computational cost than the filter approach. They use independent criteria to identify optimal subsets for a known cardinality. The learning algorithm is then used to select the final optimal subset across different cardinalities [3].

Regardless of the approach chosen, feature selection can be viewed as an optimization problem as it searches for the best-evaluated feature subset [4]. Different search strategies can be used, including sequential search (greedy approach), exponential search (exhaustive search, beam search, or branch and bound), and random search [3]. On the other hand, dynamic programming (DP) is not as commonly applied to feature selection compared to other methods. This popular optimization approach breaks a problem into smaller subproblems and uses their solutions to construct the solution to the larger problem. An optimal solution can be found if the problem exhibits optimal substructure. This means that an optimal solution to the problem contains optimal solutions to subproblems [5,6]. However, DP is usually computationally demanding, so for reasons of feasibility, acceptable speed, and availability to handle problems with higher dimensionality, it is also required that the number of subproblems is not too high and that the subproblems overlap, suggesting that it makes sense to record their solutions in a table and reuse them [6].

In this paper, we highlight the possibilities of using DP in feature selection, analyze the difficulties of existing (rare) approaches, and propose alternative solutions. An evaluation criterion based on feature quality, correlation, and/or statistics does not generally provide an optimal substructure since, e.g., the union of two optimal subsets is not necessarily optimal due to possible high correlations between pairs of features, one from each subset. It is possible to achieve an optimal solution for specific problems by adapting the evaluation criterion, but this spoils generality, which is among our primary goals. We thus focused on finding the best possible suboptimal solution. We studied approximate (ADP) [7] and iterative [8] dynamic programming (IDP) methods and developed a solution which we called alternating suboptimal dynamic programming (ASDP). The method has good convergence properties, as it finds the optimal solution in more than 90% cases, and the solution found in each iteration is never worse than the one found in the previous iteration.

The Introduction is followed by four sections. In the second one, we survey existing solutions in feature evaluation and selection, the use of DP in feature selection, and suboptimal DP algorithms. In the most research-intensive third section, we first summarise our preliminary filter method for feature selection based on graph cuts, which can be used alone or as a preprocessing for the new ASDP method presented afterward. In Section 4, we show and analyze the results, and in the final Section 5, we discuss the work done, its strengths, and some weaknesses that pose challenges for future research.

2. Related Works

As the topic presented here combines several challenges, the state-of-the-art review must address several areas. First, in Subsection 2.1, we address feature evaluation, i.e., procedures and metrics to assess the contribution of individual features and/or a feature subset to a machine learning model. The feature evaluation is the basis for feature selection, which we review in Subsection 2.2. The goal is to optimally select a subset of the input features that solve a given machine-learning task. We wanted to approach the problem using dynamic programming, so in Subsection 2.3, we review the use of this software design strategy in feature selection. However, such methods are rare, time-demanding, and practically always offer partial solutions only. Consequently, the solution proposed in this paper is suboptimal; thus, Subsection 2.4 briefly reviews the use of suboptimal DP for various problems, including feature selection.

2.1. Feature Evaluation

Feature evaluation is a critical step in the feature selection process. It includes assessing the contribution of input features to a machine learning model performance [2]. Features that contribute the most information to the predictive model can improve the model’s performance, reduce overfitting, and accelerate the learning process [2,9,10]. For classification purposes, feature evaluation can be achieved directly by evaluating the classification models built for each feature [2]. The choice of classifier strongly influences the evaluation results, while its learning is often time-consuming. The latter is particularly evident in cases of a large number of features [2,9,10]. Similar drawbacks are also noted for regression purposes, as feature evaluation can be achieved using computationally demanding regression approaches built for each feature.

To avoid using a computationally demanding classifier, techniques for analyzing the discriminatory power of features are introduced. Early approaches focused on the ratio between the distances of samples of different classes and samples of the same class [11]. Examples of these include the Fisher criterion [12], the maximum margin criterion [13], and the Laplacian score [14]. In the case of regression tasks, techniques are based on calculating the correlation coefficients (e.g., Pearson’s or Spearman’s) between the feature’s values and the continuous target variable [2,9]. However, the mentioned techniques for classification and regression tasks cover only linear interdependencies between feature values and the target variable.

Approaches that capture non-linear dependencies are based on the information contribution. For classification purposes, this technique evaluates features according to the ratio between the classes’ entropy and the feature values’ conditional entropy [15,16,17]. Regarding accuracy, similar results can be obtained using the computationally more efficient Gini impurity [18,19,20]. In the case of multi-class classification, Gini impurity is biased towards majority classes and prone to overfitting [20]. On the other hand, techniques based on mutual information capture non-linear relationships between features and the target variable successfully, utilizing both classifications [21] and regression [22], respectively. However, such metrics favor features with many different values, which can lead to overfitting.

2.2. Feature Selection

Overfitting negatively affects the power of machine learning methods and cripples predictive accuracy. Irrelevant features lower the predictive power of the model. Feature selection methods can overcome both limitations [23]. We divide them into three groups:

filters,
wrappers, and
embedded methods.

Filtering is usually performed by a threshold value. Although such methods are computationally very efficient, their classification power largely depends on the feature evaluation techniques [2,9,24]. The latter often consider only pairwise dependencies between features’ values and the target variable, ignoring correlations between features [2,11]. As a result, the prediction efficiency is thus limited.

In [25,26], a method calculates the efficiency of separation between different classes in the local neighborhood of selected samples to evaluate the feature. This enables low execution times because it does not use all of the samples contained in the dataset. However, calculations are usually inaccurate due to the limited number of considered samples. The method also does not consider the correlation between features. In [27], the authors proposed the approach that selects features highly correlated with the class labels and in low correlation with each other. A similar method is proposed [28] but for regression purposes. The only difference is that it selects features highly correlated with the target variable. However, neither technique considers the interaction between features and only considers the linear interdependence between feature values and target variables.

In [29], the authors propose a two-stage feature selection method, where the evaluation is based on the calculation of mutual information while at the same time considering the correlation between pairs of features. In [22], the adequacy of the mutual information for regression is considered. However, in the case of a small number of training samples, inaccurate estimates of mutual information may appear, and the method is biased towards features with a large number of different values due to the use of this metric. In [30], a feature selection framework for large datasets was proposed based on a cascade of methods capable of detecting nonlinear relationships between two features and designed to achieve a balance between accuracy and speed.

Wrapper methods, on the other hand, select a subset of features that maximizes the performance of a given classifier or regressor [2]. Wrappers are considered a multi-criteria optimization problem that maximizes machine learning method performance while minimizing the number of selected features. This can be addressed with several optimization techniques [2,31], such as sequential selection algorithms or nature-inspired algorithms, such as the evolutionary and genetic algorithm [32,33], particle swarm optimization [32,34], and the bees algorithm [35].

Early wrappers were based on sequential selection [36]. It starts with an empty set, adding features, and evaluating the prediction performance. The feature that gives the best results is permanently included in the set. The selection continues by adding features one by one again and keeping those that contribute the most to improving the prediction performance. The algorithm terminates when a predetermined threshold of acceptable results is reached or when a sufficient number of features are selected. In [37], the authors propose an inverse procedure where features are removed from the input set. The main limitation of these algorithms is that they do not consider the correlation between features. This limitation is eliminated in the adaptive version of the algorithm [38]. However, such a search for an optimal set with a more significant number of features soon grows into an exponentially time-consuming [11,36].

Therefore, methods that find a sub-optimal solution are proposed [32,33]. Examples of the latter are algorithms based on nature-inspired concepts. Similar to sequential feature selection methods, the evaluation function of evolutionary algorithms represents the performance of a model, while the features represent the population. The best-performing subsets are combined to achieve the desired result [33,34]. The biggest problem with these methods is their computational complexity, as it involves evaluating features by the model for each specific subset over a large number of iterations to obtain useful results [2,39].

An alternative to wrapper methods is the embedded methods, which have lower execution times [2,40]. They perform the selection of a subset of features in interaction with the model in the learning phase of the model and are thus tied to the selected machine learning algorithm [2]. Decision trees achieve feature selection based on mutual information evaluation, while support vector methods use LASSO (Least Absolute Shrinkage and Selection operator) regression analysis with Ll [40], or ridge regression with L2-regularization [41] to rank features during learning. This significantly reduces the computational complexity of both methods, as it allows for avoiding multiple repetitions of the machine learning algorithm learning process. At the same time, support vector methods are inexplicable and sensitive to many input parameters. Similar to support vector methods, the selection of features can also be achieved with neural networks, whereby learning the network, we set the weights for individual features according to their suitability [2].

2.3. Dynamic Programming-Based Feature Selection

DP can be employed since feature selection can be formulated as an optimization problem. In this context, DP solves the exhaustive search of a feature subset by breaking it down into simpler searches while storing the suboptimal subsets of features to avoid redundant calculations.

Already in 1998, Nelson and Levy [42] presented a method where optimality is defined in terms of a particular measure, the Fisher return function, providing the features were uncorrelated. In [43], a method for selecting the best subset of features for classification purposes is presented. It uses DP for divergence analysis of the features’ distributions regarding given classes, selecting the subset of the most informative features. However, this method does not consider the interaction between features and thus can choose redundant ones. The identical drawback can be noted in [44]. The approach is similar to the sequential forward feature selection, starting with an empty set of features and adding the best-performing one in each iteration. The main difference is that it can remove any previously selected features if it improves the performance of a set. In [45], the authors presented a method that uses rough sets theory and DP in order to remove redundant features from the input set while maintaining high classification performance. However, this approach is computationally intensive, especially for large datasets with a high number of features.

2.4. Suboptimal Dynamic Programming

In the literature, there are several partially overlapping concepts addressing suboptimal DP.

Approximate Dynamic Programming (ADP) is a sophisticated variant of traditional DP, representing a compromise between the method’s accuracy and computational feasibility. It aims to find near-optimal solutions to DP problems, achieved by approximating the value or policy functions using function approximation techniques such as neural networks, linear approximators, or interpolation methods [46,47]. A policy represents a strategy or set of rules that dictate the decision-making process, while the value corresponds to the expected return or benefit from following a particular policy. ADP iteratively refines both, converging towards an optimal or near-optimal solution [47]. The concept has proven itself, particularly in solving large-scale discrete-time multistage stochastic control processes, i.e., complex Markov Decision Processes (MDPs), and found applications in different fields, such as inventory control systems, financial optimization problems, robot path planning, information theory, and decision-making processes in learning agents, i.e., reinforcement learning (RL) [48,49]. Articles [7] and [50] consider feature selection in RL and MDPs, while [51] addresses feature discovery, also known as feature construction, in the context of ADP and RL. Note that adaptive dynamic programming with the same acronym ADP is sometimes found in the literature for practically the same concept [52].
Iterative dynamic programming (IDP) involves solving a problem by iteratively refining an initial solution through DP techniques. The definition can be interpreted in different ways. Most often, IDP is used to solve real-valued optimization problems in a manner that it reduces the state and control quantization to an arbitrarily small amount by first searching over a relatively coarse but large set of system inputs and states using DP, and then successively generating a denser and narrower search range centered about the previous result. Luus [53] defined this principle as reducing dimensionality by iteratively varying grid resolutions, while Lock and McKelvey [54] applied it on different time scales. In [8], IDP was used to optimize queries in database systems. IDP was also referred to as a counterweight to recursive DP, while value and policy iteration represent an intersection point of IDP with ADP [47]. Note that IDP can be either optimal or suboptimal.
Relaxed dynamic programming reduces the complexity by relaxing the demand for optimality. The distance from optimality is kept within prespecified error bounds, and the size of the bounds determines the computational complexity [55]. The bounds are chosen by the user, who can then effectively trade-off between solution time and accuracy [56]. By controlling the error in the processes of relaxed value iteration and approximate policy iteration, the relaxed DP concept is closely related to ADP and IDP [57].

3. Materials and Methods

In this section, we present a new method for feature selection based on suboptimal DP. There are exponentially many subsets of a given feature set, all of which are candidates for the feature selection solution, so the exhaustive search is only practically applicable to problems with a few dozen features. Our method processes, e.g., 200 features in 5 seconds, but for larger input sets, it makes sense to preprocess it with some faster filtering. We use our efficient and reliable graph cut-based feature selection [58], summarised in Subsection 3.1. In Subsection 3.2, we discuss the idea of using DP and the encountered difficulties and introduce an iterative suboptimal alternating solution, where the order of feature processing is inverted in each iteration. We conclude the chapter with proof of convergence and a theoretical analysis of time and space complexity.

3.1. Graph Cut-Based Feature Selection

This section describes a graph cut-based feature selection approach, presented in [58] that allows for extracting a subset of high-quality dissimilar features. Depending on the defined feature estimation measurement, it can be used for classification and regression purposes. Graph vertices represent features with associated weights that define their quality (as proposed in [58]), while graph edge weights define similarities between them. The method relies on two input parameters,

T_{Δ}

and

T_{p}

, used for graph definition. The former defines the necessary level of features’ quality (i.e., maximal allowed class overlap) to be included in the output feature space, and the latter determines the minimal level of dissimilarity between them.

Let

F S

denote an input feature space

F S = 〈f_{i}〉

. A feature

f_{i}

, referred to by an index

i \in [1, n]

, is given as a mapping function

f_{i} : Z \to R

. An index

m \in [1, M]

refers to a sample, i.e., a feature vector defined as

{\vec{x}}_{m} = 〈f_{i, m}〉

. An undirected graph used for feature selection is defined as

G = (F, E)

, where a set of vertices F is defined as

F = \{f_{i} \in F S; Δ (f_{i}) \leq T_{Δ}\}

, while an unordered set of edges

E = \{e_{i, j}; P (e_{i, j}) \geq T_{p}\}

is given by

e_{i, j} = (f_{i}, f_{j})

for all

f_{i}, f_{j} \in F

, such that

i \neq j

. A vertex-weighting function is given by

Δ (f_{i})

, as defined in [58], and the edge-weighting function is given by the absolute Pearson correlation coefficient

P : E \to [0, 1]

, formally described by (1).

P (e_{i, j}) = | \frac{\sum_{m = 1}^{M} (f_{i, m} - μ_{i}) (f_{j, m} - μ_{j})}{σ_{i} σ_{j}} |,

(1)

where

μ_{i}

denotes mean, while standard deviation

σ_{i}

of feature values is defined as

σ_{i} = \sqrt{\frac{1}{M} \sum_{m = 1}^{M} (f_{i, m} - μ_{i})}

. Both functions,

Δ

and P, are designed so lower values (closer to 0) are more favorable for selection than higher values (closer to 1).

According to the theoretical framework introduced in [58], we used the following definitions of elementary properties:

Vertices $f_{i} \in F$ and $f_{j} \in F$ are adjacent in a graph G if there exists an edge $e_{i, j} \in E$ .
A path from $f_{i_{0}}$ to $f_{i_{N}}$ is an ordered sequence of vertices $\prod_{i_{0}, i_{N}} = 〈f_{i_{0}}, f_{i_{1}}, . . ., f_{N}〉$ , such that $f_{i_{j}}$ and $f_{i_{j + 1}}$ are adjacent for all $j \in [0, N - 1]$ .
A graph G is connected if $\forall f_{i}, f_{j} \in F$ there exists a path $\prod_{i, j}$ .
A graph $G^{'} = (F^{'}, E^{'})$ is subgraph of G if $F^{'} \subseteq F$ and $E^{'} \subseteq E$ .
A neighbourhood $Z (f_{i})$ of a vertex $f_{i}$ in graph G is the subset of vertices F, defined by all the adjacent vertices of $f_{i k}$ , namely, $Z (f_{i}) = {f_{j}}; f_{j} \in F; \exists e_{i, j}$ , where $i \neq j$ .

We say that a set of vertices

C U T (F) \subseteq F

is a vertex-cut if its removal separates graph G into at least two non-empty and pairwise disconnected connected components. Obviously,

Z (f_{i})

is a graph-cut, as it separates a singleton

{f_{i}}

(i.e., an individual vertex) from the rest of the graph, thus creating a subgraph

G^{'} = (F^{'}, E^{'})

, whose vertex- and edge-sets are given formally by (2).

\begin{matrix} F^{'} = F ∖ (Z (f_{i}) \cup {f_{i}}), \\ E^{'} = {e_{h, l} \in E; f_{h}, f_{l} \in F^{'} and h \neq l} . \end{matrix}

(2)

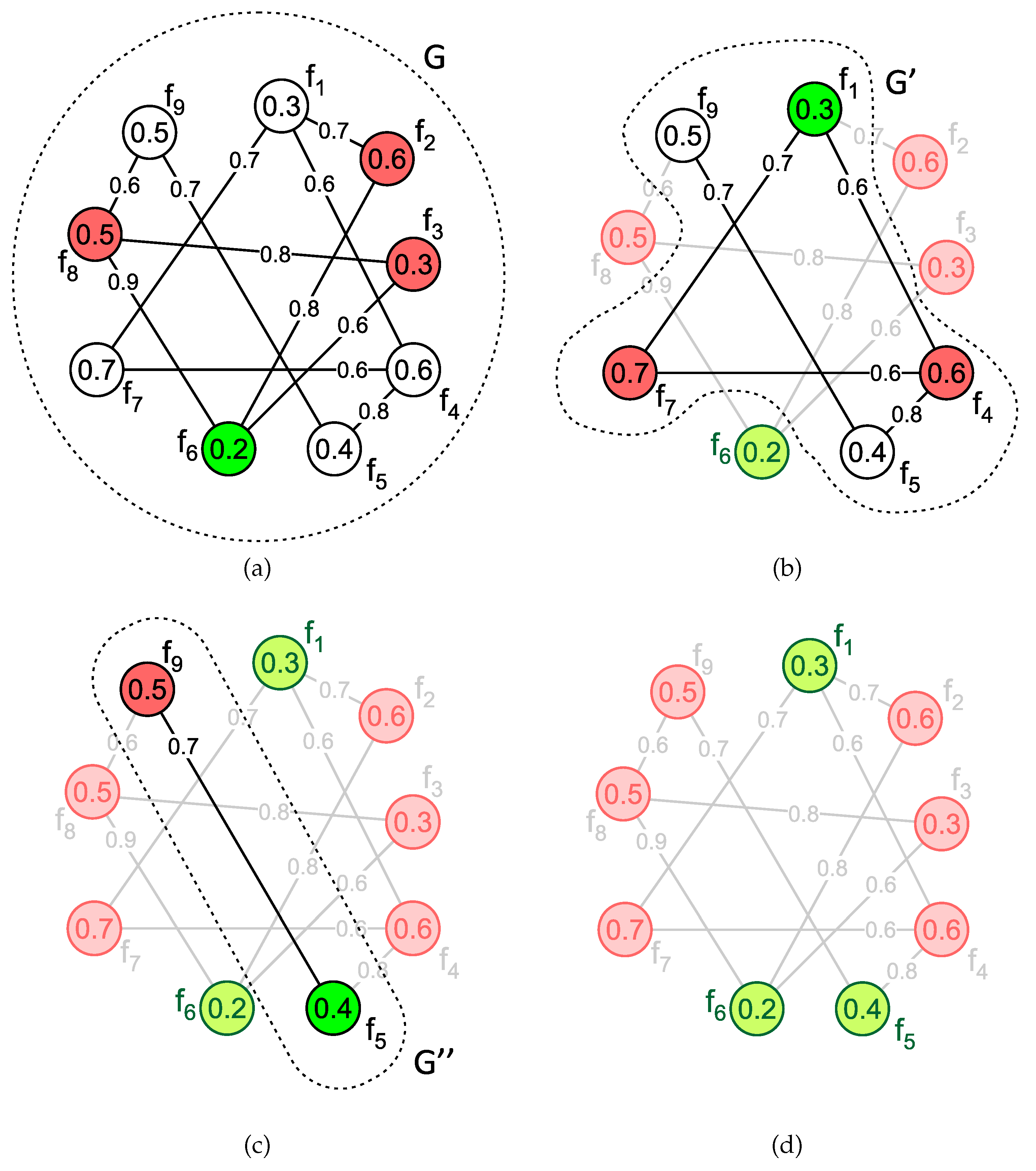
The example of vertex-cut feature selection is presented in Figure 1. Figure 1a shows an undirected graph

G = (F, E)

, constructed over a set of features

F S = {f_{1}, f_{2}, \dots, f_{9}}

, with thresholds

T_{Δ} = 0.6

and

T_{p} = 0.6

applied on the associated vertex- and edge-weighting functions

Δ

and P, accordingly. To ensure the preservation of the overall informativeness of selected features, a feature of the highest quality

\hat{f_{r}} = {arg min}_{f_{m} \in G} Δ (f_{m})

is selected first by a vertex-cut of its neighborhood

Z (\hat{f_{r}})

. The selected feature

f_{6}

is colored green. All of highly correlated adjacent features

Z (\hat{f_{6}}) = {f_{2}, f_{3}, f_{8}}

are marked red and removed from G. This results in

G^{'}

, as defined by (2), and a disconnected singleton

{f_{6}}

(see Figure 1b). The same process is then repeated on

G^{'}

, separating the feature of the highest quality, namely

f_{1}

, from the remaining graph

G^{''}

by removal of

Z (f_{1}) = {f_{4}, f_{7}}

. The final cut is performed on the graph

G^{''}

separating

f_{5}

(in green) from the remaining (empty) graph

G^{''}

by removal of

Z (f_{5}) = {f_{9}}

(in red), as shown in Figure 1c. Thus, the output subset of high-quality dissimilar features, namely

{f_{1}, f_{5}, f_{6}}

, is obtained, as shown in Figure 1d.

3.2. New Suboptimal Dynamic Programming Algorithm

The new method combines the advantages of iterative and approximate dynamic programming. It is based on a graph like the graph cut-based filtering from Subsection 3.1. We thus use the same notation, but we will extend it throughout this subsection with additional algorithm parameters and graph vertex attributes. The graph is undirected, i.e.

P (e_{i, j}) = P (e_{j, i})

. The input is the feature set

F S = 〈f_{i}〉

0 < i \leq n

, which is processed in index order, i.e., from

f_{1}

f_{n}

, so we will sometimes also speak of a sequence of features. At both ends of this sequence, the guard vertices

f_{0}

and

f_{n + 1}

are added, which do not change during the execution of the algorithm, but they simplify the implementation. There is no edge between the two guards, while the guard vertices and the edges between a guard and any other vertex are given weights 0. We stress this in the form of an Equation (3).

\begin{matrix} Δ (f_{0}) = 0, \\ Δ (f_{n + 1}) = 0, \\ P (e_{0, n + 1}) = \infty, \\ P (e_{0, i}) = 0, 0 < i \leq n, \\ P (e_{i, n + 1}) = 0, 0 < i \leq n . \end{matrix}

(3)

Each graph vertex

f_{i}

contains, in addition to the weight

Δ (f_{i})

, a set

S_{i}

that stores the "optimal" subset (feature selection result) of the vertices already processed, and the score

s_{i}

of this subset, which is obtained by the evaluation criterion. Their initialization is described by (4) and is important for the convergence proof in Subsection 3.3. The evaluation criterion described in (5) seeks a minimum for all vertices, except the guards, i.e.,

0 < i \leq n

\begin{matrix} S_{i} = \emptyset, 0 \leq i \leq n + 1, \\ s_{i} = 0, 0 \leq i \leq n + 1 . \end{matrix}

(4)

s_{i} = min_{0 \leq j < i} (s_{j} + Δ (f_{i}) + \sum_{k \in S_{j}} P (e_{k, i}))

(5)

Let r be the value of j where the minimum was identified. The corresponding

S_{i}

is calculated by (6).

S_{i} = S_{r} \cup {i}

(6)

The final score

s c o r e

and feature selection result

S o l u t i o n

are given by (7).

1.5

\begin{matrix} s c o r e = min_{0 < i \leq n} s_{i}, \\ s o l u t i o n = i, where s c o r e was found, \\ S o l u t i o n = S_{s o l u t i o n} . \end{matrix}

(7)

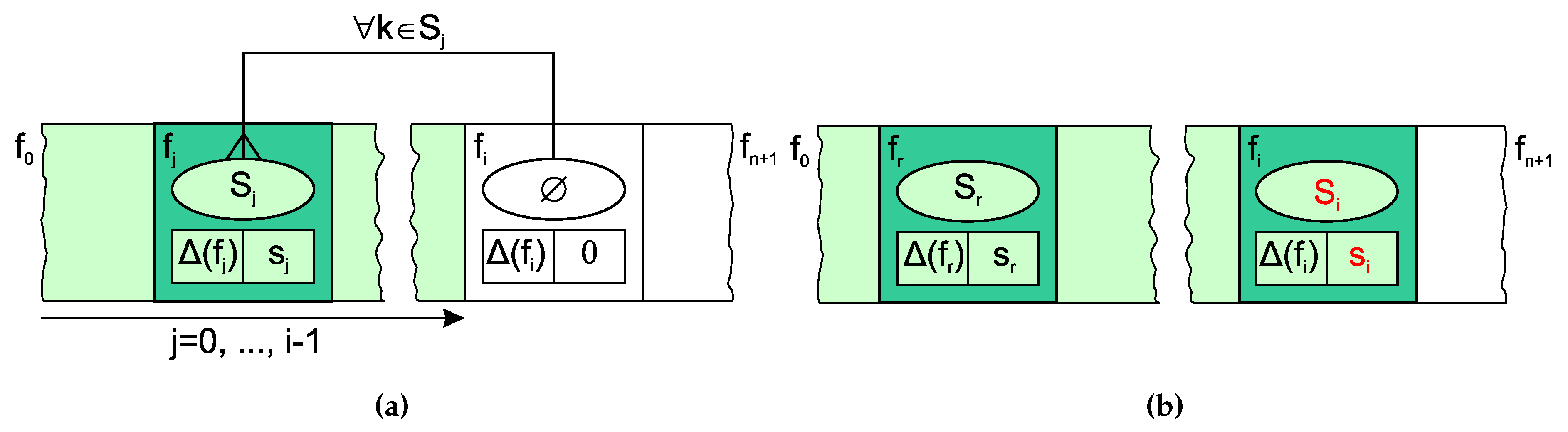
Figure 2a shows the situation immediately before the Equations (5) and (6) are applied to vertex

f_{i}

, and Figure 2b shows the situation immediately after the equations are applied. Green indicates the graph vertices that have already been processed, and white indicates those that are or will be processed. The red text indicates vertex attributes modified during the observed

f_{i}

processing.

So far, everything seems straightforward, but there are, in fact, three serious problems in the process that need to be addressed. The first is that the importance of vertices and edges might differ. For this reason, we introduce a weight w,

0 \leq w \leq 1

. This modifies the evaluation criterion (5) into (8).

s_{i} = min_{0 \leq j < i} (s_{j} + w \cdot Δ (f_{i}) + (1 - w) \cdot \sum_{k \in S_{j}} P (e_{k, i}))

(8)

The second problem is that equation (5) in its present form always leads to a trivial solution from (9). Since the weights of the graph vertices and edges are all non-negative, the minimum consists of a single vertex (without incident edges) with the lowest weight.

s c o r e = min_{0 < j \leq n} (w \cdot Δ (f_{j}))

(9)

To prevent this, we first modified the model by replacing the decreasing vertex evaluation function

Δ

with the increasing

Δ^{'} (f) = 1 - Δ (f)

. The idea was to award high vertex weights and penalize high edge weights. This resulted in the optimization function (10):

s_{i} = max_{0 \leq j < i} (s_{j} + w \cdot Δ^{'} (f_{i}) - (1 - w) \cdot \sum_{k \in S_{j}} P (e_{k, i})),

(10)

which does not tend towards the trivial solution. However, to retain complementarity with the graph cut-based method, we preferred to choose an alternative approach, which decrements all vertex and edge weights (except those of guards and their incident edges) for user-defined non-negative values

s h f t_{Δ}

and

s h f t_{P}

, respectively (see (11)). Furthermore, these two additional parameters provide new possibilities for tuning, as demonstrated in Section 4.

s_{i} = min_{0 \leq j < i} (s_{j} + w \cdot (Δ (f_{i}) - s h f t_{Δ}) + (1 - w) \cdot \sum_{k \in S_{j}} (P (e_{k, i}) - s h f t_{P}))

(11)

The third problem is the most demanding. Even if all partial solutions

S_{j}

0 < j < i

were optimal, there is no guarantee that this will be the case after adding

f_{i}

to any of these solutions. It is enough that

f_{i}

is over-correlated with a single feature from each

S_{j}

, and the optimum will likely be missed. In other words, optimization defined in this way does not guarantee an optimal substructure, one of the two fundamental assumptions of dynamic programming, along with overlapping subproblems [6]. Of course, when considering

f_{i}

, we can no longer refresh its predecessors’ attributes

S_{j}

and

s_{j}

. We tried to mitigate this problem by extending the evaluation criterion by predicting the contribution of vertices not yet visited and, most importantly, considering the correlation between the visited and predicted parts. The need to predict the contribution of unvisited nodes led us to a simple idea, which later turned out to be very successful, namely to reverse the graph traversing direction after arriving at

f_{n}

. As G is an undirected graph, the status from the previous traversal can simply be used to estimate the score

s_{i}

and partial solution

S_{i}

. The updated evaluation criterion is given by (12).

s_{f w d} = min_{n + 1 \geq j > i} (s_{j} + s_{i} + (1 - w) \cdot \sum_{k \in S_{j}, h \in S_{i}} (P (e_{k, h}) - s h f t_{P}))

(12)

When the reverse traversal reaches

f_{1}

, the direction of visiting the vertices is inverted again. The evaluation criterion (12) is slightly modified to (13), corresponding to the forward direction from

f_{1}

towards

f_{n}

. The only difference between the two equations is, of course, the direction and boundaries of the vertices’ traversal, written under the min function label.

s_{f w d} = min_{0 \leq j < i} (s_{j} + s_{i} + (1 - w) \cdot \sum_{k \in S_{j}, h \in S_{i}} (P (e_{k, h}) - s h f t_{P}))

(13)

The modified evaluation criterion significantly impacts the choice of vertex

f_{r}

(r is the value of j, providing the minimum) and thus indirectly affects the calculation of

s_{i}

and

S_{i}

. Let r be the value of j in (12) or (13) where the minimum was identified. The score

s_{i}

is then calculated by using (14), while (6) representing the solution subset

S_{i}

remains applicable.

s_{i} = s_{r} + w \cdot (Δ (f_{i}) - s h f t_{Δ}) + (1 - w) \cdot \sum_{k \in S_{r}} (P (e_{k, i}) - s h f t_{P})

(14)

However,

s_{i}

and

S_{i}

should not be directly refreshed by

s_{f w d}

and

S_{r} \cup S_{i}

, since in the treatment of subsequent vertices, we assume that

s_{i}

and

S_{i}

can only refer to vertices that were visited before

f_{i}

in the current iteration. On the other hand, it would be a pity not to make better use of the great potential that Equations (12) and (13) certainly have. Fortunately, they can be used to predict the attributes of another vertex instead of

f_{i}

, namely

f_{i_{e n d}}

, which represents the last vertex in the set

S_{i}

(the one with the lowest index in the reverse direction traversal or with the highest index in the forward traversal). However, we should not update

s_{i_{e n d}}

and

S_{i_{e n d}}

yet when we process

f_{i}

because we will need the values from the previous iteration when we process

f_{i_{e n d}}

later. As a consequence, we extend each vertex

f_{k}

with additional attributes

p r (s_{k})

and

p r (S_{k})

(

p r

stands for prediction), which store the aforementioned estimates of the score and the solution set. At the beginning of each iteration, the initialization

p r (s_{k}) = \infty, 0 < k \leq n

, is performed. Algorithm 1 shows the processing of vertex

f_{i}

, which is further explained in Figure 3. For simplicity, we assume that all the variables in Algorithm 1 are global, except i and

f o r w a r d

. The score

s_{i}

is determined as the minimum between the previously stored

p r (s_{i})

and

s_{i}

computed by (14). In the former case, the set

p r (S_{i})

is assigned to

S_{i}

, while in the latter case,

S_{i}

is determined by equation (6). Note that

p r (s_{i})

and

p r (S_{i})

can be refreshed multiple times in the same iteration since multiple sequences

S_{i}

at different i can terminate with the same vertex

f_{i_{e n d}}

Algorithm 1 Processing a Considered Graph Vertex.

1:: function ProcessVertex(i, $f o r w a r d$ )
2:: if $f o r w a r d$ then ▹ Forward direction graph traversal.
3:: $i_{e n d} = {max}_{f_{k} \in S_{i}} k$ ;
4:: $s_{f w d} = {min}_{0 \leq j < i} (s_{j} + s_{i} + (1 - w) \cdot \sum_{k \in S_{j}, h \in S_{i}} (P (e_{k, h}) - s h f t_{P}))$ ; ▹ (13)
5:: else ▹ Reverse direction graph traversal.
6:: $i_{e n d} = {min}_{f_{k} \in S_{i}} k$ ;
7:: $s_{f w d} = {min}_{n + 1 \geq j > i} (s_{j} + s_{i} + (1 - w) \cdot \sum_{k \in S_{j}, h \in S_{i}} (P (e_{k, h}) - s h f t_{P}))$ ; ▹ (12)
8:: end if
9:: $r =$ the value of j, where the minimum in line 4 or 7 was achieved;
10:: $s_{i} = s_{r} + w \cdot (Δ (f_{i}) - s h f t_{Δ}) + (1 - w) \cdot \sum_{k \in S_{r}} (P (e_{k, i}) - s h f t_{P})$ ; ▹ (14)
11:: $S_{i} = S_{r} \cup {i}$ ; ▹ (6)
12:: if $(p r (s_{i}) < s_{i})$ then ▹ Update the vertex with predictions from the same iteration.
13:: $s_{i} = p r (s_{i})$ ;
14:: $S_{i} = p r (S_{i})$ ;
15:: end if
16:: if $(s_{f w d} < p r (s_{i_{e n d}}))$ then ▹ Update the predictions of a not yet processed $f_{i_{e n d}}$ .
17:: $p r (s_{i_{e n d}}) = s_{f w d}$ ;
18:: $p r (S_{i_{e n d}}) = S_{r} \cup S_{i}$ ;
19:: end if
20:: return ▹ No value returned - all the variables are global, except i and $f o r w a r d$ .
21:: end function

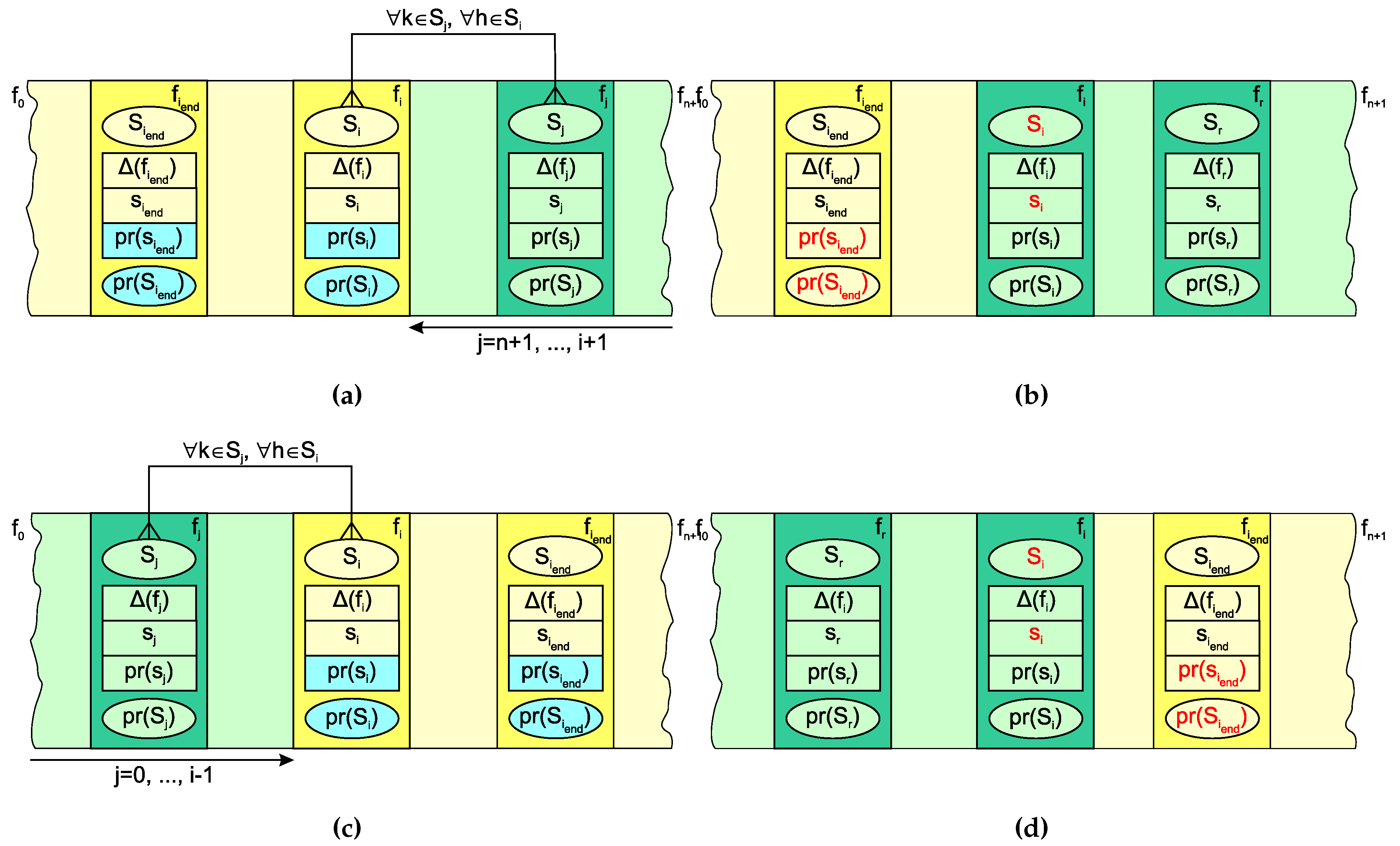
Figure 3a and Figure 3b show the situation immediately before and after the Equations (12), (14) and (6) are applied to vertex

f_{i}

, respectively. The graph traversal is performed in the reverse direction. The obvious difference between the straightforward non-iterative solution from Figure 2 is that here

S_{i}

does not contain the initial vertex

f_{i}

only, but the partial solution from the previous iteration instead. As a consequence, there is a double loop in the sum calculation. The green color indicates the graph vertices that have already been processed in the observed iteration, and the yellow color indicates those that were processed in the previous iteration (and are or will be processed later in the current iteration). Note that these yellow vertices contain the predictions (colored cyan), which might be updated earlier in the ongoing iteration. The red text indicates vertex attributes modified during the observed

f_{i}

processing. Analogously, Figure 3c and Figure 3d show the processing of vertex

f_{i}

when the graph is passed in the forward direction. (13) replaces (12) in this case.

The pseudocode in Algorithm 2 describes the overall structure of the alternating suboptimal dynamic programming method for feature selection. As mentioned, 200 features can still be processed relatively fast, but for larger input sets, it makes sense to preprocess the method with the graph cut-based feature selection filtering (line 2). The initialization in line 3 sets up the guard vertices by using (3). Partial solution sets candidates and their scores are initialized by using (4), which is needed in lines 7, 4 and 11 of Algorithm 1 within the first-iteration calls of ProcessVertex (line 11 of Algorithm 2). The value

f i n a l S c o r e

is set to some high value (∞) to provide the first comparison in line 16, and

M a x I t e r a t i o n s

is set to a user-defined value or default 100. In line 8, all predicted scores are set to a high value (∞) at the beginning of each iteration, which is needed in line 16. The main work is done in the ProcessVertex function, which is called sequentially in line 11 for each feature

f_{i}

except for the guard vertices. A direction of traversing the features is inverted in each iteration (line 23). The process terminates when the identical score is obtained three times in a row, or the number of iterations reaches

m a x I t e r a t i o n s

(line 24). If there are two (or more) solutions with the same score, the algorithm may find one during the forward direction traversal and a different one in the reverse direction traversal. In this case, it will return the last of the two solutions found.

Algorithm 2 Alternating Suboptimal Dynamic Programming.

1:: function ASDP( $Δ$ , P, n)
2:: $(Δ, P, n) =$ GraphCutBasedFeatureSelection( $Δ, P, n$ ); ▹ Optional filtering
3:: $(Δ, P, s, S, f i n a l S c o r e, m a x I t e r a t i o n s) =$ Init( $Δ, P, n$ );
4:: $s o l u t i o n R e p e a t e d = 0$ ; $i t e r a t i o n = 0$ ;
5:: $s t a r t = 1$ ; $e n d = n$ ;
6:: repeat ▹ iterations of ASDP
7:: for $i \leftarrow s t a r t$ to $e n d$ do ▹ for all features
8:: $p r (s_{i}) = \infty$ ;
9:: end for ▹ for all features
10:: for $i \leftarrow s t a r t$ to $e n d$ do ▹ for all features
11:: ProcessVertex(i, $s t a r t < e n d$ );
12:: end for ▹ for all features
13:: $s c o r e = {min}_{0 < i \leq n} s_{i}$ ; ▹ (7): this and the next two lines
14:: $s o l u t i o n = i$ , where $s c o r e$ was found;
15:: $S o l u t i o n = S_{s o l u t i o n}$ ;
16:: if $(s c o r e < f i n a l S c o r e)$ then
17:: $f i n a l S c o r e = s c o r e$ ;
18:: $s o l u t i o n R e p e a t e d = 0$ ;
19:: else
20:: $s o l u t i o n R e p e a t e d = s o l u t i o n R e p e a t e d + 1$ ;
21:: end if
22:: $i t e r a t i o n = i t e r a t i o n + 1$ ;
23:: $(s t a r t, e n d) =$ Swap $(s t a r t, e n d)$ ;
24:: until $(i t e r a t i o n = m a x I t e r a t i o n s) \lor (s o l u t i o n R e p e a t e d = 3)$ ;
25:: return ( $f i n a l S c o r e$ , $S o l u t i o n$ )
26:: end function

3.3. Convergence and Complexity Analysis

The solution found is generally suboptimal but often better than in the one-pass method, as will be confirmed by the results in the next section. In any case, the solution after several passes is not worse than the one-pass solution since the result can only improve from iteration to iteration or remain unchanged (after three consecutive such iterations, the algorithm terminates), which is confirmed by Theorem 1 below.

Theorem 1.

The score in each iteration of the proposed alternating suboptimal dynamic programming algorithm can only be lower (better) or equal to the score in the previous iteration but never higher (worse).

Proof.

The proof is conceptually straightforward since we will show that the score

s_{i}

from the previous iteration is also considered a candidate for the minimum in the observed iteration. Namely, this score is obtained in the evaluation criterion in line 7 of Algorithm 1 at

j = 0

or in line 4 at

j = n + 1

. The algorithm does not modify the parameters of the two guards, so

s_{j} = 0

and

S_{j} = \emptyset

in both cases. Consequently only

s_{i}

remains from the expression on the right of (13) or (12). If

s_{i}

is also the minimum in the current iteration, then

s_{f w d} = s_{i}

will be written first to

p r (s_{i_{e n d}})

in line 17 of Algorithm 1, then to

s_{i}

in line 13 of Algorithm 1, to

s c o r e

in line 13 of Algorithm 2, and finally to

f i n a l S c o r e

in line 17 of Algorithm 2. On the other hand, if

s_{i}

is not the minimum in the current iteration, then it can only be replaced with a lower score in some of the aforementioned lines of Algorithm 1 or Algorithm 2. This completes the proof. □

Based on Theorem 1, it makes sense to modify the initialization (line 3 of Algorithm 2). The proven convergence allows us to use the input feature set instead of the empty set as an initial solution candidate. Equation (15) introduces a recursive definition of initial values, which replaces (4). Note that the last two lines of (15) were derived from (6) and (14) by setting

r = i - 1

\begin{matrix} S_{0} = S_{n + 1} = \emptyset, s_{0} = s_{n + 1} = 0, \\ S_{1} = {1}, s_{1} = Δ (f_{1}), \\ S_{i} = S_{i - 1} \cup {i}, 2 \leq i \leq n, \\ s_{i} = s_{i - 1} + w \cdot (Δ (f_{i}) - s h f t_{Δ}) + (1 - w) \cdot \sum_{k \in S_{i - 1}} (P (e_{k, i}) - s h f t_{P}), 2 \leq i \leq n . \end{matrix}

(15)

Theorems 2–4 consider the time and space complexity of the graph-cut-based and the alternating suboptimal dynamic programming feature selection approaches.

Theorem 2.

The graph-cut-based feature selection method has the worst-case time complexity

O (n^{2})

, where n is the number of features, i.e., graph vertices.

Proof.

The algorithm gradually selects features

\hat{f_{r}}

with the highest quality, which requires at most

O (n)

steps. In each step, a neighborhood

Z (\hat{f_{r}})

is considered, which contains at most

O (n)

features. This results in

O (n) \cdot O (n) = O (n^{2})

worst-case time complexity. Note that the method removes the considered features and their highly correlated neighborhood from the graph G in each step and, consequently, the expected time complexity is much closer to

O (n \cdot log n)

, which corresponds to sorting the vertices according to their qualities. □

Theorem 3.

The proposed alternating suboptimal dynamic programming feature selection approach runs in

O (n^{4})

in the worst case, where n is the number of graph vertices (features).

Proof.

A double sum in lines 7 and 4 of Algorithm 1 contributes

O (n^{2})

time. In both cases, it is performed within the min function, which considers

O (n)

values. ProcessVertex function thus requires

O (n) \cdot O (n^{2}) = O (n^{3})

time. It is called

O (n)

times in line 11 of Algorithm 2, resulting in

O (n^{4})

time per a single iteration. Although the number of iterations (loop of lines 6 – 24) is by default set to 100, it rarely exceeds ten and practically never 15, so its time consumption may be considered constant, i.e.,

O (1)

, and the overall worst-case time complexity is proven

O (n^{4})

. □

Theorem 4.

Both considered approaches to feature selection, i.e. the graph-cut-based and the alternating suboptimal dynamic programming algorithm, require

O (n^{2})

space, where n is the number of graph vertices (features).

Proof.

In the graph-cut-based approach, the graph contains n vertices and at most

\frac{n \cdot (n - 1)}{2}

edges. Similarly, there are

n + 2

vertices and

\frac{(n + 2) \cdot (n + 1)}{2} - 1

edges in the ASDP approach. Furthermore,

n + 2

sets

S_{i}

and

p r (S_{i})

, each with

O (n)

elements, also do not exceed

O (n^{2})

space. The overall space complexity is thus

O (n^{2})

. □

4. Results

4.1. Validation Setup

The proposed method based on alternating suboptimal dynamic programming (ASDP) and the exhaustive search algorithm (brute force, BF) was implemented using C++, while the graph cut-based feature selection (Graph-FS) using python on the Microsoft^® Windows 11 operating system. All experiments were conducted on a workstation with Intel^® Core^TM i5 CPU and 16 GB of main memory. The algorithms are not yet integrated into a common application, but the results of the Graph-FS prefiltering are imported into the ASDP and BF methods via text files. The reproducibility of classification experiments is provided through the scikit-learn 1.4.1 implementation of machine learning methods. Classifiers were implemented with the following settings:

K-Nearest neighbors classifier (KNN) was assessed using default settings, where $K \in {2, 3, \dots, 8}$ were tested,
Naive Bayes classifier (NBC) was used with the default settings,
Random Forest (RF) was of maximal depth from the range $\{2, 4, 8, 16, 20\}$ , while the maximal number of iterations was from $\{5, 10, 15, 20, 25, 30\}$ , and
XGBOOST was of maximal depth from the range $\{2, 4, 8, 16, 20\}$ , while the maximal number of iterations was from $\{5, 10, 15, 20, 25, 30\}$ .

The ASDP and BF evaluation and the classification accuracy assessment were conducted on 9 well-known benchmark datasets, available at the UCI machine learning repository [59]. Table 1 summarises the characteristics of each dataset, including its name and the number of features, classes, and samples contained.

Each run of the ASDP and BF evaluation test consists of 125 experiments by employing

5 \cdot 5 \cdot 5

triplets of parameters

(w, s h f t_{Δ}, s h f t_{P})

, where

w \in {0, 0.25, 0.5, 0.75, 1}

s h f t_{Δ} \in {0, m e d_{1 / 4} (Δ), m e d (Δ), m e d_{3 / 4} (Δ), 1}

, and

s h f t_{P} \in {0, m e d_{1 / 4} (P), m e d (P),

m e d_{3 / 4} (P), 1}

. Here

m e d (Δ)

is the median of

Δ (f_{i}), 0 < i \leq n

, while

m e d_{1 / 4} (Δ)

and

m e d_{3 / 4} (Δ)

are the medians of the lower and higher half-sequences of

Δ (f_{i})

, respectively. In a similar manner, the medians

m e d_{1 / 4} (P)

m e d (P)

, and

m e d_{3 / 4} (P)

are determined.

4.2. Assessment of Scores of the Alternating Suboptimal Dynamic Programming Algorithm

The main question in the ASDP method development was how much it could improve the solution compared to a single iteration of suboptimal dynamic programming (SDP-1). At the same time, it is reasonable to compare the extent to which ASDP and SDP-1 achieve the global optimum provided by the BF approach. Results of the analysis are summarised in Table 2. Three main conclusions are listed below the table.

The third column shows that SDP-1 reaches the global optimum in 62.6 % of the tests. The fourth column then shows that ASDP significantly raises this percentage to 95.8.
The matching amount (61.4 %) between the SDP-1 and ASDP scores in the fifth column should not be below that between SDP-1 and BF (62.6 %) since ASDP never degrades the score from the first iteration, according to Theorem 1. Indeed, if we ignore rows Ds4, Ds6, Ds7, and Ds9, where we could not evaluate BF, we also obtain 62.6 % for ASDP (in brackets). Interestingly, at least for the tests performed, a conclusion can be made that whenever ASDP fails to reach the global optimum in the first iteration, it improves the score at least a little in subsequent iterations.
The last two columns confirm the empirical finding of the proof of Theorem 3 that the number of iterations of ASDP is within $O (1)$ , since in the tests performed, it does not exceed 11, and on average it is only $3.7$ , barely above the termination condition of 3 consecutive iterations with the unchanged score.

In order to further improve the results and, in particular, the feasibility in situations with a larger number of features, we preprocessed ASDP with fast and highly accurate, though still suboptimal, Graph-FS. The results are shown in Table 3, and the critical observations are listed immediately below.

The second column confirms a significantly lower number of features than before the use of Graph-FS (see Table 1).
The fourth column shows that BF did not change the Graph-FS results in 38.7 % of tests. In other words, it gets a better score of 61.3 %
The fifth column gives the first impression that ASDP performs significantly worse (34.8 % vs. 38.7) compared to BF. However, eliminating all tests on the Ds7 dataset, where BF was not viable, made both scores equal. Since ASDP cannot, according to Theorem 1 and the initialization from (15), spoil the initial score, we may also conclude here that the score was strictly improved in the remaining 61.3 % of tests. However, a better ASDP score obtained with (14) does not necessarily imply better results in practical applications. We will show this in subSection 4.3 by matching the ASDP score with the classification accuracy.
The sixth column shows that preprocessing of ASDP with Graph-FS raises the proportion of reaching the global optimum from 95.8 % in Table 2 to 98 %.
The last two columns show a maximum number of iterations of 12 and a lower number of iterations of 3.4 compared to 3.7 from Table 2.

4.3. Assessment of the Use in Classification Tasks

In this section, we demonstrated the usability of Graph-FS and ASDP for feature selection for classification tasks on real benchmark datasets displayed in Table 1. For this purpose, we compared the classification performance of the selected features for both presented methods and their combination (Graph-FS + ASDP) with the performance of the same classifiers when learning about the input feature set. The results are shown in Table 4, Table 5, Table 6 and Table 7 for each specific classifier used. All tests were conducted by ten-fold cross-validation [60], using average accuracy

a c c

to indicate the method’s efficiency. The accuracy is defined by (16):

a c c = \frac{n u m b e r o f c o r r e c t l y c l a s s i f i e d s a m p l e s}{n u m b e r o f a l l c l a s s i f i e d s a m p l e s} .

(16)

Note that the

a c c

values in the tables represent the highest achieved classification results. We also report the number of features selected and parameters

T_{Δ}

and

T_{p}

used in Graph-FS and Graph-FS + ASDP methods while obtaining the listed highest results. Since identical results were typically obtained for different combinations, we do not list ASDP parameters w,

s h f t_{Δ}

, and

s h f t_{p}

. Table 1 gives the number of input features. The highest accuracy for each dataset is emphasized in bold. Here, we considered that the same accuracy can be achieved across different methods, regardless of selected features.

Analysis has proven an improvement in accuracies regarding those achieved on the original dataset for all test cases except in the case of Ds1 for classifier RF. Furthermore, Graph-FS and ASDP scored similar classification results. However, Graph-FS showed slightly higher accuracies for Ds2, Ds3, Ds5, and Ds8 for classifier RF, while the same results as ASDP are shown in the case of Ds4, Ds5, Ds6, and Ds9. For classifier XGBOOST, similar results are obtained, where Graph-FS is slightly better in classification accuracies than ASDP in cases Ds1, Ds2, Ds3, Ds7, and Ds8. In the case of classifier NBC, Graph-FS achieved the best results in cases Ds2, Ds3, Ds5, and Ds8, while for Ds8, ASDP provides the most informative feature subset, achieving the highest accuracy among those in comparison. We observed different results for the last classifier, KNN, with the ASDP showing superior performance. It achieved highest accuracy in cases Ds1, Ds3, Ds7, and Ds8.

On the other hand, when comparing ASDP and Graph-FS + ASDP, we noticed the improved classification performance of selected classifiers in some cases. For example, in the case of Ds4 for classifier RF, we achieved the highest classification accuracy with Graph-FS + ASDP for a selected feature subset that contains only two features, while Graph-FS and ASDP achieved the same results when subsets of 10 and 14 features were selected, respectively. Similar results can be found in the case of Ds2 and Ds6 across all classifiers, Ds1 for NBC, and Ds2 and Ds3 for the KNN classifier, where the combination of Graph-FS and ASDP achieved the highest measured accuracies but with a smaller number of features than Graph-FS and ASDP individually. The most interesting result is at Ds7 for NBC, where Graph-FS and ASDP combined achieved the highest among all measured results.

5. Discussion

This paper introduces an alternating suboptimal dynamic programming (ASDP) algorithm, primarily aimed at improving feature selection, at least in some cases, and being competitive in others. It iteratively considers individual features and inverts the processing order in each iteration. This allows for improving the optimization function by using the score from the previous iteration to estimate the contribution of yet unprocessed features in the current one. We proved the convergence and a polynomial (

O (n^{4})

) time complexity. Results on nine well-known benchmark datasets for machine learning tasks demonstrated that a single iteration suboptimal dynamic programming found the global optimum in

62.6 %

cases, which was significantly improved to

95.8 %

by ASDP in only

3.7

iterations on average (and never above 12). Although ASDP is relatively slow and thus limited to 200-300 input features, we have extended its usability by preprocessing it with our fast and highly accurate graph-cut-based feature selection (Graph-FS) method. This raised the proportion of reaching the global optimum to

98 %

and reduced the average number of iterations to

3.4

We have also shown the practicality of using ASDP and the Graph-FS + ASDP combination in classification. The latter was slightly behind or equal to the Graph-FS alone when using the RF or XGBOOST classifiers and sometimes slightly better when using the NBC. The former seems contradictory to the proven convergence of ASDP, but the optimization criterion of ASDP and the classification accuracy of the used classifiers do not guarantee the perfect consistency of results. Surprisingly, the ASDP method without Graph-FS prefiltering performed best when using the KNN classifier. Finally, in all but one case for RF, the presented methods achieved better classification accuracy than the classifiers learned from the complete input feature set. Note that superior performances of Graph-FS in comparison to the state of the art were demonstrated in [58] already. We may thus conclude that ASDP and Graph-FS + ASDP are also entirely competitive.

A disadvantage of using ASDF without preprocessing is that a larger number of features makes the method too slow or, depending on the implementation, even infeasible. On the other hand, Graph-FS + ASDF restricts the solution search space to subsets of the Graph-FS solution. We will try to achieve a compromise by cascading Graph-FS over 2-5 iterations, where in each iteration, we will gradually lower the thresholds

T_{Δ}

and

T_{P}

and extend the selected set with features chosen from those not yet in the solution. We would also like to evaluate the use of ASDF in regression tasks in the future. Besides this, we expect that the idea of alternating suboptimal optimization will soon be generalized to tasks beyond feature selection as well.

Author Contributions

Conceptualization, D.P. and D.V.; methodology, D.M and D.V.; software, D.P and D.V.; validation, D.P., D.V. and B.Ž.; formal analysis, D.V. and B.Ž.; investigation, D.P., D.V., D.M. and B.Ž.; resources, D.V.; data curation, D.V.; writing—original draft preparation, D.P., D.V. and B.Ž.; writing—review and editing, D.P. and D.M.; visualization, D.P. and D.V.; supervision, B.Ž. and D.M.; project administration, B.Ž.; funding acquisition, B.Ž. and D.M. All authors have read and agreed to the published version of the manuscript.

Funding

Funding: This research was funded by the Slovene Research and Innovation Agency under Research Project J2-4458 and Research Programme P2-0041.

Data Availability Statement

No new data were created or analysed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

ADP	Approximate/Adaptive Dynamic Programming
ASDP	Alternating Suboptimal Dynamic Programming
BF	Brute Force, Brute-Force
CPU	Central Processing Unit
DP	Dynamic Programming
Graph-FS	Graph-cut-based Feature Selection
IDP	Iterative Dynamic Programming
KNN	K-Nearest Neighbours classifier
LASSO	Least Absolute Shrinkage and Selection Operator
MDP	Markov Decision Process
NBC	Naive Bayes Classifier
RF	Random Forrest
RL	Reinforcement Learning
SDP-1	Single iteration of alternating Suboptimal Dynamic Programming
UCI	University of California Irvine machine learning repository
XGBOOST	Extreme Gradient Boosting

References

Liu, H.; Motoda, H. Feature Selection for Knowledge Discovery and Data Mining; Kluwer Academic Publishers, 1998.
Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
Kumar, V.; Minz, S. Feature selection: A literature Review. SmartCR 2014, 4, 211–229. [Google Scholar] [CrossRef]
Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artificial intelligence 1997, 97, 273–324. [Google Scholar] [CrossRef]
Bellman, R. Dynamic programming. Princeton University Press 1957, 89, 92. [Google Scholar]
Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to algorithms; MIT press, 2022.
Liu, D.R.; Li, H.L.; Wang, D. Feature selection and feature learning for high-dimensional batch reinforcement learning: A survey. Int. J. Autom. Comput. 2015, 12, 229–242. [Google Scholar] [CrossRef]
Kossmann, D.; Stocker, K. Iterative dynamic programming: a new class of query optimization algorithms. ACM Trans. Database Syst. 2000, 25, 43–82. [Google Scholar] [CrossRef]
Forman, G. An Extensive Empirical Study of Feature Selection Metrics for Text Classification. J. Mach. Learn. Res. 2003, 3, 1289–1305. [Google Scholar]
Fakhraei, S.; Soltanian-Zadeh, H.; Fotouhi, F. Bias and Stability of Single Variable Classifiers for Feature Ranking and Selection. Expert Syst. Appl 2014, 41, 6945–6958. [Google Scholar] [CrossRef]
Liu, H.; Motoda, H. Computational Methods of Feature Selection; Chapman & Hall/CRC, 2007; p. 440.
Gu, Q.; Li, Z.; Han, J. Generalized Fisher Score for Feature Selection. Proceedings of the 27th Conference on Uncertainty in Artificial Intelligence, UAI 2011, 2012, pp. 266–273. [Google Scholar]
Li, H.; Jiang, T.; Zhang, K. Efficient and robust feature extraction by maximum margin criterion. Adv. Neural Inf. Process. Syst. 2003, 16. [Google Scholar] [CrossRef]
He, X.; Cai, D.; Niyogi, P. Laplacian Score for Feature Selection. Proceedings of the 18th International Conference on Neural Information Processing Systems, 2005, pp. 507–514.
Han, J.; Kamber, M.; Pei, J. , Data Mining: Concepts and Techniques; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2011; p. 744. [Google Scholar]
Cover, T.M.; Thomas, J.A. , Elements of Information Theory; Wiley-Interscience: USA, 2006; p. 792. [Google Scholar]
Verleysen, M.; Rossi, F.; François, D. Advances in Feature Selection with Mutual Information. Similarity-Based Clustering: Recent Developments and Biomedical Applications; Biehl, M., Hammer, B., Verleysen, M., Villmann, T., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2009; pp. 52–69. [Google Scholar]
Breiman, L.; Friedman, J.; Stone, C.; Olshen, R. , Classification and Regression Trees; The Wadsworth and Brooks-Cole statistics-probability series, Taylor & Francis, 1984.
Strobl, C.; Boulesteix, A.L.; Augustin, T. Unbiased split selection for classification trees based on the Gini Index. Comput. Stat. Data Anal. 2007, 52, 483–501. [Google Scholar] [CrossRef]
Raileanu, L.; Stoffel, K. Theoretical Comparison between the Gini Index and Information Gain Criteria. Ann. Math. Artif. Intell. 2004, 41, 77–93. [Google Scholar] [CrossRef]
Krakovska, O.; Christie, G.; Sixsmith, A.; Ester, M.; Moreno, S. Performance comparison of linear and non-linear feature selection methods for the analysis of large survey datasets. PLoS One 2019, 14, 1–17. [Google Scholar] [CrossRef]
Frénay, B.; Doquire, G.; Verleysen, M. Is mutual information adequate for feature selection in regression? Neural Networks 2013, 48, 1–7. [Google Scholar] [CrossRef] [PubMed]
Bishop, C.M. , Pattern Recognition and Machine Learning (Information Science and Statistics); Springer-Verlag: Berlin, Heidelberg, 2006; p. 728. [Google Scholar]
Bell, D.; Wang, H. A Formalism for Relevance and Its Application in Feature Subset Selection. Mach. Learn. 2000, 41, 175–195. [Google Scholar] [CrossRef]
Kira, K.; Rendell, L.A. A Practical Approach to Feature Selection. Proceedings of the Ninth International Workshop on Machine Learning, 1992, pp. 249–256.
Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the myopia of inductive learning algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
Hall, M.A. Correlation-based feature selection for machine learning. PhD thesis, The University of Waikato, 1999.
Yu, L.; Liu, H. Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution. Proceedings of the Twentieth International Conference on International Conference on Machine Learning, 2003, pp. 856–863.
Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
Garcia-Ramirez, I.A.; Calderon-Mora, A.; Mendez-Vazquez, A.; Ortega-Cisneros, S.; Reyes-Amezcua, I. A novel framework for fast feature selection based on multi-stage correlation measures. Mach. Learn. Knowl. Extr. 2022, 4, 131–149. [Google Scholar] [CrossRef]
Wang, L.; Zhou, N.; Chu, F. A General Wrapper Approach to Selection of Class-Dependent Features. IEEE Trans. Neural Networks 2008, 19, 1267–1278. [Google Scholar] [CrossRef]
Oliveira, L.S.; Sabourin, R.; Bortolozzi, F.; Suen, C.Y. A methodology for feature selection using multiobjective genetic algorithms for handwritten digit string recognition. Int. J. Pattern Recognit Artif Intell. 2003, 17, 903–929. [Google Scholar] [CrossRef]
Jesenko, D.; Mernik, M.; Žalik, B.; Mongus, D. Two-Level Evolutionary Algorithm for Discovering Relations between Nodes Features in a Complex Network. Appl. Soft Comput. 2017, 56, 82–93. [Google Scholar] [CrossRef]
Chuang, L.Y.; Chang, H.W.; Tu, C.J.; Yang, C.H. Improved binary PSO for feature selection using gene expression data. Comput. Biol. Chem. 2008, 32, 29–38. [Google Scholar] [CrossRef] [PubMed]
Schiezaro, M.; Pedrini, H. Data feature selection based on Artificial Bee Colony algorithm. EURASIP J. Image Video Process 2013, 47, 1–8. [Google Scholar] [CrossRef]
Narendra.; Fukunaga. A Branch and Bound Algorithm for Feature Subset Selection. IEEE Trans. Comput. 1977, C-26, 917–922. [CrossRef]
Gheyas, I.A.; Smith, L.S. Feature subset selection in large dimensionality domains. Pattern Recognit. 2010, 43, 5–13. [Google Scholar] [CrossRef]
Somol, P.; Pudil, P.; Novovicová, J.; Paclík, P. Adaptive floating search methods in feature selection. Pattern Recognit. Lett. 1999, 20, 1157–1163. [Google Scholar] [CrossRef]
Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
Zhao, P.; Yu, B. On model selection consistency of Lasso. J. Mach. Learn. Res. 2006, 7, 2541–2563. [Google Scholar]
Buteneers, P.; Caluwaerts, K.; Dambre, J.; Verstraeten, D.; Schrauwen, B. Optimized parameter search for large datasets of the regularization parameter and feature selection for ridge regression. Neural Process. Lett. 2013, 38, 403–416. [Google Scholar] [CrossRef]
Nelson, G.D.; Levy, D.M. A Dynamic Programming Approach to the Selection of Pattern Features. IEEE Transactions on Systems Science and Cybernetics 1968, 4, 145–151. [Google Scholar] [CrossRef]
Acır, N. Classification of ECG beats by using a fast least square support vector machines with a dynamic programming feature selection algorithm. Neural Comput. Appl 2005, 14, 299–309. [Google Scholar] [CrossRef]
Cheung, R.; Eisenstein, B. Feature selection via dynamic programming for text-independent speaker identification. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 397–403. [Google Scholar] [CrossRef]
Moudani, W.; Shahin, A.; Shakik, F.; Mora-Camino, F. Dynamic programming applied to rough sets attribute reduction. J. Inf. Optim. Sci. 2013, 32, 1371–1397. [Google Scholar] [CrossRef]
Bertsekas, D.; Tsitsiklis, J.N. Neuro-dynamic programming; Athena Scientific, 1996.
Approximate Dynamic Programming. https://deepgram.com/ai-glossary/approximate-dynamic-programming. Accessed: 2024-04-23.
Mes, M.; Perez Rivera, A. Approximate Dynamic Programming by Practical Examples. In Markov Decision Processes in Practice; Boucherie, R., van Dijk, N.M., Eds.; Number 248; Springer: Germany, 2017; pp. 63–101. [Google Scholar]
Loxley, P.N.; Cheung, K.W. A dynamic programming algorithm for finding an optimal sequence of informative measurements. Entropy 2023, 25, 251. [Google Scholar] [CrossRef] [PubMed]
Petrik, M.; Taylor, G.; Parr, R.; Zilberstein, S. Feature Selection Using Regularization in Approximate Linear Programs for Markov Decision Processes. Proceedings of the 27th International Conference on Machine Learning (ICML 2010); Fürnkranz, J.; Joachims, T., Eds. Omnipress, 2010, pp. 871–878.
Preux, P.; Girgin, S.; Loth, M. Feature discovery in approximate dynamic programming. 2009 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning. IEEE, 2009, pp. 109–116.
Papadaki, K.P.; Powell, W.B. Exploiting structure in adaptive dynamic programming algorithms for a stochastic batch service problem. Eur. J. Oper. Res. 2002, 142, 108–127. [Google Scholar] [CrossRef]
Luus, R. Optimal control by dynamic programming using systematic reduction in grid size. Int. J. Control 1990, 51, 995–1013. [Google Scholar] [CrossRef]
Lock, J.; McKelvey, T. A computationally fast iterative dynamic programming method for optimal control of loosely coupled dynamical systems with different time scales. IFAC-PapersOnLine 2017, 50, 5953–5960. [Google Scholar] [CrossRef]
Lincoln, B.; Rantzer, A. Suboptimal dynamic programming with error bounds. Proceedings of the 41st IEEE Conference on Decision and Control, 2002. IEEE, 2002, Vol. 2, pp. 2354–2359.
Lincoln, B.; Rantzer, A. Relaxing dynamic programming. IEEE Trans. Control Syst. Technol. 2006, 51, 1249–1260. [Google Scholar] [CrossRef]
Rantzer, A. Relaxed dynamic programming in switching systems. IEE Proceedings-Control Theory and Applications 2006, 153, 567–574. [Google Scholar] [CrossRef]
Vlahek, D.; Mongus, D. An Efficient Iterative Approach to Explainable Feature Learning. IEEE Trans. Neural Networks Learn. Syst. 2023, 34, 2606–2618. [Google Scholar] [CrossRef]
Dua, D.; Graff, C. UCI Machine Learning Repository, 2017.
Alpaydin, E. Introduction to machine learning; MIT Press, 2010; p. 537.

Figure 1. Vertex-cut-based feature selection: (a) graph G where the feature of the highest quality (coloured green) is selected and its neighbourhood (red) is removed, (b) repeating the same procedure on subgraph

G^{'}

, and (c) subgraph

G^{''}

. (d) The output result

{f_{1}, f_{5}, f_{6}}

(in green) is obtained.

G^{'}

, and (c) subgraph

G^{''}

. (d) The output result

{f_{1}, f_{5}, f_{6}}

(in green) is obtained.

Figure 2. The concept of feature selection based on dynamic programming: (a) partial solution to be stored in

f_{i}

considers the solutions stored in all its predecessors; (b) the situation after updating the status of

f_{i}

S_{i}

and

s_{i}

are calculated with (6) and (5), respectively.

Figure 2. The concept of feature selection based on dynamic programming: (a) partial solution to be stored in

f_{i}

considers the solutions stored in all its predecessors; (b) the situation after updating the status of

f_{i}

S_{i}

and

s_{i}

are calculated with (6) and (5), respectively.

Figure 3. The concept of feature selection based on alternating suboptimal dynamic programming: the situation (a) before processing

f_{i}

during the reverse direction traversal; (b) after processing

f_{i}

during the reverse direction traversal; (c) before processing

f_{i}

during the forward direction traversal; and (d) after processing

f_{i}

during the forward direction traversal.

Figure 3. The concept of feature selection based on alternating suboptimal dynamic programming: the situation (a) before processing

f_{i}

during the reverse direction traversal; (b) after processing

f_{i}

during the reverse direction traversal; (c) before processing

f_{i}

during the forward direction traversal; and (d) after processing

f_{i}

during the forward direction traversal.

Table 1. Description of test datasets.

Dataset ID	Dataset name	# features	# samples	# classes
Ds1	Abalone	8	4177	2
Ds2	Credit Approval	15	690	2
Ds3	Diabetes	8	768	2
Ds4	Ionosphere	34	351	2
Ds5	Letters	16	20000	26
Ds6	Sonar	60	208	2
Ds7	Spambase	57	4601	2
Ds8	Vehicle	18	946	4
Ds9	Wisconsin Brest Cancer Diagnostic	30	569	2

Table 2. Comparison of scores obtained by BF, SDP-1, and ASDP method.

Dataset ID	# tests	SDP-1 score = BF score [%]	ASDP score = BF score [%]	SDP-1 score = ASDP score [%]	Max. # iterations	Avg. # iterations
Ds1	125	58.4	100.0	58.4	5	3.4
Ds2	125	68.8	100.0	68.8	7	3.6
Ds3	125	76.8	100.0	76.8	7	3.3
Ds4	125	/	/	65.6	8	3.6
Ds5	125	54.4	94.4	54.4	6	3.4
Ds6	125	/	/	52.0	7	3.9
Ds7	125	/	/	50.4	11	4.4
Ds8	125	54.4	84.8	54.4	7	3.7
Ds9	125	/	/	72.0	8	3.7
Total *	1125	62.6	95.8	61.4 (62.6)		3.7

* The Tests column contains the sum, and the others contain average values.

Table 3. Comparison of scores of the Graph-FS filtering used alone or postprocessed by BF or ASDP.

Dataset ID	# features selected by Graph-FS	# tests	BF score = Graph-FS score [%]	ASDP score = Graph-FS score [%]	ASDP score = BF score [%]	Max. # iterations	Avg. # iterations
Ds1	1 or 2	250	74.0	74.0	100.0	3	3.0
Ds2	2 to 15	1250	29.8	29.8	99.1	8	3.3
Ds3	1 to 8	500	50.2	50.2	99.8	6	3.1
Ds4	2	125	32.0	32.0	100.0	3	3.0
Ds5	10 to 13	625	32.6	32.6	91.7	8	3.5
Ds6	1 to 11	625	43.7	43.7	98.7	6	3.5
Ds7	12 to 56	1375	27.2 *	22.0	94.4 *	12	4.0
Ds8	5 to 10	500	26.0	26.0	93.2	5	3.0
Ds9	1 to 7	375	53.6	53.3	99.7	5	3.3
Total **		5625	38.7	34.8	98.0		3.4

* Only 125 tests used due to the limited number of features in BF. ** The Tests column contains the sum, and the others contain average values.

Table 4. Accuracies for RF classifier after the feature selection with Graph-FS, ASDP, their combination, or when using all input features.

	Graph-FS				ASDP		Graph-FS + ASDP		Input data
Dataset ID	# selected features	acc	$T_{Δ}$	$T_{p}$	# selected features	acc	# selected features	acc	acc
Ds1	1	46.17	0.35	0.4	5	53.11	1	46.17	53.34
Ds2	7	98.55	0.4	0.4	3	97.10	3	97.10	97.10
Ds3	3	80.51	0.3	0.4	2	74.02	2	74.02	71.42
Ds4	2	100	0.3	0.4	8	100	2	100	100
Ds5	13	95.85	0.3	0.65	15	94.95	11	88.25	95.20
Ds6	10	100	0.3	0.7	14	100	6	100	100
Ds7	56	96.52	0.45	0.55	14	90.67	13	85.46	94.79
Ds8	8	78.82	0.3	0.8	13	78.82	5	77.64	74.11
Ds9	7	78.94	0.35	0.8	1	78.94	5	75.43	75.43

Table 5. Accuracies for XGBOOST classifier after Graph-FS, ASDP, Graph-FS + ASDP, or when using all input features.

	Graph-FS				ASDP		Graph-FS + ASDP		Input data
Dataset ID	# selected features	acc	$T_{Δ}$	$T_{p}$	# selected features	acc	# selected features	acc	acc
Ds1	1	55.02	0.35	0.4	5	54.54	1	55.02	53.34
Ds2	7	98.55	0.4	0.4	3	97.10	3	97.10	95.65
Ds3	3	72.72	0.3	0.4	2	71.45	2	71.42	71.42
Ds4	2	100	0.3	0.4	8	100	2	100	100
Ds5	13	95.70	0.3	0.65	15	95.70	11	90.00	95.35
Ds6	10	100	0.3	0.7	14	100	6	100	100
Ds7	56	96.52	0.45	0.55	14	89.15	13	85.68	94.79
Ds8	8	75.29	0.3	0.8	13	74.11	5	70.58	75.29
Ds9	7	78.94	0.35	0.8	1	78.94	4	77.19	75.43

Table 6. Accuracies for NBC after the feature selection with Graph-FS, ASDP, their combination, or when using all input features.

	Graph-FS				ASDP		Graph-FS + ASDP		Input data
Dataset ID	# selected features	acc	$T_{Δ}$	$T_{p}$	# selected features	acc	# selected features	acc	acc
Ds1	1	55.02	0.35	0.4	5	54.06	1	55.02	53.34
Ds2	7	98.55	0.4	0.4	3	97.10	3	97.10	95.65
Ds3	3	75.32	0.3	0.4	2	72.72	2	72.72	71.42
Ds4	2	100	0.3	0.4	8	100	2	100	100
Ds5	13	63.40	0.3	0.65	15	62.60	11	52.6	61.45
Ds6	10	100	0.3	0.7	14	100	6	100	100
Ds7	56	90.60	0.45	0.55	14	91.32	13	97.61	59.65
Ds8	8	52.94	0.3	0.8	13	56.47	5	50.58	49.41
Ds9	7	78.94	0.35	0.8	1	78.94	4	77.19	75.43

Table 7. Accuracies for KNN classifier after Graph-FS, ASDP, Graph-FS + ASDP, or when using all input features.

	Graph-FS				ASDP		Graph-FS + ASDP		Input data
Dataset ID	# selected features	acc	$T_{Δ}$	$T_{p}$	# selected features	acc	# selected features	acc	acc
Ds1	1	51.67	0.35	0.4	5	55.02	1	51.67	53.34
Ds2	7	95.65	0.4	0.4	3	95.65	3	95.65	78.26
Ds3	3	71.42	0.3	0.4	2	75.32	2	75.32	71.42
Ds4	2	100	0.3	0.4	8	100	2	100	100
Ds5	13	94.85	0.3	0.65	15	94.70	11	86.8	94.45
Ds6	10	100	0.3	0.7	14	100	6	100	100
Ds7	56	91.54	0.45	0.55	14	92.62	13	84.38	50.45
Ds8	8	67.05	0.3	0.8	13	72.94	5	63.52	69.41
Ds9	7	78.94	0.35	0.8	1	78.94	4	77.19	75.43

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A New Alternating Suboptimal Dynamic Programming Algorithm with Applications for Feature Selection

Abstract

1. Introduction

2. Related Works

2.1. Feature Evaluation

2.2. Feature Selection

2.3. Dynamic Programming-Based Feature Selection

2.4. Suboptimal Dynamic Programming

3. Materials and Methods

3.1. Graph Cut-Based Feature Selection

3.2. New Suboptimal Dynamic Programming Algorithm

3.3. Convergence and Complexity Analysis

4. Results

4.1. Validation Setup

4.2. Assessment of Scores of the Alternating Suboptimal Dynamic Programming Algorithm

4.3. Assessment of the Use in Classification Tasks

5. Discussion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe