Prerpints.org logo
Preprint
Article

Optimization Strategies for Atari Game Environments: Integrating Snake Optimization Algorithm and Energy Valley Optimization in Reinforcement Learning Models

Altmetrics

Downloads

97

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

20 May 2024

Posted:

20 May 2024

You are already at the latest version

Alerts
Abstract
This study presents a groundbreaking approach in the field of gaming AI, focusing on the classic game” Pacman” through the lens of DRL integrated with advanced optimization techniques. The core of the research involves adapting DRL models for” Pacman”, utilizing the ESO for hyper- parameter tuning. These novel adaptations significantly enhance the AI agent’s performance, demonstrating a remarkable improvement in adaptability, responsiveness, and efficiency within the game environment. A pivotal aspect of this research is the innovative integration of metaheuristic optimization techniques into the DRL framework, a first in the domain of Atari gaming AI. This integration has proven essential in fine-tuning the DRL models, leading to a more effective and dynamic gaming experience. The study thoroughly evaluates and compares the performance of these algorithms, providing empirical support for their effectiveness and setting a new benchmark in AI-driven game development. The implications of this research extend beyond gaming AI, opening up possibilities for future exploration in several directions. Expanding DRL models to other complex gaming environments, continuous algorithmic enhancements, real-time learning adaptations, and applying these principles to robotics and autonomous vehicles are examples. The research also emphasizes ethical and responsible AI use in gaming to address fairness and addiction issues.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In the realm of artificial intelligence, machine learning stands as a cornerstone, offering a diverse spectrum of ap- plications that significantly impact various sectors. Among its numerous methodologies, three distinct learning paradigms – supervised learning (SL) [1], unsupervised learning (UL) [2], and reinforcement learning (RL) [3] – dominate, each contributing uniquely to the advancement of AI technologies. Supervised learning [1], with its foundation in input-output data correlations, has been integral in developing practical applications such as spam detection [4], image recognition, object detection [5], and predictive analytics [6]. Unsupervised learning [2], on the other hand, ventures into the territory of identifying underlying patterns in unlabeled data, employing techniques like k-means clustering and principal component analysis for data classification and dimensionality reduction [7,8].
Deep learning, an extension of conventional machine learning, has emerged as a critical development, especially in its ability to automate feature extraction and process vast datasets [9]. This advancement is particularly evident in fields requiring the analysis of unstructured data types like images and audio. However, it is the dynamic and complex world of Atari gaming [10] that presents a unique challenge, one that necessitates a blend of deep reinforcement learning (DRL) and innovative optimization techniques.
This paper delves into the application of DRL, specifically the deep Q-network (DQN) approach, within the context of the Atari game” Pacman.” The focus lies on addressing the challenges inherent in training DRL agents for high- performance gameplay in complex, dynamic environments [10]. The exploration and optimization of DRL algorithms, particularly in the absence of extensive datasets and relying on real-time interactions, underscore the novelty and complexity of this research. Moreover, the integration of metaheuristic optimization techniques, such as snake optimization and Energy Valley Optimization, represents a novel approach in fine-tuning the parameters of DRL models for enhanced performance in such intricate gaming scenarios.
The significance of this study is manifold. Firstly, it con- tributes to the growing body of knowledge in the field of AI and gaming by providing a comprehensive analysis of DRL applications in Atari gaming. Secondly, it addresses the prevalent research gap in the optimization of DRL algorithms for complex gaming environments [10], offering a model that combines the strengths of DRL with advanced optimization strategies. Finally, the study sets a precedent for future re- search, paving the way for further advancements in AI-driven gaming and beyond.
In sum, this paper aims to rigorously explore, develop, and evaluate DRL models tailored for the” Pacman” game, integrating advanced optimization techniques to enhance the models’ performance. This endeavor not only challenges existing paradigms in AI gaming but also lays the groundwork for future innovations in the field.
RL has become a prominent technique in gaming, where it employs a process of learning through trial and error to optimize rewards both in the short and long term. A notable instance of this is seen in the development of an RL model for the game of Othello, which learned to play the game autonomously [11]. Furthermore, the domain of Atari games witnessed significant advancements with the adoption of DRL, wherein a combination of Q-learning and CNNs was used to process image pixels and produce value functions, leading to remarkable improvements in seven different Atari games [12]. In educational gaming platforms, RL has been instrumental in creating interactive and efficient learning experiences, offering a new dimension to educational technology [13]. The technique of self-play in RL, where agents enhance their skills by competing against themselves, has seen successful application in various gaming contexts [14].
The game of Go serves as a seminal example of RL’s capabilities. AlphaGo, developed through the integration of neural networks and Monte Carlo tree search methods, significantly outperformed existing Go programs [15]. Building upon this, the AlphaZero framework was introduced, a more generalized RL approach applicable to games such as Go, chess, and shogi, a Japanese variant of chess. AlphaZero, distinct in its ability to learn game rules without specific domain knowledge, achieved notable victories against world champions in these games [16]. RL has also made strides in real-time strategy games, exemplified by its application in Boulder Dash, where DRL methodologies like the deep Q-network (DQN) were utilized to reduce decision-making latency [17]. Additionally, the actor-critic algorithm has been refined with the inclusion of experience replay, making it suitable for a wide range of tasks, both continuous and discrete. This enhancement has been validated on benchmark platforms like Atari and Mujoco, offering an innovative approach to value function calculation that moves beyond traditional Q-learning methods [18]. StarCraft II, renowned for its complexity and competitive nature, stands as a significant subject in AI research, particularly noted for its prominence in esports [19]. In a groundbreaking development, Google’s DeepMind unveiled AlphaStar in 2019, achieving a landmark victory by defeating top professional player Grzegorz Komincz in StarCraft II with an impressive 5-0 scoreline [20].
AlphaStar’s architecture represents a sophisticated blend of deep learning (DL), reinforcement learning (RL), and deep neural networks (DNNs), capable of processing raw game data with remarkable efficiency. The system employs a unique” Transformer” AI architecture, which integrates attention mechanisms supported by recurrent neural networks (RNNs) and convolutional neural networks (CNNs) [21]. Its design is further enhanced with an LSTM core and adaptive strategies [22,23].
The training regime of AlphaStar commenced with super- vised learning techniques, observing and emulating human gameplay. DeepMind then employed a multi-agent system, allowing AI agents to engage in extensive virtual conflicts over two weeks. This process aimed to refine the agents’ capabilities to outmaneuver both individual and multiple op- ponents, applying RL methodologies such as off-policy actor- critic, experience replay, and self-imitation to optimize neural network weights [24].
In another innovative study, researchers proposed a novel deep reinforcement learning framework for text-based adventure games [25]. This system used a knowledge graph to efficiently prune actions and employed question-answering techniques for training, demonstrating superior performance over existing methods. Similarly, LeDeepChef, another DRL-based agent, exhibited its prowess in text-based gaming by securing the second position in Microsoft Research’s First TextWorld Problems competition [26].
Further expanding RL’s application, the ReBeL self-play AI framework has shown remarkable competence in imperfect- information games like Texas hold’em poker, using a combination of RL and search techniques [27]. Additionally, research efforts have been directed towards applying DRL in complex control tasks in 1v1 MOBA games, exemplified by Tencent’s development of Solo, an AI agent adept in” Honor of Kings”.
Major technology corporations, notably Google’s DeepMind and Microsoft, have consistently led the charge in developing algorithms designed to conquer popular games. Much of this pioneering work has been documented in the field of reinforcement learning [28]. While comparisons among AI agents have primarily centered on ATARI games and certain board games, the lack of standardized performance metrics in strategy or MOBA games remains a challenge. DeepMind’s research, including the effectiveness of DQN algorithms that combine Q-learning with DNNs in ATARI games, serves as a benchmark, incorporating measures of human performance for comparative analysis.

2. Materials & Methods

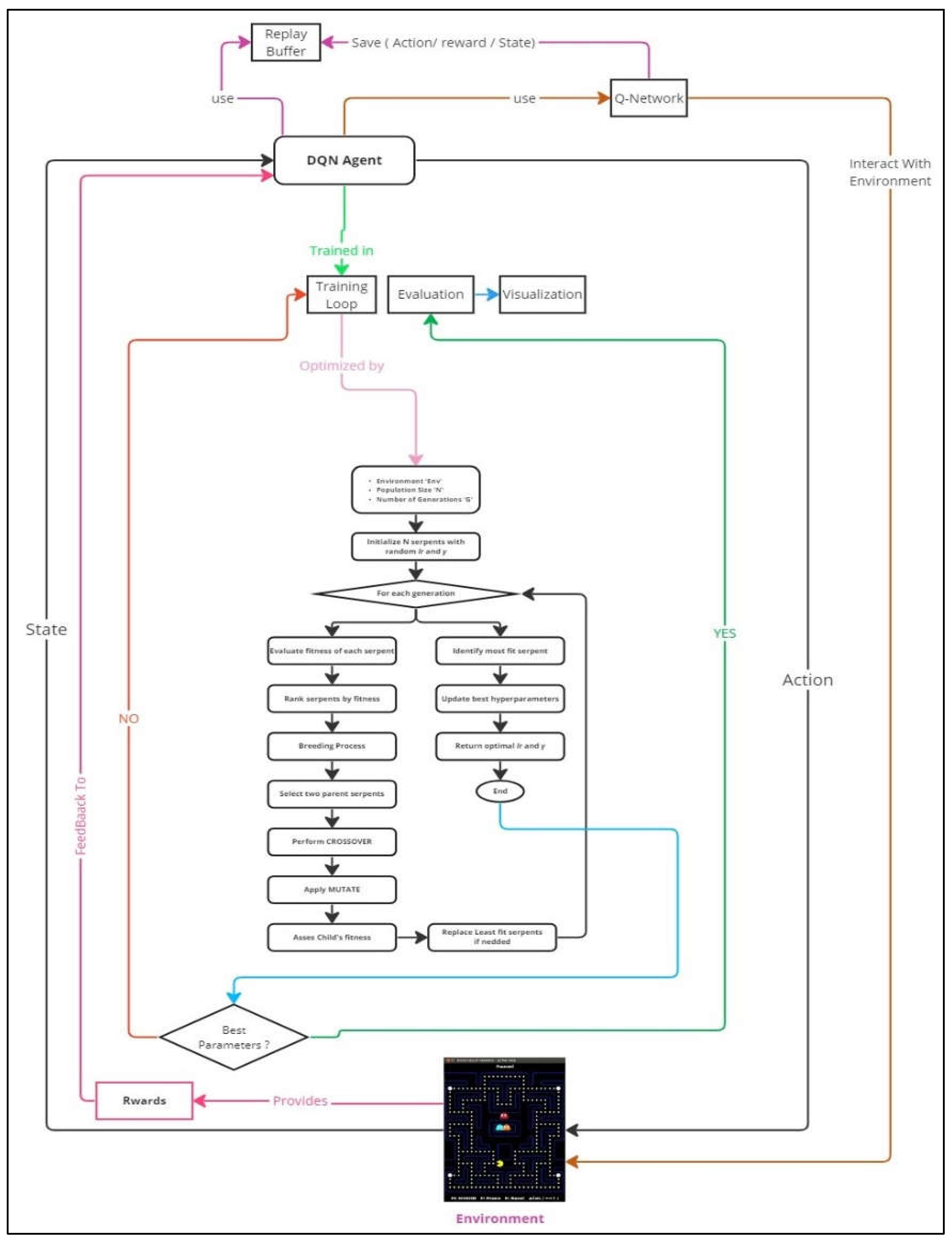
In our refined approach to mastering the Ms. Pac-Man game, we synergize deep reinforcement learning with sophisticated optimization strategies. Central to our system is the DQN Agent, leveraging a Q-Network—a convolutional neural network adept at discerning the most advantageous actions in the game scenario. This is supported by the Replay Buffer, an integral feature that archives and re-examines previous gameplay, thereby ensuring a robust and progressive learning journey.
Our technique is further refined by intertwining the Snake Optimization Algorithm (SOA) with Energy Valley Optimization (EVO), both of which are inspired by genetic-based algorithms. These advanced methods are integrated for the optimization of critical hyperparameters, enhancing the overall efficiency of our system. By merging ESO, we optimize not only the hyperparameters but also the training loop, continuously updating the DQN Agent parameters until the best ones are identified, as indicated by the rewards feedback from the environment. The interplay of these elements culminates in a comprehensive and effective solution to the challenges posed by the Ms. Pac-Man gaming environment. Each component—from the Q-Network and Replay Buffer to the innovative ESO optimization—works in concert to refine our strategy, which will be further elaborated in the subsequent sections.
Preprints 106943 g001
Figure 1. General Flowchart.
Figure 1. General Flowchart.
Preprints 106943 g001

2.1. Setup and Environment Preparation

Building a strong foundation is critical to our Ms. Pac-Man project's success. The preliminary actions made to establish a reliable and effective setup are described in this section. The installation of the required libraries and pack-ages marks the start of the procedure. These assets not only make it possible for our procedures to run smoothly but also offer vital utility functions that are necessary for the experiment's later phases. Using the most recent versions of these tools ensures compatibility and maximizes efficiency.
Next, we used OpenAI's Gym toolbox to put up the Ms. Pac-Man gaming setting. In the field of reinforcement learning, Gym is well-known for its standardised interface, which makes it easier to interact with the game, process observations, and put actions into action. This standardization is key to ensuring that our experiments are replicable and align with broader research efforts. Following this, we define key parameters of our experiment, including the action space (possible movements for Ms. Pac- Man), observation space (how the game’s state is represented), and the reward structure. These parameters are critical as they inform the learning process of our DQN agent, guiding its decision-making and strategy development.
In sum, the setup and environment preparation stage lays the groundwork for our experiment. This meticulous preparation ensures that the later stages, including the training of the Q-Network and the application of the Snake Optimization Algorithm for hyperparameter tuning, are built on a well- defined and robust platform, setting the stage for successful outcomes.

2.2. Design and Functionality of the Q-Network

At the core of our approach to mastering Ms. Pac-Man is the Q-Network, a CNN specifically designed for this task. The Because Q-Network is responsible for computing Q-values for various game states, it is an essential component of our reinforcement learning approach. In order to direct the agent toward activities that maximize benefits over time, it is essential to accurately estimate these Q-values, which stand for the anticipated rewards in the future for taking particular actions in given states.
Our Q-Network is tailored to the specific requirements of Atari-style games like Ms. Pac-Man. It uses convolutional layers to effectively interpret the pixel-based visual inputs of the game. These layers excel in identifying and understanding spatial relationships and patterns, such as the maze layout, ghost positions, and pellet locations in Ms. Pac-Man. The network processes this visual information and feeds it through additional layers, culminating in a dense layer that produces Q-values for every possible action available to the agent.
Training the Q-Network involves using a loss function, typ- ically Mean Squared Error (MSE), to measure the difference between the predicted and target Q-values. These target values are calculated using the Bellman equation, a cornerstone concept in reinforcement learning that relates current Q-values to future rewards and the maximal Q-values of subsequent states. The learning process of the Q-Network is dynamic and ongoing. As the agent interacts with the game environment and gathers new experiences, the network is continuously up- dated, refining its Q-value predictions and enhancing decision- making capabilities.
Delving deeper into the Q-Network’s structure, we have devised an architecture that aligns with the demands of Ms. Pac-Man. The network consists of two primary sections: a convolutional segment and a fully connected (dense) segment. The convolutional part includes three layers. The first layer processes raw pixel inputs using 32 filters of size 8x8 and a stride of 4, followed by a Rectified Linear Unit (ReLU) activation function for non-linearity. The second layer uses 64 filters of size 4x4 with a stride of 2, and the third layer employs 128 filters of size 3x3 with a stride of 1, each accompanied by a ReLU activation. These layers adeptly capture complex spatial patterns and hierarchies in the game’s visuals.
Following the convolutional stage, the processed data is flattened and directed to the dense segment. This begins with a linear layer connecting the convolutional output to 512 neurons, with a subsequent ReLU activation. A dropout layer with a 0.5 probability is included to prevent overfitting and add regularization. The information then passes through 256 neurons and finally to a linear layer that outputs the Q-values for each action available to the agent in the game.
This architecture, with its blend of convolutional and dense layers, provides a comprehensive system to process visual inputs, discern complex patterns within the game, and convert these insights into actionable strategies for optimal game performance.

2.3. Implementing Experience Replay for Stable Learning

Experience replay stands as a critical component in our reinforcement learning strategy, especially in addressing challenges like temporal correlations and the evolving nature of data in such environments. This approach deviates from the traditional method of learning directly from consecutive experiences, which could lead to correlated data and unstable learning paths. The core concept of experience replay involves storing individual experiences, or transitions, and later revisiting them randomly. These transitions are composed of tuples containing the current state, the action taken, the resultant reward, the following state, and an indicator of whether the game concluded after the action. These tuples are then stored in a Replay Buffer, a repository that serves as a memory bank, continuously filled as the agent interacts with the game.
When it’s time for the agent to learn or update its Q- Network, it doesn’t solely depend on recent experiences. Instead, it randomly selects a batch of experiences from the Replay Buffer. This approach helps in breaking the chain of closely correlated experiences and incorporates older but valuable memories into the learning process. The result is a more stable and effective learning trajectory.
The Replay Buffer also allows for the repeated utilization of data, enabling the agent to learn multiple times from a single experience. This feature is particularly beneficial in complex environments like Ms. Pac-Man, where some crucial but infrequent experiences hold significant learning potential. In essence, experience replay, facilitated through the Replay Buffer, introduces a level of randomness and diversity to the learning process. This approach effectively counters issues such as temporal correlation, enriching the agent’s learning with a wide array of past interactions. This mechanism, in conjunction with the Q-Network, forms a solid foundation for our deep reinforcement learning methodology in mastering Ms. Pac-Man.

2.4. Role and Functions of the DQN Agent

The DQN Agent is pivotal in orchestrating the complex interactions between the agent and the Ms. Pac-Man game environment. It carries the dual responsibility of deciding the agent’s actions and training the Q-Network based on the outcomes of these actions. Action selection within the DQN Agent operates on a principle balancing exploration and exploitation. Initially, when the agent’s knowledge of the environment is limited, and its Q-values are unrefined, the agent emphasizes exploration. This is typically managed through an epsilon-greedy strategy. The agent randomly selects actions with a probability defined by epsilon to explore the environment and relies on the highest Q- value actions for the remaining decisions, exploiting its current knowledge. As the agent’s familiarity with the environment improves, and the reliability of its Q-values increases, epsilon is progressively reduced, tilting the balance towards exploitation.
Following action execution, the DQN Agent plays a crucial role in training the Q-Network. It leverages the Replay Buffer, sampling a random batch of experiences to compute target Q-values based on the rewards received and the projected Q- values of subsequent states. The goal is to minimize the gap between these target Q-values and those predicted by the Q- Network, usually using gradient descent or its variants as the optimization method. This ongoing cycle of action selection, experience accumulation, and network updating constitutes the learning loop that gradually enhances the agent’s game strategy and understanding.
A key element in this process is the periodic update of target Q-values. Rather than continuously adjusting them, which could lead to instability, these updates are spaced out to ensure a more consistent and stable learning path.
In summary, the DQN Agent is central to our approach, effectively bridging exploration and learning. It adeptly navigates the Ms. Pac-Man environment, adapting its strategies and continually refining the Q-Network. This dynamic interplay of actions, feedback, and learning equips the agent with the necessary capabilities to master the game environment.

2.5. Execution and Maintenance of the Training Loop

The training loop marks the dynamic phase where our reinforcement learning strategy is actualized. In this iterative process, the DQN Agent interacts with the Ms. Pac-Man game environment, making decisions, assimilating feedback, storing experiences, and iteratively improving its decision- making capabilities by updating the Q-Network. This section explores the intricate aspects and workflow of the training loop.
This loop encompasses numerous episodes, each representing a full game of Ms. Pac-Man from start to end. At the beginning of each episode, the game environment is reset, presenting a new challenge for the agent. During the episode, the agent observes the current state, decides on an action influenced by its epsilon-greedy policy, and implements that action in the game. Subsequently, the game environment transitions to a new state and awards a reward based on the action’s effectiveness. These elements – the state transition, chosen action, received reward, and the game’s end status – are recorded as an experience in the Replay Buffer.
Once a sufficient number of experiences are collected, the agent utilizes a randomly selected batch from the Replay Buffer for Q-Network training. This training involves adjusting the network’s weights to reduce the discrepancy between the predicted Q-values and the target Q-values. This feedback- driven approach ensures that the agent continuously hones its strategy for progressively improved performance.
A crucial aspect of the training loop is the conservation of the Q-Network’s weights. Given that the agent may go through countless iterations, it’s vital to periodically save these weights. These saved checkpoints serve several pur- poses. Firstly, they provide a fallback in case of disruptions, preventing complete loss of progress. Secondly, they allow for periodic assessment of the agent’s performance, offering insights into its learning progression. Finally, saved weights can be used for transferring learning to similar tasks or for further refinement in future tasks.
In essence, the training loop is where the agent’s interaction with the environment and consequent learning converts into practical gameplay strategy. Through ongoing engagement, feedback analysis, and adaptive learning, the agent transitions from a novice to an adept Ms. Pac-Man player, all while ensuring that its accumulated knowledge is regularly saved for future use and evaluation.

2.6. Performance Evaluation of the Agent

Following the intensive training loop, assessing the agent’s performance is crucial. This evaluation not only verifies the agent’s proficiency in the Ms. Pac-Man environment but also identifies potential areas for improvement. The evaluation process is structured to precisely measure the agent’s effectiveness.
The first step in this evaluation is to switch the agent to a purely exploitative mode, which involves disabling the random action selection feature (i.e., setting epsilon to zero in the epsilon-greedy policy). This mode forces the agent to solely depend on its acquired knowledge, choosing actions based entirely on the Q-values provided by the Q-Network. This approach offers an accurate representation of the agent’s learning and its application skills.
In this phase, the agent engages in a set number of episodes, mirroring the training process but with two key distinctions. First, there is no learning or adjustment of the Q-Network’s weights based on the agent’s actions. Second, detailed records are kept of every action, state transition, and reward received. The primary indicator of the agent’s performance is the total cumulative reward accumulated in each episode.
Nevertheless, relying on a single metric might not fully encapsulate the agent’s abilities. Therefore, additional metrics are considered. These could include the number of levels completed, the average number of ghosts eaten per episode, or the frequency of bonus fruit captures. These additional metrics offer a more nuanced view of the agent’s strategic gameplay. Given the inherent randomness in games like Ms. Pac- Man, where ghost behaviors and fruit appearances vary, it’s important to average the agent’s performance across multiple episodes. This approach smooths out random fluctuations and provides a more consistent measure of the agent’s true capabilities.
During the evaluation stage, visual aids frequently support the quantitative analysis. Heatmaps showing the agent's most-traveled paths through the maze or graphs showing the trajectory of accumulated rewards over episodes can provide important visual insights on the agent's strategic routines and behaviors.

2.7. Visualizing the Agent’s Gameplay

Seeing our reinforcement learning agent's gameplay in Ms. Pac-Man provides a clearer understanding of our model's efficacy. Comparable to seeing a human player navigate a maze, this visual method offers an interesting and thorough narrative of the agent's tactics, difficulties, and opportunities for development.
The agent tells a tale through its interactions with the Ms. Pac-Man surroundings, going beyond simple labyrinth navigation to include learned habits, threat assessments, and pivotal decision-making moments. We are able to thoroughly analyze and comprehend the agent's path thanks to this visual representation.
In order to do this, we created a simulated screen that records the agent playing in real time. This covers every step, near-death experience, and power pellet usage accomplished. This visual record fulfills numerous important functions: First of all, it serves as an easy-to-use, direct method of validation. It allows researchers, developers, enthusiasts, and other stake- holders to see the results of the training process in a dynamic and tangible way. It answers critical questions about the agent’s strategy: How effectively does it navigate through tight spots? Does it use power pellets strategically to pursue ghosts, or does it focus on clearing the maze? How does it respond to the sudden appearance of bonus fruits?
Additionally, this visual representation aids in debugging and fine-tuning the agent’s behavior. Anomalies or patterns of suboptimal decisions, which might be less apparent in numerical data, become immediately obvious in a visual format. This can lead to quicker and more intuitive adjustments and improvements.
Finally, these visual recordings have significant outreach potential. They can be shared with the broader community, included in presentations, or utilized in educational settings to demonstrate the principles of deep reinforcement learning in a relatable and engaging way.
In conclusion, visualizing the agent’s gameplay not only brings the abstract elements of deep reinforcement learning to life but also serves as a critical tool for validation, refinement, and education. It provides a vivid depiction of the agent’s abilities, offers valuable insights for improvements, and underscores the effectiveness of deep reinforcement learning in navigating complex environments like Ms. Pac-Man.

2.8. Proposed Optimization Algorithm for Hyperparameter Tuning

In our innovative framework, we synergize the robust methodologies of the Snake Optimization Algorithm (SOA) and the Energy Valley Optimization (EVO) into a unified approach, aptly named the Energy Serpent Optimizer (ESO). By leveraging these two algorithms, we aim to finely tune key hyperparameters, especially the learning rate (lr) and the discount factor (gamma), which are crucial for the DQN Agent’s learning efficacy and strategic foresight.
Snake Optimization (SO) is a novel intelligent optimization algorithm conceptualized by Hashim et al., which draws inspiration from the natural behaviors of snakes, particularly their feeding, fighting, and mating patterns. The uniqueness of this algorithm lies in its emulation of the complex survival strategies of snakes. Distinct from other metaheuristic algorithms, SO categorizes the population into males and females. It commences with randomly generated populations and incorporates the influence of temperature, a critical factor for cold-blooded animals like snakes, in their feeding and mating behavior. The algorithm operates in two phases: the exploration phase, where snakes search randomly for food in an environment with inadequate food supply, and the exploitation phase, where enough food is available, guiding the search behavior. The exploration and exploitation phases are mathematically modeled, with specific equations governing the positions of male and female individuals in each phase. The algorithm also features unique modes like fight and mating modes, triggered based on environmental conditions, particularly temperature, further adding to its complexity and efficacy in optimization.
Energy Valley Optimization, on the other hand, is inspired by the principles of particle physics, particularly the behavior of subatomic particles. It revolves around the concept of stability and decay of particles. In the universe, most particles are unstable, tending to emit energy and transform into more stable forms. This optimization method focuses on the concept of an 'energy valley,' which is a metaphorical representation of the state where particles are in their most stable form, bound by optimal levels of neutrons (N) and protons (Z). The principle underlying this optimization technique is that particles aim to increase their stability by adjusting their N/Z ratio, moving towards this energy valley or stability band. This concept is particularly crucial for understanding the stability of heavier particles, which require a higher N/Z ratio for stability. The optimization process in Energy Valley Optimization mimics this natural tendency of particles, leveraging the idea of stability and transformation to guide the search towards optimal solutions in a given problem space. It's an innovative approach that applies the fundamental aspects of particle physics to the realm of algorithmic optimization.
The implementation begins with the SOA initializing a diverse population of 'snakes', each representing a unique set of hyperparameters. These snakes navigate a metaphorical landscape that mirrors the DQN Agent's performance under varied hyperparameter configurations. Concurrently, the EVO introduces a separate population that undergoes a similar evaluation, where each individual's performance in managing the game character is assessed.
The next phase involves the fusion of SOA and EVO methodologies, where the top-performing snakes from the SOA are combined with the leading individuals from the EVO population. This integration allows for the crossover of robust hyperparameters, creating offspring that are potentially superior to their predecessors. Mutation is applied to both populations, introducing variability and ensuring a broad search across the hyperparameter space.
As the evolutionary process progresses across generations, both SOA and EVO work in tandem to refine the hyperparameters towards an optimal set that promises enhanced performance in the Ms. Pac-Man environment. This iterative process continues until a convergence criterion is met or a predetermined number of generations have passed.
The optimized hyperparameters, a product of this dual-algorithm approach, are then used to configure the DQN Agent. The agent undergoes rigorous training within the game environment, with its performance meticulously tracked and optimized over numerous episodes. To validate the effectiveness of the ESO tuned hyperparameters, an extensive evaluation is conducted. This not only involves a quantitative assessment of the rewards but also includes a qualitative analysis through visualized gameplay, offering insights into the agent’s decision-making and strategic gameplay the detailed steps is shown in Figure 2.
Preprints 106943 g002
Figure 2. Energy Serpent Optimizer pseudocode.
Figure 2. Energy Serpent Optimizer pseudocode.
Preprints 106943 g002
The Energy Serpent Optimizer (ESO) (as shown in Figure 3 pseudocode) is an evolutionary algorithm tailored for optimizing the learning rate and discount factor in reinforcement learning models. It commences with establishing a virtual environment where a population of serpents, each representing a unique set of hyperparameters, is initialized. As the algorithm progresses through generations, each serpent is evaluated on how effectively its hyperparameters perform in the given environment, with performance typically gauged by the agent's reward accumulation.
Serpents are ranked by their fitness, and the ones with superior hyperparameter configurations are identified as the most fit. These leading serpents then undergo a breeding process where genetic operations such as crossover and mutation are applied. Crossover involves blending the hyperparameters of two parent serpents to generate offspring, while mutation introduces random changes to these offspring, ensuring diversity and aiding in the exploration of the hyperparameter space.
This process of evaluation, selection, breeding, and mutation continues over a series of generations, steadily honing the hyperparameters. The algorithm seeks to replace less fit serpents with more promising offspring, iteratively pushing the entire population towards optimal hyperparameter combinations.
The ESO concludes its run after a pre-defined number of generations, at which point it presents the optimal learning rate and discount factor, reflecting the most effective hyperparameter set discovered. This culmination represents a refined approach to training reinforcement learning agents, ensuring they are primed for maximum efficiency in complex decision-making environments.
In summary, the combined ESO approach for hyperparameter tuning is a dynamic and exploratory journey that strategically adjusts the parameters critical to the learning process. This synergy ensures that the DQN Agent is equipped with the best possible strategy, enabling it to navigate the Ms. Pac-Man maze with enhanced proficiency and intelligence.

3. Results

3.1. Outcomes of the ESO Algorithm

In our application of the ESO, we set it within a complex maze-based game setting, where an AI agent was tasked with navigating through a labyrinth filled with unique challenges and goals. The game board was distinguished by its elaborate blue passageways, which had a range of themes such as characters in motion, snake emblems, and skulls. The AI agent's primary objective was to navigate this maze as fast as it could while dodging hazards and engaging with particular icons to score points.
Table 1 provides a clear depiction of the iterative training process for three distinct optimization algorithms: the Snake Optimizer Algorithm (SOA), the Energy Valley Optimizer (EVO), and the Evolved Snake Optimizer (ESO). Across the span of eight iterations, each algorithm's performance is evaluated based on the reward obtained, which serves as a proxy for its optimization efficacy.
Initially, in the first iteration, ESO establishes a strong lead with a reward of 400.0, significantly outpacing the SOA and EVO, which start with rewards of 200.0 and 150.0, respectively. As the iterations progress, all three algorithms exhibit an increasing trend in their rewards, indicating that each is effectively learning and improving its strategy to navigate the problem space.
By the second iteration, the SOA and EVO show signs of progress with rewards of 350.0 and 250.0, yet the ESO continues to dominate, extending its lead with a reward of 550.0. This pattern of incremental improvement continues consistently, with the SOA and EVO making steady gains in their respective reward values.
Despite these gains, the ESO consistently outperforms the other two, suggesting a more efficient optimization process. By the fourth iteration, the ESO's reward reaches 750.0, while the SOA and EVO lag with rewards of 450.0 and 350.0. The gap in performance underscores the ESO's superior ability to quickly identify and exploit high-reward strategies. Upon reaching the seventh iteration, the rewards for SOA and EVO are 700.0 and 500.0, while the ESO breaks the four-digit barrier with a reward of 1050.0, showcasing its accelerated learning curve.
The culmination of this progression is marked by the eighth iteration, where the SOA and EVO attain rewards of 800.0 and 550.0, respectively. Meanwhile, the ESO achieves a reward of 1100.0, cementing its leading position. This final iteration is particularly noteworthy as it underscores the computational limitations imposed by the GPU hardware within the server. Despite the restricted computing environment, the ESO's algorithmic design allows it to utilize the available resources more efficiently, reaching a superior level of optimization compared to its counterparts. The ESO's performance in this context implies that it is not only a potent optimization tool but also one that is well-suited to environments where computational resources are at a premium.
The ESO was utilized to evolve many hyperparameter setups using a genetic algorithm. Finding the ideal set of hyperparameters to increase the agent's ability to achieve the highest score while efficiently managing time was the aim of this evolution. It needed 32 seconds to finish the ESO process, involving multiple revisions and iterations. With a noteworthy score of 1100.0, the AI agent concluded this session and showed how the modified hyperparameters improved its performance and decision-making.
Preprints 106943 g003
Figure 3. Reward Score of ESO.
Figure 3. Reward Score of ESO.
Preprints 106943 g003
The portrayal in Figure 4 illustrates the progressive evolution of the agent's gaming at different times. This image visually depicts the agent's path through the maze and emphasizes the strategies and challenges it encounters. A thorough understanding of the the agency's decision-making process, the variety of obstacles it encounters, and the notable strides it takes toward peak performance can be obtained by looking at this image. Tracking the agent's journey requires having a clear and complete picture of the gaming dynamics, which this visual tool offers.
In this comparative analysis of the Energy Valley Optimizer (EVO) and the Snake Optimizer Algorithm (SOA), we observe distinct outcomes in terms of the rewards achieved through their respective operational paradigms. The SOA, which is inspired by the foraging behavior of snakes, has demonstrated a commendable performance with a reward score of 840.0. This score is indicative of the algorithm's efficient search and optimization capability within the solution space, possibly due to its strategic balance between exploration and exploitation phases.
On the other hand, the EVO, which draws on the concept of potential energy minimization to navigate through the search space, yielded a reward of 640.0. While this score is lower compared to that of the SOA, it still reflects a notable level of effectiveness in reaching a near-optimal solution. The discrepancy in the rewards between the two algorithms could be attributed to the inherent differences in their search heuristics and convergence properties.
In the domain of algorithmic optimization, the comparative analysis, as Table 2 illustrate, of the Snake Optimizer Algorithm (SOA), Energy Valley Optimizer (EVO), and ESO is strikingly telling. The SOA, while robust in its mimicry of natural foraging strategies, achieved a moderate reward of 840.0 but required a relatively prolonged duration of 45 seconds to converge upon a solution. The EVO, although innovative in its approach to minimizing potential energy to determine optimal paths, presented a lower reward score of 640.0 and even surpassed the SOA in time consumption with a completion time of 50 seconds. These figures suggest a less efficient optimization process in scenarios where quick convergence is paramount.
The ESO emerges as a superior optimization tool in this comparative study, not only outperforming the aforementioned algorithms with a reward of 1100.0 but also demonstrating expedited computational efficiency by completing its process in a mere 32 seconds. This performance leap is attributed to the ESO's adept use of a genetic algorithm to evolve hyperparameter configurations, showcasing its heightened adaptability and learning efficiency. The evolutionary aspect of the ESO allows for a dynamic and continuous improvement of the agent's decision-making capabilities, which is pivotal in achieving higher scores in a shorter timeframe.
The limitations of the SOA and EVO, while apparent in this context, may stem from their less dynamic adaptation mechanisms. These algorithms, despite their potential, fall short when tasked with rapidly evolving environments or problems that demand quick iterative improvements. The ESO's genetic algorithm framework provides a tangible advantage in this regard, offering an evolutionary edge that is clearly reflected in the results. Such findings underscore the importance of algorithmic flexibility and learning speed in the pursuit of peak optimization performance.

4. Discussion & Implications

The application of the combined Snake Optimization Algorithm and Energy Valley Optimization (ESO) in a complex maze-based game environment offers insightful revelations about adaptive artificial intelligence strategies and their implications in dynamic settings. The AI agent’s task of navigating intricate pathways and engaging with various game elements underlines the algorithm's ability to fine-tune decision-making processes under tight constraints, such as time and the presence of hazards.
The success of ESO in evolving hyperparameters is evident from the agent's ability to achieve a significant score within the stipulated time frame. This accomplishment not only demonstrates the effectiveness of the genetic algorithm-based approach but also highlights the criticality of selecting and adjusting the right hyperparameters. The learning rate and discount factor, in particular, have shown to be instrumental in shaping the agent's learning curve and its proficiency in maximizing rewards while minimizing risks.
The visualization of the agent's journey through the maze, as indicated in Figure 2, serves as a powerful tool for analyzing the behavioral patterns and strategic adaptations of the AI. It provides a granular view of the agent’s interactions within the game, revealing the nuanced approaches taken to overcome obstacles and optimize paths. The implications of this visualization are twofold: it not only facilitates a deeper understanding of the agent’s tactics but also assists in identifying potential areas for further optimization.
Moreover, the score of 1100.0 achieved by the AI agent sets a benchmark for performance, opening up avenues for comparative analysis with other reinforcement learning models or optimization techniques. This performance metric serves as a tangible outcome of the evolutionary process, allowing for empirical assessments of different hyperparameter configurations.
The implications of our findings extend beyond the realm of gaming. The methodologies employed here can be adapted for various real-world applications where autonomous decision-making is crucial, such as in robotics, autonomous vehicles, and complex system management. The ability to rapidly evolve and adapt to changing conditions is a hallmark of advanced AI systems, and the ESO approach exemplifies this capacity.
In conclusion, the deployment of ESO in a maze-based game environment has provided valuable insights into the capabilities of AI agents in complex and variable settings. It underscores the importance of continuous learning and adaptation, hallmarks of intelligent behavior, which are essential for the development of sophisticated AI systems capable of navigating the myriad challenges of both virtual and real-world environments.
The exploration of the individual capabilities of the Snake Optimization Algorithm (SOA) and the Energy Valley Optimizer (EVO) within the same complex maze-based game environment further enriches our understanding of adaptive optimization strategies in dynamic and constrained settings. The SOA, with its biologically inspired approach, emphasizes a strategic balance between exploration and exploitation, mimicking the foraging behavior of snakes. This method allows the AI to navigate through the maze with an intuitive understanding of space but can sometimes lead to suboptimal decision-making when faced with highly complex environments or abrupt changes in the game's dynamics. On the other hand, the EVO, which leverages the concept of energy minimization to find optimal paths, shows promise in navigating through the maze by systematically reducing the potential energy states. However, its performance can be hindered by its sometimes overly deterministic approach, which might not always account for the stochastic nature of dynamic obstacles or changing game conditions effectively.
While both SOA and EVO exhibit unique strengths in navigating through the maze and engaging with its elements, they also face limitations that can affect their overall effectiveness in achieving high scores within the designated time frames. The SOA’s reliance on a heuristic balance may not always yield the most efficient path, especially in mazes with highly irregular and unpredictable patterns. Similarly, EVO’s deterministic nature might limit its adaptability in rapidly changing or highly stochastic environments, potentially leading to less-than-optimal exploration strategies.
In contrast, the ESO emerges as a more robust and adaptable solution by integrating the strengths of both SOA and EVO while mitigating their weaknesses through the application of a genetic algorithm. This approach enables the ESO to dynamically evolve hyperparameters, thereby enhancing the AI agent's decision-making processes to be more responsive and efficient in the face of complex challenges. The ESO's ability to achieve a significant score of 1100.0 in the maze-based game underscores its superior performance, attributed to its adaptive learning rate, discount factor adjustments, and overall strategic flexibility. By learning from the limitations of SOA and EVO, the ESO demonstrates a heightened ability to navigate through the maze with improved efficiency and effectiveness, showcasing the potential of hybridized and evolved optimization strategies in complex and dynamic environments.
Thus, while SOA and EVO provide valuable insights into the optimization capabilities in constrained settings, the ESO stands out for its adaptive, integrated approach, offering a compelling model for advanced AI systems that require rapid adaptation and learning in diverse and unpredictable situations.

5. Conclusion & Future Work

In this paper, we have presented an innovative approach that harnesses the combined power of the Snake Optimization Algorithm and Energy Valley Optimization (ESO) to elevate the performance of reinforcement learning agents in complex environments. Our exploration within the challenging confines of a maze-based game has not only validated the robustness of the reinforcement learning model but has also underscored the novelty of the ESO combination in effectively tuning hyperparameters to optimize the agent's learning and decision-making abilities. The environment presented to the agents was rich and dynamic, providing a rigorous testing ground for the algorithms to perform and evolve.
The novelty of our approach lies in its adaptive complexity and the nuanced understanding of the agent's interactions within the game, which is made possible by the detailed analysis of the agent's performance and the strategic evolution of hyperparameters. The ESO framework demonstrates a significant advancement in the field by allowing for a more nuanced and fine-tuned approach to the evolution of the learning parameters.
For future work, we aim to transcend the domain of games to apply our findings to more intricate and practical applications such as autonomous systems, logistics, and complex problem-solving scenarios, where AI agents must make decisions in unpredictable and multifaceted environments. We anticipate that addressing the limitations observed, such as the need for extensive computational resources and the potential for overfitting to specific types of environments, will be crucial in advancing the ESO framework. Further, we aim to explore the scalability of the approach, its applicability to multi-agent systems, and its effectiveness in multi-objective optimization scenarios. By doing so, we hope to pave the way for reinforcement learning models that are not only efficient and robust but also versatile in their application to the ever-growing challenges faced in the realm of artificial intelligence.

References

  1. Kadhim, A.I. Survey on supervised machine learning techniques. Artif. Intell. Rev. 2019, 52, 273–292. [Google Scholar] [CrossRef]
  2. Yau, K.A.; Elkhatib, Y.; Hussain, A.; Al-fuqaha, A.L.A. Unsupervised machine learning for networking: Techniques, applications and research challenges. IEEE Access 2019, 7, 65579–65615. [Google Scholar]
  3. Singh, B.; Kumar, R.; Singh, V.P. Reinforcement learning in robotic applications: A comprehensive survey. Artif. Intell. Rev. 2022, 55, 1–46. [Google Scholar]
  4. Rao, S.; Verma, A.K.; Bhatia, T.A. Review on social spam detection: Challenges, open issues, and future directions. Expert Syst. Appl. 2021, 186, 115742. [Google Scholar] [CrossRef]
  5. Sahil, S.; Zaidi, A.; Samar, M.; Aslam, A.; Kanwal, N.; Asghar, M.; Lee, B. A survey of modern deep learning based object detection models. Digit. Signal Process. 2022, 126, 103514. [Google Scholar]
  6. Bochenek, B.; Ustrnul, Z. Machine learning in weather prediction and climate analyses—applications and perspectives. Atmosphere 2022, 13, 180–2022. [Google Scholar] [CrossRef]
  7. Keerthana, S.; Santhi, B. Survey on applications of electronic nose. J. Comput. Sci. 2020, 16, 314–320. [Google Scholar] [CrossRef]
  8. Razzaghi, P.; Tabrizian, A.; Guo, W.; Chen, S.; Taye, A.; Thompson, E.; Wei, P. A survey on reinforcement learning in aviation applications. arXiv 2022, arXiv:2211.02147. [Google Scholar]
  9. Sivamayil, K.; Rajasekar, E.; Aljafari, B.; Nikolovski, S.; Vairavasun- daram, S.; Vairavasundaram, I. A systematic study on reinforcement learning based applications. Energies 2023, 16, 1512. [Google Scholar] [CrossRef]
  10. Gronauer, S.; Diepold, K. Multi-agent deep reinforcement learning: a survey. Artif. Intell. Rev. 2022, 1–49. [Google Scholar]
  11. Nvan Eck, J.; van Wezel, M. Application of reinforcement learning to the game of othello. Comput. Oper. Res. 2008, 35, 1999–2017. [Google Scholar] [CrossRef]
  12. Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wier- stra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
  13. Rajendran, D.; Santhanam, P. Towards digital game-based learning content with multi-objective reinforcement learning. Mater. Today Proc. 2021. [CrossRef]
  14. Liu, S.; Cao, J.; Wang, Y.; Chen, W.; Liu, Y. Self-play reinforcement learning with comprehensive critic in computer games. Neurocomputing 2021, 449, 207–213. [Google Scholar] [CrossRef]
  15. Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M. Mastering the game of go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
  16. Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T. A general rein- forcement learning algorithm that masters chess, shogi, and go through self-play. Science 2018, 362, 1140–1144. [Google Scholar] [CrossRef]
  17. Nu, C.; Ferna, J.; Perez, R. Learning to select goals in automated planning with deep-q learning. Expert Syst. Appl. 2022, 202, 117265. [Google Scholar]
  18. Gong, X.; Yu, J.; Lu, S.; Lu, H. Actor-critic with familiarity-based trajectory experience replay. Inf. Sci. 2022, 582, 633–647. [Google Scholar] [CrossRef]
  19. Such, F.; Madhavan, V.; Conti, E.; Lehman, J.; Stanley, K.; Clune, J. Deep neuroevolution: Genetic algorithms are a competitive alternative for training deep neural networks for reinforcement learning. arXiv 2017, arXiv:1712.06567. [Google Scholar]
  20. Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q–learning. In Proceedings of the AAAI Conference on Artificial Intelligence 2016, 30. [Google Scholar] [CrossRef]
  21. OpenAI; Berner, C. ; Brockman, G.; Chan, B.; Cheung, V.; Debiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S. Dota 2 with large scale deep reinforcement learning. Dota 2 with large scale deep reinforcement learning. arXiv arXiv:1912.06680, 2019.
  22. Vinyals, O.; Fortunato, M.; Pointer networks, N.J. 2015; arXiv:1506.03134.
  23. Lee, J.; Lee, Y.; Kim, J.; Kosiorek, A.; Choi, S.; Teh, Y.W. Set trans- former: A framework for attention-based permutation-invariant neural networks. In Proceedings of the International Conference on Machine Learning; 2018. [Google Scholar]
  24. Ammanabrolu, P.; Riedl, M.O. Playing text–adventure games with graph–based deep reinforcement learning. arXiv 2018, arXiv:1812.01628. [Google Scholar]
  25. Adolphs, L.; Hofmann, T. Ledeepchef: Deep reinforcement learning agent for families of text–based games. In Proceedings of the AAAI Conference on Artificial Intelligence; 2019. [Google Scholar]
  26. Brown, N.; Bakhtin, A.; Lerer, A.; Gong, Q. Combining deep reinforcement learning and search for imperfect–information games. arXiv arXiv:2007.13544, 2020.
  27. Ye, D.; Liu, Z.; Sun, M.; Shi, B.; Zhao, P.; Wu, H.; Yu, H.; Yang, S.; Wu, X.; Guo, Q. Mastering complex control in moba games with deep reinforcement learning. Proc. AAAI Conf. Artif. Intell. 2020, 34, 6672–6679. [Google Scholar] [CrossRef]
  28. Roy, B. An analysis of temporal–difference learning with function approximation. Autom. Control. IEEE Trans. 1997, 42, 674–690. [Google Scholar]
Table 1. Iterative Reward Comparison: Showcases ESO's superior optimization efficiency over SOA and EVO.
Table 1. Iterative Reward Comparison: Showcases ESO's superior optimization efficiency over SOA and EVO.
Iteration SOA Reward EVO Reward ESO Reward
1 200.0 150.0 400.0
2 350.0 250.0 550.0
3 400.0 300.0 650.0
4 450.0 350.0 750.0
5 500.0 400.0 850.0
6 600.0 450.0 950.0
7 700.0 500.0 1050.0
8 800.0 550.0 1100.0
Table 2. Comparative Performance of SOA, EVO, and ESO: Reward scores and computational times.
Table 2. Comparative Performance of SOA, EVO, and ESO: Reward scores and computational times.
Algorithm Reward Achieved Time Taken (seconds)
SOA 840.0 45
EVO 640.0 50
ESO 1100.0 32
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated