Masterminding the Giant : Shannonian Entropic Threshold Perplexity AI

Preprint

Article

Masterminding the Giant : Shannonian Entropic Threshold Perplexity AI

Altmetrics

Downloads

141

Views

Comments

Dr Ismail A Mageed^*

This version is not peer-reviewed

This preprints belongs to the Topic

Artificial Intelligence Models, Tools and Applications

Submitted:

19 May 2024

Posted:

20 May 2024

You are already at the latest version

Alerts

Abstract

Undoubtedly, there is a potential impact of large language models like ChatGPT in revolutionizing information retrieval and knowledge discovery, particularly in the context of the vast amount of electronic material available. On another strong note, the current work offers a first time ever mathematical approach to accurately fine tune perplexity AI, which sets a giant step ahead towards accurate next generations AI. Having started this world leading discovery, the upper and lower bounds of perplexity AI, namely , , respectively, are obtained for the first-time ever. Concluding remarks combined with emerging open problems and next research phase are provided.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

Introduction

This hot burning topic needs more exploration, especially, when we investigate the evaluation of two versions of ChatGPT, which would reveal that they still lack the ability to handle the intricacies of complex topics due to limited access to the entire scientific literature. However, they will soon be valuable for assisting scientists in surveys, literature reviews, and teaching [1].

Entropy [2] as a powerful tool of fine-tuning uncertainty can efficiently impact ChatGPT-4’s advancement including other futuristic ChatGPT forms. For example, to improve the accuracy of the generated thoughts, there are some proposed filtering them based on uncertainty, such as answer entropy, which measures the uncertainty of the answers, and filters out thoughts with higher uncertainty, so filtering by answer entropy leads to slightly higher accuracy compared to filtering by the number of consistent paths used in previous work.

Perplexity[3] is a statistical metric used in Natural Language Processing (NLP) to measure how well a language model predicts a sample. A lower perplexity score indicates that the language model is more accurate and confident in its predictions.

In NLP, encoding refers to representing text as numerical vectors, which can be used as input for machine learning models. Embeddings capture the relationships between words or phrases in a text corpus.

Entropy can steer the advancement of both existing and futuristic ChatGPT to higher levels of accuracy. Based, on my world-leading mathematical discovery, Perplexity AI, can be fine-tuned through obtaining entropic thresholds corresponding to perplexity expression. Notably, Shannonian entropic formula, will be the very basic to target, then taking a higher-level step ahead, my innovative entropy formula, namely, Ismail’s second entropy[5], will provide a novel link between Entropy Theory, Statistical Mechanics, and AI. My lecture will travel through a visionary spotlight to employing another three entropies in the literature, under my name, Ismail’s entropy 1,3, and 4(c.f., [6,7,8]).

My innovative mathematical approach has the great potential to steer AI into a higher level of accuracy, which will be highly influential to be applied to all fields of human knowledge.

The current work reads:

2. Crossroads between Perplexity AI, and Shannonian Entropy

When assessing language models, one popular statistic to utilise is ambiguity [9]. Consider the built-in metric of perplexity in scikit-learn’s implementation of the topic-modelling algorithm Latent Dirichlet Allocation.

In numerous Natural Language challenges, a common configuration [9] is to have a language L and aim to construct a model M for it. A particular genre or corpus, such as “English Wikipedia,” “Nigerian Twitter,” or “Shakespeare,” or (at least conceptually) a general term, such as “French,” could constitute the “language.”

Specifically [9], by a language L, we mean a process for generating text. Given a history h consisting of a series of previous words in a sentence, the language L is the probability that the next word is w:

h a s e r i e s o f w o r d s (w_{1}, w_{2}, \dots, w_{n - 1})

L (w| h) = P r o b (n e x t w o r d i s w| p r e v i o u s w o r d s a r e h)

(1)

A l a n g u a g e m o d e l i s a c o l l e c t i o n o f p r o b a i l i t y d i s t r i b u t i o n s

If L is “English,” for instance, I’m ready to bet that:

➢: L(dog | The swift brown fox leaps over the slow brown) ≈ 1.
➢: L(ipsum | Lorem) ≈ 1.
➢: L(wings | Buffalo buffalo buffalo Buffalo buffalo) ≈ 0

L (s) = L (w_{1}| w_{0}) \times L (w_{2}| w_{0} w_{1}) \dots \times (w_{n}| w_{0} w_{1} \dots w_{n - 1}) {= \prod}_{k = 1}^{n} L (w_{k}| w_{0} w_{1} \dots w_{k - 1})

(2)

T h e l a n g u a g e L g i v e s t h e p r o b a b i l i t y o f a s e n t e n c e s

Nonetheless, it is typical practice to omit the product’s initial phrase as well, or even to utilise an even longer beginning context [9].Obtaining an impeccable imitation of

L

in, instance, spoken American English is surprisingly simple. Simply signal any person who is fluent in English as they pass by. Typically, our goal is to teach the model to a computer, which is why machine learning was created. Thus,

M

will represent any language model that we have been able to construct computationally. This configuration, comprising of a language

L

and a model

M

, is highly versatile and is utilised in numerous Natural Language jobs such as speech-to-text, autocorrection, autocomplete, machine translation, and so forth.

Given the words someone has entered so far, autocomplete is the most obvious example; pick the completion with the highest probability and try to estimate what they could type next.

Eventually [9], if given a model

M

, the perplexity on a sentence

s

, reads:

P e r p l e x i t y (M) = {(\prod_{k = 1}^{n} (\frac{1}{M (w_{k}| w_{0} w_{1} \dots w_{k - 1})}))}^{\frac{1}{n}}

(3)

P e r p l e x i t y o f a l a n g u a g e m o d e l M

This is the opposite of the geometric mean of the terms in the product’s denominator, as the second line makes clear. This can be understood as a per-word metric since the likelihood of each word is only computed once, contingent upon the history. This indicates that sentence length has no bearing on the level of bewilderment, other things being equal. We want our odds to be high, which denotes less confusion. The perplexity would be 1 and the model would accurately predict the text if all the probability were 1. Conversely, there will be more confusion with worse language models.

The language itself sets a lower bound on bewilderment. However, this highlights a typical aspect of NLP metrics: a simple metric, such as perplexity, may not always be the best indicator of a model’s actual performance. For development (validation), confusion is beneficial, but not always for evaluation. Human evaluation is still considered the gold standard in evaluation.

Entropy

While entropy is a difficult notion in physics, information theory makes sense of it very easily. Assume you have a procedure (e.g., a word-generating language

L

). There is a chance p that the event or the thing that happened was going to happen at every stage of the process. The unexpected number is

- l o g (p),

where you can take the logarithm in any base by altering the units. Events with little likelihood are highly surprising. There are zero surprises in events that were expected to occur (

p = 1

). Unfeasible events (

p = 0

) have infinite surprise.

The expected value of the surprise over all potential events, indexed by i, is known as the entropy, namely,

H (p)

H (p) = - \sum_{i} p_{i} l n p_{i}

(4)

Relationship between Perplexity and Entropy

Now all that remains to do is show the relationship between the two. Assuming we took the logarithm in base e:

P e r p l e x i t y (M) = e^{H (L, M)}

(5)

If we took the logarithm in base 2, use 2 for the base, etc.

In summary, therefore:

1. We construct a language model

M

for the real language, L, that is producing the data.

2. We calculate

M' s

(with respect to L) perplexity or, equivalently, cross-entropy.

3. The actual language

L' s

perplexity limits

M' s

perplexity below (see, cross-entropy).

How “random” our model is is measured by the perplexity. If each word has a perplexity of 3, it indicates that the model’s average chance of correctly predicting the next word in the text was one in three. It is occasionally referred to as the average branching factor for this reason.

Key Features and Advantages

1. Accuracy: Perplexity AI delivers high accuracy rates and can be fine-tuned [10].

2. Efficiency: The platform offers several natural language processing (NLP) features, making it an efficient and reliable way to find information quickly [11].

3. User-friendly interface: Perplexity AI is easy to use and navigate, with a clean and well-designed interface [12,13].

4. Credibility: The platform provides citations for the information it returns, allowing users to verify the reliability of the information [14].

5. Real-time information: Perplexity AI can provide real-time information, outperforming other AI chatbots like ChatGPT [15].

Limitations

Perplexity AI’s limitations include its sensitivity to the specific test set used, which may not always provide a consistent evaluation of its performance [16]. Additionally, while it can sometimes generate incorrect answers, it makes it easy for users to check the sources themselves [12].

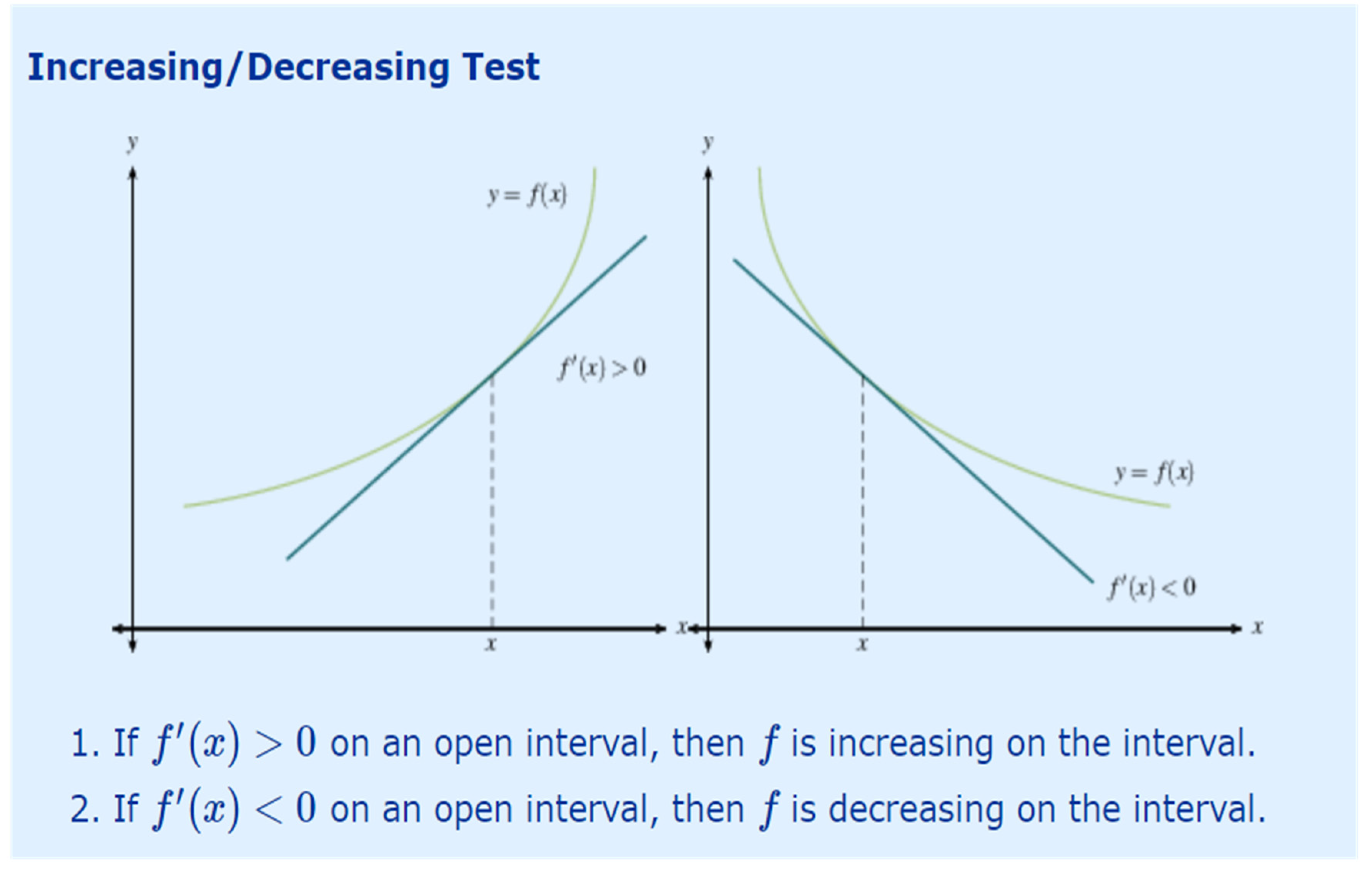
The threshold approach is pivotally based on the derivative test, where increasability phase exists for regions of positive derivatives, while decreasability exists in negative derivative zones, as shown by figure (c.f.[17]). Notably, this is the corner stone of this current work, namely the Increasing/Decreasing test, or (IDT).

Figure 1. Increasing and decreasing test.

3. Results and Experimental Validation

Theorem 1. The Shannonian perplexity AI,

ω (p (n)) = 2^{H (p (n)}, H (p (n)) = - \sum_{n = 1}^{N} p (n) l n p (n)

(6)

(i) Increases forever in

λ

if and only if

\exists λ > 0

satisfying that:

p (n) = e^{- (λ + 1)}, ω (p (n)) = 2^{(λ + 1)}, λ = - l n p (n) - 1, p (n) \in [0,1], H (0) = 0

(7)

(ii) Decreases forever in

ρ

if and only if

\exists ρ > 0

satisfying that:

p (n) = e^{(ρ - 1)}, ω (p (n)) = 2^{(1 - ρ)}, ρ = l n p (n) + 1, p (n) \in [0,1], H (0) = 0

(8)

Proof

Let

ω (x),

defines perplexity,

ω (p (n)) = 2^{H (p (n))}, H (p (n)) d e f i n e s t h e S h a n n o i a n e n t r o p y o f (c . f ., (4))

(9)

H (p (n)) = - \sum_{n = 1}^{N} p (n) l n p (n)

(10)

\frac{d ω}{d p (n)} = 2^{H (p (n))} (- \sum_{n = 1}^{N} (1 + l n p (n)))

(11)

Communicating(11), and IDT, one gets

\frac{d ω}{d p (n)} > 0 ⟺ 2^{H (p (n))} (- \sum_{n = 1}^{N} (1 + l n p (n))) > 0

(12)

Since

2^{H (p (n))} > 0,

\frac{d ω}{d p (n)} > 0 ⟺ 1 + l n p (n) < 0

(13)

1 + l n p (n) < 0

translates to the existence of a positive real number, say

λ

, satisfying:

1 + l n p (n) = - λ

(14)

p (n) = e^{- (λ + 1)}

(15)

The normalization property implies:

\sum_{n = 1}^{N} p (n) = 1

(16)

Engaging (7), and (16), it is implied that:

N e^{- (λ + 1)} = 1 \to N = e^{(λ + 1)}

(17)

(17) translates to

λ = \ln (- 1 (c . f ., (7))

(18)

Wrapping up (9), (15),(17), and (18) yields:

ω (λ) = 2^{H (p (n))} = 2^{- (\sum_{n = 1}^{N} e^{- (λ + 1)} (- (λ + 1)))} = 2^{(λ + 1) N e^{- (λ + 1)}} = 2^{(λ + 1)} (c.f., (7))

Moreover,

\frac{d ω}{d p (n)} < 0 ⟺ 2^{H (p (n))} (- \sum_{n = 1}^{N} (1 + l n p (n))) > 0

(19)

Equation (19) holds only if

\exists

a positive real number

ρ

, such that:

1 + l n p (n) = ρ

(20)

Engaging the same logic as in (i), the proof of (ii) follows.

Experimental setup:

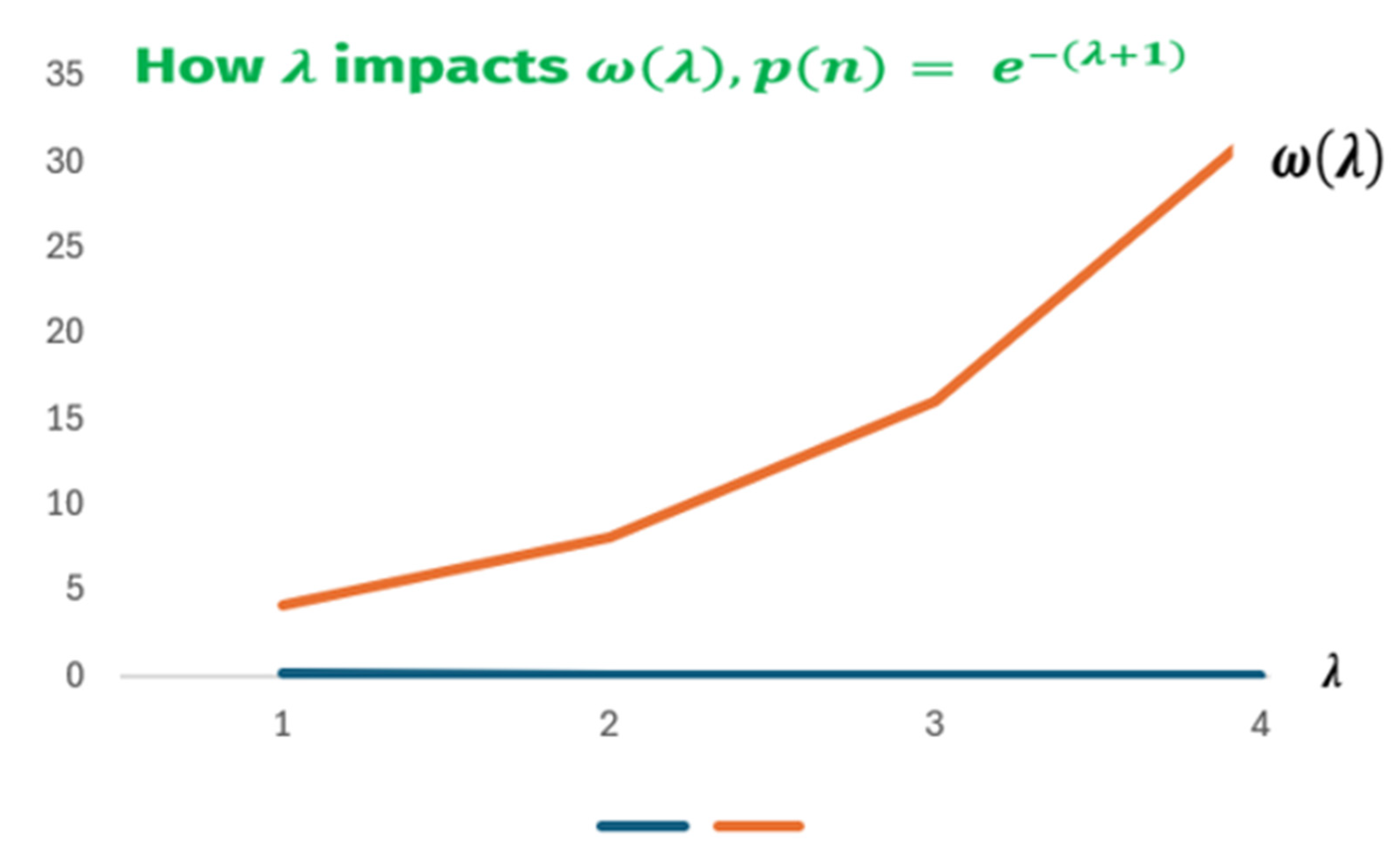
The increasability zones

Observing Figure 2, it can be seen perplexity AI increases by the progressive increase of the fine- tuner,

λ

On another separate note, reading the represented data of Table 1, the only permitted case, is for

ρ = 1

, otherwise, this violates the axiomatic probability logic.

Theorem 2. The upper and lower bounds of Shannonian perplexity AI,

{U B}_{P e r p l e x i t y A I} {, U B}_{P e r p l e x i t y A I},

respectively, are given by the following inequality:

{U B}_{P e r p l e x i t y A I} = {(1 + \frac{H (p (n)}{n})}^{(n + H (p (n))} > ω (p (n)) > H (p (n) = {L B}_{P e r p l e x i t y A I}

(21)

H (p (n)) = - \sum_{n = 1}^{N} p (n) l n p (n)

Proof

Following Taylor’s expansion of the exponential function,

e^{x}

, for

x > 0

e^{x} = \sum_{k = 0}^{\infty} (\frac{x^{k}}{k!}) > x

(22)

Moreover, engaging Lehmer’s inequality(c.f., [18]),

e^{x} \leq {(1 + \frac{x}{n})}^{(\frac{x + n}{2})} for x, n > 0

(23)

Since,

{(1 + \frac{x}{n})}^{(\frac{x + n}{2})} < {(1 + \frac{x}{n})}^{(x + n)} holds for all x, n > 0

(24)

Setting

x = H (p (n)),

combined with communicating (22)-(24), the proof follows.

4. Conclusion, Open Problems, and Next Research Phase

The current influential work showcases for the first time ever, the fine-tuning of AI, is revealed by using a novel revolutionary mathematical approach. The analytic findings are validated numerically. Notably, the upper and lower bounds of Perplexity AI are calculated.

The following are some emerging open problems:

Assuming other media, such as “Twitter” or “Spoken English,” and other languages, such as “Russian,” the true entropy of written English text remains undetermined.
Can we replace $H (x)$ , by other entropies, such as Rényi, Tsallis, or $Z$ - entropies to fine tune the perplexity? The question is still open.
Is it feasible to calculate strict upper and lower bounds for perplexity AI?

The next phase of research includes attempting to solve the proposed complex-still-open to solve problems, as well as the exploration of more unprecedented innovative mathematical techniques to advance AI.

References

Pimentel, et al., “ Challenging ChatGPT with Chemistry-Related Subjects,”, 2023.
X. Li X and X. Qiu, “ MoT: Pre-thinking and Recalling Enable ChatGPT to Self-Improve with Memory-of-Thoughts,” arXiv preprint arXiv:2305.05181, 2023.
Vasilatos, et al., “ HowkGPT: Investigating the Detection of ChatGPT-generated University Student Homework through Context-Aware Perplexity Analysis, ” arXiv preprint arXiv:2305.18226, 2023.
J. Yang, et al., “Harnessing the power of LLMS in practice: A survey on ChatGPT and beyond,” arXiv preprint arXiv:2304.13712, ” 2023.
A. Mageed, “Fractal Dimension(D f ) Theory of Ismail’s Second Entropy(H q I ) with Potential Fractal Applications to ChatGPT, Distributed Ledger Technologies(DLTs) and Image Processing(IP). 2023 International Conference on Computer and Applications (ICCA), Cairo, Egypt, 2023, pp. 1-6, doi: 10.1109/ICCA59364.2023.10401817.
A. Mageed, “Fractal Dimension (D f ) of Ismail’s Fourth Entropy (H IV ⁽ q,a 1 , a 2 ,..,a k ⁾) with Fractal Applications to Algorithms, Haptics, and Transportation,” 2023 International Conference on Computer and Applications (ICCA), Cairo, Egypt, 2023, pp. 1-6, doi: 10.1109/ICCA59364.2023.10401780.
A. Mageed and Q. Zhang, “An Information Theoretic Unified Global Theory For a Stable Queue With Potential Maximum Entropy Applications to Energy Works,” 2022 Global Energy Conference (GEC), Batman, Turkey, 2022, pp. 300-305, doi: 10.1109/GEC55014.2022.9986719.
I.A.Mageed, D.I. “Fractal Dimension of Ismail’s Third Entropy with Fractal Applications to CubeSat Technologies and Education,”, Preprints 2024, 2024020954. https://doi.org/10.20944/preprints202402.0954.v1. [CrossRef].
Ravi. “The Relationship Between Perplexity And Entropy In NLP,” 2021.[Last accessed 2024]. Available online: https://www.topbots.com/perplexity-and-entropy-in-nlp/.
https://www.cloudbooklet.com/perplexity-ai-the-ai-powered-search-engine/.
https://digitalbeech.com/perplexity-ai/.
https://www.producthunt.com/products/perplexity-ai/reviews.
https://apps.apple.com/us/app/perplexity-ask-anything/id1668000334.
https://findmyaitool.com/tool/perplexity-ai.
https://www.pcguide.com/apps/perplexity-ai/.
https://www.producthunt.com/products/perplexity-ai/reviews.
A. Mageed and Q. Zhang, “Threshold Theorems for the Tsallisian and Rényian (TR) Cumulative Distribution Functions (CDFs) of the Heavy-Tailed Stable Queue with Tsallisian and Rényian Entropic Applications to Satellite Images (SIs),”, electronic Journal of Computer Science and Information Technology, 9(1), 2023,41-47.
L. Kozma, “Useful inequalities,”, 2020, online source[ Last accessed 2024]. Available at http://www.Lkozma.net/inequalities_cheat_sheet.

Figure 2. The increasability zones of perplexity AI.

Table 1. Data showcasing the impossibility of existing zones of decreasability.

$ρ$	$p (n) = 2^{(ρ - 1)}$	$ω (ρ) = 2^{(1 - ρ)}$
1	1	1
2	2.718281828	0.5
3	7.389056099	0.25
4	20.08553692	0.125

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Masterminding the Giant : Shannonian Entropic Threshold Perplexity AI

Abstract

Introduction

2. Crossroads between Perplexity AI, and Shannonian Entropy

Entropy

Relationship between Perplexity and Entropy

Limitations

3. Results and Experimental Validation

4. Conclusion, Open Problems, and Next Research Phase

References

MDPI Initiatives

Important Links

Subscribe